Lavoro ed energia: testi degli esercizi svolti

Dinamica del punto materiale: Lavoro ed energia in Meccanica classica

Home » Lavoro ed energia: testi degli esercizi svolti

La presente raccolta di 82 esercizi svolti è stata elaborata con l’intento di offrire un supporto didattico sistematico per l’approfondimento dei concetti di lavoro ed energia nell’ambito della meccanica classica. In essa è possibile reperire un’ampia gamma di esercizi relativi sia alle forze conservative sia a quelle non conservative, con l’obiettivo di fornire una trattazione rigorosa e metodologicamente strutturata. La selezione degli esercizi non si limita a una mera esposizione di problemi, ma costituisce un percorso finalizzato al consolidamento delle conoscenze teoriche e delle capacità applicative dello studente.

Gli esercizi proposti sono tratti da testi di riferimento ampiamente riconosciuti nella letteratura scientifica, tra cui:

Rosati, Luigi – Fisica Generale
Mencuccini, C., Silvestrini, G. – Fisica
Mazzoldi, P., Nigro, M., Voci, C. – Elementi di Fisica
Resnick, R., Halliday, D., Walker, J. – Fundamentals of Physics
Goldstein, H. – Classical Mechanics
Griffiths, D.J. – Introduction to Electrodynamics
Landau, L.D., Lifshitz, E.M. – Mechanics

Oltre agli esercizi selezionati da fonti accademiche consolidate, la raccolta include una serie di problemi originali e quesiti estratti da prove d’esame universitarie. Tale approccio consente una trattazione completa delle problematiche inerenti al lavoro e all’energia, permettendo allo studente di confrontarsi con situazioni diversificate e di affinare le proprie competenze analitiche e risolutive.

Il capitolo successivo, in linea con l’ordine didattico, è dedicato agli esercizi svolti sui moti relativi, dove potrete trovare 37 esercizi svolti, selezionati con la consueta cura. Il capitolo precedente, dedicato agli esercizi svolti sulle leggi della dinamica, contiene 58 esercizi svolti.

Potete accedere all’intero corso di meccanica classica, frutto del lavoro del nostro team negli ultimi quattro anni. Ulteriori dettagli sugli autori e i revisori sono disponibili nella sezione dedicata alla fisica.

$\,$

Lavoro ed energia: autori e revisori

Leggi...

Autori e Revisori:

Valerio Brunetti, Giuseppe Palaia.

Autori:

Romano Rotonda, Daniele Massaro, Andrea Corradini, Davide Vignotto, Cosimo Tommasi.

Revisori:

Cesare Malagù, Nicola Fusco.

Autori in collaborazione:

Giulia Romoli, Antonio Figura, Christian Magliano.

Ex Autori & Revisori:

Patrizio Di Lorenzo, Simone Brozzesi, Nicola Santamaria, Vittorio Larotonda, Leonardo Rebeschini, Simone Romiti, Antonio Junior Iovino, Daniele Bjørn Malesani, Tiziano Schiavone, Serena Lezzi, Marco Chilioiro.

Testi degli esercizi su lavoro ed energia

Esercizio 1 $(\bigstar \largewhitestar\largewhitestar \largewhitestar\largewhitestar)$ . Un punto materiale può muoversi all’interno di una guida circolare di raggio $R$ liscia, vincolata nel punto $A$ e di massa trascurabile posta in un piano verticale. Calcolare che velocità deve avere il punto materiale in $A$ per restare in contatto con la guida in $B$ .

Rendered by QuickLaTeX.com

Figura 1: schema del problema lavoro ed energia 1.

Schema di un punto materiale che si muove all'interno di una guida circolare liscia di raggio R, vincolata nel punto A e situata in un piano verticale. Il punto materiale deve avere una certa velocità iniziale v_A per restare in contatto con la guida in B.

Svolgimento esercizio 1.

Esercizio 2 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Un anellino di massa $m$ è vincolato a scorrere lungo un’asta verticale in presenza di una forza di attrito costante $\vec{F}_{a}$ ed è inizialmente fermo alla base dell’asta. A seguito dell’applicazione di un impulso $\vec{J}$ , l’anellino viene lanciato verso l’alto, fino a raggiungere la quota $h$ . Successivamente, ricade e arriva alla base dell’asta con velocità $\vec{v}$ . Calcolare il modulo dell’impulso $\vec{J}$ .
Eseguire i calcoli per: $m=30\,\text{g}$ , $h=3\,\text{m}$ , $v=2\,\text{m}\cdot\text{s}^{-1}$ .

Rendered by QuickLaTeX.com

Figura 2: schema del problema lavoro ed energia 2.

Schema di un anellino di massa m che scorre lungo un’asta verticale. L’anellino è inizialmente fermo alla base dell’asta e viene lanciato verso l’alto con un impulso J, raggiungendo la quota h prima di ricadere alla base con velocità v.

Svolgimento esercizio 2.

Esercizio 3 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Una massa puntiforme $m$ è inizialmente in quiete su un piano orizzontale con coefficiente di attrito statico $\mu_s$ ed attrito dinamico $\mu_d$ . Alla massa viene applicata all’istante $t=0\,\text{s}$ una forza orizzontale con direzione e verso costanti ed il cui modulo varia nel tempo secondo la legge $F=Kt$ . Si determinino:

(i) il tempo $t_0$ al quale $m$ comincia a muoversi;

(ii) il lavoro totale compiuto dalle forze agenti su $m$ dall’istante iniziale fino al tempo $t=\tau$ .

Eseguire i calcoli per: $\tau =10\,\text{s},\,$ $m=1\,\text{kg},\,$ $\mu_s=0,2,\,$ $\mu_d=0,1,\,$ $K=2\,\text{N}\cdot\text{s}^{-1}$ .

Rendered by QuickLaTeX.com

Figura 3: schema del problema lavoro ed energia 3.

Svolgimento esercizio 3.

Esercizio 4 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Un corpo di massa $m$ si muove di moto rettilineo uniforme su un piano orizzontale liscio con velocità $V$ verso una delle estremità di una molla (di massa trascurabile) a riposo, come mostrato in figura 4. La molla non è ideale, ma esercita sul corpo una forza di richiamo $F=-kx-\alpha x^{3}$ , dove $x$ indica la compressione della molla e $\alpha$ è una costante avente unità di misura $\text{N}\cdot \text{m}^{-3}$ . Calcolare la massima compressione subita dalla molla.

Rendered by QuickLaTeX.com

Figura 4: schema del problema lavoro ed energia 4.

Svolgimento esercizio 4.

Esercizio 5 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Una massa puntiforme $m$ è vincolata a muoversi su un piano orizzontale. Ad essa è collegata una molla di massa trascurabile, avente costante elastica $k$ e lunghezza a riposo $\ell_{0}$ fissata ad una parete verticale come in figura 5. Inizialmente la molla è nella posizione di riposo; ad un certo punto per mezzo di un’opportuna forza esterna si sposta il corpo $m$ di una quantità $\Delta x$ rispetto alla parete verticale. Determinare l’energia potenziale di $m$ in funzione dello spostamento $\Delta x$ dalla parete e dimostrare che per piccole oscillazioni l’energia potenziale è proporzionale ad $(\Delta x)^{4}$ .

Rendered by QuickLaTeX.com

Figura 5: schema del problema lavoro ed energia 5.

Svolgimento esercizio 5.

Esercizio 6 $(\bigstar \largewhitestar\largewhitestar \largewhitestar\largewhitestar)$ . Un’autocisterna fuori controllo per un guasto ai freni sta salendo con una velocità $V$ su di una rampa di emergenza priva di attrito, con inclinazione di $\theta$ , come in figura 6. Quale deve essere la lunghezza minima $L_{min}$ della rampa per esser certi che riesca ad arrestare la cisterna?

Rendered by QuickLaTeX.com

Figura 6: schema del problema lavoro ed energia 6.

Svolgimento esercizio 6.

Esercizio 7 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Ad un blocco di massa $m$ in quiete su un piano orizzontale viene applicato un impulso $\vec{J}$ , orientato come in figura 7. A seguito di ciò il blocco scivola lungo il piano orizzontale liscio incontrando l’inizio di una guida circolare liscia di raggio $R$ nel punto $A$ . La velocità del corpo nel punto $A$ è tale da consentire al blocco di arrivare in un punto $B$ della guida. Il raggio $R$ che congiunge il centro della guida con $B$ forma un angolo $\dfrac{\pi}{2}<\theta<\pi$ con la verticale. Calcolare la reazione vincolare della guida nel punto $B$ .

Rendered by QuickLaTeX.com

Figura 7: schema del problema lavoro ed energia 7.

Svolgimento esercizio 7.

Esercizio 8 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Un blocco di massa $m$ viene spinto contro una molla ideale di costante elastica $k$ non nota e lunghezza a riposo $y_0$ comprimendo la molla di una quantità $y_{\text{eq}}$ , in modo che il sistema rimanga in equilibrio. Si determini $k$ in funzione di $m$ , g e $y_{\text{eq}}$ . Successivamente, il blocco di massa $m$ viene spinto verso il basso da una opportuna forza di un ulteriore spazio $\Delta \tilde{y}$ e poi rilasciato. Determinare l’energia totale del sistema subito prima del rilascio in funzione di $m$ , $g$ , $\Delta \tilde{y}$ e $y_{\text{eq}}$ . Inoltre, calcolare fino a che altezza oltre la posizione di rilascio arriverà il blocco in funzione di $\Delta \tilde{y}$ e $y_{\text{eq}}$ .

Rendered by QuickLaTeX.com

Figura 8: schema del problema lavoro ed energia 8.

Svolgimento esercizio 8.

Esercizio 9 $(\bigstar\bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Una molla ideale (priva di massa) di costante elastica $k$ e lunghezza a riposo $y_0$ è posta verticalmente lungo un piano orizzontale. Ad un’altezza $D$ dalla molla si trova un blocco di massa $m$ tenuto in sospensione verticale mediante un apposito filo. Ad un certo punto il filo viene tagliato ed il blocco cade verso la molla la quale è dotata di un particolare supporto per cui il blocco resta incollata ad essa. Una volta che il corpo $m$ rimane attaccato alla molla, si determini:

a) l’altezza massima $h_{max}$ e l’altezza minima $h_{min}$ del corpo rispetto al suolo sfruttando la conservazione dell’energia e da esse dedurre la legge oraria del blocco;

b) applicando le leggi della dinamica la legge oraria del blocco e successivamente calcolare $h_{max}$ ed $h_{min}$ .

Si ipotizzi che nell’urto tra $m$ e la molla si conservi l’energia.

Rendered by QuickLaTeX.com

Figura 9: schema del problema lavoro ed energia 9.

Svolgimento esercizio 9.

Esercizio 10 $(\bigstar \largewhitestar \largewhitestar \largewhitestar\largewhitestar)$ . Un blocco di ghiaccio è lasciato scivolare dal bordo in una coppa semisferica di raggio $r$ , priva di attrito come illustrato in figura 10. Che velocità possiede il blocco quando arriva in fondo alla coppa?

Rendered by QuickLaTeX.com

Figura 10: schema del problema lavoro ed energia 10.

Un blocco di ghiaccio è lasciato scivolare dal bordo di una coppa semisferica di raggio r, priva di attrito. Il problema richiede di determinare la velocità del blocco quando arriva in fondo alla coppa. La figura mostra una coppa semisferica con un blocco posizionato sul bordo, pronto a scivolare verso il punto più basso, con il centro della sfera indicato come O e il raggio r evidenziato.

Svolgimento esercizio 10.

Esercizio 11 $(\bigstar \bigstar \bigstar \largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ si muove con velocità $V_0$ diretta lungo un piano orizzontale ed è attaccato ad una molla ideale di costante elastica $k$ , inizialmente nella posizione di riposo (supporre che la posizione di riposo della molla sia $x_0$ ). Tra il punto materiale e la superficie orizzontale di appoggio c’è attrito con coefficienti di attrito statico e dinamico rispettivamente $\mu_S$ e $\mu_d$ . Si determini la relazione che deve sussistere tra il modulo $V_0$ della velocità e le grandezze $m,k,\mu_S$ e $\mu_d$ affinché il punto materiale rimanga ferma nella posizione corrispondente al massimo allungamento della molla.

Rendered by QuickLaTeX.com

Figura 11: schema del problema lavoro ed energia 11.

Svolgimento esercizio 11.

Esercizio 12 $(\bigstar\largewhitestar \largewhitestar \largewhitestar\largewhitestar)$ . Ad un filo ideale (filo inestensibile e di massa trascurabile) di lunghezza $L$ , opportunamente fissato in un punto $O$ , è legata una palla. Ad una distanza verticale $d$ dal punto $O$ è posto un piolo individuato dal punto $P$ . Quando la palla, inizialmente ferma, è lasciata libera, oscillerà lungo l’arco tratteggiato in rosso, come illustrato in figura 12. Quando il filo tocca il piolo la massa descriverà l’arco tratteggiato in blu di raggio $r$ . Calcolare la velocità della palla dopo che il filo sarà rimasto impigliato nel piolo quando:

raggiungerà il punto più basso della traiettoria;
raggiungerà il punto più alto della traiettoria.

Si assuma che nell’urto con il piolo si conservi l’energia del sistema. Esprimere i risultati in funzione di $g$ , $d$ e $L$ .

Rendered by QuickLaTeX.com

Figura 12: schema del problema lavoro ed energia 12.

Svolgimento esercizio 12.

Esercizio 13 $(\bigstar \bigstar \largewhitestar \largewhitestar\largewhitestar)$ . Una molla ideale, con lunghezza a riposo $\ell_0$ , può essere compressa di una quantità $\Delta \ell$ da un’opportuna forza esterna $F$ . Un blocco di massa $m$ è inizialmente fermo in cima ad un piano inclinato privo di attrito, formante un angolo $\theta$ con il piano orizzontale. Ad un certo punto viene lasciato libero di scorrere lungo il piano. Il blocco si arresta momentaneamente dopo aver compresso la molla di una quantità $\Delta \tilde{\ell}$ .
Calcolare di quanto si è spostato il corpo $m$ lungo il piano inclinato e qual è la sua velocità quando tocca la molla. Supporre che nell’urto tra la molla e il punto materiale $m$ si conservi l’energia.

Rendered by QuickLaTeX.com

Figura 13: schema del problema lavoro ed energia 13.

Svolgimento esercizio 13.

Esercizio 14 $(\bigstar \bigstar \bigstar \largewhitestar\largewhitestar)$ . Un blocco di $m$ , partendo da fermo, scivola per una distanza $d$ giù per un piano privo di attrito inclinato di $\theta$ , fino ad imbattersi in una molla. Il blocco continua a scivolare per $\Delta x$ prima di essere momentaneamente arrestato dalla compressione della molla la cui costante è $k$ .
Si richiedere di determinare il valore di $d$ e la distanza fra il punto di primo contatto e il punto in cui il blocco raggiunge la velocità massima.

Rendered by QuickLaTeX.com

Figura 14: schema del problema lavoro ed energia 14.

Svolgimento esercizio 14.

Esercizio 15 $(\bigstar \bigstar \bigstar \largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ parte con velocità nulla dalla posizione $A$ e scende lungo un piano inclinato di $\theta$ , privo di attrito. Nella posizione $B$ il piano è raccordato a una guida circolare di centro $O$ e raggio $R$ , anch’essa priva di attrito. Il segmento $AB$ è tangente alla guida.
Si vuole che il punto si stacchi dalla guida in corrispondenza dell’angolo $\alpha$ (punto $C$ sulla guida). Si calcoli di quanto la quota di $A$ deve superare la quota di $B$ .

Rendered by QuickLaTeX.com

Figura 15: schema del problema lavoro ed energia 15.

Svolgimento esercizio 15.

Esercizio 16 $(\bigstar \bigstar\bigstar \largewhitestar\largewhitestar)$ . Un giovane ragazzo è seduto sulla sommità di un blocco di ghiaccio a forma di semisfera, come mostrato nella figura 16. Dopo aver ricevuto una leggera spinta, inizia a scivolare verso il basso. Dimostrare che, se il ghiaccio è privo di attrito, egli si staccherà dal ghiaccio in un punto che si trova ad un’altezza di $\dfrac{2}{3}R$ rispetto al suolo. Si consideri il blocco di ghiaccio fisso al suolo.

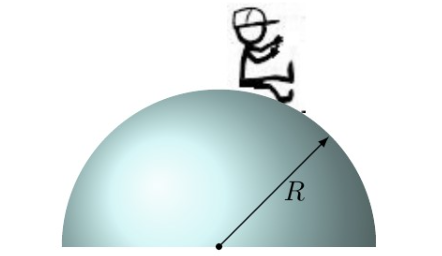
Figura 16: schema del problema lavoro ed energia 16.

Svolgimento esercizio 16.

Esercizio 17 $(\bigstar \bigstar\bigstar \largewhitestar\largewhitestar)$ . Un corpo posto sul punto più alto di una calotta sferica fissa di raggio $R=\text{2,50} \,\text{m}$ viene messo in moto con velocità $v_0=\text{0,30} \,\text{m}\cdot \text{s}^{-1}$ . Se la calotta è liscia, calcolare:

(i) l’altezza rispetto al piano orizzontale in cui il blocco si stacca dalla calotta;

(ii) la distanza orizzontale percorsa una volta che il blocco ha lasciato la calotta;

(iii) la velocità finale $\vec{v}_{f}$ del corpo quando tocca il suolo.

Rendered by QuickLaTeX.com

Figura 17: schema del problema lavoro ed energia 17.

Svolgimento esercizio 17.

Esercizio 18 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ .Un punto materiale $P$ di massa $m$ , inizialmente in quiete, viene lasciato scivolare lungo uno scivolo liscio costituito da un piano inclinato di un angolo $\theta$ raccordato ad una guida orizzontale, posta alla quota $a$ rispetto al suolo, come in figura 18. Calcolare:

la velocità $\overrightarrow{V}_A$ che $P$ deve possedere all’uscita dello scivolo ( $A$ ) per colpire il bersaglio $B$ , posto sul suolo ad una distanza $d$ dalla fine dello scivolo;
l’angolo di impatto $\phi$ di $P$ con il suolo;
la quota $h$ da cui bisogna lasciare $P$ da fermo affinché esso colpisca il bersaglio;
la quota $h'$ da cui bisognerebbe lasciare $P$ da fermo se il piano inclinato fosse scabro, con coefficiente di attrito dinamico $\mu_d$ , e la guida orizzontale liscia.

Nota. Il piano inclinato si raccorda con il piano orizzontale in modo tale da far conservare l’energia di $P$ .

Rendered by QuickLaTeX.com

Figura 18: schema del problema lavoro ed energia 18.

Svolgimento esercizio 18.

Esercizio 19 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ viene lasciato scivolare con velocità iniziale nulla dalla sommità di un piano inclinato scabro, avente altezza $h$ , angolo di base $\theta$ e coefficiente di attrito dinamico $\mu_d$ (punto $A$ ). Alla fine del piano inclinato (punto $B$ ), il punto materiale percorre un tratto di lunghezza $d$ su un piano orizzontale scabro, con lo stesso coefficiente di attrito dinamico $\mu_d$ . Giunto alla fine di tale tratto (punto $C$ ), il punto viene fermato in $D$ da una molla di costante elastica $k$ . Trascurando l’attrito radente dinamico nel tratto in cui agisce la forza della molla, calcolare:

la velocità del punto in $B$ ;
l’accelerazione nel tratto $AB$ ;
la variazione della sua energia cinetica nel tratto $BC$ ;
il massimo valore della compressione della molla.

Nota. La fine del piano inclinato si raccorda con il piano orizzontale in moto tale da far conservare l’energia di $P$ .

Rendered by QuickLaTeX.com

Figura 19: schema del problema lavoro ed energia 19.

Svolgimento esercizio 19.

Esercizio 20 $(\bigstar \bigstar\bigstar \largewhitestar\largewhitestar)$ . Una molla ideale di costante elastica $k$ si trova su di un piano orizzontale ad un’altezza $h$ dal suolo. In un esperimento si spara una palla di massa $m$ , comprimendo la molla di una quantità $\Delta x_1$ per colpire un bersaglio che si trova al suolo ad una distanza $\Delta x_2$ dalla base del piano orizzontale. Purtroppo, la sfera manca il bersaglio di una distanza pari ad $\Delta x_3$ . Al secondo tentativo, qual’è la quantità $\Delta x$ di cui deve essere compressa la molla affinché la sfera colpisca il bersaglio? Si richiede di esprimere $\Delta x$ in funzione di $\Delta x_1$ , $\Delta x_2$ e $\Delta x_3$ .
Nota. Si consideri il sistema conservativo e la sfera puntiforme.

Rendered by QuickLaTeX.com

Figura 20: schema del problema lavoro ed energia 20.

Svolgimento esercizio 20.

Esercizio 21 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Un corpo viene lanciato con velocità $\vec{V}$ nel punto $A$ del tratto orizzontale $\overline{AB}$ di lunghezza $\ell$ , in modo che percorra tale tratto e poi il tratto $\overline{BC}$ , di lunghezza uguale al precedente, inclinato di un angolo $\theta$ rispetto all’orizzontale. Tra il corpo ed i due tratti succitati vi è attrito con coefficiente di attrito dinamico $\mu_d$ . Calcolare il modulo $V$ della velocità del corpo, se quest’ultimo arriva in $C$ con velocità nulla. Inoltre, supporre che la fine del piano inclinato si raccordi con il piano orizzontale in moto tale da far conservare l’energia del punto materiale $m$ .

Rendered by QuickLaTeX.com

Figura 21: schema del problema lavoro ed energia 21.

Svolgimento esercizio 21.

Esercizio 22 $(\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar)$ . Su un container inizialmente fermo agiscono tre forze di modulo pari a $\vec{F}_1,\vec{F}_2$ e $\vec{F}_3$ orientate come in figura 22. Calcolare il lavoro svolto dal risultante delle forze durante uno spostamento $d$ del container. Esprimere il lavoro in funzione di, $F_1$ , $F_2$ , $F_3$ , $\theta_2$ , $\theta_3$ , e $d$ .

Rendered by QuickLaTeX.com

Figura 22: schema del problema lavoro ed energia 22.

Svolgimento esercizio 22.

Esercizio 23 $(\bigstar \largewhitestar \largewhitestar \largewhitestar\largewhitestar)$ . Una molla ideale di costante elastica $k$ , disposta su un piano orizzontale liscio, ha un’estremità fissata ad una parete ed è compressa di $\delta$ . Si appoggia all’altra estremità della molla un corpo di massa $m$ (si veda figura 23) e si taglia il filo che tiene compressa la molla.
In corrispondenza dell’istante in cui la lunghezza della molla è quella di riposo, si calcoli: il lavoro compiuto dalla molla sul corpo, la velocità di quest’ultimo ed il modulo dell’impulso complessivo esercitato dalla molla sul corpo in tale istante. Inoltre, si dimostri che il moto è armonico semplice.

Rendered by QuickLaTeX.com

Figura 23: schema del problema lavoro ed energia 23.

Svolgimento esercizio 23.

Esercizio 24 $(\bigstar \bigstar \largewhitestar \largewhitestar\largewhitestar)$ . Una pallina di massa $m$ si muove di moto circolare uniforme con periodo $T$ su un piano orizzontale liscio; la pallina è collegata al centro della traiettoria da un filo elastico di costante elastica $k$ e lunghezza di riposo $\ell_0$ . Quanto vale l’energia meccanica della pallina?

Rendered by QuickLaTeX.com

Figura 24: schema del problema lavoro ed energia 24.

Svolgimento esercizio 24.

Esercizio 25 $(\bigstar \bigstar \bigstar \bigstar\largewhitestar)$ . Una palla di massa $m$ viene appoggiata su un piano orizzontale liscio e attaccata ad una molla ideale e di costante elastica $k$ , come in figura 25. Si assuma la molla attaccata ad un estremo fisso $O$ e di lunghezza a riposo nulla. Scelto un sistema di riferimento fisso $Oxy$ , posizionando la pallina in un generico punto $(x_0,y_0)$ e imprimendo una velocità iniziale $\vec{v}=v_{i,x}\, \hat{x}+v_{i,y}\, \hat{y}$ alla pallina, si determini sotto quale condizione il moto della pallina descrive un’ellisse centrata nell’origine con gli assi coincidenti con gli assi coordinati. Inoltre, applicando le coordinate polari si scrivano le equazioni del moto della pallina e si determini se la pallina possa descrivere un moto circolare uniforme.

Rendered by QuickLaTeX.com

Figura 25: schema del problema lavoro ed energia 25.

Svolgimento esercizio 25.

Esercizio 26 $(\bigstar \bigstar \largewhitestar \largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ scende lungo un piano inclinato liscio. Alla fine del piano inclinato scorre su un tratto orizzontale scabro, con coefficiente di attrito dinamica $\mu$ , andando ad urtare una molla, di massa trascurabile e costante elastica $k$ fissata ad un vincolo verticale; il piano inclinato è fatto in modo tale da raccordare la fine di esso con il piano orizzontale in modo che si conservi l’energia. La molla ha una lunghezza a riposo $\ell_0$ e una costante elastica $k$ . La distanza tra la fine del piano inclinato e il vincolo è $d$ . Se il punto all’istante iniziale è fermo, determinare l’altezza $h$ da cui deve scendere affinché, dopo aver urtato la molla, possa toccare la parete del vincolo. Si supponga che nell’urto tra molla e punto si conservi l’energia, e che nella parte in cui è presente la molla non ci sia attrito.

Rendered by QuickLaTeX.com

Figura 26: schema del problema lavoro ed energia 26.

Svolgimento esercizio 26.

Esercizio 27 $(\bigstar \bigstar\bigstar \largewhitestar\largewhitestar)$ . Due punti materiali con la stessa massa sono collegati da un filo, come in figura 27. Il piano inclinato forma un angolo $\theta$ con il piano orizzontale ed è scabro, con coefficiente di attrito dinamico $\mu_d$ . Ad un certo istante, il sistema viene lasciato libero di muoversi e si osserva che la massa sospesa ad un’altezza $h$ rispetto al suolo comincia a scendere. Calcolare la distanza totale $s$ percorsa dalla massa che si trova sul piano inclinato per arrestarsi. Si assuma il piano inclinato fisso.

Rendered by QuickLaTeX.com

Figura 27: schema del problema lavoro ed energia 27.

Svolgimento esercizio 27.

Esercizio 28 $(\bigstar \bigstar\bigstar \largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ poggia su di un piano orizzontale ed è attaccato ad una molla ideale di costante elastica $k$ . Inizialmente il corpo $m$ ha velocità $\vec{V}_0$ e la molla è a riposo, come in figura 28. Tra la cassa e la superficie orizzontale di appoggio c’è attrito, con coefficienti di attrito statico e dinamico rispettivamente pari a $\mu_s$ e $\mu_d$ . Si determini la relazione che deve esistere tra il modulo $V_0$ della velocità della cassa e le grandezze $m,k,\mu_s$ e $\mu_d$ affinché la cassa rimanga ferma nella posizione corrispondente al massimo allungamento della molla.

Rendered by QuickLaTeX.com

Figura 28: schema del problema lavoro ed energia 28.

Svolgimento esercizio 28.

Esercizio 29 $(\bigstar \bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un blocco di massa $m$ si trova in un piano verticale, ed è vincolato a muoversi su una semicirconferenza di raggio $R$ , come in figura 29. Inizialmente il corpo si trova sulla sommità della semicirconferenza e ha una velocità $\vec{v}_0$ parallela al piano orizzontale, come si può dedurre dalla figura 29, e comincia a scendere lungo la guida. Nella prima metà la guida oppone al moto una forza tangenziale di attrito con modulo costante $F$ , nella seconda metà la guida è liscia. Calcolare la reazione della guida nell’istante in cui il blocco passa nella posizione individuata dall’angolo $\theta$ .

Rendered by QuickLaTeX.com

Figura 29: schema del problema lavoro ed energia 29.

Svolgimento esercizio 29.

Esercizio 30 $(\bigstar \bigstar\bigstar\largewhitestar\largewhitestar)$ . Una molla è legata per un’estremità al punto più alto di una guida circolare di raggio $R$ disposta verticalmente e per l’altra estremità ad un anello di massa $m$ e raggio trascurabile in grado di scorrere senza attrito lungo la guida circolare. La lunghezza della molla a riposo è $\ell<2R$ . Quando viene stirata, la molla reagisce con una forza elastica $F=-k\Delta\ell$ . Si determini

i valori assunti dall’angolo $\phi$ tra l’elastico e la verticale nelle posizioni di equilibrio dell’anello;
la condizione che deve soddisfare la costante elastica $k$ affinché l’anello sia in equilibrio ad un angolo $\phi\neq0$ .

Rendered by QuickLaTeX.com

Figura 30: schema del problema lavoro ed energia 30.

Svolgimento esercizio 30.

Esercizio 31 $(\bigstar \bigstar\bigstar\largewhitestar\largewhitestar)$ . Un corpo approssimabile a un punto materiale di massa $m$ è agganciato a due molle; la prima, di costante elastica $k_1$ , ha l’altro estremo fissato sulla parte superiore di una scatola, mentre l’altra di costante elastica $k_2$ ha l’altro estremo agganciato alla parte inferiore della stessa scatola. La scatola è alta $\ell_0$ e tale lunghezza è pari anche alla lunghezza a riposo di entrambe le molle. Il corpo è vincolato a muoversi lungo la direzione verticale, le molle sono ideali e possono comprimersi fino ad avere lunghezza nulla. Si supponga la scatola ferma.

Si appoggi $m$ alla base della scatola e si determini il valore minimo $k_{2,{\min}}$ di $k_2$ necessario affinché la massa $m$ possa essere in equilibrio senza essere appoggiata alla base della scatola (reazione vincolare nulla).
Il corpo viene lasciato da fermo dalla posizione iniziale $y_0=\ell_0/2$ . Si calcoli la velocità massima $v_{\max}$ che ha il corpo durante il moto e il periodo del moto.

Rendered by QuickLaTeX.com

Figura 31: schema del problema lavoro ed energia 31.

Svolgimento esercizio 31.

Esercizio 32 $(\bigstar \bigstar\bigstar\largewhitestar\largewhitestar)$ . Due punti materiali $1$ e $2$ , ciascuno di massa $m$ , sono vincolati a scorrere senza attrito lungo due binari in un piano orizzontale che formano tra di loro un angolo fisso $2\theta$ e che giacciono su un piano orizzontale.
I due punti materiali sono connessi da una molla ideale, di lunghezza a riposo nulla, di costante elastica $k$ , e di massa trascurabile. Le due masse si muovono in modo da mantenere le rispettive distanze dal punto di giunzione dei due binari uguali tra loro. Calcolare:

Il modulo della forza esercitata dalla molla su ciascuna massa quando le masse distano $\ell$ dal punto in comune dei due binari;
il periodo del moto quando le masse vengono messe ad una distanza generica $x^\prime$ dal punto di intersezione delle due guide.

Si trascuri ogni forma di attrito e supporre che quando i due punti si urtino nel punto di intersezione delle due guide non ci sia dissipazione di energia. In altri termini, supporre che il moto sia periodico anche se sussiste un urto nella posizione di equilibrio $x^\prime=0$ , ovvero quando i due punti materiali si incontrano nel punto di intersezione tra le due guide.

Rendered by QuickLaTeX.com

Figura 32: schema del problema lavoro ed energia 32.

Svolgimento esercizio 32.

Esercizio 33 $(\bigstar \bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un bue traina una slitta con un carico complessivo di massa $m$ su una strada ripida, con pendenza $\theta$ , mediante una fune inestensibile e di massa trascurabile. Il coefficiente di attrito dinamico fra la slitta e la strada è $\mu_d$ . Il bue durante il traino eroga una potenza $P$ .

Calcolare il modulo costante della velocità con cui il bue riesce a tirare la slitta diretta parallelamente al piano inclinato.
Calcolare la potenza dissipata per effetto dell’attrito e la corrispondente frazione rispetto alla potenza $P$ erogata dal bue.
Calcolare la potenza per compiere lavoro contro la forza di gravità e la corrispondente frazione rispetto alla potenza $P$ erogata dal bue.
Si verifichi che si conserva la potenza, in ogni istante $t>0$ .

Rendered by QuickLaTeX.com

Figura 33: schema del problema lavoro ed energia 33.

Svolgimento esercizio 33.

Esercizio 34 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Un alpino di massa $m$ si arrampica mediante una fune inestensibile e di massa trascurabile a velocità costante su una parete verticale alta $h$ . Per raggiungere la sommità impiega un tempo pari a $\Delta t$ . Si calcoli la potenza $P$ che devono fornire i muscoli dell’alpino in un generico istante $t>0$ . Inoltre, si consideri l’alpino come un punto materiale.

Rendered by QuickLaTeX.com

Figura 34: schema del problema lavoro ed energia 34.

Svolgimento esercizio 34.

Esercizio 35 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un corpo di massa $m$ entra con velocità $\vec{v}_A$ in una guida verticale circolare liscia di raggio $R$ . La velocità $\vec{v}_A$ è parallela al piano orizzontale sul quale poggia $m$ prima di entrare nella guida, come rappresentato in figura 35.

Calcolare:

il modulo della velocità nei punti $B$ e $C$ della guida;
il modulo della reazione vincolare generato dalla guida su $m$ nei punti $A$ , $B$ e $C$ ;
il valore minimo del modulo della velocità $v_A$ affinché il corpo arrivi nel punto $C$ mantenendo il contatto con la guida.

Si supponga che sia soddisfatta la seguente condizione $v_A^2> 5gR$ .

Rendered by QuickLaTeX.com

Figura 35: schema del problema lavoro ed energia 35.

Svolgimento esercizio 35.

Esercizio 36 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Due corpi $A$ e $B$ , di masse $m_A=m_B=m$ , si trovano su un piano scabro inclinato di $\alpha$ rispetto all’orizzontale, sono collegati da una molla ideale di massa trascurabile, e costante elastica $k$ . Inizialmente i due corpi sono tenuti fermi ad una distanza relativa pari alla lunghezza di riposo della molla; inoltre, il corpo $A$ si trova ad una quota maggiore rispetto al corpo $B$ , come illustrato in figura 36. Ad un certo istante si lascia il corpo $B$ libero di muoversi mentre $A$ è tenuto fermo mediante un opportuno vincolo esterno: $B$ scende verso il basso e prima di fermarsi percorre un tratto $\delta>0$ .

Calcolare:

il coefficiente di attrito dinamico $\mu_d$ comune ai due corpi.

Nell’istante in cui $B$ si ferma esso viene bloccato con un opportuno vincolo esterno mentre $A$ è libero di muoversi. Si calcoli:

lo spazio $\ell$ percorso da $A$ prima di fermarsi la prima volta;
l’energia cinetica massima raggiunta da $A$ nella fase di discesa.

Supporre che valga la condizione $2 mg\sin\alpha-k\delta>0$ e che $A$ ed $B$ non si scontrino mai.

Rendered by QuickLaTeX.com

Figura 36: schema del problema lavoro ed energia 36.

Svolgimento esercizio 36.

Esercizio 37 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Due blocchi di massa $m_1$ e $m_2$ , collegati tra loro da una molla ideale di costante elastica $k$ , sono appoggiati su un piano inclinato di un angolo $\theta$ . Il piano è scabro nella parte superiore dove si trova $m_1$ con coefficiente di attrito statico $\mu_s$ , ed è liscio nella parte inferiore dove si trova $m_2$ . Nell’istante iniziale $m_1$ è in quiete, $m_2$ ha velocità di modulo $v_0$ e la molla è al riposo. La velocità di modulo $v_0$ è diretta parallelamente al piano inclinato, come in figura 1. Calcolare, nell’istante iniziale

l’accelerazione di $m_2$ ;
la forza di attrito agente su $m_1$ .

In un certo istante successivo $m_1$ entra in moto. Calcolare in tale istante:

l’allungamento della molla;
la velocità di $m_2$ .

Supporre $mu_s\cos\theta-\sin\theta>0$ e $\left(2+\dfrac{m_1}{m_2}\right)\sin\theta-\dfrac{m_1}{m_2}\mu_s\cos\theta>0.$

Rendered by QuickLaTeX.com

Figura 37: schema del problema lavoro ed energia 37.

Svolgimento esercizio 37.

Esercizio 38 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Un corpo di massa $m$ è attaccato ad un filo inestensibile, di lunghezza $\ell$ e massa trascurabile, a un punto $P$ della superficie laterale di un disco di raggio $R<\ell/\pi$ e con l’asse di simmetria parallelo al suolo. Si assuma che il disco sia fermo e che inizialmente il corpo pende liberamente sotto l’azione della forza peso (si veda la figura 38). Si mette in movimento il corpo con velocità $\vec{v}_0$ perpendicolare al filo e all’asse del disco, dopo di che, il filo si avvolge attorno al disco. Si chiami $\theta$ l’angolo che forma il raggio $R$ con l’orizzontale, nel verso indicato nella figura 38, assumendo che $\theta\in[0,\pi]$ . Si richiede di determinare

il modulo della tensione $\vec{\tau}$ del filo in funzione dell’angolo $\theta$ ;
il valore minimo $\vec{v}_{\min}$ del modulo della velocità iniziale tale per cui il corpo riesca ad avvolgersi intorno a metà circonferenza.

Rendered by QuickLaTeX.com

Figura 38: schema del problema lavoro ed energia 38.

Svolgimento esercizio 38.

Esercizio 39 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Siano un sistema di riferimento fisso $Oxy$ e un punto materiale di massa $m$ tale per cui $m$ giaccia nel piano $xy$ . Il piano $xy$ coincide con un piano orizzontale privo di attrito. Tale punto materiale è attaccato ad un filo, a sua volta fissato ad un palo di raggio $R$ , intorno al quale può avvolgersi. All’istante $t=0$ la posizione del punto è $(R,L)$ dove $L$ è la lunghezza del filo. Il filo è fissato al palo nel punto $(R,0)$ . La velocità del punto, sempre a $t=0$ è $(-v_0,0)$ . Si determini la posizione del punto in funzione del tempo e la sua velocità. Inoltre, determinare dopo quanto tempo il punto urta il palo. Supporre $L>R\pi$ .

Rendered by QuickLaTeX.com

Figura 39: schema del problema lavoro ed energia 39.

Un punto materiale di massa m è attaccato a un filo che si avvolge attorno a un palo di raggio R in un piano orizzontale privo di attrito. Il punto parte dalla posizione (R, L) con una velocità iniziale orizzontale e si muove verso il palo. Il problema richiede di determinare la posizione e la velocità del punto nel tempo, oltre al momento in cui urta il palo.

Svolgimento esercizio 39.

Esercizio 40 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Un corpo di massa $m$ è in quiete in un punto $O$ , su di una guida rettilinea orizzontale liscia; viene messo in moto tramite l’applicazione di una botta. La botta ha una durata di tempo $\Delta t>0$ molto breve. Dopo la botta, la massa $m$ , ha una velocità $\vec{v}_0$ parallela al piano orizzontale, come rappresentato in figura 40. Si richiede di calcolare

il valor medio della forza applicata durante la botta di durata molto breve.

Dopo la botta, il corpo scivola lungo la guida rettilinea orizzontale liscia fino al punto $A$ , come rappresentato in figura 40. Raggiunto il punto $A$ la guida orizzontale si raccorda con una guida scabra, posta in un piano verticale, avente la forma di un quarto di circonferenza di raggio $R$ . Il lavoro della forza di attrito lungo il percorso curvilineo $AB$ vale $L_{\text{att}}<0$ .
Si richiede di calcolare

supponendo che valga $v_{0}^2+2\left(\dfrac{L_{\text{att}}}{m}-gR\right)>0$ , il modulo della velocità $\vec{v}_B$ del corpo nel punto $B$ ;
la reazione normale della guida nel punto $A$ , ovvero nel punto che raccorda la guida orizzontale con la guida scabra circolare.

Rendered by QuickLaTeX.com

Figura 40: schema del problema lavoro ed energia 40.

Un punto materiale di massa m è collegato a un punto fisso O da un filo inestensibile, descrivendo una traiettoria circolare in un piano verticale. Il sistema è soggetto a forze conservative come la forza gravitazionale e la tensione del filo. Il punto materiale passa per le posizioni A, B e C, evidenziando le variazioni di energia cinetica e potenziale lungo il percorso.

Svolgimento esercizio 40.

Esercizio 41 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ , collegato ad un punto fisso $O$ da un filo inestensibile e di massa trascurabile, descrive una circonferenza di raggio $R>0$ posta in un piano verticale. Nel punto $A$ la tensione del filo applicata ad $m$ vale $T_A>0$ , e che nel punto $B$ la velocità di $m$ vale $v_B>0$ . Si richiede di calcolare

il valore del raggio $R$ ;
il modulo $T_C$ che esercita il filo su $m$ in $C$ .

Rendered by QuickLaTeX.com

Figura 41: schema del problema lavoro ed energia 41.

Svolgimento esercizio 41.

Esercizio 42 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un corpo di massa $m$ è in quiete sostenuto da due fili inestensibili e entrambi di massa trascurabile. Il filo 1 forma un angolo $\beta$ con la verticale, mentre il filo 2 forma un angolo $\alpha$ con la verticale, come illustrato in figura 42. Il sistema fisico composto dai due fili e la massa $m$ è in equilibrio. Si richiede di calcolare

i moduli $T_1$ e $T_2$ che i due fili esercitano su $m$ .

Successivamente si taglia il filo 2, ed il corpo inizia ad oscillare rispetto alla verticale. La velocità massima raggiunta dal corpo durante le oscillazioni è $v>0$ . Calcolare:

la lunghezza $\ell$ del filo 1.

Rendered by QuickLaTeX.com

Figura 42: schema del problema lavoro ed energia 42.

Un corpo di massa m è sostenuto da due fili inestensibili di massa trascurabile. Il filo 1 forma un angolo β con la verticale, mentre il filo 2 forma un angolo α con la verticale. Il sistema è in equilibrio. Dopo il taglio del filo 2, il corpo inizia a oscillare. Si richiede di calcolare i moduli delle tensioni T1 e T2 e la lunghezza ℓ del filo 1.

Svolgimento esercizio 42.

Esercizio 43 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un blocco di massa $M$ viene trascinato mediante una fune inestensibile e di massa trascurabile su un piano orizzontale scabro, per un tratto $d$ . Alla fune è applicata una forza $\vec{F}$ costante in modulo, direzione e verso. La forza $\vec{F}$ è rappresentata nella figura 43 e la sua direzione forma un angolo costante $\alpha$ con l’orizzontale. Sapendo che il blocco si muove con velocità costante, si richiede di calcolare:

il lavoro compiuto sul blocco dalla forza d’attrito;
il coefficiente di attrito dinamico fra blocco e piano.

Rendered by QuickLaTeX.com

Figura 43: schema del problema lavoro ed energia 43.

Un blocco di massa M è trascinato su un piano orizzontale scabro mediante una fune inestensibile. Alla fune è applicata una forza F costante in modulo, direzione e verso, formando un angolo α con l'orizzontale. Il blocco si muove con velocità costante. Si richiede di calcolare il lavoro della forza d'attrito e il coefficiente di attrito dinamico.

Svolgimento esercizio 43.

Esercizio 44 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un pendolo semplice di massa $m$ e lunghezza $\ell$ , oscilla intorno al punto $A$ con un’ampiezza iniziale rispetto alla verticale pari a $\theta_0=\pi/2$ . Si richiede di calcolare, in funzione del generico angolo $\theta$ che il pendolo semplice forma con la verticale al piano di sospensione:

il modulo $v$ della velocità $\vec{v}$ di $m$ ;
il modulo $a$ dell’accelerazione $\vec{a}$ di $m$ ;
il modulo $T$ della tensione $\vec{T}$ del filo esercitata sul corpo di massa $m$ .

Rendered by QuickLaTeX.com

Figura 44: schema del problema lavoro ed energia 44.

Un pendolo semplice di massa m e lunghezza l oscilla attorno al punto A con un'ampiezza iniziale rispetto alla verticale pari a θ₀ = π/2. Il pendolo è sospeso a un punto fisso e forma un angolo generico θ con la verticale. Si richiede di calcolare la velocità, l'accelerazione e la tensione del filo esercitata sulla massa m.

Svolgimento esercizio 44.

Esercizio 45 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un corpo di massa $m$ è agganciato ad un supporto fisso da una molla di costante elastica $k$ . Il sistema è inizialmente in quiete sopra un piano orizzontale che è liscio alla destra del punto $O$ e scabro alla sua sinistra. Ad un certo istante con un’opportuna forza esterna si imprime al corpo una velocità $\vec{v}_0$ nel verso indicato in figura 45. Si richiede di calcolare

di quanto è allungata la molla nell’istante in cui il corpo si ferma.

Il corpo ripassa per $O$ con velocità $-\vec{v}_0$ , orientata come in figura 45, e si ferma dopo aver percorso da $O$ la distanza $x'$ , nel piano scabro. Si richiede di calcolare

il valore del coefficiente di attrito dinamico $\mu$ .

Supporre che valga $mv_0^2-kx'^2>0.$

Rendered by QuickLaTeX.com

Figura 45: schema del problema lavoro ed energia 45.

Svolgimento esercizio 45.

Esercizio 46 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Due masse $m_1$ ed $m_2$ sono collegate tra loro tramite una carrucola da un filo ideale di massa trascurabile, come rappresentato in figura 46. Si assuma che tra filo e carrucola non ci sia attrito. La massa $m_2$ è collegata al piano orizzontale mediante una molla ideale, di lunghezza a riposo nulla, posta in verticale e di costante elastica $k$ , allungata di una quantità $y>0$ . Il sistema complessivamente è in quiete sotto l’azione della forza $\vec{F}$ . La forza $\vec{F}$ è costante in modulo, direzione e verso. Si richiede di calcolare

il valore di $y$ .

Ad un certo istante si sgancia la molla ed il sistema entra in movimento. Si richiede di calcolare:

il valore $\vec{R}$ della forza totale agente su $m_1$ durante il moto.

Si osserva che dopo un tempo $\Delta t>0$ dall’inizio del moto, il corpo $m_1$ è avanzato di $h$ . Si richiede di calcolare

nell’intervallo di tempo $\Delta t>0$ il lavoro $W$ svolto dalla forza $F$ ;
la variazione di energia potenziale $\Delta U_2$ della massa $m_2$ ;
il valore di $\Delta t>0$ ;
l’energia cinetica totale del sistema $K_{\text{tot}}$ all’istante $\Delta t>0$ .

Supporre che valga $F>m_2g$ .

Rendered by QuickLaTeX.com

Figura 46: schema del problema lavoro ed energia 46.

Due masse collegate tramite una carrucola con un filo ideale. La massa m1 è posta su un piano orizzontale ed è soggetta a una forza F. La massa m2 è collegata a una molla verticale di costante elastica k. Il sistema è inizialmente in equilibrio.

Svolgimento esercizio 46.

Esercizio 47 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un blocco di massa $m$ poggia su di un piano orizzontale, ed è soggetto ad una forza $\vec{F}(t)$ di direzione costante parallela al piano orizzontale, modulo variabile nel tempo, e verso indicato in figura 47. L’energia cinetica del corpo cresce nel tempo secondo la legge $K(t)=\alpha t^3$ , con $\alpha$ costante.
Si calcoli la costante $\alpha$ e l’intensità della forza all’istante $t=\tau>0$ , sapendo che l’impulso della forza nell’intervallo di tempo $(0,\tau)$ ha modulo $J>0$ . L’energia cinetica va riferita rispetto ad un sistema di riferimento fisso $Ox$ , con l’asse delle $x$ coincidente con il piano orizzontale sul quale poggia $m$ .

Rendered by QuickLaTeX.com

Figura 47: schema del problema lavoro ed energia 47.

Un blocco di massa m poggia su un piano orizzontale ed è soggetto a una forza F(t) di direzione costante, parallela al piano orizzontale. L’energia cinetica del corpo cresce nel tempo secondo la legge K(t) = αt³, con α costante.

Svolgimento esercizio 47.

Esercizio 48 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un corpo di massa $m$ poggia su di un piano orizzontale ed è soggetto ad una forza $\vec{F}$ parallela al piano orizzontale, modulo variabile e direzione costante. Si scelga un sistema di riferimento fisso $Ox$ , con l’asse delle $x$ coincidente con il piano orizzontale; rispetto a tale sistema di riferimento si assuma che, il corpo di massa $m$ si muova di moto rettilineo e che il modulo della sua quantità di moto sia $p(t)=ct^2$ , con $c$ costante avente unità di misura $\text{kg}\cdot \text{m}\cdot \text{s}^{-3}$ . Tale moto può essere prodotto:

da una forza $\vec{F}(t)$ dipendente dal tempo;
da una forza $\vec{F}(x)$ dipendente dalla posizione del corpo, con $x$ posizione generica del punto materiale nel sistema di riferimento scelto.

Si determini nei due casi il modulo della forza in funzione del tempo o della posizione. Inoltre, si assuma che, la massa $m$ non dipenda dal tempo.

Rendered by QuickLaTeX.com

Figura 48: schema del problema lavoro ed energia 48.

Svolgimento esercizio 48.

Esercizio 49 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Un punto materiale di massa $m$ è soggetto ad una forza $\vec{F}=\vec{c}\wedge\vec{v},$ dove $\vec{v}$ e $\vec{c}$ sono rispettivamente la sua velocità rispetto ad un sistema di riferimento fisso e un vettore di modulo, direzione e verso costante, come rappresentato in figura 49. Inoltre, l’unità di misura del vettore $\vec{c}$ è $\text{kg}\cdot \text{s}^{-1}$ . Si determinino le possibili traiettorie del punto di materiale di massa $m$ rispetto ad un sistema di riferimento fisso $Oxyz$ .

Rendered by QuickLaTeX.com

Figura 49: schema del problema lavoro ed energia 49.

Un punto materiale di massa m è soggetto a una forza F data dal prodotto vettoriale tra il vettore c e la velocità v. Il sistema di riferimento Oxyz è rappresentato con il vettore c in direzione dell'asse z e il vettore v nel piano xy.

Svolgimento esercizio 49.

Esercizio 50 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Una massa puntiforme $m$ si muove su un piano orizzontale, privo di attrito, collegata all’estremità libera di una molla ideale di costante elastica $k$ e lunghezza a riposo $\ell_0$ . La seconda estremità della molla è fissata in un punto $C$ sul piano, e, quando la lunghezza della molla è pari a quella a riposo, la velocità della massa, di modulo $v_0$ , forma un angolo $\theta$ rispetto all’orientazione della molla, come mostrato in figura 50. Quando la molla raggiunge la sua massima lunghezza, $\ell_M$ , la velocità della massa ha modulo $v\neq 0$ . Determinare il valore di $v_0$ e $v$ . Supporre che valga ${(1-\alpha)}/{\left(1-\alpha^2\sin^2\theta\right)}>0$ , dove $\alpha=\ell_M/\ell_0$ .

Rendered by QuickLaTeX.com

Figura 50: schema del problema lavoro ed energia 50.

Una massa puntiforme m si muove su un piano orizzontale, privo di attrito, collegata all'estremità di una molla ideale fissata in un punto C. La velocità iniziale della massa ha modulo v0 e forma un angolo θ rispetto all'orientazione della molla.

Svolgimento esercizio 50.

Esercizio 51 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Da un sistema di riferimento fisso $Oxy$ si osserva un punto materiale di massa $m$ muoversi sotto l’azione della forza peso lungo una guida liscia, la cui forma è rappresentato dal grafico della funzione $f:\mathbb{R}\to\mathbb{R}$ tale che $y=f(x)$ , dove per convenienza l’asse $y$ è stato diretto verso il basso. All’istante iniziale $t=0$ , il punto materiale è nell’origine $O$ con velocità iniziale diretta parallelamente all’asse $y$ e di modulo pari a $v_0$ . Si determini

la scrittura analitica delle funzione $f$ affinché il punto materiale di massa $m$ si muova di moto rettilineo uniforme lungo l’asse delle $y$ ;
le componenti lungo l’asse delle $x$ e delle $y$ della reazione vincolare $\vec{R}$ generata dal vincolo sul punto materiale di massa $m$ .

Rendered by QuickLaTeX.com

Figura 51: schema del problema lavoro ed energia 51.

Un punto materiale di massa m si muove lungo una guida liscia rappresentata dal grafico della funzione y = f(x). All'istante iniziale t = 0, il punto è nell'origine O con velocità iniziale v0 diretta lungo l'asse y.

Svolgimento esercizio 51.

Esercizio 52 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ giace in quiete nel punto $A$ sul fondo di una guida liscia fissa con profilo semicircolare nel piano verticale di raggio $R$ . A partire da un certo istante al corpo $m$ è applicata una forza orizzontale di modulo $F$ costante. Calcolare:

il modulo $v_B$ della velocità $\vec{v}_B$ di $m$ quando raggiunge il punto $B$ più alto della guida;
la reazione vincolare della guida nello stesso istante.

Rendered by QuickLaTeX.com

Figura 52: schema del problema lavoro ed energia 52.

Un punto materiale di massa m si trova in quiete nel punto A sul fondo di una guida liscia con profilo semicircolare di raggio R. Una forza orizzontale F è applicata al corpo, spingendolo lungo la guida fino al punto B, il punto più alto della guida.

Svolgimento esercizio 52.

Esercizio 53 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . In un sistema di riferimento inerziale $Ox$ un punto materiale di massa $m=6$ kg è vincolato a muoversi lungo l’asse $x$ . Esso è soggetto ad una forza conservativa la cui energia potenziale è $U(x)=kx^2$ , dove $x$ è espresso in metri e $k=3 \text{ J}\cdot \text{m}^{-2}$ . L’energia totale (cinetica $+$ potenziale) del punto materiale è $E=30$ J per ogni istante $t>0$ . È possibile che il punto materiale si trovi nella posizione di ascissa $x=2$ m? In caso affermativo, in questa posizione, calcolare il modulo della velocità.

Svolgimento esercizio 53.

Esercizio 54 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Dato un sistema di riferimento inerziale $Ox$ , un punto materiale di massa $m=1$ kg vincolato all’asse $x$ si muove lungo quest’ultima. Nella posizione $x_A = 2$ m, la sua velocità è $v_A = 4\, \text{m}\cdot\text{s}^{-1}$ ; nella posizione $x_B = 7$ m, la sua velocità è $v_B$ . Il lavoro dissipato per attrito nel tratto che va da $x_A$ ad $x_B$ è $L_{\text{attr}}=-6$ J. Calcolare la velocità $v_B$ del punto materiale.

Svolgimento esercizio 54.

Esercizio 55 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Dato un sistema di riferimento inerziale $Oy$ , si consideri un punto materiale di massa $m=5$ kg. All’istante $t=0$ s il punto materiale si trova fermo ad un’altezza $y_i = 100$ m rispetto all’origine del sistema di riferimento, ovvero il suolo. Durante gli istanti successivi, quindi per $t>0$ , esso cade liberamente. Giunto ad un’altezza $y_f = 30$ m dal suolo, la sua velocità è di $v_f = 31 \text{ m} \cdot \text{s}^{-1}$ . Calcolare l’energia dissipata per attrito con l’aria.

Svolgimento esercizio 55.

Esercizio 56 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dato un sistema di riferimento inerziale $Ox$ , un punto materiale di massa $m=3\,\text{kg}$ vincolato a muoversi lungo l’asse delle $x$ si muove di moto armonico semplice con ampiezza $A = 15\,\text{cm}$ e frequenza angolare $\omega = 3 \text{ rad}\cdot \text{s}^{-1}$ . Assumendo che il sistema sia conservativo, calcolare l’energia meccanica $E$ del sistema.

Svolgimento esercizio 56.

Esercizio 57 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dato un sistema di riferimento fisso $Oxyz$ , per ogni istante $t\geq 0$ un punto materiale di massa $m = 2$ kg è vincolato a muoversi lungo l’asse delle $x$ secondo la seguente legge oraria

(1) $\begin{equation*} x(t) = 4t^3 + t^2 + 2t - 3, \end{equation*}$

valida per $t\geq 0$ .
Si consideri che i coefficienti numerici dell’equazione sopra riportata vanno intesi con le opportune unità di misura affinché la posizione $x(t)$ , dove il tempo $t$ è espresso in secondi, abbia come unità di misura il metro. Calcolare il lavoro compiuto dalla risultante delle forze $\vec{F}(t)$ agenti sul punto materiali nell’intervallo di tempo $t\in[1,3]\,\text{s}$ .

Svolgimento esercizio 57.

Esercizio 58 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dato un sistema di riferimento fisso $Oxy$ , si consideri un punto materiale vincolato a muoversi sulla curva $\Gamma$ di equazione $y=x^3$ , dove $x\in\mathbb{R}$ . Il punto materiale è sottoposto ad una forza costante $\vec{F}=-30\,\hat{x}\,\text{ N}+ 15\,\hat{y}\,\text{ N}$ , dove $\hat{x}$ e $\hat{y}$ sono rispettivamente i versori dell’asse delle $x$ e delle $y$ . Calcolare il lavoro compiuto dalla forza sul punto materiale lungo il tratto di curva con $x \in [0,2]\,\text{m}$ .

Svolgimento esercizio 58.

Esercizio 59 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Un punto materiale di massa $m=6$ kg è vincolato a muoversi lungo una retta. Si scelga un sistema di riferimento fisso $Ox$ tale per cui l’asse delle $x$ coincida con la retta e la posizione del punto materiale sia indicata con $x$ . Sul punto materiale agisce la sola forza conservativa $\vec{F}$ a cui è associata l’energia potenziale $U(x) = kx^2$ , dove $k = 3 \text{ J} \cdot \text{m}^{-2}$ è una costante. Si richiede di calcolare l’accelerazione del corpo nella posizione $x=-4\,\text{m}$ .

Svolgimento esercizio 59.

Esercizio 60 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Una sferetta di massa $m = 100$ g è agganciata ad una molla ideale, di costante elastica $k = \text{19,6}$ N $\cdot$ m $^{-1}$ , lunghezza a riposo $L = 40$ cm, priva di massa il cui secondo estremo è fissato nel punto $A$ , come mostrato in figura 60. Il sistema è posto su un piano orizzontale scabro (coefficiente di attrito dinamo $\mu = \text{0,5}$ ). Se si allunga la molla di un tratto $\Delta\ell_0 = 20$ cm e si lascia quindi muovere la sferetta sotto l’azione della molla, si determini la distanza minima da $A$ raggiunta dalla sferetta nel suo moto.

Rendered by QuickLaTeX.com

Figura 60: schema del problema lavoro ed energia 60.

Una sferetta di massa m è agganciata a una molla ideale di costante elastica k e lunghezza a riposo L. Il sistema è su un piano orizzontale scabro con coefficiente di attrito dinamico μ. La molla viene allungata di un tratto Δℓ0 e poi rilasciata, mettendo in moto la sferetta.

Svolgimento esercizio 60.

Esercizio 61 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Una molla ideale, priva di massa, è appesa ad un estremo in posizione verticale (figura 61.1). All’estremo libero viene agganciato un blocco di massa $M$ . All’equilibrio l’allungamento subito dalla molla è $\Delta \ell$ . La stessa molla viene poi disposta su un piano inclinato di angolo $\theta$ e privo di attrito, come mostrato in figura 61.2. Un corpo di massa $m$ è appoggiato alla molla e spinto in modo da comprimerla di un tratto $\Delta L$ . Il corpo viene poi lasciato libero di muoversi sul piano inclinato, partendo da fermo. Si calcoli la distanza percorsa dal corpo lungo il piano inclinato prima di invertire il suo moto.

Rendered by QuickLaTeX.com

Una molla ideale è appesa verticalmente con un'estremità fissata e l'altra con una massa M. L'allungamento della molla all'equilibrio è Δℓ.

Figura 61.1: schema del problema lavoro ed energia 61.1.

Rendered by QuickLaTeX.com

Una molla ideale è fissata a un piano inclinato di angolo θ. Una massa m è compressa contro la molla di un tratto ΔL e poi lasciata libera di muoversi lungo il piano inclinato.

Figura 61.2: schema del problema lavoro ed energia 61.2.

Svolgimento esercizio 61.

Esercizio 62 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dato un sistema di riferimento fisso $Oxyz$ , per ogni istante $t \geq 0$ un punto materiale di massa $m = 2\,\text{kg}$ è vincolato a muoversi lungo l’asse delle $x$ secondo la seguente legge oraria

(2) $\begin{equation*} x(t) = 4t^3 +t^2+2t-3. \end{equation*}$

La precedente equazione è valida per $t\geq0$ . Si consideri che i coefficienti numerici dell’equazione sopra riportata vanno intesi con le
opportune unità di misura affinché la posizione $x(t)$ , dove il tempo $t$ è espresso in secondi, abbia come unità di misura il metro. Calcolare la potenza media sviluppata dalla risultante delle forze agenti sul punto materiale nell’intervallo di tempo $t\in[0,5]\,\text{s}$ .

Svolgimento esercizio 62.

Esercizio 63 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Una molla ideale di massa trascurabile con costante elastica $k=1300 \text{ N} \cdot \text{m}^{-1}$ è disposta verticalmente e fissata con un suo estremo al suolo, mentre all’altro suo estremo è fissato un piattello di massa trascurabile. La molla è inizialmente in posizione di riposo. Da un’altezza di $h = 7$ m dal piattello, nell’istante $t=0$ , viene lasciato cadere un corpo di massa $m = 3$ kg che è inizialmente fermo. Trascurando la perdita di energia in seguito all’urto e l’attrito del corpo con l’aria, calcolare la massima compressione della molla.

Rendered by QuickLaTeX.com

Una molla ideale con costante elastica k è fissata al suolo con un piattello sopra di essa. Un corpo di massa m viene lasciato cadere da un'altezza h sopra il piattello. L'obiettivo è calcolare la massima compressione della molla.

Figura 63: schema del problema lavoro ed energia 63.

Svolgimento esercizio 63.

Esercizio 64 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Siano un sistema di riferimento inerziale $Oxyz$ e un punto materiale di massa $m$ soggetto ad una forza $\vec{F}$ . Siano $x(t)$ , $y(t)$ e $z(t)$ rispettivamente la posizione di $m$ lungo l’asse delle $x$ , la posizione di $m$ lungo l’asse delle $y$ e la posizione di $m$ lungo l’asse delle $z$ . La forza $\vec{F}$ agente su $m$ , ne causa il moto descritto dalle seguenti equazioni parametriche:

(3) $\begin{equation*} \begin{cases} x(t)=c_1t^3\\ y(t)=c_2t^2\\ z(t)=c_3t, \end{cases} \end{equation*}$

dove $c_1$ è una costante avente unità di misura $\text{m}\cdot \text{s}^{-3}$ , $c_2$ è una costante avente unità di misura $\text{m}\cdot \text{s}^{-2}$ e $c_3$ è una costante avente unità di misura in $\text{m}\cdot \text{s}^{-1}$ . Il precedente sistema è valido per $t\geq0$ . Si richiede di determinare la potenza sviluppata dalla forza $\vec{F}$ nel generico istante $t\geq 0$ .

Svolgimento esercizio 64.

Esercizio 65 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Da un sistema di riferimento inerziale si osserva un’automobile di massa $m$ percorrere ad una velocità $\vec{v}$ con moto rettilineo uniforme una strada in salita, inclinata di un angolo $\theta$ rispetto all’orizzontale. Il modulo della forza di attrito $\vec{f}_A$ dipende dal modulo della velocità $\vec{v}$ dell’automobile secondo la relazione $f_A=(a+bv)$ , con $a$ e $b$ costanti, e $v$ il modulo della velocità. Si calcoli la potenza erogata dal motore in funzione di $v$ , $\theta$ , $a$ , $b$ , $m$ e $g$ .

Rendered by QuickLaTeX.com

Un'automobile di massa m percorre una strada inclinata di un angolo θ con velocità v. La forza di attrito f_A è diretta lungo il piano inclinato, opposta al moto dell'auto. L'obiettivo è calcolare la potenza erogata dal motore.

Figura 65: schema del problema lavoro ed energia 65.

Svolgimento esercizio 65.

Esercizio 66 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ .Una locomotiva, che sviluppa una potenza costante $P$ , accelera un treno da una velocità iniziale di modulo $v_0$ ad una velocità finale di modulo $v_f$ in un intervallo di tempo $\Delta t$ . Trascurando ogni forma di attrito, si calcoli la massa del treno in funzione di $P$ , $\Delta t$ , $v_f$ e $v_0$ .

Rendered by QuickLaTeX.com

Una locomotiva sviluppa una potenza costante P per accelerare un treno lungo un binario. Il treno passa da una velocità iniziale v0 a una velocità finale vf in un intervallo di tempo Δt.

Figura 66: schema del problema lavoro ed energia 66.

Svolgimento esercizio 66.

Esercizio 67 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Una guida $ABC$ è costituita da un arco di circonferenza $AB$ di raggio $R$ e da un tratto rettilineo $BC$ . Il tratto curvilineo è liscio, mentre il tratto rettilineo è scabro con coefficiente di attrito dinamico $\mu_d$ . Un corpo viene lasciato libero di scivolare da fermo dal punto $A$ . Si determini la distanza percorsa dal corpo sul tratto rettilineo prima di fermarsi. Si supponga che la guida si raccordi perfettamente con il piano orizzontale.

Rendered by QuickLaTeX.com

Una guida ABC è composta da un arco di circonferenza AB di raggio R e da un tratto rettilineo BC. Il tratto curvilineo è liscio, mentre il tratto rettilineo è scabro con coefficiente di attrito dinamico μ_d. Un corpo di massa m parte da fermo dal punto A e scivola lungo la guida.

Figura 67: schema del problema lavoro ed energia 67.

Svolgimento esercizio 67.

Esercizio 68 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un corpo di massa $m$ si muove di moto rettilineo rispetto ad un sistema di riferimento inerziale $Oxy$ , lungo l’asse delle $x$ . Il corpo è soggetto ad una forza $\vec{F}$ diretta lungo l’asse delle $x$ . Sia $x$ la posizione di $m$ lungo l’asse delle $x$ . La velocità del corpo è funzione della posizione $x$ , cioè $v(x)=Ax^{1/2}$ , con $x>0$ e $A$ costante. Si richiede di calcolare

la potenza $P$ fornita al corpo dalla forza nella posizione $x=\tilde{x}>0$ ;
l’impulso $J$ della forza nel percorso da $x_0$ ad $\tilde{x}$ .

Rendered by QuickLaTeX.com

Un corpo di massa m si muove lungo un piano orizzontale ed è soggetto a una forza F diretta lungo l'asse x. Il corpo si muove con velocità v, rappresentata da un vettore nella direzione del moto.

Figura 68: schema del problema lavoro ed energia 68.

Svolgimento esercizio 68.

Esercizio 69 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un corpo di massa $m$ viene lanciato con velocità iniziale di modulo $v_0>0$ lungo un piano inclinato scabro, con coefficiente di attrito dinamico $\mu_d$ , partendo dal bordo inferiore del piano, come rappresentato in figura 69. Sapendo che l’angolo di inclinazione del piano è $\alpha$ , si calcoli la massima altezza raggiunta dal corpo ed il corrispondente lavoro della forza d’attrito. Le risposte vanno fornite in funzione dei parametri $\alpha$ , $v_0$ , $m$ e $\mu_d$ . Inoltre, la velocità $v_0$ è stata misurata da un sistema di riferimento fisso solidale con il suolo.

Rendered by QuickLaTeX.com

Figura 69: schema del problema lavoro ed energia 69.

Un corpo di massa m viene lanciato con velocità iniziale v0 lungo un piano inclinato con angolo α. Il piano è scabro e ha un coefficiente di attrito dinamico μ_d. L'obiettivo è calcolare la massima altezza raggiunta dal corpo e il lavoro della forza d'attrito.

Svolgimento esercizio 69.

Esercizio 70 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un blocco di massa $m$ si muove su un piano orizzontale scabro avente un coefficiente di attrito dinamico $\mu_d$ . Inizialmente il blocco ha una velocità $\vec{v}_0$ diretta parallelamente al piano orizzontale (si veda la figura 70) e si trova ad una distanza $d$ da una molla ideale di costante elastica $k$ e massa trascurabile. Un’estremità della molla è fissata ad un piano verticale, mentre l’altra estremità è libera. Determinare quale condizione deve essere soddisfatta affinché il blocco urti contro la molla. In tale scenario si calcoli la massima compressione della molla. Si supponga che nell’urto tra massa $m$ e molla non ci sia dissipazione di energia.

Rendered by QuickLaTeX.com

Un blocco di massa m si muove su un piano orizzontale scabro con coefficiente di attrito dinamico μ_d. Il blocco ha velocità iniziale v0 e si trova a una distanza d da una molla ideale di costante elastica k fissata a un piano verticale. L'obiettivo è calcolare la massima compressione della molla.

Figura 70: schema del problema lavoro ed energia 70.

Svolgimento esercizio 70.

Esercizio 71 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un punto materiale di massa incognita è sospeso tramite un filo verificale ed è collegato al suolo da una molla di costante elastica $k$ . La molla è inizialmente a riposo. Sia $T$ la tensione del filo. Calcolare

la massa del punto in funzione di $T$ e $g$ .

Ad un certo istante si taglia il filo, calcolare:

la massima distanza percorsa dal punto in funzione di $T$ e $k$ ;
la posizione in cui la velocità è massima in funzione di $T$ e $k$ ;
il valore massimo della sua velocità in funzione di $T$ , $k$ e $g$ .

Rendered by QuickLaTeX.com

Un punto materiale di massa m è sospeso tramite un filo verticale ed è collegato al suolo da una molla di costante elastica k. La molla è inizialmente a riposo. L'obiettivo è calcolare la massa del punto in funzione della tensione T del filo e l'effetto del taglio del filo.
Una molla orizzontale con costante elastica k ha un'estremità fissa e l'altra colpita da un blocco di massa m, che la comprime di un tratto Δx. Il blocco è inizialmente messo in moto da una forza F inclinata di un angolo θ rispetto all'orizzontale. L'obiettivo è calcolare la velocità del blocco e il valore minimo della forza F per metterlo in moto.

Figura 71: schema del problema lavoro ed energia 71.

Esercizio 72 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Una molla di costante elastica $k$ e massa trascurabile é disposta orizzontalmente con una estremità fissa. All’altra estremità è colpita da un blocco di massa $m$ che la comprime di un tratto $\Delta x$ . Il blocco di massa $m$ è messo inizialmente in moto da una forza $\vec{F}$ che forma un angolo $\theta$ con l’orizzontale.
Sapendo che il coefficiente di attrito dinamico è $\mu_d$ tra il blocco e la superficie, calcolare

la velocità del blocco nell’instante in cui comincia a comprimere la molla in funzione di $\Delta x$ , $\mu_d$ , $m$ , $g$ e $k$ ;
il valore minimo $F_{\min}$ del modulo della forza $\vec{F}$ necessario per mettere in moto il corpo se il coefficiente di attrito statico fosse $\mu_s$ . Si esprima $F_{\min}$ in funzione di $\mu_s$ , $m$ , $g$ e $\theta$ .

Rendered by QuickLaTeX.com

Figura 72: schema del problema lavoro ed energia 72.

Una molla orizzontale con costante elastica k ha un'estremità fissa e l'altra colpita da un blocco di massa m, che la comprime di un tratto Δx. Il blocco è inizialmente messo in moto da una forza F inclinata di un angolo θ rispetto all'orizzontale. L'obiettivo è calcolare la velocità del blocco e il valore minimo della forza F per metterlo in moto.

Svolgimento esercizio 72.

Esercizio 73 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Si consideri un sistema di riferimento fisso $Ox$ . Un punto materiale di massa $m=1$ kg è vincolato a muoversi lungo l’asse $x$ , come illustrato in figura 73. Nella posizione $A$ la sua velocità è $v_A = 4 \text{ m}\cdot\text{s}^{-1}$ ; nella posizione $B$ la sua velocità è $v_B$ . Il lavoro dissipato per attrito nel tratto $AB$ ammonta a $L_{\text{diss}} = 6$ J . Calcolare la velocità $v_B$ del punto materiale.

Rendered by QuickLaTeX.com

Un corpo A di massa m_A è collegato a un corpo B di massa m_B tramite una fune inestensibile e una carrucola O. Il corpo B è inizialmente appoggiato su un piano orizzontale, mentre il corpo A è sospeso con il filo teso ed orizzontale. L'obiettivo è determinare di quanto si abbassa il corpo A prima che B si stacchi dal piano.

Figura 73: schema del problema lavoro ed energia 73.

Un punto materiale di massa m = 1 kg si muove lungo l'asse x. Alla posizione A ha una velocità vA = 4 m/s, mentre alla posizione B ha una velocità vB da determinare. Il lavoro dissipato per attrito lungo il tratto AB è L_diss = 6 J.

Svolgimento esercizio 73.

Esercizio 74 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un corpo $A$ di massa $m_A = 2$ kg è collegato tramite una fune inestensibile di massa trascurabile, di lunghezza $2\ell = 4$ m, ad un corpo $B$ di massa $m_B = 3$ kg tramite una carrucola $O$ . Tra filo e carrucola non è presente attrito. Inizialmente il corpo $B$ è appoggiato su un piano orizzontale ed il tratto di filo $OB$ è verticale, mentre il corpo $A$ , in quiete, è tenuto col tratto di filo $OA$ teso ed orizzontale, come illustrato in figura 74. Finché il corpo $B$ rimane a contatto con il piano orizzontale vale $\overline{OA} = \overline{OB} = \ell$ . Ad un certo istante si lascia libero il corpo $A$ . Si determini di quanto si abbassa il corpo $A$ , in verticale, prima che il corpo $B$ si stacchi dal piano d’appoggio.

Rendered by QuickLaTeX.com

Figura 74: schema del problema lavoro ed energia 74.

Esercizio 75 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un corpo di massa $m$ e dimensioni trascurabili è libero di muoversi senza attrito lungo un profilo circolare di raggio $R$ , disposto verticalmente. Una molla ideale (massa trascurabile e che rispetta la legge di Hooke) ha un estremo attaccato ad un punto fisso $A$ del profilo circolare e l’altro estremo è attaccato al punto materiale di massa $m$ , come rappresentato in figura 75. Il corpo, sottoposto alla forza peso, può scivolare senza attrito lungo il profilo. Inizialmente il corpo si trova fermo nel punto $B$ con $\theta=\theta_0$ ed in tale posizione la molla è a riposo.

Determinare i valori delle componenti normale e tangenziale dell’accelerazione del corpo nei punti $B$ e $C$ indicati in figura 75, supponendo che la costante elastica della molla sia $k$ . I risultati vanno forniti in funzione di $k$ , $g$ , $R$ , $\theta_0$ e $m$ .
Quale valore deve avere la costante $k$ della molla affinché sia nulla la forza esercitata sul profilo quando il corpo, in movimento, si trova al punto $C$ ? I risultati vanno forniti in funzione di $g$ , $R$ , $\theta_0$ e $m$ .

Rendered by QuickLaTeX.com

Figura 75: schema del problema lavoro ed energia 75.

Un corpo di massa m è libero di muoversi senza attrito lungo un profilo circolare di raggio R, disposto verticalmente. Una molla è attaccata a un punto fisso A del profilo e al corpo in movimento. Il corpo parte dal punto B con angolo θ0. L'obiettivo è determinare le componenti dell'accelerazione nei punti B e C e il valore della costante elastica k.

Svolgimento esercizio 75.

Esercizio 76 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un punto materiale di massa $2m$ è attaccato, tramite una molla ideale di costante elastica $k$ e lunghezza a riposo $\ell_0$ , ad un altro punto materiale di massa $m$ . Il sistema fisico composto dalle due masse è posto verticalmente con il punto materiale di massa $2m$ posto ad altezza $h$ dal suolo, come mostrato in figura 76. La molla è inizialmente a riposo. Determinare l’altezza $h$ massima affinché la massa $2m$ una volta raggiunto il suolo rimanga appoggiata su di esso. Il risultato va espresso in funzione di $m$ , $g$ e $k$ .

Rendered by QuickLaTeX.com

Un punto materiale di massa 2m è attaccato a una molla ideale di costante elastica k e lunghezza a riposo ℓ0, connesso a un altro punto materiale di massa m. Il sistema è disposto verticalmente, con la massa 2m inizialmente a un'altezza h dal suolo. L'obiettivo è determinare l'altezza massima h affinché la massa 2m rimanga appoggiata al suolo.

Figura 76: schema del problema lavoro ed energia 76.

Svolgimento esercizio 76.

Esercizio 77 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ viene lanciato con velocità $\vec{v}_0$ dalla sommità di un piano inclinato fisso con angolo $\alpha$ rispetto all’orizzontale, come rappresentato in figura 77. La velocità $\vec{v}_0$ è diretta parallelamente al piano inclinato.

Se tra punto materiale e piano si sviluppa un attrito dinamico con coefficiente pari a $\mu_d$ costante, trovare sotto quale condizione il punto materiale $m$ si ferma.
A che distanza dalla sommità del piano inclinato il punto materiale si ferma?
Quanto spazio deve percorrere $m$ prima di raggiungere la velocità massima lungo il piano inclinato?
Quanto spazio deve percorrere $m$ affinché l’energia totale iniziale sia dimezzata?
Rispondere alle precedenti domande supponendo che il coefficiente di attrito dinamico cresca linearmente con la legge $\mu_d=kx$ con $k$ costante, con unità di misura è $\text{m}^{-1}$ , dove $x$ è la posizione lungo l’asse delle $x$ di un sistema di riferimento fisso $Ox$ tale per cui l’asse delle $x$ sia coincidente con il piano inclinato e avente origine $O$ all’apice del piano inclinato.

Rendered by QuickLaTeX.com

Un punto materiale di massa m viene lanciato con velocità iniziale v0 dalla sommità di un piano inclinato con angolo α rispetto all'orizzontale. La velocità v0 è diretta parallelamente al piano inclinato. L'obiettivo è determinare la distanza percorsa e le condizioni per l'arresto del corpo considerando l'attrito dinamico.

Figura 77: schema del problema lavoro ed energia 77.

Svolgimento esercizio 77.

Esercizio 78 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Un punto materiale di massa $m$ è posto alla sommità di un semianello circolare rigido in cui può muoversi senza attrito, inoltre è collegato a due molle di lunghezza a riposo nulla e costante elastica $k$ , le quali sono ancorate nei punti $A$ e $B$ , come mostrato in figura 78. Le molle sono vincolate a scorrere lungo il semianello rigido come si può dedurre dalla figura 78. Se il punto materiale viene sposrmini la reazione vincolare in funzione dell’angolo $\theta$ che forma il raggio che congiunge il punto materiale con la verticale. Si determini il periodo delle piccole oscillatato leggermente dalla posizione di equilibrio si detezioni intorno alla posizione di equilibrio (cioè $\theta=0^{\circ}$ ). Supporre che valga la condizione $mg<2kR$ .

Rendered by QuickLaTeX.com

Un punto materiale di massa m è posto alla sommità di un semianello circolare rigido in cui può muoversi senza attrito. È collegato a due molle di lunghezza a riposo nulla e costante elastica k, ancorate nei punti A e B. L'obiettivo è determinare la reazione vincolare e il periodo delle oscillazioni intorno alla posizione di equilibrio.

Figura 78: schema del problema lavoro ed energia 78.

Svolgimento esercizio 78.

Esercizio 79 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un punto materiale di massa $m$ è vincolato a muoversi lungo un’asta rigida senza attrito che forma un angolo di ${\pi}/{4}$ con il piano orizzontale, come rappresentato in figura 79. Il punto materiale di massa $m$ è attaccato a due molle di lunghezza a riposo nulla e costante elastica $k$ fissate ai punti $A\equiv(d,0)$ e $B\equiv (0,\ell)$ . Se il punto materiale parte da un punto generico $(x_0,y_0)$ , si determini in quale punto dell’asta la velocità è massima, poi si determini l’espressione analitica del modulo della reazione vincolare generata dell’asta sul punto materiale $m$ in funzione della posizione e, inoltre, si determini l’espressione analitica della reazione vincolare nel caso in cui $d=\ell$ . Per la risoluzione del problema si scelga un sistema di riferimento $Oxy$ , come rappresentato sempre in figura 79.

Rendered by QuickLaTeX.com

Figura 79: schema del problema lavoro ed energia 79.

Un punto materiale di massa m è vincolato a muoversi lungo un’asta rigida senza attrito inclinata di π/4 rispetto all'orizzontale. Il punto è attaccato a due molle di lunghezza a riposo nulla e costante elastica k, fissate nei punti A e B. L'obiettivo è determinare il punto di massima velocità e la reazione vincolare dell'asta.

Svolgimento esercizio 79.

Esercizio 80 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Nell’origine $O$ di un sistema di riferimento fisso $Oxy$ è posizionata una molla ideale di lunghezza a riposo nulla e costante elastica $k$ . All’estremo libero della molla è attaccato un punto materiale di massa $m$ che si trova a una distanza $d$ da un piano inclinato con angolo $\alpha$ rispetto all’orizzontale, come rappresentato in figura 80.
Se al punto materiale si fornisce una velocità iniziale $\vec{v}_0$ diretta parallelamente all’asse delle $x$ , si determini lo spazio percorso sul piano inclinato prima di fermarsi e si dimostri che la reazione vincolare del piano inclinato è costante in ogni istante $t>0$ . Si trascuri ogni forma di attrito.

Rendered by QuickLaTeX.com

Figura 80: schema del problema lavoro ed energia 80.

Una molla ideale con costante elastica k è fissata all'origine O di un sistema di riferimento Oxy. All'estremo libero della molla è attaccato un punto materiale di massa m, situato a distanza d da un piano inclinato con angolo α. L'obiettivo è determinare lo spazio percorso dal corpo sul piano inclinato prima di fermarsi.

Svolgimento esercizio 80.

Esercizio 81 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Due punti materiali di massa $m_1$ ed $m_2$ collegati da una molla di costante elastica $k$ e lunghezza a riposo nulla si trovano alla sommità di due aste rigide di lunghezza rispettivamente $\ell_1$ e $\ell_2$ con un vertice in comune e formanti un angolo di $90^o$ , come rappresentato in figura 81. Le aste si trovano in un piano verticale, sono ancorate sul piano sul quale poggiano e su di esse non è presente attrito. Sapendo che inizialmente il sistema è in quiete trovare la posizione di equilibrio delle due masse. Inoltre, se si mantiene fissa la massa $m_1$ determinare il modulo della velocità iniziale $\vec{v}_0$ diretta parallelamente all’asta di lunghezza $\ell_2$ che deve avere $m_2$ affinché raggiunga la base della barretta con velocità nulla.

Rendered by QuickLaTeX.com

Figura 81: schema del problema lavoro ed energia 81.

Svolgimento esercizio 81.

Esercizio 82 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Si osserva da un sistema di riferimento fisso $Oxy$ un punto materiale di massa $m$ vincolato a muoversi nel piano $xy$ . Il punto materiale all’istante $t=0$ si trova in $O$ , ed è soggetto ad un campo di forze $F=-(kx,ky)=-\left(F_1,F_2\right)$ . Il punto ha una velocità iniziale di modulo $v_0$ . Determinare i punti del piano dove la velocità del punto materiale si annulla. Se il punto viene spostato nel punto generico $(x_0,y_0)$ , sempre con velocità di modulo $v_0$ , determinare nuovamente dove si annulla la velocità e i punti dove il modulo della velocità è massima.

Svolgimento esercizio 82.

Esercizi di Meccanica classica

Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.

Leggi..

Tutti gli esercizi di elettromagnetismo

Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di

Elettromagnetismo. Questa raccolta include spiegazioni dettagliate e gli esercizi sono organizzati in base al livello di difficoltà, offrendo un supporto completo per lo studio e la pratica.

Leggi...

Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.

Esercizi di Meccanica razionale

Se siete interessati ad approfondire argomenti inerenti alla Meccanica razionale, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.

Leggi...

Ulteriori risorse didattiche per la fisica

Leggi...

Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.

Document

Menu

Chiudi

Lavoro ed energia: testi degli esercizi svolti

Lavoro ed energia: autori e revisori

Leggi...

Testi degli esercizi su lavoro ed energia

Esercizi di Meccanica classica

Leggi..

Tutti gli esercizi di elettromagnetismo

Leggi...

Esercizi di Meccanica razionale

Leggi...

Ulteriori risorse didattiche per la fisica

Leggi...

Suggerimenti, refusi ed errori