Login Abbonati
Accedi ai contenuti scaricabili
a

Menu

M

Chiudi

Esercizio lavoro ed energia 16

Dinamica del punto materiale: Lavoro ed energia in Meccanica classica

Home » Esercizio lavoro ed energia 16

L’esercizio 16 sul lavoro e l’energia fa parte della raccolta inclusa nella cartella Dinamica del punto materiale: Lavoro ed energia in Meccanica classica. Questo esercizio segue Esercizio lavoro ed energia 15 ed è il precedente di Esercizio lavoro ed energia 17. Questo esercizio è progettato per studenti che frequentano un corso di Fisica 1, indirizzato a chi studia ingegneria, fisica o matematica.

 

Testo lavoro ed energia 16

Esercizio 16 (\bigstar \bigstar\bigstar \largewhitestar\largewhitestar). Un giovane ragazzo è seduto sulla sommità di un blocco di ghiaccio a forma di semisfera, come mostrato nella figura 1. Dopo aver ricevuto una leggera spinta, inizia a scivolare verso il basso. Dimostrare che, se il ghiaccio è privo di attrito, egli si staccherà dal ghiaccio in un punto che si trova ad un’altezza di \dfrac{2}{3}R rispetto al suolo. Si consideri il blocco di ghiaccio fisso al suolo.

 

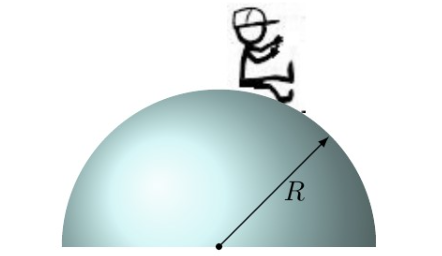
Lavoro ed energia: Un ragazzo seduto su un blocco di ghiaccio che scivola verso il basso
 

Figura 1: schema del problema.

Svolgimento.

Chiamiamo h la distanza tra il suolo e il punto di distacco. Dobbiamo dimostrare che h = \frac{2}{3}R.

Consideriamo un sistema di riferimento inerziale Otn con l’asse t tangente alla traiettoria del ragazzo e l’asse n perpendicolare all’asse t. Il sistema di riferimento è scelto tale per cui in un generico isante t>0, il ragazzo si trova sull’asse n, come mostrato nella figura 2. Utilizzando la seconda legge della dinamica lungo l’asse normale, possiamo scrivere:

    \[-mg \sin \theta + N = - m \dfrac{v^2}{R},\]

dunque

    \[-mg \sin \theta +N = - m \dfrac{v^2}{R}.\]

   

Lavoro ed energia: Diagramma con le forze agenti su un blocco di ghiaccio mentre un ragazzo scivola

   

Nel punto in cui avviene il distacco, la forza normale N è zero poiché non c’è più la reazione normale della superficie. Pertanto, possiamo scrivere

    \[ mg \sin \theta = m \dfrac{v_f^2}{R}, \]

da cui

(1)   \begin{equation*} v_f^2 = Rg \sin \theta. \end{equation*}

Applicando il principio di conservazione dell’energia meccanica, valido in questo caso poiché sono presenti solo forze conservative, abbiamo:

(2)   \begin{equation*} K_i + U_i = K_f + U_f, \end{equation*}

dove il pedice i indica lo stato iniziale, il pedice f lo stato finale, U l’energia potenziale (abbiamo posto l’energia potenziale nulla rispetto al livello del suolo.) e K l’energia cinetica. Poiché K_i = 0 e K_f = \frac{1}{2}mv_f^2, dall’equazione \eqref{ce} otteniamo:

(3)   \begin{equation*} mgR = \dfrac{1}{2}mv_f^2 + mgh. \end{equation*}

Mettendo a sistema \eqref{1} e \eqref{2} otteniamo

    \[\begin{cases} mgR = \dfrac{1}{2}mv_f^2 + mgh\\[10pt] v_f^2 = gR \sin \theta,\\[10pt] \end{cases}\]

conseguentemente

    \[1 = \dfrac{1}{2} \sin \theta +\sin \theta\quad \Leftrightarrow\quad \sin \theta = \dfrac{2}{3}.\]

Osserviamo dalla geometria del problema che h = R \sin \theta; di conseguenza dalla precedente equazione otteniamo:

    \[\boxcolorato{fisica}{ h = \dfrac{2}{3}R, }\]

come richiesto dal problema.

Fonte.

D.Halliday, R.Resnick, J.Walker – Fondamenti di fisica, Meccanica, Zanichelli


 
 

Scarica gli esercizi svolti

Ottieni il documento contenente 82 esercizi risolti, contenuti in 255 pagine ricche di dettagli, per migliorare la tua comprensione del lavoro ed energia in meccanica classica.

 
 

Esercizi di Meccanica classica

Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.

Leggi..


 
 

Tutti gli esercizi di elettromagnetismo

Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di

  • Elettromagnetismo. Questa raccolta include spiegazioni dettagliate e gli esercizi sono organizzati in base al livello di difficoltà, offrendo un supporto completo per lo studio e la pratica.

    Leggi...

    Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.


     
     

    Esercizi di Meccanica razionale

    Se siete interessati ad approfondire argomenti inerenti alla Meccanica razionale, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.

    Leggi...


     
     

    Ulteriori risorse didattiche per la fisica

    Leggi...

    • Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
    • ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
    • Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
    • Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
    • The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
    • American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
    • Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
    • Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
    • Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
    • Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.






    Document