50% di sconto su tutto fino al 31/12/2024

Il mio account
Accedi ai contenuti scaricabili
a

Menu

M

Chiudi

Lavoro ed energia: esercizio 3

Dinamica del punto materiale: Lavoro ed energia in Meccanica classica

Home » Lavoro ed energia: esercizio 3

Esercizio lavoro ed energia 3

L’esercizio 3 sul lavoro e l’energia è il terzo della raccolta inclusa nella cartella Dinamica del punto materiale: Lavoro ed energia in Meccanica classica. Questo esercizio è il successivo di Esercizio lavoro ed energia 2 ed è il precedente di Esercizio lavoro ed energia 4. Questo esercizio è progettato per studenti che frequentano un corso di Fisica 1, indirizzato a chi studia ingegneria, fisica o matematica.

 

Testo lavoro ed energia 3

Esercizio 3 (\bigstar \bigstar\largewhitestar \largewhitestar\largewhitestar). Una massa puntiforme m è inizialmente in quiete su un piano orizzontale con coefficiente di attrito statico \mu_s ed attrito dinamico \mu_d. Alla massa viene applicata all’istante t=0\,\text{s} una forza orizzontale con direzione e verso costanti ed il cui modulo varia nel tempo secondo la legge F=Kt. Si determinino:

(i) il tempo t_0 al quale m comincia a muoversi;

(ii) il lavoro totale compiuto dalle forze agenti su m dall’istante iniziale fino al tempo t=\tau.

Eseguire i calcoli per: \tau =10\,\text{s},\, m=1\,\text{kg},\, \mu_s=0,2,\, \mu_d=0,1,\, K=2\,\text{N}\cdot\text{s}^{-1}.

 

Rendered by QuickLaTeX.com

Diagramma vettoriale di un corpo che si muove su una guida circolare

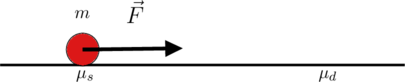
Svolgimento punto (i).

Innanzitutto scegliamo un sistema di riferimento cartesiano Oxy fisso e costruiamo il diagramma di corpo libero come in figura 1. Sul corpo di massa m agiscono la forza \vec{F} e la forza di attrito statico (poiché il corpo è inizialmente fermo) \vec{f}_{a,s}.

 

Rendered by QuickLaTeX.com

Grafico temporale della forza applicata

 

Ricordiamo che la forza di attrito statico è una forza che si oppone al moto del corpo ed istante per istante è uguale in modulo ad F(t) ma opposta in verso. Tuttavia, esiste un valore soglia oltre il quale la forza di attrito statico non è più in grado di controbilanciare la sollecitazione indotta da \vec{F}(t) ed in particolare

(1)   \begin{equation*} f_{a,s}\leq\mu_{s}N, \nonumber \end{equation*}

dove N=mg è il modulo della reazione vincolare causata dal contatto tra il corpo m ed il piano di appoggio. Definiamo f_{a,s,max}\equiv\mu_{s}N= mg\mu_{s}, per cui affinché il corpo m cominci a muoversi ad un istante di tempo t, la forza \vec{F} valutata in questo istante di tempo deve eccedere, in modulo, la forza di attrito statico massima \vec{f}_{a,s,max}, ossia

(2)   \begin{equation*} F(t)\geq f_{a,s,max}. \end{equation*}

In virtù di ciò, il corpo m comincerà a muoversi non appena la forza \vec{F} avrà eguagliato in modulo la forza di attrito statico, ossia

(3)   \begin{equation*} F(t_0)=f_{a,s,max}\quad \Leftrightarrow\quad Kt_0=mg\mu_{s}, \nonumber \end{equation*}

da cui otteniamo che

    \[\boxcolorato{fisica}{ t_0=\frac{mg\mu_{s}}{K}=0,981\,\text{s}\simeq1\,\text{s}.}\]

 

 Di seguito riportiamo il grafico dell’evoluzione temporale del modulo di \vec{F}, dove sulle ascisse abbiamo il tempo e sulle ordinate il modulo della forza \vec{F}.

 

Rendered by QuickLaTeX.com

Diagramma di corpo libero su piano orizzontale

 

Si osservi che l’intersezione tra la retta rossa e la retta blu rappresenta l’istante di tempo in cui il modulo della forza \vec{F} raggiunge il valore massimo della forza di attrito.

 


Svolgimento punto (ii).

Per calcolare il lavoro totale compiuto dalle forze agenti sul corpo m ad un certo istante t=\tau si può determinare applicando il teorema delle forze vive. In particolare dal succitato teorema segue che il lavoro compiuto dal risultante delle forze che agisce sul corpo m vale

(4)   \begin{equation*} L=K_{fin}-K_{ini}, \end{equation*}

dove K_{fin} e K_{ini} rappresentano l’energia cinetica posseduta dal corpo rispettivamente al tempo t=\tau e al tempo iniziale t=0\,\text{s}. Poiché all’inizio il corpo è in quiete (v_{ini}=0) allora K_{ini}=0. Quindi l’equazione (4) diventa

(5)   \begin{equation*} L=\dfrac{1}{2}mv^2(\tau). \end{equation*}

Dobbiamo calcolare la velocità del corpo in corrispondenza del tempo t=\tau. Dalla cinematica sappiamo che

(6)   \begin{equation*} a(t)=\dfrac{dv(t)}{dt} . \end{equation*}

Nel caso specifico, come visto, il corpo m è in quiete fino all’istante t_0 a partire dal quale comincia un moto accelerato. La velocità del corpo m all’istante di tempo t=\tau sarà data da

(7)   \begin{equation*} v(\tau)=\int^{\tau}_{t_0}\, a(t)\,dt. \end{equation*}

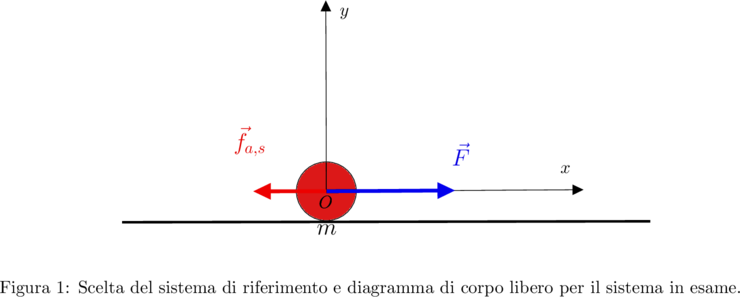
Bisogna calcolare l’espressione dell’accelerazione del corpo a partire dal tempo t=t_0. Usiamo lo stesso sistema di riferimento cartesiano fisso Oxy di figura 1, e costruiamo il diagramma di corpo libero per il corpo m. Questa volta, poiché il corpo è già in moto, su di esso agirà (oltre alla solita forza \vec{F}) la forza di attrito dinamico \vec{f}_{a,d}=-mg\mu_{d}\hat{v}, dove \hat{v} è il versore del vettore velocità \vec{v}(t) del corpo m (vedi figura 3), in altri termini la forza di attrito dinamico ha la stessa direzione del vettore velocità ma verso opposto.

 

Rendered by QuickLaTeX.com

Diagramma di forze per il calcolo del lavoro ed energia in un esercizio di fisica

 

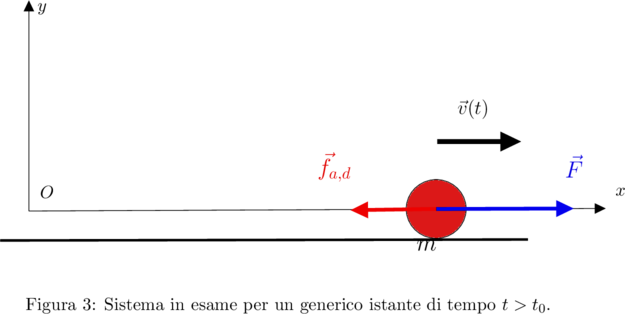
Dal II principio della dinamica segue che

(8)   \begin{equation*} ma(t)=F(t)-mg\mu_{d}=Kt-mg\mu_{d} \end{equation*}

da cui

(9)   \begin{equation*} a(t)=\dfrac{K}{m}t-g\mu_{d}. \end{equation*}

Inserendo l’equazione (9) nell’equazione (7) si ottiene

    \[\begin{aligned} v(\tau)=\int^{\tau}_{t_0} \left( \dfrac{K}{m}t-g\mu_{d}\right)dt&=\dfrac{K}{m}\int^{\tau}_{t_0}t\,dt-g\mu_{d}\int^{\tau}_{t_0} dt=\\ &=\dfrac{K}{m}\dfrac{t^2}{2}\biggr\rvert^{\tau}_{t_0}-g\mu_{d}t\biggr\rvert^{\tau}_{t_0}=\\ &=\dfrac{K}{2m}(\tau^2-t_0^2)-g\mu_{d}(\tau-t_0). \end{aligned}\]

Dunque, valutando t=\tau l’equazione (5) e sfruttando il valore v(\tau), ottenuto nella precedente relazione, otteniamo che il lavoro totale compiuto dalle forze agenti sul corpo m al tempo t=\tau vale

    \[\boxcolorato{fisica}{ L=\dfrac{1}{2}m\left(\dfrac{K}{2m}(\tau^2-t_0^2)-g\mu_{d}(\tau-t_0)\right)^2=4065\,\text{J}.}\]

 


Fonte.

Fonte: esercizio numero 1 dell’esame di Fisica 1 del 24 Febbraio 2017 del corso di Fisica dell’Università di Roma Tor Vergata.

 
 

Esercizi di Meccanica classica

Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.

Leggi..


 
 

Tutti gli esercizi di elettromagnetismo

Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di

  • Elettromagnetismo. Questa raccolta include spiegazioni dettagliate e gli esercizi sono organizzati in base al livello di difficoltà, offrendo un supporto completo per lo studio e la pratica.

    Leggi...

    Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.


     
     

    Esercizi di Meccanica razionale

    Se siete interessati ad approfondire argomenti inerenti alla Meccanica razionale, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.

    Leggi...


     
     

    Ulteriori risorse didattiche per la fisica

    Leggi...

    • Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
    • ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
    • Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
    • Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
    • The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
    • American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
    • Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
    • Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
    • Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
    • Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.

     
     

    Lavoro ed energia nelle energie rinnovabili: fondamenti per un futuro sostenibile

    Leggi...

    L’energia è un concetto fondamentale che pervade tutti gli aspetti della vita moderna, dall’alimentazione delle abitazioni e delle industrie, alla mobilità e alla comunicazione globale. Con l’emergere delle preoccupazioni legate al cambiamento climatico e all’esaurimento delle risorse fossili, le energie rinnovabili sono diventate un tema centrale nella ricerca di soluzioni sostenibili per il futuro energetico del pianeta. Questo articolo esplora i concetti di lavoro ed energia nell’ambito delle energie rinnovabili, evidenziando il loro ruolo cruciale nella transizione verso una produzione energetica più pulita e sostenibile.

    Il concetto di lavoro in fisica si riferisce al trasferimento di energia attraverso l’applicazione di una forza su un corpo che si muove nella direzione della forza stessa. In termini di energia rinnovabile, il lavoro viene svolto ogni volta che una fonte naturale di energia, come il vento, il sole, o l’acqua, viene convertita in una forma di energia utilizzabile, come l’elettricità. Ad esempio, nelle turbine eoliche, il lavoro è compiuto dal vento che esercita una forza sulle pale, facendole ruotare. Questa rotazione viene convertita in energia elettrica attraverso un generatore. Il vento compie lavoro sulle pale, trasferendo loro l’energia cinetica necessaria per generare elettricità. Nei pannelli fotovoltaici, i fotoni provenienti dal sole “spingono” gli elettroni attraverso un semiconduttore, generando corrente elettrica. Anche se il concetto di lavoro qui è meno intuitivo rispetto all’eolico, l’energia solare svolge un lavoro fondamentale nel liberare gli elettroni necessari per produrre energia. Nelle centrali idroelettriche, l’acqua che cade da un’altezza compie lavoro sulle turbine situate alla base delle dighe. Questo lavoro, dovuto all’energia potenziale dell’acqua, viene trasformato in energia cinetica e infine in energia elettrica.

    L’energia è la capacità di un sistema di compiere lavoro. Nelle energie rinnovabili, la sfida principale è catturare e convertire l’energia disponibile nell’ambiente in una forma utilizzabile. Le principali forme di energia coinvolte nelle tecnologie rinnovabili includono l’energia cinetica, come quella del vento e dell’acqua in movimento, che può essere convertita direttamente in energia elettrica, l’energia solare, che può essere convertita in energia elettrica attraverso pannelli fotovoltaici o utilizzata per riscaldare fluidi in impianti solari termici, e l’energia potenziale, come l’energia immagazzinata nell’acqua dietro una diga, che può essere rilasciata per generare energia elettrica.

    Uno degli obiettivi principali nello sviluppo delle tecnologie rinnovabili è migliorare l’efficienza con cui queste tecnologie convertono l’energia disponibile in energia utilizzabile. L’efficienza è spesso definita come il rapporto tra l’energia prodotta e l’energia disponibile, e può essere limitata da vari fattori, tra cui le perdite energetiche sotto forma di calore e l’inefficienza dei componenti meccanici ed elettrici. La sostenibilità delle energie rinnovabili non dipende solo dall’efficienza, ma anche dalla capacità di queste tecnologie di ridurre l’impatto ambientale rispetto alle fonti fossili. A differenza del carbone, del petrolio e del gas naturale, le fonti rinnovabili non emettono direttamente gas serra durante la produzione di energia e possono essere sfruttate in modo continuo senza esaurirsi nel tempo.

    Mentre il mondo si sposta verso un futuro più sostenibile, l’importanza delle energie rinnovabili continuerà a crescere. Gli sviluppi tecnologici stanno rendendo queste fonti di energia sempre più competitive rispetto alle fonti tradizionali, riducendo i costi e migliorando l’affidabilità. Con il continuo progresso nella scienza dei materiali e nelle tecnologie di stoccaggio dell’energia, le energie rinnovabili sono destinate a svolgere un ruolo centrale nel soddisfare le esigenze energetiche globali, contribuendo al contempo a mitigare il cambiamento climatico. In conclusione, il concetto di lavoro ed energia è intrinsecamente legato alle energie rinnovabili, fornendo una base per comprendere come queste tecnologie catturano e trasformano le risorse naturali in energia utilizzabile. Con l’aumento della consapevolezza ambientale e la pressione per ridurre le emissioni di carbonio, le energie rinnovabili rappresentano non solo una soluzione necessaria, ma anche una strada percorribile verso un futuro energetico sostenibile.


     

    Lavoro ed energia: l’evoluzione storica e scientifica di due concetti fondamentali della fisica

    Leggi...

    Il concetto di lavoro ed energia ha radici profonde nella storia della fisica e della filosofia naturale, evolvendosi attraverso secoli di osservazioni e teorie che hanno cercato di spiegare il funzionamento del mondo naturale. Il concetto di lavoro in fisica, come misura del trasferimento di energia attraverso l’applicazione di una forza, è relativamente recente nella storia della scienza, risalente al XVIII secolo. Prima di questo periodo, i filosofi naturali, come Aristotele, avevano concetti più rudimentali di movimento e forza, senza una chiara distinzione tra energia e lavoro. Il termine “lavoro” in senso fisico fu formalmente introdotto dal matematico francese Gaspard-Gustave Coriolis nel 1829. Coriolis definì il lavoro come il prodotto della forza applicata su un corpo e dello spostamento del corpo nella direzione della forza. Questa definizione permise di quantificare il lavoro meccanico e divenne un concetto fondamentale nella meccanica classica.

    Il concetto di energia ha una storia più lunga e complessa. L’idea che il movimento e le forze potessero essere legate a una sorta di “capacità di compiere lavoro” risale all’antichità, ma il concetto moderno di energia iniziò a prendere forma solo nel XVII secolo. Un passo importante fu fatto con i lavori di Gottfried Wilhelm Leibniz e Émilie du Châtelet nel XVII e XVIII secolo. Leibniz sviluppò il concetto di vis viva (forza viva), che corrisponde all’energia cinetica moderna, come il prodotto della massa di un corpo e del quadrato della sua velocità. Questo concetto fu ulteriormente sviluppato da Émilie du Châtelet, che chiarì il ruolo dell’energia potenziale, contribuendo a formare la base del principio di conservazione dell’energia.

    Nel XIX secolo, scienziati come Joule, Helmholtz, e Thomson (Lord Kelvin) consolidarono il concetto di energia come quantità fisica conservata. Joule, in particolare, dimostrò l’equivalenza tra lavoro meccanico e calore, stabilendo il principio di conservazione dell’energia, noto come la prima legge della termodinamica.

    La formalizzazione del lavoro e dell’energia come concetti interconnessi permise agli scienziati di sviluppare una comprensione più profonda dei processi fisici. In meccanica classica, il lavoro svolto su un sistema è strettamente legato alle variazioni di energia del sistema, e questa comprensione è alla base di molte applicazioni in ingegneria e fisica. Nel tempo, questi concetti sono diventati fondamentali non solo nella meccanica, ma anche in altre branche della fisica, come la termodinamica e l’elettromagnetismo, fornendo un linguaggio comune per descrivere e analizzare un’ampia gamma di fenomeni naturali.






    Document



    • error: Il contenuto è protetto!!