Integrali impropri – Teoria

Home » Integrali impropri – Teoria

L’integrazione secondo Riemann è uno strumento potente e con una relativa semplicità d’uso. Possiede però dei limiti: esso permette di integrare soltanto funzioni limitate su intervalli limitati. È possibile però estendere la nozione di integrale a una classe più ampia di funzioni, anche su intervalli illimitati, mediante un procedimento combinato di integrazione e limite, ottenendo i cosiddetti integrali impropri o generalizzati.

Questa dispensa è dedicata a tale importante tema e si focalizza sui seguenti punti:

Come si definiscono formalmente gli integrali generalizzati?
Quali sono le proprietà di questi strumenti e quali caratteristiche mantengono in comune con gli integrali “classici”?
In cosa consistono i criteri di convergenza degli integrali impropri detti del confronto, della convergenza assoluta, della serie numerica?
Cosa riguarda il criterio di Abel-Dirichlet sull’integrazione impropria di un prodotto e cosa sono le funzioni a variazione limitata?

Se desideri approfondire questi argomenti con spiegazioni chiare e numerosi esempi ed esercizi svolti, questa dispensa è quello di cui hai bisogno!

La conoscenza dei contenuti relativi agli integrali definiti e indefiniti è necessaria al fine di comprendere questo articolo.

Come ulteriori letture teoriche sul medesimo tema, consigliamo le seguenti, estratte dalla lista completa alla fine dell’articolo:

Segnaliamo inoltre le seguenti raccolte di esercizi svolti:

Autori e revisori

Leggi...

Autori: Maicol Caponi

Revisori: Matteo Talluri.

Integrali impropri

Definizione e proprietà.

Dato un intervallo chiuso e limitato $[a,b]\subset\mathbb R$

e una funzione $f\colon[a,b]\to\mathbb R$

limitata su $[a,b]$

e continua su $[a,b]\setminus N$

, con $N$

sottoinsieme finito di $[a,b]$

sappiamo che è possibile definire l’integrale di Riemann di $f$

su $[a,b]$

. Inoltre, tale integrale è continuo rispetto a uno qualunque dei due estremi, cioè

$\int_a^bf(t)\,dt=\lim_{x\to a^+}\int_x^bf(t)\,dt=\lim_{y\to b^-}\int_a^yf(t)\,dt.$

Infatti, poiché $f$ è limitata, se chiamiamo

$M:=\sup_{t\in[a,b]}|f(t)|<+\infty,$

vale

$\begin{align*} &\left|\int_a^b f(t)\,dt-\int_x^b f(t)\,dt \right|\le\int_a^x|f(t)|\,dt\le M(x-a)\to 0\quad\text{per $x\to a^+$},\\ &\left|\int_a^b f(t)\,dt-\int_a^y f(t)\,dt \right|\le\int_y^b|f(t)|\,dt\le M(b-y)\to 0\quad\text{per $y\to b^-$}. \end{align*}$

Si noti che l’integrale di Riemann può essere definito solo per una classe molto esigua di funzioni (limitate e definite su intervalli chiusi e limitati). In queste dispense vogliamo estendere la nozione di integrale in modo da includere funzioni illimitate o definite su intervalli illimitati. Per esempio, data la funzione

$f(x):=\frac{1}{x^2}\quad\text{per $x\in[1,+\infty)$},$

ci chiediamo se sia possibile definire il suo integrale sull’intervallo $[1,+\infty)$ . Si noti che, fissato $x\in(1,+\infty)$ , la funzione $f$ è integrabile su $[1,x]$ e risulta

$\int_1^x\frac{1}{t^2}\,dt=\left[-\frac{1}{t}\right]_1^x=1-\frac{1}{x}.$

Poiché la quantità a destra ammette limite per $x\to+\infty$ , ha senso definire

$\int_1^{+\infty}\frac{1}{t^2}\,dt=\lim_{x\to +\infty}\int_1^x\frac{1}{t^2}\,dt=\lim_{x\to +\infty}\left(1-\frac{1}{x}\right)=1.$

Questo tipo di integrale si chiama integrale generalizzato (o improprio) di $f$ su $[1,+\infty)$ .

Più in generale, dato un intervallo $I\subseteq\mathbb R$ e una funzione $f\colon I\to\mathbb R$ possiamo dare le seguenti definizioni.

$\quad$

Definizione 1 (locale integrabilità). Sia $I\subseteq\mathbb R$

un intervallo (non necessariamente aperto o chiuso) e $f\colon I\to\mathbb R$

. La funzione $f$

è localmente (Riemann) integrabile su $I$

se $f$

è integrabile secondo Riemann su ogni sottointervallo chiuso e limitato $J$

di $I$

$\quad$

Osservazione 1. Se $I\subseteq\mathbb R$ è un intervallo e $f\colon I\to\mathbb R$ è continua, allora $f$ è localmente integrabile su $I$ . Infatti, $f$ è integrabile secondo Riemann su ogni sottointervallo chiuso e limitato $J$ di $I$ , essendo $f$ continua e limitata su $J$ .

$\quad$

Definizione 2 (integrale generalizzato). Sia $I:=[a,b)\subset\mathbb R$

con $-\infty < a < b \le +\infty$

e sia $f\colon [a,b)\to\mathbb R$

una funzione localmente integrabile sull’intervallo $[a,b)$

¹. La funzione $f$

è integrabile in senso generalizzato (o improprio) su $\overline I$

(la chiusura di $I$

) se esiste finito il limite

$\lim_{x\to b^-}\int_a^xf(t)\,dt.$

In tal caso si pone

$\int_a^bf(t)\,dt:=\lim_{x\to b^-}\int_a^xf(t)\,dt,$

e l’integrale generalizzato (o improprio) di $f$ è detto convergente su $\overline I$ . Se invece

$\lim_{x\to b^-}\int_a^xf(t)\,dt=\pm \infty,$

si dice che l’integrale generalizzato di $f$ è divergente su $\overline I$ .

Quindi $f$ è integrabile secondo Riemann su $[a,x]$ per ogni $x\in(a,b)$ . ↩

$\quad$

Osservazione 2. Se $[a,b]\subset\mathbb R$ è un intervallo chiuso e limitato e $f\colon [a,b]\to\mathbb R$ è integrabile secondo Riemann su $[a,b]$ , allora $f$ è integrabile in senso generalizzato su $[a,b]$ e i due integrali coincidono.

Osservazione 3. In queste dispense l’intervallo dove è definito l’integrale generalizzato di $f\colon I:=[a,b)\to\mathbb R$ è indicato con $\overline I$ (la chiusura di $I$ ). Dunque, se $b\in\mathbb R$ , allora $\overline I=[a,b]$ , mentre se $b=+\infty$ allora $\overline I=[a,+\infty)$ . In molti libri l’intervallo dove $f$ è integrabile in senso generalizzato viene denotato anche con $I$ , senza aggiungere la chiusura.

Analogamente, se $I:=(a,b]\subset\mathbb R$ con $-\infty \le a < b < +\infty$ e $f\colon (a,b]\to \mathbb R$ è una funzione localmente integrabile sull’intervallo $(a,b]$ ², allora $f$ è integrabile in senso generalizzato su $\overline I$ se esiste finito il limite

$\lim_{x\to a^+}\int_x^bf(t)\,dt,$

e si pone

$\int_a^bf(t)\,dt:=\lim_{x\to a^+}\int_x^bf(t)\,dt.$

Si noti che $f\colon I:=(a,b]\to\mathbb R$ è integrabile in senso generalizzato su $\overline I$ se e solo se la funzione la funzione $g\colon J:=[-b,-a)\to\mathbb R$ definita come

$g(x):=f(-x)\quad\text{per $x\in [-b,-a)$}$

è integrabile in senso generalizzato su $\overline J$ .

Esempio 1. Sia $f\colon [0,+\infty)\to\mathbb R$ definita da

$f(x)=xe^{-x^2}\quad\text{per $x\in[0,+\infty)$}.$

La funzione $f$ è continua su $[0,+\infty)$ , dunque è localmente integrabile su $[0,+\infty)$ . Andiamo a vedere se è integrabile in senso generalizzato su $[0,+\infty).$ Per ogni $x\in(0,+\infty)$ abbiamo che

$\int_0^xte^{-t^2}\,dt=\left[-\frac{e^{-t^2}}{2}\right]_0^x=\frac{1-e^{-x^2}}{2}.$

Poiché

$\lim_{x\to+\infty}\int_0^x te^{-t^2}\,dt=\lim_{x\to+\infty}\frac{1-e^{-x^2}}{2}=\frac{1}{2},$

ne deduciamo che $f$ è integrabile in senso generalizzato su $[0,+\infty)$ .

Esempio 2. Sia $f\colon (-\dfrac{\pi}{2},0]\to\mathbb R$ definita da

$f(x)=\tan x\quad\text{per $x\in \left(-\frac{\pi}{2},0\right]$}.$

La funzione $f$ è continua su $(-\dfrac{\pi}{2},0]$ , dunque è localmente integrabile su $(-\dfrac{\pi}{2},0]$ . Andiamo a vedere se è integrabile in senso generalizzato su $[-\dfrac{\pi}{2},0].$ Per ogni $x\in(-\dfrac{\pi}{2},0)$ abbiamo che

$\int_x^0\tan t\,dt=\int_x^0\frac{\sin t}{\cos t}\,dt=\left[-\ln(\cos t)\right]_x^0=\ln(\cos x).$

Poiché

$\lim_{x\to-\frac{\pi}{2}^+}\int_x^0\tan t\,dt=\lim_{x\to-\frac{\pi}{2}^+} \ln(\cos x)=-\infty,$

ne deduciamo che $f$ non è integrabile in senso generalizzato su $[-\dfrac{\pi}{2},0]$ (in questo caso l’integrale generalizzato di $f$ su $[-\dfrac{\pi}{2},0]$ diverge).

Esempio 3. Sia $\alpha\in\mathbb R$ e consideriamo la funzione $f\colon (0,+\infty)\to\mathbb R$ definita come

$f(x):=\frac{1}{x^\alpha}=x^{-\alpha}\quad\text{per $x\in(0,+\infty)$}.$

Andiamo a determinare valori di $\alpha$ per cui la funzione $f$ risulta integrabile in senso generalizzato su $[0,1]$ oppure su $[1,+\infty)$ . Chiaramente $f$ è localmente integrabile sia su $(0,1]$ che su $[1,+\infty)$ . Inoltre, fissato $x\in(0,1)$ risulta che

$\int_x^1f(t)\,dt= \begin{cases}\dfrac{1-x^{1-\alpha}}{1-\alpha}&\text{per $\alpha\neq 1$},\\ -\ln x&\text{per $\alpha= 1$}. \end{cases}$

Quindi il limite per $x\to 0^+$ esiste finito se e solo se $\alpha<1$ . Fissato invece $y\in (1,+\infty)$ abbiamo che

$\int_1^yf(t)\,dt= \begin{cases}\dfrac{y^{1-\alpha}-1}{1-\alpha}&\text{per $\alpha\neq 1$},\\ \ln y&\text{per $\alpha= 1$}. \end{cases}$

Dunque il limite per $y\to+\infty$ esiste finito se e solo se $\alpha>1$ .

Perciò l’integrale generalizzato di $f$ su $[0,1]$ è convergente se e solo se $\alpha<1$ e risulta

$\int_0^1 f(t)\,dt=\frac{1}{1-\alpha},$

mentre l’integrale generalizzato di $f$ su $[1,+\infty)$ è convergente se e solo se $\alpha>1$ e risulta

$\int_1^{+\infty} f(t)\,dt=\frac{1}{\alpha-1}.$

Più in generale, fissato $a\in\mathbb R$ , per ogni $\alpha\in\mathbb R$ possiamo considerare la funzione $f\colon (a,+\infty)\to\mathbb R$ definita come

$f(x):=\frac{1}{(x-a)^\alpha}\quad\text{per $x\in(a+\infty)$}.$

In maniera analoga a prima, per ogni $c\in(a,+\infty)$ abbiamo che l’integrale generalizzato di $f$ su $[a,c]$ converge se e solo se $\alpha<1$ , mentre diverge per $\alpha\ge 1$ . Invece l’integrale generalizzato di $f$ su $[c,+\infty)$ converge se e solo se $\alpha>1$ , mentre diverge per $\alpha\le 1$ .

Si noti che negli esempi precedenti abbiamo sempre considerato funzioni $f$ illimitate o definite su intervalli illimitati. Infatti, nel caso in cui sia la funzione $f$ che il suo intervallo di definizione $I$ siano limitati, allora $f$ risulta sempre integrabile in senso generalizzato su $\overline I$ .

Teorema 1. Siano $-\infty < a < b < +\infty$

e sia $f\colon [a,b)\to\mathbb R$

una funzione limitata e localmente integrabile su $[a,b)$

. Allora qualunque prolungamento di $f$

ad $[a,b]$

è integrabile secondo Riemann su $[a,b]$

e il suo integrale su $[a,b]$

coincide con l’integrale generalizzato di $f$

su $[a,b]$

(in particolare l’integrale su $[a,b]$

di un qualsiasi prolungamento è lo stesso).

$\quad$

Dimostrazione. Ricordiamo che se $I\subset\mathbb R$ è un intervallo chiuso e limitato e $f\colon I\to\mathbb R$ è una funzione limitata, allora $f$ è integrabile secondo Riemann su $I$ se e solo se per ogni $\varepsilon >0$ esiste una partizione $P:=\{x_0,\dots,x_n\}$ di $I$ tale che

$S(P,f)-s(P,f)<\varepsilon,$

dove

$\begin{align*} &S(P,f):=\sum_{j=0}^{n-1}M_j(x_{j+1}-x_j),\qquad M_j:=\sup_{t\in[x_j,x_{j+1}]}f(t)\quad\text{per $j=0,\dots,n-1$},\\ &S(p,f):=\sum_{j=0}^{n-1}m_j(x_{j+1}-x_j),\qquad m_j:=\inf_{t\in[x_j,x_{j+1}]}f(t)\quad\text{per $j=0,\dots,n-1$},\\ \end{align*}$

Siano $-\infty<a<b<+\infty$ e sia $f\colon [a,b)\to\mathbb R$ una funzione limitata e localmente integrabile su $[a,b)$ . Sia inoltre $\tilde f\colon [a,b]\to \mathbb R$ un qualsiasi prolungamento di $f$ , cioè

$\tilde f(x):= \begin{cases} f(x)&\text{per $x\in[a,b)$},\\ w\in\mathbb R&\text{per $x=b$}. \end{cases}$

Chiaramente anche la funzione $\tilde f$ è limitata, quindi esiste una costante $\tilde M>0$ tale che

$|\tilde f(x)|\le \tilde M\quad\text{per ogni $x\in[a,b]$}.$

Fissato $\varepsilon>0$ , sia $c\in (a,b)$ tale che

$b-c<\frac{\varepsilon}{4\tilde M}.$

Poiché la funzione $f$ è integrabile secondo Riemann su $[a,c]$ , allora esiste una partizione $P:=\{x_0,\dots,x_n\}$ di $[a,c]$ che soddisfa

$S(P,f)-s(P,f)<\frac{\varepsilon}{2}.$

Chiaramente $\tilde P:=\{x_0,\dots,x_n,b\}$ è una partizione di $[a,b]$ e per costruzione

$\begin{align*} &S(\tilde P,\tilde f)=S(P,f)+\sup_{t\in[c,b]}\tilde f(t)(b-c)\le S(P,f)+\tilde M(b-c)\le S(P,f)+\frac{\varepsilon}{4},\\ &s(\tilde P,\tilde f)=s(P,f)+\inf_{t\in[c,b]}\tilde f(t)(b-c)\ge s(P,f)-\tilde M(b-c)\ge s(P,f)-\frac{\varepsilon}{4}. \end{align*}$

Allora

$S(\tilde P,\tilde f)-s(\tilde P,\tilde f)\le S(P,f)-s(P,f)+\frac{\varepsilon}{2}<\varepsilon,$

e quindi $\tilde f$ è integrabile secondo Riemann su $[a,b]$ . In particolare

$\int_a^b \tilde f(t)\,dt=\lim_{x\to b^-}\int_a^x\tilde f(t)\,dt=\lim_{x\to b^-}\int_a^xf(t)\,dt=:\int_a^bf(t)\,dt.$

Ne segue che $f$ è integrabile in senso generalizzato su $[a,b]$ e l’integrale generalizzato di $f$ su $[a,b]$ coincide con l’integrale di Riemann di $\tilde f$ su $[a,b]$ .

$\quad$

Esempio 4. Sia $f\colon (0,1]\to\mathbb R$ definita da

$f(x):=\sin\left(\frac{1}{x}\right)\quad\text{per $x\in(0,1]$}.$

La funzione $f$ è continua e limitata su $(0,1]$ , essendo $|f(x)|\le 1$ per ogni $x\in(0,1]$ . Allora, per il Teorema 1 abbiamo che $f$ è integrabile in senso generalizzato su $[0,1]$ .

Osservazione 4. Se $f\colon [a,b)\to\mathbb R$ è continua su $[a,b)$ ed esiste finito

$\lim_{x\to b^-}f(x)=L\in\mathbb R,$

allora $f$ è prolungabile con continuità in $[a,b]$ e dunque è limitata su $[a,b)$ . In particolare, per il Teorema 1 la funzione $f$ è sempre integrabile in senso generalizzato su $[a,b]$ e il suo prolungamento continuo è integrabile secondo Riemann.

Sia $I:=[a,b)$ con $-\infty \le a < b \le +\infty$ e sia $f\colon [a,b)\to\mathbb R$ una funzione localmente integrabile sull’intervallo $[a,b)$ . Si può facilmente osservare che $f$ è integrabile in senso generalizzato su $\overline I$ se e solo se lo è in un intorno sinistro di $b$ , cioè se comunque preso $c\in(a,b)$ e $J:=[c,b)$ , la funzione $f$ è integrabile in senso generalizzato su $\overline J$ . Inoltre vale

$\int_a^bf(t)\,dt=\int_a^cf(t)\,dt+\int_c^bf(t)\,dt.$

Possiamo dunque definire l’integrale generalizzato per una funzione $f$ definita su un intervallo aperto $(a,b)$ con $-\infty \le a < b \le +\infty$ nel seguente modo.

Quindi $f$ è integrabile secondo Riemann su $[x,b]$ per ogni $x\in(a,b)$ . ↩

$\quad$

Definizione 3. Sia $I:=(a,b)$

con $-\infty \le a < b \le +\infty$

e sia $f\colon (a,b)\to\mathbb R$

una funzione localmente integrabile su $(a,b)$

³. La funzione $f$

è integrabile in senso generalizzato su $\overline I$

se comunque preso $c\in(a,b)$

, $I_1:=(a,c]$

e $I_2:=[c,b)$

la funzione $f$

è integrabile in senso generalizzato su $\overline I_1$

e $\overline I_2$

. In tal caso si pone

$\int_a^bf(t)\,dt:=\int_a^cf(t)\,dt+\int_c^bf(t)\,dt=\lim_{x\to a^+}\int_x^cf(t)\,dt+\lim_{y\to b^-}\int_c^yf(t)\,dt.$

Quindi $f$ è integrabile secondo Riemann su $[c,d]$ per ogni $a<c<d<b$ .. ↩

$\quad$

Esempio 5. Fissato $\alpha\in\mathbb R$ consideriamo di nuovo la funzione $f\colon (0,+\infty)\to\mathbb R$ definita come

$f(x):=\frac{1}{x^\alpha}\quad\text{per $x\in(0,+\infty)$}.$

Nell’esempio 3 abbiamo già visto che tale funzione è integrabile in senso generalizzato su $[0,1]$ se e solo se $\alpha<1$ , mentre è integrabile in senso generalizzato su $[1,+\infty)$ se e solo se $\alpha>1$ . Dunque per ogni $\alpha\in\mathbb R$ la funzione $f$ non è mai integrabile in senso generalizzato su tutto $[0,+\infty)$ .

Esempio 6. Sia $f\colon (-1,1)\to\mathbb R$ definita da

$f(x):=\frac{1}{\sqrt{1-x^2}}\quad\text{per $x\in(-1,1)$}.$

Si osservi che la funzione $f$ è continua su $(-1,1)$ , e dunque è localmente integrabile su tale intervallo. Se scegliamo il punto $c:=0\in(-1,1)$ abbiamo che

$\begin{align*} &\int_x^0\frac{1}{\sqrt{1-t^2}}\,dt=[\arcsin t]_x^0=-\arcsin x\quad\text{per ogni $x\in(-1,0)$},\\ &\int_0^y\frac{1}{\sqrt{1-t^2}}\,dt=[\arcsin t]_0^y=\arcsin y\quad\text{per ogni $y\in(0,1)$}. \end{align*}$

Poiché esistono entrambi i limiti per $x\to -1^+$ e $y\to 1^-$ , ne deduciamo che $f$ è integrabile in senso generalizzato su $[-1,1]$ e

$\begin{aligned} \int_{-1}^1 \frac{1}{\sqrt{1-t^2}}\,dt &= \lim_{x \to -1^+} \int_x^0 \frac{1}{\sqrt{1-t^2}}\,dt + \lim_{y \to 1^-} \int_0^y \frac{1}{\sqrt{1-t^2}}\,dt \\ &= \lim_{x \to -1^+} (-\arcsin x) + \lim_{y \to 1^-} \arcsin y \\ &= \frac{\pi}{2} + \frac{\pi}{2} \\ &= \pi. \end{aligned}$

Come abbiamo osservato prima, l’integrabilità in senso generalizzato di una funzione $f\colon I:=(a,b)\to\mathbb R$ non dipende dalla scelta di $c\in (a,b)$ . In particolare, la funzione $f$ risulta integrabile in senso generalizzato su $\overline I$ se e solo se esiste finito

$\lim_{\substack{x\to a^+\\y\to b^-}}\int_x^yf(t)\,dt\in\mathbb R,$

cioè esiste $l\in\mathbb R$ tale che per ogni $\varepsilon >0$ esistono $a<a_\varepsilon<b_\varepsilon<b$ con la proprietà che

$\left|\int_x^yf(t)\,dt-l\right|<\varepsilon\quad\text{per ogni $a<x<a_\varepsilon$ e $b_\varepsilon<y<b$}.$

In questo caso sarà $l=\int_a^bf(t)\,dt$ .

Osservazione 5. Si noti che la funzione

$(x,y)\mapsto \int_x^y f(t)\,dt$

deve essere vista come una funzione di due variabili e i limiti in $x$ e $y$ devono essere calcolati in maniera indipendente l’uno dall’altro. Per esempio, se consideriamo la funzione $f\colon \mathbb R\to \mathbb R$ definita da

$f(x):=\sin x\quad\text{per $x\in\mathbb R$},$

abbiamo che $f$ è localmente integrabile su $\mathbb R$ , ma non è integrabile in senso generalizzato su $\mathbb R$ . Infatti, preso $x\in (0,+\infty)$ abbiamo

$\int_0^x\sin t\,dt=[-\cos t]_0^x=1-\cos x,$

che non ammette limite per $x\to +\infty$ . D’altra parte $f$ è una funzione dispari, dunque per ogni $x\in(0,+\infty)$

$\int_{-x}^x\sin t\,dt=[-\cos t]_{-x}^x=0,$

è dunque esiste finito il limite

$\lim_{x\to+\infty}\int_{-x}^x\sin t\,dt=0.$

Teorema 2. Sia $I:=(a,b)\subseteq\mathbb R$

con $+\infty \le a < b \le +\infty$

. Sia $f\colon (a,b)\to\mathbb R$

una funzione continua su $(a,b)$

e sia $F\colon (a,b)\to\mathbb R$

una primitiva di $f$

in $(a,b)$

⁴. Allora $f$

è integrabile in senso generalizzato su $\overline I$

se e solo se esistono finiti i limiti

$\lim_{x\to a^+}F(x),\qquad\lim_{y\to b^-}F(y).$

In tal caso, si pone

$\int_a^bf(t)\,dt=[F(t)]_a^b:=\lim_{y\to b^-}F(y)-\lim_{x\to a^+}F(x).$

è derivabile su $(a,b)$ e $F'(x)=f(x)$ per ogni $x\in (a,b)$ . ↩

$\quad$

Dimostrazione. Fissato $c\in (a,b)$ , dal teorema fondamentale del calcolo integrale abbiamo

$\int_x^c f(t)\,dt =F(c)-F(x)\quad\text{per ogni $x\in(a,c)$},\qquad \int_c^yf(t)\,dt=F(y)-F(c)\quad\text{per ogni $y\in(c,b)$}.$

Dunque, la funzione $f$ è integrabile in senso generalizzato su $\overline I$ se e solo se esistono finiti i limiti

$\lim_{x\to a^+}F(x),\qquad\lim_{y\to b^-}F(y),$

e risulta

$\begin{aligned} \int_a^b f(t)\,dt &= \int_a^c f(t)\,dt + \int_c^b f(t)\,dt \\ &= F(c) - \lim_{x \to a^+} F(x) + \lim_{y \to b^-} F(y) - F(c) \\ &= \lim_{y \to b^-} F(y) - \lim_{x \to a^+} F(x). \end{aligned}$

La notazione adottata nel teorema precedente è molto utilizzata per il calcolo degli integrali impropri, ma è necessario fare attenzione nell’adoperarla. Esempio 7. Sia $f\colon (0,+\infty)\to\mathbb R$ definita da

$f(x):=\frac{\ln x}{(x+1)^2}\quad\text{per $x\in(0,+\infty)$}.$

La funzione $f$ è localmente integrabile su $(0,+\infty)$ e vediamo se è integrabile in senso generalizzato su $[0,+\infty)$ . Determiniamo una primitiva di $f$ in $(0,+\infty)$ e integrando per parti otteniamo che

$\int\frac{\ln t}{(t+1)^2}\,dt=-\frac{\ln t}{t+1}+\int \frac{1}{t(t+1)}\,dt.$

Osserviamo che per il primo termine a destra dell’uguale risulta

$\lim_{t\to 0^+}\frac{\ln t}{t+1}=-\infty.$

Ciò non implica che la funzione $f$ non sia integrabile in senso generalizzato su $[0,+\infty)$ , poiché l’integrale a destra dell’uguale può contribuire con ulteriori termini che possono rendere finito il limite della primitiva di $f$ per $x\to 0^+$ . Andiamo a determinare due numeri $A,B\in\mathbb R$ tali che

$\frac{A}{t}+\frac{B}{t+1}=\frac{1}{t(t+1)}.$

Abbiamo che

$\frac{(A+B)t+A}{t(t+1)}=\frac{1}{t(t+1)}\quad\Leftrightarrow\quad\text{$A=1$ e $B=-1$},$

da cui otteniamo

$\begin{aligned} \int\frac{\ln t}{(t+1)^2}\,dt=-\frac{\ln t}{t+1}+\int\left(\frac{1}{t}-\frac{1}{t+1}\right)\,dt=\ln t-\frac{\ln t}{t+1}-\ln(t+1)+c,\quad c\in\mathbb R. \end{aligned}$

Dunque, una primitiva di $f$ è data da

$F(t):=\ln t-\frac{\ln t}{t+1}-\ln(t+1)\quad\text{per $t\in(0+\infty)$}.$

Poiché⁵

$\begin{aligned} &\lim_{t\to 0^+}\left(\ln t-\frac{\ln t}{t+1}-\ln(t+1)\right)=\lim_{t\to 0^+}\left(\frac{t\ln t}{t+1}-\ln(t+1)\right)=0, \\ &\lim_{t\to +\infty}\left(\ln t-\frac{\ln t}{t+1}-\ln(t+1)\right)=\lim_{t\to +\infty}\left(-\frac{\ln t}{t+1}-\ln \left(1+\frac{1}{t}\right)\right)=0, \end{aligned}$

allora $f$ risulta integrabile in senso generalizzato su $[0,+\infty)$ e con la notazione del teorema 2 si ha

$\int_0^{+\infty}\frac{\ln t}{(t+1)^2}\,dt=\left[\ln t-\frac{\ln t}{t+1}-\ln(t+1)\right]_0^{+\infty}=0.$

Supponiamo ora di avere una funzione $f$ definita su un intervallo $I\subseteq\mathbb R$ eccetto in un punto $c\in I$ . In questo caso possiamo decomporre

$I\setminus\{c\}=I_1\cup I_2$

con $I_1,I_2\subset\mathbb R$ intervalli disgiunti e possiamo definire l’integrale generalizzato di $f$ su $\overline I$ richiedendo che $f$ sia integrabile in senso generalizzato su $\overline I_1$ e $\overline I_2$ e ponendo

$\int_{\overline I}f(t)\,dt:=\int_{\overline I_1}f(t)\,dt+\int_{\overline I_2}f(t)\,dt.$

Più in generale possiamo considerare una funzione $f$ definita su $I\setminus N$ , con $N$ sottoinsieme finito di $I$ , e dare la seguente definizione.

Ricordiamo che $\displaystyle\lim_{y\to 0^+}y\ln y=0$ . ↩

$\quad$

Definizione 4. Sia $I\subseteq\mathbb R$

un intervallo, sia $N$

un sottoinsieme finito di $I$

e sia

$I\setminus N=\bigcup_{j=1}^nI_j,$

con $I_j\subset \mathbb R$ per $j=1,\dots,n$ intervalli a due a due disgiunti. Sia $f\colon I\setminus N \to\mathbb R$ una funzione localmente integrabile su $I\setminus N$ ⁶. La funzione $f$ è integrabile in senso generalizzato su $\overline I$ se è integrabile in senso generalizzato su ogni intervallo $\overline I_j$ per $j=1,\dots,n$ . In tal caso l’integrale generalizzato di $f$ su $\overline I$ è definito come

$\int_{\overline I}f(t)\,dt:=\sum_{j=1}^n\int_{\overline I_j}f(t)\,dt.$

Quindi $f$ è localmente integrabile su ogni intervallo $I_j$ per $j=1,\dots,n$ . ↩

Esempio 8. Sia $f\colon\mathbb R\setminus\{0\}\to\mathbb R$ definita da

$f(x):=\frac{1}{\sqrt{|x|}(|x|+1)}\quad\text{per $x\in\mathbb R\setminus\{0\}$}.$

La funzione $f$ è localmente integrabile nel suo dominio di definizione è andiamo a vedere se è integrabile in senso generalizzato su $\mathbb R$ . Abbiamo che $\mathbb R\setminus\{0\}=(-\infty,0)\cup(0,+\infty)$ e vediamo se $f$ è integrabile in senso generalizzato su $[0,+\infty)$ . Iniziamo con il determinare una primitiva di $f$ in $(0,+\infty)$ e osserviamo che

$f(x)= \frac{1}{\sqrt{|x|}(|x|+1)}=\frac{1}{\sqrt{x}(x+1)}\quad\text{per $x\in(0,+\infty)$}.$

Tramite la sostituzione $s=\sqrt{t}$ otteniamo che $dt=2s\,ds$ e quindi

$\int f(t)\,dt =\int \frac{1}{\sqrt{t}(t+1)}\,dt=\int\frac{2}{s^2+1}\,ds=2\arctan s+c=2\arctan\sqrt{t}+c,\quad c\in\mathbb R.$

Dato che

$\lim_{t\to +\infty}2\arctan\sqrt{t}=\pi,\qquad \lim_{t\to 0^+}2\arctan\sqrt{t}=0,$

abbiamo che $f$ è integrabile in senso generalizzato su $[0,+\infty)$ e

$\int_0^{+\infty}f(t)\,dt=\pi.$

Inoltre la funzione $f$ è pari su $\mathbb R\setminus\{0\}$ , quindi

$\int_x^yf(t)\,dt=\int_{-y}^{-x}f(t)\,dt\quad\text{per ogni $-\infty<x<y<0$}.$

Per $x\to-\infty$ e $y\to 0^+$ possiamo dedurre che $f$ è integrabile in senso generalizzato su $(-\infty,0]$ e

$\int_{-\infty}^0f(t)\,dt=\int_0^{+\infty}f(t)\,dt=\pi.$

Quindi la funzione $f$ è integrabile su $\mathbb R$ e

$\int_{-\infty}^{+\infty}f(t)\,dt=2\pi.$

Dalla linearità dell’integrale di Riemann e dalla linearità del limite risulta che anche l’integrale generalizzato è lineare. Più precisamente, se $f,g\colon I\setminus N\to\mathbb R$ sono due funzioni integrabili in senso generalizzato su $\overline I$ , allora per ogni $\alpha,\beta\in\mathbb R$ anche la funzione $\alpha f+\beta g\colon I\setminus N\to\mathbb R$ è integrabile in senso generalizzato su $\overline I$ e

$\int_{\overline I}(\alpha f(t)+\beta g(t))\,dt=\alpha\int_{\overline I}f(t)\,dt+\beta\int_{\overline I}g(t)\,dt.$

Osservazione 6. Per vedere se una funzione $f\colon I\setminus N\to \mathbb R$ è integrabile in senso generalizzato su $\overline I$ , è necessario calcolare i limiti di ogni singolo integrale generalizzato in maniera indipendente. Si consideri per esempio la funzione

$f(x)=\frac{1}{x}\quad\text{per $x\in[-1,1]\setminus\{0\}$}.$

Già sappiamo che questa funzione non è integrabile in senso generalizzato su $[-1,1]$ perché non lo è su $[0,1]$ . D’altra parte, per ogni $x\in(0,1)$ abbiamo che

$\int_{-1}^{-x}\frac{1}{t}\,dt+\int_x^1\frac{1}{t}\,dt=\ln x-\ln x=0.$

Dunque esiste finito

$\lim_{x\to 0^+}\left(\int_{-1}^{-x}\frac{1}{t}\,dt+\int_x^1\frac{1}{t}\,dt\right)=0.$

Osservazione 7. Abbiamo visto che le funzioni $f(x):=\sin x$ e $g(x):=\frac{1}{x}$ non sono integrabili in senso generalizzato su $\mathbb R$ e $[-1,1]$ , rispettivamente, ma è possibile assegnare a questi due integrali un valore numerico calcolando il limite in maniera opportuna. Questo particolare tipo di integrazione prende il nome di valore principale di Cauchy e di solito si denota aggiungendo le lettere $P.V.$ di fronte all’integrale. Esso viene utilizzato in alcuni ambiti della matematica per dare un valore all’integrale di funzioni definite su $\mathbb R$ e/o con una singolarità isolata, nel caso in cui non siano integrabili in senso generalizzato. Più precisamente, per una funzione localmente integrabile $f\colon \mathbb R\to\mathbb R$ si definisce

$P.V.\int_{-\infty}^{+\infty}f(t)\,dt:=\lim_{R\to+\infty}\int_{-R}^Rf(t)\,dt$

se tale limite esiste finito, mentre per una funzione localmente integrabile $f\colon[a,b]\setminus\{c\}\to\mathbb R$ con $a<c<b$ si definisce

$P.V.\int_a^bf(t)\,dt:=\lim_{\varepsilon\to 0^+}\left(\int_a^{c-\varepsilon}f(t)\,dt+\int_{c+\varepsilon}^b f(t)\,dt\right)$

se tale limite esiste finito. Infine, per una funzione localmente integrabile $f\colon \mathbb R\setminus\{c\}\to\mathbb R$ si definisce

$P.V.\int_{-\infty}^{+\infty}f(t)\,dt:=\lim_{\varepsilon\to 0}\left(\int_{c-\frac{1}{\varepsilon}}^{c-\varepsilon}f(t)\,dt+\int_{c+\varepsilon}^{c+\frac{1}{\varepsilon}}f(t)\,dt\right)$

se tale limite esiste finito. In particolare, per i due esempi precedenti abbiamo che

$P.V.\int_{-\infty}^{+\infty}\sin t\,dt=0,\qquad P.V.\int_{-1}^1\frac{1}{t}\,dt=0.$

Nell’Esempio 8 abbiamo utilizzato le formule di sostituzione per calcolare la primitiva della funzione $f$ . In realtà, la stessa formula di sostituzione può essere usata anche per calcolare direttamente l’integrale generalizzato di $f$ .

Teorema 3. (Integrazione per sostituzione). Siano $I:=(a,b)\subseteq\mathbb R$

e $J:=(c,d)\subseteq\mathbb R$

due intervalli aperti e sia $f\colon (a,b)\to\mathbb R$

una funzione continua su $(a,b)$

. Sia $\phi\colon (c,d)\to (a,b)$

una funzione strettamente crescente e derivabile con derivata continua su $(c,d)$

tale che

$\lim_{x\to c^+}\phi(x)=a,\qquad\lim_{x\to d^-}\phi(x)=b.$

Allora la funzione $f$ è integrabile in senso generalizzato su $\overline I$ se e solo se la funzione

$g(x):= f(\phi(x))\phi'(x)\quad \text{per $x\in (c,d)$}$

è integrabile in senso generalizzato su $\overline J$ e risulta

$\int_a^bf(t)\,dt=\int_c^dg(s)\,ds=\int_c^df(\phi(s))\phi'(s)\,ds.$

$\quad$

Dimostrazione. Poiché $\phi\colon (c,d)\to (a,b)$ è derivabile con derivata continua su $(c,d)$ e $f\colon (a,b)\to\mathbb R$ è continua su $(a,b)$ , allora la funzione $g$ è continua su $(c,d)$ . In particolare, $g$ è localmente integrabile su $(c,d)$ . Fissati $c<x<y<d$ , dal teorema di integrazione per sostituzione per l’integrale di Riemann risulta

$\int_x^yg(s)\,ds=\int_x^yf(\phi(s))\phi'(s)\,ds=\int_{\phi(x)}^{\phi(y)}f(t)\,dt.$

Poiché $f$ è integrabile in senso generalizzato su $\overline I$ e

$\lim_{x\to c^+}\phi(x)=a,\qquad\lim_{x\to d^-}\phi(x)=b,$

ne deduciamo che

$\int_a^bf(t)\,dt=\lim_{\substack{w\to a^+,\\z\to b^-}}\int_w^zf(t)\,dt=\lim_{\substack{x\to c^+,\\y\to d^-}}\int_{\phi(x)}^{\phi(y)}f(t)\,dt.$

Quindi esiste finito il limite

$\lim_{\substack{x\to c^+,\\y\to d^-}}\int_x^yg(s)\,ds=\lim_{\substack{x\to c^+,\\y\to d^-}}\int_{\phi(x)}^{\phi(y)}f(t)\,dt=\int_a^bf(t)\,dt.$

Allora $g$ è integrabile in senso generalizzato su $\overline J$ e

$\int_c^d g(s)\,ds=\int_a^bf(t)\,dt.$

Infine, per ottenere l’altra implicazione osserviamo che la funzione $\phi\colon (c,d)\to (a,b)$ è invertibile (essendo strettamente crescente su $(c,d)$ ) e la sua inversa $\phi^{-1}\colon (a,b)\to (c,d)$ soddisfa ancora le ipotesi del teorema (l’inversa di una funzione strettamente crescente e derivabile con derivata continua è anche essa strettamente crescente e derivabile con derivata continua). Dunque, se $g$ è integrabile in senso generalizzato su $\overline J$ , allora la funzione

$g(\phi^{-1}(x))(\phi^{-1})'(x)=f(x)\phi'(\phi^{-1}(x))(\phi^{-1})'(x)=f(x)\quad\text{per $x\in I$}$

risulta integrabile in senso generalizzato su $\overline I$ .

Si noti che se abbiamo una funzione $\phi\colon (c,d)\to (a,b)$ derivabile con derivata continua che soddisfa $\phi'(x)>0$ per ogni $x\in (c,d)$ , allora $\phi$ è strettamente crescente. Inoltre questo teorema rimane vero se $\phi\colon (c,d)\to (a,b)$ è strettamente decrescente (per esempio quando $\phi'(x)<0$ per ogni $x\in (c,d)$ ) e

$\lim_{x\to c^+}\phi(x)=b,\qquad\lim_{x\to d^-}\phi(x)=a.$

In questo caso abbiamo

$\int_a^bf(t)\,dt=\int_d^cf(\phi(s))\phi'(s)\,ds=-\int_c^df(\phi(s))\phi'(s)\,ds.$

Esempio 9. Consideriamo la funzione $f\colon (4,+\infty)\to\mathbb R$ data da

$f(x):=\frac{1}{x\sqrt{x-4}}\quad\text{per $x\in(4,+\infty)$}.$

Se consideriamo il cambio di variabili $\phi\colon (0,+\infty)\to (4,+\infty)$ definito come

$\phi(x):=x^2+4\quad\text{per $x\in(0,+\infty)$},$

abbiamo che $\phi$ soddisfa le ipotesi del teorema precedente e

$\lim_{x\to 0^+}\phi(x)=4,\qquad \lim_{x\to +\infty}\phi(x)=+\infty.$

Dunque

$\int_4^{+\infty}\frac{1}{t\sqrt{t-4}}\,dt=\int_0^{+\infty}\frac{2}{s^2+4}\,ds=\left[\arctan \frac{s}{2}\right]_0^{+\infty}=\frac{\pi}{2}.$

A volte per calcolare un integrale per sostituzione è più semplice utilizzare l’inversa di $\phi$ . Infatti, se nell’esempio precedente poniamo $s=\sqrt{t-4}=\phi^{-1}(t)$ , da cui $t=s^2+4=\phi(s)$ , deduciamo immediatamente che $dt=2s\,ds$ e che i nuovi estremi di integrazione per $g(s):=\frac{2}{s^2+4}$ sono

$\lim_{t\to 4^+}\sqrt{t-4}=0,\qquad \lim_{t\to +\infty}\sqrt{t-4}=+\infty,$

da cui otteniamo

$\int_4^{+\infty}\frac{1}{t\sqrt{t-4}}\,dt=\int_0^{+\infty}\frac{2}{s^2+4}\,ds=\frac{\pi}{2}.$

Si noti che tramite il metodo di integrazione per sostituzione è possibile trasformare un integrale generalizzato in un integrale di Riemann e viceversa. Per esempio, se nell’esempio 6 consideriamo il cambio di variabili $\phi\colon (0,\pi)\to (-1,1)$ dato da

$\phi(x):=\cos x\quad\text{per $x\in (0,\pi)$},$

otteniamo

$\int_{-1}^1\frac{1}{1-t^2}\,dt=\int_0^{\pi}\frac{\sin s}{\sqrt{1-\cos^2 s}}\,ds =\int_0^{\pi}\,ds=\pi.$

Osservazione 8. Il teorema 3 può anche essere usato per ricondurre lo studio dell’integrabilità di una funzione illimitata su un dominio limitato a quello di una funzione su un dominio illimitato, e viceversa. Infatti, siano $-\infty<a<b<+\infty$ e sia $f\colon[a,b)\to\mathbb R$ una funzione continua su $[a,b)$ . Se consideriamo la funzione $\phi\colon (\dfrac{1}{b-a},+\infty)\to (a,b)$ definita come

$\phi(x):=b-\frac{1}{x}\quad\text{per $x\in\left(\frac{1}{b-a},+\infty\right)$},$

questa soddisfa le ipotesi del teorema precedente. Dunque $f$ è integrabile in senso generalizzato su $[a,b]$ se e solo se la funzione

$g(x):=\frac{f\left(b-\frac{1}{x}\right)}{x^2}\quad\text{per $x\in\left[\frac{1}{b-a},+\infty\right)$}$

è integrabile in senso generalizzato su $[\dfrac{1}{b-a},+\infty)$ e

$\int_a^bf(t)\,dt=\int_{\frac{1}{b-a}}^{+\infty}\frac{f\left(b-\frac{1}{t}\right)}{t^2}\,dt.$

Criteri di convergenza.

Molto spesso non è possibile calcolare il valore esatto dell’integrale di Riemann generalizzato di una funzione, soprattutto quando non si riesce a determinare una primitiva esplicita in termini di funzioni elementari. Per questo motivo vogliamo introdurre dei criteri che permettano di studiare la convergenza dell’integrale generalizzato di $f$

su $\overline I$

senza dover calcolare il suo integrale di Riemann su ogni sottointervallo. Per semplicità ci riduciamo al caso in cui $I:=[a,b)$

con $-\infty< a < b \le +\infty$

(gli altri casi possono essere facilmente dedotti da questo per quanto osservato precedentemente).

Sia $I:=[a,b)$ con $-\infty< a< b \le +\infty$ e sia $f\colon [a,b)\to[0,+\infty)$ una funzione non negativa e localmente integrabile su $[a,b)$ . Allora la funzione

$F(x):=\int_a^xf(t)\,dt$

è non decrescente su $[a,b)$ e dunque esiste sempre il limite

$\lim_{x\to b^-}F(x):=\int_a^b f(t)\,dt\in\mathbb R\cup\{+\infty\}.$

Quindi l’integrale generalizzato di $f$ risulta convergente su $\overline I$ se e solo se tale limite è finito.

Teorema 4 (criterio del confronto). Sia $I:=[a,b)$

con $-\infty< a < b \le +\infty$

e siano $f,g\colon [a,b)\to[0,+\infty)$

due funzioni non negative e localmente integrabili su $[a,b)$

. Assumiamo che

$0\le f(x)\le g(x)\quad\text{per ogni $x\in [a,b)$}.$

Se l’integrale generalizzato di $g$ è convergente su $\overline I$ , allora anche l’integrale generalizzato di $f$ è convergente su $\overline I$ e si ha

$0\le\int_a^b f(t)\,dt\le \int_a^b g(t)\,dt.$

Se invece l’integrale generalizzato di $f$ è divergente su $\overline I$ , allora anche l’integrale generalizzato di $g$ è divergente su $\overline I$ .

$\quad$

Dimostrazione. Dalla disuguaglianza $0\le f(x)\le g(x)$ per ogni $x\in [a,b)$ , possiamo dedurre che

$0\le\int_a^xf(t)\,dt\le \int_a^xg(t)\,dt\quad\text{per ogni $x\in (a,b)$},$

e dunque

$\int_a^bf(t)\,dt=\lim_{x\to b^-}\int_a^xf(t)\,dt\le \lim_{x\to b^-}\int_a^x g(t)\,dt=\int_a^bg(t)\,dt$

(entrambi i limiti esistono in $\mathbb R\cup\{+\infty\}$ per quanto osservato prima). Quindi se l’integrale di $g$ converge su $\overline I$ , allora anche l’integrale di $f$ converge su $\overline I$ , mentre se l’integrale di $f$ diverge su $\overline I$ , allora anche l’integrale di $g$ diverge su $\overline I$ .

Vediamo come possiamo applicare questo risultato per studiare l’integrabilità in senso generalizzato di una funzione $f$ .

Esempio 10. Consideriamo al funzione

$f(x):=\frac{\cos^2(x^2+1)e^{-x}}{\sqrt{x}+|\sin x|}.$

La funzione $f$ è ben definita e continua su $(0,+\infty)$ (il denominatore si annulla solo in $x=0$ ) e dunque ha senso chiedersi se $f$ sia integrabile in senso generalizzato su $[0,+\infty)$ . Poiché non è semplice determinare una primitiva esplicita di $f$ in termini di funzioni elementari (e non è detto che si possa fare), non possiamo argomentare come abbiamo fatto precedentemente. D’altra parte $f$ è non negativa su $(0,+\infty)$ , perciò possiamo applicare il criterio del confronto.

Iniziamo studiando l’integrabilità in senso generalizzato in un intorno destro di $0$ . Osserviamo che

$0\le f(x)\le \frac{e^{-x}}{\sqrt{x}}\le \frac{1}{\sqrt{x}}\quad\text{per ogni $x\in(0,1]$}.$

Poiché la funzione $x\mapsto\dfrac{1}{\sqrt{x}}$ è integrabile in senso generalizzato su $[0,1]$ (come dimostrato nell’esempio 3), dal teorema del confronto otteniamo che anche $f$ è integrabile in senso generalizzato su $[0,1]$ .

Analizziamo ora il comportamento di $f$ in un intorno di $+\infty$ . In questo caso abbiamo che

$f(x)\le \frac{e^{-x}}{\sqrt{x}}\le e^{-x}\quad\text{per $x\in[1,+\infty)$}.$

Poiché

$\int_1^x e^{-t}\,dt=\left[-e^{-t}\right]_1^x=e^{-1}-e^{-x}\to e^{-1}\quad\text{per $x\to+\infty$},$

ne segue che la funzione $x\mapsto e^{-x}$ è integrabile in senso generalizzato su $[1+\infty)$ , e dunque anche $f$ lo è dal teorema del confronto. Quindi la funzione $f$ è integrabile in senso generalizzato su tutto $[0,+\infty)$ .

Esempio 11. Consideriamo la funzione

$f(x):=\frac{(3x+\arctan x)^2}{\sqrt[3]{x^2}+e^{\frac{1}{x}}}.$

La funzione $f$ è ben definita su $\mathbb R\setminus\{0\}$ , dove è anche continua e dunque ci possiamo chiedere se $f$ è integrabile in senso generalizzato su $\mathbb R$ . Poiché la funzione $f$ è non negativa, possiamo applicare il criterio del confronto.

Per prima cosa controlliamo la convergenza dell’integrale generalizzato in un intorno sinistro e destro di $0$ .

Dato che

$f(x)\le \frac{(3+\arctan 1)^2}{\sqrt[3]{x^2}+e^{\frac{1}{x}}}\le\dfrac{(3+\dfrac{\pi}{4})^2}{\sqrt[3]{x^2}}\quad\text{per $x\in(0,1]$}$

e la funzione $x\mapsto\dfrac{1}{\sqrt[3]{x^2}}$ è integrabile in senso generalizzato su $[0,1]$ (come dimostrato all’interno dell’esempio 3, essendo $\alpha=\dfrac{2}{3}<1$ ), dal teorema del confronto ne consegue che $f$ è integrabile in senso generalizzato su $[0,1]$ . Analogamente $f$ è integrabile in senso generalizzato su $[-1,0]$ , perché

$f(x)\le \frac{(-3-\arctan 1)^2}{\sqrt[3]{x^2}+e^{\frac{1}{x}}}\le\frac{(3+\frac{\pi}{4})^2}{\sqrt[3]{x^2}}\quad\text{per $x\in[-1,0)$},$

e $x\mapsto\dfrac{1}{x^{\frac{2}{3}}}$ è integrabile in senso generalizzato su $[-1,0]$ .

Invece, $f$ non è integrabile in senso generalizzato in un intorno di $+\infty$ , in quanto

$f(x)\ge \frac{9x^2}{\sqrt[3]{x^2}+e}\ge\frac{9x^2}{\sqrt[3]{x^2}+e\sqrt[3]{x^2}}=\frac{9}{1+e}\sqrt[3]{x^4}\quad\text{per $x\in[1,+\infty)$}$

e $x\mapsto \sqrt[3]{x^4}$ non è integrabile in senso generalizzato su $[1,+\infty)$ (ciò si può vedere sia calcolando la primitiva sia usando l’esempio 3 essendo $\alpha=-\dfrac{4}{3}\le 1$ ). Analogamente la funzione $f$ non è integrabile in senso generalizzato in un intorno di $-\infty$ . In particolare $f$ non è integrabile in senso generalizzato su $\mathbb R$ .

Come abbiamo visto, per studiare l’integrabilità di una funzione $f\colon [a,b)\to [0,+\infty)$ , è sufficiente controllare il comportamento della funzione in un intorno sinistro di $b$ . Di conseguenza, dal criterio del confronto possiamo dedurre il seguente criterio di integrabilità.

Corollario 1. Sia $I:=[a,b)$

con $-\infty< a < b \le +\infty$

e siano $f,g\colon [a,b)\to[0,+\infty)$

due funzioni non negative e localmente integrabili su $[a,b)$

. Supponiamo che $f$

sia un O-grande di $g$

per $x\to b^-$

, cioè che esista $c\in(a,b)$

e una funzione limitata $k\colon [c,b)\to\mathbb R$

tale che

$f(x)=k(x)g(x)\quad\text{per $x\in[c,b)$}.$

Se l’integrale generalizzato di $g$ è convergente su $\overline I$ , allora anche l’integrale generalizzato di $f$ è convergente su $\overline I$ . Se invece l’integrale generalizzato di $f$ è divergente su $\overline I$ , allora anche l’integrale generalizzato di $g$ è divergente su $\overline I$ .

$\quad$

Dimostrazione. La dimostrazione segue direttamente dal criterio del confronto. Infatti, poiché le funzioni $f$ e $g$ sono integrabili secondo Riemann su $[a,x]$ per ogni $x\in(a,b)$ , è sufficiente studiare il comportamento di $f$ e $g$ in un intorno sinistro di $b$ . Siccome $f$ è un O-grande di $g$ , allora esiste $c\in(a,b)$ e una funzione limitata $k\colon J:=[c,b)\to\mathbb R$ tale che

$0\le f(x)=k(x)g(x)\le Mg(x)\quad\text{per ogni $x\in [c,b)$},\qquad M:=\sup_{x\in [c,b)}k(x)\in[0,+\infty).$

Dal criterio del confronto segue che se l’integrale generalizzato di $g$ è convergente su $\overline J$ , allora anche l’integrale generalizzato di $f$ è convergente su $\overline J$ , mentre se l’integrale generalizzato di $f$ è divergente su $\overline J$ , allora anche l’integrale generalizzato di $g$ è divergente su $\overline J$ .

Un’altra conseguenza del Teorema 4 è il criterio del confronto asintotico.

$\quad$

Teorema 5 (criterio del confronto asintotico). Sia $I:=[a,b)$

con $-\infty < a < b \le +\infty$

e consideriamo due funzioni non negative $f,g\colon [a,b)\to[0,+\infty)$

localmente integrabili su $I$

. Supponiamo che $g$

sia strettamente positiva in un intorno sinistro di $b$

e che $f$

e $g$

siano asintoticamente equivalenti per $x\to b^-$

( $f\sim g$

per $x\to b^-$

), cioè che esista finito e non nullo il limite

$\lim_{x\to b^-}\frac{f(x)}{g(x)}=\lambda\in(0,+\infty).$

Allora l’integrale generalizzato di $f$ è convergente (divergente) su $\overline I$ se e solo se l’integrale generalizzato di $g$ è convergente (divergente) su $\overline I$ .

$\quad$

Dimostrazione. Poiché le funzioni $f$ e $g$ sono integrabili secondo Riemann su $[a,x]$ per ogni $x\in(a,b)$ , allora è sufficiente studiare il comportamento di $f$ e $g$ in un intorno sinistro di $b$ . Siccome $g$ è strettamente positiva vicino a $b$ , allora il rapporto $\dfrac{f(x)}{g(x)}$ è ben definito in un intorno opportuno di $b$ . In particolare,

$\lim_{x\to b^-}\frac{f(x)}{g(x)}=\lambda\in(0,+\infty),$

e dalla definizione di limite possiamo trovare $c\in(a,b)$ tale che

$\left|\frac{f(x)}{g(x)}-\lambda\right|\le \frac{\lambda}{2}\quad\text{per ogni $x\in J:=[c,b)$},$

e dunque

$0\le \frac{\lambda}{2}g(x)\le f(x)\le \frac{3\lambda}{2}g(x)\quad\text{per ogni $x\in [c,b)$}.$

Applicando il criterio del confronto prima ad $f$ e poi a $g$ otteniamo che l’integrale generalizzato di $f$ è convergente (divergente) su $\overline J$ se e solo se l’integrale generalizzato di $g$ è convergente (divergente) su $\overline J$ .

Nel caso in cui

$\lim_{x\to b^-}\frac{f(x)}{g(x)}=0,$

allora abbiamo solo che $f$ è un O-grande di $g$ per $x\to b^-$ . Infatti, dalla definizione di limite esiste $c\in(a,b)$ tale che la funzione

$k(x):=\frac{f(x)}{g(x)}\quad\text{per $x\in [a,b)$}$

è limitata e banalmente

$f(x)=k(x)g(x)\quad\text{per $x\in[c,b)$}.$

In questo caso possiamo quindi applicare il Corollario 1.

Esempio 12. Consideriamo la funzione

$f(x)=\frac{\arctan(x^4+\sqrt[3]{x})}{x^2+\ln(1+\sqrt{x})}.$

Abbiamo che $f$ è ben definita e continua su $(0,+\infty)$ (il denominatore si annulla solo in $x=0)$ . Dunque, ha senso studiare la convergenza dell’integrale generalizzato di $f$ su $[0,+\infty)$ . Abbiamo che $f$ è non negativa su $(0,+\infty)$ e inoltre⁷

$f(x)=\frac{\arctan(x^4+\sqrt[3]{x})}{x^2+\ln(1+\sqrt{x})}\sim \frac{x^4+\sqrt[3]{x}}{\sqrt{x}}\sim \frac{\sqrt[3]{x}}{\sqrt{x}}=\frac{1}{x^\frac{1}{6}}\quad\text{per $x\to 0^+$}.$

Poiché la funzione $x\mapsto\dfrac{1}{x^\frac{1}{6}}$ è integrabile in senso generalizzato su $[0,1]$ , dal criterio del confronto asintotico otteniamo che $f$ è integrabile in senso generalizzato su $[0,1]$ . Inoltre

$f(x)=\frac{\arctan(x^4+\sqrt[3]{x})}{x^2+\ln(1+\sqrt{x})}\sim \frac{1}{x^2}\quad\text{per $x\to+\infty$},$

e la funzione $x\mapsto\dfrac{1}{x^2}$ è integrabile in senso generalizzato su $[1,+\infty)$ . Dunque $f$ è integrabile in senso generalizzato su $[1,+\infty)$ per il criterio del confronto asintotico. In particolare, $f$ è integrabile in senso generalizzato su tutto $[0,+\infty)$ .

Ricordiamo che $\displaystyle\lim_{y\to 0}\frac{\ln(1+y)}{y}=\lim_{y\to 0}\frac{\arctan y}{y}=1.$ ↩

Combinando il criterio del confronto asintotico con l’esempio 3 possiamo dedurre il seguente risultato.

$\quad$

Corollario 2.

Sia $f\colon [a,+\infty)\to [0,+\infty)$ una funzione non negativa e localmente integrabile su $[a,+\infty)$ . Supponiamo che esista $\alpha\in\mathbb R$ tale che
$\lim_{x\to +\infty}x^\alpha f(x)=\lambda\in(0,+\infty).$

Se $\alpha>1$ l’integrale generalizzato di $f$ converge su $[a,+\infty)$ , mentre se $\alpha\le 1$ l’integrale di $f$ diverge su $[a,+\infty)$ .

Sia $f\colon [a,b)\to [0,+\infty)$ una funzione non negativa e localmente integrabile su $[a,b)$ . Supponiamo che esista $\beta\in\mathbb R$ tale che
$\lim_{x\to b^-}(b-x)^\beta f(x)=\lambda\in(0,+\infty).$

Se $\beta<1$ l’integrale generalizzato di $f$ converge su $[a,b]$ , mentre se $\beta\ge 1$ l’integrale di $f$ diverge su $[a,b]$ .

$\quad$

Dimostrazione.

Poiché
$\lim_{x\to +\infty}x^\alpha f(x)=\lambda\in(0,+\infty),$

abbiamo che $f$ è asintoticamente equivalente a $g(x):=\dfrac{1}{x^\alpha}$ per $x\to +\infty$ . Dunque dal criterio del confronto asintotico l’integrale generalizzato di $f$ è convergente (divergente) su $[a,+\infty)$ se e solo se l’integrale generalizzato di $g$ è convergente (divergente) su $[a,+\infty)$ . Dall’esempio 3 l’integrale generalizzato di $g$ converge per $\alpha>1$ , mentre diverge per $\alpha\le 1$ .

Poiché
$\lim_{x\to b^-}(b-x)^\alpha f(x)=\lambda\in\mathbb R\setminus\{0\},$

abbiamo che $f$ è asintoticamente equivalente a $g(x):=\dfrac{1}{(b-x)^\alpha}$ per $x\to b^-$ . Dunque dal criterio del confronto asintotico l’integrale generalizzato di $f$ è convergente (divergente) su $[a,b]$ se e solo se l’integrale generalizzato di $g$ è convergente (divergente) su $[a,b]$ . In maniera analoga a quanto mostrato nell’esempio 3, abbiamo che l’integrale generalizzato di $g$ converge per $\alpha<1$ , mentre diverge per $\alpha\ge 1$ .

Si noti che tutti i risultati precedenti rimangono validi anche per un una funzione $f\colon I\to (-\infty,0]$ non positiva. Infatti, è sufficiente considerare la funzione $-f$ e osservare che l’integrale generalizzato di $f$ converge (diverge) su $\overline I$ se e solo se l’integrale generalizzato di $-f$ converge (diverge) su $\overline I$ .

Sia ora $f\colon I\to\mathbb R$ una qualsiasi funzione localmente integrabile su un intervallo $I\subseteq\mathbb R$ . Se $f$ non ha segno costante su $I$ , allora non possiamo applicare i criteri precedenti per studiare la convergenza del suo integrale generalizzato su $\overline I$ . Se consideriamo però il suo modulo $|f|\colon I\to\mathbb R$ , questa è una funzione non negativa ed è ancora localmente integrabile su $I$ (se $f$ è integrabile secondo Riemann su un intervallo chiuso e limitato $J$ , allora anche $|f|$ è integrabile secondo Riemann su $J$ ). Dunque a $|f|$ possiamo applicare i criteri precedenti, e da ciò dedurre delle informazioni su $f$ .

Teorema 6. Sia $I:=[a,b)$

con $-\infty<a<b\le +\infty$

e sia $f\colon I\to\mathbb R$

una funzione localmente integrabile su $I$

. Se $|f|\colon I\to [0,+\infty)$

è integrabile in senso generalizzato su $\overline I$

, allora anche $f$

è integrabile in senso generalizzato su $\overline I$

. In particolare

$\left|\int_a^b f(t)\,dt\right|\le \int_a^b|f(t)|\,dt.$

$\quad$

Dimostrazione. Consideriamo le due funzioni

$f^+(x):=\max\{f(x),0\}\quad\text{per $x\in[a,b)$},\qquad f^-(x):=-\min\{f(x),0\}\quad\text{per $x\in[a,b)$}.$

Abbiamo che $f^+,f^-\colon I\to [0,+\infty)$ sono non negative e localmente integrabili su $I$ e

$0\le f^+(x)\le |f(x)|\quad\text{per $x\in[a,b)$},\qquad 0\le f^-(x)\le |f(x)|\quad\text{per $x\in[a,b)$}.$

Dal criterio del confronto segue che se $|f|$ è integrabile in senso generalizzato su $\overline I$ , allora anche $f^+$ e $f^-$ sono integrabili in senso generalizzato su $\overline I$ . Inoltre

$f(x)=f^+(x)-f^-(x)\quad\text{per $x\in[a,b)$},$

quindi $f$ è integrabile in senso generalizzato su $I$ . Infine, per ogni $x\in(a,b)$ abbiamo che

$-\int_a^x|f(t)|\,dt\le \int_a^x f(t)\,dt\le \int_a^x|f(t)|\,dt.$

Facendo il limite per $x\to b^-$ otteniamo

$\left|\int_a^b f(t)\,dt\right|\le \int_a^b|f(t)|\,dt.$

$\quad$

Definizione 5. Sia $I\subseteq\mathbb R$

un intervallo e sia $f\colon I\to \mathbb R$

una funzione localmente integrabile su $I$

. Se l’integrale generalizzato di $|f|\colon I\to[0,+\infty)$

su $\overline I$

è convergente, allora l’integrale generalizzato di $f$

su $\overline I$

si dice assolutamente convergente.

$\quad$

Esempio 13. Consideriamo la funzione

$f(x):=\frac{x^4-5x-\sin x}{\sqrt{(e^x-1)^3}}.$

Abbiamo che $f$ è ben definita e continua su $(0,+\infty)$ , ma non ha segno costante. Se consideriamo il suo modulo abbiamo che⁸

$0\le |f(x)|\le \frac{x^4+5|x|+|\sin x|}{\sqrt{(e^x-1)^3}}\sim \frac{x}{\sqrt{x^3}}=\frac{1}{\sqrt{x}}\quad\text{per $x\to 0^+$}$

(si noti che $|x|=x$ e $|\sin x|=\sin x$ per $x\to 0^+$ ). Applicando il criterio del confronto asintotico e quello del confronto otteniamo che $|f|$ è integrabile in senso generalizzato su $[0,1]$ poiché $x\mapsto\dfrac{1}{\sqrt{x}}$ lo è. Inoltre

$0\le |f(x)|\le \frac{x^4+5|x|+|\sin x|}{\sqrt{(e^x-1)^3}}\sim \frac{x^4}{\sqrt{e^{3x}}}=x^4e^{-\frac{3}{2}x}\quad\text{per $x\to +\infty$}.$

Abbiamo che la funzione $g(x):=x^4e^{-\frac{3}{2}x}$ è integrabile in senso generalizzato su $[1,+\infty)$ . Ciò può essere dimostrato usando la definizione e integrando per parti, oppure osservando che $g$ è un O-grande di $x\mapsto e^{-x}$ per $x\to+\infty$ , essendo

$\lim_{x\to +\infty}\frac{x^4 e^{-\frac{3}{2}x}}{e^{-x}}=\lim_{x\to +\infty}x^4 e^{-\frac{x}{2}}=0,$

e che $e^{-x}$ è integrabile in senso generalizzato su $[1,+\infty)$ . Quindi $|f|$ è integrabile in senso generalizzato su $[1,+\infty)$ . Allora l’integrale generalizzato di $f$ su $[0,+\infty)$ è assolutamente convergente, e quindi convergente.

Ricordiamo che $\displaystyle\lim_{y\to 0}\frac{e^y-1}{y}=\lim_{y\to 0}\frac{\sin y}{y}=1.$ ↩

Si noti che il viceversa del teorema 6 è falso, cioè esistono funzioni $f\colon I\to \mathbb R$ i cui integrali generalizzati su $\overline I$ sono convergenti, ma non assolutamente convergenti.

Esempio 14 (integrale di Dirichlet). Consideriamo la funzione $f\colon (0,+\infty)\to\mathbb R$ definita da

$f(x):=\frac{\sin x}{x}\quad\text{per $x\in(0,+\infty)$}.$

Abbiamo che $f$ è continua su $(0,+\infty)$ e facciamo vedere l’integrale generalizzato di $f$ converge su $[0,+\infty)$ . Per prima cosa osserviamo $f$ è prolungabile con continuità a destra in $x=0$ , poiché

$\lim_{x\to 0^+}\frac{\sin x}{x}=1,$

dunque la funzione $f$ è integrabile in senso generalizzato su $[0,1]$ . Rimane dunque da studiare l’integrabilità di $f$ su $[1,+\infty)$ . Fissato $x\in(1,+\infty)$ , integrando per parti otteniamo che

$\int_1^x\frac{\sin t}{t}\,dt=\left[-\frac{\cos t}{t}\right]_1^x-\int_1^x\frac{\cos t}{t^2}\,dt=\cos 1-\frac{\cos x}{x}-\int_1^x\frac{\cos t}{t^2}\,dt.$

Osserviamo che esiste finito il limite

$\lim_{x\to +\infty}\left(\cos 1-\frac{\cos x}{x}\right)=\cos 1.$

Dunque, la funzione $f$ risulta integrabile in senso generalizzato su $[1,+\infty)$ se e solo se la la funzione

$g(x):=\frac{\cos x}{x^2}\quad\text{per $x\in[1,+\infty)$}$

è integrabile in senso generalizzato su $[1,+\infty)$ . Poiché

$0\le |g(x)|\le \frac{1}{x^2}\quad\text{per $x\in[1,+\infty)$},$

dal teorema del confronto risulta che l’integrale generalizzato di $g$ è assolutamente convergente su $[1,+\infty)$ , e dunque convergente. Pertanto $f$ è integrabile in senso generalizzato su tutto $[0,+\infty)$ .

D’altra parte abbiamo che l’integrale generalizzato di $|f|$ è divergente su $[0,+\infty)$ . Infatti, fissato $m\in\mathbb N$ con $m\ge 2$ possiamo scrivere

$\int_\pi^{m\pi}|f(t)|\,dt=\int_{\pi}^{m\pi}\frac{|\sin t|}{t}\,dt=\sum_{k=2}^m\int_{(k-1)\pi}^{k\pi}\frac{|\sin t|}{t}\,dt.$

La funzione $x\mapsto\dfrac{1}{x}$ è non crescente in $(0,+\infty)$ , dunque

$\frac{1}{x}\ge \frac{1}{k\pi}\quad\text{per ogni $x\in[(k-1)\pi,k\pi]$ e $k=2,\dots,m$}.$

Poiché $x\mapsto|\sin x|$ è una funzione periodica di periodo $\pi$ , allora

$\int_{(k-1)\pi}^{k\pi}|\sin t|\,dt=\int_0^{\pi}|\sin t|\,dt=[-\cos t]_0^\pi=2\quad\text{per ogni $k=2,\dots,m$}.$

Perciò

$\int_\pi^{m\pi}\frac{|\sin t|}{t}\,dt\ge\sum_{k=2}^m\int_{(k-1)\pi}^{k\pi}\frac{|\sin t|}{k\pi}\,dt=\frac{2}{\pi}\sum_{k=2}^m\frac{1}{k}.$

Poiché $|f|$ è non negativa, esiste il limite

$\int_{\pi}^{+\infty}\frac{|\sin t|}{t}\,dt=\lim_{x\to+\infty}\int_\pi^x\frac{|\sin t|}{t}\,dt=\lim_{m\to+\infty}\int_\pi^{m\pi}\frac{|\sin t|}{t}\,dt\in\mathbb R\cup\{+\infty\}$

(si noti che il primo limite è fatto sui reali, mentre il secondo è fatto sui naturali). Dunque, per $m\to+\infty$ otteniamo

$\int_{\pi}^{+\infty}\frac{|\sin t|}{t}\,dt\ge \lim_{m\to+\infty}\frac{2}{\pi}\sum_{k=2}^m\frac{1}{k}=\frac{2}{\pi}\sum_{k=2}^{+\infty}\frac{1}{k}.$

$\quad$

Figura 1: grafico di $f(x)=\dfrac{\sin x}{x}$ su $\mathbb R$ .

$\quad$

Poiché la serie $\sum_{k=1}^{+\infty}\frac{1}{k}$ diverge, ne segue che l’integrale generalizzato di $|f|$ è divergente su $[\pi,+\infty)$ , e quindi anche su $[0,+\infty)$ .

L’integrale generalizzato

$\int_0^{+\infty}\frac{\sin t}{t}\,dt$

è chiamato integrale di Dirichlet ed è possibile dimostrare che

$\int_0^{+\infty}\frac{\sin t}{t}\,dt=\frac{\pi}{2}.$

Andiamo ora ad introdurre dei criteri per studiare il comportamento dell’integrale generalizzato di una funzione definita su un dominio illimitato. Come abbiamo visto nell’esempio precedente, è possibile ricondurre lo studio della convergenza dell’integrale di $f$ su $[a,+\infty)$ alla convergenza di una opportuna serie.

$\quad$

Teorema 7 (criterio della serie). Sia $n_0\in\mathbb N$

e $f\colon[n_0,+\infty)\to[0,+\infty)$

una funzione non negativa e non crescente su $[n_0,+\infty)$

. Allora

$\int_{n_0}^{+\infty}f(t)\,dt\quad\text{converge}\quad\Leftrightarrow\quad \sum_{k=n_0}^\infty f(k)\quad\text{converge}.$

$\quad$

Dimostrazione. Per prima cosa osserviamo che se $f\colon[n_0,+\infty)\to[0,+\infty)$ è una funzione non crescente su $[n_0,+\infty)$ , allora $f$ è localmente integrabile su $I$ . Dimostriamo intanto che

$\int_{n_0}^{+\infty}f(t)\,dt\quad\text{converge}\quad\Rightarrow\quad \sum_{k=n_0}^\infty f(k)\quad\text{converge}.$

Sia $m\in\mathbb N$ con $m\ge n_0+1$ , allora

$\sum_{k=n_0}^mf(k)=f(n_0)+\sum_{k=n_0+1}^m(k-(k-1))f(k)=f(n_0)+\sum_{k=n_0+1}^m\int_{k-1}^kf(k)\,dt.$

Poiché $f$ è non crescente, allora

$f(k)\le f(t)\quad\text{per ogni $t\in[k-1,k]$ e $k=n_0+1,\dots,m$}.$

Perciò

$\sum_{k=n_0}^mf(k)\le f(n_0)+\sum_{k=n_0+1}^m\int_{k-1}^kf(t)\,dt=f(n_0)+\int_{n_0}^m f(t)\,dt.$

Poiché $f$ è non negativa, abbiamo che esistono i limiti

$\begin{aligned} \sum_{k=n_0}^{+\infty} f(k) &= \lim_{m \to +\infty} \sum_{k=n_0}^m f(k) \in \mathbb{R} \cup \{+\infty\}, \\ \int_{n_0}^{+\infty} f(t)\,dt &= \lim_{x \to +\infty} \int_{n_0}^x f(t)\,dt = \lim_{m \to +\infty} \int_{n_0}^m f(t)\,dt \in \mathbb{R} \cup \{+\infty\}. \end{aligned}$

Per $m\to+\infty$ otteniamo che

$\sum_{k=n_0}^{+\infty}f(k)\le f(n_0)+\int_{n_0}^{+\infty}f(t)\,dt,$

e dunque se l’integrale generalizzato di $f$ converge su $[n_0,+\infty)$ , allora la serie $\sum_{k=n_0}^{+\infty}f(k)$ è convergente.

Dimostriamo ora che

$\sum_{k=n_0}^\infty f(k)\quad\text{converge}\quad\Rightarrow\quad\int_{n_0}^{+\infty}f(t)\,dt\quad\text{converge}.$

Sia $m\in\mathbb N$ con $m\ge n_0+1$ , allora

$\int_{n_0}^m f(t)\,dt=\sum_{k=n_0}^{m-1}\int_k^{k+1}f(t)\,dt.$

Siccome la funzione $f$ è non crescente, abbiamo

$f(t)\le f(k)\quad\text{per ogni $t\in[k,k+1]$ e $k=n_0,\dots, m-1$}.$

Perciò

$\int_{n_0}^m f(t)\,dt\le \sum_{k=n_0}^{m-1}\int_k^{k+1}f(k)\,dt=\sum_{k=n_0}^{m-1}f(k).$

Poiché $f$ è non negativa, sappiamo che esistono i limiti

$\begin{aligned} \sum_{k=n_0}^{+\infty} f(k) &= \lim_{m \to +\infty} \sum_{k=n_0}^{m-1} f(k) \in \mathbb{R} \cup \{+\infty\}, \\ \int_{n_0}^{+\infty} f(t)\,dt &= \lim_{x \to +\infty} \int_{n_0}^x f(t)\,dt = \lim_{m \to +\infty} \int_{n_0}^m f(t)\,dt \in \mathbb{R} \cup \{+\infty\}. \end{aligned}$

Per $m\to+\infty$ otteniamo che

$\int_{n_0}^{+\infty} f(t)\,dt\le\sum_{k=n_0}^{+\infty}f(k),$

e dunque se la serie $\sum_{k=n_0}^{+\infty}f(k)$ è convergente, allora l’integrale generalizzato di $f$ converge su $[n_0,+\infty)$ .

Esempio 15. Sia $f\colon [1,+\infty)\to \mathbb R$ definita da

$f(x)=x^{-x}e^x\quad\text{per $x\in[1,+\infty)$}.$

La funzione $f$ è continua su $[1,+\infty)$ è vediamo se è integrabile in senso generalizzato su tale intervallo. Osserviamo che $f$ è non crescente su $[1,+\infty)$ . Infatti

$f(x)=x^{-x}e^x=e^{\ln(x^{-x})}e^x=e^{x-x\ln x}=e^{x(1-\ln x)},$

e quindi

$f'(x)=-e^{x(1-\ln x)}\ln x\le 0\quad\text{per $x\in[1,+\infty)$}.$

Quindi possiamo applicare il criterio della serie e ottenere che

$\int_1^{+\infty}x^{-x}e^x\,dt\quad\text{converge}\quad\Leftrightarrow\quad \sum_{k=1}^{+\infty}\frac{e^n}{n^n}\quad\text{converge}.$

Osserviamo che tale serie converge dal criterio del rapporto, infatti

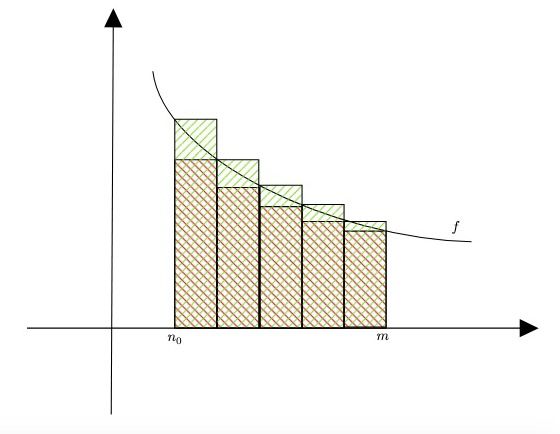
$\frac{f(k+1)}{f(k)}=\frac{e^{k+1}}{(k+1)^{k+1}}\frac{k^k}{e^k}=\frac{e}{k+1}\frac{1}{\left(1+\frac{1}{k}\right)^k}\to 0\quad\text{per $k\to +\infty$}.$

$\quad$

Figura 2: Il grafico mostra la relazione tra la somma parziale della serie e l’integrale della funzione $f(x)$ su un intervallo $[n_0, m]$ . I rettangoli rappresentano i termini della serie, confrontati con l’area sotto la curva della funzione decrescente $f(x)$ .

$\quad$

Dunque l’integrale generalizzato di $f$ è convergente su $[1,+\infty)$ .

Si noti che la convergenza dell’integrale di $f$ su $[1,+\infty)$ può essere dedotta anche dal criterio del confronto. Infatti, se ci mettiamo su $[e^2,+\infty)$ abbiamo che

$1-\ln x\le 1-\ln e^2=-1\quad\text{per ogni $x\in[e^2,+\infty)$}\quad\Rightarrow\quad x(1-\ln x)\le -x\quad\text{per ogni $x\in[e^2,+\infty)$},$

e dunque

$0\le f(x)\le e^{-x}\quad\text{per ogni $x\in[e^2,+\infty)$}.$

Poiché l’integrale di $x\mapsto e^{-x}$ converge su $[e^2,+\infty)$ , ne segue che $f$ è integrabile in senso generalizzato su $[e^2,+\infty)$ e dunque anche su $[1,+\infty)$ .

In genere, il criterio della serie viene utilizzato al contrario, cioè per dedurre la convergenza (divergenza) di una serie a partire dalla convergenza (divergenza) dell’integrale generalizzato. Infatti, combinando il criterio della serie con l’esempio 3 ritroviamo che

$\sum_{k=1}^{+\infty}\frac{1}{k^\alpha}\quad\text{converge}\quad\Leftrightarrow\quad \alpha<1.$

Inoltre, è possibile stimare il valore della serie a tramite il valore dell’integrale generalizzato associato e viceversa, in quanto all’interno della dimostrazione del criterio della serie abbiamo provato che

$\int_{n_0}^{+\infty}f(t)\,dt\le \sum_{k=n_0}^{+\infty}f(k)\le f(n_0)+\int_{n_0}^{+\infty}f(t)\,dt.$

Teorema 8. Sia $a\in\mathbb R$

e sia $f\colon[a,+\infty)\to\mathbb R$

una funzione localmente integrabile su $[a,+\infty)$

. Se esiste non nullo il limite

$\lim_{x\to+\infty}f(x)=L\in(\mathbb R\cup\{\pm\infty\})\setminus\{0\},$

allora l’integrale generalizzato di $f$ su $[a,+\infty)$ diverge.

$\quad$

Dimostrazione. Supponiamo che $L\in (0,+\infty]$ (il caso $L\in[-\infty,0)$ è analogo). Poiché

$\lim_{x\to+\infty}f(x)=L>0,$

dalla definizione di limite esiste $c\in[a,+\infty)$ ed esiste $\varepsilon>0$ tale che

$f(x)\ge\varepsilon \quad\text{per ogni $x\in[c,+\infty)$}.$

Quindi, per ogni $x\in(c,+\infty)$ abbiamo

$\int_a^xf(t)\,dt=\int_a^cf(t)\,dt+\int_c^xf(t)\,dt\ge \int_a^c f(t)\,dt+(x-c)\varepsilon.$

Per $x\to+\infty$ otteniamo che esiste il limite

$\lim_{x\to+\infty}\int_a^x f(t)\,dt=+\infty.$

Dunque l’integrale generalizzato di $f$ su $[a,+\infty)$ diverge.

Il teorema precedente può essere riformulato nel seguente modo: se l’integrale generalizzato di una funzione $f\colon [a,+\infty)\to \mathbb R$ è convergente su $[a,+\infty)$ ed esiste

$\lim_{x\to+\infty}f(x)=L\in\mathbb R\cup\{\pm\infty\},$

allora $L=0$ . Questo risultato è quindi in analogia con la nota condizione necessaria per le serie convergenti. Si noti però, che al contrario di ciò che accade per le serie, l’integrale generalizzato di $f$ su $[a,+\infty)$ può convergere anche quando il limite di $f$ per $x\to+\infty$ non esiste.

Esempio 16 (Integrale di Fresnel). Consideriamo la funzione $f\colon \mathbb R\to\mathbb R$ definita da

$f(x):=\sin(x^2)\quad\text{per $x\in\mathbb R$}.$

Abbiamo che non esiste il limite di $f$ per $x\to +\infty$ , e facciamo vedere che $f$ è integrabile in senso generalizzato su $[0,+\infty)$ . Poiché $f$ è continua su $[0,+\infty)$ , è sufficiente far vedere che l’integrale generalizzato di $f$ converge su $[1,+\infty)$ . Fissato $x\in(1,+\infty)$ , integrando per parti, abbiamo

$\begin{aligned} \int_1^x \sin(t^2)\,dt &= \int_1^x \frac{1}{t} \cdot t\sin(t^2)\,dt \\ &= \left[-\frac{\cos(t^2)}{2t}\right]_1^x - \int_1^x \frac{\cos(t^2)}{2t^2}\,dt \\ &= \frac{\cos 1}{2} - \frac{\cos(x^2)}{2x} - \int_1^x \frac{\cos(t^2)}{2t^2}\,dt. \end{aligned}$

Poiché esiste finito

$\lim_{x\to +\infty}\left(\frac{\cos 1}{2}-\frac{\cos (x^2)}{2x}\right)=\frac{\cos 1}{2},$

possiamo dedurre che $f$ è integrabile in senso generalizzato su $[1,+\infty)$ se e solo se la funzione

$g(x)=\frac{\cos (x^2)}{2x^2}\quad\text{per $x\in[1,+\infty)$}$

è integrabile in senso generalizzato su $[1,+\infty)$ . Osserviamo che

$0\le |g(x)|\le \dfrac{1}{2x^2}\quad\text{per $x\in[1,+\infty)$}$

e che l’integrale di $x\to\frac{1}{2x^2}$ su $[1,+\infty)$ è convergente. Allora l’integrale di $g$ su $[1,+\infty)$ e assolutamente convergente, e quindi $f$ è integrabile in senso generalizzato su $[0,+\infty)$ . Si noti infine che la funzione $f$ è pari, dunque $f$ è integrabile in senso generalizzato su tutto $\mathbb R$ . Analogamente, è possibile provare che anche la funzione $x\mapsto\cos(x^2)$ è integrabile in senso generalizzato su tutto $\mathbb R$ .

Le funzioni integrali

$S(x)=\int_0^x\sin(t^2)\,dt\quad\text{per $x\in[0,+\infty)$},\qquad C(x)=\int_0^x\cos (t^2)\,dt\quad\text{per $x\in[0,+\infty)$},$

sono chiamate integrali di Fresnel ed è possibile dimostrare che

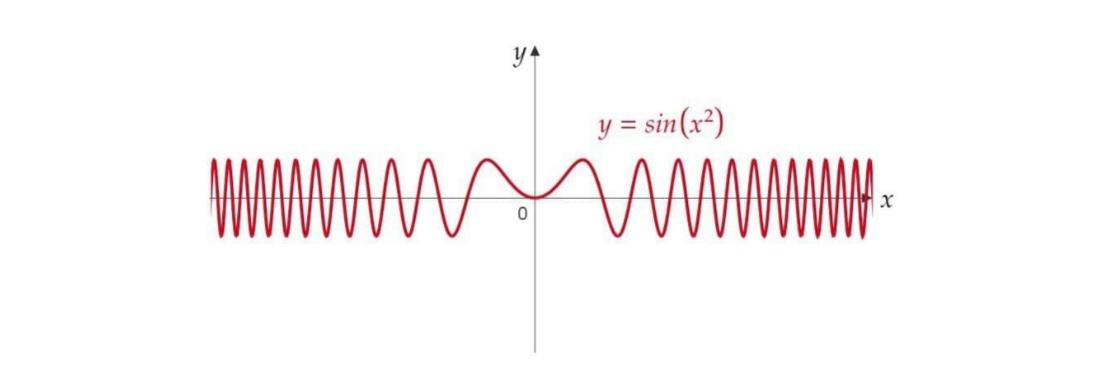
$\int_0^{+\infty}\sin (t^2)\,dt=\int_0^{+\infty}\cos (t^2)\,dt=\sqrt{\frac{\pi}{8}}.$

$\quad$

Figura 3: grafico di $f(x)=\sin(x^2)$ su $\mathbb R$ . Al contrario di $x\mapsto \sin x$ la funzione $f$ risulta integrabile su $\mathbb R$ , grazie al fatto che oscilla sempre più rapidamente per $x\to\pm\infty$ .

$\quad$

Si noti che negli esempi 14 e 16 per dimostrare la convergenza degli integrali generalizzati, abbiamo integrato per parti e sfruttato il fatto che il nuovo integrale così ottenuto convergeva. Questo tipo di ragionamento può essere formulato in maniera più generale. Prima di tutto diamo la seguente definizione.

$\quad$

Definizione 6 (funzione a variazione limitata). Sia $I\subseteq\mathbb R$

un intervallo, sia $N$

un sottoinsieme finito di $I$

e sia $f\colon I\setminus N\to\mathbb R$

una funzione derivabile con derivata continua su $I\setminus N$

. La funzione $f$

ha variazione limitata su $\overline I$

se l’integrale generalizzato di $f'$

è assolutamente convergente su $\overline I$

, cioè

$\int_{\overline I}|f'(t)|\,dt<+\infty.$

$\quad$

Osservazione 9. Se $I=(a,b)\subseteq\mathbb R$ con $-\infty\le a<b<\le +\infty$ è un intervallo e $f\colon (a,b)\to\mathbb R$ è monotona (non decrescente o non crescente) e derivabile con derivata continua su $(a,b)$ , allora $f$ ha variazione limitata su $\overline I$ se e solo se è limitata. Infatti, se assumiamo che $f$ sia non decrescente, allora per ogni $a<x<y<b$ risulta

$\int_x^y|f'(t)|\,dt=\int_x^yf'(t)\,dt=f(y)-f(x).$

Dunque $f$ ha variazione limitata su $\overline I$ se e solo se esistono finiti i limiti

$\lim_{x\to a^+}f(x)=\inf_{x\in (a,b)}f(x),\qquad \lim_{x\to b^-}f(x)=\sup_{x\in (a,b)}f(x),$

e ciò accade se e solo se $f$ è limitata. Analogamente, lo stesso ragionamento si può applicare se $f$ è non decrescente.

Teorema 9 (criterio di Abel-Dirichlet). Sia $I:=[a,b)$

con $-\infty<a<b\le +\infty$

e siano $f,g\colon [a,b)\to \mathbb R$

due funzioni continue su $[a,b)$

. Supponiamo che $f$

abbia una primitiva limitata su $[a,b)$

, cioè che esista $F\colon [a,b)\to\mathbb R$

continua e limitata su $[a,b)$

e derivabile su $(a,b)$

con $F'(x)=f(x)$

per ogni $x\in(a,b)$

, e che $g$

sia derivabile con derivata continua su $(a,b)$

, abbia variazione limitata su $\overline I$

e sia infinitesima per $x\to b^-$

. Allora la funzione $fg$

è integrabile in senso generalizzato su $\overline I$

$\quad$

Dimostrazione. Poiché $f$ ha una primitiva $F$ limitata su $[a,b)$ , allora

$M:=\sup_{x\in[a,b)}|F(x)|<+\infty.$

Fissato $x\in (a,b)$ , dalla formula di integrazione per parti su $[a,x]$ otteniamo

$\int_a^x f(t)g(t)\,dt=[F(t)g(t)]_a^x-\int_a^x F(t)g'(t)\,dt=F(x)g(x)-F(a)g(a)-\int_a^x F(t)g'(t)\,dt.$

Per ipotesi, $g$ è infinitesima per $x\to b^-$ e $F$ è limitata, dunque

$\lim_{x\to b^-}\left(F(x)g(x)-F(a)g(a)\right)=-F(a)g(a).$

Quindi $fg$ è integrabile in senso generalizzato su $\overline I$ se e solo se $Fg'$ è integrabile in senso generalizzato su $\overline I$ . Poiché

$0\le |F(x)g'(x)|\le M|g'(x)|\quad\text{per ogni $x\in[a,b)$}$

e $g$ ha variazione limitata su $\overline I$ , ne consegue che $F'g$ è assolutamente integrabile su $\overline I$ per il criterio del confronto. Dunque $fg$ è integrabile in senso generalizzato su $\overline I$ .

Grazie al criterio di Abel-Dirichlet otteniamo immediatamente che le funzioni

$f_1(x):=\frac{\sin x}{x}\quad\text{per $x\in[1,+\infty)$},\qquad f_2(x):=\sin (x^2)\quad\text{per $x\in [1,+\infty)$}$

sono integrabili in senso generalizzato su $[0,+\infty)$ , essendo

$\begin{aligned} &f_1(x)=\frac{1}{x}\cdot \sin x\quad\text{per $x\in[1,+\infty)$},\qquad f_2(x)=\frac{1}{x}\cdot x\sin (x^2)\quad\text{per $x\in[1,+\infty)$}, \end{aligned}$

e la funzione $x\mapsto \dfrac{1}{x}$ è a variazione limitata su $[1,+\infty)$ (essendo monotona non crescente e limitata) e infinitesima per $x\to+\infty$ , mentre $x\mapsto\sin x$ e $x\mapsto x\sin(x^2)$ hanno una primitiva limitata su $[1,+\infty)$ (rispettivamente $x\mapsto-\cos x$ e $x\mapsto-\dfrac{1}{2}\cos(x^2)$ ).

Esempio 17. Sia $\alpha>2$ e sia $f\colon [0,+\infty)\to\mathbb R$ definita da

$f(x):=x\cos(x^\alpha)\quad\text{per $x\in [0,+\infty)$}.$

La funzione $f$ è continua su $[0,+\infty)$ e vediamo se integrabile in senso generalizzato su $[0,+\infty)$ . Abbiamo che

$f(x)=\frac{1}{x^{\alpha-2}}x^{\alpha-1}\cos(x^\alpha)\quad\text{per $x\in[1,+\infty)$},$

e per $\alpha>2$ la funzione $x\mapsto \dfrac{1}{x^{\alpha-2}}$ è a variazione limitata su $[1,+\infty)$ e infinitesima per $x\to+\infty$ , mentre $x\mapsto x^{\alpha-1}\cos (x^\alpha)$ ha una primitiva limitata su $[1,+\infty)$ (la funzione $x\mapsto \frac{1}{\alpha}\sin (x^\alpha)$ ). Allora per il criterio di Abel-Dirichlet otteniamo che $f$ è integrabile in senso generalizzato su $[1,+\infty)$ , e quindi su $[0,+\infty)$ .

Osservazione 10. Si noti che la funzione $f(x):=x\cos(x^\alpha)$ per $\alpha>2$ è integrabile in senso generalizzato su $[0,+\infty)$ , ma è illimitata in ogni intorno di $+\infty$ .

Le ipotesi del teorema 9 possono essere ridotte, richiedendo per $f\colon [a,b)\to\mathbb R$ solo che sia localmente integrabile su $[a,b)$ e che esista una funzione $F\colon [a,b)\to\mathbb R$ continua e limitata su $[a,b)$ e derivabile su $(a,b)\setminus N$ con $F'(x)=f(x)$ per $x\in (a,b)\setminus N$ , dove $N$ è sottoinsieme finito di $(a,b)$ (o al più numerabile con accumulazione $+\infty$ se $f$ è definita su $[a,+\infty)$ ). Sotto queste ipotesi infatti, la formula di integrazione per parti continua a valere grazie alla proprietà di additività dell’integrale, e quindi il criterio di Abel-Dirichlet può essere dimostrato in maniera analoga a prima.

Esempio 18. Sia $f\colon [1,+\infty)\to\mathbb R$ definita da

$f(x):=\frac{(-1)^{\lfloor x \rfloor}}{x}\quad\text{per $x\in[1,+\infty)$},$

dove $\lfloor x \rfloor$ denota la parte intera inferiore di $x\in\mathbb R$ , cioè

$\lfloor x \rfloor:=n\quad\text{per $x\in[n,n+1)$ e $n\in\mathbb Z$}.$

Fissato $x\in(1,+\infty)$ abbiamo che la funzione $f$ risulta integrabile secondo Riemann su $[1,x]$ essendo limitata e continua eccetto in un numero finito di punti. Ha quindi senso chiedersi se $f$ sia integrabile in senso generalizzato su $[1,+\infty)$ . Se definiamo

$F(x):=\int_1^x (-1)^{\lfloor t \rfloor}\,dt\quad\text{per $x\in\mathbb [1,+\infty)$},$

abbiamo che la funzione $F$ risulta continua su $[1,+\infty)$ e derivabile su $(1,+\infty)\setminus \mathbb N$ con $F'(x)=(-1)^{\lfloor x \rfloor}$ per ogni $x\in (1,+\infty)\setminus \mathbb N$ . Inoltre $F$ è limitata su $[1,+\infty)$ , essendo compresa tra $-1$ e $0$ ( $F$ nei punti dispari vale $0$ , nei punti pari vale $-1$ ed è lineare sugli intervalli $[k,k+1]$ per ogni $k\in\mathbb N$ con $k\ge 2$ ). Poiché

$f(x)=\frac{1}{x}\cdot (-1)^{\lfloor x\rfloor}$

e $x\mapsto\dfrac{1}{x}$ ha variazione limitata ed è infinitesima per $x\to +\infty$ , dal criterio di Abel-Dirichlet otteniamo che $f$ è integrabile in senso generalizzato su $[1,+\infty)$ .

Teorema 10. Sia $a\in\mathbb R$

e sia $f\colon [a,+\infty)\to [0,+\infty)$

una funzione continua, non negativa, non identicamente nulla e periodica su $[a,+\infty)$

(cioè esiste $T>0$

tale che $f(x)=f(x+T)$

per ogni $x\in[a,+\infty)$

). Allora l’integrale generalizzato di $f$

su $[a,+\infty)$

diverge.

$\quad$

Dimostrazione. Sia $T$ il periodo della funzione $f$ , cioè

$f(x)=f(x+T)\quad\text{per ogni $x\in[a,+\infty)$}.$

Poiché la funzione $f$ è continua, non negativa e non identicamente nulla su $[a,a+T]$ (se fosse nulla su $[a,a+T]$ , sarebbe nulla su tutto $[a,+\infty)$ ), allora

$\int_a^{a+T}f(t)\,dt=\varepsilon>0.$

Fissato $m\in\mathbb N$ con $m\ge 1$ , dal fatto che $f$ è periodica di periodo $T$ otteniamo

$\int_a^{a+mT}f(t)\,dt=\sum_{k=1}^m\int_{a+(k-1)T}^{a+kT}f(t)\,dt=\sum_{k=1}^m\int_a^{a+T}f(t)\,dt=m\varepsilon.$

Siccome $f$ è non negativa, allora esiste il limite

$\int_a^{+\infty}f(t)\,dt=\lim_{x\to+\infty}\int_a^xf(t)\,dt=\lim_{m\to+\infty}\int_a^{a+mT}f(t)\,dt.$

Per $m\to+\infty$ otteniamo

$\int_a^{+\infty}f(t)\,dt=\lim_{m\to+\infty}\int_a^{a+mT}f(t)\,dt=\lim_{m\to+\infty}m\varepsilon=+\infty,$

e dunque l’integrale generalizzato di $f$ diverge su $[a,+\infty)$ .

Osservazione 11. Nel teorema 10 è importante assumere che $f$ abbia segno costante per dedurre che l’integrale diverge. Infatti, la funzione $f(x)=\sin x$ è periodica su $[0,+\infty)$ , ma l’integrale di $f$ su $[0,+\infty)$ non diverge (e nemmeno converge), in quanto non esiste il limite per $x\to +\infty$ di

$\int_0^x \sin t\,dt =1-\cos x.$

Concludiamo questa sottosezione con tre esempi significativi.

Esempio 19. Siano $\alpha,\beta,\gamma\in\mathbb R$ e sia $f\colon (0,+\infty)\setminus\{1\}\to\mathbb R$ definita come

$f(x):=\frac{1}{x^\alpha|\ln x|^\beta e^{\gamma x}}\quad\text{per $x\in(0,+\infty)\setminus\{1\}$}.$

Andiamo a determinare per quali valori di $\alpha,\beta,\gamma$ la funzione $f$ è integrabile in senso generalizzato in un intorno di $+\infty$ , $0$ e $1$ (sia da sinistra che da destra).

Fissato $a>1$ , studiamo l’integrabilità di $f$ su $[a,+\infty)$ . Per $\gamma<0$ e $\alpha,\beta\in\mathbb R$ abbiamo che esiste
$\lim_{x\to +\infty}f(x)=\lim_{x\to +\infty}\frac{e^{-\gamma x}}{x^\alpha(\ln x)^\beta}=+\infty.$

Dunque, dal teorema 8 l’integrale generalizzato di $f$ su $[a,+\infty)$ è divergente.

Per $\gamma>0$ e $\alpha,\beta\in\mathbb R$ abbiamo che

$\lim_{x\to +\infty}\frac{f(x)}{e^{-\frac{\gamma}{2}x}}=\frac{e^{-\frac{\gamma}{2}x}}{x^\alpha(\ln x)^\beta}=0,$

dunque $f$ è un O-grande di $g(x):=e^{-\frac{\gamma}{2}x}$ per $x\to +\infty$ . Inoltre $g$ è integrabile in senso generalizzato su $[a,+\infty)$ , poiché

$\int_a^xg(t)\,dt=\left[-\frac{2}{\gamma}e^{-\frac{\gamma}{2}t}\right]_a^x=\frac{2}{\gamma}e^{-\frac{\gamma}{2}a}-\frac{2}{\gamma}e^{-\frac{\gamma}{2}x}\to \frac{2}{\gamma}e^{-\frac{\gamma}{2}a}\quad\text{per $x\to +\infty$}.$

Dunque l’integrale generalizzato di $f$ su $[a,+\infty)$ converge.

Per $\gamma=0$ otteniamo che

$f(x)=\frac{1}{x^\alpha(\ln x)^\beta}.$

Fissato $x\in(a,+\infty)$ , tramite la sostituzione $t=e^s$ otteniamo $dt=e^s\,ds$ e

$\int_a^{+\infty}\frac{1}{t^\alpha(\ln t)^\beta}\,dt=\int_{\ln a}^{+\infty}\frac{1}{e^{s(\alpha-1)}s^\beta}\,ds.$

Quindi, dal teorema 3 abbiamo che $f$ è integrabile in senso generalizzato su $[a,+\infty)$ se e solo se la funzione

$g(x):=\frac{1}{e^{s(\alpha-1)}s^\beta}$

è integrabile in senso generalizzato su $[\ln a,+\infty)$ . Per quanto osservato prima, abbiamo che se $\alpha<1$ e $\beta\in\mathbb R$ , allora l’integrale di $g$ su $[\ln a,+\infty)$ diverge, mentre se $\alpha>1$ e $\beta\in\mathbb R$ l’integrale di $g$ su $[\ln a,+\infty)$ converge. Infine, se $\alpha=1$ , allora

$g(x)=\frac{1}{x^\beta}\quad\text{per $x\in[\ln a,+\infty)$}$

e dunque l’integrale di $g$ su $[\ln a,+\infty)$ , converge se $\beta>1$ , mentre diverge se $\beta\le 1$ . Dunque per $\gamma=0$ l’integrale generalizzato di $f$ converge su $[a,+\infty)$ se $\alpha>1$ e $\beta\in\mathbb R$ oppure $\alpha=1$ e $\beta>1$ , mentre diverge se $\alpha<1$ e $\beta\in\mathbb R$ oppure $\alpha=1$ e $\beta\le 1$ .

Fissato $a\in(0,1)$ , studiamo l’integrabilità di $f$ su $[0,a]$ . Osserviamo che
$f(x)\sim \frac{1}{x^\alpha(-\ln x)^\beta}\quad\text{per $x\to 0^+$},$

dunque per il criterio del confronto asintotico l’integrale di $f$ converge su $[0,a]$ se e solo se l’integrale di

$g(x):=\frac{1}{x^\alpha(-\ln x)^\beta}\quad\text{per $x\in(0,a]$}$

converge su $[0,a]$ . Fissato $x\in(a,+\infty)$ , tramite la sostituzione $s=\frac{1}{t}$ otteniamo $dt=-\frac{1}{s^2}\,ds$ e

$\int_0^a\frac{1}{t^\alpha(-\ln t)^\beta}\,dt=\int_{\frac{1}{a}}^{+\infty}\frac{1}{s^{2-\alpha}(\ln s)^\beta}\,ds$

(si noti che $\ln(\dfrac{1}{s})=-\ln s$ ). Dal teorema 3 deduciamo quindi che l’integrale di $g$ converge su $[0,a]$ se e solo se l’integrale di

$h(x):=\frac{1}{x^{2-\alpha}(\ln x)^\beta}\quad\text{per $x\in\left[\frac{1}{a},+\infty\right)$}$

converge su $[\dfrac{1}{a},+\infty)$ . Dal punto $(1)$ abbiamo che l’integrale di $h$ converge su $[\dfrac{1}{a},+\infty)$ se $\alpha<1$ e $\beta\in\mathbb R$ , oppure $\alpha=1$ e $\beta>1$ , mentre diverge se $\alpha>1$ e $\beta\in\mathbb R$ oppure $\alpha=1$ e $\beta\le 1$ . Quindi l’integrale generalizzato di $f$ su $[0,a]$ converge se $\alpha<1$ e $\beta,\gamma\in\mathbb R$ , oppure $\alpha=1$ , $\beta>1$ e $\gamma\in\mathbb R$ , mentre diverge se $\alpha>1$ e $\beta,\gamma\in\mathbb R$ oppure $\alpha=1$ , $\beta\le 1$ e $\gamma\in\mathbb R$ .

Fissato $a\in(0,1)$ studiamo l’integrabilità di $f$ su $[a,1]$ . Osserviamo che
$f(x)\sim\frac{1}{(-\ln x)^\beta}\sim \frac{1}{(1-x)^\beta}\quad\text{per $x\to 1^-$},$

essendo $\ln x\sim x-1$ per $x\to 1$ . Dunque, dal criterio del confronto asintotico otteniamo che l’integrale generalizzato di $f$ converge su $[a,1]$ se $\beta<1$ e $\alpha,\gamma\in\mathbb R$ , mentre diverge se $\beta\ge 1$ e $\alpha,\gamma\in\mathbb R$ .

Analogamente, fissato $a\in(1,+\infty)$ , l’integrale generalizzato di $f$ converge su $[1,a]$ se $\beta<1$ e $\alpha,\gamma\in\mathbb R$ , mentre diverge se $\beta\ge 1$ e $\alpha,\gamma\in\mathbb R$ .

$\quad$

Possiamo riepilogare i precedenti risultati nella seguente tabella.

$\quad$

Esempio 20. Siano $\alpha,\beta\in\mathbb R$ e sia $f\colon (0,+\infty)\to\mathbb R$ definita come

$f(x):=x^\alpha\sin(x^\beta)\quad\text{per $x\in(0,+\infty)$}.$

Andiamo a determinare per quali valori di $\alpha,\beta\in\mathbb R$ la funzione $f$ è integrabile in senso generalizzato in un intorno di $+\infty$ e $0$ .

Fissato $a\in (0,+\infty)$ , studiamo l’integrabilità di $f$ su $[a,+\infty)$ . Per $\beta=0$ abbiamo che
$f(x)=x^\alpha\sin 1\quad\text{per $x\in[a,+\infty)$},$

dunque l’integrale generalizzato di $f$ converge su $[a,+\infty)$ se e solo se $\alpha<-1$ .

Se $\beta\neq 0$ , allora tramite la sostituzione $s=t^\beta$ otteniamo $ds=\beta t^{\beta-1}\,dt$ e

$\int_a^{+\infty} t^\alpha\sin(t^\beta)\,dt=\frac{1}{\beta}\int_{a^\beta}^{+\infty}s^{\frac{\alpha-\beta+1}{\beta}}\sin s\,ds.$

Dunque, per il teorema 3 $f$ è integrabile in senso generalizzato su $[a,+\infty)$ se e solo se $g(x):=x^{\frac{\alpha-\beta+1}{\beta}}\sin x$ è integrabile in senso generalizzato su $[a^\beta,+\infty)$ .

Se $\alpha-\beta<-1$ , allora la funzione $x\mapsto x^\frac{\alpha-\beta+1}{\beta}$ ha variazione limitata su $[a,+\infty)$ ed è infinitesima per $x\to+\infty$ . Inoltre, la funzione $x\mapsto\sin x$ ha una primitiva limitata su $[a,+\infty)$ (la funzione $x\mapsto-\cos x$ ). Dunque, per il criterio di Abel-Dirichlet l’integrale generalizzato di $f$ converge su $[a,+\infty)$ .

Se $\alpha-\beta=-1$ , per $x\in(a^\beta,+\infty)$ otteniamo che

$\int_{a^\beta}^x g(s)\,ds=\int_{a^\beta}^x \sin s\,ds=\cos(a^\beta)-\cos(x),$

che non ammette limite per $x\to +\infty$ . Dunque $f$ non è integrabile in senso generalizzato su $[a,+\infty)$ .

Infine, se $\alpha-\beta<-1$ , fissato $m\in\mathbb N$ con $m\ge 2$ abbiamo che

$\int_{\pi}^{m\pi}s^{\frac{\alpha-\beta+1}{\beta}}\sin s\,ds=\sum_{k=1}^{m-1}\int_{k\pi}^{(k+1)\pi}s^{\frac{\alpha-\beta+1}{\beta}}\sin s\,ds.$

Poiché $x\mapsto \sin x$ ha segno costante in $[k\pi,(k+1)\pi]$ , allora per il teorema della media ponderata esisterà $c_k\in[k\pi,(k+1)\pi]$ tale che

$\int_{k\pi}^{(k+1)\pi}s^{\frac{\alpha-\beta+1}{\beta}}\sin s\,ds=c_k^{\frac{\alpha-\beta+1}{\beta}}\int_{k\pi}^{(k+1)\pi}\sin s\,ds=2c_k^{\frac{\alpha-\beta+1}{\beta}}(-1)^k\quad\text{per $k=1,\dots,m-1$}.$

Quindi

$\int_{\pi}^{m\pi}s^{\frac{\alpha-\beta+1}{\beta}}\sin s\,ds=\sum_{k=1}^{m-1}2c_k^{\frac{\alpha-\beta+1}{\beta}}(-1)^k.$

Poiché $\alpha-\beta> -1$ e $c_k\in[k\pi,(k+1)\pi]$ , allora

$\lim_{k\to+\infty}c_k^{\frac{\alpha-\beta+1}{\beta}}=+\infty.$

In particolare, non esiste il limite

$\lim_{k\to+\infty}2c_k^{\frac{\alpha-\beta+1}{\beta}}(-1)^k,$

e dunque la serie

$\sum_{k=1}^{+\infty}2c_k^{\frac{\alpha-\beta+1}{\beta}}(-1)^k$

non converge (è indeterminata). Ne consegue che non esiste il limite

$\lim_{m\to+\infty}\int_{\pi}^{m\pi}s^{\frac{\alpha-\beta+1}{\beta}}\sin s\,ds,$

e dunque $g$ non è integrabile in senso generalizzato su $[\pi,+\infty)$ . In particolare, $f$ non è integrabile in senso generalizzato su $[a,+\infty)$ .

Quindi la funzione $f$ è integrabile in senso generalizzato su $[a,+\infty)$ se e solo se $|\beta|>\alpha+1$ .

Fissato $a\in(0,+\infty)$ , studiamo l’integrabilità di $f$ su $[0,a]$ . Tramite la sostituzione $s=\frac{1}{t}$ otteniamo $ds=-\frac{1}{t^2}\,dt$ e
$\int_0^a t^\alpha\sin(t^\beta)\,dt=\int_{\frac{1}{a}}^{+\infty}s^{-\alpha-2}\sin (s^{-\beta})\,ds.$

Dunque, per il teorema 3 abbiamo che $f$ è integrabile in senso generalizzato su $[0,a]$ se e solo se la funzione

$g(x):=x^{-\alpha-2}\sin(x^{-\beta})\quad\text{per $x\in\left[\frac{1}{a},+\infty\right)$}$

è integrabile in senso generalizzato su $[\dfrac{1}{a},+\infty)$ . Per quanto visto prima ciò accade se e solo se $|-\beta|>-\alpha-2+1$ , cioè $|\beta|>-\alpha-1$ .

Possiamo riepilogare i precedenti risultati nella seguente tabella.

$\,$

Esempio 21. Sia $\alpha\in\mathbb R$ e consideriamo l’integrale improprio

$\int_{\pi}^{+\infty}|\sin t|^{t^\alpha}\,dt.$

Andiamo a determinare per quali valori di $\alpha$ tale integrale è convergente. Osserviamo che la funzione integranda

$f(x):=|\sin x|^{x^\alpha}$

è ben definita è continua su $[\pi,+\infty)$ . Quindi dobbiamo studiare l’integrabilità in senso generalizzato di $f$ in un intorno di $+\infty$ . Se $\alpha\le 0$ si ha

$x^\alpha\le 1\quad\text{per ogni $x\in[\pi,+\infty)$}\quad\Rightarrow\quad |\sin x|^{x^\alpha}\ge |\sin x|\quad\text{per ogni $x\in[\pi,+\infty)$},$

poiché $|\sin x|\in[0,1]$ per ogni $x\in [\pi,+\infty)$ . Di conseguenza

$\int_{\pi}^{+\infty}|\sin t|^{t^\alpha}\,dt\ge \int_{\pi}^{+\infty}|\sin t|\,dt$

che diverge per il teorema 10, essendo $x\mapsto |\sin x|$ una funzione periodica di periodo $\pi$ .

Il caso $\alpha>0$ è più difficile da studiare. Per prima cosa, possiamo scrivere

$\int_{\pi}^{+\infty}|\sin t|^{t^\alpha}\,dt=\sum_{k=1}^{+\infty}\int_{k\pi}^{(k+1)\pi}|\sin t|^{t^\alpha}\,dt$

e inoltre

$\begin{aligned} &\lfloor k^\alpha\pi^\alpha\rfloor \le x^\alpha\le \lceil(k+1)^\alpha\pi^\alpha\rceil\quad\text{per ogni $x\in[k\pi,(k+1)\pi]$ e $k\in\mathbb N$ con $k\ge 1$},\\ &\int_{k\pi}^{(k+1)\pi}|\sin t|^m\,dt=\int_0^{\pi}|\sin t|^m\,dx=2\int_0^{\frac{\pi}{2}}(\sin t)^m\,dt\quad\text{per ogni $m\in\mathbb N$ e $k\in\mathbb N$ con $k\ge 1$}, \end{aligned}$

dove $\lfloor y\rfloor$ e $\lceil y \rceil$ denotano, rispettivamente la parte intera inferiore e superiore di $y$ , cioè

$\lfloor y\rfloor=n\quad\text{per $y\in[n,n+1)$ e $n\in\mathbb Z$},\qquad\lceil y\rceil=n+1\quad\text{per $y\in(n,n+1]$ e $n\in\mathbb Z$}.$

Di conseguenza

$\sum_{k=1}^{+\infty}2\int_0^{\frac{\pi}{2}}(\sin t)^{\lceil(k+1)^\alpha\pi^\alpha\rceil}\,dt\le\int_{\pi}^{+\infty}|\sin t|^{t^\alpha}\,dt\le \sum_{k=1}^{+\infty}2\int_0^{\frac{\pi}{2}}(\sin t)^{\lfloor k^\alpha\pi^\alpha\rfloor}\,dt.$

Definiamo

$I_m:=\int_0^{\frac{\pi}{2}}(\sin t)^m\,dt\quad\text{per $m\in\mathbb N$}.$

Per ogni $m\in\mathbb N$ con $m\ge 2$ risulta che

$\begin{aligned} I_m&=\int_0^{\pi}{2}(\sin t)^{m-1}\sin t\,dt=\left[-\cos t(\sin t)^{m-1}\right]_0^{\frac{\pi}{2}}+(m-1)\int_0^{\frac{\pi}{2}}(\sin t)^{m-2}(\cos t)^2\,dt\\ &=(m-1)\int_0^{\frac{\pi}{2}}(\sin t)^{m-2}\,dt-(m-1)\int_0^{\frac{\pi}{2}}(\sin t)^m\,dt=(m-1)I_{m-2}-(m-1)I_m. \end{aligned}$

Dunque, abbiamo

$I_m:=\frac{m-1}{m}I_{m-2}\quad\text{per $m\in\mathbb N$ con $m\ge 2$},$

da cui per induzione si può ricavare che

$\begin{aligned} &I(2n)=\frac{(2n-1)!!}{(2n)!!}I(0)=\frac{(2n-1)!!}{(2n)!!}\frac{\pi}{2}\quad\text{per $m=2n$ con $n\in\mathbb N$},\\ &I(2n+1)=\frac{(2n)!!}{(2n+1)!!}I(1)=\frac{(2n)!!}{(2n+1)!!}\quad\text{per $m=2n+1$ con $n\in\mathbb N$}, \end{aligned}$

dove $m!!$ è il semifattoriale di $m$ , definito come il prodotto dei numeri positivi minori di $m$ avente stessa parità di $m$ , cioè

$\begin{aligned} &(2n)!!=(2n)(2n-2)(2n-4)\cdot\cdots\cdot 2\quad\text{per $m=2n$ con $n\in\mathbb N$},\\ &(2n+1)!!=(2n+1)(2n-1)(2n-3)\cdot\cdots\cdot 1\quad\text{per $m=2n+1$ con $n\in\mathbb N$}. \end{aligned}$

Grazie alla formula di Stirling

$n!\sim \sqrt{2\pi n}\left(\frac{n}{e}\right)^n\quad\text{per $n\to+\infty$}$

e al fatto che $(2n)!!=2^nn!$ per $n\in\mathbb N$ , abbiamo che

$\begin{aligned} &I(2n) = \frac{(2n-1)!!}{(2n)!!} \frac{\pi}{2} = \frac{(2n)!}{(2n)!!(2n)!!} \frac{\pi}{2} = \frac{(2n)!}{2^{2n} (n!)^2} \frac{\pi}{2} \\ &\sim \sqrt{4\pi n} \frac{\left(\frac{2n}{e}\right)^{2n}}{2^{2n} 2\pi n \left(\frac{n}{e}\right)^{2n}} \frac{\pi}{2} = \sqrt{\frac{\pi}{4n}} \quad \text{per $n \to +\infty$},\\ &I(2n+1) = \frac{(2n)!!}{(2n+1)!!} = \frac{2^{2n} (n!)^2}{(2n+1)!} = \frac{2^{2n} (n!)^2}{(2n)!} \frac{2}{\pi} \frac{\pi}{2(2n+1)} \\ &\sim \sqrt{\frac{4n}{\pi}} \frac{\pi}{2(2n+1)} \sim \sqrt{\frac{\pi}{2(2n+1)}} \quad \text{per $n \to +\infty$}. \end{aligned}$

Quindi, risulta

$I_m:=\int_0^{\frac{\pi}{2}}(\sin t)^m\,dt\sim \sqrt{\frac{\pi}{2m}}\quad\text{per $m\to+\infty$}.$

Ne consegue che

$\begin{aligned} &2\int_0^{\frac{\pi}{2}}(\sin t)^{\lceil(k+1)^\alpha\pi^\alpha\rceil}\,dt\sim \frac{\sqrt{2\pi}}{\sqrt{\lceil(k+1)^\alpha\pi^\alpha\rceil}}\sim \sqrt{2\pi^{1-\alpha}}\frac{1}{k^\frac{\alpha}{2}}\quad\text{per $k\to+\infty$},\\ &2\int_0^{\frac{\pi}{2}}(\sin t)^{\lfloor k^\alpha\pi^\alpha\rfloor}\,dt\sim \frac{\sqrt{2\pi}}{\sqrt{\lfloor k^\alpha\pi^\alpha\rfloor}}\sim \sqrt{2\pi^{1-\alpha}}\frac{1}{k^\frac{\alpha}{2}}\quad\text{per $k\to+\infty$}. \end{aligned}$

Dunque, otteniamo

$\int_{\pi}^{+\infty}|\sin t|^{t^\alpha}\,dt\quad\text{converge}\quad\Leftrightarrow\quad\sum_{k=1}^{+\infty}\frac{1}{k^{\frac{\alpha}{2}}}\quad\text{converge}\quad\Leftrightarrow\quad\alpha>2.$

Esercizi svolti

Leggi...

Esercizio 1 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dato il seguente integrale improprio

$\int_0^4\frac{\ln |t-1|}{\sqrt{t}}\,dt,$

dire se converge e in caso positivo calcolarne il valore.

$\quad$

Soluzione. Se consideriamo la funzione

$f(x):=\frac{\ln|x-1|}{\sqrt{x}}$

abbiamo che $f$ è ben definita su $I:=(0,1)\cup (1,+\infty)$ ed è continua su tale insieme, quindi localmente integrabile. Per vedere se $f$ è integrabile in senso generalizzato su $[0,4]$ , dobbiamo dunque studiare la convergenza dell’integrale improprio negli intervallo $[0,1]$ e $[1,4]$ .

Iniziamo studiando l’integrabilità di $f$ in senso generalizzato su $[1,4]$ . Fissato $x\in(1,4)$ , integrando per parti abbiamo che

$\int_x^4\frac{\ln (t-1)}{\sqrt{t}}\,dt=[2\sqrt{t}\ln(t-1)]_x^4-\int_x^4\frac{2\sqrt{t}}{t-1}\,dt.$

Se nel secondo integrale facciamo la sostituzione $s=\sqrt{t}$ , otteniamo $dt=2s\,ds$ e

$\int_x^4\frac{2\sqrt{t}}{t-1}\,dt=\int_{\sqrt{x}}^2\frac{4s^2}{s^2-1}\,ds=\int_{\sqrt{x}}^2\left(4+\frac{4}{s^2-1}\right)\,ds.$

Andiamo a determinare due numeri $A,B\in\mathbb R$ tali che

$\frac{A}{s-1}+\frac{B}{s+1}=\frac{4}{s^2-1}.$

Abbiamo che

$\frac{(A+B)s+A-B}{s^2-1}=\frac{4}{s^2-1}\quad\Leftrightarrow\quad\begin{cases} A+B=0,\\A-B=4.\end{cases}$

Dunque $A=2$ e $B=-2$ , da cui otteniamo

$\begin{aligned} \int_x^4\frac{\ln (t-1)}{\sqrt{t}}\,dt&=[2\sqrt{t}\ln(t-1)]_x^4-\int_{\sqrt{x}}^2\left(4+\frac{2}{s-1}-\frac{2}{s+1}\right)\,ds=\\ &=2\sqrt{t}\ln(t-1)]_x^4-[4s+2\ln(s-1)-2\ln(s+1)]_{\sqrt{x}}^2=\\ &=4\sqrt{x}-2\sqrt{x}\ln(x-1)+2\ln(\sqrt{x}-1)-2\ln(\sqrt{x}+1)+6\ln 3-8. \end{aligned}$

Se calcoliamo il limite per $x\to 1^+$ otteniamo

$\begin{aligned} &\lim_{x\to 1^+}(4\sqrt{x}-2\sqrt{x}\ln(x-1)+2\ln(\sqrt{x}-1)-2\ln(\sqrt{x}+1)+6\ln 3-8)\\ &\lim_{x\to 1^+}(4\sqrt{x}-2\sqrt{x}\ln((\sqrt{x}-1)(\sqrt{x}+1))+2\ln(\sqrt{x}-1)-2\ln(\sqrt{x}+1)+6\ln 3-8)\\ &=\lim_{x\to 1^+}(4\sqrt{x}+2(1-\sqrt{x})\ln (\sqrt{x}-1)-2(1+\sqrt{x})\ln(\sqrt{x}+1)+6\ln 3-8)=6\ln 3-4\ln 2-4. \end{aligned}$

Dunque $f$ è integrabile in senso generalizzato su $[1,4]$ e

$\int_1^4\frac{\ln (t-1)}{\sqrt{t}}\,dt=6\ln 3-4\ln 2-4.$

Vediamo ora se $f$ è integrabile in senso generalizzato su $[0,1]$ e per fare ciò andiamo a determiniamo una primitiva di $f$ su $(0,1)$ . Integrando per parti otteniamo che

$\int\frac{\ln (1-t)}{\sqrt{t}}\,dt=2\sqrt{t}\ln(1-t)+\int\frac{2\sqrt{t}}{1-t}\,dt.$

Nel secondo integrale, se facciamo la sostituzione $s=\sqrt{t}$ otteniamo $dt=2s\,ds$ e

$\int\frac{2\sqrt{t}}{1-t}\,dt=\int\frac{4s^2}{1-s^2}\,ds=\int\left(\frac{4}{1-s^2}-4\right)\,ds.$

Come prima andiamo a determinare due numeri $A,B\in\mathbb R$ tali che

$\frac{A}{1-s}+\frac{B}{1+s}=\frac{4}{1-s^2}.$

Abbiamo che

$\frac{(A-B)s+A+B}{1-s^2}=\frac{4}{1-s^2}\quad\Leftrightarrow\quad\begin{cases} A-B=0,\\A+B=4.\end{cases}$

Dunque $A=B=2$ e otteniamo

$\int\frac{4s^2}{1-s^2}\,ds=\int\left(\frac{2}{1-s}+\frac{2}{1+s}-4\right)\,ds=2\ln(1+s)-2\ln(1-s)-4s+c,\quad c\in\mathbb R.$

Quindi

$\int\frac{\ln (1-t)}{\sqrt{t}}\,dt=2\sqrt{t}\ln(1-t)+2\ln(1+\sqrt{t})-2\ln(1-\sqrt{t})-4\sqrt{t}+c,\quad c\in\mathbb R.$

Se ci calcoliamo i limiti per $x\to 0^+$ e $x\to 1^-$ , in maniera analoga a prima otteniamo

$\begin{aligned} &\lim_{t\to 0^+}(2\sqrt{t}\ln(1-t)+2\ln(1+\sqrt{t})-2\ln(1-\sqrt{t})-4\sqrt{t})=0,\\ &\lim_{t\to 1^-}(2\sqrt{t}\ln(1-t)+2\ln(1+\sqrt{t})-2\ln(1-\sqrt{t})-4\sqrt{t})\\ &=\lim_{t\to 1^-}(2(\sqrt{t}-1)\ln(1-\sqrt{t})+2(\sqrt{t}+1)\ln(1+\sqrt{t}))-4\sqrt{t})=4\ln 2-4. \end{aligned}$

Ne consegue che $f$ è integrabile in senso generalizzato su $[0,1]$ e

$\int_0^1\frac{\ln|t-1|}{\sqrt{t}}\,dt=[2\sqrt{t}\ln(1-t)+2\ln(1+\sqrt{t})-2\ln(1-\sqrt{t})-4\sqrt{t}]_0^1=4\ln 2-4.$

Pertanto, l’integrale generalizzato di $f$ converge su $[0,4]$ e

$\int_0^4\frac{\ln |t-1|}{\sqrt{t}}\,dt=4\ln 2-4+6\ln 3-4-4\ln 2=6\ln 3- 8.$

$\quad$

Esercizio 2 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

.Dato il seguente integrale improprio

$\int_{-\infty}^{+\infty}\frac{e^{-t}}{e^{-2t}+2e^{-t}+2}\,dt,$

dire se converge e in caso positivo calcolarne il valore.

$\quad$

Soluzione. Se consideriamo la funzione

$f(x):=\frac{e^{-x}}{e^{-2x}+2e^{-x}+2},$

abbiamo che $f$ è ben definita e continua su tutto $\mathbb R$ (il denominatore non si annulla mai), e dunque è localmente integrabile su $\mathbb R$ . Per vedere se $f$ è integrabile in senso generalizzato su $\mathbb R$ andiamoci a calcolare una primitiva su tale insieme. Grazie alla sostituzione $s=e^{-t}$ otteniamo $ds=-e^{-t}\,dt$ e

$\begin{aligned} &\int\frac{e^{-t}}{e^{-2t}+2e^{-t}+2}\,dt=-\int\frac{1}{s^2+2s+2}\,ds=-\int\frac{1}{(s+1)^2+1}\,ds=\\ &=-\arctan (s+1)+c=-\arctan(e^{-t}+1)+c,\quad c\in\mathbb R. \end{aligned}$

Poiché

$\lim_{t\to -\infty}(-\arctan(e^{-t}+1))=-\frac{\pi}{2},\qquad\lim_{t\to +\infty}(-\arctan(e^{-t}+1))=-\frac{\pi}{4},$

otteniamo che $f$ è integrabile in senso generalizzato su $\mathbb R$ e

$\int_{-\infty}^{+\infty}\frac{e^{-t}}{e^{-2t}+2e^{-t}+2}\,dt=[-\arctan(e^{-t}+1)]_{-\infty}^{+\infty}=-\frac{\pi}{4}+\frac{\pi}{2}=\frac{\pi}{4}.$

$\quad$

Esercizio 3 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Data la funzione

$f(x)=\frac{1}{\sqrt{2x\sqrt{x}-x^2}},$

dire se è integrabile in senso generalizzato nel suo dominio e in caso positivo calcolarne il valore.

$\quad$

Soluzione. Il dominio della funzione $f$ è dato da

$\begin{cases} x>0,\\ 2x\sqrt{x}-x^2>0, \end{cases} \quad\Leftrightarrow\quad \begin{cases} x>0,\\ 2\sqrt{x}>x, \end{cases} \quad\Leftrightarrow\quad \begin{cases} x>0,\\ 4x-x^2>0, \end{cases} \quad\Leftrightarrow\quad 0<x<4.$

Quindi il dominio di $f$ è l’intervallo $(0,4)$ , dove è anche continua, e vediamo se $f$ è integrabile in senso generalizzato su $[0,4]$ . Tramite la sostituzione $s=\sqrt{t}$ otteniamo $dt=2s\,ds$ e

$\begin{aligned} \int\frac{1}{\sqrt{2t\sqrt{t}-t^2}}\,dt&=\int\frac{1}{\sqrt{t}\sqrt{2\sqrt{t}-t}}\,dt=\int\frac{2}{\sqrt{2s-s^2}}\,ds=\int\frac{2}{\sqrt{1-(s-1)^2}}\,ds\\ &=\arcsin (s-1)+c=\arcsin(\sqrt{t}-1)+c,\quad c\in\mathbb R. \end{aligned}$

Poiché

$\lim_{t\to 0^+}\arcsin(\sqrt{t}-1)=-\frac{\pi}{2},\qquad \lim_{t\to 4^-}\arcsin(\sqrt{t}-1)=\frac{\pi}{2},$

deduciamo che $f$ è integrabile in senso generalizzato su $[0,4]$ e

$\int_0^4\frac{1}{\sqrt{2t\sqrt{t}-t^2}}\,dt=[\arcsin(\sqrt{t}-1)]_0^4=\pi.$

$\quad$

Esercizio 4 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Dato il seguente integrale improprio

$\int_{1}^{+\infty} \frac{1}{\cosh ^2 t}\,dt$

dire se converge e in caso positivo calcolarne il valore.

$\quad$

Soluzione. La funzione integranda

$f(x):=\frac{1}{\cosh ^2 x}$

è continua su $\mathbb R$ e controlliamo se è integrabile in senso generalizzato in un intorno destro di $+\infty$ . Abbiamo che

$0\le f(x) = \frac{4e^{2x}}{(1+e^{2x})^2} \le \frac{4}{e^{2x}}\quad \text{per $x\in [1,+\infty)$},$

quindi $f$ è integrabile in senso generalizzato su $[1,+\infty)$ per il criterio del confronto. Calcoliamo il valore dell’integrale di $f$ su $[1,+\infty)$ e abbiamo

$\int_{1}^{+\infty} \frac{1}{\cosh ^2 t } \, dt = \int_{1}^{+\infty} \frac{4e^{2t}}{(1+e^{2t})^2}\, dt= \left[-\frac{2}{1+e^{2t}} \right]_{1}^{+\infty} = \frac{2}{1+e^2}.$

Alternativamente potevamo utilizzare che

$\int_{1}^{+\infty} \frac{1}{\cosh ^2 t} \, dt = \left[\tanh x \right]_{1}^{+\infty} = 1-\frac{e^2-1}{1+e^2} = \frac{2}{1+e^2}.$

$\quad$

Esercizio 5 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dato il seguente integrale improprio

$\int_{-1}^0 \frac{\arcsin t}{\sqrt{1+t}} \, dt,$

dire se converge e in caso positivo calcolarne il valore.

$\quad$

Soluzione. Ponendo $s = t+1$ abbiamo

$\int_{-1}^0 \frac{\arcsin t}{\sqrt{1+t}} \, dt=\int_0^1 \frac{\arcsin(s-1)}{\sqrt{s}} \, ds.$

Se consideriamo la funzione integranda

$f(x):=\frac{\arcsin(x-1)}{\sqrt{x}},$

abbiamo che $f$ è ben definita e continua su $(0,2]$ . Dunque dobbiamo controllare l’integrabilità in senso generalizzato di $f$ in un intorno destro di 0. Per $x\to 0^+$ abbiamo

$f(x) \sim \frac{1}{\sqrt{x}},$

quindi per il criterio del confronto asintotico $f$ è integrabile in senso generalizzato su $[0,1]$ . Dunque l’integrale

$\int_{-1}^0 \frac{\arcsin t}{\sqrt{1+t}} \, dt$

è convergente. Concludiamo calcolando il valore di tale integrale e abbiamo

$\begin{aligned} \int_{-1}^0 \frac{\arcsin t}{\sqrt{1+t}} \, dt&=\int_0^1 \frac{\arcsin(s-1)}{\sqrt{s}} \, ds = \left[2\sqrt{s} \arcsin(s-1) \right]_0^1 - \int_0^1 2\sqrt{s} \cdot\frac{1}{\sqrt{1-(s-1)^2} } \, ds\\ & = -\int_0^1 \frac{2 \sqrt{s}}{\sqrt{-s^2+2s}}\, ds = - 2 \int_0^1 \frac{1}{\sqrt{-s+2}} \, ds = \left[4 \sqrt{-s+2}\right]_0^1 = 4-4 \sqrt{2}. \end{aligned}$

$\quad$

Esercizio 6 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Al variare di $\alpha \in \mathbb{R}$

discutere la convergenza dell’integrale improprio

$\int_0^{\frac{1}{2}} \frac{(\sin t)^{t+2}|\ln t |^{\alpha}}{\ln(1+t^3)} \, dt.$

$\quad$

Soluzione. Calcoliamo per prima cosa il dominio della funzione integranda

$f(x):=\frac{(\sin x)^{x+2} |\ln x|^{\alpha}}{\ln(1+x^3)}$

e abbiamo che è dato da

$\begin{cases} 1+x^3>0,\\ \ln(1+x^3)\neq0,\\ x>0, \end{cases} \quad \Leftrightarrow \quad \begin{cases} x>-1,\\ x \neq 0, \\ x>0. \end{cases}$

Pertanto $f$ è definita e continua su $(0,+\infty)$ . Dobbiamo perciò controllare se $f$ sia integrabile in senso generalizzato in un intorno destro di $0$ . Per $x\to 0^+$ abbiamo che

$\begin{aligned} f(x) & = \frac{(\sin x)^{x+2}| \ln x |^\alpha}{\ln(1+x^3)} \sim \frac{x^{x+2} | \ln x |^{\alpha}}{x^3}= \frac{1}{x} x^x | \ln x |^\alpha = \frac{1}{x} e^{x \ln x} | \ln x |^\alpha \sim \frac{1}{x |\ln x |^{-\alpha}}, \end{aligned}$

grazie al fatto che $\ln(1+x^3)\sim x^3$ e $\sin x\sim x$ per $x\to 0^+$ . Per il criterio del confronto asintotico e dall’esempio 19 concludiamo che

$\int_0^{\frac{1}{2}} f(t) \, dt < + \infty \quad \Leftrightarrow \quad \alpha<-1.$

$\quad$

Esercizio 7 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Al variare di $\alpha \in \mathbb{R}$

discutere la convergenza dell’integrale improprio

$\int_0^{+\infty} \frac{\ln(1+\sqrt{t})}{t^\alpha(2+\sqrt{t})^{2\alpha+1}}\,dt.$

$\quad$

Soluzione. Osserviamo che la funzione integranda

$f(x):=\frac{\ln(1+\sqrt{x})}{x^\alpha(2+\sqrt{x})^{2\alpha+1}}$

è ben definita e continua su $(0,+\infty)$ . Dobbiamo quindi studiare l’integrabilità in senso generalizzato di $f$ in un intorno destro di $0$ e in un intorno di $+\infty$ . Per $x \to 0^+$ si ha

$f(x)=\frac{\ln(1+\sqrt{x})}{x^\alpha(2+\sqrt{x})^{2\alpha+1}} \sim \frac{\sqrt{x}}{x^\alpha}=\frac{1}{x^{\alpha-\frac{1}{2}}}.$

Dunque per il criterio del confronto asintotico

$\int_0^1f(t)\,dt<+\infty\quad\Leftrightarrow\quad \alpha<\frac{3}{2}.$

Per $x \to + \infty$ abbiamo

$f(x)=\frac{\ln(1+\sqrt{x})}{x^\alpha(2+\sqrt{x})^{2\alpha+1}}\sim\frac{\ln x}{x^{2\alpha+\frac{1}{2}}},$

essendo

$\lim_{x\to+\infty}\frac{\ln(1+\sqrt{x})}{\ln x}=\lim_{x\to+\infty}\frac{\ln\left(\sqrt{x}\left(1+\frac{1}{\sqrt{x}}\right)\right)}{\ln x}=\lim_{x\to+\infty}\frac{\ln\sqrt{x}+\ln\left(1+\frac{1}{\sqrt{x}}\right)}{\ln x}=\lim_{x\to+\infty}\frac{\ln\sqrt{x}}{\ln x}=\frac{1}{2}.$

Quindi per il criterio del confronto asintotico e l’esempio 19 si ha

$\int_1^{+\infty}f(t)\,dt<+\infty\quad\Leftrightarrow\quad \alpha>\frac{1}{4}.$

Mettendo a sistema i valori trovati abbiamo

$\begin{cases} \alpha>\dfrac{1}{4},\\ \alpha<\dfrac{3}{2}, \end{cases} \quad \Leftrightarrow \quad \alpha \in \left(\frac{1}{4},\frac{3}{2} \right).$

Si conclude che $f$ è integrabile in senso generalizzato su $[0,+\infty)$ se e solo se $\alpha \in (\frac{1}{4},\frac{3}{2})$ .

$\quad$

Esercizio 8 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Consideriamo il seguente l’integrale improprio

$\int_1^{+\infty} \frac{t^{\alpha}+3}{t^4+t^2} \, dt.$

Determinare per quali valori del parametro $\alpha >0$ l’integrale converge.

Calcolare il valore dell’integrale nel caso particolare $\alpha =1$ .

$\quad$

Soluzione.

Osserviamo che la funzione integranda
$f(x):=\frac{x^{\alpha}+3}{x^4+x^2}$

è ben definita e continua su $[1+\infty)$ . Dobbiamo dunque controllare per quali valori di $\alpha>0$ è integrabile in senso generalizzato in un intorno di $+\infty$ . Per $x\to +\infty$ abbiamo

$f(x)=\frac{x^{\alpha}+3}{x^4+x^2}\sim \frac{1}{x^{4-\alpha}},$

dunque per il criterio del confronto asintotico l’integrale di $f$ è convergente su $[1,+\infty)$ se e solo se $\alpha<3$ .

Se poniamo $\alpha=1$ (quindi l’integrale generalizzato di $f$ è convergente su $[1,+\infty)$ ), abbiamo
$\int_1^{+\infty} \frac{t+3}{t^2(t^2+1)} \, dt.$

Andiamo a determinare quattro numeri $A,B,C,D\in\mathbb R$ tali che

$\frac{At+B}{t^2+1}+\frac{C}{t^2}+\frac{D}{t}=\frac{t+3}{t^2(t^2+1)}.$

Abbiamo che

$\frac{(A+D)t^3+(B+C)t^2+Dt+C}{t^2(t^2+1)}=\frac{t+3}{t^2(t^2+1)}\quad\Leftrightarrow\quad\begin{cases} A+D=0,\\B+C=0,\\D=1,\\C=3.\end{cases}$

Dunque $A=-1$ , $B=-3$ , $C=3$ e $D=1$ , da cui otteniamo

$\begin{aligned} \int_1^{+\infty} \frac{t+3}{t^2(t^2+1)} \, dt &= \int_1^{+\infty} \left( -\frac{t+3}{t^2+1} + \frac{3}{t^2} + \frac{1}{t} \right) \, dt \\ &= \int_1^{+\infty} \left( - \frac{t}{t^2+1} - \frac{3}{t^2+1} + \frac{3}{t^2} + \frac{1}{t} \right) \, dt \\ &= \left[- \frac{\ln (t^2+1)}{2} - 3 \arctan t - \frac{3}{t} + \ln |t| \right]_1^{+\infty} \\ &= \left[\ln \left( \frac{|t|}{\sqrt{t^2+1}} \right) - 3 \arctan t - \frac{3}{t} \right]_1^{+\infty} \\ &= \ln 1 - \frac{3\pi}{2} - \ln \frac{1}{\sqrt{2}} + \frac{3\pi}{4} + 3 \\ &= 3 - \frac{3\pi}{4} + \frac{1}{2}\ln 2. \end{aligned}$

Riferimenti bibliografici

[1] Giuseppe De Marco: Analisi 1. Zanichelli, 1996.

[2] Enrico Giusti: Analisi Matematica 1, Bollati Boringhieri, 2002.

[3] Marco Pavone: Integrali impropri e funzioni integrali. Aracne, 1992.

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Document

Menu

Chiudi

Integrali impropri – Teoria

Autori e revisori

Leggi...

Integrali impropri

Definizione e proprietà.

Criteri di convergenza.

Esercizi svolti

Leggi...

Riferimenti bibliografici

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi