50% di sconto su tutto fino al 31/12/2024

Il mio account
Accedi ai contenuti scaricabili
a

Menu

M

Chiudi

Il teorema di Weierstrass

Teoria sulle Funzioni continue-lipschitziane-holderiane

Home » Il teorema di Weierstrass

Il teorema di Weierstrass

Il teorema di Weierstrass è un concetto fondamentale nell’analisi matematica, che esprime un’importante proprietà delle funzioni continue di una variabile reale. Esso infatti garantisce l’esistenza di valori massimi e minimi per una funzione continua in un un intervallo chiuso e limitato.
Per tale motivo, questo risultato costituisce uno strumento teorico di notevole utilità, permettendo di stabilire a priori l’esistenza di tali massimi e minimi e aprendo così la strada alla loro determinazione.

L’articolo spiega in maniera chiara la sua formulazione e ne espone la dimostrazione, soffermandosi poi su esempi espliciti che illustrano situazioni in cui le ipotesi del teorema non sono verificate, proponendo quindi una trattazione completa dell’argomento.

Per tali ragioni, il materiale è consigliato a studenti dei corsi di Analisi 1 e appassionati che desiderano approfondire tutti gli aspetti legati a questo importante risultato dell’Analisi Matematica.

Consigliamo i seguenti articoli di esercizi:

Risultano invece di interesse le seguenti risorse aggiuntive di teoria, delle quali è possibile reperire una lista completa alla fine dell’articolo:

 

Autori e revisori

Leggi...

Autori:Daniele Fakhoury, Luigi De Masi, Giuseppe Palaia, Silvia Lombardi.  

Revisori: Valerio Brunetti, Sara Sottile, Sergio Fiorucci, Matteo Talluri, Chiara Bellotti.  

 

Introduzione

Leggi...

Le funzioni continue possiedono numerose proprietà. Tra di esse, assume notevole rilevanza quella stabilita dal teorema di Weierstrass, che è il risultato principale di questo articolo.

 

Teorema 1 (Weierstrass). Sia A \subseteq \mathbb{R} un insieme chiuso e limitato, e sia f\colon A \to \mathbb{R} una funzione continua. Allora f ammette massimo e minimo assoluti in A, ovvero esistono x_m, \, x_M \in A tali che

    \[ f(x_m)\leq f(x) \leq f(x_M) \qquad \forall x \in A. \]

In particolare la conclusione è vera se A=[a,b], ossia se A è un intervallo chiuso è limitato.

 

Osserviamo che \inf_A f e \sup_A f esistono sempre in quanto estremo inferiore e superiore dell’insieme f(A)=\operatorname{Im}f, si veda [1, Funzioni elementari — Volume 1, sezione 2.8.3]. Per una funzione generica, però, \inf_A f e \sup_A f non appartengono all’immagine di f, cioè non costituiscono rispettivamente minimo e massimo di f. In particolare, \inf_A f e \sup_A f possono anche essere infiniti.

Il teorema 1 afferma quindi che, sotto le ipotesi che A sia chiuso e limitato e f sia continua, invece \min_A f e \max_A f esistono e sono finiti. In altre parole, f assume i valori estremi \inf_A f e \sup_A f nei punti rispettivamente pari a x_m e x_M, si veda anche la figura 1. Questa conclusione è falsa anche rimuovendo soltanto una delle ipotesi suddette, come mostreremo con opportuni esempi.

   

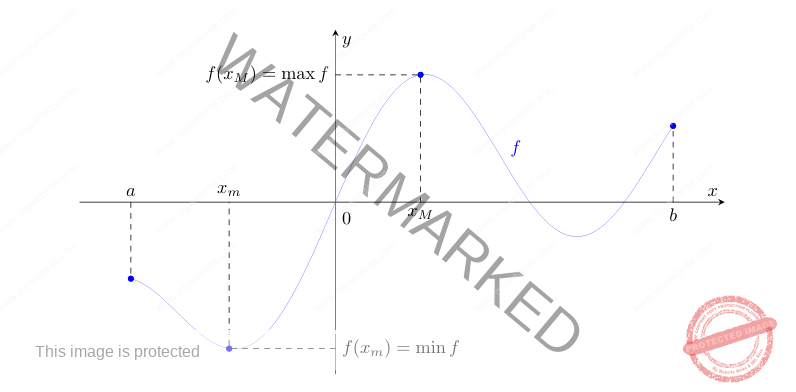
il teorema di Weierstrass

 

Figura 1: illustrazione del teorema di Weierstrass; la funzione f \colon [a,b] \to \mathbb{R} è continua, quindi assume valori massimo e minimo, in corrispondenza rispettivamente dei punti di massimo e minimo x_M,x_m \in [a,b].

   

Il lavoro è così organizzato: nella sezione 1 presentiamo le definizioni e i risultati necessari alla trattazione che segue. Nella sezione 2 dimostriamo il teorema 1, mentre nella sezione 3 facciamo vedere, con alcuni esempi, che ciascuna delle ipotesi del teorema è necessaria affinché la tesi sia valida.

 

Risultati preliminari

Leggi...

Cominciamo col richiamare la definizione di massimo e minimo assoluti per una funzione e di punti di massimo e minimo.  

Definizione 2 (massimi e minimi assoluti). Sia f \colon A \to \mathbb{R} una funzione. Un punto x_M è detto punto di massimo assoluto per f se

(1)   \begin{equation*} f(x) \leq f(x_M) \qquad \forall x \in A. \end{equation*}

Il valore f(x_M) è detto massimo assoluto di f ed è indicato col simbolo \max_A f.

Analogamente si definisce un punto di minimo x_m e il valore minimo f(x_m)=\min_A f di f.

 

Osserviamo che, mentre il valore \max_A f è unico, possono esistere molti (anche infiniti) punti di massimo assoluto.

Presentiamo inoltre un risultato riguardante le successioni che utilizzeremo nella dimostrazione del teorema 1: il teorema di Bolzano-Weierstrass. Esso afferma che una successione \{x_n\}_n a valori in un insieme chiuso e limitato (come il dominio A di f nelle ipotesi del teorema di Weierstrass) possiede una sottosuccessione convergente. Rimandiamo a [3, teorema di Bolzano-Weierstrass] per una dimostrazione.

 

Teorema 3 (Bolzano-Weierstrass). Sia A \subseteq \mathbb{R} un insieme chiuso e limitato, e sia \{x_n\}_{n \in \mathbb{N}} una successione a valori in A. Allora esiste una sua sottosuccessione convergente a un elemento di A.

 

Riportiamo la caratterizzazione della continuità per successioni stabilita in [2, Funzioni continue, teorema 3.3], che utilizziamo nella dimostrazione del teorema 1.

 

Teorema 4 (caratterizzazione della continuità per successioni). Sia A \subseteq \mathbb{R}, sia f \colon A \to \mathbb{R} e sia x_0 \in A. Allora le due affermazioni seguenti sono equivalenti:  

  1. f è continua in x_0;
  2. per ogni successione \{x_n\}_{n \in \mathbb{N}} a valori in A tale che x_n \to x_0, si ha

    (2)   \begin{equation*} \displaystyle \lim_{n \to +\infty}f(x_n)=f(x_0). \end{equation*}

 

 

Dimostrazione del teorema di Weierstrass

Leggi...

In questa sezione dimostriamo il teorema 1.

 

Dimostrazione. Sia m = \inf_{A} f; per definizione di estremo inferiore, esiste una successione y_n \in \operatorname{Im} f tale che y_n \to m. Poiché y_n \in f(A), esiste una successione x_n \in A tale che

(3)   \begin{equation*} f(x_n) = y_n \qquad \forall n \in \mathbb{N}. \end{equation*}

Poiché A è chiuso e limitato, per il teorema 3, esiste una sottosuccessione x_{n_k} convergente in A, cioè esiste x_m \in A tale che

(4)   \begin{equation*} \lim_{k \to \infty} x_{n_k}=x_m. \end{equation*}

Si ha

(5)   \begin{equation*} f(x_m) = \lim_{k \to \infty} f(x_{n_k}) = \lim_{k \to \infty} y_{n_k} = m, \end{equation*}

dove la prima uguaglianza segue dalla continuità di f in x_m e dal teorema 4, mentre la terza uguaglianza segue dal fatto che y_n \to m e y_{n_k} è una sottosuccessione di y_n. L’equazione (5) mostra che m \in f(A) (in particolare m > - \infty) e quindi m=\min_A f.

Analogamente si mostra che f ha massimo in A.

 

Necessità delle ipotesi del teorema di Weierstrass

Leggi...

La conclusione del teorema 1 non è valida rimuovendo anche una sola delle ipotesi. Andiamo infatti ad analizzare alcuni controesempi che lo dimostrano.

Chiusura del dominio

L’ipotesi di chiusura del dominio è essenziale, come mostrato dall’esempio 5. Inoltre, l’esempio 6 prova che anche assumendo per ipotesi la limitatezza della funzione, essa può non assumere minimo e/o massimo.

 

Esempio 5 (dominio non chiuso). Sia f \colon (0,1] \to \mathbb{R} la funzione definita da

(6)   \begin{equation*} f(x)=\dfrac{1}{x} \qquad \forall x \in (0,1], \end{equation*}

rappresentata in figura 2, è continua e ammette valore minimo pari a 1, ma non ammette massimo.

   

 

Figura 2: la funzione f dell’esempio 5; si vede che \min f=1 (assunto in corrispondenza di x=1), ma che f è illimitata superiormente, per cui non ammette massimo.

   

Infatti, è chiaro che f è decrescente, quindi

(7)   \begin{equation*} f(x) \geq f(1) \qquad \forall x \in (0,1], \end{equation*}

da cui segue, per la definizione 2, che x=1 è un punto di minimo per f e che 1= \min_{(0,1]} f. D’altra parte, sempre per la monotonia di f si ha che

(8)   \begin{equation*} \sup_{(0,1]} f = \lim_{x \to 0^+}f(x) = +\infty, \end{equation*}

quindi f non ammette valore massimo.

 

Esempio 6 (dominio non chiuso e funzione limitata). La funzione f \colon (1,2] \to \mathbb{R} definita da f(x)=x per ogni x \in (1,2] è continua, limitata, ma non ammette minimo. Infatti

(9)   \begin{equation*} \max_{(1,2]} f = 2, \qquad \inf_{(1,2]} f = 1, \end{equation*}

ma il valore 1 non è assunto da f, come mostrato in figura 3.

   

 

Figura 3: la funzione f dell’esempio 6; si vede che \max f=2 (assunto in corrispondenza di x=2), ma che f non ammette minimo in quanto il valore 1 non appartiene all’immagine di f.

Limitatezza del dominio.

L’esempio 7 mostra che, se il dominio della funzione è illimitato, essa può non assumere massimo oppure minimo. L’esempio 8 assicura che neppure la limitatezza della funzione basta ad ottenere l’esistenza del massimo e/o del minimo.

 

Esempio 7 (dominio illimitato). La funzione f \colon \mathbb{R} \to \mathbb{R} definita da f(x)=x per ogni x \in \mathbb{R} è continua, il suo dominio è chiuso, ma non ammette né massimo né minimo in quanto

(10)   \begin{equation*} \inf_\mathbb{R}f = -\infty, \qquad \sup_\mathbb{R}f = +\infty. \end{equation*}

 

Esempio 8 (dominio illimitato e funzione limitata). La funzione f \colon [1,+\infty) \to \mathbb{R} definita da

(11)   \begin{equation*} f(x)=\frac{1}{x} \qquad \forall x \in [1,+\infty) \end{equation*}

(rappresentata in figura 4) è continua, il suo dominio è chiuso e

(12)   \begin{equation*} \max_{[1,+\infty)}f = 1, \qquad \inf_{[1,+\infty)}f = 0, \end{equation*}

ma f non ha minimo in quanto f(x)>0 per ogni x \in [1,+\infty).

 

   

 

Figura 4: la funzione f dell’esempio 8; si vede che \max f=1 (assunto in corrispondenza di x=1) e che \inf f=0, ma poiché tale valore non è assunto f non ammette minimo.

   

Continuità della funzione.

L’esempio 9 mostra che, anche se il dominio della funzione è chiuso e limitato, se questa non è continua può non assumere massimo o minimo.

 

Esempio 9 (funzione non continua). La funzione f \colon [-2,2] \to \mathbb{R} definita da

(13)   \begin{equation*} f(x)= \begin{cases} 0 & \text{se } x \in [-2,1] \cup [1,2]\\ x & \text{se } x \in (-1,1), \end{cases} \end{equation*}

il cui grafico è mostrato in figura 5, è definita su un dominio chiuso e limitato, ha delle discontinuità di salto in -1 e 1 e non ammette né massimo né minimo, infatti

(14)   \begin{equation*} \inf_{[-2,2]}f = -1, \qquad \sup_{[-2,2]}f = 1, \end{equation*}

ma tali valori non appartengono all’immagine di f.

   

 

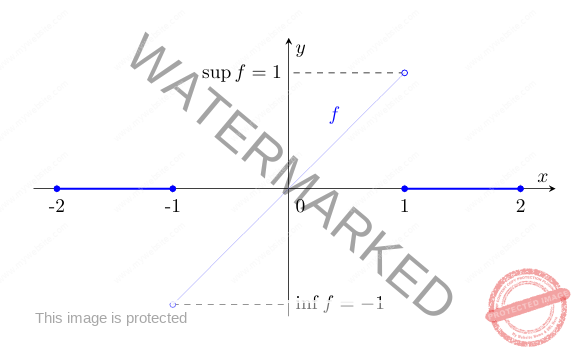
Figura 5: la funzione f dell’esempio 9; si vede che \inf f=-1 e \sup f=1, ma tali valore non sono assunti e quindi f non ammette minimo. Si notino le discontinuità di salto di f in x=-1 e x=1.

   

 

Riferimenti bibliografici

[1] Qui Si Risolve Funzioni elementari — Volume 1.

[2] Qui Si Risolve Funzioni continue.

[3] Qui Si Risolve Teorema di Bolzano-Weierstrass per successioni.

 
 

Tutta la teoria di analisi matematica

Leggi...

  1. Teoria Insiemi
  2. Il metodo della diagonale di Cantor
  3. Logica elementare
  4. Densità dei numeri razionali nei numeri reali
  5. Insiemi Numerici \left(\mathbb{N},\, \mathbb{Z},\, \mathbb{Q}\right)
  6. Il principio di induzione
  7. Gli assiomi di Peano
  8. L’insieme dei numeri reali: costruzione e applicazioni
  9. Concetti Fondamentali della Retta Reale: Sintesi Teorica
  10. Costruzioni alternative di \mathbb{R}
  11. Binomio di Newton
  12. Spazi metrici, un’introduzione
  13. Disuguaglianza di Bernoulli
  14. Disuguaglianza triangolare
  15. Teoria sulle funzioni
  16. Funzioni elementari: algebriche, esponenziali e logaritmiche
  17. Funzioni elementari: trigonometriche e iperboliche
  18. Funzioni goniometriche: la guida essenziale
  19. Teorema di Bolzano-Weierstrass per le successioni
  20. Criterio del rapporto per le successioni
  21. Definizione e proprietà del numero di Nepero
  22. Limite di una successione monotona
  23. Successioni di Cauchy
  24. Il teorema ponte
  25. Teoria sui limiti
  26. Simboli di Landau
  27. Funzioni continue – Teoria
  28. Il teorema di Weierstrass
  29. Il teorema dei valori intermedi
  30. Il teorema della permanenza del segno
  31. Il teorema di Heine-Cantor
  32. Il teorema di esistenza degli zeri
  33. Il metodo di bisezione
  34. Teorema ponte versione per le funzioni continue
  35. Discontinuità di funzioni monotone
  36. Continuità della funzione inversa
  37. Teorema delle contrazioni o Teorema di punto fisso di Banach-Caccioppoli
  38. Teoria sulle derivate
  39. Calcolo delle derivate: la guida pratica
  40. Teoria sulle funzioni convesse
  41. Il teorema di Darboux
  42. I teoremi di de l’Hôpital
  43. Teorema di Fermat
  44. Teoremi di Rolle e Lagrange
  45. Il teorema di Cauchy
  46. Espansione di Taylor: teoria, esempi e applicazioni pratiche
  47. Polinomi di Taylor nei limiti: istruzioni per l’uso
  48. Integrali definiti e indefiniti
  49. Teorema fondamentale del calcolo integrale (approfondimento)
  50. Integrali ricorsivi
  51. Formule del trapezio, rettangolo e Cavalieri-Simpson
  52. Teoria sugli integrali impropri
  53. Funzioni integrali – Teoria
  54. Introduzione ai numeri complessi – Volume 1 (per un corso di ingegneria — versione semplificata)
  55. Introduzione ai numeri complessi – Volume 1 (per un corso di matematica o fisica)
  56. Serie numeriche: la guida completa
  57. Successioni di funzioni – Teoria
  58. Teoremi sulle successioni di funzioni
    1. 58a. Criterio di Cauchy per la convergenza uniforme
    2. 58b. Limite uniforme di funzioni continue
    3. 58c. Passaggio al limite sotto il segno di integrale
    4. 58d. Limite uniforme di funzioni derivabili
    5. 58e. Piccolo teorema del Dini
    6. 58f. Procedura diagonale e teorema di Ascoli-Arzela
  59. Serie di funzioni – Teoria
  60. Serie di potenze – Teoria
  61. Serie di Fourier – Teoria e applicazioni
  62. Integrali multipli — Parte 1 (teoria)
  63. Integrali multipli — Parte 2 (teoria e esercizi misti)
  64. Regola della Catena — Teoria ed esempi.
  65. Jacobiano associato al cambiamento di coordinate sferiche
  66. Guida ai Massimi e Minimi: Tecniche e Teoria nelle Funzioni Multivariabili
  67. Operatore di Laplace o Laplaciano
  68. Teoria equazioni differenziali
  69. Equazione di Eulero
  70. Teoria ed esercizi sulla funzione Gamma di Eulero
  71. Teoria ed esercizi sulla funzione Beta
  72. Approfondimento numeri complessi
  73. Diverse formulazioni dell’assioma di completezza
  74. Numeri di Delannoy centrali
  75. Esercizi avanzati analisi

 
 

Tutte le cartelle di Analisi Matematica

Leggi...

  1. Prerequisiti di Analisi
    1. Ripasso algebra biennio liceo
    2. Ripasso geometria analitica
    3. Ripasso goniometria e trigonometria
    4. Errori tipici da evitare
    5. Insiemi numerici N,Z,Q,R
    6. Funzioni elementari
    7. Logica elementare
    8. Insiemi
  2. Successioni
    1. Teoria sulle Successioni
    2. Estremo superiore e inferiore
    3. Limiti base
    4. Forme indeterminate
    5. Limiti notevoli
    6. Esercizi misti Successioni
    7. Successioni per ricorrenza
  3. Funzioni
    1. Teoria sulle funzioni
    2. Verifica del limite in funzioni
    3. Limite base in funzioni
    4. Forme indeterminate in funzioni
    5. Limiti notevoli in funzioni
    6. Calcolo asintoti
    7. Studio di funzione senza derivate
    8. Dominio di una funzione
    9. Esercizi misti Funzioni
    10. Esercizi misti sui Limiti
  4. Funzioni continue-lipschitziane-holderiane
    1. Teoria sulle Funzioni continue-lipschitziane-holderiane
    2. Continuità delle funzioni
    3. Continuità uniforme
    4. Teorema degli zeri
    5. Esercizi sul teorema di Weierstrass senza l’uso delle derivate
  5. Calcolo differenziale
    1. Derivate
    2. Calcolo delle derivate
    3. Retta tangente nel calcolo differenziale
    4. Punti di non derivabilità nel calcolo differenziale
    5. Esercizi sul teorema di Weierstrass con l’uso delle derivate
    6. Studio di funzione completo nel calcolo differenziale
    7. Esercizi teorici nel calcolo differenziale
    8. Metodo di bisezione
    9. Metodo di Newton
  6. Teoremi del calcolo differenziale
    1. Teoria sui Teoremi del calcolo differenziale
    2. Teorema di Rolle
    3. Teorema di Lagrange
    4. Teorema di Cauchy
    5. Teorema di De L’Hôpital
  7. Calcolo integrale
    1. Integrale di Riemann
    2. Integrali immediati
    3. Integrale di funzione composta
    4. Integrali per sostituzione
    5. Integrali per parti
    6. Integrali di funzione razionale
    7. Calcolo delle aree
    8. Metodo dei rettangoli e dei trapezi
    9. Esercizi Misti Integrali Indefiniti
    10. Esercizi Misti Integrali Definiti
  8. Integrali impropri
    1. Teoria Integrali impropri
    2. Carattere di un integrale improprio
    3. Calcolo di un integrale improprio
  9. Espansione di Taylor
    1. Teoria Espansione di Taylor
    2. Limiti di funzione con Taylor
    3. Limiti di successione con Taylor
    4. Stime del resto
  10. Funzioni integrali (Approfondimento)
    1. Teoria Funzioni integrali (Approfondimento)
    2. Studio di funzione integrale
    3. Limiti con Taylor e De L’Hôpital
    4. Derivazione di integrali parametrici (Tecnica di Feynmann)
  11. Numeri Complessi
    1. Teoria Numeri complessi
    2. Espressioni con i numeri complessi
    3. Radice di un numero complesso
    4. Equazioni con i numeri complessi
    5. Disequazioni con i numeri complessi
    6. Esercizi misti Numeri complessi
  12. Serie numeriche
    1. Teoria Serie numeriche
    2. Esercizi Serie a termini positivi
    3. Esercizi Serie a termini di segno variabile
    4. Esercizi Serie geometriche e telescopiche
  13. Successioni di funzioni
    1. Teoria Successioni di funzioni
    2. Esercizi Successioni di funzioni
  14. Serie di funzioni
    1. Teoria Serie di funzioni
    2. Esercizi Serie di funzioni
  15. Serie di potenze
    1. Teoria Serie di potenze
    2. Esercizi Serie di potenze
  16. Serie di Fourier
    1. Teoria Serie di Fourier
    2. Esercizi Serie di Fourier
  17. Trasformata di Fourier
    1. Teoria Trasformata di Fourier
    2. Esercizi Trasformata di Fourier
  18. Funzioni di più variabili
    1. Teoria Funzioni di più variabili
    2. Massimi e minimi liberi e vincolati
    3. Limiti in due variabili
    4. Integrali doppi
    5. Integrali tripli
    6. Integrali di linea di prima specie
    7. Integrali di linea di seconda specie
    8. Forme differenziali e campi vettoriali
    9. Teorema di Gauss-Green
    10. Integrali di superficie
    11. Flusso di un campo vettoriale
    12. Teorema di Stokes
    13. Teorema della divergenza
    14. Campi solenoidali
    15. Teorema del Dini
  19. Equazioni differenziali lineari e non lineari
    1. Teoria equazioni differenziali lineari e non lineari
    2. Equazioni differenziali lineari e non lineari del primo ordine omogenee
  20. Equazioni differenziali lineari
    1. Del primo ordine non omogenee
    2. Di ordine superiore al primo,a coefficienti costanti,omogenee
    3. Di ordine superiore al primo,a coefficienti costanti,non omogenee
    4. Di Eulero,di Bernoulli,di Clairaut,di Lagrange e di Abel
    5. Non omogenee avente per omogenea associata un’equazione di Eulero
    6. Sistemi di EDO
  21. Equazioni differenziali non lineari
    1. A variabili separabiliO
    2. A secondo membro omogeneo
    3. Del tipo y’=y(ax+by+c)
    4. Del tipo y’=y(ax+by+c)/(a’x+b’y+c’)
    5. Equazioni differenziali esatte
    6. Mancanti delle variabili x e y
    7. Cenni sullo studio di un’assegnata equazione differenziale non lineare
    8. Di Riccati
    9. Cambi di variabile: simmetrie di Lie
  22. Analisi complessa
    1. Fondamenti
    2. Funzioni olomorfe
    3. Integrale di Cauchy e applicazioni
    4. Teorema della curva di Jordan e teorema fondamentale dell’Algebra
    5. Teorema di inversione di Lagrange
    6. Teorema dei Residui
    7. Funzioni meromorfe
    8. Prodotti infiniti e prodotti di Weierstrass
    9. Continuazione analitica e topologia
    10. Teoremi di rigidità di funzioni olomorfe
    11. Trasformata di Mellin
  23. Equazioni alle derivate parziali
    1. Equazioni del primo ordine
    2. Equazioni del secondo ordine lineari
    3. Equazioni non-lineari
    4. Sistemi di PDE
  24. Funzioni speciali
    1. Funzione Gamma di Eulero
    2. Funzioni Beta,Digamma,Trigamma
    3. Integrali ellittici
    4. Funzioni di Bessel
    5. Funzione zeta di Riemann e funzioni L di Dirichlet
    6. Funzione polilogaritmo
    7. Funzioni ipergeometriche
  25. Analisi funzionale
    1. Misura e integrale di Lebesgue
    2. Spazi Lp,teoremi di completezza e compattezza
    3. Spazi di Hilbert,serie e trasformata di Fourier
    4. Teoria e pratica dei polinomi ortogonali
    5. Spazi di Sobolev
  26. Complementi
    1. Curiosità e approfondimenti
    2. Compiti di analisi
    3. Esercizi avanzati analisi
  27. Funzioni Convesse

 
 

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.


Algebra lineare.


Geometria analitica.


Geometria differenziale.


 
 

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

  • Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
  • Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
  • MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
  • PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
  • Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
  • The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
  • Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
  • Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
  • Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
  • Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.






Document









Document



error: Il contenuto è protetto!!