Massimi e minimi vincolati – Esercizi – Volume 2

Home » Massimi e minimi vincolati – Esercizi – Volume 2

In questo secondo volume di esercizi sui massimi e minimi vincolati per funzioni in più variabili presentiamo ulteriori 9 problemi sulla ricerca dei punti di massimo e minimo di una funzione su un insieme compatto $D \subset \mathbb{R}^n$ . Come in Massimi e minimi vincolati – Esercizi – Volume 1, lo studio riguarda sia la parte interna di $D$ , sia particolarmente il bordo $\partial D$ , mediante parametrizzazione o il metodo dei moltiplicatori di Lagrange.

Gli esercizi sono completamente risolti, offrendo spesso più soluzioni alternative per aumentare la varietà di tecniche mostrata al lettore.
Questo secondo volume arricchisce e completa quindi il lavoro contenuto nella prima porzione di esercizi, ed è rivolto a studenti e appassionati.

Segnaliamo il seguente materiale su argomenti correlati:

Buona lettura!

Autori e revisori

Leggi...

Autori: Giulio Binosi.

Revisori: Matteo Talluri, Davide La Manna, Jacopo Garofali, Daniele Bjørn Malesani, Silvia Lombardi, Valerio Brunetti.

Introduzione

Leggi...

La seguente dispensa è una collezione di esercizi riguardanti il problema della determinazione del massimo e del minimo di una funzione su un insieme compatto di $\mathbb{R}^3$ . Essa è composta da esercizi di varia difficoltà ed è rivolta a studenti di Ingegneria, Fisica e Matematica che desiderano affrontare l’esame di Analisi 2. Tutti gli esercizi presentano una soluzione convenzionale, mentre alcuni ne hanno altre più ad hoc. L’obiettivo è quello di suggerire allo studente strade alternative per risolvere l’esercizio più velocemente. Gli strumenti utilizzati sono il Teorema di Fermat per quanto riguarda la parte interna dell’insieme, mentre per la sua frontiera adotteremo il metodo della parametrizzazione, qualora possibile, o il metodo dei moltiplicatori di Lagrange, quando il vincolo è espresso come luogo di zeri.

Richiami di teoria

Leggi...

Prima delle soluzioni, richiamiamo alcuni risultati fondamentali, che saranno utilizzati nella risoluzione degli esercizi:

Teorema 1 (teorema di Weierstrass). Sia $K\subset\mathbb{R}^n$ un insieme compatto e sia $f:K\rightarrow\mathbb{R}$ una funzione continua. Allora $f$ ammette massimo e minimo su $K$ .

Teorema 2 (teorema di Heine-Borel). Un insieme $E\subset\mathbb{R}^n$ è compatto se e solo se è chiuso e limitato.

Teorema 3 (teorema di Fermat). Siano $A\subset\mathbb{R}^n$ un insieme aperto, $f:A\rightarrow\mathbb{R}$ e $x_0\in A$ tale che $f$ è differenziabile in $x_0$ . Allora, se $x_0$ è un punto di massimo o minimo relativo per $f$ su $A$ , vale $\nabla f(x_0)=0$ .

Corollario 1. Sia $f:A\subset\mathbb{R}^n\rightarrow\mathbb{R}$ una funzione differenziabile su tutto $A$ , insieme aperto. Allora, tutti i punti di massimo o minimo relativo di $f$ su $A$ sono, in particolare, punti critici.

Teorema 4 (teorema dei moltiplicatori di Lagrange). Siano $f,g:\mathbb{R}^n\rightarrow\mathbb{R}$ due funzioni di classe $\mathcal{C}^1$ , sia $\Gamma:=\{x\in\mathbb{R}^n\mid g(x)=0\}$ . Supponiamo che $x_0\in\Gamma$ sia un punto di massimo o minimo di $f$ su $\Gamma$ e che $\nabla g(x_0)\neq0$ , allora $\exists\lambda\in\mathbb{R}$ tale che $\nabla f(x_0)=\lambda\nabla g(x_0).$

Corollario 2. siano $f,g_1,...,g_k:\mathbb{R}^n\rightarrow\mathbb{R}$ funzioni differenziabili e sia

$\begin{equation*} \Gamma:=\{\overline{x}\in\mathbb{R}^n\mid g_1(\overline{x})=...=g_k(\overline{x})=0\}. \end{equation*}$

Supponiamo che $\overline{x}_0\in\Gamma$ sia punto di massimo o di minimo relativo per $f$ su $\Gamma$ e che i vettori $\nabla g_i(\overline{x}_0)$ non siano linearmente dipendenti. Allora, definita la Lagrangiana $\mathcal{L}:\mathbb{R}^n\times\mathbb{R}^k\rightarrow\mathbb{R}$ ,

$\begin{equation*} \mathcal{L}(x_1,...,x_n,\lambda_1,...,\lambda_k):=f(x_1,...,x_n)-\lambda_1g_1(x_1,...,x_n)-...-\lambda_kg_k(x_1,...,x_n), \end{equation*}$

vale

$\begin{equation*} \nabla\mathcal{L}(\overline{x}_0,\lambda_1,...,\lambda_k)=(0,...,0), \end{equation*}$

cioè $\overline{x}_0$ è un punto critico della Lagrangiana.

Esercizi

$\quad$

Esercizio 1 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^3\rightarrow\mathbb{R},$ definita da

$f(x,y,z):=4x+y+z^2,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2\leq z\leq 4\}.$

Svolgimento 1.

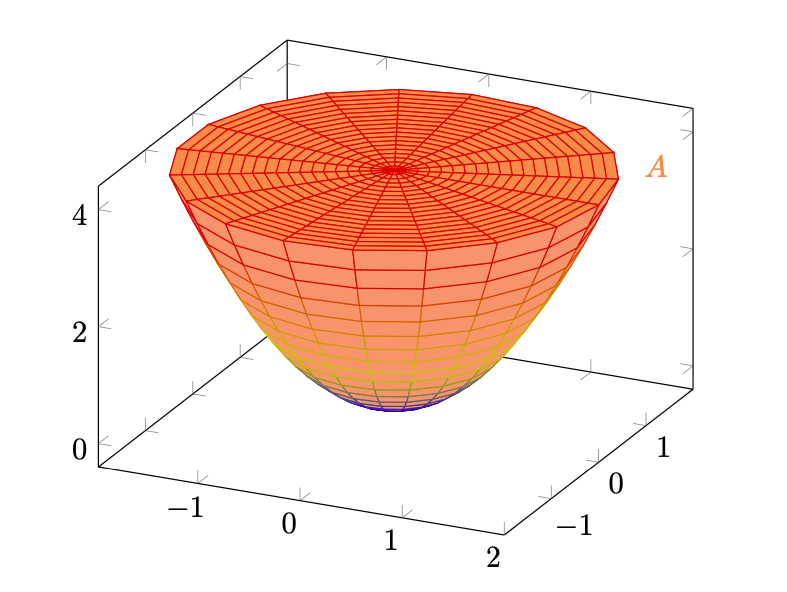
Figura 1: l’insieme $A$ .

$\quad$

Osserviamo che $f$ è un polinomio, pertanto è una funzione continua su $\mathbb{R}^3$ , mentre l’insieme $A$ è chiuso e limitato. La chiusura segue dal fatto che $A$ è intersezione di controimmagini di insiemi chiusi di $\mathbb{R}$ tramite funzioni continue, mentre per la limitatezza notiamo che esso è un settore di paraboloide ellittico, contenuto in una sfera di raggio $2\sqrt{5}$ . Infatti, dalle equazioni definenti $A$ , per ogni $(x,y,z)\in A$ risulta

$\begin{equation*} ||(x,y,z)||=\sqrt{x^2+y^2+z^2}\leq\sqrt{z+z^2}\leq\sqrt{4+16}=2\sqrt{5}. \end{equation*}$

Dunque è un chiuso e limitato di $\mathbb{R}^3$ , compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$A^\circ$ ) Essendo $f$ differenziabile sull’insieme aperto $A^\circ$ , il teorema di Fermat ci assicura che gli estremi relativi di $f$ in $A^\circ$ vanno ricercati tra i suoi eventuali punti critici in $A^\circ$ , ovvero i punti $P\in A^\circ$ tali che $\nabla f(P)=(0,0,0)$ e scartare tutti i punti che non soddisfano tale condizione. Calcoliamo il gradiente di $f$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=4\\\\ \dfrac{\partial f}{\partial y}(x,y)=1\\\\ \dfrac{\partial f}{\partial z}(x,y)=2z, \end{cases}$

dunque $\nabla f(x,y,z)=(4,1,2z)$ , che non si annulla per nessuna scelta di $(x,y,z)\in A^\circ$ . Ciò significa che non vi sono punti critici.

$\partial A$ ) La frontiera di $A$ sarà descritta dalle equazioni, le cui disequazioni associate definiscono $A$ . Dunque

$\begin{equation*} \partial A=\left\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2=z, 0\leq z\leq4\right\}\cup\left\{(x,y,z)\in\mathbb{R}^3\mid z=4, x^2+y^2\leq z\right\}. \end{equation*}$

Possiamo distinguere $\partial A$ in due componenti: $\partial A=B\cup C$ , dove

$\begin{equation*} B=\left\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2=z, 0\leq z\leq4\right\} \end{equation*}$

$\begin{equation*} C=\left\{(x,y,z)\in\mathbb{R}^3\mid z=4, x^2+y^2\leq z\right\}. \end{equation*}$

$\quad$

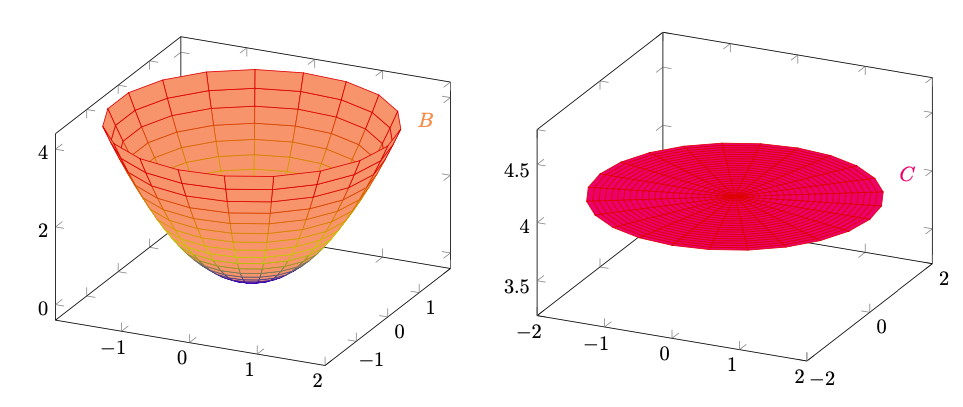
massimi e minimi vincolati

Figura 2: Gli insiemi $B$ e $C$ che compongono la frontiera di $A$ .

$\quad$

A questo punto, studiamo il comportamento di $f$ su $B$ e $C$ : dovremo trovare due parametrizzazioni $\varphi$ di $B$ e $\psi$ di $C$ e studiare massimi e minimi delle funzioni composte $f\circ\varphi$ e $f\circ\psi$ sui loro rispettivi domini.

$B$ ) È immediato osservare che $B$ è unione di circonferenze di raggio $\sqrt{z}$ a quota $z$ , per $z\in[0,4]$ . Dunque, una sua possibile parametrizzazione è la seguente:

$\begin{equation*} \begin{array}{rcl} \varphi:[0,2\pi]\times[0,2]& \rightarrow&\mathbb{R}^3 \\ (\theta,\rho) & \mapsto&(\rho\cos\theta,\rho\sin\theta,\rho^2). \end{array} \end{equation*}$

$\quad$

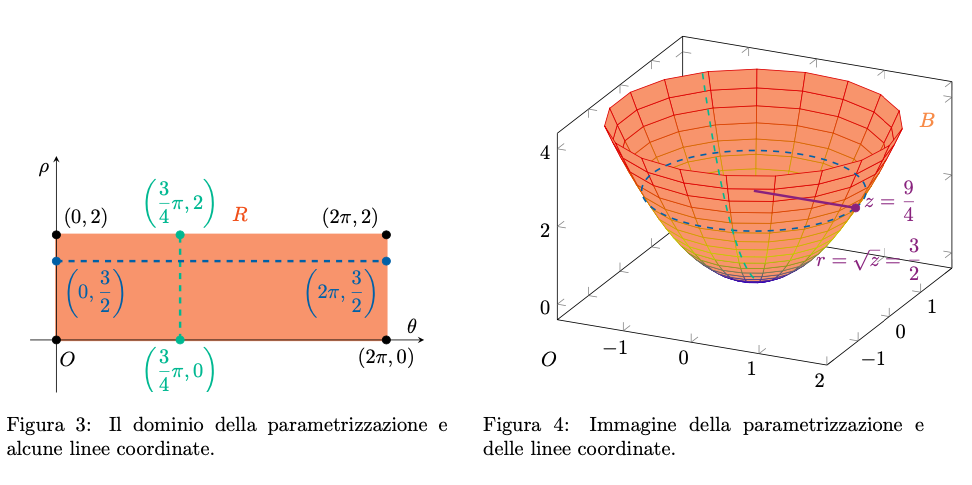
massimi e minimi vincolati

$\quad$

Calcoliamo allora $(f\circ\varphi)(\theta,\rho)$ :

$\begin{equation*} f(\varphi(\theta,\rho))=f(\rho\cos\theta,\rho\sin\theta,\rho^2)=4\rho\cos\theta+\rho\sin\theta+\rho^4. \end{equation*}$

Sia $R:=[0,2\pi]\times[0,2]$ il dominio della parametrizzazione. Osserviamo che $f\circ\varphi$ è somma e prodotto di funzioni continue e $R$ è un chiuso e limitato di $\mathbb{R}^2$ , dunque compatto. Per il teorema di Weierstrass, esisteranno il massimo ed il minimo di $f\circ\varphi$ su $R$ . Per trovarli, distinguiamo nuovamente l’insieme nella sua parte interna, $R^\circ=(0,2\pi)\times(0,2)$ e la sua frontiera, formata dai 4 lati del rettangolo.

Per quanto riguarda l’insieme aperto $R^\circ$ , essendo $f\circ\varphi$ una funzione differenziabile, il teorema di Fermat afferma che condizione necessaria affinchè $P\in R^\circ$ sia un punto di massimo o di minimo è che $\nabla (f\circ\varphi)(P)=(0,0)$ . Calcoliamo allora il gradiente di $f\circ\varphi$ tramite le derivate parziali:

$\begin{cases} \dfrac{\partial (f\circ\varphi)}{\partial \theta}(\theta,\rho)=-4\rho\sin\theta+\rho\cos\theta\\\\ \dfrac{\partial (f\circ\varphi)}{\partial \rho}(\theta,\rho)=4\cos\theta+\sin\theta+4\rho^3. \end{cases}$

Dunque

(1) $\begin{equation*} \nabla (f\circ\varphi)(\theta,\rho)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} -4\rho\sin\theta+\rho\cos\theta=0\\\\ 4\cos\theta+\sin\theta+4\rho^3=0 \end{array} \right.\Leftrightarrow\displaystyle\left\{\begin{array}{l} \rho(\cos\theta-4\sin\theta)=0\\\\ 4\cos\theta+\sin\theta+4\rho^3=0. \end{array} \right. \end{equation*}$

Poichè $\rho\in(0,2)$ , la prima equazione si annulla solamente se $\cos\theta=4\sin\theta$ . Da tale relazione è possibile recuperare il valore di $\sin\theta$ e $\cos\theta$ risolvendo il sistema

$\begin{equation*} \left\{\begin{array}{l} X^2+Y^2=1 \\\\ X=4Y, \end{array} \right. \end{equation*}$

in cui $X$ rappresenta $\cos\theta$ e $Y$ $\sin\theta$ . Dunque si ha

$\begin{equation*} \left\{\begin{array}{l} X^2+Y^2=1 \\\\ X=4Y, \end{array} \right.\Leftrightarrow \left\{\begin{array}{l} 16Y^2+Y^2=1 \\\\ X=4Y, \end{array} \right.\Leftrightarrow \left\{\begin{array}{l} 17Y^2=1 \\\\ X=4Y, \end{array} \right.\Leftrightarrow \left\{\begin{array}{l} Y=\pm\dfrac{1}{\sqrt{17}} \\\\ X=4Y=\pm\dfrac{4}{\sqrt{17}}. \end{array} \right. \end{equation*}$

$\quad$

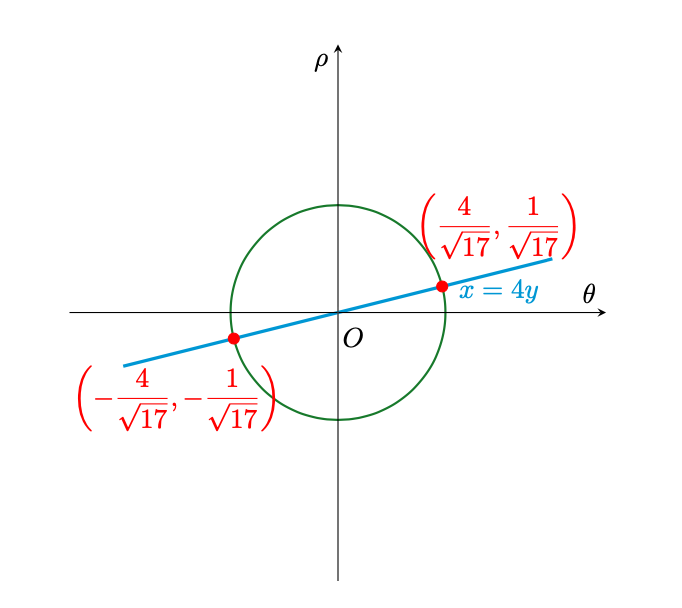
massimi e minimi vincolati

Figura 5: soluzioni dell’equazione lineare goniometrica.

$\quad$

Abbiamo dunque trovato che la prima equazione di (1) è verificata per $\left(\cos\theta,\sin\theta\right)=\pm\left(\dfrac{4}{\sqrt{17}},\dfrac{1}{\sqrt{17}}\right)$ .

Inseriamo questi valori nella seconda equazione di (1) per trovare $\rho$ :

$\begin{equation*} 4\rho^3\pm4\dfrac{4}{\sqrt{17}}\pm\dfrac{1}{\sqrt{17}}=0\Leftrightarrow4\rho^3\pm\dfrac{17}{\sqrt{17}}=0\Leftrightarrow\rho^3=\mp\dfrac{\sqrt{17}}{4}\Leftrightarrow\rho=\mp\sqrt[3]{\dfrac{\sqrt{17}}{4}} \end{equation*}$

Possiamo accettare solo il valore $\rho=+\sqrt[3]{\dfrac{\sqrt{17}}{4}}\approx 1\in(0,2)$ .

Abbiamo trovato dunque il punto critico di $f\circ\varphi$ su $R^\circ$

$\Tilde{P}_1=\left(\arccos{\left(-\dfrac{4}{\sqrt{17}}\right)},\sqrt[3]{\dfrac{\sqrt{17}}{4}}\right),$

a cui corrisponde il punto $P_1$ su $B$

$\begin{equation*} P_1=\varphi\left(\Tilde{P}_1\right)=\left(-\sqrt[3]{\dfrac{\sqrt{17}}{4}}\dfrac{4}{\sqrt{17}},-\sqrt[3]{\dfrac{\sqrt{17}}{4}}\dfrac{1}{\sqrt{17}},\sqrt[3]{\dfrac{17}{16}}\right)=\left(-\sqrt[3]{\dfrac{16}{17}},-\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},\sqrt[3]{\dfrac{17}{16}}\right). \end{equation*}$

$\quad$

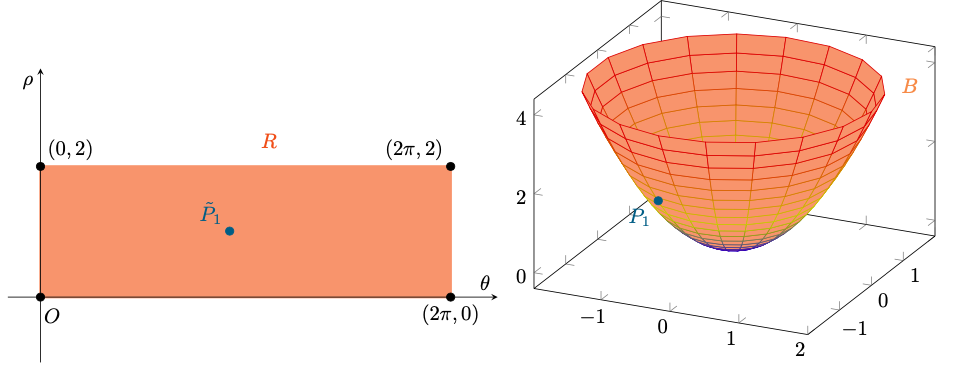
massimi e minimi vincolati

Figura 6: il punto critico $\tilde{P}_1$ della funzione parametrizzata $f\circ\varphi$ a cui corrisponde il punto $P_1$ su $B\subset\partial A$ .

$\quad$

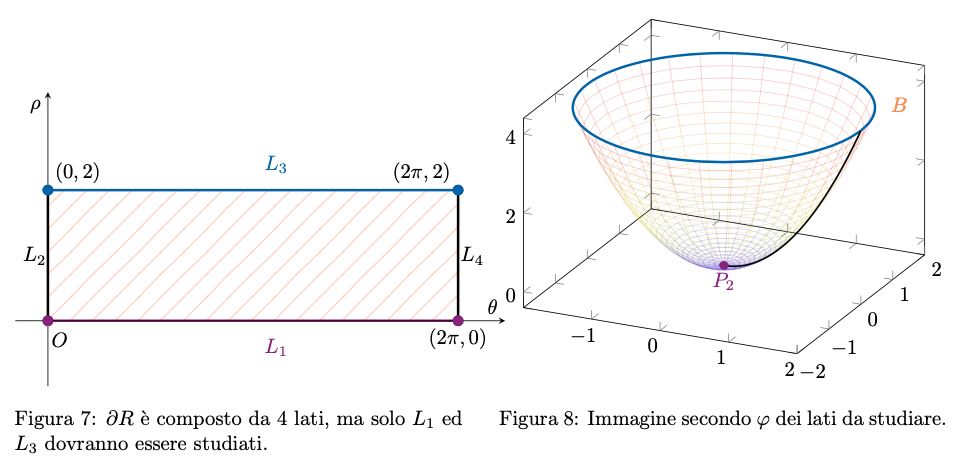
Per quanto riguarda la frontiera $\partial R$ , essa è composta dai $4$ lati $L_1,L_2,L_3$ e $L_4$ , come mostrato in figura. Notiamo, tuttavia, che non è necessario studiare $f\circ\varphi$ su $L_2$ e $L_4$ , i lati corrispondenti ai valori di $\theta=0$ , $\theta=2\pi$ , poichè la funzione $f\circ\varphi$ è $2\pi$ -periodica rispetto a $\theta$ . Infatti, avremmo potuto parametrizzare $B$ tramite $\tilde{\varphi}:[-\pi,\pi]\times[0,2]$ , con $\tilde{\varphi}(\theta,\rho)=\varphi(\theta,\rho)$ , laddove entrambe definite. In tal modo la parte di frontiera relativa a $\theta=0$ non avrebbe svolto alcun ruolo nella ricerca dei massimi e minimi di $f\circ\varphi$ su $R$ . Lo stesso discorso vale analogamente per $\theta=2\pi$ .

$\quad$

massimi e minimi vincolati

$\quad$

Il lato $L_1$ , corrispondente al settore $\rho=0$ viene parametrizzato da

$\begin{equation*} \begin{array}{rcl} \alpha_1:[0,2\pi] & \rightarrow&\mathbb{R}^2 \\ t&\mapsto&(t,0) \end{array} \end{equation*}$

$\begin{equation*} (f\circ\varphi)(\alpha_1(t))=f(\varphi(t,0))=f(0,0,0)=0. \end{equation*}$

Ciò significa che $f\circ\varphi$ è costante su $L_1=[0,2\pi]\times\{0\}$ che risulta quindi un insieme di punti critici per $f\circ\varphi$ , a cui corrisponde su $B$ il solo punto $\{(0,0,0)\}=\varphi(L_1)$ , che denotiamo con $P_2$ .

Per quanto riguarda $L_3=[0,2\pi]\times\{2\}$ , parametrizzato da

$\begin{equation*} \begin{array}{rcl} \alpha_3:[0,2\pi] & \rightarrow&\mathbb{R}^2 \\ t&\mapsto&(t,2). \end{array} \end{equation*}$

calcoliamo $(f\circ\varphi)(\alpha_3(t))$ e i suoi punti critici.

$\begin{equation*} (f\circ\varphi)(\alpha_3(t))=f(2\cos t,2\sin t,4)=8\cos t+2\sin t+16, \end{equation*}$

$\begin{equation*} ((f\circ\varphi)\circ\alpha_3)'(t)=-8\sin t+2\cos t. \end{equation*}$

Dunque i punti critici di $((f\circ\varphi)\circ\alpha_3)$ , ovvero i punti che annullano la sua derivata prima, sono i valori di $t\in[0,2\pi]$ per cui vale

$\begin{equation*} \cos t=4\sin t, \end{equation*}$

equazione risolta in precedenza, dove abbiamo ottenuto i valori

$\begin{equation*} t_k=\arccos{\left(\dfrac{4}{\sqrt{17}}\right)}+k\pi,\qquad k\in\mathbb{Z} \end{equation*}$

Di tale successioni, solo $t_0,t_1\in[0,2\pi]$ , dominio della parametrizzazione. I punti su $R$ corrispondenti a $t_0$ e $t_1$ sono rispettivamente $\Tilde{P}_3$ e $\Tilde{P}_4$ definiti da

$\begin{equation*} \Tilde{P}_3=\alpha_3\left(\arccos{\left(\dfrac{4}{\sqrt{17}}\right)}\right)=\left(\arccos{\left(\dfrac{4}{\sqrt{17}}\right)},2\right) \end{equation*}$

$\begin{equation*} \Tilde{P}_4=\alpha_3\left(\arccos{\left(\dfrac{4}{\sqrt{17}}\right)}+\pi\right)=\left(\arccos{\left(\dfrac{4}{\sqrt{17}}\right)}+\pi,2\right), \end{equation*}$

a cui corrispondono a loro volta i punti su $B$

$\begin{equation*} P_3=\varphi\left(\arccos{\left(\dfrac{4}{\sqrt{17}}\right)},2\right)=\left(\dfrac{8}{\sqrt{17}},\dfrac{2}{\sqrt{17}},4\right) \end{equation*}$

$\begin{equation*} P_4=\varphi\left(\arccos{\left(\dfrac{4}{\sqrt{17}}\right)}+\pi,2\right)=\left(-\dfrac{8}{\sqrt{17}},-\dfrac{2}{\sqrt{17}},4\right). \end{equation*}$

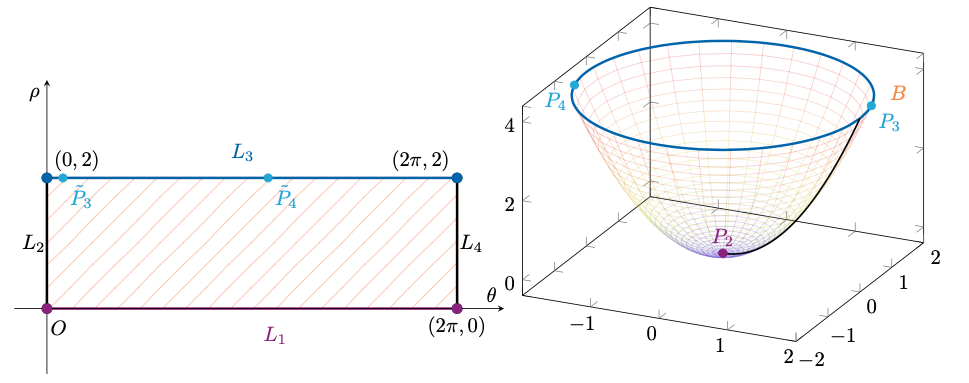
massimi e minimi vincolati

Figura 9: rappresentazione dei punti interessanti trovati su $\partial R$ e la loro immagine su $\partial A$ .

$\quad$

Questo conclude lo studio di $f$ su $B$ che ha portato alla nostra attenzione $4$ candidati ad essere punti di massimo o di minimo di $f$ su $A$ : i punti $P_1,P_2,P_3$ e $P_4$ .

$C$ ) Osserviamo immediatamente che $C$ è un cerchio di raggio $2$ a quota $z=4$ . Pertanto esso è parametrizzabile da

$\begin{equation*} \begin{array}{rcl} \psi:R=[0,2\pi]\times[0,2] & \rightarrow&\mathbb{R}^3 \\ (\theta,\rho) & \mapsto&(\rho\cos\theta,\rho\sin\theta,4). \end{array} \end{equation*}$

$\quad$

massimi e minimi vincolati

Figura 10: parametrizzazione di $C$ . Vengono rappresentate alcune linee coordinate per aiutare la visualizzazione della mappa $\psi$ .

$\quad$

Calcoliamo $f\circ\psi$

$\begin{equation*} (f\circ\psi)(\theta,\rho)=f(\rho\cos\theta,\rho\sin\theta,4)=4\rho\cos\theta+\rho\sin\theta+16. \end{equation*}$

Analogamente a quanto detto in precedenza, anche per $f\circ\psi$ il teorema di Weierstrass garantisce l’esistenza del massimo e del minimo su $R$ . Studiamo inizialmente il comportamento di $f\circ\psi$ sull’insieme aperto $R^\circ$ tramite la ricerca dei punti critici, per poi studiare $f\circ\psi$ su $\partial R$ .

Calcoliamo le derivate parziali di $f\circ\psi$ :

$\begin{cases} \dfrac{\partial (f\circ\psi)}{\partial \theta}(\theta,\rho)=-4\rho\sin\theta+\rho\cos\theta\\\\ \dfrac{\partial (f\circ\psi)}{\partial \rho}(\theta,\rho)=4\cos\theta+\sin\theta. \end{cases}$

Dunque

(2) $\begin{equation*} \nabla (f\circ\psi)(\theta,\rho)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} -4\rho\sin\theta+\rho\cos\theta=0\\\\ 4\cos\theta+\sin\theta=0 \end{array} \right.\Leftrightarrow\displaystyle\left\{\begin{array}{l} \rho(\cos\theta-4\sin\theta)=0\\\\ 4\cos\theta+\sin\theta=0. \end{array} \right. \end{equation*}$

Se $(\theta,\rho)\in R^\circ$ , $\rho>0$ e il precedente sistema è equivalente a

$\begin{equation*} \left\{\begin{array}{l} \cos\theta-4\sin\theta=0\\\\ 4\cos\theta+\sin\theta=0. \end{array} \right.\Leftrightarrow\displaystyle\left\{\begin{array}{l} \cos\theta=4\sin\theta\\\\ \cos\theta=-\dfrac{1}{4}\sin\theta, \end{array} \right. \end{equation*}$

che non ammette soluzioni: ciò significa che non ci sono punti critici di $f\circ\psi$ su $R^\circ$ .

Potevamo giungere a questa conclusione osservando che la restrizione di $f$ a $C$ è affine, dunque non può ammettere punti critici.

Per quanto riguarda $\partial R$ , poichè anche $f\circ\psi$ è $2\pi$ -periodica rispetto a $\theta$ , lo stesso discorso fatto in precedenza ci autorizza ad ignorare i lati corrispondenti ai valori $\theta=0$ e $\theta=2\pi$ . I lati rimasti sono $M_1=[0,2\pi]\times\{0\}$ e $M_3=[0,2\pi]\times\{2\}$ . Osserviamo tuttavia che $\psi(M_1)=\{(0,0,4)\}$ , dunque anziché parametrizzare il lato $M_1$ e studiare $f\circ\psi$ attraverso tale parametrizzazione, a mio avviso è più rapido annettere il punto $P_5=(0,0,4)$ tra i possibili candidati e semplicemente valutare $f(P_5)$ .

Infine, per quanto riguarda $M_3$ , osserviamo che $f\circ\psi|_{M_3}=f\circ\varphi|_{L_3}$ , che abbiamo ampiamente studiato in precedenza.

$\quad$

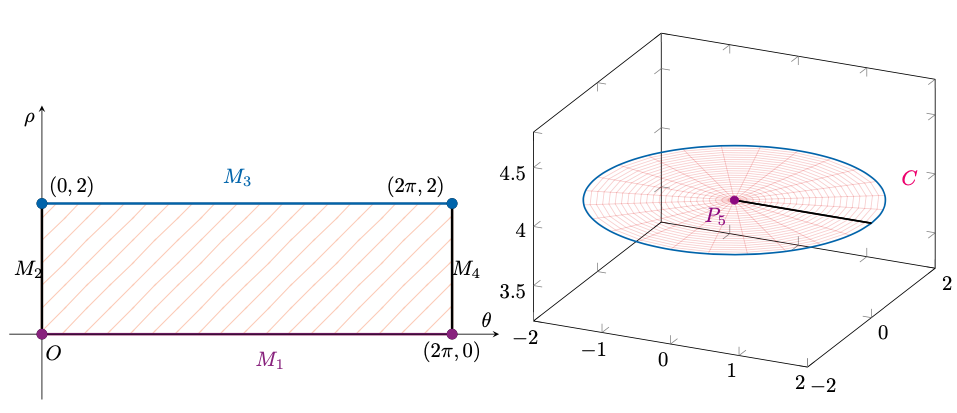
massimi e minimi vincolati

Figura 11: immagine di $\partial R$ attraverso $\varphi$ . Come si evince, non vi è nulla di speciale in $\psi(M_2)=\psi(M_4)$ rappresentati in nero.

$\quad$

Questo conclude lo studio di $\partial A=B\cup C$ .

I possibili candidati ad essere punti di massimo o di minimo di $f$ su $A$ sono i seguenti

$\begin{equation*} \begin{split} &P_1=\left(-\sqrt[3]{\dfrac{16}{17}},-\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},\sqrt[3]{\dfrac{17}{16}}\right),\qquad P_2=(0,0,0),\qquad P_3=\left(\dfrac{8}{\sqrt{17}},\dfrac{2}{\sqrt{17}},4\right),\\ & P_4=\left(-\dfrac{8}{\sqrt{17}},-\dfrac{2}{\sqrt{17}},4\right),\qquad P_5=(0,0,4), \end{split} \end{equation*}$

$\quad$

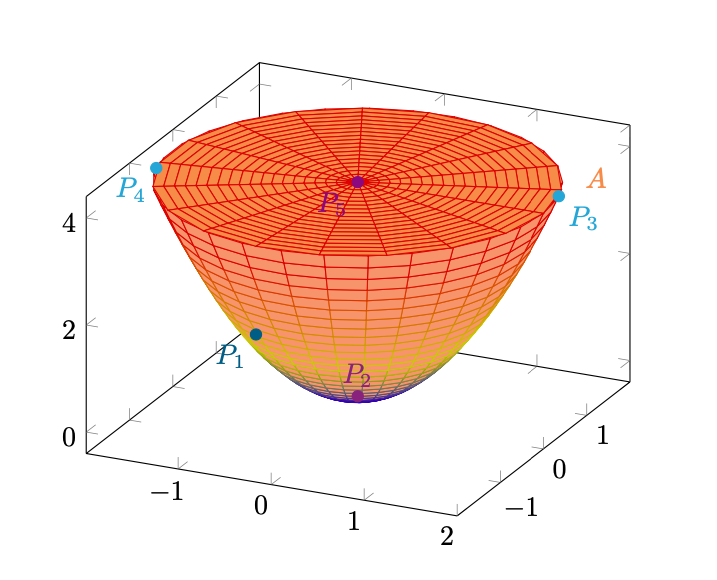
massimi e minimi vincolati

Figura 12: tutti i possibili candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

i cui valori rispetto a $f$ sono

$\begin{equation*} \begin{split} &f(P_1)=-\dfrac{3}{4}\left(\dfrac{17}{2}\right)^{\frac{2}{3}}\approx-3.1,\qquad f(P_2)=0,\qquad f(P_3)=16+2\sqrt{17}\approx 24.2,\\ &f(P_4)=16-2\sqrt{17}\approx 7.8,\qquad f(P_5)=16. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $16+2\sqrt{17}$ , assunto nel punto $P_3=\left(\dfrac{8}{\sqrt{17}},\dfrac{2}{\sqrt{17}},4\right)$ e valore minimo $-\dfrac{3}{4}\left(\dfrac{17}{2}\right)^{\frac{2}{3}}$ , assunto in $P_1=\left(-\sqrt[3]{\dfrac{16}{17}},-\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},\sqrt[3]{\dfrac{17}{16}}\right)$ .

Svolgimento 2.

Occupiamoci della frontiera di $A$ , questa volta utilizzando il metodo dei moltiplicatori di Lagrange, anziché passare attraverso la parametrizzazione.

Possiamo separare la frontiera di $A$ in questo modo:

$\begin{equation*} \partial A=D\sqcup E\sqcup F, \end{equation*}$

dove

$\begin{equation*} D:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2=z, z<4\} \end{equation*}$

$\begin{equation*} E:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2<z, z=4\} \end{equation*}$

$\begin{equation*} F:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2=z=4\}=\overline{D}\cap\overline{E}. \end{equation*}$

$\quad$

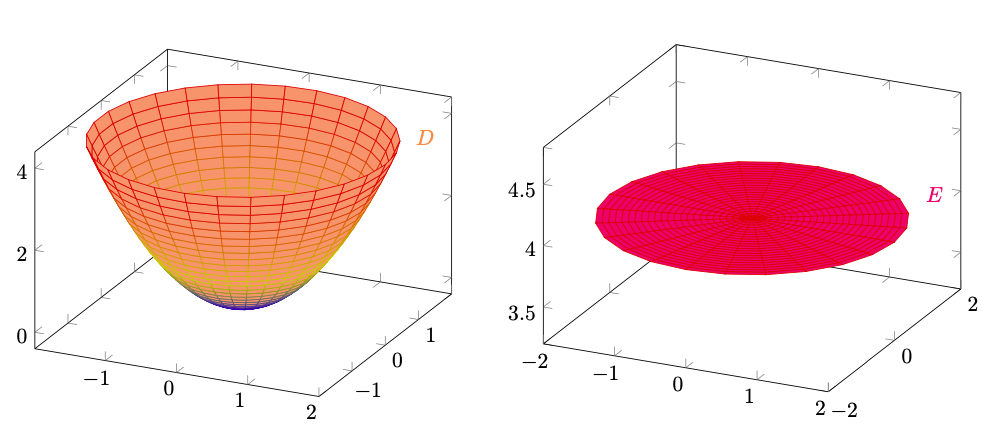
massimi e minimi vincolati

Figura 13: gli insiemi $D$ , $E$ ed $F$ , che compongono $\partial A$ .

$\quad$

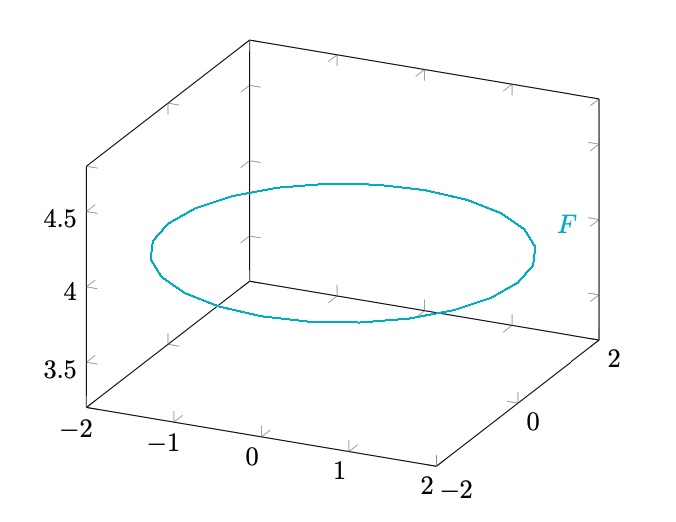
massimi e minimi vincolati

Figura 14: si nota che $F=\overline{D}\cap\overline{E}$ .

$\quad$

Sarà quindi necessario costruire tre Lagrangiane, $\mathcal{L}_D$ , $\mathcal{L}_E$ e $\mathcal{L}_F$ , per ciascun vincolo.

$D)$ Consideriamo la funzione

$\begin{equation*} \begin{array}{rcl} g:\mathbb{R}^3& \rightarrow&\mathbb{R} \\ (x,y,z) & \mapsto& x^2+y^2-z \end{array} \end{equation*}$

e restringiamola al cilindro aperto $\mathcal{C}:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2< 4\}$ . Notiamo che $B=\{(x,y,z)\in\mathcal{C}\mid g(x,y,z)=0\}$ . Abbiamo cioè espresso il vincolo $B$ come luogo di zeri della funzione $g$ . A questo punto possiamo costruire la Lagrangiana $\mathcal{L}_D$

$\begin{equation*} \begin{split} \mathcal{L}_D(x,y,z,\lambda):&=f(x,y,z)-\lambda g(x,y,z)\\ &=4x+y+z^2-\lambda(x^2+y^2-z). \end{split} \end{equation*}$

Troviamo i punti critici della Lagrangiana, secondo il teorema dei moltiplicatori di Lagrange:

$\begin{equation*} \begin{split} \nabla\mathcal{L}_D(x,y,z,\lambda)=(0,0,0,0) \\ & \iff \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}_D}{\partial x}=4-2\lambda x=0 \\\\ \dfrac{\partial\mathcal{L}_D}{\partial y}=1-2\lambda y=0 \\\\ \dfrac{\partial\mathcal{L}_D}{\partial z}=2z+\lambda=0 \\\\ \dfrac{\partial\mathcal{L}_D}{\partial \lambda}=-(x^2+y^2-z)=0 \end{array}\right. \\ &\iff \left\{\begin{array}{l} 4+4zx=0 \\\\ 1+4z y=0 \\\\ \lambda=-2z \\\\ x^2+y^2=z \end{array}\right. \\ & \iff \left\{\begin{array}{l} z=-\dfrac{1}{x} \\\\ z=-\dfrac{1}{4y} \\\\ \lambda=-2z \\\\ x^2+y^2=z. \end{array}\right. \end{split} \end{equation*}$

Le prime due equazioni impongono la relazione $y=\dfrac{x}{4}$ e, considerato che $z=-\dfrac{1}{x}$ , l’ultima equazione diventa

$\begin{equation*} x^2+\dfrac{x^2}{16}=-\dfrac{1}{x}\Leftrightarrow \dfrac{17}{16}x^3=-1\Leftrightarrow x=-\sqrt[3]{\dfrac{16}{17}}. \end{equation*}$

Recuperiamo i valori delle altre coordinate:

$\begin{equation*} y=\dfrac{-\sqrt[3]{\dfrac{16}{17}}}{4}=-\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},\qquad z=-\dfrac{1}{-\sqrt[3]{\dfrac{16}{17}}}=\sqrt[3]{\dfrac{17}{16}}. \end{equation*}$

Abbiamo quindi trovato il punto critico $P_1=\left(-\sqrt[3]{\dfrac{16}{17}},-\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},\sqrt[3]{\dfrac{17}{16}}\right)\in D$ . Osserviamo anche che

$\nabla g(P_1)=\left(-2\sqrt[3]{\dfrac{16}{17}},-2\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},-1\right)\neq(0,0,0).$

$\quad$

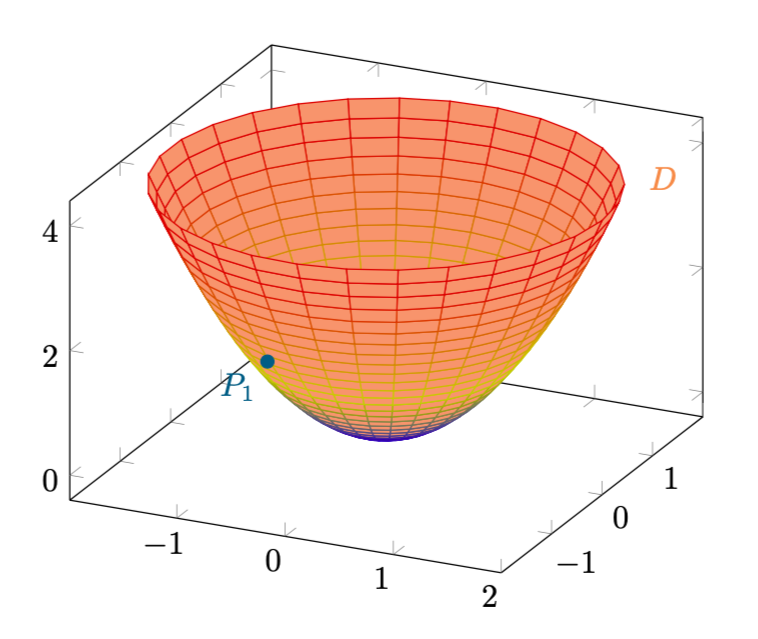
massimi e minimi vincolati

Figura 15: l’unico punto critico su $D$ .

$\quad$

$E)$ Ricordando che $E:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2<z=4\}$ , possiamo esprimere $E$ come luogo di zero della funzione $h:\mathcal{C}\rightarrow\mathbb{R}$ , definita semplicemente $h(x,y,z):=z-4$ . Ripetendo i passi del punto precedente, calcoliamo la Lagrangiana $\mathcal{L}_E$ e i suoi punti critici.

$\begin{equation*} \begin{split} \mathcal{L}_E(x,y,z,\mu):&=f(x,y,z)-\mu h(x,y,z)\\ &=4x+y+z^2-\mu(z-4) \end{split} \end{equation*}$

$\begin{equation*} \nabla\mathcal{L}_E=(0,0,0,0)\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial\mathcal{L}_E}{\partial x}=4=0 \\\\ \dfrac{\partial\mathcal{L}_E}{\partial y}=1=0 \\\\ \dfrac{\partial\mathcal{L}_E}{\partial z}=2z-\mu=0 \\\\ \dfrac{\partial\mathcal{L}_E}{\partial \mu}=-(z-4)=0. \end{array}\right. \end{equation*}$

Il sistema è evidentemente impossibile.

Rimane da studiare il vincolo unidimensionale $F$ , ottenuto come intersezione tra (la chiusura de) i due vincoli $D$ ed $E$ .

Applichiamo 2 sfruttando le funzioni che definivano i precedenti vincoli: $g$ e $h$ . Vale infatti

$\begin{equation*} \begin{split} F&=\{(x,y,z)\in\mathcal{C}\mid x^2+y^2=z, \ z=4\}\\ &=\{(x,y,z)\in\mathcal{C}\mid g(x,y,z)=0, \ h(x,y,z)=0\}. \end{split} \end{equation*}$

Seguendo l’enunciato, costruiamo la Lagrangiana $\mathcal{L}_F:\mathcal{C}\times\mathbb{R}^2\subset\mathbb{R}^5\rightarrow\mathbb{R}$

$\begin{equation*} \begin{split} \mathcal{L}_F(x,y,z,\lambda,\mu):&=f(x,y,z)-\lambda g(x,y,z)-\mu h(x,y,z)\\ &=4x+y+z^2-\lambda(x^2+y^2-z)-\mu(z-4) \end{split} \end{equation*}$

ed, infine, i suoi punti critici:

$\begin{equation*} \nabla\mathcal{L}(x,y,z,\lambda,\mu)=(0,0,0,0,0)\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial\mathcal{L}_F}{\partial x}=4-2\lambda x=0 \\\\ \dfrac{\partial\mathcal{L}_F}{\partial y}=1-2\lambda y=0 \\\\ \dfrac{\partial\mathcal{L}_F}{\partial z}=2z+\lambda+\mu=0 \\\\ \dfrac{\partial\mathcal{L}_F}{\partial \lambda}=-(x^2+y^2-z)=0 \\\\ \dfrac{\partial\mathcal{L}_F}{\partial \mu}=-(z-4)=0. \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \lambda=\dfrac{2}{x} \\\\ \lambda=\dfrac{1}{2y} \\\\ \lambda+\mu=8 \\\\ x^2+y^2=4 \\\\ z=4. \end{array}\right. \end{equation*}$

Confrontando le prime due equazioni troviamo la relazione $x=4y$ . Utilizzandola nella quarta equazione si ricava

$\begin{equation*} 16y^2+y^2=4\Leftrightarrow y=\pm\dfrac{2}{\sqrt{17}}. \end{equation*}$

Ricaviamo anche le altre coordinate:

$\begin{equation*} x=\pm\dfrac{8}{\sqrt{17}},\qquad z=4. \end{equation*}$

Abbiamo quindi trovato altri due punti critici: $P_2=\left(\dfrac{8}{\sqrt{17}},\dfrac{2}{\sqrt{17}},4\right)$ e $P_3=\left(-\dfrac{8}{\sqrt{17}},-\dfrac{2}{\sqrt{17}},4\right)$ . Infine, per accettare i punti trovati, dobbiamo verificare che i gradienti delle funzioni definenti i vincoli non siano linearmente dipendenti in quei punti. Vale

$\begin{equation*} \nabla g(P_2)=\left(\dfrac{16}{\sqrt{17}},\dfrac{4}{\sqrt{17}},-1\right),\qquad \nabla h(P_2)=(0,0,1), \end{equation*}$

$\begin{equation*} \nabla g(P_3)=\left(-\dfrac{16}{\sqrt{17}},-\dfrac{4}{\sqrt{17}},-1\right),\qquad\nabla h(P_3)=(0,0,1). \end{equation*}$

I gradienti delle funzioni non sono linearmente dipendenti nè in $P_2$ nè in $P_3$ , che quindi possono essere accettati.

$\quad$

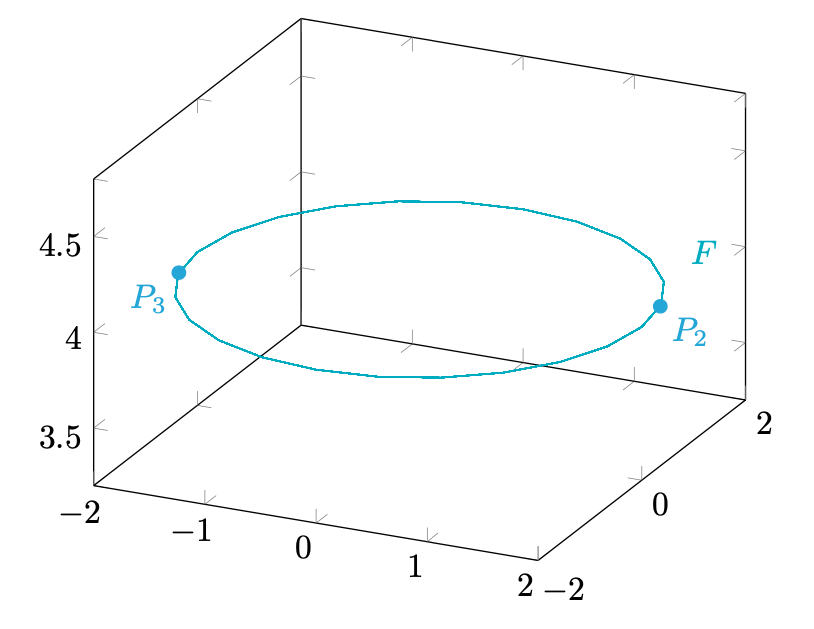
massimi e minimi vincolati

Figura 16: i due punti critici su $F$ .

$\quad$

Abbiamo trovato $3$ candidati ad essere massimo e minimo di $f$ su $A$ :

$\begin{equation*} P_1=\left(-\sqrt[3]{\dfrac{16}{17}},-\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},\sqrt[3]{\dfrac{17}{16}}\right),\qquad P_2=\left(\dfrac{8}{\sqrt{17}},\dfrac{2}{\sqrt{17}},4\right),\qquad P_3=\left(-\dfrac{8}{\sqrt{17}},-\dfrac{2}{\sqrt{17}},4\right). \end{equation*}$

Calcoliamo il valore di $f$ su ciascuno di essi e confrontiamoli.

$\begin{equation*} \begin{gathered} f(P_1)=f\left(-\sqrt[3]{\dfrac{16}{17}},-\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},\sqrt[3]{\dfrac{17}{16}}\right)=-\dfrac{3}{4}\left(\dfrac{17}{2}\right)^{\dfrac{2}{3}}, \\ f(P_2)=f\left(\dfrac{8}{\sqrt{17}},\dfrac{2}{\sqrt{17}},4\right)=16+2\sqrt{17},\\ f(P_3)=f\left(-\dfrac{8}{\sqrt{17}},-\dfrac{2}{\sqrt{17}},4\right)=16-2\sqrt{17}. \end{gathered} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $16+2\sqrt{17}$ , assunto nel punto $P_2=\left(\dfrac{8}{\sqrt{17}},\dfrac{2}{\sqrt{17}},4\right)$ e valore minimo $-\dfrac{3}{4}\left(\dfrac{17}{2}\right)^{\dfrac{2}{3}}$ , assunto in $P_1=\left(-\sqrt[3]{\dfrac{16}{17}},-\dfrac{1}{4}\sqrt[3]{\dfrac{16}{17}},\sqrt[3]{\dfrac{17}{16}}\right)$ .

Esercizio 2 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^3\rightarrow\mathbb{R},$ definita da

$f(x,y,z):=xy^2z,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\left\{(x,y,z)\in\mathbb{R}^3\mid x+z=0, \ \dfrac{x^2}{4}+\dfrac{y^2}{9}+z^2=1\right\}.$

Svolgimento 1.

$\quad$

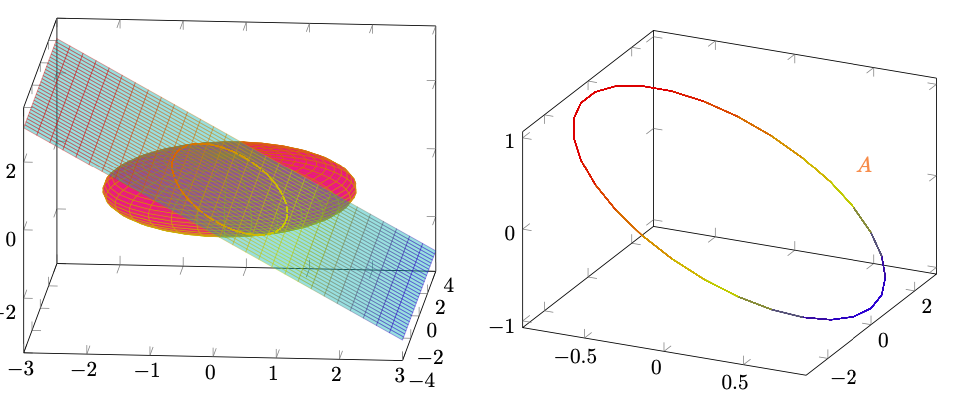
massimi e minimi vincolati

Figura 19: l’insieme $A$ , intersezione delle superfici precedenti.

$\quad$

Osserviamo che $f$ è un monomio, pertanto è una funzione continua su $\mathbb{R}^3$ , mentre l’insieme $A$ è chiuso e limitato. La chiusura segue dal fatto che $A$ è intersezione di controimmagini di insiemi chiusi di $\mathbb{R}$ tramite funzioni continue, mentre per la limitatezza notiamo che esso è intersezione tra un piano e un’ellissoide, quest’ultimo fornisce la limitatezza ad $A$ . Dunque è un chiuso e limitato di $\mathbb{R}^3$ , compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Osserviamo anche che $A^\circ=\emptyset$ , ovvero $A=\partial A$ : l’intero problema, si riduce quindi a studiare il massimo ed il minimo di $f$ attraverso i metodi che abbiamo solitamente utilizzato per studiare la frontiera di $A$ .

Come detto, $A$ è intersezione tra il piano $z=-x$ e l’ellissoide $\dfrac{x^2}{4}+\dfrac{y^2}{9}+z^2=1$ . Cerchiamo una parametrizzazione di questa curva, mettendo a sistema le due equazioni.

$\begin{equation*} \left\{\begin{array}{l} z=-x \\\\ \dfrac{x^2}{4}+\dfrac{y^2}{9}+z^2=1 \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} z=-x \\\\ \dfrac{x^2}{4}+\dfrac{y^2}{9}+x^2=1 \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} z=-x \\\\ \dfrac{x^2}{\left(\dfrac{2}{\sqrt{5}}\right)^2}+\dfrac{y^2}{3^2}=1 \end{array}\right. \end{equation*}$

Possiamo riconoscere che la seconda equazione descrive un’ellisse di semiassi $\dfrac{2}{\sqrt{5}}$ e $3$ , la cui parametrizzazione è

$\begin{equation*} \begin{array}{rcl} \alpha:[0,2\pi]& \rightarrow&\mathbb{R}^2 \\ t & \mapsto&\left(\dfrac{2}{\sqrt{5}}\cos t,3\sin t\right). \end{array} \end{equation*}$

$\quad$

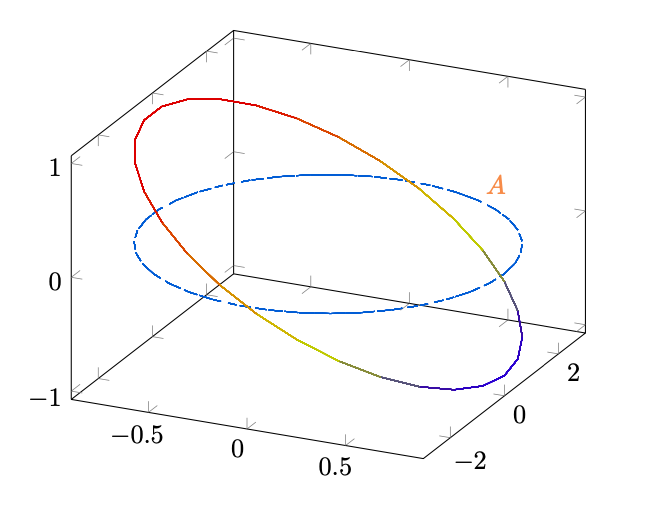
massimi e minimi vincolati

Figura 20: tratteggiata in blu la proiezione di $A$ sul piano $z=0$ .

$\quad$

Essa è la proiezione su $\mathbb{R}^2$ di $A$ , che invece vive in $\mathbb{R}^3$ , più precisamente nel piano $z=-x$ . Ecco dunque che una parametrizzazione di $A$ è la seguente:

$\begin{equation*} \begin{array}{rcl} \beta:[0,2\pi] & \rightarrow&\mathbb{R}^3 \\ t & \mapsto&\left(\dfrac{2}{\sqrt{5}}\cos t,3\sin t,-\dfrac{2}{\sqrt{5}}\cos t\right) \end{array} \end{equation*}$

A questo punto, esplicitiamo $f\circ\beta$ e studiamo il suo massimo e minimo su $[0,2\pi]$ . Essendo $f\circ\beta$ composizione di funzioni continue e l’intervallo $[0,2\pi]$ compatto, il teorema di Weierstrass garantisce nuovamente il massimo ed il minimo di $f\circ\beta$ su $[0,2\pi]$ .

Calcoliamo dunque $f\circ\beta$ :

$\begin{equation*} (f\circ\beta)(t)=f\left(\dfrac{2}{\sqrt{5}}\cos t,3\sin t,-\dfrac{2}{\sqrt{5}}\cos t\right)=\dfrac{2}{\sqrt{5}}\cos t(3\sin t)^2\left(-\dfrac{2}{\sqrt{5}}\cos t\right)=-\dfrac{36}{5}\cos^2t\sin^2t. \end{equation*}$

Seguendo le indicazioni del teorema di Fermat, i possibili punti di massimo e di minimo vanno ricercati tra i punti critici di $f\circ\beta$ nella parte interna del dominio della parametrizzazione, tra gli eventuali punti di non derivabilità e tra gli estremi $\{0\}$ e $\{2\pi\}$ . Essendo $f\circ\beta$ derivabile, non vi sono punti di non derivabilità. Cerchiamo allora i punti critici, ovvero i valori $t\in(0,2\pi)$ tali per cui accade $(f\circ\beta)'(t)=0$ .

$\begin{equation*} \begin{split} &(f\circ\beta)'(t)=\dfrac{72}{5}\cos t\sin t(\sin^2 t-\cos^2 t)=0\Leftrightarrow\\ &\cos t=0\lor\sin t=0\lor \cos t=\sin t\lor\cos t=-\sin t. \end{split} \end{equation*}$

I valori di $t$ per cui ciò accade sono $t_k=\dfrac{k}{4}\pi$ , con $k=1,...,8$ , ovvero

$\begin{equation*} \begin{gathered} t_1=0,\qquad t_2=\dfrac{\pi}{4},\qquad t_3=\dfrac{\pi}{2},\qquad t_4=\dfrac{3}{4}\pi, \\ t_5=\pi,\qquad t_6=\dfrac{5}{4}\pi, \qquad t_7=\dfrac{3}{2}\pi,\qquad t_8=\dfrac{7}{4}\pi. \end{gathered} \end{equation*}$

$\quad$

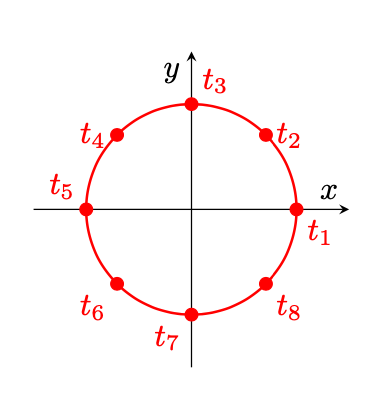
massimi e minimi vincolati

Figura 21: istanti corrispondenti a punti critici della mappa $f\circ\beta$ , la rilettura di $f$ su $A$ .

$\quad$

Nonostante $t_1\notin(0,2\pi)$ , avremo comunque dovuto considerarlo tra gli estremi del dominio, assieme a $t_9=2\pi$ . A questi istanti $t_1$ , corrispondono i punti $P_i=\beta(t_i)$ su $A$ :

$\begin{equation*} \begin{split} &P_1=\beta(0)=\left(\dfrac{2}{\sqrt{5}},0,-\dfrac{2}{\sqrt{5}}\right),\qquad P_2=\beta\left(\dfrac{\pi}{4}\right)=\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right),\qquad P_3=\beta\left(\dfrac{\pi}{2}\right)=(0,3,0),\\ &P_4=\beta\left(\dfrac{3}{4}\pi\right)=\left(-\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right),\qquad P_5=\beta(\pi)=\left(-\dfrac{2}{\sqrt{5}},0,\dfrac{2}{\sqrt{5}}\right),\\ & P_6=\beta\left(\dfrac{5}{4}\pi\right)=\left(-\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right),\\ &P_7=\beta\left(\dfrac{3}{2}\pi\right)=(0,-3,0),\qquad P_8=\beta\left(\dfrac{7}{8}\pi\right)=\left(\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right),\qquad P_9=\beta(2\pi)=P_1. \end{split} \end{equation*}$

$\quad$

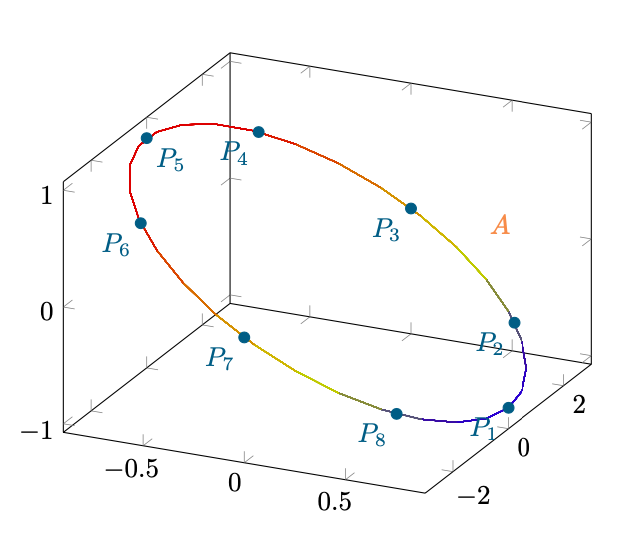
massimi e minimi vincolati

Figura 22: rappresentazione di tutti i candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

Abbiamo trovato 8 candidati ad essere massimo e minimo di $f$ su $A$ . Calcoliamo il loro valore attraverso $f$ e confrontiamoli.

$\begin{equation*} \begin{split} &f(P_1)=f\left(\dfrac{2}{\sqrt{5}},0,-\dfrac{2}{\sqrt{5}}\right)=0,\qquad f(P_2)=f\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)=-\dfrac{9}{5},\qquad f(P_3)=f(0,3,0)=0\\ &f(P_4)=f\left(-\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right)=-\dfrac{9}{5},\qquad f(P_5)=f\left(-\dfrac{2}{\sqrt{5}},0,\dfrac{2}{\sqrt{5}}\right)=0,\qquad f(P_6)=f\left(-\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right)=-\dfrac{9}{5}\\ &f(P_7)=f(0,-3,0)=0,\qquad f(P_8)=f\left(\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)=-\dfrac{9}{5}. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $0$ , assunto nei punti ${P_1=\left(\dfrac{2}{\sqrt{5}},0,-\dfrac{2}{\sqrt{5}}\right)}$ , $P_3=(0,3,0)$ , $P_5=\left(-\dfrac{2}{\sqrt{5}},0,\dfrac{2}{\sqrt{5}}\right)$ e $P_7=(0,-3,0)$ e valore minimo $-\dfrac{9}{5}$ , assunto in $P_2=\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)$ , $P_4=\left(-\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right)$ , $P_6=\left(-\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right)$ e $P_8=\left(\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)$ .

Svolgimento 2.

Risolviamo l’esercizio attraverso il teorema dei moltiplicatori di Lagrange riferendoci ad $A$ come vincolo, il quale può essere espresso come intersezione di due vincoli: $A=\mathcal{P}\cap\mathcal{E}$ , dove $\mathcal{P}$ è il piano

$\begin{equation*} \mathcal{P}:=\{(x,y,z)\in\mathbb{R}^3\mid x+z=0\}, \end{equation*}$

mentre $\mathcal{E}$ è l’ellissoide

$\begin{equation*} \mathcal{E}:=\left\{(x,y,z)\in\mathbb{R}^3\mid \dfrac{x^2}{4}+\dfrac{y^2}{9}+z^2=1\right\}. \end{equation*}$

Osserviamo che $\mathcal{P}=\{(x,y,z)\in\mathbb{R}^3\mid g(x,y,z)=0\}$ e $\mathcal{E}=\{(x,y,z)\in\mathbb{R}^3\mid h(x,y,z)=0\}$ , dove $g(x,y,z):=x+z$ e $h(x,y,z)=\dfrac{x^2}{4}+\dfrac{y^2}{9}+z^2-1$ .

Il teorema dei moltiplicatori di Lagrange, declinato in questo contesto, afferma che, in corrispondenza dei punti di massimo e di minimo relativi di $f$ su $A=\mathcal{P}\cap\mathcal{E}$ succede un fenomeno che possiamo rileggere sia in chiave geometrica che algebrica: geometricamente lo si può interpretare dal fatto che i gradienti di $f$ , $g$ ed $h$ sono complanari. Da un punto di vista algebrico, detto $(x,y,z)$ un punto di estremo relativo, esisteranno $\lambda,\mu\in\mathbb{R}$ tali che

$\begin{equation*} \nabla f(x,y,z)=\lambda\nabla g(x,y,z)+\mu\nabla h(x,y,z). \end{equation*}$

Per questo motivo, costruiamo la Lagrangiana $\mathcal{L}:\mathbb{R}^5\rightarrow\mathbb{R}$ , definita tramite

$\begin{equation*} \mathcal{L}(x,y,z,\lambda,\mu):=f(x,y,z)-\lambda g(x,y,z)-\mu h(x,y,z). \end{equation*}$

Il teorema dei moltiplicatori di Lagrange garantisce che i punti critici di $\mathcal{L}$ corrisponderanno esattamente agli estremi relativi di $f$ su $A$ . Calcoliamo la Lagrangiana:

$\begin{equation*} \begin{split} \mathcal{L}(x,y,z,\lambda,\mu):=xy^2z-\lambda(x+z)-\mu\left(\dfrac{x^2}{4}+\dfrac{y^2}{9}+z^2-1\right). \end{split} \end{equation*}$

Andiamo a cercare i suoi punti critici, risolvendo con attenzione il seguente sistema

$\begin{equation*} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}}{\partial x}=y^2z-\lambda-\dfrac{1}{2}\mu x=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial y}=2xyz-\dfrac{2}{9}\mu y=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial z}=xy^2-\lambda-2\mu z=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \lambda}=-(x+z)=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \mu}=-\left(\dfrac{x^2}{4}+\dfrac{y^2}{9}+z^2-1\right)=0. \\\\ \end{array}\right. \end{equation*}$

Dalla quarta equazione troviamo la relazione $z=-x$ da utilizzare in ciascuna delle altre equazioni:

$\begin{equation*} \left\{\begin{array}{l} -xy^2-\lambda-\dfrac{1}{2}\mu x=0 \\\\ -2x^2y-\dfrac{2}{9}\mu y=0 \\\\ xy^2-\lambda+2\mu x=0 \\\\ z=-x \\\\ \dfrac{x^2}{4}+\dfrac{y^2}{9}+x^2=1 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} -xy^2-\lambda-\dfrac{1}{2}\mu x=0 \\\\ y\left(x^2+\dfrac{1}{9}\mu\right)=0 \\\\ xy^2-\lambda+2\mu x=0 \\\\ z=-x \\\\ \dfrac{5}{4}x^2+\dfrac{y^2}{9}=1. \\\\ \end{array}\right. \end{equation*}$

La seconda equazione si annulla se $y=0$ oppure se $\mu=-9x^2$ . Supponiamo inizialmente $y=0$ , l’ultima equazione diventa

$\begin{equation*} \dfrac{5}{4}x^2=1\Leftrightarrow x=\pm\dfrac{2}{\sqrt{5}} \end{equation*}$

e, ricordando che $z=-x$ , troviamo $z=\mp\dfrac{2}{\sqrt{5}}$ . Abbiamo, al momento, trovato due punti critici:

$\begin{equation*} P_1=\left(\dfrac{2}{\sqrt{5}},0,-\dfrac{2}{\sqrt{5}}\right)\qquad e \qquad P_2=\left(-\dfrac{2}{\sqrt{5}},0,\dfrac{2}{\sqrt{5}}\right). \end{equation*}$

A questo punto, possiamo supporre $y\neq0$ e dunque assumere $\mu=-9x^2$ . Inseriamo questa informazione nel sistema, dopo aver sostituito la prima equazione con la somma tra di essa e la terza equazione:

$\begin{equation*} \left\{\begin{array}{l} -2\lambda+\dfrac{3}{2}\mu x=0 \\\\ y\left(x^2+\dfrac{1}{9}\mu\right)=0 \\\\ xy^2-\lambda+2\mu x=0 \\\\ z=-x \\\\ \dfrac{5}{4}x^2+\dfrac{y^2}{9}=1 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} -2\lambda-\dfrac{27}{2} x^3=0 \\\\ \mu=-9x^2 \\\\ xy^2-\lambda-18x^3=0 \\\\ z=-x \\\\ \dfrac{5}{4}x^2+\dfrac{y^2}{9}=1. \\\\ \end{array}\right. \end{equation*}$

Dalla prima equazione risulta

$\begin{equation*} \lambda=-\dfrac{27}{4}x^3, \end{equation*}$

che, inserito nella terza equazione, dà

$\begin{equation*} xy^2+\dfrac{27}{4}x^3-18x^3=0\Leftrightarrow x\left(y^2-\dfrac{45}{4}x^2\right)=0. \end{equation*}$

Quest’ultima equazione è soddisfatta se $x=0$ , oppure se $y^2=\dfrac{45}{4}x^2$ , cioè $y=\pm\dfrac{3\sqrt{5}}{2}x$ . Ricaviamo velocemente le soluzioni derivanti da $x=0$ : l’ultima equazione risulta

$\begin{equation*} \dfrac{y^2}{9}=1\Leftrightarrow y=\pm3. \end{equation*}$

Poiche $z=-x=-0$ , abbiamo trovato altri due punti critici:

$\begin{equation*} P_3=(0,3,0)\qquad e \qquad P_4=(0,-3,0). \end{equation*}$

Infine, indipendentemente dal segno che sussiste nella relazione tra $x$ ed $y$ , inseriamo $y^2=\dfrac{45}{4}x^2$ nell’ultima equazione per ricavare le ultime soluzioni del sistema:

$\begin{equation*} \dfrac{5}{4}x^2+\dfrac{\dfrac{45}{4}x^2}{9}=1\Leftrightarrow\dfrac{5}{4}x^2+\dfrac{5}{4}x^2=1\Leftrightarrow\dfrac{5}{2}x^2=1\Leftrightarrow x=\pm\sqrt{\dfrac{2}{5}}. \end{equation*}$

Ricaviamo le altre coordinate attraverso le precedenti relazioni, facendo attenzione a tutte le possibili combinazioni di segni: poichè $z=-x$

$\begin{equation*} x=\pm\sqrt{\dfrac{2}{5}}\Rightarrow z=\mp\sqrt{\dfrac{2}{5}}; \end{equation*}$

inoltre, da $y=\pm\dfrac{3\sqrt{5}}{2}x$ ,

$\begin{equation*} x=\sqrt{\dfrac{2}{5}}\Rightarrow y=\pm\dfrac{3\sqrt{5}}{2}\sqrt{\dfrac{2}{5}}=\pm\dfrac{3\sqrt{2}}{2}, \end{equation*}$

$\begin{equation*} x=-\sqrt{\dfrac{2}{5}}\Rightarrow y=\pm\dfrac{3\sqrt{5}}{2}\sqrt{\dfrac{2}{5}}=\pm\dfrac{3\sqrt{2}}{2}. \end{equation*}$

Abbiamo quindi trovato altri quattro punti critici:

$\begin{equation*} \begin{split} &P_5=\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right),\qquad P_6=\left(\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)\\ &P_7=\left(-\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right),\qquad P_8=\left(-\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right). \end{split} \end{equation*}$

Abbiamo trovato 8 candidati ad essere massimo e minimo di $f$ su $A$ .

Mettiamo in evidenza una sostanziale differenza che sussiste tra i primi quattro candidati e gli altri. I punti $P_1$ , $P_2$ , $P_3$ e $P_4$ sono in realtà punti critici di $f$ che si trovano su $A$ . Il teorema dei moltiplicatori di Lagrange rileva banalmente anche gli stessi punti critici di $f$ ¹ appartenenti al vincolo, poiché il vettore nullo è complanare ad ogni coppia di vettori: basta prendere $\lambda=\mu=0$ per ottenere la combinazione lineare banale

$0=\nabla f(x,y,z)=0\nabla g(x,y,z)-0\nabla h(x,y,z).$

I punti $P_5$ , $P_6$ , $P_7$ e $P_8$ sono conclusioni non banali del teorema dei moltiplicatori di Lagrange. Dimostriamo esplicitamente che in tali punti il gradiente di $f$ è complanare con quello di $g$ ed $h$ , ovvero che esiste una combinazione lineare (non nulla) di $\nabla g$ e $\nabla h$ che ricava $\nabla f$ . Iniziamo da $P_5$ :

$\begin{equation*} \begin{split} \nabla f(x,y,z)=(y^2z,2xyz,xy^2)\Rightarrow&\nabla f(P_5)=\nabla f\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)=\left(-\dfrac{9}{\sqrt{10}},-\dfrac{6\sqrt{2}}{5},\dfrac{9}{\sqrt{10}}\right);\\ \nabla g(x,y,z)=(1,0,-1)\Rightarrow&\nabla g(P_5)=\nabla g\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)=(1,0,1);\\ \nabla h(x,y,z)=\left(\dfrac{x}{2},\dfrac{2}{9}y,2z\right)\Rightarrow&\nabla h(P_5)=\nabla h\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)=\left(\dfrac{1}{\sqrt{10}},\dfrac{\sqrt{2}}{3},-\dfrac{4}{\sqrt{10}}\right). \end{split} \end{equation*}$

A questo punto dovremo trovare $\lambda,\mu\in\mathbb{R}$ tali che $\nabla f(P_5)=\lambda \nabla g(P_5)+\mu\nabla h(P_5)$ . Osserviamo che essendo vettori in $\mathbb{R}^3$ , si tratta di un sistema con tre equazioni e due incognite, ovvero un sistema sovradeterminato. Sarà proprio il fatto che $P_5$ è soluzione del teorema di Lagrange a rendere risolvibile il sistema risolvibile.

Dobbiamo dunque trovare $\lambda,\mu\in\mathbb{R}$ tali che

$\begin{equation*} \left\{\begin{array}{l} -\dfrac{9}{\sqrt{10}}=\lambda +\mu\dfrac{1}{\sqrt{10}}\\\\ -\dfrac{6\sqrt{2}}{5}=\mu\dfrac{\sqrt{2}}{3}\\\\ \dfrac{9}{\sqrt{10}}=\lambda-\mu\dfrac{4}{\sqrt{10}}. \end{array}\right. \end{equation*}$

Dalla seconda equazione troviamo subito $\mu=-\dfrac{18}{5}$ . Inseriamo il valore di $\mu$ nella prima equazione per calcolare $\lambda$ :

$\begin{equation*} -\dfrac{9}{\sqrt{10}}=\lambda -\dfrac{18}{5\sqrt{10}}\Leftrightarrow\lambda=\dfrac{-45+18}{5\sqrt{10}}=-\dfrac{27}{5\sqrt{10}}. \end{equation*}$

A questo punto vediamo se la terza equazione è soddisfatta. Ciò implicherebbe la complanarità dei tre vettori gradienti in $P_5$ :

$\begin{equation*} \dfrac{9}{\sqrt{10}}=\lambda-\mu\dfrac{4}{\sqrt{10}}=-\dfrac{27}{5\sqrt{10}}+\dfrac{18}{5}\dfrac{4}{\sqrt{10}}=\dfrac{45}{5\sqrt{10}}=\dfrac{9}{\sqrt{10}}. \end{equation*}$

$\quad$

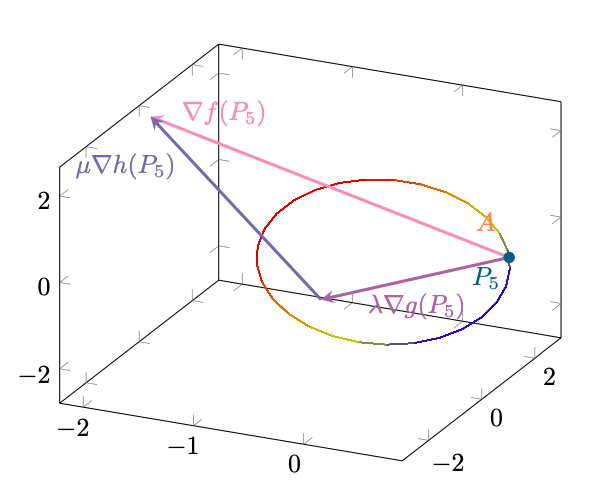
massimi e minimi vincolati

Figura 23: illustrazione della complanarità dei gradienti di $f$ , $g$ e $h$ in $P_5$ . La stessa situazione si verifica per $P_6$ , $P_7$ e $P_8$ .

$\quad$

La complanarità dei punti $P_6$ , $P_7$ e $P_8$ si dimostra in modo del tutto analogo.

Giunti a questo punto, non ci resta che calcolare il valore attraverso $f$ degli otto candidati e confrontarli.

$\begin{equation*} \begin{split} &f(P_1)=f\left(\dfrac{2}{\sqrt{5}},0,-\dfrac{2}{\sqrt{5}}\right)=0,\qquad f(P_2)=f\left(-\dfrac{2}{\sqrt{5}},0,\dfrac{2}{\sqrt{5}}\right)=0,\qquad f(P_3)=f(0,3,0)=0\\ &f(P_4)=f(0,-3,0)=0,\qquad f(P_5)=f\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)=-\dfrac{9}{5}, \qquad f(P_6)=f\left(\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)=-\dfrac{9}{5}\\ &f(P_7)=f\left(-\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right)=-\dfrac{9}{5},\qquad f(P_8)=f\left(-\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right)=-\dfrac{9}{5}. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $0$ , assunto nei punti $P_1=\left(\dfrac{2}{\sqrt{5}},0,-\dfrac{2}{\sqrt{5}}\right)$ , $P_2=\left(-\dfrac{2}{\sqrt{5}},0,\dfrac{2}{\sqrt{5}}\right)$ , $P_3=(0,3,0)$ e $P_4=(0,-3,0)$ e valore minimo $-\dfrac{9}{5}$ , assunto in $P_5=\left(\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)$ , $P_6=\left(\sqrt{\dfrac{2}{5}},-\dfrac{3\sqrt{2}}{2},-\sqrt{\dfrac{2}{5}}\right)$ , $P_7=\left(-\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right)$ e $P_8=\left(-\sqrt{\dfrac{2}{5}},\dfrac{3\sqrt{2}}{2},\sqrt{\dfrac{2}{5}}\right)$ .

Tra le ipotesi del teorema dei moltiplicatori di Lagrange vi è che il punto in questione non dev’essere punto critico delle funzioni definenti i vincoli, ma non vi è alcuna ipotesi riguardo il gradiente della funzione di cui si sta calcolando massimo e minimo. Al contrario, ogni suo punto critico soddisfaciente l’equazione del vincolo sarà in particolare punto critico della Lagrangiana con moltiplicatori nulli. ↩

Esercizio 3 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^3\rightarrow\mathbb{R},$ definita da

$f(x,y,z):=x^2+y^2+y(z+x-1),$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\left\{(x,y,z)\in\mathbb{R}^3\mid x+y+z=0, \ x^2+y^2=1\right\}.$

Svolgimento 1.

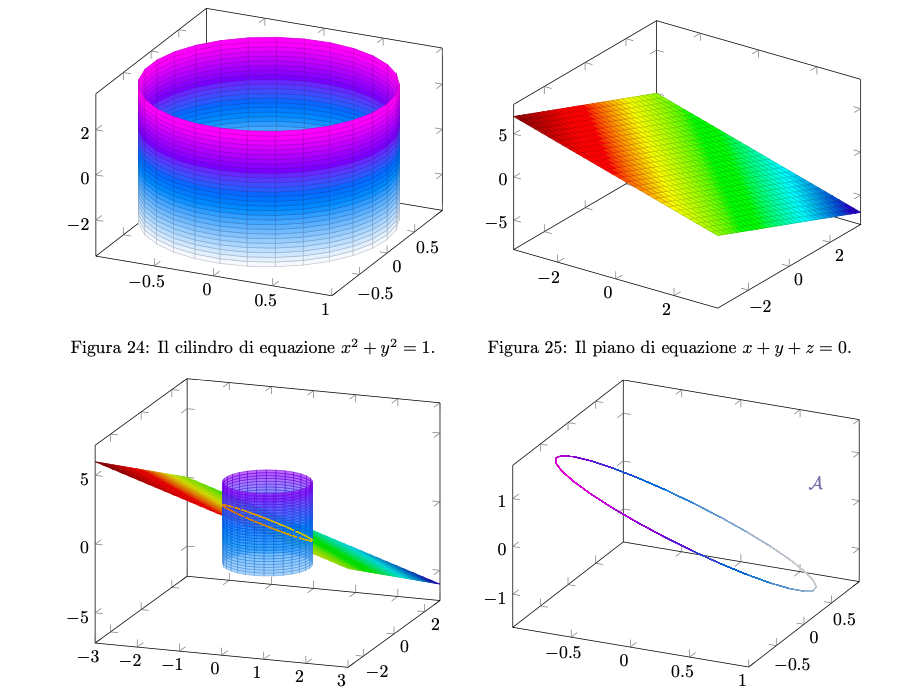
Figura 26: $A$ è l’ellisse intersezione tra il cilindro e il piano.

$\quad$

Osserviamo che $f$ è un polinomio, pertanto è una funzione continua su $\mathbb{R}^3$ , mentre l’insieme $A$ è chiuso e limitato. La chiusura segue dal fatto che $A$ è intersezione di controimmagini di insiemi chiusi di $\mathbb{R}$ tramite funzioni continue, mentre per la limitatezza dimostriamo che esso è contenuto in una palla di raggio $R=\sqrt{3}$ . Sia infatti $(x,y,z)\in A$ qualsiasi, stimiamo il quadrato della sua norma:

$\begin{equation*} ||(x,y,z)||^2=x^2+y^2+z^2=1+z^2, \end{equation*}$

dove abbiamo sfruttato il fatto che su $A$ vale $x^2+y^2=1$ .

L’altra relazione definente $A$ implica $z=-x-y$ , che inserita nella precedente equazione ci dà

$\begin{equation*} ||(x,y,z)||^2=1+x^2+y^2-2xy=2-2xy. \end{equation*}$

Ora non ci resta che valutare il contributo di $h(x,y):=xy$ su $A$ . Possiamo parametrizzare la proiezione $A'=\pi(A)\subset\mathbb{R}^2$ di $A$ sul piano $xy$ mediante

$\begin{equation*} \gamma(t):=(\cos t,\sin t), \qquad t\in[0,2\pi], \end{equation*}$

dunque stimare $h$ su $A$ studiando $h\circ\gamma$ su $[0,2\pi]$ :

$\begin{equation*} (h\circ\gamma)(t)=\cos t\sin t, \end{equation*}$

$\begin{equation*} \begin{split} &(h\circ\gamma)'(t)=\cos^2(t)-\sin^2(t)=(\cos t+\sin t)(\cos t-\sin t)=0\Leftrightarrow\\ &\Leftrightarrow \cos t=\pm\sin t\Leftrightarrow t_1=\dfrac{\pi}{4}\lor t_2=\dfrac{3}{4}\pi\lor t_3=\dfrac{5}{4}\pi\lor t_4=\dfrac{7}{4}\pi. \end{split} \end{equation*}$

Su ciascuno di questi valori $t_k$ osserviamo che $|h(t_k)|=\dfrac{1}{2}$ . Ciò significa che $-\dfrac{1}{2}\leq xy\leq\dfrac{1}{2}$ . Tale informazione può essere utilizzata per stimare definitivamente la norma di $(x,y,z)$ :

$\begin{equation*} ||(x,y,z)||^2=2-2xy\leq2+1=3 \end{equation*}$

e questo conclude la dimostrazione del fatto che $A$ è un insieme limitato, contenuto in una sfera di raggio $R=\sqrt{3}$ .

Per il teorema di Heine-Borel $A$ è un insieme compatto di $\mathbb{R}^3$ . Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Notiamo che $A^\circ=\emptyset$ , cioè $A$ coincide con la sua frontiera. Utilizziamo il teorema dei moltiplicatori di Lagrange, osservando che $A$ è intersezione di due vincoli: $A=\mathcal{C}\cap\mathcal{P}$ , dove $\mathcal{C}$ è il cilindro

$\begin{equation*} \mathcal{C}:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2=1\} \end{equation*}$

e $\mathcal{P}$ è il piano di equazione $x+y+z=0$ .

$\quad$

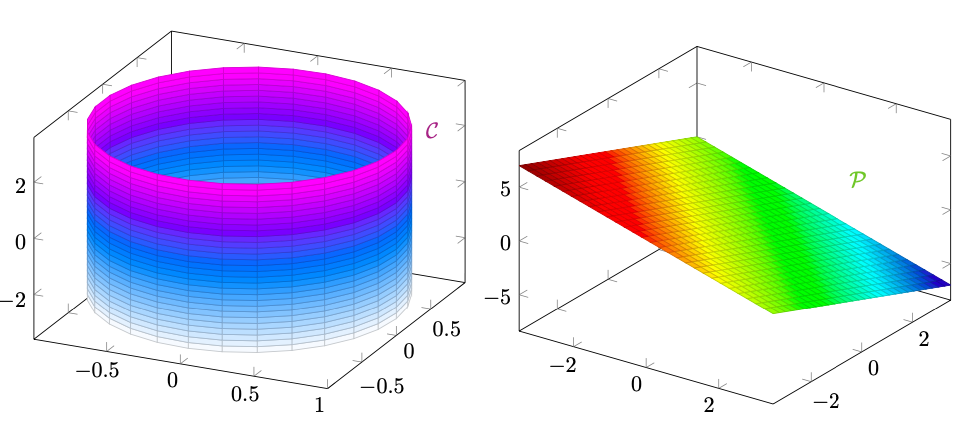
massimi e minimi vincolati

$\quad$

Esprimiamo i vincoli come luoghi di zeri di funzioni per applicare il metodo dei moltiplicatori:

$\begin{equation*} \mathcal{C}:=\{(x,y,z)\in\mathbb{R}^3\mid g(x,y,z)=0\}, \end{equation*}$

con

$\begin{equation*} g(x,y,z):=x^2+y^2-1 \end{equation*}$

$\begin{equation*} \mathcal{P}:=\{(x,y,z)\in\mathbb{R}^3\mid h(x,y,z)=0\}, \end{equation*}$

con

$\begin{equation*} h(x,y,z):=x+y+z. \end{equation*}$

$\begin{equation*} \nabla f(x,y,z)=\lambda\nabla g(x,y,z)+\mu\nabla h(x,y,z). \end{equation*}$

Per questo motivo, costruiamo la Lagrangiana $\mathcal{L}:\mathbb{R}^5\rightarrow\mathbb{R}$ , definita tramite

$\begin{equation*} \mathcal{L}(x,y,z,\lambda,\mu):=f(x,y,z)-\lambda g(x,y,z)-\mu h(x,y,z). \end{equation*}$

Il teorema dei moltiplicatori di Lagrange garantisce che i punti critici di $\mathcal{L}$ corrisponderanno esattamente agli estremi relativi di $f$ su $A$ . Infatti, calcolare i punti critici di $\mathcal{L}$ significa risolvere il sistema

$\begin{equation*} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}}{\partial x}=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial y}=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial z}=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \lambda}=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \mu}=0 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial f}{\partial x}-\lambda\dfrac{\partial g}{\partial x}-\mu\dfrac{\partial h}{\partial x}=0 \\\\ \dfrac{\partial f}{\partial y}-\lambda\dfrac{\partial g}{\partial y}-\mu\dfrac{\partial h}{\partial y}=0 \\\\ \dfrac{\partial f}{\partial z}-\lambda\dfrac{\partial g}{\partial z}-\mu\dfrac{\partial h}{\partial z}=0 \\\\ g=0 \\\\ h=0.\\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \nabla f=\lambda\nabla g+\mu\nabla h \\\\\\ g=0 \\\\ h=0.\\\\ \end{array}\right. \end{equation*}$

Le prime tre equazioni affermano proprio che $\nabla f$ appartiene al piano individuato da $\nabla g$ e $\nabla h$ . Le ultime equazioni assicurano che il punto si trovi su $\partial A=\{g\equiv 0\}\cap\{h\equiv0\}$ .

Calcoliamo la Lagrangiana:

$\begin{equation*} \begin{split} \mathcal{L}(x,y,z,\lambda,\mu):=x^2+y^2+y(z+x-1)-\lambda(x^2+y^2)-\mu(x+y+z). \end{split} \end{equation*}$

Andiamo a cercare i suoi punti critici, risolvendo con attenzione il seguente sistema

$\begin{equation*} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}}{\partial x}=2x+y-2\lambda x-\mu=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial y}=2y+z+x-1-2\lambda y-\mu=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial z}=y-\mu=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \lambda}=-(x^2+y^2-1)=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \mu}=-\left(x+y+z\right)=0 \\\\ \end{array}\right. \end{equation*}$

La terza equazione impone immediatamente $\mu=y$ , che sostituiamo laddove è utile:

$\begin{equation*} \left\{\begin{array}{l} 2x+y-2\lambda x-y=0 \\\\ 2y+z+x-1-2\lambda y-y=0 \\\\ \mu=y \\\\ x^2+y^2-1=0 \\\\ x+y+z=0. \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} 2x(1-\lambda)=0 \\\\ y+z+x-1-2\lambda y=0 \\\\ \mu=y \\\\ x^2+y^2-1=0 \\\\ x+y+z=0. \\\\ \end{array}\right. \end{equation*}$

Confrontando l’ultima equazione con la seconda, possiamo riscrivere il sistema in questo modo:

$\begin{equation*} \left\{\begin{array}{l} x(1-\lambda)=0 \\\\ -1-2\lambda y=0 \\\\ \mu=y \\\\ x^2+y^2-1=0 \\\\ x+y+z=0. \\\\ \end{array}\right. \end{equation*}$

A questo punto, osserviamo la prima equazione: essa è soddisfatta solamente se $x=0$ oppure se $\lambda =1$ . Se supponiamo $x=0$ , il sistema si risolve immediatamente

$\begin{equation*} \left\{\begin{array}{l} x=0 \\\\ \lambda y=\mp\dfrac{1}{2} \\\\ \mu=\pm1 \\\\ y^2=\pm1 \\\\ z=\mp1. \\\\ \end{array}\right. \end{equation*}$

Abbiamo quindi trovato i primi due punti critici della Lagrangiana:

$P_1=(0,1,-1)\qquad \text{e}\qquad P_2=(0,-1,1).$

Supponiamo invece $\lambda=1$ , da cui risulta

$\begin{equation*} \left\{\begin{array}{l} \lambda=1 \\\\ -1-2 y=0 \\\\ \mu=y \\\\ x^2+y^2-1=0 \\\\ x+y+z=0 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \lambda=1 \\\\ y=-\dfrac{1}{2} \\\\ \mu=-\dfrac{1}{2} \\\\ x^2+\dfrac{1}{4}-1=0 \\\\ x-\dfrac{1}{2}+z=0 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \lambda=1 \\\\ y=-\dfrac{1}{2} \\\\ \mu=-\dfrac{1}{2} \\\\ x=\pm\dfrac{\sqrt{3}}{2} \\\\ z=\dfrac{1\mp\sqrt{3}}{2}. \\\\ \end{array}\right. \end{equation*}$

Abbiamo trovato altri due punti critici, ovvero

$\begin{equation*} P_3=\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right)\qquad\text{e}\qquad P_4=\left(\dfrac{-\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right). \end{equation*}$

Abbiamo trovato quattro candidati ad essere punti di massimo e di minimo di $f$ su $A$ .

$\quad$

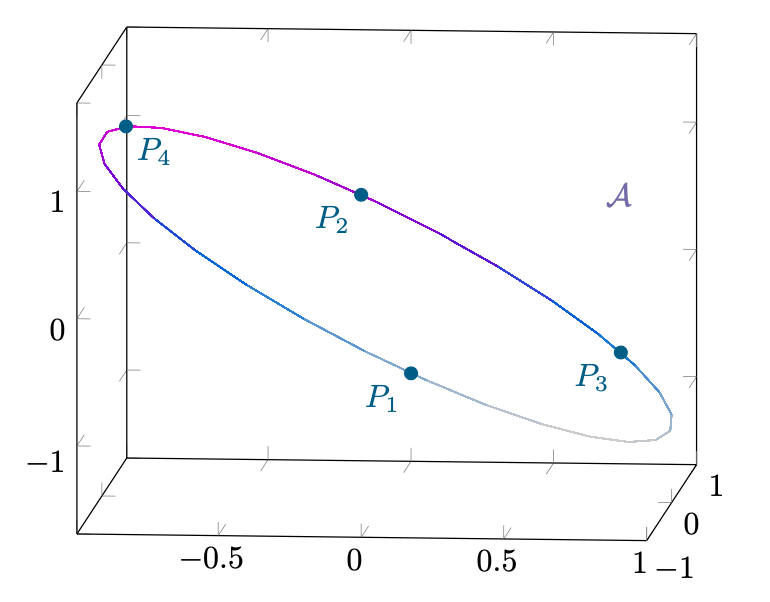
massimi e minimi vincolati

Figura 27: tutti i candidati ad essere punti di massimo e di minimo di $f$ su $A$ .

$\quad$

Calcoliamo i loro valori tramite $f$ e confrontiamoli:

$\begin{equation*} \begin{split} f(P_1)&=f(0,1,-1)=-1,\qquad f(P_2)=f(0,-1,1)=1,\\ f(P_3)&=f\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right)=\dfrac{5}{4} \qquad\text{e}\qquad f(P_4)=f\left(\dfrac{-\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right)=\dfrac{5}{4}. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\dfrac{5}{4}$ , assunto nei punti $P_3=\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right)$ e $P_4=\left(\dfrac{-\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right)$ e valore minimo $-1$ , assunto in $P_1=(0,1,-1)$ .

Svolgimento 2.

Possiamo risolvere il problema in maniera puramente algebrica. Infatti, utilizzando le equazioni dei vincoli

$\begin{equation*} \left\{\begin{array}{l} x^2+y^2=1\\\\ x+y+z=0, \end{array}\right. \end{equation*}$

la funzione diventa

$\begin{equation*} f(x,y,z)=x^2+y^2+y(z+x+y-y-1)=1+y(-y-1)=-y^2-y+1,\qquad\text{con }y\in[-1,1]. \end{equation*}$

L’espressione della funzione si semplifica estremamente, risultando funzione della sola variabile $y$ . Definiamo (con abuso di notazione) la funzione di una singola variabile

$\begin{equation*} \begin{array}{rcl} f:[-1,1]\subset\mathbb{R} & \rightarrow&\mathbb{R} \\ y & \mapsto&-y^2-y+1 \end{array} \end{equation*}$

Possiamo pertanto studiare il massimo ed il minimo di $f$ sull’intervallo $[-1,1]$ . Tale problema ha sicuramente soluzione, grazie al teorema di Weierstrass, essendo $f$ continua e $[-1,1]$ compatto. Una volta trovati i valori di $y$ basterà trovare i punti corrispondenti appartenenti al vincolo.

A tal fine, essendo $f$ anche differenziabile, il teorema di Fermat ci fornisce uno strumento per riconoscere eventuali punti di massimo o minimo di $f$ per quanto riguarda l’insieme aperto $(-1,1)=[-1,1]^\circ$ : tali punti, saranno in particolare punti critici di $f$ . Nulla possiamo invece dire su $\partial[-1,1]=\{-1\}\cup\{1\}$ : questi due valori andranno studiati separatamente.

Come indicato dal teorema di Fermat, studiamo i punti critici di $f$ , ovvero i valori $y\in(-1,1)$ tali che $f'(y)=0$ :

$\begin{equation*} f'(y)=-2y-1=0\Leftrightarrow y=-\dfrac{1}{2}. \end{equation*}$

Abbiamo dunque trovato il valore $y=-\dfrac{1}{2}$ , a cui corrispondono i punti soluzione del sistema precedente, con $y=-\dfrac{1}{2}$ :

$\begin{equation*} \left\{\begin{array}{l} x^2+\dfrac{1}{4}=1\\\\ x-\dfrac{1}{2}+z=0, \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} x=\pm\dfrac{\sqrt{3}}{2}\\\\ z=\dfrac{1\mp\sqrt{3}}{2}. \end{array}\right. \end{equation*}$

Abbiamo quindi trovato due candidati:

$\begin{equation*} P_1=\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right)\qquad\text{e}\qquad P_2=\left(\dfrac{-\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right). \end{equation*}$

Dobbiamo aggiungere manualmente i punti corrispondenti agli estremi $y=\pm1$ , poiché non abbiamo alcun motivo per escluderli. Risolviamo nuovamente il sistema con $y=\pm1$ :

$\begin{equation*} \left\{\begin{array}{l} x^2+1=1\\\\ x\pm1+z=0, \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} x=0\\\\ z=\mp1 \end{array}\right. \end{equation*}$

Abbiamo trovato altri due candidati

$\begin{equation*} P_3=(0,1,-1)\qquad \text{e} \qquad P_4=(0,-1,1). \end{equation*}$

Calcoliamo i loro valori tramite $f$ e confrontiamoli:

$\begin{equation*} \begin{split} f(P_1)&=f\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right)=\dfrac{5}{4},\qquad f(P_2)=f\left(\dfrac{-\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right)=\dfrac{5}{4},\\ f(P_3)&=f(0,1,-1)=-1 \qquad\text{e}\qquad f(P_4)=f(0,-1,1)=1. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\dfrac{5}{4}$ , assunto nei punti $P_1=\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right)$ e $P_2=\left(\dfrac{-\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right)$ e valore minimo $-1$ , assunto in $P_3=(0,1,-1)$ .

Svolgimento 3.

Il terzo modo per risolvere il problema sfrutta l’esplicita prametrizzazione di $A$ . Per trovarla, indaghiamo il sistema contenente le equazioni dei vincoli:

$\begin{equation*} \left\{\begin{array}{l} x^2+y^2=1\\\\ x+y+z=0, \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} x^2+y^2=1\\\\ z=-x-y. \end{array}\right. \end{equation*}$

La prima equazione suggerisce di parametrizzare le prime due variabili attraverso le coordinate polari: $(x,y)=(\cos\theta,\sin\theta)$ , con $\theta\in[0,2\pi]$ , mentre dall’ultima equazione otteniamo $z=-\cos\theta-\sin\theta$ . Ecco dunque ottenuta la parametrizzazione di $A=\gamma([0,2\pi])$ , con

$\begin{equation*} \begin{array}{rcl} \gamma:[0,2\pi]&\rightarrow&\mathbb{R}^3 \\ \theta&\mapsto&(\cos\theta,\sin\theta,-\cos\theta-\sin\theta). \end{array} \end{equation*}$

$\quad$

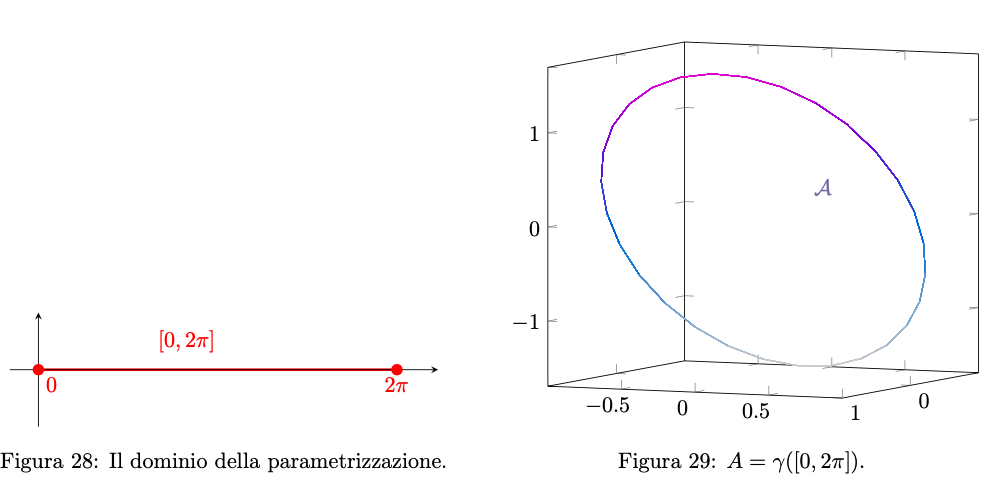
massimi e minimi vincolati

$\quad$

A questo punto, basterà studiare la funzione composta $f\circ\gamma$ sull’intervallo $[0,2\pi]$ . Essendo $f$ e $\gamma$ continue, anche la loro composizione lo è, inoltre $[0,2\pi]$ è un insieme compatto, quindi per il teorema di Weierstrass troveremo il massimo ed il minimo di $f\circ\gamma$ su $[0,2\pi]$ . Poichè la parametrizzazione $\gamma$ è $2\pi$ -periodica, non sarà necessario studiare gli estremi del dominio $\{0\}$ e $\{2\pi\}$ (questo è facilmente intuibile dal fatto che la periodicità permette di traslare a piacimento il dominio della parametrizzazione, cambiando in questo modo gli estremi del dominio), ma sarà sufficiente studiare i punti critici di $f\circ\gamma$ .

Calcoliamo dunque la funzione composta e la sua derivata:

$\begin{equation*} f(\gamma(\theta))=f(\cos\theta,\sin\theta,-\cos\theta-\sin\theta)=\cos^2(\theta)+\sin^2(\theta)+\sin(\theta)(-\cos(\theta)-\sin(\theta)+\cos(\theta)-1)=1-\sin^2(\theta)-\sin(\theta), \end{equation*}$

$\begin{equation*} (f\circ\gamma)'(\theta)=-2\sin(\theta)\cos(\theta)-\cos(\theta)=-\cos(\theta)(1+2\sin(\theta)) \end{equation*}$

Dunque i punti critici di $f\circ\gamma$ soddisfano

$\begin{equation*} \cos(\theta)=0\qquad\lor\qquad\sin(\theta)=-\dfrac{1}{2} \end{equation*}$

a cui corrispondono i valori di $\theta\in[0,2\pi]$

$\begin{equation*} \theta_1=\dfrac{\pi}{2},\qquad\theta_2=\dfrac{3}{2}\pi,\qquad\theta_3=\dfrac{7}{6}\pi,\qquad\theta_4=\dfrac{11}{6}\pi. \end{equation*}$

Calcoliamo le corrispondenti immagini attraverso la parametrizzazione:

$\begin{equation*} \begin{split} &P_1=\gamma(\theta_1)=(0,1,-1),\qquad P_2=\gamma(\theta_2)=(0,-1,1)\\ &P_3=\gamma(\theta_3)=\left(\dfrac{-\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right),\qquad P_4=\gamma(\theta_4)=\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right). \end{split} \end{equation*}$

$\quad$

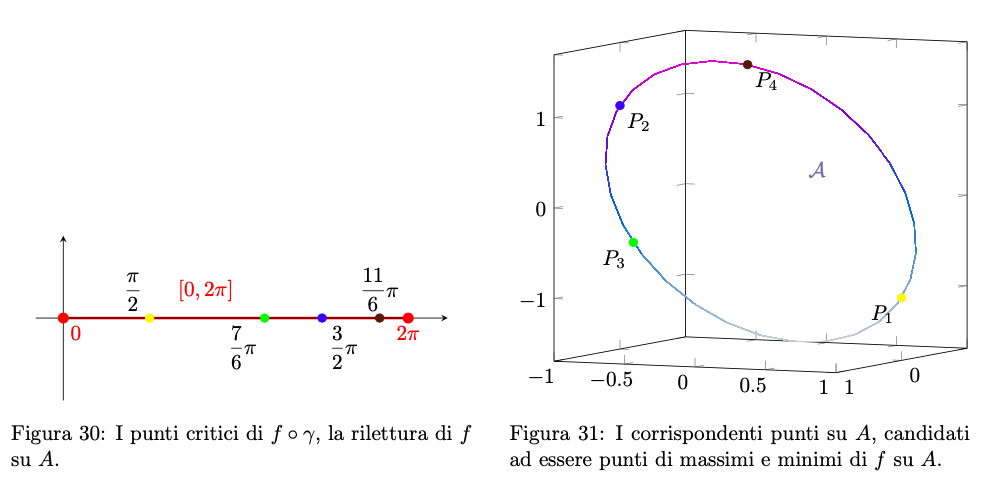
massimi e minimi vincolati

$\quad$

Calcoliamo i loro valori tramite $f$ e confrontiamoli:

$\begin{equation*} \begin{split} f(P_1)&=f(0,1,-1)=-1,\qquad f(P_2)=f(0,-1,1)=1,\\ f(P_3)&=f\left(-\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right)=\dfrac{5}{4} \qquad\text{e}\qquad f(P_4)=f\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right)=\dfrac{5}{4}. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\dfrac{5}{4}$ , assunto nei punti $P_3=\left(-\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1+\sqrt{3}}{2}\right)$ e $P_4=\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2},\dfrac{1-\sqrt{3}}{2}\right)$ e valore minimo $-1$ , assunto in $P_1=(0,1,-1)$ .

Esercizio 4 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^3\rightarrow\mathbb{R},$ definita da

$f(x,y,z):=2xy+xz^2,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\left\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2+z^2\leq3, \ x^2+z^2-y^2\leq 1\right\}.$

Svolgimento.

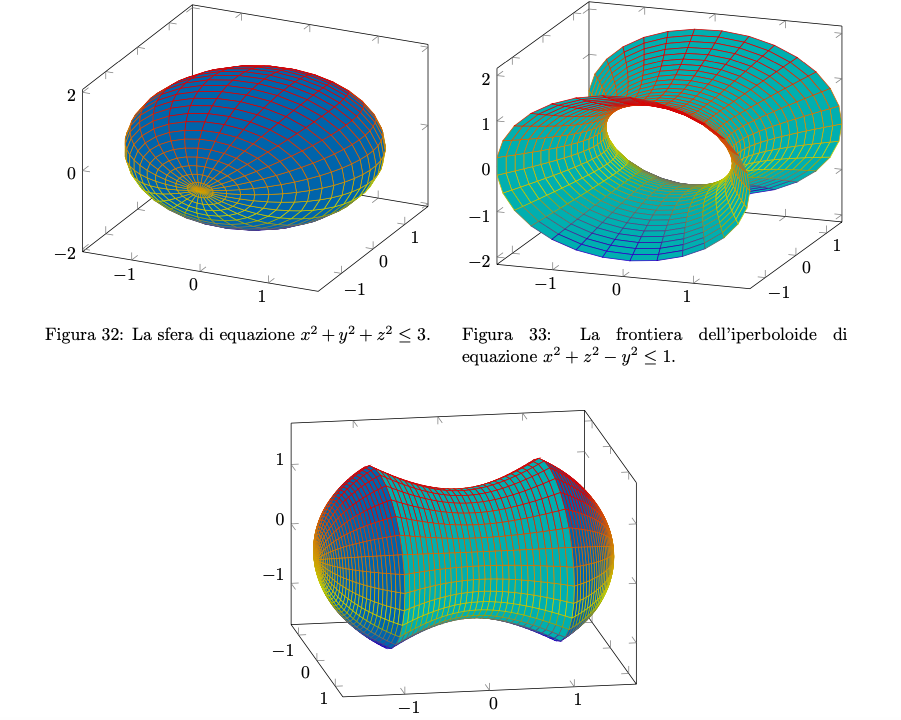
Figura 34: l’insieme $A$ .

$\quad$

Osserviamo che $f$ è un polinomio, pertanto è una funzione continua su $\mathbb{R}^3$ , mentre l’insieme $A$ è chiuso e limitato. La chiusura segue dal fatto che $A$ è intersezione di controimmagini di insiemi chiusi di $\mathbb{R}$ tramite funzioni continue, mentre per la limitatezza, la prima condizione assicura che $A$ è contenuto nella palla di centro l’origine e raggio $\sqrt{3}$ . Dunque è un chiuso e limitato di $\mathbb{R}^3$ , compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ , dove

$\begin{equation*} A^\circ:=\left\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2+z^2<3, \ x^2+z^2-y^2< 1\right\} \end{equation*}$

$\begin{equation*} \partial A=A\setminus A^\circ. \end{equation*}$

Studiamo separatamente e in maniera differente le due componenti.

$A^\circ)$ Essendo $f$ differenziabile sull’insieme aperto $A^\circ$ , il teorema di Fermat ci assicura che gli estremi relativi di $f$ in $A^\circ$ vanno ricercati tra i suoi eventuali punti critici in $A^\circ$ , ovvero i punti $P\in A^\circ$ tali che $\nabla f(P)=(0,0,0)$ e scartare tutti i punti che non soddisfano tale condizione. Calcoliamo il gradiente di $f$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=2y+z^2\\\\ \dfrac{\partial f}{\partial y}(x,y)=2x\\\\ \dfrac{\partial f}{\partial z}(x,y)=2xz, \end{cases}$

dunque

$\nabla f(x,y,z)=(2y+z^2,2x,2xz).$

Pertanto, i punti critici di $f$ soddisfano

$\begin{equation*} \begin{cases} 2y+z^2=0\\\\ 2x=0\\\\ 2xz=0 \end{cases}\Leftrightarrow \begin{cases} y=-\dfrac{z^2}{2}\\\\ x=0. \end{cases} \end{equation*}$

Possiamo allora parametrizzare i punti critici di $f$ attraverso la curva

$\begin{equation*} \gamma(t):=\left(0,-\dfrac{t^2}{2},t\right). \end{equation*}$

Naturalmente, siamo interessati alla porzione di curva che giace in $A^\circ$ . Indaghiamo la natura di questi punti critici attraverso lo studio della matrice Hessiana, valutata sui punti della curva.

Ricordiamo, prima di svolgere esplicitamente i calcoli, l’importante teorema che sta alla base di questo procedimento:

Sia $f:A\subset\mathbb{R}^n\rightarrow\mathbb{R}$ di classe $\mathcal{C}^2(A)$ , con $A$ sottoinsieme aperto e $x_0\in A$ un punto critico di $f$ . Sia $\mathcal{H}_f(x_0)$ la matrice Hessiana di $f$ valutata in $x_0$ , allora se

$\cdot$ $\mathcal{H}_f(x_0)$ è definita positiva, $x_0$ è un punto di minimo relativo per $f$

$\cdot$ $\mathcal{H}_f(x_0)$ è definita negativa, $x_0$ è un punto di massimo relativo per $f$

$\cdot$ $\mathcal{H}_f(x_0)$ è indefinita, $x_0$ è un punto di sella per $f$ .

Ricordiamo infine cosa significa per una matrice simmetrica (come la matrice Hessiana di una funzione di classe $\mathcal{C}^2$ ) essere definita o indefinita:

una matrice simmetrica si dice definita positiva (negativa rispettivamente) se tutti i suoi autovalori sono positivi (negativi risp.)

una matrice simmetrica si dice indefinita se esistono almeno due autovalori di segno opposto.

Consci del precedente teorema, calcoliamo la matrice Hessiana di $f$ in un generico punto $(x,y,z)$ :

$\begin{equation*} \mathcal{H}_f(x,y,z)=\begin{pmatrix} 0&2&2z\\ 2&0&0\\ 2z&0&2x \end{pmatrix} \end{equation*}$

e valutiamola, dunque, nei punti appartenenti alla curva

$\begin{equation*} \mathcal{H}_f(\gamma(t))=\begin{pmatrix} 0&2&2t\\ 2&0&0\\ 2t&0&0 \end{pmatrix}. \end{equation*}$

A questo punto, per indagare la natura dei punti critici giacenti sulla curva, dovremo studiare la definitezza della matrice Hessiana su ciascuno di questi punti. Per farlo, calcoliamo il segno degli autovalori della matrice, che saranno in funzione del parametro $t$ , di evoluzione della curva. Per definizione, gli autovalori della matrice $\mathcal{H}_f(\gamma(t))$ sono i valori $\lambda\in\mathbb{R}$ , radici del polinomio caratteristico (possiamo affermare che gli autovalori saranno numeri reali, poiché la matrice Hessiana è una matrice simmetrica):

$\begin{equation*} P(\lambda):=\det(\mathcal{H}_f(\gamma(t)-\lambda I_3), \end{equation*}$

dove $I_3$ è la matrice identità di dimensione 3.

Calcoliamo $P(\lambda)$ e cerchiamo le sue radici.

$\begin{equation*} \mathcal{H}_f(\gamma(t))-\lambda I_3=\begin{pmatrix} 0&2&2t\\ 2&0&0\\ 2t&0&0 \end{pmatrix}-\lambda\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix}=\begin{pmatrix} -\lambda&2&2t\\ 2&-\lambda&0\\ 2t&-0&-\lambda \end{pmatrix}, \end{equation*}$

quindi

$\begin{equation*} P(\lambda)=\det \begin{pmatrix} -\lambda&2&2t\\ 2&-\lambda&0\\ 2t&0&-\lambda \end{pmatrix}=-\lambda^3+4\lambda-4\lambda t^2=-\lambda(\lambda^2-4-4t^2). \end{equation*}$

I valori che annullano $P(\lambda)$ sono

$\begin{equation*} \lambda_1=0, \end{equation*}$

$\begin{equation*} \lambda_{2,3}=\pm2\sqrt{1+t^2}. \end{equation*}$

Osserviamo che, indipendentemente dal parametro $t$ , gli autovalori $\lambda_2$ e $\lambda_3$ hanno segno opposto, ovvero la matrice Hessiana $\mathcal{H}_f(\gamma(t))$ è ovunque indefinita e per il teorema sopra citato, ne evinciamo che tutti i punti sulla curva sono punti di sella, che dunque non possono essere ne massimi ne minimi relativi.

Questo conclude lo studio di $A^\circ$ .

$\partial A)$ Innanzitutto, dobbiamo capire com’è fatto $\partial A$ . Osserviamo che

$\begin{equation*} \begin{split} \partial A &= \{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2+z^2=3, \ x^2+z^2-y^2\leq 1\}\cup \\ & \quad \cup \{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2+z^2\leq3, \ x^2+z^2-y^2= 1\}. \end{split} \end{equation*}$

Analizziamo la prima componente, mettendo a sistema l’equazione con la disequazione:

$\begin{equation*} \left\{\begin{array}{l} x^2+y^2+z^2=3 \\\\ x^2+z^2-y^2\leq 1 \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} x^2+z^2=3-y^2 \\\\ 3-2y^2\leq 1 \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} x^2+z^2=3-y^2 \\\\ y^2\geq 1 \end{array}\right. \Leftrightarrow\left\{\begin{array}{l} x^2+z^2=3-y^2 \\\\ y\leq -1\lor y\geq 1. \end{array}\right. \end{equation*}$

Ovviamente, affinché la prima equazione abbia soluzione nel campo dei reali, si richiede anche $y\in\left[-\sqrt{3},\sqrt{3}\right]$ . Pertanto, la prima componente rappresenta due porzioni di sfera di raggio $\sqrt{3}$ , $S^\pm$ , definite tramite

$\begin{equation*} S^+:=\left\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2+z^2=3, \ y\in\left[1,\sqrt{3}\right]\right\} \end{equation*}$

$\begin{equation*} S^-:=\left\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2+z^2=3, \ y\in\left[-\sqrt{3},-1\right]\right\}. \end{equation*}$

$\quad$

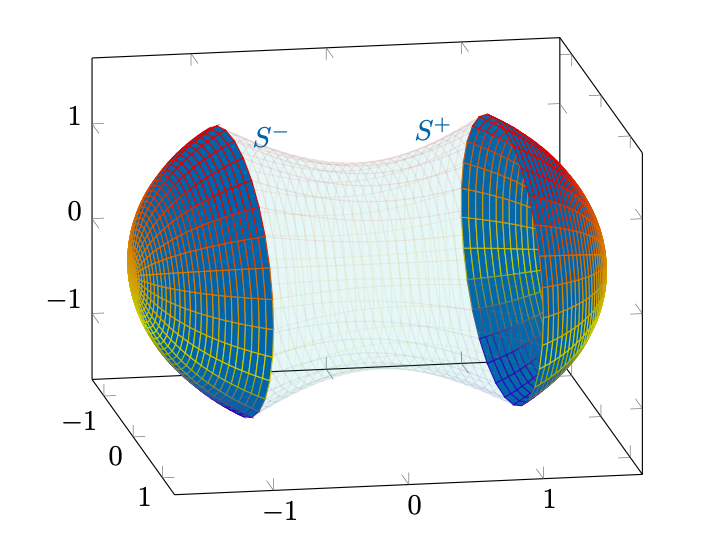
massimi e minimi vincolati

Figura 35: le due parti di sfera che compongono la frontiera di $A$ .

$\quad$

Ripetiamo lo stesso ragionamento anche per la seconda componente, mettendo a sistema l’equazione e la disequazione che la definiscono

$\begin{equation*} \left\{\begin{array}{l} x^2+y^2+z^2\leq3 \\\\ x^2+z^2-y^2= 1 \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} 1+2y^2\leq 3\\\\ x^2+z^2=1+y^2 \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} y^2\leq 1\\\\ x^2+z^2=1+y^2 \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} -1\leq y\leq1\\\\ x^2+z^2=1+y^2. \end{array} \right. \end{equation*}$

Abbiamo trovato che la seconda componente è una porzione di iperboloide $I$ , rappresentato da

$\begin{equation*} I:=\left\{(x,y,z)\in\mathbb{R}^3\mid x^2+z^2-y^2=1, \ y\in\left[-1,1\right]\right\}. \end{equation*}$

$\quad$

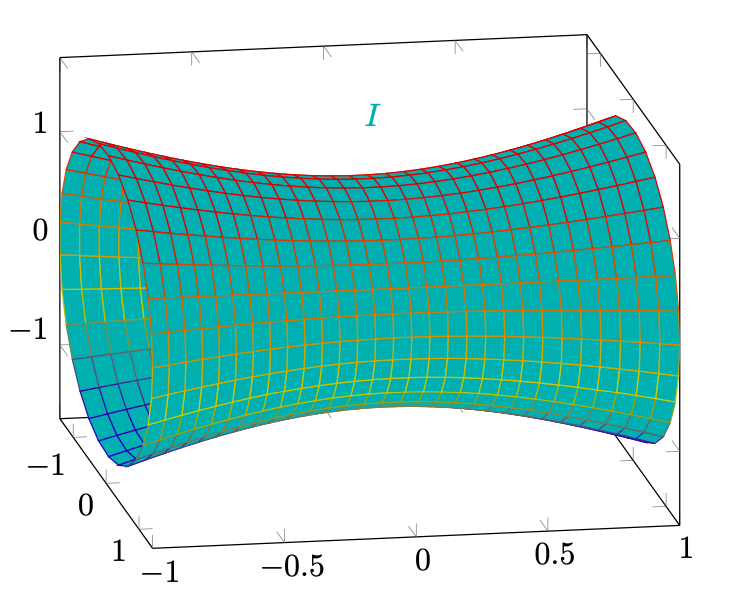
massimi e minimi vincolati

Figura 36: la parte di ipeboloide che compone il resto di $\partial A$ .

$\quad$

Siamo dunque in grado di esprimere $\partial A$ attraverso

$\begin{equation*} \partial A=S^-\cup I\cup S^+. \end{equation*}$

A questo punto, studiamo separatamente il comportamento di $f$ ristretto a $S^\pm$ e $I$ , separatamente.

$S^+)$ Essendo $S^+$ una porzione di sfera, utilizziamo le coordinate sferiche

$\begin{equation*} \psi(\theta,\varphi):=\left(\sqrt{3}\cos\theta\sin\varphi,\sqrt{3}\cos\varphi,\sqrt{3}\sin\theta\sin\varphi\right), \end{equation*}$

prendendo inizialmente come dominio $(\theta,\varphi)\in[0,2\pi]\times[0,\pi]$ . In questo modo, tuttavia, otteniamo una parametrizzazione dell’intera sfera di centro l’origine e raggio $\sqrt{3}$ . Per parametrizzare $S^+$ , dovremo restringere il dominio della parametrizzazione $\psi$ . In particolare, notiamo che $S^+$ è definito dal vincolo $y\in\left[1,\sqrt{3}\right]$ , da cui troviamo

$\begin{equation*} \begin{cases} \sqrt{3}\cos\varphi\geq1\\\\ \sqrt{3}\cos\varphi\leq\sqrt{3} \end{cases} \Leftrightarrow \begin{cases} \cos\varphi\geq\dfrac{\sqrt{3}}{3}\\\\ \cos\varphi\leq1 \end{cases} \Leftrightarrow \varphi\in\bigcup_{k\in\mathbb{Z}}\left[-\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}+2k\pi,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}+2k\pi\right]. \end{equation*}$

Intersecando il vincolo appena trovato con il dominio di partenza relativo a $\varphi$ , $\varphi\in[0,\pi]$ , otteniamo

$\varphi\in\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right].$

Nessun vincolo, invece, riguarda $\theta$ , libero di variare in $[0,2\pi]$ . Affermiamo che una parametrizzazione regolare di $S^+$ sarà

$\begin{equation*} \begin{array}{ccl} \psi^+:[0,2\pi]\times\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]&\rightarrow&\mathbb{R}^3 \\\\ (\theta,\varphi)&\mapsto& \left(\sqrt{3}\cos\theta\sin\varphi,\sqrt{3}\cos\varphi,\sqrt{3}\sin\theta\sin\varphi\right), \end{array} \end{equation*}$

infatti, detto $U:=(0,2\pi)\times\left(0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right)$ , risulta che $U$ è un aperto, la cui chiusura è compatta, $\psi^+|_U$ è iniettiva e di classe $\mathcal{C}^1$ su U, $\det J_{\psi^+}\neq 0$ su $U$ ed infine vale

$\psi^+\left([0,2\pi]\times\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]\right)=S^+.$

$\quad$

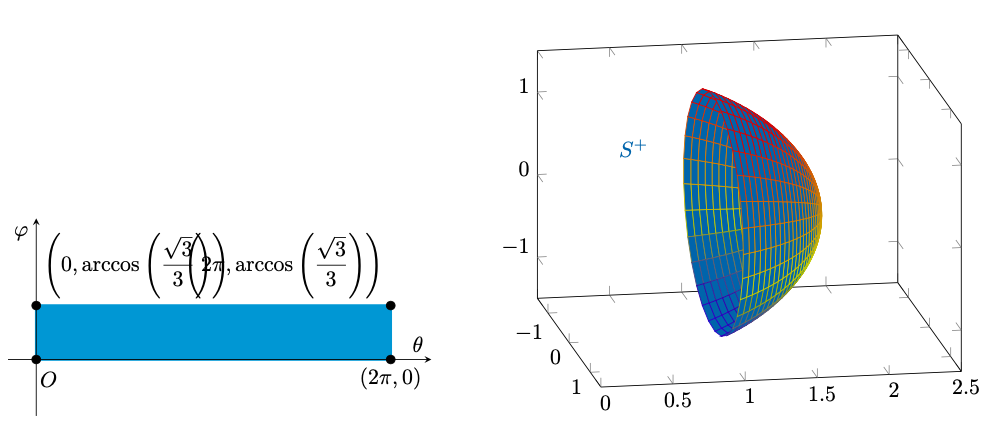
massimi e minimi vincolati

Figura 37: la parametrizzazione di $S^+$ .

$\quad$

Questo ragionamento ci permette di rimpiazzare lo studio del massimo e del minimo di $f$ sulla varietà $S^+\subset\mathbb{R}^3$ con lo studio della funzione composta $f\circ\psi^+$ sulla regione $[0,2\pi]\times\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]\subset\mathbb{R}^2$ , il che comporta un vantaggio notevole, vista la semplicità del dominio.

Per prima cosa, calcoliamo esplicitamente la composizione delle due funzioni:

$\begin{equation*} (f\circ\psi^+)(\theta,\varphi)=f\left(\sqrt{3}\cos\theta\sin\varphi,\sqrt{3}\cos\varphi,\sqrt{3}\sin\theta\sin\varphi\right)=6\cos\theta\sin\varphi\cos\varphi+3\sqrt{3}\cos\theta\sin^2\theta\sin^3\varphi. \end{equation*}$

Cerchiamo, dunque, il massimo ed il minimo della funzione $f\circ\psi^+$ su $[0,2\pi]\times\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]$ . Essendo $f$ e $\psi^+$ di classe $\mathcal{C}^1$ , sono a fortiori continue, cosi come lo è la loro composizione, inoltre $[0,2\pi]\times\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]$ è un compatto di $\mathbb{R}^2$ , dunque per il Teorema di Weierstrass, esisterà il massimo ed il minimo di $f\circ\psi^+$ su $[0,2\pi]\times\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]$ .

Vorremmo distinguere la parte interna di $[0,2\pi]\times\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]$ , che abbiamo denotato con $U$ e la sua frontiera, che andranno studiate in maniera diversa. Osserviamo tuttavia che la frontiera della varietà $S^+$ è parametrizzata da

$\partial S^+=\psi^+\left([0,2\pi]\times\left\{\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right\}\right).$

Ciò significa che è possibile riparametrizzare $S^+$ in maniera tale che i valori di $\theta=0,2\pi$ e $\varphi=0$ non siano più estremi del dominio, ma stiano nella sua parte interna. Dunque, detti $R:=[0,2\pi]\times\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]$ ed $L:=[0,2\pi]\times\left\{\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right\}$ , per lo studio dei punti di massimo e minimo è conveniente distinguere $R\setminus L$ , da affrontare mediante il teorema di Fermat ed $L$ , attraverso una sua esplicita parametrizzazione.

$\quad$

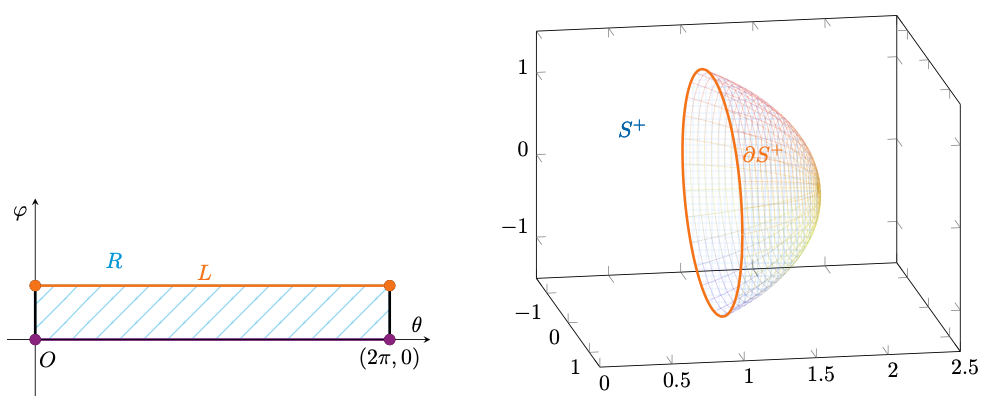
massimi e minimi vincolati

Figura 38: studio della frontiera di $S^+$ .

$\quad$

$R\setminus L)$ Utilizziamo il teorema di Fermat per trovare gli eventuali punti di massimo e minimo relativo di $f\circ\psi^+$ su $R\setminus L$ , nonostante esso non sia un insieme aperto, per le considerazioni fatte in precedenza. Su $R\setminus L$ , condizione necessaria affinché un punto $(\theta_0,\varphi_0)\in U$ sia punto di massimo o minimo relativo della funzione differenziabile $f\circ\psi^+$ su $U$ è che esso sia un suo punto critico, ovvero che si verifichi $\nabla(f\circ\psi^+)(\theta_0,\varphi_0)=(0,0)$ . Calcoliamo allora il gradiente di $f\circ\psi^+$ attraverso il calcolo delle derivate parziali:

$\begin{equation*} \begin{split} \dfrac{\partial}{\partial\theta}(f\circ\psi^+)&=-6\sin\theta\sin\varphi\cos\varphi-3\sqrt{3}\sin^3\theta\sin^3\varphi+6\sqrt{3}\cos^2\theta\sin\theta\sin^3\varphi\\ &=3\sin\theta\sin\varphi\left(-2\cos\varphi-\sqrt{3}\sin^2\theta\sin^2\varphi+2\sqrt{3}\cos^2\theta\sin^2\varphi\right), \end{split} \end{equation*}$

$\begin{equation*} \begin{split} \dfrac{\partial}{\partial\varphi}(f\circ\psi^+)&=6\cos\theta\left(\cos^2\varphi-\sin^2\varphi\right)+9\sqrt{3}\cos\theta\sin^2\theta\cos\varphi\sin^2\varphi\\ &=3\cos\theta\left(2\cos^2\varphi-2\sin^2\varphi+3\sqrt{3}\sin^2\theta\cos\varphi\sin^2\varphi\right), \end{split} \end{equation*}$

dunque

$\begin{equation*} \begin{split} \nabla (f\circ\psi^+)=&\left(3\sin\theta\sin\varphi\left(-2\cos\varphi-\sqrt{3}\sin^2\theta\sin^2\varphi+2\sqrt{3}\cos^2\theta\sin^2\varphi\right),\right.\\ &\qquad\left.3\cos\theta\left(2\cos^2\varphi-2\sin^2\varphi+3\sqrt{3}\sin^2\theta\cos\varphi\sin^2\varphi\right)\right). \end{split} \end{equation*}$

Calcoliamo allora i punti critici, ovvero i punti che annullano il gradiente:

(3) $\begin{equation*} \left\{\begin{array}{l} 3\sin\theta\sin\varphi\left(-2\cos\varphi-\sqrt{3}\sin^2\theta\sin^2\varphi+2\sqrt{3}\cos^2\theta\sin^2\varphi\right)=0 \\\\ 3\cos\theta\left(2\cos^2\varphi-2\sin^2\varphi+3\sqrt{3}\sin^2\theta\cos\varphi\sin^2\varphi\right)=0. \end{array}\right. \end{equation*}$

Osserviamo immediatamente che la prima equazione si annulla se $\sin\theta=0$ o $\sin\varphi=0$ . Supponiamo inizialmente $\sin\theta=0$ , che si verifica per $\theta=0,\pi$ , nei quali casi $\cos\theta=\pm1$ e inserendo quest’informazione nella seconda equazione troviamo

$\begin{equation*} \pm3\left(2\cos^2\varphi-2\sin^2\varphi\right)=0, \end{equation*}$

che si annulla se e solo se

$\begin{equation*} \cos\varphi=\pm\sin\varphi\Leftrightarrow\varphi=\dfrac{\pi}{4}+k\dfrac{\pi}{2}. \end{equation*}$

Notiamo che per $k=0$ ,

$\varphi=\dfrac{\pi}{4}\in\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right],$

dunque abbiamo trovato i primi punti da considerare:

$\begin{equation*} \tilde{P}_1=\left(0,\dfrac{\pi}{4}\right),\qquad \tilde{P}_2=\left(\pi,\dfrac{\pi}{4}\right), \end{equation*}$

a cui corrispondono i punti

$\begin{equation*} P_1=\psi^+\left(\tilde{P}_1\right)=\left(\dfrac{\sqrt{6}}{2},\dfrac{\sqrt{6}}{2},0\right),\qquad P_2=\psi^+\left(\tilde{P}_2\right)=\left(-\dfrac{\sqrt{6}}{2},\dfrac{\sqrt{6}}{2},0\right) \end{equation*}$

su $S^+$ .

Se invece $\sin\varphi=0$ , che per l’intervallo interessato da $\varphi$ si verifica solamente per $\varphi=0$ , la seconda equazione si riduce a

$\begin{equation*} 6\cos\theta=0\Leftrightarrow\theta=\dfrac{\pi}{2},\dfrac{3}{2}\pi. \end{equation*}$

Abbiamo trovato in questo modo altri due punti da considerare:

$\begin{equation*} \tilde{P}_3=\left(\dfrac{\pi}{2},0\right),\qquad \tilde{P}_4=\left(\dfrac{3}{2}\pi,0\right). \end{equation*}$

Essi hanno la stessa immagine rispetto a $\psi^+$ e indivuano il punto

$\begin{equation*} P_3=\psi^+\left(\tilde{P}_3\right)=\psi^+\left(\tilde{P}_4\right)=\left(0,\sqrt{3},0\right). \end{equation*}$

La seconda equazione si annulla se $\cos\theta=0$ , ovvero per $\theta=\dfrac{\pi}{2},\dfrac{3}{2}\pi$ , che inserito nella prima equazione implica

$\begin{equation*} \pm3\sin\varphi\left(-2\cos\varphi-\sqrt{3}\sin^2\varphi\right)=0. \end{equation*}$

Questa equazione si annulla se $\sin\varphi=0$ , che ci porta a ritrovare i punti $\tilde{P}_3$ e $\tilde{P}_4$ , oppure se

$\begin{equation*} -2\cos\varphi-\sqrt{3}\sin^2\varphi=0. \end{equation*}$

Risoviamo l’equazione:

$\begin{equation*} 0=2\cos\varphi+\sqrt{3}\sin^2\varphi=2\cos\varphi+\sqrt{3}-\sqrt{3}\cos^2\varphi. \end{equation*}$

Definiamo $t:=\cos\varphi$ , dunque l’equazione precedente risulta essere

$\begin{equation*} 0=2t+\sqrt{3}-\sqrt{3}t^2=3t^2-2\sqrt{3}t-3, \end{equation*}$

che si annulla per

$\begin{equation*} t_{1,2}=\dfrac{\sqrt{3}\pm\sqrt{3+9}}{3}=\dfrac{\sqrt{3}\pm2\sqrt{3}}{3}=\begin{cases} t_1=\sqrt{3}\\\\ t_2=-\dfrac{\sqrt{3}}{3}. \end{cases} \end{equation*}$

Poiché $t=\cos\varphi\in[-1,1]$ , la prima soluzione non è accettabile, mentre la seconda implica

$\begin{equation*} \varphi=\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\notin\left[0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right]. \end{equation*}$

Ciò detto, possiamo supporre $\sin\theta,\cos\theta,\sin\varphi\neq0$ , dunque il sistema (3) si riduce a

$\begin{equation*} \left\{\begin{array}{l} -2\cos\varphi-\sqrt{3}\sin^2\theta\sin^2\varphi+2\sqrt{3}\cos^2\theta\sin^2\varphi=0 \\\\ 2\cos^2\varphi-2\sin^2\varphi+3\sqrt{3}\sin^2\theta\cos\varphi\sin^2\varphi=0. \end{array}\right. \end{equation*}$

A questo punto, è conveniente moltiplicare entrambi i membri della prima equazione per $\cos\varphi$ e per farlo, dobbiamo supporre $\cos\varphi\neq0$ , secondo i principi delle equazioni. Tuttavia, prima dobbiamo controllare che non perdiamo soluzioni: se fosse $\cos\varphi=0$ , la seconda equazione implicherebbe $\sin\varphi=0$ , ma nelle nostre ipotesi, $\sin\varphi\neq0$ . Siamo quindi liberi per moltiplicare la prima equazione per $\cos\varphi$ :

$\begin{equation*} \left\{\begin{array}{l} -2\cos^2\varphi-\sqrt{3}\sin^2\theta\cos\varphi\sin^2\varphi+2\sqrt{3}\cos^2\theta\cos\varphi\sin^2\varphi=0 \\\\ 2\cos^2\varphi-2\sin^2\varphi+3\sqrt{3}\sin^2\theta\cos\varphi\sin^2\varphi=0. \end{array}\right. \end{equation*}$

e sommiamo nella prima riga le due equazioni del sistema:

$\begin{equation*} \left\{\begin{array}{l} -2\sin^2\varphi+2\sqrt{3}\cos^2\theta\cos\varphi\sin^2\varphi=0 \\\\ 2\cos^2\varphi-2\sin^2\varphi+3\sqrt{3}\sin^2\theta\cos\varphi\sin^2\varphi=0, \end{array}\right. \end{equation*}$

$\begin{equation*} \left\{\begin{array}{l} -2\sin^2\varphi\left(1-\sqrt{3}\cos^2\theta\cos\varphi\right)=0 \\\\ 2\cos^2\varphi-2\sin^2\varphi+3\sqrt{3}\cos\varphi\sin^2\varphi-3\sqrt{3}\cos^2\theta\cos\varphi\sin^2\varphi=0. \end{array}\right. \end{equation*}$

Poiché $\sin\varphi\neq0$ , la prima equazione comporta

$\begin{equation*} \sqrt{3}\cos^2\theta\cos\varphi=1, \end{equation*}$

che, inserito nella seconda equazione, ci porta all’equazione nella sola variabile $\varphi$

$\begin{equation*} 2\cos^2\varphi-2\sin^2\varphi+3\sqrt{3}\cos\varphi\sin^2\varphi-3\sin^2\varphi=2\cos^2\varphi-5\sin^2\varphi+3\sqrt{3}\cos\varphi\sin^2\varphi=0. \end{equation*}$

Utilizzando ancora l’identità fondamentale goniometrica, troviamo

$\begin{equation*} 2\cos^2\varphi+5\cos^2\varphi+3\sqrt{3}\cos\varphi-3\sqrt{3}\cos^3\varphi=0 \end{equation*}$

$\begin{equation*} \cos\varphi\left(-3\sqrt{3}\cos^2\varphi+7\cos\varphi+3\sqrt{3}\right)=0 \end{equation*}$

Ricordando che $\cos\varphi\neq0$ , la precedente equazione si annulla se

$\begin{equation*} -3\sqrt{3}\cos^2\varphi+7\cos\varphi+3\sqrt{3}=9\cos^2+7\sqrt{3}\cos\theta-9=0, \end{equation*}$

che si verifica per

$\begin{equation*} \cos\theta_{1,2}=\dfrac{7\sqrt{3}\pm\sqrt{147+324}}{18}\notin\left[\dfrac{\sqrt{3}}{3},1\right]. \end{equation*}$

Questo conclude lo studio di $R\setminus L$ .

$L)$ Osserviamo che su $L$ , $f\circ\psi^+$ si riduce a

$\begin{equation*} (f\circ\psi^+)|_L(\theta)=f\left(\sqrt{2}\cos\theta,1,\sqrt{2}\sin\theta\right)=2\sqrt{2}\cos\theta(1+\sin^2\theta). \end{equation*}$

Essendo una funzione derivabile di una variabile, periodica sul suo dominio, basterà studiare i punti che annullano la sua derivata prima:

$\begin{equation*} \begin{split} (f\circ\psi^+)'|_L(\theta)&=2\sqrt{2}\left[-\sin\theta\left(1+\sin^2\theta\right)+2\sin\theta\cos\theta\right]\\ &=2\sqrt{2}\sin\theta\left(3\cos^2\theta-2\right), \end{split} \end{equation*}$

che si annulla solamente se

$\begin{equation*} \sin\theta=0,\qquad\cos\theta=\pm\sqrt{\dfrac{2}{3}}, \end{equation*}$

ovvero per

$\begin{equation*} \theta=0,\pi,2\pi,\arccos{\left(\sqrt{\dfrac{2}{3}}\right)},\arccos{\left(-\sqrt{\dfrac{2}{3}}\right)},2\pi-\arccos{\left(\sqrt{\dfrac{2}{3}}\right)},2\pi-\arccos{\left(-\sqrt{\dfrac{2}{3}}\right)}. \end{equation*}$

Troviamo i corrispondenti punti su $\partial S^+$ :

$\begin{equation*} \begin{split} &P_4=\psi^+\left(0,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right)=\psi^+\left(2\pi,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right)=\left(\sqrt{2},1,0\right),\\ &P_5=\psi^+\left(\pi,\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right)=\left(-\sqrt{2},1,0\right),\\ &P_6=\psi^+\left(\arccos{\left(\sqrt{\dfrac{2}{3}}\right)},\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right)=\left(\dfrac{2}{\sqrt{3}},1,\sqrt{\dfrac{2}{3}}\right),\\ &P_7=\psi^+\left(\arccos{\left(-\sqrt{\dfrac{2}{3}}\right)},\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right)=\left(-\dfrac{2}{\sqrt{3}},1,\sqrt{\dfrac{2}{3}}\right),\\ &P_8=\psi^+\left(2\pi-\arccos{\left(\sqrt{\dfrac{2}{3}}\right)},\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right)=\left(\dfrac{2}{\sqrt{3}},1,-\sqrt{\dfrac{2}{3}}\right),\\ &P_9=\psi^+\left(2\pi-\arccos{\left(-\sqrt{\dfrac{2}{3}}\right)},\arccos{\left(\dfrac{\sqrt{3}}{3}\right)}\right)=\left(-\dfrac{2}{\sqrt{3}},1,-\sqrt{\dfrac{2}{3}}\right). \end{split} \end{equation*}$

Questo conclude lo studio di $S^+$ .

$\quad$

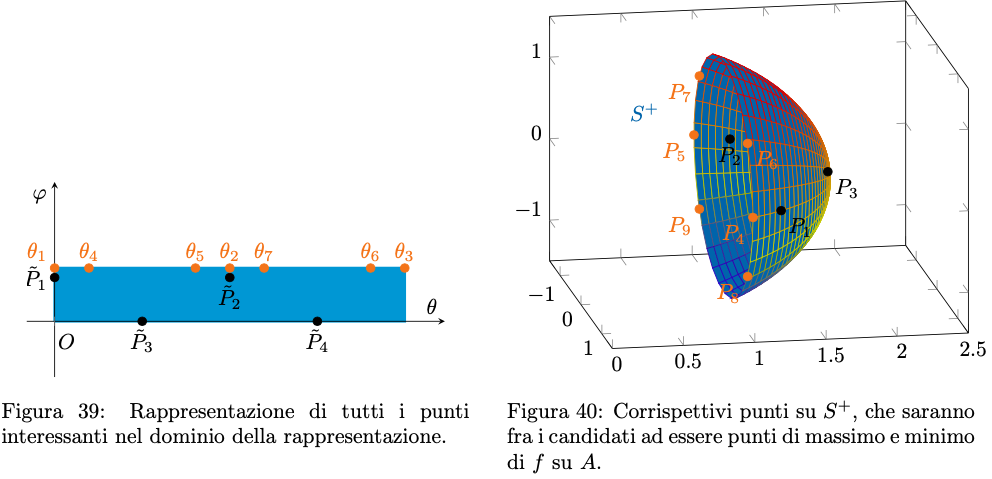
$S^-)$ La situazione è inizialmente molto simile rispetto allo studio di $S^+$ , infatti anche $S^-$ è una porzione di sfera di raggio $\sqrt{3}$ . Utilizziamo nuovamente le coordinate sferiche

$\begin{equation*} \psi(\theta,\varphi):=\left(\sqrt{3}\cos\theta\sin\varphi,\sqrt{3}\cos\varphi,\sqrt{3}\sin\theta\sin\varphi\right), \end{equation*}$

e selezioniamo accuratamente il dominio di queste coordinate per ottenere una parametrizzazione regolare di $S^-$ . Poiché $S^-$ è definito dal vincolo $y\in\left[-\sqrt{3},-1\right]$ , avremo

$\begin{equation*} \begin{split} \begin{cases} \sqrt{3}\cos\varphi\leq-1\\\\ \sqrt{3}\cos\varphi\geq-\sqrt{3} \end{cases} & \iff \begin{cases} \cos\varphi\leq-\dfrac{\sqrt{3}}{3}\\\\ \cos\varphi\geq-1 \end{cases} \\ & \iff \varphi\in\bigcup_{k\in\mathbb{Z}}\left[\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}+2k\pi,-\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}+2(k+1)\pi\right]. \end{split} \end{equation*}$

Intersecando con il naturale dominio della parametrizzazione della sfera completa, per cui solitamente vale $\varphi\in[0,\pi]$ , si ha

$\begin{equation*} \varphi\in\left[\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)},\pi\right]. \end{equation*}$

Di nuovo, la variabile $\theta$ non ha vincoli. Possiamo allora affermare, riprendendo le giustificazioni fornite al passaggio precedente, che una parametrizzazione regolare di $S^-$ è la seguente

$\begin{equation*} \begin{array}{ccl} \psi^-:[0,2\pi]\times\left[\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)},\pi\right]&\rightarrow&\mathbb{R}^3 \\\\ (\theta,\varphi)&\mapsto& \left(\sqrt{3}\cos\theta\sin\varphi,\sqrt{3}\cos\varphi,\sqrt{3}\sin\theta\sin\varphi\right). \end{array} \end{equation*}$

Questo ragionamento ci permette nuovamente di semplificare lo studio del massimo e minimo di $f$ sulla varietà $S^-$ attraverso il più comodo problema di determinare massimo e minimo della funzione composta $f\circ\psi^-$ sulla regione $[0,2\pi]\times\left[\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)},\pi\right]$ .

Osserviamo che, essendo l’espressione funzionale di $\psi^-$ uguale a quella di $\psi^+$ , si trova come prima

$\begin{equation*} (f\circ\psi^+)(\theta,\varphi)=6\cos\theta\sin\varphi\cos\varphi+3\sqrt{3}\cos\theta\sin^2\theta\sin^3\varphi. \end{equation*}$

Ciò che cambia rispetto a prima è ovviamente il dominio.

Essendo il dominio compatto e la funzione continua, il Teorema di Weierstrass garantisce l’esistenza dei punti di massimo e minimo. Come prima, definiamo $R':=[0,2\pi]\times\left[\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)},\pi\right]$ e $L':=[0,2\pi]\times\left\{\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\right\}$ e distinguiamo $R'\setminus L'$ da $L'$ che andranno studiati in maniera diversa.

$\quad$

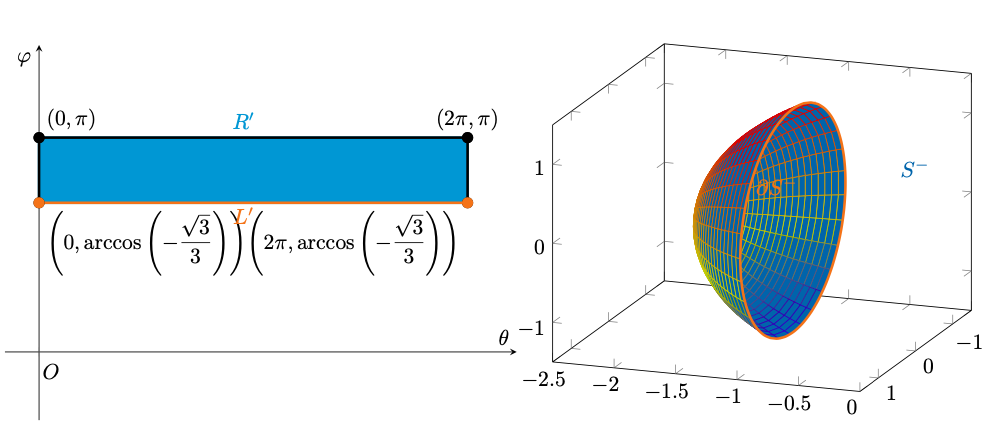
Figura 41: parametrizzazione di $S^-$ .

$\quad$

$R'\setminus L')$ Lo strumento che ci è d’aiuto in queste situazioni è sempre il Teorema di Fermat: poiché $f\circ\psi^-$ è differenziabile su $R'\setminus L'$ , per trovare i suoi punti di massimo e minimo, dovremo andare alla ricerca dei punti critici di $f\circ\psi^-$ su $R'\setminus L'$ . Calcoliamo dunque il gradiente di $f\circ\psi^-$ e i punti che lo annullano.

Possiamo avvalerci di tutti i calcoli svolti in precedenza, dal momento che la funzione da studiare è esattamente la stessa:

Affrontiamo lo studio dei punti critici come abbiamo fatto in precedenza, con l’unica differenza che ora $\varphi\in\left[\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)},\pi\right]$ : supponendo $\sin\theta=0$ , abbiamo trovato $\varphi=\dfrac{\pi}{4}+k\dfrac{\pi}{2}$ , che solo per $k=1$ può appartenere a $V$ . Abbiamo dunque trovato due punti da considerare:

$\begin{equation*} \tilde{P}_{10}=\left(0,\dfrac{3}{4}\pi\right),\qquad\tilde{P}_{11}=\left(\pi,\dfrac{3}{4}\pi\right), \end{equation*}$

a cui corrispondono i punti su $S^-$

$\begin{equation*} P_{10}=\psi^-\left(\tilde{P}_{11}\right)=\left(\dfrac{\sqrt{6}}{2},-\dfrac{\sqrt{6}}{2},0\right),\qquad P_{11}=\psi^-\left(\tilde{P}_{12}\right)=\left(-\dfrac{\sqrt{6}}{2},-\dfrac{\sqrt{6}}{2},0\right). \end{equation*}$

Supponiamo poi $\sin\varphi=0$ , che può verificarsi solo per $\varphi=\pi$ , che porta a $\theta=\dfrac{\pi}{2},\dfrac{3}{2}\pi$ e dunque ai punti

$\begin{equation*} \tilde{P}_{12}=\left(\dfrac{\pi}{2},\pi\right),\qquad \tilde{P}_{13}=\left(\dfrac{3}{2}\pi,\pi\right), \end{equation*}$

i quali ambedue individuano il punto su $S^-$

$\begin{equation*} P_{12}=\psi^-\left(\tilde{P}_{12}\right)=\psi^-\left(\tilde{P}_{13}\right)=\left(0,-\sqrt{3},0\right). \end{equation*}$

Supponendo invece $\cos\theta=0$ , cioè $\theta=\dfrac{\pi}{2},\dfrac{3}{2}\pi$ troviamo

$\begin{equation*} \cos\varphi=\left\{\begin{array}{l} \sqrt{3} \\\\ -\dfrac{\sqrt{3}}{3} , \end{array}\right. \end{equation*}$

in cui solo l’ultima soluzione è accettabile e comporta $\varphi=\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}$ , a cui corrispondono i punti

$\begin{equation*} \tilde{P}_{14}=\left(\dfrac{\pi}{2},\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\right),\qquad \tilde{P}_{15}=\left(\dfrac{3}{2}\pi,\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\right), \end{equation*}$

che tuttavia appartengono ad $L'$ , sui cui il Teorema di Fermat non ha valenza.

Procedendo come prima, troviamo che l’ultima possibile soluzione al sistema si verifica per

$\begin{equation*} \cos\theta_{1,2}=\dfrac{7\sqrt{3}\pm\sqrt{147+324}}{18}\notin\left[-1,-\dfrac{\sqrt{3}}{3}\right] \end{equation*}$

quindi non si hanno altre soluzioni.

$L')$ Poiché su $L'$ vale $\cos\varphi=-\dfrac{\sqrt{3}}{3}$ e $\sin\varphi=\sqrt{\dfrac{2}{3}}$ , la restrizione di $f\circ\psi^-$ su $L'$ vale

$\begin{equation*} \begin{split} (f\circ\psi^-)|_{L'}(\theta)=f\left(\sqrt{2}\cos\theta,-1,\sqrt{2}\sin\theta\right)=-2\sqrt{2}\cos\theta+2\sqrt{2}\sin^2\theta\cos\theta=-2\sqrt{2}\cos^3\theta, \end{split} \end{equation*}$

che assume punti critici per $\theta=k\dfrac{\pi}{2}$ , con $k=0,1,2,3,4$ . Ad essi, corrispondono i punti su $\partial S^-$

$\begin{equation*} \begin{split} &P_{13}=\psi^-\left(0,\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\right)=\psi^-\left(2\pi,\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\right)=\left(\sqrt{2},-1,0\right),\\ &P_{14}=\psi^-\left(\dfrac{\pi}{2},\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\right)=\left(0,-1,\sqrt{2}\right),\\ &P_{15}=\psi^-\left(\pi,\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\right)=\left(-\sqrt{2},-1,0\right),\\ &P_{16}=\psi^-\left(\dfrac{3}{2}\pi,\arccos{\left(-\dfrac{\sqrt{3}}{3}\right)}\right)=\left(0,-1,-\sqrt{2}\right). \end{split} \end{equation*}$

Questo conclude lo studio della seconda varietà, $S^-$ .

$\quad$

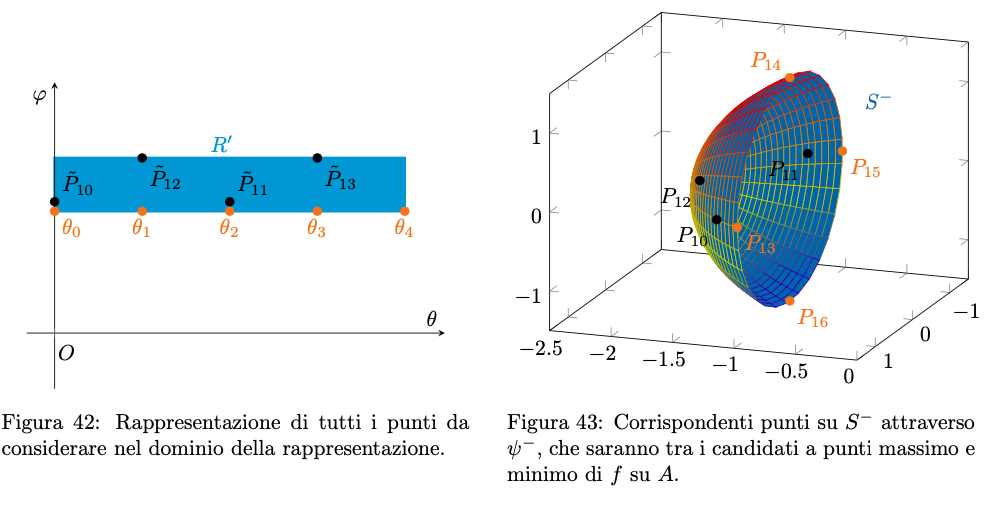
$I)$ Notiamo che $I$ è un iperboloide, ottenibile come superficie di rivoluzione della curva

$\begin{equation*} \gamma(t):=\left(\sqrt{1+t^2},t\right),\qquad t\in[-1,1]. \end{equation*}$

Pertanto, una parametrizzazione regolare di $I$ è la seguente:

$\begin{equation*} \begin{array}{rcl} \Phi:[0,2\pi]\times[-1,1]&\rightarrow&\mathbb{R}^3 \\ (\theta,t)&\mapsto&\left(\sqrt{1+t^2}\cos\theta,t,\sqrt{1+t^2}\sin\theta\right). \end{array} \end{equation*}$

Osserviamo anche che $\partial I=\partial S^+\cup\partial S^-$ , che sono già state precedentemente studiate. Dunque sarà necessario occuparsi esclusivamente di $I^\circ=\Phi\left([0,2\pi]\times(-1,1)\right)$ .

$\quad$

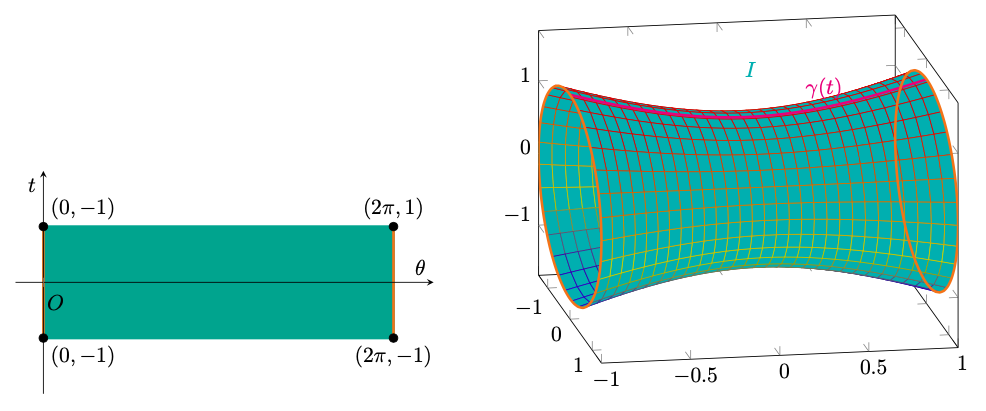
Figura 44: parametrizzazione di $I$ .

$\quad$

Servendoci del teorema di Fermat, andiamo ad indagare l’insieme dei punti critici della funzione composta $f\circ\Phi$ per trovare i punti di massimo o minimo relativi di $f$ su $I$ . Per prima cosa calcoliamo $f\circ\Phi$ :

$\begin{equation*} \begin{split} (f\circ\Phi)(\theta,t)&=f\left(\sqrt{1+t^2}\cos\theta,t,\sqrt{1+t^2}\sin\theta\right)=2t\cos\theta\sqrt{1+t^2}+(1+t^2)^{\frac{3}{2}}\sin^2\theta\cos\theta\\ &=\sqrt{1+t^2}\cos\theta\left(2t+(1+t^2)\sin^2\theta\right). \end{split} \end{equation*}$

Ora, calcoliamo il suo gradiente, per trovare i punti su $[0,2\pi]\times(-1,1)$ che lo annullano:

$\begin{equation*} \begin{split} \dfrac{\partial}{\partial\theta}\left(f\circ\Phi\right)(\theta,t)&=-\sqrt{1+t^2}\sin\theta\left(2t+(1+t^2)\sin^2\theta\right)+2\sin\theta\cos^2\theta(1+t^2)^{\frac{3}{2}}\\ &=\sqrt{1+t^2}\sin\theta\left[-2t-(1+t^2)\sin^2\theta+2(1+t^2)\cos^2\theta\right]\\ &=\sqrt{1+t^2}\sin\theta\left[-2t-3(1+t^2)\sin^2\theta+2(1+t^2)\right]\\ &=\sqrt{1+t^2}\sin\theta\left[(1+t^2)(2-3\sin^2\theta)-2t\right], \end{split} \end{equation*}$

$\begin{equation*} \begin{split} \dfrac{\partial}{\partial t}\left(f\circ\Phi\right)(\theta,t)&=\dfrac{t}{\sqrt{1+t^2}}\cos\theta\left(2t+(1+t^2)\sin^2\theta\right)+\left(2+2t\sin^2\theta\right)\sqrt{1+t^2}\cos\theta\\ &=\sqrt{1+t^2}\cos\theta\left[\dfrac{2t^2+(1+t^2)t\sin^2\theta}{1+t^2}+2+2t\sin^2\theta\right]\\ &=\dfrac{\sqrt{1+t^2}\cos\theta}{1+t^2}\left[2t^2+(1+t^2)t\sin^2\theta+2(1+t^2)+2t(1+t^2)\sin^2\theta\right]\\ &=\dfrac{\cos\theta}{\sqrt{1+t^2}}\left[3t(1+t^2)\sin^2\theta+4t^2+2\right], \end{split} \end{equation*}$

da cui

$\begin{equation*} \nabla (f\circ\Phi)(\theta,t)=\left(\sqrt{1+t^2}\sin\theta\left[(1+t^2)(2-3\sin^2\theta)-2t\right],\dfrac{\cos\theta}{\sqrt{1+t^2}}\left[3t(1+t^2)\sin^2\theta+4t^2+2\right]\right). \end{equation*}$

I punti critici di $f\circ\Phi$ sono le coppie $(\theta,t)$ che soddisfano

$\begin{equation*} \left\{\begin{array}{l} \sqrt{1+t^2}\sin\theta\left[(1+t^2)(2-3\sin^2\theta)-2t\right]=0\\\\ \dfrac{\cos\theta}{\sqrt{1+t^2}}\left[3t(1+t^2)\sin^2\theta+4t^2+2\right]=0. \end{array}\right. \end{equation*}$

Consideriamo prima le possibili soluzioni banali: la prima equazione si annulla se $\sin\theta=0$ , che inserito nella seconda fornisce

$\begin{equation*} \dfrac{\cos\theta}{\sqrt{1+t^2}}\left[4t^2+2\right]=0\Leftrightarrow\cos\theta=0, \end{equation*}$

che è chiaramente incompatibile con l’ipotesi $\sin\theta=0$ . Allo stesso modo, la seconda equazione si annulla per $\cos\theta=0$ , da cui $\sin\theta=\pm1$ , dunque la prima equazione diventerebbe

$\begin{equation*} \pm\sqrt{1+t^2}(-1-t^2-2t)=0\Leftrightarrow t=-1, \end{equation*}$

valore che non possiamo accettare poiché si trova sulla frontiera del dominio considerato e non nella sua parte interna.

A questo punto, è lecito supporre $\sin\theta,\cos\theta\neq0$ , dunque, osservando che $\sqrt{1+t^2}\neq 0$ il sistema precedente si riduce a

$\begin{equation*} \left\{\begin{array}{l} (1+t^2)(2-3\sin^2\theta)-2t=0 \\ 3t(1+t^2)\sin^2\theta+4t^2+2=0. \end{array}\right. \end{equation*}$

Converrebbe moltiplicare la prima equazione per $t$ , tuttavia è necessario supporre $t\neq0$ , per il secondo principio delle equazioni. Prima, però, dobbiamo controllare se il caso $t=0$ comporta delle soluzioni: la seconda equazione diventerebbe impossibile per $t=0$ , dunque possiamo supporre $t\neq0$ e moltiplicare la prima equazione del sistema per $t$ :

$\begin{equation*} \left\{\begin{array}{l} 2t+2t^3-3t(1+t^2)\sin^2\theta-2t^2=0 \\ 3t(1+t^2)\sin^2\theta+4t^2+2=0. \end{array}\right. \end{equation*}$

Sommando nella prima riga le equazioni tra loro risulta

$\begin{equation*} \left\{\begin{array}{l} 2t^3+2t^2+2t+2=0 \\ 3t(1+t^2)\sin^2\theta+4t^2+2=0. \end{array}\right. \end{equation*}$

La prima equazione è nella sola variabile $t$ e può essere risolta esplicitamente, infatti

$\begin{equation*} 2t^3+2t^2+2t+2=2(t+1)(t^2+1)=0\Leftrightarrow t=-1, \end{equation*}$

che di nuovo non accettiamo. Questo significa che su $I$ non vi sono punti interessanti.

Abbiamo trovato in tutto $16$ candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

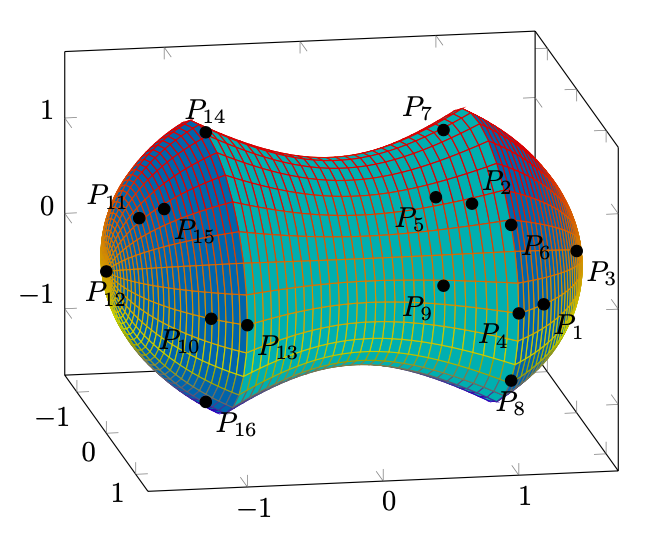
Figura 45: illustrazione di tutti i 16 punti, candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

Calcoliamo i loro valori secondo $f$ e confrontiamoli.

$\begin{equation*} \begin{split} f(P_1)&=f\left(\dfrac{\sqrt{6}}{2},\dfrac{\sqrt{6}}{2},0\right)=3,\qquad f(P_2)=f\left(-\dfrac{\sqrt{6}}{2},\dfrac{\sqrt{6}}{2},0\right)=-3,\\ f(P_3)&=f\left(0,\sqrt{3},0\right)=0,\qquad f(P_4)=f\left(\sqrt{2},1,0\right)=2\sqrt{2},\\ f(P_5)&=f\left(-\sqrt{2},1,0\right)=-2\sqrt{2},\qquad f(P_6)=f\left(\dfrac{2}{\sqrt{3}},1,\sqrt{\dfrac{2}{3}}\right)=\dfrac{16}{9}\sqrt{3},\\ f(P_7)&=f\left(-\dfrac{2}{\sqrt{3}},1,\sqrt{\dfrac{2}{3}}\right)=-\dfrac{16}{9}\sqrt{3},\qquad f(P_8)=f\left(\dfrac{2}{\sqrt{3}},1,-\sqrt{\dfrac{2}{3}}\right)=\dfrac{16}{9}\sqrt{3},\\ f(P_9)&=f\left(-\dfrac{2}{\sqrt{3}},1,-\sqrt{\dfrac{2}{3}}\right)=-\dfrac{16}{9}\sqrt{3},\qquad f(P_{10})=f\left(\dfrac{\sqrt{6}}{2},-\dfrac{\sqrt{6}}{2},0\right)=-3\\ f(P_{11})&=f\left(-\dfrac{\sqrt{6}}{2},-\dfrac{\sqrt{6}}{2},0\right)=3,\qquad f(P_{12})=f\left(0,-\sqrt{3},0\right)=0,\\ f(P_{13})&=f\left(\sqrt{2},-1,0\right)=-2\sqrt{2},\qquad f(P_{14})=f\left(0,-1,\sqrt{2}\right)=0,\\ f(P_{15})&=f\left(-\sqrt{2},-1,0\right)=2\sqrt{2},\qquad f(P_{16})=f\left(0,-1,\sqrt{2}\right)=0. \end{split} \end{equation*}$

$\quad$

Si evince che la soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\dfrac{16}{9}\sqrt{3}\cong3.1$ , assunto nei punti $P_6=\left(\dfrac{2}{\sqrt{3}},1,\sqrt{\dfrac{2}{3}}\right)$ e $P_8=\left(\dfrac{2}{\sqrt{3}},1,-\sqrt{\dfrac{2}{3}}\right)$ , mentre il minimo vale $-\dfrac{16}{9}\sqrt{3}$ assunto in $P_7=\left(-\dfrac{2}{\sqrt{3}},1,\sqrt{\dfrac{2}{3}}\right)$ e in $P_9=\left(-\dfrac{2}{\sqrt{3}},1,-\sqrt{\dfrac{2}{3}}\right)$ .

Esercizio 5 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^3\rightarrow\mathbb{R},$ definita da

$f(x,y,z):=\dfrac{x^2+y^2+z^2}{2},$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y,z)\in\mathbb{R}^3\mid x+y+1=0, \ y+z+1=0\}.$

Svolgimento.

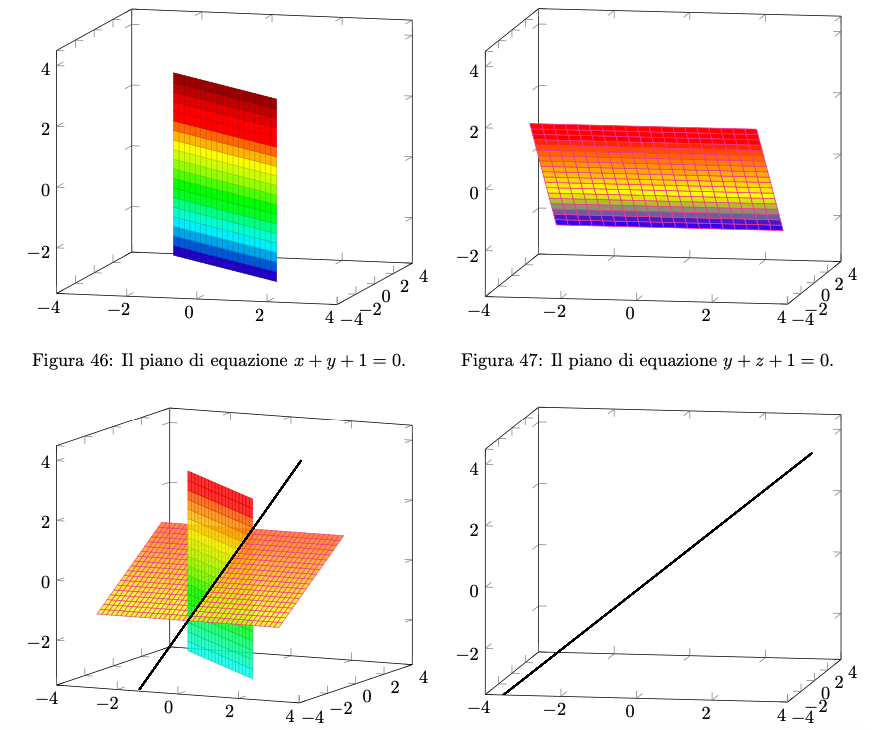
Figura 48: la loro intersezione è l’insieme $A$ , raffigurato in nero.

$\quad$

Osserviamo che l’insieme $A$ è intersezione di piani non paralleli, pertanto forma una retta in $\mathbb{R}^3$ . Ciò significa che non è un sottoinsieme limitato di $\mathbb{R}^3$ e quindi non possiamo applicare il teorema di Weierstrass. Tuttavia, osserviamo che $f$ è strettamente convessa e $A$ è un insieme chiuso e convesso di $\mathbb{R}^3$ , quindi possiamo quantomeno affermare che $f$ assume il minimo su $A$ .

Osserviamo che $A^\circ=\emptyset$ , dunque $A=\partial A$ .

Cerchiamo una parametrizzazione $\varphi$ di $A$ e studiamo la funzione composta $f\circ\varphi$ . Per trovare la parametrizzazione, risolviamo il sistema formato dalle equazioni definenti $A$ :

$\begin{equation*} \left\{\begin{array}{l} x+y+1=0 \\\\ y+z+1=0 \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} y+1=-x \\\\ y+1=-z. \end{array}\right. \end{equation*}$

Confrontando le equazioni tra loro, troviamo $x=z$ e $y=-x-1$ . Allora, una possibile parametrizzazione di $A$ è la seguente:

$\begin{equation*} \varphi:(-\infty,+\infty)\rightarrow\mathbb{R}^3 \end{equation*}$

$\begin{equation*} \varphi(t):=(t,-t-1,t). \end{equation*}$

Calcoliamo $f\circ\varphi:\mathbb{R}\rightarrow\mathbb{R}$ e il suo punto critico (l’unicità segue dalla convessità di $f$ e l’iniettività di $\varphi$ ).

$\begin{equation*} (f\circ\varphi)(t)=f(t,-t-1,t)=\dfrac{3t^2+2t+1}{3}. \end{equation*}$

Dunque

$\begin{equation*} (f\circ\varphi)'(t)=\dfrac{6t+2}{2}=3t+1, \end{equation*}$

da cui

$\begin{equation*} (f\circ\varphi)'(t)=0\Leftrightarrow t=-\dfrac{1}{3}. \end{equation*}$

Abbiamo dunque trovato un solo punto critico, come annunciato, il quale non può che essere il punto minimizzante la funzione $f$ su $A$ . Esso corrisponde al punto

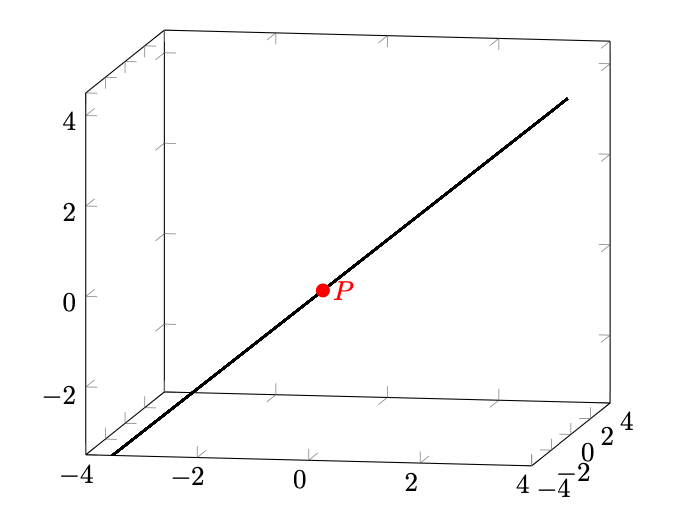
$\begin{equation*} P=\varphi\left(-\dfrac{1}{3}\right)=\left(-\dfrac{1}{3},-\dfrac{4}{3},-\dfrac{1}{3}\right). \end{equation*}$

$\quad$

Figura 49: $P$ è l’unico punto critico di $f\circ\varphi$ .

$\quad$

Il valore di $f$ in quel punto è

$\begin{equation*} f(P)=f\left(-\dfrac{1}{3},-\dfrac{2}{3},-\dfrac{1}{3}\right)=\dfrac{1}{3}. \end{equation*}$

Osserviamo, invece, che non esiste il massimo di $f$ su $A$ . In particolare, proveremo che $\sup_Af=+\infty$ e ciò è sufficiente a garantire che $f$ non assuma su $A$ il suo estremo superiore, ovvero che il massimo non esista.

Abbiamo già parametrizzato $A$ tramite $\varphi$ e calcolato $(f\circ\varphi)(t)=\dfrac{3t^2+2t+1}{3}$ . Calcoliamo allora

$\begin{equation*} \lim_{t\to\pm\infty}(f\circ\varphi)(t)=\lim_{t\to\pm\infty}\dfrac{3t^2+2t+1}{3}=+\infty. \end{equation*}$

Ciò dimostra effettivamente che $\sup_Af=+\infty$ e che dunque $f$ non ammette massimo su $A$ .

La soluzione dell’esercizio è la seguente: $f$ ha minimo su $A$ pari a $\dfrac{1}{3}$ , assunto nel punto $P=\left(-\dfrac{1}{3},-\dfrac{2}{3},-\dfrac{1}{3}\right)$ , mentre $f$ non ha massimo su $A$ .

Esercizio 6 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Tra tutti i triangoli di fissato perimetro $2p$ , trovare quello di area massima.

Svolgimento 1.

Sia $\overset{\triangle}{ABC}$ un triangolo generico di vertici $A=(x_A,y_A)$ , $B=(x_B,y_B)$ e $C=(x_C,y_C)$ . Osserviamo che con una rototraslazione possiamo sempre supporre $C=(0,0)$ e $y_A=0$ . Infatti, consideriamo l’isometria di $\mathbb{R}^2$

$\begin{equation*} F:\mathbb{R}^2\rightarrow\mathbb{R}^2 \end{equation*}$

$\begin{equation*} F:=R\circ T, \end{equation*}$

dove $T:\mathbb{R}^2\rightarrow\mathbb{R}^2$ è la traslazione

$\begin{equation*} T(x,y):=(x-x_C,y-y_C), \end{equation*}$

che trasla il piano $\mathbb{R}^2$ in modo tale che il punto $C$ nell’origine e la rotazione $R:\mathbb{R}^2\rightarrow\mathbb{R}^2$ è della forma

$\begin{equation*} R(x,y):=R_{\overline{\theta}}\cdot (x,y)^t, \end{equation*}$

dove $R_{\overline{\theta}}$ è la matrice

$\begin{equation*} R_{\overline{\theta}}:=\begin{pmatrix} \cos\overline{\theta}&-\sin\overline{\theta}\\ \sin\overline{\theta}&\cos\overline{\theta} \end{pmatrix}, \end{equation*}$

con $\overline{\theta}$ un opportuno angolo definito dalla relazione

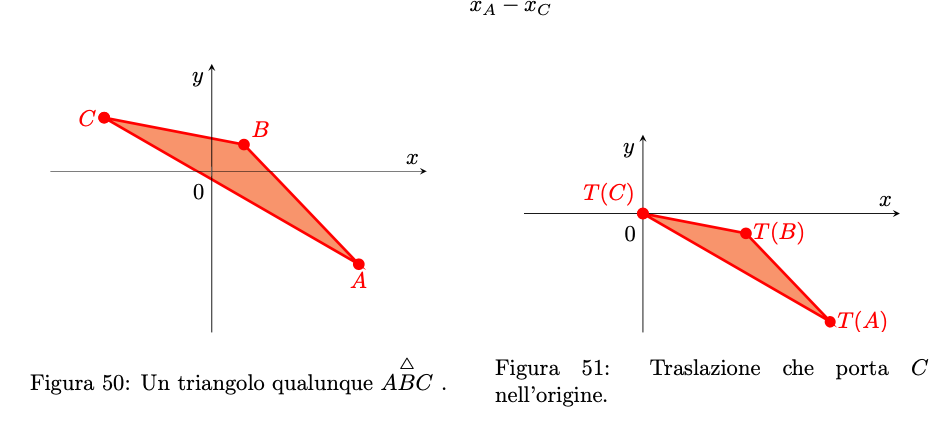
$\begin{equation*} \tan\overline{\theta}=\dfrac{y_C-y_A}{x_A-x_C} \end{equation*}$

$\quad$

Si dimostra immediatamente che $F(C)=(0,0)$ , mentre

$\begin{equation*} \begin{split} F(A)&= R_{\overline{\theta}}\cdot (x_A-x_C,y_A-y_C)^t= \\ &= (\cos\overline{\theta}(x_A-x_C)-\sin\overline{\theta}(y_A-y_C),\sin\overline{\theta}(x_A-x_C)+\cos\overline{\theta}(y_A-y_C))^t= \\ &= \cos\overline{\theta}\left(x_A-x_C+\dfrac{(y_A-y_C)^2}{x_A-x_C},y_C-y_A+y_A-y_C\right)^t= \\ &= \cos\overline{\theta}\left(x_A-x_C+\dfrac{(y_A-y_C)^2}{x_A-x_C},0\right)^t, \end{split} \end{equation*}$

in particolare, $F_2(A)=0$ .

$\quad$

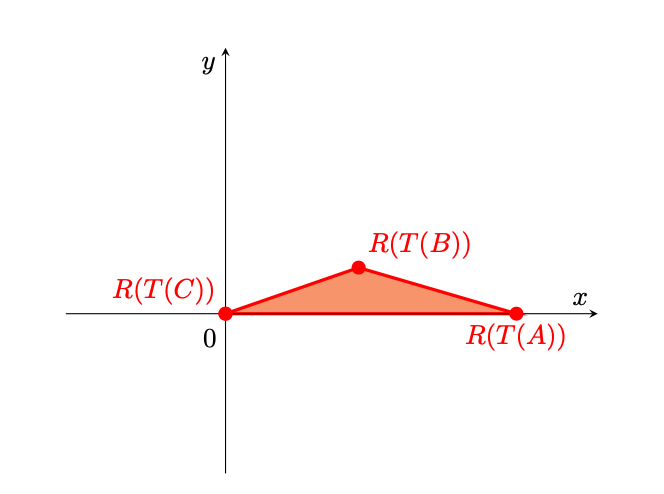
Figura 52: rotazione che sposta la traslazione di $A$ sull’asse $x$ , ottenendo la configurazione descritta.

$\quad$

Poiché $F$ è un’isometria, essa lascia inalterate aree e lunghezze. Per questo motivo possiamo dunque supporre, senza perdita di generalità, che il triangolo sia della forma $\overset{\triangle}{OAB}$ , con $O=(0,0)$ , $A=(x_A,0)$ e $B=(x_B,y_B)$ .

Introduciamo le variabili $x,y,z$ per esprimere le coordinate dei punti:

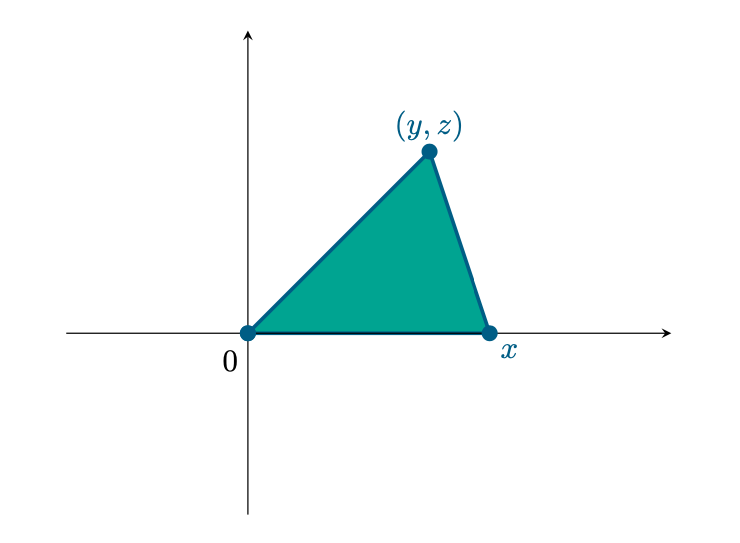
$\begin{equation*} \left\{\begin{array}{l} x:=x_A \\\\ y:=x_B\\\\ z:=y_B \end{array}\right. \end{equation*}$

$\quad$

Figura 53: le coordinate $x$ , $y$ e $z$ corrispondono rispettivamente alla prima coordinata di $A$ e alle coordinate di $B$ .

$\quad$

A questo punto, è facile esprimere il perimetro e l’area del triangolo $\overset{\triangle}{OAB}$ in queste coordinate:

$\begin{equation*} 2p=|x|+\sqrt{y^2+z^2}+\sqrt{(x-y)^2+z^2}, \end{equation*}$

e l’area, indicata con $\mathcal{A}$

$\begin{equation*} \mathcal{A}(x,y,z)=\dfrac{1}{2}|xz|. \end{equation*}$

Supponiamo per semplicità $x,z>0$ . Ciò è sempre possibile, utilizzando, se necessario, le riflessioni

$\begin{equation*} D_x(x,y,z):=(-x,y,z),\qquad D_z(x,y,z):=(x,y,-z), \end{equation*}$

essendo perimetro e area invarianti per riflessioni. Possiamo cosi esprimere il problema, inizialmente geometrico, in un problema di ottimizzazione vincolata, ovvero trovare il massimo della funzione

$\mathcal{A}=\dfrac{1}{2}xz$

soggetta al vincolo

$\begin{equation*} \mathcal{P}_p:=\{(x,y,z)\in\mathbb{R}^3\mid g_p(x,y,z)=0\}, \end{equation*}$

dove

$\begin{equation*} g_p(x,y,z):=x+\sqrt{y^2+z^2}+\sqrt{(x-y)^2+z^2}-2p. \end{equation*}$

$\quad$

Utilizziamo a tal fine il metodo dei moltiplicatori di Lagrange, costruendo la funzione Lagrangiana $\mathcal{L}(x,y,z):\mathbb{R}^4\rightarrow\mathbb{R}^4$ ,

$\begin{equation*} \mathcal{L}(x,y,z,\lambda):=\dfrac{1}{2}xz+\lambda\left(x+\sqrt{y^2+z^2}+\sqrt{(x-y)^2+z^2}-2p\right). \end{equation*}$

Dal teorema dei moltiplicatori di Lagrange sappiamo che ai punti critici della funzione $\mathcal{A}$ vincolata all’insieme $\mathcal{P}_p$ corrispondono i punti critici non vincolati della funzione $\mathcal{L}$ . Ricerchiamo allora questi ultimi, cioè i punti $(x,y,z,\lambda)\in\mathbb{R}^4$ tali che

$\begin{equation*} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}}{\partial x}(x,y,z,\lambda)=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial y}(x,y,z,\lambda)=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial z}(x,y,z,\lambda)=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \lambda}(x,y,z,\lambda)=0. \\\\ \end{array}\right. \end{equation*}$

Applicato alla nostra Lagrangiana, il sistema diventa

$\begin{equation*} \left\{\begin{array}{l} \dfrac{z}{2}+\lambda+\dfrac{\lambda(x-y)}{\sqrt{(x-y)^2+z^2}}=0 \\\\ \dfrac{\lambda y}{\sqrt{y^2+z^2}}+\dfrac{\lambda(y-x)}{\sqrt{(x-y)^2+z^2}}=0\\\\ \dfrac{x}{2}+\dfrac{\lambda z}{\sqrt{y^2+z^2}}+\dfrac{\lambda z}{\sqrt{(x-y)^2+z^2}}=0\\\\ x+\sqrt{y^2+z^2}+\sqrt{(x-y)^2+z^2}=2p\\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \dfrac{z}{2}+\lambda+\dfrac{\lambda(x-y)}{\sqrt{(x-y)^2+z^2}}=0 \\\\ \lambda\left[\dfrac{y}{\sqrt{y^2+z^2}}+\dfrac{y-x}{\sqrt{(x-y)^2+z^2}}\right]=0\\\\ \dfrac{x}{2}+\dfrac{\lambda z}{\sqrt{y^2+z^2}}+\dfrac{\lambda z}{\sqrt{(x-y)^2+z^2}}=0\\\\ x+\sqrt{y^2+z^2}+\sqrt{(x-y)^2+z^2}=2p.\\\\ \end{array}\right. \end{equation*}$

Osserviamo che la prima equazione si annulla se $\lambda=0$ , tuttavia di conseguenza tutte le altre variabili si annullerebbero producendo un triangolo di area nulla, che non può chiaramente rappresentare il massimo dell’area possibile.

Possiamo allora supporre $\lambda\neq0$ e ridurre il precedente sistema a

$\begin{equation*} \left\{\begin{array}{l} \dfrac{z}{2}+\lambda+\dfrac{\lambda(x-y)}{\sqrt{(x-y)^2+z^2}}=0 \\\\ \dfrac{y}{\sqrt{y^2+z^2}}=\dfrac{x-y}{\sqrt{(y-x)^2+z^2}}\\\\ \dfrac{x}{2}+\dfrac{\lambda z}{\sqrt{y^2+z^2}}+\dfrac{\lambda z}{\sqrt{(x-y)^2+z^2}}=0\\\\ x+\sqrt{y^2+z^2}+\sqrt{(x-y)^2+z^2}=2p.\\\\ \end{array}\right. \end{equation*}$

Manipoliamo algebricamente la seconda equazione per ottenere la prima informazione preziosa:

$\begin{equation*} \begin{split} \dfrac{y}{\sqrt{y^2+z^2}}&=\dfrac{x-y}{\sqrt{(y-x)^2+z^2}}\Leftrightarrow \dfrac{y^2}{y^2+z^2}=\dfrac{(x-y)^2}{(y-x)^2+z^2}\Leftrightarrow \\\\ \dfrac{y^2+z^2-z^2}{y^2+z^2}&=\dfrac{(x-y)^2+z^2-z^2}{(x-y)^2+z^2}\Leftrightarrow 1-\dfrac{z^2}{y^2+z^2}=1-\dfrac{z^2}{(x-y)^2+z^2}\Leftrightarrow\\\\ \dfrac{1}{y^2+z^2}&=\dfrac{1}{(x-y)^2+z^2}\Leftrightarrow y^2+z^2=(x-y)^2+z^2. \end{split} \end{equation*}$

Ma questo implica che i denominatori della seconda equazione coincidono, pertanto coincideranno anche i numeratori:

$\begin{equation*} y=x-y\Leftrightarrow y=\dfrac{x}{2}. \end{equation*}$

Quest’informazione esprime geometricamente che il triangolo $\overset{\triangle}{OAB}$ è isoscele. Dobbiamo mostrare che si tratta di un triangolo equilatero, caso più particolare di un triangolo isoscele.

Risolviamo il sistema, con le relazioni $y=\dfrac{x}{2}$ , $y^2+z^2=(x-y)^2+z^2$ :

$\begin{equation*} \left\{\begin{array}{l} \dfrac{z}{2}+\lambda+\dfrac{\lambda(x-y)}{\sqrt{(x-y)^2+z^2}}=0 \\\\ x=2y\\\\ \dfrac{x}{2}+\dfrac{\lambda z}{\sqrt{y^2+z^2}}+\dfrac{\lambda z}{\sqrt{(x-y)^2+z^2}}=0\\\\ x+\sqrt{y^2+z^2}+\sqrt{(x-y)^2+z^2}=2p\\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \dfrac{z}{2}+\lambda+\dfrac{\lambda y}{\sqrt{y^2+z^2}}=0 \\\\ x=2y\\\\ y+\dfrac{2\lambda z}{\sqrt{y^2+z^2}}=0\\\\ x+2\sqrt{y^2+z^2}=2p.\\\\ \end{array}\right. \end{equation*}$

Dall’ultima equazione risulta

$\begin{equation*} \sqrt{y^2+z^2}=p-\dfrac{x}{2}=p-y, \end{equation*}$

che inserita nelle altre equazioni comporta

$\begin{equation*} \left\{\begin{array}{l} \dfrac{z}{2}+\lambda+\dfrac{\lambda y}{p-y}=0 \\\\ x=2y\\\\ y+\dfrac{2\lambda z}{p-y}=0\\\\ \sqrt{y^2+z^2}=p-y.\\\\ \end{array}\right. \end{equation*}$

Esplicitiamo $z$ nella prima equazione:

$\begin{equation*} \dfrac{z}{2}=-\lambda\left(1+\dfrac{y}{p-y}\right)=-\left(\dfrac{\lambda p}{p-y}\right), \end{equation*}$

da cui

(4) $\begin{equation*} z=\dfrac{2\lambda p}{y-p}. \end{equation*}$

Sostituiamo questa espressione nella terza equazione per ottenere $\lambda$ :

$\begin{equation*} y+\dfrac{2\lambda\dfrac{2\lambda p}{y-p}}{p-y}=0\Leftrightarrow y-\dfrac{4\lambda^2 p}{(p-y)^2}=0\Leftrightarrow \lambda=\pm\dfrac{p-y}{2}\sqrt{\dfrac{y}{p}}. \end{equation*}$

Sostituiamo questa espressione in (4) per trovare

$\begin{equation*} z=\mp\sqrt{\dfrac{y}{p}}p=\mp\sqrt{yp}, \end{equation*}$

da cui

$\begin{equation*} z^2=yp. \end{equation*}$

Sostituendo quest’espressione nell’ultima equazione, finalmente ricaviamo $y$ :

$\begin{equation*} \sqrt{y^2+yp}=p-y\Leftrightarrow y^2+yp=p^2+y^2-2yp\Leftrightarrow 3yp=p^2\Leftrightarrow y=\dfrac{p}{3}. \end{equation*}$

Possiamo immediatamente trovare le altre variabili:

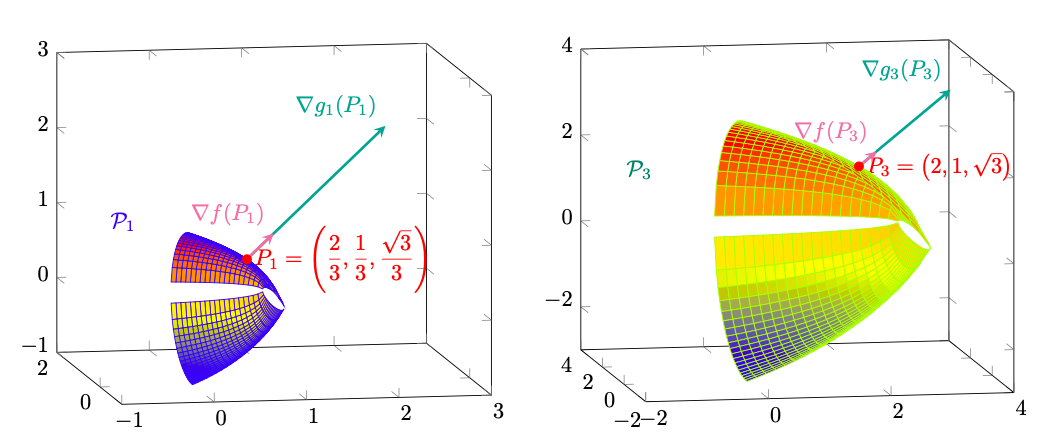
$\begin{equation*} x=\dfrac{2}{3}p,\qquad z=\dfrac{\sqrt{3}}{3}p. \end{equation*}$

$\quad$

Figura 56: in entrambe le situazioni i gradienti di $f$ e $g_p$ nei punti prestabiliti sono linearmente dipendenti, essendo paralleli.

$\quad$

Abbiamo dunque trovato il triangolo $\overset{\triangle}{OAB}$ di coordinate

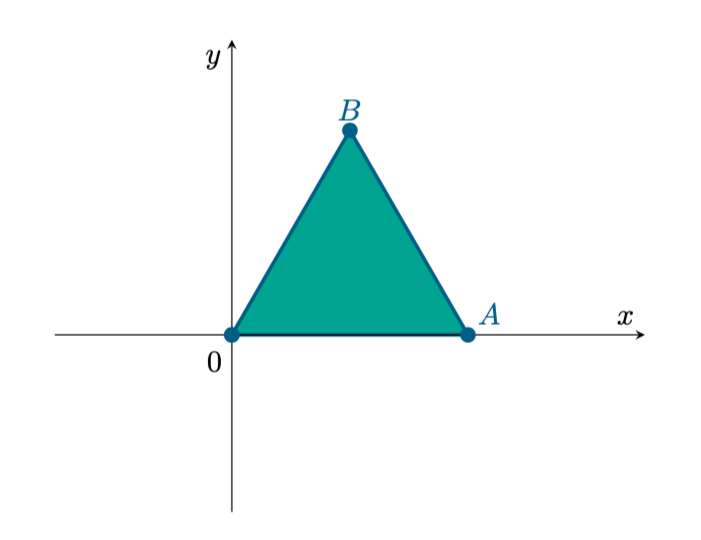
$\begin{equation*} O=(0,0),\qquad A=\left(\dfrac{2}{3}p,0\right),\qquad C=\left(\dfrac{p}{3},\dfrac{\sqrt{3}}{3}p\right). \end{equation*}$

$\quad$

Figura 57: il triangolo $\overset{\triangle}{OAB}$ è equilatero.

$\quad$

Notiamo che esse individuano un triangolo equilatero di perimetro $2p$ , infatti i lati hanno lunghezza uguale

$\begin{equation*} \overline{OA}=x_A=x=\dfrac{2}{3}p, \end{equation*}$

$\begin{equation*} \overline{OB}=\sqrt{x_B^2+y_B^2}=\sqrt{y^2+z^2}=\dfrac{2}{3}p, \end{equation*}$

$\begin{equation*} \overline{AB}=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}=\sqrt{(x-y)^2+z^2}=\dfrac{2}{3}p. \end{equation*}$

e perimetro assegnato, avendo

$\begin{equation*} \overline{OA}+\overline{OB}+\overline{AB}=\dfrac{2}{3}p+\dfrac{2}{3}p+\dfrac{2}{3}p=2p. \end{equation*}$

Svolgimento 2.

Questo esercizio si poteva risolvere per via del tutto algebrica, facendo uso della disuguaglianza tra media aritmetica e geometrica. Ricordiamo infatti il seguente fatto: Siano $x_1,...,x_n\in\mathbb{R}^+$ , allora vale

$\begin{equation*} \sqrt[n]{x_1\cdot...\cdot x_n}\leq\dfrac{x_1+...+x_n}{n}, \end{equation*}$

con l’uguaglianza che sussiste se e solo se $x_1=...=x_n$ .

Consideriamo allora un triangolo di perimetro $2p$ e, detti $x$ , $y$ e $z$ le lunghezze dei suoi lati, risulta $\dfrac{x+y+z}{2}=p$ .

Ricordiamo, infine, la formula di Erone, che esprime l’area di un triangolo in funzione del perimetro e dei suoi lati:

$\begin{equation*} \mathcal{A}(x,y,z)=\sqrt{p(p-x)(p-y)(p-z)}. \end{equation*}$

Utilizziamo allora la disuguaglianza precedente con $n=3$ , $x_1:=p-x$ , $x_2:=p-y$ e $x_3:=p-z$ , ottenendo

$\begin{equation*} \sqrt[3]{(p-x)(p-y)(p-z)}\leq \dfrac{p-x+p-y+p-z}{3}=\dfrac{p}{3}. \end{equation*}$

D’altra parte,

$\begin{equation*} \sqrt[3]{(p-x)(p-y)(p-z)}=\sqrt[3]{\dfrac{\mathcal{A}(x,y,z)^2}{p}}, \end{equation*}$

da cui

$\begin{equation*} \mathcal{A}(x,y,z)\leq \dfrac{\sqrt{3}}{9}p^2. \end{equation*}$

Osserviamo infine che l’uguaglianza e quindi il valore di area massima, si ottiene solamente se $p-x=p-y=p-z$ , ovvero se il triangolo è equilatero.

Esercizio 7 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^3\rightarrow\mathbb{R},$ definita da

$f(x,y,z):=x-2y+z,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+z^2\leq y\leq 1\}.$

Svolgimento.

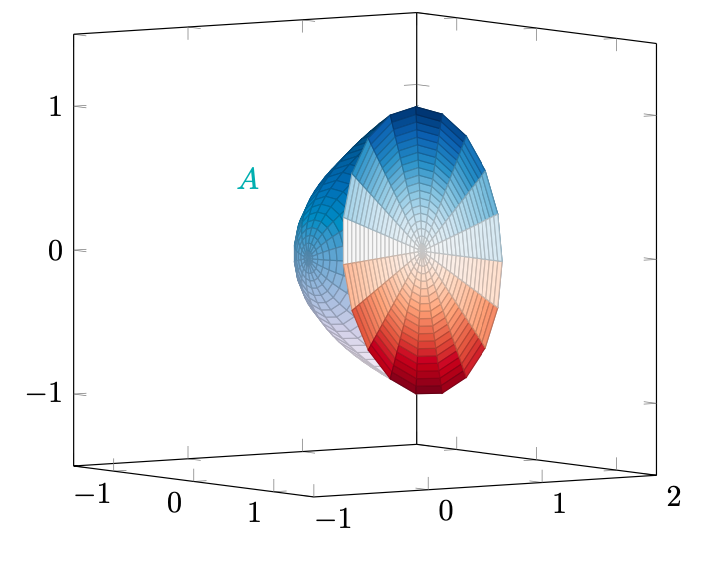
Figura 58: l’insieme $A$ .

$\quad$

$\begin{equation*} A:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+z^2-y\leq 0\}\cap \{(x,y,z)\in\mathbb{R}^3\mid 0\leq y\leq 1\}, \end{equation*}$

le funzioni $h_1(x,y,z):=x^2+z^2-y$ e $h_2(x,y,z)=y$ sono funzioni continue e gli intervalli $(-\infty,0]$ , $[0,1]$ sottoinsiemi chiusi di $\mathbb{R}$ , per cui si verifica $A=h^{-1}_1((-\infty,0])\cap h^{-1}_2([0,1])$ . Per la limitatezza, osserviamo che ciascun punto $(x,y,z)\in A$ soddisfa

$\begin{equation*} x^2+y^2+z^2\leq 1+y^2\leq 2, \end{equation*}$

da cui $A$ è contenuto in una sfera di raggio $\sqrt{2}$ . Dunque è un chiuso e limitato di $\mathbb{R}^3$ , compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$A^\circ)$ Essendo $f$ differenziabile sull’insieme aperto $A^\circ$ , il teorema di Fermat ci assicura che gli estremi relativi di $f$ in $A^\circ$ vanno ricercati tra i suoi eventuali punti critici in $A^\circ$ , ovvero i punti $P\in A^\circ$ tali che $\nabla f(P)=(0,0,0)$ e scartare tutti i punti che non soddisfano tale condizione. Osserviamo tuttavia che $f$ , in qualità di funzione lineare, non ammette punti critici. Pertanto, lo studio di $A^\circ$ non comporta alcun punto da annotare.

$\partial A)$ Possiamo descrivere $\partial A$ come unione di due componenti, ovvero $\partial A=B\cup C$ , con

$\begin{equation*} B:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+z^2=y, x^2+z^2\leq 1\}, \end{equation*}$

$\begin{equation*} C:=\{(x,y,z)\in\mathbb{R}^3\mid y=1, x^2+z^2\leq 1\}. \end{equation*}$

$\quad$

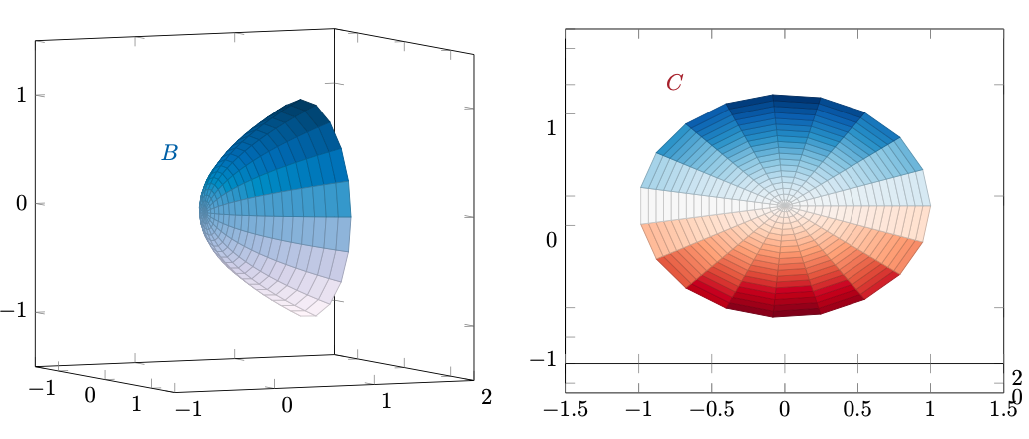
Figura 59: $B$ e $C$ , le due componenti della frontiera di $A$ .

$\quad$

Al fine di risolvere l’esercizio è utile trovare una parametrizzazione regolare per ciascuna delle componenti, $\psi_B$ e $\psi_C$ e studiare le funzioni composte $f\circ\psi_B$ e $f\circ\psi_C$ .

$B$ ) È immediato osservare che $B$ è unione di circonferenze parallele al piano $xz$ di raggio $y$ , dunque una sua possibile parametrizzazione è la seguente:

$\begin{equation*} \psi_B:[0,1]\times[0,2\pi]\rightarrow\mathbb{R}^3 \end{equation*}$

$\begin{equation*} \psi_B(\rho,\theta):=(\rho\cos\theta,\rho^2,\rho\sin\theta). \end{equation*}$

$\quad$

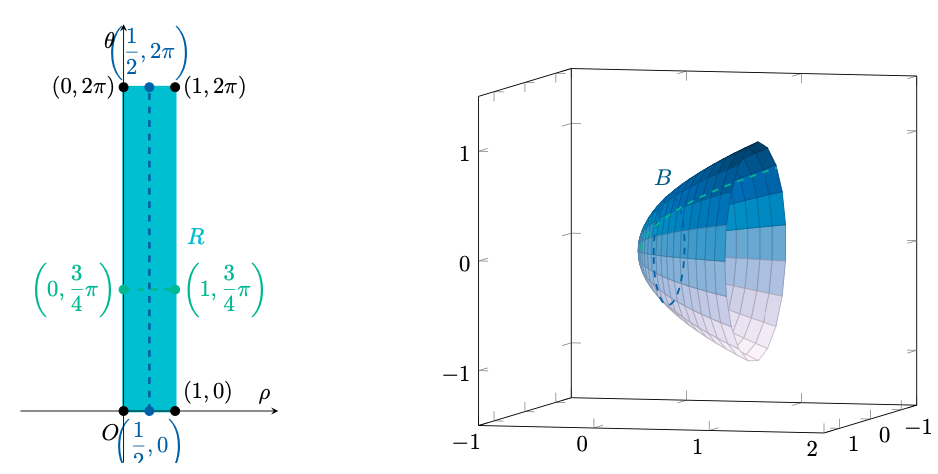
Figura 60: la parametrizzazione di $B$ con rappresentazione di alcune linee coordinate.

$\quad$

Sia $R:=[0,1]\times[0,2\pi]$ il dominio della parametrizzazione e $R^\circ=(0,1)\times(0,2\pi)$ la sua parte interna. $\psi_B$ è una parametrizzazione regolare di $B$ poiché $\psi_B|_{R^\circ}$ è iniettiva e di classe $\mathcal{C}^1$ su $R^\circ$ , $\det J_{\psi_B}\neq 0$ su $R^\circ$ ed infine vale

$\psi_B(R)=B.$

Osserviamo che sia $f$ sia $\psi_B$ sono funzioni continue, dunque lo è anche la loro composizione. Infine, $R$ è un chiuso e limitato di $\mathbb{R}^2$ , dunque compatto. Per il teorema di Weierstrass, esisteranno il massimo ed il minimo di $f\circ\psi_B$ su $R$ . Per trovarli, distinguiamo nuovamente l’insieme nella sua parte interna, $R^\circ$ e la sua frontiera, formata dai 4 lati del rettangolo.

Per quanto riguarda l’insieme aperto $R^\circ$ , essendo $f\circ\psi_B$ una funzione differenziabile, il teorema di Fermat afferma che condizione necessaria affinchè $P\in R^\circ$ sia un punto di massimo o di minimo è che $\nabla (f\circ\psi_B)(P)=(0,0)$ . Calcoliamo allora il gradiente di $f\circ\psi_B$ tramite le derivate parziali:

$\begin{equation*} (f\circ\psi_B)(\rho,\theta)=f(\rho\cos\theta,\rho^2,\rho\sin\theta)=\rho(\sin\theta+\cos\theta-2\rho), \end{equation*}$

$\begin{cases} \dfrac{\partial (f\circ\psi_B)}{\partial \rho}(\rho,\theta)=\cos\theta+\sin\theta-4\rho\\\\ \dfrac{\partial (f\circ\psi_B)}{\partial \theta}(\rho,\theta)=-\rho\sin\theta+\rho\cos\theta. \end{cases}$

Dunque

(5) $\begin{equation*} \nabla (f\circ\psi_B)(\rho,\theta)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} \cos\theta+\sin\theta-4\rho=0\\\\ -\rho\sin\theta+\rho\cos\theta=0 \end{array} \right.\Leftrightarrow\displaystyle\left\{\begin{array}{l} \cos\theta+\sin\theta-4\rho=0\\\\ \rho(\cos\theta-\sin\theta)=0. \end{array} \right. \end{equation*}$

Poiché su $R^\circ$ , $\rho>0$ , la seconda equazione si annulla solamente se $\cos\theta=\sin\theta$ , cioè per $\theta_1=\dfrac{\pi}{4}$ , $\theta_2=\dfrac{5}{4}\pi$ . Dalla prima equazione risulta

$\begin{equation*} \rho=\pm\dfrac{\sqrt{2}}{4}, \end{equation*}$

che possiamo accettare solo con segno positivo. Abbiamo trovato il punto critico di $f\circ\psi_B$ :

$\begin{equation*} \Tilde{P}_1:=\left(\dfrac{\sqrt{2}}{4},\dfrac{\pi}{4}\right), \end{equation*}$

a cui corrisponde il punto su $B$

$\begin{equation*} P_1=\psi_B\left(\dfrac{\sqrt{2}}{4},\dfrac{\pi}{4}\right)=\left(\dfrac{1}{4},\dfrac{1}{8},\dfrac{1}{4}\right). \end{equation*}$

$\quad$

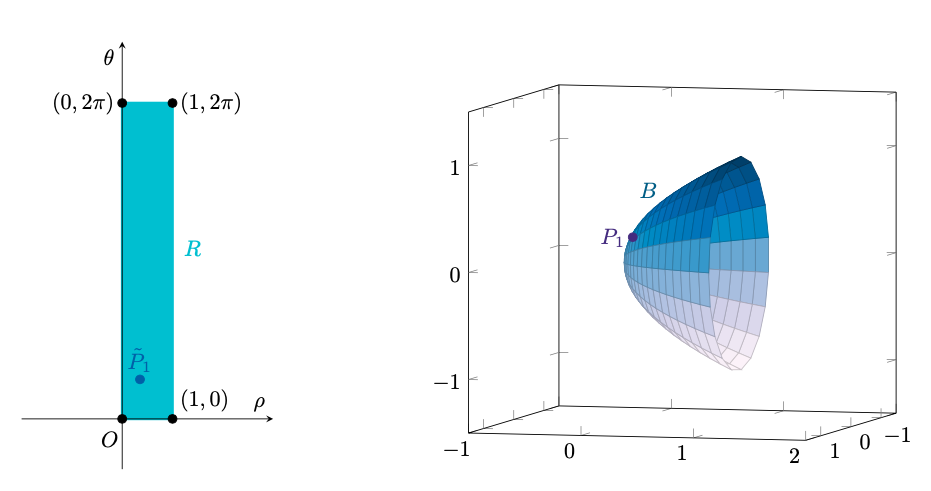
Figura 61: $\tilde{P}_1$ è l’unico punto critico di $f\circ\psi_B$ . Il suo corrispondente punto su $B$ è $P_1=\psi_B\left(\tilde{P}_1\right)$ .

$\quad$

Per quanto riguarda la frontiera $\partial R$ , essa è composta dai $4$ lati $L_1,L_2,L_3$ e $L_4$ , come mostrato in figura. Notiamo, tuttavia, che non è necessario studiare $f\circ\psi_B$ su $L_2$ e $L_4$ , i lati corrispondenti ai valori di $\theta=0$ , $\theta=2\pi$ , poichè la funzione $f\circ\psi_B$ è $2\pi$ -periodica rispetto a $\theta$ . Infatti, avremmo potuto parametrizzare $B$ tramite $\psi_B':[0,1]\times[-\pi,\pi]$ , con $\psi_B'(\rho,\theta)=\psi_B(\rho,\theta)$ , laddove entrambe definite. In tal modo la parte di frontiera relativa a $\theta=0$ non avrebbe svolto alcun ruolo nella ricerca dei massimi e minimi di $f\circ\psi_B$ su $R$ . Lo stesso discorso vale analogamente per $\theta=2\pi$ .

$\quad$

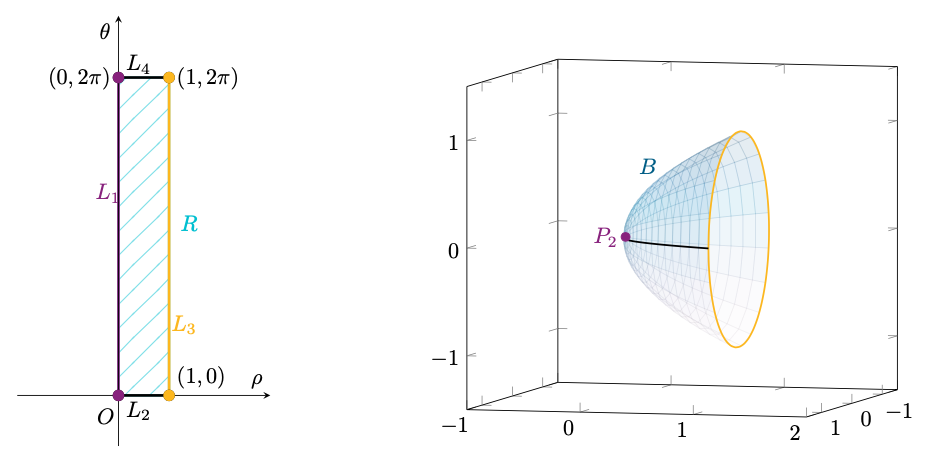
Figura 62: studio di $\partial B$ attraverso la sua parametrizzazione. Basterà studiare i lati $L_1$ e $L_3$ .

$\quad$

Il lato $L_1$ , corrispondente al settore $\rho=0$ viene parametrizzato da

$\begin{equation*} \begin{array}{rcl} \alpha_1:[0,2\pi] & \rightarrow&\mathbb{R}^2 \\ t&\mapsto&(0,t) \end{array} \end{equation*}$

$\begin{equation*} (f\circ\psi_B)(\alpha_1(t))=f(\psi_B(0,t))=f(0,0,0)=0. \end{equation*}$

Ciò significa che $f\circ\psi_B$ è costante su $L_1=\{0\}\times[0,2\pi]$ che risulta quindi un insieme di punti critici per $f\circ\psi_B$ , a cui corrisponde su $B$ il solo punto $\{(0,0,0)\}=\psi_B(L_1)$ , che denotiamo con $P_2$ .\ Per quanto riguarda $L_3=\{1\}\times[0,2\pi]$ , parametrizzato da

$\begin{equation*} \begin{array}{rcl} \alpha_3:[0,2\pi] & \rightarrow&\mathbb{R}^2 \\ t&\mapsto&(1,t). \end{array} \end{equation*}$

calcoliamo $(f\circ\psi_B)(\alpha_3(t))$ e i suoi punti critici.

$\begin{equation*} (f\circ\psi_B)(\alpha_3(t))=f(\cos t,1,\sin t)=\cos t+\sin t-2, \end{equation*}$

$\begin{equation*} ((f\circ\psi_B)\circ\alpha_3)'(t)=-\sin t+\cos t. \end{equation*}$

Dunque i punti critici di $((f\circ\psi_B)\circ\alpha_3)$ , ovvero i punti che annullano la sua derivata prima, sono i valori di $t\in[0,2\pi]$ per cui vale

$\begin{equation*} \cos t=\sin t, \end{equation*}$

cioè per $t=\dfrac{\pi}{4}$ e $t=\dfrac{5}{4}\pi$ . Troviamo dunque i punti

$\Tilde{P}_3=\left(1,\dfrac{\pi}{4}\right),\qquad \Tilde{P}_4=\left(1,\dfrac{5}{4}\pi\right),$

a cui corrispondono su $B$ i punti

$\begin{equation*} P_3=\psi_B\left(1,\dfrac{\pi}{4}\right)=\left(\dfrac{\sqrt{2}}{2},1,\dfrac{\sqrt{2}}{2}\right),\qquad P_4=\psi_B\left(1,\dfrac{5}{4}\pi\right)=\left(-\dfrac{\sqrt{2}}{2},1,-\dfrac{\sqrt{2}}{2}\right). \end{equation*}$

$\quad$

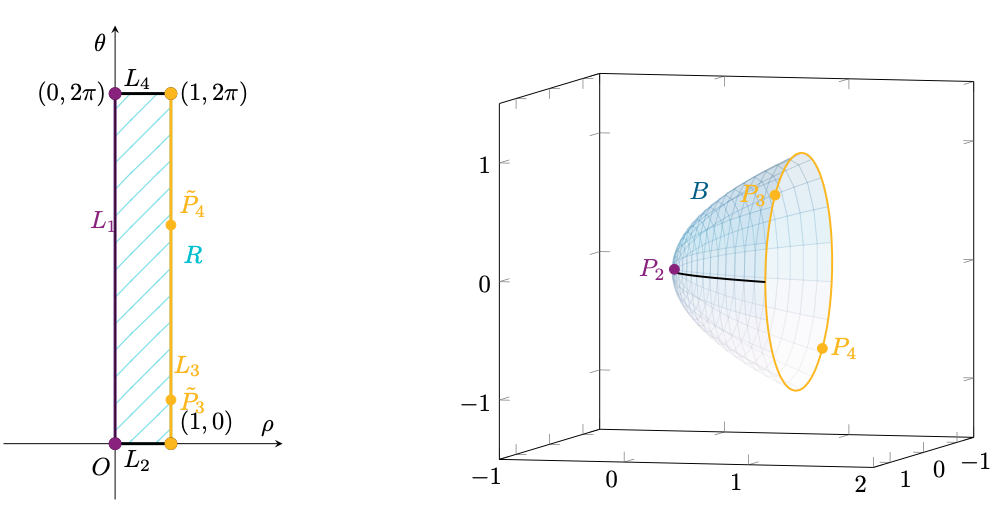
Figura 63: $P_3$ e $P_4$ corrispondono a punti critici su $L_3$ e il punto $P_2$ è immagine del lato $L_1$ .

$\quad$

Questo conclude lo studio di $f$ su $B$ che ha portato alla nostra attenzione $4$ candidati ad essere punti di massimo o di minimo di $f$ su $A$ : i punti $P_1,P_2,P_3$ e $P_4$ .

$C$ ) Osserviamo immediatamente che $C$ è un cerchio di raggio $1$ a quota $y=1$ . Pertanto esso è parametrizzabile da

$\begin{equation*} \psi_C:R \rightarrow\mathbb{R}^3 \end{equation*}$

$\begin{equation*} \psi_C(\rho,\theta):=(\rho\cos\theta,1,\rho\sin\theta). \end{equation*}$

$\quad$

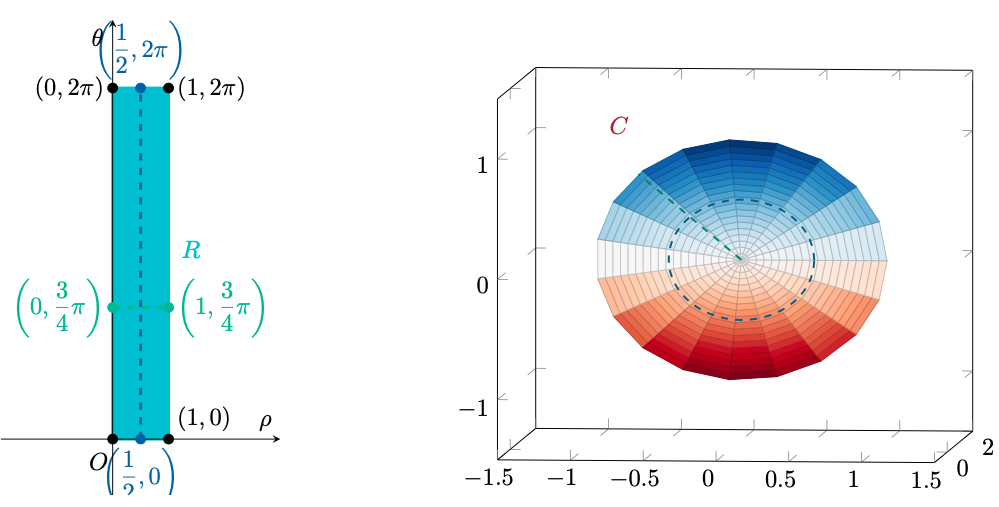
Figura 64: la parametrizzazione di $C$ , con alcune linee coordinate.

$\quad$

Calcoliamo $f\circ\psi_C$ :

$\begin{equation*} (f\circ\psi_C)(\rho,\theta)=f(\rho\cos\theta,1,\rho\sin\theta)=\rho\cos\theta+\rho\sin\theta-2. \end{equation*}$

Analogamente a quanto detto in precedenza, anche per $f\circ\psi_C$ il teorema di Weierstrass garantisce l’esistenza del massimo e del minimo su $R$ . Studiamo inizialmente il comportamento di $f\circ\psi_C$ sull’insieme aperto $R^\circ$ tramite la ricerca dei punti critici, per poi studiare $f\circ\psi_C$ su $\partial R$ .

Calcoliamo le derivate parziali di $f\circ\psi_C$ :

$\begin{cases} \dfrac{\partial (f\circ\psi_C)}{\partial \rho}(\rho,\theta)=\cos\theta+\sin\theta\\\\ \dfrac{\partial (f\circ\psi_C)}{\partial \theta}(\rho,\theta)=-\rho\sin\theta+\rho\cos\theta. \end{cases}$

Dunque

(6) $\begin{equation*} \nabla (f\circ\psi_C)(\rho,\theta)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} \cos\theta+\sin\theta=0\\\\ -\rho\sin\theta+\rho\cos\theta=0, \end{array} \right. \end{equation*}$

ma questo sistema non ha soluzioni: ciò significa che non ci sono punti critici di $f\circ\psi_C$ su $R^\circ$ . Per quanto riguarda $\partial R$ , poichè anche $f\circ\psi_C$ è $2\pi$ -periodica rispetto a $\theta$ , lo stesso discorso fatto in precedenza ci autorizza ad ignorare i lati corrispondenti ai valori $\theta=0$ e $\theta=2\pi$ . I lati rimasti sono $M_1=\{0\}\times[0,2\pi]$ e $M_3=\{1\}\times[0,2\pi]$ . Osserviamo tuttavia che $\psi_C(M_1)=\{(0,1,0)\}$ , dunque annotiamo per semplicità $P_5=(0,1,0)$ tra i possibili candidati.

Infine, per quanto riguarda $M_3$ , osserviamo che $f\circ\psi_C|_{M_3}=f\circ\psi_B|_{L_3}$ , che abbiamo ampiamente studiato in precedenza.

Questo conclude lo studio di $\partial A=B\cup C$ .

$\quad$

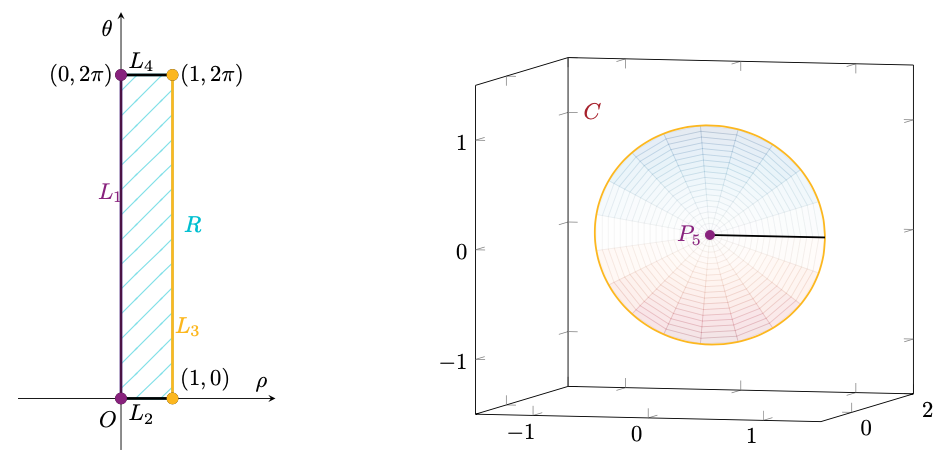
Figura 65: studio della frontiera di $C$ . Anche in questo caso, i lati $L_2$ e $L_4$ non svolgono alcun ruolo.

$\quad$

I possibili candidati ad essere punti di massimo o di minimo di $f$ su $A$ sono i seguenti

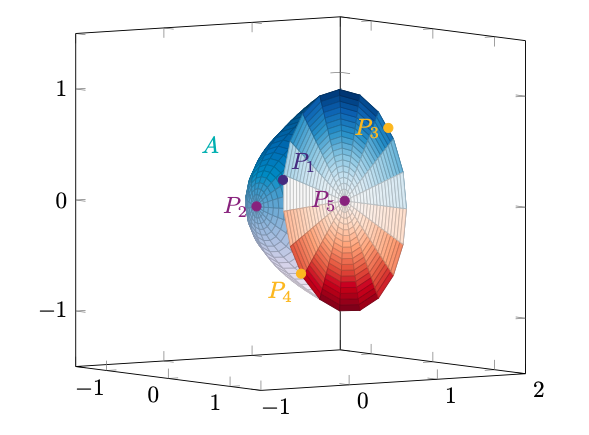
$\begin{equation*} \begin{split} &P_1=\left(\dfrac{1}{4},\dfrac{1}{8},\dfrac{1}{4}\right),\qquad P_2=(0,0,0),\qquad P_3=\left(\dfrac{\sqrt{2}}{2},1,\dfrac{\sqrt{2}}{2}\right),\\ & P_4=\left(-\dfrac{\sqrt{2}}{2},1,-\dfrac{\sqrt{2}}{2}\right),\qquad P_5=(0,1,0), \end{split} \end{equation*}$

$\quad$

Figura 66: tutti i candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

i cui valori rispetto a $f$ sono

$\begin{equation*} \begin{split} &f(P_1)=\dfrac{1}{4},\qquad f(P_2)=0,\qquad f(P_3)=\sqrt{2}-2,\\ &f(P_4)=-\sqrt{2}-2,\qquad f(P_5)=-2. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\dfrac{1}{4}$ , assunto nel punto $P_1=\left(\dfrac{1}{4},\dfrac{1}{8},\dfrac{1}{4}\right)$ e valore minimo $-\sqrt{2}-2$ , assunto in $P_4=\left(-\dfrac{\sqrt{2}}{2},1,-\dfrac{\sqrt{2}}{2}\right)$ .

Esercizio 8 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^3\rightarrow\mathbb{R},$ definita da

$f(x,y,z):=x^3+y^3+z^3,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2-z^2=1, \ x+y=1, \ -2\leq z\leq 2\}.$

Svolgimento.

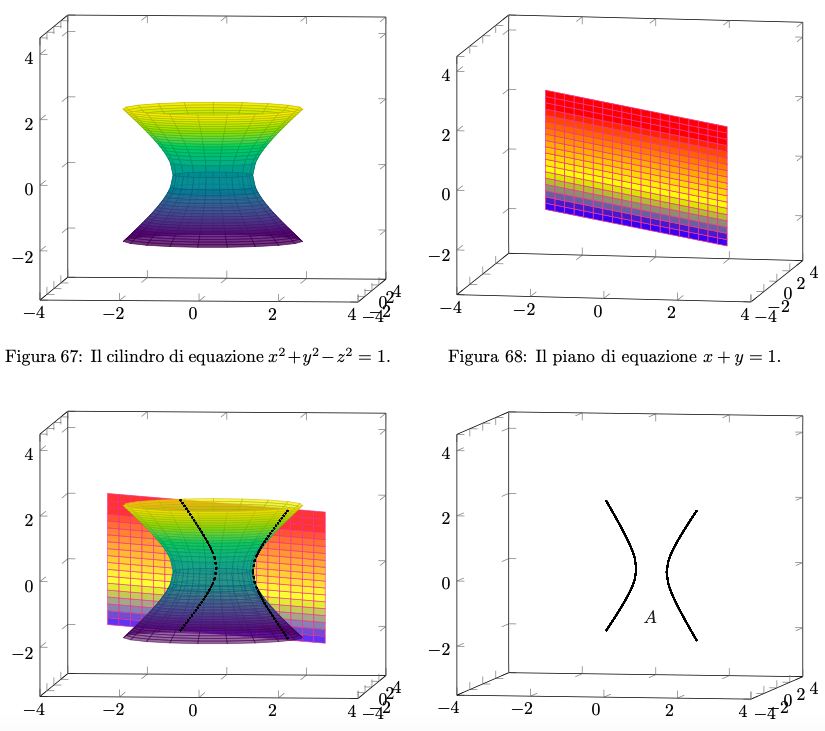
Figura 69: l’insieme $A$ , in nero, ottenuto come intersezione tra il cilindro e il piano, con vincolo $-2\leq z\leq 2$ .

$\quad$

$\begin{equation*} x^2+y^2=1+z^2\leq5, \end{equation*}$

da cui possiamo affermare che l’insieme $A$ è contenuto in una sfera di raggio $r=\sqrt{5+5+4}=\sqrt{14}$ , in particolare $A$ è un insieme limitato. Abbiamo dunque trovato che $A$ è un chiuso e limitato di $\mathbb{R}^3$ , compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Osserviamo che $A^\circ=\emptyset$ , ovvero $A$ è un insieme chiuso che coincide con la sua frontiera. È utile, tuttavia, separare $A$ tramite le due componenti

$\begin{equation*} A_1:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2-z^2=1, \ x+y=1, \ -2< z< 2\}, \end{equation*}$

$\begin{equation*} A_2:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2-z^2=1, \ x+y=1, \ z=\pm2\}, \end{equation*}$

$\quad$

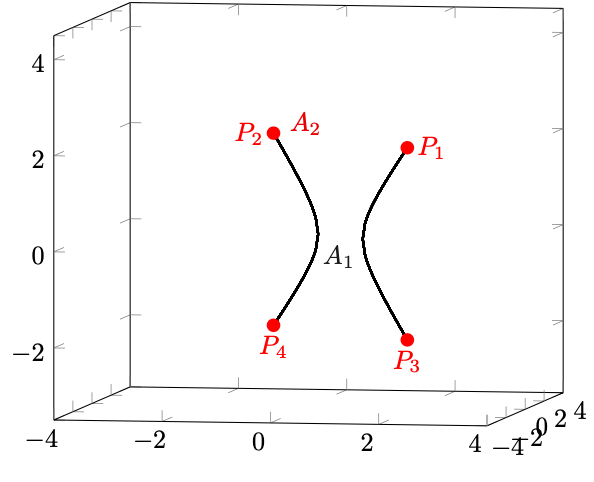
Figura 70: raffigurati i due insiemi che formano $A$ : $A_1$ in nero e $A_2$ composto dai 4 punti rossi.

$\quad$

da cui risulta

$\begin{equation*} A=A_1\cup A_2. \end{equation*}$

Ricerchiamo i punti di massimo e minimo di $f$ su $A_1$ attraverso il metodo dei moltiplicatori di Lagrange, mentre indaghiamo $A_2$ in maniera diretta, essendo unione di punti isolati, come vedremo. Osserviamo che il vincolo $A_1$ si può esprimere come intersezione di luogo di zeri di due funzioni: siano $g,h:\mathbb{R}^3\rightarrow\mathbb{R}$ definite da

$\begin{equation*} g(x,y,z):=x^2+y^2-z^2-1, \end{equation*}$

$\begin{equation*} h(x,y,z):=x+y-1. \end{equation*}$

Detti

$\begin{equation*} B:=\{(x,y,z)\in\mathbb{R}^2\times(-2,2)\mid g(x,y,z)=0\} \end{equation*}$

$\begin{equation*} C:=\{(x,y,z)\in\mathbb{R}^2\times(-2,2)\mid h(x,y,z)=0\}, \end{equation*}$

$\quad$

Figura 71: si applica il metodo dei moltiplicatori di Lagrange ai vincoli $B$ e $C$ , la cui intersezione è il vincolo effettivo.

$\quad$

vale

$\begin{equation*} A_1=B\cap C. \end{equation*}$

Il metodo dei moltiplicatori di Lagrange ci induce a studiare la funzione Lagrangiana

$\mathcal{L}(x,y,z,\lambda,\mu):=f(x,y,z)-\lambda g(x,y,z)-\mu h(x,y,z)$

e ricercare i suoi punti critici non vincolati. Infatti, per il teorema dei moltiplicatori di Lagrange, ad essi corrisponderanno i punti critici vincolati di $f$ su $A_1$ . Dovremo dunque risolvere il sistema

Nel nostro caso

$\begin{equation*} \mathcal{L}(x,y,z,\lambda,\mu)=x^3+y^3+z^3-\lambda(x^2+y^2-z^2-1)-\mu(x+y-1), \end{equation*}$

i cui punti critici devono soddisfare il sistema

$\begin{equation*} \left\{\begin{array}{l} 3x^2+2\lambda x+\mu=0 \\\\ 3y^2+2\lambda y+\mu=0 \\\\ 3z^2-2\lambda z=0 \\\\ x^2+y^2-z^2=1 \\\\ x+y=1 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} 3x^2+2\lambda x+\mu=0 \\\\ 3y^2+2\lambda y+\mu=0 \\\\ (3z-2\lambda) z=0 \\\\ x^2+y^2-z^2=1 \\\\ x+y=1. \\\\ \end{array}\right. \end{equation*}$

Sostituiamo nella prima riga la differenza tra le prime due equazioni e utilizziamo il prodotto notevole $x^2-y^2=(x+y)(x-y)$ :

$\begin{equation*} \left\{\begin{array}{l} 3(x^2-y^2)+2\lambda(x-y)=0 \\\\ 3y^2+2\lambda y+\mu=0 \\\\ (3z-2\lambda) z=0 \\\\ x^2+y^2-z^2=1 \\\\ x+y=1 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} (x-y)\left[3(x+y)+2\lambda\right]=0 \\\\ 3y^2+2\lambda y+\mu=0 \\\\ (3z-2\lambda) z=0 \\\\ x^2+y^2-z^2=1 \\\\ x+y=1 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} (x-y)\left(3+2\lambda\right)=0 \\\\ 3y^2+2\lambda y+\mu=0 \\\\ (3z-2\lambda) z=0 \\\\ x^2+y^2-z^2=1 \\\\ x+y=1, \\\\ \end{array}\right. \end{equation*}$

dove abbiamo utilizzato l’equazione $x+y=1$ per semplificare la prima equazione. Osserviamo che la terza equazione si annulla solamente se $z=0$ o $\lambda=\dfrac{3}{2}z$ . Supponiamo prima $z=0$ , da cui il sistema risulta

$\begin{equation*} \left\{\begin{array}{l} (x-y)\left(3+2\lambda\right)=0 \\\\ 3y^2+2\lambda y+\mu=0 \\\\ z=0 \\\\ x^2+y^2=1 \\\\ x+y=1 \\\\ \end{array}\right.\implies\left\{\begin{array}{l} z=0\\\\ x^2+y^2=1 \\\\ x+y=1 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} z=0\\\\ x=1 \\\\ y=0 \\\\ \end{array}\right.\lor\left\{\begin{array}{l} z=0\\\\ x=0 \\\\ y=1 \\\\ \end{array}\right. \end{equation*}$

Abbiamo allora trovato i primi due punti interessanti: $P_5=(1,0,0)$ e $P_6=(0,1,0)$ .

Supponendo, invece, $\lambda=\dfrac{3}{2}z$ , il sistema diventa

$\begin{equation*} \left\{\begin{array}{l} (x-y)\left(3+3z\right)=0 \\\\ 3y^2+3z y+\mu=0 \\\\ \lambda=\dfrac{3}{2}z \\\\ x^2+y^2-z^2=1 \\\\ x+y=1. \\\\ \end{array}\right. \end{equation*}$

La prima equazione si annulla solo se $x=y$ o $z=-1$ . Se fosse $x=y$ , l’ultima equazione implicherebbe $x,y=\dfrac{1}{2}$ , ma dalla quarta equazione avremmo

$\begin{equation*} z^2=x^2+y^2-1=\dfrac{1}{4}+\dfrac{1}{4}-1=-\dfrac{1}{2}, \end{equation*}$

che è chiaramente impossibile. Se, invece, $z=-1$ , focalizziamoci ancora sulle ultime due equazioni del sistema che si riducono a

$\begin{equation*} \left\{\begin{array}{l} x^2+y^2=2 \\\\ x+y=1. \\\\ \end{array}\right. \end{equation*}$

Ricavando $y=1-x$ , otteniamo l’equazione in funzione della sola variabile $x$

$\begin{equation*} 2x^2+1-2x=2\Leftrightarrow2x^2-2x-1=0\Leftrightarrow x_{1,2}=\dfrac{1\pm\sqrt{1+2}}{2}=\dfrac{1\pm\sqrt{3}}{2}, \end{equation*}$

da cui

$\begin{equation*} y_{1,2}=1-\dfrac{1\pm\sqrt{3}}{2}=\dfrac{1\mp\sqrt{3}}{2}. \end{equation*}$

Abbiamo quindi trovato altri 2 punti da considerare:

$\begin{equation*} P_7=\left(\dfrac{1+\sqrt{3}}{2},\dfrac{1-\sqrt{3}}{2},-1\right),\qquad P_8=\left(\dfrac{1-\sqrt{3}}{2},\dfrac{1+\sqrt{3}}{2},-1\right). \end{equation*}$

Questo conclude lo studio di $A_1$ .

Occupiamoci ora di $A_2$ e osserviamo che è composto da $4$ punti isolati. Infatti, dalle equazioni che definiscono $A_2$ , troviamo

$\begin{equation*} \left\{\begin{array}{l} x^2+y^2-z^2=1 \\\\ x+y=1\\\\ z=\pm2 \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} x^2+y^2=5 \\\\ x+y=1\\\\ z=\pm2. \end{array} \right. \end{equation*}$

Sostituiamo $y=1-x$ nella prima equazione per trovare $x$ :

$\begin{equation*} 2x^2-2x+1=5\Leftrightarrow x^2-x-2=0\Leftrightarrow(x-2)(x+1)=0\Leftrightarrow x=2\lor x=-1, \end{equation*}$

da cui si trova

$\begin{equation*} y=-1\lor y=2. \end{equation*}$

Pertanto,

$\begin{equation*} A_2=P_1\cup P_2\cup P_3\cup P_4, \end{equation*}$

dove

$\begin{equation*} P_1=(2,-1,2),\qquad P_2=(-1,2,2),\qquad P_3=(2,-1,-2),\qquad P_4=(-1,2,-2). \end{equation*}$

Abbiamo trovato otto candidati ad essere punti di massimo e di minimo di $f$ su $A$ .

$\quad$

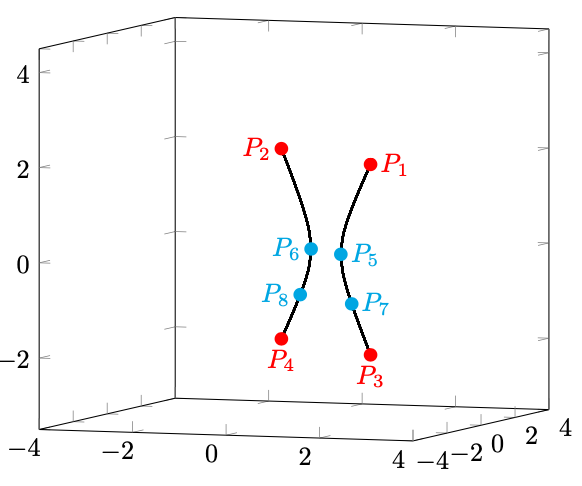
Figura 72: tutti i candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

Calcoliamo i loro valori tramite $f$ e confrontiamoli:

$\begin{equation*} \begin{split} f(P_1)=f(2,-1,2)=15,&\qquad f(P_2)=f(-1,2,2)=15,\\ f(P_3)=f(2,-1,-2)=-1,&\qquad f(P_4)=f(-1,2,-2)=-1,\\ f(P_5)=f\left(1,0,0\right)=1,&\qquad f(P_6)=f\left(0,1,0\right)=1,\\ f(P_7)=f\left(\dfrac{1+\sqrt{3}}{2},\dfrac{1-\sqrt{3}}{2},-1\right)=\dfrac{3}{2},&\qquad f(P_8)=f\left(\dfrac{1-\sqrt{3}}{2},\dfrac{1+\sqrt{3}}{2},-1\right)=\dfrac{3}{2}.\\ \end{split} \end{equation*}$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $15$ , assunto nei punti $P_1=(2,-1,2)$ e $P_2=(-1,2,2)$ valore minimo $-1$ , assunto nei punti $P_3=(2,-1,-2)$ e $P_4=(-1,2,-2)$ .

Esercizio 9 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^3\rightarrow\mathbb{R},$ definita da

$f(x,y,z):=z-x,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2+z=1, \ x^2+z^2=3\}.$

Svolgimento.

Figura 73: tratteggiato, in nero, l’insieme $A$ , ottenuto come intersezione tra un cilindro e un paraboloide.

$\quad$

Osserviamo che $f$ è un polinomio, pertanto è una funzione continua su $\mathbb{R}^3$ , mentre l’insieme $A$ è chiuso e limitato. La chiusura segue dal fatto che $A$ è intersezione di controimmagini di insiemi chiusi di $\mathbb{R}$ tramite funzioni continue, la limitatezza dalle equazioni che definiscono $A$ . Infatti, dalla seconda condizione possiamo immediatamente affermare che $x,z\in[-3,3]$ , da cui $x^2\in[0,9]$ , pertanto dalla prima equazione possiamo ottenere una stima di $y$ :

$\begin{equation*} y^2=1-x^2-z\in[-11,4], \end{equation*}$

da cui $y\in[-2,2]$ . Abbiamo trovato che ciascun punto $(x,y,z)$ in $A$ dev’essere contenuto in un parallelepipedo di centro l’origine e lati $6,4$ e $6$ , a sua volta contenuto in una sfera di raggio $r=\sqrt{3^2+2^2+3^2}=\sqrt{22}$ . Ciò dimostra la limitatezza di $A$ . Abbiamo dunque trovato che $A$ è un chiuso e limitato di $\mathbb{R}^3$ , compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Osserviamo che $A^\circ=\emptyset$ , ovvero $A$ è un insieme chiuso che coincide con la sua frontiera. Ricerchiamo i punti di massimo e minimo di $f$ su $A$ attraverso il metodo dei moltiplicatori di Lagrange. Osserviamo che il vincolo $A$ si può esprimere come intersezione di luogo di zeri di due funzioni: siano $g,h:\mathbb{R}^3\rightarrow\mathbb{R}$ definite da

$\begin{equation*} g(x,y,z):=x^2+y^2+z-1, \end{equation*}$

$\begin{equation*} h(x,y,z):=x^2+z^2-3. \end{equation*}$

Detti

$\begin{equation*} \Gamma:=\{(x,y,z)\in\mathbb{R}^3\mid g(x,y,z)=0\} \end{equation*}$

$\begin{equation*} \Sigma:=\{(x,y,z)\in\mathbb{R}^3\mid h(x,y,z)=0\}, \end{equation*}$

$\quad$

vale

$\begin{equation*} A=\Gamma\cap\Sigma. \end{equation*}$

Il teorema dei moltiplicatori di Lagrange afferma che in corrispondenza dei punti di massimo o minimo di $f$ su $A$ , che non siano punti critici dei vincoli $g$ ed $h$ , i gradienti delle funzioni $f$ , $g$ e $h$ risultano complanari. Ciò significa che, se $x_0\in A$ è punto di massimo o minimo di $f$ su $A$ e tale che $\nabla g(x_0),\nabla h(x_0)\neq 0$ , esistono $\lambda,\mu\in\mathbb{R}$ tali che

$\begin{equation*} \nabla f(x_0)=\lambda\nabla g(x_0)+\mu\nabla h(x_0). \end{equation*}$

È conveniente, al fine di utilizzare questo metodo risolutivo, costruire direttamente la funzione Lagrangiana

$\mathcal{L}(x,y,z,\lambda,\mu):=f(x,y,z)-\lambda g(x,y,z)-\mu h(x,y,z)$

e ricercare i suoi punti critici non vincolati. Ad essi corrisponderanno i punti critici vincolati di $f$ su $A$ . Dovremo dunque risolvere il sistema

Nel nostro caso

$\begin{equation*} \mathcal{L}(x,y,z,\lambda,\mu)=z-x-\lambda(x^2+y^2+z-1)-\mu(x^2+z^2-3), \end{equation*}$

i cui punti critici devono soddisfare il sistema

$\begin{equation*} \left\{\begin{array}{l} -1+2\lambda x+2\mu x=0 \\\\ 2\lambda y=0 \\\\ 1+\lambda+2\mu z=0 \\\\ x^2+y^2+z=1 \\\\ x^2+z^2=3 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} 2\lambda x+2\mu x=1 \\\\ \lambda y=0 \\\\ \lambda+2\mu z=-1 \\\\ x^2+y^2+z=1 \\\\ x^2+z^2=3 \\\\ \end{array}\right. \end{equation*}$

Osserviamo che la seconda equazione si annulla solamente se $\lambda=0$ o $y=0$ . Supponiamo inizialmente $\lambda=0$ , allora il sistema diventa

$\begin{equation*} \left\{\begin{array}{l} 2\mu x=1 \\\\ \lambda=0 \\\\ 2\mu z=-1 \\\\ x^2+y^2+z=1 \\\\ x^2+z^2=3. \\\\ \end{array}\right. \end{equation*}$

Confrontando tra loro la prima e la terza equazione, dovrà necessariamente risultare $x=-z$ . Inserendo quest’informazione nell’ultima equazione del sistema, troviamo

$\begin{equation*} 2x^2=3\implies x=\pm\sqrt{\dfrac{3}{2}}. \end{equation*}$

Osserviamo che la soluzione $x=-\sqrt{\dfrac{3}{2}}$ non è accettabile, poiché risulterebbe $z=\sqrt{\dfrac{3}{2}}>1$ , ma dalla quarta equazione sappiamo sicuramente che $z=1-x^2-y^2\leq 1$ . Risolviamo il sistema per $x=\sqrt{\dfrac{3}{2}}$ e $z=-\sqrt{\dfrac{3}{2}}$ , trovando dalla quarta equazione

$\begin{equation*} y^2=1-\dfrac{3}{2}+\sqrt{\dfrac{3}{2}}\implies y=\pm\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}}. \end{equation*}$

Per completezza, troviamo il moltiplicatore di Lagrange $\mu$ :

$\begin{equation*} \mu=\dfrac{1}{2\sqrt{\dfrac{3}{2}}}=\dfrac{1}{\sqrt{6}}. \end{equation*}$

Abbiamo trovato i primi punti critici della Lagrangiana

$\left(\sqrt{\dfrac{3}{2}},\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}},-\sqrt{\dfrac{3}{2}},0,\dfrac{1}{\sqrt{6}}\right),\qquad\left(\sqrt{\dfrac{3}{2}},-\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}},-\sqrt{\dfrac{3}{2}},0,\dfrac{1}{\sqrt{6}}\right),$

a cui corrispondono i punti su $A$

$\begin{equation*} P_1=\left(\sqrt{\dfrac{3}{2}},\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}},-\sqrt{\dfrac{3}{2}}\right),\qquad P_2=\left(\sqrt{\dfrac{3}{2}},-\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}},-\sqrt{\dfrac{3}{2}}\right). \end{equation*}$

Supponendo, invece $y=0$ , possiamo restringere la nostra attenzione alle ultime due equazioni del sistema per trovare le altre due variabili:

$\begin{equation*} \left\{\begin{array}{l} x^2+z=1 \\\\ x^2+z^2=3 \\ \end{array}\right. \end{equation*}$

per confronto tra le due equazioni troviamo

$\begin{equation*} x^2=1-z=3-z^2, \end{equation*}$

ovvero

$\begin{equation*} z^2-z-2=0\Leftrightarrow(z-2)(z+1)=0\Leftrightarrow\left\{\begin{array}{l} z=2 \\\\ z=-1 \end{array}\right. \end{equation*}$

Il valore $z=2$ non comporta alcuna soluzione reale per $x^2=1-z$ , per cui verrà eslcuso, mentre per $z=-1$ otteniamo $x=\pm\sqrt{2}$ , ovvero i punti

$\begin{equation*} P_3=\left(\sqrt{2},0,-1\right),\qquad P_4=\left(-\sqrt{2},0,-1\right), \end{equation*}$

corrispondenti ai punti critici della Lagrangiana

$\begin{equation*} \left(\sqrt{2},0,-1,\dfrac{\sqrt{2}-2}{6},\dfrac{4+\sqrt{2}}{12}\right),\qquad \left(-\sqrt{2},0,-1,\dfrac{-\sqrt{2}-2}{6},\dfrac{4-\sqrt{2}}{12}\right). \end{equation*}$

Abbiamo trovato quattro candidati ad essere punti di massimo e di minimo di $f$ su $A$ .

$\quad$

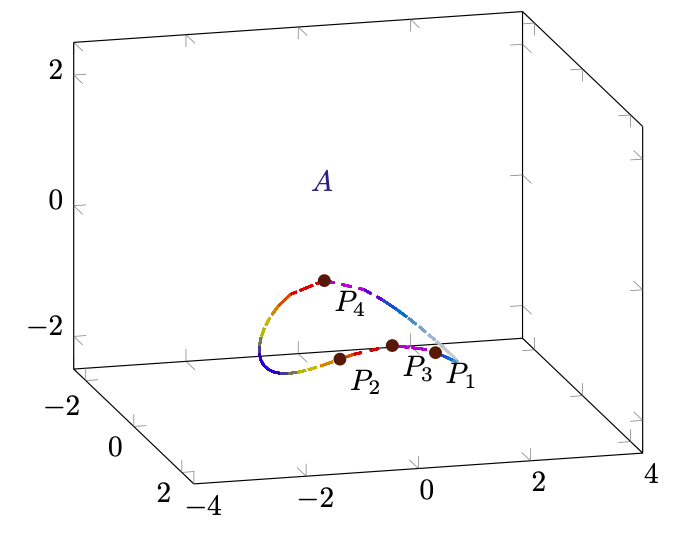
Figura 76: tutti i punti candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

Mostriamo che, come prevede il teorema dei moltiplicatori di Lagrange, i gradienti di $f$ , $g$ e $h$ sono complanari nei punti precedentemente trovati:

$\quad$

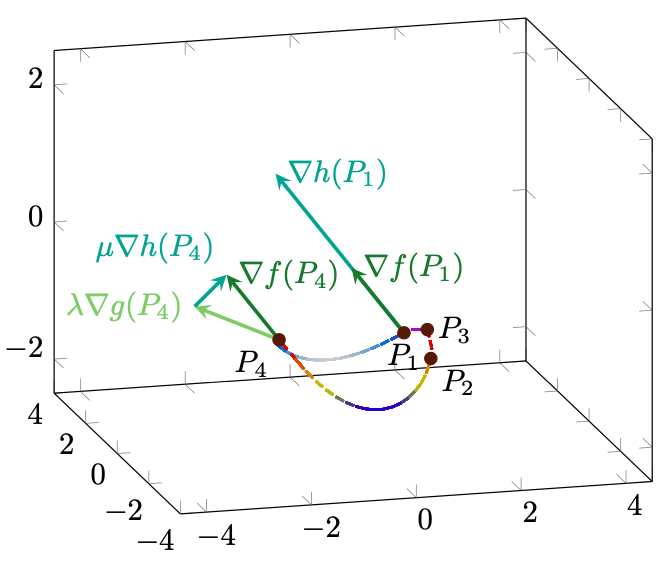
Figura 77: vi è una differenza tra $P_1$ e $P_4$ : in $P_1$ i gradienti di $f$ e $h$ sono paralleli, mentre in $P_4$ sono complanari assieme al gradiente di $g$ . Ciò significa che $P_1$ sarebbe da considerare anche nella ricerca di massimi e minimi di $f$ sulla superficie $\Sigma$ , mentre $P_4$ solo in relazione al vincolo più restrittivo $\Sigma\cap\Gamma$ .

$\quad$

Calcoliamo i loro valori tramite $f$ e confrontiamoli:

$\begin{equation*} \begin{split} f(P_1)=f\left(\sqrt{\dfrac{3}{2}},\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}},-\sqrt{\dfrac{3}{2}}\right)=-\sqrt{6},&\qquad f(P_2)=f\left(\sqrt{\dfrac{3}{2}},-\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}},-\sqrt{\dfrac{3}{2}}\right)=-\sqrt{6}\\ f(P_3)=f\left(\sqrt{2},0,-1\right)=-1-\sqrt{2},&\qquad f(P_4)=f\left(-\sqrt{2},0,-1\right)=\sqrt{2}-1. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\sqrt{2}-1$ , assunto nel punto $P_4=\left(-\sqrt{2},0,-1\right)$ e valore minimo $-\sqrt{6}$ , assunto nei punti $P_1=\left(\sqrt{\dfrac{3}{2}},\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}},-\sqrt{\dfrac{3}{2}}\right)$ e $P_2=\left(\sqrt{\dfrac{3}{2}},-\sqrt{\sqrt{\dfrac{3}{2}}-\dfrac{1}{2}},-\sqrt{\dfrac{3}{2}}\right)$ .

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Document

Menu

Chiudi

Massimi e minimi vincolati – Esercizi – Volume 2

Autori e revisori

Leggi...

Introduzione

Leggi...

Richiami di teoria

Leggi...

Esercizi

Svolgimento 1.

Svolgimento 2.

Svolgimento 1.

Svolgimento 2.

Svolgimento 1.

Svolgimento 2.

Svolgimento 3.

Svolgimento.

Svolgimento.

Svolgimento 1.

Svolgimento 2.

Svolgimento.

Svolgimento.

Svolgimento.

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi