Massimi e minimi vincolati – Esercizi – Volume 1

Home » Massimi e minimi vincolati – Esercizi – Volume 1

Benvenuti nel primo volume di esercizi sulla ricerca di massimi e minimi vincolati per funzioni in più variabili. L’articolo consiste in una raccolta di 10 esercizi sulla ricerca dei punti di massimo e minimo di una funzione su un insieme compatto $D \subset \mathbb{R}^n$ . Viene studiata la presenza di eventuali punti di estremo sia nell’interno di $D$ , grazie al teorema di Fermat e alle tecniche classiche come lo studio della matrice hessiana, sia sul bordo $\partial D$ , grazie a tecniche di parametrizzazione o utilizzando il metodo dei moltiplicatori di Lagrange.
Gli esercizi presentano soluzioni complete, quasi sempre più di una soluzione, per offrire al lettore una panoramica ampia di tecniche risolutive così da permettere di confrontarle e affinare le sue capacità di problem solving.
La raccolta è quindi particolarmente indicata per gli appassionati e per gli studenti dei corsi di Analisi Matematica 2, in vista della preparazione dell’esame.

Oltre a Massimi e minimi vincolati – Esercizi – Volume 2, segnaliamo il seguente materiale su argomenti correlati:

Buona lettura!

Autori e revisori

Leggi...

Autori: Giulio Binosi.

Revisori: Matteo Talluri, Davide La Manna, Jacopo Garofali, Daniele Bjørn Malesani, Silvia Lombardi, Valerio Brunetti.

Introduzione

Leggi...

La seguente dispensa è una collezione di esercizi riguardanti il problema della determinazione del massimo e del minimo di una funzione su un insieme compatto di $\mathbb{R}^2$ . Essa è composta da esercizi di varia difficoltà ed è rivolta a studenti di Ingegneria, Fisica e Matematica che desiderano affrontare l’esame di Analisi 2. Tutti gli esercizi presentano una soluzione convenzionale, mentre alcuni ne hanno altre più ad hoc. L’obiettivo è quello di suggerire allo studente strade alternative per risolvere l’esercizio più velocemente. Gli strumenti utilizzati sono il Teorema di Fermat per quanto riguarda la parte interna dell’insieme, mentre per la sua frontiera adotteremo il metodo della parametrizzazione, qualora possibile, o il metodo dei moltiplicatori di Lagrange, quando il vincolo è espresso come luogo di zeri.

Richiami di teoria

Leggi...

Richiamiamo alcuni risultati fondamentali, che saranno utilizzati nella risoluzione degli esercizi:

Teorema 1 (teorema di Weierstrass). Sia $K\subset\mathbb{R}^n$ un insieme compatto e sia $f:K\rightarrow\mathbb{R}$ una funzione continua. Allora $f$ ammette massimo e minimo su $K$ .

Teorema 2 (teorema di Heine-Borel). Un insieme $E\subset\mathbb{R}^n$ è compatto se e solo se è chiuso e limitato.

Teorema 3 (teorema di Fermat). Siano $A\subset\mathbb{R}^n$ un insieme aperto, $f:A\rightarrow\mathbb{R}$ e $x_0\in A$ tale che $f$ è differenziabile in $x_0$ . Allora, se $x_0$ è un punto di massimo o minimo relativo per $f$ su $A$ , vale $\nabla f(x_0)=0$ .

Corollario 4. Sia $f:A\subset\mathbb{R}^n\rightarrow\mathbb{R}$ una funzione differenziabile su tutto $A$ , insieme aperto. Allora, tutti i punti di massimo o minimo relativo di $f$ su $A$ sono, in particolare, punti critici.

Teorema 5 (teorema dei moltiplicatori di Lagrange). Siano $f,g:\mathbb{R}^n\rightarrow\mathbb{R}$ due funzioni di classe $\mathcal{C}^1$ , sia $\Gamma:=\{x\in\mathbb{R}^n\mid g(x)=0\}$ . Supponiamo che $x_0\in\Gamma$ sia un punto di massimo o minimo di $f$ su $\Gamma$ e che $\nabla g(x_0)\neq0$ , allora $\exists\lambda\in\mathbb{R}$ tale che $\nabla f(x_0)=\lambda\nabla g(x_0).$

Proposizione 6. Sia $f=g\circ h$ . Se la funzione $g$ è strettamente crescente, i punti di massimo di $f$ corrispondono a punti di massimo per $h$ , ugualmente per i punti di minimo. Viceversa, se $g$ è strettamente decrescente, i punti di massimo di $f$ corrispondono a punti di minimo per $h$ e viceversa.

$\quad$

Dimostrazione. Dimostriamolo attraverso la definizione: un punto $P\in A$ si dice punto di massimo per $f$ su $A$ se e solo se $f(P)\geq f(x,y)$ , $\forall (x,y)\in A$ (analogamente per punto di minimo). Ma allora, essendo $f=g\circ h$ , con $g$ strettamente crescente si ha

$\begin{equation*} \begin{split} g(h(P))&=f(P)\geq f(x,y)=g(h(x,y))\qquad\forall(x,y)\in\mathbb{R}^2\\ &\Leftrightarrow h(P)\geq h(x,y)\qquad\forall(x,y)\in\mathbb{R}^2 \end{split} \end{equation*}$

Viceversa, se $g$ è strettamente decrescente

$\begin{equation*} \begin{split} g(h(P))&=f(P)\geq f(x,y)=g(h(x,y))\qquad\forall(x,y)\in\mathbb{R}^2\\ &\Leftrightarrow h(P)\leq h(x,y)\qquad\forall(x,y)\in\mathbb{R}^2 \end{split} \end{equation*}$

Esercizi

$\quad$

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=x^2+3y^2+\dfrac{1}{2}x,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$E:=\{(x,y)\in\mathbb{R}^2\mid x^2+4y^2\leq4\}.$

Svolgimento 1.

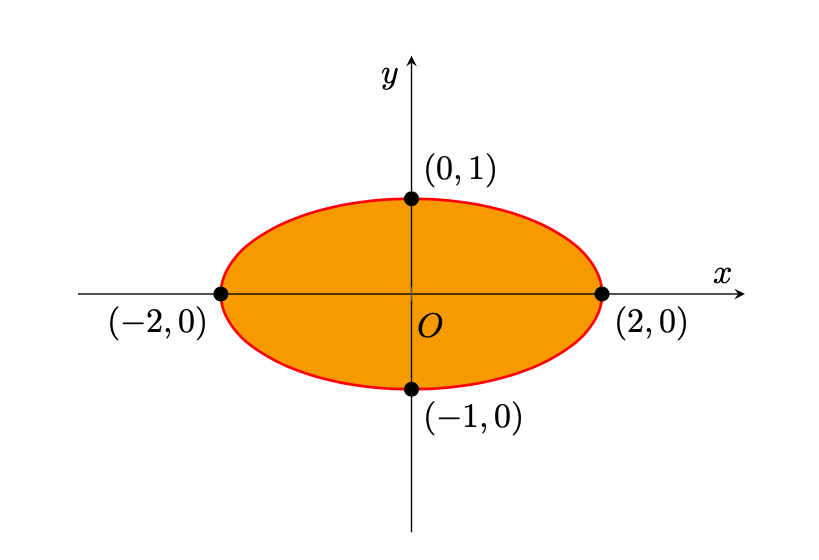
Figura 1: L’insieme $E$ .

$\quad$

Osserviamo immediatamente che $f$ , essendo un polinomio, è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $E$ è compatto, poiché rappresenta un’ellisse piena. Più precisamente, esso è limitato in quanto ogni suo punto è contenuto nella palla di centro l’origine e raggio $2$ , mentre è chiuso poiché controimmagine dell’intervallo chiuso $[0,4]$ tramite la funzione continua $(x,y)\mapsto x^2+4y^2$ . Pertanto, il teorema di Weierstrass assicura l’esistenza del massimo e del minimo di $f$ su $E$ , come richiesto.

Per indagare tali punti, di cui abbiamo mostrato l’esistenza, ricorriamo al Teorema di Fermat, per il quale condizione necessaria per essere un punto di massimo o minimo è quella di essere punto critico. È importante sottolineare che tale comportamento si applica a funzioni differenziabili su un insieme aperto. Il più grande aperto contenuto in $E$ , al quale possiamo applicare il teorema di Fermat è $E^\circ$ ¹. Dovremo studiare diversamente $\partial E$ ², in modo da esaminare l’intero insieme $E=E^\circ\sqcup\partial E$ ³.

Indaghiamo gli eventuali punti critici di $f$ in $E^\circ$ , ovvero i punti $P\in E^\circ$ tali che $\nabla f(P)=(0,0)$ . Calcoliamo il gradiente di $f$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=2x+\dfrac{1}{2}\\\\ \dfrac{\partial f}{\partial y}(x,y)=6y. \end{cases}$

Dunque

$\nabla f(x,y)=(0,0)\quad \Leftrightarrow \quad \displaystyle\left\{\begin{array}{l} 2x+\dfrac{1}{2}=0\\\\ 6y=0 \end{array} \right.\quad \Leftrightarrow \quad\displaystyle\left\{\begin{array}{l} x=-\dfrac{1}{4}\\ y=0. \end{array} \right.$

Ciò significa che l’unico punto critico di $f$ è $P_1=\left(-\dfrac{1}{4},0\right)$ , il quale appartiene a $E^\circ$ , poiché soddisfa la disequazione stretta $x^2+4y^2<4$ .

Consideriamo ora la frontiera di $E$ . Presentiamo due modi per trovare il massimo e minimo di $f$ su $\partial E$ : attraverso il metodo dei moltiplicatori di Lagrange o con la parametrizzazione della frontiera. In questo caso conviene il secondo metodo, essendo $\partial E$ un’ellisse con i fuochi sull’asse $x$ e semiassi $a=2$ , $b=1$ . Una parametrizzazione di $\partial E$ è la seguente:

$\begin{aligned} \alpha:[0,2\pi] & \longrightarrow \mathbb{R}^2\\ t & \longmapsto (2\cos(t),\sin(t)). \end{aligned}$

A questo punto sarà sufficiente studiare i punti di massimo e minimo assoluti della funzione, dipendente da una variabile, $f\circ\alpha:[0,2\pi]\rightarrow\mathbb{R}$ . Osserviamo che $f\circ\alpha$ è composizione di funzioni continue, quindi anch’essa continua su $\mathbb{R}$ e l’intervallo $[0,2\pi]$ è compatto, pertanto il teorema di Weierstrass assicura nuovamente l’esistenza di massimo e minimo di $f$ su $\partial E$ . Essi si possono trovare in corrispondenza dei punti critici di $f\circ\alpha$ , ovvero i punti $\alpha(t)$ tali che $(f\circ\alpha)'(t)=0$ oppure nei punti di frontiera della curva $\alpha$ , che solitamente si trovano negli estremi del dominio della curva. In questo caso, essendo $\alpha$ una curva chiusa, la sua frontiera è vuota e per questo possiamo evitare di studiare gli estremi del dominio.

Esplicitamente,

$\begin{equation*} \begin{split} f\circ\alpha(t)&=f(2\cos(t),\sin(t))=(2\cos(t))^2+3\sin^2(t)+\cos(t)\\ &=\cos^2(t)+\cos(t)+3, \end{split} \end{equation*}$

dunque, cerchiamo le soluzioni dell’equazione $(f\circ\alpha)'(t)=0$ , con $t\in[0,2\pi]$ :

$\begin{equation*} (f\circ\alpha)'(t)=-2\cos(t)\sin(t)-\sin(t)=-\sin(t)(2\cos(t)+1)=0, \end{equation*}$

che ha come soluzioni

$\begin{equation*} \sin(t)=0\ \lor \ \cos(t)=-\dfrac{1}{2} \end{equation*}$

da cui

$\begin{equation*} t=0 \ \lor \ t=\pi \ \lor \ t=2\pi \ \lor \ t=\dfrac{2}{3}\pi \ \lor \ t=\dfrac{4}{3}\pi, \end{equation*}$

$\quad$

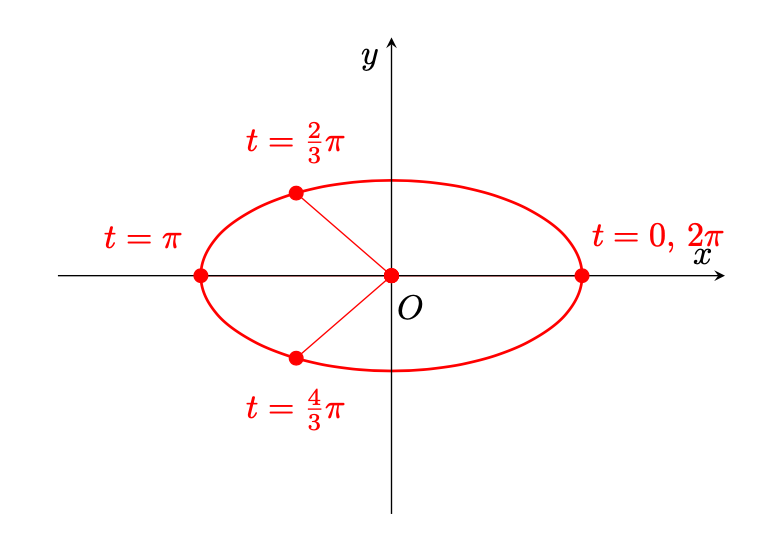
massimi e minimi vincolati

Figura 2: I punti critici di $f\circ\alpha$ .

$\quad$

a cui corrispondono i punti su $\partial E$ :

$\begin{equation*} \begin{aligned} &P_2=\alpha(0)=\alpha(2\pi)=(2,0),\qquad P_3=\alpha(\pi)=(-2,0),\\ &P_4=\alpha\left(\dfrac{2}{3}\pi\right)=\left(-1,\dfrac{\sqrt{3}}{2}\right),\qquad P_5=\alpha\left(\dfrac{4}{3}\pi\right)=\left(-1,-\dfrac{\sqrt{3}}{2}\right). \end{aligned} \end{equation*}$

Abbiamo trovato tutti i punti di $E$ che concorrono nel diventare massimo o minimo di $f$ su $E$ : calcoliamo il valore di $f$ in tali punti, così da selezionarne il massimo e il minimo.

$\quad$

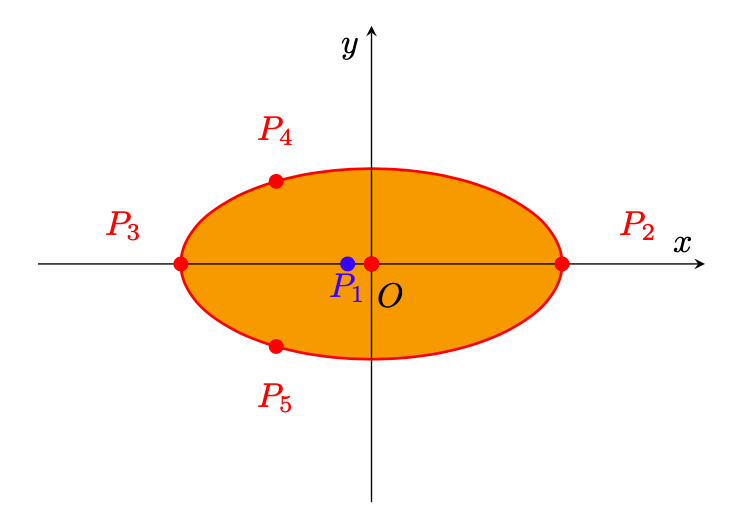
massimi e minimi vincolati

Figura 3: i punti candidati a punti di massimo o minimo di $f$ su $E$ .

$\quad$

$\begin{equation*} f(P_1)=-\dfrac{1}{16}\qquad f(P_2)=5\qquad f(P_3)=3\qquad f(P_4)=\dfrac{11}{4}\qquad f(P_5)=\dfrac{11}{4}. \end{equation*}$

Ecco dunque la soluzione al problema di massimo e minimo vincolati:

$\quad$

Il massimo di $f$ su $E$ vale 5, assunto in corrispondenza del punto $P_2=(2,0)$ , mentre il minimo è $-\dfrac{1}{16}$ , assunto in $P_1=\left(-\dfrac{1}{4},0\right)$ .

con $E^\circ$ si intende l’interno di $E$ . ↩

$\partial E$ indica la frontiera di $E$ . ↩

on $\sqcup$ s’intende unione disgiunta. ↩

Svolgimento 2.

Un’altra strada per risolvere l’esercizio è quella di parametrizzare l’ellisse piena tramite la parametrizzazione regolare

$\begin{aligned} \psi:[0,2\pi]\times[0,2] & \longrightarrow\mathbb{R}^2 \\ (\theta,\rho) & \longmapsto\left(\rho\cos{\theta},\dfrac{1}{2}\rho\sin\theta\right). \end{aligned}$

$\quad$

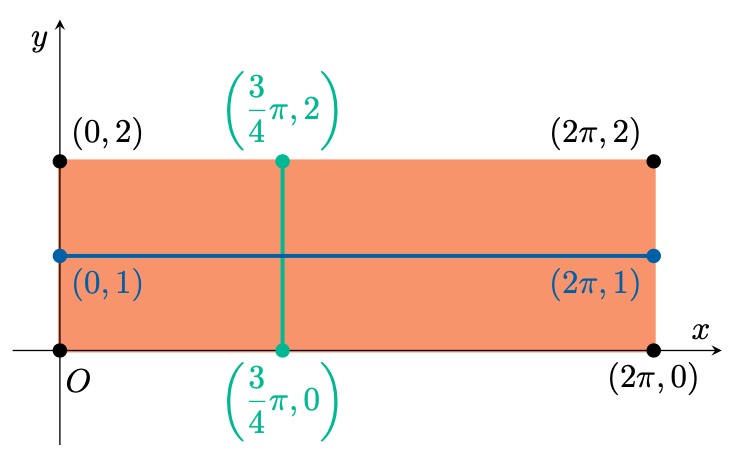
Figura 4: Dominio della parametrizzazione con linee coordinate.

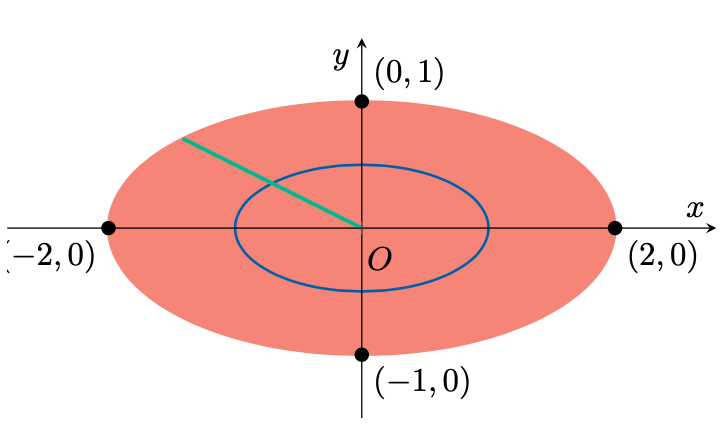
Figura 5: Immagine della parametrizzazione e delle linee coordinate.

$\quad$

In generale, diremo che una funzione $\psi:R\subset\mathbb{R}^n\rightarrow\mathbb{R}^m$ è una parametrizzazione regolare di $\Psi(R)$ se

$R$ è un sottoinsieme compatto di $\mathbb{R}^n$ ed esiste un sottoinsieme aperto $A$ di $R$ tale che $\overline{A}=R$ ⁴;

$\Psi|_A$ sia iniettiva;

$\Psi$ sia differenziabile e valga $\det J_\Psi\neq0$ su $A$ , dove

$\begin{equation*} J_\Psi(x_1,...,x_n):=\begin{pmatrix} \dfrac{\partial \Psi_1}{\partial x_1}&\cdot\cdot\cdot&\dfrac{\partial \Psi_1}{\partial x_n}\\ \cdot&\cdot&\cdot\\ \cdot&\cdot&\cdot\\ \cdot&\cdot&\cdot\\ \dfrac{\partial \Psi_m}{\partial x_1}&\cdot\cdot\cdot&\dfrac{\partial \Psi_m}{\partial x_n} \end{pmatrix}. \end{equation*}$

L’espediente di utilizzare la parametrizzazione regolare $\Psi$ permette di ricondurre lo studio dei punti critici di una funzione $f$ su $\Psi(A)\subset\Psi(R)$ allo studio dei punti critici di $f\circ\Psi$ su $A$ . Infatti, dalla regola della catena vale

$\begin{equation*} \nabla(f\circ\Psi)(x_1,...,x_n)=\nabla f(\Psi(x_1,...,x_n))\cdot J_\Psi(x_1,...,x_n) \end{equation*}$

e dall’ipotesi di non singolarità della matrice Jacobiana di $\Psi$ risulta

$\begin{equation*} \nabla f(\Psi(x_1,...,x_n))=0\Leftrightarrow\nabla(f\circ\Psi)(x_1,...,x_n)=0\qquad\forall(x_1,...,x_n)\in A. \end{equation*}$

Nel nostro caso, ponendo $R:=[0,2\pi]\times[0,2]$ , $\psi$ è una parametrizzazione regolare di $E$ . Infatti vale

$E=\psi(R)$ ;

posto $A:=[0,2\pi)\times(0,2]$ , $\overline{A}=R$ ;

$\psi|_A$ è iniettiva;

$\psi$ è differenziabile e

$\begin{equation*} J_\psi(\theta,\rho):=\begin{pmatrix} \dfrac{\partial\psi_1}{\partial\theta}&\dfrac{\partial\psi_1}{\partial\rho}\\\\ \dfrac{\partial\psi_2}{\partial\theta}&\dfrac{\partial\psi_2}{\partial\rho} \end{pmatrix}=\begin{pmatrix} -\rho\sin\theta&\cos\theta\\\\ \dfrac{1}{2}\rho\cos\theta&\dfrac{1}{2}\sin\theta, \end{pmatrix} \end{equation*}$

dunque

$\begin{equation*} \det J_\psi(\theta,\rho)=-\dfrac{1}{2}\rho\sin^2\theta-\dfrac{1}{2}\rho\cos^2\theta=-\dfrac{1}{2}\rho\neq 0 \end{equation*}$

poiché su $A$ , $\rho\neq0$ .

Il ragionamento appena illustrato permette di sostituire la ricerca dei punti critici di $f$ su $E\setminus\{(0,0)\}=\psi(A)$ a quella dei punti critici di $f\circ\psi$ su $A$ .

$\quad$

Figura 6: Rappresentazione di $A$ , il più grande sottoinsieme su cui $\psi$ è iniettiva.

Figura 7: L’immagine secondo $\psi$ di $A$ è l’ellisse piena, esclusa l’origine.

$\quad$

Calcoliamo, allora, la funzione composta $f\circ\psi$ :

$\begin{equation*} (f\circ\psi)(\theta,\rho)=f\left(\rho\cos{\theta},\dfrac{1}{2}\rho\sin\theta\right)=\rho^2\cos^2\theta+\dfrac{3}{4}\sin^2\theta+\dfrac{1}{2}\rho\cos\theta=\dfrac{3}{4}\rho^2+\dfrac{1}{4}\rho^2\cos^2\theta+\dfrac{1}{2}\rho\cos\theta, \end{equation*}$

le sue derivate parziali

$\begin{equation*} \begin{cases} \dfrac{\partial (f\circ\psi)}{\partial \theta}(\theta,\rho)=-\dfrac{1}{2}\rho^2\sin\theta\cos\theta-\dfrac{1}{2}\rho\sin\theta\\\\ \dfrac{\partial (f\circ\psi)}{\partial \rho}(\theta,\rho)=\dfrac{3}{2}\rho+\dfrac{1}{2}\rho\cos^2\theta+\dfrac{1}{2}\cos\theta \end{cases} \end{equation*}$

e i suoi punti critici, ovvero i punti in cui si annulla il gradiente, il vettore formato dalle derivate parziali appena calcolate:

$\begin{equation*} \begin{aligned} \nabla(f\circ\psi)(\theta,\rho)=0 & \iff \displaystyle\left\{\begin{array}{l} -\dfrac{1}{2}\rho^2\sin\theta\cos\theta-\dfrac{1}{2}\rho\sin\theta=0\\ \dfrac{3}{2}\rho+\dfrac{1}{2}\rho\cos^2\theta+\dfrac{1}{2}\cos\theta=0 \end{array} \right. \\ & \iff \displaystyle\left\{\begin{array}{l} -\dfrac{1}{2}\rho\sin\theta\left(\rho\cos\theta+1\right)=0\\ \dfrac{3}{2}\rho+\dfrac{1}{2}\rho\cos^2\theta+\dfrac{1}{2}\cos\theta=0. \end{array} \right. \end{aligned} \end{equation*}$

Ricordando che su $A$ , $\rho\in(0,2]$ e $\theta\in[0,2\pi)$ , la prima equazione si annulla solamente se

$\begin{equation*} \sin\theta=0 \end{equation*}$

oppure

$\begin{equation*} \rho\cos\theta=-1. \end{equation*}$

Nel primo caso $\theta=0\lor\theta=\pi$ : se $\theta=0$ la seconda equazione non si annulla, in quanto

$\begin{equation*} \dfrac{3}{2}\rho+\dfrac{1}{2}\rho\cos^2(0)+\dfrac{1}{2}\cos(0)=\dfrac{3}{2}\rho+\dfrac{1}{2}\rho+\dfrac{1}{2}>0; \end{equation*}$

se, invece, $\theta=\pi$ , la seconda equazione diventa

$\begin{equation*} \dfrac{3}{2}\rho+\dfrac{1}{2}\rho\cos^2(\pi)+\dfrac{1}{2}\cos(\pi)=\dfrac{3}{2}\rho+\dfrac{1}{2}\rho-\dfrac{1}{2}=2\rho-\dfrac{1}{2} \end{equation*}$

e si annulla per $\rho=\dfrac{1}{4}$ . Abbiamo così trovato il punto critico $P_1=\left(\pi,\dfrac{1}{4}\right)$ di $f\circ\psi$ su $A$ , che corrisponde al punto critico $\left(-\dfrac{1}{4},0\right)=\psi(P_1)$ di $f$ trovato nel primo svolgimento. Nel secondo caso, $\rho\cos\theta=-1$ , dunque la seconda equazione diventa

$\begin{equation*} \dfrac{3}{2}\rho+\dfrac{1}{2}\rho\cos^2\theta+\dfrac{1}{2}\cos\theta= \dfrac{3}{2}\rho-\dfrac{1}{2}\cos\theta+\dfrac{1}{2}\cos\theta= \dfrac{3}{2}\rho \end{equation*}$

che non si annulla mai su $A$ . A questo punto possiamo considerare concluso lo studio del comportamento di $f$ su $\psi(A)^\circ=E^\circ\setminus\{(0,0)\}$ , attraverso la parametrizzazione $\psi$ . Abbiamo trovato come unico punto critico $\psi(P_1)=\left(-\dfrac{1}{4},0\right)$ .

$\quad$

massimi e minimi vincolati

Figura 8: $P_1$ punto critico di $f\circ\psi$ , a cui corrisponde $\psi(P_1)$ su $E$ come candidato.

$\quad$

Il punto $(0,0)$ è un punto singolare della parametrizzazione $\psi$ e conviene valutare $f$ su $(0,0)$ e confrontare il suo valore con gli altri competitori.

Rimane infine da studiare $f$ su $\partial E$ . Osservando che $\partial E=\psi\left([0,2\pi),\{2\}\right)$ basterà studiare $\psi$ su $R_2:=[0,2\pi)\times\{2\}$ . Introduciamo la parametrizzazione regolare di $\partial E$

$\begin{equation*} \begin{array}{rcl} \varphi:[0,2\pi)&\rightarrow&\mathbb{R}^2 \\ \theta&\mapsto&\psi(\theta,2)=(2\cos\theta,\sin\theta), \end{array} \end{equation*}$

osservando che $\psi|_{R_2}=\varphi$ .

$\quad$

massimi e minimi vincolati

$\quad$

Applichiamo il ragionamento precedente alla funzione $f\circ\varphi$ . I punti critici di $f$ su $\partial E$ , infatti, saranno in corrispondenza con i punti critici di $f\circ\varphi$ su $[0,2\pi)$ .

Calcoliamo esplicitamente $f\circ\varphi$ :

$\begin{equation*} (f\circ\varphi)(\theta)=f(2\cos\theta,\sin\theta)=3+\cos^2\theta+\cos\theta, \end{equation*}$

la cui derivata è

$\begin{equation*} (f\circ\varphi)'(\theta)=-2\cos\theta\sin\theta-\sin\theta=-\sin\theta(2\cos\theta+1) \end{equation*}$

che si annulla se e solo se

$\begin{equation*} \sin(\theta)=0\ \lor \ \cos(\theta)=-\dfrac{1}{2} \end{equation*}$

da cui

$\quad$

massimi e minimi vincolati

Figura 10: rappresentazione goniometrica dei punti cirtici della mappa $f\circ\varphi$ .

$\quad$

$\begin{equation*} \theta=0 \ \lor \ \theta=\pi \ \lor \ \theta=\dfrac{2}{3}\pi \ \lor \ \theta=\dfrac{4}{3}\pi, \end{equation*}$

a cui corrispondono i punti su $R_2$

$\begin{equation*} P_2=(0,2),\qquad P_3=(\pi,2),\qquad P_4=\left(\dfrac{2}{3}\pi,2\right),\qquad P_5=\left(\dfrac{4}{3}\pi,2\right) \end{equation*}$

e su $\partial E$ :

$\begin{equation*} \begin{aligned} &\tilde{P}_2=\psi\left(P_2\right)=(2,0),\qquad \tilde{P}_3=\psi\left(P_3\right)=(-2,0),\\\\ &\tilde{P}_4=\psi\left(P_4\right)=\left(-1,\dfrac{\sqrt{3}}{2}\right),\qquad \tilde{P}_5=\psi\left(P_5\right)=\left(-1,-\dfrac{\sqrt{3}}{2}\right), \end{aligned} \end{equation*}$

trovati nello svolgimento precedente.

Abbiamo trovato tutti i punti di $R$ che concorrono nel diventare massimo o minimo di $f\circ\psi$ su $R$

$\quad$

massimi e minimi vincolati

Figura 12: i corrispondenti punti mappati dalla parametrizzazione $\psi$ su $E$ .

$\quad$

Calcoliamo il valore di $f\circ\psi$ in tali punti, così da selezionarne il massimo e il minimo. Essi corrisponderanno ai valori di massimo e minimo di $f$ su $E$ . Infine tali valori saranno assunti nell’immagine secondo $\psi$ dei punti di massimo e minimo di $f\circ\psi$ su $R$ .

$\begin{equation*} \begin{gathered} (f\circ\psi)(P_1)=(f\circ\psi)\left(\pi,\dfrac{1}{4}\right)=-\dfrac{1}{16},\qquad (f\circ\psi)(P_2)=(f\circ\psi)\left(0,2\right)=5, \\ (f\circ\psi)(P_3)=(f\circ\psi)\left(\pi,2\right)=3,\\ (f\circ\psi)(P_4)=(f\circ\psi)\left(\dfrac{2}{3}\pi,2\right)=\dfrac{11}{4},\qquad(f\circ\psi)(P_5)=(f\circ\psi)\left(\dfrac{4}{3}\pi,2\right)=\dfrac{11}{4}. \end{gathered} \end{equation*}$

Ecco dunque la soluzione al problema di massimo e minimo vincolati:

Il massimo di $f$ su $E$ vale 5, assunto in corrispondenza del punto $\psi(P_2)=(2,0)$ , mentre il minimo è $-\dfrac{1}{16}$ , assunto in $\psi(P_1)=\left(-\dfrac{1}{4},0\right)$ .

con $\overline{A}$ intendiamo la chiusura di $A$ , ovvero il più piccolo insieme chiuso contenente $A$ . ↩

Svolgimento 3.

Un modo per semplificare notevolmente l’esercizio è quello di riscrivere $f$ come

$\begin{equation*} f(x,y)=x^2+4y^2-y^2+\dfrac{1}{2}x \end{equation*}$

e suddividere $E$ in infinite ellissi $E_k$ di equazione

$\begin{equation*} E_k:=\{(x,y)\in\mathbb{R}^2\mid x^2+4y^2=k\}, \end{equation*}$

notando che

$\begin{equation*} E=\bigcup_{k\in[0,4]}E_k. \end{equation*}$

$\quad$

massimi e minimi vincolati

Figura 13: suddivisione di $E$ in ellissi concentriche.

$\quad$

Su ciascuna ellisse $E_k$ , si ha

$f_k(x,y)=-y^2+\dfrac{1}{2}x+k\qquad\forall (x,y)\in E_k.$

Studiamo quindi ciascuna $f_k$ su $E_k$ utilizzando il metodo dei moltiplicatori di Lagrange. Per prima cosa dovremo esprimere ciascun vincolo come luogo di zeri di una funzione:

$E_k=\{(x,y)\in\mathbb{R}^2\mid g_k(x,y)=0\},$

dove

$g_k(x,y):=x^2+4y^2-k.$

Il teorema dei moltiplicatori di Lagrange afferma che in corrispondenza dei punti di massimo e minimo di $f_k$ su $E_k=\{g_k\equiv0\}$ , i gradienti di $f_k$ e $g_k$ sono paralleli (purché $\nabla g_k\neq0$ in quei punti). Questa è la motivazione alla base della costruzione della funzione Lagrangiana $\mathcal{L}_k(x,y,\lambda):=f_k(x,y)-\lambda g_k(x,y)$ . Per il teorema di Lagrange, i punti di massimo e minimo di $f_k$ vincolati alla frontiera di A in cui $\nabla g_k \neq (0,0)$ vanno ricercati tra i punti critici della Lagrangiana. Da cui occorre risolvere il sistema

$\begin{equation*} \nabla\mathcal{L}_k=(0,0,0)\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial\mathcal{L}_k}{\partial x}=0 \\\\ \dfrac{\partial\mathcal{L}_k}{\partial y}=0 \\\\ \dfrac{\partial\mathcal{L}_k}{\partial \lambda}=0 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial f_k}{\partial x}-\lambda\dfrac{\partial g_k}{\partial x}=0 \\\\ \dfrac{\partial f_k}{\partial y}-\lambda\dfrac{\partial g_k}{\partial y}=0 \\\\ g_k=0. \\\\ \end{array}\right. \end{equation*}$

Le prime due equazioni affermano proprio che $\nabla f_k$ è multiplo di $\nabla g_k$ , ovvero che i due gradienti sono paralleli. L’ultima equazione assicura che il punto si trovi su $E_k=\{g_k\equiv 0\}$ .

Calcoliamo la Lagrangiana. Nel nostro caso

$\begin{equation*} \mathcal{L}_k(x,y,\lambda):=-y^2+\dfrac{1}{2}x+k-\lambda(x^2+4y^2-k) \end{equation*}$

e osserviamo che $\nabla g_k(x,y)=(2x,8y)\neq(0,0)$ se $(x,y)\neq(0,0)$ . Ciò significa che l’origine non soddisfa le ipotesi del teorema di Lagrange e l’allineamento dei gradienti non sarà, dunque, condizione necessaria per la ricerca di massimi e minimi. Essa andrà valutata separatamente. Calcoliamo ora i punti critici della Lagrangiana:

$\begin{equation*} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}_k}{\partial x}=\dfrac{1}{2}+2\lambda x=0 \\\\ \dfrac{\partial\mathcal{L}_k}{\partial y}= -2y+8\lambda y=0 \\\\ \dfrac{\partial\mathcal{L}_k}{\partial \lambda}=-(x^2+4y^2-k)=0\\\\ \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} 4\lambda x=-1 \\\\ 2y(4\lambda-1)=0\\\\ x^2+4y^2=k.\\\\ \end{array} \right. \end{equation*}$

La seconda equazione si annulla per $y=0$ oppure $\lambda=\dfrac{1}{4}$ . Distinguiamo i due casi:

supponiamo $y=0$ : l’ultima equazione dà $x=\pm\sqrt{k}$ . Abbiamo dunque trovato i punti critici

$\begin{equation*} P^+_k=\left(\sqrt{k},0\right)\qquad P^-_k=\left(-\sqrt{k},0\right),\qquad k\in(0,4]. \end{equation*}$

Se, invece, $\lambda=\dfrac{1}{4}$ , dalla prima equazione risulta $x=-1$ e dalla terza, $y=\pm\dfrac{\sqrt{k-1}}{2}$ , che ha senso per $k\geq1$ . Abbiamo ottenuto un altro insieme di punti critici

$\begin{equation*} Q^+_k=\left(-1,\dfrac{\sqrt{k-1}}{2}\right)\qquad Q^-_k=\left(-1,-\dfrac{\sqrt{k-1}}{2}\right)\qquad k\in [1,4]. \end{equation*}$

Abbiamo ottenuto 4 insiemi di punti critici, soddisfacienti la condizione necessaria del teorema di Lagrange.

$\quad$

massimi e minimi vincolati

Figura 14: rappresentazione dei 4 segmenti critici di $f$ su $E$ .

$\quad$

Possiamo parametrizzare tali insiemi per studiare il comportamento di $f$ . Una proposta di parametrizzazioni è la seguente:

$\begin{equation*} \begin{array}{rcl} \alpha^\pm:(0,4]&\rightarrow & \mathbb{R}^2 \\ t & \mapsto&\left(\pm\sqrt{t},0\right); \end{array} \end{equation*}$

relativa ai punti $P^\pm_k$ e

$\begin{equation*} \begin{array}{rcl} \beta^\pm:[1,4]&\rightarrow & \mathbb{R}^2 \\ t & \mapsto&\left(-1,\pm\dfrac{\sqrt{t-1}}{2}\right). \end{array} \end{equation*}$

relativa ai punti $Q^\pm_k$ .

Studiamo quindi le funzioni composte

$f\circ\alpha^\pm:(0,4]\rightarrow\mathbb{R},\qquad f\circ\beta^\pm:[1,4]\rightarrow\mathbb{R}.$

$f\circ\alpha^+)$

$\begin{equation*} (f\circ\alpha^+)(t)=f\left(\sqrt{t},0\right)=t+\dfrac{1}{2}\sqrt{t}, \end{equation*}$

che è strettamente crescente, dunque verrà studiato solo il punto estremale

$P^+_4=\alpha^+(4)=(2,0).$

$f\circ\alpha^-)$

$\begin{equation*} (f\circ\alpha^-)(t)=f\left(-\sqrt{t},0\right)=t-\dfrac{1}{2}\sqrt{t}. \end{equation*}$

Per calcolare il massimo e minimo della funzione $f\circ\alpha^-$ , derivabile su $(0,4]$ , calcoliamone la derivata prima e dove questa si annulla:

$\begin{equation*} (f\circ\alpha^-)'(t)=1-\dfrac{1}{4\sqrt{t}}=0\Leftrightarrow t=\dfrac{1}{16}, \end{equation*}$

a cui corrisponde il punto critico $P^-_{1/16}=\alpha^-\left(\dfrac{1}{16}\right)=\left(-\dfrac{1}{4},0\right)$ . Oltre al punto critico, va considerato anche l’estremo della parametrizzazione $P^-_4=\alpha^-(4)=(-2,0)$ .

$f\circ\beta^+)$

$\begin{equation*} (f\circ\beta^+)(t)=f\left(-1,\dfrac{\sqrt{t-1}}{2}\right)=1+k-1-\dfrac{k-1}{4}-\dfrac{1}{2}=\dfrac{3}{4}k-\dfrac{1}{4}, \end{equation*}$

che è una funzione lineare, quindi monotona. Pertanto, gli unici punti da considerare saranno gli estremi della parametrizzazione, ovvero

$Q^+_1=\beta^+(1)=\left(-1,0\right)\qquad\text{e}\qquad Q^+_4=\beta^+(4)=\left(-1,\dfrac{\sqrt{3}}{2}\right).$

$f\circ\beta^-)$ Notiamo che $f$ è pari in $y$ , da cui

$\begin{equation*} (f\circ\beta^-)(t)=f\left(-1,-\dfrac{\sqrt{t-1}}{2}\right)=f\left(-1,\dfrac{\sqrt{t-1}}{2}\right)=(f\circ\beta^+)(t). \end{equation*}$

Dunque, i punti da valutare, seguendo il procedimento di $(f\circ\beta^+)(t)$ sono

$Q^-_1=\beta^-(1)=(-1,0)=Q^+_1\qquad\text{e}\qquad Q^-_4=\beta^-(4)=\left(-1,-\dfrac{\sqrt{3}}{2}\right).$

Abbiamo terminato la ricerca dei potenziali punti di massimo e minimo di $f$ su $E$ : calcoliamo il valore di $f$ in tali punti, così da selezionarne il massimo e il minimo.

$\quad$

massimi e minimi vincolati

Figura 15: rappresentazione di tutti i candidati e le rispettive orbite.

$\quad$

$\begin{equation*} \begin{gathered} f(0,0)=0\qquad f(P_4^+)=f(2,0)=5, \\f\left(P_{1/16}^-\right)=f\left(-\dfrac{1}{4},0\right)=-\dfrac{1}{16}, \qquad f(P_4^-)=f(-2,0)=3,\\ f(Q^+_1)=f(-1,0)=\dfrac{1}{2}\qquad f(Q^+_4)=f\left(-1,\dfrac{\sqrt{3}}{2}\right)=\dfrac{11}{4}\qquad f(Q^-_4)=f\left(-1,-\dfrac{\sqrt{3}}{2}\right)=\dfrac{11}{4}. \end{gathered} \end{equation*}$

Ecco dunque la soluzione al problema di massimo e minimo vincolati:

Il massimo di $f$ su $E$ vale 5, assunto in corrispondenza del punto $P_4^+=(2,0)$ , mentre il minimo è $-\dfrac{1}{16}$ , assunto in $P_{1/16}^-=\left(-\dfrac{1}{4},0\right)$ .

Esercizio 2 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=xy+2x^2-x,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$E:=\{(x,y)\in\mathbb{R}^2\mid x\geq -1, -1\leq y\leq 2-2x\}$

Svolgimento.

Figura 16: l’insieme $E$ e le rette che lo delimitano.

$\quad$

Osserviamo immediatamente che $f$ , essendo un polinomio, è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $E$ è compatto, poiché rappresenta l’interno di un triangolo unito alla sua frontiera. Pertanto, il teorema di Weierstrass assicura che il problema ha soluzione.

Distinguiamo l’insieme $E$ nella sua parte interna e la sua frontiera: $E=E^\circ\sqcup\partial E$ . Studiamo separatamente le due componenti.

$E^\circ$ ) Per quanto riguarda l’insieme aperto $E^\circ$ , il teorema di Fermat ci permette di indagare gli eventuali punti critici di $f$ in $E^\circ$ , ovvero i punti $P\in E^\circ$ tali che $\nabla f(P)=(0,0)$ e scartare tutti i punti che non soddisfano tale condizione. Calcoliamo il gradiente di $f$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=y+4x-1\\\\ \dfrac{\partial f}{\partial y}(x,y)=x, \end{cases}$

dunque

$\nabla f(x,y)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} y+4x-1=0\\ x=0 \end{array} \right.\Leftrightarrow\displaystyle\left\{\begin{array}{l} x=0\\ y=1. \end{array} \right.$

Ciò significa che l’unico punto critico di $f$ è $P_1=\left(0,1\right)$ , il quale appartiene a $E^\circ$ , poiché soddisfa le disequazioni strette $x> -1, -1< y< 2-2x$ .

$\quad$

massimi e minimi vincolati

Figura 17: rappresentati la parte interna di $E$ e l’unico punto critico di $f$ , $P_1$ .

$\quad$

$\partial E$ ) Per quanto riguarda la frontiera, invece, notiamo che essa rappresenta un triangolo, dotato quindi di 3 lati ${\partial E=L_1\cup L_2\cup L_3}$ , come in figura.

$\quad$

massimi e minimi vincolati

Figura 18: $\partial E$ composto dai 3 lati $L_1$ , $L_2$ e $L_3$ .

$\quad$

Cerchiamo una parametrizzazione per ognuno di essi. Un modo universale per parametrizzare un generico segmento $\overline{PQ}$ è il seguente: date le coordinate degli estremi $P=(x_P,y_P)$ e $Q=(x_Q,y_Q)$ del segmento, una sua parametrizzazione sarà definita tramite la combinazione convessa di $P$ e $Q$ :

$\begin{equation*} \begin{array}{rcl} \alpha_{\overline{PQ}}:[0,1]&\rightarrow&\mathbb{R}^2 \\ t & \mapsto&\left(x_P+t(x_Q-x_P),y_P+t(y_Q-y_P)\right). \end{array} \end{equation*}$

In questo caso, applicando il ragionamento sopra descritto, forniamo una possibile scelta di parametrizzazioni dei lati $L_1$ , $L_2$ e $L_3$ , con $t\in[0,1]$ :

$\begin{equation*} \begin{aligned} &\alpha_1(t):=\left(-1+\dfrac{5}{2}t,-1\right)\\ & \alpha_2(t):=\left(\dfrac{3}{2}-\dfrac{5}{2}t,-1+5t\right)\\ &\alpha_3(t):=\left(-1,4-5t\right). \end{aligned} \end{equation*}$

Per ciascuna parametrizzazione, studiamo i punti critici della funzione composta $f\circ\alpha_i$ e gli estremi del dominio $\alpha_i(0)$ e $\alpha_i(1)$ , con $i=1,2,3$ , che corrispondono ai vertici del triangolo.

$L_1\bigg)$

$\begin{equation*} \begin{split} (f\circ\alpha_1)(t)=f\left(-1+\dfrac{5}{2}t,-1\right)=1-\dfrac{5}{2}t+2\left(-1+\dfrac{5}{2}t\right)^2+1-\dfrac{5}{2}t=\dfrac{25}{2}t^2-15t+4, \end{split} \end{equation*}$

dunque calcoliamo

$\begin{equation*} 0=(f\circ\alpha_1)'(t)=25t-15\iff t=\dfrac{3}{5}. \end{equation*}$

Alternativamente, essendo $f\circ\alpha$ una parabola, il punto critico sarà esattamente in corrispondenza della $x$ del suo vertice. Come conferma, infatti, $x_V=-\dfrac{b}{2a}=-\dfrac{-15}{25}=\dfrac{3}{5}$ .

Ecco dunque che il punto $P_2=\alpha_1\left(\dfrac{3}{5}\right)=\left(\dfrac{1}{2},-1\right)$ è candidato per essere massimo o minimo di $f$ su $E$ .

$L_2\bigg)$

$\begin{equation*} \begin{split} (f\circ\alpha_2)(t)&=f\left(\dfrac{3}{2}-\dfrac{5}{2}t,-1+5t\right)=\left(\dfrac{3}{2}-\dfrac{5}{2}t\right)(-1+5t)+2\left(\dfrac{3}{2}-\dfrac{5}{2}t\right)^2-\dfrac{3}{2}+\dfrac{5}{2}t\\ &=-\dfrac{3}{2}+\dfrac{15}{2}t-\dfrac{25}{2}t^2+\dfrac{9}{2}+\dfrac{25}{2}t^2-15t-\dfrac{3}{2}+\dfrac{5}{2}t=-5t+\dfrac{3}{2}. \end{split} \end{equation*}$

La funzione $f\circ\alpha_2(t)$ è affine e non nulla, quindi non ha punti critici.

$L_3\bigg)$

$\begin{equation*} (f\circ\alpha_3)(t)=f(-1,4-5t)=5t-1, \end{equation*}$

concludiamo per lo stesso motivo di $L_2$ . La scelta della parametrizzazione non è mai unica. Proponiamo un’altra parametrizzazione per ciascun segmento con l’obiettivo di mostrare che le conclusioni ottenute in precedenza non dipendono dalla scelta della parametrizzazione.

Il lato $L_1$ si poteva parametrizzare tramite

$\begin{aligned} \beta_1:\left[-1,\dfrac{3}{2}\right]&\longrightarrow\mathbb{R}^2 \\ t & \longmapsto(t,-1), \end{aligned}$

per cui risulta

$\begin{equation*} (f\circ\beta_1)(t)=f(t,-1)=-t+2t^2-t=2t(t-1), \end{equation*}$

la cui equazione corrisponde ad una parabola con concavità positiva e vertice in $t=\dfrac{1}{2}$ . Valutando $\beta_1$ in tale valore, ritroviamo

$\beta_1\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2},-1\right)=P_2,$

in accordo con il risultato fornito in precedenza dalla parametrizzazione $\alpha_1$ .

Un’altra parametrizzazione di $L_2$ è la seguente

$\begin{aligned} \beta_2:\left[-1,\dfrac{3}{2}\right] & \longrightarrow\mathbb{R}^2 \\ t & \longmapsto(t,-2t+2), \end{aligned}$

da cui

$\begin{equation*} (f\circ\beta_2)(t)=f(t,-2t+2)=-2t^2+2t+2t^2-t=t, \end{equation*}$

funzione lineare, non nulla, come risulta per $f\circ\alpha_2$ .

Infine, per $L_3$ si poteva procedere attraverso la parametrizzazione

$\begin{equation*} \begin{array}{rcl} \beta_3:\left[-1,4\right] & \rightarrow&\mathbb{R}^2 \\ t & \mapsto&(-1,t), \end{array} \end{equation*}$

e la composizione

$\begin{equation*} (f\circ\beta_3)(t)=f(-1,t)=-t+2+1=-t+3, \end{equation*}$

è nuovamente affine e non nulla.

Elenchiamo, a questo punto, tutti i canditati ad essere massimo o minimo per $f$ su $E$ : $P_1=(0,1)$ , punto critico di $f$ in $E^\circ$ , $P_2=\left(\dfrac{1}{2},-1\right)$ , punto critico di $f\circ\alpha_1$ su $\partial E$ e i vertici di $\partial E$ , $A=(-1,4)$ , $B=(-1,-1)$ e $C=\left(\dfrac{3}{2},-1\right)$ .

$\quad$

massimi e minimi vincolati

Figura 19: l’insieme $E$ e i 4 candidati

$\quad$

Calcoliamo il valore di $f$ su ciascuno di questi punti per determinarne il massimo e il minimo:

$\begin{equation*} f(P_1)=0\qquad f(P_2)=-\dfrac{1}{2}\qquad f(A)=-1\qquad f(B)=4\qquad f(C)=\dfrac{3}{2}. \end{equation*}$

$\quad$

Concludiamo quindi che il massimo di $f$ su $E$ vale 4, assunto nel punto $B=(-1,-1)$ , mentre il minimo è -1, assunto nel punto $A=\left(-1,4\right)$ .

Esercizio 3 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=(2y+3)e^{2x^2+y^2},$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\left\{(x,y)\in\mathbb{R}^2\mid 2x^2+y^2\leq1\right\}.$

Svolgimento 1.

massimi e minimi vincolati

Figura 20: raffigurato l’insieme $A$ .

$\quad$

Osserviamo che $f$ è composizione, prodotto e somma di funzioni continue, pertanto è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $A$ è un’ellisse piena, in particolare è un chiuso e limitato di $\mathbb{R}^2$ , dunque compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$A^\circ$ ) Per quanto riguarda l’insieme aperto $A^\circ$ , essendo $f$ differenziabile su $A^\circ$ , il teorema di Fermat ci assicura che gli estremi relativi di $f$ vanno ricercati tra i suoi eventuali punti critici in $A^\circ$ , ovvero i punti $P\in A^\circ$ tali che $\nabla f(P)=(0,0)$ e scartare tutti i punti che non soddisfano tale condizione. Calcoliamo il gradiente di $f$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=4x(2y+3)e^{2x^2+y^2}\\\\ \dfrac{\partial f}{\partial y}(x,y)=[2+2y(2y+3)]e^{2x^2+y^2}. \end{cases}$

Dunque, ricordando che l’esponenziale è una funzione sempre positiva,

$\nabla f(x,y)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} 4x(2y+3)=0\\\\ 2+2y(2y+3)=0 \end{array} \right.\Leftrightarrow\displaystyle\left\{\begin{array}{l} x=0\vee y=-\dfrac{3}{2}\\\\ y=-1\vee y=-\dfrac{1}{2}. \end{array} \right.$

Le soluzioni del sistema saranno i punti $P_1=\left(0,-\dfrac{1}{2}\right)$ e $Q=(0,-1)$ . Osserviamo però che, mentre $P_1\in A^\circ$ , $Q\in\partial A$ , poiché $2x_Q^2+y_Q^2=1$ , pertanto non è interno ad $A$ e quindi verrà analizzato nello studio di $\partial A$ .

$\quad$

massimi e minimi vincolati

Figura 21: il punto critico $P_1$ appartiene ad $A^\circ$ , mentre $Q$ sta sulla frontiera.

$\quad$

$\partial A$ ) Occupiamoci ora della frontiera di $A$ . Potremmo parametrizzare facilmente $\partial A$ , essendo un’ellisse, vogliamo però utilizzare il metodo dei moltiplicatori di Lagrange. Per prima cosa dovremo esprimere il vincolo come luogo di zeri di una funzione: $\partial A=\{(x,y)\in\mathbb{R}^2\mid g(x,y)=0\}$ , dove $g(x,y):=2x^2+y^2-1$ .

Il teorema dei moltiplicatori di Lagrange afferma che in corrispondenza dei punti di massimo e minimo di $f$ su $\partial A=\{g\equiv0\}$ , i gradienti di $f$ e $g$ sono paralleli⁵. Questa è la motivazione alla base della costruzione della funzione Lagrangiana $\mathcal{L}(x,y,\lambda):=f(x,y)-\lambda g(x,y)$ . Per il teorema di Lagrange, i punti di massimo e minimo di f vincolati alla frontiera di A in cui $\nabla g \neq (0,0)$ vanno ricercati tra i punti critici della Lagrangiana. Da cui occorre risolvere il sistema

$\begin{equation*} \nabla\mathcal{L}=(0,0,0)\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial\mathcal{L}}{\partial x}=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial y}=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \lambda}=0 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial f}{\partial x}-\lambda\dfrac{\partial g}{\partial x}=0 \\\\ \dfrac{\partial f}{\partial y}-\lambda\dfrac{\partial g}{\partial y}=0 \\\\ g=0. \\\\ \end{array}\right. \end{equation*}$

Calcoliamo la Lagrangiana e i suoi punti critici. Nel nostro caso

$\begin{equation*} \mathcal{L}(x,y,\lambda):=(2y+3)e^{2x^2+y^2}-\lambda(2x^2+y^2), \end{equation*}$

$\begin{equation*} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}}{\partial x}=4x(2y+3)e^{2x^2+y^2}-4\lambda x=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial y}= (2y(2y+3)+2)e^{2x^2+y^2}-2\lambda y=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \lambda}=-(2x^2+y^2-1)=0\\\\ \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} 4x[(2y+3)e^{2x^2+y^2}-\lambda]=0\\\\ (4y^2+6y+2)e^{2x^2+y^2}-2\lambda y=0\\\\ 2x^2+y^2=1.\\\\ \end{array} \right. \end{equation*}$

Inserendo l’ultima equazione nelle altre, l’esponenziale $e^{2x^2+y^2}$ è costantemente pari a $e$ , dunque il precedente sistema risulta

$\begin{equation*} \left\{\begin{array}{l} 4x[(2y+3)e-\lambda]=0\\\\ (4y^2+6y+2)e-2\lambda y=0\\\\ 2x^2+y^2=1.\\\\ \end{array} \right. \end{equation*}$

La prima equazione si annulla per $x=0$ oppure $\lambda=(3+2y)e$ . Inserendo $x=0$ nell’ultima equazione otteniamo $y=\pm 1$ , inserendo invece $\lambda=(3+2y)e$ nella seconda equazione si ottiene la contraddizione $2e=0$ . Abbiamo allora trovato due punti critici per $f$ su $\partial A$ : $P_2=(0,1)$ e $Q=(0,-1)$ , che avevamo trovato in precedenza. Osserviamo infine che

$\begin{equation*} \nabla g(P_2)=(0,2)\neq(0,0)\qquad\text{e}\quad\nabla g(Q)=(0,-2)\neq(0,0). \end{equation*}$

Abbiamo calcolato tutti i punti che concorrono nel diventare massimo o minimo di $f$ su $A$ : $P_1=\left(0,-\dfrac{1}{2}\right)$ , $P_2=(0,1)$ e $Q=(0,-1)$ .

$\quad$

massimi e minimi vincolati

Figura 22: i tre punti candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

Calcoliamo infine il valore di $f$ su tali punti:

$\begin{equation*} f(P_1)=2e^{1/4}\qquad f(P_2)=5e\qquad f(Q)=e. \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $5e$ , assunto nel punto $P_2=(0,1)$ e minimo $2e^{1/4}$ , assunto in $P_1=\left(0,-\dfrac{1}{2}\right)$ .

Purché $\nabla g\neq0$ in quei punti. ↩

Svolgimento 2.

Un modo alternativo per svolgere l’esercizio è osservare che

$\begin{equation*} A=\bigcup_{k\in[0,1]}A_k, \end{equation*}$

dove

$\begin{equation*} A_k:=\{(x,y)\in\mathbb{R}^2\mid 2x^2+y^2=k\}. \end{equation*}$

$\quad$

massimi e minimi vincolati

Figura 23: rappresentazione di $A$ mediante unione continua di ellissi concentriche.

$\quad$

Ciò comporta il notevole vantaggio che su ciascuna ellisse $A_k$ ,

$f_k(x,y)=(2y+3)e^k\qquad\forall (x,y)\in A_k.$

Per massimizzare $f$ su $A$ , sarà sufficiente ottimizzare i fattori $2y+3$ e $e^{2x^2+y^2}$ , separatamente.

Il secondo fattore è costante su ciascun’ellisse $A_k$ ed il suo valore, $e^k$ , è strettamente crescente rispetto al parametro $k$ , dunque raggiunge il suo massimo nell’ellisse esterna, corrispondente al valore $k=1$ .

Il primo fattore, invece, è direttamente proporzionale a $y$ , pertanto sarà massimo quando lo è $y$ . Osservando che il massimo valore di $y$ corrisponde al punto $(0,1)$ , che si trova sull’ellisse esterna, proprio dove il fattore $e^{2x^2+y^2}$ è massimo, possiamo concludere che il punto $(0,1)$ è il punto di massimo di $f$ su $A$ .

Per quanto riguarda il minimo di $f$ su $A$ è bene osservare che entrambi i fattori sono positivi su $A$ , pertanto il minimo sarà anch’esso positivo. Tuttavia, non possiamo procedere come abbiamo fatto per la ricerca del massimo, in quanto i due fattori non si minimizzano nel medesimo luogo, come avveniva invece per il massimo. Possiamo però studiare il comportamento di $f_k$ su ciascun $A_k$ utilizzando nuovamente il metodo dei moltiplicatori di Lagrange che in precedenza abbiamo applicato solamente su $\partial A=A_1$ .

In questo caso, ciascuna ellisse $A_k$ può essere espressa come luoghi di zeri della funzione $g_k(x,y):=2x^2+y^2-k$ , il cui gradiente vale

$\begin{equation*} \nabla g_k(x,y)=(4x,2y)\neq(0,0)\qquad\text{se }(x,y)\neq(0,0). \end{equation*}$

Pertanto, possiamo utilizzare il metodo dei moltiplicatori di Lagarange per ciascun $A_k$ , con $k\in(0,1]$ . Ad ogni $A_k$ , associamo la funzione Lagrangiana

$\begin{equation*} \mathcal{L}_k(x,y,\lambda):=f_k(x,y)-\lambda g_k(x,y)=f_k(x,y)=(2y+3)e^k-\lambda\left(2x^2+y^2-k\right) \end{equation*}$

Calcoliamo ora i punti critici della Lagrangiana:

$\begin{equation*} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}_k}{\partial x}=-4\lambda x=0 \\\\ \dfrac{\partial\mathcal{L}_k}{\partial y}=2e^k-2\lambda y=0 \\\\ \dfrac{\partial\mathcal{L}_k}{\partial \lambda}=-(2x^2+y^2-k)=0\\\\ \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} 4\lambda x=0 \\\\ 2\lambda y=2e^k\\\\ 2x^2+y^2=k.\\\\ \end{array} \right. \end{equation*}$

La prima equazione si annulla per $\lambda=0$ oppure per $x=0$ , ma se $\lambda=0$ , la seconda equazione non ha soluzione, dunque vale necessariamente $x=0$ .

$\quad$

massimi e minimi vincolati

Figura 24: vengono rappresentati i gradienti delle funzioni $f_k$ (in blu) e $g_k$ (in rosso) su punti particolari di alcune ellissi. Si può notare che essi risultano paralleli sull’asse $y$ .

$\quad$

Il metodo dei moltiplicatori di Lagrange assicura che il minimo, così come il massimo, di $f$ su $A$ si trova sulla retta $x=0$ . Possiamo notare che $A_0=\{(0,0)\}$ , la regione su cui il teorema dei moltiplicatori falliva, è compresa in tale retta, dunque per completare l’esercizio basterà studiare $f$ imponendo $x=0$ . Sia, dunque, $Z:=A\cap\{x=0\}$ . $Z$ può essere parametrizzato tramite

$\begin{equation*} \begin{array}{rcl} \alpha:[-1,1] & \rightarrow&\mathbb{R}^2 \\ t & \mapsto&(0,t). \end{array} \end{equation*}$

$\quad$

massimi e minimi vincolati

Figura 25: raffigurato l’insieme $Z$ , su cui si troveranno i candidati.

$\quad$

Calcoliamo allora $f\circ\alpha$ per determinare il minimo di $f$ su $Z$ . Esso potrà essere assunto negli estremi della parametrizzazione, $(0,\pm 1)$ e nei punti critici, ovvero i punti interni a $[-1,1]$ che annullano la derivata prima di $f\circ\alpha$ :

$\begin{equation*} (f\circ\alpha)(t)=f(0,t)=(2t+3)e^{t^2}, \end{equation*}$

$\begin{equation*} (f\circ\alpha)'(t)=f(0,t)=[2+2t(2t+3)]e^{t^2}. \end{equation*}$

La derivata prima si annulla solamente se

$\begin{equation*} 2+2t(2t+3)=4t^2+6t+2=4\left(t+\dfrac{1}{2}\right)(t-1)=0\Leftrightarrow t=-\dfrac{1}{2}\lor t=-1. \end{equation*}$

Solo il valore $t=-\dfrac{1}{2}$ è interno a $[-1,1]$ , mentre $t=-1$ è un punto di frontiera. Perciò, l’unico punto critico di $f$ su $A_0$ è $\alpha\left(-\dfrac{1}{2}\right)=\left(0,-\dfrac{1}{2}\right)$ .

I possibili punti di minimo sono $(0,1)$ , $(0,-1)$ e $\left(0,-\dfrac{1}{2}\right)$ .

$\quad$

massimi e minimi vincolati

Figura 26: i candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

Calcoliamo $f$ su tali punti:

$\begin{equation*} f(0,1)=5e,\qquad f(0,-1)=e,\qquad f\left(0,-\dfrac{1}{2}\right)=2e^{1/4}. \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $5e$ , assunto nel punto $(0,1)$ e minimo $2e^{1/4}$ , assunto in $\left(0,-\dfrac{1}{2}\right)$ .

Esercizio 4 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=2\log(2+x^2+y^2)-xy,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\left\{(x,y)\in\mathbb{R}^2\mid x^2+y^2\leq4\right\}.$

Svolgimento 1.

Figura 27: l’insieme $A$ .

$\quad$

Osserviamo che $f$ è composizione, prodotto e somma di funzioni continue, pertanto è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $A$ è un cerchio chiuso di raggio 2, in particolare è un chiuso e limitato di $\mathbb{R}^2$ , dunque compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$A^\circ$ ) Per quanto riguarda l’insieme aperto $A^\circ$ , essendo $f$ differenziabile su $A^\circ$ , il teorema di Fermat ci assicura che gli estremi relativi di $f$ in $A^\circ$ vanno ricercati tra i suoi eventuali punti critici in $A^\circ$ , ovvero i punti $P\in A^\circ$ tali che $\nabla f(P)=(0,0)$ e scartare tutti i punti che non soddisfano tale condizione. Calcoliamo il gradiente di $f$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=\dfrac{4x}{2+x^2+y^2}-y\\\\ \dfrac{\partial f}{\partial y}(x,y)=\dfrac{4y}{2+x^2+y^2}-x, \end{cases}$

dunque,

$\nabla f(x,y)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} \dfrac{4x}{2+x^2+y^2}-y=0\\\\ \dfrac{4y}{2+x^2+y^2}-x=0. \end{array} \right.$

Per risolvere il sistema, studiamo per prima cosa il comportamento sugli assi. Supponiamo inizialmente $x=0$ , allora il sistema diventa

$\begin{equation*} \left\{\begin{array}{l} y=0\\\\ \dfrac{4y}{2+y^2}=0 \end{array} \right.\Leftrightarrow \ y=0. \end{equation*}$

Dunque l’origine $P_0=(0,0)\in A^\circ$ è un punto critico di $f$ . Viceversa, supponendo $y=0$ si ottiene $x=0$ , ovvero nuovamente l’origine.

Una volta studiati gli assi cartesiani, possiamo suppore $x\neq0$ e $y\neq 0$ e moltiplichiamo entrambi i membri delle due equazioni del sistema rispettivamente per $y$ e per $x$ : ciò è possibile poiché stiamo moltiplicando per una quantità diversa da zero. Il sistema così ottenuto sarà più semplice da risolvere, infatti

$\begin{equation*} \left\{\begin{array}{l} \dfrac{4xy}{2+x^2+y^2}-y^2=0\\\\ \dfrac{4xy}{2+x^2+y^2}-x^2=0 \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} y^2=\dfrac{4xy}{2+x^2+y^2}\\\\ x^2=\dfrac{4xy}{2+x^2+y^2}, \end{array} \right. \end{equation*}$

da cui per confronto tra le due equazioni deduciamo

$\begin{equation*} x^2=y^2\qquad\Leftrightarrow\qquad \begin{aligned} x&=y\\ &\ \lor\\ x&=-y. \end{aligned} \end{equation*}$

Se assumiamo $x=y$ , la prima equazione diventa

$\begin{equation*} y^2=\dfrac{4y^2}{2+2y^2}\Leftrightarrow 2+2y^2=4\Leftrightarrow y=\pm1. \end{equation*}$

Abbiamo trovato due punti critici: $P_1=(1,1)$ e $P_2=(-1,-1)$ . Osserviamo che entrambi i punti sono interni ad $A$ .

Se, invece, assumiamo $x=-y$ , la prima equazione diventa

$\begin{equation*} y^2=\dfrac{-4y^2}{2+2y^2}\Leftrightarrow 2+2y^2=-4, \end{equation*}$

che non ha soluzione reale. Ciò conclude lo studio di $A^\circ$ , che porta la nostra attenzione a $3$ punti critici: $P_0$ , $P_1$ e $P_2$ .

$\quad$

massimi e minimi vincolati

Figura 28: i punti critici di $f$ su $A^\circ$ .

$\quad$

$\partial A$ ) $\partial A$ è la circonferenza di un cerchio di raggio $2$ e centro l’origine, dunque una sua parametrizzazione è la seguente:

$\begin{equation*} \begin{array}{rcl} \alpha:[0,2\pi] &\rightarrow&\mathbb{R}^2 \\ t & \mapsto&\left(2\cos t,2\sin t\right), \end{array} \end{equation*}$

infatti, notiamo che ogni punto di $\alpha(t)$ soddisfa l’equazione definente $\partial A$

$\begin{equation*} (2\cos t)^2+(2\sin t)^2=4(\cos^2t+\sin^2t)=4. \end{equation*}$

Calcoliamo la funzione composta $(f\circ\alpha)(t)$ che esprime il comportamento di $f$ su $\partial A$ :

$\begin{equation*} \begin{split} (f\circ\alpha)(t)=f(2\cos t,2\sin t)=2\log(2+4\cos^2t+4\sin^2t)-4\cos t\sin t=2\log(6)-4\cos t\sin t. \end{split} \end{equation*}$

A questo punto, siamo in grado di studiare i potenziali punti di massimo o di minimo di $f$ su $\partial A$ : essi si trovano solo in corrispondenza dei punti critici di $f\circ\alpha$ . In generale, vanno indagati, oltre a tali punti critici, anche i punti di non derivabilità di $f\circ\alpha$ e i punti di frontiera di $\alpha([0,2\pi])$ , ma essendo $f\circ\alpha$ derivabile e $\alpha$ una curva chiusa, l’insieme di punti siffatti è vuoto.

Studiamo allora i punti critici di $f\circ\alpha$ , ovvero i punti che soddisfano $(f\circ\alpha)'(t)=0$ :

$\begin{equation*} 0=(f\circ\alpha)'(t)=4\sin^2t-4\cos^2t=-4\cos(2t). \end{equation*}$

Tale equazione è soddisfatta quando

$\begin{equation*} 2t=\dfrac{\pi}{2}+k\pi\quad k\in\mathbb{Z}\Leftrightarrow t_k=\dfrac{\pi}{4}+k\dfrac{\pi}{2}\quad k\in\mathbb{Z}. \end{equation*}$

Osseviamo che i valori interi di $k$ per cui $t_k\in[0,2\pi]$ sono $\{0,1,2,3\}$ :

$\begin{equation*} t_0=\dfrac{\pi}{4},\qquad t_1=\dfrac{3}{4}\pi,\qquad t_2=\dfrac{5}{4}\pi,\qquad t_3=\dfrac{7}{4}\pi, \end{equation*}$

a cui corrispondono i punti su $\partial A$

$\begin{equation*} \begin{aligned} &P_3=\alpha(t_0)=\left(\sqrt{2},\sqrt{2}\right),\qquad P_4=\alpha(t_1)=\left(-\sqrt{2},\sqrt{2}\right)\\ &P_5=\alpha(t_2)=\left(-\sqrt{2},-\sqrt{2}\right),\qquad P_6=\alpha(t_3)=\left(\sqrt{2},-\sqrt{2}\right). \end{aligned} \end{equation*}$

$\quad$

massimi e minimi vincolati

Figura 29: tutti i candidati ad essere punti di massimo o minimo di $f$ su $A$ .

$\quad$

Abbiamo trovato $7$ candidati ad essere massimo e minimo di $f$ su $A$ : calcoliamo il valore di ciascuno di essi e confrontiamoli.

$\begin{equation*} \begin{aligned} &f(P_0)=f(0,0)=2\log(2),\qquad f(P_1)=f(1,1)=2\log(4)-1,\qquad f(P_2)=f(-1,-1)=2\log(4)-1,\\ &f(P_3)=f\left(\sqrt{2},\sqrt{2}\right)=2\log(6)-2,\qquad f(P_4)=f\left(-\sqrt{2},\sqrt{2}\right)=2\log(6)+2,\\ &f(P_5)=f\left(-\sqrt{2},-\sqrt{2}\right)=2\log(6)-2,\qquad f(P_6)=f\left(\sqrt{2},-\sqrt{2}\right)=2\log(6)+2. \end{aligned} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $2\log(6)+2$ , assunto nei punti $P_4=\left(-\sqrt{2},\sqrt{2}\right)$ e $P_6=\left(\sqrt{2},-\sqrt{2}\right)$ e minimo $2\log(2)$ , assunto in $P_0=(0,0)$ .

Svolgimento 2.

Un modo alternativo per svolgere l’esercizio è osservare che

$\begin{equation*} A=\bigcup_{k\in[0,4]}A_k, \end{equation*}$

dove

$\begin{equation*} A_k:=\{(x,y)\in\mathbb{R}^2\mid x^2+y^2=k\}. \end{equation*}$

$\quad$

massimi e minimi vincolati

Figura 30: rappresentazione di $A$ come unione continua di circonferenze concentriche.

$\quad$

Osserviamo che su ciascuna ellisse $A_k$ ,

$f_k(x,y)=2\log(2+k)-xy\qquad\forall (x,y)\in A_k.$

Poichè il primo addendo della funzione è costante su ciascuna ellisse, sarà sufficiente studiare la funzione $h(x,y):=-xy$ soggetta al vincolo $(x,y)\in A_k$ . Utilizziamo il metodo dei moltiplicatori di Lagrange: ciascuna ellisse $A_k$ può essere espressa come luoghi di zeri della funzione $g_k(x,y):=x^2+y^2-k$ , il cui gradiente vale

$\begin{equation*} \nabla g_k(x,y)=(2x,2y)\neq(0,0)\qquad\text{se }(x,y)\neq(0,0). \end{equation*}$

Pertanto, tale metodo vale per ciascun $A_k$ , con $k\in(0,1]$ . Ad ogni $A_k$ , associamo la funzione Lagrangiana

$\begin{equation*} \mathcal{L}_k(x,y,\lambda):=h(x,y)-\lambda g_k(x,y)=-xy-\lambda\left(x^2+y^2-k\right) \end{equation*}$

Calcoliamo ora i punti critici della Lagrangiana:

$\begin{equation*} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}_k}{\partial x}=-y-2\lambda x=0 \\\\ \dfrac{\partial\mathcal{L}_k}{\partial y}=-x-2\lambda y=0 \\\\ \dfrac{\partial\mathcal{L}_k}{\partial \lambda}=-(x^2+y^2-k)=0\\\\ \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} y=-2\lambda x \\\\ x+2\lambda y=0\\\\ x^2+y^2=k.\\\\ \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} y=-2\lambda x \\\\ x-4\lambda^2 x=0\\\\ x^2+y^2=k.\\\\ \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} y=-2\lambda x \\\\ x(1-4\lambda^2)=0\\\\ x^2+y^2=k.\\\\ \end{array} \right. \end{equation*}$

La seconda equazione si annulla per $x=0$ oppure per $\lambda=\pm\dfrac{1}{2}$ , ma se $x=0$ , la prima equazione implica $y=0$ , ma in $(0,0)$ abbiamo già osservato che non possiamo applicare il metodo, poiché si annulla $\nabla g_k$ .

Supponiamo, allora, $\lambda=\pm\dfrac{1}{2}$ e dalla prima equazione otteniamo $y=\mp x$ . Il metodo dei moltiplicatori di Lagrange assicura, pertanto, che il minimo, così come il massimo, di $f$ su $A$ si trovano sulle rette $y=\pm x$ . Siano, dunque,

$\begin{equation*} A^+:=A\cap\{y=x\}\qquad\text{e}\qquad A^-:=A\cap\{y=-x\}. \end{equation*}$

$\quad$

massimi e minimi vincolati

Figura 31: i punti di massimo o minimo di $f$ su $A$ saranno necessariamente contenuti nei segmenti $A^+$ e $A^-$ .

$\quad$

Per trovare le parametrizzazioni di $A^+$ e $A^-$ occorre calcolare i punti di intersezione tra le rette $y=\pm x$ e $\partial A$ . Per $A^+$ abbiamo

$\begin{equation*} \left\{\begin{array}{l} y=x \\\\ x^2+y^2=4 \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} y=x \\\\ 2x^2=4 \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} y=x \\\\ x^2=2 \end{array}\right.\left\{\begin{array}{l} y=\pm\sqrt{2} \\\\ x=\pm\sqrt{2}. \end{array}\right. \end{equation*}$

Dunque troviamo gli estremi $P_1=(\sqrt{2},\sqrt{2})$ e $P_2=(-\sqrt{2},-\sqrt{2})$ .

Similmente, per $A^-$

$\begin{equation*} \left\{\begin{array}{l} y=-x \\\\ x^2+y^2=4 \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} y=-x \\\\ 2x^2=4 \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} y=-x \\\\ x^2=2 \end{array}\right.\left\{\begin{array}{l} y=\mp\sqrt{2} \\\\ x=\pm\sqrt{2}. \end{array}\right. \end{equation*}$

Su $A^-$ gli estremi sono $P_3=(\sqrt{2},-\sqrt{2})$ e $P_4=(-\sqrt{2},\sqrt{2})$ .\ Le parametrizzazioni di $A^+$ e $A^-$ saranno rispettivamente

$\begin{equation*} \begin{array}{rcl} \alpha^+:[-\sqrt{2},\sqrt{2}]&\rightarrow&\mathbb{R}^2 \\ t &\mapsto&(t,t) \end{array} \end{equation*}$

$\begin{equation*} \begin{array}{rcl} \alpha^-:[-\sqrt{2},\sqrt{2}]&\rightarrow&\mathbb{R}^2 \\ t &\mapsto&(t,-t) . \end{array} \end{equation*}$

Calcoliamo allora $f\circ\alpha^\pm$ per determinare il massimo ed il minimo di $f$ su $A^\pm$ . Esso potrà essere assunto negli estremi della parametrizzazione, ovvero i punti $P_1$ , $P_2$ , $P_3$ e $P_4$ , calcolati in precedenza oltre che nei punti critici, ovvero i punti interni a $[-1,1]$ che annullano la derivata prima di $f\circ\alpha^\pm$ .

$f\circ\alpha^+)$

$\begin{equation*} (f\circ\alpha^+)(t)=f(t,t)=2\log(2+2t^2)-t^2 \end{equation*}$

la cui derivata prima è

$\begin{equation*} (f\circ\alpha^+)'(t)=\dfrac{8t}{2+2t^2}-2t=\dfrac{2t(1-t^2)}{1+t^2}, \end{equation*}$

che si annulla per $t=-1,0,1$ , valori interni a $[-\sqrt{2},\sqrt{2}]$ , a cui corrispondono i punti

$\begin{equation*} P_5=\alpha^+(-1)=(-1,-1),\qquad P_6=\alpha^+(0)=(0,0),\qquad P_7=\alpha^+(1)=(1,1). \end{equation*}$

$f\circ\alpha^-)$

$\begin{equation*} (f\circ\alpha^-)(t)=f(t,-t)=2\log(2+2t^2)+t^2, \end{equation*}$

da cui

$\begin{equation*} (f\circ\alpha^-)'(t)=\dfrac{8t}{2+2t^2}+2t=\dfrac{2t(3+t^2)}{1+t^2}, \end{equation*}$

che si annulla solamente per $t=0$ a cui corrisponde però il punto $P_6$ già investigato in precedenza.

I possibili punti di massimo e minimo sono

$\begin{equation*} \begin{split} &P_1=(\sqrt{2},\sqrt{2}),\qquad P_2=(-\sqrt{2},-\sqrt{2}), \qquad P_3=(\sqrt{2},-\sqrt{2}), \\ &P_4=(-\sqrt{2},\sqrt{2}),\qquad P_5=(-1,-1),\qquad P_6=(0,0),\qquad P_7=(1,1). \end{split} \end{equation*}$

$\quad$

massimi e minimi vincolati

Figura 32: rappresentazione di tutti i candidati ad essere massimo o minimo di $f$ su $A$ . Come annunciato, essi si trovano sui segmenti $A^+$ e $A^-$ .

$\quad$

Calcoliamo $f$ su tali punti:

$\begin{equation*} \begin{split} &f(P_1)=f\left(\sqrt{2},\sqrt{2}\right)=2\log(6)-2,\qquad f(P_2)=f\left(-\sqrt{2},-\sqrt{2}\right)=2\log(6)-2,\\ &f(P_3)=f\left(\sqrt{2},-\sqrt{2}\right)=2\log(6)+2,\qquad f(P_4)=f\left(-\sqrt{2},\sqrt{2}\right)=2\log(6)+2,\\ &f(P_5)=f(-1,-1)=2\log(4)-1,\qquad f(P_6)=f(0,0)=2\log(2),\qquad f(P_7)=f(1,1)=2\log(4)-1. \end{split} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $2\log(6)+2$ , assunto nei punti $P_3=(\sqrt{2},-\sqrt{2})$ e $P_4=(-\sqrt{2},\sqrt{2})$ e minimo $2\log(2)$ , assunto in $P_6=(0,0)$ .

Esercizio 5 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=x+2y\cos x,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y)\in\mathbb{R}^2\mid 0\leq x\leq\pi, \ 0\leq y\leq\sin x\}.$

Svolgimento 1.

Figura 33: raffigurazione dell’insieme $A$ .

$\quad$

Osserviamo che $f$ è prodotto e somma di funzioni continue, pertanto è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $A$ è chiuso e limitato. La chiusura segue dal fatto che $A$ è intersezione di controimmagini di insiemi chiusi di $\mathbb{R}$ tramite funzioni continue, mentre per la limitatezza notiamo che esso è contenuto nel rettangolo con vertice l’origine, di base $\pi$ e altezza $1$ , il quale a sua volta è contentuto in una palla di centro l’origine e raggio $2\pi$ . Per la caratterizzazione degli insiemi compatti di $\mathbb{R}^n$ del teorema di Heine-Borel, $A$ è un compatto di $\mathbb{R}^2$ . Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=1-2y\sin x\\\\ \dfrac{\partial f}{\partial y}(x,y)=2\cos x, \end{cases}$

dunque,

$\nabla f(x,y)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} 1-2y\sin x=0\\\\ 2\cos x=0 \end{array} \right.\Leftrightarrow \displaystyle\left\{\begin{array}{l} y=\dfrac{1}{2\sin x}\\\\ x=\dfrac{\pi}{2}+k\pi\quad k\in\mathbb{Z}. \end{array} \right.\Leftrightarrow \displaystyle\left\{\begin{array}{l} y=\pm\dfrac{1}{2}\\\\ x=\dfrac{\pi}{2}+k\pi\quad k\in\mathbb{Z}. \end{array} \right.$

Osserviamo che la seconda equazione si annulla per $x=\dfrac{\pi}{2}+k\pi$ , con $k\in\mathbb{Z}$ i cui valori, inseriti nella prima equazione, danno come risultato $y=\dfrac{1}{2}$ se $k$ è pari, $y=-\dfrac{1}{2}$ se $k$ è dispari. Abbiamo così trovato due successioni di punti critici:

$\begin{equation*} \begin{aligned} &P_k=\left(\dfrac{\pi}{2}+2k\pi,\dfrac{1}{2}\right)\qquad k\in\mathbb{Z},\\ &Q_k=\left(\dfrac{\pi}{2}+(2k+1)\pi,-\dfrac{1}{2}\right)=\left(\dfrac{3\pi}{2}+2k\pi,-\dfrac{1}{2}\right) \qquad k\in\mathbb{Z}. \end{aligned} \end{equation*}$

La cosa che ora ci interessa è capire quali di questi punti appartiene ad $A^\circ$ . Notiamo immediatamente che, poiché $A$ è contenuto nel semipiano $y\geq0$ , nessuno dei punti $Q_k$ può stare in $A$ (e tantomeno in $A^\circ$ ), mentre dalla condizione $0\leq x\leq \pi$ , osserviamo che solo $P_0=\left(\dfrac{\pi}{2},\dfrac{1}{2}\right)$ ha la possibilità di appartenere ad $A^\circ$ : dal fatto che

$0<\dfrac{1}{2}=y_{P_0}<\sin\left(x_{P_0}\right)=1,$

concludiamo che $P_0$ è l’unico punto critico di $f$ in $A^\circ$ .

$\quad$

Figura 34: rappresentazione delle due successioni di punti critici. Solo l’elemento $P_0$ appartiene ad $A^\circ$ .

$\quad$

$\partial A$ ) È immediato verificare che $\partial A=\gamma_1\cup\gamma_2$ è composto da un segmento orizzontale $\gamma_1$ e da una curva $\gamma_2$ , grafico della funzione $y=\sin x$ . Le loro parametrizzazioni sono le seguenti

$\begin{equation*} \begin{aligned} &\begin{array}{rcl} \alpha_1 :[0,\pi]& \rightarrow&\mathbb{R}^2 \\ t & \mapsto&(t,0) \end{array}\\ & \begin{array}{rcl} \alpha_2 :[0,\pi]& \rightarrow&\mathbb{R}^2 \\ t & \mapsto&(t,\sin t). \end{array} \end{aligned} \end{equation*}$

Dobbiamo necessariamente considerare i punti di intersezione $\gamma_1\cap\gamma_2$ , poiché in tali punti non vi è alcuna condizione necessaria da soddisfare per essere punti di massimo o minimo⁶. Essi sono $P_1=(0,0)$ e $P_2=(\pi,0)$ .

$\quad$

Figura 35: l’insieme $\partial A$ descritto mediante 2 curve, $\gamma_1$ e $\gamma_2$ .

$\quad$

Per tutti gli altri punti, invece, vige una condizione necessaria da soddisfare in modo da essere possibili candidati di punti di massimo o minimo, ovvero essere punti critici della funzione $f\circ\alpha_i$ . I punti cercati sono, cioè, i punti $\alpha_i(t)$ che soddisfano $(f\circ\alpha_i)'(t)=0$ , con $i=1,2$ .

Per quanto riguarda il lato orizzontale $\gamma_1$ , con parametrizzazione $\alpha_1$ , si ha

$\begin{equation*} (f\circ\alpha_1)(t)=t, \end{equation*}$

che non ha punti critici. Sulla curva $\gamma_2$ , invece, si ha

$\begin{equation*} (f\circ\alpha_2)(t)=t+2\sin t\cos t, \end{equation*}$

dunque i suoi punti critici sono le soluzioni di

$\begin{equation*} (f\circ\alpha_2)'(t)=1+2\left(\cos^2t-\sin^2t\right)=1+2\cos(2t). \end{equation*}$

La precedente funzione si annulla quando $\cos(2t)=-\dfrac{1}{2}$ , il che significa

$\begin{equation*} 2t=\dfrac{2}{3}\pi+2k\pi\lor2t=\dfrac{4}{3}\pi+2k\pi\Leftrightarrow t=\dfrac{\pi}{3}+k\pi\lor t=\dfrac{2}{3}\pi+k\pi\qquad k\in\mathbb{Z}. \end{equation*}$

$\quad$

Figura 36: valori critici della funzione $f\circ\alpha_2$ .

$\quad$

Tuttavia, essendo $[0,\pi]$ il dominio della parametrizzazione, possiamo considerare solamente i valori $t_1=\dfrac{\pi}{3}$ e $t_2=\dfrac{2}{3}\pi$ , a cui corrispondono i punti su $\partial A$

$\begin{equation*} P_3=\alpha_2(t_1)=\left(\dfrac{\pi}{3},\dfrac{\sqrt{3}}{2}\right),\qquad P_4=\alpha_2(t_2)=\left(\dfrac{2}{3}\pi,\dfrac{\sqrt{3}}{2}\right). \end{equation*}$

$\quad$

Figura 37: insieme di tutti i candidati ad essere punti di massimo o minimo di $f$ su $A$ . $P_0$ è un suo punto critico, mentre $P_1$ , $P_2$ , $P_3$ e $P_4$ corrispondono ai valori critici precedentemente trovati.

$\quad$

Abbiamo trovato $5$ candidati ad essere massimo e minimo di $f$ su $A$ : calcoliamo il valore di ciascuno di essi e confrontiamoli.

$\begin{equation*} \begin{aligned} &f(P_0)=f\left(\dfrac{\pi}{2},\dfrac{1}{2}\right)=\dfrac{\pi}{2},\qquad f(P_1)=f(0,0)=0,\qquad f(P_2)=f(\pi,0)=\pi,\\ &f(P_3)=f\left(\dfrac{\pi}{3},\dfrac{\sqrt{3}}{2}\right)=\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{2},\qquad f(P_4)=f\left(\dfrac{2}{3}\pi,\dfrac{\sqrt{3}}{2}\right)=\dfrac{2}{3}\pi-\dfrac{\sqrt{3}}{2}. \end{aligned} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\pi$ , assunto nel punto $P_2=\left(\pi,0\right)$ e valore minimo $0$ , assunto in $P_1=(0,0)$ .

Più precisamente, $\partial A$ è una curva regolare a tratti, in cui i punti di non regolarità corrispondono esattamente all’intersezione di $\gamma_1$ e $\gamma_2$ . ↩

Svolgimento 2.

Proponiamo ora un modo puramente algebrico per risolvere l’esercizio in maniera astuta.

Per prima cosa, separiamo l’insieme $A$ in due regioni $B$ e $C$ in questo modo

$\begin{equation*} B:=\{(x,y)\in A\mid \cos x\geq0\},\qquad C:=\{(x,y)\in A\mid \cos x<0\}. \end{equation*}$

$\quad$

Figura 38: suddivisione di $A$ in due zone $B$ e $C$ .

$\quad$

Procediamo con ordine alla soluzione del problema, ricercando prima il minimo di $f$ e poi il massimo, facendo sempre riferimento alla regione nella quale stiamo studiando $f$ .

Minimo:

$B)$ Osserviamo che su $B$ $\cos x\geq 0$ e $x,y\geq0$ , dunque vale

$\begin{equation*} f(x,y)\geq0\qquad\forall(x,y)\in B. \end{equation*}$

$C)$ Su $C$ , invece, $\cos x<0$ e $x>\dfrac{\pi}{2}$ , mentre $0\leq y\leq \sin x$ , dunque si ha

$\begin{equation*} f(x,y)\geq x+2\sin(x)\cos(x)=x+\sin(2y)\geq \dfrac{\pi}{2}-1>0\qquad\forall(x,y)\in C. \end{equation*}$

Ciò significa che $f(x,y)\geq 0$ su $A$ . Si noti, tuttavia, che $f(0,0)=0$ , dunque $0$ è il minimo di $f$ su $A$ , raggiunto in $(0,0)$ .

Massimo:

$B)$ Su $B$ sappiamo che $\cos(x)\geq0$ , $x\geq\dfrac{\pi}{2}$ e $0\leq y\leq \sin x$ , dunque si ha

$\begin{equation*} f(x,y)\leq x+2\sin(x)\cos(x)=x+\sin(2x)\leq\dfrac{\pi}{2}+1<\pi\qquad\forall(x,y)\in B. \end{equation*}$

$C)$ Su $C$ , poiché $y\geq0$ e $\cos x<0$ vale

$\begin{equation*} f(x,y)\leq f(x,0)=x\leq\pi\qquad\forall(x,y)\in C, \end{equation*}$

ricordando che $x\leq\pi$ su $C$ . Abbiamo dunque mostrato che $f(x,y)\leq\pi$ su $A$ . Tuttavia, $f(\pi,0)=\pi$ , dunque $f$ assume il suo massimo $\pi$ nel punto $(\pi,0)$ .

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\pi$ , assunto nel punto $P_2=\left(\pi,0\right)$ e valore minimo $0$ , assunto in $P_1=(0,0)$ .

Esercizio 6 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=\arctan(x^2+y^2+xy-3y),$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y)\in\mathbb{R}^2\mid x^2+y^2\leq9\}.$

Svolgimento.

Figura 39: rappresentazione dell’insieme $A$ .

$\quad$

Osserviamo che $f$ è composizione, prodotto e somma di funzioni continue, pertanto è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $A$ è un cerchio chiuso di raggio 3, in particolare è un chiuso e limitato di $\mathbb{R}^2$ , dunque compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Si osservi che l’arcotangente è una funzione crescente, quindi grazie alla proposizione 6, i punti di massimo e di minimo per $f$ su $A$ corrispondono ai punti di massimo e di minimo della funzione $h(x,y)= x^2+y^2+xy-3y$ . D’ora in avanti, quindi, studieremo la funzione $h(x,y)$ , i cui punti critici corrispondono a quelli di $f$ , grazie alla differenziabilità di $g$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$A^\circ$ ) Per quanto riguarda l’insieme aperto $A^\circ$ , essendo $f$ differenziabile su $A^\circ$ , per il teorema di Fermat, gli eventuali massimi e minimi relativi vanno ricercati tra i punti critici di h nell’interno di A, ovvero i punti $P\in A^\circ$ tali che $\nabla h(P)=(0,0)$ e scartare tutti i punti che non soddisfano tale condizione. Calcoliamo il gradiente di $h$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial h}{\partial x}(x,y)=2x+y\\\\ \dfrac{\partial h}{\partial y}(x,y)=2y+x-3, \end{cases}$

dunque, il gradiente di $h$ si annulla solamente se

$\nabla h(x,y)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} 2x+y=0\\\\ 2y+x-3=0 \end{array} \right.\Leftrightarrow \displaystyle\left\{\begin{array}{l} y=-2x\\\\ y=-\dfrac{x}{2}+\dfrac{3}{2}. \end{array} \right.$

Ciascuna equazione del sistema definisce una retta, la cui intersezione è costituita dal punto $P_1=(-1,2)\in A^\circ$ , che risulta, quindi, punto critico di $h.$

$\quad$

Figura 40: il punto critico $P_1$ , ottenuto come intersezione tra le rette $y=-2x$ , e $y=-\dfrac{x}{2}+\dfrac{3}{2}$ appartiene effettivamente ad $A^\circ$ .

$\quad$

$\partial A$ ) $\partial A$ è la circonferenza di un cerchio di raggio $3$ e centro l’origine, dunque una sua parametrizzazione è la seguente:

$\begin{equation*} \begin{array}{rcl} \alpha:[0,2\pi] &\rightarrow&\mathbb{R}^2 \\ t & \mapsto&\left(3\cos t,3\sin t\right), \end{array} \end{equation*}$

Calcoliamo la funzione composta $(h\circ\alpha)(t)$ che esprime il comportamento di $h$ su $\partial A$ :

$\begin{equation*} \begin{split} (h\circ\alpha)(t)&=h(3\cos t,3\sin t)=9\cos^2t+9\sin^2t+9\cos t\sin t-9\sin t\\ &=9+9\cos t\sin t-9\sin t. \end{split} \end{equation*}$

Ora, essendo $h$ una funzione differenziabile e $\alpha$ una curva chiusa, i punti di massimo o di minimo di $h$ su $\partial A$ si trovano solo in corrispondenza dei punti critici di $h\circ\alpha$ , ovvero i punti che soddisfano $(h\circ\alpha)'(t)=0$ .

$\begin{equation*} ( h\circ\alpha)'(t)=9\cos^2t-9\sin^2t-9\cos t=9(\cos^2t-\sin^2t)-9\cos t=9\cos(2t)-9\cos t=0\Leftrightarrow\cos(2t)=\cos t. \end{equation*}$

Gli unici valori di $t\in[0,2\pi]$ tali che $\cos(2t)=\cos(t)$ sono $t=0$ , $t=\dfrac{2}{3}\pi$ e $t=\dfrac{4}{3}\pi$ , a cui corrispondono i punti su $\partial A$

$\begin{equation*} P_2=\alpha(0)=(3,0),\qquad P_3=\alpha\left(\dfrac{2}{3}\pi\right)=\left(-\dfrac{3}{2},\dfrac{3\sqrt{3}}{2}\right),\qquad P_4=\alpha\left(\dfrac{4}{3}\pi\right)=\left(-\dfrac{3}{2},-\dfrac{3\sqrt{3}}{2}\right). \end{equation*}$

$\quad$

Figura 41: rappresentazione di tutti e 4 i candidati a punti di massimo o minimo di $f$ su $A$ .

$\quad$

Abbiamo trovato $4$ candidati ad essere massimo e minimo di $h$ su $A$ , che per quanto detto in precedenza, tali punti sono i candidati anche per $f$ .

Calcoliamo il valore di $f$ su ciascuno di essi e confrontiamoli.

$\begin{equation*} \begin{aligned} &f(P_1)=f(-1,2)=-3,\qquad f(P_2)=f(3,0)=9,\\ &f(P_3)=f\left(-\dfrac{3}{2},\dfrac{3\sqrt{3}}{2}\right)=9-\dfrac{27\sqrt{3}}{4},\qquad f(P_4)=f\left(-\dfrac{3}{2},-\dfrac{3\sqrt{3}}{2}\right)=9+\dfrac{27\sqrt{3}}{4}. \end{aligned} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\arctan\left(9+\dfrac{27\sqrt{3}}{4}\right)$ , assunto nel punto $P_4=\left(-\dfrac{3}{2},-\dfrac{3\sqrt{3}}{2}\right)$ e valore minimo $\arctan(-3)$ , assunto in $P_1=(-1,2)$ .

Esercizio 7 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=e^{2x^2+3|y|},$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y)\in\mathbb{R}^2\mid 0\leq x\leq 3, x\geq|y|\}.$

Svolgimento 1.

Osserviamo che $f$ è composizione, prodotto e somma di funzioni continue⁷, pertanto è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $A$ è l’interno di un triangolo isoscele unito alla sua frontiera, in particolare è un chiuso e limitato di $\mathbb{R}^2$ , dunque compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$\quad$

Figura 42: raffigurato l’insieme $A$ .

$\quad$

$A^\circ$ ) Discutiamo con precisione l’enunciato del Teorema di Fermat:

Sia $\Omega\subset\mathbb{R}^n$ aperto e $f:\Omega\rightarrow\mathbb{R}$ funzione differenziabile su $\Omega$ , allora ogni punto di massimo o minimo di $f$ su $\Omega$ è in particolare un punto critico di $f$ .

In questo caso, la funzione $f(x,y)=e^{2x^2+3|y|}$ non è differenziabile sull’asse $x$ , cioè per $y=0$ . infatti mostreremo che non esiste $\nabla f(x,0)$ , $\forall x\in\mathbb{R}$ , in particolare non esiste $\dfrac{\partial f}{\partial y}(x,0)$ .

Dalla definizione di derivata parziale, si ha per ogni valore di $x$ ⁸

$\begin{equation*} \begin{split} \dfrac{\partial f}{\partial y}(x,0)&=\lim_{h\to0^{\pm}}\dfrac{f(x,h)-f(x,0)}{h}=\lim_{h\to0^{\pm}}\dfrac{e^{2x^2+3|h|}-e^{2x^2}}{h}=\lim_{h\to0^{\pm}}\dfrac{e^{2x^2}\left(e^{3|h|}-1\right)}{h}\\ &=e^{2x^2}\lim_{h\to0^{\pm}}\dfrac{e^{3|h|}-1}{3|h|}\dfrac{3|h|}{h}=3e^{2x^2}\lim_{h\to0^{\pm}}\dfrac{|h|}{h}=\pm3e^{2x^2}. \end{split} \end{equation*}$

Limite destro e sinistro non coincidono mai, dunque la derivata non esiste e $f$ non è differenziabile quando $y=0$ .

Tuttavia, se $y\neq 0$ , la funzione è differenziabile, dunque il più grande aperto contenuto in $A$ su cui applicare il teorema di Fermat è $\Tilde{A}:=\{(x,y)\in A^\circ\mid y\neq0\}$ .

Seguendo l’indicazione fornita dal teorema di Fermat indaghiamo i punti di massimo e minimo di $f$ su $\Tilde{A}$ ricercando i suoi punti critici, ovvero i punti $P\in \tilde{A}$ tali che $\nabla f(P)=(0,0)$ . Calcoliamo il gradiente di $f$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=4xe^{2x^2+3|y|}\\\\ \dfrac{\partial f}{\partial y}(x,y)=3\sigma(y)e^{2x^2+3|y|}, \end{cases}$

dove

$\sigma(y)=\left\{\begin{array}{l} \ \ 1\qquad\text{se }y>0 \\\\ \ \ 0\qquad\text{se }y=0\\\\ -1\qquad\text{se }y<0 \end{array}\right.$

è la funzione segno.

Osserviamo che la seconda equazione non si annulla mai per $y\neq0$ e in particolare non si annulla su $\tilde{A}$ . Questo significa che non ci sono punti critici di $f$ su $\Tilde{A}$ .

Il nostro studio di $A^\circ$ non è ancora finito, poiché mancano da studiare i punti di non differenzialità di $f$ , ovvero $A_0:=\{(x,y)\in A^\circ \mid y=0\}$ .

$\quad$

Figura 43: vengono rappresentati la parte interna di $A$ e i punti di $A^\circ$ su cui $f$ non risulta differenziabile. Su tali punti non potremo usare il Teorema di Fermat.

$\quad$

Questa regione è un segmento che possiamo parametrizzare tramite

$\begin{equation*} \begin{array}{rcl} \gamma:[0,3] & \rightarrow&\mathbb{R}^2 \\ t& \mapsto&(t,0). \end{array} \end{equation*}$

Calcoliamo $f$ lungo $A_0$ mediante la funzione composta $(f\circ\gamma)(t)=f(t,0)=e^{2t^2}$ . Si tratta di una composizione di funzioni monotone crescenti per $t\in[0,3]$ , dunque non vi saranno punti critici nemmeno su $A_0$ . Questo conclude il nostro studio di $A^\circ$ .

$\partial A$ ) Per quanto riguarda la frontiera, un triangolo, è composta da 3 lati $\partial A=L_1\cup L_2\cup L_3$ , come in figura.

$\quad$

Cerchiamo una parametrizzazione per ognuno di questi segmenti. Esse saranno rispettivamente

$\begin{equation*} \begin{aligned} &\alpha_1(t):=\left(t,t\right)\qquad t\in[0,3]\\ & \alpha_2(t):=\left(t,-t\right)\qquad t\in[0,3]\\ &\alpha_3(t):=\left(3,t\right)\qquad t\in[-3,3]. \end{aligned} \end{equation*}$

Per ciascuna parametrizzazione, studiamo i punti critici o di non derivabilità delle funzioni composte $f\circ\alpha_i$ e gli estremi del dominio $\alpha_i(0)$ e $\alpha_i(1)$ , con $i=1,2,3$ , che corrispondono ai vertici del triangolo.

$L_1\bigg)$

$\begin{equation*} \begin{split} (f\circ\alpha_1)(t)=f\left(t,t\right)=e^{2t^2+3t} \end{split} \end{equation*}$

dunque calcoliamo

$\begin{equation*} (f\circ\alpha_1)'(t)=(4t+3)e^{2t^2+3t}, \end{equation*}$

che non si annulla mai per $t\in[0,3]$ .

$L_2\bigg)$ Per lo studio di $L_2$ è sufficiente osservare che $f$ è una funzione pari rispetto a $y$ , dunque $f\circ\alpha_2=f\circ\alpha_1$ e quindi concludiamo come al passo precedente.

$L_3\bigg)$

$\begin{equation*} (f\circ\alpha_3)(t)=f(3,t)=e^{18}e^{3|t|}. \end{equation*}$

$f\circ\alpha_3$ non è derivabile in $0$ , dunque bisognerà calcolare il valore di $f$ nel punto $P_1=\alpha_3(0)=(3,0)$ . Per $t\neq0$ , ricerchiamo i punti critici di $f\circ\alpha_3$ :

$\begin{equation*} (f\circ\alpha_3)'(t)=3\sigma(t)e^{18}e^{3|t|}, \end{equation*}$

che non si annulla mai per $t\neq0$ . Infine, per quanto detto in precedenza, anche i vertici del triangolo $O=(0,0)$ , $B=(3,-3)$ e $C=(3,3)$ devono essere valutati.

$\quad$

Figura 44: il punto $P_1$ e i tre vertici del triangolo sono i candidati a punto di minimo e di massimo di $f$ su $A$ .

$\quad$

Abbiamo quindi trovato $4$ punti che competono ad essere massimo o minimo di $f$ su $A$ , calcoliamo i loro valori e confrontiamoli.

$\begin{equation*} \begin{gathered} f(P_1)=f(3,0)=e^{18},\qquad f(O)=f(0,0)=1, \\ f(B)=f(3,-3)=e^{27},\qquad f(C)=f(3,3)=e^{27}. \end{gathered} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $e^{27}$ , assunto nei punti $B=(3,-3)$ e $C=(3,3)$ e valore minimo $1$ , assunto in $O=(0,0)$ .

Il modulo è una funzione continua, ma non ovunque differenziabile. ↩

Useremo il limite notevole $\lim_{t\to0}\dfrac{e^t-1}{t}=1$ . ↩

Svolgimento 2.

Offriamo ora un modo alternativo per risolvere l’esercizio bypassando la difficoltà causata dalla presenza del modulo. Sfrutteremo la parità rispetto alla variabile $y$ sia della funzione $f$ , sia dell’insieme $A$ . Separiamo, infatti, l’insieme $A$ in due regioni, $A^+$ e $A^-$ , simmetriche tra di loro rispetto all’asse $x$ :

$\begin{equation*} A^+:=\{(x,y)\in\mathbb{R}^2\mid 0\leq x\leq 3, 0\leq y\leq x\} \end{equation*}$

$\begin{equation*} A^-:=\{(x,y)\in\mathbb{R}^2\mid 0\leq x\leq 3, -x\leq y\leq 0\}. \end{equation*}$

Osserviamo che $A=A^+\cup A^-$ e

$\begin{equation*} A^-=\{(x,y)\in\mathbb{R}^2\mid (x,-y)\in A^+\}. \end{equation*}$

$\quad$

Figura 45: separiamo l’insieme $A$ nelle due componenti $A^+$ e $A^-$ .

$\quad$

Dalla parità di $f$ rispetto a $y$ , sarà sufficiente studiare $f$ unicamente su $A^+$ ed estendere i risultati ad $A^-$ per parità.

Il notevole vantaggio di queste considerazioni sta nel fatto che $f$ su $(A^+)^\circ$ è una funzione differenziabile, di espressione

$\begin{equation*} f_{A^+}(x,y)=e^{2x^2+3y}. \end{equation*}$

Determiniamo, allora, il massimo e il minimo di $f$ su $A^+$ , studiando separatamente la sua parte interna $(A^+)^\circ$ e la sua frontiera $\partial A^+$ .

$\quad$

Figura 46: mettiamo in evidenza la parte interna e la frontiera di $A^+$ .

$\quad$

$(A^+)^\circ$ Per quanto riguarda l’insieme aperto $(A^+)^\circ$ , il teorema di Fermat ci permette di indagare gli eventuali punti critici di $f$ in $(A^+)^\circ$ , ovvero i punti $P\in (A^+)^\circ$ tali che $\nabla f(P)=(0,0)$ e scartare tutti i punti che non soddisfano tale condizione. Calcoliamo il gradiente di $f$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=4xe^{2x^2+3y}\\\\ \dfrac{\partial f}{\partial y}(x,y)=3e^{2x^2+3y}. \end{cases}$

Ricordando che l’esponenziale è una funzione strettamente positiva, la seconda coordinata del gradiente, $\dfrac{\partial f}{\partial y}$ , non si annulla mai su $(A^+)^\circ$ , dunque non vi sono punti critici di $f$ su $(A^+)^\circ$ .

$\partial A^+)$ Per quanto riguarda la frontiera, un triangolo, è composta da 3 lati $\partial A^+=L_1\cup L_2\cup L_3$ , come in figura.

$\quad$

Figura 47: la frontiera di $A^+$ è composta da tre lati $L_1$ , $L_2$ e $L_3$ .

$\quad$

Cerchiamo una parametrizzazione per ognuno di questi segmenti. Esse saranno rispettivamente

$\begin{equation*} \begin{aligned} &\alpha_1(t):=\left(t,t\right)\qquad t\in[0,3]\\ & \alpha_2(t):=\left(t,0\right)\qquad t\in[0,3]\\ &\alpha_3(t):=\left(3,t\right)\qquad t\in[0,3]. \end{aligned} \end{equation*}$

Per ciascuna parametrizzazione, studiamo punti critici o di non derivabilità delle funzioni composte $f\circ\alpha_i$ e gli estremi del dominio $\alpha_i(0)$ e $\alpha_i(1)$ , con $i=1,2,3$ , che corrispondono ai vertici del triangolo.

$L_1\bigg)$

$\begin{equation*} \begin{split} (f\circ\alpha_1)(t)=f\left(t,t\right)=e^{2t^2+3t} \end{split} \end{equation*}$

dunque calcoliamo

$\begin{equation*} (f\circ\alpha_1)'(t)=(4t+3)e^{2t^2+3t}=0\Leftrightarrow t=-\dfrac{3}{4}\notin[0,3], \end{equation*}$

dunque $f\circ\alpha_1$ non ha punti critici.

$L_2\bigg)$ Per lo studio di $L_2$ è sufficiente osservare che $f$ è una funzione pari rispetto a $y$ , dunque $f\circ\alpha_2=f\circ\alpha_1$ e quindi concludiamo come al passo precedente.

$L_3\bigg)$

$\begin{equation*} (f\circ\alpha_3)(t)=f(3,t)=e^{18}e^{3|t|}. \end{equation*}$

$f\circ\alpha_3$ non è derivabile in $0$ , dunque bisognerà calcolare il valore del punto $P_1=\alpha_3(0)=(3,0)$ . Per $t\neq0$ , ricerchiamo i punti critici di $f\circ\alpha_3$ :

$\begin{equation*} (f\circ\alpha_3)'(t)=3\sigma(t)e^{18}e^{3|t|}, \end{equation*}$

che non si annulla mai per $t\neq0$ .

Infine, per quanto detto in precedenza, anche i vertici del triangolo $O=(0,0)$ , $B=(3,-3)$ e $C=(3,3)$ devono essere valutati. end{enumerate} Abbiamo quindi trovato $3$ punti che competono a diventare massimo o minimo di $f$ su $A^+$ , calcoliamo i loro valori e confrontiamoli.

$\begin{equation*} f(O)=f(0,0)=1,\qquad f(B)=f(3,0)=e^{18}\qquad f(C)=f(3,3)=e^{27} \end{equation*}$

Per quanto riguarda $A$ , dobbiamo estendere per parità i risultati ottenuti su $A^+$ considerando $D=(3,-3)$ , il punto simmetrico di $C$ rispetto a $y$ , il cui valore è $e^{27}$ come per $C$ .

$\quad$

Figura 48: rappresentiamo i candidati trovati su $A^+$ e per simmetria, quelli su $A^-$ .

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $e^{27}$ , assunto nei punti $C=(3,3)$ e $D=(3,-3)$ e valore minimo $1$ , assunto in $0=(0,0)$ .

Esercizio 8 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=\displaystyle{e^{x^2+\frac{y^2}{2}+y}},$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y)\in\mathbb{R}^2\mid x^2+\dfrac{y^2}{2}\leq1, y\geq|\sqrt{2}x|\}.$

Svolgimento.

Figura 49: l’insieme $A$ , in giallo.

$\quad$

Osserviamo che $f$ è composizione, prodotto e somma di funzioni continue, pertanto è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $A$ è chiuso e limitato. La chiusura segue dal fatto che $A$ è intersezione di controimmagini di insiemi chiusi di $\mathbb{R}$ tramite funzioni continue, mentre per la limitatezza notiamo che esso è contenuto in un’ellisse. Dunque è un chiuso e limitato di $\mathbb{R}^2$ , compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$\begin{cases} \dfrac{\partial f}{\partial x}(x,y)=2xe^{x^2+\frac{y^2}{2}+y}\\\\ \dfrac{\partial f}{\partial y}(x,y)=(y+1)e^{x^2+\frac{y^2}{2}+y}. \end{cases}$

Dunque, ricordando che l’esponenziale è una funzione sempre positiva,

$\nabla f(x,y)=(0,0)\Leftrightarrow\displaystyle\left\{\begin{array}{l} 2x=0\\\\ y+1=0 \end{array} \right.\Leftrightarrow\displaystyle\left\{\begin{array}{l} x=0\\\\ y=-1. \end{array} \right.$

Abbiamo trovato il punto critico $(0,-1)$ , che tuttavia non appartiene ad $A^\circ$ .

$\quad$

Figura 50: la parte interna di $A$ e l’unico punto critico di $f$ , che non vi appartiene.

$\quad$

$\partial A$ ) Concentriamoci ora sulla frontiera di $A$ . Essa è un “settore ellittico”, composto da due segmenti e un arco di ellisse. La prima cosa da trovare sono i vertici del settore ellittico tramite i quali calcoleremo il dominio della parametrizzazione dell’arco. I due vertici superiori sono dati dall’intersezione delle curve che delimitano A, cioè dalle soluzioni del sistema

$\begin{cases} y=\pm\sqrt{2}x\\\\ x^2+\dfrac{y^2}{2}=1 \end{cases}\Rightarrow 2x^2=1\Rightarrow x=\pm\dfrac{\sqrt{2}}{2}, y=1.$

Chiamiamo $C=\left(\dfrac{\sqrt{2}}{2},1\right)$ e $B=\left(-\dfrac{\sqrt{2}}{2},1\right)$ .

$\quad$

Figura 51: la frontiera di $A$ è composta da due segmenti e un arco di ellisse.

$\quad$

$\begin{equation*} \begin{array}{rcl} \alpha_1:[0,2\pi] & \rightarrow&\mathbb{R}^2 \\ t & \mapsto&\left(\cos t,\sqrt{2}\sin t\right) \end{array} \end{equation*}$

basterà restringere il suo dominio per parametrizzare l’arco. Il dominio è $\left[\dfrac{\pi}{4},\dfrac{3}{4}\pi\right]$ , infatti

$\begin{equation*} \alpha_1\left(\dfrac{\pi}{4}\right)=\left(\dfrac{\sqrt{2}}{2},1\right)=C \qquad\text{e}\qquad \alpha_1\left(\dfrac{3}{4}\pi\right)=\left(-\dfrac{\sqrt{2}}{2},1\right)=B. \end{equation*}$

Le parametrizzazioni dei segmenti sono invece

$\begin{equation*} \begin{array}{rcl} \alpha_2:\left[0,\dfrac{\sqrt{2}}{2}\right] & \rightarrow&\mathbb{R}^2 \qquad\qquad\text{ per }\overline{OC}\\ t & \mapsto&\left(t,\sqrt{2}t\right) \end{array} \end{equation*}$

$\begin{equation*} \begin{array}{rcl} \alpha_3:\left[-\dfrac{\sqrt{2}}{2},0\right] & \rightarrow&\mathbb{R}^2 \qquad\qquad\text{ per }\overline{OB}\\ t & \mapsto&\left(t,-\sqrt{2}t\right) \end{array} \end{equation*}$

Finalmente possiamo studiare il comportamento di $f$ su $\partial A$ : oltre ad indagare i punti critici delle funzioni composte $f\circ\alpha_1$ , $f\circ\alpha_2$ e $f\circ\alpha_3$ , dovremo valutare anche i vertici del settore ellittico $O$ , $C$ , $B$ .

$\widehat{CB}\bigg)$

$\begin{equation*} (f\circ\alpha_1)(t)=f\left(\cos t,\sqrt{2}\sin t\right)=e^{\sqrt{2}\sin t+1}, \end{equation*}$

$\begin{equation*} (f\circ\alpha_1)'(t)=\sqrt{2}(\cos t)e^{\sqrt{2}\sin t+1}=0\Leftrightarrow t=\dfrac{\pi}{2}+k\pi\qquad k\in\mathbb{Z}. \end{equation*}$

Poiché $\alpha_1:\left[\dfrac{\pi}{4},\dfrac{3}{4}\pi\right]\rightarrow\mathbb{R}^2$ , l’unico valore a cui siamo interessati è $t=\dfrac{\pi}{2}$ , a cui corrisponde il punto $P_1=(0,\sqrt{2})$ .

$\overline{OC}\bigg)$

$\begin{equation*} (f\circ\alpha_2)(t)=f\left(t,\sqrt{2}t\right)=e^{2t^2+\sqrt{2}t}. \end{equation*}$

$\begin{equation*} (f\circ\alpha_2)'(t)=(4t+\sqrt{2})e^{2t^2+\sqrt{2}t}=0\Leftrightarrow t=-\dfrac{\sqrt{2}}{4}\notin\left[0,\dfrac{\sqrt{2}}{2}\right]. \end{equation*}$

Ciò significa che $f\circ\alpha_2$ non ha punti critici nel suo dominio di definizione.

$\overline{OB}\bigg)$ Poiché $f$ è pari rispetto a $x$ , $f\circ\alpha_3=f\circ\alpha_2$ , che abbiamo già studiato al punto precedente.

$\quad$

Figura 52: tutti i candidati ad essere massimo o minimo di $f$ su $A$ .

$\quad$

Abbiamo quindi trovato $4$ punti da valutare: $P_1=(0,\sqrt{2})$ , $O=(0,0)$ , $C=\left(-\dfrac{\sqrt{2}}{2},1\right)$ e $B=\left(\dfrac{\sqrt{2}}{2},1\right)$ . Calcoliamo i loro valori e confrontiamoli

$\begin{equation*} \begin{gathered} f(O)=f(0,0)=1,\qquad f(P_1)=f(0,\sqrt{2})=e^{\sqrt{2}+1}, \\ f(C)=f\left(-\dfrac{\sqrt{2}}{2},1\right)=e^{2},\qquad f(B)=f\left(-\dfrac{\sqrt{2}}{2},1\right)=e^{2}. \end{gahtered} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $e^{\sqrt{2}+1}$ , assunto nel punto $P_1=(0,\sqrt{2})$ e valore minimo $1$ , assunto in $O=(0,0)$ .

Esercizio 9 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=x-y,$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y)\in\mathbb{R}^2\mid 5(x^2+y^2)+8xy-8=0\}.$

Svolgimento 1.

Figura 53: l’insieme $A$ .

$\quad$

Osserviamo che $f$ è un polinomio di primo grado, pertanto è una funzione continua su $\mathbb{R}^2$ , mentre, se definiamo la funzione continua

$h(x,y):=5(x^2+y^2)+8xy-8,$

l’insieme $A$ è definito come luogo di zeri di $h$ , dunque è un chiuso di $\mathbb{R}^2$ .

Inoltre, affermiamo che $A$ è un’ellisse con gli assi obliqui: dimostriamolo riducendo $A$ in forma canonica. Per farlo, dovremo diagonalizzare una sottomatrice della matrice dei coefficienti che descrivono l’ellisse e trovare la matrice ortogonale di trasformazione formata dagli autovettori della sottomatrice. In generale, data un’ellisse di equazione

$a_{11}x^2+a_{22}y^2+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0,$

la matrice dei coefficienti sarà

$\begin{equation*} M:= \begin{pmatrix} a_{11}&a_{12}&a_{13}\\ a_{12}&a_{22}&a_{23}\\ a_{13}&a_{23}&a_{33} \end{pmatrix} \end{equation*}$

e la sottomatrice da diagonalizzare è quella formata dai termini di grado 2, ovvero

$\begin{equation*} M':= \begin{pmatrix} a_{11}&a_{12}\\ a_{12}&a_{22} \end{pmatrix}. \end{equation*}$

In questo caso

$\begin{equation*} M= \begin{pmatrix} 5&4&0\\ 4&5&0\\ 0&0&-8 \end{pmatrix} \end{equation*}$

$\begin{equation*} M'= \begin{pmatrix} 5&4\\ 4&5 \end{pmatrix}. \end{equation*}$

Osserviamo che $M'$ è simmetrica, dunque sempre diagonalizzabile. Essa si diagonalizza nel seguente modo: calcoliamo gli autovalori di $M'$ , che sono le radici del polinomio caratteristico $p(\lambda)=\det{M'-\lambda I_2}$ , dove $I_2$ è la matrice identità di dimensione $2$

$\begin{equation*} \begin{gathered} p(\lambda)=\det\begin{pmatrix} 5-\lambda&4\\ 4&5-\lambda \end{pmatrix}=25+\lambda^2-10\lambda-16=\lambda^2-10\lambda+9=0 \\ \iff \\ \lambda_{1,2}=5\pm\sqrt{25-9}=\left\{\begin{array}{l} \lambda_1=1 \\\\ \lambda_2=9. \end{array}\right. \end{gathered} \end{equation*}$

Troviamo gli autovettori corrispondenti a tali autovalori, ovvero i vettori $\Vec{v}_j$ che soddisfano $(M'-\lambda_jI_2)\cdot\Vec{v}_j=\Vec{0}$ , per $j=1,2$ .

Iniziamo con $\lambda_1=1$ :

$\begin{equation*} \begin{pmatrix} 5&4\\ 4&5 \end{pmatrix}- 1\begin{pmatrix} 1&0\\ 0&1 \end{pmatrix}=\begin{pmatrix} 4&4\\ 4&4 \end{pmatrix}, \end{equation*}$

dunque il primo autovettore $\Vec{v}_1=(x,y)$ deve soddisfare

$\begin{equation*} \left\{\begin{array}{l} 4x+4y=0 \\ 4x+4y=0 \end{array}\right.\Leftrightarrow x=-y, \end{equation*}$

perciò $\Vec{v}_1=(-y,y)$ . Troviamo ora, in maniera analoga, il secondo autovettore $\Vec{v}_2$ , relativo a $\lambda_2=9$ .

$\begin{equation*} \begin{pmatrix} 5&4\\ 4&5 \end{pmatrix}- 9\begin{pmatrix} 1&0\\ 0&1 \end{pmatrix}=\begin{pmatrix} -4&4\\ 4&-4 \end{pmatrix}, \end{equation*}$

da cui $\Vec{v}_2=(x,y)$ soddisfa

$\begin{equation*} \left\{\begin{array}{l} -4x+4y=0 \\ 4x-4y=0 \end{array}\right.\Leftrightarrow x=y, \end{equation*}$

cioè $\Vec{v}_2=(y,y)$ . Abbiamo dunque trovato che, per ogni valore di $y\in\mathbb{R}$ , la matrice

$\begin{equation*} R_y=\begin{pmatrix} -y&y\\ y&y \end{pmatrix} \end{equation*}$

diagonalizza $M'$ . Tuttavia, affinchè $R_y$ sia una matrice ortogonale, dobbiamo avere $\det(R_y)=\pm1$ , che si verifica se

$\begin{equation*} \pm1=\det(R_y)=\det\begin{pmatrix} -y&y\\ y&y \end{pmatrix}=-2y^2, \end{equation*}$

che viene soddisfatto solo se $y=\pm\dfrac{1}{\sqrt{2}}$ , a cui corrispondono le matrici

$\begin{equation*} R_{\pm\frac{1}{\sqrt{2}}}=\pm \begin{pmatrix} -\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}} \end{pmatrix}. \end{equation*}$

Notiamo che in entrambi i casi, $\det\left(R_{\pm\frac{1}{\sqrt{2}}}\right)=-1$ , ciò significa che $R_{\pm\frac{1}{\sqrt{2}}}$ è una riflessione.

Scegliamo per comodità $y=\dfrac{1}{\sqrt{2}}$ . La trasformazione che riduce $A$ in forma canonica sarà dunque la seguente:

$\begin{equation*} T:\mathbb{R}^2\rightarrow\mathbb{R}^2, \end{equation*}$

$\begin{equation*} T(x,y)=R_{\frac{1}{\sqrt{2}}}\cdot\begin{pmatrix} x\\ y \end{pmatrix}=\begin{pmatrix} \dfrac{y-x}{\sqrt{2}}\\\\ \dfrac{x+y}{\sqrt{2}} \end{pmatrix}. \end{equation*}$

Graficamente possiamo notare che $T$ esprime la riflessione rispetto alla retta di equazione $y=(1+\sqrt{2})x$ .

$\quad$

Figura 54: l’immagine degli estremi dei semiassi di $A$ vengono mappati dalla riflessione $T$ sugli assi cartesiani. Vedremo che $T$ è proprio la trasformazione che riduce $A$ in forma canonica.

$\quad$

Essa, in particolare, sarà l’inversa di sè stessa, infatti

$\begin{equation*} \begin{split} (T\circ T)(x,y) &= T\left(\dfrac{y-x}{\sqrt{2}},\dfrac{y+x}{\sqrt{2}}\right)=\left(\dfrac{\dfrac{y+x}{\sqrt{2}}-\dfrac{y-x}{\sqrt{2}}}{\sqrt{2}},\dfrac{\dfrac{y+x}{\sqrt{2}}+\dfrac{y-x}{\sqrt{2}}}{\sqrt{2}}\right)= \\ & = \left(\dfrac{\dfrac{2x}{\sqrt{2}}}{\sqrt{2}},\dfrac{\dfrac{2y}{\sqrt{2}}}{\sqrt{2}}\right)=\left(\dfrac{2x}{2},\dfrac{2y}{2}\right)=(x,y) \end{split} \end{equation*}$

questo dimostra che $T^{-1}=T$ .

Inoltre, se $(x,y)\in A$ soddisfa

$5(x^2+y^2)+8xy-8=0,$

$T(x,y)=(T_1(x,y),T_2(x,y))$ soddisfa

$\begin{equation*} 5(T_1^2(x,y)+T_2^2(x,y))+8T_1(x,y)T_2(x,y)-8=0, \end{equation*}$

cioè

$\begin{equation*} \begin{split} 5\left(\left(\dfrac{y+x}{\sqrt{2}}\right)^2+\left(\dfrac{y-x}{\sqrt{2}}\right)^2\right)+8\left(\dfrac{y-x}{\sqrt{2}}\right)\left(\dfrac{y+x}{\sqrt{2}}\right)-8&=0\\ \dfrac{5}{2}\left(x^2+y^2+2xy+x^2+y^2-2xy\right)+\dfrac{8}{2}(y^2-x^2)-8&=0\\ 5x^2+5y^2-4x^2+4y^2-8&=0\\ x^2+9y^2-8&=0. \end{split} \end{equation*}$

Ciò significa che $T(A)=\mathcal{C}$ , dove $\mathcal{C}$ è l’ellisse, in forma canonica, di equazione

$\begin{equation*} \mathcal{C}:=\left\{(x,y)\in\mathbb{R}^2\mid \dfrac{x^2}{8}+\dfrac{9y^2}{8}=1\right\}. \end{equation*}$

$\quad$

Figura 55: $\mathcal{C}=T(A)$ è l’ellisse in forma canonica corrispondente ad $A$ . Sarà molto più facile studiare il problema variazionale della ricerca di massimo e minimo di $f\circ T^{-1}$ su $\mathcal{C}$ , rispetto a quello originale.

$\quad$

Con questo ragionamento, l’affermazione iniziale è stata dimostrata. In particolare, $A$ è un chiuso (luogo di zeri di una funzione continua) e limitato di $\mathbb{R}^2$ , dunque compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Se definiamo la funzione $g:=f\circ T^{-1}:\mathcal{C}\rightarrow\mathbb{R}^2$ , allora sarà sufficiente studiare il problema di massimo e minimo di $g$ su $\mathcal{C}$ e riportare quanto trovato ad $A$ attraverso la trasformazione $T$ .

Calcoliamo $g$

$\begin{equation*} g(x,y)=f(T^{-1}(x,y))=f(T(x,y))=f\left(\dfrac{y-x}{\sqrt{2}},\dfrac{y+x}{\sqrt{2}}\right)=-\dfrac{2}{\sqrt{2}}x=-\sqrt{2}x. \end{equation*}$

Risulta quindi molto facile trovare il massimo e il minimo di $g$ su $\mathcal{C}$ . Infatti

$\begin{equation*} \max_\mathcal{C}g=g(-2\sqrt{2},0)=4, \end{equation*}$

assunto nel punto $Q_1=(-2\sqrt{2},0)$ e

$\begin{equation*} \min_\mathcal{C}g=g(2\sqrt{2},0)=-4, \end{equation*}$

assunto nel punto $Q_2=(2\sqrt{2},0)$ .

A questo punto non rimane altro che scoprire a che punti su $A$ corrispondono i punti di massimo e minimo $Q_1$ e $Q_2$ trovati su $\mathcal{C}$ :

$\begin{equation*} P_1=T^{-1}(Q_1)=T(Q_1)=T(-2\sqrt{2},0)=\left(\dfrac{0-(-2\sqrt{2})}{\sqrt{2}},\dfrac{0+(-2\sqrt{2})}{\sqrt{2}}\right)=(2,-2), \end{equation*}$

$\begin{equation*} P_2=T^{-1}(Q_2)=T(Q_2)=T(2\sqrt{2},0)=\left(\dfrac{0-2\sqrt{2}}{\sqrt{2}},\dfrac{0+2\sqrt{2}}{\sqrt{2}}\right)=(-2,2). \end{equation*}$

$\quad$

Figura 56: raffigurati l’insieme dei candidati al problema canonica di $f\circ T^{-1}$ , $Q_1$ e $Q_2$ e i corrispondenti punti su $A$ , $P_1$ e $P_2$ .

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $4$ , assunto nel punto $P_1=(2,-2)$ e valore minimo $-4$ , assunto in $P_2=(-2,2)$ .

Svolgimento 2.

Figura 57: l’ellisse $A$ e la sua forma canonica $\mathcal{C}$ .

$\quad$

Abbiamo già osservato nella risoluzione precedente che $A$ è un’ellisse con gli assi obliqui. Osserviamo che l’insieme $A$ ha interno vuoto, dunque non è possibile applicare il teorema di Fermat per la ricerca di punti critici. Utilizzeremo, invece, il teorema dei moltiplicatori di Lagrange per l’intero esercizio.

Abbiamo già espresso $A$ come luogo di zeri della funzione $h$ , di classe $\mathcal{C}^1$ , il cui gradiente non è mai nullo su $A$ . Il metodo dei moltiplicatori di Lagrange ci suggerisce di costruire la funzione Lagrangiana $\mathcal{L}(x,y,\lambda):=f(x,y)-\lambda h(x,y)$ . Per il teorema di Lagrange, i punti critici di $\mathcal{L}$ saranno esattamente i punti critici di $f$ su $\partial A$ , calcoliamoli risolvendo il sistema che segue

$\begin{equation*} \nabla\mathcal{L}=(0,0,0)\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial\mathcal{L}}{\partial x}=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial y}=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \lambda}=0 \\\\ \end{array}\right.\Leftrightarrow\left\{\begin{array}{l} \dfrac{\partial f}{\partial x}-\lambda\dfrac{\partial h}{\partial x}=0 \\\\ \dfrac{\partial f}{\partial y}-\lambda\dfrac{\partial h}{\partial y}=0 \\\\ h=0.\\\\ \end{array}\right. \end{equation*}$

Calcoliamo la Lagrangiana e i suoi punti critici. Nel nostro caso

$\begin{equation*} \mathcal{L}(x,y,\lambda):=x-y-\lambda(5(x^2+y^2)+8xy-8) \end{equation*}$

$\begin{equation*} \begin{aligned} \left\{\begin{array}{l} \dfrac{\partial\mathcal{L}}{\partial x}=1-\lambda(10x+8y)=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial y}=-1-\lambda(10y+8x)=0 \\\\ \dfrac{\partial\mathcal{L}}{\partial \lambda}=-(5(x^2+y^2)+8xy-8)=0\\\\ \end{array} \right. & \iff \left\{\begin{array}{l} 10\lambda x+8\lambda y-1=0 \\\\ 8\lambda x+10\lambda y+1=0\\\\ 5(x^2+y^2)+8xy-8=0\\\\ \end{array} \right. \\ & \iff \left\{\begin{array}{l} 18\lambda (x+y)=0 \\\\ 8\lambda x+10\lambda y+1=0\\\\ 5(x^2+y^2)+8xy-8=0\\\\ \end{array} \right. \end{aligned} \end{equation*}$

dove nell’ultimo passaggio alla prima equazione abbiamo sostituito la somma tra la prima e la seconda equazione.

Se assumiamo $\lambda=0$ , la seconda equazione è impossibile, possiamo allora suppore $\lambda\neq0$ , quindi

$\begin{equation*} \left\{\begin{array}{l} x=-y \\\\ 2\lambda y+1=0\\\\ 10y^2-8y^2-8=0\\\\ \end{array} \right.\Leftrightarrow\left\{\begin{array}{l} x=-y \\\\ \lambda=\pm\dfrac{1}{4}\\\\ y=\pm2.\\\\ \end{array} \right. \end{equation*}$

$\quad$

Figura 58: si può notare come nei due punti trovati con il metodo dei moltiplicatori di Lagrange i gradienti delle due funzioni sono effettivamente linearmente dipendenti.

$\quad$

Dunque abbiamo trovato i punti $P_1=(-2,2)$ e $P_2=(2,-2)$ . Notiamo in figura che $\nabla f$ e $\nabla g$ sono paralleli in $P_1$ e $P_2$ . Calcoliamo i loro valori e confrontiamoli

$\begin{equation*} f(P_1)=f(-2,2)=-4,\qquad f(P_2)=f(2,-2)=4. \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $4$ , assunto nel punto $P_2=(2,-2)$ e valore minimo $-4$ , assunto in $P_1=(-2,2)$ .

Esercizio 10 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Data la funzione $f:\mathbb{R}^2\rightarrow\mathbb{R},$ definita da

$f(x,y):=\ln(1+y^2+|x|),$

determinare, se esistono, il massimo e il minimo di $f$ sull’insieme

$A:=\{(x,y)\in\mathbb{R}^2\mid |y|\leq x\leq2-y^2\}.$

Svolgimento.

Figura 59: l’insieme $A$ .

$\quad$

Osserviamo che $f$ è composizione, prodotto e somma di funzioni continue, pertanto è una funzione continua su $\mathbb{R}^2$ , mentre l’insieme $A$ è un settore parabolico limitato, in particolare è un chiuso e limitato di $\mathbb{R}^2$ , dunque compatto per il teorema di Heine-Borel. Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

Possiamo allora applicare il teorema di Weierstrass, il quale garantisce l’esistenza del massimo e del minimo di $f$ su $A$ .

È molto utile, per il proseguo dell’esercizio, osservare che la funzione $g(t):=\ln(t)$ è monotona crescente e che $f=g\circ h$ , dove

$h(x,y):=1+y^2+|x|.$

Dunque, possiamo applicare proposizione 6, che ci permette studiare la funzione $h$ anziché $f$ .

Distinguiamo l’insieme $A$ nella sua parte interna e la sua frontiera: $A=A^\circ\sqcup\partial A$ . Studiamo separatamente e in maniera differente le due componenti.

$A^\circ$ ) Discutiamo con precisione l’enunciato del Teorema di Fermat:

Sia $\Omega\subset\mathbb{R}^n$ aperto e $h:\Omega\rightarrow\mathbb{R}$ funzione differenziabile su $\Omega$ , allora ogni punto di massimo o minimo di $h$ su $\Omega$ è in particolare un punto critico di $h$ .

In questo caso, la funzione $h(x,y)=1+y^2+|x|$ non è differenziabile sull’asse $y$ , cioè per $x=0$ . infatti mostreremo che $\nexists\nabla h(0,y)$ , $\forall y\in\mathbb{R}$ , in particolare che $\nexists\dfrac{\partial h}{\partial x}(0,y)$ .

Dalla definizione di derivata parziale, $\forall y\in\mathbb{R}$

$\begin{equation*} \begin{split} \dfrac{\partial h}{\partial x}(0,y)&=\lim_{t\to0^{\pm}}\dfrac{h(t,y)-h(0,y)}{t}=\lim_{t\to0^{\pm}}\dfrac{1+y^2+|t|-(1+y^2)}{t}=\lim_{t\to0^{\pm}}\dfrac{|t|}{t}=\pm1. \end{split} \end{equation*}$

Limite destro e sinistro non coincidono, dunque la derivata non esiste e $h$ non è differenziabile quando $x=0$ .

In ogni caso, $A^\circ$ è contenuto nel semipiano aperto $x>0$ , dunque $A^\circ$ non contiene punti di non derivabilità di $h$ , per cui possiamo applicare il teorema di Fermat a tutto $A^\circ$ .

$\quad$

Figura 60: notiamo come l’insieme dei punti di non differenziabilità di $f$ non intersechi la parte interna di $A$ .

$\quad$

Ricerchiamo i punti critici di $h$ , ovvero i punti $P\in A^\circ$ tali che $\nabla h(P)=(0,0)$ . Calcoliamo il gradiente di $h$ svolgendo le derivate parziali:

$\begin{cases} \dfrac{\partial h}{\partial x}(x,y)=\sigma(x)\\\\ \dfrac{\partial h}{\partial y}(x,y)=2y, \end{cases}$

dove

$\sigma(x)=\left\{\begin{array}{l} \ \ 1\qquad\text{se }x>0 \\\\ \ \ 0\qquad\text{se }x=0\\\\ -1\qquad\text{se }x<0 \end{array}\right.$

è la funzione segno.

Osserviamo che la prima equazione non si annulla mai per $x\neq0$ e in particolare non si annulla su $A^\circ$ . Questo significa che non ci sono punti critici di $h$ su $A^\circ$ .

$\partial A$ ) Concentriamoci ora sulla frontiera di $A$ . Essa è un settore di parabola, composto da due segmenti e un arco di parabola. La prima cosa da trovare sono i vertici del settore di parabola, tramite i quali calcoleremo il dominio della parametrizzazione dell’arco.

$\begin{cases} x=\pm y\\\\ x=2-y^2 \end{cases}\Rightarrow y^2\pm y-2=0\Rightarrow y=\dfrac{\mp1\pm\sqrt{1+8}}{2}\Rightarrow\begin{cases} y=2,\qquad x=-2\\\\ y=1,\qquad x=1\\\\ y=-1,\qquad x=1\\\\ y=-2,\qquad x=-2. \end{cases}$

Osserviamo che, poichè $A$ è contenuto nel semipiano $x\geq0$ , i vertici del settore di parabola sono $B=(1,1)$ e $C=(1,-1)$ .

$\quad$

Figura 61: i punti di intersezione tra la parabola e i segmenti. In questo modo possiamo trovare le parametrizzazioni del bordo di $A$ ..

$\quad$

Ora è possibile individuare le parametrizzazioni dei lati. La funzione

$\begin{equation*} \begin{array}{rcl} \alpha_1:(-\infty,\infty)&\rightarrow&\mathbb{R}^2 \\ t&\mapsto& (2-t^2,t) \end{array} \end{equation*}$

parametrizza la parabola e per selezionare il settore che compone $\widehat{BC}$ basterà ridurre il suo dominio a $[-1,1]$ , infatti

$\begin{equation*} \alpha_1(-1)=(1,-1)=C\qquad\text{e }\qquad \alpha_1(1)=(1,1)=B. \end{equation*}$

Possiamo parametrizzare i due segmenti tramite un’unica curva:

$\begin{equation*} \begin{array}{rcl} \alpha_2:[-1,1] &\rightarrow&\mathbb{R}^2 \\ t &\mapsto&(|t|,t). \end{array} \end{equation*}$

Si tratta di una curva regolare a tratti, i cui tratti sono $[-1,0]$ e $[0,1]$ , mentre $t=0$ è un punto singolare della curva poiché non esiste il vettore tangente in $\alpha_2(0)$ , a causa del fatto che la funzione modulo non è ivi derivabile.

Per la ricerca dei punti di massimo o minimo di $h$ su $\partial A$ dovremo studiare i punti critici delle funzioni composte $h\circ\alpha_1$ e $h\circ\alpha_2$ , gli estremi di tali parametrizzazioni, $B$ e $C$ e i punti singolari delle curve, ovvero $O:=\alpha_2(0)=(0,0)$ .

$\widehat{BC}$ )

$\begin{equation*} (h\circ\alpha_1)(t)=h\left(2-t^2,t\right)=1+t^2+|2-t^2|=3, \end{equation*}$

è una funzione costante, i cui punti sono critici per definizione.

$\overline{CB}$ )

$\begin{equation*} (h\circ\alpha_2)(t)=h\left(|t|,t\right)=1+t^2+|t|. \end{equation*}$

Per $t>0$ $h\circ\alpha_2$ è strettamente crescente, mentre per $t<0$ è strettamente decrescente, mentre per $t=0$ , valore che dovremo già studiare, non è derivabile.

Abbiamo trovato tutti i punti dell’arco di parabola $\widehat{BC}$ come punti critici di $h$ su $\partial A$ .

$\quad$

massimi e minimi vincolati

Figura 62: l’insieme dei punti candidati a punti di massimo o minimo di $f$ su $A$ . Da notare che tutto l’arco $\widehat{BC}$ compete.

$\quad$

I punti che meritano la nostra attenzione sono $O=(0,0)$ , $B=(1,1)$ , $C=(1,-1)$ e l’arco di parabola $\widehat{BC}$ . Calcoliamo i loro valori e confrontiamoli.

$\begin{equation*} \begin{gathered} f(O)=f(0,0)=0,\qquad f(B)=f(1,1)=\ln(3), \\ f(C)=f(1,-1)=\ln(3)\qquad f(x,y)=\ln(3)\quad\forall(x,y)\in\widehat{BC}. \end{gathered} \end{equation*}$

$\quad$

La soluzione dell’esercizio è la seguente: $f$ ha massimo su $A$ pari a $\ln(3)$ , assunto su tutto l’arco di parabola $\widehat{BC}$ e valore minimo $0$ , assunto in $O=(0,0)$ .

e non sia un forum, è una risorsa eccellente per la teoria matematica.

The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.

Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.

Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.

Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.

Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

[/learn_more]

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Document

Menu

Chiudi

Massimi e minimi vincolati – Esercizi – Volume 1

Autori e revisori

Leggi...

Introduzione

Leggi...

Richiami di teoria

Leggi...

Esercizi

Svolgimento 1.

Svolgimento 2.

Svolgimento 3.

Svolgimento.

Svolgimento 1.

Svolgimento 2.

Svolgimento 1.

Svolgimento 2.

Svolgimento 1.

Svolgimento 2.

Svolgimento.

Svolgimento 1.

Svolgimento 2.

Svolgimento.

Svolgimento 1.

Svolgimento 2.

Svolgimento.

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi