Il teorema di esistenza degli zeri

Teoria sulle Funzioni continue-lipschitziane-holderiane

Home » Il teorema di esistenza degli zeri

Il teorema di esistenza degli zeri afferma che, se una funzione continua su un intervallo assume valori di segno diverso, allora assume anche valore nullo. Esso è uno strumento utilissimo nel provare l’esistenza di soluzioni a equazioni non facilmente risolubili esplicitamente. Presentiamo una dimostrazione costruttiva del teorema che fornisce un metodo pratico per la ricerca approssimata di tali soluzioni, oltre a una breve ed elegante dimostrazione di carattere più teorico. Se desideri conoscere i dettagli di questo strumento dalle infinite potenzialità, questo conciso articolo è quanto cercavi!

Oltre all’esaustiva lista reperibile alla fine dell’articolo, segnaliamo il seguente materiale teorico di riferimento:

Di seguito, inoltre, le raccolte di esercizi su argomenti correlati:

Sommario

Leggi...

In questo articolo trattiamo il teorema di esistenza degli zeri e ne presentiamo due dimostrazioni: una di tipo più teorico e un’altra di tipo costruttivo. Riportiamo inoltre dei controesempi sulla necessità delle ipotesi e un’applicazione alla risoluzione qualitativa di equazioni.

Autori e revisori

Leggi...

Autore: Daniele Fakhoury, Luigi De Masi, Silvia Lombardi, Giuseppe Palaia.

Revisori: Sara Sottile, Matteo Talluri, Valerio Brunetti, Sergio Fiorucci, Chiara Bellotti.

Introduzione

Leggi...

Questo articolo tratta una formalizzazione matematica del seguente concetto pratico e intuitivo: “tracciando una linea continua che cominci da una parte di una retta e termini dall’altra, la linea deve attraversare la retta.” Per secoli si è ritenuto che questo genere di conclusioni fossero talmente evidenti da non necessitare una dimostrazione. Soltanto quando divenne necessario definire cosa significasse matematicamente l’espressione “linea continua”, ci si rese conto che, di conseguenza, anche queste informazioni così semplici andavano giustificate e dimostrate rigorosamente.

Il teorema di esistenza degli zeri consiste appunto nella formalizzazione dell’idea intuitiva esposta sopra. In esso, per linea continua si intende il grafico di una funzione continua, mentre la retta è data dall’asse delle ascisse. Le due zone da una parte e dall’altra di esso sono il semipiano delle $y$ negative e quello delle $y$ positive. Quindi, una funzione continua che assuma valori di segno opposto agli estremi di un intervallo interseca necessariamente l’asse delle $x$ ; esiste cioè un punto $x_0$ tale che $f(x_0)=0$ . $x_0$ viene quindi detto uno zero di $f$ , cioè un punto in cui $f$ assume il valore $0$ . Si veda la figura 1.

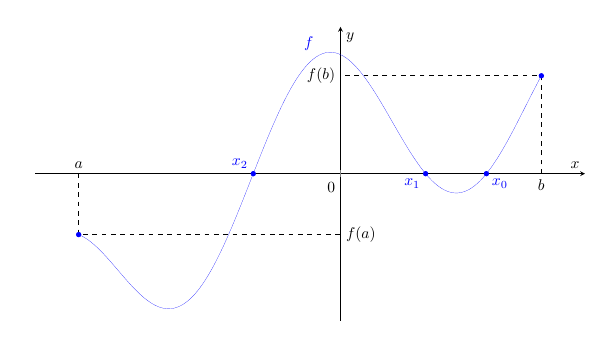
Figura 1: rappresentazione del teorema 1. Poiché $f(a)<0$ , $f(b)>0$ e $f$ è continua, il grafico di $f$ interseca l’asse $x$ in almeno un punto $x_0 \in (a,b)$ . Si noti che, nonostante il teorema 1 assicuri l’esistenza di almeno un punto $x_0$ tale che $f(x_0)=0$ , esso può non essere unico, come nel caso in esame in cui sono presenti anche gli zeri $x_1$ e $x_2$ di $f$ .

Teorema 1 (teorema di esistenza degli zeri). Sia $f\colon [a,b]\subset \mathbb{R} \to \mathbb{R}$ una funzione continua e si supponga che $f(a)\cdot f(b) < 0$ . Allora esiste $x_0\in \left(a,b\right)$ tale che $f(x_0)=0$ .

Osserviamo che la condizione $f(a) \cdot f(b)<0$ è semplicemente un modo compatto per esprimere il fatto che $f(a)$ e $f(b)$ hanno segno opposto: infatti ciò è equivalente a richiedere che $f(a) \cdot f(b)<0$ .

Notiamo infine che il punto $x_0$ in cui $f$ si annulla potrebbe anche non essere unico, come nell’esempio rappresentanto in figura 1.

Dopo aver richiamato le definizioni e i risultati preliminari nella sezione 1, presentiamo due dimostrazioni del teorema 1: la prima, nella sezione 2, di tipo più teorico, mentre la seconda di tipo costruttivo è riportata nella sezione 3. Nella sezione 4 notiamo come le ipotesi del teorema siano necessarie affinché la tesi sia valida. Infine, nella sezione 5 presentiamo un corollario che risulta molto utile nella risoluzione qualitativa di equazioni che sarebbero difficilmente trattabili al fine di trovare la soluzione esplicita.

Definizioni preliminari

Leggi...

In questa sezione richiamiamo, per comodità del lettore, la definizione e i risultati sulle funzioni continue che utilizzeremo nel seguito. Rimandiamo alla dispensa [2, Funzioni continue] per una trattazione completa dell’argomento. Riportiamo la caratterizzazione della continuità per successioni stabilita in [2, Funzioni continue], che utilizziamo nelle dimostrazioni del teorema 1.

Teorema 2 (caratterizzazione della continuità per successioni). Sia $A \subseteq \mathbb{R}$ , sia $f \colon A \to \mathbb{R}$ e sia $x_0 \in A$ . Allora le due affermazioni seguenti sono equivalenti:

$f$ è continua in $x_0$ ;
per ogni successione $\{x_n\}_{n \in \mathbb{N}}$ a valori in $A$ tale che $x_n \to x_0$ , si ha
(1) $\begin{equation*} \displaystyle \lim_{n \to +\infty}f(x_n)=f(x_0). \end{equation*}$

Un ulteriore risultato dalla teoria delle funzioni continue che utilizzeremo è il teorema della permanenza del segno [2, Funzioni continue, corollario 5.2].

Teorema 3 (permanenza del segno per funzioni continue). Sia $f\colon A \subseteq \mathbb{R}\to \mathbb{R}$ e sia $x_0\in A$ un punto di continuità per $f$ . Allora se $f(x_0)>0$ esiste un intorno $I_{x_0}$ tale che

$f(x)>0 \qquad \forall x\in I_{x_0}\cap A.$

Vale un risultato analogo se $f(x_0)<0$ .

Dimostrazione del teorema 1

Leggi...

La prima dimostrazione del teorema 1 che presentiamo è di carattere più formale e determina il punto $x_0$ come estremo superiore dell’insieme $E$ dei punti $x$ tali che $f(x)<0$ . L’idea intuitiva soggiacente è che tale estremo superiore $x_0$ deve essere proprio un punto in cui $f$ cambia segno e quindi, per la continuità di $f$ , è tale che $f(x_0)=0$ . Si veda la figura 2.

Più formalmente, esso non può soddisfare $f(x_0)<0$ né $f(x_0)>0$ perché altrimenti, per il teorema 3 della permanenza del segno, vi sarebbe un intorno $I$ di $x_0$ in cui $f$ assume lo stesso segno, contro il fatto che $x_0$ sia l’estremo superiore dei punti tali che $f(x)<0$ .

Figura 2: rappresentazione del teorema 1. Poiché $f(a)<0$ , $f(b)>0$ e $f$ è continua, il grafico di $f$ interseca l’asse $x$ in almeno un punto $x_0 \in (a,b)$ , ottenuto come estremo superiore dell’insieme $E= \{x \in [a,b] \colon f(x) \leq 0\}$ (rappresentato in rosso). Si noti che, nonostante il teorema 1 assicuri l’esistenza di almeno un punto $x_0$ tale che $f(x_0)=0$ , esso può non essere unico, come nel caso in esame in cui sono presenti anche gli zeri $x_1$ e $x_2$ di $f$ .

Dimostrazione del teorema 1 Supponiamo che $f(a)<0$ e $f(b)>0$ . Il caso opposto si dimostra in maniera analoga. Definiamo l’insieme

(2) $\begin{equation*} E = \{ x \in [a,b] \colon f(x) \leq 0\}, \end{equation*}$

rappresentato in rosso in figura 2. Osserviamo che $a\in E$ , dunque $E$ è non vuoto e inoltre $E\subset [a,b]$ , dunque è limitato superiormente. Allora per la completezza dei numeri reali (si veda [1, Funzioni elementari — Volume 1, assioma 2.57]) esiste

(3) $\begin{equation*} x_0= \sup E \in [a,b]. \end{equation*}$

Proviamo che $f(x_0)=0$ .

Per definizione di estremo superiore, esiste una successione $x_n \in E$ tale che $x_n \to x_0$ , da cui segue, per la continuità di $f$ e per il teorema 2, che

(4) $\begin{equation*} f(x_0) \leq 0. \end{equation*}$

In particolare ciò mostra che $x_0< b$ .

Supponiamo che $f(x_0)<0$ , allora per il teorema 3, esisterebbe $x_1>x_0$ con $x_1\in [a,b]$ tale che $f(x_1)<0$ , contraddicendo il fatto che $x_0=\sup E$ . Da tale contraddizione segue che

(5) $\begin{equation*} f(x_0)=0. \end{equation*}$

Dimostrazione costruttiva del teorema 1

Leggi...

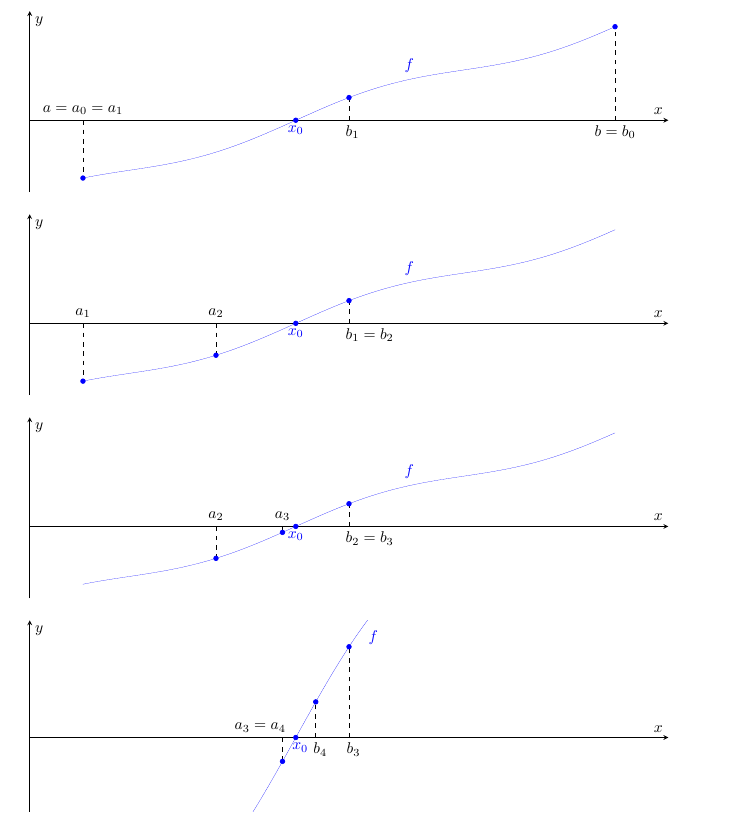
Viene presentata ora una dimostrazione alternativa di tipo costruttivo. In essa si costruisce una successione di intervalli $[a_n,b_n]$ di lunghezza via via dimezzata, ai cui estremi $f$ assume segno opposto. Poiché all’aumentare di $n$ l’ampiezza dell’intervallo diminuisce, al limite per $n \to + \infty$ $a_n$ e $b_n$ convergono allo stesso numero reale $x_0$ che ci si aspetta sia lo zero che si stava cercando. Si veda la figura 3. per una rappresentazione dell’idea della dimostrazione.

Figura 3: i primi passi nella costruzione degli intervalli $[a_n,b_n]$ descritti nella dimostrazione alternativa del teorema 1 (per maggiore chiarezza, l’ultimo grafico è dilatato verticalmente di un fattore 15). Si noti come, dimezzando l’ampiezza dell’intervallo a ogni passo, le successioni $a_n$ e $b_n$ convergano rapidamente a uno zero $x_0$ di $f$ .

Dimostrazione costruttiva del teorema 5.3 Per ipotesi si ha $f(a)\cdot f(b) < 0$ . Vogliamo costruire induttivamente una successione di intervalli $[a_n,b_n]$ con la proprietà che

(6) $\begin{equation*} [a_{n+1},b_{n+1}] \subset [a_n,b_n], \quad \,\, f(a_n) \cdot f(b_n) < 0 \qquad \forall n \in \mathbb{N}, \end{equation*}$

ovvero che essi siano “inscatolati” e che il segno delle successioni $\{f(a_n)\}$ e $\{f(b_n)\}$ sia costante e discorde. Si avrà poi che $a_n$ e $b_n$ convergeranno allo stesso limite $x_0$ che, per la continuità di $f$ , sarà lo zero cercato.

Costruzione degli intervalli $[a_n, b_n]$ . Procediamo per induzione. Come primo passo, poniamo

(7) $\begin{equation*} \left[a_0,b_0\right]\coloneqq \left[a,b\right]. \end{equation*}$

Per ipotesi, $f(a_0)\cdot f(b_0)<0$ . Come passo successivo, supposto di aver costruito l’intervallo $[a_n,b_n]$ tale che $f(a_n) \cdot f(b_n) < 0$ procediamo a costruire $[a_{n+1},b_{n+1}]$ nel seguente modo: se $f\left(\frac{a_n+b_n}{2}\right)=0$ , poniamo $x_0=\frac{a_n+b_n}{2}$ e abbiamo finito; in caso contrario definiamo

(8) $\begin{equation*} [a_{n+1},b_{n+1}]= \begin{cases} \left[a_n,\dfrac{a_n+b_n}{2}\right] & \mbox{se } f(a_n)\cdot f\left( \dfrac{a_n+b_n}{2}\right) <0,\\[8pt] \left[\dfrac{a_n+b_n}{2},b_n\right] & \mbox{altrimenti. } \end{cases} \end{equation*}$

Queste scelte sono illustrate nella figura 3.
$a_n$ e $b_n$ convergono a $x_0$ . Osserviamo che

(9) $\begin{equation*} a \leq a_n \leq a_{n+1} \leq b_{n+1}\leq b_n \leq b \qquad \forall n \in \mathbb{N}, \end{equation*}$

dunque $\{a_n\}$ e $\{b_n\}$ sono due successioni monotone e limitate, quindi esse sono convergenti; chiamiamo $\alpha$ e $\beta$ i limiti rispettivamente di $\{a_n\}$ e $\{b_n\}$ .

Mostriamo ora che $\alpha=\beta$ . Infatti, osserviamo che per costruzione l’intervallo $[a_{n+1},b_{n+1}]$ si ottiene bisecando $[a_n,b_n]$ , quindi

(10) $\begin{equation*} 0 < b_n-a_n= \dfrac{b-a}{2^n}\quad \forall n\in \mathbb{N}. \end{equation*}$

Passando al limite per $n \to +\infty$ nella precedente relazione, si ottiene

(11) $\begin{equation*} 0 \leq \beta - \alpha \leq \lim_{n \to +\infty} \dfrac{b-a}{2^n} = 0, \end{equation*}$

ossia $\beta=\alpha$ . Chiamamo $x_0$ questo limite comune di $a_n$ e $b_n$ .
$f(x_0)=0$ . Occorre ora dimostrare che $f(x_0)=0$ . Ancora per costruzione abbiamo che $f(a_n)$ e $f(b_n)$ hanno segno costante e discorde e quindi $0 > f(a_n) \cdot f(b_n)$ , da cui, passando al limite¹

(12) $\begin{equation*} 0 \geq \lim_{n \to +\infty} \big( f(a_n) \cdot f(b_n) \big) = f(x_0)\cdot f(x_0) = f(x_0)^2, \end{equation*}$

dove nella prima uguaglianza si è usata la continuità di $f$ e il teorema 2. Dato che $y^2 \geq 0$ per ogni $y \in \mathbb{R}$ , da (12) segue necessariamente $f(x_0)^2=0$ , ossia

(13) $\begin{equation*} f(x_0)=0. \end{equation*}$

$\[\]$

Ricordiamo che il limite di una successione è un punto della chiusura dell’insieme immagine della successione. Nel nostro caso l’immagine è contenuta nell’insieme $(-\infty,0)$ , quindi a priori il limite appartiene $[-\infty,0]$ . Sostanzialmente la disuguaglianza $f(a_n)f(b_n)<0$ al limite per $n\to+\infty$ diventa $\displaystyle\lim_{n\to+\infty}f(a_n)f(b_n)\leq 0$ . ↩

Necessità delle ipotesi del teorema 1

Leggi...

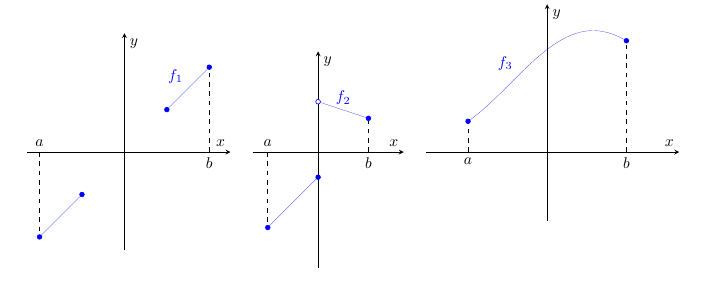
Osserviamo in figura 4 che le ipotesi del teorema degli zeri sono necessarie.

Figura 4: le ipotesi del teorema di esistenza degli zeri sono necessarie. A sinistra, $f_1$ è una funzione continua e assume valori di segno opposto agli estremi del suo dominio, ma questo non è un intervallo. Al centro, $f_2$ è definita su un intervallo e assume valori di segno opposto agli estremi, ma non è continua. A destra, $f_3$ è continua e definita su un intervallo, ma non assume valori di segno opposto agli estremi.

Applicazione: risoluzione di equazioni

Leggi...

Il teorema di esistenza degli zeri è uno strumento utile per dimostrare l’esistenza di soluzioni di equazioni che risulta impossibile determinare analiticamente, come mostra il seguente semplice corollario e il relativo esempio.

Corollario 4. Siano $f,g \colon [a,b] \to \mathbb{R}$ due funzioni continue tali che

(14) $\begin{equation*} f(a)>g(a) \qquad \text{e} \qquad f(b) < g(b), \end{equation*}$

oppure

(15) $\begin{equation*} f(a)<g(a) \qquad \text{e} \qquad f(b) > g(b). \end{equation*}$

Allora esiste $x_0 \in (a,b)$ tale che

(16) $\begin{equation*} f(x_0)=g(x_0). \end{equation*}$

In altre parole, se i valori assunti da $f$ e $g$ in $a$ e $b$ sono in rapporti di ordine diverso, esiste almeno una soluzione $x_0$ dell’equazione $f(x)=g(x)$ .

Dimostrazione. La funzione $h \colon [a,b] \to \mathbb{R}$ definita da

(17) $\begin{equation*} h(x)=f(x)-g(x) \qquad \forall x \in [a,b] \end{equation*}$

è continua e, per l’ipotesi sull’ordine di $f(a),g(a),f(b),g(b)$ , è tale che $h(a)$ e $h(b)$ hanno segno opposto. Il teorema 1 prova quindi l’esistenza di $x_0$ tale che $h(x_0)=0$ , ovvero la conclusione.

Applichiamo questo risultato a un esempio pratico.

Esempio 5. Determiniamo il numero di soluzioni dell’equazione nella variabile $x$

(18) $\begin{equation*} e^{-x}=x, \end{equation*}$

fornendone anche eventualmente una stima. Innanzitutto si osserva che la funzione $f \colon x \in \mathbb{R} \mapsto e^{-x} \in \mathbb{R}$ (il cui grafico è rappresentato in rosso in figura 5) è strettamente decrescente, mentre la funzione definita da $g \colon x \in \mathbb{R} \mapsto x \in \mathbb{R}$ (il cui grafico è rappresentato in blu in figura 5) è strettamente crescente, quindi l’equazione (18) possiede al più una soluzione.

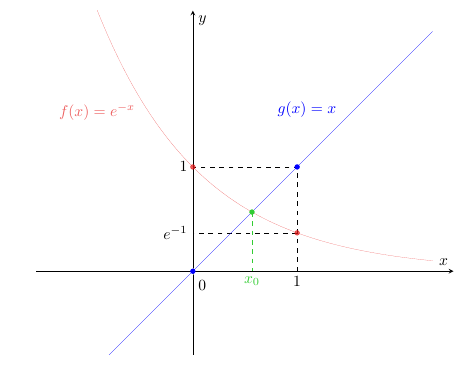
Figura 5: le funzioni $f$ e $g$ (rispettivamente in rosso e blu) dell’esempio 5. L’equazione (18) possiede una soluzione $x_0$ (in verde) poiché $f(0)>g(0)$ e $f(1)<g(1)$ per il corollario 4. Tale soluzione è unica per la monotonia opposta di $f$ e $g$ .

Per stabilire che una soluzione effettivamente esiste, osserviamo che

(19) $\begin{equation*} f(0)=1 > 0=g(0) \qquad \text{e} \qquad f(1)=e^{-1}<1 =g(1), \end{equation*}$

da cui l’esistenza di $x_0 \in (0,1)$ garantita dal corollario 4.

Si poteva anche procedere utilizzando direttamente il teorema 1, considerando la funzione $h \colon [0,1] \to \mathbb{R}$ definita da

(20) $\begin{equation*} h(x)= f(x)-g(x) = e^{-x}-x \qquad \forall x \in [0,1]. \end{equation*}$

Risolvere l’equazione (18) è equivalente a determinare gli zeri di $h$ , ossia i numeri reali $x$ tali che $h(x)=0$ . Osserviamo che

(21) $\begin{equation*} h(0)=e^{0}-0=1>0, \qquad h(1)=e^{-1}-1<0. \end{equation*}$

Poiché $h$ è continua, per il teorema di esistenza degli zeri esiste $x_0 \in (0,1)$ tale che $h(x_0)=0$ , cioè tale che

(22) $\begin{equation*} e^{-x_0}=x_0. \end{equation*}$

Tale punto è rappresentato in verde in figura 5 e una sua stima è che esso è compreso tra 0 e 1.

Riferimenti bibliografici

[1] Qui Si Risolve, Funzioni elementari — Volume 1.

[2] Qui Si Risolve, Funzioni continue.

Scarica la teoria

Ottieni il documento contenente la dimostrazione del teorema di esistenza degli zeri.

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Document

Menu

Chiudi

Il teorema di esistenza degli zeri

Sommario

Leggi...

Autori e revisori

Leggi...

Introduzione

Leggi...

Definizioni preliminari

Leggi...

Dimostrazione del teorema 1

Leggi...

Dimostrazione costruttiva del teorema 1

Leggi...

Necessità delle ipotesi del teorema 1

Leggi...

Applicazione: risoluzione di equazioni

Leggi...

Riferimenti bibliografici

Scarica la teoria

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi