Funzioni continue – Teoria

Teoria sulle Funzioni continue-lipschitziane-holderiane

Home » Funzioni continue – Teoria

Le funzioni continue sono forse tra le più importanti della matematica. Il concetto di continuità esprime infatti l’idea che il valore di un oggetto in un punto sia “vicino” ai valori assunti in punti vicini, ossia la nozione intuitiva di variazione “senza scatti istantanei”.
Questa proprietà implica numerose altre caratteristiche, essenziali nello studio degli oggetti matematici che le possiedono.

Questa dispensa completa espone il concetto di continuità per funzioni reali di una variabile reale, discutendo i seguenti argomenti fondamentali:

Definizione di continuità;
Continuità delle funzioni elementari e operazioni con le funzioni continue;
Caratterizzazione della continuità per successioni, ossia la versione del teorema ponte per funzioni continue;
Discontinuità e loro classificazione, inclusa la caratterizzazione delle discontinuità di funzioni monotone;
Teoremi sulle funzioni continue, tra cui il teorema della permanenza del segno, il teorema di esistenza degli zeri e dei valori intermedi, il teorema di Weierstrass sui massimi e minimi;
Il concetto di continuità uniforme e relativo teorema di Heine-Cantor;
Funzioni lipschitziane, hölderiane, loro relazioni col concetto di continuità uniforme e teorema delle contrazioni.

Il testo, oltre a offrire una presentazione chiara della teoria, ne fornisce delle spiegazioni intuitive e motivate da numerosi esempi, figure ed esercizi.

Se desideri scoprire questi affascinanti concetti della matematica, preparati a sfogliare questa dispensa completa e accessibile!

Oltre all’esaustiva lista alla fine dell’articolo, segnaliamo le seguenti raccolte di esercizi su questo importante argomento:

Sommario

Leggi...

Questa dispensa riguarda la continuità di funzioni reali di variabile reale. Dopo aver discusso la continuità delle funzioni elementari e la sua caratterizzazione mediante le successioni (attraverso il cosiddetto “teorema ponte”), presentiamo i principali teoremi riguardanti le funzioni continue, seguiti dalle nozioni di continuità uniforme, lipschitzianità e hölderianità. Gli esercizi relativi agli argomenti qui trattati sono raccolti nella dispensa [15, esercizi sulla continuità].

Autori e revisori

Leggi...

Autori: Daniele Fakhoury, Luigi De Masi, Silvia Lombardi, Giuseppe Palaia

Revisori: Sara Sottile, Sergio Fiorucci, Matteo Talluri, Chiara Bellotti.

Introduzione

Leggi...

La parola “funzione” appare per la prima volta verso la fine del XVII secolo, nella corrispondenza tra Leibniz (1646 – 1716) e Johann Bernoulli (1667 – 1748); tuttavia, è solo con Eulero (1707 – 1783) che questo concetto si afferma come uno dei principali strumenti dell’analisi. Proprio ad Eulero si deve, infatti, la prima sistemazione della meccanica newtoniana nel linguaggio del calcolo differenziale. L’idea che Eulero e i matematici del Settecento hanno della matematica è comunque lontana da quella moderna: per loro le funzioni elementari note sono poche e una funzione è semplicemente un’espressione analitica, ovvero una combinazione lineare o una composizione di funzioni elementari. Per Eulero, una funzione continua è una funzione che è espressa con un un’unica espressione analitica su tutto il dominio. In tal senso, per esempio, la funzione $|x|$ definita a tratti come

$|x| = \begin{cases} x \; \; \quad \mbox{ se } x \geq 0,\\ - x \quad \mbox{altrimenti} \end{cases}$

è discontinua. All’inizio dell’ottocento vi è una revisione del concetto di funzione, necessaria per la dimostrazione rigorosa di alcuni risultati, come ad esempio il teorema degli zeri sulle funzioni continue. Si inizia dunque ad affermare la concezione moderna di funzione come corrispondenza tra due insiemi.

In concomitanza a tale ampliamento di vedute, si fanno sempre più sentire esigenze di precisione: nel secolo precedente tutte le funzioni, in ogni caso quelle che valesse la pena studiare, erano quantomeno continue; tuttavia, con l’introduzione di funzioni più generali e sempre più irregolari, diventa necessario precisare la nozione di continuità e rendere esplicite le condizioni che garantiscono la validità dei teoremi. Un primo esempio di “nuove funzioni” di questo periodo è la celebre funzione introdotta da Dirichlet (1805 – 1859) da cui prende il nome e che vale $1$ sui punti razionali e $0$ nei punti irrazionali:

$D(x) = \begin{cases} 1 \quad \mbox{se $ x \in \mathbb{Q}$,} \\ 0 \quad \mbox{se $x \in \mathbb{R} \setminus \mathbb{Q}.$} \end{cases}$

In questo contesto, dapprima prevale l’impostazione di Lagrange (1736 – 1813), che richiede che tutte le funzioni siano sviluppabili in serie di potenze, cioè siano esprimibili nella forma

$f(x) = \sum_{n=0}^{\infty} a_n (x-x_0)^n.$

Successivamente, si afferma la visione di Cauchy (1789 – 1857) che è, con minime variazioni, quella ancora in uso. Nel suo Course d’analyse, Cauchy introduce la nozione di funzione continua mediante l’uguaglianza tra il valore della funzione in un punto e quello del limite della funzione nel punto stesso, come presentata ad esempio in [6].

La dispensa si sviluppa nel modo seguente. Nella sezione 2 viene definito il concetto di funzione continua e, successivamente, viene dimostrata la continuità delle funzioni elementari e della composizione di funzioni continue. La sezione 3 è interamente dedicata alla caratterizzazione della continuità mediante l’uso di successioni ed alle sue applicazioni. Nella sezione 4 viene enunciata la definizione di discontinuità seguita dall’analisi dei diversi tipi di discontinuità. Successivamente, la sezione 5 contiene gli enunciati e le dimostrazioni dei principali teoremi riguardanti le funzioni continue: il teorema della permanenza del segno, il teorema degli zeri, il teorema dei valori intermedi e il teorema di Weierstrass. La sezione 6 è dedicata interamente al concetto di uniforme continuità. Nella sezione 6.2 viene enunciato e dimostrato il teorema di Heine-Cantor, che lega il concetto di uniforme continuità e continuità. Infine, nelle sezioni 6.3 e 6.4 sono introdotti i concetti di funzione lipschitziana e funzione hölderiana, rispettivamente, e le loro relazioni con i concetti di continuità e uniforme continuità. Diverse tipologie di esercizi sugli argomenti trattati in questa dispensa sono raccolte nella dispensa [15, esercizi sulla continuità].

Continuità

Definizione.

Dal punto di vista informale, una funzione $f$ è continua in un punto $x_0$ se i valori $f(x)$ sono “vicini” a $f(x_0)$ quando $x$ è “vicino” a $x_0$ . Formalizziamo questa idea nella definizione rigorosa di funzione continua.

Definizione 2.1 (funzione continua in un punto). Sia $A \subseteq \mathbb{R}$ . Una funzione $f: A \to \mathbb{R}$ si dice continua in $x_0\in A$ se $x_0$ è un punto isolato di $A$ oppure se

$\lim_{x \to x_0} f(x) = f(x_0).$

$\quad$

Tale definizione conferma l’intuizione che una funzione $f$ è continua in $x_0$ se ci possiamo avvicinare arbitrariamente al valore della funzione $f(x_0)$ valutando $f$ in punti opportunamente vicini a $x_0$ .

Osservazione 2.2 (continuità nei punti isolati). La definizione di continuità distingue quindi il caso in cui $x_0$ sia isolato. Il motivo di tale distinzione è che nel caso in cui il punto $x_0$ è isolato, il limite di $f$ in $x_0$ non è definito. Ciononostante, se $x_0$ è isolato, è intuitivamente chiaro che $f(x)$ è vicino a $f(x_0)$ per $x$ vicino a $x_0$ , in quanto l’unico $x$ arbitrariamente vicino a $x_0$ è $x_0$ stesso.

$\quad$

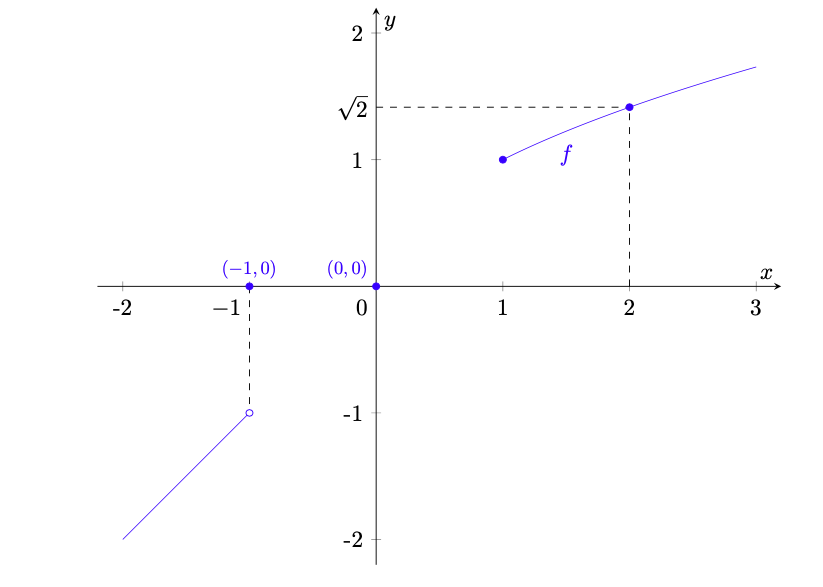
funzioni continue

Figura 1: grafico (in blu) della funzione $f$ dell’esempio 2.3. Si osservi che $f$ è continua in $0$ (in quanto punto isolato del dominio) e in $2$ , ma non è continua in $-1$ . Intuitivamente, se $x$ è vicino a $2$ , allora $f(x)$ è vicino a $f(2)$ ; invece se $x$ è vicino a $-1$ , $f(x)$ non è vicino a $f(-1)$ .

$\quad$

Esempio 2.3. Sia $A=[-2,1] \cup \{0\} \cup [1,3]$ e sia $f \colon A \to \mathbb{R}$ la funzione definita da

(1) $\begin{equation*} f(x) = \begin{cases} x & \text{se } x \in [-2,-1)\\ 0 & \text{se } x =-1 \text{ oppure } x =0\\ \sqrt{x} & \text{se } x \in [1,3]. \end{cases} \end{equation*}$

Il grafico di $f$ è rappresentato in blu in figura 1. Facciamo le seguenti osservazioni.

$\quad$

$f$ è continua in $x=2$ in quanto
(2) $\begin{equation*} \lim_{x \to 2} f(x)=f(2). \end{equation*}$

Proveremo in seguito la validità di questo limite e, più in generale, che la funzione radice quadrata è continua.

$f$ è continua in $x=0$ in quanto $0$ è un punto isolato del dominio;

$f$ non è continua in $x=-1$ in quanto è chiaro che $\displaystyle \lim_{x \to -1} f(x)=-1$ , ma $f(-1)=0$ .

Proposizione 2.4. Siano $A \subseteq \mathbb{R}$ , $f \colon A \to \mathbb{R}$ e sia $x_0 \in A$ . Allora $f$ è continua in $x_0$ se e solo se, per ogni $\varepsilon>0$ , esiste $\delta>0$ tale che

$\begin{equation*} |f(x)-f(x_0)|< \varepsilon \qquad \forall x \in (x_0-\delta,x_0+\delta) \cap A. \end{equation*}$

$\quad$

Infine, enunciamo la definizione di funzione continua in un insieme.

Definizione 2.5 (funzione continua). Sia $A \subseteq \mathbb{R}$ . Una funzione $f\colon A \to \mathbb{R}$ si dice continua in $E \subseteq A$ se è continua in ogni punto di $E$ . La funzione $f$ si dice continua se è continua in tutto il suo dominio $A$ e in tal caso si scrive

(3) $\begin{equation*} f \in C^0(A) \qquad \text{oppure} \qquad f \in C(A). \end{equation*}$

I simboli $C^0(A)$ e $C(A)$ denotano l’insieme delle funzioni continue in $A$ .

$\quad$

Continuità delle funzioni elementari.

La prima funzione elementare di cui dimostriamo la continuità è la funzione identità, cioè $f \colon \mathbb{R} \to \mathbb{R}$ definita da

(4) $\begin{equation*} f(x) = x \qquad \forall x \in \mathbb{R}. \end{equation*}$

Proposizione 2.6 (continuità dell’identità). La funzione identità $f\colon \mathbb{R} \to \mathbb{R}$ definita da

$f(x) = x \qquad \forall x \in \mathbb{R}$

è continua in $\mathbb{R}$ .

$\quad$

Dimostrazione. Dobbiamo dimostrare che per ogni $x_0\in \mathbb{R}$ si ha $\lim_{x \to x_0} x = x_0.$ Siano $x_0 \in \mathbb{R}$ e $\varepsilon>0$ . Cerchiamo $\delta>0$ tale che

(5) $\begin{equation*} |x-x_0|<\delta \quad \Longrightarrow \quad |f(x)-f(x_0)|< \varepsilon. \end{equation*}$

Poiché $f(x)=x$ per ogni $x \in \mathbb{R}$ , basta scegliere $\delta=\varepsilon$ . Infatti si ha

$\begin{equation*} |f(x)-f(x_0)|=|x-x_0| < \varepsilon \qquad \forall x \in (x_0-\varepsilon,x_0+\varepsilon). \end{equation*}$

Ciò mostra che $\lim_{x\to x_0} f(x)=x_0$ , cioè che $f$ è continua in $x_0$ . Per l’arbitrarietà di $x_0\in \mathbb{R}$ , $f$ è continua in $\mathbb{R}$ . In figura 2 si ha la rappresentazione grafica della dimostrazione.

$\quad$

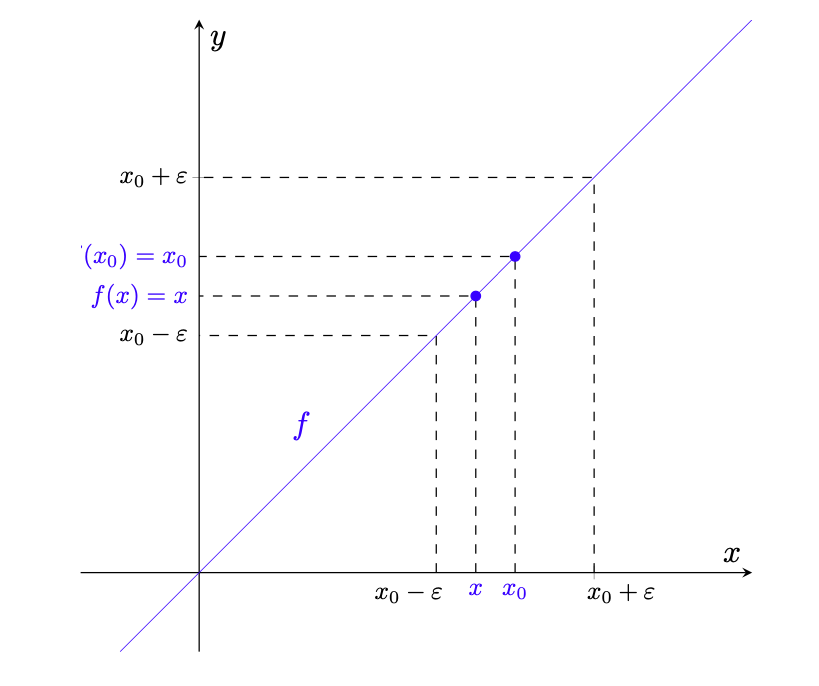
funzioni continue

Figura 2: rappresentazione della dimostrazione della proposizione 2.6. In blu il grafico della funzione identità; si nota che, se $x \in (x_0-\varepsilon,x_0+\varepsilon)$ , allora $f(x) \in (x_0-\varepsilon,x_0+\varepsilon)$ .

$\quad$

Segue direttamente che le funzioni potenza sono continue, come esplicitato dal risultato seguente.

Proposizione 2.7 (continuità della funzione potenza). Sia $n\in \mathbb{N}$ . La funzione potenza $f\colon \mathbb{R} \to \mathbb{R}$ definita da

$\begin{equation*} f(x)=x^n \qquad \forall x \in \mathbb{R}, \end{equation*}$

è continua in $\mathbb{R}$ .

$\quad$

Dimostrazione. Siano $n \in \mathbb{N}$ e $x_0\in \mathbb{R}$ . Consideriamo $f\colon \mathbb{R}\to\mathbb{R}$ tale che $f(x)=x^n$ per ogni $x \in \mathbb{R}$ . Tale funzione è il prodotto della funzione identità per se stessa ripetuto $n$ volte, dunque:

$\lim_{x \to x_0} x^n = \lim_{x \to x_0} \underbrace{x\cdot x\cdot \dots\cdot x}_{n \text{ volte}}= \underbrace{\lim_{x \to x_0} x\cdot \lim_{x \to x_0} x\cdot\dots \cdot\lim_{x \to x_0} x}_{n \text{ volte}} = \underbrace{x_0 \cdot x_0 \cdot \dots \cdot x_0}_{n \text{ volte}} = x_0 ^n,$

dove nella seconda disuguaglianza si è usato [3, teorema 4.10] e nella terza si è usata la proposizione 2.6. Ciò prova che la funzione potenza $f$ è continua in $x_0 \in \mathbb{R}$ , dunque per l’arbitrarietà di $x_0$ essa è continua in $\mathbb{R}$ .

Il risultato precedente ci permette di dimostrare che i polinomi e i loro quozienti sono funzioni continue.

Proposizione 2.8 (continuità dei polinomi e del quoziente di polinomi).

Siano $n \in \mathbb{N}$ e $a_i \in \mathbb{R}\; \forall i =0,\dots, n$ . Allora la funzione polinomiale $P\colon \mathbb{R} \to \mathbb{R}$ definita da
$\begin{equation*} P(x)=a_nx^n + a_{n-1}x^{n-1}+\dots + a_0 \qquad \forall x\in \mathbb{R} \end{equation*}$

è continua in $\mathbb{R}$ .

Siano inoltre $m \in \mathbb{N}$ , $b_i \in \mathbb{R}\; \forall i =0,\dots, m$ e sia $Q\colon \mathbb{R}\to \mathbb{R}$ la funzione polinomiale definita da
$\begin{equation*} b_nx^n + b_{n-1}x^{n-1}+\dots + b_0 \qquad \forall x\in \mathbb{R}. \end{equation*}$

Sia $A\coloneqq \{ x \in \mathbb{R} \colon Q(x) \neq 0 \}$ . Allora la funzione $g\colon A\to \mathbb{R}$ tale che $g(x) = \dfrac{P(x)}{Q(x)}$ è continua in $A$ .

$\quad$

Dimostrazione. Sia $x_0\in \mathbb{R}$ . La funzione polinomiale $P\colon \mathbb{R} \to \mathbb{R}$ è combinazione lineare di funzioni potenza tramite i coefficienti $a_i \in \mathbb{R}\; \forall i =0,\dots n.$ Utilizzando le proprietà dei limiti sul prodotto di funzioni per delle costanti e sulla somma di funzioni ([3, teorema 4.10]), si ha che

$\begin{aligned} \lim_{x \to x_0} P(x) =& \lim_{x \to x_0} a_n x^n + a_{n-1}x^{n-1} + \dots + a_0 \\ =& \;a_n \lim_{x \to x_0} x^n + a_{n-1}\lim_{x \to x_0} x^{n-1} + \dots a_0 \\ =& \; a_n x_0^n + a_{n-1}x_{0}^{n-1}+ \dots a_0 \\ =& \; P(x_0), \end{aligned}$

dove abbiamo utilizzato la proposizione 2.7 sulla continuità delle funzioni potenza. Segue che la funzione polinomiale $P$ è continua in $x_0\in \mathbb{R}$ , dunque per l’arbitrarietà di $x_0$ essa è continua in $\mathbb{R}$ .

Consideriamo ora la funzione polinomiale $Q \colon \mathbb{R} \to \mathbb{R}$ e sia $A\coloneqq \{ x \in \mathbb{R} \colon Q(x) \neq 0 \}$ . Definiamo $g\colon A \to \mathbb{R}$ tale che $g(x) = \dfrac{P(x)}{Q(x)}$ e consideriamo inoltre $x_0 \in A$ . Si noti che, per il teorema 5.1 di permanenza del segno (si veda anche [13]), in un intorno di $x_0\in A$ si ha che $Q(x)\neq 0$ . Utilizzando la proprietà sui limiti di funzioni quoziente [3, teorema 4.10], si ha che

$\lim_{x \to x_0} g(x) = \lim_{x \to x_0} \frac{P(x)}{Q(x)} = \frac{\lim_{x \to x_0} P(x)}{\lim_{x \to x_0} Q(x)}= \frac{P(x_0)}{Q(x_0)} = g(x_0),$

dove la penultima uguaglianza segue dalla prima parte della dimostrazione.

La funzione quoziente $g$ è continua in $x_0 \in A$ , e dunque per l’arbitrarietà di $x_0$ essa è continua in $A$ .

Proposizione 2.9 (continuità della funzione seno). La funzione $f\colon \mathbb{R} \to \mathbb{R}$ definita da

$f(x) = \sin x \qquad \forall x \in \mathbb{R}$

è continua in $\mathbb{R}$ .

$\quad$

Dimostrazione. Siano $x, x_0 \in \mathbb{R}$ , allora dalle formule di prostaferesi ([8, sezione 2B, proprietà 11]) si ha:

(6) $\begin{equation*} \sin x - \sin x_0 = 2 \sin \Big( \frac{x - x_0}{2} \Big) \cos \Big( \frac{x + x_0}{2} \Big). \end{equation*}$

Ricordando che $|\cos(\alpha)| \leq 1$ e $|\sin(\alpha)| \leq |\alpha|$ ([8, sezione 2B, proprietà 3]) per ogni $\alpha \in \mathbb{R}$ , passando ai moduli in (6), si ha

(7) $\begin{equation*} |\sin x - \sin x_0 | \leq 2 \Big| \frac{x - x_0}{2} \Big| = |x- x_0|. \end{equation*}$

Vogliamo usare tale disuguaglianza per dimostrare che $\lim_{x \to x_0} f(x)=f(x_0)$ . Fissato $\varepsilon >0$ , vogliamo determinare $\delta>0$ tale che, se $|x-x_0|< \delta$ , allora $|f(x)-f(x_0)|<\varepsilon$ . Da (7) segue che si può scegliere $\delta=\varepsilon$ , infatti

$|x-x_0| < \varepsilon \Longrightarrow|\sin x - \sin x_0 | < \varepsilon.$

Ciò prova che

$\lim_{x \to x_0} \sin x = \sin x_0, \qquad \forall x_0 \in \mathbb{R}.$

In figura 3 si ha la rappresentazione grafica della dimostrazione.

$\quad$

funzioni continue

Figura 3: rappresentazione della dimostrazione della proposizione 2.9. In blu il grafico della funzione $\sin$ ; si nota che $|\sin x - \sin x_0| \leq |x - x_0|$

$\quad$

In maniera analoga si dimostra lo stesso risultato per la funzione coseno.

Proposizione 2.10 (continuità della funzione coseno). La funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da

$f(x) = \cos x \qquad \forall x \in \mathbb{R}$

è continua in $\mathbb{R}$ .

$\quad$

Dimostrazione. Siano $x, x_0 \in \mathbb{R}$ , allora per le formule di prostaferesi si ha:

$\cos x - \cos x_0 = - 2 \sin \Big( \frac{x - x_0}{2} \Big) \sin \Big( \frac{x + x_0}{2} \Big).$

La dimostrazione è analoga a quella della proposizione 2.9.

Dimostriamo ora la continuità della funzione esponenziale, iniziando con un lemma preliminare.

Lemma 2.11 (continuità dell’esponenziale in zero). Sia $a > 0$ un numero reale, allora

$\lim_{x \to 0} a^x = 1 .$

$\quad$

Dimostrazione. Se $a=1$ , l’enunciato è ovvio. Fissiamo quindi $a>1$ e $\varepsilon \in (0,1)$ . Dai noti limiti

(8) $\begin{equation*} \lim_{n \to + \infty}(1-\varepsilon)^n=0, \qquad \lim_{n \to + \infty}(1+\varepsilon)^n=+\infty, \end{equation*}$

segue che esiste $n \in \mathbb{N}$ tale che

(9) $\begin{equation*} 0<(1-\varepsilon)^n<a^{-1}<a < (1+\varepsilon)^n \iff 1-\varepsilon < a^{-\frac{1}{n}} < a^{\frac{1}{n}} < 1+\varepsilon. \end{equation*}$

Da ciò e dalla monotonia della funzione esponenziale segue la disuguaglianza (rappresentata in figura 4)

(10) $\begin{equation*} 1-\varepsilon < a^{-\frac{1}{n}} < a^x< a^{\frac{1}{n}} < 1+\varepsilon \qquad \forall x \in \left(-\frac{1}{n}, \frac{1}{n}\right). \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ e dalla definizione di limite otteniamo la tesi.

Il caso $a \in (0,1)$ si ottiene osservando che $a^x=\left(\dfrac{1}{a}\right)^{-x}$ per ogni $x \in \mathbb{R}$ .

$\quad$

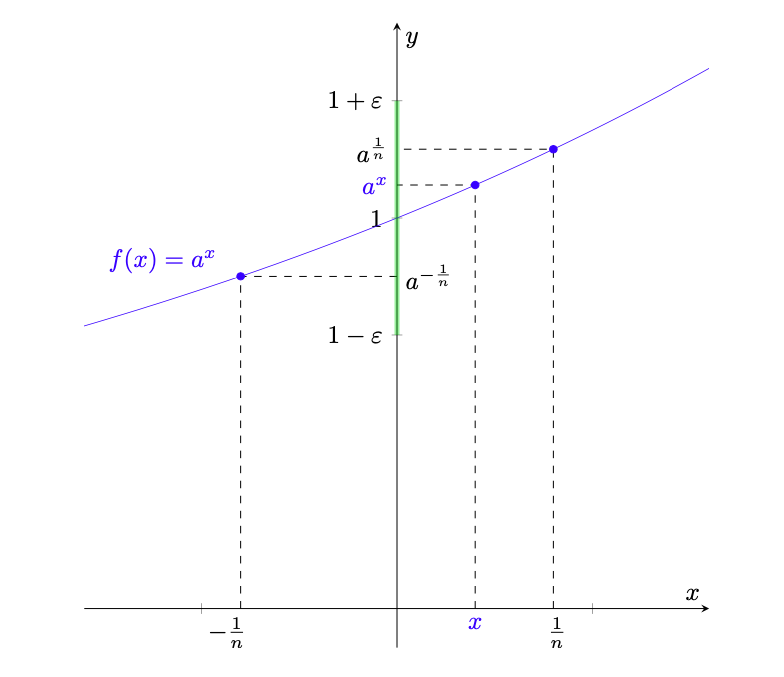
funzioni continue

Figura 4: rappresentazione della dimostrazione del lemma 2.11. In blu è rappresentato il grafico della funzione esponenziale, mentre in verde è rappresentato l’intorno $(1-\varepsilon,1+\varepsilon)$ .

$\quad$

Proposizione 2.12 (continuità della funzione dell’esponenziale). Sia $a > 0$ un numero reale. La funzione $f\colon \mathbb{R} \to \mathbb{R}$ definita da

$f(x) = a^x \qquad \forall x \in \mathbb{R}$

è continua in $\mathbb{R}$ .

$\quad$

Dimostrazione. Fissato $x_0 \in \mathbb{R}$ si ha che

$\lim_{x \to x_0} a^x - a^{x_0} = \lim_{x \to x_0} a^{x_0}( a^{x - x_0} - 1).$

Effettuando il cambio di variabile $y=x - x_0$ si ottiene

$\lim_{x \to x_0} a^{x_0}( a^{x - x_0} - 1 )= a^{x_0} \lim_{y \to 0} a^y - 1 = 0,$

avendo utilizzato il lemma 2.11. Ciò prova che

$\lim_{x \to x_0} a^x = a^{x_0},$

da cui segue che la funzione esponenziale è continua in $x_0$ . Per l’arbitrarietà di $x_0 \in \mathbb{R}$ segue che la funzione esponenziale è continua in $\mathbb{R}$ .

Date due funzioni continue $f,g \colon A \to \mathbb{R}$ , risulta naturale chiedersi se le funzioni $f+g, fg, \dfrac{f}{g}$ risultino continue. Ciò è vero, come mostra la proposizone seguente, che costituisce una generalizzazione della proposizione 2.8. Infatti, quest’ultima poteva anche essere ottenuta dalla proposizione 2.13 e dalla proposizione 2.6.

Proposizione 2.13 (continuità di somma, prodotto e quoziente di funzioni continue). Sia $A \subseteq \mathbb{R}$ , e siano $f,g \colon A \to \mathbb{R}$ . Consideriamo le funzioni $f+g, fg \colon A \to \mathbb{R}$ definite da

$(f+g)(x)\coloneqq f(x)+g(x) \quad \text{e} \quad (fg)(x) \coloneqq f(x)g(x) \qquad \forall x \in \mathbb{R},$

inoltre detto $B\coloneqq \{x\in A \colon g(x) \neq 0 \}$ consideriamo $\dfrac{f}{g}\colon B \to \mathbb{R}$ tale che $\dfrac{f}{g}(x) \coloneqq \dfrac{f(x)}{g(x)} \; \forall x \in B$ .

Se $f$ e $g$ sono funzioni continue, allora $f+g$ , $fg$ e $\dfrac{f}{g}$ sono funzioni continue nei loro domini.

$\quad$

Dimostrazione. La dimostrazione segue dalle proprietà sui limiti ([3, teorema 4.10]). Sia $x_0\in A$ . Se $x_0$ è isolato la dimostrazione è banale. Se invece $x_0$ è di accumulazione per $A$ , allora dall’ipotesi di continuità di $f$ e $g$ in $x_0$ si ha

$\lim_{x \to x_0}f(x)=f(x_0)\qquad \text{ e } \qquad \lim_{x \to x_0}g(x)=g(x_0).$

Segue che

$\lim_{x \to x_0} (f+g)(x) = \lim_{x \to x_0} f(x) +g(x) = f(x_0)+g(x_0) = (f+g)(x_0)$

La dimostrazione per prodotto e quoziente è analoga.

Dai risultati precedenti segue inoltre il seguente corollario.

Corollario 2.14 (continuità della funzione tangente). La funzione $f\colon \mathbb{R}\setminus \left\{ \frac{\pi}{2} + k \pi \colon k \in \mathbb{Z} \right\} \to \mathbb{R}$ definita da

$f(x) = \tan x \coloneqq \dfrac{\sin x}{\cos x} \qquad \forall x \in \mathbb{R}\setminus \left\{ \frac{\pi}{2} + k \pi \colon k \in \mathbb{Z} \right\}$

è continua nel suo dominio.

$\quad$

Dimostrazione. Poiché la funzione $\tan x$ viene definita come rapporto delle funzioni $\sin x$ e $\cos x$ che sono continue per le proposizioni 2.9 e 2.10, rispettivamente, la tesi segue dalla proposizione 2.13.

Continuità delle funzioni composte.

In questa ultima parte della sezione consideriamo le funzioni composte, in particolare si prova che la funzione composta di due funzioni continue è una funzione continua.

Proposizione 2.15 (continuità della funzione composta). Siano $f\colon A \to \mathbb{R}$ e $g\colon B \to \mathbb{R}$ funzioni tali che $f(A) \subseteq B$ . Se $f$ è continua in $x_0\in A$ e $g$ è continua in $y_0 \coloneqq f(x_0)\in B$ , allora la funzione composta $g \circ f$ è continua in $x_0$ .

$\quad$

Questa proposizione è diretto corollario della proposizione seguente, che afferma che le funzioni continue preservano il limite.

Proposizione 2.16. Siano $f\colon A\subseteq\mathbb{R} \to \mathbb{R}$ e $g\colon B\subseteq\mathbb{R} \to \mathbb{R}$ tali che $f(A) \subseteq B$ . Sia $x_0 \in \mathbb{R}$ di accumulazione per $A$ . Se $\lim_{x \to x_0} f(x) = y_0$ e se $g$ è una funzione continua in $y_0$ allora

$\lim_{x \to x_0} g(f(x)) = g(y_0).$

$\quad$

Dimostrazione. Sia $\varepsilon>0$ . Poiché $g$ è continua in $y_0$ , allora per la proposizione 2.4 esiste $\gamma_\varepsilon$ tale che

$|g(y) - g(y_0) | \qquad \forall y \in(y_0-\gamma_\varepsilon,y_0 +\gamma_\varepsilon)\cap B.$

Inoltre, poiché $\lim_{x \to x_0} f(x) = y_0$ esiste $\delta_\varepsilon$ tale che

$|f(x) - y_0| < \gamma_\varepsilon \qquad \forall x \in(x_0-\delta_\varepsilon,x_0 +\delta_\varepsilon)\cap A.$

Segue quindi che

$|g(f(x)) - g(y_0)|< \varepsilon \qquad \forall x \in(x_0-\delta_\varepsilon,y_0 +\delta_\varepsilon)\cap B,$

da cui la tesi.

Concludiamo la sezione osservando che l’esistenza e la continuità delle funzioni inverse di alcune funzioni elementari sarà studiato nella sezione 5.3, come conseguenza dei risultati provati nella sezione 4. Pertanto, nonostante negli esempi tale esistenza e continuità (ad esempio di radici e logaritmi) sarà data per scontata, essa verrà provata nella sezione annunciata.

Continuità e successioni: il teorema ponte

Introduzione.

In questa sezione viene presentato un risultato che lega il concetto di continuità definito nella sezione 2 e le successioni.

Per richiami di teoria sui limiti di successioni si veda [3, 8, 6]. Ricordiamo la seguente definizione prima di enunciare il risultato principale della sezione.

Definizione 3.1. Sia $\{x_n\}_{n\in \mathbb{N}}$ una successione. Una proprietà si dice valida definitivamente per la successione $\{x_n\}$ se esiste $N\in \mathbb{N}$ tale che la proprietà è valida $\forall n \geq N$ .

Teorema 3.2 (teorema ponte). Sia $A \subseteq \mathbb{R}$ , sia $f \colon A \to \mathbb{R}$ e sia $x_0 \in \mathbb{R} \cup \{\pm \infty\}$ un punto di accumulazione per $A$ . Allora le due affermazioni seguenti sono equivalenti:

$\quad$

vale
(11) $\begin{equation*} \lim_{x \to x_0} f(x) = \ell \in \mathbb{R} \cup \{\pm \infty\}; \end{equation*}$

esiste $\ell \in \mathbb{R} \cup \{\pm \infty\}$ tale che, per ogni successione $\{x_n\}_{n \in \mathbb{N}}$ a valori in $A$ tale che $x_n \to x_0$ , con $x_n \neq x_0$ definitivamente, si ha
(12) $\begin{equation*} \lim_{n \to +\infty} f(x_n)= \ell. \end{equation*}$

$\quad$

Non riportiamo la dimostrazione di questo teorema (per la quale rimandiamo su il teorema ponte), anche perché essa è analoga a quella del seguente risultato, che esprime la medesima proprietà per le funzioni continue.

Teorema 3.3 (caratterizzazione della continuità per successioni). Sia $A \subseteq \mathbb{R}$ , sia $f \colon A \to \mathbb{R}$ e sia $x_0 \in A$ . Allora le due affermazioni seguenti sono equivalenti:

$\quad$

$f$ è continua in $x_0$ ;

per ogni successione $\{x_n\}_{n \in \mathbb{N}}$ a valori in $A$ tale che $x_n \to x_0$ , si ha
(13) $\begin{equation*} \displaystyle \lim_{n \to +\infty}f(x_n)=f(x_0). \end{equation*}$

$\quad$

Dimostrazione. Proviamo separatamente le due implicazioni.

$\quad$

Sia $f$ continua in $x_0$ , si consideri una successione $\{x_n\}_{n \in \mathbb{N}}$ a valori in $A$ tale che $x_n \to x_0$ e sia $\varepsilon>0$ . Per la continuità di $f$ , esiste $\delta>0$ tale che

(14) $\begin{equation*} |f(x)-f(x_0)|< \varepsilon \qquad \forall x \in (x_0-\delta,x_0+\delta) \cap A. \end{equation*}$

Poiché $x_n$ è a valori in $A$ e $x_n \to x_0$ , esiste $N \in \mathbb{N}$ tale che

(15) $\begin{equation*} x_n \in (x_0-\delta,x_0+\delta) \cap A \qquad \forall n \geq N, \end{equation*}$

come rappresentato in figura 5. Da (14) e (15) segue che

(16) $\begin{equation*} |f(x_n)-f(x_0)| < \varepsilon \qquad \forall n \geq N, \end{equation*}$

ossia, per l’arbitrarietà di $\varepsilon$ , che $\lim_{n \to +\infty}f(x_n)=f(x_0)$ .

Supponiamo viceversa che $f$ non sia continua in $x_0$ . Allora per definizione di continuità esiste $\varepsilon>0$ con la proprietà che
(17) $\begin{equation*} \exists x_n \in \left(x_0-\frac{1}{n},x_0+\frac{1}{n} \right ) \cap A \,\,\,\, \text{tale che} \,\,\,\, |f(x_n)-f(x_0)|>\varepsilon \qquad \forall n \in \mathbb{N}. \end{equation*}$

La successione $\{x_n\}_{n \in \mathbb{N}}$ è a valori in $A$ e, da $|x_n-x_0|<\dfrac{1}{n}$ , segue che converge a $x_0$ . Ciononostante, essa non soddisfa $\lim_{n \to + \infty} f(x_n)=x_0$ .

$\quad$

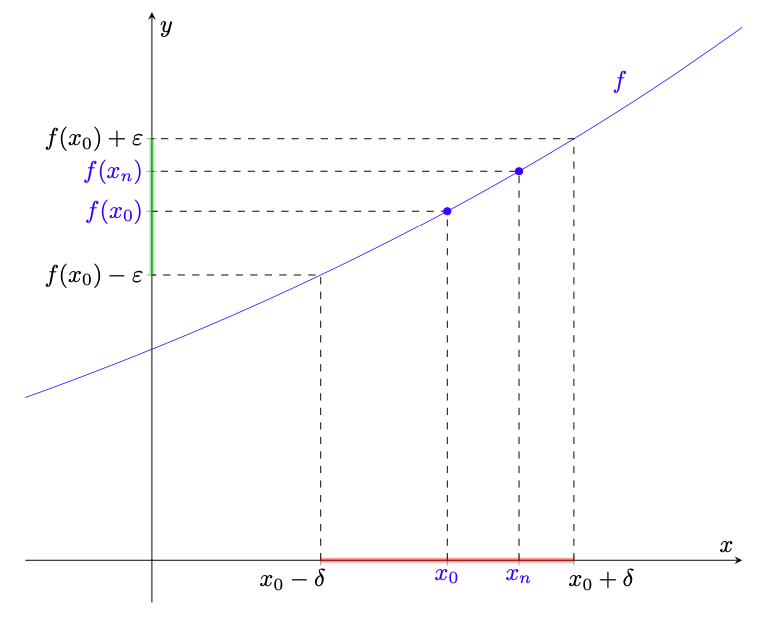
funzioni continue

Figura 5: rappresentazione della dimostrazione del teorema 3.3; l’intorno $(x_0-\delta,x_0+\delta)$ è rappresentato in rosso, mentre in verde è rappresentato l’intorno $(f(x_0)-\varepsilon, f(x_0)+\varepsilon)$ .

$\quad$

Esempi di applicazione.

Il teorema 3.3 si rivela uno strumento utile per mostrare la non esistenza del limite di una funzione, e dunque può essere utilizzato per mostrare che una funzione non è continua in un punto.

Vengono presentati ora due esempi di applicazione del teorema per provare la non esistenza di un limite; in particolare, data una funzione $f\colon A \subseteq \mathbb{R}\to \mathbb{R}$ , la strategia è quella di trovare due successioni $\{x_n\}_{n\in \mathbb{N}}$ e $\{y_n\}_{n\in \mathbb{N}}$ a valori in $A$ che convergono allo stesso limite $x_0$ che sia un punto di accumulazione per $A$ tali che

$\lim_{n \to +\infty}f(x_n)\neq \lim_{n\to +\infty}f(y_n).$

Per il teorema 3.2 segue dunque che non esiste $\lim_{x \to x_0}f(x)$ .

Esempio 3.4. Consideriamo la funzione $f\colon \mathbb{R} \to \mathbb{R}$ definita da

$f(x) = \sin x \qquad \forall x \in \mathbb{R}$

e dimostriamo che non esiste

$\lim_{x \to +\infty} \sin x.$

L’intuizione che questo limite non esista è dovuta alla natura oscillatoria e periodica della funzione $f$ i cui valori $f(x)$ sembrano “non avvicinarsi”, per $x \to + \infty$ , ad alcun numero reale fissato.

Consideriamo le successioni $\{x_n\}_{n\in \mathbb{N}}$ e $\{y_n\}_{n\in \mathbb{N}}$ di termini generali rispettivamente

$x_n = 2 \pi n\quad \text{e} \quad y_n = 2\pi n + \frac{\pi}{2}, \qquad \forall n\in \mathbb{N}.$

Tali successioni sono rappresentate graficamente in figura 6. Vale

$\lim_{n \to +\infty} x_n = \lim_{n \to +\infty} y_n = +\infty,$

tuttavia

$\sin(x_n) = 0 \quad \mbox{ e } \quad \sin(y_n) = 1, \qquad \forall n \in \mathbb{N},$

e di conseguenza

$\lim_{n \to +\infty} \sin(x_n) = 0 \quad \mbox{ e } \quad \lim_{n \to +\infty} \sin(y_n) = 1.$

Poiché la condizione $2.$ del teorema 3.3 non è soddisfatta, segue che $\lim_{x\to + \infty} \sin x$ non esiste.

$\quad$

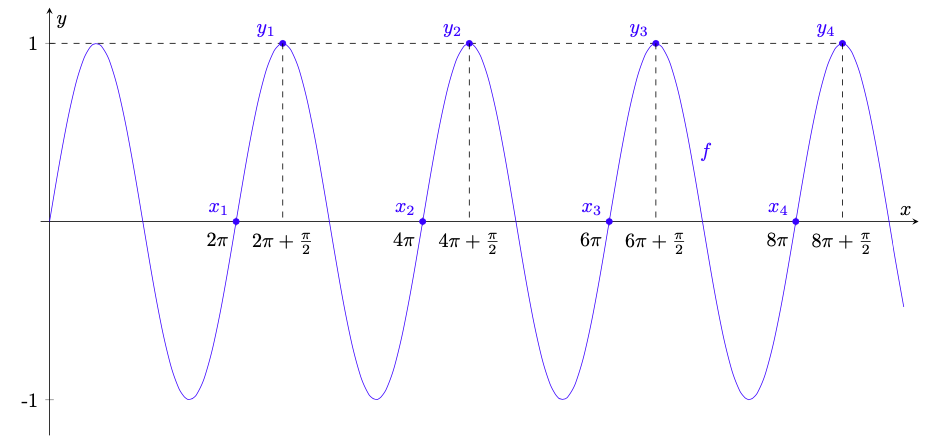
funzioni continue

Figura 6: le due successioni $x_n$ e $y_n$ dell’esempio 3.4; si vede che $\sin x_n=0$ e $\sin y_n=1$ per ogni $n \in \mathbb{N}$ . Da ciò e dal teorema 3.2 segue che $\displaystyle \lim_{x \to +\infty}\sin x$ non esiste.

$\quad$

Esempio 3.5. Consideriamo la funzione $f\colon \mathbb{R} \setminus \{0\} \to \mathbb{R}$ definita da

$f(x) = \frac{1}{x} \qquad \forall x \in \mathbb{R} \setminus \{0\}$

e dimostriamo che non esiste

$\lim_{x \to 0} \frac{1}{x}.$

Consideriamo due successioni $\{x_n\}_{n \in \mathbb{N}}$ e $\{y_n\}_{n \in \mathbb{N}}$ di termini generali

$x_n = \frac{1}{n} \quad \text{e}\quad y_n = - \frac{1}{n}, \qquad \forall n \in \mathbb{N}.$

Tali successioni sono rappresentate graficamente in figura 7. Allora si ha

$\lim_{n \to +\infty} x_n = \lim_{n \to +\infty} y_n = 0.$

Tuttavia,

$f(x_n) = n \quad \mbox{ e } \quad f(y_n) = -n, \qquad \forall n \in \mathbb{N},$

e di conseguenza

$\lim_{n \to +\infty} f(x_n) = +\infty \quad \mbox{ e } \quad \lim_{n \to +\infty} f(y_n) = -\infty.$

Ciò implica che $\lim_{x \to 0} \dfrac{1}{x}$ non esiste.

$\quad$

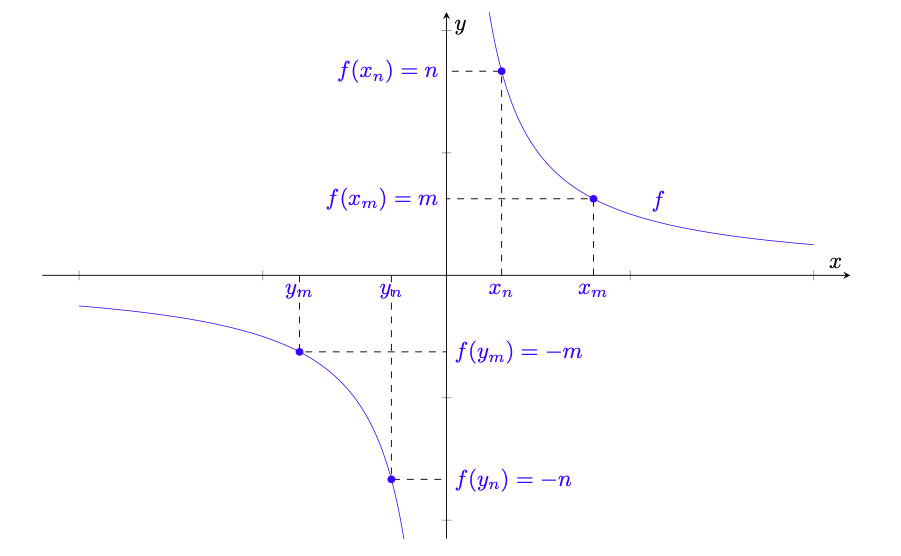
funzioni continue

Figura 7: le due successioni $x_n$ e $y_n$ dell’esempio 3.5; da $f(x_n)\to +\infty$ , $f(y_n) \to -\infty$ e dal teorema 3.2 segue che $\displaystyle \lim_{x \to 0}f(x)$ non esiste.

$\quad$

Discontinuità

Introduzione.

In questa sezione viene data la definizione di discontinuità di una funzione in un punto e la classificazione dei diversi tipi di discontinuità.

Definizione 4.1 (discontinuità). Sia $f\colon A \subseteq \mathbb{R}\to \mathbb{R}$ e sia $x_0 \in A$ . La funzione $f$ si dice discontinua in $x_0$ se non è continua in $x_0$ .

$\quad$

Osservazione 4.2. Secondo la definizione data un punto di discontinuità appartiene al dominio della funzione. Tuttavia, in alcuni testi, la definizione di discontinuità in un punto viene data in maniera differente: una funzione $f\colon A\subseteq \mathbb{R}\to \mathbb{R}$ può essere definitiva discontinua anche in punti non appartenenti al dominio.

Riteniamo inopportuna quest’ultima accezione in quanto essa richiede che il dominio della funzione debba essere a priori considerato come un sottoinsieme di uno spazio più grande e inoltre perché contrasta con la definizione, più generale, di continuità di funzioni tra spazi topologici.

Si consiglia dunque al lettore, nel consultare diversi manuali, di prestare attenzione al tipo di definizione che viene data in ciascun contesto. In particolare, si fa riferimento a [9] per un approfondimento sulla questione.

Nel riferirsi a funzioni definite discontinue in punti non appartenenti al dominio, tali autori utilizzano in maniera implicita il seguente concetto. Presentiamo quindi questa nozione, seguita da esempi che chiariscono quanto anticipato.

Definizione 4.3 (funzione prolungabile con continuità). Dati $A \subset \mathbb{R}$ e $x_0 \in \mathbb{R}\setminus A$ di accumulazione per $A$ , una funzione continua $f \colon A \to \mathbb{R}$ si dice estendibile o prolungabile con continuità in $x_0$ se esiste finito $\displaystyle \ell=\lim_{x \to x_0}f(x)$ , ossia se la funzione $\tilde{f} \colon A \cup \{x_0\} \to \mathbb{R}$ , ottenuta ponendo

(18) $\begin{equation*} \tilde{f}(x) = \begin{cases} f(x) & \text{se } x \in A\\ \ell & \text{se } x=x_0, \end{cases} \end{equation*}$

è continua. Tale $\tilde{f}$ è detta estensione continua di $f$ in $x_0$ . In caso contrario, $f$ si dice non estendibile con continuità in $x_0$ .

$\quad$

In altre parole, una funzione $f$ è estendibile con continuità in un punto se essa coincide con la restrizione di una funzione $\tilde{f}$ continua in tale punto.

La definizione 4.3 chiarisce forse la diversità di opinioni riguardo funzioni definite “discontinue” in punti non appartenenti al dominio: tali autori si riferiscono a quelle che abbiamo definito funzioni non prolungabili con continuità in tali punti.

Esempio 4.4. Secondo le nostre definizioni, la funzione $f \colon \mathbb{R} \setminus \{0\}$ definita da $f(x)= \frac{1}{x}$ per ogni $x \neq 0$ è continua, ma non è prolungabile con continuità in $0$ in quanto

(19) $\begin{equation*} \lim_{x \to 0} f(x) = \lim_{x \to 0} \dfrac{1}{x} \quad \text{non esiste,} \end{equation*}$

come mostrato nell’esempio 3.5 e in figura 7. Equivalentemente, (19) mostra che non può esistere alcuna funzione continua $\tilde{f} \colon \mathbb{R} \to \mathbb{R}$ che coincida con $f$ in $\mathbb{R} \setminus \{0\}$ .

Esempio 4.5. La funzione $f \colon \mathbb{R} \setminus \{0\} \to \mathbb{R}$ rappresentata in figura 8 e definita da

(20) $\begin{equation*} f(x) = x \sin \left( \dfrac{1}{x}\right) \qquad \forall x \in \mathbb{R} \setminus \{0\}, \end{equation*}$

$\quad$

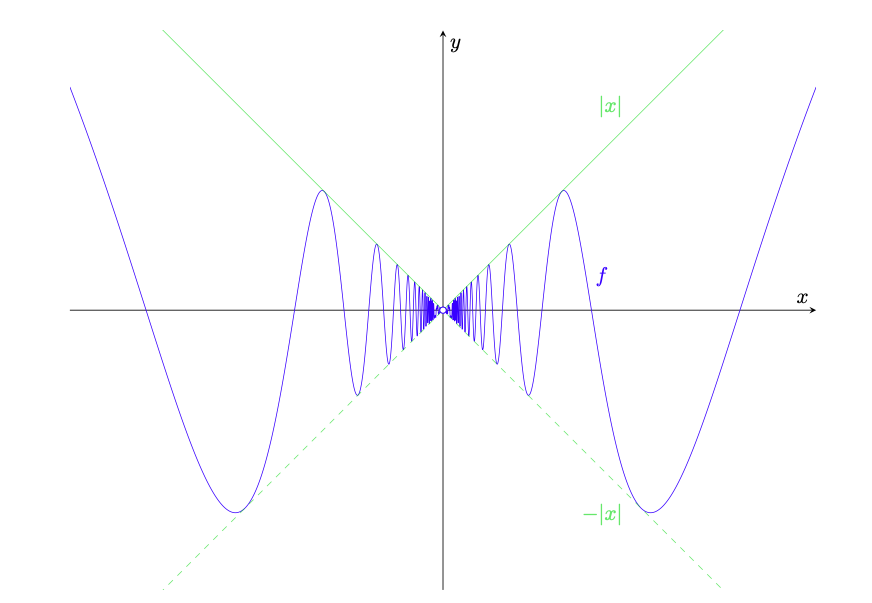
funzioni continue

Figura 8: la funzione $f$ dell’esempio 4.5 (in blu) e il suo confronto con le funzioni $x \mapsto \pm|x|$ (in verde). Nonostante $f$ non sia definita in $0$ , si vede che $\displaystyle \lim_{x \to 0} f(x)=0$ , quindi essa è estendibile con continuità.

$\quad$

è estendibile con continuità in $x=0$ . Infatti si ha

(21) $\begin{equation*} 0 \leq \left| x \sin \left( \dfrac{1}{x}\right) \right| \leq |x| \quad \forall x \in \mathbb{R} \setminus \{0\}, \qquad \lim_{x \to 0} |x|=0. \end{equation*}$

Da tali relazioni, per il teorema del confronto si ottiene

(22) $\begin{equation*} \lim_{x \to 0} f(x)=0, \end{equation*}$

da cui $f$ è estendibile con continuità in $0$ e la funzione $\tilde{f} \colon \mathbb{R} \to \mathbb{R}$ definita da

(23) $\begin{equation*} \tilde{f}(x) = \begin{cases} x \sin \left( \dfrac{1}{x}\right) & \text{se } x \neq 0\\ 0 & \text{se } x =0 \end{cases} \end{equation*}$

è la sua estensione continua in $0$ .

Tipi di discontinuità.

Procediamo ora con la classificazione dei diversi tipi di discontinuità, cui seguiranno degli esempi.

$\quad$

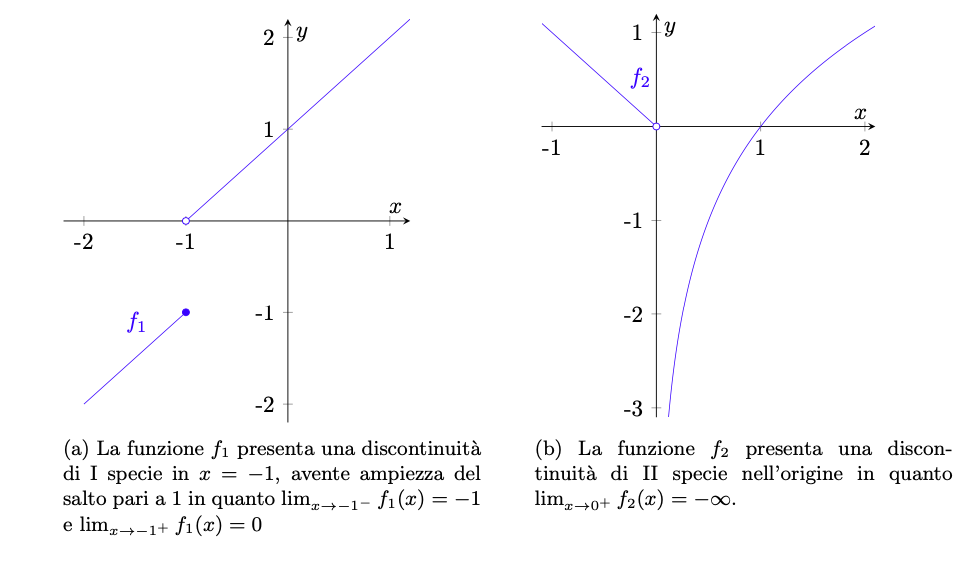
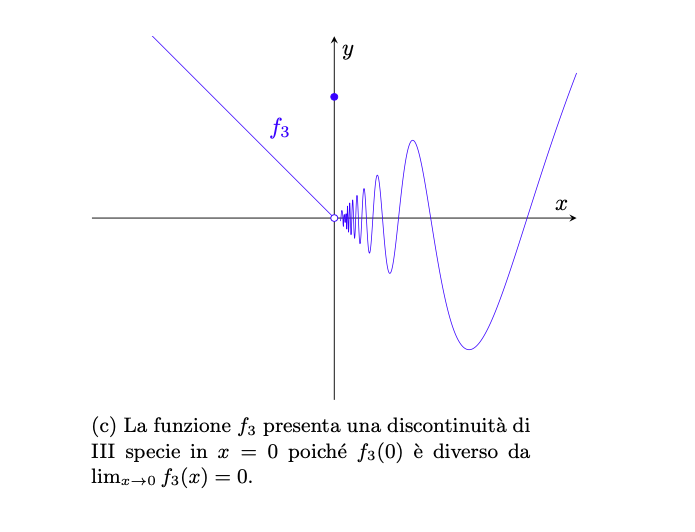
funzioni continue

Figura 9: discontinuità di I, II e III specie.

$\quad$

Definizione 4.6 (discontinuità di I specie o di salto, figura 9a). Una funzione $f\colon A \subseteq \mathbb{R}\to \mathbb{R}$ ha una discontinuità di prima specie o di salto in $x_0\in A$ se se esistono finiti i limiti destro e sinistro per $x\to x_0$ ma essi sono diversi, cioè

(24) $\begin{equation*} \lim_{x \to x_0^-} f(x) = \ell_- \in \mathbb{R}, \quad \lim_{x \to x_0^+} f(x) = \ell_+ \in \mathbb{R} \quad \text{e} \quad \ell_- \neq \ell_+. \end{equation*}$

Si definisce ampiezza del salto la differenza

(25) $\begin{equation*} \ell_+ - \ell_-. \end{equation*}$

Definizione 4.7 (discontinuità di II specie, figura 9b). Si dice che una funzione $f\colon A \subseteq \mathbb{R}\to \mathbb{R}$ ha una discontinuità di seconda specie in $x_0\in A$ se almeno uno tra $\displaystyle \lim_{x \to x_0^-}f(x)$ e $\displaystyle \lim_{x \to x_0^+}f(x)$ non esiste o è pari a $\pm \infty$ .

Definizione 4.8 (discontinuità di III specie o eliminabile, figura 9c). Si dice che una funzione $f\colon A \subseteq \mathbb{R}\to \mathbb{R}$ ha una discontinuità di III specie o eliminabile in $x_0$ se esiste finito il limite per $x\to x_0$ di $f$ ma esso è diverso da $f(x_0)$ , cioè

(26) $\begin{equation*} \lim_{x \to x_0} f(x) = \ell \in \mathbb{R} \quad \text{e} \quad \ell \neq f(x_0). \end{equation*}$

$\quad$

Osservazione 4.9. L’ultimo tipo di discontinuità si chiama “eliminabile” proprio perché, ridefinendo il valore della funzione nel punto $x_0$ e ponendolo uguale al valore del limite $\ell$ si ottiene una nuova funzione continua.

Procediamo ora con alcuni esempi.

Esempio 4.10 (discontinuità di salto).

Si consideri la funzione funzione $f\colon \mathbb{R} \to \mathbb{R}$ definita da
$f(x) \coloneqq \chi_{(a,b)}(x) = \begin{cases} 1 \quad \mbox{ se } a < x < b,\\ 0 \quad \; \mbox{altrimenti,} \end{cases}$

rappresentata a sinistra in figura 10. Tale funzione prende il nome di funzione caratteristica dell’intervallo $(a,b)$ .

$\quad$

$\quad$

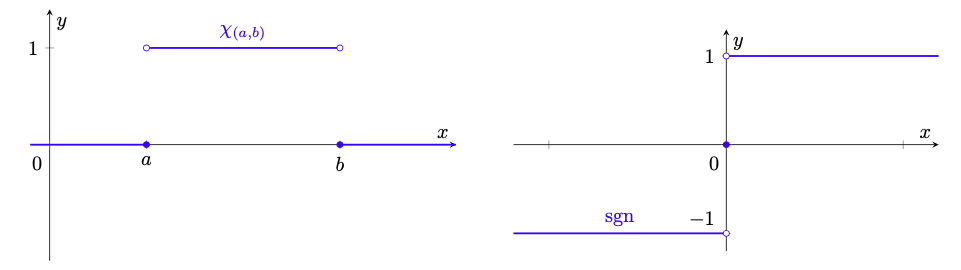
Figura 10: le due funzioni dell’esempio 4.10. A sinistra, il grafico della funzione $\chi_{(a,b)}$ caratteristica dell’intervallo $(a,b)$ : si notino le discontinuità di prima specie in $a$ e $b$ con salti rispettivamente pari a $1$ e $-1$ . A destra, il grafico della funzione $\operatorname{sgn}$ , avente una discontinuità di prima specie in $0$ con salto pari a $2$ .

$\quad$

$\quad$

Si ha

$\lim_{x \to a^+} f(x) = 1, \qquad \lim_{x \to a^-} f(x) = 0,$

mentre

$\lim_{x \to b^+} f(x) = 0, \qquad \lim_{x \to b^-} f(x) = 1.$

Segue che $f$ ha un salto sia in $a$ che in $b$ di ampiezza $1$ e $-1$ , rispettivamente.

Consideriamo la funzione $f\colon \mathbb{R} \to \mathbb{R}$ definita da
$f(x) \coloneqq \text{sgn}(x) = \begin{cases} 1 \quad \mbox{ se } x>0,\\ 0 \quad \mbox{ se } x = 0,\\ -1 \quad \mbox { se } x<0, \end{cases}$

rappresentata a destra in figura 10. Tale funzione prende il nome di funzione segno. Studiando i limiti destro e sinistro in $x=0$ , è immediato verificare che $f$ ha una discontinuità di salto in tale punto con ampiezza del salto pari a ampiezza $2$ .

Esempio 4.11 (discontinuità di seconda specie).

Consideriamo la funzione $f\colon \mathbb{R}\to \mathbb{R}$ definita da
$f(x) = \begin{cases} 1 & \text{se } x \leq 0,\\[7pt] \dfrac{1}{x} & \text{se } x > 0, \end{cases}$

rappresentata a sinistra in figura 11. In questo caso si ha una discontinuità di seconda specie in $x=0$ , poiché

$\lim_{x \to 0^+} f(x) = + \infty .$

Sia $a\in \mathbb{R}$ e consideriamo la funzione $f\colon \mathbb{R}\to \mathbb{R}$ definita da
$f(x) = \begin{cases} \sin\dfrac{1}{x} \qquad \text{se }x\neq 0,\\[7pt] a \qquad \quad \; \; \text{se }x = 0, \end{cases}$

rappresentata a destra in figura 11. In questo caso si ha una discontinuità di seconda specie in $x=0$ per ogni $a\in \mathbb{R}$ , poiché non esiste $\lim_{x \to 0} f(x)$ .

$\quad$

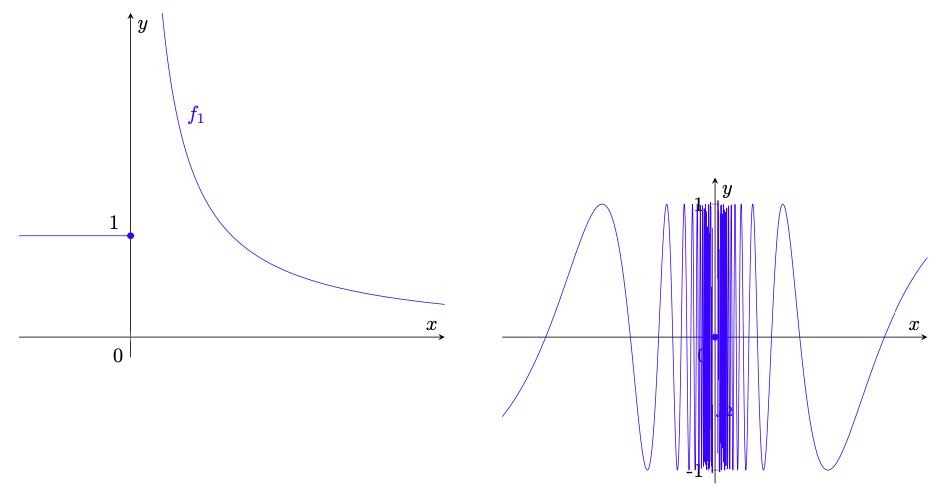
funzioni continue

Figura 11: le due funzioni dell’esempio 4.11. $f_1$ possiede una discontinuità di seconda specie in quanto $\lim_{x \to +}f_1(x)=+\infty$ , mentre $f_2$ ha una discontinuità di seconda specie in quanto $\lim_{x \to 0}f_2(x)$ non esiste.

$\quad$

Esempio 4.12 (discontinuità eliminabile). Consideriamo la funzione $f\colon \mathbb{R}\to \mathbb{R}$ definita da

$f(x)\coloneqq \text{sgn}^2(x) = \begin{cases} 0 \quad \mbox{ se } x =0,\\ 1 \quad \mbox{ altrimenti, } \end{cases}$

rappresentata in figura 12. Tale funzione ha una discontinuità eliminabile in $x=0$ , infatti

$\lim_{x \to 0} \text{sgn}^2(x) = 1 \neq \text{sgn}^2(0) = 0.$

Tuttavia, possiamo definire una nuova funzione a partire da $f$ , $\widetilde{f} \colon \mathbb{R}\to \mathbb{R}$ nel modo seguente

$\widetilde{f}(x)\coloneqq 1 \qquad \forall x \in \mathbb{R},$

eliminando così la discontinuità.

$\quad$

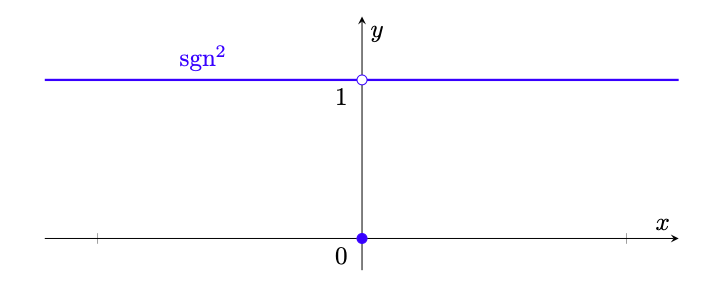
funzioni continue

Figura 12: la funzione $\operatorname{sgn}^2$ dell’esempio 4.12. Poiché essa assume valore $1$ ovunque tranne che in $x=0$ , in tale punto possiede una discontinuità eliminabile.

$\quad$

Discontinuità di funzioni monotone.

Una trattazione a parte riguarda le funzioni monotone definite in un intervallo, in quanto tali funzioni ammettono solo discontinuità di salto. Per i richiami sulle funzioni monotone si rimanda alla dispensa [11, funzioni elementari – volume 1, sezione 2.9].

Teorema 4.13 (discontinuità di funzioni monotone). Sia $f \colon [a, b] \to \mathbb{R}$ una funzione monotona. Allora essa possiede esclusivamente discontinuità di prima specie, con salti di ampiezza positiva se $f$ è crescente e di ampiezza negativa se $f$ è decrescente.

Inoltre, l’insieme dei punti di discontinuità di f possiede cardinalità finita o numerabile.

$\quad$

Dimostrazione. Dimostriamo il risultato nel caso di una funzione crescente, poiché l’altro caso si dimostra in maniera analoga.

Sia $x_0 \in [a,b]$ un punto di discontinuità per $f$ . Allora, poiché $f$ è una funzione monotona crescente si ha che

$\lim_{x \to x_0^+} f(x) = \inf_{x \in (x_0,b]} f(x)\eqqcolon \alpha(x_0) \quad \text{e} \quad \lim_{x \to x_0^-} f(x) = \sup_{x \in [a,x_0)} f(x)\eqqcolon \beta(x_0),$

inoltre vale

$f(a) \leq \beta(x_0) \leq f(x_0) \leq \alpha(x_0) \leq f(b).$

Dunque segue che $\alpha(x_0) , \beta(x_0) \in \mathbb{R}$ . Abbiamo escluso quindi la possibilità di avere discontinuità di seconda o terza specie.

Poiché $\beta(x_0) \leq f(x_0) \leq \alpha(x_0)$ , se $\alpha(x_0) = \beta(x_0)$ allora $x_0$ non sarebbe un punto di discontinuità per $f$ . Segue dunque che l’unica possibilità rimasta è $\alpha(x_0) \neq \beta(x_0)$ , dunque $x_0$ è un punto di discontinuità di salto per $f$ .

$\quad$

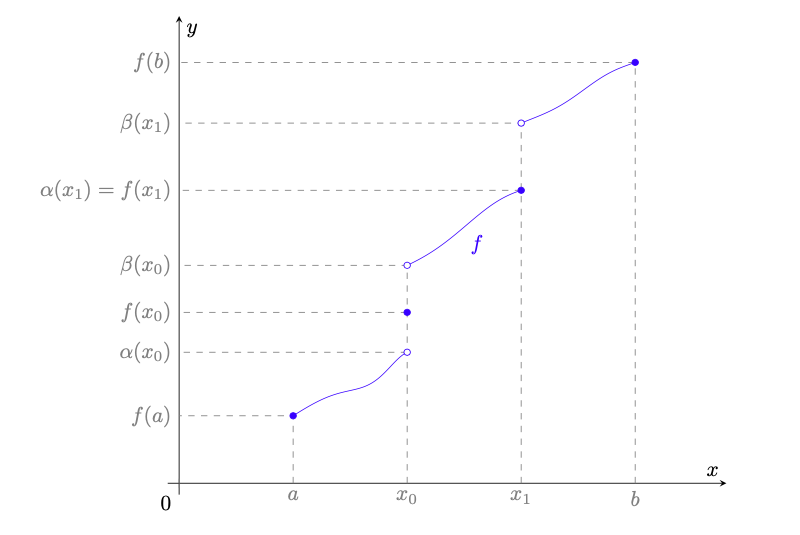
funzioni continue

Figura 13: discontinuità di una funzione monotona $f \colon [a,b] \to \mathbb{R}$ . Si noti che gli intervalli $(\alpha(x_i),\beta(x_i))$ sono tutti contenuti in $[f(a),f(b)]$ e sono a due a due disgiunti.

$\quad$

Mostriamo ora che l’insieme $D \coloneqq \{x \in [a,b] \colon x \text{ è di discontinuità per f}\}$ è finito o numerabile. A tal fine, consideriamo la funzione $g \colon D \to \mathbb{Q}$ definita come segue

(27) $\begin{equation*} g(x) = q_x \in \big(\alpha(x),\beta(x)\big) \cap \mathbb{Q} \qquad \forall x \in D, \end{equation*}$

dove $q_x$ è scelto in maniera arbitraria nell’insieme $(\alpha(x),\beta(x)) \cap \mathbb{Q}$ . Osserviamo che tale insieme non è vuoto in quanto $x$ è di discontinuità per $f$ , per cui $\alpha(x)< \beta(x)$ , e per la densità di $\mathbb{Q}$ in $\mathbb{R}$ . Notiamo inoltre che la possibilità di effettuare tali scelte dipende, nel caso in cui $D$ sia infinito, dall’assioma della scelta. La funzione $g$ risulta quindi ben definita.

Osserviamo ora che $g$ è iniettiva. Infatti, siano $x_0,x_1 \in D$ con $x_0<x_1$ (l’altro caso è analogo). Per la monotonia di $f$ si ha

(28) $\begin{equation*} \alpha(x_0) < \beta(x_0) \leq \alpha(x_1) < \beta(x_1). \end{equation*}$

Gli intervalli $(\alpha(x_0), \beta(x_0))$ e $(\alpha(x_1), \beta(x_1))$ sono dunque disgiunti e quindi $g(x_0) \neq g(x_1)$ . Dall’iniettività di $g$ e dalla numerabilità di $\mathbb{Q}$ segue che $D$ è al più numerabile. Si veda figura 13 per la rappresentazione grafica della dimostrazione.

Scarica la teoria

Ottieni il documento contenente la teoria sulle funzioni continue.

Teoremi sulle funzioni continue

Introduzione.

In questa sezione presentiamo alcuni fondamentali teoremi riguardanti le funzioni continue: il teorema della permanenza del segno e il teorema degli zeri, il teorema dei valori intermedi e il teorema di Weierstrass. Vengono presentati esempi di applicazione di tali teoremi, anche in ambito computazionale con l’ausilio di MATLAB.

Il teorema della permanenza del segno.

Richiamiamo dapprima un risultato di teoria dei limiti, che poi applicheremo al caso di funzioni continue.

Teorema 5.1 (permanenza del segno). Sia $f\colon A\subseteq \mathbb{R}\to \mathbb{R}$ e sia $x_0$ un punto di accumulazione per $A$ . Supponiamo che esista

$\lim_{x \to x_0} f(x)=\ell \in \mathbb{R} \quad \text{con} \quad \ell \neq 0.$

Allora esiste un intorno $I_{x_0}$ di $x_0$ tale che la funzione $f$ assume in $I_{x_0} \setminus \{x_0\}$ valori di segno costante e uguale al segno di $\ell$ .

$\quad$

Dimostrazione. Poiché $\ell \neq 0$ , esiste $\varepsilon>0$ tale che $0 \notin (\ell - \varepsilon,\ell+\varepsilon)$ , cioè ogni numero reale di tale insieme ha lo stesso segno di $\ell$ . Per definizione di limite esiste un intorno $I$ di $x_0$ tale che

(29) $\begin{equation*} f(x) \in (\ell-\varepsilon,\ell+\varepsilon) \qquad \forall x \in I\setminus \{x_0\}, \end{equation*}$

cioè, per come è stato scelto $\varepsilon$ , $f(x)$ assume lo stesso segno di $\ell$ per ogni $x \in I\setminus \{x_0\}$ . Si veda figura 14 per una rappresentazione grafica.

$\quad$

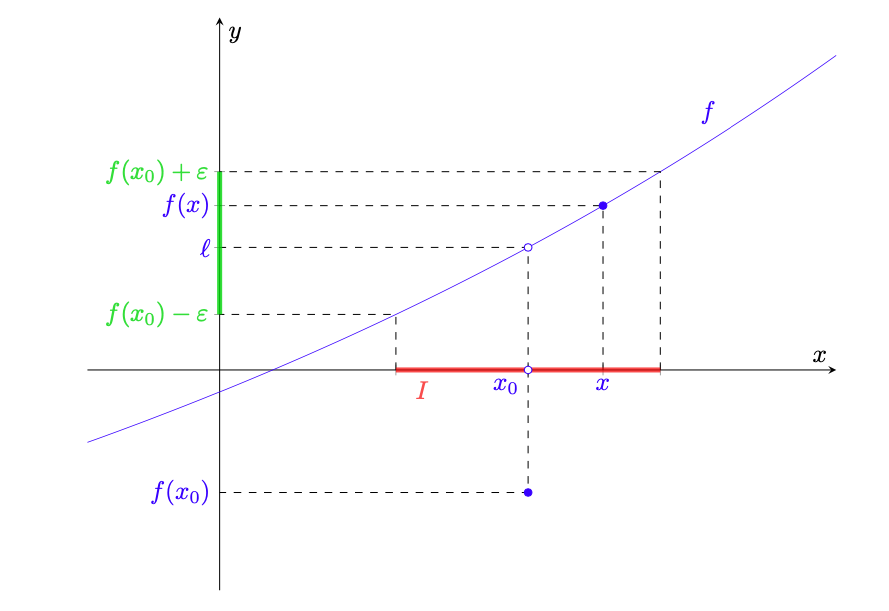
funzioni continue

Figura 14: rappresentazione del teorema 5.1. Poiché $\ell>0$ , per ogni $x \in I \setminus \{x_0\}$ $f(x)$ ha lo stesso segno di $\ell$ . Si noti l’indipendenza di ciò dal segno di $f(x_0)$ , che può anche essere diverso.

$\quad$

Segue direttamente il seguente risultato per funzioni continue.

Corollario 5.2 (permanenza del segno per funzioni continue). Sia $f\colon A \subseteq \mathbb{R}\to \mathbb{R}$ e sia $x_0\in A$ un punto di continuità per $f$ . Allora se $f(x_0)>0$ esiste un intorno $I_{x_0}$ tale che

$f(x)>0 \qquad \forall x\in I_{x_0}\cap A.$

Vale un risultato analogo se $f(x_0)<0$ .

$\quad$

Il teorema di esistenza degli zeri.

L’enunciato del seguente teorema, chiamato anche “teorema degli zeri” è estremamente intuitivo: esso infatti afferma che una funzione continua definita su un intervallo che assume valori di segno opposto ai suoi estremi deve necessariamente assumere il valore $0$ all’interno dell’intervallo stesso: si veda la figura 15 per un esempio grafico. In altre parole, se il grafico di una funzione continua si trova in parte al di sotto e in parte al di sopra dell’asse delle ascisse, deve necessariamente attraversarlo.

Teorema 5.3 (teorema di esistenza degli zeri). Sia $f\colon [a,b]\subset \mathbb{R} \to \mathbb{R}$ una funzione continua e si supponga che $f(a)\cdot f(b) < 0$ . Allora esiste $x_0\in \left(a,b\right)$ tale che $f(x_0)=0$ .

$\quad$

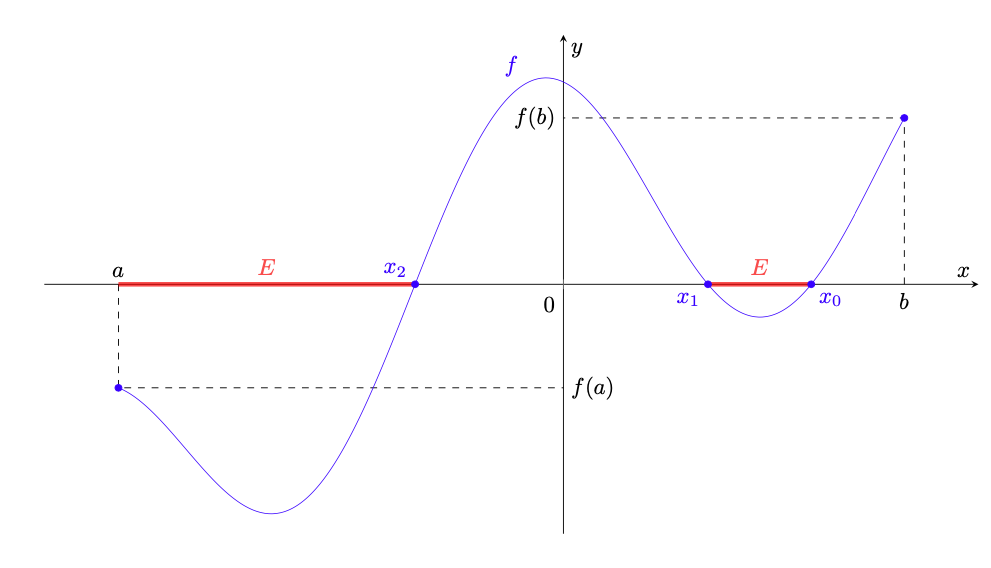
funzioni continue

Figura 15: rappresentazione del teorema 5.3. Poiché $f(a)<0$ , $f(b)>0$ e $f$ è continua, il grafico di $f$ interseca l’asse $x$ in almeno un punto $x_0 \in (a,b)$ , ottenuto come estremo superiore dell’insieme $E= \{x \in [a,b] \colon f(x) \leq 0\}$ (rappresentato in rosso). Si noti che, nonostante il teorema 5.3 assicuri l’esistenza di almeno un punto $x_0$ tale che $f(x_0)=0$ , esso può non essere unico, come nel caso in esame in cui sono presenti anche gli zeri $x_1$ e $x_2$ di $f$ .

$\quad$

Dimostrazione. Supponiamo che $f(a)<0$ e $f(b)>0$ . Il caso opposto si dimostra in maniera analoga. Definiamo l’insieme

(30) $\begin{equation*} E = \{ x \in [a,b] \colon f(x) \leq 0\}, \end{equation*}$

rappresentato in rosso in figura 15. Osserviamo che $a\in E$ , dunque $E$ è non vuoto e inoltre $E\subset [a,b]$ , dunque è limitato superiormente. Allora per la completezza dei numeri reali (si veda [11, funzioni elementari – volume 1, assioma 2.57]) esiste

(31) $\begin{equation*} x_0= \sup E \in [a,b]. \end{equation*}$

Proviamo che $f(x_0)=0$ .

Per definizione di estremo superiore, esiste $x_n \in E$ tale che $x_n \to x_0$ , da cui segue, per la continuità di $f$ e per il teorema 3.3, che

(32) $\begin{equation*} f(x_0) \leq 0. \end{equation*}$

In particolare ciò mostra che $x_0< b$ .

Supponiamo che $f(x_0)<0$ , allora per il corollario 5.2, esisterebbe $x_1>x_0$ con $x_1\in [a,b]$ tale che $f(x_1)<0$ , contraddicendo il fatto che $x_0=\sup E$ . Da tale contraddizione segue che

(33) $\begin{equation*} f(x_0)=0. \end{equation*}$

Viene presentata ora una dimostrazione alternativa di tipo costruttivo.

$\quad$

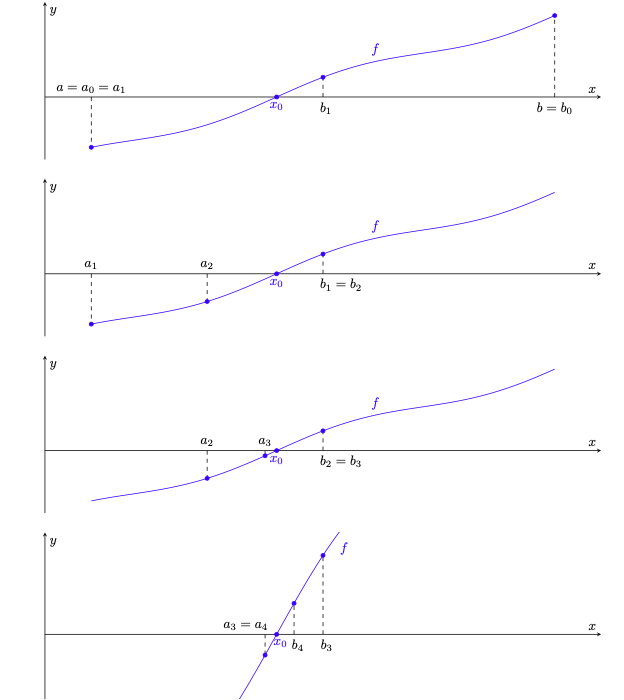
funzioni continue

Figura 16: i primi passi nella costruzione degli intervalli $[a_n,b_n]$ descritti nella dimostrazione alternativa del teorema 5.3 (per maggiore chiarezza, l’ultimo grafico è dilatato verticalmente di un fattore 15). Si noti come, dimezzando l’ampiezza dell’intervallo a ogni passo, le successioni $a_n$ e $b_n$ convergano rapidamente a uno zero $x_0$ di $f$ .

$\quad$

Dimostrazione alternativa del teorema 5.3. Per ipotesi si ha $f(a)\cdot f(b) < 0$ . Vogliamo costruire induttivamente una successione di intervalli $[a_n,b_n]$ con la proprietà che

(34) $\begin{equation*} [a_{n+1},b_{n+1}] \subset [a_n,b_n], \quad \,\, f(a_n) \cdot f(b_n) < 0 \qquad \forall n \in \mathbb{N}, \end{equation*}$

ovvero che essi siano “inscatolati” e che il segno delle successioni $\{f(a_n)\}$ e $\{f(b_n)\}$ sia costante. Procediamo per induzione. Come primo passo, poniamo $\left[a_0,b_0\right]:=\left[a,b\right]$ . Per ipotesi, $f(a_0)\cdot f(b_0)<0$ . Come passo successivo, supposto di aver costruito l’intervallo $[a_n,b_n]$ tale che $f(a_n) \cdot f(b_n) < 0$ procediamo a costruire $[a_{n+1},b_{n+1}]$ nel seguente modo: se $f\left(\dfrac{a_n+b_n}{2}\right)=0$ , poniamo $x_0=\dfrac{a_n+b_n}{2}$ e abbiamo finito; in caso contrario definiamo

(35) $\begin{equation*} [a_{n+1},b_{n+1}]= \begin{cases} \left[a_n,\dfrac{a_n+b_n}{2}\right] & \mbox{se } f(a_n)\cdot f\left( \dfrac{a_n+b_n}{2}\right) <0,\\[8pt] \left[\dfrac{a_n+b_n}{2},b_n\right] & \mbox{altrimenti. } \end{cases} \end{equation*}$

Queste scelte sono illustrate nella figura 16. Osserviamo che

(36) $\begin{equation*} a \leq a_n \leq a_{n+1} \leq b_{n+1}\leq b_n \leq b \qquad \forall n \in \mathbb{N}, \end{equation*}$

dunque $\{a_n\}$ e $\{b_n\}$ sono due successioni monotone e limitate, quindi esse sono convergenti; chiamiamo $\alpha$ e $\beta$ i limiti rispettivamente di $\{a_n\}$ e $\{b_n\}.$

Mostriamo ora che $\alpha=\beta$ . Infatti, osserviamo che per costruzione l’intervallo $[a_{n+1},b_{n+1}]$ si ottiene bisecando $[a_n,b_n]$ , quindi

(37) $\begin{equation*} 0 < b_n-a_n= \dfrac{b-a}{2^n}\quad \forall n\in \mathbb{N}. \end{equation*}$

Passando al limite per $n \to +\infty$ nella precedente relazione, si ottiene

(38) $\begin{equation*} 0 \leq \beta - \alpha \leq \lim_{n \to +\infty} \dfrac{b-a}{2^n} = 0, \end{equation*}$

ossia $\beta=\alpha$ . Chiamato $x_0$ questo limite comune di $a_n$ e $b_n$ , ci manca da dimostrare che $f(x_0)=0$ .

Ancora per costruzione abbiamo che $f(a_n)$ e $f(b_n)$ hanno segno costante e discorde e quindi $0 > f(a_n) \cdot f(b_n)$ , da cui, passando al limite¹

(39) $\begin{equation*} 0 \geq \lim_{n \to +\infty} \big( f(a_n) \cdot f(b_n) \big) = f(x_0)\cdot f(x_0) = f(x_0)^2, \end{equation*}$

dove nella prima uguaglianza si è usata la continuità di $f$ e il teorema 3.3. Dato che $y^2 \geq 0$ per ogni $y \in \mathbb{R}$ , da (39) segue necessariamente $f(x_0)^2=0$ , ossia

(40) $\begin{equation*} f(x_0)=0. \end{equation*}$

Osservazione 5.4. Osserviamo in figura 17 che le ipotesi del teorema degli zeri sono necessarie.

$\quad$

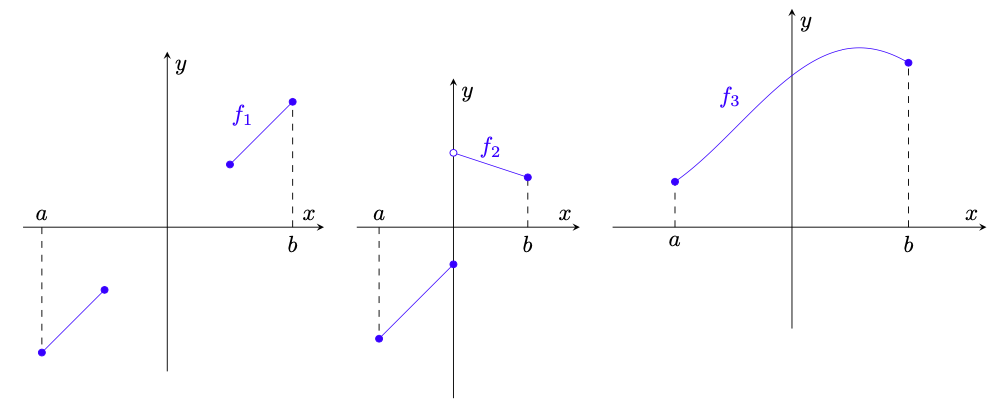
funzioni continue

Figura 17: le ipotesi del teorema di esistenza degli zeri sono necessarie. A sinistra, $f_1$ è una funzione continua e assume valori di segno opposto agli estremi del suo dominio, ma questo non è un intervallo. Al centro, $f_2$ è definita su un intervallo e assume valori di segno opposto agli estremi, ma non è continua. A destra, $f_3$ è continua e definita su un intervallo, ma non assume valori di segno opposto agli estremi.

$\quad$

Il teorema di esistenza degli zeri è uno strumento utile per dimostrare l’esistenza di soluzioni di equazioni che risulta impossibile calcolare analiticamente, come mostra il seguente semplice corollario e il relativo esempio.

Corollario 5.5. Siano $f,g \colon [a,b] \to \mathbb{R}$ due funzioni continue tali che

(41) $\begin{equation*} f(a)>g(a) \qquad \text{e} \qquad f(b) < g(b), \end{equation*}$

oppure

(42) $\begin{equation*} f(a)<g(a) \qquad \text{e} \qquad f(b) > g(b). \end{equation*}$

Allora esiste $x_0 \in (a,b)$ tale che

(43) $\begin{equation*} f(x_0)=g(x_0). \end{equation*}$

$\quad$

In altre parole, se i valori assunti da $f$ e $g$ in $a$ e $b$ sono in rapporti di ordine diverso, esiste almeno una soluzione $x_0$ dell’equazione $f(x)=g(x)$ .

Dimostrazione. La funzione $h \colon [a,b] \to \mathbb{R}$ definita da

(44) $\begin{equation*} h(x)=f(x)-g(x) \qquad \forall x \in [a,b] \end{equation*}$

è continua e, per l’ipotesi sull’ordine di $f(a),g(a),f(b),g(b)$ , è tale che $h(a)$ e $h(b)$ hanno segno opposto. Il teorema 5.3 prova quindi l’esistenza di $x_0$ .

Applichiamo questo risultato in un esempio pratico.

Esempio 5.6. Determiniamo il numero di soluzioni dell’equazione nella variabile $x$

(45) $\begin{equation*} e^{-x}=x, \end{equation*}$

fornendone anche eventualmente una stima. Innanzitutto si osserva che la funzione $f \colon x \in \mathbb{R} \mapsto e^{-x} \in \mathbb{R}$ (il cui grafico è rappresentato in rosso in figura 18) è strettamente decrescente, mentre la funzione definita da $g \colon x \in \mathbb{R} \mapsto x \in \mathbb{R}$ (il cui grafico è rappresentato in blu in figura 18) è strettamente crescente, quindi l’equazione (45) possiede al più una soluzione.

$\quad$

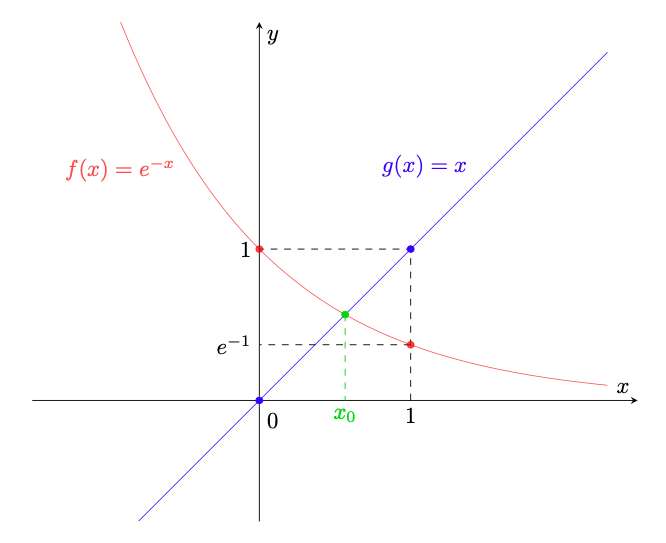
funzioni continue

Figura 18: le funzioni $f$ e $g$ (rispettivamente in rosso e blu) dell’esempio 5.6. L’equazione (45) possiede una soluzione $x_0$ (in verde) poiché $f(0)>g(0)$ e $f(1)<g(1)$ per il corollario 5.5. Tale soluzione è unica per la monotonia di $f$ e $g$ .

$\quad$

Per stabilire che una soluzione effettivamente esiste, osserviamo che

(46) $\begin{equation*} f(0)=1 > 0=g(0) \qquad \text{e} \qquad f(1)=e^{-1}<1 =g(1), \end{equation*}$

da cui l’esistenza di $x_0 \in (0,1)$ garantita dal corollario 5.5.

Si poteva anche procedere utilizzando direttamente il teorema 5.3, considerando la funzione $h \colon [0,1] \to \mathbb{R}$ definita da

(47) $\begin{equation*} h(x)= f(x)-g(x) = e^{-x}-x \qquad \forall x \in [0,1]. \end{equation*}$

Risolvere l’equazione (45) è equivalente a determinare gli zeri di $h$ , ossia i numeri reali $x$ tali che $h(x)=0$ . Osserviamo che

(48) $\begin{equation*} h(0)=e^{0}-0=1>0, \qquad h(1)=e^{-1}-1<0. \end{equation*}$

Poiché $h$ è continua, per il teorema di esistenza degli zeri esiste $x_0 \in (0,1)$ tale che $h(x_0)=0$ , cioè tale che

(49) $\begin{equation*} e^{-x_0}=x_0. \end{equation*}$

Tale punto è rappresentato in verde in figura 18 e una sua stima è che esso è compreso tra 0 e 1.

Il metodo di bisezione

Il teorema degli zeri 5.3 garantisce l’esistenza di (almeno) uno zero della funzione, se le ipotesi sono soddisfatte. Si è visto come questo strumento sia utile per risolvere equazioni del tipo

$f(x) = 0,$

dove $f \colon [a,b]\subset \mathbb{R}\to \mathbb{R}$ è una funzione continua che assume valori di segno discorde agli estremi o come nel corollario 5.5. Tuttavia a livello pratico non sempre è possibile calcolare analiticamente la soluzione dell’equazione e bisogna ricorrere all’aiuto di programmi di calcolo, che forniscono una approssimazione della soluzione richiesta.

Esistono vari algoritmi che implementano quanto richiesto, ma uno dei più intuitivi è il metodo di bisezione che sfrutta direttamente la dimostrazione alternativa del teorema degli zeri.

Per spiegare più in dettaglio il metodo, supponiamo senza perdita di generalità che $f(a)<0$ e $f(b)>0$ . Come nella dimostrazione costruttiva del teorema 5.3, si costruiscono tre successioni di numeri reali $a_n$ , $b_n$ e $x_n$ soddisfacenti $f(a_n)<0$ e $f(b_n)>0$ per ogni $n$ . Tali successioni sono costruite per ricorrenza ponendo

(50) $\begin{equation*} a_0=a, \qquad b_0=b, \qquad x_0 = \frac{a_0+b_0}{2} \end{equation*}$

e, una volta definiti $a_n, b_n, x_n$ si valuta $f(x_n)$ procedendo come segue:

$\quad$

se $f(x_n)=0$ , allora $x_n$ è la soluzione cercata e l’algoritmo si arresta.

Se $f(x_n)>0$ , allora, per il teorema degli zeri, l’intervallo $[a_n,x_n]$ contiene uno zero di $f$ e si pone
(51) $\begin{equation*} a_{n+1}=a_n, \qquad b_{n+1}=x_n, \qquad x_{n+1} = \frac{a_{n+1}+b_{n+1}}{2}. \end{equation*}$

Se $f(x_n)<0$ , allora, per il teorema degli zeri, l’intervallo $[x_n,b_n]$ contiene uno zero di $f$ e si pone
(52) $\begin{equation*} a_{n+1}=x_n, \qquad b_{n+1}=b_n, \qquad x_{n+1} = \frac{a_{n+1}+b_{n+1}}{2}. \end{equation*}$

Il processo appena descritto può in generale non arrestarsi mai nel caso in cui la soluzione non cada esattamente in uno dei punti medi degli intervalli trovati. Esistono perciò diversi “criteri di arresto” che forzano la conclusione del processo.

Per arrestare l’algoritmo, una scelta consiste nel fissare a priori il numero massimo $N$ di iterazioni che desideriamo che esso compia. Nel caso in cui si arrivi a compiere tutte le $N$ iterazioni ammesse, si conviene che il valore

(53) $\begin{equation*} x_{N} = \dfrac{a_N+b_N}{2}, \end{equation*}$

ossia il punto medio dell’intervallo $N$ -esimo determinato dall’algoritmo, sia la soluzione approssimata fornita in uscita.

Osserviamo che, poiché gli estremi $a,b$ dell’intervallo $(a,b)$ sono noti, fissare $N$ equivale a determinare l’errore massimo tra lo zero reale $x^*$ della funzione e il suo valore approssimato $x_N$ . Infatti, poiché $x^* \in (a_N,b_N)$ e $x_N$ è il punto medio di tale intervallo, si ha

(54) $\begin{equation*} |x^* - x_N| \leq \dfrac{b_N-a_N}{2} = \dfrac{b-a}{2^{N+1}}, \end{equation*}$

dove l’ultima uguaglianza segue dal fatto che a ogni passo l’ampiezza dell’intervallo è dimezzata e può essere facilmente dimostrata per induzione.

Quindi, se si desidera che l’errore massimo $|x^* - x_N|$ commesso dall’algoritmo sia inferiore a $\tau>0$ , occorre impostare

(55) $\begin{equation*} \dfrac{b-a}{2^{N+1}} \leq \tau \iff 2^{N+1} \geq \dfrac{b-a}{\tau} \iff N \geq \log_2 \left( \dfrac{b-a}{\tau}\right) - 1. \end{equation*}$

Esempio 5.7. Il seguente esempio ha il solo scopo di illustrare i passaggi del metodo, in un caso in cui la soluzione $x^*$ dell’equazione $f(x^*)=0$ sia già nota. Consideriamo la funzione $f\colon \left[\dfrac{1}{2}\,, 2\right] \to \mathbb{R}$ definita da

$f(x) = \ln x \qquad \forall x \in \left[\dfrac{1}{2}\,, 2\right].$

Si vuole trovare una soluzione nel suo dominio fissando la tolleranza $\tau = 0.01$ . \\ Si vede facilmente che $f(1/2)\cdot f(2) < 0$ per cui deve esistere $x_0 \in (1/2 \, , \, 2)$ tale che $f(x_0) = 0$ . Nella seguente tabella sono riportate le iterazioni dell’algoritmo precedentemente discusso creando per ogni passo un nuovo intervallo più piccolo $[a_n, b_n]$ contenente il punto $x_0$ .

$\begin{equation*} \begin{array}{c|c|c|c|c|c|c} \text{Passo } n & a_n & b_n & b_n - a_n & x_n & f(x_n)& e_n \\[3pt] \hline $0$ & $0.500000$ & $2.000000$ & $1.500000$ & $1.250000$ & $0.223144$ & $0,750000$ \\ $1$ & $0.500000$ & $1.250000$ & $0.750000$ & $0.875000$ & $-0.133531$ & $0.187500$\\ $2$ & $0.875000$ & $1.250000$ & $0.375000$ & $1.062500$ & $0.060625$ & $0.046875$\\ $3$ & $0.875000$ & $1.062500$ & $0.187500$ & $0.968750$ & $-0.031749$ & $0.011719$\\ $4$ & $0.968750$ & $1.062500$ & $0.093750$ & $1.015625$ & $0.015504$ & $0.002830$\\ \end{array} \end{equation*}$

La tolleranza $\tau=0.01 > e_4$ quindi possiamo prendere $x_{4} = 1.01$ come zero di $f$ . Osserviamo che $f(x_{4}) = 0.0155$ , che è molto vicino allo zero. Questo non ci sorprende in quanto è noto che lo zero di $f$ è $x_0 = 1$ .

Di seguito sono presentati l’andamento dell’errore e l’andamento degli estremi dell’intervallo $[a_n,b_n]$ .

$\quad$

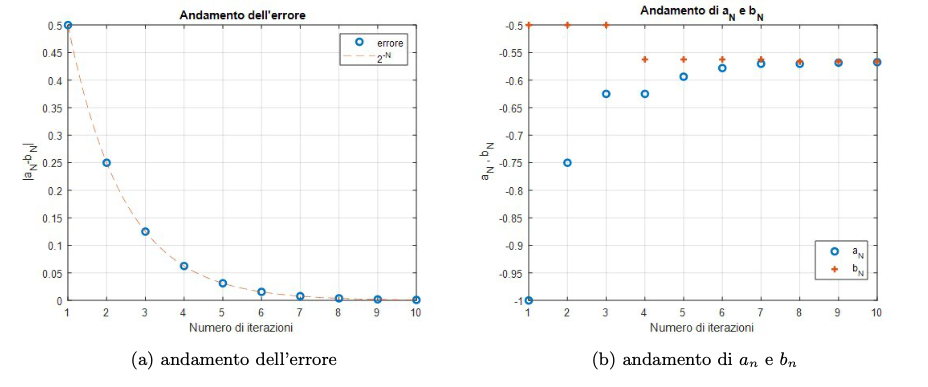
funzioni continue

Figura 19: errori e andamento dell’intervallo al variare delle iterazioni.

$\quad$

Esempio 5.8. Vediamo ora un esempio di implementazione del metodo di bisezione nel linguaggio MATLAB, imponendo come condizione di arresto che l’errore , dato dalla variabile err, sia inferiore ad un certa tolleranza, dato dalla variabile toll,.

Tale codice serve per trovare un’approssimazione dello zero della funzione definita da $f(x)=e^x + x$ nell’intervallo $[-1,0]$ che non può essere determinata con metodi analitici classici.

Il codice risulta diviso in tre parti:

$\quad$

Dati di input: vengono inizializzati tutti gli elementi necessari (e.g. a, b, toll);

Algoritmo di bisezione: implementa il codice di bisezione tenendo conto della condizione di arresto err toll;

Post-processing: vengono graficati alcuni andamenti necessari ad una valutazione della correttezza del codice. In particolare, sono stati considerati gli andamenti di $a_N$ e $b_N$ e l’andamento dell’errore.

%------- Dati di input ---------------------------------------------------

f =@(x) exp(x)+x; %definisco la funzione f(x)=e^x+x a =-1 ; b = 0 ; toll = 10^(-3) ; %definisco la tolleranza err = b-a ; %inizializzo l'errore a_memo = [] ; %vettore di memorizzazione di aN b_memo = [] ; %vettore di memorizzazione di bN err_memo = [] ; %vettore di memorizzazione dell'errore %------ Algoritmo di bisezione -------------------------------------------- while err>toll m = (a+b)/2; %calcolo il valor medio if f(a)*f(m)<0 a=a; b=m; a_memo = [a_memo a]; b_memo = [b_memo b]; elseif f(m)== 0 break else a=m; b=b; a_memo = [a_memo a]; b_memo = [b_memo b]; end err = abs(a-b); err_memo = [err_memo err]; end x=(a+b)/2; % valore della soluzione %------- Post-processing ------------------------------------------------- plot(a_memo,'o','LineWidth',2) hold on plot(b_memo,'+','LineWidth',2) grid on box on legend('a_N','b_N') xlabel('Numero di iterazioni') ylabel('a_N , b_N') title('Andamento di a_N e b_N') figure plot(err_memo,'o','LineWidth',2) hold on plot([1\colon 0.1\colon length(err_memo)], 2.^([-1\colon -0.1\colon -length(err_memo)]),'--') grid on box on xlabel('Numero di iterazioni') ylabel('|a_N-b_N|') title('Andamento dell''errore')

legend('errore','2^{-N}')

Ricordiamo che il limite di una successione è un punto della chiusura dell’insieme immagine della successione. Nel nostro caso l’immagine è contenuta nell’insieme $(-\infty,0)$ , quindi a priori il limite appartiene $[-\infty,0]$ . Sostanzialmente la disuguaglianza $f(a_n)f(b_n)<0$ al limite per $n\to+\infty$ diventa $\displaystyle\lim_{n\to+\infty}f(a_n)f(b_n)\leq 0$ . ↩

Il teorema dei valori intermedi.

In questa sezione presentiamo un risultato che discende direttamente dal teorema degli zeri, il teorema dei valori intermedi.

Teorema 5.9 (dei valori intermedi). Sia $I\subset \mathbb{R}$ un intervallo e sia $f\colon I \to \mathbb{R}$ una funzione continua. Siano

$m = \inf_I f, \qquad M = \sup_I f$

l’estremo inferiore e l’estremo superiore dei valori assunti da $f$ in $I$ , rispettivamente.

Allora per ogni $c \in (m, M)$ esiste $x_0 \in I$ tale che $f(x_0) = c$ . In altri termini la funzione assume tutti i valori compresi tra $m$ e $M$ .

$\quad$

funzioni continue

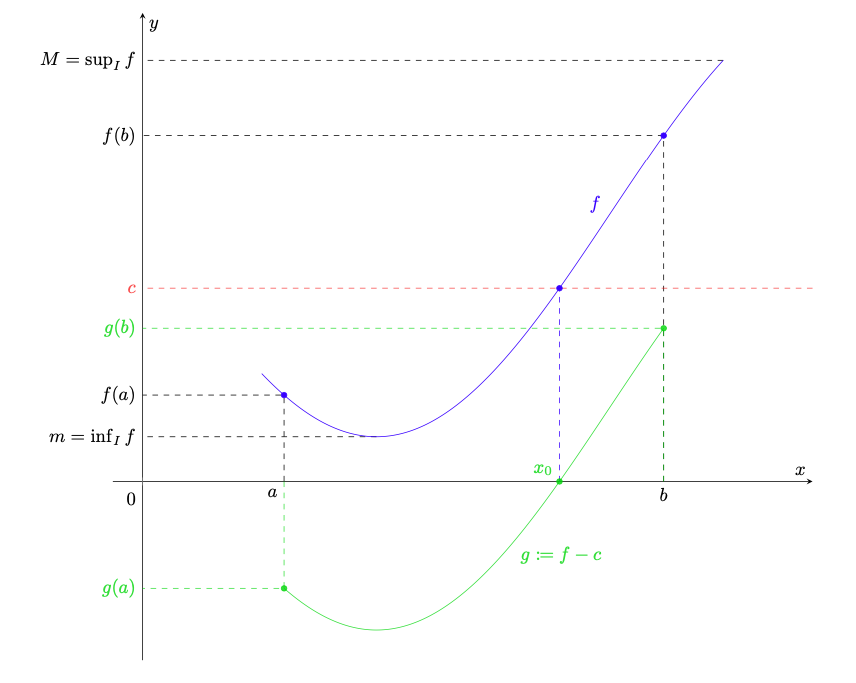
Figura 20: rappresentazione del teorema 5.9; si determinano $a,b \in I$ con $f(a)<c<f(b)$ e si applica il teorema 5.3 alla funzione $g \coloneqq f-c$ (in verde), ottenendo uno zero $x_0$ di $g$ . Per costruzione si ha quindi $f(x_0)=c$ .

$\quad$

Dimostrazione. Sia $c \in (m,M)$ e dimostriamo che esiste $x_0 \in I$ tale che $f(x_0)=c$ . Definiamo una funzione $g\colon I \to \mathbb{R}$ tale che

$g(x) \coloneqq f(x) - c \qquad \forall x \in I,$

il cui grafico è rappresentato in verde nella figura 20. Osserviamo che $g$ è continua in quanto somma di funzioni continue. Poiché $c>m$ , allora $c$ non è un minorante di $\text{Im}(f)$ e deve dunque esistere un valore $a \in I$ tale che $f(a) < c$ , ovvero $g(a) = f(a) - c < 0$ .

Analogamente, poiché $c<M$ non è un maggiorante di Im $(f)$ , deve esistere $b\in I$ tale che $f(b) > c$ , da cui $g(b)=f(b)-c>0$ .

Supponiamo $a < b$ (l’altro caso è analogo). Allora per il teorema degli zeri

$\exists x_0 \in (a,b) \colon g(x_0)=0, \text{ cioè }f(x_0) = c.$

Osservazione 5.10. Una diretta conseguenza del teorema dei valori intermedi è che, se $f$ è una funzione continua, allora l’immagine di un intervallo $I$ è a sua volta un intervallo, come precisato dal prossimo corollario, i cui estremi sono

$m = \inf_I f, \qquad M = \sup_I f .$

Tuttavia, occorre osservare che il teorema dei valori intermedi non dà informazioni riguardo l’appartenenza di $m$ e $M$ all’intervallo $J$ .

Corollario 5.11. Sia $f \colon A \to \mathbb{R}$ una funzione continua e sia $J \subseteq A$ un intervallo. Allora $f (J)$ è un intervallo.

$\quad$

Dimostrazione. Per mostrare che $f(J)$ è un intervallo, occorre mostrare che, dati $\alpha,\beta \in f(J)$ con $\alpha \leq \beta$ e dato $c \in (\alpha,\beta)$ , allora anche $c \in f(J)$ , ossia esiste $x_0 \in J$ tale che $f(x_0)=c$ . Definiti

(56) $\begin{equation*} m=\inf_J f, \qquad M = \sup_J f, \end{equation*}$

a tal fine osserviamo che, da $\alpha,\beta \in f(J)$ , per definizione di estremi inferiore e superiore segue che $c \in (m,M)$ . Quindi possiamo applicare il teorema 5.9 all’intervallo $J$ , ottenendo che esiste $x_0 \in J$ tale che $f(x_0)=c$ , cioè la tesi.

Il teorema 5.9 afferma che la proprietà dei valori intermedi è implicata dalla continuità. Risulta naturale chiedersi se valga il viceversa, ossia se una funzione $f \colon I \to \mathbb{R}$ tale che l’immagine tramite $f$ di un intervallo sia un intervallo debba allora essere continua. Ciò è falso, come mostra il seguente esempio.

Esempio 5.12. Si consideri la funzione $f \colon [-1,1] \to \mathbb{R}$ definita da

(57) $\begin{equation*} f(x) = \begin{cases} \sin \left( \dfrac{1}{x} \right) &\text{se } x \in [-1,1] \setminus \{0\}\\ 0 & \text{se } x =0, \end{cases} \end{equation*}$

rappresentata in figura 21.

$\quad$

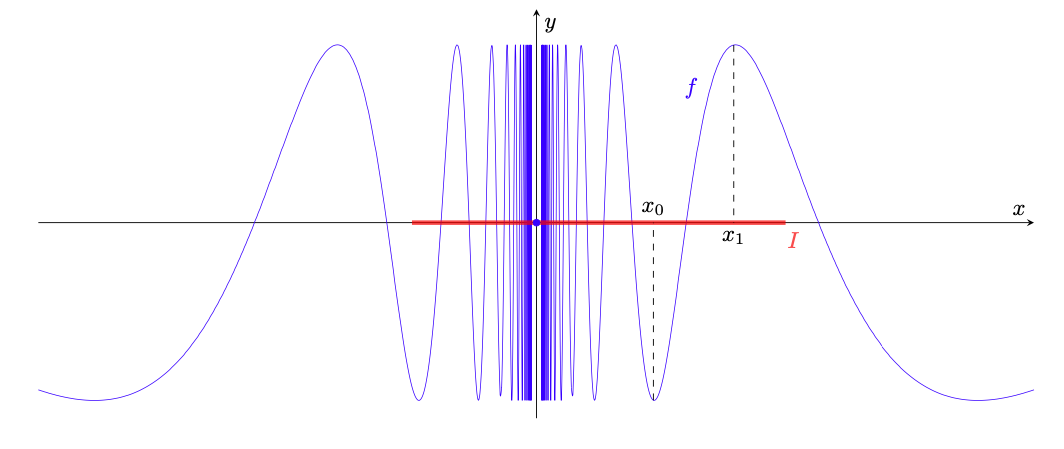
funzioni continue

Figura 21: la funzione dell’esempio 5.12. Se l’intervallo $I$ (in rosso) contiene $0$ , allora esistono $x_0, x_1 \in I$ con $f$ continua in $[x_0,x_1]$ e tali che $f(x_0)=-1$ e $f(x_1)=1$ , da cui si vede quindi che $f(I)=[-1,1]$ .

$\quad$

Poiché $\displaystyle \lim_{x \to 0} f(x)$ non esiste, $f$ non è continua in $x=0$ . Mostriamo però che essa possiede la proprietà dei valori intermedi. A tal fine, sia $I \subseteq [-1,1]$ un intervallo. Se $0 \notin I$ , allora $f(I)$ è un intervallo in quanto $f$ è continua in $I$ . Se invece $0 \in I$ , mostriamo che $f(I)=[-1,1]$ . L’idea è che esistono numeri reali dello stesso segno e arbitrariamente vicini a $0$ in cui $f$ assume valori pari a $-1$ e $1$ . Da $0 \in I$ , segue che esiste $n \in \mathbb{N}$ tale che

(58) $\begin{equation*} \left[\dfrac{1}{2n\pi + \dfrac{3\pi}{2}}, \dfrac{1}{2n\pi + \dfrac{\pi}{2}} \right] \subset I, \end{equation*}$

da cui $[-1,1] \subseteq f(I)$ per la continuità di $f$ in $\left[\dfrac{1}{2n\pi + {3\pi}/{2}}, \dfrac{1}{2n\pi + {\pi}/{2}} \right]$ e per il teorema 5.9. D’altronde, per costruzione di $f$ , poiché il seno assume solo valori compresi tra $-1$ e $1$ , si ha $f(I) \subseteq [-1,1]$ , da cui

(59) $\begin{equation*} f(I) = [-1,1], \end{equation*}$

e in particolare $f(I)$ è un intervallo.

Di seguito viene mostrato un esempio di calcolo dell’immagine di una funzione usando il teorema dei valori intermedi.

Esempio 5.13. Si consideri la funzione $f \colon (-2, +\infty) \to \mathbb{R}$ rappresentata in figura 22 definita da

(60) $\begin{equation*} f(x) = \dfrac{x+1}{x+2} \qquad \forall x \in (-2, +\infty). \end{equation*}$

$\quad$

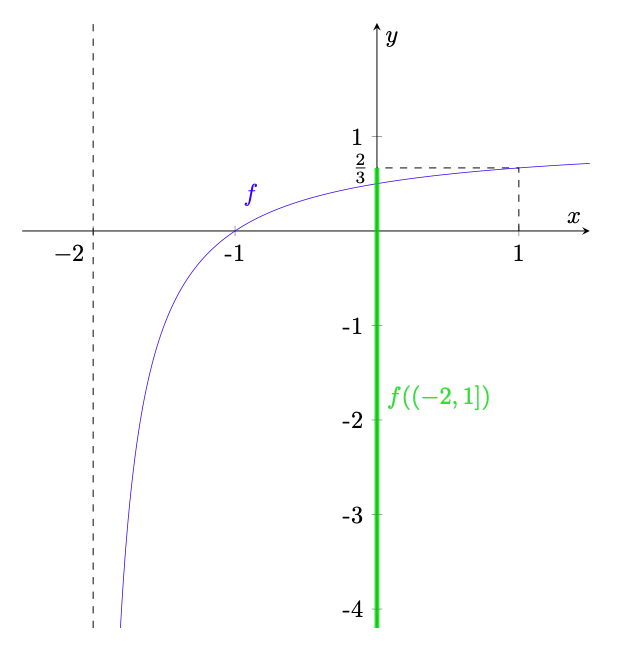
funzioni continue

Figura 22: la funzione dell’esempio 5.13. Poiché $f$ è crescente e continua, dallo studio fatto segue che $f((-2,1])$ è pari all’intervallo $(\infty,\dfrac{2}{3}]$ , rappresentato in verde.

$\quad$

Determiniamo $f((-2,1])$ . Osserviamo che $f$ è continua per la proposizione 2.7 e che

(61) $\begin{equation*} \lim_{x \to -2^+} f(x) = \lim_{x \to -2^+} \dfrac{x+1}{x+2} = -\infty, \qquad \lim_{x \to 1} f(x) = f(1)=\frac{2}{3}. \end{equation*}$

Inoltre $f$ è crescente in $(-2,+\infty)$ in quanto

(62) $\begin{equation*} f(x) = \dfrac{x+1}{x+2} = \dfrac{x+2 - 1}{x+2} = 1 - \dfrac{1}{x+2} \qquad \forall x \in (-2,+\infty) \end{equation*}$

e la funzione $x \mapsto \dfrac{1}{x+2}$ è decrescente in $(-2,+\infty)$ . Dalla monotonia di $f$ e da (61) segue che

(63) $\begin{equation*} \inf_{x \in (-2,1]} f(x) = -\infty, \qquad \sup_{x \in (-2,1]} f(x) = \max_{x \in (-2,1]} f(x) = f(1)=\frac{2}{3}. \end{equation*}$

Da (63) e dal teorema 5.9 si ha

(64) $\begin{equation*} f((-2,1]) = \left(-\infty, \dfrac{2}{3} \right). \end{equation*}$

Continuità della funzione inversa.

Il teorema dei valori intermedi è uno strumento utile per dimostrare che la funzione inversa di una funzione continua è anch’essa continua. Per le funzioni continue e definite su un intervallo, l’iniettività è equivalente alla stretta monotonia, come mostrato dal seguente lemma, che sarà poi utilizzato nella dimostrazione della continuità delle funzioni inverse.

Lemma 5.14. Sia $I \subseteq \mathbb{R}$ un intervallo e sia $f \colon I \to \mathbb{R}$ una funzione continua. Allora $f$ è iniettiva se e solo se è strettamente monotona, schematicamente:

(65) $\begin{equation*} f \text{ iniettiva} \iff f \text{ strettamente monotona.} \end{equation*}$

$\quad$

Chiaramente l’implicazione $f$ strettamente monotona $\Rightarrow$ $f$ iniettiva è banale e va mostrata solo l’altra.

Dimostrazione. Sia $a,b \in I$ con $a < b$ e, supponendo che $f(a) < f(b)$ , mostriamo che $f$ è crescente in $[a,b]$ , che mostrerà poi che $f$ è crescente in $I$ . Se invece $f(a)<f(b)$ , in maniera simile si mostra che $f$ è decrescente. Se esistessero $x_1,x_2 \in (a,b)$ tali che

(66) $\begin{equation*} x_1 < x_2, \qquad f(x_1) > f(x_2), \end{equation*}$

distinguiamo due casi.

$\quad$

Se fosse $f(a)< f(x_1)$ , allora esisterebbe $c \in \big(f(a),f(x_1)\big) \cap \big(f(x_2),f(x_1)\big)$ e, per il teorema 5.9, esisterebbero $\xi_1 \in (a,x_1)$ e $\xi_2 \in (x_1,x_2)$ tali che
(67) $\begin{equation*} f(\xi_1) = f(\xi_2)= c, \end{equation*}$

ma ciò contraddirebbe l’iniettività di $f$ .

Se invece fosse $f(a)>f(x_1)$ , in maniera simile si prova che esistono $\xi_1 \in (x_1,x_2)$ e $\xi_2 \in (x_2,b)$ tali che
(68) $\begin{equation*} f(\xi_1) = f(\xi_2). \end{equation*}$

Di nuovo ciò contraddirebbe l’iniettività di $f$ .

Tali contraddizioni provano che $f$ è crescente in $[a,b]$ .

Se $[c,d] \subseteq I$ è tale che $[a,b] \subseteq [c,d]$ , per il ragionamento di sopra $f$ è monotona su $[c,d]$ , quindi deve essere crescente. Per l’arbitrarietà dell’intervallo $[c,d] \subseteq I$ , $f$ è crescente in $I$ .

Teorema 5.15 (continuità della funzione inversa). Siano $I,J \subseteq \mathbb{R}$ intervalli e sia $f\colon I \to J$ una funzione continua e invertibile; allora $f^{-1}$ è continua.

$\quad$

Dimostrazione. Per il lemma 5.14 $f$ è monotona. Supponiamo che $f$ sia crescente (se $f$ è decrescente la dimostrazione è analoga). Per il corollario 5.11, $J = f(I)$ è un intervallo. La funzione $f^{-1}\colon J \to I$ deve essere anch’essa crescente (perché inversa di una funzione crescente) e $f^{-1}(J) = I$ è un intervallo.

Supponiamo per assurdo che esista $y_0 \in J = f(I)$ tale che $f^{-1}$ non sia continua in $y_0$ . Dal teorema 4.13 segue che la discontinuità è di salto e quindi almeno uno tra i limiti destri e sinistri di $f^{-1}$ in $y_0$ è diverso da $f^{-1}(y_0)$ . Supponiamo senza perdita di generalità che

$\ell^+ \coloneqq \lim_{y \to y_0^+}f^{-1}(y) = \inf_{y>y_0} f^{-1}(y) \neq f^{-1}(y_0).$

Allora, per monotonia di $f^{-1}$ , se $y > y_0$ si ha $f^{-1}(y) > \ell^+$ . D’altro canto se $y < y_0$ si ha $f^{-1}(y) < f^{-1}(y_0)$ . Ma ciò implica che $f^{-1}$ non assume alcun valore compreso tra $f^{-1}(y_0)$ e $\ell$ . Quest’ultima osservazione contraddice il fatto che l’immagine di $f^{-1}$ sia un intervallo.

Osservazione 5.16. La conclusione del teorema 5.15 non è valida se il dominio di $f$ non è un intervallo, come mostrano i seguenti esempi.

Esempio 5.17 (inversa con discontinuità di salto). Sia $f \colon [0,1] \cup (2,+\infty) \to [0,+\infty)$ definita da

(69) $\begin{equation*} f(x) = \begin{cases} x^2 & \text{se } x \in [0,1]\\ x-1 & \text{se } x \in (2,+\infty). \end{cases} \end{equation*}$

La funzione $f$ , rappresentata a sinistra in figura 23, risulta continua, oltre che strettamente crescente e quindi iniettiva. Inoltre dal teorema 5.7 segue che

(70) $\begin{equation*} f([0,1])=[0,1], \qquad f((2,+\infty))=(1,+\infty), \end{equation*}$

da cui $\operatorname{Im} f = [0,+\infty)$ , quindi $f$ è suriettiva ed è dunque invertibile. Ciononostante, la sua inversa $f^{-1} \colon [0,+\infty) \to [0,1] \cup (2,+\infty)$ definita da

(71) $\begin{equation*} f^{-1}(x) = \begin{cases} \sqrt{x} & \text{se } x \in [0,1]\\ x+1 & \text{se } x \in (1,+\infty) \end{cases} \end{equation*}$

e rappresentata a destra in figura 23, possiede una discontinuità di salto in $x=1$ .

$\quad$

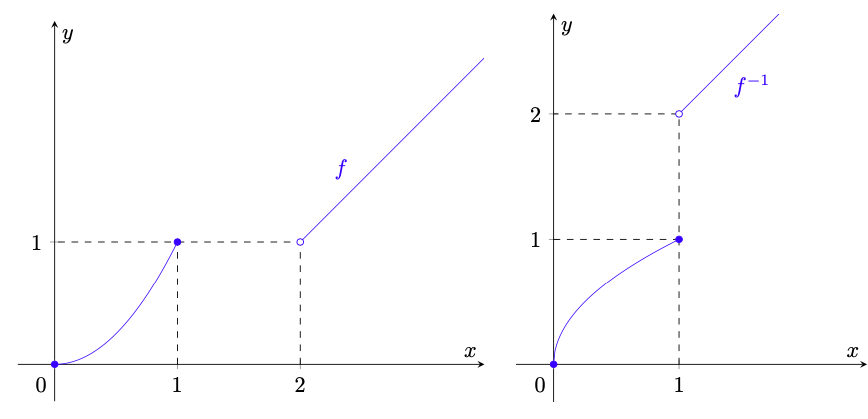
Figura 23: le funzioni $f$ e $f^{-1}$ dell’esempio 5.17. Nonostante $f$ sia continua e invertibile, poiché il suo dominio non è un intervallo, la sua inversa $f^{-1}$ possiede una discontinuità di salto.

$\quad$

Esempio 5.18 (inversa con discontinuità di seconda specie). Sia $f \colon (-\infty,-1] \cup (0,+\infty) \to \mathbb{R}$ la funzione definita da

(72) $\begin{equation*} f(x) = \begin{cases} x+1 & \text{se } x \in (-\infty,-1]\\[7pt] \dfrac{1}{x} & \text{se } x \in (0,+\infty), \end{cases} \end{equation*}$

rappresentata a sinistra in figura 24.

$\quad$

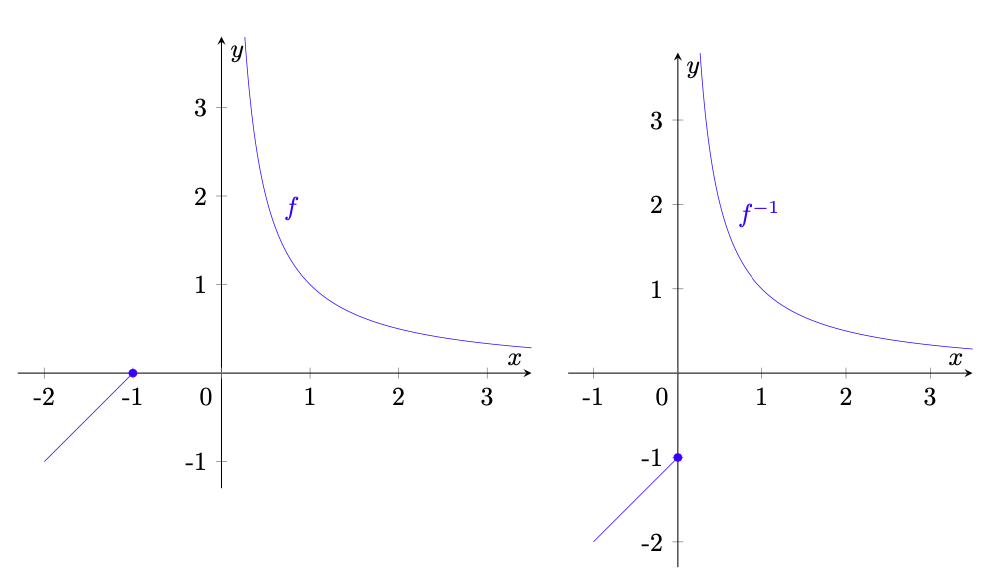
Figura 24: le funzioni $f$ e $f^{-1}$ (rispettivamente a sinistra e a destra) dell’esempio 5.18. Si vede che $f$ è continua e invertibile ma la sua inversa $f^{-1}$ possiede una discontinuità di seconda specie.

$\quad$

La funzione $f$ è strettamente crescente in $(-\infty,-1]$ e strettamente decrescente in $(0,+\infty)$ . Inoltre

(73) $\begin{equation*} f(-1)=0, \qquad \lim_{x \to +\infty}f(x) = 0, \end{equation*}$

da cui segue

(74) $\begin{equation*} f((-\infty,-1]) \subseteq (-\infty,0], \qquad f((0,+\infty)) \subseteq (0,+\infty). \end{equation*}$

Quindi $f$ è iniettiva. Dato che

(75) $\begin{equation*} \lim_{x \to - \infty}f(x)=-\infty, \qquad \lim_{x \to 0^+} f(x)=+\infty, \end{equation*}$

dal teorema 5.9 si ha

(76) $\begin{equation*} f((-\infty,-1]) = (-\infty,0], \qquad f((0,+\infty)) = (0,+\infty), \end{equation*}$

dunque $\operatorname{Im}f= \mathbb{R}$ e quindi $f$ è suriettiva, perciò è invertibile. La sua inversa, ossia la funzione $f^{-1}\colon \mathbb{R} \to (-\infty,-1] \cup (0,+\infty)$ rappresentata a destra in figura 24, possiede un punto di discontinuità di seconda specie in $x=0$ in quanto

(77) $\begin{equation*} \lim_{x \to 0^+} f(x)=+\infty. \end{equation*}$

Funzioni radici n-esime e logaritmo.

Come applicazione dei precedenti risultati, mostriamo ora l’invertibilità di alcune funzioni elementari, provando inoltre la continuità delle loro inverse. Ciò permetterà di definire l’esistenza e le proprietà delle funzioni radice $n$ -esima e di logaritmo. Sebbene molto probabilmente il lettore conosca già queste nozioni, sottolineiamo che esse rispondono alle domande seguenti, che affrontano l’inversione delle funzioni potenza a esponente intero ed esponenziale.

Domanda 5.19. Dati $n \in \mathbb{N}$ e $a \in \mathbb{R}$ , esiste $b$ $\in \mathbb{R}$ tale che $b^n=a$ ? Dati $a,y \in \mathbb{R}$ , esiste $x \in \mathbb{R}$ tale che $a^x=y$ ? Tali $b,x$ sono univocamente determinati? Si può inoltre dire che essi variano con continuità in funzione dei numeri $a$ e $y$ ?

Per quanto il lettore sia abituato alle risposte note quali radici $n$ -esime e logaritmi, occorre osservare che la loro esistenza e le loro proprietà non sono scontate e seguono fondamentalmente dalla continuità delle funzioni potenza ed esponenziale.

L’idea degli argomenti che permettono di ottenere le risposte alle domande di sopra risiede nell’uso del teorema dei valori intermedi per mostrare la suriettività di funzioni continue definite su intervalli. Poiché spesso l’iniettività di tali funzioni viene ottenuta da considerazioni elementari riguardo la loro monotonia, ciò permette di dedurne l’invertibilità.

Cominciamo dall’inversa della funzione potenza a esponente naturale, detta radice $n$ -esima.

Proposizione 5.20 (invertibilità delle potenze $n$ -esime). Sia $n \in \mathbb{N}$ .

$\quad$

Se $n$ è pari, allora per ogni $a \in [0,+\infty)$ esiste un unico $b \in [0,+\infty)$ tale che $b^n=a$ .

Se $n$ è dispari, allora per ogni $a \in \mathbb{R}$ esiste un unico $b \in \mathbb{R}$ tale che $b^n=a$ .

In particolare, le funzioni potenza $n$ -esima definite da

(78) $\begin{equation*} \begin{aligned} f_n \colon x \in [0,+\infty) \mapsto & \,\,x^n \in [0,+\infty) \qquad \text{se $n$ è pari}, \\ f_n \colon x \in \mathbb{R} \mapsto& \,\, x^n \in \mathbb{R} \qquad \qquad \text{se $n$ è dispari} \end{aligned} \end{equation*}$

sono invertibili e le loro inverse sono continue.

$\quad$

Dimostrazione. Le funzioni $f_n$ definite in (78) e rappresentate nella colonna di sinistra in figura 25 sono ovviamente strettamente monotone e quindi iniettive. Definendo

(79) $\begin{equation*} m_n\coloneqq \inf f_n, \quad M_n \coloneqq \sup f_n \qquad \forall n \in \mathbb{N}, \end{equation*}$

si ha

(80) $\begin{equation*} (m_n,M_n) = \begin{cases} (0,+\infty) & \text{se } n \text{ è pari}\\ \mathbb{R} & \text{se } n \text{ è dispari}. \end{cases} \end{equation*}$

Se $b \in (m_n,M_n)$ , dalla continuità delle funzioni $f_n$ provata nella proposizione 2.7 e dal teorema 5.9 segue l’esistenza di $b$ tale che $b^n=a$ e quindi la suriettività delle funzioni $f_n$ , che risultano dunque invertibili con inverse $f_n^{-1}$ . Per il teorema 5.15, le funzioni $f_n^{-1}$ sono continue.

$\quad$

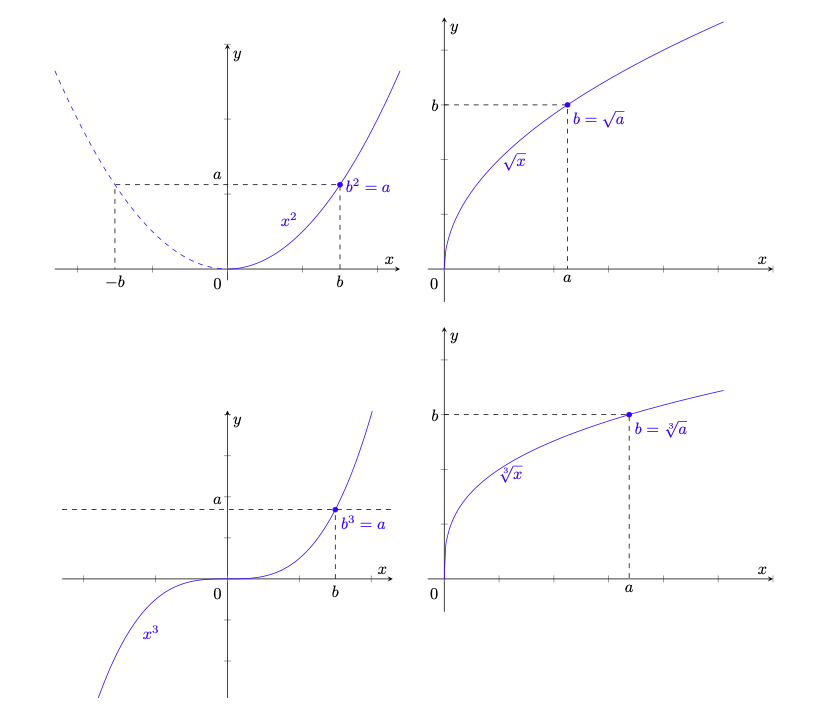
Figura 25: a sinistra, rispettivamente in alto e in basso, le funzioni $x \mapsto x^2$ e $x \mapsto x^3$ . A destra, rispettivamente in alto e in basso, le loro inverse $x \mapsto \sqrt{x}$ e $x \mapsto \sqrt[3]{x}$ . Il punto $b$ , soddisfacente $b^n=a$ è la radice $n$ -esima di $a$ .

$\quad$

La proposizione 5.20 motiva la seguente definizione, probabilmente già familiare al lettore.

Definizione 5.21 (radice $n$ -esima). Sia $n \in \mathbb{N}$ e sia $a \in \mathbb{R}$ se $n$ è dispari, altrimenti sia $a \in [0,+\infty)$ se $n$ è pari. L’unico numero $b \in \mathbb{R}$ fornito dalla proposizione 5.20 tale che $b^n=a$ viene detto radice $n$ -esima di $a$ e viene denotato con il simbolo $\sqrt[n]{a}$ .

La funzione continua $f_n^{-1}$ inversa della funzione $f_n$ definita in (78), che associa al numero reale $a$ la sua radice $n$ -esima, è detta funzione radice $n$ -esima.

$\quad$

I grafici di tali funzioni sono riportati a destra in figura 25.

Utilizzando gli stessi strumenti, proseguiamo mostrando l’invertibilità della funzione esponenziale, che implica l’esistenza e la continuità della funzione logaritmo.

Proposizione 5.22 (invertibilità della funzione esponenziale). Sia $a \in (0,1) \cup (1,+\infty)$ . Allora per ogni $y_0 \in (0,+\infty)$ esiste un unico $x_0 \in \mathbb{R}$ tale che $a^{x_0}=y_0$ . In particolare, la funzione esponenziale $f_a \colon \mathbb{R} \to (0,+\infty)$ definita da

(81) $\begin{equation*} f_a(x)=a^x \qquad \forall x \in \mathbb{R} \end{equation*}$

è invertibile e la sua inversa $f_a^{-1}$ è continua.

$\quad$

Dimostrazione. Sia $a \in (0,1) \cup (1,+\infty)$ . La funzione $f_a$ definita in (81) e rappresentata a sinistra in figura 26 è strettamente crescente se $a>1$ e strettamente decrescente se $a \in (0,1)$ , in particolare è iniettiva. Poiché

(82) $\begin{equation*} 0= \inf_\mathbb{R} f_a, \quad +\infty = \sup_\mathbb{R} f_a, \end{equation*}$

se $y_0 \in (0,+\infty)$ , dalla continuità della funzione $f_a$ provata nella proposizione 2.12 e dal teorema 5.9, segue l’esistenza di $x_0 \in \mathbb{R}$ tale che $f_a(x)=a^{x_0}=y_0$ . Quindi $f_a$ risulta suriettiva e invertibile con inversa $f_a^{-1}$ , che è continua per il teorema 5.15.

$\quad$

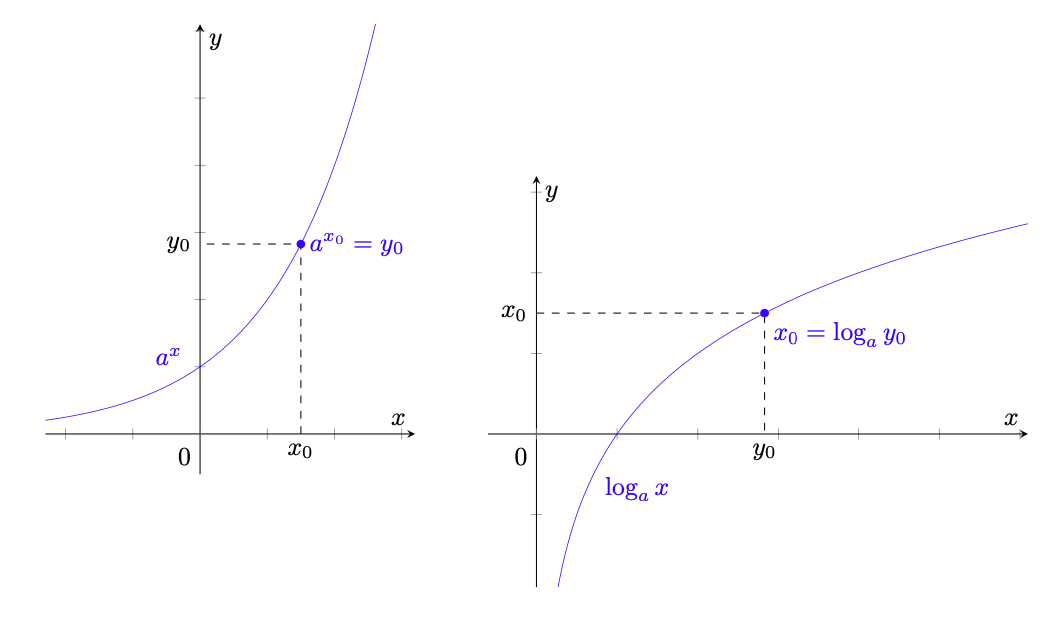
Figura 26: a sinistra la funzione esponenziale di base $a>1$ e a destra la sua inversa, la funzione $\log_a$ detta logaritmo in base $a$ . Dato $y_0>0$ , l’unico punto $x_0$ tale che $a^{x_0}=y_0$ è detto logaritmo in base $a$ di $y_0$ e indicato con $\log_a y_0$ .

$\quad$

La proposizione 5.20 permette di dare la seguente definizione di logaritmo, anch’essa probabilmente già nota al lettore.

Definizione 5.23 (logaritmi). Sia $a \in (0,1) \cup (1,+\infty)$ e sia $y_0 \in (0,+\infty)$ . L’unico numero $x_0 \in \mathbb{R}$ fornito dalla proposizione 5.22 tale che $a^{x_0}=y_0$ viene detto logaritmo in base $a$ di $y_0$ e viene denotato con il simbolo $\log_a y_0$ .

La funzione continua $f_a^{-1} \colon (0,+\infty) \to \mathbb{R}$ definita da

(83) $\begin{equation*} f_a^{-1}\colon y \in (0,+\infty) \mapsto \log_a(y) \in \mathbb{R}, \end{equation*}$

inversa della funzione esponenziale $f_a$ definita in (81) è detta funzione logaritmica e viene indicata con lo stesso simbolo $\log_a$ .

Se $a=e$ , con $e$ il numero di Nepero, $\log_e y$ è detto logaritmo naturale, denotato con $\log y$ .

$\quad$

Il grafico della funzione $\log_a$ è riportato a destra in figura 26. Dalla discussione precedente segue inoltre il seguente risultato.

Proposizione 5.24. Siano $f,g \colon A \subseteq \mathbb{R} \to \mathbb{R}$ funzioni continue con $f>0$ . Allora la funzione $f^g$ è continua.

$\quad$

Dimostrazione. Si ha

(84) $\begin{equation*} f(x)^{g(x)} = e^{\log (f(x)^{g(x)})} = e^{g(x) \log (f(x))} \qquad \forall x \in A, \end{equation*}$

dove nella prima uguaglianza si è usato il fatto che la funzione $\log$ è l’inversa dell’esponenziale di base $e$ , mentre nella seconda si è usata la nota proprietà dei logaritmi $\log(a^b)=b \log a$ . Da (84), dalla proposizione 2.12 e dalla proposizione 5.22, segue che $f^g$ è composizione e prodotto di funzioni continue, quindi è continua.

Osservazione 5.25. Usando (84) e le proprietà dei limiti dei prodotti e delle composizioni di funzioni, si può mostrare più in generale che, se $\displaystyle \lim_{x \to x_0} f(x) = L$ e $\displaystyle\lim_{x \to x_0}g(x)=M$ , allora

(85) $\begin{equation*} \lim_{x \to x_0} f(x)^{g(x)} = L^M, \end{equation*}$

escludendo però i casi

(86) $\begin{equation*} L\in \{0,+\infty\},\,M=0, \quad \text{e} \quad L=1,\, M= \pm \infty, \end{equation*}$

che danno luogo a forme indeterminate. Invitiamo il lettore a svolgere per esercizio la dimostrazione.

Funzioni trigonometriche inverse

In questa sezione discutiamo i risultati di esistenza e continuità delle funzioni trigonometriche inverse. Ricordiamo che le funzioni $\sin x$ , $\cos x$ e $\tan x$ sono funzioni periodiche nei loro domini e dunque non ammettono un’inversa in quanto non sono iniettive; possiamo però considerare le relative restrizioni del dominio in cui tali funzioni sono strettamente monotone, e dunque iniettive per il lemma 5.14. La loro suriettività può essere dedotta come nelle proposizioni 5.20 e 5.22; pertanto non dimostriamo la prossima proposizione, invitando il lettore a ricostruire gli argomenti in questi casi.

Proposizione 5.26. Le funzioni $f\colon [-\dfrac{\pi}{2},\dfrac{\pi}{2}]\to [-1,1]$ , $g\colon [0,\pi]\to [-1,1]$ e $h\colon (-\dfrac{\pi}{2},\dfrac{\pi}{2})\to \mathbb{R}$ definite rispettivamente da

$\begin{aligned} f(x)=& \sin x \quad \forall x \in \left[-\frac{\pi}{2},\frac{\pi}{2}\right],\\ g(x)=&\cos x \quad \forall x \in \left[0,\pi\right],\\ h(x)=&\tan x \quad \forall x \in \left(-\frac{\pi}{2},\frac{\pi}{2}\right)\\ \end{aligned}$

sono invertibili e le loro inverse $f^{-1},g^{-1}, h^{-1}$ sono continue.

$\quad$

Le inverse $f^{-1},g^{-1}, h^{-1}$ prodotte dal precedente risultato rivestono notevole importanza nelle applicazioni e sono le cosiddette funzioni trigonometriche inverse.

Definizione 5.27 (funzioni trigonometriche inverse). Le funzioni continue

(87) $\begin{gather*} \arcsin = f^{-1} \colon [-1,1] \to \left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right], \\ \arccos = g^{-1} \colon [-1,1] \to \left[0, \pi\right] \\ \arctan = h^{-1} \colon \mathbb{R} \to \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right). \end{gather*}$

fornite dalla proposizione 5.26 sono dette rispettivamente arcoseno, arcocoseno e arcotangente.

$\quad$

Il prefisso $\operatorname{arc}$ nelle funzioni $\arcsin, \arccos, \arctan$ è giustificato dal fatto che esse, essendo le inverse delle restrizioni rispettivamente delle funzioni $\sin,\cos,\tan$ , forniscono l’arco $x_0$ di circonferenza associato a un determinato valore $y_0$ rispettivamente del seno, del coseno e della tangente, come chiarito dalla figura 27.

$\quad$

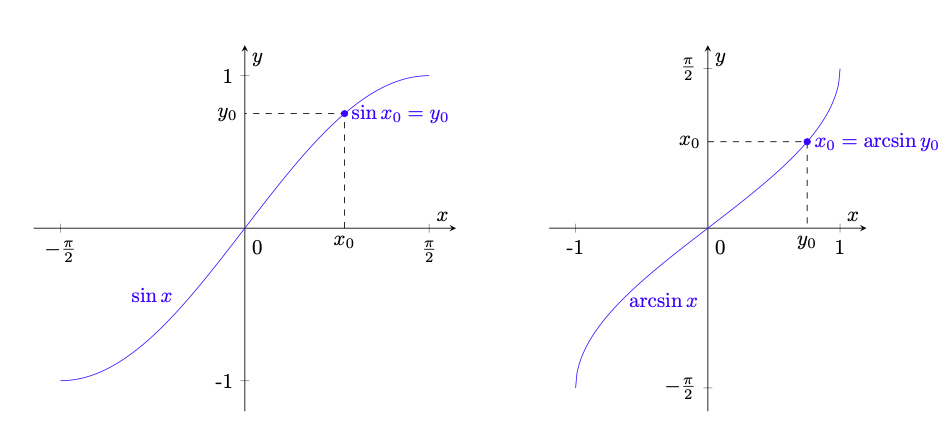
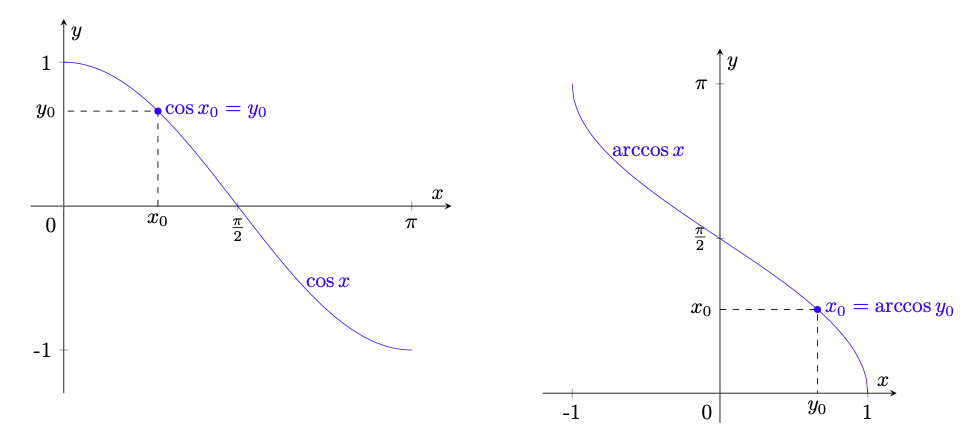
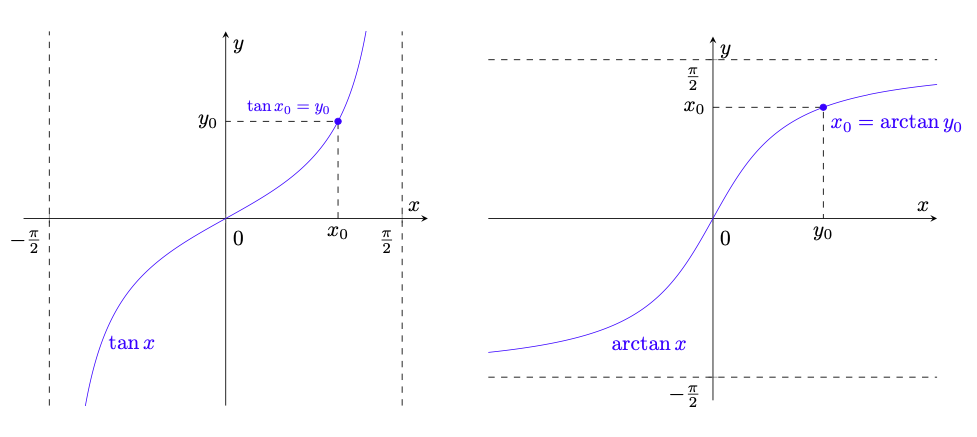
Figura 27: principali funzioni trigonometriche (nella colonna sinistra) e rispettive inverse (nella colonna destra).

$\quad$

Osservazione 5.28. Osserviamo che la scelta dei domini su cui restringiamo le funzioni trigonometriche per ottenere funzioni strettamente monotone è arbitraria. Difatti, essendo tali funzioni periodiche, si potrebbero definire le relative funzioni inverse su qualsiasi sottoinsieme del dominio in cui le funzioni sono monotone.

Massimi e minimi: il teorema di Weierstrass.

Prima di enunciare il teorema di Weierstrass, su cui si basa questa sezione, diamo la seguente definizione di massimi e minimi assoluti.

Definizione 5.29 (massimi e minimi assoluti). Sia $f \colon A \to \mathbb{R}$ una funzione. Un punto $x_M$ è detto punto di massimo assoluto per $f$ se

(88) $\begin{equation*} f(x) \leq f(x_M) \qquad \forall x \in A. \end{equation*}$

Il valore $f(x_M)$ è detto massimo assoluto di $f$ ed è indicato col simbolo $\max_A f$ .

Analogamente si definisce un punto di minimo $x_m$ e il valore minimo $f(x_m)=\min_A f$ di $f$ .

$\quad$

Osserviamo che, mentre il valore $\max_A f$ è unico, possono esistere molti (anche infiniti) punti di massimo assoluto.

Enunciamo ora un importante teorema che lega la continuità di una funzione all’esistenza di punti di massimo e minimo assoluti, illustrato in figura 28.

Teorema 5.30 (Weierstrass). Siano $a, b \in \mathbb{R}$ con $a \leq b$ e sia $f: [a,b] \to \mathbb{R}$ una funzione continua. Allora $f$ ammette massimo e minimo assoluti $[a,b]$ , ovvero esistono $x_m, x_M \in [a,b]$ tali che

$\begin{aligned} f(x_m) \leq f(x) \leq f(x_M) \qquad \forall x \in [a,b]. \end{aligned}$

$\quad$

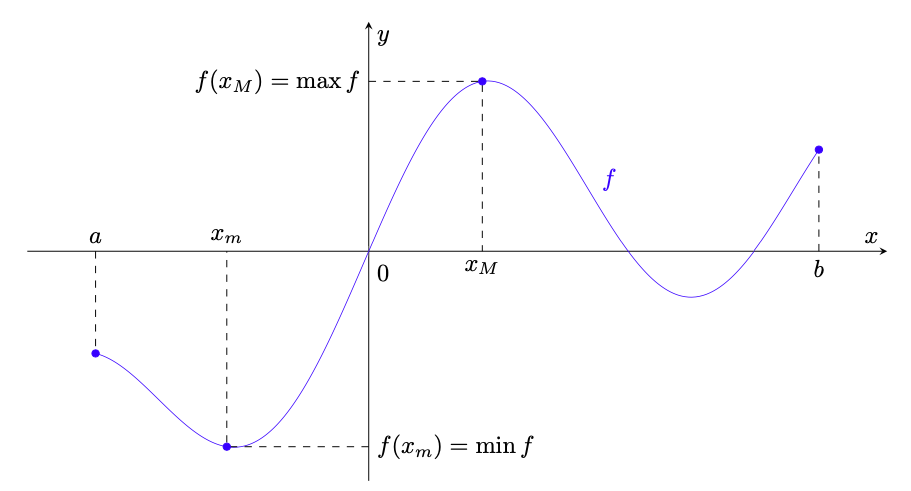
Figura 28: illustrazione del teorema di Weierstrass; la funzione $f \colon [a,b] \to \mathbb{R}$ è continua, quindi assume valori massimo e minimo, in corrispondenza rispettivamente dei punti $x_M,x_m \in [a,b]$ .

$\quad$

Dimostrazione. Sia $m = \inf_{[a,b]} f$ ; per definizione di estremo inferiore, esiste una successione $y_n \in \operatorname{Im} f$ tale che $y_n \to m$ . Poiché $y_n \in f([a,b])$ , esiste una successione $x_n \in [a,b]$ tale che

(89) $\begin{equation*} f(x_n) = y_n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Poiché $[a,b]$ è chiuso e limitato, per [14, teorema di Bolzano-Weierstrass], esiste una sottosuccessione $x_{n_k}$ convergente in $[a,b]$ , cioè esiste $x_m \in [a,b]$ tale che

(90) $\begin{equation*} \lim_{k \to \infty} x_{n_k}=x_m. \end{equation*}$

Si ha

(91) $\begin{equation*} f(x_m) = \lim_{k \to \infty} f(x_{n_k}) = \lim_{k \to \infty} y_{n_k} = m, \end{equation*}$

dove la prima uguaglianza segue dalla continuità di $f$ in $x_m$ e dal teorema 3.3, mentre la terza uguaglianza segue dal fatto che $y_n \to m$ e $y_{n_k}$ è una sottosuccessione di $y_n$ . L’equazione (91) mostra che $m \in f([a,b])$ (in particolare $m > - \infty$ ) e quindi $m=\min f$ .

Analogamente si mostra che $f$ ha massimo in $[a,b]$ .

Osservazione 5.31. Il teorema di Weierstrass si può enunciare e dimostrare in maniera analoga nel caso più generale in cui il dominio di $f$ sia un sottoinsieme chiuso e limitato di $\mathbb{R}$ .

Le ipotesi del teorema di Weierstrass sono tutte necessarie, come si evince dal seguente schema riassuntivo.

$\quad$

$\bullet$ chiusura del dominio Questa ipotesi è essenziale, come mostrato dall’esempio 5.32. Inoltre, l’esempio 5.33 prova che anche assumendo per ipotesi la limitatezza della funzione, essa può non assumere minimo e/o massimo.

$\bullet$ limitatezza del dominio L’esempio 5.34 mostra che, se il dominio della funzione è illimitato, essa può non assumere massimo oppure minimo. L’esempio 5.35 assicura che neppure la limitatezza della funzione basta ad ottenere l’esistenza del massimo e/o del minimo.

$\bullet$ continuità della funzione L’esempio 5.36 mostra che, anche se il dominio della funzione è chiuso e limitato, se questa non è continua può non assumere massimo o minimo.

Esempio 5.32 (dominio non chiuso). Sia $f \colon (0,1] \to \mathbb{R}$ la funzione definita da

(92) $\begin{equation*} f(x)=\dfrac{1}{x} \qquad \forall x \in (0,1], \end{equation*}$

rappresentata in figura 29, è continua e ammette valore minimo pari a $1$ , ma non ammette massimo. Infatti, è chiaro che $f$ è decrescente, quindi

(93) $\begin{equation*} f(x) \geq f(1) \qquad \forall x \in (0,1], \end{equation*}$

da cui segue, per la definizione 5.29, che $x=1$ è un punto di minimo per $f$ e che $1= \min_{(0,1]} f$ . D’altra parte, sempre per la monotonia di $f$ si ha che

(94) $\begin{equation*} \sup_{(0,1]} f = \lim_{x \to 0^+}f(x) = +\infty, \end{equation*}$

quindi $f$ non ammette valore massimo.

$\quad$

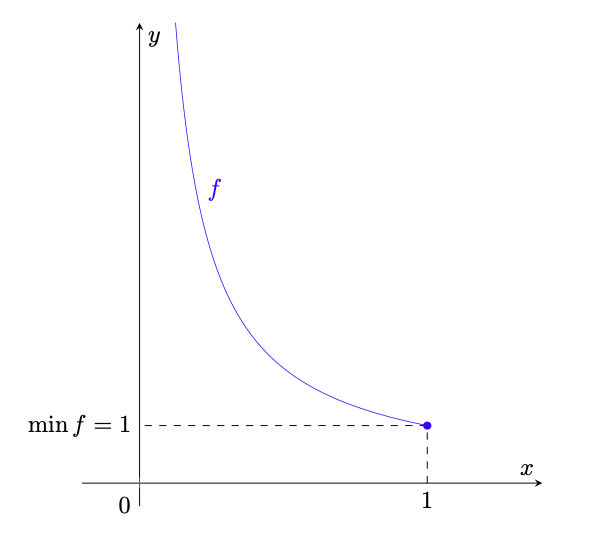
Figura 29: la funzione $f$ dell’esempio 5.32; si vede che $\min f=1$ (assunto in corrispondenza di $x=1$ ), ma che $f$ è illimitata superiormente, per cui non ammette massimo.

$\quad$

Esempio 5.33 (dominio non chiuso e funzione limitata). La funzione $f \colon (1,2] \to \mathbb{R}$ definita da $f(x)=x$ per ogni $x \in (1,2]$ è continua, limitata, ma non ammette minimo. Infatti

(95) $\begin{equation*} \max_{(1,2]} f = 2, \qquad \inf_{(1,2]} f = 1, \end{equation*}$

ma il valore $1$ non è assunto da $f$ , come mostrato in figura 30.

$\quad$

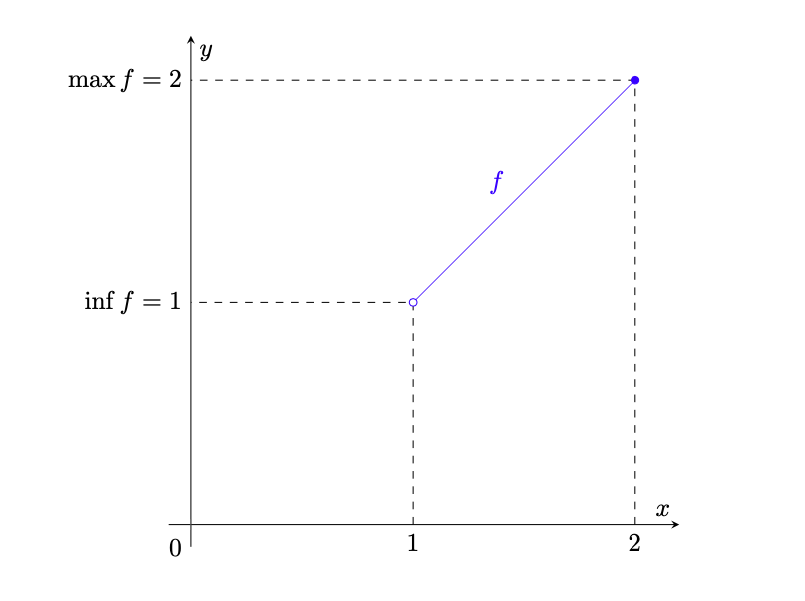
Figura 30: la funzione $f$ dell’esempio 5.33; si vede che $\max f=2$ (assunto in corrispondenza di $x=2$ ), ma che $f$ non ammette minimo in quanto il valore $1$ non appartiene all’immagine di $f$ .

$\quad$

Esempio 5.34 (dominio illimitato). La funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da $f(x)=x$ per ogni $x \in \mathbb{R}$ è continua, il suo dominio è chiuso, ma non ammette né massimo né minimo in quanto

(96) $\begin{equation*} \inf_\mathbb{R}f = -\infty, \qquad \sup_\mathbb{R}f = +\infty. \end{equation*}$

Esempio 5.35 (dominio illimitato e funzione limitata). La funzione $f \colon [1,+\infty) \to \mathbb{R}$ definita da

(97) $\begin{equation*} f(x)=\frac{1}{x} \qquad \forall x \in [1,+\infty) \end{equation*}$

(rappresentata in figura 31) è continua, il suo dominio è chiuso e

(98) $\begin{equation*} \max_{[1,+\infty)}f = 1, \qquad \inf_{[1,+\infty)}f = 0, \end{equation*}$

ma $f$ non ha minimo in quanto $f(x)>0$ per ogni $x \in [1,+\infty)$ .

$\quad$

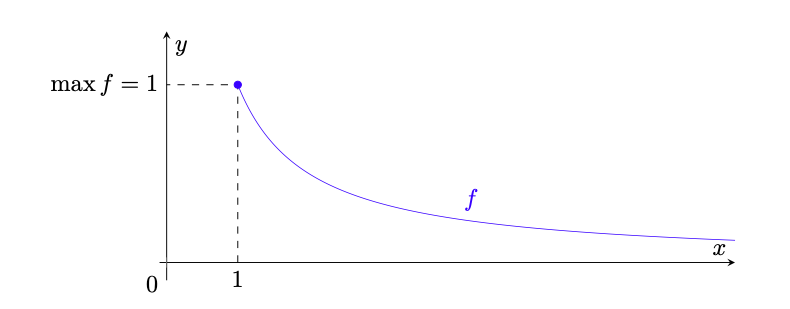
Figura 31: la funzione $f$ dell’esempio 5.35; si vede che $\max f=1$ (assunto in corrispondenza di $x=1$ ) e che $\inf f=0$ , ma poiché tale valore non è assunto $f$ non ammette minimo.

$\quad$

Esempio 5.36 (funzione non continua). La funzione $f \colon [-2,2] \to \mathbb{R}$ definita da

(99) $\begin{equation*} f(x)= \begin{cases} 0 & \text{se } x \in [-2,1] \cup [1,2]\\ x & \text{se } x \in (-1,1), \end{cases} \end{equation*}$

il cui grafico è mostrato in figura 32, è definita su un dominio chiuso e limitato, ha delle discontinuità di salto in $-1$ e $1$ e non ammette né massimo né minimo, infatti

(100) $\begin{equation*} \inf_{[-2,2]}f = -1, \qquad \sup_{[-2,2]}f = 1, \end{equation*}$

ma tali valori non appartengono all’immagine di $f$ .

$\quad$

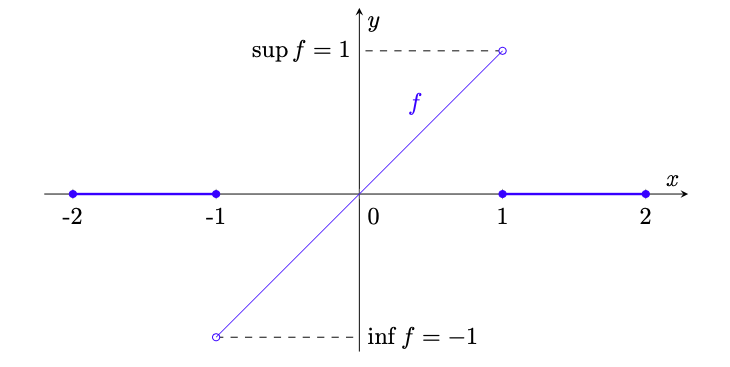
Figura 32: la funzione $f$ dell’esempio 5.36; si vede che $\inf f=-1$ e $\sup f=1$ , ma tali valore non sono assunti e quindi $f$ non ammette minimo. Si notino le discontinuità di salto di $f$ in $x=-1$ e $x=1$ .

$\quad$

Continuità uniforme e teorema di Heine-Cantor

Definizione ed esempi.

Introduciamo in questa sezione il concetto di “continuità uniforme”. Osserviamo che il concetto di continuità di una funzione è una proprietà locale: difatti, quando viene definita la continuità di una funzione in tutto il suo dominio si intende che tale funzione è continua in ogni suo punto.

Considerata una funzione $f\colon A\subseteq \mathbb{R}\to \mathbb{R}$ , ricordiamo dalla definizione 2.4 che essa è detta continua in $A$ se e solo se, per ogni $x_0 \in A$ e per ogni $\varepsilon>0$ , esiste $\delta=\delta(x_0,\varepsilon)>0$ tale che

(101) $\begin{equation*} |f(x)-f(x_0)| \qquad \forall x \in (x_0-\delta,x_0+\delta) \cap A. \end{equation*}$

Segue che la scelta di $\delta$ dipende sia da $\varepsilon$ che dal particolare punto $x_0$ in cui si vuole provare la continuità di $f$ . Il concetto di uniforme continuità, invece, è una proprietà globale. Esso infatti vuole slegare la scelta di $\delta$ dal particolare punto $x_0$ in questione. In altre parole, si desidera che la misura della variazione dei valori di $f(x)$ sia controllata solo dalla variazione della variabile $x$ e non dal particolare punto $x$ che si sta considerando.

Diamo ora la definizione rigorosa di uniforme continuità.

Definizione 6.1 (continuità uniforme). Sia $A\subseteq\mathbb{R}$ . Una funzione $f\colon A\rightarrow \mathbb{R}$ si dice uniformemente continua in $A$ se se per ogni $\varepsilon>0$ esiste $\delta>0$ tale che

(102) $\begin{equation*} x,y \in A, \;|x-y| < \delta \quad \Longrightarrow \quad|f(x)-f(y)|<\varepsilon. \end{equation*}$

$\quad$

Osservazione 6.2. Una funzione $f\colon A \to \mathbb{R}$ è quindi uniformemente continua se la distanza $|f(x)-f(y)|$ si controlla solo con la distanza $|x-y|$ tra $x,y$ indipendentemente dai punti $x,y$ scelti ed è infinitesima per $|x-y|\to 0$ . In altre parole, se esiste una funzione $\sigma \colon [0,+\infty) \to (0,+\infty)$ soddisfacente $\lim_{t \to 0} \sigma(t)=0$ e tale che

(103) $\begin{equation*} |f(x)-f(y)| \leq \sigma(|x-y|) \qquad \forall x,y \in A. \end{equation*}$

Una tale funzione $\sigma$ viene anche detta un modulo di continuità della funzione $f$ . Intuitivamente quindi, il modulo di continuità $\sigma$ “quantifica” la continuità di $f$ esprimendo quanto possano essere distanti al massimo $f(x)$ e $f(y)$ in base alla distanza $|x-y|$ .

Facciamo qualche esempio di funzioni uniformemente continue e analizziamo il legame tra la continuità uniforme e semplice.

Esempio 6.3. Le funzioni $\sin \colon \mathbb{R} \to \mathbb{R}$ e $\cos \colon \mathbb{R} \to \mathbb{R}$ sono uniformemente continue. Infatti, dalle dimostrazioni delle proposizioni 2.9 e 2.10, segue che

(104) $\begin{equation*} |x-y| < \varepsilon \qquad \Longrightarrow \qquad |\sin x - \sin y|< \varepsilon, \quad |\cos x - \cos y|< \varepsilon. \end{equation*}$

Quindi, per le funzioni $\sin$ e $\cos$ , il $\delta$ nella definizione 6.1 può essere scelto pari a $\varepsilon$ .

Esempio 6.4. La funzione $f \colon [0,+\infty) \to \mathbb{R}$ definita da

(105) $\begin{equation*} f(x) = \sqrt{x} \qquad \forall x \in [0,+\infty) \end{equation*}$

è uniformemente continua. Infatti, siano $a,b \in [0,+\infty)$ con $a<b$ ; si ha

(106) $\begin{equation*} |f(b)-f(a)| = \sqrt{ (f(b)-f(a))^2 } = \sqrt{ b-2\sqrt{ab}+a } \leq \sqrt{ b-a}, \end{equation*}$

dove la disuguaglianza deriva da $\sqrt{ab}\geq a$ . La disuguaglianza (106) (illustrata in figura 33) mostra che un modulo di continuità per $f$ esiste ed è la funzione $f$ stessa, provando quindi che $f$ è uniformemente continua.

Per vedere ciò esplicitamente, fissiamo $\varepsilon>0$ ; se $|a-b|<\varepsilon^2$ , dalla disuguaglianza (106) segue che

(107) $\begin{equation*} |f(a)-f(b)| \leq \sqrt{|a-b|} \leq \sqrt{\varepsilon^2} = \varepsilon, \end{equation*}$

che mostra che $f$ è uniformemente continua.

$\quad$

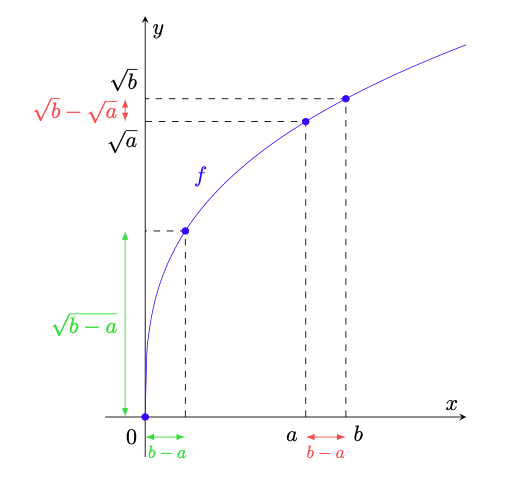
Figura 33: la funzione $f$ dell’esempio 6.4. Si noti come $\sqrt{b}-\sqrt{a} \leq \sqrt{b-a}$ .

$\quad$

Relazione con la continuità

In questa sezione indaghiamo la relazione tra continuità uniforme e continuità semplice, riassunti dall’osservazione seguente.

Osservazione 6.5. L’uniforme continuità implica la continuità di una funzione in quanto per ogni punto $x \in A$ e per ogni $\varepsilon>0$ , basta scegliere il $\delta$ dato dalla definizione 6.1 in 2.4. Tuttavia non vale il viceversa, come mostrato dai seguenti controesempi.

Esempio 6.6. Consideriamo la funzione $f\colon \mathbb{R}\to \mathbb{R}$ tale che $f(x)=x^2$ per ogni $x\in \mathbb{R}$ , rappresentata in figura 34. Sappiamo già che tale funzione è continua e proviamo che non è uniformemente continua. Negando la definizione di uniforme continuità, ciò si traduce nel dimostrare la seguente proprietà:

(108) $\begin{equation*} \exists \varepsilon>0\colon \;\forall \delta>0\;\exists x,y\in A\colon \\ |x-y| < \delta \text{ e } |f(x)-f(y)|\geq \varepsilon. \end{equation*}$

Fissiamo $\varepsilon=1$ e sia $\delta>0$ , consideriamo $x=\dfrac{1}{\delta}\text{ e } y=\dfrac{\delta}{2}+\dfrac{1}{\delta}$ . Chiaramente $|x-y|=\dfrac{\delta}{2}<\delta$ ma

$|f(x)-f(y)|=\left|\dfrac{1}{\delta^2}-\left(\dfrac{\delta}{2}+\frac{1}{\delta}\right)^2\right|=\left \vert \dfrac{\delta^2}{4}+1\right \vert>1.$

Dunque, abbiamo dimostrato che vale (108) in corrispondenza di $\varepsilon = 1$ .

$\quad$

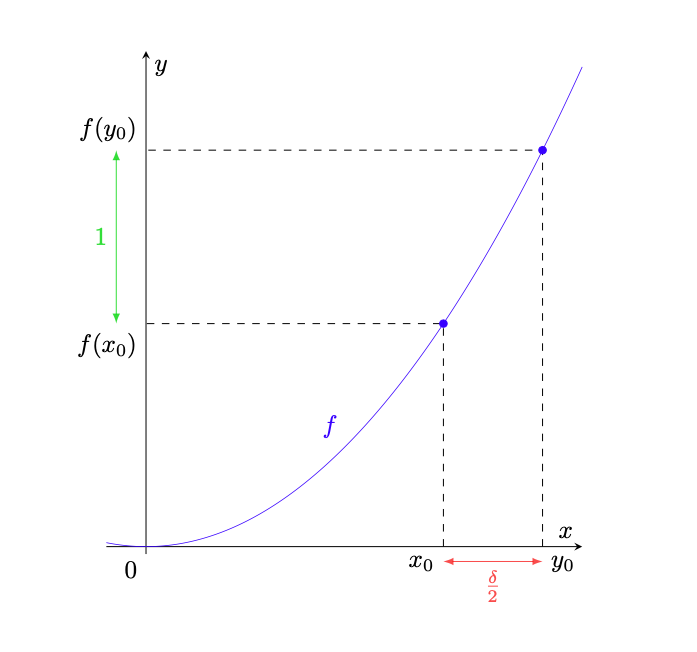
Figura 34: la funzione $f$ dell’esempio 6.6. Poiché la pendenza del grafico $f$ aumenta al crescere di $x$ , per $x$ molto grandi si riesce a trovare $x_0$ e $y_0$ a distanza $\delta/2$ (con $\delta$ arbitrariamente piccolo), ma tali che $f(x_0)$ e $f(y_0)$ hanno distanza $1$ . Ciò mostra che $f$ non è uniformemente continua.

$\quad$

Anche se il dominio di una funzione continua $f$ è limitato, essa può non essere uniformemente continua, come mostra il prossimo esempio.

$\quad$

Figura 35: la funzione $f$ dell’esempio 6.7. Poiché $\lim_{x \to 0^+}f(x)=+\infty$ , per ogni $n \in \mathbb{N}$ esistono punti a distanza $\dfrac{1}{n}$ le cui immagini hanno distanza $n;$ quindi $f$ non è uniformemente continua.

$\quad$

Esempio 6.7. La funzione $f \colon (0,1] \to \mathbb{R}$ definita da

(109) $\begin{equation*} f(x) = \dfrac{1}{x} \qquad \forall x \in (0,1] \end{equation*}$

e rappresentata nella figura 35 è continua per la proposizione 2.7, ma non è uniformemente continua.

Mostriamo infatti che non esiste alcun $\delta>0$ tale che

(110) $\begin{equation*} |x-y| < \delta \Rightarrow |f(x)-f(y)|<1. \end{equation*}$

Sia quindi $\delta >0$ e sia $n \in \mathbb{N}$ tale che $\dfrac{1}{2n}< \delta$ . Scegliendo $x=\dfrac{1}{n}$ e $y= \dfrac{1}{2n}$ si ha

(111) $\begin{equation*} |x-y|= \frac{1}{2n} \qquad \text{e} \qquad |f(x)-f(y)| = 2n-n=n \geq 1. \end{equation*}$

La situazione non cambia anche se la funzione $f$ è limitata.

Esempio 6.8. Si consideri la funzione $f \colon (0,1] \to \mathbb{R}$ definita da

(112) $\begin{equation*} f(x) = \sin \left( \dfrac{1}{x} \right) \qquad \forall x \in (0,1], \end{equation*}$

rappresentata in figura 36.

$\quad$

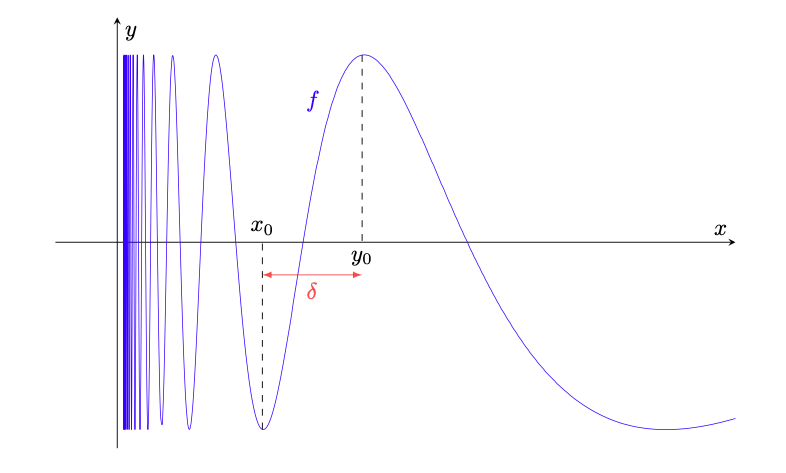
Figura 36: la funzione $f$ dell’esempio 6.8. Poiché i punti in cui $f$ assume valori $-1$ e $1$ si accumulano verso l’origine, si possono esibire $x_0$ e $y_0$ arbitrariamente vicini tali che $f(x_0)=-1$ e $f(y_0)=1$ . Quindi $f$ non è uniformemente continua.

$\quad$

Essa è continua perché composizione e rapporto di funzioni continue il cui denominatore non si annulla. Ciononostante, anche se il suo dominio è limitato, essa non è uniformemente continua. Infatti, $f$ assume infinite volte i valori $-1$ e $1$ in un intorno dell’origine. Ciò implica che, qualunque sia $\delta>0$ , esistono $x_0,y_0 \in [0,1]$ tali che

(113) $\begin{equation*} |x_0-y_0| < \delta, \qquad |f(x_0)-f(y_0)|=2. \end{equation*}$

Ciò prova che $f$ non è uniformemente continua.

Una funzione uniformemente continua possiede un tasso di crescita al più affine, come precisa la prossima proposizione. Tale comportamento differisce da quello delle funzioni continue che, come evidente dall’esempio 6.6, possono non rispettare questa condizione.

Proposizione 6.9. Sia $A \subseteq \mathbb{R}$ e sia $f \colon A \to \mathbb{R}$ una funzione uniformemente continua. Allora esistono $a,b\geq 0$ tali che

(114) $\begin{equation*} |f(x)| \leq a + b|x| \qquad \forall x \in A. \end{equation*}$

$\quad$

Dimostrazione. Sia $x_0 \in A$ , si fissi $\varepsilon>0$ e sia $\delta>0$ dato dalla definizione di uniforme continuità di $f$ . Per ogni $x \in A$ con $x > x_0$ , esiste $n \in \mathbb{N}$ tale che

(115) $\begin{equation*} (n-1) \delta < |x-x_0| \leq n \delta. \end{equation*}$

Poiché $f$ è uniformemente continua, abbiamo

(116) $\begin{equation*} |f(x_0+k \delta) - f(x_0 + (k-1) \delta)| < \varepsilon \quad \forall k \leq n-1, \qquad |f(x) - f(x_0+(n-1) \delta)| < \varepsilon. \end{equation*}$

Da ciò segue che

(117) $\begin{equation*} |f(x)- f(x_0)| \leq |f(x) - f(x_0+(n-1) \delta)| + \sum_{k=1}^{n-1} |f(x_0+k \delta) - f(x_0 + (k-1) \delta)| \leq n \varepsilon \end{equation*}$

e dunque

(118) $\begin{equation*} |f(x)| \leq |f(x_0)| + \varepsilon \leq |f(x_0)| + \varepsilon + \dfrac{|x-x_0|}{\delta} \leq \Big( |f(x_0)| + \varepsilon + \dfrac{|x_0|}{\delta} \Big)+ \dfrac{|x|}{\delta}. \end{equation*}$

Ponendo

(119) $\begin{equation*} a \coloneqq |f(x_0)| + \varepsilon + \dfrac{|x_0|}{\delta}, \qquad b \coloneqq \dfrac{1}{\delta}, \end{equation*}$

per l’arbitrarietà di $x > x_0$ si ottiene la tesi (il caso $x < x_0$ è analogo).

Il teorema di Heine-Cantor.

Abbiamo evidenziato nell’osservazione 6.5 che una funzione continua non è necessariamente uniformemente continua. I domini delle funzioni continue mostrate negli esempi sono illimitati o non chiusi e quindi ci si chiede se particolari proprietà geometriche del dominio, insieme alla continuità della funzione, possano implicare l’uniforme continuità.

Il teorema di Heine-Cantor risponde a questa domanda. Tale risultato afferma che ogni funzione continua definita su un insieme chiuso e limitato $A\subset \mathbb{R}$ è anche uniformemente continua, fornendo dunque una condizione sufficiente affinché una funzione continua sia anche uniformemente continua. Ne forniamo prima una versione su intervalli (teorema 6.10) che fa uso del teorema di Bolzano-Weierstrass, per poi studiarne una dimostrazione di carattere topologico, con cui ne proveremo la generalizzazione a insiemi chiusi e limitati (teorema 6.16).

Teorema 6.10 (Heine-Cantor). Siano $a,b\in \mathbb{R}$ e sia $f\colon [a,b]\rightarrow \mathbb{R}$ una funzione continua. Allora $f$ è uniformemente continua.

$\quad$

Dimostrazione. Supponiamo per assurdo che $f$ non sia uniformemente continua, cioè che esista $\varepsilon>0$ tale che

$\forall n \in \mathbb{N}\quad \exists x_n,y_n \in A \colon \qquad |x_n-y_n|<\frac{1}{n} \quad \text{e} \quad |f(x_n)-f(y_n)|\geq \varepsilon.$

Dato che la successione $x_n$ è limitata, per il teorema di Bolzano-Weiestrass esiste una sottosuccessione $x_{n_k}$ convergente a un numero reale $\ell$ , che appartiene ad $[a,b]$ in quanto tale insieme è chiuso. Poiché $|x_n-y_n|< \dfrac{1}{n}$ per ogni $n \in \mathbb{N}$ , si ha

(120) $\begin{equation*} x_{n_k} - \dfrac{1}{n_k} < y_{n_k} < x_{n_k} + \dfrac{1}{n_k} \qquad \forall k \in \mathbb{N}. \end{equation*}$

Da ciò deriva, per il teorema del confronto, che anche $y_{n_k}$ converge a $\ell$ . Poiché per ipotesi $f$ è continua, per il teorema 3.2 si ha che

$\lim_{k \to +\infty} f(x_{n_k})=\lim_{k \to +\infty}f(y_{n_k})=f(\ell).$

Questo contraddice l’assunzione

$|f(x_{n_k})-f(y_{n_k})|\geq\varepsilon \quad \forall k\in \mathbb{N},$

dimostrando il teorema.

Approfondimento: il punto di vista topologico

Forniamo adesso una dimostrazione alternativa del teorema di Heine-Cantor di carattere topologico, che non fa uso delle successioni e del teorema di Bolzano-Weierstrass.

Fin’ora abbiamo lavorato con intervalli chiusi e limitati di $\mathbb{R}$ . Per estendere i risultati già discussi introduciamo alcuni concetti topologici, a partire dalla definizione di insieme aperto.

Definizione 6.11 (insieme aperto). Sia dato un sottoinsieme $A\subseteq \mathbb{R}$ . Si dice che $A$ è aperto se per ogni $x \in A$ esiste $r>0$ tale che

$(x-r,x+r) \subseteq A.$

$\quad$

Diamo ora la definizione topologica di insieme compatto, a partire da quella di ricoprimenti aperti.

Definizione 6.12 (ricoprimento aperto). Sia dato un sottoinsieme $A\subseteq \mathbb{R}$ . Si dice ricoprimento aperto di $A$ una qualunque famiglia di sottoinsiemi aperti $\{U_i\}_{i\in I}$ di $\mathbb{R}$ con la proprietà che

$A\subseteq\bigcup_{i\in I}U_i.$

$\quad$

Definizione 6.13 (compattezza). Un sottoinsieme $A\subset \mathbb{R}$ si dice compatto se per ogni ricoprimento aperto $\{U_i\}_{i\in I}$ di $A$ esiste un sottoricoprimento finito, ovvero un sottoinsieme di indici $J\subseteq I$ , con $J$ finito, tale che

$A\subseteq\bigcup_{i\in J}U_i.$

$\quad$

Vediamo un esempio di insieme non compatto e poi enunciamo un teorema che caratterizza tali insiemi.

Esempio 6.14 Sia $A=(0,1]$ . Per ogni $n\in\mathbb{N}$ definiamo $U_n=\big(\dfrac{1}{n},2\big)$ . La famiglia di insiemi $\{U_n\}_{n\in \mathbb{N}}$ è un ricoprimento aperto di $A$ che non ammette un sottoricoprimento finito, ovvero per cui non esiste un sottoinsieme finito di indici $J\subseteq I$ tale che

$A\subseteq\bigcup_{i\in J}U_i.$

Infatti, se un tale $J$ esistesse, allora preso $n_0\coloneqq \max{J}$ , si avrebbe che

$A=(0,1]\subset\bigcup_{i\in J}U_i = \Big(\frac{1}{n_0},2\Big).$

Questo è evidentemente un assurdo.

La compattezza in $\mathbb{R}$ si caratterizza con la chiusura e la limitatezza, come mostra il prossimo risultato di cui omettiamo la dimostrazione (si veda [10, teorema 2.41] in cui si trova un enunciato più generale in $\mathbb{R}^N$ ).

Teorema 6.15 (Heine-Borel). Un sottoinsieme $A\subset \mathbb{R}$ è compatto se e solo se è chiuso e limitato.

$\quad$

Diamo adesso una dimostrazione diretta del teorema di Heine-Cantor che fa uso della definizione di compattezza.

Teorema 6.16 (Heine-Cantor). Sia $A\subset\mathbb{R}$ un insieme compatto. Se $f\colon A\rightarrow \mathbb{R}$ è una funzione continua, allora $f$ è uniformemente continua.

$\quad$

Dimostrazione. Poiché $f$ è continua, sappiamo che, fissato $\varepsilon>0$ , si ha che

(121) $\begin{equation*} \forall x\in A \; \exists \delta_{x}>0\colon \;y\in(x-2\delta_x,x+2\delta_x)\cap A\Rightarrow|f(x)-f(y)|<\frac{\varepsilon}{2}. \end{equation*}$

Osserviamo che la famiglia $\{(x-\delta_x,x+\delta_x)\}_{x\in A}$ è un ricoprimento aperto di $A$ , in quanto ogni $x \in A$ è contenuto in qualcuno degli intervalli della famiglia. Pertanto, essendo $A$ compatto, per la definizione 6.13 esiste un sottoinsieme finito $\{x_1,\dots,x_n\}\subseteq A$ tale che

(122) $\begin{equation*} A\subseteq\bigcup_{i=1}^{n}{(x-\delta_{x_i},x+\delta_{x_i})}. \end{equation*}$

Vogliamo trovare un $\delta>0$ tale che, presi $x,y \in A$ tali che $|x-y|<\delta$ , risulti $|f(x)-f(y)|<\varepsilon$ . A tal fine poniamo

$\delta\coloneqq \min_{1\leq i\leq n}\delta_{x_i}>0$

e fissiamo $x,y\in A$ tali che $|x-y|<\delta$ . Notiamo che, grazie alla (122), sicuramente esiste un $i\in \{1, \dots,n\}$ tale che

(123) $\begin{equation*} |x-x_i|<\delta_{x_i}, \end{equation*}$

inoltre, per la disuguaglianza triangolare, si ha che

(124) $\begin{equation*} |y-x_i|\leq |x-x_i|+|x-y|<\delta_{x_i}+ \delta\leq 2\delta_{x_i}. \end{equation*}$

Per la (121) e la (123) abbiamo che

$|f(x)-f(x_i)|<\frac{\varepsilon}{2},$

mentre da (121) e (124) segue che

$|f(y)-f(x_i)|<\frac{\varepsilon}{2}.$

Per concludere ci basta notare che, applicando nuovamente la disuguaglianza triangolare, si ha:

$|f(x)-f(y)|\leq |f(y)-f(x_i)|+|f(x)-f(x_i)|<\varepsilon.$

Ciò prova l’uniforme continuità di $f$ su $A$ .

In questa dispensa diamo la definizione di compattezza come nella definizione 6.13 utilizzando i ricoprimenti; per questo, viene chiamata anche “compattezza per ricoprimenti”. In particolare, questa terminologia è necessaria poiché esiste anche una definizione di “compattezza sequenziale”.

Definizione 6.18 (compatezza sequenziale). Sia $A\subset \mathbb{R}$ . Diremo che $A$ è compatto sequenzialmente se e solo se ogni successione a valori in $A$ ammette una sottosuccessione convergente a un punto di $A$ .

$\quad$

Tuttavia in $\mathbb{R}$ (e in generale in ogni spazio metrico) le due definizioni sono equivalenti. Per ulteriori approfondimenti si rimanda a [7].

Funzioni lipschitziane.

Abbiamo introdotto la proprietà di uniforme continuità come proprietà globale. Introduciamo ora un ulteriore concetto legato, intuitivamente, al “controllo” nell’incremento di una funzione, che risulta un caso particolare delle funzioni uniformemente continue.

Una funzione lipschitziana è una funzione per cui il rapporto tra la distanza tra i valori della funzione e la distanza tra i punti del dominio è limitato da un numero reale non-negativo detto “costante di Lipschitz”, che prende il nome dal matematico tedesco Rudolf Lipschitz (1832-1903).

Definizione 6.19 (funzione lipschitziana). Sia $A\subseteq\mathbb{R}$ . Una funzione $f\colon A\rightarrow \mathbb{R}$ si dice lipschitziana se esiste una costante $L \geq 0$ tale che

(125) $\begin{equation*} |f(x)-f(y)|\leq L |x-y| \quad \forall x, y\in A. \end{equation*}$

Inoltre la più piccola costante $L$ che soddisfa tale condizione si dice costante di Lipschitz della funzione $f$ e si indica con $\operatorname{Lip}(f)$ .

Osservazione 6.20. Osserviamo che se $f\colon A\subseteq \mathbb{R}\to \mathbb{R}$ è lipschitziana, allora la costante di Lipschitz esiste sempre. Consideriamo infatti l’insieme

$D \coloneqq \{L\in [0,+\infty) \colon |f(x)-f(y)|\leq L |x-y| \quad \forall x, y\in A\}.$

Dobbiamo dimostrare che tale insieme $D$ ammette minimo, che è proprio la costante di Lipschitz. Osserviamo che $D\subseteq \mathbb{R}^+$ è non vuoto, poiché per ipotesi $f$ è lipschitziana, dunque esiste $m = \inf(D)$ . Sia $L= \inf D$ e sia $L_n$ una successione in $D$ tale che $L_n \to L$ . Si ha

(126) $\begin{equation*} L |x-y| = \lim_{n \to +\infty} L_n|x-y| \geq |f(x)-f(y)| \qquad \forall x,y \in A, \end{equation*}$

dove la disuguaglianza segue da $L_n \in D$ . Quindi $L \in D$ e pertanto $L=\min D$ .

Esempio 6.21. La funzione identità $f \colon \mathbb{R} \to \mathbb{R}$ definita da $f(x)=x$ per ogni $x \in \mathbb{R}$ è lipschitziana con $\operatorname{Lip}(f)=1$ . Infatti

(127) $\begin{equation*} |f(x)-f(y)|=|x-y| \qquad \forall x,y \in \mathbb{R}. \end{equation*}$

Esempio 6.22. La funzione $\sin \colon \mathbb{R} \to \mathbb{R}$ è lipschitziana, infatti da (7) segue che

(128) $\begin{equation*} |\sin x - \sin y| \leq |x-y| \qquad \forall x,y \in \mathbb{R}. \end{equation*}$

Si può mostrare² che $\operatorname{Lip}(\sin)=1$ .

Esempio 6.23. La funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da $f(x)=|x|$ per ogni $x \in \mathbb{R}$ è lipschitziana con costante di Lipschitz pari a $1$ . Infatti

(129) $\begin{equation*} |f(x)-f(y)| = ||x|-|y|| \leq |x-y| \qquad \forall x,y \in \mathbb{R}, \end{equation*}$

il che prova che $f$ è lipschitztiana con $\operatorname{Lip}(f) \leq 1$ . Il fatto che $\operatorname{Lip}(f) = 1$ segue invece scegliendo $x,y>0$ :

(130) $\begin{equation*} |f(x)-f(y)| = ||x|-|y|| = |x-y|. \end{equation*}$

Geometricamente, una funzione $f \colon A \to \mathbb{R}$ è lipschitziana di costante $L$ , se per qualunque punto $x_0 \in A$ , il grafico di $f$ è contenuto nel cono di vertice $(x_0,f(x_0))$ e delimitato dalle rette aventi coefficiente angolare $L,-L$ passanti per tale punto, come mostrato dalla figura 37.

$\quad$

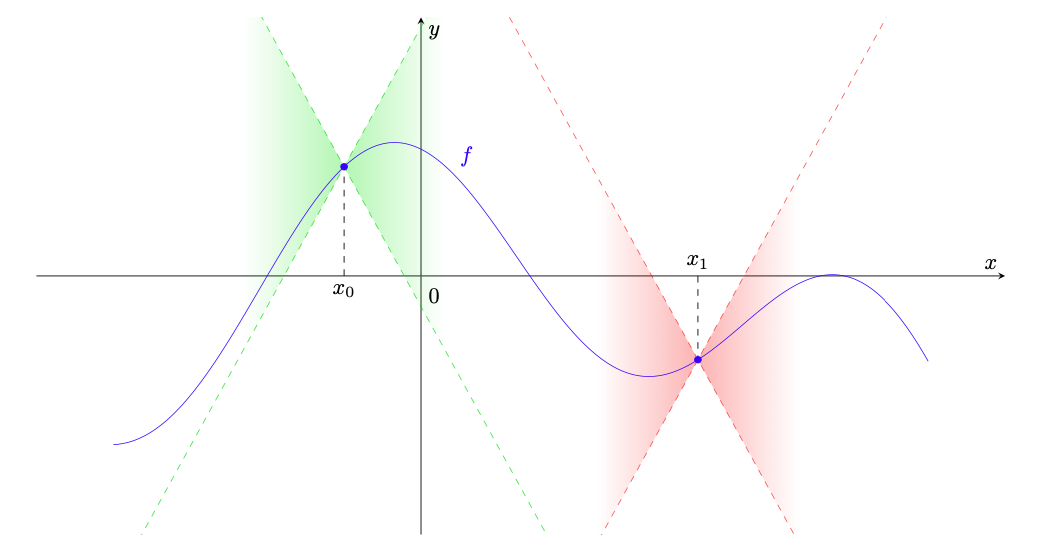
Figura 37: la funzione $f$ è lipschitziana di costante $L$ in quanto il suo grafico è contenuto in coni (ombreggiati in verde e in rosso) delimitati da rette di pendenza $L$ e $-L$ (tratteggiate) e centrati su di esso.

$\quad$

Infatti, fissato $x_0 \in A$ possiamo scrivere la condizione di Lipschitz come

(131) $\begin{equation*} \begin{split} |f(x)-f(x_0)| \leq L |x-x_0| & \iff -L|x-x_0| \leq f(x) - f(x_0) \leq L |x-x_0| \\ & \iff f(x_0) - L|x-x_0| \leq f(x) \leq f(x_0) + L |x-x_0| \qquad \forall x \in A. \end{split} \end{equation*}$

Se ad esempio $x>x_0$ , l’ultima condizione diventa

(132) $\begin{equation*} f(x_0) - L(x-x_0) \leq f(x) \leq f(x_0) + L (x-x_0), \end{equation*}$

ossia il punto $(x,f(x))$ deve essere compreso tra le rette passanti per $(x_0,f(x_0))$ aventi coefficienti angolari $L$ e $-L$ , tratteggiate in verde e in rosso in figura 37. La stessa conclusione vale se $x< x_0$ .

La condizione di Lipschitz può essere equivalentemente definita attraverso il concetto di rapporto incrementale.

Definizione 6.24 (rapporto incrementale). Consideriamo $f\colon A\subseteq\mathbb{R}\rightarrow \mathbb{R}$ . Si definisce rapporto incrementale di $f$ la funzione $R_f\colon A\times A\rightarrow\mathbb{R}$ definita da

(133) $\begin{equation*} R_f(x,y) = \begin{dcases} 0 & \text{se } x=y, \\ \frac{f(x) - f(y)}{x-y} & \text{se }x\neq y. \end{dcases} \end{equation*}$

$\quad$

Il rapporto incrementale $R_f(x,y)$ rappresenta quindi il coefficiente angolare della retta passante per i punti $(x,f(x))$ e $(y,f(y))$ . Si vede subito che una funzione è lipschitziana se e solo se esiste $L\geq0$ tale che

(134) $\begin{equation*} |R_f(x,y)|\leq L \quad \forall x, y\in A, \end{equation*}$

ossia se e solo se il rapporto incrementale è limitato.

Mostriamo ora un esempio del fatto che la lipschitzianità di una funzione dipenda dal dominio su cui essa è definita.

Esempio 6.25. Sia $a \in (0,+\infty)$ e sia $f\colon [-a,a] \to \mathbb{R}$ definita da

$f(x) = x^2, \qquad \forall x \in [-a,a].$

Affermiamo che $f$ è lipschitziana con costante di Lipschitz pari a $2a$ .

$\quad$

$\bullet$ $f$ è lipschitziana. Fissati arbitrariamente $x, y \in [-a,a])$ , si ha

$|f(x) - f(y)| = |x^2 - y^2| = |x + y| |x-y| \leq |a + a| |x-y| = 2a |x-y|,$

quindi $f$ è lipschitziana con $\operatorname{Lip}(f) \leq 2a$ .

$\bullet$ $\operatorname{Lip}(f) = 2a$ . A tal fine, mostriamo che ogni costante $L <2a$ non soddisfa (125): fissando $\delta >0$ tale che $L < 2a-\delta$ , abbiamo

(135) $\begin{equation*} |f(a)-f(a-\delta)| = |a^2-(a^2-2a\delta + \delta^2)| = |2a - \delta| |\delta| > L |a - (a-\delta)|. \end{equation*}$

La lipschitzianità però viene meno nel momento in cui la stessa funzione viene definita su tutto $\mathbb{R}$ : la funzione $f\colon \mathbb{R} \to \mathbb{R}$ definita da

$f(x) =x^2, \qquad \forall x \in \mathbb{R}$

non è lipschitziana. Per dimostrarlo, facciamo vedere che nessun $L \geq 0$ soddisfa (125) esibendo $x,y \in \mathbb{R}$ tali che $|f(x)-f(y)| >L|x-y|$ . Fissiamo $L \geq 0$ arbitrariamente; scegliendo $x=2L$ e $y=0$ si ha infatti

(136) $\begin{equation*} |f(x)-f(y)| = |f(2L) - f(0)| = 4L^2 > L |2L-0| = L|x-y|. \end{equation*}$

usando il limite notevole $\lim_{x \to 0} \dfrac{\sin x}{x}=1$ o usando le derivate. ↩

$\quad$

Relazioni con l’uniforme continuità

Come anticipato nell’introduzione, le funzioni lipschitziane sono uniformemente continue e quindi continue, come stabilito dal prossimo risultato.

Proposizione 6.26. Sia $A\subseteq\mathbb{R}$ . Se $f\colon A\rightarrow \mathbb{R}$ è lipschitziana, allora essa è uniformemente continua. In particolare $f$ è continua.

$\quad$

Dimostrazione. Sia $\varepsilon>0$ . Poiché $f$ è lipschitziana esiste $L \geq 0$ tale che

(137) $\begin{equation*} |f(x)-f(y)|\leq L |x-y| \quad \forall x, y\in A. \end{equation*}$

Scegliendo $\delta = \varepsilon/L$ e $x,y\in A$ tali che $|x-y|<\delta$ , da tale disuguaglianza abbiamo che

(138) $\begin{equation*} |f(x)-f(y)| \leq L |x-y| < L \frac{\varepsilon}{L} = \varepsilon, \end{equation*}$

cioè $f$ è uniformemente continua.

Il viceversa di tale proposizione non è vero: esistono funzioni lipschitziane che non sono uniformemente continue, come mostrato dall’esempio 6.27.

Esempio 6.27. Sia $\alpha \in (0,1)$ e consideriamo la funzione $f\colon [0,1] \to \mathbb{R}$ definita da

(139) $\begin{equation*} f(x)=x^\alpha \qquad \forall x \in [0,1] \end{equation*}$

e rappresentata in figura 38.

$\quad$

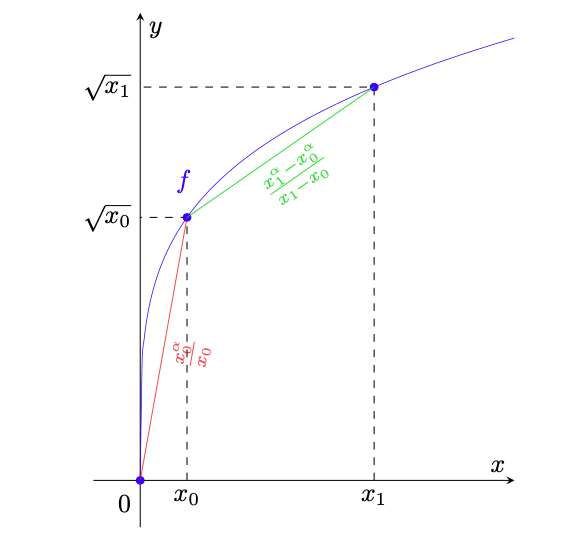
Figura 38: la funzione $f$ dell’esempio 6.27. Si vede che i rapporti incrementali per punti vicini a $0$ sono illimitati, rappresentati dalla pendenza $\frac{x_0^\alpha}{x_0}$ arbitrariamente grande del segmento in rosso. Se invece i punti sono lontani dall’origine i rapporti incrementali sono limitati, come si vede dalla pendenza $\dfrac{x_1^\alpha-x_0^\alpha}{x_1-x_0}$ del segmento in verde.

$\quad$

Proviamo prima che $f$ è uniformemente continua. Infatti per le proprietà dei logaritmi possiamo riscrivere $f$ in $(0,1]$ nel seguente modo:
(140) $\begin{equation*} f(x) = e^{\alpha \log x} \qquad \forall x \in (0,1]. \end{equation*}$

Quindi $f$ è continua in $(0,1]$ perché composizione di esponenziale e logaritmo, che sono funzioni continue. Poiché da tale espressione segue anche che

(141) $\begin{equation*} \lim_{x \to 0} f(x) = 0 = f(0), \end{equation*}$

$f$ risulta continua anche in $0$ e quindi è continua in $[0,1]$ . Per il teorema 6.10, $f$ è quindi uniformemente continua.

$f$ non è però lipschitziana. Infatti si ha
(142) $\begin{equation*} R_f(x,0) = \dfrac{f(x)-f(0)}{x-0} = \dfrac{x^\alpha}{x} = \dfrac{1}{x^{1-\alpha}} \qquad \forall x \in (0,1]. \end{equation*}$

Quindi

(143) $\begin{equation*} \lim_{x \to 0^+} R_f(x,0)=+\infty, \end{equation*}$

cioè il rapporto incrementale di $f$ non è limitato in un intorno di $0$ , per cui $f$ non è lipschitziana.

La funzione $f$ dell’esempio 6.27 è però lipschitziana se ci si allontana dal punto $x=0$ , ossia considerando come dominio insiemi del tipo $[\delta,+\infty)$ con $\delta>0$ . Lo mostriamo prima per $\alpha=\dfrac{1}{2}$ (la cui dimostrazione risulta più immediata) e poi nel caso generale.

Esempio 6.28. Dato $\delta>0$ , la funzione $f\colon [\delta,+\infty) \to \mathbb{R}$ definita da

(144) $\begin{equation*} f(x)=\sqrt{x} \qquad \forall x \in [\delta,+\infty) \end{equation*}$

è lipschitziana. Infatti, se $x,y \in [\delta,+\infty)$ con $x \neq y$ , si ha

(145) $\begin{equation*} |f(x)-f(y)| = |\sqrt{x}- \sqrt{y}| = \dfrac{|(\sqrt{x}- \sqrt{y})(\sqrt{x}+ \sqrt{y})|}{\sqrt{x}+ \sqrt{y}} = \dfrac{|x-y|}{\sqrt{x}+ \sqrt{y}} \leq \dfrac{|x-y|}{2\sqrt{\delta}}, \end{equation*}$

dove nella prima uguaglianza abbiamo moltiplicato e diviso per $\sqrt{x}+\sqrt{y}$ , mentre nella disuguaglianza abbiamo usato che $x,y \geq \delta$ , per cui $\sqrt{x}+\sqrt{y} \geq 2 \sqrt{\delta}$ .

Esempio 6.29. Dati $\alpha \in (0,1)$ e $\delta>0$ , la funzione $f\colon [\delta,+\infty) \to \mathbb{R}$ definita da

(146) $\begin{equation*} f(x)=x^\alpha \qquad \forall x \in [\delta,+\infty) \end{equation*}$

è lipschitziana. Infatti, se $x,y \in [\delta,+\infty)$ con $x \neq y$ , si ha

(147) $\begin{equation*} \begin{split} |f(x)-f(y)| &= |y^\alpha - x^\alpha| \\ &= \dfrac{|(y^\alpha - x^\alpha)(y^{1-\alpha}+x^{1-\alpha})|}{y^{1-\alpha}+x^{1-\alpha}} \\ &\leq \dfrac{|y-x| + |y^{\alpha}y^{1-\alpha} - x^{\alpha}x^{1-\alpha}|}{2\delta^{1-\alpha}} \\ &\leq \dfrac{|y-x|}{\delta^{1-\alpha}}, \end{split} \end{equation*}$

dove nella prima uguaglianza abbiamo moltiplicato e diviso per ${y^{1-\alpha}+x^{1-\alpha}}$ , nella prima disuguaglianza abbiamo usato la disuguaglianza triangolare al numeratore e il fatto che $x,y \geq \delta$ al denominatore, mentre nella seconda disuguaglianza abbiamo sfruttato il fatto che, se ad esempio $x<y$ , allora

(148) $\begin{equation*} \begin{gathered} x = x^\alpha x^{1-\alpha} \leq y^{\alpha}x^{1-\alpha} \leq y^\alpha y^{1-\alpha} = y, \\ x = x^\alpha x^{1-\alpha} \leq x^{\alpha}y^{1-\alpha} \leq y^\alpha y^{1-\alpha} = y, \end{gathered} \end{equation*}$

quindi la distanza tra i numeri $y^{\alpha}x^{1-\alpha}$ e $x^{\alpha}x^{1-\alpha}$ è minore o uguale a quella tra $x$ e $y$ , ovvero gli estremi dell’intervallo $[x,y]$ in cui tali numeri sono contenuti. Da (147) segue che $f$ è una funzione lipschitziana con costante di Lipschitz minore o uguale a $\delta^{\alpha - 1}$ (si veda anche la figura 38).

Il teorema delle contrazioni.

La costante di Lipschitz $L$ di una funzione $f$ fornisce intuitivamente una misura di quanto $f$ “dilati” le distanze tra punti. Se $L<1$ , segue che $f$ contrae le distanze tra i punti; per questo motivo, le funzioni lipschitziane con costante di Lipschitz strettamente minore di $1$ sono dette contrazioni.

Questa proprietà di contrazione, avvicinando punti che sono inizialmente a una distanza maggiore, intuitivamente suggerisce che, partendo da un punto qualsiasi $x_0$ e applicando ripetutamente $f$ , il risultato si “stabilizza” verso un certo punto $\bar{x}$ che risulta un punto fisso di $f$ , ossia tale che $f(\bar{x})=\bar{x}$ . Questa intuizione è formalizzata dal prossimo importante risultato, detto teorema delle contrazioni, che è dovuto ai matematici Stefan Banach (1892-1945) e Renato Caccioppoli (1904-1959).

Teorema 6.30 (Banach-Caccioppoli o delle contrazioni). Sia $C \subseteq \mathbb{R}$ un insieme chiuso e sia $f \colon C \to C$ una contrazione, cioè una funzione lipschitziana con costante di Lipschitz $L<1$ . Allora esiste uno e un solo punto fisso $\bar{x} \in C$ di $f$ , ossia tale che

(149) $\begin{equation*} f(\bar{x})=\bar{x}. \end{equation*}$

$\quad$

Dimostrazione. Proviamo in primo luogo che un punto fisso di $f$ esiste e successivamente ne dimostriamo l’unicità.

$\bullet$ Esistenza Si fissi $x_0 \in C$ e si costruisca la successione $\{x_n\}_n$ definita per ricorrenza da

(150) $\begin{equation*} x_{n+1}= f(x_n) \qquad \forall n \in \mathbb{N}. \end{equation*}$

Poiché $f \colon C \to C$ , tale successione è ben definita. Inoltre, da (150) e dal fatto che $f$ è lipschitziana di costante $L$ otteniamo

(151) $\begin{equation*} \begin{split} |x_{n+1} - x_n| &= |f(x_n) - f(x_{n-1})| \\ &\leq L |x_n - x_{n-1}| \\ &= L |f(x_{n-1}) - f(x_{n-2})| \\ &\leq L^2 |x_{n-1} - x_{n-2}| \quad \forall n \geq 2. \end{split} \end{equation*}$

Continuando in questo modo, otteniamo per induzione

(152) $\begin{equation*} |x_{n+1} - x_n| \leq L^n |x_1 - x_0 | \qquad \forall n \in \mathbb{N}. \end{equation*}$

Mostriamo che la successione $x_n$ è di Cauchy e quindi ha limite. Infatti

(153) $\begin{equation*} |x_{n+k}-x_n| \leq \sum_{i=n}^{n+k-1}|x_{i+1}-x_{i}| \leq \sum_{i=n}^{n+k-1} L^{i}|x_1-x_0| = \left( \sum_{i=n}^{n+k-1} L^{i} \right)|x_1-x_0| \qquad \forall n,k \in \mathbb{N}, \end{equation*}$

dove nella prima disuguaglianza abbiamo usato la disuguaglianza triangolare, mentre nella seconda abbiamo usato (152).

Utilizzando la nota formula per la somma di una serie geometrica in (153) si ottiene

(154) $\begin{equation*} |x_{n+k}-x_n| \leq \dfrac{L^n-L^{n+k}}{1-L}|x_1-x_0| \leq \dfrac{L^n}{1-L} \qquad \forall n,k \in \mathbb{N}, \end{equation*}$

dove nella seconda disuguaglianza abbiamo usato il fatto che $L<1$ per stimare il numeratore della frazione. Poiché $L \in (0,1)$ , si ha

(155) $\begin{equation*} \lim_{n \to + \infty} \frac{L^n}{1-L}=0, \end{equation*}$

quindi, fissato $\varepsilon>0$ esiste $N \in \mathbb{N}$ tale che

(156) $\begin{equation*} |x_{n+k}-x_n| \leq \varepsilon \qquad \forall n \geq N, \,\,\, \forall k \in \mathbb{N}, \end{equation*}$

cioè la successione $x_n$ è di Cauchy, pertanto ha limite $\bar{x} \in \mathbb{R}$ . Poiché la successione $x_n$ ha valori in $C$ e $C$ è un insieme chiuso, anche il suo limite $\bar{x} \in C$ .

Mostriamo ora che $\bar{x}$ è un punto fisso di $f$ . Infatti si ha

(157) $\begin{equation*} \bar{x} = \lim_{n\to +\infty} x_{n+1} = \lim _{n\to +\infty}f(x_n) = f\left(\lim_{n\to +\infty} x_n\right) = f(\bar{x}), \end{equation*}$

dove la penultima uguaglianza segue dalla continuità di $f$ e dal teorema 3.3. (157) mostra che $\bar{x}$ è un punto fisso per $f$ .

$\bullet$ Unicità Supponiamo per assurdo che $a,b \in C$ siano dei punti fissi di $f$ con $a \neq b$ ; allora si ha

(158) $\begin{equation*} |a-b|= |f(a)-f(b)| \leq L |a-b|, \end{equation*}$

dove nella prima uguaglianza si è usato il fatto che $a,b$ sono dei punti fissi per $f$ e nella disuguaglianza si è sfruttato il fatto che $f$ è lipschitziana di costante $L$ . Dividendo entrambi i membri della disuguaglianza per $|a-b|$ si ottiene

(159) $\begin{equation*} 1 \leq L, \end{equation*}$

che contraddice l’ipotesi iniziale $L<1$ . Da tale contraddizione segue che non possono esistere due punti fissi distinti $a,b$ di $f$ .

Forniamo di seguito un esempio di applicazione del teorema delle contrazioni.

Esempio 6.31. Mostriamo che l’unica soluzione $\bar{x}$ non negativa dell’equazione

(160) $\begin{equation*} (\sin^2 x) \dfrac{1-e^{-x}}{2e} = x \end{equation*}$

è data da $\bar{x}=0$ . È chiaro che $\bar{x}=0$ è una soluzione. Per mostrarne l’unicità, definiamo la funzione $f \colon [0,+\infty) \to [0,+\infty)$ definita da

(161) $\begin{equation*} f(x) = ( \sin^2 x) \dfrac{1-e^{-x}}{2e} \qquad \forall x \in [0,+\infty) \end{equation*}$

e rappresentata in blu in figura 39.

$\quad$

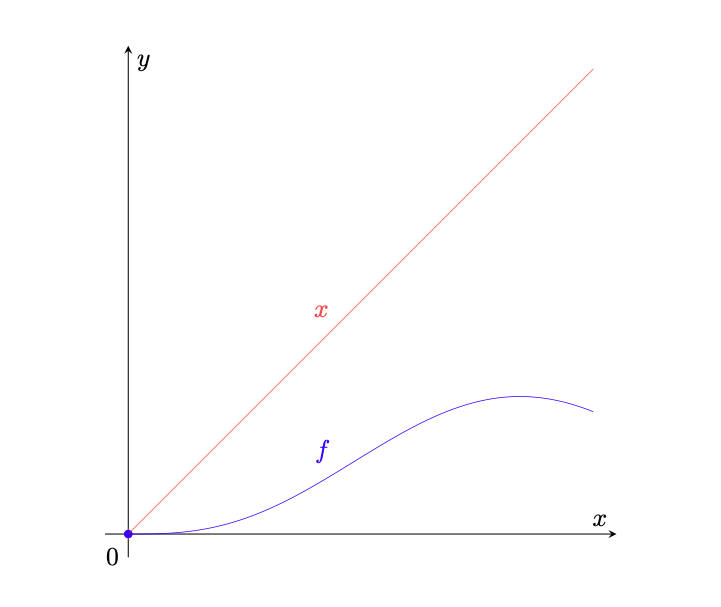
Figura 39: le soluzioni dell’equazione (160) sono i punti fissi della funzione $f$ (in blu), ossia le intersezioni del suo grafico con quello della funzione identità (in rosso). La funzione $f$ è una contrazione poiché la pendenza del suo grafico è sempre strettamente minore di $1$ , quindi l’equazione (160) possiede una e una sola soluzione, data da $\bar{x}=0$ . Si nota infatti che i due grafici si intersecano solo nell’origine.

$\quad$

Osserviamo che le soluzioni dell’equazione (160) sono tutti e soli i punti fissi di $f$ , ossia le ascisse delle intersezioni tra il grafico di $f$ e quello della funzione identità. Per dimostrare che ne esiste una sola, mostriamo che $f$ è una contrazione e usiamo il teorema 6.30 per ottenere l’unicità dei punti fissi di $f$ .

Per farlo, osserviamo innanzitutto che le funzioni $g,h \colon [0,+\infty) \to [0,+\infty)$ definite da

(162) $\begin{equation*} g(x)=e^{-x}, \quad h(x)=\dfrac{\sin^2 x}{2} \qquad \forall x \in [0,+\infty) \end{equation*}$

sono lipschitziane di costante di Lipschitz minore o uguale a $1$ .

$\quad$

Per quanto riguarda $g$ , si ha
(163) $\begin{equation*} \begin{split} |g(x)-g(y)| &= |e^{-x} - e^{-y}| \\ &= |e^{-x}| |1 - e^{-(y-x)}| \\ &\leq |e^{-x}| |1 - (1 - (-(y - x)))| \\ &\leq |x - y|, \qquad \forall x, y \in [0, +\infty), \end{split} \end{equation*}$

dove la prima disuguaglianza è ottenuta a partire dalla nota disuguaglianza $e^a \geq 1+a$ per³ ogni $a \in \mathbb{R}$ e la seconda dal fatto che $x \geq 0$ , quindi $e^{-x} \leq 1$ . Quindi $g$ è lipschitziana con costante di Lipschitz minore o uguale a 1.

Riguardo a $h$ , per ogni $x,y \in [0,+\infty)$ abbiamo
(164) $\begin{equation*} \begin{split} |h(x)-h(y)| = & \dfrac{|\sin^2 x - \sin^2y|}{2} \\ \leq & \dfrac{|\sin^2 x - \sin x \sin y| + |\sin x \sin y - \sin^2y|}{2} \\ = & \dfrac{|\sin x|}{2}|\sin x - \sin y| + \dfrac{|\sin y|}{2} |\sin x - \sin y| \\ \leq & \dfrac{|x-y|}{2} + \dfrac{|x-y|}{2} \\ = & |x-y|, \end{split} \end{equation*}$

dove nella prima disuguaglianza si è usata la disuguaglianza triangolare, mentre nella seconda si è usato il fatto che la funzione seno è lipschitziana, provato nella dimostrazione della proposizione 2.9.

Ritornando a $f$ , per ogni $x,y \in [0,+\infty)$ si ha

(165) $\begin{equation*} \begin{split} |f(x)-f(y)| = & \left|\sin^2 x \dfrac{1-e^{-x}}{2e} - \sin^2 y \dfrac{1-e^{-y}}{2e}\right| \\ \leq & \left| \sin^2 x \dfrac{1-e^{-x}}{2e} - \sin^2 y \dfrac{1-e^{-x}}{2e} \right| + \left|\sin^2 y \dfrac{1-e^{-x}}{2e} - \sin^2 y \dfrac{1-e^{-y}}{2e}\right| \\ \leq & \left| \dfrac{1-e^{-x}}{2e} \right| |\sin^2 x - \sin^2y| + |\sin^2y| \left|\dfrac{1-e^{-x}}{2e} - \dfrac{1-e^{-y}}{2e}\right| \\ \leq & \dfrac{1}{e}|{|x-y|} + \dfrac{1}{2e}|x-y| \\ =& \dfrac{3}{2e}|x-y|. \end{split} \end{equation*}$

Poiché $\dfrac{3}{2e} < 1$ , $f$ è lipschitziana con costante di Lipschitz minore di 1 e quindi è una contrazione. Poiché $[0,+\infty)$ è un insieme chiuso, il teorema 6.30 implica che $f$ ha un unico punto fisso $\bar{x}$ , ossia tale che

(166) $\begin{equation*} \bar{x} = f(\bar{x}) = (\sin^2 \bar{x}) \dfrac{1-e^{-\bar{x}}}{2e}. \end{equation*}$

Ciò mostra che l’equazione (160) possiede l’unica soluzione $x=0$ .

Tale disuguaglianza si ottiene da

(167) $\begin{equation*} 1+a = 1+ n\frac{a}{n} \leq \left( 1+ \frac{a}{n}\right)^n \xrightarrow[n \to +\infty]{} e^a, \end{equation*}$

dove la disuguaglianza deriva dalla disuguaglianza di Bernoulli e il limite dalla definizione dell’esponenziale. Dal fatto che la successione $\left( 1+ \dfrac{a}{n}\right)^n$ è crescente si ottiene il risultato finale. ↩

Funzioni hölderiane.

Concludiamo la sezione introducendo il concetto di funzioni hölderiane, particolari funzioni uniformemente continue che generalizzano il concetto di funzione lipschitziana.

Definizione 6.32 (funzione hölderiana). Sia $A\subseteq\mathbb{R}$ e $\alpha>0$ . Una funzione $f\colon A\rightarrow \mathbb{R}$ si dice $\alpha$ -hölderiana se esiste una costante $L \geq 0$ tale che

(168) $\begin{equation*} |f(x)-f(y)| \leq L |x-y|^\alpha \qquad \forall x,y \in A. \end{equation*}$

La più piccola costante $L$ che soddisfa tale condizione si dice costante di Hölder della funzione $f$ .

$\quad$

Osservazione 6.33. Osserviamo che se $f\colon A\rightarrow \mathbb{R}$ è hölderiana, allora la costante di Hölder esiste sempre. La dimostrazione è analoga a quella vista nell’osservazione 6.20 sull’esistenza della costante di Lipschitz.

Il “prototipo” di funzione $\alpha$ -hölderiana è fornito dal prossimo esempio.

Esempio 6.34. Se $\alpha\in (0,1]$ , la funzione $f\colon \mathbb{R} \to \mathbb{R}$ definita da

$f(x) = |x|^\alpha \qquad \forall x \in \mathbb{R}$

è $\alpha$ -hölderiana, con costante di Hölder pari a $1$ .

$\quad$

Consideriamo $x,y \in \mathbb{R}$ e supponiamo, senza perdita di generalità, che $|x|>|y|$ (nel caso valga l’uguaglianza, l’equazione (168) è banalmente vera). Allora si ha

(169) $\begin{equation*} \dfrac{|f(x)-f(y)|}{|x-y|^\alpha} = \dfrac{ \left| 1 - \dfrac{|y|^\alpha}{|x|^\alpha} \right|}{\left| 1 - \dfrac{|y|}{|x|} \right|^\alpha} \leq 1 \end{equation*}$

dove nell’uguaglianza si è raccolto $|x|^\alpha$ al numeratore e al denominatore; la disuguaglianza segue invece dal fatto che $0 \leq \dfrac{|y|}{|x|}<1$ e quindi

(170) $\begin{gather*} 0 \leq \frac{|y|}{|x|} \leq \frac{|y|^\alpha}{|x|^\alpha} < 1 \quad \Longrightarrow \quad 0 < \left| 1 - \frac{|y|^\alpha}{|x|^\alpha} \right| \leq \left| 1 - \frac{|y|}{|x|} \right| \\ 0 < \left| 1 - \frac{|y|}{|x|} \right| %= %1 - \frac{|y|}{|x|} \leq 1 \quad \Longrightarrow \quad \left| 1 - \frac{|y|}{|x|} \right| \leq \left| 1 - \frac{|y|}{|x|} \right|^\alpha, \end{gather*}$

dove si è usato che, poiché $\alpha \in (0,1]$ , si ha $t^\alpha\geq t$ per $t \in [0,1]$ . (169) mostra che $f$ è $\alpha$ -hölderiana con costante di Hölder minore o uguale a $1$ .

Per vedere che la costante di Hölder è pari a $1$ , si osservi che
(171) $\begin{equation*} |f(x)-f(0)| = ||x|^\alpha| = |x-0|^\alpha \qquad \forall x \in \mathbb{R}. \end{equation*}$

In particolare, l’esempio precedente per $\alpha = 1$ implica che la funzione valore assoluto definita da

$f(x) = |x| \qquad \forall x \in \mathbb{R}$

è lipschitziana, come già visto nell’esempio 6.23.

Relazioni con l’uniforme continuità e criteri di hölderianità

In questa sezione discutiamo il rapporto tra funzioni hölderiane, lipschitziane e funzioni uniformemente continue. Inoltre presentiamo una condizione sufficiente affinché una funzione $f \colon I \to \mathbb{R}$ sia hölderiana, relativa alla lipschitzianità delle sue potenze. Cominciamo con le seguenti osservazioni.

Osservazione 6.35. Dalle definizioni 6.32 e 6.19 segue che una funzione è lipschitziana se e solo se è $1$ -hölderiana.

Osservazione 6.36.Esistono funzioni $\alpha$ -hölderiane ma non lipschitziane: se $\alpha \in (0,1]$ , abbiamo visto nell’esempio 6.34 che la funzione $f\colon [0, +\infty) \to \mathbb{R}$ definita da

$f(x) = x^\alpha \qquad \forall x \in [0, +\infty)$

è $\alpha$ -hölderiana. Essa non è però lipschitziana se $\alpha \in (0,1)$ , come osservato nell’esempio 6.27.

Come anticipato nell’introduzione, le funzioni hölderiane sono uniformemente continue. Tale proprietà viene stabilita dalla seguente proposizione.

Proposizione 6.37. Se $f\colon A \subseteq \mathbb{R} \to \mathbb{R}$ è $\alpha$ -hölderiana, allora è uniformemente continua.

$\quad$

Dimostrazione. Poiché $f$ è $\alpha$ -hölderiana, esiste $L\geq 0$ tale che

$|f(x)- f(y)| \leq L |x - y |^\alpha \qquad \forall x,y \in A.$

Se $L=0$ , allora $f$ è costante e dunque uniformemente continua. Supponiamo quindi che $L\neq 0$ e fissiamo $\varepsilon>0$ . Scelto

$\delta = \left(\dfrac{\varepsilon}{L}\right)^{\frac{1}{\alpha}},$

per ogni $x,y \in A$ con $|x-y|< \delta$ si ha che

$|f(x)- f(y)| \leq L |x - y |^\alpha < L \delta^\alpha = \varepsilon.$

Viceversa, esistono funzioni uniformemente continue che non sono hölderiane, come si evince dal seguente esempio.

Esempio 6.38. Si consideri la funzione $f \colon \left[0,\dfrac{1}{2}\right] \to \mathbb{R}$ definita da

(172) $\begin{equation*} f(x) = \begin{cases} \dfrac{1}{\log x} & \text{se } x \in (0,\frac{1}{2}]\\[6pt] 0 & \text{se } x =0. \end{cases} \end{equation*}$

Tale funzione è continua in $\left(0,\dfrac{1}{2} \right]$ , inoltre $f$ è anche continua in $x=0$ poiché

$\lim_{x\to 0^+} \dfrac{1}{\log x} = 0$

e dunque, per il teorema di Heine-Cantor 6.10, $f$ è uniformemente continua. Supponiamo per assurdo che $f$ sia $\alpha$ -hölderiana per un qualche $\alpha \in (0,1]$ ; allora esisterebbe $L\geq 0$ tale che

$|f(x)-f(0)| \left|\dfrac{1}{\log x} - 0\right| \leq L |x|^\alpha \qquad \forall x \in \left(0,\frac{1}{2}\right].$

Ciò equivale a

$L |x|^\alpha |\log x | \geq 1, \qquad \forall x \in \left(0,\frac{1}{2}\right],$

ma ciò è assurdo poiché

$\lim_{x \to 0^+} L |x|^\alpha |\log x | = 0.$

Da tale contraddizione segue che $f$ non è $\alpha$ -hölderiana per nessun $\alpha\in (0,1]$ .

Presentiamo ora un criterio di hölderianità: una funzione $f$ è hölderiana se una sua qualche potenza $f^{\frac{1}{\alpha}}$ , con $\alpha \in (0,1)$ è lipschitziana.

Proposizione 6.39. Sia $I \subseteq \mathbb{R}$ un intervallo e sia $f \colon I \to \mathbb{R}$ una funzione continua. Se esiste $\alpha \in (0,1)$ tale che la funzione $|f|^{\frac{1}{\alpha}} \colon I \to \mathbb{R}$ è lipschitziana, allora $f$ è $\alpha$ -hölderiana.

$\quad$

Dimostrazione. Supponiamo che $|f|^{\frac{1}{\alpha}} \colon I \to \mathbb{R}$ sia lipschitziana per qualche $\alpha \in (0,1)$ con costante di Lipschitz pari a $L \geq 0$ , ossia

(173) $\begin{equation*} \big| |f(x)|^{\frac{1}{\alpha}} - |f(y)|^{\frac{1}{\alpha}} \big| \leq L|x-y| \qquad \forall x,y \in I. \end{equation*}$

Mostreremo che $f$ è $\alpha$ -hölderiana con costante di Hölder al più pari a $2L$ . A tal fine, fissiamo arbitrariamente $x,y \in I$ e distinguiamo due casi.

$\bullet$ $f(x)$ e $f(y)$ hanno stesso segno⁴. Ricordiamo innanzitutto che, come mostrato nell’esempio 6.34, la funzione $g \colon \mathbb{R} \to \mathbb{R}$ definita da $g(x)= |x|^\alpha$ per ogni $x \in \mathbb{R}$ è $\alpha$ -holderiana con costante di Hölder pari a $1$ . Quindi

(174) $\begin{equation*} \big| |a|^\alpha - |b|^\alpha \big| \leq |a-b|^\alpha \qquad \forall a,b \in \mathbb{R}. \end{equation*}$

Ritornando alla stima di $f$ , si ha

(175) $\begin{equation*} \begin{split} |f(x) - f(y)| &= \big| |f(x)| - |f(y)| \big| \\ &= \Big| \big( |f(x)|^{\frac{1}{\alpha}} \big)^\alpha - \big( |f(y)|^{\frac{1}{\alpha}} \big)^\alpha \Big| \\ &\leq \big| |f(x)|^{\frac{1}{\alpha}} - |f(y)|^{\frac{1}{\alpha}} \big|^\alpha \\ &\leq L |x - y|^\alpha, \end{split} \end{equation*}$

dove nella prima uguaglianza si è usato che $f(x)$ e $f(y)$ hanno stesso segno, mentre nella seconda si è usata l’identità $|t|=\big(|t|^{\frac{1}{\alpha}}\big)^\alpha$ ; inoltre la prima disuguaglianza segue da (174) applicata a $a = |f(x)|^{\frac{1}{\alpha}}$ e $b = |f(y)|^{\frac{1}{\alpha}}$ , mentre la seconda disuguaglianza è dovuta a (173).

$\bullet$ $f(x)$ e $f(y)$ hanno stesso diverso. Senza perdita di generalità supponiamo $x < y$ . In tal caso, per la continuità di $f$ e per il teorema 5.3 di esistenza degli zeri, esiste $\zeta \in (x,y)$ tale che $f(\zeta)=0$ . Possiamo quindi applicare il punto precedente alle coppie $x,\zeta$ e $\zeta,y$ , ottenendo

(176) $\begin{equation*} |f(x)-f(y)| \leq |f(x) - f(\zeta)| + |f(\zeta)-f(y)| \leq L |x-\zeta|^\alpha + L |\zeta - y|^\alpha \leq 2L |x-y|^\alpha, \end{equation*}$

dove la prima disuguaglianza è dovuta alla disuguaglianza triangolare, la seconda si ottiene applicando il punto precedente alle coppie $x,\zeta$ e $\zeta,y$ (le cui immagini tramite $f$ hanno segno concorde), mentre la terza segue dal fatto che $\zeta \in (x,y)$ , quindi $|x-\zeta| \leq |x-y|$ , $|y-\zeta| \leq |x-y|$ , e che la funzione $t \in [0+\infty) \mapsto t^\alpha$ è crescente.

Ciò mostra che $f$ è $\alpha$ -hölderiana con costante di Hölder pari al più a $2L$ .

Dalla dimostrazione che segue è chiaro che l’argomento copre anche il caso in cui qualcuno tra $f(x)$ e $f(y)$ sia pari a $0$ . ↩

$\quad$

Proprietà degli esponenti di Hölder

Su insiemi limitati, la proprietà di essere $\alpha$ -hölderiana implica quella di essere $\beta$ -hölderiana per tutti gli esponenti minori, come precisato dalla prossima proposizione.

Proposizione 6.40. Sia $A\subseteq \mathbb{R}$ limitato e sia $f\colon A \to \mathbb{R} \to \mathbb{R}$ $\alpha$ -hölderiana, con $\alpha\in (0,1]$ . Allora $f$ è $\beta$ -hölderiana per ogni $\beta \in (0,\alpha]$ .

$\quad$

Dimostrazione. Sia $\alpha\in (0,1]$ e sia $L \geq 0$ tale che

(177) $\begin{equation*} |f(x)-f(y)| \leq L |x-y|^\alpha \qquad \forall x,y \in A. \end{equation*}$

Se $\beta \in (0, \alpha]$ , si ha

(178) $\begin{equation*} |f(x)-f(y)| \leq L |x-y|^\alpha = L |x-y|^{\alpha-\beta} |x-y|^\beta \qquad \forall x,y \in A \end{equation*}$

Poiché $A$ è limitato, esiste $M>0$ tale che $A \subseteq [-M,M]$ , da cui segue che

$L|x-y|^{\alpha-\beta} \leq L(2M)^{\alpha-\beta} \qquad \forall x,y \in A.$

Detta $L' \coloneqq L (2M)^{\alpha-\beta}$ e inserendo tale disuguaglianza in (178), si ottiene

(179) $\begin{equation*} |f(x)-f(y)| \leq % L |x-y|^\alpha = L |x-y|^{\alpha-\beta} |x-y|^\beta L' |x-y|^\beta \qquad \forall x,y \in A, \end{equation*}$

cioè $f$ è $\beta$ -hölderiana.

Le ipotesi $\beta \in (0,\alpha]$ e di limitatezza di $A$ nella proposizione 6.40 sono essenziali, come mostrano i seguenti esempi.

Esempio 6.41. Dato $\alpha \in (0,1]$ , la funzione definita da $x \in [0,1] \mapsto |x|^\alpha \in [0,1]$ è $\alpha$ -hölderiana come visto nell’esempio 6.34, ma non è $\beta$ -hölderiana se $\beta>\alpha$ . Infatti

(180) $\begin{equation*} \dfrac{| f(x)- f(0)|}{| x - 0 |^\beta} = \dfrac{ |x|^\alpha}{| x|^\beta} = \dfrac{1}{|x|^{\beta-\alpha}} \qquad \forall x \neq 0 \end{equation*}$

e, poiché per $\beta> \alpha$ si ha

$\lim_{x \to 0^+} \dfrac{1}{|x|^{\beta-\alpha}} = +\infty,$

non può esistere alcuna costante $L$ soddisfacente (168). Quindi $f$ non è $\beta$ –hölderiana.

Esempio 6.42. Sia $f \colon \mathbb{R} \to \mathbb{R}$ la funzione identità definita da $f(x)=x$ per ogni $x \in \mathbb{R}$ . Essa è lipschitziana (quindi $1$ -hölderiana), ma non è $\alpha$ -hölderiana per nessun $\alpha \in (0,1)$ . Infatti

(181) $\begin{equation*} \dfrac{|f(x)-f(0)|}{|x-0|^\alpha} = \dfrac{|x|}{|x|^\alpha} = |x|^{1-\alpha} \qquad \forall x \neq 0 \end{equation*}$

e $\displaystyle \lim_{x \to +\infty}|x|^{1-\alpha}=+\infty$ , da cui segue che $f$ non è $\alpha$ -hölderiana.

La condizione di Hölder risulta scarsamente interessante per esponenti maggiori di $1$ , come si evince dalla seguente proposizione.

Proposizione 6.43. Sia $J\subseteq \mathbb{R}$ un intervallo e sia $f\colon J \to \mathbb{R}$ una funzione $\alpha$ -hölderiana per qualche $\alpha>1$ . Allora $f$ è costante.

$\quad$

Dimostrazione. Siano $x,y \in J$ con $x < y$ . Per ogni $n \in \mathbb{N}$ si ha

(182) $\begin{equation*} \begin{split} |f(x)-f(y)| &\leq \sum_{j=1}^n \left| f\left( x + j\frac{y-x}{n} \right) - f\left( x + (j-1)\frac{y-x}{n} \right) \right| \\ &\leq \sum_{j=1}^n \left( \frac{y-x}{n} \right)^\alpha \\ &= \frac{n}{n^\alpha} (y - x), \end{split} \end{equation*}$

dove la prima disuguaglianza deriva dalla disuguaglianza triangolare, mentre la seconda dalla condizione di $\alpha$ -hölderianità. Da $\alpha>1$ si ottiene

(183) $\begin{equation*} \lim_{n \to + \infty} \frac{n}{n^\alpha} (y-x) = 0 \end{equation*}$

e, poiché (182) è vera per ogni $n \in \mathbb{N}$ , deve valere

(184) $\begin{equation*} |f(x)-f(y)|=0. \end{equation*}$

Per l’arbitrarietà di $x$ e $y$ , $f$ è costante.

Riepilogo.

Concludiamo presentando il seguente schema, che riassume le relazioni tra le varie nozioni introdotte.

$\quad$

Riferimenti bibliografici

[1] Berretti, A., Analisi Matematica 1, Universitaria (2018).

[2] Bertsch, M., Dal Passo, R., Giacomelli, L., Analisi Matematica , McGraw-Hill (2009).

[3] Canuto, C., Tabacco, A., Analisi Matematica 1, Springer (2021).

[4] De Marco, G., Analisi, Zanichelli (1996).

[5] Fiorenza, R., Greco, D., Lezioni di Analisi Matematica, Liguori Editore (1995).

[6] Giusti, E., Analisi Matematica 1, Bollati Boringhieri (2002).

[7] Kelley, J., General Topology, Springer (1975).

[8] Marcellini, P., Sbordone, C., Calcolo, Liguori Editore (2002).

[9] Polizzi, F., Un blog matematico, $f(x)=1/x$ } ha una discontinuità in { $x=0$ ?}, Web page.

[10] Rudin, W., Principi di Analisi Matematica, McGraw-Hill (1991).

[11] Qui Si Risolve, funzioni elementari – volume 1

[12] Qui Si Risolve, successioni — teoria

[13] Qui Si Risolve, teorema della permanenza del segno

[14] Qui Si Risolve, teorema di Bolzano-Weierstrass per successioni

[15] Qui Si Risolve, esercizi sulla continuità

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Document