0 Elementi

Esercizi sulla verifica dei limiti 6

Verifica del limite in funzioni

Home » Esercizi sulla verifica dei limiti 6

Presentiamo nel seguito i richiami di teoria utili allo svolgimento dell’esercizio. Per richiami più completi si veda la dispensa richiami di teoria.

Definizione 1 (limiti di funzioni) 
Sia A \subseteq \mathbb{R}, sia x_0 \in \overline{\mathbb{R}} un punto di accumulazione per A, sia f \colon A \to \mathbb{R} una funzione e sia \ell \in \overline{\mathbb{R}}. Si dice che \ell è il limite di f per x che tende a x_0 se, per ogni intorno V di \ell, esiste un intorno U di x_0 tale che

(1)   \begin{equation*} f(x) \in V \qquad \forall x \in U \cap A \setminus \{x_0\}. \end{equation*}

In tal caso si scrive

(2)   \begin{equation*} \lim_{x \to x_0} f(x) = \ell. \end{equation*}

Risulta utile vedere come si scrive esplicitamente la definizione 1 suddividendo le casistiche in cui x_0 \in \mathbb{R}, x_0 = -\infty, x_0=+\infty e \ell \in \mathbb{R}, \ell = -\infty, \ell=+\infty.

 

Testo dell’esercizio

Esercizio 6  (\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar).

Verificare, mediante la definizione, i seguenti limiti:

  1. \displaystyle \lim_{x \to 1} \log x = 0;
  2. \displaystyle \lim_{x \to +\infty} \log x = +\infty;
  3. \displaystyle \lim_{x \to 0^+} \log x = -\infty.

 

Svolgimento.
L’esercizio può essere risolto utilizzando il fatto che la funzione \log \colon (0,+\infty) \to \mathbb{R} è la funzione inversa di \exp \colon \mathbb{R} \to (0,+\infty).

  1. Siamo nel primo caso della tabella 1 con x_0=1 e \ell=0. Fissiamo dunque \varepsilon>0. Poiché \log è l’inversa di \exp, si ha

    (3)   \begin{equation*} -\varepsilon<\log x < \varepsilon \iff e^{-\varepsilon} < x < e^\varepsilon. \end{equation*}

    Dato che e^{-\varepsilon} < 1 < e^\varepsilon, esiste \delta>0 tale che

    (4)   \begin{equation*} e^{-\varepsilon} < 1-\delta < 1+\delta < e^\varepsilon, \end{equation*}

    si veda la figura 6a. Da tale scelta e da (3) segue

    (5)   \begin{equation*} x \in (1-\delta,1+\delta) \implies |\log x - \ell| = |\log x| < \varepsilon. \end{equation*}

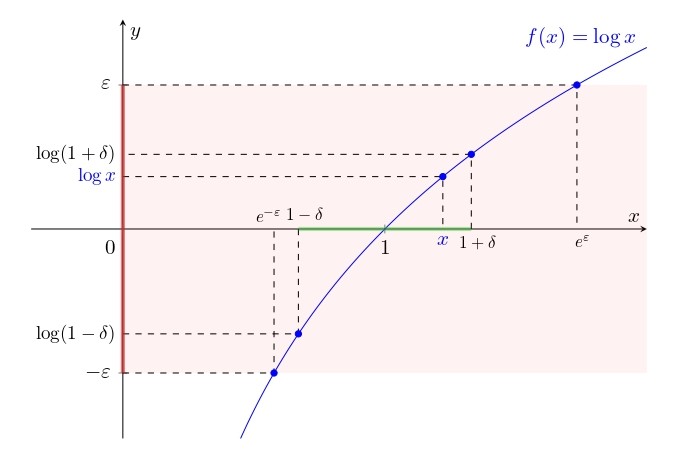
    Figura 6a: rappresentazione del punto 1 dell’esercizio 6. In rosso è rappresentato l’intorno (-\varepsilon,\varepsilon) di \ell=0 e in verde è rappresentato l’intorno \left(1-\delta,1+\delta\right) di x_0=1.

     

  2. Vogliamo verificare la formula al caso 9 della tabella 1. Fissiamo dunque M \in \mathbb{R}. Dalla relazione tra \log e \exp si ha

    (6)   \begin{equation*} \log x > M \iff x > e^M. \end{equation*}

    Dunque il valore di H cercato è H=e^M.

  3. Dobbiamo verificare che valga la condizione enunciata nel caso 2 della tabella 1 con x_0=0. Fissiamo dunque M \in \mathbb{R}. Di nuovo dalla relazione di invertibilità tra \log e \exp si ha

    (7)   \begin{equation*} \log x < M \iff 0< x < e^M. \end{equation*}

    Dunque il valore di \delta cercato è \delta=e^M.

Osservazione. La soluzione di questo esercizio è notevolmente più breve di quella dell’esercizio 5. Poiché la relazione di invertibilità tra \log e \exp è simmetrica, si potrebbe essere tentati di applicare un argomento simile anche per risolvere l’esercizio 5, evitando tra l’altro di dover dimostrare il Lemma 1. Questa sorta di apparente “gratuità” di entrambe le dimostrazioni è un segnale del fatto che ciò non sarebbe corretto, poiché condurrebbe a un argomento circolare. Infatti, la suriettività della funzione \exp \colon \mathbb{R} \to (0,+\infty) e quindi l’esistenza stessa della funzione \log sono conseguenze dei risultati dell’esercizio 5.

Precisamente, la suriettività della funzione \exp si ottiene grazie al fatto che

(8)   \begin{equation*} \inf_{x \in \mathbb{R}} e^x = 0, \qquad \sup_{x \in \mathbb{R}} e^x = +\infty \end{equation*}

e grazie alla sua continuità, ossia che in ogni punto x_0 \in \mathbb{R} si ha

(9)   \begin{equation*} \lim_{x \to x_0} e^x = e^{x_0}, \end{equation*}

che sono proprio i risultati dell’esercizio 5. Per maggiori dettagli si vedano proposizione 2.12, proposizione 5.22, definizione 5.23 della dispensa di teoria sulle funzioni continue.
Pertanto non si può utilizzare la funzione \log nella soluzione dell’esercizio 5: ciò sarebbe equivalente a usare una conseguenza di un teorema per dimostrare il teorema stesso, cioè un argomento circolare.

error: Il contenuto è protetto!!