Successioni di funzioni – Teoria

Home » Successioni di funzioni – Teoria

È possibile considerare successioni, ossia liste ordinate, di oggetti matematici diversi dai numeri reali? La nozione di successione di funzioni è quindi un naturale sviluppo di questa curiosità, carica di risvolti e applicazioni teoriche e pratiche nella Matematica.

In questa guida completa studiamo in profondità tale tema, rivolgendo la nostra attenzione ai seguenti argomenti:

Convergenza puntuale e uniforme e loro caratterizzazioni, come le condizioni di Cauchy;
Analisi dettagliata con esempi che mostrano come le proprietà di continuità, integrabilità e derivabilità non passino al limite puntuale di una successione;
Teoremi di passaggio al limite per la convergenza uniforme relativi alla continuità, derivabilità e integrabilità del limite uniforme di funzioni;
Criteri di convergenza uniforme come i teoremi del Dini, il teorema di Ascoli-Arzelà e la procedura diagonale;
Gli spazi normati delle funzioni limitate o continue e interpretazione dei teoremi di convergenza in questo contesto generale;
Il teorema di convergenza dominata di Arzelà, che mostra come si possa passare al limite l’integrale di una successione di funzioni sotto sole ipotesi di convergenza puntuale.

Ogni risultato viene introdotto da domande intuitive e spiegato da esempi e illustrazioni chiare, proponendo inoltre esercizi teorici risolti che rendono il discorso interattivo e stimolante. Questo articolo è quindi un viaggio nel cuore dell’Analisi Matematica moderna: non ti resta che iniziarlo!

Oltre alla raccolta
Esercizi sulle successioni di funzioni segnaliamo il seguente materiale teorico:

Autori e revisori

Leggi...

Autori: Luigi De Masi

Revisori: Roberto Castorini, Matteo Talluri, Valerio Brunetti, Sergio Fiorucci.

Notazioni

Leggi...

$\emptyset$	Insieme vuoto;
$\mathbb{N}$	Insieme dei numeri naturali positivi;
$\mathbb{Z}$	Insieme dei numeri interi;
$\mathbb{R}$	Insieme dei numeri reali;
$f_n \xrightarrow[n \to \infty]{\text{punt.}} f$	Convergenza puntuale della successione $f_n$ a $f$ ;
$f_n \xrightarrow[n \to \infty]{\text{punt.}(F)} f$	Convergenza puntuale sull’insieme $F$ della successione $f_n$ a $f$ ;
$f_n \xrightarrow[n \to \infty]{\text{unif.}} f$	Convergenza uniforme della successione $f_n$ a $f$ ;
$f_n \xrightarrow[n \to \infty]{\text{unif.}(F)} f$	Convergenza uniforme sull’insieme $F$ della successione $f_n$ a $f$ ;
$\operatorname{dist}(x,A)$	$= \inf\{\|x-y\| \mid y \in A\}$ : distanza di $x \in \mathbb{R}^d$ dall’insieme $A \subseteq \mathbb{R}^m$ ;
$\operatorname{dist}(A,B)$	$= \inf\{\|x-y\| \mid x \in A, \, y \in B\}$ , distanza tra gli insiemi $A,B \subseteq \mathbb{R}^m$ ;
$\chi_A$	funzione caratteristica dell’insieme $A \subseteq \mathbb{R}^m$ , definita da: (1) $\begin{equation} \chi_A(x) = \begin{cases} 1 & \text{se } x \in A, \\ 0& \text{se } x \notin A; \end{cases} \end{equation}$
$s(f,P), S(f,P)$	somme di Riemann inferiore e superiore della funzione $f$ rispetto alla suddivisione $P$ ;
$A \setminus B$	$=\{x \in A \mid x \notin B \}$ : differenza insiemistica tra $A$ e $B$ ;
$A^c$	$=\mathbb{R}^m \setminus A$ : complementare dell’insieme $A \subseteq \mathbb{R}^m$ ;
$\|I\|$	se $I \subset \mathbb{R}$ è costituito dall’unione di un numero finito di intervalli disgiunti, $\|I\|$ è la somma delle lunghezze di tali intervalli. Corrisponde alla cosiddetta misura di Peano-Jordan dell’insieme $I$ ;
$\sup_A f$	estremo superiore della funzione $f$ sull’insieme $A$ ;
$\inf_A f$	estremo inferiore della funzione $f$ sull’insieme $A$ ;
$\max_A f$	massimo della funzione $f$ sull’insieme $A$ ;
$\min_A f$	minimo della funzione $f$ sull’insieme $A$ ;
$\mathscr{B}(E,\mathbb{R})$	spazio vettoriale delle funzioni reali limitate con dominio $E$ ;
$C_b(E,\mathbb{R})$	spazio vettoriale delle funzioni reali continue e limitate con dominio $E$ ;
$d(x,y)$	distanza tra i punti $x,y$ ;
$\\| x \\|$	norma del vettore $x$ ;
$\\| f \\|_\infty$	norma infinito della funzione $f \in \mathscr{B}(E,\mathbb{R})$ ;
$d_\infty(\cdot, \cdot)$	distanza infinito indotta dalla norma $\\| \\|_\infty$ su $\mathscr{B}(E,\mathbb{R})$ ;
$B_r(x)$	$= \{y \in X \mid d(x,y) < r\}$ : palla aperta di centro $x$ e raggio $r$ nello spazio metrico $(X,d)$ ;

Introduzione

Leggi...

Nel corso dello studio dell’Analisi Matematica si studiano successioni e serie in cui il termine generale è un numero reale o complesso. Cosa possiamo dire invece se il termine generale è una funzione reale $f_n: \mathbb{R} \rightarrow \mathbb{R}$ (o una complessa $f_n: \mathbb{C} \rightarrow \mathbb{C}$ )? E soprattutto, è necessario indagare questo tipo di astrazione? La storia e le applicazioni della matematica hanno dato una risposta affermativa. Consideriamo di seguito alcuni esempi di queste situazioni.

$\quad$

Una procedura standard per calcolare il valore di una funzione con un certo grado di precisione è di approssimare la funzione usando dei polinomi “vicini” alla funzione e calcolare il valore di tali approssimanti. Questa procedura si esegue, ad esempio, quando la funzione da approssimare è trascendente. Può sembrare sorprendente, ma questo è il metodo usato sia nei moderni calcolatori che dai matematici dei secoli passati. Osserviamo che ciò presuppone di aver definito rigorosamente cosa si intende per approssimare una funzione e di essere certi che il suo valore puntuale si ottiene come limite del valore puntuale dei polinomi approssimanti.

Un caso ancor più estremo si verifica quando non si riesce ad esprimere la funzione $f$ che descrive un particolare fenomeno tramite funzioni elementari. Un caso esemplificativo di particolare importanza è l’equazione del calore. Un modo per risolvere il problema consiste nell’approssimare $f$ con combinazioni lineari di opportune funzioni sufficientemente semplici per essere trattabili. Ci si aspetta che, facendo crescere all’infinito il numero di funzioni elementari utilizzate, si ottenga un’approssimazione sempre migliore di $f$ .

Un altro caso in cui il concetto di approssimazione è molto utile è di tipo teorico. Un metodo per dimostrare la validità di un risultato per una certa classe $\mathcal{C}$ di funzioni consiste nel dimostrare che esso vale per una sua particolare sottoclasse $\mathcal{S}$ che però risulta abbastanza diffusa da essere “densa” nella classe originaria, nello stesso senso in cui i numeri razionali sono densi nei numeri reali. Chiaramente spesso ciò risulta più semplice rispetto al provare il risultato originario. Successivamente, approssimando opportunamente la generica funzione in $\mathcal{C}$ con una successione di funzioni in $\mathcal{S}$ , si riesce più facilmente a provare che essa soddisfa la proprietà desiderata.

Questi esempi mostrano l’utilità del concetto di successione di funzione e di definire in quale (in realtà quali) senso si intende il loro limite.

Concludiamo questa introduzione con una breve descrizione dell’organizzazione della dispensa:

$\quad$

Nella sezione 2 descriviamo la convergenza puntuale, che è una nozione abbastanza naturale di convergenza per successioni di funzioni; una volta definita questa convergenza è naturale chiedersi quali proprietà delle funzioni della successione passino al limite: continuità, integrabilità, derivabilità, etc.. Tali questioni costituiscono il leitmotiv che guida lo sviluppo di gran parte della dispensa.

Noteremo la parziale inadeguatezza della convergenza puntuale attraverso numerosi esempi ed esercizi. Come eccezione segnaliamo la sezione 2.1.3 in cui presentiamo un poco noto risultato di convergenza per gli integrali dovuto a Cesare Arzelà, il teorema 2.1.6.

Nella sezione 3 analizziamo dunque la nozione di convergenza uniforme, che risulta essere più forte della convergenza puntuale e che permette di sviluppare una teoria adeguata del passaggio al limite: mostriamo infatti nella sezione 3.2 come la convergenza uniforme assicuri una risposta affermativa alle questioni che ci siamo posti al riguardo della convergenza puntuale.
Una volta ottenuti questi risultati di convergenza, risulta evidente l’importanza di stabilire se una successione di funzioni converga uniformemente. Nella sezione 3.3 analizziamo alcune condizioni sufficienti per la convergenza uniforme. Oltre ai teoremi basati su criteri di monotonia della successione della sezione 3.3.1, nella sezione 3.3.2 presentiamo l’importante nozione di equicontinuità e mostriamo col teorema 3.56 come essa in un certo senso catturi l’essenza del passaggio dalla convergenza puntuale a quella uniforme.

Nella sezione 3.3.3 presentiamo il teorema di Ascoli-Arzelà, che è una sorta di analogo del teorema di Bolzano-Weierstrass per la convergenza uniforme, e dove l’equicontinuità della successione risulta essere di nuovo essenziale.

Nella sezione 4 osserviamo come la convergenza uniforme sia in realtà indotta da una cosiddetta metrica sullo spazio delle funzioni limitate, che permette cioè di misurare la distanza tra due qualunque funzioni. Inquadriamo i risultati ottenuti nelle precedenti sezioni in tale ottica, che ci permette di avere una visione globale e generale della situazione; questa visione si presta a essere utilizzata anche in altri contesti e studi futuri.
Nonostante il suo notevole interesse, a volte tale materiale viene escluso dai programmi dei corsi di Analisi 2, quindi il lettore può decidere in base alle sue necessità e gusti personali se dedicarsi o meno a tale approfondimento.

Nella sezione 5 raccogliamo alcune soluzioni di esercizi proposti nel testo.

Nell’appendice A presentiamo il concetto di misura di intervalli in maniera elementare, insieme ad alcune semplici proprietà utilizzate nella dispensa.

Nell’appendice B rispondiamo (negativamente) alla domanda 2.10 descrivendo una successione di funzioni continue convergente puntualmente a una funzione non integrabile secondo Riemann.

Nell’appendice C dimostriamo il teorema 2.16 di convergenza dominata di Arzelà, che fornisce condizioni sufficienti affinché si abbia convergenza degli integrali di funzioni integrabili sotto ipotesi di convergenza puntuale della successione di funzioni.

Convergenza puntuale

Introduzione.

Consideriamo $E \subseteq \mathbb{R}$ e una successione di funzioni $f_n \colon E \to \mathbb{R}$ . Quali significati possiamo dare al concetto di convergenza della successione $(f_n)_{n \in \mathbb{N}}$ a una opportuna funzione $f \colon E \to \mathbb{R}$ ?

In tutto il corso di questo capitolo ci interesseremo di funzioni reali di una sola variabile; tuttavia, molti dei risultati che dimostreremo valgono anche nel caso di funzioni in più variabili.

L’idea che può venire in mente è quella di estendere il concetto di convergenza di una successione numerica al caso delle funzioni. Infatti osserviamo che, fissato un elemento $x \in E$ , otteniamo una successione di numeri reali $(f_n(x))_{n \in \mathbb{N}}$ per la quale conosciamo già la nozione di convergenza. Supponiamo che essa sia convergente a un numero reale che scegliamo di chiamare $f(x)$ . Se ciò avviene per ogni $x \in E$ il valore $f(x)$ rappresenta una funzione $f : E \rightarrow \mathbb{R}$ che chiameremo limite puntuale della successione di funzioni $f_n$ .

Definizione 2.1 (convergenza puntuale). Data una successione di funzioni $f_n \colon E \to \mathbb{R}$ e una funzione $f \colon E \to \mathbb{R}$ , diciamo che $f_n$ converge puntualmente a $f$ se per ogni $x \in E$ la successione numerica $\big( f_n(x)\big)_{n \in \mathbb{N}}$ converge a $f(x)$ , cioé se si ha:

(2) $\begin{equation*} \lim_{n\to+\infty} f_n(x) = f(x) \qquad \forall x \in E. \end{equation*}$

In simboli scriviamo

(3) $\begin{equation*} f_n \xrightarrow[n \to \infty]{\text{punt.}} f, \quad \text{oppure} \quad f_n \xrightarrow{\text{punt.}} f. \end{equation*}$

Se (2) è verificata per ogni $x \in F$ , dove $F \subset E$ , diciamo che $f_n$ converge puntualmente a $f$ in $F$ . In simboli scriviamo

(4) $\begin{equation*} f_n \xrightarrow[n \to \infty]{\text{punt.} (F)} f, \quad \text{oppure} \quad f_n \xrightarrow{\text{punt.}(F)} f. \end{equation*}$

$\quad$

Osservazione 2.2. Usando la definizione di limite, la convergenza puntuale di $f_n$ a $f$ è equivalente a dire che

(5) $\begin{equation*} \forall \varepsilon > 0, \, \forall x \in E, \, \exists N \in \mathbb{N}\, \text{ tale che }\, \forall n > N \quad |f_n(x) - f(x))| < \varepsilon. \end{equation*}$

Sottolineiamo che il numero $N$ nella definizione di sopra dipende, oltre che da $\varepsilon$ , anche dal punto $x$ fissato.

Osservazione 2.3. Poiché l’eventuale limite puntuale $f$ di una successione di funzioni $f_n$ è definito punto per punto come limite di una successione di numeri reali, e poiché il limite di una successione di numeri reali, se esiste, è unico, otteniamo che, se $f_n$ ha limite puntuale $f$ , questo è unico.

Facciamo ora qualche esempio relativo alla convergenza puntuale.

Esempio 2.4. Consideriamo la successione di funzioni $f_n(x) \colon[0,1] \to \mathbb{R}$ definita da $f_n(x)=x^n$ . La successione $f_n$ converge puntualmente alla funzione $f \colon [0,1] \to \mathbb{R}$ definita da

(6) $\begin{equation*} \begin{cases} 0 & \text{se $0 \leq x < 1$,}\\ 1 & \text{se $x=1$.} \end{cases} \end{equation*}$

Infatti, per $x=1$ $f_n(1)=1$ per ogni $n \in \mathbb{N}$ e quindi non vi è nulla da dimostrare.

Se invece $x \in [0,1)$ , si ha

(7) $\begin{equation*} \lim_{n \to \infty} f_n(x) = \lim_{n \to \infty} x^n = 0. \end{equation*}$

Esercizio 2.5 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $E \subseteq \mathbb{R}$ , sia $g \colon E \to \mathbb{R}$ una funzione e sia $\alpha_n$ una successione di numeri reali tali che $\alpha_n \to 0$ . Dimostrare che la successione di funzioni $f_n \colon E \to \mathbb{R}$ definite da

(8) $\begin{equation*} f_n(x) = \alpha_n g(x) \end{equation*}$

converge puntualmente alla funzione $f \colon E \to \mathbb{R}$ identicamente nulla.

$\quad$

Rimandiamo alla sezione 5 per la soluzione.

Limiti della convergenza puntuale: continuità e passaggio al limite.

Ora che abbiamo definito una nozione di convergenza per successione di funzioni, risulta naturale chiedersi quali proprietà delle funzioni $f_n$ siano soddisfatte anche dal limite puntuale $f$ .

Domanda 2.6. Sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni continue che converga puntualmente a una funzione $f \colon E \to \mathbb{R}$ . Si può dire che $f$ è continua?

La risposta alla domanda 2.6 è negativa: in generale, il limite puntuale di una successione di funzioni continue non è necessariamente continuo, come mostra l’esempio 2.4. Infatti in tale esempio, la funzione limite $f$ non è continua nel punto $x=1$ .

Osservazione 2.7. Il problema enunciato nella domanda 2.6 corrisponde a chiedersi se è possibile scambiare l’ordine in cui si calcolano due limiti. Infatti, per rispondere alla domanda 2.6, si può stabilire se per ogni $x_0 \in E$ di accumulazione per $E$ vale la seguente uguaglianza:

(9) $\begin{equation*} \lim_{x \rightarrow x_0} f(x) \stackrel{?}{=} f(x_0) \end{equation*}$

Usando la continuità delle funzioni $f_n$ e il fatto che la successione delle $f_n$ converge puntualmente a $f$ , la precedente uguaglianza si riscrive nel seguente modo:

(10) $\begin{equation*} \lim_{x \rightarrow x_0} \Big( \lim_{n\to+\infty} f_n(x) \Big) \stackrel{?}{=} \lim_{n\to+\infty} \Big( \lim_{x \rightarrow x_0} f_n(x)\Big), \end{equation*}$

che appunto è equivalente a chiedersi se è possibile scambiare l’ordine con cui si calcolano due limiti.

Visto nella prospettiva dell’osservazione 2.7, nell’esempio 2.4 scambiare l’ordine in cui si calcolano i due limiti seguenti dà luogo a risultati diversi, infatti:

(11) $\begin{equation*} \begin{gathered} \lim_{x \rightarrow 1^{-}} \Big( \lim_{n\to+\infty} f_n(x)\Big) = \lim_{x \rightarrow 1^{-}} f(x) \\ \lim_{n\to+\infty} \Big( \lim_{x \rightarrow 1^{-}} f_n(x) \Big) = \lim_{n\to+\infty} f_n(1) = 1. \end{gathered} \end{equation*}$

Ci si potrebbe chiedere se la commutatività dei limiti fallisca a causa del fatto che il limite puntuale $f$ non è continuo; ci si potrebbe cioè porre la seguente questione.

Domanda 2.8. Sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni (non necessariamente continue) che converga puntualmente a una funzione $f \colon E \to \mathbb{R}$ continua. Vale, per ogni $x_0 \in E$ , l’uguaglianza

(12) $\begin{equation*} \lim_{x \rightarrow x_0} \Big( \lim_{n\to+\infty} f_n(x)\Big) = \lim_{n\to+\infty} \Big( \lim_{x \rightarrow x_0} f_n(x) \Big) ? \end{equation*}$

Notiamo che, rispetto alla domanda 2.6, nella domanda 2.8 si sta rinunciando alla continuità delle $f_n$ ma si sta assumendo per ipotesi che il limite $f$ sia continuo e ci si chiede se, in tal caso, l’operazione di limite sia commutativa.

Purtroppo, di nuovo la risposta è negativa, come mostra il seguente esempio.

Esempio 2.9. Consideriamo la successione di funzioni $f_n \colon [0,1) \to \mathbb{R}$ definita da

(13) $\begin{equation*} f_n(x) = \begin{cases} 0 & \text{se } x=0 \text{ oppure } \dfrac{2}{n} \leq x \leq 1, \\[5pt] 1 & \text{se $0 < x < \dfrac{1}{n}$,}\\[6pt] 2 - nx & \text{se $\dfrac{1}{n} \leq x < \dfrac{2}{n}$.} \end{cases} \end{equation*}$

Essa converge puntualmente alla funzione $f(x) \equiv 0$ . Infatti si ha $f_n(0)=0$ per ogni $n \in \mathbb{N}$ ; Se invece $x>0$ , per ogni $n > \dfrac{2}{x}$ si ha $\dfrac{2}{n} < x$ e ciò implica $f_n(x)=0$ ; da cui

(14) $\begin{equation*} \begin{gathered} \lim_{n \to +\infty} f_n(x) = 0. \end{gathered} \end{equation*}$

Poiché $f$ è ovviamente continua, ciò mostra che scambiare l’ordine in cui si calcolano i due limiti seguenti dà luogo a risultati diversi:

(15) $\begin{equation*} \begin{gathered} \lim_{x \rightarrow 0} \Big( \lim_{n\to+\infty} f_n(x)\Big) = \lim_{x \rightarrow 0} 0 = 0, \\ \lim_{n\to+\infty} \Big( \lim_{x \rightarrow 0} f_n(x) \Big) = \lim_{n\to+\infty} 1 = 1. \end{gathered} \end{equation*}$

$\quad$

Figura 1: La funzione $f_n$ dell’esempio 2.9.

$\quad$

Limiti della convergenza puntuale: integrazione.

Si può indagare come si comportano le proprietà relative all’integrazione rispetto alla convergenza puntuale di una successione di funzioni. La prima questione che occorre affrontare è se il limite puntuale di una successione di funzioni integrabili secondo Riemann è a sua volta integrabile.

Domanda 2.10. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni integrabili secondo Riemann che converga puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ . $f$ risulta integrabile?

La risposta è negativa anche assumendo la continuità delle $f_n$ , come mostra l’esempio B.2 riportato nell’appendice B.

Osservazione 2.11. L’esempio B.2 può essere visto come un rafforzamento di quanto mostrato nell’esempio 2.4. Infatti esso mostra che il limite puntuale di funzioni continue non solo non è necessariamente continuo, ma può non essere neppure integrabile secondo Riemann, che è una proprietà più debole della continuità.

Ci si può chiedere se, assumendo per che il limite puntuale di una successione di funzioni continue sia integrabile, allora il valore degli integrali converga al valore dell’integrale del limite. Più precisamente ci poniamo la seguente questione.

Domanda 2.12. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni integrabili secondo Riemann che converga puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ integrabile secondo Riemann. Si può concludere che

(16) $\begin{equation*} \lim_{n \to +\infty} \int_a^b f_n(x) \,\mathrm{d}x = \int_a^b f(x) \,\mathrm{d}x \, ? \end{equation*}$

Ci si sta chiedendo, cioè, se le operazioni di integrazione e di limite siano in quache modo commutative.

Ancora otteniamo una risposta negativa, perfino se le funzioni $f_n$ e $f$ sono continue, come mostra il seguente esempio.

Esempio 2.13. Consideriamo la successione di funzioni $f_n \colon [0,1] \to \mathbb{R}$ definita da

(17) $\begin{equation*} f_n(x) = \begin{cases} n^2x & \text{se $0 \leq x < \dfrac{1}{n}$,}\\[8pt] 2n - n^2x & \text{se $\dfrac{1}{n} \leq x < \dfrac{2}{n}$,}\\[8pt] 0 & \text{se $\dfrac{2}{n} \leq x \leq 1$.} \end{cases} \qquad \forall n \geq 2. \end{equation*}$

Si osserva che $f_n(x)$ converge puntualmente alla funzione $f(x)=0$ . Ma notiamo che

(18) $\begin{equation*} \lim_{n\to+\infty} \int_0^1 f_n(x) \,\mathrm{d}x = \lim_{n\to+\infty} 1 = 1 \,\,\,\,\, \text{e} \,\,\,\,\, \int_0^1 \Big( \lim_{n\to+\infty} f_n(x) \Big) \,\mathrm{d}x = \int_0^1 0 \,\mathrm{d}x = 0. \end{equation*}$

$\quad$

Figura 2: La funzione $f_n$ dell’esempio 2.13.

$\quad$

Il teorema di convergenza dominata di Arzelà

Si può notare che le funzioni $f_n$ dell’esempio 2.13 sono limitate, ma per ogni $n \in \mathbb{N}$ si ha

(19) $\begin{equation*} \sup_{x \in [0,1]} |f_n(x)| = n \xrightarrow[n \to \infty]{} +\infty. \end{equation*}$

A un’osservazione attenta, ciò provoca in questo caso una “concentrazione” dell’area sottesa al grafico di $f_n$ in un intervallo sempre più stretto, nonostante il valore di tale area rimanga costantemente pari a $1$ . Al limite, quest’area scompare e questa potrebbe essere la ragione del fatto che gli integrali $\int f_n$ non convergono a $\int f$ .

Ci si potrebbe chiedere se, richiedendo una limitatezza “uniforme” delle $f_n$ , si possano prevenire questi fenomeni di concentrazione e quindi ottenere la convergenza degli integrali.

Domanda 2.14. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni integrabili secondo Riemann; si supponga che esista $M>0$ tale che

(20) $\begin{equation*} \sup_{x \in [a,b]} |f_n| \leq M \qquad \forall n \in \mathbb{N}. \end{equation*}$

Si supponga inoltre che $f_n$ converga puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ integrabile secondo Riemann. Si può concludere che

(21) $\begin{equation*} \lim_{n \to +\infty} \int_a^b f_n(x) \,\mathrm{d}x = \int_a^b f(x) \,\mathrm{d}x \, ? \end{equation*}$

Osservazione 2.15. La condizione (20) si può esprimere dicendo che le funzioni $f_n$ sono equilimitate; per maggiori dettagli, si veda la definizione 3.57, dove si può trovare una discussione approfondita sull’importanza di tale proprietà rispetto alla convergenza uniforme.

La risposta alla domanda 2.14 è affermativa, come mostra il seguente notevole risultato dovuto al matematico italiano Cesare Arzelà (1847 – 1912).

Teorema 2.16. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni integrabili secondo Riemann e si supponga che esista $M>0$ tale che

(22) $\begin{equation*} \sup_{x \in [a,b]} |f_n| \leq M \qquad \forall n \in \mathbb{N}. \end{equation*}$

Si supponga inoltre che $f_n$ converga puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ integrabile secondo Riemann. Allora si ha

(23) $\begin{equation*} \lim_{n \to +\infty} \int_a^b f_n(x) \,\mathrm{d}x = \int_a^b f(x) \,\mathrm{d}x. \end{equation*}$

$\quad$

Rimandiamo la dimostrazione all’appendice C.

Limiti della convergenza puntuale: derivazione.

È naturale chiedersi cosa possiamo dire della derivabilità del limite puntuale di una successione di funzioni. Cominciamo con l’analizzare la seguente domanda:

Domanda 2.17. Sia $f_n \colon (a,b) \to \mathbb{R}$ una successione di funzioni derivabili che converge puntualmente a $f \colon (a,b) \to \mathbb{R}$ . $f$ risulta derivabile?

La risposta è negativa, come mostra il seguente esempio.

Esempio 2.18. Consideriamo la successione di funzioni $f_n \colon (-1,1) \to \mathbb{R}$ definita da

$f_n(x) = \sqrt{x^2 + \frac{1}{n^2}}.$

Si osserva facilmente che $f_n$ è derivabile (con derivata continua), e che il limite puntuale di $f_n$ è $f(x) = |x|$ (che non è derivabile in $x=0$ ). Infatti, sia $x \in (-1,1)$ ; se $x \geq 0$ (l’altro caso è analogo) si ha

(24) $\begin{equation*} |f_n(x) - f(x)| = \frac{\Big(\sqrt{x^2 + \dfrac{1}{n^2}} - x \Big)\Big(\sqrt{x^2 + \dfrac{1}{n^2}} + x\Big)}{\Big(\sqrt{x^2 + \dfrac{1}{n^2}} + x \Big)} \leq \frac{\dfrac{1}{n^2}}{\dfrac{1}{n}+x } \leq \frac{1}{n} \end{equation*}$

che converge a $0$ per $n\to \infty$ .

Si potrebbe pensare che, assumendo per ipotesi la derivabilità della funzione limite, si possa concludere che la successione delle derivate converga almeno puntualmente. Più precisamente possiamo porci la seguente domanda.

Domanda 2.19. Sia $f_n \colon (a,b) \to \mathbb{R}$ una successione di funzioni derivabili che converge puntualmente a $f \colon (a,b) \to \mathbb{R}$ derivabile. Si può affermare che la successione $f_n'$ converge puntualmente a una funzione $g$ ?

La risposta è ancora negativa, come mostrato dal seguente esempio.

Esempio 2.20. Sia $f_n \colon [-2\pi,2\pi] \to \mathbb{R}$ la successione di funzioni definite da

(25) $\begin{equation*} f_n(x)= \frac{1}{n}\sin(2^nx). \end{equation*}$

Abbiamo

(26) $\begin{equation*} |f_n(x)| \leq \frac{1}{n} \qquad \forall n \in \mathbb{N}, \,\,\, \forall x \in [-2\pi,2\pi], \end{equation*}$

che prova la convergenza puntuale delle $f_n$ alla funzione $f$ identicamente nulla; $f$ è chiaramente derivabile con derivata nulla, tuttavia si ha

(27) $\begin{equation*} f_n'(\pi) = \frac{2^n}{n}\cos(2^n \pi) = \frac{2^n}{n}, \end{equation*}$

che diverge per $n \to \infty$ .

Come ultima domanda, ci si può chiedere se assumendo anche la convergenza delle derivate, si possa affermare che il limite delle $f_n$ sia pari a $f'$ .

Domanda 2.21. Sia $f_n \colon (a,b) \to \mathbb{R}$ una successione di funzioni derivabili che converge puntualmente a $f \colon (a,b) \to \mathbb{R}$ derivabile, sia $x_0 \in (a,b)$ e si supponga che la successione $f_n'$ converga puntualmente a una funzione $g$ . Si può concludere che $g=f'$ ? In altre parole, si può affermare che

(28) $\begin{equation*} \lim_{n \to \infty} f_n'(x_0) = f'(x_0)? \end{equation*}$

Anche la risposta a questa domanda è negativa, come mostrato dal seguente esempio.

Esempio 2.22. Sia $f_n \colon [-1,1] \to \mathbb{R}$ la successione di funzioni definita da

(29) $\begin{equation*} f_n(x) = \begin{cases} -\dfrac{1}{n} & \text{se } x \in \left[-1,-\dfrac{\pi}{2n}\right)\\[8pt] \dfrac{1}{n} \sin(nx) & \text{se } x \in \left[-\dfrac{\pi}{2n},\dfrac{\pi}{2n}\right]\\[8pt] \dfrac{1}{n} & \text{se } x \in \left(\dfrac{\pi}{2n},1\right]. \end{cases} \qquad \forall n \geq 2. \end{equation*}$

Si può verificare che $f_n$ risulta derivabile in $[-1,1]$ (controllando che $f'(\pm \pi/2n)=0$ ). Inoltre, per ogni $n \geq 2$ si ha

(30) $\begin{equation*} |f_n(x)| \leq \frac{1}{n} \qquad \forall x \in[-1,1]. \end{equation*}$

Ciò mostra che $f_n$ converge puntualmente alla funzione $f$ identicamente nulla, che ovviamente risulta derivabile e $f' \equiv 0$ . Tuttavia si può facilmente vedere che

(31) $\begin{equation*} f_n'(0)=1 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Si vede che $f_n'$ converge puntualmente alla funzione $g \colon [-1,1] \to \mathbb{R}$ definita da

(32) $\begin{equation*} g(x) = \begin{cases} 0 & \text{se } x \in [-1,0) \cup (0,1]\\[4pt] 1 & \text{se } x=0. \end{cases} \end{equation*}$

Si ha $g \neq f'$ e la (28) è quindi falsa per $x_0=0$ .

Convergenza uniforme

Introduzione.

La convergenza puntuale di una successione di funzioni $f_n$ è molto debole e ciò comporta dei pro e dei contro: da un lato essa è facilmente ottenibile e verificabile; di contro, come dimostrano gli esempi riportati sopra, il limite puntuale $f$ può non godere delle proprietà delle funzioni $f_n$ (si pensi agli esempi 2.4 e 2.18 e B.2), oppure, anche quando $f$ soddisfa le proprietà di continuità, integrabilità e derivabilità delle $f_n$ , può non esserci una loro convergenza quantitativa: gli esempi 2.9, 2.13, 2.20 e 2.22 chiariscono il significato di tale affermazione.

La mancanza di teoremi di passaggio al limite ci mostrano che la nozione di convergenza puntuale non è adeguata alla maggior parte degli scopi dell’Analisi Matematica e ci spingono a ricercarne delle altre.

Si può iniziare tale ricerca chiedendosi quale sia il “difetto” della convergenza puntuale. Sia quindi $E \subseteq \mathbb{R}$ e consideriamo una successione di funzioni

(33) $\begin{equation*} f_n \colon E \to \mathbb{R} \end{equation*}$

che converge puntualmente a una funzione $f \colon E \to \mathbb{R}$ . Si potrebbe pensare che, per quanto le funzioni $f_n$ convergano a $f$ in senso puntuale, esse non siano “sufficientemente vicine” a $f$ affinché le loro proprietà passino al limite. In che senso si può intendere questa frase?

La risposta risiede appunto nell’aggettivo puntuale: la convergenza puntuale afferma che, fissato un punto $x \in E$ , allora da un certo $N$ in poi, le funzioni $f_n$ calcolate nel punto $x$ sono vicine alla $f$ calcolata nel punto $x$ . Cambiando il punto $x$ , potrebbe essere necessario variare il numero naturale $N$ . In altre parole, potrebbe non esistere un unico numero naturale $N$ per cui, per $n>N$ le funzioni $f_n$ siano vicine almeno $\varepsilon$ alla funzione $f$ in ogni punto $x$ .

Una nuova nozione di convergenza potrebbe quindi richiedere questo controllo uniforme su $N$ che non dipenda cioè dal punto $x$ scelto e che sia appunto uniforme sull’intero insieme $E$ . Allora, fissato un valore di $\varepsilon$ la condizione $|f_n(x) - f(x)| < \varepsilon$ sarebbe verificata per ogni $n > N$ , qualsiasi sia $x \in E$ .

Questa nuova nozione dà luogo a una teoria ricca e ciò motiva la definizione di convergenza uniforme.

Definizione e prime proprietà.

Definizione 3.1 (convergenza uniforme). Sia $E \subset \mathbb{R}$ , $f_n \colon E \to \mathbb{R}$ una successione di funzioni e sia $f \colon E \to \mathbb{R}$ ; si dice che $f_n$ converge uniformemente a $f$ se, per ogni $\varepsilon>0$ , esiste $N \in \mathbb{N}$ tale che

(34) $\begin{equation*} |f_n(x) - f(x))| < \varepsilon \qquad \forall n \geq N, \,\, \forall x \in E. \end{equation*}$

In simboli scriviamo

(35) $\begin{equation*} f_n \xrightarrow[n \to +\infty]{\text{unif}} f, \quad \text{oppure} \quad f_n \xrightarrow{\text{unif}} f. \end{equation*}$

Se (34) è verificata per ogni $x \in F$ , dove $F \subseteq E$ , diciamo che la successione $f_n$ converge uniformemente in $F$ a $f$ e scriviamo

(36) $\begin{equation*} f_n \xrightarrow[n \to +\infty]{\text{unif}(F)} f, \quad \text{oppure} \quad f_n \xrightarrow{\text{unif}(F)} f. \end{equation*}$

$\quad$

Osservazione 3.2. Scrivendo la definizione di convergenza uniforme in formule, abbiamo che $f_n$ converge uniformemente a $f$ se e solo se

(37) $\begin{equation*} \forall \varepsilon >0 \,\, \exists N \in \mathbb{N} \, \text{ tale che }\, \forall n \geq N \,\, \forall x \in E \quad |f_n(x) - f(x))| < \varepsilon. \end{equation*}$

La (37), pur sembrando simile alla (5), che definisce la convergenza puntuale, differisce da essa in maniera sostanziale: nella (37) il numero naturale $N$ è scelto senza tener conto del punto $x$ (e infatti l’esistenza di $N$ è affermata prima di scegliere il punto $x$ ), mentre nella (5) il numero $N$ dipende dal particolare punto $x$ scelto (e infatti l’esistenza di un siffatto $N$ è affermata dopo aver scelto $x$ ).

Per meglio comprendere il significato della convergenza uniforme, facciamo qualche considerazione di carattere grafico e successivamente analizziamo un esempio concreto.

Osservazione 3.3. La nozione di convergenza uniforme è raffigurata in figura 3. Dato $\epsilon > 0$ esiste un $N$ tale che per ogni $n > N$ il grafico di $f_n$ (rappresentato con il tratto rosso) è compreso fra i grafici di $f + \epsilon$ e $f - \epsilon$ (rappresentati tratteggiati).

In altre parole, $f_n$ converge uniformemente a $f$ se, dato $\varepsilon>0$ e immaginando una striscia di ampiezza $\varepsilon$ intorno al grafico di $f$ (dai contorni tratteggiati in figura 3), allora da un certo $N$ in poi il grafico di $f_n$ è compreso nella suddetta striscia.

$\quad$

Figura 3: Convergenza uniforme di una successione di funzioni $f_n$ a $f$ .

$\quad$

Quanto visto nell’osservazione precedente non avviene invece nel caso della convergenza puntuale, come mostra il prossimo esercizio che esamina la successione di funzioni dell’esempio 2.4 dal punto di vista della convergenza uniforme.

Esempio 3.4. Sia $f_n : [0,1) \rightarrow \mathbb{R}$ definite da $f_n(x) = x^n$ . Allora si può vedere che $f_n$ converge puntualmente ma non uniformemente alla funzione $f \equiv 0$ . La convergenza delle $f_n$ a $f$ è però uniforme in ogni intervallo del tipo $[0,\alpha]$ con $0 <\alpha < 1$ .

La prima parte dell’enunciato è già stata dimostrata nell’esempio 2.4. Dunque la successione di funzioni converge puntualmente alla funzione identicamente nulla.

$f_n$ non converge però uniformemente a $f$ . Infatti, fissiamo un qualunque $n \in \mathbb{N}$ . Poiché si ha

(38) $\begin{equation*} \lim_{x \to 1^-} f_n(x)=1, \end{equation*}$

esiste $x_n \in [0,1)$ tale che $f_n(x_n) > \dfrac{1}{2}$ . Ciò implica che, se $\varepsilon \in \big(0,\dfrac{1}{2} \big)$ , allora non esiste nessun $n \in \mathbb{N}$ per cui

(39) $\begin{equation*} f_n(x) = |f_n(x) - f(x)| < \varepsilon \qquad \forall x \in [0,1). \end{equation*}$

Ciò nega la convergenza uniforme delle $f_n$ a $f$ .

Per verificare l’ultima asserzione, si consideri $\alpha \in (0,1)$ . Poiché ognuna delle funzioni $f_n$ è crescente, si ha

(40) $\begin{equation*} |f_n(x) - f(x)| = f_n(x) \leq f_n(\alpha) = \alpha^n \qquad \forall n \in \mathbb{N},\,\, \forall x \in [0,\alpha]. \end{equation*}$

Sia $\varepsilon>0$ . Allora, poiché $\lim_{n \to \infty} \alpha^n=0$ , esiste $N \in \mathbb{N}$ tale che, per ogni $n \geq N$ , si ha $\alpha^n < \varepsilon$ . Ma allora, per (40), per ogni $n \geq N$ si ha

(41) $\begin{equation*} |f_n(x) - f(x)| \leq \alpha^n < \varepsilon \qquad \forall x \in [0, \alpha]. \end{equation*}$

Ciò prova che

(42) $\begin{equation*} f_n \xrightarrow[n \to \infty]{\text{unif}([0,\alpha])} f. \end{equation*}$

$\quad$

Figura 4: Convergenza non uniforme della successione $f_n(x)=x^n$ a $f \equiv 0$ ; se $0 < \varepsilon < 1$ , il grafico delle $f_n$ non è contenuto nella striscia di ampiezza $\varepsilon$ intorno al grafico di $f \equiv 0$ .

$\quad$

Esercizio 3.5 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dimostrare con un esempio che la convergenza dell’esercizio 2.5 può non essere uniforme.

Esercizio 3.6 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $E \subseteq \mathbb{R}$ , sia $g \colon E \to \mathbb{R}$ una funzione limitata e sia $\alpha_n$ una successione di numeri reali tali che $\alpha_n \to 0$ . Dimostrare che la successione di funzioni $f_n \colon E \to \mathbb{R}$ definite da

(43) $\begin{equation*} f_n(x) = \alpha_n g(x) \end{equation*}$

converge uniformemente alla funzione $f \colon E \to \mathbb{R}$ identicamente nulla.

$\quad$

Rimandiamo alla sezione 5 per le soluzioni.

Definizione e prime proprietà: caratterizzazione equivalente della convergenza uniforme.

Come primo semplice risultato riguardante la convergenza uniforme, enunciamo una sua semplice caratterizzazione che si rivela utile nei casi pratici.

Proposizione 3.7 (caratterizzazione della convergenza uniforme). Sia $E \subset \mathbb{R}$ , $f_n \colon E \to \mathbb{R}$ una successione di funzioni e sia $f \colon E \to \mathbb{R}$ ; Allora $f_n$ converge uniformemente a $f$ se e solo se

(44) $\begin{equation*} \lim_{n \to + \infty} \, \sup \big\{ |f_n(x) - f(x)| \mid x \in E \big\} = 0. \end{equation*}$

$\quad$

Osservazione 3.8. Spesso, in luogo della (44), si useranno le sue abbreviazioni

(45) $\begin{equation*} \lim_{n \to + \infty} \sup_{x \in E} |f_n(x) - f(x)|, \quad \text{ oppure } \quad \lim_{n \to + \infty} \sup_{E} |f_n - f|. \end{equation*}$

Dimostrazione della proposizione 3.7. Se $f_n$ converge uniformemente a $f$ , allora per definizione, per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ tale che

(46) $\begin{equation*} |f_n(x) - f(x)| < \varepsilon \qquad \forall n \geq N,\,\, \forall x \in E. \end{equation*}$

Ciò implica che, per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ tale che

(47) $\begin{equation*} \sup_{x \in E} |f_n(x) - f(x)|< \varepsilon \qquad \forall n \geq N. \end{equation*}$

Per definizione di limite, quindi, la quantità di sopra converge a $0$ per $n \to \infty$ . In formule

(48) $\begin{equation*} \lim_{n \to + \infty} \sup_{x \in E} |f_n(x) - f(x)| = 0. \end{equation*}$

Poiché tutte le implicazioni dimostrate sono in realtà delle equivalenze, ciò dimostra anche l’altra parte dell’enunciato. Per chiarezza e comodità del lettore, però, scriviamo comunque la dimostrazione per esteso.

Supponiamo quindi verificata la (44). Per definizione di limite ciò implica che per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ tale che

(49) $\begin{equation*} \sup_{x \in E} |f_n(x) - f(x)|< \varepsilon \qquad \forall n \geq N. \end{equation*}$

Ciò ovviamente implica che per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ tale che

(50) $\begin{equation*} |f_n(x) - f(x)|< \varepsilon \qquad \forall n \geq N, \,\, \forall x \in E, \end{equation*}$

che è proprio la definizione di convergenza uniforme delle $f_n$ a $f$ .

Definizione e prime proprietà: relazione con la convergenza puntuale.

Una volta introdotto un nuovo oggetto, spesso in Matematica si analizzano le sue relazioni con oggetti precedentemente studiati. Per quanto riguarda la convergenza uniforme, possiamo chiederci quale sia la sua relazione con la nozione di convergenza puntuale.

Domanda 3.9. L’eventuale limite uniforme di una successione di funzioni è unico? Che relazione esiste tra la convergenza puntuale e uniforme? Una implica l’altra? Nel caso siano verificate entrambe le convergenze, i limiti coincidono?

Analizzando il modo in cui abbiamo definito la nozione di convergenza uniforme di una successione di funzioni, si può intuire che questa sia più forte di quella puntuale, come precisa il prossimo risultato.

Proposizione 3.10. Sia $E \subset \mathbb{R}$ ; se una successione di funzioni $f_n \colon E \to \mathbb{R}$ converge uniformemente a una funzione $f \colon E \to \mathbb{R}$ , allora $f_n$ converge puntualmente a $f$ .

In particolare, il limite uniforme di una successione di funzioni, se esiste, coincide con il limite puntuale e quindi è unico.

$\quad$

Dimostrazione. Assumiamo che $f_n$ converga uniformemente a $f$ e fissiamo un qualunque $x_0 \in E$ . Allora ovviamente si ha

(51) $\begin{equation*} |f_n(x_0) - f(x_0)| \leq \sup_{x \in E} |f_n(x) - f(x)| \qquad \forall n \in \mathbb{N}. \end{equation*}$

Poiché per l’ipotesi di convergenza uniforme il membro di destra tende a $0$ per $n \to \infty$ , si ha

(52) $\begin{equation*} \lim_{n \to \infty} |f_n(x_0) - f(x_0)| = 0, \end{equation*}$

che prova la convergenza puntuale delle $f_n$ a $f$ . L’ultima asserzione segue facilmente dalla prima parte dell’enunciato e dall’unicità del limite puntuale.

Osservazione 3.11. La proposizione 3.10, oltre al fatto che la convergenza uniforme è più forte di quella puntuale, asserisce che, quando esistono, i due limiti sono uguali. Ciò è utile nei casi pratici: infatti, per studiare la convergenza uniforme di una successione, se ne può studiare prima la convergenza puntuale (che, essendo più debole è solitamente più semplice da ottenere) e poi, in virtù della proposizione 3.10, verificare se il limite puntuale ottenuto è anche uniforme.

Esercizio 3.12 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $f_n \colon \mathbb{R} \to \mathbb{R}$ la successione di funzioni definita da

(53) $\begin{equation*} f_n(x) = \arctan(x-n). \end{equation*}$

Dimostrare che la successione converge puntualmente alla funzione costante $f = -\dfrac{\pi}{2}$ ; dimostrare inoltre che la convergenza non è uniforme su $\mathbb{R}$ ma che lo è su ogni intervallo del tipo $(-\infty,R]$ con $R \in \mathbb{R}$ .

$\quad$

Rimandiamo alla sezione 5 per la soluzione.

Definizione e prime proprietà: condizioni di Cauchy.

In alcuni casi non è possibile calcolare esattamente il limite puntuale o uniforme di una successione di funzioni $f_n$ , oppure non è agevole farlo; inoltre, può capitare di essere interessati alla convergenza di una successione e che non sia essenziale determinare la funzione limite.

In tali casi può essere utile avere a disposizione dei criteri per dimostrare i due tipi di convergenza introdotti. Questi prendono il nome di criteri di Cauchy, in quanto si rifanno al noto criterio di Cauchy per le successioni numeriche, che richiamiamo qui di seguito. Per una dimostrazione rimandiamo il lettore a [1, Teorema 5.48].

Teorema 3.13 (criterio di Cauchy per le successioni numeriche). Una successione $(x_n)_{n \in \mathbb{N}}$ di numeri reali è convergente se e solo se, per ogni $\varepsilon>0$ , esiste $N \in \mathbb{N}$ tale che

(54) $\begin{equation*} |x_n - x_m| < \varepsilon \qquad \forall n,m \geq N. \end{equation*}$

Definizione 3.14. Una successione numerica che soddisfa la condizione del teorema 3.13 è detta di Cauchy.

$\quad$

Osservazione 3.15. Il teorema 3.13 costituisce una formulazione equivalente dell’assioma di completezza di $\mathbb{R}$ , [1, Assioma 3.12, Teorema 3.15].

Il teorema 3.13 produce i seguenti risultati per le successioni di funzioni.

Proposizione 3.16 (criterio di Cauchy per la convergenza puntuale). Sia $E \subset \mathbb{R}$ e una successione di funzioni $f_n \colon E \to \mathbb{R}$ . Allora $f_n$ converge puntualmente a una funzione $f \colon E \to \mathbb{R}$ se e solo se, per ogni $x \in E$ e per ogni $\varepsilon>0$ , esiste $N \in \mathbb{N}$ tale che

(55) $\begin{equation*} |f_n(x) - f_m(x)| < \varepsilon \qquad \forall n,m \geq N. \end{equation*}$

$\quad$

Osservazione 3.17. Il numero $N$ dipende sia dal punto $x \in E$ sia da $\varepsilon$ .

Dimostrazione della proposizione 3.16. Se $f_n$ converge puntualmente a $f$ , allora per ogni $x \in E$ fissato, la successione numerica $f_n(x)$ è convergente, quindi per il teorema 3.13 è di Cauchy, cioè per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ per cui la (55) è soddisfatta.

Viceversa, se per ogni $x \in E$ e per ogni $\varepsilon$ esiste $N \in \mathbb{N}$ per cui vale la (55), allora per ogni $x \in E$ la successione $f_n(x)$ è di Cauchy, quindi converge per il teorema 3.13 e, chiamando per ogni $x \in E$ $f(x)$ il limite di tale successione, risulta definita una funzione $f \colon E \to \mathbb{R}$ che è proprio il limite puntuale delle $f_n$ .

Proposizione 3.18 (criterio di Cauchy per la convergenza uniforme). Sia $E \subset \mathbb{R}$ e una successione di funzioni $f_n \colon E \to \mathbb{R}$ . Allora $f_n$ converge uniformemente a una funzione $f \colon E \to \mathbb{R}$ se e solo se, per ogni $\varepsilon>0$ , esiste $N \in \mathbb{N}$ tale che

(56) $\begin{equation*} \sup_{x \in E}|f_n(x) - f_m(x)| \leq \varepsilon \qquad \forall n,m \geq N. \end{equation*}$

$\quad$

Dimostrazione. Supponiamo che $f_n$ converga uniformemente a $f$ . Allora per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ tale che, per ogni $n \geq N$ , si ha

(57) $\begin{equation*} \sup_{x \in E}|f_n(x) - f(x)| < \frac{\varepsilon}{2}. \end{equation*}$

Ma allora, per ogni $x \in E$ e per ogni $n, m \geq N$ , vale

(58) $\begin{equation*} \begin{split} |f_n(x) - f_m(x)| \leq & |f_n(x) - f(x)| + |f(x) - f_m(x)| \\ \leq & \sup_{x \in E}|f_n(x) - f(x)| + \sup_{x \in E}|f_m(x) - f(x)| \\ < & {\varepsilon}. \end{split} \end{equation*}$

Passando all’estremo superiore per il membro di sinistra, si ottiene

(59) $\begin{equation*} \sup_{x \in E}|f_n(x) - f_m(x)| \leq \varepsilon. \end{equation*}$

Viceversa, se per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ per cui vale (56), allora in particolare per ogni $x \in E$ la successione $f_n(x)$ è di Cauchy, quindi per il teorema 3.13 converge a un numero reale $f(x)$ che definisce una funzione $f \colon E \to \mathbb{R}$ . Quindi

(60) $\begin{equation*} |f_n(x) - f_m(x)| \leq \varepsilon \qquad \forall x \in E, \,\,\, \forall n,m \geq N. \end{equation*}$

Facendo tendere $m \to \infty$ nell’equazione sopra, si ottiene

(61) $\begin{equation*} |f_n(x) - f(x)| \leq \varepsilon \qquad \forall x \in E, \,\,\, \forall n \geq N. \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ , $f_n$ converge uniformemente a $f$ .

Teoremi di convergenza.

Una delle proprietà importanti della convergenza uniforme consiste nel fatto che essa è stabile rispetto al passaggio al limite, all’integrazione e alla derivazione. I risultati che esplicitano tale stabilità sono detti teoremi di convergenza e sono l’oggetto di questa sezione.

Teoremi di convergenza: continuità e limiti.

In questa sezione indagheremo le relazioni tra continuità e convergenza uniforme. Il primo risultato afferma che la situazione dell’esempio 2.4 non è possibile ipotizzando la convergenza uniforme della successione; infatti, in tal caso, la continuità “passa al limite”.

In altre parole, la domanda 2.6 ha una risposta affermativa se cambiamo l’avverbio “puntualmente” in “uniformemente”.

Teorema 3.19 (limite uniforme di funzioni continue). Sia $E \subset \mathbb{R}$ e sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni continue convergente uniformemente alla funzione $f \colon E \to \mathbb{R}$ . Allora $f$ è una funzione continua.

$\quad$

Osservazione 3.20. Il teorema 3.19 mostra anche che, se le $f_n$ sono continue e $f$ non lo è, $f_n$ non può convergere uniformemente a $f$ . Ciò costituisce un criterio per mostrare che una successione non converge uniformemente.

Dimostrazione del teorema 3.19. Sia $x_0 \in E$ un punto di accumulazione di $E$ e consideriamo una successione $x_j \in E$ che converga a $x_0 \in E$ . Per provare il teorema occorre mostrare che

(62) $\begin{equation*} \lim_{j \to \infty} f(x_j) = f(x_0). \end{equation*}$

Utilizzando la disuguaglianza triangolare, abbiamo

(63) $\begin{equation*} |f(x_j) - f(x_0)| \leq |f(x_j) - f_n(x_j)| + |f_n(x_j) - f_n(x_0)| + |f_n(x_0) - f(x_0)| \qquad \forall n \in \mathbb{N}. \end{equation*}$

Fissiamo ora $\varepsilon>0$ ; l’idea della dimostrazione è di stimare dall’alto i tre termini nel membro di destra della (63) per ottenere che $|f(x_j) - f(x_0)| < \varepsilon$ per $j$ sufficientemente grande.

Per la convergenza uniforme, esiste $N \in \mathbb{N}$ tale che

(64) $\begin{equation*} |f_n(x) - f(x)| < \frac{\varepsilon}{3} \qquad \forall x \in E, \,\, \forall n \geq N. \end{equation*}$

Fissiamo quindi $n \geq N$ ; si ha quindi

(65) $\begin{equation*} |f(x_j) - f_n(x_j)| < \frac{\varepsilon}{3} \quad \forall j \in \mathbb{N}, \qquad |f_n(x_0) - f(x_0)| < \frac{\varepsilon}{3}. \end{equation*}$

Poiché $f_n$ è una funzione continua, esiste $J \in \mathbb{N}$ tale che

(66) $\begin{equation*} |f_n(x_j) - f_n(x_0)| < \frac{\varepsilon}{3} \qquad \forall j \geq J. \end{equation*}$

Allora, utilizzando (65) e (66) in (63) con $n \geq N$ , si ottiene che

(67) $\begin{equation*} |f(x_j) - f(x_0)| < \varepsilon \qquad \forall j \geq J, \end{equation*}$

che prova la conclusione.

Rimandiamo alla sezione 4, e in particolare alla proposizione 4.25 per la riformulazione del teorema appena dimostrato nel contesto degli spazi metrici.

Ci si può chiedere se anche per la domanda 2.8 accada qualcosa di simile alla domanda 2.6 richiedendo la convergenza uniforme al posto di quella puntuale.

Domanda 3.21. Sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni (non necessariamente continue) che converga uniformemente a una funzione $f \colon E \to \mathbb{R}$ e sia $x_0 \in E$ un punto di accumulazione di $E$ . Si può affermare che vale l’uguaglianza

(68) $\begin{equation*} \lim_{x \rightarrow x_0} \Big( \lim_{n\to+\infty} f_n(x)\Big) = \lim_{n\to+\infty} \Big( \lim_{x \rightarrow x_0} f_n(x) \Big) ? \end{equation*}$

La risposta in questo caso è affermativa. Infatti, il seguente risultato, che è una generalizzazione del teorema 3.19, afferma la possibilità di scambiare i limiti, qualora le quantità in gioco esistano.

Teorema 3.22 (scambio di limiti per la convergenza uniforme). Sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni che converga uniformemente a una funzione $f \colon E \to \mathbb{R}$ e sia $x_0 \in E$ un punto di accumulazione di $E$ . Se i limiti $\lim_{x \rightarrow x_0} f_n(x)$ esistono per ogni $n \in \mathbb{N}$ , allora il limite $\lim_{x \rightarrow x_0} f(x)$ esiste e inoltre vale

(69) $\begin{equation*} \lim_{x \rightarrow x_0} f(x) \lim_{n\to+\infty} \Big( \lim_{x \rightarrow x_0} f_n(x) \Big). \end{equation*}$

$\quad$

Dimostrazione. La dimostrazione si basa su una variazione dell’argomento mostrato nella dimostrazione del teorema 3.19. Chiamiamo

(70) $\begin{equation*} L_n := \lim_{x \rightarrow x_0} f_n(x) \qquad \forall n \in \mathbb{N}. \end{equation*}$

La tesi è equivalente a dimostrare che il limite $L_0:= \lim_{n \to \infty} L_n$ esiste e che vale

(71) $\begin{equation*} L_0 = \lim_{x \rightarrow x_0} f(x). \end{equation*}$

$\quad$

Caso 1: Esiste $M \in \mathbb{N}$ tale che $L_n \in \mathbb{R}$ per ogni $n \geq M$
A meno di troncare i primi $M$ elementi della successione $f_n$ , possiamo supporre che tutti i numeri $L_n$ siano finiti.

Dimostriamo prima che $L_n$ è una successione di Cauchy, quindi convergente per il teorema 3.13. Infatti, sia $\varepsilon>0$ ; poiché la successione $f_n$ converge uniformemente, per la proposizione 3.18

(72) $\begin{equation*} |L_n - L_m| = \lim_{x \to x_0} |f_n(x) - f_m(x)| \leq \sup_{x \in E} |f_n(x) - f_m(x)| < \varepsilon \qquad \forall n, m \geq N. \end{equation*}$

Ciò prova che la successione $L_n$ è di Cauchy, per cui converge a un numero reale $L_0$ .

Dimostriamo ora che vale la (71). A tal fine, consideriamo $x_j$ una successione di elementi di $E$ convergente a $x_0$ . La tesi è provata se si dimostra che

(73) $\begin{equation*} \lim_{j \to \infty} f(x_j)=L_0. \end{equation*}$

Per la disuguaglianza triangolare si ha

(74) $\begin{equation*} |f(x_j) - L_0| \leq |f(x_j) - f_n(x_j)| + |f_n(x_j) - L_n| + |L_n - L_0| \qquad \forall n \in \mathbb{N}. \end{equation*}$

Fissiamo ora $\varepsilon>0$ e stimiamo dall’alto i tre termini nel membro di destra della (74) per ottenere che $|f(x_j) - L_0| < \varepsilon$ per $j$ sufficientemente grande.

Per la convergenza uniforme e per la convergenza $L_n \to L_0$ , esiste $N \in \mathbb{N}$ tale che

(75) $\begin{equation*} |f(x_j) - f_n(x_j)| + |L_n - L_0| < \frac{2}{3}\varepsilon \qquad \forall j \in \mathbb{N}, \,\, \forall n \geq N. \end{equation*}$

Fissiamo quindi $n \geq N$ ; per definizione di $L_n$ , esiste $J \in \mathbb{N}$ tale che

(76) $\begin{equation*} |f_n(x_j) - L_n| \leq \frac{\varepsilon}{3} \qquad \forall j \geq J. \end{equation*}$

Utilizzando (75) e (76) in (74) con $n \geq N$ si ottiene che

(77) $\begin{equation*} |f(x_j) - L_0| < \varepsilon \qquad \forall j \geq J, \end{equation*}$

che prova la conclusione.

Caso 2: esiste una sottosuccessione tale che $L_{n_k}=+\infty$ per ogni $k \in \mathbb{N}$ .
Dimostriamo che allora esiste $M \in \mathbb{N}$ tale che $L_n= + \infty$ per ogni $n \geq M$ . Infatti, per la proposizione 3.18, per ogni $\varepsilon>0$ esiste $M \in \mathbb{N}$ tale che

(78) $\begin{equation*} \sup_{x \in E} |f_n(x) - f_m(x)| < \varepsilon \qquad \forall n,m \geq M. \end{equation*}$

Si fissi $n=n_k \geq M$ ; poiché $\lim_{x \to x_0} f_{n_k}(x)=+\infty$ , per ogni $R>0$ esiste $\delta>0$ tale che

(79) $\begin{equation*} f_{n_k}(x) \geq R \qquad \forall x \in E \cap (x_0-\delta, x_0 + \delta). \end{equation*}$

Da (78) e (79) si ottiene

(80) $\begin{equation*} f_{m}(x) > R - \varepsilon \qquad \forall m \geq M, \,\, \forall x \in E \cap (x_0-\delta, x_0 + \delta). \end{equation*}$

Poiché $R$ è arbitrario, ciò prova che

(81) $\begin{equation*} L_m = \lim_{x \to x_0} f_m(x)= + \infty \qquad \forall m \geq M. \end{equation*}$

Quindi $L_0= \lim_{m \to \infty}L_m$ esiste e vale $L_0=+\infty$ .

Occorre ora dimostrare la (71). Sia $x_j \to x_0$ una successione e consideriamo un qualunque numero reale $R>0$ . Per convergenza uniforme, esiste $N \in \mathbb{N}$ tale che

(82) $\begin{equation*} |f(x_j) - f_n(x_j)| \leq 1 \qquad \forall n \geq N,\,\, \forall j \in \mathbb{N}. \end{equation*}$

Poiché $L_n= +\infty$ , mandando $j \to \infty$ nella (82), si ottiene $L_0 \geq L_n - 1$ , cioè $L_0= +\infty$ .

Poiché il caso $L_{n_k}=-\infty$ è analogo, ciò conclude la dimostrazione.

Proponiamo ora un’altra versione del teorema 3.22, molto utile nelle applicazioni.

Teorema 3.23. Sia $f_n:[a,b]\rightarrow \mathbb{R}$ una successione di funzioni uniformemente convergente ad una funzione $f$ , sia $\{x_n\}_n$ una successione in $[a,b]$ convergente a $x_0 \in [a,b]$ e supponiamo che $f$ sia continua in $x_0$ . Allora

(83) $\begin{equation*} \lim_{n\to+\infty} f_n(x_n) = f(x_0). \end{equation*}$

$\quad$

Osservazione 3.24. Facciamo notare che il teorema 3.23 non è una semplice conseguenza del teorema 3.22, in quanto quest’ultimo richiede l’esistenza dei limiti $\lim_{x \to x_0} f_n(x)$ , mentre nel teorema 3.23 non si ipotizza l’esistenza di alcun limite. L’esistenza del limite $\lim_{n \to \infty} f_n(x_n)$ è parte della tesi. Ad esempio, la successione di funzioni $f_n \colon [-1,1] \to \mathbb{R}$ definite da

(84) $\begin{equation*} f_n(x)= \begin{cases} \dfrac{1}{n} \sin \Big(\dfrac{1}{x} \Big) & \text{se } x \neq 0\\[8pt] 0 & \text{se } x = 0; \end{cases} \end{equation*}$

converge uniformemente alla funzione $f \equiv 0$ e soddisfa le ipotesi del teorema 3.23 ma non quelle del teorema 3.22, in quanto ognuna delle $f_n$ non ha limite per $x \to 0$ .

Dimostrazione del teorema 3.23. Per la disuguaglianza triangolare, per ogni $n \in \mathbb{N}$ si ha

(85) $\begin{equation*} |f(x_0) - f_n(x_n)| \leq |f(x_0) - f(x_n)| + |f(x_n) - f_n(x_n)|. \end{equation*}$

Vogliamo stimare i due termini al membro di destra di tale disuguaglianza. Sia $\varepsilon>0$ ; poiché $f$ è continua in $x_0$ e per la convergenza uniforme di $f_n$ a $f$ , esiste $N \in \mathbb{N}$ tale che

(86) $\begin{gather*} |f(x_0) - f(x_n)| < \frac{\varepsilon}{2} \quad \text{e} \quad |f(x_n) - f_n(x_n)| < \frac{\varepsilon}{2} \qquad \forall n \geq N. \end{gather*}$

Unendo (85) e (86) si ottiene

(87) $\begin{equation*} |f(x_0) - f_n(x_n)| < \varepsilon \qquad \forall n \geq N, \end{equation*}$

cioè la (83).

Osservazione 3.25. Tale risultato, essendo una condizione necessaria per la convergenza uniforme, è utilizzabile come criterio per mostrare che una successione di funzioni $f_n$ non converge uniformemente a una funzione $f$ . Infatti, consideriamo ad esempio il caso in cui $E=[a,b]$ e che $f$ sia continua in $[a,b]$ ; supponiamo di trovare una successione $x_n$ che converga a $x_0 \in [a,b]$ e tale che

(88) $\begin{equation*} \lim_{n \to \infty}f_n(x_n) \neq f(x_0), \end{equation*}$

oppure tale che $\lim_{n \to \infty}f_n(x_n)$ non esista; il teorema 3.23 mostra allora che la $f_n$ non converge uniformemente a $f$ .

Esempio 3.26. Nell’esempio 3.4 si può mostrare che la convergenza non è uniforme considerando la successione $x_n=2^{-\frac{1}{n}}$ .

Esercizio 3.27 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Verificare che la successione di funzioni $f_n \colon [0,1] \to \mathbb{R}$ definita da

(89) $\begin{equation*} f_n(x) = \frac{x^2}{x^2 + (1-nx)^2}, \end{equation*}$

converge puntualmente alla funzione $f \equiv 0$ , ma che la convergenza non è uniforme.

$\quad$

Rimandiamo alla sezione 5 per la soluzione.

Teoremi di convergenza: integrazione.

Si può indagare quale sia la risposta alle domande 2.10 e 2.12 sostituendo la convergenza uniforme a quella puntuale: il limite uniforme di funzioni integrabili è integrabile? In caso affermativo, l’integrale del limite è pari al limite degli integrali?

Contrariamente alla convergenza puntuale, la risposta a tali domande è affermativa, come mostra il seguente risultato.

Teorema 3.28 (Passaggio al limite sotto il segno di integrale). Sia $f_n\colon [a,b] \to \mathbb{R}$ una successione di funzioni integrabili secondo Riemann che converga uniformemente a una funzione $f \colon [a,b] \to \mathbb{R}$ . Allora $f$ risulta integrabile secondo Riemann e vale

(90) $\begin{equation*} \lim_{n\to+\infty} \int_{a}^{b} f_n(x)\,\mathrm{d}x = \int_{a}^{b} f(x)\,\mathrm{d}x. \end{equation*}$

$\quad$

Osservazione 3.29. Il teorema appena enunciato si potrebbe generalizzare considerando $E \subset \mathbb{R}$ un insieme limitato e misurabile secondo Peano-Jordan e una successione $f_n \colon E \to \mathbb{R}$ di funzioni integrabili secondo Riemann.

In realtà, la dimostrazione di quest’ultimo risultato si riconduce facilmente al caso del teorema 3.28, in quanto se $E \subset \mathbb{R}$ è misurabile secondo Peano-Jordan, una funzione $g \colon E \to \mathbb{R}$ si dice integrabile secondo Riemann se e solo se per ogni intervallo $[a,b] \supseteq E$ la funzione $\tilde{g} \colon [a,b] \to \mathbb{R}$ definita da

(91) $\begin{equation*} \tilde{g}= \begin{cases} g(x) & \text{se $x \in E$,}\\ 0 & \text{se $x \in [a,b] \setminus E$} \end{cases} \end{equation*}$

è integrabile e in tal caso si pone

(92) $\begin{equation*} \int_E g(x) \,\mathrm{d}x = \int_a^b \tilde{g}(x)\, \mathrm{d}x. \end{equation*}$

Dimostrazione del teorema 3.28. Senza ledere la generalità possiamo supporre $[a,b]=[0,1]$ .

Per la disuguaglianza triangolare, per ogni suddivisione

(93) $\begin{equation*} \begin{split} |S(f,P) - s(f,P)| \leq & |S(f,P) - S(f_n,P)| + |S(f_n,P) - s(f_n,P)| \\ & + |s(f_n,P) - s(f,P)|, \end{split} \end{equation*}$

dove con $S(f,P), s(f,P)$ si sono indicate rispettivamente le somme superiori e inferiori di $f$ relative alla suddivisione $P$ . L’idea della dimostrazione è mostrare, stimando i tre termini al membro di destra della (93), che essi possono essere resi piccoli a piacere scegliendo opportunamente la suddivisione $P$ e $n \in \mathbb{N}$ .

Sia fissato $\varepsilon>0$ . Poiché $f_n$ converge uniformemente a $f$ , esiste $N \in \mathbb{N}$ tale che

(94) $\begin{equation*} |f_n(x) - f(x)| < \frac{\varepsilon}{3} \qquad \forall x \in [0,1],\,\, \forall n \geq N. \end{equation*}$

In particolare, poiché ogni $f_n$ è limitata (perché integrabile secondo Riemann), (94) prova che $f$ è limitata. Occorre ora mostrare che essa è integrabile secondo Riemann. Fissiamo quindi $n \geq N$ ; poiché $f_n$ è integrabile, esistono

(95) $\begin{equation*} a=x_0 < x_1 < \dots < x_M = 1 \end{equation*}$

tali che la suddivisione

(96) $\begin{equation*} P = \{ I_i:= [x_{i-1}, x_i] \mid i=1, \dots, M \} \end{equation*}$

soddisfi

(97) $\begin{equation*} 0 \leq S(f_n,P) - s(f_n,P) = \sum_{i=1}^M \big( \sup_{I_i} f_n - \inf_{I_i} f_n \big)(x_i - x_{i-1}) < \frac{\varepsilon}{3}. \end{equation*}$

Mostriamo ora che si ha

(98) $\begin{equation*} \Big| \sup_{x \in I_i} f_n(x) - \sup_{x \in I_i} f(x) \Big| \leq \frac{\varepsilon}{3}, \quad \Big| \inf_{x \in I_i} f_n(x) - \inf_{x \in I_i} f(x) \Big| \leq \frac{\varepsilon}{3} \qquad \forall i=1, \dots, M. \end{equation*}$

Infatti, per ogni $\eta>0$ esiste $\xi \in I_i$ tale che $f_n(\xi)> \sup_{I_i}f_n - \eta$ ; Quindi

(99) $\begin{equation*} \sup_{I_i}f \geq f(\xi) > f_n(\xi) - \frac{\varepsilon}{3} > \sup_{I_i}f_n - \eta - \frac{\varepsilon}{3}, \end{equation*}$

dove nella seconda disuguaglianza si è usata (94); da ciò si ricava

(100) $\begin{equation*} \sup_{I_i}f_n - \sup_{I_i}f < \frac{\varepsilon}{3} + \eta. \end{equation*}$

Poiché la disuguaglianza $- \sup_{I_i}f_n + \sup_{I_i}f < \dfrac{\varepsilon}{3} + \eta$ si ottiene scambiando i ruoli di $f_n$ e di $f$ nel ragionamento di sopra, e per l’arbitrarietà di $\eta$ , risulta provata

(101) $\begin{equation*} \Big| \sup_{x \in I_i} f_n(x) - \sup_{x \in I_i} f(x) \Big| \leq \frac{\varepsilon}{3}. \end{equation*}$

Un ragionamento analogo dimostra la disuguaglianza per gli estremi inferiori in (98).

La (98) implica che

(102) $\begin{equation*} \begin{split} |S(f_n,P) - S(f,P)| \leq & \sum_{i=1}^M \big| \sup_{I_i} f_n - \sup_{I_i} f \big|(x_i - x_{i-1}) \\ \leq & \frac{\varepsilon}{3} \sum_{i=1}^M (x_i - x_{i-1}) \\ = & \frac{\varepsilon}{3}. \end{split} \end{equation*}$

Similmente vale

(103) $\begin{equation*} |s(f_n,P) - s(f,P)| \leq \frac{\varepsilon}{3}. \end{equation*}$

Inserendo (102), (97), e (103) in (93), si ottiene

(104) $\begin{equation*} |S(f,P) - s(f,P)| < \varepsilon. \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ , ciò prova che $f$ è integrabile.

Per dimostrare la (90), basta osservare che, per la versione integrale della disuguaglianza triangolare si ha

(105) $\begin{equation*} \begin{split} \Big| \int_0^1 f(x) \mathrm{d}x - \int_0^1 f_n(x) \mathrm{d}x \Big| \leq & \int_0^1 |f(x) - f_n(x)| \mathrm{d}x \leq \int_0^1 \frac{\varepsilon}{3} \mathrm{d}x = \frac{\varepsilon}{3} \quad \forall n \geq N. \end{split} \end{equation*}$

Di nuovo l’arbitrarietà di $\varepsilon$ implica la (90).

Osservazione 3.30. Come si può osservare, la gran parte della dimostrazione del teorema 3.28 serve a dimostrare l’integrabilità del limite. Se avessimo ipotizzato che le $f_n$ fossero continue, la dimostrazione sarebbe stata molto più breve. Infatti avremmo potuto concludere, grazie al teorema 3.19, che anche $f$ sarebbe stata continua e quindi integrabile. La (90) si sarebbe ottenuta come sopra.

Osservazione 3.31. Nella dimostrazione del teorema 3.28 abbiamo usato l’ipotesi che l’intervallo $[a,b]$ fosse limitato, supponendo di poterci ridurre senza perdita di generalità al caso in cui $[a,b]=[0,1]$ . Se, invece, l’intervallo non è limitato, non siamo più nel caso dell’integrale di Riemann vero e proprio e occorre riferirsi alla nozione di integrale improprio.

In tale fattispecie, non è detto che il limite sia integrabile in senso improprio. Inoltre, anche assumendo che il limite lo sia, il risultato di convergenza è falso e non si può passare al limite sotto il segno di integrale, come mostrano i seguenti esercizi, le cui soluzioni sono nella sezione 5.

Esercizio 3.32 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Esibire una successione di funzioni $f_n \colon [0,+\infty) \to \mathbb{R}$ integrabili in senso improprio che converga uniformemente a una funzione $f \colon [0,+\infty) \to \mathbb{R}$ che non sia integrabile in senso improprio.

Esercizio 3.33 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Esibire una successione di funzioni $f_n \colon [0,+\infty) \to \mathbb{R}$ integrabili in senso improprio che converga uniformemente a una funzione $f \colon [0,+\infty) \to \mathbb{R}$ integrabile in senso improprio ma tale che

(106) $\begin{equation*} \lim_{n\to+\infty} \int_{0}^{+\infty} f_n(x)\,\mathrm{d}x \neq \int_{0}^{+\infty} f(x)\,\mathrm{d}x. \end{equation*}$

$\quad$

Teoremi di convergenza: derivazione.

Possiamo chiederci come si comporta la derivabilità rispetto alla convergenza uniforme; ad esempio possiamo indagare le seguenti questioni, che sono le versioni analoghe di quelle relative alla convergenza puntuale, analizzate nella sezione 2.1.4.

Domanda 3.34. Sia $f_n \colon (a,b) \to \mathbb{R}$ una successione di funzioni derivabili che converga uniformemente a una funzione $f_n \colon (a,b) \to \mathbb{R}$ . Si può dire che $f$ è derivabile? In caso affermativo, si può affermare che la successione delle derivate $f_n'$ converga almeno puntualmente? E in tal caso, si può affermare che il limite delle $f_n'$ è pari a $f'$ ?

Esaminando gli esempi 2.18, 2.20 e 2.22 si può notare che, in tutti e tre i casi, la convergenza delle $f_n$ a $f$ è in realtà uniforme e la si era in realtà già provata.

L’esempio 2.18 mostra che il limite uniforme di funzioni derivabili non è necessariamente derivabile. L’esempio 2.20 mostra che anche assumendo la derivabilità del limite uniforme, la successione delle derivate può non essere convergente. L’esempio 2.22 mostra che anche assumendo la convergenza uniforme delle $f_n$ a una funzione $f$ derivabile e la convergenza puntuale delle $f_n'$ a una funzione $g$ , si può avere $g \neq f'$ .

Per ottenere delle proprietà di passaggio al limite delle derivate, si devono fare delle ipotesi più forti sulla convergenza, come illustra il seguente risultato.

Teorema 3.35 (limite uniforme di funzioni derivabili). Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni derivabili tali che la successione delle derivate prime $f_n'$ converga uniformemente ad una funzione $g \colon [a,b] \to \mathbb{R}$ ; supponiamo inoltre che esista $x_0 \in [a,b]$ e $y_0 \in \mathbb{R}$ tale che

(107) $\begin{equation*} \lim_{n \to \infty} f_n(x_0) = y_0. \end{equation*}$

Allora esiste una funzione derivabile $f \colon [a,b] \to \mathbb{R}$ tale che

$\quad$

$f_n$ converge uniformemente a $f$ ;

$f'=g$ .

$\quad$

Prima di dimostrare il teorema, facciamo alcune osservazioni.

Osservazione 3.36. Il teorema 3.35 afferma in sostanza che la convergenza uniforme delle derivate implica la convergenza uniforme delle funzioni e la derivabilità del limite. Si dice, in maniera piuttosto eloquente, che la convergenza delle derivate controlla quella delle funzioni.

Osservazione 3.37. Facciamo notare che il teorema 3.35 non assume alcuna ipotesi sulle derivate $f_n'$ ; esso risulta pertanto un rafforzamento poco noto di quello generalmente proposto, in cui si richiede la continuità delle derivate $f_n'$ e la cui dimostrazione risulta piuttosto semplificata, come mostra l’esercizio 3.38.

Dimostrazione del teorema 3.35.

Step 1: $f_n$ converge uniformemente a una funzione $f$ .
Sia $\varepsilon>0$ ; Poiché la successione numerica $f_n(x_0)$ è di Cauchy e poiché la successione delle derivate $f_n'$ converge uniformemente a $g$ , per la proposizione 3.18 esiste $N \in \mathbb{N}$ tale che

(108) $\begin{equation*} \begin{gathered} \sup_{z \in [a,b]}|f_n'(z) - f_m'(z)| < \varepsilon, \quad |f_n(x_0) - f_m(x_0)|< \varepsilon \qquad \forall n,m \geq N. \end{gathered} \end{equation*}$

Siano, quindi $n,m \in \mathbb{N}$ soddisfacenti tali relazioni; poiché la funzione $f_n - f_m$ è derivabile, possiamo applicare a essa il teorema di Lagrange e ottenere che per ogni $x \in [a,b]$ esiste $\xi = \xi(x,n,m) \in [x_0,x]$ tale che

(109) $\begin{equation*} \begin{split} |f_n(x) - f_m(x) - f_n(x_0) + f_m(x_0)| = & |f_n'(\xi) - f_m'(\xi)||x-x_0| \\ \leq & (b-a)\sup_{z \in [a,b]}|f_n'(z) - f_m'(z)| \\ < & \varepsilon(b-a). \end{split} \end{equation*}$

Poiché per la disuguaglianza triangolare si ha

(110) $\begin{equation*} |f_n(x) - f_m(x)| \leq |f_n(x) - f_m(x) - f_n(x_0) + f_m(x_0)| + |f_n(x_0) - f_m(x_0)|, \end{equation*}$

unendo (109) e (110) si ottiene

(111) $\begin{equation*} |f_n(x) - f_m(x)| < \varepsilon (1+ b-a). \end{equation*}$

Per la proposizione 3.18, la successione $f_n$ converge uniformemente a una funzione $f$ .

Step 2: $f$ è derivabile e $f'=g$ .
Fissiamo un punto $x \in [a,b]$ ; per qualunque $z \in [a,b]\setminus \{ x\}$ , per la disuguaglianza triangolare abbiamo

(112) $\begin{equation*} \begin{split} \left| \frac{f(x) - f(z)}{x-z} - g(x) \right| \leq & \left| \frac{f(x) - f(z)}{x-z} - \frac{f_n(x) - f_m(z)}{x-z} \right| \\ & + \left| \frac{f_n(x) - f_n(z)}{x-z} - f_n'(x) \right| + |f_n'(x) - g(x)|. \end{split} \end{equation*}$

Vogliamo stimare i tre termini al membro di destra. Fissiamo $\varepsilon>0$ ; innanzitutto osserviamo che per un ragionamento analogo a quello appena fatto, ricordando la convergenza uniforme delle $f_n'$ e applicando il teorema di Lagrange, esiste $N \in \mathbb{N}$ tale che, per ogni $n,m \geq N$ e per ogni $z \in [a,b]\setminus \{ x\}$ si ha

(113) $\begin{gather*} |f_n'(x) - g(x)| < \varepsilon, \\ \end{gather*}$

(114) $\begin{gather*} \left| \frac{f_n(x)- f_n(z)}{x-z} - \frac{f_m(x)- f_m(z)}{x-z} \right| = |f_n'(\xi) - f_m'(\xi)| < \varepsilon. \end{gather*}$

dove $\xi$ è il punto dato dal teorema di Lagrange. Quindi, per la proposizione 3.18, la successione di funzioni definita da

(115) $\begin{equation*} \varphi_n(z) := \frac{f_n(x)- f_n(z)}{x-z} \end{equation*}$

converge uniformemente in $[a,b] \setminus \{ x\}$ ; inoltre, per la convergenza uniforme delle $f_n$ a $f$ il limite uniforme delle $\varphi_n$ è la funzione $\varphi(z):=\dfrac{f(x)- f(z)}{x-z}$ . Si ha quindi

(116) $\begin{equation*} \left| \frac{f(x) - f(z)}{x-z} - \frac{f_n(x) - f_m(z)}{x-z} \right| \leq \varepsilon \qquad \forall n \geq N. \end{equation*}$

Fissiamo ora $n \geq N$ . Poiché $f_n$ è derivabile in $x$ , esiste $\delta>0$ tale che

(117) $\begin{equation*} \left| \frac{f_n(x) - f_n(z)}{x-z} - f_n'(x) \right| < \varepsilon \qquad \forall z \in \{ z \in [a,b] \mid |z-x|< \delta, \, z \neq x\}. \end{equation*}$

Unendo (112), (113), (114) e (117), si ottiene

(118) $\begin{equation*} \left| \frac{f(x) - f(z)}{x-z} - g(x) \right| < 3 \varepsilon \qquad \forall z \in \{ z \in [a,b] \mid |z-x|< \delta, \, z \neq x\}. \end{equation*}$

Ciò mostra che $f$ è derivabile in $x$ e che $f'(x)=g(x)$ .

Esercizio 3.38 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Dimostrare più brevemente il teorema 3.35 assumendo la continuità delle derivate $f_n'$ .

Suggerimento: usare il teorema fondamentale del calcolo integrale. Vedi sezione 5.

$\quad$

Osservazione 3.39. L’ipotesi di convergenza puntuale delle $f_n$ in un punto $x_0$ nel teorema 3.35 è essenziale affinché la tesi sia vera: si consideri infatti la successione di funzioni $f_n \colon [0,2\pi] \to \mathbb{R}$ definita da

(119) $\begin{equation*} f_n(x)= n + \sin x. \end{equation*}$

Osservazione 3.40. Nella dimostrazione del teorema 3.35 si è usato il fatto che il dominio $I$ delle $f_n$ è limitato. Se $I$ non è limitato possiamo solo concludere che $f_n(x)$ converge uniformemente a una funzione $f(x)$ sui sottoinsiemi limitati di $I$ , e che $f$ è una funzione derivabile la cui derivata è pari a $g$ ; in generale però, la convergenza di $f_n$ ad $f$ può non essere uniforme in $I$ , come mostra il seguente esempio.

Esempio 3.41. Sia $g_n \colon \mathbb{R} \to \mathbb{R}$ la successione di funzioni definita da (figura 5)

(120) $\begin{equation*} g_n(x) = \begin{cases} 0 & \text{se $x < 2^n$,}\\[6pt] \dfrac{x-2^n}{2^{2n}} & \text{se $2^n \leq x \leq 2^{n+1}$,}\\[8pt] \dfrac{1}{2^{n}} & \text{se $x > 2^{n+1}$.} \end{cases} \end{equation*}$

$\quad$

Figura 5: La funzione $g_n$ dell’esempio 3.41.

$\quad$

Dal momento che

(121) $\begin{equation*} \sup_{x \in \mathbb{R}} |g_n(x)| = \frac{1}{2^n} \qquad \forall n \in \mathbb{N}, \end{equation*}$

$g_n$ converge uniformemente alla funzione $g$ identicamente nulla. Se definiamo

(122) $\begin{equation*} f_n(x) = \int_{0}^{x}g_n(t)\,\mathrm{d}t = \begin{cases} 0 & \text{se $x < 2^{n}$,}\\[6pt] \dfrac{(x-2^n)^2}{2^{2n+1}} & \text{se $2^n \leq x \leq 2^{n+1}$}\\[8pt] \dfrac{1}{2} + \dfrac{x-2^{n+1}}{2^n} & \text{se $x > 2^{n+1}$} \end{cases} \qquad \forall n \in \mathbb{N}, \end{equation*}$

$f_n$ converge alla funzione $f$ identicamente nulla uniformemente sui sottoinsiemi limitati di $\mathbb{R}$ (e quindi puntualmente in $\mathbb{R}$ ); $f$ risulta essere una primitiva di $g$ , ma la convergenza delle $f_n$ a $f$ non è uniforme su $\mathbb{R}$ dato che

(123) $\begin{equation*} \sup_{x \in \mathbb{R}} |f_n(x) - f(x)| = + \infty \qquad \forall n \in \mathbb{N}. \end{equation*}$

Criteri di convergenza uniforme.

Abbiamo visto nel paragrafo precedente che le proprietà come continuità e integrabilità si conservano in presenza di convergenza uniforme (mentre in generale si perdono sotto ipotesi di convergenza puntuale). Risulta quindi evidente la necessità di avere strumenti in grado di stabilire la convergenza uniforme di una successione di funzioni. Abbiamo già dato alcune semplici caratterizzazioni della convergenza uniforme con le proposizioni 3.7 e 3.18.

Siamo in grado di dare altre condizioni sufficienti su una successione di funzioni affinché la convergenza sia uniforme?

Criteri di convergenza uniforme: criteri di monotonia.

Alcune condizioni sufficienti per la convergenza uniforme riguardano la monotonia della successione. Un risultato in tal senso è costituito dal piccolo teorema del Dini.

Teorema 3.42 (piccolo teorema del Dini). Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione crescente di funzioni continue, cioè tale che

(124) $\begin{equation*} f_n(x) \leq f_{n+1}(x), \qquad \forall n \in \mathbb{N}, \,\,\, \forall x \in [a,b]. \end{equation*}$

Si supponga inoltre che il limite puntuale $f\colon [a,b] \to \mathbb{R}$ della successione $f_n$ sia continuo.

Allora $f_n$ converge uniformemente a $f$ . Analogo risultato vale se la successione $f_n$ è decrescente.

$\quad$

Osservazione 3.43. Poiché per ogni $x \in [a,b]$ la successione $f_n(x)$ è crescente, il limite $\lim_{n \to \infty} f_n(x)$ esiste certamente; non è in generale vero che tale limite definisca una funzione $f\colon [a,b] \to \mathbb{R}$ , in quanto in qualche punto esso potrebbe essere infinito; l’ipotesi di continuità del teorema, in virtù del teorema di Weiestrass, implica che $f$ sia ovunque finita. Il fatto che $f$ sia limitata è inoltre equivalente all’assunzione che le $f_n$ siano equilimitate (definizione 3.57).

Dimostrazione del teorema 3.42. Supponiamo per assurdo che la convergenza non sia uniforme, cioè che esista $\varepsilon>0$ , una successione crescente di numeri naturali $n_k$ e una successione di punti $x_k \in [a,b]$ tali che

(125) $\begin{equation*} |f(x_k) - f_{n_k}(x_k)| = f(x_k) - f_{n_k}(x_k) \geq \varepsilon, \end{equation*}$

dove la prima uguaglianza segue dal fatto che per ogni $x \in [a,b]$ si ha $f(x) \geq f_n(x)$ , poiché la successione $f_n(x)$ è crescente. Sempre per la monotonia della successione $f_n(x)$ , si ha

(126) $\begin{equation*} f(x_k) - f_{j}(x_k) \geq \varepsilon \qquad \forall k \in \mathbb{N}, \,\, \forall j \leq n_k \end{equation*}$

Poiché $[a,b]$ è compatto, a meno di passare ulteriormente a sottosuccessioni possiamo assumere che $x_k \to x_0$ . Fissiamo $j \in \mathbb{N}$ ; passando al limite per $k \to \infty$ nella (126), per la continuità di $f_j$ e di $f$ si ottiene

(127) $\begin{equation*} f(x_0) - f_j(x_0) \geq \varepsilon. \end{equation*}$

Poiché $j$ è arbitrario, ciò nega la convergenza puntuale delle $f_j$ in $x_0$ , che è assurdo.

È possibile mostrare un analogo risultato nel caso in cui valga la proprietà di monotonia delle funzioni $f_n(x)$ rispetto ad $x$ (nel teorema precedente si assume la monotonia rispetto ad $n$ ).

Teorema 3.44. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni crescenti, cioè tali che

(128) $\begin{equation*} x \leq y \Longrightarrow f_n(x) \leq f_n(y) \qquad \forall n \in \mathbb{N}. \end{equation*}$

Supponiamo che $f_n$ converga puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ continua. Allora la convergenza di $f_n$ a $f$ è uniforme. Vale un analogo risultato se le funzioni $f_n$ sono decrescenti.

$\quad$

Dimostrazione. Sia $\varepsilon>0$ . Poiché $f$ è continua e $[a,b]$ è chiuso e limitato, essa è uniformemente continua per il teorema di Heine-Cantor (teorema 3.51); allora esiste $\delta>0$ tale che

(129) $\begin{equation*} |f(x) - f(y)| < \varepsilon \qquad \text{se } |x-y|< \delta. \end{equation*}$

Consideriamo una suddivisione di $[a,b]$ data da

(130) $\begin{equation*} a = x_0 < x_1 < \dots < x_M = b. \end{equation*}$

e tale che $x_{j} - x_{j-1} < \delta$ per ogni $j=1,\dots,M$ . Mostreremo la convergenza uniforme su ciascuno degli intervalli $[x_{j-1},x_j]$ ; essendo questi intervalli in numero finito, ciò proverà la convergenza uniforme su $[a,b]$ . Fissiamo quindi $j \in \{1,\dots,M \}$ . Per la disuguaglianza triangolare, per ogni $n \in \mathbb{N}$ e per ogni $x \in [x_{j-1},x_j]$ , abbiamo

(131) $\begin{equation*} \begin{split} |f(x) - f_n(x)| \leq & |f(x) - f(x_j)| + |f(x_j) - f_n(x_j)| + |f_n(x_j) - f_n(x)|. \end{split} \end{equation*}$

Vogliamo stimare uniformemente in $x$ i termini al membro di destra per ottenere la convergenza uniforme.

Per il primo termine osserviamo che, da $x \in [x_{j-1},x_j]$ , si ricava $|x-x_j|< \delta$ ; per (129) si ottiene

(132) $\begin{equation*} |f(x)-f(x_j)| < \varepsilon \qquad \forall x \in [x_{j-1},x_j]. \end{equation*}$

Per il secondo termine, poiché la successione $f_n$ converge puntualmente a $f$ , esiste $N \in \mathbb{N}$ tale che

(133) $\begin{equation*} \begin{gathered} |f_n(x_j) - f(x_j)| < \varepsilon \qquad \forall n \geq N, \\ |f_n(x_{j-1}) - f(x_{j-1})| < \varepsilon \qquad \forall n \geq N. \end{gathered} \end{equation*}$

Per il terzo termine, sfruttando la monotonia delle $f_n$ , la disuguaglianza triangolare, la (133) e la (129), per ogni $n \geq N$ si ha

(134) $\begin{equation*} \begin{split} f_n(x_{j}) - f_n(x_{j-1}) = & |f_n(x_{j}) - f_n(x_{j-1})| \\ \leq & |f_n(x_j) - f(x_j)| + |f(x_j) - f(x_{j-1})| \\ & + |f(x_{j-1}) - f_n(x_{j-1})| \\ < & 3\varepsilon. \end{split} \end{equation*}$

Allora, sempre per la monotonia delle $f_n$ si ha

(135) $\begin{equation*} |f_n(x_j) - f_n(x)| = f_n(x_j) - f_n(x) < 3\varepsilon \qquad \forall n \geq N, \,\, \forall x \in [x_{j-1},x_j]. \end{equation*}$

Inserendo la (132), la (133) e la (135) nella (131), si ottiene

(136) $\begin{equation*} \begin{split} |f(x) - f_n(x)| < & 5 \varepsilon \qquad \forall x \in [x_{j-1},x_j], \,\, \forall n \geq N. \end{split} \end{equation*}$

Ciò mostra che $f_n$ converge uniformemente a $f$ .

Esempio 3.45. La successione $f_n \colon [0,1] \to \mathbb{R}$ definita da $f_n(x)= x^n$ dell’esempio 2.4 converge puntualmente alla funzione $f \colon [0,1] \to \mathbb{R}$ definita da

(137) $\begin{equation*} f(x) = \begin{cases} 0 & \text{se } x \in [0,1)\\ 1 & \text{se } x = 1. \end{cases} \end{equation*}$

Poiché $f$ non è continua, il teorema 3.19 assicura che la convergenza non è uniforme.

Chiaramente, ciò implica che non si può applicare né il il teorema 3.42, né il teorema 3.44; infatti, nonostante per ogni $x \in [0,1]$ la successione numerica $f_n(x)$ sia decrescente, e nonostante ognuna delle $f_n$ sia crescente, il limite puntuale $f$ non è continuo e questa è un’ipotesi essenziale in entrambi i teoremi.

Restringendo il dominio delle $f_n$ all’intervallo $[0,1)$ si ricade nell’esempio 3.4 in cui si è mostrato che di nuovo la convergenza non è uniforme. Qui, anche se il limite puntuale $f \equiv 0$ è continuo e ognuna delle $f_n$ è crescente, le ipotesi dei teoremi 3.42 e 3.44 non sono soddisfatte in quanto l’intervallo $[0,1)$ non è chiuso.

Se, invece, restringiamo ulteriormente l’intervallo considerando $[0,\alpha]$ con $\alpha \in (0,1)$ , sono soddisfatte le ipotesi di entrambi i teoremi e quindi la convergenza è uniforme, come si era già provato nell’esempio 3.4.

Criteri di convergenza uniforme: equicontinuità.

I casi esposti dai teoremi 3.42 e 3.44 sono piuttosto particolari e sarebbe desiderabile un criterio che ci permetta di ottenere la convergenza uniforme di una successione di funzioni in ipotesi più generali. Chiaramente, poiché la convergenza uniforme è strettamente più forte della convergenza puntuale, occorre aggiungere qualche altra ipotesi sulla successione per ottenerla.

Supponiamo quindi che $[a,b] \subset \mathbb{R}$ , consideriamo una successione di funzioni $f_n \colon [a,b] \to \mathbb{R}$ che converga puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ . Anche assumendo che le $f_n$ e la $f$ siano funzioni continue, come mostrato dall’esercizio 3.27, la convergenza uniforme non è garantita. Ricordiamo che nell’esercizio 3.27 si ha una successione di funzioni $f_n \colon [0,1] \to \mathbb{R}$ definita da

(138) $\begin{equation*} f_n(x) = \frac{x^2}{x^2 + (1-nx)^2}, \end{equation*}$

che converge puntualmente, ma non uniformemente alla funzione $f \equiv 0$ .

La situazione non cambia richiedendo la continuità uniforme delle funzioni, in quanto sempre nell’esercizio 3.27 tutte le funzioni sono uniformemente continue, come ci apprestiamo a verificare. Per meglio fissare le idee ricordiamo la definizione di funzione uniformemente continua.

Definizione 3.46 (continuità uniforme, modulo di continuità). Sia $g \colon [a,b] \to \mathbb{R}$ ; $g$ si dice uniformemente continua se esiste una funzione $\sigma \colon [0,+\infty) \to [0,+\infty)$ , detta modulo di continuità di $g$ che soddisfi le seguenti condizioni:

$\quad$

$\sigma$ è monotona non decrescente;

$\lim_{\varepsilon \to 0}\sigma(\varepsilon) = \sigma(0) = 0$ ;

Si ha
(139) $\begin{equation*} |g(x) - g(y)| \leq \sigma(|x-y|) \qquad \forall x,y \in [a,b]. \end{equation*}$

$\quad$

Osservazione 3.47. Una funzione uniformemente continua è ovviamente continua. Infatti, si può tradurre la definizione 3.46 dicendo che $f$ è uniformemente continua se per ogni $\varepsilon>0$ , esiste $\delta>0$ tale che

(140) $\begin{equation*} |x-y| < \delta \Longrightarrow |f(x) - f(y)|< \varepsilon. \end{equation*}$

Osservazione 3.48. In altre parole, una funzione è uniformemente continua se la distanza tra $g(x)$ e $g(y)$ è controllata solo dalla distanza tra $x$ e $y$ ed è indipendente dai particolari punti scelti (mentre per una semplice funzione continua questo controllo dipende in generale dai punti considerati).

Osservazione 3.49. Un modulo di continuità (che, per una determinata funzione, non è unico), in un certo senso “quantifica la continuità” della funzione $g$ ; infatti $\sigma(d)$ è il valore massimo della distanza tra $g(x)$ e $g(y)$ , se $|x-y|=d$ . Se $\sigma$ è un modulo di continuità di $g$ e $\tau$ è un modulo di continuità della funzione $h$ , la disuguaglianza $\sigma \leq \tau$ dice quindi in qualche modo che “ $g$ è più continua di $h$ ”, in quanto, a parità di distanza tra i punti nel dominio, i valori di $g$ sono tra loro più vicini rispetto a quelli assunti da $h$ .

Osservazione 3.50. Se $f$ è uniformemente continua, non esiste un suo unico modulo di continuità. Infatti, se $\sigma$ è un modulo di continuità per $f$ , allora ogni funzione $\tau \geq \sigma$ risulta ovviamente essere un modulo di continuità per $f$ .

Vale il seguente importante risultato.

Teorema 3.51 (Heine-Cantor). Sia $f \colon [a,b] \to \mathbb{R}$ una funzione continua; allora $f$ è uniformemente continua.

$\quad$

Dal teorema 3.51 segue quindi che le funzioni dell’esercizio 3.27 sono uniformemente continue. Neanche questa condizione, quindi, è sufficiente a garantire la convergenza uniforme. Per risolvere la questione, possiamo chiederci cosa “va storto” in questo esempio, analizzando più da vicino le funzioni $f_n$ in questione. Chiamiamo quindi, per ogni $n \in \mathbb{N}$ , $\sigma_n$ il modulo di continuità di $f_n$ e cerchiamo di capire come essi si comportano al variare di $n$ .

Si può osservare che, per ogni $n \in \mathbb{N}$ , vale

(141) $\begin{equation*} f_n(0)=0, \quad f_n \Big( \frac{1}{n} \Big) = 1. \end{equation*}$

Ciò implica che

(142) $\begin{equation*} \sigma_n \Big( \frac{1}{n} \Big) \geq 1 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Traducendo queste informazioni, otteniamo che, pur essendo tutte le $f_n$ uniformemente continue, non vi è un unico modulo di continuità $\sigma$ adeguato a tutte le $f_n$ ; infatti un tale $\sigma$ dovrebbe soddisfare $\sigma \geq \sigma_n$ per ogni $n \in \mathbb{N}$ , e cioè

(143) $\begin{equation*} \sigma \Big( \frac{1}{n} \Big) \geq 1 \qquad \forall n \in \mathbb{N}, \end{equation*}$

ma ciò contraddirebbe il fatto che $\lim_{\varepsilon \to 0}\sigma(\varepsilon)=0$ . In poche parole, la stima di continuità delle $f_n$ degenera al crescere di $n.$

Analizziamo dallo stesso punto di vista l’esempio 2.4, dove non si ha convergenza uniforme e il limite puntuale non è continuo. Anche qui, chiamando $\sigma_n$ i moduli di continuità delle funzioni $f_n$ , si vede che essi degenerano al crescere di $n$ : osservando la figura 4, intuitivamente si vede $x^n$ rimane circa pari a $0$ per un intervallo sempre più grande, e poi ha una variazione repentina che la porta ad ottenere $f_n(1)=1$ . Più precisamente, per ogni $n \in \mathbb{N}$ si ha

(144) $\begin{equation*} f_n \Big( \frac{1}{\sqrt[n]{n}} \Big) = \frac{1}{n}, \quad f_n(1)=1 \end{equation*}$

e vale

(145) $\begin{equation*} 1 - \frac{1}{\sqrt[n]{n}} \xrightarrow[n \to \infty]{} 0, \qquad 1 - \frac{1}{n} \xrightarrow[n \to \infty]{} 1. \end{equation*}$

Anche in questo esempio, quindi, non può esistere un modulo di continuità $\sigma$ universale per tutte le $f_n$ ; infatti un tale $\sigma$ dovrebbe soddisfare

(146) $\begin{equation*} \sigma \Big( 1 - \frac{1}{\sqrt[n]{n}} \Big) \geq 1 - \frac{1}{n}, \qquad \forall n \in \mathbb{N}, \end{equation*}$

che di nuovo contraddirebbe il fatto che $\lim_{\varepsilon \to 0}\sigma(\varepsilon)=0$ . Anche in questo esempio, quindi, la continuità uniforme delle $f_n$ degenera al crescere di $n$ .

Ci si può chiedere se vi sia un legame tra la convergenza uniforme di una successione di funzioni e l’esistenza di un unico modulo di continuità per tutte le funzioni $f_n$ . Quest’ultima proprietà è talmente importante da meritare una definizione.

Definizione 3.52 (equicontinuità). Sia $X$ un insieme di funzioni (continue) definite sull’intervallo $[a,b]$ e a valori reali. $X$ si dice equicontinuo se esiste $\sigma \colon [0,+\infty) \to [0,+\infty)$ tale che, per ogni $f \in X$ , $\sigma$ è un modulo di continuità per $f$ .

Osservazione 3.53. Si può tradurre la definizione 3.52 dicendo che $X$ è equicontinuo se per ogni $\varepsilon>0$ , esiste $\delta>0$ tale che

(147) $\begin{equation*} |x-y| < \delta \Longrightarrow |f(x) - f(y)|< \varepsilon \qquad \forall f \in X, \,\, \forall x,y \in [a,b]. \end{equation*}$

Infatti, se $X$ è equicontinuo e $\varepsilon>0$ , basta scegliere $\delta>0$ tale che $\sigma(\delta)< \varepsilon$ . Se invece per ogni $\varepsilon>0$ , esiste $\delta>0$ per cui vale la (147), si può porre

(148) $\begin{equation*} \sigma(\varepsilon) := \min \Big\{ \varepsilon, \, \sup \{ \delta >0 \mid \delta \text{ soddisfa 145} \}) \Big\}. \end{equation*}$

Si può verificare per esercizio che $\sigma$ risulta un modulo di continuità, chiaramente comune a tutte le funzioni in $X$ .

Osservazione 3.54. Una famiglia $X=\{f_n\}_{n=1}^N$ finita di funzioni $f_n \colon [a,b] \to \mathbb{R}$ uniformemente continue è chiaramente equicontinua; infatti, se $\sigma_n$ è un modulo di continuità per $f_n$ , è facile verificare che la funzione $\sigma \colon [0,+\infty) \to [0,+\infty)$ definita da

(149) $\begin{equation*} \sigma(\varepsilon) = \max \{\sigma_1(\varepsilon), \dots, \sigma_N(\varepsilon) \} \end{equation*}$

è un modulo di continuità per ognuna delle $f_n$ . Ciò è ovvio in quanto $\sigma(\varepsilon) \geq \sigma_i(\varepsilon)$ per ogni $\varepsilon>0$ e per ogni $i \in \{1, \dots, N \}$ .

Ci possiamo ora chiedere se l’esistenza di uno stesso modulo di continuità per tutte le funzioni di una successione garantisca la convergenza uniforme. Più precisamente, ci poniamo la seguente domanda.

Domanda 3.55. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni continue (e quindi uniformemente continue per il teorema 3.51) che convergono puntualmente a una funzione $f$ . Se la successione $f_n$ è equicontinua, si può dire che la convergenza è uniforme?

La risposta alla domanda è affermativa come mostrato dal seguente teorema; inoltre esso afferma che l’equicontinuità è una condizione equivalente alla convergenza uniforme. In un certo senso, quindi, l’equicontinuità cattura l’essenza della convergenza uniforme per le funzioni continue.

Teorema 3.56. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni continue che converge puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ . Allora le seguenti condizioni sono equivalenti:

$\quad$

Le funzioni $f_n$ sono equicontinue;

$f_n$ converge uniformemente a $f$ .

$\quad$

Dimostrazione.

1. $\Rightarrow$ 2.
Poiché le $f_n$ sono equicontinue, sia $\sigma$ un modulo di continuità comune a tutte le $f_n$ . Vogliamo dimostrare che la successione delle $f_n$ soddisfa la proposizione 3.18. Sia allora $\varepsilon>0$ ; poiché $\sigma$ soddisfa $\lim_{\varepsilon \to 0}\sigma(\varepsilon)=0$ , allora esiste $\bar{\delta}>0$ tale che

(150) $\begin{equation*} \sigma(\delta) < \frac{\varepsilon}{3} \qquad \forall \delta \in [0,\bar{\delta}]. \end{equation*}$

In altre parole, si ha

(151) $\begin{equation*} |f_n(x)-f_n(y)|< \frac{\varepsilon}{3} \qquad \forall n \in \mathbb{N},\,\, \forall x,y \in [a,b] \text{ tali che } |x-y| \leq \bar{\delta}. \end{equation*}$

Sia allora $a=x_0 < x_1 < \dots < x_M = b$ una sequenza di punti tali che

(152) $\begin{equation*} x_i - x_{i-1} < \bar{\delta} \qquad \forall i=1, \dots, M. \end{equation*}$

Poiché $f_n$ converge puntualmente a $f$ , esiste $N \in \mathbb{N}$ tale che

(153) $\begin{equation*} |f_n(x_i)-f_m(x_i)| < \frac{\varepsilon}{3} \qquad \forall n,m \geq N, \,\, \forall i=0, \dots, M. \end{equation*}$

Siano quindi siano $n,m \geq N$ . Per qualunque $x \in [a,b]$ si ha ovviamente $x \in [x_{i-1},x_i]$ per qualche $i \in \{1, \dots, M\}$ . Per la disuguaglianza triangolare, la (151), la (152) e la (153) si ha

(154) $\begin{equation*} \begin{split} |f_n(x)-f_m(x)| \leq & |f_n(x)-f_n(x_i)| + |f_n(x_i)-f_m(x_i)| + |f_m(x_i)-f_m(x)| \\ < & \, \varepsilon. \end{split} \end{equation*}$

Per la proposizione 3.18, allora $f_n$ converge uniformemente a una funzione, che chiaramente corrisponde a $f$ per l’ipotesi di convergenza puntuale e la proposizione 3.10.

2. $\Rightarrow$ 1.
Supponiamo per assurdo che la successione $f_n$ non sia equicontinua; per l’osservazione 3.53, esiste $\varepsilon>0$ tale che, per ogni $k \in \mathbb{N}$ esistono dei punti $x_k,y_k \in [a,b]$ e ${n_k} \in \mathbb{N}$ tali che

(155) $\begin{equation*} |x_k - y_k| < \frac{1}{k} \quad \text{e} \quad |f_{n_k}(x_k) - f_{n_k}(y_k)| \geq \varepsilon \qquad \forall k \in \mathbb{N}. \end{equation*}$

Poiché per l’osservazione 3.54 una famiglia finita di funzioni uniformemente continue è equicontinua, $(n_k)_{k \in \mathbb{N}}$ non è superiormente limitato. Senza perdita di generalità, quindi, a meno di passare ulteriormente a una sottosuccessione, si può supporre che la funzione

(156) $\begin{equation*} k \in \mathbb{N} \mapsto n_k \in \mathbb{N} \end{equation*}$

sia crescente. Poiché $[a,b]$ è chiuso e limitato, per il teorema di Bolzano-Weiestrass esiste una ulteriore sottosuccessione (che per semplicità di notazione indichiamo sempre con $n_k$ ) e dei punti $x,y \in [a,b]$ tali che

(157) $\begin{equation*} \lim_{k \to \infty} x_k = x, \qquad \lim_{k \to \infty} y_k = y \end{equation*}$

e inoltre $x=y$ per la prima disuguaglianza in (155). Poiché la convergenza è uniforme, $f$ è continua e, applicando il teorema 3.23 alle successioni $x_k, f_{n_k}$ e $y_k, f_{n_k}$ , si ha

(158) $\begin{equation*} \lim_{k \to \infty} f_{n_k}(x_k) = f(x) = \lim_{k \to \infty} f_{n_k}(y_k), \end{equation*}$

ma ciò contraddice la seconda disuguaglianza in (155).

Criteri di convergenza uniforme: Il teorema di Ascoli-Arzelà.

Come vedremo, la nozione di equicontinuità è collegata a una questione di compattezza per successioni di funzioni. Infatti è ben noto che una successione numerica $x_n$ convergente è necessariamente limitata. Il viceversa non è in generale vero, ma se $x_n$ è una successione limitata, per il teorema di Bolzano-Weierstrass si può dire che esiste sempre una sua sottosuccessione convergente.

Per provare a mantenere il parallelo tra successioni numeriche e successioni di funzioni, dobbiamo innanzitutto chiarire cosa intendiamo per successione limitata e in che senso intendiamo la convergenza. Diamo quindi la seguente definizione.

Definizione 3.57 (equilimitatezza). Sia $E \subseteq \mathbb{R}$ ; una successione di funzioni $f_n \colon E \to \mathbb{R}$ si dice equilimitata se esiste $M >0$ tale che

(159) $\begin{equation*} \sup_{x \in E} |f_n(x)| \leq M \qquad \forall n \in \mathbb{N}. \end{equation*}$

$\quad$

In altre parole, una successione di funzioni è equilimitata se le $f_n$ sono limitate dallo stesso numero reale $M>0$ .

Ora che abbiamo definito la nozione di limitatezza, possiamo chiederci se e in quale senso valga il parallelo tra successioni numeriche e successioni di funzioni riguardo la limitatezza e la convergenza. Cominciamo col chiederci se una successione convergente è necessariamente equilimitata.

Domanda 3.58. Sia $E \subseteq \mathbb{R}$ e una successione di funzioni $f_n \colon E \to \mathbb{R}$ limitate convergente puntualmente a una funzione $f \colon E \to \mathbb{R}$ limitata. Si può affermare che le $f_n$ sono equilimitate? E se la convergenza è uniforme?

La prima domanda ha risposta negativa, come mostra l’esempio 2.13: la successione $f_n$ converge puntualmente alla funzione nulla, le $f_n$ sono singolarmente limitate, ma non equilimitate in quanto

(160) $\begin{equation*} \sup_{x \in [0,1]} |f_n(x)| = n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Richiedendo invece la convergenza uniforme, la risposta alla domanda diventa affermativa, come mostra la seguente proposizione.

Proposizione 3.59. Sia $E \subseteq \mathbb{R}$ e una successione di funzioni limitate $f_n \colon E \to \mathbb{R}$ convergente uniformemente a una funzione $f \colon E \to \mathbb{R}$ . Allora le $f_n$ sono equilimitate.

$\quad$

Dimostrazione. Poiché ogni famiglia finita di funzioni limitate è equilimitata (basta considerare il massimo tra gli estremi superiori), è sufficiente dimostrare che esiste $N \in \mathbb{N}$ e $M >0$ tale che

(161) $\begin{equation*} \sup_{x \in E} |f_n(x)| \leq M \qquad \forall n \geq N. \end{equation*}$

Per la proposizione 3.18, scegliendo $\varepsilon=1$ , esiste $N \in \mathbb{N}$ tale che

(162) $\begin{equation*} \sup_{x \in E} |f_n(x) - f_m(x)| < 1 \qquad \forall n,m \geq N. \end{equation*}$

Fissiamo $m \geq N$ . Poiché $f_m$ è limitata, esiste $M >0$ tale che

(163) $\begin{equation*} \sup_{x \in E} |f_m(x)| \leq M. \end{equation*}$

Le (163) e (162) implicano che

(164) $\begin{equation*} \sup_{x \in E} |f_n(x)| < M + 1 \qquad \forall n \geq N, \end{equation*}$

cioè l’equilimitatezza delle $f_n$ .

Chiediamoci ora se per le successioni di funzioni vale un analogo del teorema di Bolzano-Weierstrass. Precisamente, analizziamo la seguente questione.

Domanda 3.60. Sia $E \subseteq \mathbb{R}$ e sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni equilimitate. Esiste una funzione $f \colon E \to \mathbb{R}$ e una sottosuccessione $f_{n_k}$ che converga uniformemente o almeno puntualmente a $f$ ?

La risposta è negativa, anche se si suppone la continuità delle $f_n$ , come mostrato dal seguente esercizio, per la cui soluzione rimandiamo alla sezione 5.

Esercizio 3.61 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Sia $f_n \colon [0,1] \to \mathbb{R}$ la successione di funzioni definita da

(165) $\begin{equation*} f_n(x) = \begin{cases} 2^n \bigg( x - \dfrac{k}{2^n} \bigg) & \text{se } x \in \bigg[\dfrac{k}{2^n},\dfrac{k+1}{2^n}\bigg), \,\, k \in \{ 0,1, \dots, 2^{n}-1\}, \text{ $k$ pari}, \\[10pt] 1 -2^n \bigg( x - \dfrac{k}{2^n} \bigg) & \text{se } x \in \bigg[\dfrac{k}{2^n},\dfrac{k+1}{2^n}\bigg), \,\, k \in \{ 0,1, \dots, 2^{n}-1\}, \text{ $k$ dispari}. \\[10pt] 0 & \text{se } x=1. \end{cases} \end{equation*}$

Provare che ogni sua sottosuccessione non converge puntualmente.

$\quad$

La conclusione di questo esercizio mostra che l’analogo del teorema di Bolzano-Weiestrass non vale sotto la sola ipotesi di equilimitatezza della successione di funzioni. Occorre aggiungere ulteriori condizioni alla successione per garantire l’esistenza di una sottosuccessione convergente. La condizione giusta risulta essere proprio l’equicontinuità, come mostra il notevole risultato dovuto ai matematici italiani Giulio Ascoli (1843 — 1896) e Cesare Arzelà (1847 — 1912). Per dimostrarlo, però, premettiamo il seguente utile lemma, noto come procedura diagonale e che costituisce una generalizzazione del teorema di Bolzano-Weiestrass.

Lemma 3.62 (procedura diagonale). Sia $E \subseteq \mathbb{R}$ , sia $q_j$ una successione di numeri in $E$ e sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni tale che, per ogni $j \in \mathbb{N}$ , la successione numerica $f_n(q_j)_{n \in \mathbb{N}}$ sia limitata. Allora esiste una funzione $\varphi \colon \mathbb{N} \to \mathbb{N}$ strettamente crescente tale che per ogni $j \in \mathbb{N}$ , la successione $f_{\varphi(k)}(q_j)_{k \in \mathbb{N}}$ è convergente a un numero reale $f(q_j)$ .

$\quad$

Osservazione 3.63. Se le ipotesi del lemma 3.62 sono verificate, il teorema di Bolzano-Weiestrass implica che per ogni $j$ fissato, la successione $f_n(q_j)_{n}$ ammette un’estratta convergente. La successione estratta dipende, ovviamente, dal particolare $j$ fissato. Il lemma 3.62 afferma invece che esiste un’estratta fissata $f_{\varphi(n)}$ per cui ognuna delle successioni $f_{\varphi(n)}(q_j)_n$ sia convergente.

Prima di procedere con la dimostrazione formale, è conveniente spiegare euristicamente l’idea sottostante. Essa consiste nel formare per ricorrenza una matrice infinita, in modo che sulla riga $j$ ci sia una sottosuccessione di $f_n$ estratta da quella presente alla riga $j-1$ , scelta in modo che sia convergente se valutata su $q_j$ . La sottosuccessione costruita considerando la diagonale di tale matrice risulta essere un’estratta di ognuna delle sottosuccessioni nelle righe e quindi è convergente se valutata su ognuno dei $q_j$ . Per una visualizzazione di tale idea, si veda l’osservazione 3.64.

Dimostrazione del lemma 3.62. Ci accingiamo a definire $\varphi$ per ricorrenza. Poiché la successione $f_n(q_1)_n$ è limitata, esiste una sua estratta $f_{n(k,1)}(q_1)_{k \in \mathbb{N}}$ convergente a un numero reale che chiamiamo $f(q_1)$ . Poniamo

(166) $\begin{equation*} \varphi(1)=n(1,1). \end{equation*}$

Successivamente, supponiamo definita la successione $f_{n(k,j)}(q_j)_k$ , $f(q_j)$ e $\varphi(j)$ e consideriamo la successione $f_{n(k,j)}(q_{j+1})_{k \in \mathbb{N}}$ . Poiché anch’essa è limitata, esiste una sua estratta $f_{n(k,j+1)}(q_{j+1})_{k \in \mathbb{N}}$ convergente a un numero reale $f(q_{j+1})$ . Poniamo quindi $\varphi(j+1)=n(j+1,j+1)$ . Poiché la successione $n(k,j+1)_{k \in \mathbb{N}}$ è un’estratta della successione $n(k,j)_{k \in \mathbb{N}}$ , si ha

(167) $\begin{equation*} \varphi(j+1) = n(j+1,j+1) \geq n(j+1,j) > n(j,j) = \varphi(j), \end{equation*}$

e ciò prova che la funzione $\varphi$ è strettamente crescente. Per il modo in cui è stata costruita la funzione $\varphi$ , per ogni $j \in \mathbb{N}$ la successione $\varphi(k)_{k \in \mathbb{N}}$ è un’estratta della successione $n(k,j)_{k \in \mathbb{N}}$ . Per tale ragione si ha

(168) $\begin{equation*} \lim_{k \to \infty}f_{\varphi(k)}(q_j) = f(q_j) \qquad \forall j \in \mathbb{N}. \end{equation*}$

Osservazione 3.64. Come è stato già anticipato, il lemma 3.62 è detto procedura diagonale in quanto possiamo immaginare di disporre le varie successioni in una sorta di matrice infinita dove, nella riga $j$ , la sottosuccessione $n(k,j)_{k \in \mathbb{N}}$ scelta è estratta dalla sottosuccessione $n(k,j-1)_{k \in \mathbb{N}}$ della riga superiore, e la funzione $\varphi$ è costruita scegliendo l’estratta determinata dalla “diagonale principale” della matrice.

(169) $\begin{equation*} \begin{matrix} \colorbox{tau}{$f_{n(1,1)}(q_1)$} & f_{n(2,1)}(q_1) & f_{n(3,1)}(q_1) & \dots & f_{n(j,1)}(q_1) & \dots & \to & f(q_1) \\ f_{n(1,2)}(q_2) & \colorbox{tau}{$f_{n(2,2)}(q_2)$} & f_{n(3,2)}(q_2) & \dots & f_{n(j,2)}(q_2) & \dots & \to & f(q_2) \\ f_{n(1,3)}(q_3) & f_{n(2,3)}(q_3) & \colorbox{tau}{$f_{n(3,3)}(q_3)$} & \dots & f_{n(j,3)}(q_3) & \dots & \to & f(q_3)\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ f_{n(1,j)}(q_j) & f_{n(2,j)}(q_j) & f_{n(3,j)}(q_j) & \dots & \colorbox{tau}{$f_{n(j,j)}(q_j)$} & \dots & \to & f(q_j) \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \end{matrix} \end{equation*}$

Possiamo ora enunciare e dimostrare il teorema di Ascoli-Arzelà.

Teorema 3.65 (Ascoli-Arzelà). Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni continue. Allora le due seguenti condizioni sono equivalenti:

$\quad$

le funzioni $f_n$ sono equilimitate e equicontinue;

da ogni sottosuccessione $f_{n_k}$ se ne può estrarre una convergente uniformemente.

$\quad$

Dimostrazione.

1. $\Rightarrow$ 2.
Supponiamo che le $f_n$ siano equilimitate dalla costante $M>0$ ed equicontinue, e scegliamo quindi un loro modulo di continuità $\sigma \colon [0,+\infty) \to [0,+\infty)$ . Per mostrare l’implicazione basta dimostrare che $f_n$ possiede un’estratta convergente: infatti, una volta provato ciò, è sufficiente applicare questo risultato a una qualunque sottosuccessione $f_{n_k}$ .

Sia $q \colon \mathbb{N} \to \mathbb{Q} \cap [a,b]$ una funzione biunivoca; indicando con $q_j$ il valore $q(j)$ , $q_j$ risulta una successione che assume una sola volta tutti i valori razionali appartenenti all’intervallo $[a,b]$ . Ciò è possibile in quanto i numeri razionali formano un insieme detto numerabile, cioè in corrispondenza biunivoca con i numeri naturali. Una tale successione $q_j$ è detta una enumerazione dei razionali.

Poiché le funzioni $f_n$ sono equilimitate, possiamo applicare il lemma 3.62 e ottenere l’esistenza di una sottosuccessione $f_{\varphi(n)}$ e di una funzione $f \colon \mathbb{Q} \cap [a,b] \to \mathbb{R}$ (cioè definita su ognuno dei $q_j$ ) per cui si abbia

(170) $\begin{equation*} \lim_{n \to \infty}f_{\varphi(n)}(q_j) = f(q_j) \qquad \forall j \in \mathbb{N}. \end{equation*}$

In altre parole, $f$ è il limite puntuale della successione di funzioni $f_{\varphi(n)}$ sull’insieme $\mathbb{Q} \cap [a,b]$ , cioè sui razionali appartenenti all’intervallo $[a,b]$ . Dimostriamo ora che la successione $f_{\varphi(n)}$ converge puntualmente su $[a,b]$ . Per alleggerire la notazione, supponiamo che

(171) $\begin{equation*} \varphi(n)=n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Sia quindi $x \in [a,b]$ ; vogliamo provare che la successione $f_{n}(x)_{n \in \mathbb{N}}$ è di Cauchy. Sia quindi $\varepsilon>0$ ; per ogni $n,m,j \in \mathbb{N}$ , per la disuguaglianza triangolare si ha

(172) $\begin{equation*} \begin{split} |f_{n}(x) - f_{m}(x)| \leq & |f_{n}(x) - f_{n}(q_j)| + |f_{n}(q_j) - f_{m}(q_j)| \\ & + |f_{m}(q_j) - f_{m}(x)|. \end{split} \end{equation*}$

L’idea consiste nello stimare i termini del membro di destra della (172). Sia quindi $\delta>0$ tale che $\sigma(\delta) < \dfrac{\varepsilon}{3}$ ; per la densità di $\mathbb{Q}$ in $\mathbb{R}$ , fissiamo $j \in \mathbb{N}$ tale che

(173) $\begin{equation*} |q_j - x| < \delta. \end{equation*}$

Poiché $\sigma$ è un modulo di continuità per tutte le $f_n$ si ha

(174) $\begin{equation*} |f_{n}(x) - f_{n}(q_j)| < \frac{\varepsilon}{3}, \quad |f_{m}(q_j) - f_{m}(x)| < \frac{\varepsilon}{3}, \qquad \forall n,m \in \mathbb{N}. \end{equation*}$

D’altra parte, poiché $f_{n}(q_j)$ è convergente, essa è di Cauchy e quindi esiste $N \in \mathbb{N}$ tale che

(175) $\begin{equation*} |f_{n}(q_j) - f_{m}(q_j)| < \frac{\varepsilon}{3} \qquad \forall n,m \geq N. \end{equation*}$

Inserendo (174) e (175) in (172), si ottiene

(176) $\begin{equation*} |f_{n}(x) - f_{m}(x)| < \varepsilon \qquad \forall n,m \geq N, \end{equation*}$

che prova che la successione $f_{n}(x)$ è di Cauchy. Per tale ragione essa converge a un numero reale che indichiamo con $f(x)$ . In tal modo, risulta definita la funzione $f \colon [a,b] \to \mathbb{R}$ tale che

(177) $\begin{equation*} \lim_{n \to \infty} f_{n}(x) = f(x); \end{equation*}$

$f$ è quindi il limite puntuale della successione $f_{n}$ (che, lo si ricorda, corrisponde in realtà alla successione $f_{\varphi(n)}$ , cf. (171)). Il teorema 3.56 implica che la convergenza è uniforme.

2. $\Rightarrow$ 1.
Se da ogni sottosuccessione $f_{n_k}$ se ne può estrarre una uniformemente convergente, supponiamo per assurdo che $f_n$ non sia equilimitata; supponiamo cioè che per ogni $k \in \mathbb{N}$ esista $x_k \in [a,b]$ e $n_k \in \mathbb{N}$ tale che

(178) $\begin{equation*} f_{n_k}(x_k) \geq k \end{equation*}$

A meno di definire $n_k$ in modo tale che $n_{k+1} > n_k$ , otteniamo una sottosuccessione $f_{n_k}$ di $f_n$ e, a meno di passare ulteriormente a una sottosuccessione, per l’ipotesi possiamo supporre che $f_{n_k}$ converge uniformemente a una funzione $f$ . Poiché le funzioni $f_n$ sono tutte limitate, in quanto sono funzioni continue un intervallo chiuso e limitato, la proposizione 3.59 implica che la successione $f_{n_k}$ è equilimitata, che contraddice (178).

Supponiamo ora per assurdo che la successione $f_n$ non sia equicontinua. Allora, per l’osservazione 3.53, esiste $\varepsilon>0$ tale che, per ogni $k \in \mathbb{N}$ , esistono $x_k, y_k \in [a,b]$ e $n_k \in \mathbb{N}$ tali che

(179) $\begin{equation*} |x_k - y_k| < \frac{1}{k}, \qquad |f_{n_k}(x_k) - f_{n_k}(y_k)| \geq \varepsilon. \end{equation*}$

A meno di definire $n_k$ in modo tale che $n_{k+1} > n_k$ , otteniamo una sottosuccessione $f_{n_k}$ di $f_n$ e, a meno di passare ulteriormente a una sottosuccessione, per l’ipotesi possiamo supporre che $f_{n_k}$ converge uniformemente a una funzione $f$ . Per il teorema 3.56, la successione $f_{n_k}$ è equicontinua, ma ciò contraddice la (179).

Scarica la teoria

Ottieni la dispensa teorica di 59 pagine sulle successioni di funzioni.

Gli spazi normati $\mathscr{B}(E,\mathbb{R})$ e $C_b(E,\mathbb{R})$

Introduzione.

La nozione di convergenza uniforme può essere inquadrata in un contesto più ampio e dai risvolti teorici e pratici molto importanti. Infatti, l’analogia tra la convergenza di successioni di punti e di successioni di funzioni non è soltanto un’utile similitudine, ma affonda le sue radici nel fatto che è possibile immaginare le funzioni come elementi di uno spazio $X$ e definire una nozione di distanza tra di essi, del tutto analoga alla distanza di due numeri reali $x,y$ definita da $d(x,y)=|x-y|$ . Si può quindi immaginare la successione di funzioni come una successione di punti in questo spazio $X$ e definire la nozione di convergenza rispetto a questa distanza.

Questa idea è così utile che diviene il concetto centrale della cosiddetta Analisi funzionale, la branca dell’Analisi Matematica che si occupa dello studio dei vari spazi di funzioni, delle loro proprietà e delle relazioni tra essi.

Noi esamineremo solo qualcuno di questi spazi di funzioni, e cioè quelli relativi alla convergenza uniforme di successioni di funzioni.

A tal fine, cominciamo col definire precisamente il concetto di distanza e di spazio metrico. Durante il corso di questa sezione, se non diversamente specificato, $E$ denota un sottoinsieme di $\mathbb{R}$ .

Spazi metrici e normati.

Definizione 4.1 (spazio metrico). Sia $X$ un insieme non vuoto e sia $d \colon X \times X \to [0,+\infty)$ una funzione; la coppia $(X,d)$ si dice uno spazio metrico se la funzione $d$ , detta {distanza, soddisfa le seguenti condizioni:

$d(x,y)=0$ se e solo se $x=y$ ;

Simmetria: per ogni $x,y \in X$ si ha $d(x,y)=d(y,x)$ ;

Disuguaglianza triangolare:
(180) $\begin{equation*} d(x,z) \leq d(x,y) + d(y,z) \qquad \forall x,y, z \in X. \end{equation*}$

Esempio 4.2. Se, come anticipato nell’introduzione, definiamo la funzione

(181) $\begin{equation*} d \colon (x,y) \in \mathbb{R} \times \mathbb{R} \mapsto |x-y| \in [0,+\infty), \end{equation*}$

essa risulta una distanza su $\mathbb{R}$ (verificarlo per esercizio), per cui la coppia $(\mathbb{R},d)$ risulta uno spazio metrico.

Esempio 4.3. La naturale estensione dell’esempio precedente è la funzione

(182) $\begin{equation*} d \colon (x,y) \in \mathbb{R}^m \times \mathbb{R}^m \mapsto |x-y|:=\Big( \sum_{i=1}^m (x_i-y_i)^2 \Big)^{\frac{1}{2}} \in [0,+\infty), \end{equation*}$

che risulta essere una distanza su $\mathbb{R}^m$ ; cioè la coppia $(\mathbb{R}^m,d)$ è uno spazio metrico.

È possibile parlare di successioni convergenti in uno spazio metrico, che è l’estensione dello stesso concetto per successioni di numeri reali.

Definizione 4.4 (successioni convergenti). Sia $(X,d)$ uno spazio metrico, sia $(x_n)$ una successione in $X$ e sia $x \in X$ ; diciamo che $x_n$ converge a $x$ e scriviamo $x_n \to x$ se per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ tale che

(183) $\begin{equation*} d(x_n,x) < \varepsilon \qquad \forall n \geq N. \end{equation*}$

$x$ è detto limite della successione $x_n$ e si scrive

(184) $\begin{equation*} \lim_{n \to \infty} x_n = x. \end{equation*}$

$\quad$

Osservazione 4.5. Il limite di una successione in uno spazio metrico, se esiste, è unico. Infatti, siano $x,y$ limiti della successione $x_n$ . Allora per ogni $\varepsilon>0$ , dato $N \in \mathbb{N}$ per cui vale (183), si ha

(185) $\begin{equation*} d(x,y) \leq d(x,x_n) + d(x_n,y) \leq 2 \varepsilon. \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ , si ha $d(x,y)=0$ e dalla proprietà 1 della definizione 4.1, si ottiene $x=y$ .

Su uno spazio vettoriale reale (o complesso), è possibile definire una norma, che è intuitivamente un modo per misurare le lunghezze dei vettori.

Definizione 4.6 (norma). Sia $V$ uno spazio vettoriale reale. Una funzione $\| \cdot\| \colon V \to [0,+\infty)$ è detta una norma se soddisfa le seguenti 3 condizioni:

$\| v \| =0$ se e solo se $v =0$ ;

1-omogeneità: per ogni $v \in V$ e per ogni $\lambda \in \mathbb{R}$ , si ha
(186) $\begin{equation*} \| \lambda v \| = |\lambda| \| v\|; \end{equation*}$

per ogni $v, w \in V$ vale la disuguaglianza triangolare:
(187) $\begin{equation*} \|v + w \| \leq \|v \| + \| w \|. \end{equation*}$

Se $\| \cdot \|$ è una norma su $V$ , la coppia $(V, \| \cdot \|)$ si dice uno spazio normato.

$\quad$

Esempio 4.7. Con riferimento agli esempi 4.2 e 4.3, la funzione

(188) $\begin{equation*} \| \cdot \| \colon x \in \mathbb{R}^m \mapsto |x| \in [0,+\infty) \end{equation*}$

è una norma su $\mathbb{R}^m$ .

La situazione descritta nel precedente esempio non è una mera coincidenza, infatti ci si può aspettare che i concetti di distanza su un insieme e di norma su uno spazio vettoriale siano collegati: una norma su $V$ permette di definire una distanza tra i punti di esso, definita come la lunghezza della traslazione che porta uno nell’altro, come mostra la seguente proposizione.

Proposizione 4.8 (distanza indotta). Sia $V$ uno spazio normato con norma $\| \cdot\|$ . Allora la funzione $d \colon V \times V \to [0,+\infty)$ definita da

(189) $\begin{equation*} d(v,w) = \|v - w \| \qquad \forall v,w \in V \end{equation*}$

è una distanza, detta distanza indotta dalla norma $\| \cdot \|$ .

$\quad$

Dimostrazione. Occorre verificare che $d$ soddisfa le 3 proprietà richieste dalla definizione 4.1. La proprietà 1 è una banale conseguenza della proprietà 1 della definizione 4.6. Per quanto riguarda la simmetria, si ha

(190) $\begin{equation*} d(x,y) = \| x-y\| = \|(-1) (y - x) \| = \|y-x\|, \end{equation*}$

dove l’ultima uguaglianza è dovuta alla condizione 2 sulle norme. Riguardo la 3, si ha

(191) $\begin{equation*} d(x,z) = \|x-z \| = \|x-y + y - z \| \leq \|x-y \| + \|y - z \| = d(x,y) + d(y,z), \end{equation*}$

dove si è usata la proprietà 3 della definizione 4.6.

Osservazione 4.9. Il viceversa della proposizione 4.8 non è in generale vero: esistono cioè distanze su spazi vettoriali che non sono indotte da alcuna norma, come mostra il prossimo esempio.

Esempio 4.10 Sia $V=\mathbb{R}$ e sia $d \colon \mathbb{R} \times \mathbb{R} \to [0,+\infty)$ la funzione definita da

(192) $\begin{equation*} d(x,y) = \sqrt{|x-y|}. \end{equation*}$

Per provare che $d$ è una distanza, verifichiamo che essa soddisfa le condizioni della definizione 4.1:

$\quad$

$d(x,y)=0$ se e solo se $x=y$ ;

$d(x,y)=d(y,x)$ per ogni $x,y \in \mathbb{R}$ per la simmetria del valore assoluto;

Per ogni $x,y,z \in \mathbb{R}$ si ha
(193) $\begin{equation*} d(x,z) = \sqrt{|x-z|} \leq \sqrt{|x-y| + |y-z|} \leq \sqrt{|x-y|} + \sqrt{|y-z|} = d(x,y) + d(y,z), \end{equation*}$

dove la prima disuguaglianza segue dalla disuguaglianza triangolare per il valore assoluto e dal fatto che la funzione $t \mapsto \sqrt{t}$ è crescente e la seconda disuguaglianza segue dal fatto che la funzione $t \mapsto \sqrt{t}$ è concava (oppure si può dimostrare semplicemente elevando al quadrato i due membri).

Quindi $d$ è una distanza su $\mathbb{R}$ . Per dimostrare che essa non è indotta da alcuna norma, proviamo che essa non è $1$ -omogenea, cioè che una tale norma non potrebbe soddisfare la condizione 2 della definizione 4.1. Infatti, supponiamo per assurdo che esista una norma $\| \cdot \|$ che induca $d$ ; allora, per la proposizione 4.8, essa sarebbe definita da $\| x \|= d(x,0) = \sqrt{x}$ . Ma allora si avrebbe

(194) $\begin{equation*} \|\lambda x \| = \sqrt{|\lambda x|} = \sqrt{|\lambda|} \sqrt{|x|} = \sqrt{|\lambda|} \| x\| \neq |\lambda| \| x \| \qquad \quad \forall \lambda \in \mathbb{R} \setminus \{0,1, -1 \},\,\, \forall x \in \mathbb{R} \setminus \{ 0 \}, \end{equation*}$

che contraddice la condizione 2 della definizione 4.6. Da tale assurdo segue che $d$ non è indotta da alcuna norma.

Gli spazi delle funzioni limitate.

Applichiamo ora questi concetti astratti a un caso concreto che esamineremo nel seguito della trattazione; definiamo quindi lo spazio vettoriale delle funzioni limitate su un sottoinsieme $E$ di $\mathbb{R}$ .

Definizione 4.11 ( $\mathscr{B}(E,\mathbb{R})$ ). Sia $E \subset \mathbb{R}$ ; si definisce

(195) $\begin{equation*} \mathscr{B}(E,\mathbb{R}) = \{ f \colon E \to \mathbb{R} \mid f \text{ è limitata} \} \end{equation*}$

lo spazio vettoriale delle funzioni limitate su $E$ con le usuali operazioni di somma e prodotto per uno scalare.

$\quad$

Osservazione 4.12. Si può fare lo stesso discorso anche se $E \subseteq \mathbb{R}^m$ per $m >1$ .

Si può dotare lo spazio $\mathscr{B}(E,\mathbb{R})$ di una norma, detta norma infinito o uniforme.

Definizione 4.13 (norma e distanza infinito). Sia $f \in \mathscr{B}(E,\mathbb{R})$ ; allora la quantità

(196) $\begin{equation*} \|f \|_{\infty} = \sup_{x \in E} |f(x)| \end{equation*}$

viene detta norma infinito o norma uniforme della funzione $f$ . La distanza che, per la proposizione 4.8, tale norma induce su $\mathscr{B}(E,\mathbb{R})$ è detta distanza infinito e si denota con $d_\infty$ .

$\quad$

Osservazione 4.14. Poiché ogni $f \in \mathscr{B}(E,\mathbb{R})$ è limitata, la quantità $\| f\|_\infty$ risulta ben definita.

Il fatto di averla chiamata norma è giustificato dalla seguente proposizione, la cui dimostrazione è lasciata come esercizio per il lettore.

Proposizione 4.15. Sia $E \subseteq \mathbb{R}$ . Allora $\| \cdot \|_\infty$ è una norma su $\mathscr{B}(E,\mathbb{R})$ .

$\quad$

Abbiamo introdotto la distanza infinito su $\mathscr{B}(E,\mathbb{R})$ perché essa è precisamente la distanza che induce la convergenza uniforme, come chiarisce la seguente proposizione. Ciò giustifica il nome di norma uniforme.

Proposizione 4.16 (convergenza uniforme e in $(\mathscr{B}(E,\mathbb{R}),d_\infty)$ ). Sia $f_n \in \mathscr{B}(E,\mathbb{R})$ una successione di funzioni e sia $f \in \mathscr{B}(E,\mathbb{R})$ . Allora $f_n$ converge uniformemente a $f$ se e solo se $f_n$ è una successione convergente nello spazio metrico $(\mathscr{B}(E,\mathbb{R}),d_\infty)$ e il suo limite è $f$ .

$\quad$

Dimostrazione. Si ha

(197) $\begin{equation*} d_\infty(f_n,f) = \| f_n - f \|_\infty = \sup_{x \in E} |f_n(x)- f(x)|. \end{equation*}$

Per definizione, $f_n$ converge uniformemente a $f$ se e solo se l’ultima quantità tende a $0$ per $n \to \infty$ . Ma ciò è equivalente al fatto che

(198) $\begin{equation*} \lim_{n \to \infty} d_\infty(f_n,f) = 0, \end{equation*}$

cioè è equivalente alla convergenza della successione $f_n$ a $f$ in $(\mathscr{B}(E,\mathbb{R}),d_\infty)$ .

Osservazione 4.17. Cosa si può dire riguardo alla convergenza puntuale? Si può dimostrare che non è possibile definire una distanza $d_p$ su $\mathscr{B}(E,\mathbb{R})$ in modo che valga un analogo della proposizione 4.16 per la convergenza puntuale. In altre parole, la convergenza puntuale non è indotta da una distanza. Per una dimostrazione rimandiamo a e [2, IX.7.1]

Un sottospazio di $\mathscr{B}(E,\mathbb{R})$ di particolare importanza è costituito dalle funzioni continue e limitate su $E$ .

Definizione 4.18 ( $C_b(E,\mathbb{R})$ ). Sia $E \subset \mathbb{R}$ ; si definisce $C_b(E,\mathbb{R})$ come il sottospazio di $\mathscr{B}(E,\mathbb{R})$ costituito dalle funzioni continue. $C_b(E,\mathbb{R})$ è quindi lo spazio delle funzioni continue e limitate su $E$ .

$\quad$

Osservazione 4.19. Poiché $C_b(E,\mathbb{R})$ è un sottospazio di $\mathscr{B}(E,\mathbb{R})$ , allora la norma infinito è una norma anche su $C_b(E,\mathbb{R})$ .

Essendo spazi vettoriali normati, per la proposizione 4.8 sia $C_b(E,\mathbb{R})$ che $\mathscr{B}(E,\mathbb{R})$ sono spazi metrici.

Successioni di Cauchy e completezza.

Anche in spazi metrici astratti si può introdurre il concetto di successione di Cauchy.

Definizione 4.20 (successione di Cauchy). Sia $(X,d)$ uno spazio metrico e sia $(x_n)_n$ una successione di elementi di $X$ ; $x_n$ è detta di Cauchy se per ogni $\varepsilon>0$ esiste $N \in \mathbb{N}$ tale che

(199) $\begin{equation*} d(x_n,x_m) < \varepsilon \qquad \forall n,m \geq N. \end{equation*}$

$\quad$

Tra gli spazi metrici, una classe importante è costituita dagli spazi metrici completi. Il concetto di completezza è un’estensione della nozione di completezza di $\mathbb{R}$ e infatti, come ci accingiamo a vedere, esso è perfettamente analogo al criterio di Cauchy per le successioni di numeri reali.

Definizione 4.21 Uno spazio metrico $(X,d)$ si dice completo se ogni successione di Cauchy di elementi di $X$ è convergente.

$\quad$

Esempio 4.22. Lo spazio metrico $(\mathbb{R}, d)$ definito nell’esempio 4.2 è uno spazio metrico completo per il teorema 3.13.

Esercizio 4.23 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dimostrare che gli spazi metrici $(\mathbb{R}^m, d)$ definiti nell’esempio 4.3 sono completi per ogni $m \in \mathbb{N}$ .

$\quad$

Esempio 4.24. Lo spazio metrico $(\mathscr{B}(E,\mathbb{R}), d_\infty)$ è completo per la proposizione 3.18.

Osserviamo come la continuità del limite uniforme di una successione di funzioni continue stabilita dal teorema 3.19 possa essere riformulata nel linguaggio degli spazi metrici.

Proposizione 4.25. Lo spazio metrico $(C_b(E,\mathbb{R}), d_\infty)$ è completo.

$\quad$

Dimostrazione. Sia $f_n$ una successione di Cauchy in $C_b(E,\mathbb{R})$ . Allora ognuna delle $f_n$ è una funzione continua e limitata su $E$ . Per il criterio di Cauchy per la convergenza uniforme dato dalla proposizione 3.18, $f_n$ converge uniformemente a una funzione $f$ che risulta continua per il teorema 3.19 e limitata (proposizione 3.59).

Per la proposizione 4.16, la successione $f_n$ converge a $f$ nello spazio metrico $(C_b(E,\mathbb{R}), d_\infty)$ , che risulta quindi completo.

(Equi)limitatezza di funzioni.

Nel contesto degli spazi metrici si può introdurre la nozione di limitatezza di un insieme. Per farlo, però, prima definiamo il concetto di palla.

Definizione 4.26 (palla). Sia $(X,d)$ uno spazio metrico, sia $x_0 \in X$ e sia $r > 0$ . Si definisce palla di centro $x_0$ e raggio $r$ l’insieme

(200) $\begin{equation*} B_r(x_0) = \{ x \in X \mid d(x,x_0) < r \}. \end{equation*}$

$\quad$

Passiamo ora alla definizione di insieme limitato.

Definizione 4.27 (insiemi limitati). Sia $(X,d)$ uno spazio metrico e sia $Y \subseteq X$ . Si dice che $Y$ è limitato se esiste $x_0 \in X$ e $r>0$ tale che

(201) $\begin{equation*} Y \subset B_r(x_0). \end{equation*}$

In maniera analoga si dice che una successione $x_n$ di elementi di $X$ si dice limitata se se esiste $x_0 \in X$ e $r>0$ tale che

(202) $\begin{equation*} x_n \in B_r(x_0) \qquad \forall n \in \mathbb{N}. \end{equation*}$

$\quad$

Osservazione 4.28. Se $Y \subseteq X$ è limitato, cioè se esiste $x_0 \in X$ e $r>0$ che soddisfano la definizione 4.27, allora per ogni $x \in X$ vi è una palla centrata in $x$ contenente $Y$ , infatti

(203) $\begin{equation*} Y \subseteq B_r(x_0) \subseteq B_{r + d(x,x_0)}(x) \qquad \forall x \in X. \end{equation*}$

Data questa definizione, la discussione sull’equilimitatezza fatta all’inizio della sezione 3.3.3 si può riformulare nel seguente modo.

Proposizione 4.29. Sia $f_n \colon E \to \mathbb{R}$ una successioni di funzioni limitate. Essa è equilimitata se e solo se è limitata come successione in $\mathscr{B}(E,\mathbb{R})$ .

$\quad$

Dimostrazione. La successione $f_n$ è equilimitata se e solo se esiste $M>0$ tale che

(204) $\begin{equation*} \sup_{x \in E} |f_n(x)| \leq M \qquad \forall n \in \mathbb{N}. \end{equation*}$

Ciò è equivalente a dire che

(205) $\begin{equation*} \| f_n - f_0 \|_\infty \leq M \qquad \forall n \in \mathbb{N}, \end{equation*}$

dove $f_0$ denota la funzione identicamente nulla su $E$ . A sua volta, questo è equivalente a

(206) $\begin{equation*} f_n \in B_M(f_0) \qquad \forall n \in \mathbb{N}, \end{equation*}$

dove la palla è intesa nella distanza $d_\infty$ di $\mathscr{B}(E,\mathbb{R})$ .

Negli spazi metrici vale il risultato, analogo del caso $X=\mathbb{R}$ , che afferma la limitatezza di una successione convergente.

Proposizione 4.30. Sia $(X,d)$ uno spazio metrico e sia $x_n$ una successione convergente in $X$ . Allora $x_n$ è limitata.

$\quad$

Dimostrazione. Sia $x= \lim_{n \to \infty} x_n$ . Per definizione di limite, esiste $N \in \mathbb{N}$ tale che

(207) $\begin{equation*} x_n \in B_1(x) \qquad \forall n \geq N. \end{equation*}$

Definiamo ora

(208) $\begin{equation*} r = \max \{d(x,x_n) \mid n = 1, \dots, N \}, \quad R = \max \{1, r \}. \end{equation*}$

Per (207) si ha

(209) $\begin{equation*} x_n \in B_R(x) \qquad \forall n \in \mathbb{N}. \end{equation*}$

Osservazione 4.31. La proposizione 3.59, che afferma l’equilimitatezza di una successione uniformemente convergente, può essere quindi vista come una semplice conseguenza delle proposizioni 4.29 e 4.30.

Compattezza di funzioni continue e limitate.

In questa sezione trasportiamo la discussione fatta nella sezione 3.3.3 a proposito del parallelo tra il teorema di Bolzano-Weierstrass e l’estrazione di una sottosuccessione convergente da una successione di funzioni $f_n$ nel contesto generale degli spazi metrici. L’esercizio 3.61 mostra che una successione $f_n$ in $C_b([a,b],\mathbb{R})$ limitata può non avere estratte puntualmente convergenti (e quindi uniformemente). La proprietà di poter sempre estrarre una sottosuccessione convergente in uno spazio metrico è importante al punto da meritare una definizione.

Definizione 4.32 (Relativa compattezza). Sia $(X,d)$ uno spazio metrico e sia $Y \subseteq X$ . Si dice che $Y$ è relativamente compatto se, per ogni successione $f_n$ di elementi di $Y$ , esiste una sua sottosuccessione convergente in $X$ .

$\quad$

Osservazione 4.33. Il teorema di Bolzano-Weiestrass si può quindi riformulare dicendo che una successione $x_n$ in $\mathbb{R}$ limitata è relativamente compatta.

Una estensione del teorema di Bolzano-Weiestrass è il seguente risultato, la cui dimostrazione è lasciata per esercizio.

Teorema 4.34 (Heine-Borel). Sia $d \in \mathbb{N}$ con $d \geq 1$ . Per un sottoinsieme $E \subset \mathbb{R}^d$ sono equivalenti le seguenti condizioni:

$\quad$

$E$ è limitato;

$E$ è relativamente compatto.

Esercizio 4.35 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Dimostrare il teorema di Heine-Borel. Hint: usare il teorema di Bolzano-Weierstrass e la proposizione 4.30.

$\quad$

Osservazione 4.36. Il teorema di Bolzano-Weierstrass corrisponde all’implicazione $i) \Rightarrow ii)$ nel caso in cui $X= \mathbb{R}$ e $E$ è costituito da una successione.

L’esercizio 3.61 mostra quindi che un analogo del teorema di Heine-Borel non è valido per qualunque spazio metrico, in particolare se $(X,d)=\big(C_b([a,b],\mathbb{R}),d_\infty \big)$ . In altre parole, non tutte le successioni limitate in $\big(C_b([a,b],\mathbb{R}),d_\infty \big)$ possiedono estratte convergenti. Abbiamo però visto col teorema 3.65 che, aggiungendo alla limitatezza l’ipotesi di equicontinuità, si ottiene l’esistenza di estratte convergenti. Possiamo quindi riformulare il teorema di Ascoli-Arzelà nella seguente forma.

Teorema 4.37 (Ascoli-Arzelà). Sia $\mathcal{F} \subset C_b([a,b],\mathbb{R})$ . Allora le seguenti condizioni sono equivalenti:

$\quad$

$\mathcal{F}$ è limitato in $\big(C_b([a,b],\mathbb{R}),d_\infty \big)$ e equicontinuo;

$\mathcal{F}$ è relativamente compatto in $\big(C_b([a,b],\mathbb{R}),d_\infty \big)$ .

$\quad$

Esercizi

Svolgimento esercizio 2.5.

Per ogni $x \in E$ si ha

(210) $\begin{equation*} \lim_{n \to \infty} f_n(x) = \lim_{n \to \infty} \alpha_n g(x) = 0. \end{equation*}$

Svolgimento esercizio 3.5.

Si consideri la funzione $g \colon (0,1) \to \mathbb{R}$ definita da $g(x) = \dfrac{1}{x}$ . Allora si ha

(211) $\begin{equation*} f_n(x) = \frac{\alpha_n}{x} \qquad \forall n \in \mathbb{N},\,\, \forall x \in (0,1). \end{equation*}$

Poiché il limite puntuale delle $f_n$ è la funzione $f$ identicamente nulla (come mostrato nell’esercizio 2.5), otteniamo

(212) $\begin{equation*} \sup_{x \in (0,1)} |f_n(x) - f(x)| = \sup_{x \in (0,1)} |f_n(x)| + \infty, \end{equation*}$

per cui la convergenza non è uniforme.

Svolgimento esercizio 3.6.

Poiché $g$ è limitata, esiste $M>0$ tale che

(213) $\begin{equation*} \sup_{x \in E} |g(x)| \leq M. \end{equation*}$

Per ogni $n \in \mathbb{N}$ si ha quindi

(214) $\begin{equation*} \sup_{x \in E} |f_n(x)| = \alpha_n \sup_{x \in E} |g(x)| \leq \alpha_n M \xrightarrow[n \to \infty]{} 0. \end{equation*}$

Ciò dimostra la convergenza uniforme delle $f_n$ alla funzione $f$ identicamente nulla.

Svolgimento esercizio 3.12.

Per ogni $x \in \mathbb{R}$ si ha

$\lim_{n\to+\infty} \arctan(x-n) = -\frac{\pi}{2}.$

Ciò dimostra la convergenza puntuale alla funzione $f$ . Per quanto riguarda la convergenza uniforme, osserviamo che

(215) $\begin{equation*} \sup_{x \in \mathbb{R}}|f_n(x)- f(x)| \geq |f_n(n)- f(n)| = \arctan 0 + \frac{\pi}{2} = \frac{\pi}{2}. \end{equation*}$

Ciò vuol dire che $\sup_{x \in \mathbb{R}}|f_n(x)- f(x)|$ non converge a $0$ per $n \to \infty$ , quindi la proposizione 3.7 implica che la convergenza non è uniforme. In virtù della proposizione 3.10, la successione $f_n$ non converge uniformemente a nessuna funzione.

Per quanto riguarda l’ultima asserzione, essa si può dimostrare osservando che per ogni $n \in \mathbb{N}$ la funzione $f_n$ è crescente, per cui, se $R \in \mathbb{R}$ , si ha

(216) $\begin{equation*} \sup_{x \in (-\infty,R]}|f_n(x)- f(x)| = f_n(R) + \frac{\pi}{2} \xrightarrow[n \to \infty]{} 0, \end{equation*}$

dove l’ultimo limite vale per la convergenza puntuale delle $f_n$ a $f$ . Di nuovo per la proposizione 3.7, si ha che $f_n$ converge uniformemente a $f$ su $(-\infty,R]$ .

Svolgimento esercizio 3.27.

Per ogni $x \in [0,1]$ si ha

(217) $\begin{equation*} \lim_{n \to \infty} f_n(x) = \lim_{n \to \infty} \frac{x^2}{x^2 + 1 - 2nx + n^2x^2} = 0, \end{equation*}$

quindi $f_n$ converge puntualmente alla funzione $f \equiv 0$ . Si consideri la successione $x_n=\frac{1}{n}$ . Si ha

(218) $\begin{equation*} \lim_{n\to+\infty} f_n \left(\frac{1}{n} \right) = \lim_{n\to+\infty} 1 = 1 \neq 0 = f(0). \end{equation*}$

Per il teorema 3.23, la convergenza non è uniforme.

Svolgimento esercizio 3.32.

Sia $f_n \colon [0,+\infty) \to \mathbb{R}$ la successione di funzioni definita da

(219) $\begin{equation*} f_n(x) = \sum_{k=1}^{2n}(-1)^k 2^{-k+1}\chi_{[2^{k-1},2^k)}(x), \end{equation*}$

dove, se $E \subseteq \mathbb{R}$ , $\chi_{E}$ denota la funzione caratteristica dell’insieme $E$ , cioè

(220) $\begin{equation*} \chi_E(x) = \begin{cases} 1 & \text{se $x \in E$,}\\ 0 & \text{se $x \notin E$.} \end{cases} \end{equation*}$

$\quad$

Figura 6: la funzione $f_2$ definita in (219).

$\quad$

Per come è definita, la funzione $f_n$ è integrabile e si ha

(221) $\begin{equation*} \begin{split} \int_0^{+\infty} f_n(x) \mathrm{d}x = \sum_{k=1}^{2n}(-1)^k 2^{-k+1}\cdot 2^{k-1} = \sum_{k=1}^{2n}(-1)^k = \, 0 \qquad \forall n \in \mathbb{N}. \end{split} \end{equation*}$

Mostriamo che la successione delle $f_n$ converge uniformemente alla funzione $f \colon [0,+\infty) \to \mathbb{R}$ definita da

(222) $\begin{equation*} f(x) = \sum_{k=1}^{+\infty}(-1)^k 2^{-k+1}\chi_{[2^{k-1},2^k)}(x) \end{equation*}$

(notare che per ogni $x \geq 1$ vi è un solo $k \in \mathbb{N}$ per cui $\chi_{[2^{k-1},2^k)}(x) \neq 0$ , quindi la convergenza della serie è assicurata). Infatti si ha

(223) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in [0,+\infty)} |f_n(x) - f(x)| = & \lim_{n \to +\infty} \sup_{x\in [2^{2n},+\infty)} |f(x)| \\ = & \lim_{n \to +\infty} 2^{-2n} \\ = & \, 0. \end{split} \end{equation*}$

Tuttavia per ogni $N \in \mathbb{N}$ si ha

(224) $\begin{equation*} \begin{gathered} \int_0^{2^{2N}} f(x) \,\mathrm{d}x = \sum_{k=1}^{2N}(-1)^k 2^{-k+1}2^{k-1} = 0, \\ \int_0^{2^{2N + 1}} f(x)\, \mathrm{d}x = \sum_{k=1}^{2N+1}(-1)^k 2^{-k+1}2^{k-1} = -1. \end{gathered} \end{equation*}$

Ciò prova che $\lim_{R \to +\infty} \int_0^R f(x)\, \mathrm{d}x$ non esiste e quindi $f$ non risulta integrabile in senso improprio.

Svolgimento esercizio 3.33.

Sia $f_n \colon [0,+\infty) \to \mathbb{R}$ la successione di funzioni definita da

(225) $\begin{equation*} f_n(x) = \begin{cases} \frac{1}{n} & \text{se $0 \leq x < n$,}\\ 0 & \text{se $x>n$.} \end{cases} \end{equation*}$

Essa converge uniformemente alla funzione $f$ identicamente nulla, infatti

(226) $\begin{equation*} \lim_{n \to \infty} \Big( \sup_{x \in [0,+\infty)} |f_n(x) - f| \Big) = \lim_{n \to \infty} \frac{1}{n} = 0. \end{equation*}$

D’altra parte,

$\int_{0}^{\infty} f_n(x) \mathrm{d}x = n \cdot \frac{1}{n} = 1, \qquad \int_{0}^{\infty} f(x)\,\mathrm{d}x = 0,$

e quindi non si verifica la convergenza degli integrali.

Svolgimento esercizio 3.38.

Siccome $g$ è il limite uniforme di una successione di funzioni continue, è continua per il teorema 3.19 e quindi integrabile. Risulta allora ben definita la funzione $f \colon [a,b] \to \mathbb{R}$ tale che

(227) $\begin{equation*} f(x) := y_0 + \int_{x_0}^{x} g(t) \mathrm{d}t, \qquad \forall x \in [a,b]. \end{equation*}$

Per il teorema fondamentale del calcolo $f$ è derivabile in $[a,b]$ e vale

(228) $\begin{equation*} f'(x) = g(x) \qquad \forall x \in [a,b]. \end{equation*}$

Occorre pertanto mostrare solo la convergenza uniforme delle $f_n$ a $f$ . A tal fine, si consideri $\varepsilon>0$ ; poiché $f_n'$ converge uniformemente a $g$ e $f_n(x_0) \to y_0$ esiste $N \in \mathbb{N}$ tale che

(229) $\begin{equation*} \begin{gathered} |f'_n(x) - g(x)|< \varepsilon \qquad \forall n \geq N, \,\, \forall x \in [a,b]; \\ |f_n(x_0)- y_0| < \varepsilon \qquad \forall n \geq N. \end{gathered} \end{equation*}$

Si fissi un tale $n \in \mathbb{N}$ ; per la disuguaglianza triangolare e per ogni $x \in [a,b]$ , si ha

(230) $\begin{equation*} \begin{split} |f_n(x) - f(x)| \leq & |f_n(x_0)-y_0| + \int_{x_0}^{x} |f_n'(t) - g'(t)|\mathrm{d}t \\ \leq & \varepsilon + \varepsilon \int_{x_0}^{x} \mathrm{d}t \\ \leq & (1+ b-a) \varepsilon. \end{split} \end{equation*}$

Ciò mostra la convergenza uniforme delle $f_n$ a $f$ .

Svolgimento esercizio 3.61.

$\quad$

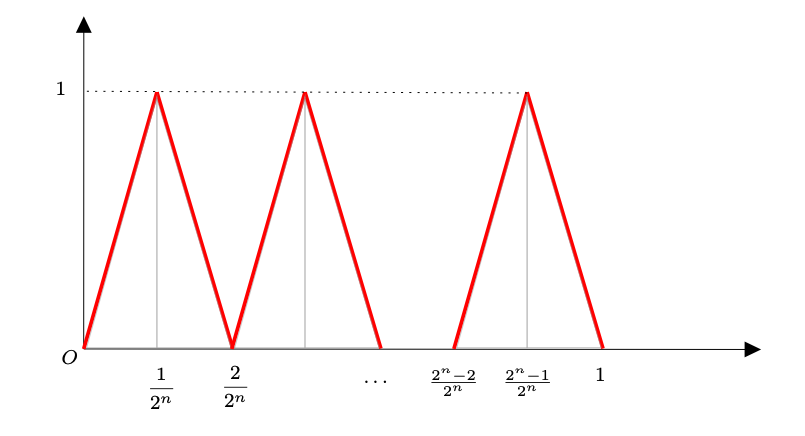
Figura 7: la funzione $f_n$ dell’esercizio 3.61.

$\quad$

La generica funzione $f_n$ è rappresentata nella figura 7. Per dimostrare che essa non possiede sottosuccessioni convergenti puntualmente, consideriamo una sua qualunque sottosuccessione $f_{n_k}$ ; vogliamo estrarre da essa una opportua ulteriore sottosuccessione $f_{n_{k_j}}$ e trovare un punto $x \in [0,1]$ tale che il limite $\lim_j f_{n_{k_j}}(x)$ non esista. Il punto $x$ sarà ottenuto come limite di una successione $x_j$ : informalmente, l’idea è di scegliere $x_j$ ricorsivamente tale che

(231) $\begin{equation*} f_{n_{k_j}}(x_j)=(-1)^j \qquad \forall j \in \mathbb{N}, \end{equation*}$

in modo che $f_{n_{k_j}}(x)$ sia vicino al valore $(-1)^j$ per ogni $j \in \mathbb{N}$ . Ciò dimostrerà che la successione $f_{n_k}(x)$ non è convergente.

Per semplicità di notazione, si illustrerà l’argomento per la sottosuccessione $n_k=k$ , ma sarà chiaro che esso può essere ripetuto per qualunque sottosuccessione $f_{n_k}$ , in quanto ogni passaggio della costruzione ricorsiva dipenderà solo dalla possibilità di scegliere $n_{k_{j+1}}$ sufficientemente grande rispetto a $n_{k_j}$ .

Un’osservazione semplice, ma fondamentale, è la seguente: se $f_n(y)=0$ oppure $f_n(y)=1$ , allora $f_m(y)=0$ per ogni $m > n$ . Ciò segue chiaramente dalla definizione delle $f_n$ .

Si definisce ${k_1}= {1}$ , ${k_2}= {2}$ e

(232) $\begin{equation*} x_1=x_2= \frac{1}{2} \quad \Longrightarrow \quad f_{k_1}(x_1)=1, \,\,\, f_{{k_2}}(x_2)=0, \end{equation*}$

dove l’ultima uguaglianza segue dall’osservazione fondamentale.

Una volta definito ${k_{2j}}$ , si sceglie ${k_{2j+1}}$ tale che

(233) $\begin{equation*} \frac{1}{2^{{k_{2j+1}} }} < \frac{1}{2^{2{k_{2j}+1}}} \end{equation*}$

e $k_{2j+2}=k_{2j+1}+1$ Si pone

(234) $\begin{gather*} x_{k_{2j+1}} = x_{k_{2j+2}} = x_{k_{2j}} + \frac{1}{2^{{k_{2j+1}} }}. \end{gather*}$

Poiché per l’osservazione fatta all’inizio si ha $f_{k_{2j+1}}(x_{2j})=0$ , otteniamo

(235) $\begin{equation*} f_{k_{2j+1}} ( x_{k_{2j+1}}) = 1, \qquad f_{k_{2j+2}} ( x_{k_{2j+2}}) = 0. \end{equation*}$

La successione $x_j$ risulta di Cauchy; infatti, se $J \in \mathbb{N}$ , si ha

(236) $\begin{equation*} |x_j - x_J| \leq \sum_{\ell = 2k_{J}+1}^\infty \frac{1}{2^\ell} = \frac{1}{2^{2k_J}} \qquad \forall j \geq J. \end{equation*}$

Quindi esiste $x \in [0,1]$ tale che $x_j \to x$ ; (236) implica anche che

(237) $\begin{equation*} |x - x_j| \leq \frac{1}{2^{2k_j}}, \qquad \forall j \in \mathbb{N}. \end{equation*}$

Poiché per ogni $k \in \mathbb{N}$ $f_k$ soddisfa

(238) $\begin{equation*} |f_k(y) - f_k(z)| \leq 2^k|y-z| \qquad \forall y,z \in [0,1], \end{equation*}$

otteniamo

(239) $\begin{equation*} |f_{k_j}(x) - f_{k_j}(x_j)| \leq 2^{k_j}|x-x_j| \leq \frac{1}{2^{k_j}}, \qquad \forall j \in \mathbb{N}. \end{equation*}$

dove per l’ultima disuguaglianza abbiamo usato (237). Otteniamo quindi

(240) $\begin{equation*} \begin{gathered} 0 \leq f_{k_{2j}}(x) \leq f_{k_{2j}}(x_{2j}) + \frac{1}{2^{k_j}} = \frac{1}{2^{k_j}}, \qquad \forall j \in \mathbb{N}, \\ 1 \geq f_{k_{2j+1}}(x) \geq f_{k_{2j+1}}(x_{2j+1}) - \frac{1}{2^{k_j}} = 1 - \frac{1}{2^{k_j}}, \qquad \forall j \in \mathbb{N}. \end{gathered} \end{equation*}$

Tali relazioni dimostrano quindi che la successione $\big(f_{k_j}(x)\big)_j$ non è convergente, poiché possiede due estratte convergenti a limiti diversi ( $1$ e $0$ ).

Appendice A: Misura di unioni finite di intervalli

Leggi...

Prima di presentare i risultati delle prossime appendici, definiamo l’utile concetto di misura di un insieme costituito dall’unione finita di intervalli e ne enunciamo qualche proprietà. Tale idea è un caso particolare della cosiddetta misura di Peano-Jordan di un insieme, che permette appunto di assegnare a un insieme un numero reale non negativo che, in un certo senso, corrisponde alla sua idea intuitiva di estensione.

In alcune dimostrazioni dei risultati che seguono (in particolare nella costruzione dell’esempio B.2 e nella dimostrazione del teorema 2.16) abbiamo bisogno di tale concetto di misura di un insieme.

Non tratteremo però il concetto di misura nella sua generalità poiché esso esula dagli scopi di questa dispensa (rimandando il lettore a testi specifici sull’argomento) e preferiamo restringerci al caso particolare di insiemi costituiti da una unione finita di intervalli, sostanzialmente per due ragioni:

$\quad$

Essi costituiscono una cosiddetta algebra: complementari, unioni e intersezioni finite di insiemi costituiti da unioni finite di intervalli sono ancora costituiti da unioni finite di intervalli. Quindi, anche trattando solo questo caso particolare, siamo in grado di “misurare” complementari, unioni e intersezioni finite di insiemi.

Tale famiglia di insiemi è sufficiente a concludere le dimostrazioni dei risultati di cui abbiamo bisogno.

Definizione A.1. Sia $E \subset \mathbb{R}$ un insieme costituito dall’unione finita di intervalli disgiunti (aperti o chiusi) limitati, cioè tale che $E = \bigcup_{k=1}^N J_k$ , con $N \in \mathbb{N}$ e $J_k = [(a_k,b_k)]$ (con tale simbolo indichiamo che l’intervallo $J_k$ può essere aperto o chiuso a sinistra e a destra); definiamo la misura $|E|$ di $E$ come

(241) $\begin{equation*} |E| = \sum_{k=1}^N (b_k - a_k). \end{equation*}$

$\quad$

Si può verificare che tale definizione non dipende dalla decomposizione di $E$ in intervalli disgiunti scelta. Inoltre la misura appena definita soddisfa alcune semplici proprietà, riportate nel seguente risultato.

Lemma A.2. Siano $E, F, A, B \subset \mathbb{R}$ costituiti dall’unione finita di intervalli disgiunti e limitati. Valgono le seguenti proprietà:

Se $E=(a,b)$ , allora $|E|=b-a$ ;

Se $E \subseteq F$ , allora $|E| \leq |F|$ ;

Se $E= A \cup B$ e $A \cap B = \emptyset$ , allora $|E| = |A| + |B|$ .

$\quad$

Dimostrazione.

È una conseguenza immediata della definizione A.1;

Sia $E = \bigcup_{i=1}^L I_i$ e $F= \bigcup_{j=1}^M J_j$ e supponiamo $E \subseteq F$ . Allora
(242) $\begin{equation*} |F| = \sum_{j=1}^M |J_j| \geq \sum_{j=1}^M \left( \sum_{i \colon I_i \subseteq J_j}|I_i|\right) = |E|, \end{equation*}$

dove la disuguaglianza deriva dal fatto che gli intervalli $I_i$ sono disgiunti e l’ultima uguaglianza dal fatto che $E \subseteq F$ .

Se $A \cap B = \emptyset$ e $E= A \cup B$ , allora si può trovare una decomposizione di $E$ in un numero finito di intervalli $\{I_i\}_{i=1}^L$ e un numero $0 \leq M \leq L$ tali che
(243) $\begin{equation*} E = \bigcup_{i=1}^L I_i, \qquad A= \bigcup_{i=1}^M I_i, \qquad B= \bigcup_{i=M+1}^L I_i \end{equation*}$

(basta scegliere tre decomposizioni di $A,B,E$ e definire gli $I_i$ come le intersezioni possibili degli intervalli che le compongono, e poi eventualmente riordinarli). Da ciò si ottiene

(244) $\begin{equation*} |A| + |B| = \sum_{i=1}^M |I_i| + \sum_{i=M+1}^L |I_i| = \sum_{i=1}^L |I_i| = |E|. \end{equation*}$

Appendice B: Una funzione non integrabile

Leggi...

In questa appendice esibiamo l’esempio B.2, che mostra come una successione di funzioni continue $f_n \colon [0,1] \to \mathbb{R}$ (e quindi integrabili secondo Riemann) possa convergere puntualmente a una funzione $f$ non integrabile.

Premettiamo alla costruzione il prossimo utile lemma, che afferma che l’intersezione di una famiglia decrescente di chiusi e limitati non vuoti è non vuota.

Lemma B.1. Sia $\{K_n \}_{n \in \mathbb{N}}$ una successione di insiemi tali che $K_n$ è non vuoto, chiuso, limitato e $K_{n+1} \subset K_n$ per ogni $n \in \mathbb{N}$ . Allora si ha

(245) $\begin{equation*} \bigcap_{k = 1}^{\infty}K_n \neq \emptyset. \end{equation*}$

$\quad$

Dimostrazione. Chiamiamo $K= \bigcap_{k = 1}^{\infty}K_n$ . Per ogni $n \in \mathbb{N}$ scegliamo $x_n \in K_n$ ; poiché $K_1$ è chiuso e limitato e per ogni $n$ si ha $K_n \subseteq E_1$ , per il teorema di Bolzano-Weierstrass possiamo assumere che $x_n$ (a meno di passare a una sottosuccessione) converga a $x \in K_1$ . Poiché per ogni $n \in \mathbb{N}$ si ha

(246) $\begin{equation*} x_{n+k} \in K_n \qquad \forall k \in \mathbb{N} \end{equation*}$

e poiché $K_n$ è chiuso, otteniamo

(247) $\begin{equation*} x \in K_n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Ciò dimostra che $x \in K$ , che risulta quindi non vuoto.

Possiamo quindi esibire una successione di funzioni continue che converge puntualmente a una funzione non integrabile secondo Riemann.

Esempio B.2 (limite puntuale di funzioni continue non integrabile). La costruzione è suddivisa in vari step.

$\quad$

Costruzione della successione $f_n$ e dell’insieme $C$ .
Consideriamo la successione di funzioni $f_n \colon [0,1] \to \mathbb{R}$ definita, per $n \geq 1$ , da

(248) $\begin{equation*} f_n(x) = \max \Big\{ 0, 1- (8^{n+1}) \operatorname{dist}(x, E_n) \Big\}, \end{equation*}$

dove $E_n$ è definito ricorsivamente:

(249) $\begin{equation*} \begin{gathered} E_0 = [0,1], \\ E_1 = E_0 \setminus \left(\frac{1}{2}-\frac{1}{8}, \frac{1}{2}+\frac{1}{8} \right), \\ E_2 = E_1 \setminus \Bigg( \bigg( \frac{\dfrac{1}{2}-\dfrac{1}{8}}{2} - \frac{1}{8^2}, \frac{\dfrac{1}{2}-\dfrac{1}{8}}{2} + \frac{1}{8^2} \bigg) \cup \bigg( \frac{\dfrac{1}{2}+\dfrac{1}{8}}{2} - \frac{1}{8^2}, \frac{\dfrac{1}{2}+\dfrac{1}{8}}{2} + \frac{1}{8^2} \bigg) \Bigg); \\ \vdots \end{gathered} \end{equation*}$

In altre parole, $E_{n+1}$ è ottenuto sottraendo da ognuno degli intervalli costituenti $E_n$ un intervallo aperto centrale di ampiezza pari a $2\cdot 8^{-n}$ . Per un certo $n$ fissato, fa funzione $f_n$ vale $1$ su $E_n$ e decresce linearmente al valore $0$ , assunto nei punti aventi distanza da $E_n$ maggiore o uguale a $8^{-n-1}$ . In particolare, poiché la funzione distanza da un insieme è continua (è 1-Lipschitziana) e il massimo tra due funzioni continue è continuo, ogni funzione $f_n$ è continua, quindi integrabile.

Si vede che per ogni $x \in [0,1]$ , la successione $(f_n(x))_n$ è decrescente e ciò implica che esiste il limite $f(x)$ , che è per definizione il limite puntuale della successione $f_n$ calcolato nel punto $x$ .

Definiamo l’insieme $C$ come l’intersezione di tutti gli $E_n$ :

(250) $\begin{equation*} C = \bigcap_{n=1}^{+\infty} E_n. \end{equation*}$

$C$ è non vuoto
Per come è definito, si ha $C= \bigcap_{n=1}^\infty E_n$ , dove $\{E_n\}_{n \in \mathbb{N}}$ è una successione decrescente di chiusi e limitati non vuoti. Applicando il lemma B.1 con $K_n=E_n$ , si ottiene $C \neq \emptyset$ .

$f$ è la funzione caratteristica di $C$
Affermiamo che $f \colon [0,1] \to \mathbb{R}$ è la funzione caratteristica dell’insieme $C$ :

(251) $\begin{equation*} f(x) = \chi_C(x) = \begin{cases} 1 & \text{se } x \in C, \\ 0& \text{se } x \notin C. \end{cases} \end{equation*}$

Infatti, chiaramente $f(x)=1$ per ogni $x \in C$ , visto che $f_n(x)=1$ per ogni $x \in E_n$ e $C \subset E_n$ per ogni $n \in \mathbb{N}$ .

D’altra parte, se $x \in [0,1] \setminus C$ , allora esiste $N \in \mathbb{N}$ tale che $x \notin E_N$ . Dato che $E_N$ è compatto, esiste $\delta>0$ tale che

(252) $\begin{equation*} \operatorname{dist}(x,E_N) > \delta. \end{equation*}$

Inoltre, poiché per ogni $n \in \mathbb{N}$ vale $E_{n+1} \subset E_n$ , si ha

(253) $\begin{equation*} \operatorname{dist}(x,E_{n+1}) \geq \operatorname{dist}(x,E_{n}) > \delta \qquad \forall n \geq N. \end{equation*}$

Per ogni $n \geq N$ tale che $8^{-n-1} < \delta$ , per definizione delle $f_n$ si ha allora $f_n(x)=0$ ; poiché la successione $f_n(x)$ è definitivamente nulla, si ha $f(x)=0$ .

$f$ non è integrabile secondo Riemann.
Affermiamo ora che la funzione $f = \chi_C$ non è integrabile secondo Riemann. Poiché l’insieme $C$ non contiene nessun intervallo (provarlo per esercizio), per ogni suddivisione $P$ dell’intervallo $[0,1]$ la somma inferiore $s(f,P)$ di $f$ su $P$ è nulla.

Per quanto riguarda le somme superiori, vogliamo dimostrare che per ogni suddivisione $P$ di $[0,1]$ , si ha $S(f,P) \geq \frac{1}{2}$ , che proverebbe appunto la non integrabilità di $f$ .

Si consideri quindi una suddivisione $P$ dell’intervallo $[0,1]$ definita da

(254) $\begin{equation*} P = \{ I_i:= [x_{i-1}, x_i] \mid i=1, \dots, k \} \qquad \text{con} \qquad 0=x_0 < x_1 < \dots < x_k = 1. \end{equation*}$

Scegliamo un $\varepsilon>0$ e chiamiamo, per ogni $i=1, \dots, k$ ,

(255) $\begin{equation*} J_i = \Big(x_{i-1} - \frac{\varepsilon}{2k} , x_i + \frac{\varepsilon}{2k}\Big). \end{equation*}$

Gli intervalli aperti $J_i$ sono degli “allargamenti” degli $I_i$ in modo che la lunghezza totale aggiunta sia pari a $\varepsilon$ .

Abbiamo quindi la seguente stima per la somma superiore $S(f,P)$ di $f$ relativa a $P$ :

(256) $\begin{equation*} \begin{split} S(f,P) = & \sum_{i \mid I_i \cap C \neq \emptyset} (x_i - x_{i-1}) \\ \geq & - \varepsilon + \sum_{i \mid I_i \cap C \neq \emptyset} \Big(x_i + \frac{\varepsilon}{2k} - x_{i-1} + \frac{\varepsilon}{2k} \Big) \\ = & - \varepsilon + \sum_{i \mid I_i \cap C \neq \emptyset} |J_i|, \end{split} \end{equation*}$

dove con $|J_i|$ si indica la misura dell’intervallo $J_i$ che, come nella definizione A.1, è pari alla differenza tra i suoi estremi: $|(a,b)|= b-a$ . Definendo l’insieme

(257) $\begin{equation*} U= \bigcup_{i \mid I_i \cap C \neq \emptyset} J_i, \end{equation*}$

si ha

(258) $\begin{equation*} \operatorname{dist}(C, U^c) \geq \frac{\varepsilon}{2k}, \end{equation*}$

(dove $\operatorname{dist}(C, U^c)$ è la distanza tra i due insiemi $C,U^c$ , definita nella sezione Notazioni) poiché l’insieme $\bigcup_{i \mid I_i \cap C \neq \emptyset} I_i$ ricopre $C$ . Ma allora, poiché $\operatorname{dist}(C, E_n^c) \leq 8^{-n-1}$ , si ha

(259) $\begin{equation*} E_n \subset U \qquad \text{per ogni } n \in \mathbb{N} \text{ tale che } \frac{1}{8^{n+1}} < \frac{\varepsilon}{2k}. \end{equation*}$

Poiché per ogni $n \in \mathbb{N}$ $E_n$ è costituito da un’unione finita di intervalli chiusi la cui somma delle lunghezze è pari a (verificarlo per esercizio)

(260) $\begin{equation*} |E_n| = 1 - \sum_{h=1}^n \frac{1}{4^h} > \frac{1}{2} \end{equation*}$

(dove $|E_n|$ qui indica la somma delle lunghezze degli intervalli che costituiscono l’insieme $E_n$ , cioè la misura di $E_n$ data dalla definizione A.1), da (259) si ottiene

(261) $\begin{equation*} |U| = \sum_{i \mid I_i \cap C \neq \emptyset} |J_i| \geq \frac{1}{2}. \end{equation*}$

Unendo (256) e (261), si ottiene.

(262) $\begin{equation*} S(f,P) \geq \frac{1}{2} - \varepsilon. \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ , si ottiene

(263) $\begin{equation*} S(f,P) \geq \frac{1}{2}, \end{equation*}$

che appunto implica la non integrabilità di $f$ secondo Riemann.

Osservazione B.3. La parte della costruzione in cui si mostra che $C \neq \emptyset$ non è strettamente necessaria. Infatti, successivamente viene provato che la funzione caratteristica di $C$ non è integrabile, e ciò in particolare implica che $C$ non è vuoto, altrimenti si avrebbe $\chi_C \equiv 0$ che è addirittura continua. Abbiamo però inserito la dimostrazione diretta di quel punto in quanto la riteniamo istruttiva e applicabile anche in altri contesti.

Osservazione B.4. L’insieme $C$ definito nel precedente esempio è un cosiddetto fat Cantor set, in quanto la sua costruzione è modellata sulla base del famoso insieme di Cantor. L’aggettivo fat è dovuto al fatto che, differentemente dal classico insieme di Cantor, l’insieme $C$ costruito sopra ha misura di Lebesgue positiva. In termini euristici, ciò può essere spiegato notando che, come si può intuire dalla dimostrazione di sopra, un qualsiasi insieme aperto che ricopra $C$ ha una somma delle lunghezze dei suoi intervalli maggiore o uguale a $\dfrac{1}{2}$ .

Chiaramente tali nozioni non possono essere discusse in dettaglio in quanto esulano dagli scopi della presente dispensa.

Appendice C: il teorema di convergenza dominata di Arzelà

Introduzione.

In questa sezione dimostriamo il teorema 2.16. A tal fine, premettiamo due utili lemmi: il primo è un risultato di topologia della retta reale, mentre il secondo è un risultato nello spirito della cosiddetta Teoria della Misura, che viene però dimostrato con metodi elementari e utilizzando soltato gli strumenti sviluppati nell’appendice A.

Risultati preliminari.

Cominciamo con la definizione di insieme aperto

Definizione C.1 (insieme aperto). Un insieme $U \subseteq \mathbb{R}$ si dice aperto se esso è costituito dall’unione di una famiglia di intervalli aperti.

$\quad$

Osservazione C.2. Si può facilmente verificare che la definizione C.1 è equivalente alla seguente: un insieme $U \subseteq \mathbb{R}$ si dice aperto se per ogni $x \in U$ , esiste un intervallo aperto $(a,b) \subseteq U$ tale che $x \in (a,b)$ .

Il primo risultato che presentiamo consiste nell’ottenere una scrittura di ogni insieme aperto come unione di una famiglia al più numerabile (cioè finita o in corrispondenza biunivoca con i numeri naturali) di intervalli aperti disgiunti.

Lemma C.3. Sia $U \subset \mathbb{R}$ un insieme aperto. Allora esiste una famiglia $\mathcal{G}$ al più numerabile di intervalli aperti $(a_k, b_k)_{k =1}^N$ (dove $N \in \mathbb{N}$ oppure $N= +\infty$ ) disgiunti e contenuti in $U$ tali che

(264) $\begin{equation*} U = \bigcup_{k=1}^{N}(a_k,b_k). \end{equation*}$

$\quad$

Osservazione C.4. È importante notare che la parte interessante del lemma C.3 consiste nell’aggettivo disgiunti. Infatti, è facile dimostrare che un qualsiasi intervallo aperto $(a,b)$ è unione al più numerabile di intervalli aperti con estremi razionali. Poiché tali intervalli costituiscono un insieme numerabile (in quanto tali sono i numeri razionali), l’enunciato seguirebbe facilmente.

Come ulteriore osservazione sul lemma, si noti che esso è falso in $\mathbb{R}^n$ per $n \geq 2$ : un insieme costituito dall’unione di palle aperte non può in generale essere scritto come unione al più numerabile di palle disgiunte. Il lettore può cercare degli esempi per esercizio.

Dimostrazione del lemma C.3. L’idea della dimostrazione consiste nel considerare una famiglia $\mathcal{F}$ di intervalli la cui unione dà $U$ e nell’unire tutti gli intervalli che sono collegati con altri intervalli in $\mathcal{F}$ in modo da formare degli intervalli più grandi che risultino disgiunti e in quantità numerabile.

$\quad$

Costruzione della famiglia $\mathcal{G}$
Sia $\mathcal{F}$ un insieme qualsiasi i cui elementi siano intervalli tali che

(265) $\begin{equation*} U = \bigcup_{I \in \mathcal{F}} I. \end{equation*}$

Dati $I,J \in \mathcal{F}$ , diciamo che $I$ e $J$ sono collegati se, esistono un numero finito di intervalli $I_1, \dots, I_M \in \mathcal{F}$ tali che

(266) $\begin{equation*} I_{i-1} \cap I_{i} \neq \emptyset \qquad \forall i=1, \dots, M+1, \end{equation*}$

dove abbiamo posto $I_0=I$ e $I_{M+1}=J$ . Gli intervalli $I_1, \dots, I_M$ sono detti una serie di collegamento di $I$ e $J$ . In altre parole, $I$ e $J$ sono collegati se esiste una successione finita di elementi di $\mathcal{F}$ a due a due non disgiunti che porti da $I$ a $J$ .

Si vede facilmente che ogni intervallo $I \in \mathcal{F}$ è collegato a sé stesso, che se $I$ e $J$ sono collegati e $J$ e $H$ sono collegati, allora $I$ e $H$ sono collegati. Ciò mostra che la proprietà di essere collegati è una cosiddetta relazione di equivalenza.

Sia $I \in \mathcal{F}$ e consideriamo l’insieme $V_I$ definito da

(267) $\begin{equation*} V_I \coloneqq \bigcup_{J \text{ collegato a } I} J. \end{equation*}$

Dati $I, J \in \mathcal{F}$ , dalle proprietà della relazione di essere collegati, si ha subito che $V_I = V_J$ se e solo se $I$ e $J$ sono collegati.

Consideriamo quindi la famiglia $\mathcal{G}$ costituita dagli insiemi $V_I$ al variare di $I \in \mathcal{F}$ , cioè

(268) $\begin{equation*} \mathcal{G} \coloneqq \{V_I \colon I \in \mathcal{F} \}. \end{equation*}$

$\bigcup_{V \in \mathcal{G}} V = U$ .
Per come sono definiti gli elementi $V$ di $\mathcal{G}$ (cioè unioni di intervalli contenuti in $U$ ), ovviamente si ha $\bigcup_{V \in \mathcal{G}} V \subseteq U$ .

Per dimostrare l’altra inclusione, consideriamo $x \in U$ . Poiché $U$ è l’unione degli intervalli di $\mathcal{F}$ , esiste $I \in \mathcal{F}$ tale che $x \in I$ . Ma allora $x \in V_I$ , e quindi $x \in \bigcup_{V \in \mathcal{G}} V$ .

Gli elementi $V_I$ di $\mathcal{G}$ sono intervalli aperti
Sia $I \in \mathcal{F}$ e dimostriamo che $V_I$ è un intervallo. Proveremo che, dati $x, y \in V_I$ con $x < y$ , allora $[x,y] \subset V_I$ . Siano $I_x, I_y \in \mathcal{F}$ due intervalli collegati a $I$ che contengono rispettivamente $x$ e $y$ . Poiché appunto entrambi sono collegati a $I$ , $I_x$ e $I_y$ sono collegati tra loro e la loro serie di collegamento $I_1, \dots, I_M$ è costituita tutta da intervalli collegati a $I$ . Quindi la loro unione

(269) $\begin{equation*} W = I_x \cup I_1 \cup \dots, \cup I_M \cup I_y \end{equation*}$

è contenuta in $V_I$ . $W$ è ovviamente un intervallo, in quanto in (269) ogni intervallo ha intersezione non vuota dal precedente e dal successivo. Si ha inoltre $[x,y] \subset W \subset V_I$ . Da ciò segue che $V_I$ è un intervallo.

Per provare che $V_I$ è aperto, siano $a,b$ gli estremi di $V_I$ , con $a < b$ e proviamo che entrambi non appartengono a $V_I$ . Supponiamo infatti per assurdo che $a \in V_I$ . Allora esisterebbe un intervallo aperto $J \in \mathcal{F}$ collegato a $I$ tale che $a \in J$ . Ma poiché $J$ è aperto, esiste $x \in J$ tale che $x < a$ . Ma allora $x \in V_I$ e ciò contraddice l’ipotesi che $a$ sia l’estremo sinistro di $V_I$ .

Per tale motivo, $V_I$ è aperto.

Se $I, J \in \mathcal{F}$ non sono collegati, allora $V_I \cap V_J = \emptyset$
Supponiamo per assurdo che $I$ e $J$ non siano collegati e che esista $x \in V_I \cap V_J$ . Allora esiste $I'$ collegato a $I$ e $J'$ collegato a $J$ tali che

(270) $\begin{equation*} x \in I', \qquad x \in J'. \end{equation*}$

Quindi $I' \cap J' \neq \emptyset$ . Ma poiché due intervalli che si intersecano sono collegati, ciò mostra che anche $I$ e $J$ sono collegati, e ciò è assurdo.

Gli intervalli $V_I \in \mathcal{G}$ sono una quantità al più numerabile
Ogni $V_I$ contiene almeno un numero razionale e, poiché i $V_I$ sono disgiunti, ogni numero razionale appartiene ad al più un $V_I$ per qualche $I \in \mathcal{F}$ . Ciò mostra che gli elementi $V_I$ di $\mathcal{G}$ sono in quantità al più numerabile.

Il prossimo lemma esprime una condizione sufficiente affinché l’intersezione di una famiglia numerabile decrescente $\{U_n\}_{n \in \mathbb{N}}$ di insiemi aperti abbia intersezione non vuota. Ciò in generale non è vero: si pensi all’esempio $U_n = (0,1/n)$ .

Lemma C.5. Sia $\{U_n\}_{n \in \mathbb{N}}$ una famiglia numerabile di insiemi aperti limitati decrescente, cioè tale che, per ogni $n \in \mathbb{N}$ , $U_{n+1} \subseteq U_n$ . Supponiamo inoltre che esista $\varepsilon>0$ tale che, per ogni $n \in \mathbb{N}$ , $U_n$ contenga l’unione $V_n$ di una famiglia finita di intervalli aperti disgiunti $\{ I_i^n\}_{i=1}^{L_n}$ la cui somma delle lunghezze sia maggiore di $\varepsilon$ . Allora si ha

(271) $\begin{equation*} \bigcap_{n = 1}^\infty U_n \neq \emptyset. \end{equation*}$

$\quad$

Dimostrazione. L’idea della dimostrazione consiste nell’esibire una successione $\{K_n\}_{n \in \mathbb{N}}$ di insiemi chiusi e limitati non vuoti, tali che

(272) $\begin{equation*} K_n \subseteq K_{n-1} \quad \text{e} \quad K_n \subset U_n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Poiché l’intersezione di una tale famiglia non è vuota per il lemma B.1 ed è certamente contenuta in $\bigcap_{n \in \mathbb{N}}U_n$ , anche quest’ultima risulta non vuota.

Poiché gli aperti $U_n$ sono limitati e la famiglia è decrescente, a meno di riscalare e traslare, senza perdita di generalità possiamo supporre che

(273) $\begin{equation*} U_n \subset [0,1] \qquad \forall n \in \mathbb{N}. \end{equation*}$

$\quad$

Stime sulle lunghezze degli intervalli costituenti gli $U_n$
Per il lemma C.3, consideriamo per ogni $n \in \mathbb{N}$ la decomposizione di $U_n$ in intervalli aperti disgiunti, cioè

(274) $\begin{equation*} U_n = \bigcup_{k=1}^{N_n} (a_k^n, b_k^n) \qquad \forall n \in \mathbb{N}, \end{equation*}$

dove $N_n \in \mathbb{N}$ oppure $N_n = +\infty$ . Fissiamo ora $n \in \mathbb{N}$ . Poiché gli intervalli $(a_k^n, b_k^n)$ sono a due a due disgiunti, ognuno degli intervalli disgiunti della famiglia $\{ I_i^n\}_{i=1}^{L_n}$ è contenuto in esattamente uno degli $(a_k^n, b_k^n)$ . Questo implica che

(275) $\begin{equation*} 1 \geq S_n \coloneqq \sum_{k=1}^{N_n} |b_k^n - a_k^n| > \varepsilon, \end{equation*}$

dove:

$\quad$

La prima disuguaglianza deriva dal fatto che $U_n \subset [0,1]$ , quindi le somme parziali della serie non eccedono $1$ , poiché per il punto 2 del lemma A.2 ogni somma finita di lunghezze di intervalli disgiunti contenuti in $[0,1]$ non può eccedere il valore $1$ :
(276) $\begin{equation*} \sum_{k=1}^N |b_k^n - a_k^n| = \Big| \bigcup_{k=1}^N (a_k^n, b_k^n) \Big| \leq 1 \qquad \forall N \in \mathbb{N}, \,\, N \leq N_n. \end{equation*}$

Da ciò segue $S_n \leq 1$ .

La seconda disuguaglianza deriva dal fatto che per ogni $n \in \mathbb{N}$ esiste $N \in \mathbb{N}$ tale che
(277) $\begin{equation*} \bigcup_{k=1}^N (a_k^n, b_k^n) \supseteq \bigcup_{i=1}^{L_n} I_i. \end{equation*}$

Poiché $\sum_{i=1}^{L_n} |I_i| > \varepsilon$ , per il punto 2 del lemma A.2 si ottiene

(278) $\begin{equation*} \sum_{k=1}^N (b_k^n - a_k^n) \geq \sum_{i=1}^{L_n} |I_i| > \varepsilon, \end{equation*}$

da cui $S_n > \varepsilon$ .

$\quad$

Definizione dei compatti $K_n \subset U_n$ tali che $\emptyset \neq K_n \subseteq K_{n-1}$ .
Definiamo $K_n$ per ricorrenza.

$\quad$

Esiste $M_1 \in \mathbb{N}$ tale che $M_1 \leq N_1$ e una famiglia di intervalli chiusi $[\alpha_k^1,\beta_k^1]_{k=1}^{M_1}$ e disgiunti tali che
(279) $\begin{equation*} \begin{gathered} [\alpha_k^1,\beta_k^1] \subset (a_k^1, b_k^1) \qquad \forall k=1, \dots, M_1; \\ |K_1| = \sum_{k=1}^{M_1} (\beta_k^1 - \alpha_k^1) > S_1 - \frac{\varepsilon}{2}, \end{gathered} \end{equation*}$

dove abbiamo posto

(280) $\begin{equation*} K_1 = \bigcup_{k=1}^{M_1} \, [\alpha_k^1,\beta_k^1]. \end{equation*}$

Poiché $S_1 > \varepsilon$ , si ha $K_1 \neq \emptyset$ .

Supponiamo definito $K_{n-1}$ , costituito da un’unione finita di intervalli chiusi disgiunti e supponiamo che esso soddisfi
(281) $\begin{equation*} |K_{n-1}| > S_{n-1} - \varepsilon\bigg( 1 - \frac{1}{2^{n-1}}\bigg). \end{equation*}$

In particolare da ciò segue che:

(a) $K_{n-1} \neq \emptyset$ , in quanto $S_{n-1}> \varepsilon$ per (275);

(b) $U_{n - 1} \setminus K_{n-1}$ è costituito dall’unione al più numerabile di intervalli disgiunti la cui serie delle lunghezze soddisfa

(282) $\begin{equation*} S_{n-1} - |K_{n-1}| < \varepsilon\bigg( 1 - \frac{1}{2^{n-1}}\bigg). \end{equation*}$

Ciò si può verificare considerando che $K_{n-1}$ è ottenuto sottraendo da $U_{n-1}$ una quantità finita di intervalli chiusi, che ognuno di tali intervalli chiusi è contenuto in uno solo tra gli intervalli $(a_k^{n-1},b_k^{n-1})$ costituenti $U_{n-1}$ e applicando il punto 3 del lemma A.2.

Vogliamo definire $K_n \subset K_{n-1} \cap U_n$ , costituito dall’unione finita di intervalli chiusi disgiunti e soddisfacente

(283) $\begin{equation*} |K_n| > S_n - \varepsilon \bigg( 1 - \frac{1}{2^n}\bigg). \end{equation*}$

Come sopra, esiste $M_n \in \mathbb{N}$ tale che $M_n \leq N_n$ e una famiglia di intervalli chiusi e disgiunti $[\alpha_k^n,\beta_k^n]_{k=1}^{M_n}$ tali che

(284) $\begin{gather*} [\alpha_k^n,\beta_k^n] \subset (a_k^n, b_k^n) \qquad \forall k=1, \dots, M_n; \\ |\tilde{K}_n| = \sum_{k=1}^{M_n} (\beta_k^n - \alpha_k^n) > S_n - \frac{\varepsilon}{2^{n+1}}, \end{gather*}$

dove abbiamo posto $\tilde{K}_n \coloneqq \bigcup_{k=1}^{M_n} [\alpha_k^n,\beta_k^n]$ . Per come è definito, $\tilde{K}_n \subset U_n$ .

Definiamo $K_n \coloneqq \tilde{K_n} \cap K_{n-1}$ . Chiaramente $K_n$ è costituito dall’unione finita di intervalli chiusi disgiunti e si ha $K_n \subseteq K_{n-1} \cap U_n$ . Dimostriamo che

(285) $\begin{equation*} |K_n|=|\tilde{K}_n \cap K_{n-1}| > S_n - \varepsilon \bigg( 1 - \frac{1}{2^n}\bigg). \end{equation*}$

Infatti si ha

(286) $\begin{equation*} |\tilde{K}_n \cap K_{n-1} | = |\tilde{K}_n| - |\tilde{K}_n \cap \big( U_{n-1} \setminus K_{n-1} \big)|, \end{equation*}$

dove l’uguaglianza deriva dal fatto che $\tilde{K}_n = (\tilde{K}_n \cap K_{n-1}) \cup \big(\tilde{K}_n \cap ( U_{n-1} \setminus K_{n-1})\big)$ , che tale unione è disgiunta, dal fatto che i due insiemi sono costituiti dall’unione finita di intervalli chiusi e dal punto 3 del lemma A.2.

Poiché $\tilde{K}_n \cap ( U_{n-1} \setminus K_{n-1})$ è costituito da un’unione finita di intervalli contenuti in $U_{n-1} \setminus K_{n-1}$ , per (282) si ha

(287) $\begin{equation*} |\tilde{K}_n \cap ( U_{n-1} \setminus K_{n-1})| < \varepsilon\bigg( 1 - \frac{1}{2^{n-1}}\bigg). \end{equation*}$

Unendo (286), (284) e (287) si ottiene

(288) $\begin{equation*} |\tilde{K}_n \cap K_{n-1} | > S_n - \frac{\varepsilon}{2^{n+1}} - \varepsilon\bigg( 1 - \frac{1}{2^{n-1}}\bigg) > S_n - \varepsilon \bigg( 1 - \frac{1}{2^n}\bigg). \end{equation*}$

$\quad$

$\bigcap_{n = 1}^\infty U_n \neq \emptyset$
Poiché per ogni $n \in \mathbb{N}$ si ha $K_n \neq \emptyset$ , $K_n \subseteq K_{n-1}$ , si ottiene

(289) $\begin{equation*} \emptyset \neq \bigcap_{n = 1}^\infty K_n \subseteq \bigcap_{n = 1}^\infty U_n, \end{equation*}$

dove la prima disuguaglianza è dovuta al lemma B.1 e l’inclusione segue dal fatto che $K_n \subset U_n$ per ogni $n \in \mathbb{N}$ .

Dimostrazione del teorema 2.16.

Abbiamo ora gli strumenti necessari per dimostrare il teorema 2.16.

Dimostrazione del teorema 2.16. L’idea della dimostrazione consiste nel ridursi al caso di $f_n$ non negative convergenti e $f \equiv 0$ e poi ragionare per assurdo: se non si avesse convergenza degli integrali, esisterebbe per ogni $n$ una famiglia finita $\{I_i^n\}_{i=1}^{L_n}$ di intervalli aperti su cui $f_n > \varepsilon > 0$ e tale che

(290) $\begin{equation*} \sum_{i=1}^{L_n} |I_i^n| > \varepsilon \end{equation*}$

Per ottenere tale stima è cruciale l’ipotesi che

(291) $\begin{equation*} |f_n(x)|\leq M \qquad \forall n \in \mathbb{N}, \,\, \forall x \in [a,b] \end{equation*}$

(da cui l’aggettivo dominata nel nome del teorema). La stima (290) permette di applicare il lemma C.5 e trovare un punto $\xi \in [a,b]$ per cui $f_n(\xi)$ non converge a $0$ . Da tale contraddizione con la convergenza puntuale segue la tesi.

$\quad$

Si può supporre $f\equiv 0$ , $f_n \geq 0$ , $M=1$ e $[a,b]=[0,1]$
Senza ledere la generalità, a meno di sostituire $f_n$ con $g_n \colon [0,1] \to \mathbb{R}$ definita da

(292) $\begin{equation*} g_n(x) \coloneqq \frac{1}{M} \Big( f_n\big(a + (b-a)x\big) - f\big(a + (b-a)x\big) \Big) \qquad \forall x \in [0,1], \end{equation*}$

possiamo supporre che $f$ sia la funzione identicamente nulla, che $M=1$ e che $[a,b]=[0,1]$ . Inoltre, possiamo limitarci a dimostrare il risultato assumendo che

(293) $\begin{equation*} f_n(x) \geq 0 \qquad \forall n \in \mathbb{N}, \,\, \forall x \in [a,b]. \end{equation*}$

Infatti, poiché $|f_n|\geq 0$ e per la disuguaglianza triangolare $\int_0^1 |f_n(x)| \, \mathrm{d}x \geq \big| \int_0^1 f_n(x) \, \mathrm{d}x \big|$ , l’assunzione (293) non è restrittiva.

Supponiamo per assurdo che $\limsup_{n \to \infty} \int_0^1 f_n(x) \, \mathrm{d}x >0$ . A meno di passare a una opportuna sottosuccessione, possiamo assumere che esista $\varepsilon>0$ tale che

(294) $\begin{equation*} \int_0^1 f_n(x) \, \mathrm{d}x > 2\varepsilon \qquad \forall n \in \mathbb{N}. \end{equation*}$

Definizione delle famiglie $\{I_i^n\}_{i=1}^{L_n}$ e stima $\sum_{i=1}^{L_n} |I_i^n| > \varepsilon$
Da (294) segue che per ogni $n \in \mathbb{N}$ esiste una suddivisione $P_n$ dell’intervallo $[0,1]$ definita da

(295) $\begin{equation*} P_n = \{ J_i^n:= (x_{i-1}^n, x_i^n) \mid i=1, \dots, M_n \} \qquad \text{con} \qquad 0=x_0^n < x_1^n < \dots < x_{M_n}^n = 1 \end{equation*}$

e tale che

(296) $\begin{equation*} s(f_n,P_n) = \sum_{i=1}^{M_n} |J_i^n| \big( \inf_{J_i^n}f_n \big) > 2\varepsilon. \end{equation*}$

Vogliamo stimare la misura dell’unione degli intervalli $J_i^n$ su cui $f_n \geq \varepsilon$ . Si ha

(297) $\begin{equation*} \begin{split} 2\varepsilon < & \sum_{i=1}^{M_n} |J_i^n| \big( \inf_{J_i^n}f_n \big) \\ \leq & \sum_{\substack{i=1 \\[2pt] i \colon \inf_{J_i^n}f_n \leq {\varepsilon}}}^{M_n} |J_i^n|{\varepsilon} + \sum_{\substack{i=1 \\[2pt] i \colon \inf_{J_i^n}f_n > {\varepsilon}}}^{M_n} |J_i^n| \cdot 1 \\ \leq & \,\,{\varepsilon} + \sum_{\substack{i=1 \\[2pt] i \colon \inf_{J_i^n}f_n > {\varepsilon}}}^{M_n} |J_i^n|, \end{split} \end{equation*}$

dove nella seconda disuguaglianza abbiamo utilizzato il fatto che $f_n \leq 1$ e nella terza disuguaglianza abbiamo sfruttato il fatto che gli intervalli $J_i^n$ sono disgiunti e contenuti in $[0,1]$ e il punto 2 del lemma A.2. Chiamiamo $\{I_i^n\}_{i=1}^{L_n}$ gli intervalli $J_i^n$ tali che $\inf_{J_i^n}f_n > {\varepsilon}$ . Definendo

(298) $\begin{equation*} V_n \coloneqq \bigcup_{i=1}^{L_n} I_i^n, \end{equation*}$

la disuguaglianza (297) diventa quindi

(299) $\begin{equation*} |V_n| = \sum_{i=1}^{L_n} |I_i^n| > \varepsilon. \end{equation*}$

Definizione degli aperti $U_n$ ed esistenza di $\xi \in \bigcap_{n=1}^\infty U_n$
Per ogni $n \in \mathbb{N}$ , definiamo

(300) $\begin{equation*} U_n = \bigcup_{m \geq n} V_m. \end{equation*}$

Ogni $U_n$ è un insieme aperto in quanto è costituito dall’unione di intervalli aperti (poiché tale è ogni $V_m$ ) e soddisfa $U_n \subset U_{n-1}$ . Inoltre si ha $U_n \supseteq V_n$ con $V_n = \bigcup_{i=1}^{L_n}$ , dove $\{I_i^n\}_{i=1}^{L_n}$ è una famiglia finita di intervalli aperti disgiunti tali che $\sum_{i=1}^{L_n}|I_i^n|> \varepsilon$ . Possiamo applicare quindi il lemma C.5 e concludere che esiste $\xi \in \bigcap_{n=1}^\infty U_n$ .

$\limsup_{n \to \infty} f_n(\xi) \geq \varepsilon$
Osserviamo che, se $x \in U_n$ , allora esiste $m \geq n$ tale che

(301) $\begin{equation*} f_m(x) > \varepsilon. \end{equation*}$

Infatti, se $x \in U_n$ , esiste $m \geq n$ tale che $x \in V_m$ e $V_m$ è costituito dall’unione degli intervalli $I_i^m$ tali che $\inf_{I_i^m}f_m \geq \varepsilon$ .

Quindi, poiché $\xi \in \bigcap_{n=1}^\infty U_n$ , per ogni $n \in \mathbb{N}$ esiste $m \geq n$ tale che $f_m(\xi) > \varepsilon$ . Ciò chiaramente implica che

(302) $\begin{equation*} \limsup_{n \to \infty} f_n(\xi) \geq \varepsilon, \end{equation*}$

che contraddice il fatto che $f_n$ converge puntualmente alla funzione nulla.

Riferimenti bibliografici

[1] Acerbi, E. & Buttazzo, G., Primo corso di Analisi Matematica Pitagora Editrice, (1997).

[2] Dugundji, J., Topology Allyn and Bacon, (1966).

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Document

Successioni di funzioni – Teoria

Autori e revisori

Leggi...

Notazioni

Leggi...

Introduzione

Leggi...

Convergenza puntuale

Introduzione.

Limiti della convergenza puntuale: continuità e passaggio al limite.

Limiti della convergenza puntuale: integrazione.

Limiti della convergenza puntuale: derivazione.

Convergenza uniforme

Introduzione.

Definizione e prime proprietà.

Definizione e prime proprietà: caratterizzazione equivalente della convergenza uniforme.

Definizione e prime proprietà: relazione con la convergenza puntuale.

Definizione e prime proprietà: condizioni di Cauchy.

Teoremi di convergenza.

Teoremi di convergenza: continuità e limiti.

Teoremi di convergenza: integrazione.

Teoremi di convergenza: derivazione.

Criteri di convergenza uniforme.

Criteri di convergenza uniforme: criteri di monotonia.

Criteri di convergenza uniforme: equicontinuità.

Criteri di convergenza uniforme: Il teorema di Ascoli-Arzelà.

Scarica la teoria

Gli spazi normati e

Introduzione.

Spazi metrici e normati.

Gli spazi delle funzioni limitate.

Successioni di Cauchy e completezza.

(Equi)limitatezza di funzioni.

Compattezza di funzioni continue e limitate.

Esercizi

Svolgimento esercizio 2.5.

Svolgimento esercizio 3.5.

Svolgimento esercizio 3.6.

Svolgimento esercizio 3.12.

Svolgimento esercizio 3.27.

Svolgimento esercizio 3.32.

Svolgimento esercizio 3.33.

Svolgimento esercizio 3.38.

Svolgimento esercizio 3.61.

Appendice A: Misura di unioni finite di intervalli

Leggi...

Appendice B: Una funzione non integrabile

Leggi...

Appendice C: il teorema di convergenza dominata di Arzelà

Introduzione.

Risultati preliminari.

Dimostrazione del teorema 2.16.

Riferimenti bibliografici

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Gli spazi normati $\mathscr{B}(E,\mathbb{R})$ e $C_b(E,\mathbb{R})$