Successioni di funzioni – Esercizi

Home » Successioni di funzioni – Esercizi

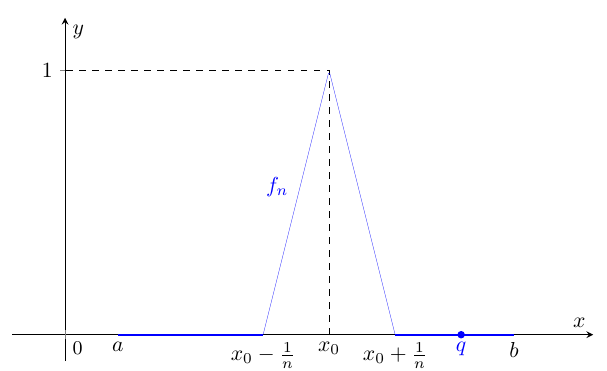
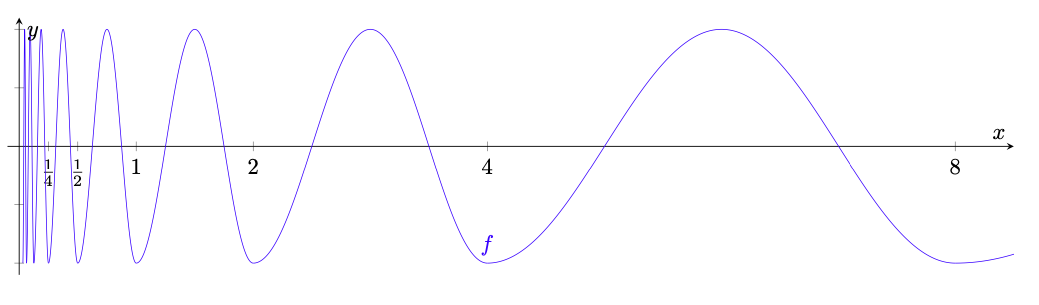
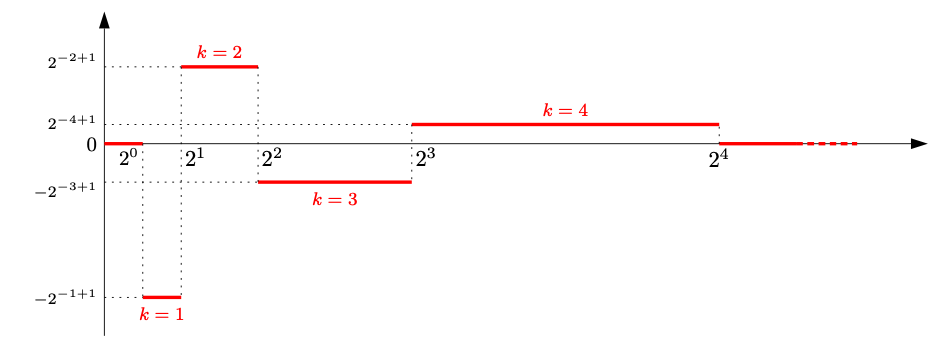
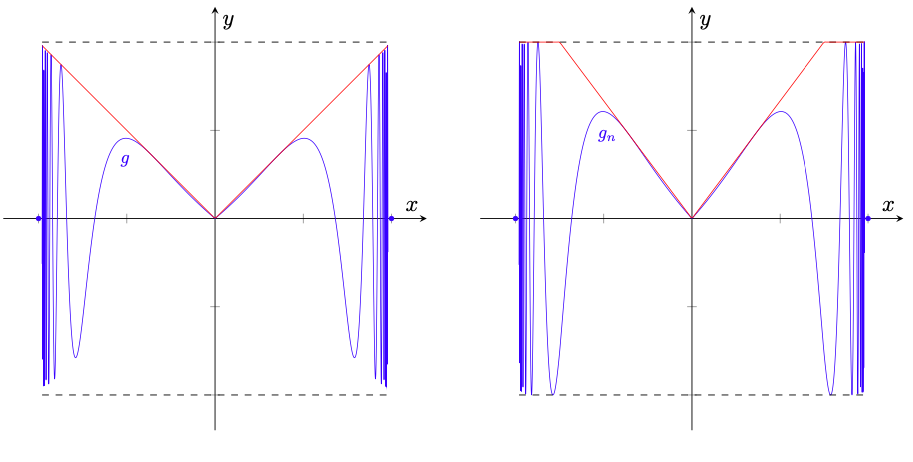
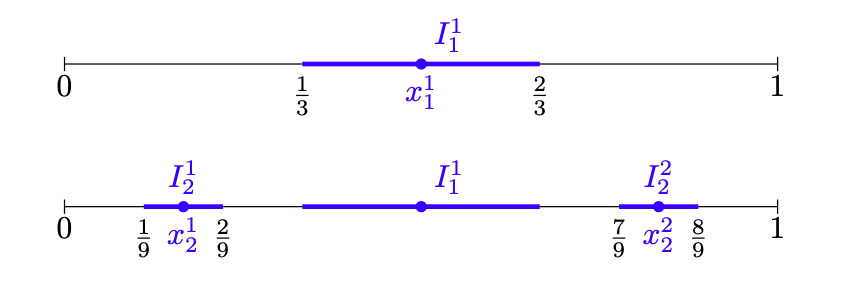
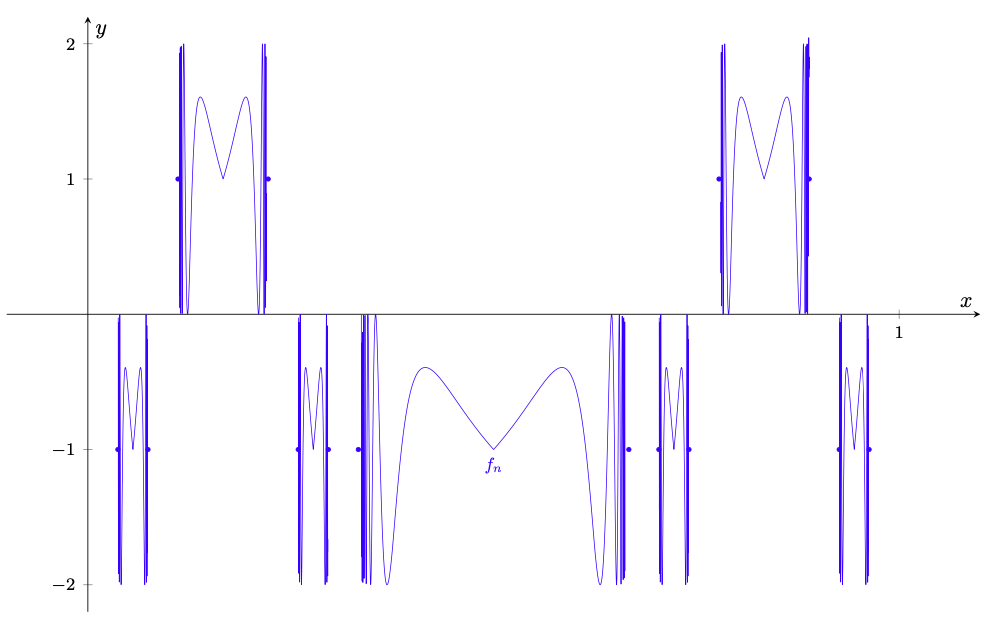
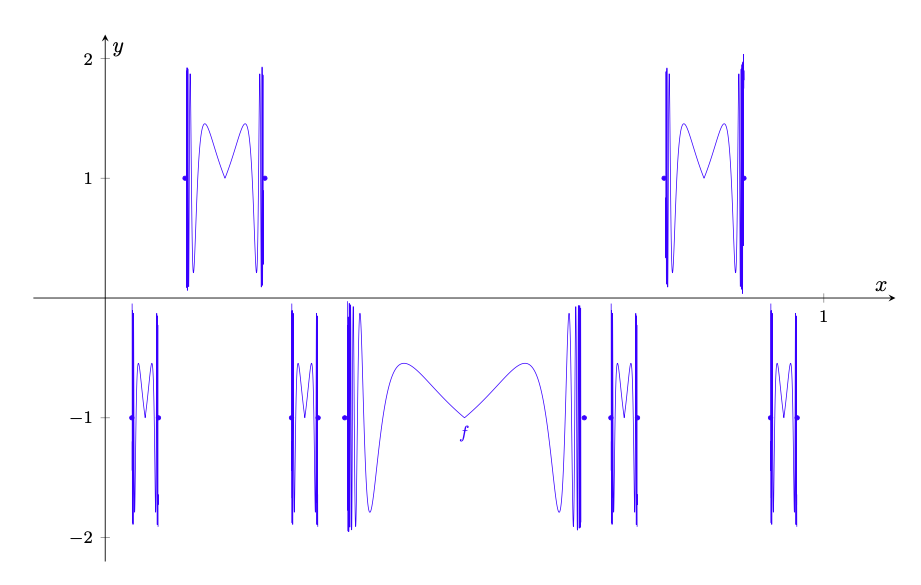
Benvenuti nella nostra raccolta di esercizi sulle successioni di funzioni. In questo articolo presentiamo 42 esercizi su questo importante argomento, ordinati per difficoltà crescente. Gli esercizi sono corredati di una soluzione completa, per consentire al lettore di confrontare le sue soluzioni con quelle da noi riportate, e coprono ampiamente il programma relativo a questo tema svolto nei corsi universitari di Analisi Matematica per tutte le facoltà scientifiche.

La teoria necessaria è reperibile nell’articolo completo Successioni di funzioni – Teoria. Segnaliamo inoltre i seguenti articoli:

Sommario

Leggi...

Questa dispensa è una raccolta di esercizi riguardanti le successioni di funzioni. I problemi, di natura sia teorica che pratica, sono ordinati per difficoltà crescente e sono tutti completamente risolti. Essi presentano un ampio spettro di difficoltà e di tecniche, oltre a toccare la maggior parte degli argomenti relativi usualmente trattati in un corso di Analisi Matematica 2. Di numerosi esercizi vengono fornite più soluzioni alternative che utilizzano anche strumenti di non comune applicazione.

Autori e revisori

Leggi...

Autori: Luigi De Masi, Roberto Castorrini.

Revisori: Valerio Brunetti, Sergio Fiorucci, Chiara Bellotti, Nicola Fusco, Matteo Talluri.

Notazioni

Leggi...

$\mathbb{N}$	Insieme dei numeri naturali positivi: $\{1, 2, \dots\}$
$\exp(x)$	$e^x$
$\chi_A$	Funzione caratteristica dell’insieme $A \subseteq \mathbb{R}$ , definita da: $\chi_A(x) = \begin{cases} 1 & \text{se } x \in A, \\ 0 & \text{se } x \notin A; \end{cases}$

Introduzione

Leggi...

Questa dispensa è una raccolta di problemi risolti sulle successioni di funzioni e, in particolare, riguardanti la convergenza puntuale e uniforme. Essi coprono una parte abbastanza estesa dei relativi argomenti teorici e spesso sono presentate soluzioni alternative che fanno uso di strumenti a volte meno utilizzati. Gli esercizi sono proposti in ordine di difficoltà crescente; invitiamo il lettore a cimentarsi anche con i più difficili prima di leggere le soluzioni riportate. Come riferimento per la parte di teoria, rimandiamo il lettore alla dispensa Successioni di funzioni (teoria); ci riferiremo spesso ai risultati di tale volume (che abbiamo raccolto nella sezione “Richiami di teoria” per comodità) nelle risoluzioni degli esercizi.

Richiami di teoria

Leggi...

In questa sezione richiamiamo le definizioni principali e i teoremi che utilizzeremo nel seguito. Il lettore può riferirsi a Successioni di funzioni (teoria) per una trattazione completa degli argomenti. Riportiamo i teoremi senza dimostrazione, rimandando ai rispettivi punti in Successioni di funzioni (teoria).

$\quad$

Definizione 1.1 (convergenza puntuale). Dato $E \subseteq R$ , data una successione di funzioni $f_n \colon E \to \mathbb{R}$ e una funzione $f \colon E \to \mathbb{R}$ , diciamo che $f_n$ converge puntualmente a $f$ se per ogni $x \in E$ la successione numerica $\big( f_n(x)\big)_{n \in \mathbb{N}}$ converge a $f(x)$ , cioè se si ha:

(1) $\begin{equation*} \lim_{n\to+\infty} f_n(x) = f(x) \qquad \forall x \in E. \end{equation*}$

Se $F \subseteq E$ , diciamo che $f_n$ converge puntualmente a $f$ in $F$ se e solo se

(2) $\begin{equation*} \lim_{n\to+\infty} f_n(x) = f(x) \qquad \forall x \in F. \end{equation*}$

$\quad$

Definizione 1.2 (convergenza uniforme). Sia $E \subset \mathbb{R}$ , $f_n \colon E \to \mathbb{R}$ una successione di funzioni e sia $f \colon E \to \mathbb{R}$ ; si dice che $f_n$ converge uniformemente a $f$ se, per ogni $\varepsilon>0$ , esiste $N \in \mathbb{N}$ tale che

(3) $\begin{equation*} |f_n(x) - f(x))| < \varepsilon \qquad \forall n \geq N, \,\, \forall x \in E. \end{equation*}$

Se $F \subseteq E$ , diciamo che $f_n$ converge uniformemente a $f$ in $F$ se e solo se per ogni $\varepsilon>0$ , esiste $N \in \mathbb{N}$ tale che

(4) $\begin{equation*} |f_n(x) - f(x))| < \varepsilon \qquad \forall n \geq N, \,\, \forall x \in F. \end{equation*}$

$\quad$

Il prossimo risultato consiste in una semplice caratterizzazione della convergenza uniforme e spesso si usa per mostrare che una successione converge uniformemente. Per una dimostrazione, rimandiamo il lettore a Successioni di funzioni (teoria), proposizione 3.7.

$\quad$

Proposizione 1.3 (caratterizzazione della convergenza uniforme). Sia $E \subset \mathbb{R}$ , $f_n \colon E \to \mathbb{R}$ una successione di funzioni e sia $f \colon E \to \mathbb{R}$ ; allora $f_n$ converge uniformemente a $f$ se e solo se

(5) $\begin{equation*} \lim_{n \to + \infty} \, \sup_{x \in E} \big\{ |f_n(x) - f(x)| \big\} = 0. \end{equation*}$

$\quad$

Un’altra caratterizzazione della convergenza uniforme, che può risultare comoda in quanto non fa uso esplicito del limite uniforme, è il seguente criterio. Per una dimostrazione, rimandiamo a Successioni di funzioni (teoria), proposizione 3.18.

$\quad$

Proposizione 1.4 (criterio di Cauchy per la convergenza uniforme). Sia $E \subset \mathbb{R}$ e sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni. Allora $f_n$ converge uniformemente a una funzione $f \colon E \to \mathbb{R}$ se e solo se, per ogni $\varepsilon>0$ , esiste $N \in \mathbb{N}$ tale che

(6) $\begin{equation*} \sup_{x \in E}|f_n(x) - f_m(x)| \leq \varepsilon \qquad \forall n,m \geq N. \end{equation*}$

$\quad$

Il prossimo risultato è utile per mostrare che una successione di funzioni continue converge puntualmente ma non uniformemente al suo limite puntuale. Rimandiamo il lettore a Successioni di funzioni (teoria), teorema 3.19 per una dimostrazione.

$\quad$

Teorema 1.5 (limite uniforme di funzioni continue). Sia $E \subset \mathbb{R}$ e sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni continue convergente uniformemente alla funzione $f \colon E \to \mathbb{R}$ . Allora $f$ è una funzione continua.

$\quad$

Risulta spesso utile una generalizzazione del teorema precedente, dimostrata in Successioni di funzioni (teoria), teorema 3.22.

$\quad$

Teorema 1.6 (scambio di limiti per la convergenza uniforme). Sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni che converga uniformemente a una funzione $f \colon E \to \mathbb{R}$ e sia $x_0 \in \mathbb{R}$ un punto di accumulazione di $E$ . Se i limiti $\lim_{x \rightarrow x_0} f_n(x)$ esistono per ogni $n \in \mathbb{N}$ , allora il limite $\lim_{x \rightarrow x_0} f(x)$ esiste e inoltre vale

(7) $\begin{equation*} \lim_{x \rightarrow x_0} f(x) = \lim_{n\to+\infty} \Big( \lim_{x \rightarrow x_0} f_n(x) \Big). \end{equation*}$

$\quad$

Il seguente risultato afferma il fatto che, sotto ipotesi di convergenza uniforme, l’integrale del limite è pari al limite dell’integrale. Per una dimostrazione il lettore può riferirsi a Successioni di funzioni (teoria), teorema 3.28.

$\quad$

Teorema 1.7 (Passaggio al limite sotto il segno di integrale). Sia $f_n\colon [a,b] \to \mathbb{R}$ una successione di funzioni integrabili secondo Riemann che converga uniformemente a una funzione $f \colon [a,b] \to \mathbb{R}$ . Allora $f$ risulta integrabile secondo Riemann e vale

(8) $\begin{equation*} \lim_{n\to+\infty} \int_{a}^{b} f_n(x)\,\mathrm{d}x = \int_{a}^{b} f(x)\,\mathrm{d}x. \end{equation*}$

$\quad$

Il teorema che segue mette in evidenza il collegamento tra la convergenza uniforme delle derivate $f_n'$ di una successione di funzioni, la convergenza uniforme delle $f_n$ e la derivabilità del limite delle $f_n$ . Una dimostrazione è in Successioni di funzioni (teoria), teorema 3.35.

$\quad$

Teorema 1.8 (limite uniforme di funzioni derivabili). Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni derivabili tali che la successione delle derivate prime $f_n'$ converga uniformemente a una funzione $g \colon [a,b] \to \mathbb{R}$ ; supponiamo inoltre che esista $x_0 \in [a,b]$ e $y_0 \in \mathbb{R}$ tale che

(9) $\begin{equation*} \lim_{n \to \infty} f_n(x_0) = y_0. \end{equation*}$

Allora esiste una funzione derivabile $f \colon [a,b] \to \mathbb{R}$ tale che

$\quad$

$f_n$ converge uniformemente a $f$ ;

$f'=g$ .

$\quad$

Il prossimo teorema mostra che la convergenza puntuale di una successione $f_n$ di funzioni continue a una funzione $f$ continua, sotto ipotesi di monotonia della successione $f_n$ , è in realtà uniforme. Per una dimostrazione, si veda Successioni di funzioni (teoria), teorema 3.42.

$\quad$

Teorema 1.9 (piccolo teorema del Dini). Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione crescente di funzioni continue, cioè tale che

(10) $\begin{equation*} f_n(x) \leq f_{n+1}(x), \qquad \forall n \in \mathbb{N}, \,\,\, \forall x \in [a,b]. \end{equation*}$

Si supponga inoltre che il limite puntuale $f\colon [a,b] \to \mathbb{R}$ delle $f_n$ sia continuo. Allora $f_n$ converge uniformemente a $f$ . Analogo risultato vale se la successione $f_n$ è decrescente.

$\quad$

La stessa conclusione del teorema precedente vale sotto l’ipotesi che ogni funzione $f_n$ sia monotona: si veda Successioni di funzioni (teoria), teorema 3.44.

$\quad$

Teorema 1.10. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni crescenti, cioè tali che

(11) $\begin{equation*} x \leq y \Longrightarrow f_n(x) \leq f_n(y) \qquad \forall n \in \mathbb{N}. \end{equation*}$

Supponiamo che $f_n$ converga puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ continua. Allora la convergenza di $f_n$ a $f$ è uniforme. Vale un analogo risultato se le funzioni $f_n$ sono decrescenti.

$\quad$

Definiamo ora i concetti di continuità uniforme, modulo di continuità e di equicontinuità, che sono centrali nella teoria delle funzioni continue. Per una discussione più approfondita, si veda Successioni di funzioni (teoria), sezione 3.3.2.

$\quad$

Definizione 1.11 (continuità uniforme, modulo di continuità). Sia $g \colon [a,b] \to \mathbb{R}$ ; $g$ si dice uniformemente continua se esiste una funzione $\sigma \colon [0,+\infty) \to [0,+\infty)$ , detta modulo di continuità di $g$ che soddisfi le seguenti condizioni:

$\quad$

$\sigma$ è monotona non decrescente;

$\lim_{\varepsilon \to 0}\sigma(\varepsilon) = \sigma(0) = 0$ ;

si ha
(12) $\begin{equation*} |g(x) - g(y)| \leq \sigma(|x-y|) \qquad \forall x,y \in [a,b]. \end{equation*}$

$\quad$

Definizione 1.12 (equicontinuità). Sia $X$ un insieme di funzioni (continue) definite sull’intervallo $[a,b]$ e a valori reali. $X$ si dice equicontinuo se esiste $\sigma \colon [0,+\infty) \to [0,+\infty)$ tale che, per ogni $f \in X$ , $\sigma$ è un modulo di continuità per $f$ .

$\quad$

L’equicontinuità di una successione di funzioni è strettamente legata alle sue proprietà di convergenza uniforme. Riportiamo i seguenti fondamentali risultati, per una cui dimostrazione si rimanda a Successioni di funzioni (teoria), teoremi 3.56 e 3.65.

$\quad$

Teorema 1.13. Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni continue che converge puntualmente a una funzione $f \colon [a,b] \to \mathbb{R}$ . Allora le seguenti condizioni sono equivalenti:

$\quad$

Le funzioni $f_n$ sono equicontinue;

$f_n$ converge uniformemente a $f$ .

$\quad$

Teorema 1.14 (Ascoli-Arzelà). successione di funzioni continue. Allora le due seguenti condizioni sono equivalenti:

$\quad$

le funzioni $f_n$ sono equilimitate e equicontinue;

da ogni sottosuccessione $f_{n_k}$ se ne può estrarre una convergente uniformemente .

$\quad$

Riportiamo inoltre la seguente definizione, usata in alcuni esercizi proposti.

$\quad$

Definizione 1.15 (proprietà di Darboux). Una funzione $f \colon [a,b] \to \mathbb{R}$ si dice avere la proprietà di Darboux o dei valori intermedi se, per ogni $x,y \in [a,b]$ tali che $x<y$ e per ogni $t$ compreso tra $f(x)$ e $f(y)$ , esiste $z \in [x,y]$ tale che $f(z)=t$ .

$\quad$

Osservazione 1.16. Equivalentemente, $f$ ha la proprietà di Darboux se e solo se l’immagine $f(I)$ di ogni intervallo $I \subseteq [a,b]$ è a sua volta un intervallo.

Esercizi

$\quad$

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definite da

$f_{n}(x)=\frac{n+\cos x}{2 n+\sin ^{2} x} \qquad \forall n \in \mathbb{N},\,\, n\geq 1,\,\, \forall x \in \mathbb{R},$

Soluzione.

Poiché $|\cos x|\leq 1$ e $0 \leq |\sin^2 x| \leq 1$ per ogni $x \in \mathbb{R}$ , si ha

(13) $\begin{equation*} \frac{n-1}{2n+1} \leq f_n(x) \leq \frac{n+1}{2n} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}. \end{equation*}$

Dato che $\dfrac{n-1}{2n+1} < \dfrac{1}{2}< \dfrac{n+1}{2n}$ per ogni $n\in \mathbb{N}$ e per ogni $x \in \mathbb{R}$ , ponendo $f \colon \mathbb{R} \to \mathbb{R}$ la funzione definita da $f(x)= \dfrac{1}{2}$ per ogni $x \in \mathbb{R}$ , da (13) si ottiene

(14) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} \left| f_n(x) - f(x) \right| \leq \lim_{n \to +\infty} \left( \frac{n+1}{2n-1} - \frac{n-1}{2n+1} \right) = \frac{1}{2}-\frac{1}{2} = 0. \end{equation*}$

Per la proposizione 1.3, $f_n$ converge uniformemente (e quindi anche puntualmente) in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ tale che $f(x)= \dfrac{1}{2}$ per ogni $x \in \mathbb{R}$

Esercizio 2 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Data una successione $a_n$ di numeri reali, si consideri la successione $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da¹

(15) $\begin{equation*} f_n(x) = a_n \chi_{[n,n+1)}(x) \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}. \end{equation*}$

Studiare la convergenza puntuale e uniforme della successione $f_n$ in $\mathbb{R}$ .

$\,$

dove $\chi_{A}$ indica la funzione caratteristica dell’insieme $A$ , che vale $1$ nell’insieme e $0$ altrove. ↩

Soluzione.

Poiché $f_n(x)=0$ per ogni $x < n$ , si ha

(16) $\begin{equation*} \lim_{n \to \infty} f_n(x) = 0 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Pertanto $f_n$ converge puntualmente alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla.

Per la convergenza uniforme, osserviamo che

(17) $\begin{equation*} \sup_{x \in\mathbb{R}} |f_n(x)-f(x)| = a_n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Pertanto, la convergenza di $f_n$ a $f$ è uniforme se e solo se $\lim_{n \to +\infty} a_n=0$ .

Esercizio 3 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon [0,1] \to \mathbb{R}$ definita da

$f_n(x) = x^n \qquad \forall n \in \mathbb{N}, \,\, \forall x \in [0,1],$

nei seguenti insiemi:

$\,$

nell’intervallo $[0,1]$ ;

nell’intervallo $[0,1)$ ;

negli intervalli del tipo $[0,\alpha]$ con $\alpha \in [0,1)$ .

Soluzione.

Osserviamo che, se $x \in [0,1]$ , si ha

$\lim _{n\to +\infty} f_{n}(x)=\lim _{n\to +\infty} x^{n}= \begin{cases} 0 & \text{se } 0 \leq x<1 \\ 1 & \text{se } x=1, \end{cases}$

da cui segue la convergenza puntuale alla funzione $f \colon [0,1] \to \mathbb{R}$ definita da

$f(x) = \begin{cases} 0 & \text{se } 0 \leq x<1 \\ 1 & \text{se } x=1. \end{cases}$

Studiamo ora la convergenza uniforme nei tre casi indicati.

Soluzione punto 1.

Poichè ogni funzione $f_n$ e continua, mentre il limite puntuale $f$ e una funzione discontinua in $1$ , dal teorema 1.5 segue che la convergenza non è uniforme nell’intervallo $[0,1]$ .

Soluzione punto 2.

Affermiamo che la convergenza non è uniforme neanche nell’intervallo $[0,1)$ . Infatti, per ogni $n \in \mathbb{N}$ , si ha

(18) $\begin{equation*} \lim_{x \to 1^-} x^n = 1. \end{equation*}$

(19) $\begin{equation*} \sup_{x \in [0,1)} |f_n(x) - f(x)| = \sup_{x \in [0,1)} |x^n| = 1 \qquad \forall n \in \mathbb{N}, \end{equation*}$

e ciò in particolare prova che

(20) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in [0,1)} |f_n(x) - f(x)| = 1 \neq 0. \end{equation*}$

Per la proposizione 1.3, $f_n$ non converge uniformemente a $f$ in $[0,1)$ .

Soluzione punto 3.

Fissiamo $\alpha \in [0,1)$ ; allora si ha

(21) $\begin{equation*} \sup_{x \in [0,\alpha]} |f_n(x) - f(x)| = \sup_{x \in [0,\alpha]} x^n = \alpha^n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Da ciò segue che

(22) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in [0,\alpha]} |f_n(x) - f(x)| = \lim_{n \to +\infty} \alpha^n = 0, \end{equation*}$

dove l’ultima uguaglianza segue dalla convergenza puntuale di $f_n$ a $0$ in $[0,\alpha]$ . La convergenza uniforme segue quindi dalla proposizione 1.3.

Esercizio 4 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definite da

$f_n(x) = \frac{n^2+x^n}{n^2} \qquad \forall n \in \mathbb{N},\,\ \forall x \in \mathbb{R}.$

Inoltre verificare che il seguente limite esiste e calcolarne il valore:

(23) $\begin{equation*} \lim_{n \rightarrow +\infty} \int_{1}^{5} f_n(x) \, \mathrm{d} x. \end{equation*}$

Soluzione.

Osserviamo che

$\lim_{n\to +\infty} f_n(x) = \lim_{n\to +\infty} 1+\frac{x^n}{n^2} = \begin{cases} \text{non esiste} & \text{se } x<-1\\ 1 & \text{se } x\in [-1,1]\\ +\infty & \text{se } x>1 \end{cases}.$

Dunque $f_n$ converge puntualmente alla funzione $f \colon [-1,1] \to \mathbb{R}$ identicamente pari a 1 su $[-1,1]$ e non converge puntualmente al di fuori di tale insieme.

Affermiamo che la convergenza è anche uniforme su $[-1,1]$ , infatti

(24) $\begin{equation*} \lim_{n\to +\infty} \sup_{x\in [-1,1]}|f_n(x)-f(x)| = \lim_{n\to +\infty} \sup_{x\in [-1,1]} \frac{|x^n|}{n^2} = \lim_{n\to +\infty} \frac{1}{n^2}=0, \end{equation*}$

dove si è usato che $|x^n|\leq 1$ per ogni $x \in [-1,1]$ .

Per calcolare il limite (23), non si può far ricorso al teorema 1.7, in quanto non si ha convergenza uniforme (nemmeno puntuale) delle funzioni $f_n$ in $[1,5]$ . D’altra parte, calcoliamo

(25) $\begin{equation*} \int_{1}^{5} f_n(x)\dif x = \int_{1}^{5} \left(1 +\frac{x^n}{n^2} \right) \dif x = 4+\left[\frac{x^{n+1}}{n^2(n+1)}\right]^5_1 = 4+\frac{5^{n+1}-1}{n^2(n+1)} \qquad \forall n \in \mathbb{N}. \end{equation*}$

Passando al limite per $n \to +\infty$ , si ottiene

(26) $\begin{equation*} \lim_{n\to +\infty} \int_{1}^{5} f_n(x)\, \mathrm{d} x = \lim_{n \to +\infty} \left( 4+\frac{5^{n+1}-1}{n^2(n+1)} \right) = +\infty. \end{equation*}$

Esercizio 5 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Data una successione $a_n$ di numeri reali, si consideri la successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

(27) $\begin{equation*} f_n(x) = \begin{cases} a_n(1-nx) & \text{se $0 \leq x < 1/n$}\\ 0 & \text{altrimenti} \end{cases} \qquad \forall n \in \mathbb{N}. \end{equation*}$

Studiare la convergenza puntuale e uniforme di $f_n$ nei seguenti casi:

$\,$

$a_n = 1/n$ ;

$\quad$

$a_n$ è una successione convergente.

Soluzione punto 1.

Dato che $a_n=\dfrac{1}{n}$ , poiché $0 \leq (1-nx)\leq 1$ per ogni $n \in \mathbb{N}$ e per ogni $x \in \left[0,\dfrac{1}{n}\right]$ , si ha

(28) $\begin{equation*} \lim_{n \to +\infty} \,\sup_{x \in\mathbb{R}} \left| f_n(x) \right| \leq \lim_{n \to +\infty}|a_n| = \lim_{n \to +\infty} \frac{1}{n} = 0, \end{equation*}$

da cui segue la c da cui segue la convergenza uniforme di $f_n$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla.

Soluzione punto 2.

Supponiamo che $\lim_{n\to +\infty} a_n=a \in R$ ; se $x \neq 0$ , si ha che $x \notin \left[0,\dfrac{1}{n}\right]$ per ogni $n > \dfrac{1}{x}$ ; pertanto $f_n(x)=0$ per ogni $n > \dfrac{1}{x}$ e quindi $f_n$ converge puntualmente alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da

(29) $\begin{equation*} f(x) = \begin{cases} a & \text{se } x=0 \\ 0 & \text{se } x \ne 0. \end{cases} \end{equation*}$

Poiché per ogni $n \in \mathbb{N}$ si ha $\lim_{x \to 0^+}f_n(x)=a_n$ , si ottiene

(30) $\begin{equation*} \sup_{x \in\mathbb{R} \setminus \{0\}} |f_n(x) - f(x)| %=\max \left\{|a_n-a|, \sup_{x \in(0,+\infty)} |f_n(x)| %\right\} = a \qquad \forall n \in \mathbb{N}. \end{equation*}$

Poiché per ipotesi

(31) $\begin{equation*} \lim_{n \to + \infty} |f_n(0)-f(0)| = \lim_{n \to +\infty} |a_n-a| = 0, \end{equation*}$

da (30) segue quindi che $\lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |f_n(x) - f(x)|=0$ se e solo se $a=0$ ; pertanto si ha convergenza uniforme di $f_n$ a $f$ se e solo se $a=0$ .

Alternativamente, per studiare la convergenza uniforme di $f_n$ a $f$ , si poteva anche osservare che le $f_n$ sono continue in $[0,+\infty)$ , mentre la funzione $f$ è continua in $0$ solo se $a=0$ , pertanto per il teorema 1.5 non si ha convergenza uniforme se $a \neq 0$ . Riguardo il caso $a=0$ , si poteva procedere osservando che le funzioni $f_n$ sono decrescenti in $[0,1]$ , quindi in tale intervallo si ha convergenza uniforme a $f$ per il teorema 1.10. Poiché le $f_n$ sono identicamente nulle in $\mathbb{R} \setminus [0,1]$ , è chiaro che la convergenza di $f_n$ a $f$ è uniforme in $\mathbb{R}$ .

Esercizio 6 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \dfrac{x^2+nx}{2x^2+n^2} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti casi:

$\,$

in $\mathbb{R}$ ;

negli intervalli del tipo $[-R,R]$ con $R>0$ .

Soluzione punto 1.

Studiamo separatamente i due casi. alcoliamo il limite puntuale della successione $f_n$ ; a tal fine, fissiamo $x \in \mathbb{R}$ e osserviamo che

$\lim_{n\to +\infty} \dfrac{x^2+nx}{2x^2+n^2} =\lim_{n\to +\infty}\dfrac{\dfrac{x^2}{n}+x}{n\left( \dfrac{2x^2}{n^2}+1\right)} =0.$

Quindi la successione converge puntualmente alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da $f(x)=0$ per ogni $x \in \mathbb{R}$ .

Per studiarne la convergenza uniforme, osserviamo che si ha

(32) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in \mathbb{R}} |f_n(x)-f(x)| \geq \lim_{n \to +\infty} f_n(n) %= %\frac{2n^2}{3n^2} = \frac{2}{3}. \end{equation*}$

Da ciò e dalla proposizione 1.3, segue che la convergenza non è uniforme.

Soluzione punto 2.

Fissiamo $R>0$ ; per il punto precedente, il limite puntuale della successione in $[-R,R]$ è la funzione $f$ .

Per studiare la convergenza uniforme, osserviamo che si ha

(33) $\begin{gather*} |x^2+nx| \leq x^2 + n|x| \leq R^2 + nR \qquad \forall x \in [-R,R], \,\, \forall n \in \mathbb{N}, \\ 2x^2 + n^2 \geq n^2 \qquad \forall x \in [-R,R], \,\, \forall n \in \mathbb{N}. \end{gather*}$

Da ciò segue che Da ciò segue che

(34) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in [-R,R]} |f_n(x) - f(x)| \leq \lim_{n \to +\infty} \frac{R^2 + nR}{n^2} =0. \end{equation*}$

Da tale relazione e dalla proposizione 1.3, segue che la convergenza di $f_n$ a $f$ in $[-R,R]$ è uniforme.

Esercizio 7 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

(35) $\begin{equation*} f_n(x) = e^{-(n+ 4x)^2} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}, \end{equation*}$

nei seguenti insiemi:

$\,$

in $\mathbb{R}$ ;

negli intervalli del tipo $[R,+\infty]$ , con $R \in \mathbb{R}$

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Per ogni $x \in \mathbb{R}$ si ha $\lim_{n \to +\infty} (n+4x)=+\infty$ , pertanto

(36) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \lim_{n \to +\infty} e^{-(n+ 4x)^2} = 0 \qquad \forall x \in \mathbb{R}. \end{equation*}$

Quindi $f_n$ converge puntualmente in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla. La convergenza non è però uniforme; infatti osserviamo che, poiché $e^{0}=1$ , si ha

(37) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |f_n(x)| \geq \lim_{n \to +\infty} f_n\left(-\frac{n}{4}\right) = \lim_{n \to +\infty} e^{-(n + n)} = 1. \end{equation*}$

Per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme.

Soluzione punto 2.

Sia $\mathbb{R} \in \mathbb{R}$ . Se $n\geq 4|R|$ , si ha

(38) $\begin{equation*} n+4x \geq 4|R|+ 4R \geq 0 \qquad \forall x \in [R,+\infty) \end{equation*}$

e, dalla monotonia della funzione esponenziale, segue che $f_n$ è decrescente in $[R,+\infty)$ . Quindi

(39) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[R,+\infty)} |f_n(x)| = \lim_{n \to +\infty} f_n(R) = 0, \end{equation*}$

dove nell’ultima uguaglianza abbiamo usato la convergenza puntuale di $f_n$ a $0$ . Di nuovo per la proposizione 1.3, la convergenza di $f_n$ a $f$ è uniforme in $[R,+\infty)$ .

Esercizio 8 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $E \subseteq R$ , sia $f_n \colon E \to \mathbb{R}$ una successione di funzioni convergente uniformemente a una funzione $f \colon E \to \mathbb{R}$ e sia $g \colon E \to \mathbb{R}$ una funzione.

$\,$

Studiare la convergenza puntuale e uniforme della successione di funzioni $g \cdot f_n$ .

$\quad$

Come cambia la risposta al punto precedente assumendo che la funzione $g$ sia limitata?

Soluzione punto 1.

Rispondiamo separatamente alle due questioni.

Poiché in particolare $f_n$ converge puntualmente a $f$ , si ha

(40) $\begin{equation*} \lim_{n \to +\infty} g(x)f_n(x) = g(x)f(x) \qquad \forall x \in E. \end{equation*}$

La convergenza può tuttavia non essere uniforme. Si considerino ad esempio $E=\left[0,\dfrac{\pi}{2}\right)$ e le funzioni $f_n,g \colon E \to \mathbb{R}$ definite da

(41) $\begin{equation*} f_n(x)=\frac{1}{n}, \quad g(x)=\tan x \qquad \forall n \in \mathbb{N}, \,\,\forall x \in E. \end{equation*}$

Si ha che $f_n$ converge uniformemente su $E$ a $f \colon E \to \mathbb{R}$ identicamente nulla, ma

(42) $\begin{equation*} \sup_{x \in E} |g(x)f_n(x)| = \sup_{x \in [0,\frac{\pi}{2})}\dfrac{\tan x}{n} = +\infty \qquad \forall n \in \mathbb{N}. \end{equation*}$

Per la proposizione 1.3, $g f_n$ non converge uniformemente a $gf$ in $E$ .

Soluzione punto 2.

Se $g$ è limitata, in particolare valgono i risultati del punto precedente, ossia $gf_n$ converge puntualmente a $gf$ . In questo caso, però, la convergenza è anche uniforme. Infatti, sia $M=\sup_E |g|$ , che è finito per ipotesi. Si ha

(43) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in E} |gf_n(x) - gf(x)| \leq & \lim_{n \to +\infty} \left( \sup_{x \in E}|g(x)| \cdot \sup_{x \in E} |f_n(x)-f(x)| \right) \\ \leq & M \lim_{n \to +\infty} \sup_{x \in E} |f_n(x)-f(x)| \\ = & 0, \end{split} \end{equation*}$

dove nella seconda disuguaglianza si è usato che $\supx{E}|g(x)|=M$ e nell’uguaglianza si è usata la convergenza uniforme di $f_n$ a $f$ . La proposizione 1.3 e (43) provano quindi che $gf_n$ converge uniformemente a $gf$ in $E$ .

Esercizio 9 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \frac{x}{x^2 + \dfrac{1}{n}} \qquad \forall n \in \mathbb{N},\,\, \forall x \in [0, +\infty),$

nei seguenti insiemi:

$\,$

in $[0, +\infty)$ ;

$\quad$

in $(0,+\infty)$ ;

$\quad$

negli intervalli del tipo $[a,+\infty)$ con $a>0$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Se $x=0$ si ha banalmente $f_n(0)=0$ per ogni $n \in \mathbb{N}$ . Se $x \ne 0$ si ha $\lim_{n\to +\infty} f_n(x)=\dfrac 1x$ poiché $\lim_{n \to +\infty} \frac 1n = 0$ . Da ciò segue che il limite puntuale $f \colon [0,+\infty) \to \mathbb{R}$ della successione $f_n$ è dato da

$f(x)=\begin{cases} 0 & \text{se } x = 0\\ \dfrac 1x & \text{se } x \neq 0. \end{cases}$

Poichè le $f_n$ sono continue e $f$ è discontinua, dal teorema 1.5 segue che la convergenza non è uniforme.

Soluzione punto 2.

Dato che 0 è un punto di accumulazione di $(0,+\infty)$ e vale

(44) $\begin{equation*} \lim_{x \to 0^+} f_n(x) = 0 \quad \forall n \in \mathbb{N}, \qquad \lim_{x \to 0^+} f(x) = +\infty, \end{equation*}$

dal teorema 1.6 segue che la convergenza di $f_n$ a $f$ non è uniforme in $(0,+\infty)$ .

Si poteva mostrare che la convergenza di $f_n$ a $f$ non è uniforme in $(0,+\infty)$ anche osservando che da (44) segue

(45) $\begin{equation*} \supx{(0,+\infty)} \vdiff = +\infty \qquad \forall n \in \mathbb{N}, \end{equation*}$

oppure che

(46) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in (0,+\infty)} |f_n(x) - f(x)| \geq \lim_{n \to +\infty} \left| f_n \left(\frac{1}{\sqrt{n}} \right) - f \left(\frac{1}{\sqrt{n}} \right) \right| = \lim_{n \to +\infty} \left| \frac{\sqrt{n}}{2} - \frac{\sqrt{n}}{1} \right| = +\infty. \end{equation*}$

In entrambi i casi, la tesi segue dalla proposizione 1.3.

Soluzione punto 3.

Si ha

(47) $\begin{equation*} \left|f_{n}(x)-f(x)\right|=\left|\frac{x}{x^{2}+\dfrac{1}{n}}-\frac{1}{x}\right|=\left|\frac{-\dfrac{1}{n}}{x\left(x^{2}+\dfrac{1}{n}\right)}\right| \leq \frac{1}{na^3} \qquad \forall n \in \mathbb{N},\,\, \forall x \in [a,+\infty), \end{equation*}$

dove la disuguaglianza segue dal fatto che

(48) $\begin{equation*} x\left(x^{2}+\frac{1}{n}\right) \geq x^{3} \geq a^{3} \qquad \forall x \in [a,+\infty),\,\, \forall n \in \mathbb{N}. \end{equation*}$

Da (47) si ha che

(49) $\begin{equation*} 0 \leq \lim_{n \to +\infty} \sup _{x \in[a,+\infty)}\left|f_{n}(x)-f(x)\right| \leq \lim_{n \to +\infty} \frac{1}{na^3} = 0, \end{equation*}$

da cui abbiamo la convergenza uniforme di $f_n$ a $f$ in $[a,+\infty)$ .

Esercizio 10 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \frac{nx}{1+n^2 x^2} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti insiemi:

$\quad$

in $\mathbb{R}$ ;

$\quad$

negli insiemi del tipo $(-\infty,-a] \cup [a,+\infty)$ con $a>0$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi. Innanzitutto osserviamo che ognuna delle $f_n$ è dispari, quindi basta studiare la convergenza puntuale e uniforme negli insiemi del tipo $[a,+\infty)$ con $a \geq 0$ .

Si ha

$\lim_{n\to +\infty} f_n(x)= \lim_{n\to \infty} \frac{nx}{1+n^2 x^2}=0 \qquad \forall x\in [0,+\infty),$

dunque la successione $f_n$ converge puntualmente in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla.

Affermiamo che la convergenza non è però uniforme. Per mostrarlo, poiché ognuna delle $f_n$ è derivabile in $\mathbb{R}$ studiamo $f_n'$ :

$f_{n}^{\prime}(x)= \frac{n(1+n^2x^2) - nx(2n^2x)}{\left(1+n^{2} x^{2}\right)^{2}} = \frac{n\left(1-n^{2} x^{2}\right)}{\left(1+n^{2} x^{2}\right)^{2}} \geq 0 \iff x \in \left[0,\frac{1}{n}\right]\,\,\, \forall n \in \mathbb{N}.$

Quindi ogni $f_n$ è crescente nell’intervallo $\left[0,+\dfrac{1}{n}\right]$ e decrescente in $\left[\dfrac{1}{n},+\infty\right)$ . Poiché $f_n(x) \geq 0$ per ogni $x \in [0,+\infty)$ , il punto $\dfrac{1}{n}$ è di massimo assoluto per la funzione $|f_n|$ . Da tali considerazioni si ottiene

(50) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[0,+\infty)} |f_n(x)-f(x)| = \lim_{n \to +\infty} f_n \left(\frac{1}{n}\right) = \frac{1}{2} \neq 0. \end{equation*}$

Per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme in $\mathbb{R}$ .

Soluzione punto 2.

Sia $a>0$ ; affermiamo che $f_n$ converge uniformemente a $f$ in $[a,+\infty)$ . Poiché

(51) $\begin{equation*} f_{n}^{\prime}(x)=\frac{n\left(1-n^{2} x^{2}\right)}{\left(1+n^{2} x^{2}\right)^{2}} \leq 0 \qquad \forall n \in \mathbb{N} ,\,\, \forall x \in \left[\frac{1}{n},+\infty \right), \end{equation*}$

si ha

(52) $\begin{equation*} \max_{x \in [a,+\infty)} f_n(x)= f_n(a) \qquad \forall n \geq \frac{1}{a}. \end{equation*}$

Dato che $f_n(x)\geq 0$ per $x \in [a,+\infty)$ per ogni $n \in \mathbb{N}$ , da (52) segue che

(53) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[a,+\infty)} |f_n(x)-f(x)| = \lim_{n \to +\infty} f_n(a) = 0, \end{equation*}$

dove l’ultima uguaglianza deriva dalla convergenza puntuale di $f_n$ alla funzione nulla. Per (53) e per la proposizione 1.3, la convergenza è uniforme su $(-\infty,-a] \cup [a,+\infty)$ (in quanto $f_n$ e $f$ sono dispari).

Scarica gli esercizi svolti

Ottieni il documento contenente 42 esercizi risolti, contenuti in 69 pagine ricche di dettagli, per migliorare la tua comprensione delle successioni di funzioni

Esercizio 11 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \left(1+\sin^2(nx) \right)e^{-nx} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti insiemi:

$\quad$

in $\mathbb{R}$ ;

$\quad$

in $[0,+\infty)$ ;

$\quad$

in $[0,+\infty)$ ;.

$\quad$

negli intervalli del tipo $[a,+\infty)$ con $a>0$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Poiché

(54) $\begin{equation*} 1 \leq 1 + \sin^2(nx) \leq 2 \qquad \forall n \in \mathbb{N},\,\,\forall x \in \mathbb{R}, \end{equation*}$

calcoliamo il limite puntuale della successione $f_n$ :

(55) $\begin{equation*} \lim_{n\to \infty} f_n(x) = \lim_{n\to \infty} \left(1+\sin^2(nx) \right)e^{-nx} = \begin{cases} +\infty & \text{se } x \in (-\infty,0)\\ 1 & \text{se } x=0\\ 0 & \text{se } x \in(0,+\infty). \end{cases} \end{equation*}$

Da ciò segue che non vi è convergenza puntuale (e quindi nemmeno uniforme) in $\mathbb{R}$ .

Soluzione punto 2.

Da (55) si vede che la successione $f_n$ converge puntualmente in $[0,+\infty)$ alla funzione $f \colon [0,+\infty)$ definita da

(56) $\begin{equation*} f(x) = \begin{cases} 1 & \text{se } x=0\\ 0 & \text{se } x \in(0,+\infty). \end{cases} \end{equation*}$

Poiché ogni $f_n$ è una funzione continua e dato che $f$ è discontinua in $x=0$ , dal teorema 1.5 si deduce che la convergenza di $f_n$ a $f$ non è uniforme in $[0,+\infty)$ .

Soluzione punto 3.

Di nuovo da (55), chiaramente $f_n$ converge puntualmente in $(0,+\infty)$ alla funzione $f$ . Poiché 0 è un punto di accumulazione di $(0,+\infty)$ e vale

(57) $\begin{equation*} \lim_{x \to 0^+} f_n(x) = 1 \quad \forall n \in \mathbb{N}, \qquad \lim_{x \to 0^+} f(x) = 0, \end{equation*}$

dal teorema 1.6 segue che la convergenza di $f_n$ a $f$ non è uniforme.

Un altro modo per mostrare che la convergenza di $f_n$ a $f$ non è uniforme consiste nel notare che, poiché $f(x) = 0$ per ogni $x \in (0,+\infty)$ e $\lim_{x \to 0^+}f_n(x)=1$ per ogni $n \in \mathbb{N}$ , segue che

(58) $\begin{equation*} \sup_{x \in (0,+\infty)} |f_n(x) - f(x)| \geq 1 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è quindi uniforme.

Soluzione punto 4.

Sia $a>0$ . Da (55), $f_n$ converge puntualmente alla funzione nulla $f$ . Per studiare la convergenza uniforme, osserviamo che, da (54) si ha

(59) $\begin{equation*} |f_n(x)| \leq 2 e^{-nx} \leq 2e^{-na} \qquad \forall n \in \mathbb{N},\,\, \forall x \in [a,+\infty) \end{equation*}$

dove l’ultima disuguaglianza segue dal fatto che la funzione $x \mapsto e^{-nx}$ è decrescente in $[a,+\infty)$ per ogni $n \in \mathbb{N}$ . Da ciò segue che

(60) $\begin{equation*} 0 \leq \lim_{n \to \infty} \sup_{x \in [a,+\infty)}|f_n(x)-f(x)| \leq 2\lim_{n \to \infty} 2e^{-na} = 0, \end{equation*}$

dove l’ultima uguaglianza è conseguenza del fatto che $a>0$ . Da (60) e dalla proposizione 1.3, si ha che $f_n$ converge uniformemente a $f$ su $[a,+\infty)$ .

Esercizio 12 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $f \colon \mathbb{R} \to \mathbb{R}$ una funzione e si assuma che la successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

(61) $\begin{equation*} f_n(x) = f(nx) \qquad \forall n \in \mathbb{N},\,\,\forall x \in \mathbb{R} \end{equation*}$

sia equicontinua (si veda la definizione 1.12). Cosa si può concludere su $f$ ?

Soluzione.

Affermiamo che $f$ è una funzione costante. Si consideri $\sigma \colon [0,+\infty) \to [0,+\infty)$ un modulo di continuità (si veda la definizione 1.11) per tutte le funzioni $f_n$ , si fissi $\varepsilon>0$ e sia $\delta>0$ tale che

(62) $\begin{equation*} \sigma(|t-s|)< \varepsilon \qquad \forall t,s \in \mathbb{R} \colon |t-s|< \delta. \end{equation*}$

Siano $x,y \in \mathbb{R}$ e si fissi $n \in \mathbb{N}$ tale che

(63) $\begin{equation*} \left| \dfrac{x}{n} - \dfrac{y}{n}\right| < \delta. \end{equation*}$

Allora si ha

(64) $\begin{equation*} |f(x)-f(y)| = \left| f \left(n\cdot\frac{x}{n}\right) - f \left(n\cdot\frac{y}{n}\right)\right| = \left| f_n \left(\frac{x}{n}\right) - f_n \left(\frac{y}{n}\right)\right| < \sigma\left(\left| \frac{x}{n}- \frac{y}{n}\right| \right) < \varepsilon, \end{equation*}$

dove la prima disuguaglianza segue dal fatto che $\sigma$ è un modulo di continuità per ognuna delle $f_n$ , mentre la seconda è dovuta a (63) e (62).

Per l’arbitrarietà di $\varepsilon >0$ e di $x,y \in \mathbb{R}$ , (64) mostra che $f$ è costante.

Esercizio 13 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \frac{nx}{1 + n^4 x^2} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti insiemi:

$\,$

in $\mathbb{R}$ ;

negli intervalli del tipo $[-R,R]$ , con $R>0$ .

Studiare infine la validità della seguente uguaglianza:

(65) $\begin{equation*} \lim_{n \to +\infty} \int_{0}^{1} f_n(x) \dif x = \int_{0}^{1} \lim_{n \to +\infty} f_n(x) \dif x. \end{equation*}$

Soluzione.

Si ha

(66) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \lim_{n \to +\infty} \frac{nx}{1 + n^4 x^2} = 0 \qquad \forall x \in \mathbb{R}, \end{equation*}$

quindi le $f_n$ convergono puntualmente in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla.

La convergenza è anche uniforme; infatti innazitutto osserviamo che le funzioni $f_n$ sono dispari, quindi basta mostrare la convergenza uniforme in $[0,+\infty)$ . In secondo luogo, osserviamo che per ogni $n \in \mathbb{N}$ si ha

(67) $\begin{equation*} f_n(0)=0, \qquad \lim_{x \to +\infty} f_n(x)=0, \qquad f_n(x) \geq 0 \quad \forall x \geq 0, \end{equation*}$

pertanto

(68) $\begin{equation*} \supx{[0,+\infty)}|f_n|= \max_{[0,+\infty)}f_n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Per determinare tale massimo, poiché le $f_n$ sono derivabili, studiamo

(69) $\begin{equation*} f_n'(x)= \frac{n\left(n^{4} x^{2}+1\right)-2 n^{4} x \cdot n x}{\left(1+n^{4} x^{2}\right)^{2}}=\frac{n\left(1-n^{4} x^{2}\right)}{\left(1+n^{4} x^{2}\right)^{2}}, \end{equation*}$

da cui

$f_n'(x) \ge 0 \iff |x|\le \frac{1}{n^2} \qquad \forall n \in \mathbb{N}.$

Da ciò e da (68) segue che

(70) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[0,+\infty)}|f_n| = \lim_{n \to +\infty} f_n\left(\frac{1}{n^2} \right) = \lim_{n \to +\infty} \frac{1}{2n} = 0. \end{equation*}$

Questo prova la convergenza uniforme delle $f_n$ a $f$ . Per il teorema 1.7, si ha quindi che (65) è valida.

Esercizio 14 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $f_n \colon \mathbb{R} \to \mathbb{R}$ la successione di funzioni definita da

$f_n(x) = \arctan \left(\frac{x}{n} \right) \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}.$

$\quad$

Mostrare che la successione delle derivate $f_n'$ converge uniformemente in $\mathbb{R}$

Mostrare che la successione delle $f_n$ non converge uniformemente in $\mathbb{R}$ .

In quali intervalli $f_n$ converge uniformemente?

Soluzione punto 1.

Rispondiamo separatamente alle questioni poste.

Ognuna delle $f_n$ è derivabile e si ha

(71) $\begin{equation*} f_n'(x) = \frac{\dfrac 1n}{1+\left(\dfrac{x}{n}\right)^2} \qquad \forall n \in \mathbb{N}, \,\, \forall x\in \mathbb{R}. \end{equation*}$

Dato che $1+\left(\dfrac{x}{n}\right)^2 \geq 1$ , si ha

(72) $\begin{equation*} |f_n'(x)| \leq \frac{1}{n} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}, \end{equation*}$

da cui segue che

(73) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |f_n'(x)| \leq \lim_{n \to +\infty} \frac{1}{n} = 0 \end{equation*}$

e, per la proposizione 1.3, $f_n'$ converge uniformemente alla funzione $g \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla.

Soluzione punto 2.

Dalla continuità della funzione $\arctan$ si ha

$\lim_{n\to\infty} f_n(x)= \lim_{n \to +\infty} \arctan \left(\frac{x}{n} \right) = \arctan(0)=0 \qquad \forall x\in \mathbb{R},$

da cui si ha che $f_n$ converge puntualmente in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla. Mostriamo che la convergenza non è uniforme. Infatti, si ha

(74) $\begin{equation*} \lim_{x \to +\infty} f_n(x) = \lim_{x \to +\infty} \arctan \left(\frac{x}{n} \right) = \frac{\pi}{2} \qquad \forall n \in \mathbb{N}. \end{equation*}$

Pertanto

(75) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |f_n(x)-f(x)| = \frac{\pi}{2} \neq 0, \end{equation*}$

e, per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme.

Soluzione punto 3.

Come si è visto, la successione delle derivate $f_n'$ converge uniformemente in $\mathbb{R}$ alla funzione $g \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla, e inoltre $\lim_{n \to +\infty} f_n(0)=0$ . Il teorema 1.8 implica allora che $f_n$ converge uniformemente a $f$ su ogni intervallo del tipo $[-R,R]$ per $R>0$ .

Un’altra conseguenza del teorema 1.8 è inoltre che $f$ è derivabile e $f'=g$ , ma ciò segue banalmente anche dal fatto che $f=g$ .

$\,$

Osservazione 3.1.

Questo esempio, poiché $\lim_{n \to +\infty} f_n(0)=0$ , mostra che l’ipotesi di limitatezza dell’intervallo $[a,b]$ nel teorema 1.8 è essenziale.

Esercizio 15 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definite da

(76) $\begin{equation*} f_n(x) = n \sin \left( \dfrac{e^{-nx^2}}{n}\right) \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}, \end{equation*}$

nei seguenti insiemi:

$\,$

in $\mathbb{R}$ .

$\quad$

negli insiemi del tipo $(-\infty,r] \cup [r,+\infty)$ , con $r >0$ .

Soluzione punto 1.

Cominciamo col notare che ogni $f_n$ è una funzione pari, quindi è sufficiente limitarci a studiarne la convergenza in insiemi del tipo $[r,+\infty)$ con $r \geq 0$ .

Per quanto riguarda la convergenza puntuale in $[0,+\infty)$ , si ha

(77) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \lim_{n \to +\infty} e^{-nx^2} \dfrac{\sin \left( \dfrac{e^{-nx^2}}{n}\right)}{\dfrac{e^{-nx^2}}{n}} = \begin{cases} 1 & \text{se } x=0\\ 0 & \text{se } x\neq 0, \end{cases} \end{equation*}$

dove la seconda uguaglianza segue da

(78) $\begin{equation*} \lim_{n \to +\infty} {e^{-nx^2}} = \begin{cases} 1 & \text{se } x=0\\ 0 & \text{se } x\neq 0, \end{cases} \qquad \lim_{n \to +\infty} \dfrac{e^{-nx^2}}{n} = 0 \quad \forall x \in \mathbb{R}, \qquad \text{e} \qquad \lim_{t \to 0} \dfrac{\sin t}{t}=1. \end{equation*}$

Quindi $f_n$ converge puntualmente in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da

(79) $\begin{equation*} f(x) = \begin{cases} 1 & \text{se } x=0\\ 0 & \text{se } x\neq 0, \end{cases} \end{equation*}$

Poiché ogni $f_n$ è una funzione continua mentre $f$ non lo è, per il teorema 1.5 la convergenza di $f_n$ a $f$ non può essere uniforme in $[0,+\infty)$ .

Soluzione punto 2.

Sia $r>0$ . Affermiamo che la convergenza di $f_n$ a $f$ in $[r,+\infty)$ è uniforme. A tal fine, osserviamo che la funzione $g_n \colon [0,+\infty) \to \mathbb{R}$ definita da $g_n(x)= \dfrac{e^{-nx^2}}{n}$ è decrescente e soddisfa

(80) $\begin{equation*} g_n(0)=1, \qquad \lim_{x \to +\infty} g_n(x) = 0. \end{equation*}$

Inoltre, la funzione $t \mapsto \sin t$ è crescente e positiva in $[0,1]$ . Poiché $f_n(x)= n \sin (g_n(x))$ , da tali considerazioni segue quindi che ognuna delle funzioni $f_n$ è decrescente e positiva in $[r,+\infty)$ . Pertanto

(81) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in [r,+\infty)} |f_n(x)-f(x)| = \lim_{n \to +\infty} f_n(r) = 0, \end{equation*}$

dove l’ultima uguaglianza segue dalla convergenza puntuale di $f_n$ a $0$ . La proposizione 1.3 e la (81) implicano la convergenza uniforme di $f_n$ a $f$ in $[r,+\infty)$ .

Esercizio 16 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon [0,+\infty) \to \mathbb{R}$ definita da

(82) $\begin{equation*} f_n(x) = \int_0^{\frac{x}{n}} \frac{\dif t}{(\sin^2 t + 1)\sqrt{t+1}} \qquad \forall n \in \mathbb{N},\,\, \forall x \in [0,+\infty), \end{equation*}$

nei seguenti insiemi:

$\,$

in $[0,+\infty)$ ;

$\quad$

negli intervalli del tipo $[0,R]$ , con $R >0$ .

Soluzione punto 1.

Distinguiamo i diversi casi.

Si ha

(83) $\begin{equation*} |f_n(x)| = \int_0^{\frac{x}{n}} \frac{\dif t}{(\sin^2 t + 1)\sqrt{t+1}} \leq \frac{x}{n} \sup_{t \in[0,\frac{x}{n}]} \frac{1}{(\sin^2 t + 1)\sqrt{t+1}} \leq \frac{x}{n} \qquad \forall n \in \mathbb{N}, \,\, \forall x \geq 0, \end{equation*}$

dove la prima disuguaglianza segue dal fatto che $\int_0^a g(t) \dif t \leq |a| \cdot \sup_{[0,a]}|g|$ , mentre la seconda disuguaglianza segue dal fatto che $\sin^2 t +1 \geq 1$ e $\sqrt{t+1}\geq 1$ per ogni $t \geq 0$ .

Da (83) segue che $\lim_{n \to +\infty} f_n(x) = 0$ ², pertanto $f_n$ converge puntualmente alla funzione $f \colon [0,+\infty) \to \mathbb{R}$ identicamente nulla.

La convergenza non è però uniforme, in quanto

(84) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in[0,+\infty)} |f_n(x)| \geq & \lim_{n \to +\infty} f_n\left( \frac{n\pi}{2}\right) \\ \geq & \frac{\pi}{2} \, \min_{t \in [0,\frac{\pi}{2}]}\,\frac{1}{(\sin^2 t + 1)\sqrt{t+1}} \\ = & \frac{\pi}{2} \, \frac{1}{2 \cdot \sqrt{\frac{\pi}{2}+1}}, \end{split} \end{equation*}$

dove la seconda disuguaglianza segue dal fatto che $\int_0^a g(t) \dif t \geq |a| \cdot \inf_{[0,a]}|g|$ , mentre la terza disuguaglianza segue dal fatto che le funzioni $t \mapsto \sin^2 t+1$ e $t \mapsto \sqrt{t+1}$ sono crescenti in $\left[0,\dfrac{\pi}{2}\right]$ . (84) e la proposizione 1.3 implicano che la convergenza di $f_n$ a $f$ non è uniforme in $[0,+\infty)$ .

$\,$

Tale uguaglianza poteva anche dedursi dal fatto generale che, se $g \colon \mathbb{R} \to \mathbb{R}$ è limitata, allora la funzione integrale

(85) $\begin{equation*} y \mapsto \int_0^y f(t) \dif t \end{equation*}$

è continua. ↩

Soluzione punto 2.

Sia $R>0$ ; la convergenza di $f_n$ a $f$ è uniforme in $[0,R]$ . Per provarlo, osserviamo che la funzione $g \colon [0,+\infty) \to \mathbb{R}$ definita da

(86) $\begin{equation*} g(t) = \frac{1}{(\sin^2 t + 1)\sqrt{t+1}} \qquad \forall t \geq 0, \end{equation*}$

è positiva per ogni $t \geq 0$ . Pertanto ognuna delle $f_n$ è crescente: se $x \leq y$ , allora si ha

(87) $\begin{equation*} f_n(y) - f_n(x) = \int_{\frac{x}{n}}^{\frac{y}{n}} \frac{\dif t}{(\sin^2 t + 1)\sqrt{t+1}} \geq 0 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Poiché ognuna delle $f_n$ è crescente e il limite puntuale $f$ è continuo, per il teorema 1.10 la convergenza di $f_n$ a $f$ è uniforme in $[0,R]$ .

Esercizio 17 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dati $b > a >0$ , calcolare il seguente limite:

(88) $\begin{equation*} \lim_{n \to +\infty} \int_a^b n^2 \sin \frac{1}{n^2x} \, \mathrm{d} x. \end{equation*}$

Soluzione.

Chiamando $f_n \colon (0,+\infty) \to \mathbb{R}$ la funzione definita da

(89) $\begin{equation*} f_n(x) = n^2\sin \frac{1}{n^2x} \qquad \forall n \in \mathbb{N},\,\, \forall x >0, \end{equation*}$

osserviamo che si ha

(90) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \frac{1}{x} \lim_{n \to +\infty} \frac{\sin \frac{1}{n^2x}}{\frac{1}{n^2x}} = \frac{1}{x} \qquad \forall x >0. \end{equation*}$

Pertanto $f_n$ converge puntualmente in $(0,+\infty)$ alla funzione $f \colon (0,+\infty) \to \mathbb{R}$ definita da $f(x)=\dfrac{1}{x}$ .

Affermiamo che la convergenza è anche uniforme in $[a,b]$ . Infatti

(91) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in[a,b]} |f_n(x)-f(x)| = & \lim_{n \to +\infty} \sup_{x \in[a,b]} \frac{1}{x} \left(1 - \frac{\sin \dfrac{1}{n^2x}}{\dfrac{1}{n^2x}} \right) \\ \leq & \frac{1}{a}\lim_{n \to +\infty} \sup_{t \in [\frac{1}{n^2b}, \frac{1}{n^2a}]} \left(1 - \frac{\sin t}{t} \right) \\ = & 0, \end{split} \end{equation*}$

dove nella disuguaglianza abbiamo usato che $\dfrac{1}{x} \leq \dfrac{1}{a}$ in $[a,b]$ e abbiamo effettuato la sostituzione $t=\dfrac{1}{n^2x}$ , mentre nell’uguaglianza abbiamo usato il limite notevole $\lim_{t \to 0} \dfrac{\sin t}{t}=1$ . Per (91) e la proposizione 1.3, la convergenza di $f_n$ a $f$ è uniforme in $[a,b]$ .

Possiamo quindi usare il teorema 1.7 e affermare che

(92) $\begin{equation*} \lim_{n \to +\infty} \int_a^b n^2 \sin \frac{1}{n^2x} \, \mathrm{d} x = \int_a^b \frac{1}{x} \, \mathrm{d} x = \left[\log x \right]_a^b = \log \frac{b}{a}. \end{equation*}$

Esercizio 18 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data una successione $a_n$ di numeri reali non negativi, si consideri la successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = x^n e^{-a_n x} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}.$

Si determinino gli eventuali intervalli di convergenza puntuale e uniforme della successione $f_n$ nei seguenti casi:

$\,$

$a_n = n$ ,

$a_n = \sqrt{n}$ .

Soluzione punto 1.

Affermiamo che esiste $a<0$ tale che

$\quad$

$f_n$ converge puntualmente in $(a,+\infty)$ alla funzione $f \colon (a,+\infty) \to \mathbb{R}$ identicamente nulla e non converge puntualmente in $(-\infty,a]$ .

$f_n$ converge uniformemente a $f$ negli intervalli del tipo $[a+\eta,+\infty)$ per ogni $\eta>0$ .

$f_n$ non converge uniformemente a $f$ in $(a,+\infty)$ .

Osserviamo che la funzione $\varphi \colon \mathbb{R} \to \mathbb{R}$ definita da

(93) $\begin{equation*} \varphi(x) = xe^{-x} \qquad \forall x \in \mathbb{R} \end{equation*}$

è continua, soddisfa $\lim_{x \to -\infty} \varphi_n(x)=-\infty$ , è crescente in $(-\infty,1]$ e decrescente in $[1,+\infty)$ . Pertanto

(94) $\begin{equation*} \max_{x \in \mathbb{R}} \varphi(x) = \varphi(1) = e^{-1}. \end{equation*}$

Inoltre vale $\lim_{x \to +\infty} \varphi(x)=0$ . Da queste considerazioni, segue che esiste $a<0$ tale che

(95) $\begin{equation*} \varphi(a)=-1, \qquad \varphi(x) \in (-1,e^{-1}] \iff x \in (a,+\infty). \end{equation*}$

$\quad$

Per provare l’affermazione 1, scriviamo
(96) $\begin{equation*} f_n(x) = x^n e^{-n x} = \big( xe^{-x}\big)^n = \big( \varphi(x)\big)^n \qquad \forall n \in \mathbb{N},\,\,\forall x \in \mathbb{R} \end{equation*}$

e osserviamo che la successione $(xe^{-x})^n$ converge a zero se e solo se $xe^{-x} \in (-1,1)$ . Da (95) e da $e^{-1}<1$ segue che $f_n$ converge puntualmente in $(a,+\infty)$ alla funzione $f \colon (a,+\infty) \to \mathbb{R}$ identicamente nulla.

Se $\eta>0$ , dalle proprietà di monotonia di $\varphi$ considerate sopra segue che
(97) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[a+\eta,+\infty)}|f_n(x)| = \lim_{n \to +\infty} \max\{|\varphi(a+\eta)^n|,e^{-n} \} = 0, \end{equation*}$

dove si è usato che $|\varphi(a+\eta)|<1$ . Dalla proposizione 1.3, $f_n$ converge uniformemente a $f$ in $[a+\eta,+\infty)$ .

Dalla continuità di $\varphi$ e dal fatto che $\varphi(a)=-1$ segue che
(98) $\begin{equation*} \lim_{x \to a^+} f_n(x) = \lim_{x \to a^+} (xe^{-x})^n = (-1)^n \qquad \forall n \in \mathbb{N}. \end{equation*}$

Da ciò si ottiene

(99) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in(a,+\infty)} |f_n(x)-f(x)| \geq 1 \neq 0, \end{equation*}$

quindi $f_n$ non converge uniformemente a $f$ in $(a,+\infty)$ .

Soluzione punto 2.

$\quad$

$f_n$ converge puntualmentein $(-1,1]$ alla funzione $f\colon (-1,1] \to \mathbb{R}$ identicamente nulla e non converge puntualmente al di fuori di tale intervallo;

$f_n$ converge uniformemente a $f$ negli intervalli del tipo $[-a,a]$ per ogni $a \in [0,1)$ ;

$f_n$ non converge uniformemente $f$ in $(-1,1)$ .

Proviamo separatamente le affermazioni fatte.

$\quad$

Scriviamo la successione di funzioni come
(100) $\begin{equation*} f_n(x) = \left(x\exp\left(-\frac{x}{\sqrt{n}}\right)\right)^n \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}. \end{equation*}$

Poiché per ogni $x \in \mathbb{R}$ si ha $\lim_{n \to +\infty} \exp\left(-\dfrac{x}{\sqrt{n}}\right)=1$ , otteniamo che

(101) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \begin{cases} \text{non esiste} & \text{se } x \leq -1\\ 0 & \text{se } x \in (-1,1]\\ %1 & \text{se } x=1\\ + \infty & \text{se } x >1. \end{cases} \end{equation*}$

Quindi $f_n$ converge puntualmente in $(-1,1]$ alla funzione $f\colon (-1,1] \to \mathbb{R}$ identicamente nulla e non converge al di fuori di questo intervallo.

Sia $a>0$ . Ogni $f_n$ è derivabile in $[-a,a]$ e vale
(102) $\begin{equation*} f_{n}^{\prime}(x)=\sqrt{n} x^{n-1} e^{-\sqrt{n} x}(\sqrt{n}-x) \qquad \forall n \in \mathbb{N},\,\, \forall x \in [-a,a]. \end{equation*}$

Dallo studio del segno di $f_n'$ , si vede che ogni $f_n$ è monotona negli intervalli $[-a,0]$ e in $[0,a]$ ; da ciò, insieme al fatto che $f_n(0)=0$ , si ottiene che

(103) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[-a,a]}|f_n(x)| = \lim_{n \to +\infty} \max\{|f_n(-a)|,|f_n(a)| \} = 0, \end{equation*}$

dove l’ultima uguaglianza segue dalla convergenza puntuale di $f_n$ a $0$ in $[-a,a]$ .

La convergenza di $f_n$ a $f$ non è uniforme in $(-1,1)$ in quanto
(104) $\begin{equation*} \lim_{x \to -1^+} f_n(x) = (-1)^ne^{\sqrt{n}} \qquad \forall n \in \mathbb{N}. \end{equation*}$

Da ciò segue che

(105) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in(-1,1)}|f_n(x)-f(x)| \geq \lim_{n \to +\infty} e^{\sqrt{n}} = +\infty. \end{equation*}$

Quindi la convergenza di $f_n$ a $f$ non è uniforme in $(-1,1)$ .

Esercizio 19 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right] \to \mathbb{R}$ definita da

(106) $\begin{equation*} f_n(x) = \left( \frac{1}{n} + \sin^2 x\right)^n \qquad \forall n \in \mathbb{N},\,\, \forall x \in \left[-\frac{\pi}{2},\frac{\pi}{2}\right], \end{equation*}$

nei seguenti insiemi:

$\,$

in $\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$ ;

negli intervalli del tipo $[-a,a]$ , con $a \in \left[0,\dfrac{\pi}{2}\right)$ ;

in $\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Se $x \in \left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ , allora $\sin^2x \in [0,1)$ , da cui esistono $N \in \mathbb{N}$ e $\alpha<1$ (dipendenti da $x$ ) tali che

(107) $\begin{equation*} 0 \leq \frac{1}{n} + \sin^2 x \leq \alpha < 1 \qquad \forall n \geq N. \end{equation*}$

Da ciò segue che

(108) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \lim_{n \to +\infty} \left( \frac{1}{n} + \sin^2 x\right)^n \leq \lim_{n \to +\infty} \alpha^n = 0 \qquad \forall x \in \left(-\frac{\pi}{2},\frac{\pi}{2}\right). \end{equation*}$

Se $x\in \left\{-\dfrac{\pi}{2},\dfrac{\pi}{2}\right\}$ , si ha invece $\sin^2 x=1$ e

(109) $\begin{equation*} \lim_{n \to +\infty} \left( \frac{1}{n} + 1\right)^n = e. \end{equation*}$

Per cui $f_n$ converge puntualmente alla funzione $f \colon \left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right] \to \mathbb{R}$ definita da

(110) $\begin{equation*} f(x) = \begin{cases} 0 & \text{se } x \in \left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\\[5pt] e & \text{se } x \in \left\{-\dfrac{\pi}{2},\dfrac{\pi}{2}\right\}. \end{cases} \end{equation*}$

Poiché ogni $f_n$ è continua, mentre $f$ non lo è, per il teorema 1.5 la convergenza non è uniforme.

Soluzione punto 2.

Sia $a \in \left[0,\dfrac{\pi}{2}\right)$ . Poiché tutte le funzioni $f_n$ sono pari, basta limitarci a studiare la convergenza uniforme in $[0,a]$ . Osserviamo che ogni $f_n$ è crescente in $[0,a]$ e il limite puntuale $f$ è continuo in $[0,a]$ ; pertanto, il teorema 1.10 implica che la convergenza di $f_n$ a $f$ è uniforme in $[0,a]$ .

Tale risultato poteva provarsi anche usando la proposizione 1.3 e osservando che, per la monotonia e la positivitità di $f_n$ in $[0,a]$ , si ha

(111) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[0,a]} |f_n(x)-f(x)| = \lim_{n \to +\infty} f_n(a) = 0, \end{equation*}$

dove l’ultima uguaglianza segue dalla convergenza puntuale di $f_n$ a $0$ in $a$ .

Soluzione punto 3.

La convergenza non è uniforme in $\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ in quanto

(112) $\begin{equation*} \lim_{x \to \frac{\pi}{2}} f_n(x) = \left( \frac{1}{n} + 1\right)^n >1 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Da ciò segue che

(113) $\begin{equation*} \sup_{x \in\left(-\frac{\pi}{2},\frac{\pi}{2}\right)} |f_n(x)-f(x)| \geq 1 \qquad \forall n \in \mathbb{N}, \end{equation*}$

per cui la convergenza di $f_n$ a $f$ non è uniforme in $\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ .

Esercizio 20 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . tudiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita per ricorrenza da

(114) $\begin{equation*} \begin{cases} f_0(x)=1\\ f_n(x)= f_{n-1}(x) + (3x)^n \end{cases} \qquad \forall x \in \mathbb{R},\,\, \forall n \in \mathbb{N}. \end{equation*}$

e determinarne l’eventuale limite.

Soluzione.

Calcoliamo i primi termini della successione per $x \in \mathbb{R}$ :

(115) $\begin{equation*} f_0(x)=1, \qquad f_1(x)=3x, \qquad f_2(x)=3x + (3x)^2, \qquad f_3(x)=3x + (3x)^2+(3x)^3. \end{equation*}$

Questi primi termini della successione sembrano suggerire che

(116) $\begin{equation*} f_n(x)= \sum_{k=0}^n (3x)^k \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}. \end{equation*}$

Ciò corrisponde al vero, e la dimostrazione è una semplice conseguenza del principio di induzione. Infatti, chiaramente si ha $f_1(x)= 1 + (3x)^1$ per ogni $x \in \mathbb{N}$ . Assumendo che $f_{n-1}(x)= \sum_{k=0}^{n-1} (3x)^k$ per ogni $x \in \mathbb{R}$ , si ha

(117) $\begin{equation*} f_{n}(x)= f_{n-1}(x)+ (3x)^n = \left( \sum_{k=0}^{n-1} (3x)^k \right) + (3x)^n = \sum_{k=0}^{n} (3x)^k \qquad \forall x \in \mathbb{R}. \end{equation*}$

Il principio di induzione assicura quindi la validità di (116).

$f_n(x)$ coincide dunque con la somma parziale di una serie geometrica di ragione $r= 3x$ . Da (116), utilizzando la nota formula³

(118) $\begin{equation*} \sum_{k=0}^n r^k = \frac{1-r^{n+1}}{1-r} \qquad \forall r \neq 1,\,\, \forall n \in \mathbb{N}, \end{equation*}$

si ottiene

(119) $\begin{equation*} f_n(x) = \begin{cases} \dfrac{1 - (3x)^{n+1}}{1-3x} & \text{se } x \neq \dfrac{1}{3}\\[10pt] n+1 & \text{se } x = \dfrac{1}{3} \end{cases} \qquad \forall n \in \mathbb{N}. \end{equation*}$

Si ha quindi

(120) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \begin{cases} \text{non esiste} & \text{se } x \leq -\dfrac{1}{3}\\[8pt] \dfrac{1}{1-3x} & \text{se } |x| < \dfrac{1}{3}\\[8pt] +\infty & \text{se } x \geq \dfrac{1}{3}. \end{cases} \end{equation*}$

Dunque $f_n$ converge puntualmente in $\left(-\dfrac{1}{3},\dfrac{1}{3}\right)$ alla funzione $f \colon \left(-\dfrac{1}{3},\dfrac{1}{3}\right) \to \mathbb{R}$ definita da

(121) $\begin{equation*} f(x) = \frac{1}{1-3x} \qquad \forall x \in \left( -\frac{1}{3},\frac{1}{3}\right). \end{equation*}$

Affermiamo che la convergenza è uniforme negli intervalli del tipo $[-a,a]$ con $a \in \left[0,\dfrac{1}{3}\right)$ . Infatti, fissato $a \in \left[0,\dfrac{1}{3}\right)$ , si ha

(122) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[-a,a]} |f_n(x)-f(x)| = \lim_{n \to +\infty} \sup_{x \in[-a,a]} \dfrac{|3x|^{n+1}}{1-3x} \leq \lim_{n \to +\infty} \frac{(3a)^{n+1}}{1-3a} = 0, \end{equation*}$

dove nella disuguaglianza abbiamo usato che $|3x|\leq 3a$ e che $1-3x \geq 1-3a>0$ per ogni $x \in [-a,a]$ . Da (122) e dalla proposizione 1.3, otteniamo la convergenza uniforme di $f_n$ a $f$ in $[-a,a]$ .

Affermiamo infine che la convergenza non è uniforme in $\left( -\dfrac{1}{3},\dfrac{1}{3}\right)$ .

(123) $\begin{equation*} \lim_{x \to (\frac{1}{3})^-} |f(x)-f_n(x)| = \lim_{x \to (\frac{1}{3})^-} \frac{|3x|^{n+1}}{1-3x} = +\infty \qquad \forall n \in \mathbb{N}. \end{equation*}$

Da ciò segue che

(124) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\left( -\frac{1}{3},\frac{1}{3}\right)} |f_n(x)-f(x)| = +\infty, \end{equation*}$

mostrando che la convergenza non è uniforme in $\left( -\dfrac{1}{3},\dfrac{1}{3}\right)$ .

$\,$

Che si può mostrare osservando che, ponendo $S(n)= \sum_{k=0}^n r^k$ , si ha $S(n)-r S(n)= 1-r^{n+1}$ , da cui si ricava $S(n)$ . ↩

Esercizio 21 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \frac{nx}{e^{nx}} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti insiemi:

$\quad$

in $\mathbb{R}$ ;

negli intervalli del tipo $(0,a]$ con $a>0$ .

negli intervalli del tipo $[a,+\infty)$ con $a>0$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Siccome si ha

$\lim_{n\to +\infty} n xe^{-n x} = \begin{cases} 0 &\text{se }x\ge 0 \\ -\infty &\text{se } x<0, \end{cases}$

la successione non converge puntualmente (e quindi nemmeno uniformemente) su $\mathbb{R}$ .

Soluzione punto 2.

Per quanto osservato al punto precedente, la successione converge puntualmente in $[0,+\infty)$ alla funzione $f \colon [0,+\infty) \to \mathbb{R}$ identicamente nulla e, in particolare, negli intervalli del tipo $(0,a]$ , con $a>0$ .

Si fissi quindi $a>0$ . Affermiamo che la convergenza delle $f_n$ a $f$ non è uniforme su $(0,a]$ . Osserviamo che ogni $f_n$ è derivabile e che vale

(125) $\begin{equation*} f_n'(x)=n(1-nx)e^{-nx} \qquad \forall n \in \mathbb{N},\,\, \forall x \in (0,a]. \end{equation*}$

Poiché

(126) $\begin{equation*} f_n'(x) \geq 0 \iff x \in \left(0,\frac{1}{n} \right] \qquad \forall n \in \mathbb{N}, \end{equation*}$

si ha

(127) $\begin{equation*} \max_{x \in (0,a]}f_n(x) = \begin{cases} f(a) & \text{se } \dfrac{1}{n}\geq a\\[7pt] f\left(\dfrac{1}{n}\right)=e^{-1} & \text{se } \dfrac{1}{n}< a \end{cases} \end{equation*}$

Da ciò, poiché $f_n(x) \geq 0$ per ogni $n \in \mathbb{N}$ e per ogni $x \in (0,a]$ , si ha

(128) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in (0,a]}|f_n(x)-f(x)| = \lim_{n \to +\infty} \max_{x \in (0,a]}f_n(x) = \lim_{n \to +\infty} e^{-1} = e^{-1}. \end{equation*}$

Per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme in $(0,a]$ .

Soluzione punto 3.

Sia $a>0$ ; affermiamo che la convergenza di $f_n$ a $f$ è uniforme in $[a,+\infty)$ . Per (126), $f_n$ è decrescente in $[a,+\infty)$ se $\dfrac{1}{n}< a$ . Ciò implica che

(129) $\begin{equation*} \max_{x \in [a,+\infty)}f_n(x) = f_n(a) \qquad \forall n> \frac{1}{a}. \end{equation*}$

Unendo a (129) il fatto che $f_n(x) \geq 0$ per ogni $n \in \mathbb{N}$ e per ogni $x \in [a,+\infty)$ , si ottiene

(130) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[a,+\infty)}|f_n(x)-f(x)| = \lim_{n \to +\infty} f_n(a) = 0, \end{equation*}$

dove l’ultima uguaglianza dalla convergenza puntuale di $f_n$ a $0$ . La proposizione 1.3 implica quindi la convergenza uniforme delle $f_n$ a $f$ su $[a,+\infty)$ .

$\,$

Esercizio 22 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon (0,+\infty) \to \mathbb{R}$ definite da

(131) $\begin{equation*} f_n(x) = \left( 1 - \cos \dfrac{x}{n}\right)^{\frac{1}{n^2}} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}, \end{equation*}$

nei seguenti insiemi:

$\,$

negli insiemi del tipo $[r,R]$ , con $0<r<R$ ;

negli insiemi del tipo $(0,r]$ , con $r >0$ ;

negli insiemi del tipo $[R,+\infty)$ con $R>0$ .

Soluzione punto 1.

Studiamo separatamente i vari casi. Si fissino $0<r<R$ . Si ha

(132) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \lim_{n \to +\infty}\left( \dfrac{1 - \cos \dfrac{x}{n}}{\dfrac{x^2}{n^2}}\right)^{\frac{1}{n^2}} \left( \dfrac{x^2}{n^2}\right)^{\frac{1}{n^2}} = 1 \qquad \forall x \in [r,R], \end{equation*}$

dove l’ultima uguaglianza segue da

(133) $\begin{equation*} \lim_{t \to 0} \dfrac{1-\cos t}{t^2}=\frac{1}{2}, \qquad \text{e da} \qquad \lim_{n \to +\infty} n^{\frac{1}{n}}= \lim_{n \to +\infty} y^{\frac{1}{n}}=1 \quad \forall y >0. \end{equation*}$

Da (132) si ha che $f_n$ converge puntualmente in $[r,R]$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente pari a $1$ . Dall’arbitrarietà di $r$ e $R$ , segue che $f_n$ converge puntualmente a $f$ in $(0,+\infty)$ .

Affermiamo che la convergenza è anche uniforme in $[r,R]$ . Infatti osserviamo che, poiché la funzione $t \mapsto 1- \cos t$ è crescente e positiva in $(0,\pi/2]$ e la funzione $y \to y^{\frac{1}{n^2}}$ è crescente per ogni $n \in \mathbb{N}$ , ognuna delle funzioni $f_n$ è crescente in $(0,n\pi/2]$ e inoltre in tale intervallo si ha $f_n(x)\leq 1$ . Poiché per ogni $n \geq \dfrac{2R}{\pi}$ si ha $[r,R] \subset (0,n\pi/2]$ , otteniamo

(134) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in [r,R]}|f_n(x)-f(x)| = \lim_{n \to +\infty}\big( 1 - f_n(r)\big) = 0, \end{equation*}$

dove l’ultima uguaglianza segue dalla convergenza puntuale di $f_n$ a $f$ . Da (134) e dalla proposizione 1.3, si ha la convergenza uniforme di $f_n$ a $f$ in $[r,R]$ .

Soluzione punto 2.

Sia $r>0$ . Affermiamo che la convergenza di $f_n$ a $f$ non è uniforme in $(0,r]$ . Infatti, poiché

(135) $\begin{equation*} \lim_{x \to 0^+} f_n(x)=0 \qquad \forall n \in \mathbb{N}, \end{equation*}$

si ha

(136) $\begin{equation*} \sup_{x \in (0,r]} |f_n(x)-f(x)| = 1 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Di nuovo per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme in $(0,r]$ .

Soluzione punto 3.

Sia $R>0$ . Affermiamo che anche in $[R,+\infty)$ la convergenza di $f_n$ a $f$ non è uniforme. Infatti, sia $k \in \mathbb{N}$ tale che $2k\pi \geq R$ . Allora si ha $f_n(2nk\pi)=0$ per ogni $n \in \mathbb{N}$ e quindi

(137) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in [R,+\infty)} |f_n(x)-f(x)| \geq \lim_{n \to +\infty} \big( 1 - f_n(2nk\pi) \big) = 1. \end{equation*}$

Ancora la proposizione 1.3 implica che la convergenza di $f_n$ a $f$ non è uniforme in $[R,+\infty)$ .

Esercizio 23 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Esibire una successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ continue che soddisfi contemporaneamente le seguenti condizioni:

$\,$

per ogni $n \in \mathbb{N}$ l’integrale improprio $\int_{-\infty}^{+\infty} f_n(x) \dif x$ converge;

la successione $f_n$ converge uniformemente in $\mathbb{R}$ a una funzione $f \colon \mathbb{R} \to \mathbb{R}$ ;

l’integrale improprio $\int_{-\infty}^{+\infty} f(x) \dif x$ converge;

vale
(138) $\begin{equation*} \lim_{n \to +\infty} \int_{-\infty}^{+\infty} f_n(x) \, \mathrm{d} x \neq \int_{-\infty}^{+\infty} f(x) \, \mathrm{d} x. \end{equation*}$

Soluzione punto 1.

Di questo esercizio presentiamo due svolgimenti.

Consideriamo la successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

(139) $\begin{equation*} f_n(x)=\frac{\dfrac 1n}{1+\left(\dfrac{x}{n}\right)^2} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}. \end{equation*}$

Le funzioni $f_n$ sono continue. Mostriamo ora che esse soddisfano tutte le condizioni richieste.

$\quad$

Per ogni $n \in \mathbb{N}$ una primitiva di $f_n$ è la funzione $g_n \colon \mathbb{R} \to \mathbb{R}$ definita da
(140) $\begin{equation*} g_n(x)= \arctan \left(\frac xn\right) \qquad \forall x \in \mathbb{R}. \end{equation*}$

Per definizione di integrale improprio si ha

(141) $\begin{equation*} \begin{split} \int_{-\infty}^{+\infty} f_n(x) \dif x = & \lim_{b \to + \infty} \left( \int_{-b}^{0} f_n(x) \dif x \right) + \lim_{b \to + \infty} \left( \int_{0}^{b} f_n(x) \dif x \right) \\ = & \lim_{b \to + \infty} \left[\arctan\left(\frac xn\right) \right]_{-b}^0 + \lim_{b \to + \infty} \left[\arctan\left(\frac xn\right) \right]_{0}^b \\ = & \,\pi \qquad \forall n \in \mathbb{N}, \end{split} \end{equation*}$

da cui la convergenza dell’integrale improprio $\int_{-\infty}^{+\infty} f_n(x) \dif x$ per ogni $n \in \mathbb{N}$ .

Dato che $1+\left(\dfrac{x}{n}\right)^2 \geq 1$ , si ha
$|f_n(x)| \leq \frac{1}{n} \quad \text{per ogni } n, \forall x \in \mathbb{R},$

da cui segue che

$\lim_{n \to \infty} \sup_{x \in \mathbb{R}} |f_n(x)| \leq \lim_{n \to \infty} \frac{1}{n} = 0$

e, per la proposizione 1.3, $f_n$ converge uniformemente alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla.

Dato che $f$ è la funzione nulla, ovviamente si ha

(142) $\begin{equation*} \int_{-\infty}^{+\infty} f(x) \, \mathrm{d} x = 0. \end{equation*}$

Per (141) e (142) si ha
$\lim_{n \to \infty} \int_{-\infty}^{+\infty} f_n(x) \, \mathrm{d} x = \pi \neq 0 = \int_{-\infty}^{+\infty} f(x) \, \mathrm{d} x.$

Soluzione punto 2.

Sia $f_n \colon \mathbb{R} \to \mathbb{R}$ la successione di funzioni definita da

(143) $\begin{equation*} f_n(x) = \begin{cases} \dfrac{1}{n} & \text{se } x \in [-n,n]\\[7pt] \dfrac{1}{n}+n - x & \text{se } x \in \left(n,n+ \dfrac{1}{n}\right]\\ \dfrac{1}{n}+n + x & \text{se } x \in \left[-n- \dfrac{1}{n},-n\right)\\ 0 & \text{altrimenti}. \end{cases} \qquad \forall n \in \mathbb{N}. \end{equation*}$

$\,$

Figura 1: una delle funzioni $f_n$ definite in (143).

$\,$

Ognuna delle $f_n$ è una funzione continua, come si vede in figura 1.

$\quad$

Poiché
(144) $\begin{equation*} f_n(x) = 0 \qquad \forall |x| \geq n+1,\,\,\, \forall n \in \mathbb{N}, \end{equation*}$

l’integrale improprio $\int_{-\infty}^{+\infty} f_n(x) \dif x$ converge per ogni $n \in \mathbb{N}$ . In particolare, poiché ognuna delle $f_n$ è una funzione pari, si ha

(145) $\begin{equation*} \int_{-\infty}^{+\infty} f_n(x) \, \mathrm{d} x = 2\int_0^n \frac{1}{n} \, \mathrm{d} x + 2\int_n^{n+ \frac{1}{n}} \left(\frac{1}{n}+n - x\right) \, \mathrm{d} x = 2\cdot 1 + 2 \frac{1}{2n^2}= 2 + \frac{1}{n^2}. \qquad \forall n \in \mathbb{N}. \end{equation*}$

item Si ha

(146) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}}|f_n(x)| = \lim_{n \to +\infty} \frac{1}{n} = 0, \end{equation*}$

quindi $f_n$ converge uniformemente in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla. Dato che $f$ è la funzione nulla, ovviamente si ha

(147) $\begin{equation*} \int_{-\infty}^{+\infty} f_n(x) \, \mathrm{d} x = 0. \end{equation*}$

Da (145) e (147), segue che
(148) $\begin{equation*} \lim_{n \to +\infty} \int_{-\infty}^{+\infty} f_n(x) \, \mathrm{d} x = 2 \neq 0 = \int_{-\infty}^{+\infty} f(x) \, \mathrm{d} x. \end{equation*}$

Esercizio 24 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Si consideri la successione di funzioni $f_n\colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \frac{1}{\sqrt n} \sin(nx) \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}.$

$\,$

Studiare la convergenza puntuale e uniforme della successione $f_n$ .

Studiare la convergenza puntuale e uniforme della successione delle derivate $f_n'$ .

Soluzione punto 1.

Si mostrerà che la successione $f_n$ converge uniformemente in $\mathbb{R}$ , ma la successione delle derivate non converge in alcun punto.

Poiché $|\sin t| \leq 1$ per ogni $t \in \mathbb{R}$ , osserviamo che

(149) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}}|f_n(x)| \leq \lim_{n \to +\infty} \frac{1}{\sqrt{n}} = 0, \end{equation*}$

per cui la successione $f_n$ converge uniformemente in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla.

Soluzione punto 2.

Studiamo ora la successione delle derivate, dato che $f_n$ è derivabile per ogni $n\in \mathbb{N}$ :

$f_n'(x)=\frac{1}{\sqrt n} (n \cos nx)=\sqrt n\cos(n x) \qquad \forall n \in \mathbb{N}, \,\, \forall x \in \mathbb{R}.$

Facciamo ora le seguenti osservazioni.

Se $x= 2k\pi$ per qualche $k \in \mathbb{Z}$ , allora $\cos(nx)=1$ per ogni $n \in \mathbb{N}$ , quindi

(150) $\begin{equation*} \lim_{n \to +\infty} \sqrt n\cos(n x) = +\infty. \end{equation*}$

Se $x = q \pi$ per qualche $q=\dfrac{h}{m} \in \mathbb{Q} \setminus \{2k \colon k \in \mathbb{Z} \}$ con $h,m$ coprimi e $m \neq 0$ , allora la successione $\cos(nx)$ è ciclica di periodo $2m$ al variare di $n \in \mathbb{N}$ , assumendo sia valori positivi che negativi, pertanto $\lim_{n \to +\infty} \sqrt n\cos(n x)$ non esiste.

Se invece $x \neq q \pi$ per qualche $q \in \mathbb{Q}$ , allora per [1, proposizione 5.46], l’insieme

(151) $\begin{equation*} \{nx + m(2\pi) \colon n,m \in \mathbb{Z}\} \end{equation*}$

è denso in $\mathbb{R}$ , da cui segue che la successione $\cos(nx)$ possiede sottosuccessioni convergenti a qualsiasi numero reale in $[-1,1]$ . Pertanto $\lim_{n \to +\infty} \sqrt n\cos(n x)$ non esiste. Riassumendo:

(152) $\begin{equation*} \lim_{n \to \infty} f'_n(x) \begin{cases} =+\infty & \text{se $x=2k\pi$ per qualche $k \in \mathbb{Z}$}\\ \text{non esiste} & \text{altrimenti}. \end{cases} \end{equation*}$

Da ciò segue che la successione delle derivate non converge nemmeno puntualmente su $R$ .

Esercizio 25 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = e^{-\left(x- 1/n\right)^2} \cos\left(e^{-\left(x- 1/n\right)^2} \right). \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}.$

Soluzione punto 1.

Osserviamo che

$\lim_{n\to \infty} e^{-(x-1/n)^2} \cos(e^{-(x-1/n)^2}) = e^{-x^2}\cos(e^{-x^2}) \qquad \forall x \in \mathbb{R},$

da cui segue la convergenza puntuale delle funzioni $f_n$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da

(153) $\begin{equation*} f(x) = e^{-x^2}\cos(e^{-x^2}) \qquad \forall x \in \mathbb{R}. \end{equation*}$

Proviamo che la convergenza è anche uniforme. Osserviamo che

(154) $\begin{equation*} f_n(x) = f\left( x - \frac{1}{n}\right) \qquad \forall n \in \mathbb{N},\,\,\forall x \in \mathbb{R}. \end{equation*}$

Poiché $f$ è continua e derivabile in $\mathbb{R}$ , dal teorema di Lagrange segue che, per ogni $x \in \mathbb{R}$ e per ogni $n \in \mathbb{N}$ , esiste $\xi \in \left(x-\dfrac{1}{n},x\right)$ tale che

(155) $\begin{equation*} |f_n(x)-f(x)| = \left| f\left(x-\frac{1}{n}\right) - f(x)\right| = \frac{1}{n} |f'(\xi)|. \end{equation*}$

Pertanto si ha

(156) $\begin{equation*} \sup_{x \in\mathbb{R}} |f_n(x)-f(x)| \leq \frac{1}{n} \sup_{x \in\mathbb{R}} |f'(x)| \qquad \forall n \in \mathbb{N}. \end{equation*}$

Poiché

(157) $\begin{equation*} f'(x) = -2xe^{-x^2}\cos(e^{-x^2}) -2xe^{-2x^2}\sin(e^{-x^2}) \qquad \forall x \in \mathbb{R}, \end{equation*}$

si ottiene che $f'$ è continua e vale $\lim_{x\to \pm\infty}f'(x)=0$ . Da ciò segue che esiste finito $L=\max_{x \in \mathbb{R}}|f'(x)|$ . Unendo questa informazione a (156), si ottiene

(158) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |f_n(x)-f(x)| \leq \lim_{n \to +\infty} \frac{L}{n} = 0, \end{equation*}$

da cui la convergenza uniforme di $f_n$ a $f$ in $\mathbb{R}$ .

Lo studio della convergenza uniforme poteva anche svolgersi nel seguente modo.

Soluzione punto 2.

Per quanto riguarda la convergenza uniforme di $f_n$ a $f$ , dividiamo lo studio in due fasi.

$\quad$

Proviamo che la convergenza è uniforme sugli intervalli del tipo $[-R,R]$ con $R>0$ . A tal fine, fissiamo $R>0$ . Notiamo che
(159) $\begin{equation*} f_n(x) = f\left( x - \frac{1}{n}\right) \qquad \forall n \in \mathbb{N},\,\,\forall x \in \mathbb{R}. \end{equation*}$

Poiché $f$ è continua e derivabile in $\mathbb{R}$ , dal teorema di Lagrange segue che, per ogni $x \in \mathbb{R}$ e per ogni $n \in \mathbb{N}$ , esiste $\xi \in \left(x-\dfrac{1}{n},x\right)$ tale che

(160) $\begin{equation*} |f_n(x)-f(x)| = \left| f\left(x-\frac{1}{n}\right) - f(x)\right| = \frac{1}{n} |f'(\xi)|. \end{equation*}$

Pertanto si ha

(161) $\begin{equation*} \sup_{x \in[-R,R]} |f_n(x)-f(x)| \leq \frac{1}{n} \sup_{x \in[-R-1,R+1]} |f'(x)| \qquad \forall n \in \mathbb{N}. \end{equation*}$

Poiché $f$ è di classe $C^1(\mathbb{R})$ , esiste finito $L=\max_{x [-R-1,R+1]}|f'(x)|$ . Unendo questa informazione a (156), si ottiene

(162) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[-R,R]} |f_n(x)-f(x)| \leq \lim_{n \to +\infty} \frac{L}{n} = 0, \end{equation*}$

da cui la convergenza uniforme di $f_n$ a $f$ in $[-R,R]$ .

Proviamo ora che la convergenza è uniforme su $\mathbb{R}$ . Si fissi $\varepsilon>0$ . Poiché $\lim_{x \to \infty}e^{-x^2}=0$ , esiste $R>0$ tale che
(163) $\begin{equation*} |f(x)|\le e^{-x^2} < \frac{\varepsilon}{2} \quad \text{e} \quad |f_n(x)|\le e^{-(x-\frac 1n)^2} < \frac{\varepsilon}{2} \qquad \forall n \in \mathbb{N},\,\, \forall x \in (-\infty,-R]\cup [R,+\infty). \end{equation*}$

Da ciò segue che

(164) $\begin{equation*} \sup_{x \in\{|x|\geq R\}} |f_n(x)-f(x)| \leq \sup_{x \in\{|x|\geq R\}} (|f_n(x)|+|f(x)|) < \varepsilon \qquad \forall n \in \mathbb{N}. \end{equation*}$

D’altra parte, per il punto precedente $f_n$ converge uniformemente a $f$ su $[-R,R]$ , quindi esiste $N \in \mathbb{N}$ tale che

(165) $\begin{equation*} \sup_{x \in[-R,R]}|f_n(x)-f(x)| < \varepsilon \qquad \forall n \geq N. \end{equation*}$

Unendo (164) e (165), si ottiene

(166) $\begin{equation*} \sup_{x \in\mathbb{R}} |f_n(x)-f(x)| < \varepsilon \qquad \forall n \geq N. \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ , (166) implica che $\lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |f_n(x)-f(x)|=0$ , e quindi, per la proposizione 1.3, $f_n$ converge uniformemente a $f$ in $\mathbb{R}$ .

Esercizio 26 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) =n^2x^2(1-x)^n \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti insiemi:

$\,$

in $\mathbb{R}$ ;

negli intervalli del tipo $(0,a)$ con $a\in (0,2)$ .

negli intervalli del tipo $[a,b]$ con $0<a<b<2$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Si ha

(167) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \begin{cases} +\infty & \text{se } x < 0\\ 0 & \text{se } x \in [0,2)\\ \text{non esiste} & \text{se } x \geq 2. \end{cases} \end{equation*}$

Per verificarlo, osserviamo che, se $x<0$ , allora $(1-x)^n>1$ e quindi $n^2x^2(1-x)^n>n^2x^2$ , da cui

(168) $\begin{equation*} \lim_{n \to +\infty} f_n(x) > \lim_{n \to +\infty} n^2x^2 = +\infty \qquad \forall x < 0. \end{equation*}$

Se $x=0$ , allora $f_n(x)=0$ per ogni $n \in \mathbb{N}$ . Per $x \in (0,2)$ si ha $|1-x|<1$ e quindi, per le note proprietà degli esponenziali, otteniamo

(169) $\begin{equation*} \lim_{n \to +\infty} n^2|1-x|^n = 0 \qquad \forall x \in (0,2). \end{equation*}$

Per cui si ha $\lim_{n \to +\infty} f_n(x)=0$ .

Se invece $x\geq 2$

(170) $\begin{equation*} \lim_{n \to +\infty} n^2x^2=+\infty \qquad \text{e} \qquad |1-x|^n\geq 1 \quad \forall n \in \mathbb{N}, \end{equation*}$

quindi $\lim_{n \to +\infty} |f_n(x)|=+\infty$ , ma poiché $(1-x)^n$ ha segno alternante, il limite $\lim_{n \to +\infty} f_n(x)$ non esiste.

In sintesi $f_n$ converge puntualmente solo in $[0,2)$ e inoltre il suo limite puntuale è la funzione $f \colon [0,2) \to \mathbb{R}$ identicamente nulla.

Soluzione punto 2.

Sia $a \in (0,2)$ ; dal punto precedente sappiamo che $f_n$ converge puntualmente a $f$ in $(0,a)$ .

Affermiamo che la convergenza non è uniforme. A tal fine, osserviamo che la forma di $f_n$ suggerisce di sostituire $x=\dfrac{1}{n}$ (se $\dfrac{1}{n}<a$ ). Osservando infatti che begin{equation} n^2 left(frac{1}{n}right) =1 quad forall n in mathbb{N}, qquad lim_{n to +infty} left(1-frac{1}{n}right)^n = e^{-1}, end{equation} si ricava

(171) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in(0,a)} |f_n(x)-f(x)| \geq \lim_{n \to +\infty} f_n\left(\frac{1}{n}\right) = e^{-1} \neq 0 \end{equation*}$

Per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme.

Un altro metodo (meno rapido) per ottenere una stima dal basso su $\supx{(0,a)} |f_n(x)-f(x)|$ consiste nello studiare il segno della la derivata

$f_n'(x) = n^{2}\left(2 x(1-x)^{n}-n x^{2}(1-x)^{n-1}\right) = n^{2} x(1-x)^{n-1}(2-2 x-n x) \qquad \forall n \in \mathbb{N} ,\,\, \forall x \in (0,a),$

ottenendo che

(172) $\begin{equation*} f_n'(x)\geq 0 \qquad \forall x \in \left(0, \frac{2}{2+n}\right]. % %\iff %\begin{cases} %x \in \left(0, \frac{2}{2+n}\right] & \text{se $n$ è dispari}\\[10pt] %x\in \left(0, \frac{2}{2+n}\right] \cup [1,a) & \text{se $n$ è pari} %\end{cases} \end{equation*}$

Poiché ogni $f_n$ è crescente e positiva in $\left(0, \dfrac{2}{2+n}\right]$ , si ha che

(173) $\begin{equation*} \max_{x \in (0,a)} |f_n(x)-f(x)| \geq f_n \left( \frac{2}{2+n}\right) = \frac{4n^2}{(n+2)^{2}}\left(\frac{n}{n+2}\right)^{n} \qquad \text{se } \frac{2}{2+n}<a. \end{equation*}$

Osservando che

$\lim_{n\to \infty} \left(1+\frac{y}{n}\right)^n=e^y \quad \forall y \in \mathbb{R}, \qquad \lim_{n\to \infty} \frac{4n^2}{(n+2)^{2}}=4,$

da (173) si ottiene

(174) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in(0,a)}|f_n(x)-f(x)| \geq \lim_{n \to +\infty} \frac{4n^2}{(n+2)^{2}}\left(\frac{n}{n+2}\right)^{n} = 4 e^{-2} \neq 0. \end{equation*}$

Per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme.

Soluzione punto 3.

Siano $0<a<b<2$ ; affermiamo che la convergenza di $f_n$ a $f$ è uniforme su $[a,b]$ . Un primo modo nel vederlo consiste nell’effettuare uno studio del segno più accurato delle derivate $f_n'$ :

(175) $\begin{equation*} f_n'(x)\geq 0 \iff \begin{cases} x \in \left(a, \dfrac{2}{2+n}\right] & \text{se $n$ è dispari}\\[10pt] x\in \left(a, \dfrac{2}{2+n}\right] \cup [1,b) & \text{se $n$ è pari} \end{cases} \end{equation*}$

Poiché

(176) $\begin{equation*} \frac{2}{2+n} \notin [a,b] \qquad \forall n > \frac{2}{a}-2, \end{equation*}$

i massimi e i minimi delle funzioni $f_n$ sull’intervallo $[a,b]$ vanno quindi ricercati tra i valori

(177) $\begin{equation*} f_n(1)=0,\quad f_n(a),\quad f_n(b). \end{equation*}$

Poiché per la convergenza puntuale di $f_n$ a $f$ si ha

(178) $\begin{equation*} \lim_{n \to +\infty} f_n(a) = \lim_{n \to +\infty} f_n(b) = 0, \end{equation*}$

si ottiene

(179) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[a,b]}|f_n(x)-f_(x)| = \lim_{n \to +\infty} \max\{f_n(a),f_n(b)\} = 0, \end{equation*}$

da cui la convergenza uniforme delle $f_n$ a $f$ .

Un altro metodo che avrebbe condotto alla soluzione è osservare che la successione numerica dei moduli $\{|f_n(x)|\}_{n \in \mathbb{N}}$ è decrescente per $n$ sufficientemente grande, infatti, da $x \in [a,b] \subset (0,2)$ , segue

(180) $\begin{equation*} \lim_{n \to +\infty} \frac{|f_{n+1}(x)|}{|f_n(x)|} = \lim_{n \to +\infty} \frac{(n+1)^2|1-x|}{n^2} = |1-x| < 1. \end{equation*}$

Poiché la successione delle funzioni $|f_n|$ converge puntualmente su $[a,b]$ alla funzione $f$ nulla, che è continua, e l’intervallo $[a,b]$ è chiuso e limitato, il teorema 1.9 implica che $|f_n|$ converge uniformemente alla funzione nulla $f$ . D’altra parte, ciò implica che anche la successione delle $f_n$ converge uniformemente a $f$ su $[a,b]$ .

Esercizio 27 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_{n}(x)=\frac{1}{n} x \sin x+x+\cos \frac{1}{n} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti insiemi:

$\,$

in $\mathbb{R}$ ;

negli intervalli del tipo $[-R,R]$ , con $R>0$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Si ha

(181) $\begin{equation*} \lim_{n\to +\infty} f_n(x)=x+1, \qquad \forall x\in \mathbb{R}, \end{equation*}$

da cui la convergenza puntuale in $R$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da

(182) $\begin{equation*} f(x)= x+1 \qquad \forall x \in \mathbb{R}. \end{equation*}$

Affermiamo che la convergenza non è uniforme. Per mostrarlo, un’idea consiste nel notare che il termine $\dfrac{1}{n} x \sin x$ scompare, quando si effettua il limite puntuale. Esso però non è “uniformemente piccolo”: un’intuizione può essere scegliere una successione $x_n$ divergente affinché $\lim_{n \to +\infty} \frac{x_n}{n}=+\infty$ e tale che $\sin x_n=1$ per ogni $n \in \mathbb{N}$ .

Tale intuizione è appunto confermata dalla scelta $x_n= \dfrac{\pi}{2}+2n^2\pi$ ; infatti si ha

(183) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |f_n(x)-f(x)| \geq & \lim_{n \to +\infty} \left|f_n\left(\frac{\pi}{2}+2n^2\pi \right) - f\left(\frac{\pi}{2}+2n^2\pi \right) \right| \\ =& \lim_{n \to +\infty} \left| \frac{\pi + 4n^2}{2n} + \cos \frac{1}{n}- 1 \right| = +\infty. \end{split} \end{equation*}$

Per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme.

Soluzione punto 2.

Fissiamo $R>0$ . Si ha

(184) $\begin{equation*} \begin{split} \left|f_{n}(x)-f(x)\right|&=\left|\frac{1}{n} x \sin x+\cos \frac{1}{n}-1\right| \\ &\leq \frac{|x \sin x|}{n}+\left|\cos \frac{1}{n}-1\right| \\ &\leq \frac{R}{n}+\left|\cos \frac{1}{n}-1\right| \qquad \forall n \in \mathbb{N} , \,\, \forall x \in [-R,R], \end{split} \end{equation*}$

dove nella prima disuguaglianza abbiamo usato la disuguaglianza triangolare, mentre nella seconda il fatto che $|\sin x|\leq 1$ e che $|x| \leq R$ . Da (184) si ottiene

(185) $\begin{equation*} \lim_{n\to +\infty}\sup_{x\in [-R,R]}\left|f_{n}(x)-f(x)\right|\le \lim_{n\to +\infty} \frac{R}{n}+\left|\cos \frac{1}{n}-1\right|=0, \end{equation*}$

da cui concludiamo che $f_n$ converge ad $f$ uniformemente su $[-R,R]$ .

Esercizio 28 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Si consideri la successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \sqrt{x^2 + \frac{1}{n}} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}.$

$\,$

Studiare la convergenza puntuale e uniforme della successione $f_n$ .

Studiare la convergenza puntuale e uniforme della successione $f_n'$ nei seguenti insiemi:

$\,$

$\mathbb{R}$ ;
$\mathbb{R} \setminus \{0\}$ ;
$(-\infty,-a] \cup [a,+\infty)$ per $a>0$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Si ha

$\lim_{n\to\infty} f_n(x) = \lim_{n\to\infty}\sqrt{x^2 + \frac{1}{n}}=\sqrt{x^2}=|x| \qquad \forall x \in \mathbb{R}.$

da cui segue la convergenza puntuale delle $f_n$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da $f(x)=|x|$ .

La convergenza è anche uniforme. Infatti

(186) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}}|f_n(x)-f(x)| = & \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} \left|\frac{\left(\sqrt{x^2+\dfrac{1}{n}}-|x|\right)\left(\sqrt{x^2+\dfrac{1}{n}}+|x|\right)}{\sqrt{x^2+\dfrac{1}{n}}+|x|} \right| \\ = & \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} \frac{\dfrac{1}{n}}{\sqrt{x^2+\dfrac{1}{n}}+|x|} \\ \leq & \lim_{n \to +\infty} \frac{1}{\sqrt{n}} \\ = & \, 0, \end{split} \end{equation*}$

dove nella disuguaglianza abbiamo usato il fatto che

(187) $\begin{equation*} \sqrt{x^2+\dfrac{1}{n}}+|x| \geq \frac{1}{\sqrt{n}} \qquad \forall x \in \mathbb{R},\,\,\forall n \in \mathbb{N}. \end{equation*}$

La convergenza uniforme delle $f_n$ a $f$ segue quindi dalla proposizione 1.3.

Soluzione punto 2.

Poiché le $f_n$ sono tutte derivabili, consideriamo la successione delle derivate $f_n' \colon \mathbb{R} \to \mathbb{R}$ :

$f_n'(x)= \frac{x}{\sqrt{x^2 + \dfrac{1}{n}}} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}.$

le quali sono tutte funzioni continue. Abbiamo $f_n'(0)=0$ per ogni $n\in \mathbb{N}$ . Per $x\neq 0$ , vale

$\lim_{n\to +\infty}f'_n(x)=\frac{x}{\sqrt{x^2}}=\frac{x}{|x|}=\begin{cases} 1 \quad &{\text{se}}\quad x> 0\\ -1 \quad &{\text{se}}\quad x< 0. \end{cases}$

Concludiamo che la successione $f_n'$ delle derivate converge puntualmente alla funzione $g \colon \mathbb{R} \to \mathbb{R}$ definita da

$g(x) =\begin{cases} 1 \quad &{\text{se}}\quad x> 0\\ 0 \quad &{\text{se}}\quad x=0 \\-1 \quad &{\text{se}}\quad x< 0, \end{cases}$

Osserviamo che il limite puntuale $g$ delle derivate esiste in $x=0$ , mentre la funzione $f$ limite uniforme delle $f_n$ non è derivabile in $x=0$ . D’altra parte, si ha $g(x)=f'(x)$ per ogni $x \neq 0$ , ossia per ogni $x$ in cui $f$ è derivabile.

$\quad$

Poiché $g$ è discontinua in $0$ , per il teorema 1.5 la convergenza delle $f_n'$ a $g$ non può essere uniforme in qualsiasi intorno di $0$ , quindi nemmeno in $\mathbb{R}$ .

Proviamo ora che la convergenza delle $f_n'$ a $g$ non è uniforme nemmeno in $\mathbb{R} \setminus \{0\}$ . Infatti si ha
(188) $\begin{equation*} \lim_{x \to 0} f_n'(x) = \lim_{x \to 0} \frac{x}{\sqrt{x^2 + \dfrac{1}{n}}} = 0 \qquad \forall n \in \mathbb{N}, \end{equation*}$

da cui, tenendo presente che invece $\lim_{x \to 0^+}g(x)=1$ , segue

(189) $\begin{equation*} \sup_{x \in\mathbb{R} \setminus \{0\}} |f_n'(x) - g(x)| \geq 1 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Pertanto, per la proposizione 1.3, la convergenza di $f_n'$ a $g$ non è uniforme in $\mathbb{R} \setminus \{0\}$ .

Sia $a>0$ e dimostriamo che la convergenza delle $f_n'$ a $g$ è uniforme in $(-\infty,-a] \cup [a,+\infty)$ . Innanzitutto, per la parità delle $f_n'$ e di $g$ sull’insieme considerato, basta dimostrare la convergenza uniforme solo su $[a,+\infty)$ . Osserviamo che per ogni $n \in \mathbb{N}$ e ogni $x \geq a$ si ha

(190) $\begin{equation*} |g(x) - f_n'(x)| = 1- \frac{x}{\sqrt{x^2 + \dfrac{1}{n}}} = \frac{\sqrt{x^2 + \dfrac{1}{n}}-x}{\sqrt{x^2 + \dfrac{1}{n}}} = \frac{\dfrac{1}{n}}{\left(\sqrt{x^2 + \dfrac{1}{n}} + x\right)\sqrt{x^2 + \dfrac{1}{n}}} \leq \frac{1}{2na^2}, \end{equation*}$

dove nella disuguaglianza abbiamo usato che $x \geq a$ per ottenere una stima dal basso sul denominatore della frazione. Da (190) si ottiene

(191) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[a,+\infty)} |g(x) - f_n'(x)| \leq \lim_{n \to +\infty} \frac{1}{2na^2} = 0, \end{equation*}$

e quindi la convergenza delle $f_n'$ a $g$ è uniforme in $(-\infty,-a] \cup [a,+\infty)$ per la proposizione 1.3.

Esercizio 29 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . er ogni $n \in \mathbb{N}$ , sia $f_n \colon \mathbb{R} \to \mathbb{R}$ la soluzione del problema di Cauchy

(192) $\begin{equation*} \begin{cases} f_n'(t)= f_n(t) + t + 2^{-n}\\[10pt] f_n(0)=-1. \end{cases} \end{equation*}$

$\,$

Studiare la convergenza puntuale e uniforme di $f_n$ negli intervalli $[-R,R]$ , con $R > 0$ .

Studiare la convergenza puntuale e uniforme di $f_n$ in $\mathbb{R}$ .

Soluzione punto 1.

Studiamo separatamente le due questioni.

L’equazione è lineare e ha senso per ogni $t \in \mathbb{R}$ , pertanto la soluzione $f_n$ di (192) è definita in $\mathbb{R}$ .

Calcoliamo ora l’espressione di $f_n$ al fine di studiarne la convergenza. Moltiplicando per $e^{-t}$ l’equazione si ottiene

(193) $\begin{equation*} \begin{split} \begin{cases} e^{-t}f_n'(t)= \big(f_n(t) + t + 2^{-n}\big)e^{-t}\\[10pt] f_n(0)=-1. \end{cases} \iff & \begin{cases} e^{-t}f_n'(t) - e^{-t} f_n(t) = (t + 2^{-n})e^{-t}\\[10pt] f_n(0)=-1. \end{cases} \\ \iff & \begin{cases} \frac{\, \mathrm{d}}{\, \mathrm{d} t} \left(e^{-t}f_n(t)\right) = (t + 2^{-n})e^{-t}\\[10pt] f_n(0)=-1. \end{cases} \end{split} \end{equation*}$

Integrando entrambi i membri dell’equazione tra $0$ e $t$ e utilizzando la formula di integrazione per parti al secondo membro, si ottiene

(194) $\begin{equation*} e^{-t}f_n(t) +1 = 2^{-n} - (t + 2^{-n})e^{-t} - e^{-t} + 1 \qquad \forall n \in \mathbb{N},\,\, \forall t \in \mathbb{R}, \end{equation*}$

che è equivalente a

(195) $\begin{equation*} f_n(t)= 2^{-n}e^t - (t+2^{-n}+1) \qquad \forall n \in \mathbb{N},\,\, \forall t \in \mathbb{R}. \end{equation*}$

Sia $f \colon \mathbb{R} \to \mathbb{R}$ la funzione definita da

(196) $\begin{equation*} f(t)= -(t+1) \qquad \forall t \in \mathbb{R}. \end{equation*}$

Si ha

(197) $\begin{equation*} \lim_{n \to +\infty} f_n(t) = \lim_{n \to +\infty} \Big( 2^{-n}e^t - (t+2^{-n}+1) \Big) = -(t+1) =f(t) \qquad \forall t \in \mathbb{R}. \end{equation*}$

Pertanto $f_n$ converge a $f$ puntualmente in $\mathbb{R}$ e quindi in ogni intervallo del tipo $[-R,R]$ con $R>0$ . Si fissi quindi $R\geq 0$ ; si ha

(198) $\begin{equation*} \lim_{n \to +\infty} \sup_{t \in [-R,R]} |f_n(t) - f(t)| = \lim_{n \to +\infty} \sup_{t \in [-R,R]} 2^{-n}|e^t -1| \leq \lim_{n \to +\infty} 2^{-n} \max\{1,e^R-1\} = 0, \end{equation*}$

dove nella disuguaglianza si è usato il fatto che la funzione $t \mapsto e^t$ è crescente e positiva in $[-R,R]$ . Da 1 e dalla proposizione 1.3 segue la convergenza uniforme di $f_n$ a $f$ .

Soluzione punto 2.

La convergenza di $f_n$ a $f$ non è uniforme in $\mathbb{R}$ , in quanto

(199) $\begin{equation*} \sup_{t \in\mathbb{R}} |f_n(t) - f(t)| = \sup_{t \in\mathbb{R}} 2^{-n}|e^t -1| = +\infty \qquad \forall n \in \mathbb{N}. \end{equation*}$

Esercizio 30 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon [0,+\infty) \to \mathbb{R}$ definita da

(200) $\begin{equation*} f_n(x) = \int_{0}^{x} \frac{t}{1+n^2 t} \dif t \qquad \forall n \in \mathbb{N},\,\, \forall x \in [0,+\infty), \end{equation*}$

nei seguenti insiemi:

$\,$

in $[0,+\infty)$ ;

negli intervalli del tipo $[a,+\infty)$ , con $a >0$ .

Soluzione punto 1.

Di questo esercizio presentiamo due svolgimenti: nel primo calcoliamo esplicitamente l’integrale in (200) e usiamo la rappresentazione esplicita di $f_n$ per studiarne la convergenza puntuale e uniforme; nel secondo svolgimento usiamo delle stime sulla funzione integranda per ottenere i risultati desiderati. Questo secondo metodo è forse maggiormente versatile, in quanto in molti casi il calcolo esplicito degli integrali risulta poco agevole e inoltre l’uso di stime può spesso semplificare i calcoli.

$\quad$

Notiamo che la funzione integranda è continua in $\mathbb{R}$ per ogni $n\in \mathbb{N}$ ; in particolare l’integrale è ben definito per ogni $x \ge 0$ e $f_n(0)=0$ per ogni $n\in \mathbb{N}$ . Troviamo una formula esplicita per la successione calcolando l’integrale:
$\begin{split} \int_{0}^{x} \frac{t}{1+n^2 t} \, \mathrm{d} t &= \frac{1}{n^2}\int_{0}^{x} \frac{n^2t}{1+n^2 t}\, \mathrm{d} t \\ & = \frac{1}{n^2}\int_{0}^{x}1-\frac{1}{1+n^2 t} \, \mathrm{d} t \\ &= \frac{1}{n^2}\left(\int_{0}^{x}1-\frac{1}{n^2}\int_0^x\frac{n^2}{1+n^2 t} \, \mathrm{d} t \right) \\ &= \frac{1}{n^2}\left[t-\frac{1}{n^2}\log(1+n^2t) \right]_0^x \\ &= \frac{1}{n^2}\left( x-\frac{1}{n^2}\log(1+n^2x) \right). \end{split}$

Quindi si ha

$f_n(x)=\frac{x}{n^2}-\frac{1}{n^4}\log(1+n^2x) \qquad \forall n \in \mathbb{N},\,\, \forall x \ge 0.$

Di conseguenza, otteniamo

$\lim_{n\to +\infty} f_n(x)=\lim_{n\to +\infty}\frac{x}{n^2}-\frac{1}{n^4}\log(1+n^2x)=0, \qquad \forall x \ge 0,$

da cui la convergenza puntuale delle $f_n$ alla funzione $f \colon [0,+\infty) \to \mathbb{R}$ identicamente nulla.

Affermiamo che la convergenza non è uniforme in $[0,+\infty)$ . Infatti, la funzione $f_n(x)$ è illimitata superiormente in $[0,+\infty)$ , poiché si ha

$\lim_{x\to + \infty} f_n(x) = \lim_{x\to +\infty} \frac{x}{n^2}-\frac{1}{n^4}\log(1+n^2x) = \lim_{x\to +\infty} x \left( \frac{1}{n^2}-\frac{\log(1+n^2x)}{n^4 x}\right) =+\infty \qquad \forall n\in \mathbb{N},$

dove si è usato il fatto che $\lim_{x\to +\infty} \dfrac{\log(1+n^2x)}{x}=0$ per ogni $n\in \mathbb{N}$ . Pertanto

(201) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[0,+\infty)}|f_n(x)-f(x)| = +\infty \end{equation*}$

e, per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme.

Fissiamo $R>0$ e proviamo che la convergenza è uniforme in $[0,R]$ . Osserviamo innanzitutto che, dal teorema fondamentale del calcolo integrale (si veda ad esempio il teorema 4.1 nella dispensa Teorema fondamentale del calcolo integrale ), si ha che $f_n$ è derivabile per ogni $n \in \mathbb{N}$ e vale
(202) $\begin{equation*} f_n'(x)=\frac{x}{1+n^2 x} \qquad \forall n \in \mathbb{N},\,\, \forall x\geq 0. \end{equation*}$

Pertanto ogni $f_n$ è crescente; da ciò e dal fatto che $f_n(0)=0$ per ogni $n \in \mathbb{N}$ segue che

(203) $\begin{equation*} \sup_{x\in [0,R]} |f_n(x)-0|= f_n(R) \qquad \forall n \in \mathbb{N}. \end{equation*}$

Per stimare $f_n(R)$ , osserviamo che per il teorema di Lagrange, per ogni $n \in \mathbb{N}$ esiste $\xi_n \in (0,R)$ tale che

(204) $\begin{equation*} f_n(R)=f_n(R) - f_n(0) = R f_n'(\xi_n) = R \frac{\xi_n}{1+n^2 \xi_n} \leq \frac{R}{n^2} \qquad \forall n \in \mathbb{N}, \end{equation*}$

dove nella terza uguaglianza si è usato che $f_n'(x) = \dfrac{x}{1+n^2x}$ e nella disuguaglianza si è usato che $1+n^2 \xi_n \geq n^2 \xi_n$ . Da ciò e da (203) segue

$\lim_{n\to+\infty}\sup_{x\in [0,R]} |f_n(x)-0|=\lim_{n\to+\infty} f(R) \leq \lim_{n \to +\infty} \frac{R}{n^2} = 0,$

da cui la convergenza uniforme delle $f_n$ a $f$ in $[0,R]$ per la proposizione 1.3.

Presentiamo ora il secondo svolgimento dell’esercizio, in cui si prescinde dal calcolo esplicito dell’integrale in (200).

Soluzione punto 2.

Da $1+n^2t \geq n^2t$ per ogni $n \in \mathbb{N}$ e ogni $t \geq 0$ segue che

(205) $\begin{equation*} 0 \leq \frac{t}{1+n^2 t} \leq \frac{1}{n^2} \qquad \qquad \forall n \in \mathbb{N},\,\, \forall t\geq 0. \end{equation*}$

Pertanto, se $R>0$ , si ha

(206) $\begin{equation*} |f_n(x)| = \int_0^x \frac{t}{1+n^2 t} \, \mathrm{d} t \leq \int_0^R \frac{1}{n^2} \, \mathrm{d} t = \frac{R}{n^2} \qquad \forall n \in \mathbb{N},\,\, \forall x \in [0,R], \end{equation*}$

e ciò implica che

(207) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[0,R]}|f_n(x)| \leq \lim_{n \to +\infty} \frac{R}{n^2} = 0, \end{equation*}$

da cui segue la convergenza uniforme in $[0,R]$ di $f_n$ alla funzione $f \colon [0,+\infty) \to \mathbb{R}$ identicamente nulla per la proposizione 1.3. Per l’arbitrarietà di $R$ , ciò implica anche che $f_n$ converge puntualmente a $f$ in $[0,+\infty)$ .

Per provare che la convergenza di $f_n$ a $f$ non è uniforme su $[0,+\infty)$ , osserviamo che

(208) $\begin{equation*} \lim_{t \to +\infty} \frac{t}{1+n^2t} = \frac{1}{n^2} \qquad \forall n \in \mathbb{N}. \end{equation*}$

Pertanto, per ogni $n \in \mathbb{N}$ esiste $R_n>0$ tale che

(209) $\begin{equation*} \frac{t}{1+n^2t} \geq \frac{1}{2n^2} \qquad \forall t \geq R_n. \end{equation*}$

Pertanto si ha

(210) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |f_n(x)| \geq & \lim_{n \to +\infty} f_n(2n^2 + R_n) \\ = & \lim_{n \to +\infty} \int_{0}^{2n^2 + R_n} \frac{t}{1+n^2t} \, \mathrm{d} t \\ \geq & \lim_{n \to +\infty} \int_{R_n}^{2n^2 + R_n} \frac{1}{2n^2} \, \mathrm{d} t \\ = & \lim_{n \to +\infty} \frac{2n^2 + R_n - R_n}{2n^2} \\ = & 1, \end{split} \end{equation*}$

dove nella seconda disuguaglianza si è usato (209) e il fatto che la funzione integranda è positiva. Da (210) e dalla proposizione 1.3, segue che $f_n$ non converge a $f$ uniformemente in $[0,+\infty)$ .

Esercizio 31 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon (0,+\infty) \to \mathbb{R}$ definite da

(211) $\begin{equation*} f_n(x) = \begin{cases} \sqrt{n} & \text{se } x \in \left(0,\dfrac{1}{n}\right)\\[10pt] \dfrac{1}{\sqrt{x+\dfrac{1}{n^2}}} & \text{se } x \in \left[\dfrac{1}{n},n^2\right)\\[15pt] \dfrac{1}{\sqrt{x+n}} & \text{se } x \in \left[n^2,+\infty\right) \end{cases} \qquad \forall n \in \mathbb{N}, \end{equation*}$

nei seguenti insiemi:

$\,$

in $(0,+\infty)$ ;

negli intervalli del tipo $[a,+\infty)$ , con $a >0$ .

Soluzione punto 1.

Studiamo separatamente le due richieste.

La successione $f_n$ converge puntualmente in $(0,+\infty)$ alla funzione $f_n \colon (0,+\infty) \to \mathbb{R}$ definita da

(212) $\begin{equation*} f(x) = \dfrac{1}{\sqrt{x}} \qquad \forall (0,+\infty). \end{equation*}$

Infatti, per ogni $x \in (0,+\infty)$ esiste $N \in \mathbb{N}$ tale che

(213) $\begin{equation*} x \in \left[\dfrac{1}{n},n^2\right) \qquad \forall n \geq N. \end{equation*}$

Pertanto

(214) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = \lim_{n \to +\infty} \dfrac{1}{\sqrt{x+\frac{1}{n^2}}} = \dfrac{1}{\sqrt{x}} \qquad \forall x \in (0,+\infty). \end{equation*}$

La convergenza non è però uniforme in quanto

(215) $\begin{equation*} \sup_{x \in(0,+\infty)} |f_n(x)-f(x)| \geq \sup_{x \in\left(0,\frac{1}{n}\right)} \left| \sqrt{n} - \dfrac{1}{\sqrt{x}}\right| = +\infty \qquad \forall n \in \mathbb{N}, \end{equation*}$

dove si è sfruttata (211). Da (215) e dalla proposizione 1.3, $f_n$ non converge uniformemente a $f$ in $(0,+\infty)$ .

Soluzione punto 2.

Dal punto precedente segue che $f_n$ converge puntualmente a $f$ in $[a,+\infty)$ per ogni $a>0$ . Affermiamo che la convergenza in tali insiemi è anche uniforme. Infatti, si fissi $a >0$ . Se $n > \dfrac{1}{a}$ , si ha $(a,+\infty) \subset \left(\frac{1}{n},+\infty \right)$ e quindi

(216) $\begin{equation*} \begin{split} \sup_{x \in[a,+\infty)} |f(x) - f_n(x)| = \max \left\{ \sup_{x \in[a,n^2)} \left|\dfrac{1}{\sqrt{x}} - \dfrac{1}{\sqrt{x+\frac{1}{n^2}}}\right|, \sup_{x \in[n^2,+\infty)}\left| \dfrac{1}{\sqrt{x}} - \dfrac{1}{\sqrt{x+n}} \right| \right\} \end{split}. \end{equation*}$

Per studiare i due estremi superiori in (216) osserviamo che, se $0 < x \leq y$ , si ha

(217) $\begin{equation*} \dfrac{1}{\sqrt{x}} - \dfrac{1}{\sqrt{y}} = \dfrac{\sqrt{y} - \sqrt{x}}{\sqrt{xy}} = \dfrac{\left(\sqrt{y} - \sqrt{x}\right)\left(\sqrt{y} + \sqrt{x}\right)}{\sqrt{xy}\left(\sqrt{y} + \sqrt{x}\right)} = \dfrac{y-x}{\sqrt{xy}\left(\sqrt{y} + \sqrt{x}\right)} \leq \dfrac{y-x}{2x^{\frac{3}{2}}}, \end{equation*}$

dove nella disuguaglianza si è usato che $x \leq y$ e quindi $\sqrt{xy}\geq x$ e $\sqrt{y} + \sqrt{x} \geq 2 \sqrt{x}$ . Poiché per ogni $n\in \mathbb{N}$ e per ogni $x \in [a,+\infty)$ si ha $a \leq x < x + \dfrac{1}{n^2}$ e $x < x+n$ , si può applicare (217) a (216), ottenendo

(218) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in[a,+\infty)} |f(x) - f_n(x)| \leq & \lim_{n \to +\infty} \max \left\{ \sup_{x \in[a,n^2)} \dfrac{\dfrac{1}{n^2}}{2\sqrt{x^3}}, \sup_{x \in[n^2,+\infty)} \dfrac{n}{2\sqrt{x^3}} \right\} \\ = & \lim_{n \to +\infty} \max \left\{ \dfrac{1}{2 n^2 \sqrt{a^3}}, \dfrac{n}{2\sqrt{n^6}} \right\} \\ = & 0. \end{split}. \end{equation*}$

Da (218) e dalla proposizione 1.3, si ha che $f_n$ converge uniformemente a $f$ in $[a,+\infty)$ .

Esercizio 32 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = 1 + n \sin \left(\frac{x \arctan(x) \ln (x^2+1)}{n^2}\right) \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti insiemi:

$\,$

in $\mathbb{R}$ ;

negli insiemi del tipo $[-R,R]$ con $R>0$ .

Soluzione punto 1.

Trattiamo separatamente i diversi casi.

Osservando che

$\lim_{n\to +\infty} \frac{x \arctan(x) \ln (x^2+1)}{n^2}=0 \qquad \forall x \in \mathbb{R},$

e ricordando lo sviluppo di Taylor $\sin t= t+o(t)$ per $t \to 0$ ,⁴ si ha

$\lim _{n \rightarrow+\infty} n \sin \left(\frac{x \arctan (x) \ln \left(x^{2}+1\right)}{n^{2}}\right)= \lim _{n \rightarrow+\infty} \left( \frac{x \arctan (x) \ln \left(x^{2}+1\right)}{n}+o\left(\frac 1n \right) \right) =0,$

da cui segue che $f_n$ converge puntualmente in $\mathbb{R}$ alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente pari a $1$ .

Osserviamo che la convergenza di $f_n$ a $f$ non è però uniforme. Infatti, per ogni $n \in \mathbb{N}$ la funzione $\varphi_n \colon \mathbb{R} \to \mathbb{R}$ definita da

(219) $\begin{equation*} \varphi_n(x) = \frac{x \arctan(x) \ln (x^2+1)}{n^2} \qquad \forall x \in \mathbb{R} \end{equation*}$

è continua e soddisfa $\varphi_n(0)=0$ e $\lim_{x \to \infty}\varphi(x)=+\infty$ . Per il teorema dei valori intermedi (si veda [1, teorema 6.29]), per ogni $n \in \mathbb{N}$ esiste $x_n \in [0,+\infty)$ tale che

(220) $\begin{equation*} \varphi_n(x_n)=\frac{\pi}{2}. \end{equation*}$

Pertanto si ha

(221) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}}|f_n(x)-f(x)| \geq \lim_{n \to +\infty} |f_n(x_n)-f(x_n)| = \lim_{n \to +\infty} \left|1+ n \sin\left(\frac{\pi}{2} \right) - 1\right| = +\infty. \end{equation*}$

Per la proposizione 1.3, la convergenza di $f_n$ a $f$ non è uniforme in $\mathbb{R}$ .

$\,$

Per la definizione e le proprietà degli infinitesimi $o(t)$ , si rimanda a [1, sezione 6.6]; in questa sede è sufficiente ricordare che, per definizione di $o$ -piccolo, vale $\lim_{t\to 0} o(t)/t=0$ ↩

Soluzione punto 2.

Sia $R>0$ ; chiaramente anche in $[-R,R]$ si ha convergenza puntuale delle $f_n$ a $f$ .

Affermiamo che la convergenza è anche uniforme in $[-R,R]$ . Si ha infatti

(222) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in[-R,R]} |f_n(x)-f(x)| = & \lim_{n \to +\infty} \sup_{x \in[-R,R]} \left| n \sin \left(\frac{x \arctan (x) \ln \left(x^{2}+1\right)}{n^{2}}\right) \right| \\ \leq & \lim_{n \to +\infty} \sup_{x \in[-R,R]} \left|\frac{x \arctan (x) \ln \left(x^{2}+1\right)}{n}\right| \\ = & \lim_{n \to +\infty} \frac{R \arctan (R) \ln \left(R^{2}+1\right)}{n} \\ = & \,0, \end{split} \end{equation*}$

dove nella disuguaglianza abbiamo usato la nota disuguaglianza $|\sin t| \leq |t|$ per ogni $t \in \mathbb{R}$ , mentre nella seconda uguaglianza abbiamo usato il fatto che la funzione $x \mapsto x \arctan(x) \ln (x^2+1)$ è pari e crescente in $[0,R]$ .

Da (222) e dalla proposizione 1.3 segue che $f_n$ converge uniformemente a $f$ in $[-R,R]$ .

Un modo alternativo per concludere era osservare che, appunto dalla monotonia e dalla continuità della funzione $x \mapsto x \arctan(x) \ln (x^2+1)$ in $[0,R]$ e da $\lim_{n \to +\infty} \frac{1}{n^2}=0$ , segue che esiste $N \in \mathbb{N}$ tale che

(223) $\begin{equation*} 0\leq \frac{x \arctan (x) \ln \left(x^{2}+1\right)}{n^{2}} \leq \frac{\pi}{2} \qquad \forall n \geq N, \,\,\, \forall x \in [0,R]. \end{equation*}$

Poiché la funzione $t \mapsto \sin t$ è crescente in $\left[0,\dfrac{\pi}{2}\right]$ , si ha che $f_n$ è crescente in $[0,R]$ per ogni $n \geq N$ . Dato che $f_n \geq 1$ , si ottiene quindi

(224) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[-R,R]} |f_n(x)-f(x)| = \lim_{n \to +\infty} |f_n(R) - f(R)| = 0, \end{equation*}$

dove l’ultima uguaglianza segue dalla convergenza puntuale di $f_n$ a $f$ .

Esercizio 33 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon [-1,1] \to \mathbb{R}$ definita da

(225) $\begin{equation*} f_n(x) = \left( 1-\frac{x^2}{n} + \dfrac{1}{n^2} \right)^{n^2} \qquad \forall n \in \mathbb{N},\,\,\,\forall x \in [-1,1] \end{equation*}$

nei seguenti insiemi:

$\,$

in $[-1,1]$ ;

negli insiemi del tipo $[-1,-\delta] \cup [\delta,1]$ , con $0 < \delta < 1$ .

Si calcoli poi

(226) $\begin{equation*} \lim_{n \to +\infty} \int_{-1}^1 f_n(x) \, \mathrm{d} x. \end{equation*}$

Soluzione punto 1.

Risolviamo separatamente i vari punti.

Se $x \in [-1,1] \setminus \{0\}$ , dato che $\lim_{n \to +\infty} \frac{1}{n^2} \frac{n}{x^2}=0$ , esiste $N \in \mathbb{N}$ tale che

(227) $\begin{equation*} 0 < 1-\frac{x^2}{n} + \dfrac{1}{n^2} < 1- \frac{x^2}{2n} \qquad \forall n \geq N. \end{equation*}$

Quindi

(228) $\begin{equation*} 0 \leq \lim_{n \to +\infty} f_n(x) \leq \lim_{n \to +\infty} \left(1- \frac{x^2}{2n}\right)^{n^2} = \lim_{n \to +\infty} \left(1- \frac{x^2}{2n}\right)^{2n \cdot \frac{n^2}{2n}} = 0, \end{equation*}$

dove nell’ultima uguaglianza si è usato il limite notevole $\lim_{n \to +\infty} \left(1- \frac{x^2}{2n}\right)^{2n}=e^{-x^2}$ , il fatto che $0<e^{-x^2}<1$ e che $\lim_{n \to +\infty} \frac{n^2}{2n}=+\infty$ . Se invece $x= 0$ , si ha

(229) $\begin{equation*} \lim_{n \to +\infty} f_n(0) = \lim_{n \to +\infty} \left(1 + \dfrac{1}{n^2}\right)^{n^2} = e. \end{equation*}$

Da tali considerazioni segue che $f_n$ converge puntualmente in $[-1,1]$ alla funzione $f \colon [-1,1] \to \mathbb{R}$ definita da

(230) $\begin{equation*} f(x) = \begin{cases} 0 & \text{se } x \in [-1,1] \setminus \{0\}\\ e & \text{se } x = 0. \end{cases} \end{equation*}$

Poiché ogni $f_n$ è una funzione continua mentre $f$ non è continua in $0$ , per il teorema 1.5 la convergenza di $f_n$ a $f$ non è uniforme.

Soluzione punto 2.

Sia $\delta>0$ . Affermiamo che la convergenza di $f_n$ a $f$ è uniforme in $[-1,-\delta] \cup [\delta,1]$ . A tal fine, osserviamo preliminarmente che ogni $f_n$ è una funzione pari, quindi è sufficiente provare la convergenza uniforme in $[\delta,1]$ .

Poiché la funzione $x \mapsto 1-\dfrac{x^2}{n} + \dfrac{1}{n^2}$ è decrescente e positiva in $[\delta,1]$ , anche $f_n$ lo è e quindi

(231) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[\delta,1]} |f_n(x)-f(x)| = \lim_{n \to +\infty} f_n(\delta) = 0, \end{equation*}$

dove l’ultima uguaglianza segue dalla convergenza puntuale di $f_n$ a $f$ . La proposizione 1.3 e 231 implicano la convergenza uniforme di $f_n$ a $f$ in $[\delta,1]$ .

Poiché $f_n$ non converge uniformemente a $f$ in $[-1,1]$ , non si può applicare il teorema 1.7 per concludere che il limite (226) sia pari a $0$ . Per superare questa difficoltà, osserviamo innanzitutto che per la parità delle funzioni $f_n$ si ha

(232) $\begin{equation*} \int_{-1}^1 f_n(x) \, \mathrm{d} x = 2 \int_0^1 f_n(x) \, \mathrm{d} x \qquad \forall n \in \mathbb{N}. \end{equation*}$

Dato che $f_n$ converge uniformemente a $f$ in $[\delta,1]$ per ogni $\delta>0$ , si ottiene

(233) $\begin{equation*} \lim_{n \to +\infty} \int_{\delta}^1 f_n(x) \, \mathrm{d} x = \int_{\delta}^1 f(x) \, \mathrm{d} x = 0 \qquad \forall \delta \in (0,1), \end{equation*}$

dove la prima uguaglianza deriva dal teorema 1.7. Inoltre, poiché ognuna delle $f_n$ è decrescente e positiva in $[0,1]$ e $\lim_{n \to +\infty} f_n(0)=e$ , le $f_n$ sono equilimitate, ovvero esiste $M>0$ tale che

(234) $\begin{equation*} |f_n(x)|\leq M \qquad \forall n \in \mathbb{N},\,\,\forall x \in [0,1]. \end{equation*}$

Utilizzando queste osservazioni preliminari dimostriamo quindi che il limite in (226) è pari a $0$ . A tal fine, fissiamo $\varepsilon>0$ , e scegliamo $\delta>0$ tale che $M \delta < \dfrac{\varepsilon}{2}$ . Per (233), esiste $N \in \mathbb{N}$ tale che

(235) $\begin{equation*} 0 \leq \int_{0}^1 f_n(x) \, \mathrm{d} x = \int_{0}^\delta f_n(x) \, \mathrm{d} x + \int_{\delta}^1 f_n(x) \, \mathrm{d} x \leq M \delta + \frac{\varepsilon}{2} \leq \varepsilon \qquad \forall n \geq N. \end{equation*}$

dove la seconda disuguaglianza deriva da $|f_n|\leq M$ e da (233), mentre la terza deriva da $M \delta \leq \dfrac{\varepsilon}{2}$ . Per l’arbitrarietà di $\varepsilon$ , si ha

(236) $\begin{equation*} \lim_{n \to +\infty} \int_{-1}^1 f_n(x) \, \mathrm{d} x = 2 \lim_{n \to +\infty} \int_0^1 f_n(x) \, \mathrm{d} x = 0. \end{equation*}$

Esercizio 34 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni continue tali che

(237) $\begin{equation*} \lim_{n \to +\infty} f_n(x) = f(x) \qquad \forall x \in [a,b] \cap \mathbb{Q}, \end{equation*}$

dove $f \colon [a,b] \to \mathbb{R}$ è una funzione continua.

$\,$

Si può dire che $f_n$ converge puntualmente a $f$ in $[a,b]$ ?

Cosa si può dire sulla convergenza di $f_n$ a $f$ in $[a,b]$ assumendo invece che $f_n$ converga uniformemente a $f$ in $[a,b] \cap \mathbb{Q}$ ?

Soluzione punto 1.

Rispondiamo separatamente alle due domande.

La risposta è negativa, come mostra il seguente esempio. Sia $x_0 \in [a,b] \setminus \mathbb{Q}$ un numero irrazionale, e si consideri la successione di funzioni $f_n \colon [a,b] \to \mathbb{R}$ rappresentate in figura 2 e definite da

(238) $\begin{equation*} f_n(x) = \max\left\{ 0, 1 - n|x-x_0|\right\} \qquad \forall n \in \mathbb{N},\,\, \forall x \in [a,b]. \end{equation*}$

Ogni $f_n$ è una funzione continua essendo massimo di funzioni continue, e si ha

(239) $\begin{equation*} f_n(x) = 0 \qquad \forall x \in [a,b] \colon |x-x_0|\geq \frac{1}{n}, \quad \forall n \in \mathbb{N}. \end{equation*}$

Sia $q \in [a,b] \cap \mathbb{Q}$ . Poiché $|q-x_0|>0$ , da (238) segue che

(240) $\begin{equation*} f_n(x)=0 \qquad \forall n \geq \frac{1}{|q-x_0|}, \end{equation*}$

pertanto $f_n$ converge puntualmente in $[a,b] \cap \mathbb{Q}$ alla funzione $f \colon [a,b] \to \mathbb{R}$ identicamente nulla. Chiaramente però $f_n$ non converge a $f$ puntualmente in $[a,b]$ , in quanto da (239) segue che $f_n(x_0)=1$ per ogni $n \in \mathbb{N}$ .

Soluzione punto 2.

$\,$

Figura 2: una delle funzioni $f_n$ definite in (238). Se $x_0 \notin \mathbb{Q}$ e $q \in \mathbb{Q}$ , per $n$ sufficientemente grande si ha $f_n(q)=0$ . Si noti inoltre che, poiché esistono numeri razionali arbitrariamente vicini a $x_0$ , in tali punti $f_n$ assume valori arbitrariamente vicini a $1$ , quindi $f_n$ non converge uniformemente alla funzione identicamente nulla su $[a,b] \cap \mathbb{Q}$ .

$\,$

Se $f_n$ converge a $f$ uniformemente in $[a,b] \cap \mathbb{Q}$ , affermiamo che $f_n$ converge uniformemente a $f$ in $[a,b]$ . Infatti, si scelga $\varepsilon>0$ . Dall’ipotesi di convergenza uniforme in $[a,b] \cap \mathbb{Q}$ , esiste $N \in \mathbb{N}$ tale che

(241) $\begin{equation*} |f_n(y)-f(y)|< \frac{\varepsilon}{3} \qquad \forall n \geq N,\,\, \forall y \in [a,b] \cap \mathbb{Q}. \end{equation*}$

Sia ora $x \in [a,b]$ e sia $n \geq N$ ; dalla disuguaglianza triangolare si ha

(242) $\begin{equation*} |f_n(x)-f(x)| \leq |f_n(x)-f_n(y)| + |f_n(y)-f(y)| + |f(y)-f(x)| \qquad \forall y \in [a,b]. \end{equation*}$

Dalla densità di $\mathbb{Q}$ in $R$ e dalla continuità di $f_n$ e di $f$ , si può scegliere $y \in [a,b] \cap \mathbb{Q}$ tale che

(243) $\begin{equation*} |f_n(x)-f_n(y)| < \frac{\varepsilon}{3}, \qquad |f(y)-f(x)| < \frac{\varepsilon}{3}. \end{equation*}$

Con tale scelta di $y$ , inserendo (241) e (243) in (242), si ottiene

(244) $\begin{equation*} |f_n(x)-f(x)| \leq |f_n(x)-f_n(y)| + |f_n(y)-f(y)| + |f(y)-f(x)| < \varepsilon. \end{equation*}$

Dall’arbitrarietà di $\varepsilon$ , di $x$ e di $n \geq N$ e dalla definizione 1.2, segue la convergenza uniforme di $f_n$ a $f$ in $[a,b]$ .

Esercizio 35 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Sia $f_n \colon \mathbb{R} \to \mathbb{R}$ una successione di funzioni limitate convergenti uniformemente a una funzione $f \colon \mathbb{R} \to \mathbb{R}$ e sia $g \colon \mathbb{R} \to \mathbb{R}$ una funzione continua.

$\,$

Cosa si può dire sulla convergenza puntuale e uniforme della successione $g \circ f_n$ ?

Come cambia la risposta alla domanda precedente rimuovendo l’ipotesi che le funzioni $f_n$ siano limitate?

Soluzione punto 1.

Rispondiamo separatamente alle domande.

Per la proposizione 3.59 in Esercizi Successioni di funzioni, una successione di funzioni limitate convergente uniformemente è equilimitata, ossia esiste $M >0$ tale che

(245) $\begin{equation*} |f_n(x)| \leq M \qquad \forall n \in \mathbb{N}, \,\, \forall x \in \mathbb{R}. \end{equation*}$

Per convenienza del lettore, riportiamo qui un accenno di dimostrazione di questa affermazione.

Poichè ognuna delle $f_n$ è limitata, per ogni $n \in \mathbb{N}$ esiste $M_n>0$ tale che

(246) $\begin{equation*} |f_n(x)| \leq M_n \qquad \forall x \in \mathbb{R}. \end{equation*}$

Per ogni $\varepsilon>0$ , per la convergenza uniforme di $f_n$ a $f$ e per la proposizione 1.4, esiste $N \in \mathbb{N}$ tale che

(247) $\begin{equation*} |f_{N}(x) - f_n(x)|< \varepsilon \qquad \forall n \geq N,\,\, \forall x \in \mathbb{R}. \end{equation*}$

Da (246) e (247) segue che

(248) $\begin{equation*} |f_n(x)| < |f_{N}(x)|+ \varepsilon \leq M_{N}+ \varepsilon \qquad \forall n \geq N,\,\, \forall x \in \mathbb{R}, \end{equation*}$

pertanto esiste $M >0$ tale che

(249) $\begin{equation*} |f_n(x)| \leq M \qquad \forall n \in \mathbb{N}, \,\, \forall x \in \mathbb{R}. \end{equation*}$

Passando al limite per $n\to +\infty$ in (249), si ottiene che anche

(250) $\begin{equation*} |f(x)| \leq M \qquad \forall x \in \mathbb{R}. \end{equation*}$

Poiché $g$ è continua, per il teorema di Heine-Cantor [1, Teorema 6.41], essa è uniformemente continua ristretta all’intervallo $[-M,M]$ : fissato $\varepsilon>0$ , esiste $\delta>0$ tale che

(251) $\begin{equation*} |g(s)-g(t)|< \varepsilon \qquad \forall s,t \in [-M,M], \text{ con } |s-t|< \delta. \end{equation*}$

Poiché $f_n$ converge uniformemente a $f$ in $\mathbb{R}$ , esiste $N \in \mathbb{N}$ tale che

(252) $\begin{equation*} |f_n(x)-f(x)|< \delta \qquad \forall n \geq N,\,\, \forall x \in \mathbb{R}. \end{equation*}$

Da (252), (249), (250) e (251) segue che

(253) $\begin{equation*} |g(f_n(x)) - g(f(x))| < \varepsilon \qquad \forall n \geq N,\,\, \forall x \in \mathbb{R}. \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ e per la definizione 1.2,, $g \circ f_n$ converge uniformemente (e quindi anche puntualmente) a $g \circ f$ in $\mathbb{R}$ .

Soluzione punto 2.

Se le funzioni $f_n$ non sono limitate, in generale $g \circ f$ non converge uniformemente a $g \circ f$ . Infatti, consideriamo la successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definite da

(254) $\begin{equation*} f_n(x) = x+\frac{1}{n} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}, \end{equation*}$

e la funzione $g \colon \mathbb{R} \to \mathbb{R}$ definita da $g(y)=y^2$ .

$f_n$ converge uniformemente alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ definita da $f(x)=x$ e $g$ è una funzione continua. Si ha però

(255) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}} |g(f_n(x)) - g(f(x))| \geq \lim_{n \to +\infty} |g(f_n(n^2)) - g(f(n^2))| = \lim_{n \to +\infty} \left|2n + \frac{1}{n^2}\right| = +\infty, \end{equation*}$

da cui $g \circ f_n$ non converge uniformemente a $g \circ f$ in $\mathbb{R}$ .

D’altra parte, osserviamo che $g \circ f_n$ converge puntualmente a $g \circ f$ in $\mathbb{R}$ . Infatti, poiché $g$ è continua e $f_n$ converge puntualmente a $f$ , si ha

(256) $\begin{equation*} \lim_{n \to +\infty} g(f_n(x)) = g(f(x)) \qquad \forall x \in \mathbb{R}. \end{equation*}$

Osserviamo che in quest’ultima parte abbiamo usato la sola convergenza puntuale di $f_n$ a $f$ .

Esercizio 36 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Per ogni $n \in \mathbb{N}$ , sia $f_n \colon (1-\delta_n,1+\delta_n) \to \mathbb{R}$ , con $\delta_n>0$ , la soluzione locale del problema di Cauchy

(257) $\begin{equation*} \begin{cases} y'= \dfrac{1+y^2}{2t^2y}\\[10pt] y(1)=e^{-n}. \end{cases} \end{equation*}$

Si dica se ogni $f_n$ è estendibile in $[1,+\infty)$ e si studi la convergenza puntuale e uniforme di $f_n$ su tale intervallo.

Soluzione punto 1.

Presentiamo due svolgimenti diversi di questo esercizio. Il primo utilizza il calcolo esplicito delle soluzioni $f_n$ di (257) e del loro limite $f$ , mentre il secondo giunge alle stesse conclusioni evitando però sia il calcolo esplicito delle $f_n$ , sia quello di $f$ .

Nonostante tale secondo approccio possa in qualche modo sembrare limitante, esso si rivela in realtà molto utile; infatti, spesso è più importante ottenere informazioni qualitative sulle soluzioni di un’equazione differenziale e sulle convergenze che esse soddisfano, piuttosto che calcolare esplicitamente tali soluzioni e i loro limiti. Questa indagine qualitativa risulta inoltre essenziale quando i calcoli espliciti sono impossibili oppure non forniscono le informazioni necessarie.

Poiché la funzione $F \colon (0,+\infty)\times (0,+\infty) \to (0,+\infty)$ definita da

(258) $\begin{equation*} F(t,y)=\frac{1+y^2}{2t^2y} \qquad \forall (t,y) \in (0,+\infty)\times (0,+\infty) \end{equation*}$

è localmente lipschitziana in un intorno di $(1,e^{-n})$ per ogni $n \in \mathbb{N}$ , per il teorema di esistenza e unicità di Cauchy-Lipschitz [2, teorema 5.14] esiste $\delta_n>0$ tale che il problema (257) abbia un’unica soluzione $f_n \colon (1-\delta_n,1+\delta_n) \to \mathbb{R}$ in tale intorno. Calcoliamo $f_n$ integrando l’equazione, che risulta essere a variabili separabili. Per ogni $t \in (1-\delta_n,1+\delta_n)$ si ha

(259) $\begin{equation*} \begin{split} \begin{cases} \dfrac{2 f_n(t) f_n'(t)}{1+f_n^2(t)} = \dfrac{1}{t^2}\\[10pt] f_n(1)=e^{-n} \end{cases} \iff & \int_1^t \dfrac{2 f_n(\tau) f_n'(\tau)}{1+f_n^2(\tau)} \dif \tau = \int_1^t \dfrac{1}{\tau^2} \dif \tau \\[5pt] \iff & \log \left( 1+f_n^2(t) \right) - \log \left( 1+e^{-2n} \right) = 1-\frac{1}{t} \\[8pt] \iff & f_n(t) = \sqrt{(1+e^{-2n})e^{1-\frac{1}{t}} - 1}, \end{split} \end{equation*}$

dove nella prima equivalenza si è integrata l’equazione tra $1$ e $t$ . Dall’espressione delle $f_n$ , risulta che ognuna di esse è ben definita per ogni $t \geq 1$ e inoltre $f_n \geq 0$ . Pertanto ogni $f_n$ è prolungabile su $(1-\delta_n, + \infty)$ rimanendo soluzione del problema (257). Si ha

(260) $\begin{equation*} \begin{equation*} \lim_{n \to +\infty} f_n(t) = \lim_{n \to +\infty} \sqrt{(1+e^{-2n})e^{1-\frac{1}{t}} - 1} = \sqrt{e^{1-\frac{1}{t}} - 1} \qquad \forall t \in [1,+\infty). \end{equation*}$

Pertanto $f_n$ converge puntualmente in $[1,+\infty)$ alla funzione $f \colon [1,+\infty) \to \mathbb{R}$ definita da

(261) $\begin{equation*} f(t) = \sqrt{e^{1-\frac{1}{t}} - 1} \qquad \forall t \in [1,+\infty). \end{equation*}$

Poiché la funzione $f$ è continua e la successione $f_n(t)$ è decrescente per ogni $t \in [1,+\infty)$ , per il teorema 1.9 la convergenza di $f_n$ a $f$ è uniforme in ogni intervallo del tipo $[1,T]$ con $T>1$ .

Osserviamo ora che $\lim_{t \to +\infty}f(t) = \sqrt{e-1}>1$ . Da tale relazione e da $f_n \geq f$ segue quindi l’esistenza di $T>1$ tale che

(262) $\begin{equation*} f_n(t) \geq f(t) \geq 1 \qquad \forall t \geq T. \end{equation*}$

Fissando un tale $T$ , si ha

(263) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{t \in [T,+\infty)} |f_n(t)-f(t)| = & \lim_{n \to +\infty} \sup_{t \in [T,+\infty)} \dfrac{f_n^2(t) - f^2(t)}{f_n(t)+f(t)} \\[10pt] \leq & \lim_{n \to +\infty} \sup_{t \in [T,+\infty)} \dfrac{e^{-2n}e^{1-\frac{1}{t}}}{2} \\ = & \lim_{n \to +\infty} \dfrac{e^{-2n+1}}{2} \\ =& 0, \end{split} \end{equation*}$

dove nella prima uguaglianza si è sfruttato $f_n > f$ (la disuguaglianza segue facilmente dalle espressioni di $f_n$ e di $f$ ) e si è moltiplicato e diviso per $f_n(t)+f(t)$ (che è non nullo in quanto sia le $f_n$ sia $f$ sono strettamente positive in $(1,+\infty)$ ), mentre nella disuguaglianza è stata usata (262). Ciò mostra, per la proposizione 1.3, la convergenza uniforme di $f_n$ a $f$ anche in $[T,+\infty)$ e quindi la convergenza uniforme di $f_n$ a $f$ in $[1,+\infty)$ .

Soluzione punto 2.

Poiché la funzione $F \colon (0,+\infty)\times (0,+\infty) \to (0,+\infty)$ definita da

(264) $\begin{equation*} F(t,y)=\frac{1+y^2}{2t^2y} \qquad \forall (t,y) \in (0,+\infty)\times (0,+\infty) \end{equation*}$

è localmente lipschitziana in un intorno di $(1,e^{-n})$ per ogni $n \in \mathbb{N}$ , per il teorema di esistenza e unicità di Cauchy-Lipschitz [2, teorema 5.14]. esiste $\delta_n>0$ tale che il problema (257) abbia un’unica soluzione $f_n \colon (1-\delta_n,1+\delta_n) \to \mathbb{R}$ in tale intorno.

Dall’equazione (257) e da $F>0$ , segue che ogni $f_n$ è crescente in tutto il suo intervallo massimale $[1-\delta_n',M_n)$ di esistenza, con $\delta_n' \leq \delta_n$ e $M_n \geq 1+\delta_n$ .

Mostriamo ora che tale intervallo contiene $[1,+\infty)$ . A tal fine, poiché dalla monotonia di $f_n$ esiste il limite $\lim_{t \to M_n} f_n(t)$ e $F$ è definita in $(0,+\infty)\times (0,+\infty)$ , il teorema di fuga dai compatti [2, teorema 5.8]. implica che è sufficiente dimostrare che $f_n$ è limitata in $[1,M_n)$ .

Se $f_n(t) \leq 1$ per ogni $t \in [1,M_n)$ , è chiaro che $f_n$ è limitata. Invece, se esiste $T_n \in [1,M_n)$ tale che $f_n(t) \geq 1$ per ogni $t \in [T_n,M_n)$ , allora si ha

(265) $\begin{equation*} f_n'(t) = F(t,f_n(t)) = \dfrac{1+f_n^2(t)}{2t^2 f_n(t)} \leq \dfrac{2f_n^2(t)}{2t^2 f_n(t)} = \dfrac{f_n(t)}{t^2} \qquad \forall t \in [T_n,M_n), \end{equation*}$

dove nella disuguaglianza si è sfruttato $f_n(t) \geq 1$ per $t \in [T_n,M_n)$ per ottenere $1+f_n^2(t) \leq 2f_n^2(t)$ . Per il teorema del confronto [2, teorema 5.17], si ha

(266) $\begin{equation*} f_n(t) \leq g_n(t) \qquad \forall t \in [1,R_n), \end{equation*}$

dove $g_n \colon [1,R_n) \to \mathbb{R}$ è la soluzione massimale del problema di Cauchy

(267) $\begin{equation*} \begin{cases} y' - \dfrac{y}{t^2} = 0\\[7pt] y(1)=e^{-n}. \end{cases} \end{equation*}$

È facile calcolare $g_n$ esplicitamente, in quanto l’equazione differenziale in (267) è lineare. Moltiplicandola per $e^{\frac{1}{t}}$ si ottiene

(268) $\begin{equation*} \begin{split} \begin{cases} e^{\frac{1}{t}}y' - e^{\frac{1}{t}}\dfrac{y}{t^2} = \dfrac{\dif}{\dif t}\left(e^{\frac{1}{t}}y(t) \right) = 0 \\[7pt] y(1)=e^{-n} \end{cases} \iff & \begin{cases} e^{\frac{1}{t}}y(t) = c_n \\[7pt] y(1)=e^{-n} \end{cases} \\ \iff & \begin{cases} y(t) = c_n e^{-\frac{1}{t}} \\[7pt] y(1)=e^{-n}, \end{cases} \end{split} \end{equation*}$

dove la costante $c_n \in \mathbb{R}$ deve essere calcolata in base alla condizione iniziale $y(1)=e^{-n}$ . Da tale relazione infatti segue che $c_n=e^{1-n}$ . Pertanto si ha

(269) $\begin{equation*} g_n(t)=e^{1-n} e^{-\frac{1}{t}} \qquad \forall n \in \mathbb{N},\,\, \forall t \in [1,R_n). \end{equation*}$

Poiché tale funzione è positiva e limitata in $[1,+\infty)$ , essa è soluzione dell’equazione (267) per ogni $t \geq 1$ . Pertanto $R_n =+\infty.$ Poiché $g_n$ è limitata in $[1,+\infty)$ , da (266) segue che anche $f_n$ lo è. Da ciò segue che ogni $f_n$ è prolungabile su $[1,+\infty)$ . Inoltre, dato che ogni $f_n$ è crescente, per ogni $n \in \mathbb{N}$ esiste

(270) $\begin{equation*} \lim_{t \to +\infty} f_n(t) = \ell_n < +\infty. \end{equation*}$

Studiamo ora la convergenza delle funzioni $f_n$ in $[1,+\infty)$ . Da $f_m(1) > f_n(1)$ se $m \leq n$ e dall’unicità della soluzione, si ha anche

(271) $\begin{equation*} f_m(t) > f_n(t) > 0 \qquad \forall t \geq 1,\,\, \forall m \leq n. \end{equation*}$

Da ciò segue che, per ogni $t \in \mathbb{N}$ , la successione $\{f_n(t)\}_{n \in \mathbb{N}}$ è decrescente. Ciò mostra che $f_n$ converge puntualmente a una funzione $f \colon [1,+\infty) \to [0,+\infty)$ .

Si mostrerà ora che $f_n$ converge uniformemente a $f$ in $[1,+\infty)$ . A tal fine, si studierà separatamente la convergenza di $f_n$ a $f$ in opportuni intervalli del tipo $[1,1+\eta], [\eta,T], [T,+\infty)$ .

Si fissi $\varepsilon>0$ . Poiché ogni $f_n$ è una funzione continua e per ogni $t \in \mathbb{N}$ la successione $\{f_n(t)\}_{n \in \mathbb{N}}$ è decrescente, da $\lim_{n \to +\infty} f_n(1)= \lim_{n \to +\infty} e^{-n}=0$ si ha che esiste $N_1\in \mathbb{N}$ e $\eta>0$ tale che

(272) $\begin{equation*} f_n(t) \leq \varepsilon \qquad \forall n \geq N_1,\,\, \forall t \in [1,1+\eta]. \end{equation*}$

Determiniamo ora un opportuno $T>1+\eta$ e studiamo la convergenza uniforme di $f_n$ a $f$ in $[T,+\infty)$ . A tal fine, cerchiamo di ricavare preliminarmente una stima dal basso sul valore di $f_n$ in $[1+\eta,+\infty)$ .

Poiché ogni $f_n$ è limitata e per ogni $t \in [1,+\infty)$ la successione $\{f_n(t)\}_{n \in \mathbb{N}}$ è decrescente, esiste $M>0$ tale che

(273) $\begin{equation*} f_n(t) \leq M \qquad \forall n \in \mathbb{N},\,\,\forall t \in [1,+\infty). \end{equation*}$

Quindi, dall’equazione differenziale in (257) segue che

(274) $\begin{equation*} f_n'(t) \geq \frac{1}{2t^2 y} \geq \frac{1}{2(1+\eta)^2 M} \qquad \forall n \in \mathbb{N},\,\, \forall t \in [1,1+\eta]. \end{equation*}$

Applicando il teorema di Lagrange a ogni $f_n$ nell’intervallo $[1,1+\eta]$ e usando (274), si ottiene

(275) $\begin{equation*} f_n(t) \geq \frac{\eta}{2(1+\eta)^2 M} \qquad \forall n \in \mathbb{N},\,\, \forall t \geq 1+\eta. \end{equation*}$

Unendo (273) e (275) si ottiene l’esistenza di una costante $c>0$ tale che

(276) $\begin{equation*} f_n'(t)=\frac{1+f_n^2(t)}{2t^2f_n(t)} \leq \frac{c}{t^2} \qquad \forall n \in \mathbb{N},\,\, \forall t \geq 1+\eta. \end{equation*}$

Per ogni $T>1+\eta$ e per ogni $n \in \mathbb{N}$ si può quindi stimare

(277) $\begin{equation*} \begin{split} \sup_{t \in [T,+\infty)} |f_n(t)-f(t)| \leq & \ell_n - f(T) \\ = & \ell_n - f_n(T) + f_n(T) - f(T) \\ = & \int_T^{+\infty} f_n'(t) \dif t + f_n(T) - f(T) \\ \leq & \int_T^{+\infty} \frac{c}{t^2}\dif t + f_n(T) - f(T) \\ = & \frac{c}{T} + f_n(T) - f(T), \end{split} \end{equation*}$

dove nella prima disuguaglianza abbiamo sfruttato la monotonia di $f_n$ e di $f$ , nella seconda uguaglianza abbiamo usato il teorema fondamentale del calcolo integrale, mentre nella terza disuguaglianza abbiamo usato (276).

Per (277) e per la convergenza puntuale di $f_n$ a $f$ , esiste $N_2 \in \mathbb{N}$ e $T \geq 1+\eta$ tale che

(278) $\begin{equation*} \sup_{t \in [T,+\infty)} |f_n(t)-f(t)| \leq \varepsilon \qquad \forall n \geq N_2. \end{equation*}$

Occorre ora studiare la convergenza uniforme in nell’intervallo $[1+\eta, T]$ . Osserviamo che, per (276), la successione $f_n$ è equicontinua (definizione 1.12) in $[1+\eta,T]$ . Infatti, dati $t,s \in [1+\eta,T]$ e $n \in \mathbb{N}$ , per il teorema di Lagrange esiste $\tau$ compreso tra $t,s$ tale che

(279) $\begin{equation*} |f_n(t) - f_n(s)| = |f_n'(\tau)||t-s| \leq c\frac{|t-s|}{(1+\eta)^2}, \end{equation*}$

dove nella disuguaglianza si è usato (276) e $\tau \geq 1+\eta$ . Poiché per $0 \leq f_n$ e (273) la successione $f_n$ è anche equilimitata, per il teorema 1.13, essa converge uniformemente in $[1+\eta,T]$ .

Unendo quest’ultima informazione a (272) e (178), e dall’arbitrarietà di $\varepsilon$ , si ottiene la convergenza uniforme di $f_n$ in $[1,+\infty)$ .

Esercizio 37 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definita da

$f_n(x) = \left(\dfrac{nx^2+3}{nx^2+1}\right)^n \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R},$

nei seguenti insiemi:

$\,$

in $\mathbb{R}$ ;

in $\mathbb{R} \setminus \{0\}$ ;

negli intervalli del tipo $(-\infty, -a] \cup [a,+\infty)$ con $a>0$ .

Soluzione punto 1.

Trattiamo separatamente i casi proposti.

Per $x=0$ si ha

(280) $\begin{equation*} \lim_{n \to \infty} f_n(0)=\lim_{n \to \infty}3^n=+\infty, \end{equation*}$

dunque $f_n$ non converge puntualmente (e quindi nemmeno uniformemente) in $\mathbb{R}$ .

Soluzione punto 2.

Si ha

(281) $\begin{equation*} f_n(x) = \left(1+ \dfrac{2}{nx^2+1}\right)^n = \left( \left(1+ \dfrac{2}{nx^2+1}\right) ^{\frac{nx^2+1}{2}}\right)^\frac{2n}{nx^2+1} \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R} \setminus \{0\}, \end{equation*}$

quindi

(282) $\begin{equation*} \lim_{n \to \infty} f_n(x) = \lim_{n \to \infty} \left( \left(1+ \dfrac{2}{nx^2+1}\right) ^{\frac{nx^2+1}{2}}\right)^\frac{2n}{nx^2+1} = \exp \left(\frac{2}{x^2} \right) \qquad \forall x \in \mathbb{R} \setminus \{0\}. \end{equation*}$

Ciò implica che la successione $f_n$ converge puntualmente in $\mathbb{R} \setminus \{0\}$ alla funzione $f \colon \mathbb{R} \setminus \{0\} \to \mathbb{R}$ definita da

(283) $\begin{equation*} f(x) = \exp \left(\frac{2}{x^2} \right) \qquad \forall x \in \mathbb{R} \setminus \{0\}. \end{equation*}$

Studiamo ora la convergenza uniforme di $f_n$ a $f$ in $\mathbb{R} \setminus\{0\}$ ; innanzitutto osserviamo che, dalla parità delle $f_n$ e di $f$ , è sufficiente studiare la convergenza uniforme di $f_n$ a $f$ in $(0,+\infty)$ . Calcolando $f_n$ e $f$ in $\dfrac{1}{\sqrt{n}}$ si ottiene

(284) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in (0,+\infty)} |f_n(x) - f(x)| \geq \lim_{n \to +\infty} \left\vert f_n\left(\frac{1}{\sqrt{n}} \right) - f\left(\frac{1}{\sqrt{n}} \right) \right\vert = \lim_{n \to +\infty} |2^n - e^{2n}| = +\infty, \end{equation*}$

quindi la convergenza di $f_n$ a $f$ non è uniforme in $(0,+\infty)$ , e quindi nemmeno in $\mathbb{R} \setminus \{0\}$ .

Soluzione punto 3.

Fissato $a>0$ , affermiamo che $f_n$ converge uniformemente a $f$ su $(-\infty,-a] \cup [a,+\infty)$ . Per la parità di $f_n$ e di $f$ , è sufficiente provare la convergenza uniforme sull’insieme $[a,+\infty)$ .

Facciamo ora delle osservazioni preliminari sulle funzioni $f_n$ .

$\quad$

Per ogni $n \in \mathbb{N}$ , $f_n$ è decrescente in $[a,+\infty)$ . Ciò segue dalla scrittura di $f_n$ in (280) e dal fatto che, fissato $n \in \mathbb{N}$ , la funzione $x \mapsto \frac{2}{nx^2+1}$ è decrescente in $[a,+\infty)$ .

Si ha
(285) $\begin{equation*} \lim_{x \to \infty}f_n(x) = \lim_{x \to \infty} \left(1+ \dfrac{2}{nx^2+1}\right)^n = 1 \qquad \forall n \in \mathbb{N}. \end{equation*}$

Per ogni , la successione è crescente, ossia le convergono a crescendo; ciò può essere dedotto dalla scrittura di data in (280). Infatti, è noto che converge crescendo a se la successione è crescente e inoltre la successione degli esponenti
(286) $\begin{equation*} \frac{2n}{nx^2+1}= \frac{2}{x^2} \frac{1}{1+\frac{1}{nx^2}} \end{equation*}$

è crescente. end{enumerate} Unendo le osservazioni fatte si ha quindi

(287) $\begin{equation*} 1 \leq f_n(x) \leq f(x) \qquad \forall n \in \mathbb{N}, \,\, \forall x \in [a,+\infty), \end{equation*}$

dove la prima disuguaglianza segue dalle osservazioni 1 e da 2, mentre la seconda segue dall’osservazione 3.

Fissiamo ora $\varepsilon>0$ . Dato che $f$ è decrescente in $[a,+\infty)$ e $\lim_{x \to +\infty} f(x)=1$ , esiste $R\geq a$ tale che

(288) $\begin{equation*} 1 \leq f(x) \leq 1 + \frac{\varepsilon}{3} \qquad \forall x \geq R. \end{equation*}$

$f_n$ segue che Da (287) e da (288) segue che

(289) $\begin{equation*} 1 \leq f_n(x) \leq f(x) \leq 1+\varepsilon \qquad \forall n \in \mathbb{N}, \,\, \forall x \geq R. \end{equation*}$

Sull’intervallo $[a,R]$ , per la continuità delle $f_n$ e di $f$ e per il fatto che $f_n$ converge crescendo a $f$ , si può applicare il teorema 1.9 e concludere⁵. che $f_n$ converge uniformemente a $f$ su $[a,R]$ . Quindi esiste $N \in \mathbb{N}$ tale che

(290) $\begin{equation*} |f_n(x) - f(x)| \leq \varepsilon \qquad \forall n \geq N, \,\, \forall x \in [a,R]. \end{equation*}$

Unendo (289) e (290), si ha

(291) $\begin{equation*} |f_n(x) - f(x)| \leq \varepsilon \qquad \forall n \geq N, \,\, \forall x \in [a,+\infty). \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ , ciò prova la convergenza uniforme di $f_n$ a $f$ su $[a,+\infty)$ .

$\,$

$\,$
1. poiché ogni $f_n$ è decrescente su $[a,R]$ , si poteva anche applicare il teorema 1.10 ↩

Esercizio 38 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Studiare la convergenza puntuale e uniforme della successione di funzioni $f_n \colon \mathbb{R} \to \mathbb{R}$ definite da

(292) $\begin{equation*} f_n(x) = \dfrac{e^{-n^\alpha |x|}}{\sqrt{n}} (1+nx^2) \qquad \forall n \in \mathbb{N},\,\, \forall x \in \mathbb{R}, \end{equation*}$

al variare del parametro $\alpha \in (0,+\infty)$ , nei seguenti insiemi:

$\,$

negli insiemi del tipo $(-\infty,-r]\cup[r,+\infty)$ , con $r >0$ ;

in $\mathbb{R}$ .

Soluzione punto 1.

Presentiamo due soluzioni di questo esercizio. La prima utilizza il calcolo delle derivate delle $f_n$ per determinarne gli estremi locali, mentre la seconda fa uso di maggiorazioni ottenute dall’espressione delle funzioni $f_n$ . Riteniamo entrambi gli approcci interessanti e istruttivi per il lettore.

Entrambe le soluzioni cominciano col notare che lo studio della convergenza della successione $f_n$ può essere ridotto a quello di una successione $h_n$ la cui espressione risulta più semplice da trattare. Commentiamo brevemente tale idea nell’osservazione 3.2 e spieghiamo che essa, pur essendo utile, non è strettamente necessaria ai fini della soluzione dell’esercizio.

Osserviamo in primo luogo che per ogni $n \in \mathbb{N}$ si può scrivere $f_n = g_n + h_n$ , con $g_n, h_n \colon \mathbb{R} \to \mathbb{R}$ definite da

(293) $\begin{equation*} g_n(x) = \dfrac{e^{-n^\alpha |x|}}{\sqrt{n}}, \quad h_n(x) = \dfrac{\sqrt{n}x^2}{e^{n^\alpha |x|}} \qquad \forall x \in \mathbb{R}. \end{equation*}$

Fissiamo $\alpha>0$ . Poiché $e^{-n^\alpha |x|} \leq 1$ per ogni $x \in \mathbb{R}$ , si ha

(294) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in\mathbb{R}}|g_n(x)| \leq \lim_{n \to +\infty} \dfrac{1}{\sqrt{n}} = 0, \end{equation*}$

ossia la successione di funzioni $g_n$ converge uniformemente in $\mathbb{R}$ alla funzione $g \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla. Ne segue che, per qualunque insieme $E \subseteq \mathbb{R}$ , la successione $f_n$ converge puntualmente o uniformemente in $E$ a una funzione $f \colon E \to \mathbb{R}$ se e solo se $h_n$ converge rispettivamente puntualmente o uniformemente in $E$ alla medesima funzione $f$ .

Osservando inoltre che ogni $f_n$ e ogni $h_n$ è una funzione pari, deduciamo che il problema è equivalente a studiare la convergenza puntuale e uniforme di $h_n$ al variare di $\alpha>0$ negli intervalli del tipo $[r,+\infty)$ , con $r\geq 0$ .

$\,$

Per quanto riguarda la convergenza puntuale, se $x >0$ vale

(295) $\begin{equation*} \begin{split} \lim_{n \to +\infty} h_n(x) = & \dfrac{\sqrt{n}x^2}{e^{n^\alpha x}} \\ \leq & \begin{cases} \displaystyle\lim_{n \to +\infty} \dfrac{\sqrt{n}x^2}{e^{n^{\frac{1}{4}} x}} & \text{se } \alpha \geq \dfrac{1}{4}\\[12pt] \displaystyle\lim_{n \to +\infty} \dfrac{\sqrt{n}x^2}{e^{n^{\alpha} x^{4\alpha}}} & \text{se } 0< \alpha < \dfrac{1}{4} \end{cases} \\[7pt] = & \,0 \qquad \forall \alpha>0, \end{split} \end{equation*}$

dove l’ultima uguaglianza deriva dal limite notevole⁶

(296) $\begin{equation*} \lim_{t \to +\infty} \frac{t^\beta}{e^t}=0 \quad \forall \beta>0. \end{equation*}$

Da 1 e dal fatto che $h_n(0)=0$ per ogni $n \in \mathbb{N}$ , segue che $h_n$ (e quindi anche $f_n$ ) converge puntualmente in $[0,+\infty)$ alla funzione $h \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla.
Per studiare la convergenza uniforme di $h_n$ a $h$ , studiamo le derivate delle funzioni $h_n$ per determinarne i rispettivi estremi. Si ha

(297) $\begin{equation*} h_n'(x) = -{n^\alpha}e^{-n^\alpha x}\sqrt{n}x^2+ {e^{-n^\alpha x}}2{\sqrt{n}}x = {\sqrt{n}}{e^{-n^\alpha x}}x \left( -n^\alpha x +2 \right) \qquad \forall n \in \mathbb{N},\,\, \forall x > 0. \end{equation*}$

Quindi, per ogni $n \in \mathbb{N}$ e per $x \in [0,+\infty)$ si ha

(298) $\begin{equation*} \begin{split} h_n'(x) \leq 0 \overset{x \geq 0 }{\iff} & n^{\alpha}x -2 \geq 0 \iff x \geq 2 n^{-\alpha}. \end{split} \end{equation*}$

Quindi ogni $h_n$ è crescente in $[0,2n^{-\alpha}]$ e decrescente in $[2n^{-\alpha},+\infty)$ , pertanto $x=2n^{-\alpha}$ è un suo punto di massimo assoluto e, poiché assume valori non negativi, segue che

(299) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[0,+\infty)}|h_n(x)| = \lim_{n \to +\infty} h_n(2n^{-\alpha}) = \lim_{n \to +\infty} \dfrac{4 \sqrt{n} n^{-2\alpha}}{e^2} = \begin{cases} + \infty &\text{se } \alpha < \frac{1}{4}\\ 4 e^{-2} &\text{se } \alpha = \frac{1}{4}\\ 0 &\text{se } \alpha > \frac{1}{4}. \end{cases} \end{equation*}$

Da ciò segue che $h_n$ (e quindi $f_n$ ) converge uniformemente in $[0,+\infty)$ alla funzione $h$ se e solo se $\alpha > \dfrac{1}{4}$ .

D’altra parte, poiché ogni $h_n$ è decrescente in $[2n^{-\alpha},+\infty)$ e $\lim_{n \to +\infty} 2n^{-\alpha}=0$ , se $r >0$ si ottiene

(300) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in [r,+\infty)} |h_n(x)| = \lim_{n \to +\infty} h_n(r) = 0 \qquad \forall \alpha>0, \end{equation*}$

dove l’ultima uguaglianza segue dalla convergenza puntuale di $h_n$ a $h$ . Ciò mostra che $h_n$ (e quindi $f_n$ ) converge uniformemente a $f$ in ogni insieme del tipo $[r,+\infty)$ , con $r>0$ , per ogni $\alpha>0$ .

Ricapitolando, abbiamo ottenuto le seguenti conclusioni.

$\quad$

$f_n$ converge puntualmente alla funzione $h \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla per ogni $\alpha>0$ .

Se $\alpha> \dfrac{1}{4}$ , allora $f_n$ converge uniformemente a $h$ in $\mathbb{R}$ .

Se $0 <\alpha\leq \dfrac{1}{4}$ , allora $f_n$ non converge uniformemente a $h$ in $\mathbb{R}$ , ma vi converge uniformemente in tutti gli intervalli del tipo $(-\infty,r] \cup [r,+\infty)$ con $r>0$ .

Osserviamo che la suddivisione in casi in 1 serve proprio a utilizzare il limite notevole 1. ↩

Osservazione 3.2.

L’osservazione iniziale sul fatto che $f_n = g_n + h_n$ , con $g_n$ convergente uniformemente in $\mathbb{R}$ alla funzione nulla ha ridotto il problema allo studio della convergenza puntuale e uniforme di $h_n$ ; ciò è stato quindi utile ai fini della soluzione, ma non è strettamente necessario. Infatti, lo stesso studio applicato alla successione $f_n$ invece che a $h_n$ avrebbe portato al medesimo risultato. Invitiamo il lettore a convincersene osservando però che lo studio del segno di $f_n'$ risulta più complicato di quello di $h_n'$ . Infatti

(301) $\begin{equation*} f_n'(x) = -\dfrac{n^\alpha}{\sqrt{n}}e^{-n^\alpha x}(1+nx^2)+ \dfrac{e^{-n^\alpha x}}{\sqrt{n}}2nx = \dfrac{e^{-n^\alpha x}}{\sqrt{n}} \left( -n^\alpha -n^{\alpha+1}x^2 +2nx \right) \qquad \forall n \in \mathbb{N},\,\, \forall x > 0. \end{equation*}$

Quindi, per ogni $n \in \mathbb{N}$ si ha

(302) $\begin{equation*} \begin{split} f_n'(x) \leq 0 \iff & n^{\alpha+1}x^2 -2nx + n^\alpha \geq 0 \\ \iff & \begin{cases} \forall x > 0 & \text{se } \alpha\geq\dfrac{1}{2}\\[10pt] \forall x \in \left(0,\dfrac{n-\sqrt{n^2-n^{2\alpha+1}}}{n^{\alpha+1}}\right] \cup \left[\dfrac{n+\sqrt{n^2-n^{2\alpha+1}}}{n^{\alpha+1}},+\infty\right) & \text{se } 0<\alpha <\dfrac{1}{2}. \end{cases} \end{split} \end{equation*}$

Nonostante da tale relazione si ottengano, con argomenti simili a quelli presentati, ovviamente le stesse conclusioni, il lettore può notare che l’osservazione iniziale ha semplificato notevolmente il procedimento successivo.

Presentiamo ora il secondo svolgimento dell’esercizio, che è basato su stime per le funzioni $f_n$ e non utilizza le derivate per studiarne la convergenza uniforme.

Soluzione punto 2.

Scrivendo $f_n=g_n + h_n$ come all’inizio dello svolgimento precedente, le stesse osservazioni mostrano che l’esercizio è equivalente a studiare la convergenza puntuale e uniforme di $h_n$ al variare di $\alpha>0$ , negli intervalli del tipo $[r,+\infty)$ , con $r\geq 0$ .

Consideriamo $r>0$ e $n \in \mathbb{N}$ . Si ha

(303) $\begin{equation*} \begin{split} \sup_{x \in[r,+\infty)} |h_n(x)| = & \sup_{x \in[r,+\infty)} \dfrac{\sqrt{n}x^2}{e^{n^\alpha x}} \\[7pt] \leq & \begin{cases} \displaystyle\sup_{x \in[r,+\infty)}\dfrac{\sqrt{n}x^2}{e^{n^{\frac{1}{4}} x}} & \text{se } \alpha \geq \dfrac{1}{4}\\[12pt] \displaystyle\sup_{x \in[r,+\infty)}\dfrac{\sqrt{n}x^2}{e^{n^{\alpha} x^{4\alpha}}} & \text{se } 0< \alpha < \dfrac{1}{4} \end{cases} \\ = & \begin{cases} \displaystyle \sup_{t \in [\sqrt[4]{n}r,+\infty)}\dfrac{t^2}{e^{t}} & \text{se } \alpha \geq \dfrac{1}{4}\\[12pt] \displaystyle\sup_{t \in [n^\alpha r^{4\alpha},+\infty)}\dfrac{t^{\frac{1}{2\alpha}}}{e^{t}} & \text{se } 0< \alpha < \dfrac{1}{4}, \end{cases} \end{split} \end{equation*}$

dove nella disuguaglianza si sono effettuati i cambi di variabile $t=\sqrt[4]{n}x$ al rigo superiore e $t=n^\alpha x^{4\alpha}$ al rigo inferiore. Poiché

(304) $\begin{equation*} \lim_{n \to +\infty} \sqrt[4]{n}r = \lim_{n \to +\infty} n^\alpha r^{4\alpha} = +\infty \quad \forall \alpha >0 \qquad \text{e} \qquad \lim_{t \to +\infty} \frac{t^\beta}{e^t}=0 \quad \forall \beta>0, \end{equation*}$

da (303) segue che

(305) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in[r,+\infty)} |h_n(x)| = 0, \end{equation*}$

pertanto $h_n$ (e quindi $f_n$ ) converge uniformemente (e quindi anche puntualmente) in $[r,+\infty)$ alla funzione $h \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla per ogni $\alpha>0$ . Osserviamo che i due casi $\alpha \geq \dfrac{1}{4}$ e $\alpha < \dfrac{1}{4}$ in (303) sono stati considerati al fine di ricondursi al secondo limite notevole in (304).
Per la convergenza uniforme di $h_n$ a $h$ negli insiemi del tipo $[r,+\infty)$ con $r>0$ ottenuta al punto precedente, si ha che $h_n$ converge puntualmente a $h$ in $(0,+\infty)$ per ogni $\alpha>0$ . In $x=0$ si ha $h_n(0)=0$ per ogni $n \in \mathbb{N}$ , per cui $h_n$ (e quindi $f_n$ ) converge puntualmente a $h$ in $[0,+\infty)$ per ogni $\alpha>0$ .
Per studiare la convergenza uniforme di $h_n$ a $h$ in $[0,+\infty)$ , in virtù del punto precedente, è sufficiente condiderare insiemi del tipo $[0,r]$ con $r>0$ . Si fissi quindi $r>0$ .

Al fine di ottenere un’intuizione al riguardo, osserviamo che dalla proposizione 1.3 segue che, se $h_n$ converge uniformemente alla funzione $h \colon [0,r] \to \mathbb{R}$ identicamente nulla, deve aversi 1 per ogni $\lim_{n \to +\infty} h_n(x_n)=0$ successione reale $x_n$ . Notiamo che la forma di $h_n$ suggerisce di studiare la successione $h_n(n^{-\beta})$ per $\beta>0$ . Si ha

(306) $\begin{equation*} \lim_{n \to +\infty} h_n(n^{-\beta}) = \lim_{n \to +\infty} \dfrac{n^{\frac{1}{2}-2\beta}}{e^{n^{\alpha - \beta}}} = 0 \quad \forall \beta>0 \iff \alpha > \frac{1}{4}. \end{equation*}$

Infatti, se $\alpha\leq \dfrac{1}{4}$ , si ha

(307) $\begin{equation*} \lim_{n \to +\infty} h_n(n^{-\beta}) = \lim_{n \to +\infty} \dfrac{n^{\frac{1}{2}-2\beta}}{e^{n^{\alpha - \beta}}} \geq \begin{cases} \displaystyle \lim_{n \to +\infty}\dfrac{1}{e} & \text{se } \beta= \dfrac{1}{4}\\[7pt] \displaystyle \lim_{n \to +\infty} \dfrac{n^{\frac{1}{2}-2\beta}}{e} & \text{se } \alpha\leq \beta < \dfrac{1}{4} \end{cases} = \begin{cases} \displaystyle {e^{-1}} & \text{se } \beta= \dfrac{1}{4}\\[7pt] +\infty & \text{se } \alpha\leq\beta < \dfrac{1}{4}. \end{cases} \end{equation*}$

Viceversa, se $\alpha>\dfrac{1}{4}$ si ha

(308) $\begin{equation*} \lim_{n \to +\infty} h_n(n^{-\beta}) = \lim_{n \to +\infty} \dfrac{n^{\frac{1}{2}-2\beta}}{e^{n^{\alpha - \beta}}} \leq \begin{cases} \displaystyle \lim_{n \to +\infty} n^{\frac{1}{2}-2\beta} & \text{se } \beta> \dfrac{1}{4}\\ \displaystyle \lim_{n \to +\infty} \dfrac{n^{\frac{1}{2}-2\beta}}{e^{n^{\alpha-\beta}}} & \text{se } \beta \leq \dfrac{1}{4} \end{cases} \,\,\, = 0, \end{equation*}$

dove l’ultima uguaglianza per il rigo inferiore segue dal secondo limite notevole in (304). Ciò fornisce un’intuizione al riguardo del fatto che $\alpha=\frac{1}{4}$ potrebbe essere il valore di soglia oltre il quale si ha convergenza uniforme di $h_n$ a $h$ in $[0,r]$ . Tale intuizione è corretta e la mostriamo rigorosamente.
Se $0<\alpha\leq \dfrac{1}{4}$ , da (307), da $\lim_{n \to +\infty} n^{-\beta}=0$ e dalla proposizione 1.3, segue che $h_n$ non converge uniformemente a $h$ in $[0,r]$ .
Se $\alpha> \dfrac{1}{4}$ , chiaramente (308) non implica la convergenza uniforme di $h_n$ a $h$ in $[0,r]$ . Tale equazione suggerisce però di scegliere $\dfrac{1}{4}< \beta < \alpha$ e suddividere l’intervallo $[0,r]$ in $[0,n^{-\beta}]$ e $[n^{-\beta},r]$ . Usando tale suddivisione, per ogni $n \in \mathbb{N}$ si ha

(309) $\begin{equation*} \begin{split} \sup_{x \in [0,r]}|f_n| = & \max \left\{ \sup_{x \in [0,n^{-\beta}]} \dfrac{\sqrt{n}x^2}{e^{n^\alpha x}} , \sup_{x \in [n^{-\beta},r]}\dfrac{\sqrt{n}x^2}{e^{n^\alpha x}} \right\}. \end{split} \end{equation*}$

Stimiamo separatamente i due estremi superiori al membro di destra di (309). Per quanto riguarda il primo si ha

(310) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in [0,n^{-\beta}]}\dfrac{ \sqrt{n}x^2}{e^{n^\alpha x}} \leq \lim_{n \to +\infty} \sqrt{n}n^{-2\beta} = \lim_{n \to +\infty} n^{\frac{1}{2}-2\beta} = 0, \end{split} \end{equation*}$

dove l’ultima uguaglianza è dovuta al fatto che $\beta > \dfrac{1}{4}$ e nella disuguaglianza si è usato che

(311) $\begin{equation*} x \leq n^{-\beta}, \quad e^{n^\alpha x}\geq 1 \qquad \forall n \in \mathbb{N}, \,\, \forall x \in \left[0,n^{-\beta}\right]. \end{equation*}$

Per quanto riguarda il secondo estremo superiore in (309), otteniamo

(312) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in [n^{-\beta},r]}\dfrac{\sqrt{n}x^2}{e^{n^\alpha x}} \leq \lim_{n \to +\infty} r^2 \dfrac{n^{\frac{1}{2}}}{e^{n^{\alpha- \beta}}} = 0, \end{split} \end{equation*}$

dove nella disuguaglianza si è usato il fatto che $x \leq r$ al numeratore e che $x \geq n^{-\beta}$ al denominatore, mentre l’ultima uguaglianza segue dall’ultimo limite notevole in (304).

Inserendo (310) e (312) in (309), si ottiene

(313) $\begin{equation*} \lim_{n \to +\infty} \sup_{x \in [0,r]}|h_n(x)| = 0, \end{equation*}$

che implica la convergenza uniforme di $h_n$ (e quindi di $f_n$ ) a $h$ in $[0,r]$ per $\alpha> \dfrac{1}{4}$ .

Esercizio 39 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Sia $f \colon (0,+\infty) \to \mathbb{R}$ una funzione, sia $a_n$ una successione di numeri reali positivi e si assuma che la successione di funzioni $f_n \colon (0,+\infty) \to \mathbb{R}$ definita da

(314) $\begin{equation*} f_n(x) = f(a_n x) \qquad \forall n \in \mathbb{N},\,\,\forall x \in \mathbb{R} \end{equation*}$

converga uniformemente a una funzione $g \colon (0,+\infty) \to \mathbb{R}$ .

$\,$

Se $a_n=n$ e $g$ è continua, dimostrare che esiste $\ell = \lim_{x \to +\infty}f(x)$ e che $g$ è costantemente pari a $\ell$ .

Se $a_n=2^n$ e $g$ è continua,provare con un esempio che il limite $\lim_{x \to \infty}f(x)$ può non esistere e $g$ può non essere costante.

Se $a_n=n$ e $g$ non è continua, provare con un esempio che il limite $\lim_{x \to \infty}f(x)$ può non esistere.

Soluzione punto 1.

Risolviamo separatamente i vari punti. Sia $y \in (0,+\infty)$ ; poiché $g$ è continua, per ogni $\varepsilon>0$ esiste $\delta>0$ tale che

(315) $\begin{equation*} |g(x)-g(y)|< \varepsilon \qquad \forall x \in [y-\delta,y+\delta]. \end{equation*}$

Inoltre, per l’ipotesi di convergenza uniforme di $f_n$ a $g$ , esiste $N_1 \in \mathbb{N}$ tale che

(316) $\begin{equation*} |f_n(x) - g(x)| < \varepsilon \qquad \forall n \geq N_1, \forall x \in (0,+\infty). \end{equation*}$

Quindi

(317) $\begin{equation*} \begin{gathered} |f_n(x)-g(y)| \leq |f_n(x)-g(x)|+ |g(x)-g(y)| < 2\varepsilon \qquad \forall x \in [y-\delta,y+\delta],\,\,\forall n \geq N_1, \end{gathered} \end{equation*}$

dove la prima disuguaglianza segue dalla disuguaglianza triangolare, mentre la seconda da (316) e da (315). Ricordando che $f_n(x)=f(a_n x)$ e che $a_n=n$ , da (317) si ricava

(318) $\begin{equation*} \begin{gathered} |f(t)-g(y)|< 2\varepsilon \qquad \forall t \in I_n \coloneqq [ny-n\delta,ny+n\delta],\,\,\forall n \geq N_1. \end{gathered} \end{equation*}$

Poiché $\delta >0$ , esiste $N \geq N_1$ tale che

(319) $\begin{equation*} n \delta > \frac{y}{2} \qquad \forall n \geq N. \end{equation*}$

Dato che $(n+1)y - ny= y$ per ogni $n \in \mathbb{N}$ , da (319) segue che

(320) $\begin{equation*} I_n \cap I_{n+1} \neq \emptyset \qquad \forall n \geq N, \end{equation*}$

e ciò implica, poiché ovviamente $\lim_{n \to +\infty} ny = + \infty$ , che

(321) $\begin{equation*} [Ny,+\infty) \subset \bigcup_{n=N}^{+\infty} I_n. \end{equation*}$

Quindi (321) e (318) mostrano che

(322) $\begin{equation*} |f(x)-g(y)|< 2\varepsilon \qquad \forall x \geq Ny. \end{equation*}$

Dall’arbitrarietà di $\varepsilon$ , questo prova che esiste il limite

(323) $\begin{equation*} \ell = \lim_{x \to + \infty} f(x) = g(y). \end{equation*}$

D’altra parte, per l’arbitrarietà di $y \in (0,+\infty)$ , l’equazione precedente mostra che $g$ è costante.

Soluzione punto 2.

Consideriamo una funzione $h \colon \mathbb{R} \to \mathbb{R}$ , continua, periodica di periodo $1$ e non costante e definiamo $f \colon (0,+\infty) \to \mathbb{R}$ come

(324) $\begin{equation*} f(x) = h\left( \dfrac{x-2^k}{2^k} \right) \qquad \text{se } x \in [2^k,2^{k+1}),\,\,\, k \in \mathbb{Z}. \end{equation*}$

$\,$

Figura 3: grafico (in blu) della funzione $f$ ; si noti che il grafico di $f$ consiste di copie scalate di fattori $2^k$ del grafico di $h$ , corrispondente alla porzione rappresentata nell’intervallo $[1,2]$ .

$\,$

In altre parole, $f$ consiste di “copie” del grafico $h$ ristretto all’intervallo $[0,1]$ , scalate in orizzontale di fattori $2^k$ e “affiancate” l’una all’altra. Per come è definita e per il fatto che $h$ è continua, periodica e non costante, $f$ è continua e $\lim_{x \to +\infty} f(x)$ non esiste.

Affermiamo inoltre che la successione di funzioni $f_n \colon (0,+\infty) \to \mathbb{R}$ definita da $f_n(x)=f(2^n x)$ soddisfa $f_n=f$ per ogni $n \in \mathbb{N}$ .

Ciò si può mostrare osservando che, se $x \in (0,+\infty)$ , esiste un unico $k \in \mathbb{Z}$ tale che $x \in [2^k,2^{k+1})$ , quindi $2^n x \in [2^{k+n},2^{k+n+1})$ per ogni $n \in \mathbb{N};$ da questo segue che

(325) $\begin{equation*} f_n(x) = f(2^n x) = h\left( \dfrac{2^nx-2^{k+n}}{2^{k+n}} \right) = h\left( \dfrac{x-2^{k}}{2^{k}} \right) = f(x) \qquad \forall n \in \mathbb{N}. \end{equation*}$

Pertanto $f_n$ converge uniformemente alla funzione continua $g=f$ , che però non è costante.

Soluzione punto 3.

Sia $a_n=n$ . Consideriamo la funzione $f \colon (0,+\infty) \to \mathbb{R}$ definita da

(326) $\begin{equation*} f(x) = \begin{cases} 1 & \text{se } x \in \mathbb{Q} \cap (0,+\infty)\\ 0 & \text{altrimenti}. \end{cases} \end{equation*}$

$f$ è la funzione indicatrice dei numeri razionali, anche detta funzione di Dirichlet. Chiaramente $\lim_{x \to +\infty} f(x)$ non esiste. Poiché $x \in \mathbb{Q}$ se e solo se $nx \in \mathbb{Q}$ per ogni $n \in \mathbb{N}$ , si ha

(327) $\begin{equation*} f_n(x) = f(nx) = f(x) \qquad \forall n \in \mathbb{N},\,\,\,\forall x \in (0,+\infty), \end{equation*}$

quindi $f_n=f$ per ogni $f \in \mathbb{N}$ . Ovviamente $f_n$ converge uniformemente a $g=f$ .

Osservazione 3.3.

istruttivo confrontare le affermazioni di questo esercizio con quella dell’esercizio 12 alla luce del teorema 1.13, che lega la convergenza uniforme di una successione di funzioni continue all’equicontinuità della successione.

Mentre l’esercizio 12 afferma che $f$ è costante, il primo punto del presente esercizio afferma l’esistenza del limite $\lim_{x \to +\infty} f(x)$ , che può essere interpretato come una sorta di “costanza all’infinito” di $f$ .

Il lettore è invitato a riflettere sulle seguenti domande: come mai le conclusioni dei due esercizi sono diverse? Come cambierebbero le risposte a questo esercizio se il dominio delle funzioni trattate fosse $[0,+\infty)$ ?

Esercizio 40 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Calcolare il limite

(328) $\begin{equation*} \lim_{n \to +\infty} \int_n^{+\infty} \dfrac{n^2x^2}{1+x^2} \arctan \dfrac{1}{nx^2} \, \mathrm{d} x . \end{equation*}$

Soluzione.

Al fine di eliminare la dipendenza da $n$ degli estremi di integrazione, si effettua il cambio di variabili $x= ny$ , con il quale l’integrale in (328) diventa

(329) $\begin{equation*} \int_n^{+\infty} \dfrac{n^2x^2}{1+x^2} \arctan \dfrac{1}{nx^2} \dif x = \int_1^{+\infty} \dfrac{n^5y^2}{1+n^2y^2} \arctan \dfrac{1}{n^3y^2} \dif y \qquad \forall n \in \mathbb{N}. \end{equation*}$

Definiamo la successione di funzioni $f_n \colon [1,+\infty) \to \mathbb{R}$ definite da

(330) $\begin{equation*} f_n(y) = \dfrac{n^5y^2}{1+n^2y^2} \arctan \dfrac{1}{n^3y^2} \qquad \forall n \in \mathbb{N},\,\, \forall y \in [1,+\infty) \end{equation*}$

e si fissi $\varepsilon>0$ . Per il limite notevole $\lim_{t \to 0}\dfrac{\arctan t}{t}=1$ , esiste $\delta>0$ tale che

(331) $\begin{equation*} (1-\varepsilon)t \leq \arctan t \leq (1+\varepsilon)t \qquad \forall t \in (0,\delta). \end{equation*}$

Poiché $\dfrac{1}{n^3y^2} \leq \dfrac{1}{n^3}$ per ogni $n \in \mathbb{N}$ e per ogni $y \geq 1$ , esiste $N_1 \in \mathbb{N}$ tale che

(332) $\begin{equation*} 0 < \frac{1}{n^3y^2} < \delta \qquad \forall n \geq N_1,\,\,\, \forall y \geq 1. \end{equation*}$

Da ciò e da (331) segue che

(333) $\begin{equation*} \dfrac{1-\varepsilon}{n^3y^2} \leq \arctan \dfrac{1}{n^3y^2} \leq \dfrac{1+\varepsilon}{n^3y^2} \qquad \forall n \geq N_1, \,\,\, \forall y \in [1,+\infty). \end{equation*}$

Ciò mostra che

(334) $\begin{equation*} (1-\varepsilon) \dfrac{n^2}{1+n^2y^2} \leq f_n(y) %\dfrac{n^5y^2}{1+n^2y^2} \arctan \dfrac{1}{n^3y^2} \leq (1+\varepsilon) \dfrac{n^2}{1+n^2y^2} \qquad \forall n \geq N_1,\,\,\, \forall y \geq 1, \end{equation*}$

che è equivalente a

(335) $\begin{equation*} \dfrac{1}{y^2}\dfrac{1-\varepsilon}{1 + \dfrac{1}{y^2n^2}} \leq f_n(y) %\dfrac{n^5y^2}{1+n^2y^2} \arctan \dfrac{1}{n^3y^2} \leq \dfrac{1}{y^2}\dfrac{1+\varepsilon}{1 + \dfrac{1}{y^2n^2}} \qquad \forall n \geq N_1,\,\,\, \forall y \geq 1. \end{equation*}$

Poiché $0 \leq \dfrac{1}{n^2y^2} \leq \dfrac{1}{n^2}$ per ogni $n \in \mathbb{N}$ e per ogni $y \geq 1$ , esiste $N_2 \in \mathbb{N}$ tale che

(336) $\begin{equation*} 1 < 1+ \frac{1}{y^2n^2} < 1+\varepsilon \qquad \forall n \geq N_2,\,\,\, \forall y \geq 1. \end{equation*}$

Definendo $N\coloneqq \max\{N_1,N_2\}$ e inserendo (336) in (335), si ottiene

(337) $\begin{equation*} \dfrac{1}{y^2}\dfrac{1-\varepsilon}{1 + \varepsilon} \leq f_n(y) %\dfrac{n^5y^2}{1+n^2y^2} \arctan \dfrac{1}{n^3y^2} \leq \dfrac{1}{y^2}(1+\varepsilon) \qquad \forall n \geq N,\,\,\, \forall y \geq 1. \end{equation*}$

Poiché la funzione $f \colon [1,+\infty) \to \mathbb{R}$ definita da

(338) $\begin{equation*} f(y) = \frac{1}{y^2} \qquad \forall y \geq 1. \end{equation*}$

è integrabile in senso improprio in $[1,+\infty)$ , (337) prova innanzitutto che ogni $f_n$ è integrabile in senso improprio in $[1,+\infty)$ . Inoltre, da (329), (337) e dall’arbitrarietà di $\varepsilon$ , segue che

(339) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \int_n^{+\infty} \dfrac{n^2x^2}{1+x^2} \arctan \dfrac{1}{nx^2} \, \mathrm{d} x = & \lim_{n \to +\infty} \int_1^{+\infty} f_n(y) \, \mathrm{d} y \\ = & \int_1^{+\infty} \dfrac{1}{y^2} \, \mathrm{d} y \\ = & 1. \end{split} \end{equation*}$

Osservazione 3.4.

Dato che la funzione $f$ è limitata in $[1,+\infty)$ e $\varepsilon>0$ è arbitrario, si può notare che la (337) prova in particolare che $f_n$ converge uniformemente in $[1,+\infty)$ alla funzione $f$ , che è integrabile in senso improprio. Quest’ultimo fatto non è però sufficiente neppure a garantire che le funzioni $f_n$ siano integrabili in senso improprio per qualche $n \in \mathbb{N}$ , come mostra l’esempio della successione di funzioni $g_n \colon [1,+\infty) \to \mathbb{R}$ definite da

(340) $\begin{equation*} g_n(x) = \frac{1}{x^2} + \frac{1}{nx} \qquad \forall n \in \mathbb{N}, \,\, \forall x \geq 1. \end{equation*}$

Infatti, la successione delle $g_n$ converge uniformemente a $f$ , ma nessuna delle $g_n$ è integrabile in senso improprio. Ciò mostra che, nel teorema 1.7 di passaggio al limite sotto al segno di integrale nel caso di convergenza uniforme, l’ipotesi di limitatezza dell’intervallo $[a,b]$ non si può rimuovere.

La (337), la limitatezza e l’integrabilità della funzione limite $f$ costituiscono quindi una condizione più forte della convergenza uniforme che è sufficiente a garantire la convergenza degli integrali anche quando questi sono calcolati su un intervallo illimitato. Ciò può essere generalizzato nella seguente proposizione, che costituisce una sorta di analogo del teorema di convergenza dominata per l’integrale di Lebesgue.

Preposizione 3.5.

Sia $I \subseteq \mathbb{R}$ un intervallo illimitato e sia $f_n \colon I \to \mathbb{R}$ una successione di funzioni limitate e integrabili sugli intervalli limitati contenuti in $I$ . Supponiamo che esistano due successioni $a_n,b_n$ di numeri reali positivi e una funzione $f \colon I \to \mathbb{R}$ integrabile in senso improprio tali che

(341) $\begin{equation*} \lim_{n \to +\infty} a_n = \lim_{n \to +\infty} b_n = 1, \qquad a_n f(x) \leq f_n(x) \leq b_n f(x) \quad \forall n \in \mathbb{N},\,\, \forall x \in I. \end{equation*}$

Allora la successione $f_n$ converge uniformemente a $f$ in $I$ , ognuna delle $f_n$ è integrabile in senso improprio in $I$ e vale

(342) $\begin{equation*} \lim_{n \to +\infty} \int_I f_n(x) \, \mathrm{d} x = \int_I f(x) \, \mathrm{d} x. \end{equation*}$

Esercizio 41 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Sia $f_n \colon [0,+\infty) \to \mathbb{R}$ una successione di funzioni limitate, integrabili in senso improprio, convergenti uniformemente a una funzione $f \colon [0,+\infty) \to \mathbb{R}$ e tali che esista finito il limite

(343) $\begin{equation*} \lim_{n \to +\infty} \int_{0}^{+\infty}f_n(x) \, \mathrm{d} x = \ell \in \mathbb{R}. \end{equation*}$

$\,$

Si può concludere che $f$ sia integrabile in senso improprio?

Cosa si può dire sull’esistenza e sull’eventuale valore di $\int_{0}^{+\infty}f(x) \dif x$ se, oltre alle ipotesi fatte, si assume anche che $f_n(x) \geq 0$ per ogni $n \in \mathbb{N}$ e ogni $x \in [0,+\infty)$ ?

Soluzione punto 1.

La risposta è negativa. Per mostrarlo, consideriamo la successione di funzioni $f_n \colon [0,+\infty) \to \mathbb{R}$ definita da

(344) $\begin{equation*} f_n(x) = \sum_{k=1}^{2n}(-1)^k 2^{-k+1}\chi_{[2^{k-1},2^k)}(x) \qquad \forall n \in \mathbb{N},\,\, \forall x \in [0,+\infty), \end{equation*}$

(si veda la figura 4) dove, se $E \subseteq \mathbb{R}$ , $\chi_{E}$ denota la funzione caratteristica dell’insieme $E$ , cioè

(345) $\begin{equation*} \chi_E(x) = \begin{cases} 1 & \text{se $x \in E$,}\\ 0 & \text{se $x \notin E$.} \end{cases} \end{equation*}$

$\,$

Figura 4: La funzione $f_2$ definita in (344)

$\,$

Per come è definita, la funzione $f_n$ è integrabile e per ogni $n \in \mathbb{N}$ si ha

(346) $\begin{equation*} \begin{split} \int_0^{+\infty} f_n(x) \mathrm{d}x = \sum_{k=1}^{2n}(-1)^k 2^{-k+1}2^{k-1} = \, 0. \end{split} \end{equation*}$

Mostriamo che la successione delle $f_n$ converge uniformemente alla funzione $f \colon [0,+\infty) \to \mathbb{R}$ definita da

(347) $\begin{equation*} f(x) = \sum_{k=1}^{+\infty}(-1)^k 2^{-k+1}\chi_{[2^{k-1},2^k)}(x) \qquad \forall x \in [0,+\infty) \end{equation*}$

(notare che per ogni $x \geq 1$ vi è un solo $k \in \mathbb{N}$ per cui $\chi_{[2^{k-1},2^k)}(x) \neq 0$ , quindi la convergenza della serie è assicurata). Infatti si ha

(348) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in [0,+\infty)} |f(x) - f_n(x)| = & \lim_{n \to +\infty} \sup_{x \in [0,+\infty)} \sum_{k=2n+1}^{+\infty}2^{-k+1}\chi_{[2^{k-1},2^k)}(x) \\ = & \lim_{n \to +\infty} 2^{-2n} \\ = & \,0. \end{split} \end{equation*}$

Tuttavia per ogni $N \in \mathbb{N}$ si ha

(349) $\begin{equation*} \begin{gathered} \int_0^{2^{2N}} f(x) \,\mathrm{d}x = \sum_{k=1}^{2N}(-1)^k 2^{-k+1}2^{k-1} = 0, \\ \int_0^{2^{2N + 1}} f(x)\, \mathrm{d}x = \sum_{k=1}^{2N+1}(-1)^k 2^{-k+1}2^{k-1} = -1. \end{gathered} \end{equation*}$

Ciò prova che $\lim_{R \to +\infty} \int_0^R f(x)\, \mathrm{d}x$ non esiste e quindi $f$ non risulta integrabile in senso improprio.

Soluzione punto 2.

Se in aggiunta alle precedenti ipotesi si assume che $f_n \geq 0$ per ogni $n \in \mathbb{N}$ , affermiamo che l’integrale $\int_{0}^{+\infty}f(x) \dif x$ esiste, è finito e soddisfa

(350) $\begin{equation*} 0 \leq \int_{0}^{+\infty}f(x) \, \mathrm{d} x \leq \lim_{n \to +\infty} \int_{0}^{+\infty}f_n(x) \, \mathrm{d} x. \end{equation*}$

Per provarlo, innanzitutto osserviamo che, poiché $f_n \geq 0$ , anche $f \geq 0$ . Da ciò segue che la funzione integrale $x \mapsto \int_0^x f(t) \dif t$ è (debolmente) crescente e quindi l’integrale improprio

(351) $\begin{equation*} \int_{0}^{+\infty}f(x) \dif x = \lim_{x \to +\infty}\int_0^x f(t) \dif t \end{equation*}$

esiste. Vogliamo dimostrare che è finito. A tal fine, fissiamo $R >0$ e $\varepsilon>0$ ; per la convergenza uniforme di $f_n$ a $f$ su $[0,R]$ , per il teorema 1.7 e per (343), esiste $N \in \mathbb{N}$ tale che

(352) $\begin{gather*} \int_{0}^{R}f(x) \, \mathrm{d} x \leq \varepsilon + \int_{0}^{R}f_n(x) \, \mathrm{d} x \qquad \forall n \geq N, \\ \label{eq:23:stima_int_2} \int_{0}^{+\infty}f_n(x) \, \mathrm{d} x \leq \ell + \varepsilon \qquad \forall n \geq N. \end{gather*}$

Scegliendo $n \geq N$ e unendo (352) e (??), si ottiene

(353) $\begin{equation*} \int_{0}^{R}f(x) \dif x \leq \varepsilon + \int_{0}^{R}f_n(x) \dif x \leq \varepsilon + \int_{0}^{+\infty}f_n(x) \dif x \leq 2\varepsilon + \ell. \end{equation*}$

Da (351) e (353) e dall’arbitrarietà di $R$ e $\varepsilon$ , si ottiene

(354) $\begin{equation*} \int_{0}^{+\infty}f(x) \, \mathrm{d} x \leq \lim_{n \to +\infty} \int_{0}^{+\infty}f_n(x) \, \mathrm{d} x. \end{equation*}$

Osserviamo che la disuguaglianza (354) può essere stretta, come mostra l’esempio della successione di funzioni $f_n=2^{-n}\chi_{[2^n,2^{n+1}]}$ . Infatti ognuna delle funzioni $f_n$ è positiva, integrabile con $\int_0^{+\infty} f_n(x) \dif x=1$ , ma la successione delle $f_n$ converge uniformemente alla funzione $f \colon \mathbb{R} \to \mathbb{R}$ identicamente nulla, che ovviamente ha integrale nullo.

Esercizio 42 $(\bigstar\bigstar\bigstar\bigstar\bigstar)$ . Sia $f_n \colon [a,b] \to \mathbb{R}$ una successione di funzioni aventi la proprietà di Darboux (definizione 1.15) convergenti uniformemente a una funzione $f \colon [a,b] \to \mathbb{R}$ .

Si può dire che $f$ ha la proprietà di Darboux?

Soluzione.

La risposta è negativa, come mostra il seguente esempio. Dividiamo la costruzione della successione $f_n$ e del limite uniforme $f$ in vari passi. L’idea consiste nell’usare una successione di funzioni $g_n$ convergenti uniformemente a una funzione $g$ . La differenza principale tra le funzioni $g_n$ e $g$ è che le prime assumono i valori $-1$ e $1$ , mentre $g$ non li assume.

Si costruisce poi la successione $f_n$ “affiancando” delle copie opportunamente traslate e riscalate dei grafici delle $g_n$ , in modo che le funzioni $f_n$ assumano il valore $0$ , a differenza del loro limite uniforme $f$ . Poiché le immagini di $f_n$ e di $f$ contengono sia valori positivi che negativi, $f$ non possiederà la proprietà di Darboux.

Costruzione delle funzioni $g_n$ convergenti uniformemente a $g$ . Consideriamo la funzione $g \colon [-1,1] \to (-1,1)$ definita da

(355) $\begin{equation*} g(x) = \begin{cases} |x|\sin \left( \dfrac{1}{1-|x|} \right) & \text{se } x \in (-1,1)\\[7pt] 0 & \text{se } x \in \{-1,1\}, \end{cases} \end{equation*}$

il cui grafico è rappresentato a sinistra nella figura ??. Osserviamo che $g$ è una funzione continua.

Consideriamo poi, per ogni $n \in \mathbb{N}$ , le funzioni $g_n \colon [-1,1] \to [-1,1]$ (si noti che in questo caso il codominio è chiuso) definite da

(356) $\begin{equation*} g_n(x) = \begin{cases} \min\left\{1, \left(1+\frac{1}{n}\right)|x| \right\} \sin \left( \dfrac{1}{1-|x|} \right) & \text{se } x \in (-1,1)\\[7pt] 0 & \text{se } x \in \{-1,1\}. \end{cases} \end{equation*}$

Il grafico di una delle funzioni $g_n$ è rappresentato a destra nella figura 5.

$\,$

Figura 5: sulla sinistra in blu il grafico della funzione $g$ , mentre in rosso il grafico della funzione $x \mapsto |x|$ . Si noti che $g$ non assume mai i valori $-1$ e $1$ .\ Sulla destra il grafico (in blu) di una delle funzioni $g_n$ , mentre in rosso il grafico della funzione $x \mapsto \min\left\{1, \left(1+\dfrac{1}{n}\right)|x| \right\}$ . Si osservi che $g_n$ assume i valori $-1$ e $1$ infinite volte.

$\,$

il cui grafico è rappresentato a sinistra nella figura 5. Osserviamo che $g$ è una funzione continua. Consideriamo poi, per ogni $n \in \mathbb{N}$ , le funzioni $g_n \colon [-1,1] \to [-1,1]$ (si noti che in questo caso il codominio è chiuso) definite da

(357) $\begin{equation*} g_n(x) = \begin{cases} \min\left\{1, \left(1+\dfrac{1}{n}\right)|x| \right\} \sin \left( \dfrac{1}{1-|x|} \right) & \text{se } x \in (-1,1)\\[7pt] 0 & \text{se } x \in \{-1,1\}. \end{cases} \end{equation*}$

Il grafico di una delle funzioni $g_n$ è rappresentato a destra nella figura 5. Si ha che $g_n$ converge uniformemente a $g$ . Infatti

(358) $\begin{equation*} \begin{split} \lim_{n \to +\infty} \sup_{x \in[-1,1]} |g_n(x)-g(x)| = & \lim_{n \to +\infty} \sup_{x \in(-1,1)} \left| \min\left\{1, \left(1+\frac{1}{n}\right)|x| \right\} - |x| \right|\cdot \left| \sin \left( \dfrac{1}{1-|x|} \right) \right| \\ \leq & \lim_{n \to +\infty} \sup_{x \in(-1,1)} \left|\left(1+\frac{1}{n} \right)|x| - |x| \right| \\ \leq & \lim_{n \to +\infty} \frac{1}{n} \\ = & 0, \end{split} \end{equation*}$

dove nella prima disuguaglianza sono stati usati la disuguaglianza $|\sin t| \leq 1$ , la parità di $g_n$ e di $g$ e il fatto che che la funzione $x \mapsto \left(1+\dfrac{1}{n}\right)|x|$ è crescente in $[0,1)$ .

Osserviamo che sia le funzioni $g_n$ che la funzione $g$ possiedono la proprietà di Darboux; inoltre, le $g_n$ assumono infinite volte i valori $-1$ e $1$ , mentre $g$ non lo assume mai.

Costruzione dei punti $x_k^j$ e degli intervalli $I_k^j$ Consideriamo ora l’intervallo $[0,1]$ e costruiamo ricorsivamente i punti $x_k^j \in [0,1]$ come segue:

(359) $\begin{gather*} x_1^1= \frac{1}{2}, \\ x_{k+1}^{2j-1} = x_k^j - \frac{1}{3^k}, \quad x_{k+1}^{2j} = x_k^j + \frac{1}{3^k} \qquad \forall k \in \mathbb{N},\,\, \forall j \in \{1,\dots,2^{k-1}\}. \end{gather*}$

I punti $x_k^j$ sono i punti centrali degli intervalli che ricorsivamente vengono sottratti a $[0,1]$ per ottenere il famoso insieme di Cantor⁸. Definiamo poi gli intervalli

(360) $\begin{equation*} I_{k}^j \coloneqq \left[x_k^j - \dfrac{1}{2 \cdot 3^k}, x_k^j + \dfrac{1}{2 \cdot 3^k} \right] \qquad \forall k \in \mathbb{N},\,\,\forall j \in \{1,\dots,2^{k-1}\}, \end{equation*}$

e osserviamo che essi, al variare di $k \in \mathbb{N}$ e $j \in \{1,\dots,2^{k-1}\}$ , hanno ampiezza $\dfrac{1}{3^k}$ e sono a due a due disgiunti. I punti $x_k^j$ e gli intervalli $I_k^j$ sono rappresentati in figura 6.

$\,$

Figura 6: Gli insiemi $I_1^1,I_2^1,I_2^2$ e i rispettivi punti centrali $x_1^1,x_2^1,x_2^2$ rappresentati in blu nell’intervallo $[0,1]$ .

$\,$

$D\coloneqq [0,1] \setminus \bigcup_{k=1}^{+\infty} \bigcup_{j=1}^{2^{k-1}}I_k^j$ non contiene alcun intervallo. Infatti, se indichiamo con $|I_k^j|= \frac{1}{3^k}$ l’ampiezza di ciascun intervallo $I_k^j$ , si ha⁹

$\begin{equation}\label{eq:32:somma_lunghezze} $$ \sum_{k=1}^{+\infty} \sum_{j}^{2^{k-1}} |I_k^j| = $$ $$ \sum_{k=1}^{+\infty} \sum_{j}^{2^{k-1}} \frac{1}{3^k} = $$ $$ \sum_{k=1}^{+\infty} \frac{2^{k-1}}{3^k} = $$ $$ \frac{1}{2} \sum_{k=1}^{+\infty} \left(\frac{2}{3}\right)^k = $$ $$ \frac{1}{2} \cdot \frac{2}{3} \cdot \frac{1}{1-\frac{2}{3}} = 1 $$. \end{equation}$

In altre parole, la serie delle lunghezze degli intervalli $I_k^j$ è pari a $1$ . Da (??) e dal fatto che gli $I_k^j$ sono a due a due disgiunti, segue che l’insieme

(361) $\begin{equation*} D\coloneqq [0,1] \setminus \left( \bigcup_{k=1}^{+\infty} \bigcup_{j=1}^{2^{k-1}}I_k^j \right) \end{equation*}$

non contiene alcun intervallo.

Costruzione della successione di funzioni $f_n$ aventi la proprietà di Darboux Sia $f_n \colon [0,1] \to [-2,2]$ la successione di funzioni definita da

(362) $\begin{equation*} f_n(x) = \begin{cases} (-1)^k + g_n \left( 2 \cdot 3^k(x-x_k^j)\right) & \text{se } x \in I_k^j \text{ per qualche } k \in \mathbb{N}, \,\, j \in \{1,\dots,2^{k-1}\} \\[16pt] 1 & \text{altrimenti}. \end{cases} \end{equation*}$

Osserviamo che, in virtù del fatto che gli intervalli $I_k^j$ sono a due a due disgiunti, $f_n$ risulta ben definita. Il grafico delle funzioni $f_n$ è rappresentato in figura 7.

$\,$

Figura 7: Grafico (in blu) delle funzioni $f_n$ , in cui però per semplicità abbiamo rappresentato solamente le parti relative agli intervalli $I_k^j$ per $k=1,2,3$ . Osserviamo che $f_n$ assume infinite volte il valore $0$ e possiede la proprietà di Darboux.

$\,$

Se $x$ o $y$ non appartiene a nessuno degli intervalli $I_k^j$ , supponiamo senza perdita di generalità che ciò sia vero per $x$ .

Poiché $D$ non contiene alcun intervallo, all’intervallo $(x,y)$ deve appartenere l’estremo sinistro di un $I_k^j$ : esiste cioè $I_k^j$ tale che

(363) $\begin{equation*} x < x_k^j - \frac{1}{2 \cdot 3^k} \leq y. \end{equation*}$

Di nuovo dal fatto che $D$ non contiene alcun intervallo, esiste $I_h^i$ tale che

(364) $\begin{equation*} I_h^i \subset \left( x, x_k^j - \frac{1}{2 \cdot 3^k} \right). \end{equation*}$

Senza ledere la generalità, possiamo supporre che $h \geq k$ . Allora l’intervallo $I_{h+1}^{2i}$ è strettamente compreso tra $I_h^i$ e $I_k^j$ . Riassumendo, abbiamo determinato due intervalli $I_h^i$ e $I_{h+1}^{2i}$ strettamente compresi tra $x$ e $y$ ¹⁰.

Poiché

(365) $\begin{equation*} f\left(I_h^i \right) \cup f\left(I_{h+1}^{2i}\right) = [-2,2], \end{equation*}$

esiste $z \in [x,y]$ tale che $f(z)=t$ . In tutti i casi possibili quindi, esiste $z \in [x,y]$ tale che $f(z)=t$ . Pertanto $f_n$ ha la proprietà di Darboux.

Il limite uniforme $f$ delle $f_n$ non ha la proprietà di Darboux. Affermiamo che $f_n$ converge uniformemente alla funzione $f \colon [0,1] \to \mathbb{R}$ (il cui grafico è rappresentato in figura 8 definita da

(366) $\begin{equation*} f(x) = \begin{cases} (-1)^k + g \left( 2 \cdot 3^k(x-x_k^j)\right) & \text{se } x \in I_k^j \text{ per qualche } k \in \mathbb{N}, \,\, j \in \{1,\dots,2^{k-1}\} \\[16pt] 1 & \text{altrimenti}. \end{cases} \end{equation*}$

$\,$

Figura 8: Grafico (in blu) della funzione $f$ , in cui

$\,$

per semplicità abbiamo rappresentato solamente le parti relative agli intervalli $I_k^j$ per $k=1,2,3$ . Osserviamo che $f$ non assume il valore $0$ e pertanto non possiede la proprietà di Darboux.

Infatti si ha

(367) $\begin{gather*} f_n(x) = f(x) \qquad \forall n \in \mathbb{N},\,\, \forall x \in D, \\ \supx{I_k^j}\vdiff = \supx{[-1,1]}|g_n(x)-g(x)| \leq \frac{1}{n} \qquad \forall k,n \in \mathbb{N}, \,\, \forall j \in \{1,\dots,2^{k-1}\}, \end{gather*}$

dove l’uguaglianza segue dalla definizione di $f_n$ e di $f$ e la disuguaglianza segue da (358). Affermiamo che $f$ non possiede la proprietà di Darboux. Infatti, poiché $\operatorname{Im}g=(-1,1)$ e dalla definizione di $f$ , segue che

(368) $\begin{equation*} \operatorname{Im}f =(-2,0) \cup (0,2). \end{equation*}$

Poiché $0 \notin \operatorname{Im}f$ , ma $f$ assume sia valori positivi che negativi, segue che $f$ non ha la proprietà di Darboux.

$\,$

si veda ad esempio questa pagina. per la sua definizione e le sue principali proprietà. ↩

ove si è usata la nota formula

(369) $\begin{equation*} \sum_{k=1}^{+\infty} r^k = r \frac{1}{1-r} \qquad \forall r \in (-1,1). \end{equation*}$

↩

Se fosse stato $k \geq h$ , i due intervalli in questione sarebbero stati $I_{k+1}^{2j-1}$ e $I_{k+2}^{4j-1}$ . ↩

$\,$

Riferimenti bibliografici

[1] Acerbi, E. & Buttazzo, G. Primo corso di Analisi Matematica, Pitagora Editrice, (1997).

[2] Acerbi, E. & Buttazzo, G. Primo corso di Analisi Matematica, Pitagora Editrice, (2016).

[3] Qui Si Risolve, Successioni di funzioni – Teoria.

[4] Qui Si Risolve, Teorema fondamentale del calcolo integrale .

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Document