Esercizi avanzati di analisi matematica

Home » Esercizi avanzati di analisi matematica

Benvenuti nella nostra raccolta di esercizi avanzati di Analisi Matematica! In questo articolo presentiamo 72 problemi di tipo avanzato che toccano varie sezioni di questa importante branca della Matematica, alcune anche poco note. Gli esercizi sono di difficoltà mista, alcuni di essi sono anche molto complessi e richiedono una conoscenza profonda e dettagliata dell’Analisi Matematica a 360°. Essi risultano quindi appropriati per gli specialisti del settore e, più in generale, per chi intenda mettere alla prova in modo completo e deciso la propria preparazione in questo ambito.
Di ogni esercizio offriamo una o più soluzioni complete, per consentire al lettore di confrontarle e scegliere quelle maggiormente di suo gusto.

Cosa aspetti allora? Se desideri qualcosa di davvero arduo e stimolante, prova a risolvere qualcuno di questi problemi!

Oltre ai richiami teorici sugli esercizi avanzati, consigliamo il seguente materiale teorico di riferimento:

Buona lettura!

Sommario

Leggi...

In questo articolo presentiamo alcuni esercizi di Analisi Matematica di carattere avanzato, di cui proponiamo soluzioni che utilizzano strumenti particolare e di difficile reperibilità.

Autori e revisori

Leggi...

Autori: Valerio Brunetti, Gianmarco Bramanti, Giulio Francot, Jacopo Garofali, Daniele Bjørn Malesani..

Esercizi

$\quad$

Esercizio 1 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare tutte le radici distinte della seguente equazione:

$1-\begin{pmatrix} n\\2 \end{pmatrix} x^2 + \begin{pmatrix} n\\4 \end{pmatrix}x^4 - \begin{pmatrix} n\\6 \end{pmatrix} x^6+ \dots + (-1)^j \begin{pmatrix} n\\2j \end{pmatrix} x^{2j}=0,$

dove

$j = \begin{cases} n/2, \qquad &\text{se } \, n \, \text{è pari}\\ (n-1)/2, \qquad &\text{se } \, n \, \text{è dispari}.\\ \end{cases}$

Svolgimento.

Ricordiamo la formula del binomio di Newton

(1) $\begin{equation*} (a+b)^n=\sum_{k=0}^n \begin{pmatrix} n \\ k \end{pmatrix} a^{n-k} b^k. \end{equation*}$

Osserviamo adesso che la nostra equazione può essere riscritta al modo seguente

$\sum_{k=0}^{[n/2]}\begin{pmatrix} n \\ 2k\end{pmatrix} (-1)^k x^{2k}=0,$

dove

$[n/2]=\left\{\begin{array}{lcl} n/2 & & n\textrm{ pari}\\ & & \\ (n-1)/2 & & n\textrm{ dispari.} \end{array}\right.$

Se scriviamo $-1=i^2$ l’equazione assume la forma

$\sum_{k=0}^{[n/2]}\begin{pmatrix} n \\ 2k\end{pmatrix} (ix)^{2k}=0$

per cui, confrontandola con la formula (1) si osserva che essa contiene solo le potenze pari dello sviluppo del polinomio $(1+ix)^n$ . Poiché risulta

(2) $\begin{equation*} \begin{aligned} (1+ix)^n &=\sum_{k=0}^n \begin{pmatrix} n \\ k \end{pmatrix} (ix)^{k}=\\ &=\sum_{k=0}^{[n/2]} \begin{pmatrix} n \\ 2k \end{pmatrix}(ix)^{2k}+ \sum_{k=0}^{[n/2]} \begin{pmatrix} n \\ 2k+1 \end{pmatrix}(ix)^{2k+1}=\\ &=\sum_{k=0}^{[n/2]} \begin{pmatrix} n \\ 2k \end{pmatrix}(-1)^k x^{2k}+i \sum_{k=0}^{[n/2]} \begin{pmatrix} n \\ 2k+1 \end{pmatrix}(-1)^k x^{2k+1}, \end{aligned} \end{equation*}$

la nostra equazione assume la forma compatta seguente:

$\mathrm{Re}\left[(1+ix)^n\right]=0,$

con $\mathrm{Re}$ che indica la parte reale del numero complesso. Per risolverla, scriviamo il numero complesso $1+ix$ in forma trigonometrica

$1+ix=\rho(\cos\theta+i\sin\theta),\quad \rho=\sqrt{1+x^2},\ \theta\in[0,2\pi).$

Allora

$0=\mathrm{Re}\left[\rho^n(\cos(n\theta)+i\sin(n\theta))\right] \iff \rho^n\cos(n\theta)=0,$

e pertanto, avendosi $\rho\neq 0$ per ogni scelta di $x$ ,

$\cos(n\theta)=0 \implies \theta=\frac{\pi}{2n}+h\frac{\pi}{n},\ h=0,\ldots,2n-1.$

Essendo poi, per la posizione fatta

$1=\rho\cos\theta,\qquad x=\rho\sin\theta,$

si ottiene

$x=\tan\theta=\tan\left(\frac{\pi}{2n}+h\frac{\pi}{n}\right),\ h=0,\ldots,n-1,$

avendo diminuito le scelte per $h$ a causa della periodicità della funzione tangente. Inoltre, per tali soluzioni va escluso l’indice $h=(n-1)/2$ quando $n$ è dispari, in quanto in tal caso

$\theta=\frac{\pi}{2n}+(n-1)\frac{\pi}{2n}=n\cdot\frac{\pi}{2n}=\frac{\pi}{2},$

e la tangente perde di significato.

Esercizio 2 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Si consideri l’equazione differenziale ordinaria del secondo ordine lineare omogenea a coefficienti variabili

$Py\equiv(3x^2+x-1)y''-(9x^2+9x-2)y'+(18x+3)=0.$

$\quad$

Determinare una soluzione non nulla;

Determinare la soluzione generale dell’equazione;

Si consideri la funzione $y=f(x)$ , soluzione dell’equazione non omogenea
$Py=6(6x+1),$

che soddisfa le condizioni

$f(0)=1,\qquad [f(-1)-2]\cdot[f(1)-6]=1.$

Si determinino tutte le terne di numeri interi $a,b,c\in\mathbb{Z}$ tali che

$[f(-2)-a]\cdot[f(2)-b]=c.$

Svolgimento.

Riportiamo la soluzione dei diversi punti.

Svolgimento punto 1.

La presenza dei coefficienti sotto forma di polinomi suggerisce di determinare una soluzione di tipo polinomiale. Per prima cosa, vediamo se ci sono condizioni da porre al grado di tale funzione. Supponiamo che la nostra soluzione sia della forma

$y=ax^n+q_{(n-1)}(x),$

dove $q_{(n-1)}(x)$ è un polinomio di grado minore di $n$ (indichiamo tra parentesi in basso $n-1$ per tenere conto di questo fatto) e $a\neq 0$ . Abbiamo allora

$y'=anx^{n-1}+q'_{(n-2)}(x),\qquad y''=an(n-1)x^{n-2}+q''_{(n-3)}(x),$

dove, come prima, abbiamo indicato a pedice delle derivate del polinomio $q$ quale sia il grado massimo presente. Sostituendo nell’equazione abbiamo

$\begin{aligned} & 3an(n-1)x^n+an(n-1)x^{n-1}-an(n-1)x^{n-2}+Q_{(n-1)}(x)\\ & -9anx^{n+1}-9anx^n+2anx^{n-1}+Q_{(n)}(x)\\ & +18ax^{n+1}+3ax^{n}+Q_{(n)}(x)=0, \end{aligned}$

dove con $Q_{(i)}$ si è indicato il polinomio che si ottiene come prodotto dei coefficienti variabili e delle derivate di $q$ e il grado massimo $i$ presente in esso. Possiamo osservare che appaiono solo due termini di grado $n+1$ : al fine di ottenere una soluzione, dovrà essere

$-9anx^{n+1}+18ax^{n+1}=0 \implies 9ax^{n+1}(-n+2)=0,$

e quindi deve essere $n=2$ .

In base a quanto detto in precedenza, ipotizziamo che la nostra soluzione sia del tipo

$y=ax^2+bx+c \implies y'=2ax+b,\ y''=2a,$

da cui sostituendo

$\begin{aligned} & 6ax^2+2ax-2a-18ax^3-9bx^2-18ax^2-9bx+4ax+2b\\ & +18ax^3+18bx^2+18cx+3ax^2+3bx+3c=0, \end{aligned}$

e semplificando

$(-9a+9b)x^2+(6a-6b+18c)x+(-2a+2b+3c)=0,$

da cui ricaviamo

$\begin{cases} -9a+9b=0\\ 6a-6b+18c=0\\ -2a+2b+3c=0 \end{cases}\implies a=b,\ c=0.$

Se ne deduce che la soluzione polinomiale cercata è della forma

(3) $\begin{equation*} \boxcolorato{analisi}{ y=ax^2+ax=a(x^2+x),\qquad a\in\mathbb{R}. } \end{equation*}$

Svolgimento punto 2.

Per determinare la soluzione generale della funzione, abbiamo bisogno di una seconda soluzione $z(x)$

che risulti linearmente indipendente dalla soluzione appena trovata. Per fare ciò ricordiamo il seguente notevole risultato.

Teorema 3.1 (Abel). Sia data l’equazione differenziale ordinaria del secondo ordine lineare omogenea a coefficienti variabili

$y''+p(x) y'+q(x)=0,$

con soluzione generale $y(x)=C_1 y_1(x)+C_2 y_2(x)$ , dove $y_1, y_2$ sono linearmente indipendenti e $C_1, C_2$ costanti arbitrarie. Allora il Wronskiano delle soluzioni si può scrivere come

$W(x)=y_1(x)\cdot y'_2(x)-y'_1(x)\cdot y_2(x)=\exp\left[-\int p(x)\ dx\right].$

$\quad$

Portiamo allora la nostra equazione nella forma richiesta dal teorema 3.1:

$y''-\frac{9x^2+9x-2}{3x^2+x-1} y'+\frac{18x+3}{3x^2+x-1} y=0,$

per cui

$p(x)=-\frac{9x^2+9x-2}{3x^2+x-1}=-\frac{3(3x^2+x-1)+6x-1}{3x^2+x-1}=-3-\frac{6x+1}{3x^2+x-1}.$

Calcoliamo ora il Wronskiano secondo il teorema: abbiamo

$\begin{aligned} W(x) &=\exp\left[-\int p(x)\ dx\right]=\\ &=\exp\left[\int\left(3+\frac{6x+1}{3x^2+x-1}\right)\ dx\right]=\\ &=\exp\left[3x+\ln|3x^2+x+1|+c\right]=\\ &=e^{3x}\cdot(3x^2+x+1). \end{aligned}$

D’altra parte, se poniamo

$y_1(x)=x^2+x,\qquad y_2(x)=z(x),$

allora

$W(x)=y_1(x)\cdot y'_2(x)-y'_1(x)\cdot y_2(x)=(x^2+x)\cdot z'(x)-(2x+1)\cdot z(x),$

e quindi uguagliando otteniamo la seguente equazione differenziale ordinaria del primo ordine lineare

$(x^2+x) z'(x)-(2x+1)\cdot z(x)=e^{3x}(3x^2+2x-1).$

Tale equazione diventa

$z'(x)-\frac{2x+1}{x^2+x}\cdot z(x)=e^{3x}\frac{3x^2+2x-1}{x^2+x},$

che è della forma

$z'+a(x) z=b(x),$

la cui soluzione generale è

$z(x)=e^{-A(x)}\left[\int b(x) e^{A(x)}\ dx+c\right],\qquad A(x)=\int a(x)\ dx.$

Nel nostro caso

$a(x)=-\frac{2x+1}{x^2+x},\qquad b(x)=e^{3x}\frac{3x^2+2x-1}{x^2+x},$

per cui

$A(x)=\int-\frac{2x+1}{x^2+x}\ dx=-\ln|x^2+x|$

$\begin{aligned} \int b(x) e^{A(x)}\ dx &=\int e^{3x}\frac{3x^2+x-1}{(x^2+x)^2}\ dx=\\ &=\int e^{3x}\frac{3(x^2+x)-(2x+1)}{(x^2+x)^2}\ dx=\\ &=\int e^{3x}\left(\frac{3}{x^2+x}-\frac{2x+1}{(x^2+x)^2}\right)\ dx=\\ &=\int \frac{3e^{3x}}{x^2+x}\ dx-\int e^{3x}\frac{2x+1}{(x^2+x)^2}\ dx. \end{aligned}$

Integrando per parti il primo integrale con

$f'=3e^{3x},\ g=\frac{1}{x^2+x} \implies f=e^{3x},\ g'=-\frac{2x+1}{(x^2+x)^2},$

si ha

$\begin{aligned} \int b(x) e^{A(x)}\ dx &=e^{3x}\frac{1}{x^2+x}+\int e^{3x}\frac{2x+1}{(x^2+x)^2}\ dx -\int e^{3x}\frac{2x+1}{(x^2+x)^2}\ dx=\\ &=e^{3x}\frac{1}{x^2+x}, \end{aligned}$

da cui

$z(x)=(x^2+x)\left[e^{3x}\frac{1}{x^2+x}+c\right]=e^{3x}+c(x^2+x).$

La soluzione generale dell’equazione $Py=0$ risulta allora

(4) $\begin{equation*} \boxcolorato{analisi}{y(x)=C_1(x^2+x)+C_2 e^{3x}.} \end{equation*}$

Svolgimento punto 3.

Determiniamo una soluzione particolare per $Py=6(6x+1)$

: la scelta di una soluzione polinomiale porterebbe a pensare di usare un polinomio di primo grado. Tuttavia, come abbiamo visto all’inizio, conviene concentrare l’attenzione su un generico polinomio di secondo grado. Ripetendo i calcoli già effettuati, avendo questa volta un termine noto non nullo, si perviene alle condizioni sui coefficienti del generico polinomio $y(x)=ax^2+bx+c$

seguenti:

$\begin{cases} -9a+9b=0\\ 6a-6b+18c=36\\ -2a+2b+3c=6 \end{cases} \implies a=b,\ c=2,$

e pertanto la soluzione particolare assume la forma $y=a(x^2+x)+2,\ a\in\mathbb{R}$ che, inglobata nella soluzione dell’equazione omogenea conduce a

$y(x)=C_1(x^2+x)+C_2 e^{3x}+2.$

Per determinare la soluzione cercata, imponiamo le condizioni:

$f(0)=1 \implies 1=C_2+2 \implies C_2=-1,$

$[f(-1)-2]\cdot[f(1)-6]=1 \implies [-e^{-3}]\cdot[2C_1-e^3-4]=1 \implies C_1=2,$

e quindi la soluzione cercata

$f(x)=2(x^2+x)-e^{3x}+2=2(x^2+x+1)-e^{3x}.$

Per ricavare gli interi cercati, osserviamo che

$f(2)=14-e^6,\qquad f(-2)=6-e^{-6},$

pertanto deve essere

$[6-e^{-6}-a]\cdot[14-e^6-b]=c,$

che semplificata diventa

$(6-a)(14-b)-(6-a)e^6-(14-b)e^{-6}+1-c=0.$

La relazione precedente si può pensare come un polinomio nelle variabili $e^6,\ e^{-6}$ : per il principio di identità tutti i suoi coefficienti devono essere pari a zero. Pertanto

$\begin{cases} (6-a)(b-14)+1-c=0\\ -(6-a)=0\\ -(14-b)=0 \end{cases} \implies a=6,\ b=14,\ c=1$

quindi

(5) $\begin{equation*} \boxcolorato{analisi}{a=6,\ b=14,\ c=1. } \end{equation*}$

Esercizio 3 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Trovare le soluzioni positive delle equazioni

$x^{x+y}=y^a \qquad \mbox{e} \qquad y^{x+y}=x^{4a},$

dove $a>0$ .

Svolgimento.

Possiamo prendere i logaritmi ad ambo i membri delle due equazioni ottenendo

$\begin{cases} (x+y) \ln x=a\ln y\\ (x+y) \ln y=4a\ln x. \end{cases}$

Notiamo che la coppia $(x,y)=(1,1)$ risulta una soluzione del sistema. Osserviamo poi che, dovendo essere $x,y>0$ , allora si ha pure $x+y>0$ : pertanto possiamo dividere membro a membro le due equazioni (avendo escluso il caso $x=y=1$ ) ottenendo

$\frac{\ln y}{\ln x}=4\frac{\ln x}{\ln y},$

da cui

$\ln^2 y=4\ln^2 x \implies (\ln y-2\ln x)(\ln y+2\ln x)=0.$

Si hanno pertanto due equazioni:

(6) $\begin{equation*} \begin{gathered} \ln y=2\ln x \implies y=x^2, \\ \ln y=-2\ln x \implies y=\frac{1}{x^2}. \end{gathered} \end{equation*}$

Sostituendo $y=x^2$ nella prima delle due equazioni originali si ha

$(x+x^2)\ln x=2a\ln x \implies x^2+x-2a=0 \quad (x\neq 1),$

che ha soluzioni

$x_{1,2}=\frac{-1\pm\sqrt{1+8a}}{2},$

di cui solo quella col segno positivo prima della radice risulta accettabile. Si ricava poi che

$y=\left(\frac{-1+\sqrt{8a+1}}{2}\right)^2=\frac{4a+1-\sqrt{8a+1}}{2}.$

Sostituendo invece $y=1/x^2$ nella prima delle due equazioni originali si ricava

$\left(x+\frac{1}{x^2}\right)\ln x=-2a\ln x \implies x^3+2ax^2+1=0 \quad (x\neq 1),$

la quale non ammette soluzioni positive in quanto, se $x>0$ , risulta somma di tre quantità sempre maggiori di zero.

Possiamo qundi concludere che le soluzioni del sistema originale sono date dalle due coppie

(7) $\begin{equation*} \boxcolorato{analisi}{\displaystyle (1,1)\qquad\left(\frac{\sqrt{1+8a}-1}{2},\frac{{4a+1}-\sqrt{1+8a}}{2}\right), } \end{equation*}$

che coincidono quando $a=1$ , come è facile verificare.

Esercizio 4 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Trovare tutte le soluzioni delle equazioni simulteanee:

$\begin{aligned} & y=x+\sqrt{x+\sqrt{x+\dots+\sqrt{x+\sqrt{y}}}}\\ & x+y=6, \end{aligned}$

dove nella prima equazione compaiono 1975 radici quadrate.

Svolgimento.

Osserviamo che deve essere necessariamente $y\ge 0$

: pertanto si ha pure $x\le 6$

. Inoltre, se ragioniamo in termini di possibili soluzioni intere, si vede subito che la coppia $(x,y)=(2,4)$

soddisfa il sistema. Andiamo allora ad analizzare i due casi $4< y\le 6$

e $0\le y< 4$

Caso 1.

$4< y\le 6$

: poniamo $y=4+h, 0<h\le 2$

da cui $x=2-h$

. Ovviamente

$y=4+h < 4+4h+h^2=(2+h)^2,$

e quindi

$x+\sqrt{y}< 2-h+2+h=4.$

Di conseguenza

$x+\sqrt{x+\sqrt{y}}<2-h+2=4-h<4,$

$x+\sqrt{x+\sqrt{x+\sqrt{y}}}<2-h+2=4-h<4.$

Ciò porta ad un assurdo, in quanto per ipotesi $y>4$ , ma iterando il procedimento si avrà che il membro destro della prima equazione risulti sempre minore di $4$ .

Caso 2.

$0< y\le 4$

: consideriamo per prima cosa $y<3$

: dalla prima equazione ricaviamo che $y>x$

( $y$

si ottiene da $x$

sommando una quantità positiva), tuttavia se $y<3$

allora $x=6-y>3$

e quindi si crea un assurdo. Pertanto deve essere $3 \le y < 4$

. Se poniamo $y=4-h,\ 0< h \le 1$

abbiamo $x=2+h$

e anche

$y=4-h>4-2h+h^2=(2-h)^2,$

$x+\sqrt{y}>2+h+2-h=4,$

$x+\sqrt{x+\sqrt{y}}>2-h+2=4-h>4,$

$x+\sqrt{x+\sqrt{x+\sqrt{y}}}>2-h+2=4-h,$

e quindi, iterando il procedimento, il membro destro risulta strettamente maggiore di $4$ , mentre $y<4$ , che porta ad un altro assurdo.

Possiamo concludere, infine, che l’unica soluzione del sistema risulta la coppia

(8) $\begin{equation*} \boxcolorato{analisi}{(x,y)=(2,4). } \end{equation*}$

Esercizio 5 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare il seguente integrale definito

$\int_0^{\pi/2} (\ln(2\sin x))^2 \, dx.$

Svolgimento.

È nota l’identità

$\ln (\sin (x))=-\sum\limits_{k\geq 1}\frac{\cos (2kx)}{k}-\ln (2),$

dunque

(9) $\begin{equation*} \begin{split} \int_{0}^{\frac{\pi }{2}}\ln ^{2}(2\sin (x))dx &= \int_{0}^{ \frac{\pi }{2}}\left( \sum_{k\geq 1}\frac{\cos (2kx)}{k}\right) ^{2}dx \\ &= \int_{0}^{\frac{\pi }{2}}\sum_{k\geq 1}\sum_{h\geq 1}\frac{\cos (2kx)\cos (2hx)}{kh}dx \\ &= \sum_{k\geq 1}\sum_{h\geq 1}\int_{0}^{\frac{\pi }{ 2}}\frac{\cos (2kx)\cos (2hx)}{kh}dx. \end{split} \end{equation*}$

Per le relazioni di ortoganalità

$\int_{0}^{\frac{\pi }{4}}\frac{\cos (2kx)\cos (2hx)}{kh}dx= \begin{cases} \frac{\pi }{4k^2} &\text{ se }k= h \\ 0 &\text{ se }k\neq h \end{cases}$

e dunque l’ultima somma si riduce a¹

(10) $\begin{equation*} \boxcolorato{analisi}{\displaystyle \frac{\pi }{4}\sum_{k\geq 1}\frac{1}{k^{2}}=\frac{\pi ^{3}}{24}. } \end{equation*}$

Si ricorda che

$\sum_{k\geq1}\dfrac{1}{k^2}=\dfrac{\pi^2}{6}$

↩

Esercizio 6 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare l’integrale triplo

$\iiint_D \ln\left(\dfrac{xy}{z}\right) \, dx \, dy \, dz,$

dove $D=\{ (x,y,z) : x \in [1,e], \, 4 \le yz, \; 0 \le y+z \le 5 \}$ .

Svolgimento.

Posto

$I=\iiint_{D}\ln \left(\frac{xy}{z}\right)dxdydz,$

per simmetria si ha pure

$I=\iiint_{D}\ln \left(\frac{xz}{y}\right)dxdydz$

e dunque

$\begin{aligned} 2I &=\iiint_{D}\left(\ln \left(\frac{xy}{z}\right)+\ln \left(\frac{xz}{y}\right)\right)dxdydz= \\ &=\iint_{A}\left(\int_{1}^{e}\ln \left(x^{2}\right)dx\right)dydz, \end{aligned}$

dove $A=\{(y,z):4\leq zy$ , $0\leq z+y\leq 5\}$ . Perciò

$\begin{aligned} 2I &=\int_{1}^{e}\ln \left(x^{2}\right)dx\iint_{A}dydz \\ &=\int_{1}^{e}\ln \left(x^{2}\right)\int_{1}^{4}\left(y+5-\frac{4}{y}\right)dy \\ &=2\left(\frac{15}{2}-8\ln 2\right) \end{aligned}$

e dunque

(11) $\begin{equation*} \boxcolorato{analisi}{\displaystyle I=\frac{15}{2}-8\ln 2. } \end{equation*}$

Esercizio 7 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Siano $a_1<a_2<\dots<a_n$

dei numeri interi positivi. Dimostrare che

$1+\prod_{k=1}^{n} \left(1+\dfrac{1}{a_k}\right) \le 2 \prod_{k=1}^{n} \left(1+\dfrac{1}{a_k+1}\right).$

Svolgimento.

Ponendo

(12) $\begin{equation*} h_n \coloneqq \left( 1+\frac{1}{a_{1}} \right)\cdots \left(1+\frac{1}{a_{n}}\right), \qquad k_n \coloneqq \left (1+\frac{1}{a_{1}+1}\right )\ldots \left (1+\frac{1}{a_{n}+1}\right ), \end{equation*}$

la disuguaglianza da provare diventa

(13) $\begin{equation*} 1+h_{n}\leq 2k_{n}. \end{equation*}$

Premettiamo prima le seguenti disuguaglianze:

(14) $\begin{equation*} 1\leq k_{n}\leq h_{n}\leq n+1. \end{equation*}$

Le prime due sono ovvie, mentre per la terza, tenendo conto delle limitazioni del problema, si ha che

$h_{n}\leq (1+1)\left(1+\frac{1}{2}\right)\ldots \left(1+\frac{1}{n}\right)=n+1.$

Procediamo adesso per induzione su $n$ per dimostrare (13). Il passo base si riduce a

$2+\frac{1}{a_{1}}\leq 2+\frac{2}{a_{1}+1}$

e cioè

$1\leq a_{1}$

che è certamente vera.

Siano adesso $a_{1}\ldots a_{n}$ fissati e $x=a_{n+1}$ (si tenga presente che deve essere $x\geq n+1$ ). Si deve provare che

$1+h_{n}\left( 1+\frac{1}{x}\right)\leq 2k_{n}\left(1+\frac{1}{x+1}\right),$

che, dopo qualche passaggio, si riduce a

(15) $\begin{equation*} x^{2}(2k_{n}-h_{n}-1)+x(4k_{n}-2h_{n}-1)-h_{n}\geq 0. \end{equation*}$

Osserviamo che per l’ipotesi induttiva con $n$ , ovvero $2k_n-h_n-1\ge0$ per un certo $n$ arbitrario, abbiamo

$2k_{n}-h_{n}-1>0 \quad \mbox{e} \quad 4k_{n}-2h_{n}-1>1,$

mentre per (14) otteniamo $-h_n \ge -(n+1)$ , dunque (15) diviene

$x^{2}(2k_{n}-h_{n}-1)+x(4k_{n}-2h_{n}-1)-h_{n}\ge (n+1) \cdot 1-(n+1)\geq 0,$

pertanto (13) è provata.

Esercizio 8 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare

$I = \int_0^{+\infty} \int_{y=x}^{+\infty} e^{-(x-y)^2} \; \sin^2(x^2+y^2) \; \dfrac{x^2-y^2}{(x^2+y^2)^2} \, dx \, dy.$

Svolgimento.

Passando alle coordinate polari si ha

$\begin{aligned} I &=\int_{0}^{+\infty }\int_{\frac{\pi }{4}}^{\frac{\pi }{2}% }e^{-\rho ^{2}(\cos \theta -\sin \theta )^{2}}\frac{\sin ^{2}(\rho ^{2})}{% \rho ^{4}}\rho ^{2}(\cos ^{2}\theta -\sin ^{2}\theta )\rho d\rho d\theta \\ &=\int_{0}^{+\infty }\int_{\frac{\pi }{4}}^{\frac{\pi }{2}% }e^{-\rho ^{2}(1-\sin 2\theta )}\frac{\sin ^{2}(\rho ^{2})}{\rho }(\cos 2\theta )d\rho d\theta \\ &=\int_{0}^{+\infty }e^{-\rho ^{2}}\frac{\sin ^{2}(\rho ^{2})}{\rho }\left( \int_{\frac{\pi }{4}}^{\frac{\pi }{2}}e^{\rho ^{2}(\sin 2\theta )}(\cos 2\theta ))d\theta \right) d\rho . \end{aligned}$

Ora risulta che

$\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}e^{\rho ^{2}(\sin 2\theta )}(\cos 2\theta ))d\theta =\frac{1-e^{\rho ^{2}}}{2\rho ^{2}},$

dunque

(16) $\begin{equation*} \begin{split} I &= \int_{0}^{+\infty }e^{-\rho ^{2}}\frac{\sin ^{2}(\rho ^{2})}{% \rho }\frac{1-e^{\rho ^{2}}}{2\rho ^{2}}d\rho \\ &= \int_{0}^{+\infty }e^{-\rho ^{2}}\frac{\sin ^{2}(\rho ^{2})}{% 2\rho ^{3}}d\rho -\int_{0}^{+\infty }\frac{\sin ^{2}(\rho ^{2})}{% 2\rho ^{3}}d\rho \\ &= A-B. \end{split} \end{equation*}$

Si ha che

(17) $\begin{equation*} A = \frac{1}{16}(4\arctan (2)-\ln 5), \qquad B =\frac{\pi }{8}. \end{equation*}$

In definitiva

(18) $\begin{equation*} \boxcolorato{analisi}{\displaystyle I=\frac{1}{16}(4\arctan (2)-\ln 5)-\frac{\pi }{8}. } \end{equation*}$

Esercizio 9 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Se $x_1,\,x_2,\,x_3,\,x_4,$

e $x_5$

sono tutti numeri positivi, dimostrare che

$\begin{equation*} (x_1+x_2+x_3+x_4+x_5)^2\ge4(x_1x_2+x_2x_3+x_3x_4+x_4x_5+x_5x_1). \end{equation*}$

Svolgimento.

Dobbiamo provare che

(19) $\begin{equation*} (x_1+x_2+x_3+x_4+x_5)^2-4(x_1x_2+x_2x_3+x_3x_4+x_4x_5+x_5x_1)\ge0. \end{equation*}$

Ponendo $x_1=y_1+y_2,\, x_2=y_2+y_3,...,x_5=y_5+y_1$ con $y_1,\, y_2,...,y_5$ positivi, (19) diventa:

$\begin{equation*} 4y_1y_3+4y_1y_4+4y_2y_4+4y_2y_5+4y_3y_5\ge0, \end{equation*}$

che è chiaramente soddisfatta.

Esercizio 10 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare il seguente limite di successione, se esiste:

$\begin{equation*} \lim_{x\to+\infty}n \ln \left( \dfrac{(n+1)!e^{n+2}}{(n+2)^{n+1}\sqrt{2\pi (n+1)}}\right). \end{equation*}$

Svolgimento.

Si ricorda che

(20) $\begin{equation*} n!=\sqrt{2\pi n}\left( \dfrac{n}{e}\right)^n \left(1+\dfrac{1}{12n}+o\left( \dfrac{1}{n}\right) \right) \,\mbox{per }n\to+\infty. \end{equation*}$

Quindi

(21) $\begin{equation*} (n+1)!=(n+1)n!=(n+1)\sqrt{2\pi n}\left(\dfrac{n}{e} \right)^n\left(1+\dfrac{1}{12n}+o\left(\dfrac{1}{n} \right) \right) \quad \mbox{per } \, n\to +\infty. \end{equation*}$

Tornando al limite,

$\begin{aligned} & \lim_{n\to+\infty}n\ln \left( \dfrac{(n+1)! \; e^{n+2}}{(n+2)^{n+1}\sqrt{2\pi (n+1)}}\right)= \\ & \qquad = \lim_{n\to+\infty}n\ln \left(\dfrac{e^ne^2(n+1)\sqrt{2\pi n}\left( \dfrac{n}{e}\right)^n\left(1+\dfrac{1}{12n}+o\left(\dfrac{1}{n} \right) \right)}{n^n\left(1+\dfrac{2}{n} \right)^n(n+2)\sqrt{2\pi(n+1)}} \right)=\\ & \qquad= \lim_{n\to+\infty}n\ln \left(\dfrac{e^2 (n+1)\left(1+\dfrac{1}{12n}+o\left( \dfrac{1}{n}\right) \right)}{e^{n\ln \left(1+\frac{2}{n} \right)}(n+2)\sqrt{1+\dfrac{1}{n}}} \right)=\\ &\qquad= \lim_{n\to+\infty}n\ln \left(\dfrac{\left(1+\dfrac{1}{n} \right)}{\left(1-\left(-\dfrac{2}{n} \right) \right)} \dfrac{e^2 \left (1+\dfrac{1}{12n}+o\left( \dfrac{1}{n}\right)\right )}{e^2e^{n\left(\frac{1}{2}\left(\frac{4}{n^2}+o\left(\frac{1}{n^2} \right) \right) \right)}\left(1+\dfrac{1}{n} \right)^{\frac{3}{2} }}\right)= \\ &\qquad= \lim_{n\to+\infty}n\ln \left(\dfrac{\left(1-\dfrac{2}{n}+o\left(\dfrac{1}{n} \right) \right)\left( 1+\dfrac{1}{n}\right)\left( 1+\dfrac{1}{12n}+o\left(\dfrac{1}{n} \right)\right)}{\left(1-\dfrac{2}{n}+o\left(\dfrac{1}{n} \right) \right)\left(1+\dfrac{1}{2n}+o\left(\dfrac{1}{n} \right) \right)} \right)=\\ &\qquad= \lim_{n\to+\infty}n\ln\Bigg( \left(1-\dfrac{2}{n}+o\left(\dfrac{1}{n} \right) \right)\left(1+\dfrac{1}{n} \right)\left(1+\dfrac{1}{12n}+\left( \dfrac{1}{n}\right) \right)\cdot \\ & \qquad \qquad \qquad \cdot \left( 1+\dfrac{2}{n}+o\left(\dfrac{1}{n} \right)\right)\left(1-\dfrac{1}{2n}+o\left(\dfrac{1}{n} \right) \right) \Bigg)=\\ &\qquad= \lim_{n\to+\infty}n\ln \left( 1+\dfrac{7}{12n}+o\left( \dfrac{1}{n}\right)\right)= \\ &\qquad= \lim_{n\to+\infty}n\left(\dfrac{7}{12n}+o\left(\dfrac{1}{n} \right) \right)= \\ & \qquad= \dfrac{7}{12}. \end{aligned}$

Quindi

$\boxcolorato{analisi}{\lim_{n\to+\infty}n\ln \left( \dfrac{(n+1)! \; e^{n+2}}{(n+2)^{n+1}\sqrt{2\pi (n+1)}}\right)=\dfrac{7}{12}.}$

Esercizio 11 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Sia $D$

il compatto dello spazio $xyz$

definito dalle limitazioni

$\begin{equation*} \begin{cases} x^2+y^2+z^2\le r^2\\ z\ge\sqrt{x^2+y^2}. \end{cases} \end{equation*}$

Calcolare il momento di inerzia di $D$ rispetto all’asse $z$ , nell’ipotesi che la densità $\mu(x,y,z)$ sia proporzionale alla distanza del punto $(x,y,z)$ dall’origine. Esprimere il risultato in termini della massa $M$ del solido.

Svolgimento 1.

$D$

è rappresentato in figura 1.

$\quad$

Figura 1: l’insieme dell’esercizio 11.

$\quad$

Il momento d’inerzia è

$\begin{equation*} I=\int R^2 dm, \end{equation*}$

dove

$\begin{equation*} \dfrac{dm}{d\tau}=\mu(x,y,z)=k\sqrt{x^2+y^2}, \end{equation*}$

quindi

(22) $\begin{equation*} I=\iint_\tau k\sqrt{x^2+y^2}R^2dxdydz, \end{equation*}$

dove $k$ è costante. Calcoliamo ora $k$ come segue

$\begin{aligned} m &= \iiint_\tau k\sqrt{x^2+y^2}dxdydz = \\ &=\int_{0}^{2\pi}d\theta \int_{0}^{\frac{\pi}{4}}d\phi\int_0^{r}k\rho\vert \sin\phi\vert \rho^2\sin\phi \rho= \\ & = 2\pi k\int_{0}^{\frac{\pi}{4}}\sin^2 \phi \; d\phi\int_{0}^r \rho^3d\rho= \\ &= 2\pi k \dfrac{r^4}{4}\left(\dfrac{\pi}{8}-\dfrac{1}{4} \right)= \\ &= \pi k r^4 \; \dfrac{\pi-2}{16}, \end{aligned}$

ovvero

(23) $\begin{equation*} k= \dfrac{16}{\pi r^4} \; \dfrac{m}{\pi-2}. \end{equation*}$

L’integrale (22) diventa

$\begin{aligned} I&=\int_0^{2\pi}d\theta \int_0^{\frac{\pi}{2}}d\phi\int_0^r k\underbrace{\sqrt{x^2+y^2}}_{\rho\sin\phi} \rho^2 \sin^2\phi \; \rho^2\sin \phi \; d\rho=\\ &=2\pi k\int_0^{\frac{\pi}{4}}\sin^4 \phi \; d\phi \int_0^r \rho^5 d\rho= \\ &=\left(\dfrac{2\pi kr^6}{6}\right) \left(\dfrac{3\pi-8}{32}\right) . \end{aligned}$

Sostituendo (23) otteniamo

(24) $\begin{equation*} \boxcolorato{analisi}{I= \dfrac{16}{\pi r^4} \; \dfrac{m}{\pi-2} \; \dfrac{2\pi r^6}{6} \; \dfrac{3\pi-8}{32} = \dfrac{mr^2 (3\pi-8)}{6(\pi-2)}. } \end{equation*}$

Svolgimento 2.

Alternativamente si poteva procedere come segue:

$\begin{aligned} m &=\int_0^{2\pi}d\theta \int_0^{\frac{r}{\sqrt{2}}}dz\int_0^z k\rho^2d\rho+\int_0^{2\pi}d\theta\int_{\frac{r}{\sqrt{2}}}^rdz\int_0^{\sqrt{r^2-z^2}}k\rho^2d\rho=\\ &=2\pi k\left(\int_0^{\frac{r}{\sqrt{2}}} \dfrac{z^3}{3}dz + \int_{\frac{r}{\sqrt{2}}}^{r} \dfrac{(\sqrt{r^2-z^2})^3}{3}dz\right)=\\ &=2\pi k\left( \dfrac{3\pi}{96}r^4-\dfrac{8}{96}r^4+\dfrac{r^4}{48}\right), \end{aligned}$

ossia

(25) $\begin{equation*} \begin{aligned} m & = 2\pi k\left(\dfrac{3\pi}{96}r^4-\dfrac{r^4}{16} \right)=\\ &=\dfrac{2\pi k}{16}r^4\left( \dfrac{1}{2}\pi-1\right) =\\ &=\dfrac{\pi kr^4}{8} \; \dfrac{\pi-2}{2}= \\ &= \dfrac{\pi kr^4(\pi-2)}{16}, \end{aligned} \end{equation*}$

che è equivalente a

(26) $\begin{equation*} k=\dfrac{16m}{\pi r^4(\pi-2)}, \end{equation*}$

da cui

$\begin{aligned} I&=\int_0^{2\pi}d\theta \int_0^{\frac{\pi}{\sqrt{2}}}dz\int_0^z k\rho^4 d\rho+\int_0^{2\pi}d\theta \int_{\frac{r}{\sqrt{2}}}^r dz\int_0^{\sqrt{r^2-z^2}}k\rho^4 d\rho=\\ &=2\pi \left(\int_0^{\frac{r}{\sqrt{2}}}k\dfrac{z^5}{5}dz+\int_{\frac{r}{\sqrt{2}}}^r k\dfrac{(r^2-z^2)^{\frac{5}{2}}}{5}dz \right)=\\ &=2\pi r^6k\left(\dfrac{15\pi}{960}-\dfrac{44}{960}+\dfrac{1}{240} \right)=\\ &=2\pi r^6 k\left( \dfrac{15}{960}\pi-\dfrac{1}{24}\right)= \\ &= \dfrac{\pi r^6(3\pi-8)k}{96}. \end{aligned}$

Quindi

(27) $\begin{equation*} \boxcolorato{analisi}{I=\dfrac{\pi r^6(3\pi-8)}{96} \; \dfrac{16m}{\pi r^4(\pi-2)} =\dfrac{mr^2(3\pi-8)}{6(\pi-2)}. } \end{equation*}$

Esercizio 12 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Sia $ABC$

un triangolo avente in $A$

un angolo retto. Sia $M$

il punto medio di $AB$

e sia $D$

posto sul lato $BC$

in modo tale che $BD=BA$

; infine sia $P$

sulla circonferenza che circoscrive il triangolo $ADC$

di modo che l’angolo $APB$

sia retto.

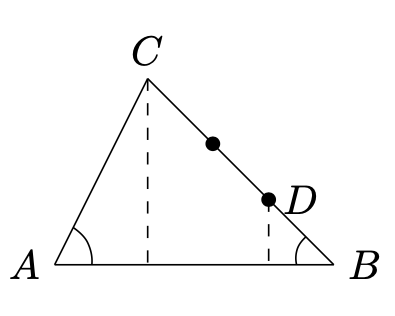
Sia $U$ un punto su $AP$ posto in modo tale che $BU$ sia perpendicolare a $MP$ ed infine sia $V$ posto su $DP$ di modo che $BV$ sia parallelo a $MP$ .

Dimostrare che $\dfrac{PU}{PV}=\dfrac{BU}{BV}$ e che il segmento $CP$ biseziona $UV$ .

Svolgimento.

Premettiamo due lemmi alla soluzione vera e propria del problema.

Lemma 3.2.

Lemma 3.2. Sia $Q$

il punto di intersezione tra la circonferenza circoscritta ad $ABP$

ed il segmento $AD$

. Allora vale che $AQP\sim PDC$

e $PQD\sim APC$

$\quad$

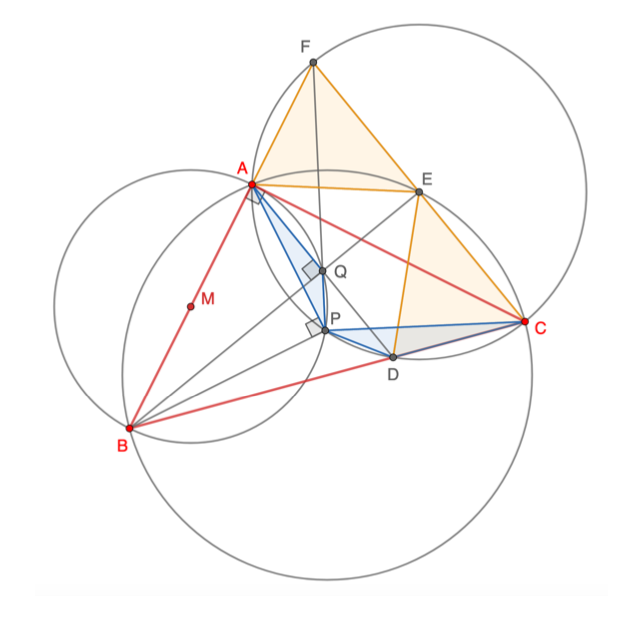
Figura 2: lemma 3.2.

$\quad$

Dimostrazione del lemma 3.2. Indichiamo con $E$ il centro della circonferenza $ACD$ e prolunghiamo il raggio $CE$ fino ad incontrare la circonferenza nel punto $F$ . Pertanto $CF$ è diametro della circonferenza $ACD$ .

Osserviamo i seguenti fatti:

(28) $\begin{equation*} \text{$B$, $A$ ed $F$ sono allineati.} \end{equation*}$

È sufficiente osservare che gli angoli $\widehat{BAC}$ e $\widehat{CAF}$ sono entrambi retti e dunque $\widehat{BAF} = \widehat{BAC}+\widehat{CAF} = 180^\circ$ .

Osserviamo poi che

(29) $\begin{equation*} \text{$AEF$ e $CDE$ sono congruenti.} \end{equation*}$

Risulta infatti $EF=EA=EC=ED$ in quanto raggi e $\widehat{DEC}=90^\circ-\widehat{BED}=90^\circ-\widehat{BEA}=\widehat{AEF}$ in virtù di (28) e in quanto $E$ sta sull’asse di $AD$ .

Notiamo che $Q$ appartiene al segmento $BE$ . Infatti l’angolo $\widehat{AQB}$ è retto perché insiste sul diametro della circonferenza $ABP$ . Ne segue che $Q$ è il centro del rombo $ABDE$ , ed in particolare appartiene alla diagonale $BE$ .

(30) $\begin{equation*} \text{$P$, $Q$ ed $F$ sono allineati.} \end{equation*}$

Si ha infatti che $\widehat{PQD}=\widehat{QFE}$ in quanto angoli corrispondenti e dunque $\widehat{PQD}+\widehat{EQF}=\widehat{QFE}+\widehat{EQF}=90^\circ$ . Questo dimostra la collinearità.

Per dimostrare ora che $AQP\sim PDC$ osserviamo che $\widehat{PAQ} = \widehat{PAD}= \widehat{DCP}$ in quanto angoli che insistono sullo stesso arco $PD$ . Inoltre $\widehat{APQ}=\widehat{APF}=\widehat{DPC}$ , dove la prima uguaglianza sussiste in forza della (30) e la seconda della (29).

Per provare che $PQD\sim APC$ si nota che $\widehat{PDA}=\widehat{PCA}$ in quanto angoli insistenti sullo stesso arco $AP$ e $\widehat{CPA}=\widehat{CPF}+\widehat{FPA}=\widehat{CPF}+\widehat{DPC}=\widehat{QPD}$ , dove si è ancora utilizzata la (29).

Lemma 3.3.

Lemma 3.3. Se $X^\prime$

indica l’inverso del punto $X$

rispetto alla circonferenza di centro $P$

e raggio $PB$

, risulta $A^\prime=U$

e $D^\prime=V$

$\quad$

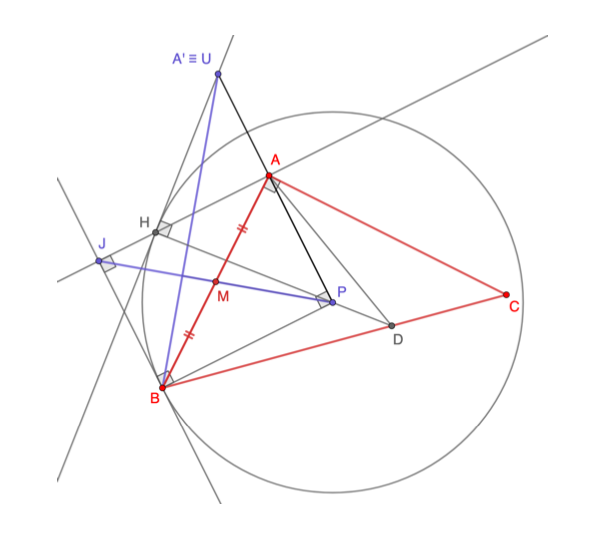
Figura 3: lemma 3.3.

$\quad$

Dimostrazione del lemma 3.3. L’inverso del punto $A$ è definito come il punto sulla retta $PA$ per cui risulti $PA\cdot PA^{\prime}=PB^2$ . Per determinarlo si usa il secondo teorema di Euclide con la seguente costruzione: si manda la perpendicolare per $A$ alla retta $AP$ che incontra la circonferenza nel punto $H$ e da questo punto si traccia la tangente alla circonferenza. L’intersezione tra la retta tangente e la retta passante per $A$ e $P$ è l’inverso di $A$ . Per dimostrare che il punto $U$ , costruito seguendo il testo del problema, è proprio l’inverso di $A$ , occorre far vedere che $UB \perp PM$ .

Diamo una dimostrazione basata sul calcolo vettoriale. Nel seguito indicheremo con $\bullet$ il prodotto scalare. Dobbiamo provare che:

$BU\bullet PJ=0,$

dove $J$ è il punto di incontro della retta $AH$ e della perpendicolare a $BP$ passante per $B$ (è facile constatare che $BPAJ$ è un rettangolo). Si ha:

$\begin{aligned} BU\bullet PJ&= (BP+PU)\bullet (BJ-BP) =\\ &=BP\bullet BJ-\vert BP\vert^2+PU\bullet BJ-PU\bullet BP =\\ &=-\vert BP\vert^2+PU\bullet BJ =\\ &=-\vert BP\vert^2+(AP+AU)\bullet BJ =\\ &=-\vert BP\vert^2+\vert AP\vert^2+AU\bullet AP =\\ &=-\vert BP\vert^2+\vert AP\vert^2+\vert AH\vert^2 =\\ &=-\vert BP\vert^2+\vert PH\vert^2 =\\ &=0, \end{aligned}$

dove si sono utilizzati il secondo teorema di Euclide (applicato al triangolo $PUH$ ) ed il teorema di Pitagora (applicato al triangolo $PAH$ ). Analogamente si dimostra che $V$ è l’inverso di $D$ .

Soluzione del problema principale.

Dal lemma 3.3, per definizione di inversione, seguono le uguaglianze

$AP\cdot PU=PB^2\quad\mbox{ e } \quad PD\cdot PV=PB^2.$

Dividendo membro a membro:

$\dfrac{PU}{PV}=\dfrac{PD}{AP}.$

$\quad$

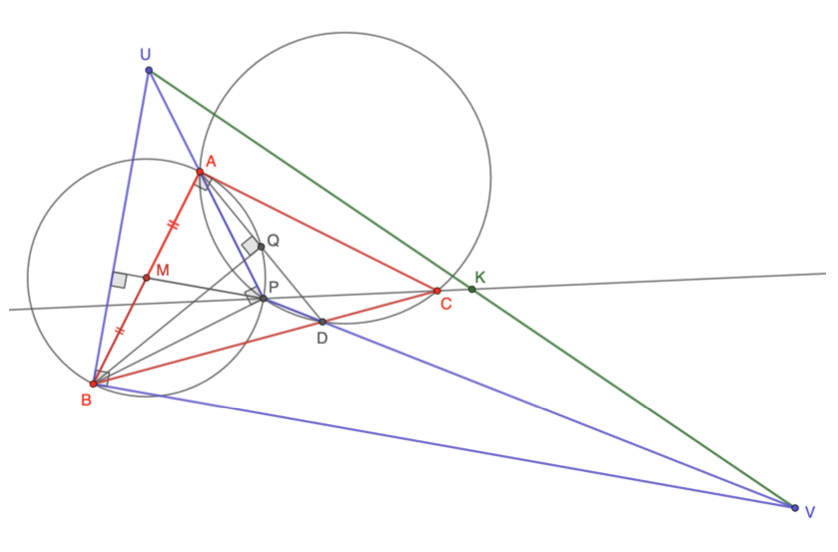
Figura 4: soluzione dell’esercizio 12.

$\quad$

Inoltre per la formula della distanza nell’inversione si ha:

$\begin{aligned} BU=\dfrac{BP^2\cdot AB}{BP\cdot AP}=BP\cdot\dfrac{AB}{AP},\qquad BV=\dfrac{BP^2\cdot BD}{BP\cdot PD}=BP\cdot\dfrac{BD}{PD}, \end{aligned}$

cioè

$\dfrac{BU}{BV}=\dfrac{AB}{AP}\dfrac{PD}{BD}.$

Ma $AB=BD$ e dunque

$\dfrac{BU}{BV}=\dfrac{PD}{AP}=\dfrac{PU}{PV},$

che era quanto si doveva provare.

Per la seconda parte del problema notiamo adesso che il punto $K$ , intersezione tra il segmento $UV$ e la retta che passa per $P$ e $C$ è l’inverso del punto $C$ . Sappiamo infatti che $A$ , $P$ , $D$ e $C$ sono conciclici e che la circonferenza di appartenenza passa per $P$ che è il centro di inversione. Una proprietà dell’inversione ci assicura ora che le inversioni dei punti appartenenti a questa circonferenza giacciono tutte sulla medesima retta. Per questa proprietà, dunque, $K$ , $U$ e $V$ devono essere allineati, quindi $K$ giace su $UV$ . Inoltre, per costruzione $K$ appartiene alla retta che passa per $P$ e $C$ . Questi due fatti ci permettono di concludere che $K$ è l’inverso di $C$ .

Segue dalla formula sulla distanza nell’inversione che

$\begin{aligned} UK=\dfrac{BP^2\cdot AC}{AP\cdot PC}, \qquad VK=\dfrac{BP^2\cdot DC}{PD\cdot PC}, \end{aligned}$

e dunque

$\dfrac{UK}{VK} = \dfrac{PD \cdot AC}{AP \cdot DC}.$

Per il lemma 3.2 si ha pure

$\dfrac{AC}{QD}=\dfrac{PC}{PD} \quad \mbox{ e } \quad \dfrac{AP}{PC}=\dfrac{AQ}{DC},$

cioè

$AC\cdot PD=PC \cdot QD \quad \mbox{ e } \quad AP\cdot DC=AQ\cdot PC.$

Dividendo membro a membro le due equazioni, e ricordando che $AQ = QD$ :

$\dfrac{AC\cdot PD}{AP\cdot DC}=\dfrac{PC\cdot QD}{AQ\cdot PC}=1.$

Si conclude che

$\frac{UK}{VK} = \dfrac{AC \cdot PD}{AP \cdot DC} = 1,$

che completa la dimostrazione.

Esercizio 13 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Se $a,b,c,d\in(0,1)$

, dimostrare che

$\begin{equation*} \left(\dfrac{a+b}{2} \right)^{\frac{c+d}{2}}+\left( \dfrac{b+c}{2}\right)^{\frac{d+a}{2}}+\left( \dfrac{c+d}{2}\right)^{\frac{a+b}{2}}+\left(\dfrac{d+a}{2} \right)^{\frac{b+c}{2}}>2. \end{equation*}$

Svolgimento.

Il risultato desiderato si ottiene con una semplice applicazione della seguente disuguaglianza

(31) $\begin{equation*} x^y>\dfrac{x}{x+y}\qquad \quad \text{per } x,y\in(0,1). \end{equation*}$

Ponendo $a+b+c+d=t$ otteniamo immediatamente

(32) $\begin{equation*} \begin{split} \text{LHS} > \dfrac{a+b}{t}+\dfrac{b+c}{t}+\dfrac{c+d}{t}+\dfrac{d+a}{t}= \dfrac{2t}{t}=2. \end{split} \end{equation*}$

Esercizio 14 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Dimostrare che

$\begin{equation*} \int_{0}^{1}\dfrac{\ln\left(1+x^6\right)}{x^2+1}\,dx=\dfrac{\pi}{4}\ln 2-6\sum_{n=0}^{+\infty}\dfrac{\left(-1\right)^n}{\left(2n+1\right)}\sum_{k=0}^{+\infty}\dfrac{\left(-1\right)^k}{\left(2n+6k+7\right)}. \end{equation*}$

Svolgimento.

Procediamo integrando per parti

$\begin{aligned} \int_{0}^{1}\dfrac{\ln\left(1+x^6\right)}{x^2+1}\,dx &= \arctan x \ln \left(1+x^6\right)\bigg \vert^1_0-\int_{0}^{1}\arctan x\cdot \dfrac{6x^5}{1+x^6}\,dx=\\ &=\dfrac{\pi}{4}\ln 2 -6 \int_{0}^{1}\dfrac{x^5\arctan x}{1+x^6}\,dx \eqqcolon I. \end{aligned}$

Sviluppiamo in serie i vari termini della funzione integranda

$\begin{aligned} I&=\dfrac{\pi}{4}\ln 2 -6\int_{0}^{1}x^5\sum_{n=0}^{+\infty}\left(-1\right)^n\dfrac{x^{2n+1}}{2n+1}\,\sum_{k=0}^{+\infty}\left(-1\right)^kx^{6k}\,dx=\\ &=\dfrac{\pi}{4}\ln 2 -6\sum_{n=0}^{+\infty}\dfrac{\left(-1\right)^n}{2n+1}\sum_{k=0}^{+\infty}\left(-1\right)^k\int_{0}^{1}x^{2n+6+6k}\,dx=\\ &=\dfrac{\pi}{4}\ln 2 -6\sum_{n=0}^{+\infty}\dfrac{\left(-1\right)^n}{2n+1}\sum_{k=0}^{+\infty}\dfrac{\left(-1\right)^k}{2n+6k+7}, \end{aligned}$

da cui segue l’asserto.

Esercizio 15 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Provare che se $a, b$

e c sono numeri complessi tale che $a+b+c=0$

e $|a|=|b|=|c|$

, allora $a^{3}=b^{3}=c^{3}$

. Questo risultato può essere esteso a più di tre numeri?

Svolgimento.

Se $a=0$

, dalla condizione sull’uguaglianza dei moduli segue $b=c=0$

e la tesi è ovviamente verificata.

Se $a \neq 0,$ dividendo per $a$ la condizione $a+b+c=0$ otteniamo $1+x+y=0,$ dove abbiamo posto $x=\dfrac{b}{a}$ e $y=\dfrac{c}{a}$ .

Osservando che $|x|=|y|=1$ si avrà

$x=\cos (\alpha)+i \sin (\alpha), \quad \mbox{per } \, \alpha \in[0,2 \pi[$

$y=\cos (\beta)+i \sin (\beta)\quad \mbox{per } \, \beta \in[0,2 \pi[.$

Dunque $1+\cos (\alpha)+i \sin (\alpha)+\cos (\beta)+i \sin (\beta)=0$ cioè, separando parte reale e parte immaginaria,

$\begin{cases} \cos (\alpha)+\cos (\beta)=-1 \\ \sin (\alpha)+\sin (\beta)=0, \end{cases}$

le cui soluzioni sono $\alpha=\dfrac{2}{3} \pi, \beta=\dfrac{4}{3} \pi$ o viceversa.

In definitiva i numeri complessi che soddisfano le condizioni date sono $1, e^{i \frac{2}{3} \pi}, e^{i \frac{4}{3} \pi}$ che effettivamente verificano la tesi.

Se $n>3$ la tesi non è verificata. Basta considerare le radici $n$ -esime dell’unità $z_{k}=e^{i \frac{2 k}{n} \pi}$ per $k=0,1, \ldots, n-1 .$ Questi numeri verificano l’equazione $z^{n}=1$ dunque hanno tutti lo stesso modulo ed inoltre, $z^{n}-1=\left(z-z_{1}\right)\left(z-z_{2}\right) \ldots\left(z-z_{n}\right),$ da cui, per il principio di identità dei polinomi, $z_{1}+z_{2}+\ldots+z_{n}=0 .$

Dunque, entrambe le condizioni sono soddisfatte ma non è vero che $z_{k}^{3}=e^{i \frac{6 k}{n} \pi}$ assume sempre lo stesso valore.

Esercizio 16 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare tutte le funzioni polinomiali $f$

tali che

(33) $\begin{equation*} (x-1) f(x+1)-(x+2) f(x) \equiv 0. \end{equation*}$

Svolgimento.

Sostituiamo $x=1$

e $x=-2$

in (33) e otteniamo

$f(1)=0\quad \text{e}\quad f(-1)=0,$

pertanto $x=1$ e $x=-2$ sono radici di $f$ e quindi possiamo riscriverlo come

$f(x)=(x-1)(x+1)g(x),$

dove $g(x)$ è una funzione polinomiale.

Sostituiamo l’espressione appena ottenuta in (33) e otteniamo

$x(x+2)(x-1)g(x+1)-(x+2)(x-1)(x+1)g(x)=0,$

che è equivalente a

(34) $\begin{equation*} (x-1)(x+2)\left(xg(x+1)-(x+1)g(x) \right)=0 \end{equation*}$

Notiamo che sostituendo $x=0$ in (34) si ottiene

$g(0)=0.$

Quindi $x=0$ è una radice di $g$ e possiamo scrivere $f$ come

$f(x)=x(x-1)\underbrace{(x+1)n(x)}_{g(x)},$

dove $n(x)$ è una funzione polinomiale. Sostituiamo l’espressione appena ottenuta di $g$ in (34) e giungiamo a

$\begin{aligned} (x-1)(x+2)\left(x(x+2)g(x+1)-x(x+1)g(x) \right)=0, \end{aligned}$

ossia

(35) $\begin{equation*} x(x-1)(x+2)^2\left(g(x+1)-g(x) \right)=0. \end{equation*}$

Il seguente

(36) $\begin{equation*} x(x-1)(x+2)^2\left(g(x+1)-g(x) \right)=0 \end{equation*}$

si annulla per $g(x+1)=g(x)$ , quindi $g(x)=c\in\mathbb{R}$ .

Si conclude che le funzioni polinomiali certate sono le seguenti:

(37) $\begin{equation*} \boxcolorato{analisi}{f(x)=c\left(x^3-x \right)\quad \text{con}\,\,c \in \mathbb{R}. } \end{equation*}$

Esercizio 17 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare il seguente integrale indefinito:

$\int \frac{2 x+1-2 \sqrt{x^{2}+x}}{4 \sqrt{x}+5 \sqrt{1+x}} d x.$

Svolgimento.

Con la sostituzione $x=t^2$

troviamo

$\int 2t\cdot\dfrac{2t^2+1-2t\sqrt{t^2+1}}{4t+5\sqrt{1+t^2}} \; d t$

da cui, ponendo

$t^{2}+1=(u+t)^{2} \iff t=\dfrac{1}{2}\left(\dfrac{1}{u}-u\right),$

si ottiene

$\begin{aligned} &\int \dfrac{2t^2+1-2t\sqrt{t^2+1}}{4t+5\sqrt{1+t^2}} \; 2t \; d t = \\ &=\int \dfrac{2 \; \dfrac{1}{4}\left(\dfrac{1}{u}- u \right)^{2} + 1 -2 \, \dfrac{1}{2} \left(\dfrac{1}{u}-u\right)(u+t)}{2 \; \dfrac{1}{2} \; \left(\dfrac{1}{u}-u\right)+5\left(u+t\right)} \; 2 \; \dfrac{1}{2}\; \left(\dfrac{1}{u}-u\right) \cdot \\ & \qquad \cdot \dfrac{1}{2}\left(-\dfrac{1}{u^2}-1\right) du =\\ & = \int \dfrac{\dfrac{1}{2}\left(\dfrac{1-u^{2}}{u}\right)^{2}+1-\left(\dfrac{1-u^{2}}{u}\right)\left(\dfrac{u^{2}+1}{2 u}\right)\left(\dfrac{1}{u}-u\right) \dfrac{1}{2}\left(\dfrac{-1-u^{2}}{u^{2}}\right)}{2\left(\dfrac{1-u^{2}}{u}\right)+5\left(\dfrac{u^{2}+1}{2 u}\right)} \; du= \\ &= \int \dfrac{\left(\dfrac{1-u^{2}}{u}\right)\left[\dfrac{1}{2}\left(\dfrac{1-u^{2}}{u}\right)-\left(\dfrac{u^{2}+1}{2u}\right)\right]+1}{\dfrac{4-4 u^{2}+5 u^{2}+5}{2 u}}\left(\dfrac{1}{u}-u\right) \dfrac{1}{2}\left(\dfrac{-1-u^{2}}{u^{2}}\right) \; d u = \\ & = \int \dfrac{\dfrac{1-u^{2}}{u}\left(\dfrac{1-u^{2}-u^{2}-1}{2 u}\right)+1}{\dfrac{9+u^{2}}{2 u}}\left(\dfrac{1}{u}-u\right) \dfrac{1}{2}\left(\dfrac{-1-u^{2}}{u^{2}}\right) d u = \\ & = \int\left(u^{2}-1+1\right) \dfrac{2 u}{u^{2}+9}\left(\dfrac{1}{u}-u\right) \dfrac{1}{2}\left(-\dfrac{1-u^{2}}{u^{2}}\right) \; d u = \\ & = \int \dfrac{2u^{3}}{u^2+9} \; \left(\dfrac{1-u^2}{u}\right) \; \dfrac{1}{2} \left(\dfrac{-1-u^2}{u^2}\right) \; du =\\ & = \int \dfrac{u^4-1}{u^2+9} \; du. \end{aligned}$

Ora possiamo scrivere

$\dfrac{u^4-1}{u^2+9} = u^2-9+\dfrac{80}{u^2+9},$

ottenendo quindi

$\begin{aligned} \int \dfrac{u^4-1}{u^2+9} \; du & = \int\left( u^2-9+\dfrac{80}{u^2+9}\right) \; du = \dfrac{u^3}{3}-9u+80 \int \dfrac{1}{u^2+9} \, du. \end{aligned}$

Ponendo

$u=3v \implies du = 3dv,$

si ha

$\begin{aligned} \dfrac{u^3}{3}-9u+80 \int \dfrac{1}{u^2+9} \, du = \dfrac{u^3}{3}-9u+80 \int \dfrac{3}{9(v^2+1)} \, dv = \dfrac{u^3}{3}-9u+\dfrac{80}{3}\arctan({v}). \end{aligned}$

Pertanto, ponendo $X=\sqrt{1+x}-\sqrt{x}$ , concludiamo

(38) $\begin{equation*} \boxcolorato{analisi}{\displaystyle \int \frac{2 x+1-2 \sqrt{x^{2}+x}}{4 \sqrt{x}+5 \sqrt{1+x}} d x = \dfrac{X^3}{3}-9X+\dfrac{80}{3}\arctan\left(\dfrac{X}{3}\right) + c,} \end{equation*}$

con $c \in \mathbb{R}$ costante.

Esercizio 18 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Denotiamo con $\mathbb{R}^+$

l’insieme dei numeri reali positivi. Trovare tutte le funzioni strettamente monotone $f: \mathbb{R}^+ \to \mathbb{R}^+$

tali che

$f\left(\dfrac{x^2}{f(x)}\right) = x \qquad \forall x \in \mathbb{R}^+.$

Svolgimento.

Dimostriamo che le uniche soluzioni dell’equazione sono le funzioni del tipo $f(x)=k x$

Osserviamo preliminarmente che $f$ è iniettiva perchè monotona crescente e suriettiva perchè, dato $y>0$ , risulta che

$\frac{y^{2}}{f(y)}>0 \quad \mbox{e} \quad f\left(\frac{y^{2}}{f(y)}\right)=y.$

Se $x>0,$ possiamo dunque scrivere $x=f(t),$ e l’equazione di partenza diventa

$f\left(\frac{f^{2}(t)}{f(f(t))}\right)=f(t)$

e, applicando l’inversa,

$f^{2}(t)=t f(f(t)).$

Poniamo adesso $f(t)=t \, g(t)$ nell’ultima equazione ottenendo

$t^{2} g^{2}(t)=t^{2} g(t) g(t\, g(t)),$

cioè

(39) $\begin{equation*} g(t)=g(tg(t)). \end{equation*}$

Ponendo invece $f(t)=t\, g(t)$ nell’equazione di partenza otteniamo

$\frac{t}{g(t)} g\left(\frac{t}{g(t)}\right)=t,$

cioè

(40) $\begin{equation*} g(t)=g\left(\frac{t}{g(t)}\right). \end{equation*}$

Cerchiamo adesso quali sono le soluzioni di (39) e (40) considerando $t$ reale. Notiamo che $g=1$ è una soluzione accettabile. Sia ora invece $g$ non identicamente uguale a $1$ . Esiste allora $x>0$ con $g(x)=a \neq 1$ . Osserviamo che, per induzione, (39) ci dà

$g\left(x a^{n}\right)=a \text { per ogni } n \geq 0,$

mentre (40)

$g\left(\frac{x}{a^{n}}\right)=a \text { per ogni } n \geq 0.$

Se $a>1$ , passando a limite per $n \to +\infty$ , otteniamo $g(x)=g(0)$ , e dunque $g$ è costante.

Se $a<1$ , utilizzando (39) e passando al limite, otteniamo allo stesso modo $g(x)=g(0).$ In definitiva $g$ è costante e le uniche soluzioni dell’equazione di partenza sono $f(x)=kx$ .

Esercizio 19 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare

(41) $\begin{equation*} \ell = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2+\sqrt{2}}}{2} \cdot \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}\cdots . \end{equation*}$

Svolgimento.

Proponiamo due soluzioni, una puramente analitica e una geometrica. Per entrambe, il primo passo è lo stesso.

Svolgimento 1.

Per prima cosa, definiamo la seguente successione:

$\begin{aligned} a_1 {} & = \frac{\sqrt{2}}{2}; \\ a_n {} & = \frac{\displaystyle\sqrt{2+2a_{n-1}}}{2} \quad (n > 1). \end{aligned}$

Allora il limite cercato si può riscrivere in forma più compatta come

(42) $\begin{equation*} \ell = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2+\sqrt{2}}}{2} \cdot \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \cdots = \prod_{n=1}^{+\infty} a_n. \end{equation*}$

Primo passo. Il punto di partenza è riscrivere la successione in (41) in una forma più maneggevole. Possiamo notare che $\cos(\pi/4) = \sqrt{2}/2 = a_1$ e che, usando la formula di bisezione del coseno, $\cos(\alpha/2) = \sqrt{(1+\cos\alpha)/2}$ , si ha pure

(43) $\begin{equation*} \cos\left(\frac{\pi}{8}\right) = \sqrt{\frac{1+\cos(\pi/4)}{2}} = \sqrt{\frac{1+\sqrt{2}/2}{2}} = \frac{\sqrt{2+\sqrt{2}}}{2} = a_2. \end{equation*}$

Sulla base di queste osservazioni, possiamo concludere che in generale vale

(44) $\begin{equation*} a_n = \cos\left(\frac{\pi}{2^{n+1}}\right). \end{equation*}$

Questo si può formalizzare per induzione. Infatti, assumendo vera la (44), si ha

$\begin{aligned} a_{n+1} &= \frac{\sqrt{2+2a_n}}{2}= \\ &\overset{(\star)}{=} \frac{\displaystyle\sqrt{2+2\cos\frac{\pi}{2^{n+1}}}}{2} =\\ &= \sqrt{\frac{\displaystyle 1+\cos\frac{\pi}{2^{n+1}}}{2}} = \\ &\overset{(\circ)}{=} \cos\left(\frac{\pi}{2^{n+1}}\middle/2\right) = \\ &= \cos\left(\frac{\pi}{2^{n+2}}\right), \end{aligned}$

dove nel passaggio $(\star)$ si è usata l’ipotesi di induzione (44) e nel passaggio $(\circ)$ la formula di bisezione del coseno.

Usiamo una formula dovuta (come tante!) ad Eulero. In generale per ogni $m \in \mathbb{N}$ e $x \in \mathbb{R}$ , applicando $m$ volte la formula di duplicazione del seno $\sin \alpha = 2\sin(\alpha/2)\cos(\alpha/2)$ , si trova:

(45) $\begin{equation*} \begin{aligned} \sin(x) & = 2\sin\left(\frac{x}{2}\right)\cos\left(\frac{x}{2}\right) = \\ &= 2\left[2\sin\left(\frac{x}{4}\right)\cos\left(\frac{x}{4}\right)\right]\cos\left(\frac{x}{2}\right) = \cdots = \\ &= 2^m \sin\left(\frac{x}{2^m}\right)\prod_{n=1}^{m}\cos\left(\frac{x}{2^n}\right). \end{aligned} \end{equation*}$

Se $m \to +\infty$ , $\sin\left(x/2^m\right) \sim x/2^m$ , per cui, passando al limite nella (45), si ha

(46) $\begin{equation*} \sin(x) = x \prod_{n=1}^{+\infty}\cos\left(\frac{x}{2^n}\right). \end{equation*}$

Inserendo $x = \pi/2$ nella (46), si ha

(47) $\begin{equation*} \prod_{n=1}^{+\infty}\cos\left(\frac{\pi/2}{2^n}\right) = \prod_{n=1}^{+\infty}\cos\left(\frac{\pi}{2^{n+1}}\right) = \prod_{n=1}^{+\infty} a_n = \frac{\sin(\pi/2)}{\pi/2} = \frac{2}{\pi}. \end{equation*}$

Svolgimento 2.

Questo procedimento si basa sul confronto tra le aree dei poligoni regolari inscritti in una circonferenza di raggio unitario e aventi $2^m$

lati. In figura sono disegnati come esempio un quadrato, un ottagono regolare ed un esadecagono regolare (16 lati). Calcoliamo l’area $A_m$

del poligono con $2^m$

lati. Considerando l’ottagono come guida nelle nostre considerazioni, si prenda in esame il triangolo isoscele $QOA$

. L’angolo $\widehat{OQR} = \alpha_m$

vale $(2\pi/2^m)/2 = \pi/2^m$

, per cui la base misura $\overline{OA} = 2\sin\alpha_m$

, mentre l’altezza misura $\overline{QR} = \cos\alpha_m$

. L’area di $QOA$

misura pertanto $\overline{OA}\times\overline{QR}/2 = \sin\alpha_m\cos\alpha_m$

, e l’area del poligono è $A_m = 2^m\sin\alpha_m\cos\alpha_m$

Calcoliamo ora il rapporto $R_m$ tra le aree di due poligoni successivi. Si ha, usando la formula di duplicazione del seno:

$\begin{aligned} R_m = \frac{A_m}{A_{m+1}} = & {} \frac{\displaystyle 2^m\sin\left(\frac{\pi}{2^m}\right)\cos\left(\frac{\pi}{2^m}\right)} {\displaystyle 2^{m+1}\sin\left(\frac{\pi}{2^{m+1}}\right)\cos\left(\frac{\pi}{2^{m+1}}\right)} =\\ = &\frac{\displaystyle \left[2 \sin\left(\frac{\pi}{2^{m+1}}\right)\cos\left(\frac{\pi}{2^{m+1}}\right)\right]\cos\left(\frac{\pi}{2^m}\right)}{\displaystyle 2\sin\left(\frac{\pi}{2^{m+1}}\right)\cos\left(\frac{\pi}{2^{m+1}}\right)} = \nonumber \\[2pt] = & {} \cos\left(\frac{\pi}{2^m}\right). \end{aligned}$

Il rapporto tra l’area del quadrato ( $m=2$ ) e quella del poligono con $2^m$ lati è invece:

(48) $\begin{equation*} \frac{A_2}{A_m} = \frac{A_2}{A_3}\times\frac{A_3}{A_4}\times\cdots\times\frac{A_{m-2}}{A_{m-1}}\times\frac{A_{m-1}}{A_m} = \prod_{k=2}^{m-1}R_k = \prod_{n=1}^{m-2}R_{n+1}. \end{equation*}$

Possiamo considerare il cerchio come il caso limite dei poligoni per $m \to +\infty$ . La sua area è $A_\infty = \pi$ . Prendendo quindi il limite per $m \to +\infty$ della (48), abbiamo

(49) $\begin{equation*} \frac{2}{\pi} = \frac{A_2}{A_\infty} = \lim_{m\to{+\infty}}\frac{A_2}{A_m} = \prod_{n=1}^{+\infty}R_{n+1} = \prod_{n=1}^{+\infty}\cos\left(\frac{\pi}{2^{n+1}}\right) = \prod_{n=1}^{+\infty} a_n = \ell. \end{equation*}$

Esercizio 20 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

. Dimostrare che

(50) $\begin{equation*} \lim_{x\to+\infty} \left[\Gamma\left(1+\frac{1}{x}\right)\right]^x=e^{-\gamma}. \end{equation*}$

Svolgimento.

$\Gamma$

è una funzione speciale, detta funzione $\Gamma$

di Eulero, che generalizza il fattoriale a valori non interi: se $n \in \mathbb{N}$

, si ha infatti $\Gamma(n+1) = n! = n\cdot(n-1)\cdots2\cdot1$

, ma in generale $\Gamma$

si può definire su tutto $\mathbb{R}$

, tranne che in 0 e sugli interi negativi, in termini del seguente integrale:

(51) $\begin{equation*} \Gamma(x) = \int_0^{+\infty} t^{x-1}e^{-t}\,\mathrm{d}{t}. \end{equation*}$

Dato che $\Gamma(1) = 0! = 1$ , il limite è una forma indeterminata del tipo $1^\infty$ . Si può semplificare usando il teorema di de l’Hôpital:

$\begin{aligned} \lim_{x\to+\infty} \left[\Gamma\left(1+\frac{1}{x}\right)\right]^x = {} & \lim_{x\to+\infty} \exp\left[x\ln\Gamma\left(1+\frac{1}{x}\right)\right] = \nonumber \\ = {} & \lim_{x\to+\infty} \exp\left[\frac{\ln\Gamma\left(1+1/x\right)}{1/x}\right] = \nonumber \\ \overset{\text{(H)}}{=} {} & \lim_{x\to+\infty}\exp\left[\frac{\displaystyle\frac{\,\mathrm{d}}{\,\mathrm{d}{x}}\left[\ln\Gamma\left(1+\frac{1}{x}\right)\right]} {\displaystyle\frac{\mathrm{d}}{\mathrm{d}}\frac{1}{x}}\right] = \nonumber \\ = {} & \lim_{x\to+\infty}\exp\left[\frac{\displaystyle\frac{\Gamma'(1+1/x)}{\Gamma(1+1/x)}\cancel{\left(-1/x^2\right)}}{\displaystyle \cancel{-1/x^2}}\right] = \nonumber \\ = {} & \exp\left[\frac{\Gamma'(1)}{\Gamma(1)}\right] = e^{\Gamma'(1)}. \end{aligned}$

Nel passaggio (H), la regola di de l’Hôpital viene usata per risolvere la forma indeterminata $0/0$ che appare nell’argomento dell’esponenziale. Questo passaggio è legittimo perché quel limite esiste finito e la funzione $\exp(x)$ è continua.

Per completare il calcolo del limite (50), dobbiamo quindi valutare $\Gamma'(1)$ , che si può esprimere in termini della costante $\gamma$ di Eulero-Mascheroni, una delle costanti fondamentali in matematica:

(52) $\begin{equation*} \gamma = \lim_{n\to+\infty}\left(\sum_{k=1}^{n}\frac{1}{k} - \ln n \right). \end{equation*}$

Numericamente si ha $\gamma \approx 0$ ,5772. L’equazione (52) mostra che la serie armonica diverge a $+\infty$ con la stessa rapidità del logaritmo, in quanto la loro differenza tende ad una costante. Per calcolare $\Gamma'(1)$ , possiamo usare la definizione (51), derivando sotto il segno di integrale (la funzione integranda è di classe $C^{\infty}$ per $t > 0$ , $x \in \mathbb{R}$ ), ottenendo il risultato:

(53) $\begin{equation*} \frac{\mathrm{d}}{\mathrm{d}{x}}\Gamma(x) = \frac{\mathrm{d}}{\mathrm{d}{x}} \int_0^{+\infty} t^{x-1}e^{-t}\,\mathrm{d}{t} = \int_0^{+\infty} \frac{\partial}{\partial x}\left(t^{x-1}e^{-t}\,\mathrm{d}{t}\right)\,\mathrm{d}{t} = \int_0^{+\infty} t^{x-1}e^{-t}\ln t\,\mathrm{d}{t}. \end{equation*}$

Per proseguire, è utile ricordare il teorema della convergenza dominata. Sia $\{f_n\}_{n\geqslant1}$ una successione di funzioni convergente puntualmente alla funzione $f$ ( $f,f_n$ : $A \subseteq \mathbb{R} \to \mathbb{R}$ ), ed esista una funzione $g$ : $A\to\mathbb{R}$ tale che $\int_A g(x)\,\mathrm{d}{x}$ è finito e che $|f_n(x)| \leqslant g(x)$ $\forall x \in A$ e $\forall n \geqslant 1$ . Allora $f$ è integrabile su $A$ e si possono scambiare limite ed integrale:

(54) $\begin{equation*} \lim_{n\to+\infty}\int_A f_n(x)\,\mathrm{d}{x} = \int_A \lim_{n\to+\infty}f_n(x)\,\mathrm{d}{x} = \int_A f(x)\,\mathrm{d}{x}. \end{equation*}$

Se in particolare $A = (a,+\infty)$ (con $a \in \mathbb{R}$ ), vale anche questa formulazione del risultato (54):

(55) $\begin{equation*} \int_a^{+\infty} \lim_{n\to+\infty}f_n(x)\,\mathrm{d}{x} = \lim_{n\to+\infty}\int_a^{n} f_n(x)\,\mathrm{d}{x}. \end{equation*}$

Siamo finalmente pronti per il calcolo finale². Alcuni passaggi sono commentati alla fine.

$\begin{aligned} \Gamma'(1) = \int_0^{+\infty}\ln(t)e^{-t}\,\mathrm{d}{t} & {} \overset{(\odot)}{=} \lim_{n\to+\infty}\int_0^n\ln(t)\left(1-\frac{t}{n}\right)^n\,\mathrm{d}{t}=\\ & {} \overset{(\ast)}{=}\lim_{n\to+\infty}n\int_0^1\ln(n\tau)\,(1-\tau)^n\,\mathrm{d}{\tau} =\\ & = \lim_{n\to+\infty}n\int_0^1[\ln(n)+\ln(1-y)]\,y^n\,\mathrm{d}{y} =\\ & {} \overset{(\otimes)}{=}\lim_{n\to+\infty}\left[\frac{n}{n+1}\ln(n)-n\int_0^1\sum_{k=1}^{+\infty}\frac{y^k}{k} y^n\,\mathrm{d}{y}\right] = \\ & {} \overset{(+)}=\lim_{n\to+\infty}\left[\frac{n}{n+1}\ln(n)-n\sum_{k=1}^{+\infty}\frac{1}{k}\int_0^1 y^{k+n}\,\mathrm{d}{y}\right] = \\ & {} =\lim_{n\to+\infty}\left[\frac{n}{n+1}\ln(n)-n\sum_{k=1}^{+\infty}\frac1{k(n+k+1)}\right] = \\ & {} \overset{(\star)}{=}\lim_{n\to+\infty}\left[\frac{n}{n+1}\ln(n)-\frac{n}{n+1}\sum_{k=1}^{+\infty}\left(\frac1k-\frac1{n+k+1}\right)\right] = \\ & {} \overset{(\diamond)}{=}\lim_{n\to+\infty}\frac{n}{n+1}\left[\ln(n)-\sum_{k=1}^{n+1}\frac{1}{k}\right] =\lim_{n\to+\infty}\left[\ln(n)-\sum_{k=1}^{n+1}\frac{1}{k}\right]=\\ & = \lim_{n\to+\infty}\left[\ln(n)-\sum_{k=1}^{n}\frac{1}{k}\right] - \lim_{n\to+\infty} \frac{1}{n+1} =-\gamma. \end{aligned}$

$(\odot)$ : Si usa qui il teorema della convergenza dominata (55), usando come funzione dominante $g(t) = \ln(t)e^{-t}$ . Infatti $(1-t/n)^n \leqslant e^{-t}$ $\forall t \in \mathbb{R}$ e $\forall n \geqslant 1$ .

$(\ast)$ : Si effettua il cambio di variabile $\tau = t/n$ ; nel passaggio successivo, $y = 1-\tau$ .

$(\otimes)$ : Si usa qui lo sviluppo in serie di Taylor $\displaystyle \ln(1-y) = -\sum_{k=1}^{+\infty}\dfrac{y^k}{k}$ ; il primo termine invece si è integrato ricordando che $\int_0^1 y^n\ dy=\left[\dfrac{y^{n+1}}{n+1}\right]_0^1=\dfrac{1}{n+1}$

$(+)$ : Si è usato anche qui il teorema della convergenza dominata, ricordando che una serie è il limite per $n\to+\infty$ di una somma finita di $n$ termini.

$(\star)$ : Si usa la decomposizione in frazioni parziali:

$\begin{displaymath} \frac{1}{k(n+k+1)} = \frac{A}{k} + \frac{B}{n+k+1} = \frac{(A+B)k+A(n+1)}{k(n+k+1)}, \end{displaymath}$

da cui si ricava $A = -B = 1/(n+1)$ .

$(\diamond)$ : La somma è telescopica: tutti i termini si cancellano, eccetto i primi $(n+1)$ addendi $1/k$ .

Dunque concludiamo che

(56) $\begin{equation*} \boxcolorato{analisi}{\displaystyle \lim_{x\to+\infty} \left[\Gamma\left(1+\frac{1}{x}\right)\right]^x = e^{-\gamma}. } \end{equation*}$

Tratto da questo link. ↩

Esercizio 21 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che

$\int_{0}^{\frac{\pi}{2}} \frac{ \{ \tan(x) \} }{\tan(x)}\, dx = \frac{\pi}{2}-\frac{1}{2}\ln \left(\frac{ \sinh(\pi)}{\pi} \right),$

dove $\{\tan(x)\}$ indica la parte decimale di $\tan(x)$ .

Svolgimento.

Scriviamo la parte decimale di $\tan(x)$

come

$\left \{ \tan(x) \right \} = \tan(x)- \left [\tan(x) \right ],$

dove le parentesi quadre indicano la parte intera di $\tan{x}$ , quindi l’integrale diventa

$\int_{0}^{\frac{\pi}{2}} \frac{\left \{ \tan(x) \right \}}{\tan(x)} dx = \int_{0}^{\frac{\pi}{2}} 1-\frac{\left [ \tan(x) \right ]}{\tan(x)} dx = \frac{\pi}{2}-\int_{0}^{\frac{\pi}{2}}\frac{\left [ \tan(x) \right ]}{\tan(x)} dx.$

La funzione $\left[\tan(x)\right]$ assume valori interi $n$ quando $x$ è compreso tra $\arctan(n)$ e $\arctan\left(n+1\right)$ . Dunque possiamo spezzare l’integrale della riga precedente come una sommatoria infinita di integrali:

$\begin{aligned} I & = \int_{0}^{\frac{\pi}{2}}\frac{\left [ \tan(x) \right ]}{\tan(x)} dx = \\ &=\int_{0}^{\arctan(1)}\frac{0}{\tan(x)} dx + \int_{\arctan(1)}^{\arctan(2)}\frac{1}{\tan(x)} dx + \cdots + \int_{\arctan(n)}^{\arctan(n+1)}\frac{n}{\tan(x)} dx +\cdots =\\ & = \sum_{n=1}^{+\infty} n \int_{\arctan(n)}^{\arctan(n+1)}\frac{1}{\tan(x)} dx. \end{aligned}$

L’integrale nella sommatoria si può calcolare agevolmente essendo l’integrale della cotangente

$I= \sum_{n=1}^{+\infty} n \left[ \ln(\sin(\arctan(n+1)))-\ln(\sin(\arctan(n))) \right].$

Usando le identità trigonometriche si può provare³ che $\sin(\arctan(x))= \dfrac{x}{\sqrt{1+x^{2}}}$ . Sostituendo quanto appena ottenuto nell’ultima espressione di $I$ si ricava

$\begin{aligned} I & = \sum_{n=1}^{+\infty} \left( n \ln \left( \frac{n+1}{\sqrt{1+(n+1)^{2}}} \right) -n\ln \left( \frac{n}{\sqrt{1+n^{2}}} \right)\right) = \\ & = \sum_{n=1}^{+\infty} \left( \frac{n}{2} \ln \left( 1 +\frac{1}{n^{2}} \right)- \frac{n}{2} \ln \left( 1 +\frac{1}{(n+1)^{2}} \right) \right) = \\ & = \sum_{n=1}^{+\infty} \left( \frac{n}{2} \ln \left( 1 +\frac{1}{n^{2}} \right)- \frac{n+1}{2} \ln \left( 1 +\frac{1}{(n+1)^{2}} \right)+ \frac{1}{2} \ln \left( 1 +\frac{1}{(n+1)^{2}} \right)\right). \end{aligned}$

I primi due termini della sommatoria a destra rappresentano una serie telescopica, quindi si elidono lasciando solo il termine per $n=1$ cioè $\dfrac{\ln(2)}{2}$ :

$I=\frac{\ln(2)}{2} + \frac{1}{2} \sum_{n=1}^{+\infty} \ln \left( 1 +\frac{1}{(n+1)^{2}} \right) =\frac{1}{2} \sum_{n=1}^{+\infty} \ln \left( 1 +\frac{1}{n^{2}} \right).$

Per il calcolo dell’ultima serie definiamo la funzione

$F(z)= \sum_{n=1}^{+\infty} \ln \left( 1 +\frac{z^{2}}{n^{2}} \right).$

Effettuando la derivata di $F(z)$ rispetto a $z$ , si ha

$\frac{dF}{dz}= \sum_{n=1}^{+\infty} \frac{2z}{n^{2}+z^{2}}.$

Quest’ultima sommatoria è analiticamente definita e risulta pari a⁴

$\frac{dF}{dz}= \sum_{n=1}^{+\infty} \frac{2z}{n^{2}+z^{2}} = -\frac{1}{z}+\pi \coth{\pi z},$

da cui, integrando e tenendo presente che $F(0)=0$ , otteniamo

$F(z)= \sum_{n=1}^{+\infty} \ln \left( 1 +\frac{z^{2}}{n^{2}} \right) = \ln \left( \frac{\sinh(\pi z)}{\pi z} \right).$

Per il nostro problema deve essere $z =1$ , pertanto

$I=\sum_{n=1}^{+\infty} \ln \left( 1 +\frac{1}{n^{2}} \right) = F(1)= \ln \left( \frac{\sinh(\pi)}{\pi} \right),$

da cui il risultato finale

(57) $\begin{equation*} \boxcolorato{analisi}{\displaystyle \int_{0}^{\frac{\pi}{2}} \frac{\left \{ \tan(x) \right \}}{\tan(x)} dx = \frac{\pi}{2} - I = \frac{\pi}{2} - \ln \left( \frac{\sinh(\pi)}{\pi} \right). } \end{equation*}$

È sufficiente porre $y = \arctan(x)$ allora $\sin(y) = \dfrac{\tan(y)}{\sqrt{1+\tan^{2}(y)}}$ . ↩

Nota la relazione

$\pi \cot(\pi z)=\dfrac{1}{z}+2z \sum_{n=1}^{+\infty} \frac{1}{z^2-n^2},$

si può osservare che la sostituzione $z\to iz$ permette di scrivere, utilizzando le espressioni di Eulero per la cotangente e la definizione di cotangente iperbolica

$\cot(\pi iz)=\frac{\cos(\pi iz)}{\sin(\pi i z)}=i\frac{e^{-\pi z}+e^{\pi z}}{e^{-\pi z}-e^{\pi z}}=-i\coth(\pi z),$

da cui

$-i\pi\coth(z)=\frac{1}{iz}+2iz\sum_{n=1}^{+\infty}\frac{1}{-z^2-n^2},$

e, moltiplicando tutto per $i$ ,

$\pi\coth(z)=\frac{1}{z}+2z\sum_{n=1}^{+\infty}\frac{1}{z^2+n^2}.$

↩

Esercizio 22 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che

$\int_{0}^{1} \frac{x \ln(1+x)}{1+x^{2}}\,dx = \frac{\pi^{2}}{96}+ \frac{\ln^{2}(2)}{8}.$

Svolgimento.

Sia

$F(\alpha ) = \int_{0}^{1} \frac{x \ln(1+\alpha x)}{1+x^{2}} dx.$

Per $\alpha=0$ risulta che $F(0)=0$ , di conseguenza l’integrale può essere riscritto come

$\int_{0}^{1} \frac{x \ln(1+x)}{1+x^{2}} dx = \int_{0}^{1} \dfrac{dF( \alpha)}{d \alpha} d \alpha = \int_{0}^{1}\int_{0}^{1} \frac{x^{2}}{(1+x^{2})(1+ \alpha x)} \ dx\ d \alpha,$

dove nella seconda uguaglianza abbiamo sfruttato il fatto che integranda e derivata sono continue. Scomponendo in fratti semplici otteniamo

$\int_{0}^{1}\int_{0}^{1} \frac{x^{2}}{(1+x^{2})(1+ \alpha x)}\ dx\ d \alpha = \int_{0}^{1}\int_{0}^{1} \left [ \frac{A}{(1+ \alpha x)} + \frac{Bx+C}{(1+x^{2})} \right ]\ dx\ d \alpha,$

da cui

$\begin{aligned} \int_{0}^{1}\int_{0}^{1} & \frac{x^{2}}{(1+x^{2})(1+ \alpha x)}\ dx \ d \alpha =\\ &=\int_{0}^{1}\int_{0}^{1} \frac{(A+ \alpha B)x^{2}+ (B+ \alpha C)x+(A+C)}{(1+ \alpha x)(1+x^{2})}\ dx \ d \alpha. \end{aligned}$

Dal principio d’identità dei polinomi con

$x^2=(A+ \alpha B)x^{2}+ (B+ \alpha C)x+(A+C),$

otteniamo

$\begin{cases} A= \dfrac{1}{1+\alpha^{2}} \\[9pt] B= \dfrac{\alpha}{1+\alpha^{2}} \\[9pt] C= - \dfrac{1}{1+\alpha^{2}} \end{cases}$

per cui possiamo scrivere

$\int_{0}^{1}\int_{0}^{1} \frac{x^{2}}{(1+x^{2})(1+ \alpha x)} dx d \alpha = \int_{0}^{1} \frac{1}{1+\alpha^2}\int_{0}^{1} \left [ \frac{1}{(1+ \alpha x)} + \frac{\alpha x - 1}{(1+x^{2})} \right ] dx d \alpha.$

Ora integriamo rispetto ad $x$ ,

$\begin{aligned} \int_{0}^{1}\int_{0}^{1} \frac{x^{2}}{(1+x^{2})(1+ \alpha x)} dx d \alpha & = \int_{0}^{1} \frac{1}{1+\alpha^2} \left [ \frac{ \ln(1 + \alpha x)}{\alpha} \right ]_{x=0}^{x=1} d \alpha \; + \\ & \quad + \int_{0}^{1}\frac{\alpha}{1+\alpha^2} \left [ \frac{ \ln(1 + x^{2})}{2} \right ] _{x=0}^{x=1} d \alpha \; +\\ & \quad - \int_0^1 \frac{1}{1+\alpha^{2}}\left [ \arctan(x) \right ]_{x=0}^{x=1}\ d\alpha, \end{aligned}$

arrivando a

$\int_{0}^{1} \frac{x \ln(1+x)}{1+x^{2}} \; dx = \int_{0}^{1} \frac{\ln (1+\alpha)}{(1+\alpha^2) \alpha} d \alpha + \int_{0}^{1} \frac{\alpha \ln (2) }{2(1+\alpha^2)} d \alpha - \int_{0}^{1} \frac{\pi}{4(1+\alpha^2)} d \alpha.$

Il secondo e il terzo addendo al membro di destra dell’ultima equazione possono essere calcolati agevolmente come segue:

$\int_{0}^{1} \frac{\alpha \ln (2)}{2(1+\alpha^2)} d \alpha = \left [ \frac{ \ln (2) \ln (1+\alpha^2) }{4} \right ] _{\alpha=0}^{\alpha=1} = \frac{\ln^{2}(2)}{4},$

$\int_{0}^{1} \frac{\pi}{4(1+\alpha^2)} d \alpha = \left [ \frac{ \pi \arctan(\alpha) }{4} \right ]_{\alpha=0}^{\alpha=1} =\frac{ \pi^{2}}{16}.$

Sostituendo quanto appena ottenuto nell’espressione precedente abbiamo

$\int_{0}^{1} \frac{x \ln(1+x)}{1+x^{2}} \; dx = \int_{0}^{1} \frac{\ln (1+\alpha)}{(1+\alpha^2) \alpha} d \alpha +\frac{\ln^{2}(2)}{4} - \frac{ \pi^{2}}{16}.$

Ora, per calcolare l’integrale di $\dfrac{\ln (1+\alpha)}{(1+\alpha^2) \alpha}$ , scomponiamo $\dfrac{1}{(1+\alpha^2) \alpha}$ in fratti semplici

$\begin{aligned} \int_{0}^{1} \frac{\ln (1+\alpha)}{(1+\alpha^2) \alpha} d \alpha &= \int_{0}^{1} \ln(1+\alpha) \left ( \frac{1}{\alpha}- \frac{\alpha}{1+\alpha^{2}} \right ) d\alpha =\\ &= \int_{0}^{1} \frac{\ln(1+\alpha)}{\alpha} d\alpha - \int_{0}^{1} \frac{\alpha \ln(1+ \alpha)}{1+\alpha^{2}} d \alpha. \end{aligned}$

Osserviamo che l’ultimo integrale presente nella precedente espressione risulta uguale a quello che vogliamo calcolare, eccezion fatta per la presenza della variabile $\alpha$ che sostituisce la variabile $x$ . L’integrale di $\dfrac{\ln(1+\alpha)}{\alpha}$ può essere calcolato utilizzando lo sviluppo in serie di $\ln(1+\alpha)$ dato che l’intervallo di integrazione è contenuto nell’insieme di convergenza della serie. Si ha

$\begin{aligned} \int_{0}^{1} \frac{\ln(1+\alpha)}{\alpha} d\alpha &= \int_{0}^{1} \sum_{n=1}^{+ \infty } \frac{(-1)^{n+1}}{n} \alpha^{n-1} d \alpha =\\ &=\sum_{n=1}^{+ \infty } \frac{(-1)^{n+1}}{n} \int_{0}^{1} \alpha^{n-1} d \alpha= \sum_{n=1}^{+ \infty } \frac{(-1)^{n+1}}{n^{2}}. \end{aligned}$

La serie ottenuta è la serie armonica di ordine 2 a segni alterni che è pari alla metà della serie del problema di Basilea⁵ e quindi vale $\dfrac{\pi^{2}}{12}$ . Sostituendo il tutto nell’identità per il calcolo del nostro integrale otteniamo

$\begin{aligned} \int_{0}^{1} \frac{x \ln(1+x)}{1+x^{2}}\ dx &= \int_{0}^{1} \frac{\ln (1+\alpha)}{(1+\alpha^2) \alpha}\ d \alpha +\frac{\ln^{2}(2)}{4} - \frac{ \pi^{2}}{16} =\\ &=\frac{\pi^{2}}{12} - \int_{0}^{1} \frac{x \ln(1+ x)}{1+x^{2}}\ dx +\frac{\ln^{2}(2)}{4} - \frac{ \pi^{2}}{16}. \end{aligned}$

In definitiva isolando l’integrale a sinistra e dividendo per $2$ otteniamo

(58) $\begin{equation*} \boxcolorato{analisi}{\displaystyle \int_{0}^{1} \frac{x \ln(1+x)}{1+x^{2}} = \frac{\pi^{2}}{24}-\frac{\pi^{2}}{32}+ \frac{\ln^{2}(2)}{8} = \frac{\pi^{2}}{96}+ \frac{\ln^{2}(2)}{8}. } \end{equation*}$

Il problema di Basilea, posto da Pietro Mengoli nel 1644 e risolto da Eulero nel 1735, è legato al determinare una somma esplicita della serie armonica di secondo ordine. Eulero dimostrò che

$\sum_{n=1}^{+\infty}\frac{1}{n^2}=\frac{\pi^2}{6}.$

Qui si sfrutta il fatto che, posto

$A=\sum_{n=1}^{+\infty}\frac{(-1)^{n+1}}{n^2},\qquad B=\sum_{n=1}^{+\infty}\frac{1}{n^2},$

si può scrivere

$\begin{aligned} B &=\sum_{n=1}^{+\infty}\frac{1}{(2n)^2}+\sum_{n=1}^{+\infty}\frac{1}{(2n-1)^2}=2\sum_{n=1}^{+\infty}\frac{1}{(2n)^2}-\sum_{n=1}^{+\infty}\frac{1}{(2n)^2}+\sum_{n=1}^{+\infty}\frac{1}{(2n-1)^2}=\\ &=\frac{1}{2}\sum_{n=1}^{+\infty}\frac{1}{n^2}+\left[-\sum_{n=1}^{+\infty}\frac{1}{(2n)^2}+\sum_{n=1}^{+\infty}\frac{1}{(2n-1)^2}\right]=\\ &=\frac{1}{2}B+\sum_{n=1}^{+\infty}\frac{(-1)^{n+1}}{n^2}=\frac{1}{2}B+A, \end{aligned}$

da cui

$A=\frac{1}{2} B=\frac{\pi^2}{12}.$

↩

Esercizio 23 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare il seguente integrale:

(59) $\begin{equation*} I=\int_{0}^{1}\left( \dfrac{\ln x}{x-1}\ln \left(1+x\right)\ln\left(1-x\right)+2\right)\dfrac{x-1}{\ln x }\,dx. \end{equation*}$

Svolgimento.

Riscriviamo (59) come

$I=\underbrace{\int_{0}^{1}\ln \left(1-x\right)\ln\left(1+x\right)\,dx}_{I_1}+2\underbrace{\int_{0}^{1}\dfrac{x-1}{\ln x}\,dx}_{I_2}.$

Calcoliamo $I_1$ . Sia

$f:(-1,1)\rightarrow \mathbb{R}$

tale che

$f(x)=\ln \left(1-x\right)\ln \left(1+x\right)$

e osserviamo che $f$ è funzione pari, infatti

$f(-x)=f(x),$

da cui possiamo scrivere

$I_1=\dfrac{1}{2}\int_{-1}^{1}\ln\left(1+x\right)\ln\left(1-x\right)\,dx.$

Operiamo la sostituzione $1+x=2t$ e otteniamo

$\begin{aligned} I_1&=\dfrac{1}{2}\int_{0}^{1}\ln\left(2t\right)\ln\left(1-\left(2t-1\right)\right)\,2dt= \\ &=\int_{0}^{1}\ln\left(2t\right)\ln\left(2-2t\right)\,dt= \\ &=\int_{0}^{1}\left(\ln 2+\ln t\right)\left(\ln 2 +\ln \left(1-t\right)\right)\,dt=\\ &=\int_{0}^{1}\left(\ln^2 2 +\ln 2 \ln\left(1-t\right) +\ln 2 \ln t +\ln t \ln \left(1-t\right)\right)\,dt=\\ &=\ln^2 2 +\ln 2 \int_{0}^{1}\ln\left(1-t\right)\,dt+\ln 2 \int_{0}^{1}\ln t \, dt+\int_{0}^{1}\ln t \ln \left(1-t\right)\,dt=\\ &=\ln^22+\ln 2 (-1)+\ln 2(-1)+\int_{0}^{1}\ln t \ln \left(1-t\right)\,dt =\\ &=\ln^2 2 -2\ln 2 +\underbrace{\int_{0}^{1}\ln t \ln \left(1-t\right)\,dt}_{I_3}. \end{aligned}$

Calcoliamo $I_3$ . Ricordiamo che

$\ln \left(1-t\right)=-\sum_{n=0}^{+\infty}\dfrac{t^{n+1}}{n+1}\quad \forall x \in [-1,1),$

da cui⁶

$I_3=-\int_{0}^{1}\sum_{n=0}^{+\infty}\dfrac{t^{n+1}}{n+1}\ln t \, dt=-\sum_{n=0}^{+\infty}\dfrac{1}{n+1}\int_{0}^{1}t^{n+1}\ln t\,dt=-\sum_{n=1}^{+\infty}\dfrac{1}{n}\int_{0}^{1}t^n\ln t \,dt.$

Ricordiamo la seguente formula facilmente ottenibile con l’integrazione per parti:

$\int t^n\ln t \, dt=\dfrac{t^{n+1}\left(\left(n+1\right)\ln t-1\right)}{\left(n+1\right)^2}+\text{costante}\quad \text{con}\,\, n \in \mathbb{N},$

da cui

(60) $\begin{equation*} \int^{1}_{0} t^n\ln t \, dt=-\dfrac{1}{\left(n+1\right)^2}. \end{equation*}$

Applicando (60) a $I_3$ otteniamo⁷

$\begin{aligned} I_3&=\sum_{n=1}^{+\infty}\dfrac{1}{n\left(n+1\right)^2}= \\ &=\sum_{n=1}^{+\infty}\left(\dfrac{1}{n}-\dfrac{1}{n+1}-\dfrac{1}{\left(n+1\right)^2}\right)= \\ &=\lim_{N\rightarrow +\infty}\sum_{n=1}^{N}\left(\dfrac{1}{n}-\dfrac{1}{n+1}\right)-\sum_{n=1}^{+\infty}\dfrac{1}{\left(n+1\right)^2}=\\ &=\lim_{N \rightarrow +\infty}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dots -\dfrac{1}{N+1}\right)+1-1-\sum_{n=2}^{+\infty}\dfrac{1}{n^2}= \\ &=2-\sum_{n=1}^{+\infty}\dfrac{1}{n^2}= \\ &=2-\dfrac{\pi^2}{6}, \end{aligned}$

concludendo che

(61) $\begin{equation*} \boxcolorato{analisi}{I_1=\ln^2 2 -2 \ln 2 +2-\dfrac{\pi^2}{6}. } \end{equation*}$

Ora calcoliamo $I_2$ . A tale proposito, consideriamo $F:(0,+\infty) \rightarrow \mathbb{R}$ tale che

$F(\alpha)=\int_{0}^{1}\dfrac{x^\alpha-1}{\ln x }\,dx= \int_{0}^{1}f(x,\alpha)\,dx\qquad \text{con}\,\, \alpha >0.$

Con l’intento di derivare la funzione sotto il segno di integrale, ricordiamo il seguente risultato.

Teorema 3.4 (derivazione sotto il segno di integrale). Sia $F:[a,b]\rightarrow \mathbb{R}$

definita da

$F(\alpha)=\int_{t_1(\alpha)}^{t_2 (\alpha)}f(x,\alpha )\,dx.$

Se $f(x,\alpha)$ e $\dfrac{\partial f}{\partial \alpha}(x,\alpha)$ sono continue in $\left\{(x,\alpha):a\leq \alpha \leq b,\,t_1(\alpha)\leq x \leq t_2(\alpha)\right\}$ ed inoltre $t_1(\alpha)$ e $t_2(\alpha)$ sono di classe $C^1$ in $[a,b]$ , allora

$\dfrac{dF}{d\alpha}(\alpha)=\int_{t_1(\alpha)}^{t_2(\alpha)}\dfrac{\partial f}{\partial \alpha }(x,\alpha)\,dx+f(t_2(\alpha),\alpha)\, \dfrac{dt_2}{d\alpha}(\alpha)-f(t_1(\alpha),\alpha)\,\dfrac{dt_1}{d\alpha}(\alpha).$

$\quad$

Osserviamo che

$\lim_{x \rightarrow 0^+}f(x,\alpha)=0 \qquad \mbox{e} \qquad \lim_{x \rightarrow 1^-}f(x,\alpha)=\alpha$

e definiamo

$\tilde{f}(x,\alpha)= \begin{cases} f(x,\alpha), \quad & \text{per} \,\, x \in (0,1)\\ 0, & \text{per}\,\, x=0\\ \alpha, & \text{per}\,\, x=1, \end{cases}$

allora $\tilde{f}(x,\alpha)$ e $\dfrac{\partial \tilde{f}}{\partial \alpha}(x,\alpha)=x^\alpha$ sono continue in $[0,1]$ con $\alpha \in (0,+\infty)$ , quindi le ipotesi del teorema 3.4 sono soddisfatte ed applicandolo otteniamo

(62) $\begin{equation*} \hspace{-0.5cm}\dfrac{dF}{d \alpha}(\alpha)=\int_{0}^{1}\dfrac{\partial f}{\partial \alpha}(x,\alpha)\,dx= \int_{0}^{1} \dfrac{x^\alpha \, \ln x}{\ln x }\,dx=\int_{0}^{1}x^\alpha\, dx =\dfrac{x^{\alpha+1}}{\alpha+1}\bigg \vert^1_0=\dfrac{1}{\alpha+1}. \end{equation*}$

Ora integriamo rispetto ad $\alpha$ e otteniamo

$F(\alpha)=\int \dfrac{1}{\alpha+1}\,d \alpha =\ln \left \vert 1+\alpha \right \vert +\text{costante}.$

Nella precedente poniamo $\alpha=0$ arrivando a

$F(0)=0=\ln 1+\text{costante} \iff \text{costante} =0,$

da cui

$F(\alpha)=\ln(1+\alpha ).$

Ponendo ora $\alpha=1$ in (62) otteniamo

$F(1)=\int_{0}^{1}\dfrac{x-1}{\ln x }\,dx=\ln2.$

Dunque possiamo concludere che

(63) $\begin{equation*} \boxcolorato{analisi}{I_2= \int_{0}^{1}\dfrac{x-1}{\ln x}\,dx=\ln 2 . } \end{equation*}$

Sommando i risultati di $I_1$ e $I_2$ concludiamo che

$I=\ln^2 2 -2 \ln 2 +2-\dfrac{\pi^2}{6}+\ln 2 =\ln^2 2 - \ln 2 +2-\dfrac{\pi^2}{6},$

ovvero

(64) $\begin{equation*} \boxcolorato{analisi}{I=\ln^2 2 - \ln 2 +2-\dfrac{\pi^2}{6}. } \end{equation*}$

Lo scambio della serie con l’integrale si dimostra facilmente applicando il teorema della convergenza dominata. ↩

Il problema di Basilea, posto da Pietro Mengoli nel 1644 e risolto da Eulero nel 1735, è legato al determinare una somma esplicita della serie armonica di secondo ordine. Eulero dimostrò che

$\sum_{n=1}^{+\infty}\frac{1}{n^2}=\frac{\pi^2}{6}.$

↩

Esercizio 24 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare il seguente integrale:

(65) $\begin{equation*} I=\int_{0}^{1}\dfrac{\ln\left(1-x\right)}{1+x}\,dx. \end{equation*}$

Svolgimento.

Con la sostituzione $1-x=t$

l’integrale (65) diventa

$I=\int_{0}^{1}\dfrac{\ln t}{2-t}\, dt=\dfrac{1}{2}\int_{0}^{1}\dfrac{\ln t}{1-\frac{t}{2}}\,dt.$

Ora ricordiamo che

$\dfrac{1}{1-x}=\sum_{n=0}^{+\infty}x^n \qquad \forall x \in \left(-1,1\right),$

da cui⁸

$I=\dfrac{1}{2}\int_{0}^{1}\ln t \sum_{n=0}^{+\infty}\left(\dfrac{t}{2}\right)^n\,dt=\dfrac{1}{2}\sum_{n=0}^{+\infty}\dfrac{1}{2^n}\int_{0}^{1}t^n \ln t \, dt.$

Ricordiamo la seguente formula facilmente ottenibile con l’integrazione per parti:

$\int t^n\ln t \, dt=\dfrac{t^{n+1}\left(\left(n+1\right)\ln t-1\right)}{\left(n+1\right)^2}+\text{costante}\quad \text{con}\,\, n \in \mathbb{N},$

per cui possiamo scrivere

(66) $\begin{equation*} \int^{1}_{0} t^n\ln t \, dt=-\dfrac{1}{\left(n+1\right)^2}, \end{equation*}$

quindi

$I=-\dfrac{1}{2}\sum_{n=0}^{+\infty}\dfrac{1}{2^n\left(n+1\right)^2}.$

Ora ricordiamo la definizione di polilogaritmo:

(67) $\begin{equation*} \mathrm{Li}_k(y)=\sum_{n=1}^{+\infty}\dfrac{y^n}{n^k} \quad \forall y \in (-1,1), \,\,\,k \in \mathbb{R} \end{equation*}$

e riscriviamo (65) come

(68) $\begin{equation*} I=-\dfrac{1}{2}\sum_{n=1}^{+\infty}\dfrac{2^{-n+1}}{n^2}=-\sum_{n=1}^{+\infty}\dfrac{2^{-n}}{n^2}. \end{equation*}$

Confrontando (68) con la definizione di polilogaritmo (67), giungiamo a

$I=-\mathrm{Li}_2\left(\dfrac{1}{2}\right).$

Com’è noto, grazie ad Eulero, si ha la seguente identità :

$\text{Li}_2\left(\dfrac{1}{2}\right)=\dfrac{\pi^2}{12}-\dfrac{\ln^22}{2},$

pertanto concludiamo che

(69) $\begin{equation*} \boxcolorato{analisi}{I=-\left(\dfrac{\pi^2}{12}-\dfrac{\ln^22}{2}\right).} \end{equation*}$

Lo scambio della serie con l’integrale si dimostra facilmente applicando il teorema della convergenza dominata. ↩

Esercizio 25 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare i seguenti limiti:

(70) $\begin{equation*} a) \lim_{n \to +\infty} n \sin(2\pi e n!); \end{equation*}$

(71) $\begin{equation*} b) \lim_{n \rightarrow +\infty}\dfrac{n^2}{\left(\prod_{k=1}^{n}k^k\right)^{4/n^2}}. \end{equation*}$

Svolgimento di a.

Ricordiamo che

$e = \sum_{k=0}^{+\infty} \dfrac{1}{k!} = \sum_{k=0}^{n} \dfrac{1}{k!}+\sum_{k=n+1}^{+\infty} \dfrac{1}{k!},$

dunque (70) può essere riscritta come

$\begin{aligned} \lim_{n \to +\infty} n \sin(2\pi e n!)& = \lim_{n \to +\infty} n \sin\left(2\pi n!\left(\sum_{k=0}^{n} \dfrac{1}{k!}+\sum_{k=n+1}^{+\infty} \dfrac{1}{k!}\right)\right)=\\ & = \lim_{n \to +\infty} n \sin\left(2\pi n!\sum_{k=0}^{n} \dfrac{1}{k!}+2\pi n!\sum_{k=n+1}^{+\infty} \dfrac{1}{k!}\right). \end{aligned}$

Osserviamo che

$\begin{aligned} 2\pi n! \sum_{k=0}^n \dfrac{1}{k!} & = 2\pi n! \left( \dfrac{1}{n!}+ \dfrac{1}{(n-1)!}+ \dfrac{1}{(n-2)!}+ \dots + 1\right) = \\ &= 2\pi\dfrac{n!}{n!} \left( 1+ n + n(n-1)+\dots + n!\right) = \\ & =2\pi\left( 1+ n + n(n-1)+\dots + n! \right) = 2\pi m \quad \text{con}\,\, m \in \mathbb{N}. \end{aligned}$

Vogliamo dimostrare che⁹

$\lim_{n \rightarrow +\infty}\dfrac{n!\displaystyle\sum_{k=n+1}^{+\infty} \dfrac{1}{k!}-\frac{1}{n}}{\frac{1}{n}}=0 \iff n!\sum_{k=n+1}^{+\infty} \dfrac{1}{k!}=\dfrac{1}{n}+o\left(\dfrac{1}{n}\right)\quad \text{per}\,\, n\rightarrow +\infty .$

Osserviamo quanto segue:

$\begin{aligned} 0 &\leq \left \vert n\left(n!\sum_{k=n+1}^{+\infty}\dfrac{1}{k!}-\dfrac{1}{n}\right)\right \vert = \\ &=n\left \vert \left(\sum_{k=n+1}^{+\infty}\dfrac{n!}{k!}-\dfrac{1}{n}\right)\right \vert = \\ &= n\left \vert \left(\dfrac{n!}{(n+1)!}-\dfrac{1}{n}+\sum_{k=n+2}^{+\infty}\dfrac{n!}{k!}\right)\right \vert =\\ & = n\left \vert \left(\dfrac{1}{n+1}-\dfrac{1}{n}+\sum_{k=n+2}^{+\infty}\dfrac{n!}{k!}\right)\right \vert = \\ &= n\left \vert \left(\underbrace{\dfrac{1}{n+1}-\dfrac{1}{n}}_{b_n}+\left(\dfrac{n!}{(n+2)!}+\dfrac{n!}{(n+3)!}+\dots\right)\right)\right \vert =\\ &= n\left \vert \left(b_n+\left(\dfrac{1}{(n+2)(n+1)}+\dfrac{1}{(n+3)(n+2)(n+1)}+\dots\right)\right)\right \vert \leq \\ &\leq \left \vert nb_n\right \vert +\left \vert n\left(\dfrac{1}{n^2}+\dfrac{1}{n^3}+\dots\right)\right \vert =\\ &=n\left \vert b_n \right \vert + n \sum_{k=2}^{+\infty} \dfrac{1}{n^k} =n\left \vert b_n \right \vert+ \dfrac{\left(\frac{1}{n}\right)^2}{1-\frac{1}{n}} = \\ &= n\left \vert b_n \right \vert+ \dfrac{1}{n\left(n-1\right)}, \end{aligned}$

dove nel penultimo passaggio abbiamo utilizzato il fatto che¹⁰

$\sum_{k=k_0}^{+\infty}x^k = \dfrac{x^{k_0}}{1-x}, \qquad x \in (-1,1).$

Effettuando il limite del risultato precedente, otteniamo

$\lim_{n \rightarrow +\infty}\left(n\left \vert b_n\right \vert +\dfrac{1}{n-1}\right)=0,$

per cui

$n!\sum_{k=n+1}^{+\infty}\dfrac{1}{k!}-\dfrac{1}{n}=o\left(\dfrac{1}{n}\right) \quad \text{per} \,\, n \rightarrow +\infty .$

Dunque

$\begin{aligned} \lim_{n \to +\infty} n \sin(2\pi e n!)& = \lim_{n \to +\infty} n \sin\left( 2\pi \left(m+\dfrac{1}{n}+o\left(\dfrac{1}{n}\right)\right)\right) = \\ &= \lim_{n \to +\infty} n\sin \left(2 \pi m +\dfrac{2\pi}{n}+o\left(\dfrac{1}{n}\right)\right) =\\ & =\lim_{n \rightarrow +\infty}n\sin \left(\dfrac{2\pi}{n}+o\left(\dfrac{1}{n}\right)\right)= \\ &= \lim_{n \rightarrow +\infty}n \left(\dfrac{2\pi}{n}+o\left(\dfrac{1}{n}\right)\right)= \\ &=2\pi. \end{aligned}$

Pertanto concludiamo che

(72) $\begin{equation*} \boxcolorato{analisi}{\lim_{n \to +\infty} n \sin(2\pi e n!)=2\pi.} \end{equation*}$

È sufficiente ricordare la definizione di o-piccolo. ↩

$\sum_{k=k_0}^{+\infty}x^k = x^{k_0} \sum_{k=k_0}^{+\infty}x^{k-k_0} = x^{k_0} \sum_{t=0}^{+\infty}x^{t} = \dfrac{x^{k_0}}{1-x}, \qquad \forall x \in (-1,1).$

↩

Svolgimento di b.

Riscriviamo il denominatore di (71) come

(73) $\begin{equation*} \left(\prod_{k=1}^{n}k^k\right)^{\frac{4}{n^2}}=e^{\frac{4}{n^2}\ln \left(\prod_{k=1}^{n}k^k\right)} \end{equation*}$

e osserviamo che

$\begin{aligned} \ln \left(\prod_{k=1}^{n}k^k\right)&=\ln1^1+\ln2^2+\ln3^3+\dots+\ln n^n=\sum_{k=1}^{n}\ln k^k=\sum_{k=1}^{n}k\ln k. \end{aligned}$

Ora notiamo che¹¹

$\begin{aligned} \dfrac{1}{n^2}\sum_{k=1}^{n}k\ln k & = \dfrac{1}{n}\sum_{k=1}^{n}\dfrac{k}{n}\ln k= \\ &= \dfrac{1}{n}\sum_{k=1}^{n}\dfrac{k}{n}\left(\ln \dfrac{k}{n}+\ln n \right)= \\ &= \dfrac{1}{n}\sum_{k=1}^{n}\dfrac{k}{n}\ln \dfrac{k}{n}+\dfrac{\ln n }{n^2}\sum_{k=1}^{n}k=\\ &=\dfrac{1}{n}\sum_{k=1}^{n}\dfrac{k}{n}\ln \dfrac{k}{n}+\dfrac{\ln n }{2}\left(1+\dfrac{1}{n}\right), \end{aligned}$

per cui (71) diventa

$\begin{aligned} \lim_{n \rightarrow +\infty}\dfrac{n^2}{\left(\prod_{k=1}^{n}k^k\right)^{\frac{4}{n^2}}} &= \lim_{n \rightarrow +\infty}\dfrac{n^2}{e^{4\left( \frac{1}{n}\sum_{k=1}^{n}\frac{k}{n}\ln \frac{k}{n}+\frac{\ln n }{2}\left(1+\frac{1}{n}\right)\right)}}=\\ &=\lim_{n \rightarrow +\infty}\dfrac{n^2}{e^{4\left( \frac{1}{n}\sum_{k=1}^{n}\frac{k}{n}\ln \frac{k}{n}\right)}\cdot e^{4\left( \frac{\ln n }{2}\left(1+\frac{1}{n}\right)\right)}}= \\ &= \lim_{n\rightarrow +\infty}\dfrac{n^2}{e^{4\left( \frac{1}{n}\sum_{k=1}^{n}\frac{k}{n}\ln \frac{k}{n}\right)}\cdot e^{2\ln n}\cdot e^{2\frac{\ln n }{n}}}=\\ &= \lim_{n\rightarrow +\infty}\dfrac{n^2}{e^{4\left( \frac{1}{n}\sum_{k=1}^{n}\frac{k}{n}\ln \frac{k}{n}\right)}\cdot n^2\cdot e^{2\frac{\ln n }{n}}}= \\ &= \dfrac{1}{e^{4\int_{0}^{1}x \ln x \,dx}}= \\ &= \dfrac{1}{e^{4\left(-\frac{1}{4}\right)}}= \\ &= e. \end{aligned}$

Si conclude che

(74) $\begin{equation*} \boxcolorato{analisi}{\lim_{n \rightarrow +\infty}\dfrac{n^2}{\left(\prod_{k=1}^{n}k^k\right)^{\frac{4}{n^2}}}=e.} \end{equation*}$

Se $f$ è una funzione integrabile su $[0,1]$ (per esempio se è continua), allora si ha:

$\lim_{n \rightarrow +\infty}\dfrac{1}{n}\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)=\int_{0}^{1}f(x)\,dx.$

Inoltre vale

$\sum_{k=1}^{n}k=\dfrac{n^2+n}{2}.$

↩

Esercizio 26 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

. Determinare tutte le funzioni $f:\{(x,y)\in\mathbb{R}^2\ | xy>0\}\rightarrow\mathbb{R}$

soluzioni del seguente sistema di PDE’s (Partial Differential Equations, Equazioni alle derivate parziali)

$\begin{cases} \displaystyle x\cdot\frac{\partial f}{\partial x}+y\cdot\frac{\partial f}{\partial y}=xy\cdot\log(xy)\\ \displaystyle x^2\cdot\frac{\partial^2 f}{\partial x^2}+y^2\cdot\frac{\partial^2 f}{\partial y^2}=xy. \end{cases}$

Svolgimento.

Il problema rappresenta un’utile applicazione della Chain rule (regola della catena) per la derivazione di funzioni composte in più variabili. Osserviamo che la presenza ripetuta del termine $xy$

suggerisce di passare ad una nuova variabile $u=xy$

. Come scegliamo una ulteriore variabile di sostituzione? Possiamo osservare che sia nella prima che nella seconda equazione, dividendo tutti i memebri per $xy$

appariranno, moltiplicati davanti alle derivate parziali, i fattori della forma $x/y$

e $y/x$

(uno il reciproco dell’altro. Poniamo allora¹² $v=x/y$

. Osserviamo che, attraverso queste sostituzioni, si ha

$\frac{\partial u}{\partial x}=y,\qquad \frac{\partial u}{\partial y}=x,\qquad \frac{\partial v}{\partial x}=\frac{1}{y},\qquad \frac{\partial v}{\partial y}=-\frac{x}{y^2}.$

Applichiamo ora la chain rule alle derivate del primo ordine della funzione $f$ : abbiamo¹³

$\begin{aligned} \frac{\partial f}{\partial x}&=\frac{\partial f}{\partial u}\cdot\frac{\partial u}{\partial x}+ \frac{\partial f}{\partial v}\cdot\frac{\partial v}{\partial x}=y\cdot\frac{\partial f}{\partial u}+\frac{1}{y}\cdot \frac{\partial f}{\partial v},\\ \frac{\partial f}{\partial y}&=\frac{\partial f}{\partial u}\cdot\frac{\partial u}{\partial y}+ \frac{\partial f}{\partial v}\cdot\frac{\partial v}{\partial y}=x\cdot\frac{\partial f}{\partial u}-\frac{x}{y^2}\cdot \frac{\partial f}{\partial v}, \end{aligned}$

da cui, sostituendo nella prima equazione

$x\cdot\left(y\cdot\frac{\partial f}{\partial u}+\frac{1}{y}\cdot \frac{\partial f}{\partial v}\right)+y\cdot\left(x\cdot\frac{\partial f}{\partial u}-\frac{x}{y^2}\cdot \frac{\partial f}{\partial v}\right)=xy\cdot\log(xy),$

ed eseguendo le opportune semplificazioni

$2u\frac{\partial f}{\partial u}=u\cdot\log(u),$

si giunge alla nuova equazione

(75) $\begin{equation*} \frac{\partial f}{\partial u}=\frac{1}{2}\log(u). \end{equation*}$

Applichiamo adesso la chain rule alle derivate parziali seconde non miste della funzione $f$ : abbiamo

$\begin{aligned} \frac{\partial^2 f}{\partial x^2}&=\frac{\partial\ }{\partial x}\left(\frac{\partial f}{\partial x}\right) =y\cdot\frac{\partial^2 f}{\partial x\partial u}+\frac{1}{y}\cdot \frac{\partial^2 f}{\partial x\partial v}=\\ &=y\left(\frac{\partial^2 f}{\partial u^2}\cdot\frac{\partial u}{\partial x}+ \frac{\partial^2 f}{\partial v\partial u}\cdot\frac{\partial v}{\partial x}\right)+\frac{1}{y}\left( \frac{\partial^2 f}{\partial u\partial v}\cdot\frac{\partial u}{\partial x}+ \frac{\partial^2 f}{\partial v^2}\cdot\frac{\partial v}{\partial x}\right)=\\ &=y\left(y\cdot\frac{\partial^2 f}{\partial u^2}+\frac{1}{y}\cdot \frac{\partial^2 f}{\partial v\partial u}\right)+\frac{1}{y}\left( y\cdot\frac{\partial^2 f}{\partial u\partial v}+ \frac{1}{y}\cdot\frac{\partial^2 f}{\partial v^2}\right), \end{aligned}$

da cui

$\frac{\partial^2 f}{\partial x^2}=y^2\cdot\frac{\partial^2 f}{\partial u^2}+ 2\frac{\partial^2 f}{\partial v\partial u}+ \frac{1}{y^2}\cdot\frac{\partial^2 f}{\partial v^2}.$

Analogamente

$\begin{aligned} \frac{\partial^2 f}{\partial y^2}&=\frac{\partial\ }{\partial y}\left(\frac{\partial f}{\partial y}\right) =x\cdot\frac{\partial^2 f}{\partial y\partial u}-\frac{x}{y^2}\cdot \frac{\partial^2 f}{\partial y\partial v}+\frac{2x}{y^3}\cdot \frac{\partial f}{\partial v}=\\ &=x\left(\frac{\partial^2 f}{\partial u^2}\cdot\frac{\partial u}{\partial y}+ \frac{\partial^2 f}{\partial v\partial u}\cdot\frac{\partial v}{\partial y}\right)-\frac{x}{y^2}\left( \frac{\partial^2 f}{\partial u\partial v}\cdot\frac{\partial u}{\partial y}+ \frac{\partial^2 f}{\partial v^2}\cdot\frac{\partial v}{\partial y}\right)+\frac{2x}{y^3}\cdot \frac{\partial f}{\partial v}=\\ &=x\left(x\cdot\frac{\partial^2 f}{\partial u^2}-\frac{x}{y^2}\cdot \frac{\partial^2 f}{\partial v\partial u}\right)-\frac{x}{y^2}\left( x\cdot\frac{\partial^2 f}{\partial u\partial v}- \frac{x}{y^2}\cdot\frac{\partial^2 f}{\partial v^2}\right)+\frac{2x}{y^3}\cdot \frac{\partial f}{\partial v}, \end{aligned}$

da cui

$\frac{\partial^2 f}{\partial y^2}=x^2\cdot\frac{\partial^2 f}{\partial u^2}- \frac{2x^2}{y^2}\frac{\partial^2 f}{\partial v\partial u}+ \frac{x^2}{y^4}\cdot\frac{\partial^2 f}{\partial v^2}+\frac{2x}{y^3}\cdot \frac{\partial f}{\partial v}.$

Sostituendo le due espressioni trovate per le derivate parziali seconde nella seconda equazione otteniamo

$\begin{aligned} x^2&\left(y^2\cdot\frac{\partial^2 f}{\partial u^2}+ 2\frac{\partial^2 f}{\partial v\partial u}+ \frac{1}{y^2}\cdot\frac{\partial^2 f}{\partial v^2}\right)\\ &+y^2\left(x^2\cdot\frac{\partial^2 f}{\partial u^2}- \frac{2x^2}{y^2}\frac{\partial^2 f}{\partial v\partial u}+ \frac{x^2}{y^4}\cdot\frac{\partial^2 f}{\partial v^2}+\frac{2x}{y^3}\cdot \frac{\partial f}{\partial v}\right)=xy \end{aligned}$

e, dopo opportune semplificazioni,

$2u^2\cdot\frac{\partial^2 f}{\partial u^2}+ 2v^2\cdot\frac{\partial^2 f}{\partial v^2} +2v\cdot\frac{\partial f}{\partial v}=u$

si trova la nuova equazione

(76) $\begin{equation*} u^2\cdot\frac{\partial^2 f}{\partial u^2}+ v^2\cdot\frac{\partial^2 f}{\partial v^2} +v\cdot\frac{\partial f}{\partial v}=\frac{u}{2}. \end{equation*}$

Se ora deriviamo (75) rispetto alla variabile $u$ abbiamo

$\frac{\partial^2 f}{\partial u^2}=\frac{1}{2u},$

che, sostituito in (76), conduce a

$u^2\cdot\frac{1}{2u}+ v^2\cdot\frac{\partial^2 f}{\partial v^2} +v\cdot\frac{\partial f}{\partial v}=\frac{u}{2}$

e quindi

(77) $\begin{equation*} v\cdot\frac{\partial^2 f}{\partial v^2} +\cdot\frac{\partial f}{\partial v}=0. \end{equation*}$

Se invece integriamo l’equazione (75) abbiamo

(78) $\begin{equation*} f(u,v)=\frac{1}{2}\int\log(u)\ du=\frac{1}{2}\left[u\log u-\int du\right]=\frac{1}{2}\left[u\left(\log u-1\right)\right]+\varphi(v), \end{equation*}$

dove $\varphi(v)$ è una funzione dipendente dalla sola variabile $v$ . Se ora sostituiamo l’espressione appena trovata per $f$ nella equazione (77), osservando che il primo termine della sua espressione dipende solo dalla variabile $u$ , abbiamo la seguente equazione differenziale ordinaria di secondo ordine nella sola variabile $v$ :

(79) $\begin{equation*} v\cdot\varphi''(v)+\varphi'(v)=0. \end{equation*}$

Posto $z(v)=\varphi'(v)$ , l’equazione diventa

$v\cdot z'(v)+z(v)=0 \implies \left[v\cdot z(v)\right]'=0 \implies v\cdot z(v)=a,$

dove $a$ è una costante arbitraria. Ricordando la sostituzione fatta per $\varphi$ , si ha

$v\cdot\varphi'(v)=a \implies \varphi'(v)=\frac{a}{v} \implies \varphi(v)=a\log v+b,$

con $b$ altra costante arbitraria. Sostituendo questa espressione per $\varphi$ nell’espressione scritta in precedenza per $f$ in (78), otteniamo

$f(u,v)=\frac{u}{2}\left(\log u-1\right)+a\log v+b,\qquad a,b\in\mathbb{R},$

e, ricordando la posizione fatta all’inizio per le variabili $u, v$ , si ha la soluzione del problema:

$f(x,y)=\frac{xy}{2}\left(\log(xy)-1\right)+a\log\left(\frac{x}{y}\right)+b,\qquad a,b\in\mathbb{R}.$

Potremmo anche porre $v=y/x$ ottenendo lo stesso risultato. ↩

Lasciamo indicate nel seguito le variabili $x,y$ per ottenere una più rapida semplificazione una volta sostituite le derivate parziali. ↩

Esercizio 27 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Si dimostri la seguente identità per $x\in \left(-1,+\infty\right)$

(80) $\begin{equation*} \sqrt{\left( x+\dfrac{1-x}{1+\sqrt{\dfrac{2}{1+x}}}\right)^2+\left( \dfrac{1-x}{1+\sqrt{\dfrac{2}{1+x}}}\right)^2}+\dfrac{1-x}{1+\sqrt{\dfrac{2}{1+x}}}=1. \end{equation*}$

Svolgimento 1.

Posto

$q=\dfrac{1-x}{1+\sqrt{\dfrac{2}{1+x}}},$

(80) diventa

$\left(q+x\right)^2+q^2=\left(1-q\right)^2,$

ossia

(81) $\begin{equation*} \left(q+x\right)^2=1-2q. \end{equation*}$

Risolviamo (81) come segue:

(82) $\begin{equation*} \begin{split} q^2+x^2+2qx=1-2q & \iff q^2+2q\left(x+1\right)+x^2-1=0 \\ & \iff q_{1,2}=-\left(x+1\right)\pm\sqrt{\left(x+1\right)^2-\left(x^2-1\right)} \\ & \iff q_{1,2}=-\left(x+1\right)\pm\sqrt{2+2x}. \end{split} \end{equation*}$

Ora notiamo che

$q=\dfrac{1-x}{1+\sqrt{\dfrac{2}{1+x}}}=\frac{\left(1-x\right)\left(1-\sqrt{\dfrac{1}{1+x}}\right)}{1-\frac{2}{1+x}}=-\left(x+1-\dsqrt{2x+2}\right)$

e, scegliendo la soluzione positiva di (82), si ha l’asserto.

Svolgimento 2.

Poniamo

$q=q(x)=\dfrac{1-x}{1+\sqrt{\dfrac{2}{1+x}}}$

e calcoliamone l’inversa; si ha dunque:

$\begin{aligned} q\left(1+\sqrt{\dfrac{2}{1+x}} \right)=1-x \iff q + q \sqrt{\dfrac{2}{1+x}}=1-x \iff q \sqrt{\dfrac{2}{1+x}} = 1-x-q. \end{aligned}$

Elevando al quadrato ambo i membri otteniamo

$q^2\left( \dfrac{2}{1+x}\right)=q^2+2qx-2q+x^2-2x+1,$

da cui

$\begin{aligned} 2q^2=(q^2+2qx-2q+x^2-2x+1)(1+x), \end{aligned}$

ovvero

(83) $\begin{equation*} x^3+x^2(2q-1)+x(q^2-1)-q^2-2q+1=0. \end{equation*}$

Osserviamo che $x=1$ è una soluzione, quindi, effettuando la divisione per $(x-1)$ , abbiamo

$x^2+2qx+q^2+2q-1=0,$

le cui soluzioni si ricavano facilmente e sono

$x=x(q)=-q\pm \sqrt{1-2q}.$

Adesso la verifica dell’identità

$\left(-q\pm \sqrt{1-2q}+q \right)^2+q^2=(1-q)^2$

è immediata.

Esercizio 28 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare il seguente limite:

$\begin{equation*} \lim_{n\to+\infty}\int_0^n x\sin\left( \dfrac{1}{nx}\right)\dfrac{dx}{\sqrt{x^2+1}}. \end{equation*}$

Svolgimento.

Ricordando che

$\left\vert \dfrac{\sin(u)}{u} \right\vert \le 1, \qquad \forall u \in \mathbb{R} \setminus\{0\},$

risulta

(84) $\begin{equation*} \begin{aligned} 0 & \le \left\vert \int_0^n x \sin\left(\dfrac{1}{xn}\right) \; \dfrac{1}{\sqrt{x^2+1}}\; dx \right\vert \le \\ &\le \int_0^n \left\vert x \; \sin\left(\dfrac{1}{xn}\right) \right\vert \; \dfrac{1}{\sqrt{x^2+1}} \; dx = \\ & = \dfrac{1}{n} \int_0^n \left\vert xn \; \sin\left(\dfrac{1}{xn}\right) \; \dfrac{1}{\sqrt{x^2+1}} \right\vert \le \\ & \leq \dfrac{1}{n} \int_0^n \dfrac{1}{\sqrt{x^2+1}} \; dx = \\ &= \dfrac{\ln\left(n+\sqrt{n^2+1}\right)}{n}. \end{aligned} \end{equation*}$

Poichè

(85) $\begin{equation*} \lim_{n\to+\infty} \dfrac{\ln\left(n+\sqrt{n^2+1}\right)}{n} = 0, \end{equation*}$

il limite proposto vale dunque zero, pertanto concludiamo che

(86) $\begin{equation*} \boxcolorato{analisi}{\lim_{n\to+\infty}\int_0^n x\sin\left( \dfrac{1}{nx}\right)\dfrac{dx}{\sqrt{x^2+1}}=0. } \end{equation*}$

Esercizio 29 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Trovare tutti i numeri reali $t$

tali che per ogni $x>y>0$

valga

$\begin{equation*} (x-y)^t(x+y)^t=(x^t-y^t)(x^t+y^t)^{2-t}. \end{equation*}$

Svolgimento.

Supponiamo $t\ge0$

. Deve essere

$\dfrac{(x+y)^t(x-y)^t}{(x^t-y^t)(x^t+y^t)^{2-t}}=1 \qquad \forall \; x>y>0.$

Fissato $y$ , si ha

$\dfrac{(x+y)^t(x-y)^t}{(x^t-y^t)(x^t+y^t)^{2-t}}\sim\dfrac{x^{2t}}{x^{3t-t^2}}\quad \mbox{per }x\to+\infty$

e dunque $2t=3t-t^2$ . Delle soluzioni $t=0$ e $t=1$ solo la seconda verifica l’equazione ed è accettabile. Supponiamo ora $t<0$ e poniamo $t=-u$ con $u>0$ . Fissato $y$ , si ha

$\dfrac{(x+y)^{-u}(x-y)^{-u}}{(x^{-u}-y^{-u})(x^{-u}+y^{-u})^{2+u}}=\dfrac{\left(\dfrac{x^uy^u}{y^u-x^u} \right)\left(\dfrac{x^u y^u}{y^u+x^u} \right)^{2+u}}{(x+y)^u (x-y)^u} \overset{ x\to+\infty} {\sim} \dfrac{(-y^u)(y^u)^{2+u}}{x^{2u}}.$

Si vede facilmente che l’ultima frazione tende a $0$ ed in particolare è diversa da $1$ , quindi per $t<0$ non ci sono soluzioni.

Esercizio 30 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Nel triangolo $ABC$

, l’angolo $A=60^{\circ}$

e l’angolo $B=45^{\circ}$

. Se $D$

è un punto sul lato $BC$

di modo che $BD=\dfrac{BC}{3}$

, dimostrare che

$\begin{equation*} \dfrac{AB^4}{9}+\dfrac{AC^4}{36}=\tan 15^\circ \cdot AD^4. \end{equation*}$

Svolgimento.

Rappresentiamo il problema graficamente in figura 5, dove $C\hat{A}B=60^o$

e $A\hat{B}C=45^o$

$\quad$

Figura 5: illustrazione dell’esercizio 30.

$\quad$

Mettiamo a sistema ¹⁴ da cui

$BC\left(\dfrac{1}{\sqrt{3}}+1 \right)=\sqrt{2}AB, \qquad AC\dfrac{1}{\sqrt{2}}\left(1+\sqrt{3} \right)=\sqrt{2}AB,$

quindi

$BC=\dfrac{\sqrt{2}\sqrt{3}}{\sqrt{3}+1}AB=\dfrac{3-\sqrt{3}}{\sqrt{2}}AB, \qquad AC=\dfrac{2}{\sqrt{3}+1}AB=(\sqrt{3}-1)AB.$

Pertanto

$\begin{aligned} AD^2 &=\left(\dfrac{BC}{3} \cdot\dfrac{1}{\sqrt{2}}\right)^2+\left( AB-\dfrac{BC}{\sqrt{2}}\right)^2=\\ &=\left(\dfrac{3-\sqrt{3}}{3\cdot2}\right)^2 AB^2+\left(1-\dfrac{3-\sqrt{3}}{3\cdot2} \right)^2AB^2=\\ &=\left[\left(\dfrac{3-\sqrt{3}}{6} \right)^2+\left(\dfrac{3+\sqrt{3}}{6} \right)^2 \right]AB^2=\dfrac{2(9+3)}{36}AB^2=\dfrac{2}{3}AB^2. \end{aligned}$

Ora ci chiediamo se quanto segue è verificato:

$\begin{aligned} \left(\dfrac{AB^2}{3} \right)^2+\left(\dfrac{AC^2}{6} \right)^2 \overset{?}{=} (2-\sqrt{3})AD^2 & \iff \dfrac{1}{9}+\dfrac{(\sqrt{3}-1)^4}{36}\overset{?}{=} (2-\sqrt{3}) \dfrac{4}{9} \\ &\iff \dfrac{1}{9}+\dfrac{(4-2\sqrt{3})^2}{36} \overset{?}{=} \dfrac{(2-\sqrt{3})4}{9} \\ &\iff \dfrac{1}{9}+\dfrac{(2-\sqrt{3})^2}{9} \overset{?}{=} \dfrac{4(2-\sqrt{3})}{9} \\ &\iff 8 -4\sqrt{3} \overset{?}{=} 8-4\sqrt{3}. \quad \checkmark \end{aligned}$

Abbiamo applicato il teorema del seno. ↩

Esercizio 31 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Sia $f_0(x)=e^x$

e $f_{n+1}(x)=x f^\prime_n(x)$

per $n=0,1,2,...$

.
Dimostrare che

$\sum_{n=0}^{\infty}\dfrac{f_n(1)}{n!}=e^e.$

Svolgimento.

Ponendo

$g_n(x)=f_n(x)e^{-x},$

è facile ottenere la seguente successione per ricorrenza per $g_n(x)$ :

$g_{n+1}(x)=x\left(g_n(x)+g_n^\prime(x) \right).$

Questa ricorsione, insieme al dato iniziale $g_0(x)=1$ , è soddisfatta dai polinomi di Bell $B_n(x)$ la cui funzione generatrice è

$B_n(x)=e^{-x}\sum_{k\ge0} \dfrac{k^n}{k!}x^k.$

Si ha dunque

$g_n(1)=B_n(1)=\dfrac{1}{e}\sum_{k\ge0}\dfrac{k^n}{k!}.$

La somma da calcolare vale così

$\begin{aligned} \sum_{n\ge0}\dfrac{f_n(1)}{n!} &= e\sum_{n\ge0}\dfrac{g_n(1)}{n!}= \\ &= \sum_{n\ge0}\dfrac{1}{n!}\sum_{k\ge0}\dfrac{k^n}{k!}=\\ &=\sum_{k\ge0}\dfrac{1}{k!}\sum_{n\ge0}\dfrac{k^n}{n!}= \\ &= \sum_{k\ge0}\dfrac{e^k}{k!}= \\ &= e^e. \end{aligned}$

Esercizio 32 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Sia $f:[0,+\infty)\to \mathbb{R}$

una funzione di classe $C^1$

nel proprio dominio tale che $\lim_{x\to +\infty}f(x)=c\in\mathbb{R}.$

Supponendo che l’integrale

$\int _{0}^{+\infty }{\frac {f(bx)-f(ax)}{x}}\,{\rm {d}}x$

esista finito, dimostrare che vale la seguente formula:

(87) $\begin{equation*} {\displaystyle {\int_{0}^{+\infty }{\frac {f(bx)-f(ax)}{x}}\,{\rm {d}}x=(f(0)-c))\ln \left({\frac {a}{b}}\right)}}\qquad \forall a,b>0. \end{equation*}$

Nota. Gli integrali di questo tipo vengono chiamati integrali di Frullani.

Svolgimento.

La funzione $f$

è di classe $C^1$

e, applicando il teorema fondamentale del calcolo integrale, abbiamo

(88) $\begin{equation*} \int_{a}^{b}f^\prime(xt)\,dt=\dfrac{f(xt)}{x}\bigg \vert^{b}_a=\dfrac{f(bx)-f(ax)}{x}. \end{equation*}$

Consideriamo il seguente integrale:

$\int_{0}^{M}\dfrac{f(bx)-f(ax)}{x}\,dx.$

Sfruttando (88), possiamo riscriverlo come

$\int_{0}^{M}\dfrac{f(bx)-f(ax)}{x}\,dx=\int_{0}^{M}\int_{a}^{b}f^\prime(xy)\,dy \,dx.$

È immediato osservare che la funzione $f^\prime(xy)$ è continua nel rettangolo $\{(x,y)\in \mathbb{R}^2:\,0\leq x \leq M,\, a\leq y \leq b \}$ , pertanto possiamo applicare il teorema di Fubini:

$\int_{0}^{M}\dfrac{f(bx)-f(ax)}{x}\,dx=\int_{0}^{M}\int_{a}^{b}f^\prime(xy)\,dy \,dx=\int_{a}^{b}\int_{0}^{M}f^\prime(xy)\,dx\,dy\eqqcolon I(M).$

Ora procediamo nel risolvere l’integrale appena ottenuto:

$\begin{aligned} I\left(M\right)&=\int_{a}^{b}\dfrac{f\left(xy\right)}{y}\bigg\vert^{M}_{0}\,dy=\int_{a}^{b}\dfrac{f\left(My\right)-f\left(0\right)}{y}\,dy=\\ &=\int_{a}^{b}\dfrac{f(My)}{y}\,dy-\int_{a}^{b}\dfrac{f(0)}{y}\,dy=\\ &=\int_{a}^{b}\dfrac{f(My)}{y}\,dy-f(0)\ln\left(\dfrac{b}{a}\right). \end{aligned}$

Passando al limite per $M\to +\infty$ ,

$\lim_{M\to +\infty}I\left(M\right)=\lim_{M\to +\infty}\int_{a}^{b}\dfrac{f(My)}{y}-f(0)\ln\left(\dfrac{b}{a}\right).$

Osserviamo che $f$ è continua in $[0,+\infty)$ con $\lim_{\lim_{x\to +\infty}}f(x)=c\in \mathbb{R}$ quindi il $\sup_{[0,+\infty]}\vert f \vert$ esiste finito e vale

$\left \vert \dfrac{f\left(My\right)}{y}\right \vert <\dfrac{\sup _{[0,+\infty)}\vert f \vert }{y}\qquad \forall y \in [a,b].$

In particolare

$\int_{a}^{b}\dfrac{\sup_{[0,+\infty)}\vert f\vert }{y}\,dy=\displaystyle\sup_{[0,+\infty)}\vert f \vert\, \ln\left(\dfrac{b}{a}\right)<+\infty$

pertanto possiamo applicare il teorema della convergenza dominata, ottenendo

$I=\int_{a}^{b}\lim_{M\to +\infty}\dfrac{f(My)}{y}\,dy-f(0)\ln \left(\dfrac{b}{a}\right),$

per cui

$\begin{aligned} I&=\int_{a}^{b}\dfrac{c}{y}\,dy-f(0)\ln\left(\dfrac{b}{a}\right)=c \ln y \bigg \vert^b_a-f(0)\ln\left(\dfrac{b}{a}\right)=\\ &=c\ln \left(\dfrac{b}{a}\right)-f(0)\ln \left(\dfrac{b}{a}\right)=\\ &=\left(c-f(0)\right)\ln\left(\dfrac{b}{a}\right)= \\ &= \left(f(0)-c\right)\ln\left(\dfrac{a}{b}\right), \end{aligned}$

da cui segue l’asserto.

Approfondimento.

Presentiamo ora una dimostrazione alternativa della formula per l’integrale di Frullani. La motivazione è che le ipotesi su $f$

possono essere rilassate rispetto a quelle presentate nel testo del problema. In questa dimostrazione alternativa, è sufficiente richiedere la continuità di $f$

. In realtà, la caratterizzazione precisa di quali siano le ipotesi “minime” affinché la formula rimanga valida non è elementare. Per chi fosse interessato, rimandiamo a questo articolo specialistico (Arias-de-Reyna 1990, Proc. Amer. Math. Soc., 109, 165). La dimostrazione che presentiamo è tratta da questo link.

Teorema. Sia $f$

: $[0,+\infty) \to \mathbb{R}$

una funzione continua su $(0,+\infty)$

tale che esistano finiti i due limiti:

$f_0 = \lim_{x\to0^+}f(x),\quad f_\infty = \lim_{x\to+\infty}f(x).$

Allora, presi $a,b > 0$ , vale:

(89) $\begin{equation*} \int_0^{+\infty} \frac{f(ax)-f(bx)}{x}\,\mathrm{d}x = (f_0 - f_\infty)\ln\left(\frac{b}{a}\right). \end{equation*}$

$\quad$

Dimostrazione. Siano $x$ , $y > 0$ . Possiamo scrivere:

$\int_0^{+\infty} \frac{f(at)-f(bt)}{t}\,\mathrm{d}t = \lim_{\substack {x\to0^+\\y\to+\infty}} \int_x^y \frac{f(at)-f(bt)}{t}\,\mathrm{d}t.$

Questa uguaglianza vale se i due limiti nel membro di destra esistono entrambi finiti. Procediamo a verificare questa ipotesi.

(90) $\begin{equation*} \begin{aligned} \int_x^y \frac{f(at)-f(bt)}{t}\,\mathrm{d}t = {} & \int_x^y \frac{f(at)}{t}\,\mathrm{d}t - \int_x^y \frac{f(bt)}{t}\,\mathrm{d}t = \\ = {} & \int_{ax}^{ay} \frac{f(u)}{u}\,\mathrm{d}u - \int_{bx}^{by} \frac{f(u)}{u}\,\mathrm{d}u = \\ = {} & \int_{ax}^{bx} \frac{f(u)}{u}\,\mathrm{d}u + \int_{bx}^{ay} \frac{f(u)}{u}\,\mathrm{d}u - \int_{bx}^{ay} \frac{f(u)}{u}\,\mathrm{d}u - \int_{ay}^{by} \frac{f(u)}{u}\,\mathrm{d}u = \\ = {} & \underbrace{\int_{ax}^{bx} \frac{f(u)}{u}\,\mathrm{d}u}_{I_1(x)} - \underbrace{\int_{ay}^{by} \frac{f(u)}{u}\,\mathrm{d}u}_{I_2(y)}. \end{aligned} \end{equation*}$

Valutiamo ora i limiti per $x \to 0^+$ e $y\to+\infty$ di questa espressione. Fortunatamente, possiamo occuparci di un termine alla volta, perché i due limiti sono disaccoppiati. Iniziamo da $I_1$ . Essendo $f$ continua, sappiamo che esistono

$m(x) = \min_{t\in[ax,bx]} f(t), \quad M(x) = \max_{t\in[ax,bx]} f(t).$

Abbiamo in particolare

$m(x)\ln\left(\frac{b}{a}\right) \leq \int_{ax}^{bx}\frac{f(u)}{u}\,\mathrm{d}u \leq M(x)\ln\left(\frac{b}{a}\right).$

Per il teorema del confronto, dato che per $x \to 0^+$ si ha $\lim m(x) = \lim M(x) = \lim f(x) = f_0$ , si conclude

$\lim_{x\to0^+}I_1(x) = f_0\ln\left(\frac{b}{a}\right).$

Passiamo a $I_2$ . Fissiamo $\varepsilon < 0$ . Dato che $f$ ammette limite per $x \to +\infty$ , esiste $x_0 > 0$ tale che per ogni $u \geq x_0$ si ha $|f(u)-f_\infty| < \varepsilon$ . Preso dunque $Y = x_0/a$ , per ogni $y \geq Y$ si ha:

$\begin{aligned} \left|\,\int_{ay}^{by}\frac{f(u)}{u}\,\mathrm{d}u - f_{\infty}\ln\left(\frac{b}{a}\right)\right| = {} & \left|\,\int_{ay}^{by}\frac{f(u)-f_\infty}{u}\,\mathrm{d}u\right| \leq \\ \leq {} & \int_{ay}^{by}\frac{\left|f(u)-f_\infty\right|}{u}\,\mathrm{d}u \leq \\ \leqslant {} & \varepsilon\int_{ay}^{by}\frac{1}{u}\,\mathrm{d}u = \varepsilon\ln\left(\frac{b}{a}\right). \end{aligned}$

Questo dimostra, per definizione di limite, che:

$\lim_{y\to+\infty} I_2(y) = f_\infty\ln\left(\frac{b}{a}\right).$

Questo completa la dimostrazione della formula (89):

$\begin{aligned} \int_0^{+\infty} \frac{f(at)-f(bt)}{t}\,\mathrm{d}t = {} & \lim_{\substack {x\to0^+\\y\to+\infty}} \int_x^y \frac{f(at)-f(bt)}{t}\,\mathrm{d}t = \\ = {} & f_0\ln\left(\frac{b}{a}\right)-f_{\infty}\ln\left(\frac{b}{a}\right) = \\ = {} & (f_0-f_{\infty})\ln\left(\frac{b}{a}\right). \end{aligned}$

Esercizio 33 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Dimostrare che $\displaystyle I=\int_{0}^{1}\dfrac{x^3-1}{\ln x}\,dx=\ln 4.$

Svolgimento 1.

Applichiamo la sostituzione $-\dfrac{1}{\ln x}=t$

, ottenendo

$I=\int_{0}^{+\infty}\dfrac{e^{-\frac{3}{t}}-1}{-\dfrac{1}{t}}\left(\dfrac{e^{\frac{-1}{t}}}{t^2}\right)\,dt=-\int_{0}^{+\infty}\dfrac{e^{-\frac{4}{t}}-e^{-\frac{1}{t}}}{t}.$

Sia

$f:(0,+\infty)\to \mathbb{R}, \qquad \qquad f(t)=\dfrac{e^{-\frac{4}{t}}-e^{-\frac{1}{t}}}{t}.$

La sua derivata

$f^\prime(t)=\dfrac{e^{-4t}\left(e^{\frac{3}{t}}\left(t-1\right)-t+4\right)}{t^3}$

è continua in $(0,+\infty)$ . Inoltre

$\lim_{t\to 0^+}e^{-\frac{1}{t}} \qquad \text{ e } \qquad \lim_{t\to +\infty}e^{-\frac{1}{t}}=1,$

quindi possiamo applicare la nota formula dell’integrale di Frullani¹⁵ dell’esercizio 32:

$I=\int_{0}^{+\infty}\dfrac{e^{-\frac{1}{t}}-e^{-\frac{4}{t}}}{t}\,dt=\left(0-1\right)\ln\frac{1}{4}=\ln 4,$

da cui segue l’asserto.

Gli integrali di Frullani sono integrali del tipo

$\int_{0}^{+\infty}\dfrac{f\left(\alpha x\right)-f\left(\beta x\right)}{x}\,dx$

dove $f:[0,+\infty)\to \mathbb{R}$ è una funzione tale che $\displaystyle\lim_{x\to +\infty}f(x)$ esiste finito e $f^\prime(x)$ risulta continua nel dominio di $f$ . Allora se l’integrale improprio converge vale la seguente formula

$\int_{0}^{+\infty}\dfrac{f\left(\alpha x\right)-f\left(\beta x\right)}{x}\,dx=\left(f(0)-\lim_{x\to+\infty}f(x)\right)\ln\left(\dfrac{\beta}{\alpha}\right).$

Nel caso particolare in cui $f$ non sia definita in $x=0$ ma $\displaystyle\lim_{x \to 0^+}f(x)$ esiste finito e l’integrale improprio converge, allora vale

$\int_{0}^{+\infty}\dfrac{f\left(\alpha x\right)-f\left(\beta x\right)}{x}\,dx=\left(\lim_{x\to 0^+}f(x)-\lim_{x\to+\infty}f(x)\right)\ln\left(\dfrac{\beta}{\alpha}\right).$

Il nostro caso presenta $\alpha=1$ e $\beta=\dfrac{1}{4}$ . ↩

Svolgimento 2.

Prima di presentare la risoluzione dell’esercizio, ricordiamo il seguente teorema.

Teorema 3.5 (derivazione sotto segno di integrale). Sia $F:[a,b]\rightarrow \mathbb{R}$

definita da

$F(\alpha)=\int_{t_1(\alpha)}^{t_2 (\alpha)}f(x,\alpha )\,dx.$

$\quad$

Consideriamo $F:(0,+\infty) \rightarrow \mathbb{R}$ tale che

$F(\alpha)=\int_{0}^{1}\dfrac{x^\alpha-1}{\ln x }\,dx= \int_{0}^{1}f(x,\alpha)\,dx\qquad \text{con}\,\, \alpha >0.$

Osserviamo che

$\lim_{x \rightarrow 0^+}f(x,\alpha)=0 \qquad \mbox{e} \qquad \lim_{x \rightarrow 1^-}f(x,\alpha)=\alpha$

e, definendo

$\tilde{f}(x,\alpha)= \begin{cases} f(x,\alpha), \quad & \text{per} \,\, x \in (0,1)\\ 0, & \text{per}\,\, x=0\\ \alpha, & \text{per}\,\, x=1, \end{cases}$

$\dfrac{dF}{d \alpha}(\alpha)=\int_{0}^{1}\dfrac{\partial f}{\partial \alpha}(x,\alpha)\,dx= \int_{0}^{1} \dfrac{x^\alpha \, \ln x}{\ln x }\,dx=\int_{0}^{1}x^\alpha\, dx =\dfrac{x^{\alpha+1}}{\alpha+1}\bigg \vert^1_0=\dfrac{1}{\alpha+1}.$

Ora integriamo rispetto al $\alpha$ e otteniamo

$F(\alpha)=\int \dfrac{1}{\alpha+1}\,d \alpha =\ln \left \vert 1+\alpha \right \vert +\text{costante}.$

Poniamo $\alpha=0$ e otteniamo

$F(0)=0=\ln 1+\text{costante} \iff \text{costante} =0,$

da cui

$F(\alpha)=\ln(1+\alpha ),$

ponendo ora $\alpha=1$ otteniamo

$F(3)=\int_{0}^{1}\dfrac{x^3-1}{\ln x }\,dx=\ln4,$

che è proprio il risultato cercato.

Esercizio 34 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che

$I= \int_{0}^{+\infty}\dfrac{e^{-ax}-e^{-bx}}{x}\sin\left(kx\right)\,dx=\arctan\left(\dfrac{b}{k}\right)-\arctan\left(\dfrac{a}{k}\right),$

con $a,b,k\in\left(0,+\infty\right)$ .

Svolgimento.

Consideriamo

$\int_{0}^{+\infty}e^{-\alpha x}\sin\left(kx\right)\,dx.$

Integrando per parti otteniamo

(91) $\begin{equation*} \int_{0}^{+\infty}e^{-\alpha x}\sin \left(kx\right)\,dx=\dfrac{k}{\alpha^2+k^2}\qquad \text{con}\,\,\alpha>0,\,k\in \mathbb{R}. \end{equation*}$

Osserviamo che

$\begin{aligned} \int_{0}^{+\infty}\dfrac{e^{-ax}-e^{-bx}}{x}\sin\left(kx\right)\,dx&=\int_{0}^{+\infty}dx\int_{a}^{b}e^{-\alpha x}\sin\left(kx\right)\,d\alpha=\\ &=\lim_{M\to +\infty}\int_{0}^{M}dx\int_{a}^{b}e^{-\alpha x}\sin \left(kx\right)\,d\alpha. \end{aligned}$

È chiaro che la funzione integranda $e^{-\alpha x}\sin\left(kx\right)$ nel dominio $\{(x,\alpha)\in \mathbb{R}^2:\,a\leq \alpha \leq b,\,0\leq x \leq M\}$ risulta integrabile, quindi possiamo applicare il teorema di Fubini:

$\int_{0}^{M}dx\int_{a}^{b}e^{-\alpha x}\sin\left(kx\right)\,d\alpha=\int_{a}^{b}d\alpha\int_{0}^{M}e^{-\alpha x}\sin \left(kx\right)\,dx.$

Osserviamo che, sfruttando (91), abbiamo

$\begin{aligned} &\int_{0}^{+\infty}dx\int_{a}^{b}e^{-\alpha x}\sin\left(kx\right)\,d\alpha=\int_{a}^{b}d\alpha\int_{0}^{+\infty}e^{-\alpha x}\sin\left(kx\right)\,dx, \end{aligned}$

che è equivalente a¹⁶

(92) $\begin{equation*} \begin{split} \int_{0}^{+\infty}\dfrac{e^{-a x}-e^{-bx}}{x}\sin\left(kx\right)\,dx &=\int_{a}^{b}\dfrac{k}{\alpha^2+k^2}\,d\alpha= \\ & = \arctan\left(\dfrac{\alpha}{k}\right)\bigg \vert^b_a= \\ &=\arctan\left(\dfrac{b}{k}\right)-\arctan\left(\dfrac{a}{k}\right), \end{split} \end{equation*}$

da cui segue l’asserto.

Nelle ipotesi di validità del teorema di Fubini per scambiare limite e integrale basta l’esistenza dell’integrale improprio dopo lo scambio. ↩

Esercizio 35 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Dimostrare che

(93) $\begin{equation*} I= \int_{0}^{a}\dfrac{\ln\left(x+a\right)}{x^2+a^2}\,dx=\dfrac{\pi}{8a}\ln 2+\dfrac{\pi\ln a}{4a}, \end{equation*}$

con $a>0.$

Svolgimento.

Riscriviamo $I$

come segue:

$I=\underbrace{\int_{0}^{a}\dfrac{\ln a}{x^2+a^2}\,dx}_{I_1}+\dfrac{1}{a^2}\underbrace{\int_{0}^{a}\dfrac{\ln\left(1+\dfrac{x}{a}\right)}{1+\dfrac{x^2}{a^2}}\,dx}_{I_2}.$

Calcoliamo $I_1$

$I_1=\dfrac{\ln a}{a}\arctan\left(\dfrac{x}{a}\right)\bigg \vert^1_0=\dfrac{\pi\ln a}{4 a}$

e poi calcoliamo $I_2$ operando la sostituzione $\dfrac{x}{a}=\tan \theta$ :

$I_2=a\int_{0}^{\frac{\pi}{4}}\ln \left(1+\tan\theta\right)\,d\theta.$

Operiamo una nuova sostituzione $\dfrac{\pi}{4}-\theta=\alpha$ e otteniamo

$\begin{aligned} I_2&=a\int_{0}^{\frac{\pi}{4}}\ln\left(1+\tan \left(\frac{\pi}{4}-\alpha\right)\right)\,d \alpha=\\ &=a\int_{0}^{\frac{\pi}{4}}\left(1+\frac{1-\tan\alpha}{1+\tan \alpha}\right)\,d\alpha=\\ &=a\int_{0}^{\frac{\pi}{4}}\ln 2 \,d\alpha -\underbrace{a\int_{0}^{\frac{\pi }{4}}\ln \left(1+\tan\alpha\right)\,d\alpha}_{I_2}, \end{aligned}$

ossia

(94) $\begin{equation*} I_2=\dfrac{a\pi }{8}\ln 2, \end{equation*}$

ottenendo infine

$I=I_1 + \dfrac{1}{a^2}\; I_2 = \dfrac{\pi}{8a}\ln 2+\dfrac{\pi\ln a}{4a},$

che è ciò che volevamo ottenere.

Esercizio 36 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Dimostrare che

$\begin{equation*} \int_{0}^{1}\dfrac{\ln\left(1+x^6\right)}{x^2+1}\,dx=-\sum_{n=1}^{+\infty}\dfrac{36n^2+36n+13}{3\left(2n+1\right)\left(6n+1\right)\left(6n+5\right)}\left(-1\right)^nH_n, \end{equation*}$

dove $H_n$ è l’n-esimo numero armonico.

Svolgimento.

Si ha

$\frac{36k^{2}+36k+13}{(6k+1)(6k+3)(6k+5)}=\left( \frac{1}{6k+1}\frac{1}{6k+3}+\frac{1}{6k+5}\right)$

e dunque dobbiamo sommare

(95) $\begin{equation*} \sum_{k\geq 0}\left( \frac{1}{6k+1}-\frac{1}{6k+3}+\frac{1}{6k+5}\right) \left( -1\right) ^{k}H_{k}. \end{equation*}$

Ricordando che vale

$\sum_{k\geq 0}H_{k}z^{k}=-\frac{\ln (1-z)}{1-z}$

e, sostituendo $z=-x^{6}$ , otteniamo

(96) $\begin{equation*} \sum_{k\geq 0}(-1)^{k}H_{k}x^{6k}=-\frac{\ln (1+x^{6})}{1+x^{6}}. \end{equation*}$

Integrando tra $0$ e $1$ :

$\sum_{k\geq 0}(-1)^{k}H_{k}\frac{1}{6k+1}=-\int_{0}^{1}\frac{\ln (1+x^{6})}{1+x^{6}}dx.$

Moltiplicando la (96) per $x^{2}$ e $x^{4}$ e integrando tra $0$ e $1$ otteniamo rispettivamente

$\begin{gathered} \sum_{k\geq 0}(-1)^{k}H_{k}\frac{1}{6k+3} =-\int_{0}^{1}x^{2}\frac{\ln (1+x^{6})}{1+x^{6}}dx, \\[4pt] \sum_{k\geq 0}(-1)^{k}H_{k}\frac{1}{6k+5} =-\int_{0}^{1}x^{4}\frac{\ln (1+x^{6})}{1+x^{6}}dx \end{gathered}$

e, sostituendo in (95), otteniamo

(97) $\begin{equation*} \begin{split} &\sum_{k\geq 0}\left( \frac{1}{6k+1}-\frac{1}{6k+3}+\frac{1}{6k+5}\right) \left( -1\right) ^{k}H_{k} = \\ & \qquad =-\int_{0}^{1}\frac{\ln (1+x^{6})}{1+x^{6}}dx+\int _{0}^{1}x^{2}\frac{\ln (1+x^{6})}{1+x^{6}}dx-\int_{0}^{1}x^{4}\frac{\ln (1+x^{6})}{1+x^{6}}dx=\\ &\qquad = -\int_{0}^{1}\frac{\ln \left( x^{6}+1\right) }{x^{2}+1}, \end{split} \end{equation*}$

da cui segue l’asserto.

Esercizio 37 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che

$\begin{equation*} I=\int_{0}^{+\infty} \dfrac{x\left(e^xx+e^x+1\right)}{e^{2x}-1}\,dx=\dfrac{7}{4}\zeta\left(3\right)+\dfrac{\pi^2}{6}. \end{equation*}$

Svolgimento 1.

Riscriviamo $I$

come segue:

$\begin{aligned} I&=\int_{0}^{+\infty}\dfrac{2xe^x\left(x+1\right)+2x}{2\left(e^{2x}-1\right)}= \\ &= \int_{0}^{+\infty}\dfrac{x^2e^x+x^2+2xe^x+2x+x^2e^x-x^2}{2\left(e^{2x}-1\right)}\,dx=\\ &=\int_{0}^{+\infty}\dfrac{\left(x^2+2x\right)\left(e^x+1\right)+x^2\left(e^{x}-1\right)}{2\left(e^{2x}-1\right)}\,dx=\\ &=\int_{0}^{+\infty}\dfrac{x^2}{2\left(e^x-1\right)\,dx}+\int_{0}^{+\infty}\dfrac{x}{\left(e^x-1\right)}\,dx+\int_{0}^{+\infty}\dfrac{x^2}{2\left(e^x+1\right)}\,dx=\\ &=\underbrace{\int_{0}^{+\infty}\dfrac{xe^{-x}}{\left(1-e^{-x}\right)}\,dx}_{I_1}+\underbrace{\int_{0}^{+\infty}\dfrac{x^2}{2\left(e^x-1\right)\,dx}}_{I_2}+\underbrace{\int_{0}^{+\infty}\dfrac{x^2}{2\left(e^x+1\right)}\,dx}_{I_3}. \end{aligned}$

Ricordiamo

$\psi _{n}(t)=(-1)^{n+1}\int _{0}^{+\infty }{\frac {x^{n}e^{-tx}}{1-e^{-x}}}dx\ }={(-1)^{n+1}\;n!\;\sum _{k=0}^{+\infty }{\frac {1}{(t+k)^{n+1}}}}\quad \text{con}\,\, n\in \mathbb{N$

e, imponendo $n=1,t=1$ , si trova

$I_1= \psi _{1}(1)=\sum_{k=0}^{+\infty}\dfrac{1}{\left(1+k\right)^2}=\zeta\left(2\right)=\dfrac{\pi^2}{6}.$

Ora utilizziamo la formula che lega la Zeta di Riemann con la funzione Gamma di Eulero

$\zeta (x)={\frac {1}{\Gamma (x)}}\int _{{0}}^{{+\infty }}{\frac {t^{{x-1}}}{e^{t}-1}}dx \quad \text{con}\,\, x>0$

che, imponendo $x=3$ , ci dà $I_2=\zeta\left(3\right).$ Per calcolare $I_3$ si può ricorrere alla formula

$\zeta\left(x\right)\left(1-2^{1-x}\right)\Gamma(x) = \int_0^\infty \frac{t^{x-1}}{e^t+1} \, dt\quad \text{con}\,\, x>0,$

da cui, imponendo $x=3$ , si ottiene $I_3=\dfrac{3}{4}\zeta\left(3\right)$ .

Infine si ha

$I=I_1+I_2+I_2=\dfrac{7}{4}\zeta\left(3\right)+\dfrac{\pi^2}{6},$

che è ciò che volevamo dimostrare.

Svolgimento 2.

Abbiamo $\int_{0}^{+\infty} x e^{-kx}\,dx = \dfrac{1}{k^2}$

e $\int_{0}^{+\infty}x^2 e^{-kx}\,dx = \dfrac{2}{k^3}$

per ogni $k>0$

, dunque

$\begin{aligned} I &= \int_{0}^{+\infty}\frac{x(xe^x+e^x+1)}{e^{2x}-1}\,dx \\ &= \int_{0}^{+\infty}\frac{x^2}{e^{x}-1}\,dx+\int_{0}^{+\infty}\frac{x}{e^{x}-1}\,dx-\int_{0}^{+\infty}\frac{x^2}{e^{2x}-1}\,dx \\ &= \sum_{n\geq 1}\int_{0}^{+\infty}x^2 e^{-nx}\,dx+\sum_{n\geq 1}\int_{0}^{+\infty}x e^{-nx}\,dx-\sum_{n\geq 1}\int_{0}^{+\infty}x^2 e^{-2n x}\,dx \\ &= \sum_{n\geq 1}\frac{2}{n^3}+\sum_{n\geq 1}\frac{1}{n^2}-\sum_{n\geq 1}\frac{1}{4n^3} = \\ &= \color{red}{\frac{7}{4}\,\zeta(3)+\zeta(2)}. \end{aligned}$

Esercizio 38 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

. Calcolare l’integrale

(98) $\begin{equation*} \displaystyle I\left(\alpha\right)= \int_{0}^{\pi}\ln\left(1+\alpha\cos x\right)\,dx \end{equation*}$

e determinare per quali valori di $\alpha \in \mathbb{R}$ esso è ben definito.

Svolgimento 1.

Ricordiamo il seguente risultato.

Teorema 3.6 (derivazione sotto il segno di integrale – versione 1). Sia $F:[a,b] \rightarrow \mathbb{R}$

tale che

(99) $\begin{equation*} F(\alpha)=\int_{t_1(\alpha)}^{t_2 (\alpha)}f(x,\alpha )\,dx. \end{equation*}$

Se $f(x,\alpha)$ e $\dfrac{\partial f}{\partial \alpha}(x,\alpha)$ sono continue in $\{(x,\alpha):a\leq \alpha \leq b,\,t_1(\alpha)\leq x \leq t_2(\alpha)\}$ e $t_1(\alpha)$ e $t_2(\alpha)$ sono di classe $C^1$ in $[a,b]$ , allora vale

(100) $\begin{equation*} \dfrac{dF}{d\alpha}(\alpha)=\int_{t_1(\alpha)}^{t_2(\alpha)}\dfrac{\partial f}{\partial \alpha }(x,\alpha)\,dx+f(t_2(\alpha),\alpha)\, \dfrac{dt_2}{d\alpha}(\alpha)-f(t_1(\alpha),\alpha)\,\dfrac{dt_1}{d\alpha}(\alpha). \end{equation*}$

$\quad$

Definiamo

$f:[0,\pi]\times A\to \mathbb{R},\qquad f(x,\alpha)=\ln\left(1+\cos \alpha\right)$

dove $A\subseteq\mathbb{R}$ è il dominio da determinare affinché $I$ abbia senso. Osserviamo che $f$ è continua nel suo dominio e $\dfrac{\partial f}{\partial \alpha}=\dfrac{\cos x}{1+\alpha \cos x}$ è continua nel dominio di $f$ , pertanto possiamo applicare il teorema 3.6: Deriviamo $I(\alpha)$ e otteniamo

$I^\prime\left(\alpha\right)=\int_{0}^{\pi}\dfrac{\cos x }{1+\alpha \cos x}\,dx.$

Il caso banale $\alpha=0$ è ovviamente verificato perché l’integrale risulta nullo, quindi ipotizzando $\alpha\neq0$ possiamo moltiplicare e dividere per $\alpha$ così ottenendo

$\begin{aligned} I^\prime(\alpha)&=\dfrac{1}{\alpha}\int_{0}^{\pi}\dfrac{\alpha \cos x}{1+\alpha \cos x}\,dx=\dfrac{1}{\alpha}\int_{0}^{\pi}\dfrac{1-1+\alpha\cos x }{1+\alpha\cos x}\,dx=\\ &=\dfrac{\pi}{\alpha}-\dfrac{1}{\alpha}\underbrace{\int_{0}^{\pi}\dfrac{1}{1+\alpha\cos x}\,dx}_{J(\alpha)}. \end{aligned}$

Per calcolare $J(\alpha)$ applichiamo le formule parametriche

$\begin{aligned} J(\alpha)&=2\int_{0}^{\pi}\dfrac{1}{t^2\left(1-\alpha\right)+1+\alpha}\,dt=\\ &=\dfrac{2}{\sqrt{1-\alpha}}\int_{0}^{+\infty}\dfrac{\sqrt{1-\alpha}}{\left(t\sqrt{1-\alpha}\right)^2+\sqrt{\left(1+\alpha\right)^2}}\,dt=\\ &=\dfrac{2}{\sqrt{1-\alpha}}\cdot \dfrac{1}{\sqrt{1+\alpha}}\cdot \arctan\left(\dfrac{t\sqrt{1-\alpha}}{\sqrt{1+\alpha}}\right)\bigg \vert^{+\infty}_0=\\ &=\dfrac{\pi}{\sqrt{1-\alpha^2}}, \end{aligned}$

da cui

$I^\prime(\alpha)=\dfrac{\pi}{\alpha}-\dfrac{1}{\alpha}\left(\dfrac{\pi}{\sqrt{1-\alpha^2}}\right)=\pi\left(\dfrac{1}{\alpha}-\dfrac{1}{\alpha\sqrt{1-\alpha^2}}\right).$

Integriamo da entrambe le parti

$\begin{aligned} I(\alpha)=\pi \ln\left(\left \vert \alpha\right \vert\right)-\pi\underbrace{\int\dfrac{1}{\alpha\sqrt{1-\alpha^2}}\,d\alpha}_{L\left(\alpha\right)} \end{aligned}$

e, per calcolare $L(\alpha)$ adoperiamo la sostituzione $\sin t =\alpha$ ottenendo,

$\int\dfrac{1}{\alpha\sqrt{1-\alpha^2}}\,d\alpha=\int\dfrac{1}{\sin t}\,dt.$

Per l’ultimo integrale riapplicando le note formule parametriche o sostituzione di Weierstrass

$\begin{aligned} \int\dfrac{1}{\alpha\sqrt{1-\alpha^2}}\,d\alpha&=\int\dfrac{1}{\sin t}\,dt= \\ &= \ln \left \vert \tan \left(\dfrac{t}{2}\right)\right \vert+c=\\ &=\ln \left \vert \dfrac{1-\cos t }{\sin t}\right \vert+c= \\ &= \ln \left \vert \dfrac{1-\sqrt{1-\alpha^2}}{\alpha}\right \vert+c, \end{aligned}$

cioè

$\begin{aligned} I(\alpha)&=\pi \ln\left(\left \vert \alpha\right \vert\right)-\pi\ln \left \vert \dfrac{1-\sqrt{1-\alpha^2}}{\alpha}\right\vert+c=\\ &=\pi\left(\ln \left \vert \alpha \right \vert +\ln \left \vert \dfrac{\alpha}{1-\sqrt{1-\alpha^2}}\right\vert\right)+c=\\ &=\pi\ln\left \vert \dfrac{\alpha^2}{1-\sqrt{1-\alpha^2}}\right \vert=\pi \ln \left \vert\dfrac{\alpha^2\left(1+\sqrt{1-\alpha^2}\right)}{1-\left(1-\alpha^2\right)} \right \vert+t=\\ &=\pi\ln \left \vert 1+\sqrt{1-\alpha^2}\right \vert+c. \end{aligned}$

Poniamo $\alpha=0$ e troviamo $c=-\pi \ln 2$ , pertanto

$\begin{aligned} I(\alpha)&=\pi\ln \left \vert 1+\sqrt{1-\alpha^2}\right \vert-\pi \ln 2= \\ &= \pi\ln \left \vert\dfrac{1+\sqrt{1-\alpha^2}}{2} \right \vert=\\ &=\pi\ln \left( \dfrac{1+\sqrt{1-\alpha^2}}{2}\right). \end{aligned}$

In particolare, imponendo

$1+\sqrt{1-\alpha^2}> 0,$

si trova che

$\alpha\in\left(-1,1\right),$

ovvero i valori di $\alpha$ per il quale l’integrale risulta ben definito.

Ora trattiamo i casi limiti ovvero $\alpha\to \pm 1.$ Osserviamo che

$I(-\alpha)=I\left(\alpha\right),$

pertanto basta studiare il caso $\alpha\to 1^-$ . Abbiamo dunque

$\lim_{\alpha \to 1^-}I(\alpha)=\lim_{\alpha \to 1^-}\pi\ln \left( \dfrac{1+\sqrt{1-\alpha^2}}{2}\right)=-\pi\ln\left(2\right)$

e possiamo estendere per continuità il dominio di $I(\alpha)$ in $x=\pm1$ , arrivando alla conclusione cercata:

$\tilde{\alpha}=\begin{cases} \pi\ln \left( \dfrac{1+\sqrt{1-\alpha^2}}{2}\right) &\text{per } x \in (-1,1)\\[10pt] -\pi\ln2 &\text{per } x=\pm 1. \end{cases}$

Nota. Si vuole far osservare al lettore che abbiamo applicato il famoso “trucco” di Feyman per risolvere l’integrale.

Svolgimento 2.

Preso un numero naturale positivo $n$

e definito $\zeta$

come $\exp\left(\dfrac{\pi i}{n}\right)$

(radice primitiva $2n$

-esima dell’unità) abbiamo

$x^{2n}-1 = (x-1)\prod_{k=1}^{2n-1}(x-\zeta^k),$

$\frac{x^{2n}-1}{x^2-1} = \prod_{k=1}^{n-1}(x-\zeta^k)(x-\zeta^{-k})=\prod_{k=1}^{n-1}\left(x^2+1-2x\cos\frac{\pi k}{n}\right),$

$\frac{x^{2n}-1}{(x^2-1)(x^2+1)^{n-1}}=\prod_{k=1}^{n-1}\left(1-\frac{2x}{x^2+1}\cos\frac{\pi k}{n}\right).$

Per ogni $\alpha\in(-1,1)$ possiamo porre $x=\frac{1-\sqrt{1-\alpha^2}}{\alpha}$ , ottenendo

$\prod_{k=1}^{n-1}\left(1-\alpha \cos\frac{\pi k}{n}\right) = \frac{1-x^{2n}}{(1-x^2)(1+x^2)^{n-1}},$

$\sum_{k=1}^{n-1}\log\left(1-\alpha\cos\frac{\pi k}{n}\right) = \log(1-x^{2n})-\log(1-x)-(n-1)\log(1+x^2).$

Moltiplicando ambo i membri per $\dfrac{\pi}{n}$ e passando al limite per $n\to +\infty$ , otteniamo

$\int_{0}^{\pi}\log(1-\alpha\cos t)\,dt = -\pi\log(1+x^2) = -\pi\log\left(\frac{2}{\alpha^2}(1-\sqrt{1-\alpha^2})\right),$

ossia

$\int_{0}^{\pi}\log(1-\alpha\cos t)\,dt = -\pi\log(1+x^2) = {\pi\log\left(\frac{1+\sqrt{1-\alpha^2}}{2}\right)}.$

Svolgimento 3.

Per ogni numero reale $R$

per cui $|R| < 1$

, abbiamo

$\frac{1}{1-R e^{i\theta}} = \sum_{n\geq 0} R^n e^{i\theta n},\qquad\frac{1}{1-R e^{-i\theta}} = \sum_{n\geq 0} R^n e^{-i\theta n}$

e, per differenza,

(101) $\begin{equation*} \frac{R\sin\theta}{(1+R^2)-2R\cos\theta} = \sum_{n\geq 0}R^n \sin(n\theta). \end{equation*}$

Notiamo che per ogni $\theta\in(-\pi,\pi)$ le serie di Fourier ci garantiscono

(102) $\begin{equation*} \theta = \sum_{n\geq 1}2\frac{(-1)^{n+1}}{n}\sin(n\theta), \end{equation*}$

dunque per ortogonalità

(103) $\begin{equation*} \int_{0}^{\pi}\frac{\theta\,R \sin\theta}{(1+R^2)-2R\cos\theta}\,d\theta = \pi\sum_{n\geq 1}\frac{(-1)^{n+1}}{n}R^n=\pi\log(1+R). \end{equation*}$

L’integrale

(104) $\begin{equation*} \int_{0}^{\pi}\log(1-\alpha\cos\theta)\,d\theta = \int_{0}^{\pi}\log(1+\alpha\cos\theta)\,d\theta \end{equation*}$

può essere d’altro canto ricondotto a (103) attraverso un passaggio di integrazione per parti e una sostituzione.

Esercizio 39 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Una pedina può muoversi lungo una riga di una scacchiera di una casella per volta, rimanendo in orizzontale; si chiede in quanti modi distinti la pedina può essere mossa da un punto ad un altro in modo che alla fine abbia compiuto in totale $n$

passi.

Svolgimento. Il problema dei path unidimensionali su reticolo discreto.

Affrontiamo in questa sezione dei metodi per risolvere in modo generale le diverse varianti del seguente problema: una pedina può muoversi lungo una riga di una scacchiera di una casella per volta, rimanendo in orizzontale si chiede in quanti modi distinti la pedina può essere mossa da un punto ad un altro in modo che alla fine abbia compiuto in totale $n$

passi. Considereremo dapprima il caso di scacchiera infinita, poi, il caso di una scacchiera semi-infinita infine il caso di una scacchiera finita. Vedremo che l’ultimo caso richiede un cambiamento di paradigma rispetto ai ragionamenti utili ai casi precedenti.

Problema 1.

Problema 1. Determinare il numero di path che conducono ad uno spostamento di $s$

passi verso destra in $n$

passi totali rispetto alla posizione originale.

$\quad$

Soluzione. Indichiamo con $p$ il numero di passi verso destra e con $q$ il numero di passi verso sinistra allora abbiamo: $p + q = n,\, p - q = s$ il sistema ammette soluzioni intere, esse $n$ ed $s$ hanno la stessa parità. Il numero totale di cammini si riduce al numero di permutazioni con ripetizione di due simboli in numero di $p$ e $q$ ripetizioni:

$\left(\begin{matrix}p+q\\ q\end{matrix} \right)=\left(\begin{matrix}p+q\\ p\end{matrix} \right)=\left(\begin{matrix}n\\\frac{n+s}{2}\end{matrix} \right).$

In tutto quel che segue terremo sempre presente che la probabilità è nulla se $n$ ed $s$ hanno parità opposta, mentre la esprimeremo in termini di $p=\dfrac{n+s}{2}$ e $q=\dfrac{n-s}{2}$ in tutti gli altri casi.

Problema 2.

Problema 2. Determinare il numero di path che conducono ad uno spostamento di $s$

passi verso destra in $n$

passi totali senza mai più toccare la casella originale.

$\quad$

Soluzione. Applichiamo il principio di riflessione di Desire Andrè. Cominciamo perciò a contare i cammini, fra tutti quelli che constano di $p$ passi verso destra e $q$ passi verso sinistra, che iniziano con un passo verso sinistra. Questi sono ovviamente tutti i cammini che constano di $p$ passi verso destra e $q - 1$ passi verso sinistra. Osserviamo adesso con D. Andrè che il numero di cammini che procedono verso destra per poi toccare nuovamente l’origine in uno o più punti possono essere posti, ciascuno, in corrispondenza con un solo cammino che procede inizialmente verso sinistra, semplicemente riflettendo rispetto all’origine il tratto iniziale che rimane a destra dell’origine. In base a questo ragionamento il numero di cammini che toccano nuovamente l’origine sono in complesso:

$2\left(\begin{matrix}p+q-1\\ p\end{matrix} \right),$

quindi la soluzione al problema proposto è:

$\left(\begin{matrix}p+q\\ p\end{matrix} \right)-2\left(\begin{matrix}p+q-1\\p\end{matrix} \right)=\left(1-\dfrac{2q}{p+q} \right)\left(\begin{matrix}p+q\\ p\end{matrix} \right).$

L’ultima espressione può essere spiegata oltrechè come conseguenza algebrica della prima con questo semplice argomento probabilistico di tutti i cammini di $p$ passi verso destra e $q$ passi verso sinistra, la frazione che inizialmente si muove verso sinistra è data da $\dfrac{q}{p+q}$ quindi la frazione che residua dopo averli contati due volte ciascuno e tolti dal mucchio è certamente $1-\dfrac{2q}{p+q}$ . Il problema simmetrico si ottiene da questa versione ponendo $s$ negativo, si può constatare che l’effetto del cambiamento di segno di $s$ è quello di scambiare $p$ con $q$ .

Lemma 1. In seguito sarà utile una ulteriore trascrizione delle nostre formule

$\left(\begin{matrix}p+q\\p \end{matrix}\right)-2\left(\begin{matrix}p+q-1\\p \end{matrix} \right)=\left(\begin{matrix}p+q-1\\ p-1\end{matrix} \right)-\left(\begin{matrix}p+q-1\\p\end{matrix} \right).$

$\quad$

Dimostrazione. La formula altri non è se non la formula di Tartaglia in uno dei suoi più riusciti travestimenti. La rimostreremo per piena soddisfazione del lettore nella seguente forma:

$\left(\begin{matrix}p+q\\p \end{matrix}\right)-\left(\begin{matrix}p+q-1\\p \end{matrix} \right)=\left(\begin{matrix}p+q-1\\ p-1\end{matrix} \right).$

Abbiamo:

$\begin{aligned} \left(\begin{matrix}p+q\\p\end{matrix}\right)-\left(\begin{matrix}p+q-1\\ p\end{matrix}\right) &= \dfrac{(p+q)!}{p!q!}-\dfrac{(p+q-1)!}{p!(q-1)!}=\\ &=\dfrac{(p+q)(p+q-1)!}{p(p-1)!q!}-\dfrac{q(p+q-1)!}{p(p-1)!q!}=\\ &=\dfrac{(p+q-q)(p+q-1)!}{p(p-1)!q!}= \\ &= \left(\begin{matrix}p+q-1\\ p-1\end{matrix} \right). \end{aligned}$

Problema 3.

Problema 3. Determinare il numero di path di $n$

passi totali che giungono ad $s$

passi a destra dell’origine senza mai andare a sinistra dell’origine (è tuttavia ammesso, diversamente dal problema precedente, che l’origine sia toccata nuovamente).

$\quad$

Soluzione. Il problema si riconduce al precedente con un semplice stratagemma andiamo a contare cioè i cammini che sono lunghi $n + 1$ passi e cominciano però dalla prima casella a sinistra dell’origine, quindi ci siamo ricondotti certamente al caso precedente e la soluzione è quindi data dalla formula:

$\left(\begin{matrix}p+q+1\\ p\end{matrix} \right)-2\left(\begin{matrix}p+q\\p\end{matrix} \right)=\left(\begin{matrix}p+q\\p\end{matrix} \right)-\left( \begin{matrix}p+q\\ p+1\end{matrix}\right)$

Applicazione. I numeri di Catalan che contano i cammini di $n$ passi che tornano all’origine senza mai attraversarla a sinistra si ottengono facilmente da questa formula nel caso in cui $p=q$ . Infatti risulta facilmente:

$\left(\begin{matrix} 2p+1\\ p+1\end{matrix}\right)-2\left(\begin{matrix}2p\\ p+1\end{matrix} \right)=\dfrac{1}{p+1}\left(\begin{matrix} 2p\\p\end{matrix}\right).$

Problema 4.

Problema 4. Determinare il numero di path di $n$

passi totali che giungono ad $s$

passi a destra dell’origine senza mai toccare la prima casella a sinistra dell’origine.

$\quad$

Soluzione. Anche in questo caso possiamo ricondurci al problema 2 o al problema 3 con uno stratagemma. La riconduzione al problema 5 avviene andando a contare i path che partono dalla prima casella a sinistra dell’origine senza più toccarla, occorre allora incrementare di un’unità i passi a sinistra mantenendo costanti i passi a destra. Del resto il problema è ovviamente equivalente al problema 3. E quindi come per il problema 6 la soluzione è:

$\left(\begin{matrix} p+q\\p\end{matrix}\right)-\left(\begin{matrix} p+q\\p+1\end{matrix}\right) .$

Problema 5.

Problema 5. Determinare il numero di path di $n$

passi totali che giungono ad $s$

passi a destra dell’origine senza mai oltrepassare la prima casella a sinistra dell’origine (stavolta è ammesso toccare la casella a sinistra dell’origine).

$\quad$

Soluzione. Anche in questo caso possiamo ricondurci al caso precedente o al caso equivalente del problema 3 ammettendo che l’origine nominale sia effettivamente il primo posto a sinistra dell’origine effettiva ed aumentando di un’unità i passi verso sinistra. In tal modo risulta:

$\begin{aligned} \left(\begin{matrix}p+q+1\\ p+1\end{matrix} \right)-\left(\begin{matrix}p+q+1\\ p+2\end{matrix} \right) &= \left(\begin{matrix}p+q\\ p\end{matrix} \right)+\left(\begin{matrix}p+q\\p+1\end{matrix} \right)-\left(\begin{matrix} p+q\\ p+1\end{matrix}\right)-\left(\begin{matrix}p+q\\p+2\end{matrix} \right)=\\ &=\left(\begin{matrix} p+q\\p+1\end{matrix}\right)-\left(\begin{matrix} p+q\\p+2\end{matrix}\right), \end{aligned}$

dove abbiamo applicato, come di consueto la regola di Tartaglia.

Problema 6.

Problema 6. Determinare il numero di path di $n$

passi totali che giungono ad $s$

passi a destra dell’origine senza mai oltrepassare la seconda casella a sinistra dell’origine.

$\quad$

Soluzione. Stavolta la soluzione richiede una piccola complicazione. Non sarà infatti sufficiente ricondursi ancora una volta al caso precedente, ma bisognerà tener presente che i cammini che muovono inizialmente con un passo verso sinistra devono essere scartati, per contare queste ultime ci ricondurremo allora al problema 3 diminuendo di una unità i passi verso sinistra e quindi in conclusione dovremo porre $p^\prime=p+1,\, q^\prime=q-1$ . Quindi unendo le due considerazioni la soluzione è

$\left(\begin{matrix}p+q+1\\ p+1\end{matrix} \right)-\left(\begin{matrix}p+q+1\\p+3\end{matrix} \right)-\left[\left(\begin{matrix}p+q\\ p+1\end{matrix} \right)-\left(\begin{matrix}p+q\\ p+2\end{matrix} \right) \right]$

e qui, applicando ancora la regola di Tartaglia si ottiene:

$\left(\begin{matrix}p+q\\ p\end{matrix} \right)-\left(\begin{matrix} p+q\\ p+3\end{matrix}\right).$

Problema 7.

Problema 7. Determinare il numero di path di $n$

passi totali che giungono ad $s$

passi a destra dell’origine senza mai oltrepassare la terza casella a sinistra dell’origine.

$\quad$

Soluzione. In questo caso si sfruttano le soluzioni ai problemi 6 ed 5. Infatti in primis si considerano tutti i path di che non si spingono oltre la seconda casella a sinistra con $p^\prime=p+1$ e $q^\prime=q$ quindi si tolgono i path che non si spingono oltre la prima casella a sinistra con $p^\prime=p+1$ e $q^\prime=q-1$ e che corrispondono al sottoinsieme dei path precedenti in cui il primo movimento avviene verso sinistra. Abbiamo quindi

$\left(\begin{matrix}p+q+1\\ p+2\end{matrix} \right)-\left(\begin{matrix}p+q+1\\ p+4\end{matrix} \right)-\left[ \left( \begin{matrix}p+q\\ p+1\end{matrix}\right)-\left(\begin{matrix}p+q\\ p+3\end{matrix} \right)\right]$

e qui, applicando ancora la regola di Tartaglia, si ottiene:

$\left(\begin{matrix} p+q\\ p\end{matrix}\right)-\left(\begin{matrix}p+q\\ p+4\end{matrix} \right).$

Siamo ora in condizione di enunciare il seguente teorema generale.

Teorema 3.7 Il numero di path consistenti di $p$

passi a destra e $q$

passi a sinistra che non si spingono oltre la $k^a$

casella a sinistra è dato da

$\left( \begin{matrix}p+q\\ p\end{matrix}\right)-\left(\begin{matrix} p+q\\ p+k+1\end{matrix}\right).$

$\quad$

Dimostrazione. La dimostrazione si ottiene per induzione basta infatti considerare la differenza fra il numero di path di $p + 1$ passi a destra e $q$ passi a sinistra che non si spingono oltre la $(k-1)^a$ casella a sinistra e togliere i path di $p + 1$ passi a destra e $q-1$ passi a sinistra che non si spingono oltre la $(k-2)^a$ casella a sinistra contandoli in accordo alla tesi induttiva. Otteniamo allora

$\left(\begin{matrix}p+q+1\\ p+1\end{matrix} \right)-\left(\begin{matrix} p+q+1\\ p+k+1\end{matrix}\right)-\left[ \left(\begin{matrix}p+q\\p+1\end{matrix} \right)-\left( \begin{matrix}p+q\\ p+k\end{matrix}\right)\right]$

che, in accordo alla regola di Tartaglia, si riduce a

$\left(\begin{matrix} p+q\\p\end{matrix}\right)-\left(\begin{matrix} p+q\\p+k+1\end{matrix}\right).$

Poichè l’ipotesi induttiva è stata dimostrata già per il caso $k=2$ , segue coerentemente per tutti i $k$ .

Problema 8.

Problema 8. Trovare i path consistenti di $p$

passi a destra e $q$

passi a sinistra che non oltrepassano la $j^a$

cella a sinistra del punto di partenza e la $k^a$

cella a destra del punto di partenza.

$\quad$

Una prima tentazione potrebbe essere quella di sfruttare quanto imparato dall’analisi dei casi semi-infiniti precedenti e scrivere qualcosa come:

$\left(\begin{matrix}p+q\\p\end{matrix} \right)-\left(\begin{matrix} p+q\\ p+k+1\end{matrix}\right)-\left(\begin{matrix}p+q\\q+j+1\end{matrix} \right).$

Ora sebbene questa soluzione si riveli corretta per valori non troppo grandi di $p + q$ rispetto a $j + k + 1$ per valori più grandi va incontro a doppi conteggi. Infatti per $p$ e $q$ sufficientemente grandi esistono path che superano sia la $k^a$ casella a sinistra che la $j^a$ casella a destra. E queste vengono contate due volte una volta fra i path che oltrepassano la $k^a$ casella a sinistra ed una volta fra quelle che oltrepassano la $j^a$ casella a destra.

Soluzione. È possibile concepire un modo completamente diverso per risolvere il problema avvalendosi dell’opportunità offerta dal fatto che il numero di posti accessibili dai path è finito. Imposteremo il conteggio in termini matriciali come un processo di Markov. In primo luogo numeriamo le caselle da sinistra a destra con i numeri $1$ a $N = j + k + 1$ . Supponiamo quindi di conoscere in quanti modi dopo un certo numero $n$ di passi la casella $s^a$ sia raggiungibile a partire dalla casella $o^a$ e formiamo con questi path il vettore $\left(\pi_1^{n},\dots,\pi_N^{n }\right)$ . Per determinare il numero di path che raggiungono la casella $s^a$ a partire dalla $o^a$ in $n + 1$ passi distinguere il caso dei punti interni per cui risulta $\pi_s^{(n+1)}=\pi_{s-1}^{(n)}+\pi_{s+1}^{(n)}$ dal caso di frontiera per cui è invece $\pi_1^{(n+1)}=\pi_2^n$ e $\pi_N^{(n+1)}=\pi_{N-1}^n$ . Pertanto il numero di path sarà espresso semplicemente dal nuovo vettore

$\left(\pi_1^{(n+1)},...,\pi_s^{(n+1)},...\pi_N^{(n+1)} \right)=\left(\pi_2^{(n)},...,\pi_{s-1}^{(n)} +\pi_{s+1}^{(n)},...\pi_{N-1}^{(n)}\right)$

ed in forma di vettoriale otteniamo

$\begin{pmatrix} \pi_1^{(n+1)}\\ \pi_2^{(n+1)}\\ \pi_3^{(n+1)}\\ \vdots\\ \pi_{N-1}^{(n+1)}\\ \pi_N^{(n+1)} \end{pmatrix}=\begin{pmatrix} 0&1&0&\cdots&0&0\\ 1&0&1&\cdots&0&0\\ 0&1&0&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&0&1\\ 0&0&0&\cdots&1&0 \end{pmatrix}\begin{pmatrix} \pi_1^{(n)}\\ \pi_2^{(n)}\\ \pi_3^{(n)}\\ \vdots\\ \pi_{N-1}^{(n)}\\ \pi_N^{(n)} \end{pmatrix}.$

Il problema della diagonalizzazione di queste matrici tridiagonali simmetriche di Toeplitz che indicheremo con $T_N$ è ampiamente trattato in letteratura perciò è ripetere i dettagli della trattazione ci limitiamo a considerare il seguente risultato: gli autovalori della matrice $N\times N$ sono gli $N$ numeri $\lambda_k=2\cos\left( \dfrac{k\pi}{N+1}\right)$ dove $k\in\{1,...,N\}$ e l’autovettore normale associato $\textbf{v}_k$ ha componenti $(\textbf{v}_k)_j=V_{kj}=\sqrt{\dfrac{2}{N+1}}\sin \left( \dfrac{kj\pi}{N+1}\right)$ quel che si evidenzia è che la matrice del cambiamento di base $V$ , formata dagli autovettori normali, che essendo relativi ad autovalori diversi di una matrice simmetrica reale sono anche mutuamente ortogonali, risulta ortogonale, e questo risultato è generale, ma nel caso specifico risulta anche simmetrica quindi risulta $VV^T=V^2=\textbf{1}$ . Questa circostanza rende particolarmente semplice esprimere il vettore canonico di base $\textbf{e}_k$ di componenti $(\textbf{e}_k)_j = \delta_{kj}$ in termini degli autovettori, infatti risulta:

$\textbf{e}_k=\sum_{j=1}^N V_{kj}\textbf{v}_j$

e quindi

$T_N^n\textbf{e}_k=\sum_{j=1}^N V_{kj}T_N^n\textbf{v}_j=\sum_{j=1}^N V_{kj}(\lambda_j)^n \textbf{v}_j,$

ovvero

$\begin{aligned} \mathrm{path}_n^N(k,l) &=(T_N^n \textbf{e}_k)_l=\sum_{j=1}^N V_{kj}(\lambda_j)^nV_{jl}=\\ &=\sum_{j=1}^N\dfrac{2}{N+1}\sin \left( \dfrac{kj\pi}{N+1}\right)\left( 2\cos \left(\dfrac{j\pi}{N+1} \right)\right)^n\sin\left(\dfrac{jl\pi}{N+1}\right) . \end{aligned}$

Questa formula esprime quindi il numero cercato di path che conducono in $n$ passi dalla posizione $k$ alla posizione $1$ e verifica una condizione di reciprocità per cui questo è anche il numero di path che conducono in $n$ passi dalla posizione $l$ alla posizione $k$ .

Problema 9.

Problema 9. È forse di qualche interesse risalire al polinomio caratteristico delle matrici di transizione $T_N$

dal polinomio rappresentativo del poligono regolare di $N + 1$

lati inscritto nella circonferenza unitaria con un vertice coincidente con l’unità.

$\quad$

Soluzione. Le proprietà della rappresentazione di Eulero dei numeri complessi implicano che il polinomio $z^{N+1} = 1$ ammetta per soluzioni tutti e soli i numeri $z_m = e^{\frac{\text{im}\pi}{N+1}}$ in modo che $\forall m$ :

$\begin{aligned} &\left(\cos\left(\dfrac{m\pi}{N+1} \right)+i \sin \left(\dfrac{m\pi}{N+1} \right) \right)^{N+1}=\\ & \qquad = \sum_{k=0}^{N+1}\left(\begin{matrix}N+1\\k\end{matrix} \right)\left(i\sin\left(\dfrac{m\pi}{N+1} \right) \right)^k \left(\cos\left( \dfrac{m\pi}{N+1}\right) \right)^{N+1-k}= \\ & \qquad = 1. \end{aligned}$

In particolare la parte reale di questa equazione complessa si scrive al modo seguente:

$\sum_{k=0}^{\lfloor \frac{N+1}{2} \rfloor}\left(\begin{matrix}N+1\\2k\end{matrix} \right)\left(-\sin^2\left(\dfrac{m\pi}{N+1} \right) \right)^k\left(\cos\left( \dfrac{m\pi}{N+1}\right) \right)^{N+1-2k}=1,$

da cui

$\sum_{k=0}^{\lfloor \frac{N+1}{2} \rfloor}\left( \begin{matrix}N+1 \\2k\end{matrix}\right)\left( \cos^2 \left( \dfrac{m\pi}{N+1}\right)-1\right)^k\left( \cos \left( \dfrac{m\pi}{N +1}\right)\right)^{N+1-2k}=1$

ed infine

$\sum_{k=0}^{\lfloor \frac{N+1}{2} \rfloor}\left(\begin{matrix} N+1\\2k\end{matrix} \right)\left( \sum_{l=0}^k \left( \begin{matrix} k\\l \end{matrix}(-1)^l \right) \cos^{2(k-l)}\right)\left(\cos\left(\dfrac{m\pi}{N+1} \right) \right)^{N+1-2k}=1,$

che può essere espressa in modo più compatto come

$\sum_{k=0}^{\lfloor \frac{N+1}{2} \rfloor}\sum_{l=0}^k\left(\begin{matrix} N+1\\2k \end{matrix} \right)\left( \begin{matrix} k\\l \end{matrix}\right)(-1)^l \left( \cos\left(\dfrac{m\pi}{N+1} \right)\right)^{N+1-2l}=1.$

Questa infine equivale a

$\sum_{k=0}^{\lfloor \frac{N+1}{2} \rfloor}\sum_{l=0}^k\left(\begin{matrix}N+1\\ 2k \end{matrix} \right)\left( \begin{matrix} k\\l \end{matrix}\right)\left( \dfrac{1}{2^{N+1-2l}}\right)(-1)^l\left( 2\cos\left( \dfrac{m\pi}{N+1}\right)\right)^{N+1-2l}=1,$

ovvero

$\sum_{k=0}^{\lfloor \frac{N+1}{2} \rfloor}\sum_{l=0}^k\left( \begin{matrix} N+1\\ 2k \end{matrix}\right)\left( \begin{matrix} k\\l \end{matrix}\right)(-4)^l\left( 2\cos \left( \dfrac{m\pi}{N+1}\right)\right)^{N+1-2l}=2^{N+1},$

nonchè, da ultimo, cambiando l’ordine di somma,

$\sum_{l=0}^{\lfloor \frac{N+1}{2} \rfloor}\left[\sum_{k=l}^{\lfloor \frac{N+1}{2} \rfloor}\left( \begin{matrix} N+1\\2k \end{matrix}\right) \left(\begin{matrix} k\\l \end{matrix} \right) \right](-4)^l\left(2\cos \left( \dfrac{m\pi}{N+1}\right) \right)^{N+1-2l}=2^{N+1},$

il quale è un polinomio a coefficienti interi di grado $N+1$ che ammette per radici tutti e soli gli $N +1$ autovalori, al più due volte molteplici, di $T_{N+1}$ ed in più la radice $z = 1$ .

Questo deve essere allora, per il teorema di unicità della fattorizzazione dei polinomi in una variabile, a meno di un solo coefficiente moltiplicativo, esattamente il polinomio caratteristico della matrice $T_N$ per il monomio $\lambda-1$ risulta quindi provato il seguente risultato.

Teorema 3.8 Esiste $K\in\mathbb{Z}$

tale che

$\det(T_{N+1}-\lambda1)(\lambda\textbf{1})=\dfrac{1}{K}\left(\sum_{l=0}^{\lfloor \frac{N+1}{2} \rfloor} \left[ \sum_{k=l}^{\lfloor \frac{N+1}{2} \rfloor} \left( \begin{matrix}N+1\\2k\end{matrix}\right)\left(\begin{matrix} k\\l \end{matrix} \right)\right](-4)^l\lambda^{N+1-2l}-2^{N+1} \right).$

$\quad$

La circostanza che ${K}$ appartenga a $\mathbb{Z}$ discende dal fatto che si dimostra facilmente che il polinomio caratteristico, a meno d’un segno, è monico. Naturalmente tutto il ragionamento può essere ripetuto a partire dal polinomio ciclotomico $(z^{N+1}-1):(z-1)=\displaystyle\sum_{k=0}^N z^k$ che ammette per fattori solamente i numeri $z-z_k$ con $\vert z_k\vert=1$ e Re $(z_k)=\dfrac{\lambda_k}{2}$ .

Vedremo che spesso questi polinomi sono riducibili nel campo degli interi (è certamente questo il caso in cui il numero dei lati del poligono è un numero composto).

Esempio 1. Trovare il numero di path di lunghezza $n$ che connettono il punto medio allo stesso punto medio per $N=7$ .

Applichiamo la formula generale. Nel caso specifico abbiamo $k=l=(N+1)/2$ quindi la formula risolutiva si riduce a:

$\mathrm{path}_n^7(4,4)=\sum_{k=1}^N \dfrac{2}{N+1}\sin^2\left(\dfrac{k\pi}{2} \right)\left( 2\cos\left(\dfrac{k\pi}{N+1} \right)\right)^n,$

ma, poichè risulta $\cos\left( \dfrac{k\pi}{N+1}\right)=\cos\left( \pi-\dfrac{k\pi}{N+1}\right)$ , abbiamo

$\mathrm{path}_n^7(4,4)=\sum_{k=1}^{\frac{N-1}{2}}2\cdot\dfrac{2}{N+1}\sin^2 \left( \dfrac{k\pi}{2}\right)\left(2\cos\left(\dfrac{k\pi}{N+1} \right) \right)^n$

se $n$ è pari a $0$ ed $n$ è dispari, ed inoltre i termini di indice pari di questa somma si annullano. In conclusione abbiamo

$\begin{aligned} \mathrm{path}_{2m}^7(4,4) &= \dfrac{1}{2}\left(\left(2\cos\left(\dfrac{\pi}{8} \right) \right)^{2m}+\left(2\cos\left( \dfrac{3\pi}{8}\right) \right)^{2m} \right)=\\ &=\left( \dfrac{(2+\sqrt{2})^m+(2-\sqrt{2})^m}{2}\right). \end{aligned}$

Osservazione. Il polinomio associato con le radici significative si riduce in questo caso ad un polinomio di grado $2$ perchè due soli sono gli autovalori coinvolti, in particolare si tratta degli autovalori corrispondenti alle parti reali dei numeri complessi che designano i vertici del quadrato inscritto nell’ottagono associato alla matrice di Toeplitz di ordine $7$ , contate ciascuna con le rispettive molteplicità (che valgono $2$ ). Nella fattispecie si vede quindi che il fattore rilevante del polinomio caratteristico può essere associato ad una semplice ricorsione di ordine $2$ : $(x-(2+\sqrt{2}))(x-(2-\sqrt{2}))=x^2-4x+2$ ovvero $a_{n+1}=4a_n-2a_{m-1}$ relazione ricorsiva che risulta effettivamente verificata dalla sequenza: $a_m=\mathrm{path}_{2m}^7 (4,4): 1,2,6,20,68,...$

È un esercizio istruttivo tentare di ricavare questa relazione ricorsiva per via diretta, si perviene più facilmente ad una relazione ricorsiva ternaria, che tuttavia nasconde la relazione minima che è binaria, come abbiamo ottenuto per via analitica. La sequenza così ottenuta è catalogata nell’enciclopedia on-line delle sequenze intere con il codice O.E.I.S… tuttavia non risulta alcuna associazione esplicita diretta con la nostra matrice tridiagonale di Toeplitz di ordine $7$ nè con il problema dello spoglio elettorale fra due limiti nel caso di eletti in condizioni di parità.

Esercizio 40 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

. Dimostrare che

(105) $\begin{equation*} I=\int_{0}^{+\infty}\dfrac{x \sinh x}{3+4 \sinh^2x}\,dx=\dfrac{\pi^2}{24}. \end{equation*}$

Svolgimento 1.

Il problema è il numero 12199 – 07 – S. Sharma (India) della rivista American Mathematical Monthly.

Si puo’ riscrivere (105) come segue¹⁷:

(106) $\begin{equation*} \begin{aligned} I & = \dfrac{1}{2}\int_{0}^{+\infty}\dfrac{x\,e^{-x}\left(1-e^{-2x}\right)}{e^{-4x}+e^{-2x}+1}\,dx \overset{*}{=}\\ & \overset{*}{=} -\dfrac{1}{2}\int_{0}^{1}\dfrac{\ln t\left(1-t^2\right)}{t^4+t^2+1}\,dt\overset{\star}{=} \\ &\overset{\star}{=} -\dfrac{1}{2}\int_{1}^{+\infty}\dfrac{\ln z\left(1-z^2\right)}{z^4+z^2+1}\, dz, \end{aligned} \end{equation*}$

dove in $*$ si usa la sostituzione $e^{-x}=t$ , mentre in $\star$ si pone $t=1/z$ . Si osserva che

(107) $\begin{equation*} 2I=-\dfrac{1}{2}\int_{0}^{+\infty}\dfrac{\ln z \left(1-z^2\right)}{z^4+z^2+1}\, dt=-\dfrac{1}{2}\underbrace{\int_{0}^{+\infty}f(z)\, dt}_{I_1}. \end{equation*}$

Si vuole calcolare $I_1$ applicando il teorema dei residui, quindi si consideri il percorso in figura 6.

$\quad$

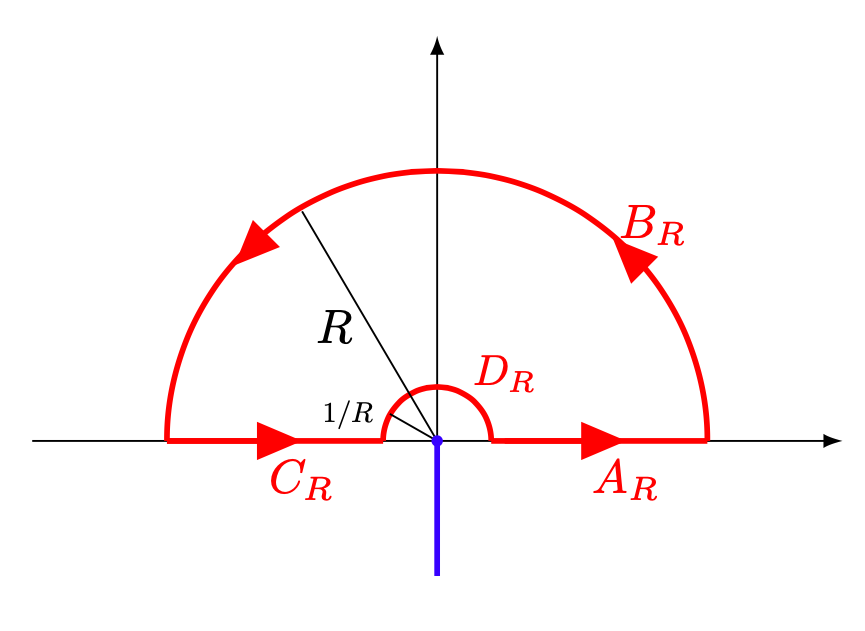
Figura 6: il percorso per l’applicazione del teorema dei residui.

$\quad$

Prendendo $\ln z=\ln \left \vert z \right \vert +i \arg z$ con $\arg z \in [-\pi/2,3/2\pi)$ , si consideri $\oint_C f(z)\, dz$ dove $C$ è il percorso chiuso in figura 6. Osserviamo che

(108) $\begin{equation*} z^4+z^2+1=0 \iff z_{1,2,3,4}=e^{\pm i \left(\frac{\pi}{3}+k\pi\right)}\quad \text{con} \,\, k=0,1, \end{equation*}$

da cui¹⁸

(109) $\begin{equation*} \begin{aligned} \oint_C f(z)\, dz &= \int_{A_R}f(z)\, dz+\int_{B_R}f(z)\, dz+\int_{C_R}f(z)\, dz+\int_{D_R}f(z)\, dz =\\ &= 2\pi i \left(\text{Res}\left(f(z),z_1\right)+\text{Res}\left(f\left(z\right),z_4\right)\right). \end{aligned} \end{equation*}$

Si nota che

(110) $\begin{equation*} \lim_{R \rightarrow +\infty}\int_{A_R}f(z)\, dz=I_1 \end{equation*}$

(111) $\begin{equation*} \lim_{R \rightarrow +\infty}\int_{C_R}f(z)\, dz=I_1+i\pi \int_{-\infty}^0\underbrace{\dfrac{1-z^2}{z^4+z^2+1}}_{g(z)}\,dz. \end{equation*}$

Ragionando sul cambio di variabile $t=1/z$ fatto in $\star$ , si ha

$\begin{aligned} \int_{-\infty}^0g(z)\,dz&=\int_{0}^{+\infty}g(z)\,dz= \\ &= \int_{0}^{1}g(z)\,dz+\int_{1}^{+\infty}g(z)\,dz=\\ &=-\int_{1}^{+\infty}g(z)\,dz+\int_{1}^{+\infty}g(z)\,dz= \\ &= 0. \end{aligned}$

Inoltre

(112) $\begin{equation*} \lim_{R \rightarrow +\infty}\int_{B_R}f(z)\, dz=0, \end{equation*}$

in quanto

(113) $\begin{equation*} \left \vert \int_{B_R}f(z)\, dz \right \vert \leq \int_{B_R} \left \vert f(z)\, dz\right \vert\leq \sup_{z \in \text{Im}\left( B_R\right)}\left \vert f(z)\right \vert \left \vert B_R\right \vert \sim \frac{\mathrm{cost}\ln R}{R} \underset{R \to +\infty}{\longrightarrow} 0. %\quad \text{per} \,\, R \rightarrow +\infty \end{equation*}$

In modo analogo si ottiene

(114) $\begin{equation*} \displaystyle\lim_{R \rightarrow +\infty}\int_{D_R}f(z)\, dz=0. \end{equation*}$

Adesso, procedendo con il calcolo dei residui, si ha

(115) $\begin{equation*} \text{Res}\left(f(z),z_1\right)=\lim_{z \rightarrow z_1}f(z)(z-z_1)=-\dfrac{\pi}{6}i \end{equation*}$

(116) $\begin{equation*} \text{Res}\left(f(z),z_4\right)=\lim_{z \rightarrow z_4}f(z)(z-z_4)=\dfrac{\pi}{3}i. \end{equation*}$

Da (109) vale

(117) $\begin{equation*} I_1+I_1=2\pi i\left(-\dfrac{\pi}{6}i+\dfrac{\pi}{3}i\right) \iff I_1=-\dfrac{1}{6}\pi^2 \end{equation*}$

e dunque (105) diviene

$2I=-\dfrac{1}{2}I_1=\dfrac{\pi^2}{12} \iff I=\dfrac{\pi^2}{24},$

da cui l’asserto.

Si ricorda che $\sinh x=\dfrac{e^{x}-e^{-x}}{2}.$ ↩

$z_1=e^{i\frac{\pi}{3}}$ , $z_4=e^{i\frac{2}{3}\pi}$ . ↩

Svolgimento 2.

Si ricorda che

(118) $\begin{equation*} I=-\dfrac{1}{2}\int_{0}^{1}\dfrac{\ln t\left(1-t^2\right)}{t^4+t^2+1}\,dt. \end{equation*}$

Osserviamo che

$\begin{aligned} \dfrac{1-t^2}{t^4+t^2+1}&=1-2t^2+t^4+t^6-2t^8+t^{10}+t^{12}-2t^{14}\dots=\\ &=\underbrace{1+t^6+t^{12}+\dots}_{t^{6n}}+\underbrace{t^{4}+t^{10}+\dots}_{t^{6n+4}}+\underbrace{-2t^2-2t^{8}-2t^{14}+\dots}_{-2t^{6n+2}}=\\ &=\sum_{n=0}^{+\infty}\left(t^{6n}+t^{6n+4}+-2t^{6n+2}\right)\quad \text{per}\,\, x \in \left(-1,1\right) , \end{aligned}$

da cui¹⁹

(119) $\begin{equation*} \begin{aligned} I & = -\dfrac{1}{2}\int_{0}^{1}\ln t \sum_{n=0}^{+\infty}\left(t^{6n}+t^{6n+4}+-2t^{6n+2}\right)\, dt=\\ & =-\dfrac{1}{2}\sum_{n=0}^{+\infty}\int_{0}^{1}\ln t \left(t^{6n}+t^{6n+4}-2t^{6n+2}\right)\, dt=\\ &=\dfrac{1}{2}\sum_{n=0}^{+\infty}\int_{0}^{1}\ln t\, t^{6n}\left(t^2-1\right)^2\,dt. \end{aligned} \end{equation*}$

Integrando per parti si ottiene

(120) $\begin{equation*} \begin{aligned} I&=-\dfrac{1}{2}\sum_{n=0}^{+\infty}\dfrac{1}{9}t^{6n+1}\Bigg(-\dfrac{9t^4}{\left(6n+5\right)^2}+\dfrac{2t^2}{\left(2n+1\right)^2}+ \\ &\qquad \qquad + 9\left(\dfrac{9t^4}{6n+5}-\dfrac{6t^2}{2n+1}+\dfrac{9}{6n+1}\right)\ln t -\dfrac{9}{\left(6n+1\right)^2}\Bigg)\Bigg \vert^1_0=\nonumber\\ &=-\dfrac{1}{18}\sum_{n=0}^{+\infty}\left(-\dfrac{9}{\left(6n+5\right)^2}+\dfrac{2}{\left(2n+1\right)^2}-\dfrac{9}{\left(6n+1\right)^2}\right)=\\ &=\underbrace{\dfrac{1}{2}\sum_{n=0}^{+\infty}\left(\dfrac{1}{\left(6n+5\right)^2}+\dfrac{1}{\left(6n+1\right)^2}\right)}_{I_1}-\underbrace{\dfrac{1}{9}\sum_{n=0}^{+\infty}\left(\dfrac{1}{\left(2n+1\right)^2}\right)}_{I_2}. \end{aligned} \end{equation*}$

Ora si noti che²⁰

(121) $\begin{equation*} \begin{aligned} I_1&=-\dfrac{1}{72}\left(\sum_{n=0}^{+\infty}\dfrac{1}{\left(n+\frac{5}{6}\right)^2}+\sum_{n=0}^{+\infty}\dfrac{1}{\left(n+\frac{1}{6}\right)^2}\right)= \\ &= -\dfrac{1}{72}\left(\psi_1\left(\dfrac{5}{6}\right)+\psi_1\left(\dfrac{1}{6}\right)\right)=\\ &=-\dfrac{1}{72}\left(\psi_1\left(1-\dfrac{1}{6}\right)+\psi_1\left(\dfrac{1}{6}\right)\right)= \\ &= -\dfrac{1}{72}\left(-1\right)\pi\left(-\dfrac{\pi}{\sin^2\left(\frac{\pi}{6}\right)}\right)= \\ &= \dfrac{\pi^2}{18} \end{aligned} \end{equation*}$

e dal problema di Basilea²¹ sappiamo che

(122) $\begin{equation*} I_2=\dfrac{1}{9}\sum_{n=0}^{+\infty}\left(\dfrac{1}{\left(2n+1\right)^2}\right)=\dfrac{1}{9}\cdot \dfrac{\pi^2}{8}=\dfrac{\pi^2}{72}. \end{equation*}$

Si può dunque riscrivere (105) come

(123) $\begin{equation*} I=\dfrac{\pi^2}{18}-\dfrac{\pi^2}{72}=\dfrac{\pi^2}{24}, \end{equation*}$

da cui la tesi.

Si dimostra facilmente grazie al teorema della convergenza dominata ↩

La funzione poligamma è data da $\psi_n(z)=(-1)^{n+1}n!\sum_{k=0}^{+\infty}\dfrac{1}{\left(z+k\right)^{n+1}}$ con $n>0$ e per ogni argomento complesso che non sia un intero negativo. Vale inoltre la regola di riflessione $\psi _{n}(1-z)+(-1)^{n+1}\psi _{n}(z)=(-1)^{n}\,\pi \,\frac{d^{n}}{dz^{n}}\cot(\pi z)$ . ↩

Vale

$\sum_{n=1}^{+\infty}\dfrac{1}{n^2}=\sum_{n=1}^{+\infty}\dfrac{1}{\left(2n\right)^2}+\sum_{n=1}^{+\infty}\dfrac{1}{\left(2n-1\right)^2}=\dfrac{1}{4}\sum_{n=1}^{+\infty}\dfrac{1}{\left(n\right)^2}+\sum_{n=1}^{+\infty}\dfrac{1}{\left(2n-1\right)^2} \iff \sum_{n=1}^{+\infty}\dfrac{1}{\left(2n-1\right)^2}=\dfrac{\pi^2}{8}. \quad$

↩

Esercizio 41 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che

(124) $\begin{equation*} \int_{0}^{+\infty} \frac{\sin(\sin(x))e^{\cos(x)}}{x}dx= \frac{\pi}{2}(e-1). \end{equation*}$

Svolgimento.

È possibile scrivere il seno di un numero complesso $z$

come parte immaginaria di $e^{iz}$

. Quindi, usando l’identità di Eulero $e^{iz}=\cos(z)+i \sin(z)$

, abbiamo

$\sin(\sin(x))= \Im(e^{i\sin(x)}),$

per cui

$\sin(\sin(x))e^{\cos(x)}= \Im\left(e^{i\sin(x)} e^{\cos(x)}\right)= \Im\left(e^{i\sin(x)+\cos(x)}\right)=\Im\left(e^{e^{ix}}\right).$

Usando l’espansione in serie della funzione esponenziale²² abbiamo

$\Im (e^{e^{ix}}) = \Im \left( \sum_{n=0}^{+\infty} \frac{e^{inx}}{n!} \right)= \sum_{n=0}^{+\infty} \frac{\Im(e^{inx})}{n!}= \sum_{n=0}^{+\infty} \frac{\sin(nx)}{n!}$

e, sostituendo quanto ottenuto nel membro di sinistra di (124), arriviamo a

$\int_{0}^{+\infty} \frac{\sin(\sin(x))e^{\cos(x)}}{x} \; dx=\int_{0}^{+\infty} \sum_{n=0}^{+\infty} \frac{\sin(nx)}{n!x} \; dx=\sum_{n=0}^{+\infty} \frac{1}{n!}\underbrace{\int_{0}^{+\infty} \frac{\sin(nx)}{x} \; dx}_{I}.$

L’integrale $I$ si puo’ risolvere con la sostituzione $t= nx$ con $n \geq 1$ , ottenendo il seguente integrale noto (detto integrale di Dirichlet)

$\int_{0}^{+\infty} \frac{\sin(t)}{t}dt,$

per il quale si sa che

(125) $\begin{equation*} \int_{0}^{+\infty} \frac{\sin(t)}{t}dt = \frac{\pi}{2}. \end{equation*}$

Si noti che, se $n=0$ , allora l’integrale è nullo. Utilizzando il risultato (125), abbiamo

$\sum_{n=1}^{+\infty} \frac{1}{n!}\int_{0}^{+\infty} \frac{\sin(nx)}{x}dx = \frac{\pi}{2} \sum_{n=1}^{+\infty} \frac{1}{n!},$

da cui il risultato finale²³

$\int_{0}^{+\infty} \frac{\sin(\sin(x))e^{\cos(x)}}{x}dx =\frac{\pi}{2}(e-1).$

Si ricorda che $e^x = {\sum_{n=0}^{+\infty} \dfrac{x^n}{n!}}$ ↩

Dalla definizione di numero di Nepero si ha

$e= \sum_{n=0}^{+\infty} \dfrac{1}{n!} \implies \sum_{n=1}^{+\infty} \dfrac{1}{n!} = e-1.$

↩

Esercizio 42 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

(126) $\begin{equation*} I=\int_{0}^{+\infty}\dfrac{\sinh x-x}{x^3 \cosh^2\left(\dfrac{x}{2}\right)}\, dx=4\sum_{n=0}^{+\infty}\dfrac{\zeta\left(2n\right)\left(1-2^{1-2n}\right)}{\left(2n+1\right)\left(2n+2\right)\left(2n+3\right)}. \end{equation*}$

Svolgimento.

Riscriviamo $I$

come²⁴

$\begin{equation*} I=\int_{0}^{+\infty}\dfrac{\sinh x-x}{x^3}\cdot\dfrac{2}{1+\cosh x }\, dx=4\int_{0}^{+\infty}\dfrac{e^x\left(\sinh x-x\right)}{x^3\left(e^x+1\right)^2}\,dx. \end{equation*}$

Ricordiamo lo sviluppo in serie del seno iperbolico:

$\begin{equation*} {\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}},} \end{equation*}$

per cui

$\begin{equation*} I=4\int_{0}^{+\infty}\sum_{n=1}^{+\infty}\,\dfrac{1}{\left(2n+1\right)!}\cdot \dfrac{e^xx^{2n-2}}{\left(e^x+1\right)^2}\, dx=4\sum_{n=1}^{+\infty}\dfrac{1}{\left(2n+1\right)!}\int_{0}^{+\infty}\dfrac{e^x\,x^{2n-2}}{\left(e^x+1\right)^2}\,dx. \end{equation*}$

Procediamo integrando per parti²⁵

$\begin{aligned} I&=4\sum_{n=1}^{+\infty}\dfrac{1}{\left(2n+1\right)!}\left(-\lim_{x\rightarrow+\infty} \left(\dfrac{x^{2n-2}}{e^x+1}+\dfrac{x^{2n-2}}{e^x+1}\right) \bigg\vert_{x=0}+\left(2n-2\right)\int_{0}^{+\infty}\dfrac{x^{2n-3}}{e^x+1}\,dx\right)=\\ &=4\sum_{n=1}^{+\infty}\dfrac{\left(2n-2\right)}{\left(2n+1\right)!}\int_{0}^{+\infty}\dfrac{x^{2n-3}}{e^x+1}\,dx= \\ &= 4\sum_{n=0}^{+\infty}\dfrac{2n}{\left(2n+3\right)!}\int_{0}^{+\infty}\dfrac{x^{2n-1}}{e^x+1}\,dx. \end{aligned}$

Si ricorda che

$\begin{equation*} \Gamma(s)\eta(s) = \int_0^{\infty} \frac{x^{s-1}}{e^x+1} \, dx \qquad \text{con}\,\, \text{Re} \left(s\right) > 0, \end{equation*}$

da cui²⁶

$\begin{aligned} I&=4\sum_{n=0}^{+\infty}\dfrac{\left(2n\right)\,\Gamma\left(2n\right)\, \eta\left(2n\right)}{\left(2n+1\right)!}= \\ &= 4\sum_{n=0}^{+\infty}\dfrac{\left(2n\right)\,\left(2n\right)!\,\eta\left(2n\right)}{\left(2n+1\right)\left(2n+2\right)\left(2n+1\right)\left(2n\right)!\left(2n\right)}=\\ &=4\sum_{n=0}^{+\infty}\dfrac{\eta\left(2n\right)}{\left(2n+1\right)\left(2n+2\right)\left(2n+3\right)}. \end{aligned}$

Utilizzando la seguente relazione notevole

$\begin{equation*} \zeta(s)=\frac{\eta(s)}{1-2^{1-s}}, \end{equation*}$

otteniamo

$\begin{equation*} I=4\sum_{n=0}^{+\infty}\dfrac{\zeta\left(2n\right)\left(1-2^{1-2n}\right)}{\left(2n+1\right)\left(2n+2\right)\left(2n+3\right)}, \end{equation*}$

da cui l’asserto.

Si ricorda che

$\cosh {\left({\frac {x}{2}}\right)}={\sqrt {\frac {1+\cosh {(x)}}{2}}}} \quad \text{e} \quad {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}.$

↩

Nel conto che segue si utilizza

$\int\dfrac{e^x}{\left(e^x+1\right)^2}\,dx=-\dfrac{1}{e^x+1}+\text{costante}.$

↩

$\Gamma\left(\left(2n\right)\right)=\dfrac{\left(2n\right)!}{2n}.$ ↩

Esercizio 43 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare l’integrale definito

(127) $\begin{equation*} I = \int_0^{+\infty}W\left(\frac{1}{x^2}\right)\mathrm{d}x, \end{equation*}$

dove $W(x) \equiv W_0(x)$ è la funzione di Lambert, definita come l’inversa della funzione $\varphi(y) = y\cdot e^y$ , con $y \geq -1/e$ .

Svolgimento.

Ricordiamo che la funzione $W$

di Lambert è l’inversa della funzione $\varphi(y) = y\cdot e^y$

. La funzione $\varphi$

non è iniettiva, per cui è necessario restringere il suo dominio per poter definire univocamente l’inversa. Come mostrato in figura, sui reali esistono quindi due rami della funzione di Lambert, indicati con $W_0(x)$

e $W_{-1}(x)$

, dove $W_0(x) \geqslant -1$

e $W_{-1}(x) \leqslant -1$

. I domini delle funzioni $W_0$

e $W_{-1}$

sono gli insiemi $[-1/e,+\infty)$

e $[-1/e,0)$

, rispettivamente. In questo esercizio, visto l’intervallo di integrazione, evidentemente $W(x) = W_0(x)$

. Per definizione di $W$

come inversa di $\varphi$

, vale la seguente proprietà fondamentale:

(128) $\begin{equation*} W(t\cdot e^t) = t \quad \forall t \in \mathbb{R}. \end{equation*}$

$\quad$

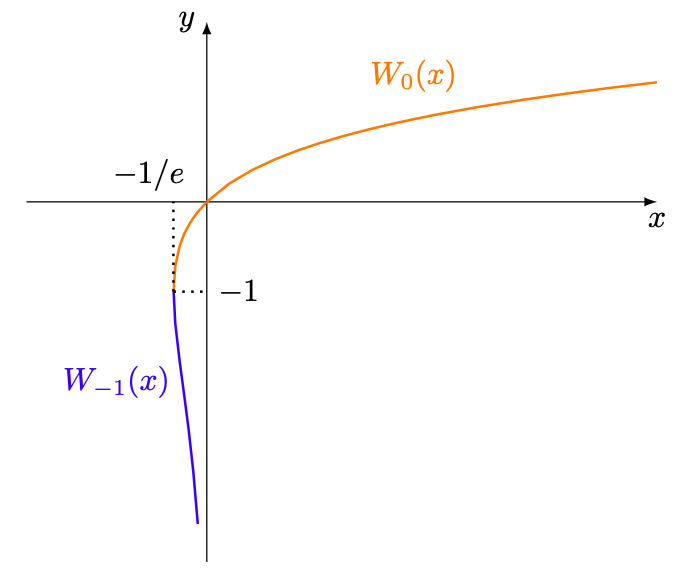
Procediamo ora al calcolo dell’integrale (127):

(129) $\begin{equation*} \begin{split} I &= \int_0^{+\infty} W\left(\frac{1}{x^2}\right)\mathrm{d}x = \\ &= \int_0^{+\infty} \frac{1}{2} W(t)\, t^{-3/2}\,\mathrm{d}t= \\ &= \frac{1}{2} \int_0^{+\infty} W(y e^y)\left(ye^y\right)^{-3/2}e^y(1+y)\,\mathrm{d}y = \\ &= \frac{1}{2} \int_0^{+\infty}\left(y^{-1/2}+y^{1/2}\right)e^{-y/2}\,\mathrm{d}y = \\ &= \int_0^{+\infty}\left(\frac{1}{\sqrt{2}}s^{-1/2} + \sqrt{2}s^{1/2}\right)e^{-s}\,\mathrm{d}s, \end{split} \end{equation*}$

dove nella seconda uguaglianza abbiamo effettuato la sostituzione $1/x^2 = t$ , e subito dopo nella terza uguaglianza abbiamo effettuato una seconda sostituzione $t = y e^y$ , da cui $\mathrm{d}t = (1+y)e^y\mathrm{d}y$ , così da sfruttare la (128) ed eliminare il riferimento a $W$ nella quarta uguaglianza.

Riconosciamo ora nell’ultimo membro della (129) la funzione $\Gamma$ di Euler, un’altra funzione speciale, che ricordiamo essere definita dal seguente integrale:

(130) $\begin{equation*} \Gamma(x) = \int_0^{+\infty} s^{x-1}e^{-s}\,\mathrm{d}s \quad \forall x > 0. \end{equation*}$

Possiamo infatti riscrivere l’ultimo membro della (129) così:

(131) $\begin{equation*} I = \frac{1}{\sqrt{2}}\,\Gamma\left(\frac{1}{2}\right) + \sqrt{2}\,\Gamma\left(\frac{3}{2}\right). \end{equation*}$

È noto che²⁷ $\Gamma(1/2) = \sqrt{\pi}$ e $\Gamma(3/2) = \sqrt{\pi}/2$ , per cui finalmente

$\boxcolorato{analisi}{\int_0^{+\infty}W\left(\frac{1}{x^2}\right)\mathrm{d}x = \sqrt{2\pi}.}$

Gli integrali nell’ultimo membro della (129) si possono ricondurre al noto integrale gaussiano. Per esempio, effettuando la sostituzione $s^{1/2} = u$ , si ha:

$\Gamma\left(\frac{1}{2}\right) = \int_0^{+\infty}s^{-1/2}e^{-s}\,\mathrm{d}s = \int_0^{+\infty} u^{-1} e^{-u^2} 2u\,\mathrm{d}u = \int_{-\infty}^{+\infty} e^{-u^2} \,\mathrm{d}u = \sqrt{\pi}.$

Il secondo integrale si ricava notando che $\Gamma(x+1) = x\,\Gamma(x)$ , per cui $\Gamma(3/2) = (1/2)\cdot\Gamma(1/2)$ . Infatti, integrando per parti:

$\Gamma(x+1) = \int_0^{+\infty}t^xe^{-t}\,\mathrm{d}t = \bcancel{\Big|-t^xe^{-t}\Big|_0^{+\infty}} + \int_0^{+\infty}xt^{x-1}e^{-t}\,\mathrm{d}t = x \int_0^{+\infty}t^{x-1}e^{-t}\,\mathrm{d}t = x\,\Gamma(x).$

↩

Esercizio 44 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

. Risolvere nei numeri interi positivi l’equazione

$\dfrac{1}{x} + \dfrac{1}{y}= \dfrac{1}{6}.$

Svolgimento 1.

Notiamo che $x=y=12$

è una soluzione; altre soluzioni intere avranno la forma generale

$(x,y)=(12,12)+t(m,n),$

dove possiamo assumere che m ed n siano interi privi di fattori comuni, che abbiamo raccolto nel parametro $t$ che, nel caso in cui cercassimo tutte le soluzioni razionali potrebbe essere un numero razionale.

Riscriviamo l’equazione:

$6(x+y)=xy$

Sostituendo la parametrizzazione con un minimo di algebra troviamo che se $t$ è non nullo (come assumiamo perché stiamo cercando soluzioni diverse da $(12,12)$ ):

$-6(m+n)=mnt \implies t=-6 \dfrac{(m+n)}{mn}.$

Quindi

$(x,y)=(12,12)+ -6 (m+n) \left( \dfrac{1}{n}, \dfrac{1}{m}. \right)$

Queste sono, al variare di $m$ ed $n$ tutte le soluzioni razionali, l’equazione è invariante per moltiplicazione di $m$ ed $n$ per un fattore comune. Adesso se cerchiamo le soluzioni intere, a parte il caso banale $m=n$ che dà la soluzione $(x,y)=(0,0)$ da rigettare, c’è il caso in cui $m$ ed $n$ siano divisori interi di $6$ , notiamo infatti che poiché abbiamo ipotizzato $m$ ed $n$ coprimi deve risultare che $\frac{m}{n}$ o la sua reciproca è una frazione irriducibile, ne consegue che se assumiamo n più grande di $m$ allora $n$ deve necessariamente dividere $6$ perché non può dividere $m+n$ , per quanto riguarda $m$ o è un’unità oppure è diverso da un’ unità e deve dividere $6$ perché non divide $m+n$ e quindi in entrambi i casi è un divisore di $6$ . Allora dovremmo cercare $m$ ed $n$ fra i divisori di $6$ se vogliamo generare tutte le soluzioni intere:

$(m,n) \in [(1,2); (2,3); (1,6); (1,3); (-1,2); (-2,3); (-1,6); (-1,3)] \quad \mbox{e simmetriche,}$

da cui

$(x,y) \in [(-6,3); (-3,2); (-30,5); (-12,4); (18,9); (15,10); (42,7); (24,8)] \quad \mbox{e simmetriche.}$

Le soluzioni cercate sono:

$(x,y) \in [(18,9); (15,10); (42,7); (24,8)] \quad \mbox{o le simmetriche}$

Svolgimento 2.

Riscrivendo l’equazione come $6(x+y)=xy$

vediamo che $6$

deve dividere $xy$

Primo caso. Se $6$ divide uno dei sue fattori, poniamo che sia $\dfrac{x}{6}=m$ ; allora l’equazione può essere riscritta come: $1= \dfrac{1}{m}+\dfrac{6}{y}$ , ovvero $\dfrac{m-1}{m}= \dfrac{6}{y}$ cioè $m-1$ divide $6$ . Quindi abbiamo le seguenti possibili soluzioni: $m-1 \in [1,2,3,6]$ , cui corrispondono subito le soluzioni

$(x,y) \in [(12,12); (18,9); (24,8); (42,7)]$

e simmetriche.

Secondo caso. Supponiamo che $x$ non è divisibile per $6$ ma per $2$ e quindi $y$ per $4$ . In tal caso ponendo $m= \dfrac{x}{2}$ e $n= \dfrac{y}{3}$ risulta $1= \dfrac{2}{m}+ \dfrac{3}{n}$ ; quindi $\dfrac{m-2}{m}= \dfrac{3}{n}$ , ovvero $m-2=3$ e $n=5$ , da cui $(x,y)=(5,10)$ .

Esercizio 45 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Dimostrare che

(132) $\begin{equation*} I=\int\left(\dfrac{\ln x \ln \left(1-x\right)}{x}\right)\,dx=\mathrm{Li}_3(x)-\mathrm{Li}_2(x)\ln x +c \end{equation*}$

e, sfruttando (132), verificare che

(133) $\begin{equation*} J=\int^1_0\left(\dfrac{\ln x \ln \left(1-x\right)}{x}\right)\,dx=\zeta\left(3\right). \end{equation*}$

Svolgimento.

Si ricorda che

$\begin{equation*} \text{Li}_{s+1}(x)=\int_{0}^{x}\dfrac{\text{Li}_{s}(t)}{t}\,dt\quad \text{con}\,\,s\in\mathbb{C} \end{equation*}$

ed in particolare, con $s=1$ , vale

(134) $\begin{equation*} \text{Li}_2(x)=-\int_{0}^{x}\dfrac{\ln\left(1-t\right)}{t}\,dt. \end{equation*}$

Calcoliamo $I$ integrando per parti e sfruttando (132) e (134):

$\begin{aligned} I&=-\text{Li}_2(x)\ln x +\int\dfrac{\text{Li}_2(x)}{x}\,dx =-\text{Li}_2(x)\ln x+\text{Li}_3(x)+c. \end{aligned}$

Calcoliamo $J$ sfruttando $I$

$\begin{aligned} J&=-\text{Li}_2(1)\ln 1 +\text{Li}_3(1)+\lim_{x\to0^+}\left(\text{Li}_3(x)-\text{Li}_2(x)\ln x\right)=\\ &=\text{Li}_3(1)+\text{Li}_3(0)+\lim_{x\to0^+}\ln x\int_{0}^{x}\dfrac{\ln \left(1-t\right)}{t}\,dt=\\ &=\text{Li}_3(1)-\lim_{x\to0^+}\ln x\int_{0}^{x}\left(1+o\left(1\right)\right)\,dt=\\ &=\text{Li}_3(1)-\underbrace{\lim_{x\to 0^+}\ln x \left(x+o\left(x\right)\right)}_{=0}=\\ &=\text{Li}_3(1). \end{aligned}$

Ricordiamo ora un’importante relazione che lega la zeta di Riemann con la funzione Polilogaritmo:

(135) $\begin{equation*} {\displaystyle \operatorname {Li} _{s}(1)=\zeta (s)\qquad (\operatorname {Re} (s)>1)}. \end{equation*}$

Con $s=3$ segue $\text{Li}_3(1)=\zeta(3)$ da cui l’asserto.

Esercizio 46 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che

(136) $\begin{equation*} I=\int_{0}^{1}\left(\dfrac{\ln \left(1-x\right) \ln \left(1+x\right)}{x}\right)\,dx=-\dfrac{5}{8}\zeta\left(3\right). \end{equation*}$

Inoltre, sfruttando (136), dimostrare che

(137) $\begin{equation*} J=\int_{0}^{1}\dfrac{\ln\left(1+x\right)\ln\left(1-x-x^2+x^3\right)}{x}\,dx=-\zeta(3). \end{equation*}$

Svolgimento.

Si ricorda il seguente fatto:

$\alpha \beta =\dfrac{1}{2}\left(\alpha+\beta\right)^2-\dfrac{1}{2}\alpha^2-\dfrac{1}{2}\beta^2.$

Ponendo $\alpha=\ln\left(1-x\right)$ e $\beta=\ln\left(1+x\right)$ , si ottiene

$I=\underbrace{\dfrac{1}{2}\int_{0}^{1}\dfrac{\ln^2\left(1-x^2\right)}{x}\,dx}_{J_1}-\underbrace{\dfrac{1}{2}\int_{0}^{1}\dfrac{\ln^2\left(1-x\right)}{x}\,dx}_{J_2}-\dfrac{1}{2}\underbrace{\int_{0}^{1}\dfrac{\ln^2\left(1+x\right)}{x}\,dx}_{J_3}.$

Osserviamo che, operando la sostituzione $x=t^2$ , l’integrale $J_2$ diventa

$J_2=\dfrac{1}{2}\int_{0}^{1}\dfrac{\ln^2\left(1-x\right)}{x}\,dx=\int_{0}^{1}\dfrac{\ln^2\left(1-t^2\right)}{t}\,dt=2J_1,$

da cui

$I=J_1-2J_1-\dfrac{1}{2}J_3 \iff I=-J_1-\dfrac{1}{2}J_3.$

Calcoliamo $J_1$ in due modi differenti.

Per prima cosa osserviamo quanto segue:

$\begin{gathered} \text{Li}_2\left(1-x^2\right)=\int_{0}^{1-x^2}-\dfrac{\ln\left(1-t\right)}{t}\,dt, \implies \text{Li}^\prime_2(1-x^2)=\dfrac{2x\ln x^2}{1-x^2}, \\ \text{Li}_3\left(1-x^2\right)=\int_{0}^{1-x^2}\dfrac{\text{Li}_2\left(t\right)}{t}\,dt \implies \text{Li}'_3\left(1-x^2\right)=\dfrac{2x\text{Li}_2\left(1-x^2\right)}{x^2-1}. \end{gathered}$

I risultati precedenti ci serviranno per calcolare $J_1$ . Procediamo integrando per parti:

$\begin{aligned} J_1&=\dfrac{1}{2}\int_{0}^{1}\dfrac{\ln^2\left(1-x^2\right)}{x}\,dx= \\ &= \dfrac{1}{2}\left(\underbrace{\ln x \ln^2\left(1-x^2\right)\bigg\vert^1_0}_{=0}-2\int_{0}^{1}\dfrac{-2x\ln\left(1-x^2\right)\ln x }{1-x^2}\right)=\\ &=\dfrac{1}{2}\int_{0}^{1}\dfrac{2x\ln x^2}{1-x^2}\cdot \ln\left(1-x^2\right)\,dx= \\ &= \dfrac{1}{2}\int_{0}^{1}\text{Li}_2^\prime\left(1-x^2\right)\cdot \ln\left(1-x^2\right)\,dx=\\ &=\underbrace{\dfrac{1}{2}\text{Li}_2\left(1-x^2\right)\ln\left(1-x^2\right)\bigg\vert^1_0}_{=0}-\dfrac{1}{2}\int_{0}^{1}\dfrac{-2x\text{Li}_2\left(1-x^2\right)}{1-x^2}\,dx. \end{aligned}$

Dunque si ottiene

$\begin{aligned} J_1 &= -\dfrac{1}{2}\int_{0}^{1}\dfrac{2x\text{Li}_2\left(1-x^2\right)}{x^2-1}\,dx= \\ &= -\dfrac{1}{2}\int_{0}^{1}\text{Li}^\prime_3\left(1-x^2\right)\,dx=\\ &=-\dfrac{1}{2}\text{Li}_3\left(1-x^2\right)\bigg \vert^1_0= \\ &= \dfrac{1}{2}\text{Li}_3(1)= \\ &= \dfrac{1}{2}\zeta(3), \end{aligned}$

dove nell’ultimo passaggio abbiamo sfruttato il fatto che

$\text{Li}_s\left(1\right)=\zeta\left(s\right)\qquad \text{con}\,\,\text{Re}(s)>1.$

Era altresì possibile procedere come segue. Applicando la sostituzione $x^2=1-t$ , otteniamo

$\begin{aligned} J_1&\overset{\triangle}{=}\dfrac{1}{4}\int_{0}^{1}\dfrac{\ln^2 t}{1-t}\,dt= \\ &= \dfrac{1}{4}\int_{0}^{1}\sum_{k=0}^{+\infty}t^k\ln^2 t \,dt=\\ &\overset{\clubsuit}{=}\dfrac{1}{4}\sum_{k=0}^{+\infty}\int_{0}^{1}t^k\ln^2 t \,dt= \\ &= \dfrac{1}{4}\sum_{k=0}^{+\infty}\left(\dfrac{t^{k+1}}{k+1}\ln^2 t\bigg\vert^1_0-\int_{0}^{1}\dfrac{2t^{k+1}\ln t}{t\left(k+1\right)}\,dt\right)=\\ &=-\dfrac{1}{2}\sum_{k=1}^{+\infty}\dfrac{1}{k+1}\int_{0}^{1}t^k\ln t \,dt, \end{aligned}$

dove in $\triangle$ abbiamo usato lo sviluppo notevole $\sum_{k=0}^{+\infty}x^k=\dfrac{1}{1-x}$ e in $\clubsuit$ abbiamo scambiato la serie con l’integrale perché $\left \vert t^k\ln^2 t \right \vert \leq \ln^2 t \,\,\forall t \in (0,1)$ e in particolare $\int_{0}^1\ln^2 t \,dt=2$ quindi è possibile applicare il teorema della convergenza dominata. Proseguendo nei calcoli si giunge a

$\begin{aligned} J_1 &= -\dfrac{1}{2}\sum_{k=1}^{+\infty}\dfrac{1}{k+1}\left(\underbrace{\dfrac{t^{k+1}}{k+1}\ln t\bigg\vert^1_0}_{=0}-\int_{0}^{1}\dfrac{t^{k+1}}{k+1}\cdot\dfrac{1}{t}\,dt \right)=\\ &=\dfrac{1}{2}\sum_{k=0}^{+\infty}\dfrac{1}{\left(k+1\right)^2}\int_{0}^{1}t^k\,dt= \\ &= \dfrac{1}{2}\sum_{k=0}^{+\infty}\dfrac{1}{\left(k+1\right)^2}\cdot \dfrac{t^{k+1}}{k+1}\bigg\vert^1_0=\\ &=\dfrac{1}{2}\sum_{k=0}^{+\infty}\dfrac{1}{\left(k+1\right)^3}= \\ &\overset{k+1=t}{=}\dfrac{1}{2}\sum_{t=1}^{+\infty}\dfrac{1}{t^3}= \\ &= \dfrac{\zeta\left(3\right)}{2}. \end{aligned}$

Non ci resta che calcolare $J_3$ . È utile ricordare quanto segue:

$\alpha^2=\dfrac{1}{2}\left(\alpha+\beta\right)^2+\dfrac{1}{2}\left(\beta-\alpha\right)^2-\beta^2.$

Ponendo

$\alpha=\ln \left(1+x\right)\quad \text{e}\quad \beta=\ln\left(1-x\right),$

si ottiene

$\begin{aligned} \ln^2 \left(1+x\right)&=\dfrac{1}{2}\left(\ln \left(1+x\right)+\ln\left(1-x\right)\right)^2+\dfrac{1}{2}\left(\ln\left(1-x\right)-\ln \left(1+x\right)\right)^2-\ln^2\left(1-x\right)=\\ &=\dfrac{1}{2}\ln^2\left(1-x^2\right)+\dfrac{1}{2}\ln^2\left(\dfrac{1-x}{1+x}\right)-\ln^2\left(1-x\right), \end{aligned}$

da cui

$\begin{aligned} J_3&=\int_{0}^{1}\dfrac{\ln^2\left(1+x\right)}{x}\,dx=\\ &=\int_{0}^{1}\dfrac{\ln^2\left(1-x^2\right)}{2x}\,dx+\underbrace{\dfrac{1}{2}\int_{0}^{1}\frac{1}{x} \ln^2\left(\frac{1-x}{1+x}\right)\,dx}_{J_4}-\int_{0}^{1}\dfrac{\ln^2\left(1-x\right)}{x}\,dx=\\ &=J_1+J_4-4J_1= \\ &= -3J_1+J_4= \\ &= -\dfrac{3}{2}\zeta(3)+J_4. \end{aligned}$

Calcoliamo $J_4$ . Operiamo la sostituzione

$\begin{aligned} &\frac{1-x}{1+x}=t+1 \iff -1+\dfrac{2}{x+1}=t \iff \dfrac{2}{x+1}=t, \end{aligned}$

da cui si ricava

(138) $\begin{equation*} \begin{split} \dfrac{x+1}{2}=\dfrac{1}{t+1} \iff x=-1+\dfrac{2}{t+1}=\dfrac{-t+1}{t+1}, \end{split} \end{equation*}$

ovvero

(139) $\begin{equation*} dx=\dfrac{-\left(t+1\right)+t-1}{\left(t+1\right)^2}dt=\dfrac{-2dt}{\left(t+1\right)^2}, \end{equation*}$

da cui

$\begin{aligned} J_4&=\dfrac{1}{2}\int_{0}^{1}\dfrac{\ln^2\left(\dfrac{1-x}{1+x}\right)}{x}\,dx= \\ &= \dfrac{1}{2}\int_{1}^{0}\dfrac{\ln^2 t}{\dfrac{-t+1}{t+1}}\left(\dfrac{-2}{\left(t+1\right)^2}\right)dt=\\ &=\int_{0}^{1}\dfrac{\ln^2 t}{1-t^2}\,dt= \\ &\overset{\ast}{=} \int_{0}^{1}\sum_{k=0}^{+\infty}t^{2k}\ln^2 t \,dt= \\ &\overset{\star}{=} \sum_{k=0}^{+\infty}\int_{0}^{1}t^{2k}\ln^2 t \,dt, \end{aligned}$

dove in $\ast$ abbiamo applicato il noto sviluppo in serie $\sum_{k=0}^{+\infty}t^{2k}=\dfrac{1}{1-t^2}$ e in $\star$ abbiamo applicato nuovamente il teorema della convergenza dominata. Integrando per parti l’ultimo membro si ottiene

(140) $\begin{equation*} \begin{split} J_4 &= \sum_{k=0}^{+\infty}\dfrac{2}{\left(2k+1\right)^3} =2 \left(\sum_{k=1}^{+\infty}\dfrac{1}{k^3}-\sum_{k=1}^{+\infty}\dfrac{1}{\left(2k\right)^3}\right)=2\sum_{k=1}^{+\infty}\left(\dfrac{1}{k^3}-\dfrac{1}{8k^3}\right)=\\ &=\dfrac{7}{4}\sum_{k=1}^{+\infty}\dfrac{1}{k^3}=\dfrac{7}{4}\zeta(3). \end{split} \end{equation*}$

Abbiamo dunque

$J_3=-\dfrac{3}{2}\zeta(3)+J_4=-\dfrac{3}{2}\zeta(3)+\dfrac{7}{4}\zeta(3)=\dfrac{\zeta(3)}{4}$

e concludiamo che

$I=-J_1-\dfrac{1}{2}J_3=-\dfrac{\zeta(3)}{2}-\dfrac{\zeta(3)}{8}=-\dfrac{5}{8}\zeta(3),$

che è l’asserto.

Per il secondo integrale è utile riprendere la seguente scrittura

$\begin{aligned} &\; \ln\left(1-x\right)\ln\left(1+x\right)=\dfrac{1}{2} \ln^2\left(1-x^2\right)- \dfrac{1}{2} \ln^2\left(1-x\right)- \dfrac{1}{2} \ln^2\left(1+x\right)\\ \iff &\; 2\ln\left(1-x\right)\ln\left(1+x\right)+\ln^2\left(1+x\right)=\ln^2\left(1-x^2\right)-\ln^2\left(1-x\right) \\ \iff & \; \ln\left(1+x\right)\left(\ln\left(1+x^2-2x\right)+\ln\left(1+x\right)\right)=\ln^2\left(1-x^2\right)-\ln^2\left(1-x\right)\\ \iff &\; \ln\left(1+x\right)\ln\left(1-x-x^2+x^3\right)=\ln^2\left(1-x^2\right)-\ln^2\left(1-x\right), \end{aligned}$

da cui

$\begin{aligned} \int_{0}^{1}\dfrac{\ln\left(1+x\right)\ln\left(1-x-x^2+x^3\right)}{x}\,dx &= \int_{0}^{1}\dfrac{\ln^2\left(1-x^2\right)}{x}\,dx-\int_{0}^{1}\dfrac{\ln^2\left(1-x\right)}{x}\,dx=\\ &=\zeta(3)-2\zeta(3) \\ &=-\zeta(3), \end{aligned}$

che è ciò che volevamo dimostrare.

Esercizio 47 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare il seguente limite, se esiste:

$\begin{equation*} \lim_{n\to +\infty} ne^{4n} \left(n \left(1+\dfrac{1}{e^n} \right)^{\frac{1}{n}}- \ln (1+e^n) -\dfrac{1}{2ne^{2n}}+\dfrac{1}{2ne^{3n}}-\dfrac{1}{6n^2e^{3n}} \right). \end{equation*}$

Svolgimento.

Sviluppiamo in serie per $n\to+\infty$

$\begin{aligned} n \left( 1+\dfrac{1}{e^n} \right)^{\frac{1}{n}} &= ne^{\frac{1}{n}\ln \left( 1+\frac{1}{e^n} \right)}= \\ &= ne^{\frac{1}{n} \left( \sum_{k=1}^a \left( \frac{1}{k} (-1)^{k+1} \left( \dfrac{1}{e^n} \right)^k \right)+o \left( \dfrac{1}{e^{kn}} \right) \right)}=\\ &=n \left( 1+\dfrac{1}{n} \left(\sum_{k=1}^a \left(\dfrac{1}{k}(-1)^{k+1}\left( \dfrac{1}{e^n} \right)^k \right) \right)+ o\left(\dfrac{1}{e^{kn}} \right) \right)+\\ &\qquad +\dfrac{1}{2} \left( \dfrac{1}{n}\left(\sum_{k=1}^a \left(\dfrac{1}{k}(-1)^{k+1} \left(\dfrac{1}{e^n} \right)^k \right) + o\left(\dfrac{1}{e^{kn}}\right) \right) \right)^2 + \\ & \qquad + \dfrac{1}{6} \left( \dfrac{1}{n} \left( \sum_{k=1}^a \left(\dfrac{1}{k}(-1)^{k+1} \left(\dfrac{1}{e^n} \right)^k \right) +o \left(\dfrac{1}{e^{kn}} \right) \right) \right)^3=\\ &=n+\left(\sum_{k=1}^a \left(\dfrac{1}{k}(-1)^{k+1} \left(\dfrac{1}{e^n} \right)^k \right)+o \left(\dfrac{1}{e^{kn}} \right) \right)+ \\ & \qquad + \dfrac{1}{2}\cdot \dfrac{1}{n} \left(\sum_{k=1}^a \left(\dfrac{1}{k} (-1)^{k+1}\left(\dfrac{1}{e^n} \right)^k \right)+o \left(\dfrac{1}{e^{kn}} \right) \right)^2+\\ &\qquad + \dfrac{1}{6}\cdot \dfrac{1}{n^2} \left(\sum_{k=1}^a \left(\dfrac{1}{k}(-1)^{k+1} \left(\dfrac{1}{e^n} \right)^k \right)+o\left(\dfrac{1}{e^{kn}} \right) \right)^3, \end{aligned}$

con $a\in \mathbb{N} \setminus \{0,1\}$ .

Inoltre

$\begin{aligned} - \ln (1+e^n) &= -n-\ln \left( 1+\dfrac{1}{e^n} \right)= \\ &= -n-\sum_{k=1}^a \dfrac{1}{k} (-1)^{k+1} \left(\dfrac{1}{e^{nk}} \right)+o\left(\dfrac{1}{e^{nk}} \right)\qquad \mbox{con} \quad a\in \mathbb{N} \setminus \{0,1\}. \end{aligned}$

Osserviamo che:

$\begin{aligned} n \left( 1+\dfrac{1}{e^n} \right)^{\frac{1}{n}}-\ln (1+e^n)&= \dfrac{1}{2n} \left(\sum_{k=1}^a \left( \dfrac{1}{k} (-1)^{k+1} \left(\dfrac{1}{e^n} \right)^k \right)+o \left(\dfrac{1}{e^{kn}} \right) \right)^2+\\ & \qquad \qquad +\dfrac{1}{6} \cdot \dfrac{1}{n^2} \left(\sum_{k=1}^a \left(\dfrac{1}{k}(-1)^{k+1} \left(\dfrac{1}{e^n} \right)^k \right) +o\left(\dfrac{1}{e^{kn}} \right) \right)^3 \end{aligned}$

per $n \to +\infty$ . Posto $a=3$ :

$\begin{aligned} &\dfrac{1}{2n} \left( \dfrac{1}{e^n}-\dfrac{1}{2e^{2n}}+\dfrac{1}{3e^{3n}}+o \left(\dfrac{1}{e^{3n}} \right) \right)^2+ \dfrac{1}{6}\cdot \dfrac{1}{n^2} \left(\dfrac{1}{e^n}-\dfrac{1}{2e^{2n}}+\dfrac{1}{3e^{3n}}+o \left(\dfrac{1}{e^{3n}} \right) \right)^3=\\ &= \dfrac{1}{2ne^{2n}}-\dfrac{1}{2ne^{3n}}+\dfrac{1}{6n^2e^{3n}}+\dfrac{11}{24ne^{4n}}+o \left(\dfrac{1}{ne^{4n}} \right) \quad \mbox{per}\quad n\to+\infty. \end{aligned}$

Tornando al limite si ottiene:

$\begin{aligned} &\lim_{n\to+\infty} ne^{4n} \bigg( \dfrac{1}{2ne^{2n}}-\dfrac{1}{2ne^{3n}}+\dfrac{1}{6n^2e^{3n}}+ \dfrac{11}{24ne^{4n}}-\dfrac{1}{2ne^{2n}}+ \\ &\qquad +\dfrac{1}{2ne^{3n}}-\dfrac{1}{6n^2e^{3n}}+o \left(\dfrac{1}{ne^{4n}} \right) \bigg)=\\ &\quad =\lim_{n\to+\infty} ne^{4n} \left( \dfrac{11}{24ne^{4n}}+o \left(\dfrac{1}{ne^{4n}} \right) \right)= \\ &\quad = \dfrac{11}{24}. \end{aligned}$

Si conclude che

(141) $\begin{equation*} \boxcolorato{analisi}{\lim_{n\to +\infty} ne^{4n} \left(n \left(1+\dfrac{1}{e^n} \right)^{\frac{1}{n}}- \ln (1+e^n) -\dfrac{1}{2ne^{2n}}+\dfrac{1}{2ne^{3n}}-\dfrac{1}{6n^2e^{3n}} \right)=\dfrac{11}{24}.} \end{equation*}$

Esercizio 48 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

. Si calcoli:

$L = \lim_{n\to+\infty} \sqrt[\stackrel{p_n}{}]{2\cdot3\cdot5\cdots p_n} = \lim_{n\to+\infty} \sqrt[p_n]{\displaystyle\prod\limits_{k=1}^{n}p_k},$

dove $p_i$ è la successione dei numeri primi ( $p_i = 2, 3, 5, 7, \ldots$ ).

Svolgimento.

Si ricorda che, se $\pi(n)$

denota la funzione che conta il numero di numeri primi più piccoli di $n$

, un teorema fondamentale afferma che:²⁸

$\pi(n) \sim \frac{n}{\ln(n)}\qquad\text{per $n \to +\infty$.}$

Questa relazione asintotica si può invertire, cioè si può trovare quanto vale, asintoticamente, il valore dell’ $n$ -esimo numero primo. Sia $f(x) = x\ln(x)$ . Allora, tenendo conto che per definizione $\pi(p_n) = n$ , si ha per $n \to +\infty$ :

(142) $\begin{equation*} \begin{aligned} f(n) &= f(\pi(p_n)) \sim \\ & \sim \frac{p_n}{\ln(p_n)}\cdot\ln\frac{p_n}{\ln(p_n)} =\\ & = \frac{p_n}{\ln(p_n)}\cdot\left(\ln(p_n) - \ln\ln(p_n)\right) \sim \\ &\sim \frac{p_n}{\ln(p_n)}\cdot \ln(p_n) = \\ &= p_n, \end{aligned} \end{equation*}$

dove abbiamo utilizzato il fatto che, se $a_n \sim b_n \to +\infty$ , allora anche $\ln(a_n) \sim \ln(b_n)$ . Riassumendo, concludiamo che

$p_n \sim n\ln(n) \qquad \text{per }n \to +\infty.$

Usiamo questo fatto per calcolare $L$ . Passiamo per praticità di scrittura al logaritmo.

(143) $\begin{equation*} \begin{aligned} \ln \sqrt[p_n]{\displaystyle\prod_{k=1}^{n}p_k} &= \frac{1}{p_n} \ln \prod_{k=1}^{n}p_k = \\ &= \frac{1}{p_n}\sum_{k=1}^{n}\ln(p_k) =\\ &= \frac{1}{p_n}\sum_{k=1}^{n}\ln(k) + \frac{1}{p_n}\sum_{k=1}^{n}\ln\frac{p_k}{k}=\\ &= \frac{1}{p_n}\ln(n!) + \frac{1}{p_n}\sum_{k=1}^{n}\ln\frac{p_k}{k}. \end{aligned} \end{equation*}$

Per la (142), si ha $p_n \sim n\ln(n)$ per $n \to +\infty$ , e quindi $\lim \dfrac{p_n}{n\ln(n)} = 1$ . La successione $\dfrac{p_n}{n\ln(n)}$ (per $n \geq 2$ ) è dunque convergente e come tale limitata, per cui possiamo porre:

$M = \sup_{n \geq 2}\frac{p_n}{n\ln(n)}.$

Allora naturalmente $\dfrac{p_k}{k} \leq M\ln(k)$ per $k \geq 2$ . La seconda somma nella (143) si può dunque maggiorare così:

$\begin{aligned} \frac{1}{p_n}\sum_{k=1}^{n}\ln\frac{p_k}{k} &= \frac{1}{p_n}\left(\ln(p_1)+\sum_{k=2}^{n}\ln\frac{p_k}{k}\right) \leq \\ &\leq \frac{1}{p_n}\left(\ln(2)+\sum_{k=2}^{n}\ln(M\ln(k))\right) \leq\\ &\leq \frac{1}{p_n}\left(\ln(2)+\sum_{k=2}^{n}\ln(M\ln(n))\right) =\\ &= \frac{\ln(2)+(n-1)\ln(M\ln(n))}{p_n} \sim \\ &\sim n\frac{\ln(M)+\ln\ln(n)}{n\ln(n)} \sim\\ &\sim \frac{\ln\ln(n)}{\ln(n)} \to 0 \qquad\text{per $n \to +\infty$.} \end{aligned}$

Per il teorema del confronto, concludiamo che la seconda sommatoria nella (143) tende a $0$ per $n\to+\infty$ . Per quanto riguarda la prima sommatoria, ricordiamo la formula di Stirling: $n! \sim n^ne^{-n}\sqrt{2\pi n}$ per $n \to +\infty$ , da cui $\ln(n!) \sim n\ln(n)-n+\ln\sqrt{2\pi n} \sim n\ln(n)$ . Sostituendo nella (143), abbiamo finalmente:

$\ln \sqrt[p_n]{\displaystyle\prod_{k=1}^{n}p_k} \sim \frac{\ln(n!)}{p_n}\sim \frac{n\ln(n)}{n\ln(n)} = 1.$

Abbiamo quindi mostrato che $\ln(L) = 1$ , ossia:

(144) $\begin{equation*} \boxcolorato{analisi}{\lim_{n\to+\infty} \sqrt[p_n]{\displaystyle\prod_{k=1}^{n}p_k} = e. } \end{equation*}$

Ricordiamo che due successioni $\{a_n\}$ e $\{b_n\}$ si dicono asintotiche, e si scrive $a_n \sim b_n$ , se:

$\lim_{n\to+\infty} \frac{a_n}{b_n} = 1.$

↩

Esercizio 49 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Risolvere il seguente problema di Cauchy:

$\begin{cases} y^{\prime \prime}-\dfrac{3}{x}y^\prime+\dfrac{4}{x^2}y=\dfrac{x}{\ln x}\\ y(1)=0\\ y^\prime(1)=1. \end{cases}$

Svolgimento.

Consideriamo la seguente sostituzione $y=x^2z$

e deriviamola due volte, ottenendo

$y=x^2z\quad \implies \quad y^\prime=2xz+x^2z^{\prime}\quad \implies \quad y^{\prime\prime}=2z+4xz^\prime+x^2z^{\prime\prime},$

da cui

$z^\prime=\dfrac{y^\prime}{x^2}-\dfrac{2z}{x^2}=\dfrac{y^\prime}{x^2}-\dfrac{2y}{x^3},$

cioè

$2z+4xz^\prime+x^2z^{\prime\prime}-6z-3xz^\prime+4z=\dfrac{x}{\ln x} \iff x^2z^{\prime\prime}+xz^\prime=\dfrac{x}{\ln x}.$

Applichiamo ora la nuova sostituzione

$z^\prime=t \implies z^{\prime\prime}=t^\prime.$

Pertanto

(145) $\begin{equation*} t^\prime+\dfrac{1}{x}t=\dfrac{1}{x \ln x}\quad \text{per}\,\,x>0. \end{equation*}$

L’integrale generale di (145) si trova procedendo come segue:

(146) $\begin{equation*} t = \dfrac{1}{x}\left(\int_{1}^{x}\dfrac{1}{\ln t}\,dt+1\right)=z^\prime=\dfrac{y^\prime}{x^2}-\dfrac{2y}{x^3} de \iff y^\prime-\dfrac{2}{x}y=x\left(\int_{1}^{x}\dfrac{1}{\ln t}\,dt+1\right), \end{equation*}$

che implica

$\begin{aligned} y &=x^2\left(\int_{1}^{x}\dfrac{1}{\alpha^2}\cdot\alpha\left(\int_{1}^{\alpha}\dfrac{1}{\ln t}\,dt+1\right)d\alpha\right) =\\ & =x^2\left(\ln \alpha \int_{1}^{\alpha}\dfrac{1}{\ln t}\,dt\bigg \vert^x_1-\int_{1}^{x}\ln \alpha\cdot \dfrac{1}{\ln \alpha}\,d \alpha+\ln \alpha\bigg \vert^{x}_1 \right)=\\ &=x^2\left(\ln x \int_{1}^{x}\dfrac{1}{\ln t}\,dt-x+1+\ln x\right)=\\ &=x^2\ln x \int_{1}^{x}\dfrac{1}{\ln t}\,dt-x^3+x^2+x^2\ln x, \end{aligned}$

Si conclude che

(147) $\begin{equation*} $$\boxcolorato{analisi}{y(x)=x^2\ln x \int_{1}^{x}\dfrac{1}{\ln t}\,dt-x^3+x^2+x^2\ln x. } \end{equation*}$

Esercizio 50 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare il seguente integrale:

$\int_{0}^{+\infty}\displaystyle\prod_{k=1}^{n}\left(x^q+\alpha^2_k\right)^{-1}\,dx,$

dove gli $\alpha_k$ e sono tutti diversi tra loro e non nulli.

Svolgimento.

Per capire come trattare questo integrale particolare partiamo prima da un caso semplice. Consideriamo il seguente integrale

$\int_{0}^{+\infty}\dfrac{1}{\left(x^2+1\right)\left(x^2+4\right)}\,dx$

e decomponiamo in fratti semplici la funzione integranda

(148) $\begin{equation*} \dfrac{1}{\left(x^2+1\right)\left(x^2+4\right)}=\dfrac{A}{x^2+1}+\dfrac{B}{x^2+4}. \end{equation*}$

Moltiplichiamo ambo le parti di (148) per $x^2+1$ e valutiamo tale espressione in $x=i$ con $i$ unità immaginaria, ottenendo

$A=\dfrac{1}{x^2+4}\bigg\vert_{x=i}=\dfrac{1}{3}.$

Di nuovo moltiplichiamo ambo le parti di (148) per $x^2+4$ e valutiamo tale espressione in $x=2i$ con $i$ unità immaginaria, ottenendo

$B=\dfrac{1}{x^2+1}\bigg\vert_{x=2i}=-\dfrac{1}{3},$

da cui

$\begin{aligned} \int_{0}^{+\infty}\dfrac{1}{\left(x^2+1\right)\left(x^2+4\right)}\,dx&=\int_{0}^{+\infty}\left(\dfrac{1}{3\left(x^2+1\right)}-\dfrac{1}{3\left(x^2+4\right)}\right)dx=\\ &=\dfrac{1}{3}\left(\arctan x-\dfrac{1}{2}\arctan\left(\dfrac{x}{2}\right)\right)\bigg \vert^{+\infty}_0=\\ &=\dfrac{1}{3}\left(\dfrac{\pi}{2}-\dfrac{\pi}{8}\right)=\dfrac{1}{8}\pi. \end{aligned}$

Ora che abbiamo capito l’idea di base, procediamo decomponendo in fratti semplici

$\left(\displaystyle\prod_{k=1}^{n}\left(x^2+\alpha^2_k\right)\right)^{-1}=\sum_{k=1}^{n}\dfrac{\beta_k}{x^2+\alpha_k^2}$

e moltiplichiamo da entrambe le parti per $x^2+\alpha_j^2$ con $1\leq j\leq n$ ottenendo

$\begin{aligned} &\;\prod_{k=1}^{n}\dfrac{x^2+\alpha_j^2}{x^2+\alpha^2_k}=\sum_{k=1}^{n}\dfrac{\left(x^2+\alpha_j^2\right)\beta_k}{x^2+\alpha_k^2}\\ \iff& \;\dfrac{x^2+\alpha_j^2}{\left(x^2+\alpha_1^2\right)\dots\left(x^2+\alpha_j^2\right)\dots\left(x^2+\alpha_n^2\right)} = \\ & \quad = \dfrac{\beta_1\left(x^2+\alpha_j^2\right)}{x^2+\alpha_1^2}+\dots\dfrac{\beta_j\left(x^2+\alpha_j^2\right)}{x^2+\alpha_j^2}+\dots\dfrac{\beta_n\left(x^2+\alpha_j^2\right)}{x^2+\alpha_n^2}\\ \iff &\;\prod_{k=1}^{j-1}\dfrac{1}{x^2+\alpha^2_k}\cdot\prod_{k=j+1}^{n}\dfrac{1}{x^2+\alpha^2_k}=\dfrac{\beta_1\left(x^2+\alpha_j^2\right)}{x^2+\alpha_1^2}+\beta_j+\dots\dfrac{\beta_n\left(x^2+\alpha_j^2\right)}{x^2+\alpha_n^2}. \end{aligned}$

Sostituiamo $x=i\alpha_j$ con $i$ unità immaginaria

$\beta_j=\prod_{k=1}^{j-1}\dfrac{1}{\alpha^2_k-\alpha_j^2}\cdot\prod_{k=j+1}^{n}\dfrac{1}{\alpha^2_k-\alpha_j^2},$

da cui

$\begin{aligned} \int_{0}^{+\infty}\left(\displaystyle\prod_{k=1}^{n}\left(x^2+\alpha^2_k\right)\right)^{-1}\,dx&= \int_{0}^{+\infty} \sum_{k=1}^{n}\dfrac{\beta_k}{x^2+\alpha_k^2}\,dx=\\ &=\sum_{k=1}^{n}\beta_k\int_{0}^{+\infty} \dfrac{1}{x^2+\alpha_k^2}\,dx=\\ &=\sum_{k=1}^{n}\beta_k\left(\dfrac{1}{\left \vert \alpha_k\right \vert }\right)\arctan\left(\dfrac{x}{\left \vert\alpha_k\right \vert}\right)\bigg \vert^{+\infty}_0=\\ &=\sum_{k=1}^{n}\left(\dfrac{\pi\beta_k}{2\left \vert \alpha_k\right \vert }\right)=\\ &=\sum_{k=1}^{n}\left(\dfrac{\pi}{2\left \vert \alpha_k\right \vert }\right)\prod_{j=1}^{k-1}\dfrac{1}{\alpha^2_j-\alpha_k^2}\cdot\prod_{j=k+1}^{n}\dfrac{1}{\alpha^2_j-\alpha_k^2}. \end{aligned}$

Concludiamo dunque

(149) $\begin{equation*} $$\boxcolorato{analisi}{\int_{0}^{+\infty}\left(\displaystyle\prod_{k=1}^{n}\left(x^2+\alpha^2_k\right)\right)^{-1}\,dx=\sum_{k=1}^{n}\left(\dfrac{\pi}{2\left \vert \alpha_k\right \vert }\right)\prod_{j=1}^{k-1}\dfrac{1}{\alpha^2_j-\alpha_k^2}\cdot\prod_{j=k+1}^{n}\dfrac{1}{\alpha^2_j-\alpha_k^2}. } \end{equation*}$

Esercizio 51 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare il seguente limite:

(150) $\begin{equation*} \lim_{n\to+\infty} \left(\dfrac{4^{2n}(n!)^4}{2n^4 (2n!)^2} \sum_{k=1}^n (2k-1)^2 \right)^{\displaystyle\frac{1}{4}\prod_{k=1}^{n}\int_{0}^{k}\frac{2x^4-4x^2-4kx+2}{2k\left(x^2-1\right)^2}\,dx}. \end{equation*}$

Svolgimento.

Riscriviamo l’integranda come

$\begin{aligned} \frac{2x^4-4x^2-4kx+2}{2k\left(x^2-1\right)^2}&=\dfrac{kx^2-2kx-kx^2-k-2kx+k+2x^4-4x^2+2}{2k\left(x^2-1\right)^2}=\\ &=\dfrac{kx^2-2kx-k\left(x+1\right)^2+k+2x^4-4x^2+2}{2k\left(x^2-1\right)^2}=\\ &=\dfrac{-k\left(x+1\right)^2+\left(x-1\right)^2k+2\left(x^2-1\right)^2}{2\left(x-1\right)^2\left(x+1\right)^2k}=\\ &=\dfrac{1}{k}-\dfrac{1}{2\left(x-1\right)^2}+\dfrac{1}{2\left(x+1\right)^2}, \end{aligned}$

per cui

$\begin{aligned} \int_{0}^{k}\left(\dfrac{1}{k}-\dfrac{1}{2\left(x-1\right)^2}+\dfrac{1}{2\left(x+1\right)^2}\right)\,dx &= 1+\dfrac{1}{2\left(k-1\right)}-\dfrac{1}{2\left(k+1\right)}= \\ &= \dfrac{2k^2-2+k+1-k+1}{2\left(k^2-1\right)}= \\ &= \dfrac{k^2}{k^2-1} \end{aligned}$

e quindi²⁹

$\prod_{k=1}^{+\infty}\dfrac{4k^2}{k^2-1}=\dfrac{\pi}{2}.$

Ora notiamo che

$\begin{aligned} \sum_{k=1}^n (2k-1)^2 &= 4\sum_{k=1}^n k^2+n-4\sum_{k=1}^n k= \\ &= 4 \; \dfrac{n(2n+1)(n+1)}{6} + n - 4\; \dfrac{n(n+1)}{2} = \\ &= \dfrac{n(2n-1)(2n+1)}{3}, \end{aligned}$

per cui (150) diventa

$\lim_{n\to+\infty} \dfrac{4^{2n}(n!)^4}{2n^4(2n!)^2} \; \sum_{k=1}^n (2k-1)^2 = \lim_{n\to+\infty} \dfrac{\pi}{2} \; \dfrac{4^{2n}(n!)^4}{2n^4(2n!)^2} \; \dfrac{n(2n-1)(2n+1)}{3}.$

Applicando l’approssimazione di Stirling si ha:

$\begin{aligned} \lim_{n\to+\infty} \dfrac{4^{2n}\left(\dfrac{\sqrt{2\pi n}(n^n)}{e^n} \right)^4 \left(\dfrac{n^3}{3} \left(1+o\left(1\right)\right)\right)}{2n^4 \left(\dfrac{\sqrt{4\pi n}((2n)^{2n})}{e^{2n}} \right)^2} &= \lim_{n\to+\infty} \dfrac{4^{2n}\,4\pi^2n^2\,n^{4n}\,e^{4n}}{2n^4\,4\pi n\,\left(2n\right)^{4n}\,e^{4n} }\cdot\dfrac{4n^3}{3}(1+o(1))= \\ &= \dfrac{\pi}{6}. \end{aligned}$

Pertanto concludiamo che

(151) $\begin{equation*} \boxcolorato{analisi}{\lim_{n\to+\infty} \left(\dfrac{4^{2n}(n!)^4}{2n^4 (2n!)^2} \sum_{k=1}^n (2k-1)^2 \right)^{\displaystyle\frac{1}{4}\prod_{k=1}^{n}\int_{0}^{k}\frac{2x^4-4x^2-4kx+2}{2k\left(x^2-1\right)^2}\,dx}=\left(\dfrac{\pi}{6}\right)^{\frac{\pi}{2}}. } \end{equation*}$

Riconosciamo il prodotto di Wallis. ↩

Esercizio 52 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare l’integrale

$\begin{equation*} I(\alpha)=\int_{0}^{\frac{\pi}{2}}\ln\left(1-\alpha\sin^2x\right)\,dx \end{equation*}$

e determinare per quali valori di $\alpha\in\mathbb{R}$ esso è ben definito.

Svolgimento.

Questo è un classico esempio di integrali che risolvono con il famoso trucco di Feynman.

Lasciamo al lettore il piacere di verificare che la funzione integranda verifica le condizioni del teorema di derivazione sotto il segno di integrale³⁰. Abbiamo dunque

$\begin{aligned} I^\prime(\alpha) &= \int_{0}^{\frac{\pi}{2}}-\dfrac{\sin^2x}{1-\alpha\sin^2 x}\,dx= \\ &= \dfrac{1}{\alpha}\int_{0}^{\frac{\pi}{2}}\dfrac{\alpha\sin^2 x+1-1}{\alpha\sin^2 x-2}\,dx= \\ &= \dfrac{1}{\alpha}\left(\dfrac{\pi}{2}+\int_{0}^{\frac{\pi}{2}}\dfrac{1}{\sin^2x}\cdot\dfrac{1}{\alpha-\frac{1}{\sin^2 x}}\,dx\right)=\\ &=\dfrac{1}{\alpha}\left(\dfrac{\pi}{2}+\int_{0}^{\frac{\pi}{2}}\dfrac{1}{\sin^2x}\cdot\dfrac{1}{\alpha-1-\cot^2x }\,dx\right)= \\ &\overset{\cot x \mapsto x }{=}\dfrac{1}{\alpha}\left(\dfrac{\pi}{2}+\int_{0}^{\frac{\pi}{2}}\dfrac{1}{\alpha-1-x^2 }\,dx\right). \end{aligned}$

È facile notare che se $\alpha\geq 1$ l’integrale diverge, mentre se $\alpha<1$ l’integrale converge, pertanto

$\begin{aligned} I^\prime(\alpha)\overset{\clubsuit}{=}\dfrac{\pi}{2\alpha}-\dfrac{1}{\alpha\sqrt{1-\alpha}}\arctan\left(\dfrac{x}{\sqrt{1-\alpha}}\right)\bigg\vert^{+\infty}_{0}=\dfrac{\pi}{2\alpha}-\dfrac{\pi}{2\alpha\sqrt{1-\alpha}}, \end{aligned}$

dove in $\clubsuit$ abbiamo utilizzato l’integrale notevole $\int \dfrac{f^\prime(x)}{k^2+f^2(x)}\,dx=\dfrac{1}{\left \vert k \right \vert }\arctan\left(\dfrac{f(x)}{\left \vert k \right \vert }\right)+c,\,\,\text{con}\,\,k\neq 0$ . Calcoliamo $I(\alpha)$ :

$\begin{aligned} I(\alpha)&= \int\left(\dfrac{\pi}{2\alpha}-\dfrac{\pi}{2\alpha\sqrt{1-\alpha}}\right)\,d\alpha= \\ &\overset{\sqrt{1-\alpha}=t}{=}\dfrac{\pi}{2}\ln\left \vert \alpha \right \vert -\dfrac{\pi}{2}\int\dfrac{2}{1-t^2}\,dt= \\ &= \dfrac{\pi}{2}\ln\left \vert \alpha \right \vert-\dfrac{\pi}{2}\ln\left \vert \dfrac{t-1}{t+1}\right \vert +c= \\ & = \dfrac{\pi}{2}\ln\left \vert \alpha \right \vert-\dfrac{\pi}{2}\ln\left \vert \dfrac{\sqrt{1-\alpha}-1}{\sqrt{1-\alpha}+1}\right \vert +c= \\ &= -\dfrac{\pi}{2}\ln\left \vert \dfrac{\sqrt{1-\alpha}-1}{\alpha\left(\sqrt{1-\alpha}+1\right)} \right \vert +c= \\ &= -\dfrac{\pi}{2}\ln\left \vert \dfrac{-\alpha}{\alpha\left(\sqrt{1-\alpha}+1\right)^2}\right \vert+c=\\ & = \pi\ln\left(\sqrt{1-\alpha}+1\right)+c \end{aligned}$

e imponiamo $I(0)=0=\pi+\ln 2 +c \iff c=-\pi\ln2$ , da cui

$I(\alpha)=\pi\ln\left(\sqrt{1-\alpha}+1\right)-\pi\ln2=\pi\ln\left(\dfrac{\sqrt{1-\alpha}+1}{2}\right).$

Concludiamo dunque

(152) $\begin{equation*} \boxcolorato{analisi}{\int_{0}^{\frac{\pi}{2}}\ln\left(1-\alpha\sin^2x\right)\,dx=\pi\ln\left(\dfrac{\sqrt{1-\alpha}+1}{2}\right)\qquad \text{con}\,\,\alpha<1.} \end{equation*}$

Sia $F:[a,b] \rightarrow \mathbb{R}$ tale che

(153) $\begin{equation*} F(\alpha)=\int_{t_1(\alpha)}^{t_2 (\alpha)}f(x,\alpha )\,dx. \end{equation*}$

Se $f(x,\alpha)$ e $\frac{\partial f}{\partial \alpha}(x,\alpha)$ sono continue in $\{(x,\alpha):a\leq \alpha \leq b,\,t_1(\alpha)\leq x \leq t_2(\alpha)\}$ e $t_1(\alpha)$ e $t_2(\alpha)$ sono di classe $C^1$ in $[a,b]$ , allora vale

(154) $\begin{equation*} \dfrac{dF}{d\alpha}(\alpha)=\int_{t_1(\alpha)}^{t_2(\alpha)}\dfrac{\partial f}{\partial \alpha }(x,\alpha)\,dx+f(t_2(\alpha),\alpha)\, \dfrac{dt_2}{d\alpha}(\alpha)-f(t_1(\alpha),\alpha)\,\dfrac{dt_1}{d\alpha}(\alpha) \end{equation*}$

↩

Esercizio 53 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

. Sia $\Gamma_0$

circonferenza di raggio $\overline{AO}_0=1,$

ed $A$

ed $R$

giacenti su $r$

. Sia $\Gamma_1$

la circonferenza tangente a $\Gamma_0$

in $A$

di diametro pari a $1$

e siano $\Gamma_2$

, $\Gamma_3$

, $\Gamma_4$

,…, $\Gamma_n...$

una successione infinita di circonferenze che godono delle seguenti proprietà:

$\quad$

$\Gamma_2$ è tangente alla retta $r$ ed alla circonferenza $\Gamma_0$ ;

$\Gamma_n$ è tangente a $\Gamma_{n-1},\,\Gamma_0$ e $\Gamma_1$ per $n\ge3$ ;

La successione $\Gamma_n$ è infinita;

Le circonferenze $\Gamma_n^\prime$ sono la riflessione delle $\Gamma_n$ rispetto alla retta $r$ .

Si determini:

$\quad$

il valore di $r_n$ , raggio della circonferenza $\Gamma_n$ ;

il valore della serie
$C=\sum_{n=1}^{+\infty}C_n+\sum_{n=1}^{+\infty}C_n^\prime,$

dove $C_n$ è la lunghezza della circonferenza $\Gamma_n$ e $C_n^\prime$ la lunghezza della circonferenza $\Gamma_n^\prime$ .

$\quad$

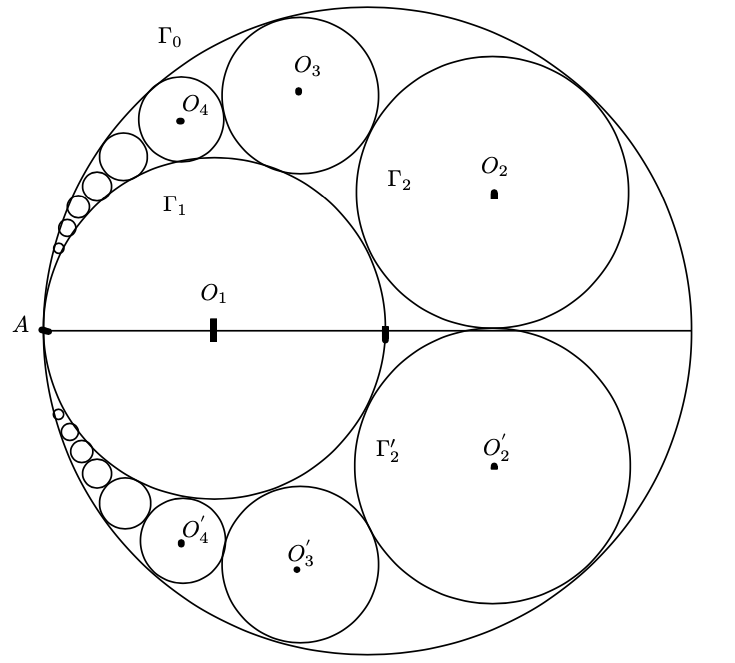
Svolgimento punto 1.

Consideriamo la figura 7 e determiniamo $r_2$

$\quad$

Figura 7: primo passo nella soluzione dell’esercizio 53.

$\quad$

Osserviamo che Il segmento $\overline{O_1O_2}$ passa per il punto $B$ di tangenza tra $\Gamma_1$ e $\Gamma_2$ e il punto $F$ di tangenza tra $\Gamma_0$ e $\Gamma_2$ giace sulla congiungente tra $O_0 O_2$ .

Siano³¹ $x = \overline{O_0G}$ , $r_2 = \overline{O_2G} = \overline{O_2F}$ , $r_1 = \overline{O_1B} = \overline{O_1 O_0} = \dfrac{1}{2}r_0$ , dunque, applicando il teorema di Pitagora a $O_0 O_2 G$ , ne segue che

$\overline{O_2G}^2=\overline{O_0O_2}^2-\overline{O_0G}^2,$

da cui

(155) $\begin{equation*} r_2^2=(r_0-r_2)^2-x^2. \end{equation*}$

Inoltre, applicando nuovamente il teorema di Pitagora al triangolo $\overset{\triangle}{O_0 O_2 G}$ , abbiamo

$\overline{O_2G}^2=\overline{O_1O_2}^2-\overline{O_0G}^2,$

cioè

(156) $\begin{equation*} r_2^2=\left(\dfrac{1}{2}r_0+r_2\right)^2-\left(\dfrac{1}{2}r_0+x\right)^2. \end{equation*}$

Risolvendo il sistema delle equazioni (155) e (156) si ottiene

$\begin{equation*}\label{53_3} x=\dfrac{1}{3}r_0=\dfrac{1}{3} \qquad \mbox{e} \qquad r_2=\dfrac{4}{9r_0}=\dfrac{4}{9}. \end{equation*}$

Invocando il teorema dei $4$ cerchi tangenti di Cartesio possiamo determinare $r_2$ , $r_3$ , $r_4$ , $...$ , $r_n$ come segue:

$\begin{equation*}\label{53_4} \left(\dfrac{1}{r_n}+\dfrac{1}{r_{n-1}}-\dfrac{1}{r_0}+\dfrac{1}{r_1}\right)^2=2\left(\dfrac{1}{r_n^2}+\dfrac{1}{r_{n-1}^2}+\dfrac{1}{r_0^2}+\dfrac{1}{r_1^2}\right). \end{equation*}$

Pertanto

(157) $\begin{equation*} \dfrac{1}{r_n}=\dfrac{1}{r_{n-1}}+1+2\sqrt{\dfrac{1}{r_{n-1}}-2}. \end{equation*}$

Si può notare che partendo da $r_2=\dfrac{4}{9}$ e sostituendo nella (157) il valore di $r_2$ si ottengono $r_3=\dfrac{4}{17}$ , $r_4=\dfrac{4}{33},\dots$ .

I termini sembrano della forma $r_n=\dfrac{4}{(2n-1)^2+8}$ ed infatti sostituendo questa espressione in (157) si ottiene che $r_{n+1}=\dfrac{4}{(2(n+1)-1)^2+8}$ . Quindi per $n\ge2$ si ha³²

(158) $\begin{equation*} \boxcolorato{analisi}{r_n=\dfrac{4}{(2n-3)^2+8}. } \end{equation*}$

Si può facilmente verificare per induzione quanto ottenuto. ↩

$G$ è il piede della perpendicolare condotta da $0_2$ al diametro della circonfenza più grande come in figura 7. ↩

Svolgimento punto 2.

Vista la simmetria rispetto alla retta $r$

ed il valore di $r_n$

ottenuto in precedenza, abbiamo

(159) $\begin{equation*} C=2\pi\cdot2\sum_{n=1}^{+\infty}\dfrac{4}{(2n-1)^2+8}, \end{equation*}$

cioè

(160) $\begin{equation*} \begin{aligned} &\;\sum_{n=1}^{+\infty}\dfrac{4}{(2n-1)^2+8}=\sum_{n=1}^{+\infty}\dfrac{4}{n^2+8}-\sum_{n=1}^{+\infty}\dfrac{4}{(2n)^2+8} \\ \iff &\; \sum_{n=1}^{+\infty}\dfrac{4}{(2n-1)^2+8}=4\sum_{n=1}^{+\infty}\dfrac{1}{n^2+8}-\sum_{n=1}^{+\infty}\dfrac{1}{n^2+2}. \end{aligned} \end{equation*}$

Dalla letteratura è noto che³³

$\sum_{n=1}^{+\infty}\dfrac{1}{k^2+a^2}=\dfrac{\pi\coth\left(\pi a\right)}{2a}-\dfrac{1}{2a^2}\quad \text{con}\,\,a\geq 0,$

perciò

$\begin{aligned} C&=4\left(\dfrac{\pi\coth\left(2\sqrt{2}\pi\right)}{4\sqrt{2}}-\dfrac{1}{16}\right)-4\left(\dfrac{\pi\coth\left(\sqrt{2}\pi\right)}{2\sqrt{2}}-\dfrac{1}{4}\right)= \\ &= \pi\sqrt{2}\left(2\coth\left(2\sqrt{2}\pi\right)-\coth\left(\sqrt{2}\pi\right)\right). \end{aligned}$

Concludiamo dunque

(161) $\begin{equation*} \boxcolorato{analisi}{C=\pi\sqrt{2}\left(2\coth\left(2\sqrt{2}\pi\right)-\coth\left(\sqrt{2}\pi\right)\right). } \end{equation*}$

Lasciamo al lettore il piacere di dimostrare l’identità citata ricordando che un’applicazione $f : \Omega \to \mathbb{C}$ si dice meromorfa se è olomorfa in $\Omega$ , eccetto che per singolarità polari. Vale inoltre il seguente

$\quad$

Teorema. Sia $f$ meromorfa in tutto il piano complesso $\mathbb{C}$ avente solo un numero finito di poli $z_1, \dots,z_\nu$ con $z_j \notin \mathbb{Z}$ , per ogni $j=1,\dots,\nu$ . Supponiamo $\vert f(z) \vert = o(\vert z \vert^{-\alpha})$ per $z \to \infty$ , con $\alpha>1$ . Definiamo

$g(z):=\pi f(z)\cot(\pi z), \qquad h(z):=\dfrac{\pi f(z)}{\sin(\pi z)}.$

Allora

$\begin{aligned} \sum_{k=-\infty}^{+ \infty} f(k)=-\sum_{j=1}^\nu \mathrm{Res}(g(z),z_j) \qquad \sum_{k=-\infty}^{+ \infty} (-1)^k \, f(k)=-\sum_{j=1}^\nu \mathrm{Res}(h(z),z_j). \end{aligned}$

$\quad$

↩

Svolgimento alternativa punto 2.

Altrimenti per determinare le due sommatorie si poteva procedere ricordando che

(162) $\begin{equation*} \pi\cot(\pi x)=\dfrac{1}{x}+2x\sum_{n=1}^{+\infty}\dfrac{1}{x^2-n^2} \end{equation*}$

e sostituendo $x=iz$ in (162) dove $i$ è l’unità immaginaria avremo

(163) $\begin{equation*} \pi\cot(\pi iz)=\dfrac{1}{iz}-2iz\sum_{n=1}^{+\infty}\dfrac{1}{z^2+n^2}. \end{equation*}$

Ricordando che $\cot(\pi iz)=i\coth(\pi z)$ , sostituendo in (163), con pochi passaggi di calcolo abbiamo

$\sum_{n=1}^{+\infty}\dfrac{1}{z^2+n^2}=\dfrac{\pi\coth (\pi z)}{2z}-\dfrac{1}{2z^2}\implies\sum_{n=1}^{+\infty}\dfrac{1}{2+n^2}=\dfrac{\pi\coth(\sqrt{2}\pi)}{2\sqrt{2}}-\dfrac{1}{4}$

$\sum_{n=1}^{+\infty}\dfrac{1}{8+n^2}=\dfrac{\pi\coth(2\sqrt{2}\pi)}{4\sqrt{2}}-\dfrac{1}{16},$

da cui

$\begin{aligned} C&=4\pi\sum_{n=1}^{+\infty}\dfrac{4}{(2n-1)^2+8}= \\ &= 16\pi\sum_{n=1}^{+\infty}\dfrac{1}{n^2+8}-4\pi\sum_{n=1}^{+\infty}\dfrac{1}{n^2+2}=\\ & = 2\cdot 2\dfrac{\pi^2\coth(2\sqrt{2}\pi)}{\sqrt{2}}-1-\dfrac{2\pi^2\coth(\sqrt{2}\pi)}{\sqrt{2}}+1\\ &=\dfrac{2\pi^2}{\sqrt{2}}(2\coth(2\sqrt{2}\pi)-\coth(\sqrt{2}\pi)). \end{aligned}$

Quest’ultima espressione si può semplificare ulteriormente sfruttando la formula di duplicazione della cotangente iperbolica ed anche $\cosh^2(x)-\sinh^2(x)=1$ , ottenendo

(164) $\begin{equation*} \boxcolorato{analisi}{C=\dfrac{2\pi^2\tanh(2\sqrt{2}\pi)}{\sqrt{2}}. } \end{equation*}$

Esercizio 54 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Se $a,\, b,\,c$

e $d$

sono numeri reali, dimostrare che

$\begin{equation*} \begin{cases} a^2+b^2=2\\ c^2+d^2=2\\ ac=bd \end{cases}\quad \text{se e solo se}\quad \begin{cases} a^2+c^2=2\\ b^2+d^2=2\\ ab=cd. \end{cases} \end{equation*}$

Svolgimento.

Siano $a,\, b,\,c,\, d$

soluzioni del primo sistema. Dalle prime due equazioni si deduce che esistono $\alpha,\,\beta$

nell’intervallo $[0,2\pi]$

per cui risulta

$a=\sqrt{2}\cos(\alpha), \quad b=\sqrt{2}\sin (\alpha), \quad c=\sqrt{2}\cos(\beta), \quad d=\sqrt{2}\sin(\beta).$

La terza equazione ci dice che

(165) $\begin{equation*} ac-bd=2\cos(\alpha)\cos(\beta)-2\sin(\alpha)\sin(\alpha)=2\cos (\alpha+\beta)=0 \end{equation*}$

e dunque $\alpha=-\beta +\dfrac{k\pi }{2}$ per $k\in\mathbb{Z}$ . Abbiamo allora

$a=\sqrt{2}\cos(-\beta+\dfrac{k\pi}{2})=\pm\sqrt{2}\sin \beta =\pm d$

$b=\sqrt{2}\sin \left( \beta+\dfrac{k\pi}{2}\right)=\pm \sqrt{2}\cos (\beta)=\pm c.$

In conclusione le soluzioni del primo sistema sono del tipo $(a,b,\pm b,\pm a)$ e si verifica facilmente che queste siano soluzioni anche del secondo sistema.

Esercizio 55 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Risolvere il seguente problema di Cauchy:

$\begin{cases} \displaystyle\left(\int_{0}^{+\infty}dx\int_{0}^{1}\dfrac{x\cosh\left(xy\right)}{3+4\sinh^2 x}\,dy \right)\dfrac{dz}{dt}(t)=\int_{0}^{+\infty}\dfrac{x^{z-1}}{1+x}\,dx\\\\ z(0)=0. \end{cases}$

Svolgimento.

Osserviamo quanto segue

$\int_{0}^{+\infty}dx\int_{0}^{1}\dfrac{x\cosh\left(xy\right)}{3+4\sinh^2 x}\,dy=\int_{0}^{+\infty}\dfrac{x \sinh x}{3+4 \sinh^2x}\,dx.$

In virtù della formula di integrazione per parti si ha

$\int_{0}^{+\infty}\frac{\sinh(x)}{3+4\sinh^2(x)}\,dx=\frac{1}{4}\int_{0}^{+\infty}\log\left(\frac{2\cosh x+1}{2\cosh x-1}\right)\,dx$

e il membro destro può anche essere espresso come

$\frac{1}{4}\int_{0}^{+\infty}\log\left(\frac{e^{2x}+e^x+1}{e^{2x}-e^x+1}\right)\,dx,$

oppure come

$\frac{1}{4}\int_{1}^{+\infty} \frac{\log(t^2+t+1)-\log(t^2-t+1)}{t}\,dt =\frac{1}{4}\int_{0}^{1}\frac{\log(t^2+t+1)-\log(t^2-t+1)}{t}\,dt.$

Poiché sia $t^2+t+1$ che $t^2-t+1$ sono polinomi ciclotomici (rispettivamente $\Phi_3(t)$ e $\Phi_6(t)$ ) il risultato è immediata conseguenza della seguente identità:

$\int_{0}^{1}\frac{-\log(1-t^k)}{t}\,dt = \sum_{n\geq 1}\int_{0}^{1}\frac{t^{nk-1}}{n}=\sum_{n\geq 1}\frac{1}{kn^2}=\frac{\pi^2}{6k}.$

In particolare si ha

$\int_{0}^{+\infty}\frac{\sinh(x)}{3+4\sinh^2(x)}\,dx=\frac{\pi^2}{24}.$

Ora riscriviamo il seguente integrale come

$\int_{0}^{+\infty}\dfrac{x^{c-1}}{1+x}\; dx=\int_{0}^{1}\dfrac{x^{c-1}}{1+x}dx+\int_{1}^{+\infty}\dfrac{x^{c-1}}{1+x}dx.$

Abbiamo dunque i due integrali:

(166) $\begin{equation*} \int_{0}^{1}\dfrac{x^{c-1}}{1+x}dx \end{equation*}$

(167) $\begin{equation*} \int_{1}^{+\infty}\dfrac{x^{c-1}}{1+x}dx. \end{equation*}$

Consideriamo (167) e operiamo la seguente sostituzione:

$t=\dfrac{1}{x} \iff x=\dfrac{1}{t} \implies dx=-\dfrac{1}{t^2}ds.$

Allora (167) diventa

$\int_{1}^{+\infty}\dfrac{x^{c-1}}{1+x}dx=-\int_{1}^{0}\dfrac{t \cdot t^{1-c}}{1+t} \; \left(\dfrac{1}{t^2}\right)dt=\int_{0}^{1}\dfrac{t^{-c}}{1+t}dt,$

da cui

$\int_{0}^{+\infty}\dfrac{x^{c-1}}{1+x} \; dx =\int_{0}^{1}\dfrac{x^{c-1}}{1+x}dx+\int_{0}^{1}\dfrac{x^{-c}}{1+x}dx=\int_{0}^{1}\dfrac{x^{-c}+x^{c-1}}{1+x}dx,$

Ricordiamo il seguente sviluppo in serie:

(168) $\begin{equation*} \dfrac{1}{1+x}=\sum_{n=0}^{+\infty}(-1)^nx^n\quad \text{per}\,\, \left \vert x \right \vert <1. \end{equation*}$

Applicando la (168) si ha

$\int_{0}^{1}\dfrac{x^{-c}+x^{c-1}}{1+x}dx=\int_{0}^{1}\,\sum_{n=0}^{+\infty}(-1)^n\left(x^{-c+n}+x^{c-1+n}\right)dx.$

Tramite il teorema della convegenza dominata si dimostra facilmente che si può scambiare la serie con l’integrale, dunque

$\begin{aligned} \int_{0}^{1}\,\sum_{n=0}^{+\infty}(-1)^n\left(x^{-c+n}+x^{c-1+n}\right)dx= &= \sum_{n=0}^{+\infty}(-1)^n\int_{0}^{1}\,\left(x^{-c+n}+x^{c-1+n}\right)dx=\\ &=\sum_{n=0}^{+\infty}(-1)^n\left(\dfrac{1}{n+c}+\dfrac{1}{n+1-c}\right)= \\ &= \dfrac{1}{c}+\sum_{n=1}^{+\infty}\dfrac{(-1)^n}{n+c}-\sum_{n=1}^{+\infty}\dfrac{(-1)^n}{n-c}= \\ &= \dfrac{1}{c}-2c\sum_{n=1}^{+\infty}\dfrac{(-1)^n}{n^2-c^2}. \end{aligned}$

Ora ricordiamo che un’applicazione $f : \Omega \to \mathbb{C}$ si dice meromorfa se è olomorfa in $\Omega$ , eccetto che per singolarità polari. Vale il seguente risultato.

$\quad$

Teorema. Sia $f$

meromorfa in tutto il piano complesso $\mathbb{C}$

avente solo un numero finito di poli $z_1, \dots,z_\nu$

con $z_j \notin \mathbb{Z}$

, per ogni $j=1,\dots,\nu$

. Supponiamo $\vert f(z) \vert = o(\vert z \vert^{-\alpha})$

per $z \to \infty$

, con $\alpha>1$

. Definiamo

$g(z):=\pi f(z)\cot(\pi z), \qquad h(z):=\dfrac{\pi f(z)}{\sin(\pi z)}.$

Allora

$\begin{aligned} \sum_{k=-\infty}^{+ \infty} f(k)=-\sum_{j=1}^\nu \mathrm{Res}(g(z),z_j), \qquad \sum_{k=-\infty}^{+ \infty} (-1)^k \, f(k)=-\sum_{j=1}^\nu \mathrm{Res}(h(z),z_j). \end{aligned}$

$\quad$

Vogliamo dimostrare, applicando il teorema precedente, che

$\dfrac{1}{c}-2c\sum_{n=1}^{+\infty}\dfrac{(-1)^n}{n^2-c^2} = \dfrac{\pi}{\sin(\pi c)} \iff \sum_{n=1}^{+\infty} \dfrac{(-1)^n}{n^2-c^2} = \dfrac{1}{2c^2}-\dfrac{\pi}{2c \sin(\pi c)},\quad \forall c \in (0,1).$

Chiamiamo $f(z)=\dfrac{1}{z^2-c^2}$ , da cui vale la seguente uguaglianza

(169) $\begin{equation*} \sum_{n=-\infty }^{+\infty} \dfrac{(-1)^n}{n^2-c^2}=- \left( \mbox{Res}(h(z),c)+\mbox{Res}(h(z),-c) \right), \quad \forall c \in (0,1). \end{equation*}$

Calcoliamo i residui

$\begin{aligned} &\mbox{Res}(h(z),c) \; \;= \;\lim_{z\to c} (z-c) \;\;\, \dfrac{1}{z^2-c^2} \; \dfrac{\pi}{\sin(\pi z)} = \dfrac{\pi}{2c} \; \dfrac{1}{\sin(\pi z)},\\ &\mbox{Res}(h(z),-c)=\lim_{z\to -c} (z+c) \; \dfrac{1}{z^2-c^2} \; \dfrac{\pi}{\sin(\pi z)} = \dfrac{\pi}{2c} \; \dfrac{1}{\sin(\pi c)}. \end{aligned}$

e tornando alla (169) abbiamo

$\begin{aligned} \sum_{n=-\infty}^{+\infty} \dfrac{(-1)^n}{n^2-c^2}= - \dfrac{\pi}{c \; \sin(\pi c)} & \iff - \dfrac{1}{c^2} + 2 \sum_{n=1}^{+\infty} \dfrac{(-1)^n}{n^2-c^2}= - \dfrac{\pi}{c \; \sin(\pi c)} \\ &\iff \sum_{n=1}^{+\infty} \dfrac{(-1)^n}{n^2-c^2}= \dfrac{1}{2c^2} - \dfrac{\pi}{2c \; \sin(\pi c)}, \end{aligned}$

da cui

(170) $\begin{equation*} \int_{0}^{+\infty} \dfrac{x^{c-1}}{1+x} \; dx =\dfrac{\pi}{\sin (c\pi)} \quad \text{ con}\,c\in \left(0,1\right). \end{equation*}$

Abbiamo dunque

$\dfrac{\pi^2}{24}\dfrac{dz}{dt}\left(t\right)=\dfrac{\pi}{\sin\left(\pi z\right)},$

cioè

$-\cos\left(\pi z\right)=24t+\text{c}.$

Dal problema di Cauchy si trova $\text{c}=-1$ , dunque concludiamo con la seguente soluzione

(171) $\begin{equation*} $$\boxcolorato{analisi}{z=-\dfrac{\arccos\left(24t-1\right)}{\pi}. } \end{equation*}$

Esercizio 56 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$

. Sia dato un triangolo rettangolo di cateti $a,\,b$

e ipotenusa $c$

. Determinare $a,\,b,\,c$

soddisfacenti le seguenti proprietà.

$\quad$

sia il più piccolo numero primo maggiore di tali che:
$\quad$
1. $2^a-1$ sia anch’esso primo (cioè $2^a-1$ sia un numero primo di Mersenne);
2. $2a+1$ sia pure primo (cioè $a$ sia un numero primo di Sophie Germain).

$c$

sia un numero primo esprimibile come segue: $c=d^2+60^2=f^2+g^2$

dove $d$

è il più piccolo intero positivo primo che restituisce un numero primo di Mersenne e che si può esprimere come la somma del quadrato di due numeri interi consecutivi, $f$

e $g$

sono due numeri interi positivi consecutivi.

Trovati i valori di $a,\,b,\,c$ rispondere alle seguenti domande.

$\quad$

$a$ verifica il teorema di Fermat sulle somme di due quadrati?

$a$ è un numero di Fibonacci?

esistono uno o più collegamenti tra gli elementi dei seguenti insiemi: $\{21,\,87,\,57,\,69\}$ e $\{a,\,b,\,c\}$ ?

Svolgimento.

Per risolvere l’esercizio è importante procede per passi che numereremo per facilità di lettura. Ci teniamo a far presente al lettore che questo non è un problema classico e richiede quindi oltre che adeguate conoscenze teoriche anche un buon intuito.

Passo 1.

In questo passo risolviamo il primo quesito posto.

Ricordiamo che un numero di Mersenne è un numero primo inferiore di uno rispetto ad una potenza di $2$ , cioè:

$M_p=2^p-1,$

con $p$ intero positivo primo che nel nostro caso è proprio il valore $a$ . Per orientarsi nella ricerca del cateto $a$ è conveniente fare una griglia con i primi $10$ numeri primi di Mersenne come in tabella 1:

Tabella Numeri di Mersenne

p	2	3	5	7	13	17	19	31	61	89
M_p	2²-1	2³-1	2⁵-1	2⁷-1	2¹³-1	2¹⁷-1	2¹⁹-1	2³¹-1	2⁶¹-1	2⁸⁹-1

Tabella 1: Numeri Primi di Mersenne

Ricordiamo anche che un numero di Sophie Germain è un numero primo $p$ tale che anche $2p+1$ lo sia e, analogamente a prima, riportiamo di seguito la tabella 2:

p	2	3	5	11	29	41	53	83	89	113
2p+1	5	7	11	23	59	83	107	167	179	227

Tabella 2: Numeri di Sophie Germain

Confrontando i valori delle tabelle 1 e 2 risulta chiaro che il valore cercato è $89$ , quindi $a=89$ .

Passo 2.

Per la seconda domanda del problema ipotizziamo che $g=f+1$

da cui $2f^2+2f+1-60^2=d^2$

. Per determinare $c$

è importante ricordare che è un numero intero positivo che restituisce un numero primo di Mersenne e pertanto si può procedere per trovare tale valore impostando ad esempio le seguenti equazioni:

$\begin{aligned} &1)\,2f^2+2f+1-60^2=4;\quad 2)\,2f^2+2f+1-60^2=9;\quad 3)\,2f^2+2f+1-60^2=25\\ &4)\,2f^2+2f+1-60^2=49;\quad 5)\,2f^2+2f+1-60^2=169;\quad 6)\,2f^2+2f+1-60^2=17^2\\ &7)\,2f^2+2f+1-60^2=19^2;\quad 8)\,2f^2+2f+1-60^2=31^2;\quad 9)\,2f^2+2f+1-60^2=61^2;\\ &10)\,2f^2+2f+1-60^2=89^2. \end{aligned}$

Si nota che la numero $7)$ ha soluzione $f=44$ e la numero $9)$ ha soluzione $n=60$ . Abbiamo dunque che $d^2=19^2$ da cui $19^2+60^2=c^2=3961=44^2+45^2$ che era proprio quello che volevamo. In particolare applicando il teorema di Pitagora si ha che $c^2-a^2=b^2=3960^2$ . È interessante osservare che $c-b=1$ . Per completezza rappresentiamo il triangolo rettangolo (non in scala) in figura 8.

$\quad$

Figura 8: triangolo rettangolo

Passo 3.

Dobbiamo verificare se $a$

(trovato al passo precedente) soddisfa il teorema di Fermat sulle somme di due quadrati; la risposta a questa domanda risulta affermativa perché $89\equiv1\,\,(\text{mod}\,\,4)$

. Per completezza riportiamo le seguenti rappresentazioni $89^2=39^2+80^2$

e $89=5^2+8^2$

Passo 4.

Ricordiamo che la successione di Fibonacci $F:\mathbb{N}\to\mathbb{N}$

è una successione che restituisce un numero intero tale che si possa rappresentare come la somma dei due termini precedenti delle successione ad eccezione di $F_0=0$

e $F_n=1$

che sono dati per definizione. Abbiamo dunque

$\begin{aligned} &0=F_0\\ &1=F_1\\ &0+1=1=F_2\\ &1+1=2=F_3\\ &2+1=3=F_4\\ &3+2=5=F_4\\ &5+3=8=F_5\\ &8+5=13=F_6\\ &13+8=21=F_7\\ &21+13=34=F_8\\ &34+21=55=F_9\\ &55+34=89=F_{10}. \end{aligned}$

Osserviamo che $F_{10}=89=a$ .

Passo 5.

Osserviamo che $21^2+57^2=3960=b$

e che $a+b+c=8010=21^2+87^2=57^2+69^2$

Osservazione 3.8. Esiste un test per stabilire se un numero è di Fibonacci o no senza calcolarli tutti. Un numero è di Fibonacci se almeno uno tra $5n^2+4$ e $5n^2-4$ è un quadrato perfetto³⁴. Nel nostro caso, $5\cdot89^2-4 = 199^2$

Un quadrato perfetto o numero quadrato è un numero intero che può essere espresso come il quadrato di un altro numero intero. ↩

Esercizio 57 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che la funzione generatrice della successione di Fibonacci $F_j$

, definita da $F_0=0,\,F_1=1$

e $F_j=F_{j-1}+F_{j-2}$

per $j\ge2$

, è uguale a:

$F(x)=\sum_{j=0}^{+\infty}F_j x^j=\dfrac{x}{1-x-x^2}.$

L’espressione vale per $\vert x\vert<1/\varphi$ dove $\varphi=(1+\sqrt{5})/2\simeq1,618$ è la sezione aurea.

Svolgimento.

In generale, data una successione ${a_j}$

con $j \ge 0$

, si dice funzione generatrice della successione, se esiste, la somma $S$

della seguente serie:

$S(x)=\sum_{j=0}^{+\infty}a_jx^j.$

Se la serie converge per qualche valore di $x>0$ , allora converge per tutti i valori dell’intervallo $(-x,x)$ . I coefficienti $a_j$ sono naturalmente collegati con i termini dello sviluppo in serie di Taylor della funzione $S$ .

Occupiamoci ora della funzione generatrice dei numeri di Fibonacci:

(172) $\begin{equation*} F(x)=\sum_{j=0}^{+\infty}F_jx^j. \end{equation*}$

Innanzitutto, ricordiamo la formula di Binet:

(173) $\begin{equation*} F_j=\dfrac{1}{\sqrt{5}}\left[\varphi^j-\left(-\dfrac{1}{\varphi} \right)^j \right]. \end{equation*}$

Si vede che per $j\to+\infty$ si ha $F_j\sim\varphi^j/\sqrt{5}$ dato che il secondo termine è trascurabile (infatti $\vert1/\varphi\vert<1$ ). Il termine generale della serie è pertanto asintotico a $(c\varphi)^j/\sqrt{5}$ . Il criterio del confronto asintotico ci permette quindi di concludere che la serie (172) converge se $\vert\varphi x\vert<1$ , cioè $\vert x\vert<1/\varphi$ (la serie non converge per $x=\pm1/\varphi$ ).

Stabilito il raggio di convergenza della (172), passiamo a calcolarne esplicitamente la somma. Ricordiamo la definizione dei numeri di Fibonacci (per $j\ge2$ ):

(174) $\begin{equation*} F_j=F_{j-1}+F_{j-2}, \end{equation*}$

da cui:

$\begin{aligned} F(x)&=\sum_{j=0}^{+\infty}F_jx^j= \\ &= 0+x+\sum_{j=2}^{+\infty}F_jx^j= \\ &= x+\sum_{j=2}^{+\infty}(F_{j-1}+F_{j-2})x^j=\\ &=x+\sum_{k=1}^{+\infty}F_kx^{k+1}+\sum_{k=0}^{+\infty}F_kx^{k+2}= \\ &= x+x\sum_{k=0}^{+\infty}F_kx^k+x^2\sum_{k=0}^{+\infty}F_kx^k=\\ &=x+xF(x)+x^2F(x). \end{aligned}$

Abbiamo quindi trovato un’equazione per $F$ :

$F(x)=x+xF(x)+x^2F(x)\implies F(x)(1-x-x^2)=x.$

In conclusione:

(175) $\begin{equation*} \boxcolorato{analisi}{F(x)=\sum_{j=0}^{+\infty}F_jx^j=\dfrac{x}{1-x-x^2}. } \end{equation*}$

Bonus. Usando la funzione generatrice, possiamo calcolare la somma di qualche serie curiosa. Per esempio:

$\sum_{k=0}^{+\infty}\dfrac{F_j}{2f}=F\left(\dfrac{1}{2} \right)=\dfrac{1/2}{1-1/2-(1/2)^2}=2.$

Esercizio 58 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che

$\displaystyle\left(e^\pi-1\right)^2\left(\dfrac{1}{2}-\sum_{k=1}^{+\infty}\dfrac{\zeta\left(4n\right)}{2^{4n}}\right)=\pi^2 e^\pi\prod_{n=2}^{+\infty}\left(1-\dfrac{1}{n^4}\right).$

Svolgimento.

Calcoliamo $\sum_{k=1}^{+\infty}\frac{\zeta\left(4n\right)}{2^{4n}}$

. Applicando la definizione di Zeta di Riemann si ha:

$\begin{aligned} \sum_{n=1}^{+\infty}\dfrac{\zeta\left(4n\right)}{2^{4n}}&=\sum_{n=1}^{+\infty}\sum_{k=1}^{+\infty}\dfrac{1}{\left(16k^4\right)^n}= \\ &= \sum_{k=1}^{+\infty}\sum_{n=1}^{+\infty}\dfrac{1}{\left(16k^4\right)^n}\overset{\clubsuit}{=} \\ &\overset{\clubsuit}{=} \sum_{k=1}^{+\infty}\dfrac{\dfrac{1}{16k^4}}{1-\dfrac{1}{16k^4}}= \\ &= \sum_{k=1}^{+\infty}\dfrac{1}{16k^4-1}\overset{\heartsuit}{=}\\ &\overset{\heartsuit}{=}\sum_{n=1}^{+\infty}\left(\dfrac{1}{4\left(2n-1\right)}-\dfrac{1}{2n+1}\right)-\dfrac{1}{2}\sum_{n=1}^{+\infty}\dfrac{1}{4n^2+1}=\\ &=\underbrace{\sum_{n=1}^{+\infty}\left(\dfrac{1}{4\left(2n-1\right)}-\dfrac{1}{4\left(2n+1\right)}\right)}_{I}-\underbrace{\dfrac{1}{8}\sum_{n=1}^{+\infty}\dfrac{1}{n^2+\dfrac{1}{4}}}_J, \end{aligned}$

dove in $\clubsuit$ abbiamo applicato la serie geometrica e in $\heartsuit$ abbiamo decomposto in fratti semplici. Osserviamo che $I=\dfrac{1}{4}$ perché è una serie telescopica. Dalla letteratura è noto che

$\sum_{k=1}^{+\infty}\dfrac{1}{k^2+a^2}=\dfrac{1}{2}\left(\dfrac{\pi}{a}\coth\left(\pi a\right)-\dfrac{1}{a^2}\right)\quad \text{con}\,\,a> 0.$

Infatti, ponendo $a=\dfrac{1}{2}$ , si trova che

$\sum_{k=1}^{+\infty}\dfrac{1}{k^2+\dfrac{1}{4}}=\pi\coth\left(\dfrac{\pi}{2}\right)-2=\pi\left(\dfrac{e^\pi+1}{e^\pi -1}\right)-2,$

da cui

$\sum_{n=1}^{+\infty}\dfrac{\zeta\left(4n\right)}{2^{4n}}=\dfrac{1}{4}-\dfrac{1}{8}\left(\pi\left(\dfrac{e^\pi+1}{e^\pi -1}\right)-2\right)=\dfrac{1}{2}-\dfrac{\pi}{8}\left(\dfrac{e^\pi+1}{e^\pi -1}\right).$

Calcoliamo $\displaystyle \prod_{n=2}^{+\infty}\left(1-\dfrac{1}{n^4 }\right)$ . Ricordiamo i seguenti fatti:

$\begin{aligned} &\frac{\sin(\pi x)}{\pi x}=\prod_{n=1}^{+\infty} \left(1-\frac{x^2}{n^2}\right)=\left(1-x^2 \right)\prod_{n=2}^{+\infty} \left(1-\frac{x^2}{n^2}\right) \iff \prod_{n=2}^{+\infty} \left(1-\frac{x^2}{n^2}\right)=\dfrac{\sin(\pi x)}{\pi x \left(1-x^2 \right)} \end{aligned}$

$\begin{aligned} & \frac{\sinh(\pi x)}{\pi x}=\prod_{n=1}^{+\infty}\left(1+\frac{x^2}{n^2}\right)=\left(1+x^2 \right)\prod_{n=2}^{+\infty}\left(1+\frac{x^2}{n^2}\right) \iff \prod_{n=2}^{+\infty}\left(1+\frac{x^2}{n^2}\right)=\dfrac{\sinh(\pi x)}{\pi x(1+x^2)}, \end{aligned}$

da cui

$\begin{aligned} &\prod_{n=2}^{+\infty} \left(1-\frac{x^2}{n^2}\right) \cdot \prod_{n=2}^{+\infty}\left(1+\frac{x^2}{n^2}\right)=\dfrac{\sin(\pi x)}{\pi x \left(1-x^2 \right)} \cdot \dfrac{\sinh(\pi x)}{\pi x(1+x^2)}, \end{aligned}$

che è equivalente a

(176) $\begin{equation*} \prod_{n=2}^{+\infty} \left(1-\frac{x^4}{n^4}\right) =\dfrac{\sin(\pi x)\cdot \sinh(\pi x)}{\left(\pi x\right)^2 \left(1-x^4 \right)}, \end{equation*}$

cioè

(177) $\begin{equation*} \prod_{n=2}^{+\infty} \left(1-\frac{x^4}{n^4}\right) =\dfrac{\sin(\pi x)\cdot \sinh(\pi x)}{\left(\pi x\right)^2 \left(1-x^4 \right)}. \end{equation*}$

Passando al limite per $x\rightarrow 1$ ambo i membri di (177) si ottiene

$\begin{aligned} \prod_{n=2}^{+\infty} \left(1-\frac{1}{n^4}\right) &= \lim_{x\rightarrow 1}\left( \dfrac{\sin(\pi x)\cdot \sinh(\pi x)}{\left(\pi x\right)^2 \left(1-x^4 \right)}\right) \\ &= \lim_{x\rightarrow 1}\left( \dfrac{\sin(\pi x)}{1-x} \cdot \dfrac{\sinh (\pi x)}{(\pi x)^2 (1+x^2)(1+x)}\right) \\ &= \dfrac{\sinh(\pi )}{4 \pi }, \end{aligned}$

ovvero

(178) $\begin{equation*} \prod_{n=2}^{+\infty} \left(1-\frac{1}{n^4}\right)=\dfrac{\sinh(\pi )}{4 \pi }, \end{equation*}$

dunque

(179) $\begin{equation*} \prod_{n=2}^{+\infty} \left(1-\frac{1}{n^4}\right)=\dfrac{\sinh(\pi )}{4 \pi }=\dfrac{e^{2\pi}-1}{8 \pi e^\pi}. \end{equation*}$

Si ha quindi:

$\begin{aligned} &\; -\left(e^\pi-1\right)^2\left(-\dfrac{1}{2}+\sum_{k=1}^{+\infty}\dfrac{\zeta\left(4n\right)}{2^{4n}}\right)=\pi^2 e^\pi\prod_{n=2}^{+\infty}\left(1-\dfrac{1}{n^4}\right) \\ \iff &\; -\displaystyle\left(e^\pi-1\right)^2\left(-\dfrac{\pi}{8}\left(\dfrac{e^\pi+1}{e^\pi -1}\right)\right)=\pi^2 e^\pi\left(\dfrac{e^{2\pi}-1}{8 \pi e^\pi}\right) \\ \iff &\; \dfrac{\pi\left(e^{2\pi}-1\right)}{8}=\dfrac{\pi\left(e^{2\pi}-1\right)}{8}, \end{aligned}$

cioè l’asserto.

Esercizio 59 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare la somma dei seguenti integrali:

$J= \int_{\mathbb{R}}\,dy\int_{\mathbb{R}}e^{-\left(\alpha x^2+\beta xy+\gamma y^2\right)}\,dx+\int_{0}^{+\infty}\dfrac{e^{-a x}-e^{-bx}}{x}\cos\left(kx\right)\,dx,$

dove $\alpha,\,\beta >0$ , $\beta^2-4\alpha\gamma<0$ e $a,b>0,\,k\in \mathbb{R}.$

Svolgimento.

È noto che

$\int_{\mathbb{R}}e^{-\alpha x^2+\beta x+\gamma}\,dx=\sqrt{\dfrac{\pi}{\alpha}}\,e^{\frac{\beta^2}{4\alpha}+\gamma}\quad \text{con}\,\, \alpha>0,\,\beta,\gamma\in\mathbb{R},$

da cui si evince

$\begin{aligned} \int_{\mathbb{R}}\,dy\int_{\mathbb{R}}e^{-\left(\alpha x^2+\beta xy+\gamma y^2\right)}\,dx&=\int_{\mathbb{R}}e^{-\gamma y^2}\,dy\int_{\mathbb{R}}e^{-\alpha x^2-\beta xy} \,dx= \\ &= \int_{\mathbb{R}}e^{-\gamma y^2}\cdot \sqrt{\dfrac{\pi}{\alpha}}\cdot e^{\frac{\beta^2 y^2}{4\alpha}}\,dx=\\ &=\sqrt{\dfrac{\pi}{\alpha}}\int_{\mathbb{R}}e^{-\gamma y^2+\frac{\beta^2 y^2}{4\alpha}}\,dx= \\ &= \sqrt{\dfrac{\pi}{\alpha}}\int_{\mathbb{R}}e^{y^2\left(\frac{-4\alpha \gamma +\beta^2}{4\alpha}\right)}\,dy=\\ &=\sqrt{\dfrac{\pi}{\alpha}}\cdot \sqrt{\dfrac{\pi}{\dfrac{\beta^2-4\alpha\gamma }{4\alpha}}}= \\ &= \sqrt{\dfrac{\pi}{\alpha}}\cdot \sqrt{\dfrac{4\alpha\pi}{\beta^2-4\alpha \gamma }}= \\ &= \dfrac{2\pi}{\sqrt{\beta^2-4\alpha\gamma }}. \end{aligned}$

Consideriamo

$\int_{0}^{+\infty}e^{-\alpha x}\cos\left(kx\right)\,dx.$

Integrando per parti otteniamo

(180) $\begin{equation*} \int_{0}^{+\infty}e^{-\alpha x}\cos\left(kx\right)\,dx=\dfrac{\alpha}{\alpha^2+k^2}\quad \text{con}\,\,\alpha>0,\,k\in \mathbb{R}. \end{equation*}$

Osserviamo che

$\begin{aligned} \int_{0}^{+\infty}\dfrac{e^{-ax}-e^{-bx}}{x}\cos\left(kx\right)\,dx &= \int_{0}^{+\infty}dx\int_{a}^{b}e^{-\alpha x}\cos\left(kx\right)\,d\alpha= \\ &= \lim_{M\to +\infty}\int_{0}^{M}dx\int_{a}^{b}e^{-\alpha x}\cos\left(kx\right)\,d\alpha. \end{aligned}$

È chiaro che la funzione integranda $e^{-\alpha x}\cos\left(kx\right)$ nel dominio $\{(x,\alpha)\in \mathbb{R}^2:\,a\leq \alpha \leq b,\,0\leq x \leq M\}$ risulta integrabile, quindi possiamo applicare il teorema di Fubini

$\int_{0}^{M}dx\int_{a}^{b}e^{-\alpha x}\cos\left(kx\right)\,d\alpha=\int_{a}^{b}d\alpha\int_{0}^{M}e^{-\alpha x}\cos\left(kx\right)\,dx$

e osserviamo che, sfruttando (180), abbiamo³⁵

$\begin{aligned} &\int_{0}^{+\infty}dx\int_{a}^{b}e^{-\alpha x}\cos\left(kx\right)\,d\alpha=\int_{a}^{b}d\alpha\int_{0}^{+\infty}e^{-\alpha x}\cos\left(kx\right)\,dx, \end{aligned}$

ossia

(181) $\begin{equation*} \begin{split} \int_{0}^{+\infty}\dfrac{e^{-a x}-e^{-bx}}{x}\cos\left(kx\right)\,dx &= \int_{a}^{b}\dfrac{\alpha}{\alpha^2+k^2}\,d\alpha \\ &= \dfrac{1}{2}\ln\left(\alpha^2+k^2\right)\bigg \vert^b_a \\ &= \dfrac{1}{2}\ln\left(\dfrac{b^2+k^2}{a^2+k^2}\right), \end{split} \end{equation*}$

da cui segue

$\boxcolorato{analisi}{J=\dfrac{2\pi}{\sqrt{\beta^2-4\alpha\gamma }}+\dfrac{1}{2}\ln\left(\dfrac{b^2+k^2}{a^2+k^2}\right). }$

Nelle ipotesi di validità del teorema di Fubini per scambiare limite e integrale basta l’esistenza dell’integrale improprio dopo lo scambio. ↩

Esercizio 60 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che il periodo di un pendolo semplice è

$T=4\sqrt{\dfrac{\ell}{g}}\int_{0}^{\dfrac{\pi}{2}}\dfrac{d\theta}{\sqrt{1-\sin^2\left(\frac{\theta_0}{2}\right)\sin^2 \theta}},$

dove $\theta_0$ è l’angolo iniziale che forma il pendolo semplice con la verticale e $\ell$ è la lunghezza del pendolo semplice.

Svolgimento.

È noto che

$\dfrac{d^2\theta}{dt^2}=-\dfrac{g}{\ell}\sin \theta .$

Operiamo la sostituzione $\dot{\theta}=N\left(\theta\right)$ e otteniamo

$\dot{N}N=-\dfrac{g}{\ell}\sin\theta,$

cioè

$\frac{N^2}{2}=\dfrac{g}{\ell}\cos\theta+\text{c}\quad \text{c}\in\mathbb{R}.$

Imponendo $\theta=\theta_0\,\text{rad}$ e $\dot{\theta}=0\,\frac{\text{rad}}{\text{s}}$ , si ottiene

$\text{c}=-\dfrac{g}{\ell}\cos\theta_0,$

per cui

$\begin{aligned} \left(\dot{\theta}\right)^2=\dfrac{2g}{\ell}\left(\cos\theta-\cos\theta_0\right) & \iff \dot{\theta}=\sqrt{\dfrac{2g}{\ell}\left(\cos\theta-\cos\theta_0\right)} \\ & \iff \dfrac{\dot{\theta}}{\sqrt{\cos\theta-\cos\theta_0}}=\sqrt{\dfrac{2g}{\ell}}. \end{aligned}$

Per determinare $\dfrac{T}{4}$ risulta chiaro che $\theta$ deve variare tra $\theta_0$ e $0\,\text{rad}$ , pertanto si ha

$\int_{0}^{\frac{T}{4}}\dfrac{\dot{\theta}\,dt}{\sqrt{\cos\theta-\cos\theta_0}}=\dfrac{T}{4}\sqrt{\dfrac{2g}{\ell}}.$

e operando la sostituzione $\theta=k$ abbiamo

$\int_{\theta_0}^{0}\dfrac{dk}{\sqrt{\cos k-\cos\theta_0}}=\dfrac{T}{4}\sqrt{\dfrac{2g}{\ell}}.$

Risulta chiaro che $T>0$ , pertanto

$T=4\sqrt{\dfrac{\ell}{2g}}\left \vert \int_{\theta_0}^{0}\dfrac{dk}{\sqrt{\cos k-\cos\theta_0}} \right \vert = 4\sqrt{\dfrac{\ell}{2g}} \int_{0}^{\theta_0}\dfrac{dk}{\sqrt{\cos k-\cos\theta_0}}$

e, tenendo conto che $\cos k=1-2\sin^2\left(\dfrac{k}{2}\right)$ e in modo analogo $\cos\theta_0$ , si ottiene

(182) $\begin{equation*} \begin{split} T &= 4\sqrt{\dfrac{\ell}{2g}} \int_{0}^{\theta_0}\dfrac{dk}{\sqrt{1-2\sin^2\left(\dfrac{k}{2}\right)-\left(1-2\sin^2\left(\dfrac{\theta_0}{2}\right)\right)}} \\ &= 4\sqrt{\dfrac{\ell}{2g}}\int_{0}^{\theta_0}\dfrac{dk}{\sqrt{2\sin^2\left(\dfrac{\theta_0}{2}\right)-2\sin^2\left(\dfrac{k}{2}\right)}}. \end{split} \end{equation*}$

Successivamente poniamo $\sin\left(\dfrac{k}{2}\right)=\sin\left(\dfrac{\theta_0}{2}\right)\sin z$ :

$\begin{aligned} T&=4\sqrt{\dfrac{\ell}{2g}}\int_{0}^{\frac{\pi}{2}}\dfrac{1}{\sqrt{2\sin^2\left(\dfrac{\theta_0}{2}\right)-2\sin^2\left(\dfrac{\theta_0}{2}\right)\sin^2 z}}\cdot \dfrac{2\sin\left(\dfrac{\theta_0}{2}\right)\cos z}{\sqrt{1-\sin^2\left(\dfrac{\theta_0}{2}\right)\sin^2 z}}=\\ &=4\sqrt{\dfrac{\ell}{2g}}\int_{0}^{\frac{\pi}{2}}\dfrac{1}{\sqrt{2}\sin\left(\dfrac{\theta_0}{2}\right)\cos z}\cdot \dfrac{2\sin\left(\dfrac{\theta_0}{2}\right)\cos z}{\sqrt{1-\sin^2\left(\dfrac{\theta_0}{2}\right)\sin^2 z}}\,dz \\ &= 4\sqrt{\dfrac{\ell}{g}}\int_{0}^{\frac{\pi}{2}}\dfrac{1}{\sqrt{1-\sin^2\left(\dfrac{\theta_0}{2}\right)\sin^2 z}}\,dz, \end{aligned}$

cioè la tesi.

Esercizio 61 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Sia $f:[0,1]\to\mathbb{R}$

una funzione di classe $C^1([0,1])$

tale che

$\int_{0}^{1}f(x)\,dx=2\quad \text{e}\quad \int_{0}^{1}x\,f(x)\,dx=3.$

Dimostrare che

$\int_{0}^{1}\left(f^\prime(x)\right)^2\,dx\geq \dfrac{4\left(440\pi\right)^3}{3\sqrt{3}\,\Gamma^9\left(\dfrac{1}{3}\right)}.$

Svolgimento.

Applichiamo la disuguaglianza di H $\ddot{o}$

lder:

$\int_{0}^{1}x\left(1-x\right)f^\prime(x)\,dx\leq \left(\int_{0}^{1}\left(x-x^2\right)^{\frac{4}{3}}\,dx\right)^{\frac{3}{4}}\left(\int_{0}^{1}\left(f^\prime\left(x\right)\right)^4\,dx\right)^{\frac{1}{4}},$

da cui

$\int_{0}^{1}\left(f^\prime(x)\right)^4\,dx\geq \dfrac{\left(\int_{0}^{1}x\left(1-x\right)f^\prime(x)\,dx\right)^4}{\left(\int_{0}^{1}\left(x-x^2\right)^{\frac{4}{3}}\,dx\right)^{3}}.$

Calcoliamo $\int_{0}^{1}x\left(1-x\right)f^\prime(x)\,dx$ integrando per parti:

$\begin{aligned} \int_{0}^{1}x\left(1-x\right)f^\prime(x)\,dx &= \underbrace{f(x)\left(x-x^2\right)\bigg\vert^1_0}_{=0}-\int_{0}^{1}f(x)\left(1-2x\right)dx= \\ &= -\int_{0}^{1}f(x)\,dx+2\int_{0}^{1}xf(x)\,dx= \\ &= 4. \end{aligned}$

Calcoliamo $\left(\int_{0}^{1}\left(x-x^2\right)^{\frac{4}{3}}\,dx\right)^{3}$ tramite la definizione di funzione $\beta$ :

$\int_{0}^{1}x^{\frac{4}{3}}\left(1-x\right)^{\frac{4}{3}}\,dx=\beta\left(\dfrac{7}{3},\,\dfrac{7}{3}\right)=\dfrac{\beta^2\left(\dfrac{7}{3}\right)}{\beta\left(\dfrac{14}{3}\right)}=\dfrac{\sqrt{3}\Gamma^3\left(\dfrac{1}{3}\right)}{110\pi}.$

Abbiamo dunque

$\int_{0}^{1}\left(f^\prime(x)\right)^4\,dx\geq\dfrac{\left(\int_{0}^{1}x\left(1-x\right)f^\prime(x)\,dx\right)^4}{\left(\int_{0}^{1}\left(x-x^2\right)^{\frac{4}{3}}\,dx\right)^{3}}=\dfrac{4^4}{\left(\dfrac{\sqrt{3}\Gamma^3\left(\dfrac{1}{3}\right)}{110\pi}\right)^3}=\dfrac{4\left(440\pi\right)^3}{3\sqrt{3}\,\Gamma^9\left(\frac{1}{3}\right)},$

cioè la tesi.

Esercizio 62 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Dimostrare che

$\sum_{n=0}^{+\infty}\left(\dfrac{3^{-2n-1}\left(4\cdot3^n\,n^2+2n^2+4\cdot3^n\cdot n+4n+3^n+2\right)}{2\left(4n^4+12n^3+13n^2+6n+1\right)}\right) =\dfrac{\pi^2}{12}-\dfrac{\ln^2\left(3\right)}{4}.$

Svolgimento.

Riscriviamo la serie come segue:

$\sum_{n=0}^{+\infty}\left(\dfrac{3^{-2n-1}\left(4\cdot3^n\,n^2+2n^2+4\cdot3^n\cdot n+4n+3^n+2\right)}{2\left(4n^4+12n^3+13n^2+6n+1\right)}\right)= \underbrace{\sum_{n=0}^{+\infty}\dfrac{\left(3\right)^{-2n-1}}{\left(2n+1\right)^2}}_{:=I}+\underbrace{\sum_{n=0}^{+\infty}\dfrac{\left(3\right)^{-n-1}}{2\left(n+1\right)^2}}_{:=J}.$

Si osserva che

$\int_{0}^{\frac{1}{3}}\dfrac{1}{x}\,dx\int_{0}^{x}t^{2n}\,dt=\dfrac{\left(3\right)^{-2n-1}}{\left(2n+1\right)^2},$

da cui

$\begin{aligned} I &\coloneqq \sum_{n=0}^{+\infty}\dfrac{\left(3\right)^{-2n-1}}{\left(2n+1\right)^2}= \\ &= \sum_{n=0}^{+\infty}\int_{0}^{\frac{1}{3}}\dfrac{1}{x}\,dx\int_{0}^{x}t^{2n}\,dt= \\ &= \int_{0}^{\frac{1}{3}}\dfrac{1}{x}\,dx\int_{0}^{x}\sum_{n=0}^{+\infty}t^{2n}\,dt=\\ &=\int_{0}^{\frac{1}{3}}\dfrac{1}{x}\,dx\int_{0}^{x}\dfrac{1}{1-t^2}\,dt= \\ &= \dfrac{1}{2}\int_{0}^{\frac{1}{3}}\dfrac{1}{x}\,dx\int_{0}^{x}\left(\dfrac{1}{t+1}+\dfrac{1}{1-t}\right)\,dt=\\ &=\dfrac{1}{2}\int_{0}^{\frac{1}{3}}\dfrac{1}{x}\left(\ln\left(1+x\right)-\ln\left(1-x\right)\right)dx=\\ &=\dfrac{1}{2}\underbrace{\int_{0}^{\frac{1}{3}}\dfrac{\ln\left(1+x\right)}{x}\,dx}_{:=I_1}- \dfrac{1}{2}\underbrace{\int_{0}^{\frac{1}{3}}\dfrac{\ln\left(1-x\right)}{x}\,dx}_{:=I_2}. \end{aligned}$

Invocando la definizione di Dilogaritmo³⁶ si ha

$I_1\overset{-x=t}{\coloneqq}-\left(-\int_{0}^{-\frac{1}{3}}\dfrac{\ln\left(1-t\right)}{t}\,dt\right)=-\text{Li}_2\left(-\frac{1}{3}\right)$

$I_2:=-\left(-\int_{0}^{\frac{1}{3}}\dfrac{\ln\left(1-x\right)}{x}\right)=-\text{Li}_2\left(\frac{1}{3}\right),$

donde

$I:=\dfrac{1}{2}I_1-\dfrac{1}{2}I_2=\dfrac{1}{2}\left(-\text{Li}_2\left(-\frac{1}{3}\right)+\text{Li}_2\left(\frac{1}{3}\right)\right).$

Analogamente per $J$ si ha

$J=\dfrac{1}{2}\text{Li}_2\left(\frac{1}{3}\right).$

Poiché è noto che (vedi il libro di Lewin Polylogarithms and Associated Functions)

$2\text{Li}\left(\dfrac{1}{3}\right)-\text{Li}_2\left(-\dfrac{1}{3}\right)=\dfrac{\pi^2}{6}-\dfrac{\ln^2\left(3\right)}{2},$

si ha

$\begin{aligned} \sum_{n=0}^{+\infty}\left(\dfrac{\left(6n^2+8n+3\right)\left(3\right)^{-2n-1}}{2\left(4n^4+12n^3+13n^2+6n+1\right)}\right) &= \dfrac{1}{2}\left(-\text{Li}_2\left(-\frac{1}{3}\right)+\text{Li}_2\left(\frac{1}{3}\right)\right)+\dfrac{1}{2}\text{Li}_2\left(\frac{1}{3}\right)=\\ &=\dfrac{1}{2}\left(-\text{Li}_2\left(-\frac{1}{3}\right)+2\text{Li}_2\left(\frac{1}{3}\right)\right)= \\ &= \dfrac{1}{2}\left(\dfrac{\pi^2}{6}-\dfrac{\ln^2\left(3\right)}{2}\right)= \\ &= \dfrac{\pi^2}{12}-\dfrac{\ln^2\left(3\right)}{4}, \end{aligned}$

cioè l’asserto.

$\operatorname {Li} _{2}(z)=-\int _{0}^{z}{\ln(1-u) \over u}\,du{\text{, }}z\in \mathbb {C}$ ↩

Esercizio 63 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Si determini esplicitamente il valore della serie $\sum_{n\geq 1}\frac{H_n^2}{n^2},$

dove $H_n \coloneqq \sum_{k=1}^n \frac{1}{k}$

è l’ $n$

-esimo numero armonico.

Svolgimento.

Posto $H_n^{(2)}=\sum_{k=1}^{n}\frac{1}{k^2}$

, notiamo preliminarmente che

$\sum_{n\geq 1}\frac{H_n^{(2)}}{n^2} = \sum_{n\geq 1}\frac{1}{n^2}\sum_{k=1}^{n}\frac{1}{k^2}=\frac{1}{2}\left(\left(\sum_{k\geq 1}\frac{1}{k^2}\right)^2+\sum_{k\geq 1}\frac{1}{k^4}\right)=\frac{7\pi^4}{360}$

per simmetria e per i valori espliciti di $\zeta(2)=\sum_{k\geq 1}\frac{1}{k^2}=\frac{\pi^2}{6}$ e $\zeta(4)=\sum_{k\geq 1}\frac{1}{k^4}=\frac{\pi^4}{90}$ . Osserviamo inoltre che per ogni $n\in\mathbb{N}$ si ha

$\int_{0}^{1}x^n \log^2(1-x)\,dx = \lim_{\alpha\to 0^+}\frac{d^2}{d\alpha^2}\int_{0}^{1}x^n(1-x)^{\alpha}\,dx = \lim_{\alpha\to 0^+}\frac{d^2}{d\alpha^2}\left(\frac{\Gamma(\alpha+1)\Gamma(n+1)}{\Gamma(n+\alpha+2)}\right),$

dunque per ogni $n\in\mathbb{N}^+$ abbiamo

(183) $\begin{equation*}\int_{0}^{1}x^{n-1} \log^2(1-x)\,dx = \frac{H_n^2+H_n^{(2)}}{n} \end{equation*}$

e la nostra serie ammette la seguente rappresentazione integrale:

$\sum_{n\geq 1}\frac{H_n^2}{n^2} = -\frac{7\pi^4}{360}+\int_{0}^{1}\log^2(1-x)\sum_{n\geq 1}\frac{x^{n-1}}{n}\,dx = -\frac{7\pi^4}{360}-\int_{0}^{1}\frac{\log^3(1-x)}{x}.$

D’altra parte è evidente (attraverso la sostituzione $x\mapsto 1-x$ ) che l’ultimo integrale coincida con

$-\int_{0}^{1}\frac{\log^3(x)}{1-x} = \sum_{n\geq 0}\int_{0}^{1}x^n(-\log x)^3\,dx = 6\sum_{n\geq 1}\frac{1}{n^4}=\frac{\pi^4}{15}$

e ciò conduce alla conclusione

$\boxcolorato{analisi}{\sum_{n\geq 1}\frac{H_n^2}{n^2} = \frac{17\pi^4}{360}.}$

Esercizio 64 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Data la successione $\{a_n\}_{n\geq 2}$

, con $a_n = \dfrac{\log\left(\cos^2 n\right)}{\log n}$

, si stabilisca se questa converge.

Svolgimento.

Rammentiamo che $\{\cos n\}_{n\geq 0}$

è densa in $[-1,1]$

. Abbiamo infatti che $\pi$

è una quantità irrazionale, dunque la successione data da $e_n = e^{in}$

è densa nella circonferenza unitaria. La proiezione data da $\cos(x)=\text{Re}(e^{ix})$

è continua e pertanto preserva la densità.

Abbiamo pertanto che per una qualche sottosuccessione $\cos^2(n_k)$ converge a $1$ e pertanto $a_{n_k}$ converge a zero. Mostriamo tuttavia che $\lim_{n\to +\infty} a_n$ non esiste.

Consideriamo $\dfrac{p_n}{q_n}$ come uno dei convergenti della frazione continua di $\dfrac{\pi}{2}$ . Per le proprietà generali delle frazioni continue

$\left| \frac{p_n}{q_n}-\frac{p_{n+1}}{q_{n+1}}\right| = \frac{1}{q_n q_{n+1}} < \frac{1}{q_n^2}$

e almeno uno tra $q_n$ e $q_{n+1}$ è certamente dispari: senza perdita di generalità possiamo supporre lo sia $q_n$ . Poiché le successioni dei convergenti di indice pari e dispari convergono monotonamente a $\frac{\pi}{2}$ abbiamo

$\left|\frac{p_n}{q_n}-\frac{\pi}{2}\right|<\frac{1}{q_n^2}\quad\Longrightarrow\quad\left|p_n-q_n\frac{\pi}{2}\right| < \frac{1}{q_n}\leq \frac{2}{p_n}.$

Posto $g(x)=|\!\cos x|$ la $1$ -lipschitzianità di $g(x)$ comporta che

$\left|g(p_n)-g\left(q_n \frac{\pi}{2}\right)\right|=|g(p_n)|=g(p_n)\leq \frac{2}{p_n},$

dunque passando ai logaritmi

$\log g(p_n) \leq \log(2)-\log(p_n)$

e questo comporta

$\liminf_{n\geq 2}\frac{\log\left(\cos^2 n\right)}{\log(n)}\leq -2,$

da cui segue la non esistenza del limite iniziale.

Esercizio 65 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare

$I=\iiint_{\Omega} \sqrt{x^2+y^2+z^2} \, dx \, dy \, dz,$

dove $\Omega = \{(x,y,z) \in \mathbb{R}^3 \, :z\geq x\,,\,(x+z)^2+2y^2\leq 2(x^2+y^2+z^2)^2\leq 2 \}$ .

Svolgimento.

È utile operare la seguente sostituzione:

(184) $\begin{equation*} \begin{cases} \alpha=x+z\\ \beta=x-z\\ \sqrt{2}y=t. \end{cases} \end{equation*}$

Prima di tutto dobbiamo determinare le variabili $x$ e $y$ in funzione di $\alpha$ e $\beta$ e quindi andiamo ad impostare il sistema

(185) $\begin{equation*} \begin{cases} \alpha=x+z\\ \beta=x-z \end{cases} \iff \begin{cases} x=\dfrac{\alpha+\beta}{2}\\[9pt] z=\dfrac{\alpha-\beta}{2}, \end{cases} \end{equation*}$

da cui

(186) $\begin{equation*} \begin{cases} \dfrac{\alpha-\beta}{2}\geq\dfrac{\alpha+\beta}{2}\\[10pt] \alpha^2+t^2\leq 2 \left( \left(\dfrac{\alpha+\beta}{2} \right)^2+ \left(\dfrac{\alpha-\beta}{2} \right)^2+\dfrac{t^2}{2}\right) ^2\\[10pt] 2 \left( \left(\dfrac{\alpha+\beta}{2} \right)^2+ \left(\dfrac{\alpha-\beta}{2} \right)^2+\dfrac{t^2}{2}\right) ^2\leq 2. \end{cases} \end{equation*}$

Riscriviamo (186) $_1$ come

$\dfrac{\alpha-\beta}{2}\geq\dfrac{\alpha+\beta}{2} \iff \beta \leq 0,$

Ora riscriviamo (186) $_2$ come segue:

$\begin{aligned} &\; \alpha^2+t^2\leq 2 \left( \left(\dfrac{\alpha+\beta}{2} \right)^2+ \left(\dfrac{\alpha-\beta}{2} \right)^2+\dfrac{t^2}{2}\right) ^2\\ \iff &\; \alpha^2+t^2\leq 2\left(\dfrac{\alpha^2+\beta^2+2\alpha\beta+\alpha^2+\beta^2-2\alpha\beta}{4}+\dfrac{t^2}{2}\right)^2 \\ \iff & \; \alpha^2+t^2\leq 2 \left( \dfrac{\alpha^2+\beta^2}{2}+\dfrac{t^2}{2}\right)^2 \\ \iff & \; 2 \left(\alpha^2+t^2\right)\leq \left(\alpha^2+\beta^2+t^2 \right)^2. \end{aligned}$

Non ci resta che (186) $_3$ ; sfruttando i precedenti calcoli si ha

$2 \left( \left(\dfrac{\alpha+\beta}{2} \right)^2+ \left(\dfrac{\alpha-\beta}{2} \right)^2+\dfrac{t^2}{2}\right) ^2\leq 2 \iff \left(\alpha^2+\beta^2+t^2 \right)^2\leq 4.$

Ricordando che

$dx\,dy\,dz=\vert J \vert d\alpha\,d \beta \, d t,$

dove

$\vert J \vert =\left \vert \text{det}\begin{vmatrix} \dfrac{\partial x}{\partial \alpha} & \dfrac{\partial x}{\partial \beta} & \dfrac{\partial x}{\partial t}\\\\ \dfrac{\partial y}{\partial \alpha} & \dfrac{\partial y}{\partial \beta} & \dfrac{\partial y}{\partial t}\\\\ \dfrac{\partial z}{\partial \alpha} & \dfrac{\partial z}{\partial \beta} & \dfrac{\partial z}{\partial t} \end{vmatrix}\right \vert = \left \vert\text{det} \begin{vmatrix} \dfrac{1}{2}&\dfrac{1}{2}&0\\\\0&0&\dfrac{1}{\sqrt{2}}\\\\\dfrac{1}{2}&-\dfrac{1}{2}&0 \end{vmatrix} \right \vert = \dfrac{1}{2\sqrt{2}},$

possiamo riscrivere $I$ come

(187) $\begin{equation*} I=\iiint_{\Omega} \sqrt{x^2+y^2+z^2} \, dx \, dy \, dz=\dfrac{1}{4}\iiint_{\tilde{\Omega}} \sqrt{\alpha^2+\beta^2+t^2}\, d \alpha \, d \beta \, dt, \end{equation*}$

dove

$\tilde{\Omega} = \{(\alpha,\beta,t) \in \mathbb{R}^3 \, :\beta\leq 0\,,\,2 \left(\alpha^2+t^2\right)\leq\left(\alpha^2+\beta^2+t^2 \right)^2\,,\,\left(\alpha^2+\beta^2+t^2 \right)^2\leq 4 \}.$

Ora applichiamo le coordinate sferiche per parametrizzare $\tilde{\Omega}$ :

$\begin{cases} \alpha=\rho \cos \theta \sin \phi \\ t=\rho \sin \theta \sin \phi \\ \beta=\rho \cos \phi \end{cases}$

e dunque otteniamo

$\begin{cases} \beta\leq 0\\ 2 \left(\alpha^2+t^2\right)\leq \left(\alpha^2+\beta^2+t^2 \right)^2\\ \left(\alpha^2+\beta^2+t^2 \right)^2\leq 4 \\ \theta \in [0,2 \pi] \end{cases} \iff \begin{cases} \rho \cos \phi \leq 0\\ 2 \rho^2 \sin^2 \phi \leq \rho^4\\ \rho^4 \leq 4 \\ \theta \in [0,2 \pi] \end{cases} \iff \begin{cases} \phi \in \left[\dfrac{\pi}{2},\pi\right]\\ \rho\geq \sqrt{2}\sin \phi \\ 0 \leq \rho \leq \sqrt{2}\\ \theta \in \left[0,2 \pi\right]. \end{cases}$

Dal sistema si ottiene

$\begin{cases} \phi \in \left[\dfrac{\pi}{2},\pi\right]\\[9pt] \rho \in \left[\sqrt{2} \sin \phi , \sqrt{2}\right]\\[9pt] \theta \in \left[0,2 \pi\right]. \end{cases}$

Ricordando che

$d\alpha \, d \beta \, d t= \rho^2 \sin \phi \, d \rho \, d \theta \, d \phi ,$

possiamo riscrivere (187) come

$I=\dfrac{1}{4}\iiint_{\tilde{\Omega}} \sqrt{\alpha^2+\beta^2+t^2}\, d \alpha \, d \beta \, dt=\dfrac{1}{4}\iiint_{\Omega^\star}\rho^3 \sin \phi \, \, d \rho \, d \theta \, d \phi ,$

dove $\Omega^\star = \left\{(\theta,\phi,\rho) \in \mathbb{R}^3 \, :\phi \in \left[\dfrac{\pi}{2},\pi\right]\,,\,\rho \in [\sqrt{2} \sin \phi , \sqrt{2}]\,,\, \theta \in [0,2 \pi]\right\}.$ Procediamo con il calcolo:

$\begin{aligned} I&=\dfrac{1}{4}\int_{0}^{2\pi}d \theta \int_{\frac{\pi}{2}}^{\pi}\sin \phi \, d \phi \int_{\sqrt{2} \sin \phi }^{\sqrt{2}}\rho^3 \, d \rho =\dfrac{2\pi}{4}\int_{\frac{\pi}{2}}^{\pi}\left(\sin \phi -\sin^5 \phi \right) d\phi = \\ &= \dfrac{\pi}{2}\left( -\cos \phi \bigg \vert^\pi_\frac{\pi}{2}- \int_{\frac{\pi}{2}}^{\pi} \sin\phi \left(\dfrac{1-\cos (2 \phi) }{2} \right)^2\, d \phi \right)= \\ &=\dfrac{\pi}{2}\left( 1-\int_{\frac{\pi}{2}}^{\pi}\sin \phi \cdot \frac{1+\cos^2 (2 \phi )-2 \cos (2 \phi )}{4} \, d \phi\right)=\\ &=\dfrac{\pi}{2}\left( 1- \dfrac{1}{4}+\dfrac{1}{2}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot \cos (2 \phi) \, d \phi -\dfrac{1}{4}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot \cos^2 (2 \phi )\, d \phi \right)= \\ &=\dfrac{\pi}{2}\left( \dfrac{3}{4}+\dfrac{1}{2}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot (2\cos^2\phi-1) \, d \phi -\dfrac{1}{4}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot (2\cos^2\phi-1)^2 \, d \phi \right)= \\ &=\dfrac{\pi}{2}\Bigg( \dfrac{3}{4}-\dfrac{1}{2}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \, d\phi + \int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot \cos^2\phi \, d \phi+ \\ &\quad - \dfrac{1}{4}\left(\int_{\frac{\pi}{2}}^{\pi} (4 \sin \phi \cdot \cos^4 \phi + \sin\phi - 2 \sin \phi \cos^2\phi) \; d\phi \right)\Bigg) = \\ &=\dfrac{\pi}{2}\left( \dfrac{3}{4}-\dfrac{\cos\phi}{2}\bigg\vert_{\frac{\pi}{2}}^{\pi} +\dfrac{\cos^3\phi}{3} \bigg\vert_{\frac{\pi}{2}}^{\pi} + \left(\dfrac{\cos^5\phi}{5}+\dfrac{\cos\phi}{4}-\dfrac{2\cos^3\phi}{12}\right)\bigg\vert_{\frac{\pi}{2}}^{\pi} \right)= \\ &=\dfrac{\pi}{2}\left( \dfrac{3}{4}- \dfrac{1}{6} + \dfrac{7}{60} \right)= \dfrac{7\pi}{30}. \end{aligned}$

Concludiamo che

(188) $\begin{equation*} \boxcolorato{analisi}{I=\dfrac{7}{30}\pi.} \end{equation*}$

Esercizio 66 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Calcolare il valore del seguente integrale:

$\int_{0}^{1}dx\int_{0}^{1}\dfrac{\ln^2\left(xy\right)}{1-xy}\,dy.$

Svolgimento.

Lasciamo al lettore il piacere di verificare che la funzione integranda sia integrabile nel rettangolo $(0,1)\times(0,1)$

, e che sia possibile scambiare la serie con l’integrale (e viceversa), specificando l’opportuno teorema da applicare.

Riscriviamo l’integrale come segue:

$\begin{aligned} \int_{0}^{1}dx\int_{0}^{1}\dfrac{\ln^2\left(xy\right)}{1-xy}\,dy&=\int_{0}^{1}dx\int_{0}^{1}\ln^2\left(xy\right)\sum_{n=0}^{+\infty}\left(xy\right)^k\,dy)=\sum_{n=0}^{+\infty}\int_{0}^{1}y^k\,dy\int_{0}^{1}\ln^2\left(xy\right)\,x^k\,dx. \end{aligned}$

Integrando per parti si ottiene:

$\begin{aligned} \int_{0}^{1}\ln^2\left(xy\right)\,x^k\,dx &= \dfrac{x^{k+1}\ln^2\left(xy\right)}{k+1}\bigg\vert^1_0-2\int_{0}^{1}\dfrac{x^{k}}{\left(k+1\right)}\ln\left(xy\right)\,dx= \\ &= \dfrac{\ln^2\left(y\right)}{k+1}-2\int_{0}^{1}\dfrac{x^{k}}{\left(k+1\right)}\ln\left(xy\right)\,dx=\\ &=\dfrac{\ln^2\left(y\right)}{k+1}-2\left(\dfrac{\ln\left(y\right)}{\left(k+1\right)^2}-\int_{0}^{1}\dfrac{x^k}{\left(k+1\right)^2}\,dx\right)= \\ &= \dfrac{\ln^2 y }{\left(k+1\right)}-2\dfrac{\ln\left(y\right)}{\left(k+1\right)^2}+\dfrac{2}{\left(k+1\right)^3}, \end{aligned}$

da cui

$\sum_{n=0}^{+\infty}\int_{0}^{1}y^k\,dy\int_{0}^{1}\ln^2\left(xy\right)\,x^k\,dx= \underbrace{\sum_{n=0}^{+\infty}\int_{0}^{1}\dfrac{y^k\ln^2\left(y\right)}{\left(k+1\right)}\,dy}_{:=I_1}+\underbrace{\sum_{n=0}^{+\infty}\int_{0}^{1}\dfrac{-2\ln \left(y\right)y^k}{\left(k+1\right)^2}}_{:=I_2}+\underbrace{\sum_{n=0}^{+\infty}\dfrac{2}{\left(k+1\right)^3}\int_{0}^{1}y^k\,dy}_{:=I_3},$

i.e.

$\int_{0}^{1}dx\int_{0}^{1}\dfrac{\ln^2\left(xy\right)}{1-xy}\,dy=I_1+I_2+I_3.$

Integrando per parti è facile verificare che

$I_1=I_2=I_3=\sum_{k=0}^{+\infty}\dfrac{2}{\left(k+1\right)^4}$

e, ricordando la definizione di Zeta di Riemann, si ha

$I_1=I_2=I_3=\sum_{k=0}^{+\infty}\dfrac{2}{\left(k+1\right)^4}=2\zeta\left(4\right)=2\cdot \dfrac{\pi^4}{90}=\dfrac{\pi^4}{45}.$

Si conclude che

(189) $\begin{equation*} \boxcolorato{analisi}{\int_{0}^{1}dx\int_{0}^{1}\dfrac{\ln^2\left(xy\right)}{1-xy}\,dy=3\cdot \dfrac{\pi^4}{45}=\dfrac{\pi^4}{15}. } \end{equation*}$

Esercizio 67 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare il seguente limite:

(190) $\begin{equation*} \lim_{n\to+\infty}\dfrac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}\dfrac{i^2+j^2}{i^3+j^3}. \end{equation*}$

Svolgimento.

Si consideri il limite

(191) $\begin{equation*} \lim_{n\to+\infty}\dfrac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}\quad \text{con}\,\,k\in\mathbb{N}, \end{equation*}$

di cui (190) risulta essere un caso particolare (basta porre $k=2$ ).

Applichiamo il teorema di Stolz Cesaro a (191) ottenendo:

$\begin{aligned} &\lim_{n\to+\infty}\dfrac{\displaystyle\sum_{i=1}^{n+1}\sum_{j=1}^{n+1}\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}-\sum_{i=1}^{n}\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}}{n+1-n}= \\ &\qquad = \lim_{n\to+\infty}\left(\displaystyle\sum_{i=1}^{n+1}\sum_{j=1}^{n+1}\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}-\sum_{i=1}^{n}\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}\right)= \\ &\qquad \coloneqq I. \end{aligned}$

Osserviamo che

$\begin{aligned} \sum_{i=1}^{n+1}\sum_{j=1}^{n+1}\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}} &= \sum_{i=1}^{n+1}\left(\dfrac{i^k+1}{i^k+1}+\dots+\dfrac{i^k+n^k}{i^{k+1}+n^{k+1}}+\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)=\\ &=\sum_{i=1}^{n}\left(\dfrac{i^k+1}{i^k+1}+\dots+\dfrac{i^k+n^k}{i^{k+1}+n^{k+1}}+\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)+\\ &\quad +\left(\dfrac{\left(n+1\right)^k+1}{\left(n+1\right)^{k+1}+1}+\dots+\dfrac{\left(n+1\right)^k+n^k}{\left(n+1\right)^{k+1}+n^{k+1}}+\dfrac{\left(n+1\right)^k+\left(n+1\right)^k}{\left(n+1\right)^{k+1}+\left(n+1\right)^{k+1}}\right)=\\ &=\sum_{i=1}^{n}\left(\dfrac{i^k+1}{i^k+1}+\dots+\dfrac{i^k+n^k}{i^{k+1}+n^{k+1}}\right)+\sum_{i=1}^{n}\left(\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)+\\ &\quad+ \left(\dfrac{\left(n+1\right)^k+1}{\left(n+1\right)^{k+1}+1}+\dots+\dfrac{\left(n+1\right)^k+n^k}{\left(n+1\right)^{k+1}+n^{k+1}}+\dfrac{\left(n+1\right)^k+\left(n+1\right)^k}{\left(n+1\right)^{k+1}+\left(n+1\right)^{k+1}}\right)=\\ &=\sum_{i=1}^{n}\sum_{j=1}^{n}\left(\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}\right)+\sum_{i=1}^{n}\left(\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)+ \\ &\quad+ \sum_{i=1}^{n}\left(\dfrac{\left(n+1\right)^k+i^k}{\left(n+1\right)^{k+1}+j^{k+1}}\right)+\dfrac{\left(n+1\right)^k+\left(n+1\right)^k}{\left(n+1\right)^{k+1}+\left(n+1\right)^{k+1}}=\\ &=\sum_{i=1}^{n}\sum_{j=1}^{n}\left(\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}\right)+2\sum_{i=1}^{n}\left(\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)+\dfrac{2}{\left(n+1\right)+\left(n+1\right)}=\\ &=\sum_{i=1}^{n}\sum_{j=1}^{n}\left(\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}\right)+2\sum_{i=1}^{n}\left(\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)+\dfrac{1}{\left(n+1\right)}, \end{aligned}$

da cui

$\begin{aligned} I&=\lim_{n\to+\infty}\Bigg( \sum_{i=1}^{n}\sum_{j=1}^{n}\left(\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}\right)+2\sum_{i=1}^{n}\left(\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)+ \\ &\qquad + \dfrac{1}{\left(n+1\right)}-\sum_{i=1}^{n}\sum_{j=1}^{n}\left(\dfrac{i^k+j^k}{i^{k+1}+j^{k+1}}\right)\Bigg)=\\ &=\lim_{n\to+\infty}2\sum_{i=1}^{n}\left(\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)+\underbrace{\lim_{n\to+\infty}\left(\dfrac{1}{n+1}\right)}_{=0}=\\ &=\lim_{n\to+\infty}2\sum_{i=1}^{n}\left(\dfrac{i^k+\left(n+1\right)^k}{i^{k+1}+\left(n+1\right)^{k+1}}\right)= \\ &= \lim_{n\to+\infty}\dfrac{2}{n+1}\sum_{i=1}^{n}\dfrac{1+\left(\dfrac{i}{n+1}\right)^k}{1+\left(\dfrac{i}{n+1}\right)^{k+1}}= \\ &= 2\int_{0}^{1}\dfrac{1+x^k}{1+x^{k+1}}\,dx. \end{aligned}$

Infine ponendo $k=2$ si ottiene

$\begin{aligned} \lim_{n\to+\infty}\dfrac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}\dfrac{i^2+j^2}{i^3+j^3}&=2\int_{0}^{1}\dfrac{1+x}{1+x^{2}}\,dx= \\ &= 2\int_{0}^{1}\dfrac{1}{1+x^{2}}\,dx+2\int_{0}^{1}\dfrac{x}{1+x^{2}}\,dx=\\ &=2\arctan x +\ln\left(1+x^2\right)\bigg\vert^1_0 \\ &= \dfrac{\pi}{2}+\ln \left(2\right). \end{aligned}$

Si conclude che

(192) $\begin{equation*} \boxcolorato{analisi}{\lim_{n\to+\infty}\dfrac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}\dfrac{i^2+j^2}{i^3+j^3}=\dfrac{\pi}{2}+\ln \left(2\right).} \end{equation*}$

Esercizio 68 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare

$I=\sum_{n=1}^{+\infty}\left(\left(\dfrac{1}{n^2}+\dfrac{1}{\left(n+2\right)^2}+\dfrac{1}{\left(n+4\right)^2}+\dots\right)-\dfrac{1}{2n}\right).$

Svolgimento 1.

Riscriviamo $I$

come segue:³⁷

$\begin{aligned} I&=\lim_{N\rightarrow+\infty} \sum_{n=1}^{2N}\,\left(\sum_{k=0}^{+\infty}\dfrac{1}{\left(n+2k\right)^2}-\dfrac{1}{2n}\right)=\\ &=\lim_{N\rightarrow+\infty}\left(\sum_{n=1}^{N}\,\sum_{k=0}^{+\infty}\dfrac{1}{\left(2n+2k\right)^2}-\dfrac{1}{4n}+\sum_{n=1}^{N}\,\sum_{k=0}^{+\infty}\dfrac{1}{\left(2n-1+2k\right)^2}-\dfrac{1}{2\left(2n-1\right)}\right)=\\ &=\lim_{N\rightarrow+\infty}\left(\dfrac{1}{4}\sum_{n=1}^{N}\,\sum_{k=0}^{+\infty}\dfrac{1}{\left(n+k\right)^2}+\sum_{n=1}^{N}\,\sum_{k=0}^{+\infty}\dfrac{1}{\left(2\left( n+k\right)-1\right)^2}-\sum_{n=1}^{N}\left(\dfrac{1}{4n}+\dfrac{1}{2\left(2n-1\right)}\right)\right). \end{aligned}$

Concentriamoci sul primo termine della serie:

$I_1=\dfrac{1}{4}\sum_{n=1}^{N}\,\sum_{k=0}^{+\infty}\dfrac{1}{\left(n+k\right)^2}.$

Consideriamo la doppia somma simultaneamente (essendo a termini positivi, possiamo permutare arbitrariamente gli addendi). Vogliamo determinare quante volte compare ciascun termine $1/(n+k)^2$ , o, equivalentemente, quante coppie $(n, k)$ restituiscono un valore fissato di $n+k$ , con $1 \leqslant n \leqslant N$ e $k \geqslant 0$ . Osserviamo che

$n+k=1 \iff \begin{cases} n=1\\k=0 \end{cases}$

$n+k=2 \iff \begin{cases} n=1\\ k=1 \end{cases} \vee \quad\begin{cases} n=2\\ k=0. \end{cases}$

Questo procedimento può essere ripetuto fino ad $N$ :

$n+k=N \iff \begin{cases} n=1\\ k=N-1 \end{cases} \vee\quad\begin{cases} n=2\\ k=N-2 \end{cases} \vee \dots \vee\quad \begin{cases} n=N\\ k=0. \end{cases}$

In generale, fissato $\ell$ intero positivo, impostiamo l’equazione:

$n+k=\ell.$

Se $1\leq\ell \leq N$ , risulta immediato che facendo scorrere l’indice $n$ tra 1 ed $N$ , c’è un solo $k$ che soddisfa l’equazione se e solo se $n\leq \ell$ (ovvero $k=\ell -n$ ). Se invece $n>\ell$ , allora nessun $k$ realizza l’equazione (infatti verrebbe $k=\ell-n<0$ che è impossibile). Quindi il termine $1/\ell^2$ viene ripetuto $\ell$ volte, una per ogni $n=1,\dots,\ell$ .

Se invece $\ell>N$ il termine $1/\ell^2$ viene contato solo $N$ volte nella somma; infatti, equivale a capire, fissato $\ell>N$ , quanti indici $n,k$ realizzano $n+k=\ell$ . Per ogni $n=1,\dots,N$ esiste uno ed un solo $k\geq 0$ che realizza l’equazione ovvero $k=\ell-n$ .

Graficamente rappresentiamo quanto detto nella figura 9.

$\quad$

Figura 9: conteggio.

$\quad$

Pertanto abbiamo

(193) $\begin{equation*} I_1=\dfrac{1}{4}\sum_{n=1}^{N}\dfrac{n}{n^2}+\dfrac{1}{4}\sum_{k=N+1}^{+\infty}\dfrac{N}{n^2}. \end{equation*}$

Lo stesso ragionamento si applica alla seconda serie:

(194) $\begin{equation*} I_2=\sum_{n=1}^{N}\,\sum_{k=0}^{+\infty}\dfrac{1}{\left(2\left(n+k\right)-1\right)^2} =\sum_{n=1}^{N}\dfrac{n}{\left(2n-1\right)^2}+\sum_{n=N+1}^{+\infty}\dfrac{N}{\left(2n-1\right)^2}. \end{equation*}$

Torniamo a $I$ e utilizzando la (193) e la (194) abbiamo

$\begin{aligned} I&=\lim_{N\to +\infty}\left(\dfrac{1}{4}\sum_{n=1}^{N}\dfrac{n}{n^2}+\dfrac{1}{4}\sum_{n=N+1}^{+\infty}\dfrac{N}{n^2}+\sum_{n=1}^{N}\dfrac{n}{\left(2n-1\right)^2}+\sum_{n=N+1}^{+\infty}\dfrac{N}{\left(2n-1\right)^2}+\right.\\ &\qquad -\left.\sum_{n=1}^{N}\left(\dfrac{1}{4n}+\dfrac{1}{2(2n-1)}\right)\right)=\\ &=\lim_{N\to +\infty}\sum_{n=N+1}^{+\infty}\left(\dfrac{N}{\left(2n\right)^2}+\dfrac{N}{\left(2n-1\right)^2}\right)+\lim_{N\to +\infty}\sum_{n=1}^{N}\left(\dfrac{n}{\left(2n-1\right)^2}-\dfrac{1}{2\left(2n-1\right)}\right) =\\ &=\underbrace{\lim_{N\to +\infty}\sum_{n=2N+1}^{+\infty}\dfrac{N}{n^2}}_{J_1}+\underbrace{\lim_{N\to +\infty}\sum_{n=1}^{N}\dfrac{1}{2\left(2n-1\right)^2}}_{J_2}. \end{aligned}$

Nell’ultimo passaggio abbiamo usato il fatto che:

$\begin{aligned} \sum_{n=N+1}^{+\infty}& \left(\dfrac{N}{\left(2n\right)^2}+\dfrac{N}{\left(2n-1\right)^2}\right) = \\ &= \dfrac{N}{\left(2N+2\right)^2}+\dfrac{N}{\left(2N+1\right)^2}+\dfrac{N}{\left(2N+4\right)^2}+\dfrac{1}{\left(2N+3\right)^2}+\cdots = \\ &=\sum_{n=2N+1}^{+\infty}\dfrac{N}{n^2}. \end{aligned}$

Calcoliamo ora $J_1$ :

$\sum_{n=2N+1}^{+\infty} \frac{N}{n^2} = \sum_{n=1}^{+\infty} \frac{N}{(n+2N)^2} = \frac{1}{N}\sum_{k=1}^{+\infty}\dfrac{1}{(2+k/N)^2}.$

Prendendo il limite per $N \to +\infty$ , abbiamo:³⁸

$J_1 = \lim_{N\to+\infty} \frac{1}{N}\sum_{k=1}^{+\infty}\dfrac{1}{(2+k/N)^2} = \int_0^{+\infty}\frac{1}{(2+x)^2}\,\mathrm{d}x = \frac{1}{2}.$

La trasformazione della serie in integrale è l’analogo del limite di una somma di Riemann, ma sull’intervallo illimitato $[0,+\infty)$ . In appendice, calcoliamo $J_1$ in modo alternativo e più elementare.

Passiamo ora a $J_2$ . Osserviamo la seguente uguaglianza:

$\sum_{n=1}^{+\infty}\dfrac{1}{n^2}=\sum_{n=1}^{+\infty}\left(\dfrac{1}{\left(2n\right)^2}+\dfrac{1}{\left(2n-1\right)^2}\right)=\dfrac{1}{4}\sum_{n=1}^{+\infty}\dfrac{1}{n^2}+\sum_{n=1}^{+\infty}\dfrac{1}{\left(2n-1\right)^2},$

da cui

(195) $\begin{equation*} \sum_{n=1}^{+\infty}\dfrac{1}{\left(2n-1\right)^2}=\dfrac{3}{4}\sum_{n=1}^{+\infty}\dfrac{1}{n^2} = \frac{3}{4}\cdot\frac{\pi^2}{6} = \frac{\pi^2}{8}, \end{equation*}$

dove abbiamo sfruttato il noto risultato del problema di Basilea³⁹. Si conclude quindi che:

(196) $\begin{equation*} J_2=\frac{1}{2} \sum_{n=1}^{+\infty}\frac{1}{(2n-1)^2} = \dfrac{\pi^2}{16}. \end{equation*}$

Pertanto finalmente giungiamo alla conclusione

(197) $\begin{equation*} \boxcolorato{analisi}{I=J_1+J_2=\dfrac{1}{2}+\dfrac{\pi^2}{16}.} \end{equation*}$

Si noti che, sommando per $n$ fino a $2N$ , stiamo calcolando il limite solo sulla sottosuccessione pari delle somme parziali. Questa operazione è lecita perché la serie (su $n$ ) è a termini positivi, per cui ammette senz’altro limite (finito o infinito), che quindi è lo stesso per qualsiasi sottosuccessione. Infatti, consideriamo questa serie telescopica:

$\frac{1}{n} = \sum_{k=0}^{+\infty}\left(\frac{1}{n+2k}-\frac{1}{n+2k+1}\right).$

Allora:

$\begin{aligned} \sum_{k=0}^{+\infty}\frac{1}{(n+k)^2} - \frac{1}{2n} = {} & \sum_{k=0}^{+\infty}\left(\frac{1}{(n+k)^2} - \frac{1}{2(n+2k)}+\frac{1}{2(n+2k+1)}\right) = \\ ={} & \sum_{k=0}^{+\infty}\frac{4 k + 7 k^2 + 2 n + 6 k n + n^2}{2 (k + n)^2 (2 k + n) (1 + 2 k + n)} > 0. \end{aligned}$

↩

Se $f$ è una funzione positiva non crescente tale che $\int_0^{+\infty}f(x)\,\mathrm{d}x$ esiste finito. Allora:

$\lim_{N \to +\infty} \frac{1}{N}\sum_{k=1}^{+\infty}f\left(\frac{k}{N}\right) = \int_0^{+\infty}f(x)\,\mathrm{d}x.$

↩

Problema di Basilea:

${\sum _{n=1}^{+\infty }{\frac {1}{n^{2}}}=\displaystyle {\frac {\pi ^{2}}{6}.$

↩

Appendice.

Proponiamo qui un metodo alternativo per calcolare la somma $J_1$

. Scriviamo innanzitutto:

$\sum_{n=2N+1}^{+\infty}\dfrac{N}{n^2}=\dfrac{N}{\left(2N+1\right)^2}\cdot 1+\dfrac{N}{\left(2N+2\right)^2}\cdot 1+\dfrac{N}{\left(2N+3\right)^2}\cdot 1+\dfrac{N}{\left(2N+4\right)^2}\cdot 1+\cdots.$

Possiamo interpretare $J_1$ come la l’area della somma di infiniti rettangoli giustapposti di base $1$ (compresa tra $k$ e $k+1$ ) e altezza $N/\left(2N+k\right)^2$ , con $k=0,1,2,\dots$ . Come evidente dalla figura 10 risulta:

$\quad$

Figura 10: metodo alternativo di calcolo di $J_1$

$\quad$

$\begin{aligned} &\int_{2N+1}^{+\infty}\dfrac{N}{x^2}\,\mathrm{d}x\leq \sum_{N=2N+1}^{+\infty}\dfrac{N}{n^2}\leq \int_{2N+1}^{+\infty}\dfrac{N}{\left(x-1\right)^2}\,\mathrm{d}x \iff \dfrac{N}{2N+1}\leq \sum_{N=2N+1}^{+\infty}\dfrac{N}{n^2}\leq \dfrac{N}{2N}. \end{aligned}$

Passando al limite per $N\to +\infty$ , grazie al teorema del doppio confronto:

$\lim_{N\to +\infty}\dfrac{N}{2N+1} = \frac{1}{2} \leq\lim_{N\to +\infty} \sum_{N=2N+1}^{+\infty}\dfrac{N}{n^2}\leq \lim_{N\to +\infty}\dfrac{N}{2N} = \frac{1}{2}.$

Possiamo quindi confermare il risultato precedente:

$J_1 = \lim_{N\to +\infty} \sum_{N=2N+1}^{+\infty}\dfrac{N}{n^2}=\dfrac{1}{2}.$

Svolgimento 2.

Osserviamo che

$\int_{0}^{+\infty}\dfrac{1}{\left(n+2x\right)^2}\,\mathrm{d}x= -\dfrac{1}{2\left(n+2x\right)}\bigg \vert^{+\infty}_{0}=\dfrac{1}{2n}$

$\begin{aligned} \frac{1}{2n} = {} & \int_{0}^{+\infty}\dfrac{1}{\left(n+2x\right)^2}\,\mathrm{d}x = \\ = {} & \sum_{k=0}^{+\infty}\int_{k}^{k+1}\dfrac{1}{\left(n+2x\right)^2}\,\mathrm{d}x = \\ = {} & -\dfrac{1}{2}\sum_{k=0}^{+\infty} \left(\dfrac{1}{n+2k}-\dfrac{1}{n+2\left(k+1\right)}\right) = \\ = {} & -\sum_{ k=0}^{+\infty}\dfrac{n+2k-n-2k-2}{2\left(n+2\left(k+1\right)\right)\left(n+2k\right)}= \\ = {} & \sum_{k=0}^{+\infty}\dfrac{1}{\left(n+2\left(k+1\right)\right)\left(n+2k\right)}. \end{aligned}$

Fissato $m$ intero, in questa somma doppia tutti i termini per cui $n+2k = m$ sono ripetuti più volte. Se $m$ è pari ( $m = 2S$ ), allora ci sono $S$ coppie $(n,k)$ ( $n \geqslant 1$ , $k\geqslant 0$ ) che soddisfano il vincolo, cioè $S = m/2$ ripetizioni. Se $m$ è dispari ( $m = 2S+1$ ), ci sono invece $S+1$ coppie di soluzioni, cioè $S = m/2+1/2$ termini ripetuti. Mettendo tutto assieme:

$\begin{aligned} I = {} &\sum_{\substack{m=1,\\\text{$m$ pari}}}^{+\infty}\dfrac{m}{2}\left(\dfrac{1}{m^2}-\dfrac{1}{m\left(m+2\right)}\right)+\sum_{\substack{m=1,\\\text{$m$ dispari}}}^{+\infty}\left(\frac{m}{2}+\frac{1}{2}\right)\left(\dfrac{1}{m^2}-\dfrac{1}{m\left(m+2\right)}\right)=\\ ={} & \sum_{m=1}^{+\infty}\dfrac{m}{2}\left(\dfrac{1}{m^2}-\dfrac{1}{m\left(m+2\right)}\right)+\dfrac{1}{2}\sum_{S=0}^{+\infty}\left(\dfrac{1}{\left(2S+1\right)^2}-\dfrac{1}{\left(2S+1\right)\left(2S+3\right)}\right)=\\ ={} &\dfrac{1}{2}\sum_{m=1}^{+\infty}\left(\dfrac{1}{m}-\dfrac{1}{m+2}\right)+\dfrac{1}{2}\sum_{S=0}^{+\infty}\dfrac{1}{\left(2S+1\right)^2}+\sum_{S=0}^{+\infty}\dfrac{1}{4}\left(\dfrac{1}{2S+3}-\dfrac{1}{2S+1}\right)=\\ ={} & \dfrac{3}{4}+\dfrac{1}{2}\dfrac{\pi^2}{8}-\dfrac{1}{4}=\dfrac{1}{2}+\dfrac{\pi^2}{16}. \end{aligned}$

Concludiamo nuovamente che

(198) $\begin{equation*} \boxcolorato{analisi}{I=\dfrac{1}{2}+\dfrac{\pi^2}{16}.} \end{equation*}$

Svolgimento 3.

Considerata la funzione trigamma definita da $\psi'(z)=\dfrac{d^2}{dz^2}\log\Gamma(z)$

, è ben noto che

$\psi'(z)=\sum_{n\geq 0}\frac{1}{(n+z)^2} = \int_{0}^{1}x^{z-1}\frac{-\log x}{1-x}\,\mathrm{d}x.$

In particolare la nostra serie può essere rappresentata come

$S=\sum_{n\geq 1}\left(\frac{1}{4}\psi'\left(\dfrac{n}{2}\right)-\frac{1}{2n}\right)=\frac{1}{4}\sum_{n\geq 1}\int_{0}^{1} x^{n/2-1}\left(\frac{-\log x}{1-x}-1\right)\mathrm{d}x,$

oppure come

$\frac{1}{4}\int_{0}^{1}\frac{1}{\sqrt{x}(1-\sqrt{x})}\left(\frac{-\log x}{1-x}-1\right)\mathrm{d}x = \frac{1}{2}\int_{0}^{1}\frac{1}{1-x}\left(\frac{-2\log x}{1-x^2}-1\right)\mathrm{d}x.$

A questo punto è sufficiente considerare la serie di Maclaurin di $\dfrac{1}{(1-x)(1-x^2)}$ e integrarla termine a termine contro $x^2-1-2\log(x)$ . Così facendo otteniamo

$S = \frac{1}{2}\sum_{n\geq 0}\frac{2n+3+(-1)^n}{(n+1)^2(n+3)}=\frac{1}{2}\sum_{n\geq 0}\frac{4n+4}{(2n+1)^2(2n+3)}+\frac{1}{2}\sum_{n\geq 1}\frac{4n}{4n^2(2n+2)},$

dove l’ultima serie è multipla della serie di Mengoli. Per la precedente serie vale invece

$\sum_{n\geq 0}\frac{2n+2}{(2n+1)^2(2n+3)}=\frac{1}{2}\sum_{n\geq 0}\frac{1}{(2n+1)(2n+3)}+\frac{1}{2}\sum_{n\geq 0}\frac{1}{(2n+1)^2},$

dove il primo termine del membro destro è una serie telescopica e l’ultimo è un noto multiplo di $\zeta(2)$ . Riassemblando tutti i contributi deduciamo ancora una volta che:

$\boxcolorato{analisi}{I=\dfrac{1}{2}+\dfrac{\pi^2}{16}.}$

Somme di Riemann con integrale improprio.

Sia $f$

: $[0,+\infty)$

è una funzione continua, positiva, non crescente, tale che $\int_0^{+\infty}f(x)\,\mathrm{d}x$

esista finito. Allora si ha

$\lim_{N\to+\infty}\left(\frac{1}{N}\sum_{n=0}^{+\infty}f\left(\frac{n}{N}\right)\right) = \int_0^{+\infty}f(x)\,\mathrm{d}x.$

Si noti come il membro di sinistra può essere interpretata come il limite di una somma di Riemann applicata all’intervallo illimitato $[0,+\infty)$ .

Dimostrazione. È un risultato noto della teoria delle serie⁴⁰ che, se $g$ soddisfa le ipotesi sopra, si ha:

$\int_0^{+\infty}g(x)\,\mathrm{d}x \leq \sum_{n=0}^{+\infty}g(n) \leq g(0) + \int_0^{+\infty}g(x)\,\mathrm{d}x.$

Applicando questa disuguaglianza alla funzione $g(x) = f(x/N)$ :

$\int_0^{+\infty}f\left(\frac{x}{N}\right)\mathrm{d}x \leq \sum_{n=0}^{+\infty}f\left(\frac{n}{N}\right) \leq f(0) + \int_0^{+\infty}f\left(\frac{x}{N}\right)\mathrm{d}x.$

Cambiando variabile nell’integrale $x = Nt$ :

$N\int_0^{+\infty}f(t)\,\mathrm{d}t \leq \sum_{n=0}^{+\infty}f\left(\frac{n}{N}\right) \leq f(0) + N\int_0^{+\infty}f(t)\,\mathrm{d}t$

e quindi

$\int_0^{+\infty}f(t)\,\mathrm{d}t \leq \frac{1}{N}\sum_{n=0}^{+\infty}f\left(\frac{n}{N}\right) \leq \frac{f(0)}{N} + \int_0^{+\infty}f(t)\,\mathrm{d}t.$

Il risultato segue dal teorema del doppio confronto, dato che per $N \to +\infty$ si ha $f(0)/N \to 0$ .

Si veda per esempio questo link. ↩

Osservazione.

L’indice inferiore della sommatoria è ininfluente, dato che:

$\begin{aligned} \lim_{N\to+\infty}\frac{1}{N}\sum_{n=n_0}^{+\infty}f\left(\frac{n}{N}\right) = {}& \lim_{N\to+\infty}\left(\frac{1}{N}\sum_{n=0}^{+\infty}f\left(\frac{n}{N}\right)-\frac{1}{N}\sum_{n=0}^{n_0-1}f\left(\frac{n}{N}\right)\right) = \\ = {} & \lim_{N\to+\infty}\left(\frac{1}{N}\sum_{n=0}^{+\infty}f\left(\frac{n}{N}\right)\right). \end{aligned}$

Nel nostro caso

$\begin{aligned} \lim_{N\to+\infty}\sum_{n=2N+1}^{+\infty}\frac{N}{n^2} &= \lim_{N\to+\infty}\left(\sum_{n=2N}^{+\infty}\frac{N}{n^2} - \frac{N}{(2N)^2}\right) = \\ &= \lim_{N\to+\infty}\sum_{k=N}^{+\infty}\frac{N}{(k+N)^2} = \\ &= \lim_{N\to+\infty}\frac{1}{N}\sum_{k=N}^{+\infty}\frac{1}{(1+k/N)^2} = \\ &= \int_1^{+\infty} \frac{1}{(1+x)^2}\mathrm{d}x = \frac{1}{2}. \end{aligned}$

Esercizio 69 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Calcolare il seguente integrale:

(199) $\begin{equation*} I=\int_{0}^{1}\left( \dfrac{\ln x}{x-1}\ln \left(1+x\right)\ln\left(1-x\right)+2\right)\dfrac{x-1}{\ln x }\,dx. \end{equation*}$

Svolgimento.

Riscriviamo (199) come segue:

$I=\underbrace{\int_{0}^{1}\ln \left(1-x\right)\ln\left(1+x\right)\,dx}_{I_1}+2\underbrace{\int_{0}^{1}\dfrac{x-1}{\ln x}\,dx}_{I_2}.$

Calcoliamo $I_1$ . Sia

$f:(-1,1)\rightarrow \mathbb{R}$

tale che

$f(x)=\ln \left(1-x\right)\ln \left(1+x\right)$

e osserviamo che $f$ è funzione pari, infatti

$f(-x)=f(x),$

da cui possiamo scrivere

$I_1=\dfrac{1}{2}\int_{-1}^{1}\ln\left(1+x\right)\ln\left(1-x\right)\,dx.$

Operiamo la sostituzione $1+x=2t$ e otteniamo

$\begin{aligned} I_1&=\dfrac{1}{2}\int_{0}^{1}\ln\left(2t\right)\ln\left(1-\left(2t-1\right)\right)\,2dt= \\ &= \int_{0}^{1}\ln\left(2t\right)\ln\left(2-2t\right)\,dt= \\ &= \int_{0}^{1}\left(\ln 2+\ln t\right)\left(\ln 2 +\ln \left(1-t\right)\right)\,dt=\\ &=\int_{0}^{1}\left(\ln^2 2 +\ln 2 \ln\left(1-t\right) +\ln 2 \ln t +\ln t \ln \left(1-t\right)\right)\,dt=\\ &=\ln^2 2 +\ln 2 \int_{0}^{1}\ln\left(1-t\right)\,dt+\ln 2 \int_{0}^{1}\ln t \, dt+\int_{0}^{1}\ln t \ln \left(1-t\right)\,dt=\\ &=\ln^22+\ln 2 (-1)+\ln 2(-1)+\int_{0}^{1}\ln t \ln \left(1-t\right)\,dt =\\ &=\ln^2 2 -2\ln 2 +\underbrace{\int_{0}^{1}\ln t \ln \left(1-t\right)\,dt}_{I_3}. \end{aligned}$

Calcoliamo $I_3$ . Ricordiamo che

$\ln \left(1-t\right)=-\sum_{n=0}^{+\infty}\dfrac{t^{n+1}}{n+1}\quad \forall x \in [-1,1),$

da cui⁴¹

$I_3=-\int_{0}^{1}\sum_{n=0}^{+\infty}\dfrac{t^{n+1}}{n+1}\ln t \, dt=-\sum_{n=0}^{+\infty}\dfrac{1}{n+1}\int_{0}^{1}t^{n+1}\ln t\,dt=-\sum_{n=1}^{+\infty}\dfrac{1}{n}\int_{0}^{1}t^n\ln t \,dt.$

Ricordiamo la seguente formula facilmente ottenibile con l’integrazione per parti:

$\int t^n\ln t \, dt=\dfrac{t^{n+1}\left(\left(n+1\right)\ln t-1\right)}{\left(n+1\right)^2}+\text{costante}\quad \text{con}\,\, n \in \mathbb{N},$

da cui

(200) $\begin{equation*} \int^{1}_{0} t^n\ln t \, dt=-\dfrac{1}{\left(n+1\right)^2}. \end{equation*}$

Applicando (200) a $I_3$ ,⁴² otteniamo

$\begin{aligned} I_3&=\sum_{n=1}^{+\infty}\dfrac{1}{n\left(n+1\right)^2}= \\ &= \sum_{n=1}^{+\infty}\left(\dfrac{1}{n}-\dfrac{1}{n+1}-\dfrac{1}{\left(n+1\right)^2}\right) = \\ &= \lim_{N\rightarrow +\infty}\sum_{n=1}^{N}\left(\dfrac{1}{n}-\dfrac{1}{n+1}\right)-\sum_{n=1}^{+\infty}\dfrac{1}{\left(n+1\right)^2}=\\ &=\lim_{N \rightarrow +\infty}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dots -\dfrac{1}{N+1}\right)+1-1-\sum_{n=2}^{+\infty}\dfrac{1}{n^2}= \\ &= 2-\sum_{n=1}^{+\infty}\dfrac{1}{n^2}= \\ &= 2-\dfrac{\pi^2}{6}, \end{aligned}$

concludendo che

(201) $\begin{equation*} \boxcolorato{analisi}{I_1=\ln^2 2 -2 \ln 2 +2-\dfrac{\pi^2}{6} . } \end{equation*}$

Ora calcoliamo $I_2$ .⁴³ A tale proposito, consideriamo $F:(0,+\infty) \rightarrow \mathbb{R}$ tale che

$F(\alpha)=\int_{0}^{1}\dfrac{x^\alpha-1}{\ln x }\,dx= \int_{0}^{1}f(x,\alpha)\,dx\qquad \text{con}\,\, \alpha >0.$

Osserviamo che

$\lim_{x \rightarrow 0^+}f(x,\alpha)=0 \qquad \mbox{e} \qquad \lim_{x \rightarrow 1^-}f(x,\alpha)=\alpha$

e definiamo

$\tilde{f}(x,\alpha)= \begin{cases} f(x,\alpha), \quad & \text{per} \,\, x \in (0,1)\\ 0, & \text{per}\,\, x=0\\ \alpha, & \text{per}\,\, x=1. \end{cases}$

Allora $\tilde{f}(x,\alpha)$ e $\frac{\partial \tilde{f}}{\partial \alpha}(x,\alpha)=x^\alpha$ sono continue in $[0,1]$ con $\alpha \in (0,+\infty)$ , quindi le ipotesi della regola di derivazione sotto il segno di integrale soddisfatte e, applicandola, abbiamo

(202) $\begin{equation*} \dfrac{dF}{d \alpha}(\alpha)=\int_{0}^{1}\dfrac{\partial f}{\partial \alpha}(x,\alpha)\,dx= \int_{0}^{1} \dfrac{x^\alpha \, \ln x}{\ln x }\,dx=\int_{0}^{1}x^\alpha\, dx =\dfrac{x^{\alpha+1}}{\alpha+1}\bigg \vert^1_0=\dfrac{1}{\alpha+1}. \end{equation*}$

Ora integriamo rispetto ad $\alpha$ e otteniamo

$F(\alpha)=\int \dfrac{1}{\alpha+1}\,d \alpha =\ln \left \vert 1+\alpha \right \vert +\text{costante}.$

Nella precedente poniamo $\alpha=0$ arrivando a

$F(0)=0=\ln 1+\text{costante} \iff \text{costante} =0,$

da cui

$F(\alpha)=\ln(1+\alpha ).$

Ponendo ora $\alpha=1$ in (202) otteniamo

$F(1)=\int_{0}^{1}\dfrac{x-1}{\ln x }\,dx=\ln2.$

Dunque possiamo concludere che

(203) $\begin{equation*} \boxcolorato{analisi}{I_2= \int_{0}^{1}\dfrac{x-1}{\ln x}\,dx=\ln 2 . } \end{equation*}$

Sommando i risultati di $I_1$ e $I_2$ concludiamo che

$I=\ln^2 2 -2 \ln 2 +2-\dfrac{\pi^2}{6}+\ln 2 =\ln^2 2 - \ln 2 +2-\dfrac{\pi^2}{6},$

ovvero

(204) $\begin{equation*} \boxcolorato{analisi}{\displaystyle I=\ln^2 2 - \ln 2 +2-\dfrac{\pi^2}{6}. } \end{equation*}$

Scambio della serie con l’integrale. Sia $\{f_n\}_{n \in \mathbb{N}}\subset \mathcal{R}[a,b]$ dove $\sum_{k=1}^{+\infty}f_k$ converge uniformemente a $f$ in $[a,b]$ . Allora $f \in \mathcal{R}[a,b]$ e $\int_{a}^{b}\sum_{k=1}^{+\infty}f_k(t)\,dt=\sum_{k=1}^{+\infty}\int_{a}^{b}f_k(t)\,dt$ . ↩

Il problema di Basilea, posto da Pietro Mengoli nel 1644 e risolto da Eulero nel 1735, è legato al determinare una somma esplicita della serie armonica di secondo ordine. Eulero dimostrò che

$\sum_{n=1}^{+\infty}\frac{1}{n^2}=\frac{\pi^2}{6}.$

↩

Derivazione sotto segno di integrale Sia $F:[a,b]\rightarrow \mathbb{R}$ definita da

$F(\alpha)=\int_{t_1(\alpha)}^{t_2 (\alpha)}f(x,\alpha )\,dx.$

Se $f(x,\alpha)$ e $\frac{\partial f}{\partial \alpha}(x,\alpha)$ sono continue in $\left\{(x,\alpha):a\leq \alpha \leq b,\,t_1(\alpha)\leq x \leq t_2(\alpha)\right\}$ ed inoltre $t_1(\alpha)$ e $t_2(\alpha)$ sono di classe $C^1$ in $[a,b]$ , allora

$\dfrac{dF}{d\alpha}(\alpha)=\int_{t_1(\alpha)}^{t_2(\alpha)}\dfrac{\partial f}{\partial \alpha }(x,\alpha)\,dx+f(t_2(\alpha),\alpha)\, \dfrac{dt_2}{d\alpha}(\alpha)-f(t_1(\alpha),\alpha)\,\dfrac{dt_1}{d\alpha}(\alpha).$

↩

Esercizio 70 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Siano

$a_n = \sum_{k=1}^{n} \dfrac{1}{k^2} \qquad \text{e} \qquad b_n = \sum_{k=1}^{n} \dfrac{1}{\left(2k-1\right)^2}.$

Dimostrare che

(205) $\begin{equation*} \lim_{n\to +\infty} n \left( \dfrac{b_n}{a_n} - \dfrac{3}{4} \right) = \dfrac{3}{\pi^2}. \end{equation*}$

Svolgimento.

Presentiamo tre diverse dimostrazioni per mostrare (205). La prima utilizza le somme di Riemann, nella seconda applichiamo il teorema di Stolz-Cesàro, e infine la terza è più complessa e utilizza la funzione poligamma. Questo documento è stato inviato a The American Mathematical Monthly Problems and Solutions.

Svolgimento 1.

Per $n\in \mathbb{N}$

, definiamo $c_n:=\sum_{k=1}^{n}1/(2k)^2$

. È facile vedere che $c_n=\dfrac{a_n}{4}$

e anche che $b_n+c_n=a_{2n}=a_n+ \sum_{k=n+1}^{2n}1/k^2$

. Di conseguenza otteniamo

$b_n= \frac{3}{4}a_n + \sum_{k=n+1}^{2n}\frac{1}{k^2},$

e quindi

$\frac{b_n}{a_n}= \frac{3}{4} + \frac{\sum_{k=n+1}^{2n}1/k^2}{a_n}.$

Inoltre, notiamo che

$n\left( \sum_{k=n+1}^{2n}1/k^2 \right)=\frac{1}{n}\sum_{k=n+1}^{2n}\frac{1}{\left( k/n \right)^2},$

è una somma di Riemann che converge a

$\int_{1}^{2}\frac{1}{x^2}\,dx=\frac{1}{2}.$

Concludiamo che

$\begin{aligned} \lim_{n \to +\infty} n\left( \frac{b_n}{a_n}-\frac{3}{4}\right)&= \lim_{n \to +\infty} \frac{n\left( \sum_{k=n+1}^{2n}1/k^2 \right)}{a_n}=\\ &=\frac{\lim_{n \to +\infty}n\left( \sum_{k=n+1}^{2n}1/k^2 \right)}{\lim_{n \to +\infty}a_n}=\frac{1/2}{\pi^2/6}=\frac{3}{\pi^2}, \end{aligned}$

come affermato.

Svolgimento 2.

Abbiamo

$\lim_{n\to +\infty}n\left(\dfrac{b_n}{a_n}-\dfrac{3}{4}\right)=\lim_{n\to+\infty}\left(\dfrac{4b_n-3a_n}{\frac{4a_n}{n}}\right),$

dove

$c_n:=4b_n-3a_n$

$d_n:=\dfrac{4a_n}{n}$

sono successioni infinitesime. Infatti, dal problema di Basilea vediamo immediatamente che

$\lim_{n\to+\infty}d_n=0,$

mentre per l’altra otteniamo

$\lim_{n\to +\infty}c_n=4\cdot\dfrac{\pi^2}{8}-3\cdot\dfrac{\pi^2}{6}=\dfrac{\pi^2}{2}-\dfrac{\pi^2}{2}=0.$

Per mostrare che $d_n$ è non crescente, notiamo innanzitutto che per $n>1$

(206) $\begin{equation*} \begin{aligned} \frac{1}{4}\left( d_{n}-d_{n-1} \right) &= \dfrac{a_n}{n}- \dfrac{a_{n-1}}{n-1}=\\ &= \dfrac{(n-1)a_n-na_{n-1}}{n(n-1)}=\\ &= \dfrac{(n-1)(a_{n-1}+\frac{1}{n^2})-na_{n-1}}{n(n-1)} = &=\dfrac{\frac{1}{n}-a_{n-1}-\frac{1}{n^2}}{n(n-1)} . \end{aligned} \end{equation*}$

Osserviamo poi che

(207) $\begin{equation*} a_n = \sum_{k=1}^n \frac{1}{k^2} \geq \frac{1}{n} \end{equation*}$

per ogni $n\in \mathbb{N}$ , il che si ottiene maggiorando dal basso ogni termine della somma (207) con $\frac{1}{n^2}$ . Di conseguenza, abbiamo

$\frac{1}{n}-a_{n-1} -\frac{1}{n^2} \leq \frac{1}{n}-\frac{1}{n-1}-\frac{1}{n^2} \leq 0,$

\noindent cioè $d_n$ è non crescente. Inoltre, da (206) otteniamo anche che per $n \to +\infty$

$d_n-d_{n-1}= 4\left( -\dfrac{\pi^2}{6} +o(1)\right)\left( \dfrac{1}{n^2} + o\left( \dfrac{1}{n^2} \right)\right)= -\dfrac{2\pi^2}{3n^2}(1+o(1)).$

La tesi segue ora dal teorema di Stolz-Cesàro, poiché abbiamo

$\begin{aligned} \lim_{n\to+\infty}\dfrac{c_n-c_{n-1}}{d_n-d_{n-1}} &= \lim_{n\to +\infty}\dfrac{4(b_n-b_{n-1})-3(a_n-a_{n-1})}{d_n-d_{n-1}}=\\ &=\lim_{n\to +\infty}\dfrac{\dfrac{4}{\left(2n-1\right)^2}-\dfrac{3}{n^2}}{d_n-d_{n-1}}=\\ &= \lim_{n\to +\infty} \dfrac{-\dfrac{2}{n^2}(1+o(1))}{-\dfrac{2\pi^2}{3n^2}(1+o(1))}=\\ &= \dfrac{3}{\pi^2}. \end{aligned}$

Svolgimento 3.

Denotando con $\psi^m$

la funzione poligamma di ordine $m$

, ricordiamo che

$\psi^1\left(n+\dfrac{1}{2}\right)=\dfrac{\pi^2}{2}-4\sum_{k=1}^{n}\dfrac{1}{\left(2k-1\right)^2}\quad \text{per}\,\,n\in \mathbb{N}.$

Usando lo sviluppo asintotico della funzione poligamma

$\psi^1(x)= \dfrac{1}{x}+o\left(\dfrac{1}{x}\right) \quad \text{per}\,\, x \to +\infty,$

otteniamo, per $n\to+\infty$

$\begin{aligned} \sum_{k=1}^{n}\dfrac{1}{\left(2k-1\right)^2}&=\dfrac{\pi^2}{8}-\dfrac{1}{4}\psi^1\left(n+\dfrac{1}{2}\right)=\\ &=\dfrac{\pi^2}{8}-\dfrac{1}{4}\left(\dfrac{1}{n+\frac{1}{2}}\right)+o\left(\dfrac{1}{n}\right)= \\ &= \dfrac{\pi^2}{8}-\dfrac{1}{4n}+o\left(\dfrac{1}{n}\right). \end{aligned}$

Usando la seguente relazione

$\dfrac{\psi^m\left(n\right)}{(-1)^{m+1}m!}=\sum_{k=n}^{+\infty}\dfrac{1}{k^{m+1}}\quad \text{per}\,n\in\mathbb{N}\setminus\{0\},\,m\in\mathbb{N}$

per $m=1$ , otteniamo

$\psi^1\left(n\right)=\sum_{k=n}^{+\infty}\dfrac{1}{k^2},$

ossia

$\psi^1\left(n+1\right)=\sum_{k=1}^{+\infty}\dfrac{1}{k^2}-\sum_{k=1}^{n}\dfrac{1}{k^2}.$

Ora, dallo sviluppo asintotico della funzione poligamma e dal problema di Basilea, possiamo scrivere

$\sum_{k=1}^{n}\dfrac{1}{k^2}=\dfrac{\pi^2}{6}-\dfrac{1}{n+1}+o\left(\dfrac{1}{n}\right)=\dfrac{\pi^2}{6}-\dfrac{1}{n}+o\left(\dfrac{1}{n}\right)\quad \text{per}\,\,n\to +\infty.$

Quindi, otteniamo

$\begin{aligned} \lim_{n\to +\infty}n\left(\dfrac{b_n}{a_n}-\dfrac{3}{4}\right)=\lim_{n\to+\infty}n\left(\left(\dfrac{\pi^2}{8}-\dfrac{1}{4n}+o\left(\dfrac{1}{n}\right)\right)\left(\dfrac{\dfrac{6}{\pi^2}}{1-\dfrac{6}{\pi^2n}+o\left(\dfrac{1}{n}\right)}\right)-\dfrac{3}{4}\right) \end{aligned}$

e poiché

$\left(1-\frac{6}{\pi^2n}+o\left(\frac{1}{n}\right)\right)^{-1}= 1+\dfrac{6}{\pi^2n}+o\left(\dfrac{1}{n}\right)\quad \text{per}\,\,n\to+\infty,$

concludiamo che

$\begin{aligned} \lim_{n\to +\infty}n\left(\dfrac{b_n}{a_n}-\dfrac{3}{4}\right) &= \lim_{n\to+\infty}n\left(\dfrac{6}{\pi^2}\left(\dfrac{\pi^2}{8}-\dfrac{1}{4n}+o\left(\dfrac{1}{n}\right)\right)\left(1+\dfrac{6}{\pi^2n}+o\left(\dfrac{1}{n}\right)\right)-\dfrac{3}{4}\right)=\\ &=\lim_{n\to +\infty}n\left(\dfrac{3}{4}+\dfrac{9}{2\pi^2n}-\dfrac{3}{2\pi^2n}-\dfrac{3}{4}+o\left(\dfrac{1}{n}\right)\right)=\\ &=\lim_{n\to +\infty}n\left(\dfrac{3}{\pi^2n}+o\left(\dfrac{1}{n}\right)\right)= \\ &= \dfrac{3}{\pi^2}, \end{aligned}$

come affermato.

Esercizio 71 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Dimostrare che

(208) $\begin{equation*} \int_0^1 \dfrac{\log(x^6+1)}{x^2+1}\,dx = \dfrac{\pi \log(6)}{2} - 3G, \end{equation*}$

dove $G$ è la costante di Catalan definita come

$G = \sum_{k=0}^{\infty} \frac{(-1)^k}{(2k+1)^2}.$

Svolgimento.

Presentiamo due diverse dimostrazioni per mostrare (208). La prima utilizza l’integrazione complessa, mentre la seconda applica il metodo di integrazione di Feynman.

Svolgimento 1.

Sia $f(x) :=\dfrac{\log(x^6+1)}{x^2+1}$

e $I= \displaystyle \int_0^1 f(x)\,dx$

. Abbiamo

(209) $\begin{equation*} I=\int_0^1 \dfrac{\log(x^6)+\log(x^{-6}+1)}{x^2+1}\,dx =6\int_0^1 \dfrac{\log(x)}{x^2+1}\,dx+ \int_0^1 \dfrac{\log(x^{-6}+1)}{x^2+1}\,dx. \end{equation*}$

Usando la sostituzione $x=1/t$ , otteniamo

(210) $\begin{equation*} \int_0^1 \dfrac{\log(x^{-6}+1)}{x^2+1}\,dx.= \int_1^{+\infty} f(x)\,dx= \int_0^{+\infty} f(x)\,dx -I. \end{equation*}$

Combinando (209) e (210) otteniamo

(211) $\begin{equation*} I=3\int_0^1 \dfrac{\log(x)}{x^2+1}\,dx+ \frac{1}{2}\int_0^{+\infty} f(x)\,dx. \end{equation*}$

È noto che

$G=-\int_0^1 \dfrac{\log(x)}{x^2+1}\,dx,$

che può essere verificato usando l’espansione in serie di $(1+x^2)^{-1}$ . Resta da dimostrare che

$\int_0^{+\infty} f(x)\,dx=\pi\log(6),$

o, equivalentemente, usando la simmetria $x \mapsto -x$ , che

$\int_{\mathbb{R}} f(x)\,dx=2\pi\log(6).$

Inoltre, osservando che

$\log(x^6+1)=\log(x^2+1)+ \log(x^4-x^2+1),$

è sufficiente dimostrare quanto segue:

$\quad$

$I_1 \coloneqq \displaystyle \int_{\mathbb{R}} \dfrac{\log(x^2+1)}{x^2+1}\,dx=2\pi\log(2);$

$I_2 \coloneqq \displaystyle \int_{\mathbb{R}} \dfrac{\log(x^4-x^2+1)}{x^2+1}\,dx=2\pi\log(3).$

Usiamo i metodi di integrazione complessa per calcolare i suddetti integrali.

Per il primo, notiamo che

$\log(x^2+1)=\Re \left( 2 \text{Log}( x+i) \right),$

per qualche ramo del logaritmo. Poiché il punto di ramo della funzione complessa

$g(z):= \displaystyle \frac{\text{Log}(z+i)}{z^2+1}$

è in $z=-i$ , esiste un ramo di $g$ olomorfo nel semipiano superiore. Pertanto, integrando sul semicerchio superiore chiuso, per il Teorema dei Residui otteniamo

$I_1= \Re\left( 4\pi i \,\text{Res}(g(z),i) \right)=\Re\left( 2\pi \,\text{Log}(2i) \right)=2\pi\log(2),$

dove abbiamo usato il fatto che l’integrale sul semicerchio di raggio $R$ si annulla nel limite $R \to +\infty$ , poiché $|f(Re^{i\theta})| \sim \frac{\log R}{R^2}$ .

Per l’ultimo, notiamo analogamente che

$\log(x^4-x^2+1)=\log((x^2-1)^2+x^2)=\Re(2\text{Log}(x^2-1+ix)).$

Osserviamo, come prima, che i punti di ramo della funzione complessa

$h(z):= \displaystyle \frac{\text{Log}(z^2-1+iz)}{z^2+1}$

sono lontani dal semipiano superiore. Pertanto, l’integrazione sul semicerchio superiore chiuso dà

$I_2=\Re(4\pi i \,\text{Res}(h(z),i))=\Re(2\pi \text{Log}(-3))=2\pi\log(3),$

come affermato.

Svolgimento 2.

Ricordiamo che abbiamo

$G=-\int _{{0}}^{{1}}{\frac {\log x}{1+x^{2}}}{\mbox{ d}}x.$

Ne consegue che

$\begin{aligned} \int_0^1 \dfrac{\log(x^6+1)}{x^2+1}\,dx=\dfrac{\pi\log(6)}{2}-3G & \iff \int_{0}^{1}\frac{-3\log(x)+\log(1+x^6)}{1+x^2}\,dx=\dfrac{\pi\log(6)}{2} \\ &\iff \int_{0}^{1}\log\left(x^3+\frac{1}{x^3}\right)\frac{dx}{1+x^2}=\dfrac{\pi\log(6)}{2}. \end{aligned}$

Usando la sostituzione $x\mapsto \tan x$ , l’integrale sopra diventa

$\begin{aligned} \int_{0}^{\frac{\pi}{4}}\log\left(\tan^3 x+\frac{1}{\tan^3 x}\right)\,dx. \end{aligned}$

Notiamo ora che

$\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\log\left(\tan^3x+\frac{1}{\tan^3x}\right)\,dx= \int_{0}^{\frac{\pi}{4}}\log\left(\tan^3x+\frac{1}{\tan^3x}\right)\,dx,$

per cui abbiamo

$\int_{0}^{\frac{\pi}{4}}\log\left(\tan^3x+\frac{1}{\tan^3x}\right)\,dx=\dfrac{1}{2}\int_{0}^{\frac{\pi}{2}}\log\left(\tan^3x+\frac{1}{\tan^3x}\right)\,dx.$

Resta da dimostrare che

$\int_{0}^{\frac{\pi}{2}}\log\left(\tan^3x+\frac{1}{\tan^3x}\right)\,dx=\pi\log(6),$

il che è equivalente a

$\int_{0}^{\frac{\pi}{2}}\log\left(\sin^6 x+\cos^6 x\right)\,dx-3\int_{0}^{\frac{\pi}{2}}\log \cos x\,dx-3\int_{0}^{\frac{\pi}{2}}\log \sin x\,dx=\pi\log(6).$

Ricordiamo che

$\int_{0}^{\frac{\pi}{2}}\log\left(b\cos x\right)\,dx=\int_{0}^{\frac{\pi}{2}}\log\left(b\sin x\right)\,dx=\dfrac{\pi}{2}\log\left(\dfrac{b}{2}\right)\quad \text{per}\,\,b>0,$

e quindi

$\int_{0}^{\frac{\pi}{2}}\log \sin x\,dx=\int_{0}^{\frac{\pi}{2}}\log \cos x\,dx=-\dfrac{\pi}{2}\log 2.$

Infine, dobbiamo calcolare

$\begin{aligned} \int_{0}^{\frac{\pi}{2}}\log\left(\sin^6 x+\cos^6 x\right)\,dx &= \int_{0}^{\pi/2}\log(1-3\sin^2x\cos^2x)\,dx=\\ &=\int_{0}^{\pi/2}\log\left(1-\frac{3}{4}\sin^2(2x)\right)\,dx=\\ &= \int_{0}^{\pi/2}\log\left(1-\frac{3}{4}\sin^2x\right)\,dx, \end{aligned}$

dove l’ultima uguaglianza usa la sostituzione $x \mapsto 2x$ e le simmetrie di $\sin^2(x)$ .

Notiamo che, per $\alpha<1$ , gli integrali $\displaystyle F(\alpha):=\int_0^{\frac{\pi}{2}}\log(1-\alpha \sin^2x)\,dx$ possono essere calcolati usando il metodo di Feynman. Infatti,

$\begin{aligned} F'(\alpha) &= \int_0^{\frac{\pi}{2}}\frac{\partial}{\partial \alpha}\log(1-\alpha \sin^2x)\,dx=\\ &= \frac{1}{\alpha}\int_0^{\frac{\pi}{2}}\left( 1-\frac{1}{1-\alpha \sin^2x}\,dx \right)=\\ &= \frac{\pi}{2\alpha} -\frac{1}{\alpha}\int_0^{\frac{\pi}{2}} \frac{1}{1+(1-\alpha)\tan^2(x)}\,d(\tan(x))=\\ &= \frac{\pi}{2\alpha} - \frac{\pi}{2} \frac{1}{\alpha\sqrt{1-\alpha}}. \end{aligned}$

Osservando che $F(0)=0$ , abbiamo il seguente

$F(\alpha)= \pi\log\left( \frac{1+\sqrt{1-\alpha}}{2} \right).$

Concludiamo che

$\int_{0}^{\pi/2}\log\left(1-\frac{3}{4}\sin^2x\right)\,dx=\pi\log 3 -2\pi\log 2,$

per cui la tesi è dimostrata.

Esercizio 72 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Siano $\alpha_1,\dots,\alpha_n \in \left [0,\dfrac{\pi}{2}\right ]$

degli archi tali che

(212) $\begin{equation*} \alpha_1 + \cdots + \alpha_n = \frac{\pi}{2}. \end{equation*}$

Determinare per quale scelta di $\alpha_1,\dots,\alpha_n$ la quantità

(213) $\begin{equation*} \cos^2 (\alpha_1) \cdot \cos^2 (\alpha_2) \cdots \cos^2 (\alpha_n) \end{equation*}$

è massima.

Richiami teorici.

In questo esercizio useremo i concetti di media aritmetica e media geometrica di numeri reali.

Definizione 3.9 (media aritmetica e media geometrica). Siano $x_1,\dots,x_n$

$n$

numeri reali non negativi. Si definisce media aritmetica di $x_1,\dots,x_n$

la quantità

(214) $\begin{equation*} \frac{x_1 + \dots + x_n}{n} = \frac{1}{n} \sum_{i=1}^n x_i. \end{equation*}$

Si definisce invece media geometrica di $x_1,\dots,x_n$ la quantità

(215) $\begin{equation*} \sqrt[n]{x_1 \cdots x_n}. \end{equation*}$

$\quad$

Sussiste la seguente notevole disuguaglianza tra le medie aritmetica e geometrica.

Proposizione 3.10 (disuguaglianza AM-GM). Dati $n$

numeri reali positivi $x_1,\dots,x_n$

, vale la disuguaglianza

(216) $\begin{equation*} \sqrt[n]{x_1 \cdots x_n} \leq \frac{x_1 + \dots + x_n}{n}. \end{equation*}$

Inoltre, l’uguaglianza vale se e solo se $x_1=x_2= \cdots=x_n$ .

$\quad$

Definiamo ora i concetti di funzione convessa e concava.

Definizione 3.11 (funzioni convesse e concave). Sia $I \subseteq \mathbb{R}$

un intervallo e sia $f \colon I \to \mathbb{R}$

una funzione. $f$

si dice convessa se vale

(217) $\begin{equation*} f\big( t x + (1-t)y\big) \leq \alpha f(x) + (1-t)f(y) \qquad \forall x,y \in I,\,\,\,\forall t \in [0,1]. \end{equation*}$

$f$ si dice strettamente convessa se

(218) $\begin{equation*} f\big( t x + (1-t)y\big) < \alpha f(x) + (1-t)f(y) \qquad \forall x,y \in I \text{ con $x \neq y$},\,\,\,\forall t \in (0,1). \end{equation*}$

La funzione $f$ si dice concava o strettamente concava, se valgono rispettivamente (217) e (218) con le disuguaglianze invertite.

$\quad$

La definizione significa che una funzione è convessa se il suo grafico è “curvato” verso l’alto, ossia se esso giace al di sotto della retta passante per due suoi punti. Analogamente, una funzione è concava se il suo grafico è “curvato” verso il basso, ossia se esso giace al di sopra della retta passante per due suoi punti. Si vede facilmente che $f$ è convessa se e solo se $-f$ è concava e similmente per la stretta convessità e concavità.

Osservazione 3.12. Una funzione $f$ derivabile due volte è concava se e solo se $f'' \leq 0$ ; inoltre, se $f''<0$ , essa è strettamente concava.

Per le funzioni convesse e concave vale la seguente notevole disuguaglianza, detta di Jensen. La scriviamo per le funzioni concave, ma dall’osservazione appena compiuta risulta evidente che vale la disuguaglianza opposta per funzioni convesse.

Proposizione 3.13 (disuguaglianza di Jensen). Sia $I \subseteq \mathbb{R}$

un intervallo, sia $f \colon I \to \mathbb{R}$

una funzione concava, siano $x_1,\dots,x_n \in I$

e $t_1,\dots,t_n \in [0,1]$

tali che $t_1+t_2+\cdots + t_n=1$

. Allora si ha

(219) $\begin{equation*} f\big( t_1 x_1 + \cdots + t_n x_n \big) \geq t_1 f(x_1) + \cdots + t_n f(x_n). \end{equation*}$

Se $f$ è strettamente concava, l’uguaglianza è verificata se e solo se $x_1=x_2=\cdots=x_n$ oppure se i $t_i$ sono tutti nulli tranne uno, che è pari a $1$ .

$\quad$

Svolgimento.

Cominciamo osservando che, per l’ipotesi che $\alpha_1,\dots,\alpha_n \in \left [0,\dfrac{\pi}{2}\right ]$

, tutti i coseni di tali archi sono numeri positivi. Si ha dunque

(220) $\begin{equation*} \sqrt[n]{\cos (\alpha_1) \cdots \cos(\alpha_n)} \leq \frac{\cos (\alpha_1) + \cdots + \cos (\alpha_n) }{n} \leq \cos \left ( \frac{\alpha_1+\cdots+\alpha_n}{n} \right ) = \cos \left ( \frac{\pi}{2n} \right ), \end{equation*}$

dove la prima disuguaglianza segue dalla disuguaglianza tra media geometrica e aritmetica data dalla proposizione 3.10, mentre la seconda disuguaglianza segue dalla disuguaglianza di Jensen data dalla proposizione 3.13 con $t_1=t_2=\cdots=t_n=\dfrac{1}{n}$ , in quanto la funzione coseno è concava nell’intervallo $\left [0, \dfrac{\pi}{2} \right ]$ : infatti la sua derivata seconda è ovunque minore o uguale a $0$ .

Elevando alla potenza $2n$ il primo e l’ultimo membro di (220), si ottiene dunque

(221) $\begin{equation*} \cos^2 (\alpha_1) \cdots \cos^2(\alpha_n) \leq \cos^{2n} \left ( \dfrac{\pi}{2n} \right ), \end{equation*}$

che limita dall’alto i valori possibili dell’espressione che desideriamo studiare.

Poiché però, scegliendo $\alpha_1=\alpha_2=\cdots=\alpha_n= \dfrac{\pi}{2n}$ , si ottiene

(222) $\begin{equation*} \cos^2 (\alpha_1) \cdots \cos^2(\alpha_n) = \cos^{2n} \left ( \dfrac{\pi}{2n} \right ), \end{equation*}$

cioè l’uguaglianza in (221), ciò assicura che il valore $\cos^{2n} \left ( \dfrac{\pi}{2n} \right )$ è effettivamente raggiunto e quindi il massimo valore dell’espressione che volevamo studiare è $\cos^{2n} \left ( \dfrac{\pi}{2n} \right )$ .

Come considerazione finale osserviamo che tale valore massimo è ottenuto solo per la scelta $\alpha_1=\alpha_2=\cdots=\alpha_n= \dfrac{\pi}{2n}$ . Infatti, le uguaglianze nella disuguaglianza AM-GM e nella disuguaglianza di Jensen (poiché il coseno è strettamente concavo in $\left [0,\dfrac{\pi}{2}\right ]$ ) valgono solo se i numeri di cui si calcola la media sono tutti uguali. Ciò prova che la disuguaglianza in (221) è sempre stretta, se gli $\alpha_i$ non sono tutti uguali.

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Document