Test di ingresso per Oxford
Autori e revisori
Leggi...
Quesito 2007-A
è un numero intero?
.
.
.
.
Soluzione.
Se , i due esponenti sono entrambi numeri non negativi, per cui
è un numero intero. Se
, invece,
è una frazione (non apparente).
La risposta corretta è dunque la .
Quesito 2007-B
al variare di ?
.
.
.
.
Soluzione.
Il massimo della funzione è quindi 49, che viene raggiunto per quei valori di
tali che
.
La risposta corretta è dunque la .
Quesito 2007-C
nell’intervallo ?
1.
2.
3.
4.
Soluzione.
Posto , si tratta quindi di risolvere l’equazione algebrica di secondo grado
, che ha soluzioni
e
. Tornando ad
, dato che
, la prima radice si deve scartare, e le uniche soluzioni valide corrispondono a
. Restringendosi all’intervallo
si trova
e
.
La risposta corretta è dunque la .
Quesito 2007-D
risulta più vicino alla circonferenza di equazione
.
.
.
.
Soluzione.
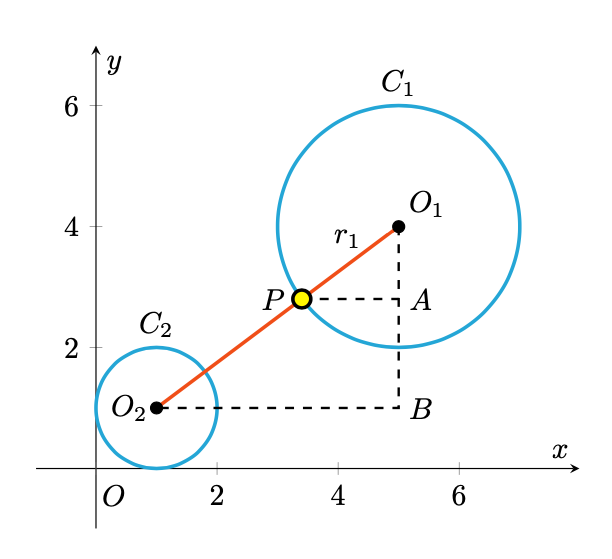
Il punto , di coordinate
, giace quindi sul segmento
, a distanza
da
. Sfruttando la similitudine dei triangoli
e
, possiamo scrivere:
La risposta corretta è dunque la .
Quesito 2007-E
è negativa quando
e
.
è negativa quando
è dispari e
.
è negativa quando
è multiplo di 3 e
.
è negativa quando
è pari e
.
Soluzione.
Per confermare che l’opzione rimanente è corretta, notiamo che, se , tutti i termini tra parentesi nel prodotto che definisce
sono negativi. Per
dispari, elevando a potenza, tre dei fattori restano negativi e due diventano positivi, per cui il prodotto è nel complesso negativo.
Per completezza, notiamo che per dispari
è negativa anche per
con
.
La risposta corretta è dunque la .
Quesito 2007-F
Nessuna soluzione reale.
Una soluzione reale.
Due soluzioni reali.
Tre soluzioni reali.
Soluzione.
Ponendo :
Dunque ci sono tre possibili soluzioni ,
,
, ma quest’ultima non è accettabile perché
. Le due restanti possibilità per
corrispondono a due soluzioni per
.
La risposta corretta è dunque la .
Quesito 2007-G
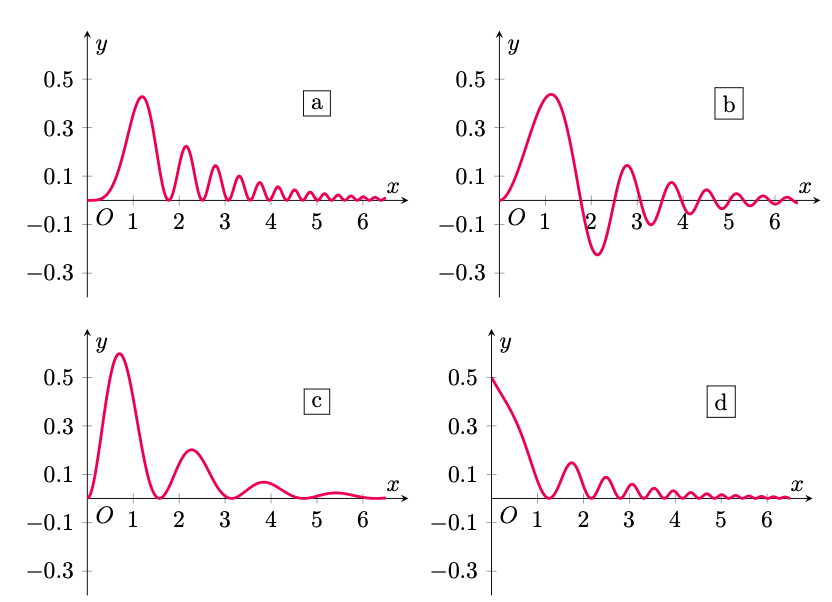
Soluzione.
Per distinguere tra i due casi rimanenti, notiamo che gli zeri della funzione rappresentata dal grafico sono equispaziati, mentre gli zeri di
si addensano per
. Questo succede nel primo grafico ma non nel terzo, in cui gli zeri hanno una distanza approssimativamente costante. Per esclusione si conclude che il grafico di
è rappresentato nella prima figura.
La risposta corretta è dunque la .
Quesito 2007-H
Quanto vale ?
.
0.
.
2.
Soluzione.
Dobbiamo quindi risolvere questo sistema per trovare :
La risposta corretta è dunque la .
Quesito 2007-I
Dati
qual è il più grande possibile valore di ?
.
1.
.
.
Soluzione.
La risposta corretta è dunque la .
Quesito 2007-J
Si sa che la disuguaglianza
è valida per ogni intero. Cosa possiamo concludere su
?
.
.
.
.
Soluzione.
Abbiamo utilizzato la formula che restituisce la somma dei primi numeri interi:
La risposta corretta è dunque la .
Quesito 2008-A
Quanti punti stazionari ha ?
Nessuno.
Uno.
Due.
Tre.
Soluzione.
L’espressione è un’equazione algebrica di secondo grado che ha come discriminante
. Si conclude che l’equazione ha due soluzioni distinte, quindi
ha due punti stazionari. Per completezza riportiamo il grafico di
evidenziando in giallo i due punti stazionari.
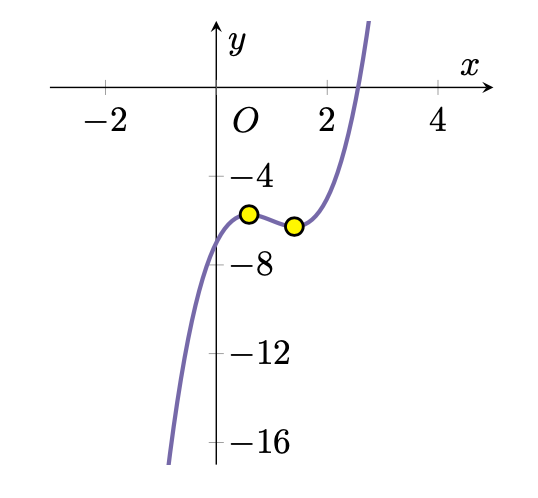
In generale, data una cubica
si può verificare facilmente che la curva presenta due punti stazionari distinti se , un solo punto stazionario se
, e nessun punto stazionario se
. Nell’esercizio proposto,
.
La risposta corretta è dunque la .
Quesito 2008-B
.
.
.
.
Soluzione.
Questo ci dice che e
. Infine, essendo
:
cioè . Graficamente:
La risposta corretta è dunque la .
Quesito 2008-C
Per quali valori di il sistema ha soluzioni?
Per ogni valore di
.
Con l’eccezione di un solo valore di
.
Con l’eccezione di due soli valori di
.
Con l’eccezione di tre soli valori di
.
Soluzione.
Due rette di equazioni e
sono parallele se e solo se
. Usando i parametri del testo, questo si traduce nella condizione:
Si vede facilmente che questa equazione è impossibile, dato che equivale a , cioè
. Concludiamo che le rette non sono mai parallele.
Alternativamente, in modo più formale, si introduce in algebra il concetto di determinante di un sistema di equazioni lineari. Nel nostro caso, esso vale:
Il sistema ha una soluzione unica ogniqualvolta , condizione in questo caso trivialmente verificata. Si vede che la condizione è la stessa di quella ricavata col procedimento geometrico.
La risposta corretta è dunque la .
Quesito 2008-D
Quanto vale il resto della divisione polinomiale di
per
?
2000.
2500.
3000.
3500.
Soluzione.
dove abbiamo usato il fatto che la somma dei primi numeri dispari è pari a
. Per chi non la conoscesse, questa formula si può ricavare ad esempio così:
dove abbiamo utilizzato la formula per la somma della progressione aritmetica.
Se non si sa il teorema del resto, si può cercare di “indovinare” il risultato. Sia:
Calcoliamo il resto della divisione tra
e
per valori piccoli di
. Per
si ha
. Per
abbiamo
, dato che:
Per ed
effettuiamo esplicitamente la divisione polinomiale:
