Test di ingresso per Oxford

Test di Ingresso – Esercizi risolti e simulazioni

Home » Test di ingresso per Oxford

Test di ingresso per Oxford

Autori e revisori

Leggi...

Autori: Daniele Malesani.

Quesito 2007-A

Siano $r$ ed $s$ dei numeri interi. In quali casi la quantità

$K = \frac{6^{r+s}\times12^{r-s}}{8^r\times9^{r+2s}}$

è un numero intero?

$\fbox{a}$ $r+s \leq 0$ .

$\fbox{b}$ $s \leq 0$ .

$\fbox{c}$ $r \leq 0$ .

$\fbox{d}$ $r \geq s$ .

Soluzione.

Ricordando le proprietà delle potenze, si ha:

$\begin{aligned} K = {} & \frac{6^{r+s}\times12^{r-s}}{8^r\times9^{r+2s}} = \\[5pt] = {} & \frac{(2^{r+s}\times3^{r+s})\times(2^{2r-2s}\times3^{r-s})}{2^{3r}\times3^{2r+4s}} = \\[5pt] = {} & 2^{r+s+2r-2s-3r}\times3^{r+s+r-s-2r-4s} = \\[5pt] = {} & 2^{-s}\times3^{-4s}. \end{aligned}$

Se $s \leq 0$ , i due esponenti sono entrambi numeri non negativi, per cui $K$ è un numero intero. Se $s > 0$ , invece, $K$ è una frazione (non apparente).

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2007-B

Qual è il valore massimo assunto dalla funzione

$f(x) = \left[3\sin^2(10x+11)-7\right]^2$

al variare di $x \in \mathbb{R}$ ?

$\fbox{a}$ $-9$ .

$\fbox{b}$ $16$ .

$\fbox{c}$ $49$ .

$\fbox{d}$ $100$ .

Soluzione.

Per ogni $\alpha \in \mathbb{R}$ , si ha $0 \leq \sin^2(\alpha) \leq 1$ , e quindi $0 \leq 3\sin^2(\alpha) \leq 3$ e infine $-7 \leq 3\sin^2(\alpha)-7 \leq -4$ . Elevando al quadrato, e tenendo conto dei segni, si ha allora $16 \leq [\sin^2(\alpha)-7]^2 \leq 49$ .

Il massimo della funzione $f$ è quindi 49, che viene raggiunto per quei valori di $x$ tali che $\sin(10x+11) = 0$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2007-C

Quante soluzioni ha l’equazione

$7\sin(x) + 2\cos^2(x) = 5$

nell’intervallo $0 \leq x < 2\pi$ ?

$\fbox{a}$ 1.

$\fbox{b}$ 2.

$\fbox{c}$ 3.

$\fbox{d}$ 4.

Soluzione.

Ricordando che $\cos^2(x) = 1-\sin^2(x)$ , l’equazione proposta è equivalente a:

$2\sin^2(x) - 7\sin(x) + 3 = 0.$

Posto $\sin(x) = t$ , si tratta quindi di risolvere l’equazione algebrica di secondo grado $2t^2-7t+3 = 0$ , che ha soluzioni $t = 3$ e $t = 1/2$ . Tornando ad $x$ , dato che $\sin(x) \leq 1$ , la prima radice si deve scartare, e le uniche soluzioni valide corrispondono a $\sin(x) = 1/2$ . Restringendosi all’intervallo $[0,2\pi)$ si trova $x = \pi/6$ e $x = 5\pi/6$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2007-D

Quali dei punti che giace sulla circonferenza $C_1$ di equazione

$(x-5)^2+(y-4)^2 = 4$

risulta più vicino alla circonferenza $C_2$ di equazione

$(x-1)^2 + (y-1)^2 = 1?$

$\fbox{a}$ $\left(\dfrac{17}{5},\, \dfrac{14}{5}\right)$ .

$\fbox{b}$ $(3,\,4)$ .

$\fbox{c}$ $(5,\,2)$ .

$\fbox{d}$ $\left(\dfrac{19}{5},\,\dfrac{12}{5}\right)$ .

Soluzione.

La circonferenza $C_1$ ha raggio $r_1 = 2$ e centro in $O_1 = (x_1,y_1) = (5,4)$ , mentre la circonferenza $C_2$ ha centro in $O_2 = (x_2,y_2) = (1,1)$ . La minima distanza di $C_1$ da $C_2$ viene raggiunta nel punto $P$ su $C_1$ che giace sul segmento $O_1O_2$ , che ha lunghezza:

$\overline{O_1O_2} = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} = 5.$

$\quad$

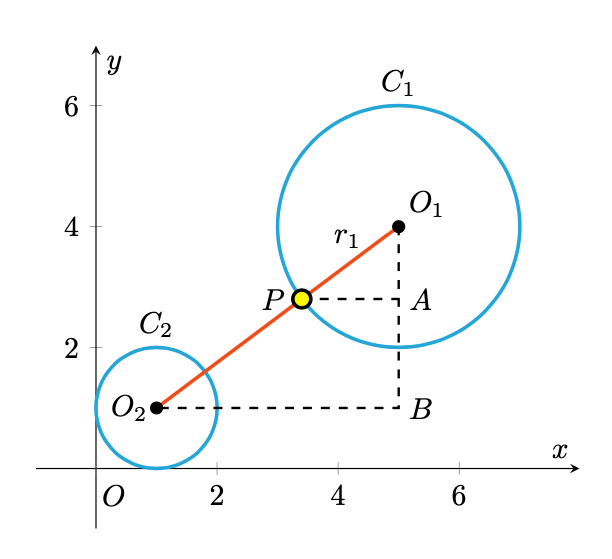
Il punto $P$ , di coordinate $(x_P,y_P)$ , giace quindi sul segmento $O_1O_2$ , a distanza $r_1$ da $O_1$ . Sfruttando la similitudine dei triangoli $O_1O_2B$ e $O_1PA$ , possiamo scrivere:

$\begin{cases} \dfrac{\overline{PA}}{\overline{O_2B}} = \dfrac{\overline{PO_1}}{\overline{O_2O_1}}; \\[10pt] \dfrac{\overline{AO_1}}{\overline{BO_1}} = \dfrac{\overline{PO_1}}{\overline{O_2O_1}}; \end{cases} \implies \quad \begin{cases} \dfrac{x_1-x_P}{x_1-x_2} = \dfrac{r_1}{5}; \\[10pt] \dfrac{y_1-y_P}{y_1-y_2} = \dfrac{r_1}{5}; \end{cases} \implies\quad \begin{cases} x_P = \dfrac{17}{5}; \\[10pt] y_P = \dfrac{14}{5}. \\ \end{cases}$

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2007-E

Sia $n$ un numero intero non negativo e $x \in \mathbb{R}$ . Si consideri la quantità

$K = (1-x)^n(2-x)^{2n}(3-x)^{3n}(4-x)^{4n}(5-x)^{5n}.$

$\fbox{a}$ $K$ è negativa quando $n > 5$ e $x < 5$ .

$\fbox{b}$ $K$ è negativa quando $n$ è dispari e $x > 5$ .

$\fbox{c}$ $K$ è negativa quando $n$ è multiplo di 3 e $x > 5$ .

$\fbox{d}$ $K$ è negativa quando $n$ è pari e $x < 5$ .

Soluzione.

Cominciamo osservando che, se $n$ è pari, $K$ non può essere negativa perché tutti gli esponenti sono pari, per cui $K$ è il prodotto di 5 termini non negativi. Questo esclude immediatamente le risposte $\fbox{a}$ , $\fbox{c}$ e $\fbox{d}$ , in cui alcuni o tutti i valori di $n$ sono pari.

Per confermare che l’opzione rimanente è corretta, notiamo che, se $x > 5$ , tutti i termini tra parentesi nel prodotto che definisce $K$ sono negativi. Per $n$ dispari, elevando a potenza, tre dei fattori restano negativi e due diventano positivi, per cui il prodotto è nel complesso negativo.

Per completezza, notiamo che per $n$ dispari $K$ è negativa anche per $1 < x < 3$ con $x \ne 2$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2007-F

Quante soluzioni ha la seguente equazione?

$8^x+4 = 4^x + 2^{x+2}.$

$\quad$

$\fbox{a}$ Nessuna soluzione reale.

$\fbox{b}$ Una soluzione reale.

$\fbox{c}$ Due soluzioni reali.

$\fbox{d}$ Tre soluzioni reali.

Soluzione.

Sfruttando le proprietà delle potenze, possiamo riscrivere equivalentemente l’equazione in questo modo:

$\begin{gather*} 2^{3x} + 4 = 2^{2x} + 4\cdot2^x; \\ 2^{3x} - 2^{2x} - 4\cdot2^x + 4 = 0. \end{gather*}$

Ponendo $2^x = t$ :

$\begin{gather*} t^3 - t^2 - 4t + 4 = 0; \\ t^2(t-1) - 4(t-1) = 0; \\ (t-1)(t^2-4) = 0; \\ (t-1)(t-2)(t+2) = 0. \end{gather*}$

Dunque ci sono tre possibili soluzioni $t = 1$ , $t = 2$ , $t = -2$ , ma quest’ultima non è accettabile perché $t = 2^x > 0$ . Le due restanti possibilità per $t$ corrispondono a due soluzioni per $x$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2007-G

Quale dei disegni mostrati sotto rappresenta il grafico della funzione

$f(x) = 2^{-x} \sin^2\left(x^2\right)?$

$\quad$

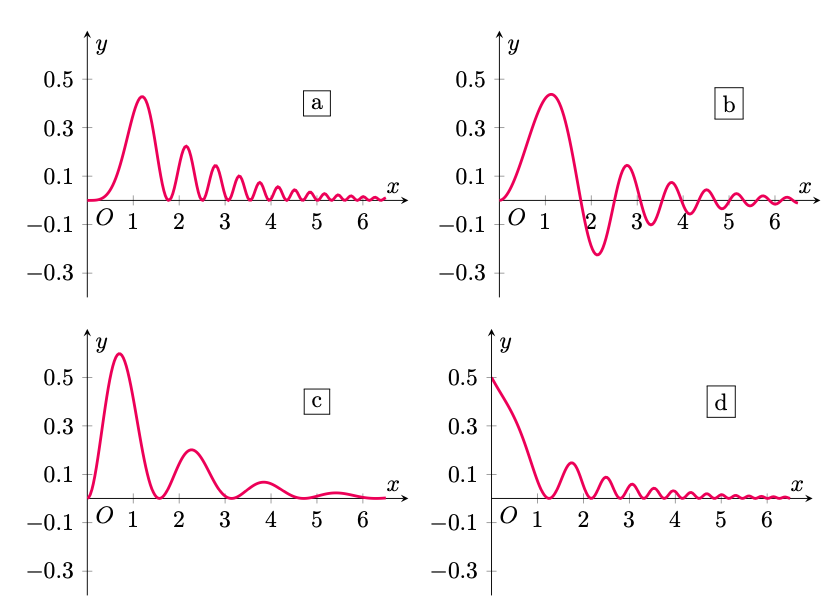
Soluzione.

Per prima cosa, notiamo che $f$ è una funzione non negativa, per cui possiamo escludere la $\fbox{b}$ . Inoltre, $f(0) = 0$ , che ci permette di escludere anche la $\fbox{d}$ .

Per distinguere tra i due casi rimanenti, notiamo che gli zeri della funzione rappresentata dal grafico $\fbox{c}$ sono equispaziati, mentre gli zeri di $\sin\left(x^2\right)$ si addensano per $x \to +\infty$ . Questo succede nel primo grafico ma non nel terzo, in cui gli zeri hanno una distanza approssimativamente costante. Per esclusione si conclude che il grafico di $f$ è rappresentato nella prima figura.

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2007-H

Sia $f$ : $[0,2] \to \mathbb{R}$ una funzione integrabile tale che:

$\begin{gather*} \int_0^1 3f(x)\,\mathrm{d}x + \int_1^2 2f(x)\,\mathrm{d}x = 7; \\ \int_0^2 f(x)\,\mathrm{d}x + \int_1^2 f(x)\,\mathrm{d}x = 1. \end{gather*}$

Quanto vale $\displaystyle\int_0^2f(x)\,\mathrm{d}x$ ?

$\quad$

$\fbox{a}$ $-1$ .

$\fbox{b}$ 0.

$\fbox{c}$ $\dfrac{1}{2}$ .

$\fbox{d}$ 2.

Soluzione.

Poniamo $\displaystyle A = \int_0^2f(x)\,\mathrm{d}x$ e $\displaystyle B = \int_0^1f(x)\,\mathrm{d}x$ . Possiamo quindi scrivere:

$\begin{multline*} \int_0^1 3f(x)\,\mathrm{d}x + \int_1^2 2f(x)\,\mathrm{d}x = \\ = \int_0^1 f(x)\,\mathrm{d}x + \int_0^1 2f(x)\,\mathrm{d}x + \int_1^2 2f(x)\,\mathrm{d}x = B + 2A = 7; \end{multline*}$

$\begin{multline*} \int_0^2 f(x)\,\mathrm{d}x + \int_1^2 f(x)\,\mathrm{d}x = \\ = \int_0^2 f(x)\,\mathrm{d}x + \int_0^2 f(x)\,\mathrm{d}x - \int_0^1 f(x)\,\mathrm{d}x = 2A - B = 1. \end{multline*}$

Dobbiamo quindi risolvere questo sistema per trovare $A$ :

$\begin{cases} 2A + B = 7; \\ 2A - B = 1; \end{cases} \implies\quad \begin{cases} A = 2; \\ B = 3. \end{cases}$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2007-I

Dati $a$ e $b$ reali positivi tali che

$4(\log_{10} a)^2 + (\log_{10}b)^2 = 1,$

qual è il più grande possibile valore di $a$ ?

$\quad$

$\fbox{a}$ $\dfrac{1}{10}$ .

$\fbox{b}$ 1.

$\fbox{c}$ $\sqrt{10}$ .

$\fbox{d}$ $10^{\sqrt{2}}$ .

Soluzione.

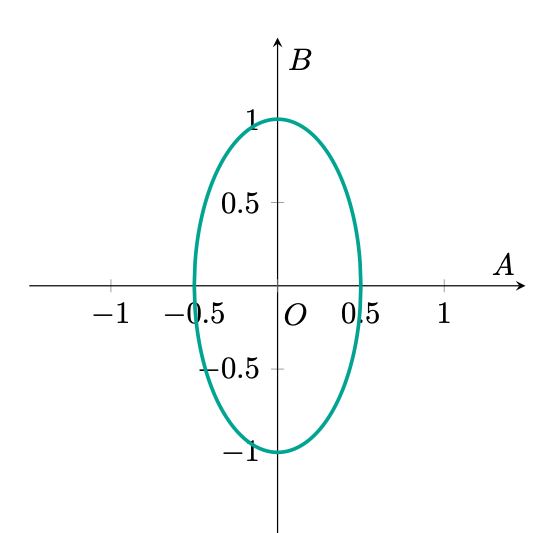
Posto $A = \log_{10}(a)$ e $B = \log_{10}(b)$ , la condizione imposta corrisponde ad un’ellisse nel piano $(A,B)$ , centrata nell’origine e con semiasse orizzontale di lunghezza $1/2$ . Il massimo valore di $a$ si ha in corrispondenza del massimo valore di $A$ , che è proprio $A = 1/2$ . Quindi il massimo di $a = 10^A$ è $10^{1/2} = \sqrt{10}$ .

$\quad$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2007-J

Si sa che la disuguaglianza

$(n+1) + (n^4+2) + (n^9+3) + (n^{16}+4) + \cdots + (n^{10000} + 100) > k$

è valida per ogni $n \geq 1$ intero. Cosa possiamo concludere su $k$ ?

$\quad$

$\fbox{a}$ $k < 1300$ .

$\fbox{b}$ $k^2 < 101$ .

$\fbox{c}$ $k \geq 101^{10000}$ .

$\fbox{d}$ $k < 5150$ .

Soluzione.

Ciascun addendo della somma nel membro di sinistra è una funzione crescente di $n$ , e quindi lo è a maggior ragione l’intera somma. Affinché la disuguaglianza rimanga valida per ogni $n$ , $k$ deve pertanto rispettare il vincolo per il più piccolo valore possibile di $n$ , cioè $n = 1$ . Sostituendo $n=1$ nella condizione, si ha:

$\begin{multline*} (1+1) + (1^4+2) + (1^9+3) + (1^{16}+4) + \cdots + (1^{10000} + 100) = \\ = \underbrace{1+1+1+1+\cdots+1}_{\text{100 volte}} + \sum_{i=1}^{100}i = 100 + \frac{100\times101}{2} = 5150. \end{multline*}$

Abbiamo utilizzato la formula che restituisce la somma dei primi $N$ numeri interi:

$\sum_{i=1}^{N} i = \frac{N(N+1)}{2}.$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2008-A

Si consideri la seguente funzione:

$f(x) = 2x^3 - 6x^2 + 5x - 7.$

Quanti punti stazionari ha $f$ ?

$\quad$

$\fbox{a}$ Nessuno.

$\fbox{b}$ Uno.

$\fbox{c}$ Due.

$\fbox{d}$ Tre.

Soluzione.

Essendo un polinomio, $f$ è naturalmente derivabile e i suoi punti stazionari soddisfano per definizione $f'(x) = 0$ . Calcolando la derivata prima si ha:

$f'(x) = 6x^2 - 12x + 5.$

L’espressione $f'(x) = 0$ è un’equazione algebrica di secondo grado che ha come discriminante $\Delta = 12^2 - 4\times6\times5 = 24 > 0$ . Si conclude che l’equazione ha due soluzioni distinte, quindi $f$ ha due punti stazionari. Per completezza riportiamo il grafico di $f$ evidenziando in giallo i due punti stazionari.

$\quad$

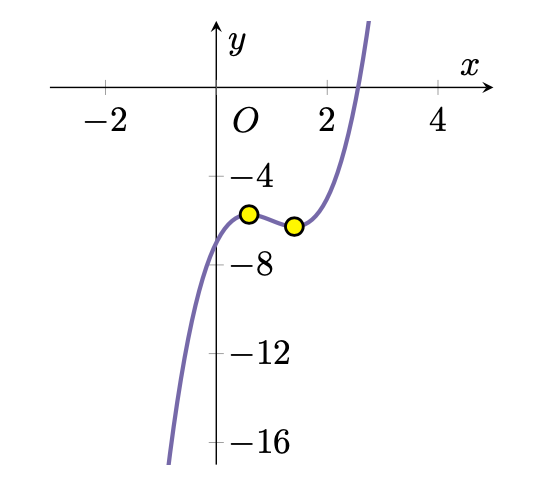
In generale, data una cubica

$y = ax^3 + bx^2 + cx + d,$

si può verificare facilmente che la curva presenta due punti stazionari distinti se $b^2 - 3ac > 0$ , un solo punto stazionario se $b^2 - 3ac = 0$ , e nessun punto stazionario se $b^2 - 3ac < 0$ . Nell’esercizio proposto, $b^2-3ac = 6 > 0$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2008-B

Senza usare la calcolatrice, stabilire quale dei seguenti numeri è il più piccolo.

$\quad$

$\fbox{a}$ $\log_{10} (\pi)$ .

$\fbox{b}$ $\sqrt{\log_{10}(\pi^2)}$ .

$\fbox{c}$ $\left[\dfrac{1}{\log_{10}(\pi)}\right]^3$ .

$\fbox{d}$ $\dfrac{1}{\log_{10}\left(\sqrt{\pi}\right)}$ .

Soluzione.

Posto $x = \log_{10} (\pi)$ , dato che $1 < \pi < 10$ , abbiamo $0 < x < 1$ . Questo ci permette di concludere immediatamente che $1/[\log_{10}(\pi)] > 1$ , e quindi:

$\begin{gather*} \left[\frac{1}{\log_{10}(\pi)}\right]^3 > 1; \\ \frac{1}{\log_{10}\left(\sqrt{\pi}\right)} = \frac{2}{\log_{10}(\pi)} > 2. \end{gather*}$

Questo ci dice che $\fbox{a} < \fbox{c}$ e $\fbox{a} < \fbox{d}$ . Infine, essendo $x < 2$ :

$\sqrt{\log_{10}(\pi^2)} = \sqrt{2\cdot x} > \sqrt{x\cdot x} = x,$

cioè $\fbox{a} < \fbox{b}$ . Graficamente:

$\quad$

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2008-C

Sia $\vartheta \in [0,2\pi)$ un parametro reale, e si consideri il sistema nella variabili $x$ e $y$ :

$\begin{cases} (\cos\vartheta)x - (\sin\vartheta)y = 2; \\ (\sin\vartheta)x + (\cos\vartheta)y = 1. \end{cases}$

Per quali valori di $\vartheta$ il sistema ha soluzioni?

$\quad$

$\fbox{a}$ Per ogni valore di $\vartheta \in [0,2\pi)$ .

$\fbox{b}$ Con l’eccezione di un solo valore di $\vartheta \in [0,2\pi)$ .

$\fbox{c}$ Con l’eccezione di due soli valori di $\vartheta \in [0,2\pi)$ .

$\fbox{d}$ Con l’eccezione di tre soli valori di $\vartheta \in [0,2\pi)$ .

Soluzione.

Il sistema si può interpretare geometricamente come l’intersezione nel piano $xy$ di due rette. In generale, la soluzione sarà unica, a meno che le due rette risultino parallele (nel qual caso non c’è nessuna soluzione, oppure infinite se le rette sono sovrapposte).

Due rette di equazioni $a_1y+b_1x+c_1 = 0$ e $a_2y+b_2x+c_2 = 0$ sono parallele se e solo se $a_1b_2 = a_2b_1$ . Usando i parametri del testo, questo si traduce nella condizione:

$\cos^2\vartheta = - \sin^2\vartheta.$

Si vede facilmente che questa equazione è impossibile, dato che equivale a $\cos^2\vartheta + \sin^2\vartheta = 0$ , cioè $1 = 0$ . Concludiamo che le rette non sono mai parallele.

Alternativamente, in modo più formale, si introduce in algebra il concetto di determinante di un sistema di equazioni lineari. Nel nostro caso, esso vale:

$D = \left|\begin{matrix}\cos\vartheta & -\sin\vartheta \\ \sin\vartheta & \cos\vartheta\end{matrix}\right| = \cos^2\vartheta+\sin^2\vartheta = 1.$

Il sistema ha una soluzione unica ogniqualvolta $D \ne 0$ , condizione in questo caso trivialmente verificata. Si vede che la condizione è la stessa di quella ricavata col procedimento geometrico.

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2008-D

Si consideri il polinomio:

$P(x) = 1 + 3x + 5x^2 + 7x^3 + \cdots + 99x^{49} = \sum_{k=1}^{50}(2k-1)x^{k-1}.$

Quanto vale il resto $R$ della divisione polinomiale di $P(x)$ per $(x-1)$ ?

$\quad$

$\fbox{a}$ 2000.

$\fbox{b}$ 2500.

$\fbox{c}$ 3000.

$\fbox{d}$ 3500.

Soluzione.

Il teorema del resto permette di risolvere rapidamente questo problema: il resto $R$ della divisione di un polinomio $P$ per il binomio $(x-k)$ è pari a $R = P(k)$ . Nel nostro caso $k = 1$ , quindi il resto è dato da:

$R = P(1) = 1 + 3 + 5 + \cdots + 99 = \sum_{k=1}^{50} (2k-1) = 50^2 = 2500,$

dove abbiamo usato il fatto che la somma dei primi $n$ numeri dispari è pari a $n^2$ . Per chi non la conoscesse, questa formula si può ricavare ad esempio così:

$\sum_{k=1}^{50} (2k-1) = 2\cdot\sum_{k=1}^{50}k - \sum_{k=1}^{50}1 = 2\cdot\frac{50\cdot(50+1)}{2} - 50 = 50\cdot50 = 2500,$

dove abbiamo utilizzato la formula per la somma della progressione aritmetica.

Se non si sa il teorema del resto, si può cercare di “indovinare” il risultato. Sia:

$P_n(x) = 1 + 3x + \cdots + (2n-1)x^{n-1} = \sum_{k=1}^{n}(2k-1)x^{k-1} \qquad (n\geq 1).$

Calcoliamo il resto $R_n$ della divisione tra $P_n(x)$ e $(x-1)$ per valori piccoli di $n$ . Per $n = 1$ si ha $R_1 = 1$ . Per $n=2$ abbiamo $R_2 = 4 = 1+3$ , dato che:

$P_2(x) = 3x+1 = 3(x-1)+4.$

Per $n = 3$ ed $n = 4$ effettuiamo esplicitamente la divisione polinomiale:

$\displaystyle\begin{array}{r|l} 5x^2+3x+1 & x-1 \\ \cline{2-2} -5x^2+5x\phantom{{}+1} & 5x + 8 \\ \cline{1-1} 8x+1 & \\ -8x+8 & \\ \cline{1-1} 9 \end{array}$

$\displaystyle\begin{array}{r|l} 7x^3+\phantom{1}5x^2+\phantom{1}3x+\phantom{1}1 & x-1 \\ \cline{2-2} \\[\dimexpr-\normalbaselineskip+0.5\jot] -7x^3+\phantom{1}7x^2\phantom{{}+13x+11} & 7x^2+12x + 15 \\ \cline{1-1} \\[\dimexpr-\normalbaselineskip+0.5\jot] 12x^2+\phantom{1}3x\phantom{{}+11} & \\ -12x^2+12x\phantom{{}+11} & \\ \cline{1-1} \\[\dimexpr-\normalbaselineskip+0.5\jot] 15x+\phantom{1}1 & \\ -15x+15 & \\ \cline{1-1} \\[\dimexpr-\normalbaselineskip+0.5\jot] 16 \end{array}$

Quindi $R_3 = 9 = 1+3+5$ e $R_4 = 16 = 1+3+5+7$ . In tutti i 4 casi esaminati il resto è pari alla somma dei primi $n$ numeri dispari, che ci spinge ad ipotizzare:

$R = R_{50} = \sum_{k=1}^{50}(2k-1) = 2500,$

che è lo stesso risultato trovato prima. Questa affermazione andrebbe però dimostrata per $n$ generico, per esempio per induzione.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2008-E

Qual è il monomio di grado più alto che compare in questo polinomio?

$P(x) =\left\{\left[\left(2x^6+7\right)^3+\left(3x^8-12\right)^4\right]^5+\left[\left(3x^5-12x^2\right)^5+\left(x^7+6\right)^4\right]^6\right\}^3.$

$\quad$

$\fbox{a}$ $x^{424}$ .

$\fbox{b}$ $x^{450}$ .

$\fbox{c}$ $x^{500}$ .

$\fbox{d}$ $x^{504}$ .

Soluzione.

Elevando un polinomio di grado $n$ ad una potenza intera $m$ , si ottiene un polinomio di grado $n \cdot m$ (volendo, questa affermazione si può verificare per induzione). Inoltre, il grado della somma di più polinomi è naturalmente il massimo tra i gradi dei singoli addendi. Poniamo per brevità:

$A = 2x^6+7, \quad B = 3x^8-12, \quad C = 3x^5-12x^2, \quad D = x^7+6.$

Se $X$ è un polinomio, indichiamo con $\partial X$ il suo grado, per cui $\partial A = 6$ , $\partial B = 8$ , $\partial C = 5$ e $\partial D = 7$ . Seguendo le parentesi dall’interno verso l’esterno, abbiamo il seguente schema:

$\begin{displaymath} \left.\begin{matrix} \left.\begin{matrix}\partial(A^3) = 6\cdot3 = 18 \\\partial(B^4) = 8\cdot4 = 32\end{matrix}\right\} \Rightarrow \partial[(A^3+B^4)^5] = 32\cdot5=160 \\[10pt] \left.\begin{matrix}\partial(C^5) = 5\cdot5 = 25 \\\partial(D^4) = 7\cdot4 = 28\end{matrix}\right\} \Rightarrow \partial[(C^5+D^4)^6] = 28\cdot6=168 \\ \end{matrix}\right\}\Rightarrow\partial P = 168\cdot3 = 504. \end{displaymath}$

Resta da determinare il coefficiente numerico del monomio di grado 504 di $P$ . Questo proviene dal ripetuto elevamento a potenza del termine $x^7$ in $D$ , che ha coefficiente unitario. Quindi anche il risultato deve avere coefficiente pari ad $1$ . In definitiva, $P$ contiene proprio il monomio $1\cdot x^{504}$ .

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2008-F

Sia $f$ : $\mathbb{R} \to \mathbb{R}$ una funzione integrabile. Si vuole stimare il valore approssimato di

$I = \int_0^1 f(x)\diff{x}.$

Allo scopo, dopo aver diviso l’intervallo $[0,1]$ in $n$ parti uguali (con $n$ opportuno), si applica il metodo dei trapezi, ottenendo come risultato il valore $I_0$ . Sapendo che $I_0$ è una sovrastima del valore esatto $I$ (cioè $I_0 > I$ ), quale dei seguenti integrali verrebbe sottostimato applicando nuovamente il metodo dei trapezi (sempre dividendo l’intervallo di integrazione in $n$ parti uguali)?

$\quad$

$\fbox{a}$ $\displaystyle\int_0^1 2f(x)\diff{x}$ .

$\fbox{b}$ $\displaystyle\int_0^1 [f(x)-1]\diff{x}$ .

$\fbox{c}$ $\displaystyle\int_1^2 f(x-1)\diff{x}$ .

$\fbox{d}$ $\displaystyle\int_0^1 [1-f(x)]\diff{x}$ .

Soluzione.

Oltre alla rappresentazione grafica, riportiamo l’espressione esplicita di $I_0$ stimato col metodo dei trapezi. Su $[0,1]$ , posto $x_k = k/n$ ( $0 \leq k \leq n$ ), si ha:

$I_0 = \sum_{k=0}^{n-1}\frac{f(x_k)+f(x_{k+1})}{2n}.$

Usando questa formula, si può verificare che la stima col metodo dei trapezi è un’operazione lineare. Inoltre, per una funzione costante $f(x) = k$ , la stima di $I_0$ su $[0,1]$ vale $k$ . Valutiamo ora le quattro opzioni una alla volta.

$\quad$

$\fbox{a}$ Applicato a $2f$ , il metodo dei trapezi restituisce come risultato $2I_0$ , che è una sovrastima del valore esatto $2I$ . $\fbox{b}$ Applicato a $f-1$ , il metodo dei trapezi fornisce come risultato $I_0 - 1$ , che è una sovrastima del valore esatto $I-1$ . $\fbox{c}$ Essendo $f(x-1)$ la traslazione di $f(x)$ di 1 verso destra, il metodo dei trapezi applicato a $f(x-1)$ sull’intervallo $[1,2]$ (in questo caso $x_k = 1 + k/n$ ) fornisce proprio $I_0$ , che è una sovrastima del valore esatto $I$ . $\fbox{d}$ Applicato a $1-f$ , il metodo dei trapezi fornisce come risultato $1-I_0$ , che è effettivamente una sottostima del valore esatto $1-I$ . La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2008-G

Determinare quale dei seguenti diagrammi rappresenta (qualitativamente) il grafico della curva definita dall’equazione

$y = \frac{1}{4x-x^2-5}.$

$\quad$

Soluzione.

Un modo per procedere è notare la seguente uguaglianza:

$y = \frac{1}{4x-x^2-5} = -\frac{1}{(x-2)^2+1}.$

Questo mostra che la funzione è sempre negativa ed è definita su tutto $\mathbb{R}$ . Il termine $(x-2)^2 + 1$ è una parabola che ha minimo assoluto per $x = 2$ , per cui anche l’opposto del suo inverso, $y = -1 / [(x-2)^2 + 1]$ , ha un minimo assoluto in $x = 2$ .

Le prime due risposte sono dunque escluse perché il loro grafico è positivo. La quarta opzione è esclusa perché il minimo si ha per $x < 0$ . Almeno qualitativamente, il terzo grafico rispetta invece tutte le proprietà di $y$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2008-H

Al variare del parametro $k$ , in quali casi l’equazione

$9^x - 3^{x+1} = k$

ha soluzioni reali?

$\quad$

$\fbox{a}$ $k \geq -\dfrac{9}{4}$ .

$\fbox{b}$ $k>0$ .

$\fbox{c}$ $k\leq-1$ .

$\fbox{d}$ $k\geq\dfrac{5}{8}$ .

Soluzione.

Possiamo riscrivere l’equazione assegnata nel modo seguente, seguendo l’idea di completare il quadrato di un binomio:

$\begin{gather*} 3^{2x} - 3\cdot3^{x} = k; \\ \left(3^x\right)^2 - 2\cdot\frac{3}{2}\cdot3^x + \frac{9}{4} = k + \frac{9}{4};\\ \left(3^x-\frac{3}{2}\right)^2 = k + \frac{9}{4}. \end{gather*}$

Dato che il membra di sinistra non è mai negativo, condizione necessaria affinché questa equazione abbia soluzione è che:

$k \geq -\frac{9}{4}.$

Se questa condizione viene rispettata, si ha:

$3^x = \frac{3}{2} \pm \sqrt{k+\frac{9}{4}}.$

Prendendo il segno +, il membro di destra è sicuramente positivo per $k \geq -9/4$ , per cui esiste sicuramente almeno una soluzione per $x$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2008-I

Si consideri la seguente funzione definita per ogni intero non negativo $n$ :

$S(n) = \text{somma delle cifre di $n$ (in base 10).}$

Per esempio, $S(125) = 1+2+5 = 8$ . Si calcoli il valore della somma:

$\sum_{n=1}^{99} S(n) = S(1)+S(2)+\cdots+S(98)+S(99).$

$\quad$

$\fbox{a}$ $746$ .

$\fbox{b}$ $862$ .

$\fbox{c}$ $900$ .

$\fbox{d}$ $924$ .

Soluzione.

Chiamiamo per brevità $S_\textrm{0-9} = S(0)+S(1)+S(2)+\cdots+S(9)$ . $S_\textrm{0-9}$ si può calcolare meccanicamente oppure usando la formula per la somma della progressione aritmetica:

$S_\textrm{0-9} = \frac{9(9+1)}{2} = 45.$

Considerando tutti gli interi appartenenti ad una certa decina, per esempio 20, 21, \ldots, 29, abbiamo:

$S(20)+S(21)+\cdots+S(29) = (2+0)+(2+1)+(2+2)+\cdots+(2+9) = 2\cdot10 + S_\textrm{0-9}.$

Lo stesso avviene per tutte le altre decine, per cui:

$\begin{aligned} \phantom{=} {} & S(1)+S(2)+\cdots+S(98)+S(99) = \\ = {} & (0 + S_\textrm{0-9}) + (1\cdot10 + S_\textrm{0-9}) + (2\cdot10 + S_\textrm{0-9}) + \cdots + (9\cdot10 + S_\textrm{0-9}) = \\ = {} & (1+2+\cdots+9)\cdot10 + 10 S_\textrm{0-9} = \\ = {} & 20S_\textrm{0-9} = 900. \end{aligned}$

Un modo alternativo per visualizzare questo risultato è disporre i numeri tra 0 e 99 nella seguente tabella, scrivendo in ogni riga una decina diversa:

$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$
$10$	$11$	$12$	$13$	$14$	$15$	$16$	$17$	$18$	$19$
$20$	$21$	$22$	$23$	$24$	$25$	$26$	$27$	$28$	$29$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$80$	$81$	$82$	$83$	$84$	$85$	$86$	$87$	$88$	$89$
$90$	$91$	$92$	$93$	$94$	$95$	$96$	$97$	$98$	$99$

In ciascuna riga, la somma delle cifre delle unità è uguale a $S_\textrm{0-9}$ . In ogni colonna, la somma delle cifre delle decine è anch’essa uguale a $S_\textrm{0-9}$ . Dato che ci sono 10 righe e 10 colonne, la somma di tutte le cifre presenti nella tabella è quindi pari a:

$10\cdot S_\textrm{0-9} + 10\cdot S_\textrm{0-9} = 20\cdot45 = 900.$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2008-J

Quante soluzioni reali possiede l’equazione

$(3+\cos x)^2 = 4 - 2\sin^8 x$

nell’intervallo $0 \leq x < 2\pi$ ?

$\quad$

$\fbox{a}$ Nessuna.

$\fbox{b}$ Una.

$\fbox{c}$ Due.

$\fbox{d}$ Tre.

Soluzione.

Dato che $-1 \leq \cos x \leq 1$ , il membro di sinistra è compreso tra $(3-1)^2$ e $(3+1)^2$ , cioè tra 4 e 16. Inoltre, dato che $0 \leq \sin^8x \leq 1$ , il membro di destra è compreso tra $(4-2)$ e 4, cioè tra 2 e 4. L’unica possibilità affinché l’equazione sia verificata è che esistano dei valori di $x$ per cui entrambi i membri siano uguali a 4. Nell’intervallo $[0,2\pi)$ , il primo termine è uguale a 4 se:

$(3+\cos x)^2 = 4 \iff \cos x = -1 \iff x = \pi.$

Sostituendo nel secondo membro, si vede che effettivamente $x = \pi$ è una soluzione dato che $4 - 2\sin^8\pi = 4$ .

La figura rappresenta graficamente la situazione (l’area grigia identifica l’intervallo da considerare $0 \leq x < 2\pi$ ).

$\quad$

Rendered by QuickLaTeX.com

$\quad$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009-A

Sia $a$ un parametro reale. Stabilire, al variare di $a$ , qual è il valore minimo della quantità

$I(a) = \int_0^1\left(x^2-a\right)^2\mathrm{d}x.$

$\quad$

$\fbox{a}$ $\dfrac{3}{20}$ .

$\fbox{b}$ $\dfrac{4}{45}$ .

$\fbox{c}$ $\dfrac{7}{13}$ .

$\fbox{d}$ $1$ .

Soluzione.

Conviene valutare direttamente l’integrale:

$\begin{aligned} I(a) = {} & \int_0^1\left(x^2-a\right)^2\mathrm{d}x = \int_0^1\left(x^4+a^2-2ax^2\right)\mathrm{d}x = \\ = {} & \left|\frac{x^5}{5}+a^2x-\frac{2}{3}ax^3\right|_0^1 = \frac{1}{5} +a^2 - \frac{2}{3}a = \\ = {} & a^2 - \frac{2}{3}a + \frac{1}{9} - \frac{1}{9}+\frac{1}{5} = \left(a-\frac{1}{3}\right)^2 + \frac{4}{45}. \end{aligned}$

Tra la seconda e la terza riga, abbiamo sfruttato la tecnica del completamento del quadrato. Scritto così, si vede facilmente che il valore minimo di $I(a)$ corrisponde ad $a = 1/3$ e vale $4/45$ .

Alternativamente, dopo aver calcolato l’integrale, sarebbe stato possibile trovare gli zeri della derivata dell’espressione in funzione di $a$ :

$I(a) = \frac{1}{5} +a^2 - \frac{2}{3}a \implies I'(a) = 2a - \frac{2}{3}.$

La derivata $I'(a)$ si annulla per $a = 1/3$ e la derivata seconda $I''(1/3) = 2$ è positiva, permettendoci di concludere che il valore minimo di $I$ è $I(1/3) = 1/5 + 1/9 - 2/9 = 4/45$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009-B

Si consideri la circonferenza di equazione:

$x^2 + y^2 + 6x + 8y = 75.$

Qual è la sua distanza minima dall’origine degli assi cartesiani?

$\quad$

$\fbox{a}$ 3.

$\fbox{c}$ 4.

$\fbox{d}$ 5.

$\fbox{e}$ 10.

Soluzione.

Completando i quadrati, possiamo riscrivere l’equazione della circonferenza nel seguente modo:

$\begin{gather*} (x+3)^2 - 9 + (y+4)^2 - 16 = 75; \\ (x+3)^2 + (y+4)^2 = 10^2. \end{gather*}$

Riconosciamo quindi che si tratta di una circonferenza di centro $C = (-3,-4)$ e raggio $r = 10$ . Il suo punto $P$ più vicino all’origine deve trovarsi necessariamente sulla retta che passa per $C$ e per $O$ .

Dato che la distanza di $C$ dall’origine è pari a $\sqrt{(-3)^2+(-4)^2} = 5$ , si conclude che la distanza tra $P$ e $O$ è pari a $r-5 = 5$ .

$\quad$

Rendered by QuickLaTeX.com

$\quad$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2009-C

Sia data la seguente equazione:

$x^4 = (x-c)^2,$

dove $c$ è una costante reale. Per quali valori di $c$ l’equazione ha quattro soluzioni reali (alcune delle quali eventualmente coincidenti)?

$\quad$

$\fbox{a}$ $c \leq \dfrac{1}{4}$ .

$\fbox{b}$ $-\dfrac{1}{4} \leq c\leq \dfrac{1}{4}$ .

$\fbox{c}$ $c \leq -\dfrac{1}{4}$ .

$\fbox{d}$ Per ogni valore di $c$ .

Soluzione.

Contiamo le soluzioni in funzione di $c$ risolvendo direttamente l’equazione. Riscriviamola usando la formula della differenza di quadrati:

$\begin{gather*} x^4 - (x-c)^2 = 0; \\ (x^2-x +c)\cdot(x^2+x-c) = 0. \end{gather*}$

Per la legge di annullamento del prodotto, questa equazione è verificata se uno o entrambi i fattori a primo membro sono nulli. Abbiamo dunque due equazioni di secondo grado; per avere in tutto quattro soluzioni (alcune delle quali eventualmente coincidenti), entrambe devono avere due radici. Calcoliamo i loro discriminanti:

$\begin{array}{l} x^2 - x + c = 0 \implies \Delta = 1 - 4c \geq 0\text{ per }c \leq\dfrac{1}{4}; \\ x^2 + x - c = 0 \implies \Delta = 1 + 4c \geq 0\text{ per }c \geq-\dfrac{1}{4}. \end{array}$

Per avere in tutto 4 soluzioni, entrambe le condizioni devono essere soddisfatte simultaneamente, per cui concludiamo che:

$-\frac{1}{4} \leq c \leq \frac{1}{4}.$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009-D

Qual è il più piccolo numero intero $n$ tale che:

$S(n) = 1-2+3-4+5+\cdots+(-1)^{n+1}n = \sum_{j=1}^n (-1)^{j+1}j \geq 100?$

$\quad$

$\fbox{a}$ $99$ .

$\fbox{b}$ $101$ .

$\fbox{c}$ $199$ .

$\fbox{e}$ $300$ .

Soluzione.

Per capire l’andamento di $S(n)$ , calcoliamo quanto fa per i primi valori di $n$ :

$\begin{array}{l}S(1) = +1; \\ S(2) = 1-2 = -1; \\ S(3) = 1-2+3 = +2; \\ S(4) = 1-2+3-4 = -2; \\ S(5) = 1-2+3-4+5 = +3; \\ \ldots \end{array}$

Vediamo che i segni si alternano e il valore assoluto cresce di 1 ogni 2 passi. Possiamo condensare questa osservazione nella seguente ipotesi:

( $\star$ ) $\begin{equation*} S(n) = \begin{cases}-\dfrac{n}{2} & \text{se $n$ è pari;} \\[7pt] \dfrac{n+1}{2} & \text{se $n$ è dispari.}\end{cases} \end{equation*}$

Stabilito questo, è facile vedere che il pù piccolo intero tale che $S(n) \geq 100$ deve essere dispari (in modo che $S$ sia positiva) e deve quindi soddisfare:

$\frac{n+1}{2} \geq 100 \implies n \geq 199.$

Per gli amanti del rigore, resta da dimostrare la $(\star)$ , che al momento è solo una congettura. Si può procedere usando il principio di induzione.

$\quad$

L’affermazione è vera per $n=1$ (che è dispari), dato che la $(\star)$ restituisce $(1+1)/2 = 1 = S(1)$ .

Ora, supposto che la $(\star)$ sia vera per $n = k$ , dimostriamola per $n = k+1$ . Innanzitutto notiamo che per ogni $k > 1$ vale:
$\begin{aligned}S(k+1) = {} & \sum_{j=1}^{k+1} (-1)^{j+1}j = \sum_{j=1}^{k} (-1)^{j+1}j + (-1)^{k+2}(k+1) = \\ = {} & S(k) + (-1)^{k+2}(k+1).\end{aligned}$

Utilizzando questa formula, e l’ipotesi di induzione $(\star)$ per $n = k$ :

$\begin{array}{l@{\mbox{}\implies\mbox{}}l}\text{$k$ pari} & S(k+1) = -\dfrac{k}{2}+k+1 = \dfrac{(k+1)+1}{2}; \\[7pt] \text{$k$ dispari} & S(k+1) = \dfrac{k+1}{2}-k-1 = -\dfrac{(k+1)}{2}.\end{array}$

L’espressione ritrovata corrisponde proprio alla $(\star)$ per $n = k+1$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2009-E

Per $0 \leq x < 2\pi$ , si consideri l’equazione

$2^{\sin^2(x)} + 2^{\cos^2(x)} = 2.$

Quale delle seguenti affermazioni è corretta?

$\quad$

$\fbox{a}$ L’equazione non ha soluzioni.

$\fbox{b}$ L’equazione ha esattamente una soluzione.

$\fbox{c}$ L’equazione ha esattamente due soluzioni.

$\fbox{d}$ L’equazione è valida per ogni $x$ .

Soluzione.

Notiamo che $0 \leq \sin^2(x) \leq 1$ e $0 \leq \cos^2(x) \leq 1$ . Quindi:

$2^0 + 2^0 = 2 \leq 2^{\sin^2(x)} + 2^{\cos^2(x)} \leq 2^1 + 2^1 = 4.$

L’unica possibilità in cui il membro di sinistra è uguale a 2 è che entrambi gli addendi siano uguali a 1, quindi che $\sin^2(x) = \cos^2(x) = 0$ . Ma questa condizione non è mai verificata, per cui l’equazione proposta non ha soluzioni.

Un procedimento alternativo, ma con più calcoli, è il seguente. Dato che $\sin^2(x) = 1-\cos^2(x)$ , possiamo riscrivere l’equazione in questo modo:

$2^{1-\cos^2(x)} + 2^{\cos^2(x)} = \frac{2}{2^{\cos^2(x)}} + 2^{\cos^2(x)} = 2.$

Posto $2^{\cos^2(x)} = t$ , abbiamo allora:

$\begin{gather*} \frac{2}{t} + t = 2; \\ t^2-2t+2 = 0; \\ (t-1)^2 + 1 = 0. \end{gather*}$

È evidente che questa equazione non ha soluzioni reali, dato che il membro di sinistra è sempre positivo e non può quindi annullarsi. Non ha pertanto soluzioni neppure l’equazione di partenza.

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2009-F

Per quali valori del parametro reale $k$ questa equazione ha quattro soluzioni reali distinte?

$3x^4 - 16x^3 + 18x^2 + k = 0.$

$\quad$

$\fbox{a}$ $-27 < k < 5$ .

$\fbox{b}$ $5 < k < 27$ .

$\fbox{c}$ $-27 < k < -5$ .

$\fbox{d}$ $-5 < k < 0$ .

Soluzione.

Non è banale risolvere questa equazione di quarto grado, ma possiamo studiare il segno dei massimi e dei minimi della funzione $f(x) = 3x^4 - 16x^3 + 18x^2 + k$ e, da questo, dedurre il numero dei suoi zeri. La derivata prima è:

$f'(x) = 12x^3-48x^2+36x = 12x(x^2-4x+3) = 12x(x-1)(x-3).$

Il segno di $f'$ è determinato da quello dei suoi fattori. Osservando il diagramma qui sotto, concludiamo che $f'(x) > 0$ se $0 < x < 1$ e $x > 3$ (intervalli marcati in azzurro).

$\quad$

Studiamo ora l’andamento di $f$ : tende a $+\infty$ (ed è quindi positiva) per $x \to \pm \infty$ ; decresce su $(-\infty,0)$ e $(1,3)$ mentre cresce su $(0,1)$ e $(3,+\infty)$ . Essendo continua, il numero degli zeri di $f$ dipende dal segno che assume nei suoi punti estremanti, che sono 0, 1 e 3:

$f(0) = k, \qquad f(1) = 5+k, \qquad f(3) = -27+k.$

La funzione $f$ avrà 4 zeri se simultaneamente $f(0) < 0$ , $f(1) > 0$ e $f(3) < 0$ , che si traduce nelle condizioni:

$k < 0 \quad \land \quad 5+k > 0 \quad \land \quad -27+k < 0 \implies -5 < k < 0.$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2009-G

Si consideri il grafico dei punti di coordinate $(x,y)$ che soddisfano l’equazione:

$\sin(x) = \sin(y).$

Quale dei seguenti diagrammi rappresenta le soluzioni dell’equazione?

$\quad$

Soluzione.

L’equazione $\sin(x) = \sin(y)$ ha due famiglie di soluzioni:

$x = y + 2k\pi \quad \vee \quad x = \pi - y + 2h\pi,$

dove $k$ e $h$ sono numeri interi arbitrari. La prima famiglia è composta da rette parallele alla bisettrice del primo e terzo quadrante, separate verticalmente di $2\pi;$ una di queste rette passa per l’origine. La seconda è composta da rette parallele alla bisettrice del secondo e quarto quadrante, sempre spaziate verticalmente di $2\pi;$ nessuna di queste rette passa per l’origine.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2009-H

Quanto vale la stima di questo integrale:

$\int_0^12^x\diff{x}$

se si usa la regola dei trapezi dividendo il dominio $[0,1]$ is $N$ sotto-intervalli equispaziati?

$\quad$

$\fbox{a}$ $\dfrac{1}{2N}\left(1+\dfrac{1}{2^{1/N}+1}\right)$ .

$\fbox{b}$ $\dfrac{1}{2N}\left(1+\dfrac{2}{2^{1/N}-1}\right)$ .

$\fbox{c}$ $\dfrac{1}{N}\left(1-\dfrac{1}{2^{1/N}-1}\right)$ .

$\fbox{d}$ $\dfrac{1}{2N}\left(\dfrac{5}{2^{1/N}+1}-1\right)$ .

Soluzione.

L’integrale definito di una funzione positiva rappresenta l’area compresa tra l’asse delle ascisse ed il grafico della funzione. Il metodo dei trapezi consiste nell’approssimare questa superficie con la somma di tanti trapezi rettangoli con le basi ortogonali all’asse delle ascisse e le altezze giacenti su di esso.

Si divide l’intervallo di integrazione $[0,1]$ in $N$ intervalli uguali $[x_k,x_{k+1}]$ , dove $x_k = k/N$ per $k = 0, \ldots, N$ . Preso $f(x) = 2^x$ , l’area dei trapezi è quindi:

$\begin{aligned} \int_0^1f(x)\diff{x} \approx {} & \sum_{k=0}^{N-1} \frac{1}{2}\cdot\left[f(x_k)+f(x_{k+1})\right]\cdot\frac{1}{N} = \frac{1}{2N}\sum_{k=0}^{N-1}\left(2^{k/N}+2^{(k+1)/N}\right) = \\ = {} & \frac{1}{2N}\sum_{k=0}^{N-1}2^{k/N}\cdot\left(1+2^{1/N}\right) = \frac{1+2^{1/N}}{2N}\sum_{k=0}^{N-1}\left(2^{1/N}\right)^k = \\ = {} & \frac{1+2^{1/N}}{2N} \frac{\left(2^{1/N}\right)^N-1}{2^{1/N}-1} = \frac{1+2^{1/N}}{2N}\frac{1}{2^{1/N}-1} = \\ = {} & \frac{1}{2N}\frac{2^{1/N}-1+2}{2^{1/N}-1} = \frac{1}{2N}\left(1+\frac{2}{2^{1/N}-1}\right). \end{aligned}$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009-I

Si consideri il polinomio di variabile reale $x$

$P_k(x) = k^2 x^{2k+3} - 25kx^{k+1} + 150x^7,$

dove $k$ è un parametro reale. Per quali valori di $k$ il polinomio $P_k$ è divisible per $Q(x) = x^2-1$ ?

$\quad$

$\fbox{a}$ Per nessun valore di $k$ .

$\fbox{b}$ Solo per $k = 10$ .

$\fbox{c}$ Solo per $k = 15$ .

$\fbox{d}$ Solo per $k = 10$ e $k = 15$ .

Soluzione.

Dato che $Q(x) = (x-1)(x+1)$ si scompone come prodotto di due fattori di primo grado, il polinomio $P_k$ avrà $Q$ come fattore se e solo se ha come fattori sia $(x-1)$ che $(x+1)$ . Questo significa che $P_k(x)$ deve avere come radici $+1$ e $-1$ . Come prima condizione, cominciamo ad imporre che $P_k(1) = 0$ :

$k^2 - 25k + 150 = 0 \implies k = \frac{25\pm\sqrt{25^2-4\cdot150}}{2}=\frac{25\pm5}{2}.$

Imponiamo ora che $P_k(-1) = 0$ :

$-k^2 - 25k(-1)^{k+1} - 150 = 0,$

dove abbiamo usato il fatto che $2k+3$ è senz’altro dispari e quindi $(-1)^{2k+3} = -1$ . Non occorre risolvere questa equazione, basta verificarla per i due unici valori permessi $k = 10$ e $k = 15$ trovati sopra:

$\begin{gather*} \begin{array}{ll} k = 1\text{0:} & -10^2 + 25\cdot10 - 150 = -100 + 250 - 150 = 0; \\ k = 1\text{5:} & -15^2 - 25\cdot15 - 150 < 0. \end{array} \end{gather*}$

Come si vede, solo $k = 10$ soddisfa simultaneamente $P_k(1) = P_k(-1) = 0$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009-J

Determinare il numero di coppie di interi positivi $(x,y)$ che soddisfano l’equazione diofantea:

$x^3 + 6x^2y + 12xy^2 + 8y^3 = 2^{30}.$

$\quad$

$\fbox{a}$ $0$ .

$\fbox{b}$ $2^6$ .

$\fbox{c}$ $2^9-1$ .

$\fbox{d}$ $2^{10}+2$ .

Soluzione.

Nonostante l’equazione appaia minacciosa, è relativamente semplice riportarla ad una forma più maneggevole:

$\begin{gather*} x^3 + 6x^2y + 12xy^2 + 8y^3 = 2^{30}; \\ (x+2y)^3 = 2^{30}; \\ x+2y = \sqrt[3]{2^{30}} = 2^{10}; \\ x = 2^{10} - 2y. \end{gather*}$

Dato che $x \geq 1$ , deve essere $2y \leq 2^{10}-1$ e quindi $y \leq 2^9 - 1/2$ , cioè $y \leq 2^9 - 1$ essendo $y$ intero. Per ogni valore intero di $y$ tale che $1 \leq y \leq 2^9 - 1$ , che sono $2^9 - 1$ possibilità, si ritrova sempre una soluzione intera per $x$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2009(S1)-A

Quanto vale l’area della regione del piano delimitata dalle curve $y = x^2$ e $y = x+2$ ?

$\quad$

$\fbox{a}$ $\dfrac{7}{3}$ .

$\fbox{b}$ $\dfrac{7}{2}$ .

$\fbox{c}$ $\dfrac{9}{2}$ .

$\fbox{d}$ $\dfrac{11}{2}$ .

Soluzione.

Come prima cosa, risulta utile visualizzare i grafici delle due curve, che sono riportati in figura. Ci sono due intersezioni $P$ e $Q$ che si trovano risolvendo l’equazione $x^2 = x+2$ , cioè $x_P = -1$ e $x_Q = 2$ . La regione la cui area va calcolata è indicata in rosa nella figura.

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Il primo metodo è ricorrere al calcolo integrale. Se $f$ e $g$ sono due funzioni positive tali che $f(x) \geq g(x)$ , i cui grafici si intersecano in punti di ascissa $x_P$ e $x_Q$ ( $x_P < x_Q$ ), allora l’area compresa tra i loro grafici è in generale data da:

$\mathcal{A} = \int_{x_P}^{x_Q} [f(x)-g(x)]\diff{x}.$

Applicato al nostro caso, con $f(x) = x+2$ e $g(x) = x^2$ , abbiamo:

$\begin{displaymath} \mathcal{A} = \int_{-1}^2\left(x+2-x^2\right)\mathrm{d}x = \left.\left(\frac{x^2}{2}+2x-\frac{x^3}{3}\right)\right|_{-1}^{+2} = \frac{9}{2}. \end{displaymath}$

Un procedimento alternativo è utilizzare, se la si conosce, la formula per l’area del segmento parabolico. Data una parabola di equazione $y = ax^2+bx+c$ , l’area compresa tra l’arco di parabola ed una retta che interseca la parabola nei punti $P$ e $Q$ è data da:

$\begin{displaymath} \mathcal{A} = \frac{1}{6}\cdot|a|\cdot(x_Q-x_P)^3. \end{displaymath}$

Sostituendo $a = 1$ , $x_P = -1$ , $x_Q = 2$ , si trova ancora $\mathcal{A} = 9/2$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2009(S1)-B

Qual è valore minimo della funzione:

$f(x) = 2x^3-9x^2+12x+3$

nell’intervallo $0 \leq x \leq 2$ ?

$\quad$

$\fbox{a}$ 1.

$\fbox{b}$ 3.

$\fbox{c}$ 5.

$\fbox{d}$ 7.

Soluzione.

Essendo la funzione $f$ continua su un intervallo compatto, per il teorema di Weierstrass ammette senz’altro minimo assoluto. Questo minimo può trovarsi o in corrispondenza di uno degli estremi dell’intervallo, oppure può essere un punto interno stazionario (tale cioè che $f'(x) = 0$ ). Iniziamo dunque a calcolare la derivata di $f$ e a studiarne il segno:

$f'(x) = 6x^2 -18x+12 = 6(x^2-3x+2).$

Si ha $f'(x) > 0$ se $x < 1$ e $x > 2$ . La funzione $f$ è quindi crescente per $x < 1$ e $x > 2$ , mentre è decrescente per $1 < x < 2$ . I punti $x = 1$ e $x = 2$ sono di massimo e minimo relativi, rispettivamente.

Ora che conosciamo gli intervalli di crescenza e decrescenza di $f$ , è facile stabilire il suo minimo assoluto sull’intervallo richiesto. Con riferimento allo schema qui sotto, e dato che $f(0) = 3$ e $f(2) = 7$ , si conclude che il minimo di $f$ sull’intervallo $[0,2]$ è 3.

$\quad$

Rendered by QuickLaTeX.com

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009(S1)-C

Quali sono le coordinate del punto $Q$ , speculare di $P\ (3,4)$ rispetto alla retta $r$ di equazione $3x + 4y = 50$ ?

$\quad$

$\fbox{a}$ (9,12).

$\fbox{b}$ (6,8).

$\fbox{c}$ (12,16).

$\fbox{d}$ (16,12).

Soluzione.

Il punto $Q$ giace sulla retta $s$ perpendicolare ad $r$ e passante per $P$ . La retta $r$ è infatti l’asse del segmento $PQ$ .

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Per prima cosa, ricaviamo l’equazione di $s$ . Il coefficiente angolare della retta $r$ è $m_r = -3/4$ , per cui il coefficiente angolare di $s$ è semplicemente $m_s = -1/m_r = 4/3$ . Inoltre, dato che $s$ passa per $P$ , la sua equazione avrà la forma:

$y = y_P + m_s(x-x_P) = 4 + \frac{4}{3}(x-3) = \frac{4}{3}x.$

Consideriamo ora il punto $R$ , intersezione di $r$ ed $s$ . Le sue coordinate $x_R$ e $y_R$ sono date dalle soluzioni del sistema:

$\begin{displaymath} \begin{cases} y = \dfrac{4}{3}x; \\[7pt] 3x + 4y = 50; \end{cases} \implies\quad \begin{cases} x_R = 6; \\ y_R = 8. \end{cases} \end{displaymath}$

Essendo $R$ il punto medio di $PQ$ , le coordinate di $Q$ sono infine date da:

$\begin{displaymath} \begin{cases} x_Q = x_P + 2(x_R-x_P) = 9; \\ y_Q = y_P + 2(y_R-y_P) = 12. \\ \end{cases} \end{displaymath}$

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2009(S1)-D

Si consideri la seguente equazione polinomiale:

$x^3 - 30x^2 + 108x - 104 = 0.$

$\quad$

$\fbox{a}$ L’equazione non possiede alcuna soluzione reale.

$\fbox{b}$ L’equazione possiede esattamente una soluzione reale.

$\fbox{c}$ L’equazione possiede tre soluzioni reali distinte.

$\fbox{d}$ L’equazione ammette una soluzione con molteplicità maggiore di 1.

Soluzione.

Detto $P(x)$ il termine di sinistra, conviene studiare la sua derivata. Si ha:

$P'(x) = 3x^2-60x+108 = 3(x^2-20x+36).$

Si verifica facilmente che $P'(x) > 0$ se $x < 2$ e $x > 18$ . La funzione è quindi crescente per $x < 2$ e per $x > 18$ , mentre decresce per $2 < x < 18$ . Quindi $x = 2$ e $x = 18$ sono punti di massimo e minimo relativo, rispettivamente. Per determinare il numero delle radici, basta ora studiare il segno di $P$ in corrispondenza di questi due valori. In particolare, si vede facilmente che $f(2) = 0$ . Questo implica che $x=0$ è una radice di molteplicità doppia, dato che $f(2) = f'(2) = 0$ (il grafico di $P$ è tangente all’asse delle ascisse). Discende inoltre automaticamente che $f(18) < 0$ (dato che $f$ è decrescente per $2 < x < 18$ ), per cui esisterà una terza radice per $x > 18$ (che si trova essere $x = 26$ , ma il valore specifico non serve per rispondere al quesito). Mettendo assieme tutta l’informazione raccolta, si vede che le prime tre risposte si possono escludere.

Riportiamo anche un procedimento alternativo. Notando che $104 = 26\times4$ , si può riscrivere:

$\begin{gather*} x^3 - 4x^2 - 26x^2 + 104x + 4x - 104 = 0; \\ x^2(x-26) - 4x(x-26) + 4(x-26) = 0; \\ (x-26)(x^2-4x+4) = 0; \\ (x-26)(x-2)^2 = 0. \end{gather*}$

Da qui, si riconoscono subito le radici dell’equazione, giungendo alla medesima conclusione di prima.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2009(S1)-E

Per quale delle seguenti affermazioni il fatto che $6 \times 7 = 42$ costituisce un controesempio?

$\quad$

$\fbox{a}$ Il prodotto di due numeri dispari è sempre dispari.

$\fbox{b}$ Se il prodotto di due numeri interi non è multiplo di 4, allora i due numeri non possono essere consecutivi.

$\fbox{c}$ Se il prodotto di due interi è un multiplo di 4, allora i due interi non possono essere consecutivi.

$\fbox{d}$ Ogni numero pari può essere scritto come il prodotto di due numeri pari.

Soluzione.

Si tratta solo di leggere con attenzione le affermazioni, e verificare qual è quella corretta.

$\quad$

$\fbox{a}$ Dato che 6 e 7 non sono entrambi numeri dispari, il fatto che $6\times 7 = 42$ non ha implicazioni per questa affermazione (che è peraltro vera). $\fbox{b}$ Dato che 42 non è un multiplo di 4, e 6 e 7 sono interi consecutivi, il fatto che $6\times 7 = 42$ costituisce un controesempio per questa affermazione, mostrando che è falsa.

$\fbox{c}$ Dato che 42 non è un multiplo di 4, il fatto che $6\times 7 = 42$ non ha implicazioni per questa affermazione (che è peraltro falsa). $\fbox{d}$ Qui si afferma che un numero pari può essere scritto come il prodotto di due numeri pari, non che deve esserlo. Di principio, potrebbero infatti esistere altre fattorizzazioni di 42 composte da due numeri pari (in realtà non esistono, e questa affermazione è falsa, ma il fatto che $6\times7 = 42$ non costituisce un controesempio).

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009(S1)-F

Quanti valori di $x$ soddisfano la seguente equazione

$2\cos^2(x)+5\sin(x) = 4$

nell’intervallo $0 \leq x < 2\pi$ ?

$\quad$

$\fbox{a}$ 2.

$\fbox{b}$ 4.

$\fbox{c}$ 6.

$\fbox{d}$ 8.

Soluzione.

Ricordando che $\cos^2(x) = 1 - \sin^2(x)$ , riscriviamo l’equazione nella forma:

$2\sin^2(x) - 5\sin(x) +2 = 0,$

Posto $t=\sin(x)$ , abbiamo di un’equazione di secondo grado in $t$ , che ha soluzioni $t = 1/2$ e $t = 2$ . Dato che $t = \sin(x) \leq 1$ , la seconda soluzione va scartata, e resta da considerare per quali valori di $x$ si ha:

$\sin(x) = \frac{1}{2},$

ossia $x = \pi/6$ e $x = 5\pi/6$ (limitandoci all’intervallo $0 \leq x < 2\pi)$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2009(S1)-G

In quale intervallo risulta verificato il seguente sistema di disequazioni?

$\begin{cases} x^2 + 3x + 2 > 0; \\ x^2+x < 2. \end{cases}$

$\quad$

$\fbox{a}$ $x < -2$ .

$\fbox{b}$ $-1 <x < 1$ .

$\fbox{c}$ $x > -1.$

$\fbox{d}$ $x > -2$ .

Soluzione.

Osserviamo che, tra le quattro risposte possibili, l’unica plausibile è la 2. Infatti, la seconda disequazione rappresenta una parabola con concavità verso l’alto, che può essere negativa solo su un intervallo limitato (o vuoto). Procediamo a verificare quantitativamente questa intuizione. Usando la formula risolutiva delle equazioni di secondo grado, troviamo che:

$\begin{cases} x^2 + 3x + 2 > 0 \\ x^2+x < 2 \end{cases} \implies\quad \begin{cases} x < -2 \ \lor \ x > -1; \\ -2 < x < 1. \end{cases}$

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Come si vede dalla rappresentazione grafica, le due disequazioni sono soddisfatte simultaneamente se $-1 < x < 1$ (intervallo evidenziato in arancione), confermando l’ipotesi iniziale.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009(S1)-H

Tenendo presente che:

$\begin{aligned} \log_{10}(2) \approx 0\text{,3010} & \quad \text{(4 cifre decimali corrette)}; \\ 10^{\text{0,2}} < 2; \end{aligned}$

è possibile stabilire la validità di una delle seguenti affermazioni? È implicito che l’uso della calcolatrice non costituisce una soluzione valida.

$\quad$

$\fbox{a}$ $2^{100}$ inizia con un 1 ed ha 30 cifre.

$\fbox{b}$ $2^{100}$ inizia con un 2 ed ha 30 cifre.

$\fbox{c}$ $2^{100}$ inizia con un 1 ed ha 31 cifre.

$\fbox{d}$ $2^{100}$ inizia con un 2 ed ha 31 cifre.

Soluzione.

Non è difficile vedere che il numero di cifre (in base decimale) di un numero $x$ è dato da $N = \lfloor \log_{10}(x)\rfloor + 1$ (dove $\lfloor z \rfloor$ rappresenta la parte intera di $z$ ). Infatti, un numero $x$ di $N$ cifre è tale che $10^{N-1} \leq x < 10^{N}$ . Passando ai logaritmi, dunque:

$N-1 \leq \log_{10}(x) < N,$

e quindi, per definizione di parte intera,

$\lfloor \log_{10}(x)\rfloor = N - 1.$

Usando questa relazione, abbiamo quindi che, posto $x = 2^{100}$ :

$N = \lfloor \log_{10}(x)\rfloor + 1 = \lfloor 100\log_{10}(2)\rfloor + 1 = \lfloor\text{30,1}\rfloor + 1 = 31.$

Per determinare la prima cifra di $x$ , sfruttiamo l’altro suggerimento fornito nel testo. Innanzitutto, scriviamo $\log_{10}(2) = 0\text{,3010} + \varepsilon$ , con $|\varepsilon| < 10^{-4}$ . Proseguiamo poi così:

$2^{100} = 10^{100\log_{10}(2)} = 10^{\text{30,1}+100\varepsilon} = 10^{30}\cdot10^{\text{0,1}+100\varepsilon}.$

Ma, dato che $0 < \text{0,}1 + 100\,\varepsilon < 0\text{,2}$ , si ha:

$10^{30} < 2^{100} < 10^{30}\cdot 10^{\text{0,2}} < 2\cdot10^{30}.$

Tutte le disuguaglianze sono strette, per cui concludiamo che la prima cifra di $2^{100}$ è necessariamente 1. Si noti che questa disuguaglianza è anche sufficiente a dimostrare che $2^{100}$ ha 31 cifre, per cui la prima parte della soluzione è ridondante. Ci pareva però interessante riportare la formula che restituisce il numero di cifre.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2009(S1)-I

Nel polinomio espansione dell’espressione

$\left(1+\frac{1}{2}x\right)^{10},$

quale potenza di $x$ ha il coefficiente più grande?

$\quad$

$\fbox{a}$ $x^2$ .

$\fbox{b}$ $x^3$ .

$\fbox{c}$ $x^5$ .

$\fbox{d}$ $x^{10}$ .

Soluzione.

Dobbiamo usare la formula del binomio di Newton:

$(a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^n b^{n-k},$

che contiene i coefficienti binomiali così definiti:

$\binom{n}{k} = \frac{n!}{k!\,(n-k)!}.$

In particolare:

$\left(1+\frac{1}{2}x\right)^{10} = \left(\frac{1}{2}x+1\right)^{10} = \sum_{k=0}^{10} \binom{10}{k}\frac{1}{2^k}x^k = \sum_{k=0}^{10} a_k x^k.$

Per scoprire quale dei coefficienti $a_k$ è il maggiore, calcoliamo:

$\frac{a_k}{a_{k-1}} = \frac{10!}{k!\,(10-k)!}\frac{1}{2^k}\cdot\frac{(k-1)!\,(11-k)!}{10!}2^{k-1} = \frac{11-k}{2k}.$

Per trovare il valore massimo di $a_k$ , possiamo allora risolvere la disequazione $a_k/a_{k-1} > 1$ , che è verificata per $k < 11/3$ . Dunque $a_k > a_{k-1}$ per $k \leq 3,$ mentre $a_k < a_{k-1}$ per $k \geq 4$ . Il massimo di $a_k$ viene quindi raggiunto per $k = 3$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009(S2)-A

Quali sono le coordinate del punto $R$ che si trova tra $P = (2,3)$ e $Q = (8,-3)$ e che divide il segmento $PQ$ in due parti di lunghezza in rapporto $1:2$ ?

$\quad$

$\fbox{a}$ $(4,-1)$ .

$\fbox{b}$ $(6,-2)$ .

$\fbox{c}$ $\left(\dfrac{14}{3},2\right)$ .

$\fbox{d}$ $(4,1)$ .

Soluzione.

Il punto $R$ si trova lungo il segmento $PQ$ , che viene diviso in parti di lunghezza in rapporto $1:2$ . Questo vuol dire che $\overline{QR} = 2\overline{PR}$ , e quindi, dato che $\overline{PQ} = \overline{PR} + \overline{QR}$ , deve essere $\overline{PR} = \overline{PQ}/3$ . La medesima proporzionalità si applica alle coordinate (teorema di Talete):

$\begin{aligned} x_R = {} & x_P + \frac{1}{3}\left(x_Q-x_P\right); \\ y_R = {} & y_P + \frac{1}{3}\left(y_Q-y_P\right). \end{aligned}$

Sostituendo i valori delle coordinate di $P$ e $Q$ , si trova $R = (4,1)$ . La figura mostra graficamente la posizione dei tre punti.

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Si noti che, per come è formulata la domanda, esiste una seconda possibilità di dividere il segmento $PQ$ in due parti in rapporto $1:2$ , e cioè che $\overline{PR} = 2\overline{QR}$ . Questa seconda interpretazione porta a $R = (6,-1)$ , che non è però annoverata tra le opzioni possibili.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2009(S2)-B

Il disegno in figura mostra il grafico di una funzione $y = f(x)$ .

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Quale di questi disegni rappresenta, qualitativamente, il grafico della funzione $g(x) = -f(1+x)$ ?

$\quad$

Soluzione.

Per una generica funzione $f$ , la trasformazione $f(x) \to -f(x)$ corrisponde ad una riflessione rispetto all’asse delle ascisse. La trasformazione $f(x) \to f(x+1)$ corrisponde invece ad una traslazione verso la direzione negativa delle ascisse. Componendo le due operazioni, si conclude che $g$ è rappresentata nel primo grafico.

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2009(S2)-C

Senza utilizzare la calcolatrice, stabilire quale dei seguenti numeri è il più grande. Tutti gli angoli sono espressi in radianti.

$\quad$

$\fbox{a}$ $\tan\left(\dfrac{5\pi}{4}\right)$ .

$\fbox{b}$ $\sin^2\left(\dfrac{5\pi}{4}\right)$ .

$\fbox{c}$ $\log_{10}\left(\dfrac{5\pi}{4}\right)$ .

$\fbox{d}$ $\log_2\left(\dfrac{5\pi}{4}\right)$ .

Soluzione.

Dalla trigonometria elementare, tenendo presente che il periodo delle funzioni $y = \tan(x)$ e $y = \sin^2(x)$ è pari a $\pi$ , si ha:

$\begin{aligned} \tan\left(\frac{5\pi}{4}\right) = {} & \tan\left(\frac{\pi}{4}\right) = 1; \\ \sin^2\left(\frac{5\pi}{4}\right) = {} & \sin^2\left(\frac{\pi}{4}\right) = \left(\frac{\sqrt{2}}{2}\right)^2 = \frac{1}{2}. \end{aligned}$

Passiamo a considerare $\fbox{c}$ e $\fbox{d}$ . Ricordiamo che ogni logaritmo con base $a > 1$ è una funzione crescente del proprio argomento (nel nostro caso, $a = 2$ oppure $a = 10$ ). Inoltre, $\log_a(a) = 1$ . Dato che $3 < \pi < 4$ , possiamo quindi derivare le seguenti implicazioni:

$\begin{aligned} \frac{5\pi}{4} < \frac{5\cdot4}{4} < 10 \implies {} & \log_{10}\left(\frac{5\pi}{4}\right) < 1; \\ \frac{5\pi}{4} > \frac{5\cdot3}{4} > 2 \implies {} & \log_2\left(\frac{5\pi}{4}\right) > 1. \end{aligned}$

Mettendo insieme tutta l’informazione raccolta, si vede che $\log_2(5\pi/4)$ è l’unico numero $> 1$ , ed è quindi il più grande.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2009(S2)-D

I numeri $x$ ed $y$ soddisfano le seguenti disuguaglianze:

$\begin{aligned} 2x+3y \leq {} & 23; \\ x+2 \leq {} & 3y; \\ 3y+1 \leq {} & 4x. \end{aligned}$

Qual è il più grande valore possibile di $x$ ?

$\quad$

$\fbox{a}$ 6.

$\fbox{b}$ 7.

$\fbox{c}$ 8.

$\fbox{d}$ 9.

Soluzione.

Conviene rappresentare le tre rette sul piano cartesiano, e valutare quale regione viene identificata da ciascuna disequazione. L’insieme delle soluzioni è indicato dall’area colorata. Per disegnare le rette, forse il modo più rapido è trovare le interesezioni di ciscuna retta con gli assi cartesiani (sostituendo $x = 0$ e $y = 0$ in ciascuna equazione).

$\quad$

Si vede che il massimo valore assunto da $x$ si ha in corrispondenza del punto $C$ . Le sue coordinate si trovano risolvendo il sistema

$\begin{cases} 2x+3y = 23; \\ x+2 = 3y; \end{cases} \implies\quad \begin{cases} x = 7; \\ y = 3. \end{cases}$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009(S2)-E

Quante soluzioni ha l’equazione

$\cos(\sin x) = \frac{1}{2}$

nell’intervallo $0 \leq x < 2\pi$ ?

$\quad$

$\fbox{a}$ Nessuna soluzione.

$\fbox{b}$ Una soluzione.

$\fbox{c}$ Due soluzioni.

$\fbox{d}$ Tre soluzioni.

Soluzione.

Poniamo $\sin(x) = t$ . Ricordando che $\cos(\pi/3) = \cos(-\pi/3) = 1/2$ , l’equazione $\cos(t) = 1/2$ ha infinite soluzioni:

$\begin{aligned} t = {} & \arccos\left(\frac{1}{2}\right) + 2n\pi = \frac{\pi}{3} + 2n\pi, & n \in \mathbb{Z}; \\ t = {} & -\arccos\left(\frac{1}{2}\right) + 2m\pi = -\frac{\pi}{3} + 2m\pi, & m \in \mathbb{Z}. \end{aligned}$

Torniamo quindi alla variabile $x$ , e ricordiamo che $|\sin(x)| \leq 1$ $\forall x \in \mathbb{R}$ . Dato che $\pi/3 > 1$ e $2\pi > 6$ , si vede facilmente che per nessun $k$ si ha $|\pm\pi/3 + 2k\pi| \leq 1$ . L’equazione proposta non ha quindi nessuna soluzione reale. Il disegno illustra graficamente la situazione.

$\quad$

Rendered by QuickLaTeX.com

$\quad$

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2009(S2)-F

Dato $a \in \mathbb{R}$ , si consideri la parabola di equazione:

$y = x^2 - 2ax + 1.$

Quale valore di $a$ rende minima la distanza tra il vertice della parabola e l’origine degli assi cartesiani?

$\quad$

$\fbox{a}$ $a = 0$ .

$\fbox{b}$ $a = \pm 1$ .

$\fbox{c}$ $a = \pm\dfrac{1}{\sqrt{2}}$ or $a = 0$ .

$\fbox{d}$ $a = \pm\dfrac{1}{\sqrt{2}}$ .

Soluzione.

Le coordinate del vertice $V$ della parabola sono date dalle note formule:

$\begin{aligned} x_V = {} & -\frac{(-2a)}{2} = a; \\ y_V = {} & -\frac{(-2a)^2-4}{4} = 1-a^2. \end{aligned}$

Alternativamente, forse un modo più diretto è riscrivere l’equazione della parabola in questo modo:

$y = x^2 - 2ax + 1 = (x-a)^2 + (1-a^2).$

In questa forma, si vede che la parabola è semplicemente una traslazione di $y = x^2$ , sia in verticale che in orizzontale, e le coordinate del vertice si leggono direttamente dall’equazione. La distanza $D$ di $V$ dall’origine è data da:

$D(a) = \sqrt{a^2+(1-a^2)^2} = \sqrt{\left(a^2-\frac{1}{2}\right)^2+\frac{3}{4}}.$

Dato che la radice quadrata è una funzione monotona, è sufficiente minimizzare il suo argomento $D^2$ . Scritto come nel membro di destra, $D^2$ è uguale alla somma di due quadrati, e sarà minimo se $a^2-1/2 = 0$ , cioè se $a = \pm1/\sqrt{2}$ .

Alternativamente, se non viene in mente la scomposizione $D^2 = a^2+(1-a^2)^2 = (a^2-1/2)^2 + 3/4$ , si può naturalmente studiare il segno della derivata di $D^2$ , giungendo naturalmente allo stesso risultato.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2009(S2)-G

Il numero di quattro cifre 2652 è tale che ogni sequenza di due cifre consecutive è un multiplo di 13. Un altro numero $N$ gode della stessa proprietà, ha una lunghezza di 100 cifre, e inizia con un 9. Qual è l’ultima cifra di $N$ ?

$\quad$

$\fbox{a}$ 2.

$\fbox{b}$ 3.

$\fbox{c}$ 6.

$\fbox{d}$ 9.

Soluzione.

Limitandoci ai multipli di due cifre di 13, notiamo che 91, 13 e 39 sono le uniche possibilità che iniziano con 9, 1 e 3, rispettivamente. Le cifre del numero $N$ devono pertanto essere 9, 1, 3 in sequenza, ciclicamente. Dato che $100 = 33\times3 + 1$ ( $100 \equiv 1 \mod{3}$ ), la sequenza si ripete 33 volte completa, seguita da una cifra singola che deve essere 9.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2009(S2)-H

Quante soluzioni ha la seguente equazione?

$\left(x^2+1\right)^{10} = 2x - x^2 - 2.$

$\quad$

$\fbox{a}$ Due soluzioni.

$\fbox{b}$ Nessuna soluzione reale.

$\fbox{c}$ Un numero dispari di soluzioni reali.

$\fbox{d}$ Venti soluzioni reali.

Soluzione.

Dato che $x^2 \geq 0$ $\forall x \in \mathbb{R}$ , si conclude subito che $\left(x^2+1\right)^{10} \geq 1 > 0$ . Il membro di sinistra, dunque, risulta sempre positivo. Per quanto riguarda il membro di destra, lo possiamo riscrivere così:

$2x -x^2 - 2 = -(x-1)^2 - 1.$

È evidente che si tratta di una quantità sempre negativa, per cui l’equazione proposta non ha soluzioni reali.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009(S2)-I

Si consideri che $2^3 = 8$ , $2^5 = 32$ , $3^2 = 9$ , e $3^3 = 27$ . Cosa possiamo dedurre sul numero $\log_2(3)$ ?

$\quad$

$\fbox{a}$ È compreso tra $4/3$ e $3/2$ .

$\fbox{b}$ È compreso tra $3/2$ e $5/3$ .

$\fbox{c}$ È compreso tra $5/3$ e $2$ .

$\fbox{d}$ È compreso tra 2 e 3.

Soluzione.

Ricordiamo innanzitutto che il logaritmo (con base $a > 1$ ) è una funzione crescente del suo argomento. Sfruttando il suggerimento del testo, abbiamo:

$\begin{aligned} 27 < 32 {} & \implies 3^3 < 2^5 {} & \hspace{-1.4cm}\implies 3\log_2(3) < 5 {} & \implies \log_2(3) < \frac{5}{3}; \\ 9 > 8 {} & \implies 3^2 > 2^3 {} & \hspace{-1.4cm}\implies 2\log_2(3) > 3 {} & \implies \log_2(3) > \frac{3}{2}. \end{aligned}$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2009(S2)-J

Si considerino le seguenti tre parabole:

$\begin{aligned} y = {} & x^2; \\ y = {} & x^2 - 2x; \\ y = {} & x^2 + 2x + 2. \end{aligned}$

In quante regioni queste parabole dividono il piano?

$\quad$

$\fbox{a}$ 4.

$\fbox{b}$ 5.

$\fbox{c}$ 6.

$\fbox{d}$ 7.

Soluzione.

Risulta utile disegnare le tre parabole, le cui equazioni si possono riscrivere nel seguente modo:

$\begin{aligned} y = {} & x^2 & \text{(rosso);}\\ y = {} & (x-1)^2 - 1 & \text{(blu);} \\ y = {} & (x+1)^2 + 1 & \text{(verde).} \end{aligned}$

In questo modo si vede che tutte le parabole sono copie traslate (orizzontalmente e verticalmente) di $y = x^2$ .

$\quad$

Effettuando il sistema tra le tre coppie di equazioni, si verifica facilmente che non ci sono ulteriori intersezioni a parte quelle evidenti nella figura (il termine quadratico si cancella sempre). A questo punto, basta contare e si verifica facilmente che il piano viene diviso in 7 regioni (identificate nel grafico con dei numeri cerchiati).

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2010-A

Per quali valori del parametro reale $k$ la retta di equazione $y = kx$ interseca la parabola di equazione $y = (x-1)^2$ ?

$\quad$

$\fbox{a}$ $k \leq 0$ .

$\fbox{b}$ $k \geq -4$ .

$\fbox{c}$ $k\leq -4 \lor k \geq 0$ .

$\fbox{d}$ $-4 \leq k \leq 0$ .

Soluzione.

Per stabilire se ci sono intersezioni tra le due curve, risolviamo l’equazione:

$kx = (x-1)^2 \implies x^2 - (k+2)x +1 = 0.$

Si tratta di un’equazione di secondo grado, che ha come discriminante:

$\Delta = (k+2)^2 - 4 = k^2 + 4k.$

Esiste almeno una soluzione se $\Delta \geq 0$ , cioè se $k\leq -4$ oppure $k \geq 0$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2010-B

Si consideri la seguente successione:

$1, 1, 2, \frac{1}{2}, 4, \frac{1}{4}, 8, \frac{1}{8}, \ldots$

Quanto vale la somma dei suoi primi $2n$ termini (dove $n$ è un numero intero positivo)?

$\quad$

$\fbox{a}$ $2^n+1-2^{1-n}$ .

$\fbox{b}$ $2^n+2^{-n}$ .

$\fbox{c}$ $2^{2n}-2^{3-2n}$

$\fbox{d}$ $\dfrac{2^n-2^{-n}}{3}$

Soluzione.

Dato che viene richiesto di calcolare la somma di $2n$ termini della successione, raggruppiamoli due a due. In ciascuna coppia riconosciamo un termine della forma $2^k$ ed un termine della forma $1/2^k$ , dove $k = 0, 1, 2, \ldots, n-1$ (attenzione che le $n$ coppie vengono indicizzate con $k$ tra 0 e $n-1$ ). Ricordando la formula per la somma della progressione geometrica di ragione $q$ :

$\sum_{k=0}^{n}q^k = \frac{q^{n+1}-1}{q-1}\qquad (q \ne 1),$

possiamo scrivere la somma cercata nel seguente modo:

$\begin{aligned} \sum_{k=0}^{n-1} 2^k + \sum_{k=0}^{n-1} \left(\frac{1}{2}\right)^k = {} & \frac{2^n-1}{2-1} + \frac{(1/2)^n-1}{(1/2)-1} = \\ = {} & 2^{n} - 1 - 2\cdot(2^{-n} - 1) = \\ = {} & 2^{n} - 2^{1-n} + 1. \end{aligned}$

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2010-C

Quante soluzioni ha l’equazione

$\sin^2(x) + 3\sin(x)\cos(x) + 2\cos^2(x) = 0$

nell’intervallo $0 \leq x < 2\pi$ ?

$\quad$

$\fbox{a}$ 1.

$\fbox{b}$ 2.

$\fbox{c}$ 3.

$\fbox{d}$ 4.

Soluzione.

Manipoliamo l’equazione per renderla più semplice. Ci sono vari modi, per esempio si può procedere così:

$\begin{gather*} \sin^2(x) + 3\sin(x)\cos(x) + 2\cos^2(x) = 0; \\ \left[\sin^2(x) + 2\sin(x)\cos(x) + \cos^2(x)\right] + \sin(x)\cos(x) + \cos^2(x) = 0; \\ \left[\sin(x)+\cos(x)\right]^2 + \left[\sin(x)+\cos(x)\right]\cdot \cos(x) = 0; \\ \left[\sin(x)+\cos(x)\right]\cdot\left[\sin(x)+2\cos(x)\right] = 0. \end{gather*}$

Notiamo che, se $x$ verifica l’equazione di partenza, $\cos(x) \ne 0$ (si verifica facilmente per sostituzione diretta). È quindi lecito dividere ambo i membri per $\cos^2(x)$ , ottenendo:

$\left[\tan(x)+1\right]\cdot\left[\tan(x)+2\right] = 0.$

Le soluzioni dell’equazione di partenza soddisfano pertanto $\tan(x) = -1$ oppure $\tan(x) = -2$ . Nell’intervallo $[0,2\pi)$ , identificato in grigio nella figura, vediamo che si tratta di quattro valori distinti (rappresentati in figura con il simbolo $\star$ ).

$\quad$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2010-D

Si consideri la funzione

$f(x) = \sin^2\left(\sqrt{x}\,\right).$

$\quad$

Soluzione.

Elenchiamo alcune proprietà salienti della funzione $f$ .

$\quad$

Ha valori non negativi, il che esclude la risposta $\fbox{a}$ .

Pur essendo una funzione oscillante, $f$ non è periodica; per esempio, i suoi zeri si hanno per $\sqrt{x} = k\pi$ (con $k$ intero arbitrario non negativo), per cui la distanza tra zeri successivi cresce quadraticamente; questo esclude la risposta $\fbox{d}$ dove gli zeri sono equispaziati.

Tutti i massimi di $f$ hanno lo stesso valore (cioè 1), che si trovano dove $\sqrt{x} = \pi/2 + k\pi$ (con $k$ intero arbitrario non negativo); questo esclude la $\fbox{c}$ , dato che i due massimi visualizzati hanno valori diversi.

Qualitativamente, il grafico $\fbox{a}$ rispetta tutte le proprietà di $f$ : la funzione oscilla tra 0 ed il suo massimo (che è lo stesso per i due massimi rappresentati), e la distanza tra gli zeri (e tra i massimi) cresce con $x$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2010-E

Senza utilizzare la calcolatrice, quale dei seguenti numeri è il più grande?

$\quad$

$\fbox{a}$ $\log_2(3)$ .

$\fbox{b}$ $\log_4(8)$ .

$\fbox{c}$ $\log_3(2)$ .

$\fbox{d}$ $\log_5(10)$ .

Soluzione.

Innanzitutto notiamo che, essendo $2 < 3$ , si ha:

$\log_3(2) <\log_3(3) = 1.$

Ricordiamo ora le queste proprietà dei logaritmi:

$\begin{array}{r@{\mbox{}=\mbox{}}ll} \log(a\cdot b) & \log(a)+\log(b) & (a,b > 0); \\ \log(a^c) & c \cdot \log(a) & (a > 0,\ c \in \mathbb{R}). \end{array}$

Cominciamo ad osservare che:

$\log_4(8) = \log_4(4\cdot2) = \log_4\left(4\cdot\sqrt{4}\,\right) = \log_4\left(4^{3/2}\right) = \frac{3}{2}.$

E ancora, dato che $\log_2(x)$ è una funzione crescente e che $9 > 8$ :

$\log_2(3) = \log_2\left(\sqrt{3^2}\,\right) = \frac{1}{2}\log_2(9) > \frac{1}{2}\log_2(8) = \frac{3}{2}.$

Infine, dato che $4 < 5$ :

$\begin{aligned} \log_5(10) = {} & \log_5(5\cdot2) = \log_5(5) + \log_5(2) = 1+ \log_5(2) = \\ = {} & 1 + \log_5\left(\sqrt{2^2}\,\right) = 1 + \frac{1}{2}\log_5(4) < 1 + \frac{1}{2}\log_5(5) = \frac{3}{2}. \end{aligned}$

Mettendo assieme le quattro relazioni trovate, concludiamo che:

$\log_3(2) < 1 < \log_5(10) < \frac{3}{2} = \log_4(8) < \log_2(3).$

$\quad$

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2010-F

La figura rappresenta il grafico di una funzione $f$ : $[0,1]\to\mathbb{R}$ , che è formato da quattro segmenti. Per calcolare l’integrale definito di $f$ tra 0 e 1, viene utilizzato il metodo dei trapezi, dividendo l’intervallo $[0,1]$ in $n$ intervalli di uguale ampiezza. Per quali valori di $n$ il valore stimato col metodo dei trapezi risulta esattamente uguale all’integrale di $f$ tra 0 e 1?

$\quad$

$\fbox{a}$ Quando $n$ è multiplo di 4.

$\fbox{b}$ Quando $n$ è multiplo di 6.

$\fbox{c}$ Quando $n$ è multiplo di 8.

$\fbox{d}$ Quando $n$ è multiplo di 12.

$\quad$

Soluzione.

Il metodo dei trapezi consiste nell’approssimare la regione di piano compresa tra l’asse delle ascisse e il grafico della funzione con una serie di trapezi rettangoli, aventi l’altezza sull’asse $x$ , le basi ortogonali ad esso, e i due vertici rimanenti sul grafico della funzione. L’intervallo di integrazione $[0,1]$ viene diviso in $n$ intervalli $[x_k,x_{k+1}]$ , dove $x_k = k/n$ con $0 \leq k \leq n$ .

Se il grafico della funzione si sovrappone perfettamente ai lati obliqui dei trapezi, allora il metodo dei trapezi produce il risultato esatto. Questo è in effetti possibile nel caso di una funzione lineare a tratti, come quella proposta nell’esercizio. I vertici dei trapezi devono coincidere con i punti dove il grafico cambia pendenza. Bisogna quindi che i punti $x = 1/3$ , $x = 1/2$ e $x = 3/4$ appartengano alla suddivisione scelta per stimare l’integrale.

Intuitivamente, è facile capire che $n$ deve essere divisibile per tutti i denominatori, cioè per 3, per 2 e per 4, e quindi per il loro minimo comune multiplo 12. Un po’ più formalmente, devono esistere degli interi $k$ , $l$ , $m$ tali che:

$\begin{gather*} \frac{k}{n} = \frac{1}{3}, \quad \frac{l}{n} = \frac{1}{2}, \quad \frac{m}{n} = \frac{3}{4} \implies n = 3k = 2l = \frac{4}{3}m. \end{gather*}$

Questo mostra che $n$ deve essere multiplo di 2, 3 e 4, e quindi di 12.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2010-G

Sia $f$ una funzione definita sui numeri interi positivi, tale che $f(1) = 1$ e che, per ogni $n$ positivo:

$\begin{array}{l@{\mbox{}=\mbox{}}l} f(2n) & 2f(n); \\[1pt] f(2n+1) & 4f(n). \end{array}$

Quanti sono i valori di $n$ per cui $f(n) = 16$ ?

$\quad$

$\fbox{a}$ 3.

$\fbox{b}$ 4.

$\fbox{c}$ 5.

$\fbox{d}$ 6.

Soluzione.

Osserviamo in primo luogo che tutti i valori assunti da $f$ sono potenze intere di 2. Infatti $f(1) = 1 = 2^0$ e, per $n > 1$ , $f(n)$ è pari al doppio o al quadruplo di un numero che a sua volta appartiene all’immagine di $f$ .

Per ogni $n$ , esiste quindi un opportuno intero $k \geq 0$ tale che $f(n) = 2^k$ . Sia $N(k)$ il numero di interi $n$ tali che $f(n) = 2^k$ . Dato che $16 = 2^4$ , a noi interessa calcolare $N(4)$ . Assumiamo per cominciare che $k \geq 2$ , e riscriviamo:

$\begin{aligned} f(n) = 2^k = {} & 2\cdot 2^{k-1} = 2\cdot f(n_1) = \\ = {} & 4\cdot 2^{k-2} = 4\cdot f(n_2), \end{aligned}$

dove $n_1$ e $n_2$ sono opportuni interi (non univocamente determinati). Da questa scrittura si vede che $2^k$ si può ottenere i) in tanti modi quanti quelli con cui si può ottenere $2^{k-1}$ (prima riga) più ii) tanti modi quanti quelli con cui si può ottenere $2^{k-2}$ (seconda riga). In formule:

$N(k) = N(k-1) + N(k-2).$

Il valore di $N(k)$ si può quindi calcolare per ricorsione a partire da $N(0)$ , $N(1)$ , \ldots, $N(k-1)$ . I casi $k = 0$ e $k = 1$ vanno trattati a parte. Dato che $2^0 = 1 = f(1)$ e $f(n) > 1$ per $n > 1$ , si ha $N(0) = 1$ . Allo stesso modo si vede che anche $N(1) = 1$ , dato che $2^1 = 2 = f(2) = 2\cdot f(1)$ e che $f(n) > 2$ per $n > 2$ . Abbiamo così tutti gli elementi per calcolare $N(k)$ anche per $k \geq 2$ :

$k$	0	1	2	3	4	5	6	$\cdots$

$2^k$	1	2	4	8	16	32	64	$\cdots$
$N(k)$	1	1	2	3	5	8	13	$\cdots$

Il caso corrispondente a $f(n) = 16$ è $k = 4$ , e dalla tabella si legge $N(4) = 5$ .

Concludiamo con una curiosità: i valori di $N(k)$ formano in pratica la famosa sequenza di Fibonacci: 0, 1, 1, 2, 3, 5, 8, 13, \ldots; i numeri di Fibonacci $F_k$ soddisfano anche loro una relazione di ricorsione:

$F_k = F_{k-1} + F_{k-2}.$

L’unica differenza sta nelle “condizioni iniziali”, dato che per i numeri di Fibonacci si definisce $F_0 = 0$ e $F_1 = 1$ , mentre $N(0) = N(1) = 1$ . Ne consegue uno sfasamento tra $N$ ed $F$ , e infatti si ha $N(k) = F_{k+1}$ .

Ringraziamo il prof. Gianmarco Bramanti per aver suggerito questa soluzione.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2010-H

Siano $n$ un numero intero positivo e $k$ un parametro reale. Si consideri la seguente equazione nell’incognita reale $x$ :

$(x-1)\cdot(x-2)\cdot(x-3)\cdots(x-n) = \prod_{i=1}^{n}(x-i) = k.$

Quale delle seguenti affermazioni è senz’altro corretta?

$\quad$

$\fbox{a}$ Per $n = 3$ , esistono valori di $k$ per cui l’equazione non ha soluzioni reali.

$\fbox{b}$ Per $n$ pari, l’equazione ha almeno una soluzione reale per ogni valore di $k$ .

$\fbox{c}$ Per $k \geq 0$ , l’equazione ha sempre almeno una soluzione reale.

$\fbox{d}$ Per qualsiasi valore assegnato di $n$ e $k$ , l’equazione non ha mai una soluzione di molteplicità doppia.

Soluzione.

Esaminiano le quattro opzioni. Poniamo per brevità $P_n(x) = (x-1)\cdots(x-n)$ .

$\quad$

$\fbox{a}$ Per $n = 3$ , $P_3(x)$ è un polinomio di terzo grado. Ogni equazione polinomiale di terzo grado (ed in generale di grado dispari) ammette almeno una soluzione reale. Infatti, $P_3(x) \to -\infty$ per $x \to -\infty$ e $P_3(x) \to +\infty$ per $x \to +\infty$ . Essendo $P_3(x)$ una funzione continua, deve necessariamente assumere ogni possibile valore reale.

$\fbox{b}$ Per $n$ pari, $P_n$ è un polinomio di grado pari, il cui coefficiente di grado massimo è positivo ( $+1$ ). Ogni polinomio con queste proprietà ammette minimo assoluto $m$ su $\mathbb{R}$ , e quindi ad ogni $k < m$ non corrisponde alcuna soluzione reale per l’equazione proposta. Volendo produrre un contro-esempio esplicito, basta prendere $n = 2$ e l’equazione diventa:

$(x-1)(x-2) = x^2 -3x + 2 = \left(x-\frac{3}{2}\right)^2 - \frac{1}{4} = k,$

che non ha soluzioni se $k < -1/4$ .

$\fbox{c}$ Per ogni $n$ si ha $P_n(1) = 0$ e $P_n(x) \to +\infty$ per $x \to +\infty$ . Dato che $P_n$ è una funzione continua (è un polinomio), gode della proprietà del valore intermedio. Quindi l’equazione $P_n(x) = k$ ha sempre almeno una soluzione per $k \geq 0$ .

$\fbox{d}$ Per $n$ pari, esiste senz’altro un valore di $k$ che produce una soluzione doppia, cioè $k = \min [P_n(x)]$ . Per presentare un controesempio esplicito, scegliamo $n = 2$ . In questo caso $P_n(x) = x^2 - 3x + 2$ rappresenta una parabola con vertice nel punto $(3/2,-1/4)$ . Prendendo $k = -1/4$ , $x = 3/2$ è una soluzione di molteplicità doppia.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2010-I

Si consideri la quantità in funzione del parametro $a \geq 0$ :

$I(a) = \int_0^a\left(4-2^{x^2}\right)\mathrm{d}x.$

Stabilire per quale valore di $a$ si ha $I'(a) = 0$ .

$\quad$

$\fbox{a}$ $\dfrac{1+\sqrt{5}}{2}$ .

$\fbox{b}$ $\sqrt{2}$ .

$\fbox{c}$ $\dfrac{\sqrt{5}-1}{2}$ .

$\fbox{d}$ $1$ .

Soluzione.

Per il teorema fondamentale del calcolo integrale, essendo l’integranda una funzione continua:

$I'(a) = 4-2^{a^2}.$

Quindi:

$I'(a) = 0 \iff 2^{a^2} = 2^2 \iff a^2 = 2.$

Dato che $a \geq 0$ per ipotesi, l’unica soluzione è $a = \sqrt{2}$ .

A scanso di equivoci, ricordiamo che, per convenzione, nell’esponenziale ripetuto si procede da destra verso sinistra: $a^{b^c} = a^{(b^c)}$ . Per esempio, $2^{3^2} = 2^9 = 512$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2010-J

Siano $a$ , $b$ , $c$ numeri positivi assegnati. In quali casi la disuguaglianza

$a^x > c\, b^y$

è soddisfatta solo da un numero finito (eventualmente nullo) di coppie di valori interi positivi $(x,y)$ ?

$\quad$

$\fbox{a}$ $a > 1$ oppure $b < 1$ .

$\fbox{b}$ $a < 1$ oppure $b < 1$ .

$\fbox{c}$ $a < 1$ e $b < 1$ .

$\fbox{d}$ $a < 1$ e $b > 1$ .

Soluzione.

Osserviamo che, se $b < 1$ , la quantità $b^y$ può avvicinarsi arbitrariamente a $0$ al crescere di $y$ . Fissato $x$ , indipendentemente dal valore di $a$ ci saranno quindi infiniti valori interi di $y$ che soddisfano la disuguaglianza, e precisamente ogni intero $y > \log_b\left(a^x/c\right)$ . Questa considerazione mostra che le prime tre scelte non sono valide.

Se invece $a < 1$ e $b > 1$ , la funzione $a^x$ è decrescente come funzione di $x$ e tende a 0, mentre $c\,b^y$ è crescente come funzione di $y$ . Può esistere pertanto soltanto un numero finito di valori di $x$ tali che $a^x > c\,b^y$ , e precisamente deve essere $x < \log_a\left(c\,b^y\right)$ (a seconda dei valori di $b$ e $c$ , questa condizione potrebbe anche non essere mai verificata).

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2011-A

Quale dei seguenti diagrammi rappresenta qualitativamente il grafico della cubica di equazione $y = x^3-x^2-x+1$ ?

$\quad$

Soluzione.

Forse il modo più semplice è fattorizzare la cubica:

$\begin{aligned} y = {} & x^3 - x^2 - x + 1 = \\ = {} & x^2(x-1) - (x-1) = \\ = {} & (x^2-1)(x-1) = \\ = {} & (x-1)^2(x+1). \end{aligned}$

Questo mostra che la cubica ha una soluzione semplice negativa ( $x = -1$ ) e una soluzione doppia positiva ( $x = +1$ ). Tra le curve proposte, solo la terza gode di queste proprietà. La $\fbox{c}$ è anche consistente con l’andamento asintotico ( $y \to \pm\infty$ per $x \to \pm\infty$ ), con l’intersezione con l’asse delle ordinate ( $y = 1 > 0$ per $x = 0$ ) e con la posizone dei massimi e dei minimi ( $y' = 0$ se $3x^2 - 2x - 1 = 0$ , cioè $x = 1 > 0$ e $x = -1/3 < 0$ ).

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2011-B

Siano $P$ ed $A$ il perimetro e l’area di un rettangolo di dimensioni arbitrarie. Quale delle seguenti affermazioni è senz’altro corretta?

$\quad$

$\fbox{a}$ $P^3 > A$ .

$\fbox{b}$ $A^2 > 2P+1$ .

$\fbox{c}$ $P^2 \geq 16A$ .

$\fbox{d}$ $PA \geq A+P$ .

Soluzione.

Cominciamo osservando che l’opzione $\fbox{c}$ è l’unica disuguaglianza dimensionalmente consistente (ad ambo i membri compare il quadrato di una lunghezza), e come tale è una buona candidata ad essere corretta.

Per escludere le alternative, è sufficiente presentare dei controesempi. Per semplicità, basta considerare un quadrato. In questo caso, detto $x$ il suo lato, si ha $P = 4x$ e $A = x^2$ . Affinché le opzioni proposte siano “senz’altro corrette”, devono valere per ogni valore di $x$ positivo. Osserviamo che:

$P^3 > A \iff 64x^3 > x^2 \iff 64x > 1 \iff x > \frac{1}{64},$

che non è valida per $x$ arbitrario. In secondo luogo:

$A^2 > 2P + 1 \iff x^4 > 8x + 1,$

che non è verificata per valori piccoli di $x$ (per $x \to 0$ , il membro di sinistra tende a 0 mentre il membro di destra tende a 1). Infine:

$PA \geq A + P \iff 4x^3 \geq x^2 + 4x \iff 4x^2 \geq x + 4,$

che come prima non è verificata per $x \to 0$ .

Queste considerazioni escludono le risposte $\fbox{a}$ , $\fbox{b}$ e $\fbox{d}$ . Resta da confermare la nostra ipotesi che la terza uguaglianza sia in effetti corretta. Per un generico rettangolo, siano $a$ e $b$ le misure dei suoi lati. Allora $A = ab$ e $P = 2(a+b)$ , e quindi:

$P^2 - 16A = 4(a+b)^2 - 16ab = 4a^2+4b^2+8ab - 16ab = 4(a-b)^2 \geq 0.$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2011-C

Si consideri la successione definita per ogni $n \geq 0$ intero:

$x_n = n^3 - 9n^2 + 631.$

Qual è il più grande valore di $n$ per cui $x_n > x_{n+1}$ ?

$\quad$

$\fbox{a}$ 5.

$\fbox{b}$ 7.

$\fbox{c}$ 11.

$\fbox{d}$ 17.

Soluzione.

Il modo più semplice è valutare la derivata della funzione $f(x) = x^3 - 9x^2 + 631$ :

$f'(x) = 3x^2 - 18x = 3x(x-6).$

Abbiamo che $f'(x) > 0$ se $x < 0$ oppure $x > 6$ . Quindi la funzione decresce per $0 \leq x \leq 6$ , ed il più grande numero intero $n$ tale che $x_n = f(n) > x_{n+1} = f(n+1)$ è quindi $n = 5$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2011-D

Si considerino le seguenti disequazioni:

$\begin{gather*} \sin(x) \geq \dfrac{1}{2}; \\ \sin(2x) \geq \dfrac{1}{2}. \end{gather*}$

In quale frazione dell’intervallo $[0,2\pi]$ almeno una delle due disequazioni (cioè una o entrambe) è verificata?

$\quad$

$\fbox{a}$ $\dfrac{1}{3}$ .

$\fbox{b}$ $\dfrac{13}{24}$ .

$\fbox{c}$ $\dfrac{7}{12}$ .

$\fbox{d}$ $\dfrac{5}{8}$ .

Soluzione.

Limitandoci all’intervallo $0 \leq x \leq 2\pi$ , la prima disequazione è verificata se:

$x \in \left[\frac{\pi}{6}, \frac{5\pi}{6}\right],$

che corrisponde all’intervallo marcato dalla barra blu in basso nella figura. Per la seconda disequazione, la soluzione è simile, ma l’intervallo $[0,2\pi]$ contiene due periodi di $\sin(2x)$ . In questo caso, la soluzione è costituita dall’unione di due intervalli (indcati dalle barre verdi nella figura):

$2x \in \left[\frac{\pi}{6}, \frac{5\pi}{6}\right] \cup \left[\frac{13\pi}{6}, \frac{17\pi}{6}\right] \iff x \in \left[\frac{\pi}{12}, \frac{5\pi}{12}\right] \cup \left[\frac{13\pi}{12}, \frac{17\pi}{12}\right].$

Almeno una delle due disequazioni è quindi verificata su questo insieme (individuato dalle barre magenta nella figura):

$x \in \left[\frac{\pi}{12},\frac{5\pi}{6}\right] \cup \left[\frac{13\pi}{12},\frac{17\pi}{12}\right].$

I due intervalli misurano $5\pi/6-\pi/12 = 3\pi/4$ e $17\pi/12-13\pi/12 = \pi/3$ , rispettivamente. La frazione dell’intervallo $[0,2\pi]$ in cui almeno una disequazione è verificata è quindi:

$\frac{3\pi/4 + \pi/3}{2\pi} = \frac{13}{24}.$

$\quad$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2011-E

Nella figura sono indicate una circonferenza di centro $O$ e tre semirette che definiscono gli angoli $\alpha$ , $\beta$ e $\gamma$ . La semiretta contenente $AB$ è tangente alla circonferenza. Quale relazione sussiste tra i tre angoli?

$\fbox{a}$ $\cos(\alpha) = \sin(\beta+\gamma)$ .

$\fbox{b}$ $\sin(\beta) = \sin(\alpha)\sin(\gamma)$ .

$\fbox{c}$ $\sin(\beta)[1-\cos(\alpha)] = \sin(\gamma)$ .

$\fbox{d}$ $\sin(\alpha+\beta) = \cos(\gamma)\sin(\alpha).$

$\quad$

Soluzione.

Costruiamo il raggio $OB$ , e sia $r$ la sua lunghezza. Essendo $AB$ una tangente, il triangolo $ABO$ è rettangolo, per cui:

$r = \overline{AO}\sin(\alpha).$

Applicando poi il teorema dei seni al triangolo $AOC$ , abbiamo:

$\frac{\overline{OC}}{\sin(\beta)} = \frac{\overline{AO}}{\sin(\gamma)}.$

Combinando queste due uguaglianze ed essendo $\overline{OC} = r$ , otteniamo proprio l’equazione $\fbox{b}$ :

$\frac{\overline{AO}\sin(\alpha)}{\sin(\beta)} = \frac{\overline{AO}}{\sin(\gamma)} \implies \sin(\alpha)\sin(\gamma) = \sin(\beta).$

Si può anche verificare che le altre tre opzioni non sono valide in generale. Per semplificare il problema, conviene spostare il punto $C$ in posizioni “comode”. Per esempio, se $AC$ è tangente alla circonferenza (quindi $\alpha = \beta$ e $\gamma = 90\degr$ ), si vede che le equazioni $\fbox{c}$ e $\fbox{d}$ non sono delle identità. Allineando invece $C$ con $A$ e $O$ , si trova che l’opzione $\fbox{a}$ è falsa.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2011-F

Sia $\vartheta \in [0,\pi)$ un parametro reale, e si consideri l’equazione

$x^2 + y^2 + 4x\cos\vartheta + 8y\sin\vartheta + 10 = 0.$

Per quali valori di $\vartheta$ questa equazione rappresenta una circonferenza?

$\quad$

$\fbox{a}$ Se $0 < \vartheta < \dfrac{\pi}{3}$ .

$\fbox{b}$ Se $\dfrac{\pi}{4} < \vartheta < \dfrac{3\pi}{4}.$

$\fbox{c}$ Se $0 < \vartheta < \dfrac{\pi}{2}$ .

$\fbox{d}$ Per ogni valore di $\vartheta$ .

Soluzione.

L’equazione di una circonferenza di centro $(x_0,y_0)$ e raggio $r$ è data da:

$(x-x_0)^2 + (y-y_0)^2 - r^2 = 0.$

Cerchiamo di ricondurre a questa forma l’equazione assegnata, usando il metodo del completamento dei quadrati.

$\begin{aligned} x^2 + y^2 {} &{} + 4x\cos\vartheta + 8y\sin\vartheta + 10 = \\ {} & = (x+2\cos\vartheta)^2 - 4\cos^2\vartheta + (y+4\sin\vartheta)^2 - 16\sin^2\vartheta + 10 = \\ {} & = (x+2\cos\vartheta)^2 + (y+4\sin\vartheta)^2 - 12\sin^2\vartheta + 6. \end{aligned}$

Affinché il luogo dei punti rappresentato da questa equazione sia una circonferenza, è necessario che il termine corrispondente a $r^2$ sia positivo:

$12\sin^2\vartheta - 6 > 0 \implies \sin^2\vartheta > \dfrac{1}{2} \implies |\sin\vartheta\,| > \dfrac{1}{\sqrt{2}}.$

Limitandoci come richiesto dal testo all’intervallo $0 \leq \vartheta < \pi$ , in cui $|\sin\vartheta\,| = \sin\vartheta$ , troviamo la soluzione:

$\frac{\pi}{4} < \vartheta < \frac{3\pi}{4}.$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2011-G

Una funzione $f$ ha come grafico la spezzata rappresentata in figura. Quanto vale $\displaystyle \int_{-1}^{+1}f(x^2-1)\diff{x}$ ?

$\quad$

$\fbox{a}$ $\dfrac{1}{4}.$

$\fbox{b}$ $\dfrac{1}{3}$ .

$\fbox{c}$ $\dfrac{3}{5}$ .

$\fbox{d}$ $\dfrac{2}{3}$ .

$\quad$

Soluzione.

Sia $t = x^2 - 1$ . Notiamo che, per $x$ nel dominio di integrazione $-1 \leq x \leq 1$ , si ha $-1 \leq t \leq 0$ . Per calcolare l’integrale, ci basta quindi conoscere $f(t)$ sull’intervallo $[-1,0]$ . Per $-1 \leq t \leq 0$ , si vede facilmente dal grafico che $f(t) = 1+t$ , e quindi $f(x^2-1) = 1 + (x^2-1) = x^2$ . Possiamo quindi calcolare:

$\int_{-1}^{+1}f(x^2-1)\diff{x} = \int_{-1}^{+1} x^2\diff{x} = \left.\frac{x^3}{3}\right|_{-1}^{+1} = \frac{2}{3}.$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2011-H

Quante soluzioni reali (positive) ha la seguente equazione?

$x = 8^{\log_2(x)} - 9^{\log_3(x)} - 4^{\log_2(x)} + \log_{0\text{,5}}(0\text{,25}).$

$\quad$

$\fbox{a}$ 0.

$\fbox{b}$ 1.

$\fbox{c}$ 2.

$\fbox{d}$ 3.

Soluzione.

Per prima cosa, notiamo che affinché l’equazione sopra abbia significato, è necessario che $x > 0$ . Cerchiamo ora di renderla più maneggevole. In particolare, usando le proprietà delle potenze e dei logaritmi:

$\log_{0\text{,5}}(0\text{,25}) = \log_{1/2}\left(\frac{1}{4}\right) = \log_{1/2}\left(\frac{1}{2}\right)^{\!2} = 2.$

Possiamo ora riscrivere il membro di destra così:

$\begin{aligned} \phantom{=} {} & 8^{\log_2(x)} - 9^{\log_3(x)} - 4^{\log_2(x)} + \log_{0\text{,5}}(0\text{,25}) = \\ = {} & (2^3)^{\log_2(x)} - (3^2)^{\log_3(x)} - (2^2)^{\log_2(x)} + 2 = \\ = {} & [2^{\log_2(x)}]^3 - [3^{\log_3(x)}]^2 - [2^{\log_2(x)}]^2 + 2 = \\ % = {} & 2^{\log_2(x^3)} - 3^{\log_3(x^2)} - 2^{\log_2(x^2)} + 2 = \\ = {} & x^3 - x^2 - x^2 + 2. \end{aligned}$

L’equazione originale è pertanto equivalente alla seguente (sotto la restrizione $x > 0$ ), che si può fattorizzare facilmente:

$\begin{gather*} x^3-2x^2 - x + 2 = 0; \\ x^2(x-2) - (x-2) = 0; \\ (x^2-1)(x-2) = 0; \\ (x-1)(x+1)(x-2) = 0. \end{gather*}$

In questo modo si leggono immediatamente le tre soluzioni reali $x = -1$ , $x = 1$ , $x = 2$ . Quella negativa, come discusso all’inizio, va scartata.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2011-I

Sull’intervallo $0 \leq x < 2\pi$ , quante soluzioni ha la seguente equazione?

$\sin^8(x)+\cos^6(x) = 1.$

$\quad$

$\fbox{a}$ 3.

$\fbox{b}$ 4.

$\fbox{c}$ 6.

$\fbox{d}$ 8.

Soluzione.

Proponiamo due metodi differenti.

$\quad$

Se $y,z \in (0,1)$ (estremi esclusi), sappiamo che $y^4 < y$ e $z^3 < z$ . Assumiamo per cominciare che $\sin^2(x) \ne 0$ e $\sin^2(x) \ne 1$ , e quindi anche $\cos^2(x) \ne 0$ e $\cos^2(x) \ne 1$ (questo si traduce in $x \ne k\pi/2$ , con $k = 0, 1, 2, 3$ ). Allora, posto $y = \sin^2(x)$ e $z = \cos^2(x)$ , si ha $y,z \in (0,1)$ , e quindi:
$\sin^8(x) + \cos^6(x) < \sin^2(x) + \cos^2(x) = 1.$

Ne consegue che l’equazione proposta non può essere soddisfatta, con le possibili eccezioni $x = k\pi/2$ ( $k = 0$ , 1, 2, 3). Sostituendo, si verifica direttamente che questi quattro valori sono in effetti tutti soluzione dell’equazione.

Poniamo $\sin^2(x) = t$ , da cui $\cos^2(x) = 1-t$ . Abbiamo allora:
$\begin{gather*} t^4 + (1-t)^3 = 1; \\ t^4 + 1 -t^3 - 3t + 3t^2 = 1; \\ t(t^3 - t^2 + 3t - 3) = 0; \\ t[t^2(t-1) + 3(t-1)] = 0; \\ t(t-1)(t^2+3) = 0. \end{gather*}$

Dato che $t^2+3 \ne 0$ , restano le due soluzioni $t = 0$ e $t = 1$ . Tornando alla variabile $x$ (che ricordiamo appartenere all’intervallo semiaperto $0 \leq x < 2\pi$ ):

$\sin^2(x) = 0 \vee \sin^2(x) = 1 \iff x = 0 \vee x = \frac{\pi}{2} \vee x = \pi \vee x = \frac{3\pi}{2}.$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2011-J

Si consideri la funzione $f$ definita sui numeri interi positivi, tale che $f(1) = 1$ e che, per ogni $n$ positivo:

$\begin{array}{l@{\mbox{}=\mbox{}}l} f(2n) & f(n); \\[1pt] f(2n+1) & [f(n)]^2 - 2. \end{array}$

Calcolare il valore della somma:

$S = f(1) + f(2) + f(3) + \cdots + f(100) = \sum_{n=1}^{100} f(n).$

$\quad$

$\fbox{a}$ -86.

$\fbox{b}$ -31.

$\fbox{c}$ 23.

$\fbox{d}$ 58.

Soluzione.

È sempre conveniente calcolare a mano qualche valore di $f$ :

$n$	$f(n)$	$n$	$f(n)$	$n$	$f(n)$	$n$	$f(n)$
1	1	5	$-1$	9	$-1$	13	$-1$
2	1	6	$-1$	10	$-1$	14	$-1$
3	$-1$	7	$-1$	11	$-1$	15	$-1$
4	1	8	1	12	$-1$	16	1

Basandoci su questa tabella, effettuiamo alcune considerazioni.

$\quad$

$f(n) = \pm1$ per ogni $n \geq 1$ . Per dimostrarlo rigorosamente, si può usare il principio di induzione (forte). Se $n = 1$ , $f(n) = 1$ per ipotesi. Supponiamo ora che $f(n) = \pm1$ per ogni $n \leq k$ ( $k\geq 1$ ). Allora: se $k+1 = 2m$ è pari, $f(k+1) = f(m) = \pm1$ (per ipotesi di induzione, essendo $m \leq k$ ); se invece $k+1 = 2m+1$ è dispari, allora $f(k+1) = [f(m)]^2 - 2 = (\pm1)^2 - 2 = -1$ (anche qui sfruttando l’ipotesi di induzione, essendo $m \leq k$ ).

Se $n$ è una potenza di 2, cioè se $n = 2^k$ , allora $f(n) = 1$ . Infatti, dividendo l’argomento della funzione ripetutamente ( $k$ volte) per 2, si ha:
$\begin{aligned}f(n) = {} & f(2^k) = f(2\cdot2^{k-1}) = f(2^{k-1}) = \\ = {} & f(2\cdot2^{k-2}) = f(2^{k-2}) = \cdots = \\ = {} & f(2) = f(1) = 1. \end{aligned}$

Se $n$ non è una potenza di 2, allora $f(n) = -1$ . Se $n$ è dispari, lo abbiamo già visto al punto 1). Se $n$ è pari, deve essere $n = m \cdot 2^k$ , dove $m$ è dispari. Possiamo rimuovere via via tutte le potenze di 2:
$\begin{aligned}f(n) = {} & f(m\cdot2^k) = f(2m\cdot2^{k-1}) = f(m\cdot2^{k-1}) = \\ = {} & f(2m\cdot2^{k-2}) = f(m\cdot2^{k-2}) = \cdots = \\ = {} & f(2m) = f(m) = -1, \end{aligned}$

perché $m$ è dispari.

Possiamo ora calcolare $S$ : ci sono 7 potenze di 2 minori di 100 (da $2^0$ a $2^6$ ), in corrispondenza delle quali $f$ vale $+1$ . Su tutti gli altri valori (che sono $100-7 = 93$ ) $f$ vale $-1$ . La somma è pertanto $S = 7\cdot(+1) + 93\cdot(-1) = -86$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2012-A

Quali delle seguenti rette nel piano $xy$ sono tangenti alla circonferenza di equazione: $x^2 + y^2 = 4$ ?

$\quad$

$\fbox{a}$ $x+y=2$ .

$\fbox{b}$ $y=x-2\sqrt{2}$ .

$\fbox{c}$ $x=-\sqrt{2}$ .

$\fbox{d}$ $y=\sqrt{2}-x$ .

Soluzione.

La circonferenza ha centro nell’origine e raggio $r = 2$ . Iniziamo a disegnare le quattro rette:

$\quad$

Per quanto riguarda le rette $\fbox{a}$ , $\fbox{c}$ e $\fbox{d}$ , basta notare che contengono tutte punti interni alla circonferenza (ad esempio nei punti con $y = 1$ ), per cui non possono essere tangenti.

La retta $\fbox{b}$ ha un’inclinazione di $45^\circ$ e forma con gli assi coordinati il triangolo rettangolo isoscele $AOB$ , i cui cateti hanno lunghezza $2\sqrt{2}$ e quindi l’ipotenusa ha lunghezza 4. La distanza $\overline{OH}$ dalla retta dal punto $O$ è quindi pari ad $\overline{AB}/2 = 2$ , che è proprio la misura del raggio $r$ della circonferenza. Concludiamo che $AB$ è tangente alla circonferenza.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2012-B

Sia $N = 2^k \times 4^m \times 8^n$ , dove $k$ , $m$ e $n$ sono numeri interi positivi. Quale condizione assicura che $N$ sia un quadrato perfetto?

$\quad$

$\fbox{a}$ $k$ è pari.

$\fbox{b}$ $k+n$ è dispari.

$\fbox{c}$ $k$ è dispari ma $m+n$ è pari.

$\fbox{d}$ $k+n$ è pari.

Soluzione.

Basta usare le proprietà delle potenze. Riscriviamo $N$ nel seguente modo:

$N = 2^k \times 4^m \times 8^n = 2^k\times2^{2m}\times2^{3n} = 2^{2m+2n}\times2^{k+n}.$

Il primo fattore $2^{2m+2n}$ è il quadrato di $2^{m+n}$ . Il secondo fattore è un quadrato perfetto se e solo se $k+n$ è pari.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2012-C

Senza utilizzare la calcolatrice, stabilire quale tra i seguenti numeri è il più piccolo.

$\quad$

$\fbox{a}$ $\left(\sqrt{3}\right)^3$ .

$\fbox{b}$ $\log_3\left(9^2\right)$ .

$\fbox{c}$ $\left(3\sin\dfrac{\pi}{3}\right)^2$ .

$\fbox{d}$ $\log_2\left[\log_2\left(8^5\right)\right]$ .

Soluzione.

Valutiamo e confrontiamo i quattro numeri:

$\left(\sqrt{3}\right)^3 = \sqrt{3^3} = \sqrt{27} > \sqrt{16} = 4.$

$\log_3\left(9^2\right) = \log_3\left(3^4\right) = 4.$

$\left(3\sin\dfrac{\pi}{3}\right)^2 = \left(3\times\frac{\sqrt{3}}{2}\right)^2 = \frac{27}{4} > 4.$

$\log_2\left[\log_2\left(8^5\right)\right] = \log_2\left[\log_2\left(2^{15}\right)\right] = \log_2(15) < \log_2(16) = \log_2(2^4) = 4.$

L’unico numero minore di 4 è $\log_2\left[\log_2\left(8^5\right)\right]$ .

$\quad$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2012-D

La figura mostra un quadrato $Q$ di vertici $(0,0)$ , $(1,0)$ , $(1,1)$ e $(0,1)$ , e la retta $r$ di equazione $y = x + c$ (con $c$ parametro reale). Sia $A(c)$ l’area della regione appartenente a $Q$ e al di sotto di $r$ (cioè l’area della regione colorata). Quale dei seguenti grafici mostra l’andamento qualitativo della funzione $A(c)$ ?

$\quad$

Soluzione.

Iniziamo notando che, se $c < -1$ , la regione gialla è vuota, quindi $A(c) = 0$ , mentre se $c > 1$ l’area è costante e sempre pari a quella di $Q$ , cioè $A(c) = 1.$

Per $-1 \leq c \leq 0$ , la retta $r$ intercetta la base del quadrato in $x = -c$ e i cateti del triangolo giallo misurano $1-|c| = 1+c$ , per cui $A(c) = (1+c)^2/2$ . In particolare, la derivata di $A$ in $c=-1$ vale $A'(-1) = 0$ .

Per $0 \leq c \leq 1$ , si ha invece (per simmetria) $A(c) = 1 - A(-c) = 1 - (1-c)^2/2$ .

La $\fbox{d}$ è esclusa perché $A(c) \ne 0$ per $-1 < c < 0$ . La $\fbox{b}$ e la $\fbox{c}$ sono escluse perché $A'(c) = 0$ per $c = -1$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2012-E

Quale delle seguenti equazioni ha come grafico quello rappresentato in figura?

$\fbox{a}$ $y = (3-x)^2 (3+x)^2 (1-x)$ .

$\fbox{b}$ $y = -x^2 (x-9) (x^2-3)$ .

$\fbox{c}$ $y = (x-6) (x-2)^2 (x+2)^2$ .

$\fbox{d}$ $y = (x^2-1)^2 (3-x)$ .

$\quad$

Soluzione.

Iniziamo ad osservare che $y \to \mp\infty$ per $x \to \pm\infty$ . Per un polinomio, questo richiede che il coefficiente del monomio di grado massimo sia negativo, il che esclude la $\fbox{c}$ .

La curva non ha come radice $x = 0$ , il che esclude la $\fbox{b}$ .

La curva ha due radici di molteplicità doppia ed una singola. La radice a molteplicità singola è positiva ed è maggiore delle altre due, il che esclude la $\fbox{a}$ .

La $\fbox{d}$ presenta tutte le caratteristiche della curva rappresentata nel grafico: due soluzioni (segno opposto) di molteplicità doppia, una singola (positiva), intersezione positiva con l’asse delle ordinate, comportamento asintotico per $x \to \pm\infty$ .

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2012-F

Sia

$T = \left[\,\int_{-\pi/2}^{+\pi/2}\cos(x)\diff{x} \right] \times \left[\,\int_{\pi}^{2\pi}\sin(x)\diff{x} \right] \times \left[\int_{0}^{\pi/8}\frac{1}{\cos(3x)}\diff{x} \right].$

Quale delle seguenti affermazioni è corretta?

$\quad$

$\fbox{a}$ $T=0$ .

$\fbox{b}$ $T < 0$ .

$\fbox{c}$ $T > 0$ .

$\fbox{d}$ $T$ non esiste.

Soluzione.

Osserviamo che:

$\quad$

il primo integrale è ben definito (l’integranda è una funzione continua) e senz’altro positivo perché $\cos(x) > 0$ per $-\pi/2 < x < +\pi/2$ ;

il secondo integrale è ben definito (l’integranda è una funzione continua) e senz’altro negativo, perché $\sin(x) < 0$ per $\pi < x < 2\pi$ ;

il terzo integrale è ben definito, perché il denominatore non si annulla per $0 < x < \pi/8$ , per cui la funzione integranda è continua; inoltre, è senz’altro positivo dato che $\cos(3x) > 0$ sullo stesso intervallo.

Si conclude che $T$ esiste e che $T < 0$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2012-G

Sia $k$ un parametro reale e si consideri il sistema nella incognite $x$ e $y$

$\begin{cases} 2x+ky = 4; \\ x+y = k. \end{cases}$

Per quali valori di $k$ il sistema ammette come soluzioni coppie di interi positivi?

$\quad$

$\fbox{a}$ Per ogni valore di $k$ .

$\fbox{b}$ Per nessun valore di $k$ .

$\fbox{c}$ Solo se $k = 2$ .

$\fbox{d}$ Solo se $k > -2$ .

Soluzione.

Ricavando $x = k-y$ dalla seconda equazione e sostituendolo nella prima abbiamo:

$2(k-y) + ky = 4 \iff (k-2)y = -2(k-2).$

Se $k \ne 2$ possiamo semplificare il fattore $k-2$ ottenendo $y = -2$ . In questo caso non esistono quindi soluzioni sugli interi positivi. Se invece $k = 2$ , l’equazione è verificata per qualsiasi valore di $y$ . Sostituendo $k = 2$ nel sistema di partenza, ci si riconduce all’equazione:

$x+y = 2,$

che ammette la coppia $(x,y) = (1,1)$ come soluzione sugli interi positivi.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2012-H

Si consideri l’equazione integrale:

$\int_0^x\sin(\sin t)\diff{t} = 0.$

Quante soluzioni ha nell’intervallo $0 < x \leq 2\pi$ ?

$\quad$

$\fbox{a}$ Nessuna.

$\fbox{b}$ Una.

$\fbox{c}$ Due.

$\fbox{d}$ Tre.

Soluzione.

Consideriamo la funzione:

$F(x) = \int_0^x\sin(\sin t)\diff{t}.$

Il problema consiste nel risolvere l’equazione $F(x) = 0$ per $0 < x \leq 2\pi$ . Si ha naturalmente $F(0) = 0$ . Notiamo inoltre il seguente fatto:

$\int_{\pi}^{2\pi}\sin(\sin t)\diff{t} = \int_{0}^{\pi}\sin[\sin(u+\pi)]\diff{u} = -\int_0^{\pi}\sin(\sin u)\diff{u},$

dove abbiamo effettuato la sostituzione $t = u + \pi$ e usato l’identità trigonometrica $\sin(x+\pi) = -\sin(x)$ . Concludiamo dunque che:

$\begin{aligned} F(2\pi) = {} & \int_0^{2\pi}\sin(\sin t)\diff{t} = \int_0^{\pi}\sin(\sin t)\diff{t} + \int_{\pi}^{2\pi}\sin(\sin t)\diff{t} = \\ = {} & \int_0^{\pi}\sin(\sin t)\diff{t} - \int_0^{\pi}\sin(\sin t)\diff{t} = 0. \end{aligned}$

Anche il valore $x = 2\pi$ è dunque una soluzione dell’equazione assegnata. Mostriamo che non ce ne sono altre nell’intervallo da considerare. Per il teorema di Torricelli-Barrow, si ha infatti $F'(x) = \sin(\sin x)$ . Il segno di $F'(x)$ si può determinare così:

$F'(x) > 0 \iff 0 < \sin(x) < \pi;$

dato che $\sin(x) \leq 1$ per ogni $x$ , questa doppia disuguaglianza si riduce a:

$\sin(x) > 0 \iff 0 < x < \pi.$

Concludiamo che $F$ cresce sull’intervallo $[0,\pi]$ e decresce su $[\pi,2\pi]$ . Abbiamo quindi che $F(x) > F(0) = 0$ per ogni $x \in (0,\pi]$ e $F(x) > F(2\pi) = 0$ per ogni $x \in [\pi,2\pi)$ , e quindi $F(x) > 0$ per ogni $x \in (0,2\pi)$ . L’equazione $F(x) = 0$ non ammette quindi soluzioni nell’intervallo $0 < x < 2\pi$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2012-I

Si consideri un triangolo equilatero inscritto in un cerchio la cui circonferenza ha lunghezza 10. Detti $P$ ed $A$ il suo perimetro e la sua area, rispettivamente, quale delle seguenti affermazioni è corretta?

$\quad$

$\fbox{a}$ $\dfrac{A}{P} = \dfrac{5}{4\pi}$ .

$\fbox{b}$ $P < A$ .

$\fbox{c}$ $\dfrac{P}{A} = \dfrac{10}{3\pi}$ .

$\fbox{d}$ $P^2 \in \mathbb{Q}$ .

Soluzione.

Il raggio della circonferenza è dato da $R = 10/(2\pi) = 5/\pi$ . Calcoliamo ora il lato $L$ del triangolo in funzione di $R$ .

$\quad$

Il triangolo rettangolo $AOH$ è metà di un triangolo equilatero di lato $R$ e altezza $L/2$ . Da questo si ricava immediatamente che:

$L = \overline{AC} = 2\overline{AH} = 2\sqrt{\,\overline{OA}\mbox{}^2-\overline{OH}\mbox{}^2} = 2\sqrt{R^2-(R/2)^2} = \sqrt{3}R.$

A questo punto è facile calcolare l’area ed il perimetro del triangolo:

$\begin{array}{ll} P = 3L = 3\sqrt{3}R; \\ A = \dfrac{1}{2}L^2\sin(60^\circ) = \dfrac{3\sqrt{3}}{4}R^2. \end{array}$

Ritroviamo quindi l’espressione $\fbox{a}$ :

$\frac{A}{P} = \dfrac{3\sqrt{3}}{4}R^2 \cdot \dfrac{1}{3\sqrt{3}R} = \frac{R}{4} = \frac{5}{4\pi}.$

Questa espressione mostra anche che $A/P < 1$ , escludendo la $\fbox{b}$ .

Vale la pena menzionare che $P^2 = 27\times25/\pi^2$ è irrazionale perché $\pi^2$ è irrazionale. Questo si dimostra ricordando che $\pi$ è un numero trascendente, cioè non è soluzione di nessuna equazione algebrica a coefficienti interi. Se per assurdo $\pi^2$ fosse razionale, allora esisterebbero $p$ e $q$ interi ( $q \ne 0$ ) tali che $\pi^2 = p/q$ , da cui $q\pi^2 -p = 0$ , e quindi $x = \pi$ sarebbe soluzione dell’equazione algebrica a coefficienti interi $qx^2-p = 0$ , che è un assurdo essendo $\pi$ trascendente. Anche l’opzione $\fbox{d}$ va dunque scartata.

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2012-J

Sia $\vartheta$ un angolo assegnato ( $0 < \vartheta < 180^\circ$ ). Si consideri una circonferenza di raggio unitario e da un punto fissato $P$ si costruiscano due corde $PQ$ e $PR$ in modo che formino tra loro un angolo $\vartheta$ . Esprimendo $\vartheta$ in radianti, quanto può valere al massimo l’area della regione colorata?

$\fbox{a}$ $\vartheta\cdot\left[1+\cos\left(\dfrac{\vartheta}{2}\right)\right]$ .

$\fbox{b}$ $\vartheta + \sin(\vartheta)$ .

$\fbox{c}$ $\dfrac{\pi}{2}[1-\cos(\vartheta)]$ .

$\fbox{d}$ $\vartheta$ .

$\quad$

Soluzione.

Per ragioni di simmetria, si può intuire che la massima area si ha quando $\overline{PQ} = \overline{PR}$ , e quindi $\widehat{QPO} = \widehat{OPR} = \vartheta/2$ . Una dimostrazione più rigorosa è allegata separatamente. Riproduciamo la figura in questa configurazione, spostando i punti $Q$ ed $R$ mantenendo costante l’angolo $\widehat{QPR} = \vartheta$ .

$\quad$

L’area che ci interessa $\mathcal{A}_{PQR}$ è pari alla somma dell’area $\mathcal{A}_{OQR}$ del settore circolare $OQR$ e delle aree $\mathcal{A}_{ORP}$ e $\mathcal{A}_{OPQ}$ dei triangoli $ORP$ e $OPQ$ (che sono congruenti). In particolare, dato che $\widehat{QOR}$ è l’angolo al centro corrispondente all’angolo alla circonferenza $\widehat{QPR}$ , si ha $\widehat{QOR} = 2\widehat{QPR} = 2\vartheta$ , e quindi (misurando $\vartheta$ in radianti):

$\mathcal{A}_{OQR} = \frac{1}{2}\times\widehat{QOR}\times\overline{OQ}^2 = \vartheta.$

I triangoli $ORP$ e $OPQ$ sono entrambi isosceli, e quindi $\widehat{POR} = 180\degr - 2\times(\vartheta/2)$ . La loro area è data da:

$\mathcal{A}_{ORP} = \frac{1}{2} \overline{OP}\times\overline{OR}\times\sin(\widehat{POR}) = \frac{1}{2}\sin(180^\circ-\vartheta) = \frac{1}{2}\sin(\vartheta).$

L’area colorata $\mathcal{A}_{PQR}$ è quindi data da:

$\mathcal{A}_{PQR} = \vartheta + 2\times\frac{1}{2}\sin(\vartheta) = \vartheta + \sin(\vartheta).$

Mostriamo più rigorosamente che l’area della regione colorata $\mathcal{A}_{PQR}$ è massima quando la figura è simmetrica, cioè quando $\overline{PQ} = \overline{PR}$ . Ricordiamo che $P$ e $\vartheta$ sono fissati, mentre $Q$ ed $R$ sono liberi di muoversi lunga la circonferenza.

$\quad$

Costruiamo la corda $QR$ , che scompone l’area che ci interessa in due pezzi. L’area del segmento circolare \textcircled{\raisebox{-.9pt}1} (ombreggiato con un colore più scuro in figura) è determinata unicamente dall’angolo $\vartheta$ , che è fissato. L’area \textcircled{\raisebox{-.9pt}1} è quindi costante. Per massimizzare $\mathcal{A}_{PQR}$ , basta quindi massimizzare l’area $\mathcal{A}_{\textcircled{\scriptsize 2}}$ del triangolo $PQR$ .

Chiamiamo per brevità $\alpha = \widehat{PQR}$ . Si ha quindi $\widehat{PRQ} = 180\degr - \vartheta - \alpha$ . Per il teorema della corda, detto $d$ il diametro della circonferenza, la lunghezza delle corde $PQ$ e $PR$ è data da:

$\begin{array}{l} \overline{PQ} = d\sin(180\degr - \vartheta - \alpha) = d\sin(\vartheta+\alpha); \\[5pt] \overline{PR} = d\sin(\alpha). \end{array}$

L’area $\mathcal{A}_{\textcircled{\scriptsize 2}}$ del triangolo $PQR$ è quindi data da:

$\mathcal{A}_{\textcircled{\scriptsize 2}} = \frac{1}{2}\times\overline{PQ}\times\overline{PR}\times\sin(\vartheta) = \frac{1}{2}d^2\sin(\vartheta+\alpha)\sin(\alpha)\sin(\vartheta).$

Al variare di $\alpha$ , $\mathcal{A}_{\textcircled{\scriptsize 2}}$ sarà massima se è massima la quantità $\sin(\vartheta+\alpha)\sin(\alpha) = [\cos(\vartheta)-\cos(2\alpha+\vartheta)]/2$ (dove abbiamo usato la terza formula di Werner), che a sua volta è massima se:

$\cos(2\alpha+\vartheta) = -1 \iff 2\alpha+\vartheta = 180\degr \iff \alpha = 90\degr - \vartheta/2.$

Per questo valore di $\alpha$ si ha $\widehat{PRQ} = 180\degr - \vartheta - \alpha = 90\degr -\vartheta/2 = \alpha$ . Il triangolo $PQR$ è quindi isoscele e $\overline{PQ} = \overline{PR}$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2013-A

Sia $a$ un parametro reale, e si consideri l’equazione:

$x^2 + ax + a = 1.$

Per quali valori di $a$ l’equazione ha radici reali distinte?

$\quad$

$\fbox{a}$ $a \ne 2$ .

$\fbox{b}$ $a > 2$ .

$\fbox{c}$ $a = 2$ .

$\fbox{d}$ Per ogni $a \in \mathbb{R}$ .

Questo quesito ci è parso particolarmente semplice. Abbiamo pertanto pensato di aggiungere alcune domande supplementari a risposta aperta:

$\quad$

Per quali valori di $a$ le radici sono una il doppio dell’altra?

Per quali valori di $a$ le radici sono una l’inversa dell’altra?

Per quali valori di $a$ la somma dei reciproci delle radici è pari a 1?

Soluzione.

Il discriminante della corrispondente equazione di secondo grado è:

$\Delta = a^2 - 4(a-1) = (a-2)^2.$

Essendo un quadrato, $\Delta > 0$ per ogni valore di $a$ , ad eccezione del caso $\Delta = 0$ , cioè $a = 2$ .

Per quanto riguarda le domande supplementari, si ricordi che la somma ed il prodotto delle radici $x_1$ e $x_2$ dell’equazione $x^2 + ax + (a-1) = 0$ sono dati da:

$x_1 + x_2 = -a, \qquad x_1\cdot x_2 = a-1.$

$\quad$

Affinché $x_1 = 2x_2$ , dovremo avere:
$\begin{cases} x_1 = 2x_2; \\ x_1 + x_2 = -a; \\ x_1\cdot x_2 = a-1. \end{cases} \implies \qquad \begin{cases} x_1 = 2x_2; \\ 3x_2 = -a; \\ 2x_2^2 = a-1. \end{cases}$

Dalla seconda equazione si trova $a = -x_2/3$ , quindi sostituendo nella terza si trova $2a^2-9a+9 = 0$ che fornisce $a = 3$ oppure $a = 3/2$ . La simmetria delle equazioni porta allo stesso risultato nel caso $x_2 = 2x_1$ .

Affinché la condizione abbia significato, è necessario che $x_1,x_2 \ne 0$ . Questa condizione si traduce in $a \ne 1$ . Se $x_1 = 1/x_2$ , allora $x_1\cdot x_2 = 1$ , e quindi $a - 1 = 1$ , cioè $a = 2$ .

Anche qui richiediamo che $a \ne 1$ in modo che $x_1 \ne 0 \ne x_2$ . Per ipotesi abbiamo:
$1 = \frac{1}{x_1} + \frac{1}{x_2} = \frac{x_1+x_2}{x_1\cdot x_2} = \frac{-a}{a-1}.$

Dato che $a-1 \ne 0$ , ci riconduciamo all’equazione $-a = a-1$ e quindi $a = 1/2$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2013-B

Si consideri il grafico della funzione $y = \sin(x)$ , lo si rifletta prima rispetto alla retta $x = \pi$ e dopo rispetto alla retta $y = 2$ . Quale delle seguenti equazioni descrive il grafico risultante?

$\quad$

$\fbox{a}$ $y = \cos(x)$ .

$\fbox{b}$ $y = 2+\sin(x)$ .

$\fbox{c}$ $y=4+\sin(x)$ .

$\fbox{d}$ $y = 2 - \cos(x)$ .

Soluzione.

Forse il modo più veloce per risolvere il problema è osservare il grafico $y = \sin(x)$ ed effettuare le due trasformazioni, come indicato in figura.

$\quad$

Per dimostrarlo, si può procedere analiticamente, considerando come operano le riflessioni sul piano cartesiano. In generale, data una funzione $f(x)$ , la funzione riflessa attorno alla retta $x = a$ è data da $f(2a-x)$ , mentre la funzione riflessa attorno alla retta $y = b$ è data da $2b-f(x)$ .

Applicando le due regole sopra con $f(x) = \sin(x)$ , $a = \pi$ , $b = 2$ , abbiamo:

$\sin(x) \ \rightsquigarrow \ \sin(2\pi-x) = -\sin(x) \ \rightsquigarrow \ 2\cdot2 - [-\sin(x)] = 4+\sin(x).$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2013-C

Siano $f$ , $g$ , $h$ : $\mathbb{R} \to \mathbb{R}$ funzioni due volte derivabili che soddisfano le seguenti relazioni:

$f'(x) = g(x+1), \qquad g'(x) = h(x-1).$

Quanto vale $f''(2x)$ ?

$\quad$

$\fbox{a}$ $h(2x+1)$ .

$\fbox{b}$ $2h'(2x)$ .

$\fbox{c}$ $h(2x)$ .

$\fbox{d}$ $h(x-1)$ .

Soluzione.

Sfruttando la prima condizione, abbiamo che:

$f''(x) = \frac{\diff}{\diff x}f'(x) = \frac{\diff}{\diff x} g(x+1) = g'(x+1).$

Inoltre, data la seconda condizione:

$g'(x+1) = h(x+1-1) = h(x).$

Quindi si conclude che

$f''(2x) = h(2x).$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2013-D

Quale dei seguenti grafici rappresenta qualitativamente nel piano $xy$ la curva di equazione $x^4-y^2 = 2y + 1$ ?

$\quad$

Soluzione.

Possiamo riscrivere l’equazione proposta nel seguente modo:

$x^4 = (y+1)^2 \iff x^2 = |y+1|,$

che si scompone nella coppia di equazioni:

$\begin{cases} y = -1 + x^2, & \text{se $y \geq -1$;} \\ y = -1 - x^2, & \text{se $y < -1$.} \end{cases}$

Queste sono due parabole, una con la concavità verso l’alto e una verso il basso, entrambe con il vertice in $(0,-1)$ , e tra loro simmetriche rispetto alla retta $y = -1$ . Queste caratteristiche sono consistenti solo con il secondo grafico.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2013-E

Si consideri il polinomio così definito:

$P(x) = \frac{\diff^2}{\diff x^2}\left[(2x-1)^4(1-x)^5\right] + \frac{\diff}{\diff x}\left[(2x+1)^4(3x^2-2)^2\right].$

Di che grado è $P$ ?

$\quad$

$\fbox{a}$ 9.

$\fbox{b}$ 8.

$\fbox{c}$ 7.

$\fbox{d}$ $<7$ .

Soluzione.

Considerando il polinomio all’interno della prima parentesi quadrata, il monomio di grado massimo è $2^4(-1)^5x^4x^5 = -16x^9$ . Per il polinomio all’interno della seconda parentesi quadrata, il monomio di grado massimo è $2^43^2x^4x^4 = 16\cdot9x^8$ . Tanto il primo polinomio derivato due volte quanto il secondo polinomio derivato una volta sola hanno grado 7. La loro somma avrà pertanto grado 7, a meno che i due monomi in $x^7$ abbiano coefficienti numerici uguali ed opposti, nel qual caso la somma avrà grado strettamente minore di 7.

Derivando due volte il primo addendo, il monomio di grado massimo è dato da $9\cdot8\cdot(-16x^7)$ ; derivando una volta il secondo addendo, il monomio di grado massimo è $8\cdot(16\cdot9x^7)$ . Si vede che questi due termini sono proprio l’uno l’opposto dell’altro, e nella somma si elidono. Il polonomio somma dei due pezzi deve avere pertanto grado strettamente minore di 7.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2013-F

Tre numeri positivi $a$ , $b$ e $c$ soddisfano le relazioni:

$\begin{cases} \log_b(a) = 2; \\ \log_b(c-3) = 3; \\ \log_a(c+5) = 2. \end{cases}$

Usando questa informazione, cosa è possibile concludere?

$\quad$

$\fbox{a}$ Il valore di $a$ è univocamente determinato.

$\fbox{b}$ Ci sono due possibili valori di $a$ .>

$\fbox{c}$ Ci sono infiniti possibili valori di $a$ .

$\fbox{d}$ L’informazione fornita contiene una contraddizione logica.

Soluzione.

Innanzitutto, i valori delle incognite per cui il sistema ha significato sono $a, b \ne 1$ e $c > 3$ (condizioni che vanno aggiunte all’ipotesi $a, b, c > 0$ ). Usando la definizione di logaritmo, riscriviamo le espressioni iniziali sotto forma di potenze:

$\begin{cases} b^2 = a; \\ b^3 = c-3; \\ a^2 = c+5. \end{cases}$

Dalla prima, abbiamo $a^2 = b^4$ , mentre dalle ultime due abbiamo:

$b^3 = c-3 = (c+5) - 8 = a^2 - 8 = b^4-8.$

Questa è un’equazione per $b$ . Per trovarne le soluzioni, consideriamo la funzione $f(b) = b^4-b^3-8$ , che ha uno zero per $b = 2$ (si può trovare per tentativi usando il teorema della radici razionali). Inoltre $f'(b) = 4b^3 - 3b^2 = b^2(4b-3)$ è positiva per $b > 3/4$ . Quindi $f$ è crescente (decrescente) per $b > 3/4$ ( $b < 3/4$ ). Dato che $f(0) = -8$ , l’unica radice positiva di $f$ è proprio $b = 2$ , che è l’unica soluzione ammissibile per il sistema di partenza.

Sostituendo si ha quindi un solo valore ammesso di $a = b^2 = 4$ . Si trova anche $c = a^2-5 = 11$ . I valori trovati di $a$ , $b$ e $c$ sono consistenti con le condizioni di esistenza, per cui la (sola) soluzione trovata è accettabile.

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2013-G

Sia $n \geq 2$ un intero e sia $P_n(x)$ il polinomio definito come segue:

$P_n(x) = (x-1) + (x-2) + \cdots + (x-n) = \sum_{k=1}^{n}(x-k).$

Qual è il resto della divisione polinomiale tra $P_n(x)$ e $P_{n-1}(x)$ ?

$\quad$

$\fbox{a}$ $\dfrac{n}{2}$ .

$\fbox{b}$ $\dfrac{n+1}{2}$ .

$\fbox{c}$ $\dfrac{n^2+n}{2}$ .

$\fbox{d}$ $-\dfrac{n}{2}$ .

Soluzione.

Per prima cosa, calcoliamo esplicitamente $P_n(x)$ . Ricordiamo la formula della somma dei primi $n$ numeri naturali:

$1 + 2 + \cdots + n = \sum_{k=1}^{n}k = \frac{n(n+1)}{2}.$

Usando questo risultato, abbiamo:

$P_n(x) = \sum_{k=1}^{n}(x-k) = nx - \frac{n(n+1)}{2};$

e quindi anche:

$P_{n-1}(x) = (n-1)x - \frac{(n-1)n}{2} = (n-1)\left(x-\frac{n}{2}\right).$

Conoscendo le espressioni di $P_n$ e $P_{n-1}$ , possiamo calcolare il resto della divisione. Un modo è usare l’algoritmo della divisione polinomiale. Alternativamente, possiamo scrivere così:

$\begin{aligned} P_n(x) = {} & nx - \frac{n(n+1)}{2} = \frac{n}{n-1}(n-1)x - \frac{n}{n-1}\frac{(n-1)(n+1)}{2} = \\ = {} & \frac{n}{n-1}(n-1)x - \frac{n}{n-1}\frac{(n-1)n}{2} - \frac{n}{2} = \\ = {} & \frac{n}{n-1}\left[(n-1)x-\frac{(n-1)n}{2}\right] - \frac{n}{2} = \\ = {} & \frac{n}{n-1} P_{n-1}(x) - \frac{n}{2}. \end{aligned}$

Da questa uguaglianza si legge che, nella divisione di $P_n(x)$ per $P_{n-1}(x)$ , il resto è $-n/2$ , mentre il quoziente è $n/(n-1)$ .

Per chi lo conosce, un procedimento alternativo è ricorrere al teorema del resto: il resto della divisione di un polinomio qualunque $Q(x)$ per il binomio $(x-a)$ è dato da $Q(a)$ . Inoltre, moltiplicando il divisore di una divisione polinomiale per una costante, il resto rimane invariato (cambia invece il quoziente). Dato che $P_{n-1} = (n-1)\times(x - n/2)$ , il resto della divisione di $P_n$ per $P_{n-1}$ è lo stesso che per la divisione tra $P_n(x)$ e $(x-n/2)$ , che è dato da:

$P_n\left(\frac{n}{2}\right) = n\frac{n}{2} - \frac{n(n+1)}{2} = -\frac{n}{2}.$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2013-H

Calcolare l’area compresa tra le due curve di equazione

$\begin{array}{l} y = \sqrt{2-x^2}; \\[5pt] x + \left(\sqrt{2}-1\right)y = \sqrt{2}. \end{array}$

$\quad$

$\fbox{a}$ $\dfrac{\sin\left(\sqrt{2}\right)}{\sqrt{2}}$ .

$\fbox{b}$ $\dfrac{\pi}{4} - \dfrac{1}{\sqrt{2}}$ .

$\fbox{c}$ $\dfrac{\pi}{2\sqrt{2}}$ .

$\fbox{d}$ $\dfrac{\pi^2}{6}$ .

Soluzione.

La prima equazione rappresenta una semicirconferenza centrata nell’origine di raggio $\sqrt{2}$ (contenuta nel semipiano non-negativo delle ordinate $y \geq 0$ ). La seconda è una retta. Calcoliamo l’intersezione tra le due curve:

$\begin{gather*} x = \sqrt{2} - \left(\sqrt{2}-1\right)y \implies x^2 = 2 + \left(\sqrt{2}-1\right)^2y^2 -2\sqrt{2}\left(\sqrt{2}-1\right)y; \\ y^2 = 2-x^2 = -\left(3-2\sqrt{2}\right)y^2 + 2\sqrt{2}\left(\sqrt{2}-1\right)y; \\ \left(2\sqrt{2}-4\right)y^2 + 2\left(2-\sqrt{2}\right)y = 0; \\ y^2 - y = 0. \end{gather*}$

Abbiamo usato che $(\sqrt{2}-1)^2 = 2 + 1 - 2\sqrt{2} = 3 - 2\sqrt{2}$ . Questa equazione ha soluzioni $y = 0$ e $y = 1$ , ed essendo $x = \sqrt{2} - \left(\sqrt{2}-1\right)y$ si trovano le ascisse corrispondenti $x = \sqrt{2}$ e $x = 1$ . Possiamo ora disegnare le due curve.

$\quad$

L’area della regione compresa tra le due curve (in rosso) si può ottenere come la differenza tra l’area del settore circolare $AOB$ e l’area del triangolo $AOB$ . Per quanto riguarda la prima, essendo $A = (1,1)$ , l’angolo $\widehat{AOB}$ vale $45\degr$ , per cui il settore circolare ha come area $1/8$ dell’area del cerchio, quindi $\pi (\sqrt{2})^2/8 = \pi/4$ . L’area del triangolo $AOB$ è poi data da $\overline{OB}\cdot\overline{AH}/2 = \sqrt{2}\cdot1/2$ .

L’area della regione rossa è quindi data da:

$\frac{\pi}{4} - \frac{\sqrt{2}}{2} = \frac{\pi}{4} - \frac{1}{\sqrt{2}} \approx 0\text{,078}.$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2013-I

Consideriamo la funzione $F$ definita sui numeri interi positivi, tale che:

$F(1) = 1;\qquad F(2) = 1; \qquad F(3) = -1.$

Inoltre, per ogni $k \geq 2$ intero, si ha:

$\begin{array}{l@{\mbox{}=\mbox{}}l} F(2k) & F(k); \\ F(2k+1) & F(k). \end{array}$

Quanto vale la seguente somma?

$F(1) + F(2) + F(3) + \cdots + F(100) = \sum_{i=1}^{100}F(i).$

$\quad$

$\fbox{a}$ $-15$ .

$\fbox{b}$ $28$ .

$\fbox{c}$ $64$ .

$\fbox{d}$ $81$ .

Soluzione.

In primo luogo, notiamo che $F$ può assumere solo i valori $\pm1$ . Per un valore fissato di $k$ , sappiamo che $F(2k) = F(2k+1) = F(k)$ . Quindi, il valore assunto da $F$ in $k$ determina il valore di $F$ per i due valori $2k$ e $2k+1$ .

Lasciamo per il momento da parte il valore $F(1)$ . Partendo dai due valori “seme” $k = 2$ e $k = 3$ , abbiamo i seguenti schemi, dove $F$ ha lo stesso valore in ciascuno dei due grafi ( $+1$ a sinistra, $-1$ a destra):

$\quad$

Lungo ciascuna riga, $F$ assume i valori $+1$ e $-1$ lo stesso numero di volte, per cui la somma lungo un’intera riga è $0$ . Più formalmente, nella riga $j$ -esima ( $j \geq 1$ intero), ci sono $2^j$ valori di $n$ ( $2^j \leq n \leq 2^{j+1}-1$ ); sui primi $2^{j-1}$ valori $F$ vale $+1$ , e sui secondi $2^{j-1}$ valori $F$ vale $-1$ .

Per calcolare la somma che ci interessa, notiamo che $2^6 < 100$ e $2^7 > 100$ . La somma di $F(n)$ per $2 \leq n \leq 2^6-1$ è pertanto nulla. Ci sono poi $2^{6-1}$ valori di $n$ ( $64 \leq n \leq 95$ ) sui quali $F$ vale $+1$ , e quindi 5 valori di $n$ ( $96 \leq n \leq 100$ ) sui quali $F$ vale $-1$ . Senza dimenticarci di $n = 1$ , abbiamo quindi:

$\begin{aligned} \sum_{i=1}^{100}F(i) = {} & F(1) + 0 + \cdots + 0 + F(64)+\cdots+F(95)+F(96)+\cdots+F(100) = \\ = {} & 1 + 32\times1 + 5\times(-1) = 28. \end{aligned}$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2013-J

Sia $n$ un numero intero positivo. Calcolare il seguente integrale:

$I(n) = \int_0^n \lfloor 2^x \rfloor \diff{x}.$

Ricordiamo che, preso un numero reale $z$ , la funzione $\lfloor z \rfloor$ denota la parte intera di $z$ , cioè il più grande numero intero minore o uguale a $z$ .

$\quad$

$\fbox{a}$ $\log_2[(2^n-1)!]$ .

$\fbox{b}$ $n2^n-\log_2[(2^n)!]$ .

$\fbox{c}$ $n2^n$ .

$\fbox{d}$ $\log_2[(2^n)!]$ .

Soluzione.

La funzione $\lfloor 2^x \rfloor$ assume per definizione solo valori interi. In particolare, $\lfloor 2^x \rfloor = n$ , per $n$ intero tale che $n \leq 2^x < n+1$ , cioè $\log_2(n) \leq x < \log_2(n+1)$ . La figura mostra il grafico della funzione $\lfloor 2^x \rfloor$ .

$\quad$

L’integrale $I(n)$ (nella figura è evidenziato $n=3$ ) è pertanto la somma delle aree dei $2^n-1$ rettangoli di base $[\log_2(k+1)-\log_2(k)]$ e altezza $k$ , con $1 \leq k \leq 2^n-1$ .

Ricordiamo inoltre che, per una successione qualsiasi $a_k$ , abbiamo:

$\sum_{k=1}^{M} (a_{k+1}-a_k) = \cancel{a_2}-a_1 + \cancel{a_3}-\cancel{a_2} + \cdots + a_{M+1}-\cancel{a_M} = a_{M+1}-a_1.$

Quindi, sfruttando l’espressione sopra con $a_k = k\log_2(k)$ e $M = 2^n-1$ , si ha:

$\begin{aligned} I(n) = {} & \sum_{k=1}^{2^n-1}k\cdot\left[\log_2(k+1)-\log_2(k)\right] = \\ = {} & \sum_{k=1}^{2^n-1}\left[(k+1)\log_2(k+1)-k\log_2(k)\right] - \sum_{k=1}^{2^n-1}\log_2(k+1) = \\ = {} & 2^n\log_2(2^n) - \log_2[(2^n)!] = \\ = {} & n2^n - \log_2[(2^n)!]. \end{aligned}$

Abbiamo anche usato il fatto che (per qualunque base del logaritmo):\vspace{-3pt}

$\begin{aligned} \sum_{k=1}^{M}\log(k) = {} & \log(1)+\log(2)+\log(3)+\cdots + \log(M) = \\[-5pt] = {} & \log(1\times2\times3\times\cdots\times M) = \log(M!). \end{aligned}$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2014-A

Per quali valori di $x$ è soddisfatta la seguente disequazione?

$x^4 < 8x^2 + 9.$

$\quad$

$\fbox{a}$ $-3 < x < 3$ .

$\fbox{b}$ $0 < x < 4$ .

$\fbox{c}$ $1 < x < 3$ .

$\fbox{d}$ $-1 < x < 9$ .

$\fbox{e}$ $-3 < x < -1$ .

Soluzione.

Posto $t = x^2$ (e si ha quindi $t \geq 0$ ), abbiamo la disequazione equivalente:

$t^2 - 8t - 9 < 0.$

Usando la formula risolutiva delle equazioni di secondo grado, o semplicemente fattorizzando il polinomio $t^2 - 8t - 9 = (t+1)(t-9)$ , questa disequazione ha come soluzione l’intervallo aperto $-1 < t < 9$ . Tornando alla variabile $x$ , la condizione $-1 < x^2$ è soddisfatta automaticamente, mentre resta da considerare $x^2 < 9$ , che ha come soluzione l’intervallo $-3 < x < 3$ .

(Si noti che, tra le opzioni presentate, solo la $\fbox{a}$ è possibile; infatti, se la disequazione originale è soddisfatta da un certo valore $x$ , deve essere soddisfatta anche da $-x$ , e quindi l’intervallo delle soluzioni deve essere simmetrico rispetto al punto $x = 0$ ).

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2014-B

Quale delle seguenti figure rappresenta qualitativamente il grafico della funzione $f(x) = \log_{10}(x^2-2x+2)$ ?

$\quad$

Soluzione.

Riscriviamo opportunamente l’argomento del logaritmo:

$x^2 - 2x + 2 = 1 + (x-1)^2.$

Questa è una parabola con la concavità rivolta verso l’alto e con vertice in $(1,1)$ (che in particolare ha ascissa positiva). È quindi sempre maggiore di 1, decrescente per $x \leq 1$ e crescente per $x \geq 1$ . Applicando il logaritmo (che è una funzione monotona crescente), vengono preservate diverse proprietà del grafico: la funzione $f$ ha un minimo per $x = 1$ , è decrescente per $x < 1$ e crescente per $x > 1$ , e $f(1) = \log_{10}(1) = 0$ . In particolare, c’è un’unica intersezione (positiva) con l’asse delle ascisse. Queste caratteristiche sono consistenti solo con l’ultimo grafico.

Gli altri grafici sono facilmente esclusi. Il primo non ha intersezioni con l’asse delle ascisse. Il secondo ha un’intersezione con l’asse delle ascisse ma è negativa. Il terzo ed il quarto hanno un asintonto verticale, che la funzione $f$ non ha perché $x^2-2x+2 \ne 0$ per ogni $x \in \mathbb{R}$ .

La risposta corretta è dunque la $\fbox{e}$ .

Quesito 2014-C

Sia $k$ un parametro reale, e si consideri la cubica:

$y = kx^3 - (k+1)x^2 + (2-k)x - k.$

Per quali valori di $k$ la cubica ha un punto di minimo per $x = 1$ ?

$\quad$

$\fbox{a}$ $k > 0$ .

$\fbox{b}$ $0 < k < 1$ .

$\fbox{c}$ $k > \dfrac{1}{2}$ .

$\fbox{d}$ $k < 3$ .

$\fbox{e}$ $\forall$ $k \in \mathbb{R}$ .

Soluzione.

Detta $f$ la funzione che descrive la cubica, $f$ è una funzione derivabile definita su tutto $\mathbb{R}$ , e quindi i suoi punti di minimo devono essere punti stazionari. La derivata di $f$ rispetto ad $x$ è data da:

$f'(x) = 3kx^2 - 2(k+1)x + 2-k.$

In particolare, si ha $f'(1) = 3k - 2k-2 + 2-k = 0$ per ogni valore di $k$ . Il punto $x = 1$ è quindi sempre un punto stazionario della cubica. Per stabilire in quali casi è un minimo, consideriamo il segno della derivata seconda:

$f''(x) = 6kx - 2(k+1).$

In particolare, $f''(1) = 4k-2.$ Se quindi $k > 1/2$ , si ha $f''(1) > 0$ , e quindi $x = 1$ è un punto di minimo (relativo). Se $k = 1/2$ , si ha $f''(1) = 0$ e quindi il test della derivata seconda è inconcludente: dobbiamo considerare questo caso a parte. Notiamo che, per $k = 1/2$ , $f'(x) = (3/2)x^2-3x+3/2 = 3(x-1)^2/2$ non è mai negativa. Per $k = 1/2$ la funzione è quindi sempre crescente (con un flesso a tangente orizzontale in $x = 1$ , che non è quindi un punto di minimo).

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2014-D

Sia $m$ un parametro reale. Quali sono le coordinate del punto $Q$ riflesso rispetto alla retta $r$ di equazione $y = mx$ del punto $P$ di coordinate $(1,0)$ ?

$\quad$

$\fbox{a}$ $(1-m^2,m)$ .

$\fbox{b}$ $(1,m)$ .

$\fbox{c}$ $(1-m,m)$ .

$\fbox{d}$ $\left(\dfrac{1-m^2}{1+m^2},\dfrac{2m}{1+m^2}\right)$ .

$\fbox{e}$ $\left(\dfrac{m^2+1}{m^2-1},\dfrac{m}{m^2-1}\right)$ .

Soluzione.

Con riferimento alla figura, il punto $Q = (x_Q,y_Q)$ giace sulla retta $s$ perpendicolare ad $r$ passante per $P$ , in modo che $\overline{QC} = \overline{CP}$ . Se $m = 0$ , si ha banalmente $Q \equiv P = (1,0)$ ; assumiamo nel seguito $m \ne 0$ .

$\quad$

La retta $s$ ha coefficiente angolare $-1/m$ ; siccome passa per $P$ , ha equazione $y = (-1/m)\cdot(x-1).$ Detto $\vartheta = \widehat{POC}$ , si ha $m = \tan(\vartheta)$ e la distanza $\overline{CP}$ di $P$ da $r$ è:

$\overline{CP} = \overline{OP}\cdot|\sin(\vartheta)| = 1\cdot\frac{|\tan(\vartheta)|}{\sqrt{1+\tan^2(\vartheta)}} = \frac{|m|}{\sqrt{1+m^2}}.$

I triangoli rettangoli $OCP$ e $QXP$ sono simili (hanno due angoli congruenti), per cui vale la proporzione $\overline{CP}:\overline{XP} = \overline{OP} : \overline{QP}$ . Dato che $\overline{QP} = 2\cdot\overline{CP}$ :

$\begin{gather*} \frac{|m|/\sqrt{1+m^2}}{1-x_Q} = \frac{1}{2\cdot |m|/\sqrt{1+m^2}}; \\ 1-x_Q = 2\left(\dfrac{|m|}{\sqrt{1+m^2}}\right)^2 = \dfrac{2m^2}{1+m^2} \implies x_Q = \frac{1-m^2}{1+m^2}. \end{gather*}$

Dato che $Q$ appartiene ad $s$ , si ha infine:

$y_Q = \frac{1}{m}(1-x_Q) = \frac{2m}{1+m^2}.$

(Tra le scelte proposte, la $\fbox{d}$ sarebbe in effetti l’unica possibile: per $m \to +\infty$ , $r$ diventa verticale e $Q \to (-1,0)$ ; solo la $\fbox{d}$ ha questo andamento asintotico).

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2014-E

Si consideri la funzione

$f(x) = \left(4\sin^2 x + 4\cos x + 1\right)^2.$

Qual è il massimo valore assunto da $f$ al variare di $x$ su $\mathbb{R}$ ?

$\quad$

$\fbox{a}$ $17+12\sqrt{2}$ .

$\fbox{b}$ $36$ .

$\fbox{c}$ $48\sqrt{2}$ .

$\fbox{d}$ $64-12\sqrt{3}$ .

$\fbox{e}$ $81$ .

Soluzione.

Riscriviamo l’espressione tra parentesi in questo modo:

$4\sin^2 x + 4\cos x + 1 = 5 - 4\cos^2 x + 4\cos x = 6 - \left(2\cos x -1\right)^2.$

Abbiamo la seguente catena di disuguaglianze:

$\begin{gather*} -1 \leq \cos x \leq 1; \\ -3 \leq 2\cos x -1 \leq 1; \\ 0 \leq \left(2\cos x -1\right)^2 \leq 9; \\ -3 \leq 6 - \left(2\cos x -1\right)^2 \leq 6; \\ 0 \leq \left[6 - \left(2\cos x -1\right)^2\right]^2 \leq 36. \end{gather*}$

La funzione $f$ assume effettivamente il valore 36 se $2\cos x - 1 = 0$ , cioè $\cos x = 1/2$ , per esempio per $x = \pi/3$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2014-F

Si considerino le funzioni $S$ , $T$ , $F$ : $\mathbb{R} \to \mathbb{R}$ , così definite:

$\begin{array}{l} S(x) = x+1; \\ T(x) = -x. \end{array}$

Applicando $s$ volte $S$ e $t$ volte $T$ , in ordine non conosciuto e non necessiaramente consecutivo, si ottiene la funzione

$F(x) = 8-x.$

Quale delle seguenti affermazioni è senz’altro vera?

$\quad$

$\fbox{a}$ $s = 8$ e $t = 1$ .

$\fbox{b}$ $s$ è dispari e $t$ è pari.

$\fbox{c}$ $s$ è pari e $t$ è dispari.

$\fbox{d}$ $s$ e $t$ sono potenze di 2.

$\fbox{e}$ Nessuna delle precedenti affermazioni è necessariamente corretta.

Soluzione.

In questa risposta, data una funzione $f$ ed un intero positivo $n$ , denotiamo con $f^n$ la composizione ripetuta (e non l’elevamento a potenza o la derivazione):

$f^n(x) = \underbrace{f\circ f \circ \cdots \circ f}_{\text{$n$ volte}}(x) = \underbrace{f(f(\cdots f}_{\text{$n$ volte}}(x))).$

Osserviamo innanzitutto che:

$\begin{aligned}S^s(x) = {} & S^{s-1}(S(x)) = S^{s-1}(x+1) = \\ = {} & S^{s-2}(S(x+1)) = S^{s-2}(x + 2) = \cdots = x+s. \end{aligned}$

Inoltre, $T \circ T(x) = -(-x) = x$ , cioè $T^2$ è la funzione identità.

Analizziamo ora le varie opzioni.

$\quad$

$\fbox{a}$ La combinazione $s = 8$ e $t = 1$ permette in effetti di ottenere $F$ : per ogni $x \in \mathbb{R}$ , $S^8 \circ T(x) = S^8(-x) = -x + 8 = F(x)$ . Questa combinazione non è però unica, per esempio $S^8 \circ T^3 = S^8 \circ T \circ T^2 = S^8 \circ T = F$ . $\fbox{b}$ Il caso discusso sopra ( $s = 8$ , $t = 1$ ) è un controesempio a questa affermazione, che è quindi senz’altro falsa. $\fbox{c}$ La composizione ripetuta di $S$ e $T$ porta necessariamente ad una funzione del tipo $\pm x + m$ , dove $m$ è un numero intero (non necessariamente positivo). Ogni applicazione di $T$ comporta l’inversione del segno di $x$ (mentre $S$ lo lascia invariato). Dato che in $F$ compare $-x$ , $T$ deve essere applicata un numero dispari di volte. L’applicazione di $T$ , inoltre, non cambia la parità di $m$ (cioè se $m$ è pari o dispari), mentre $S$ la cambia ad ogni applicazione: dato che si parte da $m = 0$ , $S$ deve essere applicata un numero pari di volte per arrivare a $m = 8$ . Quindi $s$ è pari e $t$ è dispari. $\fbox{d}$ Come appena mostrato, $t$ deve essere dispari, quindi questa affermazione è falsa.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2014-G

Sia $n$ un intero positivo, e si consideri il polinomio

$(1+xy+y^2)^n.$

Qual è il coefficiente numerico del monomio $x^3y^5$ ?

$\quad$

$\fbox{a}$ $n$ .

$\fbox{b}$ $2^n$ .

$\fbox{c}$ $\displaystyle\binom{n}{3}\binom{n}{5}$ .

$\fbox{d}$ $\displaystyle4\binom{n}{4}$ .

$\fbox{e}$ $\displaystyle\binom{n}{8}$ .

Soluzione.

Ricordiamo la formula del binomio di Newton; se $m \geq 0$ è un intero positivo, e $a$ e $b$ sono numeri arbitrari, si hanno le due formule equivalenti:

$(a+b)^m = \sum_{k=0}^{m}\binom{m}{k}a^{m-k}b^k = \sum_{k=0}^{m}\binom{m}{k}a^k b^{m-k},$

dove si sfruttano i coefficienti binomiali così definiti:

$\binom{m}{k} = \frac{m!}{k!(m-k)!}.$

Applichiamo ora la formula di Newton alla nostra espressione, una prima volta con $a = 1$ , $b = xy + y^2$ e $m = n$ , e poi con $a = xy$ , $b = y^2$ e $m = k$ :

(1) $\begin{equation*} \begin{aligned}(1+xy+y^2)^n = {} & \sum_{k=0}^{n}\binom{n}{k}1^{n-k}(xy+y^2)^k = \nonumber \\ = {} & \sum_{k=0}^n \binom{n}{k} \sum_{j=0}^{k}\binom{k}{j}(xy)^j (y^2)^{k-j} = \nonumber \\ = {} & \sum_{k=0}^n \binom{n}{k} \sum_{j=0}^{k}\binom{k}{j}x^j y^{2k-j}. \end{aligned} \end{equation*}$

In questa somma, il monomio $x^3y^5$ compare quando $j = 3$ e $2k-j = 5$ , cioè $k = 4$ . Il corrispondente coefficiente è dato da:

$\binom{n}{4}\binom{4}{3} = \binom{n}{4}\frac{4!}{3!(4-3)!} = \binom{n}{4} \frac{4\cdot3!}{3!}= 4\binom{n}{4}.$

Si noti che nella somma (1) si ha $k \leq n$ . Questo implica che, se $n < 4$ , il termine $x^3y^5$ non compare nello sviluppo del polinomio, o equivalentemente il suo coefficiente è $0$ . Può essere interessante notare che la scrittura $\fbox{d}$ rimane corretta se si considera la definizione generalizzata di coefficiente binomiale, valida per $m$ arbitrario e $k$ intero non negativo:

$\binom{m}{k} = \frac{m(m-1)\cdots(m-k+1)}{k(k-1)\cdot2\cdot1} = \prod_{i=1}^{k}\frac{m+1-i}{i}.$

Questa formula è equivalente alla definizione classica se $m$ è un intero $\geq k$ , e restituisce 0 se $m <k$ (ed è applicabile anche a valori non interi di $m$ ).

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2014-H

Sia $F$ una funzione definita sugli interi positivi, tale che $F(1) = 0$ e, per ogni $n \geq 2$ intero:

$\begin{array}{ll} F(n) = F(n-1) + 2 & \text{se } n \text{ è divisibile per 2 ma non per 3;} \\ F(n) = F(n-1) + 3 & \text{se } n \text{ è divisibile per 3 ma non per 2;} \\ F(n) = F(n-1) + 4 & \text{se } n \text{ è divisibile sia per 2 che per 3;} \\ F(n) = F(n-1) & \text{se } n \text{ non è divisibile né per 2 né per 3.} \end{array}$

Quanto vale $F(6000)$ ?

$\quad$

$\fbox{a}$ 9827.

$\fbox{b}$ 10121.

$\fbox{c}$ 11000.

$\fbox{d}$ 12300.

$\fbox{e}$ 12352.

Soluzione.

Cominciamo a classificare i numeri minori o uguali a 6000 in base al comportamento di $F$ .

$\quad$

Ci sono 3000 multipli di 2 minori o uguali a 6000: $\{2, 4, 6, 8, 10, 12, \ldots\}$ . Di questi, 2 su 3 (cioè 2000) non sono multipli di 3: $\{2, 4, 8, 10, \ldots\}$ .

Ci sono 2000 multipli di 3 minori o uguali a 6000: $\{3, 6, 9, 12, 15, 18, \ldots\}$ . Di questi, 1 su 2 (cioè 1000) non \è multiplo di 2: $\{3, 9, 15, \ldots\}$ .

Ci sono quindi 1000 multipli sia di 2 che di 3 minori o uguali a 6000: $\{6, 12, 18, \ldots\}$ .

Ci sono anche 2000 numeri minori o uguali a 6000 che non sono divisibili né per 2 né per 3: $\{1, 5, 7, 11, 13, \ldots\}$ .

Incrementando $n$ a partire da 1, il valore di $F(n)$ aumenta a ciascun passo di 2, 3, 4 oppure 0, a seconda che $n$ appartenga al gruppo (1), (2), (3) oppure (4), rispettivamente. Dato che $F(1) = 0$ , si ha:

$F(6000) = 2000 \times 2 + 1000 \times 3 + 1000 \times 4 + 2000 \times 0 = 11000.$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2014-I

Si consideri la funzione

$f(x) = 2^{x^2-4x+3}.$

Come si può ottenere il suo grafico trasformando opportunamente quello della funzione $g(x) = 2^{x^2}$ ?

$\quad$

$\fbox{a}$ Un riscalamento lungo l’asse delle ordinate seguito da una traslazione lungo l’asse delle ordinate.

$\fbox{b}$ Una traslazione lungo l’asse delle ascisse seguita da un riscalamento lungo l’asse delle ordinate.

$\fbox{c}$ Una traslazione lungo l’asse delle ascisse seguita da un riscalamento lungo l’asse delle ascisse.

$\fbox{d}$ Una traslazione lungo l’asse delle ascisse seguita da una riflessione rispetto all’asse delle ordinate.

$\fbox{e}$ Una riflessione rispetto all’asse delle ordinate seguita da una traslazione lungo l’asse delle ordinate.

Soluzione.

Per evitare confusione, ricordiamo innanzitutto che la corretta lettura della notazione $2^{x^2}$ è $2^{(x^2)}$ . Detto questo, osserviamo che:

$f(x) = 2^{x^2-4x+4-1} = 2^{(x-2)^2-1} = \frac{1}{2} \times2^{(x-2)^2} = \frac{1}{2} \times g(x-2).$

In questo modo si vede come $f$ si ottiene da $g$ effettuando prima una traslazione di 2 verso la direzione positiva delle ascisse e poi una compressione di un fattore 2 (un riscalamento) lungo l’asse delle ordinate.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2014-J

Una funzione $f$ : $\mathbb{R} \to \mathbb{R}$ integrabile soddisfa la seguente condizione:

$6+f(x) = 2f(-x)+3x^2\int_{-1}^{+1}f(t)\diff{t}.$

Calcolare la quantità

$I = \int_{-1}^{+1}f(t)\diff{t}.$

$\quad$

$\fbox{a}$ 4.

$\fbox{b}$ 6.

$\fbox{c}$ 11.

$\fbox{d}$ $\dfrac{27}{2}$ .

$\fbox{e}$ 23.

Soluzione.

Per cominciare, notiamo che, effettuando il cambio di variabile $u = -x$ , si ha:

$\int_{-1}^{+1}f(-x)\diff{x} = -\int_{+1}^{-1}f(u)\diff{u} = \int_{-1}^{+1}f(u)\diff{u} = I.$

Ora, integriamo ambo i membri della condizione assegnata tra $-1$ e $+1$ :

$\begin{gather*} \int_{-1}^{+1}[6+f(x)]\diff{x} = \int_{-1}^{+1}[2f(-x)+3x^2I]\diff{x}; \\ 6x\Big|_{-1}^{+1} + \int_{-1}^{+1}f(x)\diff{x} = 2\int_{-1}^{+1}f(-x)\diff{x} + 3I\left.\frac{x^3}{3}\right|_{-1}^{+1}; \\ 12 + I = 2I + 2I. \end{gather*}$

Quest’ultima è un’equazione per $I$ , che porta alla soluzione $I = 4$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2015-A

Si scelga un numero intero arbitrario $n$ .

Gli si aggiunga 1.

Si elevi al quadrato il risultato.

Si moltiplichi il numero ottenuto per 4.

Si sottragga 3 a questo valore.

Quali delle seguenti affermazioni sono corrette indipendentemente dal valore iniziale di $n$ ?

$\quad$

I: il risultato finale è dispari;/li>

II: il risultato finale eccede di 1 un multiplo di 3;/li>

III: il risultato finale eccede di 1 un multiplo di 8;/li>

IV: il risultato finale non è un numero primo;/li>

V: il risultato finale non precede di 1 un multiplo di 3.

$\quad$

$\fbox{a}$ I, II e V.

$\fbox{b}$ I e IV.

$\fbox{c}$ II e V.

$\fbox{d}$ I, III e V.

$\fbox{e}$ I e V.

Soluzione.

Il risultato $m$ delle operazioni descritte nel testo è:

$m = 4(n+1)^2-3.$

Analizziamo le opzioni disponibili:

I: il termine $4(n+1)^2$ nell’espressione di $m$ è multiplo di 4, quindi pari, per cui, sottraendogli poi 3, $m$ risulta senz’altro dispari. Questa affermazione è vera.

II: questa affermazione non è necessariamente vera. Per esempio, per $n = 2$ , si ha $m = 33$ che è un multiplo di 3.

III: nemmeno questa affermazione è necessariamente corretta. Per esempio, per $n = 1$ , si ha $m = 13$ , e $m-1 = 12$ non è un multiplo di 8.

IV: l’esempio appena fatto con $n = 1$ mostra che $m$ può essere un numero primo. Questa affermazione non è dunque valida per tutti i valori di $n$ .

V: in baso al resto della divisione per 3, si hanno 3 casi per $n$ : $n = 3j$ , $n = 3j+1$ , $n = 3j-1$ (con $j$ intero opportuno). Si ha:

$\begin{array}{l@{\implies}l} n = 3j & m = 4(3j+1)^2 - 3 = 3(12j^2+8j) + 1; \\ n = 3j+1 & m = 4(3j+2)^2 - 3 = 3(12j^2+16j+4) + 1; \\ n = 3j-1 & m = 4(3j)^2 - 3 = 3(12j^2-1). \end{array}$

Si vede che in nessun caso $m$ precede di 1 un multiplo di 3. Questa affermazione è dunque vera. Il procedimento appena visto chiarisce anche in quali casi l’affermazione II è vera oppure falsa.

La risposta corretta è dunque la $\fbox{e}$ .

Quesito 2015-B

Siano $a$ un numero reale arbitrario e $n \geq 2$ un numero intero. Si consideri la funzione

$f(x) = (x+a)^n.$

Cosa si può dire sul numero delle intersezioni dei grafici di $f(x)$ e $f'(x)$ ?

$\quad$

$\fbox{a}$ È un numero dispari.

$\fbox{b}$ È un numero pari.

$\fbox{c}$ Dipende da $a$ ma non da $n$ .

$\fbox{d}$ Dipende da $n$ ma non da $a$ .

$\fbox{e}$ Dipende sia da $a$ che da $n$ .

Soluzione.

Si ha $f'(x) = n(x+a)^{n-1}$ . Le intersezioni dei due grafici sono date dalle soluzioni dell’equazione $f(x) = f'(x)$ :

$(x+a)^n = n(x+a)^{n-1}.$

Notiamo che $x = -a$ è sempre una soluzione (essendo $n > 1$ ); assumendo invece $x \ne -a$ , possiamo dividere ambo i membri per $(x+a)^{n-1}$ , ottendendo:

$x+a = n \iff x = n - a.$

Si noti che questa soluzione non può mai essere uguale a quella già trovata $x = -a$ . Quindi, il numero delle intersezioni tra i grafici di $f$ e $f'$ è esattamente 2 (che è naturalmente un numero pari), indipendentemente dai valori di $a$ e $n$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2015-C

Quali delle seguenti espressioni valgono per ogni $x \in \mathbb{R}$ ?

I. $\sin\left(\dfrac{\pi}{2} +x\right) = \cos\left(\dfrac{\pi}{2}-x\right)$ ;

II: $2 + 2\sin(x) - \cos^2(x) \geq 0$ ;

III: $\sin\left(x+\dfrac{3\pi}{2}\right) = \cos(\pi-x)$ ;

IV: $\sin(x)\cos(x) \leq \dfrac{1}{4}$ .

$\quad$

$\fbox{a}$ I e II.

$\fbox{b}$ I e III.

$\fbox{c}$ II e III.

$\fbox{d}$ III e IV.

$\fbox{e}$ II e IV.

Soluzione.

Analizziamo le espressioni una ad una.

I: Questa epressione è chiaramente falsa, per esempio con $x = 0$ si ha:

$\sin\left(\frac{\pi}{2}\right) = 1 \ne \cos\left(\frac{\pi}{2}\right) = 0.$

II: Questa disuguaglianza è sempre vera. Usando l’identità trigonometrica fondamentale $\sin^2(x)+\cos^2(x) = 1$ , si ha infatti per ogni $x \in \mathbb{R}$ :

$2 + 2\sin(x) - \cos^2(x) = \sin^2(x) + 2\sin(x) + 1 = [\sin(x)+1]^2 \geq 0.$

III: Questa è un’identità che discende banalmente dalle formule per gli archi associati. Per il gusto di esplorare un metodo alternativo, ricorriamo invece agli esponenziali complessi. Se $z \in \mathbb{C}$ , indichiamo con $\operatorname{Re}(z)$ e $\operatorname{Im}(z)$ le parti reale ed immaginaria $z$ , rispettivamente. Allora, per $\vartheta \in \mathbb{R}$ :

$e^{i\vartheta} = \cos(\vartheta) + i\sin(\vartheta) \implies \begin{cases}\cos(\vartheta) = \operatorname{Re}(e^{i\vartheta}); \\ \sin(\vartheta) = \operatorname{Im}(e^{i\vartheta}).\end{cases}$

Ricordiamo che per $z\in\mathbb{C}$ si ha $\operatorname{Im}(iz) = \operatorname{Re}(z)$ (la moltiplicazione per $i$ “ruota” $z$ di $90\degr$ in senso antiorario). Quindi si ha:

$\begin{aligned} \sin\left(x+\dfrac{3\pi}{2}\right) = {} & \operatorname{Im}\left(e^{ix+3\pi i/2}\right) = \operatorname{Im}\left(e^{3\pi i/2}e^{ix}\right) = \\ = {} & \operatorname{Im}\left(-ie^{ix}\right) = -\operatorname{Im}\left(ie^{ix}\right) = -\operatorname{Re}\left(e^{ix}\right) = -\cos(x). \end{aligned}$

$\begin{aligned} \cos(\pi-x) = {} & \operatorname{Re}\left(e^{\pi i -ix}\right) = \operatorname{Re}\left(e^{\pi i}e^{-ix}\right) = \\ = {} & \operatorname{Re}\left(-e^{-ix}\right) = -\operatorname{Re}\left(e^{-ix}\right) = -\cos(-x) = -\cos(x). \end{aligned}$

IV: Questa disuguaglianza non \è vera in generale, dato che:

$\sin(x)\cos(x) = \dfrac{1}{2}\sin(2x),$

che può chiaramente assumere valori $>1/4$ . Per esempio, se $x = \pi/4$ :

$\sin(x)\cos(x) = \frac{1}{2}\sin\left(2\cdot\frac{\pi}{4}\right) = \frac{1}{2} > \frac14.$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2015-D

Siano:

$f(x) = \int_0^1(xt)^2\diff{t}, \qquad g(x) = \int_0^x t^2\diff{t}.$

Se $a$ è un numero reale positivo, quale delle seguenti affermazioni è corretta?

$\quad$

$\fbox{a}$ $g(f(a)) > f(g(a))$ .

$\fbox{b}$ $f(g(a)) > g(f(a))$ .

$\fbox{c}$ $g(f(a)) = f(g(a))$ .

$\fbox{d}$ $f(g(a)) > g(f(a))$ se $a < 1$ , mentre $g(f(a)) > f(g(a))$ se $a > 1$ .

$\fbox{e}$ $g(f(a)) > f(g(a))$ se $a < 1$ , mentre $f(g(a)) > g(f(a))$ se $a > 1$ .

Soluzione.

Visto che sono così semplici, vale la pena calcolare direttamente gli integrali:

$\begin{gather*} f(x) = \int_0^1(xt)^2\diff{t} = x^2\!\int_0^1 t^2\diff{t} = \left.x^2\frac{t^3}{3}\right|_{t=0}^{t=1} = \frac{x^2}{3}; \\ g(x) = \int_0^x t^2\diff{t} = \left.\frac{t^3}{3}\right|_{t=0}^{t=x} = \frac{x^3}{3}. \end{gather*}$

E quindi:

$\begin{gather*} g(f(a)) = g\left(\frac{a^2}{3}\right) = \frac{(a^2/3)^3}{3} = \frac{a^6}{3^4}; \\ f(g(a)) = f\left(\frac{a^3}{3}\right) = \frac{(a^3/3)^2}{3} = \frac{a^6}{3^3}. \end{gather*}$

Dato che $3^4 > 3^3$ , abbiamo che per ogni $a > 0$ vale $f(g(a)) > g(f(a))$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2015-E

Si consideri l’equazione:

$\sin[2\cos(2x)+2] = 0.$

Quante soluzioni ammette nell’intervallo $0 \leq x \leq 2\pi$ ?

$\quad$

$\fbox{a}$ 2.

$\fbox{b}$ 3.

$\fbox{c}$ 4.

$\fbox{d}$ 6.

$\fbox{e}$ 8.

Soluzione.

Si ha $\sin(\alpha) = 0$ se $\alpha = k\pi$ ( $k$ intero). Posto $\alpha = 2\cos(2x)+2$ , notiamo che

$0 \leq \alpha \leq 4.$

Quindi $\alpha = k\pi$ può verificarsi solo se $k = 0$ oppure $k = 1$ , dato che per $k \geq 2$ si ha $k\pi \geq 2\pi > 4$ . Nel caso $k = 0$ , limitandoci all’intervallo specificato $0 \leq x \leq 2\pi$ , abbiamo due soluzioni (indicate in arancio nella figura):

$2\cos(2x)+2 = 0 \iff \cos(2x) = -1 \iff x = \frac{\pi}{2} \vee x = \frac{3\pi}{2}.$

Se invece $k = 1$ , l’equazione diventa:

$2\cos(2x)+2 = \pi \iff \cos(2x) = \frac{\pi}{2}-1,$

che ha 4 soluzioni nell’intervallo $0 \leq x \leq 2\pi$ (indicate in viola nella figura), come si ricava considerando il grafico della funzione $\cos(2x)$ , che ha periodo pari a $\pi$ , e tenendo presente $0 < \pi/2 - 1 < 1$ .

Nel complesso, l’equazione proposta ha quindi 6 soluzioni per $0 \leq x \leq 2\pi$ .

$\quad$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2015-F

Si consideri la funzione:

$f(x) = \frac{x}{2}-\left\lfloor\frac{x}{2}\right\rfloor$

(la notazione $\lfloor a \rfloor$ indica la parte intera di $a$ , cioè il più grande numero intero minore o uguale ad $a$ ). Si divide l’intervallo $[0,5]$ in $n$ intervalli di uguale ampiezza, e si usa il metodo dei trapezi per approssimare il seguente integrale:

$I = \int_0^5 f(x)\diff{x}.$

Qual è il più piccolo valore di $n$ per cui la stima con il metodo dei trapezi eccede il valore esatto $I$ dell’integrale?

$\quad$

$\fbox{a}$ $n=2$ .

$\fbox{b}$ $n=3$ .

$\fbox{c}$ $n=4$ .

$\fbox{d}$ $n=5$ .

$\fbox{e}$ $I$ non viene mai sovrastimato.

Soluzione.

Notiamo che, per ogni funzione lineare, il metodo dei trapezi restituisce sempre il risultato esatto dell’integrale. Quindi, per stabilire quando il metodo dei trapezi sovrastima $I$ , possiamo limitarci a considerare $g(x) = x/2 - f(x) = \lfloor x/2\rfloor$ , cercando il più piccolo valore di $n$ per cui il metodo dei trapezi sottostima quest’altro integrale (il calcolo risulta più semplice):

$J = \int_0^5 g(x)\diff{x} = \int_0^5 \left\lfloor\frac{x}{2}\right\rfloor\mathrm{d}x.$

L’andamento di $g$ è mostrato in figura, con $g(x) = 0$ , 1, 2 per $0 \leq x < 2$ , $2 \leq x < 4$ , e $4 \leq x \leq 5$ , rispettivamente. Si calcola facilmente che $J = 4$ .

$\quad$

Per stimare $J$ col metodo dei trapezi, dividiamo $[0,5]$ in $n$ intervalli di ampiezza $5/n$ . Nei casi che consideriamo, come si vede dalla figura, i trapezi si uniscono a formare dei triangoli, la cui area è più veloce da calcolare.

$n=1$ (marrone): in questo caso c’è un solo trapezio, degenerato in un triangolo; l’area è $5\cdot2/2 = 5$ , che è maggiore di $J$ .

$n=2$ (marrone): si ha $f(5/2) = 1$ , e quindi i due trapezi sono posizionati in modo da formare un unico triangolo, coincidente con quello corrispondente a $n=1$ , la cui area è, come prima, $5$ (maggiore di $J$ ).

$n=3$ (verde): si ha $f(5/3) = 0$ e $f(2\cdot5/3) = 1$ ; anche qui si forma un triangolo di area $(10/3)\cdot2/2 = 10/3$ , che è minore di $J$ .

Ringraziamo Ken Parker per l’aiuto con la soluzione di questo quesito.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2015-G

Indicare quale dei seguenti grafici rappresenta qualitativamente la curva definita dall’equazione

$\cos^2(x) = \cos^2(y).$

$\quad$

Soluzione.

L’equazione di partenza è equivalente a:

$|\cos(y)| = |\cos(x)|,$

che a sua volta si sdoppia come segue ( $k$ è un numero intero arbitrario):

$\begin{array}{l@{\iff}l@{\mbox{\ }\vee\mbox{\ }}ll} \cos(y) = +\cos(x) & y = x + 2k\pi & y = -x + 2k\pi;\\ \cos(y) = -\cos(x) = \cos(x+\pi) & y = x+\pi + 2k\pi & y = -x -\pi + 2k\pi. \end{array}$

Queste due coppie di soluzioni si possono condensare in:

$y = \pm x + k\pi \quad (k \in \mathbb{Z}).$

Questo è un fascio di rette parallele alle bisettrici dei quadranti, che intersecano gli assi delle ascisse e delle ordinate per $x = k\pi$ e $y = h\pi$ ( $k, h \in \mathbb{Z}$ ).

Il grafico $\fbox{b}$ viene escluso perché le intersezioni della curva con gli assi coordinati avvengono solo in corrispondenza dei multipli pari di $\pi$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2015-H

Quante soluzioni distinte ha la seguente equazione?

$\log_{x^2+2}(4-5x^2-6x^3) = 2.$

$\quad$

$\fbox{a}$ Nessuna.

$\fbox{b}$ 1.

$\fbox{c}$ 2.

$\fbox{d}$ 4.

$\fbox{e}$ Infinite

Soluzione.

Innanzitutto è necessario stabilire le condizioni di esistenza dell’equazione. La base del logaritmo deve essere sempre positiva e diversa da 1, che è una condizione sempre verificata perché $x^2+2 \geq 2$ . In secondo luogo, l’argomento $P(x)$ del logaritmo deve essere positivo:

( $\star$ ) $\begin{equation*} P(x) = 4-5x^2-6x^3 > 0. \end{equation*}$

Sebbene non impossibile da risolvere, questa equazione non è neppure immediata (per chi fosse curioso, la soluzione è $x < 2/3$ ). In realtà, a noi non serve strettamente risolvere questa equazione, ma ci basta tenere in mente la condizione $(\star)$ per verificare che le soluzioni trovate siano accettabili.

Osserviamo a questo punto che, per definizione di logaritmo, l’equazione di partenza è equivalente alla seguente (purché siano rispettate le condizioni di esistenza):

$4-5x^2-6x^3 = (x^2+2)^2.$

Infatti, la scrittura $\log_a(b) = c$ vuol dire che $a^c = b$ . Semplificando e fattorizzando:

$\begin{gather*} 4-5x^2-6x^3 = x^4 + 4x^2 + 4; \\ x^2(x^2+6x+9) = 0; \\ x^2(x+3)^2 = 0. \end{gather*}$

Le soluzioni sono quindi $x = 0$ e $x = -3$ . Ci resta solo da verificare che siano accettabili, cioè compatibili con la condizione $(\star)$ . In effetti, abbiamo $P(0) = 4$ e $P(-3) = 4-5\cdot9+6\cdot27 = 121$ , che sono entrambi numeri positivi, e quindi accettabili.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2015-I

Si considerino le tre funzioni nel piano cartesiano $xy$ :

$f(x) = x^3, \qquad g(x) = x^4, \qquad h(x) = x^5.$

Senza considerare gli assi cartesiani, in quante regioni dividono il piano $xy$ i grafici di queste tre funzioni?

$\quad$

$\fbox{a}$ 6.

$\fbox{b}$ 7.

$\fbox{c}$ 8.

$\fbox{d}$ 9.

$\fbox{e}$ 10.

Soluzione.

Osserviamo i seguenti fatti.

$\quad$

Le tre funzioni si intersecano simultaneamente se $x=0$ oppure $x=1$ : $f(0) = g(0) = h(0) = 0$ e $f(1) = g(1) = h(1) = 1$ .
$f$ e $h$ si intersecano anche per $x=-1$ : $f(-1) = h(-1) = -1$ . Al di fuori delle intersezioni qui elencate, non ce ne sono altre.
Per $x < -1$ , si ha $x^5 < x^3 < -1 < x^4$ . \\ Per $-1 < x < 0$ , si ha $-1 < x^3 < x^5 < 0 < x^4$ . \\ Per $0 < x < 1$ , si ha $0 < x^5 < x^4 < x^3 < 1$ . \\ Per $x > 1$ , si ha $1 < x^3 < x^4 < x^5$ .

A questo punto, abbiamo elementi sufficienti per disegnare un grafico qualitativo delle tre funzioni, e contare le regioni, che numeriamo in senso antiorario.

$\quad$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2015-J

Senza utilizzare la calcolatrice, stabilire quale dei seguenti numeri è il più grande.

$\quad$

$\fbox{a}$ $\dfrac{\sqrt{7}}{2}$ .

$\fbox{b}$ $\dfrac{5}{4}$ .

$\fbox{c}$ $\dfrac{\sqrt{10!}}{3\cdot6!}$ .

$\fbox{d}$ $\dfrac{\log_2(30)}{\log_3(85)}$ .

$\fbox{e}$ $\dfrac{1+\sqrt{6}}{3}$ .

Soluzione.

Confrontiamo le varie opzioni che ci sono presentate.

$\quad$

$\fbox{b}$ rispetto ad $\fbox{a}$ . Riportiamo a denominatore comune:
$\frac{\sqrt{7}}{2} = \frac{2\sqrt{7}}{4} = \frac{\sqrt{28}}{4} > \frac{\sqrt{25}}{4} = \frac{5}{4}.$
$\fbox{c}$ rispetto ad $\fbox{a}$ . Portando tutto sotto radice, espandendo i fattoriali, e semplificando i numerosi fattori comuni, si ha:
$\frac{\sqrt{10!}}{3\cdot6!} = \sqrt{\frac{(5\cdot2)\cdot(3^2)\cdot(2^3)\cdot7\cdot(2\cdot3)\cdot5\cdot(2^2)\cdot3\cdot2}{3^2\cdot(2\cdot3)^2\cdot5^2\cdot(2^2)^2\cdot3^2\cdot2^2}} = \frac{\sqrt{7}}{3} < \frac{\sqrt{7}}{2}.$
$\fbox{d}$ rispetto a $\fbox{b}$ . Sfruttando il fatto che la funzione $\log_2(x)$ è monotona crescente, abbiamo:
$\frac{\log_2(30)}{\log_3(85)} < \frac{\log_2(32)}{\log_3(81)} = \frac{\log_2(2^5)}{\log_3(3^4)} = \frac{5}{4}.$
$\fbox{e}$ rispetto ad $\fbox{a}$ . Elevando al quadrato ambo i membri, osserviamo che:
$\frac{1+\sqrt{6}}{3} < \frac{\sqrt{7}}{2} \iff \frac{7+2\sqrt{6}}{9} < \frac{7}{4} \iff 8\sqrt{6} < 35.$

Dato che $\sqrt{6} < \sqrt{9} = 3$ , si ha $8\sqrt{6} < 24 < 35$ , e quindi la disuguaglianza originale è verificata.

Mettendo assieme questi risultati, si conclude che il numero più grande è $\sqrt{7}/2$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2016-A

Sia $l$ un numero reale. Una successione di numeri reali $\{a_n\}_{n=1}^{+\infty}$ è definita per ricorrenza:

$\begin{array}{ll} a_1 = 1 & \text{se $n = 1$}; \\ a_n = l\cdot a_{n-1} & \text{se $n \geq 2$}. \end{array}$

Qual è il valore del prodotto $P$ dei primi 15 termini della successione?

$\quad$

$\fbox{a}$ $l^{14}$ .

$\fbox{b}$ $15+l^{14}$ .

$\fbox{c}$ $\dfrac{1-l^{15}}{1-l}$ .

$\fbox{d}$ $l^{105}$ .

$\fbox{e}$ $15+l^{105}$ .

Soluzione.

Ci si può convincere facilmente che, per ogni $n \geq 1$ intero, vale:

$a_n = l^{n-1}$

(rigorosamente, si potrebbe utilizzare il principio di induzione). Il prodotto dei primi 15 termini di $a_n$ si può quindi calcolare così:

$P = 1\cdot l\cdot l^2\cdots l^{14} = l^{1+\cdots+14} = l^{105}.$

Abbiamo usato la proprietà delle potenze $l^al^b = l^{a+b}$ e la formula che restituisce la somma dei primi $n$ numeri naturali (con $n = 14$ ):

$\sum_{k=0}^{n} k = \frac{n(n+1)}{2} = \frac{14\cdot15}{2} = 105.$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2016-B

L’esagono (irregolare) $ABCDEF$ ha tutti i lati di uguale lunghezza, ed è posizionato in un quadrato di lato 1 come mostrato in figura. Qual è la lunghezza dei lati dell’esagono?

$\fbox{a}$ $\sqrt{2}-1$ .

$\fbox{b}$ $2-\sqrt{2}$ .

$\fbox{c}$ $1$ .

$\fbox{d}$ $\dfrac{\sqrt{2}}{2}$ .

$\fbox{e}$ $2+\sqrt{2}$ .

$\quad$

Soluzione.

Detto $L$ il lato dell’esagono, notiamo che $\overline{FG} = \overline{GE} = 1-L$ . Quindi il triangolo $FGE$ è rettangolo isoscele, e $\overline{GE} = \overline{FE}/\sqrt{2} = L/\sqrt{2}$ . Dato che $\overline{GE} + \overline{ED} = 1$ , risolvendo rispetto a $L$ , abbiamo

$\begin{gather*} \frac{L}{\sqrt{2}} + L = 1; \\[5pt] L\frac{\sqrt{2}+1}{\sqrt{2}} = 1; \\[5pt] L = \frac{\sqrt{2}}{\sqrt{2}+1} = \frac{\sqrt{2}(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)} = 2-\sqrt{2}. \end{gather*}$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2016-C

Si consideri la circonferenza di equazione:

$x^2 + ax + y^2 + by = c.$

Sotto quale condizione l’origine degli assi cartesiani è un punto interno alla circonferenza?

$\quad$

$\fbox{a}$ $c > 0$ .

$\fbox{b}$ $a^2+b^2 > c$ .

$\fbox{c}$ $a^2+b^2 < c$ .

$\fbox{d}$ $a^2+b^2 > 4c$ .

$\fbox{e}$ $a^2+b^2 < 4c$ .

Soluzione.

Sfruttando la tecnica del completamento dei quadrati, riscriviamo l’equazione della circonferenza come segue:

$\begin{gather*} x^2 + 2a\frac{x}{2} + \frac{a^2}{4} + y^2 + 2b\frac{y}{2} + \frac{b^2}{4} = c + \frac{a^2}{4} + \frac{b^2}{4}; \\[5pt] \left(x+\frac{a}{2}\right)^2 + \left(y+\frac{b}{2}\right)^2 = c + \frac{a^2}{4} + \frac{b^2}{4}. \end{gather*}$

Affinché l’equazione rappresenti una circonferenza, è necessario che il termine di destra (che rappresenta il quadrato del raggio $r$ della circonferenza) sia positivo:

( $\star$ ) $\begin{equation*} c + \frac{a^2}{4}+\frac{b^2}{4} = r^2 > 0. \end{equation*}$

L’origine ( $x = y = 0$ ) appartiene all’interno della circonferenza se:

$\left(0+\frac{a}{2}\right)^2 + \left(0+\frac{b}{2}\right)^2 < r^2 \iff \frac{a^2}{4} + \frac{b^2}{4} < c + \frac{a^2}{4} + \frac{b^2}{4},$

e cioè $c > 0$ . Resta solo da controllare che la condizione $(\star)$ sia verificata, che in effetti è sempre garantito se $c > 0$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2016-D

Sia $n$ un intero positivo e si consideri l’equazione:

$\cos^n(x) + \cos^{2n}(x) = 0.$

Quante soluzioni reali esistono nell’intervallo $0 \leq x \leq 2\pi$ ?

$\quad$

$\fbox{a}$ Una soluzione indipendentemente da $n$ .

$\fbox{b}$ Due soluzioni indipendentemente da $n$ .

$\fbox{c}$ Tre soluzioni indipendentemente da $n$ .

$\fbox{d}$ Due soluzioni per $n$ pari e tre soluzioni per $n$ dispari.

$\fbox{e}$ Tre soluzioni per $n$ pari e due soluzioni per $n$ dispari.

Soluzione.

Fattorizziamo l’equazione nel modo seguente:

$\cos^n(x)\left[1+\cos^n(x)\right] = 0.$

Per la legge di annullamento del prodotto, l’equazione viene risolta se almeno uno dei fattori si annulla. Come prima opzione abbiamo (limitandoci all’intervallo $0 \leq x \leq 2\pi$ ):

$\cos^n(x) = 0 \iff \cos(x) = 0 \iff x = \frac{\pi}{2} \vee x = \frac{3\pi}{2}.$

Il secondo fattore $1+\cos^n(x)$ non si annulla mai se $n$ è pari, dato che in questo caso $1+\cos^n(x) \geq 1 > 0$ . Se invece $n$ è dispari, abbiamo:

$\cos^n(x) = -1 \iff \cos(x) = \sqrt[n]{-1} = -1 \iff x = \pi.$

In conclusione, se $n$ è pari abbiamo solo le prime 2 soluzioni, mentre se è $n$ dispari se ne aggiunge una terza.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2016-E

Indicare quale dei seguenti grafici rappresenta qualitativamente il grafico della curva definita dall’equazione

$y = (x-1)^2 - \cos(\pi x).$

$\quad$

Soluzione.

Contiamo gli zeri della curva, cioè le soluzioni dell’equazione:

$(x-1)^2 = \cos(\pi x).$

$\quad$

Utilizziamo il metodo grafico (figura di sinistra). La parabola $(x-1)^2$ ha la concavità verso l’alto, il vertice in $(1,0)$ , e interseca l’asse $y$ in $(0,1)$ . La funzione $\cos(\pi x)$ è una versione “compressa” di $\cos(x)$ , che interseca la parabola in $x = 0$ e $x = 2$ . Inoltre, la sua derivata si annulla in $x = 0$ e $x = 2$ , per cui si hanno 4 intersezioni tra le due curve (marcate in giallo).

Tra i grafici proposti, solo il primo ha 4 intersezioni con l’asse delle ascisse. Per scrupolo, si possono anche cercare i punti stazionari della curva. La derivata prima $y' = 2(x-1) + \pi\cdot\sin(\pi x)$ si annulla se (figura di destra):

$2(x-1) = -\pi\cdot\sin(\pi x),$

quindi in $x = 1$ e in due altri punti (simmetrici) negli intervalli $0 < x < 1$ e $1 < x < 2$ . Tra i grafici presentati, solo il primo ha tre punti stazionari.

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2016-F

Sia $n$ un intero positivo, e si consideri il polinomio

$P_n(x) = \left(3+x^4\right)^n - \left(x^2+3\right)^n\left(x^2-1\right)^n.$

Per quali valori di $n$ si ha che $P_n(x)$ è divisibile per $(1+x^2)$ ?

$\quad$

$\fbox{a}$ Per tutti i valori di $n$ .

$\fbox{b}$ Per $n$ pari.

$\fbox{c}$ Per $n$ dispari.

$\fbox{d}$ Per $n \geq 3$ .

$\fbox{e}$ Per nessun valore di $n$ .

Soluzione.

Se $i$ è l’unità immaginaria ( $i^2 = -1$ ), si ha:

$x^2+1 = (x-i)(x+i).$

Affinché $P_n(x)$ sia divisibile per $x^2+1$ , quindi, $P_n(x)$ deve avere $\pm i$ come radici. Sostituendo:

$\begin{aligned} P_n(\pm i) = {} & \left[3+(\pm i)^4\right]^n - \left[(\pm i)^2+3\right]^n\left[(\pm i)^2-1\right]^n = \\ = {} & (3+1)^n - (-1+3)^n(-1-1)^n = \\ = {} & 2^{2n}-2^n(-2)^n = 2^{2n}\left[1-(-1)^n\right]. \end{aligned}$

Dunque, $P_n(\pm i) = 0$ se e solo se $1-(-1)^n = 0$ . Dato che $(-1)^n = +1$ per $n$ pari e $(-1)^n = -1$ per $n$ dispari, $P_n(\pm i) = 0$ se e solo se $n$ è pari.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2016-G

Si consideri la successione $\{x_n\}_{n=0}^{+\infty}$ , tale che $x_0 = 1$ e, per $n \geq 1$ :

$x_n = x_0 + x_1 + \cdots + x_{n-1} = \sum_{k=0}^{n-1}x_k.$

Calcolare la somma della serie:

$\sum_{k=0}^{+\infty}\frac{1}{x_k}.$

$\quad$

$\fbox{a}$ $1$ .

$\fbox{b}$ $\dfrac65$ .

$\fbox{c}$ $\dfrac85$ .

$\fbox{d}$ $3$ .

$\fbox{e}$ $\dfrac{27}{5}$ .

Soluzione.

In primo luogo notiamo che, per $n \geq 2$ :

$x_n = \sum_{k=0}^{n-1}x_k = x_{n-1} + \sum_{k=0}^{n-2}x_k = x_{n-1} + x_{n-1} = 2x_{n-1}.$

Usando questa espressione, si trova facilmente la formula generica per il termine $n$ -esimo (valida per $n \geq 1$ ):

$x_n = 2x_{n-1} = 2\cdot2x_{n-2} = \cdots = 2^{n-1}x_1 = 2^{n-1}.$

La somma della serie cercata è quindi:

$\begin{aligned} \sum_{k=0}^{+\infty}\frac{1}{x_k} = {} & \frac{1}{x_0} + \sum_{k=1}^{+\infty}\frac{1}{2^{k-1}} = 1 + \sum_{j=0}^{+\infty}\frac{1}{2^j} = 1 + \sum_{j=0}^{+\infty}\left(\frac{1}{2}\right)^j = 1 + \frac{1}{1-1/2} = \\ = {} & 3. \end{aligned}$

In questo calcolo abbiamo usato la formula per la somma della serie geometrica (valida se $|q| < 1$ ) con $q = 1/2$ :

$\sum_{k=0}^{+\infty}q^k = \frac{1}{1-q}.$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2016-H

Sia $k$ un parametro reale positivo, e si considerino le due funzioni $\mathbb{R} \to \mathbb{R}$ :

$\begin{array}{l} f(x) = k - x^2; \\[3pt] g(x) = x^4 - k. \end{array}$

Per quali valori di $k$ l’area compresa tra il grafico di $f$ e l’asse delle ascisse è più grande dell’area compresa tra il grafico di $g$ e l’asse delle ascisse?

$\quad$

$\fbox{a}$ Per ogni valore di $k > 0$ .

$\fbox{b}$ $k > 1$ .

$\fbox{c}$ $k > \dfrac65$ .

$\fbox{d}$ $k > \left(\dfrac43\right)^{3/2}$ .

$\fbox{e}$ $k > \left(\dfrac65\right)^{\!4}$ .

Soluzione.

Si tratta di valutare due integrali definiti elementari. Si noti che $f$ e $g$ intersecano l’asse delle ascisse per $x = \pm\sqrt{k}$ e per $x = \pm\sqrt[4]{k}$ , rispettivamente. Nel caso di $f$ , la regione da considerare è contenuta nel semipiano positivo delle ascisse, mentre nel caso di $g$ si trova in quello negativo (per cui, va preso l’opposto del valore dell’integrale). Le aree sottese da $f$ e $g$ sono dunque, rispettivamente:

$\begin{aligned} \mathcal{A}_f = {} & \int_{-\sqrt{k}}^{+\sqrt{k}}f(x)\diff{x} = 2\int_{0}^{\sqrt{k}}(k-x^2)\diff{x} = 2\left.\left(kx-\frac{x^3}{3}\right)\right|_{0}^{\sqrt{k}} = \\ = {} & 2\left(k\sqrt{k}-\frac{\sqrt{k}^3}{3}\right)= \frac{4}{3}\sqrt{k^3} = \frac{4}{3}k^{3/2};\\[10pt] \mathcal{A}_g = {} & -\int_{-\sqrt[4]{k}}^{+\sqrt[4]{k}}g(x)\diff{x} = 2\int_{0}^{\sqrt[4]{k}}(k-x^4)\diff{x} = 2\left.\left(kx-\frac{x^5}{5}\right)\right|_{0}^{\sqrt[4]{k}} = \\ = {} & 2\left(k\sqrt[4]{k}-\frac{\sqrt[4]{k}^5}{5}\right) = \frac{8}{5}\sqrt[4]{k^5} = \frac{8}{5}k^{5/4}. \end{aligned}$

Per curiosità, la regione sottesa da $f$ è un segmento parabolico, la cui area si può calcolare alternativamente con la formula:

$\mathcal{A}_f = \frac{1}{6}\cdot|a|\cdot(x_2-x_1)^3 = \frac{1}{6}\cdot |-1| \cdot \left[\sqrt{k}-(-\sqrt{k})\right]^3 = \frac{4}{3}k^{3/2},$

dove $a$ è il coefficiente del monomio di secondo grado nell’equazione che definisce la parabola, e $x_1$ e $x_2$ ( $x_1 < x_2$ ) sono le intersezioni della parabola con l’asse delle ascisse. Naturalmente questo risultato coincide col valore trovato in precedenza.

Affinché $\mathcal{A}_f > \mathcal{A}_g$ , si deve quindi avere:

$\frac{4}{3}k^{3/2} = \frac{4}{3}k^{6/4} > \frac{8}{5}k^{5/4} \iff k^{1/4} > \frac{6}{5} \iff k > \left(\frac65\right)^{\!4}.$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2016-I

Siano $a$ e $b$ due numeri reali positivi. Se $x, y \in \mathbb{R}$ sono tali che $x^2 + y^2 \leq 1$ , qual è il massimo valore che può assumere l’espressione $ax+by$ ?

$\quad$

$\fbox{a}$ $\dfrac{1}{a}+\dfrac{1}{b}$ .

$\fbox{b}$ $\max\{a,b\}$ .

$\fbox{c}$ $\sqrt{a^2+b^2}$ .

$\fbox{d}$ $a+b$ .

$\fbox{e}$ $a^2+ab+b^2$ .

Soluzione.

Presentiamo due possibili approcci, uno algebrico e uno geometrico.

$\quad$

Si costruiscano i vettori $v = (a,b)$ e $w = (x,y)$ . Ricordiamo le definizioni di prodotto scalare (canonico) e norma in $\mathbb{R}^2$ :
$\langle v,w\rangle = ax + by; \qquad ||v|| = \sqrt{\langle a,a\rangle} = \sqrt{a^2+b^2}.$

Per ogni prodotto scalare, vale la disuguaglianza di Cauchy-Schwarz:

$\left|\langle v,w\rangle\right| \leq ||v||\cdot||w||;$

in particolare, questa relazione diventa un’uguaglianza nel caso in cui $(a,b)$ e $(x,y)$ sono paralleli, cioè se $y/b = x/a > 0$ . Possiamo ora scrivere:

$ax + by = \langle v,w\rangle \leq ||v||\cdot||w|| = \sqrt{a^2+b^2}\sqrt{x^2+y^2} \leq \sqrt{a^2+b^2},$

che fornisce un limite superiore per $ax+by$ . Se poi $ay = bx$ e $\sqrt{x^2+y^2} = 1$ , le due disuguaglianze sono uguaglianze, per cui si ha $ax + by = \sqrt{a^2+b^2}$ .

Se $x^2+y^2 \leq 1$ , il punto $P$ di coordinate $(x,y)$ si trova all’interno o sul bordo della circonferenza di equazione $x^2+y^2 = 1$ . Costruiamo la retta $r$ di equazione $ax + by = 0$ . La distanza di $P$ da $r$ è data da:
$d = \overline{PH} = \frac{|ax + by|}{\sqrt{a^2+b^2}}.$

Dato che la retta $r$ passa per l’origine, il valore massimo di $d$ al variare di $P$ all’interno del cerchio è dato dal suo raggio, cioè 1. Questo avviene quando $P = Q$ , dove $Q$ è l’intersezione tra la circonferenza e la retta $s$ perpendicolare ad $r$ passante per l’origine. Abbiamo quindi:

$ax+by \leq |ax+by| = d\cdot\sqrt{a^2+b^2} \leq \sqrt{a^2+b^2}.$

$\quad$

$\quad$

$\quad$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2016-J

Sia $n > 1$ un numero intero. Definiamo le seguenti funzioni:

$\quad$

$\Pi(n)$ restituisce il numero di fattori primi distinti di $n$ ;

$\Lambda(n)$ restituisce l’ultima cifra della rappresentazione decimale di $n$ .

Quale delle seguenti affermazioni è falsa? Nel seguito, si considera che i possibili valori di $\Lambda$ sono gli interi compresi tra 0 e 9 inclusi.

$\quad$

$\fbox{a}$ Se $\Pi(n)=1$ , esistono valori di $\Lambda(n)$ per cui $n$ non è mai primo.

$\fbox{b}$ Se $\Pi(n)=1$ , esistono valori di $\Lambda(n)$ per cui $n$ è necessariamente primo.

$\fbox{c}$ Se $\Pi(n)=1$ , non si possono ottenere tutti i possibili valori di $\Lambda(n)$ .

$\fbox{d}$ Se $\Pi(n) + \Lambda(n) = 2$ , non si può concludere se $n$

$\fbox{e}$ Se $\Pi(n)=2$ , si possono ottenere tutti i valori possibili di $\Lambda(n)$ . sia primo o meno.

Soluzione.

Per familiarizzarci con $\Pi$ e $\Lambda$ , ecco qualche esempio: $\Pi(6) = \Pi(2\cdot3) = 2$ , $\Pi(8) = \Pi(2^3) = 1$ , $\Pi(12) = \Pi(2^2\cdot3) = 2$ ; $\Lambda(5) = 5$ , $\Lambda(42) = 2$ , $\Lambda(100) = 0$ .

Valutiamo ora la correttezza delle varie opzioni una ad una.

$\fbox{a}$ Questa affermazione è vera. Se $\Lambda(n) = 4$ , 6, oppure 8, allora $n$ è pari, e ha 2 come fattore primo. Dato che $\Pi(n) = 1$ per ipotesi, 2 è il solo fattore primo, quindi $n$ deve essere della forma $2^k$ , che è primo solo se $k=1$ , nel qual caso sarebbe però $\Lambda(n) = 2$ . Quindi $n$ non è primo.

$\fbox{b}$ Questa è l’affermazione falsa. Sia $n$ tale che $\Pi(n) = 1$ . In primo luogo, notiamo che questo implica che $\Lambda(n) \ne 0$ , perché se $\Lambda(n) =0$ allora $n$ è divisibile per 10, quindi sia per 2 che per 5, cioè $\Pi(n) \geq 2$ . Se $k$ è una cifra diversa da 0, mostriamo caso per caso che esiste sempre un numero composto $n$ tale che $\Pi(n) = 1$ e $\Lambda(n) = k$ .

$n$ :	$81$	$32$	$243$	$4$	$25$	$16$	$27$	$8$	$9$
fattori:	$3^4$	$2^5$	$3^5$	$2^2$	$5^2$	$2^4$	$3^3$	$2^3$	$3^2$
$\Lambda(n)$ :	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$

$\fbox{c}$ Questa affermazione è vera. Come discusso al punto precedente, se $\Lambda(n) = 0$ , si ha $\Pi(n) \geq 2$ .

$\fbox{d}$ Questa affermazione è vera. Come esempio, se $n = 11$ (primo) oppure $n = 121 = 11^2$ (composto), in entrambi i casi si ha $\Pi(n) = 1$ e $\Lambda(n) = 1$ , da cui $\Pi(n)+\Lambda(n) = 2$ .

$\fbox{e}$ Mostriamo caso per caso che questa affermazione è vera. Per ogni cifra $k = 0, \ldots, 9$ , è possibile trovare un intero $n$ tale che $\Pi(n) = 2$ e $\Lambda(n) = k$ .

$n$ :	$21$	$12$	$33$	$14$	$15$	$6$	$57$	$18$	$39$	$10$
fattori:	$3 \cdot 7$	$3 \cdot 4$	$3 \cdot 11$	$2 \cdot 7$	$3 \cdot 5$	$3 \cdot 2$	$3 \cdot 19$	$2 \cdot 9$	$3 \cdot 13$	$2 \cdot 5$
$\Lambda(n)$ :	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$0$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2017-A

Sia $k$ un parametro reale e si consideri la funzione di variabile reale

$f(x) = 2x^3 - kx^2 + 2x - k.$

Per quali valori di $k$ la funzione $f$ presenta due punti stazionari distinti?

$\quad$

$\fbox{a}$ $-2\sqrt{3} < k < 2\sqrt{3}$ .

$\fbox{b}$ $k < -2\sqrt{3} \vee k > 2\sqrt{3}$ .

$\fbox{c}$ $k < -3-\sqrt{21} \vee k > -3+\sqrt{21}$ .

$\fbox{d}$ $-3-\sqrt{21} < k < -3+\sqrt{21}$ .

$\fbox{e}$ Per ogni valore di $k$ .

Soluzione.

La derivata prima di $f$ è

$f'(x) = 6x^2 - 2kx + 2.$

I punti stazionari di $f$ sono quelli in cui $f'$ si annulla. Dato che $f'$ è un polinomio di secondo grado, per avere due punti stazionari distinti è necessario che il discriminante dell’equazione $f'(x) = 0$ sia strettamente positivo, cioè che:

$k^2 - 12 > 0 \iff k < -\sqrt{12} \vee k > \sqrt{12} \iff k < -2\sqrt{3} \vee k > 2\sqrt{3} .$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2017-B

Calcolare il valore minimo assunto dalla funzione:

$f(x) = 9\cos^4(x) - 12\cos^2(x) + 7.$

$\quad$

$\fbox{a}$ 3.

$\fbox{b}$ 4.

$\fbox{c}$ 5.

$\fbox{d}$ 6.

$\fbox{e}$ 7.

Soluzione.

Riscriviamo l’espressione di $f$ nel seguente modo:

$f(x) = 9\cos^4(x) - 12\cos^2(x) + 4 + 3 = [3\cos^2(x)-2]^2 + 3.$

Il termine tra parentesi non è mai negativo, per cui $f(x) \geq 3$ . Il valore di minimo viene assunto se $\cos^2(x) = 2/3$ (che ha infinite soluzioni).

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2017-C

Una successione $\{a_n\}_{n=1}^{+\infty}$ di numeri reali è definita per ricorsione nel seguente modo:

$a_{n+1} = \frac{a_n}{a_{n-1}} \qquad \text{per $n \geq 2$}.$

Se $a_1 = 2$ e $a_2 = 6$ , quanto vale $a_{2017}$ ?

$\quad$

$\fbox{a}$ $\dfrac{1}{6}$ .

$\fbox{b}$ $\dfrac{1}{3}$ .

$\fbox{c}$ $\dfrac{1}{2}$ .

$\fbox{d}$ 2.

$\fbox{e}$ 3.

Soluzione.

Innanzitutto, notiamo che la definizione è ben posta dato che, se $a_1, a_2 \ne 0$ , allora $a_n \ne 0$ per ogni $n \geq 3$ . Procediamo a calcolare i primi termini della successione:

$n$	$a_n$	$n$	$a_n$
$1$	$2$	$5$	$\frac{1}{6}$
$2$	$6$	$6$	$\frac{1}{3}$
$3$	$3$	$7$	$2$
$4$	$\frac{1}{2}$	$8$	$6$

Vediamo che $a_7 = a_1$ e $a_8 = a_2$ : questo implica che la successione si ripete con periodo 6: $a_{6n+k} = a_k$ per tutti gli interi positivi $k,n$ . Dato che $2017 = 6 \times 336 + 1$ (cioè il resto della divisione di 2017 per 6 è uguale a 1), si ha necessariamente $a_{2017} = a_1 = 2$ .

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2017-D

La figura mostra il grafico di una funzione $y = f(x)$ .

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Quale dei seguenti diagrammi mostra il grafico della funzione $y = -f(-x)$ ?

$\quad$

Soluzione.

Il grafico della funzione $f(-x)$ è dato dalla riflessione del grafico di $f(x)$ rispetto all’asse delle ordinate (che coincide con la figura $\fbox{a}$ ). Per ottenere il grafico di $-f(-x)$ è poi necessario ribaltare il risultato anche attorno all’asse delle ascisse.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2017-E

Siano $a$ e $b$ interi positivi tali che:

$a+b = 20.$

Qual è il massimo valore che può assumere la quantità $Q = a^2b$ ?

$\quad$

$\fbox{a}$ 1000.

$\fbox{b}$ 1152.

$\fbox{c}$ 1176.

$\fbox{d}$ 1183.

$\fbox{e}$ 1196.

Soluzione.

Abbiamo naturalmente $b = 20 - a$ , quindi:

$Q = a^2(20-a).$

Possiamo cercare massimi e minimi della funzione $\mathbb{R} \to \mathbb{R}$ definita come $Q$ , cioè $f(x) = x^2(20-x)$ , la cui derivata prima è:

$f'(x) = -3x^2 + 40x.$

La derivata si annulla per $x = 0$ e $x = 40/3 = 13 + 1/3$ . Si verifica facilmente che $x = 40/3$ corrisponde ad un punto di massimo: la funzione cresce per $0 \leq x \leq 40/3$ e decresce per $x \geq 40/3$ . I possibili valori interi di $x$ che massimizzano $Q$ sono pertanto $a = 13$ e $a = 14$ . Calcolando esplicitamente, si ha $Q(13) = 1183 > Q(14) = 1176$ .

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2017-F

La figura rappresenta la circonferenza unitaria, dove ogni punto ha coordinate $(\cos \vartheta,\sin \vartheta)$ . Stabilire in quale dei settori indicati è valida la condizione

$\tan(\vartheta) < \cos(\vartheta) < \sin(\vartheta).$

$\fbox{a}$ $A$ .

$\fbox{b}$ $B$ .

$\fbox{c}$ $C$ .

$\fbox{d}$ $D$ .

$\fbox{e}$ $E$ .

$\quad$

Soluzione.

Nel piano $(x,y) = (\cos \vartheta, \sin \vartheta)$ , tenendo conto della definizione di tangente, la disuguaglianza diventa:

$\frac{y}{x} < x < y.$

La seconda disuguaglianza è verificata banalmente se $y > x$ , cioè al di sopra della bisettrice del primo e terzo quadrante (area tratteggiata in arancione nella figura qui sotto). Per quanto riguarda la prima disuguaglianza, invece, possiamo risolverla così:

$\frac{y}{x} < x \iff \frac{y-x^2}{x} < 0 \iff \begin{cases} y > x^2 & \text{per $x < 0$}; \\ y < x^2 & \text{per $x > 0$}. \end{cases}$

La regione corrispondente è ombreggiata in azzurro nella figura.

$\quad$

Le soluzioni accettabili sono i punti $(x,y)$ appartenenti alla circonferenza unitaria che soddisfano entrambe le disequazioni appena risolte. Si vede dalla figura che la regione ammessa identifica il settore $\textcolor{green}C$ presentato nel testo.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2017-G

Sia $\vartheta$ un parametro reale e si consideri la retta $r$ di equazione

$(y-1)\cos(\vartheta) = (x+1)\sin(\vartheta).$

Indichiamo con $\mathcal{A}$ l’area della più grande delle due regioni in cui $r$ divide il cerchio di equazione $x^2 + y^2 \leq 4$ . Per quanti valori di $\vartheta$ nell’intervallo $0 \leq \vartheta \leq 2\pi$ l’area $\mathcal{A}$ assume il suo valore massimo?

$\quad$

$\fbox{a}$ 1.

$\fbox{b}$ 2.

$\fbox{c}$ 3.

$\fbox{d}$ 4.

$\fbox{e}$ $\mathcal{A}$ è indipendente da $\vartheta$ .

Soluzione.

Il punto $P = (-1,1)$ è interno alla circonferenza (che ha raggio 2), e per ogni valore di $\vartheta$ , la retta $r$ passa per $P$ , che funge da “perno”: $r$ ruota attorno a $P$ al variare di $\vartheta$ . Se $\cos(\vartheta) \ne 0$ , l’equazione di $r$ è infatti equivalente a:

$y = 1 + (x+1)\tan(\vartheta),$

che ha coefficiente angolare $\tan(\vartheta)$ , e quindi $\vartheta$ corrisponde all’angolo formato da $r$ con l’asse delle ascisse (se $\cos\vartheta = 0$ , la retta è verticale, $x=-1$ ). Al variare di $\vartheta$ in $[0,2\pi]$ , la retta compie una rotazione completa e, per simmetria, configurazioni che differiscono di $180\degr$ sono geometricamente indistinguibili.

Geometricamente, è evidente che l’area del segmento circolare diventa massima quando $r$ è ortogonale a $OP$ . Dato che $P$ appartiene alla bisettrice del secondo e quarto quadrante, questo avviene per i due valori $\vartheta = \pi/4$ oppure $\vartheta = 3\pi/4$ . Un modo per dimostrare rigorosamente questo fatto è mostrato in figura.

$\quad$

Costruiamo l’asse $HK$ della corda $QR$ identificata da $r$ . L’area $\mathcal{A}$ del segmento circolare (colorato in giallo in figura) dipende unicamente dalla lunghezza di $HK$ (che è la cosiddetta altezza del segmento circolare): al crescere di $\overline{HK}$ , aumenta anche $\mathcal{A}$ . Massimizzare $\mathcal{A}$ equivale quindi a massimizzare $\overline{HK}$ . Dato che $HK$ è un cateto del triangolo rettangolo $KHP$ , $\overline{HK} \leq \overline{PK}$ , e quindi la sua massima lunghezza si ottiene quando $P$ coincide con $H$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2017-H

Siano $a$ e $b$ due numeri reali arbitrari, con $a \ne 0$ . Sappiamo che:

$\quad$

il resto della divisione del polinomio $P(x) = x^2 - 2ax + a^4$ per $(x+b)$ è uguale a 1;

il polinomio $Q(x) = bx^2 + x + 1$ contiene $(ax-1)$ tra i suoi fattori.

Quali sono i possibili valori di $b$ ?

$\quad$

$\fbox{a}$ 1.

$\fbox{b}$ 0 oppure $-2$ .

$\fbox{c}$ 1 oppure 2.

$\fbox{d}$ 1 oppure 3.

$\fbox{e}$ $-1$ oppure 2.

Soluzione.

Per il teorema del resto, la divisione di $P$ per $(x+b)$ restituisce 1 come resto se e solo se $P(-b) = 1$ , cioè:

$P(-b) = b^2 + 2ab + a^4 = 1.$

Alternativamente, se non si conosce il teorema del resto, si può effettuare direttamente la divisione polinomiale, giungendo alla medesima condizione.

Dato che $Q$ è divisibile per $(ax-1)$ , vuol dire che $1/a$ è una radice di $Q$ , cioè $Q(1/a) = 0$ :

$Q\left(\frac{1}{a}\right) = \frac{b}{a^2} + \frac{1}{a} + 1 = 0 \iff b = -a^2 - a.$

Sostituendo questa espressione per $b$ nella prima equazione, abbiamo:

$\begin{gather*} (-a^2-a)^2 + 2a(-a^2-a) + a^4 = 1; \\ 2a^4 - a^2 - 1 = 0; \\ 2(a^2-1)\left(a^2+\frac{1}{2}\right) = 0. \end{gather*}$

Dato che l’ultimo fattore nel membro di sinistra è sempre positivo, l’unica possibilità è che $a^2 = 1$ , cioè $a = \pm 1$ , e quindi $b = -a^2 - a$ può assumere i valori $0$ oppure $-2$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2017-I

Siano $a$ , $b$ , $c$ numeri reali positivi, con $a,b \ne 1$ . Stabilire sotto quale condizione l’equazione

$\log_b\left[(b^x)^x\right] + \log_a\left(\frac{c^x}{b^x}\right) + \log_a\left(\frac{1}{b}\right)\log_a(c) = 0$

ammette una radice di molteplicità doppia.

$\quad$

$\fbox{a}$ $b^2 = 4ac$ .

$\fbox{b}$ $b = \dfrac{1}{a}$ .

$\fbox{c}$ $c = \dfrac{b}{a}$ .

$\fbox{d}$ $c = \dfrac{1}{b}$ .

$\fbox{e}$ $a = b = c$ .

Soluzione.

Ricordiamo alcune proprietà delle potenze e dei logaritmi:

$\begin{array}{r@{\mbox{}=\mbox{}}l} (b^x)^x & b^{x\cdot x} = b^{x^2}; \\ \log(c^x) & x\log(c); \\ \log_a(c/b) & \log_a(c)-\log_a(b). \end{array}$

Possiamo allora riscrivere l’equazione assegnata nel seguente modo:

$x^2 + x\log_a\left(\frac{c}{b}\right) - \log_a(b)\log_a(c) = 0.$

Questa è un’equazione di secondo grado, che ammette una soluzione doppia se e solo se il suo discriminante $\Delta$ è nullo:

$\begin{aligned} \Delta = {} & \left[\log_a\left(\frac{c}{b}\right)\right]^2 + 4\log_a(b)\log_a(c) = \\ = {} & \left[\log_a(c) - \log_a(b)\right]^2 + 4\log_a(b)\log_a(c) = \\ = {} & \log_a^2(c) + \log_a^2(b) + 2\log_a(b)\log_a(c) = \\ = {} & \left[\log_a(b)+\log_a(c)\right]^2 = \\ = {} & \left[\log_a(bc)\right]^2. \end{aligned}$

Imponendo $\Delta = 0$ , si conclude che $\log_a(bc) = 0$ , cioè $bc = 1$ .

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2017-J

Quali dei seguenti integrali è il più grande?

$\quad$

$\fbox{a}$ $\displaystyle\int_0^2 (x^2-4)\sin^8(\pi x)\diff{x}$ .

$\fbox{b}$ $\displaystyle\int_0^{2\pi} [2+\cos(x)]^3\diff{x}$ .

$\fbox{c}$ $\displaystyle\int_0^{\pi} \sin^{100}(x)\diff{x}$ .

$\fbox{d}$ $\displaystyle\int_0^{\pi} [3-\sin(x)]^6\diff{x}$ .

$\fbox{e}$ $\displaystyle\int_0^{8\pi} 108[\sin^3(x)-1]\diff{x}$ .

Soluzione.

Ricordiamo un’applicazione del teorema del confronto per gli integrali. Se $m \leq f(x) \leq M$ e $a < b$ , si ha:

$m\cdot(b-a) \leq \int_a^b f(x)\diff{x} \leq M\cdot(b-a).$

Usando questo fatto, possiamo stimare caso per caso i 5 integrali proposti, senza dover calcolare esplicitamente le primitive.

$\quad$

$\fbox{a}$ Per $0 \leq x \leq 2$ si ha $x^2-4 \leq 0$ , per cui la funzione integranda è non positiva, e quindi il valore dell’integrale è negativo.

$\fbox{b}$ Si ha $[2+\cos(x)]^3 \leq (2+1)^3 = 27$ , per cui il valore dell’integrale è necessariamente minore di $54\pi$ .

$\fbox{c}$ Si ha $\sin^{100}(x) \leq 1$ per ogni $x$ , per cui il valore di questo integrale è minore di $\pi$ .

$\fbox{d}$ Si ha $[3-\sin(x)]^6 \geq (3-1)^6 = 64$ , per cui il valore dell’integrale è necessariamente maggiore di $64\pi$ .

$\fbox{e}$ Dato che $\sin^3(x)-1 \leq 0$ per ogni $x$ , questo integrale è necessariamente negativo.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2018-A

Calcolare l’area della regione (limitata) compresa tra la curva di equazione $y = \sqrt{x}$ , la retta $y = x-2$ , e l’asse delle ascisse.

$\quad$

$\fbox{a}$ $2$ .

$\fbox{b}$ $\dfrac{5}{2}$ .

$\fbox{c}$ $3$ .

$\fbox{d}$ $\dfrac{10}{3}$ .

$\fbox{e}$ $\dfrac{16}{3}$ .

Soluzione.

Disegniamo il grafico delle due funzioni evidenziando alcuni punti notevoli. La curva $y = \sqrt{x}$ è un arco di parabola con l’asse orizzontale, coincidente con l’asse delle ascisse. La retta interseca l’asse delle ascisse per $x = 2$ e l’arco di parabola per $x = 4$ e $y = 2$ .

$\quad$

L’area che ci interessa $OAC$ è evidenziata in viola nella figura. Per semplificare leggermente il calcolo, notiamo che l’area $OAC$ è pari all’area di $OBC$ meno l’area del triangolo $ABC$ , cioè 2. L’area di $OBC$ è data da:

$\int_0^4 \sqrt{x}\diff{x} = \frac{2}{3}x^{3/2}\Bigg|_0^4 = \frac{2}{3}4^{3/2} = \frac{16}{3}.$

Si conclude che l’area di $OBC$ è pari a $16/3 - 2 = 10/3$ .

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2018-B

Si consideri l’equazione differenziale:

$\left(\frac{\diff^2y}{\diff{x}^2}+\frac{\diff{y}}{\diff{x}}\right) \left(\frac{\diff{y}}{\diff{x}}-y\right) = y\frac{\diff{y}}{ \diff{x}}.$

Per quali valori del parametro reale $k$ la funzione $y(x) = e^{kx}$ è soluzione?

$\quad$

$\fbox{a}$ Per nessun valore di $k$ .

$\fbox{b}$ Per uno ed un solo valore di $k$ .

$\fbox{c}$ Per due soli valori distinti di $k$ .

$\fbox{d}$ Per tre soli valori distinti di $k$ .

$\fbox{e}$ Per infiniti valori distinti di $k$ .

Soluzione.

Si ha $y'(x) = k\cdot e^{kx} = k y$ e $y''(x) = k^2\cdot e^{kx} = k^2 y$ . Sostituendo direttamente, e ricordando che $y \ne 0$ per ogni $x \in \mathbb{R}$ , si trova:

$\begin{gather*} (k^2y+ky)(ky-y) = ky^2; \\ (k^2+k)(k-1) = k. \end{gather*}$

Il valore $k = 0$ è chiaramente una soluzione (in questo caso $y = e^{kx} = 1$ è una funzione costante). Supposto invece $k \ne 0$ , si ha:

$(k+1)(k-1) = 1 \iff k^2 = 2 \iff k = \pm\sqrt{2}.$

Complessivamente, ci sono quindi 3 valori di $k$ che soddisfano l’equazione assegnata.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2018-C

Siano $a$ , $b$ , $c$ , $d$ numeri reali arbitrari. Sotto quale condizione le due curve $y = ax^2+c$ e $y = bx^2 + d$ hanno esattamente due punti di intersezione?

$\quad$

$\fbox{a}$ $\dfrac{a}{b} < 1$ .

$\fbox{b}$ $\dfrac{a}{b} < \dfrac{c}{d}$ .

$\fbox{c}$ $a < b$ .

$\fbox{d}$ $c < d$ .

$\fbox{e}$ $(d-c)(a-b) > 0$ .

Soluzione.

Le intersezioni delle due curve sono le soluzioni reali dell’equazione

$ax^2 + c = bx^2 + d \iff (a-b)x^2 = d-c.$

Se $a = b$ , questa equazione non ha nessuna soluzione (se $d \ne c$ ) oppure infinite (se $d = c$ ), quindi comunque non due. Se $a \ne b$ , dividendo ambo i membri per $a-b$ otteniamo:

$x^2 = \frac{d-c}{a-b}.$

Questa equazione ha due soluzioni (reali) distinte se e solo se il membro di destra è strettamente positivo, cioè se i fattori $(d-c)$ e $(a-b)$ hanno segno concorde. Questo è equivalente alla condizione $(d-c)(a-b) > 0$ .

La risposta corretta è dunque la $\fbox{e}$ .

Quesito 2018-D

Sia data la funzione $f$ : $\mathbb{R} \to \mathbb{R}$ :

$f(x) = x^2 - 5x + 7.$

Quali sono le coordinate del punto di minimo della funzione $y = f(x-2)$ ?

$\quad$

$\fbox{a}$ $\left(\dfrac{5}{2},\dfrac{3}{4}\right)$ .

$\fbox{b}$ $\left(\dfrac{9}{2},\dfrac{3}{4}\right)$ .

$\fbox{c}$ $\left(\dfrac{1}{2},\dfrac{3}{4}\right)$ .

$\fbox{d}$ $\left(\dfrac{9}{2},-\dfrac{5}{4}\right)$ .

$\fbox{e}$ $\left(\dfrac{5}{2},-\dfrac{5}{4}\right)$ .

Soluzione.

La funzione $f$ è una parabola con la concavità rivolta verso l’alto. Sfruttando la tecnica del completamente del quadrato, possiamo riscrivere la sua equazione come:

$f(x) = x^2 - 2\frac{5}{2}x + \frac{25}{4} - \frac{25}{4} + 7 = \left(x-\frac{5}{2}\right)^2 + \frac{3}{4}.$

In questo modo, riconosciamo le coordinate del vertice $V$ di $f$ , che è anche il suo punto di minimo assoluto:

$V = \left(\frac{5}{2},\frac{3}{4}\right).$

Il grafico di $f(x-2)$ si ottiene traslando orizzontalmente di 2 unità il grafico di $f(x)$ verso la direzione positiva delle ascisse. Il punto di minimo della parabola $f(x-2)$ è quindi:

$\left(\frac{9}{2},\frac{3}{4}\right).$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2018-E

.Si consideri su un piano cartesiano un cerchio di raggio 2 centrato nell’origine. Si marchino tutti i punti del piano con entrambe le coordinate intere. Sia $n$ il numero di questi punti che sono inclusi all’interno o stanno sul bordo del cerchio. Di quanto, come minimo, deve aumentare il raggio del cerchio in modo da includere al suo interno o sul suo bordo in tutto $2n-5$ punti del reticolo?

$\quad$

$\fbox{a}$ $\sqrt{5}-2$ .

$\fbox{b}$ $\sqrt{6}-2$ .

$\fbox{c}$ $\sqrt{8}-2$ .

$\fbox{d}$ 1.

$\fbox{e}$ $\sqrt{8}$ .

Soluzione.

Disegniamo i punti a coordinate intere e la circonferenza assegnata, come mostrato in figura:

$\quad$

All’interno o sul bordo del cerchio di raggio 2 ci sono $n = 13$ punti. Non è difficile verificarlo. Per esempio, $(1,1)$ è all’interno perché $\sqrt{1^2+1^2} = \sqrt{2} < 2$ , mentre $(1,2)$ è al di fuori perché $\sqrt{1^2+2^2} = \sqrt{5} > 2$ . I punti $(0,2)$ e $(2,0)$ stanno esattamente sul bordo, e vanno quindi anche loro conteggiati. Per simmetria, si trovano subito anche i punti nei rimanenti quadranti.

La quantità $2n-5$ vale dunque 21: dobbiamo allargare il raggio della circonferenza in modo da aggiungere 8 punti. Il primo punto che incontriamo è $(1,2)$ . Per simmetria, questo comporta direttamente l’aggiunta di 8 nuovi punti in tutto, che è proprio quel che volevamo fare. Il raggio della nuova circonferenza (indicata in figura con una linea tratteggiata) è $\sqrt{1^2+2^2} = \sqrt{5}$ . Il raggio della circonferenza originaria va quindi aumentato di $\sqrt{5}-2$ .

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2018-F

Un punto $P$ si sposta nel piano $xy$ , partendo dall’origine. Ad ogni mossa, $P$ si può spostare in uno dei seguenti due modi:

$\quad$

si può muovere di 2 verso destra e 1 verso l’alto;

si può muovere di 1 verso destra e 2 verso l’alto.

Qual è la distanza minima cui $P$ può trovarsi dal punto $Q = (25,75)$ ?

$\quad$

$\fbox{a}$ 0.

$\fbox{b}$ $5\sqrt{5}$ .

$\fbox{c}$ $2\sqrt{53}$ .

$\fbox{d}$ 25.

$\fbox{e}$ 35.

Soluzione.

Date le regole per il suo movimento, il punto $P$ è vincolato a giacere all’interno della regione delimitata dalle semirette positive (incluse) $y = 2x$ e $y = x/2$ . Il punto $Q$ ha coordinate $y = 3x$ , quindi si trova al di sopra di questa regione. La posizione più vicina a $Q$ che $P$ può raggiungere deve quindi trovarsi in prossimità della retta $y = 2x$ . Cominciamo calcolando la distanza di $Q$ dal punto di coordinate $(n,2n)$ :

$D = \sqrt{(25-n)^2+(75-2n)^2}.$

La distanza minima si ha quando:

$\begin{gather*} \frac{\mathrm{d}D}{\mathrm{d}n} = 0 \iff \frac{\mathrm{d}}{\mathrm{d}n}\left[(25-n)^2+(75-2n)^2\right] = 0; \\ -2(25-n) -4(75-2n) = 0 \iff 5n = 175 \iff n = 35. \end{gather*}$

È importante notare che il minimo di $D$ si ha in corrispondenza di un intero ( $n = 35)$ : questo ci assicura che $P$ può effettivamente raggiungere questa posizione. La minima distanza di $P$ da $Q$ è quindi:

$D_{\rm min} = \sqrt{(25-35)^2+(75-2\times35)^2} = \sqrt{10^2+5^2} = 5\sqrt{2^2+1} = 5\sqrt{5}.$

$\quad$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2018-G

.Sia $c$ un numero reale e si considerino le due parabole di equazioni

$\begin{array}{r@{\mbox{}=\mbox{}}l} y_1 & x^2 + c; \\[2.5pt] y_2^2 & x. \end{array}$

Quanto vale $c$ se le due curve hanno un’unica intersezione?

$\quad$

$\fbox{a}$ $\dfrac{1}{2\sqrt{3}}$ .

$\fbox{b}$ $\dfrac{3}{4\sqrt[3]{4}}$ .

$\fbox{c}$ $-\dfrac{1}{2}$ .

$\fbox{d}$ $\sqrt{5}-\sqrt{3}$ .

$\fbox{e}$ $\sqrt{\dfrac{2}{3}}$ .

Soluzione.

Disegniamo velocemente le due parabole: la prima ha l’asse verticale, concavità verso l’alto e vertice in $(0,c)$ , la seconda ha l’asse orizzontale, concavità verso destra e vertice in $(0,0)$ .

$\quad$

Vediamo che per $c \to +\infty$ (curve gialle) non ci sono intersezioni tra le due parabole, mentre per $c \to -\infty$ (curve rosse/arancioni) ci sono due intersezioni. Si ha una sola intersezione nel caso limite in cui $y_1 = y_2$ e $y'_1 = y'_2$ . L’intersezione avviene chiaramente nel primo quadrante, per cui $y_2 > 0$ e quindi $y_2 = +\sqrt{x}$ . Abbiamo dunque:

$\begin{cases} y_1(x) = y_2(x); \\ y'_1(x) = y'_2(x); \end{cases} \implies\quad \begin{cases} x^2 + c = \sqrt{x}; \\ 2x = \dfrac{1}{2\sqrt{x}}. \end{cases}$

Dalla seconda equazione, ricaviamo $4x^{3/2} = 1$ e quindi $x = (1/4)^{2/3}$ . Inserendo questo valore nella prima:

$\left(\frac{1}{4}\right)^{4/3}+c = \left(\frac{1}{4}\right)^{1/3} \iff c = \left(\frac{1}{4}\right)^{1/3} - \frac{1}{4}\left(\frac{1}{4}\right)^{1/3} = \frac{3}{4}\left(\frac{1}{4}\right)^{1/3}.$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2018-H

Due triangoli $S$ e $T$ , aree $s$ e $t$ rispettivamente ( $s < t$ ), hanno un lato in comune e sono iscritti nella medesima circonferenza, come mostrato in figura:

$\quad$

$\fbox{a}$ $\dfrac{2}{5}$ .

$\fbox{b}$ $\dfrac{3}{5}$ .

$\fbox{c}$ $\dfrac{4}{5}$ .

$\fbox{d}$ 1.

$\fbox{e}$ $\dfrac{3}{2}$ .

Si determini il più piccolo valore possibile che può assumere la quantità:

$Q = \frac{4s^2+t^2}{5st}.$

$\quad$

Soluzione.

Presentiamo due metodi. Osserviamo che se $X$ , $Y$ sono due numeri reali qualsiasi, vale naturalmente:

$(X-Y)^2 \geq 0 \iff X^2 + Y^2 \geq 2XY.$

In particolare, la relazione è un’uguaglianza se e solo se $X = Y$ . Poniamo ora $X = 2s$ , $Y=t$ , e quindi (dato che $XY > 0$ ):

$Q = \frac{2}{5} \frac{(2s)^2+t^2}{(2s)t} = \frac{2}{5} \frac{X^2+Y^2}{XY} \geq \frac{4}{5}.$

In particolare, si ha $Q = 4/5$ se $t = 2s$ .

Presentiamo anche un metodo alternativo: notiamo che per ipotesi $0 < s \leq t$ , per cui, posto $x = s/t$ , vale $0 < x \leq 1$ . Possiamo ora riscrivere:

$Q = \frac{4s^2+t^2}{5st} = \frac{t^2}{t^2}\frac{4(s/t)^2+1}{5(s/t)} = \frac{4x^2+1}{5x}.$

Per trovare il minimo di $Q$ , calcoliamo la derivata:

$\frac{\mathrm{d}Q}{\mathrm{d}x} = \frac{1}{5}\frac{8x\cdot x-(4x^2+1)\cdot1}{x^2} = \frac{1}{5}\frac{4x^2-1}{x^2}.$

Ricordando che $0 < x \leq 1$ , la derivata prima di $Q$ è positiva se $4x^2-1 > 0$ , cioè $1/2 < x \leq 1$ . La funzione $Q$ decresce per $0 < x \leq 1/2$ e cresce per $1/2 \leq x \leq 1$ . Il valore minimo si ha quindi per $x = 1/2$ . Sostituendo nell’espressione di $Q$ , troviamo:

$Q_\mathrm{min} = \frac{4\cdot(1/2)^2+1}{5\cdot1/2} = \frac{4}{5}.$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2018-I

Indicare quale dei seguenti grafici rappresenta qualitativamente il grafico della curva definita dall’equazione

$\left(x^8 + 4yx^6 + 6y^2x^4 +4y^3x^2 + y^4\right)^2 = 1.$

$\quad$

Soluzione.

Un modo per procedere è accorgersi che:

$x^8 + 4yx^6 + 6y^2x^4 +4y^3x^2 + y^4 = (x^2 + y)^4,$

come discende dalla formula del binomio di Newton con $a = x^2$ , $b = y$ :

$(a+b)^4 = \sum_{k=0}^4\binom{4}{k}a^k b^{4-k} = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4.$

L’equazione di partenza è dunque equivalente a:

$\left(x^2+y\right)^8 = 1,$

che corrisponde alla coppia di curve:

$y = 1 - x^2 \quad \vee \quad y = -1 - x^2.$

Queste sono due parabole con asse parallelo all’asse delle ordinate, concavità verso il basso, e vertici in $(0,+1)$ e $(0,-1)$ , rispettivamente.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2018-J

Quali tra le curve abbozzate in figura possono essere il grafico dell’equazione

$P(x) + P(y) = 0,$

dove $P$ è un opportuno polinomio?

$\fbox{a}$ I e IV, ma né II né III.

$\fbox{b}$ I e II, ma né III né IV.

$\fbox{c}$ III e IV, ma né I né II.

$\fbox{d}$ I, III e IV, ma non II.

$\fbox{e}$ I, II e III, ma non IV.

$\quad$

Soluzione.

Consideriamo i quattro grafici.

I. Ogni equazione del tipo $P(x) + P(y) = 0$ è simmetrica in $x$ e $y$ : se $(x,y)$ è una soluzione, allora lo è anche $(y,x)$ . Questo vuol dire che la curva corrispondente è simmetrica rispetto alla bisettrice del primo e terzo quadrante. Questo esclude la curva I.

II. Mostriamo come sia impossibile che un tratto della curva $P(x) + P(y) = 0$ sia la funzione costante. Se infatti, per assurdo, si avesse $y(x) = y_0 = \text{costante}$ , avremmo $P(y(x)) = P(y_0) = P_0 = \text{costante}$ . Essendo poi $P(x) + P(y(x)) = 0$ , si ha $P(x) = -P(y_0) = -P_0$ e quindi $P_0 = -P_0$ , cioè $P_0 = 0$ . L’equazione di partenza si riduce quindi all’identità $0 = 0$ , che ha come soluzione (“patologica”) l’intero piano cartesiano (che non corrisponde a quanto disegnato nel grafico II)!

III. Questa è una circonferenza; detto $r$ il suo raggio, la sua equazione si può esprimere nella forma richiesta prendendo (per esempio) $P(t) = t^2 - r^2/2$ , in modo che $P(x) + P(y) = x^2 + y^2 - r^2$ .

IV. Questa retta ha equazione $x + y = 0$ , e si può esprimere nella forma richiesta prendendo (per esempio) $P(t) = t$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2019-A

Determinare quante soluzioni reali distinte possiede l’equazione

$x^3 - 300x = 3000.$

$\quad$

$\fbox{a}$ Nessuna soluzione reale.

$\fbox{b}$ Esattamente una soluzione reale.

$\fbox{c}$ Esattamente due soluzioni reali.

$\fbox{d}$ Esattamente tre soluzioni reali.

$\fbox{e}$ Infinite soluzioni reali.

Soluzione.

Sia $f(x) = x^3 - 300x - 3000$ . Le soluzione dell’equazione proposta corrispondono agli zeri di $f$ . Per non ricorrere alla complicata formula di risoluzione delle equazioni di terzo grado, notiamo che $f(x) \to \pm\infty$ per $x \to \pm \infty$ , e quindi $f$ è negativa (positiva) per $x \to -\infty$ ( $+\infty$ ). Calcoliamo la derivata prima di $f$ per trovare gli intervalli di crescenza e decrescenza:

$f'(x) = 3x^2 - 300 > 0 \iff x^2 > 100 \iff x<-10 \ \vee \ x > 10.$

Quindi $f$ cresce per $x \leq -10$ e $x \geq 10$ , e decresce per $-10 \leq x \leq 10$ . Osserviamo ora che $f(-10) = -1000 + 3000 - 3000 = -1000 < 0$ . Essendo $f$ descrescente su $[-10,10]$ , si ha $f(10) < f(-10) < 0$ . Essendo $f$ crescente per $x \geq 10$ , e $f(x) \to +\infty$ per $x \to +\infty$ , concludiamo che $f$ ha una ed una sola radice reale.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2019-B

Sia $N$ il prodotto tra un quadrato perfetto ed un un cubo perfetto. Quale delle seguenti affermazioni è corretta?

$\quad$

$\fbox{a}$ $N$ è sempre un quadrato perfetto, ma non è mai un cubo perfetto.

$\fbox{b}$ $N$ è sempre un cubo perfetto, ma non è mai un quadrato perfetto.

$\fbox{c}$ È possibile che $N$ sia un quadrato perfetto ed è possibile che $N$ sia un cubo perfetto.

$\fbox{d}$ $N$ non è mai un quadrato perfetto né un cubo perfetto.

$\fbox{e}$ $N$ è sempre sia un cubo perfetto che un quadrato perfetto.

Soluzione.

Siano $x$ ed $y$ due numeri interi, e $N = x^2y^3$ . Proviamo con un paio di esempi.

$\quad$

Per $x = 1$ e $y = 1$ , si ha $Q = 1$ , che è sia un quadrato perfetto che un cubo perfetto.

Per $x = 3$ e $y = 2$ , si ha $Q = 9\times8 = 72$ , che non è né un cubo perfetto né un quadrato perfetto.

Questi due esempi mostrano che tutte le opzioni presentate nel quesito, esclusa la terza, sono false.

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2019-C

Indicare quale dei seguenti grafici rappresenta qualitativamente il grafico della funzione

$y = \sin^2(x) + \sin^4(x) + \sin^6(x) + \cdots.$

$\quad$

Soluzione.

Notiamo che, per $x \ne \pm \pi/2$ , la funzione si può scrivere come la somma di una serie geometrica di ragione $q = \sin^2(x)$ :

$y = \sum_{k=1}^{+\infty}\sin^{2k}(x) = \sum_{k=1}^{+\infty}\left[\sin^2(x)\right]^k = \frac{1}{1-\sin^2(x)}-1 = \tan^2(x).$

Qui abbiamo usato la formula della somma della serie geometrica, valida per $|q| < 1$ , notando però che la nostra serie inizia da $k=1$ :

$\sum_{k=0}^{+\infty}q^k = \frac{1}{1-q}.$

Per $x = \pm\pi/2$ , si ha $\sin^2(x) = 1$ , e la somma diverge a $+\infty$ . Il grafico della funzione presenta pertanto degli asintoti verticali (che esclude le opzioni $\fbox{b}$ e $\fbox{c}$ ). Inoltre, $y(0) = 0$ (che esclude l’opzione $\fbox{a}$ ), e in generale $y$ non può essere negativa (che esclude l’opzione $\fbox{e}$ ).

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2019-D

Sia $a$ un parametro reale. È noto che l’area della regione compresa tra le due parabole di equazione $y_1 = x^2 + 2ax + a$ e $y_2 = a - x^2$ è pari a 9. Quali sono i possibili valori di $a$ ?

$\quad$

$\fbox{a}$ $a=1$ .

$\fbox{b}$ $a=\pm3$ .

$\fbox{c}$ $a=-3$ .

$\fbox{d}$ $a=\pm1$ .

$\fbox{e}$ $a = 1\ \vee a = 3$ .

Soluzione.

Cerchiamo per prima cosa le intersezioni tra le due parabole, cioè i punti in cui $y_1 = y_2$ :

$x^2 + 2ax + a = a - x^2 \iff x^2+ax = 0 \iff x = 0\ \vee\ x = -a.$

Come si vede, si hanno due intersezioni per ogni valore di $a$ . Si nota anche che $y_2 > y_1$ nell’intervallo compreso tra le due soluzioni, indipendentemente dal loro ordinamento. L’area $\mathcal{A}$ compresa tra le due curve è data da:

$\begin{aligned} \mathcal{A} = {} & \left|\, \int_{-a}^0 [y_2(x)-y_1(x)]\diff{x} \right| = \left|\, \int_{-a}^0 \left(x^2+2ax+a - a+x^2\right)\mathrm{d}x \right| = \\ = {} & \left|\, \int_{-a}^0 (2x^2+2ax)\diff{x}\right| = \left|\left.\left(\frac{2x^3}{3} + ax^2\right)\right|_{-a}^{0}\right| = \frac{1}{3}|a|^3. \end{aligned}$

Dal momento che l’ordinamento relativo dei due estremi di integrazione dipende da $a$ , per evitare di separare i due casi abbiamo preso il valore assoluto dell’integrale. Dato che per ipotesi $\mathcal{A} = 9$ , abbiamo $|a| = \sqrt[3]{27} = 3$ , da cui $a = \pm 3$ .

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2019-E

Si consideri il grafico dell’equazione:

$\sin(y)-\sin(x) = \cos^2(x) - \cos^2(y).$

$\quad$

$\fbox{a}$ Il grafico è vuoto.

$\fbox{b}$ Il grafico non è vuoto, ma non include nessuna retta.

$\fbox{c}$ Il grafico include una ed una sola retta.

$\fbox{d}$ Il grafico include esattamente due rette.

$\fbox{e}$ Il grafico include infinite rette

Soluzione.

Notiamo che, ovviamante, la retta $y = x$ soddisfa l’equazione assegnata. Ma, data la periodicità delle funzioni seno e coseno, anche le rette $y = x + 2k\pi$ , con $k$ intero qualsiasi, soddisfano la stessa equazione. Si noti che esistono altre famiglie di soluzioni (sia rette che non), ma non è necessario trovarle tutte per rispondere al quesito.

La risposta corretta è dunque la $\fbox{e}$ .

Quesito 2019-F

Per $0 \leq x < 2\pi$ , si consideri l’equazione

$\sin^3(x) + \cos^2(x) = 0.$

Quante soluzioni ha questa equazione?

$\quad$

$\fbox{a}$ 0.

$\fbox{b}$ 1.

$\fbox{c}$ 2.

$\fbox{d}$ 3.

$\fbox{e}$ 4.

Soluzione.

Risolviamo l’equazione per via grafica, riscrivendola in primo luogo come:

$\sin^3(x) = -\cos^2(x).$

I grafici di $\sin^3(x)$ e di $-\cos^2(x)$ sono rappresentati in figura, e sono facili da disegnare conoscendo quelli delle funzioni $\sin(x)$ e $\cos(x)$ .

$\quad$

Per costruire il grafico di $\sin^3(x)$ , basta considerare che $\sin^3(x) = -1$ se $x = 3\pi/2$ , $\sin^3(x) = 0$ se $x = 0$ oppure $x = \pi$ , e $\sin^3(x) = +1$ per $x = \pi/2$ . Dato che la trasformazione $t \to t^3$ è monotona crescente su $[-1,1]$ , $\sin^3(x)$ ha inoltre la stessa crescenza di $\sin(x)$ , quindi cresce per $0 \leq x \leq \pi/2$ e per $3\pi/2 \leq x \leq 2\pi$ , mentre descresce per $\pi/2 \leq x \leq 3\pi/2$ .

La funzione $-\cos^2(x)$ è naturalmente non positiva e varia nell’intervallo $[-1,0]$ . Dato che $\cos(x+\pi) = -\cos(x)$ , ha periodo $\pi$ . Si ha $-\cos^2(x) = 0$ per $x = \pi/2$ e $x = 3\pi/2$ , mentre $-\cos^2(x) = -1$ se $x = 0$ , $x = \pi$ , o $x = 2\pi$ . La funzione $-\cos^2(x)$ cresce per $0 \leq x \leq \pi/2$ e per $\pi \leq x \leq 3\pi/2$ , mentre decresce per $\pi/2 \leq x \leq \pi$ e $3\pi/2 \leq x \leq 2\pi$ .

Si conclude che, nell’intervallo da considerare $0 \leq x < 2\pi$ (area grigia in figura), ci sono due intersezioni (marcate dai punti viola).

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2019-G

Siano $a$ , $b$ , $c$ tre numeri reali positivi, diversi da 1. Si consideri il sistema di equazioni:

$\begin{cases} \log_a(b) = c; \\ \log_b(a) = c + \dfrac{3}{2}; \\ \log_c(a) = b. \end{cases}$

$\quad$

$\fbox{a}$ Il sistema ha un’unica terna di soluzioni.

$\fbox{b}$ Il sistema determina unicamente $c$ , ma ha infinite soluzioni per $a$ e $b$ .

$\fbox{c}$ Il sistema determina unicamente $a$ e $c$ , ma ha infinite soluzioni per $b$ .

$\fbox{d}$ Il sistema determina unicamente $a$ e $b$ , ma ha infinite soluzioni per $c$ .

$\fbox{e}$ Il sistema non ha soluzioni.

Soluzione.

Combinando le prime due equazioni, e ricordando la proprietà dei logaritmi $\log_b(a) = 1/\log_a(b)$ , abbiamo:

$\begin{gather*} c + \frac{3}{2} = \log_b(a) = \frac{1}{\log_a(b)} = \frac{1}{c}; \\ c^2 + \frac{3}{2}c = 1; \\ 2c^2 + 3c - 2 = 0. \end{gather*}$

Questa è un’equazione di secondo grado con soluzioni $c = -2$ e $c = 1/2$ , ma la prima va esclusa perché $c > 0$ . Inserendo $c = 1/2$ nelle restanti equazioni:

$\begin{cases} \log_b(a) = c+\dfrac{3}{2} = 2; \\[5pt] \log_c(a) = \log_{1/2}(a) = b; \end{cases} \implies\mbox{\quad} \begin{cases} a = b^2; \\ a = \left(\dfrac{1}{2}\right)^b = 2^{-b}. \end{cases}$

Il sistema risultante non è risolubile in termini di funzioni elementari, ma possiamo concludere graficamente che possiede una sola coppia di soluzioni reali. Infatti, la funzione $f(b) = b^2$ è crescente per $b \geq 0$ , tende a $+\infty$ per $b \to +\infty$ , e $f(0) = 0$ . Allo stesso tempo, la funzione $g(b) = 2^{-b}$ è descrescente, tende a 0 per $b\to+\infty$ , e $g(0) = 1$ . Esiste quindi un’unica intersezione tra i grafici delle due curve.

$\quad$

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2019-H

Un triangolo $ABC$ è rettangolo in $B$ . Inoltre, le lunghezze dei suoi lati formano una progressione geometrica. Quali sono i possibili valori di $\tan(\widehat{BAC})$ ?

$\quad$

$\fbox{a}$ $\sqrt{\dfrac{1\pm\sqrt{5}}{2}}$ .

$\fbox{b}$ $\sqrt{\dfrac{\sqrt{3}\pm1}{2}}$ .

$\fbox{c}$ $\sqrt{\dfrac{\sqrt{5}\pm1}{2}}$ .

$\fbox{d}$ $\pm\sqrt{\dfrac{1+\sqrt{5}}{2}}$ .

$\fbox{e}$ $\sqrt{\dfrac{1\pm\sqrt{3}}{2}}$ .

Soluzione.

L’ipotenusa del triangolo è $AC$ , che è naturalmente più lunga dei cateti $AB$ e $BC$ . Il fatto che i lati siano in progressione geometrica significa che il rapporto tra lati consecutivi è costante. Esiste quindi un numero $k > 1$ tale che:

$\overline{AC} = k\cdot\overline{AB} = k^2\cdot\overline{BC} \quad \text{oppure} \quad \overline{AC} = k\cdot\overline{BC} = k^2\cdot\overline{AB},$

a seconda che il cateto maggiore sia $AB$ (a sinistra) oppure $BC$ (a destra).

$\quad$

Il valore che dobbiamo calcolare è:

$\tan(\widehat{BAC}) = \frac{\overline{BC}}{\overline{AB}} = \begin{cases} 1/k & \text{se $\overline{AB} = k\cdot\overline{BC} > \overline{BC}$;} \\ k & \text{se $\overline{BC} = k\cdot\overline{AB} > \overline{AB}$.} \end{cases}$

Per il teorema di Pitagora, si ha $\overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2$ , e quindi:

$\begin{array}{ll} k^4\overline{BC}^2 = k^2\overline{BC}^2 + \overline{BC}^2 & \text{se $\overline{AB} = k\cdot\overline{BC}$;} \\[2.5pt] k^4\overline{AB}^2 = k^2\overline{AB}^2 + \overline{AB}^2 & \text{se $\overline{BC} = k\cdot\overline{AB}$.} \\ \end{array}$

In entrambi i casi, giungiamo alla medesima condizione $k^4 - k^2 - 1 = 0$ . Questa è un’equazione di secondo grado nell’incognita $k^2$ , che ha come soluzioni:

$k^2 = \frac{1\pm\sqrt{5}}{2};$

solo la soluzione col $+$ è accettabile perché $(1-\sqrt{5})/2 < 0$ . Estraendo la radice quadrata, l’unico valore valido di $k$ è in conclusione:

$k = \sqrt{\frac{\sqrt{5}+1}{2}}.$

Se $\overline{BC} > \overline{AB}$ , allora $\tan(\widehat{BAC}) = k$ e abbiamo finito; se invece $\overline{AB} > \overline{BC}$ :

$\tan(\widehat{BAC}) = \frac{1}{k} = \sqrt{\frac{2}{\sqrt{5}+1}} = \sqrt{\frac{2\left(\sqrt{5}-1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}} = \sqrt{\frac{\sqrt{5}-1}{2}}.$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2019-I

Si consideri l’equazione

$x\, 2^x = y\, 2^y.$

Quante coppie di interi positivi distinti $(x,y)$ sono soluzioni?

$\quad$

$\fbox{a}$ Nessuna.

$\fbox{b}$ Una sola.

$\fbox{c}$ Esattamente 2.

$\fbox{d}$ Esattamente 4.

$\fbox{e}$ Infinite.

Soluzione.

Per $x > 0$ , la funzione $f(x) = x\,2^x$ è il prodotto di due funzioni strettamente crescenti e positive ( $x$ e $2^x$ ): come tale, è a sua volta strettamente crescente, e quindi è iniettiva. Questo vuol dire che, se $f(x) = f(y)$ , allora $x = y$ . Dato che il quesito richiede il numero di coppie di interi distinti, concludiamo che non ne esiste nessuna.

La risposta corretta è dunque la $\fbox{a}$ .

Quesito 2019-J

Un triangolo equilatero ha centro $O$ e lato di lunghezza 1. Si fa passare una retta per $O$ , che intercetta i lati del triangolo in due punti $P$ e $Q$ . Qual è il minimo valore possibile della lunghezza di $PQ$ ?

$\quad$

$\fbox{a}$ $\dfrac{1}{3}$ .

$\fbox{b}$ $\dfrac{1}{2}$ .

$\fbox{c}$ $\dfrac{\sqrt{3}}{3}$ .

$\fbox{d}$ $\dfrac{2}{3}$ .

$\fbox{e}$ $\dfrac{\sqrt{3}}{2}$ .

Soluzione.

La figura mostra una rappresentazione del problema. Per simmetria, basta considerare il caso in cui il punto $P$ appartenga al segmento $CD$ . Il triangolo $OBD$ è metà di un triangolo equilatero, per cui $\overline{OB} = 2\overline{BD}/\sqrt{3} = 1/\sqrt{3}$ . Intuitivamente, la lunghezza della corda $PQ$ è minima quando è parallela ad uno dei lati del triangolo (come esemplificato dal segmento verde in figura). In questo caso, il triangolo $PQB$ è equilatero, per cui $\overline{PQ} = 2\overline{OB}/\sqrt{3} = 2/3.$

$\quad$

Dimostriamo che $2/3$ è proprio il valore minimo di $\overline{PQ}$ . Sia $\vartheta = \widehat{DOP}$ come indicato in figura. Si noti che $\widehat{QBO} = \widehat{OBP} = 30\degr$ , $\widehat{OPB} = 90\degr - \vartheta$ , $\widehat{OQB} = \vartheta + 30\degr$ . Applicando il teorema dei seni, abbiamo allora:

$\begin{array}{l@{\mbox{}\implies\mbox{}}l} \dfrac{\overline{OP}}{\sin(\widehat{OBP})} = \dfrac{\overline{OB}}{\sin(\widehat{OPB})} & \overline{OP} = \dfrac{\sin(30\degr)}{\sqrt{3}\sin(90\degr-\vartheta)} = \dfrac{1}{2\sqrt{3}\cos(\vartheta)}; \\[10pt] \dfrac{\overline{OQ}}{\sin(\widehat{QBO})} = \dfrac{\overline{OB}}{\sin(\widehat{OQB})} & \overline{OQ} = \dfrac{\sin(30\degr)}{\sqrt{3}\sin(\vartheta+30\degr)} = \dfrac{1}{2\sqrt{3}\cos(60\degr-\vartheta)}. \end{array}$

La lunghezza di $QP$ da minimizzare è quindi data da:

$\overline{QP} = \overline{OP}+\overline{OQ} = \frac{1}{2\sqrt{3}}\left[\frac{1}{\cos(\vartheta)}+\frac{1}{\cos(60\degr-\vartheta) }\right].$

Purtroppo, la studio del segno della derivata di questa espressione non è agevole. Per trovare il minimo, possiamo usare la disuguaglianza tra media aritmetica e geometrica: per ogni $a,b \geq 0$ , si ha $(a+b)/2 \geq \sqrt{ab}$ . Nel nostro caso:

$\begin{aligned} \phantom{=} {} & \frac{1}{2}\left[\frac{1}{\cos(\vartheta)}+\frac{1}{\cos(60\degr-\vartheta)}\right] \geq \sqrt{\frac{1}{\cos(\vartheta)}\frac{1}{\cos(60\degr-\vartheta)}} = \\ = {} & \frac{1}{\sqrt{\dfrac{1}{2}[\cos(60\degr)+\cos(2\vartheta-60\degr)]}} = \frac{\sqrt{2}}{\sqrt{\dfrac{1}{2}+\cos(2\vartheta-60\degr)}} \geq \frac{\sqrt{2}}{\sqrt{\dfrac{1}{2}+1}} = \frac{2}{\sqrt{3}}. \end{aligned}$

Abbiamo usato la formula di Werner $\cos(\alpha)\cos(\beta) = [\cos(\alpha+\beta)+\cos(\alpha-\beta)]/2$ e la disuguaglianza $\cos(2\vartheta-60\degr)\leq 1$ . Concludiamo finalmente che $\overline{QP} \geq 2/3$ .

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2020-A

Un quadrato ha centro nel punto di coordinate $C = (3,4)$ e uno dei vertici ha coordinate $(1,5)$ . Quale tra le seguenti coppie corrisponde alle coordinate di un altro dei vertici?

$\quad$

$\fbox{a}$ $(1,3)$ .

$\fbox{b}$ $(5,5)$ .

$\fbox{c}$ $(4,2)$ .

$\fbox{d}$ $(2,2)$ .

$\fbox{e}$ $(5,2)$ .

Soluzione.

Conviene disegnare i punti sul piano cartesiano, oppure su carta quadrettata. Un vertice del quadrato è il simmetrico di $(1,5)$ rispetto a $C$ e ha dunque coordinate $(5,3)$ . La diagonale identificata da questi punti ha pendenza $-1/2$ ; l’altra diagonale, che le è perpendicolare, ha quindi pendenza $+2$ . A partire da $C$ , si possono quindi identificare facilmente le coordinate dei vertici rimanenti $(4,6)$ e $(2,2)$ . Solo quest’ultimo punto (cerchiato in rosso) corrisponde ad una delle opzioni disponibili (le altre sono indicate dalle crocette grigie).

$\quad$

Si può alternativamente ricorrere al calcolo vettoriale. Il vettore che porta da $C$ al punto $(1,5)$ è $v_0 = (-2,1)$ . Per trovare gli altri vertici del quadrato, possiamo calcolare la rotazione di $v_0$ di 90, 180 e 270 $\degr$ , ottenendo $v_{90} = (1,2)$ , $v_{180} = (2,-1)$ e $v_{270} = (-1,-2)$ . Sommando questi tre vettori a $C$ , si ritrovano le coordinate dei tre vertici: $(4,6)$ , $(5,3)$ e $(2,2)$ .

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2020-B

Calcolare il valore del seguente integrale definito:

$\int_0^1(e^x-x)(e^x+x)\diff{x}.$

$\quad$

$\fbox{a}$ $\dfrac{3e^2-2}{6}$ .

$\fbox{b}$ $\dfrac{3e^2+2}{6}$ .

$\fbox{c}$ $\dfrac{2e^2-3}{6}$ .

$\fbox{d}$ $\dfrac{3e^2-5}{6}$ .

$\fbox{e}$ $\dfrac{e^2+3}{6}$ .

Soluzione.

Si tratta di calcolare primitive elementari. Iniziamo semplificando la funzione integranda, sfruttando il prodotto notevole della differenza di quadrati:

$(e^x-x)(e^x+x) = (e^x)^2 - x^2 = e^{2x} - x^2.$

Di conseguenza:

$\begin{aligned} \int_0^1(e^x-x)(e^x+x)\diff{x} = {} & \int_0^1(e^{2x} - x^2)\diff{x} = \\ = {} & \left.\frac{1}{2}e^{2x}\right|_0^1 - \left.\frac{1}{3}x^3\right|_0^1 = \\[5pt] = {} & \left(\frac{e^2}{2} - \frac{1}{2}\right) - \frac{1}{3} = \frac{3e^2-5}{6}. \end{aligned}$

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2020-C

Calcolare la seguente somma:

$S = 1 - 4 + 9 - 16 + \cdots + 99^2 - 100^2 = \sum_{k=1}^{100}(-1)^{k+1}k^2.$

$\quad$

$\fbox{a}$ $-101$ .

$\fbox{b}$ $-1000$ .

$\fbox{c}$ $-1111$ .

$\fbox{d}$ $-4545$ .

$\fbox{e}$ $-5050$ .

Soluzione.

Raggruppiamo i termini a due a due, notando che sono tutti differenze di quadrati (dispari e pari alternati):

$\begin{array}{r@{\mbox{}=\mbox{}}c@{\mbox{}=\mbox{}}l} 1-4 & 1^2-2^2 & -3; \\ 9-16 & 3^2-4^2 & -7; \\ 25-36 & 5^2-6^2 & -11; \\ \multicolumn{3}{c}{\ldots\qquad\ldots\qquad\ldots} \end{array}$

Riscriviamo la somma come segue (essendoci 100 addendi, ci sono 50 coppie):

$\begin{aligned} S = {} & \sum_{k=1}^{50}[(2k-1)^2 - (2k)^2] = \sum_{k=1}^{50}(4k^2+1-4k-4k^2) = \\ = {} & \sum_{k=1}^{50}(1-4k) = \sum_{k=1}^{50}1 - 4\sum_{k=1}^{50}k = \\ = {} & 50 - 4\frac{50\times51}{2} = 50\times(1-2\times51) = -5050. \end{aligned}$

Abbiamo dato per nota la formula della somma dei primi $N$ numeri naturali:

$\sum_{k=1}^{N}k = \frac{N(N+1)}{2}.$

La risposta corretta è dunque la $\fbox{e}$ .

Quesito 2020-D

Al variare del numero reale $\vartheta$ , determinare il massimo valore assunto dalla quantità:

$f(\vartheta) = 3\cos^2\vartheta + 2\sin\vartheta + 1.$

$\quad$

$\fbox{a}$ $\dfrac{11}{5}$ .

$\fbox{b}$ $\dfrac{13}{3}$ .

$\fbox{c}$ $\dfrac{12}{5}$ .

$\fbox{d}$ $\dfrac{14}{9}$ .

$\fbox{e}$ $\dfrac{12}{7}$ .

Soluzione.

Usando l’identità trigonometrica fondamentale, e sfruttando la tecnica del completamento del quadrato, riscrivamo la nostra espressione nel seguente modo:

$\begin{aligned} f(\vartheta) = {} & 3\cos^2\vartheta + 2\sin\vartheta + 1 = \\ = {} & 3 - 3\sin^2\vartheta + 2\sin\vartheta + 1 = \\ = {} & 4 - 3\left(\sin\vartheta-\frac{1}{3}\right)^2 + \frac{1}{3} = \\ = {} & \frac{13}{3} - 3\left(\sin\vartheta-\frac{1}{3}\right)^2. \end{aligned}$

Scritto in questo modo, si vede immediatamente che l’espressione raggiunge il suo valore massimo $13/3$ ogniqualvolta il termine tra parentesi quadre si annulla (cioè quando $\sin\vartheta = 1/3$ ).

Una soluzione alternativa e più “classica” è studiare gli zeri della derivata prima. La funzione $f$ è derivabile e definita su un dominio aperto, per cui tutti i suoi massimi sono punti stazionari. La derivata $f'$ si annulla se:

$f'(\vartheta) = -6\cos\vartheta\,\sin\vartheta + 2\cos\vartheta = 2\cos\vartheta\,(1-3\sin\vartheta) = 0.$

I punti stazionari sono quindi tali che $\cos\vartheta = 0$ oppure $\sin\vartheta = 1/3$ . Per stabilire quali sono massimi, è sufficiente calcolare $f$ per questi valori:

$\begin{array}{l@{\mbox{}\implies\mbox{}}l@{\mbox{}\implies\mbox{}}l} \cos\vartheta = 0 & \sin\vartheta = \pm1 & f(\vartheta) = 0 \pm 2 + 2 = 2 \pm 2; \\[2.5pt] \sin\vartheta = \dfrac{1}{3} & \cos^2\vartheta = \dfrac{8}{9} & f(\vartheta) = 3\cdot\dfrac{8}{9} + 2\cdot\dfrac{1}{3} + 1 = \dfrac{13}{3}. \end{array}$

Dato che $2\pm 2 \leq 4$ , si conclude che $13/3$ è il valore massimo di $f$ .

Ringraziamo Massimiliano Ruffini per l’aiuto con la soluzione di questo quesito.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2020-E

Una retta è tangente alla parabola di equazione $y = x^2$ nel punto di coordinate $(a,a^2)$ , dove $a > 0$ è un parametro reale. Calcolare l’area della regione di piano compresa tra la tangente, la parabola e l’asse delle ascisse.

$\quad$

$\fbox{a}$ $\dfrac{a^2}{3}$ .

$\fbox{b}$ $\dfrac{2a^2}{3}$ .

$\fbox{c}$ $\dfrac{a^3}{12}$ .

$\fbox{d}$ $\dfrac{5a^3}{6}$ .

$\fbox{e}$ $\dfrac{a^4}{10}$ .

Soluzione.

Per prima cosa, determiniamo l’equazione della retta tangente alla parabola nel punto $(a,a^2)$ . La retta avrà come coefficiente angolare la derivata della parabola in $x = a$ , cioè $2a$ . La retta passa inoltre per $(a,a^2)$ , per cui:

$y = a^2 + 2a(x-a).$

L’intersezione di questa retta con l’asse delle ascisse si ha se $a^2 + 2a(x-a) = 0$ , cioè per $x = a/2$ (in figura, è mostrato come esempio il caso $a = 2$ ).

$\quad$

L’area $\mathcal{A}$ che ci interessa è ombreggiata in azzurro più scuro nella figura. Per semplicità di calcolo, si può sottrarre l’area del triangolo azzurro chiaro dall’area della regione totale azzurra:

$\mathcal{A} = \int_0^a x^2\diff{x} - \frac{a/2\cdot{a^2}}{2} = \left.\frac{x^3}{3}\right|_0^a - \frac{a^3}{4} = \frac{a^3}{3} - \frac{a^3}{4} = \frac{a^3}{12}.$

Se la si conosce, si può alternativamente ricorrere alla formula di Archimede, evitando l’utilizzo degli integrali. Consideriamo il segmento parabolico per $-a \leq x \leq +a$ . La sua area è pari ai $2/3$ dell’area del rettangolo a sé circoscritto, denotato in figura dalla linea punteggiata. L’area interna al rettangolo al di sotto alla parabola è quindi $1/3$ dell’area dell’intero rettangolo, e l’area totale azzurra è la metà di questo valore, cioè $(1/2)\cdot(1/3)\cdot [(2a) \cdot a^2] = a^3/3$ . Come prima, da questo valore va sottratta l’area del triangolo azzurro chiaro ( $a^3/4$ ), e si ritrova il risultato $\mathcal{A} = a^3/3 - a^3/4 = a^3/12$ .

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2020-F

Quale delle seguenti espressioni è uguale a $\log_{10}(10\times9\times8\times\cdots\times2\times1)$ ?

$\quad$

$\fbox{a}$ $1+5\log_{10}(2)+4\log_{10}(6)$ .

$\fbox{b}$ $1+4\log_{10}(2)+2\log_{10}(6)+\log_{10}(7)$ .

$\fbox{c}$ $2+2\log_{10}(2)+4\log_{10}(6)+\log_{10}(7)$ .

$\fbox{d}$ $2+6\log_{10}(2)+4\log_{10}(6)+\log_{10}(7)$ .

$\fbox{e}$ $2+6\log_{10}(2)+4\log_{10}(6)$ .

Soluzione.

È sufficiente utilizzare le proprietà dei logaritmi, e raggruppare opportunamente i fattori presenti nell’argomento, mettendo in evidenza i numeri 10, 7, 6 e 2 (quelli suggeriti dalla rosa delle possibili risposte).

$\begin{aligned} \phantom{=} {} & \log_{10}(10\times9\times8\times7\times6\times5\times4\times3\times2\times1) = \\ = {} & \log_{10}({\color{Mulberry}10}\times{\color{blue}9}\times{\color{blue}8}\times{\color{ForestGreen}7}\times{\color{blue}6}\times{\color{Mulberry}5}\times{\color{Dandelion}4}\times{\color{blue}3}\times{\color{Mulberry}2}) = \\ = {} & \log_{10}({\color{Mulberry}10^2}\times{\color{blue}6^4}\times{\color{ForestGreen}7}\times{\color{Dandelion}2^2}) = \\ = {} & {\color{Mulberry}2} + 4\log_{10}({\color{blue}6}) + \log_{10}({\color{ForestGreen}7}) + 2\log_{10}({\color{Dandelion}2}). \end{aligned}$

La risposta corretta è dunque la $\fbox{c}$ .

Quesito 2020-G

Siano $a$ , $b$ , $c$ , $d$ quattro parametri reali. Il grafico di una cubica di equazione $y = x^3 + ax^2 + bx + c$ presenta due punti estremanti di coordinate $(1,2)$ e $(3,d)$ . Quanto vale $d$ ?

$\quad$

$\fbox{a}$ $-4$ .

$\fbox{b}$ $-2$ .

$\fbox{c}$ $0.$

$\fbox{d}$ $2.$

$\fbox{e}$ $4.$

Soluzione.

Essendo $y$ una funzione derivabile su un dominio aperto, i punti estremanti sono stazionari, cioè hanno derivata nulla. La derivata della cubica è:

$y' = 3x^2 + 2ax + b.$

Sappiamo che $y'(1) = y'(3) = 0$ :

$\begin{cases} 3 + 2a + b = 0; \\ 27 + 6a + b = 0; \end{cases}\implies24+4a = 0 \implies a = -6,$

dove per ricavare $a$ abbiamo sottratto la prima equazione dalla seconda. Inoltre, $b = -2a - 3 = 9$ . Ora sfruttiamo le altre due condizioni date del testo. Per primo, la cubica passa per il punto $(1,2)$ :

$1 + a + b + c = 1 - 6 + 9 + c = 2 \implies c = -2.$

Inoltre la cubica passa per il punto $(3,d)$ :

$3^3 + a\cdot3^2 + b\cdot3 + c = 27 - 6\cdot9 + 9\cdot3 - 2 = d \implies d = -2.$

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2020-H

Sono date tre funzioni differenziabili $f$ , $g$ e $h$ . Le cinque figure qui sotto mostrano, mescolati in ordine casuale, i grafici delle funzioni $f$ , $g$ , $h$ , $f'$ e $g'$ (l’apice indica la derivata prima). Qual è il grafico della funzione $h$ ?

$\quad$

Soluzione.

Ricordiamo che gli zeri di una funzione derivata corrispondono ai punti a tangente orizzontale (punti stazionari) del grafico della funzione primitiva.

$\quad$

Il grafico $\fbox{d}$ ha un unico zero, per cui può essere la derivata solo del grafico $\fbox{c}$ (che ha un unico punto stazionario), ma questo può essere escluso perché la funzione $\fbox{d}$ è positiva per $x\to-\infty$ , mentre la curva $\fbox{b}$ è descrescente per $x\to-\infty$ . Quindi $\fbox{d}$ non è la derivata di nessuno degli altri grafici.

Inoltre il grafico $\fbox{d}$ ha due punti stazionari, per cui può essere la primitiva solo del grafico $\fbox{b}$ , ma questo è ancora una volta escluso dal segno: la funzione $\fbox{b}$ è positiva per $x\to-\infty$ , mentre la curva $\fbox{d}$ è descrescente per $x\to-\infty$ .

Quindi, il grafico $\fbox{d}$ non è né la derivata né la primitiva di una delle altre funzioni, quindi deve corrispondere per forza alla funzione $h$ .

Volendo, con considerazioni analoghe, basate sul numero degl zeri, dei punti stazionari, e degli intervalli di crescenza e positività, si può anche concludere che i grafici $\fbox{c}$ ed $\fbox{e}$ sono le derivate dei grafici $\fbox{b}$ ed $\fbox{a}$ , rispettivamente.

La risposta corretta è dunque la $\fbox{d}$ .

Quesito 2020-I

Considerato $\vartheta$ nel dominio $(-\pi/2,0) \cup (0,\pi/2)$ , si consideri la seguente somma infinita:

$S(\vartheta) = \frac{1}{\tan\vartheta} + \frac{1}{\tan^2\vartheta} + \frac{1}{\tan^3\vartheta} + \cdots.$

Per quanti valori di $\vartheta$ si ha che $S$ è pari a $\tan\vartheta$ ?

$\quad$

$\fbox{a}$ 0.

$\fbox{b}$ 1.

$\fbox{c}$ 2.

$\fbox{d}$ 3.

$\fbox{e}$ 4.

Soluzione.

Per prima cosa, dobbiamo verificare per quali valori di $\vartheta$ la somma converge. Ricordiamo la formula per la somma della serie geometrica, valida se $|q| < 1$ :

$\sum_{k=0}^{+\infty}q^k = \frac{1}{1-q}.$

Nel nostro caso, possiamo esprimere $S$ come una serie geometrica di ragione $q = 1/\tan\vartheta$ , a condizione che $|1/\tan\vartheta| < 1$ , cioè $|\tan\vartheta| > 1$ . Se vale questa condizione, abbiamo (tenendo presente che la somma parte da $k=1$ ):

$\begin{aligned} S(\vartheta) = {} & \sum_{k=1}^{+\infty}\left(\frac{1}{\tan\vartheta}\right)^k = \frac{1}{1-(1/\tan\vartheta)}-1 = \\ = {} & \frac{\tan\vartheta}{\tan\vartheta-1} - 1 = \frac{1}{\tan\vartheta-1}. \end{aligned}$

L’equazione $S(\vartheta) = \tan\vartheta$ corrisponde dunque a:

$\frac{1}{\tan\vartheta-1} = \tan\vartheta \implies \tan^2\vartheta - \tan\vartheta - 1 = 0.$

Sostituendo $t = \tan\vartheta$ , si ha l’equazione di secondo grado $t^2 - t - 1 - 0$ , che ha due soluzioni:

$t = \tan\vartheta = \frac{1\pm\sqrt{5}}{2}.$

Ricordando la condizione di convergenza $|\tan\vartheta| > 1$ , solo $(1+\sqrt{5})/2$ è accettabile. Dato che nell’intervallo $-\pi/2 < \vartheta < \pi/2$ la funzione tangente è strettamente monotona e suriettiva, esiste un solo valore di $\vartheta$ che soddisfa l’equazione proposta.

La risposta corretta è dunque la $\fbox{b}$ .

Quesito 2020-J

Sono dati un quadrato di lato 2 ed un cerchio di raggio $r$ , centrati sul medesimo punto del piano. Definiamo:

$\quad$

$A(r)$ è l’area della regione interna al cerchio ma esterna al quadrato;

$B(r)$ è l’area della regione interna al quadrato ma esterna al cerchio.

Quale dei seguenti grafici mostra, qualitativamente, l’andamento della funzione $A(r) + B(r)$ ?

$\quad$

Soluzione.

Calcoliamo le funzioni $A(r)$ e $B(r)$ nei due casi “facili”.

$\quad$

Se $r < 1$ , il cerchio è interamente contenuto nel quadrato, per cui $A(r) = 0$ , $B(r) = 4 - \pi r^2$ e quindi $A+B = 4-\pi r^2$ ; si tratta di una parabola con la concavità verso il basso, che esclude l’opzione $\fbox{c}$ .

Se $r > \sqrt{2}$ , il quadrato è interamente contenuto nel cerchio, per cui $A(r) = \pi r^2-4$ , $B(r) = 0$ e quindi $A+B = \pi r^2 - 4$ ; si tratta di una parabola con la concavità verso l’alto, che esclude le opzioni $\fbox{a}$ e $\fbox{b}$ .

Per $1 < r < \sqrt{2}$ , le funzioni $A$ e $B$ sono entrambe strettamente positive, per cui non è possibile che $A(r)+B(r) = 0$ . Questo esclude le opzioni $\fbox{b}$ (di nuovo) ed $\fbox{e}$ . Resta l’opzione $\fbox{d}$ , che è qualitativamente consistente con la geometria del problema.

Per curiosità, come mostrato separatamente, è possibile calcolare analiticamente $A(r)$ e $B(r)$ per $1 \leq r \leq \sqrt{2}$ . Si trova che:

$\begin{gather*} A(r) = 4\cdot\left(r^2\arccos\frac{1}{r}-\sqrt{r^2-1}\right)\!; \\ B(r) = 4\cdot\left[1-\sqrt{r^2-1}-r^2\left(\frac{\pi}{4}-\arccos\frac{1}{r}\right)\right]\!. \end{gather*}$

Come descritto precedentemente, l’andamento di $A(r)$ e $B(r)$ per $r < 1$ e $r > \sqrt{2}$ è facile da calcolare e permette di risolvere il quesito. Concludiamo qui studiando il caso $1 \leq r \leq \sqrt{2}$ , mostrato in figura. Le aree $A(r)$ e $B(r)$ corrispondono alla regioni colorate in blu e giallo, rispettivamente. Per simmetria, ci limitiamo a calcolare le aree in un solo ottante (la regione $PCT$ in figura).

$\quad$

Per prima cosa, dato che $\overline{CR} = 1$ , il segmento $QR$ ha lunghezza:

$\overline{QR} = \sqrt{\overline{CQ}^2-\overline{CR}^2} = \sqrt{r^2-1}.$

L’angolo $\vartheta$ è dato da:

$\vartheta = \arccos\frac{\overline{CR}}{\overline{CQ}} = \arccos\frac{1}{r}.$

L’area $\mathcal{A}_{TQR}$ della regione $TQR$ si può calcolare per sottrazione, essendo pari all’area del settore circolare $TQC$ meno quella del triangolo $RQC$ . Abbiamo:

$A(r) = 8\,\mathcal{A}_{TQR} = 8\left(\frac{1}{2}\overline{CQ}^2\vartheta - \frac{1}{2}\overline{QR}\cdot\overline{CR}\right) = 4\left(r^2\arccos\frac{1}{r}-\sqrt{r^2-1}\right)\!.$

In modo simile, l’area $\mathcal{A}_{QPS}$ della regione $QPS$ si può calcolare come differenza tra l’area del triangolo $QPC$ e l’area del settore circolare $QSC$ , per cui: \begin{aligned}

$B(r) = {} & 8\,\mathcal{A}_{QPC} = 8\left[\frac{1}{2}\overline{QP}\cdot\overline{CR} - \frac{1}{2}\overline{CQ}^2\left(\frac{\pi}{4}-\vartheta\right)\right] = \\ = {} & 4\left[1-\sqrt{r^2-1}-r^2\left(\frac{\pi}{4}-\arccos\frac{1}{r}\right)\right]\!. \end{aligned}$

La figura mostra l’andamento delle funzioni $A$ , $B$ e $A+B$ . Si ha $A'(r)+B'(r) = 4r[4\arccos(1/r)-\pi/2]$ per $1 \leq r \leq \sqrt{2}$ , da cui si vede che $A+B$ ha un unico minimo per $r = 1/\!\cos(\pi/8) \approx 1\text{,082}$ .

$\quad$

La risposta corretta è dunque la $\fbox{d}$ .

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.