In questo articolo raccogliamo 120 esercizi tratti dai test d’ingresso per le facoltà di Ingegneria, o quesiti a essi ispirati. Gli esercizi coprono il programma di matematica di base tradizionalmente affrontato nei vari Istituti superiori italiani e risulta pertanto un efficace banco di prova sia per chi desidera prepararsi a tali selezioni, sia per chi ricerca semplicemente un modo per testare a 360 gradi la sua preparazione in Matematica. Di ogni esercizio forniamo una soluzione dettagliata, che non si limita a riportare l’opzione corretta, ma fornisce una discussione approfondita sul metodo risolutivo, risultando così particolarmente efficace nell’apprendimento.
Buona lettura a tutti!
Consigliamo una visita alle nostre cartelle relative al programma di Matematica della Scuola superiore per il materiale teorico di riferimento e ulteriori esercizi sui medesimi temi.
Premessa
Leggi...
Autori e revisori
Leggi...
Revisori: Valerio Brunetti, Davide Germani, Sergio Fiorucci.
Contenuti della dispensa
Leggi...
- Monomi e polinomi, incluse le tecniche di scomposizione;
- Equazioni e disequazioni di primo e secondo grado, con estensioni al grado superiore e utilizzo dei moduli;
- Sistemi di disequazioni;
- Operazioni sui radicali
- Funzioni esponenziali e logaritmiche;
- Problemi di Geometria euclidea;
- Geometria analitica (studio della retta, parabola, circonferenza, ellisse, iperbole);
- Geometria solida;
- Goniometria e trigonometria (studio delle funzioni trigonometriche, risoluzione di equazioni e disequazioni, applicazione delle formule fondamentali quali archi associati, duplicazione, somma, sottrazione e bisezione);
- Calcolo combinatorio, statistica e probabilità.
Ogni esercizio è corredato da una spiegazione approfondita e, ove opportuno, da rappresentazioni grafiche per agevolare la comprensione dei procedimenti. L’attenzione alla chiarezza e alla precisione rende questo strumento adatto agli studenti di diversi percorsi formativi, inclusi licei scientifici, classici, linguistici e istituti tecnici.
Esercizi
- una retta;
- una circonferenza;
- una parabola;
- un’ellisse;
- un’iperbole.
Svolgimento.
La distanza al quadrato fra due punti e
nel piano è
Quindi l’insieme dei punti del piano che verificano l’equazione data nell’esercizio
distano dal punto
esattamente
(vedi figura 1)
Figura 1: circonferenza centrata in e di raggio
.
Il luogo di tali punti è quindi una circonferenza e la risposta corretta è la 2.
- tutto
;
-
;
-
;
-
;
-
.
Svolgimento.
Il logaritmo di un numero in una certa base è definito solo quando l’argomento è positivo, perciò il dominio di esistenza della funzione è l’insieme dei punti
per cui
Dobbiamo studiare quindi i segni di e di
e selezionare solo l’insieme dei valori
per cui il prodotto dei loro segni è positivo.
Lavoriamo con l’usuale diagramma:
Quindi si ottiene
Il grafico della funzione è mostrato in figura 2.
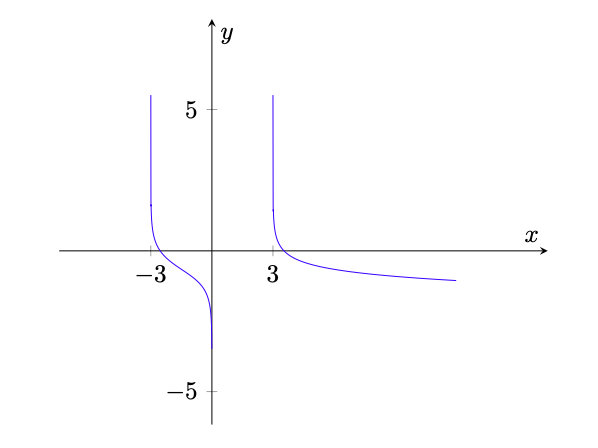
Figura 2: grafico della funzione .
La risposta giusta è quindi la 4.
- 11;
- 8;
- 10;
- 7;
- 6.
Svolgimento.
Dati una coppia di numeri ed
, una successione geometrica di ragione
e primo termine
è una successione
Una successione così fatta ha la peculiarità che il rapporto tra un termine ed il precedente è sempre costante ed è uguale alla ragione .
Nel caso dell’esericizio
e
, dobbiamo quindi risolvere
La risposta corretta è quindi la 4.
- un punto;
- una sfera non degenere;
- un cilindro non degenere;
- vuoto;
- nessuna delle precedenti.
Svolgimento.
Una somma di quadrati è sempre maggiore o uguale a zero ed è zero se e soltanto se tutti gli addendi sono uguali a . Otteniamo quindi
Il luogo è quindi un solo punto, .
- il quadrato dell’altezza per il perimetro della sua base;
- il doppio dell’area della base per l’altezza;
- tre volte il volume di una piramide avente la stessa base e altezza del prisma;
- l’area della base per il quadrato della sua altezza;
- nessuna delle precedenti.
Svolgimento.
Il volume di un prisma è uguale al prodotto dell’area di base
per la sua altezza
. D’altro canto, la formula per il calcolo del volume
di una piramide avente stessa base e altezza del prisma è
In figura 3 diamo un esempio di prisma e piramide a base pentagonale.

Figura 3: esempio di prisma e piramide a base pentagonale.
Perciò la risposta corretta è 3.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Se il parallelepipedo ha dimensioni , allora la sua area è
Invece, l’area di un parallelepipedo ottenuto dimezzandone le dimensioni pari a
è
La risposta giusta è quindi la 3.
- Alla terza settimana;
- Alla quarta settimana;
- Dopo 5 settimane;
- Non conviene mai;
- Alla seconda settimana.
Svolgimento.
Sia il prezzo iniziale e
il prezzo all’
-esima settimana. Allora
La settimana per cui conviene comprare equivale al più grande per cui
, ovvero
Perciò è la settimana più conveniente e la risposta esatta è la 1.
- Per nessun valore di
;
- Per tutti i valori di
;
- Per
;
- Per
;
- Per tutti i valori di
tranne
.
Svolgimento.
Osserviamo che è sempre positivo e
è sempre minore di
, perciò il rapporto fra
e
supera
. Dato che stiamo facendo un rapporto, dobbiamo tenere conto che il calcolo ha senso solo quando il denominatore è diverso da
, perciò solo per
. Quindi la disequazione è valida per tutti i valori di
tranne
.
-
;
-
;
-
;
-
;
- del cinquanta per cento.
Svolgimento.
Gli eventi del lancio di un dado sono fra loro indipendenti, quindi la probabilità è il prodotto delle probabilità di ottenere in sequenza. Dato che la probabilità in tutti e tre i casi è sempre
, allora la risposta è
.
- 120;
- 6;
- 2;
- 20;
- 24.
Svolgimento.
Consideriamo la prima cinquina:
Abbiamo quindi che tale numero non può superare .
D’altronde in ogni cinquina di numeri consecutivi vi deve essere un numero multiplo di
dato che sono spaziati proprio di
in
. In modo analogo, tra i cinque numeri ci deve essere almeno un multiplo di
, un multiplo di
, e infine un multiplo di
ma non di
. Dunque il loro prodotto è divisibile per
.
Scarica gli esercizi svolti
Ottieni il documento contenente 120 esercizi risolti, contenuti in 107 pagine ricche di dettagli, per i test di ingresso per ingegneria
- 1256,20 euro;
- 674,23 euro;
- 956,45 euro;
- 13455 euro;
- 728 euro.
Svolgimento.
Sia il deposito iniziale,
gli anni,
l’interesse e
le spese annue.
Infine sia
l’ammontare del conto in banca all’anno
. Quindi
. Sia
; allora
Otteniamo quindi per che il conto del cliente dopo 3 anni ammonta a
euro.
Nel caso in cui si volesse dedurre una formula per determinare automaticamente in funzione dell’anno
, basta generalizzare il caso di sopra per un qualunque
:
(1)
La formula (1) è stata solamente intuita ma per verificare che sia effettivamente quella corretta invitiamo il lettore a dimostrarla usando il principio di induzione.
Inoltre osserviamo che (1) può essere riscritta in una maniera più compatta usando il fatto che si conosce la somma parziale di una serie geometrica di ragione :
(2)
Perciò, sostistuendo la sommatoria in (1) con il valore ottenuto in (2), otteniamo
da cui si può di nuovo calcolare che euro.
Quale delle seguenti equazioni descrive una retta ortogonale ad e passante per il punto
?
-
;
-
;
-
;
-
;
-
.
Svolgimento.
L’equazione di una retta non parallela all’asse delle ordinate è
, dove
è il coefficiente angolare della retta e
è l’intercetta. Il coefficiente angolare di una retta ortogonale ad
è
. Quindi una retta ortgonale ad
e passante per un punto
ha equazione
Nel nostro caso specifico abbiamo e
, perciò la retta cercata ha equazione
In figura 4 mostriamo le due rette:
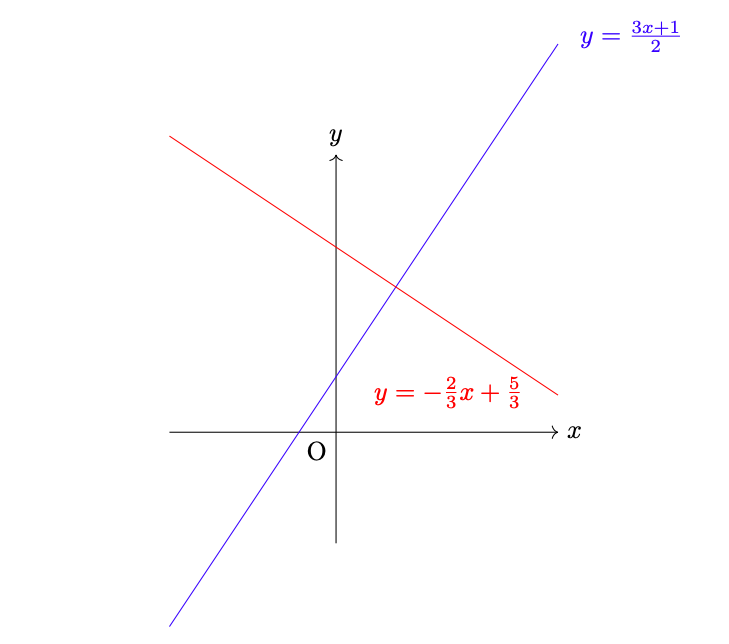
Figura 4: la retta e la sua perpendicolare per il punto
.
La risposta giusta è quindi la 4.
- non ha soluzioni nell’insieme
dei numeri interi;
- ha sempre almeno una soluzione nell’insieme
;
- non ha soluzioni nell’inisieme
dei numeri razionali;
- ha soluzioni nell’insieme
dei numeri reali ma non su
;
- non ha mai soluzione nell’insieme
.
Svolgimento.
Dall’equazione si ottiene che , che su
non può avere soluzioni, dato che
è sempre un numero pari e
è un numero dispari. Se si ragiona invece su una estensione di
come ad esempio
, una soluzione esiste ed è banalemente
.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Una funzione definita su due oggetti si può vedere come una collezione di scatole affiancate dove dentro possiamo inserire uno solo dei
oggetti del codominio, eventualmente anche ripetuti. Il numero totale di possibili inserimenti è quindi
, che è quindi anche il numero di tutte le possibili funzioni da
a
. Nel caso di funzioni iniettive invece, gli oggetti da inserire non possono essere ripetuti, perciò in totale sono solo
. Il numero di funzioni non iniettive è quindi
.
Una soluzione alternativa può essere la seguente. è composto di due soli elementi, quindi una funzione non iniettiva definita su
è tale per cui i due elementi hanno la stessa immagine. Dato che
consta di
elementi, allora ci sono solamente
funzioni non iniettive.
- Non ci sono soluzioni per
;
- Ci sono in totale
soluzioni distinte;
- Ci sono in totale
soluzioni distinte;
- C’è una sola soluzione;
- Ci sono infinite soluzioni nell’intervallo
.
Svolgimento.
Usando la formula di duplicazione del seno, l’equazione data si può riarrangiare come
Dato che la funzione seno è suriettiva nell’intervallo e
, allora sicuramente esistono soluzioni dell’equazione. L’intersezione della retta
con il grafico della funzione
consta di due punti distinti per
. Dato che la funzione
è
-periodica, allora ci sono esattamente
soluzioni distinte per
(vedi figura 5).

Figura 5: grafico della funzione e intersezione con la retta
.
La risposta giusta è quindi la 2.
-
;
-
;
-
;
-
;
- è irriducibile.
Svolgimento.
Segue dalla scomposizione . Alternativamente, si può osservare che
è divisibile per
per il teorema di Ruffini, in quanto il suo valore per
è nullo.
Applichiamo il metodo di Ruffini per dividere
per
:
Otteniamo che . Dunque il quoziente della divisione è la risposta 1.
è:
-
;
-
;
-
;
-
;
- l’insieme vuoto.
Svolgimento.
La funzione logaritmo in una certa base è definita solamente quando l’argomento è positivo. Inoltre osserviamo che il numeratore dell’argomento si può scomporre come . Supponendo
e dividendo il numeratore per il denominatore
otteniamo che l’argomento è
, il quale è positivo solo per
. Ricordando che la funzione del quesito non era ben befinita per
, il dominio di esistenza di
è
. In figura 6 mostriamo il suo grafico:

Figura 6: grafico della funzione insieme al suo asintoto verticale
.
La risposta corretta è quindi la 3.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Il primo vertice può essere colorato con tutti e i colori, quindi abbiamo
scelte. Per ciascuna di queste scelte, il secondo vertice si può colorare solo con uno dei 6 colori rimanenti, il terzo vertice solo con uno dei 5 colori rimanenti e così via. Moltiplicando tutte queste possiblità si ottiene il numero di modi di colorare i
vertici ordinati con
colori:
In figura 7 diamo un esempio di colorazione del pentagono:
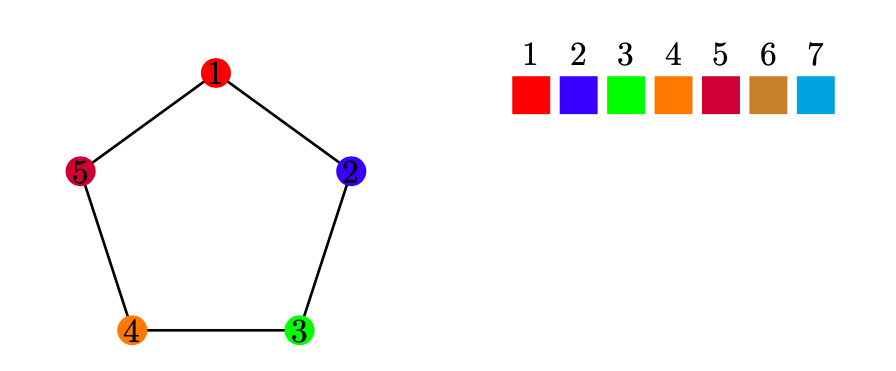
Figura 7: esempio di colorazione dei vertici del pentagono usando dei
colori disponbili.
La risposta giusta è quindi la 3.
- non incidenti;
- incidenti in più di due punti;
- incidenti in due punti;
- tangenti;
- nessuna delle precedenti.
Svolgimento.
Sostituendo l’equazione della retta in quella della circonferenza otteniamo
Dato che la loro intersezione consta di un solo punto di molteplicità , allora sono fra loro tangenti ed il punto di tangenza è
(vedi figura 8).
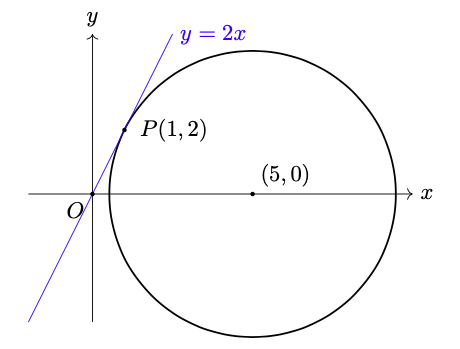
Figura 8: retta tangente alla circonferenza di centro
.
La risposta giusta è quindi la 4.
nel dominio di esistenza di ed
?
sono:
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
Nel caso 4 abbiamo che
Scrivendo le espressioni delle derivate dei restanti casi, si osserva che esse non sono uguali a .
- Circa
punti;
-
punti;
-
punti;
- Circa
punti;
-
punti.
Svolgimento.
La media del punteggio finale è
Perciò la risposta esatta è la 1.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
se e solo se
che è falso, quindi
.
è poco più di
in quanto
è circa
, quindi
. La 1 viene esclusa perché
, mentre
perché è la radice di un numero maggiore di
. Quindi la risposta corretta è la 5.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Sviluppiamo il quadrato:
Nella seconda disuguaglianza si è usata l’identità fondamentale della trigonometria e la formula di duplicazione del seno:
La risposta corretta è quindi la 4.
- Le donne sono i
degli uomini;
- Le donne sono
volte gli uomini;
- Le donne sono la metà degli uomini;
- Le donne sono
volte gli uomini;
- Le donne sono
volte gli uomini.
Svolgimento.
Sia il numero di uomini ed
il numero di donne.
Sia
e
le somme delle età degli uomini e delle donne rispettivemente. Allora si ha
Quindi
da cui .
La risposta corretta è quindi la 2.
- è 27 volte più grande;
- è 9 volte più grande;
- è 3 volte più grande;
- è 12 volte più grande;
- è 6 volte più grande.
Svolgimento.
Usando il teorema di Pitagora, si osserva che il rapporto tra la diagonale della faccia di un cubo e la lunghezza di un lato è
(vedi figura 9). In particolare, se la diagonale triplica, allora triplica anche il lato. Quindi il volume del nuovo cubo sarà
che equivale a volte il volume del cubo originario.

Figura 9: cubo di lato e quello di dimensioni triplicate.
La risposta corretta è quindi la 1.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Dal testo del quesito deduciamo che e
, ovvero
. Allora
La risposta corretta è quindi la 1.
- circonferenza;
- retta;
- parabola;
- ellisse;
- nessuna delle precedenti.
Svolgimento.
Osserviamo che l’equazione si può scrivere come un quadrato perfetto:
Quindi l’insieme dei punti che verificano tale equazione è l’insieme dei punti che verificano
ovvero una retta nel piano (vedi figura 10).

Figura 10: grafico della retta .
La risposta corretta è quindi la 2.
- 980 euro;
- 1326,7 euro;
- 1739,6 euro;
- 1121 euro;
- 598 euro.
Svolgimento.
Ciascuna delle prime notti costa
euro, per un totale di
euro. Invece ciascuna delle
notti restanti costerà
euro. Quindi il totale speso è di
euro.
- 32476;
- 12453;
- 21567;
- 26451;
- 28103.
Svolgimento.
Carl Friedrich Gauss trovò una formula per calcolare la somma dei primi
numeri consecutivi:
Calcolare la somma dei numeri da a
equivale a calcolare la differenza fra la somma dei primi
numeri e la somma dei primi
numeri:
Perciò la risposta corretta è la 5.
- infiniti valori;
-
;
-
oppure
;
- nessun valore di
;
-
.
Svolgimento.
non è mai un numero negativo, per cui non può essere minore di
.
- 2, 50;
- 4, 50;
- 6, 120;
- 4, 120;
- 6, 60.
Svolgimento.
Tali numeri si scompogono in fattori rispettivamente come segue:
Quindi il massimo comune divisore è e il minimo comune multiplo è
.
- un fascio di circonferenze concentriche;
- un fascio di circonferenze tangenti alla retta
;
- un fascio di circonferenze tangenti alla retta
;
- un fascio di circonferenze generato da due circonferenze date;
- nessuna delle precedenti.
Svolgimento.
Per ogni fissato, il luogo dei punti
che verificano l’equazione
è una circonferenza centrata nel punto
e di raggio
.
Osserviamo inoltre che la retta interseca ogni circonferenza del fascio in un solo punto
:
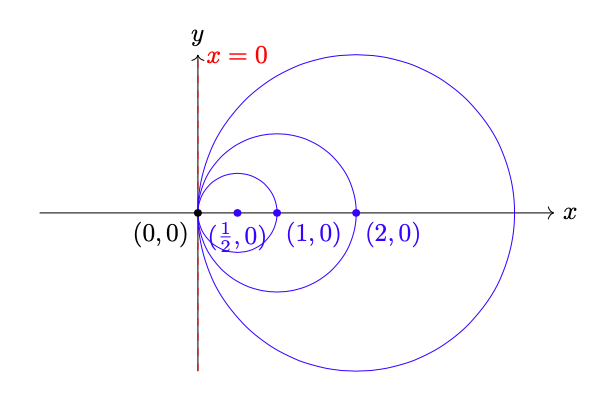
Figura 11: fascio di circonferenze tangenti alla retta .
Perciò l’equazione è quella di un fascio di circonferenze tangenti alla retta di equazione (vedi figura 11).
Pertanto la riposta coretta è la 2.
- 6, 5, 7;
- 7, 13 ,18;
- 5, 7, 1;
- 5, 12, 14;
- 5, 13, 14.
Svolgimento.
In un qualunque triangolo la somma di due lati deve essere sempre maggiore del lato rimanente (vedi figura 12). In formule, dato un triangolo di lati , allora
.
Una spiegazione può essere la seguente. Il lato di lunghezza è una porzione di linea retta, mentre i lati di lunghezza
e
descrivono una traiettoria (o meglio, una spezzata) che non è in linea retta. Pertanto la lunghezza della spezzata deve essere maggiore della lunghezza della porzione di linea retta.
Nel nostro caso specifico, possiamo notare che , quindi la terna 3 non è ammissibile.

Figura 12: triangolo di lati e
.
La risposta esatta è quindi la 3.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
1 e 2 non sono una terna di numeri che possono essere i lati di un triangolo, dato che e
. Infatti la lunghezza di ogni lato di un triangolo è sempre minore della somma dei lati rimanenti (si veda l’esercizio 33 per una spiegazione).
Inoltre anche 4 ed 5 sono da escludere in quanto il loro perimetro non è 13 cm. La riposta esatta è quindi la 3.
- 2713;
- 4591;
- 743;
- 937;
- 639.
Svolgimento.
Ricordiamo che un numero è divisibile per solo se la somma delle sue cifre è divisibile per
. Ci si può convincere di questo scrivendo un numero
, dove
indicano le sue cifre decimali:
Il numero si può scrivere come
, e in generale il numero
si può scrivere come
per un qualche numero intero
dipendente da
. Quindi il numero
può essere scritto come
Da qui si deduce che è divisibile per
solo se anche la somma delle sue cifre
è divisibile per
.
Nel caso del quesito, osserviamo che la somma delle cifre di è
, che è divisibile per
. Quindi
è divisibile per
e non è un numero primo.
La risposta corretta è quindi la 5.
- ammette infinite soluzioni;
- ammette una sola soluzione;
- non ammette alcuna soluzione;
- è risolvibile solo per
;
- è risolvibile solo per
.
Svolgimento.
Osserviamo che la seconda equazione è volte la prima. In altre parole, è ridondante e non serve per determinare lo spazio delle soluzioni del sistema, che è semplicemente l’insieme delle coppie
per cui
, ovvero l’insieme delle coppie
al variare di
nell’insieme dei numeri reali.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
La probabilità di ottenere uno stesso risultato è sempre la stessa ed uguale a
, dato che gli eventi del lancio dei dadi sono fra loro indipendenti. Dato che i tre possibili eventi sono disgiunti, allora la probabilità cercata è
, per il teorema della probabilità totale.
- è verificata per ogni valore
;
- non è verificata per alcun valore di
;
- è verificata per ogni
;
- è verificata per ogni
;
- ha una sola soluzione.
Svolgimento.
Osserviamo che è sempre positivo, quindi il suo valore assoluto è sempre
e dobbiamo risolvere
che è impossibile.
- non c’è alcuna relazione fra
e
;
-
;
-
è la terza parte di
;
-
è
volte
;
-
è
volte
.
Svolgimento.
Senza perdita di generalità, si possono posizionare i due triangoli in modo che due dei loro lati siano paralleli (vedi figura 13).
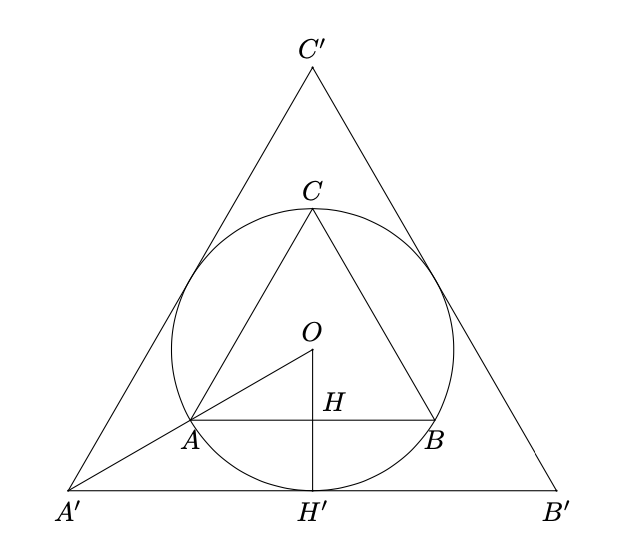
Figura 13: triangoli equilateri, uno circoscritto e l’altro inscritto alla circonferenza.
Vediamo due metodi che si possono adottare per risolvere il problema, quello di similitudine dei triangoli e quello che fa uso dei teoremi di trigonometria sui triangoli rettangoli insieme al teorema della corda.
Analizziamo il primo caso. Il triangolo è equilatero in quanto
e
hanno lunghezza
e
. Allora
è anche la mediana di
e pertanto
, da cui
.
Adesso osserviamo che i due trinagoli rettangoli e
sono simili, pertanto vale la proporzione:
Dato che e
sono rispettivemente la metà di
e
, allora
. Di conseguenza, il perimetro di
è il doppio di
.
Vediamo adesso il secondo metodo. Dal triangolo rettangolo si deduce che
Invece, applicando il toerema della corda sul lato si ottiene che
Quindi e pertanto un perimetro è il doppio dell’altro.
-
;
-
;
-
;
- dipende dalla scelta di
e da
;
- non ci sono abbastanza dati per calcolare
.
Svolgimento.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Dato che è il numero di chi mangia tutti gli stuzzichini, allora:
- il
mangia solo sia panini che noccioline;
- il
mangia solo sia noccioline che pizzette;
- il
mangia solo sia panini che pizzette.
Invece:
- il
mangia solo panini;
- il
mangia solo noccioline;
- il
mangia solo pizzette.
Se ne deduce che chi mangia qualcosa è il 1%+0%+8%+4%+17%+10%+2%=42%, quindi chi non mangia nulla è il .
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Il polinomio 5 ha tre radici distinte mentre i polinomi 1, 2, 3 sono di secondo grado e non possono quindi avere più di due radici reali distinte. Infine il polinomio 4 è , che ha una sola radice distinta
. Perciò la risposta corretta è la 5.
- i perimetri sono uguali;
- il perimetro del quadrato è minore di quello del cerchio;
- il rapporto tra il perimetro del cerchio e quello della quadrato è
;
- il rapporto tra il perimetro del quadrato e quello del cerchio è
;
- nessuna delle precedenti.
Svolgimento.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
La radice di un quadrato è il valore assoluto dell’argomento, dunque l’equazione è equivalente a . Per definizione di valore assoluto,
è
se e solo se
, che è equivalente a
.
La risposta esatta è quindi la 3.
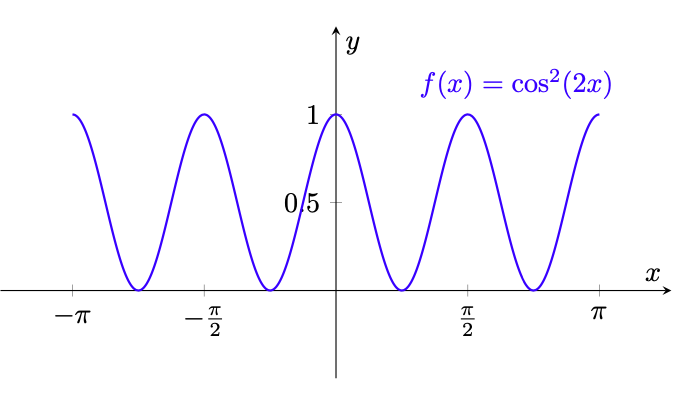
- è una funzione dispari;
- è una funzione pari;
- non è una funzione;
- si annulla negli stessi punti in cui si annulla
;
- non si annulla mai.
Svolgimento.
La funzione è sempre pari in quanto
In figura 16, mostriamo un esempio con .

Figura 16: grafici delle funzioni e
.
La risposta giusta è quindi la 2.
- descrive una traiettoria sulla sfera di
centrata nell’orgine e raggio
;
- perde di significato per alcuni valori di
;
- è una traiettoria contenuta nel piano
di
;
- è una traiettoria contenuta nel piano
di
;
- nessuna delle precedenti.
Svolgimento.
Osserviamo che la norma di ogni punto è
:
quindi la traiettoria giace sulla sfera unitaria di (vedi figura 17).

Figura 17: sfera centrata nell’origine e di raggio insieme alla traiettoria descritta da
.
Perciò la risposta esatta è la 1.
-
;
-
;
- non esiste alcuna relazione fra loro;
-
;
- sono uguali.
Svolgimento.
La formula è quella del cambio di base del logaritmo, ma volendo la si può facilemente ricavare:
Uguagliando gli esponenti del primo e dell’ultimo membro otteniamo che la 2 è la risposta corretta.
- è il luogo dei punti del piano che distano equamente da un certo punto e una certa retta data;
- è il luogo dei punti del piano che distano equamente da una coppia di punti distinti;
- è il luogo dei punti del piano la cui somma delle distanze da una coppia di punti distinti è costante;
- è il luogo dei punti del piano la cui differenza delle distanze da una coppia di punti distinti è costante;
- nessuna delle precedenti.
Svolgimento.
Si tratta proprio della definizione di parabola in geometria analitica. Partendo da un punto ed una retta (per semplicità parallela all’asse delle ascisse o all’asse delle ordinate) si ricava da tale definizione l’equazione cartesiana della parabola, che equivale a

Figura 18: costruzione di una parabola a partire dal suo fuoco e dalla sua direttrice
.
La risposta corretta è quindi la 1.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
valutata in
equivale a
perciò aumenta di
.
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
Dato che è congruo a
modulo
, cioè
diviso
ha resto di
, allora ogni numero in base
è divisibile per
semplicemente se la somma delle sue cifre è divisibile per
. Infatti, se un numero
in base
è rappresentato dalle cifre
, ovvero
allora visto che per un certo numero intero
dipendente da
, si ha
Da qui si deduce facilemente che è divisibile per
solo se la somma
è divisibile per
.
Nel nostro caso specifico abbiamo
che è divisibile per . Con ragionamenti simili si vede che il numero non è divisibile per
(e quindi neanche per
) e per
.
- quel numero che si ottiene elevando
per
;
- quel numero che si ottiene elevando
per
- quel numero che elevato ad
è uguale ad
;
- l’esponente che devi dare ad
per ottenere
;
- nessuna delle precedenti.
Svolgimento.
La 4 è proprio la definizione di logaritmo.
-
oppure
;
- la disequazione vale per ogni valore reale
tranne
;
-
oppure
;
-
;
-
.
Svolgimento.
Studiamo prima i segni del numeratore e del denominatore.
Invece, l’espressione si decompone come
. Il discriminante del fattore di secondo grado
è
, perciò il polinomio non ammette radici reali ed il suo segno è sempre positivo. Il segno di
è quindi lo stesso di
.
Facendo il prodotto dei segni con l’usuale grafico otteniamo il segno della frazione del quesito:
Pertanto la frazione assume valori non negativi per oppure per
.
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
Si osserva che
da cui si ottiene immediatamente la 4.
Un modo per dedurre la disugualianza 4 geometricamente è risolvere il seguente problema:
Trovare tra i parallelipedi aventi una diagonale di lunghezza fissa quello di superficie totale massima.
Dato un parallelipedo di lati , allora l’area totale
è
. La lunghezza della diagonale in funzione dei lati si può calcoalre applicando due volte il Teorema di Pitagora, da cui si ottiene:
(3)
Pertanto, risolvere il problema equivale a trovare il massimo della funzione in tre variabili sul vincolo
. Esistono tecniche avanzate per determinare il massimo assoluto di una funzione lungo un certo vincolo (es. metodo dei Moltiplicatori di Lagrange), ma non andremo in dettaglio. Comunque, intuitivamente si può dedurre che il parallelepipedo che massimizza l’area è un cubo, e che il suo late equivale a
(vedi 19). Quindi vale la disuguaglianza

Figura 19: un parallelepipedo ed un cubo aventi diagonale uguale.
Pertanto ricordando l’equazione (3) otteniamo la 4:
-
;
- 3;
-
;
- -3;
- 1.
Svolgimento.
Disegniamo il triangolo in un sistema di assi cartesiani :

Figura 20: triangolo di vertici ,
e
.
Notiamo che e
hanno stessa ascissa, quindi
è parallelo all’asse delle ordinate e quindi l’altezza
del triangolo
è parallela all’asse delle ascisse. Quindi la base
del triangolo è la differenza in valore assoluto
delle ordinate di
e
, mentre l’altezza del triangolo è la differenza in valore assoluto delle ascisse di
ed uno qualunque dei punti
e
, ovvero
.
Pertanto l’area del triangolo è
La risposta esatta è quindi la 2.
-
;
-
;
-
;
-
;
-
;
Svolgimento.
-
;
-
;
-
;
-
.
-
.
Svolgimento.
Il radicale si può riarrangiare come
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Tutti i numeri, tranne il 5 sono uguali a :
Invece il 5 è uguale a
che è quindi la risposta corretta.
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
Sia la distanza fra i centri
e
. Le due circonferenze
e
(vedi figura 22)
- si intersecano in due punti distinti se e solo se
;
- sono tangenti se e solo se
;
- non si intersecano se e solo se
.
Nel nostro caso l’unico punto per cui è uguale a
è 4. Infatti
Nei restanti casi, se il centro fosse 1 o 3 allora le circonferenze si incontrerebbero in due punti distinti, mentre nel restante caso 2 le circonferenze non si intersecherebbero.
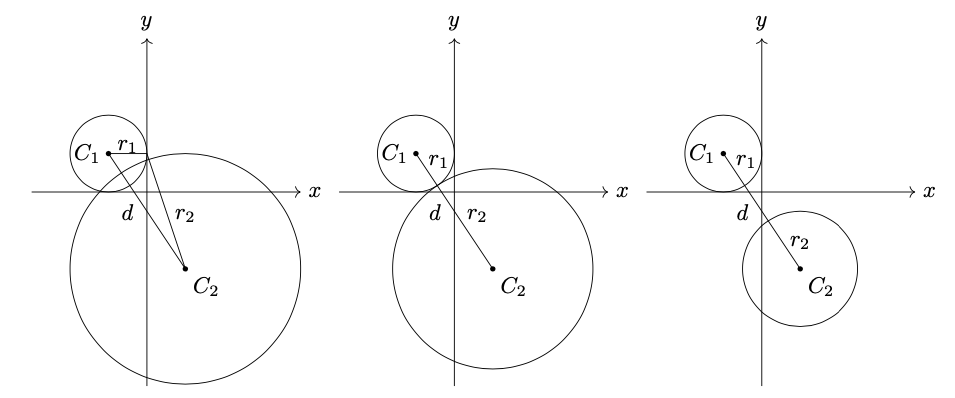
Figura 22: le tre possibili posizioni reciproche di una coppia di circonferenze.
La risposta corretta è quindi la 4.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Dobbiamo considerare la probabilità di estrarre un determinato seme ad ogni estrazione:
- Alla prima estrazione, la probabilità di estrarre un seme è
;
- Alla seconda estrazione, dobbiamo evitare il seme della prima carta. Quindi la probabilità è
, ovvero
carte disponbili diverse dal primo seme su
carte rimaste;
- Alla terza estrazione, dobbiamo evitare sia il primo che il secondo seme. Quindi la probabilità è
, ovvero
carte disponibili su
carte rimaste.
La probabilità finale è quindi:
La risposta corretta è quindi la 5.
il loro minimo comune multiplo è:
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Per calcolare il loro minimo comune multiplo occorre prendere ogni parte letterale ed elevarla al massimo esponente e poi, se i coefficienti dei monomi sono interi come in questo caso, occorre fare il minimo comunque multiplo tra loro.
Il monomio che stiamo cercando ha quindi parte letterale uguale a , mentre il coefficiente è
Perciò il minimo comune multiplo è .
-
;
-
;
-
;
-
;
-
.
Svolgimento.
La 4 e la 5 sono numeri troppo grandi perché al quadrato facciano .
Invece:
-
;
- dato che
allora
;
- dato che
allora
.
Il numero il cui quadrato si avvicina di più a è
, quindi la risposta corretta è la 2.
-
euro;
-
euro;
-
euro;
-
euro;
-
euro.
Svolgimento.
Sia il prezzo iniziale, allora
è uguale a:
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
Il radicale si può riscrivere come
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Il numero di terne possibili avendo a disposizione numeri differenti è il numero di modi di selezionare
numeri su
senza considerare il loro ordine, ovvero il numero di combinazioni di
numeri su
:
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Partiamo dai primi due numeri e
:
che è falso. Pertanto .
Invece, dato che , allora
che è falso, quindi . L’ordinamento corretto è quindi
.
La disuguaglianza si ricava come segue:
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Dato che è minore di
, allora il suo quadrato
è minore o uguale di
.
Inoltre osserviamo che e
, perciò
.
In questo intervallo ha misura positiva e osservando la figura 23 si nota che la lunghezza
della proiezione sull’asse
è sempre minore di quella sull’asse
, che è
. Quindi
e la risposta corretta è la 4.

Figura 23: la circonferenza goniometrica e il settore circolare dei punti per cui .
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
L’iperbole è il luogo dei punti del piano
per cui la differenza (in valore assoluto) tra le distanze tra due fuochi
e
è costante:
Nel caso di due fuochi e
,
, simmetrici rispetto l’asse
abbiamo che
da cui si ottiene
quindi
Facendo le opportune semplificazioni si arriva a
Perciò l’equazione dell’iperbole è del tipo e la relazione fra i coefficienti
e quelli
è la seguente:
Per definizione l’eccentricità di una iperbole è , perciò occorre risolvere il sistema
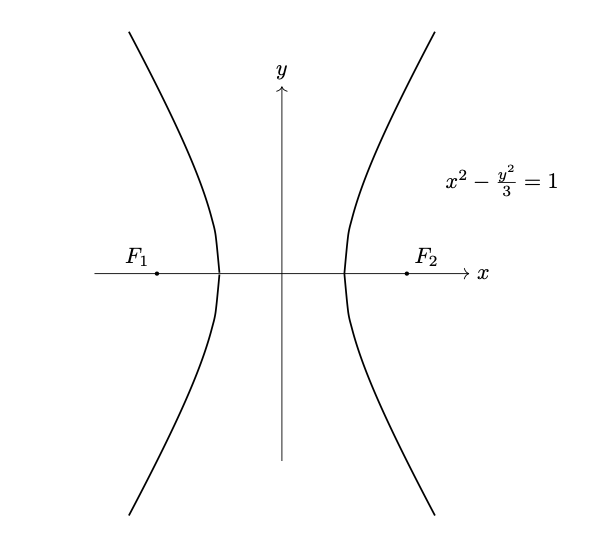
Figura 24: iperbole di fuochi e
ed eccentricità
.
Perciò l’equazione dell’iperbole è .
Un altro modo più veloce per determinare l’equazione dell’iperbole sarebbe potuto essere partire dall’equazione canonica e ricordare che valgono le relazioni
e
.
Le batterie sono state scelte a caso tra le 1000 prodotte, di cui 98 sono guaste. Qual è la probabilità che il telefono cellulare funzioni?
-
;
- circa
;
- circa
;
- circa
;
- circa
.
Svolgimento.
La probabilità che la prima delle batterie funzioni è il numero di batterie funzionanti, ovvero
, sulle
disponbiili. La probabilità che la seconda batteria funzioni è il numero delle restanti batterie funzionanti, ovvero
, su
batterie disponibili. Continuando a ragionare così, la probabilità che la terza batteria funzioni è
su
, e che la quarta funzioni è
su
. Quindi la probabilità che il telefono si accenda è
La risposta corretta è quindi la 2.
-
cm;
-
cm;
-
cm;
-
cm;
-
cm.
Svolgimento.
Indichiamo con la lunghezza di
e con
la lunghezza di
. A meno di scambiare
con
possiamo supporre che
. Dai dati abbiamo che
Allora e
sono soluzioni dell’equazione di secondo grado
:
Dunque il perimetro della Figura ?? è

Figura 25: i due quadrati costruiti sul segmento e l’area della figura.
La risposta corretta è quindi la 4.
- circa
;
-
;
-
;
-
;
-
:
Svolgimento.
Possiamo supporre che la prima moneta sia quella truccata. In questo caso, dato che la probabilità che esca un risultato qualunque dalla prima moneta è , se la probabilità che esca testa è del
, allora quella che esca croce deve essere del
, cioè rispettivamente
ed
. Allora
Perciò la probabilità che esca due volte croce e una testa è
-
;
-
;
-
;
- maggiore di
;
-
.
Svolgimento.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Dividendo l’angolo giro per
otteniamo l’angolo interno di uno dei triangoli che compongono il dodecagono (vedi figura 27). Dato che il triangolo è isoscele, allora i restanti due angoli interni al triangolo misurano entrambi
. Perciò uno degli angoli interni del dodecagono è
.

Figura 27: dodecagono regolare.
Quindi la somma delle cotagenti è
e la risposta corretta è la 1.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
-
;
-
,
;
-
,
;
-
,
;
-
,
.
Svolgimento.
La disequazione data ha senso solo per , che è dove il logaritmo esiste.
Osserviamo che , per cui ponendo
si ottiene
Le soluzioni dell’equazione sono
I valori di per cui
è non negativo sono quindi
,
. Adesso sostituiamo di nuovo
al posto di
e risolviamo le due diesquazioni:
quindi ,
.
- è un numero immaginario;
- è sempre irrazionale;
- può essere razionale;
- non è mai razionale;
- è sempre positivo.
Svolgimento.
Il prodotto di numeri irrazionali distinti può essere razionale, ad esempio , che è razionale.
-
;
-
;
-
;
-
;
-
;
Svolgimento.
Visto che è un numero negativo, allora
, perciò
.
- è
;
- è
;
- è
;
- è soluzione di un’equazione polinomiale di
grado;
- non esiste.
Svolgimento.
L’area della superficie totale del cono è , dove
è l’apotema del cono. In particolare, valore dell’apotema nel nostro caso è
, quindi la superficie totale del cono si può riscrivere come
Indichiamo con la quantità per cui il nuovo cono di altezza
e raggio
ha sempre area di superifice totale uguale a
. Allora
soddisfa l’equazione
Risolviamo l’equazione ottenuta:
Continuando a semplificare otteniamo
Come ci si poteva aspettare, una delle soluzioni è proprio , per cui escludendo questa soluzione e dividendo l’equazione di sopra per
otteniamo che altre possibili soluzioni devono essere radici del polinomio di terzo grado
Questo polinomio ha due soluzioni complesse ed una sola soluzione reale negativa, che è circa . Dato che
deve essere positivo, allora non esiste alcuna soluzione al problema.

Figura 29: il cono di altezza e raggio
a sinistra, e quello di altezza
e base
, a destra.
-
minuti;
-
minuti;
-
minuti;
-
secondi;
-
minuto.
Svolgimento.
Siano l’altezza del cono superiore e
l’altezza del cono dopo
minuti, quindi
. Siano
ed
i raggi del cono superiore all’altezza
e
rispettivamente, e
,
i volumi rispettivi dei due coni.
La quantità di sabbia uscita dal cono superiore dopo 13 minuti è il volume del tronco di cono, quindi per determinare il tempo rimanente
affinché la clessidra si svuoti completamente si può usare la proporzione:
(4)
Quindi occorre calcolare il rapporto dei volumi dei due coni.
I due triangoli in figura 30 sono simili tra loro, perciò si deduce che
Quindi
Sostituendo in (4) il valore del rapporto dei due volumi, si ottiene che il tempo rimanente è di secondi.
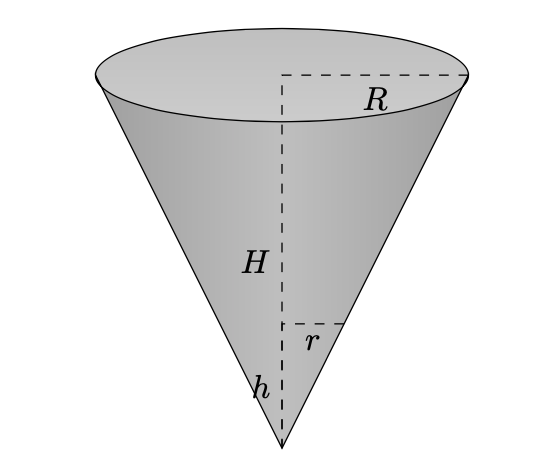
Figura 30: cono circolare, che costiuisce la parte superiore della clessidra.
La risposta corretta è quindi la 4.
- tre;
- una;
- due;
- quattro;
- non si può stabilire.
Svolgimento.
La moneta deve essere lanciata almeno tre volte. Se fosse stata lanciata esattamente due volte, potrebbe accadere che sia uscito testa e croce, quindi due lanci non bastano. Invece, al terzo lancio può uscire solamente o testa, o croce, garantendo quindi che su tre lanci sia uscito sempre almeno o due volte testa o due volte croce.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Dato che è sempre non negativo, allora
, quindi otteniamo
è sempre maggiore o uguale a zero, quindi il segno di
è quello di
, che è minore o uguale di
per
.
-
;
-
;
-
;
-
;
- i dati forniti non sono sufficienti per ottenere questa informazione.
Svolgimento 1.
Ci sono diversi metodi per risolvere il problema. Uno può essere quello di osservare che i quadrilateri, avendo angoli uguali e lati in proporzione, sono simili e quindi tracciando due diagonali corrispondenti si decompongono in triangoli simili. I lati e le altezze dei triangoli e
sono rispettivamente i
dei corrispettivi triangoli
e
. Quindi, il rapporto delle aree di
e
sono pari a
delle aree rispettivamente di
e
. La risposta corretta è quindi la 1.
Svolgimento. 2
Indichiamo con ABCD il quadrilatero più grande e con EFGH il secondo, come in figura 31. Allora
Quindi l’area dei due quadrilateri è
Adesso usiamo che ,
, e che
per ottenere

Figura 31: i due quadrilateri ABCD e EFGH.
Il risultato ottenuto mostra come il rapporto tra le areee dei due quadrilateri è uguale al rapporto tra i loro lati al quadrato. Questo risultato non è un caso in quanto è sempre vero che se due figure sono simili e il rapporto dei loro lati è , allora il rapporto delle loro aree è il quadrato
(come anche il rapporto dei loro volumi sarebbe
).
La risposta corretta è quindi la 1.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Utilizziamo la proprietà dei logaritmi per cui :
La risposta corretta è quindi la 2, plausibile è il 5.
- un’iperbole;
- un’ellisse;
- un’ellisse ed una circonferenza;
- un’ellisse ed un punto;
- nesuna delle precedenti.
Svolgimento.
Le coppie che soddisfazione l’equazione devono verificare
Tuttavia, la prima equazione non ammettte soluzioni nel campo dei numeri reali, quindi deve verificare necessariamente
che è l’equazione di un’ellisse.

Figura 32: l’insieme dei punti che verificano l’equazione .
La risposta corretta è quindi la 2.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Un approccio diretto è trovare delle radici banali del polinomio e poi usare la regola di Ruffini per scomporlo in fattori, come fatto nell’ esercizio 16. Tuttavia, in questo caso conviene ragionare per esclusione. Infatti, notiamo subito che è radice del polinomio:
Questo esclude subito 3 e 4. Inoltre, il polinomio in è uguale a
, quindi l’unico polinomio plausibile è 5.
- una diagonale che è il doppio dell’altra;
- una diagonale che è il quadruplo dell’altra;
- le due diagonali uguali, ovvero è un quadrato;
- la diagonale maggiore che è
la diagonale minore;
- nessuna delle precedenti.
Svolgimento.
Sia la diagonale minore e
la diagonale maggiore del rombo. L’area del rombo è quindi
Invece il perimetro fissato del rombo è uguale a
Osserviamo che
Quindi l’area può essere riscritta come
Visto che è sempre maggiore o uguale a zero, allora
è massima per
, ovvero per
. Abbiamo quindi ottenuto che il rombo deve essere un quadrato.

Figura 33: due rombi di uguale perimetro . Il quadrato a destra è il rombo di area massima fra quelli di perimetro fissato
.
La risposta corretta è quindi la 3.
-
-
-
;
-
-
.
Svolgimento.
Occorre trovare i punti di minimo della funzione , per
. La funzione è derivabile nel suo dominio, quindi i punti di massimo e minimo annullano la derivata, ed il suo segno determina la crescenza e decrescenza della funzione. Nell’intervallo
abbiamo che
Perciò è un punto di minimo locale per
, che è anche assoluto in
.
La risposta corretta è quindi la 3.
- non ha periodo;
-
;
-
;
-
;
-
.
Svolgimento.
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
Dimostriamo che il punto per cui la lunghezza di
è minima è tale per cui
,
ed il centro
della circonferenza sono allineati, con
dalla parte di
. Chiamiamo con
il punto per cui
,
ed
sono allineati, con
dalla parte di
. Vogliamo quindi mostrare che
per un qualunque punto
sulla circonferenza.
Indichiamo con
il punto della circonferenza ottenuto dal prolungamento del segmento
. Allora la lunghezza di
è minima se e solo se quella del segmento
è massima, cioè basta dimostrare che
per ogni punto
della circonferenza (vedi figura 35). Dato che la somma di due lati di un triangolo è sempre maggiore o uguale al terzo lato, allora deduciamo che per
vale
che è proprio ciò che volevamo dimostrare.
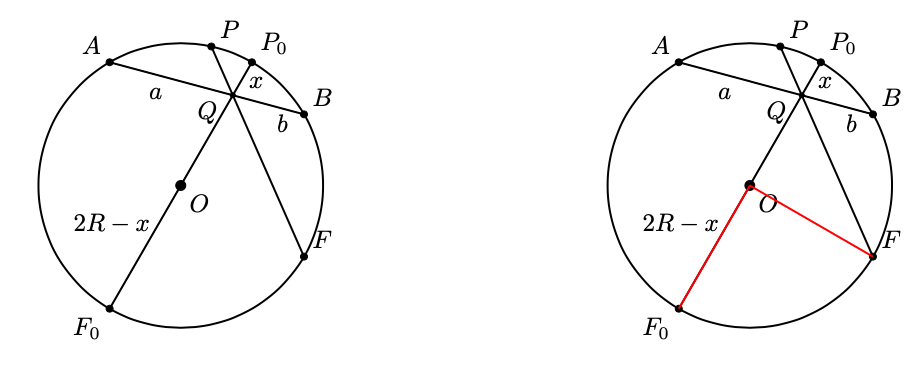
Figura 35: il segmento è quello di lunghezza massima.
Rimane da calcolare la lunghezza di . Si potrebbe usare uno dei risultati di geometria classica per cui se due corde si intersecano, i segmenti che si formano su una di esse sono i medi e i segmenti dell’altra sono gli estremi di una stessa proporzione.
Presentiamo un metodo alternativo usando un risultato equivalente, il Teorema delle Corde (Proposizione 35 del Libro III di Euclide), per cui se due corde di una circonferenza si intersecano, allora il rettangolo con lati congruenti alle due parti di una corda ha la stessa area del rettangolo con lati congruenti alle due parti dell’altra (vedi figura 36). Possiamo quindi concludere che

Figura 36: applicazione del teorema delle Corde alle corde e
.
quindi la risposta corretta è la 1.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Il volume della corona sferica è dato dalla differenza tra il volume della sfera maggiore () e quello della sfera minore (
):
Il volume del cilindro con raggio e altezza
è:
Il rapporto tra e
è:
Quindi e la risposta corretta è la 3.
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
Ricordiamo che la funzione logaritmo è strettamente crescente, quindi se , allora
.
-
, che è minore di 5.
-
.
-
.
- il logaritmo di un numero negativo non ha senso, quindi
non si può determinare.
Nessuno dei casi proposti è corretto, quindi è vera la risposta 5.
- ha infinite soluzioni positive;
- ha infinite soluzioni negative;
- non ha soluzioni;
- ha infinite soluzioni positive e infinite soluzioni negative;
- ha un numero finito di soluzioni positive.
Svolgimento.
Per risolvere , seguiamo questi passaggi:
- La radice quadrata impone la condizione
, quindi
, il che esclude 2 e 4.
- Risolviamo la disequazione
elevando al quadrato (che è possibile fare perché
e quindi
)
Portando tutto a destra:
Le soluzioni di questa disequazione di secondo grado sono
.
Intersecando l’insieme delle soluzioni con l’insieme dei valori per cui
, otteniamo che la disequazione è valida per
oppure per
.
Quindi la risposta corretta è la 1.
- Uno;
- Due;
- Infiniti;
- Nessuno;
- Quattro.
Svolgimento.
Per una retta ortogonale a un piano
è possibile condurre infiniti piani perpendicolari a
contenenti
. Ogni piano perpendicolare a
passante per la retta
può essere ruotato attorno a questa retta, generando un fascio di piani perpendicolari a
. Pertanto, la risposta corretta è la 3.
-
e
pari;
-
e
dispari;
-
e
non primi tra loro;
- per nessuna coppia di interi positivi;
-
primo e
dispari.
Svolgimento.
L’affermazione “esiste non multiplo di
tale che
è multiplo di
” implica che
non debba essere divisibile per almeno un fattore di
, ma che il prodotto
lo sia. Ciò implica che
deve avere almeno un fattore comune con
(quello che non ha con
). Quindi
e
non sono primi tra loro.
La risposta corretta è la 3.
- Nessuno;
- Uno;
- Due;
- Quattro;
- Tre;
Svolgimento.
Consideriamo ciascuna delle tre condizioni:
- La condizione
implica che
e
devono avere lo stesso segno o almeno uno dei due deve essere
. Quindi siamo nel primo e terzo quadrante compreso gli assi.
- L’equazione
rappresenta una circonferenza di raggio
e centro nell’origine.
- L’equazione
rappresenta una retta parallela alla bisettrice del secondo e quarto quadrante e passante per
.
Risolvendo il sistema:
Otteniamo i punti e
. Entrambi soddisfano
.
Pertanto, ci sono due punti che soddisfano tutte e tre le condizioni.

Figura 37: i tre insiemi descritti dalle tre equazioni e la loro intersezione.
Svolgimento.
La nona parte di equivale a moltiplicare
per
, che può essere riscritto come:
Pertanto, la risposta corretta è la 4.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Partiamo dall’equazione data:
Riscriviamo l’equazione in forma esponenziale utilizzando la definizione di logaritmo:
Poiché , possiamo scrivere:
Pertanto, la risposta corretta è la 2.
- Il cerchio con semiperimetro uguale al perimetro del poligono;
- Il cerchio circoscritto al quadrato;
- Il cerchio circoscritto al settagono;
- Il cerchio circoscritto al dodecagono;
- I tre cerchi hanno superfici identiche.
Svolgimento.
Dato che i poligoni hanno tutti lo stesso perimetro, il raggio del cerchio circoscritto diminuisce con il numero di lati del poligono. Più lati ha il poligono, più il raggio del cerchio circoscritto è piccolo. In questo caso, il quadrato ha il numero minore di lati, quindi avrà il raggio circoscritto maggiore. Pertanto, il cerchio con la superficie maggiore è quello circoscritto al quadrato.
Per giustificare meglio, calcoliamo il perimetro di un poligono regolare di
lati inscritto ad un cerchio di raggio
. Se dividiamo a spicchi il poligono regolare, osserviamo che l’angolo al centro di ciascun spicchio è 360 gradi diviso il numero
dei lati, quindi per il Teorema della Corda un lato del poligono misura
e perciò il perimetro
risulterà uguale a
Presi in considerazione due poligoni regolari inscritti in due cerchi di raggio ed
ed aventi lo stesso perimetro
, allora se il primo poligono ha più lati del secondo, ovvero
, si ha
L’ultima diseguaglianza segue da un risultato ben noto già dal liceo, ovvero che la funzione è descrescente per
. Nel nostro caso, il numero
di lati di un poligono regolare è almeno
, quindi
e perciò se
, ovvero
, allora
Possiamo concludere quindi che il cerchio circoscritto nel poligono con meno lati è anche quello che ha raggio maggiore, e quindi superficie maggiore.

Figura 38: i tre poligoni regolari di uguale perimetro circoscritti alle loro circonferenze.
La risposta corretta è la 2.
- Mai;
- Sì, con
.
- Sì, per qualsiasi valore di
e di
con lo stesso segno;
- Sì, con
e
qualsiasi;
- Sì, con
e
;
Svolgimento.
Supponiamo che e
abbiano lo stesso segno, quindi che il rapporto fra loro sia positivo.
Riscriviamo l’espressione:
dato che è sempre maggiore o uguale a zero.
La risposta corretta è la 3.
- 12;
- 4;
- 9;
- 8;
- 11.
Svolgimento.
Quando si lanciano due dadi, le somme possibili vanno da 2 a 12, e ognuna ha una probabilità diversa a seconda di quante combinazioni producono quella somma. Inoltre, più combinazione di quella somma ci sono, più è probabile che quella somma esca. Ecco le combinazioni per ogni somma:
- Somma 2:
, ovvero una combinazione;
- Somma 3:
, ovvero 2 combinazioni;
- Somma 4:
ovvero 3 combinazioni;
- Somma 5:
, ovvero 4 combinazioni;
- Somma 6:
, ovvero 5 combinazioni;
- Somma 7:
, ovvero 6 combinazioni;
- Somma 8:
, ovvero 5 combinazioni;
- Somma 9:
, ovvero 4 combinazioni;
- Somma 10:
, ovvero 3 combinazioni;
- Somma 11:
, ovvero 2 combinazioni;
- Somma 12:
, ovvero 1 combinazione.
La somma con la più alta probabilità di verificarsi tra le possibili opzioni è la somma 8, che ha 5 combinazioni.
La risposta corretta è la 4.
- Il cateto stesso e la differenza fra l’ipotenusa e l’altro cateto;
- L’ipotenusa e la proiezione dell’altro cateto sull’ipotenusa;
- la differenza fra l’ipotenusa e l’altro cateto, e la somma dell’ipotenusa con l’altro cateto;
- Il cateto stesso e la differenza delle proiezioni dei cateti sull’ipotenusa;
- Il cateto stesso e la proiezione dell’altro cateto sull’ipotenusa.
Svolgimento.
Consideriamo un triangolo di cateti e
e ipotenusa
. Per il teorema di Pitagora
La risposta corretta è la 3.
- Sia ortogonale a una retta del piano;
- Sia parallela a una retta del piano;
- I suoi punti siano equidistanti da tutti i punti del piano;
- I suoi punti non siano equidistanti dai punti del piano;
- Sia ortogonale a due rette incidenti del piano.
Svolgimento.
Una retta è ortogonale a un piano se è ortogonale a due rette incidenti del piano. Tale retta si può costruire come intersezione tra i due piani conententi una delle due rette rispettivemente ed ortogonali al piano dato.
Pertanto, la risposta corretta è la 5.
- Ha le stesse soluzioni di quella iniziale;
- Può avere meno soluzioni di quella iniziale;
- Può avere più soluzioni di quella iniziale;
- Non ha alcuna relazione con l’equazione iniziale;
- Ha infinite soluzioni.
Svolgimento.
Elevando alla quarta entrambi i membri di un’equazione, questa può avere soluzioni aggiuntive che non soddisfano l’equazione originale. Questo accade perché l’elevazione alla quarta di un numero positivo e quello di un numero negativo producono lo stesso valore. Ad esempio l’equazione ha una sola solzione, mentre
ha due soluzioni reali, ovvero
.
Pertanto, l’equazione alla quarta può avere più soluzioni rispetto a quella iniziale.
La risposta corretta è la 3.
-
;
-
;
-
;
-
;
- nessuna delle precedenti.
Svolgimento.
Poiché gli angoli del triangolo sono ordinati in modo decrescente , anche i lati opposti sono ordinati nello stesso modo, quindi
. Ciò vale per un teorema ben noto di Geometria per cui in un triangolo ad angolo maggiore si oppone lato maggiore.
La risposta corretta è la 4.
- Uno;
- Due;
- Tre;
- Più di tre;
- Più di tre, ma comunque un numero finito.
Svolgimento.
Il numero di cifre di un numero si calcola con la formula:
dove il simbolo indica la parte intera inferiore di un numero. Per parte intera inferiore di un numero
si intende il più grande numero intero più piccolo di
.
Quindi, dobbiamo risolvere la disequazione:
Poiché , la disequazione diventa:
Quindi non può superare
, ma sicuramente può superare
.
Effetivamente, con l’uso di una calcolatrice si può calcolare il primo numero per cui
ha più di
cifre, e questo è
:
La risposta corretta è la 5.
-
è inversamente proporzionale alla sesta di
;
-
è direttamente proporzionale al cubo di
;
-
è direttamente proporzionale al quadrato di
;
-
è inversamente proporzionale a
;
- La relazione tra
e
è diversa da quelle indicate nelle altre risposte.
Svolgimento.
Ci sono due relazioni:
-
è direttamente proporzionale al cubo di
, quindi:
-
è inversamente proporzionale al quadrato di
, quindi:
Allora
Dunque è inversamente proporzionale alla sesta di
.
La risposta corretta è la 1.
- Da nessun valore reale;
- Da due valori reali;
- Da un solo valore reale;
- Infiniti valori reali positivi;
- Nessuna delle risposte precedenti.
Svolgimento.
L’equazione è:
Poniamo , così che l’equazione diventi:
Risolvendo l’equazione di secondo grado:
Ora, poiché , otteniamo:
Pertanto, l’equazione ha due soluzione reali.
La risposta corretta è 2.
-
;
-
;
-
(circa);
-
;
-
.
Svolgimento.
La probabilità che A vinca è che faccia croce, ovvero:
La probabilità che B vinca è che faccia testa per la probabilità che B faccia croce (ovvero che su due tiri esca prima testa e poi croce). Dato che i due lanci sono indipendenti, allora:
La probabilità che C vinca è che faccia testa,
faccia testa e che
faccia croce (ovvero che su tre tiri esca in sequenza testa, testa croce). Di nuovo, essendo i tre lanci indipendenti, allora
La relazione fra le probabilità ottenute è:
Pertanto, la risposta corretta è la 5.
- 15;
- Più di 1000;
- 25;
- 1000;
- 100.
Svolgimento.
Quando si inscrive un quadrato dentro un altro quadrato con i punti medi dei lati, il lato del nuovo quadrato è dal teorema di Pitagora uguale a
, dove
è il lato del quadrato iniziale. Dunque il perimetro
del nuovo quadrato sarà
dove è il perimetro del quadrato iniziale. Ripetendo lo stesso procedimento per
, otteniamo
. Iterando ad ogni passo, otteniamo che l’
-esimo quadrato avrà perimetro uguale a
Dobbiamo quindi risolvere la disequazione
Quindi
Dunque si può iterare il procedimento fino ad un massimo di volte.

Figura 39: un esempio di sequenza di quadrati.
La risposta corretta è la 1.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
Ogni mazzo contiene 40 carte e 4 assi (uno per seme: cuori, quadri, fiori e picche). La probabilità di estrarre l’asso di quadri o l’asso di fiori da un mazzo è:
La probabilità di estrarre da ciascuno dei 4 mazzi un asso di quadri o un asso di fiori è:
La risposta corretta è la 4.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
La probabilità che esca il numero 16 o il 18 in una singola estrazione è . La probabilità che escano in due lanci i numeri desiderati è la probabilità che esca prima il 16 e poi il 18 oppure prima il 18 e poi il 16. Quindi:
La risposta corretta è la 2.
- due rette parallele;
- una retta e un’iperbole che non si incontrano;
- una retta e un’iperbole che si incontrano in due punti;
- una retta e una parabola che si incontrano in due punti;
- una retta e una parabola che non si incontrano.
Svolgimento.
Le equazioni date sono:
Uguagliando le due equazioni:
che non ha soluzioni reali, poiché il quadrato di un numero reale non può essere negativo.
La risposta corretta è 5.
-
;
-
;
-
;
-
;
-
.
Svolgimento.
-
Questa equazione ha due soluzioni:
e
. L’insieme è composto di due elementi.
-
Questo insieme contiene infiniti numeri reali minori o uguali a 13, quindi non è un insieme con un solo elemento.
-
Risolvendo l’equazione
, troviamo l’unica soluzione
. L’insieme contiene un solo elemento.
-
Questa equazione non ha soluzioni reali, quindi l’insieme è vuoto.
-
Le soluzioni sono
e
, quindi l’insieme contiene due elementi.
La risposta corretta è la 3.
- esiste
tale che
;
- per ogni
si ha
;
- esistono infiniti valori
per cui
;
- per rispondere occorre conoscere le espressioni di
e di
;
- nessuna delle precedenti è corretta.
Svolgimento.
L’identità data significa che per ogni valore si ha che
.
La risposta corretta è la 2.
- uguale a 0;
- minore di 0;
- uguale a
;
- uguale a
;
- uguale a
.
Svolgimento.
Calcoliamo e
:
La media aritmetica è:
La risposta corretta è C).
-
;
-
;
-
;
-
;
-
.
Svolgimento.
L’uguaglianza ha soluzione
.
Quindi la disequazione
è verificata per tutti i valori di
maggiori di
.
La risposta corretta è la 1.
-
;
-
;
- la probabilità di
non è calcolabile;
-
;
-
.
Svolgimento.
Possiamo usare la seguente formula ben nota in probabilità:
Sostituendo i valori dati:
La risposta corretta è 4.
- un punto;
- due punti;
- nessun punto;
- dipende dal segno di
;
- nessuna delle precedenti.
Svolgimento.
La curva data è l’unione di due iperboli equilatere di coefficiente e
rispettivamente.
La retta data invece è parallela alla bisettrice del secondo e quarto quadrante e passa per il punto . Ci aspettiamo quindi che per ogni valore di
la retta interseca in due punti
, mentre solo per alcuni valori di
(che dipenderanno da
) avremo che la retta interseca anche l’iperbole
.
Per determinare in modo esatto per quali valori, sostituiamo nell’equazione dell’iperbole e risolviamo l’equazione in
:
Il numero dei punti di intersezione dipendono quindi dal segno del discriminante dell’equazione di secondo grado ottenuta:
Quindi il numero di punti di intersezione fra le due curve sarà:
-
se
oppure
;
-
se
oppure
.

Figura 40: la retta e le due iperboli equilatere nel caso e
.
La risposta corretta è 5.
-
;
-
;
-
;
-
;
- Nessuna delle precedenti alternative è corretta.
Svolgimento.
Per trovare i punti di intersezione della retta data con gli assi, facciamo i seguenti calcoli:
- Intersezione con l’asse
(
):
Il punto di intersezione è
.
- Intersezione con l’asse
(
):
Il punto di intersezione è
.
L’area del triangolo è:
La risposta corretta è 4.
-
;
-
;
-
;
-
;
- Nessuna delle precedenti alternative è corretta.
Svolgimento.
Riscriviamo l’espressione:
La risposta corretta tra quelle elencate è la 2.
- per ogni
reale;
- per ogni
diverso da
;
- per ogni
diverso da
e da
;
- per
;
- per
.
Svolgimento.
La funzione non è definita dove il denominatore si annulla. La funzione è definita quindi solo quando
. Risolviamo l’equazione di secondo grado ottenendo:
Pertanto è definita per ogni
diverso da
e
. Si noti che la funzione
può essere riscritta come
che è tuttavia diversa dalla funzione . Infatti le funzioni
e
coincidono al di fuori di
ed in particolare
è un’estensione di
in
che, a differenza di
, è continua in
.

La risposta corretta è la 3.
Tutta la teoria di analisi matematica
Leggi...
- Teoria Insiemi
- Il metodo della diagonale di Cantor
- Logica elementare
- Densità dei numeri razionali nei numeri reali
- Insiemi Numerici
- Il principio di induzione
- Gli assiomi di Peano
- L’insieme dei numeri reali: costruzione e applicazioni
- Concetti Fondamentali della Retta Reale: Sintesi Teorica
- Costruzioni alternative di
- Binomio di Newton
- Spazi metrici, un’introduzione
- Disuguaglianza di Bernoulli
- Disuguaglianza triangolare
- Teoria sulle funzioni
- Funzioni elementari: algebriche, esponenziali e logaritmiche
- Funzioni elementari: trigonometriche e iperboliche
- Funzioni goniometriche: la guida essenziale
- Teorema di Bolzano-Weierstrass per le successioni
- Criterio del rapporto per le successioni
- Definizione e proprietà del numero di Nepero
- Limite di una successione monotona
- Successioni di Cauchy
- Il teorema ponte
- Teoria sui limiti
- Simboli di Landau
- Funzioni continue – Teoria
- Il teorema di Weierstrass
- Il teorema dei valori intermedi
- Il teorema della permanenza del segno
- Il teorema di Heine-Cantor
- Il teorema di esistenza degli zeri
- Il metodo di bisezione
- Teorema ponte versione per le funzioni continue
- Discontinuità di funzioni monotone
- Continuità della funzione inversa
- Teorema delle contrazioni o Teorema di punto fisso di Banach-Caccioppoli
- Teoria sulle derivate
- Calcolo delle derivate: la guida pratica
- Teoria sulle funzioni convesse
- Il teorema di Darboux
- I teoremi di de l’Hôpital
- Teorema di Fermat
- Teoremi di Rolle e Lagrange
- Il teorema di Cauchy
- Espansione di Taylor: teoria, esempi e applicazioni pratiche
- Polinomi di Taylor nei limiti: istruzioni per l’uso
- Integrali definiti e indefiniti
- Teorema fondamentale del calcolo integrale (approfondimento)
- Integrali ricorsivi
- Formule del trapezio, rettangolo e Cavalieri-Simpson
- Teoria sugli integrali impropri
- Funzioni integrali – Teoria
- Introduzione ai numeri complessi – Volume 1 (per un corso di ingegneria — versione semplificata)
- Introduzione ai numeri complessi – Volume 1 (per un corso di matematica o fisica)
- Serie numeriche: la guida completa
- Successioni di funzioni – Teoria
- Teoremi sulle successioni di funzioni
- Serie di funzioni – Teoria
- Serie di potenze – Teoria
- Serie di Fourier – Teoria e applicazioni
- Integrali multipli — Parte 1 (teoria)
- Integrali multipli — Parte 2 (teoria e esercizi misti)
- Regola della Catena — Teoria ed esempi.
- Jacobiano associato al cambiamento di coordinate sferiche
- Guida ai Massimi e Minimi: Tecniche e Teoria nelle Funzioni Multivariabili
- Operatore di Laplace o Laplaciano
- Teoria equazioni differenziali
- Equazione di Eulero
- Teoria ed esercizi sulla funzione Gamma di Eulero
- Teoria ed esercizi sulla funzione Beta
- Approfondimento numeri complessi
- Diverse formulazioni dell’assioma di completezza
- Numeri di Delannoy centrali
- Esercizi avanzati analisi
Tutte le cartelle di Analisi Matematica
Leggi...
- Prerequisiti di Analisi
- Successioni
- Funzioni
- Funzioni continue-lipschitziane-holderiane
- Calcolo differenziale
- Derivate
- Calcolo delle derivate
- Retta tangente nel calcolo differenziale
- Punti di non derivabilità nel calcolo differenziale
- Esercizi sul teorema di Weierstrass con l’uso delle derivate
- Studio di funzione completo nel calcolo differenziale
- Esercizi teorici nel calcolo differenziale
- Metodo di bisezione
- Metodo di Newton
- Teoremi del calcolo differenziale
- Calcolo integrale
- Integrali impropri
- Espansione di Taylor
- Funzioni integrali (Approfondimento)
- Numeri Complessi
- Serie numeriche
- Successioni di funzioni
- Serie di funzioni
- Serie di potenze
- Serie di Fourier
- Trasformata di Fourier
- Funzioni di più variabili
- Teoria Funzioni di più variabili
- Massimi e minimi liberi e vincolati
- Limiti in due variabili
- Integrali doppi
- Integrali tripli
- Integrali di linea di prima specie
- Integrali di linea di seconda specie
- Forme differenziali e campi vettoriali
- Teorema di Gauss-Green
- Integrali di superficie
- Flusso di un campo vettoriale
- Teorema di Stokes
- Teorema della divergenza
- Campi solenoidali
- Teorema del Dini
- Equazioni differenziali lineari e non lineari
- Equazioni differenziali lineari
- Equazioni differenziali non lineari
- Analisi complessa
- Fondamenti
- Funzioni olomorfe
- Integrale di Cauchy e applicazioni
- Teorema della curva di Jordan e teorema fondamentale dell’Algebra
- Teorema di inversione di Lagrange
- Teorema dei Residui
- Funzioni meromorfe
- Prodotti infiniti e prodotti di Weierstrass
- Continuazione analitica e topologia
- Teoremi di rigidità di funzioni olomorfe
- Trasformata di Mellin
- Equazioni alle derivate parziali
- Funzioni speciali
- Analisi funzionale
- Complementi
- Funzioni Convesse
Tutti gli esercizi di geometria
In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.
Algebra lineare.
Geometria analitica.
Geometria differenziale.
Risorse didattiche aggiuntive per approfondire la matematica
Leggi...
- Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
- Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
- MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
- PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
- Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
- The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
- Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
- Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
- Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
- Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.