Teoria sui limiti

Teoria sulle Funzioni: Concetti Fondamentali e Proprietà

Home » Teoria sui limiti

Benvenuti nella nostra guida completa alla teoria sui limiti di funzioni reali di variabile reale.
Il concetto di limite è uno dei più importanti dell’Analisi Matematica. Esso consente di dare un significato formale alla seguente domanda di carattere intuitivo:
A quale valore si avvicina una funzione $f(x)$ se $x$ si avvicina a un punto $x_0$ ?
Questa dispensa tratta in maniera completa questo argomento, affrontando le seguenti domande:

Come si formalizza l’idea di limite e qual è il suo significato?
Quali relazioni esistono tra limiti e relazioni d’ordine? Cosa afferma il teorema dei carabinieri?
Quali relazioni esistono tra i limiti e le usuali operazioni tra funzioni come somma, prodotto, quoziente, potenza e composizione?
Quali operazioni si possono estendere alla retta reale estesa, che include i simboli $-\infty$ e $+\infty$ ? Quali invece danno luogo alle cosiddette forme indeterminate?
Quali sono i limiti notevoli?
Cosa sono gli asintoti?
Cosa sono gli o-piccoli e come si opera con essi?

Il testo ti guiderà alla scoperta di questi e altri affascinanti temi, illustrando i concetti con numerosi esempi, figure e spiegazioni di carattere intuitivo, che ti consentiranno di farti un’idea chiara ed essenziale, senza rinunciare al rigore e alla completezza. Cosa aspetti, allora? Comincia pure la lettura!

Autori e revisori

Leggi...

Autore: Luigi De Masi.

Revisori: Valerio Brunetti, Sergio Fiorucci, Matteo Talluri, Sara Sottile.

Sommario

Leggi...

Questa dispensa tratta la teoria sui limiti di funzioni reali di variabile reale, illustrata con numerosi esempi e figure. Dopo le definizioni, studiamo i teoremi di limitatezza, di confronto e dei carabinieri, le operazioni con i limiti in $\overline{\mathbb{R}}$

, le forme indeterminate e alcuni argomenti collegati.

Teoria sui limiti: tabella delle notazioni

Mostra notazioni.

$\mathbb{N}$	$\qquad$ $\qquad$ Insieme dei numeri naturali
$\mathbb{Z}$	$\qquad$ $\qquad$ Insieme dei numeri interi relativi
$\mathbb{R}$	$\qquad$ $\qquad$ Insieme dei numeri reali
$\overline{\mathbb{R}}$	$\qquad$ $\qquad$ Insieme dei numeri reali estesi, ossia $\mathbb{R} \cup \{-\infty,+\infty\}$
$\operatorname{sgn}(x)$	$\qquad$ $\qquad$ Segno del numero reale $x$ , pari a $1$ se $x>0$ , a $0$ se $x=0$ e a $-1$ se $x<0$
$\sup A$ , $\inf A$	$\qquad$ $\qquad$ Estremi superiore e inferiore dell’insieme $A \subseteq \mathbb{R}$
$e$	$\qquad$ $\qquad$ Numero di Nepero
$\log x$	$\qquad$ $\qquad$ Logaritmo naturale (in base $e$ ) del numero positivo $x$
$(a,b)$	$\qquad$ $\qquad$ Intervallo aperto di estremi $a,b \in \overline{\mathbb{R}}$ , ossia l’insieme $\{x \in \mathbb{R} \colon a < x < b\}$
$[a,b]$	$\qquad$ $\qquad$ Intervallo chiuso di estremi $a,b \in {\mathbb{R}}$ , ossia l’insieme $\{x \in \mathbb{R} \colon a \leq x \leq b\}$
$\lim_{x \to x_0} f(x)$	$\qquad$ $\qquad$ Limite della funzione $f$ per $x$ che tende a $x_0$
$\lim_{x \to x_0^-} f(x)$	$\qquad$ $\qquad$ Limite sinistro della funzione $f$ per $x$ che tende a $x_0$
$\lim_{x \to x_0^+} f(x)$	$\qquad$ $\qquad$ Limite destro della funzione $f$ per $x$ che tende a $x_0$
$[\cdots]$	$\qquad$ $\qquad$ Operazioni in $\overline{\mathbb{R}}$ e forme indeterminate
$f \sim g$	$\qquad$ $\qquad$ Le funzioni $f$ e $g$ sono asintotiche
$f =o(g)$	$\qquad$ $\qquad$ $f$ è un $o$ -piccolo di $g$

Introduzione alla teoria sui limiti matematici

Leggi...

Una funzione $f \colon \mathbb{R} \to \mathbb{R}$

è un oggetto matematico che illustra l’evoluzione di una quantità $f(x)$

in relazione a una variabile $x$

, detta indipendente: si cerca cioè di stabilire un legame tra due grandezze che descrivono ad esempio un fenomeno di natura fisica, economica, etc…

Un esempio di tale processo può essere l’altezza dal suolo di un oggetto in base al tempo. In questo caso, cioè, $x$ rappresenta il tempo, e $f(x)$ è l’altezza dell’oggetto al tempo $x$ . Si supponga che la legge $f$ che descrive questo fenomeno cessi di avere validità per un tempo $x_0$ , ossia che non sia possibile calcolare l’altezza $f(x_0)$ raggiunta dal corpo al tempo $x_0$ . Ci si chiede però verso quale altezza tenda ad arrivare l’oggetto, quando il tempo si avvicina a $x_0$ . Matematicamente ciò equivale a studiare la seguente domanda.

Domanda 1. A quale valore si avvicinano i valori $f(x)$ , quando $x$ è vicino a $x_0$ ?

Nella fattispecie dell’esempio trattato, il tempo $x_0$ può essere finito, ma anche infinito. Ad esempio, una domanda ragionevole sul fenomeno è se l’oggetto tenda a stabilizzarsi verso una qualche altezza particolare al trascorrere del tempo, pur magari senza fermarsi mai del tutto. Ciò corrisponde a voler dare un significato a $f(+\infty)$ , cioè il caso $x_0=+\infty$ . È chiaro che non è possibile calcolare tout court il valore $f(+\infty)$ per alcuna funzione reale di variabile reale. Occorre pertanto costruire degli strumenti rigorosi che consentano di studiare matematicamente questa domanda.

I limiti costituiscono appunto tale mezzo. Questa dispensa è dedicata allo studio di questo importante capitolo dell’Analisi Matematica, ed è organizzata come segue.

$\[\]$

Nella sezione Intorni e punti di accumulazione nella retta reale estesa definiamo la retta reale estesa, ambiente naturale per la teoria dei limiti, e i relativi concetti di intorno e punto di accumulazione. Definiamo poi la nozione di proprietà valida definitivamente, di ampio utilizzo nello studio dei limiti.

Nella sezione Limiti definiamo il concetto di limite e lo illustriamo mediante numerosi esempi e figure. Trattiamo poi i limiti sinistri e destri, versioni “unilaterali” del concetto di limiti e i collegamenti tra tali nozioni.

Nella sezione Teoremi sui limiti presentiamo i principali risultati teorici sui limiti: i legami tra limiti e limitatezza; i teoremi di confronto, che legano disuguaglianze tra le funzioni a disuguaglianze sui limiti, e i relativi teoremi “dei carabinieri”. Trattiamo infine i limiti di funzioni monotone: stabiliremo l’esistenza di limiti sinistri e destri per funzioni monotone e ne daremo una caratterizzazione in termini di estremi inferiori e superiori.

La sezione Operazioni con i limiti è dedicata alle relazioni tra i limiti e le operazioni tra funzioni. Nella prima parte della sezione studiamo come si comportano i limiti rispetto alle operazioni algebriche di somma, prodotto e quoziente. Nella seconda parte trattiamo i limiti di funzioni composte e relativi cambi di variabile e argomenti collegati come limiti di funzioni inverse e limiti di potenze.

La sezione Forme indeterminate e limiti notevoli è costituita da uno studio completo delle cosiddette forme indeterminate, ossia dei casi non trattati dai teoremi sull’algebra dei limiti nella retta reale estesa, in cui cioè il valore del limite non si può dedurre esclusivamente dai valori dei limiti delle funzioni in esame. Ci dedicheremo a ciascuna delle 7 forme indeterminate, fornendo strategie per la loro risoluzione ed esempi svolti, oltre a trattare i cosiddetti limiti notevoli.

Nella sezione Complementi presentiamo alcuni argomenti complementari ai limiti: gli asintoti, ossia rette che approssimano bene il grafico di una funzione; le funzioni asintotiche e il relativo principio di sostituzione nel calcolo dei limiti; concludiamo infine con la nozione di $o$ -piccolo e il suo utilizzo nel calcolo dei limiti.

Intorni e punti di accumulazione nella retta reale estesa

Introduzione.

L’ambiente adatto allo studio dei limiti è la retta reale estesa $\overline{\mathbb{R}}$

, ossia l’insieme $\mathbb{R} \cup \{-\infty,+\infty\}$

, cioè l’insieme dei numeri reali a cui vengono aggiunti i simboli $-\infty$

e $+\infty$

, che vengono rispettivamente detti meno infinito e più infinito.

Non entriamo in una discussione rigorosa sulla natura di questi oggetti, ma è sufficiente tenere presente che il simbolo $-\infty$ può essere pensato come minore di ogni numero reale, mentre il simbolo $+\infty$ può essere pensato maggiore di ogni numero reale. Formalmente, l’usuale relazione d’ordine in $\mathbb{R}$ può essere estesa a una relazione d’ordine in $\overline{\mathbb{R}}$ aggiungendo le condizioni seguenti:

(1) $\begin{equation*} -\infty < x < +\infty \qquad \forall x \in \mathbb{R}. \end{equation*}$

L’uso di questi oggetti è necessario al fine di definire formalmente il significato di concetti intuitivi quali “quantità infinitamente piccola” o “infinitamente grande”.

Intorni.

Il primo passo per studiare in maniera rigorosa la domanda 1. è stabilire cosa significano espressioni come “ $x$

vicino a $x_0$

“. In altre parole, occorre stabilire cosa significa essere nelle vicinanze di un numero reale $x_0$

. A tale esigenza risponde il concetto di intorno di un elemento di $\overline{\mathbb{R}}$

Definizione 1 (intorno). Dato $x_0 \in \overline{\mathbb{R}}$

, un intorno di $x_0$

è un insieme $I \subseteq \mathbb{R}$

che contiene un intervallo aperto della forma:

$(x_0-\delta,x_0+\delta)$ , con $\delta>0$ , se $x_0 \in \mathbb{R}$ ;
$(-\infty,M)$ , con $M \in \mathbb{R}$ , se $x_0 =-\infty$ ;
$(M,+\infty)$ , con $M \in \mathbb{R}$ , se $x_0 =+\infty$ .

L’insieme $(x_0-\delta,x_0+\delta)$ è anche detto intorno circolare di $x_0$ di raggio $\delta$ e viene solitamente indicato con¹ $B_\delta(x_0)$ .

Intuitivamente, un intorno di $x_0$ è un insieme che “circonda” $x_0$ , cioè che contiene tutti i numeri reali sufficientemente vicini a $x_0$ . Poiché ogni intorno contiene un intervallo del tipo indicato nella definizione 1, spesso col termine intorno si intende proprio uno di questi intervalli.

Esempio 2.

L’insieme $I=(0,3] \cup \{4\}$ , rappresentato in blu in figura 1 è un intorno di $x_0=2$ in quanto contiene l’intervallo aperto $(1,3)=(2-1,2+1)$ . $I$ è anche un intorno di $\frac{3}{2}$ , in quanto contiene l’intervallo aperto $(1,2)= \left ( \frac{3}{2}- \frac{1}{2},\frac{3}{2}+\frac{1}{2} \right )$ . $I$ non è però un intorno di $x_0=3$ , in quanto non contiene alcun intorno circolare $B_\delta(3)$ , con $\delta>0$ . Analogamente, $I$ non è un intorno di $4$ .

$\[\]$

Figura 1: l’insieme $I$ dell’esempio 2, rappresentato in blu.

$\[\]$

L’insieme $J=[0,2) \cup [3,+\infty)$ è un intorno di $+\infty$ , in quanto contiene la semiretta destra $(5,+\infty)$ . Esso non è un intorno di $-\infty$ , in quanto non contiene alcuna semiretta sinistra. Analogamente, l’insieme $K=(-\infty,1)$ è un intorno di $-\infty$ , in quanto esso stesso è una semiretta sinistra.

$\[\]$

Figura 2: gli insiemi $J$ e $K$ dell’esempio 2, rappresentati rispettivamente in blu e in verde.

$\[\]$

L’insieme $\mathbb{R}$ è un intorno di qualunque $x_0 \in \overline{\mathbb{R}}$ .

Osservazione 3. Nel caso $x_0 \in \mathbb{R}$ , al diminuire del raggio $\delta$ dell’intorno circolare $(x_0-\delta,x_0+\delta)$ , i punti di tale intorno diventano arbitrariamente vicini a $x_0$ . In altre parole è possibile selezionare punti vicini quanto si vuole a $x_0$ , scegliendo un raggio $\delta$ sufficientemente piccolo. Ciò avviene anche con gli intorni di $-\infty$ e $+\infty$ : scegliendo $M$ sufficientemente piccolo o sufficientemente grande, le semirette $(-\infty,M)$ e $(M,+\infty)$ contengono punti arbitrariamente “vicini” rispettivamente a $-\infty$ e $+\infty$ .

$\[\]$

Mettiamo ora in luce una proprietà degli intorni che sarà molto utile nel seguito: punti di $\overline{\mathbb{R}}$ distinti possiedono intorni disgiunti.

Proposizione 4. Siano $y_1, y_2 \in \overline{\mathbb{R}}$

con $y_1 \neq y_2$

. Allora esistono un intorno $J_1$

di $y_1$

e un intorno $J_2$

di $y_2$

disgiunti.

Dimostrazione. Distinguiamo quattro casi supponendo, senza ledere la generalità, che $y_1 < y_2$ .

$y_1,y_2 \in \mathbb{R}$ . Si ha ovviamente
(2) $\begin{equation*} y_1 < y_1 + \frac{y_2- y_1}{2} = y_2-\frac{y_2-y_1}{2} < y_2 \end{equation*}$

e quindi, chiamando $\delta \coloneqq \frac{y_2-y_1}{2}$ metà della distanza tra $y_1$ e $y_2$ , segue

(3) $\begin{equation*} (y_1- \delta, y_1+\delta) \cap (y_2-\delta, y_2+\delta) = \emptyset. \end{equation*}$

I due intorni $J_1=(y_1- \delta, y_1+\delta)$ e $J_2=(y_2-\delta, y_2+\delta)$ rispettivamente di $y_1$ e $y_2$ sono disgiunti, si veda la figura 3.

$\[\]$

$\[\]$

$\[\]$

Figura 3: gli intorni $J_1$ e $J_2$ rispettivamente di $y_1$ e $y_2$ sono disgiunti.

$\[\]$

$\[\]$

$y_1\in \mathbb{R}$ e $y_2 =+\infty$ . I due intorni
(4) $\begin{equation*} J_1=(y_1-1,y_1+1), \qquad J_2= (y_1+1,+\infty) \end{equation*}$

rispettivamente di $y_1$ e $+\infty$ , sono disgiunti.

$y_1=-\infty$ e $y_2 \in \mathbb{R}$ . I due intorni
(5) $\begin{equation*} J_1=(-\infty,y_2-1), \qquad J_2= (y_2-1,y_2+1) \end{equation*}$

rispettivamente di $-\infty$ e $y_2$ , sono disgiunti.

$y_1=-\infty$ e $y_2=+\infty$ . Gli intorni
(6) $\begin{equation*} J_1=(-\infty,0), \qquad J_2=(0,+\infty) \end{equation*}$

rispettimente di $-\infty$ e $+\infty$ sono disgiunti.

$\[\]$

Dall’inglese ball. ↩

Punti di accumulazione.

La domanda 1 chiede a quale valore si avvicina $f(x)$

quando $x$

si avvicina a $x_0$

. Affinché ciò abbia senso, occorre poter calcolare $f(x)$

in punti $x$

arbitrariamente vicini a $x_0$

e diversi da esso. Intuitivamente, in ogni intorno di $x_0$

devono esserci dei punti del dominio di $f$

diversi da $x_0$

. Questo concetto si formalizza con la nozione di punto di accumulazione.

Definizione 5 (punto di accumulazione). Dato $A \subseteq \mathbb{R}$

, $x_0 \in \overline{\mathbb{R}}$

si dice punto di accumulazione per $A$

se ogni intorno di $x_0$

contiene punti di $A$

diversi da $x_0$

, ossia se ogni intorno $I$

di $x_0$

è tale che

(7) $\begin{equation*} I \cap A \setminus \{x_0\} \neq \emptyset. \end{equation*}$

Osservazione 6. Affinché $x_0$ sia un punto di accumulazione per $A \subseteq \mathbb{R}$ , in ogni intorno di $x_0$ deve esserci un punto di $A$ diverso da $x_0$ ; poiché esistono intorni di $x_0$ arbitrariamente “aderenti” a $x_0$ , risulta chiaro che a ogni intorno di $x_0$ devono appartenere infiniti punti di $A$ e quindi $A$ deve essere infinito. Viceversa, si può mostrare che ogni sottoinsieme infinito $A$ di $\mathbb{R}$ possiede almeno un punto di accumulazione: è il contenuto del famoso teorema di Bolzano-Weierstrass, la cui versione per successioni è reperibile in [4].

$\[\]$

Illustriamo l’importante concetto di punto di accumulazione mediante alcuni esempi.

Esempio 7. Consideriamo l’insieme

(8) $\begin{equation*} A = (-1,3] \cup \mathbb{N} = (-1,3) \cup \{4, 5, \dots \}, \end{equation*}$

rappresentato in blu in figura 4, e determiniamone i punti di accumulazione.

Figura 4: l’insieme $A$ dell’esempio 7, rappresentato in blu.

$\[\]$

$x_0=3$ è un punto di accumulazione per $A$ . Infatti, qualsiasi intorno di $3$ contiene un intorno circolare $I=(3-\delta,3+\delta)$ , che a sua volta contiene infiniti punti di $A$ diversi da $3$ , ad esempio tutti i punti di $I$ minori di $3$ e maggiori di $1$ : vale cioè
(9) $\begin{equation*} I \cap A \setminus \{3\} \supseteq (3-\delta,3) \qquad \forall \delta \leq 4. %\begin{cases} %(3-\delta,3) & \text{se } \delta \leq 4 %\\ %(-1,3) & \text{se } \delta > 4 %\end{cases} \end{equation*}$

In particolare $I \cap A \setminus \{3\}$ non è mai vuoto, come illustrato dalla figura 5, quindi per la definizione 5 $3$ è un punto di accumulazione di $A$ .

$\[\]$

$\[\]$

$\[\]$

Figura 5: l’intersezione dell’insieme $A$ , in blu, e dell’intorno circolare $I=(3-\delta,3+\delta)$ di $x_0=3$ , in verde, è pari a $(3-\delta,3]$ , che contiene appunto infiniti punti diversi da $3$ ; pertanto $3$ è di accumulazione per $A$ .

$\[\]$

$\[\]$

$x_0=-1$ è un punto di accumulazione per $A$ , anche se non appartiene ad $A$ . Infatti qualsiasi intorno circolare $I=(-1-\delta,-1+\delta)$ di $-1$ contiene tutti i punti di $A$ minori di $-1+\delta$ :
(10) $\begin{equation*} I \cap A \setminus \{-1\} = (-1,-1+\delta) \qquad \forall \delta \leq 4, \end{equation*}$

come si evince dalla figura 6. In questo caso è indifferente effettuare o meno la differenza insiemistica $I \cap A \setminus \{-1\}$ , in quanto $-1 \notin A$ .

$\[\]$

$\[\]$

$\[\]$

Figura 6: l’intersezione dell’insieme $A$ , in blu, e dell’intorno circolare $I=(1-\delta,1+\delta)$ di $x_0=-1$ , in verde, è pari a $(-1,-1+\delta)$ , che contiene infiniti punti di $A$ diversi a $-1$ ; dunque $-1$ è di accumulazione per $A$ .

$\[\]$

$\[\]$

Ogni punto $x_0 \in (-1,3)$ è di accumulazione per $A$ . Infatti, ogni intorno $(x_0-\delta,x_0+\delta)$ contiene l’intervallo costituito dai punti di $(-1,3)$ maggiori di $x_0-\delta$ e minori di $x_0+\delta$ , cioè infiniti punti di $A$ diversi da $x_0$ , come illustrato in figura 7 .

$\[\]$

$\[\]$

$\[\]$

Figura 7: l’intersezione dell’insieme $A$ , in blu, e di ogni intorno circolare $I=(x_0-\delta,x_0+\delta)$ di $x_0 \in (-1,3)$ , in verde, contiene un intero intervallo; dunque $x_0$ è di accumulazione per $A$ .

$\[\]$

$\[\]$

Ogni altro punto di $\mathbb{R}$ non è di accumulazione per $A$ . Infatti, se $x_0<-1$ , allora esiste $\delta>0$ sufficientemente piccolo affinché $(x_0-\delta,x_0+\delta)$ non contenga alcun punto di $A$ . Analogamente, se $x_0>3$ , allora è possibile determinare $\delta>0$ tale che $(x_0-\delta,x_0+\delta)$ contenga al più $x_0$ come unico punto di $A$ , come illustrato in figura 8 .

$\[\]$

$\[\]$

$\[\]$

Figura 8: se $x_0<-1$ , è possibile determinare un intorno di $x_0$ sufficientemente piccolo, tale da non contenere alcun punto di $A$ . Se $x_0>3$ , esiste un intorno di $x_0$ la cui intersezione con $A$ è costituita al più dal solo punto $x_0$ . In entrambi i casi, $x_0$ non è di accumulazione per $A$ .

$\[\]$

$\[\]$

$x_0=+\infty$ è un punto di accumulazione per $A$ . Infatti, qualunque intorno di $+\infty$ contiene una semiretta del tipo $(M,+\infty)$ , a cui appartengono tutti i numeri naturali maggiori di $M$ , ossia infiniti elementi di $A$ , come illustrato a destra in figura 9; in formule
(11) $\begin{equation*} (M,+\infty) \cap A \setminus \{+\infty\} = \{n \in \mathbb{N} \colon n > M\} \neq \emptyset. \end{equation*}$

Si osservi come in questo caso sia irrilevante la condizione $\setminus \{+\infty\}$ in quanto $+\infty$ , non essendo un numero reale, è già escluso a priori dall’appartenere ad $A$ .

$\[\]$

$\[\]$

$\[\]$

Figura 9: {ogni semiretta destra $(M,+\infty)$ contiene tutti i naturali maggiori di $M$ che sono tutti punti di $A$ ; dunque $+\infty$ è di accumulazione per $A$ . Invece, la semiretta sinistra $(-\infty,-2)$ non contiene alcun punto di $A$ , quindi $-\infty$ non è di accumulazione per $A$ .

$\[\]$

$\[\]$

$x_0=-\infty$ non è un punto di accumulazione per $A$ . Infatti, l’intorno $(-\infty,-2)$ non contiene alcun punto di $A$ , come illustrato a sinistra in figura 9; in formule
(12) $\begin{equation*} (-\infty,-2) \cap A \setminus \{-\infty\} = \emptyset. \end{equation*}$

Anche in questo caso escludere $\{-\infty\}$ è ininfluente ai fini del discorso.

Osservazione 8. $+\infty$ è un punto di accumulazione per un insieme $A \subseteq \mathbb{R}$ se e solo se $A$ è illimitato superiormente. Infatti, $A$ è illimitato superiormente se e solo se, per ogni $M\in \mathbb{R}$ , esiste $x \in A \cap (M+\infty)$ , ossia se e solo se ogni intorno di $+\infty$ contiene punti di $A$ .

Analogamente, $-\infty$ è di accumulazione per $A \subseteq \mathbb{R}$ se e solo se $A$ è illimitato inferiormente.

Proprietà valide definitivamente.

Nei punti di accumulazione di un insieme, si può parlare di proprietà valide definitivamente.

Definizione 9 (proprietà valide definitivamente). Sia $A \subseteq \mathbb{R}$

e sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

. Una proprietà $P$

definita per gli elementi di $A$

si dice valida definitivamente per $x \to x_0$ (o per $x$

che tende a $x_0$

) se esiste un intorno $I$

di $x_0$

tale che essa sia vera per ogni $x \in A \cap I \setminus \{x_0\}$

Intuitivamente, una proprietà è valida definitivamente se è vera per tutti punti sufficientemente vicini a $x_0$ , escluso al più $x_0$ stesso.

Esempio 10.

La disuguaglianza $x + 10\sin x > 2$ , che ha senso per ogni $x \in \mathbb{R}$ , è definitivamente vera per $x \to +\infty$ . Infatti è vera per ogni $x \in (12,+\infty)$ , che è appunto un intorno di $+\infty$ .

La relazione $\sin x \neq 0$ è definitiamente vera per $x \to 0$ . Infatti, sebbene $\sin 0=0$ , nell’intorno $I \coloneqq \left (-\frac{\pi}{2},\frac{\pi}{2}\right )$ di $x_0=0$ si ha
(13) $\begin{equation*} \sin x \neq 0 \qquad \forall x \in I \setminus \{0\}. \end{equation*}$

La proprietà $\sin x>0$ non è definitivamente vera per $x \to +\infty$ . Infatti, in ogni semiretta $(M,+\infty)$ intorno di $x_0=+\infty$ , esistono punti $x$ tali che $\sin x\leq 0$ , per la periodicità della funzione seno.

Limiti: definizione e prime proprietà

Introduzione.

Siamo ora pronti per presentare lo strumento matematico che permette di rispondere alla domanda 1. L’idea è utilizzare gli intorni per dire che $f(x)$

può essere reso arbitrariamente vicino a $\ell \in \overline{\mathbb{R}}$

se $x$

è sufficientemente vicino a $x_0$

Definizione e teorema di unicità del limite.

Definizione 11 (limite). Sia $f\colon A \subseteq \mathbb{R} \to \mathbb{R}$

e sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

. Si dice che $f$

ha limite $\ell \in \overline{\mathbb{R}}$ per $x$ che tende a $x_0$ se, per ogni intorno $J$

di $\ell$

, esiste un intorno $I$

di $x_0$

tale che

(14) $\begin{equation*} f(x) \in J \qquad \forall x \in I \cap A \setminus \{x_0\}. \end{equation*}$

In tal caso si scrive

(15) $\begin{equation*} \lim_{x \to x_0} f(x)= \ell \qquad \text{o talvolta} \qquad f(x) \xrightarrow[x \to x_0]{} \ell. \end{equation*}$

Se $\ell=\pm\infty$ , $f$ si dice divergente positivamente o negativamente per $x \to x_0$ . Se invece $\ell \in \mathbb{R}$ , $f$ si dice convergente a $\ell$ per $x \to x_0$ . Se inoltre $\ell=0$ , $f$ si dice infinitesima per $x \to x_0$ .

Intuitivamente, $f$ ha limite $\ell$ per $x \to x_0$ se, scegliendo $x$ sufficientemente vicino a $x_0$ , i valori assunti da $f(x)$ possono essere resi arbitrariamente vicini a $\ell$ . Si noti che $x_0$ può anche non appartenere al dominio $A$ di $f$ , e che il limite $\ell$ non ha alcuna relazione con l’eventuale valore $f(x_0)$ . Infatti, (14) non pone alcuna condizione su $f(x_0)$ : essa cioè richiede solo che i valori $f(x)$ assunti nell’intorno $I$ escludendo $x_0$ appartengano all’intorno $J$ di $\ell$ . In generale quindi, anche se $x_0 \in A$ , può aversi $f(x_0) \neq \ell$ , come illustrato nel grafico in alto a sinistra nella figura 10.

$\[\]$

Figura 10: illustrazione di $\lim_{x \to x_0} f(x)=\ell$ : fissato un intorno $J$ di $\ell$ , deve esistere $I$ intorno di $x_0$ tale che $f(x) \in J$ per ogni $x \in I \setminus \{x_0\}$ . Nella prima riga riportiamo il caso $x_0 \in \mathbb{R}$ , nella seconda riga $x_0 =-\infty$ e nella terza riga il caso $x_0=+\infty$ ; nella prima colonna riportiamo i casi $\ell\in \mathbb{R}$ , mentre sulla seconda colonna riportiamo i casi $\ell=+\infty$ ; non illustriamo i casi $\ell=-\infty$ , che però si ottengono riflettendo la colonna di destra rispetto all’asse $x$ .

$\[\]$

Tabella 1: versioni della definizione 11 distinguendo i vari casi tra $x_0$ e $\ell$ .

$\[\]$

La definizione 11 è molto generale e comprende tutti i casi possibili per $x_0,\ell$ reali o infiniti. Risulta però conveniente riproporre il significato di

(16) $\begin{equation*} \lim_{x \to x_0} f(x) = \ell \end{equation*}$

esplicitando, per ciascuno dei possibili casi, gli intorni di $x_0$ e $\ell$ e ottenendo così la tabella 1. I vari casi sono illustrati nella figura 10.

Un modo equivalente di enunciare la definizione di limite utilizza la nozione di distanza tra numeri reali, ottenuta mediante valore assoluto della loro differenza. Ad esempio, la definizione di $\lim_{x \to x_0} f(x)= \ell$ nel caso $x_0,\ell \in \mathbb{R}$ può essere data come segue:

per ogni $\varepsilon>0$ esiste $\delta>0$ tale che $\displaystyle x \in A \colon 0 < |x-x_0| < \delta \implies |f(x)-\ell|< \varepsilon,$

che nuovamente ha il seguente significato intuitivo: si fissi qualunque $\varepsilon>0$ ; se si desidera che la distanza tra $f(x)$ e $\ell$ sia inferiore a $\varepsilon$ , è sufficiente che la distanza tra $x$ e $x_0$ sia positiva (affinché $x \neq x_0$ ) e inferiore a $\delta$ , dove $\delta>0$ è scelto opportunamente. Riformulando la definizione di limite in questi termini per ognuno dei casi possibili su $x_0,\ell$ , si ottengono le seconde caratterizzazioni nella tabella 1. Un ottimo esercizio per familiarizzare con la definizione di limite e comprenderla meglio è provare a riscrivere tutti i casi in autonomia: invitiamo il lettore a cimentarsi e a confrontare poi i propri risultati con quelli nella tabella 1, analizzando eventuali differenze.

Una importante proprietà dei limiti è la loro unicità. Ciò consente di parlare del limite di una funzione in un punto e giustifica la scrittura

(17) $\begin{equation*} \lim_{x \to x_0} f(x)= \ell. \end{equation*}$

Tale caratteristica è strettamente correlata alla proprietà di separazione degli intorni stabilita dalla proposizione 4.

Teorema 12 (unicità del limite). Sia $f \colon A \subseteq \mathbb{R} \to \mathbb{R}$

e sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

. Se $f$

ha limite $\ell \in \overline{\mathbb{R}}$

in $x_0$

, tale limite è unico.

Dimostrazione. Supponiamo per assurdo che $\ell_1, \ell_2 \in \overline{\mathbb{R}}$ siano due limiti distinti di $f$ in $x_0$ e fissiamo due intorni $J_1,J_2$ rispettivamente di $\ell_1$ e $\ell_2$ disgiunti, che esistono per la proposizione 4 e che rappresentiamo in rosso nella figura 11.

$\[\]$

Figura 11: dimostrazione del teorema 12 di unicità del limite; per la definizione di limite, se $x \in I_1 \cap I_2$ , $f(x)$ dovrebbe appartenere simultaneamente a $J_1$ e $J_2$ , che è impossibile in quanto essi sono disgiunti.

$\[\]$

Per definizione 11 di limite, esistono intorni $I_1,I_2$ di $x_0$ tali che

(18) $\begin{equation*} f(x) \in J_1 \quad \forall x \in A \cap I_1 \setminus \{x_0\}, \qquad f(x) \in J_2 \quad \forall x \in A \cap I_2 \setminus \{x_0\}. \end{equation*}$

Dunque $f(x)$ dovrebbe appartenere simultaneamente a $J_1$ e $J_2$ se $x$ appartiene all’intersezione $I=I_1 \cap I_2$ dei due intorni di $x_0$ , che è a sua volta un intorno di $x_0$ e ha intersezione non vuota con $A \setminus \{x_0\}$ in quanto $x_0$ è un punto di accumulazione per $A$ . In formule, dovrebbe valere

(19) $\begin{equation*} f(x) \in J_1 \cap J_2 \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

che è assurdo in quanto $J_1 \cap J_2= \emptyset$ .

Osservazione 13. (definizione 11 per intorni piccoli). Poiché la nozione di limite serve per caratterizzare il comportamento di $f$ nelle vicinanze di $x_0$ , per studiare la validità della definizione 11 è sufficiente verificarla solo per intorni “sufficientemente piccoli” di $\ell$ , cioè contenuti in un fissato intorno $J_0$ di $\ell$ .

Dunque, i casi esplicitati dalla tabella 1 si possono modificare nelle seguenti forme.

$\ell \in \mathbb{R}$ . “Per ogni $\varepsilon \in (0,\varepsilon_0)$ …”, dove $\varepsilon_0>0$ è un numero fissato;

$\ell=-\infty$ . “Per ogni $M < M_0$ …”, dove $M_0 \in \mathbb{R}$ è un numero fissato;

$\ell=+\infty$ . “Per ogni $M > M_0$ …”, dove $M_0 \in \mathbb{R}$ è un numero fissato.

Utilizzeremo varie volte questa semplice osservazione nel seguito.

Primi esempi.

Illustriamo ora il concetto di limite con alcuni esempi, rimandando il lettore a [3] per un’ampia raccolta di esempi illustrati sul tema.

Esempio 14. Consideriamo $f \colon \mathbb{R} \to \mathbb{R}$ definita da

(20) $\begin{equation*} f(x) = \begin{cases} 2 & \text{se $x \neq 0$}\\ 1 & \text{se $x = 0$}. \end{cases} \end{equation*}$

Il grafico della funzione $f$ è rappresentato in blu in figura 12. Verifichiamo che

(21) $\begin{equation*} \lim_{x \to 0} f(x) = 2. \end{equation*}$

$\[\]$

Figura 12: la funzione $f$ dell’esempio 14. In rosso è evidenziato l’intorno $J=(2 - \varepsilon,2+\varepsilon)$ di $\ell=2$ . Da $f(x)=2$ per ogni $x \in \mathbb{R} \setminus \{0\}$ , segue che $\ell=\lim_{x \to 0} f(x)=2$ . Si noti che $\ell \neq f(0)$ .

$\[\]$

Poiché $x_0, \ell \in \mathbb{R}$ , dobbiamo verificare la validità della formula del primo caso della tabella 1, con $x_0=0$ e $\ell=2$ . Fissiamo dunque $\varepsilon>0$ ; poiché $f(x)=2$ per ogni $x \neq 0$ , scegliendo un qualunque $\delta>0$ vale

(22) $\begin{equation*} f(x) \in (2-\varepsilon,2+\varepsilon) \qquad \forall x \in (-\delta,\delta) \setminus \{0\}. \end{equation*}$

Per l’arbitrarietà di $\varepsilon$ abbiamo dunque la conclusione.

Esempio 15. Sia $\alpha>0$ . Verifichiamo che valgono i seguenti limiti:

$\lim_{x \to x_0} x^\alpha = x_0^\alpha \text{per ogni} x_0 \in [0,+\infty)$ ;

$\lim_{x \to +\infty} x^\alpha=+\infty$ .

Fissiamo $\alpha>0$ e definiamo la funzione $f \colon [0,+\infty) \to \mathbb{R}$ come

(23) $\begin{equation*} f(x) = x^\alpha \qquad \forall x \geq 0. \end{equation*}$

Proviamo separatamente i due limiti richiesti, che seguono dall’esistenza e dalle proprietà delle potenze a esponente reale: il lettore interessato può consultare [2 (capitolo 2, sezione 8)], [6 (sezione 5)] e [12 (appendice A)] per maggiori dettagli.

Dobbiamo verificare che vale la condizione al punto 1 della tabella 1 con . Per maggiore chiarezza espositiva separiamo i casi in cui e .
- $x_0=0$ . Fissiamo $\varepsilon>0$ , definiamo l’intorno $J=(-\varepsilon,\varepsilon)$ di $\ell=0$ e osserviamo che
  (24) $\begin{equation*} f(x) \in J \iff 0 \leq x^\alpha < \varepsilon \iff 0 \leq x < \varepsilon^{\frac{1}{\alpha}}, \end{equation*}$
  
  dove l’equivalenza segue elevando tutto alla potenza $\frac{1}{\alpha}$ e sfruttando il fatto che la potenza a esponente reale positivo è crescente, si veda il grafico a sinistra in figura 13. Scegliendo dunque $\delta= \varepsilon^{\frac{1}{\alpha}}$ , si ottiene che l’intorno $I=(-\delta,\delta)$ di $x_0=0$ è tale che
  
  (25) $\begin{equation*} f(x) \in J \qquad \forall x \in I \cap [0,+\infty)=\big[0,\varepsilon^{\frac{1}{\alpha}} \big), \end{equation*}$
  
  ovvero quanto desiderato.
  
  $\[\]$
  
  $\[\]$
  
  $\[\]$
  
  Figura 13: punto 1 dell’esempio 15, ossia il limite per $x_0 \in [0,+\infty)$ . A sinistra il caso $x_0=0$ , a destra il caso $x_0>0$ . Nonostante sia rappresentato il caso $\alpha \in (0,1)$ , gli argomenti sono indipendenti da questa proprietà e solo validi per qualunque $\alpha>0$ .
  
  $\[\]$
  
  $\[\]$
- $x_0>0$ . Sia ora $x_0>0$ e scegliamo $\varepsilon>0$ . Per l’osservazione 21 possiamo assumere $\varepsilon < x_0^\alpha$ , avendo così $x_0^\alpha - \varepsilon>0$ . Considerando l’intorno $J=(x_0^\alpha - \varepsilon,x_0^\alpha + \varepsilon)$ di $\ell=x_0^\alpha$ , si ha dunque
  
  (26) $\begin{equation*} f(x) \in J \iff x_0^\alpha - \varepsilon < x^\alpha < x_0^\alpha + \varepsilon \iff (x_0^\alpha - \varepsilon)^{\frac{1}{\alpha}} < x < (x_0^\alpha + \varepsilon)^{\frac{1}{\alpha}}, \end{equation*}$
  
  si veda il grafico a destra nella figura 13. Poiché l’intervallo aperto $\left ( (x_0^\alpha - \varepsilon)^\frac{1}{\alpha}, (x_0^\alpha + \varepsilon)^{\frac{1}{\alpha}} \right )$ contiene $x_0$ , esiste $\delta>0$ tale che
  
  (27) $\begin{equation*} (x_0^\alpha - \varepsilon)^\frac{1}{\alpha} < x_0-\delta < x_0+\delta < (x_0^\alpha + \varepsilon)^{\frac{1}{\alpha}}. \end{equation*}$
  
  Chiamando $I=(x_0-\delta,x_0+\delta)$ tale intorno di $x_0$ , per (26) e (27) si ottiene quindi
  
  (28) $\begin{equation*} f(x) \in J \qquad \forall x \in I, \end{equation*}$
  
  oppure, in altre parole,
  
  (29) $\begin{equation*} x \in (x_0-\delta,x_0+\delta) \implies |x^\alpha - x_0^\alpha|< \varepsilon, \end{equation*}$
  
  ovvero la conclusione.

Occorre provare la validità della condizione al punto 9 della tabella 1. A tal fine, fissiamo $M \in \mathbb{R}$ e, nuovamente in virtù dell’osservazione 13, possiamo limitarci a considerare il caso in cui $M>0$ . Dunque $J=(M,+\infty)$ è un intorno di $\ell=+\infty$ . Si ha

(30) $\begin{equation*} f(x) \in J \iff x^\alpha> M \iff x > M^{\frac{1}{\alpha}}, \end{equation*}$

dove di nuovo l’equivalenza segue elevando entrambi i membri a $\frac{1}{\alpha}$ (che è possibile grazie alla scelta $M>0$ ) e per la monotonia della potenza a esponente reale positivo; si veda la figura 14. Scegliendo quindi $H=M^{\frac{1}{\alpha}}$ e definendo l’intorno $I=\big( M^{\frac{1}{\alpha}}, +\infty \big)$ di $x_0=+\infty$ , (30) è equivalente a

(31) $\begin{equation*} f(x) \in J \qquad \forall x \in I, \end{equation*}$

cioè quanto volevamo provare.

$\[\]$

Figura 14: punto 2 dell’esempio 15. Si vede che, se $x> M^{\frac{1}{\alpha}}$ , allora $x^\alpha> M$ .

$\[\]$

Esempio 16 (funzione che non ammette limite). Sia $f \colon \mathbb{R} \to \mathbb{R}$ la funzione definita da

(32) $\begin{equation*} f(x) = \sin x \qquad \forall x \in \mathbb{R}. \end{equation*}$

Come provato in [3 (esercizio 11)], per ogni $x_0 \in \mathbb{R}$ si ha

(33) $\begin{equation*} \lim_{x \to x_0} \sin x = \sin x_0. \end{equation*}$

Osserviamo che

(34) $\begin{equation*} \lim_{x \to + \infty} \sin x \quad \text{non esiste.} \end{equation*}$

Infatti, notiamo innanzitutto che la funzione $\sin$ è periodica di periodo $2\pi$ e assume tutti i valori dell’intervallo $[-1,1]$ , dunque ciò è vero anche in ogni intorno di $x_0=+\infty$ . Fissiamo $\ell \in \overline{\mathbb{R}}$ e scegliamo un intorno $J$ di $\ell$ che non contienga $[-1,1]$ (illustrato in rosso in figura 15), non esiste alcun intorno $I$ di $x_0$ tale che $f(x) \in J$ per ogni $x \in I$ ; quindi $\lim_{x \to + \infty} \sin x$ non può essere pari a $\ell$ . Si veda [3 (esercizio 10)] per maggiori dettagli.

$\[\]$

Figura 15: si fissi l’intorno $J=\left (\ell-\frac{1}{4},\ell+\frac{1}{4}\right )$ , rappresentato in rosso, che non contiene l’intero $[-1,1]$ ; poiché $\operatorname{Im} \sin = [-1,1]$ , in ogni intorno $I=(H,+\infty)$ di $x_0=+\infty$ esiste $\bar{x}$ tale che $f(\bar{x}) \notin J$ .

$\[\]$

Osservazione 17. In maniera analoga si può dimostrare che ogni funzione $f \colon \mathbb{R} \to \mathbb{R}$ periodica e non costante non ha limite per $x \to +\infty$ e per $x \to -\infty$ .

$\[\]$

Figura 16: la funzione dell’esempio 18, definita da $f(x)= \sin \left ( \frac{1}{x} \right )$ , non ha limite per $x \to 0$ .

$\[\]$

Esempio 18. Un comportamento analogo ha la funzione $f \colon (0,+\infty) \to \mathbb{R}$ definita da

(35) $\begin{equation*} f(x) = \sin \left ( \frac{1}{x} \right ) \qquad \forall x \in (0,+\infty), \end{equation*}$

il cui grafico è rappresentato in figura 16. È evidente che, in ogni intorno di $0$ , $f$ assume tutti i valori dell’intervallo $[-1,1]$ e quindi non ha limite per $x \to 0$ . Infatti, fissando un intervallo $J$ contenuto strettamente in $[-1,1]$ , in ogni intorno di $x_0=0$ la funzione $f$ assume anche valori esterni a $J$ .

$\[\]$

Nella tabella 2 riepiloghiamo i limiti visti nei precedenti esempi, insieme ad altri limiti di alcune funzioni elementari di base, le cui dimostrazioni possono essere reperite in [3].

$\[\]$

Tabella 2: limiti di alcune funzioni elementari, riportati nei precedenti esempi e in [3].

$\[\]$

Limiti sinistri e destri.

Dato $x_0 \in \overline{\mathbb{R}}$

, può essere necessario studiare il comportamento di una funzione $f$

quando la variabile si avvicini a $x_0$

“da sinistra” o “da destra”, ossia quando $x$

si avvicini a $x_0$

assumendo però solo valori minori o maggiori di $x_0$

. Tale studio conduce alle nozioni di limite sinistro e destro; per presentarla, anteponiamo la seguente definizione di punti di accumulazione sinistri e destri di un sottoinsieme di numeri reali.

Definizione 19 (punti di accumulazione sinistri e destri). Dato $A \subseteq \mathbb{R}$

e $x_0 \in \mathbb{R} \cup \{+\infty\}$

, esso si dice punto di accumulazione sinistro per $A$

se esso è un punto di accumulazione dell’insieme $A \cap (-\infty,x_0)$

, ossia se e solo se per ogni $x_1 < x_0$

si ha

(36) $\begin{equation*} (x_1,x_0) \cap A \neq \emptyset. \end{equation*}$

Analogamente $x_0 \in \mathbb{R} \cup \{-\infty\}$ si dice punto di accumulazione destro se esso è un punto di accumulazione dell’insieme $A \cap (x_0,+\infty)$ , ovvero se e solo se per ogni $x_1>x_0$ si ha

(37) $\begin{equation*} (x_0, x_1) \cap A \neq \emptyset. \end{equation*}$

Segue subito dalla definizione che, se $x_0$ è un punto di accumulazione sinistro o destro per $A$ , allora esso è un punto di accumulazione per $A$ nel senso della definizione 5. Viceversa, se $x_0$ è di accumulazione per $A$ non è detto che esso sia di accumulazione destro e sinistro per $A$ , ma si può mostrare che esso è di accumulazione destro o sinistro per $A$ .

Osservazione 20. Si noti inoltre che la nozione di punto di accumulazione sinistro e destro non differisce da quella di punto di accumulazione nei casi $x_0=\pm \infty$ : $+\infty$ è di accumulazione sinistro per $A$ se e solo se è di accumulazione per $A$ , mentre $-\infty$ è di accumulazione destro per $A$ se e solo se è di accumulazione per $A$ .

$\[\]$

Utilizzando questi strumenti, possiamo definire i limiti sinistro e destro di una funzione in un punto.

Definizione 21 (limiti sinistri e destri). Sia $f \colon A\subseteq \mathbb{R} \to \mathbb{R}$

una funzione e sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione sinistro per $A$

. Si dice che $\ell \in \overline{\mathbb{R}}$

è il limite sinistro di $f$

per $x$

che tende a $x_0$

se, per ogni intorno $J$

di $\ell$

, esiste $x_1<x_0$

tale che

(38) $\begin{equation*} f(x) \in J \qquad \forall x \in (x_1,x_0) \cap A . \end{equation*}$

In tal caso si scrive

(39) $\begin{equation*} \lim_{x \to x_0^-} f(x) = \ell. \end{equation*}$

Analogamente si definisce il limite destro di $f$ per $x \to x_0$ ed esso si indica con $\displaystyle \lim_{x \to x_0^+} f(x)$ .

Osservazione 22. Il limite sinistro della funzione $f$ in $x_0$ coincide quindi col limite sinistro della restrizione $f_{| A \cap (-\infty,x_0)}$ di $f$ all’insieme $A \cap (-\infty,x_0)$ , ossia considerando $f$ definita solo per i numeri reali minori di $x_0$ . Analogamente, il limite destro di $f$ in $x_0$ coincide col limite della restrizione $f_{| A \cap (x_0,+\infty)}$ , ovvero considerando il comportamento di $f$ solo a destra di $x_0$ .

$\[\]$

Osservazione 23. Per l’osservazione 20, i limiti in $x_0=-\infty$ sono soltanto destri, mentre i limiti in $x_0=+\infty$ sono solo sinistri.

$\[\]$

Esempio 24. Verifichiamo che

(40) $\begin{equation*} \lim_{x \to 0^-} \frac{1}{x} = -\infty, \qquad \lim_{x \to 0^+} \frac{1}{x} = +\infty. \end{equation*}$

$\[\]$

Figura 17: in blu, il grafico della funzione $f$ dell’esempio 24. Si vede che, se $x$ si avvicina a $0$ da sinistra, allora i valori $f(x)$ diventano infinitamente negativi; viceversa, se $x$ si avvicina a $0$ da destra, allora i valori assunti da $f$ diventano infinitamente grandi.

$\[\]$

Vogliamo quindi calcolare i limiti della funzione $f \colon \mathbb{R} \setminus \{0\} \to \mathbb{R}$ definita da

(41) $\begin{equation*} f(x) = \frac{1}{x} \qquad \forall x \in \mathbb{R} \setminus \{0\}, \end{equation*}$

il cui grafico è rappresentato in figura 17. Osserviamo che ogni numero reale è un punto di accumulazione destro e sinistro del dominio $\mathbb{R} \setminus \{0\}$ di $f$ ; dunque i limiti richiesti sono significativi e possono essere studiati.

Occorre verificare che il limite sinistro in $x_0=0$ della funzione $f$ vale $-\infty$ . Poiché $\ell=-\infty$ , siamo nel caso 2 riportato dalla tabella 1. Scegliamo dunque $M \in \mathbb{R}$ e, in virtù dell’osservazione 13, possiamo limitarci a considerare $M<0$ , come rappresentato a sinistra in figura 18.

$\[\]$

Figura 18: limite sinistro e destro in $0$ della funzione $f$ definita da $f(x)=\frac{1}{x}$ .

$\[\]$

Dato che

(42) $\begin{equation*} f(x) < M \iff \frac{1}{x} < M \iff \frac{1}{M} < x <0, \end{equation*}$

scegliendo $\delta=|\frac{1}{M}|$ otteniamo

(43) $\begin{equation*} f(x)<M \qquad \forall x \in (-\delta,0), \end{equation*}$

cioè quanto volevamo provare. Analogamente, scegliendo $M>0$ e come illustrato a destra in figura 18, si mostra che

(44) $\begin{equation*} \lim_{x \to 0^+} \frac{1}{x} = +\infty, \end{equation*}$

Per i limiti sinistri e destri valgono tutte le proprietà studiate e che studieremo nel seguito, con le opportune modifiche che il lettore può individuare per esercizio.

L’esistenza dei limiti sinistro e destro in un punto è strettamente correlata all’esistenza del limite. Presentiamo infatti il seguente risultato, che afferma che una funzione ha limite $\ell$ in un punto se e solo se i due limiti destro e sinistro in tale punto esistono e coincidono con $\ell$ .

Proposizione 25 (relazione tra limite sinistro, destro e limite). Sia $f \colon A \subseteq \mathbb{R} \to \mathbb{R}$

, sia $x_0$

un punto di accumulazione sinistro e destro per $A$

e sia $\ell \in \overline{\mathbb{R}}$

. Le seguenti affermazioni sono equivalenti:

$\lim_{x \to x_0} f(x)= \ell;$

$\lim_{x \to x_0^+} f(x)= \lim_{x \to x_0^-} f(x) = \ell.$

Dimostrazione. Proviamo le due implicazioni, limitandoci a considerare il caso $x_0 \in \mathbb{R}$ , in quanto solo in tale fattispecie hanno senso entrambi i limiti destro e sinistro.

1) $\Rightarrow$ 2). Fissiamo un intorno $J$ di $\ell$ ; poiché $\lim_{x \to x_0} f(x)= \ell$ , esiste $\delta>0$ di $x_0$ tale che
(45) $\begin{equation*} f(x) \in J \qquad \forall x \in A \cap (x_0-\delta,x_0+\delta) \setminus \{x_0\}. \end{equation*}$

Ovviamente vale dunque

(46) $\begin{equation*} f(x) \in J \quad \forall x \in A \cap (x_0-\delta,x_0), \qquad f(x) \in J \quad \forall x \in A \cap (x_0,x_0+\delta) \end{equation*}$

e ciò mostra che i limiti sinistro e destro di $f$ in $x_0$ esistono e sono pari a $\ell$ .

2) $\Rightarrow$ 1). Fissiamo un intorno $J$ di $\ell$ ; siccome i limiti sinistro e destro di $f$ in $x_0$ sono pari a $\ell$ , esistono $\delta_-,\delta_+>0$ tali che
(47) $\begin{equation*} f(x) \in J \quad \forall x \in A \cap (x_0-\delta_-,x_0), \qquad f(x) \in J \quad \forall x \in A \cap (x_0,x_0+\delta_+). \end{equation*}$

Scegliendo $\delta \coloneqq \min \{\delta_-,\delta_+\}$ , si ha quindi

(48) $\begin{equation*} f(x) \in J \qquad \forall x \in A \cap (x_0-\delta,x_0+\delta) \setminus \{x_0\}, \end{equation*}$

che prova che $\lim_{x \to x_0} f(x)=\ell$ .

La proposizione 25 è molto utile per dimostrare l’esistenza o la non esistenza di un limite, come mostrano gli esempi seguenti.

Esempio 26. La funzione $f \colon \mathbb{R} \setminus \{0\} \to \mathbb{R}$ definita da

(49) $\begin{equation*} f(x) = \frac{1}{x} \qquad \forall x \in \mathbb{R} \setminus \{0\} \end{equation*}$

non ha limite per $x \to 0$ . Infatti, come osservato già nell’esempio 24, si ha

(50) $\begin{equation*} \lim_{x \to 0^-} \frac{1}{x} = -\infty, \qquad \lim_{x \to 0^+} \frac{1}{x} = +\infty. \end{equation*}$

Poiché i limiti destro e sinistro in $0$ esistono ma sono diversi, per la proposizione 25 il limite di $f$ in $0$ non esiste.

$\[\]$

Esempio 27. Calcoliamo $\lim_{x \to 0} f(x)$ , dove $f \colon \mathbb{R} \to \mathbb{R}$ è definita da

(51) $\begin{equation*} f(x)= \begin{cases} 0 & \text{se } x < 0 \\ 1 & \text{se } x=0 \\ x & \text{se } x >0, \end{cases} \end{equation*}$

ed è rappresentata in figura 19.

$\[\]$

Figura 19: il grafico della funzione $f$ dell’esempio 27. Sia se $x$ si avvicina a $0$ da sinistra, sia se $x \to 0$ da destra, i valori $f(x)$ si avvicinano a $0$ ; dunque il limite di $f$ in $0$ vale $0$ .

$\[\]$

Abbiamo $\lim_{x \to 0^-} f(x)= 0$ in quanto $f$ è costantemente nulla per $x<0$ , mentre $\lim_{x \to 0^+}f(x)=\lim_{x \to 0^+}x=0$ per l’esempio 15. Dunque la proposizione 25 implica

(52) $\begin{equation*} \lim_{x \to 0} f(x)=0. \end{equation*}$

Scarica la teoria

Ottieni il documento di 63 pagine sulla teoria dei limiti.

Teoremi sui limiti

Introduzione.

In questa sezione riportiamo alcuni teoremi sui limiti, che ne precisano le proprietà.

Limiti e limitatezza.

L’esistenza del limite di una funzione $f$

in un punto $x_0$

implica delle proprietà di limitatezza di $f$

in un intorno di $x_0$

Proposizione 28 (limiti e limitatezza). Sia $f \colon A \subseteq \mathbb{R} \to \mathbb{R}$

una funzione, sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

e si supponga che

(53) $\begin{equation*} \lim_{x \to x_0} f(x) = \ell \in \overline{\mathbb{R}}. \end{equation*}$

Se $\ell \in \mathbb{R}$ , allora $f$ è limitata in un intorno di $x_0$ ;

Se $\ell=+\infty$ , allora $f$ è illimitata superiormente in ogni intorno di $x_0$ ed esiste un intorno di $x_0$ in cui $f$ è limitata inferiormente;

Se $\ell=-\infty$ , allora $f$ è illimitata inferiorente in ogni intorno di $x_0$ ed esiste un intorno di $x_0$ in cui $f$ è limitata superiormente.

Dimostrazione Dimostriamo separatamente le varie affermazioni.

$\ell \in \mathbb{R}$ . In tal caso, fissiamo un intorno $J=(\ell-\varepsilon,\ell+\varepsilon)$ , dove $\varepsilon$ è un numero reale positivo tale che l’eventuale valore $f(x_0)$ appartiene a $J$ . In particolare, $J$ è un intervallo limitato. Per definizione 11, esiste un intorno $I$ di $x_0$ tale che

(54) $\begin{equation*} \ell- \varepsilon < f(x) < \ell +\varepsilon \qquad \forall x \in I \cap A. \end{equation*}$

Per la definizione di limite occorrerebbe escludere $x_0$ da $I \cap A$ , ma ciò non è necessario in quanto abbiamo scelto $J$ in modo che contenesse anche $f(x_0)$ . L’equazione (54) prova che $f$ è limitata nell’intorno $I$ di $x_0$ .

$\ell=+\infty$ . Fissiamo $M \in \mathbb{R}$ . Nuovamente per definizione 11, esiste un intorno $I$ di $x_0$ tale che
(55) $\begin{equation*} f(x) > M \qquad \forall x \in I \cap A \setminus \{x_0\}. \end{equation*}$

Dunque $f$ è limitata inferiormente in $I \cap A$ . Mostriamo ora che $f$ è illimitata superiormente in ogni intorno di $x_0$ : supponiamo per assurdo che $I$ sia un intorno di $x_0$ in cui sia superiormente limitata, cioè tale che

(56) $\begin{equation*} f(x) \leq M \qquad \forall x \in I \cap A. \end{equation*}$

Per definizione di limite, esiste un intorno $I'$ di $x_0$ tale che

(57) $\begin{equation*} f(x) > M \qquad \forall x \in I' \cap A \setminus \{x_0\}, \end{equation*}$

ma ciò contraddice (56) in $I \cap I' \cap A$ , che è non vuoto in quanto $x_0$ è di accumulazione per $A$ .

Il caso $\ell=-\infty$ è analogo a $\ell=+\infty$ .

$\[\]$

Osservazione 29. Le implicazioni della precedente proposizione non si possono invertire:

la funzione definita da $f(x)= \sin \left (\frac{1}{x}\right )$ , studiata nell’esempio 18, è limitata, ma non ha limite in $0$ ;

la funzione $f \colon (0,+\infty) \to \mathbb{R}$ definita da

(58) $\begin{equation*} f(x)=\frac{1}{\sin^2 \left ( \dfrac{1}{x} \right )+x} \qquad \forall x \in (0,+\infty) \end{equation*}$

è limitata inferiormente (è non negativa) ed è superiormente illimitata in ogni intorno di $0$ ma non ha limite in $0$ ; ciò si evince anche dalla figura 20, in cui si vede che in ogni intorno di $0$ la funzione assume sia valori arbitrariamente grandi, sia vicini a $1$ .

$\[\]$

$\[\]$

$\[\]$

Figura 20: la funzione definita in (58) è inferiormente limitata, non è superiormente limitata in ogni intorno di $0$ , ma non ha limite per $x \to 0$ .

$\[\]$

$\[\]$

Teoremi di confronto e dei carabinieri.

I teoremi di confronto stabiliscono dei legami tra le disuguaglianze soddisfatte da funzioni e disuguaglianze tra i rispettivi limiti. Il teorema della permanenza del segno afferma che una disuguaglianza stretta tra i limiti in $x_0$

implica una disuguaglianza stretta tra le funzioni in un intorno di $x_0$

Teorema 30 (permanenza del segno – versione generale). Siano $f, g \colon A \subseteq \mathbb{R} \to \mathbb{R}$

due funzioni, sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

e supponiamo che

(59) $\begin{equation*} \lim_{x \to x_0} f(x) \eqqcolon \ell_f < \ell_g \coloneqq \lim_{x \to x_0} g(x). \end{equation*}$

Allora $f(x)<g(x)$ definitivamente per $x \to x_0$ .

In particolare, se $f$ è identicamente nulla, allora $g(x)>0$ definitivamente per $x \to x_0$ . Se, invece, $g$ è identicamente nulla, allora $f(x)<0$ definitivamente per $x \to x_0$ .

Dimostrazione. Poiché $\ell_f \neq \ell_g$ , per la proposizione 4, esistono due intorni $J_f,J_g$ disgiunti di $\ell_f,\ell_g$ . Ciò, insieme a $\ell_f < \ell_g$ implica che

(60) $\begin{equation*} y < z \qquad \forall y \in J_f, \,\,\forall z \in J_g. \end{equation*}$

Per la definizione 11 di limite, esistono due intorni $I_f,I_g$ di $x_0$ tali che

(61) $\begin{equation*} f(x) \in J_f, \quad \forall x \in A \cap I_f \setminus \{x_0\}, \qquad g(x) \in J_g \quad \forall x \in A \cap I_g \setminus \{x_0\}. \end{equation*}$

Definiamo dunque $I \coloneqq I_f \cap I_g$ , che è ancora un intorno di $x_0$ ; tali relazioni, insieme a (60), implicano che

(62) $\begin{equation*} f(x) < g(x) \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

ossia che $f(x)<g(x)$ definitivamente per $x \to x_0$ . Le ultime affermazioni seguono applicando il teorema ai casi in cui le funzioni $f$ o $g$ siano identicamente nulle.

$\[\]$

Osservazione 31. È bene notare che le disuguaglianze larghe tra limiti non implicano una disuguaglianza tra le funzioni: se $\ell_f \leq \ell_g$ , non si può concludere che $f(x)\leq g(x)$ definitivamente, come mostra il seguente esempio.

$\[\]$

Esempio 32. Consideriamo le funzioni $f,g \colon \mathbb{R} \to \mathbb{R}$ definite da

(63) $\begin{equation*} f(x)=2x^2, \quad g(x)=x^2 \qquad \forall x \in \mathbb{R} \end{equation*}$

e sia $x_0=0$ . Per quanto stabilito nell’esempio 15 vale

(64) $\begin{equation*} \ell_f= \lim_{x \to 0} 2x^2 = 0 = \lim_{x \to 0} x^2 = \ell_g, \end{equation*}$

cioè $\ell_f \leq \ell_g$ , però ovviamente si ha

(65) $\begin{equation*} f(x)> g(x) \qquad \forall x \in \mathbb{R} \setminus \{0\}, \end{equation*}$

quindi in particolare non vale $f(x)\leq g(x)$ definitivamente per $x \to 0$ .

$\[\]$

Come parziale inversione del precedente teorema, vale la seguente proposizione, che prova che disuguaglianze tra le funzioni si conservano al limite.

Proposizione 33 (disuguaglianze al limite). Siano $f, g \colon A \subseteq \mathbb{R} \to \mathbb{R}$

due funzioni e sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

e supponiamo che esistano i limiti

(66) $\begin{equation*} \lim_{x \to x_0} f(x) = \ell_f, \qquad \lim_{x \to x_0} g(x) = \ell_g. \end{equation*}$

Se vale $f(x) \leq g(x)$ definitivamente per $x \to x_0$ (definizione 9), allora

(67) $\begin{equation*} \ell_f \leq \ell_g. \end{equation*}$

Dimostrazione. Se si avesse $\ell_f>\ell_g$ , per il teorema 30 dovrebbe aversi $f(x)>g(x)$ definitivamente per $x \to x_0$ , che è contro l’ipotesi $f(x) \leq g(x)$ definitivamente. Pertanto deve aversi $\ell_f \leq \ell_g$ , cioè la tesi.

$\[\]$

Osservazione 34. Evidenziamo che la proposizione 33 non assicura l’esistenza dei limiti di $f$ e $g$ , ma solo che, se essi esistono, allora soddisfano una disuguaglianza.

$\[\]$

Osservazione 35. È bene notare che le disuguaglianze strette tra funzioni non passano in generale al limite: se $f(x)< g(x)$ definitivamente, non si può concludere che $\ell_f < \ell_g$ . Basta considerare l’esempio 32 invertendo i ruoli di $f$ e $g$ . Ovviamente, se $f(x)< g(x)$ definitivamente, per la proposizione 33 si ha $\ell_f \leq \ell_g$ .

$\[\]$

Esempio 36. Siano $f,g \colon \mathbb{R} \to \mathbb{R}$ le funzioni definite da

(68) $\begin{equation*} f(x) = x^2, \quad g(x)=2x^2 \qquad \forall x \in \mathbb{R}, \end{equation*}$

ovvero le funzioni dell’esempio 32 in cui si è scambiato il ruolo di $f$ e $g$ . Come già provato, si ha $f(x)<g(x)$ definitivamente per $x \to 0$ , ma $\ell_f \not < \ell_g$ in quanto tali limiti sono entrambi nulli.

Riepiloghiamo quanto stabilito dai precedenti risultati in questo schema.

Ribadiamo che tutti i precedenti risultati non affermano l’esistenza dei limiti delle funzioni in esame: l’esistenza dei limiti è assunta per ricavarne delle disuguaglianze.

Sotto opportune ipotesi però, delle disuguaglianze tra funzioni permettono di stabilire l’esistenza di un limite. È il caso del teorema dei carabinieri: se la funzione $g$ è compresa tra le funzioni $f$ e $h$ e queste ultime hanno il medesimo limite in $x_0$ , allora anche $g$ avrà lo stesso limite in tale punto.

Teorema 37 (dei carabinieri, caso $\ell \in \mathbb{R}$ ). Siano $f,g,h \colon A\subseteq \mathbb{R} \to \mathbb{R}$ e sia $x_0 \in {\mathbb{R}}$ un punto di accumulazione per $A$ . Supponiamo inoltre che

(69) $\begin{equation*} f(x) \leq g(x) \leq h(x) \qquad \text{definitivamente per $x \to x_0$} \end{equation*}$

e che valga

(70) $\begin{equation*} \lim_{x \to x_0} f(x) = \lim_{x \to x_0} h(x) = \ell \in {\mathbb{R}}. \end{equation*}$

Allora anche $g$ ha limite per $x \to x_0$ e si ha

(71) $\begin{equation*} \lim_{x \to x_0} g(x)= \ell. \end{equation*}$

Il teorema è appunto detto “dei carabinieri” in quanto le due funzioni $f$ e $h$ “intrappolano” la funzione $g$ e la forzano ad avere lo stesso limite $\ell$ . Intuitivamente, se $g$ è compresa tra $f$ e $h$ e queste ultime “passano” per lo stesso punto, anche $g$ è costretta a farlo, si veda la figura 21.

$\[\]$

Figura 21: illustrazione del teorema 37 dei carabinieri e della sua dimostrazione. Si osservi che, come di consueto, i valori di $f(x_0),g(x_0),h(x_0)$ non hanno alcuna rilevanza per i valori dei limiti e possono anche non soddisfare le proprietà richieste dalle ipotesi.

$\[\]$

Dimostrazione del teorema 37. Fissiamo un qualunque intorno $(\ell-\varepsilon,\ell+\varepsilon)$ di $\ell$ , con $\varepsilon>0$ (rappresentato in giallo nella figura 21) e facciamo le seguenti osservazioni.

Per l’ipotesi che $f(x) \leq g(x) \leq h(x)$ definitivamente per $x \to x_0$ , esiste un intorno $I_1$ (rappresentato in blu nella figura 21) di $x_0$ tale che
(72) $\begin{equation*} f(x) \leq g(x) \leq h(x) \qquad \forall x \in A \cap I_1 \setminus \{x_0\}. \end{equation*}$

Per definizione di limite 11, esiste un intorno $I_2$ (rappresentato in verde nella figura 21) di $x_0$ tale che
(73) $\begin{equation*} \ell - \varepsilon < f(x) < \ell+\varepsilon \qquad \forall x \in A \cap I_2 \setminus \{x_0\}. \end{equation*}$

Analogamente, esiste un intorno $I_3$ (rappresentato in rosso nella figura 21) di $x_0$ tale che
(74) $\begin{equation*} \ell - \varepsilon < h(x) < \ell+\varepsilon \qquad \forall x \in A \cap I_3 \setminus \{x_0\}. \end{equation*}$

L’insieme $I \coloneqq I_1 \cap I_2 \cap I_3$ (che nella figura 21 corrisponde a $I_3$ ) è un intorno di $x_0$ e in tale intorno valgono tutte le 3 condizioni precedenti; unendole, si ottiene

(75) $\begin{equation*} \ell- \varepsilon < f(x) \leq g(x) \leq h(x) < \ell +\varepsilon \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

Abbiamo cioè mostrato che, per ogni intorno $J$ di $\ell$ , esiste un intorno $I$ di $x_0$ tale che $g(x) \in J$ per ogni $x \in A \cap I \setminus \{x_0\}$ ; per la definizione 11, ciò implica che

(76) $\begin{equation*} \lim_{x \to x_0} g(x) = \ell. \end{equation*}$

Il teorema dei carabinieri vale in realtà anche se $\ell=\pm \infty$ . In questo caso, a differenza del controllo “bilaterale” necessario se $\ell \in \mathbb{R}$ , è sufficiente un controllo “unilaterale” sulle funzioni in esame, come chiarito dalla prossima proposizione.

Proposizione 38 (dei carabinieri, caso $\ell=\pm \infty$ ). Siano $f,g \colon A \subseteq \mathbb{R} \to \mathbb{R}$ , sia $x_0 \in \overline{\mathbb{R}}$ un punto di accumulazione per $A$ e si supponga che

(77) $\begin{equation*} f(x) \leq g(x) \qquad \text{definitivamente per $x \to x_0$}. \end{equation*}$

Valgono le seguenti proprietà:

se $\displaystyle \lim_{x \to x_0}f(x)= +\infty$ , allora anche $g$ ha limite in $x_0$ e si ha $\displaystyle \lim_{x \to x_0}g(x)=+\infty$ ;
se $\displaystyle \lim_{x \to x_0}g(x)= -\infty$ , allora anche $f$ ha limite in $x_0$ e si ha $\displaystyle \lim_{x \to x_0}f(x)=-\infty$ .

Osservazione 39. Intuitivamente, il teorema afferma che, se $g$ è “al di sopra di $f$ ” e $f$ cresce all’infinito, anche $g$ è forzata a crescere all’infinto. Viceversa, se $g$ decresce a $-\infty$ , anche $f$ è forzata a farlo: si modifichi opportunamente la figura 21 e si veda la figura 23 per un esempio.

$\[\]$

Dimostrazione della proposizione 38. Dimostriamo solo il primo punto in quanto il secondo è analogo. Poiché $f(x) \leq g(x)$ definitivamente per $x \to x_0$ , esiste un intorno $I_1$ di $x_0$ tale che

(78) $\begin{equation*} f(x) \leq g(x) \qquad \forall x \in A \cap I_1 \setminus \{x_0\}. \end{equation*}$

Si fissi ora $M \in \mathbb{R}$ ; poiché $\lim_{x \to x_0}f(x)= +\infty$ , esiste un intorno $I_2$ di $x_0$ tale che

(79) $\begin{equation*} f(x)> M \qquad \forall x \in A \cap I_2 \setminus \{x_0\}. \end{equation*}$

L’insieme $I=I_1 \cap I_2$ è un nuovo intorno di $x_0$ in cui valgono entrambe le condizioni (78) e (79); pertanto si ha

(80) $\begin{equation*} g(x)\geq f(x) > M \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

che prova quindi $\lim_{x \to x_0} g(x)=+\infty$ .

$\[\]$

Il teorema 37 dei carabinieri e la proposizione 38 sono estremamente utili per provare l’esistenza di un limite sfruttando una stima della funzione in esame con altre funzioni più semplici da trattare, come mostrano i seguenti esempi.

Esempio 40. Proviamo che

(81) $\begin{equation*} \lim_{x \to 0^+} x \sin^2 \left (\frac{1}{x} \right ) \frac{2+ \arctan(\log(x))}{4} = 0. \end{equation*}$

Poiché vale

(82) $\begin{equation*} \begin{gathered} 0 \leq \sin^2 \left (\frac{1}{x} \right ) \leq 1, \qquad \forall x \in (0,+\infty), \\[5pt] 0<\frac{2-\frac{\pi}{2}}{4} < \frac{2+ \arctan(\log(x))}{4} < \frac{2+ \frac{\pi}{2}}{4} <1 \qquad \forall x \in (0,+\infty), \end{gathered} \end{equation*}$

chiamando $g \colon (0,+\infty) \to \mathbb{R}$ la funzione nell’argomento del limite in (81), si ha

(83) $\begin{equation*} 0 \leq g(x) \leq x \qquad \forall x \in (0,+\infty). \end{equation*}$

Le funzioni definite da $f(x)\equiv 0$ e $h(x)=x$ (rispettivamente in verde e in rosso nella figura 22) soddisfano $\lim_{x \to 0^+} f(x) = 0 = \lim_{x \to 0^+}h(x)$ e quindi, per il teorema dei carabinieri 37, si ha anche

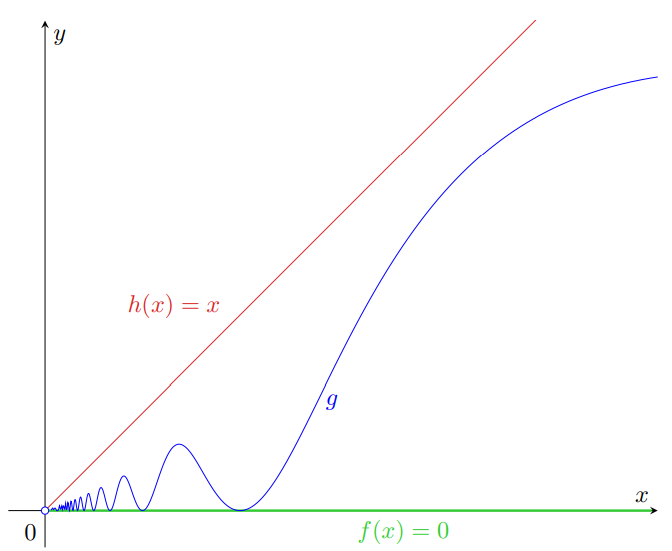
(84) $\begin{equation*} \lim_{x \to 0^+} x \sin^2 \left (\frac{1}{x} \right ) \frac{2+ \arctan(\log(x))}{4} = 0. \end{equation*}$

$\[\]$

Figura 22: la funzione $g$ (in blu) di cui si vuole calcolare il limite in $0^+$ è compresa tra la funzione identicamente nulla (in verde) e la funzione identità (in rosso). Poiché queste ultime hanno limite nullo in $0$ , anche $g$ ha limite nullo.

$\[\]$

Mostriamo ora un esempio di applicazione della proposizione 38.

$\[\]$

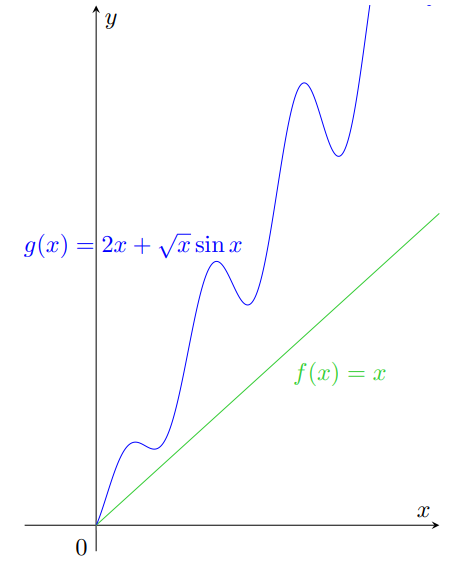
Figura 23: la funzione $g$ (in blu) dell’esempio 41 di cui si vuole calcolare il limite in $+\infty$ assume valori maggiori della funzione $f$ (in verde) per $x>1$ . Poiché $f$ ha limite $+\infty$ in $+\infty$ , anche $g$ ha limite infinito.

$\[\]$

Esempio 41. Proviamo che

(85) $\begin{equation*} \lim_{x \to +\infty} 2x +\sqrt{x}\sin x = +\infty. \end{equation*}$

Chiamiamo $g$ la funzione definita da $g(x)=2x +\sqrt{x}\sin x$ e sia $f \colon \mathbb{R} \to \mathbb{R}$ la funzione definita da $f(x)=x$ . Osserviamo che, se $x>1$ , allora $\sqrt{x}< x$ e quindi, poiché $|\sin x|\leq 1$ , vale

(86) $\begin{equation*} 2x +\sqrt{x}\sin x > x \qquad \forall x >1. \end{equation*}$

Poiché $\lim_{x \to +\infty} x = +\infty$ , come visto nell’esempio 15, la proposizione 38 prova (85).

Limiti e successioni: il teorema ponte.

Un altro oggetto matematico di cui si possono calcolare i limiti sono le successioni: una successione reale è una lista infinita e ordinata $x_n$

di numeri reali, in cui gli indici $n$

variano tra i numeri naturali. Ad esempio la successione definita da $x_n=\frac{1}{n}$

corrisponde alla lista

(87) $\begin{equation*} x_1=1, \quad x_2= \frac{1}{2}, \quad x_3= \frac{1}{3}, \quad \dots, \quad x_n= \frac{1}{n}, \quad \dots \end{equation*}$

Poiché tale lista è infinita, è naturale chiedersi verso quale valore, se ne esiste uno, si avvicinano i valori $x_n$ al crescere dell’indice $n$ . Tale eventuale valore $\ell$ viene detto limite della successione e si indica con lo stesso simbolo $\ell=\lim_{n \to +\infty} x_n$ usato per i limiti di funzioni o con la scrittura breve $x_n \to \ell$ .

Il fatto che le scritture siano le stesse non è un caso: formalmente infatti si può vedere la successione $x_n$ come la funzione $x \colon \mathbb{N} \to \mathbb{R}$ che associa a ogni numero naturale $n$ un numero reale $x(n)=x_n$ . Il termine $x_n$ è quindi l’immagine $x(n)$ del numero $n$ tramite la funzione $x$ . In tale ottica, poiché l’unico punto di accumulazione del dominio $\mathbb{N}$ della funzione $x$ è $+\infty$ , si può calcolare il limite della funzione $x$ in tale punto, che corrisponde al limite della successione. Dunque per i limiti di successioni valgono tutti i risultati stabiliti in questa dispensa, essendo queste semplicemente delle funzioni il cui dominio è il sottoinsieme $\mathbb{N}$ di $\mathbb{R}$ .

Esplicitiamo soltanto la definizione di limite di una successione in termini di indici: una successione $x_n$ ha limite $\ell$ se e solo se, per ogni intorno $J$ di $\ell$ , esiste $N \in \mathbb{N}$ tale che

(88) $\begin{equation*} x_n \in J \qquad \forall n \geq N. \end{equation*}$

Rimandiamo alla dispensa [12] per una trattazione completa di questo importante argomento dell’Analisi Matematica.

I limiti di funzioni e di successioni sono strettamente legati. Consideriamo infatti una funzione $f \colon A\subseteq \mathbb{R} \to \mathbb{R}$ e $\bar{x} \in \overline{\mathbb{R}}$ un punto di accumulazione di $A$ : studiando il limite $\lim_{x \to \bar{x}}f(x)$ , che sappiamo essere una descrizione del comportamento di $f$ negli intorni di $\bar{x}$ , ci interroghiamo sulla seguente domanda.

Domanda 42. È possibile dedurre il limite di $f$ in $\bar{x}$ “testando” $f(x_n)$ lungo successioni $x_n$ che tendono a $\bar{x}$ ?

$\[\]$

Il teorema ponte afferma che, se il limite delle successioni $f(x_n)$ esiste ed è lo stesso per ogni successione $x_n$ che tende a $\bar{x}$ , allora si può concludere che anche $\lim_{x \to \bar{x}} f(x)$ esiste e assume il medesimo valore. Viceversa, se $\lim_{x \to \bar{x}} f(x)= \ell$ , allora le successioni $f(x_n)$ hanno limite $\ell$ per ogni successione $x_n$ che tende a $\bar{x}$ .

Tale strumento è molto utile, in quanto permette di ridurre un problema per così dire “continuo” a molti problemi “discreti”, cioè allo studio di successioni. Rimandiamo a [9] per una discussione completa su questo teorema e a [5 (sezione 3.1)]] per la versione del teorema per funzioni continue e alcuni esempi di applicazione.

Teorema 43 (teorema ponte). Sia $f \colon A\subseteq \mathbb{R} \to \mathbb{R}$

, sia $\bar{x} \in \overline{\mathbb{R}}$

un punto di accumulazione di $A$

e sia $\ell \in \overline{\mathbb{R}}$

. Sono equivalenti:

$\displaystyle \lim_{x \to \bar{x}} f(x)= \ell$ ;
per ogni successione $x_n \in A \setminus \{\bar{x}\}$ tale che $x_n \to \bar{x}$ , si ha $f(x_n) \to \ell$ .

Dimostrazione. Proviamo che ciascuna delle condizioni implica l’altra.

(1) $\Rightarrow$ (2). Supponiamo che $\lim_{x \to \bar{x}} f(x)= \ell$ e fissiamo una successione $x_n$ i cui termini siano tutti in $A$ e diversi da $\bar{x}$ : vogliamo dimostrare che la successione $f(x_n)$ ha limite $\ell$ . A tal fine, fissiamo un qualunque intorno $J$ di $\ell$ . Per definizione 11 di limite, esiste un intorno $I$ di $\bar{x}$ tale che

(89) $\begin{equation*} f(x) \in J \qquad \forall x \in I \cap A \setminus \{x_0\}. \end{equation*}$

Poiché la successione $x_n$ ha limite $\bar{x}$ e $I$ è un intorno di $\bar{x}$ , esiste $N \in \mathbb{N}$ tale che

(90) $\begin{equation*} x_n \in I \qquad \forall n \geq N. \end{equation*}$

D’altra parte $x_n \in A \setminus \{x_0\}$ per ogni $n \in \mathbb{N}$ e quindi, per $n \geq N$ , il termine $x_n$ soddisfa la condizione in (89), cioè

(91) $\begin{equation*} f(x_n) \in J \qquad \forall n \geq N, \end{equation*}$

che è proprio la definizione di limite della successione $f(x_n)$ ; dunque $f(x_n) \to \ell$ .

(2) (1). In questa parte utilizzeremo la famiglia di intorni di definita come segue:
- $I_n=(-\infty,-n)$ per ogni $n \in \mathbb{N}$ se $\bar{x}=-\infty$ ;
- $I_n=\left (\bar{x} - \frac{1}{n}, \bar{x}+ \frac{1}{n} \right )$ per ogni $n \in \mathbb{N}$ se $\bar{x} \in \mathbb{R}$ ;
- $I_n=(n,+\infty)$ per ogni $n \in \mathbb{N}$ se $\bar{x}=+\infty$ .
L’osservazione fondamentale è la seguente: una successione tale che $x_n \in I_n$ per ogni $n \in \mathbb{N}$ ha limite $\bar{x}$ in ciascuno dei tre casi, grazie al teorema dei carabinieri.

Supponiamo che valga la condizione (2) e supponiamo, per assurdo, che la condizione (1) sia falsa. Dunque esiste un intorno $J$ di $\ell$ tale che, in ogni intorno $I$ di $\bar{x}$ esiste $x \in I \cap A \setminus \{\bar{x}\}$ tale che $f(x) \notin J$ . In particolare

(92) $\begin{equation*} \forall n \in \mathbb{N} \quad \exists x_n \in I_n \cap A \setminus \{\bar{x}\} \colon \quad f(x_n) \notin J, \end{equation*}$

poiché gli $I_n$ costruiti sopra sono appunto degli intorni di $\bar{x}$ . Abbiamo dunque costruito una successione $x_n$ che, come osservato sopra, tende a $\bar{x}$ e ha valori in $A \setminus\{\bar{x}\}$ . Quindi, per la condizione (2), i suoi termini dovrebbero appartenere a $J$ da un certo indice $N$ in poi, che contraddice però (92). Tale contraddizione mostra che (1) non può essere falsa.

Dal teorema ponte è possibile dedurre i limiti di numerose successioni, conoscendo i limiti delle funzioni relative.

Esempio 44. Calcoliamo il limite della successione $\sin \left (\frac{1}{n} \right )$ . La successione $x_n=\frac{1}{n}$ ha limite $0$ e tutti i suoi termini sono diversi da $0$ ; inoltre, dai risultati della tabella 2, sappiamo che $\lim_{x \to \bar{x}} \sin x= \sin(\bar{x})$ ; dunque per il teorema ponte 43 vale

(93) $\begin{equation*} \lim_{n \to +\infty} \sin \left (\frac{1}{n} \right ) = \sin 0 = 0. \end{equation*}$

$\[\]$

Un utilizzo molto importante del teorema ponte consiste nel dimostrare che una determinata funzione $f \colon A \to \mathbb{R}$ non ha limite in un certo punto $\bar{x}$ . Infatti, supponiamo di aver determinato due successioni $x_n \in A \setminus \{\bar{x}\}$ e $y_n \in A \setminus \{\bar{x}\}$ tali che le due successioni $f(x_n)$ e $f(y_n)$ non hanno lo stesso limite. Il teorema ponte 43 implica che il limite $\lim_{x \to \bar{x}}f(x)$ non può esistere, perché altrimenti il limite di $f$ dovrebbe essere lo stesso su tutte le successioni che tendono a $\bar{x}$ . Vediamo subito un esempio classico.

Esempio 45. Dimostriamo che

(94) $\begin{equation*} \lim_{x \to +\infty} \sin x \quad \text{non esiste.} \end{equation*}$

Abbiamo già verificato tale affermazione nell’esempio 16 mediante la definizione stessa di limite. Proviamola qui utilizzando il teorema ponte. Consideriamo infatti la funzione $f$ definita da $f(x)=\sin x$ e le successioni di numeri reali definite da

(95) $\begin{equation*} x_n=2n \pi, \quad y_n= \frac{\pi}{2} + 2n\pi \qquad \forall n \in \mathbb{N}. \end{equation*}$

Ovviamente entrambe le successioni hanno limite $\bar{x}=+\infty$ . Si ha però

(96) $\begin{equation*} \sin(x_n) = \sin \left ( 2n \pi \right ) = 0, \quad \sin(y_n)= \sin \left ( \frac{\pi}{2} + 2n\pi \right ) = 1 \qquad \forall n \in \mathbb{N}, \end{equation*}$

dunque la successione $\sin(x_n)$ ha costantemente valore nullo, mentre la successione $\sin(y_n)$ ha costantemente valore $1$ . Da ciò segue

(97) $\begin{equation*} f(x_n) \to 0, \qquad f(y_n) \to 1. \end{equation*}$

Poiché esistono due successioni divergenti a $\bar{x}=+\infty$ su cui $f$ ha limiti diversi, per il teorema ponte 43 il limite $\lim_{x \to +\infty} f(x)$ non esiste.

$\[\]$

Limiti di funzioni monotone.

Una funzione si dice monotòna [11 (sezione 2.6)] quando i valori assunti dalla funzione sono ordinati in maniera costante rispetto alla variabile indipendente, come ricordiamo nella seguente definizione.

Definizione 46 (monotonia). Sia $f \colon A \subseteq \mathbb{R} \to \mathbb{R}$

una funzione.

$f$ si dice crescente se $f(x) \leq f(y)$ per ogni $x,y \in A$ tali che $x < y$ .
$f$ si dice strettamente crescente se $f(x) < f(y)$ per ogni $x,y \in A$ tali che $x < y$ .
$f$ si dice decrescente se $f(x) \geq f(y)$ per ogni $x,y \in A$ tali che $x < y$ .
$f$ si dice strettamente decrescente se $f(x) > f(y)$ per ogni $x,y \in A$ tali che $x < y$ .

In ciascun caso $f$ si dice monotòna, mentre nei casi 2 e 4 $f$ si dice strettamente monotòna.

Le funzioni monotone possiedono speciali proprietà, che appaiono anche in relazione ai limiti: i limiti sinistro e destro in $x_0$ di una funzione monotona esistono sempre e si esprimono come estremi inferiore e superiore dei valori assunti a sinistra o a destra di $x_0$ , come mostrato dal seguente risultato.

Proposizione 47 (limiti di funzioni monotone). Sia $f \colon A \subseteq \mathbb{R} \to \mathbb{R}$

una funzione monotona e sia $x_0 \in \overline{\mathbb{R}}$

è un punto di accumulazione sinistro e/o destro per $A$

. Allora i limiti sinistro e/o destro di $f$

in $x_0$

esistono e valgono le seguenti proprietà:

Se $f$ è crescente, allora si ha
(98) $\begin{equation*} \lim_{x \to x_0^-} f(x) = \sup_{x<x_0} f(x), \qquad \lim_{x \to x_0^+} f(x) = \inf_{x>x_0} f(x). \end{equation*}$
Se $f$ è decrescente, allora si ha
(99) $\begin{equation*} \lim_{x \to x_0^-} f(x) = \inf_{x<x_0} f(x), \qquad \lim_{x \to x_0^+} f(x) = \sup_{x>x_0} f(x). \end{equation*}$

$\[\]$

Figura 24: limiti di una funzione monotona $f \colon (a,b) \to \mathbb{R}$ . Fissando un intorno $J$ di $\ell^-=\sup_{x \in (a,x_0)}f(x)$ e scegliendo $x_1<x_0$ tale che $f(x_1) \in J$ , per la monotonia di $f$ si ha che $f(x) \in J$ per ogni $x$ nell’intervallo $(x_1,x_0)$ , rappresentato in verde.

$\[\]$

Dimostrazione. Ci limitiamo a dimostrare l’esistenza del limite sinistro di una funzione crescente e la sua caratterizzazione, in quanto per gli altri casi si ragiona in maniera analoga. Osserviamo innanzitutto che, poiché $x_0$ è un punto di accumulazione sinistro per $A$ , abbiamo $x_0 \neq -\infty$ . Ha quindi senso definire

(100) $\begin{equation*} \ell^- \coloneqq \sup_{x<x_0} f(x) \end{equation*}$

e fissiamo un intorno $J=(\alpha,\beta)$ di $\ell^-$ , rappresentato in rosso in figura 24. Osserviamo che l’ipotesi che $f$ sia crescente implica che $\ell^-\neq -\infty$ e quindi vale $\alpha< \ell^-$ .

Per definizione di estremo superiore, esiste $x_1 \in A$ con $x_1<x_0$ e tale che $f(x_1) > \alpha$ . Poiché $f$ è crescente, si ha

(101) $\begin{equation*} \alpha < f(x_1) \leq f(x) \leq \ell^- \qquad \forall x \in (x_1,x_0) \cap A, \end{equation*}$

ossia

(102) $\begin{equation*} f(x) \in J \qquad \forall x \in (x_1,x_0) \cap A, \end{equation*}$

che è proprio la definizione 21 di limite sinistro in $x_0$ .

$\[\]$

Possiamo utilizzare questo risultato per provare l’esistenza e determinare il valore di alcuni limiti.

Esempio 48. Dimostriamo che

(103) $\begin{equation*} \lim_{x \to \left (\frac{\pi}{2}\right )^{-}} \tan x = +\infty. \end{equation*}$

$\[\]$

Figura 25: grafico della funzione $\tan$ .

$\[\]$

Infatti, la funzione $f \colon \left (-\frac{\pi}{2},\frac{\pi}{2}\right ) \to \mathbb{R}$ definita da $f(x)= \tan x$ , il cui grafico è riportato nella figura 25, è crescente e la sua immagine è $\mathbb{R}$ , [7 (sezione 1.2)], dunque

(104) $\begin{equation*} \sup_{x< \frac{\pi}{2}} \tan x = +\infty. \end{equation*}$

La proposizione 47 implica allora che il limite sinistro di $f$ in $\frac{\pi}{2}$ esiste e vale

(105) $\begin{equation*} \lim_{x \to \left (\frac{\pi}{2}\right )^{-}} \tan x = \sup_{x< \frac{\pi}{2}} \tan x = +\infty. \end{equation*}$

Analogamente si prova che $\lim_{x \to \left (-\frac{\pi}{2}\right )^{+}} \tan x = -\infty$

Operazioni con i limiti

Introduzione.

Risulta naturale chiedersi quali siano le relazioni tra l’operazione di limite e le usuali operazioni tra funzioni. Intuitivamente infatti, se $f(x)$

si avvicina a $\ell_f$

e $g(x)$

si avvicina a $\ell_g$

, è ragionevole aspettarsi che la somma $f(x)+g(x)$

si avvicini a $\ell_f+\ell_g$

e similmente per le altre operazioni algebriche come prodotti e quozienti. Ci si chiede cioè se il limite della somma di due funzioni sia pari alla somma dei limiti e così via per le altre operazioni.

Nella sezione Algebra dei limiti nell’insieme dei reali mostreremo che tali domande hanno risposte affermative quando i limiti sono numeri reali e le operazioni tra essi sono ben definite (ad esempio quando il limite della funzione al denominatore non è nullo). Nella successiva sezione Algebra dei limiti nell’insieme dei reali estesi vedremo che, sotto opportune ipotesi, tali risultati si estendono anche ai casi in cui i limiti appartengono alla retta reale estesa $\overline{\mathbb{R}}$ . Nella sezione Composizione e cambi di variabile analizziamo la relazione tra i limiti e la composizioni di funzioni, mentre nella sezione Limiti di funzioni inverse studiamo i limiti di funzioni inverse. Infine, nella sezione Limiti e potenze, utilizziamo i risultati precedenti per stabilire le relazioni tra i limiti e l’operazione di elevamento a potenza.

Algebra dei limiti nell'insieme dei reali.

Teorema 49 (algebra dei limiti in $\mathbb{R}$ ). Siano $f,g \colon A \subseteq \mathbb{R} \to \mathbb{R}$

due funzioni, sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

e supponiamo che i limiti

(106) $\begin{equation*} \ell_f \coloneqq \lim_{x \to x_0} f(x), \qquad \ell_g \coloneqq \lim_{x \to x_0} g(x) \end{equation*}$

esistano e siano finiti. Allora

(107) $\begin{equation*} \lim_{x \to x_0} \big(f(x)\pm g(x) \big) = \ell_f \pm \ell_g, \qquad \lim_{x \to x_0} f(x)\cdot g(x) = \ell_f \cdot \ell_g. \end{equation*}$

Se inoltre $\ell_g \neq 0$ , allora si ha

(108) $\begin{equation*} \lim_{x \to x_0} \frac{f(x)}{g(x)} = \frac{\ell_f}{\ell_g}. \end{equation*}$

Dimostrazione. Dimostriamo le affermazioni relative alle varie operazioni coinvolte nell’enunciato.

Somma. Dimostriamo solo la parte relativa alla somma, in quanto quella relativa alla differenza si ottiene in maniera analoga. Fissiamo un qualunque $\varepsilon>0$ e proviamo che
(109) $\begin{equation*} |f(x)+g(x) - (\ell_f+\ell_g)|< \varepsilon \qquad \text{definitivamente per $x \to x_0$.} \end{equation*}$

Infatti, per le ipotesi e per la definizione 11 di limite, esistono due intorni $I_1,I_2$ di $x_0$ tali che

(110) $\begin{gather*} |f(x)- \ell_f|< \frac{\varepsilon}{2} \qquad \forall x \in A \cap I_1 \setminus \{x_0\}, \\[4pt] |g(x)- \ell_g|< \frac{\varepsilon}{2} \qquad \forall x \in A \cap I_2 \setminus \{x_0\}. \end{gather*}$

Nell’intorno $I \coloneqq I_1 \cap I_2$ di $x_0$ queste disuguaglianze sono entrambe verificate e quindi, utilizzando la disuguaglianza triangolare, si ottiene

(111) $\begin{equation*} |f(x)+g(x) - \ell_f-\ell_g| \leq |f(x)- \ell_f| + |g(x)-\ell_g| < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

Prodotto. Fissiamo un qualunque $\varepsilon>0$ e dimostriamo che
(112) $\begin{equation*} |f(x)\cdot g(x) - \ell_f\cdot \ell_g|< \varepsilon \qquad \text{definitivamente per $x \to x_0$.} \end{equation*}$

Poiché $f$ ha limite finito in $x_0$ , per la proposizione 28 essa è limitata in un intorno $I_1$ di $x_0$ ed esiste quindi¹ $M> |\ell_g|$ tale che

(113) $\begin{equation*} |f(x)|\leq M \qquad \forall x \in A \cap I_1 \setminus \{x_0\}. \end{equation*}$

Di nuovo dalle ipotesi, esistono due intorni $I_2,I_3$ di $x_0$ tali che

(114) $\begin{equation*} \begin{gathered} |f(x)- \ell_f|< \frac{\varepsilon}{2M} \qquad \forall x \in A \cap I_2 \setminus \{x_0\}, \\ |g(x)- \ell_g|< \frac{\varepsilon}{2M} \qquad \forall x \in A \cap I_3 \setminus \{x_0\}. \end{gathered} \end{equation*}$

Nell’intorno $I \coloneqq I_1 \cap I_2 \cap I_3$ di $x_0$ le precedenti condizioni sono tutte valide. Pertanto

$\begin{aligned} |f(x) g(x) - \ell_f \ell_g| &= |f(x) g(x) - \ell_g f(x) + \ell_g f(x) - \ell_f \ell_g| = \\ &\leq |f(x) g(x) - \ell_g f(x)| + |\ell_g f(x) - \ell_f \ell_g| = \\ &= |g(x) - \ell_g| |f(x)| + |\ell_g| |f(x) - \ell_f| = \\ &\overset{\text{(eq. 114)}}{<} \frac{\varepsilon}{2M} \cdot M + |\ell_g| \cdot \frac{\varepsilon}{2M} = \\ &\overset{(|\ell_g| < M)}{\leq} \varepsilon, \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{aligned}$

dove nella prima uguaglianza abbiamo aggiunto e sottratto $\ell_g f(x)$ , mentre nella prima disuguaglianza abbiamo usato la disuguaglianza triangolare.
Quoziente. È sufficiente provare che
(115) $\begin{equation*} \lim_{x \to x_0} \frac{1}{g(x)}= \frac{1}{\ell_g}, \end{equation*}$

in quanto, per ottenere il limite di un quoziente, basta applicare il risultato sui limiti di prodotti alle funzioni $f$ e $\frac{1}{g}$ .

Fissiamo dunque $\varepsilon>0$ . Osserviamo innanzitutto che, dall’ipotesi $\ell_g \neq 0$ e dal teorema di permanenza del segno 30, segue che $g(x) \neq 0$ definitivamente per $x \to x_0$ , dunque $x_0$ è un punto di accumulazione per il dominio della funzione $\frac{1}{g}$ e il limite che stiamo cercando di calcolare ha senso. In particolare, sempre dal teorema di permanenza del segno segue che esiste un intorno $I_1$ di $x_0$ tale che

(116) $\begin{equation*} |g(x)|> \frac{|\ell_g|}{2} \qquad \forall x \in A \cap I_1 \setminus \{x_0\}. \end{equation*}$

Inoltre, dal fatto che $g$ ha limite $\ell_g$ , esiste un intorno $I_2$ di $x_0$ tale che

(117) $\begin{equation*} |g(x)- \ell_g|< \varepsilon\frac{\ell_g^2}{2} \qquad \forall x \in A \cap I_1 \setminus \{x_0\}. \end{equation*}$

Utilizzando queste disuguaglianze, valide nell’intorno $I \coloneqq I_1 \cap I_2$ , si ottiene

(118) $\begin{equation*} \left | \frac{1}{g(x)}- \frac{1}{\ell_g} \right | = \frac{|\ell_g - g(x)|}{|g(x)||\ell_g|} < \dfrac{\varepsilon\frac{\ell_g^2}{2}}{\frac{\ell_g^2}{2}} = \varepsilon \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

$\[\]$

Il teorema 49 permette di calcolare numerosi limiti di funzioni ottenute mediante operazioni tra funzioni, conoscendo i limiti di queste ultime. Tali risultati potrebbero ottenersi anche mediante l’applicazione della definizione, ma con estremo sforzo: si pensi ad esempio al lavoro che è stato necessario per ottenere i risultati dell’esempio 15 sui limiti delle potenze $x^\alpha$ .

Esempio 50. Calcoliamo

(119) $\begin{equation*} \lim_{x \to 3} \frac{2x^2 - x +1}{\sqrt{x} - \frac{1}{x}}. \end{equation*}$

Osserviamo che il numeratore è pari alla somma di potenze, eventualmente moltiplicate per dei coefficienti: per l’esempio 15 e il teorema 49, si ha quindi

(120) $\begin{equation*} \lim_{x \to 3} \big( 2x^2 - x +1 \big) = 2 \cdot \left ( \lim_{x \to 3} x^2 \right ) - \left (\lim_{x \to 3} x\right ) + 1 = 18-3+1 = 16. \end{equation*}$

Per il denominatore, osserviamo che per l’esempio 15 con $\alpha=\frac{1}{2}$ , si ha

(121) $\begin{equation*} \lim_{x \to 3} \sqrt{x} = \sqrt{3}, \end{equation*}$

mentre applicando la parte sul limite del quoziente del teorema 49, si ha

(122) $\begin{equation*} \lim_{x \to 3} \frac{1}{x} = \dfrac{1}{\lim_{x \to 3}x} = \frac{1}{3}. \end{equation*}$

Per il teorema 49, il denominatore ha limite $\sqrt{3} - \frac{1}{3}$ . Riapplicando il teorema 49 al quoziente si ottiene in definitiva

(123) $\begin{equation*} \lim_{x \to 3} \frac{2x^2 - x +1}{\sqrt{x} - \frac{1}{x}} = \dfrac{\lim_{x \to 3} \big( 2x^2 - x +1 \big)}{\lim_{x \to 3} \left ( \sqrt{x} - \frac{1}{x} \right )} = \dfrac{16}{\sqrt{3} - \frac{1}{3}}. \end{equation*}$

$\[\]$

Esempio 51 (limiti di polinomi). Sia $P(x)=a_nx^n + \dots + a_1x +a_0$ un polinomio e dimostriamo che, se $x_0 \in \mathbb{R}$ , allora si ha

(124) $\begin{equation*} \boxcolorato{analisi}{ \lim_{x \to x_0} P(x) = P(x_0). } \end{equation*}$

Infatti, $P$ è la somma delle $n$ funzioni definite da $a_k x^k$ , ognuna delle quali è il prodotto di un coefficiente costante $a_n$ e di $k$ fattori $x$ , che sappiamo soddisfare

(125) $\begin{equation*} \lim_{x \to x_0} x = x_0. \end{equation*}$

Applicando dunque il teorema 49 sul limite del prodotto si ottiene

(126) $\begin{equation*} \lim_{x \to x_0} a_k x^k = a_k \cdot \Big(\lim_{x \to x_0} x \Big) \cdots \Big(\lim_{x \to x_0} x \Big) = a_k \cdot x_0 \cdots x_0 = a_k x_0^k. \end{equation*}$

Applicando poi il teorema 49 sul limite della somma di funzioni si ottiene

$\begin{aligned} \lim_{x \to x_0} P(x) & = \Big( \lim_{x \to x_0} a_n x^n \Big) + \cdots + \Big( \lim_{x \to x_0} a_1 x \Big) + \Big( \lim_{x \to x_0} a_0 \Big) \overset{\text{(eq. 126)}}{=} \\& = a_n x_0^n + \cdots + a_1 x_0 + a_0 = \\& = P(x_0). \end{aligned}$

$\[\]$

Esempio 52 (limite della tangente). Fissiamo $x_0 \in \left ( -\frac{\pi}{2},\frac{\pi}{2}\right )$ e proviamo che vale

(127) $\begin{equation*} \lim_{x \to x_0} \tan x = \tan x_0. \end{equation*}$

Infatti $\tan x = \frac{\sin x}{\cos x}$ per ogni $x \in \left ( -\frac{\pi}{2},\frac{\pi}{2}\right )$ . Utilizzando i risultati della tabella 2 e ricordando che $\cos x_0 \neq 0$ se $x_0 \in \left ( -\frac{\pi}{2},\frac{\pi}{2}\right )$ , si può applicare il teorema 49 per concludere

(128) $\begin{equation*} \lim_{x \to x_0} \tan x = \lim_{x \to x_0} \frac{\sin x}{\cos x} \overset{\text{(thm. 49)}}{=} \frac{\lim_{x \to x_0} \sin x}{\lim_{x \to x_0} \cos x} \overset{\text{(tab. 2)}}{=} \frac{\sin x_0}{\cos x_0} = \tan x_0. \end{equation*}$

$\[\]$

Spesso eseguiremo calcoli simili a quelli mostrati nel precedente esempio senza citare esplicitamente ogni applicazione del teorema 49.

Come abbiamo anticipato, i risultati sull’algebra dei limiti possono essere estesi anche a casi non trattati dal teorema 49. La prossima proposizione è una generalizzazione del teorema sul limite del prodotto: quando uno dei fattori ha limite nullo, il prodotto ha limite nullo anche se l’altro fattore è meramente limitato.

Proposizione 53 (prodotto di funzioni limitate e infinitesime). Siano $f,g \colon A \subseteq \mathbb{R} \to \mathbb{R}$

due funzioni tali che $f$

sia limitata e $\lim_{x \to x_0} g(x) =0$

. Allora si ha

(129) $\begin{equation*} \lim_{x \to x_0} f(x)\cdot g(x)=0. \end{equation*}$

Dimostrazione. Fissiamo $\varepsilon>0$ . Poiché $f$ è limitata, esiste $M>0$ tale che

(130) $\begin{equation*} |f(x)|\leq M \qquad \forall x \in A. \end{equation*}$

Inoltre, per definizione 11 di limite nullo, esiste un intorno $I$ di $x_0$ tale che

(131) $\begin{equation*} |g(x)|<\frac{\varepsilon}{M} \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

Da queste informazioni ricaviamo che

(132) $\begin{equation*} |f(x) \cdot g(x)|<M \frac{\varepsilon}{M} = \varepsilon \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

che prova la tesi.

$\[\]$

Esempio 54. Calcoliamo

(133) $\begin{equation*} \lim_{x \to 0} x \sin \left (\frac{1}{x} \right ). \end{equation*}$

Il grafico della funzione $h \colon (0,+\infty) \to \mathbb{R}$ definita da

(134) $\begin{equation*} h(x) = x \sin \left (\frac{1}{x} \right ) \qquad \forall x \in (0,+\infty) \end{equation*}$

è rappresentato in figura 26. Osserviamo che $h(x)=f(x)g(x)$ con $f(x)=x$ e $g(x)=\sin \left (\frac{1}{x} \right )$ ; la funzione $f$ è ovviamente infinitesima per $x \to 0$ , mentre $\left | g(x)\right | \leq 1$ e quindi $g$ è limitata. Per la proposizione 53 si ottiene

(135) $\begin{equation*} \lim_{x \to 0} x \sin \left (\frac{1}{x} \right ) = 0. \end{equation*}$

$\[\]$

Figura 26: la funzione $h$ (in blu) dell’esempio 52 è il prodotto della funzione definita da $x$ , che è infinitesima per $x \to 0$ e della funzione definita da $\sin \left (\frac{1}{x} \right )$ , che è limitata per la limitatezza del seno. Dunque $h$ è infinitesima per $x \to 0$ .

$\[\]$

La scelta $M>|\ell_g|$ serve nel seguito: ovviamente la costante che limita $f$ può essere fissata arbitrariamente grande. ↩

Algebra dei limiti nell'insieme dei reali estesi.

Risultati analoghi a quelli del teorema 49 valgono anche nel caso di limiti infiniti, a volte sotto ipotesi ulteriori, altre volte in condizioni meno restrittive. Introduciamo preliminarmente una notazione con cui indichiamo che una funzione ha limite $\ell$

, ma assumendo definitivamente valori maggiori o minori di $\ell$

Definizione 55. Sia $f \colon A \subseteq \mathbb{R} \to \mathbb{R}$

, sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

; se $\lim_{x \to x_0} f(x)= \ell \in \mathbb{R}$

e se $f(x)>\ell$

definitivamente per $x \to x_0$

, allora scriviamo

(136) $\begin{equation*} \lim_{x \to x_0} f(x)= \ell^+. \end{equation*}$

Analogamente si definisce la scrittura $\lim_{x \to x_0} f(x)= \ell^-$ .

Esempio 56. Poiché $x^2 >0$ per ogni $x \neq 0$ , per l’esempio 15 si ha $\lim_{x \to 0} x^2=0^+$ .

$\[\]$

Siamo ora pronti per trattare l’algebra dei limiti in $\overline{\mathbb{R}}$ . Alla destra di ogni risultato, lo scriviamo tra parentesi quadre in una forma sintetica che estende le naturali operazioni tra numeri reali.

Teorema 57 (algebra dei limiti in $\overline{\mathbb{R}}$ ). Siano $f,g \colon A \subseteq \mathbb{R} \to \mathbb{R}$

due funzioni, sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

e supponiamo che esistano

(137) $\begin{equation*} \ell_f \coloneqq \lim_{x \to x_0} f(x), \qquad \ell_g \coloneqq \lim_{x \to x_0} g(x). \end{equation*}$

Sono valide le seguenti proprietà:

se $\ell_f= +\infty$ e se $\ell_g\neq -\infty$ , allora
(138) $\begin{flalign*} & & \lim_{x \to x_0} \big( f(x)+g(x) \big) =& +\infty; & \Big[ \infty + c=\infty \Big] \end{flalign*}$

se $\ell_f =+\infty$ e se $\ell_g \neq 0$ , allora
(139) $\begin{flalign*} & & \lim_{x \to x_0} f(x)g(x) &= \infty \cdot \operatorname{sgn}(\ell_g); & \Big[ \infty \cdot c=\operatorname{sgn}(c) \cdot \infty \Big] \end{flalign*}$

se $\ell_f \in \mathbb{R}$ e se $\ell_g = \pm \infty$ , allora
(140) $\begin{flalign*} & & \lim_{x \to x_0} \frac{f(x)}{g(x)} &= 0; & \Big[ \frac{c}{\infty}=0 \Big] \end{flalign*}$

se $\ell_f \neq 0$ e se $\ell_g = 0^+$ , allora
(141) $\begin{flalign*} & & \lim_{x \to x_0} \frac{f(x)}{g(x)} &= \operatorname{sgn}(\ell_f) \cdot \infty; & \left [ \frac{c}{0^+}=\operatorname{sgn}(c) \cdot \infty \right ] \end{flalign*}$

Valgono analoghe proprietà invertendo i segni.

Osservazione 58. Per semplicità e brevità di esposizione, abbiamo riportato soltanto i casi in cui uno dei limiti sia $+\infty$ oppure $0^+$ , ma il lettore può facilmente intuire che valgono enunciati analoghi cambiando opportunamente i segni delle ipotesi e dei risultati.

$\[\]$

Osservazione 59. Come sarà chiaro dalla dimostrazione, le tesi dei vari punti valgono sotto ipotesi più deboli dell’esistenza di entrambi i limiti di $f$ e $g$ :

$g$ limitata inferiormente in un intorno di $x_0$ ;

esiste $c>0$ (o $c<0$ ) tale che $g(x)>c$ (o $g(x)<c$ ) definitivamente per $x \to x_0$ ;

$f$ limitata in un intorno di $x_0$ ;

esiste $c>0$ (o $c<0$ ) tale che $f(x)>c$ (o $f(x)<c$ ) definitivamente per $x \to x_0$ .

$\[\]$

Osservazione 60. Il teorema non afferma nulla riguardo alle “operazioni” nella retta reale estesa

(142) $\begin{equation*} [+\infty-\infty], \quad \left [ \frac{\infty}{\infty} \right ], \quad [0 \cdot \infty], \quad \left [\frac{0}{0} \right ]. \end{equation*}$

Vedremo nella sezione Forme indeterminate e limiti notevoli che esse sono forme indeterminate.

$\[\]$

Osservazione 61. Le conclusioni dei teoremi 49 e 57 valgono ovviamente anche per limiti sinistri e destri.

$\[\]$

Dimostrazione del teorema 57. Proviamo separatamente i quattro punti.

Fissiamo $M>0$ . Poiché $\ell_g \coloneqq \lim_{x \to x_0} g(x)>-\infty$ , per la proposizione 28 $g$ è inferiormente limitata in un intorno $I_1$ di $x_0$ : esiste cioè $R \in \mathbb{R}$ tale che

(143) $\begin{equation*} g(x)>R \qquad \forall x \in A \cap I_1 \setminus \{x_0\}. \end{equation*}$

Inoltre, per la definizione 11 di limite, esiste un intorno $I_2$ di $x_0$ tale che

(144) $\begin{equation*} f(x)> M-R \qquad \forall x \in A \cap I_2 \setminus \{x_0\}. \end{equation*}$

Nell’intorno $I \coloneqq I_1 \cap I_2$ di $x_0$ queste due condizioni sono entrambe soddisfatte, pertanto si ha

(145) $\begin{equation*} f(x)+g(x) \geq M-R + R = M \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

che prova la tesi per l’arbitrarietà di $M$ .

Supponiamo senza perdita di generalità che $\ell_g>0$ in quanto l’altro caso è analogo. Fissiamo $M>0$ e osserviamo che, per la definizione di limite, esistono due intorni $I_1,I_2$ di $x_0$ tali che
(146) $\begin{gather*} g(x)> \frac{\ell_g}{2} \qquad \forall x \in A \cap I_1 \setminus \{x_0\}, \\[4pt] f(x)> \frac{2M}{\ell_g} \qquad \forall x \in A \cap I_2 \setminus \{x_0\}. \end{gather*}$

Definendo $I \coloneqq I_1 \cap I_2$ , si ha

(147) $\begin{equation*} f(x)g(x) > \frac{2M}{\ell_g} \frac{\ell_g}{2} = M \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

che è quanto si desiderava provare.

Supponiamo senza perdita di generalità che $g$ abbia limite $+\infty$ e fissiamo $\varepsilon>0$ . Poiché $f$ ha limite finito, è localmente limitata per la proposizione 28 esistono cioè $M>0$ e un intorno $I_1$ di $x_0$ tali che
(148) $\begin{equation*} |f(x)|< M \qquad \forall x \in A \cap I_1 \setminus \{x_0\}. \end{equation*}$

Dal fatto poi che $g$ ha limite infinito, esiste un intorno $I_2$ di $x_0$ tale che

(149) $\begin{equation*} g(x)> \frac{M}{\varepsilon} \qquad \forall x \in A \cap I_2 \setminus \{x_0\}. \end{equation*}$

In $I \coloneqq I_1 \cap I_2$ si ha quindi

(150) $\begin{equation*} \frac{f(x)}{g(x)} < \frac{M}{\frac{M}{\varepsilon}} = \varepsilon \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

che è quanto si voleva dimostrare.

Come sopra, supponiamo senza perdita di generalità che $\ell_f>0$ e fissiamo $M>0$ . Per la definizione di limite esistono due intorni $I_1,I_2$ di $x_0$ tali che
(151) $\begin{gather*} f(x)>\frac{\ell_f}{2} \qquad \forall x \in A \cap I_1 \setminus \{x_0\}, \\ 0 < g(x)< \frac{\ell_f}{2M} \qquad \forall x \in A \cap I_2 \setminus \{x_0\}. \end{gather*}$

Nell’intorno $I \coloneqq I_1 \cap I_2$ di $x_0$ entrambe le disuguaglianze sono valide e quindi

(152) $\begin{equation*} \frac{f(x)}{g(x)} > \frac{\frac{\ell_f}{2}}{\frac{\ell_f}{2M}} = M \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

che implica la tesi.

$\[\]$

Anche questo risultato possiede utili applicazioni nel calcolo dei limiti, anche mediante l’uso dei limiti base elencati nella tabella 2.

Esempio 62. Calcoliamo

(153) $\begin{equation*} \lim_{x \to +\infty} (x^2 - 2). \end{equation*}$

La funzione di cui si vuole calcolare il limite in $+\infty$ è costituita dalla somma di due funzioni, di espressione $x^2$ e $-2$ , che soddisfano

(154) $\begin{equation*} \lim_{x \to +\infty} x^2 \overset{\text{(es. 15)}}{=} +\infty, \qquad \lim_{x \to +\infty} (-2)=-2. \end{equation*}$

Poiché il limite del secondo addendo è diverso da $-\infty$ , il punto 1 del teorema 57 implica allora

(155) $\begin{equation*} \lim_{x \to +\infty} (x^2 - 2) = +\infty. \end{equation*}$

$\[\]$

Esempio 63. Calcoliamo

(156) $\begin{equation*} \lim_{x \to +\infty} (x + \sin x). \end{equation*}$

Qui non si ricade esattamente nel caso 1 del teorema 57 in quanto la funzione di cui si vuole calcolare il limite è costituita dalla somma di due funzioni, la seconda delle quali ( $\sin x$ ) non ha limite per $x \to +\infty$ . Però, grazie all’osservazione 59, affinché la tesi del teorema sia valida, è sufficiente che la seconda funzione sia inferiormente limitata, che è appunto il caso della funzione $\sin$ , che è in realtà limitata. Pertanto si ha

(157) $\begin{equation*} \lim_{x \to +\infty} (x +\sin x) =+\infty. \end{equation*}$

Alternativamente, si poteva utilizzare la versione per limiti infiniti del teorema dei carabinieri data dalla proposizione 38: poiché

(158) $\begin{equation*} x + \sin x \geq x -1 \qquad \forall x \in \mathbb{R}, \end{equation*}$

e dato che $\lim_{x \to +\infty} (x-1)=+\infty$ appunto per il teorema 57, la proposizione 38 implica

(159) $\begin{equation*} \lim_{x \to +\infty} (x +\sin x) =+\infty. \end{equation*}$

$\[\]$

Esempio 64. Calcoliamo

(160) $\begin{equation*} \lim_{x \to -\infty} \frac{x^3}{2}. \end{equation*}$

La funzione di cui si desidera studiare il limite è il prodotto della funzione definita $x^3$ e del fattore $\frac{1}{2}$ . Osserviamo innanzitutto che, dato che $\lim_{x \to -\infty} x =-\infty$ , applicando il punto 2 del teorema 57 al prodotto $x \cdot x \cdot x$ , si ha

(161) $\begin{equation*} \lim_{x \to -\infty} x^3=-\infty. \end{equation*}$

Poiché il fattore costante ha limite $\frac{1}{2}$ , di nuovo dal punto 2 del teorema 57 si ottiene

(162) $\begin{equation*} \lim_{x \to -\infty} \frac{x^3}{2} = - \infty. \end{equation*}$

$\[\]$

Esempio 65. Proviamo che

(163) $\begin{equation*} \lim_{x \to \left ( \frac{\pi}{2}\right )^-} \tan x = +\infty. \end{equation*}$

Tale risultato è stato già dimostrato nell’esempio 48 usando la monotonia della tangente; in questa sede calcoliamo il limite mediante il teorema 57. Per l’osservazione 59, infatti, possiamo utilizzare il teorema 57 per calcolare questo limite sinistro. La funzione $\tan$ è il rapporto delle funzioni seno e coseno, per le quali si ha

(164) $\begin{equation*} \lim_{x \to \left ( \frac{\pi}{2}\right )^-} \sin x = 1, \qquad \lim_{x \to \left ( \frac{\pi}{2}\right )^-} \cos x = 0^+, \end{equation*}$

in quanto il coseno assume valori positivi a sinistra di $\frac{\pi}{2}$ . Pertanto il punto 4 del teorema 57 prova (163). Analogamente, poiché $\lim_{x \to \left ( \frac{\pi}{2}\right )^+} \cos x= 0^-$ , si ottiene

(165) $\begin{equation*} \lim_{x \to \left ( \frac{\pi}{2}\right )^+} \tan x = -\infty. \end{equation*}$

$\[\]$

Esempio 66. Proviamo che

(166) $\begin{equation*} \lim_{x \to +\infty} \frac{1}{x} = 0. \end{equation*}$

La funzione di cui si vuole calcolare il limite è il rapporto di due funzioni, in cui il numeratore è costante e il denominatore ha limite infinito per $x \to +\infty$ in virtù dell’esempio 15, ricadendo cioè nel punto 3 del teorema 57, che implica la tesi.

$\[\]$

Esempio 67. Calcoliamo

(167) $\begin{equation*} \lim_{x \to 0} \frac{x-1}{x^2}. \end{equation*}$

Osserviamo che, per il teorema 49, il numeratore della frazione ha limite

(168) $\begin{equation*} \lim_{x \to 0} (x-1)=-1, \end{equation*}$

mentre il denominatore, in virtù dell’esempio 54, soddisfa

(169) $\begin{equation*} \lim_{x \to 0} x^2 = 0^+. \end{equation*}$

Dal punto 4 del teorema 49 si ha quindi

(170) $\begin{equation*} \lim_{x \to 0} \frac{x-1}{x^2}=-\infty. \end{equation*}$

$\[\]$

Composizione e cambi di variabile.

Abbiamo finora studiato le relazioni tra l’operatore di limite e le classiche operazioni algebriche tra funzioni. Un’altra operazione di fondamentale importanza è la composizione tra funzioni. Risulta quindi naturale chiedersi come questa si comporti relativamente all’operatore di limite, indagando cioè la seguente questione.

Domanda 68. Se $\lim_{x \to x_0} f(x) = y_0$ e $\lim_{y \to y_0} g(x) = \ell$ , si può concludere che $\lim_{x \to x_0} g(f(x))= \ell$ ?

$\[\]$

La risposta alla precedente domanda è affermativa sotto alcune ipotesi, come illustrato dal prossimo risultato.

Teorema 69 (cambio di variabile nei limiti). Siano $f \colon A \subseteq \mathbb{R} \to \mathbb{R}$

e $g \colon B \subseteq \mathbb{R} \to \mathbb{R}$

con $f(A) \subseteq B$

; si supponga che $x_0 \in \overline{\mathbb{R}}$

sia di accumulazione per $A$

, $y_0 \in \overline{\mathbb{R}}$

sia di accumulazione per $B$

e che

(171) $\begin{equation*} \lim_{x \to x_0} f(x) = y_0, \qquad \lim_{y \to y_0} g(x) = \ell \in \overline{\mathbb{R}}. \end{equation*}$

Se almeno una delle seguenti condizioni

$f(x) \neq y_0$ definitivamente per $x \to x_0$ ,

$y_0 \in B$ e $f(y_0)=\ell$ ,

è verificata, allora la composizione $g \circ f$ ha limite $\ell$ per $x \to x_0$ , ovvero si ha

(172) $\begin{equation*} \lim_{x \to x_0} g(f(x))= \ell. \end{equation*}$

Premettiamo alcune spiegazioni alla dimostrazione del teorema:

l’ipotesi $f(A) \subseteq B$ serve a garantire che la composizione $g \circ f$ sia ben definita;

la validità di almeno una tra le condizioni 1 e 2 è essenziale affinché la tesi sia vera, come vedremo nell’esempio 71;

l’ipotesi 2 richiede cioè che $g$ sia continua in $y_0$ ; si veda la dispensa [5] per una trattazione approfondita di questo affascinante argomento strettamente legato ai limiti.

Osservazione 70. Il teorema è valido anche richiedendo che esista solo il limite a sinistra di $g$ in $y_0$ . In tal caso però occorre l’ulteriore ipotesi che $f(x)\leq y_0$ definitivamente per $x \to x_0$ (oltre ovviamente a una delle condizioni 1 o 2): infatti, conoscere solo il limite a sinistra di $g$ significa avere informazioni sul comportamento di $g(y)$ solo quando $y<y_0$ ; pertanto, per studiare la composizione $g(f(x))$ , occorre che $f(x) \leq y_0$ definitivamente per $x \to x_0$ . Vale un’analoga considerazione se si conosce solo il limite a destra di $g$ .

$\[\]$

Dimostrazione del teorema 69. Fissiamo un qualunque intorno $K$ di $\ell$ e distinguiamo due casi, a seconda che sia verificata l’ipotesi 1 o 2 del teorema.

Per definizione di limite, esiste un intorno $J$ di $y_0$ tale che

(173) $\begin{equation*} g(y) \in K \qquad \forall y \in B \cap J \setminus \{y_0\}. \end{equation*}$

Poiché $\lim_{x \to x_0} f(x)=y_0$ esiste un intorno $I$ di $x_0$ tale che

(174) $\begin{equation*} f(x) \in J \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

Inoltre, per l’ipotesi 1 $f(x) \neq y_0$ definitivamente per $x \to x_0$ ; dunque, a meno di considerare un intorno $I$ di $x_0$ più piccolo, si ha

(175) $\begin{equation*} f(x) \in J \setminus \{y_0\}. \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

Dunque $f(x)$ appartiene a $B$ e a $J \setminus \{y_0\}$ , quindi $f(x)$ soddisfa la proprietà (173) e pertanto

(176) $\begin{equation*} g(f(x)) \in K \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

Per l’arbitrarietà di $K$ , questa è proprio la definizione di limite $\ell$ di $g \circ f$ per $x \to x_0$ , cioè la tesi.

Supponiamo che sia verificata la condizione 2. Poiché $g$ ha limite $\ell$ in $y_0$ , esiste un intorno $J$ di $y_0$ tale che
(177) $\begin{equation*} g(y) \in K \qquad \forall y \in B \cap J. \end{equation*}$

Si osservi che, da $g(y_0)=\ell$ , non è necessario escludere $y_0$ dalla condizione di sopra. Dato che $\lim_{x \to x_0}f(x)=y_0$ esiste un intorno $I$ di $x_0$ tale che

(178) $\begin{equation*} f(x) \in J \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

Dato che $f(x) \in B \cap J$ e per gli $y \in B \cap J$ vale $g(y) \in K$ , si ha

(179) $\begin{equation*} g(f(x)) \in K \qquad \forall x \in A \cap I \setminus \{x_0\}, \end{equation*}$

cioè la tesi.

Come anticipato, senza la validità di almeno una delle condizioni 1 o 2, la conclusione del teorema in generale è falsa, come mostrato dal seguente esempio. Il problema è che l’ipotesi $\lim_{y \to y_0} g(y)=\ell$ garantisce un controllo sui valori di $g(y)$ solo per $y \neq y_0$ , ma $f(x)$ potrebbe anche assumere costantemente valore $y_0$ in un intorno di $x_0$ ; in tal caso la composizione $g(f(x))$ potrebbe addirittura non essere definita in un intorno di $x_0$ se $y_0 \notin B$ , oppure assumere valori lontani da $\ell$ se $g(y_0) \neq \ell$ .

Vediamo questa seconda situazione illustrata nell’esempio che segue.

Esempio 71. Siano $f,g \colon \mathbb{R} \to \mathbb{R}$ le funzioni rappresentate in figura 27 e definite da

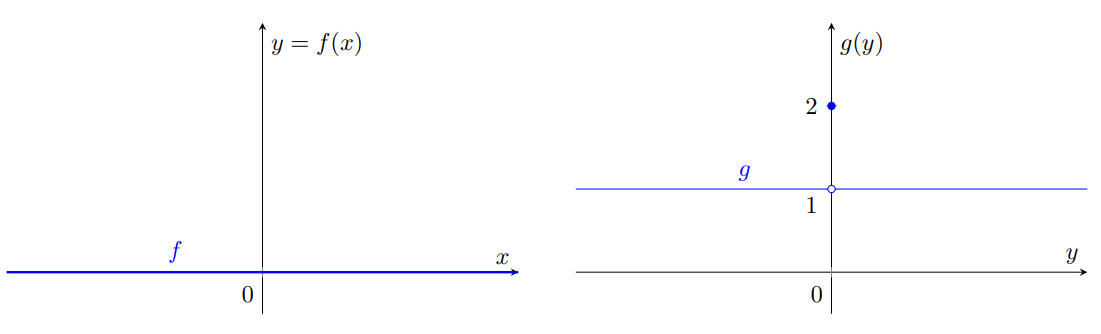
(180) $\begin{equation*} f(x)=0 \quad \forall x \in \mathbb{R}, \qquad g(y)= \begin{cases} 1 & \text{se } y \neq 0 \\ 2 & \text{se } y =0. \end{cases} \end{equation*}$

$\[\]$

Figura 27: a sinistra il grafico della funzione $f$ , identicamente nulla, mentre a destra il grafico della funzione $g$ che ha limite $1$ per $y \to 0$ , ma $g(0)=2 \neq 1$ .

$\[\]$

Scegliamo quindi $y_0=0$ e $x_0 \in \mathbb{R}$ un numero reale qualunque. Si ha

(181) $\begin{equation*} \lim_{x \to x_0} f(x)= 0 = y_0, \qquad \lim_{y \to y_0} g(x) = 1 \eqqcolon \ell. \end{equation*}$

Poiché $f(x) \equiv 0$ e $g(0)=2$ , la composizione $g \circ f$ è la funzione identicamente pari a $2$ , quindi

(182) $\begin{equation*} \lim_{x \to x_0} g(f(x))=2 \neq \ell. \end{equation*}$

La conclusione del teorema 69 non è quindi soddisfatta.

$\[\]$

Applichiamo ora il teorema 69 di cambio di variabile al calcolo di un limite. Altri utilizzi del teorema saranno illustrati nelle dimostrazioni di (267) e nell’esempio 95.

Esempio 72. Proviamo che

(183) $\begin{equation*} \lim_{x \to 0} e^{\cos x} = e. \end{equation*}$

La funzione di cui vogliamo calcolare il limite è composizione $g \circ f$ delle funzioni $f,g \colon \mathbb{R} \to \mathbb{R}$ definite da

(184) $\begin{equation*} f(x)= \cos x, \quad g(x) =e^x \qquad \forall x \in \mathbb{R}. \end{equation*}$

Per i risultati della tabella 2 si ha

(185) $\begin{equation*} \lim_{x \to 0} f(x) = \lim_{x \to 0} \cos x = 1, \qquad \lim_{y \to 1} g(y) = \lim_{y \to 1} e^y = e. \end{equation*}$

Osserviamo che in questo caso sono verificate entrambe le condizioni 1 e 2 del teorema 69: infatti

(186) $\begin{equation*} \cos x \neq 1 \quad \forall x \in (-\pi,\pi) \setminus \{ 0\}, \qquad \text{e} \qquad \lim_{y \to 1} e^y= e. \end{equation*}$

Dunque possiamo applicare il teorema di cambio di variabile 69 per ottenere

(187) $\begin{equation*} \lim_{x \to 0} e^{\cos x} = e. \end{equation*}$

$\[\]$

Limiti di funzioni inverse.

Un argomento correlato ai limiti delle funzioni composte è quello dei limiti di funzioni inverse. Studieremo in questa sezione i limiti delle funzioni inverse di una sottoclasse di funzioni invertibili, costituita dalle funzioni invertibili e monotone, ipotesi soddisfatta dalla maggioranza di funzioni invertibili con cui abitualmente si lavora. Ciò si spiega col fatto che le funzioni usualmente considerate sono continue, e dalla teoria delle funzioni continue discende [5 (lemma 5.14)] che una funzione iniettiva e continua in un intervallo è (strettamente) monotona. Dunque l’ulteriore ipotesi di monotonia, al fine di calcolare i limiti di funzioni inverse, non è particolarmente restrittiva.

Teorema 73 (limiti di funzioni inverse). Siano $A,B \subseteq \mathbb{R}$

, sia $f \colon A \to B$

una funzione invertibile e monotona, sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $A$

e supponiamo che esista

(188) $\begin{equation*} \lim_{x \to x_0} f(x) = \ell \in \overline{\mathbb{R}}. \end{equation*}$

Allora $\ell$ è un punto di accumulazione per $B$ e si ha

(189) $\begin{equation*} \lim_{y \to \ell} f^{-1}(y) = x_0. \end{equation*}$

Dimostrazione. Supponiamo senza perdita di generalità che $f$ sia crescente e osserviamo che l’ipotesi di invertibilità di $f$ implica che essa è strettamente crescente.

$\ell$ è di accumulazione per $B$ . Al fine di provare che $\ell$ sia un punto di accumulazione per $B$ , consideriamo un intorno $J$ di $\ell$ : dimostreremo che esso contiene dei punti di $B$ diversi da $\ell$ . Infatti, per definizione di limite, esiste un intorno $I$ di $x_0$ tale che

(190) $\begin{equation*} f(x) \in J \qquad \forall x \in A \cap I \setminus \{x_0\}. \end{equation*}$

Poiché $x_0$ è di accumulazione per $A$ , $I$ contiene almeno due punti distinti $x_1,x_2$ di $A$ diversi da $x_0$ e, per (190), si ha $f(x_1),f(x_2) \in B \cap J$ . Poiché $f$ è iniettiva, $f(x_1) \neq f(x_2)$ e quindi almeno uno di questi punti è distinto da $\ell$ . Abbiamo esibito un punto di $B$ , diverso da $\ell$ , che appartiene a $J$ , quindi $\ell$ è di accumulazione per $B$ .

$\lim_{y \to \ell} f^{-1}(y) = x_0$ . Poiché $f^{-1}$ è l’inversa di una funzione strettamente crescente, è anch’essa strettamente crescente; quindi, dato che $\ell$ è di accumulazione per $B$ , per la proposizione 47 il limite sinistro di $f^{-1}$ in $\ell$ esiste, e lo chiamiamo $\xi$ :
(191) $\begin{equation*} \xi \coloneqq \lim_{y \to \ell^-} f^{-1}(y). \end{equation*}$

Per dimostrare che $\xi=x_0$ , consideriamo ora le funzioni $f \colon A \to B$ e $f^{-1} \colon B \to A$ . Poiché $f$ è strettamente crescente, si ha $f(x)< \ell$ se $x<x_0$ ; dunque $f$ soddisfa la condizione 1 del teorema 69 di cambio di variabile e in particolare si ha

(192) $\begin{equation*} \lim_{x \to x_0^-} f(x)= \ell^-. \end{equation*}$

Dunque il teorema 69 può essere applicato³ alla composizione $f^{-1} \circ f$ e fornisce

(193) $\begin{equation*} \xi \overset{\text{(thm. 69)}}{=} \lim_{x \to x_0^-} f^{-1}\big(f(x)\big) = \lim_{x \to x_0^-} x = x_0, \end{equation*}$

dove la seconda uguaglianza deriva dalla definizione di funzione inversa, cioè $f^{-1}\big(f(x)\big)=x$ . Analogamente si mostra che il limite destro di $f^{-1}$ in $\ell$ è pari a $x_0$ e ciò, in virtù della proposizione 25, prova la tesi.

Il teorema 73 permette di calcolare i limiti delle inverse di numerose funzioni elementari: basta infatti osservare che quasi tutte le funzioni elementari sono monotone a tratti, ossia è possibile suddividere il loro dominio in intervalli in cui esse sono monotone.

Esempio 74. Proviamo che

(194) $\begin{equation*} \lim_{y \to y_0} \arctan y = \begin{cases} - \dfrac{\pi}{2} & \text{se } y_0 =-\infty \\[6pt] \arctan y_0 & \text{se $y_0 \in \mathbb{R}$} \\[6pt] \dfrac{\pi}{2} & \text{se } y_0 =+\infty. \end{cases} \end{equation*}$

$\[\]$

Figura 28: grafico della funzione $\arctan$ .

$\[\]$

Osserviamo che la funzione arcotangente

(195) $\begin{equation*} \arctan \colon y \in \mathbb{R} \longmapsto \arctan y \in \left (-\frac{\pi}{2}, \frac{\pi}{2} \right ), \end{equation*}$

il cui grafico è rappresentato nella figura 28, è l’inversa della funzione $\tan \colon \left (-\frac{\pi}{2}, \frac{\pi}{2} \right ) \to \mathbb{R}$ , che è strettamente crescente e invertibile; a essa si può quindi applicare il teorema 73 sui limiti delle funzioni inverse.

Distinguiamo i vari casi.

$y_0=-\infty$ . Da $\lim_{x \to \left ( -\frac{\pi}{2}\right )^+} \tan x = -\infty$ ottenuto nell’esempio 48, applicando il teorema 73 sui limiti delle funzioni inverse si ottiene
(196) $\begin{equation*} \lim_{y \to -\infty} \arctan y = - \frac{\pi}{2}. \end{equation*}$

$y_0\in \mathbb{R}$ . Consideriamo $x_0=\arctan y_0$ , cioè $y_0=\tan x_0$ e ovviamente si ha $x_0 \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right)$ . Nell’esempio 50 si è provato $\lim_{x \to x_0} \tan x = \tan x_0$ e quindi, grazie al teorema 73, abbiamo
(197) $\begin{equation*} \lim_{y \to y_0} \arctan y = \arctan y_0. \end{equation*}$

$y_0=+\infty$ . Questo risultato può essere ottenuto analogamente al caso $y_0=-\infty$ , oppure osservando che la funzione $\arctan$ è dispari e pertanto
(198) $\begin{equation*} \lim_{y \to +\infty} \arctan y = - \lim_{y \to -\infty} \arctan y = \frac{\pi}{2}. \end{equation*}$

$\[\]$

3. Nella opportuna versione per i limiti a sinistra studiata nell’osservazione 70 ↩

Limiti e potenze.

Date due funzioni $f,g$

, osservando che si può scrivere

(199) $\begin{equation*} f(x)^{g(x)} = e^{g(x) \log f(x)} \end{equation*}$

(qualora tali scritture abbiano senso), grazie al teorema sul cambio di variabili si possono studiare le relazioni tra limiti ed elevamento a potenza, come mostra il teorema seguente. In esso, ipotizziamo $f(x)>0$ affinché la potenza $f(x)^{g(x)}$ abbia senso, mentre supponiamo $g(x)>0$ in quanto il caso opposto si ottiene facilmente da

(200) $\begin{equation*} f(x)^{g(x)} = \dfrac{1}{f(x)^{-g(x)}} \end{equation*}$

e dai teoremi sull’algebra dei limiti.

Teorema 75 (limiti e potenze). Siano $f \colon A \subseteq \mathbb{R} \to (0,+\infty)$

e $g \colon A \subseteq \mathbb{R} \to \mathbb{R}$

delle funzioni, sia $x_0 \in \overline{ \mathbb{R}}$

un punto di accumulazione per $A$

e supponiamo che esistano

(201) $\begin{equation*} \lim_{x \to x_0} f(x) = \ell_f \in [0,+\infty] \qquad \lim_{x \to x_0} g(x)= \ell_g \in [0,+\infty]. \end{equation*}$

se $\ell_f,\ell_g \in [0,+\infty)$ , tranne il caso $\ell_f=\ell_g=0$ , allora $\displaystyle \lim_{x \to x_0}f(x)^{g(x)} = {\ell_f}^{\ell_g}.$

se $\ell_g = +\infty$ , allora
(202) $\begin{equation*} \lim_{x \to x_0}f(x)^{g(x)} = \begin{cases} 0 & \text{se } \ell_f \in [0,1) \\ +\infty & \text{se } \ell_f \in (1,+\infty]. \end{cases}. \end{equation*}$

Osservazione 76. Le conclusioni del punto 2 del teorema 73 possono essere sintetizzate come delle operazioni in $\overline{\mathbb{R}}$ , ovvero con le scritture

(203) $\begin{equation*} [a^{+\infty}]= \begin{cases} 0 & \text{se } a\in [0,1) \\ +\infty & \text{se } a\in (1,+\infty]. \end{cases} \end{equation*}$

Si noti però che il teorema non afferma nulla sulle “operazioni” nella retta reale estesa

(204) $\begin{equation*} [0^0], \quad [\infty^0], \quad [1^\infty]. \end{equation*}$

Vedremo nella sezione Forme indeterminate e limiti notevoli che esse sono altre forme indeterminate.

$\[\]$

Osservazione 77. Nel corso della dimostrazione sarà chiaro che, nel caso $\ell_g=+\infty$ , l’ipotesi che $f$ abbia limite non è necessaria. Vale infatti:

(205) $\begin{equation*} \lim_{x \to x_0}f(x)^{g(x)} = \begin{cases} 0 & \text{se $f(x)\leq b<1$ definitivamente per $x \to x_0$} \\[4pt] +\infty & \text{se $f(x)\geq b>1$ definitivamente per $x \to x_0$}. \end{cases} \end{equation*}$

$\[\]$

Dimostrazione del teorema 73. Come ricordato prima dell’enunciato del teorema, si ha

(206) $\begin{equation*} f(x)^{g(x)} = e^{g(x) \log f(x)} \qquad \forall x \in A. \end{equation*}$

Se $\ell_f \in (0,+\infty)$ , dal teorema 69 di cambio di variabile segue
(207) $\begin{equation*} \lim_{x \to x_0} \log \big(f(x)\big)= \log (\ell_f). \end{equation*}$

Il teorema 49 sull’algebra dei limiti in $\mathbb{R}$ fornisce quindi

(208) $\begin{equation*} \lim_{x \to x_0} g(x) \log \big(f(x)\big) = \ell_g \cdot \log (\ell_f). \end{equation*}$

Applicando nuovamente il teorema 69 si ottiene

(209) $\begin{equation*} \lim_{x \to x_0}f(x)^{g(x)} = \lim_{x \to x_0} e^{g(x) \log f(x)} \overset{\text{(thm. 69)}}{=} e^{\ell_g \log \ell_f}= {\ell_f}^{\ell_g}. \end{equation*}$

Se invece $\ell_f=0$ , il teorema di cambio di variabile 69 e il fatto che $\lim_{y \to 0^+} \log y=-\infty$ forniscono

(210) $\begin{equation*} \lim_{x \to x_0} \log f(x)=-\infty. \end{equation*}$

Dall’ipotesi $\ell_g \neq 0$ , il teorema 57 sull’algebra dei limiti in $\overline{\mathbb{R}}$ produce

(211) $\begin{equation*} \lim_{x \to x_0} g(x) \log f(x) = -\infty. \end{equation*}$

Poiché $\lim_{y \to -\infty} e^y=0$ , dal teorema 69 di cambio di variabile si ha

(212) $\begin{equation*} \lim_{x \to x_0} e^{g(x) \log f(x)} = 0 ={\ell_f}^{\ell_g}. \end{equation*}$

Distinguiamo i due casi.
- $\ell_f>1$ . Poiché $\ell_f>1$ , esiste $b >1$ tale che definitivamente per $x \to x_0$ si ha
  (213) $\begin{equation*} f(x) \geq b \implies g(x)\log f(x) \geq g(x)\log b. \end{equation*}$
  
  Poiché $\log b>0$ e $g(x) \to +\infty$ , per il teorema 57 $\lim_{x \to x_0} g(x) \log b=+\infty$ ; dunque la proposizione 38 fornisce
  
  (214) $\begin{equation*} \lim_{x \to x_0} g(x) \log f(x)= +\infty. \end{equation*}$
  
  Il teorema di cambio di variabile 69 implica quindi
  
  (215) $\begin{equation*} \lim_{x \to x_0} e^{g(x) \log f(x)} = +\infty. \end{equation*}$
- $\ell_f<1$ . Il caso $\ell<1$ si ottiene dal precedente, in quanto
  (216) $\begin{equation*} f(x)^{g(x)} = \dfrac{1}{\left (\dfrac{1}{f(x)}\right )^{g(x)}} \qquad \forall x \in A, \end{equation*}$
  
  e la funzione $\frac{1}{f(x)}$ ha limite $\frac{1}{\ell_f}>1$ per i teoremi sull’algebra dei limiti. Pertanto per il punto precedente si ha
  
  (217) $\begin{equation*} \lim_{x \to x_0} \left (\dfrac{1}{f(x)}\right )^{g(x)} = +\infty \quad \xRightarrow{\text{(thm. 57)}} \quad \lim_{x \to x_0} \dfrac{1}{\left (\dfrac{1}{f(x)}\right )^{g(x)}} = 0. \end{equation*}$

$\[\]$

Esempio 78. Calcoliamo il limite

(218) $\begin{equation*} \lim_{x \to +\infty} \left (\frac{x + \sin x}{2x^2 + x}\right )^x. \end{equation*}$

Si tratta di un limite di una potenza, in cui l’esponente tende a $+\infty$ e la base soddisfa

(219) $\begin{equation*} \lim_{x \to +\infty} \frac{x^2 + \sin x}{2x^2 + x} = \lim_{x \to +\infty} \frac{x^2 \left ( 1 + \frac{\sin x}{x} \right )}{x^2 \left ( 2 + \frac{1}{x} \right )} = \frac{1}{2}, \end{equation*}$

dove l’ultima uguaglianza deriva dal fatto che le funzioni $\frac{\sin x}{x}$ e $\frac{1}{x}$ sono infinitesime per $x \to +\infty$ in virtù rispettivamente della proposizione 53 e del teorema 57 (osservazione 59). Poiché la base dell’esponenziale tende a $\frac{1}{2}<1$ , il punto 2 del teorema 73 implica che

(220) $\begin{equation*} \lim_{x \to +\infty} \left (\frac{x + \sin x}{2x^2 + x}\right )^x = 0. \end{equation*}$

$\[\]$

Forme indeterminate e limiti notevoli

Introduzione.

Il teorema 57 permette di estendere alcuni risultati sull’algebra dei limiti a $\overline{\mathbb{R}}$

; notiamo però che esso non tratta i casi elencati di seguito.

Cosa si può dire su $\displaystyle \lim_{x \to x_0}(f(x)+g(x))$ se $\ell_f=+\infty$ e $\ell_g=-\infty$ ?

Cosa si può dire su $\displaystyle \lim_{x \to x_0} f(x) g(x)$ se $\ell_f=\infty$ e $\ell_g=0$ ?

Cosa si può dire su $\displaystyle \lim_{x \to x_0} \frac{f(x)}{g(x)}$ se $\ell_f=\infty$ e $\ell_g=\infty$ ?

Cosa si può dire su $\displaystyle \lim_{x \to x_0} \frac{f(x)}{g(x)}$ se $\ell_f=0$ e $\ell_g=0$ ?

In altre parole, il teorema 57 non dà significato alle “operazioni” in $\overline{\mathbb{R}}$

(221) $\begin{equation*} \left [ +\infty - \infty \right ], \qquad \left [ 0 \cdot \infty \right ], \qquad \left [ \frac{\infty}{\infty} \right ], \qquad \left [ \frac{0}{0} \right ]. \end{equation*}$

Analogamente, il teorema 73 consente di estendere a $\overline{\mathbb{R}}$ alcune operazioni di elevamento a potenza, come notato nell’osservazione 76. Il teorema non discute però i seguenti casi.

Cosa si può dire su $\lim_{x \to x_0}{f(x)}^{g(x)}$ se $\ell_f=0=\ell_g$ ?

Cosa si può dire su $\lim_{x \to x_0}{f(x)}^{g(x)}$ se $\ell_f=+\infty$ e $\ell_g=0$ ?

Cosa si può dire su $\lim_{x \to x_0}{f(x)}^{g(x)}$ se $\ell_f=1$ e $\ell_g=+\infty$ ?

Non vengono cioè definite le seguenti “operazioni” in $\overline{\mathbb{R}}$ :

(222) $\begin{equation*} \left [ 0^0 \right ], \qquad \left [ \infty^0 \right ], \qquad \left [1^{\infty} \right ]. \end{equation*}$

Il motivo di tali lacune è che, nei casi elencati in (221) e (222), il risultato del limite non è univocamente determinato: può cioè assumere valori diversi in base alle specifiche funzioni in esame e può anche non esistere.

In altre parole, non è possibile estendere le usuali operazioni di somma, prodotto, quoziente ed elevamento a potenza in $\overline{\mathbb{R}}$ includendo anche i casi riportati in (221) e (222), in modo che siano coerenti col calcolo dei limiti. Tali operazioni vengono dette forme indeterminate, in quanto appunto il risultato del limite non è determinato a partire dal limite dei fattori in gioco.

In questa sezione esaminiamo ognuna delle 7 forme indeterminate che abbiamo individuato (non ve ne sono altre), motivando precisamente per quale ragione esse sono classificate come tali e fornendo qualche strategia per ottenere il valore del limite, applicandole a certi esempi fondamentali. Alcuni degli esempi di forme indeterminate che studieremo per la loro importanza vengono appunto detti limiti notevoli.

Forme indeterminate più infinito meno infinito.

Mostriamo subito con un esempio che $[+\infty - \infty]$

è una forma indeterminata, esibendo delle scelte per le funzioni $f,g$

per le quali il limite della somma assuma valori diversi o addirittura non esista.

Esempio 79.

Se $f(x)=x$ e $g(x)=-x + 6$ , si ha
(223) $\begin{equation*} \lim_{x \to +\infty} f(x)= +\infty, \qquad \lim_{x \to +\infty} g(x) \overset{\text{(thm. 57)}}{=} -\infty, \end{equation*}$

ma

(224) $\begin{equation*} \lim_{x \to +\infty} \big( f(x)+g(x)\big) = \lim_{x \to +\infty} \big( x-x+6\big) = 6. \end{equation*}$

Chiaramente il valore $6$ non ha nulla di speciale e può essere sostituito da qualunque numero reale, mostrando così che, date due funzioni aventi limite rispettivamente pari a $+\infty$ e $-\infty$ , il limite della loro somma può essere pari a qualsiasi valore reale.

Se $f(x)=2x$ e $g(x)=-x$ , di nuovo si ha
(225) $\begin{equation*} \lim_{x \to +\infty} f(x)= +\infty, \qquad \lim_{x \to +\infty} g(x) = -\infty, \end{equation*}$

ma stavolta

(226) $\begin{equation*} \lim_{x \to +\infty} \big( f(x)+g(x)\big) = \lim_{x \to +\infty} \big( 2x-x\big) = \lim_{x \to +\infty} x = +\infty. \end{equation*}$

Analogamente, se $f(x)=x$ e $g(x)=-2x$ , si ottiene
(227) $\begin{equation*} \lim_{x \to +\infty} \big( f(x)+g(x)\big) = -\infty. \end{equation*}$

Se invece $f(x)=x+ \sin x$ e $g(x)=-x$ , si ha
(228) $\begin{equation*} \lim_{x \to +\infty} f(x)\overset{\text{(es. 63)}}{=} +\infty, \qquad \lim_{x \to +\infty} g(x) -\infty, \end{equation*}$

ma

(229) $\begin{equation*} \lim_{x \to +\infty} \big( f(x)+g(x)\big) = \lim_{x \to +\infty} \sin x, \end{equation*}$

che non esiste per l’esempio 16.

$\[\]$

Uno degli esempi più comuni di forma indeterminata $[+\infty-\infty]$ è costituita dal limite

(230) $\begin{equation*} \lim_{x \to +\infty} (x^\alpha - x^\beta), \end{equation*}$

dove $\alpha,\beta>0$ sono numeri reali fissati. Infatti, poiché $\alpha$ e $\beta$ sono strettamente positivi, le funzioni definite da $x^\alpha$ e $x^\beta$ hanno limite $+\infty$ e quindi (230) ricade in una forma indeterminata $[+\infty-\infty]$ . Analizziamo il tutto in maggiore dettaglio.

Esempio 80. Calcoliamo

(231) $\begin{equation*} \lim_{x \to +\infty} (x^3-5x^2 +3x). \end{equation*}$

Osserviamo che si tratta di una forma indeterminata del tipo $[\infty-\infty]$ in quanto le funzioni definite da $x^3+3x$ e $5x^2$ sono divergenti positivamente per l’esempio 15 e il teorema 57. Per determinare il valore del limite, un’idea è raccogliere il termine che tende a $\infty$ “più velocemente”, che intuitivamente è $x^3$ . Osserviamo che

(232) $\begin{equation*} \lim_{x \to +\infty} (x^3-5x^2 +3x) = \lim_{x \to +\infty} x^3\left ( 1 - {\frac{5}{x}} + {\frac{3}{x^2}} \right ) = +\infty, \end{equation*}$

dove l’ultima uguaglianza segue dal teorema 57: infatti il fattore $x^3$ ha limite $+\infty$ , mentre il fattore $1 - \frac{5}{x} + \frac{3}{x^2}$ ha limite $1$ in quanto gli addendi $\frac{5}{x}$ e $\frac{3}{x^2}$ hanno limite $0$ per il punto 3 del teorema 57.

$\[\]$

Il precedente esempio suggerisce l’idea che un polinomio all’infinito si comporta come il suo termine di grado massimo.

Più in generale, si può provare il seguente risultato:

$\boxcolorato{analisi}{\lim_{x \to +\infty} (x^\alpha - x^\beta) = \begin{cases} +\infty & \text{se } \alpha > \beta >0 \\ -\infty & \text{se } \beta > \alpha >0. \end{cases} }}$

Un altro modo per determinare il risultato di un limite che presenta una forma indeterminata $[\infty-\infty]$ consiste nell’utilizzo della seguente proposizione, che consente di studiare il limite di una forma indeterminata $[\infty-\infty]$ conoscendo il limite del rapporto tra le due funzioni.

Proposizione 81 (forme indeterminate $[+\infty-\infty]$ e $\left [ \frac{\infty}{\infty} \right ]$ ). Siano $f,g \colon A \subseteq \mathbb{R}$

, sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione di $A$

; supponiamo che

(233) $\begin{equation*} %\lim_{x \to x_0} f(x)= \lim_{x \to x_0} g(x)= +\infty, \qquad \text{e} \qquad \lim_{x \to x_0} \frac{f(x)}{g(x)}= \ell \in \overline{\mathbb{R}}. \end{equation*}$

Allora si ha

(234) $\begin{equation*} \lim_{x \to x_0} \big( f(x) - g(x) \big) = \begin{cases} + \infty & \text{se } \ell >1 \\ - \infty & \text{se } \ell \in [0,1). \end{cases} \end{equation*}$

Dimostrazione. Proviamo solo il caso $\ell>1$ in quanto l’altro è analogo. Fissando $a \in (1,\ell)$ per definizione di limite esiste un intorno $I$ di $x_0$ tale che

(235) $\begin{equation*} \frac{f(x)}{g(x)} > a \qquad \forall x \in A \cap I \setminus \{x_0\} \end{equation*}$

ovvero $f(x)>a g(x)$ definitivamente per $x \to x_0$ . Questo implica che

(236) $\begin{equation*} f(x) - g(x) > (a-1)g(x) \qquad \text{definitivamente per $x \to x_0$}. \end{equation*}$

Poiché $a-1>0$ e $\lim_{x \to x_0} g(x)=+\infty$ , per il punto 1 del teorema 57 la funzione $(a-1)g(x)$ diverge positivamente e quindi, per la proposizione 38, si ha

(237) $\begin{equation*} \lim_{x \to x_0} \big( f(x) - g(x) \big) = +\infty. \end{equation*}$

$\[\]$

Applichiamo la proposizione allo studio di un limite, usando un risultato della prossima sezione.

Esempio 82. Studiamo il limite

(238) $\begin{equation*} \lim_{x \to +\infty} (e^x - x^2). \end{equation*}$

Per i risultati nella tabella 2, esso è il limite della differenza di due funzioni entrambe divergenti positivamente, pertanto presenta una forma indeterminata del tipo $[+\infty-\infty]$ . Per risolverla, osserviamo che, come mostrato nella prossima sezione nel teorema 87, si ha

(239) $\begin{equation*} \lim_{x \to +\infty} \frac{e^x}{x^2} = +\infty. \end{equation*}$

La proposizione 81 implica allora che

(240) $\begin{equation*} \lim_{x \to +\infty} (e^x - x^2) = +\infty. \end{equation*}$

$\[\]$

Osservazione 83. Nelle ipotesi della proposizione 81, non si può concludere nulla su $\lim_{x \to x_0} (f(x)-g(x))$ se si ha $\lim_{x \to x_0} \frac{f(x)}{g(x)}=1$ .

Infatti, consideriamo ad esempio il caso in cui $f(x)=x+c$ con $c \in \mathbb{R}$ costante e $g(x)=x$ . Come si vedrà anche nella prossima sezione si ha
(241) $\begin{equation*} \lim_{x \to +\infty} \frac{f(x)}{g(x)} = \lim_{x \to +\infty} \frac{x+c}{x} = \lim_{x \to +\infty} \frac{x \left ( 1+ \frac{c}{x}\right )}{x} = 1, \end{equation*}$

ma

(242) $\begin{equation*} \lim_{x \to +\infty} \big( f(x) - g(x) \big) = \lim_{x \to +\infty} (x+c-x) = c. \end{equation*}$

Scegliendo invece $f(x)= x + \sin x$ e $g(x)=x$ , si ha nuovamente $\lim_{x \to +\infty} \frac{f(x)}{g(x)}=1$ , ma il limite di $f+g$ non esiste.

Se $f(x)=x\pm \sqrt{x}$ , vale ancora $\lim_{x \to +\infty} \frac{f(x)}{g(x)}=1$ , mentre il limite di $f+g$ è pari a $\pm \infty$ .

$\[\]$

Forme indeterminate infinito su infinito e gerarchia degli infiniti.

Cominciamo col mostrare che $\left [\frac{\infty}{\infty}\right ]$

è effettivamente una forma indeterminata, cioè che il valore del limite non possa essere determinato in maniera univoca. Riportiamo la conclusione sotto forma di esercizio svolto.

Esercizio 84. $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Provare che $\left [\frac{\infty}{\infty} \right ]$

è una forma indeterminata, esibendo dei casi in cui i limiti dei quozienti assumano valori diversi in $\overline{\mathbb{R}}$

e un caso in cui il limite del quoziente non esista.

Svolgimento. Mostriamo che, se $\lim_{x \to x_0} f(x)= \lim_{x \to x_0} g(x)=\infty$ , il limite del quoziente può assumere qualunque valore in $\overline{\mathbb{R}}$ e può anche non esistere.

Se $f(x)=c x$ con $c \in \mathbb{R} \setminus \{0\}$ e $g(x)=x$ , si ottiene
(243) $\begin{equation*} \lim_{x \to +\infty} f(x) \overset{\text{(thm. 57)}}{=} \operatorname{sgn}(c) \cdot \infty, \qquad \lim_{x \to +\infty} g(x)=+\infty, \end{equation*}$

e, per il quoziente, si ha

(244) $\begin{equation*} \lim_{x \to +\infty} \frac{f(x)}{g(x)} = \lim_{x \to +\infty} c = c. \end{equation*}$

Ciò mostra che il limite del rapporto può assumere qualsiasi valore in $\mathbb{R} \setminus \{0\}$ .

Se $f(x)=x$ e $g(x)=x^2$ , si ottiene
(245) $\begin{equation*} \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} g(x) = +\infty, \end{equation*}$

ma

(246) $\begin{equation*} \lim_{x \to +\infty} \frac{f(x)}{g(x)} = \lim_{x \to +\infty} \frac{1}{x} \overset{\text{(es. 64)}}{=} 0. \end{equation*}$

Viceversa, se $f(x)=\pm x^2$ e $g(x)=x$ , si ottiene
(247) $\begin{equation*} \lim_{x \to +\infty} \frac{f(x)}{g(x)} = \lim_{x \to +\infty} \pm x = \pm \infty. \end{equation*}$

Siano infine $f(x)=x(2+\sin x)$ e $g(x)=x$ . Dato che $2+\sin x \geq 1$ , vale $f(x) \geq x$ e quindi per la proposizione 38 si ha
(248) $\begin{equation*} \lim_{x \to +\infty} f(x) = +\infty. \end{equation*}$

D’altra parte vale

(249) $\begin{equation*} \lim_{x \to +\infty} \frac{f(x)}{g(x)} = \lim_{x \to +\infty} \frac{x(2+\sin x)}{x} = \lim_{x \to +\infty} (2+\sin x), \end{equation*}$

che non esiste. Infatti, se $\lim_{x \to +\infty} (2+\sin x)$ esistesse, per i teoremi sull’algebra dei limiti esisterebbe $\lim_{x \to +\infty} (2+\sin x - 2)$ , contro il risultato dell’esempio 16.

$\[\]$

Mostreremo ora le principali tecniche per determinare il risultato di un limite quando esso si presenti in una forma indeterminata $\left [\frac{\infty}{\infty}\right ]$ . In questo caso specifico, ciò corrisponderà a stabilire quale tra la funzione al numeratore e quella al denominatore diverga “più velocemente” a $\infty$ , cioè ad effettuare un confronto tra varie funzioni elementari e stilare una sorta di “gerarchia” delle funzioni divergenti, che viene appunto detta gerarchia degli infiniti. Cominciamo con alcuni esempi, i cui risultati potranno essere utilizzati nel seguito.

Esempio 85. Calcoliamo

(250) $\begin{equation*} \lim_{x \to - \infty} \frac{x^2 + x +2}{3x +1}. \end{equation*}$

Si osservi che il numeratore stesso presenta una forma indeterminata $+\infty-\infty$ . In ogni caso, per quanto visto nella precedente sezione e per il teorema 57, per il numeratore e il denominatore si ha

(251) $\begin{equation*} \lim_{x \to - \infty} (x^2+x+2) = \lim_{x \to -\infty} x^2\left ( 1 + \frac{1}{x} + \frac{2}{x^2} \right ) = +\infty, \qquad \lim_{x \to -\infty} (3x+1) = -\infty. \end{equation*}$

Dunque il limite richiesto presenta una forma indeterminata $\left [\frac{\infty}{\infty}\right ]$ . Per risolverla, proviamo ad applicare la strategia della precedente sezione, ossia di raccogliere il termine di grado massimo sia al numeratore che al denominatore:

(252) $\begin{equation*} \lim_{x \to - \infty} \frac{x^2 + x +2}{3x +1} = \lim_{x \to -\infty} \dfrac{x^2\left ( 1 + \frac{1}{x} + \frac{2}{x^2} \right ) }{x \left ( 3+ \frac{1}{x}\right )} = \lim_{x \to -\infty} \dfrac{x\left ( 1 + \frac{1}{x} + \frac{2}{x^2} \right ) }{ 3+ \frac{1}{x}} = -\infty, \end{equation*}$

dove l’ultima uguaglianza segue dal teorema 57 e dal fatto che $x \to -\infty$ , mentre i fattori tra parentesi tendono rispettivamente a $1$ e $3$ .

$\[\]$

Nel prossimo esempio analizziamo il caso in cui il numeratore e il denominatore abbiano lo stesso grado.

Esempio 86. Calcoliamo

(253) $\begin{equation*} \lim_{x \to - \infty} \frac{x^2 - 2x +1}{4x^2 +1}. \end{equation*}$

Mediante la stessa tecnica dell’esempio precedente otteniamo

(254) $\begin{equation*} \lim_{x \to - \infty} \frac{x^2 - 2x +1}{4x^2 +1} = \lim_{x \to -\infty} \dfrac{x^2\left ( 1 - \frac{2}{x} + \frac{1}{x^2} \right ) }{x^2 \left ( 4+ \frac{1}{x^2}\right )} = \lim_{x \to -\infty} \dfrac{1 - \frac{2}{x} + \frac{1}{x^2}}{4+ \frac{1}{x^2}} = \frac{1}{4}, \end{equation*}$

dove l’ultima uguaglianza deriva dai teoremi sull’algebra dei limiti.

$\[\]$

Se invece il grado del numeratore è inferiore a quello del denominatore, il limite è nullo, come il lettore può agevolmente verificare, sempre mediante la stessa tecnica. Riassumendo:

(255) $\begin{equation*} \boxcolorato{analisi}{\begin{aligned} \lim_{x \to +\infty} \frac{a_n x^n + \dots +a_1 x+a_0}{b_m x^m + \dots + b_1 x +b_0} & = \lim_{x \to +\infty} x^{n-m} \frac{a_n + \frac{a_{n-1}}{x} + \cdots + \frac{a_0}{x^n}}{b_m + \frac{b_{m-1}}{x} + \cdots + \frac{b_0}{x^m}} \\ & = \begin{cases} \operatorname{sgn}\frac{a_n}{b_m} \cdot \infty & \text{se } n>m \\[7pt] \dfrac{a_n}{b_n} & \text{se } n=m \\[7pt] 0 & \text{se } n<m \end{cases} \end{aligned}} \end{equation*}$

È interessante confrontare la rapidità con cui alcune funzioni divergano a $+\infty$ . Il seguente teorema afferma che le potenze divergono più rapidamente dei logaritmi, che gli esponenziali divergono più rapidamente delle potenze e che gli esponenziali della forma $x^x$ divergono a loro volta più rapidamente degli esponenziali. Esso quindi stabilisce una sorta di “gerarchia” degli infiniti, che ne giustifica il nome.

Teorema 87 (gerarchia degli infiniti). Siano $a>1$

e $\beta>0$

. Valgono i seguenti limiti notevoli:

(256) $\begin{equation*} \lim_{x \to +\infty} \frac{x^\beta}{\log_a x} = +\infty, \end{equation*}$

(257) $\begin{equation*} \lim_{x \to +\infty} \frac{a^x}{x^\beta} = +\infty, \end{equation*}$

(258) $\begin{equation*} \lim_{x \to +\infty} \frac{x^x}{a^x} = +\infty. \end{equation*}$

Dimostrazione. Il punto principale consiste nel dimostrare (257), in quanto (256) si ottiene da esso con un cambio di variabile, mentre (258) è una conseguenza del teorema 73 sui limiti di potenze.

(257). Osserviamo che il limite presenta una forma indeterminata per i risultati elencati nella tabella 2. Dimostreremo (257) sfruttando la disuguaglianza⁴

(259) $\begin{equation*} e^x>1+x \qquad \forall x \geq 0. \end{equation*}$

Distinguiamo due casi.
- $\beta \in (0,1)$ Si ha
  (260) $\begin{equation*} \frac{a^x}{x^\beta} = \frac{e^{x \log a}}{x^\beta} \overset{\text{(eq. 260)}}{\geq} \frac{1+x \log a}{x^\beta} \geq x^{1-\beta} \log a \xrightarrow[x \to +\infty]{} +\infty, \end{equation*}$
  
  dove l’ultimo limite segue da $1-\beta>0$ e dall’esempio 15. La proposizione 38 implica quindi
  
  (261) $\begin{equation*} \lim_{x \to +\infty} \frac{a^x}{x^\beta} = +\infty. \end{equation*}$
- $\beta \geq 1$ . Questo caso si ottiene dal precedente; infatti, fissiamo $N \in \mathbb{N}$ tale che $\frac{\beta}{N} < 1$ . Definendo $c\coloneqq a^{\frac{1}{N}}$ , si ha dunque $c>1$ e quindi
  (262) $\begin{equation*} \lim_{x \to +\infty} \frac{a^x}{x^\beta} = \lim_{x \to +\infty} \left ( \frac{c^x}{x^{\frac{\beta}{N}}} \right )^N = +\infty, \end{equation*}$
  
  dove la quantità tra parentesi è divergente per il punto precedente, poiché $c>1$ e $\frac{\beta}{N} <1$ , dunque l’ultima uguaglianza segue dal punto 2 del teorema 57, in quanto la funzione di cui si vuole calcolare il limite è il prodotto di $N$ funzioni divergenti positivamente.

(256). Si ha

(263) $\begin{equation*} \frac{x^\beta}{\log_a x} = \beta \frac{a^{\beta \log_a x}}{\beta \log_a x} \overset{(y=\beta \log_a x)}{=} \beta \frac{a^{y}}{y}, \end{equation*}$

quindi la funzione di cui si vuole calcolare il limite è la composizione $g \circ f$ delle funzioni

(264) $\begin{equation*} f \colon x \longmapsto y=\beta \log_a x, \qquad g \colon y \longmapsto \beta\frac{a^{y}}{y}. \end{equation*}$

A tale composizione si può applicare il teorema 69: poiché $\lim_{x \to +\infty} \beta \log_a x=+\infty$ , si ha

(265) $\begin{equation*} \lim_{x \to +\infty} \frac{x^\beta}{\log_a x} \overset{\text{(thm. 69)}}{=} \lim_{y \to +\infty} g(y) = \lim_{y \to +\infty} \beta\frac{a^{y}}{y} \overset{\text{(eq. 258)}}{=} +\infty. \end{equation*}$

Tale situazione viene riassunta col fatto che si è effettuato il cambio di variabile $y=\beta \log_a x$ .

(258). Vale

(266) $\begin{equation*} \frac{x^x}{a^x} = \left ( \frac{x}{a} \right )^x \geq 2^x \qquad \forall x \geq 2a. \end{equation*}$

Poiché la funzione definita da $\frac{x^x}{a^x}$ è definitivamente maggiore di $2^x$ , che è divergente per $x \to +\infty$ , dalla proposizione 38 segue la tesi.

Osservazione 88. Da (256), in virtù del teorema 57, segue

(267) $\begin{equation*} \lim_{x \to +\infty} \frac{\log_a x}{x^\beta} = 0 \qquad \forall a>1, \,\, \forall \beta >0. \end{equation*}$

$\[\]$

Questi risultati possono essere applicati a vari esercizi che presentano forme indeterminate $\left [ \frac{\infty}{\infty} \right ]$ .

Esempio 89. Calcoliamo

(268) $\begin{equation*} \lim_{x \to +\infty} \frac{2^{\sqrt{x}}}{x^4}. \end{equation*}$

Osserviamo che la funzione $\frac{2^{\sqrt{x}}}{x^4}$ può essere vista come la composizione $x \mapsto y=\sqrt{x} \mapsto \frac{2^y}{y^{8}}$ a cui possiamo applicare il teorema di cambio di variabile 69 in quanto $x \mapsto \sqrt{x}$ è iniettiva. In altre parole, mediante il cambio di variabile $y=\sqrt{x}$ , poiché $\lim_{x \to +\infty} \sqrt{x}=+\infty$ , il limite diventa

(269) $\begin{equation*} \lim_{x \to +\infty} \frac{2^{\sqrt{x}}}{x^4} \overset{(y=\sqrt{x})}{=} \lim_{y \to +\infty} \frac{2^{y}}{y^8} \overset{\text{(eq. 258)}}{=} +\infty. \end{equation*}$

$\[\]$

Esempio 90. Calcoliamo

(270) $\begin{equation*} \lim_{x \to +\infty} \frac{x^{\sqrt{x}}+ \sqrt{x}+ 2^x}{(\sqrt{x})^x + x^3 + e^x}. \end{equation*}$

Il limite si presenta in una forma indeterminata $\left [\frac{\infty}{\infty} \right ]$ . Per risolverla, usiamo una strategia simile a quella degli esempi precedenti, raccogliendo i termini “principali” al numeratore e al denominatore, ossia quelli che divergono più rapidamente; a tal fine occorre ovviamente individuare tali termini.

Numeratore. Dal teorema 87 sappiamo che $\lim_{x \to +\infty} \frac{\sqrt{x}}{2^x}=0$ e quindi resta da confrontare il termine $2^x$ con $x^{\sqrt{x}}$ per stabilire quale diverga più velocemente. Osserviamo che il caso non è trattato dal teorema 87, ma possiamo ricondurci agevolmente a esso usando l’identità $a^b=2^{b \log_2 a}$ , che implica
(271) $\begin{equation*} \lim_{x \to +\infty} \frac{2^x}{x^{\sqrt{x}}} = \lim_{x \to +\infty} \frac{2^x}{2^{\sqrt{x}\log_2 x}} = \lim_{x \to +\infty} 2^{x- \sqrt{x}\log_2 x} = \lim_{x \to +\infty} 2^{x \left (1- \frac{\log_2 x}{\sqrt{x}} \right )} \overset{\text{(eq. 268)}}{=} +\infty. \end{equation*}$

Ciò prova che il termine “principale” al numeratore è $2^x$ .

Denominatore. Dal teorema 87 segue che $\lim_{x \to +\infty} \frac{e^x}{x^3}=+\infty$ ; rimane dunque da confrontare il termine $e^x$ con $(\sqrt{x})^x$ per stabilire quale diverga a $+\infty$ più velocemente. Similmente allo studio del numeratore, l’identità $a^b=e^{b \log a}$ fornisce
(272) $\begin{equation*} \lim_{x \to +\infty} \frac{e^x}{(\sqrt{x})^x} = \lim_{x \to +\infty} \frac{e^x}{e^{\frac{x}{2}\log x}} = \lim_{x \to +\infty} e^{x \left (1- \frac{\log x}{2}\right )} = 0. \end{equation*}$

Ciò mostra che, al denominatore, il termine “principale” è $(\sqrt{x})^x$ .

Abbiamo dunque

(273) $\begin{equation*} \begin{split} \lim_{x \to +\infty} \frac{x^{\sqrt{x}}+ \sqrt{x}+ 2^x}{(\sqrt{x})^x + x^3 + e^x} &= \lim_{x \to +\infty} \frac{2^x \left (\frac{x^{\sqrt{x}}}{2^x}+ \frac{\sqrt{x}}{2^x}+ 1 \right )}{(\sqrt{x})^x \left (1 + \frac{x^3}{\sqrt{x})^x} + \frac{e^x}{\sqrt{x})^x} \right )} \\ &= \lim_{x \to +\infty} \left ( \frac{2}{\sqrt{x}}\right )^x \frac{\frac{x^{\sqrt{x}}}{2^x}+ \frac{\sqrt{x}}{2^x}+ 1}{1 + \frac{x^3}{(\sqrt{x})^x} + \frac{e^x}{(\sqrt{x})^x}} \\ &= 0 \end{split} \end{equation*}$

dove l’ultima uguaglianza segue dal fatto che $\lim_{x \to +\infty} \left ( \frac{2}{\sqrt{x}}\right )^x=0$ per il teorema 73 in quanto la base della potenza tende a $0$ e l’esponente a $+\infty$ , mentre la seconda frazione ha limite $1$ per quanto visto nello studio separato di numeratore e denominatore.

$\[\]$

4. Essa si può ottenere dal fatto che $e^x$ è il limite della seguente successione crescente per $x \geq 0$ :

(274) $\begin{equation*} e^x = \sup_{n \in \mathbb{N}} \left (1+\frac{x}{n}\right )^n, \end{equation*}$

che per $n=1$ fornisce la disuguaglianza desiderata. ↩

Forme indeterminate zero su zero e limiti notevoli.

Invitiamo il lettore a dimostrare per esercizio che questa è effettivamente una forma indeterminata.

Suggerimento: considerare opportuni reciproci delle funzioni usate nella soluzione dell’esercizio 82.

Come si evince dal suggerimento, in alcuni casi le forme indeterminate del tipo $\left [ \frac{0}{0}\right ]$ si riconducono a forme del tipo $\left [ \frac{\infty}{\infty}\right ]$ , considerando i reciproci o opportuni cambi di variabile.

Esempio 91. Dimostriamo che

(275) $\begin{equation*} \lim_{x \to 0^+} \frac{x}{e^{-\frac{1}{x}}} = +\infty. \end{equation*}$

Per il punto 4 del teorema 57, $\lim_{x \to 0^+} \frac{1}{x}=+\infty$ e quindi, per il teorema 69 di cambio di variabile il denominatore in (275) è infinitesimo. Il limite in (275) presenta quindi una forma indeterminata $\left [ \frac{0}{0}\right ]$ .

Osserviamo che la funzione di cui si vuole calcolare il limite è la composizione

(276) $\begin{equation*} x \,\,\overset{f}{\longmapsto}\,\, y=\frac{1}{x} \,\,\overset{g}{\longmapsto}\,\, \frac{e^y}{y} \end{equation*}$

e, poiché appunto $\lim_{x \to 0^+} \frac{1}{x}=+\infty$ , col cambio di variabile $y=\frac{1}{x}$ il teorema 69 assicura che

(277) $\begin{equation*} \lim_{x \to 0^+} \frac{x}{e^{-\frac{1}{x}}} \overset{\left (y=\frac{1}{x}\right )}{=} \lim_{y \to +\infty} \frac{e^y}{y} \overset{\text{(eq. 258)}}{=} +\infty. \end{equation*}$

$\[\]$

Vi sono però dei limiti della forma $\left [ \frac{0}{0}\right ]$ che non possono essere ricondotti in maniera immediata a dei limiti di altri tipi. Un primo esempio è costituito dal rapporto di due polinomi che si annullano nello stesso punto.

Esempio 92. Calcoliamo il limite

(278) $\begin{equation*} \lim_{x \to 3} \frac{x^2 - 4x +3}{x^2 -9}. \end{equation*}$

Dato che il numeratore e il denominatore della frazione sono dei polinomi, dall’esempio 49 sappiamo che

(279) $\begin{equation*} \lim_{x \to 3} (x^2 - 4x +3) = 3^2 - 4 \cdot 3 + 3 = 0, \qquad \lim_{x \to 3} (x^2 - 9) = 3^2 - 9 = 0, \end{equation*}$

ossia il limite in (278) è una forma indeterminata $\left [ \frac{0}{0}\right ]$ . Per risolverla osserviamo che $3$ è uno zero di entrambi i polinomi e quindi essi sono divisibili per il binomio $x-3$ , in virtù del teorema di Ruffini. Fattorizzando quindi il numeratore e il denominatore si ottiene

(280) $\begin{equation*} \lim_{x \to 3} \frac{x^2 - 4x +3}{x^2 -9} = \lim_{x \to 3} \frac{(x-3)(x-1)}{(x-3)(x+3)} = \lim_{x \to 3} \frac{x-1}{x+3} \overset{\text{(thm. 49)}}{=} \frac{1}{3}, \end{equation*}$

dove la seconda uguaglianze è dovuta al fatto che

(281) $\begin{equation*} \frac{(x-3)(x-1)}{(x-3)(x+3)} = \frac{x-1}{x+3} \qquad \forall x \in \mathbb{R} \setminus \{3,-3\}, \end{equation*}$

cioè le funzioni definite dalle espressioni $\frac{(x-3)(x-1)}{(x-3)(x+3)}$ e $\frac{x-1}{x+3}$ coincidono se $x \neq 3$ e quindi hanno lo stesso limite per $x \to 3$ .

$\[\]$

Alcuni limiti della forma $\left [ \frac{0}{0}\right ]$ sono molto importanti e vengono annoverati tra i cosiddetti limiti notevoli. Tra i più famosi vi sono quelli in cui si confrontano delle funzioni trascendenti infinitesime con delle potenze di $x$ per $x \to 0$ : ci accingiamo a esaminarli mostrando il procedimento per il loro calcolo. Vedremo nel seguito che tali limiti risultano strumenti utili nella risoluzione di molti esercizi.

Teorema 93 (limiti notevoli). Valgono i seguenti limiti:

(282) $\begin{equation*} \lim_{x \to 0} \frac{\sin x}{x} = 1; \end{equation*}$

(283) $\begin{equation*} \lim_{x \to 0} \frac{1-\cos x}{x^2} = \frac{1}{2}; \end{equation*}$

(284) $\begin{equation*} \lim_{x \to 0} \frac{e^x-1}{x} = 1; \end{equation*}$

(285) $\begin{equation*} \lim_{x \to 0} \frac{\log(1+x)}{x} = 1. \end{equation*}$

Dimostrazione. Dimostriamo i 4 limiti notevoli.

$\lim_{x \to 0} \frac{\sin x}{x}=1$ Notiamo innanzitutto che è sufficiente dimostrare l’uguaglianza per $x \to 0^+$ in quanto la funzione definita da $\frac{\sin x}{x}$ è pari poiché rapporto di due funzioni dispari [11 (sezione 2.3, lemma 2.49)].

Per dimostrare l’uguaglianza in (282) ci baseremo sulla seguente disuguaglianza

(286) $\begin{equation*} \sin x < x < \tan x \qquad \forall x \in \left( 0, \frac{\pi}{2}\right ), \end{equation*}$

che si può dedurre dalla figura 29 che rappresenta la circonferenza goniometrica di centro l’origine e raggio $1$ , e osservando che il triangolo $OAP$ è contenuto nel settore circolare $OAP$ , che è contenuto nel triangolo rettangolo $OAQ$ ; quindi le loro aree soddisfano le disuguaglianze

(287) $\begin{equation*} \operatorname{Area}(\overset{\triangle}{OAP}) \leq \operatorname{Area}(OAP) \leq \operatorname{Area}(\overset{\triangle}{OAQ}). \end{equation*}$

Indichiamo con $x$ l’arco di circonferenza orientato $AP$ e osserviamo dalla geometria elementare che

$\begin{aligned} & \operatorname{Area}(\overset{\triangle}{OAP}) = \frac{\overline{OA} \cdot \overline{BP}}{2} = \frac{\sin x}{2}, \\& \operatorname{Area}(OAP) = \pi \frac{x}{2\pi} = \frac{x}{2}, \\& \operatorname{Area}(\overset{\triangle}{OAQ}) = \frac{\overline{OA} \cdot \overline{AQ}}{2} = \frac{\tan x}{2}, \end{aligned}$

da cui si ottiene (286).

$\[\]$

$\[\]$

$\[\]$

Figura 29: dimostrazione geometrica della disuguaglianza $\sin x \leq x \leq \tan x$ . Il triangolo $OAP$ è incluso nel settore circolare $OAP$ , che è a sua volta incluso nel triangolo $OAQ$ e quindi le loro aree risultano nello stesso ordine. Scrivendo le espressioni di tali aree si ottiene la disuguaglianza desiderata.

$\[\]$

$\[\]$

Dividendo (286) per $\sin x$ e passando ai reciproci si giunge a

(288) $\begin{equation*} \cos x \leq \frac{\sin x}{x} \leq 1 \qquad \forall x \in \left( 0, \frac{\pi}{2}\right ). \end{equation*}$

Poiché $\lim_{x \to 0^+} \cos x=1$ , dal teorema dei carabinieri 37 segue $\lim_{x \to 0^+} \frac{\sin x}{x}=1$ , cioè (282).

$\lim_{x \to 0} \frac{1-\cos x}{x^2}=\frac{1}{2}$ Questo limite relativo al coseno si ricava dal precedente. Infatti, dal teorema 49 sul limite di un prodotto abbiamo

(289) $\begin{equation*} 1 = \lim_{x \to 0} \frac{\sin^2 x}{x^2} = \lim_{x \to 0} \frac{1-\cos^2 x}{x^2} = \lim_{x \to 0} \frac{(1-\cos x)(1+\cos x)}{x^2}. \end{equation*}$

Dato che $\lim_{x \to 0}(1+\cos x)=2$ , dal teorema sul limite di un quoziente segue la tesi.

$\lim_{x \to 0} \frac{e^x-1}{x}=1$ Per dimostrare questo limite faremo uso della disuguaglianza

(290) $\begin{equation*} 1+x \leq e^x \leq \frac{1}{1-x} \qquad \forall x \in (-1,1). \end{equation*}$

Osserviamo innanzitutto che $1+x \leq e^x$ è conseguenza del fatto che $e^x$ è il limite della successione $\left (1 + \frac{x}{n} \right )^n$ e che tale successione è crescente per $x>-1$ , [12]; considerando $n=1$ si ha la disuguaglianza. Fissiamo ora $x \in (-1,1)$ ; la formula $1+x \leq e^x$ in cui si abbia $-x$ al posto di $x$ fornisce

(291) $\begin{equation*} 1-x \leq e^{-x}= \frac{1}{e^x} \implies e^{x} \leq \frac{1}{1-x}, \end{equation*}$

che dimostra (290). Sottraendo $1$ e dividendo per $x$ nei tre termini in (290), si ottiene

(292) $\begin{equation*} 1 \leq \frac{e^x - 1}{x} \leq \left (\frac{1}{1-x} -1 \right )\frac{1}{x} = \frac{1}{1-x} \xrightarrow[x \to 0]{} 1. \end{equation*}$

Dunque il teorema dei carabinieri 37 prova (284).

$\lim_{x \to 0} \frac{\log(1+x)}{x}=1$ Tale limite relativo al logaritmo si ottiene da (284) mediante il cambio di variabile $y=\log(x+1)$ ; da ciò si ricava $x=e^y-1$ e quindi

(293) $\begin{equation*} \frac{\log(1+x)}{x} = \frac{y}{e^y-1}. \end{equation*}$

Quindi la funzione definita da $\frac{\log(1+x)}{x}$ è la composizione

(294) $\begin{equation*} x \,\,\overset{f}{\longmapsto}\,\, y= \log(1+x) \,\,\overset{g}{\longmapsto}\,\, \frac{y}{e^y-1}. \end{equation*}$

Dato che $\lim_{x \to 0}\log(1+x)=0$ e $f$ è strettamente crescente, soddisfa la condizione 1 del teorema 69 di cambio di variabile, per il quale si conclude

(295) $\begin{equation*} \lim_{x \to 0} \frac{\log(1+x)}{x} \overset{(y=\log(1+x))}{=} \lim_{y \to 0} \frac{y}{e^y-1} \overset{\text{(eq. 285)}}{=} 1. \end{equation*}$

$\[\]$

I limiti notevoli appena ricavati possono essere utilizzati nel calcolo di altri limiti a essi riconducibili.

Esempio 94.

Calcoliamo

(296) $\begin{equation*} \lim_{x \to 0} \frac{\tan x}{x} = \lim_{x \to 0} \frac{\sin x}{x} \frac{1}{\cos x} = 1, \end{equation*}$

dove nell’ultima uguaglianza abbiamo usato (282) e il teorema 49 sul limite di un prodotto.

Proviamo che

(297) $\begin{equation*} \lim_{x \to 0} \frac{\arctan x}{x} = 1. \end{equation*}$

Usiamo il cambio di variabile $y=\arctan x$ , ovvero scriviamo il limite come

(298) $\begin{equation*} \lim_{x \to 0} \frac{\arctan x}{x} = \lim_{x \to 0} \frac{\arctan x}{\tan(\arctan x)} \overset{(y=\arctan x)}{=} \lim_{y \to 0} \frac{y}{\tan y} \overset{\text{(eq. 298)}}{=} 1 \end{equation*}$

In altre parole il limite è stato visto come il limite della funzione composta $x \mapsto y=\arctan x \mapsto \frac{y}{\tan y}$ e si è applicato il teorema 69.

Vale
$\begin{aligned}\label{eq:lim_(sin-tan)/x^3} \lim_{x \to 0} \frac{\sin x - \tan x}{x^3} & = \lim_{x \to 0} \frac{\sin x - \frac{\sin x}{\cos x}}{x^3} = \\& = \lim_{x \to 0} \frac{\sin x}{x} \, \frac{1- \frac{1}{\cos x}}{x^2} = \\& = \lim_{x \to 0} \frac{\sin x}{x} \, \frac{\cos x-1}{x^2} \frac{1}{\cos x} = \\& =1 \cdot \left (- \frac{1}{2} \right ) \cdot 1 = \\& = -\frac{1}{2}, \end{aligned}$

dove nell’ultima uguaglianza sono stati usati i limiti notevoli (282) e (283).

$\[\]$

Forme indeterminate zero per infinito.

Come per la forma indeterminata $\left [ \frac{0}{0}\right ]$

, si può provare che anche i limiti di questa forma non sono univocamente determinati usando opportuni reciproci delle funzioni usate nella soluzione dell’esercizio 82.

Da ciò si intuisce che molte forme indeterminate del tipo $\left [0 \cdot \infty \right ]$ si risolvono riconducendosi a una forma del tipo $\left [\frac{\infty}{\infty} \right ]$ o $\left [ \frac{0}{0}\right ]$ .

Esempio 95. Proviamo che

(299) $\begin{equation*} \boxcolorato{analisi}{ \lim_{x \to -\infty} |x|^\beta a^x = 0 \qquad \forall \beta \in \mathbb{R},\,\,\forall a>1.} \end{equation*}$

Osserviamo subito che se $\beta \leq 0$ il limite non è una forma indeterminata e il risultato può essere ottenuto dalla tabella 2 e dal teorema 49 sull’algebra dei limiti in $\mathbb{R}$ , in quanto si tratta del prodotto di due funzioni che hanno limite finito.

Nel caso in cui $\beta>0$ , invece, il fattore $|x|^\beta$ è positivamente divergente e il fattore $a^x$ è infinitesimo per i risultati nella tabella 2 e siamo dunque in presenza di una forma indeterminata del tipo $[0 \cdot \infty]$ .

Per risolverla, osserviamo che si ha

(300) $\begin{equation*} \lim_{x \to -\infty} |x|^\beta a^x = \lim_{x \to -\infty} \frac{|x|^\beta}{a^{-x}} \overset{(y=-x)}{=} \lim_{y \to +\infty} \frac{y^\beta}{a^y} \overset{\text{(eq. 258)}}{=} 0 \end{equation*}$

dove alla seconda uguaglianza abbiamo usato il teorema 69 di cambio di variabile in quanto la funzione di cui si stava calcolando il limite era la composizione

(301) $\begin{equation*} x \,\,\overset{f}{\longmapsto}\,\, y=-x \,\,\overset{g}{\longmapsto}\,\, g(y)=\frac{y^\beta}{a^y}. \end{equation*}$

Dal limite in (299) discende immediatamente

(302) $\begin{equation*} \boxcolorato{analisi}{ \lim_{x \to +\infty} x^\beta a^x = 0 \qquad \forall \beta \in \mathbb{R},\,\,\forall a\in (0,1). } \end{equation*}$

Infatti, se $a \in (0,1)$ , allora $\frac{1}{a}>1$ e quindi, mediante il cambio di variabile $y=-x$ , si ha

(303) $\begin{equation*} \lim_{x \to +\infty} x^\beta a^x = \lim_{x \to +\infty} |-x|^\beta \left (\frac{1}{a}\right )^{-x} \overset{(y=-x)}{=} \lim_{y \to -\infty} |y|^\beta \left (\frac{1}{a}\right )^{y} \overset{\text{(eq. 302)}}{=} 0. \end{equation*}$

$\[\]$

Un altro limite che si affronta usando il limite notevole (257) (e le sue forme equivalenti) e un opportuno cambio di variabile è il seguente.

Esempio 96. Verifichiamo che

(304) $\begin{equation*} \boxcolorato{analisi}{\lim_{x \to 0^+} x^\beta \log_a x = 0 \qquad \forall \beta>0,\,\,\forall a\in (0,1)\cup(1,+\infty).} \end{equation*}$

Dai risultati della tabella 2 abbiamo

(305) $\begin{equation*} \lim_{x \to 0^+} x^\beta=0, \qquad \lim_{x \to 0^+} \log_a x = \begin{cases} + \infty & \text{se } a \in (0,1) \\ -\infty & \text{se } a >1, \end{cases} \end{equation*}$

dunque il limite (304) presenta una forma indeterminata del tipo $[0 \cdot \infty]$ . Basta dimostrare il risultato solo per $a>1$ in quanto l’altro caso si ottiene osservando che

(306) $\begin{equation*} \log_{\frac{1}{a}} x = - \log_a x \qquad \forall x >0. \end{equation*}$

Fissiamo dunque $a>1$ e usiamo il cambio di variabile $y=\beta \log_a x$ , cioè osserviamo che la funzione di cui si vuole calcolare il limite è la composizione

(307) $\begin{equation*} x \,\,\overset{f}{\longmapsto}\,\, y=\beta \log_a x \,\,\overset{g}{\longmapsto}\,\, g(y)=\frac{1}{\beta} a^{y} y \end{equation*}$

Infatti

(308) $\begin{equation*} g(f(x)) = \frac{1}{\beta} a^{\beta \log_a x} (\beta \log_a x) = x^\beta \log_a x \qquad \forall x >0. \end{equation*}$

Poiché

(309) $\begin{equation*} \lim_{x \to 0^+} y(x) = \lim_{x \to 0^+} \beta \log_a x = -\infty, \end{equation*}$

si ha

(310) $\begin{equation*} \lim_{x \to 0^+} x^\beta \log_a x \overset{\text{(thm. 69)}}{=} \lim_{y \to - \infty} g(y) = \lim_{y \to -\infty} \frac{1}{\beta} a^{y} y \overset{\text{(eq. 302)}}{=} 0. \end{equation*}$

$\[\]$

Forme indeterminate uno alla infinito: il numero di Nepero.

Prima di provare che l’espressione $[1^\infty]$

è effettivamente una forma indeterminata, studiamo un famoso limite di questo tipo che definisce il famoso numero di Nepero $e$

. È noto dalla teoria delle successioni [12] che il numero $e=2.71\dots$

è ottenuto dalla successione

(311) $\begin{equation*} e= \lim_{n \to +\infty} \left ( 1 + \frac{1}{n} \right )^n. \end{equation*}$

Intuitivamente ciò suggerisce che, sostituendo l’indice naturale $n$ della successione con la variabile reale $x$ , il limite per $x \to +\infty$ della funzione corrispondente sia lo stesso. Provare tale conclusione non è immediato in quanto la funzione definita da $x \mapsto \left ( 1 + \frac{1}{x} \right )^x$ potrebbe a priori assumere valori vicini a $e$ quando $x$ è un numero naturale, ma oscillare fortemente negli intervalli compresi tra due numeri naturali. Se ciò effettivamente accadesse, il limite per $x \to +\infty$ non esisterebbe, allo stesso modo in cui non esiste $\lim_{x \to +\infty}\sin x$ mentre il limite della successione $\sin(n\pi)$ è nullo. Il prossimo risultato mostra che tale circostanza non si verifica per il numero di Nepero e che la nostra intuizione iniziale è corretta.

Proposizione 97 (numero di Nepero). Vale

(312) $\begin{equation*} \lim_{x \to +\infty} \left (1 + \frac{1}{x} \right)^x = e. \end{equation*}$

Dimostrazione. Per ogni $x \in [1,+\infty)$ sia $n(x) \in \mathbb{N}$ il numero naturale tale che $n(x)\leq x < n(x)+1$ : per brevità lo chiameremo $n$ ; si ha ovviamente

(313) $\begin{equation*} \left (1+ \frac{1}{n+1}\right )^n \leq \left (1 + \frac{1}{x} \right)^x \leq \left (1+ \frac{1}{n}\right )^{n+1}, \end{equation*}$

semplicemente perché le basi delle potenze sono maggiori di $1$ e soddisfano le disuguaglianze nello stesso verso, e lo stesso vale per gli esponenti. Osserviamo ora che le due successioni in $n$ soddisfano

(314) $\begin{gather*} \lim_{n \to +\infty} \left (1+ \frac{1}{n+1}\right )^n = \lim_{n \to +\infty} \left (1+ \frac{1}{n+1}\right )^{n+1} \cdot \left (1+ \frac{1}{n+1}\right )^{-1} = e \cdot 1 = e, \\ \lim_{n \to +\infty} \left (1+ \frac{1}{n}\right )^{n+1} = \lim_{n \to +\infty} \left (1+ \frac{1}{n}\right )^{n} \cdot \left (1+ \frac{1}{n}\right ) = e \cdot 1 = e. \end{gather*}$

Dunque la funzione $x \mapsto \left (1 + \frac{1}{x} \right)^x$ è compresa tra due funzioni costanti su ciascun intervallo $[n,n+1)$ , entrambe aventi limite $e$ per $x \to +\infty$ . Il teorema 37 dei carabinieri implica quindi la tesi.

$\[\]$

Dal limite notevole (312) si ricavano facilmente esempi che mostrano che $[1^\infty]$ è una forma indeterminata.

Ovviamente $\lim_{x \to +\infty} 1^x=1$ in quanto la funzione di cui si calcola il limite è costantemente pari a $1$ .

Fissiamo un qualunque $c \in (0,1) \cup (1,+\infty)$ ; si ha
(315) $\begin{equation*} \lim_{x \to +\infty} \left (1 + \frac{1}{x} \right )^{x \log c} = \lim_{x \to +\infty} \left (\left (1 + \frac{1}{x} \right )^{x} \right )^{\log c} \overset{\text{(eq. 314)}}{=} e^{\log c} = c. \end{equation*}$

Vale
(316) $\begin{equation*} \lim_{x \to +\infty} \left (1 + \frac{1}{x} \right )^{x^2} = \lim_{x \to +\infty} \left (\left (1 + \frac{1}{x} \right )^{x} \right )^{x} = +\infty, \end{equation*}$

dove l’ultima uguaglianza segue dal fatto che $\left (1 + \frac{1}{x} \right )^{x} \to e>1$ e dal teorema 73.

Invitiamo il lettore a trovare per esercizio un esempio in cui $\lim_{x \to x_0} f(x)=1$ , $\lim_{x \to x_0}g(x)=+\infty$ , ma $\lim_{x \to x_0}{f(x)}^{g(x)}$ non esiste.

Dal limite notevole (312) è possibile ricavare altri limiti della stessa tipologia.

Esempio 98. Proviamo che

$\boxcolorato{analisi}{\lim_{x \to -\infty} \left (1 + \frac{1}{x} \right)^x = e.}$

Usando il cambio di variabile $y=-x$ , si ottiene

(317) $\begin{equation*} \lim_{x \to -\infty} \left (1 + \frac{1}{x} \right)^x \overset{(y=-x)}{=} \lim_{y \to +\infty} \left (1 - \frac{1}{y} \right)^{-y} = \lim_{y \to +\infty} \left (\frac{y}{y-1} \right)^y \end{equation*}$

Sommando e sottraendo $1$ al numeratore della frazione si ha

$\begin{aligned} \lim_{y \to +\infty} \left (\frac{y}{y-1} \right)^y & = \lim_{y \to +\infty} \left (\frac{(y-1) + 1}{y-1} \right)^y = \\& = \lim_{y \to +\infty} \left (1 + \frac{1}{y-1} \right)^{y-1}\left (1 + \frac{1}{y-1} \right) = \\& = e \cdot 1 = e, \end{aligned}$

dove alla penultima uguaglianza è stato usato il cambio di variabile $z=y-1$ e il limite notevole (312), oltre al teorema 49 sul limite di un prodotto.

$\[\]$

Esercizio 99. Provare, con argomenti simili, che

(318) $\begin{equation*} \lim_{x \to -\infty} \left (1 - \frac{1}{x} \right)^x = \frac{1}{e}. \end{equation*}$

Esempio 100. Calcoliamo

(319) $\begin{equation*} \lim_{x \to +\infty} \left ( 1+e^{-x} \right )^{e^x}. \end{equation*}$

Usiamo il cambio di variabile $y=e^x$ e osserviamo che $\lim_{x \to +\infty} y(x)=+\infty$ . Dunque

(320) $\begin{equation*} \lim_{x \to +\infty} \left ( 1+e^{-x} \right )^{e^x} = \lim_{x \to +\infty} \left ( 1+ \frac{1}{e^x} \right )^{e^x} \overset{(y=e^x)}{=} \lim_{y \to +\infty} \left ( 1+ \frac{1}{y} \right )^{y} = e. \end{equation*}$

$\[\]$

Forme indeterminate infinito alla zero.

In questa sezione mostreremo che “l’operazione” in $\overline{\mathbb{R}}$

$[\infty^0]$

non viene definita dal teorema 73 in quanto essa risulta una forma indeterminata. Spesso i limiti che si presentano in questa forma possono essere ricondotti ad altre forme indeterminate.

Esempio 101. Dimostriamo che

$\boxcolorato{analisi}{\lim_{x \to +\infty} x^\frac{1}{x} = 1.}$

Usando infatti l’uguaglianza $t=e^{\log t}$ e le proprietà dei logaritmi si ottiene

(321) $\begin{equation*} \lim_{x \to +\infty} x^\frac{1}{x} = \lim_{x \to +\infty} e^{\frac{1}{x} \log x} \end{equation*}$

Poiché da (267) si ha $\lim_{x \to +\infty} \frac{\log x}{x}=0$ e dalla tabella 2 si ha $\lim_{y \to 0} e^y=1$ , il teorema 69 sul limite delle funzioni composte prova che

(322) $\begin{equation*} \lim_{x \to +\infty} e^{\frac{1}{x} \log x} = 1. \end{equation*}$

$\[\]$

Con lo stesso procedimento, si può vedere che $[\infty^0]$ è una forma indeterminata osservando che

(323) $\begin{equation*} \lim_{x \to +\infty} x^{\frac{c}{\log x}} = e^c \qquad \forall c \in \mathbb{R}, \end{equation*}$

infatti

(324) $\begin{equation*} \lim_{x \to +\infty} x^{\frac{c}{\log x}} = \lim_{x \to +\infty} e^{\frac{c}{\log x} \log x} = \lim_{x \to +\infty} e^c = e^c. \end{equation*}$

Forme indeterminate zero alla zero.

L’ultima forma indeterminata che ci resta da analizzare è $[0^0]$

. Anche i limiti di questo tipo vengono spesso ricondotti ad altre forme indeterminate.

Esempio 102. Vale

(325) $\begin{equation*} \boxcolorato{analisi}{\lim_{x \to 0^+} x^x = 1.} \end{equation*}$

Usando nuovamente $t=e^{\log t}$ e le proprietà dei logaritmi si prova

(326) $\begin{equation*} \lim_{x \to 0^+} x^x = \lim_{x \to 0^+} e^{x \log x}. \end{equation*}$

Da (304) sappiamo che $\lim_{x \to 0^+}x\log x=0$ e quindi, per il teorema 69 sul limite delle funzioni composte e i risultati della tabella 2 si ha

(327) $\begin{equation*} \lim_{x \to 0^+}e^{x \log x} = e^0 = 1. \end{equation*}$

$\[\]$

Chiaramente $[0^0]$ è una forma indeterminata in quanto, se $a \in (0,1)$ , allora

(328) $\begin{equation*} \lim_{x \to +\infty} a^x=0, \qquad \lim_{x \to +\infty} \frac{1}{x}=0, \end{equation*}$

(329) $\begin{equation*} \lim_{x \to +\infty} \left (a^x\right )^{\frac{1}{x}} = \lim_{x \to +\infty} a = a. \end{equation*}$

Similmente

(330) $\begin{equation*} \lim_{x \to +\infty} \left (\frac{1}{x^x} \right )^{\frac{1}{x}} = \lim_{x \to +\infty} \frac{1}{x} = 0. \end{equation*}$

Usiamo questi limiti in qualche esempio.

Esempio 103. Calcoliamo

(331) $\begin{equation*} \lim_{x \to 0^+} (\sin x)^x, \end{equation*}$

che presenta una forma indeterminata $[0^0]$ . Qui sfruttiamo il limite notevole del seno (282): infatti

(332) $\begin{equation*} \lim_{x \to 0^+} (\sin x)^x = \lim_{x \to 0^+} \left (\frac{\sin x}{x} \right )^x \cdot x^x \overset{\text{(eq. 283, 328)}}{=} 1. \end{equation*}$

$\[\]$

Il prossimo risultato si affronta con una tecnica simile.

Esempio 104. Calcoliamo

(333) $\begin{equation*} \lim_{x \to 0^+} (-\log \cos x)^x, \end{equation*}$

che si presenta in una forma indeterminata $[0^0]$ in quanto $\lim_{x \to 0^+} \cos x=1$ e $\log 1=0$ . Scrivendo $\log \cos x= \log \big(1 + (\cos x - 1) \big)$ e dividendo e moltiplicando per $(1-\cos x)$ e per $x^2$ si ottiene

(334) $\begin{equation*} \begin{split} \lim_{x \to 0^+} (-\log \cos x)^x. & = \lim_{x \to 0^+} \Big(-\log \big(1 + (\cos x - 1) \big)\Big)^x = \\ & = \lim_{x \to 0^+} \left(\frac{-\log \big(1 + (\cos x - 1) \big)}{1-\cos x}\right)^x \left(\frac{1-\cos x}{x^2}\right)^x (x^{x})^2 = \\ & = 1, \end{split} \end{equation*}$

dove l’ultima uguaglianza deriva dai limiti notevoli (285), (283) e (325).

$\[\]$

Osservazione 105. Il limite $\lim_{x \to 0^+} \big(\log (\cos x) \big)^x$ non ha senso in quanto $\log (\cos x)<0$ in un intorno di $0$ e quindi non sarebbe lecito elevare tale quantità a $x$ in quanto la base di una potenza a esponente reale deve essere positiva.

$\[\]$

Complementi alla teoria dei limiti

Introduzione.

In questa sezione riportiamo alcuni argomenti strettamente legati ai limiti.

Asintoti.

I limiti consentono di studiare il comportamento di una funzione sia quando la variabile indipendente $x$

è molto grande, sia quando la funzione stessa assume valori infinitamente grandi. Quando almeno uno di questi casi si verifica, cioè quando almeno uno tra $x_0$

e $\ell$

è infinito, il grafico della funzione può assomigliare a una retta, che viene detta asintoto per la funzione. Tali rette vengono classificate in base alla loro pendenza.

Ad esempio, come si evince anche dalla figura 10 in alto a destra, se per $x_0 \in \mathbb{R}$ si ha $\lim_{x \to x_0} f(x)=\pm\infty$ , allora il grafico della funzione $f$ tende ad avvicinarsi alla retta verticale di equazione $x=x_0$ . Tale retta è detta asintoto verticale per la funzione $f$ .

Definizione 106 (asintoti verticali). Sia $f \colon A \subseteq \mathbb{R} \to \mathbb{R}$

e sia $x_0 \in \mathbb{R}$

un punto di accumulazione per $A$

. Se $\lim_{x \to x_0^-}= \pm \infty$

oppure $\lim_{x \to x_0^+}= \pm \infty$

, la retta verticale di equazione $x=x_0$

è detta asintoto verticale per $f$

$\[\]$

Figura 30: la funzione definita da $f(x)= \frac{1}{x}$ ha un asintoto verticale in $0$ ; il suo grafico è infatti approssimabile con la retta verticale $x=0$ (in verde) in un intorno di tale punto.

$\[\]$

Esempio 107. La funzione $f \colon \mathbb{R} \setminus \{0\} \to \mathbb{R}$ definita da

(335) $\begin{equation*} f(x)= \frac{1}{x} \qquad \forall x \neq 0 \end{equation*}$

ha un asintoto verticale per $x_0=0$ . Infatti

(336) $\begin{equation*} \lim_{x \to 0^-} \frac{1}{x} = -\infty, \qquad \lim_{x \to 0^+} \frac{1}{x} = +\infty, \end{equation*}$

come dimostrato nell’esempio 24 ed evidente nella figura 30.

$\[\]$

Esempio 108. La funzione $f \colon (0,+\infty) \to \mathbb{R}$ definita da

(337) $\begin{equation*} f(x)= \log (x+2) \qquad \forall x \in (0,+\infty) \end{equation*}$

ha un asintoto verticale in $x=-2$ . Per il teorema di cambio di variabile 69 si ha

(338) $\begin{equation*} \lim_{x \to (-2)^+} \log(x+2) \overset{(y=x+2)}{=} \lim_{y \to 0^+} \log y = -\infty. \end{equation*}$

$\[\]$

Un altro caso in cui una retta approssima bene il grafico di una funzione $f$ è quando $\lim_{x \to \pm \infty} f(x)=\ell$ con $\ell \in \mathbb{R}$ ; in tale circostanza, il grafico di $f$ tende infatti a essere molto vicino alla retta orizzontale di equazione $y=\ell$ , come riportato nella figura 10 al centro e in basso a sinistra.

Definizione 109 (asintoti orizzontali). Sia $A\subseteq \mathbb{R}$

un insieme illimitato superiormente, sia $f \colon A \to \mathbb{R}$

e supponiamo che $\lim_{x \to +\infty} f(x)= \ell \in \mathbb{R}$

; allora la retta orizzontale di equazione $y=\ell$

è detta asintoto orizzontale per $f$

. Analogamente si definisce l’asintoto orizzontale se $A$

è illimitato inferiormente e $\lim_{x \to -\infty} f(x)= \ell \in \mathbb{R}$

$\[\]$

Figura 31: grafico della funzione $\arctan$ . Sono tratteggiate in verde le rette orizzontali di equazione $y=\pm \frac{\pi}{2}$ , asintoti orizzontali per la funzione.

$\[\]$

Esempio 110. La funzione $f \colon \mathbb{R} \to \left ( -\frac{\pi}{2}, \frac{\pi}{2} \right )$ definita da

(339) $\begin{equation*} f(x) = \arctan x \qquad \forall x \in \mathbb{R} \end{equation*}$

possiede un asintoto orizzontale di equazione $y=-\frac{\pi}{2}$ per $x \to -\infty$ e un asintoto orizzontale di equazione $y=\frac{\pi}{2}$ per $x \to +\infty$ . Infatti, come dimostrato nell’esempio 74 e come evidente dalla figura 31, si ha

(340) $\begin{equation*} \lim_{x \to- \infty} f(x)= -\frac{\pi}{2}, \qquad \lim_{x \to+ \infty} f(x)= \frac{\pi}{2}. \end{equation*}$

$\[\]$

Il grafico di $f$ può risultare ben approssimabile anche mediante una retta obliqua (figura 32).

Definizione 111 (asintoti obliqui). Sia $A\subseteq \mathbb{R}$

un insieme illimitato superiormente e sia $f \colon A \to \mathbb{R}$

; la retta di equazione $y=mx + q$

, con $m \neq 0$

, è detta asintoto obliquo per $f$

se vale la condizione

(341) $\begin{equation*} \lim_{x \to +\infty} \big( f(x) - mx - q \big)=0. \end{equation*}$

Analogamente si definisce l’asintoto obliquo per $x \to -\infty$ .

$\[\]$

Figura 32: la retta tratteggiata in verde è un asintoto obliquo per la funzione $f$ .

$\[\]$

Si vedrà a breve che gli asintoti obliqui possono esistere solo se il limite di $f$ all’infinito è infinito (ma tale condizione non è sufficiente, come vedremo nell’osservazione 114).

Una funzione ha quindi un asintoto obliquo $y=mx+q$ se la differenza tra $f(x)$ e la retta definita da $mx+q$ è asintoticamente nulla per $x \to \pm\infty$ , cioè se il grafico di $f$ è asintoticamente indistinguibile da quello della retta.

La definizione 111 di asintoto obliquo è molto chiara, ma non esprime un modo efficiente per calcolarla: essa infatti consente di stabilire se una data retta di equazione $y=mx+q$ sia o meno asintoto obliquo, ma non fornisce alcun modo per individuare i coefficienti $m$ e $q$ della retta candidata. Risulta quindi molto utile il seguente criterio che consente di stabilire se una funzione ha un asintoto obliquo, ma al contempo fornisce anche un modo efficiente per determinare i coefficienti della retta asintoto obliquo per la funzione.

Proposizione 112. Sia $f \colon A \subseteq \mathbb{R}\to \mathbb{R}$

con $A$

illimitato superiormente. Allora $f$

ha un asintoto obliquo per $x \to +\infty$

se e solo se i seguenti limiti esistono e soddisfano le seguenti proprietà:

(342) $\begin{equation*} \lim_{x \to +\infty} \frac{f(x)}{x}\eqqcolon m \in \mathbb{R} \setminus \{0\}, \qquad \lim_{x \to +\infty} \big( f(x) -mx \big) \eqqcolon q \in \mathbb{R}. \end{equation*}$

In tal caso $y=mx +q$ è l’equazione dell’asintoto obliquo per $f$ .

In particolare, se $f$ ha asintoto obliquo per $x \to +\infty$ , allora $\lim_{x \to +\infty} f(x)=\operatorname{sgn}(m) \cdot \infty$ .

Dimostrazione. Dimostriamo separatamente le due implicazioni.

Supponiamo che $f$ abbia un asintoto obliquo per $x \to +\infty$ di equazione $y=mx+q$ con $m \neq 0$ , cioè che
(343) $\begin{equation*} \lim_{x \to +\infty} \big( f(x)-mx -q\big) = 0, \end{equation*}$

e proviamo che valgono le condizioni in (342). Si ha

$\begin{aligned} \lim_{x \to +\infty} \frac{f(x)}{x} & = \lim_{x \to +\infty} \left ( \frac{f(x) -mx - q}{x} +\frac{mx+q}{x} \right ) = \\& = \lim_{x \to +\infty} \left ( \frac{f(x) -mx - q}{x} +m+\frac{q}{x} \right ) \\ & = m, \end{aligned}$

dove nell’ultima uguaglianza abbiamo usato (341) e il teorema 57 sull’algebra dei limiti in $\overline{\mathbb{R}}$ .

La seconda condizione in (342) segue semplicemente dal teorema 49:

(344) $\begin{equation*} \lim_{x \to +\infty} \big(f(x)-mx \big) = \lim_{x \to +\infty} \big(f(x)-mx -q + q \big) = q. \end{equation*}$

Supponiamo invece che valgano le due condizioni in (342). Dalla seconda in particolare, e dal teorema 49 sull’algebra dei limiti si ha
(345) $\begin{equation*} \lim_{x \to +\infty} \big( f(x) - mx - q \big) = q-q = 0, \end{equation*}$

ovvero (341).

Per dimostrare l’ultima affermazione, notiamo che

(346) $\begin{equation*} \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{f(x)}{x} x = \operatorname{sgn}(m)\cdot \infty, \end{equation*}$

dove nell’ultima uguaglianza si è usato il punto 2 del teorema 57.

$\[\]$

Applichiamo questi strumenti al seguente esempio.

Esempio 113. Studiamo gli eventuali asintoti orizzontali o obliqui della funzione $f \colon \mathbb{R} \setminus \{-1\} \to \mathbb{R}$ definita da

(347) $\begin{equation*} f(x) = \frac{2x^2 - 3x +7}{x+1} \end{equation*}$

e rappresentata in figura 33.

$\[\]$

Figura 33: la retta $y=2x-5$ è un asintoto obliquo per la funzione $f(x)=\frac{2x^2 - 3x +7}{x+1}$ ..

$\[\]$

Dal riassunto in (255) sui limiti di quozienti di polinomi segue

(348) $\begin{equation*} \lim_{x \to +\infty} f(x)=+\infty, \qquad \lim_{x \to -\infty} f(x)=-\infty, \end{equation*}$

cioè la funzione non ha asintoti orizzontali a $+\infty$ e a $-\infty$ in quanto entrambi i limiti non sono finiti; $f$ potrebbe però possedere asintoti obliqui. Osserviamo che

(349) $\begin{equation*} \lim_{x \to \pm\infty} \frac{f(x)}{x} \overset{\text{(eq. 256)}}{=} 2 \end{equation*}$

e quindi la prima condizione in (342) è soddisfatta in quanto tale valore è finito e diverso da $0$ . Dunque gli eventuali asintoti obliqui di $f$ hanno coefficiente angolare $m=2$ . Relativamente alla seconda condizione in (342), si ha

(350) $\begin{equation*} \begin{split} \lim_{x \to \pm\infty} \big( f(x)- mx \big) & = \lim_{x \to \pm\infty} \left ( \frac{2x^2 - 3x +7}{x+1} - 2x \right ) = \\ & = \lim_{x \to \pm\infty} \left ( \frac{2x^2 - 3x +7 - 2x^2 -2x}{x+1} \right ) = \\ & = \lim_{x \to \pm\infty} \frac{-5x + 7}{x+1} = \\ & = -5. \end{split} \end{equation*}$

Dunque anche la seconda condizione in (342) è soddisfatta e fornisce $q=-5$ per $x \to \pm \infty$ . La proposizione 112 prova dunque che la retta di equazione $y=2x-5$ è un asintoto obliquo per $f$ , mostrato in verde nella figura 33.

Tale conclusione poteva anche essere ottenuta scrivendo opportunamente l’espressione della funzione $f$ : infatti per ogni $x \neq -1$ vale

$\begin{aligned} f(x) & = \frac{2x^2 - 3x +7}{x+1}= \\ & = \frac{2x^2 +2x -2x - 3x - 5 + 5 +7}{x+1}= \\ &= \frac{2x(x+1) -5(x+1) + 12}{x+1}= \\ &= 2x -5 + \frac{12}{x+1}. \end{aligned}$

Da tale scrittura l’esistenza degli asintoti obliqui di equazione $y=2x-5$ è evidente mediante la definizione 109:

(351) $\begin{equation*} \lim_{x \to \pm \infty} \big( f(x) - 2x+5 \big) = \lim_{x \to \pm \infty} \frac{12}{x+1} = 0. \end{equation*}$

$\[\]$

Osservazione 114. La condizione $\lim_{x \to +\infty} f(x)=+\infty$ non è sufficiente affinché la funzione abbia un asintoto obliquo. Consideriamo infatti la funzione logaritmo definita da $f(x)= \log x$ per ogni $x >0$ . Dai risultati nella tabella 2 sappiamo che

(352) $\begin{equation*} \lim_{x \to +\infty} \log x = +\infty, \end{equation*}$

ma ci accingiamo a verificare che $f$ non possiede asintoto obliquo per $x \to +\infty$ provando che la prima delle due condizioni in (342) non è verificata. Infatti si ha

(353) $\begin{equation*} \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{\log x}{x} \overset{\text{(eq. 268)}}{=} 0, \end{equation*}$

mentre la prima condizione in (342) richiederebbe che tale limite non sia nullo. Intuitivamente, il fatto che il limite sia nullo vuol dire che il grafico della funzione si appiattisce e la pendenza di una eventuale retta che approssimi il grafico di $f$ dovrebbe essere nulla, cioè tale retta dovrebbe essere orizzontale; d’altra parte il fatto che $\lim_{x \to +\infty} \log x=+\infty$ implica che la funzione non abbia asintoti orizzontali.

$\[\]$

Funzioni asintotiche e principio di sostituzione.

Nel calcolo di un limite per $x \to x_0$

è spesso utile rendersi conto che, al limite per $x \to x_0$

, una determinata funzione $f_1$

è “approssimativamente equivalente” a un’altra funzione $f_2$

. Conoscendo questa informazione, in alcuni casi è possibile sostituire $f_1$

con $f_2$

nel calcolo del limite desiderato (con alcune restrizioni, che vedremo a breve). Cominciamo col formalizzare la nozione di funzioni asintoticamente equivalenti.

Definizione 115 (funzioni asintotiche). Siano $f_1, f_2 \colon A \subseteq \mathbb{R} \to \mathbb{R}$

due funzioni e sia $x_0 \in \overline{\mathbb{R}}$

un punto di accumulazione per $\{x \in A \colon f_2(x) \neq 0\}$

. $f_1$

e $f_2$

si dicono asintoticamente equivalenti per $x \to x_0$

se vale

(354) $\begin{equation*} \lim_{x \to x_0} \frac{f_1(x)}{f_2(x)}= 1. \end{equation*}$

In tal caso si scrive $f_1 \sim f_2$ per $x \to x_0$ .

Poiché il rapporto di due quantità vale $1$ se e solo se le quantità sono uguali, dalla definizione di sopra si intuisce che $f_1 \sim f_2$ se e solo se esse sono “asintoticamente identiche” per $x \to x_0$ . Facciamo alcuni esempi per chiarire il concetto.

Esempio 116.

Le funzioni definite da $f_1(x)= \sin x$ e $f_2(x)=x$ sono asintoticamente equivalenti per $x \to 0$ ; infatti dal limite notevole del seno (282) segue
(355) $\begin{equation*} \lim_{x \to 0} \frac{f_1(x)}{f_2(x)} = \lim_{x \to 0} \frac{\sin x}{x} = 1 \quad \implies \quad \sin x \sim x \quad \text{per $x \to 0$.} \end{equation*}$

Analogamente, dagli altri limiti notevoli seguono le seguenti equivalenze asintotiche per $x \to 0$ :
(356) $\begin{gather*} 1 - \cos x \sim \frac{x^2}{2}, \qquad e^x - 1 \sim x, \qquad \log(1+x) \sim x. \end{gather*}$

Le funzioni definite da $f_1(x)= x^2 + x + \log x$ e $f_2(x)=x^2 - 2$ sono asintoticamente equivalenti per $x \to +\infty$ ; infatti si ha
$\begin{aligned} \lim_{x \to +\infty} \frac{f_1(x)}{f_2(x)} & = \lim_{x \to +\infty} \frac{x^2 + x +\log x}{x^2-2} = \\& = \lim_{x \to +\infty} \frac{x^2 \left (1 + \frac{1}{x} +\frac{\log x}{x^2}\right )}{x^2 \left (1 - \frac{2}{x^2}\right )} \overset{\text{(eq. 268)}}{=} 1 \end{aligned}$

$\[\]$

Le funzioni asintoticamente equivalenti possono essere sostituite nel calcolo di limiti che riguardano esclusivamente prodotti, quozienti e potenze. Vale infatti il seguente principio di sostituzione nel calcolo dei limiti.

Proposizione 117 (principio di sostituzione nel calcolo dei limiti). Sia $A \subseteq \mathbb{R}$

, siano $f_1,f_2,g_1,g_2,h_1,h_2 \colon A \to \mathbb{R}$

delle funzioni, siano $a,b,c \in \mathbb{R}$

e sia $x_0 \in \mathbb{R}$

un punto di accumulazione per $A$

. Supponiamo che $f_1 \sim f_2$

, che $g_1 \sim g_2$

e che $h_1 \sim h_2$

per $x \to x_0$

, ossia che

(357) $\begin{equation*} \lim_{x \to x_0} \frac{f_1(x)}{f_2(x)} = 1, \qquad \lim_{x \to x_0} \frac{g_1(x)}{g_2(x)} = 1, \qquad \lim_{x \to x_0} \frac{h_1(x)}{h_2(x)} = 1. \end{equation*}$

Allora dei due limiti

(358) $\begin{equation*} \lim_{x \to x_0} \frac{f_1^a(x) \cdot g_1^b(x)}{h_1^c(x)}, \qquad \lim_{x \to x_0} \frac{f_2^a(x) \cdot g_2^b(x)}{h_2^c(x)}, \end{equation*}$

uno esiste se e solo se esiste l’altro e, in tal caso, essi coincidono.

Dimostrazione. Supponiamo che esista

(359) $\begin{equation*} \lim_{x \to x_0} \frac{f_1^a(x) \cdot g_1^b(x)}{h_1^c(x)} \eqqcolon \ell \in \overline{\mathbb{R}} \end{equation*}$

e proviamo che esiste l’altro limite e che i due valori coincidono. Infatti dividendo e moltiplicando per $\frac{f_1^a(x) \cdot g_1^b(x)}{h_1^c(x)}$ si ottiene

$\begin{aligned} \lim_{x \to x_0} \frac{f_2^a(x) \cdot g_2^b(x)}{h_2^c(x)} & = \lim_{x \to x_0} \dfrac{\frac{f_2^a(x) \cdot g_2^b(x)}{h_2^c(x)}}{\frac{f_1^a(x) \cdot g_1^b(x)}{h_1^c(x)}} \,\frac{f_1^a(x) \cdot g_1^b(x)}{h_1^c(x)} = \\& = \lim_{x \to x_0} \dfrac{f_2^a(x)}{f_1^a(x)}\, \dfrac{g_2^b(x)}{g_1^b(x)}\, \dfrac{h_1^c(x)}{h_2^c(x)} \,\frac{f_1^a(x) \cdot g_1^b(x)}{h_1^c(x)} \\ & = \ell, \end{aligned}$

dove all’ultimo passaggio abbiamo usato i teoremi 49 e 57 sull’algebra dei limiti, in quanto le prime tre frazioni hanno limite $1$ , mentre la quarta ha limite $\ell$ .

$\[\]$

Applichiamo questo principio alla risoluzione di un limite.

Esempio 118. Calcoliamo

(360) $\begin{equation*} \lim_{x \to 0} \frac{\sin^2 x \cos x}{x^2 + x^3}. \end{equation*}$

Osserviamo che la frazione è ottenuta dalle tre funzioni $f(x)=\sin x$ elevata al quadrato, dalla funzione $g(x)=\cos x$ e dividendo per la funzione $h(x)=x^2+x^3$ . Si ha

(361) $\begin{equation*} \sin x \sim x, \quad \cos x \sim 1, \quad x^2+x^3 \sim x^2, \qquad \text{per $x \to 0$}. \end{equation*}$

Per il principio di sostituzione nei limiti stabilito dalla proposizione 117 si ha quindi

(362) $\begin{equation*} \lim_{x \to 0} \frac{\sin^2 x \cos x}{x^2 + x^3}. = \lim_{x \to 0} \frac{x^2 \cdot 1}{x^2} = 1. \end{equation*}$

$\[\]$

Osservazione 119. È importante notare che il principio di sostituzione non può essere applicato ai limiti in cui vi sono operazioni di somma tra funzioni, come mostra l’esempio seguente.

$\[\]$

Esempio 120. Da (??) sappiamo che

(363) $\begin{equation*} \lim_{x \to 0} \frac{\sin x - \tan x}{x^3} = - \frac{1}{2}. \end{equation*}$

Il limite notevole (282) e il principio di sostituzione implicano che

(364) $\begin{equation*} \sin x \sim x, \qquad \tan x= \frac{\sin x}{\cos x} \sim x \qquad \text{per $x \to 0$}. \end{equation*}$

Se però applicassimo (in maniera scorretta!) il principio di sostituzione alle funzioni $\sin x$ , $\tan x$ e $x^3$ , si otterrebbe

(365) $\begin{equation*} \lim_{x \to 0} \frac{\sin x - \tan x}{x^3} \textcolor{red}{ = \lim_{x \to 0} \frac{x - x}{x^3} = \lim_{x \to 0} \frac{0}{x^3} = 0, } \end{equation*}$

che è ovviamente scorretto (abbiamo evindenziato in rosso la parte sbagliata del calcolo). Il problema è che le funzioni $\sin x$ e $\tan x$ non sono uguali alla funzione $x$ : in realtà si può vedere (con gli sviluppi di Taylor [8 (esempio 1)]) che $\sin x - x$ è asintoticamente equivalente a $-\frac{x^3}{6}$ e che la differenza $\tan x - x$ è asintoticamente equivalente a $\frac{x^3}{3}$ .

$\[\]$

Infinitesimi e o-piccolo.

Il concetto di funzioni asintotiche serve dunque a esprimere l’idea intuitiva che due funzioni siano confrontabili, o approssimativamente equivalenti, per $x \to x_0$

. Risulta molto utile anche esprimere il concetto che, tra due funzioni $f$

e $g$

, $f$

“sia trascurabile” rispetto a $g$

al limite per $x \to x_0$

. Tale nozione viene espressa mediante il simbolo di $o$

-piccolo.

Definizione 121. ( $o$ -piccolo) Sia $A \subseteq \mathbb{R}$

, siano $f,g \colon A \to \mathbb{R}$

e sia $x_0 \in \mathbb{R} \cup \{-\infty,+\infty\}$

un punto di accumulazione per l’insieme $\{x \in A \colon g(x) \neq 0\}$

. Diciamo che $f$

è un $o$ -piccolo di $g$ per $x \to x_0$

(366) $\begin{equation*} \lim_{x \to x_0} \frac{f(x)}{g(x)} = 0. \end{equation*}$

In tal caso scriviamo $f=o(g)$ .

Osserviamo che, nonostante l’uso del simbolo di uguale, $o(\cdot)$ non denota una funzione precisa, ma semplicemente una funzione che soddisfa la definizione 121. In particolare, $f=o(g)$ e $h=o(g)$ non implicano $f=h$ , come è evidente nell’esempio che segue.

Esempio 122. Siano $f,g,h \colon \mathbb{R} \to \mathbb{R}$ le funzioni definite da

(367) $\begin{equation*} f(x)= (x-2)^3, \quad g(x) = x-2, \quad h(x) = (x-2)^2 \qquad \forall x \in \mathbb{R}. \end{equation*}$

Dato che $\lim_{x \to 2} \frac{f(x)}{g(x)}=0$ e $\lim_{x \to 2} \frac{h(x)}{g(x)}=0$ , si ha

(368) $\begin{equation*} f =o(g), \quad h=o(g), \qquad \text{per } x \to 2. \end{equation*}$

Invece, poiché $\lim_{x \to +\infty} \frac{g(x)}{f(x)}=0$ e $\lim_{x \to +\infty} \frac{g(x)}{h(x)}=0$ , si ha

(369) $\begin{equation*} g=o(f), \quad g=o(h), \qquad \text{per } x \to +\infty. \end{equation*}$

$\[\]$

Esempio 123. Per la definizione 121, $f=o(1)$ per $x \to x_0$ se e solo se $\lim_{x \to x_0} f(x)=0$ , cioè se e solo se $f$ è infinitesima per $x \to x_0$ .

$\[\]$

Esempio 124. Dai limiti della gerarchia degli infiniti si ottiene, per $a >1$ e $\beta>0$ , che

(370) $\begin{equation*} \log_a x = o(x^\beta), \quad x^\beta = o(a^x), \qquad \text{per $x \to +\infty$}. \end{equation*}$

$\[\]$

Dato che una strategia molto utile consiste nel confrontare le funzioni con polinomi, è essenziale essere in grado di manipolare $o$ -piccolo di quantità del tipo $(x-x_0)^n$ per $x \to x_0$ . Risultano quindi importanti le seguenti regole di calcolo, che riportiamo senza dimostrazione, proponendo al lettore di provarle come esercizio e rimandando a [1 (sezione 6.6)] e [10] per una discussione completa sull’argomento.

Proposizione 125 (algebra degli $o$ -piccolo). Sia $x_0 \in \mathbb{R}$

e siano $m,n \in \mathbb{Z}$

; valgono le seguenti proprietà.

$c\cdot o\big((x-x_0)^m\big) = o\big(c(x-x_0)^m\big)= o\big((x-x_0)^m\big)$ , per ogni $c \in \mathbb{R} \setminus \{0\}$ .

$o\big((x-x_0)^m\big) \cdot o\big((x-x_0)^n\big) = o\big((x-x_0)^{m+n}\big)$ .

$(x-x_0)^m \cdot o\big((x-x_0)^n\big) = o\big((x-x_0)^{m+n}\big)$ .

Se $m \leq n$ , allora $o\big((x-x_0)^n\big)= o\big((x-x_0)^m\big)$ ;

Se $m \leq n$ , allora $o\big((x-x_0)^m\big) + o\big((x-x_0)^n\big) = o\big((x-x_0)^m\big)$ .

Se $m < n$ , allora $o\big((x-x_0)^m\big) + (x-x_0)^n = o\big((x-x_0)^m\big)$ .

$o\big((x-x_0)^m + o((x-x_0)^m)\big)= o\big((x-x_0)^m\big)$ .

$o\big( o\big( (x-x_0)^m\big) \big)= o\big( (x-x_0)^m\big)$ .

I limiti notevoli studiati possono spesso essere riformulati in termini di $o$ -piccoli.

Esempio 126. Il limite notevole del seno (282) prova che

(371) $\begin{equation*} \lim_{x \to 0} \frac{\sin x - x}{x} = \lim_{x \to 0} \left (\frac{\sin x}{x} - 1 \right ) = 0 \quad \implies \quad \sin x - x= o(x) \quad \text{per $x \to 0$}. \end{equation*}$

In altre parole $\sin x = x + o(x)$ per $x \to 0$ , ovvero la funzione $\sin x$ è pari alla funzione $x$ a meno di un resto, un errore, che però è un $o(x)$ , ossia converge a $0$ più velocemente di $x$ .

Analogamente, dai limiti notevoli (283), (284) e (285) si hanno gli sviluppi

(372) $\begin{equation*} \cos x = 1- \frac{x^2}{2} + o(x^2), \quad e^x = 1 + x + o(x), \quad \log(1+x)= x + o(x) \qquad \text{per $x \to 0$}. \end{equation*}$

$\[\]$

Queste approssimazioni risultano spesso molto utili nel calcolo dei limiti, in quanto consentono in un certo senso di “trascurare” i termini inessenziali, concentrandosi su quelli principali.

Esempio 127. Calcoliamo

(373) $\begin{equation*} \lim_{x \to 0} \frac{\log(1+x)- \log(1-\sin x)}{x+2\sin x}. \end{equation*}$

Osserviamo che, da $\sin x =x + o(x)$ per $x \to 0$ e $\log(1+y)=y + o(y)$ per $y \to 0$ , segue che

(374) $\begin{equation*} \begin{split} \lim_{x \to 0} \frac{\log(1+x)+ \log(1-\sin x)}{x+2\sin x} & = \lim_{x \to 0} \frac{x + o(x)+ \log\big(1-x + o(x)\big)}{x+2x + o(x)} = \\ & = \lim_{x \to 0} \frac{x + o(x)+ \big(-x + o(x)\big)+ o\big(-x+o(x)\big)}{3x+ o(x)} = \\ & = \lim_{x \to 0} \frac{o(x)}{3x+ o(x)} = \\ & = 0 \end{split} \end{equation*}$

dove alla prima uguaglianza abbiamo usato $\sin x = x + o(x)$ , alla seconda uguaglianza abbiamo $\log(1+y)=y + o(y)$ per $y \to 0$ con $y=x+o(x)$ , mentre alla terza abbiamo usato le proprietà elencate nella proposizione 125. Il fatto che il limite sia nullo deriva dalla definizione di $o$ -piccolo, ad esempio dividendo numeratore e denominatore per $x$ e osservando che $\frac{o(x)}{x} \to 0$ mentre $\frac{3x+o(x)}{x} \to 3$ .

$\[\]$

Esempio 128. Calcoliamo

(375) $\begin{equation*} \lim_{x \to 0} \left (\cos x \right )^{\frac{1}{x^2}}. \end{equation*}$

Usiamo $a^b=e^{b \log a}$ e lo sviluppo $\cos x = 1 - \frac{x^2}{2} + o(x^2)$ per $x \to 0$ , ottenendo

$\begin{aligned} \lim_{x \to 0} \left (\cos x\right )^{\frac{1}{x^2}} & = \lim_{x \to 0} e^{\frac{\log \cos x}{x^2}} = \\& = \lim_{x \to 0} e^{\frac{\log \left ( 1 - \frac{x^2}{2} + o(x^2)\right )}{x^2}} = \\& = \lim_{x \to 0} e^{\frac{ \left ( - \frac{x^2}{2} + o(x^2)\right ) +o\left ( - \frac{x^2}{2} + o(x^2)\right )}{x^2}} = \\& = \lim_{x \to 0} e^{\frac{ - \frac{x^2}{2}}{x^2}} = \\& = e^{-\frac{1}{2}}, \end{aligned}$

dove alla terza uguaglianza abbiamo utilizzato lo sviluppo $\log(1+y)=y+o(y)$ per $y \to 0$ con $y=-\frac{x^2}{2}+o(x^2)$ , mentre alla quarta uguaglianza abbiamo usato la proposizione 125.

$\[\]$

Riferimenti bibliografici

[1] E. Acerbi, G. Buttazzo, Primo corso di Analisi Matematica, Pitagora Editrice, 1997.

[2] E. Giusti, Analisi Matematica 1, Bollati Boringhieri, 1988.

[3] Qui Si Risolve, Esercizi sulla verifica dei limiti.

[4] Qui Si Risolve, Il teorema di Bolzano-Weierstrass.

[5] Qui Si Risolve, Funzioni continue.

[6] Qui Si Risolve, Funzioni elementari: algebriche, esponenziali e logaritmiche.

[7] Qui Si Risolve, Funzioni goniometriche: la guida essenziale.

[8] Qui Si Risolve, Guida sull’applicazione dei polinomi di Taylor nel calcolo dei limiti.

[9] Qui Si Risolve, Il teorema ponte.

[10] Qui Si Risolve, Simboli di Laundau.

[11] Qui Si Risolve, Teoria sulle funzioni.

[12] Qui Si Risolve, Teoria sulle successioni.

Tutta la teoria di analisi matematica

Leggi...

Tutte le cartelle di Analisi Matematica

Leggi...

Tutti gli esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.

Nota a piè di pagina

Document