Questa raccolta di 69 esercizi svolti sul corpo rigido è stata sviluppata con l’obiettivo di fornire un supporto didattico strutturato e approfondito nel campo della dinamica del corpo rigido, uno dei temi centrali della meccanica classica. L’intento è quello di offrire un repertorio completo di esercizi che copra ogni aspetto fondamentale della materia, rendendo la raccolta un punto di riferimento per studenti e studiosi desiderosi di consolidare le proprie conoscenze teoriche e capacità applicative.
Gli esercizi proposti provengono da fonti accademiche riconosciute nella letteratura scientifica, tra cui:
- Rosati, Luigi – Fisica Generale
- Mencuccini, C., Silvestrini, G. – Fisica
- Mazzoldi, P., Nigro, M., Voci, C. – Elementi di Fisica
- Resnick, R., Halliday, D., Walker, J. – Fundamentals of Physics
- Goldstein, H. – Classical Mechanics
- Landau, L.D., Lifshitz, E.M. – Mechanics
Oltre agli esercizi selezionati da testi accademici di riferimento, questa raccolta include anche una serie di problemi originali e quesiti estratti da prove d’esame universitarie, con lo scopo di ampliare il ventaglio di applicazioni affrontate e rafforzare la comprensione pratica della dinamica del corpo rigido.
In linea con il percorso didattico seguito, il capitolo successivo è dedicato agli esercizi svolti sugli urti, contenente 39 esercizi svolti accuratamente selezionati. Il capitolo precedente, invece, riguarda gli esercizi svolti sui sistemi di punti materiali, per un totale di 40 esercizi svolti.
È possibile accedere all’intero corso di meccanica classica, risultato del lavoro del nostro team negli ultimi quattro anni. Maggiori dettagli sugli autori e revisori sono disponibili nella sezione dedicata alla fisica.
Corpo rigido : autori e revisori
Leggi...
Autori e Revisori:
Valerio Brunetti, Giuseppe Palaia.
Autori:
Romano Rotonda, Daniele Massaro, Andrea Corradini, Davide Vignotto, Cosimo Tommasi.
Revisori:
Autori in collaborazione:
Giulia Romoli, Antonio Figura, Christian Magliano.
Ex Autori & Revisori:
Patrizio Di Lorenzo, Simone Brozzesi, Nicola Santamaria, Vittorio Larotonda, Leonardo Rebeschini, Simone Romiti, Antonio Junior Iovino, Daniele Bjørn Malesani, Tiziano Schiavone, Serena Lezzi, Marco Chilioiro.
Testi degli esercizi sulla dinamica del corpo rigido
Esercizio 1 . Due dischi rigidi (
,
,
e
) sono connessi come in figura 1 da una cinghia indeformabile. All’asse del primo disco è connesso un motore che puo’ fornire un momento costante
, mentre sull’asse del secondo disco agisce un momento frenante costante
. Al tempo
il motore comincia ad agire facendo ruotare il primo disco.
- Calcolare la velocità angolare del secondo disco al tempo
.
- Calcolare quanto lavoro è stato fornito dal motore in questo tempo.
Si assume che la cinghia non slitti rispetto ai dischi.
Figura 1: schema del problema del corpo rigido 1.
Esercizio 2 . Sia un sistema fisico composto da tre corpi rigidi omogenei: un disco di massa
e raggio
, un’asta
(prima asta) di massa
e lunghezza
, una seconda asta di massa
e lunghezza
, come rappresentato in figura 2. L’estremo
della prima asta coincide con il centro del disco, l’estremo
coincide con il centro della seconda asta. La seconda asta è disposta ortogonalmente rispetto alla prima asta, come si può dedurre dalla figura 2. Calcolare:
1) le coordinate del centro di massa nel sistema di riferimento ;
2) il momento d’inerzia del sistema fisico in esame rispetto ad un asse passante per il punto
e ortogonale al piano
.
Si consideri un nuovo sistema di riferimento fisso tale per cui
, l’asse
sia coincidente con la seconda asta e l’asse
. Il disco e la prima asta in questa nuova configurazione ruotano con velocità angolare costante
rispetto all’asse
. Nel nuovo sistema di riferimento, si calcoli:
3) la velocità del centro di massa ;
4) il modulo della quantità di moto totale ;
5) l’energia cinetica totale e quella rispetto al centro di massa
.
Figura 2: schema della configurazione del sistema fisico.
Esercizio 3 . L’asse del cilindro rappresentato in figura 3 è fisso e il cilindro è inizialmente fermo. Il blocco di massa
si muove inizialmente verso destra senza attrito con velocità
e, passando sopra al cilindro, si porta nella posizione tratteggiata. Al primo contatto col cilindro, il blocco scivola su di esso ma l’attrito è talmente elevato che lo scivolamento cessa prima che
perda contatto col cilindro. Il cilindro ha raggio
e momento d’inerzia
.
Esprimere in funzione di
e
.
Figura 3: schema del problema del corpo rigido 1.
Esercizio 4 . Un sistema rigido è costituito da un anello di massa
kg e raggio
m, e da un disco avente uguali massa e raggio dell’anello, saldati nel punto
. Il sistema giace in un piano orizzontale ed è vincolato a ruotare, senza attrito, attorno ad un asse verticale passante per il centro
del disco. Calcolare
-
1) La posizione del centro di massa del sistema rispetto all’asse
2) Il momento d’inerzia del sistema rispetto all’asse di rotazione
Al sistema viene applicato un momento costante e il sistema entra in rotazione, si osserva che la sua velocità angolare dopo 20 giri vale
rad/s. Calcolare
-
3) Il valore del momento
Figura 4: schema del problema del corpo rigido 4.
Esercizio 5 . Due dischi coassiali aventi momenti di inerzia
kg
m
e
kg
m
rispettivamente, sono premuti uno contro l’altro; in queste condizioni il massimo momento di attrito statico è
N
m, mentre quando slittano uno rispetto all’altro il momento di attrito dinamico è
N
m. Calcolare:
-
1) l’accelerazione angolare del disco 2 se al disco 1 è applicato il momento costante
2) ripetere il calcolo se N
m.
Figura 5: schema del problema del corpo rigido 5.
Esercizio 6 . Calcolare il periodo delle piccole oscillazione del pendolo composto mostrato in figura 6, formato da due aste di masse e lunghezze
,
,
e
; la seconda asta è a
rispetto alla prima ed è fissata a questa nel centro. Considerare il sistema inizialmente in quiete e supporre che la massa sia distribuita in modo omogeneo. In particolare studiare il caso
e
.
Figura 6: schema del problema del corpo rigido 6.
Esercizio 7 . Un corpo rigido è formato da quattro aste uguali, ciascuna di massa
e lunghezza
,
disposte lungo i lati di un quadrato, che giace in un piano verticale. Calcolare
1) il momento d’inerzia del corpo rispetto ad un asse perpendicolare al piano sul quale giace il quadrato e passante per il centro O del quadrato;
2) il momento d’inerzia del corpo rispetto ad un asse perpendicolare al piano sul quale giace il quadrato e passante per il punto medio dell’asta superiore;
3) il momento d’inerzia del corpo rispetto ad un asse perpendicolare al piano sul quale giace il quadrato e passante per il punto , coincidente con il vertice superiore sinistro del quadrato;
4) calcolare inoltre il periodo delle piccole oscillazioni nel caso b).
Figura 7: schema del problema del corpo rigido 7.
Esercizio 8 . Un corpo rigido è formato da quattro aste uguali, ciascuna di massa
kg e lunghezza
m, disposte lungo i lati di un quadrato, che giace in un piano verticale. Calcolare:
1) Il momento d’inerzia del sistema rispetto ad un asse orizzontale appartenente al piano verticale e passante per il centro del quadrato;
2) Il momento d’inerzia del sistema rispetto ad un asse orizzontale appartenente al piano verticale e passante per il punto del quadrato.
Figura 8: schema del problema del corpo rigido 8.
Esercizio 9 . Un’asta rigida di massa
e lunghezza
m è incernierata nell’estremo
ed è appesa nell’estremo
a un filo collegato alla massa
kg; il sistema è in equilibrio con l’asta orizzontale. Calcolare
1) Il valore della reazione vincolare in .
Si assuma che la la fisica del problema sia tale da porre il modulo delle tensioni ai capi della carrucola uguali. Successivamente si interrompe il collegamento in e l’asta ruota sotto l’azione della forza di gravità; nel vincolo
agisce un momento che si oppone alla rotazione
, con
Nm/rad e
angolo che l’asta forma con l’asse
. Calcolare
2) La velocità angolare dell’asta quando .
Figura 9: schema del problema del corpo rigido 9.
Esercizio 10 . Un corpo rigido è costituito da un’asta, di massa
kg e lunghezza
m, e da una sfera, di massa
e raggio
, saldati nel punto
. Il sistema può ruotare senza attrito attorno ad un asse fisso uscente dal foglio passante per il punto
, ortogonale al disegno. Per mantenere in equilibrio statico il sistema, con l’asta orizzontale, nel punto
è applicata una forza verticale
. Calcolare:
1) il modulo di e della reazione normale
in
.
Viene annullata la forza e il sistema ruota sotto l’azione della forza peso, con la sfera che scende e l’asta che sale. Calcolare
2) l’accelerazione angolare un istante dopo la rimozione della forza ;
3) la velocità angolare del sistema nell’istante in cui l’asta è verticale.
Figura 10: schema del problema del corpo rigido 10.
Scarica gli esercizi svolti
Ottieni il documento contenente 69 esercizi risolti, contenuti in 242 pagine ricche di dettagli, per migliorare la tua comprensione della dinamica del corpo rigido.
Esercizio 11 . Una sbarra sottile uniforme
, lunga
m, è incernierata per un’estremità
in modo da poter spazzare su un piano verticale. La sbarra viene sollevata fino alla posizione orizzontale, poi viene lasciata cadere. Calcolare la velocità angolare della sbarra, e la velocità lineare della sua estremità libera
nell’istante in cui la sbarra ha descritto un angolo di
.
Esercizio 12 . La bacchetta omogenea, rappresentata in figura 12, lunga
m e con massa
kg, puo’ ruotare intorno a un perno orizzontale, privo di attrito posto a un’estremità. E’ lasciata libera da una posizione di riposo inclinata di
sopra l’orizzontale.
1) Qual è l’accelerazione angolare della bacchetta all’istante in cui viene lasciate libera? (Il suo momento d’inerzia rispetto al perno è kg m
).
2) Usando il principio di conservazione dell’energia trovare la velocità angolare della bacchetta all’istante in cui passa per la posizione orizzontale.
Figura 12: schema del problema del corpo rigido 12.
Esercizio 13 . Un corpo rigido è formato da tre asticelle sottili identiche di lunghezza
, unite fra loro in modo da assumere la forma della lettera
come in figura. L’insieme è libero di ruotare intorno ad un asse orizzontale fisso, che coincide con una delle gambe dell’
. Partendo da una posizione di riposo in cui il piano dell’
è orizzontale, il sistema è lasciato libero di ruotare. Qual è la velocità angolare del corpo quando il piano dell’
arriva in posizione verticale?
Figura 13: schema del problema de corpo rigido 13.
Esercizio 14 . Due masse
e
sono appese a una carrucola senza attrito di massa
e raggio
come in figura 14. La massa
viene abbandonata da ferma da un’altezza
determinare:
a) la velocità con cui tocca il suolo;
b) l’accelerazione angolare della carrucola.
Supporre che .
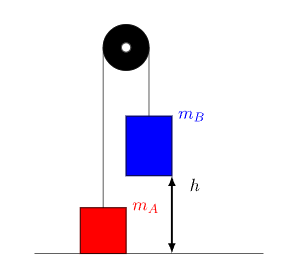
Figura 14: schema del problema del corpo rigido 14.
Esercizio 15 . Le due masse
e
della macchina di Atwood mostrata nella figura 15 sono rilasciate da ferme, con
a un’altezza
al di sopra del pavimento. Quando
colpisce il pavimento, la sua velocità è
. Assumendo che la carrucola sia un disco con la massa distribuita in modo uniforme di raggio
e che la corda, supposta priva di massa, ruoti insieme alla carrucola senza strisciare:
si determini la massa della carrucola supponendo che non vi sia alcun attrito tra il disco della carrucola e il perno centrale attorno a cui ruota.
Figura 15: schema del problema del corpo rigido 15.
Esercizio 16 . Un corpo rigido è costituito da un disco e da un’asta, disposta come in figura 16. Il disco ha massa
kg e raggio
m, l’asta ha massa
kg e lunghezza
. Calcolare:
1) dove si trova rispetto al centro dell’asta, il centro di massa del sistema;
2) Il momento d’inerzia del sistema rispetto all’asse passante per e ortogonale al piano contenente l’asta e il disco.
Supponiamo che il sistema stia in un piano verticale, per cui l’asse passante per quindi è orizzontale e sia in quiete con l’asta orizzontale. Se ad un certo istante il sistema viene lasciato libero di ruotare rispetto all’asse passante per
, calcolare:
3) La sua velocità angolare quando l’asta passa per la posizione verticale.
Figura 16: schema del problema del corpo rigido 16.
Esercizio 17 . A una carrucola, di raggio
, massa
e momento d’inerzia
rispetto all’asse passante per il suo centro e ortogonale al piano verticale in cui giace la carrucola stessa, sono sospese, tramite un filo, due masse
e
, con
. Calcolare l’accelerazione delle masse, le tensioni
e
ed infine la reazione sull’asse della carrucola. Inoltre studiare il caso particolare in cui la massa del disco sia trascurabile.
Si supponga che il filo non slitti e che non ci sia attrito sull’asse.
Figura 17: schema del problema del corpo rigido 17.
Esercizio 18 . Su un piano orizzontale è posta una massa
. La massa
viene messa in movimento tramite un filo che si avvolge su una puleggia di raggio
e quest’ultima è messa in rotazione dalla discesa, sotto l’azione del peso, di una massa
a cui è collegata da un filo avvolto su una puleggia di raggio
, coassiale e rigidamente fissata alla precedente con
. Il momento d’inerzia del sistema delle due pulegge rispetto al comune asse di rotazione vale
. Calcolare:
- la velocità
di
dopo che è scesa di
;
- le tensioni dei due fili durante il movimento;
- il valore di
se tra
e il piano ci fosse un coefficiente di attrito
.
Nota: supporre che i fili non slittino e che non ci sia attrito sull’asse.
Figura 18: schema del problema del corpo rigido 18.
Esercizio 19 . Sia un’asta rigida di lunghezza
e un sistema di riferimento fisso
come in figura 19. L’asta ha gli estremi vincolati a scorrere lungo l’asse
e lungo l’asse
. Dimostrare che il centro dell’asta descrive una circonferenza di raggio
con la stessa velocità angolare dell’asta.
Nota. Assumere trascurabili tutti gli attriti e in figura 19 è l’angolo che forza l’asta con l’asse
e
sono le coordiante del centro di massa rispetto al sistema di riferimento
e che all’iniziale è tutto in quiete .
Figura 19: schema del problema del corpo rigido 19.
Esercizio 20 . Un disco rigido, di massa
e raggio
è posto in un piano orizzontale e può ruotare attorno ad un asse verticale passante a distanza
dal centro del disco. Il bordo del disco è a contatto con un anello di raggio
che tramite un opportuno meccanismo non disegnato, può ruotare attorno allo stesso asse in modo tale che, in caso di moto relativo tra disco e anello, si sviluppi una forza di attrito radente
, tangente all’anello; la massa dell’anello è eguale a quella del disco (la forza
è l’unica forza di attrito presente nel sistema). Inizialmente disco e anello sono fermi; al tempo
viene applicato all’asse un momento costante
così che il disco entri in rotazione; l’anello viene invece mantenuto fermo.
- Calcolare la velocità angolare del disco al tempo
. Nell’istante
l’anello viene lasciato libero e inizia anch’esso a ruotare trascinato dal disco.
- Calcolare la velocità angolare dell’anello al tempo
.
Nell’istanteviene staccato dall’asse il motore che forniva il momento
e si osserva che al tempo
disco e anello hanno la stessa velocità angolare.
Calcolare: - l’energia cinetica del sistema disco-anello al tempo
;
- il lavoro complessivo svolto dalle forze interne nell’intervallo di tempo da
a
.
Figura 20: schema del problema del corpo rigido 20.
Esercizio 21 . Il sistema rappresentato in figura 21 è in equilibrio. Una massa di
è appesa all’estremità del puntone, che ha una massa di
. Gli angoli
e
sono rappresentati in figura 21. Trovare
(1) la forza di tensione nel cavo;
(2) determinare la forza generata dalla cerniera.
Nota. Supporre il filo inestensibile e di massa trascurabile.
Figura 21: schema del problema del corpo rigido 21.
Esercizio 22 . L’estremità di una trave omogenea di massa
e lunga
è incernierata ad un muro. L’altro estremo è sostenuto da un filo nella posizione indicata in figura 22. Inoltre sia
l’angolo formato dalla fune con il muro, come in figura 22.
1) Trovare la tensione generata dal filo che collega la trave al muro.
2) Trovare la reazione vincolare generata dalla cerniera per mantenere il sistema in equilibrio.
Figura 22: schema del problema del corpo rigido 22.
Esercizio 23 . Due aste omogenee e uguali, ciascuna di massa
, sono saldate insieme per un’estremità e l’angolo compreso tra le due aste è
e l’angolo
è l’angolo formato dall’asta
e il piano orizzontale (vedi figura 23 che segue). Il sistema è incernierato senza attrito in
ed è in equilibrio nella posizione di figura 23 sotto l’azione della forza verticale
applicata in
. Si calcoli l’intensità della forza
, esprimendo i risultati in funzione di
.
Figura 23: schema del problema del corpo rigido 23.
Esercizio 24 . Due aste
e
omogenee, di uguale lunghezza e massa
, vengono saldate insieme per uno dei loro estremi, una perpendicolarmente all’altra; l’estremo libero dell’asta
viene poi incernierato a un punto
(vedere la figura 24) intorno al quale l’asta può ruotare senza attrito. Si calcolino i valori dell’angolo
formato dall’asta
rispetto all’orizzontale in condizioni di equilibrio.
Figura 24: schema del problema del corpo rigido 24.
Esercizio 25 . Una scala, la cui massa è distribuita uniformemente lungo tutta la sua lunghezza
, poggia con un’estremità su un piano orizzontale scabro (
) e con l’altra contro una parete verticale liscia. Si determini l’angolo di minima inclinazione
che la scala puo’ formare col piano orizzontale senza scivolare al suolo.
Figura 25: schema del problema del corpo rigido 25.
Esercizio 26 . Un’asta rettilinea omogenea è appoggiata ad un pavimento orizzontale e a una parete verticale, entrambi perfettamente lisci, in posizione verticale. Data l’instabilità dell’equilibrio l’asta inizia a scivolare senza attrito partendo praticamente da ferma. Determinare la posizione dell’asta nell’istante in cui si distacca dalla parete verticale. Si ipotizzi che l’asta scivoli in sento antiorario come in figura 26.
Figura 26: schema del problema del corpo rigido 26.
Esercizio 27 . Due blocchi di uguale massa
sono sospesi alle estremità di un’asticella rigida e priva di peso di lunghezza
, essendo
cm e
cm. L’asticella è tenuta ferma nella posizione indicata in figura 27, e quindi lasciata libera. Calcolare l’accelerazione dei due blocchi all’istante in cui cominciano a muoversi.
Figura 27: schema del problema del corpo rigido 27.
Esercizio 28 . Una trave omogenea
di massa
kg è incernierata senza attrito in
ed è appoggiata nel punto
(come in figura 28): sia
m,
m. Due persone un uomo e una donna si muovono in versi opposti sopra la trave (vedi figura 28) e a ogni istante la distanza della donna rispetto ad
e la distanza dell’uomo rispetto ad
è la stessa; le masse delle donna e dell’uomo sono rispettivamente
kg e
kg. Determinare a quale distanza si troverà la donna quando la trave comincia a ruotare.

Figura 28: schema del problema del corpo rigido 28.
Esercizio 29 . Un cilindro di raggio
e massa
è posto sopra un piano orizzontale; il coefficiente di attrito statico vale
. In corrispondenza al centro del cilindro è scavata una fessura sottilissima in modo tale da ridurre in quella zona il raggio al valore
; si supponga che questo fatto non alteri il momento d’inerzia del cilindro. Al cilindro sono applicate le forze
e
come mostrato in figura 29. Supponendo che
sia data e
no, si richiede di
1) calcolare quanto deve valere in funzione di
,
e
, affinché il cilindro resti in equilibrio.
All’istante la forza
cessa di agire, mentre
ha il valore trovato nel punto
.
2) Trovare la relazione che deve sussistere affinché il moto sia di puro rotolamento.
Figura 29: schema del problema del corpo rigido 29.
Esercizio 30 . Un anello di acciaio di massa
e raggio
può scendere lungo un piano inclinato di acciaio (coefficiente di attrito statico
).
- Calcolare l’angolo del piano inclinato con l’orizzontale oltre il quale non è più possibile un moto di puro rotolamento, denominando tale angolo
.
- Partendo da fermo e con il centro a quota
, l’anello scende lungo tutto il piano inclinato con moto di puro rotolamento dove l’angolo di inclinazione
del piano inclinato è
. Calcolare la velocità angolare finale dell’anello.
Figura 30: schema del problema del corpo rigido 30.
Esercizio 31 . Un cilindro omogeneo di massa
e raggio
rotola senza strisciare su un piano orizzontale sotto l’azione di una forza costante
orizzontale e passante per il centro di massa del cilindro. Sapendo che il cilindro parte da fermo, determinare:
1) l’accelerazione lineare del centro di massa del cilindro;
2) l’energia cinetica del cilindro dopo un tempo dall’applicazione della forza
.
Figura 31: schema del problema del corpo rigido 31.
Esercizio 32 . Un disco di massa
e raggio
è posto sopra una guida inclinata con angolo
; all’asse del disco è collegato un filo che sostiene la massa
. Il filo è teso con la massa
bloccata a distanza
dal suolo. All’istante
si lascia libera la massa
che inizia a scendere, facendo contemporaneamente salire il disco lungo la guida. Il moto del disco è di puro rotolamento.
Calcolare:
1) l’accelerazione con cui scende la massa ;
2) la velocità con cui la massa tocca il suolo;
3) la quota massima raggiunta dal centro del disco, misurata rispetto alla quota che lo stesso centro aveva per .
Figura 32: schema del problema del corpo rigido 32.
Esercizio 33 . Un anello di massa
e raggio
viene fatto salire lungo una parete verticale tramite l’applicazione di una forza costante
, ed è tenuto premuto contro la parete verticale da una forza costante
. Le forze
e
sono orientate come in figura 33 e sono costanti in modulo, direzione e verso per tutto il moto dell’anello. Nell’ipotesi che il piano verticale sia scabro con coefficiente di attrito statico
e che l’anello si muova di puro rotolamento, si determini:
- il modulo dell’accelerazione del centro di massa dell’anello;
- il valore minimo del modulo di
affinché il moto sia di puro rotolamento.
Figura 33: schema del problema del corpo rigido 33.
Esercizio 34 . Il guscio sferico uniforme rappresentato in figura 34, di massa
e raggio
, ruota intorno a un asse verticale su cuscinetti privi di attrito. Una corda priva di massa avvolta intorno all’equatore della sfera, passando senza slittamenti sopra una puleggia, priva di attrito, avente momento d’inerzia
e raggio
, tiene appeso un piccolo oggetto di massa
, libero peraltro di cadere per effetto della forza di gravità.
La corda non slitta e il perno è privo di attrito. Quale sarà la velocità dell’oggetto dopo che sarà disceso per una distanza dalla posizione di riposo?
Figura 34: schema del problema del corpo rigido 34.
Esercizio 35 . Un disco cilindrico omogeneo, di massa
e raggio
, è sorretto, come mostrato in figura 35, da un nastro di massa trascurabile: i tratti di nastro non a contatto col disco sono verticali mentre l’asse del disco è orizzontale. Un’estremità del nastro è fissata a un sostegno, sull’altra viene esercitata una forza
diretta verso l’alto. L’attrito fra nastro e disco è trascurabile. Si calcoli:
- l’intensità
della forza
necessaria affinché sussista equilibrio e, corrispondentemente, la tensione
del tratto di filo al quale è applicata la forza
e quella
del tratto di filo fissato al sostegno;
- il modulo
dell’accelerazione con cui il disco sale e il modulo delle tensioni
e
, se
.
- Si risponda alla domanda posta in
) se il nastro presenta attrito e il disco sale rotolando senza scivolare lungo il nastro (moto di puro rotolamento).
Figura 35: schema del problema del corpo rigido 35.
Esercizio 36 . Un cilindro di massa
e raggio
è posato nel punto di mezzo di una lastra lunga
; il sistema è in quiete. Al tempo
la lastra entra in movimento con accelerazione costante
diretta come in figura 36. Calcolare l’accelerazione del cilindro rispetto alla lastra e lo spazio percorso dal cilindro rispetto al suolo da quando esso entra in moto a quando cade dalla lastra. Assumere che il moto del cilindro sia di puro rotolamento.
Figura 36: schema del problema del corpo rigido 36.
Esercizio 37 . Due cilindri
e
, di masse
e
e raggi
e
rotolano senza strisciare su due piani inclinati e sono collegati da un filo inestensibile come è mostrato in figura 37;
scende mentre
sale. Le masse del filo e della carrucola sono trascurabili. Quanto vale l’accelerazione di un punto dell’asse di
?
Figura 37: schema del problema del corpo rigido 37.
Esercizio 38 . Un cilindro di raggio
e di massa
viene fatto ruotare in senso orario con velocità angolare
. Il cilindro viene quindi posto a contatto con una superficie orizzontale con coefficiente di attrito dinamico
. Determinare il tempo impiegato dal cilindro a raggiungere la condizione di puro rotolamento, la velocità del centro di massa e la velocità angolare del sistema in tale istante.
Figura 38: schema del problema del corpo rigido 38.
Esercizio 39 . Una palla da bowling di raggio
e di massa
viene lanciata con velocità
, orientata come in figura 39, a contatto con una superficie orizzontale con coefficiente di attrito dinamico
. Determinare il tempo impiegato dalla palla a raggiungere la condizione di puro rotolamento, la velocità del centro di massa e la velocità angolare del sistema in quell’istante.
Figura 39: schema del problema del corpo rigido 39.
Esercizio 40 . Un’asta composta da due metà, ciascuna di lunghezza
e massa
, può ruotare in un piano verticale intorno ad un perno passante per il suo punto medio e posto ad una quota
da terra (vedi figura 40). La metà di sinistra ha densità lineare
uniforme, mentre quella di destra ha densità lineare
, con
distanza dal centro dell’asta. Alla rotazione si oppone un momento frenante
.
Determinare:
1) l’angolo che la barra forma con la verticale nella posizione di equilibrio statico;
2) l’energia potenziale della barra in tale posizione, calcolata rispetto a terra.
Effettuare i calcoli con ,
,
Figura 40: schema del problema del corpo rigido 40.
Esercizio 41 . Un disco circolare omogeneo, di massa
e raggio
, è vincolato a ruotare su un piano verticale, con velocità angolare costante di modulo
(supporre che il disco ruoti in senso antiorario) intorno a un asse orizzontale passante per il suo centro
. Un’asta metallica, di lunghezza
, massa
e sezione trasversale di dimensioni trascurabili, viene appoggiata con una delle estremità sul bordo superiore
del disco e su un supporto puntiforme
situato alla stessa quota di
, con
. Tra asta e disco c’è attrito, con coefficiente di attrito dinamico
.
1) Supponendo che nel contatto tra l’asta e il supporto ci sia attrito, si determini il valore minimo
del coefficiente di attrito statico affinché l’asta resti in quiete;
2) Supponendo che l’attrito tra l’asta e il supporto sia trascurabile, si determini il modulo della velocità dell’asta quando questa è spostata lungo l’orizzontale di un tratto
.
Si supponga che asta e disco siano sempre in condizione di strisciamento.
Figura 41: schema del problema del corpo rigido 41.
Esercizio 42 . Un’asta omogenea di lunghezza
è appoggiata sulla superficie di una semisfera perfettamente liscia di raggio
fissata a un piano orizzontale scabro con coefficiente di attrito statico
, come mostrato in figura 42. Dimostrare che se il sistema è in equilibrio vale la seguente relazione
(1)
dove è l’angolo che forma il segmento (raggio della sfera) che congiunge il centro della sfera (
) e il punto di contatto tra asta e sfera (
) con il piano orizzontale.
Figura 42: schema del problema del corpo rigido 42.
Esercizio 43 . Un’asta omogenea di lunghezza
è appoggiata in corrispondenza dello spigolo di un gradino di altezza
e di un piano orizzontale scabro con coefficiente di attrito statico
, come mostrato nella figura 43. Se l’asta è in equilibrio, dimostrare che vale la seguente relazione
(2)
dove è l’angolo che forma l’asta con il piano orizzontale.
Figura 43: schema del problema del corpo rigido 43.
Esercizio 44 .Una sfera omogenea di massa
e raggio
è inizialmente in quiete su un piano orizzontale. Al tempo
, la sfera viene lanciata con una velocità traslazionale iniziale di modulo
, parallela al piano. Il coefficiente di attrito dinamico tra la sfera e il piano è
. Si richiede di descrivere il moto della sfera, determinando la velocità del centro di massa
quando la sfera inizia a rotolare senza strisciare. Successivamente, calcolare il tempo
necessario per raggiungere tale condizione in funzione di
,
e
. Infine, verificare il teorema dell’energia cinetica tra gli istanti
e
.
Figura 44: schema del problema del corpo rigido 44.
Esercizio 45 . Un sistema di due corpi rigidi è costituito da una piattaforma circolare (di massa
e raggio
) che può ruotare senza attrito attorno ad un asse verticale, passante per il suo centro e fissato al suolo, e da un disco (di massa
e raggio
) che può ruotare senza attrito attorno ad un asse verticale passante per il suo centro e fissato alla piattaforma, a distanza
dal centro di quest’ultima. Le direzioni degli assi di rotazione sono fisse.
Si consideri in primo luogo il seguente stato iniziale: la piattaforma è ferma e il disco ruota con velocità angolare . Tra la piattaforma e il disco agisce una forza di attrito radente per cui dopo un certo tempo il disco non ruota più rispetto alla piattaforma. Calcolare
- il valore finale del momento angolare del sistema;
- la variazione di energia cinetica del sistema.
- Si consideri successivamente un diverso stato iniziale, in cui sia la piattaforma che il disco sono fermi, e si assuma che tra disco e piattaforma ci sia nessun attrito. Con un motore si porta la velocità angolare della piattaforma al valore
. Calcolare il lavoro fornito dal motore.
Figura 45: schema del problema del corpo rigido 45.
Esercizio 46 . Il centro
di una sbarra sottile e uniforme, di massa
e lunghezza
, è rigidamente fissato a un asse verticale
e forma con tale asse un angolo fisso pari a
. Il sistema ruota senza attrito intorno all’asse in senso antiorario con velocità angolare
costante (in modo che il vettore
giaccia lungo l’asse). Si calcolino modulo, direzione e verso del momento angolare del sistema, assumendo come polo il punto
.
Figura 46: schema del problema del corpo rigido 46.
Esercizio 47 . Un ingranaggio è costituito da due ruote dentate omogenee
e
, di spessore trascurabile e disposte nello stesso piano verticale (vedi figura 47);
e
possono ruotare intorno a due assi orizzontali passanti per i centri
e
. Le dimensioni dei denti dell’ingranaggio sono piccole e il contatto tra le due ruote può approssimarsi come puntiforme. I raggi di
e
sono rispettivamente
e
, mentre le masse sono
e
. Un filo inestensibile di massa trascurabile è avvolto sulla periferia di un disco omogeneo, di raggio
e massa
, saldato alla ruota
e concentrico a essa (vedi figura 47); all’estremità libera del filo è appeso un corpo
, di massa
. Nel punto
, intersezione con il bordo esterno di
della retta congiungente i centri
e
, è applicata una forza costante
, tangente al disco e rivolta verso l’alto. Si determini:
1) il modulo di necessario affinché l’ingranaggio resti in quiete;
2) le componenti verticali e
delle corrispondenti reazioni sviluppate dagli assi intorno ai quali ruotano
e
.
A un certo istante si annulla la forza e l’ingranaggio si mette in movimento; si determini corrispondentemente:
3) il modulo dell’accelerazione angolare della ruota ;
4) le componenti verticali delle reazioni sviluppate dagli assi di rotazione di e
.
Figura 47: schema del problema del corpo rigido 47.
Esercizio 48 . Consideriamo una sfera omogenea di raggio
e massa
, inizialmente in posizione di riposo sulla cima di una rampa che è collocata su un tavolo. Il centro di massa della sfera si trova a un’altezza
dal piano del tavolo. Lasciata libera di muoversi, la sfera rotola lungo la rampa senza slittare e, una volta raggiunta la base, prosegue con una velocità che presenta unicamente una componente orizzontale. Dopo aver lasciato il bordo del tavolo, la sfera cade verso il pavimento. Se la distanza verticale tra il piano del tavolo e il pavimento è
, si desidera determinare la distanza orizzontale
tra il bordo del tavolo e il punto in cui la sfera impatta sul pavimento.
Figura 48: schema del problema del corpo rigido 48.
Esercizio 49 . Due aste rigide
e
di uguale lunghezza
, omogenee e a sezione trasversale costante, di masse
e
, sono incernieriate fra loro con attrito trascurabile nell’estremità
, mentre le estremità
e
sono vincolate a muoversi su una guida orizzontale liscia (si veda figura 49). Tale vincolo mantiene costantemente le due aste, al di sopra della guida, in un piano verticale. Le aste sono collegate da un tirante inestensibile, di massa trascurabile e lunghezza
con punto di applicazione in corrispondenza del centro di massa delle due aste.
Se il sistema è inizialmente in equilibrio, si calcolino:
1) i moduli e
delle reazioni sviluppate dalla guida sulle due aste e la tensione
del tirante.
Nel sistema considerato, ad un certo istante il tirante si rompe. Nell’approssimazione in cui tutti gli attriti possano essere trascurati, si calcoli:
2) lo spostamento lungo la direzione orizzontale della cerniera
nell’istante in cui essa arriva a toccare la guida sulla quale scorrono
e
;
3) la velocità con cui
arriva sulla guida.
Figura 49: schema del problema del corpo rigido 49.
Esercizio 50 . La figura 50 riproduce una sezione verticale di un sistema formato da un blocco omogeneo
posato su un blocco
che, a sua volta, poggia su un piano orizzontale; la sezione verticale di
è un triangolo equilatero di lato
, le masse dei blocchi sono
e
, con
costante positiva.
- Si determini il valore massimo della distanza
e il valore minimo del coefficiente di attrito statico affinché la posizione di figura 50 sia in equilibrio.
All’istante , mentre il blocco
è in condizioni di equilibrio, si imprime a
una velocità
: il blocco
sale verso l’alto scivolando sopra
e, prima di fermarsi rispetto a questo, si sposta sopra esso di un tratto di lunghezza
. Si determini il modulo di
nei seguenti casi:
è bloccato e tra
e
non c’è attrito;
è bloccato e tra
e
c’è attrito con coefficiente di attrito dinamico
;
può scorrere senza attrito sul piano orizzontale e tra
e
non c’è attrito
può scorrere senza attrito sul piano orizzontale e tra
e
c’è attrito con coefficiente di attrito dinamico
.
La velocità va intesa rispetto ad un sistema di riferimento inerziale.
Figura 50: schema del problema del corpo rigido 50.
Esercizio 51 . Un cubo omogeneo di spigolo
è posato su un piano inclinato liscio ed è trattenuto da un piccolo scalino (supposto puntiforme) come è mostrato in figura 51. Si calcoli l’inclinazione massima
del piano inclinato per la quale il cubo resta ancora in equilibrio.
Figura 51: schema del problema del corpo rigido 51.
Esercizio 52 . Un filo inestensibile e di massa trascurabile è arrotolato intorno ad un disco di raggio
e massa
. Fissata un’estremità del filo al soffitto, si lascia cadere il disco. Il filo non slitta rispetto al bordo del disco. Determinare l’accelerazione del centro di massa
e la tensione
del filo.
Figura 52: schema del problema del corpo rigido 52.
Esercizio 53 . Un cilindro pieno di raggio
rotola senza strisciare dentro un tubo di raggio
. Nella metà di destra del tubo l’attrito è nullo. Se all’istante iniziale il cilindro è fermo nella parte di sinistra e la quota del centro di massa è
, determinare la posizione di arrivo del cilindro e la velocità angolare
. Si supponga il tubo fisso.
Figura 53: schema del problema del corpo rigido 53.
Esercizio 54 . Il sistema in figura 54 composto da un disco omogeneo di raggio
e massa
e da un’asta omogenea
di lunghezza
e massa
. Il disco è appoggiato ad una guida verticale scabra (coincidente con l’asse
). L’estremo
dell’asta è incernierato al centro del disco, mentre l’estremo
è semplicemente appoggiato su una guida orizzontale liscia (coincidente con l’asse
). Gli assi descritti definiscono un sistema di riferimento fisso
, con asse
uscente dal piano del disegno. Il sistema è contenuto nel piano verticale
, dove agisce l’accelerazione di gravità
. L’asta forma un angolo
con la guida orizzontale. Una molla ideale di costante elastica
e lunghezza a riposo nulla collega l’origine
al punto
, e una coppia di momento
è applicata al disco (
denota il versore dell’asse
). Il momento
può essere applicato rispetto ad un qualsiasi polo. Si richiede di determinare la reazione vincolare sull’asta nel punto
e il valore della coppia
affinché il sistema sia in equilibrio.
Figura 54: schema del problema del corpo rigido 54.
Esercizio 55 . Una sbarretta di lunghezza
e massa
ha un estremo incernierato ad una parete verticale nel punto
. L’estremo opposto è collegato ad una molla di costante elastica
fissata alla parete ad una distanza
da
, come rappresentato in figura 55. Il sistema è in equilibrio quando la sbarretta è in posizione orizzontale. Determinare la lunghezza a riposo
della molla e il valore della reazione vincolare
in
generata dalla cerniera. Si esprima il risultato in funzione di
,
e
.

Figura 55: schema del problema del corpo rigido 55.
Esercizio 56 . Due cilindri, aventi rispettivamente raggi
e
e momenti d’inerzia
e
, sono sostenuti da assi fissi perpendicolari al piano come mostrato in figura 56. Il cilindro grande ruota inizialmente con velocità angolare
, mentre quello piccolo si sposta verso destra finchè, giunto a contatto con quello grande, viene posto in rotazione per attrito. Cessata la fase di slittamento i cilindri ruotano con velocità costante in verso opposto.
Esprimere la velocità angolare finale in funzione di
e
.
Figura 56: schema del problema del corpo rigido 56.
Esercizio 57 . Un disco circolare omogeneo di massa
, raggio
e spessore costante è appoggiato su un piano orizzontale scabro sul quale rotola senza strisciare (moto di puro rotolamento). Il centro
del disco è collegato, mediante una molla ideale di costante elastica
e lunghezza a riposo trascurabile, a un punto
dell’asse
posto ad altezza
dal piano di appoggio. All’istante
il centro
si trova sull’asse
con velocità orizzontale
. Si determini:
- l’istante
in cui il disco si ferma per la prima volta;
- il valore minimo
del coefficiente di attrito statico necessario affinché il disco rotoli senza strisciare.
Figura 57: schema del problema del corpo rigido 57.
Esercizio 58 . Un disco omogeneo di massa
e raggio
all’istante
si trova alla base di un piano inclinato, con velocità
, come in figura 58. Il piano inclinato forma un angolo
con l’orizzontale ed è scabro, con coefficiente di attrito statico
e coefficiente di attrito dinamico
. Si calcoli
- l’istante di tempo
in cui il moto del disco diventa di puro rotolamento;
- lo spazio totale
percorso sul piano inclinato dal disco prima di fermarsi.
Figura 58: schema del problema del corpo rigido 58.
Esercizio 59 . Un disco omogeneo, di massa
e raggio
, è in quiete sopra un piano inclinato di massa
e formante un angolo
con il piano orizzontale, come in figura 59. Il disco nella discesa sul piano inclinato si muove di puro rotolamento. Inoltre, il piano inclinato può scorrere sul piano orizzontale. Si consideri il piano orizzontale liscio. Si richiede di determinare il modulo dell’accelerazione
del centro di massa del piano inclinato rispetto ad un sistema di riferimento inerziale.
Figura 59: schema del problema del corpo rigido 59.
Esercizio 60 . Un rettangolo appoggiato su un piano inclinato ha lati che misurano
e
rispettivamente lungo gli assi
e
come in figura 60. La densità superficiale di massa è
con
costante e unità di misura [
]=kg/(m
). Si determini l’angolo massimo del piano inclinato affinché il rettangolo non si stacchi dal piano.
Figura 60: schema del problema del corpo rigido 60.
Esercizio 61 . Un pendolo conico come in figura 61 è composto da un disco di massa
e raggio
, un’asta verticale di massa trascurabile e altezza
, da un filo inestensibile di lunghezza
e da una pallina di dimensioni trascurabili e massa
. Il pendolo conico è poggiato su di un piano in cui è presente un attrito sufficiente ad impedirgli di muoversi. Calcolare per quali valori di
il sistema non si distacca dal piano. Supporre il filo inestensibile e di massa trascurabile.
Figura 61: schema del problema del corpo rigido 61.
Esercizio 62 . Un punto materiale di massa
viene lanciato dalla base di un piano inclinato con velocità
. Il piano inclinato ha massa
e la forma di un triangolo isoscele di lati uguali pari ad
ed angoli alla base di ampiezza
, come mostrato in figura 62. Il piano è incernierato nel punto
. Tra piano inclinato e punto materiale non è presente attrito. Verificare che, indipendentemente dalla velocità iniziale di
, il piano non potrà mai cominciare a ruotare rispetto ad
se vale la condizione:
(3)
In caso contrario, calcolare la velocità minima che deve essere impressa ad
affinché il piano inizi a ruotare.
Figura 62: schema del problema del corpo rigido 62.
Esercizio 63 . Un disco cilindrico omogeneo, di raggio
, massa
, è appoggiato con la superficie laterale su una superficie orizzontale liscia. Un corpo di massa
, approssimabile a un punto materiale, è fissato al disco in un punto
distante
dal centro
del disco. Il disco, inizialmente in quiete nella posizione di figura 63, con il segmento
formante con la verticale un angolo
, viene lasciato libero di muoversi. Sia
l’istante in cui il punto
viene a trovarsi per la prima volta sulla verticale passante per
. In corrispondenza di tale istante, si calcoli:
1) lo spostamento del centro
del disco;
2) il modulo della velocità di
;
3) il modulo della reazione sviluppata dal piano di appoggio;
4) si determini il modulo della velocità di
quando il segmento
forma con la verticale un angolo
.
Supporre che il disco ruoti senza strisciare.
Figura 63: schema del problema del corpo rigido 63.
Esercizio 64 . Un cilindro pieno e omogeneo, di raggio
, si trova in quiete e in posizione di equilibrio a contatto con la superficie interna di un contenitore fisso cilindrico vuoto internamente, di raggio
. Nell’istante
il rullo viene messo in moto. Si assuma che il cilindro rotoli senza strisciare sulla superficie del contenitore. Si determini:
- il modulo minimo
della velocità iniziale del centro di massa del rullo affinché questo arrivi nella posizione di massima quota senza staccarsi dalla superficie del contenitore;
- il valore minimo
del coefficiente di attrito statico per cui è possibile il puro rotolamento se la velocità iniziale del centro di massa del rullo ha modulo
.
Figura 64: schema del problema del corpo rigido 64.
Esercizio 65 . Il sistema in figura 65 è formato da tre aste di uguale lunghezza
, incernierate agli estremi. Le aste
e
hanno
massa , distribuita in modo omogeneo, mentre l’asta
ha massa trascurabile. Le cerniere in
e
sono mobili, la
cerniera in è fissa nel sistema di riferimento fisso
mostrato in figura 65.
La cerniera in è vincolata tramite un carrello a muoversi lungo l’asse orizzontale
.
Tutti i vincoli sono lisci. Una molla ideale, con massa trascurabile, lunghezza a riposo nulla e di costante elastica collega il punto fisso
al carrello
. All’asta
è applicato un momento esterno
(dove
è il versore dell’asse
) nel polo
.
Determinare i valori della costante e del momento
per i quali la configurazione di equilibrio del sistema
sia quella con l’asta parallela all’asse orizzontale (come mostrato in figura 65) e l’asta
che forma con l’asse
un angolo
.
Figura 65: schema del problema del corpo rigido 65.
Esercizio 66 . Consideriamo una semisfera con base, dove la base è un disco solido di raggio
che sigilla l’apertura della semisfera, rendendo il corpo una struttura chiusa e isolata.
La superficie della sfera è caratterizzata da una densità superficiale costante , mentre la base è caratterizzata da una densità superficiale
nulla. La base della semisfera si trova in un piano orizzontale e la semisfera è vincolata a ruotare attorno al proprio asse di simmetria, con una velocità angolare iniziale
, e l’asse di rotazione non è soggetto a forze di attrito. L’asse di rotazione è fisso nello spazio e passa per il centro della semisfera.
All’istante iniziale , un uomo di massa
si trova posizionato al centro della semisfera. Successivamente, inizia a spostarsi radialmente sulla base della semisfera (al suo interno), arrivando a una distanza
dal centro al tempo
, raggiungendo tale punto con velocità nulla rispetto alla semisfera. Pertanto l’uomo si muove radialmente lungo la base della semisfera ed è vincolato a ruotare con essa.
Osservando da un sistema di riferimento fisso , determinare:
Osservando da un sistema di riferimento fisso , determinare:
- la velocità angolare finale
al tempo
del sistema composto da semisfera e uomo.
- Il lavoro compiuto dall’uomo per raggiungere la distanza di
dal centro della semisfera.
Esprimere i risultati in funzione delle variabili ,
,
, e
, dove
è il modulo della velocità angolare iniziale
. Si assuma che l’uomo cammini senza strisciare e che le forze di attrito tra esso e la semisfera siano solo di attrito statico.

Figura 66: schema del problema del corpo rigido 66.
Esercizio 67 . Un disco con raggio
e massa
, posizionato orizzontalmente su un piano, ha la capacità di ruotare senza attrito attorno a un asse verticale che passa per il suo centro. Lungo il bordo del disco è attaccata una molla ideale di massa trascurabile e costante elastica
, compressa di
, la quale collega due corpi di massa
e
. I due corpi sono vincolati a muoversi lungo il bordo del disco, scivolando senza attrito. All’istante iniziale
, la molla viene rilasciata: la massa
rimane attaccata al disco, mentre la massa
viene lanciata dalla molla. Quando la molla raggiunge la sua lunghezza di riposo, la massa
raggiunge la velocità
di modulo
rispetto ad un sistema di riferimento inerziale fisso con origine nel centro del disco.
Calcolare e il modulo
della velocità angolare
del sistema composto dal disco e dalla massa
.
Esprimere i risultati in funzione dei parametri del problema e
.
Nota: si
approssimino i due corpi come due punti materiali di massa ed
posizionati sul bordo del disco e si consideri la lunghezza a riposo della molla inferiore al diametro del disco.
Figura 67: schema del problema del corpo rigido 67.
Esercizio 68 . Un’asta
di massa
può scorrere verticalmente senza attrito lungo una guida
. L’asta ha contatto praticamente puntiforme con la parete interna, a forma di semicirconferenza di raggio
, di un blocco
di massa
. Il blocco
è libero di scorrere sopra un piano orizzontale. Si indichi con
l’angolo che forma il vettore che congiunge il centro della semicirconferenza e il punto di contatto tra guida e asta con la verticale, come rappresentato in figura 68.
-
Si determinino i valori dell’angolo
per i quali il sistema fisico costituito da asta e blocco è in equilibrio se il coefficiente di attrito statico tra il blocco e il piano vale
.
-
Sia l’attrito tra il piano e il blocco trascurabile ed il sistema venga lasciato libero di muoversi con velocità iniziali nulle nella posizione corrispondente ad un angolo iniziale pari ad
; si calcoli il modulo
della velocità dell’asta in corrispondenza del valore
.
Esprimere i risultati in funzione dei parametri del problema ed
.
Nota: nei calcoli assumere .
Figura 68: schema del problema del corpo rigido 68.
Esercizio 69 . Consideriamo una sbarra sottile di lunghezza
e massa
, uniformemente distribuita lungo la sua lunghezza. Questa sbarra è montata in modo da poter ruotare senza attrito attorno a un asse orizzontale fisso situato a un’estremità
, su un piano verticale. Inizialmente, la sbarra si trova in una posizione verticale di equilibrio instabile, come mostrato in figura 69. Viene poi applicata una forza esterna che agisce per un tempo infinitesimo (cioè il cui impulso è trascurabile) per perturbare la sbarra dalla sua posizione di equilibrio. In seguito alla perturbazione, la sbarra inizia a ruotare attorno all’asse sotto l’azione della forza di gravità.
Si consideri un sistema di riferimento cartesiano fisso , con l’origine
posta sul punto di vincolo, orientato come in figura 69. Si richiede di determinare le componenti della reazione vincolare
in
al momento in cui la sbarra raggiunge la posizione orizzontale, come illustrato in figura 69. Il risultato dovrà essere espresso in termini della massa
e dell’accelerazione gravitazionale
.

Figura 69: schema del problema del corpo rigido 69.
Esercizi di Meccanica classica
Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.
Leggi..
- Cinematica del punto materiale.
- Dinamica del punto materiale: le leggi di Newton nella meccanica classica.
- Dinamica del punto materiale: lavoro ed energia.
- Moti relativi.
- Sistemi di punti materiali.
- Dinamica del corpo rigido.
- Urti .
- Gravitazione .
- Oscillazioni e onde.
- Meccanica dei fluidi.
- Onde meccaniche.
- Statica in meccanica classica.
- Fondamenti di relatività ristretta: trasformazioni di Lorentz e principali conseguenze.
- Calcolo del centro di massa e dei momenti d’inerzia.
Tutti gli esercizi di elettromagnetismo
Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di
Leggi...
- Esercizi su lavoro elettrico e potenziale elettrico.
- Esercizi sulla legge di Gauss.
- Esercizi sui conduttori, condensatori, dielettrici ed energia elettrostatica.
- Esercizi sulla corrente elettrica.
- Esercizi sul campo magnetico e forza magnetica.
- Esercizi sulle sorgenti di un campo magnetico e legge di Ampere.
- Esercizi su campi elettrici e magnetici variabili nel tempo.
- Esercizi su oscillazione del campo elettrico e correnti alternate.
- Esercizi sulle onde elettromagnetiche.
- Esercizi sulla riflessione e rifrazione della luce.
- Esercizi sull’ ottica geometrica.
- Esercizi sull’ interferenza.
- Esercizi sulla diffrazione.
- Esercizi sulle proprietà corpuscolari e ondulatorie della materia.
Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.
Esercizi di Meccanica razionale
Se siete interessati ad approfondire argomenti inerenti alla Meccanica razionale, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.
Leggi...
Ulteriori risorse didattiche per la fisica
Leggi...
- Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
- ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
- Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
- Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
- The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
- American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
- Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
- Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
- Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
- Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.
