L’Esercizio Corpo Rigido 66 è il sessantaseiesimo nella serie dedicata agli esercizi sul corpo rigido. Segue l’Esercizio Corpo Rigido 65 e precede l’Esercizio Corpo Rigido 67. È rivolto a studenti di Fisica 1, in particolare a coloro che studiano ingegneria, fisica o matematica.
Nel percorso didattico di Fisica 1, prima di affrontare i corpi rigidi, si studiano gli esercizi sui sistemi di punti materiali. Successivamente, si passa agli esercizi sugli urti tra punti materiali e corpi rigidi, che rappresentano un momento di sintesi nel percorso formativo.
Testo dell’Esercizio Corpo Rigido 66
Esercizio 66 . Consideriamo una semisfera con base, dove la base è un disco solido di raggio
che sigilla l’apertura della semisfera, rendendo il corpo una struttura chiusa e isolata.
La superficie della sfera è caratterizzata da una densità superficiale costante , mentre la base è caratterizzata da una densità superficiale
nulla. La base della semisfera si trova in un piano orizzontale e la semisfera è vincolata a ruotare attorno al proprio asse di simmetria, con una velocità angolare iniziale
, e l’asse di rotazione non è soggetto a forze di attrito. L’asse di rotazione è fisso nello spazio e passa per il centro della semisfera.
All’istante iniziale , un uomo di massa
si trova posizionato al centro della semisfera. Successivamente, inizia a spostarsi radialmente sulla base della semisfera (al suo interno), arrivando a una distanza
dal centro al tempo
, raggiungendo tale punto con velocità nulla rispetto alla semisfera. Pertanto l’uomo si muove radialmente lungo la base della semisfera ed è vincolato a ruotare con essa.
Osservando da un sistema di riferimento fisso , determinare:
Osservando da un sistema di riferimento fisso , determinare:
- la velocità angolare finale
al tempo
del sistema composto da semisfera e uomo.
- Il lavoro compiuto dall’uomo per raggiungere la distanza di
dal centro della semisfera.
Esprimere i risultati in funzione delle variabili ,
,
, e
, dove
è il modulo della velocità angolare iniziale
. Si assuma che l’uomo cammini senza strisciare e che le forze di attrito tra esso e la semisfera siano solo di attrito statico.

Figura 1: schema del problema.
Richiami teorici.
- Il momento d’inerzia di un corpo rigido rispetto a un asse di rotazione è definito come:
(1)
dove
è la distanza perpendicolare di un elemento di massa
dall’asse di rotazione.Per corpi rigidi con una distribuzione di massa discreta, il momento d’inerzia può essere calcolato come:
(2)
dove
è la massa di ciascun punto e
è la distanza del punto
-esimo dall’asse di rotazione.Per corpi rigidi con una distribuzione di massa continua, il momento d’inerzia può essere calcolato integrando su tutto il volume
del corpo:
(3)
dove
è la densità di massa nel punto di coordinate
.La forma esatta dell’integrale dipenderà dalla geometria del corpo e dalla densità della distribuzione di massa. In altri termini la precedente equazione potrebbe rappresentare un integrale triplo, doppio, di linea di prima specie o di superficie, a seconda di com’è distribuita la massa del corpo rigido in questione.
- In un sistema di punti materiali, si verifica che la somma vettoriale delle forze interne si annulla, così come quella dei momenti interni. Tuttavia, è importante notare che le forze interne sono comunque in grado di compiere lavoro. Di conseguenza, nell’applicazione del teorema dell’energia cinetica, noto anche come teorema del lavoro-energia, per sistemi di punti materiali, è essenziale considerare anche il lavoro svolto dalle forze interne.
- Le coordinate sferiche sono un sistema di coordinate curvilinee tridimensionali in cui la posizione di un punto nello spazio è rappresentata da tre coordinate: il raggio
, l’angolo azimutale
e l’angolo polare o zenitale
.Le relazioni tra le coordinate cartesiane
e le coordinate sferiche
sono le seguenti:
dove
è la distanza dal punto all’origine,
è l’angolo azimutale misurato nel piano
dall’asse positivo
,
è l’angolo polare misurato dall’asse positivo
verso il punto.
Figura 2.
- Clicca qui per sapere di più sulle coordinate sferiche
- In coordinate sferiche, una superficie sferica è rappresentata dai punti aventi un raggio costante
, mentre gli angoli
e
variano. L’elemento di area
su una superficie sferica è dato da:
(4)
Pertanto, per calcolare l’integrale di superficie di
su una superficie sferica in coordinate sferiche, si utilizza la seguente espressione:
(5)
dove
è la funzione espressa in coordinate sferiche, e
,
, e
variano entro i limiti che definiscono la superficie
.
- La massa di un corpo rigido con una distribuzione di massa superficiale può essere definita integrando la densità di massa superficiale
su tutta la superficie
del corpo. La densità di massa superficiale è definita come la massa per unità di area, e la massa totale
è data dall’integrale di superficie di
su
:
(6)
dove
rappresenta l’elemento infinitesimale di area sulla superficie del corpo.Se il corpo ha una forma semplice e
è uniforme, l’integrale può essere semplificato moltiplicando
per l’area totale della superficie
:
(7)
Per corpi con forme più complesse o distribuzioni di massa non uniformi, l’integrale deve essere valutato considerando la variazione di
sulla superficie.
Svolgimento.
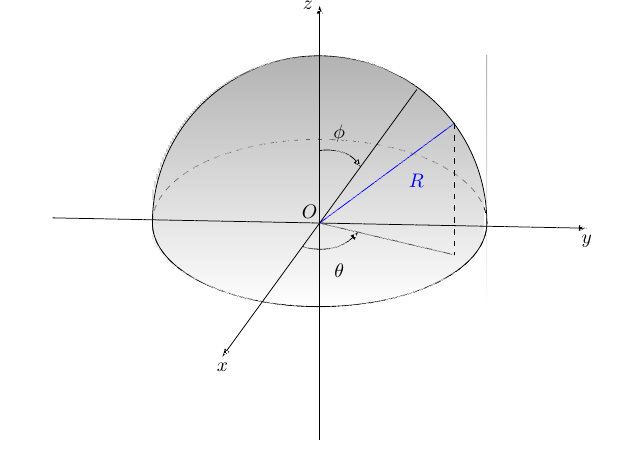
Figura 3: rappresentazione delle coordinate sferiche.
Applicando le coordinate sferiche si può parametrizzare la semisfera come segue
(8)
Inoltre, la superficie infinitesima della semisfera si può esprimere come:
(9)
L’elemento infinitesimo di massa del guscio sferico sfruttando la precedente equazione si può esprimere come:
(10)
Calcoliamo il momento d’inerzia della semisfera rispetto all’asse di rotazione applicando le equazioni (8), (9) e (10):
(11)
Consideriamo come sistema fisico l’insieme formato dal guscio sferico e dall’uomo. Le forze esterne sono le forze peso dell’uomo e del guscio sferico che agiscono lungo l’asse e la reazione vincolare generata dal vincolo applicata direttamente in
. Scegliendo come polo
, situato sull’asse
che è il polo dove passa l’asse di rotazione, i momenti di queste forze rispetto a tale asse risultano nulli, dato che le forze peso puntano lungo l’asse
e la reazione vincolare è proprio applicata al polo
. Di conseguenza, il momento angolare rispetto a questo asse si conserva.
Definiamo come il momento angolare del sistema al tempo
e
quello al tempo
, entrambi calcolati rispetto al polo
.
Al tempo , il momento angolare del sistema è dato unicamente dal guscio sferico, poiché in questo istante l’uomo si trova in
e il suo contributo al momento angolare è nullo. Pertanto, il momento angolare iniziale è:
(12)
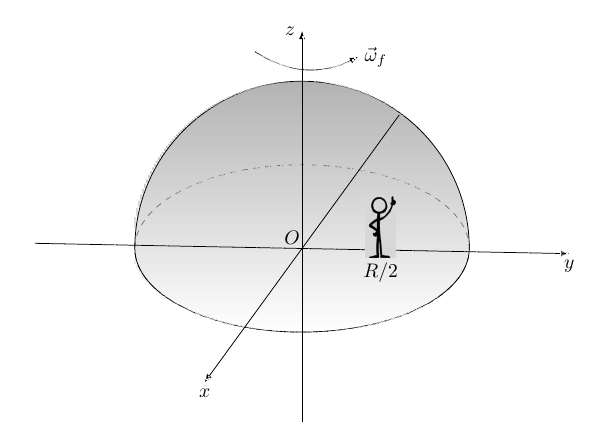
Figura 4:rappresentazione dell’uomo raggiunta la posizione finale.
Sia il modulo di
. Calcoliamo il momento angolare all’istante
rispetto al polo
. In tale istante il contributo al momento angolare totale è dato sia dal guscio sferico che dall’uomo, essendo entrambi in movimento. Il momento angolare finale è:
(13)
Dalla conservazione del momento angolare abbiamo che
(14)
Sfruttando le equazione (12) e (13) la precedente equazione diventa:
(15)
da cui
(16)
Avvalendoci dell’equazione (11) la precedente equazione si riscrive come:
(17)
Si conclude che
Nel sistema fisico considerato, le forze peso non compiono lavoro poiché sia la semisfera sia l’uomo si mantengono alla stessa quota. Le forze interne, rappresentate dalla forza di attrito , agiscono sull’uomo e sulla semisfera. Questa forza è uguale e opposta per il terzo principio della dinamica, essendo
la forza corrispondente sulla semisfera; tali forze compiono lavoro non nullo. Per calcolare il lavoro delle forze di attrito tra gli istanti
e
, applichiamo il teorema del lavoro-energia. L’energia totale del sistema fisico al tempo
è:
(18)
L’energia totale del sistema fisico all’istante è:
(19)
Applichiamo il teorema dell’energia lavoro sfruttando le due precedenti equazioni:
(20)
da cui sfruttando l’equazione (11) abbiamo
(21)
o anche
(22)
Sostituendo nella precedente equazione ottenuta al punto precedente, otteniamo:
(23)
Si conclude che il lavoro delle forze di attrito è:
Osservazione 1. Consideriamo una sfera cava con raggio e massa totale
, con la massa distribuita uniformemente sulla superficie. L’elemento di massa
su una sfera può essere espresso come:
dove è la densità di massa superficiale e
è l’elemento di area. La densità superficiale è data da:
L’elemento di area in coordinate sferiche è:
Sostituendo e integrando su tutta la superficie della sfera, otteniamo:
L’integrale di è:
pertanto
Sostituendo con
:
Per una semisfera, il momento d’inerzia rispetto allo stesso asse è:
Sostituendo nella precedente equazione , si ottiene:
Il legame tra il momento d’inerzia della sfera e quello della semisfera si osserva immediatamente confrontando le loro formule. Il momento d’inerzia della semisfera è esattamente la metà di quello della sfera:
Questo risulta dal fatto che la semisfera è essenzialmente la metà della sfera in termini di distribuzione di massa sulla superficie, considerando che la distribuzione della massa è uniforme e la distanza media dei punti dell’asse è la stessa.
Osservazione 2. Quando una persona cammina su una superficie, si verifica un’interazione dinamica fondamentale che coinvolge le forze di attrito. Consideriamo come sistema fisico l’uomo e la superficie su cui cammina. La forza di attrito che agisce tra i piedi dell’uomo e la superficie è essenziale per il movimento. Senza attrito, l’uomo scivolerebbe e non sarebbe in grado di spostarsi efficacemente. Quando l’uomo spinge il piede contro il terreno, per il terzo principio della dinamica, il terreno reagisce esercitando una forza di uguale intensità ma di direzione opposta sul piede.
- Supponiamo che la forza di attrito generata dall’uomo spingendo indietro sul terreno sia f. Questa forza è diretta verso il retro, aiutando l’uomo a spostarsi in avanti.
- Per il terzo principio della dinamica, la superficie reagisce esercitando una forza di attrito -f sull’uomo. Questa forza è diretta verso il fronte, opponendosi al movimento relativo del piede rispetto alla superficie.
Le equazioni che descrivono il movimento dell’uomo possono essere scritte considerando la somma delle forze agenti su di lui. Se è la forza netta esercitata dall’uomo contro il terreno, allora la forza netta che agisce sull’uomo è
, risultando nella seguente equazione del movimento:
dove è la massa dell’uomo e
è l’accelerazione risultante.
L’attrito non solo previene lo scivolamento, ma è anche cruciale per la trasmissione delle forze che permettono l’avanzamento. L’efficacia dell’attrito dipende dalla rugosità delle superfici in contatto e dalla forza normale esercitata, che in questo contesto è il peso dell’uomo.
Scarica gli esercizi svolti
Ottieni il documento contenente 69 esercizi risolti, contenuti in 242 pagine ricche di dettagli, per migliorare la tua comprensione della dinamica del corpo rigido.
Esercizi di Meccanica classica
Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.
Leggi..
- Cinematica del punto materiale.
- Dinamica del punto materiale: le leggi di Newton nella meccanica classica.
- Dinamica del punto materiale: lavoro ed energia.
- Moti relativi.
- Sistemi di punti materiali.
- Dinamica del corpo rigido.
- Urti .
- Gravitazione .
- Oscillazioni e onde.
- Meccanica dei fluidi.
- Onde meccaniche.
- Statica in meccanica classica.
- Fondamenti di relatività ristretta: trasformazioni di Lorentz e principali conseguenze.
- Calcolo del centro di massa e dei momenti d’inerzia.
Tutti gli esercizi di elettromagnetismo
Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di
Leggi...
- Esercizi su lavoro elettrico e potenziale elettrico.
- Esercizi sulla legge di Gauss.
- Esercizi sui conduttori, condensatori, dielettrici ed energia elettrostatica.
- Esercizi sulla corrente elettrica.
- Esercizi sul campo magnetico e forza magnetica.
- Esercizi sulle sorgenti di un campo magnetico e legge di Ampere.
- Esercizi su campi elettrici e magnetici variabili nel tempo.
- Esercizi su oscillazione del campo elettrico e correnti alternate.
- Esercizi sulle onde elettromagnetiche.
- Esercizi sulla riflessione e rifrazione della luce.
- Esercizi sull’ ottica geometrica.
- Esercizi sull’ interferenza.
- Esercizi sulla diffrazione.
- Esercizi sulle proprietà corpuscolari e ondulatorie della materia.
Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.
Esercizi di Meccanica razionale
Se siete interessati ad approfondire argomenti inerenti alla Meccanica razionale, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.
Leggi...
Ulteriori risorse didattiche per la fisica
Leggi...
- Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
- ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
- Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
- Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
- The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
- American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
- Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
- Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
- Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
- Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.
