Questa raccolta comprende 39 esercizi svolti sugli urti tra punti materiali e tra corpi rigidi, sviluppata con l’obiettivo di fornire un riferimento didattico strutturato e approfondito nel contesto della meccanica classica. L’opera si propone di coprire in modo esaustivo le diverse configurazioni di urti tra sistemi fisici, offrendo agli studenti e ai ricercatori un repertorio di problemi che facilitano la comprensione teorica e l’applicazione pratica dei principi fondamentali della dinamica.
Le esercitazioni presentate derivano da fonti accademiche di riconosciuta autorevolezza nella letteratura scientifica, tra cui:
- Rosati, Luigi – Fisica Generale
- Mencuccini, C., Silvestrini, G. – Fisica
- Mazzoldi, P., Nigro, M., Voci, C. – Elementi di Fisica
- Resnick, R., Halliday, D., Walker, J. – Fundamentals of Physics
- Goldstein, H. – Classical Mechanics
- Landau, L.D., Lifshitz, E.M. – Mechanics
Oltre agli esercizi estratti da testi accademici di riferimento, la raccolta include una selezione di problemi originali e quesiti tratti da prove d’esame universitarie, con lo scopo di ampliare il panorama applicativo e rafforzare l’acquisizione dei concetti legati alla dinamica del corpo rigido.
Nell’ambito del percorso didattico proposto, il capitolo successivo approfondisce la teoria sulla gravitazione. Una volta consolidati i principi fondamentali, il lettore potrà affrontare gli esercizi sulla gravitazione, che comprendono 15 esercizi svolti, accuratamente selezionati. Il capitolo precedente, invece, si concentra sugli esercizi svolti sui sistemi di punti materiali, che comprendono 39 esercizi svolti.
È possibile accedere all’intero corso di meccanica classica, risultato di un lavoro di ricerca e sviluppo portato avanti dal nostro team negli ultimi quattro anni. Maggiori dettagli sugli autori e revisori sono disponibili nella sezione dedicata alla fisica.
Urti: autori e revisori
Leggi...
Autori e Revisori:
Valerio Brunetti, Giuseppe Palaia.
Autori:
Romano Rotonda, Daniele Massaro, Andrea Corradini, Davide Vignotto, Cosimo Tommasi.
Revisori:
Autori in collaborazione:
Giulia Romoli, Antonio Figura, Christian Magliano.
Ex Autori & Revisori:
Patrizio Di Lorenzo, Simone Brozzesi, Nicola Santamaria, Vittorio Larotonda, Leonardo Rebeschini, Simone Romiti, Antonio Junior Iovino, Daniele Bjørn Malesani, Tiziano Schiavone, Serena Lezzi, Marco Chilioiro.
Testi degli esercizi sugli urti
Esercizio 1 Tre blocchetti di massa
kg,
,
stanno su un asse orizzontale liscio. Il blocchetto
ha velocità
, il blocchetto
è fermo, il blocchetto
ha velocità
. Nello stesso istante contemporaneamente i blocchetti
e
urtano il blocchetto
, provenendo da versi opposti rispetto alla sua posizione, e vi restano attaccati. Calcolare: a) la velocità del sistema dopo l’urto, b) la variazione della quantità di moto di
nell’urto; c) la variazione dell’energia cinetica di
nell’urto.
Figura 1: schema dell’esercizio urti 1.
Esercizio 2 . Una massa
kg, poggiata su un piano orizzontale liscio, è collegata tramite una molla ad una molla (
) ad una parete rigida. Essa esegue delle oscillazioni armoniche di ampiezza
cm. Quando si trova nel punto di massima elongazione più lontano dalla parete,
viene colpita da una massa
kg che si muove con velocità
lungo l’asse della molla. Calcolare la velocità del sistema delle due masse subito dopo l’urto e l’ampiezza
delle oscillazioni dopo l’urto. Si assuma una lunghezza a riposo della molla nulla e che l’urto tra le due masse avvenga in modo completamente anelastico.
Figura 2: schema dell’esercizio urti 2.
Esercizio 3 . Un corpo puntiforme si muove lungo un’asse orizzontale. All’istante
[s] esso passa nell’origine con velocità
diretta verso le
positive. Per
[s] il corpo è sottoposto a un’accelerazione
.
Calcolare:
a) dove si ferma.
Se durante il moto nella posizione [m], il corpo ne urta uno eguale e fermo e vi rimane attaccato, calcolare:
b) la velocità del sistema subito dopo l’urto.
Figura 3: traiettoria di un corpo puntiforme soggetto ad accelerazione variabile e urto in m.
Esercizio 4 . Un proiettile di massa
kg e velocità
m/s urta una sfera mantenuta in equilibrio da un filo inestensibile. La velocità
è orientata come in figura 4 e dopo l’urto la massa complessiva del sistema è
kg. Si consideri l’urto completamente anelastico e che avvenga in un tempo
s.
Calcolare
a) la variazione di quota della sfera dopo l’urto;
b) il valore della forza media durante l’urto.
Figura 4: schema dell’esercizio urti 4.
Esercizio 5 . Sopra un piano orizzontale liscio sono posti due punti materiali di masse
kg e
kg, a contatto tra loro. Il punto
è attaccato ad una molla di costante elastica
, in condizioni di riposo. Si sposta verso sinistra, comprimendo la molla, il punto
di una quantità
cm, mentre
resta fermo, e lo si lascia libero con velocità nulla. Il punto
ritorna verso il punto
e lo urta in modo completamente anelastico. Calcolare lo spostamento massimo verso destra del sistema rispetto alla posizione di riposo della molla.
Figura 5: schema dell’esercizio urti 5.
Esercizio 6 . Una sbarra rettilinea si trova in quiete sopra un piano orizzontale liscio; la sua lunghezza è
e la massa
. Mediante un colpo di martello dato a un estremo viene comunicata alla sbarra un impulso
orientato come nella figura che segue. Calcolare:
- la velocità del centro di massa della sbarra;
- la velocità angolare della sbarra;
- ‘energia cinetica della sbarra.
Figura 6: schema dell’esercizio urti 6.
Esercizio 7 . Un’asta lunga
e di massa
è in un piano verticale, ed è vincolata a ruotare, senza attrito, attorno al proprio centro
. Un punto materiale di massa
, lanciato verticalmente dal basso verso l’alto, colpisce l’asta a distanza
da
e vi rimane attaccato; la velocità prima dell’urto di
è
ed è diretta come in figura 7. Calcolare:
- la velocità angolare subito dopo l’urto;
- l’energia dissipata nell’urto;
- la velocità angolare del sistema quando ha compiuto una rotazione di
;
- (punto bonus) determinare il momento angolare del centro di massa rispetto ad
e del sistema
rispetto al centro di massa, un istante prima dell’urto, e dopo l’urto.
Figura 7: schema dell’esercizio urti 7.
Esercizio 8 . Siano un punto materiale di massa
e un sistema di riferimento fisso
. Il punto materiale di massa
all’istante iniziale
ha la velocità
, diretta nel verso positivo dell’asse delle
, come rappresentato in figura 8a. Successivamente il punto materiale colpisce un secondo punto materiale di uguale massa ed inizialmente fermo. Entrambi i punti materiali sono vincolati a muoversi nel piano
. Dopo l’urto, considerato elastico, la prima particella ha una velocità
formante un angolo
con l’asse delle
, come rappresentato in figura 8b. Determinare modulo e direzione della velocità
della seconda particella un’istante dopo l’urto. I risultati vanno espressi in funzione del modulo della velocità
e l’angolo
.
Esercizio 9 . Un pendolo semplice, di massa
kg e lunghezza
m, è tenuto in equilibrio statico ad angolo
rispetto alla verticale da una forza orizzontale
orientata come in figura 9. Calcolare
- a) il modulo di
.
Si rimuove e il corpo è lasciato libero di oscillare. Quando raggiunge la verticale urta contro un punto materiale di massa
kg fermo sul bordo di un gradino alto
m. Dopo l’urto l’ampiezza dell’oscillazione del pendolo è
mentre
cade sotto l’azione della forza peso. Calcolare:
- b) la velocità di
subito dopo l’urto;
- c) lo spazio orizzontale
percorso da
prima di toccare terra.
Figura 9: schema dell’esercizio urti 9.
Esercizio 10 . Si consideri un sistema costituito da due corpi
e
puntiformi, di massa
ed
, disposti agli estremi di un’asta, di massa trascurabile e lunghezza
. Il sistema è libero di ruotare senza attrito nel piano verticale, attorno ad un asse passante per
e perpendicolare al piano sul quale giace il sistema. Le distanze dei due punti
e
dal punto O sono rispettivamente
e
. Inizialmente il sistema è in quiete in posizione orizzontale. Ad un certo istante un proiettile di massa
e velocità
, inclinata di un angolo
rispetto alla direzione
, colpisce il corpo
, attraversandolo ed uscendone con una velocità
e con la stessa direzione di entrata. Per effetto dell’urto il sistema inizia a ruotare. Si imponga che valga la condizione
allora sotto questa condizione, calcolare:
a) la velocità angolare del sistema immediatamente dopo l’urto;
b) la velocità del corpo
quando raggiunge la posizione più bassa
;
c) la forza media orizzontale e verticale
della forza impulsiva generata in
durante l’urto, assunto di durata
.
d) la componente media orizzontale e verticale
della forza impulsiva generata tra la massa
e
durante l’urto, assunto di durata
.
Figura 10: schema dell’esercizio urti 10.
Scarica gli esercizi svolti
Ottieni il documento contenente 39 esercizi risolti, contenuti in 154 pagine ricche di dettagli, per migliorare la tua comprensione degli urti in meccanica classica.
Esercizio 11 . Un disco omogeneo di massa
kg e raggio
cm ruota senza attrito in un piano orizzontale intorno al suo asse di simmetria con velocità angolare
rad
s. Un proiettile di massa
g viene sparato, con direzione parallela all’asse di rotazione, sul bordo del disco, perpendicolarmente al piano del disco. Il proiettile, la cui velocità iniziale è
diretta come in figura 11, dopo l’urto rimane conficcato nel disco. Calcolare:
a) la velocità angolare del sistema dopo l’urto;
b) il lavoro delle forze non conservative durante l’urto.
Figura 11: schema dell’esercizio urti 11.
Esercizio 12 . Una palla di massa
viene fatta cadere da ferma da un’altezza
e, dopo aver rimbalzato sul pavimento, risale fino ad un’altezza
. Sapendo che nel contatto con il piano agisce una forza media
, determinare:
a) il tempo di contatto della palla con il piano;
b) l’energia dissipata nell’urto.

Figura 12: schema dell’esercizio urti 12.
Esercizio 13 . Un cannoncino inizialmente in quiete, di massa
e dimensioni trascurabili, è vincolato ad una molla di costante elastica
su un piano orizzontale senza attrito. All’istante
viene sparato un proiettile di massa
con velocità iniziale
e angolo
rispetto all’orizzonte. Il proiettile tocca terra dopo un tempo
dallo sparo e il cannoncino si muove di moto armonico con periodo
. Determinare:
a) la velocità iniziale del proiettile;
b) la velocità di rinculo del cannoncino;
c) la compressione massimale della molla.
Figura 13: schema dell’esercizio urti 13.
Esercizio 14 . Un disco di raggio
è mantenuto fermo in un piano verticale; all’istante
esso viene lasciato cadere. Quando ha percorso una distanza
il disco viene agganciato sul bordo ad un asse fisso orizzontale, ortogonale al disegno e passante per
, attorno al quale il disco ruota senza attrito. Calcolare il valore di
necessario affinché il disco compia una rotazione di
, fermandosi in tale posizione.
Figura 14: schema dell’esercizio urti 14.
Esercizio 15 . Un corpo rigido di massa
può ruotare senza attrito attorno ad un asse orizzontale, passante per
e perpendicolare al piano verticale, come in figura 15. Esso viene spostato di modo che la retta congiungente il suo centro di massa
col punto
sia orizzontale; da questa posizione viene abbandonato con velocità angolare iniziale nulla.
Quando il CM si trova sulla verticale passante per il corpo rigido urta un sistema formato da cubi a contatto; a seguito dell’urto il corpo rigido si ferma e il sistema di cubi entra in movimento, con moto traslatorio.
Le masse dei cubi valgono e
, i coefficienti di attrito rispetto al piano di scorrimento sono
e
. Si osserva che i cubi si fermano dopo un tempo
. Calcolare:
1) la forza che si esercita tra le superfici di contatto dei due cubi durante il moto;
2) la velocità iniziale del sistema dei due cubi;
3) la velocità angolare del corpo rigido al momento dell’urto.
Figura 15: schema dell’esercizio urti 15.
Esercizio 16 . Una molla di costante elastica
e massa trascurabile, viene compressa di una lunghezza
. Al suo estremo viene appoggiato un corpo di massa
su un piano orizzontale senza attrito (si veda la figura 16).
Riestendendosi, la molla lancia il corpo che urta tangenzialmente contro la periferia di un disco omogeneo di massa e raggio
. Dopo l’urto il corpo rimbalza indietro nella stessa direzione di prima dell’urto con velocità
. Si determini:
a) la velocità angolare con cui il disco ruota dopo l’urto;
b) se c’è stata nell’urto variazione di energia cinetica e, se sì, quanto vale;
c) il modulo dell’impulso ricevuto dal supporto dell’asse del disco;
d) nell’ipotesi che la massa non torni indietro e non ci siano urti successivi al primo, determinare il numero di giri fatti dal disco prima di fermarsi se sul suo asse agisce un momento di attrito
costante.
Figura 16: schema dell’esercizio urti 16.
Esercizio 17 . Due aste uguali, ciascuna di massa
e lunghezza
, sono fissate tra loro come mostrato in figura 17 (stesso centro, angolo
); esse stanno in un piano verticale e possono ruotare attorno ad un asse fisso orizzontale passante per il loro centro
e ortogonale al piano che le contiene. Inizialmente le aste sono in quiete, con l’asta
verticale. Un proiettile puntiforme, avente massa
e velocità
, in moto lungo la linea orizzontale tratteggiata, colpisce l’estremo
e vi resta conficcato. A seguito dell’urto il sistema entra in rotazione con velocità angolare
. Calcolare:
a) il valore di .
Nell’istante in cui è stato compiuto un quarto di giro, per cui l’asta è orizzontale, la velocità angolare vale
. Calcolare:
b) il valore del momento di attrito costante che agisce sull’asse di rotazione;
c) sempre nello stesso istante in cui , le componenti tangenziale e normale dell’accelerazione di
.
Figura 17: schema dell’esercizio urti 17.
Esercizio 18 . Due dischi identici di massa
kg e raggio
m sono liberi di ruotare indipendentemente attorno ad un asse orizzontale fisso passante per i loro centri. Attorno al disco
è avvolto un filo che sostiene una massa
kg. Si lascia libera
ed il disco
si mette in moto mentre il disco
resta fermo. Nell’istante in cui il disco
raggiunge la velocità angolare
il disco
viene spinto contro
e vi rimane incollato. Calcolare:
a) la velocità angolare del sistema subito dopo l’urto;
b) l’impulso trasmesso all’asse nell’urto.
Supporre che il disco sia incernierato e il disco
sia libero di scorrere lungo l’asse di rotazione; questo ci permette di spostare il disco
dalla sua posizione iniziale e con un’opportuna forza esterna spingerlo contro il blocco
.
Figura 18: schema dell’esercizio urti 18.
Esercizio 19 . Un corpo rigido formato da un’asta di massa
e lunghezza
e da un disco di eguale massa e raggio
, è posato sopra un piano orizzontale su cui può muoversi senza attrito ed è inizialmente in quiete. Un punto materiale di massa
kg, in moto con velocità
, urta il corpo rigido nel punto
distante
dall’estremo
e vi resta attaccato. Nell’ipotesi che sul corpo non agisca alcun vincolo:
a) descrivere il moto del sistema corpo-punto dopo l’urto, precisando se si tratta di moto traslatorio, rotatorio o rototraslatorio;
b) calcolare la velocità del centro di massa del sistema dopo l’urto.
Se invece il corpo è vincolato in , attorno a cui può ruotare, calcolare:
c) la velocità del centro di massa del sistema dopo l’urto;
d) l’impulso subito dal perno in durante l’urto.
Figura 19: schema dell’esercizio urti 19.
Esercizio 20 . Sopra un piano orizzontale liscio è posto un disco di massa
e raggio
, che ruota con velocità angolare costante
attorno ad un asse verticale passante per il centro
. Una sbarretta di massa
e lunghezza
si muove sul piano con velocità costante
lungo una linea retta passante per
. Ad un certo istante la sbarretta urta il bordo del disco e vi rimane attaccata in direzione radiale. Se l asse di rotazione è fisso, calcolare:
a) la velocità angolare del sistema disco-sbarretta dopo l’urto.
Se invece il disco è libero di muoversi, calcolare:
b) dopo l urto la velocità del centro di massa del sistema e la velocità angolare .
Figura 20: schema dell’esercizio urti 20.
Esercizio 21 . Consideriamo un disco di raggio
e massa
posto su un piano orizzontale che sta ruotando con velocità costante
ed un’asta di lunghezza
, massa
e spessore trascurabile, la quale procede con velocità
come in figura 21. L’asta urta il disco rimandogli attaccata (urto completamente anelastico). Determinare la velocità del centro di massa, la velocità angolare del sistema dopo l’urto e la variazione di energia cinetica prima e dopo l’urto nelle seguenti situazioni:
a) Il disco è vincolato a ruotare rispetto ad un asse passante per il proprio centro di massa e perpendicolare al piano su cui giace;
b) Il disco non ha nessun tipo di vincolo.
Si trascuri ogni forma di attrito.

Figura 21: schema dell’esercizio urti 21.
Esercizio 22 . Una guida rettilinea, inclinata rispetto all’orizzontale di un angolo
è saldata ad un blocco
appoggiato su di un piano orizzontale liscio; la massa complessiva della guida e del blocco è
.
Un corpo , di piccole dimensioni e massa
, può scorrere lungo la guida con attrito trascurabile ed è collegato all’estremità superiore della guida mediante una molla di costante elastica
e lunghezza di riposo
.
Inizialmente il sistema è in quiete e in condizioni di equilibrio, un piccolo corpo di massa è in caduta verticale, urta con velocità di modulo
contro
e vi rimane attaccato. Si determini:
- il modulo
dell’accelerazione del blocco
subito dopo l’urto.
- Il modulo
della velocità del blocca
subito dopo l’urto.
Nel disegno che segue è stato rappresento un sistema di riferimento fisso , che può essere considerato come il “laboratorio” dal quale si osserveranno gli eventi che seguiranno prima e dopo l’urto.
Figura 22: schema dell’esercizio urti 22.
Esercizio 23 . Una sferetta rigida, praticamente puntiforme e di massa
, cade lungo la verticale e urta elasticamente una semisfera rigida liscia, di massa
, nel punto
tale da formare l’angolo
(si veda la figura 23). Il modulo della velocità posseduta dalla sferetta subito prima dell’urto è
. La semisfera, prima dell’urto, è in quiete su un piano orizzontale privo di attrito. Si calcoli la quantità di moto
di
immediatamente dopo l’urto con
.
Figura 23: schema dell’esercizio urti 23.
Esercizio 24 . Un cubo di massa
e spigolo
è appoggiato su di un piano orizzontale al quale è incernierato senza attrito per uno spigolo. Un corpo di massa
, in moto con velocità
parallela al piano orizzontale (si veda la figura 24), colpisce perpendicolarmente il bordo superiore della faccia del cubo opposta allo spigolo incernierato (punto
rappresentato in figura 24). Dopo l’urto la direzione di moto del corpo si inverte, mentre il modulo della sua velocità si riduce per un fattore
. Si calcoli il valore
, con
, tale che il cubo si ribalti. Nella figura 24 è stato rappresentato un sistema di riferimento fisso
e per indicare il vettore
è stato introdotto il versore
per l’asse delle
. Inoltre, si assuma che la massa del cubo sia distribuita in modo omogeneo su tutto il suo volume, si trascuri ogni forma di attrito e sia dia per buono che il momento d’inerzia del cubo rispetto alla cerniera
sia
Figura 24: schema dell’esercizio urti 24.
Esercizio 25 . Un cubo di lato
e massa
si muove con velocità iniziale
su un tavolo liscio. La velocità
è parallela al piano orizzontale. Quando il cubo raggiunge l’estremità
del tavolo il suo spigolo rimane bloccato ed il cubo inizia a ruotare senza attrito. Il momento di inerzia del cubo rispetto ad un asse orizzontale passante per il centro di una della facce è
Calcolare:
- la velocità angolare
con cui il cubo inizia a ruotare;
- la velocità iniziale massima
tale che il cubo non si ribalti.
Figura 25: schema dell’esercizio urti 25.
Esercizio 26 . Una tavola quadrata di massa
distribuita in modo omogeneo su tutta l’area occupata dalla tavola e lato
è incernierata ad un asse verticale coincidente con il lato
. Il vincolo impone alle rotazioni un momento di attrito costante
. Il vettore
è costante in modulo, direzione e verso coincidente con l’asse di rotazione. Ortogonalmente alla tavola viene sparato un proiettile di massa
con velocità
. Questo proiettile perfora la tavola, in un tempo trascurabile, ed esce con velocità
sempre ortogonalmente alla tavola. Il foro lasciato nella tavola dista
dall’asse
. Si osserva che dopo aver percorso una distanza
lungo l’orizzontale il proiettile è sceso di una distanza
lungo la verticale rispetto al foro.
Dopo l’urto tra tavola e proiettile la tavola entra in rotazione e si ferma dopo aver percorso un angolo pari a .
Calcolare:
- il modulo
della velocità
del proiettile in funzione dei parametri
,
,
,
,
,
,
,
e
;
- il modulo
dell’impulso
subito dall’asse
nell’urto
,
,
,
,
,
,
,
,
e
.
Con si intende la componente del vettore
orientata lungo l’asse di rotazione, che essendo un momento frenante, implica che
.
Figura 26 a: tavola con foro a distanza
dal lato incernierato
.
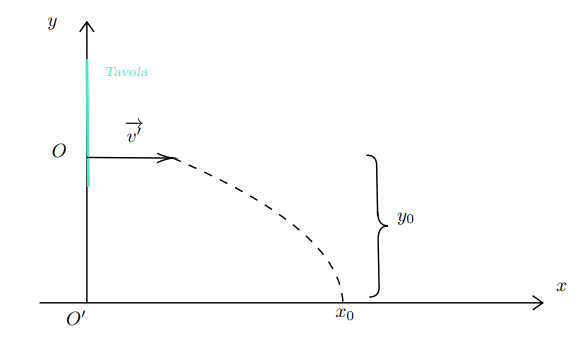
Figura 26 b: moto del proiettile all’uscita dalla tavola.
Esercizio 27 . Un disco omogeneo di massa
e raggio
è vincolato a ruotare senza attrito intorno ad un asse orizzontale fisso passante per il centro del disco
. Sull’asse è collegata una molla a spirale che esercita sul disco un momento di richiamo
, dove
è l’angolo di rotazione del disco rispetto all’asse verticale (si veda la figura 27a) e
è una costante avente unità di misura
.
Una massa urta orizzontalmente il disco con velocità
in corrispondenza del suo punto più basso
, in maniera completamente anelastica. Sia
l’angolo di rotazione massimo che percorre il disco dopo l’urto, calcolare il modulo di
in funzione di
,
e
e
.
Figura 27: situazione schematica a) del disco ruotato di un angolo e della molla a spirale che esercita il momento di richiamo; b) del sistema di disco e massa
con il sistema di riferimento fisso
.
Esercizio 28 . Un proiettile puntiforme
, di massa
, si muove, con velocità di modulo pari a
, avente direzione orizzontale e giaciente su un piano verticale
. Il proiettile si conficca istantaneamente, rimanendovi attaccato, nel punto
(si veda la figura 28) di un disco rigido e omogeneo, di massa
e raggio
, incernierato nel punto
, giacente sullo stesso piano verticare
e inizialmente in quite, con
(si veda la figura 28). Determinare il modulo
della velocità angolare del disco subito dopo l’urto in funzione dei parametri
,
,
,
,
e
.
Figura 28: schematizzazione del problema prima dell’urto (sinistra) e dopo l’urto (destra).
Esercizio 29 . Una molla ideale di costante elastica
e lunghezza a riposo
mantiene inizialmente orizzontale un’asta omogenea di lunghezza
e massa
incernierata all’altro estremo nel punto
, attorno a cui è libera di ruotare. Una massa
inizialmente ferma all’istante
cade da una quota
al di sopra dell’asta e vi si conficca, a distanza orizzontale
da
, come rappresentato in figura 1.
Determinare la velocità angolare dell’asta immediatamente dopo l’urto. Supponendo che, dopo un certo tempo, le oscillazioni dell’asta si smorzino fino ad arrestarsi ed il sistema arrivi all’equilibrio, calcolare la differenza tra la lunghezza della molla prima dell’urto e quella raggiunta al nuovo equilibrio. Si assuma che, nella nuova posizione di equilibrio dell’asta, la molla rimanga verticale (ossia l’asta possa ancora essere considerata approssimativamente orizzontale).
Figura 29: rappresentazione schematica del problema prima dell’impatto.
Esercizio 30 . Consideriamo un disco di massa
, con distribuzione omogenea di massa e raggio
, che scivola senza attrito su un piano orizzontale con una velocità orizzontale iniziale
. Immaginiamo che, ad un certo istante, un piccolo dente situato sul bordo del disco impatti contro un punto fisso
, come mostrato in figura 30. Assumendo che l’impatto tra il dente e il punto fisso
sia perfettamente elastico, vogliamo determinare la velocità finale
del centro di massa del disco e la velocità angolare
del disco subito dopo l’urto, relativamente a un sistema di riferimento inerziale.
Figura 30: illustrazione delle varie fasi avvenuto nell’urto tra disco e piolo.
Esercizio 31 . Consideriamo un anello di massa
e raggio
, inizialmente in quiete su un piano orizzontale privo di attrito.
Due corpi puntiformi, con masse rispettivamente di e
, si spostano entrambi rispettivamente alla velocità
e
, tale che
, seguendo la traiettoria illustrata nella figura 31. In un dato momento, i due corpi entrano in contatto nello stesso istante con l’anello e vi aderiscono permanentemente.
Si richiede di determinare:
- la velocità del centro di massa (CM) del sistema complessivo successivamente all’urto;
- la velocità angolare dell’intero sistema.
Figura 31: schema dell’esercizio urti 31.
Esercizio 32 . Consideriamo un anello di massa
e raggio
, che riposa in quiete su un piano orizzontale perfettamente liscio. Un proiettile di massa
, muovendosi orizzontalmente alla velocità iniziale di modulo
, colpisce tangenzialmente l’anello e rimane incastrato in esso. Si richiede di determinare:
- la velocità lineare dell’anello subito dopo l’urto.
- La velocità angolare dell’anello dopo l’urto.
- L’energia dissipata durante l’urto.
Figura 32: schema dell’esercizio urti 32.
Esercizio 33 . Un carrello di massa
può scorrere su un piano orizzontale liscio ed è sagomato in modo che la faccia superiore sia piana ed inclinata di un angolo
rispetto all’orizzontale. Una sferetta di massa
urta perpendicolarmente la faccia superiore del carrello, che inizialmente è in quiete. Il modulo della velocità prima dell’urto è
. Si calcoli la velocità
del carrello nei seguenti casi:
- nel caso in cui l’urto sia completamente anelastico;
- nel caso in cui l’urto sia perfettamente elastico.
Figura 33: schema dell’esercizio urti 33.
Esercizio 34 . Un proiettile di massa
e velocità
attraversa la massa di un pendolo semplice, emergendo con velocità
. Sia
la massa del pendolo e
la lunghezza del filo. Determinare:
- la velocità minima che deve avere la massa
del pendolo, immediatamente dopo l’urto, per poter compiere un giro completo.
- La velocità iniziale
del proiettile, prima dell’urto, assumendo che sia soddisfatta la condizione della domanda precedente.
Figura 34: schema dell’esercizio urti 34.
Esercizio 35 .Consideriamo un disco omogeneo di massa
e raggio
che ruota su un piano verticale attorno a un asse orizzontale passante per il suo centro. Questo asse oppone alla rotazione un momento di attrito
costante. Una massa
, di dimensioni trascurabili, cade verticalmente sul bordo del disco e vi rimane attaccata. La traiettoria della massa passa esattamente per l’asse di rotazione del disco, come si può dedurre dalla figura 35. Data la velocità angolare
del disco immediatamente prima dell’urto, si determini:
- la velocità angolare
del disco immediatamente dopo l’urto in funzione di
,
e
;
- il momento di attrito
, sapendo che
secondi prima dell’urto il disco ruotava con una velocità angolare
, in funzione di
,
,
,
e
;
- la velocità angolare
del disco nell’istante in cui la massa
raggiunge la posizione più bassa, in funzione di
,
,
,
,
.
Si supponga che .
Figura 35: schema dell’esercizio urti 35.
Esercizio 36 . Consideriamo un proiettile di massa
che impatta perpendicolarmente su una porta a una distanza
dai cardini, con una velocità iniziale
. La porta ha un momento d’inerzia
rispetto all’asse passante per i cardini. Dopo l’impatto, il proiettile prosegue nel suo cammino con una velocità
, mentre la porta inizia a ruotare con una velocità angolare
. Con
e
indichiamo rispettivamente i moduli di
e
. Si desidera determinare:
- la velocità finale
del proiettile, espressa in funzione di
,
,
,
, e
;
- l’energia meccanica dissipata durante l’evento, espressa in funzione di
,
,
,
, e
;
- la forza media esercitata sulla porta, se il proiettile impiega un tempo
per attraversarla, espressa in funzione di
,
,
,
,
, e
.
Si assume che .
Figura 36: schema dell’esercizio urti 36.
Esercizio 37 . \textbf{Esercizio 37}
. Consideriamo un’asta di massa
e lunghezza
che può ruotare senza attrito intorno a un asse verticale passante per il suo centro
grazie a un perno. L’asta e la massa
si trovano su di un piano orizzontale liscio. Si consideri la massa dell’asta distribuita in modo omogeneo su tutta la sua lunghezza. All’estremo dell’asta è fissata una molla di costante elastica
, inizialmente a riposo, e ancorata a un punto fisso, come rappresentato in figura 37. L’asta viene colpita in modo completamente anelastico all’estremo opposto da un proiettile di massa
e velocità iniziale
, che rimane conficcato in essa. Immediatamente dopo l’urto, il sistema composto dall’asta e dal proiettile ruota con velocità angolare
e la molla si allunga raggiungendo un’elongazione massima
. Siano
e
rispettivamente i moduli di
e
.
Le grandezze da determinare sono:
- la velocità iniziale
del proiettile in funzione di
,
e
;
- la costante elastica
della molla in funzione di
,
,
,
e
;
- il periodo
delle piccole oscillazioni del sistema in funzione di
,
e
.
Figura 37: schema dell’esercizio urti 37.
Esercizio 38 . Consideriamo un punto materiale di massa
che cade su un piano inclinato, inclinato di un angolo
rispetto all’orizzontale. Se l’urto contro il piano, situato ad un’altezza
dal punto di impatto, è elastico, si vuole calcolare l’altezza massima che la massa
raggiunge rispetto al livello del punto di impatto, assumendo che il piano inclinato sia immobile.
Figura 38: schema dell’esercizio urti 38.
Esercizio 39 . Osserviamo dal sistema di riferimento fisso Oxyz rappresentato in figura 39 un’asta rigida di massa trascurabile e lunghezza
. Questa è sospesa da un’estremità attraverso una cerniera minuta
, solidamente fissata a un punto su una guida orizzontale che coincide con l’asse
. L’asta, capace di ruotare liberamente e senza attrito attorno a
, porta due masse puntiformi
e
, collocate rispettivamente nel centro e nell’estremità libera. Inizialmente, l’asta è ferma in posizione verticale.
Consideriamo poi un corpo di massa , trattato come un punto materiale, che si muove nel piano verticale
e impatta la massa
, rimanendovi successivamente unito. La velocità
del corpo
poco prima della collisione presenta componenti
e
lungo gli assi
e
, rispettivamente. Sono richieste le determinazioni di:
- la velocità angolare
dell’asta subito dopo la collisione in funzione di
,
,
,
e
;
- l’ampiezza massima dell’angolo
che l’asta raggiunge a seguito dell’urto in funzione
,
,
,
,
,
e
;
- l’impulso
esercitato dalla reazione della cerniera durante la collisione sull’asta in funzione di
,
,
,
,
,
e
.
Figura 39: schema dell’esercizio urti 39.
Ulteriori risorse didattiche per la fisica
Leggi...
- Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
- ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
- Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
- Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
- The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
- American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
- Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
- Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
- Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
- Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.
