Questa raccolta comprende 40 esercizi svolti sui sistemi di punti materiali, concepita per offrire un riferimento didattico strutturato e approfondito nell’ambito della meccanica classica. L’opera si propone di coprire in modo esaustivo le principali tematiche relative a questo argomento, includendo esercizi di difficoltà crescente, dai più semplici ai più complessi, fino a problemi particolarmente elaborati e di difficile reperibilità. L’obiettivo è fornire agli studenti e ai ricercatori un repertorio di esercizi che favorisca la comprensione teorica e l’applicazione pratica, concentrando in un unico articolo un’ampia gamma di situazioni risolutive.
Gli esercizi presentati derivano da fonti accademiche autorevoli nella letteratura scientifica, tra cui:
- Rosati, Luigi – Fisica Generale
- Mencuccini, C., Silvestrini, G. – Fisica
- Mazzoldi, P., Nigro, M., Voci, C. – Elementi di Fisica
- Resnick, R., Halliday, D., Walker, J. – Fundamentals of Physics
- Goldstein, H. – Classical Mechanics
- Landau, L.D., Lifshitz, E.M. – Mechanics
Oltre agli esercizi tratti da testi accademici di riferimento, la raccolta include una selezione di problemi originali e quesiti provenienti da prove d’esame universitarie. Questa integrazione ha lo scopo di ampliare il panorama applicativo e rafforzare l’acquisizione dei concetti fondamentali legati ai sistemi di punti materiali.
All’interno del percorso didattico proposto, il capitolo successivo approfondisce gli esercizi sulla dinamica del corpo rigido, presentando un totale di 69 esercizi svolti. Il capitolo precedente, invece, è dedicato agli esercizi sui moti relativi, per un totale di 37 esercizi svolti.
È inoltre possibile accedere all’intero corso di meccanica classica, frutto di un lavoro di ricerca e sviluppo condotto dal nostro team negli ultimi quattro anni. Maggiori dettagli sugli autori e revisori sono disponibili nella sezione dedicata alla fisica.
Sistemi di punti materiali: autori e revisori
Leggi...
Autori e Revisori:
Valerio Brunetti, Giuseppe Palaia.
Autori:
Romano Rotonda, Daniele Massaro, Andrea Corradini, Davide Vignotto, Cosimo Tommasi.
Revisori:
Autori in collaborazione:
Giulia Romoli, Antonio Figura, Christian Magliano.
Ex Autori & Revisori:
Patrizio Di Lorenzo, Simone Brozzesi, Nicola Santamaria, Vittorio Larotonda, Leonardo Rebeschini, Simone Romiti, Antonio Junior Iovino, Daniele Bjørn Malesani, Tiziano Schiavone, Serena Lezzi, Marco Chilioiro.
Esercizio 1 . Un uomo di massa
, considerato come un punto materiale, è inizialmente in quiete sul bordo di una barca di massa
, la cui massa è distribuita in modo omogeneo e di lunghezza
, immersa nel mare.
L’uomo si sposta di una distanza rispetto al punto fisso
, senza che vi sia alcun attrito tra la barca e l’acqua.
Determinare di quanto si è spostata la barca rispetto a un sistema di riferimento fisso. L’obbiettivo è di esprimere i risultati in funzione dei parametri ,
e
.

Figura 1: schema del problema sistemi di punti materiali 1.
Esercizio 2 . Un insetto di massa
si trova all’estremo di un bastoncino lungo
e massa
posto su di un piano orizzontale liscio. L’insetto possiede una velocità iniziale
orientata come in figura 2 e al termine del proprio moto si troverà alla fine del bastoncino, per percorrere tale percorso impiega un tempo
. Determinare di quanto è arretrato il bastoncino. Si supponga la massa
del bastoncino distribuita in modo omogeneo su tutta la sua lunghezza.
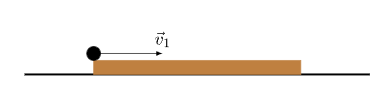
Figura 2: schema del problema sistemi di punti materiali 2.
Esercizio 3 . Tre blocchetti di masse
,
,
scendono lungo un piano inclinato liscio, con angolo
, sotto l’azione della forza peso e della forza
costante indicata in figura 3. Si sa che il modulo della forza tangente al piano a cui è sottoposto il blocchetto
è
. Calcolare il valore di
.
Si supponga ora che non ci sia la forza , ma che il piano presenti attrito, con coefficienti
,
,
rispettivamente per il blocchetto
,
,
, e che il moto sia uniforme. Calcolare il valore di
in funzioni di quest’ultimi.

Figura 3: schema del problema sistemi di punti materiali 3.
Esercizio 4 . Siano un sistema di riferimento inerziale
e due punti materiali di massa
ed
che si muovono di moto vario con leggi orarie
e
. Si richiede di verificare il teorema di König dell’energia cinetica e di determinare la condizione affinché l’energia cinetica di
sia doppia di quella di
nel sistema del centro di massa.
Esercizio 5 . Due masse, considerate puntiformi,
ed
, poste su un piano orizzontale senza attrito, comprimono una molla di costante elastica
di una lunghezza
e sono collegate da un filo di massa trascurabile. La massa
si trova inizialmente a una distanza
dal bordo di uno scalino di altezza
. All’istante
s il filo viene tagliato e la molla si decomprime. La massa
percorre la traiettoria di figura 5 e tocca terra a una distanza
dallo scalino, impiegando un tempo totale
dall’istante iniziale
s. Si determini:
- la velocità della massa
dopo la decompressione della molla;
- l’altezza
dello scalino;
- la compressione
iniziale della molla.

Figura 5: schema del problema sistemi di punti materiali 5.
Esercizio 6 . Due masse puntiformi
e
sono inizialmente ferme nell’origine dell’asse
. All’istante
la massa
inizia a muoversi con un’accelerazione
mentre
parte con una velocità
che resta costante. Determinare dopo quanto tempo il centro di massa del sistema transita nell’origine e la sua velocità in quell’istante.
Effettuare i calcoli per: ,
,
,
.
Figura 6: schema del problema sistemi di punti materiali 6.
Esercizio 7 . Una massa puntiforme
è attaccata tramite un filo di lunghezza
e massa trascurabile ad un anello di massa
. L’anello
può scorrere senza attriti lungo una guida rettilinea orizzontale. All’istante iniziale la massa
è ferma alla stessa quota dell’anello (filo orizzontale). Nell’istante in cui il filo è in direzione verticale, determinare:
a) la velocità della massa ;
b) di quanto risulta spostata la massa rispetto alla posizione iniziale.
Eseguire i calcoli numerici con ,
,
.
Figura 7: schema del problema sistemi di punti materiali 7.
Esercizio 8 . Agli estremi di un’asta di lunghezza
e massa trascurabile, sono saldati due pattini, di masse
e
, che si appoggiano su una guida circolare di raggio
, posta su un piano orizzontale. Sull’asta, a distanza
dal pattino di massa
, si trova una persona di massa
. L’asta è vincolata a ruotare rispetto al centro del disco e inizialmente possiede una velocità angolare
.
La persona si sposta, portandosi a distanza dal pattino di massa
; si calcoli la velocità angolare
del moto circolare dei pattini dopo lo spostamento della persona e il lavoro eseguito da questa per spostarsi.
Situazione inziale
Situazione finale
Figura 8: schema del problema sistemi di punti materiali 8.
Esercizio 9 . Due masse
e
, soggette alla forza peso, sono collegate da un’asticella di massa trascurabile e lunghezza
. Il sistema è libero di traslare e ruotare su un piano verticale, intorno all’asse perpendicolare al piano, passante per il centro di massa. All’istante
l’asta è posizionata come in figura 9, la massa
ha coordinate
e la massa
si trova nell’origine. In tale istante il centro di massa ha velocità
diretta nel verso positivo dell’asse delle
e la velocità angolare
(rotazione in verso antiorario).
Determinare all’istante :
- la posizione del centro di massa;
- il momento angolare del sistema rispetto al centro di massa e rispetto all’origine degli assi.
Inoltre descrivere per il moto del sistema rispetto al sistema di riferimento inerziale e il centro di massa.
Figura 9: schema del problema sistemi di punti materiali 9.
Esercizio 10 . Siano tre blocchi di massa
,
e
, tale per cui
giacca su
, ed
sia collegato ad
tramite un filo inestensibile, e di massa trascurabile, tramite una carrucola ideale. Tutti gli attriti sono trascurabili e si consideri la massa della carrucola trascurabile. Grazie ad un’opportuna forza esterna
di direzione, verso e modulo costante, il sistema composto dai tre blocchi entra in movimento. Si determini il valore di
affinché la massa
rimanga in quiete rispetto a
. Il sistema fisico in esame è rappresentato nella figura 10 che segue.
Figura 10: schema del problema sistemi di punti materiali 10.
Scarica gli esercizi svolti
Ottieni il documento contenente 40 esercizi risolti, contenuti in 178 pagine ricche di dettagli, per migliorare la tua comprensione dei sistemi di punti materiali in meccanica classica.
Esercizio 11 . Un carrello di massa
può muoversi senza attrito su di un piano orizzontale. Una persona di massa
si trova sul carrello; inizialmente il sistema è in quiete. La persona si mette a camminare sul carrello, con un’accelerazione
rispetto al carrello. L’accelerazione
ha direzione, verso e modulo costante, ed è parallela al piano orizzontale, come nella figura 11 di seguito. Si determinino le accelerazioni del carrello e della persona rispetto ad un sistema di riferimento solidale al suolo.

Figura 11: schema del problema sistemi di punti materiali 11.
Esercizio 12 . Due punti materiali di massa
e
sono collegati da una barretta rigida di massa trascurabile e lunghezza
su di un piano orizzontale. Il sistema inizialmente non è in quiete, infatti
e
hanno velocità
e
rispettivamente. Entrambe le velocità
e
vanno riferite rispetto ad un sistema di riferimento fisso. Inoltre, siano
e
i moduli rispettivamente delle velocità
e
. Le velocità
e
sono orientate come in figura 12. Sul sistema non agiscono forze esterne e all’istante
la situazione è quella mostrata in figura 12, con
, dove
è il modulo della velocità iniziale di
, ed
è il modulo della velocità iniziale di
all’istante iniziale. Si determinino le posizioni dei due punti materiali, rispetto ad un sistema di riferimento fisso, all’istante
tale che valga la seguente condizione
.
Figura 12: schema del problema sistemi di punti materiali 12.
Esercizio 13 . Un oggetto di massa
viene appoggiato su un piano metallico di massa
, sostenuto da una molla ideale di massa trascurabile, lunghezza a riposo
e costante elastica
. Si comprime, con un’opportuna forza esterna, la molla di una lunghezza
rispetto alla lunghezza di riposo. Successivamente il sistema vine rilasciato e per via della forza esercitata dalla molla risale verso l’alto. Si richiede di calcolare il massimo valore
di
affinché l’oggetto rimanga aderente al piatto.
Figura 13: schema del problema sistemi di punti materiali 13.
Esercizio 14 . Su due guide orizzontali e parallele, poste in un piano verticale e distanti tra loro
, possono scorrere senza attrito due piccoli anelli di masse
e
. I due anelli sono collegati tra loro da una molla ideale, di massa trascurabile, lunghezza a riposo trascurabile e costante elastica
. All’istante
tramite un’opportuna forza esterna l’anello di massa
si mette in moto con una velocità di modulo
diretta parallelamente alle guide, come in figura 14, mentre il secondo anello a quell’istante è in quiete. Supporre che
ed
, all’istante
siano allineati, come in figura 14. Le velocità dei due corpi all’istante iniziale vanno riferite rispetto ad un sistema di riferimento fisso. Si calcoli l’allungamento massimo della molla e il tempo minimo
che si deve attendere affinché ciò avvenga.
Figura 14: schema del problema sistemi di punti materiali 14.
Esercizio 15 . Tre masse,
,
e
, sono in moto lungo un piano orizzontale. Le masse
ed
sono connesse da una molla ideale di costante elastica
, lunghezza a riposo trascurabile e massa trascurabile, e sono soggetti rispettivamente alle forze
ed
. La massa
si trova distante dalla massa
, come si può dedurre dalla figura 15, ed è soggetta alla forza
. Le forze
,
ed
hanno direzione, verso e modulo costante, come rappresentato in figura 15. La massa
ha un’accelerazione
rispetto ad un sistema di riferimento inerziale di modulo, direzione e verso costante parallelo al piano orizzontale all’istante
, come rappresentato in figura 15. Si consideri il sistema fisico composto dalle masse
,
ed
, da cui si definisca
l’accelerazione del centro di massa di tale sistema. Inoltre, siano
e
le accelerazione rispettivamente di
ed
rispetto ad un sistema di riferimento inerziale. Si richiede di calcolare
,
,
e di quanto è allungata la molla all’istante iniziale
in funzione di
,
,
ed
.
Figura 15: schema del problema sistemi di punti materiali 15.
Esercizio 16 . Un cannone di massa
spara in orizzontale, dalla sommità di una torre di altezza
, un proiettile di massa
, che raggiunge il suolo a distanza
dalla base della torre. Trascurando la resistenza dell’aria, calcolare il modulo della forza
orizzontale e costante che un sistema di ammortizzatori deve esercitare sul cannone perché, per il rinculo, esso arretri di un tratto
prima di fermarsi. Si consideri il cannone di massa
e la massa
come due punti materiali.
Figura 16: schema del problema sistemi di punti materiali 16.
Esercizio 17 . Una pallina di massa
si trova su un piano orizzontale liscio ed è collegata, tramite un filo inestensibile, di massa trascurabile e passante per un piccolo foro
praticato nel piano, a un corpo di massa
, posto al di sotto del piano lungo la verticale passante per
. All’istante
la pallina si trova a distanza
da
e viene messa in moto lungo il piano con velocità
perpendicolare al filo e giacente sul piano orizzontale, come rappresentato in figura 17.
- Si descrivano tutte le forze che agiscono sul sistema, determinando in particolare la reazione vincolare
che il piano esercita sul filo nel punto
.
- Si determini il valore
del modulo di
tale per cui
inizia a ruotare restando a distanza
da
.
- Si trovino i valori della minima distanza
e della massima distanza
da
raggiunte da
durante il moto in funzione di
.
- Si dimostri che per qualsiasi valore di
non è possibile che
raggiunga il punto
, mentre ciò sarebbe possibile se il piano su cui si muove
presentasse attrito.
Figura 17: schema del problema sistemi di punti materiali 17.
Esercizio 18 . Due corpi di massa
e
agganciati agli estremi di una molla di massa trascurabile, si trovano su di un piano orizzontale liscio. La molla è ideale, ha costante elastica
e lunghezza a riposo
. Inizialmente la molla è tenuta compressa di un tratto
mediante un filo collegato alle due masse. Tagliato il filo, si lasciano muovere i due corpi sotto l’azione della molla. Si determini la velocità massima raggiunta dai due corpi rispetto ad un osservatore solidale al suolo. Si esprimano i risultati in funzione delle variabili
,
e
.
Figura 18: schema del problema sistemi di punti materiali 18.
Esercizio 19 . Due punti materiali di massa
, fissati alla fine di un’asta rigida di massa trascurabile e lunghezza
, formano un angolo fisso
con la verticale, come in figura 19. Il sistema è tenuto in rotazione a velocità angolare di modulo, direzione e verso costante
rispetto all’asse di rotazione passante per il centro di massa dell’asta, come rappresentato in figura 19. Si determini il momento angolare
e la sua variazione rispetto al tempo
rispetto al polo
indicato in figura 19.
Figura 19: schema del problema sistemi di punti materiali 19.
Esercizio 20 . Un blocco di massa
, costituito da un quarto di circonferenza di raggio
, è libero di muoversi senza attrito su un piano orizzontale ed è inizialmente fermo. Un punto materiale di massa
, inizialmente fermo nel punto più alto del profilo, scivola senza attrito sul profilo. Calcolare:
(i) lo spostamento del blocco rispetto alla posizione iniziale, nell’istante in cui il punto materiale ha percorso un tratto lungo l’asse orizzontale rispetto alla sua posizione di partenza;
(ii) lo spostamento del blocco rispetto alla posizione iniziale, nell’istante in cui il punto materiale ha percorso un tratto lungo lungo l’asse orizzontale rispetto ad un polo solidale al blocco stesso;
(iii) lo spostamento del blocco rispetto alla posizione iniziale quando il punto materiale ha raggiunto il piano orizzontale;
(iiii) le velocità finali del punto materiale e del blocco, rispetto al piano orizzontale quando la massa ha raggiunto il piano orizzontale stesso.
Utilizzare per i calcoli: ,
,
,
.
Figura 20: schema del problema sistemi di punti materiali 20.
Esercizio 21 . Una conca semisferica di massa
e raggio
è appoggiata ad una parete verticale e può scorrere senza attrito lungo l’asse orizzontale. Un corpo di massa
è abbandonato con velocità nulla dalla cima della conca come mostrato in figura 21. Trascurando l’attrito tra la conca e il corpo
, calcolare:
a) l’altezza massima raggiunta dal corpo dopo che la conca si è staccata dalla parete verticale;
b) la velocità della conca nell’istante in cui raggiunge l’altezza massima;
c) la velocità massima raggiunta dalla conca.
Figura 21: schema del problema sistemi di punti materiali 21.
Esercizio 22 . Un cuneo a sezione triangolare, di massa
, lunghezza
e altezza
, poggia e può scorrere senza attrito su un piano orizzontale fisso, come in figura 22. In cima al piano inclinato in quiete è poggiato un piccolo dado pesante di massa
. Si lascia libero il dado di scivolare lungo il piano inclinato. Calcolare:
a) di quanto si sarà spostato il cuneo quando il dado avrà raggiunto il piano orizzontale;
b) quanto valgono le componenti e
della velocità del dado quando la velocità del cuneo è
;
c) la velocità del cuneo all’istante in cui il dado arriva in fondo al piano inclinato, nell’ipotesi che non vi sia attrito tra cuneo e dado.
Figura 22: schema del problema sistemi di punti materiali 22.
Esercizio 23 . Un corpo di massa
scivola su un piano inclinato, tra piano e corpo c’è attrito dinamico e il coefficiente di attrito dinamico ha valore
. Il piano inclinato ha una massa distribuita in modo omogenea di valore totale
e può scorrere su un piano orizzontale privo di attrito. Calcolare le accelerazioni di
e
rispetto al laboratorio (sistema fisso) considerando che all’istante iniziale tutto è in quiete.
Figura 23: schema del problema sistemi di punti materiali 23.
Esercizio 24 . Un blocco di massa
è fermo su un cuneo di altezza
e massa
. Tutte le superfici sono senza attrito. All’inizio tutto è in quiete e il blocco di massa
si trova a quota
sul cuneo come in figura 24.
Rispetto ad un sistema di riferimento inerziale fisso, determinare:
1) di quanto si è postato il cuneo quando il punto materiale arriva alla fine di esso;
2) la velocità del cuneo quando il punto materiale si trova ad ;
3) la velocità del cuneo e del punto materiale un istante prima e dopo che il punto materiale tocca il piano orizzontale ;
4) l’accelerazione del cuneo e del punto materiale.
Figura 24: schema del problema sistemi di punti materiali 24.
Esercizio 25 . Un punto materiale di massa
viene lanciato con velocità
lungo un piano orizzontale privo di attrito. Ad un certo istante
impatta con un piano inclinato di massa
che forma un angolo
con il piano orizzontale, anch’esso libero di muoversi e privo di attrito, ed inizia a risalire lungo il piano. Si determini l’equazione che esprime la velocità assoluta del piano inclinato in funzione della quota di
e la velocità finale del sistema quando la massa
ha velocità relativa nulla rispetto al piano inclinato ovvero quando il sistema composto da
si muove all’unisono rispetto ad un osservatore fisso.
Esercizio 26 . Nel sistema rappresentato in figura 26 il blocco triangolare
di angolo alla base
e di massa
, poggia su un piano orizzontale ed è tenuto fermo dal rialzo
; i corpi
e
, di masse
e
, sono collegati da un filo inestensibile di massa trascurabile, la carrucola
ruota senza attrito e ha massa trascurabile.
a) Consideriamo trascurabile l’attrito tra il blocco e
. Si calcoli il valore minimo del coefficiente di attrito statico tra i corpi
e
necessario affinché questi, lasciati liberi con velocità nulle nella posizione di figura 26, rimangano in quiete, e le componenti orizzontale e verticale della reazione
sviluppata complessivamente dal piano
di appoggio e da
.
b) Si supponga adesso che il sistema non sia in equilibrio, che i coefficienti di attrito dinamico tra e
e tra il blocco
e
valgano
e il sistema venga lasciato libero nella posizione di figura 26 con velocità iniziali nulle. Si calcoli il modulo
dell’accelerazione di
e le componenti della reazione
.
Si supponga che sia a trascinare
Figura 26: schema del problema sistemi di punti materiali 26.
Esercizio 27 . Una corda di massa
e lunghezza
è tenuta ferma su un tavolo privo di attrito, mentre una certa porzione
della sua lunghezza pende dal bordo del tavolo.
Quanto lavoro è richiesto per tirare indietro, fino sul piano del tavolo, la parte pendente?
N.B. Per lo svolgimento dell’esercizio supporre che la massa della corda sia uniformemente distribuita lungo di essa, ossia la densità di massa della corda sia costante, cioè
(1)
dove è la massa del tratto di corda
. Inoltre, supporre che il sistema sia in quiete rispettivamente all’inizio del moto e alla fine del moto (cioè quando la corda è totalmente sul piano orizzontale).
Figura 27: schema del problema sistemi di punti materiali 27.
Esercizio 28 . Un corpo di massa
è attaccato all’estremità di una molla ideale. Esso è vincolato a muoversi verticalmente ed è in contatto con un ripiano inclinato liscio di un carrello di massa
scorrevole su un piano orizzontale privo di attrito, come illustrato in figura 28. Il ripiano forma un angolo
rispetto al piano orizzontale. La molla ha costante elastica
e quando il corpo
coincide con il punto
la molla è a riposo. All’istante
, il corpo
coincide con il punto
, ad un’altezza
rispetto al punto
, le velocità dei due corpi sono nulle e il sistema viene lasciato libero di muoversi. Si determini:
- la velocità del carrello di massa
nell’istante in cui il corpo
coincide con
;
- il modulo
della reazione vincolare del piano inclinato e il modulo
della reazione del piano orizzontale in funzione della compressione
della molla.
Figura 28: schema del problema sistemi di punti materiali 28.
Esercizio 29 . Un blocco metallico in quiete su un piano orizzontale viene spezzato, con una piccola carica di esplosivo, in tre parti
e
di massa
, che continuano a muoversi lungo lo stesso piano. Considerando un sistema di riferimento fisso inerziale
come illustrato in figura 29, con origine coincidente con la posizione del blocco metallico un istante prima dell’urto, il frammento
parte lungo l’asse
, nel verso positivo, con velocità
,
lungo l’asse
, nel verso positivo, con velocità
. Si determini il modulo e la direzione della velocità
del frammento
; si consideri il blocco metallico, così come le tre parti in cui esso è spezzato, come un punto materiale.
Figura 29: schema del problema sistemi di punti materiali 29.
Esercizio 30 . La figura 30 rappresenta la sezione verticale di un sistema formato da un cuneo
, di massa
ed apertura angolare
, posto tra due blocchi
e
di masse uguali,
, poggiati su di un piano orizzontale. Si trascuri l’attrito tra cuneo e i due blocchi.
- Si determini il valore minimo del coefficiente di attrito statico tra i blocchi
e
ed il piano d’appoggio se la situazione rappresentata in figura 30 è di equilibrio.
- L’attrito tra i due blocchi
e
ed il loro piano di appoggio sia trascurabile ed il blocco
venga lasciato libero di muoversi nella posizione di figura 30 con velocità nulla. Si calcolino i moduli della velocità e dell’accelerazione del cuneo nell’istante in cui termina il contatto tra il cuneo ed i blocchi.
Si consideri il cuneo come un triangolo isoscele e che la sua altezza sia pari ad .
Figura 30: schema del problema sistemi di punti materiali 30.
Esercizio 31 . Due masse puntiformi
e
, collegate tramite un’asta rettilinea di massa trascurabile avente lunghezza
, sono ferme in posizione verticale su un piano orizzontale privo di attrito. Se l’asta è leggermente spostata dalla sua posizione di equilibrio (instabile) e sapendo che la massa
è vincolata a muoversi sul piano orizzontale, dimostrare che il modulo della velocità angolare
con cui essa raggiunge la posizione orizzontale è data da
Figura 31: schema del problema sistemi di punti materiali 31.
Esercizio 32 . Due aste uguali, ciascuna di lunghezza
e massa trascurabile, sono vincolate a muoversi in un piano verticale e sono incernierate tra loro ad un estremo
. Gli altri due estremi
e
, vincolati a muoversi lungo un asse orizzontale, sono collegati da una molla di lunghezza di riposo trascurabile e costante elastica
. Tre corpi puntiformi, di massa
,
e
, sono saldati rispettivamente nei tre vertici
,
e
. Si assumono trascurabili tutti i possibili attriti e si consideri la molla ideale.
- Si calcoli l’altezza
, rispetto all’asse orizzontale
, del punto
nella posizione di equilibrio. Inoltre, si dica se tale equilibrio è instabile o stabile.
- Sfruttando il risultato del punto 1 si deduca qual è l’intensità minima
della forza diretta verso il basso da applicare in
, in corrispondenza della posizione di equilibrio affinché
giunga sull’asse orizzontale.
- In corrispondenza del caso 2, si determini lo spostamento
lungo l’asse orizzontale ed il modulo
della velocità con la quale vi giunge il sistema.
Figura 32: schema del problema sistemi di punti materiali 32.
Esercizio 33 . Una pallina di massa
è posta sulla sommità di una semisfera liscia di massa
e raggio
, posta a sua volta in quiete su un piano orizzontale liscio. Dimostrare che se la pallina viene spostata leggermente dalla posizione di equilibrio instabile con una velocità iniziale trascurabile, l’angolo di distacco
, ossia l’angolo che la direzione passante per il centro della semisfera e la pallina forma con la verticale, soddisfa la seguente equazione algebrica:
Figura 33: schema del problema sistemi di punti materiali 33.
Esercizio 34 . Su un’asta rigida
, di lunghezza
e di massa trascurabile, sono fissati due piccoli manicotti di masse
e
rispettivamente nei punti
e
tali che
e
. L’asta è appoggiata su un piano orizzontale e a una parete verticale; nel punto
distante
da
è applicata una forza
orizzontale, come in figura 34.
- Inizialmente l’asta è in condizioni di equilibrio nella posizione con
; si calcoli l’intensità
di
se le superfici di appoggio sono lisce.
- Si aumenta l’intensità della forza
e l’asta si sposta restando in contatto con le due superfici lisce e quando
la velocità dell’estremo
ha modulo
; si calcoli il lavoro svolto corrispondentemente dalla forza
.
- Se l’asta è in quiete nella posizione
e la forza
ha intensità
, la posizione è di equilibrio; se le superfici sono scabre con coefficiente di attrito statico
e si diminuisce l’intensità di
, per quale valore
l’asta comincia a scivolare verso il basso?
(2)
Inoltre, si supponga, che l’asta cominci a scivolare quando le forze di attrito statico sulla parete verticale e orizzontale assumano rispettivamente il valore massimo contemporaneamente.
Figura 34: schema del problema sistemi di punti materiali 34.
Esercizio 35 . Una catenella è tenuta ferma su un tavolo privo di attrito mentre un quarto della sua lunghezza pende dal bordo del tavolo.
Se la catenella ha una lunghezza totale e una massa
, quanto lavoro è richiesto per tirare indietro fino sul piano del tavolo la parte pendente?
Figura 35: schema del problema sistemi di punti materiali 35.
Esercizio 36 . Due punti materiali di massa
e
sono vincolati a muoversi su di un piano orizzontale liscio. I due punti sono fissati alle estremità di una molla ideale di costante elastica
e lunghezza a riposo
. Scelto un sistema di riferimento inerziale dal quale analizzare il sistema fisico composto dalle due masse, si definiscano
e
le posizioni rispettivamente di
e
nel sistema di riferimento scelto. Le condizioni iniziali in questo sistema di riferimento sono
,
,
e
. Si richiede di determinare le leggi orarie
e
.
Figura 36: geometria del problema sistemi di punti materiali 36 a .
Esercizio 37 . I due corpi rappresentati in figura 37 sono collegati da un filo inestensibile, di massa trascurabile e lunghezza
. Il corpo di massa
è vincolato a scorrere senza attrito lungo un’asta orizzontale; il corpo di massa
è invece libero di oscillare nel piano in cui giace il sistema delle due masse. I due corpi vengono lasciati liberi di muoversi con velocità iniziali nulle in corrispondenza di un angolo
che il filo forma con la verticale.
Calcolare:
- l’ampiezza
del moto oscillatorio del corpo di massa
in funzione di
,
,
e
;
- i moduli
e
delle velocità che i corpi possiedono quando si trovano allineati lungo la verticale in funzione di
,
,
,
e
.
Figura 37: schema del problema sistemi di punti materiali 37.
Esercizio 38 . Un punto materiale di massa
é inizialmente in quiete in cima ad un piano inclinato di un angolo
(compreso tra 0 e
), avente altezza
. Il punto esplode in due frammenti di massa
e
rispettivamente. Subito dopo l’esplosione il frammento
si muove in discesa lungo il piano inclinato con velocità di modulo
. Sapendo che il coefficiente di attrito dinamico tra il piano e
é
, e che
si ferma esattamente alla base del piano inclinato, determinare la quota massima raggiunta dal frammento
in funzione di
,
e
.
Figura 38: configurazione del sistema nell’istante che precede l’esplosione.
Esercizio 39 . Un insetto di massa
si trova inizialmente fermo all’estremità di un’asta lunga
e di massa
, posta su un piano orizzontale liscio. L’insetto inizia a muoversi verso l’altro estremo dell’asta con velocità, rispetto al piano,
. La velocità
è costante in modulo, direzione e verso, la direzione è parallela al piano orizzontale e il verso è indicato in figura 39. Determinare il tempo
impiegato dall’insetto per raggiungere l’altra estremità dell’asta.
Figura 39: schema del problema sistemi di punti materiali 39.
Esercizio 40 . Si consideri un sistema costituito da due punti materiali di massa
e
, collegati da una molla di costante elastica
e lunghezza a riposo trascurabile. Il sistema è vincolato a muoversi su un piano orizzontale liscio. Al tempo
le due masse sono poste in quiete a distanza
tra di loro e successivamente vengono lasciate libere di muoversi.
Si dimostri che per qualsiasi l’energia potenziale elastica del sistema vale
dove e
sono rispettivamente le posizioni di
e
al tempo
in un opportuno sistema di riferimento.
Figura 40: schema del problema sistemi di punti materiali 40
Esercizi di Meccanica classica
Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.
Leggi..
- Cinematica del punto materiale.
- Dinamica del punto materiale: le leggi di Newton nella meccanica classica.
- Dinamica del punto materiale: lavoro ed energia.
- Moti relativi.
- Sistemi di punti materiali.
- Dinamica del corpo rigido.
- Urti .
- Gravitazione .
- Oscillazioni e onde.
- Meccanica dei fluidi.
- Onde meccaniche.
- Statica in meccanica classica.
- Fondamenti di relatività ristretta: trasformazioni di Lorentz e principali conseguenze.
- Calcolo del centro di massa e dei momenti d’inerzia.
Tutti gli esercizi di elettromagnetismo
Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di
Leggi...
- Esercizi su lavoro elettrico e potenziale elettrico.
- Esercizi sulla legge di Gauss.
- Esercizi sui conduttori, condensatori, dielettrici ed energia elettrostatica.
- Esercizi sulla corrente elettrica.
- Esercizi sul campo magnetico e forza magnetica.
- Esercizi sulle sorgenti di un campo magnetico e legge di Ampere.
- Esercizi su campi elettrici e magnetici variabili nel tempo.
- Esercizi su oscillazione del campo elettrico e correnti alternate.
- Esercizi sulle onde elettromagnetiche.
- Esercizi sulla riflessione e rifrazione della luce.
- Esercizi sull’ ottica geometrica.
- Esercizi sull’ interferenza.
- Esercizi sulla diffrazione.
- Esercizi sulle proprietà corpuscolari e ondulatorie della materia.
Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.
Esercizi di Meccanica razionale
Se siete interessati ad approfondire argomenti inerenti alla Meccanica razionale, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.
Leggi...
Ulteriori risorse didattiche per la fisica
Leggi...
- Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
- ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
- Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
- Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
- The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
- American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
- Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
- Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
- Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
- Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.
