Login Abbonati
Accedi ai contenuti scaricabili
Qui si risolve LOGO
a

Menu

M

Chiudi

Teorema della permanenza del segno per le successioni

Teoria sulle Successioni

Home » Teorema della permanenza del segno per le successioni

Il teorema della permanenza del segno è un importante risultato della teoria dei limiti delle successioni che afferma che il segno del limite di una successione implica che, definitivamente, i termini della successione possiedono lo stesso segno. In questo articolo analizziamo il teorema e una sua generalizzazione, oltre a una sua versione contronominale, che però risulta utile esplicitare per l’utilizzo nelle applicazioni.

Oltre alle raccolte di esercizi

consigliamo gli articoli sulla teoria delle successioni, in particolare i seguenti:

Buona lettura!

 

 

Autori e revisori

Leggi...

Autore: Luigi De Masi, Martina Moro.

Revisori: Valerio Brunetti, Sergio Fiorucci.  

Teorema 1 (della permanenza del segno). Sia \{a_n\}_{n\in\mathbb{N}} una successione.

  1. Se \displaystyle \lim_{n \rightarrow +\infty} a_n=\ell>0, allora esiste N\in\mathbb{N} tale che a_n>0 per ogni n>N, ossia a_n>0 definitivamente.
  2. Se \displaystyle \lim_{n \rightarrow +\infty} a_n=\ell<0, allora esiste N\in\mathbb{N} tale che a_n<0 per ogni n>N, ossia a_n<0 definitivamente.

 

Il teorema stabilisce che, se il limite di una successione è strettamente positivo, allora la successione sarà definitivamente composta da termini positivi.

 
Dimostrazione. Mostriamo solo il caso \ell>0, in quanto l’altro caso è analogo o si ottiene, ad esempio, considerando la successione -a_n.

  • Caso \ell \in(0,+\infty). Consideriamo l’intorno I=\left(\ell-\frac{\ell}{2},\,\ell+\frac{\ell}{2}\right) di \ell; allora dalla definizione di limite di successione, esiste N tale che a_n\in I per ogni n>N, ovvero

    \begin{equation*} 0 < \ell-\frac{\ell}{2}<a_n<\ell+\frac{\ell}{2}\qquad \forall n>N. \end{equation*}

  • Caso \ell=+\infty. Consideriamo l’intorno I=(M,\,+\infty) con M>0 di \ell=+\infty; di nuovo grazie alla definizione di limite, esiste N\in\mathbb{N} tale che a_n\in I per ogni n>N, ovvero

    \begin{equation*} a_n>M>0\qquad \forall n>N. \end{equation*}

 

La prossima proposizione è una generalizzazione del teorema 1.

Proposizione 2. Sia a_n,b_n due successioni tali che a_n \to \ell_a e b_n \to \ell_b e supponiamo che \ell_a < \ell_b. Allora esiste N \in \mathbb{N} tale che

(1) \begin{equation*} a_n < b_n \qquad \forall n \geq N. \end{equation*}

 

Dimostrazione. Se \ell_b = + \infty e \ell_a=-\infty allora per definizione si ha definitivamente a_n < 0 < b_n, e la conclusione risulta ovvia. Nel caso in cui almeno uno dei limiti sia finito, consideriamo la successione b_n - a_n. Per le regole dell’algebra dei limiti si ha

(2) \begin{equation*} \lim_{n \to + \infty} (b_n - a_n) = \ell_b - \ell_a > 0. \end{equation*}

Per il teorema 1, b_n - a_n è definitivamente positivo, concludendo la dimostrazione.
 

La generalizzazione del teorema della permanenza del segno data dalla proposizione 2 si può enunciare anche nella forma equivalente seguente1, illustrata in figura 1.

Proposizione 3 (disuguaglianze al limite). Siano a_n,b_n due successioni tali che definitivamente valga a_n \leq b_n. Se a_n \to \ell_a e b_n \to \ell_b, allora si ha

(3) \begin{equation*} \ell_a \leq \ell_b. \end{equation*}

 
Dimostrazione. Se per assurdo fosse \ell_a > \ell_b, per la proposizione 2 si avrebbe a_n>b_n definitivamente, contro l’ipotesi a_n \leq b_n definitivamente.

 
 


 

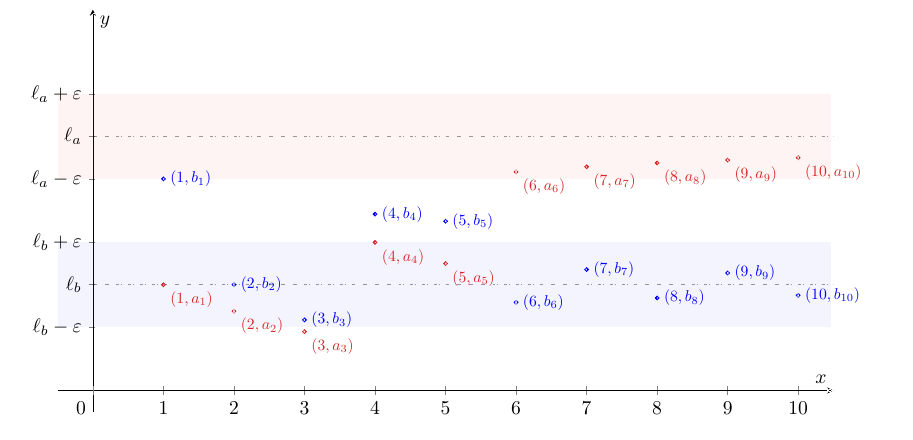
Figura 1: illustrazione della proposizione 3 nel caso \ell_a, \ell_b \in \mathbb{R}.

 
 

 
 

\[\]

  1. In logica, si dice che si tratta della contronominale della proposizione 2. ↩

 
 

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

  • Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.






Document