Login Abbonati
Accedi ai contenuti scaricabili
a

Menu

M

Chiudi

Teoremi del confronto per le successioni

Teoria sulle Successioni

Home » Teoremi del confronto per le successioni

I teoremi del confronto sono particolarmente utili nella teoria dei limiti: spesso infatti risulta arduo calcolare esplicitamente un limite, ma spesso ci si può ricondurre a confrontare, mediante disuguaglianze, il limite richiesto con altri limiti, più semplici da calcolare. In quest’ottica, i teoremi di confronto sono uno strumento essenziale da tenere presente nella risoluzione dei limiti.
In questo articolo presentiamo due versioni del teorema: una conosciuta con l’eloquente nome di “teorema dei carabinieri”, l’altra più specifica per limiti infiniti, per il quale occorrono ipotesi leggermente meno restrittive.

Oltre alle raccolte di esercizi

consigliamo gli articoli sulla teoria delle successioni, in particolare i seguenti:

Buona lettura!

 

 

Autori e revisori

Leggi...

Autore: Luigi De Masi, Martina Moro.

Revisori: Valerio Brunetti, Sergio Fiorucci.  


 

Il teorema del confronto è un principio fondamentale dell’Analisi Matematica che assume diverse forme a seconda del contesto. Esso permette di determinare il limite di una successione b_n confrontandola con altre due successioni a_n e c_n aventi lo stesso limite \ell e che la limitano dal basso e dall’alto. Conosciuto informalmente come il teorema dei due carabinieri, l’analogia descrive le successioni a_n e c_n come carabinieri che “convergono” verso lo stesso punto, costringendo necessariamente anche la successione b_n, il prigioniero, a fare altrettanto.

Teorema 1 (del confronto o dei carabinieri). Siano a_n, b_n, c_n successioni, si supponga che esista N_1\in\mathbb{N} tale che

(1)   \begin{equation*} a_n \leq b_n \leq c_n, \;\;\; \forall n \geq N_1 \end{equation*}

e che valga

    \[\lim_{n \to \infty} a_n = \lim_{n \to \infty} c_n = \ell \in \mathbb{R}.\]

Allora

    \[\lim_{n \to \infty} b_n = \ell .\]

 

Dimostrazione. Per dimostrare il teorema, consideriamo un qualsiasi \varepsilon > 0 e mostriamo che esiste N \in \mathbb{N} tale che \ell - \varepsilon \leq b_n \leq \ell + \varepsilon per tutti gli n \geq N. Fissato un \varepsilon arbitrario, dalla definizione di limite e dall’ipotesi che

    \[\lim_{n \to \infty} a_n = \lim_{n \to \infty} c_n = \ell \in \mathbb{R},\]

si deduce l’esistenza di due numeri naturali N_2 e N_3 tali che

(2)   \begin{equation*} \ell - \varepsilon \leq a_n \leq \ell + \varepsilon \quad \forall n \geq N_2, \quad \text{e} \quad \ell - \varepsilon \leq c_n \leq \ell + \varepsilon \quad \forall n \geq N_3. \end{equation*}

Scegliendo N = \max\{N_1, N_2, N_3\}, entrambe le condizioni (1) e (2) sono soddisfatte simultaneamente, quindi si ottiene

    \[\ell - \varepsilon \leq a_n \leq b_n \leq c_n \leq \ell + \varepsilon \quad \forall n \geq N,\]

completando così la dimostrazione.

 
 
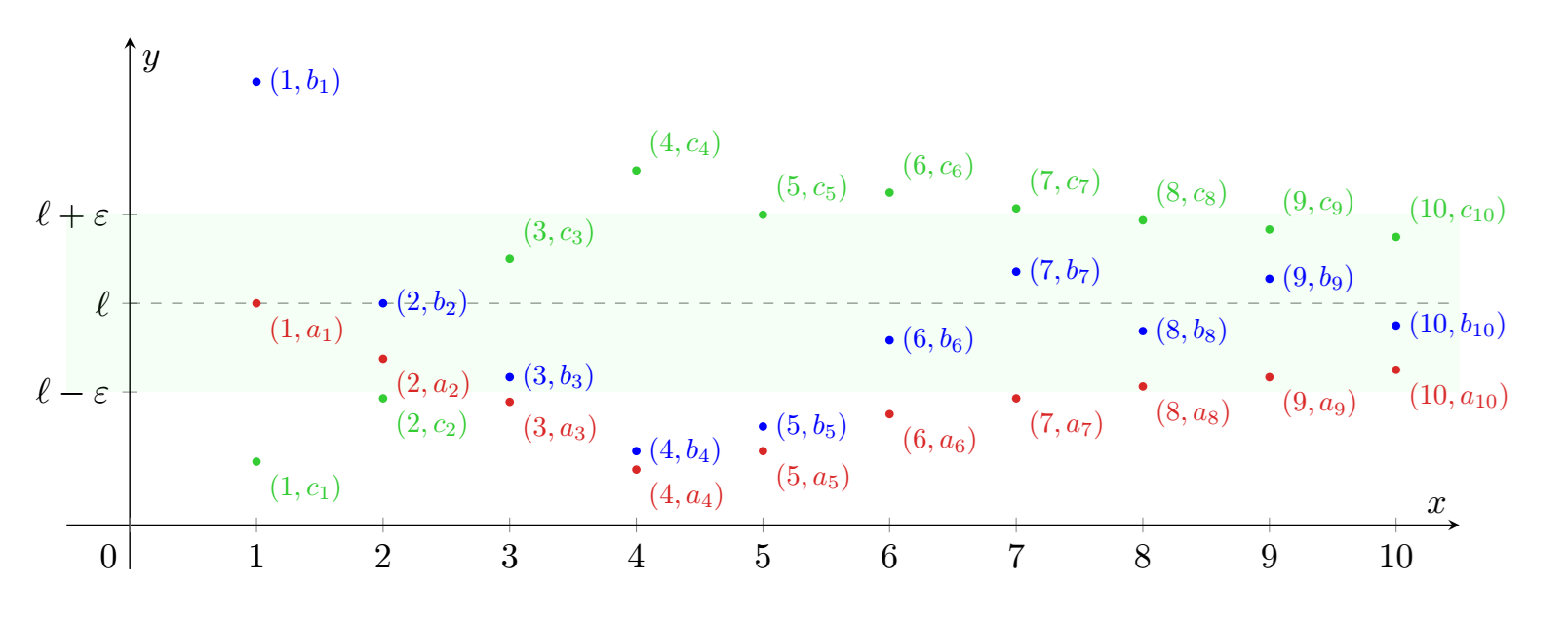
Teoremi del confronto

 

Figura 1: illustrazione del teorema 1. Le successioni a_n,b_n,c_n, rispettivamente in rosso, blu e verde, soddisfano a_n \leq b_n \leq c_n per ogni n \geq 3. Poiché per n \geq 8 vale a_n,c_n \in (\ell -\varepsilon,\ell+\varepsilon), allora anche b_n appartiene a tale intorno.

 
 

Esempio 2. Calcoliamo il seguente limite

    \[\lim_{n \rightarrow +\infty}\dfrac{\cos n}{n}.\]

Si ricorda che

    \[-1 \leq \cos n \leq 1\qquad \forall n \in \mathbb{N},\]

da cui

    \[- \frac{1}{n} \leq \frac{\cos n}{n} \leq \frac{1}{n}\qquad \forall n \in \mathbb{N}\setminus\{0\}.\]

Poiché

    \[\lim_{n \to \infty} - \frac{1}{n}= \lim_{n \to \infty} \frac{1}{n} = 0,\]

allora per il teorema 1, possiamo concludere che

    \[\lim_{n \to \infty} b_n = 0.\]

Il teorema 1 trova applicazione anche in situazioni dove il limite è infinito. In questi casi, è sufficiente limitare la successione da un solo “lato”.

 

Teorema 3 (del confronto: \ell=\pm \infty). Siano \{a_n\}_{n \in \mathbb{N}},\{b_n\}_{n \in \mathbb{N}} due successioni e supponiamo che esista N_1 \in \mathbb{N} tale che

(3)   \begin{equation*} a_n \leq b_n \qquad \forall n \geq N_1. \end{equation*}

  1. Se a_n \to +\infty, allora b_n \to + \infty.

  2. Se b_n \to - \infty, allora a_n \to - \infty.

 
In altre parole, se b_n è limitata dal basso da una successione divergente a +\infty, allora anch’essa diverge a +\infty; analogamente se a_n è limitata dall’alto da una successione divergente a -\infty, allora anch’essa diverge a -\infty.
 

Dimostrazione. Mostriamo solo il caso 1, in quanto il caso 2 si prova in modo simile oppure può essere ottenuto considerando le successioni -b_n, -a_n.

Si fissi M \in \mathbb{R}. Poiché a_n \to + \infty, esiste N \geq N_1 tale che a_n \geq M per ogni n \geq N. Per (3) si ha

(4)   \begin{equation*} b_n \geq a_n \geq M \qquad \forall n \geq N, \end{equation*}

ossia, per l’arbitrarietà di M, abbiamo che b_n \to + \infty.

 
 

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

  • Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.






Document