In questo articolo è disponibile per il download un approfondimento specialistico sul teorema fondamentale del calcolo integrale, composto da 18 pagine. I concetti di derivata e di integrale sono profondamente correlati, nonostante il loro legame non sia evidente a un primo sguardo. Infatti, mentre la derivata corrisponde all’idea intuitiva di “tasso di variazione infinitesimale” di una funzione, il concetto di integrale corrisponde a quello di “area sottesa al grafico” di una funzione. Si può però vedere che le operazioni di derivazione e di integrazione sono l’una inversa dell’altra, in un senso che viene precisato dal teorema fondamentale del calcolo integrale: sotto opportune ipotesi, la derivata in della funzione integrale è pari a e, viceversa, l’integrale della derivata è pari a .

Questo articolo è dedicato a uno studio profondo ma chiaro dei precedenti risultati, trattando i seguenti argomenti:

• Definizione di primitiva di una funzione, sue proprietà e condizioni necessarie per l’esistenza di primitive;
• Prima parte del teorema fondamentale del calcolo integrale: la funzione integrale di una funzione continua è una sua primitiva;
• Seconda parte del teorema fondamentale del calcolo integrale: la funzione integrale della derivata è pari a a meno di una costante.

Ogni teorema viene motivato da domande introduttive e illustrato da esempi e controesempi di difficile reperibilità che chiariscono il ruolo delle ipotesi. Nel testo vengono inoltre proposti esercizi le cui soluzioni sono raccolte alla fine del volume.
Il testo, scritto con precisione meticolosa e chiarezza didattica, è quindi un’utile risorsa formativa e un’avventura appassionante nel cuore del calcolo integrale. Buona lettura!
 

Teorema fondamentale del calcolo integrale: introduzione

Leggi...

Lo scopo di questa dispensa è analizzare il teorema fondamentale del calcolo integrale, che lega l’esistenza di primitive di una certa funzione a proprietà della sua funzione integrale. Questi risultati si sentono spesso riassumere nella frase “l’integrazione è l’operazione inversa della derivazione”. Ci accingiamo a studiare sotto quali ipotesi vale precisamente questa sorta di invertibilità e quali assunzioni, invece, non bastano per ottenerla.

I risultati principali di questo lavoro sono il teorema 4.1 e il teorema 5.2, costituenti la prima e la seconda parte del famoso teorema fondamentale del calcolo integrale:

   

1. Il teorema 4.1 afferma che la derivata della funzione integrale di una funzione continua è pari a ;

 

2. Il teorema 5.2 afferma che l’integrale della derivata di una funzione derivabile è pari a (a meno di una costante).

Il lavoro è così organizzato:

   

Seconda sezione

• Vengono richiamate le definizioni fondamentali utili nel seguito.

 

Terza sezione

• Viene presentata una prima proprietà delle primitive di una funzione fissata: esse differiscono per una costante. Nella sezione 3.1 viene presentato il teorema di Darboux il quale garantisce che la derivata di una funzione in un intervallo assume tuttTi i valori compresi tra e ; ciò implica che, affinché una funzione ammetta una primitiva, deve soddisfare tale proprietà, detta dei valori intermedi.

 

Sezione 4

• Viene studiata la questione dell’uguaglianza tra una funzione e la derivata della sua funzione integrale. Viene presentato il teorema 4.1, che afferma che, se è una funzione continua, allora la sua funzione integrale è derivabile e la sua derivata è proprio pari a ; si tratta, quindi, di un teorema di esistenza di primitive: una funzione continua ammette come primitiva la sua funzione integrale.

  Quarta sezione

  Analizziamo alcuni esempi che mostrano come non sia in generale possibile, rinunciando all’ipotesi di continuità, ottenere come derivata della sua funzione integrale.

 

Quinta sezione

• Presentiamo il secondo risultato principale della dispensa: il teorema 5.2; esso afferma che, se una funzione è derivabile e la sua derivata è integrabile, allora la funzione integrale di differisce da per una costante: più precisamente, vale la nota formula 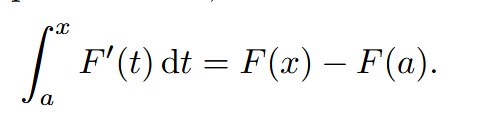Nella sezione 5.1 utilizziamo questo risultato per rispondere a una questione posta nella sezione 4.1, costruendo un ulteriore controesempio all’esistenza di primitive di una certa funzione.

Teorema fondamentale del calcolo integrale: argomenti teorici correlati

Consigliamo la lettura del seguente materiale teorico su argomenti correlati:

• Integrali definiti e indefiniti;
• Teoria sugli integrali impropri;
• Funzioni integrali – Teoria;
• Integrali ricorsivi

Teorema fondamentale del calcolo integrale: ulteriori esercizi connessi

Segnaliamo anche le seguenti raccolte di esercizi:

• Esercizi integrali definiti;
• Esercizi misti sugli integrali indefiniti;
• Esercizi sugli integrali impropri – 1
• Esercizi sugli integrali impropri – 2.