Studio di funzione: esercizi misti

Studio di funzione completo nel calcolo differenziale

Home » Studio di funzione: esercizi misti

Benvenuti nella nostra raccolta di esercizi sullo studio di funzione! In questo articolo presentiamo 24 esercizi su questo importante argomento, alcuni dei quali multipli, per un totale di 41 studi di funzione completamente svolti. Il materiale permette un approfondito studio di questo argomento, summa del programma svolto nei corsi di Analisi Matematica 1, ed è quindi particolarmente indicato per studenti universitari e appassionati.

Consigliamo il materiale teorico di riferimento:

Segnaliamo inoltre alcune raccolte di esercizi su argomenti affini:

Buona lettura!

Esercizi sullo studio di funzione: Sommario

Leggi...

Questo file contiene una raccolta ampia di esercizi dedicati allo studio di funzioni. Gli esercizi sono organizzati in ordine di difficoltà crescente, partendo da funzioni base fino ad arrivare ad espressioni più complesse. Ogni esercizio è seguito da una soluzione dettagliata. Questo materiale è ideale per studenti universitari che necessitano prepararsi per esami di analisi matematica.

Autori e revisori

Leggi...

Autori: Valerio Brunetti, Donato Ciampa, Francesco Paolo Maiale.

Revisori: Sara Sottile, Sergio Fiorucci.

Esercizi

$\quad$

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\frac{x^2-4x+3}{x-5}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità e flessi. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio della funzione è dato da tutti i numeri reali eccetto il valore che annulla il denominatore, ovvero:

$D = \mathbb{R} \setminus \{5\}$

Intersezioni con gli assi
$\quad$
- Asse x: Poniamo $f(x) = 0$ :
  $\frac{x^2 - 4x + 3}{x - 5} = 0$
  
  Il numeratore si fattorizza come $(x-3)(x-1)$ , quindi le intersezioni con l’asse $x$ sono $A=(3,0)$ e $B=(1,0)$ .
- Asse y: Calcoliamo $f(0)$ :
  $f(0) = \frac{0^2 - 4 \cdot 0 + 3}{0 - 5} = -\frac{3}{5}$
  
  L’intersezione con l’asse $y$ è pertanto $C=(0, -\frac{3}{5})$

Studio del segno La funzione è positiva quando numeratore e denominatore hanno lo stesso segno:

$\quad$
- $(x-3)(x-1) > 0$ e $(x-5) > 0$ , cioè per $x > 5$
- $(x-3)(x-1) < 0$ e $(x-5) < 0$ , cioè per $1 < x < 3$
Quindi $f(x) > 0$ per $x \in (1,3) \cup (5,+\infty)$ . Questo lo si può vedere anche graficamente con il seguente schema di studio del segno:

$\quad$

$\quad$

$\quad$

Continuità e derivabilità La funzione è continua e derivabile su tutto il suo dominio, essendo il rapporto di due polinomi.

Asintoti
$\quad$
- Asintoto orizzontale: Dato che
  $\lim_{x\to\pm\infty}f(x)=\lim_{x\to\pm\infty}\dfrac{x^2-4x+3}{x-5}=\lim_{x\to\pm\infty}\dfrac{x^2\left(1-\dfrac{4}{x}+\dfrac{3}{x^2}\right)}{x}=\lim_{x\to\pm\infty}x\left(1-\dfrac{4}{x}+\dfrac{3}{x^2}\right)=\pm\infty$
  
  la funzione $f(x)$ non ha alcun asintoto orizzontale.
- Asintoto verticale: $\lim_{x \to 5^\pm} f(x) = \pm\infty$ , quindi $x = 5$ è un asintoto verticale.
- Asintoto obliquo: Calcoliamo:
  
  $m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{x^2 - 4x + 3}{x(x-5)} = 1$
  
  $q = \lim_{x \to \pm\infty} [f(x) - mx] = \lim_{x \to \pm\infty} \left[\frac{x^2 - 4x + 3}{x-5} - x\right] = 1$
  
  L’equazione dell’asintoto obliquo è quindi $y = x + 1$ .

Massimi e minimi Calcoliamo la derivata prima:

$f'(x) = \frac{(2x-4)(x-5) - (x^2-4x+3)}{(x-5)^2} = \frac{x^2 - 10x + 17}{(x-5)^2}$

Poniamo $f'(x) = 0$ :

$x^2 - 10x + 17 = 0 \iff x_{1,2} = \frac{10 \pm \sqrt{100- 4 \cdot 17}}{2} = 5 \pm \sqrt{32},$

pertanto le soluzioni sono $x_{1,2} = 5 \pm 2\sqrt{2}$ . Il denominatore della derivata è positivo, perciò il segno di $f'$ dipende solo dal numeratore:

$\quad$
- Nell’intervallo $(5-2\sqrt 2,5 + 2 \sqrt 2)$ la derivata è negativa, dunque la funzione è decrescente.
- In $(-\infty,5-2\sqrt 2) \cup (5 + 2 \sqrt 2, \infty)$ la derivata è positiva, dunque la funzione è crescente.
Di conseguenza, in $x=5-2\sqrt 2$ abbiamo un massimo relativo

$f(5-2\sqrt{2}) = 6-4\sqrt{2},$

mentre in $x = 5 + 2\sqrt{2}$ abbiamo un minimo relativo:

$f(5+2\sqrt{2}) = 6+4\sqrt{2}.$

Notiamo che questi sono punti di massimo e minimo relativi perché nella ricerca di asintoti orizzontali abbiamo mostrato che

$\sup_{x\in D} f(x) = + \infty \quad \text{and} \quad \inf_{x \in D}f(x) =-\infty.$

Flessi Calcoliamo la derivata seconda:

$f''(x) = \frac{16}{(x-5)^3}$

Questa non si annulla mai, quindi non ci sono flessi. Dallo studio del segno del denominatore, segue che la funzione è concava per $x < 5$ e convessa per $x > 5$ .

Grafico
$\quad$

$\quad$

$\quad$

Osservazioni sul grafico: Il grafico della funzione mostra:

$\quad$
- Due intersezioni con l’asse $x$ in (1,0) e (3,0)
- Un’intersezione con l’asse $y$ in (0,-3/5)
- Un asintoto verticale in $x=5$ (in rosso)
- Un asintoto obliquo $y = x + 1$ (in verde)
- Un massimo relativo prima dell’asintoto verticale $M$
- Un minimo relativo dopo l’asintoto verticale $m$
- La funzione è concava a sinistra dell’asintoto verticale e convessa a destra

Esercizio 2 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\log \lvert x^2-8x+16\rvert.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il logaritmo richiede che l’argomento sia positivo. Osserviamo che:

$x^2-8x+16 = (x-4)^2 \ge 0$

per ogni $x \in \mathbb R$ . Di conseguenza, il modulo si può togliere

$| x^2-8x+16|=|(x-4)|^2=(x-4)^2.$

A questo punto, si deduce che $D=\mathbb{R}\setminus \{4\}$ dato che l’argomento del logaritmo è sempre non-negativo e si annulla solo in $x=4$ . Inoltre, usando le proprietà del logaritmo troviamo che

$\log \left[(x-4)^2\right] = 2 \log|x-4|,$

espressione per $f(x)$ che semplifica notevolmente i conti da fare per lo studio di funzione.

Intersezioni con gli assi
$\quad$
- Asse x: Poniamo $f(x) = 0$ :
  $2 \log |x-4| = 0 \iff |x-4| = 1$
  
  utilizzando il fatto che $\mathrm{e}^{\log y} = y$ . A questo punto possiamo risolvere sviluppando il modulo
  
  $|x-4|=1 \iff x - 4 = 1 \text{ oppure } x-4=-1 \iff x = 5 \text { oppure } x = 3$
  
  Le intersezioni con l’asse $x$ sono pertanto $A=(3,0)$ e $B=(5,0)$ .
- Asse y: Calcoliamo $f(0)$ :
  $f(0) = 2 \log(|0-4|) = 2 \log 4 = 4 \log 2$
  
  L’intersezione con l’asse $y$ è $C=(0, 4\log 2)$ .

Positività La funzione è positiva quando l’argomento del logaritmo è maggiore di uno, ovvero $|x-4| > 1$ . Togliendo il modulo si arriva alle disuguaglianze

$\begin{aligned} & x-4 > 1 & \implies x > 5 \\ & x - 4 < - 1 & \implies x < 3 \end{aligned}$

Quindi $f(x) > 0$ per $x \in (-\infty, 3) \cup (5,+\infty)$ ed $f(x)<0$ per $x \in (3,4)\cup(4,5)$ .

Continuità e derivabilità La funzione è continua e derivabile con derivata continua nel suo dominio. Questo è facile da vedere perché abbiamo una composizione

$\log(x) \circ |x-4|$

tra logaritmo e valore assoluto di un polinomio. Si noti che la funzione $h(y)=|y|$ è derivabile ovunque tranne che in $y=0$ ; nel nostro caso, il punto che annulla l’argomento del logaritmo è escluso dal dominio (i.e., $x\neq 4$ )

Asintoti
$\quad$
- Asintoti verticali:
  $\lim_{x \to 4^\pm} f(x) = \lim_{x \to 4^\pm} \log(x-4)^2 = -\infty$
  
  Quindi $x = 4$ è un asintoto verticale.
- Asintoti orizzontali:
  $\lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} \log(x-4)^2 = +\infty$
  
  Non esistono asintoti orizzontali.
- Asintoti obliqui:
  $m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{\log(x-4)^2}{x} = 0$
  
  Poiché $m = 0$ , non esistono asintoti obliqui.

Massimi e minimi Calcoliamo la derivata prima:

$f'(x) = \frac{2}{x-4}$

La derivata non si annulla mai nel dominio, quindi non ci sono massimi o minimi relativi. Dallo studio dei limiti, $\sup f(x) = +\infty$ e $\inf f(x) = -\infty$ , quindi non ci sono massimi o minimi assoluti.

Flessi e convessità Calcoliamo la derivata seconda:

$f''(x) = -\frac{2}{(x-4)^2}$

$f''(x)$ è sempre negativa nel dominio, quindi la funzione è sempre concava e non ha punti di flesso.

Grafico
$\quad$

$\quad$

$\quad$

Osservazioni sul grafico: Il grafico della funzione mostra:

$\quad$
- Due intersezioni con l’asse $x$ in (3,0) e (5,0)
- Un’intersezione con l’asse $y$ in $(0, 4\log 2)$
- Un asintoto verticale in $x=4$ (in rosso)
- La funzione tende a $+\infty$ per $x \to \pm\infty$
- La funzione è sempre concava
- La funzione è simmetrica rispetto alla retta $x=4$

Si noti che la simmetria rispetto ad $x=4$ non è stata studiata nello svolgimento dell’esercizio, ma è banale dato che

$f(x+4) = 2 \log |x|$

e la funzione $\log|x|$ è ovviamente pari e simmetrica rispetto l’origine. In particolare, lo studio di funzione si poteva svolgere limitandosi all’intervallo

$D_+ = (4,+\infty)$

per poi estendere i risultati ottenuti per simmetria (pari) rispetto l’origine.

Esercizio 3 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=e^\frac{2x-1}{x^2}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è $D=\mathbb{R}\setminus \{0\}$ dato che il denominatore dell’esponente si annulla in $x=0$ .

Intersezioni con gli assi
$\quad$
- Asse x: L’esponenziale è sempre positivo, quindi non ci sono intersezioni con l’asse $x$ .
- Asse y: $x=0$ non appartiene al dominio, quindi non c’è intersezione con l’asse $y.$

Positività L’esponenziale è una funzione sempre positiva, quindi $f(x)>0$ per ogni $x\in D$ .

Continuità La funzione è continua su tutto il suo dominio, essendo la composizione di due funzioni continue.

Asintoti
$\quad$
- Asintoto verticale:
  $\lim_{x \to 0^\pm} f(x) = \exp\left(\lim_{x \to 0^\pm} \frac{2x-1}{x^2}\right) = e^{-\infty} = 0$
  
  Quindi $x=0$ non è un asintoto verticale, ma un punto in cui la funzione può essere prolungata con continuità¹.
- Asintoto orizzontale:
  $\lim_{x \to \pm\infty} f(x) = \exp\left(\lim_{x \to \pm\infty} \frac{2x-1}{x^2}\right) = e^0 = 1$
  
  Quindi $y=1$ è un asintoto orizzontale.

Massimi e minimi Calcoliamo la derivata prima:

$f'(x) = \frac{e^{\frac{2x-1}{x^2}}(-2x+2)}{x^3}$

Studiamo il segno di $f'(x)$ :

$\quad$

$\quad$

$\quad$

La derivata cambia segno, passando da positiva a negativa, in un intorno di $x=1$ , dunque $x=1$ è un punto di massimo relativo (e assoluto) dove $f(1)=e$ .

Flessi e convessità Calcoliamo la derivata seconda:

$f''(x) = \frac{e^{\frac{2x-1}{x^2}} (4x^3- 2x^2 - 8x +4)}{x^6}$

Il segno di $f''(x)$ dipende esclusivamente dal polinomio a numeratore, in quanto il termine esponenziale e il denominatore sono sempre positivi nel dominio. Il polinomio si fattorizza come $2(2x-1)(x^2-2)$ , per cui facendo lo studio del segno si ha:

$\quad$

$\quad$

$\quad$

La funzione è concava in $(-\infty, -\sqrt{2}) \cup (\frac{1}{2},\sqrt{2})$ e convessa altrove. I punti di flesso sono:

$\begin{aligned} B &\equiv \left(-\sqrt{2}, e^{\frac{-2\sqrt{2}-1}{2}}\right) \\ C &\equiv \left(\frac{1}{2}, 1\right) \\ D &\equiv \left(\sqrt{2}, e^{\frac{2\sqrt{2}-1}{2}}\right) \end{aligned}$

Grafico
$\quad$

$\quad$

$\quad$

Osservazioni conclusive: Il grafico della funzione mostra:

$\quad$
- Nessuna intersezione con gli assi
- Un asintoto orizzontale $y=1$ per $x \to \pm\infty$ (in verde)
- Un punto di massimo assoluto in $(1,e)$
- Tre punti di flesso
- La funzione tende a 0 per $x \to 0^\pm$

Diciamo che una funzione $f(x)$ presenta una discontinuità eliminabile in un punto $x = x_0$ se esistono il limite $\lim_{x \to x_0} f(x)$ finito e assume un valore diverso da $\lim_{x \to x_0} f(x)$ . In tal caso, è possibile eliminare la discontinuità ridefinendo la funzione come segue:

$\tilde f(x) =\begin{cases} f(x) & \text{se } x \neq x_0 \\ \lim_{x \to x_0} f(x) & \text{se } x = x_0 \end{cases}$

In questo modo, la funzione diventa continua in $x = x_0$ , ovvero la discontinuità è stata eliminata. ↩

Esercizio 4 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=e^{\tan(x)}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio di $f$ corrisponde al dominio della funzione $\tan(x)$ , che risulta essere $D=\{x \in \mathbb{R}: x \ne \frac{\pi}{2} + \pi k \text{ con } k \in \mathbb{Z}\}$ .

Intersezioni con gli assi
$\quad$
- Asse x: Non esistono intersezioni con l’asse $x$ poiché $e^x > 0$ per ogni $x \in \mathbb{R}$ .
- Asse y: $f(0) = e^{\tan(0)} = e^0 = 1$ . L’intersezione è data dal punto $A = (0,1)$ .

Positività La funzione $f$ è sempre positiva su tutto il suo dominio, come menzionato in precedenza.

Continuità La funzione è continua in tutto il suo dominio $D$ essendo composizione di funzioni continue (esponenziale e tangente).

Periodicità e Asintoti
$\quad$
- Periodicità: La funzione ha periodo minimo pari a $\pi$ . Infatti, si ha
  $f(x+\pi) = e^{\tan(x+\pi)} = e^{\tan(x)} = f(x).$
- Asintoti orizzontali e obliqui: Non esistono, poiché $\lim_{x \to \pm\infty} f(x)$ non esiste. Infatti, dato che la funzione
  $h(x)= \tan(x)$
  
  oscilla per $x \to \pm \infty$ e, in particolare, ha asintoti verticali nei punti $x_k = \pi/2 + k\pi$ , tende alternativamente a $+\infty$ e $-\infty$ ogni volta che $x$ si avvicina a questi punti. Per dimostrare formalmente che il limite
  
  $\lim_{x \to +\infty} e^{\tan(x)}$
  
  non esiste, è sufficiente fornire due sotto-successioni che portano a limiti diversi:
  
  $\begin{aligned} & x_{n_k} = \frac{\pi}{2} + 2k\pi & \implies \lim_{k \to \infty} e^{\tan(x_{n_k})} = +\infty \\ & x_{m_k} = -\frac{\pi}{2} + 2k\pi & \implies \lim_{k \to \infty} e^{\tan(x_{m_k})} = 0 \end{aligned}$
  
  Un discorso analogo si può fare per il limite $\lim_{x \to - \infty}f(x)$ .
- Asintoti verticali: Calcoliamo i limiti per $x \to \frac{\pi}{2}^\pm$ :
  $\lim_{x \to \frac{\pi}{2}^+} f(x) = e^{-\infty} = 0$
  
  $\lim_{x \to \frac{\pi}{2}^-} f(x) = e^{+\infty} = +\infty$
  
  Per la periodicità di $f$ , $x = \frac{\pi}{2} + k\pi$ è asintoto verticale per ogni $k \in \mathbb{Z}$ .

Massimi e minimi Calcoliamo la derivata prima:

$f'(x) = e^{\tan(x)} \cdot \frac{1}{\cos^2(x)}$

Poiché $f'(x) > 0$ per ogni $x \in D$ , la funzione $f$ è monotona crescente su tutto il suo dominio. Dai limiti calcolati, abbiamo che $\sup f = +\infty$ e $\inf f = 0$ .

Flessi e convessità Calcoliamo la derivata seconda:

$f''(x) = e^{\tan(x)} \frac{1+2\sin x\cos(x)}{\cos^4(x)} = e^{\tan(x)} \frac{1+\sin(2x)}{\cos^4(x)}$

Il segno di $f''(x)$ è determinato da $1+\sin(2x)$ . Poiché $\sin(2x) \ge -1$ per ogni $x$ , abbiamo che $f''(x) \ge 0$ per ogni $x \in D$ . Di conseguenza, $f$ è convessa su tutto il suo dominio $D$ .

Grafico
$\quad$

$\quad$

Osservazioni conclusive: Il grafico della funzione mostra:

$\quad$
- Periodicità con periodo $\pi$
- Asintoti verticali in $x = \frac{\pi}{2} + k\pi$ , $k \in \mathbb{Z}$ (in verde)
- Monotona crescente tra due asintoti consecutivi
- Convessità su tutto il dominio
- Intersezione con l’asse $y$ nel punto $(0,1)$

Esercizio 5 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\sqrt{\log \lvert x-3 \rvert}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio della funzione è dato da:

$\begin{cases} \log|x-3| \geq 0 \\ |x-3| > 0 \end{cases} \quad \iff \quad \begin{cases} |x-3| \geq 1 \\ x \neq 3 \end{cases} \quad \iff \quad x \leq 2 \quad \text{o} \quad x \geq 4$

Quindi, $D = (-\infty, 2] \cup [4, +\infty)$ .

Intersezioni con gli assi
$\quad$
- Asse x: Si ha
  $\sqrt{\log|x-3|} = 0 \iff \log|x-3| = 0 \iff |x-3| = 1,$
  
  che ha soluzioni $x=2$ ed $x=4$ ; perciò, i punti di intersezione sono $A=(2,0)$ e $B=(4,0)$ .
- Asse y: dato che
  $f(0) = \sqrt{\log|-3|} = \sqrt{\log 3},$
  
  il punto di intersezione con l’asse y è $C=(0,\sqrt{\log 3})$ .

Positività La funzione è sempre non negativa su tutto il suo dominio $D$ .

Continuità La funzione è continua su tutto il dominio $D$ essendo composizione di funzioni continue (modulo, logaritmo e radice).

Asintoti
$\quad$
- Asintoti verticali: Non esistono, essendo la funzione continua, rispettivamente da sinistra e da destra, anche negli estremi x=2 e x=4 del dominio:
  $\begin{aligned} & \lim_{x \to 2^-} f(x) = \sqrt{ \log 1^+ } = 0 \\ & \lim_{x \to 4^+} f(x) = \sqrt{ \log 1^+ } = 0 \end{aligned}$
- Asintoti orizzontali e obliqui: Usando la continuità della radice e del logaritmo per $x$ in un intorno di $\infty$ , passiamo il limite dentro:
  $\lim_{x \to \pm\infty} f(x) = \sqrt{\log\lim_{x \to \pm\infty}|x-3|} = \sqrt{\log(+\infty)} = +\infty$
  
  Non esistono asintoti orizzontali. In realtà, non ci sono neanche asintoti obliqui dato che
  
  $\lim_{x \to \pm \infty} \frac{f(x)}{x} = 0$
  
  è una banale conseguenza del fatto che il logaritmo va ad infinito più lentamente di ogni polinomio e, pertanto, anche della funzione $h(x)=x$ .

Derivata prima e monotonia Si ha
$f'(x) = \frac{1}{2(x-3)\sqrt{\log|x-3|}}$

Studio del segno di $f'(x)$ :

$\quad$

$\quad$

La funzione è decrescente in $(-\infty,2)$ e crescente in $(4,+\infty)$ . Conseguentemente, i punti $x=2$ e $x=4$ sono di minimo assoluto.

Derivabilità in $x=2$ e $x=4$
$\quad$
- In $x=2$ : $\lim_{h \to 0^-} \frac{f(2+h)-f(2)}{h} = -\infty$
- In $x=4$ : $\lim_{h \to 0^+} \frac{f(4+h)-f(4)}{h} = +\infty$
La funzione non è derivabile in $x=2$ e $x=4$ , e il grafico ha tangenti verticali in questi punti.

Derivata seconda e convessità
$f''(x) = \frac{-2\log|x-3| -1}{4(x-3)^2 \log^{\frac{3}{2}}|x-3|}$

Il denominatore è sempre positivo dove è definito, quindi per lo studio del segno di $f''(x)$ consideriamo soltanto il numeratore:

$2 \log |x-3| + 1 \leq 0 \iff \log |x-3| \leq -\dfrac{1}{2} \iff |x-3| \leq e^{-\frac{1}{2}} \iff 3- e^{-\frac{1}{2}}\leq x \leq 3+ e^{-\frac{1}{2}}.$

Graficamente, considerando il dominio di $f''$ si ha:

$\quad$

$\quad$

$\quad$

La funzione è concava su tutto il suo dominio.

Grafico
$\quad$

$\quad$

Esercizio 6 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\log \left(\frac{x-3}{x+4}\right).$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio La condizione di esistenza del logaritmo richiede che il suo argomento sia positivo:

$\frac{x-3}{x+4} > 0$

Lo studio del segno porta al seguente diagramma:

$\quad$

$\quad$

$\quad$

Quindi, il dominio è $D = (-\infty, -4) \cup (3, +\infty)$ .

Intersezioni con gli assi
$\quad$
- Asse x: Non esistono intersezioni con l’asse $x$ , poiché
  $\log\left(\dfrac{x-3}{x+4}\right)= 0 \iff \dfrac{x-3}{x+4} = 1 \iff -3 = -4$
  
  che è ovviamente una uguaglianza falsa.
- Asse y: Non esistono intersezioni con l’asse $y$ , poiché $x=0$ non appartiene al dominio $D$ .

Positività La funzione è positiva quando l’argomento del logaritmo è maggiore di uno:

$\frac{x-3}{x+4} > 1 \quad \iff \quad \frac{-7}{x+4} > 0.$

Il numeratore è sempre negativo, perciò $f(x) > 0$ vale per $x \in (-\infty, -4)$ .

Continuità La funzione $f$ è continua su tutto il suo dominio $D$ essendo composizione di funzioni continue.

Asintoti
$\quad$
- Asintoti verticali:
  $\lim_{x \to 3^+} f(x) = -\infty \quad \text{e} \quad \lim_{x \to -4^-} f(x) = +\infty$
  
  Quindi, $x=3$ e $x=-4$ sono asintoti verticali.
- Asintoto orizzontale:
  $\lim_{x \to \pm\infty} f(x) = \log(1) = 0$
  
  Quindi, $y=0$ è un asintoto orizzontale.

Derivata prima e monotonia Si ha
$f'(x) = \frac{7}{(x-3)(x+4)}.$

Il segno di $f'(x)$ è determinato da $(x-3)(x+4)$ , che è positivo in $(-\infty, -4) \cup (3, +\infty)$ , coincidente con il dominio $D$ . In particolare:

$\quad$
- $f$ è crescente su tutto il suo dominio;
- $f$ non ammette massimi o minimi relativi.

Derivata seconda e convessità Si ha
$f''(x) = \frac{-7(2x+1)}{(x-3)^2(x+4)^2}$

Il denominatore è prodotto di termini positivi, quindi il segno di $f''(x)$ è determinato dal numeratore $-7(2x+1)$ . In particolare, otteniamo:

$\quad$
- $f''(x) > 0$ per $x < -\frac{1}{2}$
- $f''(x) < 0$ per $x > -\frac{1}{2}$
Tuttavia, $x = - 1/2$ non appartiene a $D$ , quindi non ci sono flessi. Intersecando gli intervalli ottenuti con il dominio, deduciamo che la funzione è convessa per $x < -4$ e concava per $x > 3$ .

Grafico
$\quad$

$\quad$

Esercizio 7 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\sqrt{\frac{x^3-1}{x}}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è dato dall’argomento della radice non-negativo ( $\frac{x^3-1}{x} \geq 0$ ) ed il denominatore diverso da zero ( $x \neq 0$ ). Lo studio del segno porta al seguente diagramma:

$\quad$

$\quad$

$\quad$

Quindi, il dominio è $D = (-\infty, 0) \cup [1, +\infty)$ .

Intersezioni con gli assi
$\quad$
- Asse x: Si noti che $f(x) = 0$ se e solo se $x^3 - 1=0$ , che ha come unica soluzione $x=1$ . Di conseguenza, $A=(1,0)$ è l’unico punto di intersezione con l’asse x.
- Asse y: Non ci sono intersezioni con l’asse $y$ poiché $0 \notin D$ .

Positività La funzione è sempre non negativa su tutto il suo dominio $D$ .

Continuità La funzione è continua su tutto il dominio $D$ essendo composizione di funzioni continue.

Asintoti
$\quad$
- Asintoto verticale: $\lim_{x \to 0^-} f(x) = +\infty$ , quindi $x=0$ è un asintoto verticale.
- Asintoti orizzontali: Si osserva facilmente che
  $\lim_{x \to \pm \infty} \sqrt{\frac{x^3-1}{x}} = \lim_{x \to \pm \infty} \sqrt{x^2} = + \infty,$
  
  quindi non esistono asintoti orizzontali.
- Asintoti obliqui: Iniziamo con il caso $+ \infty$ . Il coefficiente angolare è
  $m_+ = \lim_{x \to + \infty} \frac{f(x)}{x} = \lim_{x \to + \infty} \frac{|x|}{x} = 1,$
  
  dove abbiamo usato l’identità $\sqrt{x^2} = |x|$ . Segue che
  
  $q_+ = \lim_{x \to + \infty}( f(x) - m_+ x )= \lim_{x \to + \infty}( |x|-x) = 0,$
  
  quindi $y = x$ è asintoto obliquo per $x \to + \infty$ . Nel caso $- \infty$ si possono seguire gli stessi conti, osservando che
  
  $m_- = \lim_{x \to - \infty} \frac{|x|}{x} = -1 \quad \text{e} \quad q_- = 0,$
  
  da cui segue che $y=-x$ è asintoto obliquo per $x \to - \infty$ .

Derivata prima e monotonia
$f'(x) = \frac{2x^3+1}{2x^2} \sqrt{\frac{x}{x^3-1}}$

Il radicale e $2x^2$ sono entrambi termini non-negativi in $D\setminus\{1\}$ , perciò il segno di $f'$ corrisponde a quello di $2x^3+1$ . Si ha

$2x^3+1 > 0 \iff x^3 > - \frac12 \iff x > -\frac{1}{2^{1/3}}.$

Dunque, intersecando con il dominio, la funzione risulta decrescente per $x < -\frac{1}{2^{1/3}}$ e crescente per $-\frac{1}{2^{1/3}} < x < 0$ e $x > 1$ . Il punto di minimo relativo è $x = -\frac{1}{2^{1/3}}$ con $f(-\frac{1}{2^{1/3}}) = \frac{\sqrt{3}}{\sqrt[3]{2}}$ . Poiché

$f(1) = 0,$

segue che $(1,0)$ è il punto di minimo assoluto.

Derivata seconda e convessità
$f''(x) = \sqrt{\frac{x^3-1}{x}}\left(\frac{-12x^3+3}{4x^2(x^3-1)^2}\right)$

Il segno di $f''(x)$ è determinato da $-12x^3+3$ . La funzione è convessa per $x > \frac{1}{2^{2/3}}$ e concava per $x < \frac{1}{2^{2/3}}$ . Poiché $\frac{1}{2^{2/3}} \notin D$ , non ci sono punti di flesso.

Grafico
$\quad$

$\quad$

$\quad$

Osservazioni conclusive:

$\quad$
- Un asintoto verticale in $x=0$ (in rosso)
- Asintoti obliqui $y=x$ per $x \to +\infty$ e $y=-x$ per $x \to -\infty$ (in verde)
- Un punto di minimo relativo per $x = - 2^{-1/3}$ ( $m_r$ )
- Un punto di minimo assoluto in $m=(1,0)$
- Concavità che cambia, ma senza punti di flesso nel dominio

Esercizio 8 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=e^{3x} + e^{\lvert x \rvert}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è $D=\mathbb{R}$ , poiché sia il valore assoluto che l’esponenziale sono definiti per ogni numero reale.

Intersezioni con gli assi
$\quad$
- Asse x: Non ci sono intersezioni con l’asse $x$ poiché $f(x) > 0$ per ogni $x \in \mathbb{R}$ essendo somma di funzioni strettamente positive.
- Asse y: $f(0) = e^0 + e^0 = 2$ . Quindi il punto di intersezione è $A=(0,2)$ .

Positività La funzione è sempre positiva su tutto il suo dominio, come menzionato nel punto precedente.

Continuità La funzione è continua su tutto $\mathbb{R}$ in quanto somma di composizioni di funzioni continue.

Asintoti
$\quad$
- Asintoti verticali: Non esistono.
- Asintoti orizzontali: Non esistono, poiché $\lim_{x \to \pm\infty} f(x) = +\infty$ .
- Asintoti obliqui: Non esistono, poiché $\lim_{x \to \pm\infty} \frac{f(x)}{x} = +\infty$ .

Derivata prima e monotonia Sviluppando il modulo $|x|=x$ per $x > 0$ e $|x|=-x$ per $x < 0$ , otteniamo:
$f'(x) = \begin{cases} 3e^{3x}+e^x & \text{se } x > 0 \\ 3e^{3x}-e^{-x} & \text{se } x < 0 \end{cases}$

Per $x > 0$ abbiamo la somma di due termini positivi, quindi risulta sempre strettamente maggiore di zero. Per $x < 0$ , invece:

$3e^{3x} - e^{-x} = 0 \iff 3e^{4x} = 1 \iff e^{4x} = \frac13,$

e passando alla funzione inversa (ovvero il logaritmo) si ottiene

$4x = \log \frac13 = - \log 3,$

che ha come soluzione $x = - \frac14 \log 3$ . Perciò la funzione è decrescente per $x < -\frac{\log 3}{4}$ e crescente per $x > -\frac{\log 3}{4}$ . Il punto di minimo è $x = -\frac{\log 3}{4}$ con

$f(-\frac{\log 3}{4}) = \frac{4}{\sqrt[4]{3^3}}.$

Si verifica facilmente che questo è anche punto di minimo assoluto.

Derivabilità in $x = 0$ Calcoliamo il limite del rapporto incrementale in $x = 0$ . Da destra, si ha

$\lim_{h \to 0^+} \frac{f(h)-f(0)}{h} = 4.$

mentre da sinistra

$\lim_{h \to 0^-} \frac{f(h)-f(0)}{h} = 2$

Poiché i limiti destro e sinistro sono diversi, la funzione non è derivabile in x = 0, che risulta essere un punto angoloso (dato che i limiti esistono finiti ma diversi).

Derivata seconda e convessità
$f''(x) = 9e^{3x} + e^{|x|}$

Poiché $f''(x) > 0$ per ogni $x \in \mathbb{R}\setminus\{0\}$ , la funzione è convessa su tutto il suo dominio.

Grafico
$\quad$

$\quad$

Esercizio 9 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\arctan(x^2-1).$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è $D=\mathbb{R}$ , poiché la funzione arcotangente è definita per ogni numero reale.

Intersezioni con gli assi
$\quad$
- Asse x: L’arcotangente si annulla solo quando l’argomento è zero, perciò:
  $x^2 - 1 = 0,$
  
  che ha come soluzioni $x = \pm 1$ . Dunque, le intersezioni sono $A=(1,0)$ e $B=(-1,0)$ .
- Asse y: $f(0) = \arctan(-1) = -\pi/4$ , perciò il punto di intersezione è $C=(0,-\pi/4)$ .

Simmetria La funzione è pari dato che soddisfa la relazione
$f(x) = f(-x).$

Di conseguenza, possiamo limitarci a studiarne le proprietà nella semiretta positiva $D_+ := [0,+\infty)$ .

Positività La funzione è positiva quando $x^2 - 1 > 0$ , cioè per $x \in (1, +\infty)$ .

Continuità La funzione $f$ è continua su tutto il suo dominio $D_+$ essendo composizione di funzioni continue.

Asintoti
$\quad$
- Asintoti verticali: Non esistono poiché non sono presenti punti singolari o di discontinuità.
- Asintoto orizzontale: Basta ricordare che l’arcotangente soddisfa
  $\lim_{x \to+ \infty} \arctan(x) = \frac\pi2$
  
  per concludere che $y = \pi/2$ è un asintoto orizzontale per $x \to \pm\infty$ (per simmetria).
- Asintoti obliqui: Non esistono.

Derivata prima e monotonia La derivata prima è data da
$f'(x) = \frac{2x}{x^4-2x^2+2}$

Il denominatore si può scrivere come

$x^4-2x^2+2 = 1 + (-1 + x^2)^2$

ed è sempre positivo, perciò il segno di $f'(x)$ dipende solo dal numeratore $x$ . La funzione è decrescente per $x < 0$ e crescente per $x > 0$ , e questo è compatibile con il fatto che

$f(x) \text{ pari } \implies f'(x) \text{ dispari}$

Il punto di minimo (assoluto) è $x = 0$ , corrispondente al punto $C = (0,-\pi/4)$ . Non esistono massimi assoluti poiché $\sup f = \pi/2$ .

Derivata seconda e convessità
$f''(x) = \frac{2(-3x^4 + 2x^2 + 2)}{(x^4-2x^2+2)^2}$

Il denominatore è sempre positivo, perciò ci concentriamo sullo studio del segno del numeratore. Sostituendo $t = x^2$ si ha

$-3t^2 + 2t + 2 = 0$

che ha come soluzioni

$t_{1,2} = \frac{1 \pm \sqrt{7}}{3}.$

La disequazione richiede quindi $t<(1-\sqrt{7})/3$ o $t>(1+\sqrt{7} )/3$ . Passando a $x$ si trova: $x^2<(1-\sqrt{7})/3<0$ , chiaramente impossibile, e $x^2>(1+ \sqrt{7})/3$ da cui il segno di $f''(x)$ si comporta come segue:

$\quad$

$\quad$

$\quad$

La funzione è convessa per $x < -\sqrt{\frac{1+\sqrt{7}}{3}}$ e $x > \sqrt{\frac{1+\sqrt{7}}{3}}$ , e concava per $-\sqrt{\frac{1+\sqrt{7}}{3}} < x < \sqrt{\frac{1+\sqrt{7}}{3}}$ .

I punti di flesso sono:

$x = \pm \sqrt{\frac{1+\sqrt{7}}{3}} \quad \text{con} \quad y = \arctan\left(\frac{\sqrt{7}-1}{2}\right)$

Grafico
$\quad$

$\quad$

Esercizio 10 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\begin{cases} \sin x+x & x>0\\ x&x\le 0 \end{cases}$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è $D=\mathbb{R}$ , poiché entrambe le parti della funzione sono definite per ogni numero reale.

Intersezione con gli assi La funzione interseca gli assi cartesiani solo nell’origine $O=(0,0)$ . Infatti, è facile verificare che

$\sin x + x = 0 \iff x = - \sin x,$

e questa ha come unica soluzione $x = 0$ , che però appartiene all’altro ramo della funzione a tratti.

Positività
$\quad$
- Per $x > 0$ : $f(x) = \sin x + x > 0$ sempre, poiché $\sin x > -x$ per $x > 0$ . Si può verificare banalmente osservando che
  $f(0)=0 \quad \text{e} \quad f'(x) = \cos (x) + 1,$
  
  quindi la funzione è strettamente crescente in $\cup_{k \in \mathbb N}(0, 2k \pi)$ .
- Per $x \leq 0$ : $f(x) = x \leq 0$ .
$\quad$

$\quad$

Continuità La funzione è continua in $x = 0$ poiché:

$\lim_{x \to 0^+} (\sin x + x) = \lim_{x \to 0^-} x = f(0) = 0$

Di conseguenza, $f$ è continua su tutto il suo dominio.

Asintoti La funzione non ammette asintoti orizzontali dato che
$\begin{aligned} & \lim_{x \to + \infty} f(x) = \lim_{x \to + \infty} (\sin x + x) = + \infty, \\ & \lim_{x \to - \infty} f(x) = \lim_{x \to - \infty} x = - \infty. \end{aligned}$

Il primo limite è una conseguenza banale del fatto che la funzione $\sin x$ è limitata, perciò

$x-1 \le x + \sin x \le x +1,$

e prendendo il limite per $x \to + \infty$ il teorema del confronto ci permette di concludere.

Non sono neanche presenti asintoti verticali dato che $f$ è definita su tutto l’insieme dei numeri reali. Per quanto riguarda gli obliqui:

$\quad$
- Per $x \to + \infty$ si ha coefficiente angolare
  $m_+ = \lim_{x \to + \infty} \frac{f(x)}{x} = \lim_{x \to + \infty} \frac{\sin x + x}{x} = 1,$
  
  per cui
  
  $q_+ = \lim_{x \to + \infty} (f(x) - m_+ x) = \lim_{x \to + \infty} \sin x,$
  
  che non esiste. Pertanto, non ci sono asintoti obliqui a destra.
- Per $x \to - \infty$ si ha coefficiente angolare
  $m_- = \lim_{x \to - \infty} \frac{f(x)}{x} = \lim_{x \to - \infty} \frac{x}{x} = 1,$
  
  per cui
  
  $q_ = \lim_{x \to - \infty} (f(x) - m_- x) = \lim_{x \to + \infty} (x - x) = 0,$
  
  perciò $y = x$ è (banalmente) un asintoto obliquo per $x \to - \infty$ .

Derivata prima e monotonia
$f'(x) = \begin{cases} \cos(x) + 1 & \text{se } x > 0 \\ 1 & \text{se } x < 0 \end{cases}$

$f$ ha un punto angoloso in $x = 0$ poiché i limiti da destra e sinistra esistono ma non coincidono:

$\lim_{x \to 0^+} f'(x) = \cos 0 + 1 = 2 \neq 1 = 1 = \lim_{x \to 0^-} f'(x)$

La funzione è crescente su tutto il suo dominio poiché $f'(x) > 0$ per ogni $x \neq 0$ .

Derivata seconda e convessità
$f''(x) = \begin{cases} -\sin x & \text{se } x > 0 \\ 0 & \text{se } x \leq 0 \end{cases}$

$\quad$
- Per $x \leq 0$ : la funzione non è né concava né convessa dato che coincide con una retta ( $y = x$ , nello specifico).
- Per $x > 0$ : la funzione è concava nell’intervallo $(0, \pi]$ , convessa nell’intervallo $[\pi, 2\pi]$ , e questo comportamento si ripete con periodicità $2\pi$ .
I punti di flesso sono $x_k = k\pi$ con $k \in \mathbb{N}$ , dove $f(k\pi) = k\pi$ .

Grafico
$\quad$

$\quad$

$\quad$

Osservazioni conclusive:

$\quad$
- Una parte lineare per $x \leq 0$
- Una parte sinusoidale sovrapposta a una retta per $x > 0$
- Un punto angoloso nell’origine
- Crescita monotona su tutto il dominio

Esercizio 11 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Sia

$f(x)=e^{-\frac{1}{x^2}}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio e simmetrie Il dominio è $D=\mathbb{R}\setminus\{0\}$ , poiché la funzione $1/x^2$ non è definita per $x=0$ . Inoltre, è facile vedere che

$f(-x) = e^{- 1/(-x)^2} = e^{- 1/x^2} = f(x),$

quindi la funzione è pari e, di conseguenza, possiamo limitarci a studiarne il comportamento nella semiretta positiva $D_+ = (0,\infty)$ .

Intersezioni con gli assi
$\quad$
- Asse x: Non esistono intersezioni con l’asse x poiché $f(x) > 0$ per ogni $x \in D_+$ .
- Asse y: Non esistono intersezioni con l’asse y poiché $x=0$ non appartiene al dominio.

Positività La funzione è positiva su tutto il suo dominio $D_+$ essendo un esponenziale.

Continuità La funzione $f$ è continua su tutto il suo dominio $D_+$ in quanto composizione di funzioni continue. In effetti, $h(x)=1/x^2$ è continua quando $x \neq 0$ .

Asintoti E’ facile verificare che:
$\quad$
- Asintoto orizzontale: Per $x \to+ \infty$ si ha
  $\lim_{x \to + \infty} e^{-\frac{1}{x^2}} = e^0 = 1,$
  
  perciò $y = 1$ è un asintoto orizzontale sia per $+ \infty$ che (simmetria) per $-\infty$ .
- Asintoto verticale: Poiché per $x\to 0$ i limiti da destra e sinistra coincidono e si ha:
  $\lim_{x \to 0^+} e^{-\frac{1}{x^2}} = e^{-\infty} = 0,$
  
  non c’è asintoto verticale e la funzione è prolungabile con continuità in questo punto.

Derivata prima e monotonia
$f'(x) = \frac{2}{x^3} e^{-\frac{1}{x^2}}$

La funzione esponenziale è positiva, quindi il segno di $f'(x)$ dipende solo da $x^3$ :

$\quad$
- $f'(x) < 0$ per $x < 0$ (funzione decrescente)
- $f'(x) > 0$ per $x > 0$ (funzione crescente)
Questo comportamento si poteva dedurre anche dal fatto che, come menzionato in un esercizio precedente,

$f \text { pari } \implies f' \text{ dispari } \implies f'' \text { pari } \implies \cdots$

Inoltre, si verifica facilmente che $\inf f = 0$ è ottenuto per $x \to 0$ e $\sup f = 1$ per $x \to + \infty$ . Non ci sono punti di massimo o minimo relativo/assoluto.

Derivata seconda e convessità Utilizzando la formula per la derivata di un prodotto, si trova:
$f''(x) = \frac{4-6x^2}{x^6} e^{-\frac{1}{x^2}}$

In questo caso, l’esponenziale e il denominatore sono positivi, perciò il segno di $f''(x)$ dipende dal polinomio di secondo grado $4-6x^2$ :

$\quad$

$\quad$

$\quad$

La funzione risulta dunque essere

$\quad$
- convessa in $(-\sqrt{\frac{2}{3}}, \sqrt{\frac{2}{3}}) \setminus \{0\}$
- concava in $(-\infty, -\sqrt{\frac{2}{3}}) \cup (\sqrt{\frac{2}{3}}, +\infty)$
ed i corrispondenti punti di flesso sono

$A=\left(-\sqrt{\frac{2}{3}}, e^{-\frac{3}{2}}\right) \quad \text{e} \quad B=\left(\sqrt{\frac{2}{3}}, e^{-\frac{3}{2}}\right)$

Grafico
$\quad$

$\quad$

Esercizio 12 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\sqrt{x^2-3x+7}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è determinato dalla condizione $x^2-3x+7 \geq 0$ , ovvero argomento della radice non negativo. Poiché il discriminante è $\Delta = 9 - 4\cdot 7 = -19 < 0$ , il polinomio $x^2-3x+7$ risulta essere sempre positivo. Quindi, il dominio è $D=\mathbb{R}$ .

Intersezioni con gli assi
$\quad$
- Asse x: Non esistono intersezioni con l’asse $x$ come verificato nel calcolo precedente.
- Asse y: $f(0) = \sqrt{7}$ , quindi il punto di intersezione è $A=(0,\sqrt{7})$ .

Positività La funzione è sempre positiva su tutto il suo dominio $\mathbb{R}$ . Infatti, ricordiamo che la radice quadrata soddisfa

$\sqrt{ h(x) } \ge 0 \qquad \text{per ogni $x$ nel dominio}.$

Continuità La funzione $f$ è continua su tutto $\mathbb{R}$ in quanto composizione di funzioni continue.

Asintoti
$\quad$
- Asintoti verticali: Non ci sono punti di discontinuità o singolari, pertanto non ci sono asintoti verticali.
- Asintoti orizzontali: Non esistono, poiché
  $\lim_{x \to \pm\infty} f(x) = +\infty.$
- Asintoti obliqui:
  $\quad$
  - Per $x \to +\infty$ , il coefficiente angolare è
    $m_+ = \lim_{x \to + \infty} \frac{f(x)}{x} = \lim_{x \to + \infty} \frac{\sqrt{x^2}}{x} = \lim_{x \to + \infty} \frac{|x|}{x} = 1,$
    
    dove si è usata la solita identità $\sqrt{x^2}=|x|$ . Ne segue che
    
    $q_+ = \lim_{x \to + \infty} (f(x) - m_+ x) = \lim_{x \to + \infty} (\sqrt{x^2 - 3x + 7} - x) = - \frac32,$
    
    come si può mostrare facilmente razionalizzando. Perciò $y = x - 3/2$ è un asintoto obliquo nel limite per $x \to + \infty$ .
  - Per $x \to -\infty$ , il coefficiente angolare è
    $m_- = \lim_{x \to - \infty} \frac{f(x)}{x} = \lim_{x \to - \infty} \frac{|x|}{x} = -1,$
    
    da cui segue che
    
    $q_- = \lim_{x \to - \infty} f(x) - m_- x = \lim_{x \to - \infty}( \sqrt{x^2 - 3x + 7} + x )= \frac32,$
    
    come si può mostrare facilmente razionalizzando. Perciò $y = -x + 3/2$ è un asintoto obliquo nel limite per $x \to - \infty$ .

Derivata prima e monotonia
$f'(x) = \frac{2x-3}{2\sqrt{x^2-3x+7}}$

Il segno di $f'(x)$ dipende solo dal numeratore $2x-3$ , perciò

$\quad$
- $f'(x) < 0$ per $x < \frac{3}{2}$ (funzione decrescente)
- $f'(x) > 0$ per $x > \frac{3}{2}$ (funzione crescente)
Il punto di minimo relativo (e assoluto) è $x = \frac{3}{2}$ con $f(\frac{3}{2}) = \frac{\sqrt{19}}{2}$ .

Derivata seconda e convessità
$f''(x) = \frac{19}{4(\sqrt{x^2-3x+7})^3}$

Poiché $f''(x) > 0$ per ogni $x \in \mathbb{R}$ , la funzione è sempre convessa e non ha punti di flesso.

Grafico
$\quad$

$\quad$

Esercizio 13 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\frac{4x-12}{(x-2)^2}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è determinato dalla condizione $(x-2)^2 \neq 0$ , quindi:

$D = (-\infty, 2) \cup (2, +\infty)$

Simmetria La funzione non presenta simmetrie poiché:

$f(-x) = \frac{4(-x)-12}{(-x-2)^2} = -\frac{4x+12}{(x+2)^2} \neq \pm f(x)$

Intersezioni con gli assi
$\quad$
- Asse y: $f(0) = -3$ , quindi $A=(0,-3)$ è il punto di intersezione
- Asse x: $f(x) = 0$ se e solo se si annulla il numeratore, ovvero $4x - 12 = 0$ . Di conseguenza, il punto $B=(3,0)$ è l’unico di intersezione con l’asse $x$ .

Positività La funzione è positiva per $x \in (3, +\infty)$ in quanto il denominatore non gioca alcun ruolo nel determinare il segno.

Asintoti
$\quad$
- Asintoto orizzontale: Si vede che
  $\lim_{x \to \pm \infty} f(x) = 0$
  
  dato che il denominatore va come $x^2$ ed il numeratore come $x$ . Pertanto, la retta $y=0$ è un asintoto orizzontale per $x \to \pm \infty$ .
- {Asintoto verticale: Verifichiamo nell’unico punto singolare, ovvero $x = 2$ . Si ha
  $\lim_{x \to 2^\pm} f(x) = - \frac4{0^+} = - \infty,$
  
  quindi $x = 2$ è un asintoto verticale.

Derivata prima e monotonia
$f'(x) = \frac{4(4-x)}{(x-2)^3}$

Il denominatore è negativo per $x < 2$ e positivo per $x > 2$ , mentre il numeratore è negativo per $x > 4$ e positivo per $x < 4$ ; ne segue che:

$\quad$

$\quad$

$\quad$

La funzione cresce su $(2,4)$ e decresce su $(-\infty, 2) \cup (4, +\infty)$ . In particolare, il punto $x = 4$ risulta essere un massimo assoluto con $f(4) = 1$ .

Derivata seconda e convessità
$f''(x) = \frac{8x-40}{(x-2)^4}$

Questa volta il denominatore è sempre positivo, perciò il segno dipende unicamente dal numeratore come segue:

$\quad$

$\quad$

$\quad$

La funzione è convessa su $(5, +\infty)$ e concava su $(-\infty, 2) \cup (2,5)$ . Punto di flesso in $(5, \frac{8}{9})$ .

Grafico
$\quad$

$\quad$

Esercizio 14 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x) = \sqrt{x^3-3x}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

$\quad$

Dominio Il dominio è determinato dalla condizione $x^3-3x \geq 0$ . Il termine a sinistra si può scrivere come il prodotto $x(x^2-3)$ , perciò basta studiare il segno come segue:

$\quad$

$\quad$

$\quad$

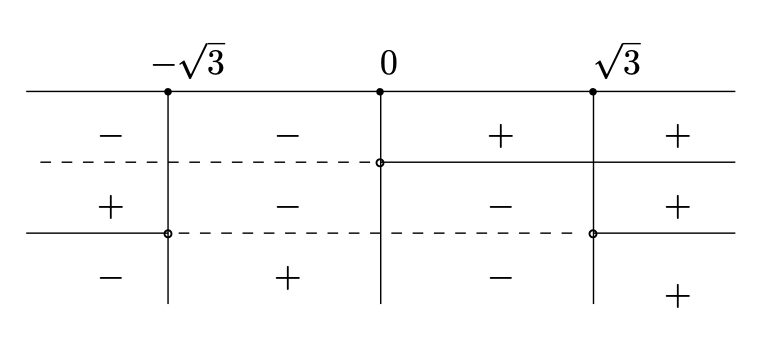
Il prodotto è positivo quando i segni dei due termini coincidono; in particolare, il dominio della funzione è dato da $D = [-\sqrt 3, 0] \cup [ \sqrt 3, + \infty)$ .

Simmetria La funzione non presenta simmetrie. Questo è immediato da verificare dato che, ad esempio, il dominio non è simmetrico.

Intersezioni con gli assi
$\quad$
- Asse x: La radice si annulla negli zeri del prodotto $x(x^2-3)$ , perciò interseca l’asse x nei punti $O=(0,0)$ , $A=(\sqrt 3, 0)$ e $B=(-\sqrt 3, 0)$ .
- Asse y: Si è già verificato sopra, l’intersezione avviene nell’origine $O$ .

Positività La funzione è sempre non negativa sul suo dominio in quanto radice quadrata. Infatti, ricordiamo che la radice quadrata soddisfa

$\sqrt{ h(x) } \ge 0 \qquad \text{per ogni $x$ nel dominio}.$

Asintoti
$\quad$
- Asintoto orizzontale: Si vede che
  $\lim_{x \to + \infty} f(x) = + \infty,$
  
  mentre per $x \to - \infty$ la funzione non è definita; di conseguenza, non ammette asintoti orizzontali.
- Asintoti verticali: Non esistono.
- Asintoti obliqui: Non ci sono asintoti obliqui poiché è facile verificare che
  $\lim_{x \to + \infty} \frac{f(x)}{x} = + \infty$
  
  in quanto $f(x)$ per $x\to +\infty$ è asintotica a $\sqrt{x^3}$ , quindi infinito di ordine superiore rispetto ad $x$ al denominatore.

Derivata prima e monotonia
$f'(x) = \frac{3(x^2-1)}{2\sqrt{x^3-3x}}$

Il denominatore è sempre positivo, quindi è sufficiente considerare il segno del numeratore. Si ha

$x^2 - 1 > 0 \iff x \in (-\infty,-1) \cup (1,+\infty),$

perciò intersecando con il dominio della funzione si verifica immediatamente che:

$\quad$
- $f'(x) > 0$ per $x \in (-\sqrt{3},-1) \cup (\sqrt{3},+\infty)$
- $f'(x) < 0$ per $x \in (-1,0)$
La funzione cresce su $(-\sqrt{3},-1) \cup (\sqrt{3},+\infty)$ e decresce su $(-1,0)$ . Dunque, in $x=-1$ c’è un massimo relativo con

$f(-1) = \sqrt 2,$

mentre $(0,0)$ e $(\pm\sqrt{3},0)$ sono punti di minimo assoluto. Si noti che la funzione risulta non derivabile in $x=0$ e $x=\pm\sqrt{3}$ .

Derivata seconda e convessità
$f''(x) = \frac{3(x^4-6x^2-3)}{4\sqrt{(x^3-3x)^3}}$

Come per la derivata prima, il denominatore non gioca alcun ruolo nello studio del segno. Per il numeratore, invece, prendiamo $t=x^2$ e troviamo

$t^2 - 6t - 3 = 0 \iff t_{1,2} = \frac{6 \pm \sqrt{36+12}}{2} = 3 \pm 2 \sqrt 3.$

Dato che $t = x^2$ è non negativo, scartiamo la soluzione negativa. Si trova perciò che

$x^4 - 6x^3 - 3 > 0 \iff x \in (-\infty, - \sqrt{3 + 2 \sqrt3}) \cup (\sqrt{3 + 2 \sqrt3}, + \infty).$

Intersecando con il dominio della funzione, deduciamo

$\quad$
- $f''(x) > 0$ per $x \in (\sqrt{3+2\sqrt{3}},+\infty)$
- $f''(x) < 0$ per $x \in (-\sqrt{3},0) \cup (\sqrt{3},\sqrt{3+2\sqrt{3}})$
La funzione è convessa su $(\sqrt{3+2\sqrt{3}},+\infty)$ e concava su $(-\sqrt{3},0) \cup (\sqrt{3},\sqrt{3+2\sqrt{3}})$ , perciò ammette un punto di flesso in

$F = (\sqrt{3+2\sqrt{3}},3\sqrt{14+8\sqrt{3}}).$

Grafico
$\quad$

$\quad$

$\quad$

Esercizio 15 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\frac{4|x-1|-x^2}{|x+1|}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio La funzione risulta non essere definita solo nei punti in cui si annulla il denominatore. In particolare,
$|x+1| \neq 0 \iff x \neq - 1,$

per cui il dominio è $D=(-\infty,-1)\cup(-1,+\infty)$ .

Simmetria La funzione non presenta simmetrie.

Intersezioni con gli assi
$\quad$
- Asse y: Si ha
  $f(0)=\frac{4 |-1|}{|1|} = 4,$
  
  perciò $A=(0,4)$ è il punto di intersezione con l’asse y.
- Asse x: Basta verificare dove si annulla il numeratore. Sviluppando il modulo si ha
  $4 |x-1| - x^2 = \begin{cases} 4x - 4 - x^2 & \text{se } x \ge 1, \\ -4x+4-x^2 & \text{se } x < 1. \end{cases}$
  
  Nel primo caso, ovvero per $x \ge 1$ , abbiamo
  
  $x^2 - 4x + 4 = 0 \iff (x-2)^2 = 0,$
  
  che ha come unica soluzione $x = 2$ (accettabile, dato che rientra nell’intervallo $(1,+\infty)$ ). Nel secondo caso, si ha
  
  $x^2 + 4x - 4 = 0 \leadsto x_{1,2} = \frac{-4 \pm \sqrt{32}}{2} = - 2 \pm 2 \sqrt 2,$
  
  ed entrambe soddisfano la condizione $x < 1$ . Perciò otteniamo tre punti di intersezione con l’asse $x$ , ovvero $B=(2,0)$ , $C=(- 2 - 2 \sqrt2, 0)$ e $D=(-2 + 2 \sqrt 2, 0)$ .

Positività Il denominatore è sempre positivo perché valore assoluto, quindi ci concentriamo sul numeratore. In base ai conti fatti per l’intersezione con gli assi, deduciamo subito che:
$f(x)>0 \iff x\in(-2(1+\sqrt{2}),-1)\cup(-1,2(\sqrt{2}-1))$

$f(x)<0 \iff x\in(-\infty,-2(1+\sqrt{2}))\cup(2(\sqrt{2}-1),+\infty)$

Asintoti
$\quad$
- Asintoti orizzontali: Al numeratore il termine dominante è $-x^2$ , perciò
  $\lim_{x \to \pm \infty} f(x) = - \lim_{x \to \pm \infty} \frac{x^2}{|x+1|} = - \infty,$
  
  perciò non ci sono asintoti orizzontali.
- Asintoti obliqui: Nel caso $x \to + \infty$ il coefficiente angolare è
  $m_+ = \lim_{x \to + \infty} \frac{f(x)}{x} = \lim_{x \to + \infty} \frac{-x^2}{x|x+1|} = - \lim_{x \to + \infty} \frac{x}{x+1} = -1,$
  
  da cui segue che
  
  $q_+ = \lim_{x \to + \infty} (f(x) - m_+ x) = \lim_{x \to + \infty} f(x) + x = \lim_{x \to + \infty} \frac{4(x-1) - x^2 + x(x+1)}{x+1} = \lim_{x \to + \infty} \frac{4x + x}{x} = 5,$
  
  perciò $y = - x +5$ è asintoto obliquo per $x \to + \infty$ . Nel caso $x \to -\infty$ , invece, il coefficiente angolare è
  
  $m_- = \lim_{x \to - \infty} \frac{f(x)}{x} = \lim_{x \to - \infty} \frac{-x^2}{x|x+1|} = \lim_{x \to - \infty} \frac{x}{x+1} = 1,$
  
  da cui segue che
  
  $q_- = \lim_{x \to - \infty} f(x) - m_- x = \lim_{x \to - \infty} f(x) - x = \lim_{x \to - \infty} \frac{-4(x-1) - x^2 + x(x+1)}{-x-1} = \lim_{x \to + \infty} \frac{-3x}{-x} = 3,$
  
  perciò $y = x +3$ è asintoto obliquo per $x \to - \infty$ .
- Asintoto verticale: Verifichiamo i limiti destro e sinistro nel punto di discontinuità $x=-1$ . Il denominatore è positivo da entrambi i lati, perciò:
  $\lim_{x \to -1^-} f(x) = \lim_{x \to -1^+} f(x) = \frac7{0^+} = + \infty,$
  
  da cui segue che $x=1$ è un asintoto verticale.

Derivata prima e monotonia In questo caso, sviluppiamo i moduli per scrivere
$f(x) = \begin{cases} - \frac{4(1-x) - x^2}{x+1} & \text{se } x \le -1 \\ \frac{4(1-x) - x^2}{x+1} & \text{se } -1 < x \le 1 \\ \frac{4(x-1) - x^2}{x+1} & \text{se } x > 1. \end{cases}$

La derivata prima si svolge in maniera simile in tutti e tre i casi:

$f'(x) = \begin{cases} \frac{8 + 2 x + x^2}{(1 + x)^2} & \text{se } x < -1 \\ - \frac{8 + 2 x + x^2}{(1 + x)^2} & \text{se } -1 < x < 1 \\ - \frac{-8 + 2 x + x^2}{(1 + x)^2} & \text{se } x > 1. \end{cases}$

Osserviamo subito che nel caso $x < -1$ il segno è determinato dal numeratore. Si ha

$x^2 + 2x + 8 = 0 \iff x_{1,2} = \frac{-2 \pm \sqrt{4 - 32}}{2},$

ed essendo il discriminante negativo, il polinomio $x^2+2x+8$ è sempre positivo. In particolare, $f'(x)$ è positivo in $(-\infty,-1)$ e negativo in $(-1,1)$ . Per $x>1$ , invece, si ha

$x^2 + 2x - 8 = 0 \iff x_{1,2} = \frac{-2 \pm \sqrt{4 + 32}}{2} = -1 \pm 3,$

da cui si prende solo la soluzione positiva $x_1=2$ e si trova che la derivata è positiva in $(1,2)$ e negativa in $(2,+\infty)$ . Ricapitolando, abbiamo:

$f'(x)>0 \iff x\in(-\infty,-1)\cup(1,2)$

$f'(x)<0 \iff x\in(-1,1)\cup(2,+\infty)$

Dato che la funzione è crescente in $(-\infty,-1)\cup(1,2)$ e decrescente in $(-1,1)\cup(2,+\infty)$ , il punto $(2,0)$ risulta essere un massimo relativo, mentre $(1,-1/2)$ un minimo relativo.

Non derivabilità e punti angolosi Verifichiamo il limite da destra e sinistra in $x=1$ della derivata definita a tratti. Si ha

$\lim_{x \to 1^-} f'(x) = -\lim_{x \to 1}\frac{8 + 2 x + x^2}{(1 + x)^2} = -\frac{11}{4},$

e, analogamente,

$\lim_{x \to 1^+} f'(x) = -\lim_{x \to 1}\frac{-8 + 2 x + x^2}{(1 + x)^2} = -\frac{-5}{4} = \frac54,$

perciò $x=1$ risulta essere un punto angoloso.

Derivata seconda e convessità La derivata seconda si può calcolare a tratti derivando individualmente i tre pezzi della derivata prima. Un semplice calcolo mostra che:

$f''(x)>0 \iff x\in(-\infty,-1)\cup(-1,1)$

$f''(x)<0 \iff x\in(1,+\infty)$

In particolare, la funzione è convessa su $(-\infty,-1)\cup(-1,1)$ e concava su $(1,+\infty)$ .

Grafico
$\quad$

$\quad$

$\quad$

Esercizio 16 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\log\left(e+\frac{1}{x}\right).$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è determinato ponendo il denominatore diverso da zero e l’argomento del logaritmo positivo. In altre parole, otteniamo il sistema:

$\left\{\begin{array}{l} x\neq 0\\ e+1/x>0 \end{array}\right.$

Risolvendo, otteniamo:

$D=\left(-\infty,-1/e\right)\cup(0,+\infty)$

Intersezioni con gli assi Per l’intersezione con l’asse delle x, cerchiamo le soluzioni dell’equazione

$\log(e + 1/x) = 0 \iff e + 1/x = 1 \iff x = \frac{1}{1-e}.$

Dunque la funzione interseca l’asse delle x in $A=(1/(1-e),0)$ . Non ci sono intersezioni con l’asse y dato che $x=0$ non appartiene al dominio.

Positività La funzione è positiva quando l’argomento del logaritmo è maggiore di uno, ovvero in:

$(-\infty,1/(1-e))\cup(0,+\infty)$

Asintoti
$\quad$
- Asintoto orizzontale: E’ facile vedere che
  $\lim_{x \to \pm \infty} \log(e+ 1/x) = \log e = 1,$
  
  quindi $y = 1$ è un asintoto orizzontale per $x \to \pm \infty$ .
- Asintoti verticali: Consideriamo i due punti singolari $-1/e$ e $0$ da sinistra e da destra rispettivamente. Nel primo caso, si ha
  
  $\lim_{x \to (-1/e)^-} \log(e + 1/x) = - \infty,$
  
  mentre nel secondo caso
  
  $\lim_{x \to 0^+} \log(e + 1/x) = \lim_{x \to 0^+} \log(1/x) = + \infty.$
  
  In particolare, $x = -1/e$ è un asintoto verticale sinistro e $x=0$ un asintoto verticale destro.

Derivata prima e monotonia Si ha
$f'(x)=-\frac{1}{x(ex+1)}.$

La funzione è sempre decrescente sul suo dominio poiché $f'(x)<0$ per ogni $x$ nel dominio, infatti studiando il segno come segue si ha

$\quad$

$\quad$

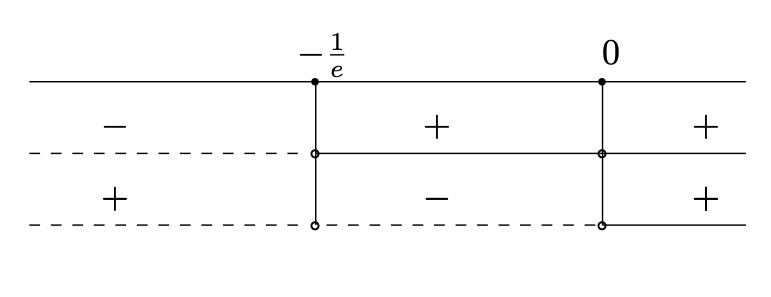
Derivata seconda e convessità Si ha
$f''(x)=\frac{2ex+1}{x^2(ex+1)^2}.$

In questo caso, il segno è determinato dal numeratore, ovvero

$2ex + 1 > 0 \iff x > - \frac{1}{2e},$

da cui segue che:

$\quad$
- $f''(x)>0$ per $x>0$
- $f''(x)<0$ per $x<-1/(2e)$
Deduciamo che $f$ è convessa su $(0,+\infty)$ e concava su $(-\infty,-1/e)$ . Non ci sono punti di flesso dato che $-1/(2e)$ non appartiene al dominio.

Grafico
$\quad$

$\quad$

$\quad$

Esercizio 17 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\cos 2x-\sin x.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio Il dominio è $\mathbb{R}$ dato che $f$ è somma di funzioni trigonometriche. Il periodo si calcola facilmente osservando che

$f(x+T)=f(x) \iff \cos(2x + T) = \cos2x \text{ e } \sin (x+T) = \sin x,$

dunque $T = 2\pi$ . Per questo motivo, limitiamo lo studio di funzione all’intervallo $[0,2\pi)$ .

Asintoti Non ci sono punti di discontinuità (perciò sono assenti asintoti verticali). Dalla periodicità segue che non ci sono neanche asintoti orizzontali/obliqui.

Segno e intersezioni con gli assi Il segno della funzione si determina risolvendo la disequazione trigonometrica
$\cos 2x - \sin x > 0.$

Per risolverla, si può sfruttare l’identità trigonometrica $\cos 2x = 1 - 2 \sin^2 x$ . In tal caso, la disequazione si riscrive come segue:

$1 - 2 \sin^2 x - \sin x > 0.$

Ponendo $t = \sin x$ si risolve come una normale disequazione di secondo grado, e poi si torna alla variabile $x$ . Un breve calcolo mostra che:

$f(x)>0 \iff x\in\left[0,\frac{\pi}{6}\right)\cup\left(\frac{5\pi}{6},2\pi\right)$

$f(x)<0 \Leftrightarrow x\in\left(\frac{\pi}{6},\frac{5\pi}{6}\right)$

L’intersezione con l’asse delle $y$ è nel punto $A=(0,1)$ , mentre le intersezioni con l’asse delle $x$ si trovano come soluzioni dell’equazione sopra e sono $B=(\frac{\pi}{6},0)$ , $C=(\frac{5\pi}{6},0)$ e $D=(\frac{3\pi}{2},0)$ .

Derivata prima e monotonia Ricordando che , abbiamo:
$f'(x)=-2\sin 2x-\cos x=-\cos x(4\sin x+1)$

La funzione cresce su $(\pi/2,\pi+\alpha)\cup(3\pi/2,2\pi-\alpha)$ e decresce altrove, dove $\alpha$ è l’angolo che soddisfa l’uguaglianza $\sin\alpha=1/4$ . In particolare:

$\quad$
- I punti $(\pi+\alpha,\frac{9}{8})$ , $(2\pi-\alpha,\frac{9}{8})$ sono massimi assoluti.
- I punti $(\frac{\pi}{2},-2)$ e $(\frac{3\pi}{2},0)$ sono, rispettivamente, minimo assoluto e minimo relativo.

Derivata seconda e convessità Si ha
$f''(x)=8\sin^2 x+\sin x-4.$

Ponendo $t = \sin x$ , risolviamo l’equazione di secondo grado associata ed osserviamo che la convessità di $f$ cambia per valori di $x$ che soddisfano:

$\sin x=\frac{-1\pm\sqrt{129}}{16}$

Grafico La funzione si disegna tra $[0,2\pi)$ e poi si estende per periodicità a tutto $\mathbb R$ . Questo è visibile nel grafico, dove ogni periodo è identificato da linee verticali tratteggiate:
$\quad$

$\quad$

Esercizio 18 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\arcsin(1-x^2).$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio e simmetrie La funzione $\arcsin x$ è definita solo per $x \in [-1,1]$ , quindi in questo caso il dominio è determinato dalla condizione:

$1 - x^2 \in [-1,1] \iff -1 \le 1-x^2 \le 1 \iff -2 \le -x^2 \le 0 \iff 0 \le x^2 \le 2,$

ovvero per $x \in [-\sqrt 2, \sqrt 2]$ . In particolare,

$D = [-\sqrt{2},\sqrt{2}].$

Inoltre, è facile vedere che $f$ è pari ( $f(-x)=f(x)$ ). Di conseguenza, possiamo limitarci a studiare la funzione sul dominio $D_+ = [0,\sqrt 2]$ .

Asintoti La funzione è definita e continua in un intervallo chiuso e limitato e ciò esclude la presenza di asintoti di qualsiasi genere.

Segno e intersezioni con gli assi La funzione è positiva quando l’argomento dell’arcoseno è positivo, perciò:
$f(x) > 0 \iff 0 < x < 1.$

L’intersezione con l’asse delle y è $A=(0,f(0))=(0,\pi/2)$ , mentre le intersezioni con l’asse delle x si ottengono come soluzioni di

$\arcsin(1-x^2) = 0,$

ovvero $x = 1$ ; in particolare, i punti di intersezione sono $B=(1,0)$ e (per simmetria) $C=(-1,0)$ .

Derivata prima e monotonia Ricordiamo che
$(\arcsin f)' = \frac{f^\prime}{\sqrt{1-f^2}},$

da cui segue

$f'(x)=-\frac{2x}{|x|\sqrt{2-x^2}}.$

Osserviamo che il denominatore della derivata si annulla nei punti $x = 0$ , $x = \sqrt{2}$ e $x = -\sqrt{2}$ . Di conseguenza, la funzione potrebbe non essere derivabile in questi punti.

In particolare, la funzione non è derivabile in $x = 0$ , che risulta essere un punto angoloso. Infatti:

$\lim_{x \to 0^-} \left(-\frac{2x}{|x|\sqrt{2-x^2}}\right) = \lim_{x \to 0^-} \frac{2}{\sqrt{2-x^2}} = \sqrt{2},$

mentre

$\lim_{x \to 0^+} \left(-\frac{2x}{|x|\sqrt{2-x^2}}\right) = \lim_{x \to 0^+} -\frac{2}{\sqrt{2-x^2}} = -\sqrt{2}.$

I limiti esistono finiti, ma non coincidono, per cui $x=0$ è punto angoloso.

Per quanto riguarda $x = \sqrt{2}$ e $x = -\sqrt{2}$ , abbiamo:

$\lim_{x \to \sqrt{2}^-} \left(-\frac{2x}{|x|\sqrt{2-x^2}}\right) = -\infty,$

e

$\lim_{x \to -\sqrt{2}^+} \left(-\frac{2x}{|x|\sqrt{2-x^2}}\right) = -\infty.$

Pertanto, in $x = \pm \sqrt{2}$ , la funzione non è derivabile. In particolare, in questi punti la tangente è verticale.

La funzione cresce su $(-\sqrt{2},0)$ e decresce su $(0,\sqrt{2})$ , perciò:

$\quad$
- Il punto $(0,\pi/2)$ è un massimo assoluto.
- I punti $(\pm \sqrt 2, - \pi/2)$ sono minimi assoluti.

Derivata seconda e convessità La derivata seconda della funzione è
$f''(x) =-\dfrac{2|x|}{\sqrt(2-x^2)^3}$

da cui segue immediatamente che la funzione $f$ è sempre concava in tutto il suo dominio.

Grafico
$\quad$

$\quad$

Esercizio 19 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$f(x)=\arctan\frac{x+1}{x-1}.$

Tracciare il grafico della funzione dopo aver determinato: il dominio $D$ , intersezione con gli assi, positività, continuità, asintoti, massimi e minimi, eventuali punti di non derivabilità, flessi, concavità e convessità. Una volta tracciato il grafico, esplicitare l’immagine di $f$ .

Svolgimento.

Dominio La funzione $\arctan x$ è definita per ogni $x$ , perciò è sufficiente porre il denominatore dell’argomento diverso da zero:

$D = (-\infty,1)\cup(1,+\infty).$

Segno e intersezioni con gli assi La funzione è positiva quando l’argomento dell’arcotangente è positivo, perciò:

$\frac{x+1}{x-1} > 0 \iff \begin{cases} x > -1 \\ x > 1 \end{cases} \text{ oppure } \begin{cases} x < - 1 \\ x < 1 \end{cases}$

e, risolvendo i due sistemi, la loro unione corrisponde a:

$f(x) > 0 \iff x \in (-\infty,-1) \cup (1,+ \infty).$

L’intersezione con l’asse delle $y$ avviene nel punto $A=(0,f(0))=(0, - \pi/4)$ , mentre con l’asse delle $x$ basta osservare che l’arcotangente si annulla solo quando l’argomento è zero, perciò in $B=(-1,0)$ .

Asintoti
$\quad$
- Asintoto orizzontale: E’ facile vedere che
  $\lim_{x \to \pm \infty} \arctan \frac{x+1}{x-1} = \arctan 1 = \frac\pi4,$
  
  perciò $y = \pi/4$ è un asintoto orizzontale per $x \to \pm \infty$ .
- Asintoto verticale: Nel punto singolare $x=1$ abbiamo
  $\lim_{x \to 1^-} \arctan\dfrac{x+1}{x-1} = - \frac\pi2,$
  
  mentre
  
  $\lim_{x \to 1^+} \arctan\dfrac{x+1}{x-1} = \frac\pi2.$
  
  Quindi, non c’è asintoto verticale.

Derivata prima e monotonia Ricordando che
$(\arctan x)' = \frac{1}{x^2+1},$

deduciamo immediatamente che:

$f'(x)=-\frac{1}{x^2+1}.$

La derivata è sempre negativa, perciò $f$ decresce su tutto il dominio.

Derivata seconda e convessità Si ha
$f''(x)=\frac{2x}{(x^2+1)^2}.$

Il segno dipende dal numeratore, ovvero da $x$ , perciò la funzione è convessa su $(0,1)\cup(1,+\infty)$ , concava su $(-\infty,0)$ . In particolare, c’è un punto di flesso in $(0,-\pi/4)$

Grafico
$\quad$

$\quad$

Esercizio 20 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare le seguenti funzioni e tracciarne un grafico qualitativo:

$\quad$

$f(x)=\frac{x^3-x}{x^2-4}$

$f(x)=\frac{\log x}{x}$

$f(x)=2x+\sqrt{x^2-1}$

$f(x)=\frac{3x+1}{x+1}-2\arctan x$

$f(x)=(x^2-4)e^{-|x|}$

$f(x)=x\cdot\frac{2\log x-3}{\log x-2}$

Svolgimento punto 1.

Consideriamo la funzione

$f(x) = \frac{x^3-x}{x^2-4}.$

Questa è definita quando il denominatore non si annulla, ovvero $x^2-4\neq 0$ . Nello specifico, ne segue che il dominio è dato da

$D=(-\infty,-2)\cup(-2,2)\cup(2,+\infty).$

Inoltre

$f(-x)=\frac{(-x)^3-(-x)}{(-x)^2-4}=\frac{-x^3+x}{x^2-4}=-\frac{x^3-x}{x^2-4}=-f(x),$

per cui la funzione è dispari e ciò permette di studiarla nel solo dominio $D_+=[0,2)\cup(2,+\infty)$ e di ottenere il suo grafico su $D\setminus D_+$ per simmetria rispetto all’origine degli assi coordinati.

Per $x=0$ si ha $f(0)=0$ , mentre $f(x)=0$ se e solo se

$x^3-x=0\iff x(x^2-1)=0\iff x=0,\ x=1,$

e quindi la funzione interseca gli assi nei punti

$O=(0,0),\quad A=(1,0).$

Risolvendo $f(x)>0$ nella parte positiva del dominio ( $D_+$ ) si trova che

$f(x)>0\iff x\in (0,1)\cup(2,+\infty).$

Inoltre, dato che il numeratore è un polinomio di ordine maggiore rispetto al denominatore, non ci sono asintoti orizzontali e vale:

$\lim_{x \to +\infty} f(x) = + \infty.$

Per quanto riguarda gli asintoti verticali, invece, calcoliamo

$\lim_{x\to 2^{\pm}} f(x)=\pm\infty,$

da cui segue che la retta $x= 2$ è asintoto verticale per $f(x)$ . Dato che il grado del numeratore supera di uno quello del denominatore, ci sono asintoti obliqui:

$m=\lim_{x\to + \infty}\frac{f(x)}{x}=\lim_{x\to\infty}\frac{x^3}{x\cdot x^2}=1,$

$q=\lim_{x\to+\infty}\left[f(x)-x\right]=\lim_{x\to+\infty}\frac{x^3-x-x^3+4x}{x^2-4}= \lim_{x\to+\infty}\frac{3x}{x^2}=0,$

segue che la retta $y=x$ è un asintoto obliquo destro. Per la derivata si può utilizzare la formula per la derivata di un rapporto per ottenere:

$f'(x)=\frac{(3x^2-1)(x^2-4)-(x^3-x)(2x)}{(x^2-4)^2}=\frac{x^4-11x^2+4}{(x^2-4)^2},$

Il denominatore non gioca alcun ruolo nel determinare il segno di $f'$ , perciò è sufficiente risolvere la disequazione:

$x^4-11x^2+4 > 0.$

Come al solito, ponendo $t=x^2$ si ottiene $t^2-11t+4 > 0$ , che ha come soluzioni

$t < \frac{11-\sqrt{105}}{2}\quad \text{e} \quad t > \frac{11+\sqrt{105}}{2},$

per cui ci riconduciamo alle disequazioni:

$x^2 < \frac{11-\sqrt{105}}{2}\quad \text{e} \quad x^2 > \frac{11+\sqrt{105}}{2}.$

Si trova

$-\sqrt{\frac{11-\sqrt{105}}{2}}\leq x\leq+\sqrt{\frac{11-\sqrt{105}}{2}}$

con la prima, e

$x\leq-\sqrt{\frac{11+\sqrt{105}}{2}},\quad x\geq+\sqrt{\frac{11+\sqrt{105}}{2}}$

con la seconda. Poiché $11^2-105=16=4^2$ , si ha

$\sqrt{\frac{11-\sqrt{105}}{2}}=\frac{1}{\sqrt{2}}\left(\sqrt{11+4}{2}-\sqrt{11-4}{2}\right)=\frac{\sqrt{15}-\sqrt{7}}{2},$

$\sqrt{\frac{11+\sqrt{105}}{2}}=\frac{1}{\sqrt{2}}\left(\sqrt{11+4}{2}+\sqrt{11-4}{2}\right)=\frac{\sqrt{15}+\sqrt{7}}{2},$

da cui

$-\frac{\sqrt{15}-\sqrt{7}}{2}\leq x\leq\frac{\sqrt{15}-\sqrt{7}}{2},$

$x\leq-\frac{\sqrt{15}+\sqrt{7}}{2},\quad x\geq\frac{\sqrt{15}+\sqrt{7}}{2},$

per cui $f'(x)\geq 0$ se e solo se

$x\in\left(-\infty,-\frac{\sqrt{15}+\sqrt{7}}{2}\right]\cup\left[-\frac{\sqrt{15}-\sqrt{7}}{2},\frac{\sqrt{15}-\sqrt{7}}{2}\right] \cup\left[\frac{\sqrt{15}+\sqrt{7}}{2},+\infty\right),$

e su tali intervalli la funzione risulta crescente. Inoltre $f$ risulta avere dei massimi relativi nei punti

$M_1=\left(-\frac{\sqrt{15}+\sqrt{7}}{2},-\frac{7\sqrt{7}+5\sqrt{15}}{8}\right), \quad M_2=\left(\frac{\sqrt{15}-\sqrt{7}}{2},\frac{-7\sqrt{7}+5\sqrt{15}}{8}\right),$

e dei minimi relativi nei punti

$m_1=\left(-\frac{\sqrt{15}-\sqrt{7}}{2},\frac{7\sqrt{7}-5\sqrt{15}}{8}\right), \quad m_2=\left(\frac{\sqrt{15}+\sqrt{7}}{2},\frac{7\sqrt{7}+5\sqrt{15}}{8}\right).$

Per la derivata seconda si ha poi

$\begin{aligned} f''(x) & =\frac{(4x^3-22x)(x^2-4)^2-(x^4-11x^2+4)2(x^2-4)(2x)}{(x^2-4)^4} \\ & =\frac{6x^3+72x}{(x^2-4)^3}=\frac{6x(x^2+12)}{(x^2-4)^3}. \end{aligned}$

La disequazione $f''(x)\geq 0$ ha soluzione in $D_+$ , dove il numeratore è sempre positivo, determinata unicamente dal denominatore:

$x \in (2,+\infty),$

dove $f$ risulta essere convessa. Inoltre $f$ ammette un punto di flesso in $O=(0,0)$ la cui tangente risulta la retta $y=x/4$ . Il grafico della funzione è riportato in figura, avendo considerato le simmetrie nella parte di dominio $D_-$ :

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 2.

La funzione

$f(x)= \frac{\log x}{x}$

è definita per $x>0$ , per cui $D=(0,+\infty)$ . Non presenta dunque simmetrie e si ha

$f(x)=0 \iff \log x=0,$

ovvero per $x=1$ . Quindi $f$ interseca l’asse delle $x$ nel punto $A=(1,0)$ .

Il denominatore è sempre positivo nel dominio $D$ , perciò $f(x)>0$ è equivalente a $\log x > 0$ , per cui $f$ risulta essere positiva su $(1,+\infty)$ . Facendo il limite in $0$ da destra otteniamo:

$\lim_{x\rightarrow 0^+}f(x) = - \infty,$

mentre il limite a $+\infty$ è dato da

$\lim_{x \to + \infty} \frac{ \log x}{x} = 0.$

In particolare, la retta $x=0$ è un asintoto verticale (da destra) mentre la retta $y=0$ un asintoto orizzontale per $x\to + \infty$ . Abbiamo poi

$f'(x)=\frac{\frac{1}{x}\cdot x-\log x}{x^2}=\frac{1-\log x}{x^2},$

per cui $f'(x) > 0$ dipende unicamente dal segno del numeratore, ovvero:

$1-\log x > 0 \iff \log x < 1\iff x < e.$

Intersecando con il dominio di $f$ , deduciamo che questa è crescente su $(0,e)$ , decrescente su $(e,+\infty)$ , e presenta un massimo (assoluto) nel punto $M=(e,1/e)$ .

La derivata seconda è data da

$f''(x)=\frac{-\frac{1}{x}\cdot x^2-(1-\log x)(2x)}{x^4}=\frac{2\log x-3}{x^3},$

ed essendo il denominatore sempre positivo sul dominio, la disequazione $f''(x) > 0$ è equivalente a

$2\log x-3 > 0\iff \log x>\frac{3}{2}\iff x> e^{3/2}=\sqrt{e^3}.$

La funzione è quindi convessa su $(\sqrt{e^3},+\infty)$ , concava su $(0,\sqrt{e^3})$ , e presenta un flesso nel punto $F=(\sqrt{e^3},3/(2\sqrt{e^3}))$ . Il grafico è riportato in figura.

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 3.

Il dominio della funzione

$f(x) = 2x + \sqrt{x^2-1}$

si ottiene imponendo la condizione $x^2-1\geq 0$ , per cui

$D=(-\infty,-1]\cup[1,+\infty).$

La funzione non ha simmetrie in quanto somma di una funzione pari e di una dispari. Inoltre, non interseca l’asse delle ordinate ( $x=0$ non appartiene al dominio), mentre

$f(x)=0 \iff 2x+\sqrt{x^2-1}=0\iff x^2-1=4x^2\iff 3x^2+1=0$

che non ha soluzioni. Quindi non ci sono intersezioni neanche con l’asse delle ascisse. Risolvendo $f(x)>0$ ci si riconduce alla coppia di sistemi:

$\begin{cases} -2x < 0 \\ x^2 -1 \ge 0 \end{cases} \quad \text{e} \qquad \begin{cases} -2x \ge 0 \\ x^2 - 1 > 4x^2 \end{cases}$

Il primo ha soluzione $x\geq 1$ , mentre il secondo non ammette alcuna soluzione. La funzione risulta allora positiva su $[1,+\infty)$ .

La funzione non ammette asintoti orizzontali dato che il limite a $\pm \infty$ è dato da

$\lim_{x\to \pm \infty}f(x)= \lim_{x\to \pm \infty}\frac{4x^2-x^2+1}{2x-\sqrt{x^2-1}}= \pm \infty,$

perciò verifichiamo eventuali asintoti obliqui. Per $x \to - \infty$ , si trova il coefficiente angolare:

$m_-=\lim_{x\to-\infty}\frac{f(x)}{x}=\lim_{x\to-\infty}\frac{3x^2+1}{2x^2-x\sqrt{x^2-1}}= \lim_{x\to-\infty}\frac{\displaystyle x^2\left(3+\frac{1}{x^2}\right)}{\displaystyle x^2\left(2+\sqrt{1-\frac{1}{x^2}}\right)}=1,$

per cui il termine noto è:

$q_-=\lim_{x\to-\infty}\left[f(x)- m_- x\right]=\lim_{x\to-\infty}\left[x+\sqrt{x^2-1}\right]= \lim_{x\to-\infty}\frac{x^2-x^2+1}{x-\sqrt{x^2-1}}=0.$

Dunque, la retta $y=x$ è un asintoto obliquo per $x \to - \infty$ . Analogamente, calcoliamo il coefficiente angolare a destra:

$m_+=\lim_{x\to+\infty}\frac{f(x)}{x}=\lim_{x\to+\infty}\left[2+\sqrt{1-\frac{1}{x^2}}\right]=3.$

Il termine noto risulta essere

$q_+=\lim_{x\to+\infty}\left[f(x)-m_+ x\right]=\lim_{x\to+\infty}\left[\sqrt{x^2-1}-x\right]= \lim_{x\rightarrow-\infty}\frac{x^2-1-x^2}{\sqrt{x^2-1}+x}=0,$

pertanto la retta $y=3x$ è un asintoto obliquo per $x\to +\infty$ . La derivata prima è

$f'(x)=2+\frac{2x}{2\sqrt{x^2-1}}=2+\frac{x}{\sqrt{x^2-1}}=\frac{2\sqrt{x^2-1}+x}{\sqrt{x^2-1}}.$

Il denominatore è sempre positivo sul dominio (escludendo i punti $x=\pm 1$ , dove si annulla), per cui la disequazione $f'(x)> 0$ è del tutto equivalente a

$2\sqrt{x^2-1}+x> 0\iff \begin{cases} -x<0\\ x^2-1> 0 \end{cases}\qquad \text{oppure} \qquad \begin{cases} -x> 0\\ 4x^2-4> x^2 \end{cases}$

Il primo sistema ha come soluzione $x> 1$ , il secondo $x<-2/\sqrt{3}$ , per cui la funzione risulta crescente su

$\left(-\infty,-\frac{2\sqrt{3}}{3}\right)\cup(1,+\infty)$

e decrescente su

$\left(-\frac{2\sqrt{3}}{3},-1\right).$

In particolare, la funzione ammette un massimo relativo nel punto

$M = \left(-\frac{2\sqrt{3}}{3},-\sqrt{3}\right),$

ed ammette due minimi relativi nei punti

$A = (-1,-2) \quad \text{e} \quad B = (1,2).$

I limiti a $\pm 1$ (da destra e sinistra rispettivamente) danno

$\lim_{x\to1^+}f'(x)=+\infty,\qquad \lim_{x\to -1^-} f'(x) = -\infty,$

perciò in tali punti la funzione ha tangente verticale ( $x=1$ e $x=-1$ rispettivamente). Infine per la derivata seconda si ha

$f''(x)=\frac{\sqrt{x^2-1}-x\frac{2x}{2\sqrt{x^2-1}}}{x^2-1}=\frac{x^2-1-x^2}{\sqrt{(x^2-1)^3}}=-\frac{1}{\sqrt{(x^2-1)^3}},$

la quale risulta sempre negativa sul dominio, perciò $f$ è concava. Il grafico è riportato nella figura che segue:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 4.

La funzione

$f(x) = \frac{3x+1}{x+1} - 2 \arctan x$

è definita per ogni valore reale ad esclusione di $x=-1$ , in cui il denominatore si annulla. Di conseguenza:

$D=(-\infty,-1)\cup(-1,+\infty).$

Si ha $f(0)=1$ , per cui interseca l’asse delle ordinate nel punto $C=(0,1)$ . Per determinare le soluzioni di $f(x)=0$ osserviamo che questa è equivalente a scrivere

$\frac{3x+1}{x+1}=2\arctan x.$

D’altra parte, il termine di sinistra si può ridurre ulteriormente facendo la divisione tra polinomi

$\frac{3x+1}{x+1}=\frac{3x+3-2}{x+1}=3-\frac{2}{x+1}.$

L’equazione si può ora risolvere valutando il grafico e facendo delle considerazioni:

$\quad$

Rendered by QuickLaTeX.com

$\quad$

La funzione $y_1=2\arctan x$ è limitata e, nello specifico, prende valori nell’intervallo $(-\pi,\pi)$ . La funzione $y_2=3-\frac{2}{x+1}$ , invece, coincide con l’iperbole equilatera $y=2/x$ traslata in modo da avere come asintoti le rette $y=3,\ x=-1$ . Ne segue che

$y_1(x)>y_2(x) \quad \text{per } x \to + \infty$

e, dato che $y_1(0)=0 < 3 = y_2(0)$ , deve esistere $\beta>0$ in cui tali curve si incontrano (teorema di esistenza degli zeri). Analogamente, dato che

$y_1(-1)=2\arctan(-1)=-\pi/2 \text{ e } y_2\to-\infty \quad \text{per } x\to-1,$

ne segue che esiste $-1<\alpha<0$ per cui le funzioni si intersecano. Ne segue che la funzione $f(x)$ interseca l’asse delle ascisse nei punti $A=(\alpha,0)$ e $B=(\beta,0)$ , risulta positiva su

$(-\infty,-1)\cup(\alpha,\beta)$

e negativa su

$(-1,\alpha)\cup(\beta,+\infty).$

Si noti che è possibile stimare il valore di $\alpha$ e $\beta$ . In particolare,

$\alpha \approx -0.488 \qquad \text{e} \qquad \beta \approx 3.026.$

I limiti a $\pm \infty$ si possono calcolare facilmente sfruttando il fatto che l’arcotangente è limitata e il rapporto tra polinomi ha lo stesso grado a numeratore e denominatore:

$\lim_{x\to\pm\infty}f(x)=\lim_{x\to\pm\infty}\left[\frac{3x}{x}-2\arctan x\right]=3-2\left(\pm\frac{\pi}{2}\right)=3\mp\pi.$

Dunque, la funzione ammette le rette $y=3-\pi$ ed $y=3+\pi$ come asintoti orizzontali a destra e sinistra rispettivamente. Nel punto singolare $x=-1$ possiamo calcolare i limiti

$\lim_{x\rightarrow-1^{\pm}}f(x)=\mp\infty+2\left(-\frac{\pi}{4}\right)=\mp\infty,$

per cui la funzione ha in $x=-1$ un asintoto verticale. La derivata prima è data da

$f'(x)=\frac{3(x+1)-(3x+1)}{(x+1)^2}-\frac{2}{x^2+1}=\frac{2}{(x+1)^2}-\frac{2}{x^2+1}=\frac{-4x}{(x^2+1)(x+1)^2},$

perciò il segno della derivata dipende unicamente dal numeratore. In particolare, la funzione $f$ risulta crescente su $(-\infty,-1)\cup(-1,0)$ , decrescente su $(0,+\infty)$ e ammette un massimo relativo in $C=(0,1)$ . La derivata seconda è data da

$\begin{aligned} f''(x) & =\frac{-4(x^2+1)(x+1)^2+4x\left[2x(x+1)^2+(x^2+1)2(x+1)\right]}{(x^2+1)^2(x+1)^4} \\ & =\frac{-4x^3-4x^2-4x-4+16x^3+8x^2+8x}{(x^2+1)^2(x+1)^3} \\ & =\frac{4(3x^3+x^2+x-1)}{(x^2+1)^2(x+1)^3}. \end{aligned}$

Il denominatore di tale derivata risulta positivo per $x\in(-1,+\infty)$ . Per il numeratore, invece, si osservi che

$3x^3+x^2+x-1 = 0$

ha un’unica soluzione, che si può ricavare con qualsiasi metodo standard di risoluzione per equazioni di terzo ordine, trovando:

$\gamma \approx 0.47.$

Ne segue che $f''(x)>0$ per $x\in(-\infty,-1)\cup(\gamma,+\infty)$ , dove la funzione è convessa, $f''(x)<0$ per $x\in(-1,\gamma)$ , dove la funzione è concava, ed $f$ ammette un flesso nel punto $F=(\gamma,f(\gamma))$ . Il grafico della funzione è riportato nella figura seguente:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 5.

Il dominio della funzione

$f(x)=(x^2-4) e^{-|x|}$

coincide con tutto l’asse reale. Inoltre, la funzione soddisfa

$f(-x)=((-x)^2-4)e^{-|-x|}=(x^2-4)e^{-|x|}=f(x),$

ovvero è pari. Inoltre $f(0)=-4$ , mentre $f(x)=0$ se e solo se

$x^2-4=0\implies x=\pm 2.$

La funzione interseca pertanto gli assi nei punti $A=(0,-4),\ B=(-2,0)$ e $C=(2,0)$ . Dato che l’esponenziale è sempre positiva, $f(x)>0$ quando $x^2-4>0$ , ovvero

$f(x) > 0 \iff x\in(-\infty,-2)\cup(2,+\infty).$

Per simmetria, possiamo limitarci al limite per $x \to + \infty$ :

$\lim_{x\to+\infty}f(x) \quad \text{è della forma} \quad [+\infty]\cdot [0],$

dato che $(x^4-4)$ tende ad infinito ed $e^{-x}$ tende a zero. Questa è una forma indeterminata, perciò applichiamo de l’Hôpital due volte ed otteniamo:

$\lim_{x\to+\infty}f(x)=\lim_{x\to+\infty}\frac{x^2-4}{e^x}=\lim_{x\to+\infty}\frac{2}{e^x}=0,$

per cui la retta $y=0$ è un asintoto orizzontale per $x \to \pm \infty$ . Non ci sono punti di discontinuità, dunque non esistono asintoti verticali.

Passando al calcolo della derivata prima, per simmetria possiamo limitarci all’intervallo $(0,+\infty)$ e sviluppare il modulo all’esponente ( $|x|=x$ ); si ha:

$f'(x)=-e^{-x}(x^2-4)+2x e^{-x}=e^{-x}(4+2x-x^2),$

per cui $f'(x)\geq 0$ su $(0,+\infty)$ equivale a

$4+2x-x^2\geq 0\iff x^2-2x-4\leq 0\iff 1-\sqrt{5}\leq x\leq 1+\sqrt{5}.$

In particolare, la derivata prima è positiva su $(0,1+\sqrt{5}]$ . La funzione è crescente in $(0,1+\sqrt{5})$ e decrescente in $(1+\sqrt{5},+\infty)$ (per simmetria, cresce su $(-\infty,-1-\sqrt{5})$ e decresce su $(-1-\sqrt{5},0)$ ) ed ammette due massimi (assoluti) nei punti

$M_1=\left(-(1+\sqrt{5}),(5+2\sqrt{5})e^{-(1+\sqrt{5})}\right),\qquad M_2=\left(1+\sqrt{5},(5+2\sqrt{5})e^{-(1+\sqrt{5})}\right),$

ed un minimo assoluto nel punto

$A=(0,-4).$

Inoltre, dato che il modulo $|x|$ non è differenziabile in $x=0$ , per verificare la differenziabilità facciamo i limiti destro e sinistro del rapporto incrementale:

$\lim_{x\to 0^{\pm}}\frac{f(x)-f(0)}{x} =\left\{\begin{array}{l} \displaystyle\lim_{x\to 0^{+}}\frac{(x^2-4)e^{-x}+4}{x}=-4 \lim_{x\to 0^{+}}\frac{e^{-x}-1}{x}=4\\ \\ \displaystyle\lim_{x\to 0^{-}}\frac{(x^2-4)e^{x}+4}{x}=-4\lim_{x\to 0^{-}}\frac{e^{x}-1}{x}=-4 \end{array}\right.$

I limiti esistono e sono finiti, ma non coincidono: dunque $x=0$ è un punto angoloso per $f$ . La derivata seconda per $x>0$ è data da

$f''(x)=-e^{-x}(4+2x-x^2)+e^{-x}(2-2x)=e^{-x}(x^2-4x-2),$

per cui risolvendo $f''(x) > 0$ con la condizione $x > 0$ si ricava

$x^2-4x-2 > 0\iff x< 2-\sqrt{6} \text{ oppure } x> 2+\sqrt{6}\iff x > 2+\sqrt{6}.$

La funzione è pertanto convessa su $(2+\sqrt{6},+\infty)$ e per simmetria su $(-\infty,-2-\sqrt{6})$ , concava su $(-2-\sqrt{6},2+\sqrt{6})$ , ed ammette flessi nei punti

$F_1=\left(-(2+\sqrt{6}),2(3+2\sqrt{6})e^{-(2+\sqrt{6})}\right),\qquad F_2=\left(2+\sqrt{6},2(3+2\sqrt{6})e^{-(2+\sqrt{6})}\right),$

in cui le tangenti hanno coefficiente angolare $\pm 2(1+\sqrt{6})e^{-(2+\sqrt{6})}$ rispettivamente. Il grafico della funzione è riportato nella figura seguente:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 6.

La funzione

$f(x) = x \cdot \frac{2 \log x - 3}{\log x - 2}$

è definita per $x > 0$ (per il logaritmo) e denominatore diverso da zero, ovvero

$\log x-2\neq 0 \iff \log x\neq 2 \iff x\neq e^2.$

In particolare, il dominio è

$D=(0,e^2)\cup(e^2,+\infty).$

La funzione non è simmetrica e interseca l’asse delle ascisse quando

$2\log x-3=0\implies x=e^{3/2},$

ovvero nel punto $A=(e^{3/2},0)$ . Inoltre, la funzione è positiva nell’unione di intervalli

$x\in(0,e^{3/2})\cup(e^2,+\infty).$

Il limite a $+ \infty$ si calcola osservando che il secondo fattore tende a $2$ :

$\lim_{x\to+\infty}f(x)=\lim_{x\to+\infty}x\cdot \underbrace{ \frac{2\log x}{\log x}}_{=2} = +\infty.$

Il coefficiente angolare di un eventuale asintoto obliquo a destra è dunque

$m=\lim_{x\to+\infty}\frac{f(x)}{x}=\lim_{x\to+\infty}\frac{2\log x}{\log x}=2,$

mentre il termine noto

$q=\lim_{x\to+\infty}\left[f(x)- m x\right]=\lim_{x\to+\infty}\frac{2x\log x-3x-2x\log x+4x}{\log x-2}= \lim_{x\to+\infty}\frac{x}{\log x-2}.$

A questo punto si applica la regola di de l’Hôpital, ottenendo:

$q =\lim_{x\to+\infty}\frac{1}{1/x}=+\infty,$

ovvero non c’è alcun asintoto obliquo. Il limite all’altro estremo del dominio di definizione è

$\lim_{x\to 0^+}f(x)\quad \text{è della forma} \quad [0]\cdot\frac{[\infty]}{[\infty]}.$

Si ha:

$\lim_{x\to 0^+} f(x)= \lim_{x\to 0^+}x \dfrac{2\log x}{\log x} =\lim_{x\to 0^+} 2x = 0.$

In particolare, $x=0$ è un punto singolare in cui la funzione può essere prolungata con continuità ponendo $f(0)=0$ . Infine, in $x=e^2$ abbiamo

$\lim_{x\rightarrow (e^2)^{\pm}} f(x)=\pm\infty,$

perciò la retta $x=e^2$ è un asintoto verticale. Per la derivata prima abbiamo

$\begin{aligned} f'(x)&=\frac{\displaystyle\left[2\log x-3+x\cdot\frac{2}{x}\right](\log x-2)-x(2\log x-3)\frac{1}{x}}{(\log x-2)^2} \\ & = \frac{(2\log x-1)(\log x-2)-2\log x+3}{(\log x-2)^2} \\ & = \frac{2\log^2 x-7\log x+5}{(\log x-2)^2}. \end{aligned}$

La disequazione $f'(x)\geq 0$ , essendo il denominatore sempre positivo sul dominio, equivale a richiederla per il numeratore:

$2\log^2 x-7\log x+5\geq 0$

sotto la condizione $x>0$ ed $x \neq e^2$ . Ponendo $t=\log x$ si ottiene una disequazione di secondo grado

$2t^2-7t+5\geq 0\iff t\leq 1 \text{ oppure } t\geq\frac{5}{2}$

e tornando alla variabile $x$ corrispondono a:

$\quad$

$\log x \le 1$ , che ha soluzione $x \le e$ ;

$\log x \ge 5/2$ , che ha soluzione $x \ge e^{5/2}$ .

Riassumendo, la funzione cresce su $(0,e)\cup(e^{5/2},+\infty)$ e decresce su $(e,e^2)\cup(e^2,e^{5/2})$ . In particolare, $f$ ha un massimo relativo in $M=(e,e)$ ed un minimo relativo in $m=(e^{5/2},4e^{5/2})$ . Inoltre, si ha

$f'(0)=\lim_{x\to 0^+}f'(x)=\lim_{x\to 0^+}\frac{2\log^2 x-7\log x+5}{(\log x-2)^2},$

e, dividendo numeratore e denominatore per $\log^2(x)$ si trova

$f'(0)=2.$

Il grafico della funzione risulta perciò essere tangente alla retta $y=2x$ nell’origine. Infine, la derivata seconda è data da

$\begin{aligned} f''(x) & =\frac{\displaystyle\left(\frac{4\log x}{x}-\frac{7}{x}\right)(\log x-2)^2-(2\log^2 x-7\log x+5)\cdot 2(\log x-2)\cdot\frac{1}{x}}{(\log x-2)^4} \\ & =\frac{(4\log x-7)(\log x-2)-2(2\log^2 x-7\log x+5)}{x(\log x-2)^3} \\ & =\frac{4\log^2 x-15\log x+14-4\log^2 x+14\log x-10}{x(\log x-2)^3}, \end{aligned}$

da cui, semplificando:

$f''(x)=\frac{4-\log x}{x(\log x-2)^3}.$

Per risolvere $f''(x) > 0$ per $x>0$ ed $x \neq e^2$ , consideriamo separatamente il segno del numeratore

$4-\log x > 0\implies \log x\le 4\implies x\leq e^4,$

e del denominatore

$x(\log x-2)^3>0\implies \log x-2>0\implies \log x>2\implies x>e^2.$

Di conseguenza, $f''(x)>0$ su $(e^2,e^4)$ , dove la funzione è convessa, $f''(x)<0$ su $(0,e^2)\cup(e^4,+\infty)$ , dove la funzione è concava, e si ha un punto di flesso in $F=(e^4,5e^4/2)$ .

$\quad$

Rendered by QuickLaTeX.com

Esercizio 21 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Studiare le seguenti funzioni e tracciarne un grafico qualitativo:

$\quad$

$f(x)=\frac{x^2}{x^2-1}$

$f(x)=e^{1/x} x^{1/3}$

$f(x)=6x\log x-(3x-2) \left[\log(3x-2)+1\right]-4\log 2$

$f(x)=x^{1/(4\log^2 x)}$

Svolgimento punto 1.

La funzione

$f(x) = \frac{x^2}{x^2-1}$

è definita per $x^2-1\neq 0$ , ovvero $x \neq \pm 1$ , per cui il dominio risulta essere:

$D=(-\infty,-1)\cup(-1,1)\cup(1,+\infty).$

Dato che $f(-x)=f(x)$ , la funzione è pari ed è pertanto sufficiente studiarla in

$D_+ = [0,1) \cup (1,+\infty).$

Inoltre interseca gli assi nella sola origine $O=(0,0)$ . Nel limite a $+\infty$ sia numeratore che denominatore asintoticamente vanno come $x^2$ , perciò

$\lim_{x\to + \infty}f(x)=1,$

mentre per $x\to 1^{\pm}$ abbiamo numeratore positivo e denominatore tendente a $0^\pm$ :

$\lim_{x\to 1^{\pm}}f(x)= \frac{1}{0^\pm} = \pm\infty.$

Di conseguenza, la retta $y=1$ è un asintoto orizzontale, mentre le rette $x=\pm 1$ (per parità $x=-1$ si comporta come $x=1$ con i segni invertiti) sono asintoti verticali. La derivata prima è data

$f'(x)=\frac{2x(x^2-1)-x^2\cdot 2x}{(x^2-1)^2}=-\frac{2x}{(x^2-1)^2},$

da cui $f'(x)=0$ se e solo se si annulla il numeratore, ovvero per $x=0$ . Dato che $f'(x)>0$ per $x<0$ e $f'(x)<0$ per $x>0$ , l’origine $O=(0,0)$ è un massimo relativo. La derivata seconda è

$f''(x)=-\frac{2(x^2-1)^2-2x\cdot 4x(x^2-1)}{(x^2-1)^4}=\frac{6x^2+2}{(x^2-1)^3}.$

Allora $f''(x)\neq 0$ per ogni $x$ nel dominio ed $f''(x)>0$ per $x\in(1,+\infty)$ , mentre $f''(x)<0$ per $x\in(0,1)$ . Estendendo l’analisi fatta sin qui per parità, si ottiene il grafico in figura:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 2.

La funzione

$f(x) = e^{1/x} \sqrt[3]{x}$

è definita per $x\neq 0$ , perciò il dominio è dato da

$D=(-\infty,0)\cup(0,+\infty).$

La funzione non interseca gli assi e non presenta simmetrie. I limiti ad infinito sono

$\lim_{x\to\pm\infty}f(x)=\pm\infty$

perché $e^{1/x} \to 0$ e $x^{1/3} \to \pm \infty$ . Il coefficiente angolare di eventuali asintoti obliqui è

$\lim_{x\to\pm\infty}\frac{f(x)}{x}= \lim_{x\to\pm\infty} e^{1/x} x^{-2/3} = 0,$

per cui la funzione non presenta asintoti obliqui od orizzontali. Nel punto $x=0$ abbiamo

$\lim_{x\to 0^-} f(x)=e^{-\infty}\cdot 0=0,$

mentre da destra si arriva ad una forma indeterminata:

$\lim_{x\to 0^+}f(x)\quad \text{del tipo}\quad [0]\cdot[\infty].$

Ponendo $t = 1/x$ il limite per $x\to 0^+$ corrisponde a $t\to +\infty$ ; usando la regola di de l’Hôpital:

$\lim_{x\to 0^+} f(x)=\lim_{t\to +\infty}\frac{e^t}{t^{1/3}}=\lim_{t\to+\infty}\frac{e^t}{t^{-2/3}/3}= \lim_{t\to+\infty}\frac{1}{3}\cdot e^t\cdot t^{2/3}=+\infty,$

per cui la retta $x=0$ è un asintoto verticale destro. La derivata prima si calcola tramite la formula di derivazione per un prodotto:

$f'(x)=-\frac{e^{1/x}}{x^2}\cdot x^{1/3}+e^{1/x}\cdot\frac{x^{-2/3}}{3}=e^{1/x}\cdot\frac{x-3}{3x^{5/3}}.$

Per cui $f'(x)=0$ se e solo se si annulla il numeratore, ovvero per $x=3$ . Dato che $f'(x)<0$ per $x\in(0,3)$ e $f'(x)>0$ per $x\in(-\infty,0)\cup(3,+\infty)$ , la funzione ha nel punto

$m=(3,e^{1/3}\sqrt[3]{3})$

un minimo relativo. La derivata seconda, invece, è data da

$\begin{aligned} f''(x) & = -\frac{e^{1/x}}{x^2}\cdot\frac{x-3}{3x^{5/3}}+e^{1/x}\cdot\frac{x^{5/3}-\frac{5}{3}(x-3) x^{2/3}}{3x^{10/3}} \\ & =\frac{e^{1/x}}{3x^{11/3}}\cdot\left(-x+3+x^2-\frac{5}{3} x^2+5x\right) \\ & =-e^{1/x}\cdot\frac{2x^2-12x-9}{9x^{11/3}}. \end{aligned}$

Si ha $f''(x)=0$ se e solo se si annulla il numeratore, ovvero

$2x^2 -12x - 9 = 0 \iff x=3\pm\frac{3\sqrt{6}}{2},$

per cui in tali punti la funzione presenta dei flessi. Dato che $f''(x)>0$ per

$x\in\left(3-\frac{3\sqrt{6}}{2},0\right)\cup\left(0,3+\frac{3\sqrt{6}}{2}\right),$

la funzione risulta convessa su tale intervallo. Il grafico è riportato in figura:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 3.

La funzione

$f(x) = 6x \log x - (3x - 2) [\log(3x-2) +1] - 4 \log 2$

è definita per $x>0$ e $3x-2>0$ . Il dominio è dunque dato da

$D=\left(\frac{2}{3},+\infty\right).$

Il limite all’estremo sinistro del dominio è dato da

$\lim_{x\to(2/3)^+} f(x)=4\log\frac{2}{3}-4\log 2=-4\log 3<0,$

mentre il limite a $+\infty$ porta ad una forma indeterminata:

$\lim_{x\to+\infty} f(x)\quad \text{del tipo}\quad \infty-\infty.$

Osserviamo dapprima che possiamo riscrivere la funzione come segue

$f(x) = [6x\log x-(3x-2)\log(3x-2)]-3x+2-4\log2,$

dove il termine $-3x+2-4\log2$ per $x\to +\infty$ è trascurabile rispetto al termine $x\log x$ ; inoltre $(3x-2)\log(3x-2)\sim 3xlog(3x)$ per $x\to + \infty$ e dunque non ci resta che calcolare il seguente limite, risolto applicando de l’Hôpital dopo alcune manipolazioni algebriche:

$\begin{aligned} \lim_{x\to+\infty}\left[6x\log x-3x\log 3x\right] & =\lim_{x\to+\infty} 3x \left[ 2 \log x - \log 3x \right]\\ &=\lim_{x\to+\infty} 3x\log x \left[ 2 - \frac{\log 3x}{\log x} \right] \\ & = \underbrace{\lim_{x\to+\infty} 3x\log x}_{=+\infty} \cdot \lim_{x\to+\infty} \left[ 2 - \underbrace{\frac{1/x}{1/x}}_{=1} \right] = + \infty. \end{aligned}$

Inoltre, è facile verificare che

$\lim_{x\to+\infty}\frac{f(x)}{x}=+\infty,$

per cui la funzione non ha asintoti orizzontali o obliqui. La derivata prima è data da

$f'(x)=6\log x+6-3\left[\log(3x-2)+1\right]-3=6\log x-3\log(3x-2)=3\log\frac{x^2}{3x-2},$

per cui $f'(x)=0$ se e solo se si annulla il logaritmo:

$\log\frac{x^2}{3x-2}=0\iff \frac{x^2}{3x-2}=1\iff x^2-3x+2=0,$

le cui soluzioni sono $x_1=1$ e $x_2=2$ . Dato che $f'(x)>0$ per $(2/3,1)\cup(2,+\infty)$ , la funzione ha un massimo (relativo) ed un minimo (relativo) rispettivamente in

$M=(1,-1-4\log 2) \quad \text{e} \quad m=(2,-4).$

Infine, la derivata seconda è

$f''(x)=3\cdot\frac{3x-2}{x^2}\cdot\frac{2x(3x-2)-3x^2}{(3x-2)^2}=\frac{3(3x-4)}{x(3x-2)},$

per cui $f''(x)=0$ se e solo se $x=4/3$ . La funzione ha allora in $F=(4/3,10\log 2-8\log 3-2)$ un flesso, e $f''(x)>0$ su $(4/3,+\infty)$ , intervallo su cui è convessa. Il grafico è riportato di seguito:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 4.

Il dominio della funzione

$f(x) = x^{\frac{1}{4 \log^2 x}}$

dipende da quello di $\log x$ , ovvero $x>0$ , e dalla condizione $\log x \neq 0$ che corrisponde dunque a:

$D=(0,1)\cup(1,+\infty).$

Il limite a $+ \infty$ è una forma indeterminata del tipo $[\infty]^{[0]}$ , quindi utilizziamo la seguente proprietà di logaritmo ed esponenziale:

$\exp \log (g(x)) = g(x).$

Si ha

$\ \lim_{x\to+\infty}f(x)=\lim_{x\to +\infty}\exp\left[\frac{\log x}{4\log^2 x}\right]=e^{0^+}=1,$

da cui segue che la retta $y=1$ è un asintoto orizzontale. Un discorso analogo si fa per il limite in $0^+$ :

$\lim_{x\to 0^+}f(x)\overset{[0]^{[0]}}{=}\lim_{x\to 0^+}\exp\left[\frac{\log x}{4\log^2 x}\right]=e^{0}=1.$

Infine, nel punto $x=1$ facciamo i limiti da sinistra e destra

$\begin{aligned} & \lim_{x\to 1^-}f(x)=\lim_{x\to 1^-}\exp\left[\frac{\log x}{4\log^2 x}\right]=e^{-\infty}=0^+, \\ & \lim_{x\to 1^+}f(x) =\lim_{x\to 1^+}\exp\left[\frac{\log x}{4\log^2 x}\right]=e^{+\infty}=+\infty, \end{aligned}$

da cui deduciamo che la retta $x=1$ è un asintoto verticale destro. La derivata prima è data da

$f'(x)=\left(\exp\left[\frac{1}{4\log x}\right]\right)'=\exp\left[\frac{1}{4\log x}\right]\cdot\frac{-1}{4x\log^2 x},$

perciò si vede subito che $f'(x) < 0$ sul dominio $D$ , ovvero $f$ è strettamente decrescente. Infine osserviamo che la funzione $f$ può essere scritta come

$f(x)=e^{g(x)},\qquad g(x)=\frac{1}{4\log x},$

per cui la derivata seconda è data dalla formula:

$f'(x)=e^{g(x)}\cdot g'(x) \implies f''(x)=e^{g(x)}\cdot[g'(x)]^2+e^{g(x)}\cdot g''(x)=e^{g(x)}\left([g'(x)]^2+g''(x)\right),$

dove

$g'(x)=-\frac{1}{4x\log^2 x}, \qquad g''(x)=\frac{\log x+2}{4x^2\log^3 x}.$

Sostituendo $g'$ e $g''$ nella formula sopra troviamo

$f''(x)=\exp\left[\frac{1}{4\log x}\right]\left(\frac{1}{16x^2\log^4 x}+\frac{\log x+2}{4x^2\log^3 x}\right)$

che, facendo alcune manipolazioni algebriche, si può riscrivere più compattamente come segue:

$f''(x)=\exp\left[\frac{1}{4\log x}\right]\cdot\frac{4\log^2 x+8\log x+1}{16x^2\log^4 x}.$

Ne segue che $f''(x)=0$ se e solo se si annulla il numeratore, ovvero

$4\log^2 x+8\log x+1=0\iff \log x=-1\pm\frac{\sqrt{3}}{2},$

e quindi per $x=e^{-1\pm\frac{\sqrt{3}}{2}}$ , punti in cui la funzione presenta due flessi come si vede dal grafico seguente:

$\quad$

Rendered by QuickLaTeX.com

Esercizio 22 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare le seguenti funzioni e tracciarne un grafico qualitativo:

$\quad$

$f(x)=1-e^{(1+\sin x)/(\sin x-1)}$

$f(x)=\frac{2^{x+1}+1}{2^x-1}$

$f(x)=\arctan\left(\frac{4x-1}{4x}-\frac{1}{4|x|}\right)$

$f(x)=\log\left(\sqrt{x^2+1}-x\right)-2\arctan\frac{1}{x}$

Svolgimento punto 1.

La funzione

$f(x) = 1 - \exp \left( \frac{\sin x + 1}{\sin x - 1}\right)$

risulta periodica di periodo $T=2\pi$ perciò ci limitiamo all’intervallo $[0,2\pi)$ . La funzione è definita per

$\sin x \neq 1 \iff x \neq \pi/2,$

e quindi il dominio risulta essere

$D=\left[0,\frac{\pi}{2}\right)\cup\left(\frac{\pi}{2},2\pi\right).$

Si ha $f(0)=1-e^{-1}$ , perciò la funzione passa per il punto $A=(0,1-1/e)$ . Inoltre

$\lim_{x\to(\pi/2)^{\pm}} f(x)=1-e^{-\infty}=1,$

per cui la funzione è prolungabile con continuità in $x=\pi/2$ ponendo $f(\pi/2)=1$ . Si noti che lo studio di asintoti orizzontali o obliqui non ha senso trattandosi di una funzione periodica.

Passiamo a calcolare la derivata prima sfruttando la formula di differenziabilità per una composizione; precisamente, si trova

$\begin{aligned} f'(x) & = -e^{(1+\sin x)/(\sin x-1)}\cdot\frac{\cos x(\sin x-1)-\cos x(\sin x+1)}{(\sin x-1)^2} \\ & =\frac{2\cos x\cdot e^{(1+\sin x)/(\sin x-1)}}{(\sin x-1)^2}, \end{aligned}$

per cui $f'(x)=0$ se e solo se $x_1=\pi/2$ o $x_2=3\pi/2$ . La funzione non è definita in $x_1$ , mentre $x_2$ risulta coincidere con il punto di minimo $m=(3\pi/2,0)$ . Infine, osserviamo che la funzione $f$ può essere scritta come

$f(x)=1-e^{g(x)},\qquad g(x)=\frac{1+\sin x}{\sin x-1},$

per cui

$f'(x)=-e^{g(x)}\cdot g'(x),$

e questo ci aiuta nel calcolo della derivata seconda grazie alla formula seguente:

$f''(x)=-e^{g(x)}\cdot[g'(x)]^2-e^{g(x)}\cdot g''(x)=-e^{g(x)}\left([g'(x)]^2+g''(x)\right).$

Si verifica facilmente che

$g'(x)=\frac{-2\cos x}{(\sin x-1)^2},\qquad g''(x)=\frac{-2(\sin x+2)}{(\sin x-1)^2},$

quindi sostituendo nell’espressione sopra si arriva alla derivata seconda di $f$ :

$\begin{aligned} f''(x) & = -e^{(\sin x+1)/(\sin x-1)}\cdot\frac{4\cos^2 x-2(\sin x+2)(\sin x-1)^2}{(\sin x-1)^4} \\ & =-e^{(\sin x+1)/(\sin x-1)}\cdot\frac{4\cos^2 x-2\sin^3 x+4\sin^2 x-2\sin x-4\sin^2 x+8\sin x-4}{(\sin x-1)^4}. \end{aligned}$

Facendo alcune semplificazioni si trova l’espressione

$f''(x)=e^{(\sin x+1)/(\sin x-1)}\cdot\frac{2\sin x(\sin x +3)}{(1-\sin x)^3},$

da cui segue che

$f''(x)\ge 0 \iff \sin x(\sin x +3)\geq 0 \iff \iff \sin x \ge 0 \iff 0\leq x \leq \pi.$

$\quad$

Rendered by QuickLaTeX.com

$\quad$

La funzione presenta punti di flesso in

$A=(0,1-1/e),\qquad B=(\pi,1-1/e),\qquad C=(2\pi,1-1/e).$

Il grafico è riportato in figura:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 2.

La funzione

$f(x) = \frac{2^{x+1}+1}{2^x-1}$

è definita quando il denominatore è diverso da zero, ovvero

$2^x - 1 \neq 0 \iff 2^x \neq 1 \iff x \neq 0.$

Il dominio risulta dunque essere

$D=(-\infty,0)\cup(0,+\infty).$

I limiti a $\pm \infty$ si calcolano banalmente ricordando che $2^x\to0$ per $x\to-\infty$ e $2^x\to+\infty$ per $x\to+\infty$ ; precisamente, si trova che

$\lim_{x\to-\infty}f(x)=\frac{0+1}{0-1}=-1,\qquad \lim_{x\to+\infty} f(x)=\lim_{x\to+\infty}\frac{2^{x+1}+1}{2^x-1}=2,$

per cui le rette $y=-1$ e $y=2$ sono asintoti orizzontali a sinistra e destra rispettivamente. Inoltre, i limiti da destra e sinistra nel punto $x=0$ sono

$\lim_{x\rightarrow 0^{\pm}}f(x)=\pm\infty,$

per cui la retta $x=0$ è un asintoto verticale. La derivata prima è data da

$f'(x)=\frac{2^{x+1}\log 2(2^x-1)-(2^{x+1}-1)2^x\log 2}{(2^x-1)^2}=\frac{-3\; 2^x\log 2}{(2^x-1)^2},$

ed è sempre negativa, perciò $f$ è decrescente nel dominio. La derivata seconda è data da

$f''(x)=-3\log 2\cdot\frac{2^x\log 2(2^x-1)^2-2^x\cdot2(2^x-1)2^x\log 2}{(2^x-1)^4},$

che si semplifica in:

$f''(x)=\frac{3\;2^x\log^2 2\cdot(2^x+1)}{(2^x-1)^3}.$

Allora $f''(x)=0$ se e solo se

$2^x-1=0 \iff x = 0,$

che però non appartiene al dominio. Dunque, il segno di $f"(x)$ dipende esclusivamente dal denominatore che risulta positivo per $x>0$ e negativo per $x<0$ , per cui la funzione risulta convessa su $(0,+\infty)$ e concava su $(-\infty,0)$ . Il grafico è riportato in figura:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 3.

Il dominio della funzione

$f(x) = \arctan \left( \frac{4x-1}{4x} - \frac{1}{4|x|} \right)$

si trova imponendo i denominatori diversi da zero, ovvero $x \neq 0$ :

$D=(-\infty,0)\cup(0,+\infty).$

La funzione si può scrivere sviluppando il modulo $|x|$ come

$f(x) = \begin{cases} f_1(x) & \text{se } x > 0, \\ f_2(x) & \text{se } x < 0,\end{cases}$

dove

$\begin{aligned} & f_1(x)=\arctan\frac{2x-1}{2x}, \\ & f_2(x)=\arctan 1= \pi/4. \end{aligned}$

In particolare, la funzione risulta costante sull’intervallo $(-\infty,0)$ . Il limite a $-\infty$ coincide con il valore della funzione su $(-\infty, 0)$ , quindi ci occupiamo solo del limite a $+\infty$ :

$\lim_{x\to +\infty} f_1(x)=\arctan 1=\frac{\pi}{4},$

dal momento che $(2x-1)/2x \sim 2x / 2x$ asintoticamente quando $x$ è sufficientemente grande. Inoltre, si vede che

$\lim_{x\to 0^+} f(x)= \lim_{x\to 0} f_1(x) = \arctan(-\infty)=-\frac{\pi}{2},$

mentre da sinistra

$\lim_{x\to 0^-} f(x)= \lim_{x\to 0} f_2(x) = \frac{\pi}{4},$

per cui la retta $y=\pi/4$ è un asintoto orizzontale destro. La derivata è nulla in $(-\infty,0)$ e

$\begin{aligned} f_1'(x) & =\frac{1}{\displaystyle 1+\left(\frac{2x-1}{2x}\right)^2}\cdot\frac{4x-4x+2}{4x^2} \\ & = \frac{4x^2}{4x^2+4x^2+1-4x}\cdot\frac{1}{2x^2} \\ & =\frac{2}{8x^2-4x+1} \end{aligned}$

in $(0,+\infty)$ . Dunque, si ha $f_1'(x)>0$ su tale intervallo e, di conseguenza, la funzione è sempre crescente per $x>0$ e costante per $x<0$ . Infine

$f_1''(x)=-\frac{2(16x-4)}{(8x^2-4x+1)^2}=-\frac{8(4x-1)}{(8x^2-4x+1)^2},$

per cui $f_1''(x)=0$ se e solo se $x=1/4$ , che appartiene al dominio di $f_1$ , da cui segue che la funzione ha un flesso nel punto $F=(1/4,-\pi/4)$ e risulta convessa per $x\in(0,1/4)$ e concava per $x\in(1/4,+\infty)$ . Il grafico è riportato in figura:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 4.

La funzione

$f(x) = \log \left( \sqrt{x^2+1} - x \right) - 2 \arctan \frac1x$

è definita per $x \neq 0$ e argomento del logaritmo positivo:

$\sqrt{1+x^2}-x>0.$

Se $x<0$ , la disequazione è certamente verificata; se $x>0$ possiamo portare $x$ a destra ed elevare al quadrato, ottenendo la disequazione

$1 + x^2 > x^2,$

che è sempre banalmente verificata. In particolare, il dominio è dato da:

$D=(-\infty,0)\cup(0,+\infty).$

Osserviamo che la funzione è positiva per $x<0$ , mentre è negativa per $x>0$ . Infatti,

$\log(\sqrt{x^2+1}-x)> 0 \iff \sqrt{x^2+1}-x >1 \iff x^2+1 > x^2 + 2x + 1 \iff x <0$

$\arctan \dfrac{1}{x} > 0 \iff x >0,$

da cui, mettendo assieme i risultati, si ha

$\log(\sqrt{x^2+1}-x) -2\arctan \dfrac{1}{x} > 0 \iff x <0.$

Il limite a $- \infty$ si calcola osservando che il termine di logaritmo logaritmico va a $+\infty$ , mentre l’altro va a $0$ :

$\lim_{x\to-\infty}f(x)=+\infty,$

perciò non c’è asintoto orizzontale sinistro. Inoltre, il coefficiente angolare di un eventuale asintoto obliquo sinistro è dato da:

$m=\lim_{x\to-\infty}\frac{f(x)}{x}=\lim_{x\to-\infty}\frac{\log(\sqrt{1+x^2}-x)}{x}= \lim_{x\to-\infty}\frac{\log(-2x)}{x}=0,$

perciò a sinistra non ammette asintoti di alcun tipo. Il limite a $+ \infty$ è più delicato, ma si può calcolare osservando che

$\sqrt{x^2+1} - x = (\sqrt{x^2+1} - x) \frac{\sqrt{x^2+1} + x}{\sqrt{x^2+1} + x} = \frac{1}{\sqrt{x^2+1} + x},$

da cui segue che:

$\lim_{x\to+\infty}f(x)=\lim_{x\to+\infty}\log\frac{1}{\sqrt{1+x^2}+x}=-\infty.$

Inoltre, il coefficiente angolare di un eventuale asintoto obliquo destro è dato da

$m=\lim_{x\to+\infty}\frac{f(x)}{x}=\lim_{x\to+\infty}\frac{1}{x} \log\frac{1}{\sqrt{1+x^2}+x} \overset{[0][ \infty]}{=} \lim_{x\to+\infty}\frac{1}{x} \log\frac{1}{x}= 0,$

dove nell’ultimo limite abbiamo usato il fatto $\lim_{x\to +\infty} \frac{\log x}{x}=0$ . Da tale risultato deduciamo che non vi sono asintoti orizzontali/obliqui. Inoltre, nel punto $x=0$ abbiamo

$\lim_{x\to 0^{\pm}}f(x)=0-2\arctan(\pm\infty)=\mp\pi,$

per cui in $x=0$ si ha un salto $-2\pi$ . La derivata prima è data da

$\begin{aligned} f'(x) & =\frac{\frac{x}{\sqrt{1+x^2}}-1}{\sqrt{1+x^2}-x}-2\frac{1}{1+\frac{1}{x^2}}\left(-\frac{1}{x^2}\right)= -\frac{1}{\sqrt{1+x^2}}+\frac{2}{1+x^2} \\[.4em] & =\frac{2-\sqrt{x^2+1}}{1+x^2}. \end{aligned}$

Dunque $f'(x)=0$ se e solo se si annulla il numeratore, ovvero:

$2\sqrt{1+x^2}-x^2-1=0 \iff 4(1+x^2)=(x^2+1)^2\iff x^2+1=4\iff x=\pm \sqrt{3}.$

Inoltre, studiando il segno di $f'$ si ha:

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Essendo $f'(x)<0$ per $(-\sqrt{3},0)\cup(0,\sqrt{3})$ , $f$ ammette un minimo in $m=(-1,\log(\sqrt{2}+1)+\pi/2)$ ed un massimo in $M = (1,\log(\sqrt{2}-1)-\pi/2)$ , entrambi relativi. Infine, potendo scrivere

$f'(x)=\frac{2\sqrt{g(x)}-g(x)}{\sqrt{[g(x)]^3}}=\frac{2}{g(x)}-\frac{1}{\sqrt{g(x)}},\qquad g(x)=x^2+1,$

la derivata seconda si calcola come segue:

$\begin{aligned} f''(x) & = -\frac{2g'(x)}{[g(x)]^2}+\frac{g'(x)}{2\sqrt{[g(x)]^3}}=\frac{g'(x)(\sqrt{g(x)}-4)}{2[g(x)]^2} \\[.4em] & =\frac{x(\sqrt{1+x^2}-4)}{(1+x^2)^2}. \end{aligned}$

Allora $f''(x)=0$ se e solo se si annulla il numeratore, ovvero $x=0$ (che non è accettabile) oppure

$\sqrt{1+x^2}-4=0\iff 1+x^2=16\iff x=\pm\sqrt{15}.$

Il segno di f” è il seguente:

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Segue che la funzione ammette due flessi in tali punti.La funzione è perciò convessa su $(-\sqrt{15},0)\cup(\sqrt{15},+\infty)$ . Il grafico della funzione è riportato in figura:

$\quad$

Rendered by QuickLaTeX.com

Esercizio 23 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Studiare le seguenti funzioni e tracciarne un grafico qualitativo:

$\quad$

$f(x)=\frac{1+|\log x|}{1-|\log x|}$

$f(x)=x+\log\cosh x-\tanh x$

$f(x)=\arcsin\sqrt{1-x^2}+\sqrt{1-x^2}$

$f(x)=\frac{2-\log^{-1} x}{\sqrt{|\log x|}}$

Svolgimento punto 1.

La funzione

$f(x)= \frac{1 + |\log x|}{1-|\log x|}$

è definita per $x>0$ e $|\log x|\neq 1$ , ovvero

$\log x \neq \pm 1 \iff x \neq 1/e \text{ e } x \neq e,$

da cui si arriva al dominio:

$D=\left(0,\frac{1}{e}\right)\cup\left(\frac{1}{e},e\right)\cup\left(e,+\infty\right).$

Sviluppando il modulo di $\log x$ si può scrivere la funzione come

$f(x) = \begin{cases} f_1(x) & \text{se } x \in [1,e) \cup (e,+\infty) \\ f_2(x) & \text{se } x \in (0,1/e) \cup (1/e,1), \end{cases}$

dove

$f_1(x)=\frac{1+\log x}{1-\log x} \quad \text{e} \quad f_2(x)=\frac{1-\log x}{1+\log x}.$

Numeratore e denominatore vanno ad infinito con la stessa velocità per $x \to + \infty$ , perciò

$\lim_{x\to+\infty}f(x)=\lim_{x\to+\infty}\frac{1/x}{-1/x}=-1,$

applicando, ad esempio, il teorema di de l’Hôpital. Inoltre, si ha

$\lim_{x\rightarrow 0^+}f(x)=\lim_{x\rightarrow 0^+}\frac{-1/x}{1/x}=-1,$

per cui la funzione è prolungabile con continuità in $x=0$ ponendo $f(0)=-1$ . Infine

$\begin{aligned} & \lim_{x\rightarrow(1/e)^-}f(x)=-\infty,\qquad \lim_{x\rightarrow(1/e)^+}f(x)=+\infty, \\ & \lim_{x\rightarrow e^-}f(x)=+\infty,\qquad \lim_{x\rightarrow e^+}f(x)=-\infty, \end{aligned}$

per cui le rette $x=1/e$ ed $x=e$ sono asintoti verticali, mentre $y=-1$ un asintoto orizzontale. Per calcolare la derivata prima di $f$ occupiamoci dei due rami $f_1$ ed $f_2$ separatamente:

$\begin{aligned} & f_1'(x)=\frac{\frac{1}{x}(1-\log x)+\frac{1}{x}(1+\log x)}{(1-\log x)^2}=\frac{2}{x(1-\log x)^2}, \\ & f'_2(x)=\frac{-\frac{1}{x}(1+\log x)-\frac{1}{x}(1-\log x)}{(1+\log x)^2}=-\frac{2}{x(1+\log x)^2}, \end{aligned}$

per cui la funzione è crescente su $(1,e)\cup(e,+\infty)$ e decrescente su $(0,1/e)\cup(1/e,1)$ . Di conseguenza, $m=(1,1)$ è un punto angoloso di minimo relativo. Infine, si ha

$\begin{aligned} & f_1''(x)=-2\frac{(1-\log x)^2-2x(1-\log x)\frac{1}{x}}{x^2(1-\log x)^4}=-\frac{2(\log x+1)}{x^2(\log x-1)^3}, \\ & f_2''(x)=2\frac{(1+\log x)^2+2x(1+\log x)\frac{1}{x}}{x^2(\log x+3)^4}=\frac{2(\log x+3)}{x^2(\log x+1)^3}, \end{aligned}$

per cui $f_1''(x)=0$ per $x=1/e$ che non appartiene al dominio, mentre $f_2''(x)=0$ per $x=1/e^3$ . La funzione ha allora un flesso nel punto $F=(1/e^3,-2)$ , risulta convessa su $(0,1/e^3)\cup(1/e,e)$ e concava su $(1/e^3,1/e)\cup(e,+\infty)$ . Il grafico è riportato in figura:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 2.

La funzione

$f(x) = x + \log \cosh x - \tanh x$

è definita quando $\cosh x>0$ , ovvero su tutto $\mathbb R$ . Inoltre $f(0)=0$ , quindi la funzione passa per l’origine degli assi. Il limite a meno infinito è una forma indeterminata:

$\lim_{x\to-\infty}f(x)=[\infty] - [\infty],$

perciò sfruttiamo il fatto che $\log ( e^x + e^{-x})$ è asintoticamente equivalente a $\log( e^{-x}) = -x$ per $x \to - \infty$ , ottenendo:

$\lim_{x\to-\infty}f(x)=\lim_{x\to-\infty}\left(x+(-x)-\log 2+1\right) =\lim_{x\to-\infty}\left(x-x-\log 2+1\right)=-\log 2+1.$

Il limite a $+ \infty$ , invece, non risulta in una forma indeterminata e si ha:

$\lim_{x\to+\infty}f(x)=+\infty.$

Cerchiamo eventuali asintoti obliqui destri; il coefficiente angolare a $+ \infty$ è dato da

$m_+=\lim_{x\to+\infty}\frac{f(x)}{x}=\lim_{x\to+\infty}\left(1+\frac{\log\cosh x}{x}-\frac{\tanh x}{x}\right)=1+1-0=2,$

mentre il termine noto è

$q=\lim_{x\to+\infty}[f(x)-m_+ x]=\lim_{x\to+\infty}\left(-x+\log(e^x+e^{-x})-\log 2-1\right) =-\log 2-1.$

Di conseguenza, la retta $y=-\log 2+1$ è un asintoto orizzontale sinistro, mentre la retta $y=2x-\log 2-1$ è un asintoto obliquo destro. Per la derivata prima si ha

$f'(x)=1+\frac{\sinh x}{\cosh x}-(1-\tanh^2 x)=\tanh x(\tanh x+1)$

usando la relazione $\sinh(x) / \cosh(x) = \tanh(x)$ . Osserviamo perciò che

$f'(x) = 0 \iff \tanh(x) = 0 \text{ oppure } \tanh(x) = -1,$

per cui $x=0$ è la soluzione della prima, mentre per la seconda si ha:

$\tanh x=-1\iff \frac{e^{2x}-1}{e^{2x}+1}=-1\iff e^{2x}-1=-e^{2x}-1,$

ovvero non ha soluzione. Dato che $f'(x)>0$ per $x>0$ , il punto $O=(0,0)$ è un minimo assoluto della funzione. La derivata seconda è data da

$f''(x)=2\tanh x(1-\tanh^2 x)+(1-\tanh^2 x)=(1-\tanh^2 x)(2\tanh x+1),$

e quindi $f''(x)=0$ in uno dei seguenti casi:

$1-\tanh^2 x=0\iff \tanh x=\pm 1\iff e^{2x}-1=\pm(e^{2x}+1),$

che non ammette soluzione, oppure

$2\tanh x+1=0\iff 2(e^{2x}-1)=-(e^{2x}+1)\iff 3e^{2x}=1\iff x=-\frac{1}{2}\log 3<0.$

La funzione presenta pertanto un flesso nel punto $F=(-(\log 3)/2, \log(2/3)+1/2)$ e risulta essere convessa su $(-(\log 3)/2,+\infty)$ e concava su $(-\infty,-(\log 3)/2)$ . Il grafico è rappresentato in figura:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 3.

La funzione

$f(x) = \arcsin \sqrt{1-x^2} + \sqrt{1-x^2}$

è definita per $0\leq \sqrt{1-x^2}\leq 1$ e $1-x^2\geq 0$ , e quindi ha per dominio

$D=[-1,1].$

È inoltre una funzione continua nel suo dominio in quanto composizione di funzioni continue. È anche facile verificare che si tratta di una funzione pari, perciò possiamo limitarci a studiarla nell’intervallo $D_+=[0,1]$ . Poiché $f(1)=0$ e $f(0)=\pi/2+1$ , la funzione passa per i punti

$A=(-1,0),\qquad B=(0,\pi/2+1),\qquad C=(1,0).$

Non dobbiamo calcolare alcun limite, perciò partiamo con il calcolo della derivata prima:

$\begin{aligned} f'(x)&=\frac{1}{\sqrt{1-(\sqrt{1-x^2})^2}}\cdot\frac{-2x}{2\sqrt{1-x^2}}+\frac{-2x}{2\sqrt{1-x^2}} \\& = -\frac{x}{\sqrt{1-x^2}}\left(\frac{1}{|x|}+1\right). \end{aligned}$

La derivata è definita in $(-1,1) \setminus \{0\}$ . Calcolando il limite da sinistra e destra rispettivamente in $\pm 1$ otteniamo:

$\lim_{x\to 1^-}f'(x)=- \infty \quad \text{e} \quad \lim_{x\to -1^+}f'(x)= \infty,$

da cui segue che in tali punti si ha una cuspide. Inoltre, in $x=0$ si ha

$\lim_{x\to 0^{\pm}} f'(x)=\lim_{x\to 0^{\pm}}-\frac{x}{|x|}=\mp 1,$

perciò $x=0$ è un punto angoloso per $f$ . La funzione risulta crescente su $[-1,0)$ e decrescente in $(0,1]$ , per cui ha due minimi assoluti nei punti $A,\ C$ e un massimo assoluto nel punto $B$ .

Infine, la derivata seconda è data da:

$f''(x)=\frac{-\sqrt{1-x^2}-(-\text{sign}(x)-x)\cdot\frac{-x}{\sqrt{1-x^2}}}{1-x^2} = \frac{-|x|-1}{\sqrt{(1-x^2)^3}}.$

E’ immediato verificare che $f''(x)<0$ per ogni $x \in (-1,0)\cup(0, 1)$ , e di conseguenza la funzione è sempre concava. Sfruttando la simmetria pari della funzione $f$ , si ottiene il grafico è riportato in figura:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 4.

La funzione

$f(x) = \frac{2 - \frac{1}{\log x}}{\sqrt{|\log x|}}$

è definita per $x>0$ e $|\log x|\neq 0$ , per cui

$D=(0,1)\cup(1,+\infty).$

Sviluppiamo il modulo e scriviamo la funzione come

$f(x) = \begin{cases} f_1(x) & \text{se } x \in (1,+\infty), \\ f_2(x) & \text{se } x \in (0,1),\end{cases}$

dove:

$f_1(x)=\frac{2\log x-1}{\sqrt{\log^3 x}} \quad \text{e} \quad f_2(x)=\frac{2\log x-1}{\sqrt{-\log^3 x}}.$

I limiti si svolgono in maniera banale osservando che in $0^+$ e $+ \infty$ il logaritmo a denomimatore è il termine dominante, mentre in $1^\pm$ abbiamo $-1/0^+$ ; riassumendo:

$\begin{aligned} & \lim_{x\rightarrow 0^+}f(x)=0^+, \\ & \lim_{x\rightarrow 1^{\pm}}f(x)=-\infty, \\ & \lim_{x\rightarrow +\infty}f(x)=0^+. \end{aligned}$

La funzione è dunque prolungabile con continuità in $x=0$ ponendo $f(0)=0$ , ammette la retta $x=1$ come asintoto verticale e la retta $y=0$ come asintoto orizzontale destro. La derivata è

$f_1'(x)=\frac{\frac{2}{x}\cdot\sqrt{\log^3 x}-(2\log x-1)\cdot\frac{1}{2\sqrt{\log^3 x}}\cdot\frac{3\log^2 x}{x}}{\log^3 x},$

che possiamo riscrivere più comodamente come segue:

$f_1'(x)=\frac{3-2\log x}{2x\sqrt{\log^5 x}}.$

In particolare, $f_1'(x)=0$ se e solo se $3-2\log x=0$ da cui $x=e^{3/2}$ ; dunque, la funzione $f_1$ è crescente su $(1,e^{3/2})$ ed ammette un massimo nel punto $M=(e^{3/2},4\sqrt{6}/9)$ . Analogamente, la derivata del secondo ramo è

$f_2'(x)=\frac{\frac{2}{x}\cdot\sqrt{-\log^3 x}-(2\log x-1)\cdot\frac{1}{2\sqrt{-\log^3 x}}\cdot\frac{-3\log^2 x}{x}}{-\log^3 x},$

che si riscrive più comodamente come segue:

$f_2'(x)=\frac{3-2\log x}{2x\sqrt{-\log^5 x}}.$

Questa funzione è strettamente positiva in $]0,1[$ , perciò $f_2$ è sempre crescente. Infine, la derivata seconda è data da

$f''_1(x)=\frac{4\log^2 x-15}{4x^2\sqrt{\log^7 x}}\quad \text{e} \quad f_2''(x)=\frac{15-4\log^2 x}{4x^2\sqrt{-\log^7 x}},$

che si annullano entrambe quando il numeratore (che è lo stesso a meno del segno) si annulla, ovvero:

$4\log^2 x-15=0\iff \log x=\pm\frac{\sqrt{15}}{2}\iff x=e^{\pm\sqrt{15}/2}.$

La prima soluzione è accettabile per $f_1$ , mentre la seconda per $f_2$ e si ha:

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Perciò, la funzione $f$ ha due flessi in tali punti ed inoltre:

$\quad$

$f_2$ è convessa su $(0,e^{-\sqrt{15}/2})$ ;

$f_1$ è convessa su $(e^{\sqrt{15}/2},+\infty)$ .

Il grafico è riportato in figura.

$\quad$

Rendered by QuickLaTeX.com

Esercizio 24 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Studiare le seguenti funzioni e tracciarne un grafico qualitativo:

$\quad$

$f(x)=|x^2-2x|e^x$

$f(x)=x^2 e^{\frac{|x|-1}{|x|}}$

$f(x)=\sin x \cdot e^{|\sin x|}$

$f(x)=\arctan\frac{\log x-1}{\log x+1}+\log(\log^2 x+1)$

Svolgimento punto 1.

La funzione

$f(x) = |x^2-2x| e^x$

risulta definita su tutto l’insieme dei numeri reali. Sviluppando il modulo, possiamo riscriverla come segue:

$f(x) = \begin{cases} (x^2-2x) e^x & \text{per } x\in(-\infty,0]\cup(2,+\infty), \\ (2x-x^2) e^x & \text{per } x\in(0,2]. \end{cases}$

La funzione interseca l’asse delle $y$ nell’origine (dato che $f(0)=0$ ) e l’asse delle $x$ in

$f(x) = 0 \iff x^2-2x=0 \iff x = 0 \text{ o } x = 2,$

ovvero nell’origine e nel punto $A=(2,0)$ . Inoltre, la funzione $f$ è non-negativa su tutto $\mathbb R$ essendo prodotto di due funzioni non-negative. Il limite a $+\infty$ è banalmente dato da

$\lim_{x\to +\infty}f(x)=+\infty,$

mentre a $-\infty$ abbiamo una forma indeterminata

$\lim_{x\to-\infty}f(x)= [+\infty] \cdot [0].$

Tuttavia, riscritta la funzione come $f(x)=\frac{|x^2-2x|}{e^{-x}}$ e ricordando che la funzione esponenziale è un infinito di ordine superiore rispetto a ogni potenza di $x$ si trova:

$\lim_{x\to-\infty}f(x) = 0.$

In particolare, la retta $y=0$ è un asintoto orizzontale sinistro. Osserviamo inoltre che

$\lim_{x\to +\infty}\frac{f(x)}{x}=+\infty,$

quindi la funzione non ammette asintoto orizzontale oppure obliquo a destra. Calcoliamo la derivata dei due “rami” della funzione separatamente, ovvero

$f'_1(x)=(2x-2)e^x+(x^2-2x)e^x=(x^2-2)e^x,$

$f'_2(x)=(2-2x)e^x+(2x-x^2)e^x=(2-x^2)e^x,$

da cui risulta che

$f'(x) = \begin{cases} (x^2-2) e^x & \text{per } x\in(-\infty,0)\cup(2,+\infty), \\ (2-x^2) e^x & \text{per } x\in(0,2). \end{cases}$

In questo caso, i punti $x=0$ ed $x=2$ vanno analizzati separatamente. Osserviamo subito che

$\lim_{x \to 0^-} f'(x) = f_1'(0) = (0-2) = -2,$

mentre

$\lim_{x \to 0^+} f'(x) = f_2'(0) = (2-0) = 2,$

perciò $x=0$ risulta essere un punto angoloso. Analogamente, si ha

$\lim_{x \to 2^-} f'(x) = f_2'(2) = (2-4)e^2 = -2e^2,$

mentre

$\lim_{x \to 2^+} f'(x) = f_1'(2) = (4-2)e^2 = 2e^2,$

perciò $x=2$ è un punto angoloso per $f$ . Inoltre

$f'(x) = 0 \iff x=\pm \sqrt2,$

dunque la funzione cresce su $(-\infty,-\sqrt{2})\cup (0,\sqrt2) \cup (2,+\infty)$ e decresce su $(-\sqrt{2},0) \cup (\sqrt{2},2)$ . La funzione presenta quindi due massimi relativi nei punti

$M_1 = (-\sqrt{2},(2+2\sqrt{2})e^{-\sqrt{2}}) \quad \text{e} \quad M_2=(\sqrt{2},(2\sqrt{2}-2)e^{\sqrt{2}})$

ed due minimi assoluti nei punti in cui si annulla, ovvero l’origine ed $A=(2,0)$ . Infine, calcoliamo la derivata seconda dei due “rami” separatamente:

$f''_1(x)=2x e^x+(x^2-2)e^x=(x^2+2x-2)e^x,$

$f''_2(x)=-2x e^x+(2-x^2)e^x=-(x^2+2x-2)e^x.$

La derivata seconda di $f$ si annulla dunque in

$x^2+2x-2=0\iff x=-1\pm\sqrt{3}.$

La funzione è convessa su $(-\infty,-1-\sqrt{3})\cup (0,-1+\sqrt{3}) \cup (2,+\infty)$ e concava altrove. Inoltre, la funzione presenta due flessi nei punti

$F_1=(-1-\sqrt{3},(6+4\sqrt{3})e^{-1-\sqrt{3}})\quad \text{e} \quad F_2=(-1+\sqrt{3},(4\sqrt{3}-6)e^{-1+\sqrt{3}}).$

Il grafico è riportato nella figura seguente:

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 2.

La funzione

$f(x) = x^2 e^{ \frac{|x|-1}{|x|}}$

è definita per $|x|\neq 0$ , ovvero il dominio è dato da

$D=(-\infty,0)\cup(0,+\infty).$

Sviluppando il modulo $|x|$ , possiamo riscrivere la funzione come segue:

$f(x) = \begin{cases}x^2 e^{\frac{x-1}{x}} & \text{per } x > 0, \\ x^2 e^{\frac{x+1}{x}} & \text{per } x < 0. \end{cases}$

Dato che la funzione è pari (ovvero, $f(-x)=f(x)$ ), possiamo limitarci a studiare uno dei due rami, ad esempio

$f_1(x) := x^2 e^{\frac{x-1}{x}} \qquad \text{per } x \in (0,+\infty).$

Il limite dell’esponente per $x\to +\infty$ si calcola facilmente essendo rapporto tra polinomi:

$\lim_{x \to + \infty} \frac{x-1}{x}=1,$

da cui segue che

$\lim_{x\to + \infty} f(x) = \lim_{x\to + \infty} f_1(x) = \lim_{x\to + \infty} x^2 = + \infty.$

In particolare, la funzione non ammette asintoti orizzontali. Un calcolo simile ci permette di affermare che non esistono neanche asintoti obliqui:

$\lim_{x\to + \infty} \frac{f_1(x)}{x} = \lim_{x\to + \infty} x e^{\frac{x - 1}{x}} = \lim_{x \to + \infty} x = \infty.$

Il limite da destra in zero si svolge osservando

$\lim_{x \to 0^+} \frac{x-1}{x} = - \infty,$

perciò sia $x^2$ che il termine esponenziale tendono a zero; in particolare, si ha:

$\lim_{x\to 0^+}f_1(x)=0\cdot \underbrace{e^{-\infty}}_{=0}=0.$

La funzione non ammette asintoti verticali e, al contrario, è prolungabile con continuità in $x=0$ ponendo $f(0)=0$ . Abbiamo poi per la derivata prima

$f_1'(x)=2x e^{\frac{x-1}{x}}+x^2 e^{\frac{x-1}{x}}\cdot\frac{x-x+1}{x^2}=(2x+1) e^{\frac{x-1}{x}}.$

Nel porre $f_1'(x) = 0$ dobbiamo ricordarci che stiamo lavorando solo sulla semiretta positiva, quindi ogni soluzione è sottoposta all’ulteriore vincolo $x>0$ . Nello specifico, si ha

$2x e^{\frac{x-1}{x}}+x^2 e^{\frac{x-1}{x}}\cdot\frac{x-x+1}{x^2}=(2x+1) e^{\frac{x-1}{x}} = 0 \iff x=-\frac12,$

e questa non è accettabile dato che non soddisfa la condizione $x>0$ . Ne deduciamo che \begin{itemize} \item $f'(x) > 0$ ed $f$ crescente in $(0,+\infty)$ ; \item $f'(x) < 0$ ed $f$ decrescente in $(-\infty, 0)$ ; \end{itemize} dato che, come menzionato in altri esercizi, $f$ pari implica $f'$ dispari. Ne deduciamo che l’origine $O=(0,0)$ è un estremo inferiore della funzione. Infine, la derivata seconda è

$f_1''(x)=2 e^{\frac{x-1}{x}}+(2x+1) e^{\frac{x-1}{x}}\cdot\frac{1}{x^2}=\frac{2x^2+2x+1}{x^2}\cdot e^{\frac{x-1}{x}}$

In questo caso, abbiamo una funzione sempre positiva e, per simmetria, la $f(x)$ risulta convessa nel suo dominio. Il grafico è riportato in figura.

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 3.

La funzione

$f(x) = \sin x e^{| \sin x|}$

è definita su tutto $\mathbb R$ e risulta periodica di periodo $T=2\pi$ . Restringiamo dunque lo studio all’intervallo $[0,2\pi)$ . Sviluppando il modulo, ovvero

$|\sin x| = \begin{cases} \sin x & \text{se } x \in [0,\pi) \\ - \sin x & \text{se } x \in [\pi,2\pi). \end{cases}$

In particolare, possiamo riscrivere la funzione come segue:

$f(x) = \begin{cases} \sin x\ e^{\sin x} & \text{se } x \in [0,\pi) \\ \sin x\ e^{-\sin x} & \text{se } x \in [\pi,2\pi). \end{cases}$

La funzione è periodica e definita ovunque, perciò non ci sono asintoti di alcun tipo. La funzione, ristretta all’intervallo scelto in precedenza, si interseca con gli assi nei punti

$O=(0,0)\quad \text{e} \quad A=(\pi,0).$

La derivata prima è data da

$f'(x) = \begin{cases} \cos x(1+\sin x)e^{\sin x}& \text{se } x \in [0,\pi) \\ \cos x(1-\sin x)e^{-\sin x} & \text{se } x \in [\pi,2\pi). \end{cases}$

Osserviamo che $f'(x)$ è ben definita in $x=\pi$ e $f'(\pi) = -1$ . Se denotiamo con $f_1'$ ed $f_2'$ i due rami della funzione derivata, osserviamo che

$f_1'(x) = 0 \iff \cos x=0 \text{ o } \sin x=-1\iff x=\frac{\pi}{2},$

ed analogamente

$f_2'(x)=0 \iff \cos x=0 \text{ o } \sin x=1\iff x=\frac{3\pi}{2}.$

Si verifica che $f_1'(x)>0$ per $x\in(0,\pi/2)$ e $f'_2(x)>0$ per $x\in (3\pi/2,2\pi)$ , da cui segue che la funzione cresce su $(0,\pi/2)\cup(3\pi/2,2\pi)$ ed ammette un massimo assoluto in $M=(\pi/2,e)$ ed un minimo assoluto in $m=(3\pi/2,-e)$ . Per la derivata seconda si ha poi

$f''(x)=\begin{cases} -e^{\sin x}(1+\sin x)(\sin^2 x+2\sin x-2) & \text{se } x \in [0,\pi) \\ e^{-\sin x}(1-\sin x)(\sin^2 x-2\sin x-2) & \text{se } x \in (\pi,2\pi) \end{cases}$

Si trova ha che

$\begin{aligned} f"(x)=0 \iff& \begin{cases} \sin x = \sqrt{3}-1 & \text{se } x \in [0,\pi)\\ \sin x= 1-\sqrt{3} & \text{se } x \in (\pi,2\pi). \end{cases} \\ \iff & \begin{cases} x = \arcsin(\sqrt{3}-1) \; \text{o} \; x =\pi - \arcsin(\sqrt{3}-1) & \text{se } x \in [0,\pi)\\ x=\pi+\arcsin(\sqrt{3}-1) o x=2\pi-\arcsin(\sqrt{3}-1) & \text{se } x \in (\pi,2\pi). \end{cases} \end{aligned}$

Tali punti risultano punti di flesso. La funzione è convessa in: $[0, \arcsin(\sqrt{3}-1)]$ , $[\pi-\arcsin(\sqrt{3}-1), \pi]$ , $[\pi+\arcsin(\sqrt{3}-1), 2\pi-\arcsin(\sqrt{3}-1)]$ e concava negli intervalli complementari in $[0,2\pi]$ . Il grafico è riportato in figura.

$\quad$

Rendered by QuickLaTeX.com

Svolgimento punto 4.

La funzione

$f(x) = \arctan \frac{\log x -1}{\log x + 1} + \log(\log^2 x + 1)$

è definita per

$\begin{cases} x > 0 \\ \log (x) + 1 \neq 0 \\ \log^2 (x) + 1 > 0 \end{cases}$

Il logaritmo è diverso da $-1$ quando l’argomento è diverso da $1/e$ , mentre $\ln^2 x+1$ è sempre maggiore o uguale a $1$ . Il dominio risulta essere:

$D=\left(0,\frac{1}{e}\right)\cup\left(\frac{1}{e},+\infty\right).$

Facciamo i limiti agli estremi del dominio. Per $x \to + \infty$ osserviamo che

$\lim_{x\to+\infty}f(x)=\lim_{x\to+\infty}\left(\arctan\frac{\log x-1}{\log x +1}+\log(\log^2 x+1)\right)=+\infty,$

dato che il primo fattore tende ad $\arctan 1 = \pi/4$ e il secondo a $+ \infty$ . Inoltre, si ha

$\lim_{x\to+\infty}\frac{f(x)}{x}=\lim_{x \to +\infty}\frac1x \left(\arctan\frac{\log x-1}{\log x +1}+\log(\log^2 x+1)\right)=0$

dato che il denominatore va a infinito più velocemente del numeratore; in particolare, la funzione non presenta asintoti obliqui od orizzontali.

Infine, ponendo $t = \log x$ abbiamo che $x \to 0^+$ corrisponde a $t \to - \infty$ da cui:

$\lim_{x\rightarrow 0^+}f(x)=\lim_{t\rightarrow-\infty}\left(\arctan\frac{t-1}{t+1}+\log(t^2+1)\right)=+\infty,$

per cui la retta $x=0$ è un asintoto verticale. Si ha poi

$\lim_{x\rightarrow(1/e)^{\pm}}f(x)=\arctan(\mp\infty)+\log 2=\mp\frac{\pi}{2}+\log 2,$

perciò la funzione in $x=1/e$ ha un punto singolare con salto $-\pi$ . Per la derivata prima, posto $g(x)=\log x$ , la funzione si scrive

$f(x)=\arctan\frac{g-1}{g+1}+\log(g^2+1).$

Derivando si ha allora

$\begin{aligned} f'(x) & = \frac{1}{1+\left(\frac{g-1}{g+1}\right)^2}\cdot\frac{g+1-g+1}{(g+1)^2}\cdot g'+\frac{2g g'}{g^2+1} \\ & =g'\left[\frac{(g+1)^2}{g^2+2g+1+g^2-2g+1}\cdot\frac{2}{(g+1)^2}+\frac{2g}{g^2+1}\right]=g'\cdot\frac{1+2g}{g^2+1}, \end{aligned}$

e sostituendo $g = \log x$ si arriva alla formula:

$f'(x)=\frac{1+2\log x}{x(\log^2 x+1)}.$

Tale derivata si annulla quando

$2 \log x + 1 = 0 \iff \log x = -\frac12 \iff x = \frac{1}{\sqrt{e}}$

e, dato che $f'(x)>0$ su $(1/\sqrt{e},+\infty)$ , la funzione cresce su tale intervallo ed ammette un minimo (assoluto) nel punto

$m= \left(\frac{1}{\sqrt{e}},\arctan(-3)+\log(5/4)\right).$

Per la derivata seconda si ha

$\begin{aligned} f''(x)& =\frac{\displaystyle\frac{2}{x}\cdot x(\log^2 x+1)-(1+2\log x)\cdot\left[\log^2 x+1+x\frac{2\log x}{x}\right]}{x^2(\log^2 x+1)^2} \\ & =\frac{2\log^2 x+2-(1+2\log x)(\log^2 x+2\log x+1)}{x^2(\log^2 x+1)^2} \\ & = -\frac{2\log^3 x+3\log^2 x+4\log x-1}{x^2(\log^2 x+1)^2}. \end{aligned}$

Per determinare gli zeri di questa derivata, poniamo ancora una volta $t=\log x$ e consideriamo il polinomio associato al numeratore:

$p(t)=2t^3+3t^2+4t-1$

definito in $(-\infty,\infty)$ . I limiti ad infinito sono

$\lim_{t\to\pm\infty}p(t)=\pm\infty,$

e la derivata è sempre positiva

$p'(t)=6t^2+6t+4=2(3t^2+3t+2)>0,$

perciò per il teorema di esistenza degli zeri esiste un’unica soluzione a $p(t)=0$ . Dato che $p(0)=-1$ e $p(1)=8$ , possiamo restringerci all’intervallo $(0,1)$ . Denotandola $t_0\in(0,1)$ , si ha

$\alpha=e^{t_0}\in(1,e)$

soluzione unica di $f''(x)=0$ . Concludiamo che $f''(x)>0$ per $x\in(0,1/e)\cup(1/e,\alpha)$ , dove la funzione risulta convessa. Infine c’è un flesso nel punto $F=(\alpha,f(\alpha))$ .

Il grafico è riportato nella figura che segue:

$\quad$

Rendered by QuickLaTeX.com

Riferimenti bibliografici

[1] Stewart, James. Calculus: Early Transcendentals. 8th ed., Cengage Learning, 2015. Chapter 4: Applications of Derivatives.

[2] Thomas, George B., Weir, Maurice D., and Hass, Joel. Thomas’ Calculus. 14th ed., Pearson, 2017.
Chapter 4: Applications of Derivatives.

[3] Larson, Ron, and Edwards, Bruce H. Calculus. 11th ed., Cengage Learning, 2017.
Chapter 4: Applications of Differentiation.

[4] OpenStax. Calculus Volume 1. OpenStax, 2016.
Chapter 4: Applications of Derivatives.

[5] Spivak, Michael. Calculus. 4th ed., Publish or Perish, 2008.

[6] Lang, Serge. A First Course in Calculus. 5th ed., Springer, 2006.
Chapter 6: Applications of the Derivative.

[7] Qui Si Risolve, Funzioni elementari.

[8] Qui Si Risolve, Funzioni elementari – volume 1.

[9] Qui Si Risolve, Funzioni elementari – volume 2.

[10] Qui Si Risolve, Funzioni goniometriche.

[11] Qui Si Risolve, La teoria delle funzioni continue.

[12] Qui Si Risolve, Teoria sui limiti.

[13] Qui Si Risolve, I teoremi di de l’Hôpital.

[14] Qui Si Risolve, Polinomi di Taylor nei limiti: istruzioni per l’uso.

[15] Qui Si Risolve, Espansione di Taylor: teoria, esempi e applicazioni pratiche.

[16] Qui Si Risolve, Funzioni convesse.

[17] Qui Si Risolve, Teoria derivate.