Esercizi sui moti vari – 2

Home » Esercizi sui moti vari – 2

Benvenuti nel secondo volume di esercizi sui moti vari. In questo articolo proponiamo 17 esercizi sulla descrizione e le proprietà dei moti che i corpi possono assumere nello spazio. I problemi sono di difficoltà varia, illustrati e ciascuno è corredato di soluzione completa, così da consentire al lettore di confrontare la sua soluzione con quella da noi proposta, per un apprendimento più efficace.

Oltre al primo volume di Esercizi sui moti vari – 1, consigliamo le seguenti raccolte di esercizi su materiale affine:

Buona lettura!

Sommario

Leggi...

Questo è il secondo volume dedicato agli esercizi sui moti vari in cinematica. Rispetto al primo, si distingue per il livello di difficoltà maggiore, presentando esercizi più complessi. Alcuni di questi esercizi, non convenzionali, richiedono astuzia e solide conoscenze matematiche. In particolare, gli esercizi finali possono costituire un valido ripasso per chi si appresta a seguire un corso di meccanica razionale o desidera prepararsi adeguatamente. Questo volume è particolarmente indicato per studenti di matematica o fisica. La dispensa presenta 17 esercizi.

Autori e revisori

Leggi...

Autori: Valerio Brunetti, Antonio Figura, Niccolò Cocciaglia.

Revisori: Cesare Malagù.

Esercizi

$\quad$

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Un punto materiale è vincolato a muoversi lungo una retta. Scelto un sistema di riferimento fisso $Ox$ tale per cui l’asse delle $x$ sia coincidente con la retta lungo la quale il punto materiale è vincolato a muoversi, la posizione del punto materiale è data dalla seguente legge oraria

(1) $\begin{equation*} x(t)=t^3-3 t+1, \end{equation*}$

dove $t$ è espresso in secondi e $x$ in metri. Calcolare l’istante $t\geq0$ in cui la velocità e l’accelerazione hanno lo stesso valore numerico.

Richiami teorici.

Di seguito ricordiamo alcuni fatti che possono tornare utili per la risoluzione dell’esercizio.

$\quad$

Sia $f:(0,+\infty) \to \mathbb{R}$ , $f(t) = t^{\alpha}$ con $\alpha \in \mathbb{R}$ , la sua derivata è $f^{\prime}(t) = \alpha\, t^{\alpha-1}$ . Inoltre, ricordiamo che la derivata di una costante è nulla.

Data un’equazione completa di secondo grado
(2) $\begin{equation*} at^2 + bt + c = 0 \end{equation*}$

con $a \in \mathbb{R} \setminus \{0\}$ e $b,\,c \in \mathbb{R}$ , la formula risolutiva è

(3) $\begin{equation*} t_{1,2} = \dfrac{-b \pm \sqrt{\Delta}}{2a}, \end{equation*}$

dove

(4) $\begin{equation*} \Delta \coloneqq b^2 - 4ac. \end{equation*}$

Il $\Delta$ si chiama discriminante. Se $\Delta > 0$ allora l’equazione ammette due soluzioni reali e distinte; se $\Delta = 0$ allora l’equazione ha due soluzioni reali e coincidenti; altrimenti, se $\Delta < 0$ , l’equazione non ammette soluzioni reali, cioè ci sono due soluzioni complesse e coniugate.

In fisica, $t_{1,2}$ rappresentano degli istanti di tempo che in generale devono essere non negativi, per cui se uno dei due tempi è negativo, va scartato.

La derivata del vettore posizione è la velocità e si denota con
(5) $\begin{equation*} \dot{x}(t) = \dfrac{dx}{dt}; \end{equation*}$

mentre la derivata seconda del vettore posizione (o la derivata prima della velocità) è l’accelerazione del corpo e si denota con

(6) $\begin{equation*} \ddot{x}(t) = \dfrac{d^2x}{dt^2}. \end{equation*}$

Svolgimento.

Utilizziamo come notazione $x(t)$ , $x^{\prime}(t)$ e $x^{\prime\prime}(t)$ per rappresentare rispettivamente la la posizione, la velocità e l’accelerazione del punto materiale. Derivando ambo i membri della legge oraria rispetto al tempo, si ricava che l’equazione della velocità è

(7) $\begin{equation*} \dot{x}(t)=3t^2-3, \end{equation*}$

mentre l’equazione dell’accelerazione

(8) $\begin{equation*} \ddot{x}(t)=6t. \end{equation*}$

Uguagliando le due precedenti equazioni, si ottiene

(9) $\begin{equation*} 3t^2-3=6t, \end{equation*}$

o anche

(10) $\begin{equation*} 3t^2-6t-3=0, \end{equation*}$

da cui Utilizziamo come notazione $x(t)$ , $x^{\prime}(t)$ e $x^{\prime\prime}(t)$ per rappresentare rispettivamente la la posizione, la velocità e l’accelerazione del punto materiale. Derivando ambo i membri della legge oraria rispetto al tempo, si ricava che l’equazione della velocità è

(11) $\begin{equation*} \dot{x}(t)=3t^2-3, \end{equation*}$

mentre l’equazione dell’accelerazione

(12) $\begin{equation*} \ddot{x}(t)=6t. \end{equation*}$

Uguagliando le due precedenti equazioni, si ottiene

(13) $\begin{equation*} 3t^2-3=6t, \end{equation*}$

o anche

(14) $\begin{equation*} 3t^2-6t-3=0, \end{equation*}$

da cui

$\boxcolorato{fisica}{t \simeq \text{2,414 s}.}$

Esercizio 2 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Un punto materiale è vincolato a muoversi lungo una retta di moto vario. Si scelga un sistema di riferimento fisso $Ox$ con l’asse delle $x$ coincidente con la retta lungo la quale il punto materiale è vincolato a muoversi. Sia $x(t)$ la legge oraria del corpo in $Ox$ . Nel sistema di riferimento $Ox$ il punto materiale ha un’accelerazione $\ddot{x}(t)=2 t-3.$ La posizione $x(t)$ soddisfa le seguenti condizioni $x(0)=0$ e $x(3)=5$ . Si richiede di calcolare dove si trova il punto materiale all’istante $t=12 \,\textbf{s}$ .

Richiami teorici.

Chiamiamo $x(t)$ , $\dot{x}(t)$ e $\ddot{x}(t)$ rispettivamente la legge oraria, la velocità e l’accelerazione del punto materiale nel sistema di riferimento $Ox$ .

Per ottenere l’equazione per la velocità è necessario integrare ambo i membri rispetto al tempo dell’equazione per l’accelerazione, e a sua volta l’equazione per la posizione è ottenuta integrando ambo i membri rispetto al tempo l’equazione della velocità. Una volta integrato ambo i membri rispetto al tempo dell’equazione considerata (accelerazione o velocità), imponendo le condizioni iniziali del problema è possibile determinare le costanti di integrazione, da cui le leggi cercate. La relazione che lega posizione, velocità e accelerazione può essere riassunta nel seguente schema rappresentato in figura.

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Inoltre, ricordiamo l’integrale di una funzione polinomiale. Sia $f:\mathbb{R}^+\to\mathbb{R},$ $f(t)=t^{\alpha}$ con $\alpha \in \mathbb{R}\setminus\{-1\}$ , il suo integrale indefinito è

(15) $\begin{equation*} \int f(t)\, dt=\frac{1}{\alpha+1} t^{\alpha+1} + c, \end{equation*}$

dove $c$ è la costante d’integrazione.

Svolgimento.

Consideriamo

(16) $\begin{equation*} \ddot{x}(t)=2 t-3. \end{equation*}$

Integrando ambo i membri rispetto al tempo la precedente equazione, si ottiene

(17) $\begin{equation*} \dot{x}(t)=t^2-3t+c, \end{equation*}$

dove $c$ è una costante di integrazione da determinare.

Integrando rispetto al tempo ambo i membri la precedente equazione, si trova

(18) $\begin{equation*} x(t)=\frac{t^3}{3}-\frac{3t^2}{2}+ct+k, \end{equation*}$

dove $k$ è una costante di integrazione da determinare.

Per poter determinare il valore numerico delle costanti $c$ e $k$ imponiamo $x(0)=0$ e $x(3)=5$ . Sfruttando la precedente equazione e imponendo le condizioni $x(0)=0$ e $x(3)=5$ , si ottiene il seguente sistema

(19) $\begin{equation*} \begin{cases} 0=k\\[10pt] 5=9-\dfrac{27}{2}+3c+k, \end{cases} \end{equation*}$

da cui

(20) $\begin{equation*} \begin{cases} k=0\\[10pt] c=\dfrac{19}{6}. \end{cases} \end{equation*}$

Sostituendo le costanti trovate nel precedente sistema nell’equazione (18), si ottiene

(21) $\begin{equation*} \boxed{x(t)=\frac{t^3}{3}-\frac{3t^2}{2}+\frac{19t}{6}.} \end{equation*}$

Sostituendo nella precedente equazione $t=12 \,\textbf{s}$ , si ha

$\boxcolorato{fisica}{x(12)=398\, \text{m}.}$

Esercizio 3 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Un punto materiale è vincolato a muoversi su di una retta. Si scelga un sistema di riferimento fisso $Ox$ con l’asse delle $x$ coincidente con la retta lungo la quale è vincolato a muoversi il punto materiale. Sia $x(t)$ la legge oraria del punto materiale in $Ox$ . L’accelerazione del punto materiale è $\ddot{x}(t)=t^2+1$ . Le condizioni del problema sono $x(0)=0$ e $\dot{x}(3)=7\,\text{m}\cdot \text{s}^{-1}$ . Calcolare la posizione del punto materiale all’istante $t=8 \,\textbf{s}$ .

Svolgimento.

Procediamo come nell’esercizio 2. Consideriamo

(22) $\begin{equation*} \ddot{x}(t)=t^2+1. \end{equation*}$

Integrando ambo i membri rispetto al tempo la precedente equazione, si ottiene

(23) $\begin{equation*} \dot{x}(t)=\frac{t^3}{3}+t+c, \end{equation*}$

dove $c$ è una costante di integrazione da determinare.

Integrando ambo i membri rispetto al tempo la precedente equazione, si ha

(24) $\begin{equation*} x(t)=\frac{t^4}{12}+\frac{t^2}{2}+ct+k, \end{equation*}$

dove $k$ è una costante d’integrazione da determinare.

Per poter determinare il valore numerico delle costanti $c$ e $k$ imponiamo le condizioni $x(0)=0$ e $\dot{x}(3)=7$ . Dalle due precedenti equazioni, imponendo $x(0)=0$ e $\dot{x}(3)=7$ , si ottiene

(25) $\begin{equation*} \begin{cases} 0=k\\[10pt] 7=9+3+c, \end{cases} \end{equation*}$

da cui

(26) $\begin{equation*} \begin{cases} k=0\\ c=-5. \end{cases} \end{equation*}$

Sostituendo le costanti determinate nel precedente sistema nell’equazione (24), si trova

(27) $\begin{equation*} \boxed{x(t)=\frac{t^4}{12}+\frac{t^2}{2}-5t.} \end{equation*}$

Sostituendo $t=8\,\textbf{s}$ nella precedente equazione, otteniamo

$\boxcolorato{fisica}{x(8)=333\, \text{m}.}$

Scarica gli esercizi svolti

Ottieni due volumi scaricabili sui moti vari in cinematica, contenenti rispettivamente 6 e 17 esercizi, completi di soluzioni dettagliate. Il primo volume è di 16 pagine, mentre il secondo è di 34.

Esercizio 4 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un punto materiale è vincolato a muoversi su di un piano orizzontale. Si scelga un sistema di riferimento fisso $Oxy$ tale per cui il piano $xy$ sia coincidente con il piano orizzontale sul quale è vincolato a muoversi il punto materiale. Il punto materiale lungo l’asse delle $x$ ha legge oraria $x(t)=t^3-3 t+1$ , mentre lungo l’asse delle $y$ ha legge oraria $y(t)=t^2+1$ . Calcolare l’istante di tempo $t\geq0$ in cui il vettore velocità e il vettore accelerazione risultino perpendicolari.

Richiami teorici.

Dati due vettori

(28) $\begin{equation*} \vec{a}=a_x\,\hat{x}+a_y\,\hat{y}+a_z\,\hat{z} \end{equation*}$

(29) $\begin{equation*} \vec{b}=b_x\,\hat{x}+b_y\,\hat{y}+b_z\,\hat{z}, \end{equation*}$

dove $a_x$ , $a_y$ , $b_x$ , $b_y$ , $a_z$ , $b_z$ $\hat{x}$ , $\hat{y}$ e $\hat{z}$ sono rispettivamente la componente del vettore $\vec{a}$ lungo l’asse delle $x$ , la componente del vettore $\vec{a}$ lungo l’asse delle $y$ , la componente del vettore $\vec{a}$ lungo l’asse delle $z$ , la componente del vettore $\vec{b}$ lungo l’asse delle $x$ , la componente del vettore $\vec{b}$ lungo l’asse delle $y$ , la componente del vettore $\vec{b}$ lungo l’asse delle $z$ , il versore dell’asse delle $x$ , il versore dell’asse delle $y$ e il versore dell’asse delle $z$ ; il loro prodotto scalare è

(30) $\begin{equation*} \vec{a}\cdot \vec{b}=a_xb_x+a_yb_y+a_zb_z. \end{equation*}$

Svolgimento.

Procediamo come nell’esercizio 2. Si ha

(31) $\begin{equation*} \begin{cases} x(t)=t^3-3t+1\\ y(t)=t^2+1, \end{cases} \end{equation*}$

da cui

(32) $\begin{equation*} \begin{cases} \dot{x}(t)=3t^2-3 \\[10pt] \dot{y}(t)=2t , \end{cases} \end{equation*}$

conseguentemente

(33) $\begin{equation*} \begin{cases} \ddot{x}(t)=6t \\[10pt] \ddot{y}(t)=2 . \end{cases} \end{equation*}$

Siano $\vec{v}(t)$ e $\vec{a}(t)$ rispettivamente la velocità e l’accelerazione del punto materiale nel sistema di riferimento $Oxy$ ; sfruttando i due precedenti sistemi, si ha

(34) $\begin{equation*} \vec{v}(t)=\left(3t^2-3\right)\hat{x}+2t\,\hat{y} \end{equation*}$

(35) $\begin{equation*} \vec{a}(t)=6t\,\hat{x}+2\,\hat{y}. \end{equation*}$

Due vettori si dicono perpendicolari se il loro prodotto scalare è nullo. Pertanto, sfruttando le due precedenti equazioni il prodotto scalare $\vec{v}\cdot\vec{a}=0$ diventa

(36) $\begin{equation*} 18t^3-18t+4t=0, \end{equation*}$

ovvero

(37) $\begin{equation*} t(18t^2-14)=0. \end{equation*}$

La precedente equazione ha come risultati $t_1=0$ , $t_{2,3}=\pm7/9\sim\text{0,8 s}$ . Scartando le soluzioni negative troviamo

$\boxcolorato{fisica}{t=0 \quad \vee \quad t \sim\text{0,8 s}.}$

Esercizio 5 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . All’istante $t=0$ , un punto materiale è vincolato a muoversi lungo una circonferenza. Si rappresenti con $s$ l’arco di circonferenza misurato in centimetri descritto dal punto materiale e con $t$ il tempo trascorso misurato in secondi. La posizione del corpo è descritto dalla legge oraria $s(t)=t^4+t^2$ . Si determini l’accelerazione tangenziale del punto all’instante di tempo $t=2,5$ $\textrm{s}$ .

Svolgimento.

L’accelerazione tangenziale si può esprimere come

(38) $\begin{equation*} a_t=\dfrac{d^2s}{dt^2}. \end{equation*}$

Pertanto sostituendo $s(t)=t^4+t^2$ nella precedente equazione otteniamo

(39) $\begin{equation*} a_t=\dfrac{d^2s}{dt^2}=\dfrac{d}{dt}\left(4t^3+2t\right)=12t^2+2. \end{equation*}$

Sostituendo $t=\text{2,5}$ $\textrm{s}$ nella precedente equazione si ricava

$\boxcolorato{fisica}{a_t=\text{77 cm}\cdot \text{s}^{-2}.}$

Esercizio 6 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un camion percorre $35$ $\textrm{km}$ verso nord, poi $10$ $\textrm{km}$ verso est e infine 6 $\textrm{km}$ verso sud. Si determini l’angolo $\alpha$ che lo spostamento complessivo forma con la direzione est.

Svolgimento.

Metodo punta-coda. Indichiamo con $\vec{s}_1$ , $\vec{s}_2$ , $\vec{s}_3$ e $\vec{s}_{\text{tot}}$ rispettivamente il primo spostamento verso nord, il secondo verso est, il finale verso sud e lo spostamento complessivo.

Scegliamo un sistema di riferimento fisso $O{xy}$ tale per cui l’origine $O$ coincide con la posizione iniziale del camion, l’asse $y$ individua la direzione nord-sud ed è orientato verso nord. Siano $\hat{x}$ , $\hat{y}$ i versori rispettivamente dell’asse delle $x$ e dell’asse delle $y$ . Analogamente l’asse delle $x$ individua la direzione est-ovest ed è orientato verso est. In virtù del sistema di riferimento adottato i vettori $\vec{s}_1,\vec{s}_2,\vec{s}_3$ e $\vec{s}_{\text{tot}}$ sono orientati come in figura 1.

$\quad$

Rendered by QuickLaTeX.com

Figura 1: schema del problema.

$\quad$

Come si evince dallo schema del problema, i vettori $\vec{s}_{\text{tot}}$ , $\vec{s}_2$ e

(40) $\begin{equation*} \vec{s}_4=\vec{s}_1+\vec{s}_3 \end{equation*}$

formano un triangolo rettangolo dove il primo vettore è l’ipotenusa, mentre gli altri due ne sono i cateti. Siccome $\vec{s}_1$ e $\vec{s}_3$ hanno verso opposto, ossia $\vec{s}_1=s_1\,\hat{y}=\text{35 km}\,\hat{y}$ e $\vec{s}_3=-s_3\,\hat{y}=-\text{6 km}\,\hat{y}$ , si ha che

(41) $\begin{equation*} \vec{s}_4=s_1\,\hat{y}- s_3\,\hat{y} =(s_1-s_3)\,\hat{y}, \end{equation*}$

da ciò segue che il modulo di $\vec{s}_4$ vale $|\vec{s}_4|=29$ $\textrm{km}$ . La relazione trigonometrica che lega il modulo del vettore $\vec{s}_2$ e il modulo dello spostamento complessivo $\vec{s}_{4}$ è

(42) $\begin{equation*} |\vec{s}_{4}|=|\vec{s}_2|\tan{\alpha}, \end{equation*}$

dove $\alpha$ è l’angolo rappresentato in figura 1 cioè l’angolo che forma $\vec{s}_{\text{tot}}$ con l’asse delle $x$ . Invertendo quest’ultima equazione si ottiene

$\boxcolorato{fisica}{\alpha=\arctan{\left(\frac{|\vec{s}_{4}|}{|\vec{s}_{2}|}\right)} \simeq 71 \mbox{\textdegree}.}$

Metodo algebrico. Come si evince dallo schema del problema si ha

(43) $\begin{equation*} \begin{cases} \vec{s}_1=\text{35 km}\,\hat{y}\\[10pt] \vec{s}_2=\text{10 km}\,\hat{x}\\[10pt] \vec{s}_3=-\text{6 km}\,\hat{y}. \end{cases} \end{equation*}$

Sommando opportunatamente membro a membro le precedenti equazioni del sistema (43) si ottiene quanto segue

(44) $\begin{equation*} \begin{cases} \vec{s}_{4}=\vec{s}=\vec{s}_1+\vec{s}_3=\text{29 km}\, \hat{y}\\ \vec{s}_{\text{tot}}=\vec{s}_1+\vec{s}_2+\vec{s}_3=\text{10 km}\,\hat{x}+\text{29 km}\,\hat{y}, \end{cases} \end{equation*}$

da cui $|\vec{s}_{\text{tot}}|\simeq30.67$ $\textrm{km}$ e $|\vec{s}_4|=29$ $\textrm{km}$ . La prosecuzione della risoluzione di quest’esercizio con questo metodo è equivalente al precedente metodo.

Esercizio 7 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . In un sistema di riferimento fisso $Ox$ , consideriamo un punto che si muove seguendo la legge oraria $x(t) = (5 - 4t)$ metri, valida per $t \geq 0$ . Si richiede di calcolare:

$\quad$

la velocità del punto nel generico istante $t\geq 0$ ;

la posizione del punto per $t = 0$ e $t = 2\,\text{s}$ ;

il tempo in cui il punto attraversa l’origine del sistema di riferimento.

$\quad$

esercizi sui moti vari

Figura 2: rappresentazione schematica del problema.

Svolgimento.

La legge oraria del punto materiale è espressa in termini di una singola coordinata spaziale. Quindi, possiamo adottare come sistema di riferimento un asse orizzontale $x$ orientato verso destra, come illustrato nella figura 2.

Indichiamo con $x_0$ la posizione del punto al tempo $t = 0$ e con $x_1$ la sua posizione al tempo $t = 2$ , come mostrato nella figura. Dato che i valori esatti di $x_0$ e $x_1$ non sono ancora noti, essi sono stati posizionati a destra dell’origine per convenzione, assumendo senza perdita di generalità che $x_0 > 0$ e $x_1 > x_0 > 0$ .

$\quad$

La velocità del punto materiale si calcola derivando la legge oraria rispetto al tempo:
$\boxcolorato{fisica}{\displaystyle v(t) = \frac{d}{dt}x(t) = -4\ \text{m}\cdot \text{s}^{-1}.}$

Dato che la velocità è costante nel tempo (non dipende da $t$ ), il punto materiale si muove in un moto rettilineo uniforme. Inoltre, poiché la velocità calcolata è negativa, il punto si sta spostando nella direzione negativa dell’asse delle $x$ . Di conseguenza, possiamo aspettarci che $x_1 < x_0$ .

Per determinare i valori numerici delle posizioni $x_0$ e $x_1$ , precedentemente definite, è necessario sostituire i valori $t = 0$ e $t = 2$ nella legge oraria. Questo ci porta ai seguenti risultati:
(45) $\begin{equation*} \begin{aligned} & x_0 = x(0) = (5 - 4 \cdot 0)\text{m}, \\ & x_1 = x(2) = (5 - 4 \cdot 2)\text{m}. \end{aligned} \end{equation*}$

Da queste, otteniamo che:

$\boxcolorato{fisica}{\displaystyle x_0 = 5\ \text{m}\, , \quad x_1 = -3\ \text{m}.}$

Concludiamo quindi che, nella figura, il punto $x_1$ si deve situare a sinistra dell’origine $O$ , in accordo con il fatto che la velocità è negativa.

Il tempo in cui il punto passa per l’origine è il valore $t=t^*$ tale per cui: $x(t^*)=0$ . Quindi:
(46) $\begin{equation*} x(t^*)=5-4t^*=0, \end{equation*}$

che ci fa trovare

$\boxcolorato{fisica}{\displaystyle t^* = 5/4\ \text{s} = \text{1,25}\ \text{s}. }$

Potevamo aspettarci a priori un valore di tempo compreso tra $0$ e $2$ , una volta considerato che l’origine è situata tra il punto $x_0$ da cui ha origine il moto a $t=0$ , ed il punto $x_1$ , raggiunto a $t=2$ .

Osservazione.

Il primo quesito e il primo punto del secondo quesito possono essere rapidamente risolti confrontando la legge oraria fornita dal problema con la formula generale del moto rettilineo uniforme:

(47) $\begin{equation*} x(t) = x_{\text{in}} + vt, \end{equation*}$

dove $x_{\text{in}}$ rappresenta la posizione iniziale del punto e $v$ la sua velocità, che è costante. Questa espressione descrive una retta in cui il coefficiente angolare corrisponde alla velocità del punto e il termine noto alla sua posizione iniziale al tempo $t = 0$ . Di conseguenza, nel nostro caso specifico, deduciamo immediatamente che $v=-4\, \text{m}\cdot \text{s}^{-1}$ e $x_0=5\ \text{m}$ .

Esercizio 8 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Si consideri su un piano orizzontale una guida liscia di forma parabolica, rappresentata dall’equazione $y(x)=5x^2$ , con $x$ e $y$ espresse in metri. Un punto P si muove con velocità costante, $v_0$ , lungo la guida. Determinare le componenti dell’accelerazione quando il punto P passa per il vertice della parabola e per il punto di ascissa $x^*$ .

$\quad$

Rendered by QuickLaTeX.com

Proposizione.

Prima di procedere allo svolgimento dell’esercizio enunciamo una proposizione che tornerà utile per lo svolgimento dell’esercizio.

$\quad$

Proposizione. Sia $x=x(t)$ derivabile in tutto il suo dominio naturale tale che $\dfrac{dx}{dt}(t)\neq0$ e sia $t=t(x)$ la sua inversa. Definiamo $a=a(t)=\dfrac{dv}{dt}(t)=\dfrac{d^2x }{dt^2}(t)$ e siano $\tilde{a}(x)=\left( a\circ t\right)(x) \,\, \text{e}\,\,\tilde{v}(x)=\left(v \circ t \right)(x)$ .

Allora si ha che

(48) $\begin{equation*} \tilde{a}(x)=\dfrac{d\tilde{v}}{dx}(x)\,\,\tilde{v}(x). \end{equation*}$

$\quad$

Dimostrazione. Abbiamo

(49) $\begin{equation*} \dfrac{d\tilde{v}}{dx}\left(x\right)=\dfrac{d\left(v\circ t\right)}{dx}\left( x\right)\overset{*}{=}\dfrac{dv}{dt}\left(t(x) \right)\,\dfrac{dt}{dx}\left(x\right), \end{equation*}$

dove in $*$ abbiamo applicato la regola della catena.

Consideriamo ora $\tilde{a}=a \circ t$ , dunque

$\tilde{a}(x)=a(t(x))=\dfrac{dv}{dt}\left(t(x)\right)$

e con (49) possiamo riscrivere

(50) $\begin{equation*} \tilde{a}(x)=\dfrac{\dfrac{d\tilde{v}}{dx}(x)}{\dfrac{dt}{dx}\left(x\right)}=\frac{d\tilde{v}}{dx}\left(x\right)\,\dfrac{1}{\dfrac{dt}{dx}\left(x\right)}. \end{equation*}$

Osserviamo che (50) è ben definita perchè per ipotesi $\dfrac{dt}{dx}\left(x\right)\neq0$ .

Per la regola della derivata della funzione inversa si ha che

(51) $\begin{equation*} \dfrac{dx}{dt}(t)=\dfrac{1}{\frac{dt}{dx}(x)} \quad \mbox{ dove } x=x(t) \end{equation*}$

ed applicando la (51) alla (50), allora (50) diventa

$\tilde{a}(x)= \tilde{v}(x)\,\frac{d\tilde{v}}{dx}\left(x\right).$

Svolgimento.

Siccome la velocità è costante in ogni istante vale

(52) $\begin{equation*} v_0^2=\tilde{v}_x^2+\tilde{v}_y^2, \end{equation*}$

dove $\tilde{v}_x$ e $\tilde{v}_y$ sono rispettivamente la componente nella direzione $x$ e $y$ della velocità.

Si osserva che

(53) $\begin{equation*} \tan \alpha=\dfrac{dy}{dx}=\dfrac{\tilde{v}_y(x)}{\tilde{v}_x(x)}=10x, \end{equation*}$

dove $\alpha$ è l’angolo che forma la componente $v_x$ della velocità tangente alla parabola con l’asse orizzontale.

Dalla (53) si ottiene

$\tilde{v}_y=10x\tilde{v}_x.$

Sostituiamo $\tilde{v}_y$ in (52) ottenendo

$\tilde{v}_x(x)=\dfrac{v_0}{\sqrt{1+100x^2}},$

da cui

$\tilde{v}_y(x)=\dfrac{10xv_0}{\sqrt{1+100x^2}}.$

Applicando (48) si ottiene

$\begin{cases} a_x(x)=\tilde{v}_x(x)\dfrac{d\tilde{v}(x)_x}{dx}=\left( \dfrac{v_0}{\sqrt{1+100x^2}}\right) \left( \dfrac{-100v_0x}{(\sqrt{1+100x^2})^3}\right)=\dfrac{-100xv_0^2}{(1+100x^2)^2};\\ a_y(x)=\tilde{v}_x(x)\dfrac{d\tilde{v}(y)}{dx}=\left( \dfrac{v_0}{\sqrt{1+100x^2}}\right)\dfrac{10v_0}{\sqrt{(1+100x^2)^3}}=\dfrac{10\left(v_0\right)^2}{(1+100x^2)^2}.\\ \end{cases}$

Dalla quale si trova che

$\boxcolorato{fisica}{\begin{cases} a_x(0)=0;\\ a_y(0)=10v_0;\\ a_x(x^*)=\dfrac{-100x^*v_0^2}{(1+100(x^*)^2)^2};\\\ a_y(x^*)=\dfrac{10v_0}{(1+100(x^*)^2)^2}.\\ \end{cases}}$

Esercizio 9 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Su un piano orizzontale sono poste due guide lisce, perpendicolari tra loro, lungo le quali posso scorrere gli estremi di un’asta $\overline{AB}$ , lunga $\ell$ . Inizialmente l’asta è disposta lungo l’asse $y$ . L’estremo $B$ viene mantenuto in moto con velocità costante $v_B$ . Determinare il modulo della velocità e dell’accelerazione dell’estremo $A$ quando $B$ raggiunge la posizione $X_B$ .

$\quad$

Rendered by QuickLaTeX.com

Svolgimento.

Dal sistema di riferimento fisso $Oxy$ possiamo scrivere la posizione di $A$ e $B$ , gli estremi dell’asta sono vincolati a muoversi sulle due guide lisce

(54) $\begin{equation*} \begin{cases} x_B=\ell \cos \theta\\ y_B=0\\ x_A=0\\ y_A=\ell \sin \theta \\ \end{cases} \end{equation*}$

Deriviamo rispetto al tempo (54)

$\begin{cases} \dot{x}_B=-\ell \dot{ \theta} \sin \theta\\ \dot{y}_B=0\\ \dot{x}_A=0\\ \dot{y}_A=\ell \dot{ \theta} \cos \theta \\ \end{cases}$

Sapendo che l’estremo $B$ è mantenuto a velocità costante $v_B$ si ha che

(55) $\begin{equation*} \dot{x}_B=-\ell \dot{ \theta} \sin \theta=v_B. \end{equation*}$

Dalla (55) si trova che

$\dot{ \theta}=-\dfrac{v_B}{\ell\sin \theta}.$

Posto $x_B=X_B$ , si trova che

$\tan \theta =\dfrac{\sqrt{\ell^2-X_B^2}}{X_B}.$

Sostituiamo $\dot{ \theta}$ in $\dot{ y}_A$ , ottenendo

$\boxcolorato{fisica}{\dot{ y}_A=\left(\ell\cos \theta\right)\left(-\dfrac{v_B}{\ell\sin \theta} \right)=-\dfrac{v_B}{\tan \theta}= -\dfrac{v_BX_B}{\sqrt{\ell^2-X_B^2}}.}$

Deriviamo nuovamente rispetto al tempo la (54)

$\begin{cases} \ddot{x}_B=-\ell(\ddot{ \theta} \sin \theta+\dot{ \theta}^2\cos \theta )=0\\ \ddot{y}_B=0\\ \ddot{x}_A=0\\ \ddot{y}_A=\ell(\ddot{ \theta} \cos \theta-\dot{ \theta}^2 \sin \theta )\\ \end{cases}$

Dal sistema ricaviamo

$\ddot{ \theta}=-\dfrac{\dot{ \theta}^2}{\tan \theta}.$

Sostituiamo $\dot{ \theta}$ e $\ddot{ \theta}$ in $\ddot{y}_A$ si ottiene

$\begin{aligned} &\text{ \boxcolorato{fisica}{\parbox{0.5cm}{$ \ddot{y}_A$}}}}=-\ell\left(\dfrac{\dot{ \theta}^2 \cos\theta}{\tan \theta}+\dot{ \theta}^2 \sin \theta\right)=\\ &=-\ell\dot{ \theta}^2\left(\dfrac{\cos\theta}{\tan \theta}+\sin \theta\right)=\\ &=-\dfrac{\ell v_B^2}{\ell^2(\sin \theta)^2}\left(\dfrac{\cos^2\theta}{\sin \theta}+\sin \theta\right)=\\ &=-\dfrac{\ell v_B^2}{\ell^2(\sin \theta)^3}=\\ &=\text{\boxcolorato{fisica}{-\left(\dfrac{v_B^2}{\ell}\right)\left(\dfrac{\ell^3}{(\sqrt{\ell^2-X_B^2})^3} \right)}}. \end{aligned}$

Si conclude che i valori cercati sono

$\boxcolorato{fisica}{\begin{cases} \dot{ y}_A=\left(\ell\cos \theta\right)\left(-\dfrac{v_B}{\ell\sin \theta} \right)=-\dfrac{v_B}{\tan \theta}= -\dfrac{v_BX_B}{\sqrt{\ell^2-X_B^2}};\\\\ \ddot{y}_A=-\left(\dfrac{v_B^2}{\ell}\right)\left(\dfrac{\ell^3}{(\sqrt{\ell^2-X_B^2})^3} \right). \end{cases}}$

Esercizio 10 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Un punto materiale $A$ si muove a velocità costante partendo dall’origine di un sistema di riferimento fisso $Oxy$ , su di una spirale di Archimede, avente equazione polare $r={(R\theta)}/{(2\pi)}$ . Un secondo punto materiale $B$ si muove lungo una circonferenza di raggio $R$ centrata nell’origine, con velocità costante $v_B$ , partendo dal punto $B\equiv (R,0)$ . Si determini la velocità $v_B$ non nulla affinché i due punti si urtino.

$\quad$

Rendered by QuickLaTeX.com

Figura 3: rappresentazione di un punto materiale A che si muove lungo una spirale di Archimede e di un punto materiale B che si muove lungo una circonferenza di raggio $R$ . L’esercizio richiede di determinare la velocità di $B$ affinché i due punti si scontrino.

Svolgimento.

Data l’equazione polare della spirale

(56) $\begin{equation*} r=\dfrac{R\theta}{2\pi}, \end{equation*}$

risulta chiaro che l’unica possibilità per far avvenire l’urto è quando $\theta=2\pi$ , ovvero nel punto $B\equiv(R,0)$ , quindi il punto materiale $B$ deve fare un giro completo lungo la circonferenza. Per questo motivo dobbiamo calcolare il tempo che il punto materiale $A$ impiega lungo la spirale di Archimede per arrivare nel punto $B$ dall’origine del sistema di riferimento in figura 3.

La velocità del punto materiale $A$ , in coordinate polari, è

(57) $\begin{equation*} v_A=v_r\,\hat{r}+v_\theta \,\hat{\theta},\quad \end{equation*}$

dove $v_r$ e $v_\theta$ sono rispettivamente la componente radiale e la componente trasversa della velocità.

Sapendo che $r=\dfrac{R\theta}{2\pi}$ , si ha:

(58) $\begin{equation*} v_r=\dfrac{dr}{dt}=\dfrac{R}{2\pi}\dot{\theta} \qquad \mbox{e} \qquad v_\theta=r\dot{\theta}=\dfrac{R\theta}{2\pi}\,\dot{\theta}, \end{equation*}$

da cui

(59) $\begin{equation*} v_A=\dfrac{R}{2\pi}\dot{\theta}\,\hat{r}+\dfrac{R}{2\pi}\,\theta\,\dot{\theta}\,\hat{\theta}. \end{equation*}$

Calcoliamo $v_A$

(60) $\begin{equation*} \begin{split} v_A&=\dfrac{R}{2\pi}\dot{\theta}\,\hat{r}+\dfrac{R}{2\pi}\,\theta\,\dot{\theta}\,\hat{\theta}. v_A=\sqrt{v_r^2+v_\theta^2}= \\ &=\sqrt{\left(\dfrac{R}{2\pi}\right)^2\dot{\theta}^2+\left(\dfrac{R}{2\pi}\right)^2\theta^2\,\dot{\theta}^2}= \\ &=\dfrac{R}{2\pi}\dot{\theta}\sqrt{1+\theta(t)^2}= \\ &=\dfrac{R}{2\pi}\dfrac{d\theta}{dt}\sqrt{1+\theta^2}, \end{split} \end{equation*}$

che è un’equazione differenziale del primo ordine a variabili separabili, da cui

(61) $\begin{equation*} v_A\,dt=\dfrac{R}{2\pi}\sqrt{1+\theta^2}\,d\theta. \end{equation*}$

Integriamo il membro sinistro di (61) tra $0$ e $t_B$ dove $t_B$ è l’istante in cui avviene l’urto tra i due punti materiali ed il membro destro di (61) tra $0$ e $2\pi$ , otteniamo:

(62) $\begin{equation*} \int_0^{t_B}v_A\,dt=\dfrac{R}{2\pi}\int_0^{2\pi}\sqrt{1+\theta^2}\,d\theta. \end{equation*}$

Ricordando l’integrale notevole:

(63) $\begin{equation*} 2\int \sqrt{1+x^2} \, dx = \text{settsinh}(x)+x\sqrt{1+x^2}, \end{equation*}$

abbiamo

(64) $\begin{equation*} v_A t_B=\dfrac{R}{2\pi}\left(\text{settsinh} (2\pi)+2\pi\sqrt{1+4\pi^2}\right), \end{equation*}$

da cui

(65) $\begin{equation*} t_B=\dfrac{R}{2\pi v_A}\left(\text{settsinh}(2\pi)+2\pi\sqrt{1+4\pi^2}\right). \end{equation*}$

Il punto materiale $B$ si muove a velocità costante $v_B$ , dunque per compiere un giro nel tempo $t_B$ deve valere

(66) $\begin{equation*} v_B=\dfrac{2\pi R}{t_B}, \end{equation*}$

cioè

(67) $\begin{equation*} v_B=\dfrac{2\pi\cancel{R}(2\pi v_A)}{\cancel{R}\left(\text{settsinh}x (2\pi)+2\pi\sqrt{1+4\pi^2}\right)} = \dfrac{4\pi^2v_A}{\text{settsinh}x (2\pi)+2\pi\sqrt{1+4\pi^2}}. \end{equation*}$

Esercizio 11 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Una persona (indicata con $P$ in figura 4 (sinistra)) porta a passeggio il suo cane (indicato con $C$ sempre in figura 4 (sinistra)). Si considerino il cane e la persona come due punti materiali. Sia $Oxy$ un sistema di riferimento fisso, rappresentato in figura 4; inoltre, siano $\hat{x}$ e $\hat{y}$ i versori rispettivamente dell’asse delle $x$ e delle $y$ . Il punto $P$ si muove a velocità $\vec{v}_0=v_0\,\hat{y}$ , dove $v_0$ è costante. All’istante $t_0=0$ si ha $O\equiv P$ . Il punto $C$ è legato a $P$ da un guinzaglio di lunghezza $\ell$ , che supponiamo inestensibile; all’istante $t_0$ , $C$ è fermo e si trova lungo l’asse $x$ nella posizione $x=\ell$ . Negli istanti successivi, $C$ si muoverà puntando costantemente verso $P$ , in modo da mantenere il guinzaglio sempre teso. Si determini il modulo $v_C$ della velocità del cane in funzione di $v_0$ e della coordinata $x$ in cui il cane si trova durante il moto.

$\quad$

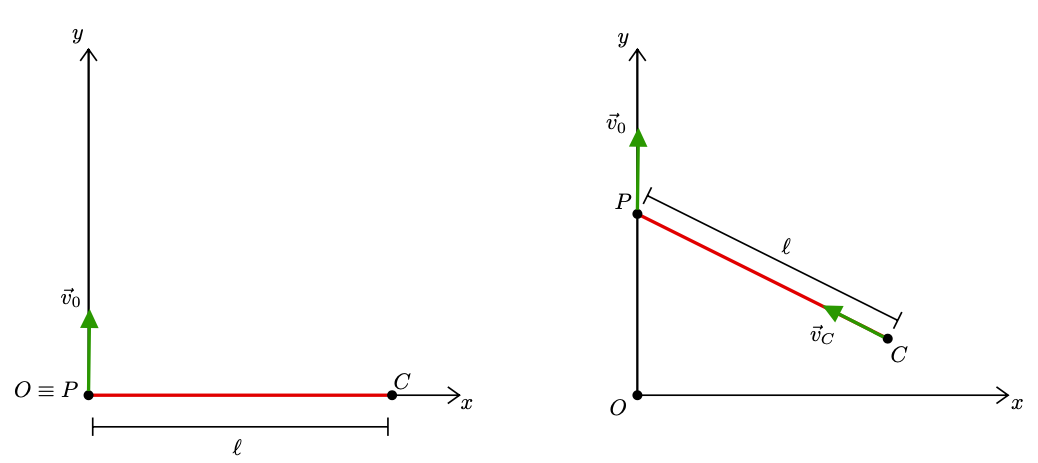
esercizi sui moti vari

Figura 4: schema del sistema per $\displaystyle t=t_{0} =0.$ e per $\displaystyle t$ generico.

Svolgimento.

Siano $x_C$ e $y_C$ rispettivamente l’ascissa e l’ordinata di $C$ , da cui $\dot{x}_C$ e $\dot{y}_C$ rappresentano rispettivamente la velocità di $C$ nelle direzioni dell’asse delle $x$ e delle $y$ . Pertanto La velocità del punto $C$ è

(68) $\begin{equation*} \vec{v}_C=\dot{x}_C\,\dot{x}+\dot{y}_C\,\hat{y}. \end{equation*}$

Inoltre, sia $y_P$ l’ordinata del punto $P$ e $\theta$ l’angolo compreso tra il guinzaglio e il segmento parallelo all’asse $x$ con un estremo nel punto $C$ , come mostra la figura 5.

$\quad$

Rendered by QuickLaTeX.com

Figura 5: schema del problema al tempo $\displaystyle t>0$ generico.

$\quad$

Il testo richiede che le componenti $\dot{x}_C$ e $\dot{y}_C$ siano espresse in funzione delle variabili $v_0$ e $x_C$ . Per fare ciò, notiamo che per ipotesi il guinzaglio (supposto inestensibile) deve essere sempre teso: questo significa che $\dot{\ell}=0$ , ossia che la lunghezza del guinzaglio non varia nel tempo. Osservando la figura 5, dalla geometria del problema, deduciamo che

(69) $\begin{equation*} \ell^2=x_C^2+(y_P-y_C)^2, \end{equation*}$

da cui, derivando rispetto al tempo ambo i membri della precedente relazione, otteniamo

(70) $\begin{equation*} 2\ell\dot{\ell}=0=2x_C\dot{x}_C+2(y_P-y_C)(\dot{y}_P-\dot{y}_C), \end{equation*}$

da cui

(71) $\begin{equation*} 0=x_C\dot{x}_C+\dot{y}_P(y_P-y_C)-\dot{y}_C(y_P-y_C), \end{equation*}$

o anche, ricordando che $y_P-y_C=\sqrt{\ell^2-x_C^2}$ e $\dot{y}_P=v_0$ , si ottiene

(72) $\begin{equation*} x_C\dot{x}_C+v_0\sqrt{\ell^2-x_C^2}-\dot{y}_C\sqrt{\ell^2-x_C^2}=0. \end{equation*}$

Dalla figura 5 si deduce che

(73) $\begin{equation*} \vec{v}_C=-v_C\cos \theta \,\hat{x}+v_C\sin \theta \,\hat{y}=\dot{x}_C \,\hat{x}+\dot{y}_C \,\hat{y}, \end{equation*}$

da cui

(74) $\begin{equation*} \begin{cases} \dot{x}_C=-v_C\cos \theta \\ \dot{y}_C=v_C\sin \theta . \end{cases} \end{equation*}$

Facendo il rapporto membro a membro delle equazioni (74) $_2$ e (74) $_1$ , si ottiene

(75) $\begin{equation*} \tan \theta=-\dfrac{\dot{y}_C}{\dot{x}_C}. \end{equation*}$

Inoltre, notiamo che

(76) $\begin{equation*} \tan \theta =\dfrac{y_P-y_C}{x_C}=\dfrac{\sqrt{\ell^2-x_C^2}}{x_C}. \end{equation*}$

Pertanto, si ha

(77) $\begin{equation*} -\dfrac{\dot{y}_C}{\dot{x}_C}=\dfrac{\sqrt{\ell^2-x_C^2}}{x_C}, \end{equation*}$

ossia

(78) $\begin{equation*} \dot{y}_C=-\dfrac{\dot{x}_C\left(\sqrt{\ell^2-x_C^2}\right)}{x_C}. \end{equation*}$

Sostituendo $\dot{y}_C$ (calcolata nell’equazione (78)) nell’equazione (72), si ottiene

(79) $\begin{equation*} \begin{split} &x_C\dot{x}_C+\dfrac{\dot{x}_C\left(\ell^2-x_C^2\right)}{x_C}+v_0\sqrt{\ell^2-x_C^2}=0\quad \Leftrightarrow\\[10pt] &\Leftrightarrow \quad x_C^2\dot{x}_C+\dot{x}_C\left(\ell^2-x_C^2\right)+v_0x_C\sqrt{\ell^2-x_C^2}=0\quad \Leftrightarrow\\[10pt] &\Leftrightarrow\quad \dot{x}_C(x_C^2+\ell^2-x_C^2)=-v_0x_C\sqrt{\ell^2-x_C^2}\quad \Leftrightarrow\\[10pt] & \Leftrightarrow\quad\dot{x}_C=-\dfrac{v_0x_C\sqrt{\ell^2-x_C^2}}{\ell^2}. \end{split} \end{equation*}$

Sostituendo $\dot{x}_C$ (calcolata nell’equazione (78)) nell’equazione (72), si trova

(80) $\begin{equation*} \dot{y}_C=-\dfrac{\dot{x}_C\left(\sqrt{\ell^2-x_C^2}\right)}{x_C}=-\dfrac{\left(\sqrt{\ell^2-x_C^2}\right)}{x_C}\left(-\dfrac{v_0x_C\sqrt{\ell^2-x_C^2}}{\ell^2}\right)=\dfrac{v_0\left(\ell^2-x_C^2\right)}{\ell^2}. \end{equation*}$

Sfruttando le equazioni (79) e (80) possiamo calcolare $v_C$ . Abbiamo dunque

(81) $\begin{equation*} v_C=\sqrt{\dot{x}_C^2+\dot{y}_C^2}, \end{equation*}$

ossia

(82) $\begin{equation*} \begin{split} v_C&=\sqrt{\dfrac{v_0^2x_C^2\left(\ell^2-x_C^2\right)}{\ell^4}+\dfrac{v_0^2\left(\ell^2-x_C^2\right)^2}{\ell^4}}= \\ &=\sqrt{\dfrac{v_0^2\left(\ell^2-x_C^2\right)\left(x_C^2+\ell^2-x_C^2\right)}{\ell^4}}= \\ &=\sqrt{\dfrac{v_0^2\ell^2\left(\ell^2-x_C^2\right)}{\ell^4}}, \end{split} \end{equation*}$

da cui

$\boxcolorato{fisica}{v_C=\dfrac{v_0}{\ell}\sqrt{\ell^2-x_C^2}.}$

Esercizio 12 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Nel meccanismo rappresentato nella figura 6, i punti $O$ , $A$ e $B$ rappresentano 3 cerniere per le aste $OA$ e $AB$ (supposte rigide e di massa trascurabile) di uguale lunghezza $\ell$ . Siano un sistema di riferimento fisso $Oxy$ e $\alpha$ l’angolo che l’asta $OA$ forma con l’asse delle $x$ . A partire dall’istante $t=0$ , l’asta $OA$ forma l’angolo $\alpha=0$ e la cerniera $B$ viene avvicinata a $O$ muovendola lungo l’asse $x$ , con velocità costante di modulo $v$ . Supponendo $O$ fisso, si calcoli in funzione del tempo

$\quad$

l’angolo $\alpha$ .

Le componenti cartesiane della velocità, nel sistema di riferimento fisso $Oxy$ , del punto $A$ .

Le componenti cartesiane dell’accelerazione, nel sistema di riferimento fisso $Oxy$ , del punto $A$ .

$\quad$

Figura 6: schema del sistema al tempo $\displaystyle t=0.$ (a sinistra) e per un tempo generico $\displaystyle t$ (a destra).

Svolgimento punto 1.

Notiamo innanzitutto che, dal momento che le aste sono supposte rigide, il triangolo ${OAB}$ è isoscele, in ogni istante del moto; segue che gli angoli alla base sono tra loro congruenti e dunque la configurazione del sistema al generico istante $t>0$ può essere rappresentata come in figura 7.

$\quad$

Rendered by QuickLaTeX.com

Figura 7: schema sistema per $\displaystyle t$ generico.

$\quad$

Dalla figura 7, è immediato dedurre che il vettore posizione del punto $B$ , vincolato a muoversi lungo l’asse $x$ , sia

(83) $\begin{equation*} \vec{r}_B=x_B\,\hat{x}=2\ell\cos\alpha\,\hat{x}, \end{equation*}$

dove $\hat{x}$ e $\hat{y}$ rappresentano rispettivamente i versori dell’asse delle $x$ e delle $y$ . Inoltre, sappiamo che il suo moto lungo l’asse delle $x$ avviene a velocità costante con modulo $v$ , dunque la cerniera $B$ si muove di moto rettilineo uniforme. Quindi

(84) $\begin{equation*} x_B=2\ell-vt, \end{equation*}$

dove $x_B=2\ell$ è la posizione iniziale della cerniera (si veda la figura 7 (a sinistra)). Confrontando l’equazione (83) con l’equazione (84), otteniamo

(85) $\begin{equation*} 2\ell\cos\alpha=2\ell-vt\quad\Leftrightarrow\quad\cos\alpha=1-\dfrac{vt}{2\ell}. \end{equation*}$

Osserviamo che l’equazione (85) per essere ben definita deve valere

(86) $\begin{equation*} -1\leq 1-\dfrac{vt}{2\ell}\leq 1, \end{equation*}$

o anche

(87) $\begin{equation*} -2\leq -\dfrac{vt}{2\ell}\leq 0, \end{equation*}$

oppure

(88) $\begin{equation*} 0\leq \dfrac{vt}{2\ell}\leq 2, \end{equation*}$

da cui

(89) $\begin{equation*} 0\leq t\leq\dfrac{4\ell}{v}. \end{equation*}$

Si conclude che

$\boxcolorato{fisica}{\alpha=\arccos\left(1-\dfrac{vt}{2\ell}\right), \quad0\leq t\leq\dfrac{4\ell}{v}.}$

Svolgimento punto 2.

Per risolvere questo punto, studiamo il moto della cerniera $A$ . Facendo riferimento alla figura 7, osserviamo che il suo vettore posizione è descritto dalle coordinate

(90) $\begin{equation*} \vec{r}_A=\ell\cos\alpha\,\hat{x}+ \ell\sin\alpha\,\hat{y}. \end{equation*}$

Grazie alla soluzione del punto $1$ , sappiamo inoltre che

(91) $\begin{equation*} \cos\alpha=1-\dfrac{vt}{2\ell}, \end{equation*}$

dunque sfruttando questo risultato e ricordando l’identità fondamentale della goniometria possiamo ricavare l’espressione della posizione di $A$ in funzione del tempo:

(92) $\begin{equation*} \begin{aligned} \vec{r}_A&=x_A\hat{x}+y_A\,\hat{y}=\\ &=\ell\left(1-\dfrac{vt}{2\ell}\right)\hat{x}+ \ell\sqrt{1-\cos^2\alpha}\,\,\hat{y}=\\ &=\left(\ell-\dfrac{vt}{2}\right)\hat{x}+ \ell\sqrt{1-\left(1-\dfrac{vt}{2\ell}\right)^2}\,\,\hat{y}=\\ &=\left(\ell-\dfrac{vt}{2}\right)\hat{x}+ \ell\sqrt{1-1-\dfrac{v^2t^2}{4\ell^2}+\dfrac{vt}{\ell}}\,\,\hat{y}=\\ &=\left(\ell-\dfrac{vt}{2}\right)\hat{x}+ \ell\sqrt{\dfrac{v}{\ell}\left(t-\dfrac{vt^2}{4\ell}\right)}\,\,\hat{y}=\\ &=\left(\ell-\dfrac{vt}{2}\right)\hat{x}+ \sqrt{v\ell\left(t-\dfrac{vt^2}{4\ell}\right)}\,\,\hat{y}. \end{aligned} \end{equation*}$

La velocità di $A$ è

(93) $\begin{equation*} \vec{v}_A=\dot{x}_A\,\hat{x}+\dot{y}_B\,\hat{y}. \end{equation*}$

Abbiamo dunque

(94) $\begin{equation*} \dot{x}_A=\dfrac{d}{dt}\left(\ell-vt\right)=-\dfrac{v}{2} \end{equation*}$

(95) $\begin{equation*} \dot{y}_A=\dfrac{d}{dt}\left(\sqrt{v\ell\left(t-\dfrac{vt^2}{4\ell}\right)}\right)=\sqrt{v\ell}\left(t-\dfrac{vt^2}{4\ell}\right)^{-\frac{1}{2}}\left(1-\dfrac{vt}{2\ell}\right). \end{equation*}$

In definitiva, avremo dunque

$\boxcolorato{fisica}{\vec{v}_A=-\dfrac{v}{2}\,\hat{x}+\sqrt{v\ell}\left(1-\dfrac{vt}{2\ell}\right)\left(t-\dfrac{vt^2}{4\ell}\right)^{-\frac{1}{2}}\hat{y}.}$

Svolgimento punto 3.

L’accelerazione di $A$ lungo la direzione dell’asse delle ${x}$ è data dalla derivata rispetto al tempo della velocità $\dot{x}_A$ ; dal momento che $\dot{x}_A=-v/2$ è costante nel tempo, avremo

$\boxcolorato{fisica}{\ddot{x}_A=0.}$

Esercizio 13 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Un punto $P$ percorre una spirale logaritmica con l’accelerazione che punta costantemente verso il centro $O$ di un sistema di riferimento fisso $Oxy$ . Ricordando che la distanza $r$ , in un generico istante $t>0$ , del punto $P$ da $O$ è data da

(96) $\begin{equation*} r=\overline{OP}=ae^{b\theta}, \end{equation*}$

dove $a$ e $b$ sono delle costanti, $\theta\in\mathbb{R}$ è l’angolo che forma $\overline{OP}$ con l’asse delle $x$ , si dimostri che il modulo dell’accelerazione è inversamente proporzionale al cubo della distanza $\overline{OP}$ .

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Rendered by QuickLaTeX.com

Svolgimento.

Ricordiamo che l’accelerazione espressa in coordinate polari è

(97) $\begin{equation*} \vec{a}=\left(\dfrac{d^2r}{dt^2}-r\left(\dfrac{d\theta}{dt}\right)^2\right)\hat{r}+ \left(\dfrac{1}{r}\dfrac{d\left(r^2\dfrac{d\theta }{dt}\right)}{dt} \right)\hat{\theta}, \end{equation*}$

dove $\hat{r}$ e $\hat{\theta}$ sono rispettivamente i versori nella direzione radiale e trasversa. Sappiamo che l’accelerazione punta sempre nella direzione radiale, pertanto deve valere

(98) $\begin{equation*} \dfrac{d\left(r^2\dfrac{d\theta }{dt}\right)}{dt}=0, \end{equation*}$

da cui

(99) $\begin{equation*} r^2\dfrac{d\theta }{dt}=\text{c}_1\in\mathbb{R}, \end{equation*}$

o anche

(100) $\begin{equation*} \dfrac{d\theta }{dt}=\dfrac{\text{c}_1}{r^2}. \end{equation*}$

Deriviamo ambo i membri della (96), rispetto al tempo, ottenendo

(101) $\begin{equation*} \dfrac{dr}{dt}=ab\dfrac{d\theta}{dt}e^{b\theta}=b\underbrace{\dfrac{d\theta}{dt}}_{=c_1/r^2}\,\underbrace{(ae^{b\theta})}_{=r}=\dfrac{b\,\text{c}_1}{r^2}\,r=\dfrac{\text{c}_2}{r}, \end{equation*}$

dove nei precedenti passaggi abbiamo sfruttato la (100) e la (96), inoltre abbiamo denotato il prodotto $b\,\text{c}_1$ con $\text{c}_2$ . Deriviamo ambo i membri della (101), rispetto al tempo, ottenendo

(102) $\begin{equation*} \dfrac{d^2r}{dt^2}=-\dfrac{\text{c}_2}{r^2}\,\underbrace{\dfrac{dr}{dt}}_{c_2/r}=-\dfrac{\text{c}_2^2}{r^3}=\dfrac{\text{c}_3}{r^3}, \end{equation*}$

dove nei precedenti passaggi abbiamo usato (101) e abbiamo denotato $-\text{c}_2^2$ con $\text{c}_3$ .

Dunque, tenendo conto di quanto ottenuto, ovvero di (100) e (102), e ricordando che la componente trasversa deve essere nulla per le ipotesi del problema, la (97) diventa

(103) $\begin{equation*} \vec{a}=\left(\dfrac{d^2r}{dt^2}-r\left(\dfrac{d\theta}{dt}\right)^2\right)\hat{r}=\left(\dfrac{\text{c}_3}{r^3}-r\,\dfrac{\text{c}_1^2}{r^4}\right)\hat{r}=\dfrac{c_3-c_1^2}{r^3}\,\hat{r}=\dfrac{\text{costante}}{r^3}\,\hat{r}, \end{equation*}$

dove abbiamo denotato $c_3-c_1^2=\text{costante}$ . Da (103), si ha

(104) $\begin{equation*} \left \vert \vec{a} \right \vert=\dfrac{\left \vert \text{costante}\right \vert}{r^3}, \end{equation*}$

che è esattamente quello che volevamo dimostrare.

Esercizio 14 $(\bigstar\bigstar\bigstar\bigstar\bigstar)$ . Un punto materiale si muove su un piano orizzontale di moto incognito e sappiamo che la componente dell’accelerazione diretta lungo il semiasse positivo delle $y$ è costante. Esprimendo il moto del punto materiale in coordinate polari secondo il sistema di riferimento fisso illustrato nella figura seguente.

$\quad$

Rendered by QuickLaTeX.com

$\quad$

giungiamo alla relazione sottostante:

$\begin{aligned} &\sqrt{2}\left(\ddot{\rho}-\rho \, \left(\dot{\theta} \right)^2 \right) \cos \left( \theta + \dfrac{\pi}{4} \right)-\sqrt{2}\left( 2 \dot{\rho}\,\dot{\theta}+\rho \, \ddot{\theta}\right)\cos \left( \theta - \dfrac{\pi}{4}\right)+k(t)=0,\\[10pt] &\text{dove}\,\,k(t)=\left(\dfrac{d^2\rho}{dt^2}-\rho\left(\dfrac{d\theta}{dt}\right)^2\right)\sin \theta- \left(\dfrac{1}{\rho}\dfrac{d\left(\rho^2\dfrac{d\theta }{dt}\right)}{dt} \right)\cos \theta. \end{aligned}$

Determinare di che moto si muove il punto materiale rispetto a tale sistema di riferimento.

Nota: nell’esercizio utilizzeremo la seguente notazione $\ddot{\rho}=\dfrac{d^2\rho}{dt^2}\,\,\text{e}\,\,\dot{\rho}=\dfrac{d\rho}{dt}$ .

Svolgimento.

Scriviamo la posizione del punto materiale in coordinate polari

$\begin{cases} x=\rho \cos \theta\\ y=\rho \sin \theta \end{cases}$

e deriviamo rispetto al tempo ottenendo

$\begin{cases} \dot{x} =\dot{\rho}\, \cos \theta + \rho \left(- \sin \theta \right) \, \dot{\theta}\\ \dot{y}=\dot{\rho}\,\sin \theta + \rho \cos \theta \, \dot{\theta}. \end{cases}$

Deriviamo nuovamente rispetto al tempo

(105) $\begin{equation*} \begin{cases} \ddot{x}=\ddot{\rho} \, \cos \theta + \dot{\rho}\,\left(-\sin \theta \right)\, \dot{\theta}+\dot{\rho}\,\left(- \sin \theta \right) \, \dot{\theta}+\rho \, \left( -\cos \theta\right)\, \left(\dot{\theta} \right)^2+\rho\, \left( -\sin \theta \right)\, \ddot{\theta}\\ \ddot{y}=\ddot{\rho}\,\sin \theta +\dot{\rho} \, \cos \theta \, \dot{\theta}+\dot{\rho}\cos \theta \,\dot{\theta}+\rho \left(-\sin \theta\right) \left( \dot{\theta}\right)^2+\rho \cos \theta \, \ddot{\theta}. \end{cases} \end{equation*}$

Ora, sottraiamo membro a membro, delle equazioni (105) $_1$ (105) $_2$ , ottenendo

$\begin{aligned} &\ddot{x}-\ddot{y}=\\ &=\left(\ddot{\rho} \, \cos \theta + \dot{\rho}\,\left(-\sin \theta \right)\, \dot{\theta}+\dot{\rho}\,\left(- \sin \theta \right) \, \dot{\theta}+\rho \, \left( -\cos \theta\right)\, \left(\dot{\theta} \right)^2+\rho\, \left( -\sin \theta \right)\, \ddot{\theta}\right)+\\ &-\left(\ddot{\rho}\,\sin \theta +\dot{\rho} \, \cos \theta \, \dot{\theta}+\dot{\rho}\cos \theta \,\dot{\theta}+\rho \left(-\sin \theta\right) \left( \dot{\theta}\right)^2+\rho \cos \theta \, \ddot{\theta} \right)=\\ &=\ddot{\rho} \, \cos \theta - \dot{\rho}\,\sin \theta \, \dot{\theta}-\dot{\rho}\,\sin \theta \, \dot{\theta}-\rho \, \cos \theta \, \left(\dot{\theta} \right)^2-\rho\, \sin \theta \, \ddot{\theta}+\\ &-\ddot{\rho}\,\sin \theta -\dot{\rho} \, \cos \theta \, \dot{\theta}-\dot{\rho}\cos \theta \,\dot{\theta}+\rho \sin \theta \left( \dot{\theta}\right)^2-\rho \cos \theta \, \ddot{\theta}=\\ &=\ddot{\rho} \, \cos \theta -2 \dot{\rho}\,\sin \theta \, \dot{\theta}-\rho \, \cos \theta \, \left(\dot{\theta} \right)^2-\rho\, \sin \theta \, \ddot{\theta}-\ddot{\rho}\,\sin \theta -2\dot{\rho} \, \cos \theta \, \dot{\theta}+\rho \sin \theta \left( \dot{\theta}\right)^2-\rho \cos \theta \, \ddot{\theta}=\\ &=\ddot{\rho} \left(\cos \theta - \sin \theta \right)-2 \, \dot{\rho} \, \dot{\theta}\left(\cos \theta +\sin \theta \right)-\rho\left(\dot{\theta} \right)^2\left( \cos \theta -\sin \theta\right)-\rho \, \ddot{\theta}\left(\cos \theta +\sin \theta \right)=\\ &=\left(\ddot{\rho}-\rho \, \left(\dot{\theta} \right)^2 \right)\left(\cos \theta - \sin \theta \right)-\left( 2 \dot{\rho}\,\dot{\theta}+\rho \, \ddot{\theta}\right)\left( \cos \theta + \sin \theta \right)=\\ &=\sqrt{2}\left(\ddot{\rho}-\rho \, \left(\dot{\theta} \right)^2 \right) \cos \left( \theta + \dfrac{\pi}{4} \right)-\sqrt{2}\left( 2 \dot{\rho}\,\dot{\theta}+\rho \, \ddot{\theta}\right)\cos \left( \theta - \dfrac{\pi}{4}\right)\quad \Leftrightarrow\\ &\Leftrightarrow\quad \ddot{x}-\ddot{y}=\sqrt{2}\left(\ddot{\rho}-\rho \, \left(\dot{\theta} \right)^2 \right) \cos \left( \theta + \dfrac{\pi}{4} \right)-\sqrt{2}\left( 2 \dot{\rho}\,\dot{\theta}+\rho \, \ddot{\theta}\right)\cos \left( \theta - \dfrac{\pi}{4}\right). \end{aligned}$

Evidenziamo il risultato appena ottenuto

(106) $\begin{equation*} \ddot{x}-\ddot{y}=\sqrt{2}\left(\ddot{\rho}-\rho \, \left(\dot{\theta} \right)^2 \right) \cos \left( \theta + \dfrac{\pi}{4} \right)-\sqrt{2}\left( 2 \dot{\rho}\,\dot{\theta}+\rho \, \ddot{\theta}\right)\cos \left( \theta - \dfrac{\pi}{4}\right). \end{equation*}$

Ricordiamo che l’accelerazione in coordinate polari si esprime come segue

$\vec{a}=\left(\dfrac{d^2\rho}{dt^2}-\rho\left(\dfrac{d\theta}{dt}\right)^2\right)\hat{r}+ \left(\dfrac{1}{\rho}\dfrac{d(\rho^2\frac{d\theta }{dt})}{dt} \right)\hat{\theta}$

e consideriamo il seguente grafico.

$\quad$

Rendered by QuickLaTeX.com

$\quad$

Dal grafico si può osservare che

$\begin{cases} \hat{r}=\cos \theta\, \hat{x}+\sin \theta \,\hat{y}\\ \hat{\theta}=-\sin \theta \,\hat{x}+\cos \theta\, \hat{y}, \end{cases}$

dove $\hat{x}$ e $\hat{y}$ sono rispettivamente i versori dell’asse delle $x$ e delle $y$ , da cui

$\begin{aligned} \vec{a}&=\left(\dfrac{d^2\rho}{dt^2}-\rho\left(\dfrac{d\theta}{dt}\right)^2\right)\left( \cos \theta \hat{x}+\sin \theta \hat{y}\right)+ \left(\dfrac{1}{\rho}\dfrac{d\left(\rho^2\dfrac{d\theta }{dt}\right)}{dt} \right)\left(-\sin \theta \hat{x}+\cos \theta \hat{y} \right)=\\[10pt] &=\hat{x}\left[\left(\dfrac{d^2\rho}{dt^2}-\rho\left(\dfrac{d\theta}{dt}\right)^2\right)\cos \theta- \left(\dfrac{1}{\rho}\dfrac{d\left(\rho^2\dfrac{d\theta }{dt}\right)}{dt} \right)\sin \theta \right]+ \\ &+\hat{y}\left[\left(\dfrac{d^2\rho}{dt^2}-\rho\left(\dfrac{d\theta}{dt}\right)^2\right)\sin \theta- \left(\dfrac{1}{\rho}\dfrac{d\left(\rho^2\dfrac{d\theta }{dt}\right)}{dt} \right)\cos \theta \right]. \end{aligned}$

Quindi

$\begin{cases} \ddot{x}=\left(\dfrac{d^2\rho}{dt^2}-\rho\left(\dfrac{d\theta}{dt}\right)^2\right)\cos \theta- \left(\dfrac{1}{\rho}\dfrac{d\left(\rho^2\dfrac{d\theta }{dt}\right)}{dt} \right)\sin \theta \\[20pt] \ddot{y}=\left(\dfrac{d^2\rho}{dt^2}-\rho\left(\dfrac{d\theta}{dt}\right)^2\right)\sin \theta- \left(\dfrac{1}{\rho}\dfrac{d\left(\rho^2\dfrac{d\theta }{dt}\right)}{dt} \right)\cos \theta. \end{cases}$

Chiamando

$k(t) = \left(\dfrac{d^2\rho}{dt^2}-\rho\left(\dfrac{d\theta}{dt}\right)^2\right)\sin \theta- \left(\dfrac{1}{\rho}\dfrac{d\left(\rho^2\dfrac{d\theta }{dt}\right)}{dt} \right)\cos \theta$

e tornando alla (106) abbiamo

$\begin{aligned} \ddot{x}&=\sqrt{2}\left(\ddot{\rho}-\rho \, \left(\dot{\theta} \right)^2 \right) \cos \left( \theta + \dfrac{\pi}{4} \right)-\sqrt{2}\left( 2 \dot{\rho}\,\dot{\theta}+\rho \, \ddot{\theta}\right)\cos \left( \theta - \dfrac{\pi}{4}\right)+\ddot{y}=\\ &=\sqrt{2}\left(\ddot{\rho}-\rho \, \left(\dot{\theta} \right)^2 \right) \cos \left( \theta + \dfrac{\pi}{4} \right)-\sqrt{2}\left( 2 \dot{\rho}\,\dot{\theta}+\rho \, \ddot{\theta}\right)\cos \left( \theta - \dfrac{\pi}{4}\right)+k(t). \end{aligned}$

Osserviamo che ponendo $\ddot{x}=0$ , si ottiene:

$\sqrt{2}\left(\ddot{\rho}-\rho \, \left(\dot{\theta} \right)^2 \right) \cos \left( \theta + \dfrac{\pi}{4} \right)-\sqrt{2}\left( 2 \dot{\rho}\,\dot{\theta}+\rho \, \ddot{\theta}\right)\cos \left( \theta - \dfrac{\pi}{4}\right)+k(t)=0,$

che è la condizione richiesta.

Ne diamo ora un’interpretazione fisica.

Avendo posto $\ddot{x}=0$ questo ci fa concludere che $\dot{x}=costante$ quindi lungo l’asse $x$ il punto materiale si muove di moto rettilineo uniforme. Mentre lungo l’asse $y$ per ipotesi sappiamo che il punto materiale si muove di moto rettilineo uniformemente accelerato. Concludiamo che il moto del punto materiale è dato dalla composizione di due moti: moto rettilineo uniforme lungo l’asse $x$ e uniformemente accelerato lungo l’asse $y$ .

Esercizio 15 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un punto materiale si trova su una piattaforma circolare di raggio $R$ e centro $O$ , che ruota con velocità angolare costante (modulo, direzione e verso) $\vec{\omega}$ in senso orario, come mostrato in figura 8. All’istante iniziale $t_0=0$ , il punto materiale si trova a una distanza $r_0$ dal centro $O$ della piattaforma e si muove verso di esso con una velocità relativa costante $\vec{v}_{r}$ rispetto alla piattaforma. Determinare, in direzione e modulo, la velocità assoluta del punto all’istante $t= t^*$ nel sistema di riferimento fisso $Oxyz$ rappresentato in figura 8.

$\quad$

Rendered by QuickLaTeX.com

Figura 8: rappresentazione del sistema fisico in esame.

Svolgimento.

Scegliamo un sistema di riferimento non inerziale $O x^\prime y^\prime z^\prime$ , solidale con la piattaforma che ruota, tale per cui il punto materiale si trovi sull’asse delle $x^\prime$ per ogni istante $t\geq 0$ e $z\equiv z^\prime$ , come illustrato in figura 8. Siano, inoltre, $\omega$ e $v_r$ rispettivamente la componente di $\vec{\omega}$ lungo l’asse $z^\prime$ e la componente di $\vec{v}_r$ lungo $x^\prime$ . Osserviamo che siccome la piattaforma si muove in senso orario $\omega<0$ e che $v_r<0$ perché il punto materiale si muove nella direzione negativa delle $x^\prime$ .

$\quad$

Rendered by QuickLaTeX.com

Figura 9: rappresentazione del sistema sistema di riferimento non inerziale $O^\prime x^\prime y^\prime$ .

$\quad$

Osservando dal sistema di riferimento $O^\prime x^\prime y^\prime$ , il corpo si muove di moto rettilineo uniforme con velocità $v_r$ diretta lungo il semiasse negativo delle $x^\prime$ . Pertanto, essendo $r_0$ la posizione iniziale del corpo, la sua legge oraria è

(107) $\begin{equation*} x^\prime (t)=r_0+v_rt,\quad \text{per $t\geq 0$}. \end{equation*}$

Per determinare la posizione del corpo all’istante $t=t^*$ , sostituiamo $t=t^*$ nella precedente equazione e otteniamo

(108) $\begin{equation*} x^\prime (t^*)=r_0+v_rt^*. \end{equation*}$

In base al teorema delle velocità relative, la velocità assoluta $\vec{v}_a$ del punto materiale nel sistema di riferimento fisso $Oxy$ , è data dalla somma della velocità radiale $\vec{v}_r$ e della velocità tangenziale $\vec{v}_t$ del corpo, cioè

(109) $\begin{equation*} \vec{v}_a = \vec{v}_r + \vec{v}_t = \vec{v}_r + \vec{\omega} \wedge \vec{r}^{\,\prime}, \end{equation*}$

dove $\vec{r}^{\,\prime}$ il vettore posizione del corpo nel sistema di riferimento $O^\prime x^\prime y$ . In questo caso particolare, queste due velocità hanno direzioni ortogonali fra di loro, pertanto il modulo della loro somma è dato da

(110) $\begin{equation*} |\vec{v}_a | = \sqrt{ |\vec{v}_r|^2 + |\vec{\omega} \wedge \vec{r}^{\,\prime}|^2}. \end{equation*}$

Essendo i vettori $\vec{\omega}$ e $\vec{r}^{\,\prime}$ ortogonali fra loro, si ha che $|\vec{\omega} \wedge \vec{r}^\prime| =\left \vert \omega\right \vert r^\prime$ , da cui

$\boxcolorato{fisica}{|\vec{v}_a | = \sqrt{ v_r^2 + (\omega r^\prime)^2}.}$

Per determinare la direzione della velocità assoluta $\vec{v}_a$ basta considerare il triangolo di ipotenusa $|\vec{v}_a|$ e i cui cateti hanno lunghezza pari a $|\vec{v}_r|$ e $|\vec{v}_t|$ , come illustrato in figura 10.

$\quad$

Rendered by QuickLaTeX.com

Figura 10: rappresentazione della direzione della velocità assoluta.

$\quad$

Per questo triangolo, vale la relazione

(111) $\begin{equation*} |\vec{v}_t| =|\vec{v}_r| \cdot \tan(\alpha), \end{equation*}$

dove $\alpha$ è l’angolo che la velocità $\vec{v}_a$ forma con la direzione radiale. Questo angolo è dato da

(112) $\begin{equation*} \alpha = \arctan \left( \dfrac{|\vec{v}_t|} {|\vec{v}_r|}\right) = \arctan\left(\dfrac{\left \vert \omega\right \vert r^\prime }{ \left \vert v_r\right \vert }\right), \end{equation*}$

in cui $r^\prime$ rappresenta la distanza percorsa nell’intervallo di tempo $\Delta t = t^*-t_0=t^*$ . Questa è data dal valore assoluto $|x^\prime (t^*)|=|r_0+v_rt^*|$ . Pertanto, l’angolo $\alpha$ è dato da

$\boxcolorato{fisica}{\alpha= \arctan \left( \dfrac{\left \vert\omega\right \vert |r_0+v_rt^*|}{\left \vert v_r\right \vert } \right).}$

Si osservi che per dedurre la direzione della velocità $\vec{v}_a$ si è usato il metodo punta-coda. È interessante osservare che $\alpha$ dipende dal tempo, pertanto istante per istante $\vec{v}_a$ cambia direzione.

Siano $\hat{x}$ e $\hat{y}$ rispettivamente i versori dell’asse delle $x$ e delle $y$ . Esprimiamo per completezza $\vec{v}_a$ rispetto ai versori $\hat{x}$ e $\hat{y}$ . Abbiamo dunque

(113) $\begin{equation*} \vec{v}_a=-\left \vert \vec{v}_a \right \vert \cos \alpha \, \hat{x}-\left \vert \vec{v}_a \right \vert \sin \alpha \, \hat{x}, \end{equation*}$

o anche

$\boxcolorato{fisica}{\begin{split} \vec{v}_a=&-\sqrt{ v_r^2 + (\omega r^\prime)^2} \cos \left(\arctan \left( \dfrac{\left \vert \omega\right \vert |r_0+v_rt^*|}{\left \vert v_r\right \vert } \right)\right) \hat{x}- \\ &-\sqrt{ v_r^2 + (\left \vert \omega\right \vert r^\prime)^2} \sin \left(\arctan \left( \dfrac{\omega |r_0+v_rt^*|}{\left \vert v_r\right \vert } \right)\right) \hat{y}.\end{split}}$

Esercizio 16 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Si consideri un punto materiale di massa $m$ su un piano orizzontale liscio soggetto ad una accelerazione espressa in coordinate polari pari ad

$\vec{a}=\dfrac{1}{r}\hat{\theta}\,\left[\dfrac{\mathrm{m}}{\mathrm{s}^2}\right].$

Con le seguenti condizioni iniziali

(114) $\begin{equation*} r(1)=1\,[\mathrm{m}] \quad \mbox{e} \quad \dfrac{d\theta }{dt}(1)=1 \end{equation*}$

verificare che le condizioni del problema soddisfano la seguente relazione:

$r^3\dfrac{dr}{dt}- 3\int r^2\left(\dfrac{dr}{dt}\right)^2dt=\dfrac{t^3}{3}+k \quad \mbox{ con } \, k\in \mathbb{R}.$

Svolgimento.

Ricordiamo come si esprime l’accelerazione in coordinate polari:

$\vec{a}=\left(\dfrac{d^2r}{dt^2}-r\left(\dfrac{d\theta}{dt}\right)^2\right)\hat{r}+ \left(\dfrac{1}{r}\dfrac{d(r^2\frac{d\theta }{dt})}{dt} \right)\hat{\theta}$

ed impostiamo il seguente problema di Cauchy

(115) $\begin{equation*} \begin{cases} \dfrac{d^2r}{dt^2}-r\left(\dfrac{d\theta}{dt}\right)^2=0\\\\ \dfrac{1}{r}\dfrac{d(r^2\frac{d\theta }{dt})}{dt}=\dfrac{1}{r}\\\\ r(1)=1\,[\mathrm{m}]\\\\ \dfrac{d\theta }{dt}(1)=1\,\left[\dfrac{\mathrm{rad}}{\mathrm{s}}\right]. \end{cases} \end{equation*}$

Risolviamo l’equazione differenziale (115) $_2$

$\begin{aligned} &\dfrac{1}{r}\dfrac{d(r^2\frac{d\theta }{dt})}{dt}=\dfrac{1}{r}\quad \Leftrightarrow\\ &\Leftrightarrow\quad\dfrac{d(r^2\frac{d\theta }{dt})}{dt}=1\quad\Leftrightarrow\\ &\Leftrightarrow \quad\int\dfrac{d(r^2\frac{d\theta }{dt})}{dt}dt=\int 1 dt\quad\Leftrightarrow\\ &\Leftrightarrow\quad r^2\frac{d\theta }{dt}=t+c_1 \quad \mbox{con } \,c_1\in \mathbb{R}\\ \end{aligned}$

e con le condizioni iniziali (114) otteniamo

$1=1+c_1 \quad\Leftrightarrow \quad c_1=0,$

quindi

$r^2\frac{d\theta }{dt}=t\Leftrightarrow \frac{d\theta }{dt}=\dfrac{t}{r^2}.$

Sostituendo $\dfrac{d\theta }{dt}$ in (115) $_1$ abbiamo

$\begin{aligned} \dfrac{d^2r}{dt^2}-r\left(\dfrac{d\theta}{dt}\right)^2=0\quad &\Leftrightarrow \quad \dfrac{d^2r}{dt^2}-r\left( \dfrac{t}{r^2}\right)^2=0 \quad\Leftrightarrow\\ &\Leftrightarrow\quad \dfrac{d^2r}{dt^2}=r\left( \dfrac{t}{r^2}\right)^2=\dfrac{t^2}{r^3}\quad\Leftrightarrow\\ &\Leftrightarrow \quad\int r^3 \dfrac{d^2r}{dt^2}dt=\int t^2dt\quad\Leftrightarrow\\ &\Leftrightarrow\quad \int \left(\dfrac{d(r^3\frac{dr}{dt})}{dt}-3r^2\left(\dfrac{dr}{dt}\right)^2\right)dt=\dfrac{t^3}{3}+c_2\quad\Leftrightarrow\\ &\Leftrightarrow \quad r^3\dfrac{dr}{dt}- 3\int r^2\left(\dfrac{dr}{dt}\right)^2dt=\dfrac{t^3}{3}+c_2 \quad \mbox{ con } \, c_2\in \mathbb{R}. \end{aligned}$

Posto $c_2=k$ si conclude che

$\boxcolorato{fisica}{r^3\dfrac{dr}{dt}- 3\int r^2\left(\dfrac{dr}{dt}\right)^2dt=\dfrac{t^3}{3}+k, \quad \mbox{ con } \, k\in \mathbb{R}. }$

Esercizio 17 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Si consideri un punto materiale di massa $m$ su un piano orizzontale liscio soggetto ad una accelerazione espressa in coordinate polari pari ad

(116) $\begin{equation*} \vec{a}=\dfrac{1}{r}\hat{\theta}\,\left[\dfrac{\mathrm{m}}{\mathrm{s}^2}\right] \end{equation*}$

con le seguenti condizioni iniziali

(117) $\begin{equation*} r(1)=1\,\,[\mathrm{m}],\quad \dfrac{d\theta }{dt}(1)=1\,\left[\dfrac{\mathrm{rad}}{\mathrm{s}}\right] \end{equation*}$

(118) $\begin{equation*} \dfrac{dr }{dt}(1)=\dfrac{4}{3}\left[\dfrac{\mathrm{m}}{\mathrm{s}}\right]. \end{equation*}$

Verificare oppure confutare che le condizioni del problema soddisfino la seguente relazione:

(119) $\begin{equation*} r^3 \dfrac{dr}{dt}-r^3=\dfrac{t^3}{3}. \end{equation*}$

Svolgimento.

Ricordiamo che l’accelerazione in coordinate polari si esprime come:

$\vec{a}=\left(\dfrac{d^2r}{dt^2}-r\left(\dfrac{d\theta}{dt}\right)^2\right)\hat{r}+ \left(\dfrac{1}{r}\dfrac{d(r^2\frac{d\theta }{dt})}{dt} \right)\hat{\theta}$

e confrontandola con (116) possiamo scrivere il seguente problema di Cauchy:

(120) $\begin{equation*} \begin{cases} \dfrac{d^2r}{dt^2}-r\left(\dfrac{d\theta}{dt}\right)^2=0\\\\ \dfrac{1}{r}\dfrac{d(r^2\frac{d\theta }{dt})}{dt}=\dfrac{1}{r}\\\\ r(1)=1\,[\mathrm{m}]\\\\ \dfrac{d\theta }{dt}(1)=1\,\left[\dfrac{\mathrm{rad}}{\mathrm{s}}\right]\\\\ \dfrac{dr }{dt}(1)=\dfrac{4}{3}\left[\dfrac{\mathrm{m}}{\mathrm{s}}\right]. \end{cases} \end{equation*}$

Risolviamo l’equazione differenziale (120) $_2$

$\begin{aligned} &\dfrac{1}{r}\dfrac{d(r^2\frac{d\theta }{dt})}{dt}=\dfrac{1}{r}\quad \Leftrightarrow\\ &\Leftrightarrow\quad\dfrac{d(r^2\frac{d\theta }{dt})}{dt}=1\quad\Leftrightarrow\\ &\Leftrightarrow \quad\int\dfrac{d(r^2\frac{d\theta }{dt})}{dt}dt=\int 1 dt\quad \Leftrightarrow\\ &\Leftrightarrow \quad r^2\frac{d\theta }{dt}=t+c_1, \quad \mbox{con } \,c_1\in \mathbb{R}. \end{aligned}$

Dalle condizioni iniziali (117) otteniamo

$1=1+c_1\quad \Leftrightarrow \quad c_1=0,$

quindi

$r^2\frac{d\theta }{dt}=t\quad \Leftrightarrow\quad \frac{d\theta }{dt}=\dfrac{t}{r^2}.$

Sostituendo $\dfrac{d\theta }{dt}$ in (120) $_1$ abbiamo

$\begin{aligned} &\dfrac{d^2r}{dt^2}-r\left(\dfrac{d\theta}{dt}\right)^2=0 \quad \Leftrightarrow \quad \\ & \Leftrightarrow \quad \dfrac{d^2r}{dt^2}-r\left( \dfrac{t}{r^2}\right)^2=0 \quad\Leftrightarrow\\ &\Leftrightarrow \quad \dfrac{d^2r}{dt^2}=r\left( \dfrac{t}{r^2}\right)^2=\dfrac{t^2}{r^3}\quad\Leftrightarrow\\ &\Leftrightarrow \quad\int r^3 \dfrac{d^2r}{dt^2}dt=\int t^2dt\quad\Leftrightarrow\\ &\Leftrightarrow \quad\int \left(\dfrac{d(r^3\frac{dr}{dt})}{dt}-3r^2\left(\dfrac{dr}{dt}\right)^2\right)dt=\dfrac{t^3}{3}+c_2\quad\Leftrightarrow\\ &\Leftrightarrow \quad r^3\dfrac{dr}{dt}- 3\int r^2\left(\dfrac{dr}{dt}\right)^2dt=\dfrac{t^3}{3}+c_2 \quad \mbox{ con } \, c_2\in \mathbb{R}\\ \end{aligned}$

Posto $c_2=k$ otteniamo la seguente relazione

$\boxcolorato{fisica}{r^3\dfrac{dr}{dt}- 3\int r^2\left(\dfrac{dr}{dt}\right)^2dt=\dfrac{t^3}{3}+k, \quad \mbox{ con } \, k\in \mathbb{R}.}$

Si osserva chiaramente che (??) differisce da (119). Questa osservazione ci fa concludere che le condizioni del problema non verificano (119). Si vuole far osservare che per arrivare alle (119) bisognava commettere il seguente errore:

$\begin{aligned} & \int r^3 \dfrac{d^2r}{dt^2}dt=\int t^2dt \quad \Leftrightarrow\\ &\Leftrightarrow\quad \int \left(\dfrac{d(r^3\frac{dr}{dt})}{dt}-3r^2\dfrac{dr}{dt}\right)dt=\dfrac{t^3}{3}+c_2\quad \Leftrightarrow\\ &\Leftrightarrow \quad r^3\dfrac{dr}{dt}-r^3=\dfrac{t^3}{3}+c_2 \quad \mbox{ con } \, c_2\in \mathbb{R}. \end{aligned}$

Dalle condizioni $r(1)=1 [\mathrm{m}],\,\dfrac{dr}{dt}(1)=\dfrac{4}{3}\left[\dfrac{\mathrm{m}}{\mathrm{s}}\right]$ otteniamo

$c_2=0,$

quindi

$\boxcolorato{fisica}{r^3\dfrac{dr}{dt}-r^3=\dfrac{t^3}{3}.}$

L’errore commesso è il seguente

$r^3 \dfrac{d^2r}{dt^2}=\dfrac{d(r^3\frac{dr}{dt})}{dt}-3r^2\dfrac{dr}{dt}.$

Chiaramente

$r^3 \dfrac{d^2r}{dt^2}\neq\dfrac{d(r^3\frac{dr}{dt})}{dt}-3r^2\dfrac{dr}{dt},$

la relazione corretta è quella che segue

$r^3\dfrac{d^2r}{dt^2}=\dfrac{d(r^3\frac{dr}{dt})}{dt}-3r^2\left(\dfrac{dr}{dt}\right)^2 .$

Tutti gli esercizi di elettromagnetismo

Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di Elettromagnetismo. Questa raccolta include spiegazioni dettagliate e gli esercizi sono organizzati in base al livello di difficoltà, offrendo un supporto completo per lo studio e la pratica.

Leggi...

Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.

Esercizi di Meccanica classica

Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.

Leggi..

Ulteriori risorse didattiche per la fisica

Leggi...

Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.

Document