Esercizio leggi della dinamica 13
L’esercizio 13 sulle leggi della dinamica è il tredicesimo della raccolta inclusa nella cartella Dinamica del punto materiale: Leggi di Newton in meccanica classica. Questo esercizio è il successivo di Esercizio leggi della dinamica 12 ed è il precedente di Esercizio leggi della dinamica 14. Questo esercizio è progettato per studenti che frequentano un corso di Fisica 1, indirizzato a chi studia ingegneria, fisica o matematica.
Testo leggi della dinamica 13
Esercizio 13 ![]() . Una massa
. Una massa ![]() è posta sopra una massa
è posta sopra una massa ![]() . Le due masse sono collegate da una fune inestensibile e di massa trascurabile tramite una carrucola. Una terza massa
. Le due masse sono collegate da una fune inestensibile e di massa trascurabile tramite una carrucola. Una terza massa ![]() è collegata alla massa
è collegata alla massa ![]() da una fune inestensibile e di massa trascurabile tramite una seconda carrucola, come illustrato in figura. Tutte le superfici di contatto sono scabre, con coefficiente di attrito dinamico
da una fune inestensibile e di massa trascurabile tramite una seconda carrucola, come illustrato in figura. Tutte le superfici di contatto sono scabre, con coefficiente di attrito dinamico ![]() . Calcolare:
. Calcolare:
- il valore del modulo dell’accelerazione di ciascuna delle tre masse;
- il modulo della tensione della fune che collega
 ad
ad 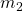 ;
; - il modulo della tensione della fune che collega
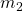 ad
ad  ;
; - il vettore risultante che agisce sul terreno su cui giace
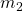 .
.
Si trascuri l’attrito tra funi e carrucole.
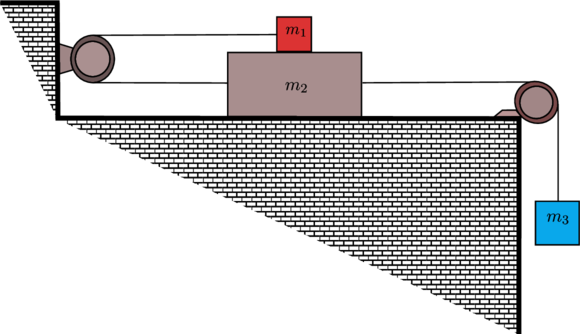
Svolgimento Punto 1.
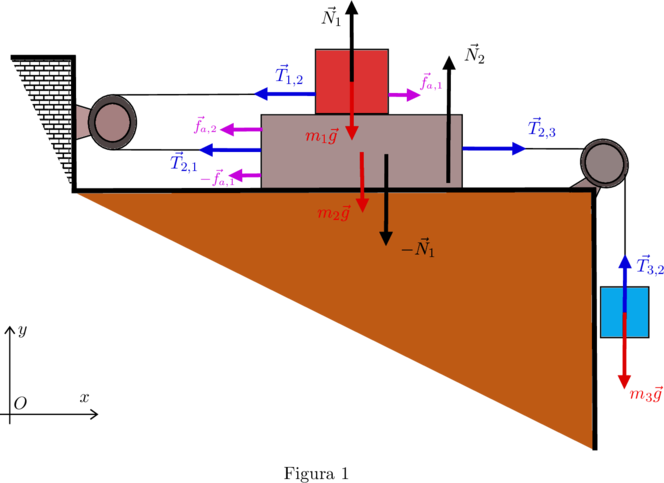
Siano ![]() il modulo della forza peso del corpo
il modulo della forza peso del corpo ![]() e
e ![]() la forza di attrito statico massima della massa
la forza di attrito statico massima della massa ![]() , dalle ipotesi del problema è chiaro che la forza peso
, dalle ipotesi del problema è chiaro che la forza peso ![]() , sicché il sistema entri in movimento. Il corpo
, sicché il sistema entri in movimento. Il corpo ![]() si muoverà nel verso negativo dell’asse delle
si muoverà nel verso negativo dell’asse delle ![]() , con accelerazione di modulo
, con accelerazione di modulo ![]() ; il corpo
; il corpo ![]() si muoverà nel verso positivo dell’asse delle
si muoverà nel verso positivo dell’asse delle ![]() , con accelerazione di modulo
, con accelerazione di modulo ![]() ; il corpo
; il corpo ![]() si muoverà nel verso negativo dell’asse delle
si muoverà nel verso negativo dell’asse delle ![]() , con accelerazione di modulo
, con accelerazione di modulo ![]() . Sul corpo
. Sul corpo ![]() lungo l’asse delle
lungo l’asse delle ![]() agiscono la forza di attrito dinamico
agiscono la forza di attrito dinamico ![]() (il verso della forza di attrito dinamico
(il verso della forza di attrito dinamico ![]() è diretto nel verso positivo dell’asse delle
è diretto nel verso positivo dell’asse delle ![]() , in quanto il corpo
, in quanto il corpo ![]() si muove nel verso negativo dell’asse delle
si muove nel verso negativo dell’asse delle ![]() ) e la tensione della corda
) e la tensione della corda ![]() (generata dalla fune che lo collega al corpo
(generata dalla fune che lo collega al corpo ![]() ). Lungo l’asse delle
). Lungo l’asse delle ![]() agiscono la forza peso
agiscono la forza peso ![]() e la reazione vincolare
e la reazione vincolare ![]() . Tutte le forze sono rappresentate in figura 1.
Il corpo
. Tutte le forze sono rappresentate in figura 1.
Il corpo ![]() scorre sopra il corpo
scorre sopra il corpo ![]() nel verso negativo dell’asse delle
nel verso negativo dell’asse delle ![]() , per cui applicando il secondo principio della dinamica al corpo
, per cui applicando il secondo principio della dinamica al corpo ![]() e proiettando le forze lungo gli assi
e proiettando le forze lungo gli assi ![]() e
e ![]() , si ha
, si ha
(1) 
Sul corpo ![]() lungo l’asse delle
lungo l’asse delle ![]() agiscono la tensione
agiscono la tensione ![]() (generata dalla fune che lo collega al corpo
(generata dalla fune che lo collega al corpo ![]() ) della corda che lo collega al corpo
) della corda che lo collega al corpo ![]() , la tensione
, la tensione ![]() (generata dalla fune che lo collega al corpo
(generata dalla fune che lo collega al corpo ![]() ) e la forza di attrito dinamico
) e la forza di attrito dinamico ![]() (il verso della forza di attrito dinamico
(il verso della forza di attrito dinamico ![]() è diretto nel verso negativo dell’asse delle
è diretto nel verso negativo dell’asse delle ![]() , in quanto il corpo
, in quanto il corpo ![]() si muove nel verso positivo dell’asse delle
si muove nel verso positivo dell’asse delle ![]() ). Inoltre, poiché quando il corpo
). Inoltre, poiché quando il corpo ![]() si muove sul corpo
si muove sul corpo ![]() si esplica una forza di attrito dinamico
si esplica una forza di attrito dinamico ![]() agente su
agente su ![]() , allora per il terzo principio della dinamica esisterà una forza
, allora per il terzo principio della dinamica esisterà una forza ![]() che agirà su
che agirà su ![]() , uguale in modulo e direzione, ma opposta in verso. Lungo l’asse delle
, uguale in modulo e direzione, ma opposta in verso. Lungo l’asse delle ![]() agiscono la forza peso
agiscono la forza peso ![]() e le reazione vincolari
e le reazione vincolari ![]() e
e ![]() , quest’ultima a causa del contatto con il terreno, orientate come in figura 1. Analogamente a quanto visto nel caso dell’asse delle
, quest’ultima a causa del contatto con il terreno, orientate come in figura 1. Analogamente a quanto visto nel caso dell’asse delle ![]() , la presenza della forza
, la presenza della forza ![]() è la conseguenza del terzo principio della dinamica in riferimento al contatto tra le superfici dei corpi
è la conseguenza del terzo principio della dinamica in riferimento al contatto tra le superfici dei corpi ![]() e
e ![]() .
Il corpo
.
Il corpo ![]() si muove lungo l’asse positivo delle
si muove lungo l’asse positivo delle ![]() , per cui applicando il secondo principio della dinamica e proiettando le forze lungo gli assi
, per cui applicando il secondo principio della dinamica e proiettando le forze lungo gli assi ![]() e
e ![]() , si ha
, si ha
(2) 
Il corpo ![]() è soggetto alla forza peso
è soggetto alla forza peso ![]() e alla tensione
e alla tensione ![]() (generata dalla fune che lo collega al corpo
(generata dalla fune che lo collega al corpo ![]() ), per cui applicando il secondo principio della dinamica e proiettando le forze lungo l’asse delle
), per cui applicando il secondo principio della dinamica e proiettando le forze lungo l’asse delle ![]() , si ha
, si ha
(3) ![]()
Abbiamo ottenuto 6 equazioni (definite nei sistemi (1, (2) e nell’equazione (3), ma con 11 incognite (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() ). Se il numero delle incognite è inferiore al numero delle equazioni il sistema risulta essere indeterminato, per cui è necessario trovare ulteriori correlazioni tra le varie incognite.
Osserviamo che poiché le due corde sono inestensibili, tese e in movimento, tutti e tre i corpi a cui sono collegate si muoveranno con la medesima accelerazione, cioè
). Se il numero delle incognite è inferiore al numero delle equazioni il sistema risulta essere indeterminato, per cui è necessario trovare ulteriori correlazioni tra le varie incognite.
Osserviamo che poiché le due corde sono inestensibili, tese e in movimento, tutti e tre i corpi a cui sono collegate si muoveranno con la medesima accelerazione, cioè
(4) ![]()
Inoltre, poiché l’attrito tra le corde e le carrucole è trascurabile significa che il ruolo svolto da quest’ultime è solamente quello di cambiare la direzione ed il verso delle tensioni preservandone il modulo. In virtù di ciò segue che
![]()
Alla luce delle osservazioni fatte, il problema si è notevolmente semplificato. Riscriviamo solo le proiezioni ![]() delle equazioni nei sistemi (1), (2) e l’equazione (3), ossia
delle equazioni nei sistemi (1), (2) e l’equazione (3), ossia
(5) 
Il sistema ottenuto è stato costruito “ad hoc”: sommando membro a membro le tre equazioni, le tensioni dei fili si elidono. Dunque, sommando membro a membro delle tre equazioni del sistema, si ottiene
(6) ![]()
Dall’equazione (1)![]() si ha
si ha
(7) ![]()
mentre dall’equazione (2)![]() , sostituendo il valore di
, sostituendo il valore di ![]() (ottenuto nell’eq.(7)), si ottiene
(ottenuto nell’eq.(7)), si ottiene
(8) ![]()
Per ottenere l’accelerazione ![]() , è necessario calcolare le forze di attrito dinamico
, è necessario calcolare le forze di attrito dinamico ![]() e
e ![]() , ossia
, ossia
(9) ![]()
(10) ![]()
dove abbiamo usato i risultati ottenuti dalle equazioni (7) e (8).
Sostituendo i valori di ![]() e
e ![]() (appena ottenuti) nella equazione (6) si giunge ad
(appena ottenuti) nella equazione (6) si giunge ad
(11) ![]()
che riscritta opportunamente diventa
![Rendered by QuickLaTeX.com \[\boxcolorato{fisica}{ a=\dfrac{g\left(m_3-\mu_d(m_2+3m_1)\right)}{m_1+m_2+m_3}.}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-74f5859e05c668a0f4b503f42349d820_l3.png)
Svolgimento Punto 2.
Svolgimento Punto 3.
![Rendered by QuickLaTeX.com \[\begin{aligned} T_2&=m_3(g-a)=\\ &=m_3\left(g-\dfrac{g}{m_1+m_2+m_3}\left(m_3-\mu_d\left(m_2+3m_1\right)\right)\right)=\\ &= \dfrac{m_3g}{m_1+m_2+m_3}(m_1+m_2+m_3-m_3+\mu_dm_2+3\mu_dm_1), \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-19c6b02fa2994b945a164b14d536a616_l3.png)
o anche
![Rendered by QuickLaTeX.com \[\boxcolorato{fisica}{ T_2=\dfrac{m_3g}{m_1+m_2+m_3}(m_1+m_2+\mu_d(m_2+3m_1)).}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-9f4b2f7eec0b233a21499f02ca88dad6_l3.png)
Si osservi che per calcolare ![]() abbiamo usato il valore di
abbiamo usato il valore di ![]() trovato nel punto
trovato nel punto ![]() .
.
Svolgimento Punto 4.

La forza ![]() che agisce sul terreno sarà dunque
che agisce sul terreno sarà dunque
(12) ![]()
da cui, sostituendo i valori di ![]() ed
ed ![]() (ottenuti nell’equazioni (10) e (8)), si ottiene
(ottenuti nell’equazioni (10) e (8)), si ottiene
![]()
dove ![]() ed
ed ![]() sono i versori rispettivamente dell’asse
sono i versori rispettivamente dell’asse ![]() e dell’asse
e dell’asse ![]() .
.
L’angolo che il vettore ![]() forma con il terrore è
forma con il terrore è
![Rendered by QuickLaTeX.com \[\boxcolorato{fisica}{\theta=\arctan\left(\dfrac{N_2}{f_{a,2}}\right)=\arctan\left(\dfrac{1}{\mu_d}\right);}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-65b6ecf42054660c70cc3f8411ba3505_l3.png)
inoltre, il modulo di ![]() è
è
![Rendered by QuickLaTeX.com \[\boxcolorato{fisica}{ R=(m_1+m_2)g\sqrt{\mu_d^2+1}.}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-da05738a9110bb8e8c71829552155d10_l3.png)
Approfondimento 1.

Poiché il filo è inestensibile e teso, le distanze tra i corpi sono costanti. In particolare, detta ![]() la distanza tra il corpo 1 e 2 ed
la distanza tra il corpo 1 e 2 ed ![]() la distanza tra il corpo 2 e 3, abbiamo che
la distanza tra il corpo 2 e 3, abbiamo che
(13) ![]()
(14) ![]()
Derivando due volte rispetto al tempo ambo i membri delle equazioni (13) e (14), si ottiene
(15) 
L’equazione (15) in sintesi ci dice che: se consideriamo un filo di massa trascurabile e inestensibile, teso e in movimento, allora l’ipotesi che il filo sia inestensibile implica che tutti i punti del filo (compresi gli estremi) abbiano la stessa accelerazione. Di conseguenza tutti i corpi in esame: ![]() ,
, ![]() e
e ![]() hanno la medesima accelerazione. Inoltre, il fatto che il filo abbia massa trascurabile implica che il prodotto
hanno la medesima accelerazione. Inoltre, il fatto che il filo abbia massa trascurabile implica che il prodotto ![]() sia nullo per il filo (e per qualsiasi posizione di esso) e quindi la risultante delle forze sul filo è nulla; di conseguenza il valore della tensione del filo durante il moto è lo stesso in qualunque punto del filo, come nel caso statico.
In virtù di ciò, riprendendo l’esempio sopra, segue che
sia nullo per il filo (e per qualsiasi posizione di esso) e quindi la risultante delle forze sul filo è nulla; di conseguenza il valore della tensione del filo durante il moto è lo stesso in qualunque punto del filo, come nel caso statico.
In virtù di ciò, riprendendo l’esempio sopra, segue che
(16) ![]()
Approfondimento 2.
Riprendendo l’espressione dell’angolo ![]() che il vettore
che il vettore ![]() forma con il terreno, studiamo i due casi che seguono.
forma con il terreno, studiamo i due casi che seguono.
- Caso 1. Consideriamo il caso in cui la forza di attrito dinamico è praticamente trascurabile, per cui
(17)
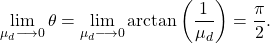
Quindi se non ci fosse forza di attrito abbiamo che
 (come è facilmente verificabile dall’eq.(12)).
(come è facilmente verificabile dall’eq.(12)). - Caso 2. Consideriamo il caso estremo in cui il coefficiente di attrito dinamico
 tende al valore di 1 (è un caso limite, non realistico). In questo caso
tende al valore di 1 (è un caso limite, non realistico). In questo caso
(18)

Poiché il coefficiente di attrito dinamico
 si ha
si ha 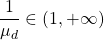 e siccome l’arcotangente è una funzione strettamente crescente nel suo dominio di definizione, deduciamo che in generale
e siccome l’arcotangente è una funzione strettamente crescente nel suo dominio di definizione, deduciamo che in generale
 Si osservi che si poteva ragionare a retroso; ovvero, partire del fatto che
Si osservi che si poteva ragionare a retroso; ovvero, partire del fatto che  e ottenere
e ottenere  , sfruttando la relazione di
, sfruttando la relazione di 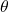 trovata nel punto
trovata nel punto 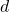 .
.
Scarica gli esercizi svolti
Ottieni il documento contenente 58 esercizi risolti, contenuti in 160 pagine ricche di dettagli, per migliorare la tua comprensione della Meccanica Newtoniana.
Esercizi di Meccanica classica
Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.
Leggi..
- Cinematica del punto materiale.
- Dinamica del punto materiale: le leggi di Newton nella meccanica classica.
- Dinamica del punto materiale: lavoro ed energia.
- Moti relativi.
- Sistemi di punti materiali.
- Dinamica del corpo rigido.
- Urti .
- Gravitazione .
- Oscillazioni e onde.
- Meccanica dei fluidi.
- Onde meccaniche.
- Statica in meccanica classica.
- Fondamenti di relatività ristretta: trasformazioni di Lorentz e principali conseguenze.
- Calcolo del centro di massa e dei momenti d’inerzia.
Tutti gli esercizi di elettromagnetismo
Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di
Leggi...
- Esercizi su lavoro elettrico e potenziale elettrico.
- Esercizi sulla legge di Gauss.
- Esercizi sui conduttori, condensatori, dielettrici ed energia elettrostatica.
- Esercizi sulla corrente elettrica.
- Esercizi sul campo magnetico e forza magnetica.
- Esercizi sulle sorgenti di un campo magnetico e legge di Ampere.
- Esercizi su campi elettrici e magnetici variabili nel tempo.
- Esercizi su oscillazione del campo elettrico e correnti alternate.
- Esercizi sulle onde elettromagnetiche.
- Esercizi sulla riflessione e rifrazione della luce.
- Esercizi sull’ ottica geometrica.
- Esercizi sull’ interferenza.
- Esercizi sulla diffrazione.
- Esercizi sulle proprietà corpuscolari e ondulatorie della materia.
Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.
Esercizi di Meccanica razionale
Se siete interessati ad approfondire argomenti inerenti alla Meccanica razionale, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.
Leggi...
Un po’ di storia sulle leggi della dinamica
Leggi...
Prima di Newton, la comprensione del movimento e delle forze era dominata dalle idee di Aristotele, un filosofo greco del IV secolo a.C. Aristotele credeva che tutti i corpi avessero un “luogo naturale” e che si muovessero solo quando una forza esterna agiva su di essi. Questa visione, conosciuta come “fisica aristotelica”, affermava che un oggetto in movimento si fermava automaticamente una volta cessata la forza che lo spingeva. Questa concezione aristotelica rimase predominante per secoli, influenzando profondamente la filosofia naturale. Tuttavia, presentava limitazioni significative, specialmente nella spiegazione di fenomeni come il moto dei pianeti o il comportamento dei proiettili. Nonostante i suoi limiti, la fisica aristotelica gettò le basi per lo sviluppo successivo delle leggi della dinamica.
Un punto di svolta nella comprensione del movimento fu segnato da Galileo Galilei, un matematico e fisico italiano del XVI secolo. Galileo sfidò molte delle idee di Aristotele, introducendo concetti che sarebbero stati fondamentali per la formulazione delle leggi della dinamica. Galileo fu il primo a dimostrare che la velocità di caduta di un oggetto non dipende dalla sua massa, ma dal tempo trascorso. Egli introdusse il concetto di inerzia, l’idea che un corpo in movimento rimane in movimento a meno che una forza esterna non intervenga. Questo principio di inerzia costituì la base della Prima legge di Newton, una delle tre leggi della dinamica che avrebbero rivoluzionato la fisica. Oltre a queste scoperte, Galileo sviluppò la metodologia scientifica basata sull’osservazione e l’esperimento, ponendo le basi per la fisica moderna. Le sue idee furono cruciali per la successiva formulazione delle leggi della dinamica da parte di Newton.
Isaac Newton, uno dei più grandi scienziati della storia, formulò le leggi della dinamica nel suo capolavoro “Philosophiæ Naturalis Principia Mathematica”, pubblicato nel 1687. Le tre leggi di Newton descrivono il comportamento del movimento e delle forze in modo preciso e matematico, fornendo una base solida per la meccanica classica. La Prima legge della dinamica, nota anche come legge dell’inerzia, afferma che un corpo in stato di quiete o di moto rettilineo uniforme rimane in tale stato finché non agisce su di esso una forza esterna. Questa legge formalizza il concetto introdotto da Galileo, stabilendo che il movimento non richiede una forza continua per essere mantenuto, ma solo per essere alterato. La legge dell’inerzia fu rivoluzionaria perché sfidava direttamente la fisica aristotelica, dimostrando che il moto non è il risultato di un’azione continua ma di una condizione naturale degli oggetti.
La Seconda legge della dinamica, forse la più famosa delle tre, stabilisce che la forza che agisce su un corpo è direttamente proporzionale alla sua massa e alla sua accelerazione, secondo la formula F = ma. Questa legge descrive come le forze influenzano il movimento degli oggetti e fornisce una base per calcolare le forze necessarie per muovere o fermare un oggetto. Questa legge è stata fondamentale per lo sviluppo della meccanica classica, permettendo di comprendere e prevedere con precisione il comportamento degli oggetti sotto l’influenza di forze diverse. È grazie a questa legge che possiamo spiegare fenomeni quotidiani, come la caduta di un oggetto o il lancio di un proiettile, con una precisione matematica.
La Terza legge della dinamica è forse la più intuitiva: afferma che per ogni azione esiste una reazione uguale e contraria. Questo significa che quando un oggetto esercita una forza su un altro, il secondo oggetto esercita una forza uguale e opposta sul primo. Questa legge è evidente in molti fenomeni quotidiani, come il rimbalzo di una palla o il funzionamento di un razzo. La comprensione di questa legge è essenziale per l’ingegneria e la tecnologia moderne, poiché spiega come le forze interagiscono in sistemi complessi.
Le leggi della dinamica di Newton hanno avuto un impatto profondo e duraturo sulla fisica classica. Prima della loro formulazione, la comprensione del movimento e delle forze era frammentaria e spesso basata su osservazioni qualitative piuttosto che su principi matematici. Le leggi di Newton hanno fornito una struttura coerente e matematica per descrivere il comportamento degli oggetti in movimento, permettendo ai fisici di fare previsioni accurate e di sviluppare nuove tecnologie. Grazie alle leggi della dinamica, è stato possibile sviluppare la meccanica celeste, che spiega il movimento dei pianeti e delle stelle. Queste leggi hanno permesso di calcolare con precisione le orbite dei corpi celesti, confermando le teorie di Keplero e contribuendo alla comprensione dell’universo. Le leggi della dinamica hanno anche gettato le basi per l’ingegneria moderna, permettendo la progettazione di macchine, edifici e veicoli con una comprensione precisa delle forze in gioco. Senza le leggi di Newton, molte delle tecnologie che diamo per scontate oggi, come gli aerei, le automobili e i ponti, non sarebbero possibili.
Con l’avvento della fisica moderna, alcune delle previsioni delle leggi della dinamica di Newton sono state riviste e ampliate. In particolare, la teoria della relatività di Einstein ha dimostrato che le leggi di Newton non sono sufficienti per descrivere il movimento a velocità prossime a quella della luce o in campi gravitazionali molto forti. Tuttavia, le leggi della dinamica rimangono valide e utili nella maggior parte delle situazioni quotidiane e continuano a essere insegnate come parte fondamentale della fisica.
Ulteriori risorse didattiche per la fisica
Leggi...
- Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
- ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
- Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
- Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
- The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
- American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
- Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
- Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
- Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
- Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.

![Rendered by QuickLaTeX.com \[\begin{aligned} &T_1=m_1a+f_{a,1}=\\ &=\dfrac{m_1g}{m_1+m_2+m_3}\left(m_3-\mu_d(m_2+3m_1)\right)+\mu_dN_1=\\ &=\dfrac{m_1g}{m_1+m_2+m_3}\left(m_3-\mu_d(m_2+3m_1)\right)+\mu_d m_1g =\\ &=m_1g\left(\dfrac{m_3-\mu_d(m_2+3m_1)}{m_1+m_2+m_3}+\mu_d\right)=\\ &=\dfrac{m_1g}{m_1+m_2+m_3}\left(m_3-\mu_dm_2-3\mu_dm_1+\mu_d\left(m_1+m_2+m_3\right)\right), \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-f20933a683d55f75e684199ef48ac1ed_l3.png)
![Rendered by QuickLaTeX.com \[\boxcolorato{fisica}{ T_1=\dfrac{m_1g}{m_1+m_2+m_3}\left(m_3+\mu_d\left(m_3-2m_1\right)\right).}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-30e9885ea322e91795230ac450aca797_l3.png)