Accedi ai contenuti scaricabili
Qui si risolve LOGO
a

Menu

M

Chiudi

Esercizi sui triangoli rettangoli – Trigonometria

Triangoli rettangoli

Home » Esercizi sui triangoli rettangoli – Trigonometria

Benvenuti nella nostra raccolta di esercizi dedicati alla risoluzione dei triangoli rettangoli, con metodi di trigonometria.
In questo articolo proponiamo alcuni esercizi su questo importante tema, applicazione geometrica delle nozioni di goniometria.
Ogni esercizio è corredato di soluzione completa, consentendo così un apprendimento dinamico e interattivo sia allo studente della scuola secondaria che desidera potenziare le sue capacità, sia a studenti universitari per un ripasso in vista dei corsi di Analisi Matematica e Fisica.

Oltre al materiale presente nella nostra cartella sulla Goniometria e al nostro Formulario di trigonometria, consigliamo i seguenti articoli su argomenti correlati:

Buona lettura!
 

Sommario

Leggi...

Esercizi di trigonometria sulla risoluzione dei triangoli rettangoli e problemi correlati.

 
 

Autori e revisori

Leggi...

Autori: Valerio Brunetti, Donato Ciampa.

Revisori: Matteo Talluri.

 
 

Esercizi

\[\quad\]

Esercizio 1 (\bigstar\bigstar\largewhitestar). In una semicirconferenza di diametro AB=2r è inscritto il triangolo ABC di perimetro r(2+\sqrt{6}). Determinare la misura degli angoli del triangolo.

Svolgimento.

Consideriamo la seguente figura:

\[\quad\]

\[\quad\]

Rendered by QuickLaTeX.com

\[\quad\]

È noto che un triangolo inscritto in una semicirconferenza è un triangolo rettangolo. Quindi A\widehat{C}B=\pi/2. Indichiamo con x=C\widehat{A}B: ne segue che 0<x<\pi/2. Abbiamo allora

\[\overline{BC}=\overline{AB} \sin x=2r\sin x,\qquad \overline{CA}=\overline{AB} \cos x=2r\cos x.\]

Possiamo scrivere quindi la seguente equazione:

\[2r+2r\sin x+2r\cos x=r(2+\sqrt{6}),\]

ossia

\[ \sin x + \cos x = \frac{\sqrt{6}}{2}. \]

Elevando al quadrato ambo i membri (ricordiamo che x \in \left (0,\frac{\pi}{2}\right ) e quindi \sin x>0 e \cos x>0) e ricordando 2\sin x \cos x= \sin (2x), si ha

\[ 1+\sin(2x)= \frac{3}{2} \iff \sin (2x)= \frac{1}{2} \iff 2x= \frac{\pi}{6} \iff x= \frac{\pi}{12}. \]

Quindi i due angoli del triangolo misurano rispettivamente

\[\boxcolorato{superiori}{ C\widehat{A}B=\frac{\pi}{12},\qquad C\widehat{B}A=\frac{5\pi}{12}. }\]


 
 

Esercizio 2 (\bigstar\bigstar\largewhitestar). Nel triangolo ABC, rettangolo in A, il cateto AC è minore del cateto AB e l’ipotenusa BC misura 2\ell. Per O, punto medio dell’ipotenusa, si tracci la perpendicolare all’ipotenusa stessa e sia M il suo punto di intersezione con il cateto AB. Determinare l’ampiezza x dell’angolo A\widehat{B}C in modo che si abbia \overline{AC}\cdot \overline{OM}=\ell^2.

Svolgimento.

Consideriamo la figura:

\[\quad\]

\[\quad\]

Rendered by QuickLaTeX.com

\[\quad\]

Dalle relazioni per i triangoli rettangoli, essendo \overline{OB}=\ell, si ha

\[\overline{AC}=2\ell\sin x,\qquad \overline{OM}=\ell\tan x.\]

Allora

\[\overline{AC}\cdot \overline{OM}=\ell^2 \iff \ell^2=2\ell^2\sin x\tan x=2\ell^2\left(\frac{\sin^2 x}{\cos x}\right)=2\ell^2\left(\frac{1-\cos^2 x}{\cos x}\right),\]

da cui, dovendo essere necessariamente \cos x\neq 0, in quanto 0<x<\pi/2,

\[2\cos^2 x+\cos x-2=0.\]

Ponendo t=\cos x, si ottiene l’equazione algebrica 2t^2+t-2=0, le cui soluzioni sono

\[t_1=\frac{-1-\sqrt{17}}{4},\qquad t_2=\frac{-1+\sqrt{17}}{4}.\]

Ricordando la posizione fatta, e osservando che t_1<-1, ne segue

\[\cos x=\frac{\sqrt{17}-1}{4},\]

da cui

\[\boxcolorato{superiori}{x=\arccos\left(\frac{\sqrt{17}-1}{4}\right), }\]

che è l’angolo cercato.


 
 

Esercizio 3 (\bigstar\bigstar\bigstar). Un triangolo ABC è rettangolo in B. Inoltre, le lunghezze dei suoi lati formano una progressione geometrica. Quali sono i possibili valori di \tan(B\widehat{A}C)?

Svolgimento.

L’ipotenusa del triangolo è AC, che è naturalmente più lunga dei cateti AB e BC. Il fatto che i lati siano in progressione geometrica significa che il rapporto tra lati consecutivi è costante. Esiste quindi un numero k > 1 tale che:

\[\overline{AC} = k\cdot\overline{AB} = k^2\cdot\overline{BC} \quad \text{oppure} \quad \overline{AC} = k\cdot\overline{BC} = k^2\cdot\overline{AB},\]

a seconda che il cateto maggiore sia AB (a sinistra) oppure BC (a destra).

\[\quad\]

\[\quad\]

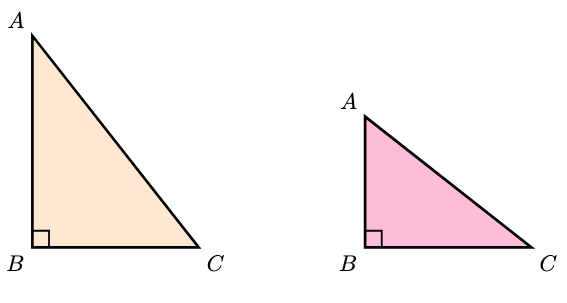
esercizi sui triangoli rettangoli

\[\quad\]

Il valore che dobbiamo calcolare è:

\[\tan(B\widehat{A}C) = \frac{\overline{BC}}{\overline{AB}} = \begin{cases} 1/k & \text{se $\overline{AB} = k\cdot\overline{BC} > \overline{BC}$;} \\ k & \text{se $\overline{BC} = k\cdot\overline{AB} > \overline{AB}$.} \end{cases}\]

Per il teorema di Pitagora, si ha \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2, e quindi: Equazione con MathJax

\[\begin{aligned} k^4 \overline{BC}^2 &= k^2 \overline{BC}^2 + \overline{BC}^2 \quad &&\text{se } \overline{AB} = k \cdot \overline{BC}; \\ k^4 \overline{AB}^2 &= k^2 \overline{AB}^2 + \overline{AB}^2 \quad &&\text{se } \overline{BC} = k \cdot \overline{AB}. \end{aligned}\]

In entrambi i casi, giungiamo alla medesima condizione k^4 - k^2 - 1 = 0. Questa è un’equazione di secondo grado nell’incognita k^2, che ha come soluzioni:

\[k^2 = \frac{1\pm\sqrt{5}}{2};\]

solo la soluzione col + è accettabile perché (1-\sqrt{5})/2 < 0. Estraendo la radice quadrata, l’unico valore valido di k è in conclusione:

\[k = \sqrt{\frac{\sqrt{5}+1}{2}}.\]

Se \overline{BC} > \overline{AB}, allora \tan(B\widehat{A}C) = k e abbiamo finito; se invece \overline{AB} > \overline{BC}:

\[\tan(B\widehat{A}C) = \frac{1}{k} = \sqrt{\frac{2}{\sqrt{5}+1}} = \sqrt{\frac{2\left(\sqrt{5}-1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}} = \sqrt{\frac{\sqrt{5}-1}{2}}.\]

In conclusione, i valori cercati sono

\[\boxcolorato{superiori}{\tan(B\widehat{A}C) = \sqrt{\frac{\sqrt{5}\pm 1}{2}} .}\]

 
 

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

  • Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
  • Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
  • MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
  • PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
  • Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
  • The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
  • Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
  • Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
  • Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
  • Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.