Accedi ai contenuti scaricabili
Qui si risolve LOGO
a

Menu

M

Chiudi

Esercizi misti sui triangoli – Trigonometria

Esercizi misti in Trigonometria

Home » Esercizi misti sui triangoli – Trigonometria

Benvenuti nella nostra raccolta di esercizi misti sui triangoli risolti con metodi trigonometrici. In questo articolo proponiamo alcuni problemi di carattere e difficoltà vari sulla risoluzione dei triangoli e a essi correlati, completamente risolti integrando strumenti della geometria euclidea e della trigonometria.
La raccolta è quindi indicata per chi desidera mettere alla prova le proprie conoscenze avendo la possibilità di spaziare su molteplici argomenti e tecniche.

Oltre al materiale presente nella nostra cartella sulla Goniometria e al nostro Formulario di trigonometria, consigliamo i seguenti articoli su temi correlati:

Buona lettura!

 
 

Sommario

Leggi...

Esercizi misti sui triangoli risolti con metodi di trigonometria.

 
 

Autori e revisori

Leggi...

Autori: Valerio Brunetti, Donato Ciampa.

Revisori: Matteo Talluri.


 
 

Testi degli esercizi

Esercizio 1 (\bigstar\bigstar\largewhitestar). Si consideri un quadrilatero di vertici A, B, C e D. Le diagonali AC e DB sono mutuamente ortogonali e si incontrano in un punto O, quest’ultimo punto dista a da A, B e C e b da D. Dimostrare che tale quadrilatero possiede una circonferenza inscritta e, detto r il suo raggio, determinare una formula per r in funzione di a e b. Determinare infine la relazione tra a e b affinché la differenza tra il perimetro e l’area del cerchio inscritto sia massima.

Svolgimento.

Innanzitutto osserviamo che, dai dati del problema, segue \overline{AD}=\overline{BD} e \overline{BC}=\overline{AC}, pertanto il quadrilatero possiede una circonferenza inscritta, di centro O' giacente su CD. Denotiamo \alpha = O\widehat{D}B e chiamiamo inoltre E e F i punti di tangenza della circonferenza inscritta rispettivamente sui lati BD e BC.

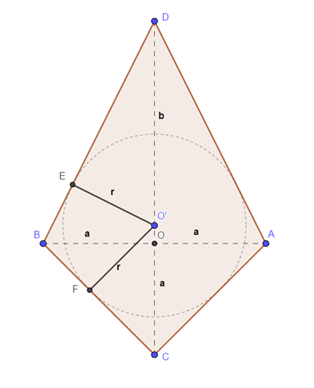
Osserviamo che il triangolo FO'C è rettangolo in F e l’angolo F \widehat{C}O' è di 45^\circ, quindi è isoscele, pertanto il segmento O'C ha lunghezza r\sqrt{2}. Invece, il triangolo O'ED è rettangolo ed è simile al triangolo BOD, avendo in comune l’angolo in D. Quindi

\[ \frac{r}{\overline{O'D}} = \frac{a}{\sqrt{a^2+b^2}} \iff \overline{O'D}= \frac{r\sqrt{a^2+b^2}}{a}. \]

Notando che a+b=\overline{CD}=\overline{CO'}+\overline{O'D}, si ha

\[ a+b = r\left (\sqrt{2}+\frac{\sqrt{a^2+b^2}}{a}\right ) \iff r= \frac{a + b}{\sqrt{2} + \frac{\sqrt{a^2 + b^2}}{a}}. \]

Si ricava quindi

\[\boxcolorato{superiori}{ r= \frac{a + b}{\sqrt{2} + \frac{\sqrt{a^2 + b^2}}{a}}. }\]

\[\quad\]

\[\quad\]

esercizi misti sui triangoli

\[\quad\]

L’espressione da massimizzare è F(r) = 2\pi r - \pi r^2. Osserviamo che 2\pi r-\pi r^2-1 = -(r-1)^2\leq 0 e tale espressione si annulla se e solo se r=1. Ne segue che anche F(r) assume valore massimo per r=1. Imponendo quindi

\[ r=\frac{a + b}{\sqrt{2} + \frac{\sqrt{a^2 + b^2}}{a}} = 1, \]

si ottiene la relazione

\[\boxcolorato{superiori}{a+b = \sqrt{2} + \frac{\sqrt{a^2 + b^2}}{a}. }\]


 
 

Esercizio 2 (\bigstar\largewhitestar\largewhitestar). Dati due quadrilateri di uguali angoli, le lunghezze del quadrilatero più piccolo sono il 75 per cento delle rispettive lunghezze del più grande. Determinare il rapporto tra l’area del quadrilatero più grande e quello più piccolo.

Svolgimento.

Indichiamo con ABCD il quadrilatero più grande e con EFGH il secondo, come in figura 1. Questi due quadrilateri sono simili e dunque, tracciando le diagonali AC e EG, anche il triangolo ABC è simile a EFG e ACD è simile a EGH. Il rapporto tra le lunghezze dei lati e altezze corrispondenti è allora \frac{4}{3}. Dalla formula dell’area del triangolo abbiamo quindi

\[ \begin{gathered} \operatorname{Area}(ABC)= \frac{4}{3} \cdot \frac{4}{3} \operatorname{Area}(EFG)= \frac{16}{9}\operatorname{Area}(EFG) \\ \operatorname{Area}(ACD)= \frac{4}{3} \cdot \frac{4}{3} \operatorname{Area}(EGH)= \frac{16}{9}\operatorname{Area}(EGH). \end{gathered} \]

Ne segue che

\[ \begin{aligned} \operatorname{Area}(ABCD) &= \operatorname{Area}(ABC)+\operatorname{Area}(ACD) \\ &= \frac{16}{9}\operatorname{Area}(EFG) + \frac{16}{9}\operatorname{Area}(EGH) \\ &= \frac{16}{9}\operatorname{Area}(EFGH). \end{aligned} \]

\[\quad\]

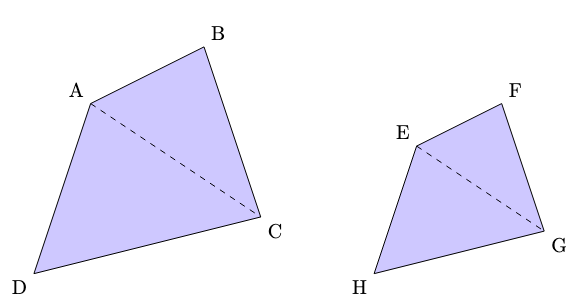
esercizi misti sui triangoli

Figura 1: i due quadrilateri ABCD e EFGH.

\[\quad\]

Il risultato ottenuto mostra come il rapporto tra le areee dei due quadrilateri è uguale al rapporto tra i loro lati al quadrato, ossia

\[\boxcolorato{superiori}{\frac{16}{9}.}\]

Decomponendo in triangoli, si può allo stesso modo mostrare che, se due poligoni sono simili e il rapporto dei loro lati è k, allora il rapporto delle loro aree è il quadrato k^2.

 
 

Risorse didattiche aggiuntive per approfondire la matematica

Leggi...

  • Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
  • Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
  • MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
  • PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
  • Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
  • The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
  • Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
  • Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
  • Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
  • Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.