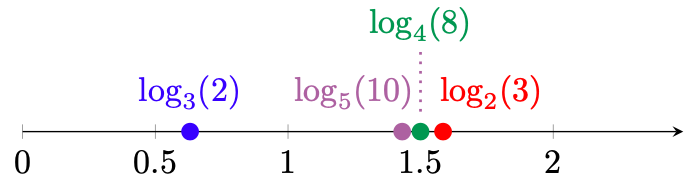Sommario
Leggi...
Raccolta di esercizi su dominio e proprietà di base dei logaritmi.
Autori e revisori
Notazioni
Leggi...
 , ,  |
Logaritmo naturale (in base  ) del numero reale ) del numero reale  . . |
Esercizi
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
Esercizio 1 
. Ricavare il valore della

applicando la definizione di logaritmo:
![Rendered by QuickLaTeX.com \[\begin{aligned} & \text{a) } \log_2 8 = x\\ & \text{b) } \log_{10} 10 = x\\ & \text{c) } \log_{25} 5 = x\\ & \text{d) } \log_x 8 = 3\\ & \text{e) } \ln x = 0. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-58b949fb5e453aeaba11482991775769_l3.svg)
Svolgimento.
La definizione di logaritmo con

,

e

è:
(1) 
Utilizziamo la definizione
![Rendered by QuickLaTeX.com \[\begin{aligned} & \text{a) } \log_2 8 = x \; \Leftrightarrow \; 2^x = 8 \; \Leftrightarrow \; 2^x = 2^3 \; \Leftrightarrow \; \boxcolorato{superiori}{ x=3 }} \\\\ & \text{b) } \log_{10} 10 = x \; \Leftrightarrow \; 10^x = 10 \; \Leftrightarrow \; \boxcolorato{superiori}{ x=1 }}\\\\ & \text{c) } \log_{25} 5 = x \; \Leftrightarrow \; 25^x = 5 \; \Leftrightarrow \;5^{2x}=5 \; \Leftrightarrow \;2x=1 \; \Leftrightarrow \; \boxcolorato{superiori}{ x=\dfrac{1}{2} }}\\\\ & \text{d) } \log_x 8 = 3 \; \Leftrightarrow \; x^3 = 8 \; \Leftrightarrow \;x^3 = 2^3 \; \Leftrightarrow \;\boxcolorato{superiori}{ x=2 }}\\\\ & \text{e) } \ln x = 0 \; \Leftrightarrow \; x=e^0 \; \Leftrightarrow \;\boxcolorato{superiori}{ x=1. }} \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-e95c98ed78ad2c60b28b7050db342499_l3.svg)
Esercizio 2 
. Ricavare il valore della

applicando la definizione di logaritmo:
![Rendered by QuickLaTeX.com \[\begin{aligned} & \text{a) } \log_5 \frac{1}{\sqrt{5}} = x\\ & \text{b) } \log_{3} \frac{3\sqrt{3}}{\sqrt[4]{3}} = x\\ & \text{c) } \log_x 1000 = 3\\ & \text{d) } \log_2 x = -3\\ & \text{e) } \log_{10} x = 0. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-b57860a2471951c9a1f634ccceffdc02_l3.svg)
Svolgimento.
La definizione di logaritmo con

,

e

è:
(2) 
Utilizziamo la definizione
![Rendered by QuickLaTeX.com \[\begin{aligned} & \text{a) } \log_5 \frac{1}{\sqrt{5}} = x \; \Leftrightarrow \; 5^x = \dfrac{1}{\sqrt{5}} \; \Leftrightarrow \; 5^x = 5^{-1/2} \; \Leftrightarrow \; \boxcolorato{superiori}{ x=-\dfrac{1}{2} }}\\\\ & \text{b) } \log_{3} \frac{3\sqrt{3}}{\sqrt[4]{3}} = x \; \Leftrightarrow \; 3^x = \frac{3\sqrt{3}}{\sqrt[4]{3}} \; \Leftrightarrow \; 3^x = \dfrac{3 \cdot 3^{1/2}}{3^{1/4}} \; \Leftrightarrow \; 3^x = 3^{1+1/2-1/4} \; \Leftrightarrow \; x = 1+\dfrac{1}{2}-\dfrac{1}{4} \; \Leftrightarrow \;\boxcolorato{superiori}{ x = \dfrac{5}{4} }} \\\\ & \text{c) } \log_x 1000 = 3 \; \Leftrightarrow \; x^3 = 1000 \; \Leftrightarrow \; x^3 = 10^3 \; \Leftrightarrow \; \boxcolorato{superiori}{ x=10 }}\\\\ & \text{d) } \log_2 x = -3 \; \Leftrightarrow \; x=2^{-3} \; \Leftrightarrow \;\boxcolorato{superiori}{ x=\dfrac{1}{8} }} \\\\ & \text{e) } \log_{10} x = 0 \; \Leftrightarrow \; x=10^0 \; \Leftrightarrow \; \boxcolorato{superiori}{ x=1. }} \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-08bec6fb816a85f7bf7d6914cbe75e3c_l3.svg)
Esercizio 3 
. Determinare il dominio della seguente funzione logaritmica

:
![Rendered by QuickLaTeX.com \[f(x)=\log_2 (x+4).\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-a5c519edb6313cce1d9e7291c33bd3c0_l3.svg)
Svolgimento.
L’argomento del logaritmo deve essere positivo, pertanto si pone

, da cui deduciamo che il dominio è
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{\mathcal{D} = \{x \in \mathbb{R} \, | \, x>-4\}. }\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-3fb380d184b174caefa65feb1e4454d2_l3.svg)
Esercizio 4 
. Determinare il dominio della seguente funzione logaritmica

:
![Rendered by QuickLaTeX.com \[f(x)=\log_3(x^2+3x+4).\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-d02c90923a2cd44dd226de742a9d043a_l3.svg)
Svolgimento.
L’argomento del logaritmo deve essere positivo, pertanto si pone

. Scriviamo l’equazione associata e la risolviamo
![Rendered by QuickLaTeX.com \[x^2+3x+4 =0 \quad \Rightarrow \quad \Delta = 9 - 16 = -7 < 0\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-4cefe36ba9ed2e0477423175733c2dec_l3.svg)
ma il discriminante è negativo, pertanto l’equazione è impossibile; ciò vuol dire che la parabola, essendo concava verso l’alto è sempre positiva, quindi la disequazione è sempre verificata.
Deduciamo dunque che il dominio è
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{\mathcal{D} = \mathbb{R}. }\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-fbea5cd59a6718b9348815f520d72472_l3.svg)
Esercizio 5 
. Determinare il dominio della seguente funzione logaritmica

:
![Rendered by QuickLaTeX.com \[f(x)=\ln(3x-1) + \ln(5-x).\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-160153ecfeec0a325ca7ad035a69e629_l3.svg)
Svolgimento.
L’argomento del logaritmo deve essere positivo, pertanto entrambi gli argomenti devono essere contemporaneamente positivi:
![Rendered by QuickLaTeX.com \[\begin{cases} 3x-1>0\\ 5-x>0 \end{cases} \quad \Rightarrow \quad \begin{cases} x>\dfrac{1}{3}\\\\ x<5. \end{cases}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-022968c3fe879915dd2000dfa7a4ac7a_l3.svg)
Deduciamo dunque che il dominio è
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{\mathcal{D} = \left\{ x \in \mathbb{R} \, \bigg\vert \, \dfrac{1}{3}<x<5\right\}. }\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-149154629d4153a4e3a44984f1135323_l3.svg)
Esercizio 6 
. Scrivi sotto forma di un unico logaritmo:
![Rendered by QuickLaTeX.com \[2 \log 4 - \log 2 + \log 8-\log 16.\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-252efa65836103d804b61104f7d80248_l3.svg)
Svolgimento.
Siano

con

.
Le proprietà dei logaritmi sono:
![Rendered by QuickLaTeX.com \[\begin{aligned} &1) \quad \log_a b + \log_a c = \log_a bc\\ &2) \quad \log_a b - \log_a c = \log_a \dfrac{b}{c}\\ &3) \quad \log_a b^N = N \; \log_a b, \qquad N \in \mathbb{R}. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-b5b837c4cd04cbfd3d404e19a6dd887d_l3.svg)
Dunque andiamo prima a portare i coefficienti dei logaritmi come esponenti, grazie alla terza proprietà:
![Rendered by QuickLaTeX.com \[\begin{aligned} & 2 \log 4 - \log 2 + \log 8-\log 16 = \\\\ & = \log 4^2 - \log 2 + \log 8-\log 16 = \\\\ & = \cancel{\log 16} - \log 2 + \log 8 - \cancel{\log 16} = \\\\ & = \log 2 + \log 8 = \\\\ & = \log \dfrac{8}{2} = \log 4. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-abbc104c35f9592e103a17cc8de087fa_l3.svg)
Quindi
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{2 \log 4 - \log 2 + \log 8-\log 16 = \log 4. }\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-b6e79e177f345a009576c1af78eacbcd_l3.svg)
Esercizio 7 
. Scrivi sotto forma di un unico logaritmo:
![Rendered by QuickLaTeX.com \[\log_3 600 -2 \log_3 2 + \dfrac{1}{2} \, \log_3 25 + \log_3 \dfrac{3}{10}.\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-638cf911b51769acc09d2e97533194e3_l3.svg)
Svolgimento.
Siano

con

.
Le proprietà dei logaritmi sono:
![Rendered by QuickLaTeX.com \[\begin{aligned} &1) \quad \log_a b + \log_a c = \log_a bc\\ &2) \quad \log_a b - \log_a c = \log_a \dfrac{b}{c}\\ &3) \quad \log_a b^N = N \; \log_a b, \qquad N \in \mathbb{R}. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-b5b837c4cd04cbfd3d404e19a6dd887d_l3.svg)
Dunque andiamo prima a portare i coefficienti dei logaritmi come esponenti, grazie alla terza proprietà:
![Rendered by QuickLaTeX.com \[\begin{aligned} & \log_3 600 -2 \log_3 2 + \dfrac{1}{2} \, \log_3 25 + \log_3 \dfrac{3}{10} = \\\\ & = \log_3 600 - \log_3 2^2 + \log_3 25^{\frac{1}{2} } + \log_3 \dfrac{3}{10} =\\\\ & = \log_3 600 - \log_3 4 + \log_3 \sqrt{25} + \log_3 \dfrac{3}{10} = \\\\ & = \log_3 600 - \log_3 4 + \log_3 5 + \log_3 \dfrac{3}{10}. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-c1e8dbc7819538f7f03766aad84559cc_l3.svg)
Utilizzando ora la prima e seconda proprietà abbiamo
![Rendered by QuickLaTeX.com \[\begin{aligned} & \log_3 600 - \log_3 4 + \log_3 5 + \log_3 \dfrac{3}{10} = \\\\ & = \log_3 \dfrac{600 \cdot \dfrac{3}{10} \cdot 5}{4} = \log_3 225 = \\\\ & = 2 \log_3 15 = 2 \log_3 (3 \cdot 5) = 2 \log_3 3 + 2\log_3 5 = 2 + 2\log_3 5. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-28bb624f484b13b518c2bf89f0a9af6e_l3.svg)
Quindi
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{\log_3 600 -2 \log_3 2 + \dfrac{1}{2} \, \log_3 25 + \log_3 \dfrac{3}{10} = 2 + 2\log_3 5. }\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-f0448e03458af2fe65a7f249a2d4855a_l3.svg)
Esercizio 8 
. Scrivi sotto forma di un unico logaritmo:
![Rendered by QuickLaTeX.com \[\log 5 - \log \sqrt{5} + \dfrac{1}{4}\; \log 25 - \dfrac{3}{2} \log \sqrt[3]{5}.\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-e6dd9f18447b27d85868b6f1341201e7_l3.svg)
Svolgimento.
Siano

con

.
Le proprietà dei logaritmi sono:
![Rendered by QuickLaTeX.com \[\begin{aligned} &1) \quad \log_a b + \log_a c = \log_a bc\\ &2) \quad \log_a b - \log_a c = \log_a \dfrac{b}{c}\\ &3) \quad \log_a b^N = N \; \log_a b, \qquad N \in \mathbb{R}. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-b5b837c4cd04cbfd3d404e19a6dd887d_l3.svg)
Dunque andiamo prima a portare i coefficienti dei logaritmi come esponenti, grazie alla terza proprietà:
![Rendered by QuickLaTeX.com \[\begin{aligned} & \log 5 - \log \sqrt{5} + \dfrac{1}{4}\; \log 25 - \dfrac{3}{2} \log \sqrt[3]{5} = \\\\ & = \log 5 - \log \sqrt{5} + \log 25^{\frac{1}{4}} - \log \left[5^{\frac{1}{3}}\right]^{\frac{3}{2}} = \\\\ & = \log 5 - \log \sqrt{5} + \log \left[5^2\right]^{\frac{1}{4}} - \log 5^{\frac{1}{2}} = \\\\ & = \log 5 - \log \sqrt{5} + \log 5^{\frac{1}{2}} - \log 5^{\frac{1}{2}} = \\\\ & = \log 5 - \log \sqrt{5} + \cancel{\log 5^{\frac{1}{2}}} \cancel{- \log 5^{\frac{1}{2}}}. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-de236d982b2ce76294e081a9793c988b_l3.svg)
Con la seconda proprietà e razionalizzando otteniamo
![Rendered by QuickLaTeX.com \[\begin{aligned} & \log 5 - \log \sqrt{5}= \log \dfrac{5}{\sqrt{5}} = \log \dfrac{5}{\sqrt{5}} \dfrac{\sqrt{5}}{\sqrt{5}} = \log \sqrt{5}. \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-080c4c072cf240ce57074eb372282718_l3.svg)
Quindi concludiamo che
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{\log 5 - \log \sqrt{5} + \dfrac{1}{4}\; \log 25 - \dfrac{3}{2} \log \sqrt[3]{5} = \log \sqrt{5}. }\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-66f60c38b0b2c9fd77a27821c47452d8_l3.svg)
Esercizio 9 
. Determinare il campo di esistenza di
![Rendered by QuickLaTeX.com \[f(x)=\log_{10}\frac{x}{x^2-9}.\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-140b69d3587b88ee109a782433f0fff9_l3.svg)
Svolgimento.
Il logaritmo di un numero in una certa base è definito solo quando l’argomento è positivo, perciò il dominio di esistenza della funzione

è l’insieme dei punti

per cui
![Rendered by QuickLaTeX.com \[ \frac{x}{x^2-9}>0. %\implies x>0 \or x^2-9>0 -3< x <0, \quad x>3. \]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-9b0a0d340b28f70cf2507e626ac07d83_l3.svg)
Dobbiamo studiare quindi i segni di  e di
e di  e selezionare solo l’insieme dei valori
e selezionare solo l’insieme dei valori  per cui il prodotto dei loro segni è positivo.
per cui il prodotto dei loro segni è positivo.
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)

![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
Quindi si ottiene
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{ -3< x <0, \quad \vee \quad x>3. }\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-74a1e3d1b91b336769f4035be441076b_l3.svg)
Il grafico della funzione  è mostrato in figura 1.
è mostrato in figura 1.
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)

Figura 1: grafico della funzione  .
.
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
Esercizio 10 
. Determinare la relazione esistente tra

e

.
Svolgimento.
La formula è quella del cambio di base del logaritmo, ma volendo la si può facilemente ricavare:
![Rendered by QuickLaTeX.com \[ b^{\log_b(a)}=a=c^{\log_c(a)}=\left(b^{\log_b(c)}\right)^{\log_c(a)}=b^{\log_b(c)\log_c(a)}. \]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-621ead0f976c2e29736ae9b736931fdf_l3.svg)
Uguagliando gli esponenti del primo e dell’ultimo membro otteniamo che
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{\log_b(a) = \log_b(c)\log_c(a).}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-3759c8139899b9b823ae6ebb50a01d9f_l3.svg)
Esercizio 11 
. Quale dei seguenti numeri differisce dagli altri?
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
 ;
;
 ;
;
 ;
;
 ;
;
![Rendered by QuickLaTeX.com \sqrt[3]{\log_2(2\cdot 4^{4})}](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-31916d8ecaeb6ae66a4ea4d746ba4368_l3.svg) .
.
Svolgimento.
Tutti i numeri tranne 5. sono uguali a

:
![Rendered by QuickLaTeX.com \[\begin{aligned} \log_3(27) &=\log_3(3^3)=3\log_33=3 \\ \ln\left (\frac{1}{e}\cdot e^{4}\right ) &= \ln(e^{-1}\cdot e^4)=\ln(e^{4-1})=3\ln(e)=3; \\ \sqrt{\log_4{\left(2^{18}\right)}}& = \sqrt{\log_4{\left(4^{9}\right)}}=\sqrt{9\log_4{4}}=3;\\ -\log_{\frac{1}{3}}(3^3) & =-\log_{\frac{1}{3}}\left(\left(\frac{1}{3}\right)^{-3}\right)=-(-3)\log_{\frac{1}{3}}\left(\frac{1}{3}\right)=3.\\ \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-ac6afceb6bec2f4fa5bd84f5b4dc9dba_l3.svg)
Invece 5. è uguale a
![Rendered by QuickLaTeX.com \[ \sqrt[3]{\log_2(2\cdot 4^{4})}=\sqrt[3]{\log_2(2^9)}=\sqrt[3]{9\log_2(2)}=\sqrt[3]{9}\neq 3, \]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-74dd242360c3098efd166dfe11e547e9_l3.svg)
che è quindi la risposta corretta.
Esercizio 12 
. Dato

,

, quanto vale il prodotto

?
Svolgimento.
Utilizziamo la proprietà dei logaritmi per cui

:
![Rendered by QuickLaTeX.com \[ \ln(a)\log_a(e)=\ln(a^{\log_a(e)})=\ln(e)=1. \]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-3755ec23398507afdd92986d4f03775b_l3.svg)
La risposta è quindi
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{\ln(a)\log_a(e)=1}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-02a959fe14fc6c0a1dbce8840c0ff632_l3.svg)
Esercizio 13 
. Senza utilizzare la calcolatrice, quale dei seguenti numeri è il più grande?
![Rendered by QuickLaTeX.com \[ \log_2(3), \quad \log_4(8), \quad \log_3(2), \quad \log_5(10). \]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-76b9b32a65bb4d20d3f0777d795ada66_l3.svg)
Svolgimento.
Innanzitutto notiamo che, essendo

, si ha:
![Rendered by QuickLaTeX.com \[\log_3(2) <\log_3(3) = 1.\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-1b2086d6a82e6a2ff91805b412a82a49_l3.svg)
Ricordiamo ora le queste proprietà dei logaritmi:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \log(a\cdot b) = \log(a)+\log(b) \quad (a,b > 0); \\[4pt] \log(a^c) = c \cdot \log(a) \quad (a > 0,\ c \in \mathbb{R}). \end{split} \end{equation*}](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-5a8034518b3a24b36f2247267a071a85_l3.svg)
Cominciamo ad osservare che:
![Rendered by QuickLaTeX.com \[\log_4(8) = \log_4(4\cdot2) = \log_4\left(4\cdot\sqrt{4}\,\right) = \log_4\left(4^{3/2}\right) = \frac{3}{2}.\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-7caf804353da9bee8fe21f2a6a42b891_l3.svg)
E ancora, dato che  è una funzione crescente e che
è una funzione crescente e che  :
:
![Rendered by QuickLaTeX.com \[\log_2(3) = \log_2\left(\sqrt{3^2}\,\right) = \frac{1}{2}\log_2(9) > \frac{1}{2}\log_2(8) = \frac{3}{2}.\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-b5d9f82deb4864cb7640ab8e7cdf47a7_l3.svg)
Infine, dato che  :
:
![Rendered by QuickLaTeX.com \[ \begin{aligned} \log_5(10) = {} & \log_5(5\cdot2) = \log_5(5) + \log_5(2) = 1+ \log_5(2) = \\ = {} & 1 + \log_5\left(\sqrt{2^2}\,\right) = 1 + \frac{1}{2}\log_5(4) < 1 + \frac{1}{2}\log_5(5) = \frac{3}{2}. \end{aligned} \]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-174239460de1e9700037534ee50f5df7_l3.svg)
Mettendo assieme le quattro relazioni trovate, concludiamo che:
![Rendered by QuickLaTeX.com \[\log_3(2) < 1 < \log_5(10) < \frac{3}{2} = \log_4(8) < \log_2(3).\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-ee887365a2d3b07dbf1f33b53d5f641a_l3.svg)
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
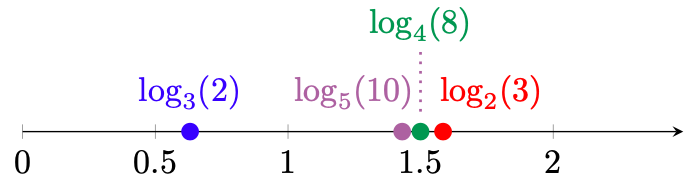
![Rendered by QuickLaTeX.com \[\quad\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-27e49cccda278470ae7436bace68813e_l3.svg)
La risposta è quindi
![Rendered by QuickLaTeX.com \[\boxcolorato{superiori}{\log_2(3).}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-aa2b28d2e0801edd996fb654506675f0_l3.svg)
Esercizio 14 
. Quale delle seguenti figure rappresenta qualitativamente il grafico della funzione

?
e di
e selezionare solo l’insieme dei valori
per cui il prodotto dei loro segni è positivo.
è mostrato in figura 1.
.
;
;
;
;
.
è una funzione crescente e che
:
: