Esercizio  .
.
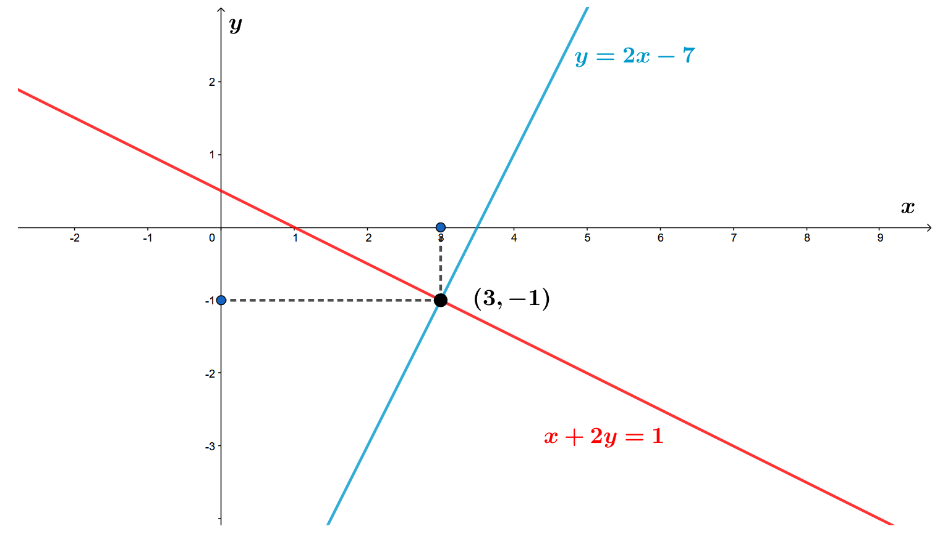
Determinare la posizione reciproca della seguente coppia di rette
Svolgimento.
Per conoscere la posizione reciproca di due rette si imposta un sistema, ottenendo così un sistema lineare di equazioni risolvibile con il metodo che più si preferisce; solitamente si utilizza il metodo di sostituzione:
dunque il sistema è determinato; ne possiamo dedurre che le rette ed
sono incidenti nel punto
.
Graficamente:
Fonte: Qui Si Risolve
