Esercizi geometria nello spazio — vettori direttori

Home » Esercizi geometria nello spazio — vettori direttori

In questo articolo presentiamo una serie di esercizi di geometria sulle rette e sui piani, focalizzandoci sull’equivalenza tra equazioni parametriche e cartesiane, nonché sulle diverse posizioni reciproche che questi possono assumere nel piano e nello spazio. Questi esercizi sono progettati per consolidare la comprensione degli strumenti matematici utilizzati per descrivere e analizzare le proprietà geometriche delle rette. Le soluzioni sono esposte in modo sintetico per incentivare l’approfondimento e la riflessione autonoma, costituendo così un valido complemento per lo studio indipendente o come supporto per un corso di Geometria I nei corsi di ingegneria, fisica e matematica.

Autori

Leggi...

Autore: Jacopo Garofali.

Testi degli esercizi

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare i vettori direttori delle seguenti rette nel piano:

$2x+3y-1=0$ ;

$6y-2x=0$ ;

$x-y+3=0$ ;

$x+y+1=0$ ;

$y-4x+8=0$ .

Svolgimento punto 1.

$(3,-2)$

Svolgimento punto 2.

$(6,2)$

Svolgimento punto 3.

$(1,1)$

Svolgimento punto 4.

$(1,-1)$

Svolgimento punto 5.

$(1,4)$

Esercizio 2 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Tra tutte le rette parallele a $r: x-2y=0$

trovare quella che

Passa per il punto $P\,(1,-1)$ ;

Interseca la retta $s: (t, 3t+1)$ nel suo punto $Q$ che ha seconda coordinata pari a $7$ .

Scrivere sia in forma parametrica che cartesiana le rette trovate.

Svolgimento punto 1.

Il vettore normale alla retta è $\nu=(1,-2)$

, dunque la retta cercata è la seguente: $(x-1)-2(y+1)=0$

, cioè $x-2y-3=0$

. Può essere espressa in forma parametrica come $(2t+3,t)$

Svolgimento punto 2.

La generica retta parallela a $r$

è data da $x-2y+\alpha=0$

. Imponendo il passaggio per $Q\,(2,7)$

, otteniamo l’equazione $2-2\cdot 7 + \alpha=0$

, da cui si ricava $\alpha=12$

. La retta cercata è dunque $x-2y+12=0$

e può essere espressa in forma parametrica come $(2t-12,t)$

Esercizio 3 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Tra tutte le rette parallele a $r: (t+1,1-t)$

trovare quella che

Passa per il punto $P\,(0,1)$ ;

Interseca la retta $s: 8x+y=0$ nel suo punto $Q$ che ha prima coordinata pari a $-1$ .

Scrivere in forma parametrica che cartesiana le rette trovate.

Svolgimento punto 1.

Il vettore direttore della retta è $v=(1,-1)$

, dunque la retta cercata è la seguente: $x+(y-1)=0$

, cioè $x+y-1=0$

. In forma parametrica può essere espressa come $(1-t,t)$

Svolgimento punto 2.

La generica retta parallela a $r$

è data da $x+y+\alpha=0$

. Imponendo il passaggio per $Q\,(-1,8)$

, otteniamo l’equazione $-1+8 + \alpha=0$

, da cui si ricava $\alpha=-7$

. La retta cercata è dunque $x+y-7=0$

e può essere espressa in forma parametrica come $(t,7-t)$

Esercizio 4 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare la posizione reciproca delle seguenti coppie di rette nel piano. Nel caso siano incidenti, trovare il punto di intersezione.

$(7-t,t)$ , $x+1=0$ ;

$(t+1, 2t+3)$ , $2x-y=0$ ;

$2x+y+12=0$ , $(-4t, 8t -12)$ ;

$(t^3, 1+t^3)$ , $(t, 1-t)$ .

Svolgimento punto 1.

Incidenti, con intersezione $P\, (-1, 8)$

Svolgimento punto 2.

Parallele.

Svolgimento punto 3.

Coincidenti.

Svolgimento punto 4.

La prima retta è $(s, 1+s)$

. Sono incidenti, con intersezione $P\,(0,1)$

Esercizio 5 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Data la retta in forma parametrica $r: (-t+1,2t+3)$

Trova le equazioni cartesiane di $r$ ;

Determinare la retta parallela a $r$ passante per il punto $P\,(1,1)$ .

Svolgimento punto 1.

Abbiamo $t=1-x$

e andando a sostituire nella seconda equazione: $y=2(1-x)+3$

, cioè $y=-2x+5$

Svolgimento punto 2.

Il vettore direttore della retta $r$

è $(-1,2)$

e quindi il vettore normale alla retta è $(2,1)$

. La retta cercata è quindi $2(x-1)+(y-1)=0$

cioè $2x+y-3=0$

Esercizio 6 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare la posizione reciproca delle seguenti coppie di rette nello spazio. Nel caso siano incidenti, trovare il punto di intersezione.

$(t,t,1)$ , $(-4t,-4t, -4)$ ;

$(t+1, 2t+3,t)$ , $(2t,-t,0)$ ;

$(2t,-t+12, 1-t)$ , $(26t, -t, -12)$ .

Svolgimento punto 1.

Coincidenti.

Svolgimento punto 2.

Sghembe.

Svolgimento punto 3.

Incidenti, con intersezione $P(26,-1-12)$

Esercizio 7 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare l’equazione parametrica e cartesiana del piano passante per $P_1\,(1,1,0), P_2\,(1,3,7),P_3\,(2,4,1)$

Svolgimento.

Il piano ha equazioni parametriche

$\makebox{\bf{x}}=\left(\begin{array}{c} 1 \\ 1 \\ 0 \end{array}\right) + t\left(\begin{array}{c} 0 \\ 2 \\ 7 \end{array}\right) + s\left(\begin{array}{c} 1 \\ 3 \\ 1 \end{array}\right)$

Sostituendo nell’ultima equazione i parametri $t$ e $s$ trovati a partire dalle prime due equazioni, troviamo le equazioni cartesiane:

$\pi: 19x-7y+2z-12=0.$

Esercizio 8 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare il piano passante per l’origine e parallelo alle rette

$r: \begin{cases} x - 2z =0 \\ y + z - 1 = 0 \end{cases} \mbox{ e } \; \; s:\begin{cases} x - 3z + 2 =0 \\ y + 2z + 4 = 0. \end{cases}$

Svolgimento.

I vettori direttori delle rette sono $v_r=(2,-1,1)$

e $v_s=(3,-2,1)$

e ovviamente costituiscono una giacitura per il piano, che ha dunque equazioni parametriche $\bf{x}=\lambda \bf{$

v_r $}+\mu \bf{$

v_s $}$

. Troviamo dunque $x+y-z=0$

Esercizio 9 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare l’equazione cartesiana del piano passante per il punto $P\,(0, 1, 2)$

e contenente la retta di equazioni

$x - 2y + 4z = 2x + y - z + 1 = 0.$

Svolgimento.

Un vettore direttore della retta è $v=(-2,9,5)$

e prendendo ad esempio $Q(0,-2,-1)$

come punto appartenente alla retta, troviamo che il piano cercato è $-2x-(y-1)+(z-2)=0$

Esercizio 10 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Per ogni $a\in \mathbb{R}$

, si consideri il piano $\pi: 2x_1-x_2+x_3=0$

e la retta $r_a$

di equazioni parametriche $x_1=t, x_2=2t+a, x_3=(a^2-a)t+2a$

. Determina al variare di $a \in \mathbb{R}$

, l’intersezione tra $\pi$

e $r_a$

. Esistono valori di $a$

per cui $r_a \subset \pi$

Svolgimento.

Sostituendo le equazioni parametriche di $r_a$

nelle equazioni cartesiane di $\pi$

e sviluppando i calcoli otteniamo $(a^2-a)t+a=0$

. Se $a^2-a\neq 0$

allora esiste un unica soluzione $t=\displaystyle \frac{1}{1-a}$

, che corrisponde a un unico punto di intersezione $P_a=\left(\displaystyle \frac{1}{1-a},\frac{a^2-a-2}{a-1},a\right)$

, mentre se $a=1$

, l’equazione diventa $1=0$

che non è mai verificata, quindi il piano e la retta sono paralleli. Infine per $a=0$

troviamo $0=0$

e dunque l’equazione è verificata per tutti i valori di $t$

, cioè $r_a \subset \pi$

Esercizio 11 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Scrivere equazioni parametriche per la retta r di equazioni cartesiane

$r: \begin{cases} x-y+z+4 =0 \\ x+y-5z+2 = 0 \end{cases}$

e trovare l’intersezione tra tale retta e il piano $\pi: 4x+6y+2z=0$ .

Svolgimento.

Un vettore direttore è $v_r=(4,6,2)$

mentre se sostituiamo $z=0$

nell’equazione troviamo che $(-3,1,0)\in r$

, dunque le equazioni parametriche sono $\makebox{\bf{x}}=(-3,1,0)+t(2,3,1)$

(che si può esplicitare come $x=-3+2t,y=1+3t,z=t$

). Sostituendo nell’equazione di $\pi$

troviamo $28t-6=0$

, che da quindi il punto $(-18/7,23/14,3/14)$

Esercizio 12 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Determinare i valori del parametro $a\in \mathbb{R}$

per i quali i seguenti piani si incontrano esattamente in un punto:

$(4 -a)y - 3z + 1 = 0,\; x + 2y - z = 0, \;2y - (1 + a)z + 2 = 0.$

Svolgimento.

Il sistema ha un’unica soluzione per ogni $a\neq 1,2$

Esercizio 13 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Trovare equazioni parametriche e cartesiane della retta $r=\alpha \cap \beta$

, dove $\alpha: x_1-2x_2-3=0$

e $\beta: \left( t, s, -2-2s \right)$

Svolgimento.

Deve essere $t-2s-3=0$

, dunque $r=\alpha \cap \beta$

ha equazioni parametriche $\left(\begin{array}{c} 2s+3 \\ s \\ -2-2s \end{array}\right)$

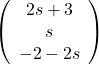D’altronde, l’equazione cartesiana di $\beta$ è $2x_2+x_3+2=0$ , dunque l’equazione cartesiana di $r$ è

$\begin{cases} x_1-2x_2-3=0 \\ 2x_2+x_3+2=0 \end{cases}.$

Ulteriori esercizi di geometria

In questa sezione vengono raccolti molti altri esercizi che coprono tutti gli argomenti di geometria proposti all’interno del sito con lo scopo di offrire al lettore la possibilità di approfondire e rinforzare le proprie competenze inerenti a tali argomenti.

Menu

Chiudi

Esercizi geometria nello spazio — vettori direttori

Autori

Leggi...

Testi degli esercizi

Svolgimento punto 1.

Svolgimento punto 2.

Svolgimento punto 3.

Svolgimento punto 4.

Svolgimento punto 5.

Svolgimento punto 1.

Svolgimento punto 2.

Svolgimento punto 1.

Svolgimento punto 2.

Svolgimento punto 1.

Svolgimento punto 2.

Svolgimento punto 3.

Svolgimento punto 4.

Svolgimento punto 1.

Svolgimento punto 2.

Svolgimento punto 1.

Svolgimento punto 2.

Svolgimento punto 3.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Ulteriori esercizi di geometria

Strutture algebriche.

Algebra lineare.

Geometria analitica.

Geometria differenziale.

Suggerimenti, refusi ed errori

Cosa dicono di noi