Esercizi svolti su correnti alternate e trasformatori ideali

Oscillazioni elettriche e correnti alternate

Home » Esercizi svolti su correnti alternate e trasformatori ideali

Questo articolo presenta 28 esercizi svolti sulle correnti alternate e trasformatori ideali, inclusi circuiti RLC, RL e RC. Gli esercizi sono risolti in modo dettagliato e minuzioso, ideali per corsi di Fisica 2 per ingegneria, fisica e matematica. Gli esercizi sono tratti dal libro ‘Elementi di Fisica. Elettromagnetismo e Onde’ di P. Mazzoldi, M. Nigro, e C. Voci. L’obiettivo di questo lavoro è fornire soluzioni chiare e dettagliate del capitolo 9.

Autori e revisori degli esercizi su oscillazioni elettriche-correnti alternate-circuiti RLC-trasformatori ideali

Leggi...

Autore: Valerio Brunetti

Revisore: Silvia Lombardi.

Testi degli esercizi su oscillazioni elettriche-correnti alternate-circuiti RLC-trasformatori ideali

Esercizio 1 $(\bigstar\bigsta\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito $LC$ con $C=64\,\mu \text{F}$ la corrente varia con la legge $i(t)=\text{1,6}\sin(2500\,t-\text{0,68})\text{A}$ (dove i 2500 sono intesi in $\text{s}^{-1}$ dato che l’argomento del seno deve essere adimensionale). Calcolare:

l’istante $t$ in cui la corrente raggiunge il suo valore massimo a partire dall’istante $t=0\,\text{s}$ ;
il valore dell’induttanza $L$ ;
l’energia totale $U$ immagazzinata nel circuito stesso.

Svolgimento punto 1.

La corrente è descritta da una funzione sinusoidale il cui massimo lo si ottiene quando l’argomento del seno è pari a $\pi/2$ , pertanto si ha

(1) $\begin{equation*} \sin(2500\,t-\text{0,68})=1 \qquad\Leftrightarrow \qquad 2500\,t-\text{0,68}={\pi\over 2} , \end{equation*}$

da cui

(2) $\begin{equation*} 2500\,t=0,68+{\pi\over 2} , \end{equation*}$

cioè

$\boxcolorato{fisica}{ t={\text{0,68}+\pi/2\over 2500\,\text{s}^{-1}}=9\cdot 10^{-4}\,\text{s}.}$

Svolgimento punto 2.

La pulsazione naturale in un circuito $LC$ in serie è

(3) $\begin{equation*} \omega={1\over \sqrt{LC}}, \end{equation*}$

che è la stessa che si trova come argomento della funzione sinusoidale della corrente ( $\omega=2500 \ \text{s}^{-1}$ ), quindi

$\boxcolorato{fisica}{L={1\over \omega^2 C}=\text{2,5}\cdot 10^{-3}\,\text{H}.}$

Svolgimento punto 3.

In assenza di resistenze non abbiamo alcuna dissipazione di energia; segue allora che la somma dell’energia immagazzinata dal condensatore e dall’induttore è costante nel tempo

(4) $\begin{equation*} U=U_C(t)+U_L(t)={q^2(t)\over 2C}+{1\over 2}L i^2(t). \end{equation*}$

Risulta chiaro che quando la carica è massima la corrente è nulla o quando la corrente è massima la carica è nulla. Pertanto essendo $i_{\max}=\text{1,6}\,\text{A}$ si ha

(5) $\begin{equation*} U={1\over 2}Li_{\max}^2={1\over 2}L (\text{1,6}\,\text{A})^2, \end{equation*}$

cioé

$\boxcolorato{fisica}{ U\approx\text{3,2}\cdot 10^{-3}\,\text{J}.}$

Esercizio 2 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Nel circuito di figura $\mathcal{E}=24\,\text{V}$ , $C=4\,\mu \text{F}$ e $L=60 \,\text{mH}$ . Inizialmente l’interruttore $T$ rimane chiuso per un tempo molto lungo nella posizione 1 e quindi commuta nella posizione 2. Calcolare:

la frequenza $\nu$ delle oscillazioni del circuito $LC$ ;
il valore massimo della corrente $i_0$ .

Figura 1: dettaglio schema esercizio 2.

Svolgimento punto 1.

Inizialmente il circuito è chiuso nella posizione $1$ ; il circuito è del tipo $RC$ con una d.d.p. data da $\mathcal{E}$ . La carica di un circuito $RC$ può essere trovata applicando la legge di Kirchoff per le tensioni alla maglia considerata. Sappiamo che il potenziale dovuto al resistore è dato dalla prima legge di Ohm, ossia

(6) $\begin{equation*} V_R(t)=Ri(t)=R\dfrac{dq}{dt}, \end{equation*}$

dove $V_R$ è il potenziale ai capi della resistenza. Il potenziale tra le due lastre del condensatore è invece, dalla definizione di capacità C di un condensatore, pari a

(7) $\begin{equation*} V_C=\frac{q}{C}. \end{equation*}$

Applicando la legge di Kircoff alle maglie si ha

(8) $\begin{equation*} \mathcal{E} -V_R-V_C=0, \end{equation*}$

ossia:

(9) $\begin{equation*} \mathcal{E}-\frac{q}{C}=R\dfrac{dq}{dt}\quad\Leftrightarrow\quad \dfrac{dt}{RC}=-\frac{dq}{\mathcal{E}C-q}. \end{equation*}$

Integriamo ambo i membri dell’equazione partendo da un tempo fissato $t_0=0\,[\text{s}]$ . A tale tempo, anche la carica $q_0$ è nulla in quanto il condensatore è scarico, dunque otteniamo

(10) $\begin{equation*} \int_{0}^{t} {\dfrac{dt}{RC}}=-\int_{0}^{q} {\frac{dq}{\mathcal{E}C-q}}. \end{equation*}$

Svolgiamo gli integrali e otteniamo:

(11) $\begin{equation*} \ln(\mathcal{E}C-q(t))-\ln(\mathcal{E}C)=-\frac{t}{RC}, \end{equation*}$

da cui

(12) $\begin{equation*} \dfrac{\mathcal{E}C-q(t)}{\mathcal{E}C}=e^{-t/RC}, \end{equation*}$

cioè

(13) $\begin{equation*} q(t)=\mathcal{E} C\big(1-e^{-t/RC}\big). \end{equation*}$

Abbiamo ottenuto la funzione che descrive la quantità di carica in funzione del tempo. Si noti che, per tempi molto lunghi, teoricamente per $t\to +\infty$ , il condensatore si carica completamente e dunque si ha $q(\infty)=\mathcal{E}C$ , sostanzialmente per tempi molto lunghi il condensatore si comporta come un circuito aperto. Quindi assumiamo il condensatore completamente carico e cambiamo la posizione dell’interruttore in $2$ ; siamo ora in presenza di un circuito $LC$ .

Abbiamo già visto nell’esercizio 1 la pulsazione naturale del circuito $LC$ , cioè $\omega=1/\sqrt{Lc}$ , ne ricaviamo la frequenza dividendo per $2\pi$ . Concludiamo con la seguente soluzione

$\boxcolorato{fisica}{\nu={1\over 2\pi\sqrt{LC}}=325\,\text{Hz}.}$

Svolgimento punto 2.

Sappiamo che l’energia iniziale è

(14) $\begin{equation*} U=\dfrac{q^2_{\max}}{2C}=\dfrac{q^2_{\infty}}{2C}=\dfrac{\mathcal{E}^2C^2}{2C}=\dfrac{\mathcal{E}^2C}{2}, \end{equation*}$

e sapendo che l’energia si conserva si ha

(15) $\begin{equation*} \dfrac{1}{2}Li^2_0=\dfrac{\mathcal{E}^2C}{2}, \end{equation*}$

da cui

(16) $\begin{equation*} i^2_0=\dfrac{\mathcal{E}^2C}{L}, \end{equation*}$

cioè

(17) $\begin{equation*} i_0=\sqrt{\dfrac{\mathcal{E}^2C}{L}}=\mathcal{E}\sqrt{\dfrac{C}{L}}=\dfrac{\mathcal{E}C}{\sqrt{LC}}=\omega\mathcal{E}C\approx\text{0,196}\,\text{A}. \end{equation*}$

Si conclude che

$\boxcolorato{fisica}{ i_0={\mathcal{E}\over \omega L}=\omega\mathcal{E}C\approx\text{0,196}\,\text{A}.}$

Esercizio 3 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito $LC$ , $L=20\,\text{mH}$ e $C=4\,\mu \text{F}$ . All’istante $t=0\,\text{s}$ la corrente vale $i=8\,\text{mA}$ e la carica sul condensatore $q=2\,\mu \text{C}$ ; il condensatore è in carica. Calcolare:

l’energia totale $U$ del circuito;
la carica massima $q_{\max}$ ;
la corrente massima $i_{\max}$ ;

Se la carica è descritta dalla relazione $q(t)=q_{\max}\cos(\omega t+\phi)$ , calcolare $\phi$ .

Svolgimento punto 1.

Conosciamo i valori iniziali della corrente e della carica depositata sul condensatore, possiamo allora calcolare l’energia utilizzando l’equazione (4) in $t=0\,\text{s}$ . Concludiamo con la seguente soluzione

$\boxcolorato{fisica}{U={1\over 2}L i^2(0)+{q^2(0)\over 2C}=\text{1,14}\cdot 10^{-6}\,\text{J}.}$

Svolgimento punto 2.

L’energia del circuito la si può calcolare anche nel caso in cui la carica nel condensatore è massima, ovvero quando la corrente è nulla.

(18) $\begin{equation*} U={q_{\max}^2\over 2C}, \end{equation*}$

da cui

$\boxcolorato{fisica}{ q_{\max}=\sqrt{2 C U}=\text{3,02}\cdot 10^{-6}\,\text{C}.}$

Svolgimento punto 3.

Analogamente possiamo calcolare $i_{\max}$ applicando la conservazione dell’energia del sistema:

(19) $\begin{equation*} U={1\over 2}L i_{\max}^2, \end{equation*}$

da cui

$\boxcolorato{fisica}{i_{\max}=\sqrt{{2 U\over L}}=\text{0,0107}\,\text{A}.}$

Per calcolare $\phi$ manipoliamo la relazione $q(t)$ . In $t=0\,\text{s}$ essa è pari a

(20) $\begin{equation*} q(0)=q_{\max}\cos(\phi) \qquad\Rightarrow\qquad \phi=\arccos\bigg({q(0)\over q_{\max}}\bigg), \end{equation*}$

pertanto

$\boxcolorato{fisica}{\phi=\arccos\bigg({q(0)\over q_{\max}}\bigg)\approx0,84\,\text{rad}=\text{0,85}^\circ.}$

Esercizio 4 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare la carica $q$ presente sulle armature di un condensatore di un circuito oscillante $LC$ , con $L= 5\,\text{mH}$ e $C=2\,\mu \text{F}$ , quando l’energia $U$ è ripartita in parti uguali tra il campo elettrostatico e il campo magnetico, in funzione della carica massima $q_{\max}$ . Calcolare anche il tempo $t$ necessario affinché si realizzi tale condizione se per $t=0\,\text{s}$ il condensatore è scarico.

Svolgimento.

Scriviamo la formula che descrive l’andamento oscillatorio della carica contenuta nel condensatore.

(21) $\begin{equation*} q(t)=q_{\max}\sin(\omega t+\phi). \end{equation*}$

E’ stata scelta la funzione sinusoidale in modo tale da rispettare la condizione iniziale $q_0=q(t=0)=0$ . Derivando questa funzione ricaviamo la corrente.

(22) $\begin{equation*} i(t)={\text{d}q(t)\over \text{d}t}=q_{\max}\omega \cos(\omega t+\phi)=i_{\max}\cos(\omega t+\phi), \end{equation*}$

quindi $q_{\max}\omega=i_{\max}$ . Siccome il condensatore è scarico si ha che

(23) $\begin{equation*} 0=q_{\max}\sin \left(\phi\right)\quad \Leftrightarrow\quad \phi =0\,\text{rad}, \end{equation*}$

pertanto

(24) $\begin{equation*} \begin{cases} q(t)=q_{\max}\sin(\omega t);\\ i(t)=i_{\max}\cos(\omega t). \end{cases} \end{equation*}$

Calcoliamo ora l’energia del condensatore

(25) $\begin{equation*} U_C=\dfrac{q^2}{2C}=\dfrac{q_{\max}^2\sin^2\left(\omega t\right)}{2C}=\dfrac{q_{\max}^2}{2C}\left(1-\cos^2\left(\omega t\right)\right)=\dfrac{q_{\max}^2}{2C}-\dfrac{q_{\max}^2}{2C}\cos^2\left(\omega t\right) \end{equation*}$

e dell’induttore

(26) $\begin{equation*} U_L=\dfrac{1}{2}Li^2=\dfrac{1}{2}Li^2_{\max}\cos^2(\omega t)=\dfrac{1}{2}L\,\omega^2q^2_{\max}\cos^2(\omega t). \end{equation*}$

Imponiamo

(27) $\begin{align*} &U_C=U_L\quad \Leftrightarrow\quad \dfrac{1}{2}L\,\omega^2q^2_{\max}\cos^2(\omega t)=\dfrac{q_{\max}^2}{2C}-\dfrac{q_{\max}^2}{2C}\cos^2\left(\omega t\right)\quad \Leftrightarrow\quad\\ &\Leftrightarrow\quad\dfrac{1}{2}L\,\omega^2\cos^2(\omega t)=\dfrac{1}{2C}-\dfrac{1}{2C}\cos^2\left(\omega t\right), \end{align*}$

ricordando che la pulsazione di un circuito $LC$ (senza generatore) è $\omega=\dfrac{1}{\sqrt{LC}}$ , si ottiene

(28) $\begin{align*} &\dfrac{1}{2}L\left(\dfrac{1}{LC}\right)\cos^2(\omega t)=\dfrac{1}{2C}-\dfrac{1}{2C}\cos^2\left(\omega t\right)\quad \Leftrightarrow \quad \dfrac{1}{2C}\cos^2(\omega t)=\dfrac{1}{2C}-\dfrac{1}{2C}\cos^2\left(\omega t\right)\quad \Leftrightarrow \quad \\ &\quad \Leftrightarrow \quad \cos^2(\omega t)=1-\cos^2\left(\omega t\right)\quad \Leftrightarrow \quad2\cos^2\left(\omega t\right)=1\quad \Leftrightarrow \quad \cos^2\left(\omega t \right)=\dfrac{1}{2}\quad \Leftrightarrow \quad\\ &\Leftrightarrow \quad\cos \left(\omega t\right)=\dfrac{\sqrt{2}}{2}\quad \Leftrightarrow \quad\omega t=\dfrac{\pi}{4}\quad \Leftrightarrow \quad t=\dfrac{\pi}{4\omega}. \end{align*}$

Concludiamo con la seguente soluzione

$\boxcolorato{fisica}{\tau={\pi\over 4\omega }={\pi \sqrt{LC}\over 4}=\text{7,85}\cdot 10^{-5}\,\text{s}.}$

A questo punto, conoscendo l’oscillazione della carica elettrica sul condensatore, possiamo calcolare la carica che $C$ possiede al tempo $\tau$ . Concludiamo con la seguente soluzione:

$\boxcolorato{fisica}{q(\tau)=q_{\max}\sin(\omega \tau)=q_{\max}\cdot \dfrac{1}{\sqrt{2}}={q_{\max}\over \sqrt{2}}.}$

Esercizio 5 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un generatore che fornisce una f.e.m. $\mathscr{E}$ di valore massimo $\mathscr{E}_{\max}=140\,\text{V}$ e frequenza $\nu=50 \,\text{Hz}$ è collegato ad un resistore $R=100 \ \Omega$ . Se la corrente all’istante $t=0\,\text{s}$ è nulla, calcolare la corrente efficace $i_\text{eff}$ all’istante $t_1=1/75 \ ,\text{s}$ e $t_2=1/50 \, \text{s}$ .

Rendered by QuickLaTeX.com

Figura 2: schema problema 5.

Svolgimento.

Il generatore fornisce una f.e.m. che ha le caratteristiche di un segnale sinusoidale, ossia un segnale il cui andamento nel tempo possa essere descritto da un’equazione del tipo

(29) $\begin{equation*} \mathscr{E}(t)=\mathscr{E}_{\max}\sin(2\pi\nu t+\phi). \end{equation*}$

Sappiamo inoltre dalla prima legge di Ohm che il potenziale $\Delta V$ ai capi di un resistore è descritta dalla relazione

(30) $\begin{equation*} \Delta V=Ri, \end{equation*}$

dove $i$ è la corrente che attraversa il circuito. Allora, applicando la legge di Kirchoff delle tensioni alla maglia in figura 2, scegliendo, per esempio, di percorrerla in senso orario, si ottiene

(31) $\begin{equation*} \mathscr{E}-\Delta V=0\quad\Leftrightarrow\quad\mathscr{E}-Ri=0\quad\Leftrightarrow\quad\mathscr{E}=Ri. \end{equation*}$

Si ottiene così, sostituendo il risultato trovato nella (29) all’interno della (31) l’espressione della corrente $i$

(32) $\begin{equation*} i(t)=\dfrac{\mathscr{E}_{\max}\sin(2\pi\nu t+\phi)}{R}. \end{equation*}$

Il testo impone inoltre che $i(0)=0\,\text{A}$ , dunque imponendo questa condizione troviamo

(33) $\begin{equation*} i(0)=\dfrac{\mathscr{E}_{\max}\sin(\phi)}{R}=0\quad\Leftrightarrow\quad\sin\phi=0\quad\Leftrightarrow\quad\phi=0, \end{equation*}$

da cui deduciamo che l’equazione che descrive l’andamendo della corrente in funzione del tempo sia

(34) $\begin{equation*} i(t)=\dfrac{\mathscr{E}_{\max}\sin(2\pi\nu t)}{R}. \end{equation*}$

A questo punto possiamo trovare i valori $i_1$ e $i_2$ della corrente ai tempi rispettivamente $t_1$ e $t_2$ . In generale, la corrente efficace $i_\text{eff}$ è

(35) $\begin{equation*} i_\text{eff}=\frac{i}{\sqrt{2}} \end{equation*}$

da cui, ricordando che $\mathscr{E}_{\max}=140 \ \text{V}$ , $\nu=50 \ \text{Hz}$ e che $R=100 \ \Omega$ , la corrente efficace all’istante $t_1=1/75 \ \text{s}$ è:

$\boxcolorato{fisica}{i_{\text{eff},1}=\frac{i_1}{\sqrt{2}}=\frac{i(t_1)}{\sqrt{2}}=\dfrac{\mathscr{E}_{\max}\left \vert \sin(2\pi\nu t_1)\right \vert }{\sqrt{2}R}\approx\text{0,86} \ \text{A}.}$

mentre invece all’istante $t_2=1/50 \ \text{s}$ si ha

$\boxcolorato{fisica}{i_{\text{eff},2}=\frac{i_2}{\sqrt{2}}=\frac{i(t_2)}{\sqrt{2}}=\dfrac{\mathscr{E}_{\max}\sin(2\pi\nu t_2)}{\sqrt{2}R}=0 \ \text{A}.}$

Esercizio 6 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare la resistenza $R_i$ di lampadine di potenza $\mathscr{P}_1=25 \,\text{W}$ , $\mathscr{P}_2=75\, \text{W}$ e $\mathscr{P}_3=100\, \text{W}$ , collegate alla linea di distribuzione domestica, $V_\text{eff}=220\, \text{V}$ .

Svolgimento.

Per risolvere questo problema è necessario notare che i valori delle potenze $\mathscr{P}_i$ forniti dal testo si riferiscono a delle potenze medie: infatti, in una linea di distribuzione domestica, la potenza ha un andamento sinusoidale in funzione del tempo a causa del fatto che essa dipende dalla tensione a cui è mantenuta la rete, la quale è a sua volta una funzione sinusoidale. Dunque in generale La potenza media è dunque

(36) $\begin{equation*} R_i=\frac{V^2_\text{eff}}{\mathscr{P}_i}, \end{equation*}$

con $i=1,2,3.$ Sostituendo i valori numerici dati dal problema otteniamo:

$\boxcolorato{fisica}{R_1=1936 \ \Omega;\quad\quad R_2=645 \ \Omega;\quad\quad R_3=484 \ \Omega.}$

Esercizio 7 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Nel circuito di figura 3, puramente induttivo, il generatore di tensione è sottoposto ad una differenza di potenziale descritto dalla legge $\mathcal{E}=V_{\max}\cos \left(\omega t -\dfrac{\pi}{2}\right)$ dove $L=60 \,\text{mH}$ , $V_{\max}=60\, \text{V}$ , $\omega=65\,\pi \,\text{rad/s}$ e $\phi =0\,\text{rad}$ . Inoltre supporre $i(0)=-\dfrac{V_{\max}}{\omega \text{L}}$ . Calcolare l’intensità di corrente $i$ all’istante $t^\star=0,0155 \,\text{s}$ .

Figura 3: dettaglio schema esercizio 7

Svolgimento.

Si ha

(37) $\begin{equation*} \mathcal{E}(t)=V_{\max}\cos \left(\omega t-\dfrac{\pi}{2}\right), \end{equation*}$

da cui

(38) $\begin{equation*} \mathcal{E}(t)=V_{\max}\cos \left(\omega t-\dfrac{\pi}{2}\right)=V_L=L\,\dfrac{di_L}{dt}, \end{equation*}$

cioè la tensione ai capi dell’induttore è uguale a quella del generatore di tensione e quindi è uguale alla derivata della corrente per l’induttanza $L$ . Si osservi che la corrente $i_L$ è la stessa corrente che attraversa il generatore, cioè la corrente di maglia, che per semplificare denoteremo con $i$ .

Integrando ambo i membri di (38) si ottiene

(39) $\begin{equation*} \dfrac{V_{\max}}{\omega}\sin\left(\omega t -\dfrac{\pi}{2}\right)=Li+c, \end{equation*}$

imponendo $i(0)=-\dfrac{V_{\max}}{\omega L}$ si ottiene $c=0$ , quindi

(40) $\begin{equation*} \dfrac{V_{\max}}{\omega}\sin\left(\omega t -\dfrac{\pi}{2}\right)=Li, \end{equation*}$

cioè

(41) $\begin{equation*} i=\dfrac{V_{\max}}{\omega\,L}\sin\left(\omega t -\dfrac{\pi}{2}\right). \end{equation*}$

Pertanto al tempo $t^*= \text{0,0155} \ \text{s}$ si ottiene

$\boxcolorato{fisica}{ i(t^)={V_{\max}\over \omega L}\sin\left(\omega t^-\dfrac{\pi}{2}\right)=\text{4,9}\,\text{A}.}$

Esercizio 8 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito puramente induttivo, la tensione massima è $V_{\max}=100\,\text{V}$ e la corrente massima alla frequenza $\nu_1=50 \,\text{Hz}$ è $i_{\max}=5\,\text{A}$ . Calcolare:

l’induttanza $L$ ;
per quale valore della frequenza $\nu_2$ abbiamo $i_{\max}=2,5\text{A}$ .

Svolgimento punto 1.

Sapendo che $2\pi\nu_1=\omega_1$ e utilizzando la relazione che lega la corrente massima alla d.d.p. massima ai capi dell’induttore, ricaviamo

(42) $\begin{equation*} i_{\max}={V_{\max}\over \omega_1 L}={V_{\max}\over(2\pi\nu_1) L}, \end{equation*}$

da cui

$\boxcolorato{fisica}{L={V_{\max}\over 2\pi\nu_1 i_{\max}}=\text{63,7}\,\text{mH}.}$

Svolgimento punto 2.

L’induttanza e la d.d.p. massima rimangono costanti, poiché immaginiamo variare solamente la frequenza del circuito. La frequenza $\nu_2$ necessaria per avere una corrente $i_{\max}=\text{2,5}$ A è pari a

$\boxcolorato{fisica}{\nu_2={V_{\max}\over 2\pi L i_{\max}}=100 \,\text{Hz}.}$

Infatti, in un circuito puramente induttivo, raddoppiando la frequenza dimezziamo la corrente massima.

Esercizio 9 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Quando un induttore è collegato ad un generatore di tensione con $V_{\max}=150\,\text{V}$ , in esso circola una corrente $i_{\max}=5\,\text{A}$ . Calcolare:

la reattanza induttiva $X_L$ ;
la corrente massima $i'_{\max}$ se la reattanza viene raddoppiata.

Svolgimento punto 1.

La reattanza induttiva è la parte immaginaria dell’impedenza complessa e in un circuito puramente induttivo essendo l’impedenza complessa associata ad un induttore $Z_L=j \omega L$ , avremo

(43) $\begin{equation*} X_{L}=\omega L, \end{equation*}$

con $\omega$ pulsazione del circuito. Sapendo che

(44) $\begin{equation*} i_{\max}=\dfrac{V_{\max}}{\omega L}, \end{equation*}$

e sostituendo la reattanza in quest’ultima relazione, si ottiene

(45) $\begin{equation*} i_{\max}={V_{\max}\over \omega L}={V_{\max}\over X_L} \quad \Leftrightarrow\quad X_{L}={V_{\max}\over i_{\max}}. \end{equation*}$

Sostituendo i valori numerici si ottiene:

$\boxcolorato{fisica}{ X_L={V_{\max}\over i_{\max}}=\text{30,6}\,\Omega.}}}$

Svolgimento punto 2.

La reattanza è inversamente proporzionale alla corrente massima, quindi se raddoppia la corrente massima si dimezza. Dall’ultima relazione ottenuta si ha

(46) $\begin{equation*} 2X_{L}={V_{\max}\over i^\prime_{\max}}\quad \Leftrightarrow\quad i^\prime_{\max}=\dfrac{V_{\max}}{2X_L}=\dfrac{i_{\max}}{2}. \end{equation*}$

Osservazione.

Si osservi che l’unità di misura della reattanza è Ohm, proprio perché la reattanza è la parte immaginare dell’impedenza complessa che ha dimensione di una resistenza.

Scarica gli esercizi svolti

Ottieni il documento contenente 28 esercizi risolti, contenuti in 24 pagine ricche di dettagli, per migliorare la tua comprensione delle correnti alternate e trasformatori ideali.

Esercizio 10 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un generatore di tensione alternata $\mathcal{E}(t)=\mathcal{E}_{\max}\sin(\omega t)$ con $\mathcal{E}_{\max}=25\,\text{V}$ e $\omega=377 \,\text{rad/s}$ è collegato ad un induttore $L=\text{12,7}\,\text{mH}$ . Inoltre ipotizzare che $i(0)=-i_{\max}$ . Calcolare:

la corrente massima $i_{\max}$ ;
Il valore di $\mathcal{E}$ quando la corrente è massima;
Il valore della corrente $i$ quando $\mathcal{E}=-\text{12,5}\, \text{V}$ e sta aumentando.

Svolgimento punto 1.

Come nei precedenti esercizi si ha

$\boxcolorato{fisica}{ i_{\max}={\mathcal{E}_{\max}\over \omega L}=\text{5,22}\,\text{A}.}$

Svolgimento punto 2.

È noto che lo sfasamento tra $i(t)$ e $\mathcal{E}(t)$ introdotto da un induttore è di $\pi/2$ . Le due funzioni considerate sono delle sinusoidi, dunque hanno semiperiodo pari a $\pi$ ; deduciamo che, quando la corrente vale $i(t)=i_{\max}$ , lo sfasamento di $\pi/2$ che stiamo trattando fa sì che $\mathcal{E}=0\,\text{V}$ . Sappiamo che

(47) $\begin{equation*} \mathcal{E}(t)=\mathcal{E}_{\max}\sin\left(\omega t\right), \end{equation*}$

da cui

(48) $\begin{equation*} \mathcal{E}_{\max}\sin\left(\omega t\right)=L\,\dfrac{di}{dt}, \end{equation*}$

da cui integrando ambo i membri, si ottiene

(49) $\begin{equation*} -\dfrac{\mathcal{E}_{\max}}{\omega}\cos\left(\omega t \right)=L\,i+c. \end{equation*}$

Ipotizzando che $i(0)=-i_{\max}=-\dfrac{\mathcal{E}}{\omega L}$ si trova $c=0\,\left[\text{V}\cdot \text{s}\right]$ , e pertanto

(50) $\begin{equation*} -\dfrac{\mathcal{E}_{\max}}{\omega}\cos\left(\omega t \right)=L\,i, \end{equation*}$

pertanto

(51) $\begin{equation*} i(t)=-\dfrac{\mathcal{E}_{\max}}{\omega L }\cos\left(\omega t \right)=.\dfrac{\mathcal{E}_{\max}}{\omega L }\sin\left(\omega t -\dfrac{\pi}{2}\right).\\[10pt] \end{equation*}$

Quindi la corrente risulta massima quando $\omega t -\dfrac{\pi}{2}=\dfrac{\pi}{2}$ , cioè $t =\dfrac{\pi}{\omega}$ . Sostituendo $t =\dfrac{\pi}{\omega}$ nella legge della tensione, si ottiene

(52) $\begin{equation*} \mathcal{E}\left(\dfrac{\pi}{\omega}\right)=\mathcal{E}_{\max}\sin\left(\omega \cdot \dfrac{\pi}{\omega}\right)=\mathcal{E}_{\max}\sin\left(\pi\right)=0\,\text{V}.\\[10pt] \end{equation*}$

Concludiamo che quando la corrente è massima la tensione è nulla.

Svolgimento punto 3.

Eleviamo al quadrato ambo i membri della (51) e otteniamo

(53) $\begin{equation*} i^2(t)=\dfrac{\mathcal{E}^2_{\max}}{\omega^2 L^2 }\cos^2\left(\omega t \right)=\dfrac{\mathcal{E}^2_{\max}}{\omega^2 L^2 }\left(1-\sin^2 \left(\omega t\right)\right)=\dfrac{\mathcal{E}^2_{\max}}{\omega^2 L^2 }\left(1-\dfrac{\mathcal{E}^2}{\mathcal{E}^2_{\max}}\right), \end{equation*}$

cioè

(54) $\begin{equation*} i(t)=\pm \dfrac{\mathcal{E}_{\max}}{\omega L }\sqrt{\left(1-\dfrac{\mathcal{E}^2}{\mathcal{E}^2_{\max}}\right)}. \end{equation*}$

Essendo la tensione e la corrente sfasate di $\dfrac{\pi}{2}$ , entrambe di periodo $2\pi$ , si deduce che la corrente è negativa nell’istante $t$ in cui la tensione vale $\mathcal{E}=-12,5\,\text{V}$ , quindi

(55) $\begin{equation*} i(t)=- \dfrac{1}{\omega L }\sqrt{\left(\mathcal{E}_{\max}^2 -\mathcal{E}^2\right)}\approx\text{-4,52}\,\text{A}. \end{equation*}$

Si conclude che

$\boxcolorato{fisica}{ \mathcal{E}=-\text{12,5}\,\text{V}\quad \Rightarrow \quad i(t) \approx-\text{4,52}\,\text{A}.}$

Esercizio 11 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare la corrente $i_{\max}$ che può erogare un generatore con $V_{\max}=50\,\text{V}$ e $\nu=50\,\text{Hz}$ quando è collegato ai capi di un condensatore $C=\text{3,7}\,\mu \text{F}$ .

Svolgimento.

Ipotizziamo che la differenza di potenziale ai capi del generatore sia

(56) $\begin{equation*} V=V_{\max}\sin \left(\omega t +\phi\right), \end{equation*}$

dove $\omega$ è la pulsazione e $\phi$ la fase iniziale.

Allora, sapendo che $i=C\,\dfrac{dV}{dt}$ , si ha

(57) $\begin{equation*} i=\omega\, C \,V_{\max} \cos \left(\omega t +\phi \right), \end{equation*}$

e quindi

(58) $\begin{equation*} i_{\max}=\omega\, C \,V_{\max}, \end{equation*}$

cioè la corrente massima è uguale alla pulsazione per la capacità del condensatore e la tensione massima ai capi del generatore di tensione (risulta chiaro che la differenza di potenziale ai capi del condensatore è la stessa del generatore). Ricordando che $\omega =2\pi \nu$ si ha

(59) $\begin{equation*} i_{\max}=\omega\, C \,V_{\max}=2\pi \nu\, C \,V_{\max}, \end{equation*}$

cioè

$\boxcolorato{fisica}{ i_{\max}=2\pi \nu\, C \,V_{\max}\approx58\,\text{mA}.}$

Esercizio 12 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito puramente capacitivo $C=20\,\mu \text{F}$ , il generatore ha una tensione massima $V_{\max}=200\,\text{V}$ e $\omega=100\pi\,\text{rad/s}$ . Ipotizzando il condensatore scarico determinare l’intensità di corrente $i$ all’istante $t=\text{0,004}\,\text{s}$ .

Svolgimento.

Ipotizziamo che la differenza di potenziale ai capi del generatore sia

(60) $\begin{equation*} V(t)=V_{\max}\sin\left(\omega t + \phi\right), \end{equation*}$

dove $\omega$ è la pulsazione e $\phi$ la fase iniziale. La tensione $V(t)$ è la stessa ai capi del condensatore per la geometria del circuito, e essendo il condensatore scarico all’istante $t=0\,\text{s}$ , ne segue che $V(0)=V_{\max}\sin\left(\phi\right)=\dfrac{q(0)}{C}=0\,\text{V}$ , cioè $\phi=0\,\text{rad}$ , e quindi

(61) $\begin{equation*} V(t)=V_{\max}\sin\left(\omega t \right). \end{equation*}$

Sapendo che

(62) $\begin{equation*} i(t)=C\,\dfrac{dV}{dt}=C\omega V_{\max}\cos\left(\omega t \right), \end{equation*}$

posto $t=t_1=\text{0,04}\,\text{s}$ si trova

$\boxcolorato{fisica}{ i(t_1)=C\omega V_{\max}\cos\left(\omega t_1 \right)\approx \text{0,39}\,\text{A}.}$

Esercizio 13 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Un generatore di tensione alternata con $V_{\max}=200\,\text{V}$ è collegato ad un condensatore $C=2\,\mu \text{F}$ . Calcolare la frequenza $\nu$ del generatore per erogare la corrente massima $i_{\max}=4\,\text{A}$ .

Svolgimento.

Dalla soluzione dell’esercizio 11 concludiamo con la seguente soluzione

$\boxcolorato{fisica}{ \nu={i_{\max}\over2\pi\, C V_{\max} }=795\,\text{Hz}.}$

Esercizio 14 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un generatore di tensione alternata $V=V_{\max}\sin(\omega t)$ con $V_{\max}=25\, \text{V}$ e $\omega=377\,\text{rad/s}$ è collegato ad un condensatore $C=\text{4,2}\,\mu \text{F}$ . Calcolare:

la corrente $i_{\max}$ ;
la tensione $V$ ai capi del condensatore quando la corrente è massima;
il valore della corrente $i$ quando il valore della tensione è $V=-\text{12,5}\,\text{V}$ e sta aumentando.

Svolgimento punto 1.

Dalla soluzione dell’esercizio 11 concludiamo con la seguente soluzione.

$\boxcolorato{fisica}{ i_{\max}=\omega\, C \,V_{\max}=\text{39,6}\,\text{mA}.}$

Svolgimento punto 2.

Un condensatore introduce uno sfasamento tra d.d.p. e corrente di $-\pi/2$ , di conseguenza quando la corrente è massima la d.d.p. è nulla.

Svolgimento punto 3.

Sapendo che

(63) $\begin{equation*} i=C\dfrac{dV}{dt}=\omega \,C\,V_{\max}\, \cos\left(\omega t\right), \end{equation*}$

e elevando al quadrato ambo i membri di quest’ultima relazione, si ottiene

(64) $\begin{equation*} i^2=\omega^2 \,C^2\,V^2_{\max}\, \cos^2\left(\omega t\right), \end{equation*}$

da cui

(65) $\begin{equation*} i^2=\omega^2 \,C^2\,V^2_{\max}\,\left(1-\sin^2\left(\omega t\right)\right)=\omega^2 \,C^2\,V^2_{\max}\,\left(1-\dfrac{V^2}{V_{\max}}\right)=\omega^2\,C^2\left(V^2_{\max}-V^2\right). \end{equation*}$

Pertanto sostituendo $V=-\text{12,5}\,\text{V}$ si ottiene

$\boxcolorato{fisica}{ i=\omega\,C\left(V^2_{\max}-V^2\right)^{\frac{1}{2}}\approx\text{0,034}\,\text{A}.}$

Esercizio 15 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare:

la frequenza $\nu$ alla quale un induttore $L=6\, \text{mH}$ e un condensatore $C= 10\,\mu \text{F}$ hanno la stessa reattanza;
la reattanza $X_{CL}$ della serie $LC$ a questa frequenza.

Svolgimento punto 1.

La reattanza di un condensatore è negativa mentre quella di un induttore è positiva, quindi possiamo trovare la frequenza $\nu$ tale per cui le reattanze sono uguali in valore assoluto

(66) $\begin{equation*} |X_{L}|=|X_{C}| \quad\Rightarrow\quad|\omega L|=\bigg|-{1\over \omega C}\bigg| \quad\Rightarrow\quad 2\pi\nu L = {1\over 2\pi\nu C}, \end{equation*}$

dove abbiamo usato l’informazione $\omega=2\pi\nu$ . Concludiamo con la seguente soluzione, ovvero abbiamo trovato la frequenza naturale del circuito in serie $LC$

$\boxcolorato{fisica}{\nu={1\over 2\pi\sqrt{LC}}=650\,\text{Hz}.}$

Svolgimento punto 2.

La reattanza del circuito $LC$ è la somma algebrica delle singole reattanze

(67) $\begin{equation*} X_{LC}=X_{L}+X_{C}, \end{equation*}$

tuttavia, alla frequenza calcolata nel punto precedente, abbiamo che $X_{L}=-X_{C}$ . Concludiamo quindi che a questa frequenza la reattanza è nulla:

$\boxcolorato{fisica}{X_{LC}=0.}$

Esercizio 16 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un condizionatore d’aria collegato alla rete $\mathcal{E}_\text{eff}= 220\,\text{V}$ è equivalente ad una resistenza $R=40\,\Omega$ e ad una reattanza induttiva $X_L =6\,\Omega$ in serie. Calcolare:

l’impedenza $Z$ del condizionatore;
la potenza media $\mathcal{P}_m$ utilizzata durante il funzionamento.

Svolgimento punto 1.

Il condizionatore è equivalente ad un resistenza, di impedenza puramente reale

(68) $\begin{equation*} Z_R=R \end{equation*}$

in serie ad un induttore avente reattanza induttiva nota (ricordiamo che la reattanza è la parte immaginaria dell’impedenza complessa e che l’impedenza di un induttore è puramente immaginaria)

(69) $\begin{equation*} Z_L=j X_L. \end{equation*}$

Essendo in serie l’impedenza totale del condizionatore non è altro che la somma delle due impedenze calcolate precedentemente. Concludiamo con la seguente soluzione

$\boxcolorato{fisica}{Z=Z_R+Z_L=R+j X_L ;\qquad |Z|=\sqrt{R^2+X_L^2}=\text{40,4} \,\Omega.}$

Svolgimento punto 2.

È noto che

(70) $\begin{equation*} P_m=R\, i_\text{eff}^2, \end{equation*}$

dove

(71) $\begin{equation*} i_\text{eff}={i_0\over \sqrt{2}} \end{equation*}$

e in particolare $i_0$ è il valore massimo assunto dalla corrente. Calcoliamo la corrente massima, essa non è altro che il rapporto tra la tensione massima con il modulo dell’impedenza complessa (prima legge di Ohm generalizzata al caso complesso), cioè

(72) $\begin{equation*} i_{0}={\mathcal{E}_0\over |Z|}={\mathcal{E}_\text{eff}\sqrt{2}\over |Z|}. \end{equation*}$

Possiamo calcolare ora la corrente efficace e di conseguenza la potenza media. Concludiamo con la seguente soluzione:

$\boxcolorato{fisica}{\mathcal{P}_m=R\bigg({\mathcal{E}_\text{eff}\over |Z|}\bigg)^2\approx1186\,\text{W}.}$

Esercizio 17 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito $RLC$ in serie, $R=20\,\Omega$ , $L=25\,\text{mH}$ , $C=20\,\mu \text{F}$ , $\mathcal{E}_{\max}=150\,\text{V}$ e $\nu=100\,\text{Hz}$ . Calcolare:

la corrente $i_{\max}$ nel circuito;
la tensione massima $V_i$ ai capi di ciascun elemento;
il fattore di potenza $\cos \phi$ del circuito ;
la potenza media $\mathcal{P}_m$ dissipata.

Figura 4: dettaglio schema esercizio 17

Svolgimento punto 1.

Calcoliamo l’impedenza complessa equivalente del circuito, per la resistenza questa vale $Z_R=R$ . Per gli altri due elementi del circuito abbiamo invece

(73) $\begin{equation*} Z_L={j\omega L},\qquad\qquad Z_C = -{j\over \omega C}, \qquad\qquad \omega =2\pi \nu. \end{equation*}$

Il circuito RLC è in serie, quindi sommiamo le varie impedenze ottenendo

(74) $\begin{equation*} Z=R+j\bigg(\omega L-{1\over \omega C}\bigg), \qquad\qquad |Z|=\sqrt{R^2+\bigg(\omega L -{1\over \omega C}\bigg)^2}\approx\text{66,93}\, \Omega. \end{equation*}$

A questo punto utilizziamo la legge di Ohm ai capi dell’impedenza $Z$ e otteniamo la corrente massima nel circuito:

$\boxcolorato{fisica}{ i_{\max}={\mathcal{E}_{\max}\over |Z|}=\text{2,24}\,\text{A}.}$

Svolgimento punto 2.

Il circuito è in serie, quindi passa la medesima corrente massima su ciascun componente. Utilizziamo anche in questo caso la prima legge di Ohm generalizzata, tuttavia dobbiamo prendere per ciascun componente il modulo della sua impedenza. Possiamo calcolare in questo modo la tensione massima $V_R$ , $V_C$ e $V_L$ su ciascun componente

$\boxcolorato{fisica}{ V_R=|Z_R|i_{\max}=R \,i_{\max}\approx\text{44,8}\,\text{V}; \qquad V_C=|Z_C|i_{\max}={1\over \omega C}\,i_{\max}\approx\text{178,3}\,\text{V};}$

$\boxcolorato{fisica}{ V_L=|Z_L|i_{\max}=\omega L \,i_{\max}\approx \text{35,2}\,\text{V}. }$

Svolgimento punto 3.

Il fattore di potenza è il coseno dell’angolo $\phi$ che forma l’impedenza complessa nel piano complesso con l’asse reale. Dalla trigonometria ricaviamo che

(75) $\begin{equation*} \left \vert z \right \vert \cos \phi=R, \end{equation*}$

da cui

$\cos \phi=\dfrac{R}{\sqrt{R^2+\left(\omega L-\dfrac{1}{\omega C}\right)^2}}=\dfrac{R}{\sqrt{R^2+\left(2\pi \nu L-\dfrac{1}{2\pi \nu C}\right)^2}},$

cioè

$\boxcolorato{fisica}{ \cos \phi\approx\text{0,3}\,\text{rad},}$

dove nell’ultimo passaggio abbiamo sostituito i valori numerici.

Svolgimento punto 4.

La potenza media sviluppata la si calcola utilizzando la corrente efficace

(76) $\begin{equation*} \mathcal{P}_m= R\,i_\text{eff}^2=R\bigg({i_{\max}\over \sqrt{2}}\bigg)^2, \end{equation*}$

cioè

$\boxcolorato{fisica}{ \mathcal{P}_m \approx\text{50,2}\,\text{W},}$

dove nell’ultimo passaggio abbiamo sostituito i valori numerici.

Esercizio 18 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito $RLC$ in serie, $R=50\,\Omega$ , $L=150 \,\text{mH}$ , $C=4\,\mu \text{F}$ , $\mathcal{E}_\text{eff}=220\,\text{V}$ e $\nu=50\,\text{Hz}$ . Calcolare:

la corrente efficace $i_\text{eff}$ nel circuito;
la tensione efficace $V_i$ ai capi di ciascun elemento;
la tensione efficace $V_{LC}$ ai capi della serie $LC$ .

Svolgimento punto 1.

La soluzione è molto simile al problema precedente. Calcoliamo prima l’impedenza complessa

(77) $\begin{equation*} Z=R+j\bigg(\omega L-{1\over \omega C}\bigg) \qquad\qquad |Z|=\sqrt{R^2+\bigg(\omega L -{1\over \omega C}\bigg)^2}=750\, \Omega. \end{equation*}$

Di conseguenza troviamo la corrente massima, utilizzando la legge di Ohm

(78) $\begin{equation*} i_\text{eff}={\mathcal{E}_\text{eff}\over |Z|}, \end{equation*}$

cioè

$\boxcolorato{fisica}{ i_\text{eff} \approx\text{0,293}\,\text{A} ,}$

dove nell’ultimo passaggio abbiamo sostituito i valori numerici.

Svolgimento punto 2.

Analogamente all’esercizio precedente troviamo che (utilizzando $\omega=2\pi\nu$ )

$\boxcolorato{fisica}{V_{R,\text{eff}}={R} \,i_{\text{eff}}\approx\text{14,65}\,\text{V}, \qquad V_{C,\text{eff}}={i_{\text{eff}}\over\omega C}\approx\text{233,2}\,\text{V}}$

$\boxcolorato{fisica}{ V_{L,\text{eff}}=\omega L \,i_{\text{eff}}\approx\text{13,8}\,\text{V}.}$

L’impedenza complessa risulta

(79) $\begin{equation*} Z_{LC}=+j\bigg(\omega L-{1\over \omega C}\bigg) \qquad\qquad |Z_{LC}|=\bigg|\omega L -{1\over \omega C}\bigg|=749\, \Omega. \end{equation*}$

Ne segue che la tensione efficace ai capi della serie LC è data da

$\boxcolorato{fisica}{ V_{LC,\text{eff}}={1\over \sqrt{2}}|Z_LC|i_{\max}=|Z_{LC}|i_{\text{eff}}=\text{219,5}\,\text{V}.}$

Esercizio 19 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Una bobina di resistenza $R=35\, \Omega$ e induttanza $L=20\,\text{mH}$ è in serie con un condensatore $C$ ed un generatore con $\mathcal{E}_{\text{eff}}=200\,\text{V}$ e frequenza $\nu=100\,\text{Hz}$ , che eroga una corrente $i_{\text{eff}}= 4\,\text{A}$ . Calcolare:

la capacità $C$
la tensione efficace $V_{\text{eff}}$ ai capi della bobina;
la potenza media $\mathcal{P}_{m}$ dissipata dalla stessa.

Svolgimento punto 1.

Una bobina è una componente RL in serie in un circuito, quindi abbiamo un circuito in serie RLC la cui impedenza complessa è nota

(80) $\begin{equation*} Z=R+j\bigg(\omega L-{1\over \omega C}\bigg) \qquad\qquad |Z|=\sqrt{R^2+\bigg(\omega L -{1\over \omega C}\bigg)^2}. \end{equation*}$

Conosciamo la tensione efficace $\mathcal{E}_{\text{eff}}$ e anche la corrente efficace $i_{\text{eff}}$ . Utilizzando la legge di Ohm generalizzata possiamo calcolare il modulo dell’impedenza complessa

(81) $\begin{equation*} |Z|={\mathcal{E}_{\text{eff}}\over i_{\text{eff}}}=50\,\Omega. \end{equation*}$

Da (80) e utilizzando il fatto che $\omega=2\pi \nu$ possiamo ricavare la capacità $C$ del condensatore

(82) $\begin{equation*} |Z|=\sqrt{R^2+\bigg(\omega L -{1\over \omega C}\bigg)^2} \quad \Leftrightarrow \quad |Z|^2-R^2=\bigg(\omega L -{1\over \omega C}\bigg)^2 , \end{equation*}$

da cui otteniamo

(83) $\begin{equation*} \sqrt{|Z|^2-R^2}=\bigg|\omega L -{1\over \omega C}\bigg|. \end{equation*}$

Consideriamo i due casi separati, nel primo l’argomento del modulo è positivo, ovvero

(84) $\begin{equation*} \omega L -{1\over \omega C}\geq 0 \quad \Leftrightarrow \quad C\geq {1\over \omega^2L}={1\over 4\pi^2\nu^2L}=\text{1,27}\cdot 10^{-4}\,\text{F}. \end{equation*}$

L’equazione (82) diventa così

(85) $\begin{align*} \sqrt{|Z|^2-R^2}&=\omega L -{1\over \omega C} \quad \iff \quad C={1\over 2\pi\nu}\bigg(2\pi\nu L-\sqrt{|Z^2|-R^2}\bigg)^{-1}=-\text{6,88}\cdot 10^{-5}\,\text{F}. \end{align*}$

Il risultato non è accettabile, dal punto di vista fisico perché una capacità negativa è priva di senso, e inoltre dal punto di vista matematico perché non soddisfa la disuguaglianza (84). Consideriamo il caso dove l’argomento del modulo è negativo, in questo caso abbiamo

(86) $\begin{equation*} \omega L -{1\over \omega C}\leq 0\quad \Leftrightarrow \quad C\leq {1\over \omega^2L}={1\over 4\pi^2\nu^2L}=\text{1,27}\cdot 10^{-4}\,\text{F}, \end{equation*}$

da cui otteniamo

(87) $\begin{align*} \sqrt{|Z|^2-R^2}&=-\omega L +{1\over \omega C}\quad \Leftrightarrow \quad C={1\over 2\pi\nu}\bigg(2\pi\nu L+\sqrt{|Z^2|-R^2}\bigg)^{-1}=\text{3,3}\cdot 10^{-5}\,\text{F}, \end{align*}$

che è accettabile in quanto verifica (86) . Concludiamo quindi con la seguente soluzione

$\boxcolorato{fisica}{ C={1\over 2\pi\nu}\bigg(2\pi\nu L+\sqrt{|Z^2|-R^2}\bigg)^{-1}\approx\text{3,3}\cdot 10^{-5}\,\text{F}.}$

Svolgimento punto 2.

Il modulo dell’impedenza complessa della bobina è dato da

(88) $\begin{equation*} Z_{bobina}=R+j\omega L \qquad\qquad |Z_{bobina}|=\sqrt{R^2+\omega^2 L^2}=\text{37,18}\,\Omega \end{equation*}$

La corrente efficace è la stessa su ogni parte del circuito, essendo questo un’unica maglia. Utilizziamo quindi la prima legge di Ohm generalizzata per trovare la tensione efficace ai capi della bobina

$\boxcolorato{fisica}{ V_{\text{eff}}=|Z_{bobina}| i_{\text{eff}}\approx\text{148,7}\,\text{V}.}$

Svolgimento punto 3.

La potenza media dissipata dalla bobina è la potenza media dissipata dalla resistenza al suo interno, abbiamo quindi (utilizzando la corrente efficace)

$\boxcolorato{fisica}{\mathcal{P}_m=R\,i_{\text{eff}}^2=560\,\text{W}.}$

Esercizio 20 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito $RLC$ in serie $i_{\text{eff}}=9\,\text{A}$ , $\mathcal{E}_{\text{eff}}=180\,\text{V}$ e la corrente è in anticipo di $\phi=37^\circ$ rispetto alla tensione. Calcolare:

la resistenza $R$ del circuito;
la reattanza $X_{LC}$ della serie LC;
la potenza media $\mathcal{P}_m$ dissipata.

Svolgimento punto 1.

Conoscendo la corrente efficace e la tensione efficace possiamo calcolare il modulo dell’impedenza complessa come segue

(89) $\begin{equation*} |Z|={\mathcal{E}_{\text{eff}}\over i_{\text{eff}}}= 20\,\Omega. \end{equation*}$

Si osserva che

(90) $\begin{equation*} Z=\dfrac{V}{I}=\dfrac{|V|e^{j\,\theta_V}}{|I|e^{j\,\theta_I}}=\dfrac{|V|}{|I|}e^{j\left(\theta_V-\theta_I\right)}, \end{equation*}$

dove $\theta_V$ è l’angolo che forma il fasore della tensione con l’asse reale e $\theta_I$ è l’angolo che forma il fasore della corrente con l’asse reale; in particolare si osserva che $\theta_V-\theta_I=\phi$ , pertanto conosciamo il fattore di potenza $\cos \phi$ , da cui

$\boxcolorato{fisica}{R=|Z|\cos\phi =\text{15,97}\,\Omega.}$

Svolgimento punto 2.

Sapendo che $Z_{L}=j X_{L}$ e $Z_{C}=j X_{C}$ (conduttore e induttanza hanno solo impedenza immaginaria) possiamo scrivere l’impedenza complessa come

(91) $\begin{equation*} Z=R+ j X_{C}+j X_{L}=R+j X_{LC} \qquad\Rightarrow\qquad |Z|^2=R^2+X_{LC}^2, \end{equation*}$

da cui

$\boxcolorato{fisica}{X_{LC}=\sqrt{|Z^2|-R^2}=\text{12,04}\,\Omega.}$

Svolgimento punto 3.

La potenza media dissipata è data dalla seguente formula

$\boxcolorato{fisica}{ D=1294\,\text{W} ,}$

$\boxcolorato{fisica}{ \mathcal{P}_{m}=\mathcal{E}_{\text{eff}}\,i_{\text{eff}}\,\cos \phi=1294\,\text{W}.}$

Esercizio 21 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Nel circuito di figura il generatore fornisce una tensione $\mathcal{E}_{\text{eff}}= 220\,\text{V}$ alla frequenza $\nu=50\,\text{Hz}$ . Con l’interruttore aperto l’amperometro $A$ misura una corrente efficace $i_{1,\text{eff}}=\text{6,22}\, \text{A}$ , con l’interruttore chiuso $i_{2,\text{eff}}=\text{7,78}\, \text{A}$ . Calcolare:

l’induttanza $L$ ;
la resistenza $R$ ;
la potenza media $\mathcal{P}_m$ dissipata con l’interruttore aperto.

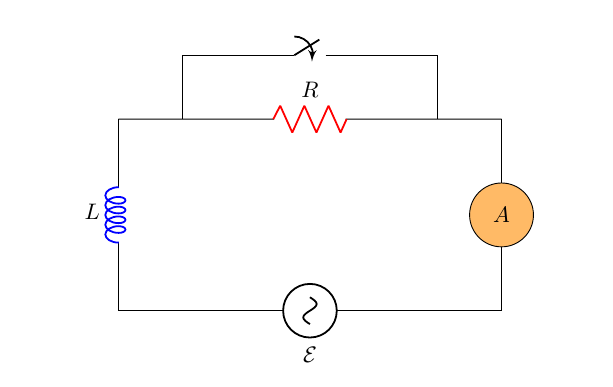
Figura 5: dettaglio schema esercizio 21.

Svolgimento punto 1.

Con l’interruttore aperto il circuito è un RL la cui impedenza complessa è data da

(92) $\begin{equation*} Z_1=R+j\omega L \qquad |Z_1|=\sqrt{R^2+\omega^2L^2}. \end{equation*}$

Chiudendo il circuito la resistenza $R$ viene circuitata (la corrente evita completamente di scorrere nel filo con resistenza $R$ passando per il filo con resistenza nulla), pertanto può essere esclusa dal circuito, e abbiamo quindi un circuito puramente induttivo $L$ la cui impedenza è data da

(93) $\begin{equation*} Z_{2}=j\omega L \qquad|Z_2|=\omega L. \end{equation*}$

Conosciamo la tensione efficace (che rimane la stessa per entrambi i circuiti, dato che l’interruttore non va ad influire sulla forza elettromotrice del generatore) e la corrente efficace $i_{2,\text{eff}}$ del circuito $L$ . Possiamo allora calcolare l’impedenza $L$

$\boxcolorato{fisica}{L={|Z_2|\over 2\pi\nu}={1\over 2\pi \nu}\cdot{\mathcal{E}_{\text{eff}}\over i_{2,\text{eff}}}\approx\text{0,090}\,\text{H}.}$

Svolgimento punto 2.

Da (92) possiamo ricavare $R$ , infatti conosciamo ora $L$ e possiamo calcolare $|Z_1|$ come

(94) $\begin{equation*} |Z_1|={\mathcal{E}_{\text{eff}}\over i_{1,\text{eff}}}, \end{equation*}$

da cui

$\boxcolorato{fisica}{R=\sqrt{|Z_1|^2-\omega^2L^2}=\sqrt{\bigg({\mathcal{E}_{\text{eff}}\over i_{1,\text{eff}}}\bigg)^2-4\pi^2\nu^2L^2}\approx\text{21,3}\,\Omega.}$

Svolgimento punto 3.

La potenza dissipata con l’interruttore aperto è data da

$\boxcolorato{fisica}{ \mathcal{P}_{m}\approx R\,i_{2,\text{eff}}^2\approx824\,\text{W}.}$

Esercizio 22 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito $RLC$ in serie ha $R=50\,\Omega$ , $L=200\,\text{mH}$ , $\nu=50\,\text{Hz}$ e $\mathcal{E}_{\max}=110\,\text{V}$ . Calcolare:

il valore della capacità $C$ per cui la potenza media $\mathcal{P}_m$ dissipata è massima;
il corrispondente valore di $\mathcal{P}_m$ ;
il fattore di potenza $\cos \phi$ .

Svolgimento punto 1.

La potenza media dissipata $\mathcal{P}_m$ ha una relazione quadratica con la corrente efficace $i_{\text{eff}}$ e quest’ultima, grazie alla legge di Ohm generalizzata, è inversamente proporzionale al modulo dell’impedenza complessa.

(95) $\begin{align*} \mathcal{P}_m\propto i_{\text{eff}}^2 && i_{\text{eff}}\propto {1\over |Z|}. \end{align*}$

Per massimizzare la potenza media dissipata dobbiamo quindi minimizzare il modulo dell’impedenza complessa. Questo si ottiene, in condizioni ideali, quando le reattanza è nulla, ovvero quando siamo in condizione di risonanza, che per un circuito RLC vale

(96) $\begin{equation*} \omega L ={1\over \omega C}. \end{equation*}$

Concludiamo con la seguente soluzione

$\boxcolorato{fisica}{C={1\over \omega^2 L}={1\over 4\pi\nu^2 L}\approx\text{5,1}\cdot 10^{-5}\,\text{F}.}$

Svolgimento punto 2.

In condizione di risonanza l’impedenza è puramente reale e vale (per un circuito RLC) $Z=R$ . Utilizziamo la legge di Ohm per calcolare la corrente efficace

(97) $\begin{equation*} i_{\text{eff}}={i_{\max}\over \sqrt{2}}={1\over \sqrt{2}}{\mathcal{E}_{\max}\over R}\approx 1,56\,\text{A}, \end{equation*}$

da cui

$\boxcolorato{fisica}{\mathcal{P}_m=R\,i_{\text{eff}}^2\approx121\,\text{W}.}$

Svolgimento punto 3.

In condizione di risonanza il fattore di potenza è massimo

$\boxcolorato{fisica}{ \cos \phi =1;}$

infatti la reattanza dell’impedenza complessa è nulla, quindi l’angolo $\phi$ che l’impedenza forma nel piano complesso è nullo. Analogamente si può vedere con la seguente relazione

(98) $\begin{equation*} \cos\phi = {R\over |Z|}={R\over R}=1. \end{equation*}$

Esercizio 23 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . In un circuito $RLC$ , con $L=14\,\mu \text{H}$ , è utilizzato per sintonizzare il segnale di una stazione radio trasmittente FM con $\nu=\text{103,2}\,\text{MHz}$ . Calcolare la capacità $C$ del circuito.

Svolgimento.

Per sintonizzare il segnale di una radio trasmittente è necessario che quest’ultima risponda al segnale di ingresso con la massima efficienza. Questo si ottiene quando la frequenza di risonanza del circuito è la stessa del segnale d’ingresso. Data l’induttanza $L$ , dobbiamo quindi aggiungere un condensatore $C$ al circuito RLC in modo tale da ottenere una frequenza di risonanza pari a $2\pi\nu$ . Concludiamo con la seguente soluzione

$\boxcolorato{fisica}{ C={1\over \omega^2L}\approx{1\over 4\pi^2\nu^2 L}=\text{1,7}\,\text{pF}.}$

Esercizio 24 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un trasformatore ideale ha $N_p=200$ spire e $N_s=1500$ spire. Se la tensione nel primario è $V_p=310\sin(\omega t)\,\text{V}$ , calcolare la tensione efficace $V_{s,\text{eff}}$ nel secondario.

Rendered by QuickLaTeX.com

Figura 6: schema problema 24

Svolgimento.

Facendo scorrere una certa corrente alternata $i(t)$ nel primario, si induce una tensione $V_p(t)$ che per un numero $N_p$ di spire, secondo la legge di Faraday-Neumann, varrà

(99) $\begin{equation*} V_p(t)=-N_p\dfrac{\text{d}\phi(\vec{B})}{\text{d}t}, \end{equation*}$

dove $\Vec{B}$ è il vettore campo magnetico che viene indotto dalla corrente $i(t)$ che scorre lungo una spira dell’avvolgimento primario $n$ e $\phi(\vec{B})$ è il flusso di questo campo attraverso la bobina. Sappiamo che un trasformatore è un dispositivo costruito in modo da far sì che la maggior parte del flusso di campo magnetico non venga disperso e dunque viaggi indisturbato all’interno del conduttore. Nel secondario avremo dunque, sempre sfruttando la legge di Faraday-Neumann, che la tensione $V_s(t)$ è

(100) $\begin{equation*} V_s(t)=-N_s\dfrac{\text{d}\phi(\vec{B})}{\text{d}t}, \end{equation*}$

dove, per quanto è stato detto, la variazione di flusso $\text{d}\phi(\vec{B})/\text{d}t$ sarà proprio quella generata dal primario. Pertanto, possiamo dividere tra di loro la (99) e la (100) ottenendo così

(101) $\begin{equation*} \dfrac{V_p(t)}{V_s(t)}=\dfrac{N_p}{N_s}\quad\Leftrightarrow\quad V_s(t)=V_p(t)\dfrac{N_s}{N_p}. \end{equation*}$

Sostituendo i dati forniti dal problema, otteniamo dunque la seguente espressione per la tensione nell’avvolgimento secondario

(102) $\begin{equation*} V_s(t)=2325\sin(\omega t)\,\text{V}. \end{equation*}$

Dunque, dal momento che $V_{s,\,\max}=2325 \ \text{V}$ , possiamo trovare la tensione efficace del secondario

$\boxcolorato{fisica}{V_{s,\text{eff}}=\dfrac{V_{s,\,\max}}{\sqrt{2}}=1650 \ \text{V}.}$

Esercizio 25 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Un trasformatore ideale ha $N_p=500$ spire e $N_s=10$ spire. Il primario è collegato ad un generatore di tensione alternata con tensione efficace $V_{p,\text{eff}}=120 \ \text{V}$ . Calcolare:

la tensione $V_{s,\text{eff}}$ in uscita ai capi del secondario aperto.

Se il secondario è chiuso su un resistore $R=20 \ \Omega$ , calcolare:

la corrente efficace $i_{p,\text{eff}}$ del primario;
la corrente efficace $i_{s,\text{eff}}$ nel secondario.

Rendered by QuickLaTeX.com

Figura 7: schema problema 25.

Svolgimento punto 1.

Con un procedimento del tutto analogo a quello del problema 24 possiamo concludere che la tensione nel primario e nel secondario in un trasformatore sono legate tra loro dall’equazione (101), ossia

(103) $\begin{equation*} V_s(t)=V_p(t)\dfrac{N_s}{N_p}. \end{equation*}$

Notiamo quindi che, essendo il rapporto $N_s/N_p$ una costante, la funzione $V_s(t)$ assumerà un massimo quando la $V_p$ sarà massima (le due funzioni sono in fase), ovvero

(104) $\begin{equation*} V_{s,\,\max}=V_{p,\,\max}\dfrac{N_s}{N_p}. \end{equation*}$

Dividendo entrambi i membri per $\sqrt{2}$ si ottengono le grandezze efficaci

(105) $\begin{equation*} \dfrac{V_{s,\,\max}}{\sqrt{2}}=\dfrac{V_{p,\,\max}}{\sqrt{2}}\cdot\dfrac{N_s}{N_p}\quad\Leftrightarrow\quad V_{s,\text{eff}}=V_{p,\text{eff}}\dfrac{N_s}{N_p}. \end{equation*}$

Concludiamo il problema con la seguente soluzione

$\boxcolorato{fisica}{V_{s,\text{eff}}=\text{2,4} \ \text{V}.}$

Osservazione.

Abbiamo ottenuto le tensioni efficaci dividendo per $\sqrt{2}$ entrambi i membri della (105). Ma attenzione, questo vale solo per grandezze sinusoidali. Il problema non assicura che la corrente sia sinusoidale, pertanto entrando nel dettaglio, per ottenere una grandezza efficace si deve calcolare una media integrale quadratica, cioè

(106) $\begin{equation*} V_{\text{eff}}=\sqrt{{1\over T}\int_0^T V^2(t)\,dt} \qquad T:\,\text{periodo}, \end{equation*}$

da cui

(107) $\begin{equation*} V_{s}(t)={V_{p}(t)}\dfrac{N_s}{N_p}\qquad \Rightarrow\qquad \sqrt{{1\over T}\int_0^T V_s^2(t)} = {N_s\over N_p}\sqrt{{1\over T}\int_0^T V_p^2(t)}, \end{equation*}$

da cui

(108) $\begin{equation*} V_{s,\text{eff}}=\dfrac{N_s}{N_p}{V_{p,\text{eff}}}. \end{equation*}$

Possiamo integrare sul medesimo periodo in quanto le due funzioni $V_{p}(t)$ e $V_{s}(t)$ differiscono soltanto per una costante moltiplicativa. La seguente relazione vale quindi per qualsiasi segnale periodico

(109) $\begin{equation*} V_{s,\text{eff}}=\dfrac{N_s}{N_p}V_{p,\text{eff}}\qquad \text{Sempre}; \end{equation*}$

mentre la relazione che lega il valore massimo da quello efficace con un fattore $\sqrt{2}$ vale solo per grandezze sinusoidali

(110) $\begin{equation*} V_{\text{eff}}={V_{\max}\over \sqrt{2}} \qquad\text{Solo grandezze sinusoidali}. \end{equation*}$

Svolgimento punto 2.

In un trasformatore ideale , sappiamo che la potenza in entrata sarà uguale alla potenza in uscita, cioè si conserva la potenza . Sapendo che la potenza vale

(111) $\begin{equation*} \mathcal{P}(t)=V(t)i(t), \end{equation*}$

possiamo scrivere, considerando il valore medio di potenza e le grandezze efficaci (sostituiamo per comodità la scritta $i_{\text{eff}}=\tilde{i}$ )

(112) $\begin{equation*} \mathcal{P}_{p,m}=\mathcal{P}_{s,m}\quad\Leftrightarrow\quad \tilde{V}_p\tilde{i}_p=\tilde{V}_s\tilde{i}_s\quad\Leftrightarrow\quad \frac{\tilde{V}_p}{\tilde{V}_s}=\frac{\tilde{i}_s}{\tilde{i}_p}=\frac{N_p}{N_s}=k, \end{equation*}$

dove è stata sfruttata la (101) per ricavare il rapporto $k$ tra la corrente che scorre secondario e quella che scorre nel primario. A questo punto, sappiamo che l’impedenza $Z_s=R$ in quanto il testo suggerisce che è il secondario ad essere chiuso sul resistore; per trovare la corrente $i_p$ dobbiamo dunque trovare l’impedenza $Z_p$ , ossia l’impedenza vista ai capi del generatore di tensione. Dalla legge di Ohm avremo dunque

(113) $\begin{equation*} Z_p=\frac{\tilde{V}_p}{\tilde{i}_p} \end{equation*}$

dove dalla (112) sappiamo che $\tilde{V}_p=k\,\tilde{V}_s$ e che $\tilde{i}_p={\tilde{i}_s}/{k}$ . Dunque otteniamo

(114) $\begin{equation*} Z_p=\dfrac{k\,\tilde{V}_s}{\dfrac{\tilde{i}_s}{k}}=k^2 \dfrac{\tilde{V}_s}{\tilde{i}_s}. \end{equation*}$

Il rapporto ${\tilde{V}_s}/{\tilde{i}_s}$ è uguale proprio all’impedenza $Z_s$ , dunque in definitiva scriviamo

(115) $\begin{equation*} Z_p=k^2Z_s=\left(\dfrac{N_p}{N_s}\right)^2R. \end{equation*}$

Possiamo ora dunque trovare la corrente che scorre nel primario; facendo riferimento alla (113)

(116) $\begin{equation*} \tilde{i}_p=\dfrac{\tilde{V}_p}{Z_p}=\dfrac{\tilde{V}_p}{R}\left(\dfrac{N_s}{N_p}\right)^2, \end{equation*}$

da cui, sostituendo i dati numerici del problema, otteniamo

$\boxcolorato{fisica}{\tilde{i}_p=\text{2,4}\ \text{mA}.}$

Svolgimento punto 3.

Una volta trovata la corrente $\tilde{i}_p$ possiamo semplicemente applicare la (112). Concludiamo con la seguente soluzione

$\boxcolorato{fisica}{\tilde{i}_s=\tilde{i}_p\dfrac{N_p}{N_s}=\text{0,12} \ \text{A}}$

Esercizio 26 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un trasformatore ideale in salita è progettato per fornire una tensione efficace in uscita $V_{s,\text{eff}}=2200 \ \text{V}$ , quando il primario è collegato alla rete elettrica $V_{p,\text{eff}}=220 \ \text{V}$ . Se nell’avvolgimento primario ci sono $N_p=70$ spire, calcolare:

le spire $N_s$ del secondario;
la corrente $i_{p,\text{eff}}$ del primario se il secondario è percorso dalla corrente $i_{s,\text{eff}}=\text{1,5} \ \text{A}$ .

Svolgimento punto 1.

Il trasformatore è in salita quindi $N_s>N_p$ . Procediamo dunque con la risoluzione del problema mediante l’uso dell’identità utilizzata nei problemi antecedenti, cioè

(117) $\begin{equation*} V_s(t)=V_p(t)\,\dfrac{N_s}{N_p} \qquad \Rightarrow\qquad V_{s,\text{eff}}=V_{p,\text{eff}}\dfrac{N_s}{N_p}, \end{equation*}$

da cui invertendo la relazione, si trova

$\boxcolorato{fisica}{N_s=N_p\,\dfrac{V_{s,\text{eff}}}{V_{p,\text{eff}}}=700.}$

Svolgimento punto 2.

In un trasformatore ideale (si veda il problema 25 per capire come si arriva all’equazione (118)) sappiamo che la corrente che scorre nel primario è legata alla corrente che scorre nel secondario dalla relazione

(118) $\begin{equation*} i_{p,\text{eff}}=i_{s,\text{eff}}\dfrac{N_s}{N_p}. \end{equation*}$

Sostituendo i valori numerici forniti dal problema e il valore di $N_s$ trovato al punto 1), otteniamo

$\boxcolorato{fisica}{i_{p,\text{eff}}=15 \ \text{A}.}$

Esercizio 27 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Nel primario di un trasformatore ideale, con ${N_s}/{N_p}=2$ , circola una corrente $i_{p,\text{eff}}=5 \ \text{A}$ e c’è una tensione efficace $V_{p,\text{eff}}=120 \ \text{V}$ . Nell’ipotesi che l’efficienza nel trasferimento della potenza sia $\text{0,95}$ , calcolare la corrente $i_{s,\text{eff}}$ e la tensione efficace $V_{s,\text{eff}}$ .

Rendered by QuickLaTeX.com

Figura 8: schema problema 27.

Svolgimento.

In questo problema, abbiamo che una certa percentuale della potenza viene dissipata nel trasferimento dal primario al secondario. Avremo, in particolare

(119) $\begin{equation*} \mathcal{P}_s=0.95\mathcal{P}_p \end{equation*}$

valida per ogni rapporto di potenza, ovvero media, istantanea o efficace. Quindi, ad esempio ricordando che la potenza efficace è $\mathcal{P}_{\text{eff}}=i_{\text{eff}}v_{\text{eff}}$ , avremo

(120) $\begin{equation*} V_{s,\text{eff}}\,i_{s,\text{eff}}=0.95\cdot V_{p,\text{eff}}\,i_{p,\text{eff}}. \end{equation*}$

Sebbene una parte della potenza venga dissipata, possiamo sfruttare l’ipotesi che il trasformatore sia ideale per affermare che il flusso di campo magnetico che attraversa il conduttore si conserva; ciò ci permette di scrivere:

(121) $\begin{equation*} V_{s,\text{eff}}=V_{p,\text{eff}}\dfrac{N_s}{N_p}\quad\Leftrightarrow\quad V_{s,\text{eff}}=2V_{p,\text{eff}}, \end{equation*}$

da cui:

$\boxcolorato{fisica}{V_{s,\text{eff}}=240 \ \text{V}.}$

Sostituendo il risultato ottenuto dalla (121) all’interno della (120), otteniamo:

(122) $\begin{equation*} 2V_{p,\text{eff}}\,i_{s,\text{eff}}=\text{0,95}\cdot V_{p,\text{eff}}\,i_{p,\text{eff}}\quad\Leftrightarrow\quad i_{s,\text{eff}}=\dfrac{\text{0,95}\cdot i_{p,\text{eff}}}{2}, \end{equation*}$

da cui si ricava

$\boxcolorato{fisica}{i_{s,\text{eff}}=\text{2,38} \ \text{A}.}$

Esercizio 28 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Un trasformatore funziona prelevando l’energia elettrica da una linea con tensione efficace $V_{p,\text{eff} }=20 \ \text{kV}$ e distribuendola a $V_{s,\text{eff}}=220 \ \text{V}$ di tensione efficace. Calcolare:

il rapporto ${N_p}/{N_s}$ del trasformatore se la potenza media assorbita è $\mathcal{P}_m=2 \ \text{MW}$ ;
la corrente $i_{p,\text{eff}}$ del primario nell’ipotesi che il fattore di potenza sia 1;
la corrente $i_{s,\text{eff}}$ del secondario nell’ipotesi che il fattore di potenza sia 1;
il carico resistivo $R_{eq}$ complessivo del secondario.

Svolgimento punto 1.

Per risolvere questo punto del problema utilizziamo lo stesso procedimento che abbiamo usato in diversi esercizi simili a questo. Sappiamo che la tensione efficace del secondario è legata a quella del primario dalla relazione

(123) $\begin{equation*} V_{s}(t)={V_{p}(t)}\dfrac{N_s}{N_p}\qquad \Rightarrow\qquad V_{s,\text{eff}}={V_{p,\text{eff}}}\dfrac{N_s}{N_p}. \end{equation*}$

Pertanto, invertendola, ricaviamo

$\boxcolorato{fisica}{\dfrac{N_p}{N_s}=\dfrac{V_{p,\text{eff}}}{V_{s,\text{eff}}}=91.}$

Svolgimento punto 2.

La potenza media si può calcolare come il prodotto tra la corrente e la tensione efficace, questo vale per definizione di grandezza efficace nel caso particolare in cui il fattore di potenza sia 1. Concludiamo quindi con la seguente soluzione

$\boxcolorato{fisica}{i_{p,\text{eff}}=\dfrac{\mathcal{P}_m}{V_{p,\text{eff}}}=100 \ \text{A}.}$

Svolgimento punto 3.

Essendo il fattore di potenza pari a 1, avremo che tutta la potenza assorbita dal primario verrà trasferita al secondario.

(124) $\begin{equation*} \mathcal{P}_p(t)=\mathcal{P}_s(t)\qquad \Rightarrow\qquad \mathcal{P}_{p,m}=\mathcal{P}_{s,m}\quad\Leftrightarrow\quad V_{p,\text{eff}}\,i_{p,\text{eff}}=V_{s,\text{eff}}\,i_{s,\text{eff}}. \end{equation*}$

Chiaramente la potenza media è definita per la legge di Galileo-Ferraris, cioè $P_M=V_{\text{eff}}\,i_{\text{eff}}\cos \phi$ , abbiamo usato il fatto che $\cos \phi=1$ (fattore di potenza pari a 1). Concludiamo quindi con la seguente soluzione

$\boxcolorato{fisica}{i_{s,\text{eff}}=\dfrac{\mathcal{P}_m}{V_{s,\text{eff}}}=\text{9,1} \ \text{kA}.}$

Svolgimento punto 4.

Utilizziamo la legge di Ohm sulle grandezze efficaci del secondario

(125) $\begin{equation*} i_{s,\text{eff}}={V_{s,\text{eff}}\over R_{eq}} \end{equation*}$

e inseriamo questo valore nell’equazione della potenza media (ricordare che il fattore di potenza è 1)

(126) $\begin{equation*} \mathscr{P}_m=i_{s,\text{eff}}\cdot V_{s,\text{eff}}=\frac{V_{s,\text{eff}}}{R_{eq}}\cdot V_{s,\text{eff}}=\dfrac{V_{s,\text{eff}}^2}{R_{eq}}, \end{equation*}$

da cui, invertendo, si ottiene:

$\boxcolorato{fisica}{R_{eq}=\dfrac{V_{s,\text{eff}}^2}{\mathcal{P}_m}=\text{24,2} \ \text{m}\Omega.}$

Notiamo che la resistenza equivalente trovata è proprio la resistenza complessiva del secondario in quanto nel procedimento è stata utilizzata la corrente e la tensione del secondario.

$\boxcolorato{fisica}{\mathscr{P}_m=V_{s,\text{eff}}\cdot i_{s,\text{eff}}=2 \, \text{W}.}$

Tutti gli esercizi di elettromagnetismo

Se si desidera proseguire con gli esercizi, di seguito è disponibile una vasta raccolta che copre interamente gli argomenti del programma di Elettromagnetismo. Questa raccolta include spiegazioni dettagliate e gli esercizi sono organizzati in base al livello di difficoltà, offrendo un supporto completo per lo studio e la pratica.

Leggi...

Per chi intende verificare le proprie competenze, è stata predisposta una raccolta di esercizi misti di elettromagnetismo.

Esercizi di Meccanica classica

Se siete interessati ad approfondire argomenti inerenti alla Meccanica Classica, di seguito troverete tutte le cartelle relative presenti sul sito Qui Si Risolve. Ciascuna cartella contiene numerosi esercizi con spiegazioni dettagliate, progettate per offrire una preparazione solida e una conoscenza approfondita della materia.

Leggi...

Ulteriori risorse didattiche per la fisica

Leggi...

Physics Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla fisica. È un’ottima risorsa per discutere e risolvere problemi di fisica a tutti i livelli, dall’elementare all’avanzato.
ArXiv – ArXiv è un archivio di preprint per articoli di ricerca in fisica (e in altre discipline scientifiche). Gli articoli non sono peer-reviewed al momento della pubblicazione su ArXiv, ma rappresentano un’importante risorsa per rimanere aggiornati sugli sviluppi più recenti nella ricerca fisica.
Phys.org – Questo sito offre notizie e aggiornamenti su una vasta gamma di argomenti scientifici, con un focus particolare sulla fisica. È una risorsa utile per rimanere aggiornati sugli ultimi sviluppi nella ricerca e nelle scoperte fisiche.
Physics Forums – Una delle comunità online più grandi per la fisica e la scienza in generale. Offre discussioni su vari argomenti di fisica, aiuto con i compiti, e discussioni su articoli di ricerca.
The Feynman Lectures on Physics – Questo sito offre accesso gratuito alla famosa serie di lezioni di fisica di Richard Feynman, un’ottima risorsa per studenti di fisica di tutti i livelli.
American Physical Society (APS) – La APS è una delle organizzazioni più importanti per i fisici. Il sito offre accesso a pubblicazioni, conferenze, risorse educative e aggiornamenti sulle novità del mondo della fisica.
Institute of Physics (IOP) – L’IOP è un’importante organizzazione professionale per i fisici. Il sito offre risorse per l’apprendimento, accesso a riviste scientifiche, notizie e informazioni su eventi e conferenze nel mondo della fisica.
Physics World – Physics World è una rivista online che offre notizie, articoli, interviste e approfondimenti su vari argomenti di fisica. È una risorsa preziosa per chiunque sia interessato agli sviluppi contemporanei nella fisica.
Quanta Magazine (sezione Fisica) – Quanta Magazine è una pubblicazione online che copre notizie e articoli di approfondimento su matematica e scienze. La sezione fisica è particolarmente interessante per i contenuti di alta qualità e le spiegazioni approfondite.
Perimeter Institute – Il Perimeter Institute è un importante centro di ricerca in fisica teorica. Il sito offre accesso a conferenze, workshop e materiale educativo, ed è un’ottima risorsa per chi è interessato alla fisica teorica avanzata.

Document