Esercizi svolti stabilità in condizione perturbate: i margini

Stabilità in condizioni perturbate: i margini

Home » Esercizi svolti stabilità in condizione perturbate: i margini

Esercizio 1 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dato il sistema in figura dove

$A(s)=\dfrac{1}{1+s},\quad R(s)=\dfrac{k}{s}\quad \text{e}\quad P(s)=\dfrac{\text{0,1}}{100s+1}.$

Si richiede di determinare la costante $k$ del regolatore affinché il sistema retroazionato sia asintoticamente stabile.

Rendered by QuickLaTeX.com

Figura 1: sistema retroazionato.

Svolgimento.

Per la soluzione del problema ci si avvale del criterio di Bode. In accordo al quale se la funzione ad anello aperto non ha poli a parte reale è positiva ed è propria il sistema retroazionato è asintoticamente stabile se il margine di fase è maggiore di zero. Nel caso in esame la funzione ad anello aperto è

$L(s)=\frac{\text{0,1}k}{s(100s+1)}.$

La funzione $L$ rispetta le condizioni per poter applicare il criterio di Bode. L’andamento della fase non risente del valore di $k$ ; per valori crescenti di $k$ , tuttavia, la pulsazione critica si sposta verso destra e associa una fase più piccola, allontanando il sistema dalla stabilità. La pulsazione limite è quella che associa una fase di $-180^\circ$ .

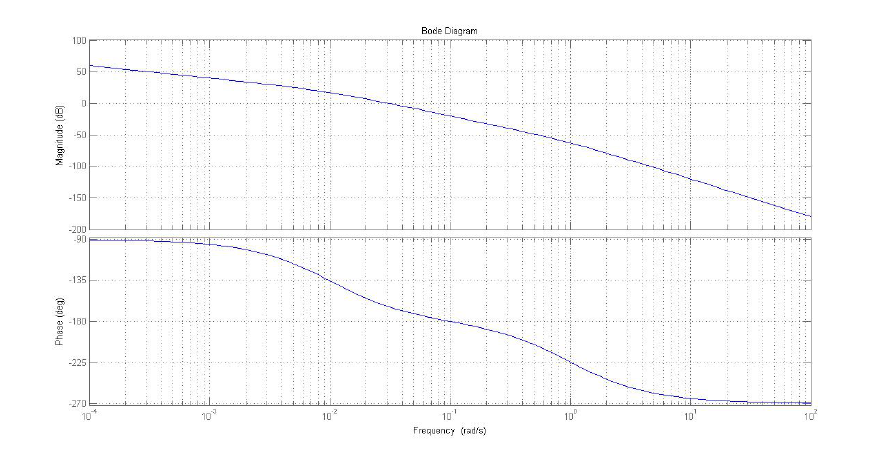
Figura 2: diagramma di Bode della funzione ad anello aperto.

Osservando il diagramma di Bode, è evidente che la pulsazione critica alla quale la fase diventa pari a $-180^\circ$ è $\omega_c = \text{0,1}\,\text{rad}\cdot\text{s}$ . Per determinare il massimo valore di $k$ per il quale il sistema rimane asintoticamente stabile secondo il criterio di Bode, si impone che il modulo della funzione ad anello aperto valutato alla pulsazione $\omega_c$ sia uguale a uno:

$\left\vert L(\text{0,1}j)\right\vert = 1.$

Sostituendo l’espressione di $L$ e valutando per $\omega=0.1$ , otteniamo:

$\frac{\left\vert \overline{k}\right\vert}{\left\vert \text{0,1}j\right\vert \left\vert 1+100\cdot\text{0,1}j\right\vert \left\vert 1+\text{0,1}j\right\vert} = 1$

$\overline{k} = \sqrt{1 + 10^2} = \sqrt{1 + 10^{-2}} \approx 10.$

Pertanto, il sistema retroazionato rimane asintoticamente stabile per valori di $k$ inferiori a $10$ . Il valore di $k=10$ può essere interpretato anche come il margine di guadagno della funzione. Per definizione:

$k_m = \frac{1}{\left\vert L(j\omega_\pi)\right\vert}$

dove $\omega_\pi$ rappresenta la pulsazione alla quale la fase diventa.

Esercizio 2 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Si consideri il sistema in figura 3, con le seguenti funzioni di trasferimento:

$A(s) = e^{-\tau s} \quad \text{con $\tau > 0$},$

$R(s) = \frac{1}{s},$

$P(s) = \frac{\text{0,1}}{1+100s}.$

Si richiede di determinare per quali valori di $\tau$ il sistema risulta asintoticamente stabile.

Rendered by QuickLaTeX.com

Figura 3: sistema retroazionato.

Svolgimento.

La funzione di anello è espressa come:

$L(s)=R\cdot A\cdot P.$

Di seguito, nella figura che segue, rappresentiamo il diagramma di Bode della funzione di anello senza ritardo di tempo.

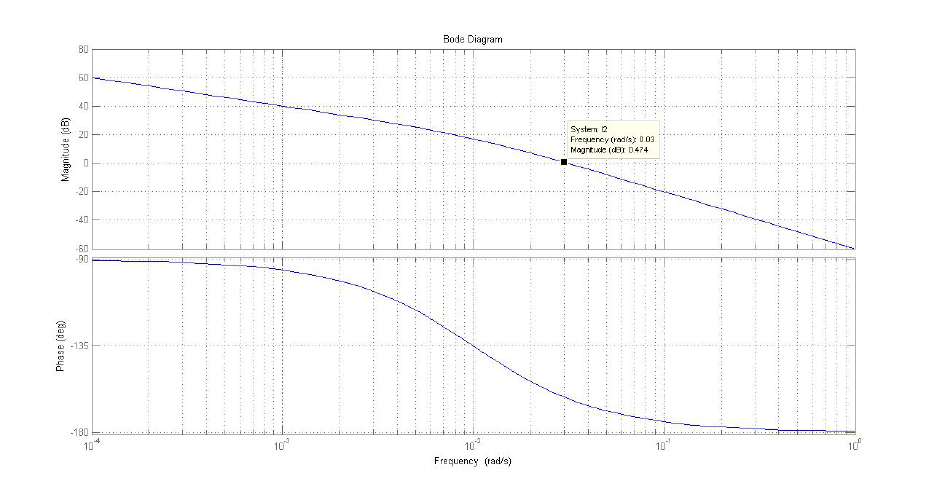
Figura 4: diagramma di Bode della funzione ad anello aperto.

La pulsazione critica alla quale il modulo del guadagno diventa unitario non è influenzata dalla presenza del ritardo di tempo. Possiamo calcolarla imponendo che il modulo della funzione di anello sia uguale a uno:

$\left\vert L(j\omega_c)\right\vert = 1.$

Da ciò otteniamo:

$\left\vert L(j\omega_c)\right\vert = \frac{\text{0,1}}{\left\vert j\omega_c\right\vert}\cdot \frac{1}{\left\vert 1+100j\omega_c\right\vert} = 1$

ovvero

$0.1 = \omega_c\sqrt{1+100\omega_c} \Rightarrow \text{0,01} = \omega_c^2\left(1+100\omega_c\right) \Rightarrow 10^4\omega_c^4+\omega_c^2-10^{-2} = 0$

che conduce a

$\omega_{c_{\text{1,2}}} = \frac{-1+\sqrt{401}}{2}\cdot 10^{-4} \approx 9\cdot 10^{-4}\,\text{rad$\cdot$s$^{-1}$}.$

Scegliendo la soluzione positiva, otteniamo

$\omega_{c_{1}} = \omega_{c} \approx 9\cdot 10^{-4}\,\text{rad$\cdot$s$^{-1}$}$

come evidenziato nella figura precedente. La fase della funzione di anello completa del ritardo di fase e valutata alla pulsazione $\omega_c$ è:

$\angle L\left(j\omega_c\right) = -90^\circ - \arctan\left(100\omega_c\right) - \tau \cdot \omega_c \cdot \frac{180^\circ}{\pi} = -90^\circ - \text{71,56}^\circ - \tau \cdot \frac{\text{0,03}\cdot 180^\circ}{\pi} = -\text{161,56} - \text{1,71}\tau.$

Quindi il margine di fase è dato da:

$\phi_m = 180^\circ - \left\vert \angle L\left(j\omega_c\right)\right\vert = \text{18,44}^\circ - \text{1,71}^\circ\tau.$

Imponendo che il margine di fase sia maggiore di zero, otteniamo che $\tau < \text{10,78}\,\text{s}$ , il che rappresenta il ritardo di tempo oltre il quale il sistema retroazionato diventa instabile.

Esercizio 3 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Data la funzione di trasferimento

$W(s)=\dfrac{4\left(1+s\right)^2}{s\left(1-s\right)^2},$

si richiede di trovare il margine di guadagno.

Svolgimento.

Il margine di guadagno rappresenta il massimo guadagno che può essere introdotto da un sistema, come per esempio un regolatore, in serie al processo tale che non rende il sistema complessivo chiuso in retroazione unitaria instabile. Il guadagno può essere valutato in tre modi:

analiticamente, come
$K_M=\dfrac{1}{\left \vert W\left(j\omega\right)\right \vert }\bigg\vert_{\omega=\omega_c},$

dove $K_M$ è il margine di guadagno e $\omega_c$ è la pulsazione per la quale vale $\angle W(j\omega_c)=\pi$ ;
graficamente dal diagramma di Bode, come la distanza tra il diagramma dei moduli e l’asse a $\text{0 dB}$ , valutata in corrispondenza della pulsazione per la quale di $W$ diventa uguale a $\pi$ ;
graficamente dal diagramma di Nyquist come la distanza tra il punto $\text{-1,0}$ e il punto di intersezione del digramma con l’asse reale.

Di seguito proporremo tutti e tre i metodi.

Svolgimento metodo 1.

La fase della funzione di trasferimento può essere scritta come

$\angle W(jw)=\angle 4 +2 \arctan \left(\omega\right)-\dfrac{\pi}{2}+2\arctan(\omega)=\pi,$

da cui

$4\arctan\left(\omega\right)=\dfrac{3}{2}\pi,$

ovvero

$\arctan\left(\omega\right)=\dfrac{3}{8}\pi,$

cioè

$\omega=\omega_c\sim \text{2,41 rad/s.}$

Abbiamo dunque

$\left \vert W(j\omega_c)\right \vert =\dfrac{4\left \vert 1+j(\text{2,41})\right \vert }{\left \vert \text{2,41}\right \vert\left \vert1-j(\text{2,41}) \right \vert }=\text{1,65},$

da cui

$K_M=\dfrac{1}{\text{1,65}}=\text{0,6},$

che può essere espresso in decibel come

$K_M\,\text{dB}=20\log_P{10}\left \vert \text{0,6}\right \vert\sim \text{-4,38} .$

Il modulo di guadagno $K_M$ rappresenta il massimo guadagno che può avere un controllore posto in serie al processo $W$ .

Svolgimento metodo 2.

Riportiamo, di seguito, i grafici della fase e del modulo dell’esercizio 4 presente nella cartella “i diagrammi di Bode”.

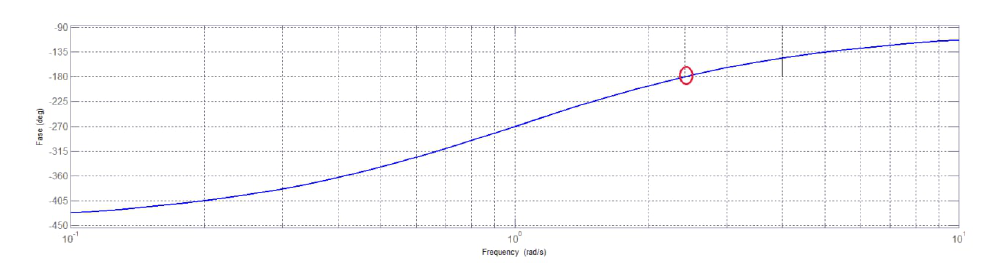
Figura 5: diagramma della fase – analisi del sistema.

Figura 6: diagramma del modulo – analisi del sistema.

Sul diagramma della fase si osserva che la fase assume il valore di $180^\circ$ in corrispondenza della pulsazione di $\text{2,4 rad/s}$ . Sul digramma del modulo la distanza tra il modulo a $\text{2,41 rad/s}$ e l’asse $\text{0 dB}$ , rappresenta il margine di guadagno della funzione anello chiuso, ovvero il massimo guadagno che può avere un regolataore posto in serie al processo da controllare.

Svolgimento metodo 3.

Per valutare il margine di guadagno dal diagramma di Nyquist, si riporta, di seguito, il diagramma ottenuto dall’esercizio 1 presente dalla cartella “I diagrammi di Nyquist”.

Figura 7: rappresentazione grafica del modulo del sistema.

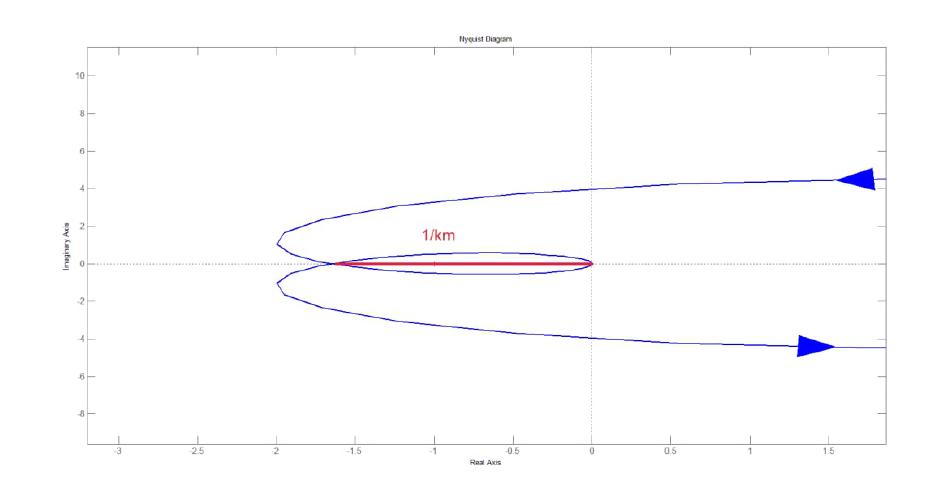
Figura 8: diagramma di Nyquist – caso 2.

Sul grafico del diagramma di Nyquist la distanza tra l’origine degli assi e il primo attraversamento con l’asse reale, rappresenta il rapporto $1/K_M$ , come rappresentato nella figura di sopra, ovvero il reciproco del margine di guadagno. La distanza in oggetto vale $\text{1,6}$ , il cui inverso vale $\text{0,6}$ e rappresenta il margine di guadagno che è lo stesso valore ottenuto nei due metodi precedenti.

Tutte le cartelle di controlli automatici

Leggi...

Document

Menu

Chiudi

Esercizi svolti stabilità in condizione perturbate: i margini

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento metodo 1.

Svolgimento metodo 2.

Svolgimento metodo 3.

Tutte le cartelle di controlli automatici

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi