Esercizi svolti schemi a blocchi e loro combinazioni

Home » Esercizi svolti schemi a blocchi e loro combinazioni

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Considerando la seguente funzione di trasferimento

$G(s) = \frac{2s^2 + s + 3}{s^3 + 3s^2 + 7s + 5}$

si richiede di determinarne una realizzazione minima.

Svolgimento.

Per iniziare, è necessario esprimere la funzione di trasferimento $G(s)$ in termini della formula canonica di riferimento:

$G(s) = \frac{b_2s^2 + b_1s + b_0}{s^3 + a_2s^2 + a_1s + a_0}.$

Optando per realizzare il sistema secondo la forma canonica di osservabilità, le matrici corrispondenti sono definite come segue:

$A = \begin{pmatrix} 0 & 0 & -a_0 \\ 1 & 0 & -a_1 \\ 0 & 1 & -a_2 \end{pmatrix} = \begin{pmatrix} 0 & 0 & -5 \\ 1 & 0 & -7 \\ 0 & 1 & -3 \end{pmatrix},$

$B = \begin{pmatrix} b_0 \\ b_1 \\ b_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix},$

$C = \begin{pmatrix} c_0 & c_1 & c_2 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 1 \end{pmatrix}.$

Con queste definizioni, la realizzazione fisica del circuito è quindi determinata.

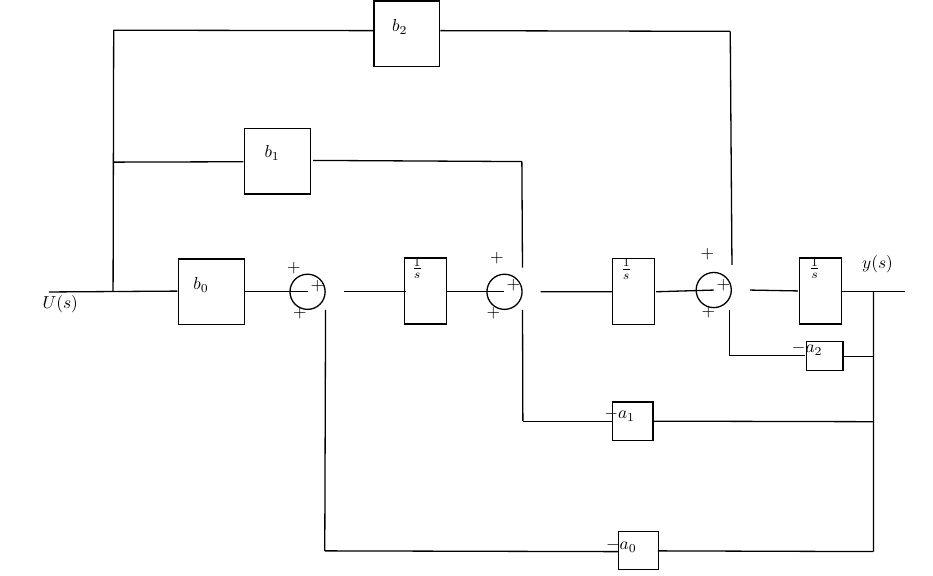
Figura 1: possibile realizzazione della funzione di trasferimento assegnata.

A partire dalle matrici $A$ , $B$ e $C$ ottenute ( $D=0$ ) si può verificare la correttezza della realizzazione ricavando la relativa funzione di trasferimento con la formula

$G(s)=\left(sI^{-1}-A\right)^{-1}B+D$

e verificando di ottenere una funzione a quella assegnata in traccia.

Esercizio 2 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Ricondurre il seguente schema a blocchi:

Figura 2.

Figura 3.

Tramite riduzioni successive.

Svolgimento.

Spostiamo il punto di diramazione a monte rispetto a $G_3$

Figura 4.

Ricaviamo il sistema equivalente della retroazione composta dai sistemi $G_2$ e $H_1$ .

Figura 5.

Consideriamo la retroazione positiva dei blocchi $H_2G_3$ e $\dfrac{G_2}{1+H_1G_2}$ .

Figura 6.

Di conseguenza, è possibile riscrivere la funzione nel blocco centrale, modificando così il sistema nel seguente modo.

Figura 7.

Possiamo effettuare il prodotto delle funzioni nella catena diretta.

Figura 8.

E dunque il sistema equivale a

Figura 9.

Questo conclude lo svolgimento dell’esercizio.

Esercizio 3 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Considerando il sistema illustrato in Figura 10, si proceda con l’identificazione di una rappresentazione in spazio di stato (ISU) per il sistema. Successivamente, si analizzi e si valuti la sua stabilità interna.

Figura 10: schema a blocchi assegnato.

Svolgimento.

Innanzitutto, è necessario trovare una rappresentazione in Spazio di Stato (ISU) per ciascun blocco che compone il sistema in esame. La rappresentazione di ogni blocco può essere espressa in una forma canonica. Facendo riferimento alla forma canonica di controllo, si ricorda la corrispondenza tra la funzione di trasferimento e le matrici del modello ISU:

$\begin{equation*} G(s) = \frac{b_n s^{n-1} + \dots + b_2 s + b_1}{s^n + a_n s^{n-1} + \dots + a_2 s + a_1}. \end{equation*}$

Le matrici in forma canonica di controllo sono definite come segue:

$A = \begin{pmatrix} 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & \dots & 0 & 1 \\ -a_1 & -a_2 & \dots & -a_{n-1} & -a_n \end{pmatrix}, \quad B = \begin{pmatrix} 0 \\ \vdots \\ 0 \\ 1 \end{pmatrix}, \quad \text{e} \quad C = \begin{pmatrix} b_1 & b_2 & \dots & b_n \end{pmatrix}.$

Per il blocco 1 si ha:

$A=-1,\quad B=1,\quad C=1.$

$\begin{cases} \dot{x}_1=-x_1+u_1=-x_1+(u-y_2) \\ y_1=x_1. \end{cases}$

Per il blocco 2 si ha:

$A=1,\quad B=1,\quad C=2.$

$\begin{cases} \dot{x}_2=x_2+u_2=x_2+y_1-y=x_2+x_1-x_3 \\ y_2=2x_2 \end{cases}$

e infine per il blocco 3:

$A=-1,\quad B=1,\quad C=1.$

$\begin{cases} \dot{x}_3=-x_3+u_3=-x_3+x_1-x_3 \\ \dot{x}_2=-2x_3+x_1 \\ y=x_3. \end{cases}$

Dunque, il sistema completo eredita le variabili di stato di ciascun sistema componente:

$\begin{cases} \dot{x}_1=-x_1-2x_2+u \\ \dot{x}_2=x_1+x_2-x_3 \\ \dot{x}_3=x_1-2x_3 \\ y=x_3. \end{cases}$

ovvero

$\dot{x}=\underbrace{\begin{pmatrix} -1 & -2 & 0 \\ 1 & 1 & -1 \\ 1 & 0 & -2 \end{pmatrix}}_A \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}+ \underbrace{\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}_Bu$

$y=\underbrace{\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}}_{C}\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}.$

Gli autovalori del sistema sono le soluzioni della seguente equazione

$\det\left(A-\lambda I\right) = 0 \quad \Rightarrow \quad \lambda^3-2\lambda^2+1=0$

da cui

$\lambda \approx \text{0,61}, \quad \lambda \approx \text{1,61}, \quad \lambda \approx -1.$

Poiché uno degli autovalori è maggiore di zero, il sistema è instabile.

In alternativa, per valutare la stabilità, si può calcolare la funzione di trasferimento del sistema complessivo:

$G(s) = C(sI - A)^{-1}B + D$

$G(s) = \frac{s - 1}{s^3 + 2s^2 - s}.$

Poiché nella funzione di trasferimento $G(s)$ non ci sono cancellazioni zero/polo, i poli di $G(s)$ coincidono con gli autovalori del sistema. Pertanto, analizzando i poli di $G(s)$ , si possono trarre conclusioni sulla stabilità interna del sistema.

Tutte le cartelle di controlli automatici

Leggi...

Document

Menu

Chiudi

Esercizi svolti schemi a blocchi e loro combinazioni

Svolgimento.

Svolgimento.

Svolgimento.

Tutte le cartelle di controlli automatici

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi