Accedi ai contenuti scaricabili
Qui si risolve LOGO
a

Menu

M

Chiudi

Esercizi svolti proprietà della risposta allo scalino

Proprietà della risposta allo scalino

Home » Esercizi svolti proprietà della risposta allo scalino

 

Esercizio 1 (\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar). Studiare la rispota allo scalino unitario del sistema descritto dalla seguente funzione di trasferimento:

\begin{equation*} G(s)=2\dfrac{s+1}{3s+1}. \end{equation*}

Svolgimento.

Il sistema analizzato è di primo ordine e non strettamente proprio. È possibile determinare il valore iniziale del sistema mediante il limite

\begin{equation*} y(0) = \lim_{s \to \infty} s \cdot \left( \frac{1}{s} \cdot 2 \frac{s+1}{3s+1} \right) = \frac{2}{3}. \end{equation*}

Dato che il polo del sistema è reale e negativo, possiamo calcolare il valore asintotico finale utilizzando il teorema del valore finale come

\begin{equation*} y_{\infty} = \lim_{s \to 0} s \cdot \left( \frac{1}{s} \cdot 2 \frac{s+1}{3s+1} \right) = 2. \end{equation*}

Il tempo di assestamento t_A, espresso in secondi, si determina come

\begin{equation*} t_A = S\tau = 5 \cdot 3 = 15 \text{ sec}, \end{equation*}

dove S\tau rappresenta il prodotto della costante di tempo 5 per il fattore 3, indicativo del tempo necessario affinché la risposta del sistema si assesti entro una certa percentuale del valore finale.

Segue la rappresentazione grafica della risposta del sistema.

   

 

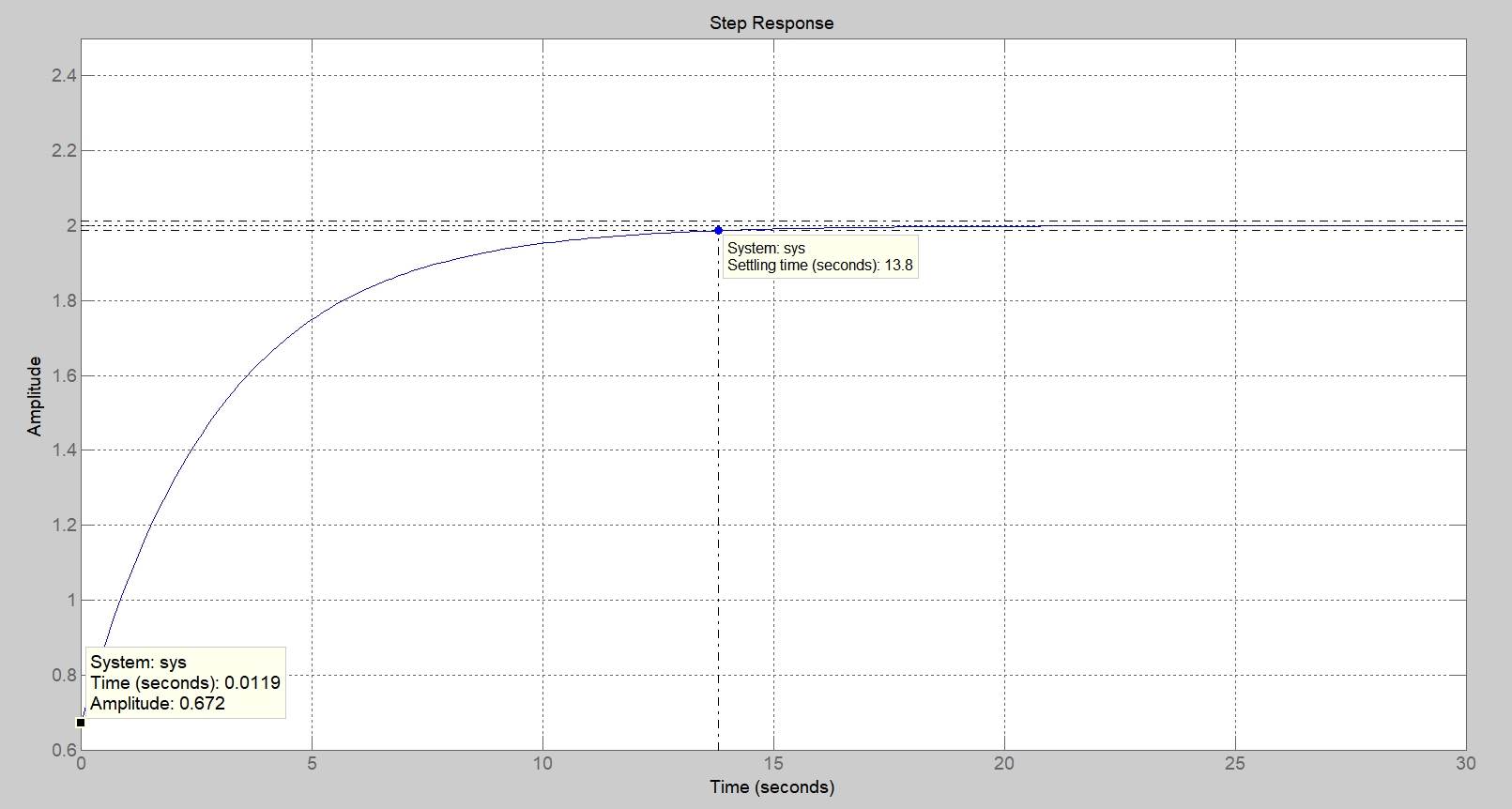
Figura 1: risposta allo scalino del problema proposto.

   

 

Esercizio 2 (\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar). Studiare la risposta allo scalino unitario del sistema avente la seguente funzione di trasferimento

\begin{equation*} G(s)=\left(\dfrac{400}{s^2+2s+4}\right). \end{equation*}

Svolgimento.

I poli del sistema sono complessi coniugati, come evidenziato dal calcolo delle radici del denominatore s^2 + 2s + 4 = 0, che risultano essere s_{1,2} = -1 \pm \sqrt{3}i. Si possono determinare il coefficiente di smorzamento \xi e la pulsazione naturale \omega_n della coppia di poli tramite l’equazione caratteristica:

\begin{align*} &s^2 + 2\xi \omega_n s + \omega_n^2 = s^2 + 2s + 4\\ &\Rightarrow \omega_n = 2, \quad \xi = \text{0,5}. \end{align*}

Utilizzando il teorema del valore iniziale, il valore iniziale dell’uscita è:

\begin{equation*} y(t = 0^+) = \lim_{s \to \infty} sY(s) = \lim_{s \to \infty} \frac{400}{s^2 + 2s + 4} = 0. \end{equation*}

Poiché i poli hanno parte reale negativa, è applicabile il teorema del valore finale:

\begin{equation*} y_{\infty} = \lim_{s \to 0} sY(s) = \lim_{s \to 0} \frac{400}{s^2 + 2s + 4} = 100. \end{equation*}

Di seguito, altri parametri significativi della risposta dinamica del sistema: a) Tempo di assestamento:

\begin{equation*} t_a \simeq \frac{5}{\xi \omega_n} = 5 \text{ s}, \end{equation*}

con \xi \omega_n che rappresenta la parte reale dei poli. b) Periodo delle oscillazioni:

\begin{equation*} T = \frac{2\pi}{\omega_n \sqrt{1-\xi^2}} = \text{3,62}\text{ s}. \end{equation*}

c) Tempo del primo picco:

\begin{equation*} t_p = \frac{1}{2}T = \text{1,81} \text{ s}. \end{equation*}

d) Ampiezza del primo picco, con \mu rappresentante il guadagno a regime pari a 100:

\begin{equation*} y_p = \mu\left[1 + \exp\left(-\frac{\xi\pi}{\sqrt{1-\xi^2}}\right)\right] = 116. \end{equation*}

Segue la rappresentazione grafica della risposta del sistema.

     

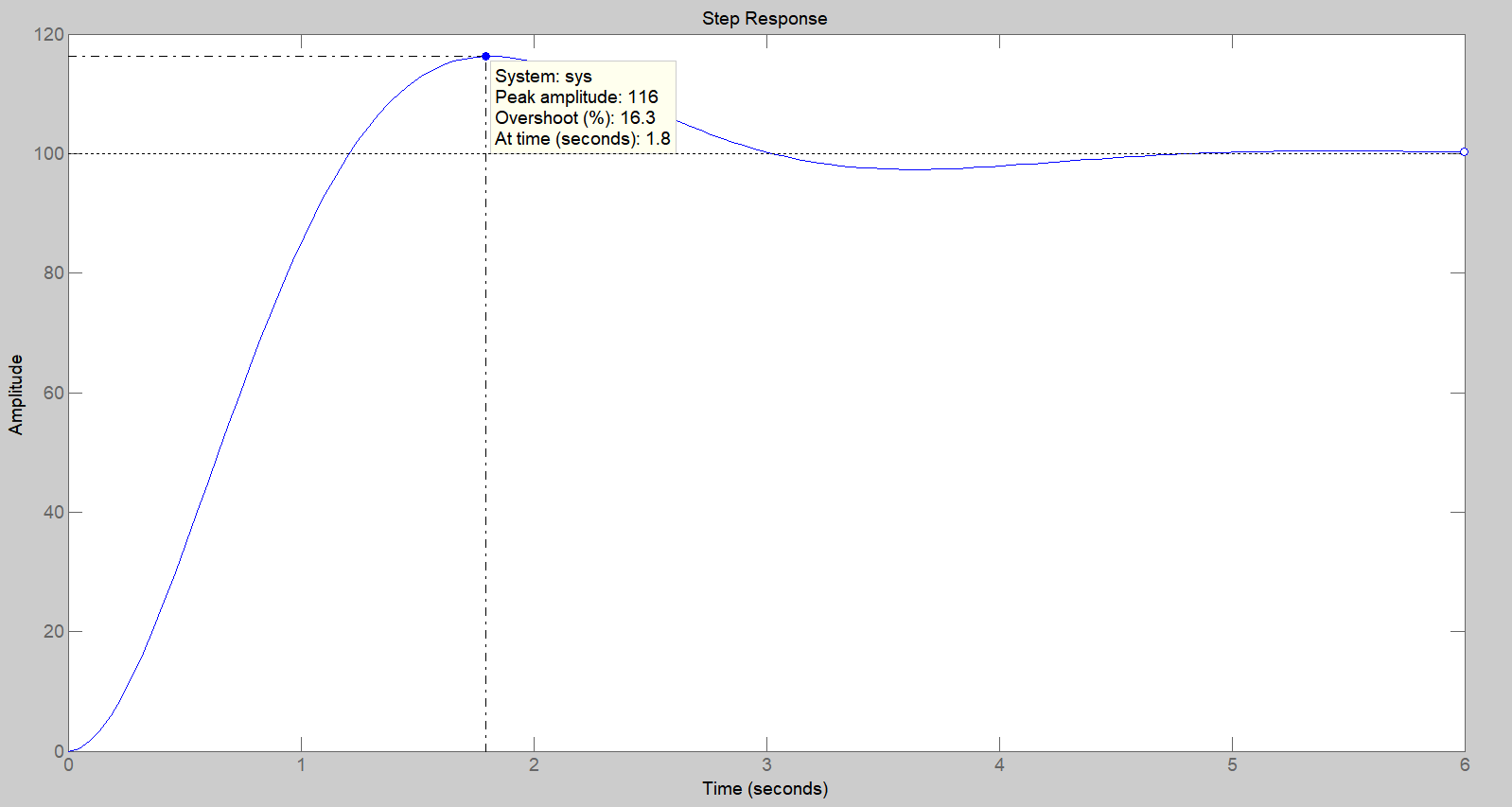
Figura 2: risposta allo scalino del sistema proposto.

   

 

 

Tutte le cartelle di controlli automatici

Leggi...

  1. Analisi nel dominio di Laplace e del tempo di sistemi dinamici LTI a tempo continuo
  2. Analisi modale di sistemi dinamici LTI a tempo continuo
  3. Linearizzazione di sistemi dinamici
  4. Analisi della Stabilità dei Sistemi LTI
  5. Stabilità dell’equilibrio di sistemi dinamici non lineari
  6. Retroazione statica dallo stato
  7. Analisi nel dominio del tempo e della trasformata Zeta di sistemi dinamici LTI a tempo discreto
  8. Trasformata Zeta
  9. La risposta in frequenza
  10. Analisi modale di sistemi dinamici LTI a tempo discreto
  11. La carta di Nichols
  12. Proprietà della risposta allo scalino
  13. Schemi a blocchi e loro combinazioni
  14. I diagrammi di Bode
  15. I diagrammi di Nyquist
  16. Il progetto del controllore
  17. Il luogo delle radici
  18. Stabilità in condizioni perturbate: i margini
  19. I regolatori PID
  20. Le reti compensatrici
  21. Modellistica dei sistemi dinamici meccanici, elettrici
  22. Proprietà strutturali dei sistemi
  23. Sintesi del modello di stato ISU
  24. Sintesi dell’osservatore asintotico dello stato






Document