Esercizi svolti reti compensatrici

Home » Esercizi svolti reti compensatrici

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Consideriamo il sistema di controllo illustrato nella figura sottostante. L’obiettivo è progettare il controllore $G(s)$

utilizzando il metodo di sintesi per tentativi in $\omega$

, con le seguenti condizioni da soddisfare:

$M_R\,\text{dB}\leq 3\,\text{dB}$ .
$B_3\sim\text{1 Hz}$ .

Il sistema è descritto dalla funzione di trasferimento di processo $P(s)$ definita come:

$P(s) = \dfrac{200(s+\text{0,1})}{s(s+2)^2}.$

Figura 1: sistema reatroazionato.

Svolgimento.

Dalla specifica sul modulo alla risonanza, è possibile ricavare il coefficiente di smorzamento $\zeta$ . Questo calcolo può essere eseguito sia in modo analitico che sfruttando le informazioni contenute nell’abaco.

Innanzitutto, considerando l’approccio analitico, dobbiamo invertire l’equazione del modulo alla risonanza:

(1) $\begin{equation*} M_R = \dfrac{\max\left \vert P(j\omega )\right \vert }{\left \vert P(j\,0)\right \vert } = \dfrac{1}{2\zeta\sqrt{1-\zeta^2}}. \end{equation*}$

La specifica che $M_R\,\text{dB}\leq3\,\text{dB}$ impone che

(2) $\begin{equation*} \dfrac{1}{M_R} \geq \text{0,707}. \end{equation*}$

Da cui possiamo ricavare:

(3) $\begin{equation*} 2\zeta\sqrt{1-\zeta^2} \geq \text{0,707}. \end{equation*}$

Questa equazione ha quattro soluzioni, tuttavia solo una di queste è accettabile, in quanto è compresa tra $0$ e $1$ , e vale $\zeta=\text{0,41}$ . Dal valore $\zeta=\text{0,41}$ è possibile determinare il margine di fase $\phi_m$ richiesto per la funzione ad anello chiuso dalla relazione:

(4) $\begin{equation*} \zeta\sim \dfrac{\phi_m}{100}. \end{equation*}$

La precedente equazione approssimata è valida solo per valori di $\phi_m\leq 70^\circ$ . Pertanto, il margine minimo richiesto dal sistema è di $41^\circ$ .

Un’alternativa a questo approccio analitico è l’utilizzo dell’analisi basata sull’abaco. Di seguito, presentiamo il grafico dell’Abaco.

Figura 2: diagramma di sovraelongazione e smorzamento.

Dall’analisi dell’abaco, possiamo dedurre che per $M_R=\text{3 dB}$ si individua un valore di circa $\text{0,4}$ .

Inoltre, considerando la specifica sulla banda passante desiderata a $\text{3 dB}$ del sistema ad anello chiuso $B_3$ , è possibile ottenere la pulsazione di attraversamento $\omega_t$ desiderata per la funzione di anello aperto utilizzando gli abachi rappresentati nelle seguenti figure.

Figura 3: banda smorzamento.

Figura 4: pulsazione di taglio e smorzamento.

Analizzando il secondo abaco e scegliendo un valore di $\zeta=\text{0,41}$ , otteniamo un valore di $B_3/\omega_n=\text{1,38}$ , dove $\omega_n$ rappresenta la pulsazione della coppia di poli complessi e coniugati del sistema ad anello chiuso. Se esprimiamo $B_3$ in radianti, con un valore di $\text{6,28 rad}$ , si calcola che $\omega_n$ è pari a $\text{4,55 rad}\cdot \text{s}^{-1}$ . Inoltre, dallo stesso abaco è possibile determinare il valore della pulsazione di attraversamento ad anello aperto, dato che $\omega_t/\omega_n=\text{0,85}$ . Di conseguenza, si ricava una pulsazione di attraversamento desiderata di $\text{3,8 rad}\cdot \text{s}^{-1}$ . Dall’analisi del diagramma di Bode del processo che segue, rappresentato in figura 6.

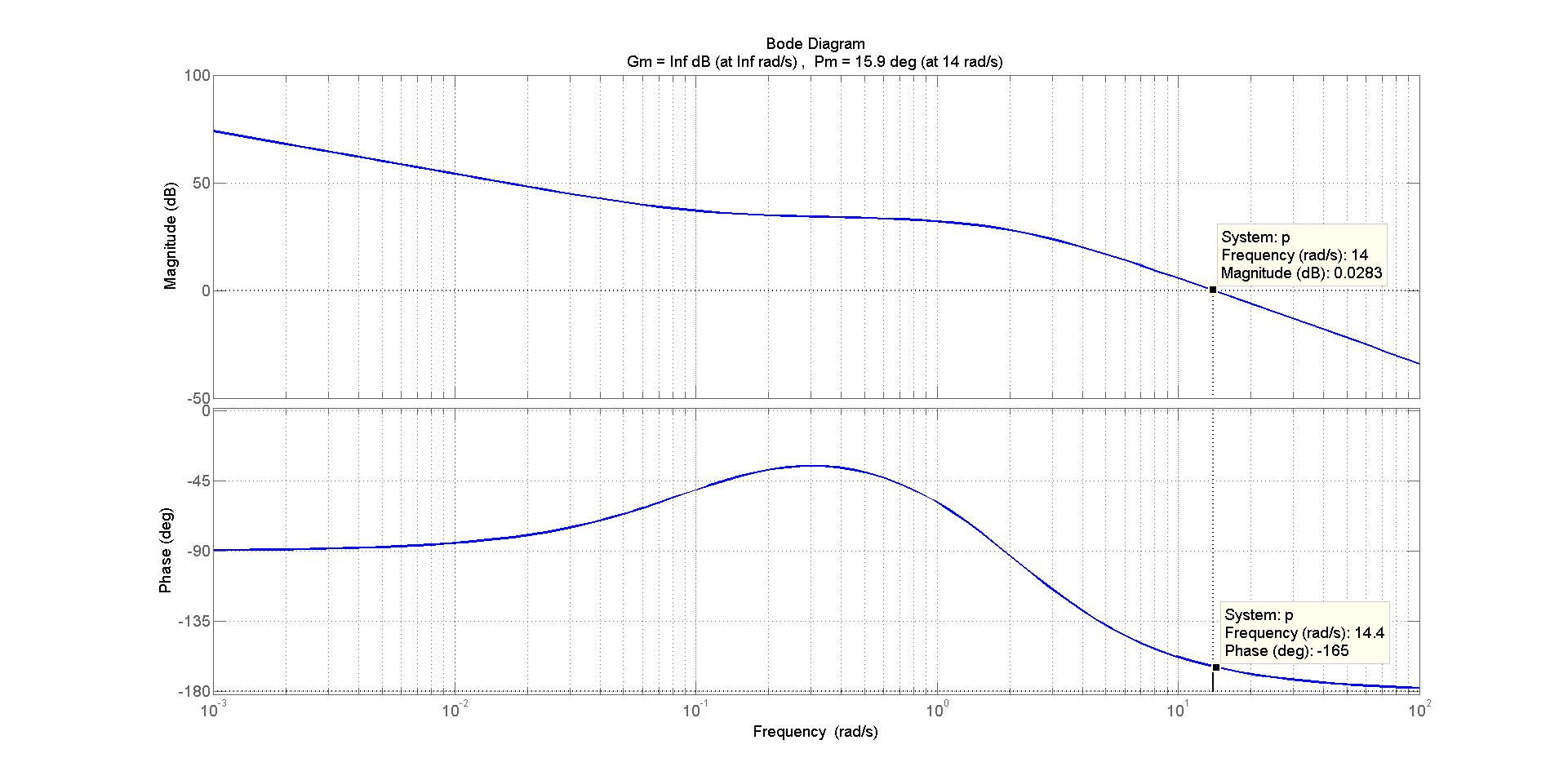
Figura 5: diagramma di bode di $P(s)$ .

Si deduce che la pulsazione di taglio va portata da 14 rad/s a 3.8 rad/sec e il margine di fase a tale pulsazione deve essere almeno di 41°.

Valutiamo il modulo di circa 20 dB alla pulsazione desiderata per il taglio si può introdurre un guadagno di -20 dB = 0.1 attraverso il regolatore.

Il diagramma di Bode per la nuova funzione di anello è rappresentato in figura 6.

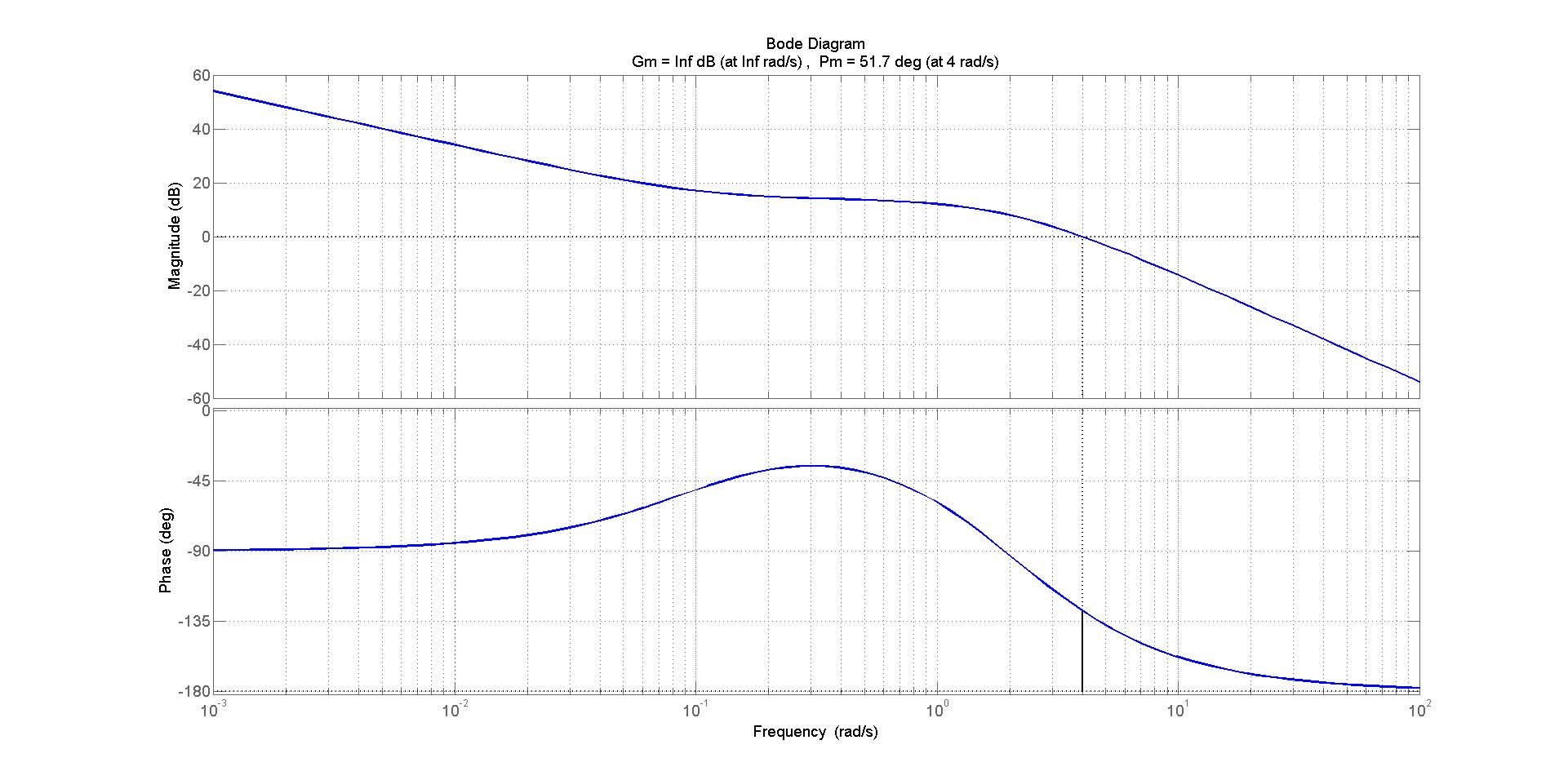
Figura 6: diagramma di bode della funzione d’anello $L(s)$ .

Si osserva che con $\omega_c = 4 \text{rad/s}$ e margine di fase di $51^\circ$ già soddisfa le richieste.

In alternativa si può dimensionare una rete ritardatrice che alla pulsazione di $3.8\text{rad/s}$ attenui il modulo di $20\text{dB}$ impattando il meno possibile sulla fase.

Consideriamo il seguente diagramma universale, rappresentato in figura 7.

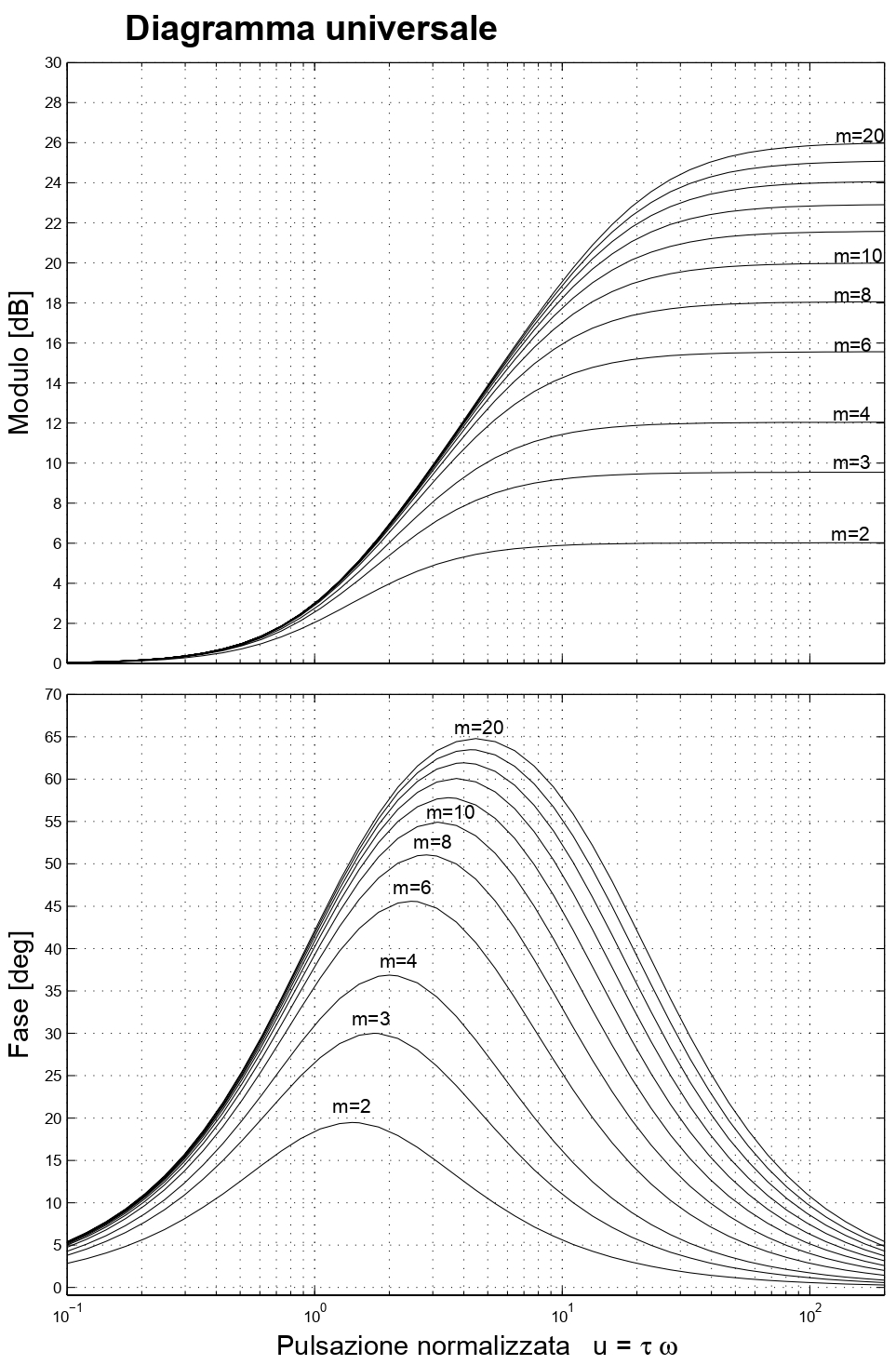
Figura 7: diagramma universale.

Si può scegliere $m =10$ , ottenendo:

$\omega_c \cdot \tau = 90, \quad \text{con } \omega_c = 3,8 \quad \Rightarrow \quad \fbox{$\tau \approx 23,6$}.$

Dunque, la funzione del regolatore è definita come:

$R(s) = \frac{1 + \left(\frac{23,68}{10}\right) s}{1 + 23,68 s}$

La funzione d’anello risultante è:

$L(s) = R(s) P(s)$

e ammette il seguente diagramma di Bode rappresentato in figura 8.

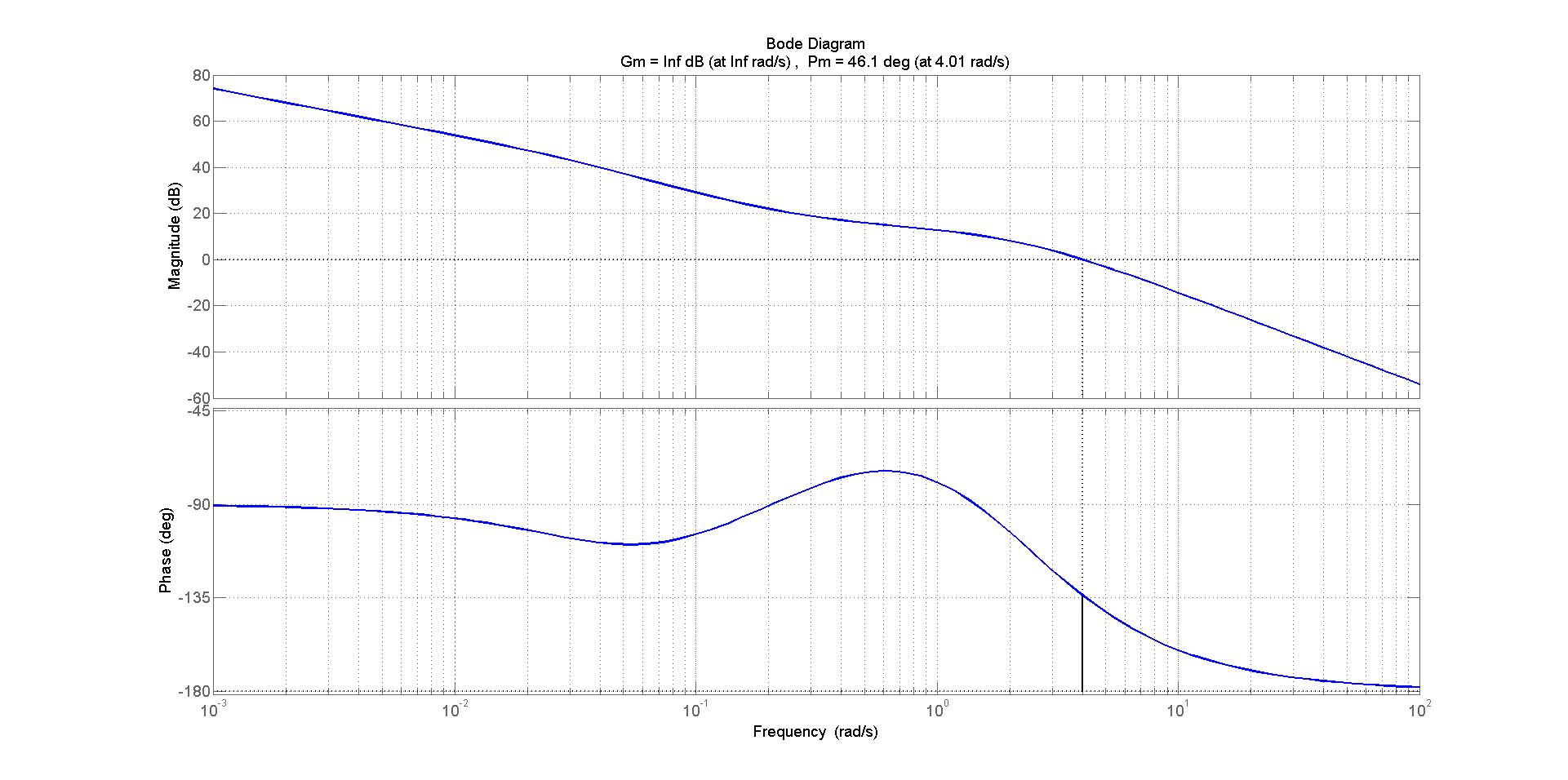
Figura 8: diagramma della funzione d’anello corretta tramite rete correttrice.

Esercizio 2 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Sia il sistema in figura 9 dove il processo è descritto dalla funzione:

$P(s)=\dfrac{100}{\left(1+\text{0,1} s\right)\left(1+\text{0,01} s\right)}.$

Si progetti il regolatore $R(s)$ con una rete compensatrice in grado di garantire un margine di fase di almeno $50^\circ$ .

Figura 9: sistema retroazionato.

Svolgimento.

Per valutare il margine di fase della funzione ad anello aperto, il primo passo è determinare la pulsazione critica $\omega_c$ alla quale il modulo diventa unitario. Successivamente, calcoliamo la fase critica $\phi_c$ della funzione ad essa associata, e calcoliamo la differenza tra $180^\circ$ e la fase critica. Questa differenza rappresenta il margine di fase.

Il margine di fase può essere calcolato sia in modo analitico che mediante l’analisi del diagramma di Bode.

Nel calcolo analitico, procediamo come segue:

Iniziamo impostando $\left \vert P(j\omega_c)\right \vert = 1$ , risolvendo l’equazione:
$\dfrac{100}{\left \vert \left(1+\text{0,1} \,\omega_c \,i\right)\left(1+\text{0,01} \,\omega_c \,i\right)\right \vert }=1,$

da cui otteniamo $\omega_c \approx \text{308 rad}\cdot \text{s}^{-1}$ .
Calcoliamo la fase critica come l’angolo $\angle P(j\omega_c)$ , ossia:
$\angle P(j\omega_c) = \angle 100 - \arctan \left\{\text{0,1}\,\omega_c\right\} - \arctan \left\{\text{0,01}\,\omega_c\right\} \approx -160^\circ.$
Di conseguenza, otteniamo un margine di fase pari a:
$\phi_m = 180^\circ - \left \vert \angle P(j\omega_c) \right \vert \approx 20^\circ.$

Dunque, l’intervento della rete correttiva deve essere in grado di aumentare la fase della funzione di trasferimento di almeno $40^\circ$ alla pulsazione critica.

Una possibile soluzione consiste nell’adottare una rete anticipatrice definita come:

$R_{\text{ant}}(s) = \dfrac{1 + \tau s}{1 - Ts},$

dove $\tau$ e $T$ rappresentano rispettivamente le costanti di tempo dello zero e del polo. Perché la rete sia effettivamente anticipatrice, è necessario che $\tau > T$ , ossia la pulsazione dello zero deve precedere quella del polo. Questo tipo di rete è in grado di introdurre un incremento nella fase.

Le tecniche di progettazione per una rete correttiva possono essere basate sull’uso di diagrammi di Bode, formule specifiche o approcci empirici. Nel nostro caso, procediamo con un approccio empirico eliminando il polo a $100\,\text{rad}\cdot\text{s}^{-1}$ del processo attraverso uno zero nella rete correttiva, e scegliamo un polo per la rete correttiva a una pulsazione di $2000\,\text{rad}\cdot\text{s}^{-1}$ . Questa scelta è basata sul fatto che la pulsazione critica del sistema diventa maggiore e di conseguenza il sistema diventa più reattivo. Inoltre, le reti anticipatrici contribuiscono positivamente alla fase, aumentando il margine di fase complessivo.

Per verificare il raggiungimento degli obiettivi desiderati, riportiamo di seguito il diagramma di Bode della cascata tra la rete anticipatrice e il processo.

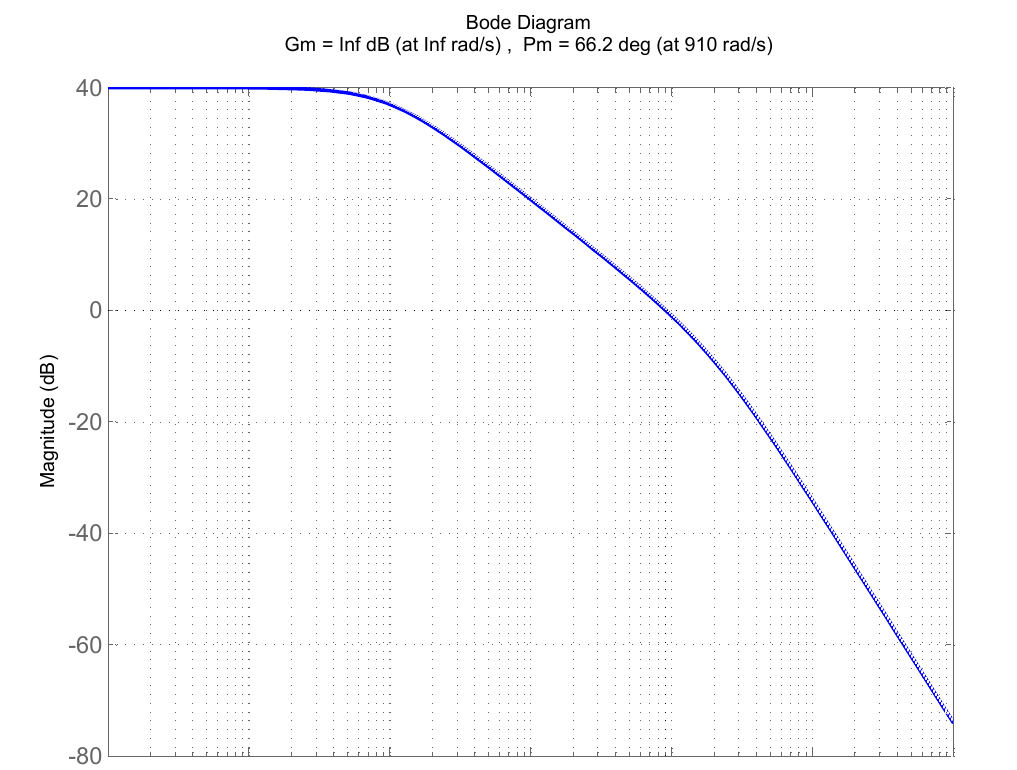
Figura 10: diagrammi di Bode di rete anticipatrice e processo.

In alternativa a questa soluzione, è possibile correggere il comportamento del processo attraverso l’uso di una rete ritardatrice, la cui funzione di trasferimento è definita come:

$R_{\text{rit}}(s) = \dfrac{1 + \tau s}{1 - Ts},$

dove $\tau$ e $T$ soddisfano la condizione $\tau < T$ . In questo caso, l’effetto del polo della rete ritardatrice avviene prima di quello dello zero. Tuttavia, il raggiungimento degli obiettivi di progetto tramite una rete ritardatrice risulta più complesso, poiché il contributo di fase della rete tende a diminuire la fase complessiva del sistema, riducendo di conseguenza il margine di fase complessivo.

L’unico modo per apportare correzioni significative utilizzando una rete ritardatrice è quello di annullare il primo polo della funzione di trasferimento con lo zero della rete ritardatrice e sostituire il polo eliminato con uno di valore inferiore. Nel caso in questione, è possibile scegliere una rete ritardatrice con la seguente forma:

$R_{\text{rit}}(s) = \dfrac{1 + 0.1s}{1 + s}.$

Di seguito, sono riportati i diagrammi di Bode del sistema complessivo per valutare l’effetto della rete ritardatrice sulla risposta del sistema.

Figura 11: diagrammi di bode di rete ritardatrice e processo.

Dalla figura 11 si evince un margine di fase di $52^\circ$ superiore ai $50^\circ$ richiesti.

Tutte le cartelle di controlli automatici

Leggi...

Document

Menu

Chiudi

Esercizi svolti reti compensatrici

Svolgimento.

Svolgimento.

Tutte le cartelle di controlli automatici

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi