Esercizi svolti carta di Nichols

Nel diagramma di Bode illustrato, il margine di guadagno, , corrisponde all’inverso del modulo della funzione di trasferimento, espressa in dB, valutata alla frequenza di attraversamento di fase, ovvero dove la fase raggiunge . Per il caso specifico, si ha .

Il margine di fase, , invece, è definito come la differenza angolare rispetto a della fase della funzione di trasferimento valutata alla frequenza di attraversamento di guadagno, dove il modulo è unitario (0 dB). Nel caso in esame, .

Figura 1: diagramma di Bode.

La carta di Nichols, utilizzando la funzione di trasferimento in anello aperto, permette di identificare importanti caratteristiche del sistema in anello chiuso con feedback unitario.

Attraverso la rappresentazione dell’andamento di modulo e fase della funzione di trasferimento in anello aperto, e confrontandoli con le curve corrispondenti al comportamento del sistema in anello chiuso, è possibile dedurre specifiche proprietà del sistema retroazionato.

Specificamente, i margini di funzionamento per la configurazione in anello aperto vengono determinati in due modi: il margine di fase () come la distanza angolare tra la fase di della funzione in anello aperto e il punto del grafico corrispondente a ; il margine di guadagno () come la distanza in decibel tra il livello di e il punto del grafico della funzione in anello aperto a . Questo approccio conferma i valori dei margini precedentemente calcolati per la configurazione in anello aperto.

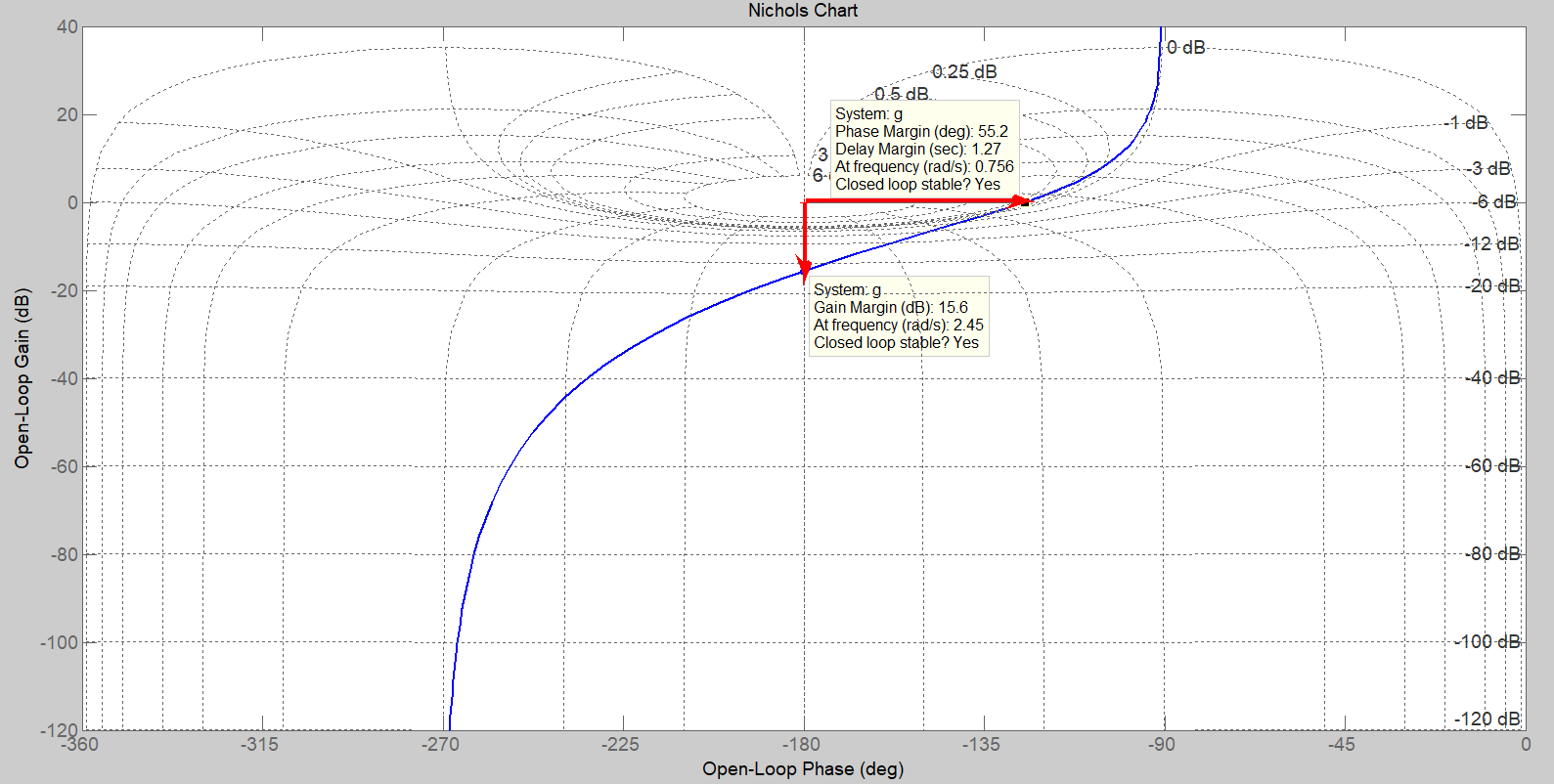
Figura 2: carta di Nichols.

Attraverso l’analisi della carta di Nichols, è possibile individuare caratteristiche significative del sistema in anello chiuso.

La banda passante a del sistema con retroazione si determina individuando il punto di intersezione tra la curva di risposta in frequenza della funzione di trasferimento in anello aperto e la linea dei , rappresentativa della attenuazione del sistema retroazionato, come illustrato nel grafico sottostante.

Questa procedura consente di stabilire la banda passante del sistema a .

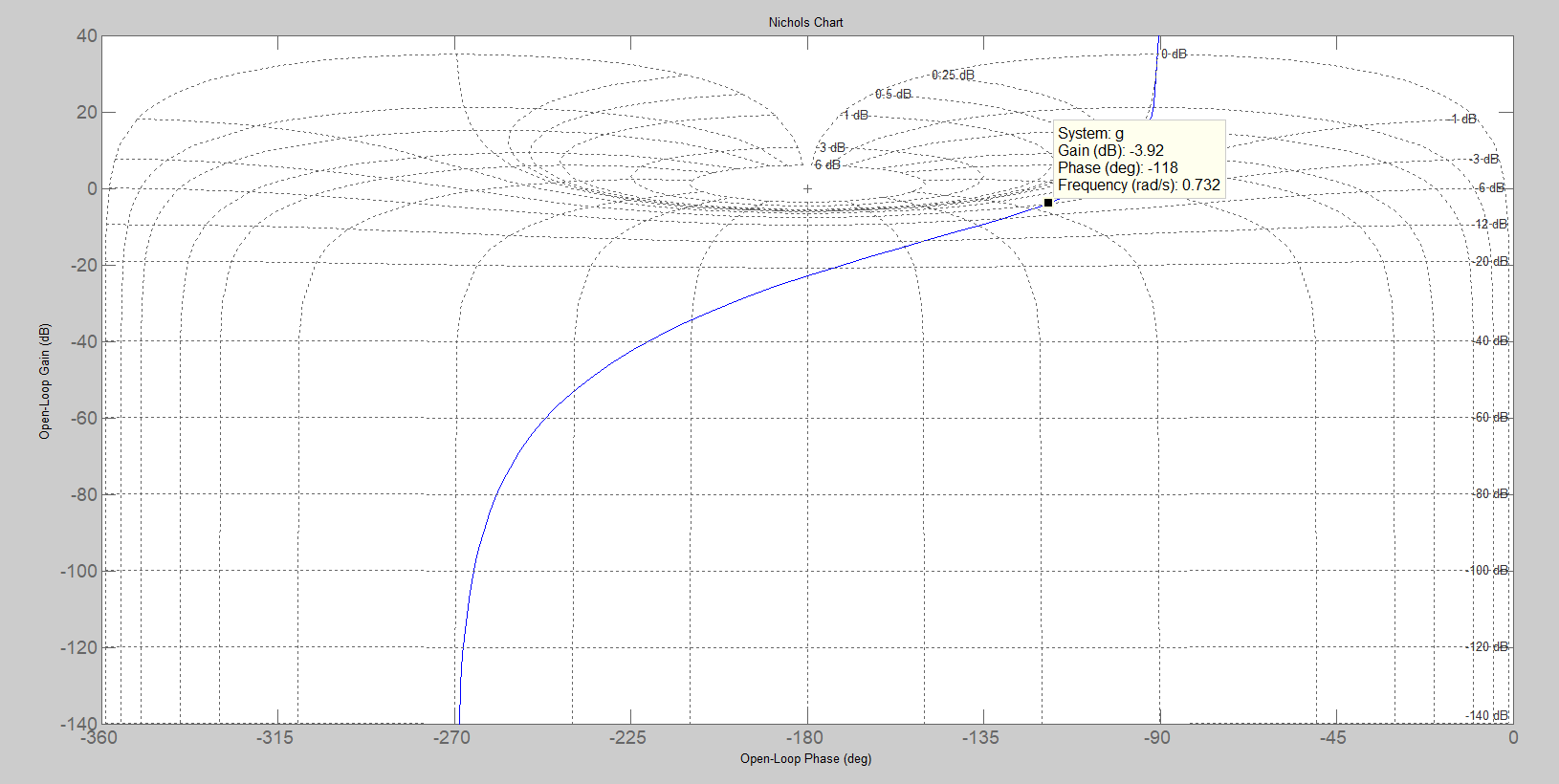
Figura 3: carta di Nichols.

È possibile ottenere lo stesso risultato analizzando il diagramma di Bode del modulo della funzione di trasferimento in anello chiuso, definita come segue:

(2)  

la cui rappresentazione grafica è illustrata nel diagramma sottostante.

Figura 4: diagramma di Bode.

Nello specifico, il margine di fase risulta essere di , mentre il margine di guadagno appare essere infinito, indicando che il sistema non raggiunge il punto di instabilità per incrementi del guadagno.

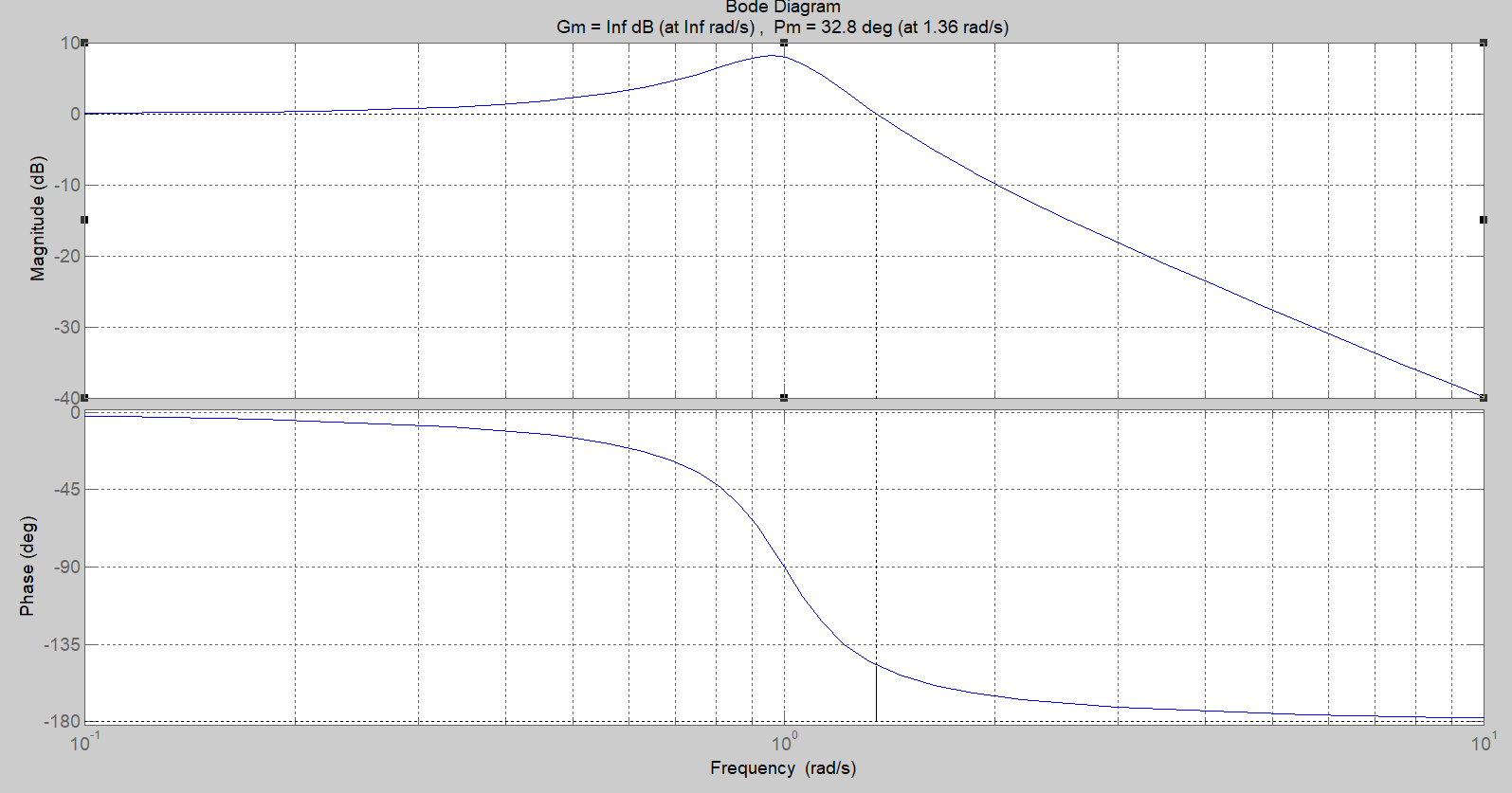
Figura 5: diagramma di Bode.

Il margine di fase può essere determinato altresì mediante il diagramma di Nichols, come illustrato nella figura seguente.

Figura 6: carta di Nichols.

La banda a dB del sistema in anello chiuso è determinabile analizzando il diagramma di Nichols, in particolare identificando il punto di intersezione con la linea corrispondente a dB. Dall’analisi del grafico, risulta che la pulsazione alla quale si verifica tale condizione, , è pari a .

Figura 7: carta di Nichols

Il modulo in condizione di risonanza può essere stimato utilizzando il diagramma di Nichols, identificando il punto sulla curva del sistema in anello chiuso che presenta il massimo valore di guadagno, posizionato il più vicino possibile alla curva relativa al sistema in anello aperto. Tale valore si aggira intorno ai .

Figura 8: carta di Nichols.

La validità di questo risultato è ulteriormente corroborata dall’esame del modulo della funzione di trasferimento in anello chiuso.

Figura 9: diagramma di Bode.

1. Analisi nel dominio di Laplace e del tempo di sistemi dinamici LTI a tempo continuo
2. Analisi modale di sistemi dinamici LTI a tempo continuo
3. Linearizzazione di sistemi dinamici
4. Analisi della Stabilità dei Sistemi LTI
5. Stabilità dell’equilibrio di sistemi dinamici non lineari
6. Retroazione statica dallo stato
7. Analisi nel dominio del tempo e della trasformata Zeta di sistemi dinamici LTI a tempo discreto
8. Trasformata Zeta
9. La risposta in frequenza
10. Analisi modale di sistemi dinamici LTI a tempo discreto
11. La carta di Nichols
12. Proprietà della risposta allo scalino
13. Schemi a blocchi e loro combinazioni
14. I diagrammi di Bode
15. I diagrammi di Nyquist
16. Il progetto del controllore
17. Il luogo delle radici
18. Stabilità in condizioni perturbate: i margini
19. I regolatori PID
20. Le reti compensatrici
21. Modellistica dei sistemi dinamici meccanici, elettrici
22. Proprietà strutturali dei sistemi
23. Sintesi del modello di stato ISU
24. Sintesi dell’osservatore asintotico dello stato