Esercizi svolti progetto del controllore

Home » Esercizi svolti progetto del controllore

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$

. Consideriamo il seguente schema retroazionato, come mostrato nella Figura 1. All’ingresso viene applicato un segnale a rampa del tipo $u(t) = 4t \cdot \text{sca}(t)$

, mentre il processo è descritto dalla funzione di trasferimento:

$P(s) = \frac{2\left(1+\frac{s}{10}\right)}{\left(1+\frac{s}{8}\right)\left(1+\frac{s}{40}\right)\left(1+\frac{s}{80}\right)}.$

Ciò che ci viene richiesto è determinare il tipo $g$ e il guadagno generalizzato $K_c$ del regolatore in modo che l’errore riferito all’uscita sia pari a $1/3$ .

Figura 1.

Svolgimento.

Per applicare il teorema del valore finale, è conveniente riscrivere la funzione di trasferimento $P(s)$

come segue:

$P(s) = 2P'(s).$

L’errore riferito all’uscita è definito come:

$e_u(t) = K_cu(t) - y(t).$

Applicando la trasformata di Laplace, otteniamo:

$E_u(s) = K_cU(s) - \dfrac{\dfrac{2K_c}{s^g}P'(s)}{1 + \dfrac{2K_cP'(s)}{3s^g}}.$

Supponiamo $K_c = 1/H = 3$ e applichiamo il teorema del valore finale per trovare $e_u(\infty)$ . Poiché:

$\mathcal{L}(s)\{4tu(t)\} = \dfrac{4}{s^2},$

otteniamo:

$e_u(\infty) = \lim_{s\to 0}s\dfrac{4}{s^2}\left(3 - \dfrac{\dfrac{2K_c}{s^g}P'(s)}{1 + \dfrac{2K_c}{3s^g}P'(s)}\right) = \lim_{s\to 0}\dfrac{4}{s}\left(3 - \dfrac{\dfrac{2K_c}{s^g}P'(s)}{1 + \dfrac{2K_c}{3s^g}P'(s)}\right).$

Per il principio del modello interno, affinché l’errore sia finito, deve esserci un solo polo in zero nella catena di andata, ovvero $g=1$ . Quindi:

(1) $\begin{equation*} \begin{aligned} e_u(\infty) &= \lim_{s\to 0}\dfrac{4}{s}\left(3 - \dfrac{\dfrac{2K_c}{s^g}P'(s)}{1 + \dfrac{2K_c}{3s^g}P'(s)}\right) \\ &= \lim_{s\to 0}\dfrac{4}{s}\left(3 - \dfrac{\dfrac{2K_c}{s^1}P'(s)}{1 + \dfrac{2K_c}{3s^1}P'(s)}\right) \\ &= \lim_{s\to 0}\dfrac{4}{s}\left(\dfrac{3 + \dfrac{2K_c}{s}P'(s) - \dfrac{2K_c}{s}P'(s)}{1 + \dfrac{2K_c}{3s}P'(s)}\right) \\ &= \lim_{s\to 0}4\left(\dfrac{3}{s + \dfrac{2K_c}{3}P'(s)}\right) \\ &= \dfrac{12}{\dfrac{2K_C}{3}} = \dfrac{18}{K_c}. \end{aligned} \end{equation*}$

Dato che per ipotesi si richiede che:

$\dfrac{18}{K_c} = \dfrac{1}{3},$

si ottiene:

$K_c = 54.$

Esercizio 2 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

. Dato lo schema rappresentato in figura 1, in cui il processo è descritto dalla funzione di trasferimento $P(s) = \frac{10}{s(s-1)}$

, l’obiettivo è progettare un regolatore con un luogo delle radici che possa stabilizzare il sistema. Inoltre, è necessario identificare il valore del guadagno $k$

del regolatore per cui il sistema retroazionato diventa asintoticamente stabile.

Figura 2: sistema retroazionato.

Svolgimento.

La prima fase nella sintesi del regolatore comporta la tracciatura del luogo delle radici del processo. Dato che la funzione di trasferimento del processo non contiene zeri, i rami che si originano dai poli si estenderanno all’infinito lungo gli asintoti che formano angoli di $90^\circ$ e $27^\circ$ con l’asse delle ascisse. Inoltre, il centro degli asintoti è localizzato nel grafico del luogo delle radici al punto con ascissa $\sigma_A = \frac{1}{2}$ .

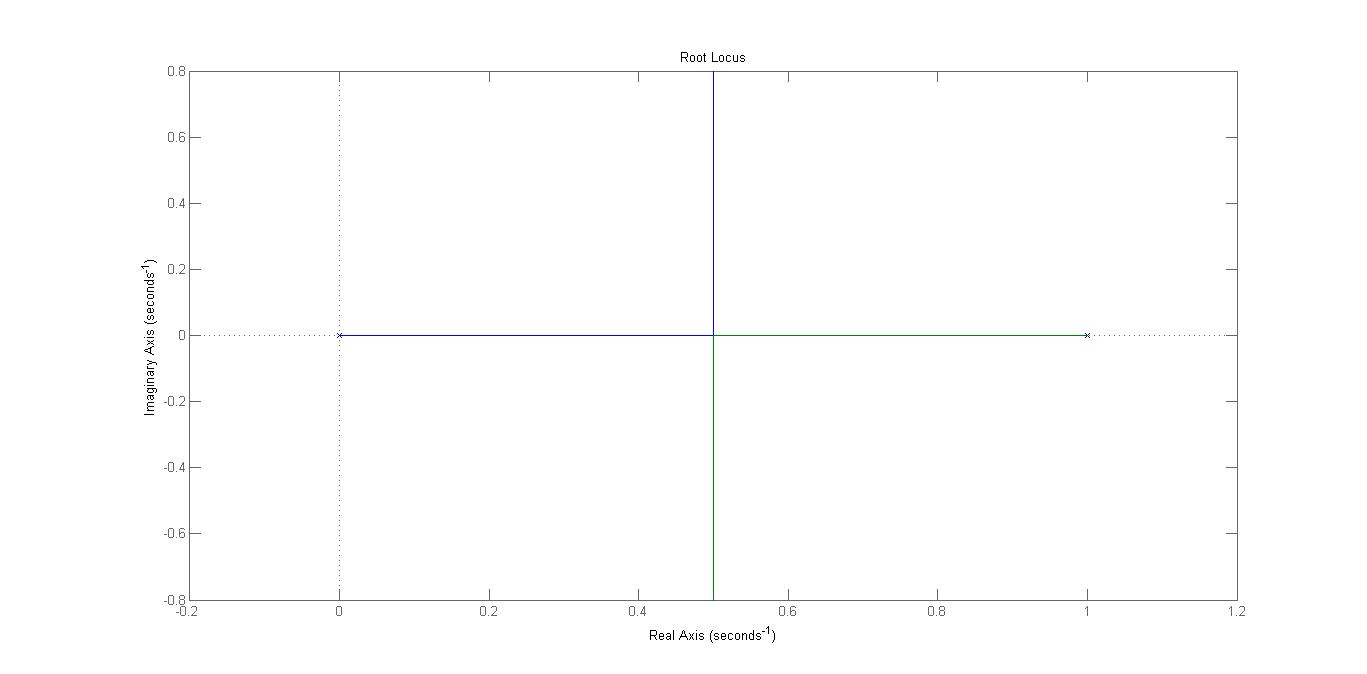
Figura 3: luogo diretto delle radici in assenza di regolatore.

Studiando il denominatore con la tabella di Routh, abbiamo:

$\begin{array}{|c|c|c|} \hline 3 & 1 & 10K - 7 \\ \hline 2 & 6 & 40K \\ \hline 1 & 3.3K - 7 & 0 \\ \hline 0 & 40K & 0 \\ \hline \end{array}$

Quindi, affinché gli elementi della prima colonna siano tutti positivi, occorre che:

$K > \frac{7}{3.3} = 2.12.$

Come si evince dal successivo diagramma del luogo delle radici.

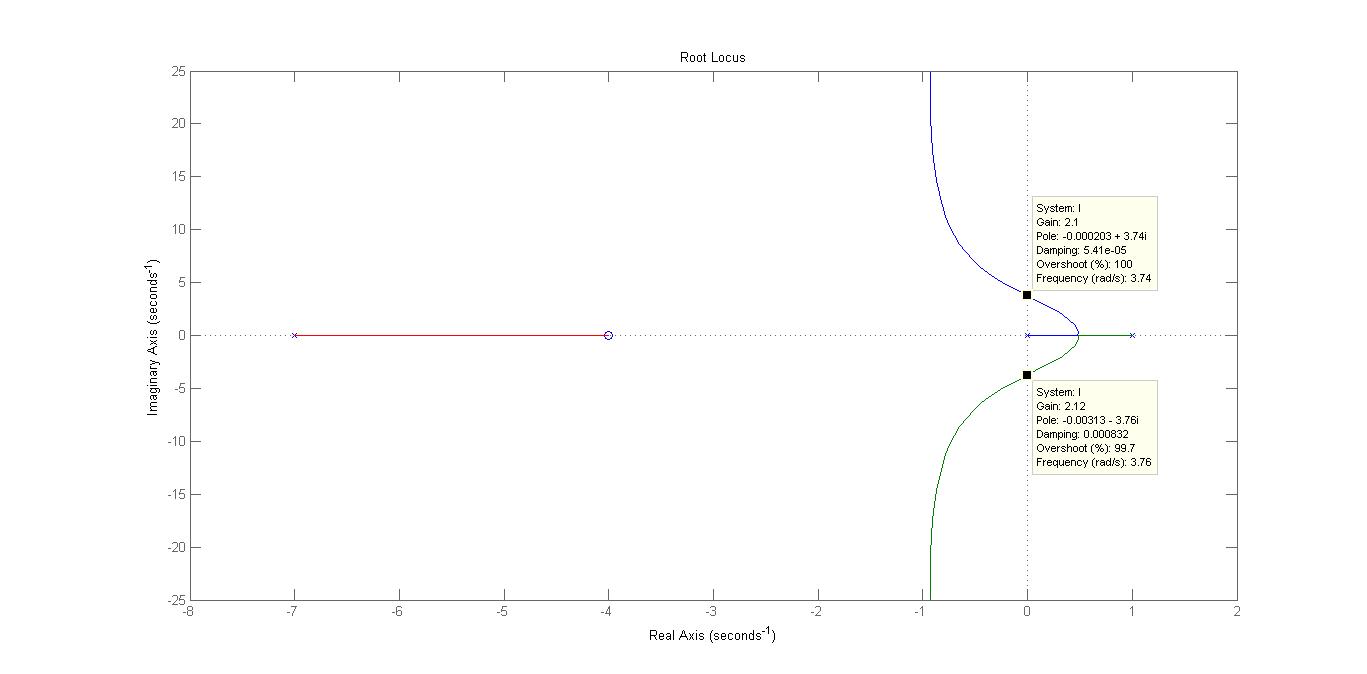
Figura 4: luogo delle radici in presenza del regolatore progettato.

Esercizio 3 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Si consideri il sistema retroazionato descritto dalla funzione di trasferimento

$W(s)=\dfrac{C(s)G(s)}{1+C(s)G(s)},$

dove

$G(s)=\dfrac{10(s+100)}{(s^2+s+10)}$

e
$C(s)$
è la funzione di trasferimento del controllore. Si richiede di svolgere i seguenti punti:

si supponga il controllore di tipo proporzionale e si studia la stabilità del sistema retroazionato quando il controllore assume valori $10^{-3}$ oppure $1$ .
Si progetti il controllore in modo da soddisfare le seguenti specifiche:
- errore a regime a risposta a gradino unitario tale che $e_\infty\leq 1/101$ ;
- pulsazione di attraversamento $\omega_c=\text{0,1}\,\text{rad}\cdot \text{s}^{-1}$ ;
- margine di fase $\phi_m\geq 60^\circ$ .

Svolgimento punto 1.

Dalla struttura della funzione di trasferimento del sistema retroazionato, in quanto manca il contributo di un trasduttore, si deduce che il sistema opera in retroazione unitaria, come rappresentato nella Figura 5.

Figura 5: sistema retroazionato.

Per valutare la stabilità del sistema in retroazione, è possibile analizzare il luogo delle radici della funzione di trasferimento G(s), considerando il controllore come il parametro che influenza la posizione dei poli del sistema retroazionato.

Figura 6: luogo delle radici.

Si osserva che per tutti i valori di guadagno positivo il luogo giace nel semipiano a parte reale negativa. Quindi vi giace per i valori proposti in traccia. Si conclude per i guadagni proposti per il controllore il sistema è asintoticamente stabile.

Svolgimento punto 2.

Il controllore si può supporre fatto di due parti: una parte per il soddisfacimento della specifica statica sull’errore a regime e una seconda parte per il soddisfacimento delle specifiche dinamiche sulla pulsazione di attraversamento sul margine di fase. Poiché si desidera un errore a regime non è necessario introdurre poli in zero nel controllore. Per cui, si può ipotizzare un controllore di tipo proporzionale $C_s(s)=k$

; pertanto l’errore a regime rispetto ad un ingresso a scalino vale $e_\infty=A/(1+\mu_L )$

dove $A$

è l’ampiezza dello scalino in ingresso e $\mu_L$

il guadagno statico della cascata costituita dal controllore e dal sistema. Il guadagno statico del sistema può essere valutato ponendo $s=0$

nella $G(s)$

, da cui risulta essere pari a $100$

. Dunque,

$e_\infty=\dfrac{1}{1+100k}\leq \dfrac{1}{101},$

da cui

$\dfrac{100k-100}{1+100k}\geq 0,$

o anche

$k\leq -\dfrac{1}{100}\quad \vee \quad k \geq 1.$

Siccome $k$ è un guadagno deve essere positivo, quindi prende solo la soluzione $k\geq 1$ .

Rappresentiamo di seguito il diagramma di Bode della funzione di anello $L(s)=R(s)G(s)$ attuale.

Figura 7: diagramma di Bode della funzione d’anello.

Si deduce che la pulsazione di attraversamento è di circa $30\,\text{rad}\cdot \text{s}^{-1}$ e il margine di fase è $\phi_m = 180^\circ - 160^\circ = 20^\circ$ . Poiché il margine di fase è inferiore a quello richiesto dalla traccia, possiamo introdurre una rete anticipatrice che aggiunge una fase di $40^\circ$ alla pulsazione di attraversamento. La struttura della rete anticipatrice è la seguente:

$C_d(s) = \frac{1 + \tau s}{1 + s\tau \,m^{-1}}$

dove $\tau$ è la costante di tempo e $m$ è un fattore di correzione del polo rispetto allo zero. Questi valori possono essere determinati consultando gli abachi noti, come quelli riportati di seguito:

Figura 8: abaco di progetto della rete anticipatrice.

Sugli abachi sono stati individuati due punti in grado di fornire un incremento di fase di $40^\circ$ con un guadagno ridotto, poiché il guadagno della funzione $G(s)$ già soddisfaceva le specifiche. Dai dati degli abachi sono stati trovati i seguenti valori:

$\tau = \frac{1}{30}$

$m = 12.$

Di conseguenza, la rete anticipatrice ha la seguente forma:

$C_d(s) = \frac{1 + \frac{s}{30}}{1 + \frac{s}{30 \cdot 12}}.$

Quindi, il controllore ha una funzione di trasferimento complessiva data dal prodotto del primo guadagno, che è stato trovato per soddisfare le specifiche statiche, e della rete anticipatrice. Con questo regolatore, il sistema retroazionato presenta un margine di fase di $73^\circ$ e una pulsazione di attraversamento di $44\,\text{rad}\,\text{s}^{-1}$ , entrambi conformi alle specifiche richieste.

Esercizio 4 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$

Figura 9.

In figura si ha lo schema del controllo a ciclo chiuso utilizzato nell’esercizio $3.2$

Con riferimento allo schema di controllo in controreazione in figura, si abbia

(2) $\begin{equation*} P(s)=\dfrac{10}{(s+1)^2},\,H(s)=\dfrac{1}{2}. \end{equation*}$

Determinare $C(s)$ con la tecnica del luogo delle radici in modo che

(3) $\begin{align*} &1.\,e_{y,\infty}\le \text{0,1}\,\mbox{per }r(t)=t\cdot1(t)\\ &2.\,e_{y,\infty}=0\,\mbox{per }d(t)=1(t) \end{align*}$

e che il sistema complessivo sia asintoticamente stabile.

Svolgimento.

Per garantire il soddisfacimento delle specifiche a regime, è necessario attenuare il disturbo a valle del processo $P(s)$ , senza introdurre tuttavia un polo in zero nel segnale risultante.

La funzione di trasferimento tra l’errore e l’uscita rispetto al riferimento e all’uscita stessa rimane la funzione di sensitività definita come:

(4) $\begin{equation*} S(s)=\dfrac{1}{1+CPH}. \end{equation*}$

Per il rispetto delle specifiche di precisione statica, è sufficiente che il regolatore presenti un polo in zero, assumendo quindi la forma:

(5) $\begin{equation*} C(s)=\dfrac{k_c}{s}. \end{equation*}$

Rispetto al segnale a rampa, è necessario imporre che l’errore di velocità sia:

(6) $\begin{equation*} e_v=\dfrac{1}{k_v}\leq \text{0,1} \end{equation*}$

con

(7) $\begin{align*} &k_v=\lim_{s\to0}\,s\cdot H\cdot P(s)C(s)\\ &k_v=\lim_{s\to0}\cancel{s}\cdot\dfrac{1}{2}\cdot\dfrac{10}{(s+1)^2}\cdot\dfrac{k_c}{\cancel{s}}=5kc\\ &e_v=\dfrac{1}{5k_c}\leq \text{0,1}\to k_c\geq 2 \end{align*}$

Si può verificare tramite il luogo delle radici se il sistema è asintoticamente stabile per $k>2$ . Dal luogo in Figura 10, per $k>0$ , si evince che per $k>2$ il sistema è instabile. Per renderlo stabile, si cancella un polo in “ $-1$ ” del processo attraverso uno zero del controllore, ottenendo:

(8) $\begin{equation*} C(s)=\dfrac{k_c(s+1)}{s} \end{equation*}$

Il sistema risultante è:

(9) $\begin{equation*} F(s)=\dfrac{10k_c}{s(s+1)}. \end{equation*}$

e come si evince dal luogo in Figura 10, è stabile per $k_c>2$ .

Figura 10: luogo delle radici.

Esercizio 5 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$

. Data la funzione ad anello aperto

(10) $\begin{equation*} L(s)=\dfrac{-0.0046275}{(s+1.68)(s-1.68)(s^2+0.0002828s+1.113)}. \end{equation*}$

Progettare un controllore in grado di garantire la stabilità del sistema ad anello chiuso con retroazione unitaria.

Svolgimento.

La funzione ad anello aperto è caratterizzata dalla presenza di un polo con parte reale positiva, indicando così la sua instabilità. Nonostante il margine di fase sia positivo, come dimostrato nella figura sottostante, che rappresenta il diagramma di Bode di $L(s)$

questa condizione non permette di dedurre automaticamente la stabilità del sistema retroazionato, in quanto sono violate le ipotesi del criterio di Bode. Il criterio di Bode, infatti, ha come condizioni per la stabilità del sistema retroazionato:

che i poli di $L(s)$ siano tutti stabili;
che il suo diagramma di Bode del modulo parta sopra l’asse 0 dB e lo tagli una volta sola;
che il guadagno generalizzato (non in decibel) sia positivo;
che il margine di fase sia positivo.

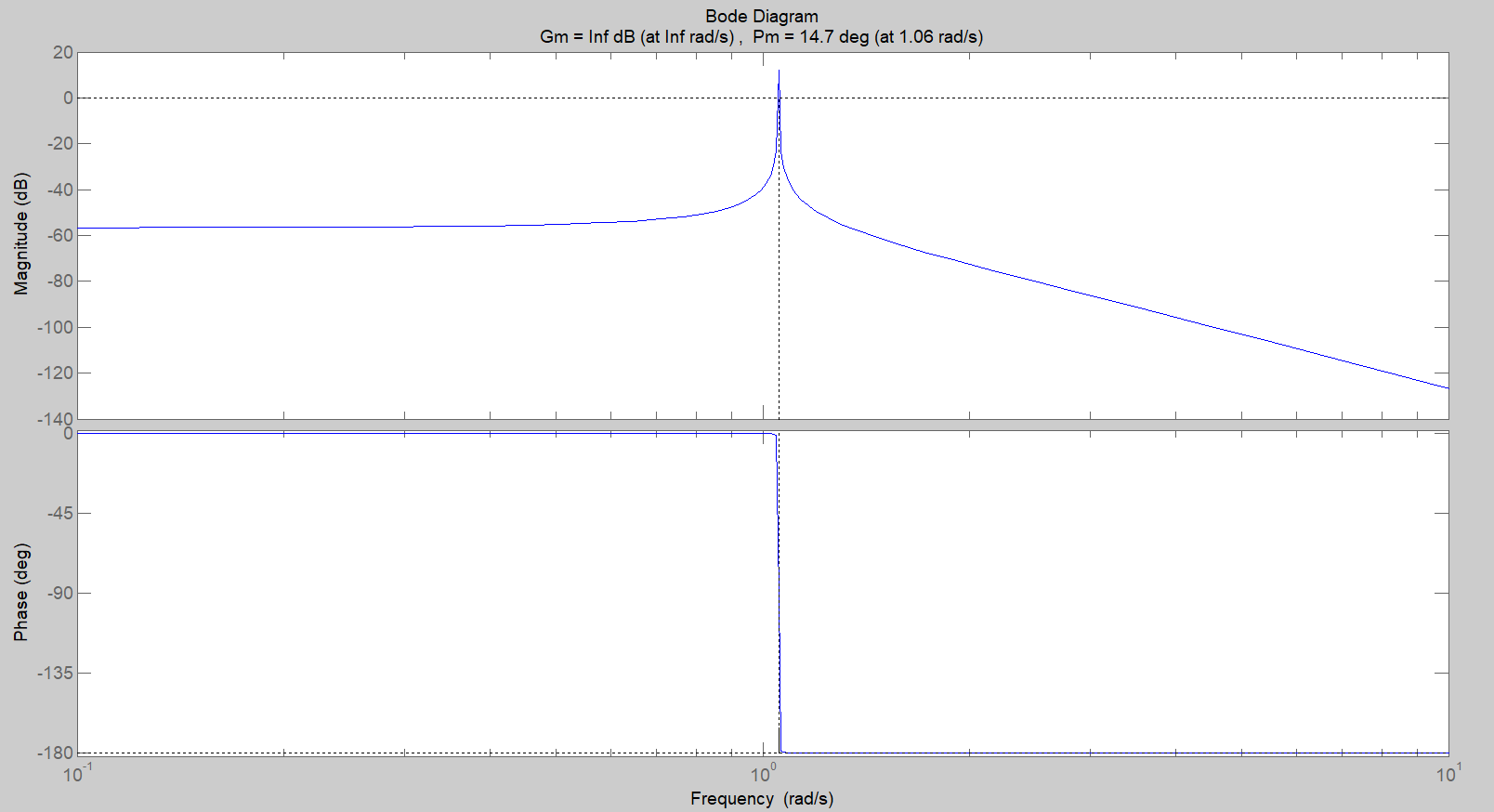
Figura 11: diagramma di Bode.

Inoltre, analizzando il diagramma di Nyquist di $L(s)$ , l’instabilità in anello chiuso è evidenziata dal fatto che la curva non circonda il punto $-1$ .

Figura 12: diagramma di Nyquist.

L’analisi del luogo delle radici rivela che l’instabilità deriva da un ramo situato costantemente nel semipiano con parte reale positiva.

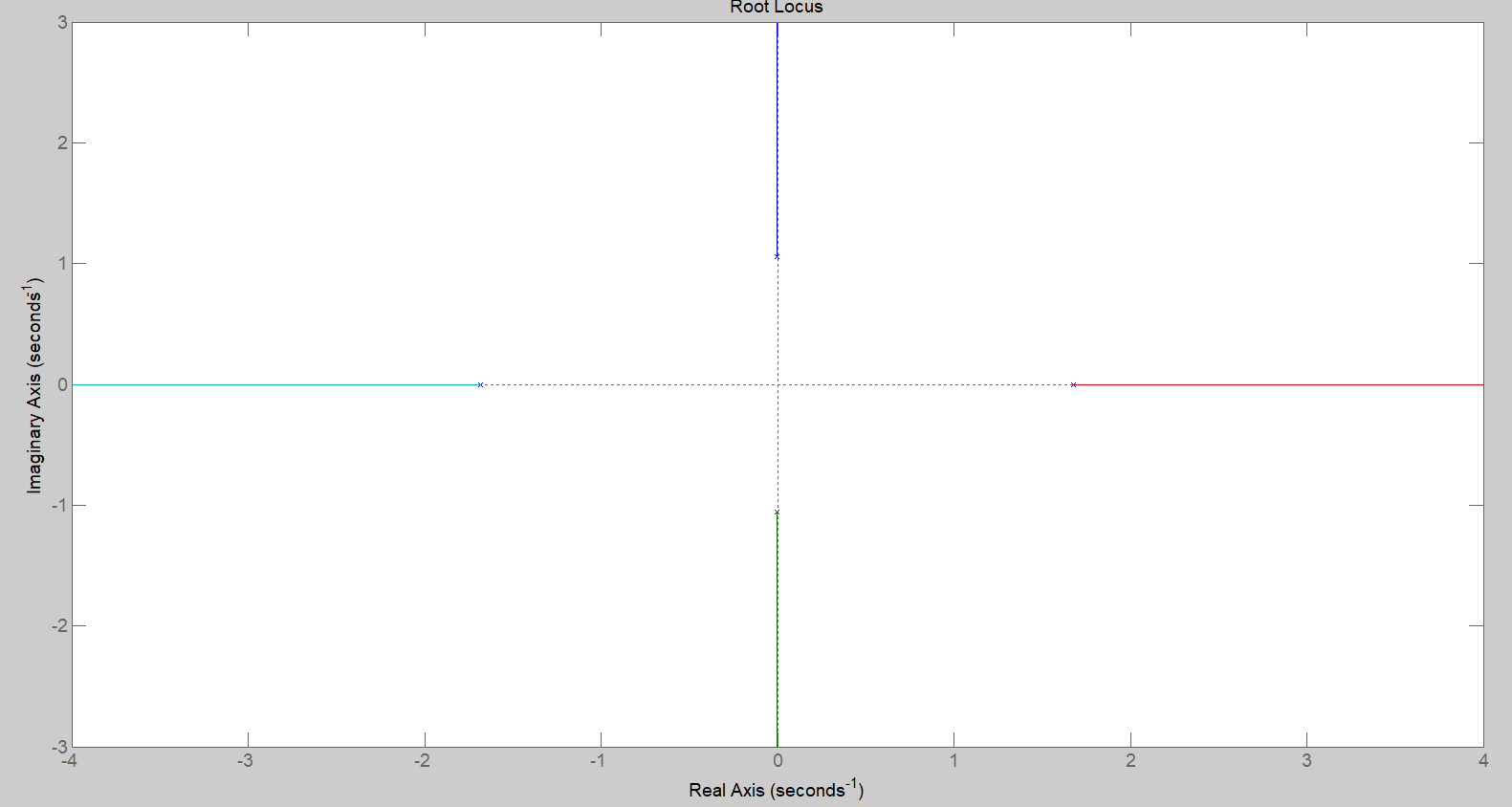
Figura 13: luogo delle radici per valori di guadagno maggiori di zero.

Figura 14: luogo delle radici per valori di guadagno minori di zero.

Prima di procedere alla sintesi del controllore $C_2$ in grado di garantire le specifiche richieste, è essenziale sviluppare un anello interno di retroazione per assicurare la stabilità del sistema. Lo schema da seguire è il seguente:

Figura 15: schema a blocchi del sistema.

Il controllore $C_1(s)$ è incaricato di stabilizzare $G(s)$ , mentre $C_2(s)$ , agendo sulla funzione stabilizzata $G_1(s)$ , garantisce il rispetto delle specifiche richieste. Analizzando il luogo delle radici, si inizia con l’applicazione di un guadagno negativo di $-1$ per invertire il ramo che si dirige verso l’infinito. Successivamente, è possibile rimuovere la coppia di poli complessi coniugati, dato che presentano una parte reale negativa, precisamente $\lambda_{1,2} = -0.0001 \pm 1.055j$ .

Figura 16: luogo delle radici.

Per spostare il luogo delle radici interamente nel semipiano delle parti reali negative, si introducono uno zero in $-1$ e un altro in $-10$ rad/sec. Di conseguenza, otteniamo:

(11) $\begin{equation*} C(s)=-\frac{10^3(1+\text{0.00036}+(\text{0,95}s)^2)(s+1)}{(\text{0,1}s+1)(\text{0,01}s+1)^2}, \end{equation*}$

includendo anche due poli ad alta frequenza per garantirne la realizzabilità fisica. Il luogo delle radici modificato è mostrato nella figura seguente.

Si ricorda che, in ogni caso, non si sarebbe potuto cancellare lo zero positivo di $L(s)$ , poiché ne avrebbe compromesso l’osservabilità.

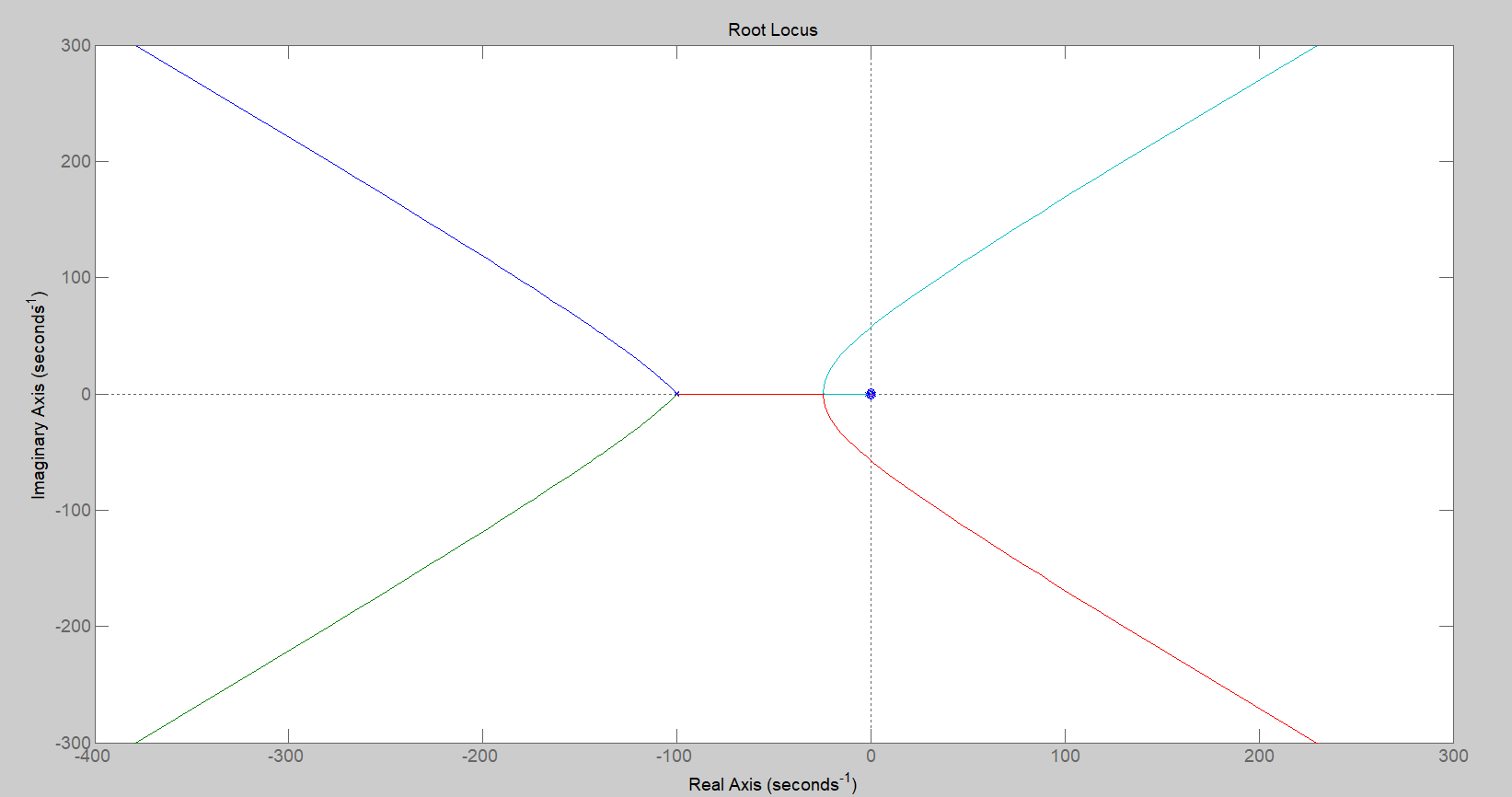
Figura 17: luogo delle radici.

Si evince la posizione stabile dei poli. Dunque è sufficiente l’anello interno a garantire l’ottemperanza alle specifiche.

Esercizio 6 $(\bigstar\bigstar\bigstar\bigstar\bigstar)$

. Sia il sistema illustrato nella Figura 18, in cui il processo è descritto dalla funzione:

$P(s) = \frac{1}{1+10s}.$

Si desidera progettare il regolatore $R(s)$ in modo che il sistema retroazionato soddisfi le seguenti specifiche:

$\left \vert e_{\infty}\right \vert=0$ per $y_0(t)=\text{sca}(t)$ (funzione gradino).
$\left \vert e_{\infty}\right \vert <0,02$ per $d(t)=\sin \left(\omega t\right)$ con $\omega=\text{0,03}\,$ rad/s;
$\omega_c$ della funzione d’anello aperto tale che $0,2\leq \omega_c \leq \,\text{rad}(\text{s})$ ;
Margine di fase $\phi_M\geq 50$ .

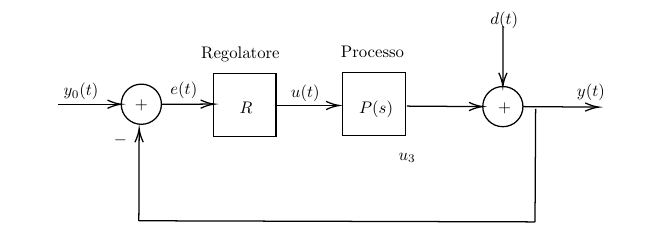
Figura 19: schema a blocchi del sistema di controllo.

Svolgimento.

La parte del regolatore che riguarda la specifica di precisione statica (specifica $a$ ) e quella relativa alla precisione dinamica possono essere progettate separatamente come segue:

$R(s) = R_S(s) \cdot R_d(s).$

Progettiamo $R_S(s)$ per soddisfare la specifica $a$ : si richiede un errore a regime nullo rispetto a un segnale a gradino che contiene un solo polo. La funzione ad anello aperto deve contenere un polo in zero, poiché nel processo manca un polo in zero, lo introduciamo nel regolatore come segue:

$R(s) = \frac{1}{s}.$

Progettiamo $R_S(s)$ per soddisfare le specifiche $b$ – $d$ come segue:

$E(s) = S(s) \cdot D(s),$

dove $S(s)$ è la funzione di sensitività complementare. Quindi, l’errore è dato da:

$E(s) = \frac{L(s) }{1 + L(s)},$

dove $L(s) = R(s) \cdot P(s)$ rappresenta la funzione d’anello.

Il disturbo agisce a basse frequenze, dove:

$\left \vert S(s) \right \vert \approx \frac{1}{\left \vert L(s) \right \vert},$

di conseguenza

$E(s) \approx \frac{D(s)}{\left \vert L(s) \right \vert }.$

È necessario che per $\omega < \text{0,03}\, \text{rad/s}$ il modulo di $L(j\omega)$ attenui il segnale di $1/(0.02) = 50 = 34\, \text{dB}$ , cioè il modulo di $L(j\omega)$ per $\omega < \text{0,03}\, \text{rad/s}$ deve essere almeno $50$ dB.

Considerando la $L(s)$ attuale: $L(s) = R(s) \cdot P(s)$ .

Figura 20: confronto tra la specifica sul disturbo e il diagramma ad anello aperto.

Dalla differenza di 16 dB tra il valore del modulo di $L(j\omega)$ valutato a $\omega=\text{0,03}$ rad/s e i 50 dB, possiamo dedurre che anche se applicassimo un guadagno in grado di far diminuire il valore di $\left \vert L(j\omega)\right \vert$ di 16 dB, la specifica $b$ verrebbe comunque soddisfatta.

D’altra parte, riducendo il valore di $\left \vert L(j\omega)\right \vert$ , sposteremmo la pulsazione di taglio verso sinistra, come richiesto dalla specifica $c$ . Questo può essere ottenuto introducendo un guadagno $\mu_R$ nel regolatore in modo che:

$-10\, \text{dB} = 20\log_{10}\left(\mu_R\right) \quad \Rightarrow \quad \mu_R = 10^{-\frac{10}{20}} = \frac{1}{\sqrt{10}} \approx \text{0,31}.$

Quindi:

$R_2(s) \approx \text{3,16}$

$L' = R_S(s)\cdot R_d(s)\cdot P(s) = \frac{\text{3,1}}{s\left(1+10s\right)}.$

Il diagramma di Bode di questa funzione è il seguente:

Figura 21: confronto tra la specifica sul disturbo e il diagramma ad anello aperto.

Dal grafico possiamo dedurre che:

$\omega \approx 0,55\, \text{rad/s}$

quindi la fase critica è:

$\phi_C = -90^\circ - \arctan(5,5) \approx -169^\circ.$

Inoltre, il margine di fase è:

$\phi_M = 180^\circ - |\phi_C| \approx 11^\circ.$

È evidente che la pulsazione di taglio $\omega_c$ deve essere spostata ulteriormente verso sinistra e il margine di fase $\phi_M$ deve essere aumentato, il che implica che la fase critica $\phi_C$ deve crescere.

Ci sono diverse tecniche che possono essere adottate per ottenere questo obiettivo. Ad esempio, è possibile cancellare il polo a $\omega=\text{0,1}$ rad/s del processo introducendo uno zero nel regolatore a $\omega=\text{0,04}$ rad/s. In tal caso, il regolatore dinamico diventerebbe:

$R_d(s) = \frac{\text{0,31}(1+10s)}{1+\dfrac{s}{\text{0,04}}}$

e la funzione di anello aperto diventerebbe:

$L'(s) = \frac{\text{3,1}}{s\left(1+\dfrac{s}{\text{0,04}}\right)}.$

Figura 22: diagramma di Bode della funzione d’anello a seguito della cancellazione del polo in \text{0,1} rad/s del processo.

Dalla Figura 22 possiamo osservare che:

$\omega_c \approx 0,3\, \text{rad/s}$

quindi

$\phi_C \approx -174^\circ$

da cui segue che

$y_M \approx 6^\circ.$

Tuttavia, la specifica sul margine di fase non è ancora soddisfatta. Per rispettarla, possiamo aggiungere uno zero nel regolatore a $\omega=\text{0,2}$ rad/s, ottenendo così il seguente regolatore: