Esercizi svolti luogo delle radici

Home » Esercizi svolti luogo delle radici

Esercizio 1 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Consideriamo lo schema di controllo mostrato nella figura. Il processo è rappresentato dalla funzione di trasferimento:

$P(s) = \frac{200}{(s + 20)(s + 4)(s - 4)}.$

Con un regolatore proporzionale definito da:

$R(s) = k,$

analizziamo la stabilità del sistema a ciclo chiuso variando $k$ , utilizzando sia il metodo del luogo delle radici che il criterio di Nyquist.

Rendered by QuickLaTeX.com

Figura 1: schema di controllo.

Svolgimento.

Si noti innanzitutto che il sistema ad anello aperto è instabile per la presenza di un polo a parte reale positiva. Tuttavia, la retroazione può rendere il sistema asintoticamente stabile. Il luogo delle radici rappresenta l’evoluzione dei poli del sistema retroazionato al variare di $k$ . Per tracciarlo, consideriamo:

I punti di diramazione, calcolati come
$N_P(s)\cdot\frac{d}{ds}(D_P(s))- D_P(s)\cdot\frac{d}{ds}(N_P(s))=0,$

dove $N_p$ e $D_P$ sono numeratore e denominatore del processo. Si ottiene

$200[(s-4)(s+4)+(s-4)(s+20)+(s+4)(s+20)]=0,$

e da ciò

$s_{1,2}=\pm \text{0,38}.$
Angoli formati dall’asse reale e il luogo delle radici, dati da
$\theta_i=\frac{180^\circ+h360^\circ}{n-m},$

con $n$ numero di poli, $m$ numero di zeri e $h=0,\dots(n-m-1)$ . Si hanno

$\theta_1=60^\circ, \quad\theta_2=180^\circ, \quad \theta_3=300^\circ.$

Per il luogo inverso,

$\theta_i=\frac{h360^\circ}{n-m},$

con

$\theta_1=0^\circ, \quad\theta_2=120^\circ, \quad \theta_3=240^\circ.$
I punti dell’asse reale con un numero dispari di poli e zeri a destra appartengono al luogo diretto, quelli con un numero pari al luogo inverso.

Basandoci su quanto precedente, possiamo affermare che il luogo diretto delle radici corrisponde a quello illustrato nella figura 2.

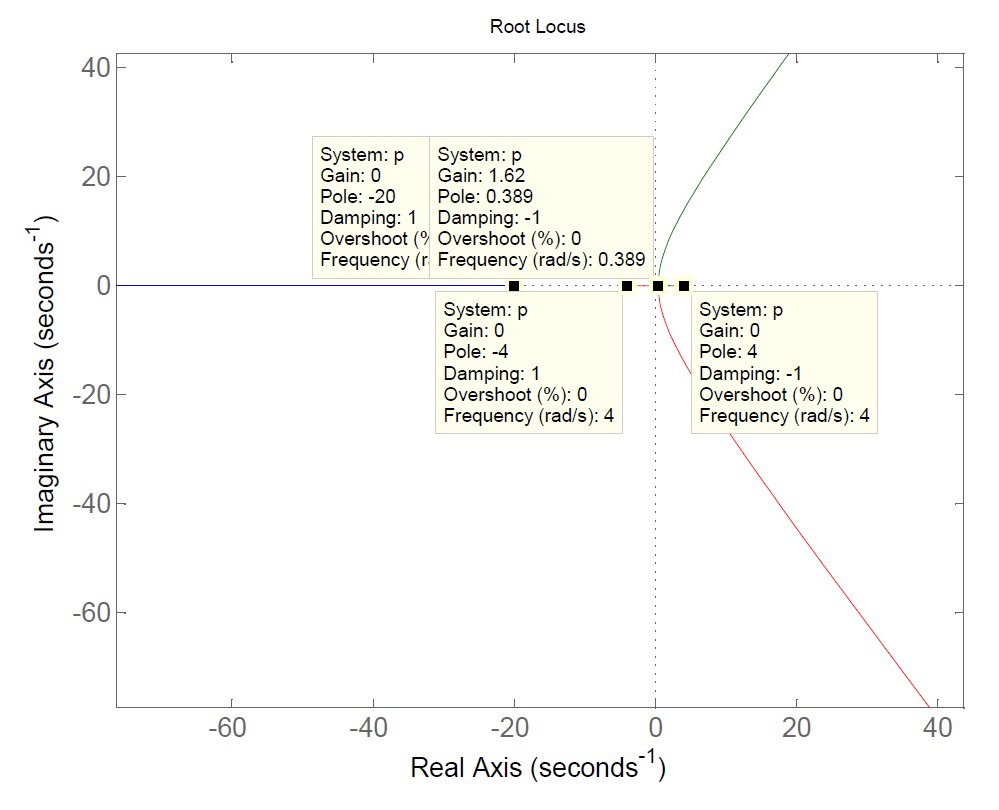
Figura 2: luogo delle radici diretto.

Dato che in $P(s)$ mancano zeri, i rami del luogo delle radici si estendono all’infinito. Analizzando il grafico 2, si evince che non esiste un valore positivo di $k$ che mantenga tutti i rami nel semipiano a parte reale negativa. Di conseguenza, il sistema non è stabilizzabile con un regolatore proporzionale a guadagno positivo.

Il luogo inverso, invece, è illustrato nella figura 3.

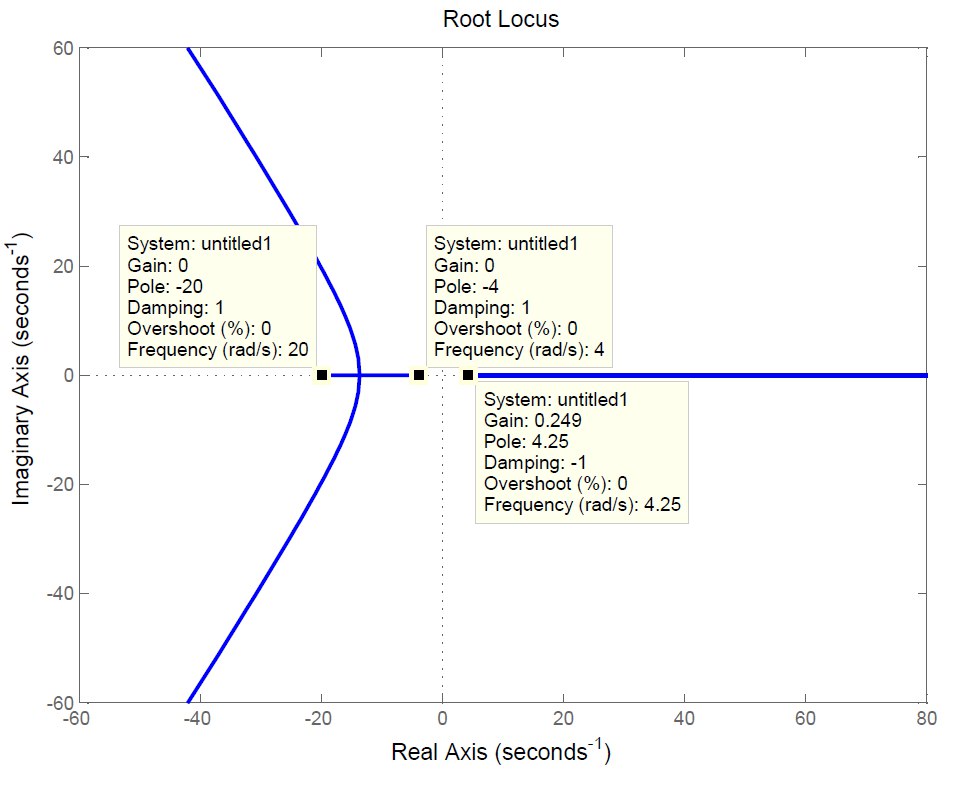
Figura 3: luogo delle radici inverso.

Anche in questo scenario, è evidente che non vi è alcun valore negativo di $k$ per cui i poli del sistema a ciclo chiuso si trovano tutti nel semipiano a parte reale negativa. Di conseguenza, il sistema non può essere stabilizzato con un guadagno negativo del regolatore. Procediamo ora con l’analisi utilizzando il criterio di Nyquist. In figura 4 è riportato il diagramma di Nyquist della funzione P(s) ad anello aperto.

Rendered by QuickLaTeX.com

Figura 4: diagramma di nyquist.

Il punto critico $-1/k$ sull’asse reale varia in base al guadagno $k$ . Tuttavia, la condizione di Nyquist non è soddisfatta a causa dell’orientamento in senso orario del diagramma. Inoltre, il criterio di Bode non è applicabile, data la presenza di un polo con parte reale positiva nel processo.

Esercizio 2 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Determinare la posizione delle radici della funzione

$L(s) = \frac{4(1 + s)^2}{s(1 - s)^2}$

e calcolare il guadagno per cui le radici del sistema in retroazione unitaria diventano instabili.

Svolgimento.

Il luogo delle radici indica la posizione dei poli del sistema al variare di un guadagno $k$ che può essere inteso introdotto da un regolatore proporzionale con retroazione unitaria. Per tracciarlo efficacemente, è importante considerare i seguenti punti:

I punti sull’asse reale appartengono al luogo diretto se a destra di essi si trovano un numero dispari di poli e zeri. Al contrario, appartengono al luogo inverso se a destra si trovano un numero pari di poli e zeri.
I punti di diramazione, dove il luogo lascia l’asse reale, si determinano imponendo:
$N_P(s)\cdot\dfrac{d}{ds}(D_P(s)) - D_P(s)\cdot\dfrac{d}{ds}(N_P(s)) = 0$

dove $N_P$ e $D_P$ sono rispettivamente il numeratore e il denominatore del processo. Per l’esempio in questione, si ha:

$2s(1-s)^2(1+s) - (1+s)^2(3s^2-4s+1) = 0,$

da cui

$s = \pm1, \quad \vee \quad s = -2 \pm \sqrt{5}.$

Secondo la regola al punto 1, i punti $s = -1$ e $s = -2 + \sqrt{5}$ appartengono al luogo inverso, mentre $s = 1$ e $s = -2 - \sqrt{5}$ appartengono al luogo diretto.
Gli angoli formati dall’asse reale con il luogo delle radici si calcolano come segue. Per il luogo diretto:
$\theta_i = \dfrac{180^\circ + h360^\circ}{n - m}$

dove $n$ è il numero di poli, $m$ è il numero di zeri e $h = 0, \dots, (n - m - 1)$ . Nel nostro caso, con $n = 3$ e $m = 0$ , e $h = 0, 1, 2$ , gli angoli sono:

$\theta_1 = 60^\circ, \quad \theta_2 = 180^\circ, \quad \text{e} \quad \theta_3 = 300^\circ.$

Per il luogo inverso, gli angoli sono dati da:

$\theta_i = \dfrac{h360^\circ}{n - m}$

Con $n = 3$ e $m = 2$ , e $h = 0$ , gli angoli risultano:

$\theta_1 = 180^\circ, \quad \theta_2 = 0^\circ.$

Segue che il luogo delle radici diretto è:

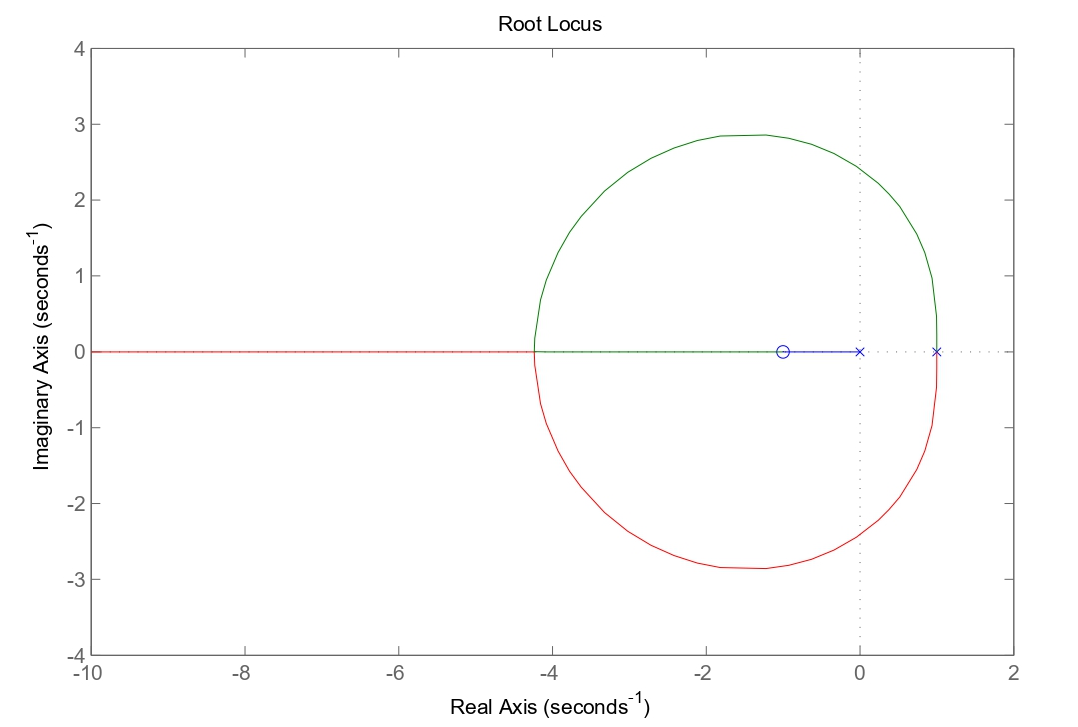
Figura 5: luogo delle radici diretto della funzione assegnata.

Il ramo originato dal polo a $0$ converge verso lo zero in $-1$ . A partire dal punto 1, dove si trovano due poli, emergono due rami che si allontanano rapidamente dall’asse reale, convergendo poi verso $-2 - \sqrt{5}$ . Da questo punto, un ramo si riconnette allo zero in $-1$ , mentre l’altro prosegue indefinitamente verso $-\infty$ lungo l’asse reale. Segue la rappresentazione del luogo inverso.

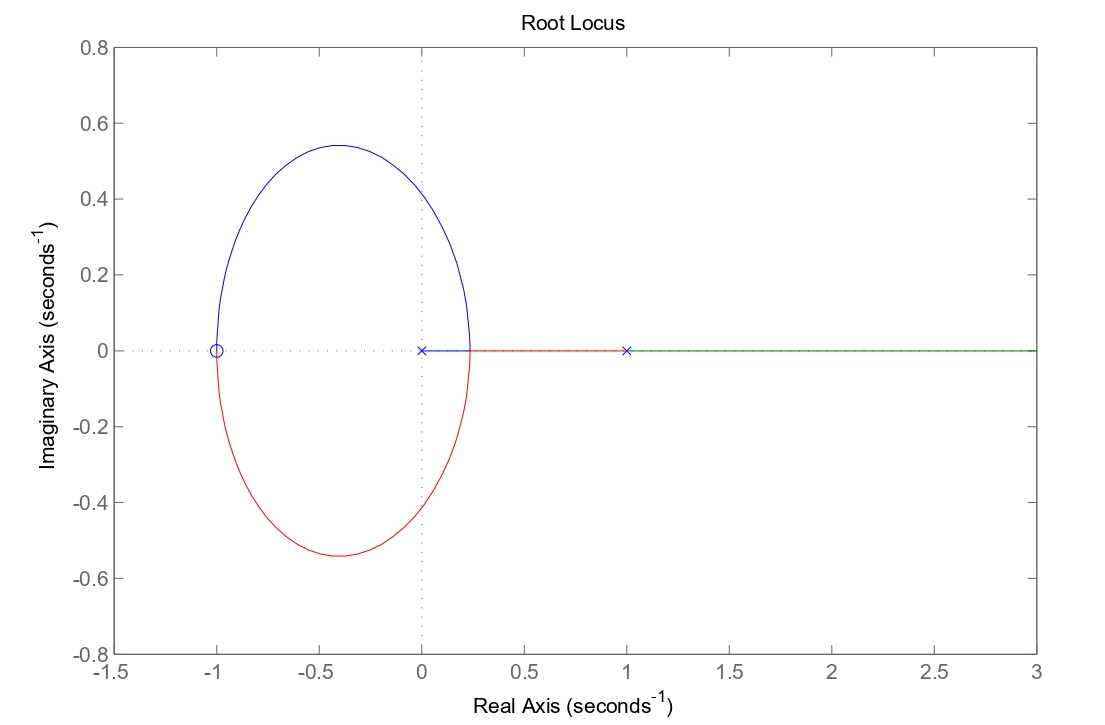
Figura 6: luogo delle radici inverso della funzione assegnata.

Dal punto in $1$ , dove sono presenti due poli ad anello aperto, partono due rami del luogo delle radici. Uno dei rami si estende all’infinito lungo l’asse reale, mentre l’altro si dirige verso il punto $-2 - \sqrt{5}$ lungo l’asse reale, per poi deviare e rientrare in asse in $-1$ , dove si trova lo zero e il ramo termina. Il ramo che inizia dal polo a zero procede lungo l’asse reale fino al punto di diramazione in $-2 + \sqrt{5}$ , dopodiché lascia l’asse reale spostandosi nel semipiano con parte reale positiva e si dirige verso lo zero in $-1$ . I poli del sistema a retroazione unitaria possono essere identificati ponendo il denominatore uguale a zero. Il denominatore con retroazione unitaria è

$x(s) = s(1-s)^2 + \rho(1+s)^2 = s^3 + (-2 + \rho)s^2 + (1 + 2\rho)s + \rho,$

dove $\rho$ è il guadagno della funzione ad anello aperto. La funzione $\rho$ può essere espressa come

$L(s) = \rho\dfrac{N(s)}{D(s)},$

dove $L(s)$ , $N(s)$ e $D(s)$ sono rispettivamente la funzione di trasferimento ad anello aperto, e $N(s)$ e $D(s)$ sono il numeratore e il denominatore della funzione di trasferimento ad anello aperto. Il valore di $\rho$ per cui le radici diventano instabili, ovvero quando il luogo delle radici si trova nel semipiano a parte reale positiva, può essere determinato applicando il criterio di Routh.

Passiamo costruire la tabella di Routh.

3	1	2ρ + 1
2	4ρ – 2	4ρ
1	(2ρ² – 4ρ – 2)/ (ρ – 2)	0
0	ρ	0

Imponendo che tutti gli elementi della seconda colonna della tabella di Routh abbiano lo stesso segno, si ottengono le seguenti condizioni:

$\begin{cases} 4\rho - 2 > 0 \\[10pt] \dfrac{2\rho^2 - 4\rho - 2}{\rho - 2} > 0 \\[10pt] \rho > 0, \end{cases}$

da cui segue che $\rho > \frac{1}{2}$ . Pertanto, per garantire che i poli del sistema retroazionato siano tutti con parte reale negativa, il guadagno del sistema deve essere maggiore di $\frac{1}{2}$ .

Esercizio 3 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Si tracci il luogo delle radici della funzione

$L(s) = \frac{s(s + 7)}{s^2 + 13s + 30}$

e si determini il valore di guadagno per cui le radici del sistema a retroazione unitaria diventano instabili.

Svolgimento.

Il luogo delle radici indica la posizione dei poli del sistema con retroazione unitaria in funzione della variazione del parametro $k$ . È utile considerare alcune regole per il suo tracciamento:

i punti sull’asse reale appartengono al luogo diretto se, a destra di essi, si trova un numero dispari di poli e zeri. Appartengono invece al luogo inverso i punti con un numero pari di poli e zeri alla loro destra.
Per identificare i punti di diramazione, dove il luogo delle radici lascia l’asse reale, si impone che:
$N_P(s) \cdot \dfrac{d}{ds}(D_P(s)) - D_P(s) \cdot \dfrac{d}{ds}(N_P(s)) = 0$

dove $N_P$ e $D_P$ sono rispettivamente il numeratore e il denominatore del processo. Per il caso in esame, si ha:

$s(s+7)(2s+13) - (s^2+13s+30)(2s+7) = 0,$

da cui si ottiene:

$s = -5 \pm \sqrt{10}\,j.$

Poiché i punti trovati presentano una parte immaginaria non nulla, non possono appartenere all’asse reale e, quindi, non rappresentano punti di diramazione. Di conseguenza, si deduce che il luogo delle radici giace interamente sull’asse reale.

I poli del sistema ad anello aperto, ovvero le radici del denominatore, si trovano in $-10$ e $-3$ .

Segue che il luogo delle radici diretto è:

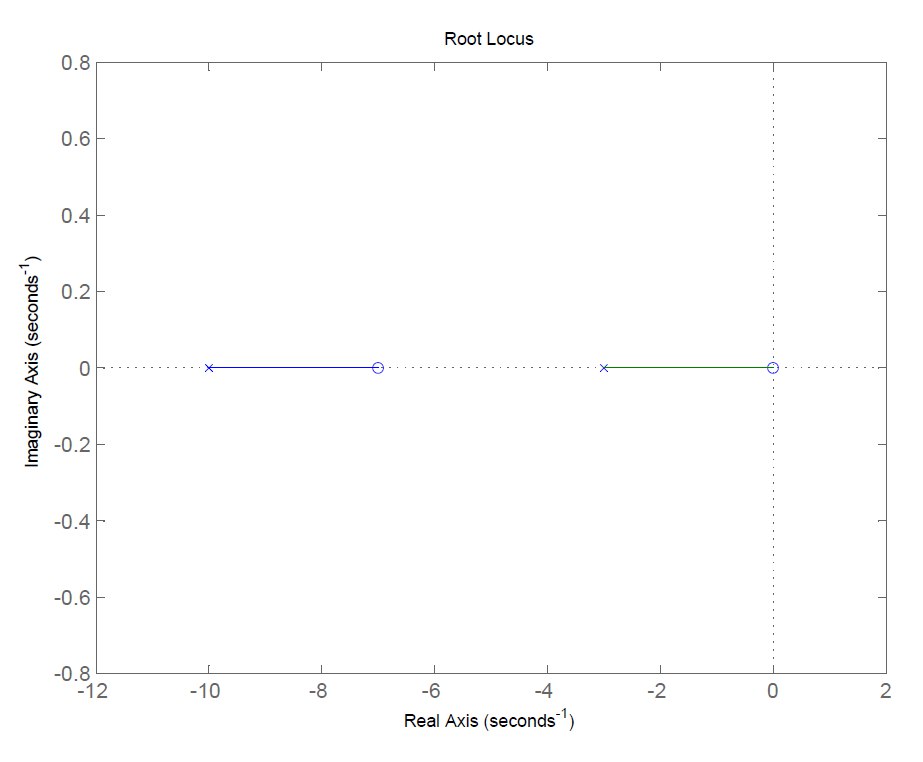
Figura 7: luogo diretto

Il ramo originato dal polo a $-10$ termina nello zero in $-7$ , mentre il ramo che parte dal polo a $-3$ si conclude nello zero a $0$ . Pertanto, non esiste un valore positivo del guadagno che possa rendere il sistema a ciclo chiuso stabile.

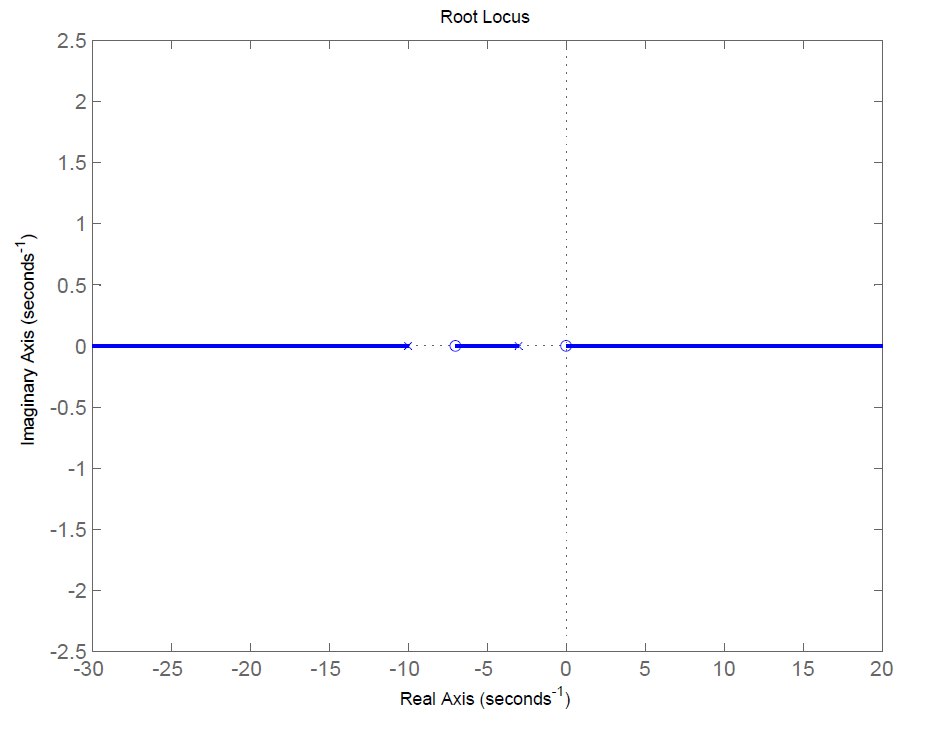
Figura 8: luogo inverso

Il polo ad anello aperto in $-10$ tende asintoticamente verso meno infinito lungo l’asse reale, poiché non occupa la parte dell’asse reale tra $-10$ e $-7$ . Invece, il polo in $-3$ termina nello zero in $-7$ , dal luogo inverso si evince che c’è sempre un ramo che ricade nella regione a parte reale positiva quando il guadagno è negativo. Per determinare l’esatto valore che rende instabile la funzione d’anello, si considera la funzione ad anello aperto in presenza di un guadagno $\rho$ . La funzione ad anello aperto è di tipo razionale fratto, con la seguente struttura:

$L(s) = \rho \frac{N(s)}{D(s)},$

dove $\rho$ è il guadagno, $N(s)$ il numeratore, e $D(s)$ il denominatore della funzione ad anello aperto. Di conseguenza, il denominatore del sistema a retroazione unitaria si presenta come:

$X(s) = D(s) + \rho N(s),$

che per il caso in questione diventa:

$X(s) = s^2 + 13s + 30 + \rho s(s + 7),$

e quindi:

$X(s) = s^2(1 + \rho) + s(13 + 7\rho) + 30.$

Il valore di $\rho$ necessario per stabilizzare il sistema può essere determinato applicando il criterio di Routh. Possiamo costruire la tabella di Routh come segue:

2	ρ + 1	7ρ + 30
1	7ρ + 13	0
0	30	0

Per garantire che tutti gli elementi della prima colonna della tabella di Routh abbiano lo stesso segno, si impongono le seguenti condizioni:

$\begin{cases} \rho + 1 > 0,\\ 7\rho + 13 > 0. \end{cases}$

Che ha come soluzione $\rho > -1$ . Pertanto, per ottenere l’asintotica stabilità del sistema retroazionato occorre che il guadagno sia maggiore di $-1$ .

Esercizio 4 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Si tracci il luogo delle radici della funzione

$L(s)=\dfrac{(s-1)(s+10)}{s(s^2+s+16)}$

e si trovi il guadagno per il quale le radici del sistema in retroazione unitaria diventa instabili.

Svolgimento.

Il luogo delle radici rappresenta la posizione dei poli del sistema a retroazione in funzione del guadagno $k$ . Per il tracciamento del luogo è utile considerare i seguenti punti:

I punti sull’asse reale appartengono al luogo diretto se, a destra di essi, si trova un numero dispari di poli e zeri. Invece, appartengono al luogo inverso i punti con un numero pari di poli e zeri alla loro destra.
I punti di diramazione, dove il luogo delle radici lascia l’asse reale, si determinano imponendo:
$N_P(s) \cdot \dfrac{d}{ds}(D_P(s)) - D_P(s) \cdot \dfrac{d}{ds}(N_P(s)) = 0$

dove $N_P$ e $D_P$ sono rispettivamente il numeratore e il denominatore del processo. Nel caso in esame, si ha:

$(s-1)(s+10)(3s^2+2s+16) - (s^3+s^2+16s)(2s-9) = 0,$

da cui si ottiene:

$s \sim \text{0,59}, \quad \vee \quad s \sim -\text{36,72}.$

Questi punti indicano dove il luogo delle radici lascia l’asse reale.

Le radici del denominatore, ovvero i poli del sistema ad anello aperto, si trovano in $0$ , e $-\frac{1}{2} \pm \text{3,96}j$ . Di seguito è rappresentato il luogo diretto.

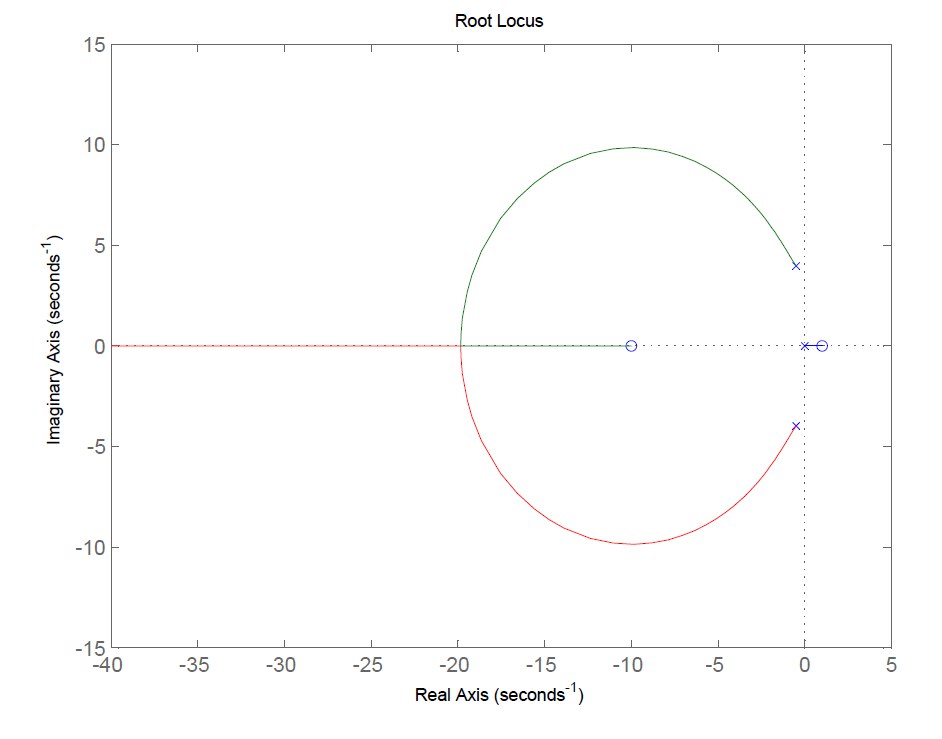
Figura 9: luogo diretto.

Si discute ora il luogo inverso. Il ramo originato dal polo in $0$ termina nello zero a $1$ . I rami hanno origine dai poli complessi coniugati intersecano l’asse delle ascisse nel punto di diramazione; successivamente, uno di questi rami si conclude nello zero a $-10$ , mentre l’altro prosegue indefinitamente lungo l’asse reale negativo.

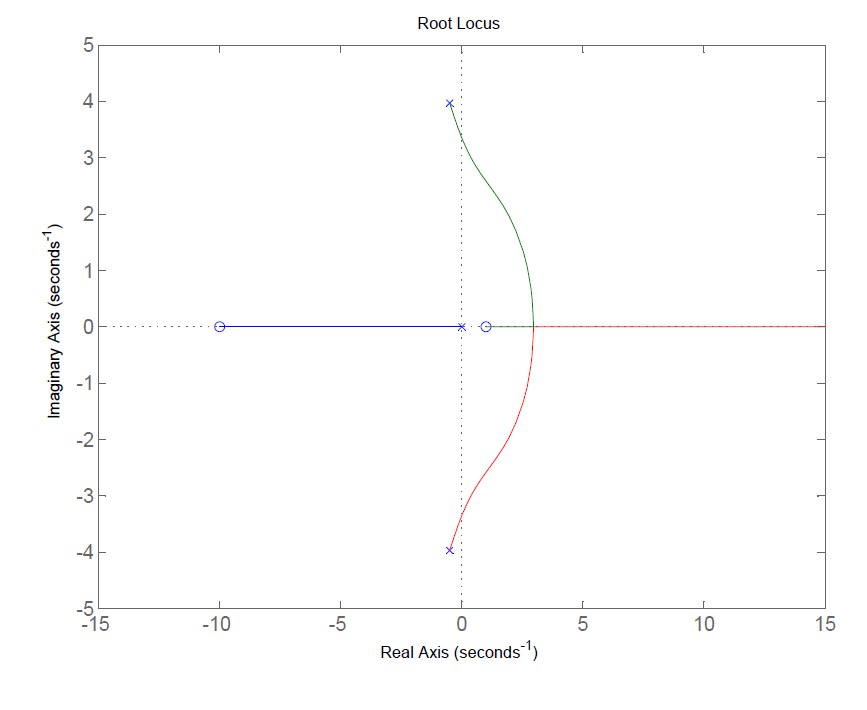
Figura 10: luogo inverso.

Il polo ad anello aperto in $0$ si sposta lungo l’asse reale negativo fino a raggiungere $-10$ , mentre i due poli complessi coniugati attraversano l’asse reale positivo nel punto di biforcazione. Successivamente, uno di essi si chiude in $1$ , mentre l’altro si dirige verso l’infinito lungo l’asse reale positivo.

La funzione ad anello aperto può essere espressa come una funzione razionale fratta:

$L(s) = \rho \dfrac{N(s)}{D(s)}$

Dove $\rho$ rappresenta il guadagno della funzione ad anello aperto, $N(s)$ è il numeratore della funzione ad anello aperto, e $D(s)$ è il denominatore della funzione ad anello aperto. Pertanto, il denominatore del sistema ad anello chiuso ha la seguente struttura:

$X(s) = D(s) + \rho N(s)$

Nel caso specifico, questa equazione diventa:

$X(s) = s^3 + s^2(1+\rho) + s(16-9\rho) - 10\rho$

Per determinare il valore di $\rho$ necessario affinché il sistema sia stabile, è possibile applicare il criterio di Routh e costruire la tabella di Routh.

3	1	16 – 9ρ
2	ρ + 1	-10ρ
1	(-9ρ² + 17ρ + 16)/(ρ + 1)	0
0	-10ρ	0

Per garantire che tutti gli elementi nella prima colonna della tabella di Routh abbiano lo stesso segno, dobbiamo soddisfare le seguenti condizioni:

$\begin{cases} \rho +1 > 0\\[10pt] \dfrac{-9\rho^2+17\rho+16}{\rho+1} > 0\\[10pt] -10\rho > 0. \end{cases}$

La soluzione di questo sistema di disequazioni è $\rho < -\frac{13}{7}$ .

Per assicurarsi che le radici del sistema a ciclo chiuso siano asintoticamente stabili, è necessario che il guadagno $\rho$ rientri nell’intervallo determinato da queste condizioni.

Tutte le cartelle di controlli automatici

Leggi...

Document

Menu

Chiudi

Esercizi svolti luogo delle radici

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Tutte le cartelle di controlli automatici

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi