Esercizi svolti regolatori PID

Home » Esercizi svolti regolatori PID

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Dato lo schema di controllo in figura:

Rendered by QuickLaTeX.com

dove:

$\begin{equation*} G(s)=\text{0,1}\dfrac{e^{-3s}}{\left(1+5s\right)\left(1+20s\right)}. \end{equation*}$

Si vuole progettare il regolatore $R(s)$ di tipo PID in modo tale che:

$e_{\infty}=0$ per $y^o(t)=sca(t)$ ;
$\phi_m\ge 40^o$ ;
$\omega_\tau$ sia la massima possibile.

Svolgimento.

Affinché l’errore a regime sia nullo, occorre che nel prodotto regolatore del processo ci sia un polo in zero, poiché manca nel processo. È necessaria un’azione integrale nel regolatore. Il regolatore PID può essere espresso in due forme alternative:

$\begin{equation*} R(s) = k_p + \frac{k_\tau}{s} + k_s s, \end{equation*}$

o alternativamente,

$\begin{equation*} R(s) = \mu_R \frac{T_i T_d s^2 + T_i s + 1}{s} = \frac{\mu_R(1 + s T_1)(1 + s T_2)}{s}, \end{equation*}$

dove $T_i$ e $T_d$ rappresentano rispettivamente le costanti di tempo integrative e derivative. Una volta selezionata una delle due formulazioni per il regolatore, è necessario aggiungere un polo ad alta frequenza per garantire la realizzabilità fisica del controllore.

Inizialmente, si può considerare che il regolatore implementi esclusivamente un’azione integrale:

$\begin{equation*} R_1(s) = \frac{1}{s}, \end{equation*}$

e procedere alla valutazione del margine di fase della funzione d’anello risultante $L(s) = G(s)R_1(s)$ .

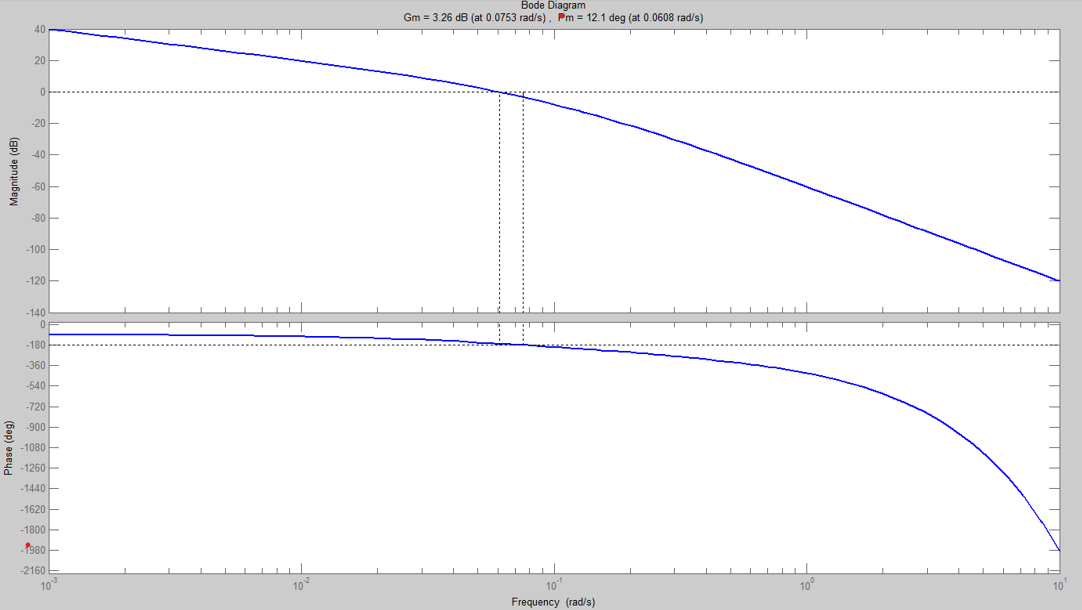
Figura 1: diagramma di Bode della funzione d’anello.

Dopo l’analisi, si osserva un margine di fase di $\phi_m = \text{12,1}^\circ$ , che risulta inferiore al valore desiderato. Pertanto, facendo riferimento alla forma espressa dall’equazione (3), le costanti di tempo degli gli zeri del regolatore vanno scelte in modo che cancellino i poli della $G(s)$ così da migliorare il margine di fase della funzione d’anello. Di conseguenza, la nuova configurazione del sistema diventa:

$\begin{align*} &L(s) = G(s) \cdot R(s) = e^{-3s} \frac{0 \cdot 1 \mu_R}{s}, \\ &\text{dove } R(s) = \mu_R \frac{(1 + 5s)(1 + 20s)}{s}. \end{align*}$

Figura 2: diagramma di Bode della funzione d’anello con l’introduzione del regolatore.

Il margine di fase ottenuto è di $\text{72,8}^\circ$ , il che soddisfa le specifiche richieste. Tuttavia, è necessario valutare il massimo valore del guadagno $\mu_R$ che può essere introdotto senza superare il margine di fase desiderato. La pulsazione critica $\omega^* = \text{0,278}\, \text{rad/sec}$ corrisponde al punto in cui il sistema raggiunge il massimo margine di fase possibile senza infrangere i requisiti specificati, ovvero:

$\begin{equation*} \phi_m = 180^\circ - \angle L(j\omega^*). \end{equation*}$

Per mantenere il guadagno entro i limiti consentiti, $\mu_R$ non deve aumentare oltre gli $8,88\, \text{dB}$ , da cui si ricava:

$\begin{equation*} \mu_R = 10^{\frac{\text{8,88}}{20}} \simeq \text{2,8}. \end{equation*}$

Per assicurare la realizzabilità fisica della funzione di trasferimento del regolatore, si può aggiungere un ulteriore polo a una pulsazione significativamente più alta rispetto a quella dei poli e degli zeri esistenti, ad esempio a $10\, \text{rad/sec}$ . Di conseguenza, la funzione di trasferimento del regolatore assume la forma:

$\begin{equation*} R(s) = \text{2,8}\frac{(1+5s)(1+20s)}{s(1+\text{0,1}s)}. \end{equation*}$

Esercizio 2 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dato il sistema descritto dalla funzione di trasferimento:

$\begin{equation*} P(s)=\dfrac{e^{-\text{0,1}s}}{s+3}. \end{equation*}$

Si progetti un controllore PID tale che assicuri:

errore a regime nullo per un ingresso a scalino;
banda a $3\,dB$ per il sistema ad anello chiuso $Bp=\text{0,6}\,Hz$ ;
sovraelongazione percentuale $s\% <10\%$ .

Svolgimento.

Per soddisfare la specifica sull’errore a regime, è necessaria l’azione integrativa. A partire dalla specifica sulla sovraelongazione, $s\% \le 10$ , si ottiene $\xi \ge \text{0,6}$ , il che implica un margine di fase $\phi_m \ge 60^\circ$ .

Dalla specifica sulla banda passante, utilizzando gli abachi, si hanno le seguenti relazioni:

$\begin{align*} \frac{B_p}{\omega_n}\Bigg\vert_{\xi=\text{0,6}} &= \text{11,5} \implies \omega_n = \text{3,26}\, \text{rad/sec}, \\ \frac{\omega_t}{\omega_n}\Bigg\vert_{\xi=\text{0,6}} &\approx \text{0,71} \implies \omega_t = \text{2,32}\, \text{rad/sec}. \end{align*}$

Valutando le caratteristiche del sistema, si ottiene:

$\begin{align*} \left| P(j\omega_t) \right| &= \frac{1}{\sqrt{9 + \omega_t^2}} = \text{0,26}, \\[10pt] \angle P(j\omega_t) &= -\text{0,1} \omega_t \frac{180}{\pi} - \arctan\left(\frac{\omega_t}{3}\right) = -51^\circ, \\[10pt] \phi_m &= 180^\circ - 51^\circ = 129^\circ. \end{align*}$

Il margine di fase prima di introdurre l’azione integrale è più di quello desiderato, quindi non occorre azione derivativa, quindi è sufficiente ricavare la costante proporzionale e quella integrativa, come segue:

$K_p = \frac{\cos(60^\circ - 129^\circ)}{|P(j\omega_t)|} = \text{1,38},$

$\frac{1}{\omega_t T_i} = \tan(60^\circ - 129^\circ) \quad \rightarrow \quad T_i = \text{0,16}\, \text{s}.$

Quindi il controllore cercato è:

$R(s) = \text{1,38} \left( 1 + \frac{1}{\text{0,16}s} \right).$

Esercizio 3 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Dato il sistema descritto da

$\begin{equation*} H(s)=\dfrac{30}{s^2+3s+1}. \end{equation*}$

Con la taratura analitica tarare un controllore PID che soddisfi le seguenti specifiche:

errore a gradino nullo;
$s\%\le30$ ;
$t_\text{salita}\le\dfrac{3}{4}$ .

Svolgimento.

Attraverso la taratura analitica, è possibile determinare le costanti per la funzione di trasferimento del PID come segue:

$\begin{align*} k_p &= \frac{\cos(\phi)}{|H(j\omega_t)|}, \\ k_d &= \frac{\sin(\phi)}{\omega_t|H(j\omega_t)|} + \frac{ki}{\omega_t^2}, \end{align*}$

dove $\phi$ rappresenta la fase che il PID deve introdurre alla pulsazione di taglio $\omega_t$ desiderata; $\omega_t$ è la pulsazione di taglio desiderata per la funzione d’anello $H\cdot R$ ; e $\phi$ può assumere valori tali che $-90\le\phi\le90$ . Se il valore di $\phi$ da introdurre è negativo, non è necessaria l’azione derivativa.

Le specifiche vengono tradotte in obiettivi da raggiungere per la funzione ad anello aperto:

$\begin{equation*} s\% \le 30 \to \xi \ge \text{0,37}, \end{equation*}$

scegliendo $\xi=\text{0,4}$ si ottiene $\phi_m=40^\circ$ .

Utilizzando gli abachi, si ottiene:

$\begin{align*} T_s \cdot B_3 \bigg|_{\xi=\text{0,4}} &= 3\quad \Rightarrow\quad B_3 = \frac{3}{3/4} - 4 \,\text{rad/sec}, \\ \frac{B3}{\omega_n} \bigg|_{\xi=\text{0,4}} &\simeq \text{1,4} \quad \Rightarrow\quad \omega_n \simeq \text{2,85} \,\text{rad/sec}, \\ \frac{\omega_t}{\omega_n} \bigg|_{\xi=\text{0,4}} &= \text{0,85}\quad \Rightarrow\quad \omega_t = \text{2,42} \,\text{rad/sec}. \end{align*}$

La specifica sull’errore a regime nullo impone l’uso dell’azione integrale. L’analisi del diagramma di Bode mostra che, in assenza di regolazione, il sistema presenta le seguenti caratteristiche a $\omega_t$ :

$\begin{align*} |H(j\omega_t)| &= \text{3,85}\,\text{dB}, \\ \phi_m &= 180 - | \angle H(j\omega t) | = \text{59,3}. \end{align*}$

Sebbene $\phi_m$ sia maggiore di quello desiderato, l’azione integrale ne risentirebbe comunque. È possibile permettere al regolatore una riduzione di fase di $19.30^\circ$ a $\omega_t$ , impostando $\phi = -\text{19,30}^\circ$ .

Di conseguenza, non occorre l’azione derivativa e le formule diventano:

$\begin{align*} k_d &= 0 = \frac{\sin(-\text{19,3}^\circ)}{\text{2,42} \cdot \text{3,85}} + \frac{k_I}{(\text{2,42})^2}, \\ k_p &= \frac{\cos(-\text{19,3}^\circ)}{\text{3,85}}, \end{align*}$

da cui si ricavano:

$\begin{align*} k_p &= \text{0,244}, \\ k_I &= \text{0,2}. \end{align*}$

Pertanto, la funzione di trasferimento del regolatore desiderato è:

$\begin{equation*} R(s) = k_p + \frac{k_I}{s} = \text{0,244} + \frac{\text{0,2}}{s}. \end{equation*}$

Tutte le cartelle di controlli automatici

Leggi...

Document

Menu

Chiudi

Esercizi svolti regolatori PID

Svolgimento.

Svolgimento.

Svolgimento.

Tutte le cartelle di controlli automatici

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi