Esercizi svolti diagrammi di Nyquist

Home » Esercizi svolti diagrammi di Nyquist

Esercizio 1 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Si tracci il diagramma di Nyquist della funzione

$L(s)=\dfrac{4\left(1+s\right)^2}{s\left(1-s\right)^2}.$

Svolgimento.

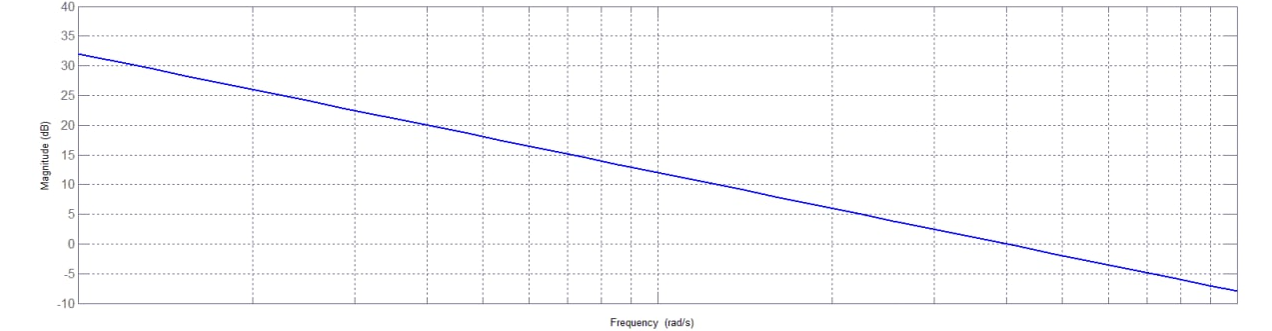
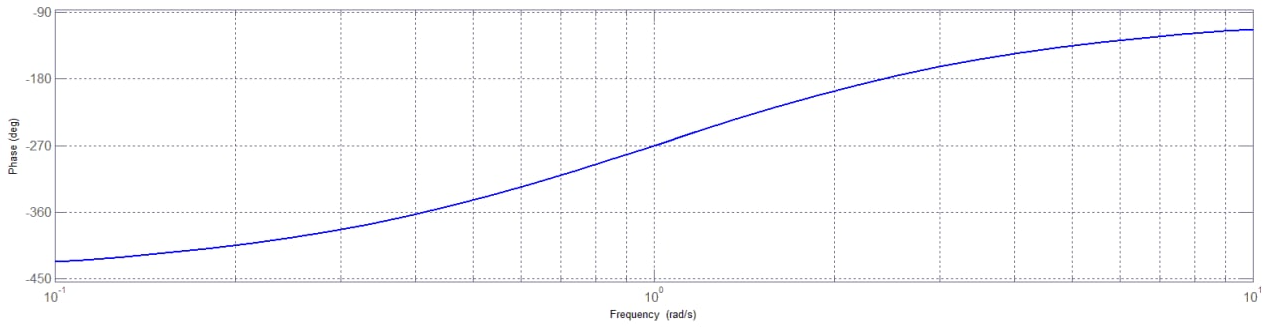
Il diagramma di Nyquist può essere agevolmente tratto dal diagramma di Bode, già esaminato nel file numero 4 della cartella ‘I diagrammi di Bode’. Ulteriori dettagli sono disponibili nei documenti successivi.

Figura 1.

Il diagramma di Nyquist è ottenuto tracciando il grafico della funzione $L(j\omega)$ in funzione della variazione della pulsazione. Questa funzione $L$ , variando $\omega$ , descrive un percorso nel piano complesso, dove la distanza di ogni punto del grafico dall’origine rappresenta il modulo di $L$ , la cui evoluzione è rappresentata dal relativo diagramma di Bode così come la fase formata con l’asse reale.

Dall’analisi del diagramma di Bode, si nota che per $\omega \to 0$ , il grafico di Nyquist parte da una distanza infinita dall’origine e con una fase di $-90^\circ$ . Quando il modulo supera $1$ , la fase raggiunge i $180^\circ$ , causando l’intersezione del grafico di Nyquist con l’asse reale negativo. Per $\omega \to \infty$ , il modulo tende a $-\infty$ e la fase a $-90^\circ$ , concludendo il grafico di Nyquist all’origine con fase di $-90^\circ$ . Essendoci un polo in zero, l’ascissa dell’asintoto per $\omega \to 0$ può essere determinata a partire da

(1) $\begin{equation*} L(s) = \frac{L^\prime(s)}{s}. \end{equation*}$

Calcoliamo:

(2) $\begin{equation*} L(0) = \lim_{s \to 0} \frac{dL^\prime(s)}{ds} = \lim_{s \to 0} \frac{16(s + 1)}{1 - s^3} = -16. \end{equation*}$

Questo permette di rappresentare il diagramma di Nyquist nella figura seguente.

Figura 2.

Il diagramma di Nyquist per $\omega < 0$ si ottiene specchiando quello per $\omega > 0$ rispetto all’asse reale. Questo implica che la parte del diagramma per frequenze negative è il riflesso di quella per frequenze positive lungo l’asse orizzontale.

Esercizio 2 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Si tracci il diagramma di Nyquist della funzione

$L(s)=\dfrac{s\left(s+7\right)}{s^2+13s+30}.$

Svolgimento.

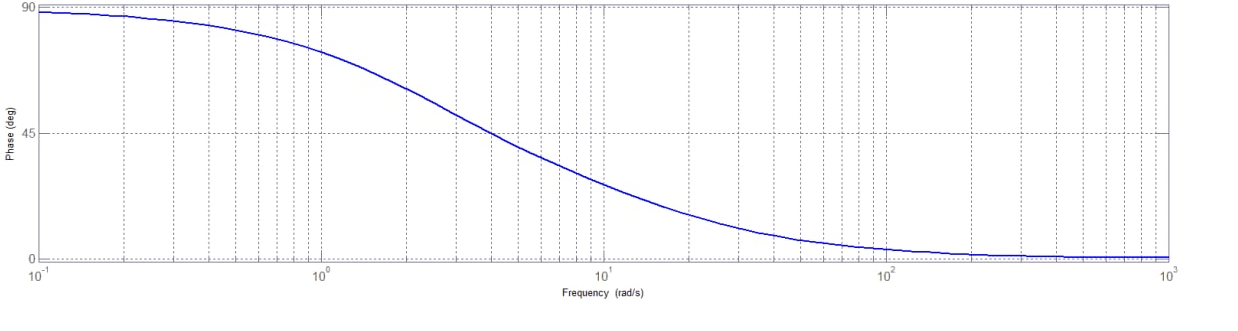
Il diagramma di Nyquist può essere facilmente dedotto dal diagramma di Bode, già analizzato nel file numero 2 della cartella “I diagrammi di Bode”.

Figura 3: diagramma di Bode del modulo della funzione assegnata.

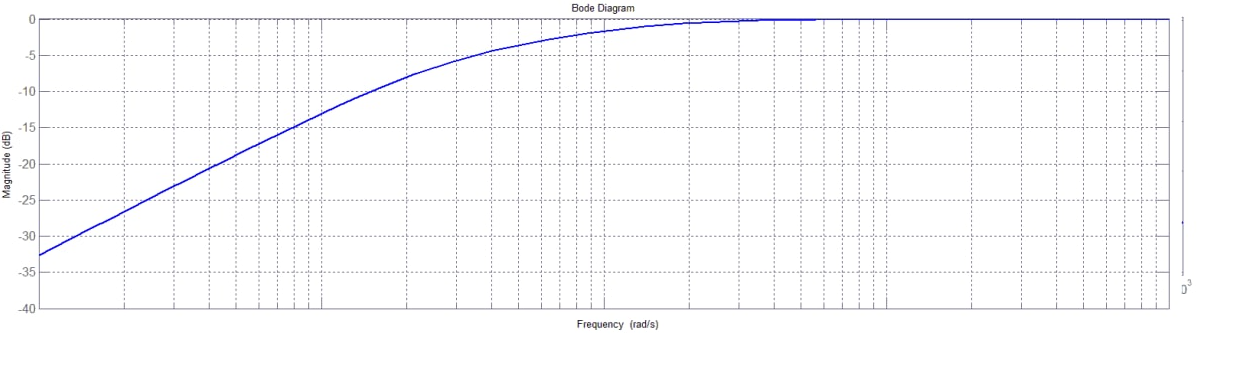
Figura 4: diagramma di Bode della fase della funzione assegnata.

Il diagramma di Nyquist traccia il grafico della funzione $L(j\omega)$ al variare della pulsazione. La funzione $L$ , variando $\omega$ , descrive un percorso nel piano complesso, dove la distanza di ogni punto del grafico dall’origine rappresenta il modulo di $L$ , leggibile anche dal diagramma dei moduli di Bode, mentre l’angolo è determinato dalla fase nel diagramma di Bode.

Dall’analisi del diagramma di Bode, si osserva che per $\omega \to 0$ , il grafico di Nyquist parte dall’origine con una fase di $90^\circ$ . La fase nel diagramma di Bode si riduce tendendo a $0^\circ$ quando il modulo raggiunge il valore massimo. Di conseguenza, il grafico di Nyquist interseca l’asse reale positivo in corrispondenza del punto $1+0j$ . Per valori negativi della pulsazione, il grafico di Nyquist è simmetrico rispetto all’asse reale.

Figura 5.

Esercizio 3 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Si tracci il diagramma di Nyquist della funzione

$L(s)=\dfrac{\left(s-1\right)\left(s+10\right)}{s\left(s^2+s+16\right)}.$

Svolgimento.

Il diagramma di Nyquist può essere facilmente derivato dall’analisi del diagramma di Bode, precedentemente esaminato nel file numero 1 della cartella “I diagrammi di Bode”. successivi.

Figura 6: diagramma di Bode del modulo della funzione assegnata.

Figura 7: diagramma di Bode della fase della funzione assegnata.

Il diagramma di Nyquist traccia il grafico della funzione $L(j\omega)$ in funzione della variazione della pulsazione. La funzione $L$ , variando $\omega$ , descrive un percorso nel piano complesso, dove la distanza di ogni punto del grafico dall’origine rappresenta il modulo di $L$ , leggibile anche dal diagramma dei moduli di Bode, mentre l’angolo è determinato dalla fase nel diagramma di Bode.

Dall’analisi del diagramma di Bode, si osserva che per $\omega \to 0$ , il grafico di Nyquist inizia a grande distanza dall’origine e con una fase di $90^\circ$ . La fase nel diagramma di Bode attraversa $0^\circ$ quando il modulo è leggermente superiore a $1$ , quindi il grafico di Nyquist intersecherà l’asse reale positivo.

Tra le pulsazioni $\omega = 2$ , $\omega = 3$ e $\omega = 5$ intervengono i poli complessi e coniugati con un fattore di smorzamento $\xi = \frac{1}{8}$ che producono una rapida riduzione della fase di $-180^{\circ}$ provocando una rapida curva del diagramma. Essendoci un polo in $0$ , possiamo trovare l’ascissa per l’asintoto quando $\omega \to 0$ :

(3) $\begin{equation*} L(s) = \frac{L^\prime(s)}{s}. \end{equation*}$

Calcoliamo:

(4) $\begin{equation*} L(0) = \lim_{s \to 0} \frac{dL^\prime(s)}{ds} = \lim_{s \to 0} \frac{-8s^2 + 52s + 154}{(s^2 + s + 16)^2} \sim \text{0,60}. \end{equation*}$

Questo permette di rappresentare il diagramma di Nyquist nella figura seguente.

Figura 8.

Tutte le cartelle di controlli automatici

Leggi...

Document

Menu

Chiudi

Esercizi svolti diagrammi di Nyquist

Svolgimento.

Svolgimento.

Svolgimento.

Tutte le cartelle di controlli automatici

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi