Esercizi svolti diagrammi di Bode

Home » Esercizi svolti diagrammi di Bode

Esercizio 1 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione di trasferimento

$W(s)=\dfrac{s\left(s+7\right)}{s^2+13s+30},$

si richiede di rappresentare il diagramma di Bode.

Svolgimento.

La funzione $W$ è rappresentata dalla forma zero-poli:

$G(s) = \frac{\rho \prod_i (s + z_i) \prod_i (s^2 + 2\zeta_i\alpha_i s + \alpha_i^2)}{s^g \prod_i (s + p_i) \prod_i (s^2 + 2\zeta_i\omega_is + \omega_i^2)},$

dove $\rho$ è la costante di trasferimento, $z_i$ gli zeri reali negativi di $G$ , $\zeta_i$ e $\alpha_i$ gli smorzamenti e le pulsazioni degli zeri complessi coniugati, rispettivamente, $g$ il grado del sistema, $p_i$ i poli reali negativi, e $\omega_i$ le pulsazioni dei poli complessi coniugati.

Con $W$ avente uno zero in $0$ e uno reale in $-7$ , il denominatore, pur essendo di secondo grado, si decompone in $(s+3)(s+10)$ , indicando due poli reali in $-3$ e $-10$ .

La funzione di trasferimento, riportata con costanti di tempo, diventa:

$G(s) = \frac{\mu \prod_i (1 + \tau_is) \prod_i (1 + 2\zeta_i\frac{s}{\alpha_i} + \frac{s^2}{\alpha_i^2})}{s^g \prod_i (1 + T_is) \prod_i (1 + 2\zeta_i\frac{s}{\omega_i} + \frac{s^2}{\omega_i^2})},$

con $\tau_i$ e $T_i$ le costanti di tempo degli zeri e dei poli, e $\mu$ il guadagno.

Quindi, $W(s)$ si riscrive come:

$W(s) = \frac{7s(\frac{s}{7} + 1)}{30(\frac{s}{3} + 1)(\frac{s}{10} + 1)}.$

Da quest’analisi, si deduce che il guadagno $\mu$ è pari a $\frac{7}{30}$ . Per ottenere il diagramma di Bode dei moduli, sommiamo i diagrammi in decibel delle singole componenti della funzione di trasferimento. Il modulo del guadagno, in decibel, è $20\log_{10}\left|\frac{7}{30}\right|$ , circa $-\text{16,6}\ dB$ . Di seguito vengono presentati i diagrammi di Bode per le varie componenti del modulo della funzione di trasferimento.

Figura 1: diagramma dei moduli delle componenti della funzione assegnata.

Di seguito spieghiamo le curve nella figura di sopra.

La curva rossa rappresenta lo zero in $-7$ che aumenta di $20\, \text{dB}/\text{dec}$ a partire da una frequenza di $7 \text{ rad/s}$ ;
La curva blu indica il guadagno costante di $-\text{4,8} \text{ dB}$ ;
La curva verde mostra lo zero in $0$ che aumenta di $20\,\text{dB}/\text{dec}$ , passando per il punto $(0\,\text{rad}, 0\,\text{dB})$ ;
La curva celeste rappresenta il polo in $-3$ che diminuisce di $20\,\text{dB}/\text{dec}$ , perdendo $3\,\text{dB}$ a una pulsazione di $3\,\text{rad/s}$ ;
La curva viola rappresenta il polo in $-10$ che diminuisce di $20\,\text{dB}/\text{dec}$ , perdendo $-3\,\text{dB}$ a una pulsazione di $10 \text{ rad/s}$ .

Il diagramma complessivo, ottenuto sommando i contributi parziali, è rappresentato nella figura successiva.

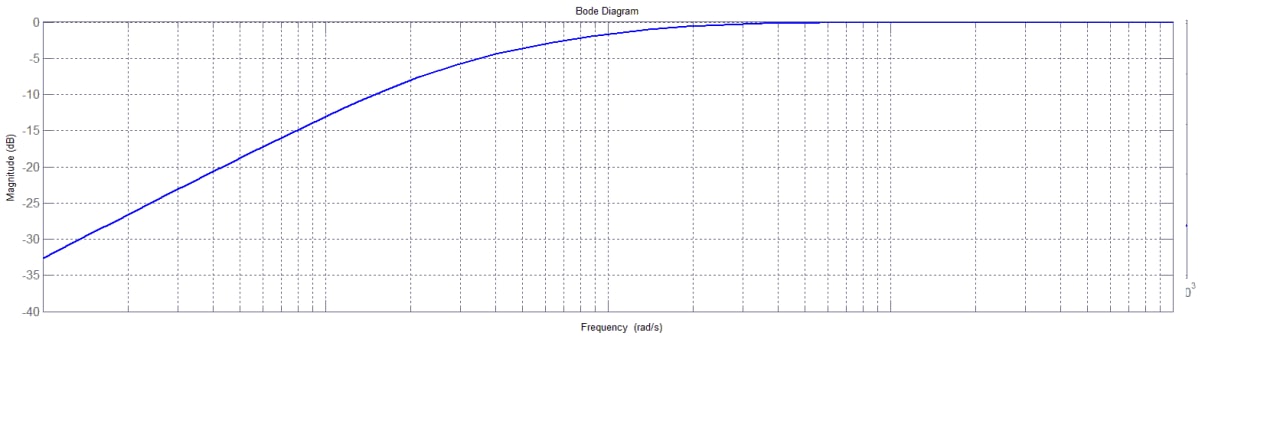
Figura 2: diagramma del modulo della funzione assegnata

Di seguito è riportato il diagramma dei contributi parziali della fase.

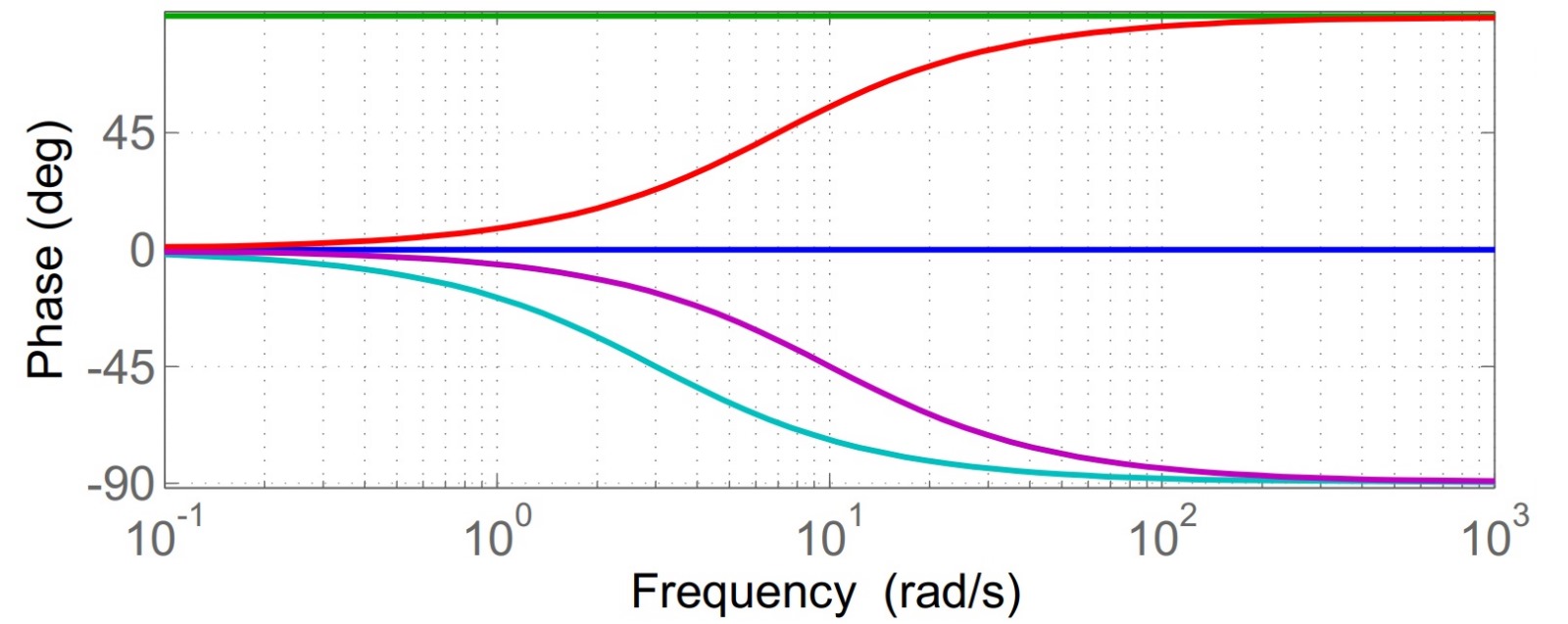
Figura 3: diagramma delle fasi delle componenti la funzione assegnata.

Di seguito spieghiamo le curve nella figura di sopra.

La curva blu rappresenta la fase del guadagno;
La curva verde indica la fase dello zero in $0$ , costante e pari a $90^\circ$ ;
La curva rossa mostra la fase dello zero in $-7$ , aumentando complessivamente di $90^\circ$ a partire da una pulsazione di $0.7 \, \text{rad/s}$ , con un incremento di $45^\circ/\text{dec}$ per $2 \, \text{decadi}$ ;
La curva azzurra rappresenta la fase del polo in $-3$ , diminuendo complessivamente di $90^\circ$ a partire da una pulsazione di $0.3 \, \text{rad/s}$ , con una perdita di $45^\circ/\text{dec}$ per $2 \, \text{decadi}$ ;
La curva viola mostra la fase del polo in $-10$ , diminuendo complessivamente di $90^\circ$ a partire da una pulsazione di $1 \, \text{rad/s}$ , con una perdita di $45^\circ/\text{dec}$ per $2 \, \text{decadi}$ ;

Sommando i vari contributi si ottiene il grafico seguente, che rappresenta la fase della funzione di trasferimento assegnata.

Figura 4: diagramma della fase della funzione assegnata.

Esercizio 2 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Data la funzione di trasferimento

$W(s)=\dfrac{\left(s-1\right)\left(s+10\right)}{s\left(s^2+s+16\right)},$

si richiede di rappresentare il diagramma di Bode.

Svolgimento.

La funzione $W$ si presenta nella forma zero poli del tipo

$G(s)=\dfrac{\rho\displaystyle \prod_i\left(s+z_i\right)\displaystyle\prod_i\left(s^2+2\zeta_i\alpha_i s+\alpha_i^2\right)}{s^g\displaystyle \prod_i\left(s+p_i\right)\displaystyle\prod_i\left(s^2+2\zeta_i\omega_is +\omega_i^2\right)},$

dove $\rho$ rappresenta la costante di trasferimento, $z_i$ sono gli zeri reali della funzione $G$ cambiati di segno, $\zeta_i$ sono gli smorzamenti delle coppie di poli complessi e coniugati, $\alpha_i$ sono le pulsazione degli zeri complessi e coniugati, $g$ è il tipo di sistema che rappresenta il numero di poli o zeri in zero, $p_i$ sono i poli reali cambiati di segno, $\zeta_i$ lo smorzamento delle coppie di poli complesse e coniugate, e $\omega_i$ la pulsazione delle coppie di poli complessi e coniugati. Pertanto la funzione $W$ presenta uno zero reale in $1$ , uno zero reale in $-10$ , un polo in $0$ , e una coppia di poli complessi e coniugati, giacché il termine quadratico al denominatore presenta radici complesse e coniugate. La pulsazione naturale delle radici di poli complessi e coniugati è in $4$ , da cui, si ha

$1=2\zeta (4) \quad \Leftrightarrow \quad \zeta=\dfrac{1}{8}.$

Occorre trovare il guadagno della funzione di trasferimento riportandola nella forma con le costanti di tempo del tipo:

$G(s)=\dfrac{\mu\displaystyle\prod_i\left(1+\tau_is\right)\displaystyle \prod_i\left(1+2\zeta_i\dfrac{s}{\alpha_i}+\dfrac{s^2}{\alpha_i^2}\right)}{s^g\displaystyle\prod_i\left(1+T_is\right)\displaystyle \prod_i\left(1+2\zeta_i\dfrac{s}{\omega_i}+\dfrac{s^2}{\omega_i^2}\right)},$

dove $\tau_i$ e $T_i$ sono rispettivamente le costanti di tempo degli zeri e dei poli, e $\mu$ rappresenta il guadagno. Dunque, la funzione di trasferimento $W(s)$ può essere riscritta come

$W(s)=-\dfrac{10(-s+1)\left(\dfrac{s}{10}+1\right)}{16s\left(\dfrac{s^2}{16}+\dfrac{s}{16}+1\right)}.$

Da quanto ottenuto deduciamo che il guadagno $\mu=-10$ . Il diagramma di Bode dei moduli si può ottenere sommando il diagramma delle componenti della funzione di trasferimento espressa in decibel. Il modulo del guadagno in $\mu \text{dB}=20\log_{10}\left\vert -\dfrac{10}{16}\right\vert \sim-\text{4,1 dB}$ .

Figura 5: diagramma dei moduli dei termini componenti la funzione assegnata.

Di sopra sono rappresentati i diagrammi di Bode delle varie componenti del modulo della funzione di trasferimento.

Di seguito spieghiamo le curve nella figura di sopra.

La curva celeste rappresenta il polo in zero che scende con pendenza costante di $-20\, \text{dB}/\text{dec}$ passando per il punto di coordinate $(1\,\text{rad}/\text{s},0\,\text{dB})$ ;
la curva blu rappresenta il guadagno costante con la frequenza di $-\text{4,8 dB}$ ;
la curva verde rappresenta lo zero in $1$ che resta pressoché costante fino alla pulsazione di $\text{1 rad/s}$ , dopo di che sale di $\text{20 dB/dec}$ ;
la curva rossa rappresenta lo zero in $-10$ costante a $\text{0 dB}$ fino alla pulsazione di $10 \,\text{rad/s}$ , dopo di che sale di $\text{20 dB/dec}$ ;
la curva viola rappresenta la coppia di poli complessi e coniugati, in prossimità della pulsazione naturale è presente un picco di risonanza, poiché il valore dello smorzamento è minore di $\text{0,5}$ . Dopo il picco la curva scende di $-40\,\text{dB/dec}$ .

Il diagramma complessivo ottenuto sommando i contributi parziali è rappresentato nella figura che segue.

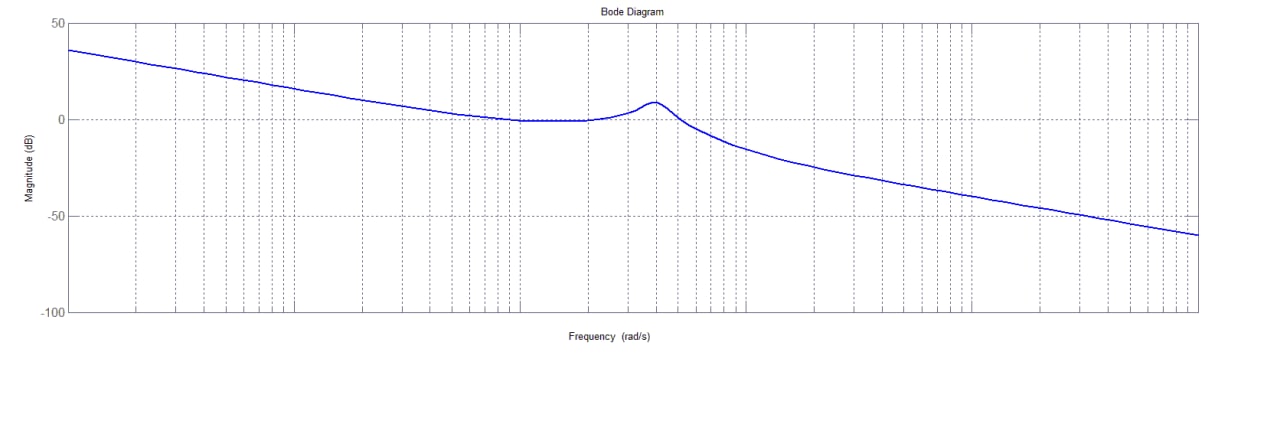
Figura 6: diagramma del modulo della funzione assegnata.

Di sopra sono rappresentati i diagrammi di Bode delle varie componenti del modulo della funzione di trasferimento.

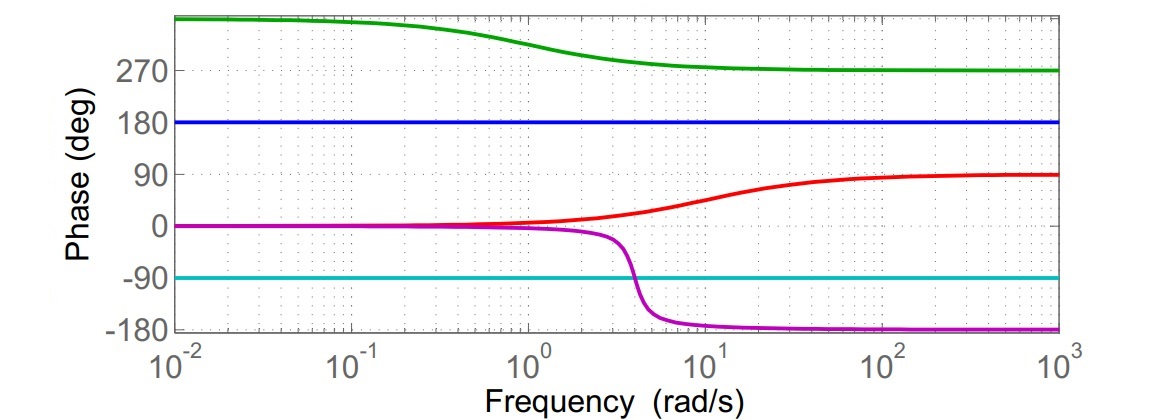
Figura 7: diagramma delle fasi dei termini componenti la funzione assegnata.

Di seguito è riportato il diagramma dei contributi parziali della fase.

Di seguito spieghiamo le curve nella figura di sopra.

La curva blu rappresenta la fase del guadagno;
la curva verde rappresenta la fase delle zero in $1$ , poiché lo zero è positivo la fase scende di $45^\circ/\text{dec}$ intorno alla pulsazione dello zero, anziché aumentare come avviene per uno zero negativo;
la curva rossa rappresenta la fase delle zero in $-10$ ;
la curva rossa rappresenta la fase del polo in zero;
la curva celeste rappresenta la fase della coppia do poli complessi e coniugati.

Sommando i vari contributi si ottiene il grafico seguente, che rappresenta la fase della funzione di trasferimento assegnata.

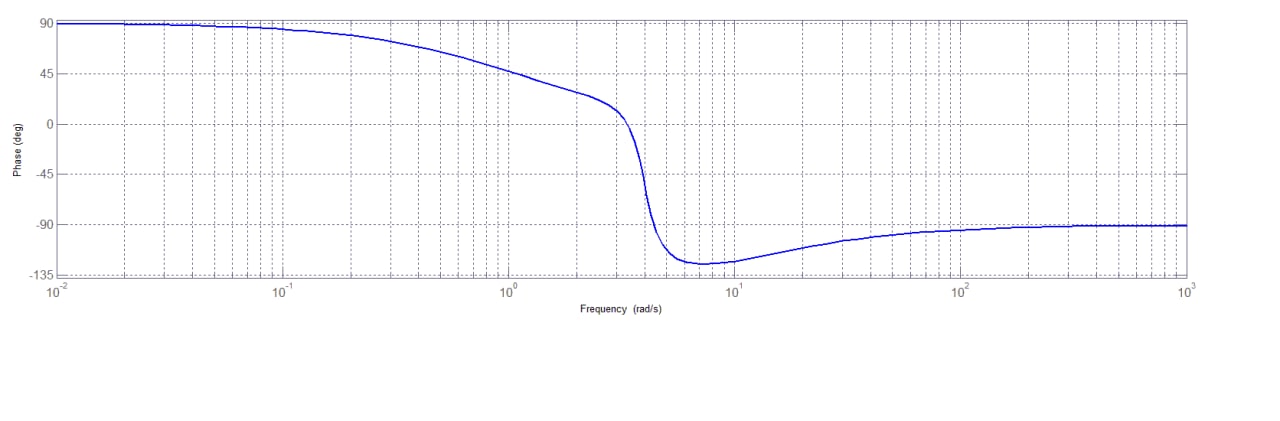
Figura 8: diagramma delle fasi della funzione assegnata.

Esercizio 3 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Data la funzione di trasferimento

$W(s)=\dfrac{4\left(1+s\right)^2}{s\left(1-s\right)^2},$

si richiede di rappresentare il diagramma di Bode.

Svolgimento.

La funzione $W$ si presenta già nella forma con le costanti di tempo del tipo:

$G(s) = \frac{\mu \prod_i (1 + \tau_i s) \prod_i \left(1 + 2\zeta_i \frac{s}{\alpha_i} + \frac{s^2}{\alpha_i^2}\right)}{s^g \prod_i (1 + T_i s) \prod_i \left(1 + 2\zeta_i \frac{s}{\omega_i} + \frac{s^2}{\omega_i^2}\right)},$

dove $\tau_i$ e $T_i$ sono rispettivamente le costanti di tempo degli zeri e dei poli, e $\mu$ rappresenta il guadagno. \newline Deduciamo che il guadagno è $\mu = 4$ . Il diagramma di Bode dei moduli si ottiene sommando il diagramma delle componenti della funzione di trasferimento espressa in decibel. Il modulo del guadagno in $\mu \text{dB} = 20\log_{10} |4| \sim \text{12,04 dB}$ . Oltre al guadagno sono presenti 2 zeri in $-1$ , un polo in $0$ , e due poli positivi in $1$ . Di seguito sono rappresentati i diagrammi di Bode delle varie componenti del modulo della funzione di trasferimento.

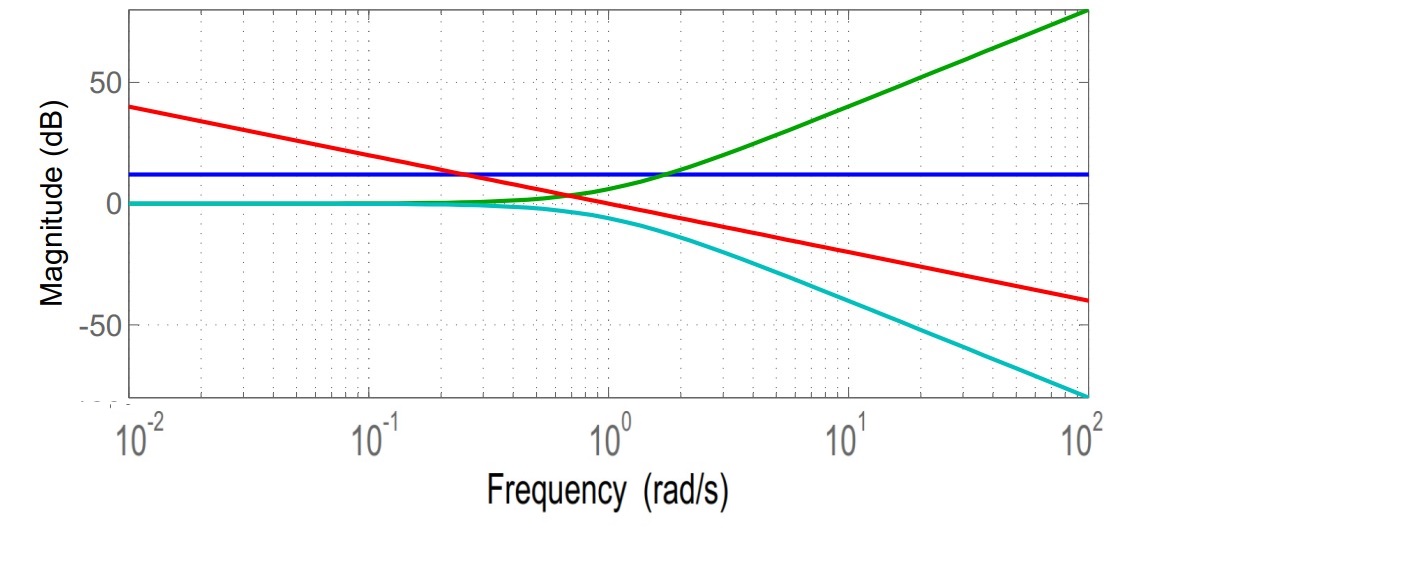
Figura 9: diagramma dei moduli delle componenti la funzione assegnata.

Di seguito spieghiamo le curve nella figura di sopra.

La curva blu rappresenta il guadagno costante di $\text{12,04 dB}$ ;
La curva rossa indica il polo in zero, che scende con una pendenza di $\text{-20 dB/dec}$ per tutte le frequenze;
La curva verde mostra la coppia di zeri in $-1$ , che sale con una pendenza di $\text{40 dB/dec}$ a partire da una pulsazione di $\text{1 rad/s}$ ;
La curva azzurra rappresenta la coppia di poli in $1$ , che scende con una pendenza costante di $\text{-40 dB/dec}$ a partire dalla pulsazione di $1$ .

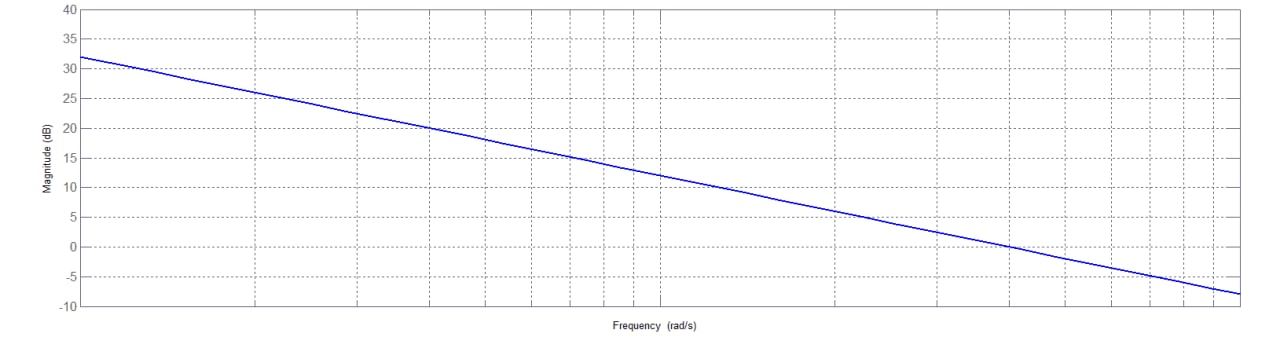
Figura 10: diagramma del modulo della funzione assegnata

Il diagramma complessivo ottenuto sommando i contributi parziali è rappresentato nella figura si sopra.

Si osserva che il diagramma dei moduli scende con una pendenza costante di $\text{-20 dB/dec}$ , a causa dell’annullamento reciproco dei contributi dei poli in $1$ e degli zeri in $-1$ .

Di seguito è riportato il diagramma dei contributi parziali della fase.

Figura 11: diagramma delle fasi delle componenti la funzione assegnata.

Di seguito spieghiamo le curve nella figura di sopra.

La curva blu rappresenta la fase del guadagno, che essendo positivo è pari a zero;
La curva verde indica la fase della coppia di poli in $1$ , che sale di $\text{90}^\circ/\text{dec}$ a partire da una pulsazione di $\text{0,1 rad/s}$ e fino a $10$ , essendo i poli a parte reale positiva;
La curva rossa mostra la fase del polo in zero, con un contributo di fase costante pari a $-90^\circ$ ;
La curva azzurra rappresenta la fase della coppia di zeri in $-1$ , che sale di $90^\circ/\text{dec}$ a partire da una pulsazione di $\text{0,1 rad/s}$ , fino a $\text{10 rad/s}$ , rimanendo poi costante.

Sommando i vari contributi si ottiene il grafico seguente, che rappresenta la fase della funzione di trasferimento assegnata.

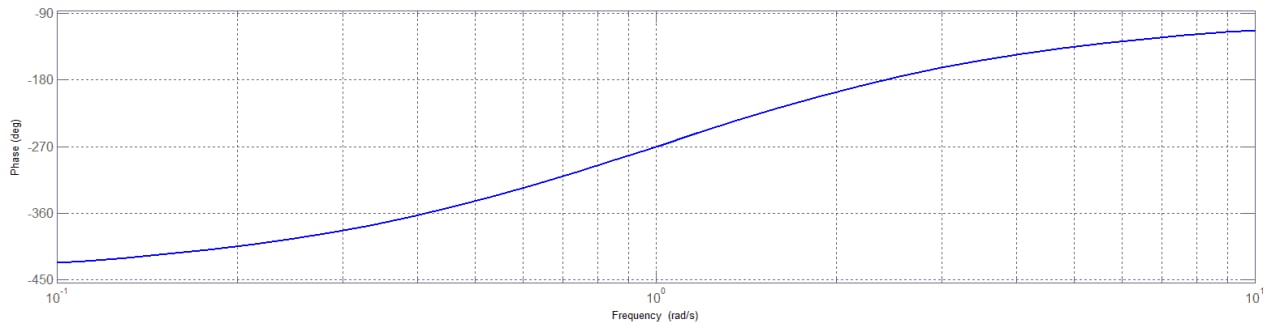
Figura 12: diagramma della fase della funzione assegnata.

In quanto i poli hanno una parte reale positiva, sia la coppia di poli sia quella di zeri contribuiscono ad un aumento progressivo della fase.

Esercizio 4 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Data la funzione di trasferimento

$W(s)=\dfrac{s\left(s-10\right)}{\left(s+100\right)\left(s^2-8s+64\right)},$

si richiede di rappresentare il diagramma di Bode.

Svolgimento.

La funzione $W$ si presenta nella forma zero poli del tipo

$G(s) = \frac{\rho \prod_i (s + z_i) \prod_i (s^2 + 2\zeta_i\alpha_i s + \alpha_i^2)}{s^g \prod_i (s + p_i) \prod_i (s^2 + 2\zeta_i\omega_i s + \omega_i^2)},$

dove $\rho$ rappresenta la costante di trasferimento, $z_i$ sono gli zeri reali della funzione $G$ cambiati di segno, $\zeta_i$ sono gli smorzamenti delle coppie di poli complessi e coniugati, $\alpha_i$ sono le pulsazioni degli zeri complessi e coniugati, $g$ è il tipo di sistema che rappresenta il numero di poli o zeri in zero, $p_i$ sono i poli reali cambiati di segno, $\zeta_i$ lo smorzamento delle coppie di poli complessi e coniugati, e $\omega_i$ la pulsazione delle coppie di poli complessi e coniugati. Pertanto la funzione $W$ presenta uno zero reale in $10$ , uno zero reale in $0$ , un polo in $-100$ , e una coppia di poli complessi e coniugati. La pulsazione naturale delle radici di poli complessi e coniugati è in $8$ , da cui, si ha

$-8 = 2\zeta (8) \quad \Leftrightarrow \quad \zeta = -\frac{1}{2}.$

Occorre trovare il guadagno della funzione di trasferimento riportandola nella forma con le costanti di tempo del tipo:

dove $\tau_i$ e $T_i$ sono rispettivamente le costanti di tempo degli zeri e dei poli, e $\mu$ rappresenta il guadagno. Dunque, la funzione di trasferimento $W(s)$ può essere riscritta come

$W(s) = -\frac{-10s \left(-\frac{s}{10} + 1\right)}{64 \cdot 100 \left(\frac{s}{100} + 1\right) \left(\frac{s^2}{64} - \frac{s}{8} + 1\right)}.$

Da quanto ottenuto deduciamo che il guadagno $\mu = -1/640$ . Il diagramma di Bode dei moduli si può ottenere sommando il diagramma delle componenti della funzione di trasferimento espressa in decibel. Il modulo del guadagno in $\mu \text{dB} = 20\log_{10} \left| -\frac{1}{640} \right| \sim -\text{\text{56,12} dB}$ . Di seguito sono rappresentati i diagrammi di Bode delle varie componenti del modulo

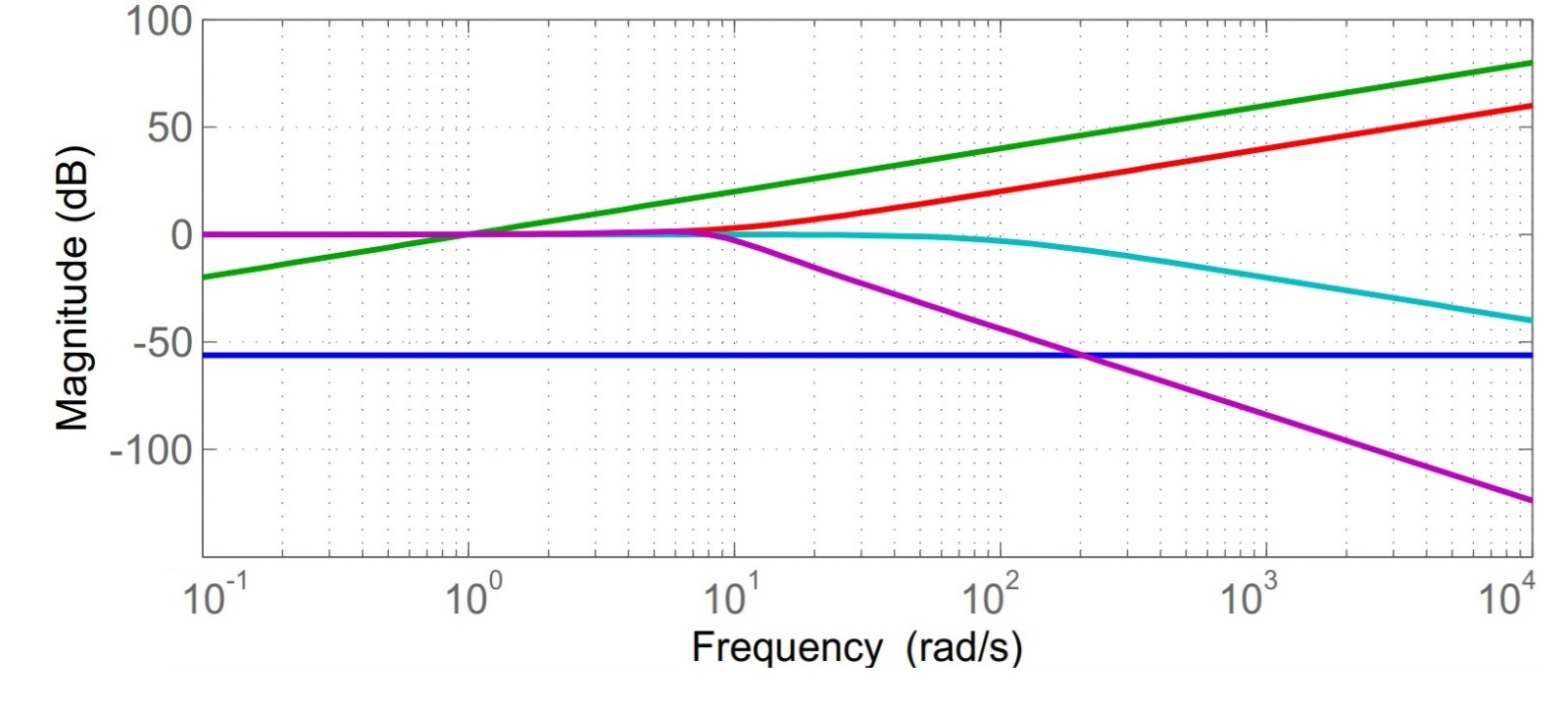
Figura 13: diagramma dei moduli delle componenti la funzione assegnata.

Di seguito spieghiamo le curve nella figura di sopra.

La curva celeste rappresenta il polo in $-100$ che scende con una pendenza costante di $-20\, \text{dB}/\text{dec}$ , passando per il punto $(100\,\text{rad/s}, 0\,\text{dB})$ ;
La curva blu indica il guadagno costante con la frequenza di $-56,12\,\text{dB}$ ;
La curva verde mostra lo zero in $0$ che sale di $20\,\text{dB/dec}$ a tutte le frequenze;
La curva rossa rappresenta lo zero in $10\,\text{rad/s}$ , costante a $0\,\text{dB}$ fino a una pulsazione di $10\,\text{rad/s}$ , dopo di che sale di $20\,\text{dB/dec}$ ;
La curva viola mostra la coppia di poli complessi e coniugati. Data la determinazione di $\zeta$ , è chiaro che non c’è picco di risonanza; fino alla pulsazione naturale di $8\,\text{rad/s}$ il modulo è costante a $0\,\text{dB}$ , e poi scende con una pendenza di $40\,\text{dB/dec}$ .

Il diagramma complessivo, ottenuto sommando i contributi parziali, è rappresentato nella figura successiva.

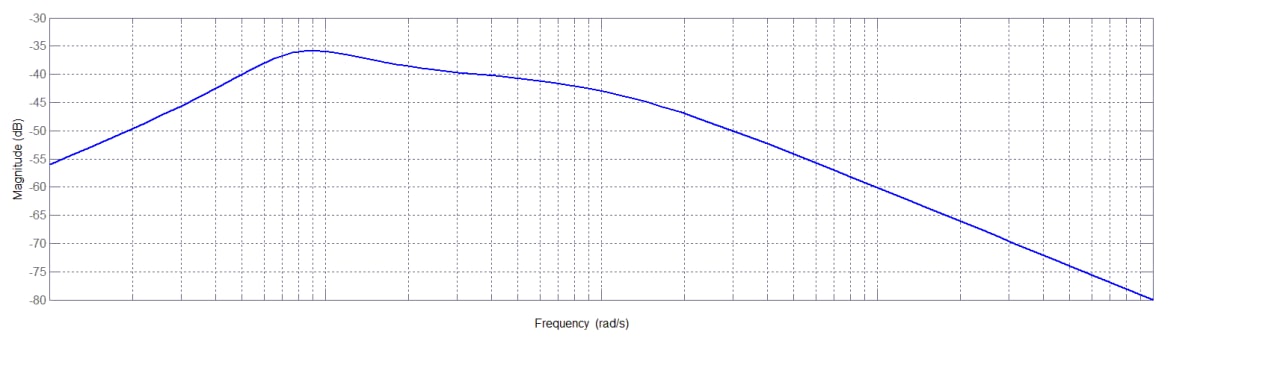
Figura 14: diagramma del modulo della funzione assegnata.

Di seguito è riportato il diagramma dei contributi parziali della fase.

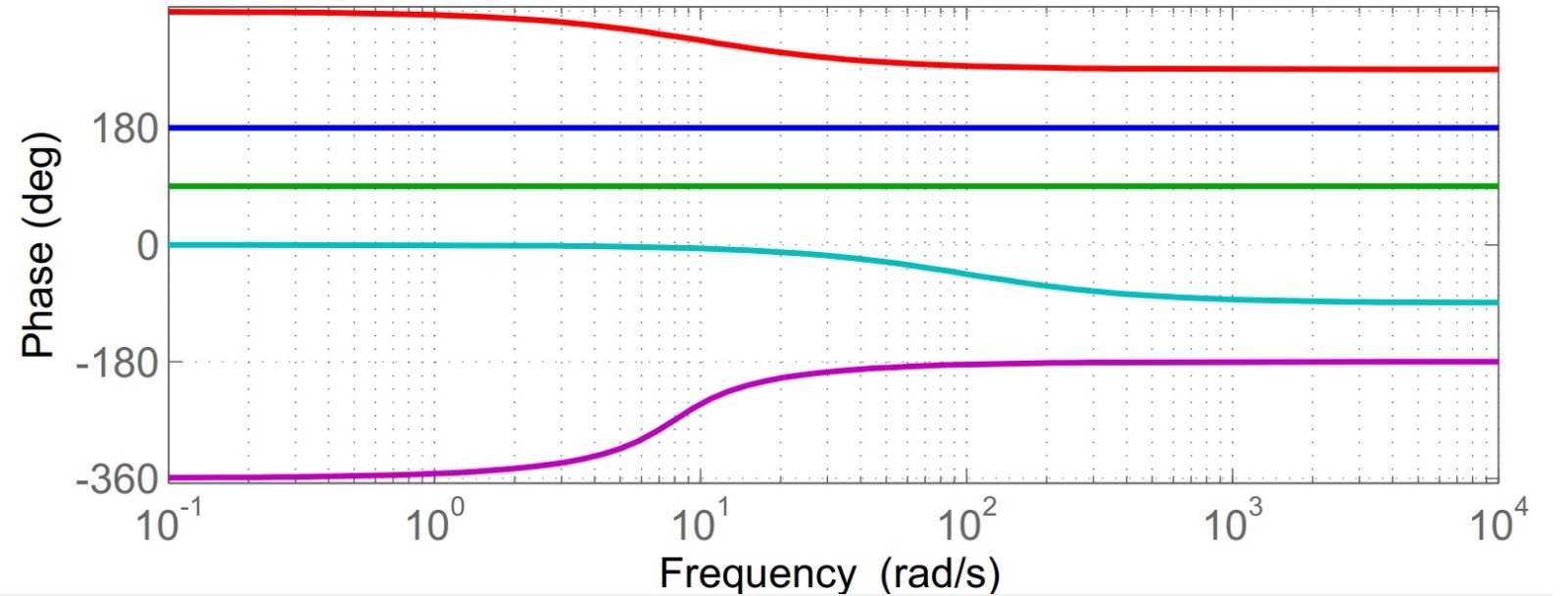
Figura 15: diagramma delle fasi delle componenti la funzione assegnata.

Di seguito spieghiamo le curve nella figura di sopra.

La curva blu rappresenta la fase di $180^\circ$ del guadagno, essendo questo negativo;
La curva verde indica la fase dello zero in zero, costante e pari a $90^\circ$ ;
La curva viola mostra la fase della coppia di poli complessi e coniugati. Con $\zeta$ negativo, la fase di questi poli cresce, a partire da una pulsazione di $0.8\,\text{rad/s}$ con pendenza approssimativamente costante di $90^\circ/\text{dec}$ per due decadi;
La curva celeste rappresenta la fase del polo in $-100$ che scende a partire da una pulsazione di $10$ per due decadi con pendenza approssimativamente costante di $45^\circ/\text{dec}$ ;
La curva rossa indica la fase dello zero positivo in $10$ , decrescente a partire da una pulsazione di $1$ per due decadi, con pendenza di circa $-45^\circ/\text{dec}$ .

Sommando i vari contributi si ottiene il grafico seguente, che rappresenta la fase della funzione di trasferimento assegnata.

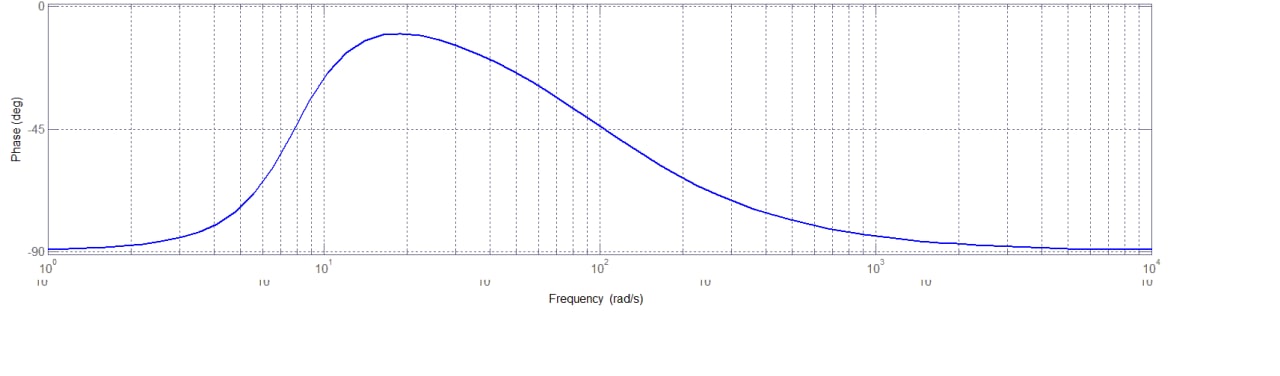
Figura 16: diagramma della fase della funzione assegnata.

Tutte le cartelle di controlli automatici

Leggi...

Document

Menu

Chiudi

Esercizi svolti diagrammi di Bode

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Tutte le cartelle di controlli automatici

Leggi...

Suggerimenti, refusi ed errori

Cosa dicono di noi