Login Abbonati
Accedi ai contenuti scaricabili
a

Menu

M

Chiudi

Esercizi svolti analisi della Stabilità dei Sistemi LTI

Analisi della Stabilità dei Sistemi LTI

Home » Esercizi svolti analisi della Stabilità dei Sistemi LTI

 

Esercizio 1 (\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar). Dato un sistema retroazionato la cui funzione d’anello aperto è

(1)   \begin{equation*} L(s)=\dfrac{300(1+ \text{0,01}s)}{(1+\text{0,1}s)(1+\text{0,001}s)}, \end{equation*}

studiare la stabilità del sistema ad anello chiuso a cui appartiene.

Svolgimento.

Poiché la funzione L(s) non presenta poli con parte reale positiva e ha un guadagno positivo, si soddisfano le condizioni necessarie all’applicazione del criterio di Bode. L’analisi della stabilità può essere effettuata esaminando il corrispondente diagramma di Bode.

   

 

Figura 1: diagramma di Bode.

   

Dal momento che l’attraversamento del diagramma di |L(j\omega)| sull’asse dei 0 dB si verifica con una pendenza di -20 dB/sec, possiamo affermare che il sistema retroazionato è asintoticamente stabile.

 

Esercizio 2 (\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar). Dato un sistema retroazionato la cui funzione d’anello aperto è

(2)   \begin{equation*} L(s)=\dfrac{20}{(1+s)^2} \end{equation*}

verificare la stabilità del sistema ad anello chiuso a cui appartiene.

Svolgimento.

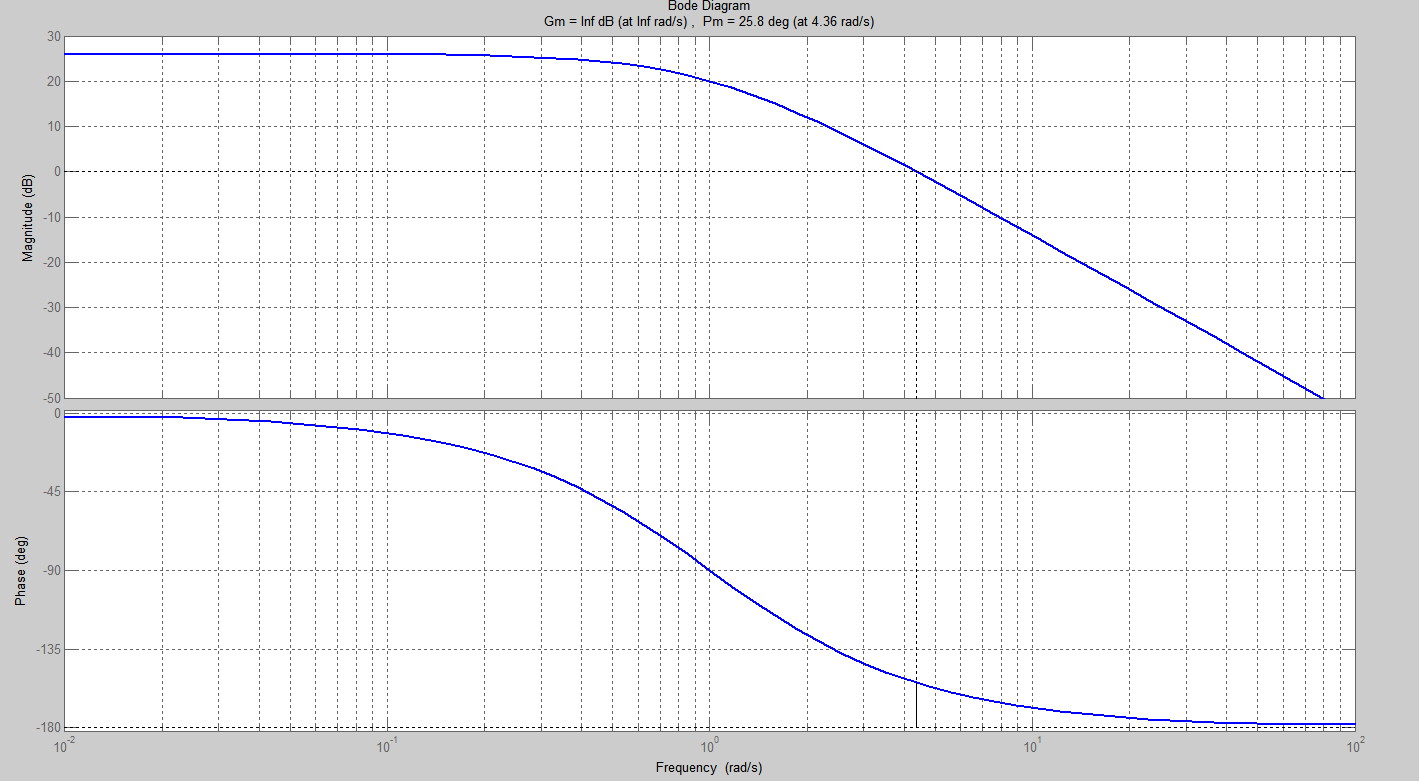
La funzione L(s), avendo un guadagno positivo e assenza di poli con parte reale positiva, rispetta le condizioni richieste dal criterio di Bode. Pertanto, si procede con la costruzione del diagramma di Bode per esaminare la stabilità del sistema.

     

Figura 2: diagramma di Bode.

   

Il diagramma del modulo interseca l’asse dei 0 dB con una pendenza di -40 dB/sec. Pertanto, il criterio di Bode non è direttamente applicabile nella sua forma semplificata. È tuttavia possibile determinare il margine di fase:

(3)   \begin{equation*} \phi_M = 180^\circ - |\phi_C| = 180^\circ - \text{154,2}^\circ = \text{25,8}^\circ. \end{equation*}

Poiché il margine di fase è positivo, secondo la formulazione completa del criterio di Bode, si conclude che il sistema in retroazione è asintoticamente stabile.

 

Esercizio 3 (\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar). Dato il sistema LTI a tempo discreto

(4)   \begin{align*} x(k+1)&=\begin{pmatrix} 4&-1&1\\5&-2&5\\0&0&-1 \end{pmatrix}x(k)+\begin{pmatrix} 0\\1\\0 \end{pmatrix}u(k)\\[10pt] y(k)&=\begin{pmatrix} 1&2&0 \end{pmatrix}x(k), \end{align*}

studiarne le prorietà di stabilità.

Svolgimento.

La stabilità di un sistema è determinata esclusivamente dalla matrice dinamica A. Per analizzare la stabilità, è necessario calcolare gli autovalori di A risolvendo l’equazione caratteristica:

(5)   \begin{equation*} \det(A - \lambda I) = 0. \end{equation*}

Ciò porta alla determinazione di due autovalori, \lambda_{1,2} = -1 con molteplicità algebrica di 2, e \lambda_3 = 3 con molteplicità algebrica di 1. La molteplicità geometria è data da:

    \[m_g(\lambda) = n - \operatorname{rank}(A - \lambda I),\]

dove n è l’ordine della matrice A e I è la matrice identità.

Per garantire la stabilità asintotica, tutti gli autovalori devono avere modulo inferiore a 1. La stabilità semplice richiede che autovalori di modulo unitario presentino molteplicità algebrica e geometrica identiche, mentre gli altri autovalori abbiano modulo minore di 1.

Dato che nessuna di queste condizioni è soddisfatta, il sistema è classificato come instabile.

 

Esercizio 4 (\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar). Si discutano, al variare di k\in\mathbb{R} le proprietà strutturali del seguente sistema.

 
 

Rendered by QuickLaTeX.com

 
 

Svolgimento.

I blocchi S_3 e S_2 sono in parallelo. La presenza di autovalori, o poli, in comune tra i due blocchi condurrebbe a dinamiche che non sono né osservabili né raggiungibili. Pertanto, se k = 0, il sistema risulta nè osservabile nè raggiungibile. Il parallelo di S_2 e S_3 produce un sistema con autovalori che corrispondono all’insieme unione degli autovalori di S_2 e S_3, risultando in poli situati in “0” e “-k” . Definendo S_{23} come il sistema risultante dal parallelo di S_2 e S_3, la funzione di trasferimento di S_{23} è la seguente:

(6)   \begin{equation*} G_{23}=\dfrac{1}{s+k}+\dfrac{1}{s}=\dfrac{2\left(s+\dfrac{k}{2}\right)}{s(s+k)}. \end{equation*}

Se k = 0, al denominatore resta un solo polo denunciando la perdita di visibilità e di effetto dell’altro polo in zero. S_{23} è in serie con il sistema S_1.

   

Rendered by QuickLaTeX.com

   

Nella connessione in serie di due sistemi:

  1. un polo di S_{23} cancellato da uno zero di S_{1} porta a una dinamica non raggiungibile,
  2. uno zero di S_{23} cancellato da un polo di S_1 comporta una dinamica non osservabile.

In tale configurazione, la cancellazione dello zero nell’origine di S_1 con un polo di S_{23} comporta la perdita di raggiungibilità, mentre la cancellazione di uno zero in S_{23} comporterebbe la perdita di osservabilità.

 

Esercizio 5 (\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar). Si studi mediante il criterio di Nyquist la stabilità ad anello chiuso con retroazione unitaria del sistema

    \[L(s)=\dfrac{4\left(1+s\right)^2}{s\left(1-s\right)^2}.\]

Svolgimento.

Per applicare il criterio di Nyquist, è fondamentale estendere il diagramma di Nyquist ottenuto nell’esercizio 1, contenuto nella cartella “I diagrammi di Nyquist” così da ottenere il diagramma polare completo della funzione ad anello aperto. Questa estensione comporta il tracciamento di una semicirconferenza percorsa in senso orario, con un raggio che tende all’infinito. Questa semicirconferenza parte dal punto L(j0^-) e giunge fino al punto L(j0^+).

     

Figura 3:diagramma di Nyquist della funzione assegnata.

   

La funzione L(s) è caratterizzata da due poli con parte reale positiva.

Poiché la funzione ad anello aperto contiene due poli a parte reale positiva, per l’analisi della stabilità del sistema ad anello chiuso occorre applicare il criterio di Nyquist in forma estesa, ovvero assicurarsi che il diagramma polare della funzione compia intorno al punto critico -1 tanti giri in senso antiorario quanti sono i poli instabili della funzione ad anello aperto, ovvero esattamente due. Il diagramma di Nyquist completo compie due giri in senso antiorario intorno al punto -1+0,j. Questo conferma che il sistema retroazionato associato è asintoticamente stabile.

 

Esercizio 6 (\bigstar\bigstar\bigstar\largewhitestar\largewhitestar). Si studi mediante il criterio di Nyquist la stabilità ad anello chiuso con retroazione unitaria del sistema

    \[L(s)=\dfrac{4\mu\left(1+s\right)^2}{s\left(1-s\right)^2},\]

al variare del parametro reale \mu.

Svolgimento.

Il caso in oggetto rappresenta l’estensione dell’esercizio 5 al caso in cui, nella funzione ad anello aperto, sia presente un guadagno \mu. Per la presenza dei poli a parte reale positiva, resta la necessità di utilizzare il criterio esteso, ma a differenza del caso precedente cambia il punto critico rispetto al quale vanno valutati i circondamenti. In questo caso è -\frac{1}{\mu}.

     

Figura 4: diagramma di Nyquist della funzione assegnata.

   

Nella figura che segue è riportato un ingrandimento della zona di interesse.

     

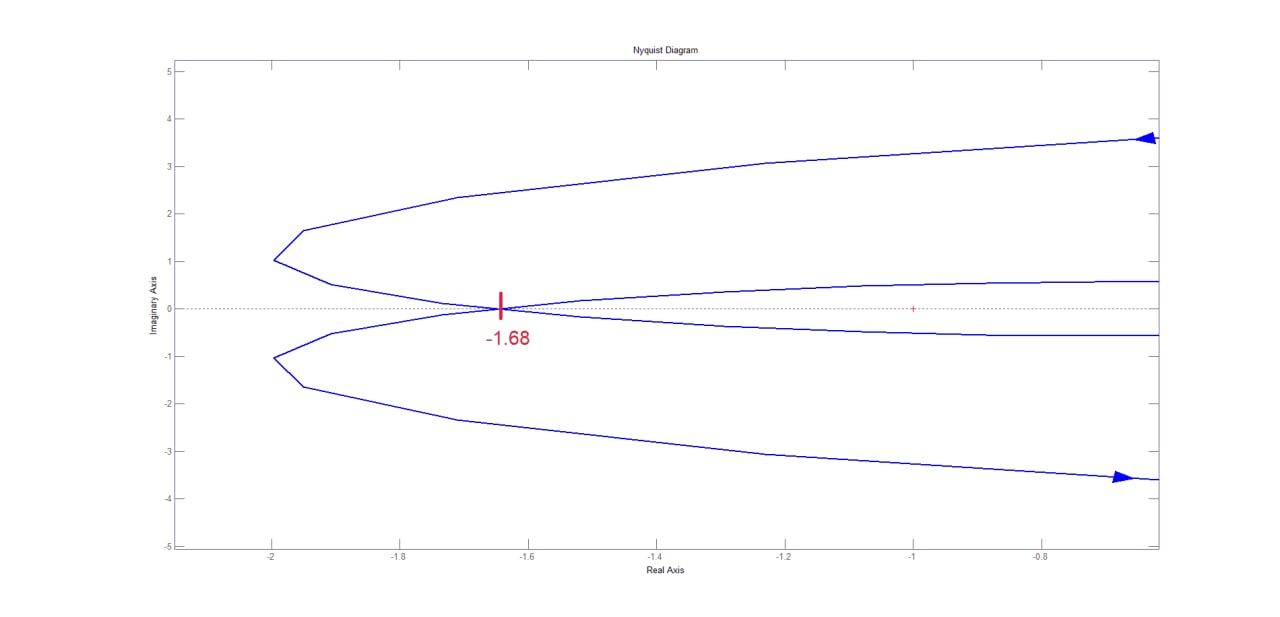
Figura 5: dettaglio del diagramma di Nyquist della funzione assegnata.

   

Dalla figura precedente, osserviamo che il punto critico può essere situato in un intervallo compreso tra -\text{1,68} e 0. Il punto critico coincide con il valore -1/\mu. Possiamo determinare il valore del guadagno \mu per cui il sistema rimane stabile ponendo -1/\mu=-\text{1,68}, da cui otteniamo: \mu\approx\text{0,6}.

Quando il guadagno \mu assume valori inferiori a \text{0,6}, il punto critico si sposta verso sinistra e il criterio di Nyquist non è più soddisfatto. Di conseguenza, il sistema retroazionato diventa instabile.

Questo criterio ci fornisce una stima, seppur qualitativa del guadagno limite che un controllore può avere prima di portare il sistema retroazionato all’instabilità. Per una valutazione più precisa, possiamo ricorrere al criterio di Routh.

 

 

Tutte le cartelle di controlli automatici

Leggi...

  1. Analisi nel dominio di Laplace e del tempo di sistemi dinamici LTI a tempo continuo
  2. Analisi modale di sistemi dinamici LTI a tempo continuo
  3. Linearizzazione di sistemi dinamici
  4. Analisi della Stabilità dei Sistemi LTI
  5. Stabilità dell’equilibrio di sistemi dinamici non lineari
  6. Retroazione statica dallo stato
  7. Analisi nel dominio del tempo e della trasformata Zeta di sistemi dinamici LTI a tempo discreto
  8. Trasformata Zeta
  9. La risposta in frequenza
  10. Analisi modale di sistemi dinamici LTI a tempo discreto
  11. La carta di Nichols
  12. Proprietà della risposta allo scalino
  13. Schemi a blocchi e loro combinazioni
  14. I diagrammi di Bode
  15. I diagrammi di Nyquist
  16. Il progetto del controllore
  17. Il luogo delle radici
  18. Stabilità in condizioni perturbate: i margini
  19. I regolatori PID
  20. Le reti compensatrici
  21. Modellistica dei sistemi dinamici meccanici, elettrici
  22. Proprietà strutturali dei sistemi
  23. Sintesi del modello di stato ISU
  24. Sintesi dell’osservatore asintotico dello stato






Document