Esercizio 1. ![]() Sono dati i due punti
Sono dati i due punti ![]() e
e ![]() . Determinare sulla semiretta bisettrice del primo quadrante un punto
. Determinare sulla semiretta bisettrice del primo quadrante un punto ![]() , in modo che il triangolo
, in modo che il triangolo ![]() risulti:
risulti:
![]() rettangolo con ipotenusa
rettangolo con ipotenusa ![]() ;
;
![]() rettangolo con ipotenusa
rettangolo con ipotenusa ![]() ;
;
![]() isoscele con base
isoscele con base ![]() .
.
Svolgimento. In figura rappresentiamo il triangolo con il vertice di coordinate generiche ![]()

Il punto ![]() appartiene alla bisettrice di equazione
appartiene alla bisettrice di equazione ![]() solo per
solo per ![]() pertanto
pertanto ![]() . Abbiamo allora, considerando il triangolo
. Abbiamo allora, considerando il triangolo ![]() , le seguenti richieste:
, le seguenti richieste:
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Poichè
![Rendered by QuickLaTeX.com \[\begin{aligned} &AB^2=(2-0)^2+(-2-2)^2=4+16=20,\\ &AC^2=(2-x)^2+(-2-x)^2=4-4x+x^2+4+4x+x^2=2x^2+8,\\ &BC^2=(0-x)^2+(2-x)^2=x^2+4-4x+x^2=2x^2-4x+4, \end{aligned}\]](https://quisirisolve.com/wp-content/ql-cache/quicklatex.com-ed1b076557c71bde99136e54295b1f74_l3.png)
segue che:
![]() abbiamo l’equazione
abbiamo l’equazione
![]()
le cui soluzioni sono ![]() , e quindi si hanno i due punti
, e quindi si hanno i due punti
![]()
Di seguito il primo triangolo

e il secondo triangolo
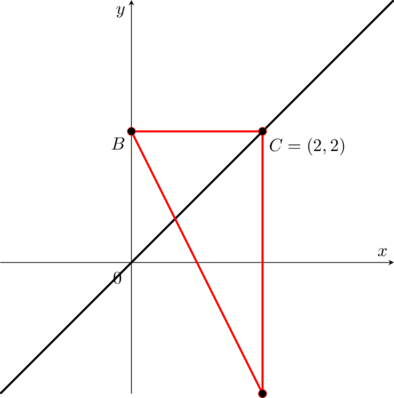
![]() abbiamo l’equazione
abbiamo l’equazione
![]()
e quindi l’unico punto ![]() ; di seguito il triangolo trovato
; di seguito il triangolo trovato

![]() abbiamo l’equazione
abbiamo l’equazione
![]()
e quindi le due soluzioni ![]() .
.
Di seguito il primo triangolo

e il secondo triangolo
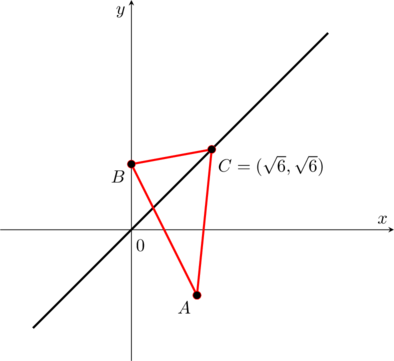
Fonte: ignota.
