Esercizi svolti sugli integrali tripli

Home » Esercizi svolti sugli integrali tripli

Esercizi svolti sugli integrali tripli

Sommario

Leggi...

Questa dispensa raccoglie 36 esercizi svolti sugli integrali tripli, concepita per gli studenti dei corsi di laurea in ingegneria, fisica e matematica, nell’ambito del corso di Analisi 2. Gli esercizi sono classificati in base alla difficoltà, suddivisa in cinque livelli distinti, indicati con un sistema di stelline che vanno da 1 (molto semplice) a 5 (estremamente complesso).

Il fine di questo materiale didattico è di offrire agli studenti un quadro esaustivo delle tecniche necessarie per la risoluzione di ogni tipologia di integrale triplo. A differenza di altre tipologie di esercizi, gli integrali tripli non si prestano a una risoluzione meccanica, in quanto richiedono notevole flessibilità nel problem solving. La sfida principale risiede nella corretta rappresentazione grafica della regione di integrazione e nella scelta della parametrizzazione più adeguata, per evitare di rendere eccessivamente complesso il procedimento risolutivo.

La varietà degli esercizi proposti, accuratamente selezionati, mira a sviluppare le competenze necessarie per affrontare con successo ogni problematica legata agli integrali tripli, permettendo allo studente di acquisire padronanza in un argomento cruciale e avanzato dell’analisi matematica.

Autori e revisori

Leggi...

Autori: Valerio Brunetti, Silvia Lombardi.

Revisori: Sara Sottile.

Esercizi

$\quad$

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Consideriamo un cono di raggio $R$ , altezza $h$ , asse sull’asse $z$ , vertice nell’origine e base nel semipiano $z>0$ . Calcolare il volume.

Svolgimento.

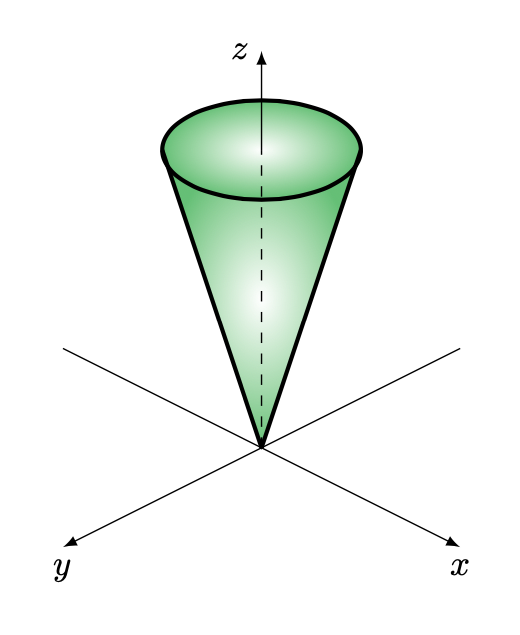
Rappresentiamo graficamente in figura 1 il cono della traccia.

$\quad$

Figura 1: cono con base circolare e altezza $h$ , vertice nell’origine.

$\quad$

Integriamo per strati.

Sia $z \in [0,h]$ e $r(z)=z\frac{R}{h}$ con

$\Omega(z) = \left\{ (x,y) \in \mathbb{R}^2 \, \vert \, x^2+y^2\le r^2(z) \right\}.$

Allora

$\tau = \int_0^h 1 \, dz \iint_{\Omega(z)}1 \, dx \, dy = \int_0^h \pi r^2(z) \, dz = \int_0^h \pi z^2 \dfrac{R^2}{h^2}\, dz=\pi \dfrac{hR^2}{3}.$

Quindi

\be

$\boxcolorato{analisi}{\tau=\pi \dfrac{hR^2}{3}. }$

Esercizio 2 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Sia la piramide a base quadrata con vertice nell’origine, altezza $h$ , asse sull’asse $z$ , base di lato $L$ posta nel semipiano $z>0$ . Calcolare il volume.

Svolgimento.

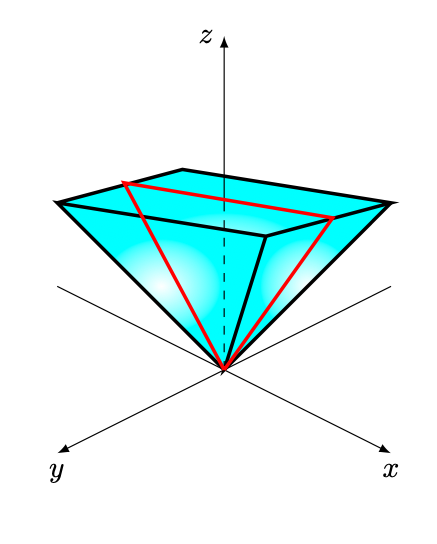
Nel grafico della Figura 2 è rappresentata la piramide descritta nella traccia, mentre il triangolo formato dall’altezza e dalla base della piramide è illustrato nella Figura 3.

$\quad$

Figura 2: piramide a base quadrata con vertice nell’origine..

$\quad$

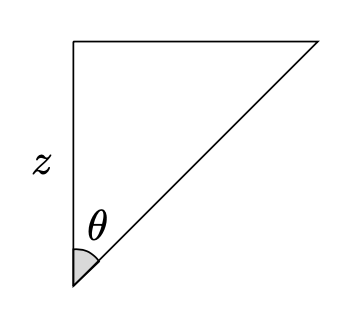
Figura 3: sezione trasversale della piramide lungo l’asse $z$ .

$\quad$

Dalla figura 3 si osserva che

(1) $\begin{equation*} \begin{split} & \tan \theta = \dfrac{\dfrac{L}{2}}{h} = \dfrac{L}{2h},\\[10pt] \end{split} \end{equation*}$

(2) $\begin{equation*} \begin{split} & y = z\tan \theta = \dfrac{Lz}{2h}. \end{split} \end{equation*}$

Sia $\Omega(z)$ un generico strato della piramide

$\Omega(z) = \left\{ (x,y) \in \mathbb{R}^2 \, : \, \vert y \vert \leq \dfrac{Lz}{2h}, \vert x \vert \leq \dfrac{Lz}{2h} \right\}.$

Procediamo ad integrare per strati per calcolare il volume della piramide

(3) $\begin{equation*} \begin{split} \tau & = \int_0^h 1 \, dz \int_{\Omega(z)} 1 \, dx \, dy = \\ & = \int_0^h \left(\dfrac{Lz}{h}\right)^2 \, dz = \\ & = \left(\dfrac{L^2}{h^2}\right) \dfrac{z^3}{3} \bigg\vert_0^h = \\ & = \dfrac{L^2 h}{3}. \end{split} \end{equation*}$

Dunque, si conclude che

$\boxcolorato{analisi}{\tau=\dfrac{L^2 h}{3}. }$

Esercizio 3 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Calcolare il seguente integrali triplo:

$\iiint_\mathcal{D} e^{\frac{x+y}{\sqrt{2}}} \, dx \, dy \, dz,$

dove il dominio è definito come

$\mathcal{D} = \{(x, y, z) \ : \ x^2 + y^2 + z^2 \leq 1\},$

e rappresentato in figura 4. Per facilitare il calcolo, si consiglia di adottare la seguente sostituzione:

(4) $\begin{equation*} \begin{cases} u = \dfrac{x + y}{\sqrt{2}}, \\[10pt] v = \dfrac{x - y}{\sqrt{2}}, \\[10pt] w = z. \end{cases} \end{equation*}$

$\quad$

Figura 4: sfera tridimensionale con centro nell’origine.

$\quad$

Svolgimento.

Parametrizziamo $\mathcal{D}$ con la parametrizzazione (4).

In questa sostituzione, il differenziale $dx \, dy \, dz$ viene espresso in termini di $du \, dv \, dw$ mediante il determinante jacobiano $\vert J \vert$ , dato da:

$\vert J \vert = \begin{vmatrix} \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} & 0\\[10pt] \dfrac{1}{\sqrt{2}} & -\dfrac{1}{\sqrt{2}} & 0\\[10pt] 0 & 0 & 1 \end{vmatrix} = 1.$

Ne consegue che il volume infinitesimale si conserva nella nuova parametrizzazione:

$dx \, dy \, dz = du \, dv \, dw.$

Dal sistema (4), si trova

$\begin{cases} x=\dfrac{u+v}{\sqrt{2}}\\\\ y=\dfrac{u-v}{\sqrt{2}}\\\\ z=w. \end{cases}$

Sostituendo nel dominio $x^2+y^2+z^2\leq 1$ , si ottiene

$\dfrac{1}{2}\left(u+v\right)^2+\dfrac{1}{2}\left(u-v\right)^2+w^2 \le 1 \quad \iff \quad u^2+v^2+w^2\leq1,$

l’integrale diventa

(5) $\begin{equation*} \begin{split} &\iiint_\mathcal{D} e^u \, du\, dv \, dw = \\ & =\int_{-1}^1 e^u\,du \iint_{v^2+w^2\le1-u^2} dv \, dw = \\ & = \int_{-1}^1 e^u \,\pi (1-u^2) \, du =\\ & = \pi \int_{-1}^1 e^u(1-u^2) \, du = \\ & = \pi \left[(1-u^2) e^u \bigg\vert_{-1}^1 + 2 \int_{-1}^1 e^u \, u \, du \right]=\\ & = 2\pi \left(e^u \, u \bigg\vert_{-1}^1 - \int_{-1}^1 e^u \, du\right) = \\ & = 2\pi \left(e^u \; u \bigg\vert_{-1}^1 - e^u \bigg\vert_{-1}^1\right) =\\ & = 2 \pi \left(e+e^{-1}-e+e^{-1}\right) =\\ & = 2\pi \; 2 \, e^{-1} =\\ & = \dfrac{4\pi}{e}. \end{split} \end{equation*}$

Quindi

$\boxcolorato{analisi}{\displaystyle\iiint_\mathcal{D} e^u \, du\, dv \, dw =\dfrac{4\pi}{e}. }$

Esercizio 4 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia il seguente insieme

$\mathcal{D} = \left\{ (x,y,z) \in \mathbb{R}^3 ) : x^2+y^2+z^2\le 1, x^2+y^2+(z-1)^2\le 1 \right\}.$

Calcolare il volume.

Svolgimento metodo 1.

L’esercizio può essere risolto applicando tre strategie differenti, che vengono di seguito illustrate. Rappresentiamo graficamente in figura 5 l’insieme dato.

$\quad$

Figura 5: intersezione di due sfere descritte dalle equazioni $x^2 + y^2 + z^2 = 1$ e $x^2 + y^2 + (z-1)^2 = 1$ .

$\quad$

Procediamo integrando per fili

(6) $\begin{equation*} \begin{split} \tau & = \iiint_{\mathcal{D}} 1 \, dx \, dy \, dz =\\ & = \iint_{\Omega} \int_{1-\sqrt{1-x^2-y^2}}^{\sqrt{1-x^2-y^2}} dz =\\ & = \iint_{\Omega}\left( \sqrt{1-x^2-y^2}-1+\sqrt{1-x^2-y^2} \right) dx \, dy =\\ & = \iint_{\Omega} \left(2 \sqrt{1-x^2-y^2}-1\right) dx \, dy, \end{split} \end{equation*}$

dove $\Omega$ è la proiezione del dominio $\mathcal{D}$ sul piano $xy$ .

Abbiamo dunque

$\begin{cases} x^2+y^2+z^2=1\\x^2+y^2+z^2-2z=0 \end{cases} \quad \iff \quad \begin{cases} x^2+y^2=1-\dfrac{1}{4} \\[10pt] 1-2z=0 \end{cases}\quad \iff \quad \begin{cases} x^2+y^2=\dfrac{3}{4}\\[10pt] z=\dfrac{1}{2}, \end{cases}$

pertanto

$\iint_{x^2+y^2\le \frac{3}{4}} \left(2\sqrt{1-x^2-y^2}-1\right) \, dx \, dy = \int_0^{2\pi} \int_0^{\frac{\sqrt{3}}{2}} \left(2\sqrt{1-\rho^2}-1\right) \rho \, d\rho = 2\pi \left(\frac{5}{24}\right) = \dfrac{5}{12}\pi.$

Svolgimento metodo 2.

Integriamo procedendo per strati

$\tau= \int_0^{\frac{1}{2}} 1 \, dz \iint_{x^2+y^2\le 1-(z-1)^2} 1 \, dx \, dy+\int_{\frac{1}{2}}^{1} 1 \, dz \iint_{x^2+y^2\le 1 -z^2} 1 \, dx \, dy$

(7) $\begin{equation*} \begin{split} \int_0^{\frac{1}{2}} 1 \, dz \iint_{x^2+y^2\le 1-(z-1)^2} 1 \, dx \, dy = \int_0^{\frac{1}{2}} \pi (1-(z-1)^2) \, dz = \dfrac{5}{24}\pi \end{split} \end{equation*}$

(8) $\begin{equation*} \begin{split} \int_{\frac{1}{2}}^{1} 1 \, dz \iint_{x^2+y^2\le 1 -z^2} 1 \, dx \, dy = \int_{\frac{1}{2}}^1 \pi (1-z^2) \, dz = \dfrac{5}{24}\pi \end{split} \end{equation*}$

quindi

$\tau = \dfrac{5}{24}\pi +\dfrac{5}{24}\pi = \dfrac{5}{12}\pi.$

Svolgimento metodo 3.

Applichiamo le coordinate sferiche

$\begin{cases} x = \rho \, \cos \theta \, \sin \phi, \\ y = \rho \, \sin \theta \, \sin \phi, \\ z = \rho \cos \phi, \end{cases}$

dove

$\dfrac{1}{2 \cos \phi} \le \rho \le 1, \quad \phi \in \left[0, \dfrac{\pi}{3}\right], \quad \theta \in [0,2\pi],$

allora

$\tau = 2 \int_0^{\frac{\pi}{3}} d\phi \int_0^{2\pi} d\theta \int_{\frac{1}{2\cos \phi}}^{1} \rho^2 \, \sin \phi \, d\rho = \dfrac{4}{3}\pi \int_0^{\frac{\pi}{3}} \left(1-\dfrac{1}{8 \cos^3 \phi}\right) \, \sin \phi \; d\phi = \dfrac{4}{3}\pi \left(\dfrac{5}{16}\right) = \dfrac{5}{12}\pi.$

Si conclude che

$\boxcolorato{analisi}{\tau = \dfrac{5}{12}\pi. }$

Esercizio 5 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia

$\mathcal{D} = \left\{(x,y,z) \in \mathbb{R}^3 : \sqrt{x^2+y^2}\le \text{min}(z,4-3z) \right\}.$

Calcolare il volume.

Svolgimento.

Si osserva che $z \le 4-3z \iff z \le 1$ , quindi

$\mbox{min}(z,4-3z) = \begin{cases} z, \qquad &\mbox{per } z \le 1\\ 4-3z, \qquad &\mbox{per } z > 1.\\ \end{cases}$

Nelle figure 6 e 7 sono rappresentate due differenti visualizzazioni del dominio dato, rispettivamente per $z \in [0,1]$ e $z\in [1,3/4]$ .

$\quad$

Figura 6: dominio cilindrico definito da $\sqrt{x^2 + y^2} \leq z$ .

$\quad$

Figura 7: dominio cilindrico definito da $\sqrt{x^2 + y^2} \leq 4 - 3z$ .

$\quad$

Applicando le coordinate cilindriche, si ottiene

(9) $\begin{equation*} \begin{split} \tau & = \int_0^1 dz \int_0^{2\pi} d\theta \int_0^z \rho \,d\rho + \int_1^{\frac{4}{3}} dz \int_0^{2\pi} d\theta \int_0^{4-3z} \rho \,d\rho = \\ & = 2\pi \int_0^1 \dfrac{z^2}{2} \, dz + 2\pi \int_1^{\frac{4}{3}} \dfrac{(4-3z)^2}{2} \, dz=\\ & = \dfrac{4\pi}{9}. \end{split} \end{equation*}$

Si conclude che

$\boxcolorato{analisi}{\tau = \dfrac{4\pi}{9}. }$

Esercizio 6 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $\mathcal{D} = \{(x,y,z) \in \mathbb{R}^3 : (x-z)^2+y^2+z^2\le z-z^2\}$ . Calcolare il volume di $\mathcal{D}$ .

Svolgimento.

Effettuiamo una trasformazione di coordinate nel modo seguente:

$\begin{cases} x-z=x^\prime\\ y=y^\prime\\ z=z^\prime \end{cases} \quad \iff \quad \begin{cases} x=z+x^\prime\\ y=y^\prime\\ z=z^\prime, \end{cases}$

con $dx\,dy\,dz = \vert J \vert \, dx^\prime \, dy^\prime \, dz^\prime = dx^\prime \, dy^\prime \, dz^\prime$ in quanto

$\vert J \vert = \left\vert \text{det} \begin{pmatrix} \dfrac{\partial x}{\partial x^\prime} & \dfrac{\partial x}{\partial y^\prime} & \dfrac{\partial x}{\partial z^\prime}\\\\ \dfrac{\partial y}{\partial x^\prime} & \dfrac{\partial y}{\partial y^\prime} & \dfrac{\partial y}{\partial z^\prime}\\\\ \dfrac{\partial z}{\partial x^\prime} & \dfrac{\partial z}{\partial y^\prime} & \dfrac{\partial z}{\partial z^\prime} \end{pmatrix} \right\vert = \left\vert \text{det} \begin{pmatrix} 1&0&1\\0&1&0\\0&0&1 \end{pmatrix} \right\vert = 1.$

Abbiamo

(10) $\begin{equation*} \begin{split} \mathcal{D}^\prime & = \left\{ (x^\prime,y^\prime,z^\prime) \in \mathbb{R}^3 \vert \left({x^\prime}\right)^2+\left({y^\prime}\right)^2 +\left({z^\prime}\right)^2 \le z^\prime - \left({z^\prime}\right)^2 \right\} = \\ & = \left\{ (x^\prime,y^\prime,z^\prime) \in \mathbb{R}^3 \vert \left({x^\prime}\right)^2+\left({y^\prime}\right)^2 \le z^\prime - 2\left({z^\prime}\right)^2 \right\}, \end{split} \end{equation*}$

e poichè

$z^\prime - 2({z^\prime})^2 \geq 0 \quad \iff \quad z' \in \left[0, \dfrac{1}{2}\right],$

ne segue che

$\mathcal{D}^\prime = \left\{ (x^\prime,y^\prime,z^\prime) \in \mathbb{R}^3 \vert \left({x^\prime}\right)^2+\left({y^\prime}\right)^2 \le z^\prime - 2\left({z^\prime}\right)^2, z' \in \left[0, \dfrac{1}{2}\right] \right\} .$

Quindi

(11) $\begin{equation*} \begin{split} &\iiint_{\mathcal{D}^\prime} dx^\prime \, dy^\prime \, dz^\prime = \\ & =\int^{\frac{1}{2}}_{0} dz^\prime \iint_{\text{\tiny{$\left({x^\prime}\right)^2+\left({y^\prime}\right)^2 \le z^\prime - 2\left({z^\prime}\right)^2$}}} dx^\prime \, dy^\prime = \\ & = \int_0^{\frac{1}{2}} \pi \left(z^\prime -2 \left(z^\prime\right)^2 \right) \; dz^\prime = \\ & = \dfrac{\pi}{24}. \end{split} \end{equation*}$

Concludiamo che

$\boxcolorato{analisi}{\displaystyle \tau= \dfrac{\pi}{24}. }$

Esercizio 7 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $\mathcal{D} = \{(x,y,z) \in \mathbb{R}^3: (z-x)^2+(y-x)^2+2x^2\le x-x^2\}$ . Calcolare il volume di $\mathcal{D}$ .

Svolgimento.

Effettuiamo una trasformazione di coordinate nel modo seguente:

$\begin{cases} x=x^\prime\\ y-x=y^\prime\\ z-x=z^\prime \end{cases} \quad \iff \quad \begin{cases} x=x^\prime\\ y=y^\prime+x\\ z=z^\prime+x, \end{cases}$

con $dx\,dy\,dz = \vert J \vert \, dx^\prime \, dy^\prime \, dz^\prime = dx^\prime \, dy^\prime \, dz^\prime$ in quanto

Abbiamo

(12) $\begin{equation*} \begin{split} \mathcal{D}^\prime = \left\{ (x^\prime,y^\prime,z^\prime) \in \mathbb{R}^3 \vert \left({z^\prime}\right)^2+\left({y^\prime}\right)^2 \le x^\prime - 3\left({x^\prime}\right)^2 \right\}, \end{split} \end{equation*}$

e poichè

$x^\prime - 3\left({x^\prime}\right)^2 \geq 0 \quad \iff \quad x' \in \left[0, \dfrac{1}{3}\right],$

ne segue che

$\mathcal{D}^\prime = \left\{ (x^\prime,y^\prime,z^\prime) \in \mathbb{R}^3 \vert \left({z^\prime}\right)^2+\left({y^\prime}\right)^2 \le x^\prime - 3\left({x^\prime}\right)^2, \; x' \in \left[0, \dfrac{1}{3}\right] \right\} .$

Allora

(13) $\begin{equation*} \begin{split} &\iiint_{\mathcal{D}^\prime} dx^\prime \, dy^\prime \, dz^\prime = \\ & = \int_0^{\frac{1}{3}} dx^\prime \iint_{\text{\tiny{$\left({z^\prime}\right)^2+\left({y^\prime}\right)^2 \le x^\prime - 3\left({x^\prime}\right)^2$}}} dy^\prime \, dz^\prime = \\ & = \int_0^{\frac{1}{3}} \pi \left(x^\prime -3 \left(x^\prime\right)^2 \right) \; dz^\prime = \\ & = \dfrac{\pi}{54}. \end{split} \end{equation*}$

Concludiamo che

$\boxcolorato{analisi}{ \tau = \dfrac{\pi}{54}. }$

Esercizio 8 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_{\mathcal{D}} 1 \, dx \,dy \, dz,$

dove $\mathcal{D}$ è la regione limitata da $0 \leq z \leq 4-x^2-y^2$ ed il piano $xy$ .

$\quad$

Figura 8: rappresentazione grafica del dominio di $\mathcal{D}$ dell’esercizio 8.

$\quad$

Svolgimento.

Per prima cosa, osserviamo che il calcolo dell’integrale triplo della funzione integranda $1$ su $\mathcal{D}$ equivale a determinare il volume di $\mathcal{D}$ , indicato con $\tau$ .

Poichè $x^2+y^2=4-z \ge 0$ allora $z \le 4$ .

Integriamo per strati

(14) $\begin{equation*} \begin{split} &\int_{0}^{4}\iint_{x^2+y^2\le 4-z} dx \, dy \int_{0}^{4} \, dz =\\ & = \int_0^4 \pi(4-z)\, dz = \\ & = \pi \left(4z-\dfrac{z^2}{2}\right)\bigg\vert_0^4 = 8\pi. \end{split} \end{equation*}$

Allora concludiamo che

$\boxcolorato{analisi}{ \tau= 8\pi. }$

Esercizio 9 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_{\mathcal{D}} 1 \, dx \,dy \, dz,$

dove $\mathcal{D}=\left\{ (x,y,z) \in \mathbb{R}^3 : x^2+y^2 \le z \le 2x \right\}$ .

$\quad$

Figura 9: rappresentazione grafica del dominio di $\mathcal{D}$ dell’esercizio 9.

$\quad$

Svolgimento.

Osserviamo che il calcolo dell’integrale triplo della funzione integranda $1$ su $\mathcal{D}$ equivale a determinare il volume di $\mathcal{D}$ , indicato con $\tau$ .

Integriamo per fili

$\iint_{x^2+y^2\le 2x} dx \, dy \int_{x^2+y^2}^{2x} \, dz = - \iint_{x^2+y^2 - 2x \le 0} (x^2+y^2-2x) \, dx \, dy.$

Parametrizziamo il precedente integrale applicando le coordinate polari, cioè

$\begin{cases} x = \rho \cos \theta + 1, \\ y = \rho \sin \theta, \end{cases}$

dove

$0 \le \rho \le 1, \quad \theta \in [0,2\pi].$

L’integrale così diventa

(15) $\begin{equation*} \begin{split} & - \iint_{x^2+y^2 - 2x \le 0} (x^2+y^2-2x) \, dx \, dy= \\ & \overset{(*)}{=} - \int_0^1 \rho \; d\rho \int_0^{2\pi} ((\rho \, \cos \theta + 1)^2 + \rho^2 \, \sin^2 \theta - 2 (\rho \cos \theta + 1)) \, d\theta = \\ & = - \int_0^1 \rho \; d\rho \int_0^{2\pi} (\rho^2 \, \cos^2 \theta + 1 + 2 \rho \cos \theta + \rho^2 \, \sin^2 \theta - 2 \rho \cos \theta -2) \, d\theta = \\ & = - 2 \pi \int_0^1 \rho(\rho^2-1) \, d\rho = \\ & = -2\pi \left( \dfrac{\rho^4}{4}-\dfrac{\rho^2}{2}\right) \bigg\vert_0^1 =\\ &= -2\pi \left(\dfrac{1}{4}-\dfrac{1}{2}\right) =\\ &= \dfrac{\pi}{2}, \end{split} \end{equation*}$

dove in $(*)$ abbiamo applicato le coordinate polari.

Si conclude che

$\boxcolorato{analisi}{ \tau=\dfrac{\pi}{2}. }$

Esercizio 10 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare l’integrale triplo

$\iiint_\mathcal{D} x\,\, dx \, dy \, dz,$

dove $\mathcal{D}=\left\{(x,y,z)\in \mathbb{R}^3:x\geq0,\,0\leq y\leq z+1,x^2+y^2+z^2 \leq 1\right\}$

Svolgimento.

Rappresentiamo l’insieme $\mathcal{D}$ in figura 10:

$\quad$

Figura 10: Sezione di un dominio sferico con vincoli $x \geq 0$ , $0 \leq y \leq z + 1$ , $x^2 + y^2 + z^2 \leq 1$ .

$\quad$

Riscriviamo l’integrale come segue

$\iiint_\mathcal{D} x\,dx\,dy\,dz=\iiint_A x\,dx\,dy\,dz+\iiint_B x\,dx\,dy\,dz,$

dove

(16) $\begin{equation*} \begin{split} &A=\left\{(x,y,z)\in \mathbb{R}^3:x\geq0,\,z\geq0,\,x^2+z^2\leq1,\,0\leq y\leq\sqrt{1-x^2-z^2}\right\}\\ &B=\left\{(x,y,z)\in \mathbb{R}^3:0\leq x \leq \sqrt{1-y^2-z^2},\ -1\leq z \leq 0 ,\,0 \leq y \leq z+1\right\}. \end{split} \end{equation*}$

L’insieme $A$ è rappresentato in figura 11.

$\quad$

Figura 11: vista del dominio tridimensionale con limite cilindrico.

$\quad$

Integrando per fili l’integrale diventa

(17) $\begin{equation*} \begin{split} \iiint_{{D}} x\,dx\,dy\,dz & =\iint_C \,dx\,dz\int_{0}^{\sqrt{1-x^2-z^2}}x\,dy+\iint_{{D}}dy\,dz \int_{0}^{\sqrt{1-y^2-z^2}}x\,dx=\\ &=\iint_C x\sqrt{1-x^2-z^2}\,dx\,dz+\iint_{{D}}\dfrac{1}{2}\left(1-y^2-z^2\right)dy\,dz, \end{split} \end{equation*}$

dove

(18) $\begin{equation*} \begin{split} &C=\left\{(x,z)\in \mathbb{R}^2:x\geq0,\,z\geq0,\,x^2+z^2\leq1\right\}\\ &D=\left\{\{(y,z)\in \mathbb{R}^2:,\ -1\leq z \leq 0 ,\,0 \leq y \leq z+1\right\}. \end{split} \end{equation*}$

Etichettiamo

(19) $\begin{equation*} \begin{split} \iint_C x\sqrt{1-x^2-z^2}\,dx\,dz\\ \label{10.2}\iint_{{D}}\dfrac{1}{2}\left(1-y^2-z^2\right)dy\,dz, \end{split} \end{equation*}$

e parametrizziamo $C$ applicando le coordinate polari

$\begin{cases} x=\rho \cos \theta\\ z=\rho \sin \theta, \end{cases}$

con

$\rho \in [0,1],\,\theta \in \left[0,\dfrac{\pi}{2}\right].$

L’integrale (19) diventa

$\iint_C x\sqrt{1-x^2-z^2}\,\,dx\,dz=\int_{0}^{\frac{\pi}{2}}d\theta\int_{0}^{1}\rho^2 \,\cos \theta \,\sqrt{1-\rho ^2} \,d\rho.$

Applicando il teorema di Fubini, si ottiene

$\int_{0}^{\frac{\pi}{2}}d\theta\int_{0}^{1}\rho^2 \,\cos \theta \,\sqrt{1-\rho ^2}\,d\rho= \int_{0}^{\frac{\pi}{2}}\cos \theta\, d\theta\int_{0}^{1}\rho^2 \,\sqrt{1-\rho ^2}\,d\rho=1\cdot\int_{0}^{1}\rho^2 \,\sqrt{1-\rho ^2}\,d\rho.$

Operando la sostituzione $\rho=\cos t$ , si trova

$\int_{0}^{\frac{\pi}{2}}(\cos t)^2\sqrt{1-(\cos t)^2}\sin t\,dt=\int_{0}^{\frac{\pi}{2}}(\cos t)^2\left \vert \sin t \right \vert \sin t\,dt.$

Si osserva che

$\left \vert \sin t \right \vert=\sin t \quad \text{per}\,\,t\in \left[0,\dfrac{\pi}{2}\right],$

da cui

$\int_{0}^{\frac{\pi}{2}}(\cos t)^2(\sin t)^2dt=\dfrac{1}{4}\int_{0}^{\frac{\pi}{2}}\left(\sin (2t)\right)^2dt,$

e ricordando che

$\sin^2 (2t) =\dfrac{1-\cos (4t)}{2}=\dfrac{1}{2}-\dfrac{\cos (4t)}{2}, \quad \forall \,t \in \mathbb{R},$

abbiamo

(20) $\begin{equation*} \begin{split} &\int_{0}^{\frac{\pi}{2}}(\cos t)^2(\sin t)^2dt =\\ & =\dfrac{1}{4}\int_{0}^{\frac{\pi}{2}}\left(\sin (2t)\right)^2dt=\\ & = \dfrac{1}{4}\int_{0}^{\frac{\pi}{2}}\dfrac{1}{2}\,dt-\dfrac{1}{4}\int_{0}^{\frac{\pi}{2}}\dfrac{\cos 4t}{2}\,dt=\\ & = \dfrac{\pi}{16}-\dfrac{1}{4}\int_{0}^{\frac{\pi}{2}}\dfrac{\cos 4t}{2}\,dt. \end{split} \end{equation*}$

Si osserva che la funzione $f(t)=\cos (4t)$ ha un periodo $T=\frac{\pi}{2}$ , quindi

$\int_{0}^{\frac{\pi}{2}}\cos (4t) \,dt=0.$

Tornando all’integrale (19), concludiamo che

$\iint_C x\sqrt{1-x^2-z^2}\,dx\,dz=\dfrac{\pi}{16}.$

Alternativamente per risolvere $\iiint_A x\,dx\,dy\,dz$ si poteva procedere applicando le coordinate sferiche

$\begin{cases} x = \rho \sin \theta \cos \phi\\ y = \rho \sin \theta \sin \phi, \\ z = \rho \cos \theta, \end{cases}$

dove

$\rho \in [0,1], \theta \in \left[0,\dfrac{\pi}{2}\right], \phi \in \left[0,\dfrac{\pi}{2}\right].$

Abbiamo dunque

(21) $\begin{equation*} \begin{split} \iiint_{A} x \, dx \, dy \, dz &= \int_{0}^{\frac{\pi}{2}} d\phi \int_{0}^{\frac{\pi}{2}} d\theta \int_0^1 (\rho \sin \theta \cos \phi) \rho^2\sin \theta \, d\rho =\\ & = \int_{0}^{\frac{\pi}{2}} \cos \phi \, d\phi \int_{0}^{\frac{\pi}{2}} \sin^2\theta \, d\theta \int_0^1 \rho^3 \, d\rho =\\ & = \bigg[ \sin \phi \bigg]_0^{\frac{\pi}{2}} \cdot \dfrac{\pi}{4} \cdot \left[ \dfrac{\rho^4}{4}\right]_0^1 =\\ & = \dfrac{\pi}{4} \cdot \dfrac{1}{4} =\\ &= \dfrac{\pi}{16}. \end{split} \end{equation*}$

Consideriamo l’integrale (??) e svolgiamo i calcoli

(22) $\begin{equation*} \begin{split} &\iint_{D}\dfrac{1}{2}\left(1-y^2-z^2\right)dy\,dz=\\ & = \dfrac{1}{2}\int_{-1}^{0}dz\int_{0}^{z+1}\left(1-y^2-z^2\right)=\\ &=\dfrac{1}{2}\int_{-1}^{0}\left(z+1-\dfrac{(z+1)^3}{3}-z^2(z+1) \right)\,dz=\\ &=\dfrac{1}{2}\cdot \dfrac{1}{3}=\\ &=\dfrac{1}{6}. \end{split} \end{equation*}$

concludiamo che

$\boxcolorato{analisi}{\iiint_{\mathcal{D}}x\, dx\,dy\,dz=\dfrac{\pi}{16}+\dfrac{1}{6}. }$

Esercizio 11 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare l’integrale triplo

$\iiint_{\mathcal{D}} \sqrt{x^2+y^2} \, dx \, dy \, dz,$

dove $\mathcal{D}=\left\{ (x,y,z) \in \mathbb{R}^3 : (2-\sqrt{x^2+y^2})^2+z^2\le1 \right\}$ .

Svolgimento.

Per parametrizzare $\mathcal{D}$ usiamo le coordiante cilindriche

$\begin{cases} x = \rho \cos \theta\\ y = \rho \sin \theta, \\ z = t, \end{cases}$

da cui

$(2-\rho)^2 + t^2 \leq 1 \quad \iff \quad (\rho-2)^2 + t^2 \leq 1.$

Rappresentiamo in figura 12 il dominio dato.

$\quad$

Figura 12: rappresentazione del solido con vincoli cilindrici descritti da $(2 - \rho)^2 + t^2 \leq 1$ .

$\quad$

Con il cambio di variabili otteniamo

$\mathcal{S} = \left\{ (t,\rho, \theta) \in \mathbb{R}^3 \; \vert \; (\rho-2)^2 + t^2 \leq 1, 0 \le \theta \le 2\pi\right\}.$

Integrando per strati si ha

$\begin{aligned} \iiint_\mathcal{D} \sqrt{x^2+y^2} \, dx \, dy \, dz & = \iiint_{\mathcal{S}} \rho^2 \, dt \, d\rho \, d\theta = \\ & = \int_0^{2\pi} d\theta \iint_{(\rho-2)^2 + t^2 \leq 1} \rho^2 d\rho \, dt. \end{aligned}$

Applichiamo le coordiante polari

$\begin{cases} \rho = \rho^\prime \cos \theta^\prime + 2, \\ t = \rho^\prime \sin \theta^\prime, \end{cases}$

dove

$\rho^\prime \in [0,1], \quad \theta^\prime \in [0,2\pi].$

Abbiamo dunque

$\begin{aligned} &\int_0^{2\pi} d\theta \iint_{(\rho-2)^2 + t^2 \leq 1} \rho^2 d\rho \, dt =\\ &=\int_0^{2\pi} d\theta \int_0^{2\pi} d\theta^\prime \int_0^1 (\rho^\prime \cos \theta^\prime + 2)^2 \, \rho^\prime \, d\rho^\prime = \\ & = 2\pi \int_0^{2\pi} d\theta \int_0^1 \left(\left(\rho^\prime\right)^3 \, \cos^2 \theta^\prime + 4 \rho^\prime + 2 \left(\rho^\prime\right)^2 \, \cos \theta^\prime \right)\, d\rho^\prime =\\ & = 2\pi \int_0^{2\pi} \left(\dfrac{1}{4} \cos^2 \theta^\prime + 2 + \dfrac{4}{3} \cos \theta^\prime \right) d\theta =\\ & = 2\pi \left(\dfrac{1}{4}\cdot \dfrac{1}{2} \cdot 2\pi + 2 \cdot 2\pi \right) = \\ &=\dfrac{17}{2}\pi^2. \end{aligned}$

Concludiamo che

$\boxcolorato{analisi}{\displaystyle\iiint_{\mathcal{D}} \sqrt{x^2 + y^2} \, dx \, dy \, dz = \dfrac{17}{2}\pi^2. }$

Esercizio 12 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare il volume del solido dato dall’intersezione del cono ottenuto ruotando il triangolo di vertici $(0,0,0)$ , $(2,0,0)$ e $(0,0,2)$ attorno all’asse $z$ , e del cilindro di asse $\{(1,0,t) \, \vert \, t \in \mathbb{R}\}$ e di raggio 1.

Svolgimento.

Rappresentiamo il solito in figura 13.

$\quad$

Figura 13: intersezione tra cono e cilindro in rotazione attorno all’asse $z$ .

$\quad$

Consideriamo il triangolo in figura mentre ruota di $360^\circ$ in figura 14.

$\quad$

Figura 14: rappresentazione della rotazione del cono attorno all’asse $z$ .

$\quad$

Osserviamo che $\tan \theta = 1$ , quindi ponendo $z^\prime = 2-z$ , abbiamo

$\tan \theta = 1 = \dfrac{z^\prime}{\rho} = \dfrac{2-z}{\rho}.$

Da cui

$\rho=2-z.$

Quindi possiamo scrivere l’equazione che descrive il sostegno della rotazione del triangolo attorno all’asse $z$

$x^2+y^2=(2-z)^2.$

Calcoliamo il volume richiesto integrando per fili

$\iint_{(x-1)^2+y^2 \le 1} dx \, dy \int_0^{2-\sqrt{x^2+y^2}} dz= \iint_{(x-1)^2+y^2\le 1}\left(2-\sqrt{x^2+y^2} \right) dx \, dy.$

Applichiamo le coordinate polari

$\begin{cases} x = \rho \, \cos \theta\\ \hspace{3cm} \rho \in [0,2 \cos \theta], \theta \in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]\\ y = \rho \, \sin \theta. \end{cases}$

L’integrale cosi diventa

$\begin{aligned} & \iint_{(x-1)^2+y^2 \le 1} \left(2-\sqrt{x^2+y^2} \right) \, dx \, dy =\\ & = -\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} d\theta \int_0^{2 \cos \theta} \left(\rho^2-2\rho\right) \, d\rho =\\ & = -\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(\dfrac{8}{3} \cos^3 \theta - 4 \cos^2 \theta \right) \, d\theta = \\ & =- \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(\dfrac{8}{3} \left(\cos \theta-\cos \theta \left(\sin \theta \right)^2 \right) - 4 \left(\dfrac{1+\cos \left(2\theta\right)}{2} \right) \right) \, d\theta = \\ & = -\left(-2\pi + \dfrac{32}{9}\right)=2\pi-\dfrac{32}{9}. \end{aligned}$

Quindi concludiamo che

$\boxcolorato{analisi}{\iint_{(x-1)^2+y^2\le 1}\left(2-\sqrt{x^2+y^2} \right) dx \, dy=2\pi-\dfrac{32}{9}. }$

Esercizio 13 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare il seguente integrale triplo:

$\iiint_{\mathcal{D}} (3x+4y+5z^2)\,dx\,dy\,dz,$

dove $\mathcal{D}$ è tronco di cono ottenuto ruotando intorno all’asse $z$ il trapezio di vertici $(0,0,0)$ , $(2,0,0)$ , $(1,0,2)$ e $(0,0,2)$ .

Svolgimento.

Rappresentiamo il solido dato in figura 15.

$\quad$

Figura 15: tronco di cono generato dalla rotazione del trapezio con vertici definiti.

$\quad$

Posto $f(x,y)=3x+4y$ si osserva che $f$ è dispari rispetto ad $x\,\, \text{e}\,\, y$ e il dominio $\mathcal{D}$ è simmetrico rispetto al piano $yz\,\, \text{e}\,\,xz$ , quindi

$\iiint_{\mathcal{D}} (3x+4y) \, dx \, dy \, dz = 0.$

Non ci resta che calcolare

(23) $\begin{equation*} \iiint_{\mathcal{D}}5z^2\,dx\,dy\,dz. \end{equation*}$

Consideriamo la sezione trapezioidale in figura 16.

$\quad$

Figura 16: sezione del tronco di cono con variazione del raggio in funzione dell’altezza.

$\quad$

Dalla geometria della figura 16, si osserva che

$\tan \theta = 2 = \dfrac{2-z}{\rho(z)}\iff \rho(z) = \dfrac{1}{2}\left(2-z\right).$

Definiamo

$\tilde{\rho}(z) = 1 + \rho(z) = 1 + 1 - \dfrac{z}{2} = 2 - \dfrac{z}{2}, \qquad \mbox{ con } z \in [0,2].$

Calcoliamo (23) integrando per strati

$\int_0^2 dz \iint_{\tiny{x^2+y^2\le \tilde{\rho}(z)}} 5z^2 \, dx \, dy = \int_0^2 5z^2 \pi \left(2-\dfrac{z}{2}\right)^2 \, dz = \dfrac{64}{3}\pi.$

Si conclude che

$\iiint_{\mathcal{D}} (3x+4y+5z^2)\,dx\,dy\,dz = \dfrac{64}{3}\pi.$

In alternativa, qualora la simmetria inizialmente evidenziata non risultasse immediatamente intuitiva, si potrebbe procedere parametrizzando $\mathcal{D}$ utilizzando le coordinate cilindriche, cioè

$\begin{cases} x = \rho \, \cos \theta\\ y = \rho \, \sin \theta\\ z = t, \end{cases}$

il dominio di integrazione diventa

$\mathcal{D} = \left[0,\dfrac{4-t}{2}\right] \times [0,2\pi] \times [0,2],$

inoltre

$\left \vert J\right \vert = \rho.$

L’integrale così diventa

$\begin{aligned} \iiint_{\mathcal{D}} (3x+4y+5z^2) \, dx \, dy \, dz & = \int_0^2 dt \, \int_0^{\frac{4-t}{2}} \rho\, d\rho \int_0^{2\pi} (3 \rho \, \cos \theta + 4 \rho \sin \theta + 5t^2) \, d\theta=\\ & = 2\pi \int_0^2 dt \int_0^{\frac{4-t}{2}} 5t^2 \, \rho \, d\rho =\\ & = \dfrac{\pi}{4} \int_0^2 5t^2 (4-t)^2 \, dt = \\ &=\dfrac{64}{3}\pi. \end{aligned}$

Nel primo passaggio, dopo il cambio di variabile, si è integrato in $d\theta$ sfruttando il fatto che l’integrale della funzione seno o coseno sull’intervallo $[0, 2\pi]$ è nullo.

Si conclude che

$\boxcolorato{analisi}{\iiint_{\mathcal{D}} (3x+4y+5z^2) \, dx \, dy \, dz =\dfrac{64}{3}\pi. }$

Esercizio 14 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare il volume del solido

$\mathcal{D} = \left\{ (x,y,z) \in \mathbb{R}^3 : (x-z)^2+4y^2 \le (1-z)^2, 0 \le z \le 1 \right\}.$

Svolgimento.

Operiamo il seguente cambio di coordinate

$\begin{cases} x^\prime=x-z\\y^\prime = 2y\\ z^\prime=z \end{cases} \iff\quad \begin{cases} x=x^\prime+z^\prime\\y=\frac{y^\prime}{2}\\z=z^\prime, \end{cases}$

per cui

$\mathcal{D}^\prime = \left\{ (x^\prime,y^\prime,z^\prime)\in \mathbb{R}^3 : \left(x^\prime\right)^2 + \left(y^\prime\right)^2 \leq (1-z^\prime)^2,\,0\leq z^\prime \leq 1\right\}.$

Calcoliamo lo jacobiano della trasformazione

$\vert J \vert = \begin{vmatrix} 1&0&1\\0&\frac{1}{2}&0\\0&0&1 \end{vmatrix} = \dfrac{1}{2} .$

Il volume cercato diventa

$\begin{aligned} \iiint_{\mathcal{D}} dx \, dy \, dz & = \iiint_{\mathcal{D}^\prime} \dfrac{1}{2} \, dx^\prime \; dy^\prime \; dz^\prime =\\ & = \int_0^1 dz^\prime \iint_{\tiny{\left(x^\prime\right)^2 + \left(y^\prime\right)^2 \leq (1-z^\prime)^2}} dx^\prime \; dy^\prime = \\ & = \dfrac{1}{2} \pi \int_0^1 (1-2z^\prime+(z^\prime)^2) \; dz^\prime = \\ & = \dfrac{\pi}{2} \left(z^\prime-(z^\prime)^2+\dfrac{(z^\prime)^3}{3}\right) \bigg\vert_0^1 = \\ & = \dfrac{\pi}{6}. \end{aligned}$

Quindi

$\boxcolorato{analisi}{\iiint_{\mathcal{D}} dx \, dy \, dz = \dfrac{\pi}{6}. }$

Esercizio 15 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare il volume del solido ottenuto dalla rotazione di un angolo $\pi$ attorno all’asse $x$ dell’insieme $1\le (x-2)^2+4y^2\le 4, y \ge 0$ .

Richiami teorici.

Il teorema di Pappo-Guldino afferma che il volume di un solido $\mathcal{D}$ , generato dalla rotazione completa di una lamina piana omogenea $E$ (dominio misurabile) attorno a un asse coordinato (ad esempio l’asse $z$ ), è pari al prodotto della lunghezza della circonferenza descritta dal baricentro della lamina $E$ per l’area di $E$ . Più precisamente:

$\text{mis}(\mathcal{D}) = \text{volume}(\mathcal{D}) = 2\pi G_x \iint_E dx \, dy,$

dove $G_x$ rappresenta la prima componente del baricentro della lamina $E$ .

Il baricentro $G_x$ è calcolato come:

$G_x = \dfrac{\iint_E x \, dx \, dy}{\iint_E dx \, dy}.$

Pertanto, il volume del solido può essere espresso come:

$\text{mis}(\mathcal{D}) = \text{volume}(\mathcal{D}) = 2\pi \iint_E x\, dx \, dy.$

Nel caso in cui la lamina $E$ giaccia nel piano $yz$ (con $y \geq 0$ ), si utilizza invece la seconda componente del baricentro, definita come:

$G_y = \dfrac{\iint_E y \, dx \, dy}{\iint_E dx \, dy}.$

Di conseguenza, il volume del solido diventa:

$\text{mis}(\mathcal{D}) = \text{volume}(\mathcal{D}) = 2\pi \iint_E y \, dx \, dy.$

Svolgimento.

Rappresentiamo il solido in figura 17.

$\quad$

Figura 17: sezione di piano che genera il solido descritto.

$\quad$

Parametrizziamo il dominio in verde nel grafico, ovvero il dominio compreso tra le due ellissi per $y\geq0$

$\begin{cases} x=2\rho \cos \theta + 2\\ y= \rho \sin \theta, \qquad \qquad \rho \in \left(\dfrac{1}{2},1\right), \theta \in (0,\pi) \end{cases}$

e quindi applichiamo il teorema di Pappo-Guldino

$\begin{aligned} \tau & = \pi \int_0^\pi d\theta \int_{\frac{1}{2}}^1 \rho \, \sin \theta \; (2\rho) \; d\rho =\\ & = 2\pi (-\cos \theta)\bigg\vert_0^\pi \; \left( \dfrac{1}{3} \rho^3 \right)\bigg\vert_{\frac{1}{2}}^1 = \\ & = \dfrac{2}{3}\pi \; 2 \; \left(1-\dfrac{1}{8}\right) =\\ & = \dfrac{7}{6}\pi. \end{aligned}$

In conclusione

$\boxcolorato{analisi}{\tau = \dfrac{7}{6}\pi. }$

Esercizio 16 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_\mathcal{D} dx \, dy \, dz,$

dove $\mathcal{D} = \left\{ (x,y,z) \in \mathbb{R}^3 : \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}\le 1 \right\}$ .

Svolgimento.

Graficamente disegniamo l’elissoide in figura 18.

$\quad$

Figura 18: elissoide rappresentato nel piano tridimensionale.

$\quad$

Possiamo riscrivere

$\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} \leq 1,$

come

$\dfrac{x^2}{a^2\left(1-\dfrac{z^2}{c^2}\right)} + \dfrac{y^2}{b^2\left(1-\dfrac{z^2}{c^2}\right)} = 1.$

scriviamo una possibile parametrizzazione di $\mathcal{D}$ :

$\begin{cases} x = a \sqrt{1 - \dfrac{z^2}{c^2}} \rho \cos \theta, \\[10pt] y = b \sqrt{1 - \dfrac{z^2}{c^2}} \rho \sin \theta, \\[10pt] z = t, \end{cases}$

dove

$\rho \in [0,1], \quad \theta \in [0,2\pi], \quad t \in [-c,c]$

in particolare

$dx\,dy\,dz= ab \left(1-\frac{z^2}{c^2}\right)\rho \;d\rho\, d\theta\, dt.$

L’integrale così diventa

$\begin{aligned} \int_{-c}^c dt \int_0^{2\pi} d\theta \int_0^1 ab \left(1-\frac{z^2}{c^2}\right) \; \rho \; d\rho & = ab \, \dfrac{2\pi}{2} \int_{-c}^c \left(1-\dfrac{z^2}{c^2}\right) \, dt =\\ & = \pi a b \left(1- \dfrac{z^3}{3c^2}\right) \bigg\vert_{-c}^c = \\ & = \pi a b \left(2c - \dfrac{2}{3}c\right) = \\ & = \dfrac{4}{3} \pi a b c. \end{aligned}$

Alternativamente si poteva procedere come segue.

Parametrizziamo $\mathcal{D}$ applicando le coordinate cilindriche

$\begin{cases} x = \rho\, a \, \cos \theta\\ y = \rho\, b \, \sin \theta,\\ z = t, \end{cases}$

dove

$\rho \in [0,1], \theta \in [0,2\pi), t \in \left[0, c \sqrt{1-\rho^2}\right],$

in particolare

$dx\,dy\,dz= ab \rho \;d\rho \,d\theta \,dt.$

L’integrale così diventa

$\begin{aligned} \tau & = 2 \int_0^{2\pi} d\theta \int_0^1 d\rho \int_0^{c\sqrt{1-\rho^2}} \rho \, a \, b \, dt =\\ & = 2 \cdot 2\pi \int_0^1 abc \rho \sqrt{1-\rho^2} \, d\rho =\\ & = 4\pi a b c \left(-\dfrac{1}{2}\right) \dfrac{(1-\rho^2)^{\frac{3}{2}}}{\frac{3}{2}} \bigg\vert_0^1 =\\ & = 4\pi a b c \left(-\dfrac{1}{2}\right) \left(\dfrac{2}{3}\right) (-1) = \\ & = \dfrac{4}{3} \pi a b c. \end{aligned}$

Nel secondo passaggio, abbiamo moltiplicato l’integrale triplo per due poiché il dominio è simmetrico rispetto al piano $xy$ . Inoltre, la funzione integranda, essendo costante e pari rispetto a qualsiasi asse, permette questa semplificazione.

In conclusione

$\boxcolorato{analisi}{\tau = \dfrac{4}{3} \pi a b c. }$

Esercizio 17 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare l’integrale triplo

(24) $\begin{equation*} \iiint_\mathcal{D} (2z-x-y^3) \, dx \, dy \, dz, \end{equation*}$

dove $\mathcal{D} = \left\{ (x,y,z) \in \mathbb{R}^3 : 0 \le z \le 2 + x, 6x-8 \le x^2+y^2 \le 4x \right\}$ .

Svolgimento.

Riscriviamo

$\iiint_\mathcal{D} (2z - x - y^3) \, dx \, dy \, dz,$

come segue:

$\underbrace{\iiint_\mathcal{D} (2z - x ) \, dx \, dy \, dz}_{I_1} + \underbrace{\iiint_\mathcal{D} (- y^3) \, dx \, dy \, dz}_{I_2}.$

Riconosciamo che

$x^2 + y^2 - 6x + 8 = 0$

è l’equazione cartesiana di un cilindro a base circolare con asse di simmetria perpendicolare al piano $xy$ e passante per il punto $(3,0,0)$ . In particolare, la circonferenza che giace sul piano $xy$ è centrata in $(3,0,0)$ e ha raggio $1$ .

L’equazione

$x^2 + y^2 - 4x = 0$

è anch’essa l’equazione cartesiana di un cilindro a base circolare con asse di simmetria perpendicolare al piano $xy$ e passante per il punto $(2,0,0)$ . In particolare, la circonferenza che giace sul piano $xy$ è centrata in $(2,0,0)$ e ha raggio $2$ .

Inoltre,

$z = 2 + x$

è l’equazione di un piano, come rappresentato in figura 19.

$\quad$

Figura 19: cilindro a base circolare con intersezione di un piano.

$\quad$

Posto $f(x,y,z)=-y^3$ si osserva che $f$ è dispari rispetto alla variabile $y$ e il dominio $\mathcal{D}$ è simmetrico rispetto al piano $xz$ , questo ci fa concludere che

$I_2= 0.$

Per calcolare $I_1$ integriamo procedendo per fili

$\begin{aligned} \iiint_\mathcal{D}\left(2z-x\right) \, dx \, dy \, dz & = \iint_{\tiny{6x-8 \le x^2+y^2 \le 4x}} dx \, dy \int_0^{2+x} (2z-x) \, dz = \\ & = \iint_{\tiny{6x-8 \le x^2+y^2 \le 4x}} \left((x+2)^2-x(x+2)\right)\, dx \, dy =\\ & = \iint_{\tiny{6x-8 \le x^2+y^2 \le 4x}} (4+2x) \, dx \, dy. \end{aligned}$

Utilizziamo le coordinate polari per la circonferenza con base centrata in $(2,0,0)$ e raggio $2$ :

$\begin{cases} x = 2 + \rho \, \cos \theta, \\ y = \rho \, \sin \theta, \end{cases}$

dove

$\rho \in [0,2], \quad \theta \in [0,2\pi].$

Per la circonferenza con base centrata in $(3,0,0)$ e raggio $1$ , procediamo in modo analogo, parametrizzandola utilizzando le coordinate polari:

$\begin{cases} x = 3 + \rho \, \cos \theta, \\ y = \rho \, \sin \theta, \end{cases}$

dove

$\rho \in [0,1], \quad \theta \in [0,2\pi].$

Inoltre, ricordando che

$dx \, dy = \rho \, d\rho \, d\theta,$

e utilizzando quanto detto, si ha

$\begin{aligned} \iint_{\tiny{6x-8 \le x^2+y^2 \le 4x}} (4+2x) \, dx \, dy & = \int_0^2 \rho \, d\rho \int_0^{2\pi}\left(4+2(2+2\rho \cos \theta)\right) d\theta - \int_0^1 \rho \, d\rho \int_0^{2\pi} (4+2(3+\rho \cos\theta)) \, d\theta = \\ & = \int_0^2 16\pi \rho \, d\rho - \int_0^1 20\pi \rho \, d\rho =\\ & = 16\pi \dfrac{\rho^2}{2} \bigg\vert_0^2 - 20\pi \dfrac{\rho^2}{2} \bigg\vert_0^1 =\\ & = 32\pi - 10\pi = \\ &=22\pi. \end{aligned}$

In conclusione

$\boxcolorato{analisi}{\iiint_{\mathcal{D}} (2z - x - y^3) \, dx \, dy \, dz= 22\pi. }$

Esercizio 18 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Calcolare l’integrale triplo

$\iiint_\mathcal{D} e^z \, dx \, dy \, dz,$

dove $\mathcal{D}$ è la piramide di vertici $(0,0,0), (0,2,0), (2,0,0), (2,2,0)$ e $(1,1,2)$ .

Svolgimento.

Graficamente rappresentiamo il solido $D$ ovvero una piramide a base quadrata rappresentato in figura 20:

$\quad$

Figura 20: piramide a base quadrata con vertici specifici per il calcolo dell’integrale triplo.

$\quad$

Applichiamo il seguente cambio di coordinate

$\begin{cases} u=x-1\\ v=y-1\\ w=z, \end{cases}$

ottenendo così $D^\prime$ ovvero una piramide di base quadrata centrata nell’origine come in figura 21.

$\quad$

Figura 21: trasformazione della piramide centrata sull’origine.

$\quad$

Consideriamo una sezione orizzontale della piramide e un punto $(0,0,\omega)$ , con $\omega \geq 0$ .

Dal punto di vista geometrico, una sezione orizzontale della piramide è rappresentata da un quadrato di lato $\ell(\omega)$ , avente semidiagonale $\rho(\omega)$ . In particolare, la base quadrata della piramide, giacente sul piano $uv$ , è caratterizzata da una semidiagonale di lunghezza $\rho(0) = \sqrt{2}$ e un lato $\ell(0) = 2$ .

Introduciamo quindi l’angolo $\theta$ , definito come l’angolo formato tra il segmento di lunghezza $\rho(0)$ e il segmento che collega i punti $(1,1,0)$ e $(0,0,2)$ , come illustrato in figura 22.

$\quad$

Figura 22: sezione orizzontale della piramide con calcolo dell’angolo.

$\quad$

Dalla geometria del problema abbiamo che

$\tan \theta = \dfrac{2}{\sqrt{2}} =\dfrac{2-w}{\rho(w)},$

da cui

$\rho(w) = \dfrac{\sqrt{2}(2-w)}{2},\qquad \mbox{con } w \in [0,2].$

Essendo $\rho(w)$ la semidiagonale della base quadrata, allora il lato del quadrato è

$\ell(\omega ) = \dfrac{2}{\sqrt{2}} \rho(w) = 2-w.$

Dunque è possibile parametrizzare $D^\prime$ come segue

$D^\prime =\left\{ \left( u,v,\omega \right) \in \mathbb{R}^3 \, : \, -\dfrac{\ell(\omega)}{2} \leq u \leq \dfrac{\ell(\omega)}{2}, \, -\dfrac{\ell(\omega)}{2} \leq v \leq \dfrac{\ell(\omega)}{2} , \, 0 \leq \omega \leq 2\right\},$

ed inoltre

$dx\,dy\,dz=du\,dv\,d\omega,$

cioè $\left\vert J \right\vert = 1$ .\newline Tornando all’integrale abbiamo

$\iiint_{\mathcal{D}} e^z \, dx \, dy \, dz = \iiint_{D^\prime} e^w \, du \, dv \, dw.$

Integrando per strati si ha che

$\begin{aligned} \iiint_{D'} e^w \, du \, dv \, dw & = \int_0^2 e^w \left(\iint_{\Omega(w)} du \, dv \right) \, dw =\\ & = \int_0^2 (2-w)^2 \, e^w \; dw = \\ & \overset{*}{=} e^w (2-w)^2\bigg\vert_0^2 + 2 \int_0^2 (2-w) \, e^w \, dw = \\ & \overset{*}{=} e^w \left((2-w)^2+2(2-w)+2\right)\bigg\vert_0^2 = \\ & = 2(e^2-5), \end{aligned}$

dove nei passaggi segnati con $*$ abbiamo utilizzato l’integrazione per parti. Ricordiamo che il solido $D$ è una piramide a base quadrata come rappresentata nella seguente figura 23.

$\quad$

Figura 23: rappresentazione piaramide a base quadrata.

$\quad$

Consideriamo il triangolo rettangolo (evidenziato in rosso nella figura 24), il cui cateto verticale coincide con l’altezza della piramide, pari a $2$ , e il cateto orizzontale misura $1$ .

Si osservi che il cateto orizzontale rappresenta il raggio della circonferenza inscritta nella base quadrata della piramide.

$\quad$

Figura 24: Sezione orizzontale della piramide con base quadrata, mostrata in corrispondenza di una quota $z$ , che evidenzia il lato della sezione e le relative proporzioni.

$\quad$

Consideriamo una sezione orizzontale della piramide a una quota $z$ e analizziamo il triangolo la cui altezza è pari a $2-z$ e il cui lato, indicato con $l(z)$ , rappresenta il raggio della circonferenza inscritta nella base quadrata della piramide a tale quota. Tale triangolo ha altezza $2-z$ e lato $l(z)$ , come illustrato nella figura 25.

Nota: in questo caso, $l(z)$ denota metà del lato della base quadrata della sezione orizzontale della piramide a una quota generica $z$ , diversamente dal procedimento iniziale in cui il lato completo era indicato con $l(z)$ .

$\quad$

Figura 25: visualizzazione del triangolo rettangolo associato alla piramide, che mostra la relazione tra l’altezza e la lunghezza del lato della base quadrata in funzione dell’altezza $z$ .

$\quad$

Consideriamo ora i due triangoli rettangoli in figura 26.

$\quad$

Figura 26: triangoli rettangoli con indicazione delle proporzioni geometriche tra il lato della base e l’altezza della piramide, utilizzati per parametrizzare il solido e calcolare il volume.

$\quad$

Osserviamo che i due triangoli rispettano le condizioni affinchè sia verificato il primo criterio di similitudine tra triangoli, quindi possiamo impostare la seguente proporzione:

$2:\left(2-z \right)=1:l \left( z \right) \iff l \left(z \right)=\dfrac{2-z}{2},$

possiamo parametrizzare $\mathcal{D}$ come segue

$\mathcal{D} =\left\{ \left( x,y,z \right) \in \mathbb{R}^3 \, : \, 0 \leq x \leq 2l(z), \, 0 \leq y \leq 2l(z) , \, 0 \leq z \leq 2\right\}.$

Siccome la funzione integranda $f(x,y,z)=e^z$ non dipende dalle variabili $x\,\, \text{e}\,\, y$ possiamo riscrivere l’integrale come segue

$\iiint_\mathcal{D} e^z \, dx \, dy \, dz=\int_{0}^{2}e^z \left \vert\omega(z) \right \vert dz,$

dove

$\omega(z)= \{(x,y)\in \mathbb{R}^2: 0 \leq x \leq 2l(z), \, 0 \leq y \leq 2l(z)\},$

da cui

$\begin{aligned} &\iiint_\mathcal{D} e^z \, dx \, dy \, dz=\\ &=\int_{0}^{2}e^z \left \vert\omega(z) \right \vert dz=\\ &=\int_{0}^{2}e^z\cdot \left( 2l(z) \right)^2dz=\\ &=\int_{0}^{2}e^z\cdot \left( 2\cdot \dfrac{2-z}{2} \right)^2\,dz=\\ &=\int_{0}^{2}e^z\left( 2-z \right)^2\,dz=\\ &=2(e^2-5). \end{aligned}$

Dunque, possiamo concludere che

$\boxcolorato{analisi}{\displaystyle \iiint_\mathcal{D} e^z \, dx \, dy \, dz=2(e^2-5). }$

Esercizio 19 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare

(25) $\begin{equation*} \iiint_\mathcal{D} y \, dx \, dy \, dz, \end{equation*}$

dove $\mathcal{D} = \left\{(x,y,z) \in \mathbb{R}^3: x^2+4x+y^2\le 0, x + 4 \ge \sqrt{3}y, \vert z \vert \le 1 \right\}$ .

Svolgimento.

Manipolando la prima equazione che definisce $\mathcal{D}$ , si ha

$x^2+4x+y^2 = 0 \quad \iff \quad (x+2)^2 + y^2 = 4,$

rappresenta un cilindro centrato in $(2,0,0)$ e raggio $2$ e altezza $2$ poichè $\left \vert z \right \vert \leq 1$ .

Analogamente, manipolando la seconda equazione che descrive $\mathcal{D}$ , si ha

$x+4 = \sqrt{3}y \quad \iff \quad y = \dfrac{x+4}{\sqrt{3}}$

rappresenta un piano.

Il solido $\mathcal{D}$ è dunque definito come l’intersezione tra il cilindro e il piano, rappresentato in figura 27.

$\quad$

Figura 27: rappresentazione di un solido cilindrico e del piano che rappresenta il solido dato.

$\quad$

Per risolvere (26) procediamo integrando per fili

(26) $\begin{equation*} \iiint_\mathcal{D} y \, dx \, dy \, dz = \iint_{D^\prime} y\, dx \, dy \int_{-1}^1 dz, \end{equation*}$

dove $D^\prime = \left\{ (x,y) \in \mathbb{R}^2 \; \vert \; (x+2)^2+y^2\le 4, \; x+ 4 \ge \sqrt{3}y \right\}$ .

Consideriamo la sezione del solido, come in figura 28.

$\quad$

Rendered by QuickLaTeX.com

Figura 28: Vista laterale del solido con il piano $x + 4 = \sqrt{3} \, y$ , evidenziando la zona di intersezione tra il cilindro e il piano.

$\quad$

L’integrale (26) diventa

$\iint_{D^\prime} y\, dx \, dy \int_{-1}^1 dz=2 \iint_{D^\prime} y \, dx \, dy .$

Mettendo a sistema la retta di equazione $y=(x+4)/\sqrt{3}$ e la circonferenza di equazione $x^2+y^2+4x=0$ si ottengono i punti $(-4,0)$ e $(-1,\sqrt{3})$ . Pertanto è possibile riscrivere l’integrale come segue

$\begin{aligned} &2 \iint_{D^\prime} y \, dx \, dy=\\ &=2\int_{-4}^{-1}dx\int_{-\sqrt{-x^2-4x}}^{\frac{x+4}{\sqrt{3}}}y\,dy+\underbrace{\int_{-1}^{0}dx\int_{-\sqrt{-x^2-4x}}^{\sqrt{-x^2-4x}}y\,dy}_{=0}=\\ &=2\int_{-4}^{-1}dx\int_{-\sqrt{-x^2-4x}}^{\frac{x+4}{\sqrt{3}}}y\,dy, \end{aligned}$

dove abbiamo sfruttato il fatto che la funzione integranda è dispari rispetto alla variabile $y$ e il dominio è simmetrico rispetto all’asse delle $x$ . Abbiamo dunque

$\begin{aligned} &2\int_{-4}^{-1}dx\int_{-\sqrt{-x^2-4x}}^{\frac{x+4}{\sqrt{3}}}y\,dy= \\ &=\int_{-4}^{-1}\left(\left(\dfrac{x+4}{\sqrt{3}}\right)^2-\left(-x^2-4x\right)\right)dx=\\ &=\int_{-4}^{-1}\left(\dfrac{x^2+16+8x}{3}+x^2+4x\right)dx=\\ &=\dfrac{1}{3}\int_{-4}^{-1}\left(4x^2+20x+16\right)dx=\\ &=\dfrac{4}{3}\left(\dfrac{x^3}{3}+\dfrac{5}{2}x^2+4x\right)\bigg\vert^{-1}_{-4}=\\ &=\dfrac{4}{3}\left(-\dfrac{1}{3}+\dfrac{5}{2}-4-\dfrac{(-4)^3}{3}-\dfrac{5}{2}(16)-(-16)\right)=\\ &=- 6. \end{aligned}$

Si conclude che

$\boxcolorato{analisi}{\iiint_{\mathcal{D}} y \, dx \, dy \, dz=- 6. }$

Esercizio 20 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_\mathcal{D}\dfrac{z}{\sqrt{x^2+y^2+z^2}}\\, dx \, dy \, dz,$

dove $\mathcal{D}=\left\{(x,y,z)\in \mathbb{R}^3: x^2+y^2+z^2\leq 4, z\geq \sqrt{3}\right\}$ .

Svolgimento.

Rappresentiamo graficamente il dominio $\mathcal{D}$ in figura 29.

$\quad$

Rendered by QuickLaTeX.com

Figura 29: calotta sferica che rappresenta il dominio $\mathcal{D}$ dato (in rosso).

$\quad$

Parametrizziamo $\mathcal{D}$ applicando le coordinate sferiche

$\begin{cases} x=\rho \cos \theta \sin \phi\\ y=\rho \sin \theta \sin \phi \\ z=\rho \cos \phi. \end{cases}$

Vogliamo trovare in quali intervalli variano le variabili $\rho, \theta$ e $\phi$ . In figura 30 rappresentiamo un punto del dominio $\mathcal{D}$ in coordinate sferiche.

$\quad$

Rendered by QuickLaTeX.com

Figura 30: Rappresentazione di un punto nel dominio $\mathcal{D}$ in coordinate sferiche, evidenziando gli angoli $\theta$ e $\phi$ .

$\quad$

In figura 31 è rappresentato l’angolo massimo assunto da $\phi$ .

$\quad$

Rendered by QuickLaTeX.com

Figura 31: visualizzazione dell’angolo massimo $\phi_{\text{max}}$ raggiunto nel dominio $D$ , utilizzato per definire i limiti di integrazione.

$\quad$

In figura 32 rappresentiamo il triangolo rettangolo per determinare l’angolo massimo della variabile $\phi$ .

$\quad$

Rendered by QuickLaTeX.com

Figura 32: triangolo rettangolo usato per calcolare l’angolo massimo della variabile $\phi$ , mostrando la relazione geometrica tra i lati e gli angoli.

$\quad$

Applicando i noti teoremi sui triangoli rettangoli, otteniamo

$\sqrt{3}=2\cos \phi_{max} \quad\iff \quad\cos \phi_{max}=\dfrac{\sqrt{3}}{2}\,\, \iff\,\, \phi_{max}=\dfrac{\pi}{6},$

quindi

$\phi \in \left[0,\dfrac{\pi}{6}\right].$

Per calcolare in quali intervalli variano $\rho$ e $\theta$ , è utile risolvere il seguente sistema

(27) $\begin{equation*} \begin{cases} \rho^2\leq 4\\ \rho \cos \phi \geq \sqrt{3} \end{cases} \qquad \iff \qquad \begin{cases} \rho^2\leq 4\\ \rho \geq\dfrac{\sqrt{3}}{\cos \phi}, \end{cases} \end{equation*}$

dove abbiamo potuto dividere per $\cos \phi$ nella seconda disequazione del sistema (27) essendo $\cos \phi>0$ per $\phi \in \left[0,\dfrac{\pi}{6}\right]$ , pertanto da (27) otteniamo

$\rho \in \left[\dfrac{\sqrt{3}}{\cos \phi },2 \right] \qquad \mbox{ e } \qquad \theta \in \left[0,2\pi\right],$

per cui possiamo concludere che la parametrizzazione di $\mathcal{D}$ in coordinate sferiche è data da

$\begin{cases} x=\rho \cos \theta \sin \phi\\ y=\rho \sin \theta \sin \phi \quad \quad \text{con}\,\, \theta \in [0,2\pi],\, \rho \in \left[\dfrac{\sqrt{3} }{\cos \phi},2\right] ,\, \phi \in \left[0,\dfrac{\pi}{6}\right].\\ z=\rho \cos \phi. \end{cases}$

Ricordando che

$dx\,dy\,dz=\rho^2 \sin \phi \,d\rho\, d\theta\, d\phi ,$

abbiamo

$\begin{aligned} \iiint_\mathcal{D} \frac{z}{\sqrt{x^2 + y^2 + z^2}} \, dx \, dy \, dz&=\int_{0}^{2\pi}d \theta\int_{0}^{\frac{\pi}{6}}d\phi \int_{\frac{\sqrt{3}}{\cos \phi }}^{2}\frac{\rho \cos \phi}{\rho}\,\rho^2\sin \phi \,d\rho=\\ &=\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{6}}d\phi \int_{\frac{\sqrt{3}}{\cos \phi }}^{2}\frac{\rho \cos \phi}{\rho}\,\rho^2\sin \phi \,d\rho=\\ &=2\pi\int_{0}^{\frac{\pi}{6}}\sin \phi \cos \phi \, d\phi \int_{\frac{\sqrt{3}}{\cos \phi }}^{2}\rho^2 \, d\rho =\\ &=\dfrac{2}{3}\pi \int_{0}^{\frac{\pi}{6}}\cos \phi \sin \phi \left(8-\dfrac{3\sqrt{3}}{\cos^3 \phi } \right) \, d\phi =\\ &=\dfrac{2\pi}{3}\int_{0}^{\frac{\pi}{6}}\left( 8 \cos \phi \sin \phi -3\sqrt{3}\dfrac{\sin \phi}{\cos^2 \phi }\right)\, d \phi =\\ &=\dfrac{2\pi}{3}\left(4 \sin^2 \phi -3\sqrt{3}\dfrac{1}{\cos\phi} \right)\bigg \vert_0^{\frac{\pi}{6}}=\\ &=\dfrac{2}{3}\pi \left(3\sqrt{3}-5 \right). \end{aligned}$

Pertanto concludiamo che

$\boxcolorato{analisi}{\displaystyle\iiint_\mathcal{D} \frac{z}{\sqrt{x^2 + y^2 + z^2}} \, dx \, dy \, dz=\dfrac{2}{3}\pi \left(3\sqrt{3}-5 \right). }$

Esercizio 21 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_{\mathcal{D}}yz\sqrt{x}\\, dx \, dy \, dz,$

dove $\mathcal{D}=\left\{(x,y,z)\in \mathbb{R}^3: \,x\geq 0 , \, y \geq 0 ,\, 0 \leq z \leq 4-x^2-y^2\right\}$ .

Svolgimento.

Vengono proposti due metodi di risoluzione dell’esercizio.

Svolgimento primo metodo.

In figura 33 rappresentiamo l’insieme $\mathcal{D}$ .

$\quad$

Rendered by QuickLaTeX.com

Figura 33: illustrazione di un dominio tridimensionale, con limiti definiti dalla superficie $z = 4 - x^2 - y^2$ , utilizzato per il calcolo dell’integrale triplo.

$\quad$

Procediamo integrando per fili:

$\iiint_\mathcal{D} yz\sqrt{x} \, dx \, dy \, dz=\iint_{\tilde{D}}y \sqrt{x}\, dx dy \int_{0}^{4-x^2-y^2}z \, dz=\dfrac{1}{2}\iint_{\tilde{\mathcal{D}}}y \sqrt{x}\, \left(4-x^2-y^2 \right)^2\,dx\, dy,$

dove $\tilde{\mathcal{D}}=\{(x,y)\in \mathbb{R}^2|\,x\geq 0 , \, y \geq 0 ,\, x^2+y^2\leq 4\}$ .

Parametrizziamo $\tilde{\mathcal{D}}$ applicando le coordinate polari

$\begin{cases} x=\rho \cos \theta \\ y=\rho \sin \theta , \end{cases}$

dove

$\theta \in \left[0,\dfrac{\pi}{2}\right],\, \rho \in [0,2]$

e ricordando che

$dx \,dy= \rho \; d \rho \, d \theta ,$

otteniamo

$\begin{aligned} \iiint_\mathcal{D} yz\sqrt{x} \, dx \, dy \, dz &= \dfrac{1}{2}\int_{0}^{\frac{\pi}{2}}d\theta \int_{0}^{2}\rho \sin \theta \sqrt{\rho \cos \theta }\left(4-\rho^2 \right)^2 \, \rho d \rho= \\ &= \dfrac{1}{2} \underbrace{\int_{0}^{\frac{\pi}{2}}\sin \theta \sqrt{\cos \theta}\, d \theta}_{I_1} \, \cdot \, \underbrace{\int_{0}^{2}\rho^{\frac{5}{2}}\left(4-\rho^2 \right)^2\, d\rho }_{I_2}. \end{aligned}$

Calcoliamo

$I_1=-\dfrac{2}{3}\left(\cos \theta \right)^{\frac{3}{2}}\bigg \vert^\frac{\pi}{2}_0=\dfrac{2}{3}$

$\begin{aligned} I_2 & =\int_{0}^{2}\rho^\frac{5}{2}\left(16+\rho^4-8\rho^2 \right)\, d \rho=\int_{0}^{2}\left(16\rho^\frac{5}{2}+\rho^\frac{13}{2}-8\rho^\frac{9}{2} \right)\, d \rho =\\ &=\dfrac{32}{7}\rho^\frac{7}{2}+\dfrac{2}{15}\rho^\frac{15}{2}-\dfrac{16}{11}\rho^\frac{11}{2}\bigg \vert^2_0=\\ &=\dfrac{32}{7}\cdot 2^\frac{7}{2}+\dfrac{2}{15}\cdot 2^\frac{15}{2}-\dfrac{16}{11}\cdot 2^\frac{11}{2}=\\ &=\dfrac{32}{7}\sqrt{2^7}+\dfrac{2}{15}\sqrt{2^{15}}-\dfrac{16}{11}\sqrt{2^{11}}=\\ &=\dfrac{32}{7}\cdot8 \sqrt{2}+\dfrac{2}{15}\cdot 2^7 \sqrt{2}-\dfrac{16}{11 }\cdot 2^5\sqrt{2}=\\ &=\sqrt{2}\left(\dfrac{256}{7}+\dfrac{256}{15}-\dfrac{512}{11}\right)=\dfrac{8192}{1155}\sqrt{2}. \end{aligned}$

Sfruttando quanto ottenuto, abbiamo:

$\iiint_\mathcal{D} yz\sqrt{x} \, dx \, dy \, dz, =\dfrac{1}{2} \; I_1\cdot I_2=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot \dfrac{8192}{1155}\sqrt{2}=\dfrac{8192}{3465}\sqrt{2},$

concludendo che

$\boxcolorato{analisi}{\displaystyle\iiint_\mathcal{D} yz\sqrt{x} \, dx \, dy \, dz = \dfrac{8192}{3465}\sqrt{2}. }$

Svolgimento secondo metodo.

Procediamo integrando per strati.

Osserviamo che dalla condizione

$z\leq 4-x^2-y^2\quad \iff\quad x^2+y^2 \leq 4-z,$

deve risultare

$z\leq 4$

e quindi con la condizione

$z\geq 0,$

abbiamo

$z\in [0,4].$

Un generico strato può essere parametrizzato come segue

$\Omega(z)=\left\{(x,y)\in \mathbb{R}^2|x\geq0 , \, y \geq 0,, \, \,x^2+y^2\leq 4-z\right\},$

dunque

$\displaystyle\iiint_\mathcal{D} yz\sqrt{x} \, dx \, dy \, dz =\int_{0}^{4}z \, dz \iint_{\Omega(z)}y\sqrt{x}\,dx\,dy.$

Parametrizziamo $\Omega(z)$ applicando le coordinate polari

$\begin{cases} x=\rho \cos \theta \\ y=\rho \sin \theta \end{cases}$

dove

$\theta \in \left[0,\dfrac{\pi}{2}\right],\, \rho \in \left[0,\sqrt{4-z}\right],$

e ricordando che

$dx\,dy\,dz=\rho \,d\rho \,d \theta ,$

abbiamo

$\begin{aligned} \displaystyle\iiint_\mathcal{D} yz\sqrt{x} \, dx \, dy \, dz &= \int_{0}^{4}z \, dz\int_{0}^{\frac{\pi}{2}}d\theta \int_{0}^{\sqrt{4-z}}\rho \sin \theta \sqrt{\rho \cos \theta }\ \rho \, d \rho=\\ &=\underbrace{\int_{0}^{\frac{\pi}{2} }\sin \theta \sqrt{\cos \theta }\, d \theta }_{I_3}\cdot \underbrace{\int_{0}^{4}z \, dz \int_{0}^{\sqrt{4-z}}\rho^\frac{5}{2} \, d \rho }_{I_4}. \end{aligned}$

Calcoliamo

$I_3=I_1=\dfrac{2}{3}$

$\begin{aligned} I_4 & = \dfrac{2}{7}\int_{0}^{4}z\left(4-z \right)^\frac{7}{4}\, dz=\\ &=\dfrac{2}{7}\left(-\dfrac{4}{11}z\left(4-z \right)^\frac{11}{4}\bigg \vert^{4}_0+\dfrac{4}{11}\int_{0}^{4}\left(4-z \right)^\frac{11}{4}\, dz \right) =\\ &=-\dfrac{2}{7}\cdot \dfrac{4}{15}\left( 4-z\right)^\frac{15}{4}\bigg \vert^4_0=\\ &=\dfrac{2}{7}\cdot\dfrac{4}{11}\cdot \dfrac{4}{15}\cdot2^\frac{15}{2}=\dfrac{4096}{1155}\sqrt{2}. \end{aligned}$

Sfruttando quanto ottenuto, abbiamo

$\displaystyle\iiint_\mathcal{D} yz\sqrt{x} \, dx \, dy \, dz =I_3\cdot I_4=\dfrac{2}{3}\cdot \dfrac{4096}{1155}\sqrt{2}=\dfrac{8192}{3465}\sqrt{2}.$

Pertanto concludiamo che

$\boxcolorato{analisi}{\displaystyle\iiint_\mathcal{D} yz\sqrt{x} \, dx \, dy \, dz =\dfrac{8192}{3465}\sqrt{2}. }$

Esercizio 22 $(\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_{\mathcal{D}} \dfrac{x^2}{x^2+z^2} \, dx \, dy \, dz,$

dove $\mathcal{D} = \{(x,y,z) \in \mathbb{R}^3 : 1\leq x^2+y^2+z^2\leq 2, \; x^2-y^2+z^2\leq 0, \; y\geq 0 \}$ .

Svolgimento.

Graficamente, rappresentiamo $\mathcal{D}$ in figura 34, considerando che è necessario includere solo la regione in cui $y \geq 0$ .

$\quad$

Figura 34: rappresentazione grafica di una sfera intersecata da una conica (in celeste), con equazioni $1 \leq x^2 + y^2 + z^2 \leq 2$ e $z^2 \leq x^2 + y^2$ , con ordinata positiva.

$\quad$

Risolviamo il seguente sistema e determiniamo l’intersezione fra la sfera di raggio $1$ e la conica di equazione $x^2+z^2=y^2$ :

$\begin{cases} x^2+y^2+z^2=1\\ x^2+z^2=y^2 \end{cases} \iff \begin{cases} x^2+z^2=\dfrac{1}{2}\\[10pt] y = \pm \dfrac{\sqrt{2}}{2} \end{cases}$

Risolviamo il seguente sistema e determiniamo l’intersezione la sfera di raggio $\sqrt{2}$ e la conica di equazione $x^2+z^2=y^2$ :

$\begin{cases} x^2+y^2+z^2=2\\x^2+z^2=y^2 \end{cases} \iff \begin{cases} x^2+z^2=1\\y=\pm 1. \end{cases}$

Riscriviamo l’integrale come segue

$\iiint_{\mathcal{D}} \dfrac{x^2}{x^2+z^2} \, dx \, dy \, dz=\underbrace{\iiint_{\Omega_1} \dfrac{x^2}{x^2+z^2} \, dx \, dy \, dz}_{I_1}+\underbrace{\iiint_{\Omega_2} \dfrac{x^2}{x^2+z^2} \, dx \, dy \, dz,}_{I_2}$

dove la parametrizzazione di $\Omega_1$ è quella che segue applicando le coordinate cilindriche

$\begin{cases} x= \rho \cos \theta\\ z=\rho \sin \theta\\ y=t, \end{cases}$

dove

$t \in \left[\frac{\sqrt{2}}{2},1\right], \theta \in [0,2\pi) , \rho \in \left[\sqrt{1-t^2},t\right].$

Analogamente, per $\Omega_2$ , abbiamo

$\begin{cases} x= \rho \cos \theta\\ z=\rho \sin \theta\\ y=t, \end{cases}$

dove

$, \qquad t \in \left[1,\sqrt{2}\right], \theta \in \left[0,2\pi\right] , \rho \in \left[0,\sqrt{2-t^2}\right].$

Inoltre, ricordando ricordando che

$dx\,dy\,dz=\rho \, d \rho \,d t\, d \theta,$

possiamo calcolare i due integrali separatamente, come segue

$\begin{aligned} & I_1=\int_{\frac{\sqrt{2}}{2}}^1 dt \int_0^{2\pi} d\theta \int_{\sqrt{1-t^2}}^t \rho \, \cos^2 \theta d\rho =\\ & = \int_0^{2\pi} \left(\dfrac{1+\cos2\theta}{2}\right) \, d\theta \int_{\frac{1}{\sqrt{2}}}^1 \dfrac{1}{2}(t^2-1+t^2) dt = \\ & = \dfrac{1}{2} \cdot 2\pi \cdot \dfrac{1}{2} \left(\dfrac{2}{3}t^3-t\right)\bigg\vert_{\frac{1}{\sqrt{2}}}^1 = \\ & = \dfrac{\pi}{2}\left(\dfrac{2}{3}-1-\dfrac{2}{3} \cdot \dfrac{2\sqrt{2}}{8}+\dfrac{\sqrt{2}}{2}\right) = \\ & = \dfrac{\pi}{2}\left(-\dfrac{1}{3}+\dfrac{\sqrt{2}}{3}\right) \end{aligned}$

$\begin{aligned} I_2&=\int_1^{\sqrt{2}}dt \int_0^{2\pi} d\theta \int_0^{\sqrt{2-t^2}} \rho \cos^2\theta \; d\theta=\\ & = \dfrac{1}{2}\int_0^{2\pi} \left(\dfrac{1+\cos(2\theta)}{2}\right) d\theta \int_{1}^{\sqrt{2}} (2-t^2) dt = \\ & = \dfrac{\pi}{2}\left(2t-\dfrac{t^3}{3}\right)\bigg\vert_1^{\sqrt{2}} =\\ & = \dfrac{\pi}{2}\left(2\sqrt{2} - \dfrac{2}{3}\sqrt{2}-2 +\dfrac{1}{3}\right) = \\ & = \dfrac{\pi}{2}\left(\dfrac{4\sqrt{2}}{3}-\dfrac{5}{3}\right), \end{aligned}$

da cui

$\begin{aligned} \iiint_{\mathcal{D}} \dfrac{x^2}{x^2+z^2} \, dx \, dy \, dz &= I_1 + I_2 =\\ &= \dfrac{\pi}{2} \left(-\dfrac{1}{3} + \dfrac{\sqrt{2}}{3} + \dfrac{4\sqrt{2}}{3} - \dfrac{5}{3}\right) \\ &= \dfrac{\pi}{2} \left(-2 + \dfrac{5\sqrt{2}}{3}\right)= \\ &= \pi \left(-1 + \dfrac{5\sqrt{2}}{6}\right) =\\ &= \dfrac{\pi}{6} \left(5\sqrt{2} - 6\right). \end{aligned}$

Concludiamo che

$\boxcolorato{analisi}{\displaystyle \iiint_{\mathcal{D}} \dfrac{x^2}{x^2+z^2} \, dx \, dy \, dz=\dfrac{\pi}{6}\left(5\sqrt{2}-6\right). }$

Esercizio 23 $(\bigstar\bigstar\bigstar\bigstar\largewhitestar)$ . Calcolare

$\iiint_{\mathcal{D}} \sqrt{x^2+y^2+z^2} \, dx \, dy \, dz,$

dove $\mathcal{D}= \{(x,y,z) \in \mathbb{R}^3 : z\geq x\,,\,(x+z)^2+2y^2\leq 2(x^2+y^2+z^2)^2\leq 2 \}$ .
Si suggerisce di operare la seguente sostituzione

(28) $\begin{equation*} \begin{cases} \alpha=x+z\\ \beta=x-z\\ \sqrt{2}y=t. \end{cases} \end{equation*}$

Svolgimento.

Si osserva che il dominio $\mathcal{D}$ presenta una natura complessa e risulta difficilmente rappresentabile graficamente. Di conseguenza, in accordo con quanto suggerito, si procede con l’applicazione della sostituzione indicata.

Il primo passo consiste nel determinare le espressioni delle variabili $x$ e $y$ in funzione dei parametri $\alpha$ e $\beta$ , mediante la definizione del seguente sistema:

(29) $\begin{equation*} \begin{cases} \alpha=x+z\\ \beta=x-z \end{cases} \quad \iff \quad \begin{cases} x=\dfrac{\alpha+\beta}{2}\\ \\ z=\dfrac{\alpha-\beta}{2}, \end{cases} \end{equation*}$

da cui, utilizzando la definizione dell’insieme dato, si ha

(30) $\begin{equation*} \begin{cases} \dfrac{\alpha-\beta}{2}\geq\dfrac{\alpha+\beta}{2}\\ \\ \alpha^2+t^2\leq 2 \left( \left(\dfrac{\alpha+\beta}{2} \right)^2+ \left(\dfrac{\alpha-\beta}{2} \right)^2+\dfrac{t^2}{2}\right) ^2\\ \\ 2 \left( \left(\dfrac{\alpha+\beta}{2} \right)^2+ \left(\dfrac{\alpha-\beta}{2} \right)^2+\dfrac{t^2}{2}\right) ^2\leq 2 . \end{cases} \end{equation*}$

Riscriviamo la prima equazione del sistema (30) come segue

$\dfrac{\alpha-\beta}{2}\geq\dfrac{\alpha+\beta}{2}\quad \iff \quad \beta \leq 0,$

Riscriviamo la seconda equazione del sistema (30) nel modo seguente

$\begin{aligned} &\alpha^2+t^2\leq 2 \left( \left(\dfrac{\alpha+\beta}{2} \right)^2+ \left(\dfrac{\alpha-\beta}{2} \right)^2+\dfrac{t^2}{2}\right) ^2\quad \iff \quad \\\\ &\iff \quad \alpha^2+t^2\leq 2\left(\dfrac{\alpha^2+\beta^2+2\alpha\beta+\alpha^2+\beta^2-2\alpha\beta}{4}+\dfrac{t^2}{2}\right)^2 \quad \iff \quad \\\\ & \iff \quad \alpha^2+t^2\leq 2 \left( \dfrac{\alpha^2+\beta^2}{2}+\dfrac{t^2}{2}\right)^2\quad \iff \quad \\\\ & 2\iff \quad \left(\alpha^2+t^2\right)\leq \left(\alpha^2+\beta^2+t^2 \right)^2, \end{aligned}$

Infine, non resta che rielaborare la terza equazione del sistema (30)¹

$2 \left( \left(\dfrac{\alpha+\beta}{2} \right)^2+ \left(\dfrac{\alpha-\beta}{2} \right)^2+\dfrac{t^2}{2}\right) ^2\leq 2 \quad \iff \quad \left(\alpha^2+\beta^2+t^2 \right)^2\leq 4.$

Ricordando che

$dx\,dy\,dz=\vert J \vert d\alpha\,d \beta \, d t,$

dove

$\vert J \vert =\left \vert \text{det}\begin{vmatrix} \dfrac{\partial x}{\partial \alpha} & \dfrac{\partial x}{\partial \beta} & \dfrac{\partial x}{\partial t}\\\\ \dfrac{\partial y}{\partial \alpha} & \dfrac{\partial y}{\partial \beta} & \dfrac{\partial y}{\partial t}\\\\ \dfrac{\partial z}{\partial \alpha} & \dfrac{\partial z}{\partial \beta} & \dfrac{\partial z}{\partial t} \end{vmatrix}\right \vert = \left \vert\text{det} \begin{vmatrix} \dfrac{1}{2}&\dfrac{1}{2}&0\\\\0&0&\dfrac{1}{\sqrt{2}}\\\\\dfrac{1}{2}&-\dfrac{1}{2}&0 \end{vmatrix} \right \vert = \dfrac{1}{2\sqrt{2}},$

possiamo riscrivere

(31) $\begin{equation*} \begin{aligned} \iiint_\mathcal{D} \sqrt{x^2 + y^2 + z^2} \, dx \, dy \, dz, &=\iiint_{\Omega} \sqrt{x^2+y^2+z^2} \, dx \, dy \, dz&=\\ =\dfrac{1}{4}\iiint_{\tilde{\Omega}} \sqrt{\alpha^2+\beta^2+t^2}\, d \alpha \, d \beta \, dt, \end{aligned} \end{equation*}$

dove

$\tilde{\Omega} = \{(\alpha,\beta,t) \in \mathbb{R}^3 \, :\beta\leq 0\,,\,2 \left(\alpha^2+t^2\right)\leq\left(\alpha^2+\beta^2+t^2 \right)^2\,,\,\left(\alpha^2+\beta^2+t^2 \right)^2\leq 4 \}.$

Applichiamo le coordinate sferiche per parametrizzare $\tilde{\Omega}$

$\begin{cases} \alpha=\rho \cos \theta \sin \phi \\ t=\rho \sin \theta \sin \phi \\ \beta=\rho \cos \phi \end{cases}$

e dunque otteniamo

$\begin{cases} \beta\leq 0\\ 2 \left(\alpha^2+t^2\right)\leq \left(\alpha^2+\beta^2+t^2 \right)^2\\ \left(\alpha^2+\beta^2+t^2 \right)^2\leq 4 \\ \theta \in [0,2 \pi] \end{cases} \quad \iff \quad \begin{cases} \rho \cos \phi \leq 0\\ 2 \rho^2 \sin^2 \phi \leq \rho^4\\ \rho^4 \leq 4 \\ \theta \in [0,2 \pi] \end{cases} \quad \iff \quad \begin{cases} \phi \in \left[\dfrac{\pi}{2},\pi\right]\\ \rho\geq \sqrt{2}\sin \phi \\ 0 \leq \rho \leq \sqrt{2}\\ \theta \in \left[0,2 \pi\right], \end{cases}$

dal sistema si ottiene

$\begin{cases} \phi \in \left[\dfrac{\pi}{2},\pi\right]\\ \\ \rho \in \left[\sqrt{2} \sin \phi , \sqrt{2}\right]\\ \\ \theta \in \left[0,2 \pi\right]. \end{cases}$

Ricordando che

$d\alpha \, d \beta \, d t= \rho^2 \sin \phi \, d \rho \, d \theta \, d \phi ,$

possiamo riscrivere (31) come segue

$\begin{aligned} \iiint_\mathcal{D} \sqrt{x^2 + y^2 + z^2} \, dx \, dy \, dz, &=\dfrac{1}{4}\iiint_{\tilde{\Omega}} \sqrt{\alpha^2+\beta^2+t^2}\, d \alpha \, d \beta \, dt=\\ &=\dfrac{1}{4}\iiint_{\Omega^\star}\rho^3 \sin \phi \, \, d \rho \, d \theta \, d \phi \end{aligned}$

dove $\Omega^\star = \left\{(\theta,\phi,\rho) \in \mathbb{R}^3 \, :\phi \in \left[\frac{\pi}{2},\pi\right]\,,\,\rho \in [\sqrt{2} \sin \phi , \sqrt{2}]\,,\, \theta \in [0,2 \pi]\right\}.$

Dunque, procediamo con il calcolo di

$\iiint_\mathcal{D} \sqrt{x^2 + y^2 + z^2} \, dx \, dy \, dz$

che sfruttando quanto ottenuto risulta

$\begin{aligned} &\dfrac{1}{4}\int_{0}^{2\pi}d \theta \int_{\frac{\pi}{2}}^{\pi}\sin \phi \, d \phi \int_{\sqrt{2} \sin \phi }^{\sqrt{2}}\rho^3 \, d \rho =\\ &=\dfrac{2\pi}{4}\int_{\frac{\pi}{2}}^{\pi}\left(\sin \phi -\sin^5 \phi \right) d\phi =\dfrac{\pi}{2}\left( -\cos \phi \bigg \vert^\pi_\frac{\pi}{2}- \int_{\frac{\pi}{2}}^{\pi} \sin\phi \left(\dfrac{1-\cos (2 \phi) }{2} \right)^2\, d \phi \right)= \\ &=\dfrac{\pi}{2}\left( 1-\int_{\frac{\pi}{2}}^{\pi}\sin \phi \cdot \frac{1+\cos^2 (2 \phi )-2 \cos (2 \phi )}{4} \, d \phi\right)=\\ &=\dfrac{\pi}{2}\left( 1- \dfrac{1}{4}+\dfrac{1}{2}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot \cos (2 \phi) \, d \phi -\dfrac{1}{4}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot \cos^2 (2 \phi )\, d \phi \right)= \\ &=\dfrac{\pi}{2}\left( \dfrac{3}{4}+\dfrac{1}{2}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot (2\cos^2\phi-1) \, d \phi -\dfrac{1}{4}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot (2\cos^2\phi-1)^2 \, d \phi \right)= \\ &=\dfrac{\pi}{2}\left( \dfrac{3}{4}-\dfrac{1}{2}\int_{\frac{\pi}{2}}^{\pi} \sin \phi \, d\phi + \int_{\frac{\pi}{2}}^{\pi} \sin \phi \cdot \cos^2\phi \, d \phi -\dfrac{1}{4}\left(\int_{\frac{\pi}{2}}^{\pi} (4 \sin \phi \cdot \cos^4 \phi + \sin\phi - 2 \sin \phi \cos^2\phi) \; d\phi \right)\right) = \\ &=\dfrac{\pi}{2}\left( \dfrac{3}{4}-\dfrac{\cos\phi}{2}\bigg\vert_{\frac{\pi}{2}}^{\pi} +\dfrac{\cos^3\phi}{3} \bigg\vert_{\frac{\pi}{2}}^{\pi} + \left(\dfrac{\cos^5\phi}{5}+\dfrac{\cos\phi}{4}-\dfrac{2\cos^3\phi}{12}\right)\bigg\vert_{\frac{\pi}{2}}^{\pi} \right)= \\ &=\dfrac{\pi}{2}\left( \dfrac{3}{4}- \dfrac{1}{6} + \dfrac{7}{60} \right)=\\ &= \dfrac{7\pi}{30}. \end{aligned}$

Concludiamo che

$\boxcolorato{analisi}{\displaystyle \iiint_\mathcal{D} \sqrt{x^2 + y^2 + z^2} \, dx \, dy \, dz =\dfrac{7}{30}\pi. }$

Utilizzando i calcoli precedentemente effettuati. ↩

Esercizio 24 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_{\mathcal{D}} \left(z^2+ze^{-x^2} \right) dx \, dy \, dz,$

dove $\mathcal{D} = \{(x,y,z) \in \mathbb{R}^3: x^2+y^2+z^2\le 1 \,, \, z^2\le x^2+y^2 \}$ .

Svolgimento.

In figura 35 è rappresentato l’insieme $\mathcal{D}$ , evidenziato come l’area colorata.

$\quad$

Figura 35: rappresentazione grafica di una sfera intersecata da una conica (in rosa), descritto dalle equazioni $x^2 + y^2 + z^2 \leq 1$ e $x^2 - y^2 + z^2 \leq 0$ .

$\quad$

Riscriviamo:

$\iiint_{\mathcal{D}} \left(z^2 + z e^{-x^2} \right) \, dx \, dy \, dz = \underbrace{\iiint_{\Omega} z^2 \, dx \, dy \, dz}_{I_1} + \underbrace{\iiint_{\Omega} z e^{-x^2} \, dx \, dy \, dz}_{I_2}.$

Si definisca la funzione $f:\mathbb{R}^3 \rightarrow \mathbb{R}$ tale che $f(x, y, z) = z e^{-x^2}$ . Poiché $f(x, y, z) = -f(x, y, -z)$ e il dominio $\Omega$ è simmetrico rispetto al piano $xy$ , si conclude che $I_2 = 0$ .

Si consideri, inoltre, la funzione $g:\mathbb{R}^3 \rightarrow \mathbb{R}$ definita come $g(x, y, z) = z^2$ . Si osserva che $g(x, y, z) = g(x, y, -z)$ e, tenendo conto della simmetria di $\Omega$ rispetto al piano $xy$ , si ottiene:

$I_1 = 2 \iiint_{\tilde{\Omega}} z^2 \, dx \, dy \, dz,$

dove

$\tilde{\Omega} = \{(x, y, z) \in \mathbb{R}^3 : x^2 + y^2 + z^2 \leq 1, \, z^2 \leq x^2 + y^2, \, z > 0\}.$

Parametrizziamo $\tilde{\Omega}$ applicando le coordinate sferiche:

$\begin{cases} x = \rho \cos \theta \sin \phi, \\ y = \rho \sin \theta \sin \phi, \\ z = \rho \cos \phi, \end{cases}$

da cui si ottiene:

$I_1 = 2 \iiint_{\Omega^\star} \tilde{g}(\rho, \theta, \phi) \, \rho^2 \sin \phi \, d\rho \, d\theta \, d\phi,$

dove

$\Omega^\star = \left\{(\rho, \theta, \phi) \in \mathbb{R}^3 : \rho \in [0, 1], \, \theta \in [0, 2\pi], \, \phi \in \left[\frac{\pi}{4}, \frac{\pi}{2} \right] \right\},$

e $\tilde{g}(\rho, \theta, \phi) = \rho^2 \cos^2 \phi$ .

Si ha che:

$\begin{aligned} I_1 &= 2 \int_{0}^{1} \rho^4 \, d\rho \int_{0}^{2\pi} d\theta \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos^2 \phi \sin \phi \, d\phi = \\ &= 2 \cdot \frac{\rho^5}{5} \Bigg|_0^1 \cdot (2\pi) \cdot \left(-\cos^3 \phi\right) \Bigg|_{\frac{\pi}{4}}^{\frac{\pi}{2}} = \\ &= \frac{\sqrt{2}}{15} \pi. \end{aligned}$

In alternativa, si poteva risolvere $I_1$ mediante integrazione per strati. Si determina l’intersezione tra le seguenti coniche:

$\begin{cases} x^2 + y^2 + z^2 = 1, \\ z^2 = x^2 + y^2, \end{cases} \quad \iff \quad \begin{cases} z = \pm \frac{\sqrt{2}}{2}, \\ x^2 + y^2 = \frac{1}{2}. \end{cases}$

Considerando solo $z \geq 0$ , si ha:

$I_1 = 2 \iiint_{\Omega^\diamond} z^2 \, dx \, dy \, dz,$

dove

$\Omega^\diamond = \left\{(x, y, z) \in \mathbb{R}^3 : z^2 \leq x^2 + y^2 \leq 1 - z^2, \, z \in \left[0, \frac{\sqrt{2}}{2}\right]\right\}.$

Si ottiene quindi:

$\begin{aligned} I_1 &= 2 \int_{0}^{\frac{\sqrt{2}}{2}} z^2 \, dz \int_{z^2 \leq x^2 + y^2 \leq 1 - z^2} 1 \, dx \, dy = \\ &= 2 \int_{0}^{\frac{\sqrt{2}}{2}} \pi z^2 \left(1 - z^2 - z^2 \right) \, dz = \\ &= 4\pi \int_{0}^{\frac{\sqrt{2}}{2}} \left(z^2 - 2z^4\right) \, dz = \\ &= 2\pi \left(\frac{z^3}{3} - \frac{2}{5}z^5\right) \Bigg|_0^{\frac{\sqrt{2}}{2}} = \\ &= 2\pi \left(\frac{2\sqrt{2}}{24} - \frac{8\sqrt{2}}{160}\right) = \\ &= 2\pi \cdot \frac{\sqrt{2}}{30} = \frac{\sqrt{2}}{15} \pi. \end{aligned}$

Si conclude che

$\boxcolorato{analisi}{\iiint_{\mathcal{D}} \left(z^2+ze^{-x^2} \right) dx \, dy \, dz=\dfrac{\sqrt{2}}{15}\pi. }$

Esercizio 25 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_{\mathcal{D}} \left(x^2+y^2 \right) dx \, dy \, dz,$

dove $\mathcal{D} = \{(x,y,z) \in \mathbb{R}^3: x^2+y^2+z^2\le 4 \,, \, x^2+y^2\geq 1 \}$ .

Svolgimento.

In figura 36 è rappresentato l’insieme $\mathcal{D}$ , evidenziato come area colorata in rosa.

$\quad$

Figura 36: visualizzazione tridimensionale del dominio $\mathcal{D}$ (in rosa), dove il vincolo $x^2 + y^2 + z^2 \leq 4$ e $1 \leq x^2 + y^2$ definisce il volume di integrazione.

$\quad$

Integriamo per strati. Determiniamo l’intersezione tra le seguenti coniche, che definiscono $\mathcal{D}$ :

$\begin{cases} x^2 + y^2 = 1, \\ x^2 + y^2 + z^2 = 4, \end{cases} \quad \iff \quad \begin{cases} x^2 + y^2 = 1, \\ z = \pm\sqrt{3}. \end{cases}$

Di conseguenza, si osserva che $z \in \left[ -\sqrt{3}, \sqrt{3} \right]$ , da cui

$I = \int_{-\sqrt{3}}^{\sqrt{3}} dz \iint_{\Omega^\star} \left( x^2 + y^2 \right) \, dx \, dy,$

dove $\Omega^\star = \{(x, y) \in \mathbb{R}^2 : 1 \leq x^2 + y^2 \leq 4 - z^2\}.$

Parametrizziamo $\Omega^\star$ applicando le coordinate polari:

$\begin{cases} x = \rho \cos \theta, \\ y = \rho \sin \theta, \end{cases}$

ottenendo

$\iiint_\mathcal{D} (x^2 + y^2) \, dx \, dy \, dz = \int_{-\sqrt{3}}^{\sqrt{3}} dz \iint_{\Omega^\star} \rho^3 \, d\rho \, d\theta,$

dove $\Omega^\star = \{(\rho, \theta) \in \mathbb{R}^2 : \theta \in [0, 2\pi], \, \rho \in [1, \sqrt{4 - z^2}]\}.$

Sfruttando quanto ottenuto finora, si ha:

$\begin{aligned} \iiint_\mathcal{D} (x^2 + y^2) \, dx \, dy \, dz & = \int_{-\sqrt{3}}^{\sqrt{3}} dz \int_{0}^{2\pi} d\theta \int_{1}^{\sqrt{4-z^2}} \rho^3 \, d\rho = \\[10pt] & = \frac{2\pi}{4} \int_{-\sqrt{3}}^{\sqrt{3}} \left( \left(4 - z^2\right)^2 - 1 \right) \, dz = \\[10pt] & \overset{\spadesuit}{=} \frac{\pi}{2} \cdot 2 \int_{0}^{\sqrt{3}} \left( 15 - 8z^2 + z^4 \right) \, dz = \\[10pt] & = \pi \left( 15z - \frac{8}{3}z^3 + \frac{z^5}{5} \right) \bigg|_{0}^{\sqrt{3}} = \\[10pt] & = \pi \left( 15\sqrt{3} - \frac{8}{3} \cdot 3\sqrt{3} + \frac{9\sqrt{3}}{5} \right) = \\[10pt] & = \pi \left( 15\sqrt{3} - 8\sqrt{3} + \frac{9}{5}\sqrt{3} \right) = \\[10pt] & = \pi \left( 7\sqrt{3} + \frac{9}{5}\sqrt{3} \right) = \\[10pt] & = \pi \left( \frac{35 + 9}{5}\sqrt{3} \right) = \frac{44}{5}\pi\sqrt{3}, \end{aligned}$

dove in $\spadesuit$ si sfrutta il fatto che l’integranda è una funzione pari su un intervallo simmetrico rispetto all’origine.

In alternativa, il calcolo di $I$ può essere eseguito integrando per fili. Si ha quindi:

$\iiint_\mathcal{D} (x^2 + y^2) \, dx \, dy \, dz = \iint_{\Omega^\diamond} dx \, dy \int_{-\sqrt{4 - x^2 - y^2}}^{\sqrt{4 - x^2 - y^2}} \left(x^2 + y^2 \right) \, dz,$

dove $\Omega^\diamond = \{(x, y) \in \mathbb{R}^2 : 1 \leq x^2 + y^2 \leq 4\}.$

Di conseguenza:

$\iiint_\mathcal{D} (x^2 + y^2) \, dx \, dy \, dz = 2 \iint_{\Omega^\diamond} \left(x^2 + y^2 \right) \sqrt{4 - x^2 - y^2} \, dx \, dy.$

Parametrizziamo $\Omega^\diamond$ applicando le coordinate polari:

$I = 2 \int_{0}^{2\pi} d\theta \int_{1}^{2} \rho^3 \sqrt{4 - \rho^2} \, d\rho.$

Il precedente integrale si risolve con la sostituzione

$\rho = 2\cos t, \quad d\rho = -2\sin t \, dt,$

ottenendo:

$\begin{aligned} I & = 2 \int_{0}^{2\pi} d\theta \int_{1}^{2} \rho^3 \sqrt{4 - \rho^2} \, d\rho = \\ & = 2 \int_{0}^{2\pi} d\theta \int_{\frac{\pi}{3}}^{0} 8 \cos^3 t \, \sqrt{4 - 4\cos^2 t} \left(-2 \sin t\right) \, dt = \\ & = 64 \cdot 2\pi \int_{0}^{\frac{\pi}{3}} \cos^3 t \, |\sin t| \, \sin t \, dt = \\ & \overset{\heartsuit}{=} 128\pi \int_{0}^{\frac{\pi}{3}} \cos^3 t \, \sin^2 t \, dt = \\ & = 128\pi \int_{0}^{\frac{\pi}{3}} \cos t \, (1 - \sin^2 t) \sin^2 t \, dt = \\ & = 128\pi \int_{0}^{\frac{\pi}{3}} \left(\cos t \sin^2 t - \cos t \sin^4 t\right) \, dt = \\ & = \frac{128}{15} \pi \left( 5\left(\frac{\sqrt{3}}{2}\right)^3 - 3\left(\frac{\sqrt{3}}{2}\right)^5 \right) = \\ & = \frac{128}{15} \pi \frac{3\sqrt{3}}{8} \left( 5 - \frac{9}{4} \right) = \\ & = \frac{16\sqrt{3}}{5} \pi \left(\frac{11}{4}\right) = \frac{44}{5} \pi\sqrt{3}, \end{aligned}$

dove $\heartsuit$ si sfrutta il fatto che $\vert \sin t \vert = \sin t$ per $t \in [0, \frac{\pi}{3}].$ Si conclude che

$\boxcolorato{analisi}{ \iiint_\mathcal{D } (x^2 + y^2) \, dx \, dy \, dz=\dfrac{44}{5}\pi\sqrt{3}. }$

Osservazione.

Si osserva che, sebbene questo secondo metodo conduca al medesimo risultato del primo, risulta meno agevole nella sua applicazione.

Esercizio 26 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Siano dati il cilindro di equazione $x^2+y^2=1$ e la sfera di equazione $x^2+y^2+z^2=R^2$ con $R>1$ . Il cilindro divide la sfera in due parti; determinare $R$ tale che le due parti abbiano misura uguale.

Svolgimento.

In figura 37 sono rappresentate le due porzioni in cui la sfera è suddivisa: una parte blu e una parte rossa.

$\quad$

Figura 37: rappresentazione delle due sezioni della sfera colorate di blu e rosso, che mostra come il volume totale viene suddiviso per calcolare i rispettivi integrali.

$\quad$

Il volume colorato di blu è dato dal seguente integrale

$\begin{aligned} \tau_{\text{blu}}=\iint_{x^2+y^2\leq1} dx\,dy \int_{-\sqrt{R^2-x^2-y^2}}^{\sqrt{R^2-x^2-y^2}}dz=2\iint_{x^2+y^2\leq 1}\sqrt{R^2-x^2-y^2}\,dx\,dy, \end{aligned}$

da cui, passando in coordinate polari, si ottiene

$\tau_{\text{blu}}=2\int_{0}^{2\pi}d\theta\int_{0}^{1}\rho\sqrt{R^2-\rho^2}\,d\rho.$

e operando la sostituzione $R^2-\rho^2=t$ , da cui $-2\rho\,d\rho=dt$ , abbiamo

$\tau_{\text{blu}}=-2\pi\int_{R^2}^{R^2-1}t^{\frac{1}{2}}\,dt=-2\pi\cdot \dfrac{2}{3}\,t^{\frac{3}{2}}\bigg\vert^{R^2-1}_{R^2}=\dfrac{4}{3}\pi\left( R^3-\sqrt{(R^2-1)^3}\right).$

Dalla geometria del problema, il volume in rosso si ottiene dalla seguente relazione

$\tau _{\text{rosso}}=\dfrac{4}{3}\pi R^3-V_{\text{blu}}.$

Imponiamo

$V_{\text{blu}}=V_{\text{rosso}},$

da cui

$\begin{aligned} 2\tau_{\text{blu}}=\dfrac{4}{3}\pi R^3\quad \iff \quad \dfrac{8}{3}\pi\left( R^3-\sqrt{(R^2-1)^3}\right)=\dfrac{4}{3}\pi R^3, \end{aligned}$

cioè

$R^3=2\sqrt{\left(R^2-1\right)^3}\quad \iff \quad R^2=\sqrt[3]{4}R^2-\sqrt[3]{4}\quad \iff \quad R^2=\dfrac{\sqrt[3]{4}}{\sqrt[3]{4}-1}\quad \iff \quad R=\dfrac{\sqrt[3]{2}}{\sqrt{\sqrt[3]{4}-1}}.$

Concludiamo con il seguente risultato

$\boxcolorato{analisi}{R=\dfrac{\sqrt[3]{2}}{\sqrt{\sqrt[3]{4}-1}} .}$

Esercizio 27 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare il volume del seguente insieme: $\mathcal{D}= \{(x, y, z) \in \mathbb{R}^3 : x^2 + y^2 \leq |z|, \ (z+1)^2 \leq 3 \}$ .

Svolgimento.

Utilizziamo le coordinate cilindriche:

$\begin{cases} x = \rho \cos\theta \\ y = \rho \sin\theta \\ z = t, \end{cases}$

dove

$\rho \in \left[ 0, \sqrt{|z|} \right], \ \theta \in [0, 2\pi], \ t \in \left[ -\sqrt{3} - 1, \sqrt{3} - 1 \right].$

\ Calcoliamo il volume:

$\tau = \int_{-\sqrt{3}-1}^{\sqrt{3}-1} \int_0^{2\pi} \int_0^{\sqrt{|z|}} \rho \, d\rho \, d\theta \, dt.$

Svolgendo i calcoli, abbiamo:

$\begin{aligned} \tau & = \int_{-\sqrt{3}-1}^{\sqrt{3}-1} 1 \, dt \int_0^{2\pi} 1 \, d\theta \int_0^{\sqrt{|t|}} \rho \, d\rho \\ & = 2\pi \int_{-\sqrt{3}-1}^{\sqrt{3}-1} \frac{1}{2} |t| \, dt =\\ & = \pi \int_{-\sqrt{3}-1}^{\sqrt{3}-1} |t| \, dt= \\ & = \pi \left( \int_{-\sqrt{3}-1}^{0} -t \, dt + \int_0^{\sqrt{3}-1} t \, dt \right)= \\ & = \pi \left( \frac{t^2}{2} \Bigg|_{-\sqrt{3}-1}^{0} + \frac{t^2}{2} \Bigg|_0^{\sqrt{3}-1} \right)= \\ & = \pi \left( \frac{0}{2} - \frac{(-\sqrt{3}-1)^2}{2} + \frac{(\sqrt{3}-1)^2}{2} \right)= \\ & = 2\pi \cdot \frac{1}{2} \cdot 4 = \\ &=4\pi. \end{aligned}$

Concludendo che

$\boxcolorato{analisi}{\tau=4\pi. }$

Esercizio 28 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare il volume del seguente insieme:

$\mathcal{D} = \{(x, y, z) \in \mathbb{R}^3 : x^2 + y^2 \leq |z|, (z + 1)^2 \leq 3\}.$

Svolgimento.

Calcoliamo i punti di intersezione tra le due curve che descrivono $\mathcal{D}$ :

$\left\{ \begin{aligned} &x^2 + y^2 \leq |z| \\ &(z + 1)^2 \leq 3 \end{aligned} \right. \quad \iff\quad \left\{ \begin{aligned} &x^2 + y^2 \leq |z| \\ &|z + 1| \leq \sqrt{3} \end{aligned} \right. \quad \iff\quad \left\{ \begin{aligned} &x^2 + y^2 \leq |z| \\ &-\sqrt{3} - 1 \leq z \leq \sqrt{3} - 1. \end{aligned} \right.$

Applicando le coordinate cilindriche, il volume $\tau$ cercato è:

$\tau = \int_{-\sqrt{3}-1}^{\sqrt{3}-1} dz \int_0^{2\pi} d\theta \int_0^{\sqrt{|z|}} \rho d\rho = \frac{2\pi}{2} \int_{-\sqrt{3}-1}^{\sqrt{3}-1} |z| dz = \pi \left( \int_{-\sqrt{3}-1}^{0} -z dz + \int_{0}^{\sqrt{3}-1} z dz \right) = 4\pi.$

Si conclude che

$\boxcolorato{analisi}{\tau =4\pi. }$

Esercizio 29 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolo del volume del seguente integrale triplo:

$\iiint_{\mathcal{D}} \frac{x^2}{x^2 + z^2} \, dx\,dy\,dz,$

dove

$\mathcal{D} = \{(x, y, z) \in \mathbb{R}^3 : 1 \leq x^2 + y^2 + z^2 \leq 2; \, x^2 - y^2 + z^2 \leq 0; \, y \geq 0 \}.$

Svolgimento.

Prima di tutto, determiniamo i punti di intersezione dei luoghi geometrici. Abbiamo:

$\begin{aligned} &\begin{cases} x^2 + y^2 + z^2 = 1 \\ x^2 + z^2 = y^2 \end{cases} \quad \iff \quad \begin{cases} x^2 + y^2 = \frac{1}{2} \\ y = \pm \frac{\sqrt{2}}{2}. \end{cases} \end{aligned}$

Proseguendo con il secondo sistema:

$\begin{aligned} &\begin{cases} x^2 + y^2 + z^2 = 2 \\ x^2 + z^2 = 1 \end{cases} \quad \iff \quad \begin{cases} x^2 + y^2 = 1 \\ y = \pm 1. \end{cases} \end{aligned}$

Sfruttando le coordinate cilindriche, l’integrale triplo diventa:

$\int_{\frac{1}{\sqrt{2}}}^{1} dt \int_{0}^{2\pi} d\theta \int_{\sqrt{1 - t^2}}^{1} \rho \cos^2\theta d\rho + \int_{1}^{\sqrt{2}} dt \int_{0}^{2\pi} d\theta \int_{0}^{\sqrt{2 - t^2}} \rho \cos^2\theta d\rho = I_1 + I_2,$

dove

$I_1 = \int_{\frac{1}{\sqrt{2}}}^{1} dt \int_{0}^{2\pi} d\theta \int_{\sqrt{1 - t^2}}^{1} \rho \cos^2\theta d\rho$

$I_2 = \int_{1}^{\sqrt{2}} dt \int_{0}^{2\pi} d\theta \int_{0}^{\sqrt{2 - t^2}} \rho \cos^2\theta d\rho.$

Calcoliamo

$\begin{aligned} I_1 &= \int_{\frac{1}{\sqrt{2}}}^{1} dt \int_{0}^{2\pi} d\theta \int_{\sqrt{1 - t^2}}^{1} \rho \cos^2\theta d\rho= \\ &= \int_{0}^{2\pi} \left( \frac{1 + \cos 2\theta}{2} \right) d\theta \int_{\frac{1}{\sqrt{2}}}^{1} \frac{1}{2} (t^2 - 1 + t^2) dt=\\ &= \frac{\pi}{2} \left(-\frac{1}{3} + \frac{1}{3}\sqrt{2}\right) \end{aligned}$

$\begin{aligned} I_2 &= \int_{1}^{\sqrt{2}} dt \int_{0}^{2\pi} d\theta \int_{0}^{\sqrt{2 - t^2}} \rho \cos^2\theta d\rho =\\ &= \frac{1}{2} \int_{0}^{2\pi} \left( \frac{1 - \cos 2\theta}{2} \right) d\theta \int_{1}^{\sqrt{2}} (2 - t^2) dt =\\ &= \frac{\pi}{2} \left( \frac{4\sqrt{2}}{3} - 2 - \frac{5}{3} \right). \end{aligned}$

Infine, otteniamo la seguente espressione finale:

$\frac{\pi}{2} \left( -\frac{1}{3} + \frac{1}{3}\sqrt{2} + \frac{4}{3}\sqrt{2} - 2 - \frac{5}{3} \right) = \frac{\pi}{2}\left(-2 + \frac{5}{6}\sqrt{2}) = \pi(-1 + \frac{5}{6}\sqrt{2}\right).$

Dunque, si conclude che

$\boxcolorato{analisi}{\iiint_{\mathcal{D}} \frac{x^2}{x^2 + z^2} \, dx\,dy\,dz=\pi\left(-1 + \frac{5}{6}\sqrt{2}\right). }$

Esercizio 30 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare

$\iiint_\mathcal{D} |x| \, dx \, dy \, dz,$

dove $\mathcal{D}= \{(x, y) : x^2 + y^2 + z^2 \leq 1, x^2 + y^2 \leq z^2\}$ , usando le coordinate sferiche.

Svolgimento.

Posto $f(x, y, z) = |x|$ , si osserva che $f(x, y, -z) = |x| = f(x, y, z)$ . Questo implica che la funzione è pari rispetto all’asse $z$ . Inoltre, poiché il dominio $\mathcal{D}$ è simmetrico rispetto al piano $xy$ , si ha:

$\iiint_\mathcal{D} |x| \, dx \, dy \, dz = 2 \iiint_{\tilde{\mathcal{D}}} |x| \, dx \, dy \, dz,$

dove

$\tilde{\mathcal{D}} = \{(x, y, z) \in \mathbb{R}^3 : x^2 + y^2 + z^2 \leq 1, \, x^2 + y^2 \leq z^2, \, z \geq 0\}.$

Parametrizziamo $\mathcal{D}$ utilizzando le coordinate sferiche definite da:

$\begin{cases} x = p \cos \theta \sin \varphi, \\ y = p \sin \theta \sin \varphi, \\ z = p \cos \varphi, \end{cases}$

con i seguenti intervalli per le variabili:

$0 \leq \theta \leq 2\pi, \quad 0 \leq \varphi \leq \frac{\pi}{4}, \quad 0 \leq p \leq 1.$

Il differenziale di volume in coordinate sferiche è dato da:

$dx \, dy \, dz = p^2 \sin \varphi \, d\theta \, d\varphi \, dp.$

Utilizzando queste informazioni, l’integrale diventa:

$\iiint_\mathcal{D} |x| \, dx \, dy \, dz = 2 \int_0^{2\pi} \int_0^{\frac{\pi}{4}} \int_0^1 p^3 \sin^2 \varphi |\cos \theta| \, dp \, d\varphi \, d\theta.$

Sfruttando la simmetria rispetto a $\theta$ , possiamo semplificare:

$\int_0^{2\pi} |\cos \theta| \, d\theta = 2 \int_0^{\frac{\pi}{2}} \cos \theta \, d\theta,$

quindi l’integrale diventa:

$\iiint_\mathcal{D} |x| \, dx \, dy \, dz = 8 \int_0^{\frac{\pi}{2}} \cos \theta \, d\theta \int_0^{\frac{\pi}{4}} \sin^2 \varphi \, d\varphi \int_0^1 p^3 \, dp.$

Calcoliamo ora ciascun integrale separatamente. Per $p$ , si ha:

$\int_0^1 p^3 \, dp = \left[ \frac{p^4}{4} \right]_0^1 = \frac{1}{4}.$

Per $\varphi$ , si ha:

$\int_0^{\frac{\pi}{4}} \sin^2 \varphi \, d\varphi = \int_0^{\frac{\pi}{4}} \frac{1 - \cos(2\varphi)}{2} \, d\varphi = \frac{1}{2} \int_0^{\frac{\pi}{4}} (1 - \cos(2\varphi)) \, d\varphi.$

Calcolando separatamente, otteniamo:

$\int_0^{\frac{\pi}{4}} 1 \, d\varphi = \frac{\pi}{4}, \quad \int_0^{\frac{\pi}{4}} \cos(2\varphi) \, d\varphi = \frac{\sin(2\varphi)}{2} \Big|_0^{\frac{\pi}{4}} = \frac{1}{2}.$

Pertanto:

$\int_0^{\frac{\pi}{4}} \sin^2 \varphi \, d\varphi = \frac{1}{2} \left( \frac{\pi}{4} - \frac{1}{2} \right).$

Per $\theta$ , si ha:

$\int_0^{\frac{\pi}{2}} \cos \theta \, d\theta = \sin \theta \Big|_0^{\frac{\pi}{2}} = 1.$

Combinando i risultati, si ottiene:

$\iiint_\mathcal{D} |x| \, dx \, dy \, dz = 8 \cdot 1 \cdot \left( \frac{\pi}{4} - \frac{1}{2} \right) \cdot \frac{1}{4}.$

Semplificando:

$\boxcolorato{analisi}{\iiint_\mathcal{D} |x| \, dx \, dy \, dz = \frac{1}{4} (\pi - 2). }$

Esercizio 31 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare il seguente integrale triplo

$\iiint_\mathcal{D} |z| \, dx \, dy \, dz,$

dove $\mathcal{D} = \{(x, y, z) \in \mathbb{R}^3 : x^2 + y^2 \leq z^2 - z^4 \}$ .

Svolgimento.

Si osserva che:

$z^2 - z^4 \geq 0 \quad \iff\quad z^4 - z^2 \leq 0 \quad \iff\quad -1 \leq z \leq 1.$

Introduciamo le coordinate cilindriche:

$\begin{cases} \begin{aligned} x &= \rho \cos \theta, \\ y &= \rho \sin \theta, \\ z &= z'. \end{aligned} \end{cases}$

dove

$\theta \in [0, 2\pi], \quad \rho \in \left[0, \sqrt{z'^2 - z'^4} \right], \quad z' \in [-1, 1].$

L’integrale così diventa:

$\begin{aligned} &\iiint_\mathcal{D} |z| \, dx \, dy \, dz = \\ &=\int_{-1}^{1} dz \int_0^{2\pi} d\theta \int_0^{\sqrt{z'^2 - z'^4}} |z'| \, \rho \, d\rho =\\ &= 2\pi \int_{-1}^{1} |z'| \left( \frac{(z'^2) - (z'^4)}{2} \right) dz' =\\ &= 4\pi \int_0^{1} z' \left( \frac{(z'^2) - (z'^4)}{2} \right) dz' =\\ &= 4\pi \int_0^1 z' \left( \frac{z'^2 - z'^4}{2} \right) dz' = \\ &=\frac{\pi}{6}. \end{aligned}$

Pertanto, la soluzione dell’integrale è:

$\boxcolorato{analisi}{\iiint_\mathcal{D} |z| \, dx \, dy \, dz = \frac{\pi}{6}. }$

Esercizio 32 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare l’integrale triplo:

$\iiint_{\mathcal{D}} (2z - x - y^3) \, dx \, dy \, dz,$

dove $\mathcal{D} = \{(x, y, z) \in \mathbb{R}^3 : 0 \leq z \leq x + 2, \, 6x - 8 \leq x^2 + y^2 \leq 4x \}$ .

Svolgimento.

Scegliamo di procedere integrando per fili:

$\begin{aligned} \iiint_\mathcal{D} (2z - x - y^3) \, dx \, dy \, dz &=\iint_B \left( \int_0^{x+2} (2z - x - y^3) \, dz \right) dx \, dy=\\ &= \iint_B \left( (x + 2)^2 - x(x + 2) - y^3(x + 2) \right) dx \, dy, \end{aligned}$

dove

$B = \{(x, y) \in \mathbb{R}^2 : 6x - 8 \leq x^2 + y^2 \leq 4x \}.$

Chiamiamo

$I_1 = \iint_B \left( (x + 2)^2 - x(x + 2) \right) dx \, dy = \iint_B g(x, y) \, dx \, dy,$

$I_2 = \iint_B \left( -y^3(x + 2) \right) dx \, dy = \iint_B f(x, y) \, dx \, dy.$

$\quad$

Rendered by QuickLaTeX.com

Figura 38: diagramma con due cerchi intersecanti su un piano cartesiano, utilizzato per determinare l’area dell’integrale doppio associato.

$\quad$

Si osserva che $I_2 = 0$ perché la funzione integranda $f$ è dispari rispetto alla variabile $y$ e $B$ è simmetrico rispetto all’asse $y$ .

Calcoliamo

$I_1 = \iint_B \left( (x + 2)^2 - x(x + 2) \right) dx \, dy = \iint_B 2(x + 2) \, dx \, dy = I_3 - I_4,$

$I_3 = \int_0^2 \int_0^{2\pi} 2\rho(p \cos \theta + 4) \, d\theta \, d\rho, \quad I_4 = \int_0^1 \int_0^{2\pi} 2\rho(p \cos \theta + 5) \, d\theta \, d\rho,$

$I_3 = \int_0^2 \int_0^{2\pi} 2\rho(p \cos \theta + 4) \, d\theta = \int_0^2 16\pi \rho \, d\rho = 32\pi,$

$I_4 = \int_0^1 \int_0^{2\pi} 2\rho(p \cos \theta + 5) \, d\theta = \int_0^1 20\pi \rho \, d\rho = 10\pi.$

Quindi

$I_1 = I_3 - I_4 = 32\pi - 10\pi = 22\pi.$

Si conclude che

$\boxcolorato{analisi}{\displaystyle\iiint_{\mathcal{D}} (2z - x - y^3) \, dx \, dy \, dz= 22\pi. }$

Esercizio 33 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Sia $\mathcal{D}$ la regione limitata nella parte superiore dalla sfera $x^2+y^2+z^2=a^2$ e nella parte inferiore dal piano $z=b$ , dove $a>b>0$ nell’ipotesi di densità costante: calcolare volume e baricentro di $\mathcal{D}$ .

Svolgimento.

La regione in considerazione è:

$\mathcal{D}=\{(x,y,z) \in \mathbb{R}^3 \; \vert \; x^2+y^2+z^2 \leq a^2, \; z\geq b, \; a>b>0 \}.$

Il volume di $\mathcal{D}$ è dato dal seguente integrale, calcolato integrando per fili:

$\begin{aligned} \tau &= \iiint_\mathcal{D} \, dx \, dy \, dz = \\ &= \iint_{x^2+y^2\leq a^2-b^2} \left(\int_{b}^{\sqrt{a^2-x^2-y^2}} dz \right) dx \, dy = \\ &= \iint_{x^2+y^2\leq a^2-b^2} \left(\sqrt{a^2-x^2-y^2}-b \right) dx \, dy. \end{aligned}$

Applicando le coordinate polari:

(32) $\begin{equation*} \begin{cases} x = \rho \cos \theta, \\ y = \rho \sin \theta, \end{cases} \end{equation*}$

dove

$\rho \in [0, \sqrt{a^2-b^2}], \; \theta \in [0, 2\pi],$

l’integrale diventa:

$\begin{aligned} & \int_{0}^{\sqrt{a^2-b^2}} d\rho \int_{0}^{2\pi} \left(\sqrt{a^2-\rho^2} - b \right) \rho \, d\theta = \\ &= 2\pi \int_{0}^{\sqrt{a^2-b^2}} \left(\rho \sqrt{a^2-\rho^2} - b\rho \right) d\rho = \\ &= \frac{\pi}{3} \left(2a^3 - 3a^2b + b^3 \right) = \\ &= \frac{\pi}{3} \left(a-b \right)^2 \left(2a+b \right). \end{aligned}$

Calcoliamo il baricentro. La definizione di baricentro, assumendo una densità volumetrica costante, è:

$\overline{r} = \frac{1}{\tau}.$

Sia $\overline{F} = (f_x, f_y, f_z) = (x, y, z)$ . Si osserva che:

$\iiint_\mathcal{D} f_x \, dx \, dy \, dz = \iiint_\mathcal{D} f_y \, dx \, dy \, dz = 0,$

poiché $f_x$ è dispari rispetto a $x$ e $\mathcal{D}$ è simmetrico rispetto al piano $yz$ , e $f_y$ è dispari rispetto a $y$ con $\mathcal{D}$ simmetrico rispetto al piano $xz$ .

Non resta dunque che calcolare:

$\overline{r} = \frac{1}{\tau} \iiint_\mathcal{D} (0, 0, z) \, dx \, dy \, dz.$

Procediamo integrando per fili:

$\begin{aligned} & \iint_{x^2+y^2\leq a^2-b^2} \left(\int_{b}^{\sqrt{a^2-x^2-y^2}} z \, dz \right) dx \, dy = \\ &= \frac{1}{2} \iint_{x^2+y^2\leq a^2-b^2} \left(a^2-x^2-y^2-b^2 \right) dx \, dy. \end{aligned}$

Applicando nuovamente le coordinate polari (32), otteniamo:

$\begin{aligned} & \frac{1}{2\tau} \iint_{x^2+y^2\leq a^2-b^2} \left(a^2-x^2-y^2-b^2 \right) dx \, dy = \\ &= \frac{1}{2\tau} \int_{0}^{\sqrt{a^2-b^2}} \left(\int_{0}^{2\pi} \left(a^2-b^2-\rho^2 \right)\rho \, d\theta \right) d\rho = \\ &= \frac{\pi}{\tau} \int_{0}^{\sqrt{a^2-b^2}} \rho \left(a^2-b^2-\rho^2 \right) d\rho = \\ &= \frac{\pi}{4\tau} \left(a^2-b^2 \right)^2 = \\ &= \frac{3\left(a+b \right)^2}{4 \left(2a+b \right)}. \end{aligned}$

Quindi

$\boxcolorato{analisi}{\frac{1}{2 \tau}\iint_{x^2+y^2\leq a^2-b^2}\left(a^2-x^2-y^2-b^2\right) \, dx \, dy= \frac{3\left(a+b\right)^2}{4 \left(2a+b\right)}. }$

Esercizio 34 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare la massa di un cilindro circolare retto di raggio a e altezza b, nell’ipotesi che la densità vari come il quadrato della distanza da un punto della circoferenza di base.

Svolgimento.

Rappresentiamo il dominio descritto dal testo dell’esercizio in figura 39.

$\quad$

Rendered by QuickLaTeX.com

Figura 39: rappresentazione di un cilindro con densità variabile, dove la distanza di un punto generico $P(x,y,z)$ dalla circonferenza di base viene utilizzata per calcolare la massa del solido.

$\quad$

Fissiamo il punto sulla circonferenza di coordinate $A=(a,0,0)$ e calcoliamo la distanza tra un generico punto $B=(x,y,z)$ del cilindro ed $A$ :

$r^2=k((x-a)^2+y^2+z^2) \quad \text{con k }\in \mathbb{R}.$

Dalle condizioni imposte per determinare la massa totale del cilindro possiamo imporre il seguente integrale di volume:

$M=k\int_{0}^{b}dz\iint_{x^2+y^2\leq a^2}\left( (x-\text{a})^2+y^2+z^2 \right)dx\,dy .$

Applichiamo le coordinate polari

$M=\int_{0}^{b}dz\int_{0}^{2\pi}d\theta\int_{0}^{a}\left((\rho \cos\theta-\text{a})^2+\rho^2 (\sin \theta)^2+z^2 \right)d\rho$

Dopo semplici passaggi si ottiene che la massa è pari ad

$\boxcolorato{analisi}{M=\frac{\pi k}{6}\text{a}^2 \text{b}\left(9\text{a}^2+2\text{b}^2\right). }$

Esercizio 35 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Dato il solido generato dalla rotazione della figura piana

$\mathcal{D}=\{(x,y,z)\in \mathbb{R}^3 : x=0, 0\le z \le \alpha^2-y^2\}.$

Trovare i valori di $\alpha>0$ tale per cui il solido abbia baricentro $(0,0,1)$ .

Svolgimento.

Dalla definizione di $\mathcal{D}$ , e considerando la condizione $0 \leq z \leq \alpha^2 - y^2$ , la figura piana da ruotare è definita dalla parabola di equazione $z = \alpha^2 - y^2$ e dalla retta $x = 0$ .

Per simmetria, le coordinate $\bar{x}$ e $\bar{y}$ del baricentro sono nulle. Rimane quindi da determinare la coordinata $\bar{z}$ , data da:

$\bar{z} = \dfrac{\iiint_\mathcal{D} z \, dx \, dy \, dz}{\iiint_\mathcal{D} dx \, dy \, dz}.$

Poiché l’insieme $\mathcal{D}$ è un solido di rotazione, possiamo applicare il teorema di Guldino (per i richiami teorici, si veda l’esercizio ex15), ottenendo:

$\iiint_\mathcal{D} dx \, dy \, dz = \int_0^{\alpha^2} \pi (\alpha^2 - z) \, dz = \pi \alpha^4 - \pi \left[\dfrac{z^2}{2}\right]_0^{\alpha^2} = \pi \dfrac{\alpha^4}{2}.$

Analogamente, per il numeratore dell’espressione di $\bar{z}$ :

$\iiint_\mathcal{D} z \, dx \, dy \, dz = \int_0^{\alpha^2} \pi z (\alpha^2 - z) \, dz = \pi \alpha^2 \left[\dfrac{z^2}{2}\right]_0^{\alpha^2} - \pi \left[\dfrac{z^3}{3}\right]_0^{\alpha^2}.$

Calcolando i termini:

$\iiint_\mathcal{D} z \, dx \, dy \, dz = \pi \dfrac{\alpha^6}{2} - \pi \dfrac{\alpha^6}{3} = \pi \dfrac{\alpha^6}{6}.$

In conclusione, la coordinata $\bar{z}$ del baricentro è:

$\bar{z} = \dfrac{\iiint_\mathcal{D} z \, dx \, dy \, dz}{\iiint_\mathcal{D} dx \, dy \, dz} = \dfrac{\pi \dfrac{\alpha^6}{6}}{\pi \dfrac{\alpha^4}{2}} = \dfrac{\alpha^2}{3}.$

Quindi

$\boxcolorato{analisi}{\alpha=\sqrt{3}. }$

Esercizio 36 $(\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)$ . Calcolare il volume del solido

$\mathcal{D}=\left\lbrace (x,y,z)\in\mathbb{R}^3 : (x-\sin(y))^2+z^2\le \sin^2\left(\frac{y}{2}\right)\right\rbrace.$

Svolgimento.

Consideriamo il piano $y = y_0$ , con $y_0 \in [0, 2\pi]$ . L’intersezione di tale piano con il dominio del solido $E$ definisce l’insieme dei punti interni al cerchio dato da:

$E_y = \left\{ (x, z) \in \mathbb{R}^2 \ : \ (x - \sin(y_0))^2 + z^2 \leq \sin^2\left(\frac{y_0}{2}\right) \right\}.$