0 Elementi

Esercizi sulla verifica dei limiti 23

Verifica del limite in funzioni

Home » Esercizi sulla verifica dei limiti 23

Presentiamo nel seguito i richiami di teoria utili allo svolgimento dell’esercizio. Per richiami più completi si veda la dispensa richiami di teoria.

Definizione 1 (limiti di funzioni) 
Sia A \subseteq \mathbb{R}, sia x_0 \in \overline{\mathbb{R}} un punto di accumulazione per A, sia f \colon A \to \mathbb{R} una funzione e sia \ell \in \overline{\mathbb{R}}. Si dice che \ell è il limite di f per x che tende a x_0 se, per ogni intorno V di \ell, esiste un intorno U di x_0 tale che

(1)   \begin{equation*} f(x) \in V \qquad \forall x \in U \cap A \setminus \{x_0\}. \end{equation*}

In tal caso si scrive

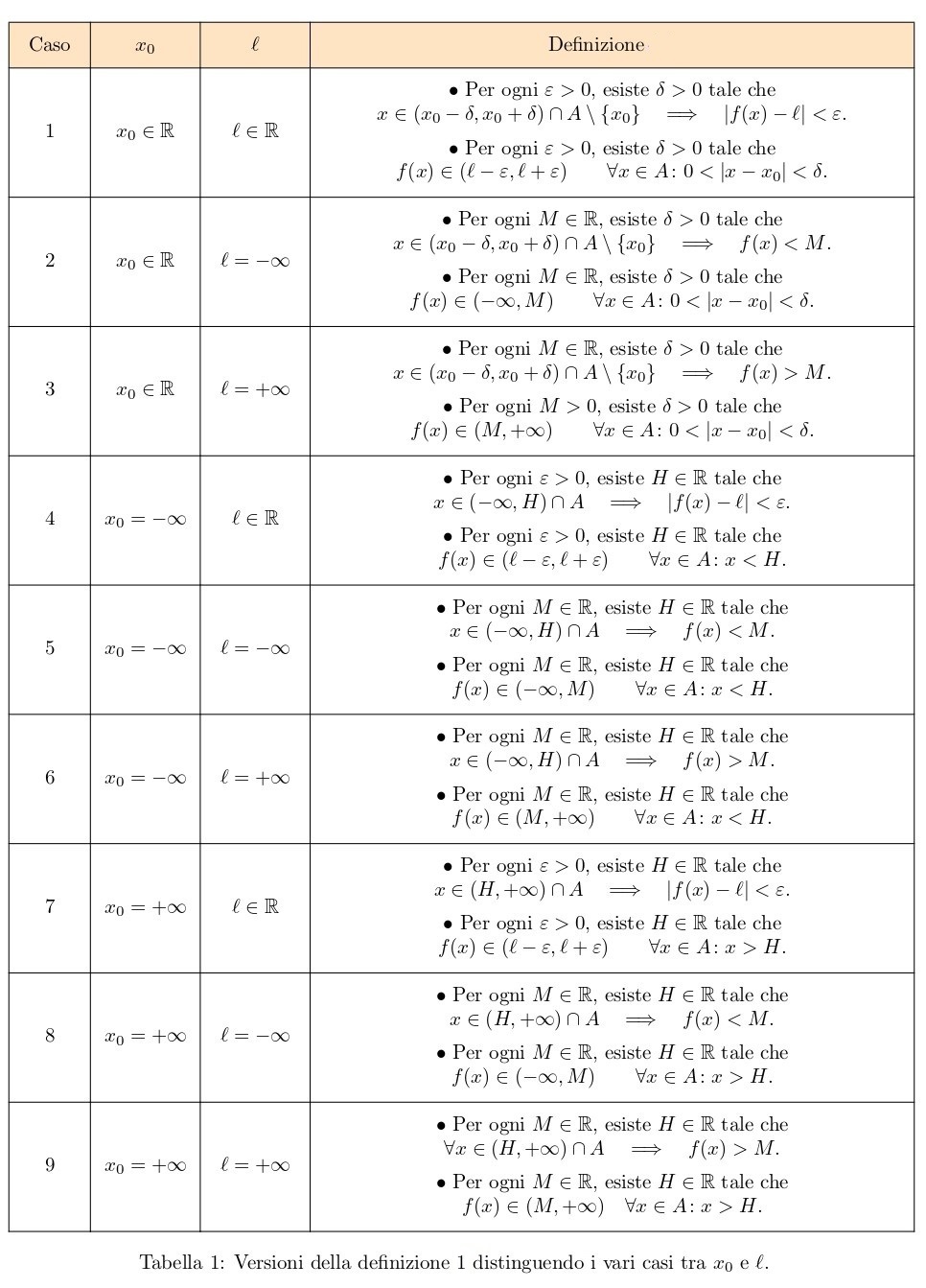
(2)   \begin{equation*} \lim_{x \to x_0} f(x) = \ell. \end{equation*}

Risulta utile vedere come si scrive esplicitamente la definizione 1 suddividendo le casistiche in cui x_0 \in \mathbb{R}, x_0 = -\infty, x_0=+\infty e \ell \in \mathbb{R}, \ell = -\infty, \ell=+\infty.

 

Testo dell’esercizio

Esercizio 23  (\bigstar\bigstar\bigstar\largewhitestar\largewhitestar).
Verificare, mediante la definizione, il seguente limite:

    \begin{equation*} \lim_{x \to 0} x \sin \left ( \frac{1}{x} \right ) = 0. \end{equation*}

 

Svolgimento .
Occorre verificare che valga la condizione al punto 1 della tabella 1 con x_0=\ell=0 e f \colon \mathbb{R} \setminus \{0\} \to \mathbb{R} definita da

(3)   \begin{equation*} f(x) = x \sin \left ( \frac{1}{x} \right ) \qquad \forall x \neq 0, \end{equation*}

il cui grafico è rappresentato in figura 23.
Anche se x_0=0 non appartiene al dominio di f, è un punto di accumulazione per esso e quindi il limite richiesto è significativo. Fissiamo quindi \varepsilon>0. Abbiamo

(4)   \begin{equation*} |f(x)-\ell|< \varepsilon \iff \left | x \sin \left ( \frac{1}{x} \right ) \right | < \varepsilon \impliedby |x|< \varepsilon, \end{equation*}

dove nell’ultima implicazione si è usato il fatto che |\sin t|\leq 1 per ogni t \in \mathbb{R} e dunque, se |x|< \varepsilon, allora \left | x \sin \left ( \frac{1}{x} \right ) \right |< \varepsilon.
Scegliendo quindi \delta=\varepsilon, si ha

(5)   \begin{equation*} x \in (-\varepsilon,\varepsilon) \setminus \{0\} \implies |f(x)|< \varepsilon, \end{equation*}

cioè la tesi.

Figura 23: la funzione f (in blu) dell’esercizio 23 e il suo confronto con le funzioni x \mapsto \pm|x| (in verde). Scegliendo \delta=\varepsilon, si vede che |x|< \varepsilon e x \neq 0 implicano |f(x)|< \varepsilon.

error: Il contenuto è protetto!!