Benvenuti nella nostra soluzione completa alla seconda prova di Matematica dell’Esame di Maturità 2025!
In questo articolo analizziamo ciascun problema e quesito della prova di Matematica e ne forniamo una soluzione completa, costituita da spiegazioni dettagliate e grafici esplicativi. Di alcuni punti offriamo più soluzioni distinte, in modo da favorire l’apprendimento e il confronto del lettore anche con metodi diversi da quelli usuali.
L’articolo è in particolare rivolto agli studenti che hanno affrontato la seconda prova di Matematica dell’Esame di Maturità, che desiderano confrontare i propri svolgimenti con delle soluzioni chiare, ma anche ad appassionati e a studenti delle classi inferiori, per i quali questo materiale può essere un utile supporto nella loro preparazione ai loro futuri esami.
Non ti resta che proseguire la lettura e scoprire come risolvere tutti i problemi e i quesiti della seconda prova di Matematica dell’Esame di Maturità 2025!
Segnaliamo anche tutto il materiale della sezione Scuola Superiore, per reperire tantissimo materiale di supporto al tuo studio.
Buona lettura!
Sommario
Leggi...
Autori e revisori
Leggi...
Revisori: Valerio Brunetti, Sergio Fiorucci, Daniele Volpe.
Traccia e svolgimento
- Verificare che
è continua ma non derivabile in
qualunque sia il valore di
.
Individuare i due valori di
in corrispondenza dei quali
delimita con il grafico di
, per opportuni valori di
, un settore circolare nel semipiano
di area
e contorno di lunghezza
.
Stabilito che
è il maggiore di tali valori, in uno stesso riferimento cartesiano
, tracciare la circonferenza
e il grafico della funzione
.
- Studiare la funzione
, specificandone dominio, simmetrie, punti di non derivabilità, intervalli di monotonia ed insieme immagine.
Verificare che il grafico di
coincide con la parte di
che si trova nel semipiano
.
Spiegare perché
non è invertibile nel suo dominio ed esplicitare l’intervallo
di ampiezza massima, con
, nel quale
ammette una funzione inversa
.
Qual è l’espressione analitica di
?
- Sia
un punto del grafico di
, situato nel I quadrante, e siano
e
le sue proiezioni ortogonali sugli assi di riferimento. Determinare le coordinate di
in modo che il quadrilatero
abbia area massima.
Dopo aver verificato che tale quadrilatero è un quadrato, dimostrare che è anche quello di perimetro massimo.
- Si consideri la funzione
con
. Determinare
e tracciare un grafico di
, dopo averne studiato monotonia e concavità.
Scrivere, inoltre, l’equazione della retta tangente al grafico di
nel suo punto di flesso.
Svolgimento.
Svolgimento punto 1.
(1)
Nella figura 1 rappresentiamo in blu il grafico di una delle funzioni .
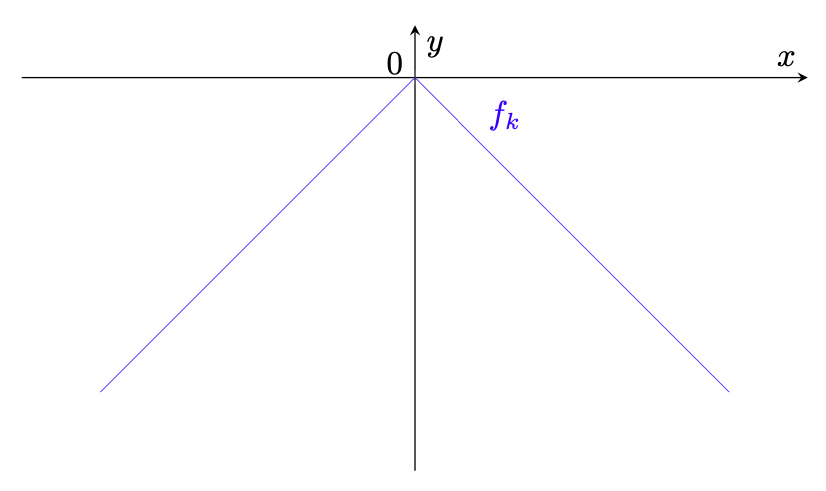
Figura 1: il grafico di una funzione .
- Fissiamo ora un qualunque
. Basandosi sulle note proprietà del valore assoluto, si può asserire che
è continua ma non derivabile in
, essendo un multiplo non nullo della funzione
, che è continua ma non derivabile in
.
In questa sede preferiamo però dimostrare queste proprietà in maniera dettagliata. Dall’espressione di
in (1), si può agevolmente verificare che essa è continua in
. Infatti
(2)
e, dall’uguaglianza dei limiti destro e sinistro, segue
(3)
Poiché ovviamente
, ne segue che la funzione è continua.
Verifichiamo ora che
non è derivabile in
. A tal fine, calcoliamo la derivata destra e sinistra di
in questo punto e mostriamo che esse sono diverse:
(4)
dove nella seconda uguaglianza abbiamo sfruttato (1). Invece, per la derivata sinistra si ha
(5)
Poiché la derivata destra e la derivata sinistra sono diverse (in quanto
visto che
),
non è derivabile in
. Più precisamente, poiché le derivate esistono, sono finite ma diverse,
presenta un punto angoloso in
.
- Rappresentiamo ora in figura 2 la circonferenza
(in verde) insieme al grafico della funzione
(in blu) ed evidenziamo in rosso il settore circolare che esamineremo in questo punto.
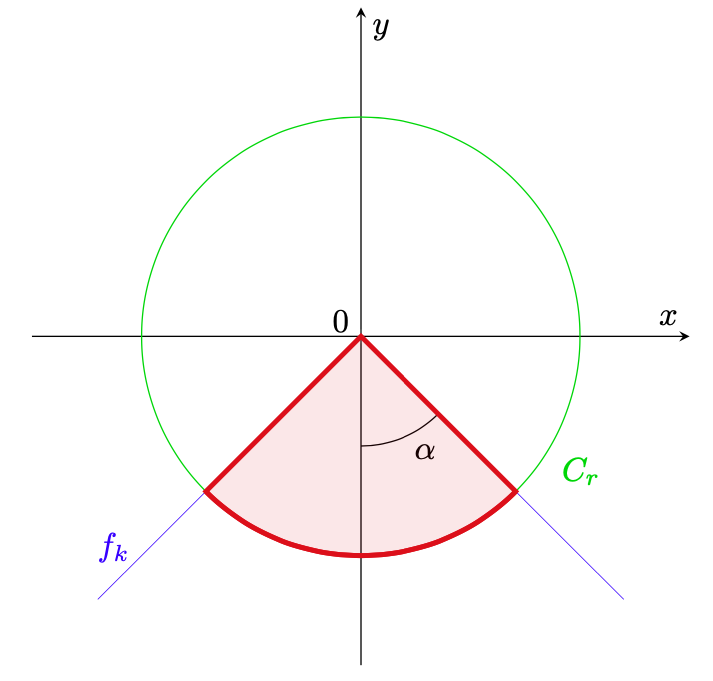
Figura 2: il grafico di una funzione
in blu, una circonferenza
in verde, mentre in rosso è evidenziato il settore circolare in esame.
Poiché il settore circolare è determinato dall’angolo al centro
dipendente dal parametro
(si veda la figura 2), la lunghezza dell’arco di circonferenza che lo delimita si ricava in proporzione alla lunghezza dell’intera circonferenza, mediante il fattore di proporzionalità
. Lo stesso si può dire dell’area del settore circolare che mantiene lo stesso fattore di proporzionalità con l’area dell’intero cerchio.
In particolare, lunghezza
dell’arco di cerchio che delimita in basso il settore è pari a
(6)
Di conseguenza, il perimetro
della regione considerata è pari alla somma di
con la lunghezza dei due raggi che costituiscono la rimanente parte del contorno:
(7)
L’area
della figura può essere ricavata in proporzione all’area totale del cerchio
in base all’angolo
determinato dal settore circolare:
(8)
Imponendo, secondo i dati del problema, che
e
, si ottiene il sistema
(9)
Dalla seconda equazione si ricava
e, sostituendo nella prima, otteniamo
(10)
Scrivendo il coefficiente di primo grado come
, si vede che due numeri il cui prodotto è
e la cui somma è
sono appunto
e
. Ne segue che le soluzioni dell’equazione sono
(11)
Alternativamente le soluzioni possono essere ricavate con la classica formula risolutiva per le equazioni di secondo grado.
Sostituendo ciascuno di tali valori nel sistema (9), si ottiene rispettivamente
(12)
- Poiché
, si ha
e quindi il maggiore tra i due raggi è
. Si osservi che il valore
a esso corrispondente si ottiene proprio quando il grafico di
è la bisettrice del secondo e del quarto quadrante, ovvero per
. Rappresentiamo dunque
e
in un grafico in figura 3.
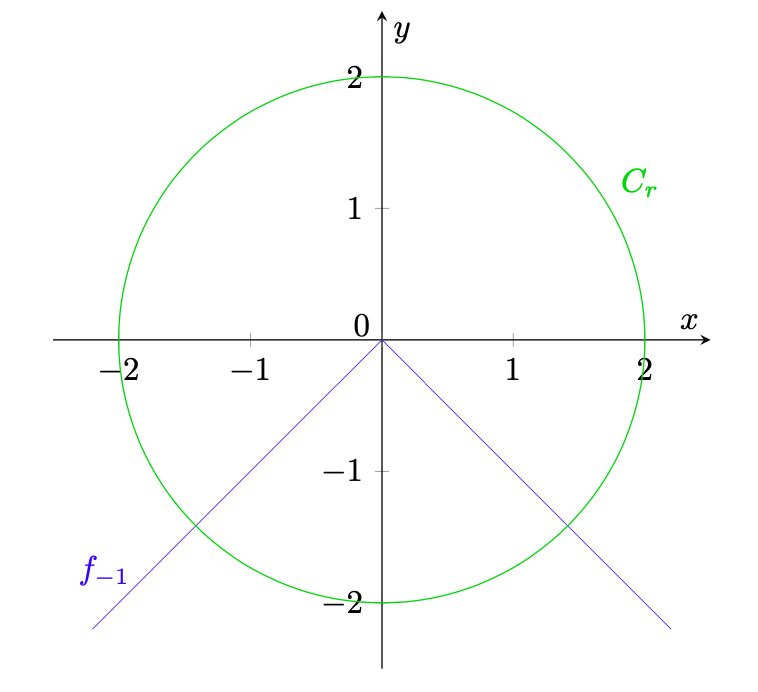
Figura 3: il grafico di
insieme alla circonferenza
.
Svolgimento punto 2.
- La funzione
(13)
è definita per i valori della
che rendono maggiore o uguale a
l’argomento della radice quadrata:
(14)
Ne segue che il dominio
della funzione
è
(15)
è, in tale intervallo, somma e composizione di funzioni continue, dunque è una funzione continua. Osserviamo inoltre che essa è una funzione pari:
(16)
La funzione
è derivabile per ogni
. Poiché
è composizione di un polinomio (derivabile per ogni
) e della funzione radice quadrata, per il teorema di derivazione delle funzioni composte
è derivabile per ogni
tale che
. Poiché
se e solo se
, ciò mostra che
è derivabile in
(17)
Inoltre lo stesso teorema afferma che la derivata di
in tale insieme è pari a
(18)
Rimane da studiare la derivabilità di
nei punti
. Per la parità di
è sufficiente studiare il punto
, in cui si ha
(19)
dove nell’ultimo passaggio abbiamo notato che il numeratore della frazione tende a
, mentre il denominatore tende a
assumendo però valori positivi. Poiché il limite della derivata per
esiste ed è infinito, per un noto teorema conseguenza del teorema di Lagrange [1, teorema 3.6] si ha che
non è derivabile in
. Per la parità di
, essa non è derivabile nemmeno per
.
Osserviamo che l’espressione di
ricavata in (18) assicura che
(20)
in quanto il denominatore della frazione è positivo per ogni
essendo il risultato di una radice quadrata, mentre il numeratore è positivo per
e negativo per
. Da tale segno della derivata e dalla continuità di
, segue che
è strettamente crescente in
e strettamente decrescente nell’intervallo
.
Da ciò segue che i punti
sono di minimo assoluto per
, mentre il punto
è di massimo assoluto per
. In particolare l’immagine
soddisfa
(21)
Poiché
è una funzione continua sull’intervallo
, per il teorema dei valori intermedi essa assume tutti i valori compresi tra
e
e quindi la precedente inclusione è in realtà un’uguaglianza:
(22)
Rappresentiamo il grafico di
nella figura 4.
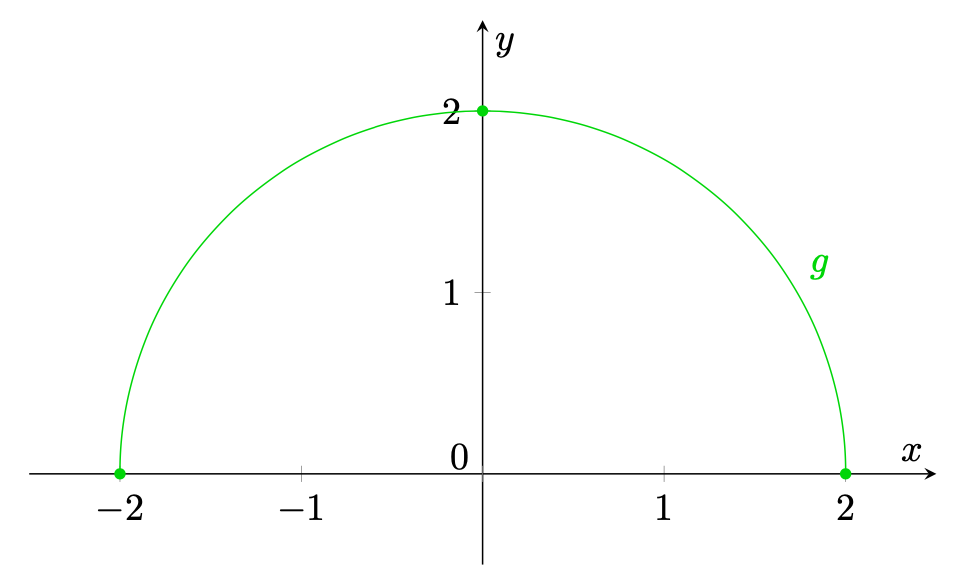
Figura 4.
- Il grafico di
è chiaramente situato nel semipiano
, in quanto la radice quadrata assume valori non-negativi, ed è costituito da tutti e soli i punti
del piano cartesiano che soddisfano l’equazione
(23)
Eleviamo ambo i membri al quadrato, tenendo traccia delle condizioni
e
. Dunque tale equazione è equivalente al sistema
(24)
Poiché la condizione
è implicata dalla prima (se fosse
, si averebbe
), il sistema è equivalente a
(25)
che è proprio l’equazione della semicirconferenza di centro l’origine e raggio
situata nel semipiano
.
- La funzione
non è invertibile nel suo dominio
in quanto non è iniettiva: ad esempio
(26)
ovvero esistono due punti distinti che hanno la stessa immagine. In generale, poiché
per ogni
nel dominio,
non è iniettiva, come tutte le funzioni pari.
Essendo però
strettamente decrescente in
, la sua restrizione a tale intervallo in particolare è iniettiva. L’immagine di tale intervallo è pari a
in quanto la funzione
è pari e
, dunque sulla parte positiva del dominio l’immagine è la stessa.
Quindi la restrizione
di
è iniettiva e suriettiva, dunque biunivoca e pertanto è invertibile.
L’intervallo
considerato ha chiaramente ampiezza
. Consideriamo ora un intervallo
avente ampiezza strettamente maggiore di
, ovvero tale che
, con
. Dunque, da
, deve aversi
. Si scelga
abbastanza piccolo in modo che
. Poiché
è pari, si ha
(27)
Quindi
non è iniettiva nell’intervallo
e pertanto non può essere invertibile in questo intervallo.
Ne segue che
non è invertibile in nessun intervallo di ampiezza strettamente maggiore di
, cioè che l’intervallo
in cui
è invertibile ha ampiezza massima.
Osserviamo infine che tale intervallo è l’unico che soddisfa i requisiti della traccia. Infatti, per un altro intervallo
di ampiezza
con
diverso da
si avrebbe necessariamente
e quindi
. Con lo stesso ragionamento di sopra, si dimostra che
non è iniettiva in tale intervallo.
- L’espressione dell’inversa
di
si ricava ponendo
ed esplicitando la
in funzione di
nell’espressione di
:
(28)
Ponendo
, l’espressione di
è data da
(29)
e coincide cioè con l’espressione di
.
Svolgimento punto 3.
- Dato che il punto
appartiene al grafico di
, le sue coordinate sono
, con
. Dunque il rettangolo
ha lati di lunghezza
e
. Ne segue che la sua area è
(30)
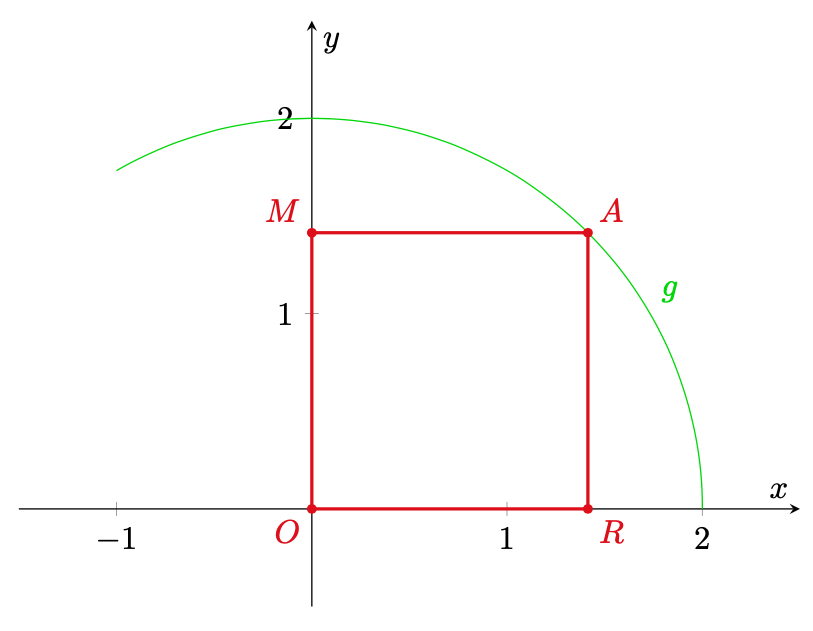
Figura 5: un quadrilatero
.
Poiché il grafico di
è costituito da una semicirconferenza centrata nell’origine e di raggio
, si ha
, ovvero la media quadratica tra
e
è costante in
e pari a
(31)
Per la disuguaglianza tra media geometrica e quadratica [2], quest’ultima è sempre maggiore o uguale alla media geometrica, che è pari proprio a
; l’uguaglianza si verifica se e solo se i due termini sono uguali. Imponendo
si ricava
(32)
Dunque il punto
che soddisfa i requisiti richiesti ha coordinate
. Poiché la diagonale
è sulla bisettrice del primo quadrante, il quadrilatero
è un quadrato.
Allo stesso risultato si può pervenire studiando la funzione
che fornisce l’area del quadrilatero al variare di
, osservando che la sua derivata è pari a
(33)
che è positiva per
e negativa per
. Dunque
ha un punto di massimo per
. Poiché
, come sopra si vede che
è un quadrato.
- Il perimetro del quadrilatero
è pari a
(34)
Si può seguire un approccio simile a quello di sopra, sostituendo però la media geometrica con quella aritmetica tra
e
, pari a
: la media quadratica tra
e
è costantemente pari a
e la media aritmetica è sempre minore o uguale a quella quadratica, con l’uguaglianza valida se e solo se
. Dunque il perimetro
assume il valore massimo
se e solo se
.
Alternativamente, studiamo la funzione
calcolandone la derivata:
(35)
che si vede essere appunto positiva per i punti dell’intervallo
in cui
e negativa per i punti dell’intervallo
in cui
. Dunque
assume valore massimo per il punto
che soddisfa
, cioè
.
Svolgimento punto 4.
- Il valore
è, per il significato geometrico dell’integrale definito, l’area (con segno) sottesa al grafico di
nell’intervallo
. Dato che il grafico di
delimita, insieme all’asse
, una semicirconferenza di raggio
nel semipiano
, il valore di tale area è
(36)
Alternativamente, era possibile determinare esplicitamente una primitiva di
mediante la sostituzione
:
(37)
dove nella quarta uguaglianza abbiamo usato la formula di bisezione del coseno e nel penultimo passaggio abbiamo usato
. Tale espressione esplicita di
, calcolata per
, fornisce ugualmente
(38)
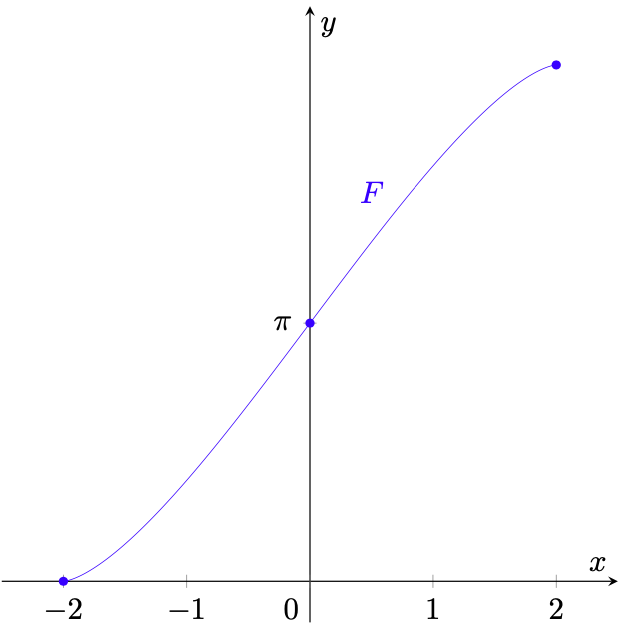
Figura 6: il grafico della funzione
.
- Si ha ovviamente
e, poiché
, vale
per ogni
.
Poiché
è continua in
, per il teorema fondamentale del calcolo integrale
è derivabile in tale intervallo e si ha
(39)
Dato che
per
e
è continua in
, essa è strettamente crescente in
.
La derivata seconda di
è dunque pari alla derivata prima di
; pertanto
è derivabile due volte in
e si ha
(40)
Come nello studio di
, si vede che essa è positiva per
e negativa per
, dunque
è convessa nell’intervallo
e concava nell’intervallo
, ovvero possiede un flesso in
, tale che
. Ciò consente di tracciare un grafico approssimativo di
, riportato in figura 6.
- Il punto di flesso ha coordinate
e la retta tangente al grafico di
in tale punto ha quindi equazione
(41)
Poiché
, l’equazione richiesta è
(42)
(43)
con e
polinomi di secondo grado.
- determinare i polinomi
e
, utilizzando le informazioni deducibili dai grafici in figura, considerando che
è ascissa di un punto stazionario di
e che
, ascissa del punto
, è uno zero di
.
- Posto che
, studiare la funzione
specificando l’equazione dell’asintoto, le ascisse dei punti stazionari e di flesso.
Verificare che la retta di equazione
è asse di simmetria per
.
Determinare l’immagine di
e indicare, al variare del parametro reale
, il numero di soluzioni dell’equazione
.
- Stabilito altresì che
, verificare che
è l’ulteriore zero di
e che il triangolo
è rettangolo.
Dimostrare che
e
hanno un unico punto di intersezione, del quale si chiedono le coordinate.
Considerati su
e
, rispettivamente, i punti
e
aventi uguale ascissa
, calcolare la lunghezza massima che può assumere il segmento
.
- Calcolare l’area della regione limitata
compresa tra
,
e l’asse delle ordinate.
Individuare, successivamente, il valore
affinché la retta
delimiti con i due grafici una regione
equivalente ad
.
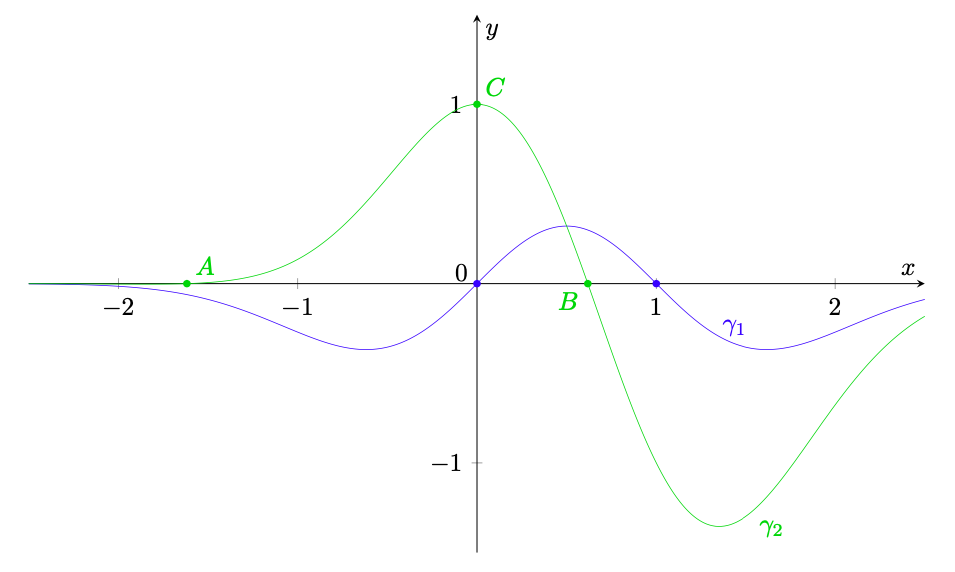
Figura 7: i grafici e
del problema 2.
Svolgimento punto 1.
(44)
con e
(altrimenti i polinomi non sarebbero di secondo grado).
- Cominciamo col determinare i coefficienti
di
. Osserviamo innanzitutto che il grafico
passa per l’origine, dunque
(45)
Dato che inoltre
passa per il punto
si ha
(46)
Sfruttiamo infine l’informazione che
ha un punto stazionario per
. Si ha
(47)
dove nell’ultima uguaglianza abbiamo inserito la condizione
ricavata prima. Affinché
, almeno uno dei fattori nell’ultimo membro deve essere nullo per
. Dato che
, l’esponenziale è sempre positivo e
si annulla per
(coerentemente col grafico), l’unico fattore che può annullarsi per
è
. Imponendo tale condizione si ottiene
(48)
Si conclude quindi che
, ovvero che
(49)
- Determiniamo ora
. Sappiamo che
passa per il punto
, per cui
e quindi
(50)
Il punto
è inoltre un punto stazionario di
. Calcoliamo
:
(51)
Imponendo che
si ha
(52)
Inoltre dalla condizione
si ottiene
(53)
Dunque
(54)
Svolgimento punto 2.
- Dato che
è il prodotto di un polinomio e di un esponenziale il cui esponente è un polinomio, essa è definita per ogni
.
è inoltre continua in
essendo prodotto e composizione di funzioni continue.
Poiché il fattore
è sempre positivo, il segno di
è uguale al segno di
:
(55)
(56)
dove l’ultima uguaglianza segue dal fatto che, sebbene
, il limite del prodotto è nullo, a causa dell’esponenziale tendente a
. Infatti, scriviamo il limite come
(57)
Esso presenta una forma indeterminata
, che può essere risolta ad esempio mediante l’applicazione del teorema di De l’Hopital; calcoliamo cioè il limite del rapporto tra le derivate del numeratore e del denominatore:
(58)
Dato che tale limite vale
, anche il limite in (56) vale
.
In maniera identica si prova (ma si veda anche la simmetria di
provata al punto successivo) che
(59)
Dunque la retta di equazione
è l’asintoto orizzontale di
per
.
Studiamo ora la derivata di
, che è derivabile in
essendo il prodotto e la composizione di funzioni derivabili. Sostituendo
in (47) si ottiene
(60)
Il fattore
è positivo per ogni
. Invece
(61)
e, risolvendo la disequazione
, si vede che gli zeri del polinomio sono
e dunque
(62)
In definitiva
(63)
Dunque
è strettamente crescente negli intervalli
e
e strettamente decrescente negli intervalli complementari. Il punto
è di massimo relativo, mentre i punti
sono di minimo relativo per
.
Osserviamo ora che tali punti sono di massimo/minimo assoluto per
. Infatti, nell’intervallo
,
è strettamente crescente e quindi
(64)
Analogamente dalla monotonia di
segue
(65)
Osservando che
, nuovamente la monotonia di
implica che essa assume valori maggiori nell’intervallo
. Concludiamo quindi che i punti
sono di minimo assoluto per
.
Analogamente si dimostra che
è di massimo assoluto per
: infatti per la monotonia di
esso è il massimo assoluto di
nell’intervallo
. Poiché nel complementare di tale intervallo vale
,
è di massimo assoluto per
sull’intero dominio
.
Calcoliamo ora la derivata seconda di
, che è derivabile due volte essendo il prodotto e la composizione di funzioni derivabili due volte. Conviene a tal fine scrivere
(66)
svolgendo i prodotti dei polinomi. Derivando questa espressione si ha
(67)
per ogni
. Si vede che il polinomio di terzo grado si annulla per
e dunque è divisibile per il polinomio
. Effettuando la divisione (mediante l’algoritmo classico o applicando la regola di Ruffini) si ottiene
(68)
Osserviamo che
(69)
dunque le radici del polinomio sono
(esse potevano anche essere ricavate mediante la classica formula) e ciò implica che
(70)
Tenendo conto che
se e solo se
ed effettuando il prodotto dei segni, si ottiene
(71)
La funzione
è convessa in ciascuno degli intervalli in cui
e concava in ognuno degli intervalli in cui
.
Le ascisse dei punti di flesso sono
(72)
- Sottraendo e aggiungendo
all’espressione di
osserviamo che
(73)
Si vede dunque che
è simmetrica rispetto all’asse
. Più precisamente, si ha
(74)
dunque
. Dato che
, vale
(75)
provando così la simmetria di
.
- Dal fatto che i punti
sono di minimo assoluto, mentre il punto
è di massimo assoluto, si ha
(76)
Ciò dimostra che
. Dato che
è una funzione continua nell’intervallo
, per il teorema dei valori intermedi, essa assume tutti i valori compresi tra
e
, pertanto
(77)
- Il punto precedente mostra che l’equazione
possiede soluzioni se e solo se
.
– Se
, occorre determinare il numero di punti
in cui
assume il suo valore minimo. Sappiamo già che vi sono esattamente due punti di minimo assoluto per
.
– Supponiamo ora
. Per il segno di
e tenendo conto dei punti di minimo assoluto, possono esistere soluzioni solo negli intervalli
(78)
Dato che
è strettamente monotona in ciascuno di questi intervalli, può esistere al più una soluzione in ognuno di essi. Proviamo che ne esiste almeno una in ogni intervallo.
Dato che
, esiste un punto
tale che
. Per il teorema dei valori intermedi applicato a
nell’intervallo
, esiste almeno un punto
in cui
.
Analogamente si dimostra che esiste una soluzione nell’intervallo
.
Inoltre, da
(79)
in virtù del teorema dei valori intermedi esiste una soluzione dell’equazione
in
. Allo stesso modo si prova che esiste un’altra soluzione in
.
Conludiamo che, per tali valori di
, esistono esattamente
soluzioni.
– Se
, occorre determinare il numero degli zeri di
. Sappiamo già che
possiede i soli due zeri
e
.
– Se
, per il teorema dei valori intermedi applicato all’intervallo
, esiste almeno una soluzione
dell’equazione
in tale intervallo. Tale soluzione è l’unica nell’intervallo per la stretta monotonia di
. Allo stesso modo, o per simmetria rispetto a
, esiste esattamente un’altra soluzione nell’intervallo
. Non esistono altre soluzioni in quanto
nel complementare di
. Dunque il numero di soluzioni per questo caso è
.
– Se
, occorre determinare il numero di punti di massimo assoluto di
, che sappiamo essere uno solo.
Svolgimento punto 3.
- Si ha
(80)
dunque
(81)
Per verificare che
è un triangolo rettangolo, calcoliamo i quadrati delle lunghezze dei lati:
(82)
Invece per
e
usiamo il teorema di Pitagora:
(83)
Si ha
(84)
Poiché la somma dei quadrati delle lunghezze di
e
è pari al quadrato della lunghezza di
, per l’inverso del teorema di Pitagora il triangolo
è rettangolo in
.
Alternativamente, si possono ricavare i coefficienti angolari delle rette
e
e verificare che il loro prodotto è pari a
. Il coefficiente angolare della retta
è pari al rapporto tra le differenze delle ordinate con le differenze delle ascisse:
(85)
Allo stesso modo si calcola il coefficiente angolare della retta
:
(86)
Ovviamente il loro prodotto è pari a
e quindi le rette
e
sono ortogonali.
- I punti di intersezione tra
e
si ottengono imponendo
, ovvero
(87)
Dunque l’unico punto di intersezione tra i due grafici ha ascissa
. Sappiamo già qual è l’ordinata corrispondente a tale punto, essendo di massimo per
. Dunque l’intersezione tra i grafici ha coordinate
(88)
- Dato che i punti
e
hanno uguale ascissa, la lunghezza del segmento verticale
è pari a
(89)
Il quesito è quindi equivalente a determinare il valore massimo di
per
. Poiché sappiamo che non vi sono intersezioni tra i grafici di
e di
oltre a
, si ha
per
, dunque è sufficiente determinare il valore massimo di
(90)
Da
(91)
si ha
(92)
Dato che il fattore
è sempre positivo, il segno di tale derivata dipende solo dal polinomio di secondo grado. Poiché le sue radici sono
e il coefficiente di secondo grado è negativo, il polinomio è positivo per
e negativo negli intervalli aperti complementari. Dato che
, osserviamo che
è crescente nell’intervallo
e decrescente nell’intervallo
. Dunque il punto
(93)
è di massimo assoluto per
nell’intervallo
. Ne segue che il valore massimo per la lunghezza del segmento
si ottiene in corrispondenza di tale ascissa. La lunghezza richiesta è
(94)
Svolgimento punto 4.
- La regione
è la porzione dei punti del piano aventi ascissa compresa tra
e
e delimitata dall’alto da
e dal basso da
, in quanto in tale intervallo
. Dunque l’area di
è l’integrale definito
(95)
Il fattore
è la derivata dell’esponente dell’esponenziale, dunque l’integrale è immediato:
(96)
dove nella prima uguaglianza abbiamo usato il teorema fondamentale del calcolo integrale.
- Analogamente, ricordando che per
si ha
, l’area di
è data dall’integrale definito
(97)
Imponendo che le due aree siano uguali, è necessario e sufficiente che
, ovvero
, da cui
(98)
in quanto la soluzione
non è maggiore di
.
Svolgimento.
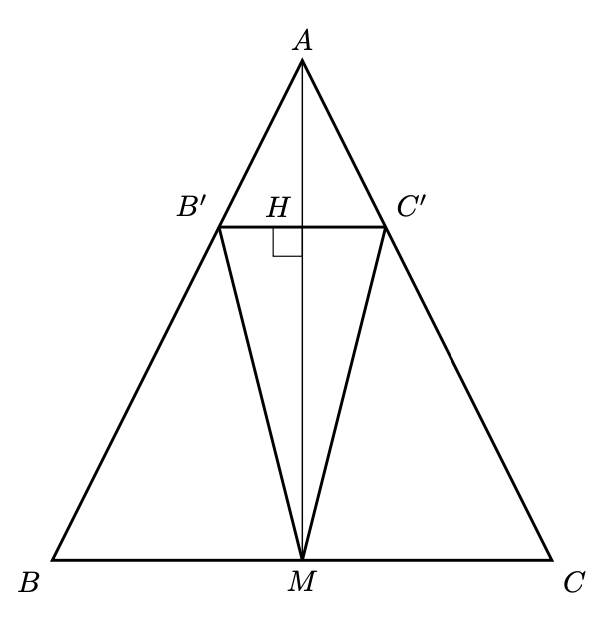
Figura 9: rappresentazione grafica della soluzione al quesito 1.
Il triangolo è simile al triangolo
avendo congruente l’angolo in
e i due lati tra cui è compreso in proporzione di
. Dunque il segmento
è parallelo al segmento
.
Dalla similitudine dei triangoli e
, segue che la mediana
passa anche per il punto medio di
, che indichiamo con
.
Assumiamo ora, come richiesto dalla traccia, che i segmenti e
siano congruenti. Se ne deduce che il triangolo
è isoscele rispetto alla base
. La mediana
di tale triangolo relativa a
è dunque anche altezza.
Dato che il segmento è perpendicolare a
e dal fatto che
è parallelo a
, concludiamo che
, e quindi
, è perpendicolare anche a
. Pertanto
è anche l’altezza del triangolo
e ciò prova che esso è isoscele rispetto alla base
in quanto la mediana e l’altezza a esse relative coincidono.
Si conclude quindi che il segmento è congruente al segmento
.
Svolgimento.
Un modo molto rapido di procedere è quello di calcolare la distanza tra il piano di equazione
e il centro
della sfera mediate la formula
(99)
e valutare se questa distanza è minore, uguale o maggiore al raggio della sfera per stabilire se il piano è rispettivamente secante, tangente o esterno a essa.
In questa sede preferiamo mostrare un’altra strategia, a essa equivalente: l’idea che seguiremo non utilizza la formula (99), che potrebbe non essere nota o sfuggire allo studente, ma si basa sul ragionamento geometrico seguente, che contiene sostanzialmente la dimostrazione della formula (99).
Un vettore normale al piano
è dato dalla terna dei coefficienti di
,
e
, dunque
(100)
La retta passante per il centro della sfera e parallela a
interseca il piano
nel suo punto
avente minima distanza da
. In base al confronto tra la distanza
tra
e
e il raggio
della sfera, si determina agevolmente la posizione reciproca dei due oggetti:
- se tale distanza è strettamente minore di
, il piano è secante alla sfera;
- se
,
è tangente alla sfera;
- se invece
, allora il piano è esterno alla sfera.
Cominciamo col determinare le coordinate di . La retta
passante per
parallela a
ha equazioni parametriche
(101)
Per calcolare l’intersezione col piano, si sostituiscono tali espressioni nell’equazione di :
(102)
Sostituendo tale valore di nelle equazioni parametriche di
si ottengono le coordinate del punto
:
(103)
Ora che abbiamo le coordinate di , possiamo calcolare la distanza tra
e il centro
della sfera. E’ più semplice calcolare il quadrato di tale distanza, con l’usuale formula
(104)
Osserviamo che
(105)
Dunque il piano è secante alla sfera per questi valori del parametro
. Imponendo
, in maniera analoga si vede che il piano è tangente alla sfera per
(106)
e che il piano è esterno alla sfera se oppure se
.
Infine, affinché il piano divida la sfera esattamente a metà, è necessario e sufficiente che esso passi per il suo centro . Ciò si può ad esempio imporre sostituendo le coordinate di
nell’equazione del piano e risolvendo rispetto a
:
(107)
Lo stesso risultato si ottiene imponendo che , dovendo cioè annullare il parametro
.
(108)
Tracciare il grafico di , dopo averne analizzato la continuità e la derivabilità nell’intervallo
.
Svolgimento.
La funzione data da è continua e derivabile in ogni punto in cui è definita, essendo somma e composizione di funzioni continue e derivabili.
Affinché essa sia definita, è necessario e sufficiente che l’argomento della tangente sia diverso da
, con
. Ricordando che la definizione di
utilizza questa espressione per
, verifichiamo che per tali valori di
l’argomento della tangente appartiene all’intervallo
. Osserviamo infatti che
(109)
dove l’ultima disuguaglianza è dovuta al fatto che e quindi
. Ciò prova che l’argomento della tangente appartiene all’intervallo
per ogni
e dunque anche il ramo destro della funzione
è ben definito per ogni
. Ne consegue che
è continua e derivabile in
.
Rimane da studiare la continuità e la derivabilità di in
.
Tenendo conto che ogni polinomio è appunto continuo in , segue che
(110)
mentre si ha
(111)
Dato che i limiti sinistro e destro di in
coincidono e sono pari a
, ne segue che
è continua in
.
La derivabilità dei polinomi in tutto il dominio implica che la derivata sinistra di in
sia pari alla derivata del polinomio
calcolata in
:
(112)
Anche la funzione è derivabile in
e dunque la sua derivata in tale punto coincide con la derivata destra di
in
:
(113)
Ciò poteva anche essere ottenuto calcolando il limite destro in della derivata di
e applicando il noto teorema secondo cui il limite destro della derivata, se esiste, è pari alla derivata destra della funzione [1, teorema 3.6]:
(114)
Poiché la derivata destra e sinistra esistono finite ma non coincidono, non è derivabile in
e possiede un punto angoloso.
Il grafico di si può quindi ottenere osservando che la parte per
è pari al grafico della tangente traslato verso l’alto di un’unità e verso sinistra di
. Invece la parte a sinistra è una parabola che può essere conveniente riscrivere come
(115)
ossia la parabola di equazione moltiplicata per un fattore
e traslata verso l’alto di
. Il grafico di
è rappresentato in figura 10.
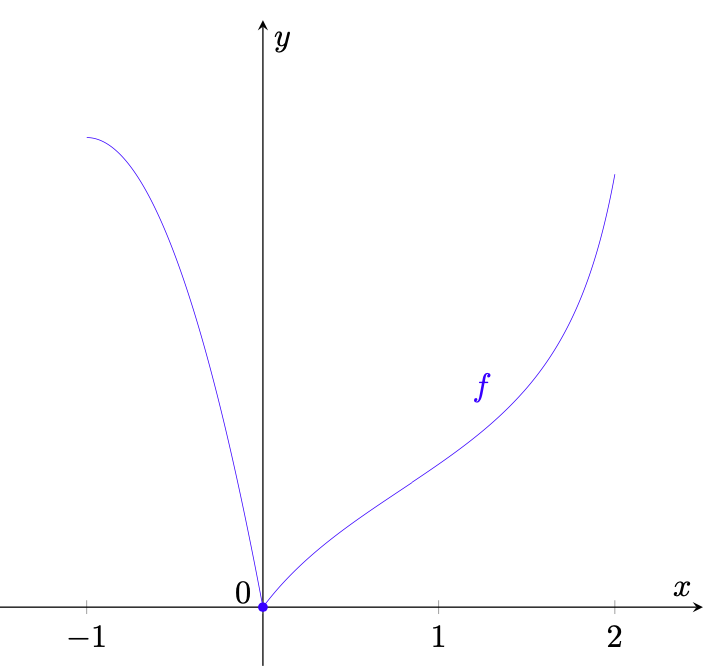
Figura 10: il gradico della funzione .
Svolgimento.
(116)
Calcoliamo ora la derivata di :
(117)
dunque
(118)
Il coefficiente angolare della retta perpendicolare al grafico di è dunque pari all’opposto del reciproco di tale derivata, ovvero a
.
Da tali informazioni si risale all’equazione richiesta:
(119)
Svolgimento.
(120)
in quanto devono passare per lo stesso punto di ascissa e avere stessa retta tangente in tale punto, ovvero stessa derivata.
Dunque un eventuale punto
di tangenza deve soddisfare il sistema
(121)
dove nel primo passaggio abbiamo sostituito la seconda equazione nella prima e nel secondo abbiamo risolto e sostituito nella seconda equazione, in quanto
.
Dato che il sistema impostato ha soluzione solo per e per
, ne segue che le due curve date sono tangenti se e solo se
nel punto di ascissa
. L’ordinata del punto di tangenza si calcola sostituendo tale valore nell’espressione di una delle due curve, ottenendo che il punto di tangenza ha coordinate
(122)
Svolgimento.
(123)
con . La retta di equazione
passa per il punto
e dunque, affinché essa sia tangente al grafico di
per
, è necessario che anche il grafico di
ci passi, ovvero
(124)
Inoltre, affinché la stessa retta sia effettivamente tangente al grafico di , la derivata
deve essere pari al coefficiente angolare della stessa retta, ovvero
(125)
Rimane da imporre il vincolo sull’integrale di :
(126)
da cui . Una funzione richiesta è dunque
(127)
Osservazione.
Il fatto che non esistano soluzioni di grado inferiore poteva essere dedotto anche a priori.
Osserviamo infatti che una funzione costante (ossia polinomiale di grado ) non può soddisfare il requisito sulla retta tangente, in quanto il suo grafico è una retta orizzontale e quindi in nessun punto la sua retta tangente è obliqua, come quella di equazione
.
Analogamente, una funzione polinomiale del tipo ha come retta tangente in ogni suo punto la retta
stessa. Dunque l’unica funzione polinomiale di grado
che soddisfi il requisito sulla retta tangente è
. Purtroppo essa non soddisfa il requisito sull’integrale, in quanto
(128)
Il ragionamento proposto nella soluzione dimostra che ne esiste una sola di grado pari a ; si può vedere che ne esistono infinite aventi grado superiore.
- la probabilità di ottenere il colpo di Venere nel lancio di
dadi;
- la probabilità di ottenere
numeri tutti uguali.
Svolgimento.
- Ogni serie di
lanci può essere pensata come una quaterna (ordinata) di numeri compresi tra
e
. Tali quaterne sono tutte equiprobabili. Contando le quaterne favorevoli e dividendo per il numero di quaterne possibili (
), si ottiene la probabilità richiesta.
- La seconda strategia si basa sull’immaginare di effettuare
lanci in sequenza dello stesso dado. Per ciascun lancio, si calcola la probabilità delle condizioni che devono verificarsi, al fine di ottenere il risultato desiderato. Poiché i lanci sono tra loro indipendenti, il prodotto di tali probabilità fornisce la probabilità richiesta.
- Osserviamo che si ottiene il colpo di Venere se gli esiti dei quattro lanci sono una permutazione dei numeri
,
,
,
, che sono in numero
, si veda anche il quesito successivo. Dunque la probabilità che si verifichi tale evento è pari al rapporto
(129)
Seguiamo ora la seconda strategia. Affinché si verifichi il colpo di Venere, il primo lancio è favorevole qualsiasi sia il valore ottenuto, dunque con probabilità
.
Il secondo lancio è favorevole se e solo se si ottiene uno dei
valori diversi da quello ottenuto al primo lancio. Dato che gli esiti di un lancio sono equiprobabili, il secondo lancio è favorevole con probabilità
.
Assumendo il secondo lancio favorevole, il terzo lancio è favorevole se e solo se si ottiene uno dei
valori diversi dai
ottenuti al primo e al secondo lancio, dunque è favorevole con probabilità
.
Assumendo secondo e terzo lancio favorevole, sono già usciti
dei
valori possibili. Il quarto lancio è quindi favorevole se e solo se si ottiene l’unico valore non ancora uscito, ovvero con probabilità
.
Moltiplicando le
probabilità, si ottiene che il colpo di Venere avviene con probabilità
(130)
- Anche a questa domanda si può rispondere contando i casi favorevoli ed effettuando il rapporto sui
casi possibili. Infatti, si ottiene l’evento richiesto se e solo se gli esiti sono una stringa di
numeri uguali:
,
, etc., che sono in numero di
. Dividendo per i
casi possibili si ottiene che la probabilità di ottenere
lanci uguali è
(131)
Mostriamo ora la seconda strategia. Come sopra, il primo lancio può assumere qualsiasi esito, ovvero è favorevole con probabilità
.
Se si desidera che i quattro lanci diano tutti lo stesso risultato, allora il secondo è favorevole se e solo se dà lo stesso esito del primo, e ciò avviene con probabilità
.
Analogamente, il terzo e il quarto lancio sono favorevoli ciascuno con probabilità
.
Moltiplicando tra loro le probabilità, si ottiene che
lanci con lo stesso risultato si verificano con probabilità
(132)
In quanti di tali anagrammi si può leggere consecutivamente la parola “ARTE”, come ad esempio in “SUARTEDI”?
Quanti sono gli anagrammi, anche senza significato, della parola “VACANZA”?
Svolgimento.
- Un anagramma della parola “STUDIARE” è costituito da un riordinamento delle sue lettere, che sono in numero di
, tutte diverse tra loro. È noto che il numero delle permutazioni di un insieme di
elementi è pari a
, ma in questa sede mostriamo come giungere al risultato in maniera diretta.
La prima lettera dell’anagramma può essere qualunque lettera della parola, dunque può venire scelta in
modi diversi. Per ciascuno di questi
modi, la seconda lettera può essere scelta tra le rimanenti
, dunque in
modi diversi. Ne segue che le prime due lettere dell’anagramma possono essere scelte in
modi diversi.
Per ciascuno di essi, la terza lettera può essere scelta in
modi diversi.
Continuando con tale ragionamento si completa l’anagramma, che può essere effettuato in
(133)
modi distinti.
- La stringa “ARTE” può essere posizionata in
posizioni diverse all’interno dell’anagramma, ovvero con la lettera “A” al primo, al secondo, al terzo, al quarto o al quinto posto.
Per ciascuna di queste
scelte (che danno luogo ad anagrammi diversi), i posizionamenti delle rimanenti
lettere si ottengono in maniera univoca ordinandole. Come visto al punto precedente, tali riordinamenti sono
. Dunque il numero degli anagrammi che contengono la parola “ARTE” è pari al prodotto
(134)
- Nella parola “VACANZA” le consonanti sono tutte e
diverse, mentre le
vocali “A” sono uguali. Supponiamo per un attimo che le tre “A” siano distinte tra loro, ovvero chiamiamole
,
e
.
Per lo stesso ragionamento fatto al primo punto, gli anagrammi della parola “V
C
NZ
” sono
(135)
In questo computo abbiamo considerato diversi gli anagrammi
(136)
che invece rappresentano la stessa parola. Abbiamo cioè contato ciascun anagramma tante volte quanti sono i modi di ordinare le tre lettere
,
e
. Poiché tali modi sono
, per ottenere il numero giusto di anagrammi occorre dividere il numero
per tale “molteplicità” di ogni anagramma. Il numero di anagrammi reale della parola “VACANZA” è quindi
(137)
Riferimenti bibliografici
[1] Qui Si Risolve, Derivate: Teoria.
[2] Wikipedia, Disuguaglianze tra le medie.
Risorse didattiche aggiuntive per approfondire la matematica
Leggi...
- Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
- Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
- MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
- PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
- Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
- The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
- Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
- Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
- Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
- Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.
