Piano cartesiano e retta: esercizi

Home » Piano cartesiano e retta: esercizi

Autori e revisori

Leggi...

Testi degli esercizi

Esercizio 1 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Determinare il perimetro e l’area del triangolo $ABC$ di vertici $A(1,2), \, B(-1,0)$ e $C(3,0)$ .

Svolgimento.

Rappresentiamo il triangolo sul piano cartesiano

Rendered by QuickLaTeX.com

Figura 1: rappresentazione triangolo.

Per determinare il perimetro abbiamo bisogno della misura dei lati AB, BC e AC, dunque con la formula della distanza tra due punti nel piano cartesiano

$d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

abbiamo

$\begin{aligned} & AB = \sqrt{(x_A-x_B)^2+(y_A-y_B)^2} = \sqrt{(1+1)^2+(0-2)^2} = \sqrt{8} = 2\sqrt{2}\\ & BC = \sqrt{(x_C-x_B)^2+(y_C-y_B)^2} = \sqrt{(3+1)^2+(0)^2} = 4\\ & AC = \sqrt{(x_A-x_C)^2+(y_A-y_C)^2} = \sqrt{(1-3)^2+(2-0)^2} = \sqrt{8} = 2\sqrt{2} \end{aligned}$

per cui il perimetro è

$P = AB + BC + AC = 2\sqrt{2} + 4 + 2\sqrt{2} = 4 + 4\sqrt{2}.$

Per calcolare l’area, prendiamo BC come base e quindi l’altezza da trovare è AH come disegnato nel grafico seguente

Rendered by QuickLaTeX.com

Figura 2: rappresentazione altezza $AH$ .

quindi è necessario calcolare la distanza tra il punto A e l’asse delle ascisse che è facilmente $y_A = 2$ . Dunque l’area del triangolo è

$\boxcolorato{superiori}{A = \dfrac{BC \cdot AH}{2} = \dfrac{4 \cdot 2}{2} = 4.}$

Esercizio 2 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Determinare il perimetro e l’area del triangolo $ABC$ di vertici $A(-1,-1), \, B(2,-1)$ e $C(-3,1)$ .

Svolgimento.

Rappresentiamo il triangolo sul piano cartesiano

Rendered by QuickLaTeX.com

Figura 3: rappresentazione triangolo.

Per determinare il perimetro abbiamo bisogno della misura dei lati AB, BC e AC, dunque con la formula della distanza tra due punti nel piano cartesiano

$d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

abbiamo

$\begin{aligned} & AB = \sqrt{(x_A-x_B)^2+(y_A-y_B)^2} = \sqrt{(-1-2)^2+(-1+1)^2} = \sqrt{9} = 3\\ & BC = \sqrt{(x_C-x_B)^2+(y_C-y_B)^2} = \sqrt{(-3-2)^2+(-1-1)^2} =\sqrt{29} \\ & AC = \sqrt{(x_A-x_C)^2+(y_A-y_C)^2} = \sqrt{(-1+3)^2+(-1-1)^2} = \sqrt{8} = 2\sqrt{2} \end{aligned}$

per cui il perimetro è

$P = AB + BC + AC = 3 + \sqrt{29} + 2\sqrt{2}.$

Per calcolare l’area, prendiamo AB come base e quindi l’altezza da trovare è CH come disegnato nel grafico seguente

Rendered by QuickLaTeX.com

Figura 4: rappresentazione altezza $CH$ .

quindi è necessario calcolare la distanza tra il punto A e il prolungamento della base AB ma essendo un segmento verticale facilmente abbiamo $CH = \vert y_c - y_a \vert = \vert 1+1 \vert = 2$ . Dunque l’area del triangolo è

$\boxcolorato{superiori}{A = \dfrac{AB \cdot CH}{2} = \dfrac{3 \cdot 2}{2} = 3.}$

Esercizio 3 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ .Determinare l’estremo $B$ del segmento $AB$ noto l’estremo $A(-1,3)$ e il punto medio $M(4,5)$ di $AB$ .

Svolgimento.

Le coordinate del punto medio di un segmento di estremi $A$ e $B$ si ricavano come segue

$M \left(\dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2}\right)$

dunque

$x_M = \dfrac{x_A+x_B}{2} \quad \Rightarrow \quad x_B =2x_M - x_A = 2 \cdot 4 - (-1) = 9$

$y_M = \dfrac{y_A+y_B}{2} \quad \Rightarrow \quad y_B =2y_M - y_A = 2 \cdot 5 - 3 = 7$

quindi

$\boxcolorato{superiori}{B(9,7).}$

Esercizio 4 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Determinare il punto medio del segmento AB di estremi $A(1,-8)$ e $B(1,-2)$ .

Svolgimento.

Le coordinate del punto medio di un segmento di estremi $A$ e $B$ si ricavano come segue

$M \left(\dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2}\right)$

dunque

$x_M = \dfrac{x_A+x_B}{2} = \dfrac{1+1}{2} = 1$

$y_M = \dfrac{y_A+y_B}{2}= \dfrac{-8-2}{2} = -5$

quindi

$\boxcolorato{superiori}{M \left(1,-5\right).}$

Esercizio 5 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ .Scrivere l’equazione della retta passante per il punto $A(0,2)$ e avente coefficiente angolare $m=3$ .

Svolgimento.

Utilizziamo l’equazione del fascio di rette passante per un punto

$y-y_A = m(x-x_A),$

da cui

$y - 2 = 3(x-0) \quad \Rightarrow \quad y - 2 = 3x.$

Dunque

$\boxcolorato{superiori}{ y = 3x + 2.}$

Esercizio 6 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ .Scrivere l’equazione della retta passante per il punto $A(-1,3)$ e avente coefficiente angolare $m=\dfrac{1}{2}$ .

Svolgimento.

Utilizziamo l’equazione del fascio di rette passante per un punto

$y-y_A = m(x-x_A),$

da cui

$y - 3 = \dfrac{1}{2}(x+1) \quad \Rightarrow \quad y - 3 = \dfrac{1}{2}x + \dfrac{1}{2} \quad \Rightarrow \quad y = \dfrac{1}{2}x + 3 + \dfrac{1}{2}.$

Quindi

$\boxcolorato{superiori}{y = \dfrac{1}{2}x + \dfrac{7}{2}.}$

Esercizio 7 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Scrivere l’equazione della retta passante per i punti $A(-4,-1)$ e $B(3,2)$ .

Svolgimento.

Per scrivere l’equazione della retta passante per $A$ e per $B$ calcoliamo dapprima il coefficiente angolare di tale retta

$m = \dfrac{\Delta y}{\Delta x} \overset{*}{=} \dfrac{y_B-y_A}{x_B-x_A} = \dfrac{2+1}{3+4} = \dfrac{3}{7}$

dove in $*$ potevamo anche scambiare l’ordine delle coordinate, cioè fare

$m = \dfrac{y_A-y_B}{x_A-x_B} = \dfrac{-1-2}{-4-3} = \dfrac{-3}{-7} = \dfrac{3}{7}$

ottenendo un risultato equivalente.

Adesso che abbiamo ottenuto il coefficiente angolare $m$ , scriviamo il fascio di rette passante per $A$ o per $B$ (la scelta è indifferente!); noi scegliamo $A$ ottenendo

$\begin{aligned} & y-y_A = m (x-x_A) \quad \Rightarrow \quad y-(-1) = \dfrac{3}{7}(x-(-4)) \quad \Rightarrow \quad y+1 = \dfrac{3}{7} (x+4) \quad \Rightarrow \quad \\ & \quad \Rightarrow \quad y= \dfrac{3}{7}x + \dfrac{12}{7}-1, \end{aligned}$

da cui

$\boxcolorato{superiori}{y = \dfrac{3}{7}x + \dfrac{5}{7}.}$

Si puo’ facilmente vedere che scegliendo il punto $B$ si ottiene lo stesso risultato:

$y-2 = \dfrac{3}{7} (x-3) \quad \Rightarrow \quad y = \dfrac{3}{7}x - \dfrac{9}{7} + 2,$

da cui

$\boxcolorato{superiori}{y = \dfrac{3}{7}x + \dfrac{5}{7}.}$

Esercizio 8 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Dire se i seguenti punti sono allineati

$A(2,1) \qquad B(-1,-3) \qquad C(0,0).$

Svolgimento.

Per controllare se tre punti sono allineati è necessario scrivere l’equazione della retta passante per due dei tre punti e vedere se il terzo punto appartiene alla retta trovata. Possiamo scrivere l’equazione della retta passante per $A$ e per $B$ : partiamo trovando il coefficiente angolare di tale retta

$m = \dfrac{y_B - y_A}{x_B - x_A} = \dfrac{-3 - 1}{-1 - 2} = \dfrac{-4}{-3} = \dfrac{4}{3}$

e scrivendo l’equazione del fascio di rette passante per $A$ o $B$ (noi scegliamo $A$ )

$y - y_A = m (x-x_A) \quad \Rightarrow \quad y - 1 = \dfrac{4}{3} (x - 2) \quad \Rightarrow \quad y = \dfrac{4}{3}x + 1 - \dfrac{8}{3} \quad \Rightarrow \quad y = \dfrac{4}{3}x - \dfrac{5}{3}$

quindi la retta passante per $A$ e $B$ è

$y = \dfrac{4}{3}x - \dfrac{5}{3}.$

Adesso controlliamo se il punto $C$ appartiene o no a tale retta. Si controlla l’appartenenza sostituendo le coordinate di $C$ nell’equazione della retta e se l’uguaglianza è verificata allora il punto appartiene, altrimenti no:

${0} = \dfrac{4}{3} \cdot 0 - \dfrac{5}{3} \quad \Rightarrow \quad 0 = - \dfrac{5}{3}$

che non è verificata, quindi i tre punti non sono allineati. Graficamente si ottiene quanto segue

Rendered by QuickLaTeX.com

Figura 5: grafico finale.

Esercizio 9 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Dire se i seguenti punti sono allineati

$A(-1,4) \qquad B(0,1) \qquad C(2,-5).$

Svolgimento.

Per controllare se due punti sono allineati è necessario scrivere l’equazione della retta passante per due dei tre punti e vedere se il terzo punto appartiene alla retta trovata. Possiamo scrivere l’equazione della retta passante per $A$ e per $B$ : partiamo trovando il coefficiente angolare di tale retta

$m = \dfrac{y_B - y_A}{x_B - x_A} = \dfrac{1-4}{0+1} = -3$

e scrivendo l’equazione del fascio di rette passante per $A$ o $B$ , noi scegliamo $A$

$y - y_A = m (x-x_A) \quad \Rightarrow \quad y - 4 = -3(x +1) \quad \Rightarrow \quad y = -3x -3 + 4 \quad \Rightarrow \quad y = -3x + 1$

quindi la retta passante per $A$ e $B$ è

$y = -3x + 1.$

$\overbrace{-5}^{y_C} = -3 \cdot \overbrace{2}^{x_C} +1 \quad \Rightarrow \quad - 5 = -5$

che è verificata, quindi i tre punti sono allineati. Graficamente si ottiene quanto segue

Rendered by QuickLaTeX.com

Figura 6: grafico finale.

Esercizio 10 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Dire se i seguenti punti sono allineati

$A(-3,1) \qquad B(0,2) \qquad C(3,3).$

Svolgimento.

$m = \dfrac{y_B - y_A}{x_B - x_A} = \dfrac{2-1}{0+3} = \dfrac{1}{3}$

e scrivendo l’equazione del fascio di rette passante per $A$ o $B$ , noi scegliamo $A$

$y - y_A = m (x-x_A) \quad \Rightarrow \quad y - 1 = \dfrac{1}{3}(x + 3) \quad \Rightarrow \quad y = \dfrac{1}{3}x +1+1 \quad \Rightarrow \quad y = \dfrac{1}{3}x + 2$

quindi la retta passante per $A$ e $B$ è

$y = \dfrac{1}{3}x + 2.$

$\overbrace{3}^{y_C} = \dfrac{1}{3} \cdot \overbrace{3}^{x_C} + 2 \quad \Rightarrow \quad 3 = 3$

che è verificata, quindi i tre punti sono allineati. Graficamente si ottiene quanto segue

Rendered by QuickLaTeX.com

Figura 7: grafico finale.

Esercizio 11 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Per quale valore di $k \in \mathbb{R}$ le seguenti rette sono perpendicolari?

$r: \quad (3-k)x+y = -5 \qquad s: \quad (k-2)y-x=2.$

Svolgimento.

Ricaviamo il coefficiente angolare da entrambe le rette

$(3-k)x+y = -5 \quad \Leftrightarrow \quad y = -(3-k)x-5 \quad \Rightarrow \quad m_r = k-3$

$(k-2)y-x=2\quad \Leftrightarrow \quad y = \dfrac{1}{k-2} x + 2 \quad \Rightarrow \quad m_s = \dfrac{1}{k-2}$

ed affinché siano parallele deve accadere

$m_r = - \dfrac{1}{m_s}$

cioè

$k-3 = - \dfrac{1}{1/(k-2)} \quad \Leftrightarrow \quad k-3 = -k+2 \quad \Leftrightarrow \quad 2k = 5,$

da cui

$\boxcolorato{superiori}{k = \dfrac{5}{2}.}$

Esercizio 12 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Determinare l’equazione dell’asse del segmento di estremi $A(0,1)$ e $B(4,5)$ .

Svolgimento.

L’asse del segmento è la retta passante per il punto medio del segmento e perpendicolare alla retta che contiene il segmento stesso. Troviamo il punto medio del segmento

$M \left(\dfrac{x_A+x_B}{2} , \dfrac{y_A + y_B}{2}\right) \quad \Rightarrow \quad M\left(\dfrac{0+4}{2} , \dfrac{1+5}{2}\right) \quad \Rightarrow \quad M\left(2,3\right).$

Ora calcoliamo il coefficiente angolare della retta passante per $A$ e $B$

$m = \dfrac{y_B-y_A}{x_B-x_A} = \dfrac{5-1}{4-0} = 1$

e poichè l’asse del segmento è la retta perpendicolare alla retta passante per $A$ e $B$ andiamo a fare l’antireciproco che nel nostro caso è

$m^\star = - \dfrac{1}{m} = - 1.$

Dunque, unendo quanto trovato, l’asse del segmento di estremi $A$ e $B$ ha equazione

$y - y_M = m^\star (x-x_M) \quad \Rightarrow \quad y - 3 = -1 (x-2) \quad \Rightarrow \quad y = -x +5.$

L’asse del segmento è la retta passante per il punto medio del segmento e perpendicolare alla retta che contiene il segmento stesso. Troviamo il punto medio del segmento

$M \left(\dfrac{x_A+x_B}{2} , \dfrac{y_A + y_B}{2}\right) \quad \Rightarrow \quad M\left(\dfrac{0+4}{2} , \dfrac{1+5}{2}\right) \quad \Rightarrow \quad M\left(2,3\right).$

Ora calcoliamo il coefficiente angolare della retta passante per $A$ e $B$

$m = \dfrac{y_B-y_A}{x_B-x_A} = \dfrac{5-1}{4-0} = 1$

e poichè l’asse del segmento è la retta perpendicolare alla retta passante per $A$ e $B$ andiamo a fare l’antireciproco che nel nostro caso è

$m^\star = - \dfrac{1}{m} = - 1.$

Dunque, unendo quanto trovato, l’asse del segmento di estremi $A$ e $B$ ha equazione

$y - y_M = m^\star (x-x_M) \quad \Rightarrow \quad y - 3 = -1 (x-2),$

da cui

$\boxcolorato{superiori}{ y = -x +5.}$

Esercizio 13 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Determinare la posizione reciproca della seguente coppia di rette

$r: \quad 2x-y=7 \qquad \qquad s: \quad x+2y = 1.$

Svolgimento.

Per conoscere la posizione reciproca di due rette si imposta un sistema, ottenendo così un sistema lineare di equazioni risolvibile con il metodo che più si preferisce; solitamente si utilizza il metodo di sostituzione:

$\begin{aligned} & \begin{cases} 2x-y=7 \\ x+2y = 1 \end{cases} \quad \Leftrightarrow \quad \begin{cases} y=2x-7 \\ x+2y = 1 \end{cases} \quad \overset{\text{sost.}}{\Leftrightarrow} \quad \begin{cases} y=2x-7 \\ x+2(2x-7) = 1 \end{cases} \quad \Leftrightarrow \quad \\ & \quad \Leftrightarrow \quad \begin{cases} y=2x-7 \\ 5x = 15 \end{cases} \quad \Leftrightarrow \quad \begin{cases} y=-1 \\ x=3 \end{cases} \end{aligned}$

dunque il sistema è determinato; ne possiamo dedurre che le rette $r$ ed $s$ sono incidenti nel punto $P(3,-1)$ . Graficamente:

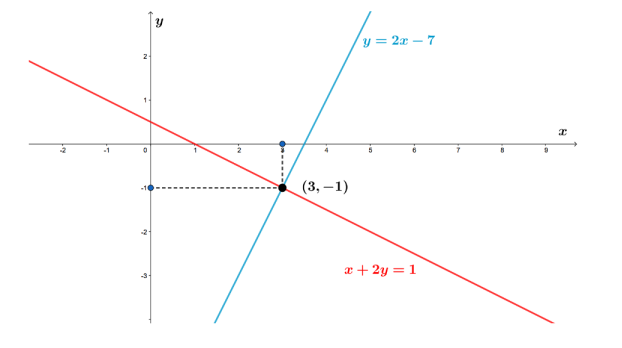
Figura 8: grafico finale.

Esercizio 14 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Scrivere l’equazione della retta $r$ passante per i punti $A(1,2)$ e $B(4,-1)$ . Calcola le distanze di questi punti dalla retta $s$ di equazione $5x + 5y + 3 = 0$ .
Come sono tra loro le rette $r$ e $s$ ?

Svolgimento.

Innanzitutto troviamo il coefficiente angolare della retta passante per i punti $A$ e $B$

$m = \dfrac{y_B - y_A}{x_B - x_A} = \dfrac{-1-2}{4-1} = \dfrac{-3}{3} = -1$

ed imponendo il passaggio per, ad esempio, il punto $A$ abbiamo

$y-y_A = m(x-x_A) \quad \Rightarrow \quad y-2 = -1(x-1) \quad \Rightarrow \quad y = x + 3.$

Nota bene: imponendo il passaggio per $B$ si ottiene la stessa retta (come ovvio). Dunque l’equazione della retta passante per $A$ e $B$ è

$\boxcolorato{superiori}{ r: y = -x + 3.}$

Ora calcoliamo la distanza di $A$ da $s$ . Osserviamo che la retta $s$ è già in forma implicita, quindi

$d_{As} = \dfrac{\vert 5 \cdot 1 + 5 \cdot 2 - 3\vert}{\sqrt{5^2+5^2}} = \dfrac{12}{\sqrt{50}} = \dfrac{12}{5\sqrt{2}} = \dfrac{6\sqrt{2}}{5}.$

Quindi

$\boxcolorato{superiori}{ d_{As} = \dfrac{6\sqrt{2}}{5}. }$

Adesso invece calcoliamo la distanza di $B$ da $s$ come segue

$d_{Bs} = \dfrac{\vert 5 \cdot 4 + 5 \cdot (-1) - 3\vert}{\sqrt{5^2+5^2}} = \dfrac{12}{\sqrt{50}} = \dfrac{12}{5\sqrt{2}} = \dfrac{6\sqrt{2}}{5}$

allora

$\boxcolorato{superiori}{ d_{Bs} = = \dfrac{6\sqrt{2}}{5} }$

quindi i punti $A$ e $B$ sono equidistanti dalla retta $s$ . Andando ad analizzare i coefficienti angolari di $r$ ed $s$ ci accorgiamo che

$m_r = -1$

$m_s = -1$

quindi le rette $r$ ed $s$ sono parallele: $r \parallel s$ .

Esercizio 15 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Determinare l’equazione della retta passante per il punto medio del segmento di estremi $A(2,4)$ e $B(-1,1)$ perpendicolare alla retta passante per $C(0,2)$ e $D(3,1)$ .

Svolgimento.

Calcoliamo il punto medio del segmento di estremi $A$ e $B$ :

$x_M = \dfrac{x_A+x_B}{2} = \dfrac{2-1}{2} = \dfrac{1}{2} \qquad \mbox{e} \qquad y_M = \dfrac{y_A+y_B}{2} = \dfrac{4+1}{2} = \dfrac{5}{2}$

quindi il punto medio è

$M\left(\dfrac{1}{2} , \dfrac{5}{2} \right).$

Ora calcoliamo il coefficiente angolare della retta passante per $C$ e $D$

$m = \dfrac{y_D-y_C}{x_D-x_C} = \dfrac{1-2}{3-0} = -\dfrac{1}{3}$

e dal momento che vogliamo la retta perpendicolare prendiamo

$m_\perp = - \dfrac{1}{m} = 3.$

Infine scriviamo l’equazione della retta

$y-y_M = m_{\perp} (x-x_M) \quad \Leftrightarrow \quad y-\dfrac{5}{2} = 3 \left(x-\dfrac{1}{2}\right),$

da cui

$\boxcolorato{superiori}{ y = 3x + 1. }$

Esercizio 16 $(\bigstar\largewhitestar\largewhitestar\largewhitestar\largewhitestar)$ . Determinare la retta passante per il baricentro del triangolo di vertici $A(1,1), B(2,5), C(3,3)$ e $D(4,-1)$ .

Svolgimento.

Determiniamo il baricentro

$x_G = \dfrac{x_A+x_B+x_C}{3} = \dfrac{1+2+3}{3} = 2 \qquad \mbox{e} \qquad y_G = \dfrac{y_A+y_B+y_C}{3} = \dfrac{1+5+3}{3} = 3$

quindi

$G(2,3).$

Ora dobbiamo scrivere l’equazione della retta passante per $G$ e per $D$ , dunque prima calcoliamo il coefficiente angolare

$m = \dfrac{y_D-y_C}{x_D-x_C} = \dfrac{-1-3}{4-2} = -2$

per cui la retta è

$y-y_D = m (x-x_D) \quad \Leftrightarrow \quad y+1 = -2(x-4),$

da cui

$\boxcolorato{superiori}{ y=-2x+7.}$

Document

Menu

Chiudi

Piano cartesiano e retta: esercizi

Autori e revisori

Leggi...

Testi degli esercizi

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Svolgimento.

Suggerimenti, refusi ed errori

Cosa dicono di noi